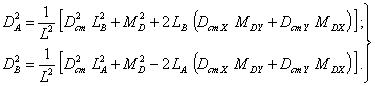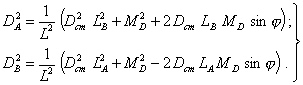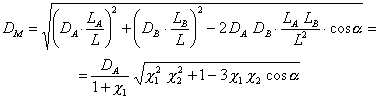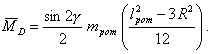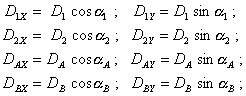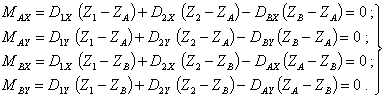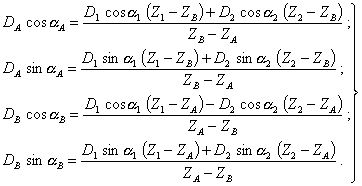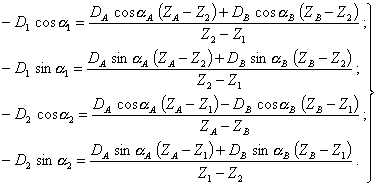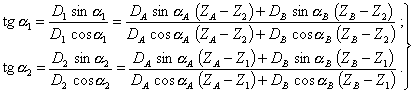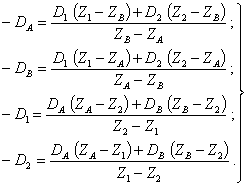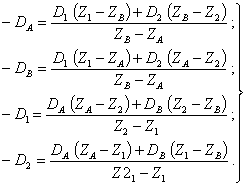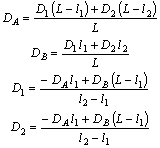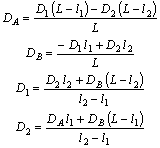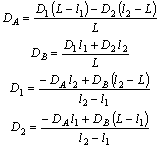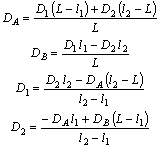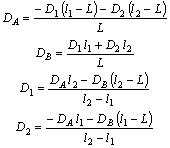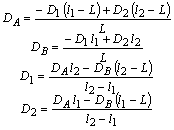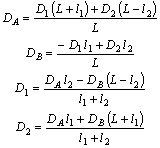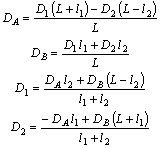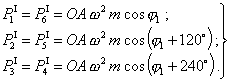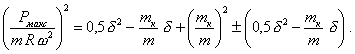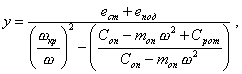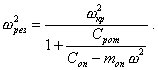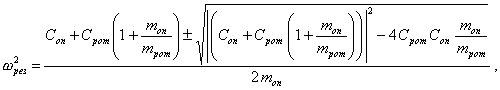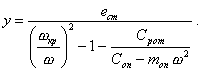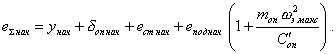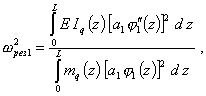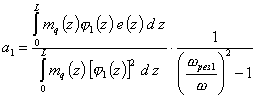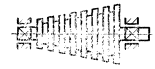МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО БАЛАНСИРОВКЕ
ЖЕСТКИХ РОТОРОВ
(К
ГОСТ 22061-76
МАШИНЫ И ТЕХНОЛОГИЧЕСКОЕ ОБОРУДОВАНИЕ.
СИСТЕМА КЛАССОВ ТОЧНОСТИ БАЛАНСИРОВКИ.
ОСНОВНЫЕ ПОЛОЖЕНИЯ)
Методические указания содержат теоретические основы построения и практического применения системы классов точности балансировки и предназначены для инженеров-расчетчиков, конструкторов и технологов, разрабатывающих нормативно-техническую документацию на балансировку «жестких роторов» (по терминологии ГОСТ 19534-74) при изготовлении или ремонте изделий.
Методические указания должны помочь избежать грубых ошибок при разработке и проведении процесса балансировки и при установлении единообразного порядка, который вводится ГОСТ 22061-76, соответствующий международному стандарту ИСО 1940.
В первой части особое внимание обращено на методы расчетов и способ определения, является ли ротор данного изделия «жестким ротором». Во второй части рассмотрены примеры различных технологических дисбалансов, их расчет и связь с точностью изготовления, а также приведены практические рекомендации.
ЧАСТЬ I
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
Раздел 1. НЕУРАВНОВЕШЕННОСТЬ
1.1. Тело, не подверженное действию внешних сил, вращающееся с постоянной угловой скоростью вокруг одной из своих главных центральных осей инерции, находится в состоянии динамического равновесия, которое характеризуется равенством нулю суммы всех неуравновешенных сил и суммы всех моментов этих сил.
где ![]() - эксцентриситет i-й массы.
- эксцентриситет i-й массы.
Можно представить на этом теле цапфы и подшипниковые опоры строго концентричные с его главной центральной осью инерции, тогда это тело превратится в ротор и сохранит свою уравновешенность.
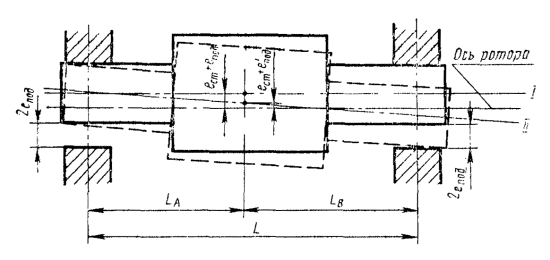
Однако, практически изготовление цапф и установка подшипников - опор всегда будет произведена с радиальной и угловой погрешностями относительно главной центральной оси инерции тела. В этом случае абсолютно жесткие опоры заставляют ротор вращаться уже вокруг другой оси ротора, не совпадающей с его главной центральной осью инерции.
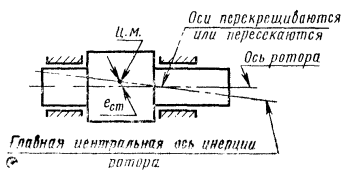
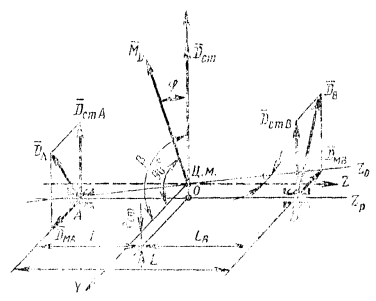
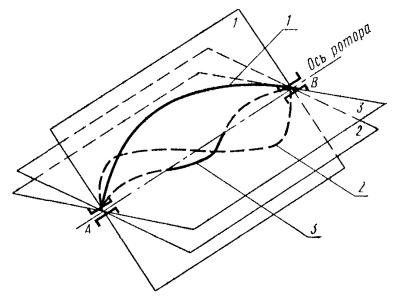
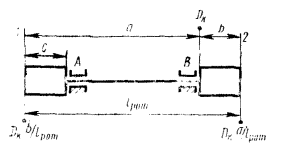
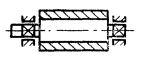
Вследствие этого ротор станет в общем случае динамически неуравновешенным (черт. 1), т.е. нарушаются равенства (1) и (2).
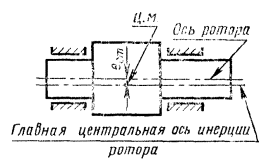
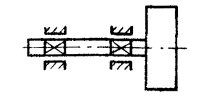
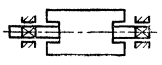
Пусть ротор - абсолютно твердое тело. Параллельное смещение оси такого ротора относительно его главной центральной оси инерции будет определять статическую неуравновешенность ротора (черт. 2), характеризуемую неравенством
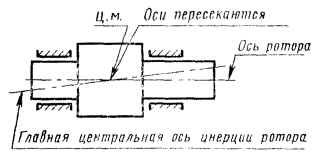
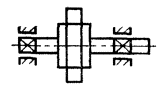
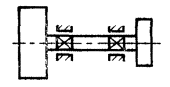
Угол между осью ротора и его главной центральной осью инерции будет вызывать моментную неуравновешенность (черт. 3), которая характеризуется неравенством:
Как при статической, так и при моментной неуравновешенностях, вращающийся с постоянной угловой скоростью ротор будет нагружать опоры силами, которые вращаются вместе с ротором. Эти переменные по направлению нагрузки опор создают изгибающие моменты, действующие на ротор и вращающиеся вместе с ним.
Черт. 1.
Черт. 2.
Черт. 3.
Разделим выражения (3) и (4) на w2, тогда
![]() (5)
(5)
![]() (6)
(6)
где ![]() - главный вектор
дисбалансов ротора;
- главный вектор
дисбалансов ротора;
![]() - главный момент дисбалансов ротора, создаваемый на плече L (расстояние между опорами) парой дисбалансов
- главный момент дисбалансов ротора, создаваемый на плече L (расстояние между опорами) парой дисбалансов ![]() ;
; ![]() - локальный
дисбаланс.
- локальный
дисбаланс.
Раздел 2. БАЛАНСИРОВКА
2.1. Балансировка - это технологический процесс совмещения главной центральной оси инерции с осью ротора.
2.2. Балансировку можно производить двумя методами.
2.2.1. Обработкой цапф так, чтобы ось вращения ротора, обычно проходящая через центры сечений цапф, совпала с главной центральной осью инерции ротора. Подобная методика балансировки, чаще всего использующая электролиз, теоретически наиболее оправдана и практически дает хорошие результаты, особенно при не очень больших начальных дисбалансах. Однако этот способ, требующий коренного изменения привычного процесса балансировки, еще мало применяется.
2.2.2. Корректировкой масс, при которой корректирующие массы перемещают по ротору, устанавливают на нем или удаляют с него таким образом, чтобы главная центральная ось инерции приближалась к оси ротора. Перемещение, добавление или удаление корректирующей массы производят в одной или нескольких точках одной плоскости коррекции, перпендикулярной оси ротора, либо в нескольких параллельных плоскостях коррекции одновременно или последовательно в каждой плоскости.
Перемещение, добавление или удаление корректирующих масс может производиться сверлением, фрезерованием, наплавкой, наваркой, завинчиванием или вывинчиванием винтов, выжиганием электрической искрой, лучом лазера, электронным пучком, электролизом, электромагнитным наплавом и т.д.
2.3. Процесс балансировки может быть последовательный, когда измерение дисбаланса и его уменьшение составляют самостоятельные операции, и совмещенный, когда измерение и корректировка масс совершаются одновременно.
Раздел 3. ДИНАМИЧЕСКАЯ НЕУРАВНОВЕШЕННОСТЬ
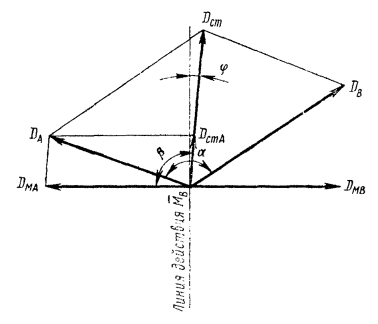
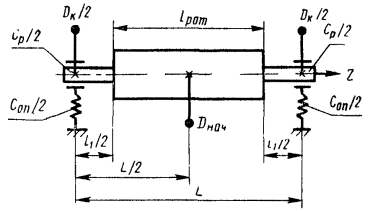
Если рассматривать две плоскости, перпендикулярные оси ротора и проходящие через середины опор А и В межопорного ротора, то главный вектор дисбалансов может быть заменен его составляющими в плоскостях опор (черт. 4), которые называют симметричными дисбалансами.
а главный момент - парой дисбалансов, действующих в тех же плоскостях, которые называют кососимметричными дисбалансами.
Таким образом, в каждой из плоскостей опор будут действовать суммарные векторы дисбалансов:
Эти два вектора вместо векторов ![]() и
и ![]() также полностью
определяют динамическую неуравновешенность ротора.
также полностью
определяют динамическую неуравновешенность ротора.
Черт. 4.
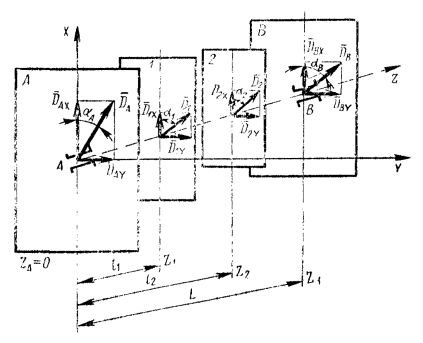
В общем случае составляющие ![]() главного вектора
дисбалансов ротора имеют разные значения, параллельны друг другу и лежат в
плоскости, содержащей ось ротора Zрот и центр его масс, тогда как векторы
дисбалансов
главного вектора
дисбалансов ротора имеют разные значения, параллельны друг другу и лежат в
плоскости, содержащей ось ротора Zрот и центр его масс, тогда как векторы
дисбалансов ![]() , определяющие главный момент дисбалансов ротора, равны по
значению, антипараллельны и лежат в другой плоскости, содержащей центральную
ось инерции Z ротора и его главную нейтральную ось инерции
Z0, причем ось Z параллельна оси ротора Zрот (черт. 4).
, определяющие главный момент дисбалансов ротора, равны по
значению, антипараллельны и лежат в другой плоскости, содержащей центральную
ось инерции Z ротора и его главную нейтральную ось инерции
Z0, причем ось Z параллельна оси ротора Zрот (черт. 4).
Первое векторное равенство (9) можно представить в координатной форме
![]()
откуда
![]()
Аналогично
![]()
Так как
![]()
то
Выражения (10) пригодны для роторов из абсолютно твердых материалов самой произвольной формы, вращающихся на абсолютно жестких опорах.
Раздел 4. ДИНАМИЧЕСКАЯ НЕУРАВНОВЕШЕННОСТЬ СИММЕТРИЧНОГО МЕЖОПОРНОГО РОТОРА
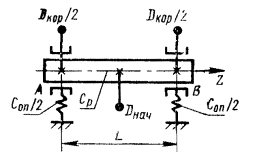
4.1. Рассмотрим ротор из абсолютно твердого материала на абсолютно жестких опорах, симметричный относительно своей главной центральной оси инерции Z0. У такого ротора любая центральная ось инерции, перпендикулярная Z0, может быть принята за главную центральную ось инерции X0.
Выберем ось X0 таким образом, чтобы она была перпендикулярна плоскости, в которой лежит угол g между главной центральной осью инерции Z0 и осью Zрот ротора (черт. 4).
В этом случае вектор ![]() лежит на оси X0 и компонента
главного момента дисбалансов по этой оси МDX = МD, а компонента МDY = 0.
лежит на оси X0 и компонента
главного момента дисбалансов по этой оси МDX = МD, а компонента МDY = 0.
Следовательно, для симметричного ротора из абсолютно твердого материала на абсолютно жестких опорах, уравнения (10) упрощаются.
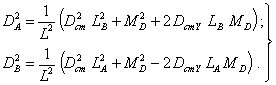
Из черт. 4
следует, что ![]()
Таким образом
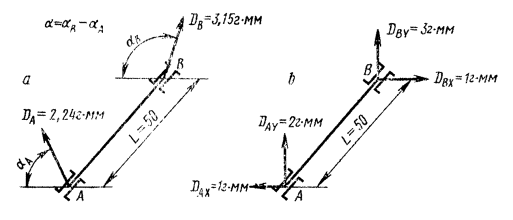
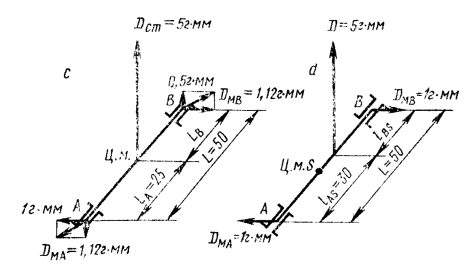
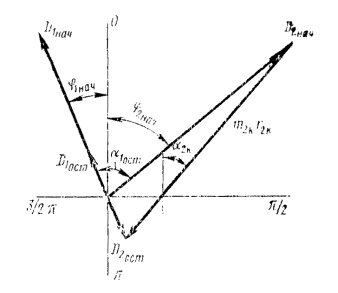
На черт. 5 показаны различные представления одной и той же неуравновешенности.
Если известны (измерены) ![]() и
и ![]() («крест дисбалансов»)
(черт. 5а) в плоскостях опор А и В или их проекции на оси X и Y (черт. 5b), то можно
определить векторы (черт. 5с и 6 вид вдоль
оси Zрот):
(«крест дисбалансов»)
(черт. 5а) в плоскостях опор А и В или их проекции на оси X и Y (черт. 5b), то можно
определить векторы (черт. 5с и 6 вид вдоль
оси Zрот):
![]() (12)
(12)
![]() (13)
(13)
Черт. 5.
Черт. 6.
На черт. 5с главный момент
дисбалансов перпендикулярен (по правилу правой руки) плоскости, в которой
расположены векторы ![]() и их модули:
и их модули:
или
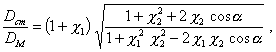 (16)
(16)
где
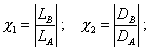
![]() - угол между дисбалансами
- угол между дисбалансами ![]() и
и ![]() .
.
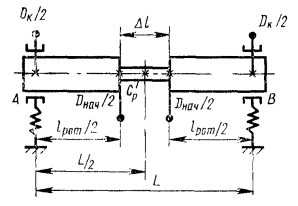
4.2. Если при балансировке уменьшение главного вектора дисбалансов
производится не по центру масс (черт. 5с), а в другой точке S на оси Zр, расстояния до которой от опор lAS и lBS, то значение DM может
быть сделано минимальным при определенном 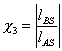 (черт. 5d). Это значение c3 можно найти, приравняв нулю первую производную выражения (15)
(черт. 5d). Это значение c3 можно найти, приравняв нулю первую производную выражения (15)
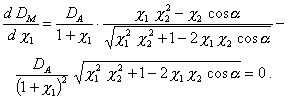 (17)
(17)
Откуда
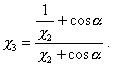
Заметим, что при коррекции дисбалансов в трех плоскостях (отдельно Dст и DM) при найденном c3 (для Dст) величины корректирующих масс будут минимальными.
4.2.1. Если DA = 0, то
Dcт = DB, ![]()
4.3. Рассмотрим формулу (11).
4.3.1. Когда угол j между ![]() и
и ![]() равен 0 или 180°,
главный момент
равен 0 или 180°,
главный момент ![]() и главный вектор
и главный вектор ![]() коллинеарны, а
дисбалансы в опорах
коллинеарны, а
дисбалансы в опорах
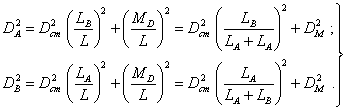 (18)
(18)
4.3.2. При j = 90 и 270°, ![]() , т.е., когда
, т.е., когда ![]() и
и ![]() коллинеарны, мы имеем случай квазистатической
неуравновешенности, при которой дисбалансы
коллинеарны, мы имеем случай квазистатической
неуравновешенности, при которой дисбалансы ![]() и
и ![]() лежат в одной
плоскости ZрAYр.
лежат в одной
плоскости ZрAYр.
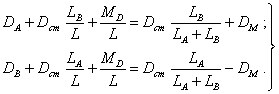 (19)
(19)
При этом возможны два случая.
4.3.2.1. a = 0, тогда ![]() , т.е. всегда Dст > DA, а
, т.е. всегда Dст > DA, а
![]() т.е. всегда DM < DA.
т.е. всегда DM < DA.
Если c1 = c2 = 1 или ![]() , то, так как DM = 0,
, то, так как DM = 0,
![]() (20)
(20)
Следовательно, имеет место только статическая неуравновешенность.
4.3.2.2. a = 180°, тогда ![]() , т.е. всегда Dст < DA. Если c2 = 1, то Dст = 0, следовательно, имеет место только моментная неуравновешенность.
, т.е. всегда Dст < DA. Если c2 = 1, то Dст = 0, следовательно, имеет место только моментная неуравновешенность.
При этом ![]() причем DM > DA.
причем DM > DA.
Если c1 = c2 = 1, то DM = DA и
![]() (21)
(21)
4.3.3. Для случая, когда a = 90° или 270°, cos a = 0,
![]()
Следовательно,
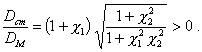
4.4. Связь между углами β или j и a.
4.4.1. Из формул (7) и (14) и черт. 6 следует, что на опору А приходится составляющая главного вектора
![]()
или
![]()
На эту же опору действует дисбаланс от момента (формула 15)
![]()
Из черт. 6
![]()
Следовательно,
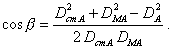
Подставив приведенные выше значения, после преобразований получим
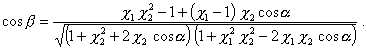 (22)
(22)
4.4.2. При квазистатической неуравновешенности, когда a = 0
![]() (23)
(23)
т.е. β = 180°, а j = 90 или
270°. В этом случае ![]() , a
, a ![]() . Для a = 180° получаются те же результаты.
. Для a = 180° получаются те же результаты.
4.4.3. Если же a = 90 или 270°, то
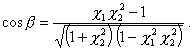 (24)
(24)
что при c1 = c2 = 1 и при ![]() дает 0, т.е. при этих
условиях β = 90 или 270°, а j = 0° или
дает 0, т.е. при этих
условиях β = 90 или 270°, а j = 0° или ![]() , a
, a ![]() .
.
Во всех остальных случаях ![]() .
.
4.4.4. Если β = 0 или 180°, a cos β = 1, то
![]() (25)
(25)
т.е. a = 90 или 270°.
Если β = 90 или 270°, a cos β = 0, то
![]() (26)
(26)
что при ![]() дает a = 180°, если c1 < 1.
дает a = 180°, если c1 < 1.
Раздел 5. ОСОБЕННОСТИ МОМЕНТНОЙ НЕУРАВНОВЕШЕННОСТИ
5.1. Рассмотрим особенности абсолютно твердого ротора, связанные с его моментной неуравновешенностью.
Для ротора произвольной формы при угле g между главной центральной осью инерции 0Z0 и осью ротора 0Zрот (черт. 4) суммарный момент неуравновешенных сил определяется формулой:
![]() (27)
(27)
где ![]() и
и ![]() - главные моменты инерции ротора
относительно ортогональных главных центральных осей инерции Х0 и Z0. Откуда, главный
момент дисбалансов ротора
- главные моменты инерции ротора
относительно ортогональных главных центральных осей инерции Х0 и Z0. Откуда, главный
момент дисбалансов ротора
Направление главного момента дисбалансов ротора ![]() определяется знаком
разности
определяется знаком
разности ![]() . Если
. Если ![]() («длинный» ротор), то
вектор
(«длинный» ротор), то
вектор ![]() будет ориентирован
вдоль положительного направления оси 0Y0; при
будет ориентирован
вдоль положительного направления оси 0Y0; при ![]() («короткий» ротор или
диск), вектор
(«короткий» ротор или
диск), вектор ![]() будет направлен в
противоположном направлении.
будет направлен в
противоположном направлении.
5.2. Для ротора в виде однородного симметричного цилиндра длины lрот и радиуса R
![]() (29)
(29)
Следовательно, если ![]() , то независимо от угловой скорости вращения и независимо от
угла g между главной центральной осью инерции и
осью ротора, главный момент дисбалансов
, то независимо от угловой скорости вращения и независимо от
угла g между главной центральной осью инерции и
осью ротора, главный момент дисбалансов ![]() однородного
цилиндрического ротора будет равен нулю.
однородного
цилиндрического ротора будет равен нулю.
Примечание. Главный момент дисбалансов ![]() однородного
цилиндрического ротора по модулю равен его центробежному моменту инерции
относительно оси ротора 0Zрот и
ей перпендикулярной главной центральной оси инерции ротора 0Y. Момент MD является моментом «внутренним», порождаемым
неуравновешенными массами ротора при его вращении.
однородного
цилиндрического ротора по модулю равен его центробежному моменту инерции
относительно оси ротора 0Zрот и
ей перпендикулярной главной центральной оси инерции ротора 0Y. Момент MD является моментом «внутренним», порождаемым
неуравновешенными массами ротора при его вращении.
5.2.1. Если предположить, что угол g ≤ 10°, то можно принять (с наибольшей
погрешностью » 1,5 %), что ![]() . В этом случае формула (30) для модуля главного момента
дисбалансов однородного симметричного цилиндра примет вид
. В этом случае формула (30) для модуля главного момента
дисбалансов однородного симметричного цилиндра примет вид
Откуда
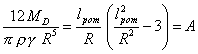
и при ![]()
Производная
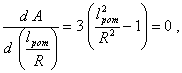
когда lрот = R, т.е. А будет иметь минимум.
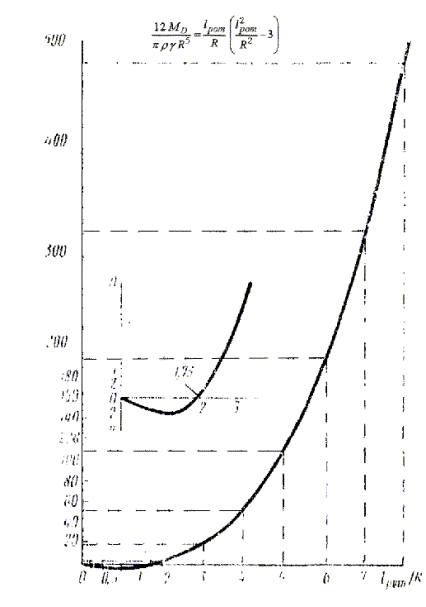
На черт. 7 показан примерный ход кривой
![]()
т.е. главного момента дисбалансов ротора при
изменении ![]() .
.
Черт. 7.
5.2.2. Пользуясь формулами (30), (7), (8) можно сравнить воздействие на опоры моментной и статической неуравновешенностей.
При одной только моментной неуравновешенности у симметричного межопорного ротора с ![]() угол
угол ![]() , где еМ
- - расстояние главной
центральной оси инерции Z0 от оси ротора Zрот на середине опоры А или В.
, где еМ
- - расстояние главной
центральной оси инерции Z0 от оси ротора Zрот на середине опоры А или В.
При одной только статической неуравновешенности у того же ротора ось Z0 будет смещена на ест параллельно оси ротора Zрот.
Нагрузки, создаваемые моментной (при малом g) и статической неуравновешенностями на каждой из двух опор ротора при его вращении с угловой скоростью w, можно выразить так:
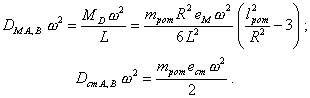
При равенстве этих нагрузок
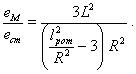 (32)
(32)
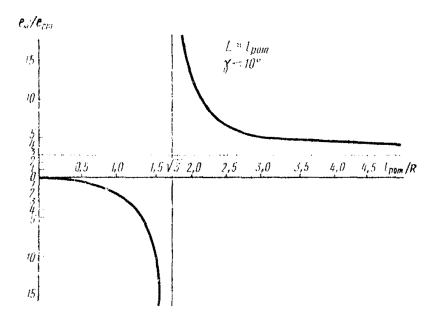
Черт. 8 показывает изменение отношения ![]() в зависимости от
в зависимости от ![]() при равенстве
нагрузок в опорах от статической и моментной неуравновешенностей, если принять L » lрот.
при равенстве
нагрузок в опорах от статической и моментной неуравновешенностей, если принять L » lрот.
5.2.3. Для посаженного без перекоса диска (например, абразивный круг) формула (31) будет выглядеть так:
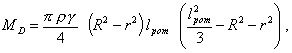
где 2r - диаметр отверстия диска.
Следовательно, при ![]() , MD = 0; MD имеет
минимум при
, MD = 0; MD имеет
минимум при ![]() . Характер же
кривых на черт. 8
остается без изменения (изменится лишь масштаб).
. Характер же
кривых на черт. 8
остается без изменения (изменится лишь масштаб).
Черт. 8.
5.3. Для абсолютно твердого ротора углы g и Q разные (черт. 9), но связаны между собой. Из (28) и формулы
![]() (33)
(33)
получаем
![]() (34)
(34)
Следовательно, увеличение угла g будет
сопровождаться также и увеличением угла Q. Знак разности моментов инерции ![]() будет определять знак
угла Q при данном угле g (на черт. 9 и 10
обозначены различные направления отсчета этих углов).
будет определять знак
угла Q при данном угле g (на черт. 9 и 10
обозначены различные направления отсчета этих углов).
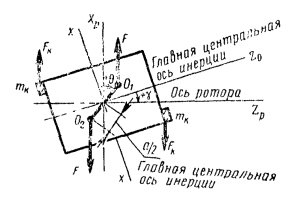
5.3.1. На черт. 9 изображен «длинный» ротор (Ix > Iz) и обозначены его оси. У таких роторов момент M0 сил F стремится не уменьшать, а увеличивать угол g, следовательно, увеличивать и угол Q.
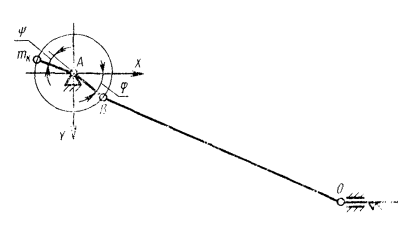
Допустим, что для уравновешивания момента М0 к ротору приложен «внешний» момент МК, например, от сил FК, возбуждаемых корректирующими массами mК. Существенно, что
этот момент МК будет
уменьшать углы Q и g и поэтому уравновешивание момента будет
иметь место при некоторых новых значениях этих углов, меньших, чем
первоначальные значения. Новым значениям углов Q и g будет соответствовать новое значение
момента, равное ![]() . Следовательно, для уравновешивания момента М0 (любого происхождения) к
нему необходимо приложить корректирующий момент
. Следовательно, для уравновешивания момента М0 (любого происхождения) к
нему необходимо приложить корректирующий момент ![]() .
.
Величина М0 зависит от формы и размеров ротора, от распределения массы в его объеме, а также и от упругих свойств ротора и от зазоров в его опорах. Для данного ротора DM0 будет определяться только изменением угла Q и расстоянием а (черт. 9), вызванным действием внешнего момента
![]()
Величину DM0 можно представить в виде функции только от
угла Q, если известна зависимость расстояния а от этого угла. Эта зависимость определяется конфигурацией
ротора и, в частности, соотношением между моментами инерции ![]() и
и ![]() .
.
01 и 02 - центры масс частей цилиндра, лежащих по обе стороны сечения плоскостью, содержащей ось ротора.
Черт. 9.
Черт. 10.
5.3.2. У «коротких» роторов (черт. 10) ![]() момент М0, создаваемый силами F, стремится уменьшить углы Q и g, следовательно, уравновешивающий его
корректирующий момент МК,
создаваемый силами FК, будет увеличивать эти углы. Таким образом,
приложение момента MК должно привести к увеличению момента М0, который необходимо
уравновесить на величину DМ0. Следовательно, процесс уравновешивания моментов закончится, когда
будет выполнено условие
момент М0, создаваемый силами F, стремится уменьшить углы Q и g, следовательно, уравновешивающий его
корректирующий момент МК,
создаваемый силами FК, будет увеличивать эти углы. Таким образом,
приложение момента MК должно привести к увеличению момента М0, который необходимо
уравновесить на величину DМ0. Следовательно, процесс уравновешивания моментов закончится, когда
будет выполнено условие
МК = М0 + DМ0.
Теоретически
возможен случай, когда МК
= DМ0, т.е., когда
корректирующий момент МК
будет полностью компенсироваться вызванным им же увеличением момента М0. В этом случае ротор будет совершенно «нечувствителен» к
моменту МК; присоединение
корректирующих масс mК и действие момента МК не вызовут изменения неуравновешенности ротора, т.е.
величина М0 останется постоянной. Очевидно, что
такая «нечувствительность» ротора будет определяться тем, как сильно изменяется
М0 в зависимости от угла Q и расстояния а. Если для данного ротора величина а представлена в виде функции от угла Q, то ![]() и «чувствительность»
ротора может быть оценена по величине
и «чувствительность»
ротора может быть оценена по величине ![]() . Можно показать, что эта производная зависит от разности
. Можно показать, что эта производная зависит от разности ![]() .
.
5.3.3. Различие в поведении «длинных» и «коротких» роторов при балансировке обусловлено тем, что у первых осью с наибольшим значением момента инерции является ось 0Х0, тогда как у «коротких» роторов - ось 0Z0. Моментная неуравновешенность вызвана неуравновешенными силами, а действие этих сил всегда направлено в сторону уменьшения угла между осью вращения и той главной центральной осью инерции, которой соответствует наибольший момент инерции. Поэтому у «длинных» роторов появление небольшого угла g приводит к появлению дополнительного момента DМ0, направленного в сторону увеличения угла g, а следовательно, увеличения угла Q и первоначального момента М0. У «коротких» роторов, наоборот, появление угла g приводит к возбуждению дополнительного момента DМ0, стремящегося уменьшить угол g и, следовательно, уменьшить первоначальный неуравновешенный момент M0.
Раздел 6. ПЕРЕСЧЕТ ДИСБАЛАНСОВ ИЗ ОДНИХ ПЛОСКОСТЕЙ В ДРУГИЕ ДЛЯ ЖЕСТКОГО ДВУХОПОРНОГО РОТОРА
6.1. Если заданы главный вектор и главный момент дисбалансов, то определить дисбалансы в любых двух плоскостях, перпендикулярных оси ротора, можно по формулам (9), (10) или (11). В тех же случаях, когда заданы (измерены) дисбалансы в двух плоскостях, перпендикулярных оси ротора, пересчитать эти дисбалансы для других параллельных плоскостей можно по приводимым ниже формулам. Эти формулы охватывают все возможное разнообразие расположения двух плоскостей опор и двух плоскостей коррекции.
Следует заметить, что при переходе от одних плоскостей к другим дисбалансы меняются не только по значениям дисбалансов, но также и по углам дисбалансов.
В этих формулах a1 и a2 - углы дисбалансов ![]() и
и ![]() в плоскостях 1 и 2, а aA и aB - углы дисбалансов
в плоскостях 1 и 2, а aA и aB - углы дисбалансов ![]() и
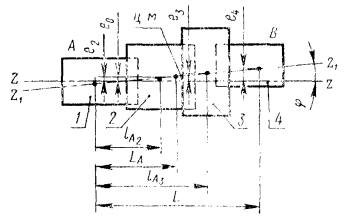
и ![]() в плоскостях опор А и В. Расстояния между плоскостями показаны на черт. 11. Все
формулы выводятся для компонентов дисбалансов по осям X и Y, которые равны:
в плоскостях опор А и В. Расстояния между плоскостями показаны на черт. 11. Все
формулы выводятся для компонентов дисбалансов по осям X и Y, которые равны:
причем отсчет углов g ведется от оси X, которая может быть представлена на роторе меткой.
Для определения DA и DB по D1 и D2 составляются уравнения моментов компонентов дисбалансов относительно центров опор А и В, а для определения D1 и D2 по DA и DB уравнения в компонентах дисбалансов по X и Y относительно точек пересечения плоскостей 1 и 2 с осью ротора.
Приведены также формулы, определяющие углы соответствующих дисбалансов.
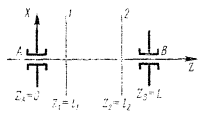
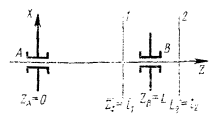
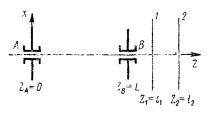
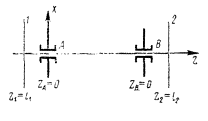
6.2. На черт. 11 представлены плоскости опор А и В и две плоскости коррекции или измерения 1 и 2 межопорного ротора и принята правая система координат XYZ, причем направление вдоль оси ротора от А к В считается положительным. Начало координат расположено в опоре А и ZA = 0. Обязательным условием последующего вывода является расположение плоскостей 1 левее 2 и A левее В.
Черт. 11.
Уравнение моментов относительно плоскостей опор А и В:
Откуда, представив из (35) компоненты векторов через углы a, получим
Следовательно, значения дисбалансов
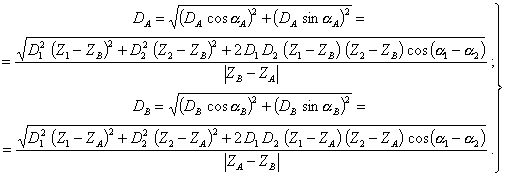 (38)
(38)
Углы aA и aB дисбалансов ![]() и
и ![]() определяются по следующим формулам, которые
вытекают из (37)
определяются по следующим формулам, которые
вытекают из (37)
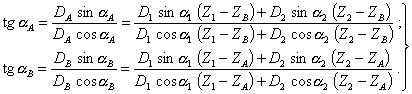 (39)
(39)
6.3. Аналогичным образом из уравнений моментов относительно точек пересечения плоскостей 1 и 2 с осью ротора:
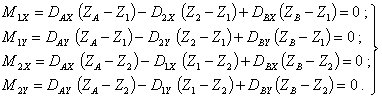 (40)
(40)
определяем компоненты векторов через их углы a:
Откуда находим значения дисбалансов:
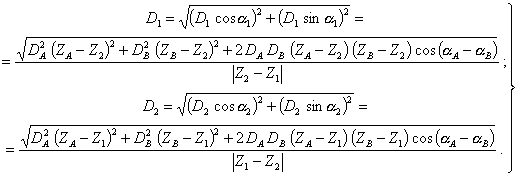 (42)
(42)
Углы a1 и a2 дисбалансов ![]() и
и ![]() определяются по следующим формулам, которые
вытекают из (41):
определяются по следующим формулам, которые
вытекают из (41):
6.4. Формулы (36) - (43) пригодны для пересчетов дисбалансов при любом расположении плоскостей А, В, 1 и 2 (при условии, что плоскость 1 левее плоскости 2, а плоскость A левее плоскости B), когда координаты Z1, Z2 и ZB подставляются в них со своими знаками.
6.5. В частных случаях, когда a1 = a2 = aA = aB, т.е. при статической неуравновешенности ротора, когда углы дисбалансов можно принять равными нулю, из (37) и (41) следует, что:
В случае, когда a1 - a2 = aA - aB = 180° имеет место моментная неуравновешенность.
Приняв a1 = aA = 0, получим для a2 = aB = 180° из (37) и (41):
6.6. По формулам (44) и (45) построена таблица.
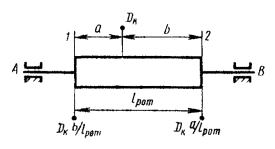
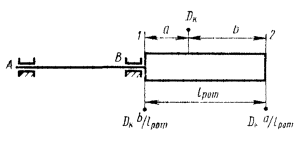
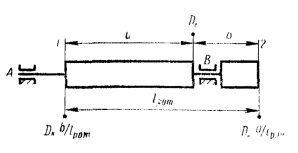
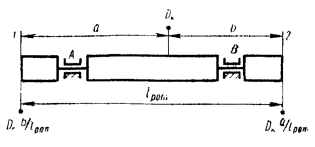
Для всех возможных случаев взаимного расположения плоскостей А, В, 1 и 2 для статической и моментной неуравновешенностей двухопорного ротора с указанием знаков координат этих плоскостей.
6.7. Из таблицы видно, что при D1 = D2 для всех межопорных (схема I) и консольных (схема III) роторов DA и DB при статической неуравновешенности больше DA и DB при моментной неуравновешенности. Лишь у роторов II и IV схем возможны обратные соотношения.
По схемам I и III построено подавляющее число изделий машиностроения, поэтому за основу принято регламентирование функционального удельного дисбаланса eст, ф ротора, обеспечивающего работоспособность подшипниковых опор и нормальное функционирование изделий. Применение этого же критерия для схем II и IV оправдано тем, что eст, ф и в этих случаях определялись по той же методике из статистически обработанных результатов измерения остаточных дисбалансов у хорошо работающих изделий.
|
Номера схем |
Схема взаимного расположения плоскости коррекции и опор |
Дисбалансы от неуравновешенности |
|
|
статической |
моментной |
||
|
I |
|
|
|
|
II |
|
|
|
|
III |
|
|
|
|
IV |
|
|
|
Раздел 7. КОЭФФИЦИЕНТ ДИСБАЛАНСА И МАЯТНИКОВЫЕ КОЛЕБАНИЯ
7.1. Допустим, что несбалансированный
абсолютно твердый ротор вращается с постоянной угловой скоростью w вокруг
горизонтальной оси на двух абсолютно жестких опорах. Эти опоры А и B
воспринимают постоянные по величине и направлению силы ![]() (сумма весовой
нагрузки
(сумма весовой
нагрузки ![]() на опору и радиальной
компоненты
на опору и радиальной
компоненты ![]() от
ремня, цепи, зубчатого колеса и т.д.) и неуравновешенные силы от дисбалансов
ротора
от
ремня, цепи, зубчатого колеса и т.д.) и неуравновешенные силы от дисбалансов
ротора ![]() в плоскостях опор А
и В, постоянные по
величине, но переменные по направлению, так как векторы сил
в плоскостях опор А
и В, постоянные по
величине, но переменные по направлению, так как векторы сил ![]() вращаются вместе с
ротором.
вращаются вместе с
ротором.
Для ротора из абсолютно твердого материала и при абсолютно жестких опорах это приведет к раскачиванию его цапф с частотой вращения ротора относительно геометрических центров подшипников.
Отношения
называются коэффициентами дисбаланса для соответствующих опор А и В.
7.2. Когда KA,B < 1,
подшипники работают по первому режиму нагружения. При таком KA,B ротор из абсолютно твердого материала
вращается вокруг своей оси и векторы неуравновешенных (динамических) сил в
опорах ![]() вращаются вместе с
ним. Благодаря этому суммарный вектор
вращаются вместе с
ним. Благодаря этому суммарный вектор ![]() сил, действующих на
опору, будет изменяться, например, при KA,B = 0,5 в
интервале
сил, действующих на
опору, будет изменяться, например, при KA,B = 0,5 в
интервале ![]() с частотой вращения
ротора. Это вызовет раскачивание цапфы с частотой вращения ротора в пределах
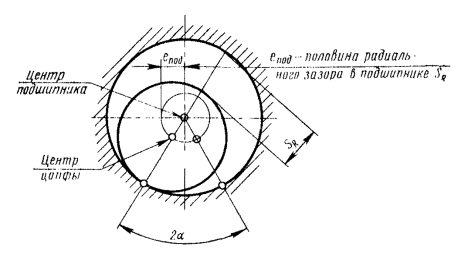
угла 2a качаний вектора
с частотой вращения
ротора. Это вызовет раскачивание цапфы с частотой вращения ротора в пределах
угла 2a качаний вектора ![]() (черт. 12).
(черт. 12).
При коэффициенте дисбаланса KA,B < 1 происходит односторонний износ подшипника и равномерный по окружности износ цапфы.
Черт. 12.
7.2.1. При первом режиме нагружения ротор прижимается к опорам с силой QA,B, значение
которой меняется от QA,B мин до QA,B макс по синусоидальному закону, причем ![]() равна удвоенной
амплитуде синусоиды или ее высоте.
равна удвоенной
амплитуде синусоиды или ее высоте.
Центр тяжести площади синусоида расположен на высоте 0,75 ее амплитуды ![]() над ограничивающей ее
линией QA,B мин.
над ограничивающей ее
линией QA,B мин.
Эквивалентные нагрузки на подшипники с учетом действия дисбалансов в опорах для определенной угловой скорости вращения w ротора определяются так:
что превышает ![]() на
на ![]() .
.
7.2.2. Обычно подбор подшипников качения ведется по нагрузкам QA,B (без учета динамических воздействий дисбалансов) по коэффициенту работоспособности подшипников
![]()
где n - частота вращения (мин-1);
h - число часов работы;
k1, k2 … - коэффициенты, определяющие условия работы подшипника.
Неучтенное в таком расчете ![]() сократит срок службы
подшипников в s раз, что адекватно
увеличению их нагрузки в s0,3 раза. Следовательно, в силу (47)
сократит срок службы
подшипников в s раз, что адекватно
увеличению их нагрузки в s0,3 раза. Следовательно, в силу (47)
Приняв среднее значение коэффициента дисбаланса ротора 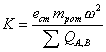 найдем из (48), что
найдем из (48), что ![]() .
.
Если регламентировано ест доп, то значение K определяется однозначно, а при подборе подшипников качения следует учесть уменьшение срока их службы в s раз
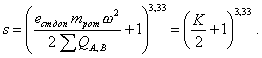 (49)
(49)
При больших различиях в нагрузках (статических и динамических) на опорах подобные расчеты следует проводить для каждой опоры в отдельности.
7.3. Если KA,B = 1, то подшипники
работают по второму режиму нагружения. В этом случае ![]() , где t - время.
, где t - время.
При K = 1 сила R будет прижимать цапфу к подшипнику, пока центр цапфы находится ниже горизонтального диаметра подшипника, и отрывать цапфу от подшипника, когда центр цапфы поднимается выше.
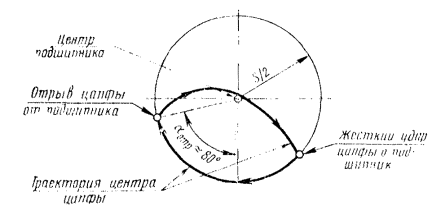
Отрыв цапфы от подшипника будет происходить, когда центр цапфы находится примерно на 10° ниже горизонтального диаметра подшипника. После отрыва цапфа движется по кривой (черт. 13), пока не ударится о подшипник и прижмется к нему. Далее процесс повторяется. Частота ударов равна частоте вращения ротора.
Работа машин с такими ударами приводит к разрушению подшипников значительно ранее их износа. Опыт показывает, что такой режим работы наступает уже вблизи K = 1.
Черт. 13.
7.4. Если ротор установлен вертикально или работает в невесомости, то ![]() может быть величиной,
большей единицы. В этом случае целесообразно применять опоры качения.
может быть величиной,
большей единицы. В этом случае целесообразно применять опоры качения.
При KA,B > 1 подшипники работают по третьему режиму нагружения. Если K > 1, то цапфа все время прижата к подшипнику и будет по нему скользить одной и той же стороной. В этом случае в подшипнике скольжения будет происходить односторонний износ цапфы, ведущий к дальнейшему увеличению K и неравномерному износу подшипника по окружности.
7.5. Из всех трех режимов нагружения для подшипников скольжения допустим лишь первый, а для подшипников качения первый и третий. Одна из задач балансировки - обеспечить эти условия работы для каждого подшипника. В общем случае коэффициенты дисбаланса различны для каждого подшипника опор A и B.
Значения коэффициентов KA,B для реальных машин должны определяться экспериментально (или теоретически, что не всегда возможно) в конце ресурсных испытаний опытного образца, так как числитель и знаменатель формулы (46) могут меняться в процессе эксплуатации.
При проектировочных расчетах следует пользоваться данными для аналогичных машин.
7.6. Если сила РА,В мала и ею можно пренебречь, то для горизонтального симметрично расположенного относительно подшипников межопорного ротора
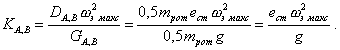
Откуда, необходимый класс точности балансировки, который обеспечивает нужный режим работы данного подшипника, находится по формуле
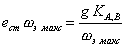 (50)
(50)
и разд. I ГОСТ 22061-76.
Чтобы не работать при втором режиме с ударами, следует избегать значений KА,В, лежащих в интервале 0,6 < KА,В < 1,4.
7.7. Рассмотрим колебания цапфы абсолютно твердого ротора в совершенно
жестких опорах без учета сил трения. Найдем сначала так называемую
восстанавливающую силу WА,В, которая равна проекции силы ![]() (п. 7.1) на
касательную к дуге, описываемой центром цапфы.
(п. 7.1) на
касательную к дуге, описываемой центром цапфы.
![]()
При первом режиме нагружения сила WА,В создает относительно центра качаний цапфы момент, который в среднем (из-за вращения цапфы) равен
![]() (51)
(51)
где ![]() - половина замеренного радиального
зазора SA,B в подшипнике А или В.
- половина замеренного радиального
зазора SA,B в подшипнике А или В.
Восстанавливающий момент при a = 1 рад принято рассматривать как жесткость С, поэтому при малых a (до 5°)
![]() , а
, а ![]()
Частоту собственных маятниковых колебаний цапфы (маятниковый резонанс) можно представить как обычно
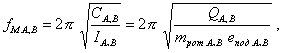 (рад/с), (52)
(рад/с), (52)
где ![]() - часть массы mрот ротора, приведенная в опоре А или В. Так как
- часть массы mрот ротора, приведенная в опоре А или В. Так как ![]() (п. 7.1), то
(п. 7.1), то
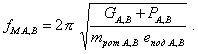
Если же ![]() , то
, то
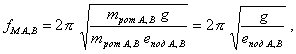 (рад/с), (53)
(рад/с), (53)
где g - ускорение силы тяжести.
Эта собственная частота маятниковых колебаний - своя для каждой опоры А или В, так как в каждой опоре свой зазор SA или SB.
Если fM в опоре А или B совпадает с частотой вращения ротора w/2p, то возникает резонанс маятниковых колебаний, амплитуда их резко возрастет и произойдет отрыв цапфы от опоры. При этом вращение в данной опоре станет неустойчивым, с ударами; ось вращения ротора начнет беспорядочно «болтаться» в опоре и поведение ротора станет неопределенным.
Маятниковые колебания ротора действуют как поглотитель энергии вращения.
7.8. При третьем режиме нагружения подшипников ротора (KA,B > 1,4) из абсолютно твердого материала на
абсолютно жестких опорах центр масс ротора постоянно находится на расстоянии ![]() от центра качаний
цапфы. В общем случае eA,B -
эксцентриситеты приведенных (не только статически) к опорам А или В частей массы
от центра качаний
цапфы. В общем случае eA,B -
эксцентриситеты приведенных (не только статически) к опорам А или В частей массы ![]() ротора, и лишь при статической неуравновешенности
ротора eA,B = eст. Поэтому для статической неуравновешенности
и третьего режима нагружения
ротора, и лишь при статической неуравновешенности
ротора eA,B = eст. Поэтому для статической неуравновешенности
и третьего режима нагружения
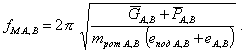 (54)
(54)
Если же ![]() , то
, то 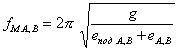 (рад/с). Маятниковые колебания в опорах при
(рад/с). Маятниковые колебания в опорах при ![]() и при KA,B > 1,4 приводит к износу некоторого участка поверхности цапфы,
симметричного относительно осевого сечения, содержащего
и при KA,B > 1,4 приводит к износу некоторого участка поверхности цапфы,
симметричного относительно осевого сечения, содержащего ![]() (п. 7.2).
(п. 7.2).
7.9. Когда маятниковый резонанс в опоре A или В выявлен, следует обеспечить несовпадение fэ с величиной ![]() , где j = 1, 2, 3, ...
, где j = 1, 2, 3, ...
Это можно сделать путем подбора подшипника, т.е. его радиального зазора 2епод = S.
Раздел 8. БАЛАНСИРОВКА КОЛЕНЧАТЫХ ВАЛОВ И УРАВНОВЕШИВАНИЕ СИЛ В ПОРШНЕВЫХ МАШИНАХ
8.1. В настоящем разделе рассматриваются особенности динамической балансировки коленчатых валов с технологическими втулками и без них, а также способы оценки неуравновешенных сил различных порядков, действующих в многоцилиндровой машине.
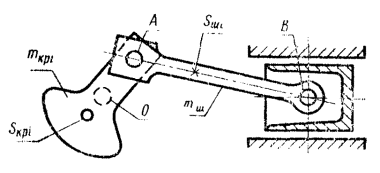
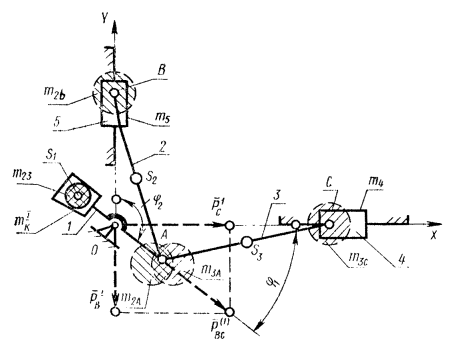
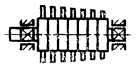
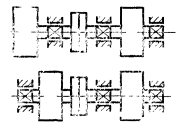
8.1.1. Если многоцилиндровая машина состоит из одинаковых центральных кривошипно-ползунных механизмов (черт. 14) и для каждого механизма справедливо условие уравновешенности вращающихся масс mкрi и тшАi, то
где OSкрi - расстояние от центра массы i-го кривошипа до оси вращения;
OAкрi - длина i-го кривошипа;
OSшi - расстояние от центра массы i-го шатуна до точки В;
АВшi - длина i-го шатуна;
mшАi - часть массы mшi i-го шатуна, статически приведенная к точке А кривошипа.
![]() (56)
(56)
mкрi - масса i-го кривошипа вместе с его корректирующей массой.
Примечание. Комплектация шатуна для определения положения его центра масс и метод этого определения должны устанавливаться в нормативно-технической документации, утвержденной в установленном порядке.
Отсюда следует, что после отсоединения от коленчатого вала шатунно-поршневых групп массы ткр1, ткр2, ... ткрk кривошипов могут оказаться неуравновешенными, вследствие чего динамическая балансировка коленчатого вала на балансировочном станке окажется невозможной без технологических втулок, которые должны закрепляться на шатунных шейках вала. Втулки делаются разъемными и имеют такие массы, чтобы их действие на коленчатый вал во время балансировки заменяло действие шатунно-поршневых групп.
На практике могут встретиться коленчатые валы, которые в зависимости от числа колен и их относительного положения должны балансироваться или с технологическими втулками или без них. На специальных балансировочных станках применяется электрическая компенсация, позволяющая обходиться без таких втулок.
Черт. 14.
8.2. Балансировка коленчатых валов без технологических втулок
8.2.1. Во время балансировки коленчатого вала на балансировочном станке масса mкрi i-го кривошипа действует на коленчатый вал с силой
![]()
где wб - угловая скорость коленчатого вала во время балансировки.
Если главный вектор и главный момент системы сил ![]() будут равны нулю
будут равны нулю
где ![]() - момент силы
- момент силы ![]() относительно произвольного центра А приведения сил;
относительно произвольного центра А приведения сил;
k - число кривошипов;
то динамическая балансировка коленчатого вала на балансировочном станке может производиться без технологических втулок.
Уравнения (57) и (58) удовлетворяются для коленчатых валов, симметричных относительно их средней плоскости (левая половина коленчатого вала является зеркальным отображением правой половины) и у которых центр системы масс mкрi лежит на оси вращения.
Например, для вала четырехцилиндровой машины с расположением кривошипов по схеме, показанной на черт. 15, или шестицилиндровой машины (черт. 16) условия (57) и (58) удовлетворяются. Поэтому балансировку таких валов следует производить без технологических втулок.
Черт. 15.
Черт. 16.
8.3. Балансировка коленчатых валов с технологическими втулками
Если условия (57) и (58) не выполняются, то балансировка коленчатого вала на балансировочном станке должна производиться с технологическими втулками.
Для того, чтобы технологические втулки действовали на коленчатый вал во время балансировки так же как и шатунно-поршневые группы, необходимо равенство дисбалансов технологической втулки и соответствующего кривошипа относительно оси вращения коленчатого вала. Отсюда следует, что масса mтi i-й технологической втулки должна быть равна в соответствии с уравнением (55)
где ![]() - длина i-го кривошипа (радиус его вращения).
- длина i-го кривошипа (радиус его вращения).
Знак минус в формуле (59) показывает, что центры масс mтi и mкрi расположены симметрично относительно оси вращения О.
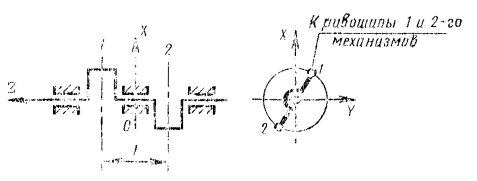
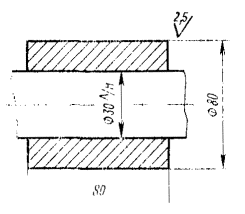
Пример 1. Рассмотрим коленчатый вал двухцилиндровой машины (черт. 17).
Черт. 17.
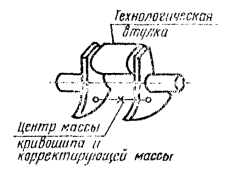
В данном случае условие (58) не выполняется, но центр массы коленчатого вала лежит на оси вращения. Перед балансировкой такого вала на балансировочном станке на каждую шатунную шейку вала необходимо надеть, как показано на черт. 18, технологическую втулку с массой mтi, определяемой формулой (59).
Черт. 18.
8.4. В некоторых случаях масса mкpi i-го кривошипа уравновешивает не только шатунную массу тшАi i-го шатуна, но и учитывает действие неуравновешенных сил первого порядка, описанных далее, в п. 8.6 настоящего раздела. Это следует учитывать при определении масс технологических втулок.
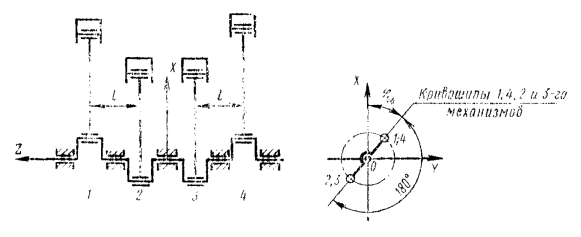
Пример 2. Рассмотрим коленчатый вал четырехцилиндровой V-образной машины с кривошипами, расположенными под углом 90°, и с углом развала цилиндров, равным также 90° (черт. 19).
Будем считать заданными массы, координаты их центров и размеры звеньев 1 - 5.
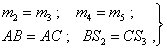 (60)
(60)
где m2, m3, m4 и т5 - массы 2, 3, 4 и 5-го звеньев.
Очевидно, что после уравновешивания вращающихся масс (черт. 19)
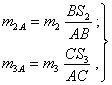 (61)
(61)
дисбаланс кривошипа будет равен
а на станину механизма будут действовать в направлении координатных осей ОХ и OY силы различных порядков, указанные в п. 8.6 I части настоящего раздела.
Силы первого порядка
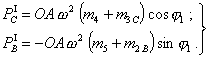 (63)
(63)
имеют равнодействующую
![]() (64)
(64)
направленную всегда по кривошипу ОА, как показано на черт. 19.
Сила ![]() может быть уравновешена путем прикрепления к
кривошипу корректирующей массы
может быть уравновешена путем прикрепления к
кривошипу корректирующей массы ![]() с дисбалансом
с дисбалансом
Таким образом, полный дисбаланс D кривошипа, необходимый для уравновешивания
как шатунных масс m2A, m3A, так и сил первого порядка ![]() ,
, ![]() , будет равен
, будет равен
![]() (66)
(66)
Черт. 19.
Подставляя сюда вместо D1 и DI выражения (62) и (65) и
принимая во внимание, что ![]() , получим
, получим
![]() (67)
(67)
Отсюда следует, что масса одной технологической втулки для рассматриваемого коленчатого вала будет равна
![]() (68)
(68)
8.5. О стационарном изгибе коленчатого вала
Стационарный изгиб коленчатого вала может возникать у статически сбалансированных коленчатых валов, симметричных относительно средней плоскости.
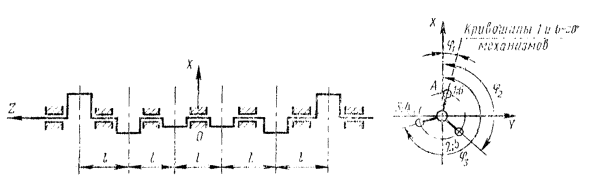
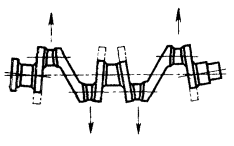
Рассмотрим коленчатый вал шестицилиндровой машины, схема которой показана на черт. 16.
Для того, чтобы неуравновешенные силы различных порядков действовали на станину машины только вдоль геометрических осей цилиндров, необходимо для каждого кривошипно-ползунного механизма выполнить условие (55). Но из черт. 16 можно видеть, что шатунные массы mшАi действуют в данном случае на коленчатый вал с силами
![]() (69)
(69)
главный вектор и главный момент которых равен нулю. По этой причине массы тшАi можно было бы в данном случае не уравновешивать корректирующими массами или противовесами. Это не изменит неуравновешенные силы, действующие на станину машины, но уменьшит массу и упростит конструкцию коленчатого вала. Этим пользуются в некоторых случаях на практике и делают коленчатые валы без противовесов.
Следует, однако, заметить, что отсутствие корректирующих масс для уравновешивания шатунных масс m2Ai даже у статически сбалансированных коленчатых валов, имеющих симметрию относительно их средней плоскости, отрицательно влияет на работу многоцилиндровой машины и прежде всего на работу самого коленчатого вала. Это объясняется тем, что при отсутствии корректирующих масс или противовесов шатунные массы тшАi и массы m1i кривошипов действуют на коленчатый вал с силами, равными
![]() (70)
(70)
где ОS1i - эксцентриситет массы m1i.
Векторы ![]() образуют две пары сил с моментами,
одинаковыми по значению, но противоположными по знаку.
образуют две пары сил с моментами,
одинаковыми по значению, но противоположными по знаку.
Для коленчатого вала, показанного на черт. 16, силы ![]() , действующие на 1, 2 и 3-й кривошипы, создают пару сил с
моментом
, действующие на 1, 2 и 3-й кривошипы, создают пару сил с
моментом
![]() (71)
(71)
где l - расстояние между геометрическими осями цилиндров.
Вектор ![]() всегда направлен по
второму кривошипу перпендикулярно его оси и вращается вместе с коленчатым
валом. Аналогично, силы
всегда направлен по
второму кривошипу перпендикулярно его оси и вращается вместе с коленчатым
валом. Аналогично, силы ![]() , действующие
на 4, 5 и 6-й кривошипы, приводятся к паре сил с моментом
, действующие
на 4, 5 и 6-й кривошипы, приводятся к паре сил с моментом
![]() (72)
(72)
направление которого противоположно моменту М1, 2, 3.
Векторы ![]() ,
, ![]() , оставаясь постоянными по модулю, вращаются вместе с
коленчатым валом и поэтому создают стационарный изгиб коленчатого вала в
плоскости, перпендикулярной к 2 и 5-му кривошипам. В таком изогнутом состоянии
коленчатый вал вращается.
, оставаясь постоянными по модулю, вращаются вместе с
коленчатым валом и поэтому создают стационарный изгиб коленчатого вала в
плоскости, перпендикулярной к 2 и 5-му кривошипам. В таком изогнутом состоянии
коленчатый вал вращается.
Это явление приводит к уменьшению ресурса машины, так как способствует увеличению интенсивности и неравномерности износа коренных и шатунных подшипников машины, появлению трещин усталости на коленчатом валу и увеличению общего уровня вибрации машины.
Чтобы коленчатый вал не имел стационарного изгиба, он должен иметь корректирующие массы или противовесы для уравновешивания шатунных масс тшАi. Целесообразность применения таких корректирующих масс в конкретных случаях должна подкрепляться также технико-экономическими расчетами.
8.6. Особенности уравновешивания в многоцилиндровых машинах неуравновешенных сил различных порядков
Будем считать, что многоцилиндровая машина состоит из одинаковых центральных кривошипно-ползунных механизмов, для которых выполняется условие (55). В этом случае на станину машины вдоль оси направляющей каждого кривошипно-ползунного механизма действует неуравновешенная сила
где А2, A4, ... - числовые коэффициенты, зависящие от ОА/АВ, представление о которых дает следующая таблица.
|
ОА/АВ |
1/3,5 |
1/4 |
1/4,5 |
1/5 |
1/6 |
1/7 |
|
А2 |
0,291800 |
0,254000 |
0,225000 |
0,202000 |
0,167800 |
0,143600 |
|
A4 |
-0,006200 |
-0,004100 |
-0,002800 |
-0,002000 |
-0,001200 |
-0,000700 |
|
A6 |
0,000126 |
0,000069 |
0,000038 |
0,000022 |
0,000009 |
0,000004 |
Слагаемые выражения (73)
![]()
и т.д. называются соответственно силами первого, второго, четвертого и более высоких порядков в зависимости от коэффициента при j.
Таким образом, в общем случае на станину центрального кривошипно-ползунного механизма, для которого выполнено условие (55), действует вдоль оси направляющей неуравновешенная сила Р, представляющая алгебраическую сумму неуравновешенных сил различных порядков.
![]() (74)
(74)
Эти силы можно рассматривать как проекции на направление движения ползуна некоторых вспомогательных векторов, равных по модулю
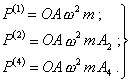 (75)
(75)
и образующих с осью X (черт. 15) углы
![]() (76)
(76)
и, следовательно, вращающихся с угловыми скоростями w; 2w; 4w.
Силу P нельзя уравновесить для отдельно взятого кривошипно-ползунного механизма путем прикрепления корректирующей массы или противовеса к кривошипу. Но в многоцилиндровых машинах вполне возможно достигнуть взаимного уравновешивания сил первого, второго, а в некоторых случаях и более высокого порядка при помощи простейших конструктивных средств, к которым относится выбор относительного расположения кривошипов и подбор значений поступательно движущихся масс.
Рассмотрим определение неуравновешенных сил в шестицилиндровой машине, у которой геометрические оси цилиндров и ось вращения коленчатого вала находятся в одной плоскости, а кривошипы расположены под углом 120°. Схема машины показана на черт. 20.
Вспомогательные векторы ![]() (i = 1, 2, ..., 6), где
(i = 1, 2, ..., 6), где ![]() направляем по
соответствующим кривошипам.
направляем по
соответствующим кривошипам.
Проектируя эти векторы на геометрические оси цилиндров, получим неуравновешенные силы первого порядка.
Так как равенства ![]() удовлетворяются
тождественно при любом значении угла j1, в чем легко убедиться путем подстановки в них выражений (77),
то заключаем, что неуравновешенные силы первого порядка приводятся в
рассматриваемой машине к двум парам сил, одинаковым по моменту, но
противоположным по знаку.
удовлетворяются
тождественно при любом значении угла j1, в чем легко убедиться путем подстановки в них выражений (77),
то заключаем, что неуравновешенные силы первого порядка приводятся в
рассматриваемой машине к двум парам сил, одинаковым по моменту, но
противоположным по знаку.
Момент ![]() пары сил, создаваемой
неуравновешенными силами
пары сил, создаваемой
неуравновешенными силами ![]() равен
равен
где а -
расстояние от геометрической оси второго цилиндра до линии действия
равнодействующей сил ![]() и
и ![]() .
.
Величину а можно определить
из уравнения моментов силы ![]() и силы
и силы ![]() , где
, где ![]() - равнодействующая
сил
- равнодействующая
сил ![]() и
и ![]() относительно точки А, лежащей на геометрической оси
второго цилиндра (черт. 20).
относительно точки А, лежащей на геометрической оси
второго цилиндра (черт. 20).
Черт. 20.
![]()
Отсюда следует
![]() (79)
(79)
Если подставить это выражение в формулу (78) и принять во внимание равенства (77), то после элементарных преобразований, получим
![]() (80)
(80)
Аналогично можно определить выражение для момента ![]() сил первого порядка,
создаваемого неуравновешенными силами
сил первого порядка,
создаваемого неуравновешенными силами ![]() и показать,
что
и показать,
что
![]() (81)
(81)
Таким образом, моменты ![]() будут вызывать
изгибные колебания коленчатого вала в плоскости, проходящей через
геометрические оси цилиндров.
будут вызывать
изгибные колебания коленчатого вала в плоскости, проходящей через
геометрические оси цилиндров.
Для оценки неуравновешенных сил второго порядка возьмем вспомогательные
векторы ![]() (i = 1, 2, ..., 6), где
(i = 1, 2, ..., 6), где ![]() и направим их под углом
2ji, к геометрическим осям соответствующих цилиндров.
и направим их под углом
2ji, к геометрическим осям соответствующих цилиндров.
Так как углы ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() , то вспомогательные
векторы
, то вспомогательные
векторы ![]() будут попарно совпадать по фазе и
направлены так, как показано на черт. 20.
будут попарно совпадать по фазе и
направлены так, как показано на черт. 20.
Проектируя эти векторы на геометрические оси цилиндров, получим неуравновешенные силы второго порядка
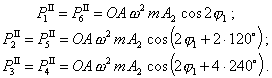
Силы ![]() приводятся к паре сил
с моментом
приводятся к паре сил
с моментом ![]() , где а определяется из уравнения моментов сил
, где а определяется из уравнения моментов сил
![]() и равнодействующей
сил
и равнодействующей
сил ![]() и
и ![]() относительно центра А, лежащего на геометрической оси второго
цилиндра
относительно центра А, лежащего на геометрической оси второго
цилиндра
![]()
Решая это уравнение относительно а, получим
![]() (82)
(82)
После этого формулу для ![]() можно записать в виде
можно записать в виде
![]() (83)
(83)
Неуравновешенные силы ![]() и
и ![]() также приводятся к
паре сил с моментом
также приводятся к
паре сил с моментом
![]() (84)
(84)
Поэтому силы второго порядка вызывают изгибные колебания коленчатого вала в плоскости, проходящей через геометрические оси цилиндров.
Такое же действие будут производить неуравновешенные силы всех четных порядков, если только порядок силы не является кратным числу 3.
Силы, порядок которых равен 3 · 2n (n = 1, 2, 3, 4, 5, ...), приводятся к равнодействующей,
в чем легко убедиться, если заметить, что вспомогательные векторы ![]() образуют с
геометрическими осями цилиндров углы
образуют с
геометрическими осями цилиндров углы
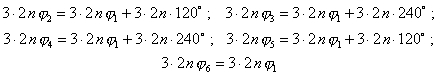
и, следовательно, совпадают по фазе. Поэтому равнодействующая
неуравновешенных сил порядка 3 · 2n, равная арифметической сумме проекций
векторов ![]() на геометрические оси
цилиндров будет
на геометрические оси
цилиндров будет
![]()
Линия действия силы ![]() проходит через
середину коленчатого вала параллельно геометрическим осям цилиндров.
проходит через
середину коленчатого вала параллельно геометрическим осям цилиндров.
8.7. Кривошипно-ползунный механизм звездообразных поршневых машин в
общем случае выполнен по схеме «звезда» или «двойная звезда» с углами развала
цилиндров, не равными углам прицепа шатунов ![]() с различными
приведенными массами по ступеням (здесь n - число цилиндров 5, 7, 9 и т.д.).
с различными
приведенными массами по ступеням (здесь n - число цилиндров 5, 7, 9 и т.д.).
Жесткие требования к уровню вибрации, генерируемому звездообразными поршневыми машинами, требуют тщательного уравновешивания результирующих сил и моментов, действующих на неподвижные части машин.
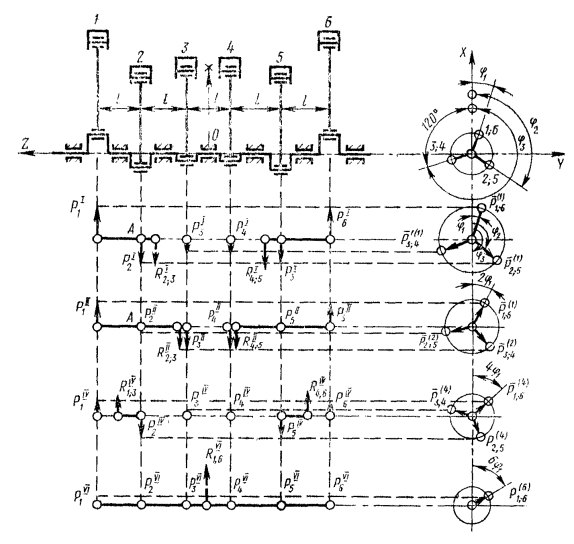
Неуравновешенная сила Рij поступательно движущейся массы в кривошипно-ползунном механизме является периодической функцией a - угла поворота коленчатого вала (черт. 21), поэтому в общем случае ее можно записать
![]()
где k - порядок гармоники;
Ajk и Bjk - амплитуды гармоник k-го порядка, пропорциональные произведению ![]() поступательно
движущейся в цилиндре массы, радиусу кривошипа и квадрату угловой скорости
вращения коленчатого вала.
поступательно
движущейся в цилиндре массы, радиусу кривошипа и квадрату угловой скорости
вращения коленчатого вала.
Черт. 21.
Сила бокового давления ![]() обусловлена в
кривошипно-ползунном механизме совместным действием неуравновешенных сил и сил
давления газа и так же как и сила инерции действует на неподвижные части
машины. Принимая за центр приведения сил неподвижную точку О коленчатого вала, имеем следующие результирующие силы и моменты.
обусловлена в
кривошипно-ползунном механизме совместным действием неуравновешенных сил и сил
давления газа и так же как и сила инерции действует на неподвижные части
машины. Принимая за центр приведения сил неподвижную точку О коленчатого вала, имеем следующие результирующие силы и моменты.
1) Неуравновешенную силу вращающихся масс Рвр, постоянную по значению и вращающуюся в плоскости, перпендикулярной оси коленчатого вала, с угловой скоростью w. Линия действия этой силы совпадает с направлением кривошипа в любой момент времени
![]()
2) Суммарную неуравновешенную силу ![]() поступательно
движущихся масс. Эта сила, изменяясь по значению и направлению, вращается в
плоскости, перпендикулярной оси коленчатого вала, в направлении вращения
кривошипа и для любого угла a
поступательно
движущихся масс. Эта сила, изменяясь по значению и направлению, вращается в
плоскости, перпендикулярной оси коленчатого вала, в направлении вращения
кривошипа и для любого угла a
![]()
3) Суммарный момент ![]() , обусловленный действием боковых составляющих
неуравновешенных сил и давления газов. Значение этого момента периодически
меняется в зависимости от угла a, а его вектор направлен по оси коленчатого
вала
, обусловленный действием боковых составляющих
неуравновешенных сил и давления газов. Значение этого момента периодически
меняется в зависимости от угла a, а его вектор направлен по оси коленчатого
вала
![]()
Неуравновешенные силы вращающихся масс полностью уравновешиваются двумя противовесами, расположенными на продолжении кривошипа
![]()
где mпр - масса противовеса;
r - расстояние до центра массы противовеса от оси О.
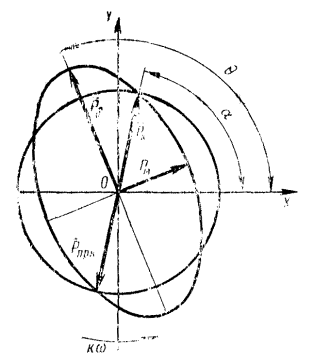
В звездообразных поршневых машинах практическое значение имеет уравновешивание суммарных неуравновешенных сил 1 и
2-го порядков. Вектор суммарной силы 1-го порядка ![]() в общем случае
изменяясь по модулю и направлению, описывает своим концом эллипс с осями,
смещенными относительно координат X, Y на угол Q, и вращается в направлении вращения
кривошипа со средней угловой скоростью w (черт. 22). В
этом нетрудно убедиться, выразив вектор
в общем случае
изменяясь по модулю и направлению, описывает своим концом эллипс с осями,
смещенными относительно координат X, Y на угол Q, и вращается в направлении вращения
кривошипа со средней угловой скоростью w (черт. 22). В
этом нетрудно убедиться, выразив вектор
![]()
При этом
где cos a и sin a - направляющие косинусы и синусы i-й неуравновешенной силы. Выражение (85) приводится к каноническому уравнению эллипса. Увеличением массы противовеса не полностью уравновешивается суммарная неуравновешенная сила 1-го порядка (черт. 22).
![]()
Величина ![]() остаточную
неуравновешенную силу на частоте вращения w.
остаточную
неуравновешенную силу на частоте вращения w.
Суммарная неуравновешенная сила 2-го порядка также не полностью может быть уравновешена при помощи соосных противовесов, располагаемых рядом с опорами коленчатого вала и вращающихся с угловыми скоростями 2w.
Неуравновешенные силы более высоких порядков остаются
неуравновешенными. В случае звездообразной поршневой машины с ![]() с равными
приведенными массами по ступеням эллипсы, описываемые векторами
неуравновешенных сил любого k-го порядка вырождаются в окружности. При
этом суммарные силы 1 и 2-го порядков уравновешиваются полностью.
с равными
приведенными массами по ступеням эллипсы, описываемые векторами
неуравновешенных сил любого k-го порядка вырождаются в окружности. При
этом суммарные силы 1 и 2-го порядков уравновешиваются полностью.
В сдвоенной звезде неуравновешенные силы уравновешиваются аналогичным
образом для каждой звезды отдельно. Гармоническая составляющая суммарного
момента 1-го порядка ![]() , в принципе, уравновешивается при помощи маятникового
противовеса, устанавливаемого около опор. Однако этот способ на практике не
применяется из-за сложности и значительного увеличения габаритов машины.
Поэтому суммарные моменты всех порядков звездообразных поршневых машин остаются
неуравновешенными. В частном случае, при
, в принципе, уравновешивается при помощи маятникового
противовеса, устанавливаемого около опор. Однако этот способ на практике не
применяется из-за сложности и значительного увеличения габаритов машины.
Поэтому суммарные моменты всех порядков звездообразных поршневых машин остаются
неуравновешенными. В частном случае, при ![]() и выровненных давлениях газа по ступеням суммарный момент
неуравновешенных сил всех порядков равен нулю.
и выровненных давлениях газа по ступеням суммарный момент
неуравновешенных сил всех порядков равен нулю.
Черт. 22.
Раздел 9. УРАВНОВЕШИВАНИЕ ДЕЗАКСИАЛЬНЫХ ПРИВОДОВ ВОЗВРАТНО-ПОСТУПАТЕЛЬНОГО ДЕЙСТВИЯ
9.1. Во время движения приводов возвратно-поступательного действия (например, режущих аппаратов косилок, жаток, зернокомбайнов, силосоуборочных и кукурузоуборочных комбайнов и др.) возникают неуравновешенные силы, которые вызывают дополнительное динамическое нагружение опор, вибрацию рамы, снижают долговечность и надежность режущих аппаратов, понижают качество технологического процесса, ухудшают условия работы водителей.
Осуществить на практике полное уравновешивание механизмов возвратно-поступательного действия не всегда удается в силу сложности конструктивного выполнения как показано в пп. 9.2 и 9.3 настоящего раздела. Поэтому в большинстве случаев неуравновешенные силы компенсируются лишь частично.
9.2. Компенсация неуравновешенных сил вращающихся масс
Неуравновешенная сила вращающихся масс на кривошипе равна (черт. 23).
![]() (86)
(86)
![]() (87)
(87)
где mвр - статически приведенная к пальцу кривошипа масса вращающихся элементов;
mкр - масса кривошипа;
mш - масса шатуна;
R - радиус кривошипа;
L - длина шатуна;
l - расстояние от шарнира А до центра массы кривошипа;
с - расстояние от шарнира у поступательно движущейся массы до центра массы шатуна;
w - угловая скорость вращения кривошипа (для сельскохозяйственных машин можно принять w = const).
Для компенсации неуравновешенных сил вращающихся масс устанавливают
противовес массой ![]() на расстоянии S, определяемом уравнением
на расстоянии S, определяемом уравнением
![]() (88)
(88)
Обычно S = R, тогда
![]() (89)
(89)
В этом случае остаются неуравновешенные силы поступательно движущихся масс звеньев и момент этих сил относительно оси, перпендикулярной плоскости движения привода.
Черт. 23.
9.3. Компенсация неуравновешенных сил поступательно движущихся масс
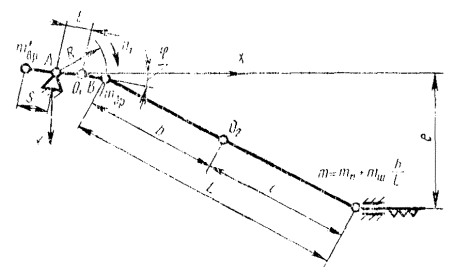
Неуравновешенные силы поступательно движущейся массы (например, ножа режущих аппаратов косилок, жаток и т.п. сельскохозяйственных машин) (черт. 23) выражаются с достаточной точностью уравнением
где ![]()
тп - поступательно движущаяся масса;
![]() - часть массы шатуна mш, приведенная к шарниру О
поступательно движущейся массы;
- часть массы шатуна mш, приведенная к шарниру О
поступательно движущейся массы;
j = wt - угол поворота кривошипа;
![]()
e/L - коэффициент дезаксиальности.
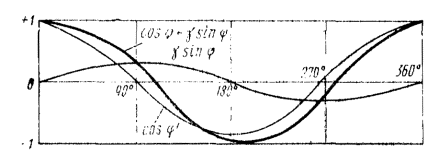
На черт. 24 представлен характер изменения неуравновешенной
силы поступательно движущейся массы за один поворот кривошипа, когда ![]() (для косилочных
аппаратов).
(для косилочных
аппаратов).
Черт. 24.
Положив g = tg j, из уравнения (90) получим
![]() (91)
(91)
где y - угол, показанный на черт. 27;
![]() - фактор увеличения неуравновешенных сил
из-за дезаксиала;
- фактор увеличения неуравновешенных сил
из-за дезаксиала;
![]() - неуравновешенная сила, которая не должна
меняться при равномерном вращении кривошипа.
- неуравновешенная сила, которая не должна
меняться при равномерном вращении кривошипа.
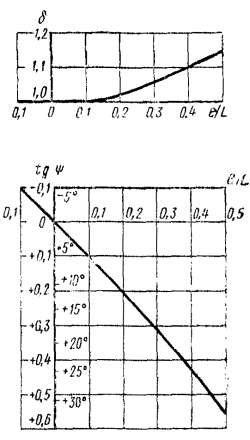
На черт. 25 изображены графики зависимости d и tg y от коэффициента дезаксиальности e/L.
Верхний график показывает, во сколько раз максимальная неуравновешенная
сила поступательно движущихся масс больше расчетной величины ![]() при отсутствии
дезаксиала. (Так, для e/L = 0,3 это превышение составляет 1,048, т.е.
4,8 %).
при отсутствии
дезаксиала. (Так, для e/L = 0,3 это превышение составляет 1,048, т.е.
4,8 %).
Для компенсации неуравновешенные силы Pп поступательно движущейся массы m могут использоваться два способа.
Черт. 25
9.3.1. Компенсирующая масса устанавливается под углом 180° к пальцу кривошипа (черт. 23).
Обозначим через mк компенсирующую массу, превышающую статически приведенную к пальцу кривошипа массу вращающихся элементов mвр.
Вводя mк/т, можно написать составляющие неуравновешенной силы по осям X и Y (черт. 23).
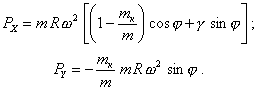
Результирующая неуравновешенная сила
![]() (92)
(92)
Откуда после ряда преобразований получим
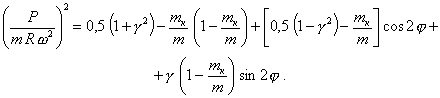 (93)
(93)
Максимальное значение неуравновешенной силы определяется из уравнения
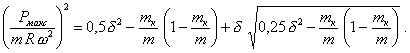 (94)
(94)
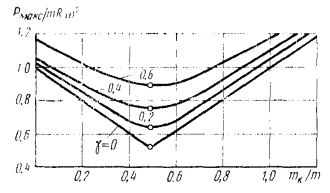
При mк/m = 0,5 величина ![]() имеет максимум, а Рмакс будет наименьшей.
Обозначим это минимальное значение Рмакс
через Р0, тогда
имеет максимум, а Рмакс будет наименьшей.
Обозначим это минимальное значение Рмакс
через Р0, тогда
![]() (95)
(95)
Для e/L = 0,3 ![]()
Наименьшего значения максимальная остаточная неуравновешенная сила для
дезаксиальных кривошипно-ползунных механизмов с расположением массы тк под углом 180° к пальцу кривошипа
достигает при ![]() о чем свидетельствуют
графики, приведенные на черт. 26.
о чем свидетельствуют
графики, приведенные на черт. 26.
Черт. 26.
9.3.2. Компенсирующая масса mк устанавливается под углом 180° - y (черт. 27).
В этом случае неуравновешенная сила будет состоять из следующих компонент:
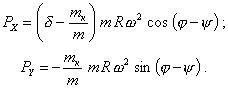 (96)
(96)
Черт. 27.
Результирующая неуравновешенная сила
![]()
Откуда, после ряда преобразований, получим
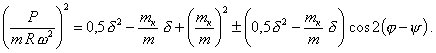
Максимальное значение неуравновешенной силы определяется из уравнения
Для ![]()
Для ![]()
При mк/m = 0,5 и e/L = 0,3, как это имело место для случая 9.3.1, получаем согласно уравнению (97)
![]()
Рассматривая уравнение (97), можно заметить, что при увеличении корректирующей массы до mк/m = 0,5d и том же значении e/L = 0,3, можно получить наименьшее максимальное значение неуравновешенной массы
![]()
Следовательно, при корректирующей массе mк, устанавливаемой под углом y, неуравновешенная сила поступательно движущихся масс значительно меньше, чем при установке ее под углом 180° по отношению к пальцу кривошипа. Для конкретных условий mк/m = 0,5, l/L = 0,3 остаточная неуравновешенная сила уменьшается на 19 %, а при тк/т = 0,5d даже на 23 %.
9.4. Компенсация неуравновешенных сил вращающихся и поступательно движущихся масс
Можно одновременно уменьшать неуравновешенные силы вращающихся и
поступательно движущихся масс, заменив корректирующие массы ![]() и mк одной уравновешивающей массой mур, которая располагается между компенсирующими массами
и mк одной уравновешивающей массой mур, которая располагается между компенсирующими массами ![]() и mк под некоторым углом 180° - x к пальцу кривошипа (между компенсирующими
массами
и mк под некоторым углом 180° - x к пальцу кривошипа (между компенсирующими
массами ![]() и mк) и определяется по формуле
и mк) и определяется по формуле
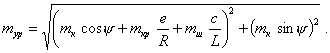 (98)
(98)
Положение массы mур определяется углом
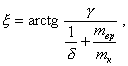 (99)
(99)
где
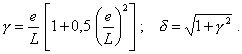
9.5. Рекомендуемый порядок расчета допустимой неуравновешенной силы кривошипно-ползунных дезаксиальных приводов сельхозмашин
Метод предусматривает следующее.
9.5.1. Определение неуравновешенной силы вращающихся масс Pвр согласно п. 9.2 настоящего раздела.
9.5.2. Определение максимального значения неуравновешенной силы поступательно движущихся масс Pп производится по п. 9.3 настоящего раздела.
9.5.3. Подсчет массы mур, уравновешивающей одновременно неуравновешенные силы вращающихся и поступательно движущихся масс, и угла расположения массы mур относительно кривошипа согласно п. 9.4 настоящего раздела.
Фактор d увеличения неуравновешенных сил можно определить по верхнему графику, а g = tgy - по нижнему графику черт. 25.
Этим методом можно скомпенсировать до 60 % неуравновешенной силы в механизмах возвратно-поступательного действия.
Раздел 10. СИСТЕМА «РОТОР - ОПОРЫ»
10.1. Рассмотрим межопорный ротор в виде массивного тонкого диска массы mрот, насаженного на упругий вал пренебрежимо малой массы, с коэффициентом жесткости Cрот, который вращается с низкой угловой скоростью вращения w без трения на упругих опорах А и В, с коэффициентом жесткости CопA и CопB
Допустим, что ротор имеет вертикальную ось вращения или, что он работает в условиях невесомости. В этом случае подшипники ротора под воздействием дисбалансов будут работать по третьему режиму нагружения с KA,B > 1,4.
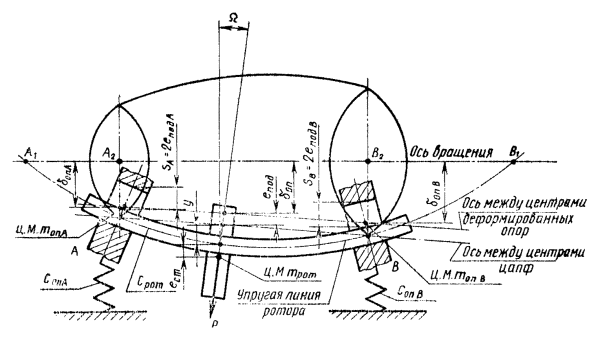
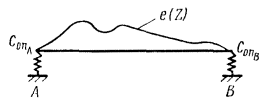
Пусть диск имеет удельный дисбаланс ест. При вращении с угловой скоростью w возникает неуравновешенная сила, которая вызовет у вала динамический прогиб y и будет деформировать опоры на величины dопА и dопВ. В результате этого ротор станет вращаться вокруг оси бочкообразной поверхности вращения, которую за каждый оборот ротора будет описывать его упругая линия, имеющая динамический прогиб (черт. 28). Влияние момента инерции диска и масляной пленки в подшипниках здесь не рассматривается.
Для реального упругого ротора на упругих опорах эта ось будет являться осью вращения ротора. В общем случае деформации опор А и В будут разные, что приведет к различным площадям оснований бочкообразной поверхности вращения. Если опоры неизотропны, то основания «бочек» вместо окружности будут иметь иную форму. Для упрощения выкладок будем считать, что деформации опор равны, т.е. dопА = dпоВ = dоп, а CпоA + CопB = Cоп.
10.2. При статической неуравновешенности ротора, работающего при третьем режиме нагружения подшипников (K > 1,4), радиальные зазоры SA,B подшипников в опорах А и В увеличат радиус вращения центра масс опор на величину
![]()
Максимальная неуравновешенная сила, развиваемая массой mрот ротора при вращении с угловой скоростью w, вызовет динамический прогиб у ротора (черт. 28).
Со стороны опор действует восстанавливающая сила ![]() состоящая из реакции
опор
состоящая из реакции
опор ![]() и неуравновешенной
силы приведенных масс
и неуравновешенной
силы приведенных масс ![]() опор, вращающихся с
той же угловой скоростью w на радиусе, равном деформации dоп опор (черт. 28)
опор, вращающихся с
той же угловой скоростью w на радиусе, равном деформации dоп опор (черт. 28)
Черт. 28.
Массы опор mопА и mопВ можно определить расчетом или экспериментально по измеренной тензометром собственной частоте свободных колебаний опор А и В после удара по ним.
Подставив (102) в (100), получим
где
![]()
wкр - критическая угловая скорость вращения упругого ротора при изгибе на абсолютно жестких опорах.
Аналогично может быть записана и критическая угловая скорость опор ![]() .
.
При равенстве нулю знаменателя выражения (103) в системе возникает резонанс по изгибу ротора. Такое возможно, когда угловая скорость w вращения ротора станет равной резонансной угловой скорости wрез вращения ротора системы «ротор - опоры», т.е. при
В формуле (102) ![]() зависящее от угловой
скорости вращения ротора, называется коэффициентом динамической жесткости опор
(без учета влияния масляной пленки), а выражение
зависящее от угловой
скорости вращения ротора, называется коэффициентом динамической жесткости опор
(без учета влияния масляной пленки), а выражение ![]() - коэффициентом
динамической жесткости системы «ротор - опоры», зависящим от угловой скорости
вращения ротора.
- коэффициентом
динамической жесткости системы «ротор - опоры», зависящим от угловой скорости
вращения ротора.
Если пренебречь в коэффициенте динамической жесткости опор слагаемым ![]() , то получим обычное выражение для коэффициента жесткости С
системы
, то получим обычное выражение для коэффициента жесткости С
системы
![]() или
или ![]()
Из (105) следует, что
т.е. существуют две действительные резонансные угловые скорости для рассматриваемой системы «ротор - опоры».
Резонансная частота системы «ротор - опоры».
![]() (107)
(107)
Из (106) видно, что, изменяя жесткости опор можно влиять на резонансную частоту системы «ротор - опоры», сдвигая ее в нужную сторону.
Если ротор работает при первом режиме нагружения подшипников (K < 0,6), то смещения епод не будет и
Если реальный ротор должен работать в широком диапазоне частот вращения, то остаточный дисбаланс в плоскостях коррекции будет зависеть от w.
10.3. Из (105), (106) и (108) следует, что:
10.3.1. При Соп ® ¥ (абсолютно жесткие опоры) и w << wрез1 упругая деформация у ротора минимальна. Как видно из формулы (108), в этом случае wрез1 ® wкр. Упругая линия ротора изогнута по первой форме (см. черт. 28 и п. 10.11.3). Если подшипники работают по третьему режиму нагружения (п. 7), то точки А и В совпадают с А3 и В3, а продолжения изогнутой упругой линии АВ пересекут ось вращения системы «ротор - опоры» за опорами А и В ротора. Ось вращения системы «ротор - опоры» с Соп ® ¥ при третьем режиме нагружения подшипников проходит через центры вкладышей подшипников скольжения или центры дорожек качения неподвижных (установленных в корпусе) колец подшипников качения.
10.3.2. При горизонтальной оси вращения в поле тяготения, если подшипники ротора с Соп ® ¥ работают на w < wрез1 по первому режиму нагружения, то ось вращения системы «ротор - опоры» проходит через центры цапф ротора в плоскостях опор скольжения или центры беговых дорожек колец подшипников качения, вращающихся вместе с ротором. В этих же центрах дорожек или цапф будут находиться и узлы А1 и В2 (точки пересечения с осью вращения системы «ротор - опоры») упругой линии ротора, изогнутой по первой форме.
10.3.3. По мере уменьшения Cоп расстояние между точками A1 и B1 пересечения (узлами), изогнутой по первой форме упругой линии ротора с осью вращения системы «ротор - опоры» возрастает, теоретически достигая ¥ при Cоп = 0 (ротор практически без опор). Одновременно wрез системы «ротор - опоры» уменьшается, как это видно из формулы (106).
10.3.4. Динамический прогиб y ротора и деформация опор sоп с ростом w возрастают
(формулы 106
и 108)
теоретически достигая ¥ при w = wрез1 (что может привести к поломке вала или опор), а при дальнейшем
возрастании w, у, don неоднократно меняют свой знак и устремляются
к ![]() . При этом центр масс вращающегося ротора приближается к оси
ротора. Это явление называется самоцентрированием массы.
. При этом центр масс вращающегося ротора приближается к оси
ротора. Это явление называется самоцентрированием массы.
Из рассмотренного следует, что, если бы в реальном роторе ест = 0, динамическое воздействие было бы равно нулю, если не учитывать прогибов от силы тяжести или радиальных нагрузок (зубчатых колес, ремней и т.п.).
10.4. Постоянно действующие поперечные силы, например, от зубчатых зацеплений, ремней и т.п. также влияют на резонансные угловые скорости системы «ротор - опоры».
Изменение первой резонансной угловой скорости системы «ротор - опоры» от действия поперечной силы Q, характеризуется коэффициентом
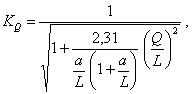
где a - расстояние от опоры А до силы Q, причем ![]()
10.5. Влияние постоянно действующей продольной силы может быть учтено коэффициентом
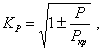
так что ![]()
где Pкр - критическая сила продольного изгиба в плоскости изгиба; при растягивающей силе берется знак плюс, при сжимающей - минус.
10.6. На значение wрез сказывается также момент инерции ротора, т.е. моменты, вызванные поворотом (см. угол W на черт. 28) отдельных масс, насаженных на вал, вследствие его изгиба. Эти влияния для особо точных роторов требуют специального рассмотрения.
10.7. В реальных условиях у ротора имеется обычно динамическая (а не
статическая) неуравновешенность; опоры имеют различные коэффициенты жесткости ![]() , следовательно,
, следовательно, ![]() и различные
радиальные зазоры в подшипниках
и различные
радиальные зазоры в подшипниках ![]() . Это приводит к возникновению маятниковых колебаний цапф в подшипниках, резонансные частоты
которых различны для обоих подшипников и не равны резонансной частоте системы
«ротор - опоры».
. Это приводит к возникновению маятниковых колебаний цапф в подшипниках, резонансные частоты
которых различны для обоих подшипников и не равны резонансной частоте системы
«ротор - опоры».
При первом режиме нагружения подшипников угловая скорость вращения центра масс ротора не равна угловой скорости вращения упругой линии ротора. Кроме того, жесткость ротора может быть неизотропна также как и жесткости опор; он может быть несимметричным в разных направлениях и т.д.
Таким образом, картина колебаний неуравновешенного вращающегося ротора резко усложняется. Трение и демпфирование также вносят свои искажения. Практически в каждом отдельном случае требуются специальные исследования.
10.8. Резонансная угловая скорость wрез1 системы «ротор - опоры» может быть определена и экспериментально, например, при помощи тензометра, укрепленного вдоль оси ротора, установленного на своих опорах. Записанная по показаниям тензометра чистота затухающих колебаний ротора, возникающих после удара по последнему, будет соответствовать первой резонансной угловой скорости вращения ротора системы «ротор - опоры». Критическая угловая скорость wкр1 собственно ротора может быть определена таким же путем, если ротор установлен на очень жесткие опоры.
Известные методы определения коэффициента жесткости ротора Cрот и коэффициентов жесткостей опор Cоп «продавливанием» здесь не рассматриваются.
10.9. Рассмотренный в пп. 10.2, 10.3 случай с одной сосредоточенной массой на гибком валу малой массы является упрощенным, но самым опасным частным случаем. В реальных системах с распределенной массой эксцентриситет ее изменяется вдоль оси Z ротора по какому-то закону e(z). Динамический прогиб y ротора по формулам (103) или (108) зависит от функции распределения начального эксцентриситета енач(z) вдоль ротора и законов изменения линейной жесткости ротора Eq(z) Iq(z) и его линейной массы mq(z). Подробнее этот вопрос рассмотрен в разд. 11.
Динамический прогиб ротора может быть уменьшен введением корректирующих масс в плоскости коррекции, если они не совпадают с плоскостями опор. Изменяя местоположение плоскостей коррекции конкретного ротора, их число и значения корректирующих масс, можно свести динамический прогиб к минимуму. Лишь в том случае, когда корректирующие дисбалансы располагаются вдоль ротора по тому же закону, что и локальные начальные дисбалансы, но под углом 180° к ним, динамический прогиб ротора может быть сведен к нулю.
Следует заметить, что функция начального эксцентриситета енач(z) зависит от конструктивного решения ротора, от принятого технологического процесса его изготовления и культуры производства.
10.10. При третьем режиме нагружения подшипников ротора со статической
неуравновешенностью (худший случай) смещение его центра масс при дорезонансной
угловой скорости вращения w определяется (черт. 28) суммой динамического прогиба
у, деформации опор dоп, удельного дисбаланса ест и половиной радиального зазора в подшипниках ![]() , т.е.
, т.е.
![]()
Начальное суммарное смещение центра масс на дорезонансной максимальной эксплуатационной угловой скорости wэ макс будет
После балансировки статически неуравновешенного двухопорного ротора на низкой (менее 1/3 резонансной) частоте вращения в двух произвольно расположенных плоскостях коррекции в плоскостях опор останутся остаточные смещения ест ост ≤ ест доп.
Корректирующие дисбалансы D1,2 кор в плоскостях коррекции, не совпадающих с плоскостями опор, вызовут на максимальной эксплуатационной угловой скорости вращения ротора динамический прогиб yкор, направленный против динамического прогиба yнач от удельного дисбаланса ест нач.
yкор будет максимальным, если ![]() расположена в
плоскости, перпендикулярной оси ротора, содержащей
расположена в
плоскости, перпендикулярной оси ротора, содержащей ![]() ; yкор - равен нулю, когда плоскости коррекции
совпадают с плоскостями опор. Наибольшее значение yкор при заданном расположении плоскостей коррекции конкретного ротора
подсчитывается методами сопротивления материалов или определяется
«продавливанием».
; yкор - равен нулю, когда плоскости коррекции
совпадают с плоскостями опор. Наибольшее значение yкор при заданном расположении плоскостей коррекции конкретного ротора
подсчитывается методами сопротивления материалов или определяется
«продавливанием».
Оптимальное положение плоскостей коррекции для некоторых функций енач(z) рассмотрены в п. 11.1.
Суммарное смещение центра масс ротора под воздействием только Dст кор при wэ макс будет
Здесь, как и ранее, ![]() должно подставляться
то, которое относится к максимальной эксплуатационной угловой скорости вращения
ротора.
должно подставляться
то, которое относится к максимальной эксплуатационной угловой скорости вращения
ротора.
Очевидно, что балансировка в двух плоскостях коррекции будет удачной, если
где
![]() - определяется по разд. 2 ГОСТ
22061-76.
- определяется по разд. 2 ГОСТ
22061-76.
Подставив в (111) выражения (109) и (110), получим
Заметим, что когда числитель формулы (112) отрицателен (т.е. когда ест ост направлено против ест нач) это легче осуществимо.
Несколько подробнее условие допустимости балансировки реального ротора как жесткого рассмотрено в разд. 11.
10.11. Рассмотренное здесь и в п. 9 позволяет оценить влияние упругости системы «ротор - опоры» на значение динамических нагрузок на опоры при различных коэффициентах дисбалансов.
10.11.1. При первом режиме работы подшипников, когда K < 0,6, в упругой системе «ротор - опоры» динамическая нагрузка на опорах от статической неуравновешенности меняется не только с частотой вращения центра масс, но и с частотой вращения упругой линии ротора (прецессии). Наибольшее значение этой динамической нагрузки на первой дорезонансной угловой скорости вращения ротора может быть представлено формулой (100), если принять епод = 0.
![]()
а в системе из абсолютно твердых материалов
![]()
Учтя (101), (102) и (108), получим
10.11.2. При статической неуравновешенности для третьего режима погружения подшипников качения упругой системы «ротор - опоры», когда K > 1,4 и ротор вращается с дорезонансной частотой, а зазор в подшипниках имеется, формулу (100) следует писать с учетом епод - половины радиального зазора SA,B в подшипниках качения.
В первом приближении ![]() , поэтому
, поэтому
Правые части равенств (113) и (114) показывают, во сколько раз динамические нагрузки от статической неуравновешенности в упругих системах «ротор - опоры» превышают динамические нагрузки в системах «ротор - опоры» из абсолютно твердых материалов.
Выражение (113) указывает на связь динамической нагрузки с зазором 2епод в подшипниках при третьем режиме их нагружения.
10.11.3. До первой резонансной угловой скорости wрез I прогиб упругой линии многомассового ротора напоминает половину синусоиды и называется первой собственной формой изгиба ротора (черт. 29 а).
Вблизи второй резонансной угловой скорости вращения ротора его упругая линия принимает вид синусоиды, показанной на черт. 29 b; опорные реакции RA и RB в плоскостях опор A и В при этом изменяются как по значению, так и по направлению (черт. 29 b).
Черт. 29.
Для ротора, эксплуатационная угловая скорость вращения которого лежит вблизи третьей резонансной угловой скорости wрез/3 форма упругой линии показана на черт. 29 с.
Плоскости, в которых происходит изгиб реального ротора по каждой из собственных форм изгиба, вообще говоря, различны (черт. 30). Совокупность таких плоскостей образует как бы «жесткую» систему, вращающуюся вместе с ротором. При изменении угловой скорости вращения ротора изменяются модули прогибов и углы между плоскостями, в которых происходит изгиб по соответствующей форме, что влечет за собой изменение значений и направлений опорных реакций.
В реальных системах «ротор - опоры» имеет место демпфирование в роторе и в опорах, которое мы не рассматривали. Под воздействием этого демпфирования плоские поверхности 1, 2, 3 (черт. 30), содержащие формы изгиба ротора, деформируются. Чаще всего этой деформацией по ее малости пренебрегают.
Черт. 30.
Раздел 11. УСЛОВИЕ ДОПУСТИМОСТИ БАЛАНСИРОВКИ РОТОРА КАК «ЖЕСТКОГО РОТОРА» НА ЧАСТОТЕ ВРАЩЕНИЯ НИЖЕ ПЕРВОЙ РЕЗОНАНСНОЙ СИСТЕМЫ «РОТОР - ОПОРЫ» И ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЭТОГО УСЛОВИЯ
Таким образом, решение о возможности балансировки конкретного типа ротора как жесткого или как гибкого зависит от частоты вращения при балансировке и положения плоскостей коррекции.
Но это не единственные исходные данные, которые влияют на решение.
Теоретическое рассмотрение условия допустимости балансировки ротора как жесткого или как гибкого изложено ниже на примере использования теории собственных функций изгиба межопорного ротора, симметричного относительно опор, работающего на дорезонансных частотах вращения при первом режиме нагружения подшипников.
Прогиб у ротора может быть представлен в виде ряда Фурье
где n - n-я форма изгиба ротора (n = 1, 2, 3, ..., n);
yn(z) - n-я собственная функция прогиба реального ротора на реальных опорах;
аn - коэффициент n-го члена ряда при n-й собственной функции.
Для разграничения жестких и гибких роторов достаточно воспользоваться только первым членом разложения y(z) по собственным функциям jn(z), так как при тех частотах вращения ротора (ниже первой резонансной системы «ротор - опоры»), при которых начинает существенно сказываться его прогиб, вызывающий индуктированный дисбаланс, описанный в п. 10.2.1, влияние членов ряда более высоких порядков пренебрежимо мало.
В общем случае даже расчет первой собственной функции j1(z) изгиба реального ротора на реальных опорах весьма трудоемок и часто требует применения ЭВМ. Поэтому для упрощения и ясности изложения ниже рассматривается симметричный относительно опор межопорный изотропный ротор ступенчатого сечения, шарнирно опирающийся на опоры равной жесткости с распределенными в одной осевой плоскости локальными дисбалансами. Распределение этих локальных дисбалансов характеризуется распределенным эксцентриситетом e(z) (черт. 31).
Черт. 31.
Потенциальная и кинетическая энергия деформации такого ротора по первой форме изгиба равна энергии, развиваемой при вращении ротора распределенными по нему дисбалансами.
![]() (116)
(116)
Заменив y(z) =a1j1(z), получим энергию первой формы изгиба.
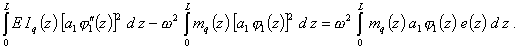
Откуда, имея в виду, что первая резонансная угловая скорость вращения ротора в системе «ротор - опоры»
получим
Энергию свободной деформации системы ротора и опор по первой форме изгиба можно представить так:
В силу симметричности ротора относительно опор третье слагаемое
![]()
В этих формулах mq(z) - линейная плотность ротора;
EIq(z) - линейная жесткость ротора;
Соп/2 = СопA = СопB - жесткость каждой опоры;
mоп/2 = mопA = mопB - приведенная масса каждой опоры.
(mon можно определить расчетом или экспериментально по собственной резонансной частоте опоры).
Первую собственную функцию j1(z) в формуле (115) реального ротора на реальных опорах можно представить в виде суммы первой собственной базисной функции f1(z) реального ротора, шарнирно опирающегося на абсолютно жесткие опоры, с собственной функцией j0(z) = 1 абсолютно твердого ротора, шарнирно опирающегося на реальные опоры, которая определяет его плоско-параллельное смещение из-за упругости опор.
Подставив (120) в (115) и (119) и вычтя равную нулю сумму динамических нагрузок и реакций опор
после сокращения на b1 ¹ 0, учитывая, что f1(0) = 0, получим
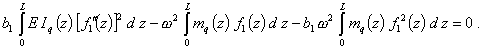
Это выражение свободных колебаний ротора при w = wрез1 резонансной угловой скорости вращения ротора системы «ротор - опоры».
Так как первая критическая угловая скорость реального ротора на абсолютно жестких опорах выражается через базисные функции так
то
Следовательно, из (120) и (123):
Поскольку локальные дисбалансы (эксцентриситеты е(z) на черт. 31) расположены в одной осевой плоскости (пространственное расположение может быть сведено к двум ортогональным плоскостям); значение главного вектора дисбалансов ротора будет
Если установить корректирующие массы в плоскостях коррекции 1 и 2, равноудаленных нa l1 = l2 от опор А и В ротора, то f1(l1) = f1(l2), так как ротор симметричен. Если даже после балансировки Dст = 0, то вследствие того, что локальные дисбалансы распределены вдоль всего ротора, а коррекция проводилась только в двух плоскостях, при вращении ротора с большой дорезонансной частотой он будет прогибаться по первой форме изгиба. В силу (118), (123) и (124) наибольший прогиб ротора по первой форме изгиба будет
Этот прогиб вызовет так называемый «индуктированный» дисбаланс (см. п. 10.2.1)
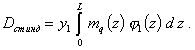 (127)
(127)
Очевидно, что, если Dст инд < Dст доп, можно не учитывать гибкость ротора.
Таким образом, критерий учета гибкости ротора
Если в (128) подставить (125) и (126) и обозначить отношение значений главного вектора начальных дисбалансов к главному вектору допустимых дисбалансов Dст нач/Dст доп = Kр, то условием допустимости балансировки реального ротора как жесткого будет
Все роторы, у которых значение левой части неравенства (129) меньше единицы, можно балансировать как жесткие в двух плоскостях коррекции.
Подставив (126) в (129) и обозначив: а) функцию, учитывающую жесткости ротора и опор при первой форме изгиба, связанную с первой резонансной угловой скоростью вращения ротора в системе «ротор - опоры», через Т
б) функцию начального эксцентриситета через ![]()
в) функцию от угловой скорости w через F
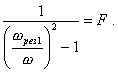 (132)
(132)
После преобразований получим
где b01 - по формуле (123) связана с собственной функцией f1(z);
j1(z) - первая собственная функция прогиба реального ротора на реальных опорах;
f1(z) - собственная базовая функция прогиба реального ротора по первой форме изгиба на абсолютно жестких опорах.
Собственно базовая функция f1(z) может быть получена методом Стодола, графическим или аналитическим путем.
Из выражения (133) видно, что фигурная скобка может обращаться в нуль, при соответствующем подборе l1, т.е. положения плоскостей коррекции. При этом условие (133) соблюдается даже вблизи резонансной частоты. Эта особенность используется для балансировки в двух плоскостях коррекции двухопорных роторов, у которых Q > 1. Такие плоскости коррекции называются оптимальными.
Корректирующие массы в оптимальных плоскостях коррекции вызывают в теле ротора минимальные изгибающие моменты и позволяют при балансировке на частоте вращения ниже первой, резонансной сохранить достигнутую уравновешенность в широком диапазоне частот вращения ротора.
Для примера рассмотрим однородный межопорный ротор постоянной жесткости
mq(z) = const, у которого
дисбаланс Dнач распределен в осевой плоскости по первой
форме изгиба (что весьма вероятно), т.е. ![]() , тогда
, тогда
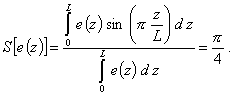
Теперь фигурная скобка выражения (133) примет вид
![]()
Откуда нетрудно найти l1 = 0,29L, которое обращает выражение (133) в нуль независимо от значения других параметров, если w ¹ wрез1.
Это и будет определять положение двух оптимально равноудаленных от опор плоскостей коррекции однородного ротора постоянного сечения при распределении его локальных дисбалансов по первой форме изгиба.
При обычном в практике балансировки 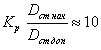 и для l1 » 0 из этого выражения следует, что для
рассмотренного случая лишь при wрез1/w ≥ 3,3 можно не учитывать прогиб ротора и
балансировать его как жесткий ротор.
и для l1 » 0 из этого выражения следует, что для
рассмотренного случая лишь при wрез1/w ≥ 3,3 можно не учитывать прогиб ротора и
балансировать его как жесткий ротор.
Если локальные дисбалансы вдоль рассмотренного ротора распределены равномерно, то оптимальные плоскости коррекции располагаются на расстоянии l1 = 0,22 L от каждой опоры.
Для других конструкций роторов и расположения их опор положение оптимальных плоскостей требует специального рассмотрения.
11.2. Рассмотрим три примера, которые являются крайними случаями
подавляющего большинства реальных межопорных роторов. Для упрощения изложения
во всех примерах рассматриваются симметричные межопорные роторы, имеющие
локальный дисбаланс Dнач в середине межопорного расстояния L и корректирующие
дисбалансы ![]() в двух плоскостях
коррекции, расположенных над опорами конечной жесткости
в двух плоскостях
коррекции, расположенных над опорами конечной жесткости ![]() .
.
11.2.1. Ротор (черт. 32) имеет жесткий участок значительной длины с
линейной плотностью mq(z) = const, установленный на валу, массой которого можно пренебречь, с жесткостью
![]() концевых участков.
концевых участков.
Вычислим значения членов уравнения (133); на участке lрот первая собственная базисная функция f1(z) = 1.
Из (123) следует, что при mq(z) = 0 на участки 0 ≤ Z ≤ l1 и L - l1 ≤ z ≤ L.
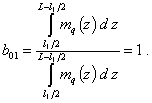
Из (123) и (124), так как b01 = 1, получим
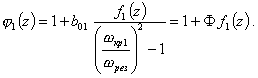
Черт. 32.
Из (130) находим
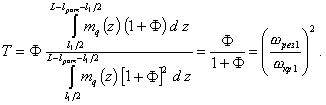
Из (131)
находим, что при ![]() , а при
, а при ![]() .
.
Таким образом, условие допустимости балансировки такого ротора как жесткого запишется так:
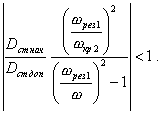
Из равенства (121) следует, что для рассматриваемого случая
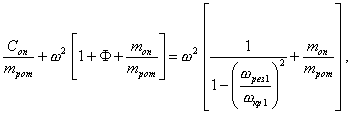
а из равенства (122) при Iq(z) = const для концов вала
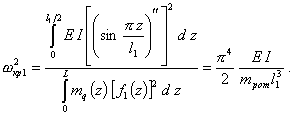
Заменив w2 на ![]() и учтя, что
и учтя, что ![]() , а для нашего случая
, а для нашего случая ![]() , получим, что
, получим, что
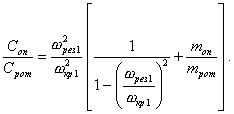
11.2.2. Однородный ротор (черт. 33) постоянной жесткости mq(z) = const. Для такого ротора первая собственная базисная функция изгиба
![]()
Черт. 33.
Вычислим значения членов уравнения (133)
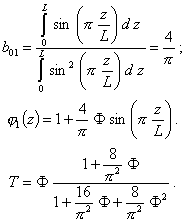
При ![]() .
.
При ![]() .
.
Приняв ![]() , получим условие (129) допустимости балансировки
подобного ротора как жесткого
, получим условие (129) допустимости балансировки
подобного ротора как жесткого
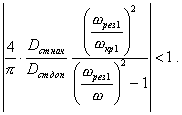
Из формулы (121) следует, что при
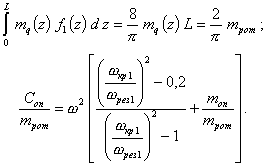
По формуле (122)
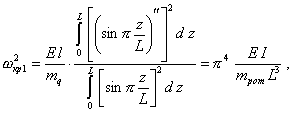
а так как ![]() , то приняв
, то приняв ![]() , получим
, получим
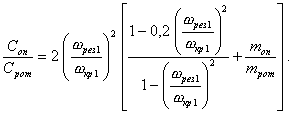
11.2.3. Ротор (черт. 34) имеет два жестких участка, соединенные гибким валом малой массы. На жестких участках mq(z) = const.
При малом Dl первая собственная
базисная функция изгиба ротора может быть представлена в виде равнобедренного
треугольника с вершинами в точках А, В и ![]() .
.
На участке от A = 0 до ![]() .
.
Вычислим значения членов уравнения (133). В силу симметрии ротора ограничимся рассмотрением только его половины
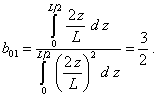
![]() в интервале
в интервале ![]() .
.
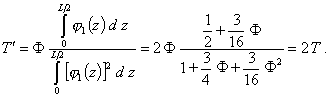
Черт. 34.
Если принять, что S[e(z)] = 1, f1(0) = 0, а 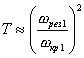 , то условием допустимости
балансировки такого ротора как жесткого ротора будет
, то условием допустимости
балансировки такого ротора как жесткого ротора будет
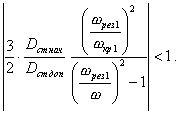
Из формулы (121) следует, что при
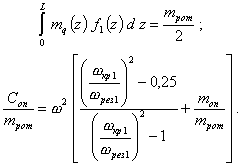 ,
,
а из равенства (122) находим
![]()
Приняв ![]() n имея в виду, что
n имея в виду, что ![]() , получим
, получим
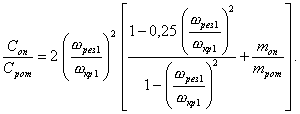
11.3. Экспериментальное определение критерия (128) учета гибкости ротора
Так как между динамической нагрузкой от дисбаланса в плоскости опоры А или В и амплитудой колебания этой опоры (если она конечной жесткости) существует в первом приближении линейная зависимость, критерий учета гибкости ротора (формула (128) настоящего раздела) можно записать так
![]()
Это и будет условием допустимости балансировки реального ротора как жесткого ротора, когда с его гибкостью можно не считаться.
Если Q > 1, то гибкость ротора при балансировке учитывать необходимо и его следует балансировать как гибкий ротор в трех или более плоскостях коррекции.
Если Q » 1, то гибкость ротора часто еще можно не учитывать, но балансировку следует проводить на частоте вращения, близкой или равной эксплуатационной частоте вращения ротора.
1) На частоте вращения, меньшей 1/3 максимальной эксплуатационной
частоты вращения ротора, провести возможно точную балансировку ротора в двух
плоскостях коррекции, определив при этом ![]() этого ротора.
этого ротора.
2) Ротор собранной и установленной машины разогнать до максимальной
эксплуатационной частоты вращения и измерить амплитуды и фазы колебаний опор ![]() и найти их сумму
и найти их сумму ![]() .
.
3) Установить в осевой плоскости ротора
систему из трех контрольных дисбалансов. Один из них ![]() , примерно равный по значению главному вектору начальных
дисбалансов
, примерно равный по значению главному вектору начальных
дисбалансов ![]() , направить против него, расположив его в месте
предполагаемого наибольшего прогиба ротора. Два других контрольных дисбаланса
установить в той же осевой плоскости, в плоскостях коррекции так, чтобы вся система трех контрольных
дисбалансов не создавала статической или моментной неуравновешенностей.
(Различные случаи установки систем контрольных дисбалансов на двухопорном
роторе показаны в таблице).
, направить против него, расположив его в месте
предполагаемого наибольшего прогиба ротора. Два других контрольных дисбаланса
установить в той же осевой плоскости, в плоскостях коррекции так, чтобы вся система трех контрольных
дисбалансов не создавала статической или моментной неуравновешенностей.
(Различные случаи установки систем контрольных дисбалансов на двухопорном
роторе показаны в таблице).
|
Номер схемы |
Расположение системы контрольных дисбалансов и плоскостей коррекции на роторе |
Примечание |
|
I |
|
Контрольный дисбаланс Dк между плоскостями коррекции 1 и 2 устанавливается в месте предполагаемого наибольшего прогиба ротора |
|
II |
|
Предполагается на участке АВ вал тонкий и без источников дисбалансов. Иначе см. случай III |
|
III |
|
Плоскость коррекции 2 может располагаться на межопорном участке у опоры В. Расположение контрольной системы остается там же |
|
IV |
|
Если плоскость коррекции расположена на межопорном участке, то контрольный дисбаланс Dк устанавливается в консоли ротора |
|
V |
|
Контрольный дисбаланс Dк устанавливается возле опор А или В на консоли, у которой b ≥ c |
Сбалансированность системы контрольных дисбалансов проверяется и исправляется на частоте вращения при балансировке, меньшей 1/3 максимальной эксплуатационной частоты вращения ротора.
4) Ротор собранной и установленной машины с системой контрольных
дисбалансов разогнать до максимальной эксплуатационной частоты вращения и
измерить амплитуду и фазы колебаний опор ![]() найти
найти ![]() .
.
5) Вычислить разности
![]()
6) Сняв систему контрольных дисбалансов, установить на роторе в той же осевой плоскости, но в плоскостях опор допустимые дисбалансы DA,B доп, рассчитанные по разд. 3 ГОСТ 22061-76.
7) Ротор собранной машины с допустимыми дисбалансами ![]() разогнать до w - меньшей 1/3 максимальной эксплуатационной
угловой скорости вращения; измерить амплитуды и фазы колебаний опор
разогнать до w - меньшей 1/3 максимальной эксплуатационной
угловой скорости вращения; измерить амплитуды и фазы колебаний опор ![]() и найти их сумму
и найти их сумму ![]() .
.
8) Посчитать Адоп при wэ макс имея в виду, что амплитуды пропорциональны а1 в формуле (118)
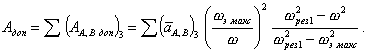
wрез1 вычисляют по формуле (117) или определяют экспериментально по п. 10.8.
Примечания:
1.
Если wрез2 > w > wрез1, то ![]() .
.
2.
Часто выгоднее (по имеющейся аппаратуре) устанавливать не DA,B доп, а ![]() и сразу измерять
амплитуды (АA,B доп)3 при wэ макс.
и сразу измерять
амплитуды (АA,B доп)3 при wэ макс.
9) Найти ![]() .
.
Примечание. Условия установки машины при всех трех измерениях амплитуд колебаний должны быть одинаковыми, без соблюдения каких-либо иных специальных требований.
11.3.2. Количество опытных роторов, подлежащих контролю по п. 11.3.1, устанавливаются по рекомендуемому приложению 4 к ГОСТ 22061-76. По этому же приложению определяется значение Q, которое характеризует опытную партию.
ЧАСТЬ II
РЕКОМЕНДАЦИИ ДЛЯ КОНСТРУКТОРА, РАСЧЕТЧИКА И ТЕХНОЛОГА
Раздел 1. РОТОРЫ, КОТОРЫЕ МОЖНО БАЛАНСИРОВАТЬ НА ЧАСТОТЕ ВРАЩЕНИЯ НИЖЕ ПЕРВОЙ РЕЗОНАНСНОЙ* СИСТЕМЫ «РОТОР - ОПОРЫ»
* Теоретическое обоснование изложено в разд. 11 I части настоящих указаний.
1.1. Роторы, у которых Q < 1 (по формуле (128) п. 11.1) можно балансировать в двух плоскостях коррекции на любых частотах вращения ниже первой резонансной системы «ротор - опоры», которая описана в п. 10.2 I части настоящих указаний.
1.2. Если Q » 1, ротор можно балансировать в двух плоскостях коррекции, но частота вращения при балансировке должна быть возможно ближе к эксплуатационной частоте вращения.
Примечание. Роторы вновь разрабатываемых изделий, у которых Q < 1, состоящие из вала и насаживаемого диска с малым отношением толщины к радиусу, даже при пренебрежимо малом главном моменте дисбалансов диска, который рассмотрен в разд. 5 I части настоящих указаний следует после сборки подвергать динамической балансировке, если торцовое биение диска после насадки на вал не соответствует установленной в технической документации точности по ГОСТ 24643-81.
Пример. Шлифовальный круг (черт. 35).
1.3. Роторы, локальные дисбалансы которых распределены, как описано в пп. 1.3.1 - 1.3.7 удается успешно балансировать в двух плоскостях коррекции.
1.3.1. Ротор имеет одну сосредоточенную массу (черт. 36), представляющую ряд деталей, устанавливаемых в одной плоскости перпендикулярной оси ротора (например, лопатки турбин, болты соединений и т.д.), а эти детали отбираются по методу селективной сборки по массе и статическим моментам.
Черт. 35.
Примечания:
1. При малом объеме производства установка деталей ротора производится методом подбора деталей (например, дисков) по фактическим их дисбалансам и устанавливаются они так, чтобы главный вектор дисбалансов не выходил за пределы допусков, рассчитанных по пп. 2 - 4 части II настоящих указаний.
2. Крепежные изделия и другие детали, расположенные на радиусе, не превышающем 5 % от наибольшего радиуса ротора, и оси которых параллельны оси ротора, допускается подбирать только по массе.
Черт. 36.
Черт. 37.
Пример. Шлифовальный круг со шкивом (черт. 37).
Примечания:
1. Две плоскости коррекции следует располагать возможно ближе к центрам сосредоточенных масс.
2. Допускается проводить балансировку по пп. 1.3.1.3 и 1.3.2.
Пример. Ротор компрессора (черт. 38).
Для такого ротора можно применить приемы балансировки, описанные в пп. 1.3.3.1 и 1.3.3.2.
1.3.3.1. Все детали ротора балансируются до сборки.
Примечания:
1. Значения остаточных дисбалансов ротора в плоскостях коррекции не должны превышать верхних значений допустимых дисбалансов, вычисленных по разд. 2 ГОСТ 22061-76.
2. При назначении допустимых дисбалансов в плоскостях коррекции каждой детали следует учитывать разд. 10 II части настоящих указаний и возможные смещения детали из-за балансировочной оправки, отклонения от соосности и отклонения посадочных поверхностей, шпоночных болтовых и других соединений, которые должны выдерживаться в пределах допусков размеров, как показано в разд. 2 - 7 II части.
3. Этот метод обеспечивает полную взаимозаменяемость; целесообразность его применения должна быть обоснована экономически.
Примечания:
1. Каждая балансировка должна обеспечивать удельный дисбаланс сборки, не превышающий принятого для данного ротора номинального значения допустимого удельного дисбаланса, определенного по п. 1.3.3 настоящего раздела.
2. Этот метод позволяет избежать тщательного контроля размеров расположения, включая и эксцентриситеты отдельных деталей.
3. Если выявляются слишком большие начальные дисбалансы одной из деталей, ее можно сбалансировать до сборки.
4. Распределение в роторе деталей (лопаток, болтов и т.п.) должно производиться с учетом п. 1.3.1 настоящего раздела.
1.3.4. Ротор, неуравновешенные массы которого сосредоточены вблизи опор
1.3.5. Ротор, симметричный относительно опор, имеющий равномерно распределенные или линейно изменяющиеся вдоль ротора локальные дисбалансы.
Пример. Барабан печатной машины (черт. 39).
Примечание. Рекомендуется использовать оптимальные плоскости коррекции по п. 11.1 I части или коррекцию в трех плоскостях по п. 1.11 настоящего раздела.
Черт. 38.
Черт. 39.
1.3.6. Ротор имеет жесткий участок значительной осевой длины, установленный на легком гибком валу, причем дисбалансы последнего пренебрежимо малы.
Пример. Барабан памяти вычислительной машины (черт. 40).
Примечание. Обе плоскости коррекции должны располагаться в пределах жесткого участка.
Черт. 40.
Черт. 41.
1.3.7. Ротор выполнен в виде роторного пакета, состоящего из ряда соединенных между собой деталей.
Пример. Ротор компрессора (черт. 41).
Возможны следующие случаи:
1.3.7.1. Роторный пакет, для обеспечения взаимозаменяемости элементов которого должны быть выполнены требования п. 1.3.3.1.
1.3.7.2. Роторный пакет допускает при сборке взаимный поворот элементов, что позволяет подбором взаимных положений элементов снизить начальные дисбалансы ротора при балансировке по п. 1.4.
1.3.7.3. Роторный пакет, проходящий последовательную сборку на валу, должен удовлетворять требованиям п. 1.3.3.2.
1.4. При неизвестном осевом распределении локальных дисбалансов межопорные роторы могут быть удовлетворительно сбалансированы на частоте вращения, меньшей, но близкой к первой резонансной частоте системы «ротор - опоры», если можно обеспечить приемлемые значения начальных дисбалансов по п. 11.1 I части настоящих указаний.
Пример. Ротор паровой турбины (черт. 42).
Примечание. Если после расчета эти приемлемые значения начальных дисбалансов окажутся слишком малыми, то необходимо использовать иной метод балансировки.
Черт. 42.
Черт. 43.
1.5. На низкой частоте вращения (ниже первой резонансной системы «ротор - опоры») можно балансировать и роторы с изменяющейся геометрией, удовлетворяющие требованиям пп. 1.1.1.2 или 1.3 II части. Они подразделяются на:
а) роторы, неуравновешенность которых изменяется непрерывно с изменением частоты вращения (например, вентилятор с резиновыми крыльями, роторы электрических машин, имеющих обмотку и т.п.);
б) роторы, неуравновешенность которых изменяется до определенной частоты вращения и остается постоянной на более высоких частотах (например, роторы асинхронных двигателей с центробежным пусковым выключателем).
1.5.1. Роторы, указанные в п. 1.5 а, следует балансировать на той частоте вращения, на которой они должны постоянно работать.
1.5.2. Роторы, указанные в п. 1.5 б, следует балансировать на частоте вращения выше той, при которой перестает изменяться неуравновешенность.
Примечание. Необходимо учитывать, что роторы с изменяющейся геометрией чаще всего бывают сбалансированы только для одной частоты вращения или только для определенного диапазона частот.
1.6. На частоте вращения ниже первой резонансной частоты системы «ротор - опоры» можно балансировать системы соединенных роторов (черт. 43), которые подразделяются на:
а) трехопорные, когда один из роторов двухопорный, а другой ротор, жестко соединенный с первым, имеет одну опору;
б) когда два двухопорных ротора соединены между собой муфтой.
Примечание. Резонансные частоты вращения системы соединенных роторов не равны резонансным частотам вращения каждого из роторов в отдельности.
1.6.1. Роторы трехопорных систем можно балансировать отдельно, если они удовлетворяют требованиям пп. 1.1; 1.2 или п. 1.3. При соединении обоих роторов рекомендуется остаточные дисбалансы в плоскостях обеих полумуфт располагать под углом 180°. После соединения полумуфт дисбалансы в плоскостях опор каждого ротора не должны превышать допустимых значений.
Примечание. Если технологически это возможно и обосновано, то балансировку таких систем можно производить в сборе.
1.6.2. Когда два двухопорных ротора, опирающиеся на собственные подшипники, соединены вместе, причем соответствующие консольно расположенные массы полумуфт малы по сравнению с массами роторов, каждый ротор можно балансировать самостоятельно, если он удовлетворяет требованиям пп. 1.1, 1.2 или 1.3.
1.6.2.1. Детали соединения (муфта и т.д.) следует балансировать отдельно, при этом должны быть установлены допуски размеров всех поверхностей вращения и их несоосность относительно посадочных поверхностей соединяемых валов роторов по разд. 2 II части.
Примечание. Допускается балансировка муфты с одним из соединенных роторов.
1.7. Роторы, удовлетворяющие пп. 1.1 - 1.6, но подшипники которых работают с коэффициентом дисбаланса K > 1,4 (т.е. по третьему режиму нагружения в соответствии с разд. 7 I части) следует балансировать, как указано в разд. 10 II части для уменьшения динамических нагрузок на опоры.
1.8. На частоте вращения ниже первой резонансной системы «ротор - опоры» балансируют колесные пары подвижного состава железных дорог. Их балансировка должна проводиться на балансировочных станках, позволяющих совмещать главную центральную ось инерции колесной пары с осью, проходящей через геометрические центры кругов качения бандажей.
1.9. Узлы коленчатых валов двигателей внутреннего сгорания в сборе, механизмы возвратно-поступательного действия, следует балансировать с учетом требований пп. 1.1 - 1.3 I части настоящих указаний.
1.10. Во время разгона или выбега прошедших балансировку роторов может повыситься уровень вибрации собранной машины при проходе резонансной частоты вращения системы «ротор - опоры». Допустимый уровень этой вибрации должен соответствовать утвержденному в технической документации.
1.11. Если двухопорный многодисковый ротор имеет wэ макс > wрез1, то для обеспечения плавного перехода через wрез1 следует, если это возможно, проводить раздельно статическую балансировку в плоскости коррекции, проходящей через центр масс ротора и моментную балансировку в двух других плоскостях коррекции.
Раздел 2. РАЗБАЛАНСИРОВКА ИЗДЕЛИЯ
2.1. Значения дисбалансов в плоскостях опор ротора в конце технического ресурса машины или перед ее капитальным ремонтом (предусматривающим балансировку) состоят из трех векторных слагаемых:
остаточных дисбалансов в плоскостях опор после балансировки (при двух
опорах ![]() );
);
технологических дисбалансов, которые возникают после балансировки при
сборке, монтаже опор, соединении машины, регулировке и т.п. (при двух опорах ![]() );
);
эксплуатационных дисбалансов, которые возникают во время работы машины
из-за износа, старения и т.п. (при двух опорах ![]() ).
).
Примечание. Пересчет из плоскостей коррекции или измерения в плоскости опор проводится по разд. 6 I части.
2.1.1. Если в партии однотипных изделий
арифметические суммы наибольших значений перечисленных дисбалансов в плоскостях
одноименных опор не превышают значений допустимых дисбалансов DA,B доп
табл от разнесения в
эти плоскости главного вектора дисбалансов ![]() для принятого по ГОСТ
22061-76 класса точности балансировки, то в данной партии изделий обеспечена полная взаимозаменяемость по
дисбалансам всех роторов в течение всего технического ресурса или до ремонта,
предусматривающего балансировку.
для принятого по ГОСТ
22061-76 класса точности балансировки, то в данной партии изделий обеспечена полная взаимозаменяемость по
дисбалансам всех роторов в течение всего технического ресурса или до ремонта,
предусматривающего балансировку.
Это условие для двухопорных роторов записывается следующими неравенствами.
![]()
где DA,B доп верхн - верхние значения допустимых дисбалансов в плоскостях опор А или В;
DA,B разб - наибольшие значения дисбалансов от разбалансировки в плоскостях опор А или В.
2.1.2. В ходе проверочного расчета после эксплуатационных испытаний опытных образцов уточняют DA,B разб, выявляют «узкие» места, т.е. технологические или эксплуатационные факторы, которые вызывают наибольшую разбалансировку и, сообразуясь с экономическими и производственными возможностями, изменяют рабочие чертежи так, чтобы обеспечить непревышение значений DA,B доп табл в конце срока службы изделия. Разбалансировка конкретного изделия будет разной при различных заданных длительностях технического ресурса. (Например, если установка на ротор подшипников после балансировки вызывает неприемлемую разбалансировку, то следует рекомендовать балансировку на собственных подшипниках или повысить класс точности изготовления посадочных мест и подшипников или даже изменить конструкцию изделия и т.д.).
Раздел 3. ТЕХНОЛОГИЧЕСКИЕ ДИСБАЛАНСЫ В ПЛОСКОСТЯХ ОПОР И УСЛОВИЕ ДОПУСТИМОСТИ СТАТИЧЕСКОЙ БАЛАНСИРОВКИ
3.1. Технологические дисбалансы в плоскостях опор ротора обусловлены рядом факторов, например: а) точностью изготовления поверхностей деталей, монтируемых на ротор после балансировки; б) монтажом подшипников после балансировки (если балансировка ротора проводилась на цапфах его вала без подшипников или, если после балансировки на своих подшипниках, последние были демонтированы и снова установлены при сборке машины); в) отклонением от соосности ротора и вала присоединяемой машины по п. 5.8 ГОСТ 22061-76.
3.2. Точность изготовления поверхностей деталей.
При обработке деталей всегда допускаются производственные погрешности. Поверхности валов и отверстий имеют отклонения формы по ГОСТ 24643-81:
в поперечном сечении - отклонение от круглости, т.е. овальность, огранку и т.п.;
в продольном сечении - конусообразность, бочкообразность, седлообразность, отклонение от прямолинейности оси.
Поверхности цилиндрической втулки и отверстий в ней имеют отклонение от соосности осей, радиальные и торцовые биения, волнистость, шероховатость и др.
Волнистость и шероховатость поверхностей деталей на неуравновешенность влияют мало. Лишь у деталей высокого класса точности балансировки состояние поверхности может играть некоторую роль, однако у таких деталей и класс шероховатости поверхности обычно очень высок, а следовательно, неровности весьма малы.
В тех случаях, когда нет «особых требований, вытекающих из условий работы, изготовления или измерения деталей», «отклонения формы и расположения поверхностей ограничиваются полем допуска размера или регламентируются в нормативных материалах на допуски, не проставляемые у размеров» (ГОСТ 24643-81).
Эти случаи наиболее распространены, поэтому при проектировании можно ориентироваться на них и лишь при проверочном расчете ужесточать предельные отклонения, если это окажется необходимым.
Все размеры обрабатываемого изделия защищены допусками - либо теми, которые стоят на чертеже, либо теми, которые соответствуют принятому на данном производстве классу точности обработки свободных размеров. Неоговоренное на чертеже радиальное биение, равное удвоенному эксцентриситету, не с одной установки обрабатываемых цилиндрических поверхностей относительно базирующих поверхностей цапф или оси, определяются точностью металлообрабатывающего станка; на современных станках оно, примерно 10 - 30 мкм, и торцовое биение - менее 10 мкм на наибольшем радиусе. В каждом конкретном случае расчета эти цифры должны уточняться по имеющемуся оборудованию.
3.2.1. Пусть цилиндрическая изотропная втулка сопрягается с валом сбалансированного ротора. Предположим, что как втулка, так и вал обрабатывались каждый не с одной установки. Пусть внешний и внутренний диаметры втулки и диаметр вала под посадку должны измеряться калибрами, микрометрами или штангенциркулями, что позволяет определить только отклонения формы трех поверхностей. В этом случае следует отдельно учесть несоосность двух цилиндрических поверхностей, указанные в п. 3.2. (При измерении, например, индикатором детали, установленной в центрах, отклонения формы и соосности измеряются совместно).
Перечисленные отклонения приводят к смещению центра масс втулки и возникновению удельного дисбаланса втулки, которое в своем максимально возможном значении может достичь арифметической полусуммы перечисленных пяти наибольших радиальных биений (три от отклонений формы и две от несоосности)
![]()
где dRi - поле допуска диаметра i-й цилиндрической поверхности или поле допуска радиального биения относительно базирующих осей или поверхностей вала и втулки.
Если цилиндрические поверхности втулки обрабатывались за одну установку, то несоосность можно не учитывать
![]()
В том случае, когда заданы радиальные биения поверхностей вала и втулки, отклонения в пределах полей допусков размеров войдут в заданные биения и
![]()
Максимально возможное смещение центра масс втулки в результате торцовых биений
![]()
где еторц j - смещение центра масс втулки в результате биения dторц j j-го торца на диаметре D.
![]()
где r - плотность материала втулки;
D и d - наружный и внутренний диаметры втулки.
Очевидно, что наибольшее возможное значение главного вектора технологических дисбалансов детали от радиальных и торцовых биений будет
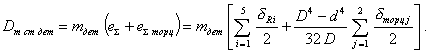
Очень часто в пределах допустимых отклонений формы и не соосности поверхностей цилиндра лежат и перекосы вызывающие моментную неуравновешенность. Однако, как это видно из разд. 5 I части настоящих указаний, детали в этом случае обычно будут вызывать значительно меньшие технологические дисбалансы в опорах, нежели наибольшие возможные технологические дисбалансы от статической неуравновешенности. Поэтому при рассмотрении максимально возможных технологических дисбалансов в плоскостях опор часто достаточно учитывать только наибольшую возможную статическую неуравновешенность детали.
Полученный результат позволяет конструктору увидеть, какой размер при намеченной точности изготовления вызовет разбалансировку наибольшей величины после посадки детали на вал. Меняя класс точности изготовления отдельных размеров, можно изменять значение технологического удельного дисбаланса детали и подобрать такой класс точности, который обеспечит приемлемые значения технологических дисбалансов в плоскостях опор. Эти требования должны увязываться с экономикой производства и c его технологическими возможностями.
Примечания:
1. Технологические дисбалансы в плоскостях опор определяются путем разнесения Dт ст дет по формулам разд. 2 ГОСТ 22061-76.
2. Неподвижные посадки и отличие от переходных недостаточно четко следуют изложенным выводам.
3.2.2. Пример. Стальной полый однородный цилиндр, поверхности которого обрабатывались не с одной установки, насаживается по напряженной посадке на вал сбалансированного ротора (черт. 44), цапфы которого и место посадки цилиндра обрабатывались также не с одной установки. Значение главного вектора остаточных дисбалансов вала Dст ост вал = 0,6 г·мм.
Материал - сталь 40 по ГОСТ 1050-88.
Черт. 44.
Так как особых требований к предельным отклонениям формы нет, по ГОСТ 24643-81 все эти отклонения ограничиваются полем допуска размера, кроме взаимного расположения поверхностей Æ 80 и Æ 30 А, которые ограничены наибольшим взаимным радиальным биением.
Определим слагаемые формулы (а).
1. Поле допуска Æ 30 Н вала ротора: d1 = 0,015 мм.
2. Поле допуска Æ 30 А отверстия цилиндра: d2 = 0,023 мм.
3. Поле допуска Æ 80 цилиндра по В5: d3макс = 0,4 мм.
4. Наибольшее радиальное биение поверхности Æ 80 относительно поверхности Æ 30 А: d4 = 0,03 мм (по п. 3.2 настоящего раздела);
5. Наибольшее радиальное биение поверхности Æ 30 Н ротора относительно поверхности его цапф d5макс = 0,03 мм (по п. 3.2 настоящего раздела).
6. Наибольшее торцовые биение цилиндра dторц1 = dторц2 = 0,01 мм на наибольшем радиусе (по п. 3.2 настоящего раздела).
Наибольшее возможное значение главного вектора дисбалансов цилиндра вследствие радиальных биений и посадки на сбалансированный вал ротора
![]()
где
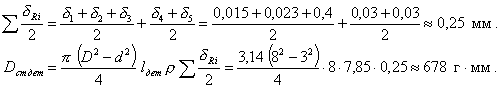
Из этого выражения видно, что d3 = 0,4 мм создает на порядок больший технологический дисбаланс, нежели остальные отклонения. Очевидно, для уменьшения технологических дисбалансов в плоскостях опор при сборке такого ротора следует в первую очередь увеличить точность изготовления Æ 80.
Наибольшее возможное значение главного вектора дисбалансов цилиндра вследствие торцовых биений
![]()
Примечание. При измерении калибром или штангенциркулем dторц примерно равно половине разности наибольших значений расстояний между торцами, измеренных по концам одного и того же диаметра; при измерении индикатором dторц равно измеренному значению торцового биения.
Главный вектор дисбалансов цилиндра вследствие технологических погрешностей его изготовления и посадки на сбалансированный вал ротора может достичь значения
![]()
Как видно из примера торцовое биение мало сказывается на неуравновешенности детали. Наибольшие технологические дисбалансы вносит радиальное биение.
3.3. Дисбалансы одной детали массы mдет определяются радиальным и угловым смещениями посадочной поверхности детали относительно главной центральной оси инерции детали. Для отдельной детали сложной формы или состоящей из нескольких элементов, жестко связанных между собой, главный вектор дисбалансов может быть найден по формуле
![]()
где ![]() и
и ![]() - главные векторы
дисбалансов детали при двух ее положениях на балансировочной оправке,
повернутых вокруг оси вращения оправки на 180°.
- главные векторы
дисбалансов детали при двух ее положениях на балансировочной оправке,
повернутых вокруг оси вращения оправки на 180°.
При таком способе определения главного вектора дисбалансов детали автоматически исключается главный вектор дисбалансов оправки.
Если же проводится измерение ![]() только при одном
положении детали на оправке, измеренный главный вектор состоит из
только при одном
положении детали на оправке, измеренный главный вектор состоит из ![]() .
.
Для этой же детали главный момент дисбалансов
![]()
где ![]() и
и ![]() - измеренные на
балансировочном станке главные моменты дисбалансов детали при двух ее положениях
на балансировочной оправке, повернутых на 180° вокруг оси, перпендикулярной оси
вращения оправки (при сохранении одной и той же общей образующей посадочных
поверхностей).
- измеренные на
балансировочном станке главные моменты дисбалансов детали при двух ее положениях
на балансировочной оправке, повернутых на 180° вокруг оси, перпендикулярной оси
вращения оправки (при сохранении одной и той же общей образующей посадочных
поверхностей).
При таком способе определения главного момента дисбалансов детали автоматически исключается главный момент дисбалансов оправки.
Если же проводится измерение ![]() только при одном
положении детали на оправке, измеренный главный момент состоит из
только при одном
положении детали на оправке, измеренный главный момент состоит из ![]() .
.
Наибольшие ожидаемые значения этих главных векторов по результатам измерений, проведенным на N деталях опытной партии, определяются как показано в пп. 9 и 10 рекомендуемого приложения 4 к ГОСТ 22061-70.
3.4. Технологические дисбалансы, вносимые балансировочной оправкой
Радиальное биение dRопр посадочной поверхности оправки измеряется индикатором для линейных измерений при прокатывании оправки на ее опорных поверхностях (обычно поверхностях цапф). Это радиальное биение является постоянной величиной для данной оправки, которое вносит ошибку в главный вектор балансируемой детали, равную:
![]()
Поверхность балансировочной оправки, на которую устанавливается балансируемая деталь, и опорные поверхности оправки должны проходить окончательную обработку за одну установку, в противном случае необходимо измерить перекос осей jопр этих поверхностей.
Балансировочная оправка должна балансироваться на один класс точности балансировки более жестко, нежели балансируемая на ней деталь.
Примечания:
1. Возможный перекос в месте посадки балансируемой детали на балансировочную оправку может вызнать существенную моментную неуравновешенность, описанную в разд. 5 I части настоящих указаний.
Она должна быть учтена как показано в п. 3.3 настоящего раздела при проектировании деталей и при назначении технологических процессов.
2. Оправку можно промерить, вставив ее другим концом в насаживаемую деталь и измерив дисбалансы до и после этого поворота.
3.4.1. Пусть двухопорный ротор массы mрот состоит из детали mдет насаженной на сбалансированный вал с массой mвал. Посадка выполнена на длине lдет с угловым g и радиальным e смещениями оси детали относительно оси, соединяющей центры поверхностей качения цапф вала ротора из-за погрешностей изготовления (деформацией ротора и опор пренебрегаем).
Угловое смещение детали собранного ротора относительно оси, проходящей через центры поверхностей качения цапф вала, в самом худшем случае будет
![]()
где ![]() - наибольшее
возможное угловое смещение оси посадочной поверхности вала относительно оси,
соединяющей центры поверхностей качения его цапф;
- наибольшее
возможное угловое смещение оси посадочной поверхности вала относительно оси,
соединяющей центры поверхностей качения его цапф;
dRвал - поле допуска посадочного (под деталь) размера вала;
![]() - наибольшее возможное угловое смещение
посадочной поверхности отверстия детали из-за отклонений его формы;
- наибольшее возможное угловое смещение
посадочной поверхности отверстия детали из-за отклонений его формы;
dRдет - поле допуска посадочного отверстия детали.
Наибольшее возможное радиальное смещение детали
![]()
Если деталь до постановки на вал проходила балансировку на оправке как
описано в п. 3.2.1,
то dRотв и gотв в настоящий расчет не входят, так как они
органически вошли в ![]() и
и ![]() .
.
Наибольшие значения главного вектора Dст и главного момента MD дисбалансов собранного ротора будут:
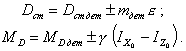
Dст дет и MD дет определяется как показано в п. 3.3 настоящего раздела либо расчетом, как показано в п. 3.2.1.
При наиболее опасной квазистатической неуравновешенности на опоры ротора будут действовать компланарные силы от главного вектора и главного момента дисбалансов ротора.
![]()
3.5. Условие допустимости только статической балансировки
При статической балансировке устанавливается такая корректирующая масса mк на радиусе rк в плоскости коррекции, чтобы
![]()
Если используется только одна плоскость коррекции и она проходит через центр масс ротора, то статическая балансировка завершается успешно, не затрагивая действие главного момента MD. Аналогичное следствие будет иметь место, если mкrк разносится (по правилам статики) в две плоскости коррекции, расположенные по обе стороны от центра масс ротора.
Если же используется одна плоскость коррекции, расположенная на расстоянии lк от центра масс ротора (например, один из торцов детали), то после такой статической балансировки возникнет момент дисбалансов от корректирующих масс
![]()
Если при статической балансировке Dст полностью скомпенсирован, то реакции опор будут
![]()
Следовательно, условием допустимости статической балансировки будет
![]()
где mрот = mвал + mдет.
Если насаживаемая на вал деталь является однородным цилиндром длиной lцил с радиусом R и радиусом посадочного отверстия r, то приближенно условие допустимости статической балансировки можно представить так
![]()
где g определяется по п. 3.4 настоящего раздела.
Следует иметь в виду, что статическая балансировка в динамическом режиме дает на порядок большую точность, нежели статическая балансировка при помощи силы тяжести (на «ножках»).
Раздел 4. ТЕХНОЛОГИЧЕСКИЕ ДИСБАЛАНСЫ В РОТОРНЫХ ПАКЕТАХ
4.1. Из всего многообразия конструкций роторов можно выделить две, имеющие принципиальное различие при расчете технологических дисбалансов:
роторы, состоящие из вала и насаженных на него деталей (например, дисков или колес);
роторы барабанной конструкции - роторные пакеты, у которых детали (диски или колеса), составляющие ротор, центрируются друг на друге, а цапфы являются элементами крайних деталей.
4.1.1. В первом случае технологические дисбалансы ![]() деталей ротора
являются независимыми случайными величинами, поэтому значения максимально
возможных технологических дисбалансов в плоскостях опор будут
деталей ротора
являются независимыми случайными величинами, поэтому значения максимально
возможных технологических дисбалансов в плоскостях опор будут
![]()
где DтA,Bj - технологический дисбаланс j-й детали, вычисляемой по п. 3.2.1 II части.
4.2.2. Во втором случае (роторный пакет) технологические дисбалансы DтA,Bj являются зависимыми случайными величинами.
Если рассматривать только главный вектор дисбалансов детали,
определяемой только технологическими причинами, то в роторном пакете из
изотропных деталей эксцентриситет ![]() массы mj каждой
последующей детали зависит от векторной суммы эксцентриситетов всех предыдущих
деталей, которые определяются накопленной радиальной и торцовой погрешностями
изготовления стыков всех n деталей роторного пакета.
массы mj каждой
последующей детали зависит от векторной суммы эксцентриситетов всех предыдущих
деталей, которые определяются накопленной радиальной и торцовой погрешностями
изготовления стыков всех n деталей роторного пакета.
4.2.3. Рассмотрим сначала радиальные отклонения, из-за которых одна
цапфа роторного пакета из n деталей сдвинется на еn параллельно оси другой
цапфы. Новая ось z1z1 (черт. 45),
соединяющая центры обеих цапф, будет повернута на угол j относительно оси zz одной
из цапф, причем, ![]() или по малости угла
или по малости угла ![]()
Максимальное значение эксцентриситета для n-й детали роторного пакета (n = 4 на черт. 45), вызванного только радиальными отклонениями, можно выразить через поля допусков размеров центрирующих поверхностей деталей и взаимные радиальные биения центрирующих поверхностей каждой детали
![]()
где i = 1, 2, 3, ... - порядковый номер детали роторного пакета, состоящий из n деталей;
dRnn, dR11 - поле допуска на радиальное биение центрирующей поверхности 1-й или n-й концевых деталей роторного пакета относительно базовой поверхности или базовой оси этих же деталей;
dRii - для неконцевых деталей радиальное биение одной центрирующей поверхности детали относительно второй центрирующей поверхности той же детали.
Черт. 45.
При обработке обеих центрирующих поверхностей с одной установки dRii » 0.
При обработке обеих центрирующих поверхностей не с одной установки и отсутствии специальных требований к соосности на чертеже dRii определяется точностью токарного или шлифовального станка.
Если на чертеже указано контролируемое радиальное биение dRii для i-й детали, то соответствующие поля допусков размеров центрирующих
поверхностей ![]() и
и ![]() этой детали в расчете
не должны учитываться, так как они уже вошли в регламентированное радиальное
биение,
этой детали в расчете
не должны учитываться, так как они уже вошли в регламентированное радиальное
биение,
где ![]() - поле допуска размера центрирующей
поверхности i-й детали в месте ее сопряжения с (i - 1)-й деталью;
- поле допуска размера центрирующей
поверхности i-й детали в месте ее сопряжения с (i - 1)-й деталью;
![]() - поле допуска размера центрирующей
поверхности i-й детали в месте сопряжения, ее с (i + 1)-й деталью;
- поле допуска размера центрирующей
поверхности i-й детали в месте сопряжения, ее с (i + 1)-й деталью;
![]() - поле допуска размера центрирующей
поверхности (i + 1) детали в месте ее сопряжения с i-й деталью.
- поле допуска размера центрирующей
поверхности (i + 1) детали в месте ее сопряжения с i-й деталью.
Максимально возможный эксцентриситет каждой k-й детали роторного пакета, зависящий только от накопленной радиальной ошибки, будет, как это видно из черт. 46
![]()
где lAk - расстояние от опоры A до центра масс k-й детали.
4.2.4. Рассмотрим торцовые отклонения в месте стыка деталей роторного пакета. Для определения наибольшей возможной погрешности сборки из-за торцовых биений в местах стыка необходимо представить себе такой роторный пакет, показанный на черт. 46. Такой пакет, только с торцовыми отклонениями, будет вращаться вокруг оси z2z2. Причем
![]()
где i =1, 2, 3, ... - порядковый номер детали роторного пакета, состоящего из n деталей.
Из-за малости углов принимаем tg y » y, поэтому
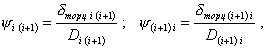
где ![]() - допуск торцового
биения i-й детали в месте ее сопряжения с (i + 1)-й деталью;
- допуск торцового
биения i-й детали в месте ее сопряжения с (i + 1)-й деталью;
![]() - допуск торцового биения (i + 1)-й детали в месте ее сопряжения с i-й деталью;
- допуск торцового биения (i + 1)-й детали в месте ее сопряжения с i-й деталью;
![]() - номинальный диаметр i-й детали в месте ее сопряжения с (i + 1)-й
деталью;
- номинальный диаметр i-й детали в месте ее сопряжения с (i + 1)-й
деталью;
![]() - номинальный диаметр (i + 1)-й детали в месте ее сопряжения с i-й деталью.
- номинальный диаметр (i + 1)-й детали в месте ее сопряжения с i-й деталью.
Допуски ![]() диаметров
диаметров ![]() и
и ![]() диаметров
диаметров ![]() должны задаваться на
чертежах или определяться как сумма полей допусков посадочных поверхностей
одной детали и радиального биения, определяемого точностью станка, на котором
изготовлялась деталь.
должны задаваться на
чертежах или определяться как сумма полей допусков посадочных поверхностей
одной детали и радиального биения, определяемого точностью станка, на котором
изготовлялась деталь.
Черт. 46.
Из черт. 46 следует, что с небольшой погрешностью из-за малости углов эксцентриситет n-й детали может быть представлен формулой
![]() или
или ![]()
а максимально возможный эксцентриситет каждой k-й детали пакета только из-за торцовых биений будет определяться так:
![]()
lAk - расстояние от опоры А до центра масс k-й детали.
Совместное влияние максимальных значений радиальных и торцовых биений приводит к суммированию углов j и y, а наибольший возможный технологический эксцентриситет k-й детали роторного пакета будет в этом случае определяться так:
![]()
Не следует допускать слишком большой угол (j + y) при проектировании роторного пакета, чтобы он не привел к существенному перекосу в подшипниках.
Наибольший возможный технологический дисбаланс роторного пакета будет
![]()
Наибольшее значение главного вектора всех дисбалансов собранного роторного пакета
![]()
где Dстi - главный вектор дисбалансов i-й детали в отдельности, определяемый расчетом или измеряемый при подетальной балансировке. (Предполагается, что в Dстi входят дисбалансы от торцовых биений каждой детали по п. 3.2.1 II части).
При больших диаметрах деталей роторного пакета необходимо учитывать и главный момент дисбалансов ротора, который, кроме главных моментов деталей пакета, содержит еще и технологический главный момент, вызванный перекосом всего пакета на угол j + y.
Изложенный метод расчета обеспечивает полную взаимозаменяемость деталей ротора по дисбалансам, если во время сборки и эксплуатации детали не претерпевают существенных деформаций.
4.2.5. При малом объеме производства следует проводить селективную сборку
или индивидуальную сборку с подбором и соответствующим расположением углов, и
значений главных векторов дисбалансов деталей. Путем поворота элементов друг
относительно друга сумма ![]() может быть сведена к
минимуму. Вектор
может быть сведена к
минимуму. Вектор ![]() может быть измерен
(по углу и значению) по специальным контрольным поверхностям каждой детали
пакета при прокатывании ротора на поверхностях его цапф.
может быть измерен
(по углу и значению) по специальным контрольным поверхностям каждой детали
пакета при прокатывании ротора на поверхностях его цапф.
Если контрольная поверхность обрабатывается не за одну установку с
центрирующей поверхностью, то ![]() ,
,
где ![]() - измеренный эксцентриситет
контрольной поверхности i-й детали относительно оси, соединяющей
центры цапф роторного пакета;
- измеренный эксцентриситет
контрольной поверхности i-й детали относительно оси, соединяющей
центры цапф роторного пакета;
![]() - измеренный эксцентриситет этой же контрольной
поверхности относительно центрирующей поверхности i-й детали при
прокатывании детали на цапфах балансировочной оправки.
- измеренный эксцентриситет этой же контрольной
поверхности относительно центрирующей поверхности i-й детали при
прокатывании детали на цапфах балансировочной оправки.
Примечание. Контрольные поверхности следует располагать на недеформирующихся участках деталей, доступных прямому контролю при прокатывании роторного пакета на поверхностях цапф.
4.3. Если удается обеспечить нужные допустимые значения технологических дисбалансов в плоскостях опор путем повышения точности изготовления или иными технологическими операциями, то все изделия при массовом производстве будут проходить по этим технологическим дисбалансам и будет иметь место полная взаимозаменяемость.
Раздел 5. ТЕХНОЛОГИЧЕСКИЕ ДИСБАЛАНСЫ, ВЫЗВАННЫЕ ПОСАДКОЙ ПОДШИПНИКОВ КАЧЕНИЯ
5.1. Подшипники качения на цапфах ротора могут устанавливаться: а) до балансировки; б) могут демонтироваться после балансировки и вновь устанавливаться в процессе сборки изделия; в) ротор может балансироваться на беговых дорожках внутренних колец подшипников, установленных на цапфах; г) подшипники могут впервые устанавливаться на ротор после его балансировки.
Наибольшие технологические дисбалансы в плоскостях опор вызывает последний случай, когда балансировка ротора проводилась на поверхностях его цапф, а подшипники устанавливались на цапфы при сборке изделия. Остальные случаи являются тем или иным упрощением (в расчете) последнего случая.
Поверхности цапф ротора, на которых проводилась балансировка, будем считать базирующими поверхностями, следовательно, их радиальные биения учтены при балансировке.
Поля допусков диаметра отверстия внутреннего или внешнего диаметра наружного кольца в местах посадок подшипника определяют возможные отклонения формы, которые приводят к радиальным биениям. При расчете максимально возможных радиальных биений от отклонений формы посадочных поверхностей подшипников качения следует учитывать поле допуска d1 диаметра в местах посадки только того кольца, которое сопрягается с ротором и вращается вместе с ним. Если это сопряжение таково, что позволяет кольцу проворачиваться во время эксплуатации, то дисбалансы ротора в плоскостях обеих опор будут меняться.
У подшипников качения беговые дорожки имеют радиальные биения относительно посадочных поверхностей своих колец. Обозначим радиальные биения беговых дорожек колец, вращающихся вместе с ротором, через d2А,В для подшипников опор А и В.
У подшипников качения имеется еще и «рабочий радиальный зазор», зависящий от типа, размера и точности изготовления подшипника.
Радиальный зазор в подшипниках качения при работе по первому режиму нагружения не сказывается на неуравновешенности ротора, однако при работе по третьему режиму радиальный зазор s значительно изменяет, как показано в разд. 10 I части неуравновешенность ротора.
Таким образом, при третьем режиме работы подшипников качения наибольшее возможное дополнительное смещение главной центральной оси инерции ротора в опоре будет
![]()
Если подшипники одинаковы в обеих опорах и нагрузки в них равны, то это выражение будет определять наибольшее возможное дополнительное смещение центра масс ротора, вызванное монтажом на сбалансированный ротор подшипников качения при работе последних по третьему режиму нагружения. Следовательно, главный вектор дисбалансов ротора может возрасти до наибольшего значения.
![]()
Примечание. При радиальных шарикоподшипниках и радиальноупорных подшипниках качения на неуравновешенности ротора указываются и осевые зазоры в подшипниках. Чтобы снизить их влияние до минимума следует устанавливать эти подшипники с предварительным осевым натягом (например, пружиной).
5.1.1. Смещение епод в ряде случаев создаст несимметричность магнитных или гидродинамических сил, действующих на ротор, т.е. вызывает дополнительные динамические нагрузки на опоры.
5.1.2. Пример. Пусть mрот = 300 кг, подшипники однорядные шариковые 310 50×110×27 мм, класса точности 0, посадка внутреннего кольца на цапфу - Пп, нагружение по третьему режиму (циркуляционное нагружение). Ротор межопорный, центр масс лежит на середине расстояния между опорами.
По ГОСТ 520-89 находим поле допуска отверстия внутреннего кольца подшипника 310 класса точности 0. d2 = 0,018 мм.
Радиальное биение беговой дорожки внутреннего кольца относительно отверстия кольца d2 = 0,015 мм.
Радиальный зазор в этом подшипнике от 12 до 29 мкм, т.е. S = 0,029 мм.
Таким образом, максимально возможное дополнительное смещение центра масс при одинаковых подшипниках может быть
![]() мм,
мм,
а вносимое ими увеличение главного вектора дисбалансов ротора
![]() г·мм.
г·мм.
Очевидно, что не учитывать такие дисбалансы нельзя.
Заметим, что здесь лишь радиальный зазор в подшипниках вызывает дисбаланс ![]() г·мм, который
проявляется только при третьем режиме нагружения.
г·мм, который
проявляется только при третьем режиме нагружения.
Раздел 6. ТЕХНОЛОГИЧЕСКИЕ ДИСБАЛАНСЫ, ВЫЗВАННЫЕ НЕСООСНОСТЬЮ СОЕДИНЕНИЯ РОТОРА И ПРИВОДА
6.1. Несоосность валов, соединяемых муфтами, приводит к значительным нагрузкам всех опор сбалансированного ротора, изгибающим моментом в роторе и проявляется в виде фиктивного условного дисбаланса, нарушающего плавный ход машины.
Требуемые точности центрирования осей соединяемых валов по смещению и углу, а также методы расчета возникающих при этом нагрузок приводятся в специальной литературе.
Раздел 7. ВЕРОЯТНОСТНЫЙ РАСЧЕТ
7.1. Вектор максимальной суммы векторов технологических дисбалансов в плоскости опоры А или В может быть с одинаковой вероятностью направлен под любым углом в полярной системе координат, связанной с осью ротора. Проекции максимального вектора во всех его положениях на ось координат, перпендикулярную оси ротора, можно считать случайными величинами, в первом приближении, распределенными по закону Гаусса в соответствии с рекомендуемым приложением 4 к ГОСТ 22061-76. В этом случае ширина e поля распределения будет равна 6s, где s - среднеквадратическое отклонение всей совокупности этих случайных величин, для опор А и В двухопорного ротора.
Для одной из проекций, например, на ось X
![]()
В этом выражении
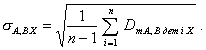
так как распределения центрированы и среднее значение их равно нулю.
Такое распределение, показанное на черт. 47, при e = 6s будет иметь
доверительную вероятность W = 0,9973, т.е. лишь в 0,0027 случаях возможны
проекции максимальных векторов сумм технологических дисбалансов превышающих ![]() . Практически это значит, что при запланированных точностях
изготовления деталей будет иметь место запланированный брак в 0,27 %,
показанный на черт. 47 зачерненными участками.
. Практически это значит, что при запланированных точностях
изготовления деталей будет иметь место запланированный брак в 0,27 %,
показанный на черт. 47 зачерненными участками.
Очень часто экономически выгоднее в массовом производстве иметь больший процент запланированного брака, но снизить класс точности изготовления продукции. В этом случае получается более пологая кривая распределения показанная на черт. 47 с шириной поля распределения e = 6s1. Сохраняя прежние максимальные значения суммы технологических дисбалансов т.е. ширину поля e, мы от этой новой кривой распределения отсечем заштрихованные участки, отражающие повышенный процент брака. Можно связать e и e1 (черт. 47) коэффициентом риска, показывающим во сколько раз уменьшается точность изготовления продукции
![]()
Черт. 47.
Процент брака и коэффициент риска Pриск для распределения Гаусса приведены в таблице.
|
Планируемый % брака |
0,27 |
1,00 |
2,00 |
3,00 |
4,00 |
5,00 |
6,00 |
8,00 |
10,00 |
|
Pриск |
1,00 |
1,16 |
1,29 |
1,38 |
1,46 |
1,52 |
1,60 |
1,71 |
1,82 |
Раздел 8. ЭКСПЛУАТАЦИОННЫЕ ДИСБАЛАНСЫ В ПЛОСКОСТЯХ ОПОР; ИХ ВИДЫ И ХАРАКТЕРИСТИКИ
8.1. Возникновение эксплуатационных дисбалансов в плоскостях опор ротора обусловлено целым рядом причин, например:
неравномерным износом деталей ротора в сборе (зубьев шестерен, соединительных муфт и т.д.);
пластическими деформациями (например, обмоток);
истиранием, выжиганием лопаток, навигационной и обычной эрозией;
возрастанием биений насадных деталей вследствие наклепа посадочных поверхностей;
смещением центра гидродинамических сил из-за изменения формы каналов и лопаток.
8.2. Все эксплуатационные дисбалансы можно разделить на:
дисбалансы ![]() , возникновение которых обусловлено вращением ротора,
например из-за изгиба вала
, возникновение которых обусловлено вращением ротора,
например из-за изгиба вала ![]() , из-за гироскопических моментов
, из-за гироскопических моментов ![]() , из-за аэродинамических сил
, из-за аэродинамических сил ![]() , из-за магнитных сил
, из-за магнитных сил ![]() , из-за неизотропности материала
, из-за неизотропности материала ![]() и т.п.
и т.п.
![]()
дисбалансы ![]() , возникновение
которых обусловлено длительной эксплуатацией, например, из-за ослабления
посадок и стыков
, возникновение
которых обусловлено длительной эксплуатацией, например, из-за ослабления
посадок и стыков ![]() , из-за смещения
крепежных и других деталей
, из-за смещения
крепежных и других деталей ![]() , из-за неравномерного износа посадочных мест
, из-за неравномерного износа посадочных мест ![]() , из-за
неравномерной ползучести, особенно в местах высоких температур
, из-за
неравномерной ползучести, особенно в местах высоких температур ![]() и т.п.
и т.п.
![]()
дисбалансы, возникновение которых обусловлено неравномерным нагревом ![]() .
.
Следовательно
![]()
Каждая составляющая этой формулы должна вычисляться или находиться в результате
эксперимента для выявления «узких мест» конструкции. Определение значения ![]() проводится как указано в п. 5.10 ГОСТ
22061-76.
проводится как указано в п. 5.10 ГОСТ
22061-76.
Раздел 9. ИЗМЕНЕНИЯ ЭКСПЛУАТАЦИОННЫХ ДИСБАЛАНСОВ И ВОЗМОЖНОСТИ УВЕЛИЧЕНИЯ ТЕХНОЛОГИЧЕСКОГО РЕСУРСА ИЗДЕЛИЙ
9.1. Если аналитически или экспериментально нет возможности найти числовые значения составляющих последней формулы (п. 8.2) предыдущего раздела на неразобранном роторе в конце технического ресурса изделия, следует их определять, разбирая ротор, выявляя все локальные дисбалансы, вызванные соответствующими эксплуатационными факторами, и по формулам разд. 2 ГОСТ 22061-76 разнести их в плоскости опор. В тех случаях, когда нет конструкторских или иных ограничений по углам дисбалансов или углы дисбалансов определить затруднительно, целесообразно все эксплуатационные дисбалансы в каждой опоре складывать арифметически, чтобы получить наибольшую разбалансировку.
9.2. На черт. 48 показан характер изменения дисбалансов ротора в процессе эксплуатации.
Черт. 48.
На участке 1 - 2 происходит увеличение дисбалансов в процессе приработки машины.
Если приращение главного вектора ![]() в результате
приработки велико, то после обкатки машин рекомендуется проводить повторную
балансировку. Кривая 2¢ - 3¢ показывает изменение Dст прир после повторной балансировки. Из черт. 48 видно,
что за счет этого можно увеличить технический ресурс ротора с tэ до
в результате
приработки велико, то после обкатки машин рекомендуется проводить повторную
балансировку. Кривая 2¢ - 3¢ показывает изменение Dст прир после повторной балансировки. Из черт. 48 видно,
что за счет этого можно увеличить технический ресурс ротора с tэ до ![]() .
.
Раздел 10. ВОЗМОЖНОСТИ УМЕНЬШЕНИЯ ДИСБАЛАНСОВ. СПОСОБ УМЕНЬШЕНИЯ ДИНАМИЧЕСКИХ НАГРУЗОК ОПОР МЕЖОПОРНОГО РОТОРА ПРИ ТРЕТЬЕМ РЕЖИМЕ НАГРУЖЕНИЯ ПОДШИПНИКОВ С РАДИАЛЬНЫМИ ЗАЗОРАМИ
10.1. При однопозиционной механической обработке нескольких поверхностей детали несоосность обработанных поверхностей будет наименьшей. Однако при планировании массового производства выгодно обрабатывать почти каждую поверхность на отдельном станке (принцип расчленения операций). Поэтому конструктор должен в первую очередь заботиться о том, чтобы центрирование детали при последующей обработке давало наименьшую несоосность.
10.1.1. Пример. Пусть тормозной барабан имеет вид и размеры, показанные на черт. 49.
Черт. 49.
Для оценки достаточно будет, пренебрегая буртиками, закруглениями и дисковой частью, написать, что главный вектор дисбалансов барабана
![]()
где DI - главный вектор дисбалансов цилиндра с параметрами:
dI, hI, eI, mI;
DII - главный вектор дисбалансов цилиндра с параметрами:
dII, hII, eII, mII;
dI - внешний диаметр;
dII - внутренний диаметр;
mI, mII - массы цилиндров;
hI, hII - высоты соответствующих цилиндров;
eI, eII - эксцентриситеты масс mI и mII, определяемые точностью станка.
Наименьшее значение главного вектора дисбалансов будет иметь место при
равенстве ![]() , т.е. когда внутренняя поверхность dII и наружная
поверхность с dI обработаны с одной установки
, т.е. когда внутренняя поверхность dII и наружная
поверхность с dI обработаны с одной установки
![]()
Наибольшее значение главного вектора дисбалансов будет иметь место,
когда ![]() , что может получиться при обработке не с одной установки
, что может получиться при обработке не с одной установки
![]()
Наконец, если ![]() , то
, то
![]() - это случай, когда центрирование при обработке
наружной поверхности ведется по dII.
- это случай, когда центрирование при обработке
наружной поверхности ведется по dII.
Для барабана, показанного на черт. 49 Dстa » 4000 г·мм, Dстβ » 30000 г·мм, Dстg » 17000 г·мм.
Как видно из этого примера, при разработке технологического процесса не считаться с этим нельзя.
Значение Dстa может быть еще уменьшено, если специально увеличить и определенным образом сориентировать эксцентриситет внутренней поверхности относительно наружной, что видно из следующего соотношения
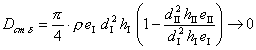
при
![]()
10.2. Конструктор, устанавливая на чертеже размеры центрирующих буртов, должен стремиться центрировать по наименьшему из возможных диаметров.
10.2.1. Пример. Пусть маховик массой 10 кг садится на коленчатый вал по посадке А/С. При наименьшем зазоре, который равен нулю для этой посадки, центрирование будет хорошим. Но при наибольшем зазоре этой посадки эксцентриситет будет равен половине зазора.
Допустим, что маховик можно центрировать по диаметру 100 А/С, либо по диаметру 30 А/С. В первом случае наибольший эксцентриситет от посадки может достигнуть 0,028 мм, во втором случае - 0,0185 мм, что может вызвать дисбалансы от посадки до 280 г·мм в первом случае или 185 г·мм во втором.
10.3. При сборке возможно возникновение деформаций, смещающих ось вращения или изменяющих положения центров масс отдельных деталей. Это может привести к возникновению дисбалансов в обеих плоскостях коррекции, т.к. внося дисбаланс в какую-либо одну плоскость (при монтаже даже хорошо отбалансированной детали) мы этим самым оказываем влияние на дисбалансы во всех плоскостях коррекции и измерения.
Например, конструктор, разрабатывая чертеж втулки, обязан предъявить жесткие требования к торцевому биению, к посадке втулки на вал и к параллельности шайбы, иначе при затягивании подшипников гайкой произойдет перекос, как это показано на черт. 50, появятся внутренние напряжения на валу, дисбалансы от искривления вала, возрастут нагрузки на опоры.
Примером неудачной центровки может служить крепление конусными гайками колеса автомобиля. В зависимости от того, какая из гаек будет затянута первой, дисбаланс может принимать то или иное значение. Естественно, что это существенно лишь для быстроходных автомобилей.
10.4. Отклонения формы и размеров деталей, а также поводка, получающиеся при механической и термической обработках, уводят центр масс изделия из его теоретического положения и создают дополнительные возмущающие силы на опорах. Возникающие в результате этого колебания во многих случаях являются причиной повреждения подшипников и усталостных поломок изделий.
Черт. 50.
Если, кроме этого, в конструкции возникают резонансные явления, то амплитуда колебаний резко возрастает.
Очевидно, что целесообразнее всего бороться с этим явлением в местах их возникновения. Это прежде всего относится к тяговым двигателям и другим машинам, связанным с относительно легкими несущими конструкциями, к машинам и станкам с повышенными требованиями к качеству работы, к приборам, работающим с малыми уровнями сигналов.
10.5. Дисбалансы, которые при работе машины вызывают колебания с частотой, равной частоте вращения изделия, могут быть уменьшены при балансировке на месте.
10.6. Если вращающиеся детали изделия состоят из нескольких частей, необходимо установить последовательность балансировки отдельных частей и их сборочных единиц, чтобы обеспечить их удовлетворительное конечное состояние и взаимозаменяемость. Правильная последовательность балансировок и сборки деталей позволяет значительно снизить требования к точности изготовления деталей изделия, экономить материал и время обработки и резко сократить стоимость изготовления.
10.7. Диски турбин и колеса компрессоров до посадки на вал следует балансировать динамически.
Значения предельных остаточных дисбалансов для них должны рассчитываться по разд. 1 - 6 II части и указываться на рабочих чертежах.
10.8. Для сопряжений прошедших балансировку деталей ротора не рекомендуется применять посадок с гарантированным зазором, если не предусмотрена балансировка собранного ротора.
Примечание. Допускается применение посадок с зазором, когда они под действием силовых или температурных деформаций переходят в посадки с гарантированным натягом или в переходные посадки.
10.9. Крепежные детали должны быть равномерно затянуты и законтрены, после чего проверяются радиальные биения головок крепежных изделий, а также одной или нескольких основных поверхностей деталей, которые крепятся ими к ротору.
Допустимые радиальные биения рассчитываются по разд. 2 - 4 II части и задают в технической документации.
10.10. Изготовляемые отдельно лопатки турбомашин должны комплектоваться для данного ротора из одной партии, особенно если они работают в условиях ползучести.
10.11. Заготовка вала должна обеспечивать его равножесткость при изгибе. Направление волокон на поверхности заготовки должно совпадать с направлением прокатывания и с осью ротора. Съем металла в радиальном направлении при обработке должен быть равномерным. При термообработке недопустимы деформации деталей ротора. Внутренние напряжения в деталях ротора должны быть сняты отжигом, старением и т.д.
10.12. Рассмотрим суммарные динамические нагрузки на опорах межопорного ротора, возникающие от дисбалансов. Для простоты рассуждений предположим, что ротор и опоры недеформируемы.
Дисбалансы ![]() и
и ![]() в плоскостях опор при
динамической неуравновешенности могут быть направлены под любым углом a между ними. Независимо от угла a между дисбалансами
в плоскостях опор при
динамической неуравновешенности могут быть направлены под любым углом a между ними. Независимо от угла a между дисбалансами ![]() и
и ![]() в плоскостях опор,
рассмотрим суммарную динамическую нагрузку как сумму
в плоскостях опор,
рассмотрим суммарную динамическую нагрузку как сумму ![]() , которая эквивалентна динамической нагрузке от главного
вектора дисбалансов
, которая эквивалентна динамической нагрузке от главного
вектора дисбалансов ![]() . Поэтому в дальнейшем будем рассматривать только статическую
и квазистатическую неуравновешенности ротора, которые характеризуются
одинаковыми главными векторами дисбалансов. Не следует забывать, что при одинаковых
значениях главных векторов дисбалансов ротора со статической или
квазистатической неуравновешенностями, динамические нагрузки в каждой из опор А или В будут в обоих случаях различными.
. Поэтому в дальнейшем будем рассматривать только статическую
и квазистатическую неуравновешенности ротора, которые характеризуются
одинаковыми главными векторами дисбалансов. Не следует забывать, что при одинаковых
значениях главных векторов дисбалансов ротора со статической или
квазистатической неуравновешенностями, динамические нагрузки в каждой из опор А или В будут в обоих случаях различными.
Однако при статической неуравновешенности (ось I на черт. 51) ротора и третьем режиме нагружения его подшипников, имеющих радиальные зазоры 2епод = S » SA » SB суммарная динамическая нагрузка на опорах при низкой (менее 1/3 резонансной) частоте вращения будет
![]()
(при eст = 0 в балансировке нет необходимости).
Черт. 51.
При квазистатической неуравновешенности (ось II на черт. 51) этой же системы суммарная динамическая нагрузка на опорах будет
![]()
где ![]() , как это видно из черт. 51, причем, епод = 0 при LB = LA. Очевидно, (Fдин)ст > (Fдин)квазист при всех
углах a между дисбалансами DA и DB в плоскостях опор А и В.
, как это видно из черт. 51, причем, епод = 0 при LB = LA. Очевидно, (Fдин)ст > (Fдин)квазист при всех
углах a между дисбалансами DA и DB в плоскостях опор А и В.
Для получения рассмотренного эффекта балансировку следует проводить на низкой (менее 1/3 резонансной) частоте вращения следующим образом.
Измерить значения D1нач и D2нач и углы a1нач - a2нач = a начальных дисбалансов ротора в плоскостях 1 и 2.
Провести корректировку масс в одной из плоскостей коррекции (например, 1) до значения остаточного дисбаланса D1ост и определить его угол a1ост, причем D1ост ≤ D1доп.
Построить векторную диаграмму по черт. 52 и определить по ней значение корректирующего дисбаланса m2кr2к и угол коррекции a2к во второй плоскости коррекции или подсчитать по формулам:
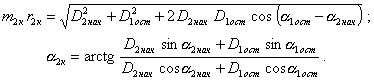
Провести корректировку масс во второй плоскости коррекции по найденным из векторной диаграммы значениям и получить таким образом во второй плоскости коррекции D2ост ≤ D2доп.
Применение описанного способа балансировки для консольных и многоопорных роторов, а также для систем, работающих на эксплуатационной частоте вращения выше первой резонансной системы, «ротор - опоры», требует специального рассмотрения.
Черт. 52.
Раздел 11. ОСОБЕННОСТИ БАЛАНСИРОВКИ ПОРШНЕВЫХ МАШИН
11.1. При балансировке роторов одноцилиндровых двигателей в сборе представляют интерес три случая.
11.1.1. Параметры колебания двигателя измеряются вдоль оси цилиндра. В этом случае можно провести коррекцию распределения вращающихся масс и добиться минимальных значений этих параметров вдоль оси цилиндра, но зато максимального размаха достигнут колебания в перпендикулярном к оси цилиндра направлении.
11.1.2. Амплитуда колебаний двигателя измеряется перпендикулярно к оси цилиндра. В этом случае можно коррекцией распределения вращающихся масс добиться минимальной амплитуды колебаний, перпендикулярно оси цилиндра, но тогда амплитуда колебаний вдоль оси цилиндра двигателя будет максимальна.
11.1.3. Амплитуда колебаний двигателя измеряется в плоскости опоры под углом 45° к оси цилиндра. В этом случае ось цилиндра двигателя наклонена под углом 45° к линии измерений и коррекцией вращающихся масс можно добиться минимальных амплитуд колебаний вдоль линии измерений, но по обе стороны под углом 45° к этой линии колебания будут иметь по 50 % своей максимальной амплитуды. Таким образом уравновешиваются только неуравновешенные силы шатунно-кривошипного механизма.
11.1.4. Конструктору поршневых машин необходимо знать не только неуравновешенные силы, действующие на опоры, но и внутренние изгибающие моменты, действующие на коленчатом валу.
Внутренние изгибающие моменты коленчатого вала (черт. 53) зависят от несоответствия массы шатунных шеек и части массы шатунов и поршней, статически приведенных к оси кривошипа, цельным или собранным противовесом коленчатого вала. У современных быстроходных короткоходовых двигателей внутреннего сгорания удается скомпенсировать лишь 40 - 50 % внутренних изгибающих моментов, зависящих от эксцентричного расположения указанных выше элементов и квадрата частоты вращения. В таких конструкциях необходимо считаться с нагрузкой на подшипники от внутренних изгибающих моментов.
Неуравновешенность внутренних изгибающих моментов усугубляется тем, что при балансировке коррекция проводится не путем добавления, а путем снятия массы. Чем больше начальные дисбалансы, тем больше приходится снимать металл с противовесов и тем самым увеличивается нагрузка коленчатого вала от внутренних изгибающих моментов. Для уменьшения значений начальных дисбалансов коленчатого вала следует либо ужесточить допуски изготовления, что весьма дорого, либо до его обработки ввести центровальную балансировку, основанную на явлении самоцентрирования массы.
Центровальная балансировка позволяет установить по необработанным поверхностям вала такую ось вращения, при которой будет сокращена до минимума последующая его механическая обработка.
11.3. Для многоопорных роторов поршневых машин трудно определить ось ротора из-за прогибов ротора и несоосности опор опорных шеек. Если измерить дисбалансы многоопорного коленчатого вала, установленного на различные пары опорных шеек, то получатся разные значения.
Для небольших коленчатых валов шестицилиндровых поршневых машин следует в качестве опор при балансировке выбирать не 1 и 7-ю коренные шейки, как это принято, а 2 и 6-ю, так как в первом случае, кроме параллельного смещения осей и прогиба вала, появляются дополнительные деформации от внутренних изгибающих моментов, зависящих от частоты вращения.
Черт. 53.
ПРИЛОЖЕНИЕ 1
ИСТОЧНИКИ ВИБРАЦИИ МАШИН
1. В реальной машине вибрацию с частотой вращения ротора n мин-1 (об/мин) могут вызвать, кроме дисбалансов, еще и, например, силы, возникающие в опорах из-за отклонения от соосности соединяемых ротором или перекоса наружных колец подшипников качения. Влияние отклонения от параллельности и пересечения осей соединенных роторов невозможно устранить с помощью балансировки.
При подозрении на отклонение от соосности или, если машина нечувствительна к балансировке, следует проверить отклонение от параллельности и пересечение осей соединений. Отклонения не должны выходить за пределы допусков, считающихся на практике удовлетворительными для типа и размера рассматриваемой машины.
2. В реальной машине может возникнуть вибрация с удвоенной частотой вращения ротора 2n из-за:
овальности шейки вала подшипника скольжения;
отклонения от круглости ротора по окружности вследствие переменного прогиба;
отклонения от круглости внутреннего кольца подшипника качения.
3. В подшипниках скольжения могут возникнуть автоколебания, обусловленные определенными условиями трения, например, фрикционные автоколебания, частоты которых бывают различны.
4. Турбулентные явления в жидком или газовом смазочном слое подшипников скольжения могут вызвать вибрацию с частотой, примерно равной 0,5n. Совместное действие этой вибрации с вибрацией частоты вращения ротора n создает так называемые «резонансные биения».
5. Подшипники качения являются источниками целой гаммы частот вибраций. Вследствие периодически повторяющейся асимметрии расположения тел качения, в подшипниках качения возникают радиальные силы с периодом, равным половине времени прохождения цапфой расстояния между телами качения. Так возбуждается вибрация с частотой
![]() с-1 (об/с)
с-1 (об/с)
где de - диаметр беговой дорожки наружного кольца подшипника качения;
di - диаметр беговой дорожки внутреннего кольца подшипника качения;
zк - число тел качения в подшипнике.
5.1. Волнистость дорожек качения или их износ вызывает вибрацию с частотой
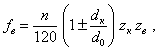
где знак «+» для внутреннего кольца;
знак «-» для внешнего кольца;
![]() - диаметр расположения центров тел качения;
- диаметр расположения центров тел качения;
zв - число гребней волн или число дефектов, расположенных вдоль дорожки качения.
5.2. Гранность тел качения или их деформация вызывает вибрацию с частотой
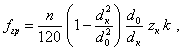
где k - число граней или деформированных участков на теле качения.
5.3. Зазоры между телами качения и кольцами подшипника приводят к ударам, в результате чего возникают свободные затухающие колебания различной частоты повторения групп этих колебаний. Наибольшая частота близка к fпк.
5.4. Сложные высокочастотные колебания цапфы в подшипнике качения могут быть разложены на ряд основных синусоидальных составляющих. Две из них могут при малейшем отклонении от параллельности системы дать биения с частотой близкой к n/60. Если нет возможности отстроиться при балансировке от этих частот, балансировка может оказаться невозможной.
5.5. Неуравновешенность сепаратора подшипников качения вызывает вибрацию с частотой
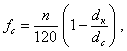 с-1 (об/с),
с-1 (об/с),
где dк - диаметр тела качения подшипника (шарика, ролика или иглы).
6. Аэродинамические, гидравлические и газодинамические силы в турбинах того или иного вида и в высокооборотных электрических машинах, могут возбудить вибрацию при трении ротора об окружающую среду от ударов потока в лопатки турбин или вентиляторов из-за кавитации, колебания, давления в маслопроводящих и охлаждающих трубопроводах, малых ресиверов и турбулизации потока и т.д.
7. В некоторых случаях и неподвижных частях машин или основаниях наблюдается резонанс при эксплуатационной частоте вращения и вибрация достигает недопустимого уровня даже в том случае, когда роторы имеют дисбалансы ниже допустимых. В этом случае для достижения удовлетворительных вибрационных характеристик машины может потребоваться исключительно точная балансировка, а иногда и изменение в конструкции машины для сдвига ее резонансной частоты.
ПРИЛОЖЕНИЕ 2
ОБОЗНАЧЕНИЯ НЕКОТОРЫХ ПАРАМЕТРОВ, ПРИМЕНЯЕМЫХ В НАСТОЯЩИХ МЕТОДИЧЕСКИХ УКАЗАНИЯХ
CопА,В - жесткости опор А и В; (Н/м) Соп = = СопА + СопВ
Cрот - средняя жесткость при изгибе ротора во всем пролете (Н/м)
![]() - значения функциональных дисбалансов в
плоскостях опор А или В ротора (г·мм; …0)
- значения функциональных дисбалансов в
плоскостях опор А или В ротора (г·мм; …0)
![]() - дисбаланс в i-й плоскости,
перпендикулярной оси ротора (г·мм; ...0)
- дисбаланс в i-й плоскости,
перпендикулярной оси ротора (г·мм; ...0)
![]() - дисбаланс в одной из двух плоскостей,
перпендикулярных оси ротора, определяющий моментную неуравновешенность ротора
(г·мм; ...0)
- дисбаланс в одной из двух плоскостей,
перпендикулярных оси ротора, определяющий моментную неуравновешенность ротора
(г·мм; ...0)
![]() - главный вектор дисбалансов ротора (г·мм;
...0)
- главный вектор дисбалансов ротора (г·мм;
...0)
![]() - компоненты главного вектора дисбалансов в
плоскостях А и B (г·мм; ...0)
- компоненты главного вектора дисбалансов в
плоскостях А и B (г·мм; ...0)
![]() - дисбалансы
в плоскостях опор А или В (г·мм; ...0)
- дисбалансы
в плоскостях опор А или В (г·мм; ...0)
![]() - дисбалансы в плоскостях коррекции 1 или 2 (г·мм; ...0)
- дисбалансы в плоскостях коррекции 1 или 2 (г·мм; ...0)
![]() - дисбалансы в плоскостях измерения I или II (г·мм;
...0)
- дисбалансы в плоскостях измерения I или II (г·мм;
...0)
![]() - начальные дисбалансы, измеренные в
плоскостях коррекции 1 и 2 при
балансировке на низкой частоте (г·мм;
...0)
- начальные дисбалансы, измеренные в
плоскостях коррекции 1 и 2 при
балансировке на низкой частоте (г·мм;
...0)
ест - удельный дисбаланс ротора (эксцентриситет массы mрот ротора относительно оси ротора) (мкм)
![]() - половина измеренного радиального зазора SA,B в подшипнике A и B (мкм)
- половина измеренного радиального зазора SA,B в подшипнике A и B (мкм)
![]() - неуравновешенная сила от i-й массы (Н)
- неуравновешенная сила от i-й массы (Н)
f - частота (Гц)
K - коэффициент дисбаланса
L - расстояние между серединами опор двухопорного ротора
LA,B - расстояние от середины опор A и B до центра масс ротора (мм)
LI, II - расстояние от середины опоры А ротора до плоскостей измерений I и II (мм)
LII - LI - расстояние между плоскостями измерения (мм)
l1, 2 - расстояние от середины опоры А до плоскостей коррекции 1 или 2 (мм)
l2 - l1 - расстояние между плоскостями коррекции 1 и 2 (мм)
li - расстояние центра i-й массы на плече неуравновешенной силы от центра масс ротора (справа от центра знак плюс) (мм)
![]() - главный момент дисбалансов ротора (г·мм; ...0)
- главный момент дисбалансов ротора (г·мм; ...0)
Mi - момент неуравновешенной силы ![]() относительно центра
массы mрот (нм;
...0)
относительно центра
массы mрот (нм;
...0)
mi - i-я масса (г)
![]() - масса ротора (г)
- масса ротора (г)
n - частота вращения ротора, мин-1 (об/мин)
nрез1 - i-я резонансная частота вращения системы «ротор - опоры», мин-1 (об/мин)
SА,В - радиальный зазор в подшипнике А или В (мкм)
![]() - среднее значение измеренных радиальных
зазоров в подшипниках А и
В (мкм)
- среднее значение измеренных радиальных
зазоров в подшипниках А и
В (мкм)
t - время (с)
y - прогиб упругой оси ротора у центра его масс (мм)
aА, aВ - углы дисбалансов ![]() и
и ![]() в плоскостях А и В (...0)
в плоскостях А и В (...0)
a = aА - aВ - угол между дисбалансами ![]() и
и ![]() в плоскостях опор А и В (...0)
в плоскостях опор А и В (...0)
a1, a2 - углы дисбалансов ![]() и
и ![]() в плоскостях 1 и 2 (...0)
в плоскостях 1 и 2 (...0)
![]() - средняя деформация опор А и В (при симметричном роторе)
(мкм)
- средняя деформация опор А и В (при симметричном роторе)
(мкм)
r - плотность материала (г/см3)
w - угловая скорость вращения ротора (рад/с)
wрез - резонансная угловая скорость вращения системы «ротор - опоры» (рад/с)
wэ - угловая скорость вращения ротора в эксплуатационных условиях (рад/с)
wэ макс - максимальная угловая скорость вращения ротора в эксплуатационных условиях (рад/с)
СОДЕРЖАНИЕ