Р 50.2.004-2000
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ
Государственная
система обеспечения единства
измерений
ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ЗАВИСИМОСТЕЙ МЕЖДУ ФИЗИЧЕСКИМИ
ВЕЛИЧИНАМИ ПРИ РЕШЕНИИ
ИЗМЕРИТЕЛЬНЫХ ЗАДАЧ
Основные положения
ГОССТАНДАРТ РОССИИ
Москва
Предисловие
1 РАЗРАБОТАНЫ И ВНЕСЕНЫ Российским Центром испытаний и сертификации - Москва (РОСТЕСТ - Москва) Госстандарта России
2 ПРИНЯТЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Госстандарта России от 17 июля 2000 г. № 191-ст
3 ВВЕДЕНЫ ВПЕРВЫЕ
СОДЕРЖАНИЕ
Р 50.2.004-2000
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ
Государственная система обеспечения единства измерений
ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ЗАВИСИМОСТЕЙ МЕЖДУ ФИЗИЧЕСКИМИ ВЕЛИЧИНАМИ ПРИ РЕШЕНИИ ИЗМЕРИТЕЛЬНЫХ ЗАДАЧ
Основные положения
Дата введения 2000-08-01
1 Область применения
Настоящие рекомендации устанавливают основные принципы определения характеристик математических моделей зависимостей между физическими величинами при решении измерительных задач.
Настоящие рекомендации распространяются на процедуры установления количественного соответствия между физическими объектами и их математическими моделями в сфере государственного метрологического контроля и надзора. Рекомендации также распространяются на используемые при этом математическое обеспечение, вычислительные и программные средства, в том числе поставляемые отдельно, характеристики которых документированы производителем или разработчиком.
2 Нормативные ссылки
В настоящих рекомендациях использованы ссылки на следующие стандарты:
ГОСТ 22.2.04-97/ГОСТ Р 22.2.04-94 Безопасность в чрезвычайных ситуациях. Техногенные аварии и катастрофы. Метрологическое обеспечение контроля состояния сложных технических систем. Основные положения и правила
ГОСТ Р 8.563-96 Государственная система обеспечения единства измерений. Методики выполнения измерений
3 Определения
3.1 В настоящих рекомендациях применяют следующие термины с соответствующими определениями:
математическая модель объекта измерений: Математическая модель зависимости между физическими величинами, характеризующими свойства объекта измерений.
измерительная задача: Задача установления количественного соответствия между свойствами физического объекта и характеристиками его математической модели в данных условиях с требуемой точностью на основе принятых систем счисления и мер физических величин.
метод решения измерительной задачи: Совокупность методов воспроизведения физических величин, измерений и вычислений для получения искомого в измерительной задаче результата.
погрешность неадекватности (математической модели объекта измерений): Величина, характеризующая разность расчетного значения данной физической величины как переменной математической модели объекта измерений и результата ее независимого измерения в соответствующих расчету условиях.
4 Общие положения
4.1 Свойства физических объектов как объектов измерений (далее - объекты) количественно выражают одноименными характеристиками их математических моделей (далее - модели). Модели зависимостей между физическими величинами следует характеризовать:
- множествами X = {Хq : q
= ![]() } входных и Y =
{Yp : р =
} входных и Y =
{Yp : р = ![]() } выходных переменных - физических величин, выражающих
причинно-следственные отношения между свойствами объекта (в вероятностных
моделях выходные переменные допускается рассматривать в качестве входных по
отношению к вероятностным характеристикам);
} выходных переменных - физических величин, выражающих
причинно-следственные отношения между свойствами объекта (в вероятностных
моделях выходные переменные допускается рассматривать в качестве входных по
отношению к вероятностным характеристикам);
- множеством Θ =
{θm : т = ![]() } параметров (числовых коэффициентов);
} параметров (числовых коэффициентов);
- структурой аналитического
выражения Ф![]() (Θ; X)
зависимости расчетного значения выходной переменной Yp от выходных переменных или
двоичным кодом структуры
(Θ; X)
зависимости расчетного значения выходной переменной Yp от выходных переменных или
двоичным кодом структуры ![]() заданной модели
максимальной сложности, описывающей класс моделей;
заданной модели
максимальной сложности, описывающей класс моделей;
- функцией погрешности Еp(X) - распределением
вероятностей разности расчетного Ф![]() (Θ; X) и
опорного
(Θ; X) и
опорного ![]() p значений переменной Yp как функцией опорных значений
p значений переменной Yp как функцией опорных значений ![]() входных переменных в
диапазонах их изменения.
входных переменных в
диапазонах их изменения.
Модель считают известной, если определены ее структура, значения параметров и размерность переменных.
4.2 Модели, характеристики которых устанавливают в ходе решения измерительной задачи, называют интерпретирующими. Такие модели, как правило, линейны по параметрам относительно системы известных базисных функций Ψ(*), в том числе ортогональных полиномов:
- в виде функции многих переменных
Ф![]() (Θ; X)
≡ Yp(Θ; X) =
(Θ; X)
≡ Yp(Θ; X) = ![]()
- в виде дифференциального оператора (уравнения)
Ф![]() (Θ; Y, Y(1), ..., Y(ω),
..., Y(Ω)) ≡
(Θ; Y, Y(1), ..., Y(ω),
..., Y(Ω)) ≡ ![]()
4.3 В качестве опорных значений физических величин следует принимать их истинные или действительные значения. Истинное значение физической величины является расчетным в рамках строгой физической теории, константы которой определены по данным измерений первичными эталонами поверочной схемы. Действительное значение физической величины является результатом ее измерения эталоном такого уровня поверочной схемы, при котором различием действительного и истинного значений в данной измерительной задаче можно пренебречь.
4.4 Погрешности моделей подразделяют:
- по источникам - на размерностно-неопределенную DNR (X) (погрешности результатов измерений, использованных для идентификации модели), структурно-неопределенную DNS (X) (погрешности неадекватности, зависящие от структуры модели) и параметрически-неопределенную DNP (X) (погрешности неадекватности, зависящие от выбора значений параметров модели, в том числе от ограничений разрядности представления чисел, прерывания вычислительных процессов и др., которые согласно ГОСТ Р 8.563 и ГОСТ 22.2.04/ГОСТ Р 22.2.04 относят к методическим погрешностям) составляющие;
- по типу математического описания - на систематическую (ее описывают однозначно, и она может быть использована в качестве поправки) и случайную (ее описывают распределением вероятностей как наиболее полной характеристикой неопределенности) составляющие.
4.5 Постановка измерительной задачи должна содержать следующее:
а) указание объекта и описание его модели, в том числе области определения и априорных значений неопределяемых параметров или переменных;
б) определение условий
измерений (характеристик влияющих величин Z = {Zk : k = ![]() }, доступности переменных модели изменениям и измерениям);
}, доступности переменных модели изменениям и измерениям);
в) формулировку цели задачи в терминах характеристик модели объекта;
г) требования к форме представления и точности искомого результата.
4.6 Измерительные задачи (далее - задачи) подразделяют:
- по направленности процедур установления количественного соответствия между свойствами физического объекта и характеристиками его математической модели - на задачи идентификации и задачи воспроизведения;
- по типам используемых математических моделей - на динамические (операторные модели), статические (функциональные модели) и вероятностно-статистические задачи;
- по целям - на размерностные (связанные с переменными) и структурно-параметрические (связанные со структурой и параметрами) задачи;
- по статусу - на прикладные (с использованием рабочих средств измерений) и метрологические (с использованием эталонов) задачи.
Размерностные задачи подразделяют по видам измерений (родам физических величин или поверочным схемам, в рамках которых определяют погрешности искомых результатов). Структурно-параметрические задачи по степени априорной неопределенности условий решения подразделяют на начальные (структура модели не задана), структурно-неопределенные (структура модели задана с точностью до класса моделей) и параметрически-неопределенные (модель задана с точностью до параметров) задачи.
4.7 Основными методами решения размерностных задач являются методы прямых, косвенных и совокупных измерений, а также прямого и косвенного воспроизведения. Структурно-параметрический метод (метод совместных измерений), а также методы программного изменения, параметрической компенсации и структурного дополнения являются соответственно методами идентификации и воспроизведения зависимостей. Они определяют типы методик решения измерительных задач (методики выполнения измерений по ГОСТ Р 8.563 - это методики косвенных измерений).
4.8 При размерностной идентификации определяют значения переменных, а при структурно-параметрической идентификации - структуру и значения или только значения параметров моделей объектов измерений.
5 Размерностная идентификация
5.1 Если по условиям измерительной задачи свойство объекта, выражаемое искомой переменной его модели, доступно сравнению с мерой соответствующей физической величины с требуемой точностью тем или иным способом (методом замещения, дополнения, дифференциальным и др.), то числовой результат такого сравнения округляют до разряда, соответствующего младшему разряду числового выражения пределов допускаемой при этом погрешности, с указанием этих пределов и доверительной вероятности (при единичной доверительной вероятности ее значение в результате решения задачи не указывают). Такой метод решения измерительной задачи называют методом прямого измерения (далее - измерением).
5.2 Если искомой в измерительной задаче является выходная переменная известной модели объекта, а измерениям доступны ее входные переменные, то в статическом случае задачу решают следующим методом: измеряют входные переменные, затем подставляют полученные данные в уравнение связи и вычисляют значение выходной переменной, округляя результат с учетом характеристик погрешностей измерений и неадекватности модели. Такой метод решения измерительной задачи называют методом косвенного измерения.
5.3 Если искомыми в
измерительной задаче являются входные переменные модели объекта, а измерениям доступны
выходные переменные, связанные с ними известными функциями ур =
Фp(Θ; x1, ..., xq, ...,
xq), p
= ![]() , то в статическом случае решение задачи при Р = Q сводят
к измерению выходных переменных с последующим решением системы уравнений
, то в статическом случае решение задачи при Р = Q сводят
к измерению выходных переменных с последующим решением системы уравнений
Фp(Θ; x1, ..., xq, ...,
xq) =
![]() , p =
, p = ![]() , (1)
, (1)
относительно входных переменных и определением характеристик погрешности результата с учетом погрешностей измерений, погрешностей неадекватности модели и погрешностей решения системы уравнений. При Р > Q используют методы наименьших квадратов (МНК) или модулей (МНМ) и другие вычислительные процедуры. Такой метод решения измерительной задачи называют методом совокупных измерений.
5.4 В динамических задачах применение метода косвенных измерений требует решения соответствующих дифференциальных уравнений, а применение метода совокупных измерений - решения соответствующих интегральных уравнений относительно искомых переменных.
6 Структурно-параметрическая идентификация
6.1
Структурно-параметрическая идентификация модели объекта измерений или
идентификация интерпретирующей модели по переменной Yp предусматривает построение
ее систематической составляющей Ф![]() (Θ; X)
(характеристики положения, смещения) и случайной составляющей Еp(X) (распределения погрешностей) как случайной функции входных переменных.
При этом оптимальность модели следует характеризовать с учетом критериев,
приведенных в приложении А.
(Θ; X)
(характеристики положения, смещения) и случайной составляющей Еp(X) (распределения погрешностей) как случайной функции входных переменных.
При этом оптимальность модели следует характеризовать с учетом критериев,
приведенных в приложении А.
6.2 Апостериорно погрешности неадекватности интерпретирующей модели определяют как погрешности экстраполяции расчетных значений ее выходной переменной на неиспользуемые для определения параметров модели данные эталонных измерений выходной переменной при соответствующих значениях входных переменных. Порядок использования данных, согласно которому параметры модели определяют по одной части данных (пробной), а погрешности модели - по другой части (контрольной), с последующим чередованием частей и объединением результатов, называют схемой перекрестного наблюдения погрешностей неадекватности. Такой метод идентификации интерпретирующих моделей объектов измерений по критериям приложения А называют методом максимума компактности (ММК).
6.3 Идентификацию интерпретирующих моделей осуществляют по данным совместных измерений и вариантам структуры, которые задают моделью максимальной сложности, приведенной к структурированному виду
Ф![]() (Θ; X)
≡
(Θ; X)
≡ ![]()
Ф![]() (Θ; Y, Y(1), ..., Y(ω),
..., Y(Ω), X) ≡
(Θ; Y, Y(1), ..., Y(ω),
..., Y(Ω), X) ≡ ![]()
где ![]() - двоичный код
структуры.
- двоичный код
структуры.
При этом структурированный вид определяют соглашением о суммировании:
а) каждый компонент
структуры модели дополняют сомножителем в виде двоичной индикаторной функции ![]() r,
r =
r,
r = ![]() , с индексом параметра, состоящим из степеней переменных I ... J ... К;
, с индексом параметра, состоящим из степеней переменных I ... J ... К;
б) совокупность двоичных
индикаторных функций ![]() =
= ![]() R
...
R
... ![]() r
...
r
... ![]() 1 образует код структуры модели - R-разрядное двоичное число,
разряды которого соответствуют порядковому положению параметров модели (прямой
код - от старших степеней к младшим, обратный
1 образует код структуры модели - R-разрядное двоичное число,
разряды которого соответствуют порядковому положению параметров модели (прямой
код - от старших степеней к младшим, обратный ![]() ’ - наоборот);
’ - наоборот);
в) компоненты модели суммируют группами (первую образуют компоненты, зависящие от степеней только одной переменной; вторую - компоненты, зависящие от степеней пар переменных; третью - от степеней троек и т.д.), упорядоченными по номерам переменных подгруппами;
г) порядок формирования вариантов структуры модели определяется последовательностью кодов (полный перебор вариантов структуры или сокращенный по какому-либо критерию оптимизации - последовательное усложнение или упрощение структуры).
6.4 Если структура интерпретирующей модели задана, а ее переменные доступны измерениям и изменениям, то параметры модели при их числе М = N определяют как решение системы уравнений
![]()
где N - число совместных измерений всех переменных модели объекта.
При М < N параметры модели определяют как результат минимизации функционалов случайной составляющей погрешности неадекватности:
Для S = 2 в формуле (2) получаемые оценки систематической составляющей модели объекта являются оценками МНК, а для S = 1 - оценками МНМ. Допускаются и другие методы параметрической идентификации.
6.5 Если структура интерпретирующей модели известна с точностью до модели максимальной сложности, то ее идентификацию осуществляют последовательной минимизацией погрешности неадекватности в схеме перекрестного наблюдения путем выбора кода структуры, метода определения параметров и правила сегментации данных.
При этом относительно характеристики положения интерпретирующей модели проверяют систему нулевых гипотез: Н0 - вырожденности (отсутствия зависимости); Н00 - непрерывности; Н000 - композиционной однородности (единой модели для ансамбля серий данных совместных измерений).
6.6 В схеме перекрестного
наблюдения характеристики погрешности неадекватности модели Ф![]() (Θ; X)
определяют с помощью экстраполяционного функционала модели по выходной
переменной
(Θ; X)
определяют с помощью экстраполяционного функционала модели по выходной
переменной
![]()
где М - число параметров модели;
кХm - т-я часть подпространства входных переменных, используемая в качестве контрольной (контрольное окно);
пΘm - множество параметров модели, определенное по данным, принадлежащим пробной части пХm = X\кХm;
П
(кХm; Х) = 
- индикаторная функция контрольного окна.
6.7 Отклонения действительных значений выходной переменной модели относительно ее экстраполяционного функционала представляют собой данные о действительных значениях погрешности модели.
В качестве оценки точности интерпретирующей модели следует использовать средний модуль погрешности неадекватности (СМПН) модели
где R - объем данных в схеме перекрестного наблюдения;
в качестве оценки правильности - среднюю не исключенную систематическую составляющую погрешности неадекватности
в качестве оценки сходимости - средний модуль случайной составляющей погрешности неадекватности как среднее абсолютное отклонение (САО)
![]()
где Θ - множество
параметров, определенное по всем данным ![]() .
.
6.8 Структурно-параметрическая идентификация характеристики положения интерпретирующей модели основана на проверке системы нулевых гипотез Н0, Н00 и Н000, а также альтернативных гипотез соответственно о наличии функциональной зависимости, о ее кусочно-непрерывном характере (наличии «разладок» - разрывов первого рода, включая производные) и о существовании индивидуальных интерпретирующих моделей для компонентов ансамбля серий данных измерений.
6.9 При проверке гипотезы Н0 выполняют следующие действия:
- делят протокол результатов
совместных измерений ![]() на блоки
на блоки ![]() таким образом, чтобы число
блоков было больше числа параметров данной структуры модели на единицу;
таким образом, чтобы число
блоков было больше числа параметров данной структуры модели на единицу;
- формируют все сочетания М
блоков как пробной выборки данных {![]() } и оставшегося блока как контрольной выборки {
} и оставшегося блока как контрольной выборки {![]() } (окна);
} (окна);
- минимизируют функционалы вида (2) на пробных выборках и вычисляют функционалы вида (4) на контрольных выборках.
В качестве наиболее правдоподобной непрерывной модели принимают модель с наименьшим значением СМПН. Затем с использованием всего протокола данных измерений окончательно определяют параметры модели оптимальной структуры - ММК-модели. При этом допускается использование функционалов (4) или (5) в зависимости от постановки задачи.
6.10 Гипотезу Н00 проверяют методом «скользящей границы», повторяя решение задачи описанным в 6.9 способом по обе стороны границы с вычислением для каждого положения границы средневзвешенного по числу измерений СМПН кусочно-непрерывной модели. Гипотезу непрерывности Н00 отклоняют, если будет найдена такая кусочно-непрерывная модель, средневзвешенный СМПН которой будет меньше значения СМПН наиболее правдоподобной непрерывной модели.
6.11 Композиционную идентификацию характеристики положения модели (проверку гипотезы Н000) осуществляют по совокупности протоколов измерений путем последовательной кластеризации ансамбля данных и построения для каждого из них ММК-модели согласно 6.9 и 6.10.
6.12 При определении параметров модели могут быть использованы МНК или МНМ. Соответствующие алгоритмы ММК-идентификации имеют обозначения ММКМНК и ММКМНМ, а интерполяционный вариант ММКМНМ, когда в качестве узлов интерполяции назначают выборочные медианы, - ММКМЕДС. В этих алгоритмах перебор вариантов структуры осуществляют методом последовательного усложнения в соответствии с соглашением о суммировании.
6.13 Идентификацию распределения погрешностей неадекватности интерпретирующей модели осуществляют путем проверки гипотез о структуре описывающего их распределения вероятностей по критерию, приведенному в приложении А при обеспечении условия эргодичности.
6.14 Условие эргодичности обеспечивают следующим образом:
- данные протокола измерений
выходной переменной модели с кодом структуры ![]() центрируют ее
экстраполяционным функционалом;
центрируют ее
экстраполяционным функционалом;
- отклонения этих данных от экстраполяционного функционала модели рассматривают в качестве погрешностей неадекватности;
- для последовательностей положительных и отрицательных погрешностей неадекватности модели согласно 6.9, 6.10 строят характеристику положения (СМПН для ММКМНК или квартальные характеристики для ММКМНМ и ММКМЕДС), которая является характеристикой масштаба;
- последовательности положительных и отрицательных погрешностей неадекватности модели нормируют характеристикой масштаба.
6.15 Для нормированных положительных и отрицательных погрешностей неадекватности, как реализаций одинаково распределенных случайных величин, по критерию воспроизводимости проверяют гипотезу о структуре распределения вероятностей. В качестве наиболее правдоподобной принимают структуру распределения с наибольшей статистикой критерия воспроизводимости (приложение А). Соответствующие алгоритмы ММК обозначают как ММКМП. При этом полученное распределение путем обратного преобразования характеристиками масштаба и положения приводят к характеристике положения интерпретирующей модели.
6.16 Окончательно функцию погрешности математической модели зависимости между физическими величинами представляют суммой размерностно-неопределенной DNR (X), структурно-неопределенной DNS (X) и параметрически-неопределенной DNP (X) составляющих:
Ep(X) = DNS(X) + DNP(X) + DNR(X).
Для функции погрешности в метрологических измерительных задачах устанавливают вероятностные характеристики (для принятого определения вероятности - аксиоматического, частотного, субъективного, интерполяционного и др.), а также соответствующие статистические характеристики в виде интервальных или точечных оценок как функций входных переменных модели. Для экспертных оценок этих характеристик (субъективные вероятности) следует различать метрические и порядковые шкалы.
При этом в методиках решения прикладных измерительных задач размерностной идентификации учитывают требования ГОСТ Р 8.563.
ПРИЛОЖЕНИЕ А
(обязательное)
Критерии идентификации
Критерием идентификации интерпретирующей модели, согласно теореме о модульном критерии (мю-критерий), является минимум математического ожидания ее смещения относительно результатов измерений выходной переменной контрольной выборки в схеме перекрестного наблюдения [1] - [3].
Если функция распределения
вероятностей Fx(x) случайной
переменной X такова, что ![]() x · Fx(x) = 0, то для характеристики положения θ
справедливо
x · Fx(x) = 0, то для характеристики положения θ
справедливо
M|X
- θ|
≡ M|X
- θ|
+2![]() (A.1)
(A.1)
Следствие. Тождество (А.1) минимизируется медианой, так как
![]()
Критерием идентификации плотности распределения вероятностей f(х) переменной X является максимум показателя ее воспроизводимости
где fп(x) и fк(x) - оценки плотности f(x) на пробной и контрольной выборках схемы перекрестного наблюдения (лемма о каппа-критерии [4] - [6]).
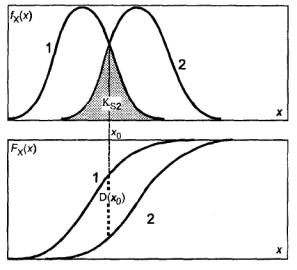
Если равенство плотностей распределений вероятностей fп(x) и fк(x) (рисунок А.1, соответственно кривые 1 и 2) случайной переменной X достигается в единственной точке x0, to показатель воспроизводимости (А.2)
где D(x) = Fп(x) - Fк(x) - разность для функций распределений вероятностей.
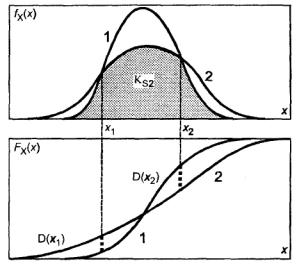
Следствие: Корням хт, т
= ![]() уравнения fп(x) и fк(x) соответствуют экстремумы
разности D(x), a
тождество (А.3) принимает вид (рисунок А.2)
уравнения fп(x) и fк(x) соответствуют экстремумы
разности D(x), a
тождество (А.3) принимает вид (рисунок А.2)
![]()
Рисунок А.1
Рисунок А.2
ПРИЛОЖЕНИЕ Б
(справочное)
Пример идентификации регрессионной модели
Возможности ММК-идентификации [7] - [14] математических моделей объектов продемонстрируем на данных [15] примера (таблица Б.1) параметрической идентификации регрессионной модели
![]()
где e - случайная величина, имитируемая датчиком «случайных» чисел, в условиях мультиколлинеарности, когда определитель информационной матрицы, соответствующей системе нормальных уравнений МНК, стремится к нулю (в данном случае он составляет £1,03 · 10-19).
Таблица Б.1 - Выход химической реакции у при времени реакции x1 и температуре x2
|
x1, мин |
x2, °С |
y, % |
Номер опыта |
x1, мин |
x2, °С |
y, % |
|
|
1 |
112 |
201 |
59,50 |
6 |
120 |
206 |
52,46 |
|
2 |
93 |
202 |
81,34 |
7 |
126 |
207 |
49,68 |
|
3 |
115 |
203 |
59,57 |
8 |
90 |
208 |
85,57 |
|
4 |
104 |
204 |
70,59 |
9 |
97 |
209 |
77,59 |
|
5 |
99 |
205 |
76,88 |
10 |
109 |
210 |
65,14 |
В этих условиях МНК со схемой Гаусса дает модель с САО < 0,735:
![]() (х1,
х2) =
-3464,336192 - 3,135112608 · х1 + 36,33886729 · х2 + 1,27819556 · 10-2
· х1х2 - 2,52413806 · 10-3 ·
(х1,
х2) =
-3464,336192 - 3,135112608 · х1 + 36,33886729 · х2 + 1,27819556 · 10-2
· х1х2 - 2,52413806 · 10-3 · ![]() - 9,12046229 ·
10-2 · х
- 9,12046229 ·
10-2 · х![]() .
.
Если же рассмотреть эту задачу как структурно-неопределенную и принять в качестве модели максимальной сложности
у (х1, x2)
= A + Bx1 + Cx2 + Dx1x2 + E![]() + Fх
+ Fх![]() ,
,
то алгоритмы
ММК-идентификации дадут модель (указан СМПН ± ![]() )
)
![]() MMKMHK(x1; х2) = -3941,1650 - 1,0450677x1 + 39,934086x2 - 0,096740127х
MMKMHK(x1; х2) = -3941,1650 - 1,0450677x1 + 39,934086x2 - 0,096740127х![]() ± 0,804.
± 0,804.
Результаты перебора вариантов
структуры (Z = A ![]() B
B ![]() C
C ![]() D
D ![]() E
E ![]() F) даны в таблице Б.2. Их
анализ показывает, что использованный для имитации датчик псевдослучайных чисел
имеет смещение, а результаты идентификации полной модели обладают существенной
структурно-неопределенной составляющей погрешности неадекватности. Лучший же
результат, выделенный в таблице Б.2, остался для авторов [15]
ненаблюдаемым.
F) даны в таблице Б.2. Их
анализ показывает, что использованный для имитации датчик псевдослучайных чисел
имеет смещение, а результаты идентификации полной модели обладают существенной
структурно-неопределенной составляющей погрешности неадекватности. Лучший же
результат, выделенный в таблице Б.2, остался для авторов [15]
ненаблюдаемым.
Таблица Б.2 - СМПН ММКМНК- и ММКМЕДС-моделей
|
Гипотеза |
||||||||||||
|
H0(Z) |
H0(AZ) |
H0(ABZ) |
H0(ABCZ) |
H0(ABCDZ) |
H0(ABCDEZ) |
|||||||
|
ММКМНК |
ММКМЕДС |
ММКМНК |
ММКМЕДС |
ММКМНК |
ММКМЕДС |
ММКМНК |
ММКМЕДС |
ММКМНК |
ММКМЕДС |
ММКМНК |
ММКМЕДС |
|
|
А |
14,73 |
15,75 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
В |
23,87 |
25,63 |
0,985 |
6,47 |
- |
- |
- |
- |
- |
- |
- |
- |
|
С |
15,07 |
16,60 |
21,14 |
78,40 |
2,10 |
3,10 |
- |
- |
- |
- |
- |
- |
|
D |
24,53 |
25,63 |
2,82 |
42,37 |
1,91 |
3,22 |
1,71 |
3,28 |
- |
- |
- |
- |
|
Е |
33,24 |
36,04 |
1,45 |
5,95 |
1,25 |
5,23 |
1,35 |
1,17 |
1,89 |
5,02 |
- |
- |
|
F |
15,89 |
17,60 |
21,22 |
78,41 |
2,11 |
3,10 |
0,804 |
0,806 |
2,19 |
6,15 |
3,16 |
29,37 |
ПРИЛОЖЕНИЕ В
(справочное)
Сравнительный анализ метрологического качества моделей функций преобразования средств измерений
В.1 При градуировке
вольтметра переменного тока [16] в пяти точках диапазона напряжение на
входе (Xi = 0,2iВ, i = ![]() ) устанавливали с погрешностью <0,002 %, а на выходе -
измеряли ni-кратно в каждой точке с
погрешностью <0,005 %. Затем определяли средние арифметическое и
квадратическое отсчетов (таблица В.1). По этим данным методом взвешенных
наименьших квадратов (МВНК) с весовыми коэффициентами ωi = ni/Si2 получена функция
преобразования
) устанавливали с погрешностью <0,002 %, а на выходе -
измеряли ni-кратно в каждой точке с
погрешностью <0,005 %. Затем определяли средние арифметическое и
квадратическое отсчетов (таблица В.1). По этим данным методом взвешенных
наименьших квадратов (МВНК) с весовыми коэффициентами ωi = ni/Si2 получена функция
преобразования
![]() bX
= 1,00004X.
bX
= 1,00004X.
Таблица В.1 - Данные градуировки
|
хi, в |
ni |
|
Si2 1010, В2 |
|
Di 105, В |
Dммкмнкi 105, В |
|
|
1 |
0,2 |
25 |
0,199946 |
8,55 |
0,200008 |
-6,2 |
0,1 |
|
2 |
0,4 |
25 |
0,400023 |
4,46 |
0,400017 |
0,6 |
-0,3 |
|
3 |
0,6 |
25 |
0,600071 |
4,31 |
0,600026 |
4,5 |
0,5 |
|
4 |
0,8 |
25 |
0,800062 |
2,82 |
0,800035 |
2,7 |
-0,3 |
|
5 |
1,0 |
50 |
1,000024 |
2,72 |
1,000044 |
-2,0 |
0,2 |
Сравнительный анализ различных вариантов (таблица В.2)
построения функции преобразования по данным таблицы В.1 показывает, что по СМПН ![]() полученная с помощью
МВНК модель функции преобразования более чем в 2
раза уступает модели, полученной с помощью ММКМНК.
полученная с помощью
МВНК модель функции преобразования более чем в 2
раза уступает модели, полученной с помощью ММКМНК.
Таблица В.2 - Данные ММК-идентификации функции преобразования
|
ммкмнк |
ММКМЕДС |
|||
|
Код |
01 |
111 |
01 |
111 |
|
СМПН |
0,000033 |
0,000015 |
0,000032 |
0,000026 |
|
Оценки параметров |
1,000052 |
-1.787195 · 10-4 1,000720 -5,18833 · 10-4 |
1,000053 |
-1,733004 · 10-4 1,000723 -5,334619 · 10-4 |
Учитывая неравноточность измерений, примем в качестве обобщенной
характеристики точности полученных вариантов функции преобразования
соответствующие значения функции правдоподобия (таблица В.3) для
распределений Гаусса  с параметрами
с параметрами ![]() .
.
Очевидно, что в данном примере алгоритм МВНК не может быть принят для получения оценок, соответствующих максимуму правдоподобия.
Вместе с тем, автором примера [17] с точки зрения выбора алгоритма высокой точности допущен ряд ошибок, оставленных без исправления в [16].
Градуировочная характеристика - это функция, обратная функции преобразования. Она позволяет пересчитывать показания средства измерений в значение измеряемой физической величины [18].
Таблица В.3 - Критерии максимального правдоподобия для функций преобразования вольтметра
|
|
|||||
|
i |
|
|
МВНК |
ММКМНК |
ММКМЕДС |
|
1 |
0,199946 |
8,55 |
1440,964664 |
13626,19449 |
13518,92125 |
|
2 |
0,400023 |
4,46 |
17880,74677 |
18666,84530 |
17722,33946 |
|
3 |
0,600071 |
4,31 |
1481,592746 |
18766,77243 |
19072,33400 |
|
4 |
0,800062 |
2,82 |
4816,842014 |
23330,50531 |
23637,51793 |
|
5 |
1,000024 |
2,72 |
15109,5573 |
24075,46676 |
21653,25886 |
|
|
2,7783181 · 1018 |
2,68122931 · 1021 |
2,33879454 · 1021 |
||
В примере не уточнена форма выражения погрешностей - относительная или приведенная. Кроме того, не ясны требования к точности градуировки вольтметра. Ограничены ли они пределом допускаемой (относительной или приведенной) погрешности измерений выходного напряжения, т.е. 0,005 %? Поэтому дальнейший анализ точности был проведен для верхней границы диапазона градуировки.
Указанное в примере критическое значение (21 · 10-5) для отклонения оценки коэффициента преобразования b от номинального значения при проверке гипотезы о его значимости не соответствует указанному в примере для данного средства измерений пределу допускаемой погрешности (0,005 % → 5 · 10-5). На верхней границе диапазона это соответствует превышению предела допускаемой погрешности более чем в 4 раза даже без учета погрешностей рабочего эталона.
Принятый в примере метод градуировки для предела допускаемой погрешности 0,005 % является неудовлетворительным уже только из-за составляющей погрешности, обусловленной построением функции преобразования. В точке i = 1 эта погрешность выходит за указанные пределы.
С учетом перечисленных обстоятельств в предпоследней колонке таблицы В.1 даны отклонения расчетных значений функции преобразования, построенной с помощью МВНК, от средних значений данных измерений в точках градуировки. В последней колонке даны аналогичные отклонения для функции преобразования, построенной с помощью ММКМНК.
В.2 При градуировке
измерительного термопреобразователя ТЭМ-1 (с помощью потенциометра Р348 класса
0,002, резистора Р321 класса 0,01 и нормального элемента класса 0,005) на его
входе устанавливали значения переменного тока (Xi = 0,3i мА, i = ![]() ), а на выходе проводили однократные измерения напряжения (
), а на выходе проводили однократные измерения напряжения (![]() мВ, i =
мВ, i = ![]() ) [16]. По этим данным (таблица В.4)
методом последовательных приближений [19] была построена функция
преобразования
) [16]. По этим данным (таблица В.4)
методом последовательных приближений [19] была построена функция
преобразования ![]() = аХ2 + bX3, где а = 0,016260, b
= -9 · 10-7.
= аХ2 + bX3, где а = 0,016260, b
= -9 · 10-7.
Сравнительный анализ
различных вариантов построения функции преобразования по данным таблицы В.4
(1-я и 2-я колонки) показывает, что по СМПН ![]() полученная с помощью
метода последовательных приближений на основе обычного МНК модель функции
преобразования (3-я и 4-я колонки) более чем на порядок уступает моделям,
полученным с помощью ММКМНК (5-я колонка) и ММКМЕДС (6-я колонка):
полученная с помощью
метода последовательных приближений на основе обычного МНК модель функции
преобразования (3-я и 4-я колонки) более чем на порядок уступает моделям,
полученным с помощью ММКМНК (5-я колонка) и ММКМЕДС (6-я колонка):
![]() = 4,843207 · 10-4 +
1,461683 · 10-4x + 1,623274
· 10-2x2 - 1,771827 · 10-13x7,
= 4,843207 · 10-4 +
1,461683 · 10-4x + 1,623274
· 10-2x2 - 1,771827 · 10-13x7, ![]() = 2,1 · 10-4,
= 2,1 · 10-4,
![]() = 8,3113555 · 10-4 +
1,6244039 · 10-2x2 - 1,2637424 · 10-8x4,
= 8,3113555 · 10-4 +
1,6244039 · 10-2x2 - 1,2637424 · 10-8x4, ![]() = 1,1 · 10-4.
= 1,1 · 10-4.
При этом следует заметить,
что ММКМНК для модели с кодом структуры ![]() = 0011 дает
= 0011 дает ![]() 0011 = 1,2 · 10-3, а с кодом
0011 = 1,2 · 10-3, а с кодом ![]() = 1011 - уже
= 1011 - уже ![]() 1011 = 4,5 · 10-4.
1011 = 4,5 · 10-4.
Таблица В.4 - Данные градуировки термопреобразователя ТЭМ-1
|
Xi, мА |
|
Yi
= a · X |
Di, мВ |
|
|
|
3 |
0,1471 |
0,1463 |
0,0008 |
0,000083 |
0,0000735 |
|
6 |
0,5856 |
0,5852 |
0,0004 |
-0,000140 |
-0,00000016 |
|
9 |
1,3167 |
1,3164 |
0,0003 |
0,000049 |
0,000185 |
|
12 |
2,3397 |
2,3393 |
0,0004 |
-0,000047 |
-0,0000107 |
|
15 |
3,6551 |
3,6555 |
-0,0004 |
0,000087 |
-0,00000014 |
|
18 |
5,2624 |
5,2630 |
-0,0006 |
-0,000015 |
-0,000173 |
|
21 |
7,1618 |
7,1623 |
-0,0005 |
-0,000073 |
-0,000195 |
|
24 |
9,3534 |
9,3533 |
0,0001 |
0,000162 |
0,000195 |
|
27 |
11,8361 |
11,8359 |
0,0002 |
-0,000145 |
0,0000805 |
|
30 |
14,6105 |
14,6097 |
0,0008 |
0,000040 |
0,000270 |
ПРИЛОЖЕНИЕ Г
(справочное)
Библиография
[2] Левин С.Ф. Основы теории контроля. - М.: МО СССР, 1983
[4] Левин С.Ф. Математическая теория измерительных задач // Контрольно-измерительные приборы и системы. - 1999: № 2 - 5. - 2000: № 1
[5] Левин С.Ф. Метрологическое аттестование и сопровождение программных средств статистической обработки результатов измерений // Измерительная техника. - 1991. - № 12
[7] Левин С.Ф. Метод максимума компактности и комплексные измерительные задачи // Измерительная техника. - 1995. - № 7
[8] Блинов А.П., Веретенин Д.А. Особенности функционального наполнения пакета прикладных программ метода максимума компактности // Измерительная техника. - 1991. - № 12
[9] Шабанов П.Г. Использование методов идентификации для оценки метрологических характеристик меры напряжения Джозефсона // Измерительная техника. - 1991. - № 12
[10] Левин С.Ф., Маркова Е.В. Планирование испытаний при метрологическом аттестовании программного обеспечения статистической обработки данных // Измерительная техника. - 1995. - № 6
[11] Левин С.Ф., Маркова Е.В., Пособило В.А. Системы метрологического сопровождения измерительных задач // Контрольно-измерительные приборы и системы. - 1997. - № 4
[12] Левин С.Ф. Метрологическое качество программных средств обработки результатов измерений // Контрольно-измерительные приборы и системы. - 1997. - № 6
[13] Левин С.Ф., Мигачев Б.С. Задача выбора точек измерительного контроля средств измерений // Измерительная техника. - 1998. - № 9
[15] Вучков И.Н., Бояджиева Л.Н., Солаков Е.Б. Прикладной линейный регрессионный анализ. - М.: Финансы и статистика, 1987
[16] Семенов Л.А., Сирая Т.Н. Методы построения градуировочных характеристик средств измерений. - М.: Изд-во стандартов, 1986
[17] Таубе Б.С. Разработка и исследование методов и средств высокой точности для автоматического измерения действующего и среднего значения переменного напряжения. Автореферат канд. диссертации, 1972
[18] Блинов А.П. Построение градуировочных характеристик средств измерений методом максимума компактности // Измерительная техника. - 1987. - № 7
[19] Безикович А.Я., Гравии О.Н. Исследование воздушных многоэлементных термопреобразователей // Тр. метрологич. ин-тов СССР. - 1965. - Вып. 82 (142)
Ключевые слова: объект измерений, математическая модель, погрешности неадекватности, размерностная идентификация, модульный критерий, критерий воспроизводимости, структурно-параметрическая идентификация