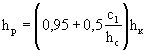|
|
ВСЕСОЮЗНЫЙ НАУЧНО-ИССЛЕДОВТЕЛЬСКИЙ ИНСТИТУТ ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ГИДРАВЛИЧЕСКОМУ РАСЧЕТУ КОСОГОРНЫХ ТРУБ
Отделение координации научно-исследовательских работ
Москва 1967
Содержание
ПРЕДИСЛОВИЕ
В настоящей работе приведены методические указания и рекомендации по гидравлическому расчету косогорных труб, подводящих сооружений (быстротоков), гасителей энергии на выходе из трубы и укреплений отводных русел.
Методические указания разработаны на основании теоретических и экспериментальных исследований, выполненных лабораторией мостовой гидравлики и гидрологии Всесоюзного научно-исследовательского института транспортного строительства (ЦНИИС), отечественных и зарубежных литературных источников, и предназначены для использования при проектировании косогорных водопропускных труб под насыпями железных и автомобильных дорог. Указания одобрены Главтранспроектом Минтрансстроя и Отделом экспертизы проектов МПС.
Указания составлены канд. техн. наук B.C. Громовым при участии инженеров Г.Я. Волченкова и В.И. Климеаова и ст. лаборанта А.С. Ефановой под общим руководством канд. техн. наук Л.Г. Бегама.
Замечания по Указаниям просьба направлять по адресу: Москва, И-329, Игарский проезд, 2, ЦНИИС, Отделение изысканий и проектирования ж.д.
ЗАМ. ДИРЕКТОРА ЦНИИС
по научной части (И.Ф. НАСЕДКИН)
РУКОВОДИТЕЛЬ ОТДЕЛЕНИЯ
изысканий и проектирования ж.д. ЦНИИС (Г.З. ВЕРЦМАН)
1. ОБЩИЕ ПОЛОЖЕНИЯ
К косогорным относятся трубы, устраиваемые при пересечении дорогами логов и водотоков под средним уклоном на участке трубы, от 0,02 и более. В косогорных трубах, как правило, на всем водопроводящем тракте или на части его, формируется гидравлически бурный поток.
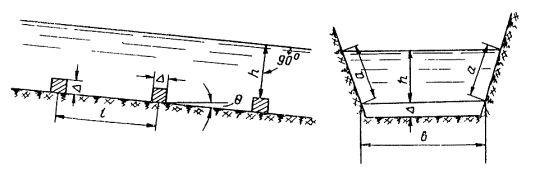
Водопропускная труба состоит из трех основных частей (рис. 1-1): а) подводящего русла, б) собственно трубы и в) выходных устройств, за которыми следует отводное русло.
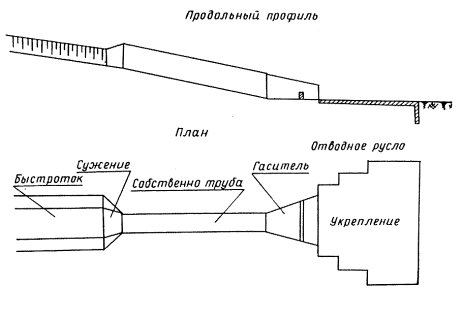
Рис. 1-1. Схема косогорной трубы
К подводящему руслу относится быстроток и входной оголовок. Собственно трубой является средняя часть сооружения, имеющая обычно постоянную ширину (диаметр). К выходным устройствам относятся: выходной оголовок, гаситель энергии и укрепление отводного русла.
Для гидравлического расчета косогорной трубы необходимо знать расходы Q и Qmax заданной СН 200-62 вероятности превышения. Эти расходы определяются гидрологическим расчетом, выполняемым в соответствии с ВСН 63-61 [8].
Гидрологический расчет отверстия трубы должен выполняться без учета аккумуляции. Учет же ее возможен лишь при индивидуальном проектировании с гидравлическим обоснованием его.
2. БЫСТРОТОКИ
2-1. Перед косогорной трубой устраивается искусственное призматическое русло (быстроток). Расчет быстротоков при равномерном движении потока производят по формуле Шези
где Q - расход воды, м3/сек;
w - площадь поперечного сечения потока, м2;
v - средняя скорость течения, м/сек;
i - уклон быстротока, то есть синус угла наклона дна к горизонту;
R - гидравлический радиус поперечного сечения, м;
С - коэффициент Шези, м0,5/сек.
2-2. Коэффициент Шези С для русел нормальной (не повышенной) шероховатости определяют по формуле Н.Н. Павловского
где n - коэффициент шероховатости, принимается по табл. 2-1;
![]() . (2-3)
. (2-3)
Значения коэффициента Шези можно определять по графику рис. 2-1.
2-3. Для уменьшения скорости течения в быстротоке может быть применена повышенная шероховатость в виде поперечных ребер квадратного сечения высотой D. Эти ребра располагают на дне поперек течения на расстоянии между осями t = 8D (рис. 2-2). Высоту ребер рекомендуется выдерживать в пределах 0,1h < D < 0,3h, где h - глубина потока над ребром, измеряемая перпендикулярно линии дна. Коэффициент Шези С в этом случае определяют из формулы О.М.Айвазяна
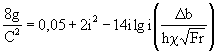 , (2-5)
, (2-5)
где
![]() - число Фруда (2-5)
- число Фруда (2-5)
c- смоченный периметр поперечного сечения потока, м:
В - ширина потока по верху, м;
b - ширина быстротока по дну, м.
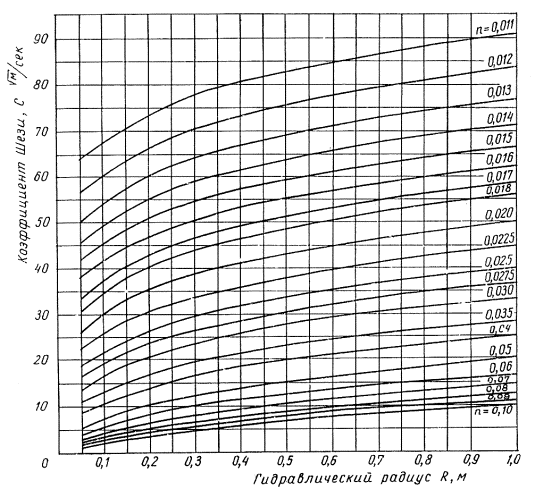
Рис. 2-1. График для определения коэффициента Шези С по полной формуле Н.Н.Павловского
Рис. 2-2. Схема быстротока с поперечными ребрами
Таблица 2-1
|
Наименование |
Коэффициент шероховатости по акад. Павловскому, n |
|
Одиночное мощение на щебне из булыжного камня размером 15-20 см |
0,020 |
|
Одиночное мощение на щебне из рваного камня размером 15-25 см |
0,025 |
|
Одиночное мощение на щебне с подборой лица и грубым приколом из камней размером 20-25 см |
0,025 |
|
Двойное мощение из рваного камня на щебне, нижний слой из камней 15 см, верхний из камней 20 см |
0,025 |
|
Облегченный бутовый лоток при h = 85 см с двухрядной укладкой камня на цементном растворе на щебеночной подготовке |
0,025 |
|
Двойное мощение на щебне в плетнях, нижний слой из камней 15 см , верхний - из камней 20 см |
0,032 |
|
Железобетонная труба без ступеней |
0,015 |
|
Каменная труба из бутовой или бутобетонной кладки без ступеней |
0,018 |
|
Лоток из сборных бетонных плит из бетона М-250, уложенных на щебеночной подготовке, толщиной 10 см |
0,016 |
|
Лоток из бутовой кладки с грубой поверхностью с применением камня крепких пород (предел прочности не менее 300 кг/см2) |
0,020 |
|
Рисберма из камня размером 20-30 см |
0,025 |
|
Лоток из бетона M-150 с грубой бетонировкой дна |
0,016 |
|
Каналы, чисто высеченные в скале |
0,020 |
|
Каналы без тщательной обработки поверхности, но с удалением резких выступов |
0,025 |
|
Каналы, грубо высеченные в скале |
0,040-0,045 |
|
Двойное мощение на цементном растворе |
0,020 |
|
Мощение бетонными плитами |
0,016 |
|
Реки и ручьи в благоприятных условиях (со свободным течением, без засорения и значительных водорослей) |
0,025 |
|
Каналы и реки в сравнительно плохих условиях (например, местами с водорослями и булыжником или заметно заросшие травой с местными обвалами откосов) |
0,030 |
|
То же, в весьма плохих условиях (с неправильным профилем, значительно засоренные камнями, водорослями и др.) |
0,035 |
|
То же, в исключительно плохих условиях (обломки скалы я крупные камни по руслу, густые корни, значительные промоины и обвалы, заросли камыша) |
0,040 |
Примечание. Значения n даны без учета аэрации потока.
2-4. Допускаемые средние скорости течения воды для разных типов укрепления и материалов принимаются по табл. 2-2, составленной на основании "Временных норм допускаемых скоростей течения воды в постоянных железнодорожных гидротехнических сооружениях".
2-5. Расчет неравномерных потоков в призматических и непризматических руслах производят по уравнению проф. В.И. Чарномского
![]() , (2-6)
, (2-6)
где hn и vn - глубина и средняя скорость течения в начале n-го участка потока;
hn+1 и vn+1 - то же в конце n-го и в начале n+1-го участков;
ln - длина n-го участка потока, измеряемая по дну;
a = (1,0 - 1,1) - коэффициент неравномерности распределения скорости течения в живом сечении потока;
![]() - средний уклон
трения на n-ом участке потока;
- средний уклон
трения на n-ом участке потока;
![]() ;
;
![]() ,
(2-7)
,
(2-7)
Величины v, С и R - те же, что и в формуле Шези (2-1), но их значения отнесены к началу n-го и n+1-го участков потока.
Уравнение проф. В.И. Чарномского (2-6) неприменимо для участков, в пределах которых поток из бурного состояния переходит в спокойное посредством гидравлического прыжка.
В призматических бетонных и железобетонных руслах прямоугольного поперечного сечения при нормальной шероховатости лотка глубину в любом сечении быстротока можно определять способом Н.Н. Павловского [3] без разбивки на участки вдоль потока.
2-6. При неодинаковых уклонах дна по длине быстротока каждый из участков рассчитывают самостоятельно. За начальное сечение последующего участка принимается конечное сечение предыдущего.
2-7. На всем протяжении быстротока надлежит обеспечивать бурный режим потока, характеризующийся тем, что в каждом его сечении глубина h меньше критической глубины hк, Критическую глубину hк потока с прямоугольным поперечным сечением определяют по формуле
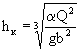 .
(2-8)
.
(2-8)
При расчете потока, имеющего непрямоугольную форму живого сечения, критическую глубину определяют подбором из уравнения
![]() .
(2-9)
.
(2-9)
2-8. Критический уклон iк потока с живым сечением любой формы в призматическом русле определяют по формуле
![]() .
(2-10)
.
(2-10)
Таблица 2-2
|
Типы грунтов или укреплений |
Размер, см |
Средние глубины потока, м |
||
|
0,4 |
1,0 |
2,0 |
||
|
1 |
2 |
3 |
4 |
5 |
|
Песок средний |
0,025-0,1 |
0,35-0,50 |
0,45-0 ,60 |
0,55-0,70 |
|
Гравий средний |
0,5-1,0 |
0,80-0,90 |
0,85-1,05 |
1,00-1,15 |
|
Галька мелкая |
1,5-2,5 |
1,10-1,25 |
1,20-1,45 |
1,35-1,65 |
|
Галька крупная |
4,0-7,5 |
1,50-2,00 |
1,85-2,40 |
2,10-2,75 |
|
булыжник мелкий |
7,5-10 ,0 |
2,00-2,45 |
2,40-2,80 |
2,75-3,20 |
|
Булыжник средний |
10,0 -15,0 |
2,45-3,00 |
2,80-3,35 |
3,20-3,75 |
|
Булыжник крупный |
15,0 -20,0 |
3,00-3,50 |
3,35-3,80 |
3,75-4,30 |
|
Глины и тяжелые суглинки среднеплотные |
объемный вес скелета грунта 1,20 - 1,66 т/м3 |
0,70 |
0,85 |
0,95 |
|
Суглинки тощие, средне плотные |
то же |
0,65 |
0,80 |
0,90 |
|
Конгломерат, мергель, сланцы |
- |
2,00 |
2,5 . |
3,0 |
|
Известняки |
- |
3,0 |
3,5 |
4,0 |
|
Песчаники и плотные известняки |
- |
4,0 |
5,0 |
6,0 |
|
Граниты и прочие твердые породы |
- |
15,0 |
18,0 |
20,0 |
|
Одерновка плашмя |
- |
0,9 |
1,2 |
1,3 |
|
Одерновка в стенку |
- |
1,5 |
1,8 |
2,0 |
|
Одиночное мощение на мху из камня |
15 |
2,0 |
2,5 |
3,0 |
|
|
20 |
2,5 |
3,0 |
3,5 |
|
|
25 |
3,0 |
3,5 |
4,0 |
|
Одиночное мощение на щебне размером камня |
15 |
2,5 |
3,0 |
3,5 |
|
|
20 |
3,0 |
3 5 |
4,0 |
|
|
25 |
3,5 |
4,0 |
4,5 |
|
|
20 |
3,5 |
4,5 |
5,0 |
|
Одиночное мощение с подбором лица и грубым приколом на щебне камня |
25 |
4,0 |
4,5 |
5,5 |
|
|
30 |
4,0 |
5,0 |
6,0 |
|
Двойное мощение из рваного камня на щебне |
15-20 |
3,5 |
4,5 |
5,0 |
|
Бутовая кладка из камня известковых пород |
- |
3,0 |
3,5 |
4,0 |
|
Бутовая кладка из камня крепких пород |
- |
6,5 |
8,0 |
10,0 |
|
Бетон как одежда |
|
|
|
|
|
марки 110 |
- |
5,0 |
6,0 |
7,0 |
|
марки 140 |
- |
6,0 |
7,0 |
8,0 |
|
марки 170 |
- |
6,5 |
8,0 |
9,0 |
|
Двойное мощение на цементом растворе |
15-20 |
6,0 |
- |
- |
|
Мощение бетонными плитами |
50x50x12 |
6,0 |
- |
- |
|
Бетонные лотки о гладкой поверхностью. Бетон марки 170 |
- |
13,0 |
16,0 |
19,0 |
|
Бетон марки 140 |
- |
12,0 |
14,0 |
16,0 |
|
Бетон марки 110 |
- |
10,0 |
12,0 |
13,0 |
Примечание. При проверке на наибольший расход Qmax пускаемые скорости повышаются на 35%.
3. СОПРЯЖЕНИЕ БЫСТРОТОКА С ТРУБОЙ
3-1. Протекание через сужение первоначально бурного потока может происходить по одной из схем:
1) с образованием перед трубой гидравлического прыжка;
2) с сохранением бурного состояния потока.
Осуществление первого или второго режима течения зависит от сочетания гидравлических характеристик потока перед сужением и геометрических характеристик сужения.
При образовании перед трубой гидравлического прыжка втекание в трубу происходит так же, как в равнинных условиях. При этом остаются справедливыми графики зависимости расхода от напора, приведенные в типовых проектах равнинных труб [1].
При сохранении бурного состояния потока (рис. 3-1) в начале сужения возникают стоячие косые волны (прыжки). Поперечный профиль потока становится вогнутым: глубина с боков оказывается значительно больше, чем в середине. Косые волны образуют с осью сооружения угол b, зависящий от гидравлических характеристик потока, геометрической формы и пряно связанный с углом сужения a0. В начале трубы, несколько ниже того сечения, где сходятся косые прыжки, поток имеет наибольшую глубину. Здесь струи частично соударяются, частично же пролетают к противоположной стенке трубы. При этом поток захватывает воздух (аэрируется). Максимальная глубина получается там, где струи встречают стенку трубы. Эта глубина может равняться наибольшей глубине на оси или даже превышать ее.
Непосредственно за входом в трубу боковые струи отрываются от стенок, и здесь образуются воздушные пазухи.
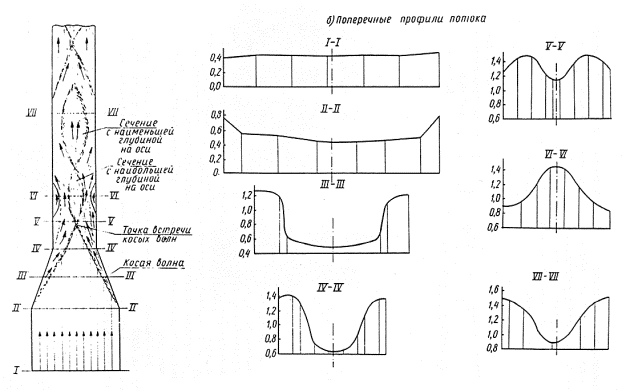
Рис. 3-1. Течение воды на переходе от прямоугольного быстротока к прямоугольной трубе меньшей ширины
На расстоянии 5-6 отверстий от входа в трубу глубины по поперечному сечению в значительной степени выравниваются и ниже поперечная неравномерность становится практически пренебрежимой. На этом же участке поток постепенно освобождается от воздуха, захваченного в зоне соударения струй (дезаэрируется).
3-2.Сопряжение быстротока с прямоугольной трубой меньшей ширины осуществляется отвесными прямыми в плане боковыми стенами, образующими с осью сооружения угол a0 (рис. 3-2 и 3-3).
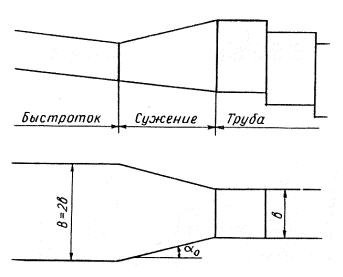
Рис. 3-2. Сопряжение прямоугольного быстротока с прямоугольной трубой
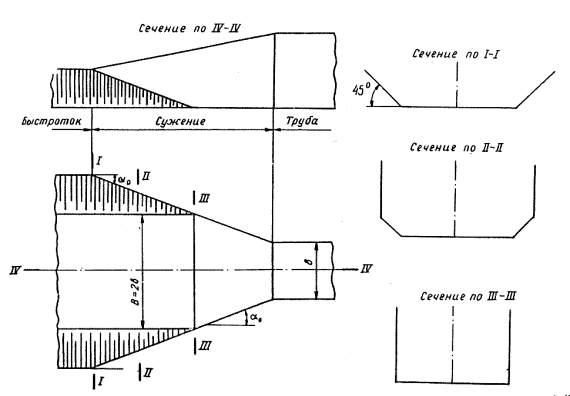
Рис. 3-3. Сопряжение трапецеидального быстротока с прямоугольной трубой
Портальные и воротниковые оголовки для косогорных сооружений недопустимы.
При расчетном расходе (табл. 3-1) угол сужения a0 принимают равным 15° или в крайнем случае 20°.
3-3. Расход, который может быть пропущен косогорной трубой нормированного просвета над поверхностью воды, согласно § 29 СН 200-62, отличается от расчетного расхода равнинных труб.
При высокой кинетичности потока и больших углах сужения на входном участке трубы получается высокий взлет струй. Необходимый зазор между уровнем воды и верхом трубы не обеспечивается. Поэтому требуется уменьшать расход против соответствующего расхода равнинных труб. При сравнительно низкой кинетичности потока и небольших углах сужения взлет струй на входном участке меньше. В этих случаях косогорные трубы имеют запас пропускной способности по сравнению с равнинными.
Расход, который протекает c сохранением в трубе над наиболее высоко взлетающими струями просвета, предусмотренного § 29 СН-200-62 , назван здесь допустимым расходом. При этом скорость потока в трубе не учитывается.
3-4. Значения допустимых расходов, установленные лабораторными опытами ЦНИИС, приведены в табл. 3-1 и 3-3 в зависимости от угла сужения a0 и кинетичности потока перед сужением; кинетичность потока характеризуется числом Фруда (2-5).
В таблицах даны значения переходного коэффициента ![]() , то есть отношения допустимого расхода к расчетному в
равнинных условиях. В табл. 3-1
приведены допустимые расходы, а в табл. 3-2 переходные коэффициенты
, то есть отношения допустимого расхода к расчетному в
равнинных условиях. В табл. 3-1
приведены допустимые расходы, а в табл. 3-2 переходные коэффициенты ![]() , для прямоугольных труб с прямоугольным быстротоком шириной,
вдвое большей отверстия трубы (см. рис. 2-2, 3-2).
Табл. 3-3 составлена для
прямоугольной трубы отверстием 1,5 м с трапецеидальным быстротоком, шириной по
дну вдвое большей отверстия трубы (см. рис. 3-3).
Для отверстий труб, не входящих в таблицы, допустимый расход определяется
умножением расчетного расхода на коэффициент К, взятый из таблиц для
геометрически подобных условий, то есть
, для прямоугольных труб с прямоугольным быстротоком шириной,
вдвое большей отверстия трубы (см. рис. 2-2, 3-2).
Табл. 3-3 составлена для
прямоугольной трубы отверстием 1,5 м с трапецеидальным быстротоком, шириной по
дну вдвое большей отверстия трубы (см. рис. 3-3).
Для отверстий труб, не входящих в таблицы, допустимый расход определяется
умножением расчетного расхода на коэффициент К, взятый из таблиц для
геометрически подобных условий, то есть
Расчетным здесь назван тот расход, который труба пропускает в равнинных условиях при безнапорной режиме с наибольшим заполнением, разрешаемым § 29 СН 200-62, при выполнении входов по типовым проектам [1]. Значения расчетных расходов, м3/сек, даны в табл. 3-4.
Таблица 3-1
|
Число Фруда перед сужением |
Угол сужения, град |
||||||||||||||
|
5 |
10 |
15 |
20 |
30 |
|||||||||||
|
отверстие трубы, м |
|||||||||||||||
|
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
|
|
Нормальное входное звено |
|||||||||||||||
|
8 |
19,0 |
22,4 |
25,7 |
9,4 |
13,45 |
17,5 |
9,4 |
13,4 |
17,5 |
9,4 |
12,6 |
15,8 |
7,9 |
10,6 |
13,2 |
|
10 |
18,8 |
22,2 |
25,6 |
9,4 |
13,35 |
17,3 |
9,4 |
13,4 |
17,3 |
9,4 |
12,6 |
15,8 |
7,8 |
10,4 |
12,9 |
|
12 |
18,6 |
22,0 |
25,4 |
9,4 |
13,20 |
17,0 |
9,4 |
13,2 |
17,0 |
9.4 |
12,6 |
15,8 |
7,2 |
9,50 |
11,8 |
|
14 |
18,5 |
21,85 |
25,2 |
9,6 |
13,25 |
16,9 |
9,4 |
13,2 |
16,9 |
9,4 |
12,6 |
15,8 |
6,5 |
8,75 |
11,0 |
|
16 |
18,5 |
21,75 |
24.9 |
10,0 |
13,25 |
16,5 |
9,4 |
13,0 |
16,5 |
9,4 |
12,5 |
15,6 |
6,0 |
8,05 |
10,1 |
|
18 |
18,3 |
21,45 |
24,6 |
10,3 |
13,25 |
16,2 |
9,4 |
12,8 |
16,2 |
9,3 |
12,3 |
15,3 |
5,5 |
7,30 |
9,1 |
|
20 |
18,1 |
21,05 |
24,0 |
10,6 |
13,2 |
15,8 |
9,4 |
12,5 |
15,6 |
9,1 |
12,1 |
15,1 |
5,0 |
6,60 |
8,2 |
|
22 |
17,2 |
20,20 |
23,2 |
10,8 |
13,2 |
15,5 |
9,4 |
12,2 |
14,9 |
8,9 |
11,7 |
14,5 |
4,6 |
6,00 |
7,4 |
|
24 |
17,0 |
19,80 |
22,6 |
11,0 |
13,1 |
15,2 |
9,4 |
11,8 |
14,3 |
8,5 |
10,8 |
13,1 |
4,3 |
5,40 |
6,5 |
|
25 |
17,0 |
19,55 |
22,1 |
11,3 |
13,05 |
14,8 |
9,4 |
11,7 |
14,0 |
8,5 |
10,6 |
12,6 |
4,0 |
5,00 |
6,0 |
|
Повышенное входное звено |
|||||||||||||||
|
8 |
24,0 |
28,5 |
33,0 |
14,3 |
19,6 |
24,9 |
13,6 |
18,2 |
22,9 |
12,7 |
17,0 |
21,3 |
9,4 |
12,6 |
15,9 |
|
10 |
23,9 |
28,3 |
32,7 |
14,1 |
19,5 |
24,9 |
13,4 |
18,2 |
22,9 |
12,7 |
17,0 |
21,3 |
9,4 |
12,6 |
15,9 |
|
12 |
23,7 |
28,0 |
32,4 |
13,6 |
19,2 |
24,9 |
13,4 |
18,2 |
22,9 |
12,6 |
17,0 |
21,3 |
9,4 |
12,6 |
15,8 |
|
14 |
23,7 |
27,8 |
32,0 |
13,6 |
19,1 |
24,6 |
13,2 |
17,9 |
22,6 |
12,5 |
16,8 |
21,2 |
9,8 |
12,3 |
15,3 |
|
16 |
23,4 |
27,6 |
31,7 |
13,5 |
18,8 |
24,2 |
13,1 |
17,8 |
22,4 |
12,5 |
16,6 |
20,8 |
8,9 |
11,8 |
14,6 |
|
18 |
23,1 |
27,2 |
31,2 |
13,5 |
18,7 |
23,5 |
13,0 |
17,5 |
22,0 |
12,4 |
16,4 |
20,4 |
8,2 |
11,5 |
14,4 |
|
20 |
22,6 |
26,4 |
30,3 |
13,4 |
18,4 |
22,9 |
12,9 |
17,1 |
21,3 |
12,0 |
15,в |
19,6 |
6,6 |
10,25 |
18,9 |
|
22 |
22,2 |
25,7 |
29,2 |
13,4 |
17,6 |
21,8 |
12,7 |
16,4 |
20,0 |
11,0 |
14,7 |
18,4 |
5,4 |
8,05 |
10,7 |
|
24 |
21,8 |
25,0 |
28,1 |
13,0 |
16,8 |
20,5 |
12,2 |
15,4 |
18,6 |
11,1 |
14,2 |
17,3 |
5,2 |
7,10 |
9,0 |
|
25 |
21,6 |
24,6 |
27,6 |
12,7 |
16,3 |
19,9 |
12,0 |
15,1 |
18,2 |
10,9 |
13,8 |
16,6 |
5,10 |
6,50 |
7,9 |
Таблица 3-2
|
Число Фруда перед сужением |
Угол сужения, град |
||||||||||||||
|
5 |
10 |
15 |
20 |
30 |
|||||||||||
|
отверстие трубы, м |
|||||||||||||||
|
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
|
|
Нормальное входное звено |
|||||||||||||||
|
8 |
2,01 |
1,82 |
1,63 |
1,0 |
1,06 |
1,11 |
1,0 |
1,06 |
1,11 |
1,0 |
1,0 |
1,0 |
0,84 |
0,84 |
0,84 |
|
10 |
1,99 |
1,80 |
1,62 |
1,0 |
1,05 |
1,10 |
1,0 |
1,05 |
1,10 |
1,0 |
1,0 |
1,0 |
0,82 |
0,82 |
0,82 |
|
12 |
1,97 |
1,79 |
1,61 |
1,0 |
1,04 |
1,08 |
1,0 |
1,04 |
1,08 |
1,0 |
1,0 |
1,0 |
0,76 |
0,76 |
0,75 |
|
14 |
1,96 |
1,78 |
1,60 |
1,02 |
1,04 |
1,07 |
1,0 |
1,04 |
1,07 |
1,0 |
1,0 |
1,0 |
0,69 |
0,70 |
0,70 |
|
16 |
1,96 |
1,77 |
1,58 |
1,06 |
1,06 |
1,05 |
1,0 |
1,02 |
1,05 |
1,0 |
1,0 |
0,99 |
0,64 |
0,64 |
0,64 |
|
18 |
1,94 |
1,75 |
1,56 |
1,09 |
1,06 |
1,03 |
1,0 |
1,02 |
1,03 |
0,98 |
0,98 |
0,97 |
0,58 |
0,58 |
0,58 |
|
20 |
1,9? |
1,72 |
1,52 |
1,12 |
1,06 |
1,00 |
1,0 |
1,00 |
0,99 |
0,96 |
0,96 |
0,96 |
0,53 |
0,58 |
0,58 |
|
22 |
1,82 |
1,64 |
1,47 |
1,14 |
1,06 |
0,98 |
1,0 |
0,98 |
0,95 |
0,94 |
0,92 |
0,90 |
0,49 |
0,48 |
0,47 |
|
24 |
1,80 |
1,62 |
1,43 |
1,17 |
1,06 |
0,96 |
1,0 |
0,96 |
0,91 |
0,90 |
0,86 |
0,83 |
0,45 |
0,43 |
0,41 |
|
25 |
1,80 |
1,60 |
1,40 |
1,20 |
1,07 |
0,94 |
1,0 |
0,94 |
0,89 |
0,90 |
0,85 |
0,80 |
0,43 |
0,40 |
0,38 |
|
Повышенное входное звено |
|||||||||||||||
|
8 |
2,54 |
2,32 |
2,09 |
1,51 |
1,54 |
1,58 |
1,44 |
1,44 |
1,45 |
1,34 |
1,34 |
1,35 |
1,00 |
1,00 |
1,01 |
|
10 |
2,53 |
2,30 |
2,07 |
1,49 |
1,54 |
1,58 |
1,42 |
1,44 |
1,45 |
1,34 |
1,34 |
1,35 |
1,0 |
1,00 |
1,01 |
|
12 |
2,51 |
2,28 |
2,05 |
1,44 |
1,50 |
1,58 |
1,42 |
1,44 |
1,45 |
1,33 |
1,34 |
1,35 |
1,0 |
1,0 |
1,0 |
|
14 |
2,51 |
2,27 |
2,03 |
1,44 |
1,50 |
1,56 |
1,40 |
1,42 |
1,43 |
1,32 |
1,33 |
1,34 |
0,98 |
0,98 |
0,97 |
|
16 |
2,47 |
2,24 |
2,01 |
1,43 |
1,48 |
1,53 |
1,39 |
1,40 |
1,42 |
1,82 |
1,32 |
1,32 |
0,94 |
0,94 |
0,93 |
|
18 |
2,44 |
2.21 |
1,98 |
1,43 |
1,48 |
1,49 |
1,38 |
1,38 |
1,39 |
1,31 |
1,30 |
1,29 |
0,37 |
0,90 |
0,92 |
|
20 |
2,39 |
2,16 |
1,92 |
1,42 |
1,46 |
1,45 |
1,37 |
1,36 |
1,35 |
1,27 |
1,26 |
1,24 |
0,70 |
0,79 |
0,88 |
|
22 |
2,35 |
2,10 |
1,85 |
1,42 |
1,40 |
1,38 |
1.34 |
1,30 |
1,27 |
1,24 |
1,20 |
1,17 |
0,57 |
0,62 |
0,68 |
|
24 |
2,31 |
2,04 |
1,78 |
1,37 |
1,34 |
1,30 |
1,29 |
1,24 |
1,18 |
1,18 |
1,14 |
1,10 |
0,55 |
0,56 |
0,57 |
|
25 |
2,29 |
2,02 |
1,75 |
1,34 |
1,30 |
1,26 |
1,27 |
1,21 |
1,15 |
1,16 |
1,10 |
1,05 |
0,54 |
0,52 |
0,50 |
Таблица 3-3
|
Число Фруда перед сужением |
Расходы, м3/сек |
Коэффициенты К = Qдоп/Qр |
|||||||||
|
Угол сужения, град |
|||||||||||
|
5 |
10 |
15 |
20 |
30 |
5 |
10 |
15 |
20 |
30 |
||
|
Нормальное входное звено |
|||||||||||
|
10 |
17,1 |
11,1 |
10,3 |
9,4 |
6,1 |
1,82 |
1,18 |
1,09 |
1,00 |
0,65 |
|
|
12 |
16,7 |
10,4 |
9,8 |
9,3 |
6,4 |
1,77 |
1,10 |
1,04 |
0,98 |
0,68 |
|
|
14 |
16,1 |
9,8 |
9,4 |
9,0 |
6,6 |
1,70 |
1,04 |
0,99 |
0,95 |
0,70 |
|
|
16 |
15,4 |
9,6 |
9,0 |
8,5 |
6,6 |
1,63 |
1,01 |
0,95 |
0,90 |
0,70 |
|
|
18 |
14,7 |
9,8 |
9,2 |
8,4 |
6,3 |
1,56 |
1,04 |
0,97 |
0,89 |
0,67 |
|
|
20 |
14,1 |
11,0 |
9,9 |
8,9 |
6,0 |
1,50 |
1,16 |
1,05 |
0,94 |
0,63 |
|
|
22 |
13,7 |
11,7 |
10,6 |
9,4, |
5,6 |
1,43 |
1,24 |
1,12 |
1,00 |
0,59 |
|
|
24 |
13,1 |
11,8 |
11,0 |
10,0 |
5,1 |
1,38 |
1,25 |
1,16 |
1,06 |
0,54 |
|
|
25 |
12,8 |
11,9 |
11,0 |
10,2 |
4,8 |
1,37 |
1,26 |
1,17 |
1,08 |
0,51 |
|
|
Повышенное входное звено |
|||||||||||
|
10 |
19,4 |
13,3 |
12,5 |
11,8 |
9,8 |
2,08 |
1,42 |
1,34 |
1,25 |
1,03 |
|
|
12 |
18,7 |
13,6 |
12,7 |
11, 9 |
9,8 |
1,99 |
1,46 |
1,36 |
1,26 |
1,03 |
|
|
14 |
17, 7 |
14,0 |
12,8 |
11,7 |
9,6 |
1,90 |
1,50 |
1,37 |
1,24 |
1,02 |
|
|
16 |
16,4 |
14,4 |
12,8 |
11,3 |
9,6 |
1,75 |
1,54 |
1,37 |
1,20 |
1,01 |
|
|
18 |
15,6 |
14,8 |
12,8 |
11,0 |
9,3 |
1,66 |
1,58 |
1,37 |
1,16 |
0,98 |
|
|
20 |
15,2 |
15,1 |
12,7 |
10,9 |
8,8 |
1,62 |
1,62 |
1,36 |
1,15 |
0,93 |
|
|
22 |
14,9 |
15,5 |
12,6 |
10,7 |
8,3 |
1,59 |
1,66 |
1,35 |
1,13 |
0,88 |
|
|
24 |
14,8 |
15,6 |
12,5 |
10,6 |
7,6 |
1,57 |
1,67 |
1,34 |
1,12 |
0,80 |
|
|
25 |
14,6 |
15,6 |
12,4 |
10,5 |
7,2 |
1,57 |
1,67 |
1,33 |
1,11 |
0,76 |
|
Таблица 3-4
|
Тип трубы |
Отверстие трубы, м |
||||
|
1,00 |
1,25 |
1,50 |
2,00 |
2,50 |
|
|
Прямоугольная Круглая |
4,60 1,40 |
5,75 2,50 |
9,45 3,90 |
12,60 8,00 |
15,75 - |
3-5. Для прямоугольных труб отверстием bтр =2,0 или 2,5 м с трапецеидальными быстротоками допустимый расход Qдоп.в определяют по выражению
![]() , (3-3)
, (3-3)
где Qдоп, 1,5 - допустимый расход для трубы отверстием 1,5 м (см. табл. 3-4) при том же типе сужения и том же числе Фруда;
Кb и К1,5 - переходные коэффициенты от расчетного расхода к допустимому, соответственно для отверстий b и 1,5 м, которые берутся теми же, что и для прямоугольного быстротока, то есть из таблицы 3-2.
3-6. Аля трубы отверстием 1,25 м с нормальным звеном допустимый расход находят по формуле (3-2), причем переходный коэффициент К принимается таким же, как и для трубы отверстием 2,0 м с повышенным звеном при том же числе Фруда и при том же типе сужения и быстротока.
3-7. Для труб отверстием 1,0 м с нормальным звеном, а также отверстием 1,0 и 1,25 м с повышенным звеном допустимый расход определяют по формуле (2-2), но коэффициент K берут таким же, как и для трубы отверстием 1,5 м с повышенным звеном при том же типе быстротока и сужения и том же числе Фруда.
3-8. Чтобы определить длину участка с повышенными входными звеньями, в случае пропуска допустимого расхода Qдоп, необходимо построить продольный профиль потока по оси в начальном участке трубы.
Продольный профиль потока строят следующим образом (рис. 3-4):
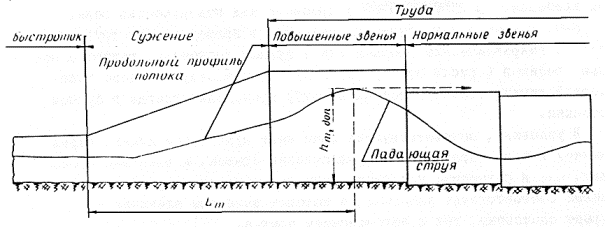
Рис. 3-4. К определению длины участка с повышенными звеньями на входе
а) Определяют положение сечения с наибольшей высотой подъема струй по формуле
![]() , (3-4)
, (3-4)
где Lm - расстояние от начала сужения до сечения с максимальной высотой подъема струй по оси трубы, м;
А1 - коэффициент, зависящий от типа быстротока и отверстия трубы.
Для прямоугольного быстротока
А1 = 0,1b - 0,063 ; (3-5)
для трапецеидального быстротока
А1 = 0,1b - 0,011 ; (3-6)
N - коэффициент, зависящий от угла сужения. Для прямоугольного быстротока
![]() ; (3-7)
; (3-7)
для трапецеидального быстротока
![]() ; (3-8)
; (3-8)
б) Вниз от сечения с наибольшей высотой подъема струй строят траекторию падающей струи, уравнение которой
![]() ; (3-9)
; (3-9)
где х1 - горизонтальное расстояние от сечения с наибольшей высотой подъема струй, м;
vbx - скорость потока на входе в сужение, м/сек;
z - высота падения струи, отсчитываемая вниз от горизонтали, проходящей через точку наибольшего подъема струй, м.
в) Графически определяют длину участка с повышенными входными звеньями, при которой в сечении перехода к нормальным звеньям выполняют требования § 29 СН 200-62 о просвете над поверхностью воды.
3-9. Вопрос о том, будет ли втекание в прямоугольную труб происходить о гидравлическим прыжком или в бурном состоянии, решают с помощью графиков (рис. 3-5). В условиях, соответствующих зоне выше оплошной линии, втекание потока в трубу происходит всегда в бурном состоянии.
В условиях, соответствующих зоне ниже пунктирной линии, перед сужением всегда образуется гидравлический прыжок, и втекание происходит, как в равнинных условиях. Зона же между пунктирной и сплошной линиями соответствует условиям, в которых возможны втекание как в бурном состоянии, так с образованием прыжка.
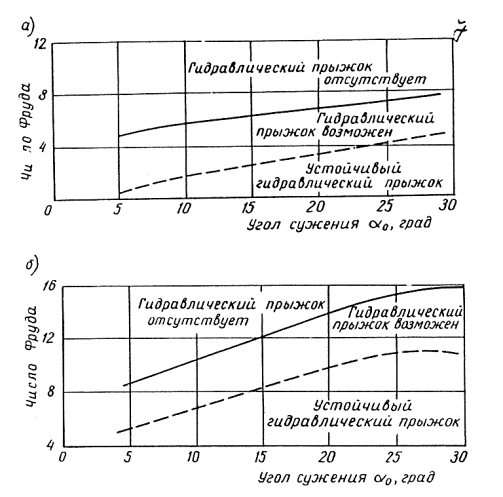
Рис. 3-5. Возникновение гидравлического прыжка в зависимости от угла сужения и кинетичности потока: a) быстроток прямоугольный; б) быстроток трапецеидальный
3-10. Сопряжение прямоугольных и трапецеидальных быстротоков с круглыми трубами рекомендуется осуществлять в соответствии со схемами (рис. 3-6 по 3-12). Сопряжения этих типов испытаны в ЦНИИСе на гидравлических моделях. При расчетных расходах, принятых в типовых проектах равнинных труб [1], работают хорошо. Они также позволяют пропустить при безнапорном режиме и удовлетворительных условиях течения расход в 1,5 раза больше расчетного.
Не рекомендуется в круглых трубах допускать расход, превышающий расчетный более чем в 1,5 раза. При таком превышении глубина на входе оказывается больше половины диаметра входного отверстия, поток ударяет в вертикальную поперечную стенку над трубой и возникают нежелательные фонтаны и водовороты.
Коническое звено на входе в круглую трубу при бурном режиме улучшает характер втекания и увеличивает запас пропускной способности. При коническом звене наибольшая глубина на входе оказывается в тех же условиях на 20-30% меньше, чем при нормальном входном звене.
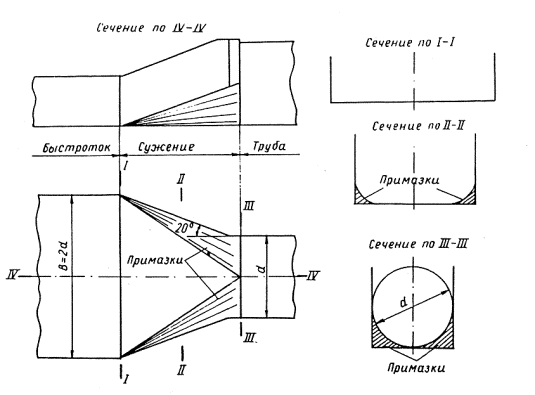
Рис. 3-6. Сопряжение прямоугольного быстротока с круглой трубой вдвое меньшей ширины, тип I
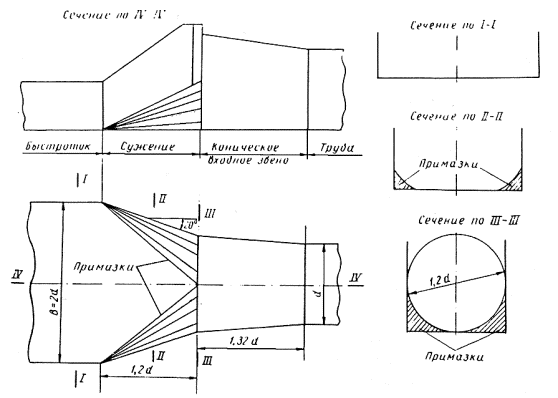
Рис. 3-7. Сопряжение прямоугольного быстротока и круглой трубы с коническим звеном, тип II
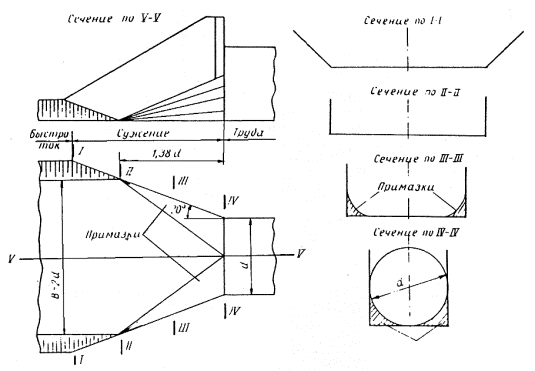
Рис. 3-8. Сопряжение трапецеидального быстротока шириной В = 2а с круглой трубой отверстием d ,тип Ш
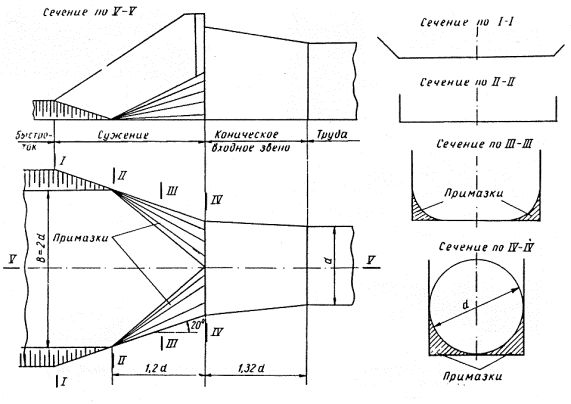
Рис. 3-9. Сопряжение трапецеидального быстротока шириной B=2d и круглой трубы отверстием a коническим входным звеном, тип IV
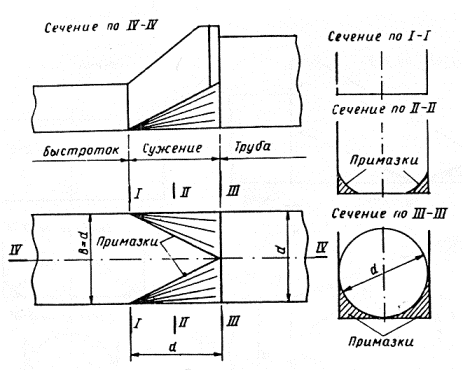
Рис. 3-10. Сопряжение прямоугольного быстротока с круглой трубой той же ширины, тип V
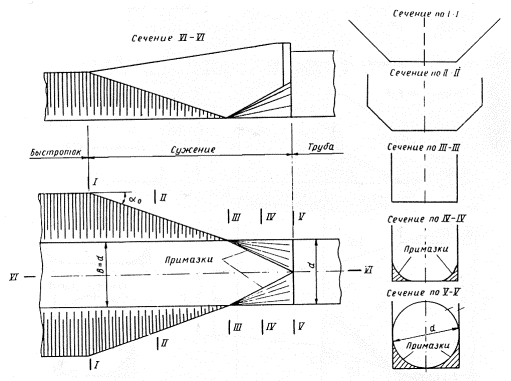
Рис. 3-11. Сопряжение трапецеидального быстротока шириной по дну B = d с круглой трубой отверстием d, тип VI
Во входном сечении трубы глубины по ширине неравномерны: на оси сооружения глубина наибольшая, по краям наименьшая. Глубины потока на входе в трубу в долях диаметра трубы при расчетном расходе показаны в табл. 3-5.
Таблица 3-5
|
Тип сопряжения быстротока с круглой трубой |
№ рис. |
Максимальная глубина |
Минимальная глубина |
Средняя глубина |
||||||
|
Числа Фруда |
||||||||||
|
12 |
18 |
25 |
12 |
18 |
25 |
12 |
18 |
25 |
||
|
I |
0,63 |
0,50 |
0,50 |
0,22 |
0,25 |
0,21 |
0,47 |
0,39 |
0,31 |
|
|
II |
0,50 |
0,46 |
0,42 |
0,09 |
0,12 |
0,16 |
0,34 |
0,33 |
0,30 |
|
|
Ш |
0,74 |
0,67 |
0,50 |
0,19 |
0,27 |
0,28 |
0,51 |
0,48 |
0,41 |
|
|
IV |
0,53 |
0,46 |
0,48 |
0,12 |
0,19 |
0,17 |
0,38 |
0,32 |
0,26 |
|
|
V |
0,36 |
0,37 |
- |
0,11 |
0,10 |
- |
0,29 |
0,26 |
- |
|
|
VI |
0,52 |
0,45 |
- |
0,08 |
0,09 |
- |
0,39 |
0,31 |
- |
|
|
VII |
0,32 |
0,35 |
0,33 |
0,30 |
0,05 |
0,31 |
0,20 |
0,21 |
0,20 |
|
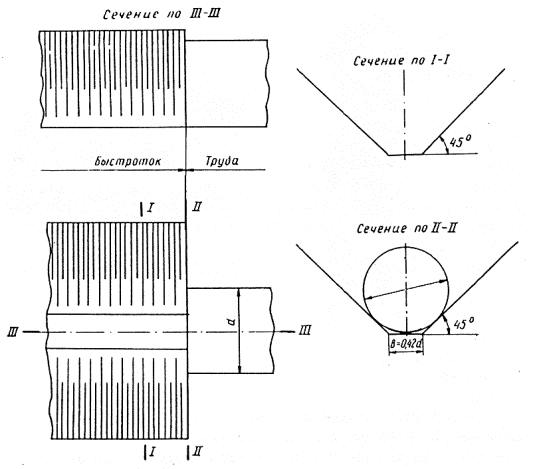
Рис. 3-12. Сопряжение трапецеидального быстротока шириной по дну В = 0,42d с круглой трубой отверстием d, тип VII
3-11. Режим втекания в круглую трубу можно определять с помощью табл. 3-6.
Таблица 3-6
|
Режим протекания |
Тип сооружения с быстротоком |
|||
|
I |
II |
III |
IV |
|
|
Только с гидравлическим прыжком при числе Фруда Fr1, менее |
7 |
6 |
8 |
7 |
|
Только в бурном состоянии при числе Фруда Fr2 более |
10 |
9 |
12 |
10 |
|
Возможны оба режима протекания при числе Фруда |
7-10 |
6-9 |
8-12 |
7-10 |
При типах сопряжения V, VI и VII протекание происходит только при бурном состоянии потока.
3-12. При необходимости резкого понижения дна сооружения могут устраиваться перед входом в трубу прямоугольные в плане водоприемные колодцы.
Гидравлический расчет прямоугольного водоприемного колодца выполняется в следующем порядке.
а) Необходимая длина колодца вдоль оси трубы при поступлении воды с торца колодца определяется по формуле
L = l0 + 0,5 (3-10)
где l0 - горизонтальное расстояние от уступа до места падения струи на дно колодца, м.
В этом случае размер колодца поперек оси трубы принимают не менее ширины подводящего лотка и не менее удвоенного отверстия трубы.
При боковом поступлении воды размер колодца вдоль оси трубы определяется шириной подводящих канав, а поперек оси трубы - дальностью падения струи l0.
б) Горизонтальное расстояние l0 определяют из уравнения
![]() , (3-11)
, (3-11)
где ![]() ;
;
h - высота уступа, м;
глубина потока h, средняя скорость v берутся в сечении над уступом;
Q - угол наклона подводящего русла к горизонту.
Расстояние l0 можно также определять по графику (см.п.5-17).
в) Глубину в сжатом сечении hc на дне колодца определяют подбором из уравнения
![]() ,
(3-12)
,
(3-12)
где ![]() - полный напор в
конце быстротока, м;
- полный напор в
конце быстротока, м;
h0 и v0 - соответственно глубина и средняя скорость течения в конце быстротока;
![]() - удельный
расход, м2/сек;
- удельный
расход, м2/сек;
b1 - ширина колодца, м.
г) Глубину h"c взаимную с глубиной в сжатом сечении, определяют по формуле
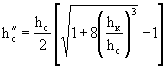 ,
(3-13)
,
(3-13)
Глубину в сжатом сечении hс и сопряженную с ней глубину h"c можно находить по графику (см. п. 5-17 б).
3-13. В случае образования гидравлического прыжка перед сужением продольный профиль потока строят в следующей последовательности (рис. 3-13).
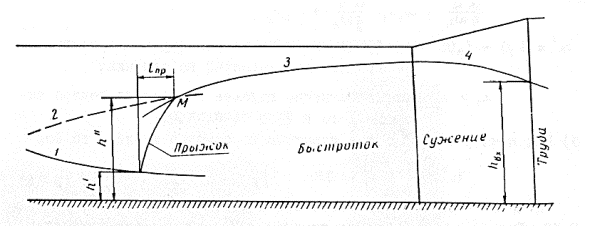
Рис. 3-13. К определению места и размеров прыжка перед сужением: 1 - кривая спада в быстротоке; 2 - кривая глубин, сопряженных с глубинами бурного потока; 3 - кривая подпора перед сужением; 4 - кривая свободной поверхности в сужении
а) Определяют глубину во входном отверстии трубы hвх.
б) Вверх от входного отверстия трубы до начала сужения строят кривую свободной поверхности 4, как в непризматическом русле (например, методом Чарномского).
б) Вверх от начала сужения наносят кривую свободной поверхности спокойного потока 3, как в призматическом русле.
г) Вниз от начала быстротока накладывают кривую спада 1, как в призматическом русле.
д) Рассчитывают кривую глубин, взаимных с глубинами бурного потока 2, на участке спада. В точке пересечения этой кривой с кривой свободной поверхности спокойного потока, проведенной вверх от сужения, будет конец прыжка.
3-14. Рассчитывать кривые свободной поверхности в призматическом русле рекомендуется способом Н.Н.Павловского [3, гл. VI] .
3-15. Построение кривой свободной поверхности в призматическом русле можно выполнять методом суммирования по формуле
![]() ,
(3-14)
,
(3-14)
где
S - расстояние между двумя сечениями;
![]() - динамическая высота
в сечении;
- динамическая высота
в сечении;
![]() - уклон трения
при глубине h и скорости v;
- уклон трения
при глубине h и скорости v;
![]() - средний уклон
трения на участка между сечениями;
- средний уклон
трения на участка между сечениями;
индекс n обозначает выше лежащее, а n+1 - ниже лежащее сечение.
Ожидаемый интервал глубин на участке построения кривой свободной поверхности разбивают на 5-10 интервалов. Построение выполняют от сечения к сечению.
3-16. Сопряженные глубины гидравлического прыжка при числе Фруда для бурного потока ≥ 3 определяют следующим образом:
а) При любой форме поперечного, сечения из уравнения прыжковой
![]() ,
(3-15)
,
(3-15)
где a' = 1,0 - 1,05 - коэффициент, учитывающий неравномерность распределения скоростей по сечению;
z1 и z2 - соответственно глубина погружения центра тяжести 1-го и 2-го сечения, м.
б) При прямоугольной форме поперечного сечения русла - по формуле
![]() ,
(3-16)
,
(3-16)
где h' и h" - глубины соответственно перед и за прыжком.
3-17. При числе Фруда перед, прыжком < 3 прыжок имеет волнистую форму без вальца. В этом случае глубину h", сопряженную с глубиной бурного потока h', определяют по формуле
![]() ,
(3-17)
,
(3-17)
3-18. Длину гидравлического прыжка определяют по формуле О.М. Айвазяна
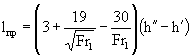 .
(3-18)
.
(3-18)
При Fr1≥3 можно также пользоваться формулой К.Д. Чертоусова
![]() (3-19)
(3-19)
или формулой Н.Н. Павловского
![]() .
(3-20)
.
(3-20)
При Fr < 3 длину волнистого прыжка определяют также по формуле Г.Т.Дмитриева
![]() .
(3-21)
.
(3-21)
4 . СОБСТВЕННО ТРУБА
4-1. При укладке звеньев труб горизонтально падение местности преодолевают за счет вертикальных уступов (ступеней) на стыках (рис. 4-1). Ступени гидравлически действуют как повышенная шероховатость.
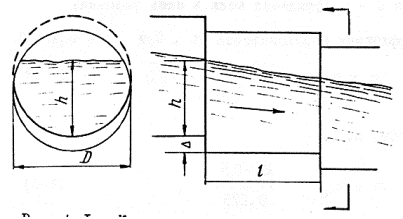
Рис. 4-1. Круглая труба со ступенями
Иногда для уменьшения скорости течения на больших уклонах повышенную шероховатость устраивают также в виде поперечных ребер (рис. 4-2).
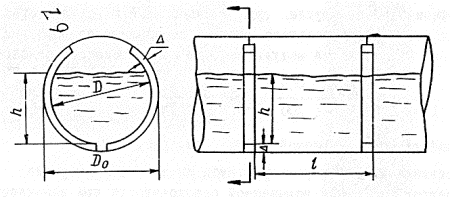
Рис. 4-2. Круглая труба с поперечными ребрами
4-2. Повышенную шероховатость практически необходимо
учитывать при относительном шаге шероховатости ![]() до 25. Здесь l -
расстояние между ступенями или ребрами; D - их высота. При l >
25 влиянием повышенной шероховатости можно пренебречь. В любом случае
коэффициент Шези С в трубе с повышенной шероховатостью не может быть больше,
чем без повышенной шероховатости.
до 25. Здесь l -
расстояние между ступенями или ребрами; D - их высота. При l >
25 влиянием повышенной шероховатости можно пренебречь. В любом случае
коэффициент Шези С в трубе с повышенной шероховатостью не может быть больше,
чем без повышенной шероховатости.
4-3. Коэффициент Шези прямоугольных труб при ступенчатом продольном профиле дна вычисляют по формуле
![]() м0,5/сек (4-1)
м0,5/сек (4-1)
При горизонтальных звеньях ![]() и
и
![]() .
(4-2)
.
(4-2)
4-4. Коэффициент Шези круглых труб при ступенчатой укладке звеньев определяют следующим методом.
а) Находят безразмерный модуль расхода при заполнении трубы наполовину
![]() ,
(4-3)
,
(4-3)
где
- безразмерный модуль расхода трубы бее повышенной шероховатости, заполненной наполовину, а С - коэффициент Шези в этих условиях.
б) Вычисляют коэффициент шероховатости n. При h ≥ 0,225D
![]() ,
(4-5)
,
(4-5)
где D - диаметр трубы, м.
При h < 0,225
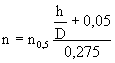 ,
(4-6)
,
(4-6)
где D - по формуле (4-5).
в) Находят коэффициент Шези по формуле
Здесь гидравлический радиус R живого сечения берется при данной глубине воды.
4-5. Коэффициент Шези круглых труб с повышенной шероховатостью в виде поперечных ребер прямоугольного сечения определят по формулам.
а) Вычисляют безразмерный модуль расхода при заполнении наполовину
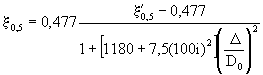 , (4-8)
, (4-8)
где D0 - полный диаметр ребристой трубы (см. рис. 4-2);
![]() - безразмерный
модуль расхода трубы из того же материала диаметром D0 без
повышенной шероховатости при заполнении на половину высоты, определяемый по
формуле (4-4);
- безразмерный
модуль расхода трубы из того же материала диаметром D0 без
повышенной шероховатости при заполнении на половину высоты, определяемый по
формуле (4-4);
б) Если l = (0,8 + 1,2)D0, находят максимальный для данных ребер коэффициент шероховатости
и вычисляют соответствующий коэффициент Шези
Здесь гидравлический радиус R живого сечения потока берут в створе ребра, где диаметр в свету D = D0 - 2D.
В случае заполнения трубы h < 0,225 D, вместо формулы (4-9) следует пользоваться формулой
Таблица 4-1
|
X |
0,00 |
0,02 |
0,04 |
0,06 |
0,08 |
|
0,1 |
0,215 |
0,243 |
0,270 |
0,295 |
0,318 |
|
0,2 |
0,342 |
0,364 |
0,386 |
0,407 |
0,428 |
|
0,3 |
0,448 |
0,468 |
0,487 |
0,506 |
0,524 |
|
0.4 |
0,543 |
0,561 |
0,578 |
0,596 |
0,613 |
|
0,5 |
0,630 |
0,647 |
0,663 |
0,679 |
0,695 |
|
0,6 |
0,711 |
0,727 |
0,743 |
0,758 |
0,773 |
|
0,7 |
0,788 |
0,811 |
0,822 |
0,833 |
0,847 |
|
0,8 |
0,862 |
0,876 |
0,890 |
0,904 |
0,918 |
|
0,9 |
0,932 |
0,946 |
0,960 |
0,973 |
0,987 |
|
1,0 |
1,000 |
1,013 |
1,027 |
1,039 |
1,053 |
|
1,1 |
1,065 |
1,078 |
1,091 |
1,104 |
1,116 |
|
1,2 |
1,129 |
1,142 |
1,154 |
1,166 |
1,179 |
|
1.3 |
1,191 |
1,203 |
1,215 |
1,227 |
1,239 |
|
1,4 |
1,251 |
1,263 |
1,275 |
1,287 |
1,299 |
|
1,5 |
1,310 |
1,322 |
1,334 |
1,345 |
1,356 |
|
1,6 |
1,368 |
1,379 |
1,390 |
1,402 |
1,413 |
|
1,7 |
1,424 |
1,435 |
1,446 |
1,457 |
1,468 |
|
1,8 |
1,480 |
1,491 |
1,501 |
1,512 |
1,524 |
|
1,9 |
1,534 |
1,545 |
1,556 |
1,567 |
1,577 |
|
2,0 |
1,587 |
1,598 |
1,608 |
1,618 |
1,629 |
|
2.1 |
1,639 |
1,650 |
1,660 |
1,671 |
1,681 |
|
2,2 |
1,691 |
1,702 |
1,712 |
1,722 |
1,732 |
|
2,3 |
1,742 |
1,752 |
1,762 |
1,772 |
1,782 |
|
2,4 |
1,792 |
1,802 |
1,812 |
1,822 |
1,832 |
|
2,5 |
1,842 |
1,852 |
1,862 |
1,872 |
1,881 |
Продолжение таблицы 4-1
|
X |
0,00 |
0,02 |
0,04 |
0,06 |
0,08 |
|
2,6 |
1,891 |
1,901 |
1,910 |
1,920 |
1,930 |
|
2,7 |
1,939 |
1,949 |
1,559 |
1,968 |
1,977 |
|
2,8 |
1,987 |
1,996 |
2,005 |
2,014 |
2,024 |
|
2,9 |
2,034 |
2,043 |
2,053 |
2,062 |
2,071 |
|
3,0 |
2,080 |
2,089 |
2,098 |
2,107 |
2,116 |
|
3,1 |
2,126 |
2,135 |
2,145 |
2,153 |
2,163 |
|
3,2 |
2,172 |
2,181 |
2,190 |
2,199 |
2,208 |
|
3,3 |
2,217 |
2,226 |
2,235 |
2,244 |
2,253 |
|
3,4 |
2,261 |
2,270 |
2,279 |
2,287 |
2,296 |
|
3,5 |
2,305 |
2,314 |
2,323 |
2,332 |
2,341 |
|
3,6 |
2,349 |
2,358 |
2,367 |
2,376 |
2,384 |
|
3,7 |
2,393 |
2,401 |
2,409 |
2,418 |
2,426 |
|
3,8 |
2,435 |
2,443 |
2,452 |
2,460 |
2,469 |
|
3,9 |
2,477 |
2,486 |
2,494 |
2,503 |
2,511 |
|
4,0 |
2,519 |
2,527 |
2,535 |
2,544 |
2,552 |
|
4,1 |
2,561 |
2,569 |
2,578 |
2,586 |
2,595 |
|
4,2 |
2,603 |
2,612 |
2,620 |
2,628 |
2,636 |
|
4,3 |
2,645 |
2,653 |
2,661 |
2,670 |
2,678 |
|
4,4 |
2,686 |
2,694 |
2,702 |
2,710 |
2,718 |
|
4,5 |
2,726 |
2,734 |
2,742 |
2,750 |
2,758 |
|
4,6 |
2,766 |
2,774 |
2,782 |
2,790 |
2,798 |
|
4,7 |
2,806 |
2,814 |
2,822 |
2,830 |
2,838 |
|
4,8 |
2,846 |
2,854 |
2,862 |
2,870 |
2,878 |
|
4,9 |
2,886 |
2,894 |
2,900 |
2,909 |
2,917 |
|
5,0 |
2,924 |
2,932 |
2,940 |
2,948 |
2,956 |
Таблица 4-2
|
X |
ех |
е-х |
X2/3 |
ех |
е-х |
|
0,00 |
1,000 |
1,000 |
0,50 |
1,649 |
0,6065 |
|
0,02 |
1,020 |
0,9802 |
0{52 |
1,682 |
0,5945 |
|
0,04 |
1,041 |
0,9608 |
0,54 |
1,716 |
0,5827 |
|
0,06 |
1,062 |
0,9418 |
0,56 |
1,751 |
0,5712 |
|
0,08 |
1,083 |
0,9231 |
0,58 |
1,786 |
0,5599 |
|
0,10 |
1,105 |
0,9048 |
0,60 |
1,822 |
0,5488 |
|
0,12 |
1,128 |
0,8869 |
0,62 |
1,859 |
0,5379 |
|
0,14 |
1,150 |
0,8694 |
0,64 |
1,897 |
0,5273 |
|
0,16 |
1,174 |
0,8521 |
0,66 |
1,935 |
0,5169 |
|
0,18 |
1,197 |
0,8353 |
0,68 |
1,974 |
0,5066 |
|
0,20 |
1,221 |
0,8187 |
0,70 |
2,014 |
0,4966 |
|
0,22 |
1,246 |
0,8025 |
0,72 |
2,054 |
0,4868 |
|
0,24 |
1,271 |
0,7866 |
0,74 |
2,096 |
0,4771 |
|
0,26 |
1,297 |
0,7711 |
0,76 |
2,138 |
0,4677 |
|
0,28 |
1,323 |
0,7558 |
0,78 |
2,182 |
0,4584 |
|
0,30 |
1,350 |
0,7408 |
0,80 |
2,226 |
0,4493 |
|
0,32 |
1,377 |
0,7261 |
0,82 |
2,271 |
0,4404 |
|
0,34 |
1,405 |
0,7118 |
0,84 |
2,316 |
0,4317 |
|
0,36 |
1,433 |
0,6977 |
0,86 |
2,363 |
0,4232 |
|
0,38 |
1,462 |
0,6839 |
0,88 |
2,411 |
0,4148 |
|
0,40 |
1,492 |
0,6703 |
0,90 |
2,460 |
0,4066 |
|
0,42 |
1,522 |
0,6570 |
0,92 |
2,509 |
0,3985 |
|
0,44 |
1,553 |
0,6440 |
0,94 |
2,560 |
0,3906 |
|
0,46 |
1,584 |
0,6313 |
0,96 |
2,612 |
0,3829 |
|
0,48 |
1,616 |
0,6188 |
0,98 |
2,665 |
0,3753 |
Продолжение таблицы 4-2
|
X |
ех |
е-х |
X |
ех |
е-х |
|
1,00 |
2,718 |
0,8679 |
1,50 |
4,482 |
0,2231 |
|
1,02 |
2,773 |
0,3606 |
1,52 |
4,572 |
0,2187 |
|
1,04 |
2,829 |
0,3535 |
1,54 |
4,665 |
0,2144 |
|
1,06 |
2,886 |
0,3465 |
1,56 |
4,759 |
0,2101 |
|
1,08 |
2,945 |
0,3396 |
1,58 |
4,855 |
0,2060 |
|
1,10 |
3,004 |
0,3329 |
1,60 |
4,953 |
0,2019 |
|
1,12 |
3,065 |
0,3263 |
1,62 |
5,053 |
0,1979 |
|
1,14 |
3,127 |
0,3198 |
1,64 |
5,155 |
0,1940 |
|
1,16 |
3,190 |
0,3135 |
1,66 |
5,259 |
0,1901 |
|
1,18 |
3,254 |
0,3073 |
1,68 |
5,366 |
0,1864 |
|
1,20 |
3,320 |
0,3012 |
1,70 |
5,474 |
0,1827 |
|
1,22 |
3,387 |
0,2952 |
1,72 |
5,585 |
0,1791 |
|
1,24 |
3,456 |
0,2894 |
1,74 |
5,697 |
0,1755 |
|
1,26 |
3,525 |
0,2837 |
1,76 |
5,812 |
0,1720 |
|
1,28 |
3,597 |
0,2780 |
1,78 |
5,930 |
0,1686 |
|
1,30 |
3,669 |
0,2725 |
1,80 |
6,050 |
0,1653 |
|
1,32 |
3,743 |
0,2671 |
1,82 |
6,172 |
0,1620 |
|
1,34 |
3,819 |
0,2618 |
1,84 |
6,297 |
0,1588 |
|
1,36 |
3,896 |
0,2567 |
1,86 |
6,424 |
0,1557 |
|
1,38 |
3,975 |
0,2516 |
1,88 |
6,554 |
0,1526 |
|
1,40 |
4,055 |
0,2466 |
1,90 |
6,686 |
0,1496 |
|
1,42 |
4,137 |
0,2417 |
1,92 |
6,821 |
0,1466 |
|
1,44 |
4,2Л |
0,2369 |
1,94 |
6,959 |
0,1437 |
|
1,46 |
4,306 |
0,2322 |
1,96 |
7,099 |
0,1409 |
|
1,48 |
4,393 |
0,2276 |
1,98 |
7,243 |
0,1381 |
Продолжение таблицы 4-2
|
X |
ех |
е-х |
X |
ех |
е-х |
|
2,00 |
7,389 |
0,1353 |
2,50 |
12,182 |
0,08208 |
|
2,02 |
7,538 |
0,1327 |
2,52 |
12,429 |
0,08046 |
|
2,04 |
7,691 |
0,1300 |
2,54 |
12,680 |
0,07887 |
|
2,06 |
7,846 |
0,1275 |
2,56 |
12,936 |
0,07730 |
|
2,08 |
8,005 |
0,1249 |
2,58 |
13,197 |
0,07577 |
|
2,10 |
8,166 |
0,1225 |
2,60 |
13,464 |
0,07427 |
|
2,12 |
8,331 |
0,1200 |
2,62 |
13,736 |
0,07280 |
|
2,14 |
8,499 |
0,1177 |
2,64 |
14,013 |
0,07136 |
|
2,16 |
8,671 |
0,1153 |
2,66 |
14,296 |
0,06995 |
|
2,18 |
8,846 |
0,1130 |
2,68 |
14,585 |
0,06856 |
|
2,20 |
9,025 |
0,1108 |
2,70 |
14,880 |
0,06721 |
|
2,22 |
9,207 |
0,1086 |
2,72 |
15,180 |
0,06587 |
|
2,24 |
9,393 |
0,1065 |
2,74 |
15,487 |
0,06457 |
|
2,26 |
9,583 |
0,1044 |
2,76 |
15,800 |
0,06329 |
|
2,28 |
9,777 |
0,1023 |
2,78 |
16,119 |
0,06204 |
|
2,30 |
9,974 |
0,1003 |
2,80 |
16,445 |
0,06081 |
|
2,32 |
10,176 |
0,09827 |
2,82 |
16,777 |
0,05961 |
|
2,34 |
10,381 |
0,09633 |
2,84 |
17,116 |
0,05843 |
|
2,36 |
10,591 |
0,09442 |
2,86 |
17,462 |
0,05727 |
|
2,38 |
10,805 |
0,09255 |
2,88 |
17,814 |
0,05613 |
|
2,40 |
II,023 |
0,09072 |
2,90 |
18,174 |
0,05502 |
|
2,42 |
11,246 |
0,08892 |
2,92 |
18,541 |
0,05393 |
|
2,44 |
11,473 |
0,08716 |
2,94 |
18,916 |
0,05287 |
|
2,46 |
11,705 |
0,08543 |
2,96 |
19,298 |
0,05182 |
|
2,48 |
11,941 |
0,08374 |
2,98 |
19,688 |
0,05079 |
Продолжение таблицы 4-2
|
X |
ех |
е-х |
X |
ех |
е-х |
|
3,00 |
20,086 |
0,04979 |
3,50 |
33,115 |
0,03020 |
|
3,02 |
20,491 |
0,04880 |
3,52 |
33,784 |
0,02960 |
|
3,04 |
20,905 |
0,04783 |
3,54 |
34,467 |
0,02901 |
|
3,06 |
21,328 |
0,04689 |
3,56 |
35,163 |
0,02844 |
|
3,08 |
21,758 |
0,04596 |
3,58 |
35,874 |
0,02788 |
|
3,10 |
22,198 |
0,04505 |
3,60 |
36,598 |
0,02732 |
|
3,12 |
22,646 |
0,04416 |
3,62 |
37,338 |
0,02678 |
|
3,14 |
23,104 |
0,04328 |
3,64 |
38,092 |
0,02625 |
|
3,16 |
23,571 |
0,04243 |
3,66 |
38,861 |
0,02573 |
|
3,18 |
24,047 |
0,04159 |
3,68 |
39,646 |
0,02522 |
|
3,20 |
24,533 |
0,04076 |
3,70 |
40,447 |
0,02472 |
|
3,22 |
25,028 |
0,03996 |
3,72 |
41,264 |
0,02423 |
|
3,24 |
25,534 |
0,03916 |
3,74 |
42,098 |
0,02375 |
|
3,26 |
26,050 |
0,03839 |
3,76 |
42,948 |
0,02328 |
|
3,28 |
26,576 |
0,03763 |
3,78 |
43,816 |
0,02282 |
|
3,30 |
27,113 |
0,03688 |
3,80 |
44,701 |
0,02237 |
|
3,32 |
27,660 |
0,03615 |
3,82 |
45,604 |
0,02193 |
|
3,34 |
28,219 |
0,03544 |
3,84 |
46,525 |
0,02149 |
|
3,36 |
28,789 |
0,03474 |
3,86 |
47,465 |
0,02107 |
|
3,38 |
29,371 |
0,03405 |
3,88 |
48,424 |
0,02065 |
|
3,40 |
29,964 |
0,03337 |
3,90 |
49,402 |
0,02024 |
|
3,42 |
30,569 |
0,03271 |
3,92 |
50,400 |
0,01984 |
|
3,44 |
31,187 |
0,03206 |
3,94 |
51,419 |
0,01945 |
|
3,46 |
31,817 |
0,03143 |
3,96 |
52,457 |
0,01906 |
|
3,48 |
32,460 |
0,03081 |
3,98 |
53,517 |
0,01869 |
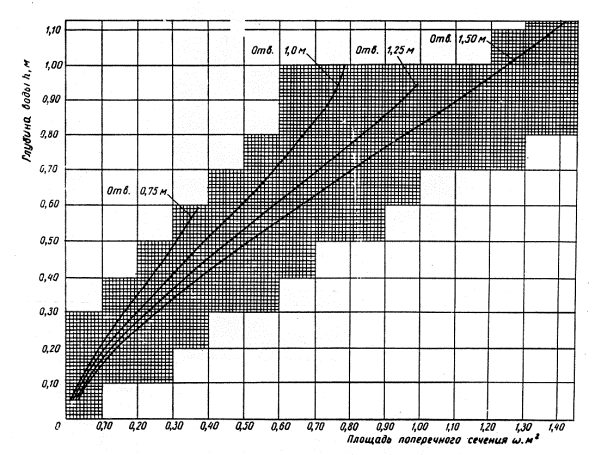
Рис. 4-3. График для определения площади поперечного сечения потока в круглой трубе
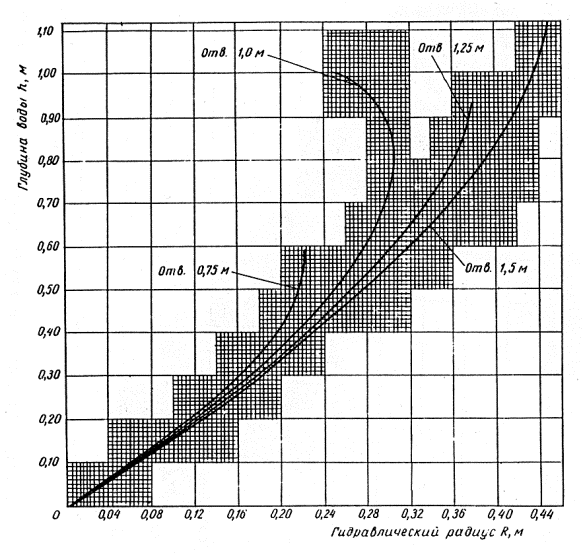
Рис. 4-4. График для определения гидравлического радиуса в круглой трубе
Рис. 4-5. График для определения критической
глубины hк в круглой трубе. График составлен по формуле ![]()
в) Если ![]() менее 0,8 или более
1,2, то вычисляют величину
менее 0,8 или более
1,2, то вычисляют величину
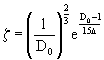 , (4-12)
, (4-12)
где е = 2,718 - основание натуральных логарифмов.
Для ускорения расчетов можно пользоваться табл. 4-1, 4-2. Далее искомый коэффициент шероховатости n находят по формуле
![]() , (4-13)
, (4-13)
где ![]() - коэффициент
шероховатости трубы диаметром D = D0–2D из того же материала, но
без повышенной шероховатости;
- коэффициент
шероховатости трубы диаметром D = D0–2D из того же материала, но
без повышенной шероховатости;
См - коэффициент Шези, вычисленный по Маннингу для тех же условий;
nм - коэффициент шероховатости материала трубы по Маннингу;
n2 - коэффициент шероховатости к формуле (4-7), вычисленный при l=D0 по формуле (4-9) или (4-11).
Остальные расчеты выполняют как обычно, но коэффициент Шези находят по формуле
![]() . (4-14)
. (4-14)
4-6. Для ускорения вычислений гидравлических характеристик потока в круглой трубе можно пользоваться графиками (рис. 4-3, 4-4 и 4-5).
5. ГАСИТЕЛИ ЭНЕРГИИ
5-1. На выходе из косогорной трубы для предотвращения размыва отводного русла, как правило, устраивают гасители энергии. Отводное русло на некоторой длине закрепляют материалом, выдерживающим скорость, с которой поток выходит из гасителя.
При прочных грунтах отводного русла вместо гасителя может быть устроен обычный оголовок. В любом случае расчетом должны быть обоснованы размеры укрепления отводного русла, то есть его плановое очертание, длина и глубина концевого устройства - зуба или погребенного откоса.
5-2. Глубину и скорость потока перед гасителем (то есть на выходе из трубы) определяют при расчете собственно трубы. При постоянном уклоне глубину и скорость на выходе можно приближенно вычислить из формулы Шези (2-1) для труб с повышенной шероховатостью (ступени по дну или поперечные ребра) при длине трубы свыше 20 м, для труб с нормальной шероховатостью при длине свыше 30 м.
При наличии в трубе участков различного уклона глубина и скорость на выходе получают в результате расчета неравномерного движения, который выполняют так же, как и для быстротоков.
5-3. В качестве гасителей энергии можно применять гаситель ЦНИИС или расширяющийся водобойный колодец (рис. 5-1 и 5-3).
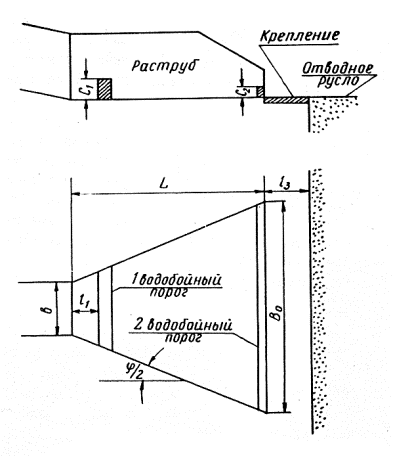
Рис. 5-1. Схема гасителя ЦНИИС
5-4. Гаситель ЦНИИС представляет собой раструб, боковые отвесные стенки которого образуют в плане с осью сооружения угол a0= 30°. Между этими стенками перпендикулярно оси сооружения устанавливают два водобойные порога: первый, высотой с1 - на относительно небольшой расстоянии l1 от начала раструба, второй, высотой с2 - на выходе из раструба. Со стороны набегающего потока водобойные пороги делают вертикальными. С низовой стороны их очертание назначают по конструктивным соображениям.
Принцип действия гасителя ЦНИИС следующий (рис. 5-2). Вытекающий из трубы бурный поток ударяется в первый водобойный порог, отклоняется вверх и, описав в воздухе кривую, близкую к параболе, падает на дно гасителя. Линия падения струй в плане дугообразная, выпуклостью вниз. Далее поток ударяется во второй водобойный порог, после чего почти ровным слоем вода изливается в отводное русло. В результате действия на поток сил реакции двух порогов и дна гасителя поток теряет значительную долю своей живой силы, его размывающая способность резко снижается. Перед первым порогом образуется поверхностный валец, который также рассеивает энергию. Лабораторные опыты показывают, что гаситель ЦНИИС гидравлически значительно эффективнее расширяющегося водобойного колодца.
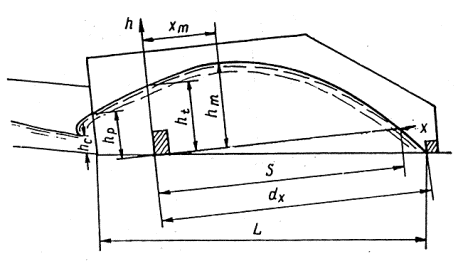
Рис.5-2. Элементы потока в гасителе ЦНИИС
5-5. Расширяющийся водобойный колодец (рис. 5-3) представляет собой раструб, образованный отвесными стенками, расходящимися в плане на угол a0 = 15-20° к оси сооружения. В конце раструба устанавливается водобойная стенка. Принцип действия гасителя этого типа состоит в том, что перед водобойной стенкой размещается затопленный подпертый гидравлический прыжок.
5-6. Гаситель ЦНИИС рекомендуется располагать на площадке с уклоном не более 0,2.
5-7. При уклоне дна гасителя до 0,05 расчет гасителя ЦНИИС выполняют в следующем порядке (см. рис. 5-2).
а) На основании расчета собственно трубы принимается глубина в начале раструба (сжатая глубина бурного потока) hс. Приближенно за эту величину можно принимать глубину равномерного движения в трубе. При сравнительно малой длине трубы неравномерного движения (кривой спада).
б) Высоту первого водобойного порога принимают в пределах
![]() . (5-1)
. (5-1)
После этого определяют глубину воды в начале раструба по формуле (4-10) или (4-11) и проверяют соблюдение в выходном участке трубы необходимого просвета над потоком. Дня этого вверх от начала раструба строят кривую подпора. Если просвет окажется недостаточным, то на соответствующей длине применяют повышенные звенья или уменьшают высоту первого водобойного порога с1.
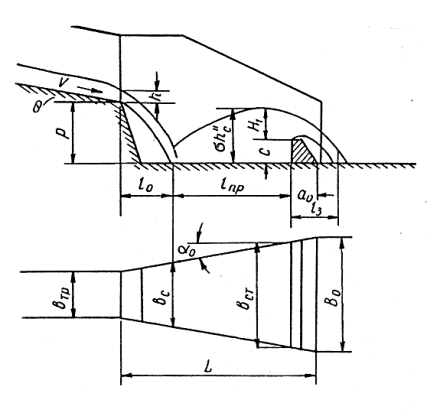
Рис. 5-3. Расширяющийся водобойный колодец
Первый водобойный порог устанавливают на расстоянии
![]() . (5-2)
. (5-2)
в) Длину всего раструба определяют как сумму расстояния до первого порога l1, и дальности падения струй S, то есть
![]() ,
(5-3)
,
(5-3)
 , (5-4)
, (5-4)
Где  .
.
Ширина раструба в конце
![]() (5-5)
(5-5)
или приближенно
![]() .
(5-6)
.
(5-6)
г) Высоту второго водобойного порога принимают в пределах
5-8. Продольный профиль потока в гасителе строят в следующем порядке.
а) Глубину потока ht в плоскости напорной грани первого водобойного порога определяют по формулам:
при ![]()
 ; (5-8)
; (5-8)
при ![]()
 . (5-9)
. (5-9)
б) Глубину воды hp в начале раструба устанавливают по формулам:
при ![]()
![]() ; (5-10)
; (5-10)
при ![]()
в) Определяют наибольшую высоту подъема струй в раструбе
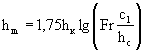 . (5-12)
. (5-12)
г) Находят горизонтальное расстояние до места наибольшего подъема струй
![]() ;
; ![]() ;
; ![]() . (5-13)
. (5-13)
д) Поверхность потока в осевой вертикальной плоскости описывается уравнением
![]() , (5-14)
, (5-14)
где ![]() ;
; ![]() ,
,
hх - высота поверхности потока на расстоянии от напорной грани первого водобойного порога, отсчитываемая от основания его напорной грани.
5-9. При необходимости допустимо придавать гасителю ЦНИИС уклон до 0,20. При этой расчет всех элементов, кроме длины и ширины раструба, выполняют так же, как при уклоне до 0,05.
Длину раструба при уклоне более 0,05 определяют по формуле
![]() ,
(5-15)
,
(5-15)
где dx - дальность падения струй по горизонтали, определяемая по формуле
![]() . (5-16)
. (5-16)
Величины А, Е и ht находят согласно п. 5-8.
5-10. При круговом сечении труб живое сечение потока на выходе принимает форму сегмента высотой h0 и площадью w0 . Высоту сегмента определяют при расчете собственно трубы.
Для расчета гасителя фактическое сегментальное сечение потока заменяют равновеликим по площади w0 прямоугольным сечением той же глубины hс и шириной
![]() .
(5-17)
.
(5-17)
5-11. Если в проекте желательно использовать элементы гасителей, рассчитанных для прямоугольных труб, то допустимо ширину динамически эквивалентных прямоугольников принимать следующим образом:
а) для труб диаметром D ≥ 2 м
b0= D–0,5 м; (5-18)
б) для труб диаметром D ≤ 1,5 м
b0= D–0,25 м; (5-19)
Тогда в качестве расчетной глубины бурного потока в эквивалентном прямоугольном сечении принимают
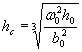 .
(5-20)
.
(5-20)
При этом эквивалентный поток прямоугольного сечения
характеризуется тем же числом Фруда ![]() , что и фактический поток сегментального сечения.
, что и фактический поток сегментального сечения.
5-12. При конструировании гасителей для круглых труб ширину раструба в начале принимает равной диаметру трубы. При этом ширина раструба в конце может быть оставлена той, как она получена по расчету. Тогда угол между открылками в плане несколько уменьшится. По конструктивным соображениям можно увеличить ширину раструба в конце на D–b0; тогда полный угол раструбности останется равным 60°.
5-13. Очертание боковых стен раструба гасителя ЦНИИС устанавливают из следующих соображений.
а) Ниже напорной грани первого водобойного порога толщину боковых стен можно принимать по конструктивным соображениям.
б) Высоту боковых стен перед водобойным порогом назначают в соответствии с п. 5-8 без каких-либо запасов. Необходимый запас обеспечивают сами расчетные формулы.
в) При угле раструбности гасителя j=60° очертание боковых струй в проекции на вертикальную плоскость, проходящую по оси сооружения, определяют по формуле
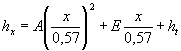 (5-21)
(5-21)
или
![]() .
.
г) Очертание боковых струй в плоскости стен, ограничивающих раструб, определяют по выражению
![]() (5-22)
(5-22)
или при j = 60°
![]() ,
(5-23)
,
(5-23)
где х - горизонтальное расстояние по оси сооружения от нижней точки напорной грани первого водобойного порога.
д) Очертание боковых стен принимают таким, чтобы они имели минимальную площадь. Отрезки, образующие профиль стен, должны касаться поверхности боковых струй (рис. 5-4).
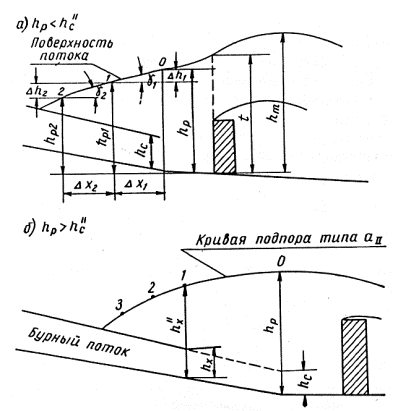
Рис.5-4. Гидравлический прыжок перед гасителем ЦНИИС
5-14. При невозможности разместить в пределах ширины лога нормальный гаситель ЦНИИС с углом раструбности j=60° возможно следующее решение. Раструбу в плане придается меньший угол между боковыми стенами в пределах 30-60°. Боковые стены делают в плане прямолинейными. Высоту и положение водобойных порогов определяют так же, как и при нормальном угле раструбности j=60°. Траектории крайних струй в проекции на плоскость симметрии сооружения строят по формуле
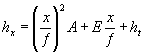 ,
(5-24)
,
(5-24)
где
![]() .
(5-25)
.
(5-25)
Величины А, Е и ht те же, что и при нормальном угле раструбности j=60° (п. 5-13).
Траекторию крайних струй в плоскости самих боковых стен строят по формуле
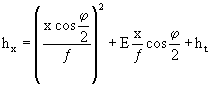 . (5-26)
. (5-26)
5-15. Гаситель ЦНИИСа вызывает некоторый подпор на выходном участке трубы. При этом возможны две схемы сопряжения:
1) hp<h"c то есть глубина в начале раструба hp, определяемая по формуле (5-11), меньше глубины h"c, сопряженной со сжатой в конце трубы (см. рис. 5-4, а);
2) hp>hc (см. рис. 5-4, б).
В схеме 1 (обычный случай) перед гасителем возникает несовершенный гидравлический прыжок, В схеме 2 между прыжком и гасителем устанавливается кривая подпора типа аII. В обоих случаях пропускная способность трубы сохраняется.
5-16. Если на выходном участке трубы необходимо строго выполнить требования § 29 СН 200-62 о просвете над поверхностью воды, то следует произвести следующий анализ.
а) Предполагая свободное истечение вычислить глубину h"c, сопряженную с глубиной в конце трубы hс, сравнить ее с глубиной в начале раструба hp при наличии гасителя и установить, происходит ли сопряжение по схемам 1 или 2 (п. 5-15).
б) При схеме 1 (п. 5-15) определяют уклон свободной поверхности потока на участке непосредственно выше раструба
![]() (5-27)
(5-27)
От точки 0 (см. рис. 5-4 а), лежащей на поверхности в начале раструба, откладывают в сторону трубы первый отрезок 0-1 с уклоном j=tgg1. Длина отрезка 0-1 должна быть небольшой, порядка 1 м;
Определяют глубину воды h'p, в конце отрезка 0-1 (в точке 1). По формуле (5-27) определяет уклон j2= tgg2 поверхности потока на следующей вышележащей участке, и к точке 1 пристраивают следующий вышележащий отрезок 1-2 и т.д.
Это построение выполняют на длине, достаточной для назначения схемы выходных устройств, обеспечивающих необходимый просвет над потоком.
в) При схеме 2 (hp>h"c), вверх от начала раструба любым способом строят кривую подпора типа аII (см. рис. 5-4 б) до того сечения, где глубина спокойного потока будет равна h"х, то есть глубине, сопряженной с глубиной hх бурного потока. Выше этого сечения располагается гидравлический прыжок. Его продольный профиль строят так же, как изложено в п. 5-16 б, но за исходную глубину в конце прыжка принимают h"х.
г) После того, как продольный профиль потока построен, можно назначить схему выходного участка трубы: применить повышенные звенья, предусмотреть перед гасителем открытую вставку, устроить уступ увеличенной высоты и т.д. (см. пример расчета гасителя ЦНИИС).
5-17. Гидравлический расчет расширяющегося водобойного колодца выполняют в следующем порядке.
а) При наличии стенки падения определяют дальность падения струи по формуле
![]() , (5-28)
, (5-28)
где ![]() , м;
, м;
h - высота стенки падения, м;
h и v - соответственно глубина и средняя скорость потока перед стенкой падения;
Q - угол наклона подводящего русла к горизонту. Для ускорения расчета можно пользоваться графиком (рис. 5-5). Пример пользования графиком.
Д а н о: v0 = 5, м/сек; i = 0,20; Q = 4 м3/сек; р = 3 м; подводящее русло прямоугольный быстроток шириной b = 2м; определить дальность падения струи l0.
Р е ш е н и е: вычисляем ![]() ; i = sinQ = 0,20, = откуда Q = 11,5°;cosQ= 0,98; V1 =5´0,2 = 1 м/сек; V2 = 5´0,98 = 4,9 м/сек.
; i = sinQ = 0,20, = откуда Q = 11,5°;cosQ= 0,98; V1 =5´0,2 = 1 м/сек; V2 = 5´0,98 = 4,9 м/сек.
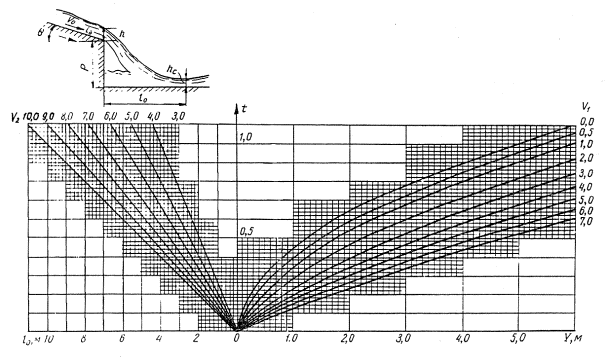
Рис. 5-5. График для определения дальности падения струй
Находим на оси точку у = 3,20, поднимаемся от нее вертикально вверх до кривой V1 = 1 м/сек, движемся по горизонтали влево до кривой V2 = 4,9 м/сек и опускаемся вертикально вниз до оси l0 , где и получаем искомое l0 = 3,4 м. При отсутствии стенки падения, l0 = 0, b2=bmp
б) Подбором из уравнения (5-28) определяют сжатую глубину в месте падения струи
![]() ,
(5-29)
,
(5-29)
где ![]() - полный напор в
конце быстротока, м;
- полный напор в
конце быстротока, м;
![]() - удельный
расход воды в месте падения струи, м2/сек;
- удельный
расход воды в месте падения струи, м2/сек;
bс - ширина колодца в месте падения струи, м.
Для ускорения расчета можно пользоваться графиком (рис. 5-6). На рис. 5-6 обозначено: h0, н v0 соответственно глубина и средняя скорость в быстротоке;
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Пример пользования графиком.
Д а н о: р=1 м; Q = 4,0 м3/сек; b = 2,0 м; v0 = 8,0 м/сек ; h0= 0,125 м.
Определить сжатую глубину и сопряженную с ней.
Р е ш е н и е: Вычисляем Т0 = 1,0+ 0,125 + ![]() = 4,38 м; q =
= 4,38 м; q = ![]() = 2,0 м2/сек;
= 2,0 м2/сек;
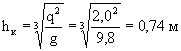 ;
; ![]() .
.
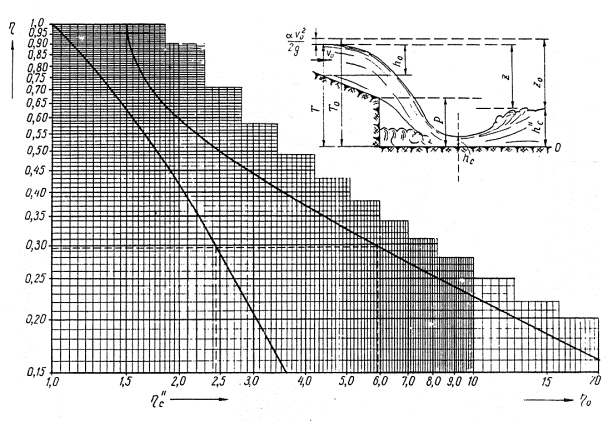
Рис. 5-6. График для определения сжатой глубины и сопряженной с ней в руслах прямоугольного сечения.
По графику находим: hс = 0,296; h" = 2,44. Определяем искомые величины: hc = h"´hk = 0,296´0,74 = 0,22 м; h"c = h"c´hk = 2,44´0,74 = 1,81 м.
При отсутствии стенки падения hc - глубина на выходе из трубы.
в) Определяем глубину h"c, сопряженную со сжатой, а также ширину водобойной стенки bст и длину прыжка lпр подбором по уравнению прыжковой функции для прямоугольного сечения
![]() , (5-30)
, (5-30)
где w1 = bсhс - площадь сжатого сечения, м2
где w2 = bстh"c - то же перед водобойной стенкой, м2.
При этом принимают
bст = bс + 2lпрtga0
Полная длина колодца будет L = l0 + 3,2h"c + a0
где a0 - толщина водобойной стенки понизу, м.
г) Определяют высоту водобойной стенки с учетом удельного расхода в сечении потока у стенки
c = sh"c – H1 (5-31)
где s = 1,05 - коэффициент затопления прыжка в водобойном колодце;
![]() - превышение уровня
воды в колодце над верхом водобойной стенки, м;
- превышение уровня
воды в колодце над верхом водобойной стенки, м;
vст - средняя скорость подхода воды к стенке, м/сек;
sh"c - глубина воды перед стенкой, м;
![]() - удельный
расход потока на стенке, м2/сек;
- удельный
расход потока на стенке, м2/сек;
H0 - полный напор над гребнем незатопленной водобойной стенки, определяемый по формуле
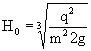 . (5-32)
. (5-32)
Здесь m = 0,42 - коэффициент расхода незатопленной водобойной стенки.
д) Вычисляют сжатую глубину за водобойной стенкой, аналогично п. 5-13 б, но при этом
Т0 = Н0 (п. 5-13 г).
е) Определяют дальность падения струи l3
переливающейся через водобойную стенку аналогично п. 5-15 а, но при этом ![]() .
.
ж) Находят ширину потока у места падения струи, переливающейся через водобойную стенку,
bc = b + 2(L+l3)tga0 (5-33)
з) Определяют скорость в сжатом сечении за водобойной стенкой
![]() . (5-34)
. (5-34)
т) За водобойной стенкой русло укрепляют на ширине b3 и длине l3 (с введением конструктивного запаса) материалом, выдерживающим скорость v3 в сжатом сечении.
Пример расчета гасителя ЦНИИС
Исходные данные. Расход Q = 9,45 м3/сек; уклон трубы и дна водобоя i = 0,15; отверстие трубы b = 1,5 м; глубина бурного потока в начале раструба hc = 0,76 м; труба прямоугольная, образована ступенями из метровых звеньев нормальной высоты - 2 м. Требуется рассчитать гаситель ЦНИИС.
Решение.
Скорость бурного потока в конце трубы
![]() .
.
Число Фруда
![]() .
.
Принимаем высоту первого порога
![]() .
.
Расстояние до первого порога
![]() .
.
Критическая глубина
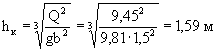 .
.
Дальность падения средней струйки
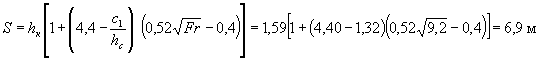 .
.
Высота второго водобойного порога
![]() .
.
Можно принять с2 = 0,20 м, что все же больше, чей меньшее значение по формуле (5-7), равное 0,25 ´ 0,76 м = 0,19 м.
Глубина в начале раструба
![]() .
.
Глубина в плоскости напорной грани первого порога
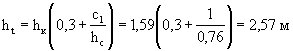 .
.
Наибольшая высота подъема струй
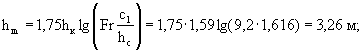
![]()
![]()
![]()
![]() .
.
Положение максимальной высоты средней струйки
![]() .
.
Очертание средней струйки
![]() .
.
Вычисление координат средней струйки приведено в табл. 5-1.
Таблица 5-1
|
x |
х2 |
Ах2 |
Ех |
h |
|
0 |
0 |
0 |
0 |
2,57 |
|
2,17 |
4,7 |
- 0,687 |
1,374 |
3,22 |
|
3 |
9 |
- 1,315 |
1,900 |
3,16 |
|
4 |
16 |
- 2,34 |
2,64 |
2,87 |
|
5 |
25 |
- 3,65 |
3,17 |
2,09 |
|
6,0 |
36 |
- 5,25 |
3,80 |
1,12 |
|
6,9 |
47,6 |
- 6,95 |
4,37 |
0,01 |
|
8,0 |
64 |
- 9,25 |
5,08 |
-1,60 |
Вычисление координат крайних струй в проекции на осевую плоскость приведено в табл. 5-2.
Таблица 5-2
|
x |
х2 |
3,07 Ах2 |
1,75 Ех |
h |
|
0 |
0 |
0 |
0 |
2,57 |
|
1,3 |
1,69 |
-0,76 |
1,44 |
2,25 |
|
2,17 |
4,7 |
-2,11 |
2,40 |
2,86 |
|
3 |
9,0 |
-4,16 |
3,32 |
1,64 |
|
4 |
1616 |
-7,18 |
4,62 |
0 |
|
5 |
25 |
-11,2 |
5,55 |
-3,08 |
По значениям х и h, приведенным в табл. 5-1, 5-2, построены траектории струй до пересечения с плоскостью дна раструба и очертание боковых стен в продольной вертикальной проекции (рис. 5-7) и графически определены плановые размеры раструба с учетом уклона русла.
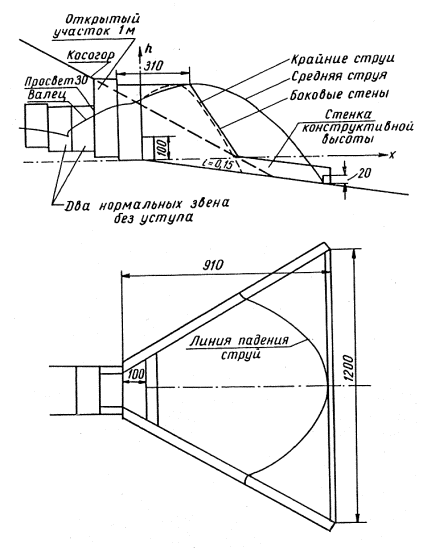
Рис. 5-7. К примеру расчета гасителя ЦНИИС
Глубина в начале раструба hр= 2,47 м, что больше высоты нормального звена. Глубина, сопряженная с глубиной бурного потока в трубе
![]() , что больше, чем hp = 2,47 м.
, что больше, чем hp = 2,47 м.
Следовательно, имеем обычный случай, и гидравлический прыжок располагается в раструбе. Однако, как показывают лабораторные опыты, валец прыжка частично размещается выше раструба и имеет в условиях данного примера обратный уклон свободной поверхности
![]() .
.
Высота поверхности воды в 1 м перед раструбом
![]() .
.
Уклон поверхности следующего вышележащего участка
![]() .
.
Высота поверхности в начале второго участка
![]() .
.
Аналогично находится высота поверхности в 3 м от раструба
![]() .
.
По этим данным на вертикальном разрезе трубы (см. рис. 5-4) наложен продольный профиль вальца. Геометрическим построением устанавливаем, что обеспечить над потоком нормированный просвет не менее 1/6 от 2 м (»30 см) можно, устроив непосредственно выше раструба открытую вставку длиной 1 м и уложив два нормальных звена без уступа между ними. Между последним звеном и открытой вставкой предусмотрен уступ двойной высоты, что позволяет получить в конце последнего звена просвет в 30 см.
6. ОТВОДНЫЕ РУСЛА
6-1. Расчет отводного русла включает определение:
а) средней скорости потока на выходе из гасителя и типа укрепления;
б) гидравлических характеристик потока в отводном русле;
в) размеров укрепления;
г) глубины зуба или погребенного относа в конце укрепления.
6-2. Среднюю скорость потока на выходе из расширяющегося водобойного колодца определяют согласно п. 5-17.
6-3. Среднюю скорость потока на выходе из гасителя ЦНИИС принимают равной
v2=0,45vc, (6-1)
где
vc- скорость бурного потока в начале гасителя, определяемая в соответствии с п. 5-2.
6-4. Гидравлические характеристики (глубину и скорость) потока в отводном русле определяют расчетом неравномерного движения по уравнению Бернулли (метод Чарномского).
6-5. При свободном растекании в нижнем бьефе ширину потока В (рис. 6-1) находят по формулам:
а) при гасителе в виде расширяющегося водобойного колодца
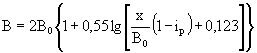 . (6-2)
. (6-2)
б) при гасителе ЦНИИС
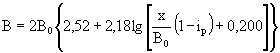 (6-3)
(6-3)
в) при гасителе ЦНШС с уменьшенным углом раструбности ширина потока уменьшается по сравнению с формулой (6-3) на величину 2L(0,577-tga0);
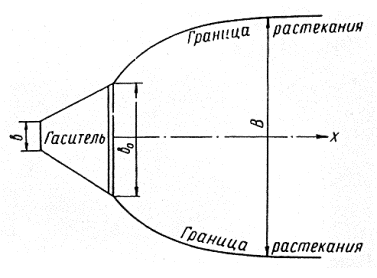
Рис. 6-1. К построению фигуры растекания потока в отводном русле за гасителем потока в отводном русле за гасителем
г) при раструбе, образованном отвесными стенами, расходящимися в плане под углом 15°-20° к оси сооружения, и имеющем дно нормальной (не усиленной) шероховатости, а также при типовом выходном оголовке, принятом в типовых проектах равнинных труб [1] ,
![]() , (6-4)
, (6-4)
где
x2 - расстояние по оси сооружения от конца раструба, м;
ip - уклон русла, по которому растекается поток.
Построение ведется от конца раструба до того cтвора, где крайняя струя пересекается с боковыми стенками русла. Ниже этого створа поток принимается заполняющим русло по всей его ширине.
Рис. 6-2. График для определения глубины, формируемой равномерным спокойным потоком
При уклоне отводного русла 1р £ 0,05 можно принимать lp = 0.
6-6. Глубину ямы местного размыва Т в неукрепленном отводном русле, образуемой потоков, стекающим с укрепления, определяют по формуле
![]() , (6-5)
, (6-5)
где
hрр - глубина, формируемая в данном грунте равномерным спокойным потоком с удельным расходом q = hivi;
hi и vi - средние глубина и скорость потока в конце укрепления;
hб - бытовая глубина нижнего бьефа;
М - коэффициент, зависящий от геометрических форм и условий работы сооружения (п. 6-8);
y - коэффициент, зависящий от устройства в конце укрепления (п. 5-8).
6-7. Глубину, формируемую равномерным спокойным потоком, определяют по формуле Б.И. Студеничникова
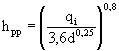 , (6-6)
, (6-6)
где
q - удельный расход потока, м2/сек, в конце укрепления;
d - средний диаметр частиц грунта, м.
Вместо формулы (6-6) можно пользоваться прилагаемым графиком (рис. 6-2).
6-8. Коэффициент М определяют по формуле
![]() , (6-7)
, (6-7)
где
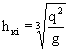 - критическая
глубина в конце укрепления.
- критическая
глубина в конце укрепления.
Значения величины m берут по графику (рис. 6-3).
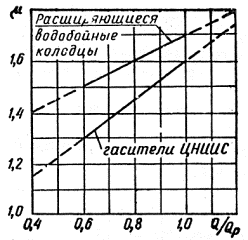
Рис. 6-3. График для определения эмпирической величины m к формуле глубины размыва
Коэффициент y принимается равным 1 при устройстве в конце укрепления отвесного зуба и 1,35 - при устройстве в конце укрепления погребенного откоса 1:1,5.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
a0- толщина водобойной стенки понизу, м;
В - ширина потока поверху, м;
b - ширина потока по дну, м;
bтр - отверстие трубы;
b0 - расчетная ширина, м, динамически эквивалентного прямоугольного сечения;
b1 - ширина водобойного колодца, м;
bс - ширина водобойного колодца в месте падении струи, м;
В0 - ширина выхода из гасителя или оголовка, м;
С - коэффициент Шези, м/сек;
с - высота водобойной стенки, м;
с1 и с2 - высота соответственно 1-го и 2-го водобойных порогов, м;
D - диаметр круглой трубы в свету, м;
D0 = D + 2D - полный диаметр ребристой трубы, м;
d - средний диаметр частиц грунта, м;
dx - дальность падения струй по горизонтали, м;
е = 2,718 - основание натуральных логарифмов;
![]() - динамическая
высота в сечении, м;
- динамическая
высота в сечении, м;
![]() - число Фруда,
характеризующее кинетичность потока;
- число Фруда,
характеризующее кинетичность потока;
Н0 - полный напор над гребнем незатопленной водобойной стенки, м;
Н1 - превышение уровня воды в водобойном колодце над гребнем водобойной стенки, м;
h - глубина воды, м;
hc- глубина воды в сжатой сечении (сжатая глубина), м;
h0- высота м, сегментального сечения потока на выходе из круглой трубы;
h' и h'' -сопряженные (взаимные) глубины при гидравлическом прыжке, м;
hm- наибольшая высота подъема струй в гасителе ЦНИИС, м;
hр - глубина воды в начале раструба гасителя энергии ЦНИИС, м;
ht - глубина воды в плоскости напорной грани 1-го водобойного порога гасителя ЦНИИС, м;
hpp - глубина, формируемая равномерным спокойным потоком, м;
hх - глубина потока в х-ом сечении;
i - уклон сооружения (быстротока, трубы) или русла, равный синусу угла наклона дна к горизонту;
![]() - уклон трения;
- уклон трения;
iƒ,cp - средний уклон трения на n-ом участке потока;
j - уклон поверхности потока перед гасителем ЦНИИС;
К - переходный коэффициент от расчетного расхода к допускаемому;
L - длина гасителя энергии, м;
l - шаг элементов повышенной шероховатости: глина ступеней или расстояние между осями ребер, м;
l0 - дальность падения струй с уступа, м;
l1 - расстояние от начала раструба до 1-го водобойного порога или водобойной стенки, м;
lпр - длина гидравлического прыжка, м;
m - коэффициент расхода при переливе через водобойную стенку;
n - коэффициент шероховатости смоченной поверхности;
h - высота уступа или стенки падения, м;
![]() - полный напор
в конце быстротока, м;
- полный напор
в конце быстротока, м;
Q - расход воды, м3/сек;
Qp- расчетный расход, м3/сек;
Qдоп - допустимый расход сооружения, проходящий с соблюдением нормированного просвета над поверхностью воды, м3/сек;
Qдоп,в - допустимый расход для трубы отверстием в, м3/сек;
q - расход, протекающий через 1 пог. м ширины сооружения (удельный расход), м3/сек;
![]() -
гидравлический радиус поперечного сечения потока, м;
-
гидравлический радиус поперечного сечения потока, м;
S - дальность падения струи в гасителе ЦНИИС от верховой грани 1-го водобойного порога, м;
v0 - средняя скорость течения в конце быстротока, м/сек;
v - средняя скорость течения, м/сек;
х,z - координаты, м;
![]() - высота
средней струйки потока перед уступом, м;
- высота
средней струйки потока перед уступом, м;
z1 и z2 - глубина погружения центра тяжести, м;
a - коэффициент, учитывающий; неравномерность скоростей в сечении при вычислении кинетической энергии по средней скорости;
![]() - угол,
образуемый стенкой входного устройства с осью сооружения, град. (угол сужения);
- угол,
образуемый стенкой входного устройства с осью сооружения, град. (угол сужения);
g - угол наклона поверхности потока перед гасителем ЦНИИС, град.
D - высота ступеней или ребер шероховатости, м;
Q - угол наклона дна потока, град.
![]() - безразмерный
модуль расхода круглой трубы;
- безразмерный
модуль расхода круглой трубы;
x0,5 - безразмерный модуль расхода круглой трубы при глубине воды h = 0,5D;
s - коэффициент затопления прыжка в водобойном колодце;
sh''c- глубина воды перед стенкой, м;
j - угол между стенками раструба гасителя или входного устройства, град;
c - смоченный периметр поперечного сечения потока, м;
w - площадь поперечного сечения потока, м2;
w0 - площадь, м2, сегментального сечения потока на выходе из круглой трубы, м2;
wк- площадь поперечного сечения потока при коитической глубине, м2.
Индексы обозначают:
к - данные величины берутся при критической глубине;
ср - среднее значение величины в сечении или на участке.
ЛИТЕРАТУРА
1. Типовой проект унифицированных сборных водопропускных труб для железных и автомобильных дорог общей сети и промышленных предприятий. Инв. № 101/1, 101/2, 180/1 и 180/2. Л., Лентрансмостпроект, 1961-1963.
2. Унифицированные косогорные водопропускные трубы для железных и автомобильных дорог. Ленгипротрансмост, 1965.
3. Руководство по гидравлическим расчетам малых искусственных сооружений и русел. М., Трансжелдориздат, 1961.
4. Студеничников Б.И. Лабораторные исследования нижних бьефов гидроузлов и вопросы методики моделирования размывов. Труды гидравлической лаборатории ВНИИ ВОДГЕО. Сборник 10, М., Госстройиздат, 1963.
5. Поклонский И.К. Протекание потока в круглых трубах с повышенной шероховатостью. - "Транспортное строительство", № 8, 1963.
6. Агроскин И.И. и др. Гидравлика. Издание четвертое, М., Госэнергоиздат, 1964.
7. Технические условия проектирования железнодорожных, автодорожных и городских мостов и труб (СН 200-62). М., Трансжелдориздат, 1962.
8. Инструкция по расчету стока с малых бассейнов. ВСН 63-61. М., Трансжелдориздат, 1962.
9. Чертоусов М.Д. Гидравлика (специальный курс), М., Госэнергоиздат, 1962.