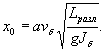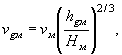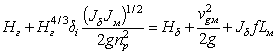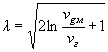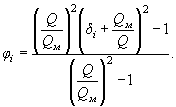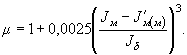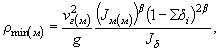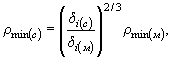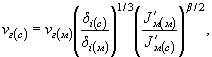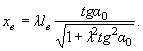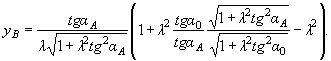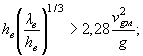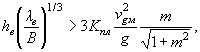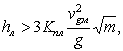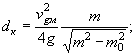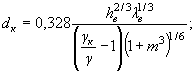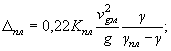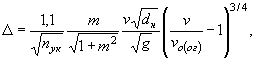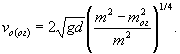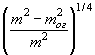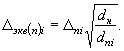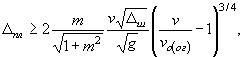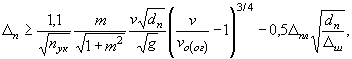В нестоящих Рекомендациях, предназначенных для использования при проектировании мостовых переходов черев равнинные реки (с поймами), рассматривается метод гидравлического расчета струенаправляющих дамб. Метод включает определение плановых размеров дамб, а также их укрепление каменной неброской и железобетонными плитами.

Работа выполнена в соответствии с программой решения научно-технической проблемы 0.85.81 "Разработать научно-технические основы и комплекс мероприятий по улучшению использования водных ресурсов и охрены вод", утвержденной Постановлением Государственного Комитете Совета Министров СССР по науке и технике № 435 от 10 декабря 1976 г.

Рекомендации разработаны в лаборатории мостовой гидравлики и гидрологии отделения изысканий и проектирования железных дорог ЦНИИСа канд. техн. наук В. Ш. Цыпиным под общим руководством канд. техн. наук В. В. Невского.

Программа расчета размеров струенаправляющих дамб для ЭВМ серии ЕС, разработанная совместно с ведущим конструктором СКТБ ЦНИИСа Л. Л. Лукьяновым, имеется в фонде программ ЦНИИСа.

Зав. отделением изысканий

и проектирования железных дорог

А. М. Козлов

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. На мостовых переходах регулирование пойменного потока должно осуществляйся сплошными незатопляемыми криволинейными в плане струенаправляющими дамбами, которые обычно состоят из верховой и низовой частей (или верховой и низовой дамб), плавно сопрягающихся в створе перехода.

Струенаправляющие верховые дамбы устраивают для уменьшения неравномерности деформаций подмостового русла, создания условий для судоходства и сплава, а также уменьшения возможного сосредоточенного размыва у вогнутого берега. Указанные цели достигаются плавным подведением пойменных вод к мостовому отверстию, устранением недопустимой косины и отжимом потока от одного из устоев.

Низовые дамбы сооружают с целью плавного вывода пойменного потока из отверстия.

1.2. Плановые размеры дамб рассчитывают на наибольшие значения гидравлических характеристик стесненного потока при расчетном расходе и возможном наиневыгоднейшем положении русла и наносных скоплениях под мостом.

Наибольшие значения требуемых гидравлических характеристик стесненного потока, - предмостового подпора и средней скорости под мостом, - имеют место на пике паводка (в начале ступени на пике схематизированного гидрографа) и определяются в процессе расчета общего размыва. Если расчет общего размыва производится не по гидрографу паводка, то с запасом предмостовой подпор и среднюю скорость потока под мостом рекомендуется определять для условий осуществления 50% полного размыва при продолжительных паводках и не менее 25% при непродолжительных.

Возможные наиневыгоднейшие положения русла и наносных скоплений под мостом определяют с учетом руслового процесса в районе перехода [1, 2].

1.3. Плавное обтекание струенаправляющих дамб* достигается при эллиптическом их очертании. Координатную ось ориентируют так, чтобы большая полуось эллипса была параллельна направлению руслового потока при расчетном расходе.

*Здесь и далее, если специально не оговорено, имеются в виду верховые дамбы.

Форма и размеры эллиптической струенаправляющей дамбы определяются большой и малой полуосью эллипса, которые принято называть соответственно длиной вылета l_в (или вылетом) и шириной разворота в (или разворотом) дамб (рис. 1).

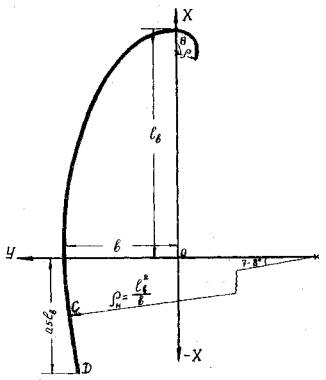
Рис. 1. Форма и размеры в осях верховой и низовой струенаправляющих дамб

1.4. Длину вылета и ширину разворота верховой струенаправляющей дамбы, принимаемые по ее бровке со стороны русла, вычисляют по формулам:

l_в = λ²ρ_min; (1)

в = λρ_min; (2)

где - отношение полуосей дамбы, определяемое согласно п. 3.5;

ρ_min - радиус кривизны токов в голове дамбы, определяемый в зависимости от гидроморфологических условий и положения трассы перехода.

Если в результате расчете по формуле (1) получится l_в ≥ L_М, то за длину вылета следует принимать ширину отверстия моста L_М (l_в = L_М), а ширину разворота вычислять по формуле

(3)

1.5. При определении координат внешней бровки (со стороны русла) верховых струенаправляющих дамб задают значение координаты x и находят координату y по формуле

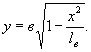(4)

Для быстрого определения безразмерной координаты рекомендуется пользоваться графиком, представленным на рис. 2. К головной чести верховой дамбы прибавляют криволинейную приставку с радиусом ρ = 0,2в и углом разворота θ = 90 - 120°(см. рис. 1).

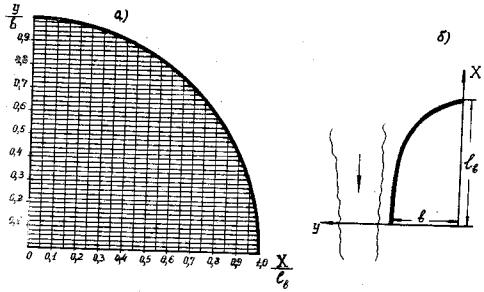
Рис. 2. Определение координат верховых струенаправляющих дамб:

а - график 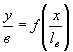; б - ориентирование осей дамб

1.6. Низовые струенаправляющие дамбы проектируют в зависимости от размеров верховых дамб. Проекцию низовой дамбы на ось x определяют по формуле

l_н = 0,5l_в. (5)

Низовую дамбу очерчивают по круговой кривой радиусом - при угле разворота 7 - 8°, а затем по прямой, касательной к круговой кривой (см. рис. 1). Безразмерные координаты точки C сопряжения касательной к кривой могут быть приняты равными а точки D конца низовой дамбы

1.7. В зависимости от ситуационных условий на мостовом переходе (наличия проток, расположения головы дамбы на относительно высоких отметках и т.п.) размеры дамбы могут корректироваться только в сторону увеличения размеров по сравнению с расчетными.

При необходимости увеличения размеров дамб в сторону от створа перехода, т.е. вылета l_в, требуется устраивать прямую вставку ∆l_в, сопрягающую расчетную длину вылета с низовой дамбой (рис. 3).

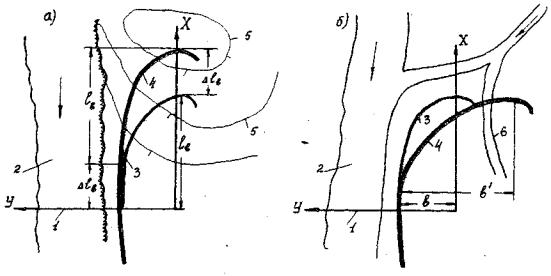
Рис. 3. Увеличение размеров дамб по ситуационным условиям:

8 - в сторону от створа перехода; б - в сторону от русла; 1 - створ перехода; 2 - русло; 3 - размеры дамбы по расчету; 4 - то же по ситуационным условиям; 5 - горизонтали; 6 - выключаемый участок протока

Увеличение размеров дамбы только за счет удлинения вылета l_в без прямой вставки не рекомендуется, так как это нарушит плавность обтекания дамбы. Увеличение размеров дамбы в сторону от русла должно достигаться увеличением ее разворота в, при этом отношение полуосей дамбы уменьшается по сравнению с расчетным значением (см. рис. 3).

1.8. В сложных случаях пересечения водотоков (при интенсивных русловых процессах, групповых отверстиях на переходе и т.д.) размеры и местоположение дамб рекомендуется уточнять по результатам физического моделирования. При этом ориентировочно можно принимать, что моделирование этих сооружений экономически оправдано* при длине вылета одной из дамб свыше 200 м.

*Под экономически оправданным моделированием понимается моделирование, результаты которого позволят снизить стоимость объекта не сумму, в пять-шесть раз превышаемую стоимость моделирования.

Объем исходных денных для моделирования, а также необходимые размеры экспериментальных установок приведены в работе [1].

1.9. Струенаправляющие дамбы выводят из грунтов близлежащих карьеров с откосами обычно не круче 1:2**. Ширина этих земляных сооружений поверху определяется с учетом организации строительных работ, но должна быть не менее 3 м. Независимо от продольного уклона водотока верх дамб на всем протяжении проектируют горизонтальной площадкой.

**Положение откосов в головной части дамб, как практикуется в настоящее время, нецелесообразно.

Отметку верха дамбы ВД определяют по следующим формулам:

с верховой стороны перехода

ВД_в = УВВ_p_% + (H_г - H_δ) + h_н + ∆; (6)

с низовой стороны моста

ВД_н = УВВ_p_% + h_н + ∆, (7)

где УВВ_p_% - уровень воды; принимается наибольшим для железных дорог и расчетным для автомобильных;

H_г - глубина потока у подошвы головы струенаправляющей дамбы, вычисляемая согласно п. 3.2 для соответствующего расхода)

H_δ - то же в бытовых условиях;

h_н - высота наката ветровой волны, определяемая по НИМП-72 [3] для соответствующего расхода;

∆ - технический запас, равный 0,25 м.

2. ОПРЕДЕЛЕНИЕ ИСХОДНЫХ ГИДРАВЛИЧЕСКИХ ХАРАКТЕРИСТИК ПОТОКА

2.1. Для расчета струенаправляющих дамб требуются следующие бытовые гидроморфологические характеристики участка перехода при расчетном расходе:

v_δ - средняя скорость по всему живому сечению нестесненного потока;

L_разл - расчетная ширина разлива; при одностороннем стеснении потока подходами L_разл принимается равной ширине разлива, а при двустороннем стеснении - половине полной ширины разлива;

J_δ - продольный уклон водной поверхности нестесненного потока в паводок;

H_δ_i - характерная глубина потока на поймах в районе голов проектируемых дамб;

n_р - коэффициент шероховатости русла.

Поскольку струенаправляющие дамбы проектируют после назначения отверстия, должны быть известны:

Q_м, Q_пп, Q_пл - расходы, проходящие при отсутствии стеснения через части живого сечения, перекрываемые соответственно отверстием моста, право- и левосторонними подходами;

Q_м/Q - относительный расход, проходящий на ширине отверстия в бытовых условиях (Q - общий расход водного потока);

- коэффициенты стеснения потока соответственно лево- и правосторонними подходами;

v_м, v_δм - скорости потока соответственно под мостом и в части живого сечения на ширине моста при отсутствии стеснения.

2.2. Предмостовой подпор находят по формуле

(8)

где K - коэффициент, определяемый в зависимости от планового положения мостового перехода.

При нормальном пересечении водотока подходами

(9)

где a - коэффициент, принимаемый по табл. 9 гл. VIII НИМП-72;

g - ускорение свободного падения (g = 9,8 м/с²).

При косом пересечении пойменного потока подходной насыпью, направленной вверх по течению (рис. 4), когда расстояние S_ов вверх от моста до выхода насыпи за пределы разлива превышает расстояние х₀

(10)

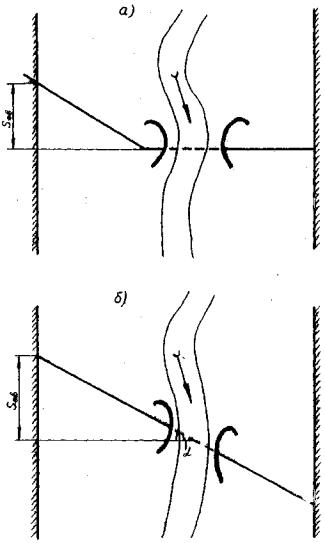
Рис. 4 Планы косого пересечения потока мостовым переходом:

а - косое пересечение поймы; б - то же русло

2.3. Расстояние x₀ от моста до вертикали, где устанавливается предмостовой подпор, определяют по формуле

(11)

2.4. Рассчетную глубину потока у подошвы струенаправляющих дамб в створе моста h_g_м определяют в зависимости от морфологических особенностей подмостового сечения и возможных плановых и глубинных деформаций.

а) В случае, когда отсутствует пойменная часть отверстия (мост перекрывает только русло) и отверстие моста L_м меньше уширенного русла B_уш, или примерно равно ему (L_м ≤ B_уш), глубины потока у подошвы струенаправляющих дамб в створе моста h_дм принимаются наибольшими в русле при побочневом типе руслового процесса и русловой многорукавности; при меандрирующих руслах всех модификаций, включая пойменную многорукавность, в качестве h_g_м принимают наибольшую глубину потока в русле только для дамбы со стороны вогнутого берега, а со стороны выпуклого - среднюю глубину потока в русле (с учетом общего размыва)

Наибольшую величину уширенного русла для несвязных грунтов при всех типах руслового процесса, кроме русловой многорукавности, вычисляют по приближенной формуле

(12)

где d - средний диаметр частиц грунта, подстилающего русло;

М₀ - коэффициент, принимаемый равным 1,06 при

при

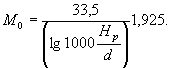(13)

Для определения M₀ и B_уш рекомендуется пользоваться графиками, представленными на рис. 5 и 6.

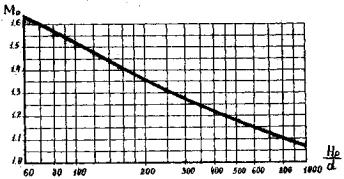
Рис.5. График для определения коэффициент М₀ при

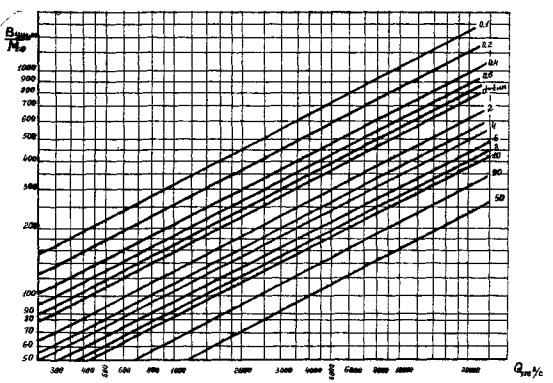
Рис. 6. График для определения уширенного русла B_уш

При русловой многорукавности за величину уширенного русла принимают наибольшую ширину многорукавного русла в его пойменных бровках на морфологически однородном участке в районе постового перехода.

б) При наличии пойменной части отверстия, когда L_м > B_уш, глубины потока у подошвы струенаправляющих дамб в створе моста принимаются наибольшими в русле только при криволинейных руслах для дамб со стороны вогнутого берега (если по прогнозу плановых деформаций в период эксплуатации перехода русло подойдет к одному из устоев); во всех остальных случаях в качестве h_g_м принимают глубину потока на пойменной части моста с учетом глубинных деформаций.

2.5. Расчетную скорость потока у подошвы струенаправляющих дамб на вертикали с глубиной h_дм рассчитывают по формуле

(14)

где Н_м - средняя по сечению моста глубина потока с учетом общего размыва.

3. НОРМАЛЬНОЕ ПЕРЕСЕЧЕНИЕ ВОДОТОКА С ОДНОЙ ПОЙМОЙ

3.1. При расчете плановых размеров струенаправляющих дамб участок реки принимают с одной поймой, если по другой проходит менее 5% расчетного расхода. Нормальный считаются пересечение водотока, когда угол отклонения створа моста от вертикали к направлению течения в бытовых условиях при расчетном расходе не превышает 5 - 10°.

3.2. Для определения уклона свободной поверхности потока перед мостом рекомендуется использовать формулу

(15)

3.3. Глубину потока у подошвы дамбы (без учета местного размыва) H_г определяют подбором из уравнения

(16)

или вычисляют по формуле (при )

H_г = H_δ + ∆h_в, (17)

где f - коэффициент, принимаемый в зависимости от коэффициента стеснения потока подходами: при δ_i > 0,5 f = 1; при 0,5 > δ_i ≥ 0,25 f = 2/3; при δ_i < 0,25 f = 1/3.

В формуле (16) все величины (H_г, g, v_g_м, L_м) следует подставлять в метрах или секундах.

Если подбором по формуле (16) получится H_г ≥ H_δ + ∆h_в, то за глубину потока у подошвы головы дамбы принимают H_г по формуле (17).

3.4. Скорость потоке в голове дамбы в створе глубиной H_г находят по формуле

(18)

где C_г - коэффициент Шези;

(19)

3.5. Отношение полуосей дамбы - определяют по формуле

(20)

или по графику (рис. 7).

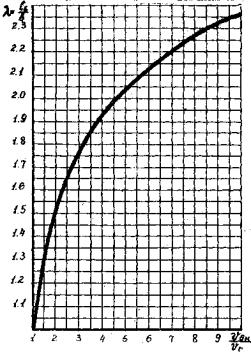
Рис. 7. График для определения полуосей дамбы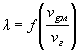

3.6. Радиус кривизны токов в голове дамбы вычисляют по формуле

(21)

где β - показатель степени;

(22)

При принимают β = 0,2.

Для быстрого нахождения величины рекомендуется пользоваться графиком (рис. 8).

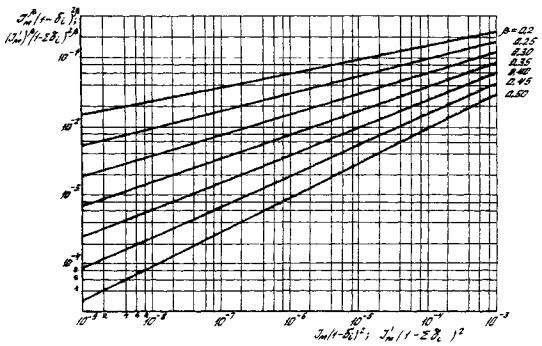
Рис. 8. График для определения величины или

3.7. Размеры и конфигурацию верховых и низовых дамб рассчитывают согласно пп. 1.4 - 1.6. При учете ситуационных условий мостового перехода следует пользоваться рекомендациями п. 1.7.

Пример расчета струенаправляющей дамбы на мостовом переходе при нормальном пересечении водотока с одной поймой приведен в приложении 1.

4. НОРМАЛЬНОЕ ПЕРЕСЕЧЕНИЕ ВОДОТОКА С ДВУМЯ ПОЙМАМИ

4.1. При величии двух пойм расчет начинают с определения размеров струенаправляющей дамбы на более мощной пойме, со стороны которой коэффициент стеснения потока подходами больше (см. п. 2.1). Если коэффициенты стеснения потоков близки между собой, то в качестве расчётной поймы принимают пойму с большим коэффициентом ζ, определяемым по формуле

(23)

Расчет размеров струенаправляющей дамбы со стороны мощной поймы производят для гидравлических условий, характеризующихся частью предмостового подпора, вызванного оттеснением мощной поймы. Эту часть предмостового подпора находят по формуле

(24)

4.2. Части предмостового подпора, вызванного стеснением мощной поймы, соответствуют уклон свободной поверхности потока перед мостом J'_м(м) и глубина потока H'_г - у подошвы головы дамбы:

(25)

(26)

Глубину потока у подошвы головы дамбы определяют по формуле (16) или (17), при этом в формуле (16) принимают коэффициент δ_i стеснения со стороны мощной поймы.

4.3. Скорость потока в голове дамбы со стороны мощной поймы определяют по формуле

(27)

где C_г - коэффициент Шези, определяемый по формуле (19) с учетом глубины потока H'_г;

μ - понижающий коэффициент;

(28)

4.4. Радиус кривизны токов в голове дамбы со стороны мощной поймы определяют по формуле

(29)

где ∑δ_i = δ_п + δ_л.

4.5. Радиус кривизны токов в голове дамбы со стороны слабой противоположной поймы вычисляют по формуле

(30)

где индексы (с) и (м) соответствуют характеристикам слабой и мощной пойм.

4.6. Скорость потока в голове дамбы со стороны слабой поймы определяют по формуле

(31)

где J'_м_(с) - уклон свободной поверхности перед мостом, который образовался бы при отсутствии мощной поймы; определяют по формуле (25) с учетом коэффициента φ_с для слабой поймы, вычисляемого по формуле (24).

Если в расчете получится v_г_(с) ≥ v_г_(м), то принимают v_г_(с) = v_г_(м). Для определения отношения v_г_(с)/v_г_(м) рекомендуется пользоваться графиком, представленным на рис. 9.

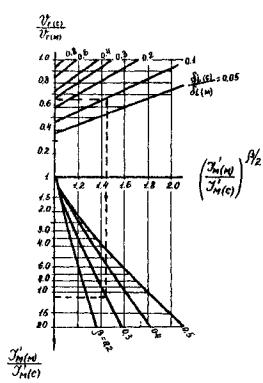
Рис. 9. График для определения отношение v_г₍_с₎/v_г₍_м₎

4.7. Дальнейший расчет размеров и конфигурации дамб производят, как и для одной поймы (см. пп. 1.4 - 1.7). При этом отношение полуосей дамб λ рассчитывают по формуле (20) или находят по графику (см. рис. 7) с учетом фактических значений скоростей v_g_м и v_г, определяемых соответственно по формулам (14) и (27) или (31).

Пример расчета струенаправляющей дамбы на мостовом переходе при нормальном пересечении водотока и наличии двух пойм приведен в приложении 2.

5. УЧЕТ КОСОГО ПЕРЕСЕЧЕНИЯ ВОДОТОКА

5.1. Различают два случая косого пересечения водотока мостовым переходом (см. рис. 4): косое пересечение пойм подходами и косое расположение отверстия моста относительно русла.

Второй случай наиболее общий, включающий и косое пересечение пойм.

5.2. При расчете струенаправляющих дамб косое пересечение пойм подходами следует учитывать, если место выхода насыпи за пределы разлива (см. рис. 4) находится выше сечения x₀, где устанавливается предмостовой подпор при нормальном пересечении пойм, т.е. S_ов > x₀. При S_ов > x₀ расчет производят согласно рекомендациям главы 3 или 4 для соответствующих условий с учетом того, что уклон свободной поверхности перед мостом находят по формуле

(32)

5.3. При косой пересечении русла оси дамб ориентируют относительно берегов русла, а расчеты по определению параметров дамб производят согласно перечисленным выше рекомендациям. При этом необходимо учитывать следующее:

в) если косина (отклонение створа моста от вертикали к направлению потока в быту) α < 10° или α > 10°, но устой со стороны мощной поймы является низовым, никаких поправок в расчетные формулы не вводят;

б) если косина 10° < α ≤ 30° при расположении устоя со стороны мощной поймы вверх по течению, то скорость потока у головы дамбы со стороны мощной поймы определяют по формуле (18) или (27) с коэффициентом 1,1^*;

^*Скорость потока со стороны слабой поймы, определяемая по формуле (31), также на 10% больше скорости при нормальном пересечении русла.

в) если устой со стороны мощной поймы расположен вверх по течению и косина α > 30°, размер дамбы следует корректировать по результатам физического моделирования.

Примеры учета косого пересечения водотока при назначении размеров струенаправляющих дамб приведены в приложении 3.

6. РЕГУЛИРОВАНИЕ РУСЛОВОГО ПОТОКА СТРУЕНАПРАВЛЯЮЩИМИ ДАМБАМИ

6.1. Под регулированием руслового потока струенаправляющими дамбами понимается такое регулирование пойменного потока, при котором предотвращается возможность возникновения неблагоприятных для мостового перехода тенденций развития руслового процесса. К ним относятся возможное приближение криволинейного русла к одному из устьев и образование осередков в подмостовом сечении.

Примечание. Наиболее интенсивное смещение криволинейного русла в сторону вогнутого берега происходит в низководные паводки, когда дамбы не работают. Поэтому струенаправляющими дамбами можно затормозить, но не ликвидировать полностью плановые деформации, русла в подмостовом сечении.

6.2. Сущность регулирования состоит в перераспределении потока под мостом при искусственно создаваемой косоструйности у дамбы специальной формы, обеспечивающей безотрывность течений при косоструйности. Косоструйность характеризуется углом отклонения токов у дамбы от нормали к створу перехода в подмостовом сечении α₀ (рис. 10). Часть расхода, которая должна поступать с поймы на прилегающей к дамбе участок l₀ (при отсутствии косоструйности), перераспределяется в подмостовом сечении за участок l₀, определяемый по приближенной формуле

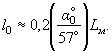(33)

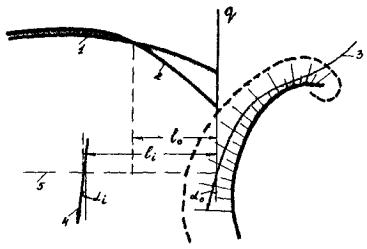
Рис. 10. Перераспределение потока под мостом при косоструйности:

1 - эпюра удельных расходов под мостом g при отсутствии косоструйности (α₀ = 0); 2 - то же при α₀ > 0: 3 - граничная струя транзитного потока у дамбы; 4 - траектория токов на расстоянии l_i от дамбы; 5 - створ перехода

По мере удаления вертикали по створу моста от дамбы, где косоструйность α₀, последняя затухает (уменьшается угол отклонения токов от нормали). На расстоянии l_i от дамбы угол отклонения токов от нормали может быть определен по формуле

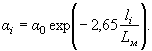(34)

6.3. Угол α₀ должен задаваться из следующих условий:

косина набегания потока на близлежащую опору α_i < 10°;

при отсутствии промежуточных опор косина потока в середине отверстия не превосходит α_i ≈ 5°.

Для удовлетворения этих условий угол α₀ необходимо назначать согласно табл. 1.

Таблица 1

№ п/п	Относительное расстояние от дамбы до ближайшей опоры	Расчетная косоструйность α₀ град
1	Промежуточные опоры отсутствуют	20
2	l_i/L_м > 0,15	15
3	l_i/L_м ≤ 0,15	10

6.4. Для принятого угла α₀ бровку дамбы определяют по точкам в той же системе координат и с учетом тех же значений λ и l_в, что и бровку дамбы без косоструйности, но створ перехода располагают выше оси y на расстоянии x = x_в, а корень дамбы - в точке M (рис. 11). Расстояние x = x_в определяют по формуле (35) или по табл. 2

(35)

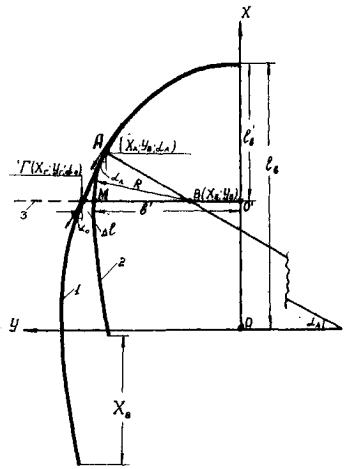
Рис. 11. Форма и размеры (в осях) струенаправляющей дамбы, создающей косоструйность течении под мостом:

1 - ось струенаправляющей дамбы для условий, не требующих отжатия потока от устоя (створ перехода совпадает с осью y) 2 - то же при отжатии потока от устоя; 3 - створ перехода

Таблица 2

α₀	λ	R/l_в	y_в/l_в	в'/l_в	y_г/l_в				x_в/l_в
10°	1,0	0,502	0,476	0,978	0,985	0,007	0,827	0,170	0,173
	1,2	0,566	0,233	0,799	0,817	0,018	0,793	0,181	0,207
	1,4	0,630	0,045	0,675	0,693	0,018	0,761	0,216	0,239
	1,6	0,679	-0,099	0,580	0,601	0,021	0,729	0,234	0,271
	1,8	0,719	-0,212	0,507	0,529	0,022	0,698	0,247	0,302
	2,0	0,745	-0,297	0,449	0,472	0,023	0,668	0,228	0,332
	2,25	0,779	-0,387	0,392	0,413	0,021	0,632	0,266	0,368
	2,5	0,790	-0,445	0,345	0,367	0,022	0,596	0,273	0,404
15°	1,0	0,389	0,555	0,944	0,965	0,021	0,741	0,148	0,259
	1,2	0,436	0,336	0,772	0,793	0,021	0,693	0,164	0,306
	1,4	0,47	0,175	0,645	0,668	0,023	0,649	0,171	0,351
	1,6	0,49	0,058	0,548	0,573	0,025	0,606	0,182	0,394
	1,8	0,496	-0,026	0,47	0,5	0,03	0,566	0,160	0,435
	2,0	0,489	-0,088	0,401	0,441	0,04	0,528	0,174	0,742
	2,25	0,49	-0,141	0,349	0,380	0,031	0,484	0,173	0,516
	2,5	0,473	-0,169	0,304	0,332	0,028	0,442	0,163	0,558
20°	1,0	0,314	0,596	0,900	0,943	0,043	0,657	0,158	0,343
	1,2	0,33	0,395	0,725	0,763	0,038	0,599	0,166	0,401
	1,4	0,345	0,256	0,601	0,638	0,037	0,545	0,172	0,455
	1,6	0,353	0,155	0,508	0,539	0,031	0,498	0,176	0,502
	1,8	0,349	0,084	0,433	0,463	0,030	0,454	0,175	0,546
	2,0	0,321	0,039	0,360	0,403	0,043	0,413	0,164	0,587
	2,25	0,312	0,001	0,313	0,345	0,032	0,365	0,155	0,635
	2,5	0,29	0,022	0,268	0,296	0,028	0,326	0,143	0,674

6.5. Верховая дамба от точки M до A описывается по окружности радиусом R, вычисляемым следующим образом:

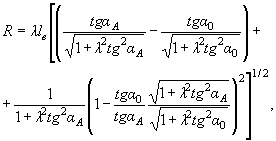(36)

где α_A = (α₀ + 10º) - угол отклонения токов от нормали к створу перехода в точке А, которая расположена выше точки M на расстоянии (вдоль оси x), равном

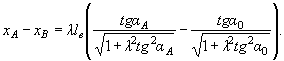(37)

Центр окружности о радиусом R лежит на линии x = x_в в точке B, отстоящей от оси x на расстоянии y_B равном

(38)

Значения R, y_B, x_B и x_А - x_B можно определять по табл. 2.

Примечание. Отрицательное значение y_B при расчете по формуле (38) означает, что центр окружности с радиусом R не лежит в одном квадрате с точками М и А.

6.6. Длину вылета l'_в и ширину разворота в' проектируемой дамбы определяют по табл. 2 или соответственно по формулам:

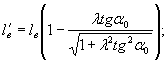(39)

в' = R + y_B. (40)

Пример расчета рассматриваемой дамбы приведен в приложении 4.

6.7. Размеры проектируемой дамбы должны удовлетворять следующему условию, практически обеспечивающему отсутствие отрывных течений (граничная струя транзитного потока, как показано на рис. 10, будет находиться на откосе дамбы):

∆l = (y_г - в') < mh_g_м, (41)

где 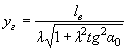- координата граничной струи транзитного потока в створе, моста;

m - коэффициент заложения откоса дамбы.

Величину левой части неравенства (40) можно определять по табл. 2.

Если неравенство (41) не удовлетворяется, то следует уменьшить принятый угол α₀. Уменьшить левую часть неравенства (41) можно также, если за угол α_А принять α_А = α₀ + ∆, где ∆ < 10º. В этом случае пользоваться табл. 2 нельзя.

6.8. Размеры низовой дамбы принимаются такими же, как дамб, не отжимающих поток.

7. УКРЕПЛЕНИЕ СТРУЕНАПРАВЛЯЮЩИХ ДАМБ

7.1. Откосы струенаправляющих дамб должны быть защищены от возможных течений вдоль сооружения, а также волновых и ледовых воздействий. Наиболее распространенными видами укреплений откосов дамб являются каменная наброска и плитные укрепления. Область применения их ограничивается обычно гидрологическими условиями, указанными в табл. 3. Определяющее силовое воздействие, при котором требуется более мощное укрепление, находят согласно пп. 7.4 - 7.6.

Таблица 3

Вид укреплений	Скорость течения, м/с	Высота волны, м	Толщина льда, м
Каменная наброске	До 4	До 1,4	Менее 0,5
Сборные железобетонные плиты толщиной до 25 см	До 4	До 3	До 0,6
Монолитные железобетонные плиты толщиной до 0,5 м	До 5	> 3	0,7 - 0,8

7.2. Каменный материал, применяемый для устройства наброски, не должен иметь признаков выветривания и трещин, прослоек мягких пород и размокаемых включений. Плотность камня должна быть не менее 2 т/м³. Требования, предъявляемые к камню по морозостойкости, приведены в табл. 4.

Таблица 4

Область применения камня и щебня	Минимальная марка камня по морозостойкости для районов с климатическими условиями
Область применения камня и щебня	умеренными и суровыми	особо суровыми
Части сооружений, находящиеся в зоне переменного уровня воды	50 - 100	150
Надводные части	25 - 50	50 - 100
Подводные части	Не нормируются

Примечание. Всем указанным требованиям обычно удовлетворяют материалы, получаемые из изверженных и метаморфических пород. Применение материалов из осадочных пород должно быть технико-экономически обосновано с учетом периодического пополнения укрепления.

7.3. Для укреплений откосов дамб рекомендуется использовать монолитный бетон и железобетон марки 200 - 250 и плиты из сборного железобетона марки 300 - 400.

Применяемый бетон должен удовлетворять требованиям ГОСТ 4795-68 (бетон гидротехнический) по прочности на сжатие и растяжение, водонепроницаемости, морозостойкости и сопротивляемости агрессивным воздействиям воды.

7.4. При сопоставлении продольных течений с волновыми воздействиями последние будут определять мощность укрепления при соблюдении неравенств:

для каменной наброски

(42)

для плитных укреплений

(43)

где h_в, λ_в - соответственно расчетные высота и длина волны, определяемые согласно СНиП II-57-75 [4];

В - длина ребра плиты или карты в направлении образующей откоса;

K_пл - коэффициент, принимаемый в зависимости от стыковки плит: при открытых швах K_пл = 1; при закрытых K_пл = 1,43.

7.5. При сопоставлении продольных течений с ледовыми воздействиями последние будут определять мощность укрепления при соблюдении неравенств:

для каменной наброски (когда расчетная ширина льдины составляет 0,1B_p):

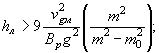(44)

для плитных укреплений

(45)

где h_л - расчетная толщина льда, определяемая по НИМП-72, а для района БАМа - по работе [5];

B_p - ширина русла на уровне подвижки льда;

m₀ - коэффициент заложения естественного откоса камня под водой; для практических расчетов принимают m₀ = 1,1 - 1,25, где большие значения соответствуют круглым, а меньшие - угловатым камням.

7.6. При сопоставлении волновых и ледовых воздействий на откосы дамб волновые воздействия будут определять мощность укрепления при соблюдении неравенств:

для каменной наброски

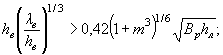(46)

для плитных укреплений

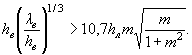(47)

7.7. По составу материала и по принципу работы каменная наброска подразделяется на однородную и неоднородную по крупности.

По принципу работы неоднородная по крупности наброска отличается от однородной тем, что в ней допускается деформация, вызываемая разделением гранулометрического состава камней на мелкие, выносимые потоком, и более крупные, вымащивающие откосы.

Каменный материал, применяемый для укрепления откосов, считается однородным:

если при воздействии продольных течений соблюдается условие

(48)

где d_н, d₁₀ - соответственно средний диаметр материала наброски и диаметр частиц, мельче которых в наброске содержится не более 10% по массе;

если при ледовых воздействиях наброска содержит неполномерных камней, имеющих массу свыше половины расчетного, не более 25% общего объема;

если при волновых воздействиях содержание камней с расчетной массой составляет более 50%, а отношение d₆₀/d₁₀ ≤ 3¸15.

При волновых воздействиях согласно СНиП II-57-75 к однородному можно, относить также материал, гранулометрический состав которого не выходит из границ зоны

(49)

где p_i - содержание по массе в наброске i-й фракции со средней крупностью частиц d_i.

Применение однородного каменного материала в наброске ограничивается диаметром окатанных камней до 50 см и неокатанных (получаемых в результата взрыва) до 70 см. Камни более крупных размеров, образующие в наброске большие щели, требуется укладывать в укреплении методом мощения (без расклинки, но с подбором лица) не менее чем в два слоя. При устройство укрепления из однородных крупных камней методом наброски (без подбора лица) необходим объем материала, обеспечивающий коэффициент оплошности укладки не менее α_сп = 1,7. Под коэффициентом оплошности понимают отношение площади проекций камней на откос к площади поверхности, на которой разместились камни.

7.8. Расчетную (требуемую) крупность однородного камня для укрепления откосов дамб определяют в зависимости от силовых воздействий по формулам:

для продольных течений

(50)

для волновых воздействий

(51)

для ледовых воздействий (в первом приближении)

(52)

или

(53)

где γ_к, γ - плотность соответственно камня и воды, которые в расчетах можно принимать γ_к = 2,65 т/м³ и γ = 1 т/м³;

Ш_л - размер льдин в направлении, перпендикулярном берегу.

7.9. К неоднородному каменному материалу относится материал, не удовлетворяющий условиям п. 7.7. В наброске должно быть не менее 15% камней (по массе) крупнее d_к.

При отсутствии данных о гранулометрическом состава несортированного камня, получаемого взрывным способом, в самом первом приближении диапазон содержания фракций в материале после взрыва средне- и слаботрещиноватых массивов [6] может быть принят по табл. 5, в которой большее содержание крупных по размеру фракций относится к более прочным породам (свыше IV - VI группы по классификации СНиП IV-13-71 [7]).

Таблица 5

Диаметр камней, см	Более 70	70 - 40	40 - 20	20 - 5 и менее
Приближенный диапазон содержания фракций % по массе	5 - 20	15 - 25	40 - 70	5 - 20

Расчет набросного укрепления из неоднородного по крупности материала при воздействии продольных течений следует производить согласно рекомендациям [8]. Несортированный каменный материал, не удовлетворяющий условиям п. 7.7, при ледовых и волновых воздействиях в набросных укреплениях использовать не рекомендуется.

7.10. По условиям устойчивости толщину железобетонных плит и карт принимают по формулам:

при продольных течениях

(54)

при воздействии льда (для предварительных расчетов и m ≥ 1,5)

(55)

при волновом воздействии

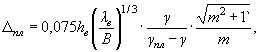(56)

где γ_пл - плотность плиты (γ_пл = 2,4 - 2,5 т/м³).

7.11. Дифференцировать мощность (или тип) укрепления вдоль дамб возможно:

при продольных течениях, когда удовлетворяется условие v_г < 0,4v_g_м;

при резко неравномерных ледовых или волновых воздействиях (голова дамбы, находящаяся на пойменном участке, располагается вне зоны ледовых воздействий; по розе ветров большая часть берегового откоса находится с теневой для волновых воздействий стороны и т.д.).

При продольных течениях по мощности укреплений выделяют два участка откосов дамбы (рис. 12).

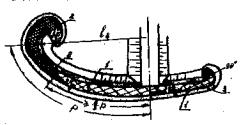
Рис. 12. Укрепление струенаправляющих дамб:

1 - участок I; 2 - участок II; 3 - укрепление подошвы

К участку I относятся низовая и более 2/3 верховой дамбы (считая от оси моста по подошве). Откосы участка I укрепляют согласно пп. 7.8 и 7.10.

К участку II относится головная часть верховой дамбы. Мощность укрепления на участке II, а также доминирующие силовые воздействия определяют по формулам (42) - (45), (50) и (54) в которых вместо v_g_м принимают увеличенную на 35% скорость v_i = 1,35v_gi потока у подошвы струенаправляющей дамбы на границе I и II участков.

Для определения скорости потока у подошвы дамб на заданной вертикали можно пользоваться формулой.

(57)

где S - расстояние по подошве струенаправляющей дамбы начиная oт створа у головы;

P - периметр по подошве верховой струенаправляющей дамбы, т.e. расстояние по подошве от вертикалей со скоростями потока v_г и v_g_м.

7.12. При назначении толщины наброски должны быть обеспечены условия:

сплошность укладки не менее α_сп = 1,7;

полная толщина не менее 1,5 d_н;

отсутствие суффозии - выноса из пор наброски частиц грунта тела дамбы; достаточным условием отсутствия суффозии является неравенство

(58)

где d - средний диаметр частиц грунта тела дамбы.

7.13. Бели не удовлетворяется неравенство (58), то требуемую толщину однородной наброски на откосе (в направлении, перпендикулярном откосу) определяют по формуле

(59)

где n_ук - число слоев наброски (при толщине одного слоя 0,7 - 0,8d_н);

v - скорость, по которой определяли крупность камня на рассматриваемом участке откоса (v_g_м или v_i = 1,35v_gi);

v_о_(ог) - размывающая скорость для частиц грунта со средним диаметром d, подстилающих наброску на откосе

(60)

Здесь m_ог - коэффициент естественного заложения грунта под водой, принимаемый по табл. 6; в ней приведены и величины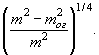

Таблица 6

Крупность частиц d, мм	m_ог
Крупность частиц d, мм	m_ог	m = 1,5	m = 2	m = 2,5
0,1 - 0,25	1,7	-	0,725	0,855
0,5 - 1	1,65 - 1,6	-	0,755 - 0,775	0,87 - 0,875
1 - 2	1,6 - 1,55	-	0,775 - 0,795	0,875 - 0,885
2 - 5	1,55 - 1,45	-	0,795 - 0,83	0,885 - 0,905
5 - 10	1,45 - 1,4	0,51 - 0,6	0,83 - 0,845	0,905 - 0,91
10 - 100	1,4 - 1,3	0,6 - 0,705	0,845 - 0,865	0,91 - 0,925
> 100	1,25	0,745	0,885	0,93

При определении требуемой толщины наброски задаются числом слоев наброски n_ук и рассчитывают величину ∆ по формуле (59), которую сопоставляют с фактической толщиной наброски в n_ук слоев

∆_ф = 0,75d_нn_ук. (61)

При ∆_ф < ∆ число слоев увеличивают и повторяют расчет до соблюдения условия ∆_ф ≥ ∆.

7.14. Для уменьшения толщины наброски устраивают подготовку (из щебня или гравийной смеси) или применяют фильтрационные полотна.

Крупность материала подготовки (или верхнего слоя при неоднородных по крупности слоях подготовки) d_п должна приниматься такой, при которой d_н/d_п < 6 - 8.

Если соблюдаются условия и то толщину подготовки следует принимать минимальной без расчета.

Если но то требуемую толщину наброски определяют по формуле

∆_н = ∆ - ∑∆_экв_(n)i, (62)

где - эквивалентная толщина i -го слоя подготовки, равная

(63)

Здесь d_ni, ∆_ni - соответственно крупность материала и толщина i -го слоя подготовки.

При определении ∆ в формуле (62) в качестве n_ук принимают суммарное число слоев (к числу слоев подготовки прибавляют отыскиваемое число слоев наброски).

7.15. Вынос частиц грунта тела дамбы из швов между плитами будет отсутствовать при ∆_ш/d < 2 - 2,5

или (64)

где ∆_ш - ширина швов.

Если указанные неравенства не соблюдаются, то требуется устраивать подготовку под плитное покрытие или применяют фильтрационные полотна. Минимальная толщина подготовки из материала крупностью d_n определяется подбором по

(65)

где n_ук - число слоев подготовки с учетом одного слоя плиты. Расчет производят до соблюдения условия ∆_n < ∆_n_(ф), где ∆_n_(ф) - задаваемая толщина подготовки.

7.16. Для обеспечения устойчивости укрепления на откосе и защиты подошвы дамбы рекомендуется устраивать рисберму.

Крупность камня в рисбермах назначается, как для откосов при воздействии продольных течений.

Объем призмы (рисбермы) для защиты подошвы дамбы от образуемого при размыве откоса на 1 м сооружения вычисляют по формуле

(66)

где h - глубина размыва у подошвы дамбы; в голове дамбы она равна местному размыву у дамбы [3], а на остальном протяжении дамбы определяется в зависимости от деформации русла под мостом с учетом руслового процесса и срезок подмостового сечения.

Упор вышележащей конструкции должен устраиваться при заложении укрепляемого откоса дамбы меньше m = 2. Приближенно дополнительный удельный объем камня для упора можно принимать равным

(67)

где W_укр - удельный (на 1 м) объем укрепления на откосе дамбы; коэффициент 1,2 принимают при m = 1,5, а 1,6 при m < 1,5.

Приложение 1

ПРИМЕР РАСЧЕТА СТРУЕНАПРАВЛЯЮЩЕЙ ДАМБЫ ПРИ НОРМАЛЬНОМ ПЕРЕСЕЧЕНИИ ВОДОТОКА С ОДНОЙ ПОЙМОЙ

Определить плановые размеры верховой дамбы на мостовом переходе через реку с одной поймой и ограниченно меандрирующим руслом (пойма находится со стороны выпуклого берега).

Русло и пойма в районе мостового перехода сложены однородным песком со средним диаметром частиц d = 1 мм; бытовой уклон водной поверхности в паводок J_δ = 0,0002. Гидрогеологические характеристики живого сечения реки в створе мостового перехода при расчетном расходе приведены в табл. 1.

Отверстие моста L_м = 320 м перекрывает русло и 70 м поймы. Коэффициент шероховатости русла n_р = 0,03.

Таблица 1

Участки живого сечения	Расход, м³/с	Средняя скорость, м/с	Ширина участка, м	Средняя глубина, м
Коренное русло	2630	1,50	250	7,0
Пойма	2100	0,35	3000	2,0
Русло и пойма	4730	0,61	3250	-

Под мостом на всю ширину пойменной части отверстия сделана срезка на глубину 1,6 м. В результате расчетов получено, что коэффициент предельного общего размыва (без учета гидрографа паводка) P = 1,3.

1. Определяем предмостовой подпор.

Предварительно находим относительный расход, проходящий на ширине отверстия в бытовых условиях:

Q_м = 2630 + 0,35·2·70 = 2689 м³/с;

Площадь под мостом в бытовых условиях

ω_м = 250·7 + 70·2 = 1890 м²;

тo же со срезкой ω_м₍_ср₎ = 250·7 + 70·(2 + 1,6) = 1750 + 250 = 2000 м².

Скорость потока на ширине отверстия моста в бытовых условиях

Скорость потока под мостом (без учета размыва)

то же с учетом осуществления 50% полного размыва

При ширине размыва L_разл = 3250 м и средней скорости по всему живому сечению нестесненного потока v_δ = 0,61 м/с (см. табл. 1) определяем параметр по табл. 9 гл. VIII НИМП-72 определяем a ≈ 1,25;

по формуле (9)

по формуле (8)

2. Определяем уклон свободной поверхности перед мостом по формуле (15).

Предварительно по формуле (11) находим

3. Определяем скорость потока у подошвы дамбы v_g_м. Предварительно надо определить среднюю по сечению моста глубину потока с учетом общего размыва H_м и глубину потока под мостом у подошвы дамбы h_g_м (с учетом общего размыва).

Средняя глубина потока под мостом без общего размыва При осуществлении 50% полного размыва (фактический коэффициент размыва Р_ф = 1+ (P - 1)·0,5 = 1 + (1,3 - l)·0,5 = 1,15)

Для конкретного мостового перехода имеет мосто неравенство L_м < B_уш, так как при (см. рис. 6), B_уш = 1,06·360 > 320 м.

Поэтому согласно п. 2.4,а принимаем, h_g_м = H_p = 7·1,15 = 8,05 м, где 1,15 - фактический коэффициент размыва.

По формуле (14)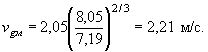

4. Определяем глубину потока у подошвы головы дамбы.

Так как то глубину потока H_г будем находить подбором из уравнения (16), в котором при принимаем f = 2/3. Вычисляем правую часть уравнения (16):

Задаемся H_г = 2,2 и определяем левую часть уравнения (16)

При H_г = H_б + ∆h_в = 2,217 м N = 2,22 < N_расч, но так как из уравнения (16) H_г > H_δ + ∆h_в, тo принимаем по формуле (17) H_г = 2,217 м.

5. По формуле (18) находим скорость потока в голове дамбы. Предварительно по формуле (19) рассчитываем

6. По формуле (20) или рис. 7 вычисляем при отношение полуосей дамбы

7. Определяем радиус кривизны токов в голове дамбы по формуле (21). Предварительно по формуле (22) находим

8. По формулам (1) и (2) длина вылета и ширина разворота верховой струенаправляющей дамбы соответственно равны:

l_в = 1,87²·32,0 = 111,6 м;

в = 1,87·32,0 = 59,6 м.

Для иллюстрации покажем на данном примере влияние врезки и общего размыва на размеры дамбы.

Без срезки имеем:

скорость потока под мостом с учетом размыва

подпор

уклон свободной поверхности перед мостом

средняя глубина потока под мостом при осуществлении 50% полного размыва

скорость потока у подошвы дамбы

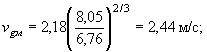
скорость потока в голове дамбы (считая H_г = H_δ + ∆h_в = 2,27 м)

отношение полуосей дамбы при

радиус кривизны токов в голова дамбы (β = 0,22)

размеры дамбы:

в = 1,9·32,6 = 61,8 м;

l_в = 1,9²·32,6 = 117,2 м.

Без размыва (со срезкой) имеем:

скорость потока под мостом

подпор

уклон свободной поверхности перед мостом

средняя глубина потока под мостом

скорость потока у подошвы дамбы (при H_p = 7 м)

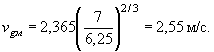
При глубине потока в голове дамбы H_г = 2,32 м левая часть уравнения (16) будет равна правой части этого уравнения

При H_г = 2,32

отношение полуосей дамбы при

радиус кривизны тонов в голова дамбы (β = 0,234)

размеры дамбы:

в = 1,88·34,5 = 64,8 м;

l_в = 1,88²·34,5 = 121,7 м.

Без размыва и срезки имеем:

скорость потока под мостом

подпор

уклон свободной поверхности перед мостом

средняя глубина потоке под мостом

скорость потока у подошвы дамбы

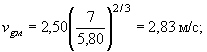
скорость потока в голове дамбы при полученной ив уравнения (16) H_г = 2,38 м

отношение полуосей дамбы при

радиус кривизны токов в голове дамбы (β = 0,236)

размеры дамбы:

в = 1,92·36,4 = 70,0 м;

l_в = 1,92²·36,4 = 134,0 м.

В табл. 2 сопоставлены размеры дамбы, подсчитанные без и с учетом срезки и общего размыва подмостового сечения, а также по методу НИМП-72.

Таблица 2

Размеры дамбы, м	По настоящим рекомендациям				По НИМП-72
Размеры дамбы, м	с учетом срезки и общего размыва	без учета срезки	без учета общего размыва.	без учета срезки и общего размыва	По НИМП-72
Длина вылета	111,6	117,2	121,7	134,0	234,0
Ширина разворота	59,6	61,8	64,8	70,0	117,0

Приложение 2

ПРИМЕР РАСЧЕТА СТРУЕНАПРАВЛЯЮЩИХ ДАМБ ПРИ НОРМАЛЬНОМ ПЕРЕСЕЧЕНИИ ВОДОТОКА С ДВУМЯ ПОЙМАМИ

Определить плановые размеры верховых дамб на мостовом переходе через реку с двумя поймами и свободно меандрирующим руслом (вогнутый берег излучины находится со стороны слабой поймы).

Русло и пойма в районе мостового перехода сложены однородным песком со средним диаметром частиц d = 1 мм; бытовой уклон водной поверхности J_δ = 0,0002; гидрогеологические характеристики живого сечения реки в створе мостового перехода при расчетном расходе приведены в таблице. Отверстие моста L_м = 320 м перекрывает русло, а также 20 м слабой (левой) и 50 м мощной (правой) поймы. Коэффициент шероховатости русла n_р = 0,03.

При расчетном расходе наибольшая глубина в русле h_max = 8,3 м (расположена у вогнутого берега). Под мостом на пойманных частях отверстия сделана срезка, при которой глубина потока при расчетном расходе (до размыва) равна 3,6 м. В результате расчетов получено, что коэффициент предельного общего размыва (без учета гидрографа паводка) Р = 1,3.

Участки живого сечения	Расход, м³/с	Средняя скорость, м/с	Ширина участка, м	Средняя глубина, м
Коренное русло	2630	1,50	250	7
Правая пойма	2100	0,35	3000	2
Левая пойма	270	0,38	350	2,03
Русло и поймы	5000	0,67	3600	-

1. Предварительно определяем относительные расходы:

на ширине отверстия моста в бытовых условиях

коэффициент стеснения потока насыпью со стороны правой поймы

то же со стороны левой поймы

2. Определяем предмостовой подпор.

Предварительно находим:

площадь под мостом в бытовых условиях

ω_м = 250·7 + 20·2,03 + 50·2 ≈ 1890 м²;

то же со срезкой

ω_м_(ср) = 250·7 + 70·3,6 = 2000 м²;

скорость потока на ширине отверстия моста в бытовых условиях

среднюю скорость потока под мостом с учетом осуществления 50% полного размыва (при фактическом коэффициенте размыва Р_ф = 1,15)

по формуле (9), где (см. п. 2.1), a = 1,19 (см. табл. 9 гл. VIII НИМП-72),

Тогда согласно формуле (8)

3. Выявляем по формуле (23), какую из пойм следует принять в качестве расчетной:

для левой поймы

для правой

Так как ζ_п > ζ_л, то правая пойма расчетная, т.е. вначале следует определять размеры дамбы со стороны этой поймы.

Примечание. Сопоставление параметров ζ_i сделано для наглядности, поскольку δ_п >> δ_л и местоположение мощной поймы не вызывает сомнения.

4. Определяем параметры φ_i по формуле (24).

Для мощной поймы ()

для слабой поймы

5. Определяем фактический и фиктивные уклоны свободной поверхности перед мостом по формулам соответственно (15) и (32).

Предварительно по формуле (11) находим

Фактический уклон свободной поверхности по формуле (15)

Для мощной поймы

для слабой поймы

6. Определяем скорость потока в голова дамбы со стороны мощной поймы по формуле (27).

Предварительно из уравнения (16) находим H_г = H_δ + ∆h_в = 2,233 м (см. определение H_г в примере приложения 1); по формуле (26)

по формуле (28)

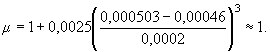
7. Определяем радиус кривизны токов в голове дамбы со стороны мощной поймы по формуле (29).

Предварительно по формуле (22) находим

по графику (см. рис. 8) при определяем (J'_м_(м))^β(1 - ∑δ_i)²^β = 0,169.

Тогда

8. Определяем скорость потока у подошвы дамбы v_g_м со стороны мощной поймы по формуле (14).

Предварительно определяем среднюю по сечению моста глубину потока H_м и глубину потока под мостом у подошвы дамбы h_g_м.

Для постового перехода имеет место неравенство L_м < B_уш (см. пример в приложении 1), поэтому согласно п. 2.4,а принимаем h_g_м = H_p = 7·1,15 = 8,05 м.

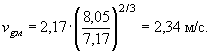
9. По формуле (20) или рис. 7 определяем при

10. По формулам (1) и (2) определяем соответственно длину вылета и ширину разворота верховой струенаправляющей дамбы со стороны мощной поймы:

l_в = 1,9²·35,3 = 127,5 м;

в = 1,9·35,3 = 67,0 м.

11. Для нахождения размеров верховой струенаправляющей дамбы со стороны слабой поймы определяем следующие параметры:

а) скорость потока в голове дамбы по формуле (31) или рис. 9 при и β = 0,213 имеем v_г_(с) = 0,64·0,53 = 0,34 м/с;

б) глубину потока у подошвы дамбы (расположенной со стороны вогнутого берега) h_g_м = h_maxP_ф = 8,3·1,15 = 9,55 м;

в) скорость потока у подошвы дамбы по формуле (14) при H_м = 7,17 м и v_м = 2,17 м/с (см. п. 8 примера)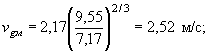

г) отношение полуосей дамбы по формуле (20) при

д) радиус кривизны токов в голове дамбы при

ρ_min(с) = 0,123^2/3·35,3 = 8,70 м;

в) ширину разворота и длину вылета дамбы соответственно по формулам (2) и (1):

в = 2,24·8,70 = 19,5 м.

l_в = 2,24²·8,70 = 43,6 м;

Приложение 3

ПРИМЕРЫ УЧЕТА КОСОГО ПЕРЕСЕЧЕНИЯ ВОДОТОКА ПРИ НАЗНАЧЕНИИ РАЗМЕРОВ СТРУЕНАПРАВЛЯЮЩИХ ДАМБ

Пример 1 (учет косого пересечения пойм).

Условия аналогичны изложенным в приложении 2. Подходная насыпь на правой пойме направлена вверх по течению. Место выхода насыпи за пределы разлива находится на расстоянии от створа моста S_ов = 1000 м (см. рис. 4,а). Найти размеры верховых струенаправляющих дамб. Так как S_ов > x₀ = 763 м, необходимо учитывать косое пересечение пойм подходами.

1. Определяем фактический и фиктивные уклоны свободной поверхности перед мостом.

Предварительно по формуле (10) находим параметр

по формуле (8) - предмостовой подпор

Фактический уклон свободной поверхности по формуле (32)

Фиктивные уклоны свободной поверхности по формуле (25):

для мощной поймы (φ_м = 0,86)

J'_м_(м) = 0,0002 + 0,86·0,000273 = 0,000435; для слабой поймы (φ_м = 0,08)

J'_м_(с) = 0,0002 + 0,08·0,000273 = 0,000221.

2. Определяем скорость потока в голове дамбы со стороны мощной поймы по формуле (27).

Предварительно из уравнения (16) находим H_г = 2,26 м; по формуле (26)

H_г = 2,26·0,86 + 2·(1 - 0,86) = 2,22 м;

по формуле (28)

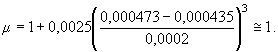
Следовательно,

3. Определяем радиус кривизны токов в голове дамбы со стороны мощной поймы по формуле (29) при β = 0,21. Предварительно по графику (см. рис. 8) при

J'_м_(м)(1 - ∑δ_i)² = 0,000435 - (1 - (0,415 + 0,051))² = 1,22·10^-4

находим:

[J'_м_(м)(1 - ∑δ_i)²]^β = 0,150;

4. По формулам (2) и (1) вычисляем ширину разворота и длину вылета верховой струенаправляющей дамбы со сторона мощной поймы

(при λ = 11,91 для ):

в = 1,91·29,4 = 56,2 м;

l_в = 1,914²·29,4 = 107,7 м.

5. Определяем размеры верховой струенаправляющей дамбы со стороны слабой поймы в такой же последовательности, как показано в п. 11 приложения 2. При этом скорость потока в голове дамбы практически равна скорости, подсчитанной без учета косины (v_г₍_c₎ = 0,34 м/с).

Поэтому λ = 2,24, Радиус кривизны токов в голове дамбы по формуле (30) δ_л_(с)/δ_п_(м) = 0,123 и ρ_min(м) = 29,4 м составляет ρ_min(с) = 0,123^2/3·29,4 = 7,25 м. Тогда в = 2,24·7,27 = 16,25 м, l_в = 2,24²·7,25 = 36,3 м.

Таким образом, расчеты показывают, что учет косого пересечения пойм подходами позволяет незначительно снизить размеры струенаправляющих дамб (см. таблицу).

Пример 2 (учет косого пересечения русла).

Условия аналогичны изложенным в приложении 2. Трасса перехода косо пересекает и поймы, и русло, как показано на рис. 4,б; S_ов = 1000 м. Определить размеры верховых струенаправляющих дамб.

Так как S_ов > x₀ = 763 м, то необходимо учитывать косое пересечение пойм подходами, что сделано в предыдущем примере. При этом устой со стороны правой мощной поймы расположен вверх по течению, а косина составляет при ширине правой поймы В_пп = 3000 м , поэтому настоящие Рекомендации позволяют рассчитывать размеры дамб. Согласно п. 5.3,б скорость потока у головы дамбы со стороны мощной поймы увеличиваем по сравнению с полученной в предыдущей примере на 10% v_г_(м) = 0,62·1,1 = 0,67 м/с. Далее для дамб со стороны мощной поймы определяем:

при по рис. 7 λ = 1,86;

по формуле (29) при [J'_м_(м)(1 - ∑δ_i)²]^β = 0,150;

по формулам (2) и (1) в = 1,86·34,2 = 63,6 м;

l_в = 1,86²·34,2 = 118,2 м.

Для слабой поймы имеем:

скорость в голове дамбы v_г_(с) = 0,53·0,67 = 0,355 м/с,

при 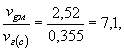λ = 2,2; радиус кривизны токов в голове дамбы при δ_л_(с)/δ_п_(м) = 0,123 и ρ_min(м) = 34,2 м равен ρ_min(с) = 0,123^2/3·34,2 = 8,45 м. Тогда в = 2,2·8,45 = 18,6 м, и l_в = 2,2²·8,45 = 40,9 м.

Следовательно, косое пересечение русла также незначительно снижает размеры струенаправляющих дамб (см. таблицу).

Размеры струенаправляющих дамб, м		Без косины	Косое пересечение поймы	Косое пересечение русла
Мощная пойма	в	67,0	56,2	63,6
Мощная пойма	l_в	127,5	107,7	118,2
Слабая пойма	в	19,5	16,25	18,6
Слабая пойма	l_в	43,6	36,3	40,9

Приложение 4

ПРИМЕР РАСЧЕТА СТРУЕНАПРАВЛЯЮЩЕЙ ДАМБЫ, ОТЖИМАЮЩЕЙ ПОТОК ОТ УСТОЯ

Определить плановые размеры верховой дамбы, расположенной со стороны вогнутого берега и предназначенной для отжатия пойменного потока от устоя. Отверстие моста L_м = 300 м; ближайшая к защищаемому устою опора находится на расстоянии l_i = 50 м. Плановые размеры верховой струенаправляющей дамбы, рассчитанные без отжатия, равны l_в = 125 м и в = 62,5 м (λ = 2); заложение откосов дамбы m = 2; глубина потока у подошвы дамбы в створе моста 5,7 м.

При по табл. 1 настоящих Рекомендаций принимаем косоструйность потока в створа моста α₀ = 15°; по табл. 2 Рекомендаций при α₀ = 15° и λ = 2 имеем в'/l_в = 0,401 и, l'_в/l_в = 0,528, откуда ширина разворота и длина вылета дамбы соответственно равны в' = 0,401·125 ≈ 50 м и l'_в = 0,528·125 = 66 м. По неравенству (41) определяем правильность принятого угла α₀. Для этого в табл. 2 Рекомендаций находим ∆l = 0,04·125 = 5 м и сопоставляем a mh_g_м = 2·5,7 = 11,4 > 5 м. Неравенство (41) соблюдается, следовательно, угол α₀ = 15° выбран правильно.

Приложение 5

ПРИМЕРЫ РАСЧЕТА УКРЕПЛЕНИЙ ОТКОСОВ СТРУЕНАПРАВЛЯЮЩИХ ДАМБ

Пример 1 (укрепление каминной наброской).

Рассчитать набросное укрепление на откосах (с коэффициентом m = 2) струенаправляющей дамбы со стороны мощной поймы. Исходные данные приведены в приложении 2. Известно также, что русловой откос дамбы необходимо защищать от волновых воздействий (расчетные высота и длина волны h_в = 0,5 м, λ_в = 3,0 м). Дамба отсыпается из среднезернистого песка с диаметром частиц d = 0,001 м.

1. Определяем доминирующие силовые воздействия по неравенству (42). Для вертикали у подошвы дамбы в створе мостового перехода v_дм = 2,34 м/с, поэтому правая часть неравенства (42) равна , что меньше левой части неравенства (42) 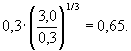Следовательно, продольные течения будут определять мощность укрепления.

2. Расчетную крупность однородного камня вычисляем по формуле (50)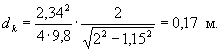

Если учитывать волновые воздействии, то по формуле (51) имеем (при γ_к/γ)

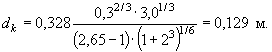
В качестве расчетной (требуемой) крупности однородного камня в наброске принимаем d_k = 0,20 м.

При необходимости дифференцирования мощности укрепления на откосах дамб на участке II (см. рис. 12) крупность камня должна быть не меньше 0,129 м (как при волновых воздействиях). Дифференцировать мощность укрепления возможно, так как удовлетворяется условие v_г < v_g_м, (64 < 0,4·2,34 = 0,94) согласно п. 7.11.

Принимаем для участка II расстояние по подошве струенаправляющей дамбы S = 1/3P. Тогда по формуле (57) скорость потока у подошвы дамбы на границе участков Скорость v_i = 1,35 v_д_i = 2,18 м/с. Для скорости v_i вычисляем правую часть неравенства (42) что больше 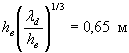. Следовательно, и на участке II определяющими будут продольные течения. По формуле (50) находим расчетную крупность однородного камня на участке II

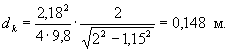В качестве расчетного принимаем камень крупностью 0,15 м.

3. Определяем требуемую конструкцию укрепления на I участке. Предварительно по формуле (60) с учетом данных табл. 6 находим размывающую скорость для части грунта в теле дамбы

Задаем наброску в три слоя, тогда по формуле (61) фактическая толщина наброски равна ∆_ф = 0,75·0,20·3 = 0,45 м.

По формуле (59) вычисляем требуемую толщину наброски

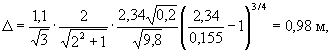, что больше ∆_ф. При семи слоях ∆_ф = 0,75·0,20·7 = 1,05 м, а 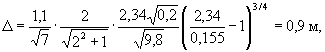что меньше ∆_ф. Следовательно, требуется устраивать наброску толщиной 1,05 м. Для уменьшения толщины слоя наброски рассмотрим вариант устройства щебеночной подготовки толщиной ∆_n = 0,15 м (крупность щебня d_n = 0,07 м). При трехслойном камне в наброске ∆_ф = 0,45 м,

Тогда по формулам (62) и (63) находим требуемую толщину наброски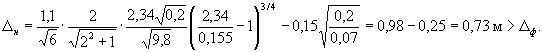

Следовательно, надо увеличивать толщину наброски или подготовку. Увеличиваем толщину подготовки до ∆_n = 0,25 м. Тогда при

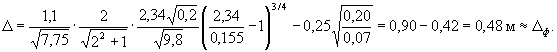
Итак, возможно использовать на участке I наброску камнем крупностью 0,2 м, уложенным в три слоя на подготовку толщиной 0,25 и из щебня крупностью 0,07 м.

Экономический расчет (с учетом производства работ) должен показать, какой из вариантов укреплений выгоден.

4. Определяем требуемую конструкцию укрепления на участке II.

Аналогичный расчет показывает, что для участка II требуется шесть слоев камня. Если принять три слоя камня и подготовку толщиной 0,25м, имеем при 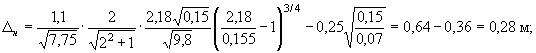при ∆_ф = 0,75·0,15·3 = 0,34 м удовлетворяется условие ∆_ф > ∆_н. Следовательно, конструкция выбрана правильно.

Пример 2 (укрепление сборными железобетонными плитами).

Рассчитать плитные укрепления на откосах дамбы для условий примера I. Длина ребра плиты в направлении образующей откоса B = 3,0 м.

1. Определяем доминирующие силовые воздействия.

Правая часть неравенства (43) равна при K_пл = 1 (плиты с открытыми швами

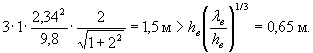
Поэтому продольные течения будут определяющими.

2. Определяем требуемую толщину железобетонных плит по формуле (54) при γ_пл = 2,4 т/м³

К расчету принимаем плиты толщиной 0,12 м.

3. Определяем конструкцию укрепления из железобетонных плит (при расчетной ширине швов ∆_ш = 0,02 м).

Конструкция плитного укрепления в данном примере требует устройства подготовки, так как не удовлетворяются неравенства;

и (64)

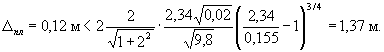
Задаем толщину щебеночной подготовки ∆_n_(ф) = 0,40 м, крупность d_n = 0,07 м и определяем по формуле (65) возможность выноса грунта из тела насыпи при такой конструкции укрепления при

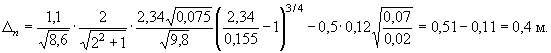
Толщина щебеночной подготовки выбрана правильно, так как ∆_n = ∆_n_(ф). Если можно использовать более мелкий щебень крупностью d_n = 0,035 м, то его потребовалось бы всего ∆_n_(ф) = 0,25 м. По Формуле (65) имеем при

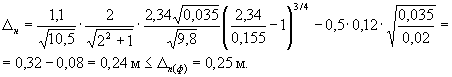
СПИСОК ЛИТЕРАТУРЫ

1. Рекомендации по регулированию потока на мостовых переходах через реки с осередковым типом руслового процесса (островного типа). М., изд. ЦНИИСа, 1977.

2. Рекомендации по регулированию потока на мостовых переходах через реки с меандрирующими руслами. М., изд. ЦНИИСа, 1978.

3. Наставление по изысканиям и проектированию железнодорожных и автодорожных мостовых переходов через водотоки (НИМП-72). М., Транспорт , 1972.

4. Строительные нормы и правила, Ч. П. Нормы проектирования. Гл. 57. Нагрузки и воздействия на гидротехнические сооружения (волновые, ледовые и от судов). СНиП II-57-75. М., Стройиздат, 1976.

5. Методические рекомендации по расчету гидрологических характеристик рек, пересекаемых трассой БАМа. М., изд. ЦНИИСа, 1976.

6. Технические указания по проектированию и производству буровзрывных работ при сооружении земляного полотна. ВСН 178-74. М., Оргтрансстрой, 1974.

7. Строительные нормы и правила. Ч.IV. Сметные нормы. Гл. 13. Буровзрывные работы. СНиП IV-13-71. М., Стройиздат, 1971.

8. Рекомендации по укреплению откосов сооружений мостовых переходов и насыпей на прижимных участках рек наброской из каменных материалов. М., изд. ЦНИИСа, 1979.