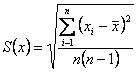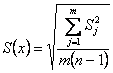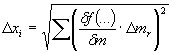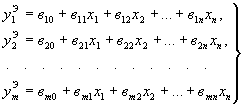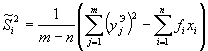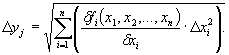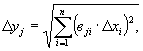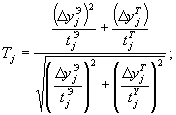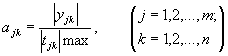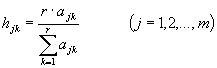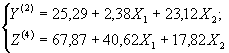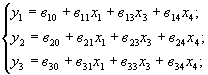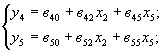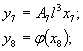НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ ГОССТРОЯ СССР (НИИСК)
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ИССЛЕДОВАНИЮ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ С ПРИМЕНЕНИЕМ МАТЕМАТИЧЕСКОГО И
ФИЗИЧЕСКОГО МОДЕЛИРОВАНИЯ
Одобрены секцией № 1
Научно-технического совета
НИИСК Госстрой СССР
Протокол № 24 от 17.09.86
КИЕВ 1987
СОДЕРЖАНИЕ
Изложены теоретические предпосылки и практические рекомендации по исследованию прочности и деформативности сложных строительных конструкций, основанные на системном анализе и функциональном моделировании. Применение методики позволит с максимальной эффективностью использовать средства автоматизации научных исследований и существенно сократить стоимость, трудоемкость и сроки их проведения.
Предназначены для научных работников, могут быть полезны инженерам-проектировщикам и аспирантам строительного профиля.
Разработаны кандидатами техн. наук Ф.В. Ярмульником и В.И. Кретовым (НИИСК Госстроя СССР).
ВВЕДЕНИЕ
Ускорение научно-технического прогресса в строительстве тесно связано с сокращением сроков исследований эффективных конструкций. Это обусловливает широкое использование ЭВМ во всем комплексе научных исследований.
Бурное развитие в последнее десятилетие численных методов строительной механики сложных пространственных сооружений, внедрение в инженерную практику разработанных на их основе универсальных программных комплексов показывают, что экономически и методически целесообразно проведение исследований сложных сооружений с применением расчетных моделей. В то же время применение математических методов сдерживается существующей в настоящее время диспропорцией между высоким уровнем автоматизации самого вычислительного процесса и отсутствием алгоритмических приемов построения расчетных схем реальных сооружений, что ставит получение результатов в зависимость от субъективных качеств исследователя.
Достоверные результаты могут быть получены экспериментально. Однако со сложностью конструкций и сооружений существенно возрастают трудоемкость, стоимость и сроки проведения исследований. Это относится и к методам физического моделирования.
В настоящих методических рекомендациях излагаются принципиальные положения оптимизации процесса исследований сложных строительных конструкций на основе системного анализа. При этом в решении поставленных задач рационально сочетаются методы физического и математического моделирования. Основной упор делается на математические методы. Физический эксперимент используется исключительно для уточнения и проверки расчетной модели объекта. Это обусловило применение целенаправленных физических моделей, разработанных на основе функционального подобия, благодаря чему существенно упрощается конструкция моделей, снижаются затраты ресурсов на эксперимент.
Максимально возможное выделение формальных методов при исследовании позволяет снизить влияние субъективных факторов на результаты, использовать автоматизацию. В то же время следует отметить, что роль неформальных методов при исследовании сложных конструкций по-прежнему остается значительной, что делает процесс проведения исследований сочетанием научных методов и искусства экспериментатора.
На современном этапе развития строительной науки, когда исследование сложных конструкций требует снижения затрат труда, времени и материальных средств, разработанные рекомендации вносят определенный вклад в создание комплексных методов исследований, позволяющих за счет ускорения испытаний и повышения информативности результатов создавать новые эффективные конструкции.
1. СИСТЕМНЫЙ ПОДХОД К ИССЛЕДОВАНИЮ СЛОЖНЫХ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ И СООРУЖЕНИЙ
1.1. Объект исследований как сложная система
1.1.1. В целях повышения эффективности исследований сложных строительных конструкций, возможности их максимальной автоматизации и снижения затрачиваемых ресурсов целесообразен подход, основанный на методологической концепции системного анализа [1...3] как одной из основных особенностей современной науки и техники. Это позволит выделить одинаковые для всех типов конструкций процедуры и этапы работ, максимально исключающие субъективность и направленные на оптимальное решение поставленных проблем.
Отсутствие единого теоретического обоснования или даже унифицированной совокупности методов, общих для всех объектов приложения системного анализа вынуждает для каждой проблемы строить свою методологию, впрочем, с обязательным включением общих принципов системности - ряда формальных и неформальных процедур.
1.1.2. Системный подход при исследовании сложных строительных конструкций носит комплексный характер. Объект исследования (конструкция или сооружение) рассматривается как сложная система со всеми необходимыми признаками: наличие подсистем (элементов), объединенных связями (физические, логические, математические), а также выполнение условия целостности функционирования.
1.1.3. В системном анализе при исследовании строительных конструкций выделяются следующие основные логические элементы - исходные категории: цель (или цели); исследования альтернативные средства достижения цели (физическое или математическое моделирование); ресурсы для решения проблемы; система связей между целями, средствами и ресурсами; критерии выбора предпочтительных альтернатив.
1.1.4. При системном подходе выбор методов исследований строительных конструкций производится с учетом их роли в целом. Оптимальные характеристики элементов системы - физических нематематических моделей-- предполагают рассмотрение их как единого средства достижения цели. Поэтому физический и численный эксперименты должны быть с самого начала согласованы между собой, ориентированы на эффективное решение задач исследований, дополняя друг друга.
1.1.5. Исследования строительных конструкций и сооружений выполняются экспериментальными методами на натурных образцах и физических моделях либо теоретическими, с использованием расчетных моделей.
Физическое моделирование, основанное на теории простого или расширенного подобия, по мере усложнения задач исследований все менее целесообразно, так как не решает задач снижения трудоемкости и стоимости изготовления моделей, соблюдения планируемых сроков эксперимента.
1.1.6. Развитием численных методов расчета сложных конструкций, применением ЭВМ, широким внедрением в инженерную практику универсальных и специальных программных комплексов обусловливается экономическая целесообразность широкого использования в исследованиях сооружений расчетных моделей с назначением достоверных расчетных схем сооружений, ориентированных на решение конкретных исследовательских задач. Однако существующей в настоящее время диспропорцией между высоким уровнем автоматизации самого расчета и методикой построения достоверных расчетных схем реального сооружения существенно снижается надежность численных исследований, вносится известная доля субъективности в получаемые результаты.
Традиционно экспериментальные и численные исследования проводятся независимо друг от друга. В лучшем случае сопоставляются результаты. При этом проведенный анализ нисколько не повлияет на саму стратегию и методику эксперимента. Все это исключает существенное ускорение и повышение результативности работ.
1.1.7. Физический и численный (математический) эксперименты рассматриваются как единая система средств (организованный комплекс), направленных на наиболее эффективное решение задач исследования.
Расчетные и физические модели, как элементы системного анализа, по сравнению с аналогичными моделями, используемыми в обычных исследованиях, характеризуются целенаправленностью и ясностью. Системный подход обусловливает применение нового класса физических моделей, разработанных с использованием функционального подобия, что существенно упрощает их конструкцию и уменьшает объем экспериментальных исследований.
1.1.8. Сочетание при исследовании сложных строительных конструкций методов физического и математического моделирования обусловливает целесообразность применения принципа декомпозиции (членения) объекта исследований на более простые элементы, раздельные испытания которых потребуют гораздо меньше ресурсов по сравнению с испытаниями всей системы. Особенно этот принцип эффективен при исследовании сооружений, состоящих из большого количества однотипных элементов и узлов.
Расчетная модель системы может быть получена путем композиции расчетных моделей подсистем с проверкой их адекватности, что существенно упрощает процедуру установления достоверности.
1.1.9. В основу декомпозиции по п. 1.1.8 настоящих методических рекомендаций должны быть положены принципы, обеспечивающие системный подход к организации исследований:
затраты ресурсов на ведение работ должны быть меньше, чем без членения;
принцип декомпозиции должен выполняться с обеспечением независимости результатов исследований отдельных подсистем;
из возможных вариантов декомпозиции предпочтительнее тот, при котором порядок членения, определяемый максимальным количеством неизвестных расчетных параметров в каждой подсистеме, будет наименьшим.
При декомпозиции сложной системы важную роль играют так называемые неформальные методы, основанные на опыте и интуиции исследователя.
1.1.10. Рассматривая процесс исследования строительных конструкций как некоторую систему, необходимо выделить в ней три основные подсистемы:
экспериментальные исследования на физических моделях;
расчетные исследования на математических моделях;
связь между экспериментом и расчетом, включающая идентификацию некоторых параметров расчетной модели, проверку ее адекватности и корректировку.
1.1.11. В научном понимании между физическими и расчетными моделями существует общность (каждая из них представляет собой упрощенное воспроизведение процессов, происходящих в реальной системе и внешней обстановке).
Различие между ними заключается в средствах представления объекта исследований: физические модели - материальные системы, математические или расчетные - знаковые.
Общность физических и математических моделей обусловливает единообразие описания их характеристик и воздействий (входные параметры), а также функциональных параметров их состояния (выходные параметры), для чего используются символика и некоторые основные понятия теорий множеств и алгоритмов.
1.1.12. Признаки, по которым исследуемый объект выделяется из ассортимента других, образуют множество параметров Р. Изменение внешних условий, влияющих на состояние объекта. характеризуется множеством воздействий нагрузок N = {nK}. Естественно, что множества Р и N включают в себя лишь свойства и воздействия, связанные с изучаемой проблемой. Как правило, они определяются вместе с постановкой задачи до начала исследований.
В расчетных моделях объекта исследований множество Р разбивается на два подмножества: М = {т2} (параметры объекта, известные априори) и Χ = {хi} (параметры, подлежащие определению в процессе исследований).
При этом Р = МUX. Таким образом, результат исследований - множество параметров напряженно-деформированного состояния Y = {yi}.
1.1.13. Множества Р, Y должны однозначно характеризовать в интересующем исследователя аспекте, состояние и поведение объекта исследований как до, так и после приложения воздействий N. При решении конкретных исследовательских задач необходимо обращать внимание на корректность их выбора, руководствуясь тем, что между множествами N, Р и У устанавливается функциональное соответствие, которое будет заключаться в следующем:
Каждые
![]()
поставлены в соответствие хотя бы одному элементу
![]() ;
;
каждому
![]()
соответствуют единственные непустые множества
![]() ,
,
причем этим подразумевается наличие некоторой функции
![]() ,
,
Примечание. В математике слово
"функция" употребляется в чрезвычайно широком смысле. В нашем же
случае под функцией у = f(х)
будем понимать
всякое правило (закон), ставящее в соответствие каждому ![]() некоторый
единственный элемент
некоторый
единственный элемент ![]() . Множество χ
- область определения функции, Y -
множество значений. Основа функции - алгоритм (предписание), позволяющий по
каждой совокупности исходных данных из некоторого числа множеств, возможных для
данного алгоритма, получить результат, если таковой существует, в противном
случае - не получить ничего.
. Множество χ
- область определения функции, Y -
множество значений. Основа функции - алгоритм (предписание), позволяющий по
каждой совокупности исходных данных из некоторого числа множеств, возможных для
данного алгоритма, получить результат, если таковой существует, в противном
случае - не получить ничего.
Совокупность всех исходных данных, к которым применим данный алгоритм, называется областью его применимости., которая совпадает с областью определения функции, задаваемой им. Два алгоритма считаются равносильными, если совпадают области применимости, а для любого объекта, взятого из этой области, сходятся результаты обоих алгоритмов. Каждый алгоритм может быть записан в конечном счете с помощью слов и необходимых математических символов.
1.2. Схема процесса исследования
1.2.1. Системный подход по разд. 1.1 позволяет строить процесс исследований напряженно-деформированного состояния сложных конструкций и сооружений (рис. 1) в виде шаговых процедур, наиболее эффективно ведущих к достижению поставленной перед исследователем цели.
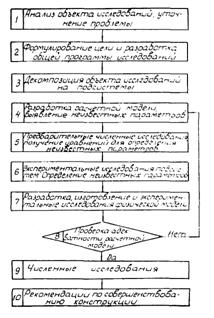
Рис. 1. Блок-схема процесса исследований
Шаг 1. Исследования сложных строительных конструкций следует начинать с подробного анализа объекта исследований и состояния вопроса по данной проблеме:
изучение рабочих чертежей и другой документации, относящейся к исследуемому объекту;
анализ условий работы и функционального назначения объекта;
выявление отличительных признаков и особенностей данного объекта по сравнению с аналогичными, ранее исследованными;
ознакомление с методиками и результатами проведенных ранее исследований.
На основании проведенного анализа оцениваются важность и новизна проблемы. Уточняется задача исследований с учетом имеющихся ресурсов, их потребности и возможных директивных ограничений на них.
Шаг 2. После уточнения задачи формулируется цель (цели) исследований, что весьма важно, так как от четкости поставленной цели зависят организация решения проблемы, ее стратегия и тактика. Правильно выбранная цель позволяет рационально распределить ресурсы. Работа исследователя на этом этапе характеризуется следующими принципами:
разбить общую цель на несколько более конкретных подцелей;
при определении цели назначить параметры, позволяющие в наиболее явной и конкретной форме представить результат;
по возможности сформулировать несколько вариантов целей в зависимости от потребности в ресурсах для их достижения, провести анализ и оценку распределения имеющихся ресурсов.
После формулировки окончательной цели разрабатывается общий план (программа) исследований - методы организации работы и решения поставленных задач.
Так как на первых этапах исследований почти нет формальных методов, они должны выполняться исполнителем высокого уровня подготовки.
Шаг 3. Производится анализ функциональных связей и особенностей работы отдельных элементов сложного объекта для возможной декомпозиции сложной системы на некоторое количество более простых подсистем.
Шаг 4. После членения для каждой подсистемы формулируются частная задача и цель исследований. В соответствии с этим для каждой i-той подсистемы выбираются наиболее подходящие априори расчетные модели и определяется своя система множеств известных Mi, неизвестных Хi, воздействий Hi и параметров напряженно-деформированного состояния Yi.
Шаг 5. Производятся экспериментальные исследования отдельных подсистем - элементов и узлов, а также экспериментально определяются параметры напряжённо-деформированного состояния Yoi, необходимые для последующего определения неизвестных параметров Xi соответствующих расчетных моделей.
Шаг 6. На расчетных моделях подсистем проводятся предварительные численные исследования. С использованием данных эксперимента определяются неизвестные параметры расчетных моделей Xi. Синтезируется общая расчетная модель объекта исследований.
Шаг 7. На основании метода функционального подобия разрабатывается физическая модель всего объекта исследований, проводятся ее экспериментальные исследования.
Шаг 8. Проверяется адекватность общей расчетной модели статистическим сопоставлением результатов эксперимента и численных исследований функционально подобной модели. Если такая проверка дала положительный результат, переходят к следующей процедуре; в противном случае анализируются причины неадекватности и уточняется общая расчетная модель вплоть до новых вариантов расчетных моделей отдельных подсистем.
Шаг 9. После того, как адекватность расчетной модели установлена, выполняются многовариантные численные исследования в объеме, необходимом для ответа на поставленные перед исследователями вопросы.
Шаг 10. Результаты исследований оформляются в установленном порядке с фиксированием достижения поставленной цели. Как правило, исследования заканчивают рекомендациями по совершенствованию конструкции.
Предложенная схема разбивки процесса исследований на шаговые процедуры не единственна: в зависимости от характера исследований некоторые шаги могут отсутствовать или, наоборот, появятся новые, изменится их порядок. Стратегия же, заключающаяся в выборе и построении расчетной модели объекта, адекватной натуре, остается неизменной.
1.2.2. Вопреки сохраняющейся ведущей роли субъективных суждений исследователя (особенно на первых шагах) в рекомендуемой схеме имеется возможность максимально выделить ряд формальных методов и процедур, что делает процесс более воспроизводимым, логически обоснованным и позволяет максимально применить автоматизацию и ЭВМ, повысив эффективность исследований, снизив трудоемкость, стоимость и сроки проведения.
1.3. Математическое моделирование работы строительной конструкции
1.3.1. Совокупность математических выражений, отражающих связь между параметрами описания и поведения системы, а также способ их преобразования, приводящий к отысканию значений параметров, принимаемых неизвестными, условимся считать математической моделью процесса, явления, системы.
Применительно к расчету строительной конструкции параметрами описания системы будут геометрия и топология системы, характеристики материалов, топология и характеристика воздействий.
Параметры поведения системы - изменения геометрии и топологии системы, характеристик материалов и напряжений.
1.3.2. Задачи, в которых известны параметры описания системы, а не известны - поведения, принято называть прямыми, решаемыми классическими методами строительной механики, теории упругости, сопротивления материалов. Для решения основных типов таких задач разработаны методы решения и составлены программы для ЭВМ, позволяющие автоматически получать результаты, изменяя исходные данные. Решение, как правило, вытекает из детерминированной системы уравнений, однозначно связывающей исходную информацию о системе с результатом расчета.
Задачи, в которых неизвестные - некоторые параметры описания системы, называются обратными [6] и решаются методами идентификации систем [7] с применением систем уравнений, количество которых существенно превышает количество неизвестных. Применительно к строительным конструкциям такие задачи возникают при экспериментальных исследованиях, в том числе при реконструкции зданий и сооружений, и связаны с определением жесткости элементов, узлов и опорных частей, а также величины действующей нагрузки [8, 9].
1.3.3. Математические модели работы строительных конструкций вытекают из следующих основных вариационных принципов механики:
возможных изменений перемещений (возможной работы); как частный случай, известный принцип Лагранжа, связанный с понятием полной потенциальной энергии деформации, получаем дифференциальные уравнения равновесия;
возможных изменений напряженного состояния (возможной дополнительной работы); частный случай - принцип Кастильяно, связанный с понятием дополнительной потенциальной энергии деформации; получаем дифференциальные уравнения равновесия [10, 11].
Построение смешанного функционала позволяет получить уравнения смешанного метода [12, 13].
Данные принципы и методы решения систем уравнений применялись для решения задач анализа континуальных систем типа пластин и оболочек. При этом для решения дифференциальных уравнений могут быть привлечены математические методы дискретизации, позволяющие свести задачу к решению дифференциальных уравнений в частных производных или к системе алгебраических уравнений [14, 15]. Сущность такого подхода в физическом смысле соответствует замене систем с бесконечным количеством степеней свободы системой c конечным числом степеней свободы, эквивалентной первой в энергетическом смысле.
1.3.3. Математическая сущность подхода к расчету конструкций на основе идеализации континуальной среды дискретными элементами, названного методом конечных элементов - МКЭ [16, 17] обоснована заменой системы дифференциальных уравнений системой алгебраических, имеющих каноническую форму (структура инвариантна по отношению к конкретному виду конструкций), в матричной форме записываемую в виде:
|
АΧ = Р + F, |
(1) |
где A - матрица коэффициентов системы, зависящая от параметров описания системы; Р - матрица, зависящая от параметров описания воздействий на систему; X - матрица неизвестных, зависящая от параметров поведения системы; F - матрица параметров начального состояния системы.
1.3.4. Наиболее распространенным МКЭ следует считать в форме метода перемещений, для которого матрица A имеет смысл матрицы реакции или жесткости системы, а Χ - матрица смещений, Р - матрица силовых воздействий, F - матрица начальных усилий.
Порядок системы уравнений (1) определяется числом степеней свободы расчетной модели. Применительно к методу перемещений ими станут возможные перемещения точек или сечений, называемых узлами, перемещения которых однозначно определяют расчетное деформированное и напряженное состояние системы, что достигается представлением континуальной среды системой элементов, имеющих конечные размеры и конечное число степеней свободы.
1.3.5. Конечные элементы (КЭ) соединяются между собой в точках или по линиям. Исходя из принципа виртуальной работы для каждого КЭ должно быть назначено возможное поле перемещений, описываемое аппроксимирующими полиномами-функциями формы [18]. Напряженное состояние каждого КЭ - производная функции формы, или независимая функция.
1.3.6. Напряженное и деформированное состояние расчетной модели рассматривается как линейная комбинация состояний отдельных элементов системы, удовлетворяющая условиям совместности деформирования и равновесия.
Расчетная модель конструкции состоит из двух частей: расчетной схемы и набора аппроксимирующих функций. Расчетной схемой можно считать графическое или зрительное представление конструкции, составленное из набора расчетных элементов, связей между ними, и граничных условий закрепления.
1.3.7. Ввиду того, что уровень теоретических разработок в области расчета конструкций МКЭ достаточно высок и доведен до практического применения, все этапы расчета и связь между ними осуществляются программно.
При выборе программы (табл. 1) необходимо, в первую очередь, определить ее возможности с точки зрения аппроксимации заданного конструктивного решения соответствующими расчетными элементами. При расчете стержневых систем альтернативы, как правило, не возникает поверхностей или трехмерных тел - появляется необходимость точного описания поверхности и опорного контура, что достигается сочетанием набора КЭ, имеющих различную форму и количество контактирующих узлов или линий. В меньшей степени представляет интерес набор аппроксимирующих функций, положенных в основу алгоритма вычисления матрицы жесткости или напряжений КЭ. Однако для некоторых модификаций МКЭ, например метода пространственных конечных элементов - МПКЭ, положенного в основу программного комплекса КОНТУР [19], выбор и назначение функций формы осуществляется индивидуально, поскольку от этого зависит конечный результат.
1.3.8. Приступая к расчету конкретной конструкции, следует представить конструктивное решение в виде расчетной схемы, удовлетворяющей условиям и требованиям по разд. 2.1, закодировать в соответствии с инструкцией к программе всю информацию о расчетной модели и получить ряд числовых массивов, каждый из которых имеет определенное смысловое содержание:
1. Общее описание системы и задачи в целом
2. Структура системы
3. Геометрия системы
4. Граничные условия
5. Характеристики материалов
6. Данные о воздействиях
7. Данные для обработки результатов.
Кроме того, может привлекаться служебная и вспомогательная информация, способствующая организации процесса обработки и счета, а также контроля исходных данных. Содержание информации может быть избыточным, но непротиворечивым. В случаях, когда это возможно, программными средствами организуется логический и смысловой контроль исходной информации.
1.3.9. Содержание числовых массивов, однозначно соответствующее расчетной модели, классифицируется как информационная или цифровая модель системы. В понятие информационной модели также входит и система логических связей между массивами, обычно реализуемых с помощью программного средства.
1.4. Физическое моделирование
1.4.1. Физическое моделирование (физический эксперимент) представляется важной частью исследований, несмотря на то, что это наиболее ресурсоёмкий процесс, требующий участия большого количества исполнителей различных специальностей и квалификации. В целях ускорения и повышения эффективности таких исследований с позиции системного подхода объем его должен быть необходимым и достаточным для решения задач:
определения и уточнения неизвестных параметров расчетных моделей;
проверки адекватности расчетной модели (устанавливается критерий оценки ее достоверности и точности).
|
Наименование программы |
Назначение |
Метод, возможности программы |
Организация-разработчик |
|
ППП АПЖБК (ЛИРА) |
Расчет пространственных систем |
МКЭ, стержни, плиты, пластины статика, динамика, сейсмика, нелинейность, РСУ, подбор арматуры |
НИИАСС Госстроя УССР (Киев) |
|
ПРОКРУСТ |
То же |
То же, суперэлементы |
Донецкий ПромстройНИИпроект Госстроя УССР |
|
МАРСС-ЕС |
Расчет пространственных стержневых систем |
МКЭ, статика, динамика сейсмика, подбор арматуры |
ЦНИИпроект Госстроя СССР, (Москва) |
|
ПРОЧНОСТЬ |
Расчет пространственных систем |
МКЭ, библиотека, КЭ, с та тика, динамика, нелинейность |
КИСИ (Киев), Минвуз УССР |
|
ИКАРУС, ФЕНИКС |
Расчет плоских и пространственных пластинчатых систем |
МКЭ, пластины, нелинейность |
Кишиневгорпроект (Горисполком) |
|
КАПРИЗ |
Расчет плит с учетом трещин |
МКЭ, нелинейность, статика |
Киев, ЗНИИЭП (Госгражданстрой) |
|
СПРИНТ |
Расчет конструкций зданий и сооружений |
МКЭ, плоские и пространственные КЭ, статика, динамика, сейсмика, температура, нелинейность |
МИИТ (Москва), Минвуз СССР |
|
КОНТУР |
Расчет зданий и сооружений как простран- |
Метод пространственных КЭ, упругие связи, нелинейность материала и основания, статика, динамика, сейсмика |
НИИСК Госстроя СССР, (Киев) |
|
ТОСТ |
Расчет зданий с несущими стенами |
Составные тонкостенные стержни, статика, динамика, сейсмика, упругое основание |
Киевпроект, (Горисполком) |
1.4.2. Физической моделью считается материальная система, свойства и параметры которой подобны реальному объекту, с контролируемыми входными и выходными параметрами, оснащенная необходимыми измерительными приборами и нагружающими устройствами. В качестве таковой может быть использован и сам объект исследований, если он подготовлен соответствующим образом к испытаниям.
1.4.3. Физическое моделирование включает:
разработку методики экспериментальных исследований, рабочих чертежей модели и приспособлений для ее испытаний;
изготовление и монтаж модели и приспособлений для испытаний;
подготовку модели к испытаниям, оснащение ее приборами и тензометрическими датчиками;
испытание модели в соответствии с методикой исследований;
обработку результатов эксперимента (не являясь окончательной целью исследований, они служат исходными данными для построения и проверки адекватности математических моделей объекта исследований).
1.4.4. Особые требования к эксперименту следует предъявлять при системном подходе к исследованиям сложных строительных конструкций с использованием прямой и обратной связи между физическим и математическим моделированием. Однако ввиду того, что результат даже наиболее тщательно подготовленного эксперимента носит случайный характер, каждый раз в обязательном порядке необходимо завершать процесс анализом и оценкой степени риска от той или иной ошибки в полученных результатах с применением методов математической статистики. Если величина ошибки или риска настораживает, рекомендуется идти по пути ее уменьшения применением более точной методики наблюдений, устранением наиболее значительных помех и т.д.
1.4.5. Наибольшие погрешности в результатах эксперимента (систематические, грубые и случайные) связаны с:
неоднородностью физико-механических и неточностью геометрических характеристик объекта исследований;
несовершенством устройств, создающих необходимое воздействие на объект;
изменением внешних условий;
погрешностью измерительного комплекса.
1.4.6. Систематическими по п. 1.4.5 считаются ошибки, повторяющиеся и одинаковые по всей серии наблюдений, проводимых единым методом с помощью одних и тех же измерительных приборов. Основная их особенность - то, что они входят в общую ошибку измерений, благодаря чему возможно в значительной степени их исключение с введением соответствующей поправки.
Один из способов уменьшения систематической ошибки - калибровка измерительных приборов до начала эксперимента. Для определения систематической ошибки измерительного комплекса во время эксперимента рекомендуется параллельно с измерением физических величин на исследуемом объекте устанавливать аналогичные величины тем же измерительным комплексом на объекте-эталоне, дающем возможность выполнять измерения другим методом, точность которого превышает точность метода, используемого в эксперименте.
1.4.7. Грубые ошибки по п. 1.4.5 настоящих методических рекомендаций вызываются резким изменением (флуктуацией) во время испытаний внешних условий, невнимательностью экспериментатора и пр. В отличие от систематической ошибки, характеризуемой неизменностью во всей серии испытаний, грубая присутствует не более чем в одном-двух испытаниях и характеризуется резким отличием по абсолютной величине от рядовых ошибок измерений.
Учесть ее заранее невозможно, поэтому необходимо повышать уровень подготовки и проведения испытаний. Если, вопреки тщательности эксперимента, появляются сомнения в каком-либо показателе, его отбрасывают. Во всех сомнительных случаях используются специальные статистические критерии, позволяющие объективно выделять в каждой серии измерений имеющиеся грубые ошибки [20].
1.4.8. Случайные ошибки (cм. п. 1.4.5) различны по величине и непредсказуемы даже при измерениях, выполняемых одинаковым способом. Однако их распределение симметрично относительно нуля, т.е. при отсутствии систематических и грубых ошибок истинный результат измерений является математическим ожиданием соответствующей случайной величины.
В соответствии с ГОСТ 8.207-76 [22] результаты прямых измерений параметров должны быть представлены в форме:
|
|
(1) |
где ![]() - результат измерений (математическое
ожидание); Δx - доверительные границы измеренной величины; Р - доверительная вероятность
(надежность выполненных измерений), обычно в экспериментах принимаемая равной
0,9 и 0,95.
- результат измерений (математическое
ожидание); Δx - доверительные границы измеренной величины; Р - доверительная вероятность
(надежность выполненных измерений), обычно в экспериментах принимаемая равной
0,9 и 0,95.
1.4.9. В подавляющем большинстве реальных испытаний при количестве повторяемых наблюдений n < 15 случайные ошибки измерений по п. 1.4.8 распределяются по нормальному закону. В этом случае характеристики измеренной величины, приведенные в (1), вычисляются по формулам:
|
|
|
|
|
где n - число результатов наблюдений одной величины; xi - i-тый результат наблюдения; t(p.f) - коэффициент Стьюдента, в зависимости от доверительной вероятности Р и числа степеней свободы f = n - 1, определяемый по таблицам t-распределения; S(х) - среднее квадратическое отклонение результата измерений, оцениваемое по формуле:
|
|
(3) |
1.4.10. Статистическая обработка результатов измерений по пп. 1.4.8 и 1.4.9 используется при оценке одной величины (например, физико-механических характеристик материалов конструкций). В процессе же экспериментальных исследований строительных конструкций проводятся измерения большой группы однородных величин, хотя не всегда имеется возможность повторять измерения по 6 - 10 раз. В случае допущения о равной точности приборов одного типа можно получить достаточно достоверные доверительные интервалы Δх, используя при обработке результаты всех наблюдений. При этом число повторных наблюдений может быть сокращено не менее чем до двух.
Пусть выполнены измерения группы из т однородных величин и повторены п раз. Для каждой величины вычисляются выборочные средние значения и выборочные дисперсии:
![]() ;
;
|
|
Так как
дисперсии равноточных измерений одинаковы, средняя квадратическая ошибка S(x) будет одинакова для всех ![]() :
:
|
|
(5) |
а доверительный интервал Δx может быть установлен по формуле (2) с определением коэффициента Стьюдента при числа степеней свободы f = n - 1.
1.4.11. В случае принятия в качестве результата экспериментальных исследований таких физико-механических характеристик объекта u = f(x1, x2,..), которые получаются в результате математических действий с несколькими случайными величинами xt, каждая из которых измерена непосредственно с доверительными интервалами Δxt при одинаковой доверительной вероятности Р, доверительный интервал функции оценивается по формуле:
|
|
(t = 1, 2, …., k).
1.5. Определение неизвестных параметров расчетных моделей
1.5.1. Для использования расчетных моделей при проведении численных исследований объекта необходимо, чтобы все параметры расчетной модели* были известны. Часть ее параметров (множество М = {mτ}) известна до начала исследований (например, геометрические размеры, граничные условия и т.д.), некоторые же (множество Χ = {xi}) не известны** и не могут быть достоверно вычислены только теоретически. Для их определения проводится специальный физический эксперимент.
* Расчетная модель считается заданной, если имеются в наличии расчетная схема и алгоритм, а при использовании ЭВМ - также программный комплекс, численно реализующий применяемый теоретический метод.
** Как правило, неизвестными параметрами расчетных моделей являются физико-механические характеристики элементов исследуемого объекта (например, жесткости отдельных участков конструкции, податливости узлов и т.д.), реже - геометрические характеристики некоторых расчетных элементов, аппроксимирующих в расчетной схеме реальный конструктивный элемент
1.5.2. Определение неизвестных параметров расчетных моделей по п. 1.5.1. с использованием результатов экспериментов выполняется двумя методами - прямым (неизвестный параметр получают непосредственно во время физического эксперимента измерением соответствующими приборами) и косвенным (неизвестные характеристики вычисляются как некоторые функции параметров, достоверно определенных в эксперименте).
1.5.3. Для дальнейшего корректного использования в расчетных моделях найденных по п. 1.5.2 параметров необходимо учитывать вероятностный характер результатов эксперимента.
1.5.4. При прямом методе определения неизвестных параметров сначала производится предварительная статистическая обработка полученных результатов, предполагающая исключение систематических погрешностей и резко выделяющихся значений (грубые ошибки измерений), затем - точечная и доверительная оценка параметра по формулам (2).
1.5.5. При косвенном методе определения неизвестных параметров возможны два случая:
неизвестный параметр - известная аналитическая функция других параметров, достоверно определяемых из эксперимента;
функциональная зависимость между неизвестными параметрами, полученными в эксперименте, не может быть представлена в виде аналитической функции.
В первом случае при:
|
xi = fi(mr), |
(7) |
(i = 1, 2, …., n; r = 1, 2, …, s)
точечная оценка неизвестного параметра:
|
|
(8) |
где ![]() - точечные оценки неизвестных
параметров;
- точечные оценки неизвестных
параметров; ![]() - точечные
оценки параметров, получаемых непосредственно в результате прямых измерений,
которые находим по формуле, аналогичной (2).
- точечные
оценки параметров, получаемых непосредственно в результате прямых измерений,
которые находим по формуле, аналогичной (2).
Доверительная оценка при заданной доверительной вероятности:
|
|
(9) |
где Δmr - доверительные интервалы параметров, получаемых непосредственно из эксперимента, которые определяем по формуле, аналогичной (2).
1.5.6. При решении задачи определения параметров расчетной модели во II случае имеем обратную функциональную зависимость:
|
yj = φj(m1, m2, …, mr, x1, x2, …, xn), |
(10) |
(j = 1, 2, …, m)
где yj - некоторый параметр напряженно-деформированного состояния конструкции, измеряемый экспериментально.
1.5.7. Как правило, количество измеряемых по п. 1.5.6 параметров должно быть больше или равно количеству неизвестных:
m > n. В этом случае задача определения неизвестных параметров расчетной модели включает:
аппроксимацию функции (10) полиномами сравнительно невысоких степеней;
приведение полученной системы m - нелинейных уравнений к избыточной m - l - линейных, причем m - l ≥ n;
определение точечных и доверительных оценок xi подстановкой в уравнение экспериментальных значений уэi - и приведением избыточной системы линейных уравнений к системе нормальных уравнений метода наименьших квадратов [21].
1.5.8. Аппроксимация функций (10) полиномами по п. 1.5.7 проводится с применением математической теории планирования экспериментов [23, 24], для чего при помощи выбранной расчетной модели объекта выполняется серия численных экспериментов-расчетов, в которых искомые неизвестные параметры расчетной модели варьируются на нескольких уровнях, назначаемых априори из опыта и по интуиции исследователя.
1.5.9. В случае, когда заранее известно, что между показателем напряженно-деформированного состояния yj и неизвестными параметрами расчетной модели существует линейная зависимость, проведение численного эксперимента осуществляется по матрицам планирования (см. приложение 1), а функция (10) аппроксимируется полиномом первой степени:
|
|
(i = 1, 2,… n; j = 1, 2, …, m)
где
|
|
![]()
N - число
расчетов - строк матрицы планирования; ![]() - расчетное значение,
параметра yj в
К-том расчете; lki - элемент
матрицы планирования на пересечении К -той строки и i-того
столбца.
- расчетное значение,
параметра yj в
К-том расчете; lki - элемент
матрицы планирования на пересечении К -той строки и i-того
столбца.
Примечания: 1. При этом неизвестные параметры расчетной модели варьируются в двух уровнях: (+1) - в верхнем и (-1) - в нижнем.
2. В зависимости от количества неизвестных параметров матрицу планирования выбираем, принимая наименьшую матрицу, число строк которой N > п, а количество столбцов равным n (лишние столбцы выбранной матрицы вычеркиваются).
1.5.10. В случае, когда устанавливается наличие линейной зависимости между yj, и xi, с точностью, достаточной для решения практических задач, функцию (10) достаточно аппроксимировать полиномом второй степени:
|
|
(i = 1, 2, …, n; j = 1, 2, …, m; K = 1, 2, …, n; K ≠ i)
с варьированием неизвестных параметров расчетной модели трех уровнях:
верхнем (+1);
среднем (0);
нижнем (-1)*.
Примечание. Матрицы планирования второго порядка и формулы для вычисления коэффициентов уравнений (13) см. в приложении 1.
* Значения неизвестных параметров расчетной модели, соответствующие среднему значению, называются также центром плана и обозначаются xoi. Натуральные значения верхнего и нижнего уровня рассматриваемого параметра определяется по формулам ximax = Χoi + Р и ximin = Χoi - P, где P - интервал варьирования параметра хi.
1.5.11.
Система нелинейных уравнений (13) может быть приведена к системе линейных, для
чего количество параметров ![]() , намеченных для измерения в физическом эксперименте, должно
быть больше количества неизвестных параметров расчетной модели, как минимум, на
число нелинейных членов. После несложных алгебраических преобразований
нелинейные члены могут быть исключены, тогда общее число уравнений в системе (13) будет т - l, где l - число нелинейных членов. Более эффективен метод обеспечения
адекватности линейных уравнений (11),
выражающийся в переходе на новую систему неизвестных параметров расчетной
модели. На основании теории подобия и размерностей можно записать безразмерные
комплексы - критерии подобия исследуемого объекта, включающие известные и
неизвестные параметры расчетной модели, причем количество используемых
критериев подобия должно быть равно числу неизвестных параметров ( к =
1, 2,.., n).
, намеченных для измерения в физическом эксперименте, должно
быть больше количества неизвестных параметров расчетной модели, как минимум, на
число нелинейных членов. После несложных алгебраических преобразований
нелинейные члены могут быть исключены, тогда общее число уравнений в системе (13) будет т - l, где l - число нелинейных членов. Более эффективен метод обеспечения
адекватности линейных уравнений (11),
выражающийся в переходе на новую систему неизвестных параметров расчетной
модели. На основании теории подобия и размерностей можно записать безразмерные
комплексы - критерии подобия исследуемого объекта, включающие известные и
неизвестные параметры расчетной модели, причем количество используемых
критериев подобия должно быть равно числу неизвестных параметров ( к =
1, 2,.., n).
1.5.12. Уравнения (10) с учетом п. 1.5.11 запишем в следующем виде:
|
|
(14) |
где πk - критерий подобия.
При переходе к новым неизвестным параметрам расчетной модели:
|
|
(15) |
параметры
напряженно-деформированного состояния yi будут линейно зависеть от ![]() .
.
1.5.13. Система линейных уравнений относительно неизвестных параметров расчетной модели xi при подстановке в левые части уравнений (11) соответствующих экспериментальных значений параметров напряженно-деформированного состояния может быть записана в виде:
|
|
(16) |
Примечание. Следует отметить, что если система (11) получена в результате преобразования из нелинейных уравнений, в левой части уравнений (16) будут линейные функции параметров напряженно-деформированного состояния.
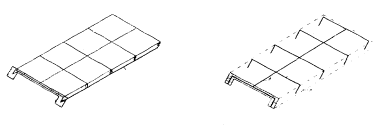
Система (16) в матричном виде:
|
Y = ВХ; |
(17) |
где
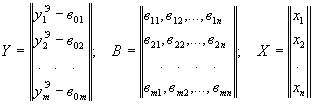
1.5.14. Для решения системы (16) как избыточной, т.е. с целью нахождения точечных и доверительных оценок xi, может быть использован метод наименьших квадратов [21] с приведением ее к полной системе нормальных уравнений:
где
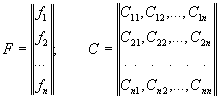
Преобразование системы (16) в (18) производится по формулам:
|
F = BTY; C = BBT |
(19) |
где ВT - транспонированная матрица В
1.5.15. Для удобства вычислений без применения ЭВМ запишем матрицы F и С в развернутом виде
![]()
|
|
(20) |
. . . . . . . . .
![]()
![]()
![]()
|
|
(21) |
![]()
. . . . . .
![]()
![]()
1.5.16.
Точечные оценки неизвестных параметров расчетной модели ![]() , находятся из решения системы нормальных уравнений (18).
, находятся из решения системы нормальных уравнений (18).
1.5.17. Доверительными
интервалами для ![]() могут считаться
границы [
могут считаться
границы [![]() -Δxi,
-Δxi, ![]() +Δxi]:
+Δxi]:
|
|
(22) |
где. tpt - коэффициент Стьюдента, определяемый по таблицам t-распределения при заданной доверительной вероятности P и числе степеней свободы j = т - п; dii - соответствующий диагональный элемент матрицы D = С-1; Si - точечная оценка стандарта σi, определяемая из выражения:
|
|
(23) |
1.5.18. Из решения системы (18) получаем значения неизвестных параметров xi в нормированном виде, переход к абсолютным значениям осуществляется с учетом выражений (14) по формулам:
Χi = Χ0i + pxi;
|
|
(24) |
1.5.19. Если предварительные численные исследования с целью получения уравнений (11) проводятся после завершения эксперимента, то нелинейную зависимость между yi и xi можно нейтрализовать, осуществив следующий итерационный процесс:
задаемся первоначальными значениями неизвестных параметров Χ0i и их интервалами варьирования Pi;
проводим численный эксперимент с целью получения уравнения (11);
подставив в уравнение (11) экспериментальные значения параметров
напряженно-деформированного состояния ![]() , по рекомендуемой методике находим первое приближение Χi и
, по рекомендуемой методике находим первое приближение Χi и ![]() ;
;
приняв ![]() за новый центр плана,
а | Χ0i -
за новый центр плана,
а | Χ0i - ![]() | за новый интервал варьирования, повторяем изложенный выше
процесс;
| за новый интервал варьирования, повторяем изложенный выше
процесс;
итерационный процесс
заканчивается, когда интервал варьирования ![]() будет меньше
доверительного
будет меньше
доверительного ![]()
1.6. Проверка адекватности расчетных моделей
1.6.1. Проверка адекватности разработанных расчетных моделей проводится сопоставлением данных экспериментальных исследований специальной физической модели с результатами численных исследований на расчетной. Так как экспериментальные данные содержат некоторую неопределенность, связанную с погрешностями измерительного комплекса, нагружающих устройств, изменением внешних условий во время эксперимента и т.д., а исходные параметры, закладываемые в расчетную модель, обладают существенной изменчивостью (физико-механические характеристики материалов, жесткости элементов и т.д.), то математически задачу проверки адекватности расчетной модели реальному объекту (физической модели) можно трактовать как проверку некоторой совокупности статистических гипотез.
1.6.2. Для практической реализации единого подхода к решению вопроса о проверке достоверности расчетной модели может быть рекомендован инженерный метод, основанный на сочетании неформальных приемов, отражающих субъективное влияние исследователя, с рядом формальных процедур проверки статистических гипотез.
В соответствии с системным подходом к исследованиям сложных строительных конструкций контроль адекватности расчетных моделей проводится в несколько этапов:
установление адекватности по одному виду параметров напряженно-деформированного состояния yi в локальной области;
то же, по всему объекту;
проверка адекватности по всем параметрам Y = {yi}.
Проверка адекватности расчетной модели по одному виду параметров yi (см. п. 1.6.1) в локальной области основана на сравнении экспериментальных и теоретических значений и их доверительных интервалов методами математической статистики*.
* См. разд. 1.4, формулы (2), (4) и (6).
1.6.3. Для получения доверительных оценок теоретических значений параметров напряженно-деформированного состояния предлагается инженерный метод, основанный на статистической динамике механических систем и математической теории планирования экспериментов, исходя из предположения о том, что, если область определения функции yi = fj(x1, x2, …, xn)), где yi - параметр НДС, xi - исходные данные расчетной модели, ограничить окрестностями xi, радиусы которых равны соответствующим доверительным интервалам Δxi, то эта функция с достаточной точностью может быть аппроксимирована полиномом вида (11) или (13). Тогда доверительные интервалы параметров yi вычисляются как погрешность функции независимых случайных величин:
|
|
(25) |
1.6.4. В реальных задачах доверительные интервалы исходных данных в большинстве своем сравнительно невелики, поэтому с точностью, достаточной для практических целей, можно ограничиться аппроксимацией функции fj полиномами первой степени (11). В этом случае доверительные интервалы yj вычисляются по более простой формуле:
|
|
(26) |
где вji - коэффициенты уравнений (11), вычисляемые по формулам (12) по результатам численных экспериментов согласно соответствующей матрице планирования (см. приложение 1).
1.6.5. При наличии
точечных и доверительных оценок параметра напряженно-деформированного состояния
yi (экспериментальные ![]() , Δ
, Δ![]() и теоретические
и теоретические ![]() и Δ
и Δ![]() установление адекватности расчетной и физической моделей
может быть сведено к проверке статистической гипотезы о равенстве средних. С
учетом возможного неравенства дисперсий (
установление адекватности расчетной и физической моделей
может быть сведено к проверке статистической гипотезы о равенстве средних. С
учетом возможного неравенства дисперсий (![]() )2 и (
)2 и (![]() )2 применим приближенный метод [20] с
несколько преобразованными расчетными формулами, согласно которому вычисляем:
)2 применим приближенный метод [20] с
несколько преобразованными расчетными формулами, согласно которому вычисляем:
где
![]() и
и ![]() - коэффициенты Стьюдента, принимаемые
по таблицам t-распределения
при доверительной вероятности 0,95 и числе степеней свободы соответственно п - 1 и N - 1, п - количество
физических экспериментов при определении Δ
- коэффициенты Стьюдента, принимаемые
по таблицам t-распределения
при доверительной вероятности 0,95 и числе степеней свободы соответственно п - 1 и N - 1, п - количество
физических экспериментов при определении Δ![]() ; N - количество строк матрицы
планирования.
; N - количество строк матрицы
планирования.
При выполнении условия:
|
|
(29) |
расчетная модель считается адекватной по параметру yj в данной точке.
1.6.5.
Для проверки адекватности расчетной модели по всему множеству параметра yj; необходимо
определить ![]() проверить неравенство
(29) для каждой пары
проверить неравенство
(29) для каждой пары ![]() и
и ![]() (j =1, 2, ..., m); К = 1,2,…, r, где r -
количество пар). Проверка не вызывает затруднений, если условие (29)
выполняется для каждой пары. В противном случае необходимо проверить
статистическую гипотезу о случайности данного явления с привлечением
непараметрических методов (U- или X-критерия),
не накладывающих ограничений на функции распределения Δ
(j =1, 2, ..., m); К = 1,2,…, r, где r -
количество пар). Проверка не вызывает затруднений, если условие (29)
выполняется для каждой пары. В противном случае необходимо проверить
статистическую гипотезу о случайности данного явления с привлечением
непараметрических методов (U- или X-критерия),
не накладывающих ограничений на функции распределения Δ![]() и Δ
и Δ![]() .
.
1.6.6. Проверке адекватности по всему параметру уj (например по всем изгибающим моментам или всем прогибам и т.д.) должен предшествовать учет превалирования зон с максимальными значениями уj (по абсолютной величине), связанного с тем, что, исходя из условия обеспечения прочности, надежности и экономичности, расчетная модель сооружения должна, в первую очередь, достоверно описывать напряженно-деформированное состояние конструкции в зонах экстремальных значений параметров НДС введением весовых коэффициентов:
|
|
(30) |
или:
|
|
(31) |
где т - количество типов параметров НДС; r - количество зон, на которые разбивается эпюра yi при проверке адекватности.
1.6.7. С учетом весовых коэффициентов определяется количество сравниваемых пар в каждой зоне:
|
|
(32) |
где r - общее количество сравниваемых пар.
Для каждой k-той пары ![]() и
и ![]() находим разность:
находим разность:
|
ejk = Rjk - Tjk |
(33) |
Приняв k(+) за число положительных разностей, а k(-) - отрицательных, расчетные модели можем считать адекватными при выполнении неравенства:
|
|
(34) |
где ![]() - критерий Фишера,
принимаемый по таблицам F-распределения
при доверительной вероятности р = 0,95 и числе степеней свободы m1 = 2(k(+)+1) и m2 = 2k(-).
- критерий Фишера,
принимаемый по таблицам F-распределения
при доверительной вероятности р = 0,95 и числе степеней свободы m1 = 2(k(+)+1) и m2 = 2k(-).
1.6.8. В ранговом методе (базирующемся на упорядочении сравниваемых величин, в нашем случае - Rjk и Тjk при k = 1, 2,..., r) с применением X-критерия, имеющем преимущество перед U-критерием по большей эффективности (при сопоставлении с двойным t-критерием он обладает асимптотической эффективностью, равной 1, при эффективности U-критерия 0,64), оценка адекватности сводится к проверке статистической гипотезы: существенно ли значения Тjk - превышают значения Rjk для всего множества параметров уj. Сначала упорядочиваются все значения Rjk и Тjk расположением в порядке их возрастания. Каждому из этих значений присваивается ранговое число, соответствующее порядковому номеру. Затем вычисляется X-критерий:
|
|
(35) |
где r - число сравниваемых пар; Sk - ранговое число Тjk;
ψ(y) = x - функция, обратная функции нормированного нормального распределения;
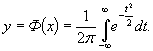
Исходя из этого, ψ(y) = x определяется как аргумент, по значению функции y = Ф(х) таблицы нормированного нормального распределения в [25]. Если статистическая гипотеза подтверждается, модели считаются адекватными:
|
Χj ≤ Χα |
(36) |
где Χα - критические значения X-критерия, принимаемые по таблице приложения 2 в зависимости от доверительной вероятности и величины 2r.
1.6.9. Один из наиболее удобных и достаточно простых способов установления глобальной адекватности как заключительного этапа проверки тождества расчетных моделей (оценка по всему множеству параметров напряженно-деформированного состояния Y) основывается на применении обобщенной функции желательности Харрингтона [26]. В основе метода - идея преобразования натуральных значений параметров в безразмерные величины dj согласно шкале желательности, или предпочтительности, назначение которой - установление соответствия между физическими и психологическими (умозрительными) параметрам (понимаются чисто субъективные оценки исследователем предпочтительности или желательности того или иного значения параметра).
Шкала желательности имеет интервал dj от 0 до 1, где dj = 1 соответствует идеальная адекватность расчетной модели по параметрам yi (см. пп. 1.6.7, 1.6.8), dj = 0 - абсолютное несовпадение расчетных и экспериментальных данных.
Сценка адекватности расчетных моделей по шкале желательности приведена в табл. 2.
Таблица 2
|
Субъективная оценка исследователем адекватности по параметрам |
Очень хорошая |
Хорошая |
Удовлетворительная |
Плохая |
Очень плохая |
|
Значение параметра yj по шкале желательности - dj |
1… |
0,8… |
0,63… |
0,37… |
0,2... |
|
0,8 |
0,63 |
0,37 |
0,2 |
0 |
Выбор оценок
0,63 и 0,37 объясняется удобством вычисления функции желательности ![]() , где
, где ![]() - относительное
значение параметра в условном масштабе.
- относительное
значение параметра в условном масштабе.
1.6.10. В случае, когда проверка адекватности по некоторому параметру yk дает отрицательный результат, а по другим, наиболее важным, параметрам адекватность моделей установлена, для оценки пригодности имеющейся расчетной модели или выбора лучшей из нескольких альтернативных можно рекомендовать применение коэффициента неадекватности:
|
|
(37) |
где nk - коэффициент неадекватности по параметру yk.
![]() - наихудшее
теоретическое значение параметра с учетом доверительного интервала;
- наихудшее
теоретическое значение параметра с учетом доверительного интервала;
![]() -
экспериментальное значение соответствующего параметра.
-
экспериментальное значение соответствующего параметра.
Затем принимаем граничные оценки для коэффициентов неадекватности:
0,95 ≤ пk ≤ 1,05 - очень хорошо;
0,9 ≤ пk ≤ 0,95; 1,05 < пk ≤ 1,1 - хорошо;
0,8 ≤ пk ≤ 0,9; 1,1 < пk ≤ 1,2 - удовлетворительно;
0,5 ≤ пk ≤ 0,8; 1,2 < пk ≤ 1,5 - плохо;
пk ≤ 0,5; пk > 1,5 - очень плохо.
Примечание Совершенно очевидно, что могут быть и другие граничные оценки. Для уменьшения влияния субъективного фактора следует воспользоваться мнением нескольких специалистов. При обобщении этих мнений и установлении степени согласованности между различными специалистами можно воспользоваться методом ранговой корреляции [23].
После назначения границ коэффициентов неадекватности определяем частный показатель желательности dj для каждого вида параметров yj расчетной модели, для чего воспользуемся графиком кривой желательности (рис. 2), на котором по оси ординат нанесены частные показатели желательности dj, а по оси абсцисс - соответствующие границы коэффициента неадекватности [nk]
После определения частных показателей функции желательности dj для каждого вида расчетных параметров вычисляем обобщенный показатель желательности по всем параметрам напряженно-деформированного состояния D, который рассматриваем как формализованную оценку пригодности расчетной модели.
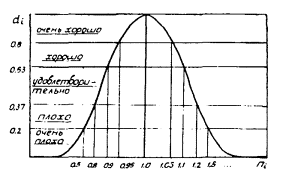
Рис. 2. График функции желательности
Ввиду того, что единого правила вычисления обобщенного показателя желательности нет, рекомендуем определять его как среднее геометрическое частных показателей желательности.
|
|
(38) |
Обобщенный показатель желательности D может быть использован в качестве критерия оптимальности расчетных моделей.
2. ПОСТРОЕНИЕ МОДЕЛЕЙ ДЛЯ ИССЛЕДОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
2.1. Расчетные модели строительных конструкций
2.1.1. Исходя из принципов системного подхода к проблеме анализа сложной системы конструкций рекомендуется назначать расчетные схемы на основе анализа их общих закономерностей.
2.1.2. Исследования сложных строительных конструкций следует начинать с анализа объекта исследований, особенностей и условий работы и др., включающего:
изучение рабочих чертежей и другой документации по исследуемому объекту;
рассмотрение функционального назначения объекта, технологических воздействий, условий работы конструкции, вида возможных предельных состояний;
выявление признаков и особенностей, отличающих данный объект от аналогичных, исследования которых проводились ранее;
ознакомление с методиками и результатами проведенных ранее исследований;
оценку новизны и важности проблемы, потенциального экономического эффекта, который может быть получен от внедрения в производство.
2.1.3. Для численных исследований сложных строительных конструкций и сооружений следует применять программные комплексы общего назначения. Наряду с этим для расчета определенных типов сооружений могут использоваться программы, в зависимости от степени специализации которых накладываются ограничения на возможность выбора расчетной схемы. Для программ общего назначения предопределен набор типов расчетных элементов, выбор которых и способ объединения для аппроксимации работы строительной конструкции зависят от инженера-исследователя, исходящего из принципов;
I - расчетная схема сооружения должна назначаться в соответствии со схемой деформирования или разрушения сооружения, подтвержденных строительной практикой;
II - поскольку расчетная схема - аналог механической модели сооружения, в нее вводятся упрощающие гипотезы, позволяющие выделить определяющие факторы, влияющие на работу конструкции (рассчитываемая конструкция находится в менее благоприятных по сравнению с действительностью условиях, кроме того, учитывается требование экономической целесообразности проектируемой конструкций);
III - для расчета некоторых конструктивных элементов или их систем целесообразно иметь несколько расчетных схем, каждая из которых имеет область применения (расчетные схемы отличаются степенью подробности аппроксимации, свойствами расчетных элементов и др.; критерием для выбора той или иной модели служит оценка результата, удовлетворяющего условиям поставленной задачи).
2.1.4. Ввиду того, что здания каркасные или с несущими стенами, массовые конструкции надземного строительства, отдельные конструктивные элементы этих несущих систем рекомендуется рассматривать с точки зрения их аппроксимации расчетными элементами моделируя:
колонны и другие элементы постоянного поперечного сечения - стержневыми конечными элементами (КЭ) с определением их жесткости по известным формулам сопротивления материалов, принимая EF - продольной или осевой жесткостью; ЕIx, EIy - изгибными жесткостями; Glкр - жесткостью кручения, а GFx, GFy - сдвига; при конструктивном обеспечении жесткого узла связи между элементами и при достаточных размерах их поперечных сечений необходимо принимать расчетные стержни с жесткими вставками, размеры которых определяются размерами жесткого узла;
ригели или другие элементы со сложной формой поперечного сечения, кроме стержневых, - набором плоских КЭ, причем потребность в этом возникает при необходимости получения более подробной картины напряженного состояния, а также учета действительных размеров их поперечного сечения; основные габаритные размеры принимаются по исходному поперечному сечению, а толщина КЭ - из решения системы уравнений (например, для крестообразного поперечного сечения по рис. 3 уравнения будут иметь вид:
Iсеч = f1(вп, hn, вст, hст),
Fсеч = f2(вп, hn, вст, hст),
где Iсеч., Fсеч. - геометрические характеристики формы исходного поперечного сечения; f1, f2 - аналитические функции размеров аппроксимирующего поперечного сечения; вn, hст известные, а вст, hn - определяемые размеры);
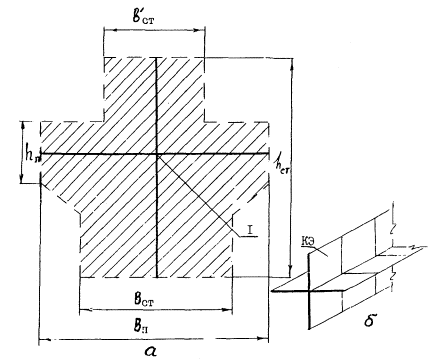
Рис. 3. Аппроксимация сечения крестообразной формы:
а - поперечное сечение; б - расчетная схема; 1 - центр тяжести сечения
балочные и стоечные элементы с отверстиями, регулярно расположенными по длине элемента, - стержневым КЭ, жесткость которого определяется из расчета участка данного элемента на краевые воздействия, как составной части основной системы (рис. 4.) после расчета участка элемента с отверстиями с помощью конечно-элементной аппроксимации на три вида воздействий получим значения перемещений, используемые как правые части системы трех уравнений, решением которых определяем величины трех характеристик жесткости аппроксимирующего стержня:
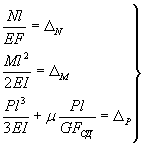
где EF осевая жесткость, ЕI - изгибная жесткость, GFСД - сдвиговая жесткость, μ - коэффициент формы сечения;
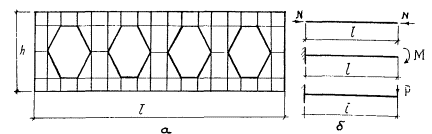
Рис. 4. К определению жесткости перфорированного элемента
а - расчетный участок элемента аппроксимации КЭ; б - единичные состояния элемента основной системы
плиты ребристые - набором КЭ оболочки нулевой кривизны, аппроксимирующих полку плиты, и стержневыми элементами, аппроксимирующими продольные ребра (рис. 5, 6). Связь между КЭ плиты и ребер осуществляется с помощью стержневых или "контактных" элементов с характеристиками жесткости на два порядка выше жесткостей ребер. Плита моделируется одним стержнем, а фактические ее размеры в поперечном направлении - стержневыми элементами повышенной жесткости. Жесткостные характеристика основного стержневого элемента равны жесткости плиты, определяемой теоретически или экспериментально;
плиты пустотные и гладкие - расчетными моделями I и II типа;
цилиндрические поверхности - КЭ оболочки нулевой кривизны прямоугольной формы;
|
|
|
|
Рис. 5. Аппроксимирующая модель ребристой плиты а - поперечное сечение; СЭ - стержневой элемент ребра; КЭ -конечный элемент связи |
6. Стержневая модель ребристой плиты а - поперечное сечение плиты; б - основной расчетный стержень; в, г - стержни |
оболочки, поверхность которых имеет кривизну в двух направлениях, - КЭ оболочки нулевой кривизны треугольной формы, при отсутствии в библиотеке таковых или по другим соображениям могут быть использованы КЭ прямоугольной формы, при этом три узла каждого КЭ лежат на поверхности, а четвертый, вне ее, - объединяется (рис. 7) с аналогичным узлом на поверхности условием равенства перемещений (происходит незначительное искажение ее формы, однако сохраняется непрерывность функций перемещений по всем сечения оболочки);
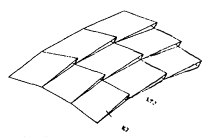
Рис. 7. Аппроксимирующая модель оболочки положительной гауссовой кривизны
КЭ - конечный элемент оболочки нулевой кривизны; KTЭ - контактный элемент, или условие равенства перемещений
эквивалентные системы, когда часть сложной системы необходимо заменить
более простой, равнозначной в определенном смысле исходной конструкции
(обычно это связано с необходимостью понизить мерность фрагмента или всей
конструкции), например, конструкцию инвентарного здания, состоящего из сборных
плит основания и металлического каркаса, в которой плиты основания,
представляются как трехслойная конструкция - верхние гладкие и нижние ребристые
соединены пространственными арматурными каркасами, а примыкание друг к другу и
сопряжение с каркасом - точечное согласно рис. 8), - моделью двух однослойных
плит, имеющих общие узлы и две группы независимых характеристик: ЕИ, tИ,
μ - характеристики изгибаемой
плиты; ЕП, tП, μ
- характеристики плиты в
плоском напряженном состоянии (каждая из них может быть получена из условия
эквивалентности трехслойной плиты при расчете на соответствующие виды
воздействий), а также когда в расчетных схемах зданий встречаются включения
типа ядер или диафрагм жесткости сложной конструктивной формы - сложной моделью, состоящей из большого количества
конечных элементов (диафрагма представлена в виде рамной системы; жесткости
элементов которой могут быть определены расчетом диафрагмы с помощью подробной
схемы на воздействие горизонтальной силы Р
единичной величины с определением значений горизонтального смещения ΔГ верхнего сечения,
дополненного расчетом рамы на действие силы Р
с определением ![]() при различных
соотношениях жесткостей колонн и ригелей (рис. 9);
при различных
соотношениях жесткостей колонн и ригелей (рис. 9);
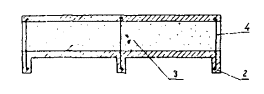
Рис. 8. Поперечное сечение трехслойной плиты
1, 2 - соответственно верхняя и нижняя плита; 3 - утеплитель; 4 - арматурный каркас
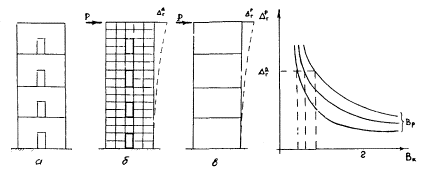
Рис. 9. К расчету диафрагм
а - диафрагма; б - подробная расчетная схема; в - рамная расчетная схема; г - график перемещений рамы
вариантные модели, когда встречаются конструктивные схемы, обладающие слабой нерегулярностью (структура системы регулярна за исключением некоторых локальных особенностей: регулярно и нерегулярно расположенные проемы, отдельные элементы повышенной и пониженной жесткости по сравнению со всей системой, необходимость расчета нескольких вариантов однотипных систем, отличающихся локальными особенностями), - кодированием расчетной схемы для всей системы без учета нерегулярных элементов (рис. 10), которые записываются как дополнительная информация по отношению к основной (при наличии проемов они могут быть описаны как расчетные элементы с отрицательными значениями толщины или модуля упругости, равными положительным значениям этих параметров, использованных при описании регулярной системы; при таком способе описания расчетной модели возможно появление узлов расчетной схемы, к которым присоединены расчетные элементы с нулевой жесткостью и которые необходимо закрепить, в пространстве от возможных смещений; для расчетных элементов, отличающихся по характеристикам жесткости, достаточно ввести в схему дополнительные элементы с тем, чтобы суммарное значение жесткости равнялось заданному, при этом действительное значение усилий необходимо определять как суммарное в исходной системе и добавочных элементах).
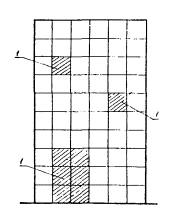
Рис. 10. Система с нарушенной регулярностью
1 - проемы
2.2. Физические модели
2.2.1. Моделирование строительных конструкций рекомендуется осуществлять на основании теории подобия и размерностей, принятых в [27, 28]. Условия подобия, лежащие в его основе, устанавливаются в результате анализа размерностей величин, характеризующих исследуемое явление, или уравнений задачи, исходя из подобия напряженно-деформированных состояний тел (напряжения, деформации, перемещения и другие величины, характеризующие изучаемое явление, в сходственных точках двух тел связаны соотношением вида αМ = СααН, где αМ и αН - значения рассматриваемой величины соответственно для модели и для натурного объекта; Сα - масштаб этой величины). При физическом моделировании различают простое и расширенное подобия.
2.2.2. При простом (геометрическом) подобии должны выполняться следующие требования:
все безразмерные величины (относительные деформации, коэффициент трения и т.д.) в модели и оригинале равны;
масштабные множители величин с одинаковой размерностью равны;
безразмерные комплексы, критерии подобия для модели и оригинала одинаковы;
модель и оригинал или их элементы геометрически подобны;
действующие на модель воздействия с учетом масштаба такие же, как и в натурной конструкции;
материал модели и ее элементов тождествен материалу натуры (для подобия в механическом смысле - это полное совпадение индикаторных диаграмм).
Строго говоря, с учетом подобия на всех стадиях работы конструкции при простом подобии произвольно может быть выбрана только одна константа - масштаб линейных размеров Cl. Масштабы других величин получают возведением Сl соответствующую степень:
Cσ = ![]() = 1; CU = Cl;
Cq = Cl; CQ = CP; Cq = CP
=
= 1; CU = Cl;
Cq = Cl; CQ = CP; Cq = CP
= ![]() ; CM =
; CM =
![]() ; CEI =
; CEI = ![]() .
.
Примечание. Соблюдение требований простого подобия весьма затрудняет моделирование, требует больших затрат ресурсов, поэтому его применение должно быть соответствующим образом обосновано.
* Cδ, CU, Cq, CQ, CP, СM, СEI - масштабы соответственно напряжений, линейных перемещений, равномерно распределенной нагрузки, перерезывающих сил, сосредоточенных нагрузок, изгибающих моментов, изгибных жесткостей.
2.2.3. Расширенное подобие [29], несколько увеличивающее возможности физического моделирования, однако требующее доказательства корректности его применения для каждого конкретного случая, характеризуется следующими условиями:
модель и оригинал, как минимум; аффинно подобны;
действующие на модель нагрузки соответствуют нагрузкам, действующим на оригинал;
масштабы величин одинаковой размерности не равны;
некоторые безразмерные величины не равны;
материал модели идентичен материалу натуры, что при подобии в механическом смысле означает гомогенность их индикаторных диаграмм.
При расширенном подобии произвольно может быть выбрано несколько масштабов, однако математические сложности, особенно требование подобия материалов, существенно ограничивают его область применения для моделирования железобетонных конструкций.
2.2.4. Ввиду того, что применение физических моделей, разработанных в соответствии с требованиями теории подобия и размерностей при исследовании сложных строительных конструкций и сооружений, из-за больших затрат ресурсов может быть не только нерациональным, но зачастую и просто невозможным (при системном подходе к исследованиям физическое моделирование уже не самостоятельный процесс, обеспечивающий достижение поставленных целей, а применим только в сочетании с расчетными исследованиями), допускается уменьшение ряда требований к конструкциям моделей, ограничиваемых лишь достаточными и необходимыми для решения задач, поставленных перед методом, - принятие в отличие от пп. 2.2.1 - 2.2.3 функционального подобия (см. приложение 3), при котором должны выполняться следующие условия:
физические явления, происходящие в рассматриваемых объектах одинаковой природы;
физическая модель и натурная конструкция имеют однотипную расчетную модель;
для модели и натурной конструкции количество определяющих критериев подобия, записываемых одинаковыми буквенными выражениями, одинаково, хотя численные их значения могут не быть равными;
при включении физико-механических характеристик материала конструкции в множество исходных данных расчетной модели материал модели должен качественно обладать теми же свойствами, что и материал натурной конструкции, т.е. определяться одинаковым набором физико-механических характеристик;
действующие на модель нагрузки не подобны, но характер вызываемого ими напряженно-деформированного состояния должен быть идентичен с натурой.
Под функционально подобной условимся понимать физическую модель, содержащую необходимое количество элементов и связей между ними, достаточное для выполнения тех же функций, что и в натурной конструкции. Эта модель однозначно может быть аппроксимирована расчетной, используемой для описания натурного объекта. Применение функционального подобия при разработке физических моделей позволяет существенно снизить материальные и трудовые затраты на изготовление и испытания моделей.
2.2.5. При простом или расширенном подобии инварианты подобных объектов - критерии подобия (безразмерные симплексы и. комплексы). При функциональном подобии инвариантами следует считать функции, алгоритмы, имеющие общие для этих объектов область определения и результат, что существенно уменьшает ограничения на выбор констант подобия - масштабов - при проектировании зданий.
Кроме того, при функциональном подобии, в отличие от простого и расширенного, геометрическое подобие объектов не обязательно, следовательно, расчетные схемы модели и натуры геометрически не подобны, разными могут быть и масштабные множители для величин с одинаковой размерностью, что существенно уменьшает ограничения на выбор констант подобия при проектировании моделей.
2.2.6. В процессе разработки физических моделей, используемых при исследовании строительных конструкций методами системного анализа, применим смешанный вид подобия - сочетание функционального с простым или расширенным.
Примечание. Тот или иной вид подобия используется в зависимости от конкретных задач, поставленных перед экспериментом, проводимым в соответствии со схемой исследования сложных конструкций (см. п. 1.1 настоящих методических рекомендаций).
2.2.7. При проведении исследований комплексным методом физическое моделирование рационально на следующих этапах:
при установлении физико-механических характеристик материалов конструкций (простое подобие: материал образцов тождествен натурному элементу, форма соответствует действующим ГОСТам, а их напряженное состояние аналогично состоянию элемента в натурной конструкции - соблюдается функциональное подобие);
при определении неизвестных параметров расчетной модели (проектирование модели осуществляется на основе смешанного подобия: простое для определяемых параметров хi и функциональное - для остальных исходных параметров mr);
при проверке адекватности расчетной и физической моделей (физическое моделирование может осуществляться исключительно на основе функционального подобия, причем, если в качестве исходных данных для расчетной модели используются интегральные характеристики элементов - жесткость, граничные условия и т.д., то эти элементы следует моделировать с применением простого или расширенного подобия).
2.3. Рекомендации по применению функционального подобия
2.3.1. Сравнительный анализ условий моделирования по видам подобия (табл. 3) позволяет рекомендовать использование функционально подобных физических моделей только при наличии расчетной, общей для модели и натурного объекта. Являясь наиболее общим видом механического подобия деформируемых систем, функциональное подобие накладывает гораздо меньше по сравнению с простым и расширенным видами подобия ограничений на выбор констант физического моделирования, что существенно упрощает разработку физических моделей сложных объектов несмотря на сужение круга задач, при решении которых оно может быть применено.
2.3.2. Основное назначение функционально подобных физических моделей следует усматривать в проверке адекватности расчетных моделей сложных объектов и сооружений с большим количеством элементов. Физические модели для этой цели разрабатываются на основе полного функционального подобия. Адекватность расчетных моделей отдельных подсистем, входящих в объект исследований, устанавливается с помощью физических моделей, разработанных на основе неполного функционального подобия.
2.3.3. Определение неизвестных параметров расчетных моделей (как правило, характеризующих жесткостные и прочностные характеристики отдельных элементов и соединений) методом функционального подобия производится при его сочетании с простым или расширенным подобием (физические же модели разрабатываются по принципу смешанного подобия).
Примечание. Так, например, для определения податливости стыков между сборными элементами вся модель в целом (конструктивная схема) выполняется функционально подобной натуре, а отдельные элементы и их стыки - по принципу простого подобия по отношению к реальным конструкциям.
Таблица 3
|
Условия моделирования |
Вицы подобия |
||
|
Простое |
Расширенное |
Функциональное |
|
|
Полное геометрическое подобие |
Обязательно по всем координатам |
Обязательно хотя бы по одной координате |
Необязательно |
|
Подобие граничных условий |
Обязательно |
Обязательно |
-"- |
|
Масштабные множители величин одной размерности |
Равны |
Неравны для некоторых величин |
Неравны для всех величин |
|
Количество независимых масштабных множителей |
Один |
Несколько |
Все |
|
Количество определяющих критериев подобия для модели и оригинала |
Равно |
Равно |
Равно |
|
Критерии подобия |
Инвариантны по величине |
Инвариантны по величине |
Инвариантные буквенные выражения |
|
Подобие воздействий |
Качественное и количественное |
Качественное и количественное |
Качественное |
|
Материал модели |
Тождествен материалу оригинала |
Подобен материалу оригинала с обязательной гомогенностью индикаторных диаграмм |
Подобен материалу оригинала |
|
Равенство безразмерных величин в модели и оригинале |
Обязательно |
В отдельных случаях необязательно |
Необязательно |
|
Требования к расчетной модели |
Идентичность уравнений связи и граничных условий |
Инвариантность функции |
|
|
Определение параметров напряженно-деформированного состояния |
Непосредственно по результатам испытания модели |
Численный эксперимент на расчетной модели |
|
2.3.4. Применение функционального подобия позволяет существенно сократить расходы ресурсов на изготовление физических моделей, которые имеют смысл и должны применяться исключительно в сочетании с расчетными моделями объекта исследований.
3. ЭКСПЕРИМЕНТАЛЬНО-ТЕОРЕТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ КОНСТРУКЦИЙ
3.1. Определение констант ортотропии элементов при плоском напряженном состоянии
3.1.1. Результаты экспериментальных исследований строительных конструкций или их моделей, как правило, включают данные испытаний образцов материала в виде кубов и призм из бетона (ГОСТ 24452-80) и арматуры (ГОСТ 12004-81), такие как Rпр, R, E (бетон) и σт, σп (арматура).
Для расчета конструкций в упругой стадии работы или оценки их несущей способности методом предельного равновесия возможно ограничиться имеющимися характеристиками материалов, полученными экспериментально или принятыми по данным нормативов.
3.1.2. Для расчетного моделирования поведения конструкций за пределами упругости рекомендуется использовать методики, в которых текущая характеристика жесткости материала определяется как функция ее начального значения и некоторых параметров нелинейности [31]. При этом для описания характеристик железобетона как композитного материала могут быть использованы усредненные данные как для однородного ортотропного материала [32], так и для материала, состоящего из бетона и арматуры с учетом их взаимодействия [33]. При моделировании конструкции, элементы которой работают в плоском напряженном состоянии, может быть использована методика, основанная на экспериментальном определении констант ортотропии железобетона как однородного материала [16, 34 - 36], исходя из следующих гипотез;
композитный материал - железобетон - может быть заменен ортотропным, деформативные характеристики которого позволяют установить интегральную зависимость между напряжениями и деформациями в пределах некоторой малой области железобетонного образца;
в пределах этой малой области константы ортотропии постоянны и зависят от соотношения средних значений напряжений по области;
константы ортотропии соответствуют мгновенно-упругому состоянию материала и подчиняются принципу квантования, принимая дискретные значения, соответствующие соотношению главных напряжений, и изменяются скачкообразно при достижении соотношения напряжений граничных значений, определяющих параметрические состояния материала;
по границам между областями выполняются условия совместности деформаций.
В качестве основы для численного решения задачи о напряженно-деформированном состоянии конструкции принимается расчетная модель МКЭ. С учетом этого в качестве области, на которую распространяются указанные гипотезы, может быть каждый КЭ.
В соответствии с этими гипотезами можно считать, что изменение констант жесткости связано с некоторыми характерными состояниями материала, зависящими от уровня и соотношения напряжений (рис. 11).
Так как в общем случае в плоском напряженном состоянии возможны воздействия в виде сдвигающих усилий, области состояний представляют собой некоторую выпуклую поверхность (согласно постулату Д. Друккера - Р. Хилда). Тогда графики рис. 11 можно рассматривать как линии пересечения этой поверхности с плоскостями σx - σy. Для получения таких кривых параметрических состояний железобетонного элемента можно использовать данные эксперимента. Полученные физические константы материала оказываются однозначно связанными с соотношением величины напряжений.
3.1.3. Для расчета конструкции, элементы которой находятся в плоском напряженном состоянии, необходимо знание таких характеристик материала: E1; E2; μ12; μ21; G12. С учетом известного соотношения:
|
μ12Е2 = μ21Е1 |
(39) |
четыре параметра из пяти независимы и могут быть определены экспериментально из уравнений закона Гука для двухосного напряженного состояния:
3.1.4. В общем случае для определения констант по п. 3.1.3 необходимо провести испытание плоского образца железобетонной конструкции при четырех независимых напряженных состояниях. Используя возможность создания одноосного напряженного состояния, получим разделяющую систему из двух уравнений, из решения которых найдем соответственно неизвестные для одного из направлений:
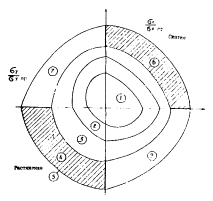
Рис. 11. Качественный график параметрических областей плоского напряженного состояния
1 - зона упруго-линейных деформаций; 2 - зона микротрещин; 3 - зона макротрещин; 4 - зона текучести арматуры; 5 - граница прочности; 6 -зона пластичности; 7 - зона прогрессирующего разрушения
Так как реализация сдвиговой нагрузки в эксперименте на образце затруднена, получаем касательные напряжения под углом 45° к осям ортотропии, создавая нагрузку разных знаков по двум перпендикулярным направлениям (рис. 12).
3.1.5. Согласно пп 3.1.3 и 3.1.4 могут быть экспериментально определены константы для области упругого поведения материала. Поскольку процессу деформирования свойственна нелинейность, экспериментальное определение констант жесткости возможно только для приращений напряжений или деформаций, в соответствии с методом "малых параметров" или "упругих решений" в задачах расчета нелинейно-деформируемого тела при следующем порядке нагружения образцов:
согласно принятому варианту в плоском напряженном состоянии повышается уровень напряжений до определенной точки на графике σx - σy;
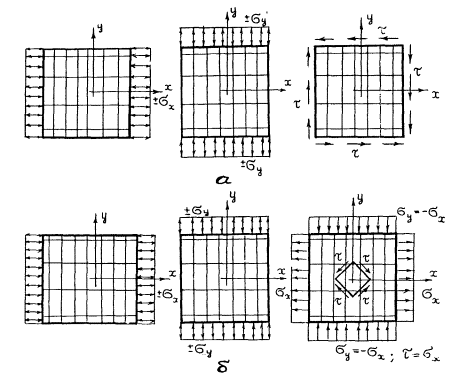
Рис. 12. Напряженные состояния для определения констант ортотропии плоского напряженного состояния
а - теоретические напряженные состояния; б - напряженные состояния, реализуемые в эксперименте
нагрузке дается приращение, достаточно малое по величине, чтобы изменить состояние материала (производятся микронагpyжения, при которых замеряются приращения деформаций и выполняются необходимые вычисления для определения констант ортотропии по зависимостям (40), (41), (42).
3.1.6. Для реализации видов напряженного состояния по п. 3.1.5 рекомендуется специальная установка, позволяющая осуществлять с помощью восьми призм нагружение железобетонного образца при двустороннем сжатии или растяжении сжатии по одной и растяжении по другой оси. Равномерность воздействия обеспечивается устройством распределительной системы, представляющей собой четыре ряда статически определимых балок на двух опорах в соотношении по рядам 8:4:2:1. Передача растягивающих напряжений на образец осуществляется через выпуски арматуры посредством системы тяжей с выходом на домкрат. Соотношение количества тяжей, считая выпуски арматуры, в последовательных группах 8:4:2:1.
Конструктивно установка (монтируется в силовой замкнутой раме) может быть в трех вариантах: УРО - устройство растяжения образцов; УСО - устройство сжатия образцов; УРСО - устройство растяжения-сжатия образцов.
3.1.7. В.соответствии с устройством, принципом действия и назначением установки может быть определен вид образцов материала. Образцы по форме представляют собой квадратные пластины размером 6,4×0,4×0,07 м, имеющие гладкую лицевую и торцовую поверхность. В случае необходимости по двум (четырем) противолежащим торцовым поверхностям имеются выпуски арматуры.
Вид армирования назначается из условий геометрического подобия натурной конструкции и образца заданных размеров. Для передачи растягивающих усилий к каждой паре выпусков арматуры привариваются скобы, которые служат захватами для нагрузочного устройства. В целях получения статистически достоверных результатов в каждой серии должно быть испытано не менее трех образцов, результаты испытаний должны быть обработаны в соответствии с требованиями ГОСТ 24452-80.
3.1.8. По результатам испытаний устанавливаются границы областей, в пределах которых параметры жесткости сохраняют постоянное значение при изменении величины соотношения напряжений.
Для описания границ этих областей могут быть использованы аналитические выражения, аппроксимирующие экспериментальные кривые в осях (±σx; ±σy).
Каждой области на графике напряжений соответствует набор из характеристик E1; E2; μ12; μ21; G, которые могут быть использованы как исходная информация к программе расчета конструкций, элементы которой работают в условиях плоского напряженного состояния. Для выполнения таких расчетов необходимо наличие в программной библиотеке КЭ расчетных модулей, позволяющих рассчитывать ортотропные КЭ. В наиболее распространенных программах (ЛИРА, ПРОКРУСТ) имеются такие типы КЭ.
3.2. Экспериментально-теоретический метод определения элементов матрицы жесткости СЭ
3.2.1. В решении задач исследования строительных конструкций блочно-регулярной структуры целесообразно использовать метод укрупненных элементов, или суперэлементов (СЭ). Расчетная модель конструкции с использованием СЭ строится по [37], а расчетные исследования могут быть выполнены с помощью существующего программного обеспечения.
3.2.2. Применение метода СЭ в экспериментальных исследованиях конструкций блочно-регулярной структуры, позволяет произвести замену испытания всей конструкции испытанием ее фрагментов (суперэлементов) с последующим объединением их на уровне расчетной модели. При этом целесообразно адекватность физической модели и ее расчетного аналога устанавливать сопоставлением матриц жесткости суперэлементов (МЖ СЭ).
3.2.3. В качестве экспериментального способа получения МЖ СЭ рекомендуется метод, теоретическое обоснование которого приведено в [38], с помощью которого МЖ СЭ может быть получена также из расчета.
3.2.4. Реализация СЭ предполагает:
изготовление физической модели фрагмента конструкции, представляющей собой СЭ;
разработку проекта испытательной установки с учетом того, что установленная в ней модель должна иметь опоры конечной жесткости Ci в направлении возможных смещений, в соответствии с которыми прикладываются силовые воздействия Рj и измеряются перемещения Vij.
3.2.5. После загружения модели поочередно силами Pj, имеющими единичные значения произвольной размерности, и измерения перемещений в каждом из направлений смещений i получим матрицу перемещений узлов модели:
|
|
(43) |
где n - полное количество направлений возможных смещений.
3.2.6. Матрица жесткости суперэлемента, определенная по результатам эксперимента, вычисляется на основании зависимости:
|
|
(44) |
где [V]-1 - матрица, обратная матрице перемещений СЭ; ┌C┘ - диагональная матрица жесткости опорных устройств. модели суперэлемента;
┌C┘ = 
Примечание. Совершенствование исследований прочности и деформативности строительных конструкций - одна из важнейших задач научно-технического прогресса в строительстве.
Предлагаемый новый подход к исследованиям сложных строительных конструкций основан на системном анализе, комплексном использовании методов математического и физического моделирования в зависимости от их экономической целесообразности и полезности для решения поставленной задачи.
Процесс исследований представлен как совокупность последовательно выполняемых этапов, содержащих формальные и неформальные процедуры. Максимально возможное выделение формальных методов и приемов позволяет снизить влияние субъективных факторов на результаты исследований. Основной упор сделан на численные исследования с применением средств автоматизации и ЭВМ на основе достоверных расчетных моделей. Физический эксперимент используется, как правило, для определения неизвестных параметров расчетной модели и проверки ее адекватности. Это дает возможность разрабатывать физические модели исследуемых объектов на основе функционального подобия, благодаря чему существенно сокращаются затраты ресурсов на физическое моделирование.
Однако комплексное применение методов математического и физического моделирования нуждается в дальнейшем углублении и совершенствовании. Можно полагать, что применение настоящих методических рекомендаций даст возможность выполнять прочностные исследования сложных строительных конструкций на единой методологической основе, что позволит снизить стоимость и трудоемкость исследований, сократить сроки их проведения, повысить достоверность и научную ценность получаемых результатов.
Приложение
1
МАТРИЦА ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
Планы первого порядка
|
п ≤ 3 |
3 < п = 7 |
||||||||||
|
№ опыта |
Χ1 |
Χ2 |
Χ3 |
№ опыта |
Χ1 |
Χ2 |
Χ3 |
Χ4 |
Χ5 |
Χ6 |
Χ7 |
|
1 |
+1 |
+1 |
+1 |
1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
|
2 |
-1 |
+1 |
-1 |
2 |
-1 |
+1 |
-1 |
+1 |
-1 |
+1 |
- |
|
3 |
+1 |
-1 |
-1 |
3 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
|
4 |
-1 |
-1 |
+1 |
4 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
|
|
5 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
|||
|
6 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
+1 |
||||
|
7 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
||||
|
8 |
-1 |
-1 |
+1 |
-1 |
+1 |
+1 |
-1 |
||||
Планы второго порядка
Уравнение
![]()
п = 2
|
№ опыта |
Χ1 |
Χ2 |
|
1 |
+1 |
+1 |
|
2 |
+1 |
-1 |
|
3 |
-1 |
+1 |
|
4 |
-1 |
-1 |
|
5 |
+1 |
0 |
|
6 |
-1 |
0 |
|
7 |
0 |
+1 |
|
8 |
0 |
-1 |
|
9 |
0 |
0 |
|
10 |
0 |
0 |
|
11 |
0 |
0 |
![]()
![]()
![]()
![]()
п = 3
|
№ опыта |
Χ1 |
Χ2 |
Χ3 |
|
1 |
+1 |
+1 |
+1 |
|
2 |
-1 |
+1 |
+1 |
|
3 |
+1 |
-1 |
+1 |
|
4 |
-1 |
-1 |
+1 |
|
5 |
+1 |
+1 |
-1 |
|
6 |
-1 |
+1 |
-1 |
|
7 |
+1 |
-1 |
-1 |
|
8 |
-1 |
-1 |
-1 |
|
9 |
+1 |
0 |
0 |
|
10 |
-1 |
0 |
0 |
|
11 |
0 |
+1 |
0 |
|
12 |
0 |
-1 |
0 |
|
13 |
0 |
0 |
+1 |
|
14 |
0 |
0 |
-1 |
|
15 |
0 |
0 |
0 |
|
16 |
0 |
0 |
0 |
|
17 |
0 |
0 |
0 |
![]()
![]()
![]()
![]()
n = 4
|
№ опыта |
Χ1 |
Χ2 |
Χ3 |
Χ4 |
|
1 |
+1 |
+1 |
+1 |
+1 |
|
2 |
-1 |
+1 |
+1 |
+1 |
|
3 |
+1 |
-1 |
+1 |
+1 |
|
4 |
-1 |
-1 |
+1 |
+1 |
|
5 |
+1 |
+1 |
-1 |
+1 |
|
6 |
-1 |
+1 |
-1 |
+1 |
|
7 |
+1 |
-1 |
-1 |
+1 |
|
8 |
-1 |
-1 |
-1 |
+1 |
|
9 |
+1 |
+1 |
+1 |
-1 |
|
10 |
-1 |
+1 |
+1 |
-1 |
|
11 |
+1 |
-1 |
+1 |
-1 |
|
12 |
-1 |
-1 |
+1 |
-1 |
|
13 |
+1 |
+1 |
-1 |
-1 |
|
14 |
-1 |
+1 |
-1 |
-1 |
|
15 |
+1 |
-1 |
-1 |
-1 |
|
16 |
-1 |
-1 |
-1 |
-1 |
|
17 |
+1 |
0 |
0 |
0 |
|
18 |
-1 |
0 |
0 |
0 |
|
19 |
0 |
+1 |
0 |
0 |
|
20 |
0 |
-1 |
0 |
0 |
|
21 |
0 |
0 |
-1 |
0 |
|
22 |
0 |
0 |
-1 |
0 |
|
23 |
0 |
0 |
0 |
+1 |
|
24 |
0 |
0 |
0 |
-1 |
![]()
![]()
![]()
![]()
Приложение
2
КРИТИЧЕСКИЕ ЗНАЧЕНИЯ Xα ДЛЯ X-КРИТЕРИЯ
|
Число |
Доверительная вероятность Р |
||
|
0,95 |
0,98 |
0,99 |
|
|
3 |
- |
- |
- |
|
4 |
2,4 |
- |
- |
|
5 |
2,6 |
3,0 |
3,2 |
|
6 |
2,86 |
3,29 |
3,6 |
|
7 |
3,11 |
3,62 |
3,94 |
|
8 |
3,39 |
3,92 |
4,26 |
|
9 |
3,63 |
4,23 |
4,6 |
|
10 |
3,86 |
4,52 |
4,94 |
|
11 |
4,08 |
4,8 |
5,26 |
|
12 |
4,29 |
5,06 |
5,55 |
|
13 |
4,5 |
5,3 |
5,83 |
|
14 |
4,69 |
5,54 |
6,09 |
|
15 |
4,88 |
5,77 |
6,35 |
|
16 |
5,07 |
5,99 |
6,6 |
|
17 |
5,25 |
6,2 |
6,84 |
|
18 |
5,42 |
6,4 |
7,06 |
|
19 |
5,59 |
6,6 |
7,28 |
|
20 |
5,75 |
6,8 |
7,5 |
|
21 |
5,91 |
6,99 |
7,72 |
|
22 |
6,06 |
7,17 |
7,93 |
|
23 |
6,21 |
7,35 |
8,13 |
|
24 |
6,36 |
7,53 |
8,32 |
|
25 |
6,5 |
7,7 |
8,51 |
приложение 3
ФУНКЦИОНАЛЬНОЕ ПОДОБИЕ КАК РАЗВИТИЕ ТЕОРИИ ПОДОБИЯ
Как было показано, свойства объекта исследований, воздействия на него и его состояние после приложения воздействий характеризуются множествами физико-механических параметров соответственно Р, N и Y. Для конкретной задачи первые два множества объединяют независимые (входные) параметры, а третье - зависимые (выходные).
Если для некоторой группы объектов эти множества тождественны, т.е. состоят из качественно одинаковых параметров, то эти объекты будут принадлежать к одному классу. Для конструкций одного класса будет общая функция Y = f(Р, N).
Все физические объекты одного класса находятся в отношении функционального подобия.
Определение. Два физических объекта находятся в отношении функционального подобия, если их свойства, внешние воздействия и параметры состояний можно однозначно соответственно описать качественно одинаковыми множествами P(1), N(1), Y(1) и Р(2), N(2), Y(2) и при этом существует такая функция f, что Y(1) = f(P(1), N(1)) и Y(2) = f(P(2), N(2)).
Функциональное подобие, так же как и другие виды подобия, может быть полным и неполным. При неполном будем иметь Y* = f(P*, N*), причем Y* = Y(1)nY(2), Р* = P(4)nP(2), N* = N(1)nN(2) (где Y(1), P(1), N(1); Y(2), P(2), N(2) - указанные множества параметров соответственно двух неполно функционально подобных объектов).
Таким образом, функциональное подобие характеризует объекты к конструкции одного класса, в которых протекают явления одинаковой физической природы. Основным требованием наличия функционального подобия является инвариантность функции Y = f(P, N) и вычисляющего ее алгоритма. Это определяет необходимость однородности функции, т.е. независимости ее от размерности элементов множеств, входящих в ее область определения и результат.
Функциональное подобие как дальнейший этап развития теории подобия, обобщения механического подобия твердых деформируемых тел на механические системы одного класса - наиболее общий вид подобия физических объектов. Простое и расширенное подобия могут быть получены в виде частных случаев функционального введением дополнительных ограничений на условия моделирования.
Применение функционального подобия при соответствующем его обосновании существенно упрощает изготовление физических моделей и уменьшает затраты ресурсов на экспериментальные исследования.
Рассмотрим основные теоретические положения функционального подобия.
Инвариантами функционально подобных объектов будут функции, поэтому первостепенное значение приобретает корректность выбора из множества параметров, которые с необходимой для данной конкретной задачи степенью идеализации определяют свойства объекта (множество Р), внешние воздействия (множество N) и параметры напряженно-деформированного состояния (множество Y).
Теорема 1: Необходимым и достаточным условием корректности выбора множеств Р, N, Y является наличие функционального соответствия (см. п. 1.1.14 настоящих методических рекомендаций) между множеством Y, с одной стороны, и множеством Р и N с другой.
Доказательство. Функциональное соответствие характеризуется наличием
функции yj = fj(P, N), где yj
= Y, ![]() ,
, ![]() ,
, ![]() , N = {nК}.
Для доказательства достаточности необходимо доказать справедливость
утверждения: "если все
, N = {nК}.
Для доказательства достаточности необходимо доказать справедливость
утверждения: "если все ![]() , то все
, то все ![]() и
и ![]() ". Так как
". Так как ![]() и
и ![]() , а
, а ![]() и
и ![]() , то, следовательно, и
, то, следовательно, и ![]() , и
, и ![]() . Для доказательства необходимости предположим, что
существуют такие
. Для доказательства необходимости предположим, что
существуют такие ![]() и
и ![]() , для которых
, для которых ![]() . Тогда, очевидно, в этих множествах имеется хотя бы по
одному элементу, соответственно
. Тогда, очевидно, в этих множествах имеется хотя бы по
одному элементу, соответственно ![]() и
и ![]() , которым нельзя поставить в соответствие ни один элементу
, которым нельзя поставить в соответствие ни один элементу ![]() , что противоречит определению функционального соответствия.
Следовательно, для любого
, что противоречит определению функционального соответствия.
Следовательно, для любого ![]() при наличии
функционального соответствия всегда найдутся такие
при наличии
функционального соответствия всегда найдутся такие ![]() и
и ![]() , что
, что ![]() . Необходимо отметить, что установление
функционального соответствия между множествами Y и P, N является
ответственной неформальной процедурой, определяющей дальнейшую стратегию и
тактику исследований.
. Необходимо отметить, что установление
функционального соответствия между множествами Y и P, N является
ответственной неформальной процедурой, определяющей дальнейшую стратегию и
тактику исследований.
Из этой теоремы вытекает одно важное следствие: для проверки алгоритма расчетной модели объекта может быть использована некоторая физическая модель, функционально подобная объекту исследований.
Для разработки функционально подобных физических моделей может быть рекомендован принцип, основанный на исследовании критериев простого подобия.
Теорема 2: Для функционального подобия объектов достаточно, чтобы количество определяющих безразмерных комплексов - критериев подобия - для этих объектов было равным, а их буквенные выражения одинаковыми.
Доказательство. Пусть свойства,
воздействия и параметры состояния двух объектов характеризуются соответственно
множествами P(1), N(1), Y(1)
и P(2), N(2), Y(2) которые являются подмножествами
соответственно множеств P, N, Y, т.е. ![]() ,
, ![]()
![]()
![]() ,
, ![]() ,
, ![]() .
.
В соответствии с
определением функционального подобия, если существует функция Y = fj(P, N), то справедливо ![]() и
и ![]() . При том, если множества P(1), N(1), и P(2), N(2)) будут соответственно качественно и
количественно одинаковы, что означает подобие в характере воздействий и
исходных параметрах объектов, то, очевидно, Y(1) и Y(2) будут также качественно и количественно
одинаковы и каждый параметр
. При том, если множества P(1), N(1), и P(2), N(2)) будут соответственно качественно и
количественно одинаковы, что означает подобие в характере воздействий и
исходных параметрах объектов, то, очевидно, Y(1) и Y(2) будут также качественно и количественно
одинаковы и каждый параметр ![]() и
и ![]() с точностью до
безразмерных коэффициентов может быть представлен в виде произведения различных
степеней элементов множеств P(1), N(1), и P(2), N(2) и,
соответственно, функции произведений различных величин являются гомогенными и,
следовательно, в соответствии с π-теоремой
теории подобия и размерностей [27]
могут быть представлены в виде зависимости между безразмерными
комплексами-критериями подобия. Функции
с точностью до
безразмерных коэффициентов может быть представлен в виде произведения различных
степеней элементов множеств P(1), N(1), и P(2), N(2) и,
соответственно, функции произведений различных величин являются гомогенными и,
следовательно, в соответствии с π-теоремой
теории подобия и размерностей [27]
могут быть представлены в виде зависимости между безразмерными
комплексами-критериями подобия. Функции ![]() и
и ![]() при записи в
критериальной форме будут отличаться только постоянными коэффициентами. А так
как количество критериев подобия и их алгебраические выражения не зависят от
постоянных, то для первого и второго объектов количество критериев подобия
будет равным, а их выражения одинаковы.
при записи в
критериальной форме будут отличаться только постоянными коэффициентами. А так
как количество критериев подобия и их алгебраические выражения не зависят от
постоянных, то для первого и второго объектов количество критериев подобия
будет равным, а их выражения одинаковы.
Эта теорема позволяет без установления функционального соответствия между множествами Y и Р, N в качестве функционально подобных применять такие физические модели, расчетные модели которых при идентичности граничных условий содержат такие же элементы (суперэлементы), что и расчетная модель натурной конструкции. При этом общие расчетные схемы модели и натуры могут быть геометрически не подобны.
Если в расчетную модель физической модели входят все элементы (суперэлементы) расчетной модели натурной конструкции, будем иметь полное функциональное подобие, в противном случае - неполное.
Физический и численный эксперименты проводятся с целью получения некоторой информации о состоянии и поведении объекта исследований при определенных внешних воздействиях. Так как параметры объекта и воздействия на него имеют стохастический характер, то и параметрам состояния объекта будет присуща некоторая неопределенность. Очевидно, что чем меньше будет эта неопределенность, тем больше будет ценность результатов исследований.
В теории информации [30] мерой априорной неопределенности является специальная характериcтика, называемая энтропией. Она вычисляется как сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком. Из двух систем меньшей неопределенностью обладает та, у которой энтропия меньше.
Теорема 3: "Из нескольких функционально подобных физических моделей, содержащих необходимое и достаточное количество элементов и связей между ними для выполнения тех же функций, что и в натурном объекте, предпочтительней та, энтропия которой будет меньше".
Доказательство. Энтропия сложной системы обладает свойством аддитивности, заключающимся в том, что при объединении независимых систем их энтропии складываются. Объект исследований - система с непрерывным числом состояний ("непрерывной системой", состояние которой описывается некоторым количеством случайных величин х1, х2,…, хп, с плотностью совместного распределения f(х1, х2,…xп). Объект исследований в этом случае можно рассматривать как объединение более простых систем Χ1, Χ2,…, Χп.
Энтропию сложной системы, (при независимых xi) можно вычислить по формуле:
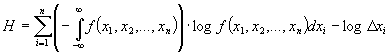
где Hi-1 - энтропия системы; Δxi -дискретность изменения xi.
Так как все энтропии одного знака, то, очевидно, что, чем меньше n, тем меньше будет общая энтропия системы.
Не вычисляя энтропии альтернативных функциональных моделей, для практических целей можем руководствоваться правилом: чем меньше изменчивых параметров содержит функциональная физическая модель, тем ее энтропия меньше, а, следовательно, сама модель предпочтительней. Применение его позволит существенно упростить физические модели сложных объектов, состоящих из однотипных элементов.
Все сказанное позволяет более объективно подойти к разработке, физических моделей, необходимых для проведения комплексных исследований сложных конструкций.
Приложение 4
примеры применения ФУНКЦИОНАЛЬНОго модЕЛирования
Исследование блоков-контейнеров
В 1984 - 1985 гг. были проведены комплексные исследования прочности и жесткости базового блока-контейнера, разработанного НИИСК Госстроя СССР, с целью:
разработки расчетной модели блока-контейнера, учитывающей совместную работу элементов каркаса и ограждающих конструкций;
проверки прочности и деформативности. основных несущих элементов отдельного блока и контейнера при действии расчетных нагрузок;
определения внутренних усилий в элементах каркаса от расчетных сочетаний нагрузок при различных конструктивных схемах зданий, собираемых из блоков-контейнеров.
Для решения поставленных задач был использован системный подход, так как применение только экспериментального либо теоретического метода не представлялось возможным из-за чрезвычайно большого объема экспериментов в первом случае и отсутствия достоверной расчетное модели - во втором. Исходя из поставленных целей, исследования проводились в три этапа:
этап I - предварительные численные исследования для получения зависимостей параметров напряженно-деформированного состояния yi в характерных точках блока-контейнера от неизвестных характеристик расчетной модели xi типа:
|
yi = fj(xi)(i = 1, 2,…, n; j = 1, 2,..., m); |
(1) |
этап II - экспериментальные исследования блока-контейнера при действии расчетных и контрольных нагрузок, определение неизвестных параметров расчетной модели и проверка ее адекватности;
этап III - численные исследования различных типов зданий, собираемых из блоков-контейнеров, для получения расчетных значений внутренних усилий; в элементах.
Численные исследования выполнялись на ЭВМ EC-1030 с применением расчетного комплекса "ПРОКРУСТ". При этом расчетная схема блока-контейнера представляла собой пространственную пластинчато-стержневую систему. Стержни расчетной схемы, элементы каркаса задавались по геометрическим осям и с соответствующими жесткостными характеристиками. Плоскостные элементы - панели стен, пола и потолка - задавались как совокупности прямоугольных плоско-напряженных КЭ с приведенными характеристиками: коэффициент Пуассона υ, модуль упругости Е и толщина t. Соединения ограждающих стеновых панелей с элементами каркаса аппроксимированы в расчетной схеме контактными элементами с неизвестными жесткостями на сдвиг - Кτ, и на растяжение-сжатие Кσ (рис. 1).
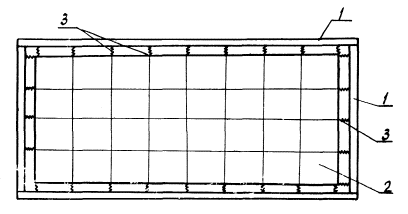
Рис. 1. Расчетная схема стены блока-контейнера
1 - каркас блока - стержневые элементы; 2 - ограждающая конструкция - плоские КЭ; 3 - связь - контактные элементы
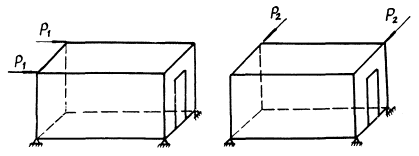
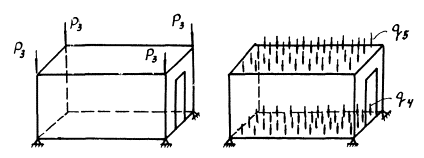
Рис. 2. Схема нагружения блока-контейнера
Для получения уравнений
(1) использована матрица планирования типа 22 (см. приложение 1)
и формулы (12)
настоящих методических рекомендаций. Для получения линейных зависимостей
перемещений от жесткостей связей в качестве неизвестных приняты не жесткости
связей, а величины им обратные: ![]() ;
; ![]() .
.
При варьировании жесткостей связей принимались уровни Kσmax = Kτmax = 10000 кН/м; Kσmin = Kτmin = 100 кН/м. При выборе вариантов нагружений и характерных параметров напряженно-деформированного состояния блока учитывалось максимальное включение в работу стеновых панелей:
перемещение верхних углов блока вдоль приложенных к ним горизонтальных сил Y(2);
прогиб середины продольного элемента панели основания от равномерно распределенной нагрузки на пол Z(4).
В результате обработки численных экспериментов после отбрасывания малозначимых членов взаимодействий получаем систему уравнений:
Экспериментальные исследования блока-контейнера были выполнены на натурном образце, изготовленном на заводе и доставленном в НИИСК по железной дороге. Блок испытывался на следующие виды воздействий (рис. 2):
горизонтальная нагрузка, приложенная к верхним углам блока, направленная вдоль длинных Р(1) и коротких Р(2) сторон;
вертикальная нагрузка, приложенная к верхним углам блока, - Р(3);
равномерно распределенная нагрузка на основание - q(4);
то же, плюс равномерно распределенная нагрузка на пол - q(5).
Нагрузки P(1), P(2), P(3) достигали своих расчетных, а нагрузки q(4) и q(5) контрольных значений. Во время эксперимента измерялись перемещения углов и середин ребер блока, а также деформации в наиболее напряженных сечениях элементов каркаса.
При всех схемах нагружения, вплоть до расчетных величин нагрузок, нарастание перемещений в характерных точках было пропорционально росту нагрузки, что свидетельствовало об упругом характере работы конструкции.
Подставив в уравнения (2)
экспериментальные значения перемещений - соответственно ![]() - 1,15 мм и
- 1,15 мм и ![]() - 5,0 мм, решив их, после
соответствующих преобразований получим реальные значения жесткостей связей: Kσ = 900 кН/м; Кτ = 2500 кН/м.
- 5,0 мм, решив их, после
соответствующих преобразований получим реальные значения жесткостей связей: Kσ = 900 кН/м; Кτ = 2500 кН/м.
Как показали экспериментальные исследования, стеновые панели, включаясь в работу, существенно разгружают элементы каркаса.
После определения всех неизвестных параметров расчетной модели были проведены численные исследования блока-контейнера.
Сначала исследовалось влияние на напряженно-деформированное состояние элементов каркаса возможных технологических дефектов при реальном осуществлении соединений с элементами каркаса.
Были рассмотрены следующие варианты: связи работают на растяжение и сдвиг; связи работают только на растяжение; связи работают только на сдвиг; связи отсутствуют.
Исследования показали, что качество выполнения связей существенно влияет на напряженно-деформированное состояние элементов каркаса, особенно стоек. При отсутствии связей или при выполнении их с отклонениями от проекта напряжения в элементах каркаса и перемещения существенно возрастают (рис. 3) и в ряде сечений могут превзойти допустимые значения.
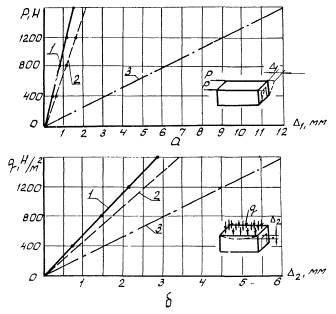
Рис. 3. Влияние стеновых панелей на деформативность блока-контейнера
а - горизонтальная нагрузка; б - вертикальная нагрузка; 1 - эксперимент; 2 - расчет с учетом стеновых панелей; 3 - то же, без учета
Исследовалось также напряженно-деформированное состояние несущих элементов каркаса в зависимости от расположения данного блока в двухэтажном здании, в том числе рассматривались варианты удаления стен (продольных или торцовых) двух смежных блоков. Анализ результатов исследований показал, что из блок-контейнеров данной конструкции можно собирать двухэтажные здания. Причем могут быть применены различные объемно-планировочные решения, в том числе и с удалением двух смежных стен.
Уточнение расчетной модели с включением в работу стен позволило улучшить его технико-экономические показатели, расход металла на блок уменьшился на 140 кг. С учетом наших рекомендаций внесены коррективы в рабочие чертежи и изготовлен по ним экспериментальный блок-контейнер. Испытания облегченного блока контрольными нагрузками подтвердили правильность принятых конструктивных решении.
Исследования каркаса здания межвидового применения серии Т.020-1/83
Каркасы межвидового применения серии 1.020-1/83 предназначены для широкой номенклатуры зданий различного назначения, что обусловливает многообразие конструктивных схем, воздействий и т.д. В этой связи для рационального проектирования конструкций необходимо разработать такие расчетные модели, которые позволяли бы достоверно определять параметры напряженно-деформированного состояния элементов и, в частности, крайних ригелей, как наиболее сложно напряженной конструкции, с учетом их реальной работы в составе диска перекрытия.
Цель исследований:
совершенствование расчетной модели крайних ригелей с учетом их пространственной работы в составе диска перекрытия;
проверка правильности конструктивных решений опирания однополочных ригелей с подрезкой;
исследование влияния на напряженно-деформированное состояние крайних (однополочных) ригелей изменения конструктивных схем здания, характера нагрузок, жесткостей элементов, возможных несовершенств строительного производства, а также ряда других факторов, возникающих в процессе монтажа и эксплуатации здания.
Для решения поставленных задач была использована методика, основанная на системном анализе и функциональном моделировании, в соответствии с положениями которой процесс исследования был разбит на ряд последовательных этапов:
I - разработка расчетной модели каркаса малоэтажного здания, учитывающей факторы, влияющие на напряженно-деформированное состояние элементов (однополочных ригелей);
II - выявление неизвестных параметров расчетной модели и проведение предварительных численных исследований для получения уравнений типа (I);
III - проведение физических экспериментов для получения данных, необходимых для определения неизвестных параметров расчетной модели и проверки ее адекватности;
IV - уточнение расчетной модели и выполнение многовариантных расчетов - численных экспериментов - в необходимом объеме.
Анализ проведенных ранее исследований показал, что расчетная модель однополочного ригеля должна учитывать следующие обстоятельства: пространственную работу; податливость крепления ригеля к колонне; совместную работу ригеля и плит; влияние замоноличивания швов между плитами; возникновение распора в плитах и ригелях; изменение жесткостных характеристик элементов при увеличении нагрузки. Вместе с тем, результат расчета должен быть получен в виде, удобном для проектирования элементов, а сама расчетная модель должна быть четкой, удобной в работе.
С учетом вышеизложенного расчетная схема каркаса с плитами была принята в виде пространственной стержневой системы, в которой основные элементы каркаса (колонны, ригели, плиты) аппроксимированы стержневыми КЭ, оси которых совпадают с физическими осями элементов, а задание реальных расстояний между точками соединения элементов моделируется стержневыми элементами бесконечной жесткости. Соединения ригеля с плитами и плит между собой аппроксимированы дискретными связями (контактными элементами), не имеющими линейных размеров, но обладающими определенной жесткостью на растяжение (сжатие) и сдвиг.
Реализация расчетной схемы выполнена с применением программного комплекса "ПРОКРУСТ" на ЭВМ EC-1030.
Рассмотренная расчетная
схема имеет десять неизвестных параметров: жесткость ригеля при изгибе в
вертикальной ![]() , и горизонтальной
, и горизонтальной ![]() плоскости; жесткость
ригеля на кручение DP; жесткость соединения ригеля с
колонной на кручение
плоскости; жесткость
ригеля на кручение DP; жесткость соединения ригеля с
колонной на кручение ![]() ; жесткость соединения ригеля с колонной при изгибе в
горизонтальной плоскости
; жесткость соединения ригеля с колонной при изгибе в
горизонтальной плоскости ![]() ; жесткость плиты при изгибе
; жесткость плиты при изгибе ![]() ; жесткость плиты на кручение DП;
высота опорного стержня плиты, определившая наличие распора, h; сдвиговая жесткость шва между плитами и ригелем КР.П; то же, между плитами КП.
Таким образом, число уравнений, в системе (1) должно быть не менее десяти.
; жесткость плиты на кручение DП;
высота опорного стержня плиты, определившая наличие распора, h; сдвиговая жесткость шва между плитами и ригелем КР.П; то же, между плитами КП.
Таким образом, число уравнений, в системе (1) должно быть не менее десяти.
Поскольку основными параметрами входящими в левые части уравнений (1), будут измеренные в эксперименте перемещения, для получения линейных зависимостей необходимо перейти к новым неизвестным параметрам расчетной модели:
![]()
![]()
Для упрощения процесса определения неизвестных параметров расчетной модели xi; (i = 1. 2,…, 10) был применен принцип декомпозиции сложной системы (каркаса) на более простые подсистемы - ригели с опорными узлами и плиты. С учетом этого (1) распалось на шесть независимых систем и отдельных уравнений.
Подсистема - ригель - при действии вертикальной нагрузки:
|
|
(3) |
|
|
(4) |
Подсистема - плита:
|
|
(5) |
|
|
(6) |
Подсистема - швы:
|
|
(7) |
где yj - параметры напряженно-деформированного состояния конструкций; у1 - вертикальный прогиб по средине ригеля; у2 - угол кручения среднего сечения ригеля; у3 - тоже, опорного; y4 - горизонтальный прогиб на средине ригеля; y5 - угол поворота в горизонтальной плоскости опорного сечения ригеля; y6 - прогиб плиты при шарнирном опирании; y7 - угол кручения по средине плиты; y8 - прогиб плиты при реальном опирании; y9 - прогиб середины ригеля в составе диска перекрытия; y10 - разность вертикальных смещений ребер двух смежных плит; вij коэффициенты уравнений регрессии, полученные методом планирования экспериментов в соответствии с матрицами планирования (см. приложение 1).
Для экспериментального определения перемещений yj были проведены испытания физических моделей со смешанным подобием: простое по отношению к неизвестным параметрам xi, и функциональное по отношению к остальным.
В соответствии с декомпозицией каркаса на подсистемы были испытаны модели:
ригелей на действие вертикальных и горизонтальных нагрузок (рис. 4,а);
плит при двух вариантах опирания (рис. 4,б);
фрагмента многоэтажного здания (рис. 4,в);
На основании анализа рабочих чертежей ригелей и плит, исходя из сортамента арматуры классов А-III и А-IV, принят масштаб моделирования Cl = 0,5.
Измеренные в эксперименте
перемещения ![]() при действии
указанных нагрузок подставлялись в соответствующие
уравнения (3) - (7), из решения которых определялись неизвестные параметры
расчетной модели xi. Причем, в зависимости
от стадии работы конструкции, при которой измерялись перемещения уj, пара метры xi были определены для
упругой стадии при действии нормативных и расчетных нагрузок и в стадии,
близкой к разрушению. Так, например, при действии расчетных нагрузок были
определены следующие значения неизвестных параметров в пересчете на натуру в
соответствии с масштабами подобия:
при действии
указанных нагрузок подставлялись в соответствующие
уравнения (3) - (7), из решения которых определялись неизвестные параметры
расчетной модели xi. Причем, в зависимости
от стадии работы конструкции, при которой измерялись перемещения уj, пара метры xi были определены для
упругой стадии при действии нормативных и расчетных нагрузок и в стадии,
близкой к разрушению. Так, например, при действии расчетных нагрузок были
определены следующие значения неизвестных параметров в пересчете на натуру в
соответствии с масштабами подобия: ![]() = 56000 кН м2;
= 56000 кН м2;
![]() = 58000 кН м2;
DP =
37000 кН м2;
= 58000 кН м2;
DP =
37000 кН м2; ![]() = 640 кН м2;
= 640 кН м2;
![]() = 2100 кН/м2;
= 2100 кН/м2;
![]() = 30000 кН м2;
DП = 31000 кН м2; h = 9 см; КРП = 18 106 кН; КП
= 13,2·105 кН.
= 30000 кН м2;
DП = 31000 кН м2; h = 9 см; КРП = 18 106 кН; КП
= 13,2·105 кН.
Кроме указанных вариантов испытаний, модель фрагмента испытывалась равномерно распределенной нагрузкой вплоть до разрушения.
После определения неизвестных параметров были выполнены расчеты модели фрагмента и проверена адекватность расчетной модели, которая показала достоверность разработанной расчетной модели.
На отлаженной расчетной модели были выполнены численные исследования и оценено влияние ряда факторов (отклонения в жесткостных характеристиках элементов, изменение высоты этажа, изменение граничных условий, качество замоноличивания, стыков и т.д.) на напряженно-деформированное состояние каркаса здания межвидового применения.
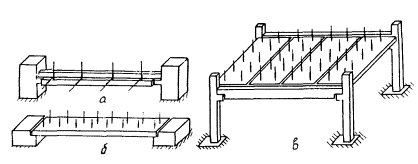
Рис. 4. Декомпозиция каркаса многоэтажного здания
а - подсистема "ригель"; б - подсистема "плита"; в - подсистема "швы"
Исследование панели сборной железобетонной градирни на транспортные нагрузки
Целью исследований было определение оптимального расположения опор на транспортном средстве, обеспечивающем трещиностойкость панелей при перевозке.
По данной методике выполнялись исследований с применением методов математического и физического моделирования следующими этапами: экспериментальные исследования на физической модели, выбор и определение неизвестных параметров расчетной модели, проверка адекватности расчетной модели, численные исследования.
Физическое моделирование осуществлялось на модели из упругого материала, так как при транспортировании возникновение трещин в панелях не допускается. Согласно заданной схеме опирания конструкции в процессе перевозки (рис. 5) в ее элементах возникают, в основном, продольные напряжения, что дает возможность при моделировании не учитывать различие коэффициентов Пуассона материалов модели и натуры. С учетом условия подобия запишем:
|
|
(8) |
где Си, СЕ, Сl, СР, Сσ, СМ - масштабы соответственно перемещений, модуля упругости, геометрических размеров, нагрузки, напряжений, изгибающих моментов. Поскольку масштабов шесть, а равенств в системе (8) имеем три, то тремя масштабами Сl, СЕ, СР, можем задаваться произвольно.
Исходя из технологических
условий принимаем Сl = 0,05. Материал модели -
эпоксидная смола ЭД-16М, следовательно, СЕ = ![]() = 0,103. Для удобства
нагружения принимаем СР = 0,0032.
= 0,103. Для удобства
нагружения принимаем СР = 0,0032.
Подставив принятые, значения Сl, СЕ, СР в систему (8), получим: Си = 0,62; Сσ = 1,28; СМ = 1,6·10-4.
Для изготовления модели применена технология точного литья в размываемые формы.
При экспериментальных исследованиях измерялись прогибы панели в узлах, а также фибровые деформации ребер и поля панели. Значения средних и доверительных оценок результатов прямых измерений прогибов и деформаций определялись по формулам (2).
Определение неизвестных параметров математической модели при транспортировке в горизонтальном положении, когда направление транспортных нагрузок перпендикулярно плоскости панели, выполняется при условии следующих допущений: нагрузка прикладывается в узлах пересечения ребер и воспринимается, в основном, ребрами, так как их жесткость на порядок выше жесткости поля панели. Таким образом, расчетная схема панели представляется в виде стержневой системы, у которой оси стержней совпадают с физическими осями ребер (см. рис. 5). Часть исходных данных известна (координаты узлов, нагрузка). Не известны жесткостные характеристики приведенного сечения ребер.
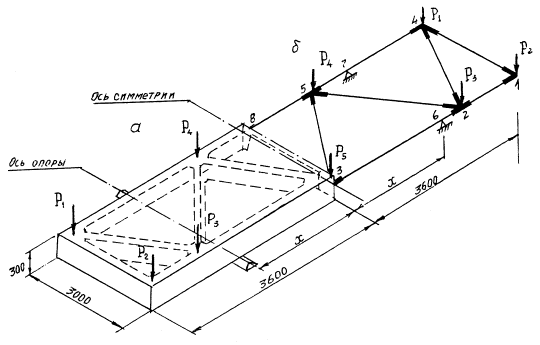
Рис. 5. Горная панель градирни а - общий вид; б - расчетная схема
Для их определения необходимо выявить расчетную ширину полки таврового сечения. В такой постановке задача решалась экспериментально-теоретически с использованием данных тензометрических измерений фибровых деформаций. При этом, если расчетную ширину полки принять за х, то, исходя из гипотезы плоских сечений, получим:
|
|
(9) |
где ![]() - усредненная по всей
ширине х деформация в полке;
- усредненная по всей
ширине х деформация в полке; ![]() =
= ![]() εР - фибровая деформация ребра; уЦ.Т(х) - расстояние центра тяжести сечения с
шириной полки х до верха плиты.
εР - фибровая деформация ребра; уЦ.Т(х) - расстояние центра тяжести сечения с
шириной полки х до верха плиты.
Решение уравнения (9) получено методом последовательных приближений. Расчетная ширина полки х. определялась для опорных и пролетных сечений ребер.
Проверка адекватности расчетной модели выполнялась сравнением критериев Т и R вычисляемых по формулам (27) и (28) методических рекомендации соответственно. Для этого сначала находили средние значения и доверительные интервалы экспериментальных и теоретических величин сравниваемых параметров соответственно. Для прогибов оценка средних и доверительных значений выполнялась по формуле (2). Для изгибающих моментов аналогичные оценки выполнялись по формулам (8) и (9) с учетом равенства (таблица).
![]()
|
Параметры НДС |
Значения |
R |
Т |
Оценка адекватности (+) или неадекватности (-) расчетной модели |
|||
|
теоретические |
экспериментальные |
||||||
|
Средние |
Доверительный интервал |
Средние |
Доверительный интервал |
||||
|
Прогибы, мм |
|||||||
|
у1 |
87,1, |
18,6 |
84,3 |
1,6 |
2,8 |
18,7 |
+ |
|
у2 |
12,4 |
7,9 |
19,4 |
0,9 |
7 |
8 |
+ |
|
у3 |
-16,7. |
10,9 |
-0,1 |
1;3 |
16,6 |
11,3 |
- |
|
у4 |
85,2 |
20,6 |
88,6 |
0,9 |
3,4 |
20,6 |
+ |
|
У5 |
-12,5 |
9,7 |
0,8 |
0,6 |
13,2 |
9,8 |
- |
|
Изгибающие моменты, Н·см |
|||||||
|
М3 |
10,1 |
3,4 |
9,6 |
2,4 |
0,5 |
5,6 |
+ |
|
М7 |
-34,5 |
2,8. |
-31,4 |
5 |
3,1 |
7,9 |
+ |
|
М8 |
-2,2 |
4,6 |
2,4 |
0,9 |
4,6 |
4,7 |
+ |
Доверительные интервалы теоретических значений параметров получены с применением математической теории планирования экспериментов по формулам (11), (12) и (26) настоящих методических рекомендаций на основании численного эксперимента. При этом учитывалась изменчивость следующих факторов:
![]()
х3 - расстояние от торца панели силы Р4; х5 - то же, Р1; х4 - расстояние от оси опоры силы Р5; х6 -то же, Р2; х7 - расстояние опоры от оси панели.
При учете влияния семи факторов
численные эксперименты проводились в соответствии с матрицей планирования 3
< n ≤ 7 (см. приложение 1).
Значения факторов в центре плана и их доверительные интервалы были
соответственно 1,5 ±0,15; 2,23 ±0,33; 6 ±
Из таблицы видно, что почти по всем параметрам расчетная модель адекватна физической. В точках неадекватности теоретические значения превышают экспериментальные, кроме того, значения параметров НДС в точках неадекватности гораздо ниже экстремальных показателей. Исходя из этого, а также цели проводимых исследований, делаем вывод о пригодности математической модели для дальнейших численных исследований.
Численные исследования проводились для определения оптимального расположения опор при транспортировании панелей. Критерием оптимальности было условие удовлетворения равнопрочности по трещиностойкости опорных и пролетных сечений. Для натурной конструкции после ряда преобразований оно запишется как:
![]()
где МОП - изгибающий момент в продольном ребре у опоры; МПР - то же, в пролете.
Выполнив серию расчетов,
в которых варьировалось расстояние опор от середины продольных ребер, находим
их оптимальные значения:
литература
1. Клиланд Д., Кинг В. Системный анализ и целевое управление. -М.; Советское радио, 1974.- 278 с.
2. Садовский В.И. Основания общей теории систем. - М.: Наука, 1974. - 215 с.
3. Блауберг И.В., Юдин Э.Г, Становление и сущность системного подхода. - М.; Наука, 1973. - 270 с.
4. Шаханович Ю.А. Введение в современную математику. - М.: Наука, 1965. - 376 с.
5. Мальцев А.И. Алгоритмы и рекурсивные функции. - М.: Наука, 1965. - 391 с.
6. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1974. - 224 с.
7. Эйкхофф П. Основы идентификации систем управления. - М.: Мир, 1975. - 683 с.
8. Дыховичный А.А., Вишневецкий А.И. Экспериментальные исследования упругих систем и математическое моделирование. - В кн.: Сопротивление материалов и теория сооружений. - Киев: БудIвельник, 1980, вып.36,.с.107-110.
9. Duhovichnuj A.A. Matematikal Modellezes a szerkezet-kutatasban. - Epitest Kutatas Feilesztes. 1982, № 4, p.209-211.
10. Безухов Н.И., Лужин О.В. Приложение методов теории упругости и пластичности к решению инженерных задач. - М.: Высшая школа, 1974.
11. Аргирос Дж. Энергетические теоремы и расчет конструкций. В кн.: Современные методы расчета сложных статически неопределимых систем. - Л: Судпромгиз., 1961.
12. Washizu
K. Variational Method in Elasticity and Plasticity. Pergamon Press,
13. Сливкер В.И. Об одной смешанной вариационной постановке задач для упругих тел. - Механика твердого тела, 1982, № 4, с. 88-97.
14. Образцов И.Ф. Вариационные методы расчета тонкостенных авиационных пространственных конструкций. - М.: Машиностроение, 1966.
15. Розин Л.А. О связи метода конечных элементов с методами Бубнова-Галеркина и Ритца. - В кн.: Строительная механика сооружений. Л.: Изд-во ЛПИ, 1971.
16. Зенкевич O.K. Метод конечных элементов в технике. - М.: Мир, 1975.
17. Розин Л.А. Метод конечных элементов в применении к упругим системам. - М.: Стройиздат, 1977.
18. Постнов В.А., Хархурим И.Я. Метод конечных элементов в расчетах судовых конструкций. - Л.: Судостроение, 1974.
19. Немчинов Ю.И. Расчет пространственных конструкций (метод конечных элементов). - К.: БудIвельник, 1980.
20. Пустыльник Е.И. Статистические методы анализа и обработки наблюдений.- М.: Наука, 1968. - 288 с.
21. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений.- М.: Физматгиз, 1962. - 352 с.
22. ГОСТ 8.207-76. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений.
23. Адлер Ю.П. Введение в планирование эксперимента. - М.: Металлургия, 1969. - 279 с.
24. Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов. - М.: Наука, 1966.
25. Шторм Р. Теория вероятностей, математическая статистика, статистический контроль качества. М.: Мир, 1979. - 368 с.
26. Harrington E.C. Indust. Quality Control, 1965, 21, № 10.
27. Кирпичёв М.В. Теория подобия. - М.: Изд. АН СССР, 1953. - 93 с.
28. Седов Л.И. Методы подобия и размерности в механике. - М.: Наука, 1972.
29. Назаров А.Г. О механическом подобии твердых деформируемых тел. - Ереван: Изд. АН АрмССР, 1965.
30. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1964. -576 с.
31.
Городецкий А.А., Здоренко B.C. Расчет физически
нелинейных плоских рамных систем. - В сб.: ЭВМ в исследованиях и проектировании
объектов строительства, вып.
32. Бондаренко В.М., Бондаренко С.В. Инженерные методы нелинейной теории железобетона. - М.: Стройиздат, 1982.
33. Гениев Г.А., Киссюк В.Н., Тюпин Г.А. Теория пластичности бетона и железобетона. - М.: Стройиздат, 1974
34. Ильюшин А.А. Пластичность. - М.: Гостехиздат, 1948.
35. Лехницкий С.Г. Теория упругости анизотропного тела. - М.: Наука, 1977.
36. Фудзии Т., Дзако М. Механика разрушения композиционных материалов. - М.: Мир, 1982.
37. Постнов В.А., Дмитриев С.А., Елтышев Б.К., Родионов А.А. Метод суперэлементов в расчетах инженерных сооружений. - Л.: Судостроение,1979.
38. Кретов В.И., Вишневецкий А.И. О получении матрицы жесткости суперэлемента. - Строительная механика и расчет сооружений, 1983, № 5