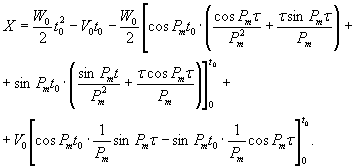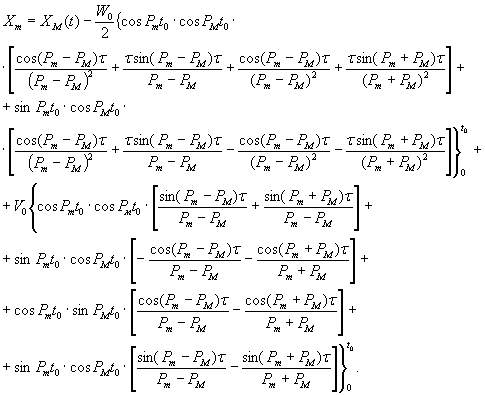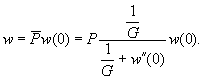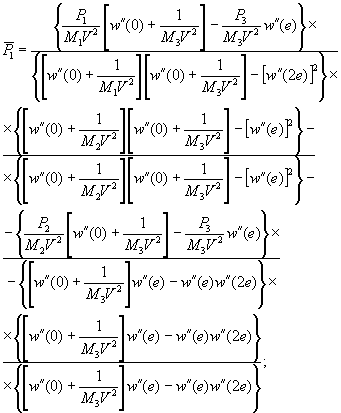Министерство образования и науки
Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический
университет
Н.Н.
Бычковский Ю.А. Гурьянов
ЛЕДОВЫЕ СТРОИТЕЛЬНЫЕ
ПЛОЩАДКИ,
ДОРОГИ И ПЕРЕПРАВЫ
Саратов 2005
Рецензенты:
Кандидат технических
наук, ведущий научный сотрудник ЦНИИСа
В.П. Величко
Кандидат технических
наук, доцент
Саратовского государственного технического университета
Ю.Н Кондюрин
Одобрено
редакционно-издательским советом
Саратовского государственного технического университета
Бычковский Н.Н.
Ледовые
строительные площадки, дороги и переправы / Н.Н. Бычковский, Ю.А. Гурьянов; под
общ. ред. Н.Н Бычковского. Саратов: Сарат. гос. техн. ун-т, 2005. 260 с.
В
книге приведены методы расчета ледяного покрова рек и водохранилищ с целью
устройства временных строительных; площадок, подъездных нукай к ним и переправ.
Дано теоретическое обоснование возможных упрощений расчетных схем при
проектировании с применением методики расчета по предельным состояниям.
Значительное
внимание уделено новым вопросам использования ледяного покрова и особенностям
его работе; под временной подвижной нагрузкой.
Обобщен
отечественный опыт проектирования временных ледовых переправ, возводимых через
большие реки и водохранилища как при производстве различных строительных работ,
так и для сезонной эксплуатации.
Предназначена
для инженерно-технических работников, занимающихся проектированием в
гидротехническом и транспортном строительстве.
Ил. 63,
Табл. 21. Библиогр. 197 назв.
По мере
дальнейшего развития гидротехнического и транспортного строительства в
восточных и северных районах нашей страны, все большие объемы работ приходится
выполнять в зимнее время, на льду и со льда рек и водохранилищ.
Примеры
использования естественного ледяного покрова известны очень давно, но изучение
работы ледяного покрова под нагрузкой и применение общих принципов строительной
механики к расчету ледяного покрова началось сравнительно недавно и вызвано
повышением веса передвигаемых по льду грузов.
Ледяные
переправы через реки и водохранилища устраивают в условиях достаточно суровой
зимы с устойчивыми отрицательными температурами воздуха. Ледяной покров должен
обладать достаточной несущей способностью (грузоподъемностью), а глубина воды
подо льдом на переправе в течение всего периода ее работы должна быть не менее
1 м при самом низком уровне воды и наибольшей толщине льда.
В нашей
стране ледяные переправы применяются с 90-х годов XIX столетия и в силу
благоприятных условий получили довольно широкое распространение. Длина переправ
колебалась от сотен метров до десятков километров (оз. Байкал).
Границы
территории, на которой возможно устройство ледяных переправ, помимо
гидрометеорологических условий, зависят также и от веса подвижного состава,
передвигающегося по льду: чем тяжелее нагрузка, тем толще должен быть лед. Если
в прежние годы по ледяным переправам передавались преимущественно легкие
двухосные вагоны и для этого достаточна была толщина льда на переправе 40-70
см, то в настоящее время переброска полногрузных четырехосных вагонов с
тепловозной тягой требует уже ледяного покрова толщиной в естественных условиях
порядка 90-100 см. Утяжеление подвижного состава вносит определенные
ограничения в область применения ледяных переправ по сравнению с той, которая
была определена для более легких нагрузок. В настоящее время существует
альтернатива железнодорожным перевозкам - автомобили большой грузоподъемности.
Переправы
по льду обычно устраивают с использованием несущей способности ледяного покрова
и укладкой пути непосредственно на лед; иногда встречается еще другой тип
переправ - свайно-ледяные, у которых нагрузка передается на дно реки через
забитые сваи. Свайно-ледяные переправы - по существу деревянные мосты, у
которых ледяной покров выполняет роль связи между сваями. Этот тип переправ
сложен и дорог в постройке и эксплуатации и малопригоден для применения на
широких и глубоких реках и водохранилищах.
Комплекс
сооружений и устройств ледяной переправы обычно неразрывно связан с комплексом
паромной переправы и включает следующие основные элементы: железнодорожные
подходы с путевым развитием; путь на льду и у берегов; сигнализацию и связь;
энергоснабжение; автомобильные дороги, здания, склады и др. Некоторые элементы
могут быть общими для паромной и ледяной переправ, например энергоснабжение,
некоторые здания, база топливо-смазочных материалов и т.п.
Место
переправы выбирают так, чтобы вблизи пути на льду отсутствовали полыньи, выходы
грунтовых вод и места сброса теплых сточных вод. При наличии полыньи трассу
ледяной переправы располагают не ближе 100 м от границы полыньи. Границей
полыньи принято считать то место, где толщина льда составляет 50% толщины
естественного льда на переправе. Желательно, чтобы длина пути на льду была
минимальной и путь не имел кривых.
В полевых
условиях рекомендуется выяснить характер образования ледяного покрова (льды
нарастания или льды нагромождения); места образования и кромки полыней в районе
переправы и ход их замерзания во времени; ход изменения толщин льда путем
регулярных замеров через 2 - 5 суток по створу ледяной переправы в естественных
условиях под снегом и на опытных площадках размером 20×20 м, очищенных от
снега; величину временного сопротивления на изгиб ледяного покрова, очищенного
от снега, при различных температурах воздуха, с одновременным описанием и
замером толщин различных слоев льда.
Рекомендуется
собрать имеющиеся многолетние данные наблюдений за температурами воздуха, воды,
толщинами льда и уровнями воды в реке. Используя годовые таблицы ежедневных
срочных наблюдений за уровнями, можно по ним построить совмещенный по годам
график зимнего хода уровня воды в отметках продольного профиля пути. Примерные
объемы основных изыскательских работ по ледяным переправам приведены в
приложении 4 [154].
Рассматривая
зимний ход уровня воды и собранные данные о толщинах льда, можно установить
ранние, средние и поздние сроки работы ледяной переправы. Начало работы переправы
приурочивают к моменту, когда толщина естественного ледяного покрова под снегом
достигает 90-100 см, а конец работы - к началу предвесеннего подъема уровня и
появлению верховодки на льду. Наивысшая отметка уровня, наблюдавшаяся в начале
работы ледяной переправы, является расчетным уровнем высокой воды (РУВВ), а
наинизшая, наблюдавшаяся в конце работы переправы, - расчетным уровнем низкой
воды (РУНВ). Разность отметок РУВВ и РУНВ даст амплитуду уровней Δ,
которую предстоит обслуживать ледяной переправе.
Современное
состояние методов расчета грузоподъемности ледяного покрова можно разделить на
три основные группы:
а) методы,
основанные на эмпирических формулах;
б)
упрощенные методы расчета, основанные на принципе аналогии;
в)
расчетные методы, основанные на положениях теорий упругости и пластичности.
В
практических расчетах ледяного покрова наиболее широкое применение получил
последний метод, основанный на теории центрального изгиба бесконечной упругой
плиты на упругом основании. Выявление действительной схемы работы ледяного
покрова под нагрузкой весьма сложно, так как приходится иметь дело с рядом
непостоянных факторов, и кроме того оно усугубляется большой математической
сложностью.
При малой
толщине или плохом состоянии льда возникает необходимость его усиления.
Известны три основных способа усиления льда: расчистка его от снега,
намораживание и усиление настилом. Возможна также и комбинация этих способов.
Проблема
увеличения грузоподъемности ледовых дорог и переправ может быть решена лучшим
образом путем усиления основного ледяного покрова способом намораживания. В
таких случаях получается плита переменной толщины, чаще всего со ступенчатым
изменением ее толщины по участкам.
В связи с
этим возникает проблема расчета плит переменной толщины, лежащих на упругом
основании. Необходимо также разработать способы определения несущей способности
таких конструкций и определить коэффициенты запаса прочности, которые они будут
иметь в период эксплуатации.
Для
всестороннего, полного исследования работы таких ледовых переправ потребовалось
поставить и решить ряд статических и динамических задач изгиба ледяного
покрова.
Как показал
опыт проектирования, строительства и эксплуатации ледовых дорог и переправ,
они, как временные транспортные сооружения, по экономическим и технологическим
показателям имеют большие перспективы развития.
С этой
целью произведены соответствующие исследования по следующим вопросам:
-
обоснование возможности расширения диапазона применения ледовых дорог и
переправ путем усовершенствования методов их расчета;
-
исследование влияния граничных условий в прибрежной зоне рек и водохранилищ, а
также изменения уровней воды в них, на несущую способность ледяного покрова;
- выявление
влияния пластических деформаций льда при определении несущей способности ледяного
покрова;
- изучение
возможности увеличения несущей способности естественного ледяного покрова с
помощью намораживания дополнительной полосы льда;
-
исследование влияния масс вибрационных и движущихся нагрузок на ледяной покров
и выявление опасных резонансных режимов эксплуатации ледовых переправ;
- изучение
влияния волновых процессов, происходящих в воде, на колебания ледяного покрова
при пропуске по нему подвижных нагрузок;
-
определение импульсов сил, возникающих при проходе подвижных нагрузок через
неровности проезжей части дороги, образующиеся в результате эксплуатации
ледовых переправ, и исследования влияния этих динамических импульсов на
поведение ледового покрова.
Исследования
производились расчетно-теоретическими и экспериментальными методами.
Исследовано
влияние граничных условий в прибрежной зоне и изменения уровней воды в реках и
водохранилищах на грузоподъемность ледяного покрова [16].
Доказана возможность усиления естественного ледяного покрова способом
намораживания дополнительного слоя льда снизу или сверху существующего ледяного
слоя [12].
Разработана конструкция усиления ледяного покрова способом намораживания и
предложены способы расчета такой конструкции при ее цилиндрическом и
центральном изгибе от действия внешних нагрузок [16,
24].
Предложен способ расчета плит переменной толщины на упругом основании по
предельным состояниям, основанный на теории малых упругопластических деформаций
[20].
Как распространение этого способа на другие конструкции, разработан способ
расчета пологих сферических и незамкнутых цилиндрических оболочек по
предельному состоянию [21].
Получены
расчетные значения разрушающих нагрузок для ледяного покрова с целью
определения запасов прочности при проектировании ледовых дорог и переправ [20].
Разработан способ расчета балок и плит на упругом основании на вибрационную
нагрузку с учетом массы действующего на них внешнего груза [14].
Предложен способ динамического расчета балок и плит на упругом основании на
воздействие движущихся нагрузок с учетом их масс [22].
Решена
задача динамического изгиба ледяного покрова от воздействия движущихся по нему
нагрузок с учетом волнового процесса, происходящего в воде, являющейся упругим
основанием. Исследовано взаимное влияние на ледяной покров нескольких
движущихся с заданным интервалом произвольных нагрузок [12].
Определены
значения импульсов сил, возникающих при проходе подвижных нагрузок через
неровности ледовых дорог и переправ, и проведена качественная и количественная
оценка влияния этих импульсов на ледяной покров [12,
18].
Экспериментально определены величины логарифмических декрементов затухания для
льда как материала и воды как упругого основания.
Результаты
исследований позволили обосновать возможность увеличения несущей способности
(грузоподъемности) строительных площадок, ледовых дорог и переправ, используя
способ намораживания дополнительной полосы льда снизу или сверху основного
ледяного слоя.
На
основании теоретических и экспериментальных исследований предложены
рациональные способы конструирования ледовых дорог и переправ, представляющих
собой ледяную плиту со ступенчатым изменением жесткости на отдельных участках.
Определены
оптимальные параметры (соотношение толщин участков плиты, их ширина и др.), при
которых достигается максимальное увеличение грузоподъемности ледяного покрова
при минимальных экономических затратах средств на их сооружение.
Учет
влияния пластических деформаций льда в настоящее время становится обязательной
составной частью расчетов ответственных ледовых дорог и переправ.
Всестороннее
исследование работы ледяного покрова под воздействием динамических нагрузок
позволяет повысить эффективность использования и надежность эксплуатации
ледовых дорог и переправ.
Авторы
выражают глубокую благодарность рецензентам за ценные замечания и пожелания,
данные ими при подготовке книги к изданию.
Книгу
написали:
инженер
Ю.А. Гурьянов - часть 1;
к.т.н.,
доцент Н.Н. Бычковский - части 2 и 3.
При
строительстве гидротехнических и транспортных сооружений большие объемы сложных
и трудоемких работ, таких как возведение перемычек, перекрытие рек, сооружение
мостовых опор и монтаж пролетных строений, прокладка трубопроводов и т.д.,
могут выполняться и в зимнее время, на льду рек и водохранилищ.
Особенно
большое значение приобретает использование ледяного покрова для устройства
ледовых строительных площадок, дорог и переправ в суровых климатических
условиях, где продолжительность периода с отрицательными температурами
составляет 200-250 дней в году. При использовании ледяного покрова для
вышеуказанных целей возникает необходимость в определении его грузоподъемности
при самых различных схемах загружения, разных граничных условиях и стадиях
работы льда как материала.
Следовательно,
изучение механических свойств льда имеет первостепенное значение для решения
перечисленного ряда задач. Состояние изученности механических свойств ледяного
покрова не всегда соответствует предъявляемым инженерной практикой требованиям.
Как правило, опубликованные в литературе лабораторные определения механических
характеристик льда не увязаны с полевыми исследованиями, из-за чего по ним не
представляется возможным охарактеризовать механические свойства ледяного
покрова.
Поэтому,
при рассмотрении недостаточно изученных вопросов, связанных с определением
физико-механических свойств ледяного покрова, авторами проводились экспериментальные
исследования в естественных полевых условиях. Результаты этих исследований
изложены в первой части книги.
Вопросам
изучения физико-механических свойств льда, исследованию проблемы расчета
ледяного покрова и увеличения его грузоподъемности посвящены работы Г.А.
Авсюка, С.А. Арцыбашева, С.А. Бернштейна, Г.Р. Брегмана, И.П. Бутягина, Б.П.
Вейнберга, К.Ф. Войтковского, С.С. Голушкевича, А.Д. Дмитриева, A.M.
Елистратовой, Н.Н. Зубова, Б.Д. Карташкина, С.В. Изюмова, К.Н. Коржавина, М.М.
Корунова, А.Н. Крылова, Б.Г. Коренева, Г.Л. Кузуба, В.В. Лаврова, П.И.
Лебедева, Б.В. Проскурякова, Д.В. Панфилова, В.Н. Пинегана, И.С. Песчанского,
Б.А. Савельева, Д.Е. Хейсина, А.Ф. Хренова, П.А. Шуйского, Г.Н. Яковлева и
многих других.
Изучены и
по необходимости использованы также наиболее интересные работы некоторых
зарубежных авторов.
Необходимо
отметить, что свойства льда по-разному проявляются на различных этапах работы
ледяного покрова, то есть зависят от характера нагружения. Под нагрузкой
ледяной покров претерпевает разные стадии деформации.
Нагрузки по
характеру воздействия их на лед можно разделить на статические и динамические.
По мнению Б.П. Вейнберга [26],
такое рассмотрение носит условный характер, поскольку переход от одной группы
нагрузок к другой происходит постепенно и, следовательно, в интервале действия
статических и динамических нагрузок существует промежуточное состояние ледяного
покрова.
В
зависимости от характера воздействия нагрузок работа ледяного слоя может быть
сведена к следующим случаям:
1. Ледяной
покров изгибается под действием статически приложенных нагрузок.
2. Ледяной
покров изгибается и подвергается колебаниям под действием движущихся нагрузок.
3. Ледяной
покров испытывает колебания от действия на него вибрационных нагрузок.
4. Ледяной
покров подвергается воздействию импульсивных нагрузок.
При
эксплуатации ледовых дорог и переправ по ним возможен пропуск нагрузок в виде автомобилей,
гусеничных машин, мотовозов, железнодорожных вагонов и других.
В
зависимости от грузоподъемности ледяного покрова и веса движущейся по нему
нагрузки, последняя может пропускаться по ледовой переправе в виде:
1)
отдельных транспортных единиц по схеме одиночного груза;
2)
транспортных колонн с определенным интервалом между движущимися единицами;
3)
условной, равномерно распределенной вдоль направления движения нагрузки.
В работе [17]
показано, что при расстоянии между отдельными грузами а ≥ 6/λ
влияние соседних грузов друг на друга при изгибе ледяного покрова практически
исключается. Здесь λ - характеристика ледяного слоя (глава 3, п. 1).
При
расстоянии 6/λ ≤ а ≤ 1/λ необходимо учитывать
взаимодействие грузов при изгибе ледяного покрова [17].
И, наконец,
при расстоянии а < 1/λ, внешнюю нагрузку можно считать условно
равномерно распределенной, численно равной весу одиночного груза, деленного на
интервал а.
При расчете
ледяного покрова на действие неподвижных одиночных грузов расчетная схема
принимается в виде плиты на упругом основании, загруженной сосредоточенной или
равномерно распределенной по окружности нагрузкой.
Радиус этой
окружности для двухосных автомобилей принимается равным половине расстояния
между центрами диагонально расположенных колес передней и задней осей.
Радиус,
окружности для трехосных автомобилей принимается равным половине расстояния
между центрами диагонально расположенных колес двух задних осей. Такое
допущение для трехосных автомобилей является оправданным, так как в груженом
состоянии у них на задние оси приходится до 80% от всей нагрузки. В зависимости
от толщины льда безразмерный радиус окружности α = r·λ изменяется в пределах
0,1÷0,2.
В практике
гидротехнического строительства нагрузки на лед могут передаваться по площадкам
разных форм и размеров, обычно заменяемым правильными равновеликими фигурами
(круг, квадрат и т.д.). Влияние характера распределения нагрузки на несущую
способность льда достаточно подробно исследовано Д.Ф. Панфиловым в работе [115].
Некоторые
авторы [17],
[41]
и другие считают, что при проведении подобных расчетов ледяной покров можно
рассматривать как упругую пластинку, опирающуюся на упругое основание, изгиб
которой описывается известным уравнением (3.3)
или (3.14) (глава 3, п. 3.1).
Как
известно, дифференциальное уравнение (3.14)
основано на гипотезе недеформированных нормалей, которая равносильна
предположению об отсутствии сдвигов в вертикальной плоскости. Некоторые же
авторы, например Н.Н. Зубов [55],
считали, что в силу специфической структуры льда в деформации плавающего
ледяного слоя большое, а может быть, преимущественное значение имеет сдвиг его
элементов в направлении действия силы. Кроме того, возможность использования уравнения
(3.14) для описания деформационного состояния
ледяного слоя нередко ставится под сомнение в связи с анизотропией льда.
С
теоретической точки зрения указанные возражения не лишены определенных
оснований.
Поэтому, с
целью оценки влияния указанных факторов, Д.Ф. Панфиловым [114]
рассматривалась задача об изгибе ледяного слоя под действием кратковременной
статической нагрузки с учетом поперечных деформаций сдвига и анизотропии льда.
Из этой работы можно сделать вывод, что роль поперечных сдвигов в деформации
ледяного слоя пренебрежимо мала.
Б.А.
Савельевым [139]
приведен расчет ледяного слоя толщиной H=1,0 м, загруженного весом P=24 тс, распределенного по кругу r=1,4 м. Сопоставляя нормальные и касательные напряжения,
возникающие в ледяном покрове, Б.А. Савельев показывает, что нормальное
напряжение в 940 раз превосходит касательное. Вопрос о практическом влиянии
анизотропии льда на расчет ледяного покрова рассматривался также А.Е. Якуниным [185].
Для
уточнения работы ледяного покрова под нагрузкой, Новосибирским филиалом ЦНИИСа
зимой 1964-1965 гг. [31]
были проведены испытания ледяного покрова на действие кратковременной нагрузки.
Лед намораживался в открытом бассейне диаметром 12 м, толщиной от 3 до 10 см.
Испытания проводились по схеме загружения одиночным грузом.
В процессе
экспериментов замерялись толщина льда, прогибы, разрушающие нагрузки и
температура наружного воздуха. Одновременно вырезались образцы льда и
определялись механические свойства ледяного покрова в бассейне.
Сравнение
экспериментальных данных с расчетными показало, что несущая способность
ледяного покрова, определенная по формулам изотропной пластинки на упругом
основании, несколько ниже, чем полученная экспериментальным путем.
И, наконец,
можно отметить работы Н.Н. Бычковского [17],
[12]
1969, 1976 гг., в которых достаточно подробно подтверждается возможность
расчета ледяного покрова как плиты на упругом основании, а имеющиеся в этих
работах многочисленные опытные данные показывают вполне удовлетворительное
совпадение экспериментальных и теоретических результатов.
Часть первая
ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА ЛЕДЯНОГО ПОКРОВА
ГЛАВА 1. ФИЗИКО-МЕХАНИЧЕСКИЕ
СВОЙСТВА ЛЬДА
1.1. Структура ледяного
покрова
Лед имеет
кристаллическое строение. Кристаллы льда оптически одноосные, принадлежат к
гексагональной сингонии [27].
Внешняя форма кристаллов разнообразна и зависит от условий их образования и
роста. Однако можно выделить три основных вида кристаллов льда: пластинчатый,
столбчатый и иглообразный. Размеры кристаллов весьма разнообразны (от долей
миллиметра до одного метра и более), они непрерывно изменяются в результате
процессов рекристаллизации, заключающихся в росте одних кристаллов за счет
других. Кристаллы льда характеризуются резко выраженной анизотропностью
механических свойств в зависимости от направления действия усилия относительно
базисной плоскости (плоскость, перпендикулярная к оптической оси кристалла).
Атомы в
пространственной решетке льда располагаются таким образом, что нарушение в
базисной плоскости вызывает разрыв только двух атомных связей на одну
элементарную ячейку, в то время как нарушение по любой другой плоскости,
перпендикулярной к базисной, требует разрыва по меньшей мере четырех связей на
одну ячейку [27].
Поэтому структуру кристалла льда можно представить как совокупность
многочисленных, очень тонких, прочных, но гибких пластинок. Промежутки между
элементарными пластинками - плоскостями наиболее густого расположения атомов -
являются плоскостями ослабления, по которым может происходить относительное
скольжение пластинок.
Ввиду
анизотропии свойств льда необходимо учитывать его строение и направление
оптических осей кристаллов.
В природе
встречаются различные виды льда, отличающиеся друг от друга по своей структуре
и по другим свойствам. Большей частью приходится иметь дело с
поликристаллическим льдом, который состоит из беспорядочно ориентированных
кристаллов, спаянных между собой (зернистый лед), или сросшихся отдельных
кристаллов, направление осей которых приблизительно параллельное.
Структура
льда зависит от способа его образования. Различают следующие основные виды
структуры льда:
• сплошная
кристаллическая структура, образуется при спокойном замерзании воды;
• игольчатая
структура, часто с наличием пузырьков воздуха, образуется в месте соприкасания
воды и льда;
• слоистая
структура, образуется при периодических замерзаниях отдельных слоев воды или
при уплотнении отдельных мокрых слоев снега;
• фирновая
(зернистая) образуется при смерзании снега;
•
мелкоагрегатная неправильная структура образуется при переменном замерзании с
перемешиванием (наблюдается в верхнем слое больших водоемов);
•
рыхло-чешуйчатая структура, наблюдается в свежевыпавшем снежном покрове, а также
при замерзании воды, конденсирующейся из пара.
В настоящее
время имеется более полная и совершенная генетическая классификация льдов,
разработанная П.А. Шумским [179],
в которой учтены все виды пресных льдов и дано подробное описание условий их
образования и залегания, структуры, ориентировки кристаллов, характера
включений воздуха, но для инженерной практики вполне достаточна приведенная
выше классификация [27].
По
характеру образования Н.Н. Зубов различает льды нарастания и льды
нагромождения. Первые образуются на реках с медленным течением в безветренную
погоду; поверхность реки почти покрывается тонкой прозрачной коркой льда;
вторые образуются на реках с быстрым течением; вода переохлаждается на всю
глубину потока, в русле скапливается большое количество шуги, внутриводного
льда и мелких битых льдин; в излучинах или узких местах русло постепенно
забивается этими образованиями и возникает затор, уровень воды поднимается,
скорость течения падает и река замерзает с образованием торосов. Начальная
толщина льда в этих условиях составляет около 10-20 см.
Нарастание
толщины прозрачного ледяного покрова при отсутствии снегопада идет снизу. При
снегопаде ледяной покров перегружается, и вода по трещинам выступает на
поверхность льда. Под снегом вода долго не замерзает, образуя впоследствии
мутный лед, насыщенный пузырьками воздуха.
Во льду
обычно встречается некоторое количество примесей - включений воздуха или газов
и солей. Газообразные включения во льду получаются или непосредственно из
атмосферы, или из замерзающей воды (рис. 1.1).

Рис.
1.1. Воздушные включения в озерном ледяном покрове
Воздушные
включения во льду бывают в виде мелких сферических полостей или удлиненных
замкнутых ячеек, встречаются также открытые поры и трещины.
При
спокойном замерзании воды в самых верхних слоях ледяного покрова преобладают
кристаллы с оптическими осями, направленными параллельно поверхности
замерзания, а ниже - кристаллы с вертикальными осями. По данным Б.А. Савельева [138],
в озерном ледяном покрове кристаллы с оптическими осями, параллельными
поверхности замерзании, встречаются примерно до глубины 18 см, а ниже все
кристаллы имеют оптические оси, перпендикулярные к плоскости замерзания. По
мере удаления от поверхности часть кристаллов выклинивается, а поперечный
размер оставшихся кристаллов увеличивается.
При
замерзании воды с перемешиванием оси кристаллов льда располагаются хаотически,
поэтому ледяной покров рек в целом можно считать изотропным.
Самый верхний
слой льда из слежавшегося снега (снеговой лед) имеет зернистую ноздреватую
структуру.
Структура
льда представляет одну из основных его характеристик, однако зависимость
прочности льда от его структуры не имеет пока точного количественного
выражения. Самым прочным является нижний слой прозрачного льда. Расположенный
выше мутный лед по прочности уступает прозрачному примерно в 1,5-2 раза.
Снеговой лед ввиду его малой прочности обычно во внимание не принимается.
1.2. Основные
закономерности деформирования льда
В случае
приложения ко льду какой-либо силы он начинает деформироваться, при этом в
зависимости от различных факторов он ведет себя как упругое, пластическое или
хрупкое тело, т.е. деформируется упруго, пластически или хрупко разрушается.
Одним из
основных характерных свойств льда по сравнению с другими кристаллическими
телами являются его отчетливо выраженные пластические свойства. Под
воздействием нагрузки лед может изменить свою форму без изменения объема, как
бы течь. Поэтому пластические деформации льда иногда сравнивают с течением
очень вязкой жидкости.
Область
проявления чисто упругих свойств настолько мала, что ее практически не удается
выделить. Обычно при любой величине напряжения наряду с упругими деформациями
наблюдаются пластические деформации. Упругие деформации происходят в момент
приложения нагрузки, а непосредственно за упругими начинаются пластические
деформации.
Общая
деформация обычно состоит из двух частей: упругой, т.е. обратимой деформации, и
пластической - остаточной. По данным К.Ф. Войтковского [27],
уже в течение первых пяти минут действия силы величины пластической деформации
льда превышают упругую деформацию.
Механические
свойства льда, т.е. способность льда сопротивляться воздействию внешних сил,
значительно изменяются в зависимости от температуры. Чем ближе температура льда
к точке его плавления, тем сильнее проявляются его пластические свойства и
уменьшается прочность.
Для льда с
ориентированным направлением кристаллов при сжатии в направлении,
перпендикулярном к направлению оптических осей кристаллов, скорость деформации
несколько больше, а предел прочности - меньше, чем при сжатии в направлении
осей кристаллов.
Если напряжение
в изгибаемом образце льда превысит некоторый предел, то вслед за стадией
установившейся скорости деформации наступает стадия ускоряющейся деформации,
заканчивающаяся разрушением образца.
Хрупкое
разрушение льда наблюдается при увеличении напряжения в нем до некоторого
предела - предела прочности, и в ряде случаев при действии динамических
нагрузок. При определении деформации ледяного покрова последний можно
рассматривать как пластинку бесконечных размеров. Такое допущение можно сделать
и для речного льда, если длина распределения круговой волны изгиба льда под
нагрузкой мала по сравнению с шириной реки. Подобное допущение вполне реально
и, кроме того, оно позволяет пренебречь влияниями краевых, условий,
предполагал, что действующие на значительном расстоянии от нагрузки внутренние
усилия стремятся к нулю.
При выводе
дифференциального уравнения изогнутой поверхности сойкой упругой плиты
предполагается, что материал ее изотропен. Ледяной покров не является
изотропным материалом и применение к нему подобного решения будет оправдано
только в том случае, если требуемые для расчета физико-механические
характеристики будут даны в виде среднеинтегральных значений для ледяного
покрова в целом. Другими словами, для упрощения задачи мы будем иметь дело с
абстрагированным изотропным ледяным покровом, основные свойства которого
соответствуют среднеинтегральным значениям характеристик действительного
ледяного покрова.
Всякое
изменение напряженного состояния льда сопровождается переходом некоторого
количества воды из одного агрегатного состояния в другое на границе раздела
воды и льда.
Пренебрегаем
влиянием перемещения нижней границы, обусловленного фазовым переходом льда в
воду под действием нагрузки на несущую способность ледяного покрова.
Принимаем,
что физико-механические свойства ледяного покрова однородны в горизонтальных
направлениях.
1.3. Упругие характеристики ледяного покрова,
модуль упругости и модуль сдвига льда
В
естественных условиях поведение ледяного покрова, лежащего на упругом жидком
основании при действии кратковременной нагрузки, приближается к упругому. С.А.
Бернштейн [8]
на основании своих наблюдений за поведением ледяного покрова под воздействием
движущейся нагрузки считает вполне допустимым в этих условиях характеризовать
ледяной покров как мнимоупругое тело. Присоединяясь к мнению С.А. Бернштейна,
С.С. Голушкевич [41]
вводит понятие «фиктивной» упругости, возникающей благодаря возвратной реакции
поверхности воды.
Несомненно,
что в ледяном покрове под воздействием нагрузки происходят процессы локального
характера, на которые указывал Б.П. Вейнберг [26],
но наличие идеально упругой подстилающей поверхности приводит к почти полному
аннулированию остаточной деформации.
Учитывая
высказанные соображения, следует отметить весьма важную особенность в работе
ледяного покрова: при кратковременном действии нагрузки, не превышающем
величины его грузоподъемности из расчета в упругой стадии, ледяной покров ведет
себя как упругое тело и к нему применимы классические дифференциальные
уравнения теории упругости.
Решение
последних возможно только в том случае, если известны следующие упругие
характеристики ледяного покрова: модуль упругости и коэффициент Пуассона. Кроме
того, необходимы сведения об изменении упругих характеристик в ледяном покрове
по слоям и во времени.
Модуль
упругости характеризует сопротивляемость льда упругой деформации при растяжении
или сжатии. При одностороннем сжатии и растяжении зависимость между
относительной деформацией и нормальными напряжениями для льда можно выразить
законом Гука.
ε=σ/Е
где ε - относительная деформация сжатия
или растяжения;
σ - величина нормального напряжения;
Е - модуль упругости, являющийся коэффициентом
пропорциональности, связывающим нормальное напряжение и относительную
деформацию.
Для
определения модуля упругости применяются два метода: статический и
динамический. Сущность статического метода заключается в измерении величины
деформации после приложения нагрузки при испытании образцов льда на сжатие,
растяжение или изгиб. Динамический метод основан на вычислении модуля упругости
по данным замеров скорости распространения по льду упругих колебаний.
Многочисленными
исследователями произведено большое количество опытов по определению модуля
упругости льда. Анализ полученных данных (приложение 1 [12])
приводит к следующему выводу: величина модуля упругости определяется в основном
размером нагрузки (напряжением), уменьшаясь по мере увеличения последней.
Разница же в структуре льда и направлении осей кристаллов относительно действия
сил не вызывает существенного различия полученных значений модуля упругости.
В теории
упругости считается, что деформации происходят в момент приложения нагрузки и
полностью исчезают при ее удалении. У льда же сильно проявляется явление
упругого последействия и обратимые деформации проявляются не сразу после
приложения нагрузки, а нарастают в течение некоторого времени. Соответственно,
при удалении нагрузки эта часть деформаций исчезает также не сразу. Поэтому величины
упругих (обратимых) деформаций льда зависят в отличие от деформаций чисто
упругих тел, от времени, в течение которого приложена нагрузка. Соответственно
будет зависеть от времени и модуль, характеризующий зависимость величины
деформации от нагрузки.
1.3.1. Опытное
определение, модуля упругости озерного льда в полевых условиях
Для
определения модуля упругости льда, авторами в период 17-18 января 1970 г.
проводились опыты, в которых применялся статический метод исследования. В
ледяном слое на озере были выпилены четыре консольные балки (рис. 1.2), размеры
и основные характеристики которых приведены в табл. 1.1.

Рис.
1.2 Ледяные консоли, подготовленные к эксперименту для определения модуля
упругости льда
Рядом
исследователей [27],
[138],
в том числе и С.К. Уховым [162],
модуль упругости определялся на основе экспериментальных данных по начальному
прогибу ледяных баночек, загруженных испытательной па-грузкой.
В наших
опытах была поставлена цель исследовать закономерность изменения значения
модуля упругости льда в зависимости от величины внешней нагрузки и
продолжительности ее действия.
Таблица 1.1
Геометрические характеристики ледяных консольных балок
|
Дата проведения опыта
|
Температура воздуха, °С
|
№ балок (консолей)
|
Размеры ледяных консольных балок, см
|
Момент сопротивления сечения, см3
|
Максимальное напряжение при изгибе
σ, кгс/см2 в зависимости от величины нагрузки Р, кгс
|
|
полная длина
|
расчетная длина
|
ширина
|
толщина
|
p
|
|
10
|
20
|
30
|
40
|
50
|
|
17.01.1970 г.
|
-10
|
1
|
141
|
120
|
50
|
13,5
|
1518
|
0,79
|
1,58
|
2,37
|
3,16
|
3,95
|
|
2
|
142
|
122
|
44,5
|
13,5
|
1352
|
0,90
|
1,80
|
2,70
|
3,60
|
4,50
|
|
18.01.1970 г.
|
-20
|
3
|
150
|
130
|
38,5
|
14,6
|
1368
|
0,95
|
1,90
|
2,85
|
3,80
|
4,75
|
|
4
|
146
|
126
|
42
|
14,6
|
1482
|
0,85
|
1,70
|
2,55
|
3,40
|
4,25
|
Нагрузка
на балку передавалась через специальную подставку размером 40×40 см,
установленную на конце консоли. Интервал изменения нагрузки 10 кгс,
максимальная нагрузка 50 кгс. В процессе нагрузки-разгрузки ледяные консоли
оставались на воде. Деформации в заделке консоли замерялись мессурами с
точностью до 0,001 мм на базе 150 мм (рис 1.2). Каждая балка подвергалась
восьмикратной нагрузке-разгрузке. Результаты экспериментов и расчеты по
определению модуля упругости льда приведены в приложении 3 [12].
В результате анализа опытных данных можно сделать следующие выводы:
а) при
небольших напряжениях (до 1 кгс/см2) и непродолжительном приложении
силы (до 1 мин) модуль упругости всегда изменяется в пределах 90-60 тыс. кгс/см2;
б) при
увеличении напряжений (до 4,75 кгс/см2) и увеличении
продолжительности приложения нагрузки (до 4-5 мин) значение модуля упругости
уменьшается до 80-55 тыс. кгс/см2
в) при
разгрузке консолей (уменьшение напряжения до 1 кгс/см2) и увеличении
времени цикла до 8 минут величина модуля упругости уменьшается в пределах 70-30
тыс. кгс/см2;
г)
зависимость между деформациями и напряжениями у льда нелинейна, и закон Гука
точно не подтверждается даже при сравнительно небольших напряжениях и
непродолжительных циклах загружения.
Следовательно,
при более или менее длительном воздействии нагрузок на ледяной покров, для
расчетов величины деформации при сжатии, растяжении и изгибе величину модуля
упругости можно принимать равной 50000-60000 кгс/см2. С.А. Бернштейн
[8]
на основе анализа работы ледяных переправ рекомендует для расчетов модуль
упругости, равный 55000 кгс/см2.
Если под
упругой деформацией льда подразумевать лишь ту часть обратимой деформации,
которая происходит мгновенно - со скоростью звука в момент приложения нагрузки,
то модуль упругости следует определять лишь на основании динамических методов
исследований. В этом случае наиболее достоверной величиной модуля упругости
льда будет Е=90000 кгс/см2.
Этой величиной рекомендуется пользоваться для расчета величин упругой
деформации льда при динамическом воздействии нагрузок [27].
1.3.2. Модуль сдвига
Модуль
сдвига характеризует сопротивляемость льда деформации сдвига. Если из массива
деформируемого льда выделить элементарный кубик, то его угловую деформацию у, в
соответствии с теорией упругости, можно выразить формулой
γ = τ/G
где τ - величина касательного
напряжения;
G - модуль сдвига.
Для:
определения модуля сдвига так же, как для определения модуля упругости,
применяются статический и динамический методы [139].
В качестве статического метода наиболее приемлемым является испытание
цилиндрических или призматических образцов льда на кручение, так как в этом
случае создаются условия для чистого сдвига.
Некоторые
результаты опытов по определению сдвига льда приведены в табл. 5 [27].
Причины значительных расхождений полученных величин в основном те же, что и при
определении модуля упругости.
Аналогично
рекомендуемым значениям модуля упругости предлагается принимать значения модуля
сдвига льда:
- для
расчетов упругой деформации при динамическом воздействии нагрузок G = (30÷34)·103
кгс/см2;
- для
расчетов начальной деформации при длительном воздействии нагрузок (деформации,
происходящей в течение первых нескольких секунд после приложения нагрузки) G = 15·103 кгс/см2.
1.4. Коэффициент Пуассона
Коэффициент
поперечной деформации, или коэффициент Пуассона, представляет собою отношение
поперечной деформации к продольной деформации образца при приложении к нему
продольных сжимающих (или растаивающих) сил и возможности свободного изменения
размеров образца в поперечных направлениях.
Коэффициент
Пуассона при упругой деформации связан с модулем упругости и модулем сдвига
зависимостью
v = Е/2G-1
Непосредственные
измерения коэффициента Пуассона для льда были произведены В.Н. Пинегиным [127].
На основании анализа результатов утих измерений, сравнения скоростей
распространения во льду продольных и поперечных колебаний и сопоставления
значений модуля упругости и модуля сдвига по данным различных исследований,
Б.П. Вейнберг [26]
установил, что наиболее близким к действительности значением коэффициента
Пуассона является v=0,36±0,13.
Значительные колебания возможных значений коэффициента Пуассона можно отчасти
объяснить тем, что упругая деформация льда происходит совместно с пластической
и трудно выделить чисто упругую часть деформации. Пластическая деформация
характеризуется изменением формы образца льда без изменения объема его и
поэтому коэффициент Пуассона при пластической деформации равен 0,5.
Следовательно, при увеличении нагрузки значение коэффициента Пуассона будет
увеличиваться. На величину коэффициента Пуассона оказывает влияние также
анизотропия льда.
Б.Д.
Карташкин [63]
на основании проведенных им экспериментов рассчитал, что коэффициент Пуассона
для льда в интервале температуры от -5 до -16°С в среднем равен 0,34.
Б. А.
Савельев [138]
рекомендует принимать для расчетов значение коэффициента Пуассона равным 0,36,
а А.Д. Дмитриев [49]
- 0,33.
По мнению
авторов, целесообразно принять к расчету значение коэффициента Пуассона равным
0,3. В этом случае можно применять при определении грузоподъемности ледяного
покрова таблицы значений функций Бесселя, прилагаемые М.Н. Ручимским [134].
1.5. Пределы прочности, расчетные значения
нормативных сопротивлений и пределов текучести льда
Пределом
прочности льда (временным сопротивлением любого материала) называется величина
напряжений, при которых он разрушается. Для льда такая величина является в
некоторой степени условной, так как его разрушение не обусловлено однозначно
достижением определенного предела напряжений. Ввиду значительной роли явлений
ползучести величины внутренних напряжений существенно зависят от скорости
приложения нагрузки, условий деформирования и других факторов.
Предел
прочности льда обычно определяется как величина максимального напряжения
(сопротивления) в испытываемом образце льда перед его разрушением при «быстром»
нагружении. В зависимости от вида деформации различают пределы прочности: при
сжатии, растяжении, срезе и изгибе.
1.5.1. Сопротивление
льда раздавливанию или сжатию
В табл. 7 [27]
приводятся основные результаты опытов по определению предела прочности льда при
одностороннем сжатии, проведенных многими исследователями. Из этих данных
видно, что сопротивление льда изменяется в широких пределах в зависимости от
структуры льда, ориентировки кристаллов относительно направления сжатия,
температуры и других факторов. При этом наблюдается значительный разброс
значений предела прочности, даже при испытаниях аналогичных по своей структуре
образцов в одинаковых условиях. Прочность естественного ледяного покрова по его
толщине не одинакова. Наиболее высоким пределом прочности обладает лед в
средней части, а наименьшей прочностью - лед в нижней части покрова.
Среднее
значение предела прочности льда при одностороннем сжатии колеблется в пределах [27]
12-32 кгс/см2 при температуре 0-5°С.
1.5.2. Сопротивление
льда разрыву или растяжению
В основном
оно зависит от тех же факторов, что и сопротивление сжатию, только величина
предела прочности значительно меньше и колеблется в меньших пределах (табл. 9) [27].
Кроме того, на величину предела прочности большое влияние оказывают различные
включения и структурные неоднородности, которые могут стать очагом разрушения.
Если при сжатии образец льда после появления трещин может допускать еще
дальнейшее увеличение нагрузки, то при растяжении образец льда разрывается
обычно без предварительного образования трещин. Среднее значение предела прочности
льда на растяжение при температуре 0-5°С равно 7-14 кгс/см2.
1.5.3. Сопротивление
льда срезу
В табл. 11 [27]
приведены основные данные о величине предела прочности льда при срезе по
материалам, опубликованным разными исследователями. Из этих данных можно
сделать вывод, что предел прочности при срезе меньше, чем при растяжении, в
среднем почти в два раза. Однако, при низких температурах в отдельных случаях
сопротивление срезу может значительно превосходить сопротивление разрыву.
Величина предела прочности при срезе так же, как и при других видах разрушения,
может изменяться в зависимости от структуры льда в направлении среза
относительно направления осей кристаллов.
Кроме того,
как показывают опыты С.С. Вялова [34],
сопротивление льда срезу зависит от величины нормального давления в плоскости
среза, увеличиваясь с ростом последнего. Среднее значение предела прочности
льда при срезе колеблется в пределах 6-13 кгс/см2 при температуре
0-15°С.
1.5.4. Прочность
смерзания льда
Прочность
смерзания льда с различными телами зависит от материала, характера его
поверхности и температуры. Некоторые значения предельных сил смерзания льда
приведены в табл. 12 [27].
Из приведенных данных видно, что силы смерзания существенно увеличиваются с
понижением температуры и при шероховатой поверхности. Силы смерзания изменяются
также в зависимости от условий смерзания льда с телом, которые обусловливают
структуру льда и направление осей кристаллов в месте контакта. При быстром
возрастании нагрузки разрушение носит хрупкий характер, причем в зависимости от
материала и состояния его поверхности разрушение может происходить не строго по
контакту, а частично проходить по льду.
Силы
смерзания льда с различными материалами, по данным некоторых авторов,
изменяются в следующих пределах [27]:
• бетон с
оштукатуренной поверхностью 13-16 кгс/см2;
• бетон с
гладкой поверхностью 10 кгс/см2;
• дерево с
гладкой поверхностью 5-22 кгс/см2.
По данным
наших многочисленных опытов, поставленных в зиму 1970-1971 гг., сила смерзания
льда со льдом весьма значительна. Разрушение смерзшихся образцов льда при
срезе, растяжении, сжатии и изгибе, как правило, происходит по льду, а не по
слою смерзания, что свидетельствует о большой прочности смерзания льда со
льдом. Это свойство льда является положительным и применимо при усилении ледяного
покрова путем намораживания дополнительного слоя. Ниже этот вопрос будет
рассмотрен более подробно.
1.5.5. Предел прочности
льда при изгибе
Сопротивление
льда излому определяется путем изгиба образцов льда или части ледяного покрова.
Наиболее вероятными очагами разрушения являются разрывы в растянутой зоне и,
соответственно, начало разрушения должно определяться достижением предельных
растягивающих напряжений.
Величина
предела прочности льда при изгибе обычно определяется как максимальное
растягивающее напряжение в изгибаемом образце перед его разрушением,
вычисляемое на основании формул для линейно-упругого тела (И.П. Бутягин [10,
11],
Д.Ф. Панфилов [121]
и др.).
При таком
подходе определяемая величина максимального напряжения оказывается больше
фактического напряжения в испытываемом образце, так как во время испытаний льда
на изгиб нагрузка доводится до разрушающей. В этом случае перед разрушением я
образце имеют место пластические деформации, при которых распределение
напряжений при изгибе изменяется.
Таким
образом, определяемый предел прочности является условной величиной, несколько
большей но сравнению с фактическим максимальным напряжением при изгибе.
Проведение
рядом исследователей ([10,
11,
17,
27,
79,
122]
и др.) многочисленных опытов по определению значения предела прочности льда при
различном силовом воздействием указывает на сложную зависимость его от целого
ряда факторов.
Из них
главнейшими являются [79]:
•
температура образца;
•
ориентировка давления относительно оси кристаллов;
• структура
образца и наличие пузырьков воздуха;
•
расположение образца по толщине льдины;
• скорость
нагружения образца;
• размеры
образца;
•
тщательность обработки образца.
Следует
отметить, что величина предела прочности льда в значительной степени зависит от
внешних условий деформирования, размеров испытываемых образцов и скорости
приложения нагрузки (или скорости деформирования), на что большинство
исследователей мало обращало внимания.
В
приложении 4 [12]
приведены значения предела прочности льда при изгибе, полученные разными
исследователями.
Зависимость
сопротивления излому от скорости нагружения образца была отмечена К.Н.
Коржавиным [79].
При увеличении скорости подачи нагрузки на образец от 2 до 20 см/мин предел прочности
льда на излом при изгибе уменьшается в 2-2,5 раза.
Сопротивление
льда при изломе в воде несколько меньше, чем при изломе «сухого» льда (Орлов,
1940). Сопротивление ледяного покрова, на примере изгиба ледяных «клавишей»,
при изгибе вниз обычно больше, чем при изгибе вверх.
Чем выше
температура льда, тем меньше его сопротивление излому (приложение 4 [12]).
Величина
предела прочности льда при изгибе весьма существенно зависит от размеров
изгибаемых образцов. Так, по данным И.П. Бутягина, предел прочности малых
образцов сечением 7×7 и 10×10 и длиной 50 см в среднем в три раза
больше, чем предел прочности крупных консольных образцов, вырезанных в ледяном
покрове. Данные исследований И.П. Бутягина, А.С. Неронова, Н.Д. Шитова,
экспериментировавших с крупными образцами льда, позволяют установить проявление
обратной пропорциональности между размерами испытываемого образца и
определяемой опытом величиной предела прочности [11].
В работе [17]
была дана экспериментальная зависимость (1.1), которой можно пользоваться в
случае необходимости
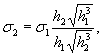 (1.1)
(1.1)
где σ1 - предел прочности
лабораторного льда;
σ2 - предел прочности
естественного льда;
h1 - толщина лабораторного льда;
h2 - толщина естественного льда.
1.5.6. Влияние тепловой
радиации на прочность льда
Б.А. Савельевым
[138]
проводилось испытание ледяного покрова на канале им. Москвы близ Химкинского
речного порта, где удалось установить влияние тепловой радиации на величину
предельного сопротивления льда изгибу при температуре, близкой к 0°. Облучение
льда осуществлялось стандартной термитной шашкой, дававшей на поверхности льда
около 7 кал/см2. Длительность облучения была порядка 100 с.
Полученные результаты показывают, что действие тепловой радиации может вызвать
резкое ослабление прочности льда. В данном случае прочность льда при изгибе
понижалась в 2 раза и направлении усилия, параллельном оптическим осям
кристаллов, и на 17% в направлении, перпендикулярном к оптическим осям.
1.5.7. Расчетные
значения нормативных сопротивлений и пределов текучести льда
По
строительным нормам и правилам СНиП
2.06.04-82* [145]
- нагрузки воздействия на гидротехнические сооружения (волновые, ледовые и от
судов), нормативные сопротивления льда растяжению Rt
сжатию Rc изгибу Rf, смятию Rb, а также пределы текучести соответственно на
сжатие Rc,y и растяжение Rt,y должны определяться по
опытным данным, согласно специальным инструкциям, например [139].
При
отсутствии опытных данных допускается, для случаев «быстрого» загружения, без
учета фактора времени:
• принимать
нормативное сопротивление льда сжатию Rc
по табл. 27* [145],
в зависимости от температуры льда;
•
определять нормативное сопротивление льда изгибу Rf для пресноводного льда
по формуле Rf=0,75 Rc;
•
определять нормативное сопротивление льда смятию Rb по формуле
Rb = Kb-Rc, (1.2)
где Kb - коэффициент,
принимаемый по таблице 28 [145];
•
принимать, пределы текучести льда на растяжение Rt,y и сжатие Rc,y по табл. 33 [145],
в зависимости от температуры льда;
•
определять средние значения пределов текучести льда при изгибе по формуле
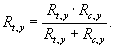 (1.3)
(1.3)
Для
расчетов ледяного покрова, деформирующегося от перепадов уровней воды во
времени [145],
допускается принимать нормативные сопротивления растяжению Rt
и сжатию Rc, определяемые
по формулам:
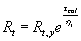 (1.4)
(1.4)
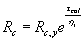 (1.5)
(1.5)
где τ - время, в течение которого
уровень поды изменяется на величину, равную толщине льда, ч;
ηi - коэффициент вязкости льда, тс·ч/м2,
определяемый по формулам:
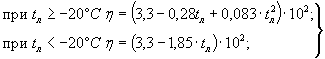 (1,6)
(1,6)
где tл -температура льда, °С [89,
145].
Для
расчетов ледяного покрова на изгиб от действия внешне приложенных нагрузок, при
кратковременном загружении, без учета фактора времени, можно принимать значения
пределов прочности и текучести льда, определенные по формулам (1.2), (1.3).
Изменение
значений пределов прочности и текучести льда в зависимости от времени действия
нагрузки отмечалось в работах Б.А. Савельева [140],
И.С. Песчанского [124] и других [145].
По нашему
мнению, наиболее удачно это явление можно охарактеризовать с помощью так
называемой функции времени [145],
определяемой по формуле:
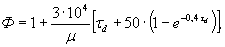 (1.7)
(1.7)
где τd - время, в течение которого происходит
деформация ледяного покрова под действием приложенной нагрузки, ч.
В
зависимости от времени τd нормативное
сопротивление и предел текучести льда при изгибе можно определять по
предлагаемым ниже формулам:
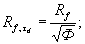 (1.8)
(1.8)
 (1.9)
(1.9)
Из
приведенных выше данных видно, что температура льда и время действия нагрузки
на лед существенно влияют на пределы прочности и текучести льда, а
следовательно, и на грузоподъемность ледяного покрова в целом. В связи с тем,
что приведенные формулы расчета пределов прочности и текучести льда уже
учитывают эти факторы, все решения задач получены в предположении, что внешняя
нагрузка действует на ледяной покров кратковременно.
Для учета,
в случае необходимости, времени действия внешней нагрузки на ледяной покров,
необходимо в окончательный результат, полученный при решении, подставить
соответствующее значение нормативного сопротивления или предела текучести льда.
Допускаемое
напряжение льда на изгиб находят путем деления величины нормативного
сопротивления на коэффициент запаса прочности, значения которого принимают
следующими [58]:
Ненарушенный
ледяной покров постоянной толщины - 1,75;
Ледяной
покров резко неравномерной толщины - 2;
Ледяной
покров с сухими трещинами - 2÷2,5.
Меньшие
значения коэффициентов запаса можно рекомендовать для переправ с небольшой интенсивностью движения.
1.6. Механические свойства намороженного
строительного льда
Сооружения
из льда возводятся посредством послойного намораживания. Одним из способов
намораживания может быть налив воды слоями с последующим замерзанием каждого из
них. При этом получается лед своеобразной структуры. По всему объему массива
такой лед пористый и слоистый. Распределение пор, заполненных воздухом, таково,
что на разрезе, сделанном перпендикулярно поверхности намораживания, отчетливо
различимы отдельные слои, соответствующие слоям при наливах воды. Степень
пористости такого льда зависит от способа налива воды. При спокойном наливе
аэрация воды невелика и пористость льда небольшая. При интенсивном
разбрызгивании воды увеличивается ее аэрация, а следовательно и пористость льда
[129].
В связи с
особенностью строения такой лед имеет и свои особенные свойства, отличающие его
от других видов льда природного происхождения (ледяного покрова водоемов).
Исследования,
проведенные Ф.И. Птухиным [129]
и A.M. Савиновым [141],
выполнялись на образцах искусственно намороженного льда, полученного спокойным
наливанием воды слоями 2-5 см. Толщина слоев менялась в зависимости от
температуры воздуха и скорости ветра. При этом последующий слой наливался
только после полного замерзания предыдущего.
Среднее
значение объемного веса по 22 образцам составило 0,875 г/см3 [129].
Средний коэффициент пористости льда как отношение объема пор к объему льда
равен 0,045 или 4,5%.
1.6.1. Предел прочности
намороженного льда на сжатие
По
результатам испытаний образцов льда при различной их температуре (от 0 до
-35°С) A.M. Савиновым [141]
получены средние значения предела прочности намороженного льда в интервале
16,9-56,3 кгс/см2 при направлении усилии параллельно слоям
намораживания, и 18,2-48,0 кгс/см2 - перпендикулярно слоям
намораживания.
1.6.2. Предел прочности
намороженного льда на изгиб
По
результатам испытаний [141]
при изменении температуры образцов от 0 до -35°С получены средние значения
предела прочности льда на изгиб в интервале 7,4-15,1 кгс/см2 при
загружении образцов параллельно слоям намораживания и 8,3-17,4 кгс/см2
- перпендикулярно слоям намораживания. Всего при испытаниях [141]
было испытано около 700 образцов намороженного льда.
1.6.3. Результаты
определения предела прочности намороженного льда на срез
Опыты по
определению предела прочности намороженного льда на срез были поставлены Ф.И.
Птухиным [129].
Образцы для испытаний на срез изготовлялись таким образом, что их больший
размер (длина) совпадал с направлением слоистости, вследствие чего поверхности
среза в обоих случаях ориентировки усилия относительно слоистости были
нормальны к слоям намораживания льда.
При
температуре образцов, близкой к 0°С, предел прочности льда на срез изменяется в
пределах 6,2-9,9 кгс/см2. Это средние данные по испытаниями
образцов.
На основе
приведенных опытных данных можно сделать следующие выводы:
•
намороженный пористый строительный лед является прочным материалом не только
при низких отрицательных температурах, но и при температуре, близкой к 0°С;
• в
диапазоне температур от 0 до -35°С прочность строительного льда на изгиб
возрастает почти по линейному закону;
• данные
результатов определения объемного веса льда свидетельствуют о достаточной
равномерности распределения
пор по объему намороженного массива.
1.7. Сопротивление льда динамическим нагрузкам
Динамическими
нагрузками обычно принято называть такие нагрузки, при действии которых
наблюдаются существенные ускорения частиц нагруженного тела или
соприкасающегося с ними другого тела, например, при ударе или при колебаниях.
При
вынужденных колебаниях, вызывающих знакопеременные напряжения, во льду могут
появиться трещины, которые постепенно растут и являются причиной разрушения. В
итоге величина предела прочности уменьшается с увеличением количества циклов
изменения напряжений.
Б.Д.
Карташкин [63]
отмечал, что ледяные балки, находящиеся под действием сравнительно небольшой
статической нагрузки, при вынужденных колебаниях в большинстве случаев
разрушаются. Наибольшее дополнительное динамическое напряжение, которое
выдерживала ледяная балка, не разрушаясь достаточно долго (10 млн. циклов) при
температуре -5-9°С и находясь под действием статической нагрузки, вызывающей
максимальное напряжение 2,5 кгс/см2 (при пределе прочности в 16
кгс/см2) было приблизительно равно 1,5 кгс/см2.
Наименьшее дополнительное динамическое напряжение, выше которого балки
разрушались почти мгновенно, было примерно равно 2,75 кгс/см2. Таким
образом, предел прочности льда при динамическом воздействии нагрузки в 3-4 раза
ниже, чем при статическом воздействии.
Характер
деформации при ударе зависит от скорости действия нагрузки (удара). Малая
скорость удара вызывает лишь упругие деформации. При возрастании скорости удара
наблюдаются упругопластические деформации, и наконец, наступает хрупкое
разрушение. Необходимо отметить, что вопросы сопротивления льда ударной нагрузке изучены еще недостаточно.
1.8. Распределение
напряжений
по толщине ледяного слоя при изгибе
С целью
определения закономерности распределения напряжений по толщине ледяного слоя
при изгибе, в период с 5 по 12 декабря 1970 г., авторами были поставлены опыты
по изгибу двух ледяных балок. Балка № 1 сечением 24×36 см и общей длиной
240 см установлена на двух опорах, при величине расчетного пролета 190 см.
Загружение балки производилось бетонными плитами весом 50 кг каждая (рис. 1.3).
Для замеров линейных деформаций льда при изгибе балки были установлены шесть
мессур (рис. 1.3).
На рис.
1.5, а дана схема установки приборов по толщине балки. Размеры даны в см.
База
приборов равна 150 мм. Точность измерения 0,001 мм. Опытные напряжения в ледяной
балке определяются по формуле
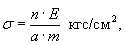
где n - показание прибора
(разность отсчетов);
E - модуль упругости
льда, равен 60000 кгс/см2;
a - коэффициент
увеличения прибора, равен 1000;
m - база прибора, равна
150 мм.

Рис.
1.3. Загружение ледяной балки испытательной нагрузкой
Тогда цена
одного деления составляет
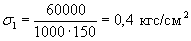
и
напряжение в балке можно определить по формуле
σ1 = 0,4·n кгс/см2.
Теоретические
напряжения в балке определим исходя из теории упругого изгиба. Момент инерции
сечения J=93320 см4.
Погонный
вес ледяной опытной балки q=0,775
кг/см.
Изгибающий
момент от собственного веса балки
Мq
= 3500кгс·см.
Напряжение
от собственного веса балки на уровне верхнего прибора равно
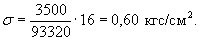
Изгибающий
момент от опытной нагрузки Р равен

Перед
каждой серией загружений балки производилось ее поддомкрачивание в середине
пролета с целью выключения собственного веса балки из работы перед снятием с
приборов нулевых отсчетов. Величина силы поддомкрачивания
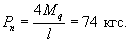
После
поддомкрачивания устанавливались приборы и брался нулевой отсчет. Затем
включался в работу собственный вес балки и брался первый отсчет по приборам.
В процессе
эксперимента фиксировались следующие величины:
вес опытной
нагрузки, кгс;
время с
момента загружения, мин.;
показания
приборов;
температура
воздуха, °С.
Балка № 2
сечением 20×23 см и общей длиной 170 см, опирается на две опоры, при
величине расчетного пролета 160 см. Четыре мессуры установлены по схеме, данной
на рис. 1.4.

Рис.
1.4. Загружение ледяной балки испытательной нагрузкой
База
приборов равна 500 мм. Цена одного деления прибора

Напряжения
в балке в результате опыта будут
σ1 = 0,12·n кгс/см2.
Момент
инерции сечения балки равен J = 20300
см4.
Погонный
вес опытной балки q
=0,41 кг/см.
Изгибающий
момент от собственного веса
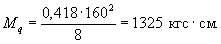
Напряжение
от собственного веса на уровне верхнего прибора равно

Изгибающий
момент от опытной нагрузки Р равен
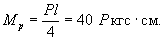
Величина
силы поддомкрачивания
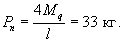
Обработка
результатов многочисленных экспериментов по загружению опытных балок
произведена в табличной форме и приведена в приложении 5 [12].
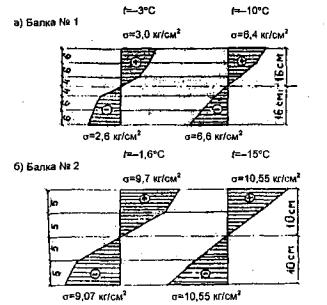
Рис. 1.5. Экспериментальные эпюры напряжений при изгибе
ледяных балок
На
основании проведенных экспериментов и используя данные К.Ф. Войтковского [29],
можно сделать следующие выводы о распределении напряжений по толщине ледяного
слоя при изгибе:
а) при
загружении ледяного слоя кратковременно действующей нагрузкой (от нескольких
секунд до одной минуты), при отрицательной температуре воздуха и льда -10°С и
ниже, закон распределения напряжений близок к упругому (рис. 1.5,а). В этом
случае почти справедлив закон Гука;
б) при
загружении ледяного слоя нагрузкой, действующей продолжительное время (от 10
минут до нескольких часов) при устойчивой отрицательной температуре, а также
при кратковременно действующей нагрузке при температуре воздуха и льда, близкой
к 0°С, явно проявляются пластические деформации. В этом случае
экспериментальная эпюра напряжений имеет вид (рис. 1.5, а,б).
Учитывая
вышеизложенные выводы и закономерность распределения температуры в толще льда,
можно предложить следующие расчетные эпюры распределения напряжений по толщине
ледяного слоя (рис. 1.6).
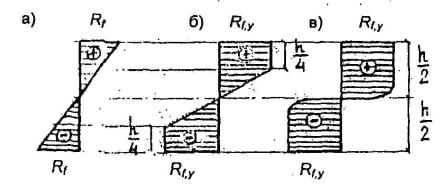
Рис. 1.6. Расчетные эпюры напряжений по толщине ледяного
покрова:
а
- для расчета упругой стадии; б - для расчета упругопластической стадии; в -
эпюры для пластической стадии
Для полосы
льда единичной ширины, значения предельных изгибающих моментов имеют следующий
вид:
для случая
a) M=Rfh2/6;
для случая
б) M=Rf,yh2/4,8;
для случая
в) M=Rf,yh2/4.
Разница
между эпюрами по схемам б) и в) составляет 20%.
Следует
отметить, что эпюра распределения напряжения (рис. 1.6, б), соответствует схеме
расчета ледяного слоя по предельному состоянию с учетом
упругопластических деформаций.
1.9. Испытания ледяного слоя на изгиб
1.9.1. Испытания
ледяного слоя до усиления
Эксперименты
проводились 19.12.1971 г. при температуре воздуха 6°С. Толщина ледяного слоя h = 8,3 см. Приборы были
установлены в мести приложения нагрузки и в 250 см от нее (рис. 1.7).

Рис.
1.7. Испытания ледяного покрова на изгиб
Теоретическое
значение прогиба под нагрузкой Р
по п. 4.6 (глава 4), при n=1

где Р -
нагрузка, кгс.
Изгибающий
момент в сечении под нагрузкой Р
по п. 4.6 (глава 4), при n=1
Мx
= Му = 0,125 (1 + v)·Р
= 0,166 Р кгс·см/см,
то есть при
расчетах плит изгибающие моменты имеют размерность силы (кгс; тс).
Напряжения
в верхних фибрах ледяного слоя
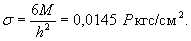
Теоретическое
значение прогиба в 250 см от нагрузки,
при ξ = λх
= 250×29,45 10-4 = 0,735, будет
w
= 0,00217 Р Wξ = 0,00147 Р см.
Изгибающие
моменты в этой же точке ледяного слоя
Мх = 0,125 Р
(UxWy + v WxUy) = 0,032 Р
кгс;
Мy
= 0,125 Р (UyWx + v
WyUx) == 0,086 Р кгс.
Напряжения
в верхних фибрах ледяного слоя


Целесообразно
провести сравнение экспериментальных данных с обоими решениями, приведенными в главе 4, и.4.6;
4.7.
В этом
случае экспериментальную нагрузку считаем распределенной по окружности радиуса r0 = 50 см. При величине l =41,61×104
см безразмерный радиус α = 0,2.
Теоретическое
значение прогиба под нагрузкой (4.32) при n=1, равно
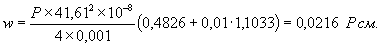
Изгибающие
моменты под нагрузкой (4.33), (4.34), при n=1,
равны
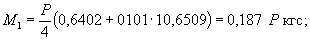
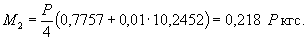
Напряжения
в верхних фибрах ледяного слоя
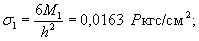
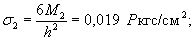
Теоретическое
значение прогиба и 250 см от нагрузки
при ξ=lx=250×41,61×10-4=1,04
будет

Изгибающие
моменты в этой же точке ледяного слоя

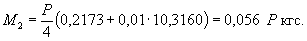
Напряжения
в верхних фибрах ледяного слоя
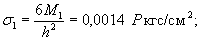

Фактические
напряжения определяются по результатам показаний мессур М-1, М-2, М-3, М-4 (табл.
1.2, 1.3).
База
мессуры равна 45 см, а цена деления ее, при модуле упругости льда Е=60000 кг/см2, составляет

Мессуры
устанавливались в плане по осям прямоугольных координат (рис. 1.7) М-1 и М-3
параллельно оси Y, М-2 и М-4 параллельно
оси X. Таким образом, фиксировались
деформации по двум взаимно перпендикулярным направлениям.
Результаты
теоретического расчета величин напряжений и прогибов в ледяном слое, а также
сравнение их с фактическими значениями, полученными в результате эксперимента,
даны в табл. 1.2, 1.3.
Во всех
случаях грузовые отсчеты по приборам брались через 5 минут после установки
нагрузок, и нулевые отсчеты через 10 минут после снятия нагрузки.
Суммарный
остаточный прогиб ледяного слоя в точке под нагрузкой после четырехкратного
загружения составил 0,35 см.
Остаточная
деформация, замеренная мессурами, составляет 0,005 мм, что соответствует
напряжению 0,67 кг/см2.
Эксперименты
были повторены 20.12.1971 г. при температуре воздуха -3°С и толщине ледяного
слоя h=8,5 см. Приборы
устанавливались в месте приложения нагрузки и в 255 см от нее по уже известной
схеме (рис. 1.7).
Результаты
теоретического расчета величин напряжений и прогибов в ледяном слое, а также
сравнение их с фактическими значениями, полученными в результате эксперимента,
даны в табл. 1.4, 1.5.
Таблица
1.2
Обработка данных
эксперимента
|
№ приборов
|
Нагрузка Р = 300 кг
|
|
Загружение № 1
|
Загружение № 2
|
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
|
нулевой.
|
грузовой
|
по п. 4.6
|
по п.4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
|
М-1
|
404
|
428
|
3,20
|
4,35
|
5,70
|
408
|
438
|
4,00
|
4,35
|
5,70
|
|
М-2
|
401
|
421
|
2,66
|
4,35
|
4,87
|
403
|
424
|
2,80
|
4,35
|
4,87
|
|
М-3
|
509
|
519
|
1,33
|
2,25
|
1,47
|
504
|
516
|
1,60
|
2,25
|
1,47
|
|
М-4
|
275
|
277
|
0,27
|
0,60
|
0,42
|
276
|
279
|
0,40
|
0,60
|
0,42
|
|
№ приборов
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
|
П-1
|
435
|
486
|
0,51
|
0,65
|
0,65
|
415
|
475
|
0,60
|
0,65
|
0,65
|
|
П-2
|
555
|
525
|
0,30
|
0,44
|
0,40
|
560
|
529
|
0,31
|
0,44
|
0,40
|
Таблица 1.3
Обработка данных
эксперимента
|
№ приборов
|
Нагрузка Р = 400 кг
|
|
Загружение № 3
|
Загружение № 4
|
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.
4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.
4.7
|
|
М-1
|
410
|
445
|
4,67
|
5,80
|
7,60
|
412
|
449
|
4,94
|
5,80
|
7,60
|
|
М-2
|
404
|
428
|
3,20
|
5,80
|
6,50
|
406
|
431
|
3,33
|
5,80
|
6,50
|
|
М-3
|
508
|
520
|
1,60
|
3,00
|
1,96
|
510
|
524
|
1,87
|
3,00
|
1,96
|
|
М-4
|
277
|
281
|
0,54
|
0,80
|
0,56
|
279
|
284
|
0,66
|
0,80
|
0,56
|
|
№ приборов
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.
4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.
4.7
|
|
П-1
|
405
|
475
|
0,70
|
0,87
|
0,86
|
400
|
472
|
0,72
|
0,87
|
0,86
|
|
П-2
|
570
|
532
|
0,38
|
0,59
|
0,56
|
575
|
535
|
0,40
|
0,59
|
0,56
|
Таблица 1.4
Обработка данных
эксперимента
|
№ приборов
|
Нагрузка Р = 400 кг
|
|
Загружение № 1
|
Загружение № 2
|
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
|
М-1
|
298
|
334
|
4,66
|
5,52
|
7,25
|
301
|
337
|
4,78
|
5,52
|
7,25
|
|
М-2
|
514
|
539
|
3,33
|
5,52
|
6,20
|
516
|
542
|
3,46
|
5,52
|
6,20
|
|
М-3
|
240
|
253
|
1,72
|
2,86
|
1,86
|
242
|
255
|
1,72
|
2,86
|
1,86
|
|
М-4
|
810
|
814
|
0,53
|
0,78
|
0,54
|
811
|
816
|
0,66
|
0,78
|
0,54
|
|
№ приборов
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
|
П-1
|
701
|
770
|
0,69
|
0,83
|
0,82
|
707
|
778
|
0,71
|
0,83
|
0,82
|
|
П-2
|
400
|
439
|
0,39
|
0,56
|
0,54
|
404
|
445
|
0,41
|
0,56
|
0,54
|
Таблица 1.5
Обработка данных
эксперимента
|
№ приборов
|
Нагрузка Р = 550 кг
|
|
Загружение № 3
|
Загружение № 4
|
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
нулевой
|
грузовой
|
по п. 4.6
по п.4.7
|
|
М-1
|
304
|
356
|
6,92
|
7,56
|
9,75
|
307
|
360
|
7,05
|
7,56
|
9,75
|
|
М-2
|
518
|
554
|
4,78
|
7,56
|
8,34
|
521
|
558
|
4,92
|
7,56
|
8,34
|
|
М-3
|
243
|
262
|
2,53
|
3,93
|
2,51
|
245
|
265
|
2,64
|
3,98
|
2,51
|
|
М-4
|
812
|
817
|
0,67
|
1,11
|
0,72
|
813
|
819
|
0,79
|
1,11
|
0,72
|
|
№ приборов
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
|
П-1
|
712
|
811
|
0,99
|
1,14
|
1,14
|
714
|
816
|
1,02
|
1,14
|
1,14
|
|
П-2
|
407
|
461
|
0,54
|
0,77
|
0,73
|
409
|
470
|
0,61
|
0,77
|
0,73
|
1.9.2. Испытания
ледяного слоя, усиленного намораживанием
С целью
экспериментальной проверки теоретических выводов, изложенных в главе 4, 4.6;
4.7,
на ледяном слое была наморожена полоса льда шириной 480 см и длиной 40 м.
Толщина льда после намораживания составила h1=11,0 см. Характеристика
λ1 в данном случае равна 24,18·104 см. Приведенная
ширина намороженной полосы составляет 2а=1,16,
приведенная длина полосы равна 3π. Испытания усиленного ледяного слоя
производились 20.12.1971 г. при t=-3°C
Толщина
основного ледяного слоя h=8,5
см. Характеристики λ=28,87·10-4
см. Отношение характеристик n=1,2.
Приборы устанавливались по такой же схеме и в таком же количестве, что и в
вышеописанном опыте, то есть в центре намороженной полосы под нагрузкой, и на
расстоянии 250 см от центра, у кромки намороженной полосы. Такая расстановка
приборов позволяет сравнить данные испытаний, полученные в первом и втором
случаях.

Рис.
1.8. Испытания намороженного ледяного покрова на изгиб
Предварительно
определим теоретические значения прогибов и напряжений в местах установки
приборов.
Прогиб в
точке под нагрузкой (2.21), при а =0,58,
равен
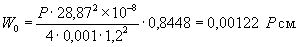
Изгибающие
моменты в сечении под нагрузкой (2.23), (2.24)
Мх = 0,182 Р кгс;
Му = 0,155 Р кгс.
Напряжения
в верхних фибрах намороженного слоя

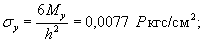
Теоретическое
значение прогиба в 250 см от нагрузки
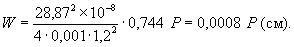
Изгибающие
моменты в этом же сечении (2.23), (2.24)
Мх = 0,0506 Р кгс;
Му = 0,0992 Р кгс.
Напряжения
в верхних фибрах намороженного слоя
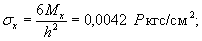
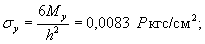
На основе
решения, изложенного в п.
4.7, имеем при h
=8,5 см l = 40,87×10-4
см, а для h1 = 11 см l1 = 34,06×10-4
см, отношение n = 1,2, а безразмерная
ширина намороженной полосы составляет 2а=1,64.
Прогиб под
нагрузкой, при а=0,82, равен (2.32)
W
= 0,00123 Р cм.
Изгибающие
моменты под нагрузкой (2.33), (2.34) соответственно равны
М1 = 0,189 Р кгс;
М2 = 0,220 Р кгс.
Напряжения
в верхних фибрах ледяного слоя
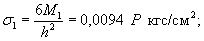
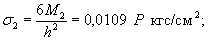
Теоретическое
значение прогиба в 250 см от нагрузки
W
= 0,0008 Р (см).
Изгибающие
моменты в этой же точке будут
М1 = 0,025 Р кгс;
М2 = 0,0875 Р кгс.
Напряжения
в верхних фибрах ледяного слоя
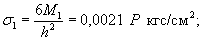
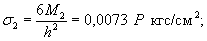
Результаты
теоретического расчета величин напряжений и прогибов в ледяном слое, а также
сравнение их с фактическими значениями, полученными в результате эксперимента,
даны в табл. 1.6, 1.7.
Отсчеты по
приборам брались с теми же интервалами времени, что и в предыдущем опыте.
21.12.1971
г. эксперименты были повторены при температуре воздуха -5°С. К моменту
окончания усиления основной ледяной слой имел толщину h=9,0 см. Ширина
намороженной полосы составляла 500 см. Толщина льда после усиления h1=12,0 см. Отношение характеристик n=1,2. Приборы
устанавливались в таком же количестве и по такой же схеме, что и в ранее
проведенном опыте.
Результаты
теоретического расчета величин напряжений и прогибов в ледяном слое, а также
сравнение их с фактическими значениями, полуденными в результате опыта, даны в
табл. 1.8, 1.9.
Из анализа
данных, полученных в результате испытаний, можно сделать следующие выводы:
1.
Закономерность изменения прогибов и напряжений в ледяном слое, полученная в
результате теоретического расчета, имеет место в действительности и
подтверждается экспериментально.
2. Почти во
всех случаях загружения фактические величины прогибов и напряжений в ледяном
слое, меньше соответствующих им теоретических значений или близки к ним.
3.
Сравнение теоретических и экспериментальных величин прогибов и напряжений дает
вполне удовлетворительные результаты.
4. Из
сравнения опытных данных в первом и втором случаях (табл. 1.2-1.9, загружение № 4) видно,
что одинаковым значениям напряжений под нагрузкой (мессура М-2), соответствуют
разные значения внешней нагрузки. В первом случае Р=400-550 кгс, во втором Р=550-1800
кгс. Следовательно, в результате намораживания ледяной полосы грузоподъемность
ледяного слоя увеличилась в 1,4 раза.
Таблица 1.6
Обработка данных
эксперимента
|
№ приборов
|
Нагрузка Р = 400 кг
|
|
Загружение № 1
|
Загружение № 2
|
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п.4.7
|
нулевой
|
грузовой
|
по п. 4.6
по п. 4.7
|
|
М-1
|
393
|
418
|
3,33
|
3,64
|
4,36
|
394
|
422
|
3,73
|
3,64
|
4,36
|
|
М-2
|
492
|
514
|
2,98
|
3,08
|
3,76
|
491
|
512
|
2,80
|
3,08
|
3,76
|
|
М-3
|
716
|
732
|
2,13
|
3,32
|
2,92
|
720
|
735
|
2,00
|
3,32
|
2,92
|
|
М-4
|
498
|
502
|
0,53
|
1,68
|
0,82
|
498
|
503
|
0,67
|
1,68
|
0,82
|
|
№ приборов
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
|
П-1
|
735
|
695
|
0,40
|
0,49
|
0,49
|
725
|
678
|
0,47
|
0,49
|
0,49
|
|
П-2
|
925
|
885
|
0,40
|
0,43
|
0,32
|
915
|
883
|
0,22
|
0,43
|
0,32
|
Таблица 1.7
Обработка данных
эксперимента
|
№ приборов
|
Нагрузка Р = 550 кг
|
|
Загружение № 1
|
Загружение № 2
|
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
нулевой
|
грузовой
|
по п. 4.6
по п. 4.7
|
|
М-1
|
396
|
432
|
4,80
|
5,01
|
6,00
|
407
|
445
|
4,92
|
5,01
|
6,00
|
|
М-2
|
490
|
521
|
4,12
|
4,28
|
5,17
|
490
|
522
|
4,25
|
4,28
|
5,17
|
|
М-3
|
725
|
760
|
4,67
|
4,56
|
4,02
|
732
|
766
|
4,54
|
4,56
|
4,02
|
|
М-4
|
500
|
508
|
1,06
|
2,31
|
1,15
|
500
|
510
|
1,33
|
2,31
|
1,15
|
|
№ приборов
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
|
П-1
|
723
|
655
|
0,68
|
0,67
|
0,68
|
710
|
640
|
0,70
|
0,67
|
0,68
|
|
П-2
|
912
|
876
|
0,36
|
0,58
|
0,44
|
905
|
860
|
0,45
|
0,58
|
0,44
|
Таблица 1.8
Обработка данных
эксперимента
|
№ приборов
|
Нагрузка Р = 550 кг
|
|
Загружение № 1
|
Загружение № 2
|
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
нулевой
|
грузовой
|
по п. 4.6
по п. 4.7
|
|
М-1
|
185
|
216
|
4,12
|
4,27
|
5,06
|
187
|
220
|
4,38
|
4,27
|
5,06
|
|
М-2
|
823
|
849
|
3,46
|
3,63
|
4,35
|
825
|
851
|
3,46
|
3,36
|
4,35
|
|
М-3
|
504
|
528
|
3,20
|
3,85
|
3,39
|
505
|
529
|
3,33
|
3,85
|
3,39
|
|
М-4
|
338
|
845
|
0,92
|
1,98
|
1,02
|
339
|
347
|
1,06
|
1,98
|
1,02
|
|
№ приборов
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
|
П-1
|
521
|
582
|
0,59
|
0,60
|
0,61
|
525
|
587
|
0,62
|
0,60
|
0,60
|
|
П-2
|
798
|
836
|
0,38
|
0,51
|
0,40
|
801
|
844
|
0,43
|
0,31
|
0,40
|
Таблица 1.9
Обработка данных
эксперимента
|
№ приборов
|
Нагрузка Р = 800 кг
|
|
Загружение № 1
|
Загружение № 2
|
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
Отсчеты
|
Фактичес. напряжен., кгс/см2
|
Теоретическ. напр.
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
нулевой
|
грузовой
|
по п. 4.6
по п. 4.7
|
|
М-1
|
189
|
235
|
6,12
|
6,20
|
7,35
|
191
|
238
|
6,25
|
6,20
|
7,35
|
|
М-2
|
827
|
867
|
5,32
|
5,28
|
6,33
|
828
|
868
|
5,32
|
5,28
|
6,33
|
|
М-3
|
508
|
549
|
5,45
|
5,60
|
4,94
|
510
|
552
|
5,58
|
5,60
|
4,94
|
|
М-4
|
341
|
351
|
1,33
|
2,88
|
1,43
|
342
|
358
|
1,47
|
2,88
|
1,43
|
|
№ приборов
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
Отсчеты
|
Фактичес. прогиб, см
|
Теоретическ. прогиб
|
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
нулевой
|
грузовой
|
по п. 4.6
|
по п. 4.7
|
|
П-1
|
528
|
313
|
0,85
|
0,87
|
0,88
|
534
|
624
|
0,90
|
0,87
|
0,88
|
|
П-2
|
804
|
875
|
0,71
|
0,74
|
0,63
|
809
|
878
|
0,69
|
0,74
|
0,63
|
5.
Сравнение приведенных решений с опытными данными показывает, что при расчете
усиленного ледяного слой на статические нагрузки, целесообразно применять
решение (4.21), (4.23), (4.24); а при
динамическом расчете - предпочтительнее решение (4.32)-(4.34). Этот вывод согласуется с физико-механическим
свойством льда (глава 1, п.
1.3), заключающимся в изменении величины модуля упругости в зависимости от
характера действующей на ледяной покров внешней
нагрузки.
1.10. Температурный режим ледяного покрова
Одним из
главнейших факторов, влияющих на физико-механические свойства льда, является
его температура. На распределение температуры по толщине ледяного покрова, а
также на величину его средней температуры, как известно, наибольшее влияние
оказывают: температура воздуха, скорость ветра, наличие снегового покрова и
толщина льда.
Тепловые
волны, распространяющиеся в ледяном покрове конечной толщины, по мере продвижения
их в толщу льда претерпевают ряд изменений, происходит непрерывное затухание
амплитуды колебаний температуры согласно закону [138]
Ah = A0e-βh,
где Ah - амплитуда тепловой волны
на глубине h;
А0 - амплитуда тепловой волны на
поверхности;
h - толщина ледяного слоя, через который прошла
волна.
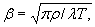
где р - плотность льда;
λ - теплопроводность льда;
Т - период колебаний.
С глубиной
также происходит увеличение сдвига фаз по следующему закону:
γh =
γ0+βh,
где γh - фаза на глубине;
γ0 - начальная фаза на
поверхности.
Дойдя до
нижней границы, тепловая волна должна была бы иметь амплитуду, равную A0e-βh, где Н - толщина ледяного покрова, в
действительности же температура на границе раздела лед - вода равна нулю. Это
могло иметь место только в том случае, если бы тепловая волна полностью
отразилась с переменной знака, когда фаза скачком изменяется на величину
π.
Но тепловые
волны не обладают способностью отражаться, в данном случае мы имеем явление
квазиотражения. Волна холода, дошедшая до границы раздела лед - вода, вызовет
фазовый переход воды в лед, при этом выделится теплота кристаллизации. Часть
этой теплоты поглотится водой, остальная часть распределится во льду.
Перераспределение теплоты кристаллизации между водой и льдом осуществляется
пропорционально их термическим свойствам.
Эпюры
распределения температур в толще льда, при отсутствии снегового покрова,
полученные из наблюдений [89],
характеризуются сложными кривыми, меняющимися во времени, которые можно разбить
на три типа:
I тип распределения наблюдается при похолодании. В
этот момент происходит отдача тепла ледяного покрова воздуху, причем верхние
слои приобретают более низкую температуру, тогда как нижеследующие слои еще
сохраняют более высокую температуру. Этот тип, как правило, характерен для начала
зимнего периода, хотя может наблюдаться и в другие периоды зимы, при наличии
резких колебаний температуры воздуха.
II тип распределения чаще встречается при потеплении. Он отвечает
обычно весеннему периоду, но (так же, как и в первый) может быть и в зимний
период.
III тип является переходным и может встречаться в течение всей
зимы.
Случай
распределения температуры по прямой, как показывают натурные наблюдения [89],
встречается очень редко. Такой тип может возникнуть при наличии длительно
установившегося периода с одинаковыми отрицательными температурами.
Ориентироваться на него нельзя и будет давильным отнести его к III типу.
Изучение
колебаний температуры ледяного слоя является довольно сложным и трудоемким
делом, в связи с большим количеством определяющих факторов (температурой воды,
влажностью воздуха, скоростью ветра, толщиной ледяного покрова и т.д.).
В связи с
этим искомые связи могут быть установлены с использованием статистических
методов и, в частности, теории корреляции. На основе анализа факторов, а также
подсчета коэффициентов корреляции, устанавливающих связь между ними, Г.Я.
Кузубом [89]
найдена следующая зависимость
t°л = t°в·0,32-1°,
где t°л, - средняя температура
ледяного покрова;
t°в - средняя отрицательная температура,
взятая за предыдущие сутки, откуда отношение t°л/t°в ≠ const.
Наиболее
интенсивное затухание амплитуды колебания температуры происходит в верхних
слоях ледяного покрова. 50% амплитуды гасит слой льда толщиной 10 см, а до
глубины 35 см доходит только 25%. В дальнейшем затухание идет медленнее. До
глубины 80 см доходит только 6% амплитуды колебания температуры воздуха в
течение суток.
Таким
образом, существенным температурным колебаниям подвержена не вся толща ледяного
покрова, а какая-то его часть, «активный слой». Размеры «активного слоя»
зависят от толщины ледяного покрова и величины температурных колебаний.
Из
графиков, построенных по экспериментальным данным Г.Я. Кузубом [89],
следует, что при малых толщинах льда (до 20 см) температурным колебаниям
подвержена вся толща ледяного покрова. До нижней поверхности льда при этом
доходит до 40% температурных колебаний воздуха. При больших толщинах (35-80 см)
ледяного покрова процент проникания температурных колебаний падает до 6.
И зимний
период ледяной покров, как правило, покрыт снегом. Наличие снега сказывается на
функции ледяного покрова как регулятора теплообмена между ложем водоема и
атмосферой.
При этом
снеговой покров, обладая незначительной теплопроводностью, принимает на себя
существенную долю теплозащитных функций. Это вызывает повышение средних
температур ледяного покрова по сравнению с температурой льда при отсутствии
снегового покрова.
Кривые
распределения температуры по толщине льда при наличии снега в общем аналогичны
кривым распределения при отсутствии его. Они также могут быть разбиты на 3
типа, характер которых обусловлен изменением температуры воздуха [89].
Выше было
указано, что колебания средней температуры ледяного покрова, при отсутствии
снега, в своем ходе отстают от колебаний температуры воздуха на одни сутки.
Снеговой покров увеличивает отставание изменения температуры льда от
температуры воздуха.
Не
останавливаясь на выводе формул для определения средней температуры ледяного
покрова при наличии снега на льду, Г.Я. Кузуб [89]
рекомендует следующую экспериментальную зависимость

где t°л - средняя температура
ледяного покрова, °С;
t°в2 - средняя температура
воздуха, взятая за предыдущие двое, суток, °С;
hл - толщина льда, см;
hc - толщина снега, см;
λл - коэффициент
теплопроводности льда, кал/см-с-град;
λс - коэффициент
теплопроводности снега, кал/см-с-град.
Анализ
натурных данных [89]
позволяет установить положение точки с температурой, равной средней по толщине
льда.
При первом
типе распределения она находится на глубине 0,45 hл от верхней поверхности
льда и при втором типе на 0,56 hл, находясь довольно
близко от нейтральной оси ледяного покрова.
1.10.1. Теплопроводность
льда и снега
Из
термических констант льда меньше всего изучена теплопроводность. Сведения о
теплопроводности пресного льда по литературным источникам весьма разноречивы. В
этом можно убедиться по значениям коэффициента теплопроводности, установленным
разными авторами и сведенными в табл. 82 [138].
Некоторые
исследователи считают коэффициент теплопроводности λл равным 2,2-10-3 кал/см-с-град.
Измерение
коэффициента теплопроводности пресного озерного льда и снежного покрова по
методу регулярного режима производила A.M. Елистратова [52].
Результаты
определения коэффициента теплопроводности, полученные A.M. Елистратовой,
показывают, что среднее его значение для прозрачного льда равно 0,0049, для
льда с вкраплением воздушных пузырьков - 0,0033 и для снежного льда - 0,0028
кал/см·с·град.
Средний
коэффициент теплопроводности снега, равный 0,000244 кал/см·с·град., примерно в
20 раз меньше коэффициента теплопроводности прозрачного льда.
В табл. 89 [139]
приведены значения коэффициентов теплопроводности λc
для различных значений плотности снега по данным разных авторов. Значения λc изменяются в пределах 0,0001-0,0009 кал/см·с·град, при изменении плотности снега от 0,12 до 0,37 кгс/см3.
1.11. Температурные напряжения и трещины в ледяном покрове
При
изменении температуры воздуха с некоторым отставанием изменяется температура
ледяного покрова. Как отмечено в предыдущем параграфе, температурным колебаниям
в основном подвержена не вся толща льда, а его «активный слой» [90].
Таким
образом, имеется постоянное неравенство температур верхних и нижних слоев льда.
Это обстоятельство обусловливает стремление ледяного покрова деформироваться и
зависимости от изменения температуры воздуха.
В
действительности, возникающий температурный изгиб происходит несвободно, ему
препятствуют давление поды, вес самого льда и горизонтальные силы, появляющиеся
благодаря стремлению ледяного покрова изменять свои размеры в плане.
Практически можно считать, что колебания температуры не вызывают заметного
изгиба ледяного покрова, по создают но толщине льда существенные сжимающие и
растягивающие напряжения.
Возникающие
напряжения приводят, при наличии сплошного ледяного покрова, к образованию
трещин и термических сжатий, в результате чего появляются торосы и гребни.
Ширину
трещин определяют деформации ледяного покрова при понижении температуры,
которые определяются формулой
Δl = αΔt°l,
где α - коэффициент линейного
расширения льда;
Δt° - понижение средней температуры ледяного
покрова;
l - длина ледяного
покрова.
Величину
возникающих напряжений от температурных изменений в толще льда, приближенно,
без учета пластических деформаций, можно определять по формуле
σ = α Δt°E,
где модуль
упругости льда Е=30000 кг/см2, с учетом продолжительности
времени, в течение которого происходит перепад температуры.
Как
известно [27],
среднее разрушающее напряжение льда на растяжение при 0-3°С составляет 8-10
кг/см2. Поэтому сравнительно быстрое понижение температуры на 5-7°
приводит к образованию трещин (рис. 1.9), часто сопровождающихся звуком,
напоминающим выстрел.
В
результате на ледяном покрове образуется весьма сложная система переплетающихся
между собой трещин. Пересекающиеся трещины образуют «карты» различной величины,
от 2-3 м2 до 20000 м , и чем крупнее трещины, тем больше карты.
В период с
3 по 17 января 1972 г. авторами проводились наблюдения за интенсивностью
намерзания озерного льда, у р. Волги в районе г. Саратова.
На
3.01.1972 г. толщина льда составляла 25 см.
За период с
3 по 11 января, то есть за 8 суток, при среднесуточной температуре t = -9-11°С, толщина льда
увеличилась на 8 см и составляла 33 см. Среднесуточное увеличение толщины и
данном случае 1 см.
При резком
похолодании с 11 по 17 января и среднесуточной температуре t =
-23-25°С, за 6 суток толщина льда увеличилась на 20 см и составляла 51-53 см.
Среднесуточное увеличение толщины льда составляет 3,3 см, снежный покров за
период наблюдений почти полностью отсутствовал. В результате резкого
температурного перепада лед покрылся сетью трещин (рис. 1.9).
Рис.
1.9. Температурные трещины в ледяном покрове
Из ста
замеров глубин незамерзшей части трещин 75% имели глубину 3÷7 см, 23% -
глубину 8÷12 см, и 2% - 20÷22 см.
В период
оттепели 25 января трещины частично или полностью заполнялись талой водой, а
затем, при понижении температуры/замерзали.
Наблюдения
за ледяным покровом этого же озера были продолжены ив январе 1974 г. Ввиду
продолжительной теплой погоды и декабре 1973 г. весь снежный покров на озере
превратился в слой снежного льда толщиной 6 см, который лежал сверху основного слоя
прозрачного льда толщиной 30 см. В этом случае температурными трещинами был
довольно интенсивно разрушен только верхний слой - слой снежного льда.
Температура наружного воздуха в период наблюдений не превышала -15°С. При этом
основной слой прозрачного льда, лежащий под верхним слоем, температурных трещин
почти не имел.
Наблюдения
за льдообразованием на этом же водоеме были повторены в зиму 2003-2004 гг. Этот
период характерен относительно теплой и малоснежной погодой, что позволяет
считать полученные результаты полезными. График наблюдений велся ежедневно с 1
декабря 2003 г. по 15 марта 2004 г. с фиксацией среднесуточной температуры
воздуха. Замеры глубин снежного покрова и толщины льда производились
еженедельно. Результаты наблюдений обобщены в графике на рис. 1.10.
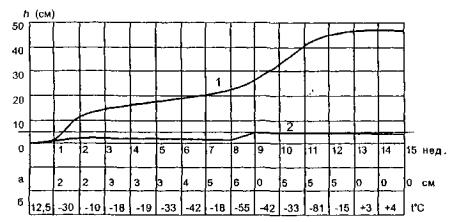
Рис. 1.10. График наблюдений за образованием льда на
водоеме с медленным течением: 1 - общая толщина льда (см); 2 - толщина мутного
льда (см);
а
- толщина снежного покрова на льду;
б - средняя температура воздуха за неделю
Замеры
производились в течение 15 недель, следовательно, за расчетный период сумма
отрицательных среднесуточных температур воздуха составляет Σt = 396°С. Для
определения скорости нарастания льда (в сантиметрах) в естественных условиях
под снежным покровом в водоемах с медленным течением возможно применение
формулы Наймана [128]
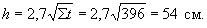
Это на 7 см
превышает фактическую толщину льда, равную 47 см. Для рек с быстрым течением
рекомендована формула Ф.И. Быдина [128]
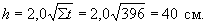
то есть
расчетная толщина меньше замеренной также на 7 см.
Следовательно,
в данном конкретном случае возможна корректировка предлагаемых формул. Тогда,
приняв за основу среднее значение, получим

Данный
пример показывает, что для конкретных рек и водохранилищ желательно иметь при
проектировании данные наблюдений за льдообразованием, тогда на их основе
возможно прогнозирование скорости нарастания льда с достаточной точностью.
Интенсивность
нарастания толщин льда, расчищенного от снежного покрова, больше на 20-40%, чем
с естественным снежным покровом. В среднем ее можно принимать 30%.
Толщина
снега на льду приблизительно пропорциональна толщине ледяного покрова. Если
принять объемный вес снега 0,2 тс/м3, то толщина его не может быть
больше 40% от толщины ледяного покрова, в противном случае наступает перегрузка льда и вода по трещинам выступает на
поверхность.
1.12. Ледовый режим рек и
водохранилищ, расчетная толщина ледяного покрова
На
основании теоретических и экспериментальных исследований процессов замерзания
выделены следующие основные типы замерзания рек и водохранилищ [61].
I тип замерзания (быстрый). Продолжительность 1-3 суток при
начальной толщине льда 0,5-2 см.
II тип замерзания (замедленный). Длительность процесса
замерзания 5-10 суток. Начальная толщина льда до 15 см.
III тип
замерзания (длительный). Продолжительность более 10 суток, толщина льда в
момент ледостава больше 20 см.
Можно
отметить, что в зависимости от характера процесса замерзания на водохранилищах
наблюдается длительность замерзания акватории, составляющая:
при I типе
3-10 суток,
при II типе
10-20 суток,
при III
типе 30-50 суток.
По данным
многочисленных наблюдений, средняя дата устойчивого ледостава на реках и
водохранилищах Европейской и Сибирской частей Российской Федерации приходится
на X-I месяцы. На водохранилищах чаще наблюдается II тип замерзания, затем I и
реже III.
Наибольшая
по средним многолетним данным [61]
интенсивность зарастания толщины льда наблюдается - в первый месяц ледостава
(1-2 см/сутки). Максимальные значения интенсивности нарастания льда составляют
для сибирских водохранилищ 3-5 см/сутки, волжских 5-6 см/сутки, днепровских 4-6
см/сутки. В последующие месяцы наблюдается равномерное уменьшение интенсивности
нарастания льда.
С ростом
интенсивности нарастания толщины льда в различные месяцы зимнего периода
наблюдается увеличение толщины ледяного покрова:
а) на
сибирских водохранилищах в октябре 10-20 см, в ноябре 20 60 см, в декабре 20-50
см, в январе 10-40 см, в феврале 10-15 см, в марте 5 10 см;
б) на
волжских и камских водохранилищах в ноябре 0-30 см, в декабре 10-35 см, в
январе 6-20 см, в феврале 10-15 см;
в) на
днепровских водохранилищах в декабре 5-35 см, в январе 5-25 см, в феврале 5-15
см.
Максимальная
толщина льда на днепровских и волгоградском водохранилищах наблюдается в конце
февраля (40-80 см). На волжских и камских водохранилищах большей частью в марте
(60-100 см), а на сибирских в конце марта (от 80 до 120 см). В холодную зиму
максимальная толщина льда в 2÷3 раза больше, чем в теплую.
На
водохранилищах изменение толщины льда по акватории составляет в среднем 20%), а
и отдельных случаях 50%. Колебания толщины льда по акватории водохранилища
значительны, однако несколько меньше, чем на речных участках. В соответствии с
этим можно отметить, что различия в условиях формирования ледяного покрова на
речных участках больше, чем на водохранилищах.
Наибольшие
различия в толщине льда наблюдаются в начальный период ледостава вследствие
неодновременности последнего по акватории, а также неоднородности характера
процессов ледообразования по участкам водохранилища.
Наибольшая толщина
льда наблюдается в мелководных зонах водохранилищ, где глубина не превышает 5-6
м, наименьшая - в зоне затопленного русла реки при максимальных глубинах воды.
Пойменные
участки водохранилищ имеют толщину льда, на 15-20% большую, чем затопленные русловые
участки. Особенно большие колебания в толщине льда могут иметь место из-за
большой неравномерности распределения снега на льду.
Снежный
покров и условия его трансформации в течение зимнего периода оказывают
значительное влияние на характер распределения толщины льда по акватории рек и
водохранилищ. При выпадении снега на лед интенсивность нарастания толщины льда
значительно уменьшается. Однако получить количественные характеристики
уменьшения толщины льда по акватории не всегда возможно, так как характер
распределения снега на льду зависит от интенсивности выпадения снега, изменения
скорости и направления ветра.
При этом
следует отметить двоякую роль снега в процессе нарастания льда. Он является не
только хорошим изолятором тепла, по и готовым материалом при образовании
снежного льда в период оттепелей. Но данным измерений на водохранилищах,
толщина снежного льда составляет 20-40% от общей толщины ледяного покрова.
В начальный
период ледостава и перед вскрытием толщина льда на водохранилищах превышает толщину
льда на реках. И середине зимы это различие невелико. Максимальная толщина
ледяного покрова на речных участках Волги, Днепра и Оби больше, чем на
соответствующих водохранилищах.
Различие
толщины льда по акватории водохранилищ меньше, чем это было на речных участках.
Вследствие
больших колебаний уровня в течение зимнего периода на водохранилищах
наблюдаются значительно большие деформации ледяного покрова, чем на реке.
1.12.1. Расчетная
толщина ледяного слоя
П.И.
Лебедев [93]
предлагает определять расчетную толщину льда по следующей формуле:
h = h1+0,5(h2+h3)k1k2,
где h - расчетная толщина льда;
h1 - толщина прозрачного слоя;
h2 - толщина мутного слоя;
h3 - толщина намороженного
слоя;
k1 - коэффициент структуры, равный при раковистой
структуре 1, а при игольчатой - 2/3;
k2 - коэффициент температуры, равный при
температуре воздуха ниже нуля - 1, а при температуре воздуха выше нуля - 4/5.
В
результате анализа данных, приведенных в п. 1.6, 1.7, можно сделать вывод,
что предел прочности намороженного льда на сжатие при изгибе приблизительно
равен пределу прочности прозрачного льда на растяжение при изгибе.
Отсюда
следует, что если мутный и намороженный лед располагается по толщине ледяного
слоя выше нейтральной оси, то при расчетах в упругой стадии можно принимать за
расчетную толщину льда полную толщину ледяного слоя, при условии, что последний
не ослаблен температурными трещинами.
При наличии
температурных трещин следует уменьшать расчетную толщину льда. В этом случае за
расчетную толщину ледяного покрова возможно принимать величину
h = 0,9H (1.10)
где H - полная толщина
ледяного покрова.
Целесообразность
определения расчетной толщины ледяного покрова но формуле (1.10) подтверждается
следующими соображениями:
Если в зону
действия внешней нагрузки попадает температурная трещина, то она может явиться
очагом местного разрушения ледяного слоя. Образовавшаяся при этом сквозная
трещина заполняется водой на 0,9 от полной толщины ледяного покрова, и при
последующем ее замерзании трещина закрывается.
Дальнейшее
уменьшение расчетной толщины льда по сравнению с выражением (1.10) явилось бы
необоснованным, так как привело бы к уменьшению расчетной грузоподъемности
ледяного покрова.
В
инструкции [60]
для увеличения грузоподъемности льда допускается послойное намораживание его
поверх ледяного покрова на толщину не более 30% его начальной толщины. В этом
случае в расчетах грузоподъемности учитывают приведенную толщину льда h=h1+0,75h2, где h1 - толщина естественного льда,
h2 - толщина искусственно
полученного льда.
1.13. Проведение
транспортных и монтажных работ в зимнее время при строительстве
автодорожного моста через р. Обь у г. Сургута
Сооружение
металлического моста через р. Обь на автодороге Нефтеюганск - Сургут - велось в
период с 1993 по 2000 гг.
Монтаж
балки жесткости вантового пролетного строения моста осуществлялся без перерыва,
независимо от времени года.
Собранные
на стапеле блоки подавали в пролет в теплое время года по воде, а зимой - по
льду (рис. 1.11). Доставка по воде производилась буксиром мощностью 400 л.с. и
двумя пеленажными катерами мощностью по 90 л.с. на барже-площадке
грузоподъемностью 480 т. В пролете, в месте установки блоков, баржу крепили с
помощью якорей и за опоры рядом расположенного железнодорожного моста. Блоки на
баржу грузили двумя кранами КН500. Зимой блоки транспортировались по льду на
санях четырехосным автомобильным тягачом МАЗ-543 «Ураган». Длина саней 20 м,
база между полозьями 11 м. Наибольшая суммарная масса одного блока и саней
составляла 95 т. Для трогания саней с места дополнительно использовали
гусеничный трактор. Толщина льда санной дороги поддерживалась в пределах
0,8-1,2 м, причем в процессе образования ледяного покрова его армировали
старогодными тросами и деревянными пластинами.

Рис. 1.11. Подача блоков в пролет по льду
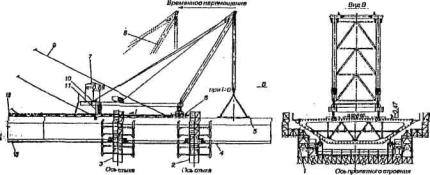
Рис.
1.12. Схема монтажа блоков: 1 - передвижные подмости; 2 - передвижные подмости
№ 1, столика 3 (масса 15,7 т); 3 - передвижные подмости № 2 (масса 15,7 т); 4 -
монтируемый блок (масса 82 т - max); 5 - траверса (масса 1,6 т); 6 - башмак
винтовой; 7 - сварочный пост и помещение для расходных материалов (масса не
более 5 т); 8 - положение агрегата при натяжении вант на блоке и перекладке
пути; 9 - натянутая ванта; 10 - проушина ванты агрегата; 11 - анкерная тяга; 12
- перекладываемая секция пути (L=10,5
м); 13 - путь катания передвижных подмостей

Рис.
1.13. Подъем блоков балки жесткости с ледовой строительной площадки
Подъем и
установка блоков балки жесткости в проектное положение в русловой части
выполнялись специальным монтажным агрегатом (рис. 1.12 и 1.13), который был
изготовлен с использованием элементов крана УМК-2, имевшегося и Мостострое-11.
Представляют интерес основные технические характеристики агрегата:
грузоподъемность 82 т, вылет на горизонтальной площадке 7,4 м.
Блок
поднимали до совмещения уровней верхних плит монтируемого блока и балки
жесткости двумя грузовыми полиспастами агрегата с помощью двух траверс.
Конструкция траверс, исключавшая возможность помех при проведении стыковочных
работ, состояла из двутавровых балок, четырех тяжей, проходивших через
специальные отверстия в верхней плите монтируемого блока, и двух балок, которые
подхватывали блок под продольными ребрами верхней плиты. Траверсы крепились на
монтируемом блоке еще до подачи его в пролет. Поперечный уклон блока
обеспечивали поочередной работой грузовых полиспастов агрегата. Следует отметить,
что расстояние между траверсами, равное 6 м, оказалось явно недостаточным и это
затруднило устранение перекосов блоков при их установке. После подъема блока до
проектной отметки регулировку его положения в плане осуществляли ручными
лебедками, располагаемыми внутри коробки на конце смонтированной части консоли.
В итоге проектное положение каждого блока фиксировалось путем прикрепления его
заднего конца с помощью передвижных подмостей к консоли, а переднего - двумя
вантами наперед заданной длины к пилону.
Операции
прикрепления навешиваемого блока к консоли проводили в таком порядке. В первую
очередь, наверху устанавливали двухсторонние накладки на вертикальных участках
обоих бортов блока. После этого грузовыми полиспастами корректировали высотное
положение свободного конца блока для обеспечения проектного положения блока и
затем фиксировали его положение понизу установкой пары двухсторонних накладок,
соединяющих нижние плиты. Для крепления двух верхних накладок использовали 40
высокопрочных болтов диаметром 22 мм и 8 пробок, для нижних накладок - 20
болтов и также 8 пробок. Далее выполняли следующие операции: затяжка
гайковертами стяжных болтов первоочередных накладок на усилие, составляющее
60-70% от проектного; геодезический контроль проектного положения
установленного блока; устройство монтажного сварного стыка по верхней плите;
закрепление вантами свободного конца блока; переезд подмостей на сечение стыка
и установка с них всех стыковых накладок и болтов (в среднем 1900 на стык) и
натяжение их гайковертами на усилие, составляющее 60÷70% от проектного;
натяжение вант гидроцилиндрами до расчетного усилия; натяжение всех стыковых
болтов динамометрическими ключами до проектного усилия; перекладка путей и
перемещение монтажного агрегата по смонтированному
блоку на следующую позицию; монтаж ветровых обтекателей.
2.1.
Общие сведения о природе поглощения энергии колебаний в твердом
материале
При
колебаниях конструкций получаемая ими извне энергия частично расходуется
материалом конструкции на неупругие (необратимые) деформации и преобразуется в
тепло [153].
Свойство
материалов поглощать и рассеивать в виде тепла долю энергии деформации при
циклических процессах нагружения и разгрузки в пределах допускаемых напряжений
является, как известно, исключительно важным фактором в работе конструкции на
динамические нагрузки. Вследствие уменьшения упругой энергии при каждом цикле
деформации собственные колебания конструкций, даже при очень малых внешних
сопротивлениях, быстро затухают, а вынужденные колебания при резонансе
оказываются ограниченными определенным конечным пределом.
Физическая
природа поглощения в твердом теле в необратимой форме доли энергии колебаний
еще мало изучена. Большинство современных физиков связывают это явление с
местными пластическими деформациями частиц материала, возникающими вследствие
неоднородности его структуры даже при небольших напряжения. Однако для
материалов, имеющих сложное строение, механизм пластических деформаций почти не
изучен. И все же отсутствие бесспорного физического объяснения механизма
поглощения энергии в твердых телах не может служить препятствием при учете
рассеяния энергии колебаний в расчетах конструкций на динамические нагрузки.
Для
обозначения свойства материалов расходовать часть энергии колебаний на
необратимые (неупругие) деформации в технической литературе употребляются
несколько терминов: «внутреннее трение», «внутреннее сопротивление»,
«внутреннее затухание», «упругий гистерезис» и другие. Более удачным, на наш
взгляд, является термин «неупругое сопротивление», данный Е.С. Сорокиным [153]
с целью отличить неупругие силы от обычных сил упругости.
Само же
явление преобразования в материале части энергии деформации в тепловую называют
обычно «поглощением» или «рассеянием» энергии. В гипотезе Сорокина [153]
применяется первый термин, с условием, что речь здесь идет о поглощении энергии
колебаний за счет свойств самого материала, а не внешних сопротивлений
(аэродинамическое и т.д.). Там, где требуется подчеркнуть это отличие, будем в
дальнейшем применять термин «внутреннее поглощение».
Правильный
учет внутреннего поглощения энергии колебаний в динамических расчетах
конструкций является важным вопросом современной динамики сооружений. Без
удовлетворительного решения этого вопроса методы расчета сооружений на динамическую
нагрузку становятся ненадежными, как только возникает вопрос о необходимости
оценки динамических напряжений или перемещении при действии переменной нагрузки
в резонансе с конструкцией.
Не менее
важное значение имеет правильный учет внутреннего поглощения при разработке
мероприятий по уменьшению вибраций.
Процесс
искания и построения новых теорий внутреннего трения нельзя считать
законченным, так как в настоящее время вряд ли можно назвать одну
общепризнанную теорию. При этих условиях важно уяснить основные опытные
закономерности внутреннего поглощения, установить степень соответствия
существующих теорий и опыта и уровень их сложности в приложении к расчетам
конструкции.
Все эти
вопросы подробно рассмотрены в работах Е.С. Сорокина [151-153],
на которые в дальнейшем мы будем ссылаться.
Учитывая
упругопластические свойства льда, будем рассматривать вполне конкретные
гипотезы внутреннего поглощения, которые непосредственно можно применять для
решения задач прикладной теории колебаний конструкций, состоящих из
упругопластического материала.
Обзору
подлежат гипотезы, учитывающие неупругое сопротивление в материале, которое
имеет решающее значение при динамических процессах деформации в области
допускаемых напряжений и проявляется:
- в виде
петли гистерезиса в диаграмме «напряжение - деформация» при циклической
нагрузке;
- в виде
затухания собственных колебаний;
- в виде
стабилизации амплитуды резонансных колебаний.
Поэтому не
будем останавливаться здесь на гипотезах, которые учитывают другие неупругие
свойства материала, имеющие значение при медленных (статических) процессах
деформации в области допускаемых напряжений [44, 62].
На
основании вышеуказанных ограничений, опускаем также рассмотрение гипотез,
высказанных применительно к случаю, когда колебания
переходят в область пластических деформаций [40].
2.2. Теории внутреннего трения
упругопластического материала
Несмотря на
разнообразие физико-механических свойств строительных материалов, опыты
обнаруживают некоторые общие закономерности, касающиеся природы внутреннего
поглощения энергии колебаний. Эти закономерности заключаются в следующем [153].
Как
показывают тщательно поставленные опыты над образцами из различных материалов
при следующих напряженных состояниях (растяжение - сжатие, изгиб, кручение) в
пределах допускаемых напряжений, зависимость между внешним усилием Р (силой, моментом) и общей деформацией
у (перемещением, углом попорота) или между напряжением (нормальным,
касательным) и относительной деформацией (удлинением, сдвигом), строго говоря,
нелинейна и различна при нагружении и разгрузке. При циклическом нагружении и
разгрузке эта зависимость для полного цикла изменения нагрузки - после
достаточного числа повторений - представляется замкнутой кривой, называемой
петлей гистерезиса (рис. 2.1).
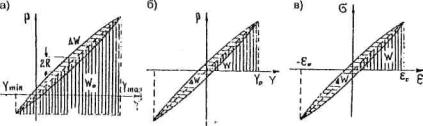
Рис. 2.1. Петли гистерезиса для циклической
нагрузки-разгрузки
По форме
петля гистерезиса напоминает очень узкий эллипс. Отрезок, отсекаемый ветвями
петли на перпендикуляре к оси деформации, характеризует собой удвоенную силу
неупругого сопротивления (2R на рис. 2.1, а).
Из вида
петли следует, что наибольшее неупругое сопротивление соответствует центру, то
есть деформации,
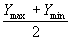
нулевое же
значение этого сопротивления отвечает концам петли, то есть деформациям Ymax и Ymin.
Площадью
петли измеряется в определенном масштабе работа, поглощенная материалом образца
за полный цикл деформации и рассеянная им и виде тепла. Отношение этой работы (ΔW) к упругой работе (W0) отвечающей удвоенной
амплитуде деформации 2Y0, определяет приближенно энергию,
израсходованную за цикл на необратимые (пластические) деформации, в долях к
полной энергии за тот же цикл (рис. 2.1, а).
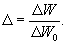
В
технической литературе обычно рассматривается не величина Δ, а величина ψ, вчетверо большая:
 (2.1)
(2.1)
где W- упругая энергия, отвечающая амплитуде
деформации (рис. 2.1,б).
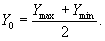
Величину ψ называют коэффициентом поглощения
энергии колебаний.
Следовательно,
петля гистерезиса, площадью которой измеряются потери энергии деформации,
представляет собой зависимость между напряжением и деформацией при циклическом
деформировании. Поэтому уравнение петли гистерезиса может быть положено в
основу описания внутреннего трения в материале.
В данном
случае коэффициентом диссипации энергии колебаний от аэродинамического
сопротивления ψаэр
пренебрегаем как весьма малым, и в дальнейшем не учитываем.
Рассмотрим
существующие в настоящее время теории внутреннего трения упругопластического
материала.
а) Теория
упругого гистерезиса.
В 1938 г.
почти одновременно были опубликованы предположения И.Л. Корчинского и Н.Н.
Давиденкова [44],
учитывающие внутреннее трение, исходя непосредственно из петли упругого
гистерезиса. И.Л. Корчинский предложил считать силу внутреннего трения
пропорциональной первой степени деформации, но имеющей знак скорости. Уравнение
петли гистерезиса в этом случае имеет вид
σ=Еε±με, (2.2)
где μ - постоянная материала.
Зависимость
между напряжением и деформацией, согласно этому предложению, имеет вид
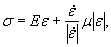 (2.3)
(2.3)
здесь отношение  дает знак скорости.
дает знак скорости.
Коэффициент
поглощения, соответствующий уравнению (2.2), по определению (2.1) будет иметь
вид
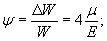 (2.4)
(2.4)
он не
зависит от скорости колебаний, что хорошо согласуется с опытом. Это является
достоинством данной теории.
С
прикладной точки зрения эта теория имеет тот недостаток, что она сильно
осложняет математический аппарат решения задач теории колебаний, так как вводит
в них нелинейность.
Тем не
менее, теория упругого гистерезиса, разработанная советской школой, явилась
значительным шагом вперед, и оказала положительное влияние на дальнейшее
развитие теории внутреннего трения.
б) Теория
неоднородного упругопластического тела.
Теории
упругого гистерезиса, принимающие ψ(ε)
= const, считали внутреннее трение следствием пластических свойств материалов.
Однако пластические характеристики материала не нашли в этих теориях явного
отражения, поскольку форма и площадь петли считались заданными. Процесс же
образования петли оставался в этих теориях не раскрытым.
С точки
зрения восполнения этого недостатка, большой интерес представляет появившаяся
позднее работа А.Ю. Ишлинского [62].
А.Ю.
Ишлинский рассматривает осевую деформацию тела, состоящего из большого
количества геометрически одинаковых волокон, ориентированных по направлению
осевой силы, характеризующихся одинаковыми значениями модуля Е, одинаковыми коэффициентами линейного
упрочнения h, но различными пределами
упругости σs. Для одного волокна
принимается следующий закон деформирования:
σ = Еε
при ε < α;
σ = Еε+h(ε-α) при ε > α, (2.5)
где 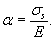
Деформация
всех волокон будет одинаковой, напряжения же в различных волокнах будут
различными. Для определения среднего напряжения в сечении тела автор применяет
статистический метод. Он вводит функцию распределения ρ(α) констант α
по сечению тела площадью F, удовлетворяющую
очевидному статистическому требованию
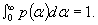
Если σ - напряжение отдельного
волокна, то среднее напряжение в сечении выразится интегралом
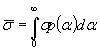 (2.6)
(2.6)
и после
подстановки в него выражений (2.5) имеем
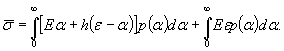 (2.7)
(2.7)
Принимая
определенную функцию распределения, можно найти σ. Зависимость σ(ε)
является законом деформирования неоднородного упругопластического тела.
А.Ю.
Ишлинский, оперируя с двумя простейшими функциями, получает соответствующие им
формы петель гистерезиса, хорошо аппроксимирующие опытные данные.
Следует
отметить, что выводы этой теории во всех своих пунктах соответствуют, по
крайней мере в качественном отношении, результатам опытов по внутреннему
трению. Но для приложений она оказывается чрезмерно сложной. И все же
теоретические предпосылки А.Ю. Ишлинского можно использовать при разработке
прикладной теории внутреннего трении, что и сделал Е.С. Сорокин [153],
давая модель неоднородного упругопластического тела,
которая положена в основу теории внутреннего трения.
2.3. Гипотеза внутреннего трения
Здесь
имеется в виду теория, опубликованная Е.С. Сорокиным [153]
в 1951 г. Для более подробного ознакомления с этой гипотезой, к трем
закономерностям, данным в п.2.2,
необходимо добавить еще следующие:
Площадь
петли гистерезиса не зависит от продолжительности цикла на широком диапазоне -
от медленных циклов (порядка нескольких минут) до очень быстрых (порядка
тысячных долей секунды). Следовательно
 . (2.8)
. (2.8)
Для данного
материала и вида напряженного состояния коэффициент ψ можно считать не зависящим от размеров и форм образца.
Коэффициент ψ в первом
приближении можно принять не зависящим от интенсивности напряженного состояния:
ψ(σ) ≈ const
и
соответственно не зависящим от амплитуды колебаний
ψ(ε0) ≈ const.
Выводы эти
подтверждаются также результатами опытов по изучению свободных затухающих
колебаний образцов из различных материалов. Логарифмический декремент затухания
практически не зависит от частоты колебаний и мало изменяется с изменением
напряжений в широких пределах. Вместе с тем между ψ и δ
существует простая приближенная зависимость
ψ ≈ 2δ. (2.9)
Эти опытные
предпосылки и были положены в основу построения данной гипотезы.
Необходимо
отметить, что в опытах по изучению внутреннего поглощения в материалах характер
циклического t изменения нагрузки во
времени был, как правило, гармоническим или близким к гармоническому.
Естественно
поэтому, что и при построении гипотезы Е.С. Сорокин исходил из рассмотрения
циклических процессов гармонического типа.
Уравнение
петли гистерезиса в диаграмме «напряжение - относительная деформация» при
гармонических колебаниях с учетом результатов опытов имеет вид [153]:
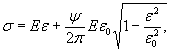 (2.10)
(2.10)
где σ - переменное
напряжение;
ε - переменная относительная деформация;
ε0 - ее амплитуда;
Е - модуль упругости материала;
ψ - постоянная материала, численно равная
коэффициенту поглощения.
Должны быть
приняты во внимание оба знака корня: знак «плюс» соответствует восходящей ветви
петли гистерезиса, знак «минус» - нисходящей ветви.
Допустим,
что деформация изменяется по закону:
ε = ε0sin[φ(t) + μ], (2.11)
где φ(t) - непрерывная
монотонная функция времени; μ -
постоянная.
Закон
(2.11) описывает колебания гармонического типа с перемен ной частотой.
Подставив (2.11) в (2.10), получим:
 (2.12)
(2.12)
Из (2.11)
следует, что

после чего
(2.12) можно представить в виде:
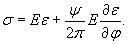 (2.13)
(2.13)
Наконец,
если процесс колебаний, определяемый уравнением (2.11), записать в комплексном
виде:
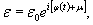 (2.14)
(2.14)
то
подставляя (2.14) в (2.13), имеем
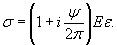 (2.15)
(2.15)
Комплексная
форма записи гипотезы обладает существенными преимуществами: она линейна и не
содержит в явном виде ни амплитуды деформации ε0, ни параметра φ, зависящего от времени. Следовательно, она неизменна для
любого периодического движения. Эту удобную запись гипотезы Е.С. Сорокина мы и
будем применять в дальнейшем.
Если
зависимость (2.9) подставим в (2.15), то
получим
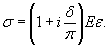 (2.16)
(2.16)
В
заключение отметим, что вывод уравнения петли гистерезиса (2.10) дан Е.С. Сорокиным в его
работе [150].
Для того
чтобы довести решение конкретной задачи динамического расчета плиты до
численного результата, необходимо иметь значение коэффициента поглощения энергии колебаний ψ для материала плиты и упругого
основания.
2.4.
Методика определения коэффициента поглощения энергии колебаний
Для
экспериментального подтверждения теории внутреннего неупругого сопротивления
Е.С. Сорокиным были поставлены многочисленные опыты [153].
Опыты производились с тремя консольными балками из железобетона, сосны и стали.
Анализ
результатов данных опыта во всех случаях удовлетворительно согласуется с
гипотезой Е.С. Сорокина.
Сравнение
опытных данных с гипотезой Фохта [153],
которая широко применялась в динамике сооружений, оказалось не в пользу
последней.
При этом
раскрылось резкое количественное и качественное противоречие гипотезы Фохта с
опытом.
Поэтому в
настоящее время гипотеза Е.С. Сорокина приобретает в динамике сооружений все
больший вес, как наиболее обоснованная в теоретическом и опытном отношениях.
Для решения
задач динамики ледяного слоя нам необходимо определить значение коэффициента
поглощения энергии колебаний ψ для льда.
В
технической литературе по этому вопросу нет ни теоретических, ни
экспериментальных данных.
Определяя
коэффициент поглощения энергии колебаний опытным путем, обычно применяют два
способа [153].
Первый способ - определение ψ по опытной петле гистерезиса (рис. 2.1).
Для этого,
на основе опытных данных, необходимо построить петлю гистерезиса в зависимости Р=f(у) или σ=f(ε) (рис. 2.1,
б,в). После этого коэффициент ψ подсчитывается по формуле (2.4). При этом основное внимание должно быть обращено не на
форму петли гистерезиса, а на зависимость площади петли от тех или иных
параметров. Нетрудно убедиться, что этот вывод является следствием анализа
формулы (2.4).
Второй
способ - определение ψ по опытному значению декремента затухания.
Е.С.
Сорокиным определялись ψ по опытному значению декремента затухания для
первого и второго тонов. Обработка экспериментальных данных и теоретические
исследования показали, что коэффициент ψ имеет) одно и то же значение для
обоих тонов. Поэтому при проведении опытов можно пользоваться только
колебаниями первого тона (рис. 2.2).
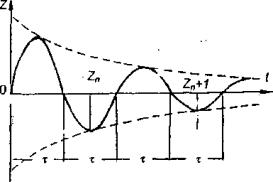
Рис. 2.2. График затухания колебаний первого тона
При
развертке затухающих колебаний (рис. 2.2) логарифмический декремент затухания
равен
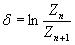 (2.17)
(2.17)
Затем,
применяя формулу (2.9), получим значение
ψ.
Е.С.
Сорокиным в работе [152]
показано, что изложенные выше два способа определения диссипации не
равнозначны.
Действительно,
из сравнения (2.1) и (2.17)
получим
W-Wn
и
ΔW=Wn-Wn+1. (2.18)
На первый
взгляд, между определениями (2.1)
и (2.17) нет противоречий. Но, как показано в работе [152],
определение (2.1) не соответствует
определению (2.17) и в некоторых случаях является источником противоречий.
По определению
(2.1), величина ψ может
быть больше единицы. Это подтверждается опытами над материалами с большим
внутренним трением (резина, грунт), а также опытами по колебаниям стержней в
сопротивляющейся среде (воздух, жидкости). По определению же (2.17), величина
ψ не может быть больше единицы.
Исходя из
вышеизложенного, можно сделать вывод, что при экспериментальном определении
коэффициента поглощения энергии колебаний, можно применять оба указанных
способа в случае, если коэффициент ψ меньше единицы. В таком случае, будет
справедливо равенство (2.9),
которое подтверждается экспериментально как опытами Е.С. Сорокина [153],
так и нашими опытами, результаты которых изложены в
следующем параграфе.
2.5. Экспериментальное
определение коэффициента поглощения энергии колебаний льда и логарифмического
декремента затухания колебаний воды как упругого основания ледяного
покрова
2.5.1. Определение
коэффициента поглощения энергии колебаний по первому способу
Для
экспериментального определения коэффициента авторами проводились опыты в
натурных условиях на озерном ледяном покрове в период с 16 по 19 января 1970 г.
Всего было
подвергнуто испытаниям 8 ледяных консольных балок «клавишей», вырезанных в
ледяном слое. Их размеры и основные характеристики приведены в табл. 2.1.
Таблица 2.1
Геометрические
характеристики консольных балок и напряжений при их изгибе
|
Дата проведения опыта
|
Температура воздуха, °С
|
№ балок (консолей)
|
Размеры консольных ледяных балок, см
|
Момент сопротивления 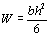
|
Максимальное напряжение при изгибе
σ, кг/см2, в зависимости от величины нагрузки Р кг
|
Средняя продолжительность цикла, мин
|
|
полная длина ln
|
расчетная длина lp
|
ширина b
|
толщина h
|
Р
|
|
10
|
20
|
30
|
40
|
50
|
|
16.01.1970
|
0
|
1
|
140
|
120
|
50,0
|
13,0
|
1408
|
0,85
|
1,70
|
2,55
|
3,40
|
4,25
|
7
|
|
2
|
120
|
100
|
49,0
|
13,0
|
1381
|
0,72
|
1,45
|
2,16
|
2,90
|
3,62
|
5
|
|
17.01.1970
|
-10
|
3
|
141
|
120
|
50
|
13,5
|
1518
|
0,79
|
1,58
|
2,37
|
3,16
|
3,95
|
8
|
|
4
|
142
|
122
|
44,5
|
13,5
|
1352
|
0,90
|
1,80
|
2,70
|
3,60
|
4,50
|
6
|
|
18.01.1970
|
-20
|
5
|
150
|
130
|
38,5
|
14,6
|
1368
|
0,95
|
1,90
|
2,85
|
3,80
|
4,75
|
8
|
|
6
|
146
|
126
|
42,0
|
14,6
|
1482
|
0,85
|
1,70
|
2,55
|
3,40
|
4,25
|
4
|
|
19.01.1970
|
-23
|
7
|
155
|
135
|
48
|
17,0
|
2300
|
0,59
|
1,18
|
1,77
|
2,36
|
2,95
|
8
|
|
8
|
160
|
140
|
52,5
|
17,0
|
2530
|
0,55
|
1,10
|
1,65
|
2,20
|
2,75
|
7
|
Нагрузка
на балку передавалась через специальную подставку размером 40×40 см,
установленную на конце консоли. Интервал изменения нагрузки 10 кг, максимальная
нагрузка на балку 50 кг. В процессе нагрузки-разгрузки ледяные консоли
оставались на воде.
Прогибы
конца консоли замерялись прогибомером системы инженера Максимова с точностью до
0,1 мм. Деформации в заделке консолей замерялись мессурой с точностью до 0,001
мм на базе 150 мм.
Прогибомеры
устанавливались на всех 8 балках, мессуры - на балках № 3-6 (табл. 2.1).
Таким
образом, для балок № 1, 2, 7, 8 получены петли гистерезиса в зависимости Р=f(у), а для балок № 3-6, в
зависимости Р=f(у) и σ=f(ε).
Каждая
балка подвергалась восьмикратной нагрузке-разгрузке. Показания приборов и
обработка опытных данных приведены в приложении 6 [12].
В
результате обработки опытных данных были получены значения коэффициента
поглощения энергии колебаний ψ, которые приведены в табл. 2.2.
Таблица
2.2
|
№ балок
|
Значение коэффициента поглощения
энергии
|
Среднее значение коэффициента ψ
|
|
№ циклов
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
0,600
|
0,588
|
0,682
|
0,580
|
0,568
|
0,519
|
0,471
|
0,445
|
0,478
|
|
2
|
0,795
|
0,379
|
0,643
|
0,468
|
0,546
|
0,492
|
0,436
|
0,306
|
0,409
|
|
3
|
0,478
0,427
|
0,466
0,362
|
0,312
0,385
|
0,213
0,358
|
0,311
0,445
|
0,296
0,314
|
0,247
0,356
|
0,232
0,243
|
0,258
0,304
|
|
4
|
0,421
0,459
|
0,391
0,398
|
0,337
0,283
|
0,291
0,332
|
0,235
0,315
|
0,322
0,230
|
0,258
0,255
|
0,240
0,244
|
0,273
0,242
|
|
5
|
0,402
0,440
|
0,394
0,416
|
0,352
0,316
|
0,392
0,354
|
0,388
0,329
|
0,229
0,311
|
0,274
0,242
|
0,207
0,323
|
0,237
0,292
|
|
6
|
0,368
0,291
|
0,314
0,312
|
0,328
0,267
|
0,266
0,286
|
0,296
0,288
|
0,214
0,256
|
0,220
0,288
|
0,209
0,269
|
0,214
0,271
|
Примечание:
в числителе дано значение коэффициента, определенное в зависимости Р= f(у), в знаменателе - σ=f(ε).
Для всех
восьми балок замкнутая петля гистерезиса получалась после 5-6-го цикла. Поэтому
в графе «Среднее значение коэффициента ψ» (табл. 2.2) дано среднее
значение для последних трех циклов загружения.
В
результате анализа опытных данных, полученных по первому способу, можно сделать
вывод, что изменение значения коэффициента ψ для льда в основном зависит
от температуры воздуха, увеличиваясь по мере повышения последней.
Эта
зависимость хорошо описывается уравнением кривой
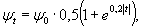 (2.19)
(2.19)
где ψ0 - коэффициент
поглощения при t = 0°С;
t - температура воздуха
со знаком «минус».
Приняв ψ0 = 0,44, получим
 (2.20)
(2.20)
По формуле
(2.20) можно определить значение ψt, для любой заданной
отрицательной температуры воздуха.
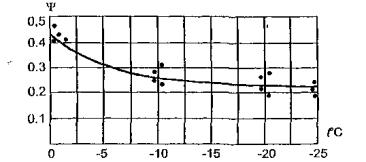
Рис.
2.3. График изменения коэффициента неупругого сопротивления льда в зависимости
от температуры окружающего воздуха
На рис. 2.3
построена кривая по формуле (2.20), отражающая изменение величины коэффициента ψ от температуры воздуха t.
2.5.2. Определение
коэффициента ψ льда и логарифмического декремента затухания δ воды по
второму способу
Опытное
определение логарифмического декремента затухания колебаний ледяного слоя,
лежащего на воде, производилось на примере колебаний ледяных консолей,
вырезанных в ледяном естественном слое. Опыты проводились 2 и 4 декабря 1970 г.
Начальная
амплитуда колебаний консоли создавалась специальным вибратором (рис. 2.4),
который устанавливался на конце консоли, а затем быстро убирался. Выведенная
таким образом из состояния статического равновесия консоль совершала колебания.
В этом колебательном процессе участвуют ледяная консоль и вода как упругое
жидкое основание.
Из
состояния покоя консоль выводилась и с помощью статической временной нагрузки,
периодически прикладываемой и снимаемой на ее конце.

Рис.
2.4. Вибрационная установка и прогибограф системы ВР-1
Колебания
консолей записывались с помощью вибрографа ВР-1 на ленту (рис. 2.5). На рис.
2.5, а записаны колебания консоли № 1, и на рис. 2.5, б - консоли № 2.

Рис.
2.5. Графики затуханий колебаний ледяных консольных балок
Вертикальный
масштаб записи равен 2:1, т.е. записанные амплитуды колебаний в 2 раза больше
действительных. Горизонтальный масштаб записи (масштаб времени) фиксировался по
счетчику времени и равен 1 с - 38 мм.
Консоль № 1
с размерами 316×53×8,8 см подвергалась 10-кратному загружению.
Частота ее колебаний из опыта равна 210 кол/мин. Период колебаний τ=0,334
с. Опыты проводились при температуре воздуха -8°С (рис. 2.5, б).
Консоль № 2
с размерами 384×54×11 см подвергалась 17-кратному загружению.
Частота колебаний из опыта равна 348 кол/мин. Период колебаний τ=0,178 с
(рис. 2.5, а).
Результаты
обработки опытных данных приведены соответственно в табл. 2.3 и 2.4, из которых
можно сделать вывод, что суммарный логарифмический декремент затухания льда и
воды изменяется в пределах 0,344-0,537.
Для опытов
по определению логарифмического декремента затухания колебаний воды как
упругого основания использовались ледяные плиты, лежащие в воде. Опыты
производились 2 и 4 декабря 1970 г.
Таблица
2.3
Опытное определение
логарифмического декремента затухания колебаний ледяной консоли, лежащей на воде.
Размеры консоли 316×53×8,8 см, температура воздуха -8°С, дата
02.12.1970 г.
|
№ п/п
|
Величины амплитуд
|
Отношения амплитуд
|
Логарифмический декремент
|
|
Z0
|
z2
|
z4
|
z6
|
Z0/Z2
|
Z2/Z4
|
Z4/Z6
|
δ0
|
δ2
|
δ4
|
|
Z1
|
z3
|
z5
|
z7
|
Z1/Z3
|
Z3/Z6
|
Z5/Z7
|
δ1
|
δ3
|
δ5
|
|
1
|
2,6
|
1,8
|
1,2
|
0,8
|
1,443
|
1,500
|
1,500
|
0,368
|
0,405
|
0,405
|
|
2,4
|
1,6
|
1,1
|
0,7
|
1,500
|
1,454
|
1,570
|
0,405
|
0,375
|
0,451
|
|
2
|
2,9
|
1,9
|
1,3
|
0,9
|
1,525
|
1,461
|
1,444
|
0,421
|
0,379
|
0,368
|
|
2,0
|
1,4
|
0,9
|
0,6
|
1,426
|
1,555
|
1,500
|
0,354
|
0,441
|
0,405
|
|
3
|
4,4
|
3,0
|
2,0
|
1,4
|
1,457
|
1,500
|
1,428
|
0,376
|
0,405
|
0,356
|
|
2,4
|
1,7
|
1,2
|
0,8
|
1,411
|
1,415
|
1,500
|
0,344
|
0,340
|
0,405
|
|
4
|
4,1
|
2,8
|
1,9
|
1,2
|
1,463
|
1,474
|
1,581
|
0,379
|
0,89
|
0,457
|
|
2,6
|
1,8
|
1,2
|
0,8
|
1,444
|
1,500
|
1,500
|
0,368
|
0,405
|
0,405
|
|
5
|
3,8
|
2,4
|
1,5
|
1,0
|
1,581
|
1,601
|
1,500
|
0,457
|
0,470
|
0,405
|
|
2,7
|
1,8
|
1,2
|
0,8
|
1,501
|
1,500
|
1,500
|
0,406
|
0,405
|
0,405
|
|
6
|
3,2
|
2,1
|
1,5
|
1,0
|
1,520
|
1,400
|
1,500
|
0,419
|
0,337
|
0,405
|
|
1,6
|
1,1
|
0,7
|
5,0
|
1,452
|
1,572
|
1,400
|
0,372
|
6,452
|
0,337
|
|
7
|
5,7
|
3,6
|
2,3
|
1,5
|
1,610
|
1,566
|
1,534
|
0,476
|
0,448
|
0,427
|
|
4,0
|
2,5
|
1,6
|
1,1
|
1,600
|
1,561
|
1,453
|
0,470
|
0,445
|
0,374
|
|
8
|
5,1
|
3,4
|
2,4
|
1,6
|
1,500
|
1,480
|
1,500
|
0,405
|
0,392
|
0,405
|
|
4,0
|
2,8
|
1,8
|
1,1
|
1,430
|
1,555
|
1,634
|
0,358
|
0,441
|
0,491
|
|
9
|
5,3
|
3,7
|
2,5
|
1,6
|
1,432
|
1,480
|
1,562
|
0,358
|
0,392
|
0,447
|
|
4,6
|
3,0
|
2,0
|
1,3
|
1,533
|
1,500
|
1,538
|
0,427
|
0,405
|
0,431
|
|
10
|
5,2
|
3,4
|
2,3
|
1,6
|
1,530
|
1,480
|
1,438
|
0,425
|
0,392
|
0,362
|
|
4,4
|
2,9
|
2,0
|
1,4
|
1,515
|
1,450
|
1,430
|
0,408
|
0,372
|
0,358
|
Таблица
2.4
Опытное определение
логарифмического декремента затухания колебаний ледяной консоли, лежащей на
воде. Размеры консоли 384×54×11 см, температура воздуха -6°С, дата
04.12.1970 г.
|
№ п/п
|
Величины амплитуд
|
Отношения амплитуд
|
Логарифмический декремент
|
|
Z0
|
z2
|
z4
|
z6
|
Z0/Z2
|
Z2/Z4
|
Z4/Z6
|
δ0
|
δ2
|
δ4
|
|
Z1
|
z3
|
z5
|
z7
|
Z1/Z3
|
Z3/Z6
|
Z5/Z7
|
δ1
|
δ3
|
δ5
|
|
1
|
6,2
|
4,0
|
2,4
|
1,6
|
1,550
|
1,664
|
1,500
|
0,438
|
0,509
|
0,405
|
|
4,6
|
2,8
|
1,7
|
1,1
|
1,645
|
1,648
|
1,545
|
0,497
|
0,497
|
0,435
|
|
2
|
5,9
|
3,6
|
2,3
|
1,5
|
1,640
|
1,565
|
1,534
|
0,495
|
0,448
|
0,427
|
|
5,1
|
3,3
|
2,2
|
1,5
|
1,544
|
1,500
|
1,468
|
1,434
|
0,405
|
0,383
|
|
3
|
5,5
|
3,7
|
2,5
|
1,6
|
1,486
|
1,480
|
1,562
|
0,396
|
0,392
|
0,445
|
|
4,0
|
2,6
|
1,6
|
1,0
|
1,537
|
1,625
|
1,600
|
0,430
|
0,484
|
0,470
|
|
4
|
6,0
|
4,0
|
2,6
|
1,7
|
1,500
|
1,528
|
1,530
|
0,405
|
0,423
|
0,425
|
|
5,3
|
3,5
|
2,3
|
1,5
|
1,515
|
1,522
|
1,534
|
0,416
|
0,42
|
0,427
|
|
5
|
7,5
|
4,7
|
2,9
|
1,8
|
1,596
|
1,622
|
1,611
|
0,468
|
0,483
|
0,476
|
|
5,7
|
3,5
|
2,2
|
1,4
|
1,625
|
1,590
|
1,572
|
0,179
|
0,464
|
0,452
|
|
6
|
5,9
|
3,8
|
2,5
|
1,6
|
1,551
|
1,519
|
1,562
|
0,438
|
0,418
|
0,445
|
|
5,0
|
3,2
|
2,2
|
1,5
|
1,562
|
1,500
|
1,465
|
0,445
|
0,405
|
0,368
|
|
7
|
6,4
|
4,3
|
2,7
|
1,7
|
1,489
|
1,593
|
1,591
|
0,398
|
0,464
|
0,463
|
|
5,0
|
3,4
|
2,1
|
1,3
|
1,470
|
1,619
|
1,616
|
0,385
|
0,482
|
0,481
|
|
8
|
7,0
|
4,4
|
2,8
|
1,7
|
1,591
|
1,571
|
1,650
|
0,464
|
0,451
|
0,501
|
|
5,4
|
3,3
|
2,0
|
1,3
|
1,636
|
1,650
|
1,538
|
0,491
|
0,501
|
0,492
|
|
9
|
5,3
|
3,7
|
2,4
|
1,5
|
1,432
|
1,543
|
1,600
|
0,359
|
0,435
|
0,470
|
|
4,8
|
3,0
|
1,9
|
1,2
|
1,533
|
1,580
|
1,584
|
0,427
|
0,459
|
0,459
|
|
10
|
6,1
|
3,8
|
2,4
|
1,4
|
1,604
|
1,652
|
1,714
|
0,472
|
0,501
|
0,537
|
|
5,3
|
3,4
|
2,1
|
1,3
|
1,560
|
1,619
|
1,615
|
0,445
|
0,482
|
0,478
|
|
11
|
5,8
|
3,5
|
2,3
|
1,5
|
1,658
|
1,590
|
1,532
|
0,507
|
0,464
|
0,427
|
|
4,3
|
2,6
|
1,6
|
1,0
|
1652
|
1,627
|
1,600
|
0,502
|
0,481
|
0,470
|
|
12
|
5,5
|
3,5
|
2,3
|
1,5
|
1,600
|
1,590
|
1,532
|
0,470
|
0,464
|
0,427
|
|
3,9
|
2,4
|
1,5
|
1,0
|
1,625
|
1,600
|
1,500
|
0,485
|
0,470
|
0,405
|
|
13
|
5,1
|
3,4
|
2,2
|
1,4
|
1,500
|
1,545
|
1,572
|
0,405
|
0,435
|
0,452
|
|
4,3
|
2,7
|
1,7
|
1,1
|
1,591
|
1,644
|
1,544
|
0,464
|
0,496
|
0,434
|
|
14
|
5,3
|
3,4
|
2,1
|
1,2
|
1,555
|
1,620
|
1,750
|
0,441
|
0,476
|
0,560
|
|
3,6
|
2,5
|
1,6
|
1,0
|
1,440
|
1,562
|
1,600
|
0,365
|
0,445
|
0,470
|
|
15
|
5,5
|
3,8
|
2,5
|
1,6
|
1,450
|
1,521
|
1,564
|
0,372
|
0,412
|
0,448
|
|
5,3
|
3,1
|
1,9
|
1,2
|
1,710
|
1,632
|
1,582
|
0,536
|
0,483
|
0,458
|
|
16
|
4,7
|
2,9
|
1,8
|
1,2
|
1,620
|
1,612
|
1,500
|
0,482
|
0,476
|
0,405
|
|
4,2
|
2,7
|
1,8
|
1,2
|
1,555
|
1,500
|
1,500
|
0,442
|
0,405
|
0,405
|
|
17
|
4,6
|
3,0
|
2,0
|
1,3
|
1,532
|
1,500
|
1,536
|
0,426
|
0,405
|
0,428
|
|
3,5
|
2,3
|
1,5
|
1,0
|
1,522
|
1,534
|
1,500
|
0,419
|
0,429
|
0,405
|
Ледяные
плиты размерами 316×53×8,8 см и 384×54×11,0 см,
свободно лежащие в воде, загружались на кромке у меньшей стороны, а затем
быстро разгружались. В результате плиты совершали в воде свободные затухающие
колебания относительно своей меньшей оси симметрии.
В процессе
опыта по прогибомерам фиксировались отсчеты, по которым определялись начальная
и конечная амплитуды колебаний. Фиксировались также количество колебаний и
время. Показания приборов и результаты обработки данных приведены в табл. 2.5 и
2.6, из которых видно, что удвоенный логарифмический декремент затухания
колебания δ, равный коэффициенту
ψ, для воды изменяется в
пределах 0,336-0,406.
Следует
отметить, что если сложить средние значения коэффициентов ψ для льда (табл. 2.2)
и ψ=26 для воды (табл. 2.5,
2.6), то получим приблизительно те же результаты, что и в опытах по колебанию
ледяных консолей на воде (табл. 2.3, 2.4), где в результате эксперимента
получено суммарное значение коэффициентов ψ
для льда и воды.
На
основании опытных данных, полученных в результате проведенных экспериментов,
можно сделать следующие выводы:
а) при
динамических расчетах ледяного покрова величину коэффициента поглощения энергии
колебаний льда можно определять по формуле (2.20);
б)
коэффициент поглощения энергии колебаний ψ
воды как упругого основания льда, изменяется в пределах
0,336-0,406 при среднем значении 0,371.
2.6.
Экспериментальное исследование динамического воздействия
движущегося автомобиля на ледяной покров
Для
проверки теоретических выводов, изложенных в данной работе, и определения
фактического воздействия движущегося автомобиля на ледяной покров, авторами
были проведены испытания ледяного слоя на грузоподъемность.
Испытания
проводились 19-20 января 1972 г. при температуре воздуха -16°С. Толщина
озерного льда в период испытаний составила 54 см при незначительном снежном
покрове, толщина которого была 8-12 см. На ледяном покрове озера, имеющего
длину около 1,5 км, была устроена временная дорога для заготовки льда. Общий
вес груженого льдом автомобиля ГАЗ-53Ф составлял 5,0-5,2 т. На расстоянии 3,0 м
от оси проезда были установлены две мессуры (М-1 перпендикулярно оси проезда и
М-2 параллельно ей), прогибомер Аистова и виброграф ВР-1.
Мессуры
были установлены на базе 60 см, цена их деления, при точности отсчета 0,001 мм
и модуле упругости льда при динамических нагрузках 90000 кгс/см2,
составляла 0,15 кгс/см2. Точность отсчетов по прогибометру Аистова
равна 0,01 мм. Виброграф ВР-1 закреплялся на неподвижной штанге, забитой в дно
озера.
Для
имитации неровностей, появляющихся в результате интенсивной эксплуатации
ледяных переправ, по всей ширине проезда был наморожен выступ снежного льда,
имеющий вид, изображенный на рис.
10.2. Высота выступа 5 см.
В табл. 2.7
даны теоретические значения динамических коэффициентов, подсчитанных по
формулам (8.9) и (8.27) без учета влияния местного препятствия;
Таблица
2.7
Определение величин
динамических коэффициентов
|
№
|
Скорость движения
|
Теоретические значения динамических
коэффициентов
|
|
км/ч
|
см/с
|
без учета местного препятствия
|
с учетом местного препятствия
|
|
по ф. 8.9
|
по ф. (8.9)
|
t0, с
|
аmax, см по ф. (10.29)
|
μ по ф. (10.28)
|
|
1
|
10
|
278
|
1,002
|
0,678
|
0,0790
|
0,0221
|
1,041
|
|
2
|
20
|
556
|
1,005
|
0,739
|
0,0395
|
0,0294
|
1,055
|
|
3
|
30
|
834
|
1,008
|
1,075
|
0,0263
|
0,0305
|
1,057
|
|
4
|
40
|
1112
|
1,014
|
0,627
|
0,0197
|
0,0316
|
1,059
|
|
5
|
50
|
1390
|
1,022
|
0,443
|
0,0158
|
0,0321
|
1,060
|
|
6
|
60
|
1668
|
1,031
|
0,365
|
0,0132
|
0,0327
|
1,061
|
Динамические
коэффициенты, найденные по формуле (10.28),
учитывают дополнительное воздействие, возникающее в результате преодоления
автомобилем вертикального препятствия. Предварительно были определены
максимальные амплитуды колебаний ледяного слоя по формуле (10.29), при ω0=4,39
Гц и ωn=13,5 Гц.
Теоретический
прогиб ледяного покрова при статическом загружении его нагрузкой 5,0 тс
составляет 0,535 см.
В табл. 2.8
даны теоретические значения прогибов и напряжений, подсчитанных по формулам (2.21) и (2.22)
с учетом динамических коэффициентов (8.9).
Приведенное расстояние от точки приложения нагрузки до; места установки
приборов составляет
а
= 300·6,625·10-4 = 0,2.
Таблица 2.8
Определение прогибов и
напряжений
|
№
|
Скорость движения км/ч
|
Динамический коэффициент μ
|
Теоретические значения
|
|
прогибов
|
напряжений, кг/см2
|
|
ω, см
|
по ф. (2.21)
|
по ф. (2.22)
|
|
σ1
|
σ2
|
σ1
|
σ2
|
|
1
|
0
|
1,000
|
0,535
|
1,221
|
1,514
|
1,901
|
2,223
|
|
2
|
10
|
1,002
|
0,536
|
1,223
|
1,517
|
1,904
|
2,228
|
|
3
|
20
|
1,005
|
0,538
|
1,227
|
1,522
|
1,910
|
2,236
|
|
4
|
30
|
1,008
|
0,540
|
1,231
|
1,526
|
1,915
|
2,244
|
|
5
|
40
|
1,014
|
0,543
|
1,238
|
1,535
|
1,930
|
2,261
|
|
6
|
50
|
1,022
|
0,547
|
1,248
|
1,547
|
1,942
|
2,279
|
|
7
|
60
|
1,031
|
0,552
|
1,259
|
1,561
|
1,959
|
2,298
|
Изгибающие
моменты от статически приложенной нагрузки соответственно равны, глава 4 п.
4.7 формулы (4.33), (4.34).
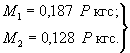 (2.21)
(2.21)
При решении
по указанным формулам для безразмерного расстояния α = 0,2
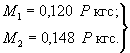 (2.22)
(2.22)
В табл. 2.9
зафиксированы отсчеты по приборам при пропуске автомобиля со скоростью от 10 до
60 км/ч по ровной ледяной дороге, и со скоростью от 10 до 40 км/ч при движении
автомобиля через местное препятствие (рис.
10.2).
В
результате обработки данных, полученных при пропуске автомобили по ледяному
покрову, получены фактические значения динамических прогибов и напряжения, а
также вычислены фактические значения динамических коэффициентов по прогибам и
напряжениям. Результаты вычислений сведены в табл. 2.10.
При
отсутствии на поверхности ледяного слоя местных неровностей и скоростях
движения от 10 до 60 км/ч колебания настолько слабы, что с помощью
установленного вибрографа нельзя было установить ни частоту, ни амплитуду
колебаний.
На рис. 2.6
записаны прогибограммы ледяного слоя при проезде автомобиля через местное
препятствие (рис.
10.2). Вертикальный масштаб 6:1. При изменении скорости движения автомобиля
от 10 до 40 км/ч амплитуды и частоты колебаний изменялись незначительно.
Динамические коэффициенты имеют большие значения, чем при соответствующих
скоростях движения по ровной дороге.

Рис.
2.6. Динамические прогибограммы, записанные прибором ВР-1
Таблица 2.9
Показания приборов при
движении автомобиля по ледовой дороге
|
Скорость движения авт.
|
Отсчеты по прогибометру
|
Отсчеты по мессурам
|
|
км/ч
|
м/с
|
нулевой
|
грузовой
|
деформация
|
М-2
|
М-1
|
|
нулевой
|
грузовой
|
деформация
|
нулевой
|
грузовой
|
деформация
|
|
При движении автомобиля без местного
препятствия
|
|
0
|
0
|
8956
|
8433
|
0,523
|
517
|
529
|
0,0120
|
724
|
733
|
0,0090
|
|
10
|
2,78
|
8914
|
8473
|
0,441
|
519
|
530
|
0,0105
|
726
|
734
|
0,0080
|
|
23
|
5,56
|
8892
|
8534
|
0,358
|
520,5
|
530
|
0,0095
|
727,5
|
735
|
0,0075
|
|
30
|
8,34
|
8870
|
8314
|
0,556
|
521,5
|
535,5
|
0,0130
|
728
|
737
|
0,0090
|
|
40
|
11,12
|
8827
|
8324
|
0,503
|
523
|
535
|
0,0120
|
729,5
|
739,5
|
0,0090
|
|
50
|
13,88
|
8713
|
8263
|
[0,450
|
524
|
535
|
0,0110
|
732
|
740
|
0,0080
|
|
60
|
16,65
|
8765
|
8427
|
0,338
|
526,5
|
547
|
0,0105
|
733,5
|
741
|
0,0075
|
|
При движении автомобиля через местное
препятствие
|
|
0
|
0
|
5992
|
5475
|
0,517
|
736
|
748
|
0,0120
|
351
|
360
|
0,0090
|
|
10
|
2,78
|
5921
|
5370
|
0,551
|
738,5
|
751
|
0,0125
|
352,5
|
362
|
0,0095
|
|
20
|
5,56
|
58,43
|
52,89
|
0,554
|
741
|
754
|
0,0130
|
355
|
365
|
0,0100
|
|
30
|
8,34
|
58,02
|
5244
|
0,558
|
744
|
757
|
0,0130
|
357,5
|
367
|
0,0095
|
|
40
|
11,12
|
57,56
|
51,93
|
0,563
|
747,5
|
761
|
0,0135
|
360
|
370
|
0,0100
|
Таблица 2.10
Определение динамических
коэффициентов по прогибам и напряжениям
|
№
|
Скорость движения автомобиля, км/ч
|
По прогибам
|
По напряжениям
|
|
ω, см
|
μ
|
σ2, кг/см2
|
μ
|
σ2, кг/см2
|
μ
|
|
При движении без местного препятствия
|
|
1
|
0
|
0,523
|
1,000
|
1,800
|
1,000
|
1,350
|
1,000
|
|
2
|
10
|
0,441
|
0,843
|
1,575
|
0,875
|
1,200
|
0,889
|
|
3
|
20
|
0,358
|
0,684
|
1,425
|
0,793
|
1,125
|
0,833
|
|
4
|
30
|
0,556
|
1,062
|
1,950
|
1,083
|
1,350
|
1,000
|
|
5
|
40
|
0,503
|
0,965
|
1,800
|
1,000
|
1,350
|
1,000
|
|
6
|
50
|
0,450
|
0,861
|
1,650
|
0,918
|
1,200
|
0,889
|
|
7
|
60
|
0,338
|
0,646
|
1,575
|
0,876
|
1,125
|
0,883
|
|
При движении через местное препятствие
|
|
8
|
0
|
0,517
|
1,000
|
1,800
|
1,000
|
1,350
|
1,000
|
|
9
|
10
|
0,499
|
0,966
|
1,871
|
1,042
|
1,425
|
1,055
|
|
10
|
20
|
0,502
|
0,971
|
1,950
|
1,084
|
1,500
|
1,111
|
|
11
|
30
|
0,558
|
1,080
|
1,950
|
1,084
|
1,425
|
1,055
|
|
12
|
40
|
0,511
|
0,989
|
2,025
|
1,123
|
1,500
|
1,111
|
Результаты обработки
прогибограмм (рис 2.6) приведены в табл. 2.11.
Таблица 2.11
Результаты расшифровки
прогибограмм
|
№ пп
|
Скорость движения, V, км/ч
|
Замеренный статический прогиб ωст,
см
|
Амплитуда, А, см
|
Замеренный динамический прогиб, ωд, см
|
Динамический коэффициент, μ
|
|
При движении через местные препятствия
|
|
1
|
20
|
0,517
|
0,038
|
0,451
|
0,872
|
|
2
|
30
|
0,517
|
0,044
|
0,561
|
1,081
|
|
3
|
40
|
0,517
|
0,041
|
0,454
|
0,879
|
Из
анализа данных, полученных в результате динамических испытаний ледяного слоя, и
сравнивая их с теоретическими данными, можно сделать следующие выводы:
1. При
движении по ровной ледовой дороге, экспериментальные значения динамических
коэффициентов по прогибам имеют значения, меньшие, чем соответствующие им
теоретические величины, определенные, по формулам (8.9) и (9.8), (табл. 2.7),
(2.10).
2. При
теоретическом определении динамических коэффициентов более удовлетворительные
результаты получены по формуле (9.8)
3. Значение
критических скоростей движения автомобиля целесообразно определять по формулам
(8.10), (9.6).
4.
Экспериментальные значения динамических коэффициентов по напряжениям, как
правило, большие, чем соответствующие им значения динамических коэффициентов по
прогибам (табл. 2.10).
5. Для
определения динамических коэффициентов по напряжениям рекомендуется
пользоваться формулами (9.13), (8.28).
6.
Дополнительные динамические воздействия, появляющиеся в результате проезда
автомобилей по дорожным неровностям, типа вертикальных препятствий, носят
импульсивный характер.
7. Значения
динамических коэффициентов, определенные в результате экспериментов при
пропуске автомобилей через вертикальное местное препятствие, удовлетворительно
согласуются с соответствующими им теоретическими величинами динамических
коэффициентов, определенными по формуле (10.28).
8.
Численное значение динамического коэффициента, определенное в результате
теоретического и экспериментального исследования, не превышает величины 1,10.
9. Несмотря
на незначительную абсолютную величину динамического коэффициента,
грузоподъемность ледяного покрова при динамическом действии нагрузки весьма
существенно уменьшается, так как при этом резко снижается предел прочности
льда.
10.
Снижение предела прочности льда при динамическом изгибе ледяного покрова
зависит от вертикальной скорости подачи нагрузки на лед, и как указывалось в
главе 1, п.
1.5, предел прочности при этом уменьшается в 2-2,5 раза.
11. В
случае преодоления автомобилем вертикального местного препятствия, величину
вертикальной скорости подачи нагрузки на лед можно определить по формуле (10.33),
так как при этом она численно равна первой
производной Х'м.
РАСЧЕТ ЛЕДЯНОГО ПОКРОВА НА ДЕЙСТВИЕ СТАТИЧЕСКИХ
НАГРУЗОК
ГЛАВА
3. РАСЧЕТ КРАЕВОГО УЧАСТКА ЛЕДЯНОГО ПОКРОВА
3.1. Методы определения грузоподъемности
ледяного покрова
Российскими
специалистами созданы методы расчета ледяного покрова под нагрузкой, которые
можно разделить на приближенные и точные. Приближенные методы рассматривают
одиночную нагрузку (короткие передачи) и основываются на эмпирических
зависимостях (П.И. Лебедев), принципе аналогии (М.М. Корунов) или являются
упрощением точных методов (М.М. Казанский и А.Р.Шульман).
Точные
методы основаны на положениях строительной механики, и плавающий ледяной покров
рассматривается как упругая плита неограниченных размеров на упругом основании.
Эти методы пригодны при ширине реки не менее 150-200 толщин льда. Лед с
известным приближением рассматривают как изотропное тело. Вода может являться
упругим основанием только до тех пор, пока прогнувшаяся верхняя поверхность
ледяного покрова не опустится ниже уровня воды, т.е. до величины прогиба,
равного примерно 0,1 толщины льда. Дальнейшее увеличение прогиба может вызвать
выступание воды по трещинам на поверхность льда и потерю его грузоподъемности.
Из числа точных методов наиболее распространены метод С.А. Бернштейна, метод
К.Е. Иванова и И.С. Песчанского. Оба эти метода позволяют вести расчет как для
одиночной нагрузки, так и для сцепа из многих единиц подвижного состава.
Нужно
отметить, что величина грузоподъемности ледяного покрова, подсчитанная точными
методами, является все же приближенной не только из-за наличия некоторых
теоретических допущений, но и ввиду того, что ряд исходных данных трудно
поддается непосредственному измерению и определяется косвенными путями, как,
например, модуль упругости льда, температура нижних слоев, временное
сопротивление льда при изгибе и др.
Даже вопрос,
как определять расчетную толщину льда, имеет различное толкование: одни (К.Е.
Иванов, И.С. Песчанский, B.C. Порожняков) считают, что верхние слои мутного
льда, имеющего меньшую прочность по сравнению с прозрачным, следует учитывать с
коэффициентом, равным 0,5; другие (Б.Л. Лагутин, М.М. Казанский, А.Р. Шульман)
считают, что в качестве расчетов нужно брать наименьшую измеренную
действительную толщину Льда без снеговых образований, так как определение
границ отдельных слоев в натуре связано со значительными трудностями и
неизбежно вносит в эти измерения элемент произвольности. Последняя рекомендация
представляется убедительной и заслуживающей внимания еще и потому, что наиболее
прочный прозрачный лед располагается в средней и нижней частях ледяного покрова,
а грузоподъемность льда определяется прочностью на разрыв именно этого слоя, в
то время как верхние менее прочные слои имеют более низкую температуру и
обладают достаточной прочностью на сжатие.
3.1.1. Основные сведения
из теории изгиба плит на упругом основании
Дифференциальное
уравнение упругой поверхности плиты
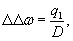 (3.1)
(3.1)
где Δ
- оператор Лапласа.
Полная
нагрузку q1=q-p
представляет собой алгебраическую сумму заданной активной нагрузки q и неизвестной реактивной нагрузки р; последняя определяется в процессе
расчета и зависит от перемещения основания.
Активная
нагрузка считается положительной, если она направлена вниз; реактивная нагрузка
считается положительной, если она направлена вверх.
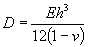 - цилиндрическая жесткость;
- цилиндрическая жесткость;
где h - толщина плиты;
Е - модуль упругости;
v - коэффициент Пуассона материала плиты.
Между
перемещениями основания и реактивными давлениями существуют следующие
соотношения:
Р(х,у) = K0w(x,y), (3.2)
P(r)
= K0w(r),
где K0 - коэффициент постели,
имеющий размерность кгс/см3 или тс/м3, и в данном случае
численно равный объемному весу воды.
3.1.2. Расчет плит в
прямоугольной системе осей координат
Как
известно, оператор Лапласа в прямоугольной системе координат имеет вид
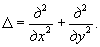
Введем вспомогательную
величину 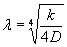 , называемую характеристикой плиты на упругом основании при
изгибе, и перейдем к безразмерной системе осей координат, где ξ=хλ, η=yλ.
, называемую характеристикой плиты на упругом основании при
изгибе, и перейдем к безразмерной системе осей координат, где ξ=хλ, η=yλ.
Значения
характеристики λ, приведены в приложении.
Уравнение
(3.1) можно записать в виде
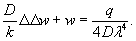 (3.3)
(3.3)
Изгибающий
момент в сечении, нормальном к оси ξ,
обозначается Мξ и определяется по формуле
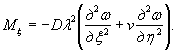 (3.4)
(3.4)
Изгибающий
момент в сечении, нормальном к оси η,
обозначается Мη и
равен
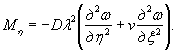 (3.5)
(3.5)
Очевидно,
что размерность изгибающих моментов, отнесенных к единице длины, будет
кгс·см/см, т.е. изгибающие моменты в плитах имеют размерность силы, кгс.
Изгибающие
моменты считаются положительными, если они вызывают растяжение в нижней части
плиты.
Вертикальные
касательные напряжения, возникающие в вышеуказанных сечениях, изменяются по
высоте плиты по параболическому закону, обращаясь в нуль при  и достигая максимума
при Z=0. Они приводятся в вертикальной силе; отношение этой силы к ширине
элементарной полоски, нормаль к которой параллельна оси ξ, называется
поперечной силой и обозначается буквой N.
Поперечная сила Nξ определяется формулой
и достигая максимума
при Z=0. Они приводятся в вертикальной силе; отношение этой силы к ширине
элементарной полоски, нормаль к которой параллельна оси ξ, называется
поперечной силой и обозначается буквой N.
Поперечная сила Nξ определяется формулой
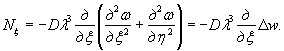 (3.6)
(3.6)
Поперечная
сила в перпендикулярном поперечном сечении, нормаль к которому оси η, обозначается Nη и определяется по
формуле
 (3.7)
(3.7)
Горизонтальные
касательные напряжения, которые изменяются по толщине плиты по линейному
закону, обращаясь в нуль в точках поперечного сечения, лежащих на половине высоты,
приводятся к паре, действующей в плоскости указанной элементарной полоски.
Отношение момента этой пары к ширине полоски называется крутящим моментом. В
элементарной полоске, нормаль к которой параллельна оси ξ, крутящий момент обозначается Hξ и определяется по формуле
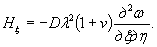 (3.8)
(3.8)
В
перпендикулярном сечении возникает крутящий момент, обозначаемый Hη; он имеет такое же
абсолютное значение, но знак его противоположный, т.е.
Hξ = -Нη.
При
неосесимметричной деформации имеют место приведенные поперечные силы, значения
которых соответственно имеют вид
 (3.9)
(3.9)
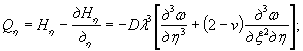 (3.10)
(3.10)
При
загружении прямоугольных или бесконечных плит равномерно распределенной по
линии или в виде узкой длинной полосы нагрузкой, плита не испытывает изгиба
вдоль линии загружения. Изгиб в данном случае происходит по цилиндрической
поверхности и называется цилиндрическим изгибом. Задачи изгиба плит в данном
случае являются одномерными, дифференциальное уравнение имеет вид
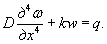 (3.11)
(3.11)
В данном
случае задачи изгиба плит решаются с помощью хорошо известных балочных
(гиперболо-тригонометрических и затухающих) функций [161],
имеющих вид
Aξ
= chξ·cos ξ; (3.12)
Bξ
= 0,5(ch ξ·sin ξ+sh ξ·cos ξ);
Cξ
= 0,5 sh ξ·sin ξ;
Dξ
= 0,25(ch ξ sin ξ - sh ξ cos ξ);
Tξ=
e-ξ cosξ; (3.13)
Uξ
= e-ξ(cosξ-sinξ);
Vξ
= e-ξsinξ;
Wξ
= e-ξ(cosξ+sinξ);
Таблицы
функций (3.12), (3.13) приведены в книге А.А. Уманского [161].
3.1.3. Расчет плит в
полярной системе осей координат
Во многих
случаях при осесимметричном загружении решение задачи дается в полярных координатах
r и φ, расположенных в средней плоскости (r
- радиус; φ - полярный угол). В
силу симметрии прогиб не зависит от угла φ
и является функцией одного лишь расстояния r.
Введем
безразмерную координату ξ = rl,
где
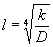 - характеристика плиты при изгибе в полярных
координатах, значения ее приведены в приложении.
- характеристика плиты при изгибе в полярных
координатах, значения ее приведены в приложении.
Уравнение (3.1) можно записать в виде
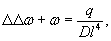 (3.14)
(3.14)
где оператор Лапласа 
Усилия,
возникающие в сечении, нормаль к которому направлена по радиусу, обозначаются M1, N1 и называются радиальными усилиями, а усилие,
возникающее в перпендикулярном сечении, называется кольцевым или тангенциальным
и обозначается М2.
Эти усилия
определяются по формулам
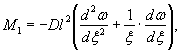 (3.15)
(3.15)
 (3.16)
(3.16)
 (3.17)
(3.17)
Однородное
уравнение, которое получается, если в (3.14)
положить q = 0, сводится к системе
двух дифференциальных уравнений второго порядка [73]
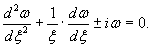 (3.18)
(3.18)
Интеграл
системы (3.18), как это следует из теории бесселевых функций, можно записать в
виде
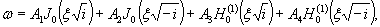
где  - функция Бесселя
первого рода нулевого порядка от того же аргумента
- функция Бесселя
первого рода нулевого порядка от того же аргумента  ;
;
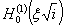 - функция Ганкеля первого рода нулевого
порядка от того же аргумента.
- функция Ганкеля первого рода нулевого
порядка от того же аргумента.
Так как
функции 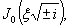
 являются
комплексными, а интеграл ω
должен быть действительным, то и постоянные A1-A4
также должны быть комплексными числами.
являются
комплексными, а интеграл ω
должен быть действительным, то и постоянные A1-A4
также должны быть комплексными числами.
Для того,
чтобы решение выразить через действительные функции, Б.Г. Кореневым [73]
введены следующие обозначения:
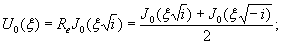 (3.19)
(3.19)

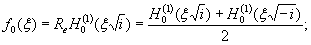
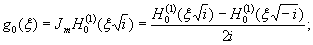
Знаки Re и Jm обозначают действительную и мнимую части этих
функций.
Тогда
ω = В1 U0(ξ) + В2 V0(ξ) + В3 f0(ξ) + B4g0(ξ). (3.20)
Так как
функции U0, V0, f0, g0
действительны, то и коэффициенты В1,
B2, B3,
B4 также будут действительными.
Функции U0, V0
вместе со всеми своими производными при ξ→0 остаются конечными, а
при ξ→∞ стремятся к бесконечности, напоминая несколько в этом
отношении функции еξ cosξ, eξ sinξ, в
теории балок на упругом основании.
Функция f0 при ξ→0 имеет особенность типа
ξ2 ln ξ, функция g0 при
ξ→0 обращается в бесконечность, как ln ξ, обе эти
функции при ξ→∞ стремятся к нулю, напоминая несколько функции
е-ξ cosξ, е-ξ sinξ в теории балок.
Между
функциями U0, V0,f0,
g0 существуют такие зависимости:
ΔU0 = V0, ΔV0 = -U0, Δf0 = g0, Δg0 = -f0. (3.21)
При
дифференцировании этих функций по формулам (3.15) (3.16), целесообразно ввести
обозначения
 (3.22)
(3.22)

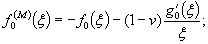
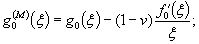
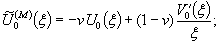 (3.23)
(3.23)
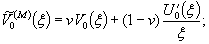
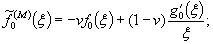
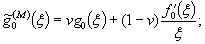
Функции U0(M), V0(M), f0(M), g0(M), Ũ0(M),  ,
,  ,
, 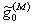 протабулированы при v=0,30. Таблицы этих функций даны в
приложении книги М.Н. Ручимского [134].
протабулированы при v=0,30. Таблицы этих функций даны в
приложении книги М.Н. Ручимского [134].
Значения
функций U0, V0, f0,
g0 и производных от них по аргументу ξ U'0, V'0, f'0, g'0,
даны в книге Б.Г. Коренева [73].
В полярной
системе координат решаются задачи изгиба круглых плит радиуса R и бесконечно протяженных с точки
зрения расчетной схемы. Активная нагрузка может быть приложена как в виде
сосредоточенной силы, так и равномерно распределенной по площади круга, по
площади кольца или по линии окружности. Во всех этих случаях изгиб плиты
происходит симметрично относительно центра (начала координат), поэтому в
литературе иногда его еще называют центральным изгибом [58].
3.1.4. Неосесимметричная
деформация плит на упругом основании
При
пользовании полярной системой координат остается в силе уравнение (3.14),
изменяется лишь вид оператора Δ, который в данном случае будет

Для решения
неосесимметричных задач изгиба плит на упругом основании, Б.Г. Кореневым [73]
введены следующие обозначения:
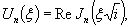 (3.24)
(3.24)

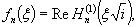

где  - цилиндрическая
функция первого рода или функция Бесселя порядка n;
- цилиндрическая
функция первого рода или функция Бесселя порядка n;
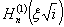 - функция Ганнеля первого рода того же
порядка.
- функция Ганнеля первого рода того же
порядка.
В книге
Б.Г. Коренева и Е.И. Черниговской [77]
приведены значения функций (3.24) первого порядка, а также
соотношения этих функций порядка n с функциями порядка 0 и 1.
3.2. Состояние вопроса и цель исследования
Расчету
грузоподъемности ледяного покрова по схеме бесконечной плиты посвящены работы
С.А. Бернштейна [8],
С.С. Голушкевича [41],
Б.В. Проскурякова и Г.Р. Брегмана [94],
А.Д. Дмитриева [48,
50]
и другие. Этот же вопрос рассматривался Н.Н. Бычковским в работах [16,
17,
20,
23].
Необходимо
отметить, что излагаемые методы не дают возможность определить несущую
способность льда у берегов, поскольку при жестком опирании льда на берег и при
свободно плавающей кромке льда возможно увеличение изгибающего момента от
временной нагрузки. Это объясняется закономерностями изгиба полубесконечной
балки на сплошном упругом основании, к расчетной схеме которой можно привести
полосу льда при цилиндрическом его изгибе под нагрузкой.
Расчет
грузоподъемности ледяного покрова, имеющего свободную прямую кромку (по схеме
полубесконечной плиты), рассмотрен в работах С.С. Голушкевича [41],
Д.Ф. Панфилова [119],
К.Н. Бычковского [13,
17]
и некоторых других.
В данной
работе поставлены и решены некоторые задачи, представляющие практический
интерес при использовании ледяного покрова для нужд гидротехнического
строительства, устройства строительных площадок, ледовых дорог и временных
переправ.
В общем
виде решение этих задач изложено в работе [16].
При
проведении статического расчета плит, лежащих на упругом основании, необходимо
обращать серьезное внимание на краевые участки.
Как
правило, краевым участком считается полоса, примыкающая к краю плиты и имеющая
приведенную ширину, равную 1,6-2.
Расчет
краевого участка плиты производится только в тех случаях, когда нагрузка
находится в пределах указанной полосы. В работах [13,
17,
23]
Н.Н. Бычковским подробно рассматривалась полубесконечная плита, имеющая
свободный край и лежащая на винклеровом основании. В данном случае исследуем
изменение грузоподъемности полубесконечной плиты на упругом основании в
зависимости от условий закрепления кромки. Для этого рассмотрим следующие три
случая закрепления: с защемленной, шарнирно-опертой и свободной кромкой.
Указанные расчетные схемы могут иметь место при расчете краевого участка
ледяного слоя, примыкающего к берегу, причальным стенкам, опорам мостов.
По методу
К.Е. Иванова и И.С. Песчанского [58]
(1949 г.), обобщивших многолетний опыт работы ледяных переправ (главным образом
в Арктике) с использованием решения Бернштейна, предлагается вначале
определить, к какому случают относится задача - к случаю центрального или
цилиндрического изгиба:
если a/b ≤ 6 - случай центрального
изгиба;
если a/b > 6 - случай цилиндрического
изгиба;
где а - длина сцепа по осям автосцепок, м;
b - длина поперечин пути на льду, но не более 6 м.
3.3. Расчет полубесконечного ледяного слоя с
защемленной кромкой
Рассмотрим
задачу изгиба полубесконечной плиты на упругом основании с защемленной кромкой,
при загружении ее на произвольном расстоянии А от кромки (рис. 3.1).
Решение
задачи сводится к отысканию интеграла дифференциального уравнения (3.3).
Граничные
условия задачи: при η=0, ω=0,  и нулевые условия на
бесконечности.
и нулевые условия на
бесконечности.
Данному
уравнению и граничным условиям удовлетворяет функция прогиба
 (3.25)
(3.25)
wлев = Wξ(VαCη-WαDη), (3.26)
wпр = Wξ(CαVη-DαWη).
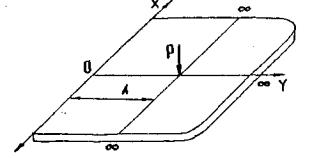
Рис. 3.1. Расчетная схема плиты
Здесь вся
плита условно разделена на две части, левую, с приведенной шириной а=А·λ, и правую, представляющую
собой полуплоскость, решение дано в затухающих и гиперболотригонометрических
функциях (3.12), (3.13).
Значение
изгибающих моментов получим, подставив функцию прогиба (3.25) в известные
дифференциальные зависимости (3.4) и (3.5)
а) для
левой части
Мξ = p[Uξ(VaCη-WaDη)+0,5vWξ(-VaAη+WaBη)], (3.27)
Mη = P[0,5Wξ(-VaAη+WaBη)+vUξ(VaCη-WaDη)],
б) для
правой части
Мξ = p[Uξ(CaVη-DaWη)+vWξ(CaTη-DaUη)], (3.28)
Мη = p[Wξ(CaTη+DaUη)+vUξ(CaVη-DaWη)],
Приведенная
поперечная сила
а) для
левой части
Qξ = 2Pλ[-Tξ(VaCη-WaDη)+0,5(2-v)Vξ(VaAη-WaBη)], (3.29)
Qη = 2Pλ[Wξ(VaDη+0,25WaAη)+0,5(2-v)Uξ(VaBη-WaCη)],
б) для
правой части
Qξ = 2Pλ[Tξ(CaVη-DaWη)+(2-v)Vξ(CaTη-DaUη)] (3.30)
Qη = 2Pλ[Wξ(-0,5CaWη+DaTη)+0,5(2-v)Uξ(CaUη-2DaVη)].
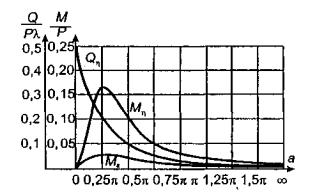
Рис. 3.2. Зависимость изгибающих моментов и поперечной силы
на кромке плиты от приведенного расстояния а
Рис. 3.3. Зависимость изгибающих моментов и поперечных сил в
сечении под силой P от приведенного расстояния а
На рис.
3.2, 3.3 приведены графики изменения внутренних усилий в ледяном слое под силой и на кромке в зависимости от приведенного
расстояния а.
3.4. Расчет полубесконечного ледяного слоя с
шарнирно-опертой кромкой
Пусть
полуплоскость на упругом основании (рис. 3.1) имеет шарнирно-опертую
кромку и загружена сосредоточенной силой, приложенной на произвольном
расстоянии b от кромки.
Решение
задачи сводится к отысканию интеграла дифференциального уравнения (3.3) при нулевых условиях на бесконечности и
следующих условиях при η=0: w=0, Мη=0.
Представим
решение уравнения (3.3), удовлетворяющее
граничным условиям задачи, в виде
 (3.31)
(3.31)
где
wлев = Wξ(VαBη-2TαDη), (3.32)
wпр = Wξ(BαVη-2DαTη),
Изгибающие
моменты соответственно равны
а) для
левой части
Mξ = 0,5Р[Uξ(VaBη - 2TaDη) + vWξ(2VaDη+TaBη)], (3.33)
Mη = 0,5P[Wξ(2VaDη+TaBη)+vUξ(VaBη-2TaDη)],
б) для
правой части
Mξ = 0,5P[Uξ(BaVη-2DaTη)+vWξ(BaTη+2DaVη)], (3.34)
Mη=0,5P[Wξ(BaTη+2DaVη)+vUξ(BaVη-2DaTη)].
Приведенная
поперечная сила
а) для
левой части
Qξ = -Pλ[Tξ(VaBη-2TaDη)+(2-v)Vξ(2VaDη+TaBη)] (3.35)
Qη=Pλ[Wξ(VaCη+0,5TaAη)+(2-v) Uξ(0,5VaAη-TaCη)]
б) для
правой части
Qξ = -Pλ[Tξ(BaVη-2DaTη)+(2-v)Vξ(BaTη+2DaVη)] (3.36)
Qη = Pλ[Wξ(-0,5BaTη+DaVη)+(2-v) Uξ(0,5BaUη+DaWη)].
На рис. 3.4
приведены графики изменения внутренних усилий в ледяном слое под силой и на
кромке в зависимости от приведенного расстояния а. Из анализа графиков,
приведенных на рис. 3.2-3.4, можно сделать вывод, что при a ≥ 1,5π условия закрепления кромки практически не влияют на грузоподъемность
ледяного слоя.
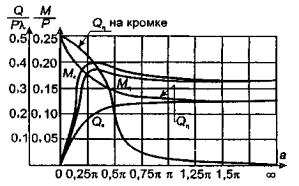
Рис.
3.4. Зависимость поперечной силы Qη
на кромке и остальных внутренних усилий в сечении под силой Р от приведенного расстояния а
3.5. Расчет полубесконечного ледяного слоя со
свободной кромкой
В
соответствии с рекомендациями Инструкции по проектированию вспомогательных
сооружений и устройств для строительства мостов (ВСН
136-78) [60]
в зимних условиях допускается устраивать ледовые дороги и размещать на льду
оборудование (копры, краны и др.). Для связи строительной площадки с берегом
устраиваются ледовые дороги. При этом сопряжение ледовой дороги с берегом
обеспечивается переходным участком (рис. 3.5).

Рис.
3.5. Сопряжение ледовой автомобильной дороги с берегом:
а
- шпальная клетка на льду; б - шпальная клетка на берегу;
1 - снежно-хворостяная гать; 2 - прогоны;
3 - снежный валик
Возникает
необходимость решения задачи изгиба полубесконечной плиты на упругом основании
со свободной кромкой (рис.
3.1). При загружении плиты на произвольном расстоянии А от кромки сосредоточенной силой Р, имеем случай центрального изгиба, при загружений равномерно
распределенной вдоль кромки нагрузкой - случай цилиндрического изгиба.
Рис.
3.6 Схемы переходного участка ледяной железнодорожной переправы:
1
- пролетные строения на подъемных опорах, обеспечивающих возможность изменения
продольного уклона i в соответствии с колебаниями уровня
воды; 2 - участок с постоянным уклоном i
для сопряжения пролетных строений с путем на льду; 3 и 4 - подошва рельсов
соответственно при РУВВ и РУНВ; 5 - лед; Δ - обслуживаемая амплитуда
уровней воды
3.5.1. Изгиб полу
бесконечной плиты со свободно опертой кромкой
При
загружений указанной плиты сосредоточенной нагрузкой Р (рис. 3.1)
на кромке (а=0) граничные условия
имеют вид при η=0 Mη=0; Qη=P и нулевые условия на бесконечности.
Уравнение
упругой поверхности, удовлетворяющее этим граничным условиям, имеет вид
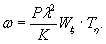
Изгибающий
момент на кромке, определяющий грузоподъемность полубесконечной плиты
Mξ=0,5P(UξTη+vWξVη).
При
удалении нагрузки Р на расстояние а ≥ 1,5π от кромки ее влияние
практически исключается и имеем случай изгиба бесконечной плиты на упругом
основании с граничными условиями в точке приложения нагрузки, куда перенесем
начало осей координат, где w'=0; Qη=P/2 и нулевые условия на бесконечности.
Уравнение
упругой поверхности, удовлетворяющее этим условиям
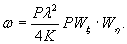
Изгибающие
моменты под силой, определяющие грузоподъемность бесконечной плиты
Мξ = 0,125 Р
(UξWη+v·WξUη); (3.37)
Mη=0,125P(WξUη+v·UξWη).
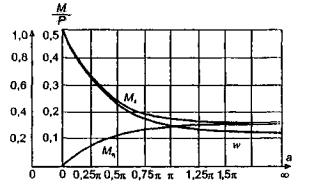
Рис. 3.7. Зависимость прогибов и изгибающих моментов в
сечении под силой P от приведенного расстояния а
Приравняв
значения изгибающих моментов величине Rfh2/6
(рис.
1.6,а), получим допускаемые величины для сосредоточенной силы P, приложенной на
расстоянии а от свободной кромки
полубесконечной плиты;
Из анализа
зависимостей, изображенных на рис. 3.8, можно делать вывод, что при удалении
сосредоточенного груза от кромки на приведенное расстояние а≈1,5π прогиб под силой уменьшается в четыре раза, а
грузоподъемность плиты увеличивается в три раза.
При
удалении груза от кромки на расстояние а>1,5π
грузоподъемность и прогиб ледяного покрова под нагрузкой практически не
изменяются.
Закономерность
изменения прогиба и грузоподъемности полубесконечной плиты со свободной кромкой
от приведенного расстояния а принята по аналогии с полубесконечной балкой на
сплошном упругом основании (п. 3.2).
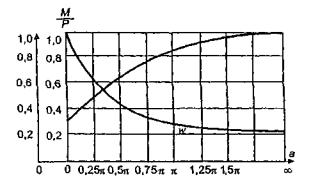
Рис. 3.8. Зависимость грузоподъемности и прогиба полубесконечной плиты в
сечении под силой Р от приведенного
расстояния а
3.6. Изгиб краевого участка ледяного покрова при
колебаниях уровня воды
При
изменении уровня воды в водоеме, в прибрежном, краевом участке ледяного слоя, в
результате цилиндрического изгиба возникают дополнительные внутренние усилия.
Для
определения этих усилий рассмотрим, как и ранее, два случая:
Защемленная
кромка (рис. 3.9)
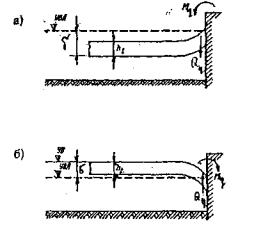
Рис. 3.9. Схемы к определению нагрузок от примерзшего к
сооружению ледяного покрова при изменении уровня воды (УВ):
a - при понижении УВ; б - при повышении
УВ; УВЛ - уровень воды при ледоставе
Решение
задачи сводится к отысканию интеграла уравнения (3.11)
при нулевых условиях на бесконечности и следующих условиях при η=0:
w = δ и w' = 0,
где δ - изменение уровня воды,
считаемся положительным при убывании воды в водоеме.
При этом
считаем, что контакт ледяного слоя с водой не нарушается по всей площади
ледяного покрова.
Решение в
общем случае имеет вид [161]
ωη=C1Tη+C2Vη (3.38)
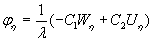
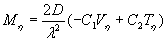
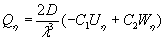
Подставляя
в (3.38) граничные условия (3.37), получим
С1 = С2 = δ
wη=δWη;


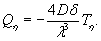
Максимальный
изгибающий момент на кромке

Подставив значение 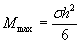 , получим
, получим 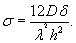
Приравняв σ среднему значению предела
текучести льда при изгибе Rfy,
получим предельное значение перемежения
 (3.40)
(3.40)
Подставляя
в (3.40) все известные величины и произведя соответствующие преобразования,
получим
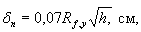 (3.41)
(3.41)
где Rf, y - имеет размерность
кгс/см2;
h - толщина ледяного
слоя, см.
Шарнирно
опертая кромка
Граничные
условия нулевые на бесконечности и при η=0:
w = δ и Мη=0. (3.42)
Подставляя
(3.42) в (3.38), получим
С1 = δ; С2
= 0,
откуда
ωη = δTη; (3.43)
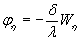
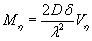
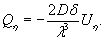
Максимальный
изгибающий момент возникает в точке, на расстоянии 0,25π от кромки и равен

Подставив
значение 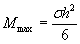 , получим
, получим 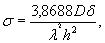 или при σ = Rf,y имеем
или при σ = Rf,y имеем
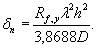 (3.44)
(3.44)
После
соответствующих преобразований
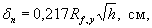 (3.45)
(3.45)
В
выражениях (3.41), (3.45) величина δn - предельное изменение
уровня воды в водоеме, при котором в ледяном покрове на
краевом участке образуются силовые трещины.
3.7. Расчет ледяного слоя, ослабленного круговым отверстием
Для
неограниченной плиты со свободным круговым отверстием приведенного радиуса а и
загруженной равномерно распределенной по кромке отверстия нагрузкой интенсивностью
q, запишем решение в виде [73]
w
= w0 + wk, (3.46)
где w0 - основное решение, представляющее собой
функцию прогиба неограниченной плиты без отверстия, загруженной вышеуказанной
нагрузкой q;
wk - решение однородного (при q=0) уравнения (3.14), которое назовем компенсирующим решением.
Представим
основное решение [73],
записанное в бесселевых функциях(3.19), в виде
при
ξ<α
 (3.47)
(3.47)
при
ξ>α
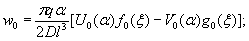 (3.48)
(3.48)
Радиальные
и кольцевые усилия в плите определяются по формулам при ξ<α
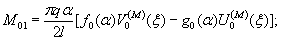 (3.49)
(3.49)
 (3.50)
(3.50)
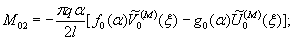 (3.51)
(3.51)
Компенсирующее
решение нужно искать в виде
wk = Af0(ξ)+Bg0(ξ).
Обозначим
изгибающий момент и поперечную силу основного решения при ξ=α через М0
и Q0, тогда постоянные А и В
определятся из граничных условий, при ξ=α,
которые в данном случае имеют вид
М1 = 0; Q1 = 0.
и
следовательно
М0-Dl2[Ag0(M)(α)+Bf0(M)(α)]=0, (3.52)
Q0-Dl3[Ag'0(α)+Bf'0(α)]=0,
откуда.
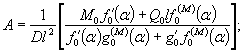 (3.53)
(3.53)
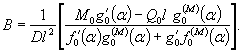
При
ξ=α получим из (3.49) и (3.50)
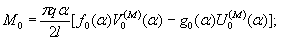
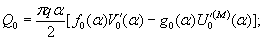
Подставим
значения М0 и Q0 в (3.53) и обозначим
выражения, заключенные в квадратные скобки, через a(α) и b(α),
тогда


Подставив
все найденные величины в (3.46), получим решение задачи в
виде:
при ξ
≥ α
 (3.54)
(3.54)
Изгибающие
моменты и поперечная сила равны
 (3.55)
(3.55)
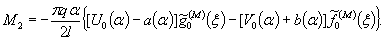 (3.56)
(3.56)
 (3,57)
(3,57)

Рис.
3.10. Зависимость прогиба и изгибающего момента от приведенного радиуса α
В
приложении 8 [12]
даны значения коэффициентов а(α) и b(α) при изменении а
от 0,1 до 2,0, а также значения изгибающего момента M2. Расчет
произведен по таблицам, приведенным М.Н. Ручимским [134]
для коэффициента Пуассона, равного 0,30.
По данным
приложения 8 [12]
построены графики изменения прогиба кромки ледяного
слоя и изгибающих моментов в ее сечениях.
3.8. Расчет ледяного слоя, имеющего жесткую вставку
В некоторых
случаях, например при расчете ледяного слоя, примыкающего к опорам мостов или
другим инженерным сооружениям, имеющим в плане круглую или близкую к этому
форму, расчетную схему можно представить в виде бесконечной плиты с круговым
защемленным отверстием [16].
Для
неограниченной плиты с защемленным круговым отверстием приведенного радиуса β, и загруженной нагрузкой,
равномерно распределенной по окружности приведенного радиуса а, решение также
запишем в виде (3.46).
Обозначим β=rol, где ro
- радиус отверстия;
α=rрl; rр - радиус окружности, по которой приложена
равномерно распределенная нагрузка Р.
Представим
компенсирующее решение в виде [73]
wk
= Af0(ξ) + Bg0(ξ)
(3.58)
Граничные
условия в данном случае имеют вид при ξ=Р
ω=0; 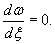
Обозначим
прогиб плиты в основном решении (3.47) при ξ=β через
 (3.59)
(3.59)
а первую
производную через
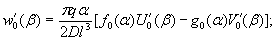 (3.60)
(3.60)
Тогда
условия (3.58) примут вид
w(β)+Af0(β) + Bg0(β) =
0;
w'(β)+Alf'0(β) + Bl g'0(β) = 0;
откуда
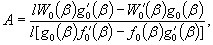 (3.61)
(3.61)

Подставив в
выражение (3.61) значения (3.59) и (3.60) и произведя необходимые
преобразования, получим
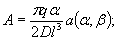 (3.62)
(3.62)

Значения a(α,β) и b(α,β) подсчитаны и представлены в табличной форме
(табл. 3.1).
Окончательно
имеем при β<ξ<α
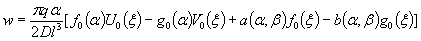 (3.64)
(3.64)
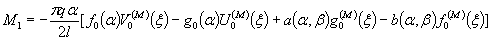 (3.65)
(3.65)
 (3.66)
(3.66)
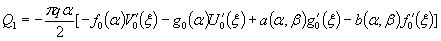 (3.67)
(3.67)
при
ξ>α
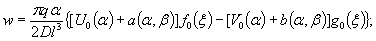 (3.68)
(3.68)
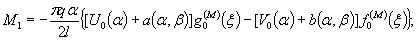 (3.69)
(3.69)
 (3.70)
(3.70)
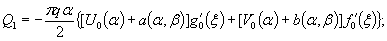 (3.71)
(3.71)
В табл. 3.1
даны значения величин a(α,β) и b(α,β), подсчитанные в пределах изменения α от 0,2 до 2,0 и β от 0,1 до 1,0.
Таблица 3.1
Значения коэффициентов а(α,β) и b(α,β) для бесконечной плиты с защемленным
отверстием
|
α
|
β
= 0,1
|
α
|
β
= 0,2
|
α
|
β
= 0,3
|
α
|
β
= 0,4
|
α
|
β
= 0,5
|
|
-а(α,β)
|
b(α,β)
|
-а(α,β)
|
b(α,β)
|
-a(α,β)
|
b(α,β)
|
-а(α,β)
|
b(α,β)
|
-а(α,β)
|
b(α,β)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
0,2
|
1,0448
|
0,0240
|
0,3
|
1,1285
|
0,0733
|
0,4
|
1,2065
|
0,1531
|
0,5
|
1,2696
|
0,2407
|
0,6
|
1,3216
|
0,3434
|
|
0,3
|
1,0054
|
0,0212
|
0,4
|
1,0750
|
0,0703
|
0,5
|
1,1393
|
0,1361
|
0,6
|
1,1946
|
0,2173
|
0,7
|
1,2312
|
0,3052
|
|
0,4
|
0,9629
|
0,0195
|
0,5
|
1,0202
|
0,0637
|
0,6
|
1,0345
|
0,1241
|
0,7
|
1,1220
|
0,1949
|
0,8
|
1,1608
|
0,2770
|
|
0,5
|
0,9167
|
0,0177
|
0,6
|
0,9642
|
0,0579
|
0,7
|
1,0093
|
0,1124
|
0,8
|
1,0522
|
0,1778
|
0,9
|
1,0716
|
0,2481
|
|
0,6
|
0,8687
|
0,0162
|
0,7
|
0,9077
|
0,0525
|
0,8
|
0,9420
|
0,1014
|
0,9
|
0,9749
|
0,1598
|
1,0
|
0,9953
|
0,2238
|
|
0,7
|
0,8195
|
0,0148
|
0,8
|
0,8504
|
0,0478
|
0,9
|
0,8807
|
0,0922
|
1,0
|
0,9051
|
0,1441
|
1,1
|
0,9221
|
0,2012
|
|
0,8
|
0,7698
|
0,0135
|
0,9
|
0,7942
|
0,0434
|
1,0
|
0,8186
|
0,0833
|
1,1
|
0,8331
|
0,1300
|
1,2
|
0,8486
|
0,1804
|
|
0,9
|
0,7200
|
0,0124
|
1,0
|
0,7415
|
0,0394
|
1,1
|
0,7582
|
0,0752
|
1,2
|
0,7605
|
0,1167
|
1,3
|
0,7790
|
0,1606
|
|
1.0
|
0,6714
|
0,0113
|
1,1
|
0,6854
|
0,0355
|
1,2
|
0,6996
|
0,0677
|
1,3
|
0,7099
|
0,1046
|
1,4
|
0,7127
|
0,1435
|
|
1,1
|
0,6232
|
0,0108
|
1,2
|
0,6333
|
0,0321
|
1,3
|
0,6258
|
0,0593
|
1,4
|
0,6486
|
0,0928
|
1,5
|
0,6526
|
0,1282
|
|
α
|
β = 0,6
|
α
|
β = 0,7
|
α
|
β = 0,8
|
α
|
β = 0,9
|
α
|
β
= 1,0
|
|
-а(α,β)
|
b(α,β)
|
-a(α,β)
|
b(α,β)
|
-а(α,β)
|
b(α,β)
|
-a(α,β)
|
b(α,β)
|
-a(α,β)
|
b(α,β)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
0,7
|
1,3451
|
0,4496
|
0,8
|
1,3502
|
0,5501
|
0,9
|
1,3520
|
0,6553
|
1,0
|
1,3334
|
0,7602
|
1,1
|
1,3098
|
0,8661
|
|
0,8
|
1,2532
|
0,4025
|
0,9
|
1,2648
|
0,4943
|
1,0
|
1,2557
|
0,5795
|
1,1
|
1,2390
|
0,6826
|
1,2
|
1,2188
|
0,7780
|
|
0,9
|
1,1656
|
0,3608
|
1,0
|
1,1751
|
0,4442
|
1,1
|
1,1667
|
0,5292
|
1,2
|
1,1487-
|
0,6114
|
1,3
|
1,1288
|
0,6973
|
|
1,0
|
1,0833
|
0,3235
|
1,1
|
1,0882
|
0,3989
|
1,2
|
1,0790
|
0,4745
|
1,3
|
1,0607
|
0,5476
|
1,4
|
1,0419
|
0,6227
|
|
1,1
|
0,9989
|
0,2880
|
1,2
|
1,0019
|
0,3559
|
1,3
|
0,9932
|
0,4241
|
1,4
|
0,9752
|
0,4876
|
1,5
|
0,9580
|
0,5542
|
|
1,2
|
0,9257
|
0,2582
|
1,3
|
0,9237
|
0,3196
|
1,4
|
0,9116
|
0,3771
|
1,5
|
0,8945
|
0,4340
|
1,6
|
0,8773
|
0,4908
|
|
1,3
|
0,8507
|
0,2295
|
1,4
|
0,8458
|
0,2843
|
1,5
|
0,8346
|
0,3395
|
1,6
|
0,8162
|
0,3345
|
1,7
|
0,8006
|
0,4335
|
|
1,4
|
0,7795
|
0,2025
|
1,5
|
0,7734
|
0,2524
|
1,6
|
0,7606
|
0,2966
|
1,7
|
0,7442
|
0,3389
|
1,8
|
0,7280
|
0,3814
|
|
1,5
|
0,7117
|
0,1788
|
1,6
|
0,7037
|
0,2237
|
1,7
|
0,6903
|
0,2613
|
1,8
|
0,6747
|
0,2974
|
1,9
|
0,6605
|
0,3344
|
|
1,6
|
0,6470
|
0,1562
|
1,7
|
0,6372
|
0,1965
|
1,8
|
0,6201
|
0,2270
|
1,9
|
0,6091
|
0,2598
|
2,0
|
0,5941
|
0,2893
|
3.9. Неосесимметричный изгиб ледяного слоя, имеющего жесткую
вставку
При расчете
ледяного слоя, примыкающего к опорам инженерных сооружений, на воздействие веса
машин и механизмов, применяемых при гидротехническом строительстве или
устройстве ледовых переправ, расчетную схему можно представить в виде
бесконечной плиты, имеющей защемленное круговое отверстие радиуса R0,
загруженной равномерной нагрузкой q,
распределенной окружности радиуса r,
в центре которой расположено начало координат (рис. 3.11).
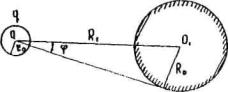
Рис. 3.11. Расчетная схема плиты с защемленным отверстием
Обозначим
расстояние между центрами указанных окружностей через R1, причем будем рассматривать случай, когда R1≥r+R0.
Угол, образующийся между прямой R1
и произвольным направлением радиуса R0,
обозначим через φ.
Представим,
как и прежде, решение задачи в виде (3.46), запишем
основное решение при ξ≥α,
где α = rl, в виде
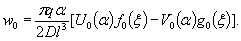 (3.72)
(3.72)
Разложим
основное решение на линии защемления в ряд
 (3.73)
(3.73)
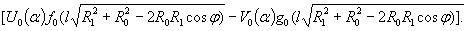
Представим
компенсирующее решение в виде
wk = Anfn(ξ)+Bngn(ξ).
Граничные
условия на линии защемления
w = 0; 
Обозначив
разложенные в ряд функции

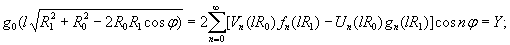
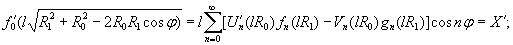
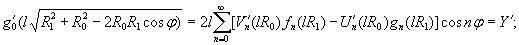
Запишем
граничные условия (3.73) в виде
 (3.74)
(3.74)
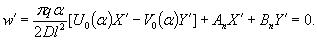
Решая
систему уравнений (3.74), получим
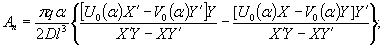 (3.75)
(3.75)
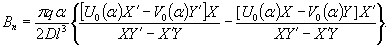
Для
упрощения записи обозначим выражения, заключенные в фигурные скобки,
соответственно через аn(αR0R1) и bn(αR0R1)и
представим функцию прогиба в окончательном виде
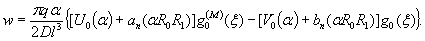 (3.76)
(3.76)
Изгибающие
моменты соответственно равны
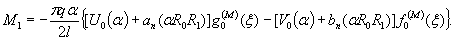 (3.77)
(3.77)
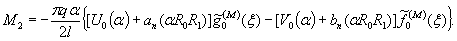 (3.78)
(3.78)
Выражение
для поперечной силы имеет вид
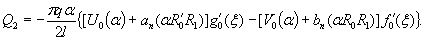 (3.79)
(3.79)
Изгибающие моменты достигают максимума при φ=0, т.е. на
линии O-O1 (рис. 3.11).
3.10. Изгиб ледяного слоя, имеющего жесткую вставку,
при колебаниях уровня воды
При
изменении уровня воды в ледяном слое, примыкающем к опорам инженерных
сооружений, в результате изгиба будут возникать дополнительные внутренние
усилия (рис.
3.9).
Как и ранее
в п.
3.6, будем считать изменение уровня воды положительным при убывании воды.
Расчетная
схема представляет собой бесконечную плиту с защемленным отверстием безразмерного
радиуса α.
Запишем
решение задачи при ξ≥α в виде
w=A(α)f0(ξ)
+ B(α)g0(ξ). (3.80)
Неизвестные
коэффициенты A(α) и В(α) найдем из граничных условий на линии
защемления:
w(α) = δ; w'(α) = 0. (3.81)
Подставляя
функцию прогиба (3.80) в выражения (3.81), получим
A(α)f0(α)
+ B(α)g0(α)=δ.
A(α)lf'0(α)
+ B(α)l g'0(α)=0.
откуда
после соответствующих преобразований имеем
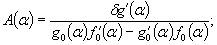 (3.82)
(3.82)

С учетом
коэффициентов (3.82) функция прогиба примет вид
 (3.83)
(3.83)
С учетом
выражений (1.15) (1.17), получим
 (3.84)
(3.84)
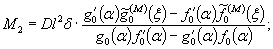 (3.85)
(3.85)
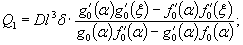 (3.86)
(3.86)
По формулам
(3.84)-(3.86) можно определить усилия, возникающие в ледяном слое, примыкающем
к опорам, при изменении уровня воды на величину δ.
Определив
максимальный изгибающий момент в месте примыкания ледяного покрова к опоре и
приравняв его величине M=Rf,yh2, можно определить предельное значение изменения уровня воды δn, при котором в ледяном
слое появляются
трещины.
3.11. Условия применения результатов полученных, решений
В практике
проектирования и строительства с использованием грузоподъемности ледяного
покрова возникает необходимость в решении конкретных задач изгиба плит на
упругом основании с расчетными схемами, отличающимися от уже рассмотренных.
В некоторых
случаях возможно применение имеющихся решений к конкретным расчетным схемам.
Например, при необходимости определения грузоподъемности ледяного покрова,
ослабленного круговым отверстием или прямоугольным в плане, и загруженного
сосредоточенным усилием на кромке, вполне оправдано применение решения,
изложенного в п. 3.5.1
- изгиб полубесконечной плиты со свободно опертой кромкой. При этом значения
изгибающих моментов (рис.
3.7) или грузоподъемность плиты (рис.
3.8) будут использованы с дополнительным коэффициентом запаса, который
будет увеличиваться с уменьшением размеров отверстия.
Запас
прочности для упрощения расчетов можно считать линейно изменяющимся от 1 при
величине безразмерного радиуса свободного отверстия, в плане большего π,
до 3, если безразмерный радиус меньше 0,1.
Для
определения грузоподъемности ледяного покрова по схеме с защемленной кромкой
(прямой по рис. 3.1
или очерченной окружностью по рис. 3.11)
вполне допустимо применение решения, изложенного в п. 3.3.
И в этом случае, так же как и ранее, значения изгибающих моментов и поперечных
сил в расчетных сечениях на кромке (рис.
3.2) или тех же усилий на сечениях под приложенной нагрузкой (рис. 3.3) будут иметь дополнительный запас прочности,
который также увеличивается с уменьшением размеров вмороженной в лед жесткой
вставки, недеформируемой с точки зрения расчетной схемы.
Однако диапазон изменения этого дополнительного
запаса прочности в данном случае менее очевиден и его можно в расчетах не
учитывать.
Необходимо
напомнить, что все решения задач, помещенных в главе 3, базируются на условии
«быстрого» загружения ледяного покрова временными нагрузками, без учета фактора
времени.
Многочисленные
исследования поведения ледяного слоя под длительно действующей нагрузкой
показывают, что с увеличением продолжительности пребывания временной нагрузки
под ней нарастают прогибы. При этом безразмерный радиус чаши прогиба не
изменяется. Когда прогиб под нагрузкой достигает предельного значения,
происходит разрушение ледяного слоя с образованием линейчатых пластических
шарниров и сквозных трещин по ним сначала радиальных, а затем и круговых с
образованием конуса. Несущая способность ледяного покрова исчерпывается и
происходит разрушение конуса, сопровождаемое провалом нагрузки.
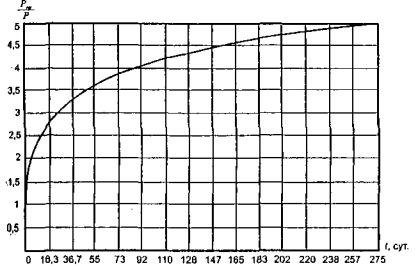
Рис.
3.12. График допускаемого времени нахождения на ледяном покрове необходимой
нагрузки в зависимости от ее отношения к предельной
Поэтому
необходимо ограничивать пребывание временной нагрузки на ледяном покрове, не
допуская ее провала.
Рекомендуется
определять допускаемое время t
(ч) нахождения нагрузки Р, найденной
по расчету или необходимой по условиям строительства, с учетом следующей
зависимости [60]:
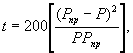
где Рпр - предельная нагрузка,
определяемая расчетом в упругой стадии, при ее кратковременном нахождении на
ледяном покрове, тс.
Для более
удобного пользования графиком расчетное время в часах переведено в сутки и
отложено по горизонтали. Безразмерное отношение предельной нагрузки к необходимой в интервале от 1 до 5 (Рпр/Р) нанесено по вертикали (рис. 3.12).
ГЛАВА 4 УСИЛЕНИЕ ЛЕДЯНОГО ПОКРОВА И ЕГО
РАСЧЕТ
4.1.
Состояние вопроса и цель исследования, конструкции усиления
ледяного покрова
Использование
ледяного покрова для производства работ при гидротехническом строительстве и
устройства ледовых переправ привлекало внимание ученых и инженеров, работы
которых по этому вопросу указаны в библиографическом списке.
В этих
работах вопрос грузоподъемности ледяного покрова рассмотрен довольно подробно.
При
практическом использовании ледяного покрова в целях гидротехнического строительства,
устройстве ледовых дорог и переправ, грузоподъемность его в естественном
состоянии не всегда обеспечивает потребность. В этом случае обеспечить
необходимую грузоподъемность ледяного покрова можно только путем его усиления.
Наиболее
рациональным представляется усиление ледяного покрова путем намораживания
дополнительного ледяного слоя.
При этом
процесс намораживания, в зависимости от естественных условий, может происходить
по следующим схемам:
а) при
глубоком снежном покрове и устойчивой отрицательной температуре воздуха - путем
расчистки снега, благодаря чему резко увеличивается теплоотдача на расчищенной
площади и происходит более интенсивное намораживание ледяного слоя снизу за
счет воды водоема, на границе лед-вода;
б) при
незначительном снежном покрове или при отсутствии его - путем послойного
намораживания льда сверху существующего ледяного покрова на величину не более
30% его начальной;
в) при
определенных обстоятельствах и благоприятных условиях, возможно комбинирующее
усиление с применением поочередно обоих способов. При этом рационально
применить сначала первый способ, затем второй.
На рис. 4.1
изображены расчетные схемы ледяного покрова, получаемые в результате его
усиления намораживанием дополнительного слоя
Усиленный
таким образом ледяной покров, по расчетной схеме представляет собой плиту,
имеющую ступенчатое изменение жесткости.
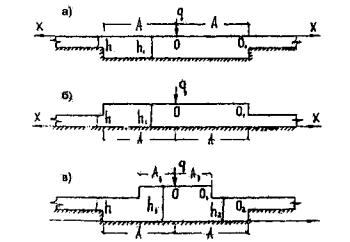
Рис. 4.1. Расчетные схемы усиленного ледяного покрова
Следует
отметить, что усиление по схеме (рис. 4.1,а) более предпочтительно, так как в
этом случае основной ледяной слой не испытывает дополнительного изгиба, который
имеет место при усилении по схеме (рис. 4.1,б). Налитая в процессе
намораживания вода является внешней нагрузкой, под действием которой в нижних фибрах ледяного слоя появляются растягивающие
напряжения.
4.2. Цилиндрический изгиб усиленного ледяного слоя
Рассмотрим
задачу изгиба плиты, лежащей на упругом основании с коэффициентом постели K, имеющей участок
шириной 2l и толщиной h1, и, уходящими от него
двумя полуплоскостями толщиной h
(рис. 4.1 ,а).
В
направлении осей X и Y плита считается
бесконечной. Обозначив жесткость первого участка плиты через D и второго соответственно через D, введем вспомогательные характеристики
[16]
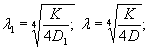 (4.1)
(4.1)
и обозначим
отношение 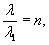
тогда
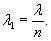
Решение
задачи изгиба плиты на упругом основании сводится к отысканию интеграла
дифференциального уравнения (3.11).
Введем
безразмерные координаты и приведенную ширину участка усиления
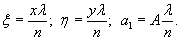
При
загружении плиты равномерно распределенной нагрузкой вдоль оси Y, будем иметь случай цилиндрического
изгиба. По методу начальных параметров [161] интеграл однородного
уравнения (3.11) равен
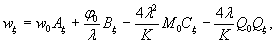 (4.2)
(4.2)
где w0, φ0, M0,
Q0 - прогиб, угол поворота, изгибающий момент и поперечная сила
в сечении, соответствующем началу координат (точка О).
Решение
дано в гиперболотригонометрических функциях (3.12).
Применяя
решение (4.2) для первого участка плиты 0≤ξ≤а, получим
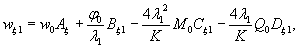 (4.3)
(4.3)
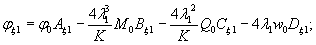

Задача
будет решена, если определим начальные параметры w0, φ0, M0, Q0 а также значения этих параметров на конце
первого участка, на лилии ξ1=a1.
В сечении О
имеем φ0=0, Q0=q/2. Параметры (ординаты
эпюр) в селении под нагрузкой будут
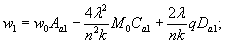 (4.4)
(4.4)
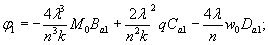
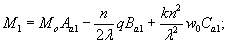
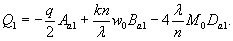
Второй
участок представляет собой полубесконечную плиту, загруженную на линии ξ1=a1 моментом
М1 и поперечной силой Q1. Перенося начало координат
на линию ξ1=a1 и
получим при ξ=λх [161]
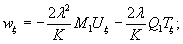 (4.5)
(4.5)

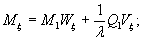

Решение
(4.5) дано в затухающих функциях (3.13).
Неизвестные
начальные параметры w0 и М0 определим из условий равенства прогибов и углов
поворота на границе двух участков, на линии ξ1=a1
 (4.6)
(4.6)

подставляя
выражения (4.4) в (4.6) и произведя необходимые преобразования, получим
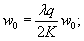 (4.7)
(4.7)

где
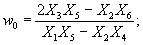 (4.8)
(4.8)
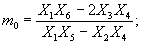
X1
= Aa1+2nBa1+2n2Ca1;
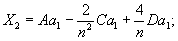
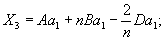 (4.9)
(4.9)
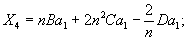

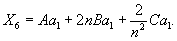
В частном
случае, при λ1=λ, в точке 0 имеем
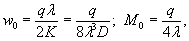
то есть
получаем значения прогиба и изгибающего момента для бесконечной плиты
постоянной толщины при цилиндрическом изгибе [161].
На рис.
4.2, 4.3 даны графики, в которых Отражены зависимость начальных параметров w0 и М0 от ширины первого участка плиты а и соотношения
жесткостных характеристик участков плиты n (4.1).
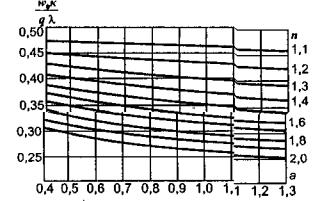
Рис. 4.2. Зависимость прогибов под нагрузкой от приведенной
ширины а
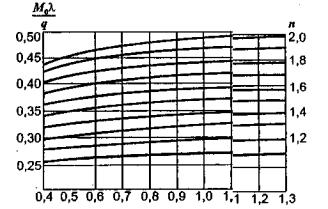
Рис. 4.3. Зависимость изгибающих моментов под нагрузкой от
приведенной ширины а

Рис. 4.4. Зависимость изгибающего момента на конце первого
участка от его приведенной ширины а1
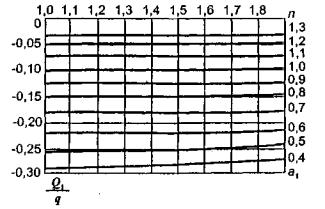
Рис. 4.5. Зависимость поперечной силы на конце первого
участка от его приведенной ширины а1
Подставляя
найденные значения начальных характеристик в выражения (4.4), получим значения
изгибающего момента М1 и
поперечной силы Q1 на
конце первого участка плиты
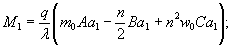
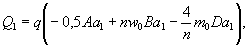
где w0 и m0
- безразмерные коэффициенты, взятые из графиков (рис. 4.2, 4.3). В заключение
отметим, что применение схемы усиления (рис.
4.1,а)
целесообразно при увеличении грузоподъемности основного
ледяного слоя в 2-2,5 раза.
4.3. Определение напряжений в ледяном
слое при намораживании дополнительной полосы льда
В случае
намораживания дополнительной полосы (рис.
4.1,
б) ледяной слой испытывает цилиндрический изгиб от веса налитой на него воды.
Расчетная схема представляет собой бесконечную плиту на упругом основании,
изгибающуюся под действием равномерно распределенной нагрузки, действующей на
участке шириной 2a1 (рис. 4.1, б) и численно равный
объемному весу слоя воды толщиной h1=h.
Решая
задачу методом начальных параметров, для первого участка плиты 0≤ξ≤a1, имеем в сечении О φ=0; Q0=0.
Тогда из (4.2) получим для сечения О1
с учетом дополнительных слагаемых от q
[88]
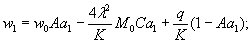 (4.10)
(4.10)
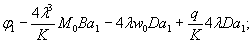


Второй
участок представляет собой полубесконечную плиту, загруженную на линии ξ=a1 поперечной силой Q1 и моментом М1.
Неизвестные
начальные параметры w0 и М0 определим из условия
равенства прогибов и углов поворота на границе двух участков, в точке О (рис. 4.1, б), куда перенесем
начало координат.
Приравняв выражения и произведя необходимые преобразования, получим
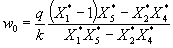 (4.11)
(4.11)
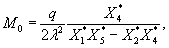 (4.12)
(4.12)
где
выражения X*1,2,3,…6 - те же, что и в (4.9), но при n=1.
По формулам
(4.10) (4.11) и (4.12) определим значения изгибающих моментов и прогибов в
начале координат и в точке О1, на конце намораживаемой полосы.
Результаты вычислений даны в табл. 4.1.
Таблица 4.1
|
а1
|
М0
|
Ма1
|
w0
|
wa1
|
|
0,3
|
0,1085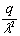
|
0,0747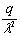
|
0,2895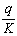
|
0,2715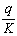
|
|
0,4
|
0,1305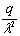
|
0,0791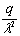
|
0,4102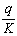
|
0,3707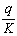
|
|
0,5
|
0,1455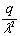
|
0,0834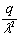
|
0,4684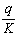
|
0,4007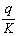
|
|
0,75
|
0,1621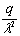
|
0,0930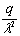
|
0,7830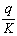
|
0,6525
|
При
толщине слоя h=25 см, a1=0,25 и толщине налитой на
лед воды hв=3 см, получим М0=258 кгс. Напряжения изгиба в растянутой зоне ледяного
слоя σu=2,48 кгс/см2.
Следовательно, можно сделать вывод, что толщина первого намораживаемого слоя
должна быть не более 3-5 см, причем тем больше, чем меньше ширина
намораживаемой полосы а1.
При таких незначительных значениях напряжений изгиба ими можно пренебречь, т.к.
процесс намораживания длительный (от одних до нескольких суток), и эти
напряжения в результате перекристаллизации льда со временем могут значительно
уменьшиться.
Каждый
последующий слой намораживается после того, как полностью закончилась
кристаллизация льда в предыдущем слое. При такой последовательности
производства работ имеем ко второму этапу уже ступенчатую плиту, загружаемую
равномерно распределенной по площади нагрузкой, решение для которой найдем в
следующем параграфе.
Если в
результате намораживания дополнительной полосы льда в основном ледяном слое
появляются значительные напряжения изгиба, то их можно уменьшить путем
временного изменения расчетной схемы (рис.
4.1).
Действительно,
так как максимальные растягивающие напряжения при изгибе возникают в нижних
слоях ледяного покрова в сечении О (рис.
4.1,
б), то их можно ликвидировать, разрезав полученную ступенчатую плиту вдоль по
оси Y (по оси симметрии). В
результате такого разреза частично уменьшится и величина температурных
напряжений в ледяном покрове, что также улучшит работу конструкции в целом.
При
устойчивой отрицательной температуре воздуха заполнившая разрез вода быстро
замерзает, и ледяной покров снова будет представлять
собой по расчетной схеме бесконечную плиту переменной толщины.
4.4. Изгиб усиленного ледяного
слоя равномерно распределенной полосовой нагрузкой
В данном
случае расчетная схема представляет собой ступенчатую плиту (рис. 4.1, б), загруженную
равномерно, распределенной нагрузкой от налитого слоя воды шириной 2а1.
Решая
задачу, как и прежде, методом начальных параметров, с учетом дополнительных
слагаемых от q, получим для первого
участка в сечении 01
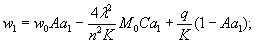
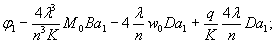 (4.13)
(4.13)
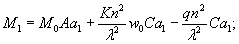
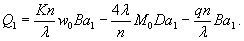
Второй
участок, как уже было сказано выше, представляет собой полубесконечную полосу,
загруженную на линии поперечной силой Q1 и моментом М1.
Неизвестные
начальные параметры получим из условия равенства прогибов и углов поворота (4.5) и (4.13).
Перенося
начало координат в точку O1, имеем, после соответствующих
преобразований
 (4.14)
(4.14)
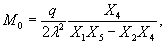 (4.15)
(4.15)
где X1,2,3,…6
- выражения (4.9).
Подставляя
начальные параметры (4.14), (4.15) в выражения (4.13), получим значения изгибающего момента и поперечной силы на конце первого участка,
в сечении O1.
4.5. Цилиндрический изгиб
ледяного слоя, усиленного комбинированным способом
Такой
способ усиления (рис. 4.1,в) целесообразно
применять в том случае, если необходимо повысить грузоподъемность существующего
ледяного слоя в 3-4 раза.
В этом
случае необходимо произвести расчет двухступенчатой плиты на упругом основании.
Введем
следующие обозначения:
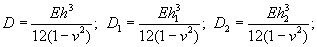


Для первого
участка 0≤ξ1≤а1,
с началом координат в точке О, справедливо выражение (4.1).
Для второго
участка a1≤ξ2≤a2. перенося начало координат в точку O
получим
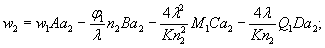 (4.16)
(4.16)
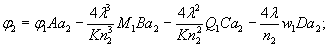
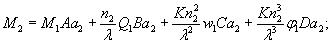
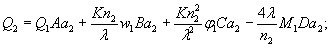
Третий
участок представляет собой полубесконечную плиту, загруженную в точке O2 моментом М2 и поперечной силой Q2.
Перенося
начало координат в точку O2, имеем
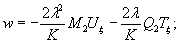 (4.17)
(4.17)
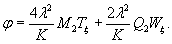
Неизвестные
начальные параметры w0 и M0 найдем из условия
равенства прогибов и узлов поворота на границе двух участков в точке О2.
Подставляя в (4.17) значения М2
и Q2 из (4.16), а вместо w1, φ1, М1,
Q1 значения (4.4), произведем
необходимые преобразования и получим
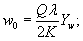 (4.18)
(4.18)
 (4.19)
(4.19)
где
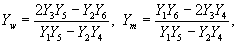 (4.20)
(4.20)
здесь Y1,2,3…6 - выражения,
аналогичные (4.9), но более сложные.
При a1=а2=0
выражения (4.18), (4.19) дают значения

то есть как
у обычной бесконечной плиты постоянной толщины при цилиндрическом изгибе.
При а2=0 имеем n2=1, и из решения (4.18), (4.19) получаем выражения (4.7), (4.8), т.е. решение для
плиты с одной ступенью усиления.
4.6. Расчет одноступенчатой ледяной плиты на
сосредоточенную нагрузку
При расчете
ледовых переправ на пропуск тяжелых транспортных единиц расчетную схему усиленного
ледяного слоя можно представить в виде бесконечной плиты со ступенчатым
изменением жесткости (рис. 4.6), загруженной сосредоточенной нагрузкой.
Считая
задачу симметричной относительно оси Y,
рассмотрим последовательно два участка плиты:
а) для
первого участка 0≤ξ1≤a1
с началом координат в точке О, функцию прогиба плиты, приближенно
удовлетворяющую уравнению (3.3), запишем в виде
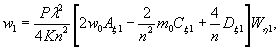 (4.21)
(4.21)
где w0 и m0 - выражения (4.8);
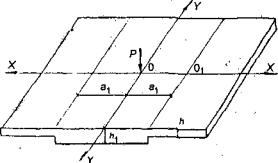
Рис. 4.6. Расчетная схема одноступенчатой плиты
б) для
второго участка плиты a1≤ξ1≤∞, перенося начало
координат в точку O1, получим
 (4.22)
(4.22)
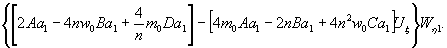
Для
определения грузоподъемности плиты достаточно иметь значения изгибающих
моментов в пределах первого участка. Применяя зависимости (3.4), (3.5) для функции прогибов (4.21), получим
 (4.23)
(4.23)
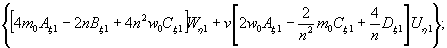
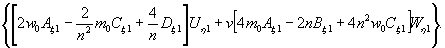 (4.24)
(4.24)
На рис.
4.7, 4.8 приведены графики изменения значений изгибающих моментов в сечениях
под силой М0(η) и в
точке O1 M1(η)
в зависимости от характеристик ступенчатой плиты а1 и n.
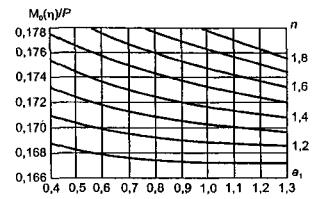
Рис. 4.7. Зависимость изгибающего момента под силой от
характеристик плиты a1 и n
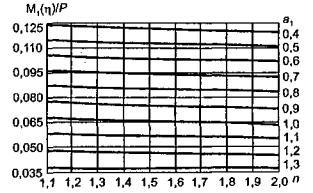
Рис. 4.8. Зависимость изгибающего момента в точке O1
от характеристик a1 и n
Изгибающие
моменты, имеющие максимальные значения, действуют на сечениях, совпадающих с
осью X, расположенных соответственно
в точках О и О1.
На рис. 4.9
построены графики оптимальных параметров одноступенчатой ледяной плиты,
полученных в результате анализа формул (4.23) и (4.24).
Оптимальными
параметрами считаем такие соотношения толщин участков плиты и их ширины, при
которых напряжения изгиба в точке О (под силой) и в начале второго участка (O1)
равны между собой.
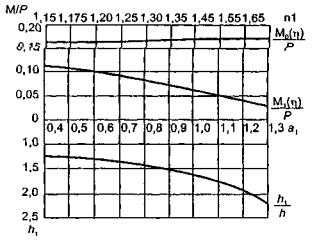
Рис.
4.9.Оптимальные параметры одноступенчатой плиты
Для
определенной, заданной величины а1,
на соответствующей ей вертикали из графика можно определить соотношение толщин
участков плиты h1/h, а
также максимальные значения изгибающих
моментов в точках О1 (на границе участков) и О (под нагрузкой).
4.7. Центральный изгиб одноступенчатой ледяной плиты
равномерно распределенной по окружности нагрузкой
В
предыдущем параграфе приведен приближенный расчет одноступенчатой ледяной плиты
на сосредоточенную силу, при этом максимально: использовались данные расчета
этой же плиты, полученные ранее при цилиндрическом изгибе.
Попытаемся,
теперь найти решение этой задачи при загружении плиты равномерно распределенной
по окружности нагрузкой. Переходя к полярной системе осей координат (рис. 4.6), введем переменную 
Обозначив
жесткость первого участка шириной 2а1
через D1, и второго
соответственно через D1 введем вспомогательные
характеристики

Их
отношение
 (4.25)
(4.25)
тогда 
Теперь
можно перейти к безразмерной координате, которая для первого участка имеет вид
 (4.26)
(4.26)
где а - половина ширины первого участка
плиты.
Основной
системой будет бесконечная полоса шириной 2а,
имеющая жесткость D1, и
две примыкающие к ней полубесконечные плиты, с жесткостью D.
Будем
считать, что нагрузка передается на плиту по окружности весьма малого радиуса r0, что соответствует безразмерной величине α=r0l1. В
этом случае сосредоточенную нагрузку Р
можно заменить эквивалентной ей нагрузкой
 (4.27)
(4.27)
Тогда для
первого участка плиты α<ξ1<ξу
можно записать решение задачи в виде, аналогичном выражению (3.38), поместив начало
координат в центре круга радиуса α.
 (4.28)
(4.28)
Для второго
участка плиты ξ>ξy, имеем
 (4.29)
(4.29)
Неизвестные
коэффициенты А(α) и В(α) определим из условия равенства
прогибов и углов поворота обоих участков плиты на границе ξy
(4.26), тогда получим
A(α)f0(ξy)-B(α)g0(ξy)=U0(α)f0(ξy)-V0(α)g0(ξy);
A(α)l1f'0(ξy)-B(α)l1g'0(ξy)=U0(α)lf'0(ξy)-V0(α)lg'0(ξy);
откуда
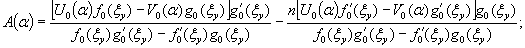 (4.30)
(4.30)
 (4.31)
(4.31)
При n=1, т.е. для плиты
постоянной толщины h,
из выражений (4.30), (4.31) получим A(α)=U0(α) и
B(α)=V0(α), а решение (4.28) превращается в известное выражение (3.48).
Для
определения грузоподъемности одноступенчатой ледяной плиты достаточно знать
значения изгибающих моментов в пределах первого участка. Тогда, произведя в
выражении (4.29) обратную замену ρ
на Р (4.27), запишем
значения прогиба и изгибающих моментов в виде
 (4.32)
(4.32)
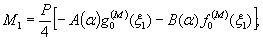 (4.33)
(4.33)
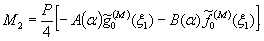 (4.34)
(4.34)
Для
большинства грузовых автомобилей (приложение 10) [12]
радиус окружности передачи нагрузки составляет 100-150 см. В этом случае при
толщине льда 35÷70 см безразмерный радиус α изменяется в пределах
0,15÷0,10, поэтому дальнейший расчет будем вести для
α=0,10÷0,15.
На рис.
4.10 построены графики оптимальных параметров одноступенчатой ледяной плиты,
полученные в результате анализа формул (4.33) и (4.34).
Значения
изгибающих моментов в сечении под нагрузкой изображены двумя верхними кривыми,
одна из которых построена для α=0,10, вторая - для α=0,15.
Две нижние
кривые отражают изменение изгибающих моментов на конце первого участка. Они
построены также для двух вышеуказанных значений α.

Рис.
4.10. Зависимость изгибающих моментов под нагрузкой и на конце первого участка а1 от его ширины и толщины
На этом же
чертеже изображены кривые (пунктирными линиями), отражающие изменение значений
изгибающих моментов по приближенному решению, данному в п.
4.6.
Для
сравнения двух приведенных решений безразмерную ширину первого участка плита а1 (п.
4.6)
нужно умножить на  , так как характеристика плиты λ
в
, так как характеристика плиты λ
в 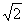 раз меньше
характеристики l.
раз меньше
характеристики l.
4.8. Расчет двухступенчатой ледяной плиты на
сосредоточенную нагрузку
Задача
также симметрична относительно оси Y.
Расчетная схема аналогична изображенной на рис. 4.6, однако сечение по оси X представляет собой фигуру,
изображенную на рис. 4.1, в.
Рассматривая,
как и прежде (п.
4.6),
плиту по участкам, получим следующие приближенные решения;
а) для
первого участка 0≤ξ1≤a1, с началом координат в точке О (рис. 4.1,в) функция прогиба
 (4.35)
(4.35)
Изгибающие
моменты соответственно равны
 (4.36)
(4.36)
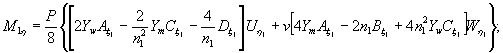 (4.37)
(4.37)
б) для
второго участка 0≤ξ1≤a2, перенося начало координат в точку O1 (рис. 4.1,в), получим выражения
для прогиба w2 и изгибающих моментов М2(ξ) и М2(η),
которые ввиду их большого объема не приводятся.
В
результате анализа формул (4.26)-(4.37) признано рациональным изменять ширину
первого участка (рис. 4.1,в) в пределах (a1=0,4÷0,8), оставляя постоянной ширину
второго участка (а2=0,5).
На рис. 4.11,
4.12 приведены графики изменения значений изгибающих моментов в сечениях под
силой М0(η), а также
в точках O1-М1(η) и O2-М2(η), в зависимости от
характеристик ступенчатой плиты n1 и n2, и ширины первого участка плиты а1.
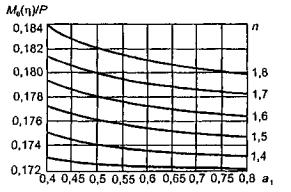
Рис.
4.11. Зависимость изгибающего момента под силой от приведенной ширины участка а1
В этом
случае максимальные изгибающие моменты так же действуют в сечениях, совпадающих
с осью X, находящихся соответственно
в точках О, О1, и O2.
На рис.
4.13 построены графики оптимальных параметров двухступенчатой плиты, полученные
в результате анализа формул (4.35)-(4.36). При этом ширина второго участка
принята постоянной (а2=0,5).
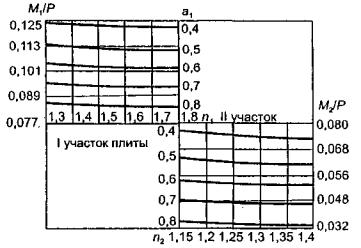
Рис.
4.12. Зависимость изгибающих моментов М1
и М2 от приведенных
параметров плиты а1; n1;
n2
при постоянном параметре а2
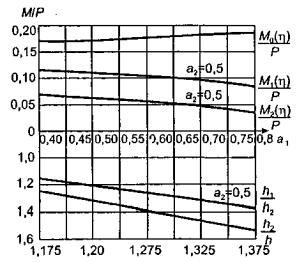
Рис.
4.13. Оптимальные параметры двухступенчатой плиты
Оптимальными
параметрами считаем такие соотношения толщин участков плиты и их ширин, при
которых напряжения изгиба в точке О (под нагрузкой), в начале второго участка
(O1) и в начале третьего участка (О2) равны между собой.
Для
определенного, заданного значения ширины первого участка из графиков легко
определяются соответствующие значения оптимальных
параметров двухступенчатой плиты.
4.9. Центральный изгиб двухступенчатой ледяной плиты
равномерно распределенной по окружности нагрузкой
При решении
данной задачи основную систему можно представить в виде бесконечной полосы
шириной 2а, с жесткостью D1, двух примыкающих к ней
бесконечных полос с приведенной шириной а2
и жесткостью D2 и двух
полуплоскостей с жесткостью D (рис. 4.1,в).
Вспомогательные
характеристики соответственно равны

Как и
прежде, целесообразно ввести обозначения
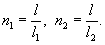 (4.38)
(4.38)
Переходя от
прямоугольной к полярной системе осей координат (рис. 4.1), введем переменную

Теперь
можно перейти к безразмерной координате, которая для первого участка имеет вид
 (4.39)
(4.39)
для второго
участка плиты
 (4.40)
(4.40)
для
третьего участка
ξ=rl. (4.41)
Уравнение
границы между первым и вторым участками будет
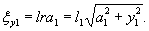 (4.42)
(4.42)
Соответственно
между вторым и третьим участками
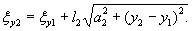 (4.43)
(4.43)
Не повторял
предпосылок, изложенных в п.
4.7,
запишем решение задачи по участкам в следующем виде
для первого
участка, при α<ξ1<ξy1
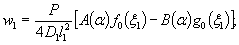 (4.44)
(4.44)
для второго
участка, при ξy1<ξ2<ξy1
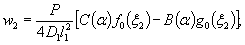 (4.45)
(4.45)
и для
третьего участка, при ξ>ξy2
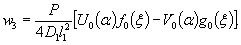 (4.46)
(4.46)
Неизвестные
коэффициенты С(α) и В(α) определим из условия равенства
прогибов и углов поворота на границе второго и третьего участков (4.43), тогда
C(α)f0(ξy2)-D(α)g0(ξy2)=U0(α)f0(ξy2)-V0(α)g0(ξy2);
C(α)l2f'0(ξy2)-D(α)l2g'0(ξy2)=U0(α)lf'0(ξy2)-V0(α)g'0(ξy2);
откуда
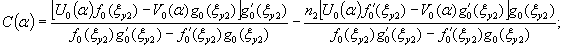 (4.47)
(4.47)
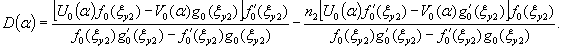 (4.48)
(4.48)
Аналогичным
способом определим неизвестные коэффициенты А(α) и B(α).
Из равенства прогибов и углов поворота на границе первого и второго участков
(4.42) получим
A(α)f0(ξy1)-B(α)g0(ξy1)=C(α)f0(ξy1)-D(α)g0(ξy1);
A(α)l1f'0(ξy1)-V(α)l1g'0(ξy1)=C(α)l2f'0(ξy1)-D(α)l2g'0(ξy1),
откуда
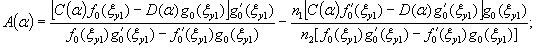 (4.49)
(4.49)
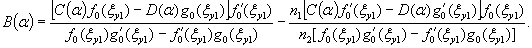 (4.50)
(4.50)
При n1=n2=1, то есть для плиты
постоянной толщины h, получим А(α)=С(α)=U0(α) и
B(α)=D(α)=V0(α).
Для
определения грузоподъемности двухступенчатой ледяной плиты достаточно знать
значения изгибающих моментов в пределах первых двух участков.
Для первого
участка получим
 (4.51)
(4.51)
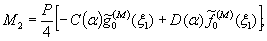 (4.52)
(4.52)
для второго
участка
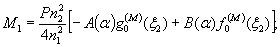 (4.53)
(4.53)
 (4.54)
(4.54)
На рис.
4.14 построены графики оптимальных параметров двухступенчатой ледяной плиты,
полученные в результате подсчета по формулам (4.52) и (4.54). Расчет произведен
для двух значений безразмерного радиуса окружности, по которой передается
нагрузка (α=0,15 и α=0,20).
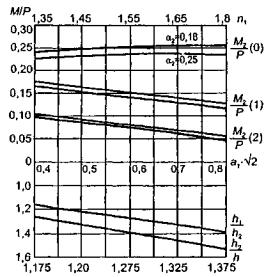
Рис.
4.14. Оптимальные параметры двухступенчатой плиты
Приведенная
ширина второго участка плиты принята постоянной и равна
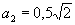 , по соображениям, изложенным в п.4.7, 4.8.
, по соображениям, изложенным в п.4.7, 4.8.
ГЛАВА
5. РАСЧЕТ УСИЛЕННОГО ЛЕДЯНОГО СЛОЯ ПО ПРЕДЕЛЬНЫМ
СОСТОЯНИЯМ
5.1.
Состояние вопроса и цель исследования
Общие методы расчета систем за пределом
упругости очень подробно разработаны для обычных конструкций, но применительно
к балкам и плитам на упругом основании необходимо провести дополнительные
исследования. Практика же инженерного проектирования настоятельно требует
создания хотя бы приближенного метода, который позволил бы проектировщикам
определять несущую способность, конструкции, расположенной на упругом
основании, при переходе ее материала за предел упругости.
Приближенные методы расчета балок и плит,
расположенных на упругом основании, за пределом упругости, даны А.П. Синицыным [143]. Основой для разработки
такого приближенного метода послужил способ Е.Н. Жемочкина, поэтому указанная
работа является распространением этого способа на задачи, в которых или
конструкции, или упругое основание переходят за предел упругости. Удобство
способа состоит в том, что позволяет довести решение любой из рассмотренных
задач до численного результата.
Метод предельного равновесия, созданный в
результате работ наших отечественных ученых В.М. Келдыша, А.А. Гвоздева, В.В.
Соколовского, Н.И. Безухова, А.Р. Ржаницына и многих других, получил всеобщее
признание и широко применяется на практике.
Трудность задачи о расчете балок и плит на
упругом основании за пределом упругости состоит в том, что нельзя
непосредственно, без специальных приемов, применить общий метод расчета
конструкции по предельному равновесию.
При загружении плиты сосредоточенной силой
наибольший момент возникает под силой, поэтому образование пластической области
в такой; плите начинается вблизи приложения нагрузки. Увеличение нагрузки
приводит к образованию линейчатых пластических шарниров, возникающие по
линейным образующим конуса, который формируется по мере роста нагрузки. Каждый
участок плиты, расположенной между двумя линейчатыми! шарнирами, начинает
работать как консоль, в результате чего быстро увеличиваются прогибы под грузом
и возрастают отрицательные моменты в плите.
У основания конуса возникает пластический шарнир
по окружности, после чего несущая способность плиты увеличивается очень слабо.
Практически можно считать, что образование конуса приводит к исчерпанию несущей
способности плиты, хотя теоретически даже при наличии радиальных и кольцевых
шарниров система остается неизменяемой за счет упругих связей основания,
которые продолжают поддерживать плиту.
Решение задачи об изгибе плиты следует начинать
с упругой стадии; для этого можно использовать решения, ранее выполненные для
плит на упругом основании.
Условия пластичности для плит значительно
усложняют расчет, и для возможности получения численных результатов приходится
искать практически приемлемые приближенные решения. В таких решениях
используется общая теорема о равенстве работ внешних и внутренних сил.
Излагаемый А.Д. Дмитриевым способ определения
несущей способности плит на упругом основании [50] основан на теории малых
упруго-пластических деформаций, разработанной А.А. Ильюшиным и изложенной в его
книге [59].
В работе [21] излагается способ определения несущей способности
сферических и незамкнутых цилиндрических оболочек, основанный на тех же предпосылках.
Как частные случаи из этой работы получаются способы расчета мембран и плит на
упругом основании с учетом упругопластических деформаций.
Кроме того, в работе [19] излагается способ
определения несущей способности балок на упругом основании, который можно
применить для расчета плит при цилиндрическом изгибе.
Принципиальной особенностью предложенного метода
является применение общего вариационного уравнения равновесия упругопластически
деформированной пластинки к плитам на упругом основании и особый прием
составления вариаций - по приращению нагрузки. Этот прием я позволяет решить
задачу определения грузоподъемности плит на упругом основании.
Особым и неизменным условием является сохранение
упругих свойств упругим основанием плиты даже тогда, когда в самой плите
появляются пластические деформации. Реакция упругого основания определяется по
гипотезе Винклера.
При расчете бесконечной плиты на упругом
основании необходимо учитывать то обстоятельство, что пластические деформации
не могут распространяться до бесконечности, и следовательно, они ограничены
некоторым радиусом аn, называемым радиусом
упругопластической зоны (рис. 5.1). Следовательно, в момент перед разрушением
предельная нагрузка Рn уравновешивается
внутренними упругопластическими силами в пределах радиуса rn чисто упругими силами
за пределами этого радиуса, и упругим основанием. При определении вариации
потенциальной энергии это учтено, и расчет произведен для чисто упругой и
упругопластической зон отдельно.
Далее принимается уже упомянутое выше положение,
что если имеется для плиты упругая форма прогиба, удовлетворяющая краевым
условиям задачи, то она может быть принята в качестве аппроксимирующей функции
для упругопластического изгиба плиты.
Затем составляется вариационное уравнение
равновесия упругопластически деформированной плиты в предельном состоянии.
Из этого уравнения и
определяется значение предельной нагрузки на бесконечную плиту.
5.2. Расчет плит переменной толщины, лежащих на упругом основании, с учетом
упругопластических деформаций
Общий метод расчета плит на упругом основании по
предельному состоянию изложен в работах [21, 49].
Задачу решаем энергетическим методом, сущность
которого заключается в том, что приращение потенциальной энергии всей системы,
полученное в результате увеличения предельной нагрузки Рn на δРn равно нулю, то есть
система находится в предельном устойчивом равновесии (рис. 5.1).
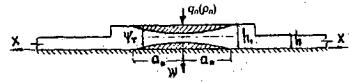
Рис. 5.1. Расчетная схема
одноступенчатой плиты
Приращение потенциальной энергии системы δU определяется выражением
δU=δT+δПу+δПn+δПос, (5.1)
где δТ
- приращение работы внешней нагрузки;
δПу - приращение потенциальной энергии внутренних сил на всей
площади чисто упругой зоны плиты;
δПn - приращение
потенциальной энергии внутренних сил на всей площади упругопластической зоны;
δПос - приращение потенциальной энергии основания на всей
площади плиты.
Следовательно, в момент перед разрушением плиты
предельная нагрузка Рn уравновешивается
внутренними упругопластическими силами в пределах границ распространения
упругопластических деформаций и упругими силами основания на всей площади
плиты.
Упругопластический прогиб плиты можно
представить в следующем виде [59]
wn = APnwxy, (5.2)
где А
- коэффициент, объединяющий постоянные для данной плиты величины;
Рn - предельная нагрузка
на плиту;
wxy - функция прогиба,
зависящая только от координат точки плиты (х,у),
то есть форма упругого прогиба плиты (5.2),
удовлетворяющая граничным условиям задачи, может быть принята в качестве
исходной и для упруго-пластического прогиба.
Вариационное уравнение плиты (5.1) получим
следующим образом:
1. Давая предельной нагрузке Рn бесконечно малое приращение δPn, получим бесконечно малое приращение прогиба плиты, которое
равно дифференциалу прогиба плиты wn по переменной Рn.
Из выражения (5.2) имеем
δwn = AδPnwxy,.
Приложенная к плите внешняя нагрузке Рn+δРn совершит на приращении
прогиба под ней работу
δТ=-(Рn + δРn)АδРn[wxy].
Пренебрегая малой величиной второго порядка,
получим выражение приращения работы внешней нагрузки
δТ=-AРn + δРn[wxy]. (5.3)
где [wxy]
- значение функции прогиба под нагрузкой.
2. Определим приращение потенциальной энергии
внутренних сил плиты в чисто упругой зоне. Потенциальная энергия внутренних сил
упруго деформированной плиты на единицу площади в прямоугольных координатах
равна [5, 21]
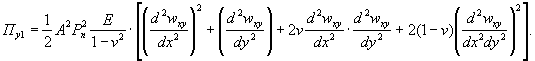 (5.4)
(5.4)
Выражение в квадратных скобках, которое зависит
только от координат точки плиты (х,у),
обозначим через Пх,у.
Тогда выражение потенциальной энергии на единицу площади упругой зоны плиты
примет вид
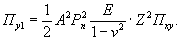
В результате приращения нагрузки на δРn потенциальная энергия
на единицу площади упругодеформированной плиты также получит приращение, равное
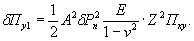
На всей площади чисто упругой зоны плиты это
приращение будет
 (5.5)
(5.5)
3. Приращение потенциальной энергии внутренних
сил упругопластически деформированной плиты на единицу ее площади равно [21, 59]
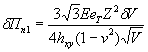
Так как при пластических деформациях коэффициент
Пуассона равен 0,5, то выражение δПп1 упрощается и принимает вид
 (5.6)
(5.6)
где
z - переменная координата
по толщине плиты;
eT -
относительная деформация предела текучести материала плиты;
EeT=σT - предел текучести
материала плиты;
V - квадратичная форма от кривизны плиты при изгибе.
Квадратичная форма V, выраженная через вторые производные от прогиба плиты (5.2), в
прямоугольных координатах равна [21, 49].
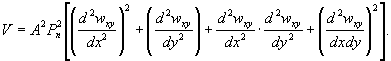 (5.7)
(5.7)
Выражение в квадратных скобках, зависящее только
от координат точки плиты (х,у), обозначим
через wxy, тогда квадратичная
форма V примет вид:
V = A2P2nwxy.
Приращение внешней нагрузки δРn вызывает приращение квадратичной формы кривизны, которое
равно
δV=2Pn δРnA2Vxy.
Подставив значения V δV в выражение (5.6),
получим
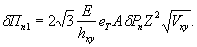
Приращение потенциальной энергии на всей площади
упругопластической зоны плиты равно
 (5.8)
(5.8)
4. Потенциальная энергия упругодеформированного
основания плиты на единицу ее площади равна
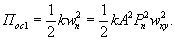
В результате приращения внешней нагрузки на δPn потенциальная энергия
основания получит приращение на единицу площади плиты, равное
δПос=kA2P2nδPnw2xy.
На всей площади плиты приращение потенциальной
энергии упругого основания будет равно
 (5.9)
(5.9)
Вариационное уравнение (3.1)
после подстановки в него всех найденных величин будет иметь следующий вид:


Разделив уравнение на АδPn, найдем величину предельной нагрузки на плиту
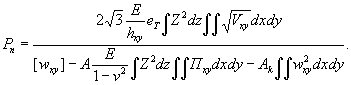 (5.10)
(5.10)
Для определения границ
упругопластической зоны плиты можно использовать известное условие [42, 59], заключающееся в том,
что на границе упругопластической и чисто упругой зоны плиты полувысота
упругого ядра ψт равна половине толщины
плиты (рис. 5.1).
Полувысота упругого ядра упругопластической зоны
[21]
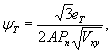
тогда

а предельная нагрузка
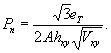 (5.11)
(5.11)
Приравняем правые части выражений (3.10), (3.11) и разделив все на 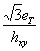 , получим уравнение для определения границ упругопластической
зоны плиты в виде
, получим уравнение для определения границ упругопластической
зоны плиты в виде
 (5.12)
(5.12)
Из этого уравнения
границы упругопластической зоны плиты определяем пробными подстановками.
5.3. Расчет усиленного ледяного слоя с учетом упругопластических деформаций при загружении равномерно
распределенной нагрузкой
Расчетная схема для данного случая загружения
дана на рис. 5.1. При ступенчатом
изменении толщины ледяного слоя получим после соответствующих преобразований
выражения (5.10)
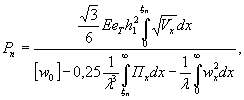 (5.13)
(5.13)
где произведение Еет равно
напряжению предела текучести материала Rf,у
Затем, подставив в выражение (5.12) все
известные величины и принимая во внимание, что 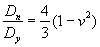 , получим уравнение для определения границ упругопластической
зоны плиты
, получим уравнение для определения границ упругопластической
зоны плиты
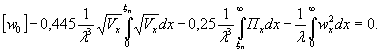 (5.14)
(5.14)
Выражения  и Пх, также существенно
упрощаются и принимают вид
и Пх, также существенно
упрощаются и принимают вид
 (5.15)
(5.15)
Принимая в качестве аппроксимирующей для первого
участка плиты (рис. 4.1,а, рис. 5.1) функцию прогиба (4.4) и подставляя в нее
значения начальных параметров w0 и М0
из (4.7), (4.8), получим после
соответствующих преобразований
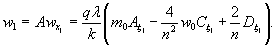
Вторая производная от функции прогиба 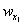
Безразмерные коэффициенты w0 и m0 определяются из графиков (рис. 4.2, 4.3).
Аппроксимирующая функция для второго участка
плиты (рис. 5.1) после подстановки в (4.5) значений M1, Q1 и
соответствующих преобразований примет вид
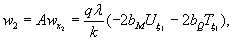
bM и bQ - безразмерные коэффициенты,
взятые из графиков (рис. 4.4, 4.5).
Вторая производная от функции прогиба равна
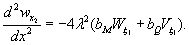
Из анализа расчета плиты с оптимальными
параметрами (глава 4, п.4.6) можно сделать вывод,
что при цилиндрическом изгибе ее, границы упругопластической зоны не выйдут за
пределы первого участка. Следовательно, можно проинтегрировать выражения,
стоящие в (5.18), и, подставив пределы,
определить их значения. С учетом всех преобразований, получим для
упругопластической зоны плиты
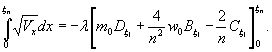
Для обоих участков упругой зоны плиты:

Для упругого основания по всей площади плиты
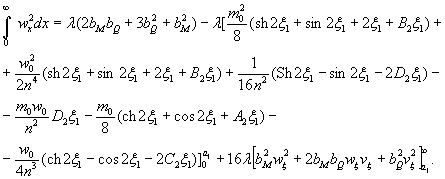
Подставляя полученные
значения интегралов в выражение (5.14), методом пробных
попыток устанавливаем, что границы упругопластической зоны аn изменяются в пределах 0,32-0,36, уменьшаясь по мере
увеличения ширины первого участка плиты a1.
На рис. 5.2 построены графики изменения
предельной нагрузки на ледяную ступенчатую плиту qn в зависимости от приведенной ширины первого участка плиты а1 и соотношения жесткостных
характеристик участков плиты n.
Дальнейшее увеличение нагрузки Рn приведет к образованию сквозной трещины в месте ее
приложения. Появление трещины приводит к весьма существенному изменению
статической схемы плиты. Для дальнейшего расчета плиты необходимо сначала найти
решение по измененной статической схеме в упругой стадии, а затем, приняв его в
качестве аппроксимирующего и применив уже известную методику, изложенную в
начале параграфа, можно определить значение разрушающей нагрузки.
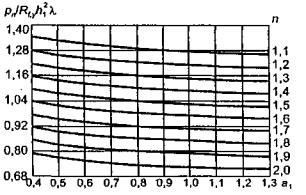
Рис. 5.2. Зависимость
предельной нагрузки на одноступенчатую плиту от параметров а1 и n
Действительно, следующая упругопластическая зона
появляется на некотором расстоянии от нагрузки Рn, в зоне действия максимального отрицательного момента. Появление
сквозной трещины в этой зоне практически приводит к
полному исчерпанию несущей способности ледяного слоя.
5.4. Расчет усиленного ледяного слоя при
цилиндрическом изгибе по предельным
состояниям без учета упругопластических деформаций
В ледяном слое, усиленном способом намораживания
дополнительной полосы, с учетом оптимальных параметров (п.4.6), от действия сосредоточенной
силы возникают одинаковые напряжения в точках О и O1 (рис. 4.6).
При загружении полученной в результате усиления
ступенчатой ледяной плиты равномерно распределенной по оси Y нагрузкой Р, будем иметь случай цилиндрического
изгиба. В этом случае существенно изменяется схема расчета, и в сечении под
нагрузкой напряжения имеют значительно большие величины, чем в сечении,
соответствующем точке О1 (рис. 4.6).
Будем увеличивать нагрузку Р до тех пор, пока в сечении под ней напряжения изгиба достигнут
предельного значения. При достаточно быстром загружении, когда пластические
деформации льда не успевают проявиться полностью, будем иметь случай хрупкого
разрушения льда, при котором в сечении под нагрузкой появится трещина.
Расчетная схема в этом случае существенно
изменяется. При дальнейшем расчете необходимо рассмотреть изгиб двух
полубесконечных плит, загруженных в месте их соединения (сечение О, в котором
образовалась трещина) нагрузкой Р.
Одним из граничных условий при этом будет равенство нулю изгибающего момента в
сечении с трещиной (сечение О).
Следовательно, к расчету принимается
полубесконечная ступенчатая плита, загруженная на кромке поперечной силой Q0=-P/2 и моментом M0=0.
Применяя решение (2.2) для первого участка
плиты 0≤ξ1≤a1
имеем при ξ1=a1
 (5.16)
(5.16)
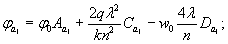
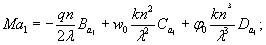
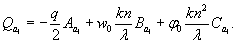
Второй участок представляет собой
полубесконечную плиту; загруженную в сечении O1 поперечной силой Q1 и изгибающим моментом М1. Перенося начало координат
в точку O1, получим при ξ=λx решение (4.5).
Неизвестные начальные параметры w0 и φ0 определим из условия равенства прогибов и углов
поворота на границе двух участков, в точке O1 (рис. 4.1).
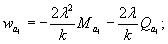 (5.17)
(5.17)
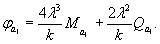
Подставляя значения  из (5.19) в (5.17),
получим
из (5.19) в (5.17),
получим
 (5.18)
(5.18)
где
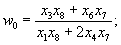 (5.19)
(5.19)
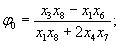
x1,2,3…6 - выражения (2.9)

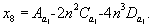
В частном случае, при λ1=λ, в точке О имеем
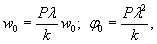
то есть получаем значения прогиба и угла
поворота для полубесконечной плиты постоянной толщины при цилиндрическом
изгибе.
На рис. 5.3, 5.4 даны графики, в которых
отражены зависимость начальных параметров w0
и φ0 от ширины
первого участка плиты а1,
и соотношения жесткостных характеристик участков плиты n. Полученное решение
можно использовать в качестве аппроксимирующего для дальнейшего расчета с
учетом упругопластических деформаций льда.
Имея значения начальных параметров, легко
определить неизвестные величины изгибающих моментов: для первого участка по
формуле (5.16), для второго - по
формуле (4.5).
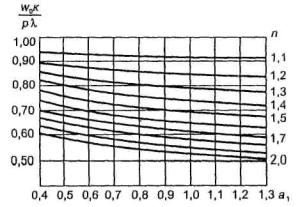
Рис. 5.3. Зависимость
начального параметра w0 от характеристик одноступенчатой плиты а1 и n
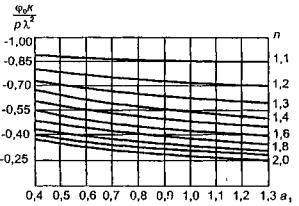
Рис. 5.4. Зависимость
начального параметра φ0
от характеристик одноступенчатой плиты а1
и n
Подставляя найденные величины начальных параметров
(5.18) в (5.16), получим значения
изгибающего момента М1 и
поперечной силы Q1 на
конце первого участка плиты
 (5.20)
(5.20)
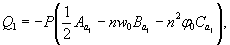
где w0
и φ0 - безразмерные
коэффициенты (5.19), взятые из графиков (рис. 5.3, 5.4).
На рис. 5.5, 5.6 даны графики, в которых
отражена зависимость М1 и Q1 от ширины первого участка
плиты а1 и соотношения
жесткостных характеристик участков плиты n.
Определяя максимальное значение изгибающего
момента и приравняв его предельному значению, найдем соответствующую данному
случаю величину внешней нагрузки О.
На рис. 5.7 даны графики (сплошными линиями), в
которых для ступенчатой ледяной плиты отражена зависимость значений разрушающей
нагрузки Р от величин а1 и n.
Приравняем значения максимальных изгибающих
моментов под силой Р (4.7) предельному моменту
при изгибе, и определим соответствующие данному случаю значения внешней
нагрузки Рn. При этом целесообразно
применить подстановку
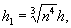
отражающую зависимость толщин участков плиты в
зависимости от соотношения жесткостных характеристик n.
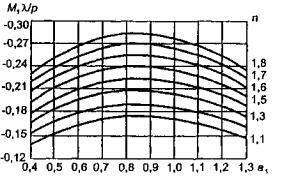
Рис. 5.5. Зависимость изгибающего момента
на конце первого участка от его ширины a1 и параметра n
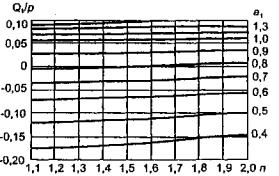
Рис. 5.6. Зависимость поперечной силы на
конце первого участка от его ширины а1,
и параметра n
На рис. 5.7 нанесены кривые (пунктирными
линиями), отражающие изменение нагрузки Р
в зависимости от приведенной ширины первого участка плиты a1 и
величины n.
Из этого графика видно, что при параметрах
плиты, соответствующих кривым, лежащим ниже пунктирной линии, появление первой
трещины ведет за собой разрушение плиты, так как без увеличения нагрузки
образуются вторые трещины (в зоне максимальных отрицательных моментов). И
наоборот, при параметрах плиты, соответствующих кривым, лежащим выше пунктирной
линии, с появлением первой трещины еще не исчерпывается полностью
грузоподъемность ледяного слоя. Сравнению подлежат кривые, соответствующие
одному и тому же значению параметра n.

Рис. 5.7. Зависимость предельной нагрузки
Рn от ширины первого участка плиты a1 и параметра n
Очевидно, несущая способность ледяной плиты
практически полностью исчерпывается с появлением второй трещины, которая
образуется в зоне действия максимального по величине
отрицательного изгибающего момента.
5.5. Расчет усиленного ледяного слоя при цилиндрическом изгибе по предельным состояниям с учетом
упругопластических деформаций
После появления трещины в сечении под нагрузкой Рn расчетная схема, как указывалось в п.5.4, существенно
изменяется.
Упругопластические деформации в данном случае
будут появляться на некотором расстоянии от точки приложения нагрузки, в зоне
действия максимальных отрицательных моментов (рис. 5.8).
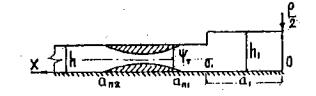
Рис. 5.8. Расчетная схема полубесконечной
ступенчатой плиты
Принимая в качестве аппроксимирующей для первого
участка плиты функцию прогиба (5.16) и подставляя в нее
значения начальных параметров w0
и φ0 из (5.18),
получим после соответствующих преобразований
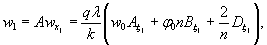 (5.21)
(5.21)
где w0
и φ0 - безразмерные
коэффициенты, взятые из графиков (рис. 5.3, 5.4).
Вторая производная от функции 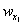
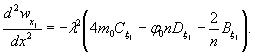
Аппроксимирующая функция для второго участка
плиты (рис. 5.8) после подстановки в (4.5) значений М1 и Q1 и соответствующих преобразований примет вид
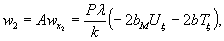 (5.22)
(5.22)
где bм и bа - безразмерные коэффициенты, взятые из графиков (рис. 5.5,
5.6).
Вторая производная от функции прогиба 
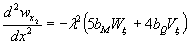
С учетом всех преобразований, получим для
упругопластической зоны плиты (рис. 5.8)
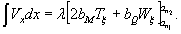
Для обоих участков упругой зоны плиты:

Для упругого основания по всей площади плиты

Подставляя полученные значения интегралов в
выражение (5.14) и определив границы
упругопластической зоны 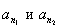 , получим из (5.13) значение разрушающей
нагрузки Р.
, получим из (5.13) значение разрушающей
нагрузки Р.
На рис. 5.9 построены графики, в которых
отражена зависимость величины разрушающей нагрузки от приведенной ширины
первого участка плиты а1 и
соотношения жесткостных характеристик участков плиты n.
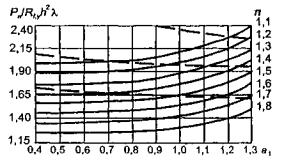
Рис. 5.9. Зависимость разрушающей
нагрузки от ширины первого участка а1
и параметра n
На этом же графике нанесены кривые (пунктирными
линями), взятые из рис. 5.2 с заменой величины h1, на h по зависимости 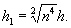 .
.
Из анализа этого графика
можно сделать вывод, что при параметрах плиты, соответствующих кривым, лежащим
ниже пунктирной линии, появление первой трещины в зоне упругопластических
деформаций под нагрузкой, приводит к разрушению плиты, так как при изменившейся
расчетной схеме, ледяная плита не выдерживает находящуюся на ней нагрузку, и
полностью проявляются упругопластические деформации в зоне максимальных
отрицательных моментов. И наоборот, при параметрах плиты, соответствующих
кривым, лежащим выше пунктирной линии, появление первой трещины еще не приводит
к исчерпанию несущей способности усиленного ледяного слоя. Сравнению подлежат кривые, соответствующие одному и тому же
значению параметра n.
5.6. Расчет усиленного ледяного слоя на сосредоточенную нагрузку по предельным состояниям без учета
упругопластических деформаций
При загружении усиленного ледяного слоя
сосредоточенной нагрузкой (рис. 4.6), максимальные
изгибающие моменты возникают в сечениях, расположенных вдоль оси X. Приравняв значения максимальных
изгибающих моментов предельному моменту при изгибе, получим соответствующие
значения внешней нагрузки, при которых в ледяном слое появляются трещины.
Дальнейшее незначительное увеличение нагрузки
или увеличение времени нахождения нагрузки на ледяном слое приводит к
распространению сквозной трещины вдоль оси X
на значительное расстояние от места приложения нагрузки. В результате расчетная
схема ледяного слоя изменяется. Трещина разделяет ледяной слон на две
полуплоскости, каждая из которых загружена половиной нагрузки, действующей на
ледяной покров. При этом рассматривается случай кратковременного действия
нагрузки, когда пластические деформации льда еще не успевают проявиться.
С учетом работы [13], представим функцию
прогиба ступенчатой полубесконечной ледяной плиты, удовлетворяющую уравнению (3.3) и граничным условиям
задачи (изгибающие моменты Мη
на кромке (рис. 4.6) равны нулю, и нулевые
условия в бесконечности), в следующем виде:
при 0<ξ1<a1
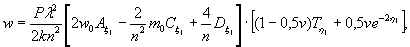 (5.23)
(5.23)
где w0 и m0 - безразмерные коэффициенты (4.8).
Применяя зависимости (3.4) (3.5) для функции прогиба
(5.23), получим

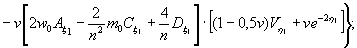 (5.24)
(5.24)
 (5.25)
(5.25)
Так как изгибающие моменты Мη на кромке равны нулю, то грузоподъемность
ступенчатой ледяной полуплоскости будет зависеть от величины изгибающего
момента Мξ.
На рис. 5.10, 5.11 построены графики изменения
значений изгибающих моментов в сечениях под силой М0(ξ) и в точке O1 M1(ξ) в зависимости от приведенной ширины первого
участка плиты а1 и
характеристики n.
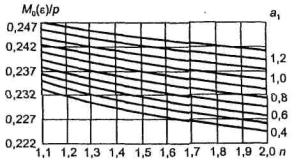
Рис. 5.10. Зависимость изгибающего
момента под силой от ширины первого участка a1
и параметра n
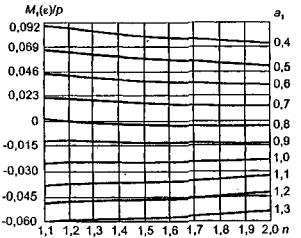
Рис. 5.11. Зависимость изгибающего
момента в конце первого участка от его ширины a1 и параметра n
Сравнение величин изгибающих моментов в сечениях
под силой (рис. 4.7, 5.10) и в сечении О (рис. 4.8, 5.11) показывает, что
грузоподъемность полу бесконечной ступенчатой ледяной плиты при загружении ее
нагрузкой P/2 меньше грузоподъемности
бесконечной усиленной ледяной плиты при загружении нагрузкой Р. Это означает, что в сечении под
нагрузкой Р/2 в ледяной полуплоскости
появится сквозная трещина вдоль оси η.
В результате расчетная схема еще раз изменится. Будем иметь четыре ступенчатые
четверть бесконечные плиты, загруженные в углах (в точке О) нагрузкой Р/4 каждая (рис. 4.6).
Граничные условия задачи следующие:
Y=0; My=0; (5.26)
Х=0; МХ=0.
С учетом работы [23] представим функцию
прогиба ступенчатой четверть бесконечной плиты, удовлетворяющую уравнению (3.3) и граничным условиям
(5.26) в следующем виде:
при 0<ξ1<a1
 (5.27)
(5.27)
где w0
и φ0 - безразмерные
коэффициенты (5.19).
Применяя зависимости (3.4), (3.5) для функции прогиба
(5.27), получим
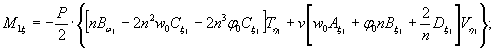 (5.28)
(5.28)
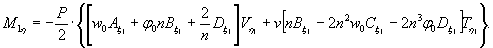 (5.29)
(5.29)
Грузоподъемность четверть бесконечной
ступенчатой ледяной плиты будет зависеть от величины изгибающего момента Мξ, так как вдоль оси X изменяется высота ледяного слоя.
На рис. 5.12 построены графики изменения
значений изгибающих моментов Мξ
в зависимости от приведенной ширины первого участка плиты а1 и характеристики n.

Рис. 5.12. Зависимость изгибающего
момента Мξ от ширины
первого участка а1 и
параметра n
Сравнение величин изгибающих моментов для
четвертьбесконечной плиты с изгибающими моментами в полубесконечной плите
показывает, что в большинстве случаев грузоподъемность первой меньше второй,
или в отдельных случаях она равна для обеих плит.
На основании проведенного анализа можно сделать
вывод, что расчет усиленного ледяного слоя следует вести таким образом, чтобы в
процессе эксплуатации не появлялись силовые трещины в ледяном покрове и не
изменялась его расчетная схема. В случае ослабления усиленного ледяного слоя
температурными или силовыми сквозными трещинами, следует учитывать уменьшение грузоподъемности и рассчитывать ее по одной из
указанных выше схем.
5.7. Расчет усиленного ледяного слоя на сосредоточенную нагрузку с учетом
упругопластических деформаций
В предыдущей главе (п.4.6-4.9) рассматривались
вопросы расчета усиленного ледяного слоя на сосредоточенную и распределенную по
окружности нагрузку, в предположении, что лед как материал работает в упругой
стадия.
Полученные
решения можно использовать в качестве аппроксимирующих при расчете усиленного
ледяного слоя с учетом упругопластических деформаций льда.
В отличие от ледяного покрова постоянной
толщины, в усиленном ледяном слое при увеличении нагрузки область
упругопластических деформаций будет появляться не только в месте приложения
нагрузки, но и около точки О1 (рис. 4.6), на границе двух
участков с разной толщиной льда.
Такая схема распространения зон
упругопластических деформаций будет иметь место при расчете усиленного ледяного
слоя как ступенчатой плиты с оптимальными параметрами. В этом случае, как
известно, напряжения изгиба в точках О и O1 равны между собой.
Поэтому по мере увеличения внешней нагрузки, вокруг точки О будет образовываться
зона упругопластических деформаций, имеющая в плане вид эллипса, а около точки
O1 эта зона будет иметь вид полуэллипса, расположенного на участке
плиты с меньшей толщиной (рис. 4.6).
Так как задача является симметричной
относительно оси Y, то таких
полуэллипсов будет два, слева и справа от места приложения нагрузки.
При расчете ледяного слоя по схеме
двухступенчатой плиты с оптимальными параметрами напряжения изгиба в точках О,
О1 и О2 равны между собой (рис. 4.1, в). Поэтому по мере
увеличения внешней нагрузки, как и прежде, вокруг точки О будет образовываться
зона упругопластических деформаций, имеющая в плане вид эллипса, а около точек
O1 и О2 эти зоны будут иметь вид полуэллипсов,
расположенных на соответственных участках плиты с толщиной h1 и h (рис.
4.18).
Применяя способ расчета плит переменной толщины
с учетом упругопластических деформаций, изложенный в п.5.2, из уравнения (5.12) можно определить
границы упругопластических зон. А имея границы упругопластических зон, из
выражения (5.10) можно определить
величину предельной нагрузки на ступенчатую ледяную плиту.
В работе [17] приведен расчет
ледяного слоя постоянной толщины, выполненный по методике, изложенной в п.5.2.
Применяя данные этого расчета, можно заранее
определить верхнюю и нижнюю границы, между которыми будет находиться величина
предельной нагрузки на ступенчатую ледяную плиту.
Для одноступенчатой ледяной плиты величина
предельной нагрузки будет больше, чем для бесконечной плиты с постоянной
толщиной h (рис. 4.1, а,б), но меньше, чем
для бесконечной плиты с постоянной толщиной h1.
Уменьшение нагрузки приблизительно составит 10-15%, если предположить, что
соотношение между грузоподъемностью ступенчатого ледяного слоя и ледяного
покрова постоянной толщины, определенное из расчета в упругой стадии, не
изменится и в упругопластической стадии работы льда под нагрузкой.
Для двухступенчатой ледяной плиты величина
предельной нагрузки соответственно будет больше, чем для бесконечной плиты с
постоянной толщиной h1 (рис. 4.1, в), но меньше, чем для
бесконечной плиты с постоянной толщиной h2.
При расчете одноступенчатой плиты по предельному
состоянию воспользуемся способом, изложенным в п.5.2. Выражение для
определения предельной силы Рn (5.10), соответствующее
первому предельному состоянию, при которой в плите появляются первые радиальные
трещины, будет для данного случая иметь вид
 (5.30)
(5.30)
и уравнение для определения границы
упругопластической (5.12) зоны, после
необходимых преобразований, примет вид
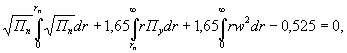 (5.31)
(5.31)
если примем в качестве аппроксимирующей функцию
прогиба (4.28), (4.29).
Запишем среднюю квадратичную от функции прогиба
в упругопластической зоне в виде
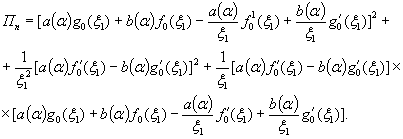 (5.32)
(5.32)
Средняя квадратичная от функции прогиба в
упругой зоне плиты будет
при 0<ξ1<ξy
 (5.33)
(5.33)
при ξy<ξ<∞
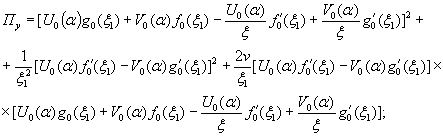 (5.34)
(5.34)
Квадрат функции прогиба плиты имеет вид:
при 0<ξ1<ξy,
w2=[a(α)f0(ξ1)-b(α)g0(ξ1)]2; (5.35)
при ξy<ξ<∞
w2=[U0(α)f0(ξ)-V0(α)g0(ξ)]2; (5.36)
Способом пробных подстановок, подставляя
вычисленные значения интегралов выражений (5.32)-(5.36) в (5.31), определим
границы упругопластических зон в ступенчатой плите, а затем, подставив эти
границы интегрирования в выражение (5.30), получим величину предельной нагрузки
Рn.
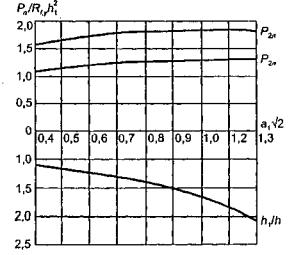
Рис. 5.13. Зависимость
предельной нагрузки от ширины первого участка a1 и параметра n
На рис. 5.15 построен график
изменения предельной нагрузки Рn в зависимости от ширины
утолщенного участка плиты, отношения толщин участков плиты h1/h и параметра n.
Появление сквозных радиальных трещин в плите под
силой Рn приводит к
существенному изменению расчетной схемы. Дальнейшее увеличение нагрузки
приведет к образованию кольцевых трещин, соответствующих второму предельному
состоянию, после чего несущая способность: плиты будет практически исчерпана.
Решая задачу в прямоугольных осях координат,
представим выражение (5.10) для определения
разрушающей силы Рn в
виде
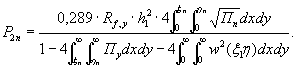 (5.37)
(5.37)
Уравнение для определения границы
упругопластической (5.12) зоны, после
необходимых преобразований примет вид
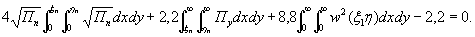 (5.38)
(5.38)
Примем в качестве аппроксимирующей функцию
прогиба (5.22) (5.27), которая в данном
случае будет иметь вид при 0<ξ1<a1
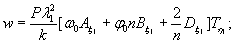 (5.39)
(5.39)
при a1<ξ<∞
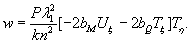 (5.40)
(5.40)
Средняя квадратичная величина от функции прогиба
(5.39) в упруго-пластической зоне примет вид
при 0<ξ1<a1
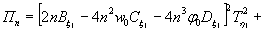
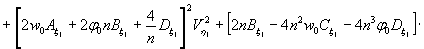

 (5.41)
(5.41)
при a1<ξ<∞
 (5.42)
(5.42)
Средняя квадратичная от функции прогиба в
упругой зоне плиты будет равна
при 0<ξ1<a1
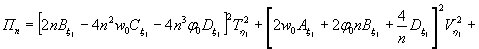
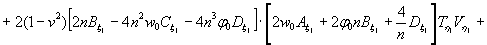
 (5.43)
(5.43)
при a1<ξ<∞
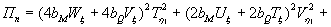

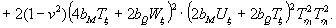 (5.44)
(5.44)
Квадрат функции прогиба плиты имеет вид
при 0<ξ1<a1
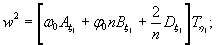 (5.45)
(5.45)
При a1<ξ<∞
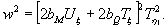 (5.46)
(5.46)
Способом пробных подстановок, подставляя
вычисленные значения интегралов выражений (5.41)-(5.46) в (5.38), найдем границы
упруго-пластических зон в ступенчатой плите, а затем, подставив эти границы
интегрирования и соответствующие им значения интегралов в (5.37), получим величину
разрушающей нагрузки Р2n.
На рис. 5.13 построен график
изменения предельной нагрузки Р1n и нагрузки Р2n в зависимости от ширины
утолщенного участка плиты, соотношения толщин участков плиты и параметра n.
Для оценки полученных результатов приведем
решение для бесконечной плиты постоянной толщины h1.
В качестве аппроксимирующей функции прогиба при
расчете по первому предельному состоянию примем решение Б.Г. Коренева [73], которое в данном
случае будет иметь вид
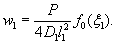 (5.47)
(5.47)
Средняя квадратичная от функции прогиба (5.47)
(рис. 5.14) в упругопластической зоне плиты имеет вид
 (5.48)
(5.48)
Средняя квадратичная от этой же функции прогиба
в чисто упругой зоне плиты будет
 (5.49)
(5.49)
Квадрат функции прогиба плиты имеет вид
w2(ξ1)=f02(ξ1). (5.50)
Равенство (5.31) выполняется ξ1n=0,62, когда входящие в
него величины имеют следующие значения:
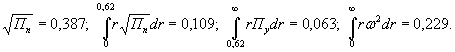
Подставляя эти значения интегралов в выражение
(5.30), получим
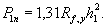 (5.51)
(5.51)
На рис. 5.14 построены графики аппроксимирующих
функций прогибов плиты постоянной толщины, принятых к расчету по первому (w1) и второму (w2) предельным состояниям.
При расчете по второму предельному состоянию
представим аппроксимирующую функцию прогиба ослабленной радиальными сквозными
трещинами плиты в виде [23] (рис. 5.14)
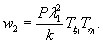 (5.52)
(5.52)
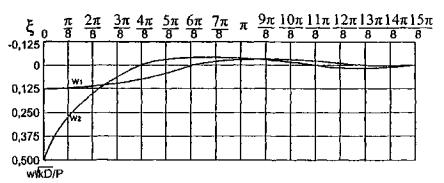
Рис. 5.14. Эпюры прогибов плиты w1, при первом и w2 при втором предельных состояниях
Безразмерную ширину утолщенного участка а1 необходимо умножить на  , так как характеристика плиты l1 в
, так как характеристика плиты l1 в  раза больше, чем λ1.
раза больше, чем λ1.
Решение (5.52) записано в прямоугольной системе
осей координат с помощью гиперболо-тригонометрических функций (3.13).
Средняя квадратичная от функции прогиба в
упругопластической зоне плиты имеет вид
 (5.53)
(5.53)
Средняя квадратичная этой же функции прогиба в
упругой зоне плиты будет
 (5.54)
(5.54)
Квадрат функции прогиба плиты будет
 (5.55)
(5.55)
Равенство (5.38) выполняется при ξn=ηn=0,98, когда входящие в него величины имеют следующие
значения:

Подставляя эти значения интегралов в выражение (5.37), получим величину
разрушающей нагрузки
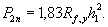 (5.56)
(5.56)
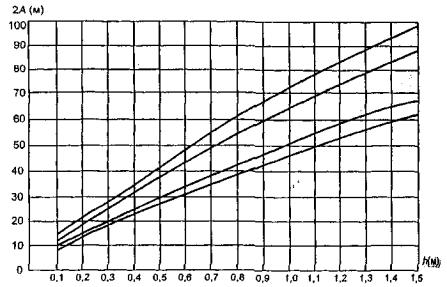
Рис. 5.15. Зависимость
ширины замораживаемого слоя 2A
от толщины ледяного покрова h:
1 - при характеристике λ с
модулем упругости льда E=6·104 кгс/см2;
2 - то же для Е=9·104
кгс/см2; 3 - при характеристике l,
с модулем упругости льда Е=6·104
кгс/см2; 4 - то же для Е=9·104
кгс/см2
Сравнивая выражения (5.51) и (5.56), можно сделать
вывод, что шик та после появления первых радиальных трещин имеет еще запас
грузоподъемности, как минимум равный 1,4.
Сравнение результатов расчета ступенчатой плиты
с плитой постоянной толщины показывает, что при безразмерной ширине утолщенного
участка a1≥1,5
грузоподъемность их становится практически одинаковой,
тогда максимальная ширина намороженной полосы льда
(рис.
4.1) равна 2А м.
Часть
третья
РАСЧЕТ
ЛЕДЯНОГО ПОКРОВА НА ДЕЙСТВИЕ ДИНАМИЧЕСКИХ НАГРУЗОК
ГЛАВА 6. ДИНАМИЧЕСКИЙ РАСЧЕТ ГИБКИХ ЛЕДОВЫХ ПЛИТ, ЛЕЖАЩИХ НА УПРУГОМ
ОСНОВАНИИ. ДИНАМИЧЕСКИЕ НАГРУЗКИ ОТ ДВИЖУЩЕГОСЯ АВТОМОБИЛЯ
ПРИ ПРОЕЗДЕ ПО НЕРОВНОСТЯМ ЛЕДОВЫХ ПЕРЕПРАВ
6.1.
Общие положения
Ледяной покров, работающий в качестве плиты на
упругом основании, при определенных режимах эксплуатации, должен рассчитываться
на действие динамических нагрузок, которые можно разделить на следующие три
группы [77]:
1) нагрузки, вызванные работой машин
периодического действия, установленных на льду;
2) подвижные нагрузки ледовых переправ;
3) нагрузки импульсивного и ударного характера,
возникающие при опускании грузов на ледовые площадки, при работе установленных
на них машин ударного действия и других.
В связи с этим рассмотрим расчет ледовых плит на
воздействие некоторых динамических нагрузок.
6.1.1. Расчет плит на упругом основании на
воздействие вибрационной нагрузки от работающих механизмов
Дифференциальное уравнение изгиба плиты, без
учета затухания колебаний, имеет вид
 (6.1)
(6.1)
где
w=w(x,y)sinωt. (6.2)
Функция w(x,y) удовлетворяет уравнению
DΔΔw + (k-mω2)ω = q(x,y). (6.3)
Это уравнение не отличается от уравнения изгиба
плиты при действии статической нагрузки, если
k>mω2, (6.4)
где m - масса плиты, приходящаяся на единицу площади.
Практически соотношение (6.4) обычно
выполняется, и в этом случае нужно во всех расчетных формулах для винклерова
основания, приведенных во второй части, заменить k величиной k-mω2.
Предполагается, что действующую на плиту внешнюю
нагрузку можно представить в виде
q(x,y,t)=q(x,y)sinωt, (6.5)
где ω
- круговая частота колебаний; t - время;
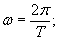
где Т
- период колебания нагрузки.
Частота колебаний нагрузки в герцах равна числу
колебаний в секунду
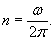
6.1.2. Расчет плит на воздействие подвижных
нагрузок
Если груз движется по плите с постоянной
скоростью, то расчетные значения усилий и прогибов отличаются от тех, которые
соответствуют случаю приложения неподвижной нагрузки. Однако методика
проведения: расчетов при этом существенно не меняется [77]. Как показано в работе [77], все задачи о движении
груза по неограниченной плите эквивалентны задачам о статическом действии
нагрузки, если считать, что на плиту действуют дополнительные равномерно
распределенные сжимающие силы, направленные по той же прямой, по которой
направлена скорость. Интенсивность этих сил равна mV2,
где m - масса, отнесенная к
единице площади, а V - скорость
движения груза.
Дифференциальное уравнение изгиба плиты (при
отсутствии затухания) имеет вид
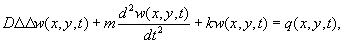 (6.6)
(6.6)
где w(x,y,t)
- прогиб плиты;
q(x,y,t) - интенсивность внешней нагрузки;
t - время.
Применяя подстановку ξ=x-vt, целесообразно перейти к новой системе координат wξy, движущейся со скоростью V относительно первоначальной системы
координат w х у. В новых координатах
уравнение (6.6) принимает вид
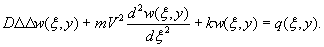 (6.7)
(6.7)
Положив q(ξ,y)=0,
получаем однородное уравнение, решение которого должно удовлетворять граничным
условиям задачи.
6.1.3. Некоторые особенности динамического
расчета плит
Основной особенностью динамического расчета,
отличающей его от статического, является необходимость учета инерционных сил,
возникающих при колебаниях. Применительно к задачам о расчете плит, лежащих на
упругом основании, следует различать инерционные силы, возникающие при
перемещении плиты, при перемещении основания, а также инерцию действующего на
плиту груза.
Учет инерции плиты при модели Винклера и модели
с двумя упругими характеристиками является сравнительно простым, однако понятие
об учете инерции основания здесь является крайне условным. В этом случае
имеется только одна возможность - присоединить распределенную массу,
учитывающую приближенно инерцию того слоя основания, который принимает участие
в колебаниях; при этом можно еще ввести фиктивное затухание, что должно
преследовать ту же цель [77].
Способ учета массы действующего груза при
динамическом расчете плит на упругом основании на воздействия вибрационных и
подвижных нагрузок изложен в работах [14, 22].
6.1.4. Учет сил внутреннего неупругого
сопротивления
С точки зрения приложений гипотезы Е.С. Сорокина
[153], важное значение имеет
то обстоятельство, что для всех материалов, в том числе и для льда, как
показано в главе 2 п. 2.5, при напряжениях, не
превышающих допускаемые, величина 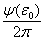 мала по сравнению с
1.
мала по сравнению с
1.
Применительно для плит на упругом основании
можно представить частоту свободных колебаний в виде
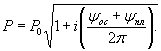
После необходимых преобразований, извлекая
корень, получим
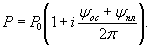
Уравнение перемещений Y системы, аналогично тому, как это сделано в работе [153], можно представить в
виде
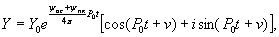 (6.8)
(6.8)
где Y0
- начальное отклонение системы;
v - угол сдвига фаз;
Р0 - частота свободных колебаний.
Из уравнения (6.8) видно, что свободные
колебания системы с учетом сил внутреннего неупругого сопротивления являются
затухающими и имеют вид, изображенный на рис. 2.2.
6.1.5. Метод решения задач динамики плит на
упругом основании с учетом сил внутреннего неупругого сопротивления
Применяем комплексную форму записи гипотезы Е.С.
Сорокина [153], согласно которой, силы
внутреннего сопротивления записываются в следующем виде:
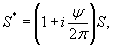
где S*
- полная внутренняя сила;
S - упругая внутренняя сила;
ψ - коэффициент поглощения энергии колебаний.
Решение различных практических задач на
основании выражения S* производится с учетом комплексного параметра 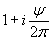 , характеризующего затухание.
, характеризующего затухание.
Таким образом, применительно к задачам динамики
плит на упругом основании, учет внутреннего неупругого сопротивления сводится к
замене упругих сил DΔΔw и k w на обобщенные силы
 (6.9)
(6.9)
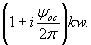
Поскольку решение дифференциальных уравнений (6.3), (6.7) с учетом обобщенных
сил (6.9) получается в комплексной форме, будем иметь в виду что действующим на
плиту действительным силам соответствует действие тельная часть комплексного
решения, которое необходимо получить.
В результате такого подхода к решению
дифференциальных уравнений мнимость раскрывается лишь в окончательных решениях,
где производится замена действительных значений D и k на обобщенные величины (6.9).
Следовательно, для того чтобы довести решение
конкретной задачи динамики плиты на упругом основании до численного результата,
необходимо иметь значения коэффициентов поглощения
энергии колебаний ψ для
материалов плиты и упругого основания.
6.2. Возмущающее воздействие неровностей дороги и
режимы движения грузовых автомобилей
При длительной или интенсивной эксплуатации на
временных зимних дорогах, устраиваемых на ледяном покрове рек и водохранилищ,
появляются значительные неровности, которые необходимо учитывать при расчете
грузоподъемности ледовых переправ. Объективная оценка ровности поверхности
дорог должна производиться с обязательным учетом влияния неровностей на
колебания автомобиля.
Динамическое воздействие автомобиля на дорогу
определяется геометрическими размерами, формой и характером чередования
неровностей.
В зависимости от длины, неровности дорог условно
разделяют на четыре группы [187]:
1. Импульсные - короткие неровности длиной до
0,3 м, воздействие которых на подвеску автомобиля аналогично приложению
импульсов вертикальной силы (ударов) к колесам в месте их контакта с дорогой.
2. Выбоины - неровности длиной 0,3-6,0 м,
вызывающие интенсивные колебания подрессоренных и неподрессоренных масс
автомобиля. Различают короткие (0,3-1,0 м) и длинные (1,0-6,0) выбоины.
Воздействие коротких выбоин при эксплуатационных скоростях движения приводит к
возникновению высокочастотных колебаний подрессоренной части автомобиля,
которые совершаются с незначительными амплитудами при высоких значениях
вертикальных ускорений. Длинные выбоины вызывают наиболее интенсивные
колебания, при которых вертикальные перемещения подрессоренной части машины
могут превышать высоты неровностей. Деление выбоины на короткие и длинные
является весьма условным, так как характер их воздействия на автомобиль (а
следовательно, и автомобиля на дорогу) во многом определяются скоростью
движения последнего.
3. Ухабы - неровности длиной 6,0-25 м.
Подрессоренная часть при движении по таким неровностям испытывает
преимущественно низкочастотные колебания, интенсивность которых возрастает по
мере повышения скорости движения.
4. Уклоны - неровности длиной свыше 25 м. Они не
оказывают существенного влияния на колебания автомобиля.
Контур профиля неровностей может быть простым,
имеющим определенную геометрическую форму (синусоидальную, трапецеидальную,
треугольную и т.п.) или сложным, описание которого не может выражаться простыми
аналитическими формулами.
Различают следующие закономерности в размещении
неровностей по длине участка на поверхности дороги:
- периодически чередующиеся неровности
одинаковых размеров и формы;
- обособленные неровности, удаленные друг от
друга на сравнительно большие расстояния;
- случайный микропрофиль - незакономерное
чередование неровностей различных размеров и формы.
Обобщенную качественную оценку неровности
автомобильных дорог в практике эксплуатации удобно производить путем условного
разделения дорог на отдельные группы, из которых следует выделить
малоизношенные дороги, на которых автомобили могут двигаться со средними
скоростями Vc,
превышающими 0,7 VM (VM-
максимальная скорость по технической характеристике машины).
Такая условная классификация автомобильных дорог
по степени ровности определяется числом, размерами и характером чередования
неровностей на поверхности дороги.
Типичными для эксплуатации грузовых автомобилей
общего назначения можно считать малоизношенные дороги, на которых среднеквадратичные
глубины выбоин не превышают 1,5 см, а максимальные - 10 см.
Типичными для эксплуатации грузовых автомобилей
повышенной проходимости можно считать дороги, среднеквадратичная глубина выбоин
на поверхности которых не превышает 3 см, максимальная - 20 см.
При расчетах плавности хода возникает
необходимость аналитического или графического представления функции
микропрофиля дороги a=f(l), отображающей изменение высоты неровностей а по длине l дорожного участка.
При анализе подрессоривания и плавности хода
автомобилей в практике наибольшее распространение получили расчеты для трех
характерных случаев движения: через обособленные неровности, по непрерывно
чередующимся периодическим неровностям и по дорогам со случайным микропрофилем.
Следует отметить, что наиболее неблагоприятным с
точки зрения возмущения колебаний будет режим движения с равномерной скоростью.
Обычно при разгоне или замедлении интенсивность колебаний автомобиля
уменьшается. Это объясняется отчасти тем, что возникающая при неравномерном
движении продольная горизонтальная составляющая силы инерции создает
дополнительную стабилизацию подрессоренной массы. В дальнейшем будет показано,
как учесть силу инерции в расчете ледяного слоя на динамическое воздействие
подвижных нагрузок.
Интенсивность колебаний автомобиля на неровных
участках дороги будет существенно изменяться в зависимости от скорости V равномерного движения. Влияние
скорости на колебания автомобиля определяется изменением возмущающей функции a(t) высот неровностей микропрофиля в зависимости
от времени t. При рассмотрении
случаев равномерного движения по дорожному участку длиной l0=2l с постоянной скоростью
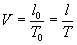 (6.10)
(6.10)
график возмущающей функции a(t) за время T0=2T
может быть получен пропорциональным изменением масштаба аргумента функции
микропрофиля а(l).
Следовательно, для получения аналитического
выражения функции a(t) необходимо подставить в
аналитическое выражение функции микропрофиля а(l) значение аргумента, выраженного равенством
l = vt. (6.11)
Для обособленной неровности характерной
синусоидальной формы, имеющей максимальную высоту а0 и максимальную длину l0,
аналитическое выражение можно представить в виде
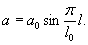 (6.12)
(6.12)
Подставляя значение l в формулу (6.12),
получим следующее аналитическое выражение для гармонических неровностей
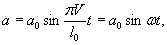 (6.13)
(6.13)
где ω
- частота изменения возмущающих сил
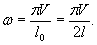 (6.14)
(6.14)
Таким образом, зная характеристики функции
микропрофиля, сравнительно просто определить соответствующие характеристики возмущающей функции для случая равномерного движения по
дорожному участку.
6.3. Определение параметров свободных колебаний подрессоренных и
неподрессоренных масс грузовых автомобилей
При проезде автомобиля через обособленные
импульсные неровности подрессорная масса совершает сложные двухкомпонентные
колебания, включающие пару составляющих колебаний синусоидальной формы с
затуханием низкой и высокой собственных частот.
Неподрессоренная масса автомобиля совершает при
этом высокочастотные колебания. Собственные колебания ледяного слоя относятся к
разряду низкочастотных (глава 7 п. 7.2, 7.3), поэтому в дальнейшем
нас будут интересовать только низкочастотные колебания подрессоренной массы,
так как при движении автомобиля по ледяному слою они будут оказывать на него
наибольшее динамическое воздействие.
Частота собственных низкочастотных колебаний
подрессоренной массы автомобиля равна [188]
 (6.15)
(6.15)
где Ср
- жесткость рессор;
Сш - радиальная жесткость шин;
М - подрессоренная масса автомобиля.
Результаты расчетного анализа указывают на то,
что для обеспечения требуемой плавности хода собственная частота колебаний
подрессоренной части автомобилей должна лежать в пределах 70-100 кол/мин
(6,7-9,6 Гц).
Определение частоты колебаний подрессоренной
массы для автомобилей общего назначения и высокой проходимости дано в
приложении 10 [12]. Как видно из расчетов и сравнения их с опытными данными,
полученными в результате стендовых испытаний [187], собственная частота
колебаний груженых автомобилей составляет 10-16 Гц, а частота колебаний-автомобилей
без груза равна 11-20 Гц. Так как наиболее характерным для работы грузовых
автомобилей является режим работы с полной нагрузкой, то следует принимать в
расчетах частоту свободных колебаний равной 10-16 Гц, что приблизительно в 1,5
раза больше значений частоты колебаний, требуемой для
обеспечения плавности хода автомобиля.
6.4.
Вынужденные колебания автомобиля при движении по неровностям
Специфической особенностью грузовых автомобилей
является большой относительный вес неподрессоренной массы [187]. Практика эксплуатации
и испытаний автомобилей указывает на то, что увеличение неподрессоренной массы
существенно ухудшает плавность хода. Это ухудшение на неровных дорогах с
выбоинами проявляется тем значительнее, чем больше скорость движения
автомобиля. При малых скоростях движения автомобиля на таких дорогах
вертикальные перемещения его подрессоренной и неподрессоренной масс совершаются
синхронно. При этом деформации подвески и шины имеют величину, обратно
пропорциональную жесткости.
Следовательно, при малых скоростях движения
автомобиля подрессоренная масса как бы испытывает колебания на пружинах
приведенной жесткости С, с
отсутствующей неподрессоренной массой. При таких колебаниях подрессоренная
масса совершает вертикальные перемещения преимущественно с частотой 1-3 Гц,
примерно соответствующей собственной частоте колебаний подрессоренной массы на
рессорах и шинах.
При дальнейшем увеличении скорости движения
синхронность колебаний ее подрессоренной и неподрессоренной масс нарушается.
Подрессоренная масса начинает испытывать высокочастотные (7-15 Гц) толчки,
интенсивность которых возрастает по мере увеличения скорости движения.
Интенсивность высокочастотных толчков достигает максимальных значений при
вспомогательном резонансе, когда частота изменения возмущающих сил будет
примерно соответствовать собственной частоте колебаний неподрессоренной массы
на рессорах и шинах. Подрессоренная масса автомобиля при этом испытывает
воздействие высокочастотных вертикальных толчков, которые характеризуются
большими значениями вертикальных ускорений при малых амплитудах вертикальных
перемещений (до 3-5 мм). При дальнейшем увеличении скорости движения амплитуды
вертикальных ускорений и перемещений подрессоренной и неподрессоренной масс
уменьшаются, а энергия воздействия неровностей дороги на колеса во все
возрастающей степени поглощается шинами.
В других существенно отличных дорожных условиях
характер колебаний может быть иным. Так, при движении автомобиля по дороге с
длинными (10-25 м) неровностями высокочастотные резонансные колебания
подрессоренной массы при эксплуатационных, скоростях не будут наблюдаться, так
как для их возмущения потребовалось бы увеличить скорость выше максимальной.
При работе автомобиля на малоизношенной ледяной
дороге без выбоин с короткими неровностями (типа булыжной мостовой) его
подрессоренная масса испытывает высокочастотные колебания при всех эксплуатационных
скоростях движения; интенсивность колебаний уменьшается по мере увеличения
скорости движения (зарезонансный режим колебаний).
На ровных гладких дорогах часто наблюдаются
вибрации (1-30 Гц) корпуса, возникающие вследствие блокировки рессор силами внутреннего
трения. При этом воздействие незначительных неровностей и шероховатостей
передается через шину на блокированные вместе подрессоренную и неподрессоренную
массы.
Таким образом, колебания автомобиля в реальных
дорожных условиях весьма разнообразны, и подрессоренная масса может испытывать
низкочастотные (1-3 Гц), высокочастотное (7-15 Гц), вибрационные (15-30 Гц)
колебания и сложные толчки.
При малых скоростях движения, когда колебания
подрессоренной массы совершаются с низкой частотой, близкой к ее собственной
частоте, отрицательное влияние величины неподрессоренной массы на плавность
хода автомобиля не проявляется.
Вредное влияние изменения величины
неподрессоренной массы на плавность хода автомобиля наиболее отчетливо
проявляется на расчетных характеристиках интенсивности колебаний автомобилей со
случайным микропрофилем.
В заключение отметим, что при расчете ледовых
дорог на динамические воздействия движущихся автомобилей особенно необходимо
исследовать влияние вынужденных колебаний
подрессоренной массы на ледяной слой.
7.1. Состояние вопроса и цели
исследования покрова
В общем случае приложение возмущающей силы Р sin ωt вызывает как вынужденные
колебания системы с угловой частотой ω,
так и свободные колебания с частотой р.
Таким образом, действительное движение системы является результатом сложения
двух простых гармонических колебаний, имеющих в общем случае различные
амплитуды, частоты и фазы. В результате получается весьма сложное движение.
Однако вследствие демпфирования, после короткого промежутка времени, свободные
колебания исчезают и остается только установившийся процесс вынужденных
колебаний, постоянно поддерживаемый действием возмущающей силы. Начальный этап сложного
движения системы, то есть первые несколько циклов, в течение которых в движении
участвуют свободные колебания, относится к переходному режиму.
В случае, когда частота возмущающей силы весьма
близка к частоте свободных колебаний системы, то есть ω≈р, возникают колебания с переменной амплитудой. Такие
колебания называют биениями.
И, наконец, для предельного случая ω=р амплитуда колебаний
неограниченно возрастает со временем. Это означает, что даже при расчете
колебаний системы без учета затухания их, когда амплитуда колебаний
неограниченно возрастает, необходимо определенное время для нарастания больших
амплитуд. Как показано С.П. Тимошенко [156], при работе
колеблющихся систем в зарезонансной области не возникает больших трудностей при
прохождении через резонанс, если это занимает незначительный промежуток
времени.
Если для какой-либо колебательной системы
установлен дорезонансный режим, то, как показывают эксперименты, становится
трудным переход через резонанс, и на это требуется больше времени.
Вводимая с этой целью дополнительная мощность
вместо разгона системы попросту расходуется на увеличение амплитуды колебаний.
Это (относится, в частности, и к случаю перехода через критическую скорость
движения (колебания ледяного слоя под действием движущихся грузов будут
рассмотрены ниже).
Динамический коэффициент становится вновь
конечным, когда частота возмущающей силы становится больше, чем частота
свободных колебаний. Его абсолютная величина уменьшается с возрастанием ω и приближается к нулю при весьма
больших значениях этого отношения. Это означает, что если на колеблющееся тело
действует гармоническая сила высокой частоты, то вызываемые его колебания имеют
малую амплитуду и во многих случаях тело можно считать неподвижным.
При рассмотрении знака выражения 1/(1-ω2/р2)
видно, что для случая ω<р это
выражение положительно, а для ω>р
оно становится отрицательным. Это показывает, что когда частота возмущающей
силы меньше частоты свободных колебаний, вынужденные колебания и возмущающая
сила все время находятся в одной фазе, когда ω>р, сдвиг фаз между вынужденными колебаниями и возмущающей
силой становится равным π.
Д.Е. Хейсиным [164] рассматривались
свободные и вынужденные, колебания плавающей упругой ледяной пластины. При этом
были получены выражения для критической (резонансной) частоты колебаний
ледяного покрова, зависящие от величины модуля упругости льда Е, толщины h и глубины водоема Н.
В работе Хейсина [163] приводится решение о
распространении изгибно-гравитационных волн малой амплитуды в ледяном покрове с
учетом влияния неупругих свойств льда. Вода при этом считается идеальной
несжимаемой однородной жидкостью, а волновое движение в ней - потенциальным. В
случае мелкого бассейна коэффициент затухания будет
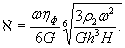
В случае глубокого бассейна
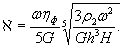
К сожалению, в этих статьях не дается четкого
разграничения бассейна на мелкий и глубокий, что затрудняет применение
приведенных формул для определения величины коэффициента затухания
изгибно-гравитационных волн. Но даже если такое разграничение будет дано, то
приведенные формулы для граничного случая дают разные значения коэффициента
затухания א. Никаких экспериментальных данных по этому вопросу в данных
статьях не приводится.
Фазовая скорость волны будет такой же, как и для
вполне упругой пластинки:

Величина K0
определяется по формуле для упругой ледяной пластины

где ρ1
- плотность льда;
ρ2 - плотность воды;
ηф - коэффициент вязкости льда при сдвиге.
Для экспериментального определения величины
логарифмического декремента затухания колебаний ледяного покрова, описанного в главе 1, нами были исследованы
свободные и вынужденные колебания ледяных консолей «клавишей», лежащих на воде
как в случае мелкого бассейна (глубина водоема составляла 1-1,5 м), так и в
случае относительно глубокого бассейна (при глубине 9-10 м). При этом
зависимость величины логарифмического декремента затухания колебаний от глубины
водоема не была обнаружена.
Практически нас интересуют как неустановившиеся,
так и установившиеся режимы вынужденных колебаний
ледяного слоя, которые в дальнейшем будут рассмотрены более подробно.
7.2. Вынужденные колебания
ледяного слоя при цилиндрическом изгибе
Если колебания ледяного слоя вызываются
гармонической равномерно распределенной нагрузкой q=q0 sin ωt, приложенной по линии, то будем иметь случай
цилиндрического изгиба в пределах распространения нагрузки.
В данном случае дифференциальное уравнение
динамического изгиба имеет вид (6.3), где функция прогиба ω зависит только от одной
координаты X.
Из анализа уравнения (6.3) можно сделать вывод,
что динамические прогибы можно получить из выражения для прогиба при
статическом изгибе, заменив действительный коэффициент постели уменьшенной
величиной k-mω2.
Используя этот результат, можно выразить
динамический прогиб ледяного слоя в виде
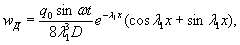 (7.1)
(7.1)
где  - характеристика
плиты при динамическом прогибе.
- характеристика
плиты при динамическом прогибе.
Максимальный прогиб возникает под нагрузкой и
определяется выражением
 (7.2)
(7.2)
После соответствующих преобразований приведем
(7.2) к виду

где λ
- характеристика плиты при статическом изгибе.
Затем, введя обозначение [161] 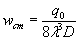 , получим
, получим
wд = wCT·μn,
то есть динамический прогиб равен статическому,
умноженному на динамический коэффициент
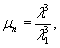
или, после соответствующих преобразований,
получим
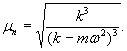 (7.3)
(7.3)
Приравняв нулю знаменатель выражения (7.3),
получим значение первой критической частоты колебаний
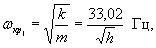 (7.4)
(7.4)
где h - толщина льда, см.
Из анализа выражения (7.4) можно сделать вывод,
что критическая частота колебаний ледяного слоя уменьшается по мере увеличения
толщины льда.
После подстановки всех известных величин в (7.4)
динамический коэффициент примет вид
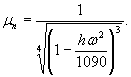 (7.5)
(7.5)
Имея функцию прогиба ледяного слоя при
цилиндрическом изгибе, легко определить значение изгибающего момента
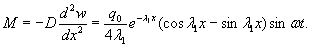 (7.6)
(7.6)
Максимальный изгибающий момент, возникающий под
нагрузкой, равен
 или
или 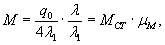
где
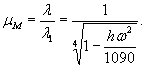 (7.7)
(7.7)
Сравнивая динамические коэффициенты для прогибов и моментов (7.5) и (7.7), убеждаемся, что первый
больше второго.
7.3. Вынужденные колебания
ледяного слоя при центральном изгибе
При воздействии на ледяной слой гармонической
сосредоточенной силы Р=Р0 sin ωt имеем случай центрального динамического изгиба.
Дифференциальное уравнение колебаний плиты на
упругом основании в данном случае имеет вид (6.3), где функция прогиба w зависит от радиуса r (в полярных
координатах).
Введем вспомогательную величину
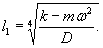 (7.8)
(7.8)
Заменяя в решении для бесконечной плиты при
статическом изгибе [73] величину l на l1
получим решение задачи о вынужденных колебаниях ледяного слоя.
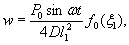 (7.9)
(7.9)
где безразмерная величина ξ1=rl1,
f0(ξ1) - функция изгиба бесконечной плиты на упругом основании,
удовлетворяющая всем граничным условиям.
Максимальный прогиб возникает под силой и равен
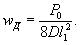
Преобразовав данное выражение, получим

где l - характеристика плиты при статическом изгибе.
Проведя замену 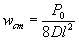 , получим
, получим
 (7.10)
(7.10)
Динамический коэффициент 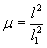 , после преобразования примет вид
, после преобразования примет вид
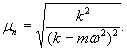 (7.11)
(7.11)
Приравняв нулю знаменатель выражения (7.11),
получим те же значения критической частоты колебаний, что и при цилиндрическом
изгибе (7.4). Преобразуя выражение
(7.11), имеем
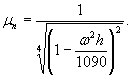 (7.12)
(7.12)
Для случая загружения ледяного слоя равномерно
распределенной нагрузкой по окружности приведенного радиуса r, динамические
коэффициенты по прогибам меньше, чем при цилиндрическом изгибе.
7.3.1. Учет сил внутреннего неупругого
сопротивления
Как отмечалось в главе 6, п. 6.15, учет сил
неупругого сопротивления сводится к замене упругих сил на обобщенные.
Подставляя в выражение динамического коэффициента (7.11) обобщенные силы (6.9), после соответствующих
преобразований по отделению действительной части выражения от мнимой, а также
пренебрегая величинами  и
и 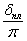 как малыми по
сравнению с единицей, получим
как малыми по
сравнению с единицей, получим
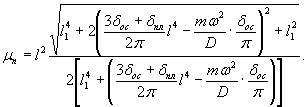 (7.13)
(7.13)
Как видно из (7.13), выражение динамического
коэффициента с учетом внутренних неупругих сил сопротивления имеет весьма
сложный и громоздкий вид. Но учитывая, что формулы (7.11) и (7.13) при
некритических значениях угловой частоты колебаний со дают почти одинаковые значения
динамического коэффициента, формулой (7.13) целесообразно пользоваться только
при критических значениях ωкр1.
Тогда, при  , получим
, получим
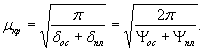 (7.14)
(7.14)
Из выражений (7.14) следует, что при критических
значениях угловой частоты колебаний, динамический коэффициент имеет вполне
определенную конечную величину.
Способ учета массы действующего груза при
динамическом расчете плит на упругом основании на
воздействия вибрационных и подвижных нагрузок изложен в работах [14, 22].
7.4. Колебания плиты на упругом основании с
учетом массы действующего на нее груза
7.4.1. Свободные колебания плиты на упругом
основании с учетом массы действующего груза
Положим, что на плиту, лежащую на упругом
основании, действует масса, сосредоточенная в точке, соответствующей началу
координат. Обозначим упругую поверхность таким образом загруженной плиты при
каком-нибудь ее главном колебании с частотой Р [14] через
w = w(r,t,p),
где r - координата произвольной точки плиты;
t - время.
Очевидно, что
w(r,tp) = V(r,p)sin p t, (7.15)
где функция V=V(r,p) представляет собой
амплитуду колебания точки r.
Воздействие массы М на плиту при колебании, представляемом уравнением (7.15), как
показано М.А. Гершгориным [39], эквивалентно действию
сосредоточенной силы
Q=Q0sin ωt = Mp2w(0)sin p t, (7.16)
равной силе
инерции данной массы.
Следовательно, можно рассматривать свободные
колебания загруженной плиты как чисто вынужденные колебания незагруженной плиты
под действием силы (7.16). В данном случае метод М.А. Гершгорина является по
существу методом сил. Отсюда следует, что
V(r,p)=p2MV(0,p)w(r,p), (7.17)
где w(r,p)
представляет собой основную функцию влияния при вынужденных колебаниях плиты на
упругом основании под действием силы P=sin pt и имеет размерность см/кгс.
Для начала координат из (7.17) получим
p2Mw(0,p) = 1, (7.18)
откуда после
соответствующих преобразований можно определить частоту собственных колебаний
плиты с учетом массы действующего на нее груза.
7.4.2. Вынужденные колебания плиты на упругом
основании с учетом массы действующего груза
Пусть на плиту, лежащую на упругом основании и
загруженную массой М в начале
координат, действует сила P=sin ωt. Обозначая упругую
поверхность плиты при возникающих чисто вынужденных колебаниях через w(r,t,p), имеем
w(r, t, ω) = V(r, ω) sin
ω t.
Аналогично предыдущему находим, что
V(r,
ω) = W(r, ω) + ω2 М V(0, ω) w(0, ω). (7.19)
Применяя равенство (7.19) к точке r=0, получим
V(0, ω) = W(0,
ω) + ω2М V(0, ω) w(0, ω),
где
 (7.20)
(7.20)
является
амплитудой колебаний точки плиты, соответствующей началу) координат.
Здесь W(0,w)
- прогиб плиты под действием силы Q=Mg·sin ωt,
g - ускорение силы тяжести.
7.5. Колебания ледяного слоя при цилиндрическом и центральном изгибе с учетом
массы действующего на него груза
7.5.1. В случае загружения бесконечной плиты на упругом основании
равномерно распределенной по линии нагрузкой, имеющей погонную, массу Mn=q/g, имеем
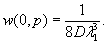 (7.21)
(7.21)
Подставляя выражение (7.21) в уравнение (7.18),
получим
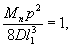
откуда после соответствующих преобразований
 (7.22)
(7.22)
Частота свободных колебаний плиты, с учетом
погонной массы груза, имеет вид

где
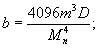

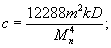
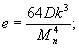

здесь у
- какой-либо действительный корень кубического уравнения
8у3-4су2
+ (2bd-8е) у+е (4с–b2)–d2 = 0,
которое решается одним из известных способов, в
частности приближенно, способом подбора.
Значение частоты свободных колебаний плиты с
учетом распределенной массы груза можно также определить непосредственно из
выражения (7.22), добиваясь равенства левой и правой частей данного уравнения
путем подстановки значений
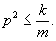
Для определения вынужденных колебаний ледяного
покрова, с учетом массы действующего груза, имеем
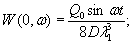 (7.23)
(7.23)

Подставив (7.23) в (7.20), получим после
соответствующих преобразований
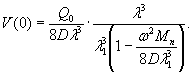 (7.24)
(7.24)
Первый сомножитель выражения (7.24) представляет
собой статический прогиб под силой Q0.
Второй - является динамическим коэффициентом, обозначим его
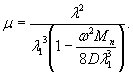 (7.25)
(7.25)
Приравняв к нулю выражение в скобках, получим
уравнение (7.18). Таким образом,
получается равенство частот свободных и вынужденных колебаний, что и должно
иметь место при резонансе.
7.5.2. Рассмотрим бесконечную плиту, загруженную сосредоточенной
массой М в начало координат. В этом
случае, для бесконечной плиты, имеем [14]
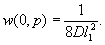 (7.26)
(7.26)
Подставляя величину (7.26) в уравнение (7.18), получим
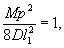
откуда после соответствующих преобразований
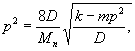
частота свободных колебаний плиты с учетом массы
груза
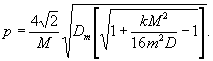 (7.27)
(7.27)
В случае вьпгужденных колебаний с учетом решения
Б.Г. Коренева [73] для статически
приложенной сосредоточенной силы
 (7.28)
(7.28)
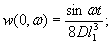
После подстановки (7.28) в (7.20) получим
 (7.29)
(7.29)
где l - характеристика плиты при статическом изгибе.
Первый сомножитель выражения (7.29) представляет
собой статический прогиб под силой Q0.
Второй - является динамическим коэффициентом
 (7.30)
(7.30)
Приравняв нулю l12, получим значение критической частоты вынужденных колебаний
без учета массы груза

Из равенства нулю выражения в скобках имеем
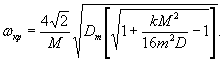 (7.31)
(7.31)
Сравнивая выражения (7.27) и (7.31), убеждаемся
в их равенстве, что и должно иметь место при резонансе.
В работе [17] показано, что
максимальная нагрузка на бесконечный ледяной слой при расчете в упругой стадии
определяется выражением
Р= 1,02 Rfh2, (7.32)
где Rf
- предел прочности льда при изгибе в упругой стадии.
С учетом (7.32) выражение (7.31) после
соответствующих преобразований принимает вид
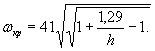
Значения критической частоты вынужденных
колебаний ледяного слоя, с учетом массы груза, определенные по формуле (7.31),
на 11-12% меньше значений частоты колебаний, определенных по формуле (7.4).
Следовательно, учет массы колеблющегося груза
приводит к уменьшению критической частоты вынужденных колебаний ледяного
покрова.
Далее следует учесть влияние сил внутреннего неупругого
сопротивления.
По методике, изложенной в главе 6, п.6.2, применительно к
данному случаю, из выражения (7.30) получим
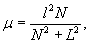 (7.33)
(7.33)

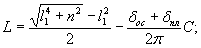
где
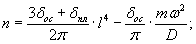
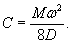
Без учета массы
колеблющегося груза, при С=0, получим
из выражения (7.33) формулу (7.13).
7.6.
Колебания ледяного слоя с учетом инерции упругого основания
Как уже указывалось в п. 7.1, учет инерции оснований
при колебаниях конструкций на упругом винклеровом основании является крайне
условным. С этой целью присоединим к колеблющейся системе (ледяной слой плюс
внешняя нагрузка) распределенную массу, учитывающую приближенно инерцию того
слоя основания, который принимает участие в колебаниях.
Будем считать, что толщина слоя основания,
принимающего участие в колебаниях, равна прогибу плиты в данной точке с
координатами х,у при максимальном
значении внешней нагрузки.
Тогда масса упругого основания, приходящаяся на
единицу площади, равна
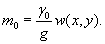 (7.34)
(7.34)
Выражая максимальный прогиб под силой Q0 sin ωt через
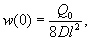 (7.35)
(7.35)
получим значение условной распределенной массы
основания в виде
 (7.36)
(7.36)
Учитывая, что масса ледяного слоя, приходящаяся
на единицу площади, равна
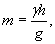 (7.37)
(7.37)
представим приведенную распределенную массу
плиты и упругого основания в виде
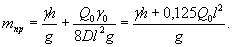 (7.38)
(7.38)
Подставив значение приведенной массы (7.33) в
формулы (7.3), (7.11), (7.25), (7.30), получим значения
динамических коэффициентов с учетом массы основания, принимающей участие в
колебаниях системы.
Для качественной и количественной оценки влияния
инерции основания на величину значений критической частоты вынужденных
колебаний ледяного покрова, подставив выражение (7.33) в формулу (7.4), получим
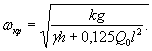 (7.39)
(7.39)
Подставив в (7.39) все известные величины и
произведя необходимые преобразования, имеем
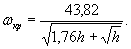 (7.40)
(7.40)
Значения критической частоты вынужденных
колебаний ледяного слоя с учетом инерции упругого основания, определенные по
формуле (5.40), на (20÷3)%
меньше значений частоты колебаний, определенных по формуле (5.4).
Влияние инерции упругого основания уменьшается с
увеличением толщины ледяного покрова.
Уже при толщине льда h=25 см, разница составляет 5%, поэтому влиянием инерции основания
при колебаниях ледяного слоя, если исходить из
предпосылок, изложенных в начале данного параграфа, можно пренебречь.
8.1.
Состояние вопроса и цели исследования
Изучение колебаний конструкций под действием
движущихся нагрузок имеет большое практическое значение. Задача о колебаниях
балок и плит (как имеющих различные опорные закрепления, так и лежащих на
упругом основании) до сих пор не потеряла своей актуальности, так как при
изучении колебаний конструкций необходимо уметь определять не только
деформации, но и напряжения в них [168].
Впервые простейшая задача о влиянии движущегося
груза на балку в предельном случае, когда весом балки, то есть силами инерции
ее, можно пренебречь, была поставлена и решена Р. Уиллисом в середине XIX века [155].
Несколько позже другое решение этой задачи было
предложено Д. Стоксом. Уравнение Стокса было проинтегрировано несколькими
исследователями различными приближенными методами. Затем было найдено решение
уравнения Стокса для балки, опертой по концам [85], однако это решение
неудобно для вычислений.
Решение задачи для другого предельного случая,
когда по весомой балке движется сила со скоростью V, впервые было получено в 1905 г. академиком А.Н. Крыловым с
помощью разложения по фундаментальным функциям, а позже, в 1912 г., методом
обобщенных координат - С.П. Тимошенко [197].
Точного решения задачи для общего случая, когда
масса балки одного порядка с движущейся сосредоточенной массой, до
настоящего" времени получить не удалось. В связи с этим был предложен ряд
методов для нахождения величин деформаций. В общем виде решение задачи сводится
к интегрированию уравнения колеблющегося стержня с грузовым членом, т.е.

где δ(x-η)
- дельта-функция, (η=Vt).
Влияние движущейся массы приближенно было учтено
К. Инглисом Метод К. Инглиса был развит в дальнейшем В.В. Болотиным и А.Б.
Моргаевским.
Уравнение колебаний балки под действием
движущегося груза многими авторами сводилось к интегродифференциальному
уравнению [168]. Однако это уравнение
из-за свойств ядра его не дает возможности находить с достаточной точностью
деформации, а тем более напряжения. Численных результатов по этому методу в
литературе не имеется.
В работе А.П. Филиппова [168] широко использован
метод интегральных уравнений в форме, позволяющей избегать указанных
трудностей. Задача сводится к решению интегральных уравнений. Для случая
движения одной массы вводятся две неизвестные функции у(η,η); d2y/dη2, благодаря чему устраняется плохая сходимость ядер
интегральных уравнений. Интегрирование систем уравнений ведется численно.
Разработанный метод позволяет находить решение уравнений с желаемой точностью
для различных сложных случаев, в том числе и для балок с нелинейными опорами.
Этот метод широко использован А.П. Филипповым для определения как деформаций,
так и напряжений.
Другой цикл задач, весьма важный для
современного развития транспорта, связан с изучением динамического воздействия
подвижных нагрузок на балки и плиты, лежащие на упругом основании. Эта задача
для балки, лежащей на линейно-упругом винклеровом основании, рассматривалась
несколькими авторами [74, 75]. Случай подрессоренных
масс и действия возмущающих гармонических сил был изучен в работе [167].
В.Е. Яровой [186] рассматривал задачу о
динамическом воздействии движущегося груза на плиту в виде бесконечной ленты
определенной ширины, лежащей на упругом основании. Однако распространение этого
решения для случая бесконечной плиты на упругом основании не представляется
возможным.
Вопросам исследования неустановившихся колебаний
бесконечной плиты на упругом основании при действии на нее различного рода
подвижных и вибрационных нагрузок посвящены работы В.В. Найвельта [105, 106] и Г.Б. Муравского [102].
Исследование колебаний различных упругих систем,
находящихся под влиянием внешних подвижных нагрузок, как с учетом инерции этих
нагрузок, так и без учета, является одним из актуальных вопросов в современной
динамике сооружений.
Вопрос о динамическом действии подвижных
нагрузок на различные сооружения имеет значительную давность. Тем не менее
следует заметить, что эта проблема еще далека от своего полного разрешения и
нуждается в теоретическом и экспериментальном изучении.
Всесторонний учет влияния подвижных нагрузок на
сооружения имеет также большое значение в связи с увеличением веса и скоростей
движущихся нагрузок.
Многие динамические явления, которыми раньше при
проектировании и строительстве можно было пренебречь, теперь в новых условиях
становятся все более существенными. Поэтому понятно, насколько актуален вопрос
о надлежащем учете динамического действия подвижных нагрузок.
Исследованию динамического действия подвижных
нагрузок на сооружения посвящен ряд работ; имеется обширная отечественная
техническая литература, посвященная теоретическому исследованию различных сторон
этой проблемы и не менее многочисленная литература, касающаяся практических
способов расчета различных конструкций и сооружений на подвижную нагрузку.
Дальнейшее развитие и уточнение упомянутой выше
проблемы в настоящее время должно вестись в направлении учета ряда новых важных
факторов, отвечающих современному состоянию знаний и возросшим требованиям к
строительным расчетам. Инженер-проектировщик должен располагать данными для
надлежащей оценки динамического действия подвижных нагрузок, то есть для учета
влияния на частоту и период колебаний (помимо других факторов) массы подвижной
нагрузки наряду с массой самой упругой системы.
Сложность решения задач в указанной здесь общей
постановке достаточно велика. Поэтому наряду с общими приемами решения должно быть
уделено внимание и приближенным методам решения этих задач.
В настоящей работе основное внимание уделено
именно этим вопросам. Излагаются способы расчета плит на упругом основании,
находящихся под воздействием подвижных сил. Далее рассмотрены вопросы,
связанные с учетом воздействия на плиты подвижных масс,
и оценены качественная и количественная стороны этого влияния.
8.2. Колебания плиты на упругом основании с
учетом массы движущегося по ней груза
Рассмотрим задачу о движении сосредоточенного
груза по бесконечной плите на упругом винклеровом основании. Определим вначале
основную функцию влияния, то есть функцию прогиба плиты от действия единичной
движущейся силы.
Решая задачу в прямоугольной системе координат w, х, у, представим основную функцию
влияния в виде
w = BF(x,y,v,t). (8.1)
Принимая направление движения единичной силы по
оси X, при постоянной скорости
движения V, целесообразно применить
подстановку
ξ = х-vt
и изучать поведение плиты под нагрузкой в новой
системе координат w, ξ, у,
движущейся со скоростью V
относительно первоначальной системы координат w, х, у.
Дифференциальное уравнение движения для
бесконечной плиты на упругом основании (при отсутствии затухания) имеет вид (6.7).
При движении груза по плите на упругом основании
на величину динамического коэффициента будут оказывать влияние силы инерции как
массы самой плиты, так и массы движущегося по ней груза, которые возникают в
результате вертикальных перемещений системы [75, 77].
Одновременный учет этих сил инерции делает
задачу столь сложной, что практически в общем виде она не имеет решения. Обычно
в литературе рассматриваются два предельных случая данной общей задачи.
Если масса плиты велика по сравнению с массой
груза, то рассматривается задача о движении идеализированного «безынерционного»
груза по весомой плите.
Если же, наоборот, масса плиты мала по сравнению
с массой груза, то ставится задача о движении груза по идеализированной
«невесомой» плите.
В обоих случаях инерция основания не учитывается.
Обозначим упругую поверхность плиты, под
действием движущейся по ней с постоянной скоростью V силой Р через
w(ξ, y, t),
где ξ,
у - координаты произвольной точки плиты.
При учете массы груза, движущейся по весомой
плите на упругом основании, полное давление груза на плиту, а следовательно и
реакция плиты заранее не известны. Упругая реакция плиты и основания должны
уравновешивать вес плиты, груза и те дополнительные инерционные силы, которые
развивают данные массы на смещении под ними, равном A(0).
Здесь начало координат принято в точке под
центром груза. Пусть прогиб определяется выражением
A=Rw(ξ, y), (8.2)
где R
- сила, передающаяся движущимся грузом на плиту;
w(ξ, y) - функция прогиба плиты
под действием движущейся единичной силы, или основная функция влияний [22].
Обозначим через w(ξ, y), - прогиб в произвольной точке весомой плиты под действием
движущейся силы Р, через w(ξ, y), - вторую производную от функции влияния.
Заметим, что в начале координат она всегда
отрицательна, так как рассматривается плита с отрицательной начальной кривизной,
то есть изогнутая вниз.
В таком случае прогиб в начале координат с
учетом массы плиты и движущегося груза можно выразить в виде
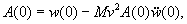 (8.3)
(8.3)
откуда
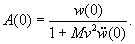 (8.4)
(8.4)
Вторая производная от основной
функции влияния 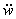 имеет размерность
1/кгс·см.
имеет размерность
1/кгс·см.
8.3. Колебания ледяного слоя под действием движущегося с постоянной скоростью
сосредоточенного груза
Решение однородного уравнения (6.7) при q=0, как показано в
работе [22], можно представить в виде
 (8.5)
(8.5)
где
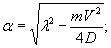
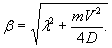
Коэффициент В
(8.1) можно получить из
условия равновесия
 (8.6)
(8.6)
Подставив значение F(ξ,y) из (8.5) в (8.6) и произведя интегрирование, получим
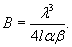
Основная функция влияния (8.1) примет вид
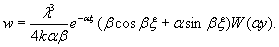 (8.7)
(8.7)
После соответствующих преобразований представим
прогиб под силой Р в виде
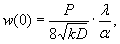 (8.8)
(8.8)
где первый сомножитель представляет собой прогиб
бесконечной плиты под силой Р при ее
статическом действии;
 (8.9)
(8.9)
является динамическим коэффициентом.
Приравняв нулю знаменатель выражения (8.9),
получим значение критической скорости движения
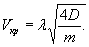
Подставив все известные величины и произведя
необходимые преобразования, получим
 (8.10)
(8.10)
где h - толщина ледяного слоя, см.
Изгибающие моменты Мξ и Му
(Мξ - в сечении,
перпендикулярном оси, вдоль которой движется сила Р) соответственно равны


В сечениях под силой Р имеем
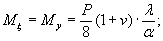
где динамический коэффициент
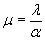
Следовательно, динамические коэффициенты по
прогибам и напряжениям равны между собой.
Выражение (8.7) учитывает только массу плиты.
Далее следует учесть влияние сил внутреннего
неупругого сопротивления.
Произведя замену упругих сил на обобщенные в
выражении (8.9), отделяя
действительную часть выражения от мнимой, а также пренебрегая
величинами  и
и  как малыми по
сравнению с единицей, получим
как малыми по
сравнению с единицей, получим

Выражение динамического коэффициента с учетом
внутренних неупругих сил сопротивления имеет сложный и громоздкий вид. Поэтому
данной формулой целесообразно пользоваться только при критических значениях
скорости V. Тогда, подставляя
значение критической скорости (8.10) и произведя соответствующие
преобразования, получим
 (8.11)
(8.11)
Используя эту формулу, можно определить конечные
значения прогиба и изгибающего момента под движущимся с критической скоростью
грузом.
8.3.1. Учет инерции упругого основания
Как указано в главе 7 п. 7.1, инерцию основания
можно свести к рассмотрению колебаний плиты с присоединенной снизу
распределенной массой, приближенно учитывающей инерцию того слоя основания,
который принимает участие в колебаниях.
Будем считать, что толщина слоя основания,
принимающего участие в колебаниях, равна прогибу плиты в данной точке с
координатами (x,у).
Тогда масса упругого основания, приходящаяся на
единицу площади
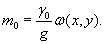 (8.12)
(8.12)
Для учета инерции основания необходимо к
распределенной массе плиты добавить распределенную массу основания, тогда в
выражениях α и β нужно добавить к величине m величину m0
Приведенная масса, приходящаяся на единицу
площади, будет иметь вид
mпр = m+m0. (8.13)
При загружении ледяного слоя сосредоточенной
силой, равной максимальному значению его грузоподъемности из расчета в упругой
стадии, величину то можно представить в виде

так как коэффициент упругого основания к
численно равен объемному весу воды γ0.
Подставив значение mпр в выражение (8.10), получим после
соответствующих преобразований
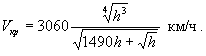 (8.14)
(8.14)
Значения критических скоростей, определенные по
формуле (8.14), в среднем на 18% меньше значений, определенных по формуле
(8.11). Следовательно, в данном случае нельзя пренебрегать инерцией упругого
основания, и поэтому динамический коэффициент и критическую скорость движения,
если вес движущейся нагрузки близок к максимальному, получаемому из расчета в
упругой стадии (7.32), нужно определять по
формулам
 (8.15)
(8.15)
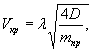 (8.16)
(8.16)
где
 (8.17)
(8.17)
Выражая прогиб под силой через 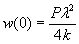 , запишем значение условной распределенной массы основания в
виде
, запишем значение условной распределенной массы основания в
виде
 (8.18)
(8.18)
Тогда учитывая, что масса плиты, приходящаяся на
единицу площади, равна
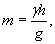 (8.19)
(8.19)
представим приведенную распределенную массу
плиты и упругого основания в виде
 (8.20)
(8.20)
Учет приведенной массы (8.20) приводит к
уменьшению значений критической скорости Vкр движущегося сосредоточенного груза на 13-15%.
8.3.2. Учет инерции движущегося по плите груза
Для учета массы движущегося груза, определим
вторую производную по ξ, от
функции (8.7) в точке ξ=0
 (8.21)
(8.21)
Подставив выражения (8.8) и (8.21) в (8.4), получим после
соответствующих преобразований
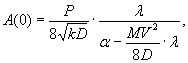
где динамический коэффициент
 (8.22)
(8.22)
учитывает как массу плиты, так и массу
движущегося по ней груза.
Для учета инерции основания можно в формуле
(8.22) заменить α на αпр (8.17). Затем
приравняв нулю знаменатель выражения (8.22), получим значение критической
скорости движения груза
 (8.23)
(8.23)
При приближении к критической скорости движения
динамический коэффициент значительно возрастает. В таких случаях необходимо
учитывать затухание колебаний, характеризующееся внутренним неупругим
сопротивлением. Применяя гипотезу внутреннего неупругого сопротивления Е.С.
Сорокина, получим
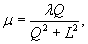 (8.24)
(8.24)
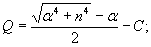
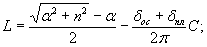
где

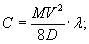
δoc и δпл
- соответственно логарифмические декременты затухания основания и плиты.
При С=0,
без учета массы движущегося груза, динамический коэффициент при критической
скорости движения равен
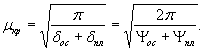 (8.25)
(8.25)
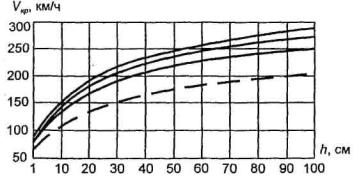
Рис. 8.1. Изменение критической скорости
движущейся силы в зависимости от толщины ледяного покрова
На рис. 8.1 изображены графики изменения
критической скорости для ледяного слоя, определенные без учета масс движущегося
груза и упругого основания, по формуле (8.11) (верхняя сплошная
линия), с учетом инерции основания, по формуле (8.16) (нижняя сплошная
линия) и с учетом массы движущегося груза по формуле (8.23) (средняя сплошная
линия). Величина груза принята максимальной из расчета грузоподъемности
ледяного слоя в упругой стадии.
По мере увеличения толщины льда влияние массы
движущегося груза на величину критической скорости уменьшается. Уже при толщине
льда h=20 см, разница между величинами критических скоростей (рис.
8.1) не превышает 12%, а при толщине h=100 см - 6,4%.
Из этого сравнения можно сделать вывод, что
влиянием массы движущегося по ледяному слою груза можно пренебречь, а
динамический коэффициент в случае необходимости определять по формуле (8.15), если вес движущейся
нагрузки существенно меньше максимального, получаемого
из расчета в упругой стадии (7.32).
8.4. Колебания ледяного слоя под действием движущейся
нагрузки, распределенной по окружности
При движении автомобиля по ледяному покрову
нагрузка от веса автомобиля, строго говоря, не является сосредоточенной в одной
точке, а передается через точки опирания колес. Поэтому более точная схема
расчета будет соответствовать случаю, когда расчетная нагрузка приложена к
ледяному слою по окружности проведенной через точки опирания автомобиля.
Вначале определим основную функцию влияния w(r,t). Принимая нагрузку от
автомобиля распределенной по окружности, получим
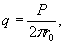 (8.26)
(8.26)
где Р
- вес автомобиля;
r0 -
радиус окружности, равный половине расстояния между двумя диагонально
расположенными колесами автомобиля.
Считаем, что расчетная нагрузка q движется по
бесконечной плите на упругом основании с постоянной скоростью V.
Обозначим через α=r0l - приведенный радиус
окружности и введем вспомогательные величины


Принимая за основу решение Б.Г. Коренева [73] для бесконечной плиты,
загруженной равномерно распределенной по окружности статической нагрузкой,
получим
при
η≤r0
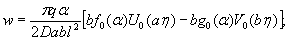
при η≥0
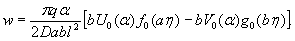
Для начала координат в точке η=0, имеем
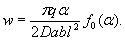
Обозначив через  статический прогиб
плиты, получим
статический прогиб
плиты, получим
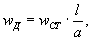 (8.27)
(8.27)
где  динамический
коэффициент по прогибам.
динамический
коэффициент по прогибам.
Изгибающие моменты в плите соответственно равны
при η≤r0
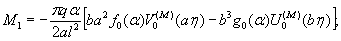
при η≥r0
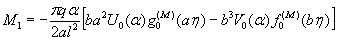
В центре плиты, при η=0, имеем
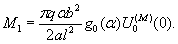
Так как изгибающий момент при статическом
загружении равен

то величина динамического коэффициента по
напряжениям в данном случае будет
 (8.28)
(8.28)
Приравняв нулю знаменатель выражения (8.28),
получим
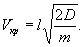 (8.29)
(8.29)
Сравнивая динамические коэффициенты (8.27) и (8.28) при
критическом значении скорости (8.29), получаем, что второй из них в  раз больше первого,
то есть динамический коэффициент по напряжениям больше, чем по прогибам.
раз больше первого,
то есть динамический коэффициент по напряжениям больше, чем по прогибам.
Из выражения (8.29), после соответствующих
преобразований, получим
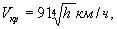
то есть получили формулу (8.11), где h - толщина льда, см.
На рис. 8.1 изображен график изменения
критической скорости (верхняя сплошная линия), построенный по формуле (8.29).
Из сравнения двух приведенных способов расчета п. 8.3; можно сделать вывод, что критические скорости движения для ледяного покрова
достаточно высоки.
8.5. Колебания ледяного слоя под действием груза,
движущегося с переменной скоростью
При равнопеременном движении груза по ледяному
слою скорость движения в момент времени t
в общем случае будет
Vt=V0±ut,
где V0
- начальная скорость;
u - ускорение движения
груза.
Решая задачу в прямоугольной системе координат,
целесообразно применить подстановку ξ=х-(V0±u t) t и изучать поведение ледяного слоя под нагрузкой в системе
координат w ξ у, движущейся с
переменной скоростью V, относительно
первоначальной системы координат w х у.
Учет массы движущегося груза при равнопеременном
движении сводится в данном случае к загружению ледяного слоя дополнительной
осевой силой инерции, равной М·u, где М - масса груза. Следовательно, мы имеем
несколько более общую задачу, чем в п. 8.2.
Введем вспомогательные величины
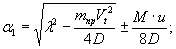

С учетом выкладок, приведенных в п.8.2, получим
динамический прогиб под нагрузкой в виде

откуда динамический коэффициент
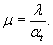 (8.30)
(8.30)
Наиболее выгодным является случай торможения,
при котором
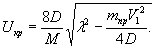 (8.31)
(8.31)
Для оценки критической величины ускорения
приведем пример расчета для случая торможения движущегося груза, вес которого
равен предельному из расчета грузоподъемности ледяного покрова в упругой
стадии, то есть P=10h2 кг и толщине льда h=25 см. Торможение
начинается при скорости движения V0=50 км/ч. В этом случае из (8.31) получим
Uкр = 8,0g,
где g
- ускорение силы тяжести.
При большей толщине льда критическое значение
ускорения будет еще большим.
Отсюда можно сделать вывод, что при эксплуатации
ледовых переправ критическое значение ускорения не может быть достигнуто.
Необходимо также заметить, что даже при
достижении критического значения ускорения не может наступить состояние
резонанса, так как время действия ускорения ничтожно
мало, а инерция ледяного покрова достаточно велика.
8.6. Колебания ледяного слоя под действием движущейся
сосредоточенной вибрационной нагрузки
Практический интерес представляет случай, когда
по бесконечному ледяному покрову движется с постоянной скоростью V гармоническая
сосредоточенная сила Р=Р0 sin ωt. Решение данной задачи может быть получено из совместного
рассмотрения уравнений (6.3) и (6.7).
Используя вспомогательные величины
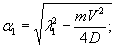
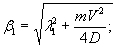
 (8.32)
(8.32)
получим с учетом выкладок, приведенных в п. 8.3, основную функцию
влияния в прямоугольных координатах в виде
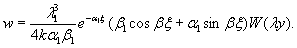 (8.33)
(8.33)
После соответствующих преобразований представим
прогиб под силой Р в виде
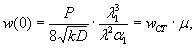
где динамический коэффициент по прогибам
 (8.34)
(8.34)
Изгибающие моменты Мξ и Му
(Мξ - в сечении,
перпендикулярном оси ξ, вдоль
которой движется сила Р),
соответственно равны
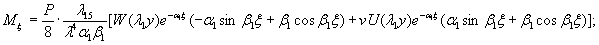
Под силой Р
после преобразований имеем изгибающий момент

где динамический коэффициент по напряжениям
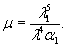 (8.35)
(8.35)
Сравнивая выражения (8.34) и (8.35), приходим к
выводу, что динамические коэффициенты по прогибам больше, чем по напряжениям.
Для определения критической скорости движения
приравняем α1 нулю,
откуда
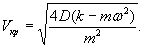 (8.36)
(8.36)
При докритических частотах колебаний ωдкр

и при закритических частотах колебаний ωзкр
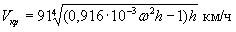
где ω
- частота колебаний нагрузки, Гц;
h - толщина ледяного слоя, см.
На рис. 8.2 даны графики изменения критических
скоростей движения вибрационной нагрузки при различных значениях частот
колебаний.
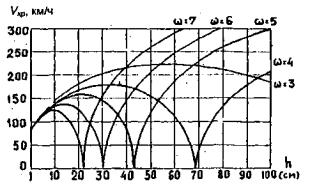
Рис. 8.2. Изменение критической скорости
движущейся вибрационной нагрузки
При приближении к критическим скоростям движения
необходимо, учитывать затухание колебаний, характеризующееся внутренним
неупругим сопротивлением льда. Применяя уже известную методику (глава 6 п.6.2), произведем преобразования
выражения (8.34) и приведем его к виду
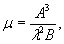 (8.37)
(8.37)
где

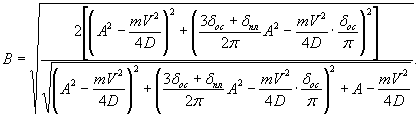
Из выражения (8.37) можно определить конечное
значение динамического коэффициента при критических
величинах скорости движения вибрационной нагрузки.
8.7. Колебания ледяного слоя под действием движущейся вибрационной
нагрузки, распределенной по окружности
При расчете ледяного слоя на динамическое
воздействие автомобиля вес последнего можно считать распределенным по
окружности и определяемым выражением (8.26). Будем считать, что
гармоническая распределенная по окружности радиуса r0
нагрузка q=q0 sin ωt движется с постоянной скоростью V по бесконечной плите на упругом основании. Решение данной задачи
может быть получено из совместного рассмотрения уравнений (6.3) и (6.7).
Решая задачу в полярных координатах и используя
вспомогательные величины
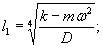
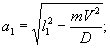
 (8.38)
(8.38)
получим с учетом выкладок, приведенных в п. 8.4, основную функцию
влияния в виде
при η≤r0

при η≥r0

В начале координат (в точке η=r0), имеем прогиб под нагрузкой q0, равный
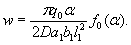 (8.39)
(8.39)
Обозначив статический прогиб плиты через
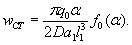
получим
 где
где 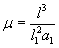 (8.40)
(8.40)
является динамическим коэффициентом по прогибам.
Изгибающие моменты в плите соответственно равны
при η≤r0
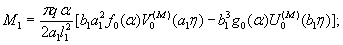
при
η≥r0
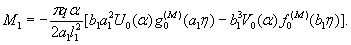
В центре плиты, при η=r0, имеем
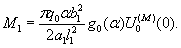
Так как статический изгибающий момент в этом
случае равен

то динамический коэффициент по напряжениям в данном
случае будет
 (8.41)
(8.41)
Приравняв нулю величину ах, стоящую в
знаменателе выражения (8.41), получим значение критической скорости
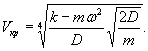 (8.42)
(8.42)
Сравнивая динамические коэффициенты (8.40) и
(8.41) при критическом значении скорости (8.42), получаем, что второй из них
больше первого, то есть динамический коэффициент по напряжениям больше, чем по
прогибам.
Из выражения (8.42), после соответствующих
преобразований, получим
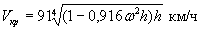
при докритических частотах колебаний, и
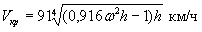
при закритических частотах колебаний.
При приближении к критическим скоростям движения
необходимо учитывать затухание колебаний, характеризующееся внутренним
неупругим сопротивлением льда.
Применяя метод решения, изложенный в главе 6 п.
6.1, и произведя необходимые преобразования выражения (8.41), получим
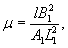 (8.43)
(8.43)
где
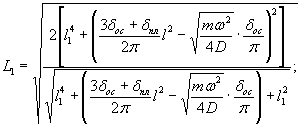
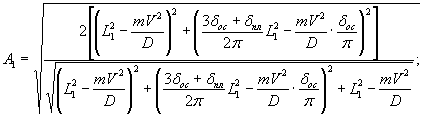
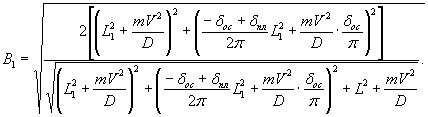
При необходимости определения динамического коэффициента по формуле (8.43) расчет следует производить
с вычисления L1.
9.1.
Состояние вопроса и цели исследования
Изучение колебаний конструкций под действием
движущихся нагрузок имеет большое практическое значение. Задача о колебаниях
балок и плит (как имеющих различные опорные закрепления, так и лежащих на
упругом основании) до сих пор не потеряла своей актуальности, так как при
изучении колебаний конструкций необходимо уметь определять не только
деформации, но и напряжения в них [168].
Изучение опытных данных, изложенных в работе
К.Е. Иванова, П.П. Кобеко и А.Р. Шульмана [56], по деформации ледяного
покрова под действием различных грузов (мотовозов, автомашин и других),
перемещавшихся с различными скоростями, показало следующее:
При скорости движения 5-15 км/ч наблюдается
упругая деформация. Возмущение от нагрузки распространяется по льду со
скоростью движения нагрузки и с той же скоростью исчезает вслед за ее проходом.
Величина прогиба под нагрузкой при этом в
1,5÷2 раза меньше, чем при чисто статических испытаниях. Таким образом,
деформация заключается в перемещении по ледовому покрову эпюры прогиба.
Благодаря кратковременности действия нагрузки
процесс прогиба ледяного покрова не успевает развиться до состояния упругого
равновесия из-за инерционности вытесняемой массы воды.
При скоростях движения более 20 км/ч в ледяном
покрове возникают волнообразные колебания, наблюдаемые даже за сотни метров от
движущегося груза. Зная расстояние между двумя приборами, установленными
перпендикулярно направлению движения [131], можно определить
скорость распространения колебаний в ледяном покрове. Экспериментами [56] установлено, что длина
ледовой волны не зависит ни от величины движущейся нагрузки, ни от скорости ее
движения, а зависит от толщины ледяного покрова и глубины воды под ледяным
покровом.
Для случая, когда длина волны значительно
превышает глубину воды подо льдом, справедливо уравнение Лагранжа  , описывающее зависимость скорости распространения волны по
поверхности воды от глубины водоема. Это позволяет предполагать, что причиной
возникновения колебаний ледяного покрова является появление гидродинамической
волны в воде от действия движущейся по льду нагрузки. Наличие же ледяного
покрова на воде обусловливает отклонение зависимости скорости распространения
волны С от уравнения Лагранжа.
Ледяной покров, деформированный под влиянием образовавшейся ледяной волны,
оказывает сверху на поверхность воды давление, определяемое величиной реакции
деформированной части ледяного покрова.
, описывающее зависимость скорости распространения волны по
поверхности воды от глубины водоема. Это позволяет предполагать, что причиной
возникновения колебаний ледяного покрова является появление гидродинамической
волны в воде от действия движущейся по льду нагрузки. Наличие же ледяного
покрова на воде обусловливает отклонение зависимости скорости распространения
волны С от уравнения Лагранжа.
Ледяной покров, деформированный под влиянием образовавшейся ледяной волны,
оказывает сверху на поверхность воды давление, определяемое величиной реакции
деформированной части ледяного покрова.
На основании закона количества движения и
импульса сил, авторы работы [56] вывели формулу скорости
распространения волны под ледовым покровом
 (9.1)
(9.1)
где Е
- модуль упругого льда, тс/м2;
h - толщина ледяного покрова, м;
γ - объемный вес воды, тс/м3;
d - высота одиночной прогрессивной волны вспучивания, м;
g - ускорение свободного падения, м/с2;
Н - глубина воды, м.
Эта формула выведена из предположении о
распространении одиночной прогрессивной волны вспучивания, образующейся
движущейся по льду нагрузкой.
Необходимо отметить, что опытные данные,
полученные этими же авторами [56], показывают, что
скорость С во многих случаях меньше;
чем теоретическая по уравнению Лагранжа. Формула (9.1), наоборот, дает только
большие результаты скорости С, так
как стоящее под знаком корня выражение в круглых скобках всегда больше единицы.
Поэтому пользоваться формулой (9.1) для определения скорости распространения
волны под ледяным покровом нельзя, так как она дает неверные результаты в
сравнении с опытными данными. Исходя из вышеизложенного следует установить, что
целью дальнейших исследований в этом вопросе является:
1) определение длины и высоты одиночной
прогрессивной волны вспучивания, а также периода ее колебаний;
2) определение скорости ее распространения под
ледяным покровом (первой критической скорости);
3) изучение колебаний ледяного покрова под
воздействием движущейся нагрузки с учетом волнового
процесса, происходящего в воде.
9.2. Определение длины волны, периода колебаний и скорости
распространения ее под ледяным покровом
Колебания системы называются свободными, если
скорость изменения состояния системы определяется только состоянием самой
системы, а именно восстанавливающей равновесное состояние силой, зависящей от
величины w, которая определяется
отклонением системы из этого состояния, и сопротивлением, пропорциональным
скорости w. Такую систему принято
называть линейным осциллятором [5].
При движении грузов по ледяному покрову вода
получает импульсы, направленные как в направлении движения, так и под углом к
нему. Получив импульс, водяная волна распространяется подо льдом со скоростью С. Из серии волн, распространяющихся под
ледяным покровом, наибольшее значение имеет первая свободная положительная
волна, которая и определяет основные параметры колебаний всей системы.
Длина свободной волны определяется из условия
распространения от источника колебаний полуволны, по очертанию равной чаше
прогиба ледяного покрова, образовавшейся в результате деформации его под
действием движущейся нагрузки. В безразмерных координатах диаметр чаши прогиба
составляет 1,5π, что равно длине полуволны. Следовательно, длина свободной
волны равна 3π. Переходя от безразмерной системы осей координат к
размерной, выразим длину волны L в
виде
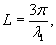 (9.2)
(9.2)
где λ1
- характеристика ледяного покрова при динамическом изгибе (глава 7. п. 7.2).
Если не учитывать сопротивлений, то уравнение
колебаний линейно-:го осциллятора, в нашем случае, будет иметь вид
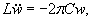 (9.3)
(9.3)
где С
- скорость распространения свободной волны.
Введя обозначение
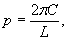 (9.4)
(9.4)
запишем решение уравнения (9.3) в следующем виде
w = А sin (p t+α).
Амплитуда колебаний А определяется начальными условиями, а период колебаний
 (9.5)
(9.5)
от начальных условий не зависит.
Необходимо отметить, что в случае действия на
ледяной покров гармонической силы с частотой колебаний ω=ρ (9.4), от места приложения нагрузки будут
распространяться волны, имеющие максимальную высоту. Следовательно, ледяной
покров будет испытывать колебания с максимальной величиной амплитуды.
Таким образом, в дополнение к выражению цервой
критической частоты колебаний ледяного покрова (7.4), следует учитывать и
вторую критическую частоту колебаний ωкр2
численно равную выражению (9.4).
С учетом внутреннего неупругого сопротивления
льда и логарифмического декремента затухания колебаний воды как упругого
основания, максимальную величину динамического коэффициента, при резонансных
колебаниях ледяного покрова можно определить из выражения (8.11).
В результате анализа опытных данных по замерам
скоростей распространения одиночных свободных волн под ледяным покровом,
опубликованных в работе [56], предлагается
полуэмпирическая формула для расчета этих скоростей. В основу этой формулы
также положено уравнение Лагранжа.
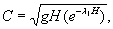 (9.6)
(9.6)
где g
- ускорение свободного падения;
Н - глубина воды;
λ1 - характеристика ледяного покрова как плиты на упругом
основании (глава 8, п. 8.2).
Выражение в скобках, в отличие от формулы (9.1) может быть меньше
единицы.
Высота одиночной прогрессивной волны, по данным
опытов [56] составляет третью часть
от прогиба, ледяного покрова под нагрузкой. Определяя прогиб под движущейся
нагрузкой по формуле (8.7), после сортветствующих преобразований, представим:
выражение для определения высоты одиночной прогрессивной волны в следующем виде
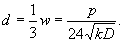
Выражение для максимальной высоты волны
вспучивания от предельного веса движущегося груза из расчета в упругой стадии
работы ледяного покрова после соответствующих преобразований примет вид
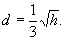 (9.7)
(9.7)
На рис. 9.1 даны графики изменения скорости
распространения свободных волн под ледяным покровом в зависимости от глубины
воды Н и толщины льда h.
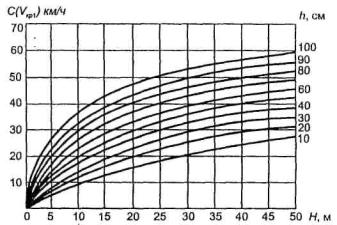
Рис. 9.1. Графики изменения скорости
распространения свободной волны под ледяным покровом
Для доказательства хорошей сходимости
результатов расчетных данных по предлагаемым формулам приведем сравнение их с
опытными данными [56]. При движении груза
весом 10,5 т со скоростью 35 км/ч по льду толщиной 60 см при глубине воды 18,8
м в опыте получены следующие величины: длина волны L=150 м, период колебаний
T=15 с. Расчетные
величины этих же параметров, по приведенным выше
формулам, соответственно равны С=33,8
км/ч, L=154 м, T=16,4 с.
9.3. Колебания ледяного слоя постоянной толщины под действием
движущегося сосредоточенного груза
Решение задачи, аналогично тому, как это сделано
в главе 8, п.8.3, дня движущегося с
постоянной скоростью V груза Р можно представить в адедующем виде:
 (9.8)
(9.8)
где при 0<V≤C

при V>C
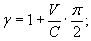 (9.9)
(9.9)
по оси координат ξ, в направлении движения
при 0<V≤C
 (9.10)
(9.10)
при V>С

по оси координат - ξ, в направлении,
противоположном движению
при 0<V≤C
 (9.11)
(9.11)
при
V>С
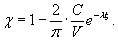
На рис. 9.2 изображена прогибограмма ледяного
покрова по оси ξ (вдоль оси движения грузов), рассчитанная по формуле (9.8), для случая, когда
скорость движения груза V равна
первой критической скорости движения нагрузки Vкр1 или скорость распространения свободной прогрессивной волны С.
Рис. 9.2. Прогибограмма ледяного покрова
при движении груза с первой критической скоростью
Кривая I - в направлении движения груза, кривая
II - в противоположном направлении ξ.
Опытными данными [56] доказано, что в случае,
когда скоросд движения груза равна скорости распространения свободной волны (V=C); прогиб под нагрузкой максимально возрастает, то есть
имеет место явление резонанса.
На рис. 9.3 дан график изменения динамического
коэффициента по прогибам для ледяного покрова под нагрузкой в зависимости от
скорости ее движения, подсчитанного на основе выражения (9.8), как отношение
динамического прогиба к статическому. Статический прогиб получен из (9.8) при скорости V=0.

Рис. 9.3. Изменение динамического
коэффициента по прогибам в зависимости от скорости движения груза по ледяному
покрову
График (кривая 1) построен для случая движения
груза Р=10,5 т по льду толщиной h=38 см, глубина воды H=6,3 м. Для этих же
данных получена экспериментальная кривая [56], которая нанесена на
рисунке пунктирной линией. Кривая 2 отражает зависимость динамического
коэффициента для льда толщиной 80 см при глубине воды 40 м.
Как видно из рис. 9.3, деформация ледяного
покрова под движущейся нагрузкой имеет сложный вид. При очень малой скорости
движения (до 3-5 км/ч) величина прогиба льда под нагрузкой почти такая же, как
и при статическом загружении.
Увеличение скорости движения приводит к уменьшению
прогиба льда под нагрузкой, это происходит до тех пор, пока скорость достигает
приблизительно 0,5 С. При этом прогиб
льда имеет минимальную величину (0,5±0,6)wСТ.
Дальнейшее увеличение скорости приводит к увеличению прогиба под нагрузкой, так
что при V=C динамический прогиб имеет
максимальную величину, несколько превышающую статический прогиб.
Скорость движения нагрузки, соответствующая
образованию максимального прогиба ледяного покрова, будем называть в дальнейшем
первой критической скоростью. При этом на расстоянии 71 впереди движущегося
груза образуется волна «вспучивания» (рис. 9.2).
Движение нагрузки со скоростью V>Vкр1 опять приводит к уменьшению прогиба ледяного покрова под
нагрузкой, которое наблюдается до тех пор, пока скорость V≤3 С.
Затем с увеличением скорости движения нагрузки
прогиб под ней вторично возрастает, достигая второго максимума при Vкр2 - второй критической скорости, величина которой определена
в главе 8, п. 8.3, формула (8.11).
Рис. 9.4. Изменение динамического
коэффициента по напряжениям в зависимости от скорости движения груза по ледяному
покрову
Выражения изгибающих моментов будут в данном
случае иметь следующий вид
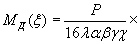
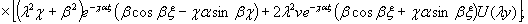 (9.12).
(9.12).


На рис. 9.4 даны графики изменения динамических
коэффициентов по напряжениям для уже описанного случая (рис. 9.3, кривая 1).
Динамические коэффициенты подсчитаны на основе выражение (9.12) по формулам

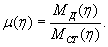 (9.13)
(9.13)
Изгибающие моменты МСТ(ξ) и МСТ(η)
получены из выражений (9.12) при скорости V=0.
Как видно из графиков, динамические коэффициенты по напряжению μ(η) больше, чем μ(ξ). Сравнение графиков на
рис. 9.3 и 9.4 показывает, что динамические коэффициенты по напряжениям μ(ξ) больше, чем по прогибам μn. Все значения
динамических коэффициентов определены для точки под грузом (начало осей
координат).
Однако, необходимо отметить, что по мере
удаления от движущегося груза амплитуда колебаний может увеличиваться и даже
превышать прогиб, полученный при статическом нагружении ледяного покрова.
Экспериментальными данными [56] установлено, что вдали
от трассы движения происходит наложение нескольких волн друг на друга, что в
отдельных случаях приводит к значительному увеличению амплитуды колебаний.
Интерференция ледяных волн может иметь большое
значение при движении нескольких грузов, при обгоне и встрече их. В этом случае
может иметь место сложение амплитуд, приводящее к разрушению ледяного покрова.
Особенно опасны такие явления при скорости движения, равной скорости
распространения свободных воли (V=С).
Такого рода явления наблюдались на Ладожской
трассе в 1942-1943 гг. Этим можно объяснить случаи внезапного провала
автомашин, в то время как до этого проходило значительное количество транспорта по льду, и следующие автомашины безаварийно
огибали место провала.
9.4. Колебания ледяного слоя переменной толщины под действием
движущегося сосредоточенного груза
Расчетную схему усиленного намораживанием
ледяного слоя можно представить в виде бесконечной плиты со ступенчатым
изменением жесткости (рис. 4.6).
Применяя подстановку η=у-vt, переходим к новой системе координат wxy, движущейся со скоростью V относительно первоначальной системы координат wxy.
Считая задачу симметричной относительно оси,
направленной вдоль линии движения нагрузки, рассмотрим последовательно два
участка плиты (глава 4, п. 4.6).
а) для первого участка 0≤λ1x≤a1 с
началом координат в точке О, функцию прогиба плиты можно представить в виде
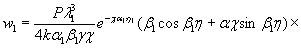
 (9.14)
(9.14)
б) для второго участка а1≤λx≤∞, перенося начало координат в точку O1 (рис. 4.6), получим

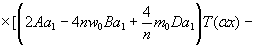
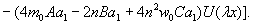 (9.15)
(9.15)
Выражения изгибающих моментов будут иметь
следующий вид
а) при 0≤α1x≤a1



 (9.16)
(9.16)
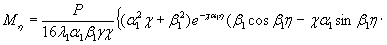
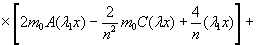
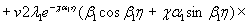
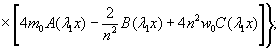 (9.17)
(9.17)
б) при а1≤λx≤∞
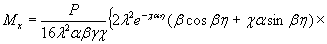




 (9.18)
(9.18)
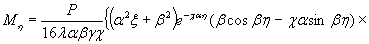

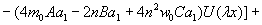
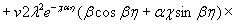
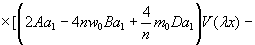
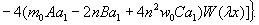 (9.19)
(9.19)
Если с полученными выражениями (9.14)-(9.19)
проделать такие же операции, что и в предыдущем параграфе, то получим значения
динамических коэффициентов для ступенчатой ледяной плиты как по прогибам, так и
по напряжениям. Существенной особенностью в данном случае будет тот факт, что
для таких плит теоретически существуют два значения как первой, так и второй
критической скорости, потому что толщина плиты на разных участках не
одинаковая. Соответственно увеличивается диапазон невыгодных скоростей движения
по ледовым переправам такой конструкции.
На основании приведенных расчетов и анализа
экспериментальных данных [56] можно сделать следующие
выводы:
1. Движение нагрузки по ледяному покрову в виде
отдельных транспортных единиц следует производить только в одном направлении,
если вес транспорта является предельным из расчета грузоподъемности ледяного
покрова в упругой стадии.
2. Интервал между отдельными транспортами должен
быть таким, чтобы время его преодоления не было близким к величине периода
колебаний отдельной прогрессивной волны (9.5).
3. Нельзя допускать у берега (за 50-70 м до
него) образования встречных (отраженных) воли, которые могут вызвать сложение
амплитуд колебаний.
4. При необходимости организации встречного
движении по ледяному покрову, при параллельном движении, расстояние между
трассами должно быть не менее 60-80 м при скорости до
20 км/ч, и не менее 200-220 м при скорости движения
больше 20 км/ч.
ГЛАВА
10. МЕСТНЫЕ ИМПУЛЬСИВНЫЕ ВОЗДЕЙСТВИЯ НА ЛЕДЯНОЙ СЛОЙ
10.1.
Постановка задачи и цель исследования
В предыдущей главе рассматривались вопросы
динамического расчета ледяного покрова при движении по нему нагрузок в
предположении, что ледяной слой имеет идеально гладкую поверхность.
В действительности же, в процессе эксплуатации
ледовых переправ, как указывалось в главе 6, п. 6.2, появляются различного
рода неровности, при проходе через которые движущийся транспорт оказывает
дополнительное воздействие на ледяной слой.
Особенность этих дополнительных воздействий в
том, что действуют они в течение очень короткого промежутка времени, однако
численная величина их может быть довольно значительна и в отдельных случаях
превышает значения динамических коэффициентов, определенных в главах 7-9.
Рассмотрим задачи о проходе массы через местное
препятствие, то есть такое препятствие, линейные размеры которого в направлении
движения достаточно малы. В пределах этого препятствия необходимо рассмотреть
кроме инерционных сил, учтенных ранее, также силы, появляющиеся непосредственно
при прохождении массы через препятствия.
Введем уже ранее принятую систему координат ξ=x-v t, жестко связанную с
движущимся грузом. Как было уже показано, в этом случае однородное
дифференциальное уравнение изгиба плиты имеет вид (6.7).
В течение всего времени движения по ледяному
слою на последний будет воздействовать постоянная сила, определяемая так, как
было показано в главе 8, п. 8.2.
Кроме этого, в течение промежутка времени, за
который груз проходит через, препятствие, на ледяной слой будут действовать
дополнительные центробежные силы [75].
Так как наибольший интерес представляет случай
быстрого перехода массы через препятствие, будем характеризовать динамическое
воздействие этих весьма кратковременных сил их импульсом. Следовательно, задача
сводится к последовательному рассмотрению двух вопросов:
1) определению импульса сил, возникающего при
прохождении через препятствие;
2) изучению действия этого импульса на ледяной слой.
10.2.
Определение импульса сил
В каждый момент того промежутка времени, в
течение которого груз проходит через препятствие, на ледяной слой будет
действовать дополнительная сила
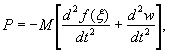 (10.1)
(10.1)
где f(ξ) - уравнение линии
очертания препятствия;
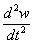 - с физической точки зрения представляет
собой дополнительное ускорение, вызванное теми перемещениями, которые
испытывает груз вследствие деформаций, возникающих в плите при прохождении
груза через препятствие.
- с физической точки зрения представляет
собой дополнительное ускорение, вызванное теми перемещениями, которые
испытывает груз вследствие деформаций, возникающих в плите при прохождении
груза через препятствие.
Так как ξ=x-v
t, а под грузом ξ=0, то
 (10.2)
(10.2)
Ввиду того, что  мало по сравнению с
мало по сравнению с 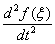 , будем этим слагаемым в дальнейшем пренебрегать.
, будем этим слагаемым в дальнейшем пренебрегать.
Таким образом, в течение промежутка времени t=l/V, где l - длина препятствия, а V
- скорость движения груза, на ледяной слой будет действовать сила
P=-MF(t). (10.3)
Импульс этой силы будет
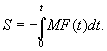 (10.4)
(10.4)
Рядом экспериментов на грузовых автомобилях [188], представляющих почти
полностью современный типаж, показано, что для практических расчетов
эквивалентная система может разбиваться на две независимые части. Это допустимо
в силу слабой связи колебаний передней и задней частей автомобиля.
Поэтому полагают, что эквивалентная
колебательная система, отображающая подрессоривание только передней или только
задней частей автомобиля, является типовой, и составляют ее в виде, показанном
на рис. 10.1.

Рис. 10.1. Эквивалентная
схема подрессоренной части автомобиля
Здесь М
- подрессоренная масса, приведенная к вертикальной плоскости над осью колес;
m - неподрессоренная масса ведущего моста;
Сp - суммарная жесткость рессор подвески данного моста;
сшр - суммарная радиальная
жесткость шин;
β - коэффициент пропорциональности
при вязком сопротивлении, имеющем место при колебаниях системы с гидравлическим
амортизатором, в котором создается сопротивление движению поршня, зависящее не
от перемещения (как это свойственно упругим связям), а от его скорости и пропорционально
ее первой степени;
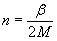 - приведенный коэффициент сопротивления в
подвеске.
- приведенный коэффициент сопротивления в
подвеске.
В данном случае вынужденные колебания системы
являются результатом движения точки крепления упругой связи. При колебаниях
точки крепления упругой связи по закону f(t) груз колеблется так,
как если бы на него действовала возмущающая сила P(t)=cf(t).
Рассмотрим конкретный пример. Аналитическое
выражение микропрофиля дороги для обособленной неровности наиболее характерной
синусоидальной формы, имеющей максимальную длину l и высоту а0, можно представить в виде
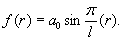 (10.5)
(10.5)
Условная частота свободных колебаний
подрессоренной массы автомобиля, определяемая по формуле (6.15), будет
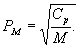 (10.6)
(10.6)
Условная частота свободных колебаний
неподрессоренной массы, возникающих за счет радиальной жесткости шин
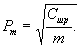 (10.7)
(10.7)
При качении колеса автомобиля по обособленной
неровности, описываемой уравнением (10.5), центр тяжести неподрессоренной массы
т за счет свободных колебаний Рm, будет описывать другую
траекторию, отличающуюся от уравнения препятствия.
Уравнение движения центра тяжести массы m, как показано в работе
Я.Г. Пановко [113], имеет вид
 (10.8)
(10.8)
Обозначение τ
введено для того, чтобы отличить время, меняющееся в интегрировании (от 0 до t), от верхнего предела t0,
который в этом процессе должен считаться постоянным.
Применяя подстановку 
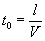 и произведя замену переменных, имеем с учетом
(10.5)
и произведя замену переменных, имеем с учетом
(10.5)
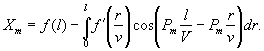 (10.9)
(10.9)
После интегрирования и необходиых
преобразований, получим уравнение движения центра массы m в виде
 (10.10)
(10.10)
где
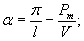

Первая производная от функции X будет
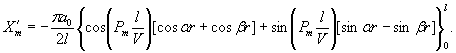 (10.11)
(10.11)
Для определения уравнения движения центра
подрессоренной массы М будем исходить
из условия жесткой связи точки подвеса рессоры с неподрессоренной массой m.
Применяя уравнение (10.9) и подставляя в него
вместо функций f(r) и f'(r) выражения (10.10), (10.11) при r=l, получим после соответствующих преобразований
 (10.12)
(10.12)
Первая производная от функции Хм
будет
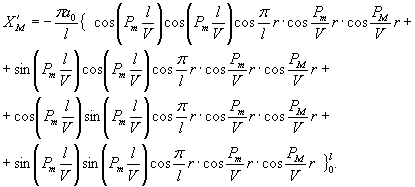 (10.13)
(10.13)
Подставляя производные (10.11) и (10.13) в
выражение (10.4) и произведя замену
переменных, получим
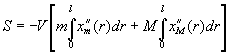
или
 (10.14)
(10.14)
После подстановки значения производных (10.11),
(10.13) в выражение (10.14), получим величину импульса, действующего на ледяной
слой в. течение времени t0
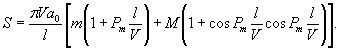 (10.15)
(10.15)
Если учесть затухание колебаний подрессоренной
массы автомобиля n, то исходное уравнение движения центра массы М примет вид [113]
 (10.16)
(10.16)
Произведя замену переменных, получим

где  - условная частота
свободных колебаний подрессоренной массы с учетом вязкого сопротивления.
Опуская промежуточные выкладки, связанные с интегрированием выражения (10.16),
представим значение импульса в виде
- условная частота
свободных колебаний подрессоренной массы с учетом вязкого сопротивления.
Опуская промежуточные выкладки, связанные с интегрированием выражения (10.16),
представим значение импульса в виде
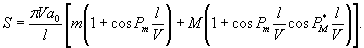
Сравнивая это выражение импульса с формулой
(10.15), приходим к выводу, что учет затухания колебаний подрессоренной массы
можно свести к замене условной частоты свободных колебаний подрессоренной массы
Рм
на величину РM*.
Для определения периода собственных колебаний
ледяного слоя следует пользоваться формулой
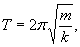
которая после подстановки всех известных величин
и необходимых преобразований принимает вид
 (10.17)
(10.17)
В выражении (10.17) величина h - толщина льда, см.
А.Н. Крыловым [85] доказано, что если
период свободных колебаний системы мал по сравнению с продолжительностью
действия силы (T<t0=t0),
то она может считаться медленно изменяющейся, а ее действие можно рассматривать
без учета динамичности, то есть считать силу приложенной статически.
Если же импульс действует в течение короткого
промежутка времени 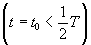 ,а затем исчезает, то, как показано В.А. Киселевым [65] и Я.Г. Пановко [113], максимальное
отклонение системы достигается после исчезновения силы. При этом импульс силы и
уравнение движения колеблющейся системы от действия этого импульса приближенно
связаны между собой уравнением, которое в нашем случае имеет вид [113]
,а затем исчезает, то, как показано В.А. Киселевым [65] и Я.Г. Пановко [113], максимальное
отклонение системы достигается после исчезновения силы. При этом импульс силы и
уравнение движения колеблющейся системы от действия этого импульса приближенно
связаны между собой уравнением, которое в нашем случае имеет вид [113]
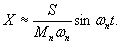
С учетом вязкого сопротивления, приводящего к
затуханию свободных колебаний, колебательный процесс подрессоренной массы
автомобиля, вызванный импульсом S,
описывается законом
 (10.18)
(10.18)
Тогда для времени t<t0 уравнение движения точки ледяного слоя, в
которой приложена движущаяся нагрузка (рис. 10.1) с учетом (6.8) и (10.18)
будет иметь вид
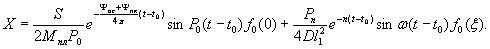 (10.19)
(10.19)
Выражение (10.19) представляет собой уравнение
неустановившихся колебаний ледяного слоя, где первая часть - свободные
колебания, вызванные действием на него импульса S, а вторая - вынужденные колебания от действия колеблющейся с
частотой ω=Рм (10.6) и движущейся со
скоростью V подрессоренной части
автомобиля.
Для учета затухания свободных колебаний в
ледяном слое значение Р0
следует брать из выражения (7.4), которое учитывает неупругое сопротивление
льда и воды как упругого основания ледяного слоя.
Затухание колебаний подрессоренной массы
автомобиля, как показали исследования [188], можно считать
пропорциональными скорости относительного перемещения моста и рамы автомобиля,
что отмечено на рис. 10.1 коэффициентом пропорциональности β.
Динамический коэффициент с учетом (10.19) будет
иметь вид
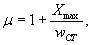 (10.20)
(10.20)
где Хmax - максимальная амплитуда колебаний ледяного слоя,
определяемая из выражения (10.19).
Максимальная амплитуда колебаний
 (10.21)
(10.21)
Время t1
определяется из условия X'=0 (для точки ξ=0), откуда имеем
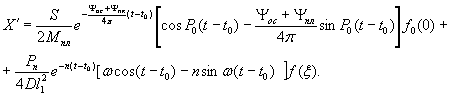 (10.22)
(10.22)
где Мn - приведенная масса
ледяного слоя, определяемая выражением
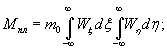
m0 -
масса плиты, приходящаяся на единицу площади;
WξWη - функция прогиба бесконечного ледяного слоя, зависящая
только от координат (глава 3, п. 3.1).
После подстановки всех известных величин и
соответствующих преобразований получим
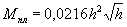 кгс·с2/см, (10.23)
кгс·с2/см, (10.23)
где h - толщина ледяного
слоя, см.
10.3. Колебания ледяного слоя, возникающие при преодолении
автомобилем вертикального препятствия
Рассмотрим упрощенную расчетную схему, по
которой колеса автомобиля одновременно наезжают на местное препятствие высотой h0
(рис. 10.2).
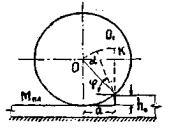
Рис. 10.2. Расчетная схема
для определения импульса силы при преодолении автомобилем местного препятствия
Попытаемся выяснить, какое влияние окажет на
прогиб ледяного слоя это местное препятствие, если колесо радиуса R движется с постоянной скоростью V.
Как показано М.Н. Ручимским [135], вертикальное
перемещение h=h(t) центра инерции
колеса может быть аппроксимировано параболой
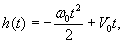
где W0
и V0 - абсолютные величины
ускорения и вертикальной составляющей скорости центра инерции колеса и
начальный момент, тогда

 (10.24)
(10.24)
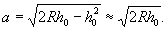
Встречу колеса с препятствием можно представить
как внезапное введение жесткой связи между колесом автомобиля и ледяным слоем,
причем высота этой связи изменяется во времени по закону
 (10.25)
(10.25)
здесь ось h направлена вниз.
Заметим, что уравнение (10.25) описывает
траекторию движения центра инерции колеса не только в случае, изображенном на рис. 10.2, но и во всех других
случаях, когда поверхность препятствия не выходит за пределы параболы (10.25).
Факт внезапного появления вертикальной начальной
скорости V0 свидетельствует о том, что воздействие колеса на
препятствие носит импульсивный характер. Для того чтобы выкладки, связанные с
импульсивностью силовых воздействий, были более наглядными, введем
дополнительную жесткую связь hф(t) таким образом, чтобы
графики скорости и ускорения центра инерции колеса имели вид, показанный на
рис. 10.3.

Рис. 10.3. Расчетная схема для
определения импульса силы при преодолении автомобилем местного препятствия
Тогда в момент времени от t=0 до t=t1,
жесткая связь изменяется по закону hф(t), а от t=t1 до t = t0
= 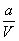 - по закону h(t).
- по закону h(t).
Действительно, графики скорости и ускорения
центра инерции колеса отличаются от графиков (рис. 10.3) лишь отсутствием
участка 0-t1 на
оси t [135].
Полагая tg
Θ→α и переходя в дальнейших выкладках к пределу при t→0 и α t1→V0, можно вернуться к действительной
схеме.
При t≤t1
уравнения движения системы, изображенной на рис. 10.3, будут иметь вид
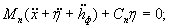
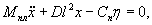
где η=х1-(х+hф) - осадка рессоры;
Х1 и X -
соответственно вертикальные перемещения масс Мn и Мпл
Сn=Сшр+Ср - суммарная жесткость подвески автомобиля;
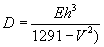 - жесткость ледяного слоя.
- жесткость ледяного слоя.
При одновременном учете
масс Мn и Мпл не представляется возможным решить данные уравнения.
Обычно, если масса плиты велика по сравнению с массой автомобиля, то
рассматривается задача о движении идеализированного «безынерционного» груза по
весомой плите. Если же масса плиты мала по сравнению с массой автомобиля, то
ставится задача о движении груза по невесомой плите.
Представим теперь уравнения в виде
при t≤t1
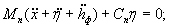

при t1≤t≤t0
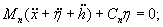
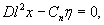
Решения этих уравнений будут иметь вид
при t≤t1
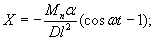
при t1≤t≤t0

Постоянные
интегрирования можно определить из следующего условия: при t=t1 величины X и Х1 должны быть соответственно
равны.
Переходя к пределу при t1→0 и αt1→V0,
a также используя соотношение V0=W0t0,
имеем 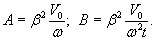
Величина β
может быть представлена в виде
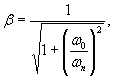
где ω0
- частота свободных колебаний бесконечной плиты с учетом массы действующего на
нее груза (7.31).
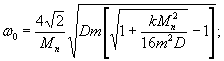
 - частота
собственных колебаний подрессоренной массы автомобиля.
- частота
собственных колебаний подрессоренной массы автомобиля.
Произведя соответствующие преобразования,
получим решение задачи в виде
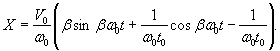
Максимум этого выражения будет
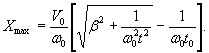 (10.26)
(10.26)
Аналогично находим, что при t≥t0

Максимум выражения равен
 (10.27)
(10.27)
Динамический коэффициент в данном случае имеет
вид
 (10.28)
(10.28)
где Amах - максимальная амплитуда колебаний ледяного слоя с учетом
как подрессоренной массы автомобиля, так и приведенной массы ледяного слоя
(10.23);
wcT - статический прогиб
ледяного слоя от веса автомобиля.
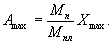 (10.29)
(10.29)
Время преодоления препятствия
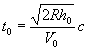
явно меньше половины
периода собственных колебаний ледяного слоя (10.17), поэтому импульс можно
считать мгновенным.
При преодолении колесом автомобиля препятствия,
описываемого уравнением (10.25), центр неподрессоренной массы m за счет свободных
колебаний Рm будет описывать другую
траекторию.
Подставляя в уравнение (10.8) первую производную по
τ от функции (10.25) и ее значение при 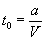 ,
получим после соответствующих преобразований
,
получим после соответствующих преобразований
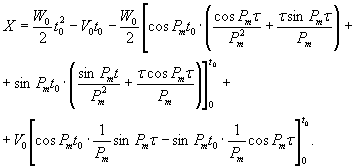 (10.30)
(10.30)
Первая производная от функции Х равна
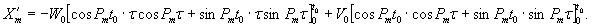 (10.31)
(10.31)
Для определения уравнения движения центра
подрессоренной массы М будем исходить
из условия жесткой связи точки подвеса рессоры с неподрессоренной массой.
Применяя уравнение (10.8) и подставляя в него
вместо функции f(t) выражение (10.30) при τ=t0 и его первую
производную по τ (10.31),
получим
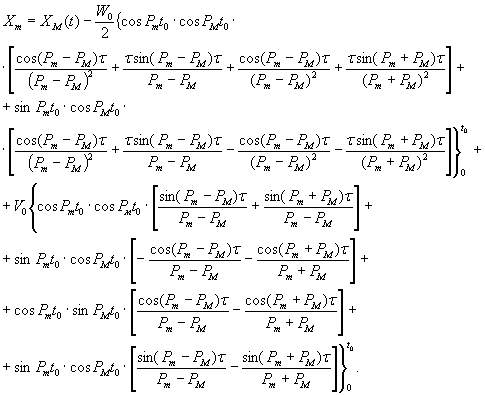 (10.32)
(10.32)
Первая производная от функции Хм
равна
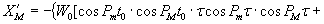
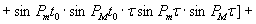
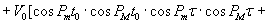
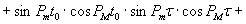

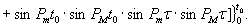 (10.33)
(10.33)
Величину импульса, возникающего при преодолении
автомобилем местного препятствия (рис. 10.2), определим из (10.14), откуда после
соответствующих преобразований получим
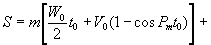
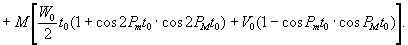 (10.34)
(10.34)
Вязкое сопротивление амортизаторов автомобиля
существенно влияет на общую силу, передающуюся ледяному покрову при свободных
колебаниях системы. Эта сила состоит из двух слагаемых, соответствующих упругой
и вязкой связи (рис. 10.1)
N = CpXМ+βx'М.
Обозначая вес подрессоренной части автомобиля
через Рn, выразим коэффициент
передачи силы в виде
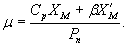 (10.35)
(10.35)
Первая производная от (10.35) по оси Хм
будет иметь вид
сpх'м +βх''M,
где Х'м - первая производная от
уравнения движения центра массы М,
дана в виде (10.33), вторая производная будет иметь вид

Чтобы
определить максимальное значение динамического коэффициента μ (10.35),
необходимо приравнять первую производную по т нулю, то
есть
сpх'м +βх''M=0
и найти соответствующее
значение времени τ=t.
10.4.
Учет взаимного влияния нескольких движущихся нагрузок
Воспользовавшись идеей М.А. Гершгорина [39], Б.Г. Коренев, имея
основную функцию влияния, дал механическую интерпретацию решения задачи изгиба
балки на упругом основании с учетом массы движущегося по ней груза [75].
В применении к нащей задаче сущность этой
интерпретации состоит в следующем.
Рассматривая задачу о движении нагрузки по
бесконечному ледяному слою, предположим, что в точке приложения груза имеется
фиктивная пружина против кривизны, то есть пружина, препятствующая нарастанию
кривизны ледяного слоя. Обозначив жесткость такой пружины через G, можно определить усилия,
воспринимаемые ледяным слоем и пружиной, приравняв их кривизны. Если усилие,
воспринимаемое ледяным слоем, равно  , то имеет место равенство
, то имеет место равенство
 (10.36)
(10.36)
откуда
 (10.37)
(10.37)
Вторая производная от основной функции влияния  имеет размерность
1/кгс·см (см. гл. 8, формула (8.4). Прогиб ледяного слоя
под нагрузкой
имеет размерность
1/кгс·см (см. гл. 8, формула (8.4). Прогиб ледяного слоя
под нагрузкой 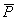 будет равен
будет равен
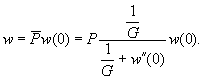 (10.38)
(10.38)
Сравнивая выражения (10.38) и (8.4), делаем вывод, что
задачу о движении груза можно рассматривать как задачу о движении нагрузки, в
точке приложения которой имеется пружина против кривизны с жесткостью G=M V2.
Принимая во внимание данный вывод, распространим
полученные выше решения на случай системы связанных движущихся грузов.
Рассмотрим движение колонны из трех грузов P1=M1g, P2=M2g и P3=M3g с
постоянной скоростью V; интервал
между грузами С, начало координат в
точке приложения первого груза Р1.
Если в точках приложения грузов передаются
нагрузки Р1, Р2 и Р3, то их можно определить из следующей системы
уравнений
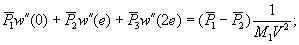
 (10.39)
(10.39)
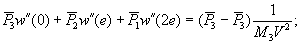
откуда
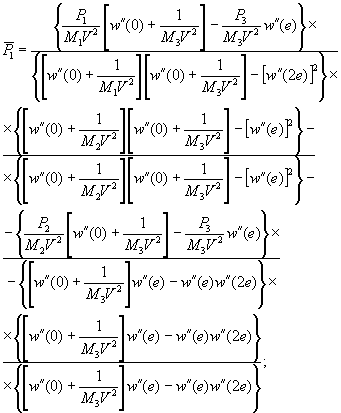 (10.40)
(10.40)

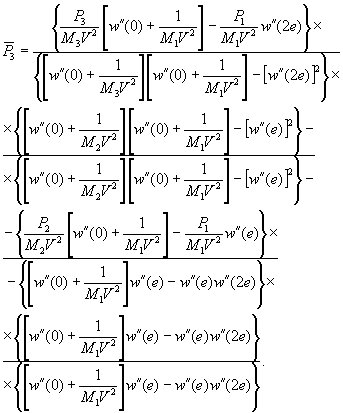
Прогибы в точках
приложения грузов будут соответственно равны

 (10.41)
(10.41)
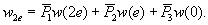
В случае Р1=Р2=Р3=Р
и М1=М2=М3=М
имеем
 (10.42)
(10.42)

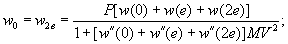
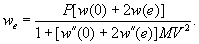
Для случая двух грузов Р1=Р2=Р с интервалом, равным С, имеем
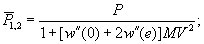 (10.43)
(10.43)
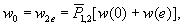
то есть получим уже известное решение для
движущейся системы, состоящей из двух грузов, приведенное Б.Г. Кореневым [75].
Приравняв нулю w(С) и w"(C), определим минимальное значение интервала С, при котором две соседние нагрузки не
будут оказывать влияния друг на друга.
w(e)=0; (10.44)
w''(e)=0.
Точное решение системы (10.44) дает значение
С→∞.
Но практически, например при решении задач в
полярных координатах с помощью функций Бесселя (глава 3, п.3.6), влияние соседнего
груза исключается уже при е=6/l.
Из выражения (10.43), получим после
соответствующей подстановки
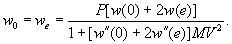 (10.45)
(10.45)
Заметим, что в начале координат (в точке 0)
вторая производная от функции прогиба w"(0)
всегда отрицательна, так как мы имеем дело с отрицательной начальной кривизной,
то есть плитой, изогнутой вниз.
Таким образом, назначая расстояние С между движущимися грузами, равными
ординате, при которой вторая производная от функции прогиба имеет максимальную
положительную величину, можно добиться уменьшения прогиба w0 за
счет разгружающего действия второго движущегося груза по отношению к первому.
Рассматривать случай движения четырех и более
грузов нецелесообразно ввиду громоздкости получаемых решений и трудности их
практического применения.
В случае пропуска колонны автомобилей через
местное препятствие ледяной покров будет испытывать действие периодических
импульсов, возникающих с интервалом времени
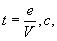 (10.46)
(10.46)
где е
- интервал между автомобилями, м;
V - скорость движения колонны, м/с.
При этом импульсы будут иметь один знак, то есть
не меняют направления действия, поэтому наиболее невыгодным будет случай, когда
интервал времени t равен периоду Т собственных колебаний ледяного
слоя.
Приравняв выражения (10.46) и (10.17), получим величину
невыгодного интервала между автомобилями
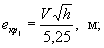 (10.47)
(10.47)
 (10.48)
(10.48)
Для того чтобы действие периодических импульсов
было сведено к минимуму, необходимо интервал между автомобилями назначать по формуле
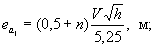 (10.49)
(10.49)
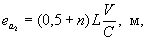
где n=1, 2, 3....
При  влияние соседнего
импульса практически исключается.
влияние соседнего
импульса практически исключается.
Полный динамический коэффициент от воздействия
периодических импульсов с учетом (10.20) будет равен
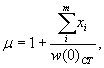 (10.50)
(10.50)
где 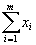 - сумма m амплитуд колебаний
ледяного слоя (10.21) или (10.29) с учетом внутренних
неупругих сопротивлений льда и жидкого упругого основания.
- сумма m амплитуд колебаний
ледяного слоя (10.21) или (10.29) с учетом внутренних
неупругих сопротивлений льда и жидкого упругого основания.
Значение времени, при котором имеет место
максимальная амплитуда колебаний, определяется для каждого импульса отдельно,
по формуле
 (10.51)
(10.51)
где i
- количество импульсов, равное количеству проходящих в колонне автомобилей,
изменяется от 1 до m;
t1 -
время, соответствующее появлению максимальной амплитуды колебаний ледяного
покрова от действия первого импульса.
В выражении (10.50) величина w(0)CT - прогиб от
статического воздействия колонны автомобилей, определяется из выражения (10.42), при значении скорости
V=0.
В данном случае формула примет вид
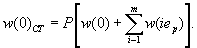 (10.52)
(10.52)
Результирующее значение динамического
коэффициента от действия движущейся колонны автомобилей
будет равно сумме динамических коэффициентов (10.20) и (10.50).
ОБЩИЕ ВЫВОДЫ И РЕКОМЕНДАЦИИ
На основании теоретических и экспериментальных
исследований, изложенных в данной книге, можно сделать следующие общие выводы и
рекомендации:
а) По физико-механическим свойствам ледяного
покрова:
1. При расчетах ледяного покрова на статическое
действие внешних нагрузок величшгу модуля упругости льда можно принимать равной
55÷60 тыс. кгс/см2 и модуль сдвига равным 15 тыс. кгс/см2.
2. Для расчетов ледяного покрова на динамическое
воздействие внешних нагрузок целесообразно принимать значение модуля упругости
льда равным 90 тыс. кгс/см2 и модуля сдвига - 30 тыс. кгс/см2.
3. Величина коэффициента Пуассона для льда при
расчетах в упругой стадии может быть принята равной 0,3 независимо от характера
внешней нагрузки.
4. Средние значения нормативного сопротивления
предела текучести при изгибе естественного льда пресных водоемов в зависимости
от устойчивой отрицательной температуры можно принимать по СНиП 2.06.04-82*.
5. Нормативное сопротивление естественного льда
на растяжение при изгибе приблизительно равно нормативному сопротивлению
намороженного строительного льда на сжатие при изгибе, что позволяет успешно
применять способ усиления ледяного покрова путем намораживания дополнительного
ледяного слоя.
6. При увеличении скорости подачи нагрузки на
лед предел прочности его уменьшается в 2-2,5 раза по сравнению со случаем
статического приложения нагрузки.
7. Предел прочности льда при динамическом
воздействии знакопеременной нагрузки в 3-4 раза ниже, чем при статическом
воздействии нагрузки.
8. Величина коэффициента неупругого сопротивления
льда в основном зависит от температуры воздуха и определяется по
экспериментальной зависимости (2.20).
9. Логарифмический декремент затухания колебаний
воды как упругого основания ледяного покрова имеет среднее значение 0,185.
б) По расчету ледяного покрова на действие
статических нагрузок:
1. В случаях, когда внешняя нагрузка находится в
пределах прибрежной зоны ледяного покрова, рекомендуется определять
грузоподъемность его краевого участка по методике расчета, изложенной в главе 3.
Грузоподъемность краевого участка ледяного
покрова, определенная по схеме полубесконечной плиты со свободной кромкой, в
три раза ниже чем грузоподъемность ледяного слоя, рассчитанная по схеме
бесконечной плиты при центральном изгибе.
При удалении груза на расстояние а>1,5π от кромки, влияние ее на грузоподъемность ледяного покрова
полностью исключается.
Колебания уровней воды в водоеме существенно
влияют на грузоподъемность ледяного покрова в прибрежной зоне и могут быть
учтены в расчете по методике, изложенной в главе 3, п. 3.6, 3.10.
2. Следует признать целесообразным и
рациональным способ усиления ледяного покрова путем намораживания
дополнительной полосы льда. При необходимости увеличения грузоподъемности
естественного ледяного покрова до двух раз, рациональной является схема
одноступенчатого усиления, и для увеличения грузоподъемности до четырех, раз
целесообразнее применение схемы двухступенчатого усиления.
3. На основании сравнения опытных данных с
расчетными (глава 1, п.
1.9), определение грузоподъемности усиленного ледяного покрова
предпочтительнее производить по методике расчета, изложенной в главе 4, п. 4.7, 4.9, где расчетная нaгрузка
от автомобиля считается распределенной по окружности приведенного радиуса, а не
сосредоточенной.
4. При расчете ледяного покрова по теории гибких
плит на упругом винклеровом основании эпюра распределения напряжений по толщине
льда в упругой стадии имеет вид (рис. 1.5, а) и при расчете в
упругопла-стическрй стадии - вид (рис. 1.5, б).
5. Предложен способ расчета ледяного покрова с
учетом упругопластических деформаций льда, на основе которого произведен расчет
ледяного покрова по двум предельным состояниям (глава 5, п. 5.2).
6. Первое предельное состояние характеризуется
появлением радиальных трещин в ледяном покрове при центральном изгибе. Второе
предельное состояние характеризуется появлением кольцевых трещин в ледяном
покрове при центральном изгибе. Несущая способность ледяного покрова после
второго предельного состояния практически полностью исчерпывается.
7. Разработана конструкция усиления ледяного
покрова и определены ее оптимальные параметры.
8. Усиление ледяного покрова способом
намораживания дополнительной полосы льда по оптимальным параметрам позволяет
достигнуть максимального увеличения грузоподъемности ледовых переправ при
минимальном объеме работ.
в) По расчету ледяного покрова на действие
динамических нагрузок:
1. Определены, по крайней мере, два значения
критической скорости движения нагрузки по ледяному покрову и два значения
критической частоты колебаний ледяного покрова.
2. Значения критических скоростей движения
нагрузки по ледяному покрову целесообразно определять по формулам (8.10), (8.29).
3. Для определения динамических коэффициентов по
напряжениям целесообразно пользоваться формулой (8.28), при этом коэффициенты
их по напряжениям получаются большими, чем по прогибам (8.9).
4. При критических значениях частоты вынужденных
колебаний ледяного покрова (7.4), (9.4) следует учитывать
затухания, характеризующиеся внутренними неупругими сопротивлениями льда и
воды. Максимальное значение динамического коэффициента можно определять по
формуле (7.14).
5. Величина критической скорости движущейся по
ледяному покрову вибрационной нагрузки зависит от частоты колебаний ю и толщины
ледяного слоя и может быть определена по формуле (8.36).
6. Дополнительные динамические воздействия,
появляющиеся в результате проезда автомобилей по дорожным неровностям, типа
вертикальных препятствий, носят импульсивный характер.
7. Значения динамических коэффициентов,
определенных в результате экспериментов при пропуске автомобилей через
вертикальное местное препятствие, удовлетворительно согласуются с
соответствующими им теоретическими величинами, подсчитанными по формуле (10.28).
8. Грузоподъемность ледяного покрова, имеющего
местные неровности, существенно уменьшается при движении по нему автомобилей,
потому что, несмотря на незначительную величину динамического коэффициента
(1.08-1.10), резко снижается предел прочности льда, так как нагрузка от
автомобиля на ледяной покров передается не статически, а с некоторой
вертикальной скоростью.
9. При динамическом расчете ледяного покрова на
вибрационную нагрузку учет массы колеблющегося груза приводит к существенному
уменьшению (до 10-12%) критической частоты колебаний ледяного слоя и увеличению
величины динамического коэффициента.
10. Учет инерции движущегося груза и инерции
упругого основания приводит к уменьшению величины второй критической скорости
движения до 13% при расчете в упругой стадии.
11. При движении автомобилей по ровной ледяной
дороге значения динамических коэффициентов, определенных
экспериментально, хорошо согласуются с теоретическими по формулам (9.13).
библиографический
список
1. Альтберг В.Я. Сила смерзания льда с
некоторыми веществами// Труды ГГИ. 1958. Вып. 4.
2. Аполлов Б.А. Учение о реках. М.: Изд-во МГУ,
1951. 552 с.
3. Арцыбашев С.А., Парфианович И.А. Определение
коэффициента теплопроводности льда// Журнал физико-химического общества. 1928.
Т. 60. Вып. 5.
4. Арцыбашев С.А., Южаков В.К. Определение
коэффициента теплопроводности снега // Известия биолого-географического НИИ при
Государственном Иркутском университете. Иркутск, 1931. Вып. 44.
5. Бабаков И.М. Теория
колебаний. М., 1968. 560 с.
6. Барнес X. Ледотехника. М.: Госэнергоиздат,
1924.
7. Баталии A.M. О морских аэродромах / Морская
гидрометеообсерватория при ВУТМС. Владивосток, 1946.
8. Бернштейн С.А.
Ледяные переправы// Сборник отдела инженерных исследований НТК НКПС.
Новосибирск, 1929. Вып. XVIII.
9. Бубырь А.А. Пористый лед как материал в
гидротехническом строительстве // Известия вузов. Строительство и архитектура.
1961. № 3.
10. Бутягин И.П. О
прочности ледяного покрова при изгибе // Труды ТЭИ ЗСФАН. Новосибирск, 1955.
Вып. V.
11. Бутягин И.П.
Прочность ледяного покрова в ледовых нагрузках на гидросооружения// Труды ТЭИ
СО АН СССР. Новосибирск, 1961. Вып. XI.
12. Бычковский Н.Н.
Вопросы статического и динамического расчета ледяного покрова при устройстве
ледовых дорог и переправ: Отчет по научно-исследовательской работе. Саратов,
1976.428 с.
13. Бычковский Н.Н.
Изгиб полубесконечной плиты на упругом основании // Материалы к III науч.-техн. конф. молодых ученых. Саратов,
1970.
14. Бычковский Н.Н.
Колебания балки на упругом основании с учетом действующего на нее груза //
Основания, фундаменты и подземные сооружения. Сборник № 68. М., 1972.
15. Бычковский Н.Н. Некоторые задачи динамики
бесконечной плиты, лежащей на упругом основании // Совершенствование
конструкций и методов расчета мостов и мостовых переходов: Межвуз. науч. сб.
Саратов, 1976. Вып. 1.
16. Бычковский Н.Н.
Некоторые задачи изгиба плит, лежащих на упругом основании // Научные труды Саратовского политехнического института.
Саратов, 1974. Вып. 67.
17. Бычковский Н.Н.
Определение грузоподъемности полубесконечного ледяного слоя / Сарат. политехн, ин-т. Саратов, 1969. 146 с.
18. Бычковский Н.Н.
Определение импульса силы, возникающего при движении автомобиля по проезжей
части моста // Научные труды Саратовского политехнического института. Саратов,
1975. Вып. 81.
19. Бычковский Н.Н. Расчет
балок на упругом основании по предельному состоянию // Расчет пространственных систем в строительной механике. Саратов: Изд-во Сарат.
ун-та, 1972.
20. Бычковский Н.Н.
Расчет бесконечной плиты на упругом основании, имеющей ступенчатое изменение
жесткости, по предельным состояниям//
Совершенствование конструкций и методов расчета искусственных сооружений на
автомобильных дорогах: Межвуз. науч. сб. Саратов, 1977. Вып. 2.
21. Бычковский Н.Н.
Расчет пологих сферических и незамкнутых цилиндрических оболочек по предельному
состоянию // Механика деформируемых сред. Саратов, 1974. Вып. 2.
22. Бычковский Н.Н.,
Богачев С.Т. Колебания балок и плит на упругом основании с учетом массы
движущегося груза // Научные труды Саратовского политехнического института.
Саратов, 1974. Вып. 67.
23. Бычковский Н.Н.,
Богачев С.Т. О расчете плит большой протяженности, лежащих на упругом основании
// Материалы к III науч.-техн. конф. молодых ученых. Саратов, 1970.
24. Бычковский Н.Н.,
Богачев СТ. Расчет плиты переменной толщины, лежащей на упругом основании, с
учетом упругопластических деформаций // Совершенствование конструкций и методов
расчета мостов и мостовых переходов. Саратов, 1976. Вып. 1.
25. Бычковский Н.Н., Ефимов Г.И. Расчет
полубесконечной балки на упругом основании по предельному состоянию// Материалы
к III науч.-техн. конф. молодых ученых. Саратов, 1970.
26. Вейнберг Б.П. Лед.
Свойства, возникновение и исчезновение льда. М.-Л.: Гостехиздат, 1940.
27. Войтковский К.Ф.
Механические свойства льда. М.: Изд-во АН СССР, 1960.564 с.
28. Войтковский К.Ф. Расчет
сооружений из льда и снега. М.: Изд-во АН СССР, 1954. 132 с.
29. Войтковский К.Ф. Экспериментальные исследования
пластических свойств льда // Сезонное промерзание грунтов и применение льда для
строительных целей. М.: Изд-во АН СССР, 1957. 146 с.
30. Вопросы ледотехники: Сб. статей
/ Под ред. К.Н. Коржавина. Новосибирск, 1955.
31. Вопросы ледотехники:
Сб. ст. / Под ред. К.Н. Коржавина. Новосибирск, 1958.
32. Временные указания по наведению и
эксплуатации ледяной переправы через Бухтарминское водохранилище у с. Кзыл-Ту /
МВССО Казахской ССР. Усть-Каменогорский строительно-дорожный институт, 1972.
33. Вялов С.С. Закономерности деформирования
льда// Советская Антарктическая экспедиция 10. Л.: Морской транспорт, 1970.
34. Вялов С.С., Ермаков
Н.Ф. Снижение прочности льда во времени // Труды координационных совещаний по
гидротехнике. М.: Энергия, 1964. Вып. X.
35. Вялов С.С., Ермаков Н.Ф. Снижение прочности
льда во времени // Труды координационных совещаний по гидротехнике. М.: Энергия,
1965. Вып. XXIII.
36. Галеркин Б.Г. Упругие тонкие плиты. М.:
Госстройиздат, 1933.
37. Гамаюнов А.И. Определение давления льда на
опоры мостов // Железнодорожное строительство. 1955. № 1.
38. Гвоздев А.А. Расчет несущей способности конструкций
по методу предельного равновесия. М.: Стройиздат, 1949. 280 с.
39. Гершгорин М.А.
Колебания пластинок, загруженных сосредоточенными массами // Прикладная
математика и механика. 1933. Т. I. Вып. I.
40. Гогенемзер К.,
Прагер В. Динамика сооружений. М.: ОНТИ, 1936.487 с.
41. Голушкевич С.С.
Некоторые вопросы расчета ледяного покрова. М.: Гостехиздат, 1947. 148 с.
42. Гольденблат И.И.
Некоторые вопросы теории упругих и пластических деформаций. М.: Стройиздат,
1950. 43 с.
43. Грандштейн И.С., Рыжик И.М. Таблицы интегралов,
сумм, рядов и произведений. М.: Госиздат ФМЛ, 1962. 684 с.
44. Давиденков Н.Н. О
рассеянии энергии при вибрациях //
Журнал технической физики. 1938. Т. VIII. Вып. 5.
45. Давыдов И.В. Изгиб балок в упруго
пластической стадии на упругом основании // Труды ХИСИ. 1958. Т. II. Вып. 8.
46. Дарков А.В. Основы теории расчета балок на
упругом основании. М: Трансжелдориздат, 1940. 88 с.
47. Динник А.Н. Приложение функций Бесселя к
задачам теории упругости. Избранные труды. Киев: Изд-во АН УкрССР, 1955. Т. И.
151с.
48. Дмитриев А.Д.
Приближенное решение задачи расчета бесконечной плиты на упругом основании при
осесимметричной нагрузке // Труды Саратовского
автомобильно-дорожного института. Сборник 13. Саратов, 1955.
49. Дмитриев А.Д. Расчет
бесконечной плиты на упругом основании при осесимметричной нагрузке по предельному состоянию // Труды Саратовского
автомобильно-дорожного института. Сборник 14. Саратов, 1956.
50. Дмитриев А.Д. Расчет
плит на упругом основании по предельному состоянию // Труды Саратовского автомобильно-дорожного института.
Сборник И. Саратов, 1951. Вып. 1.
51. Дутов
Т.Д. Расчет балок на упругом основании (новый метод). Л.: Изд-во
КУБОЧ, 1929.
52. Елистратова A.M.
Определение коэффициента теплопроводности льда и снега. Дипломная работа
физического факультета МГУ, 1946. 99 с.
53. Жемочкин Б.Н., Синицын А.П. Практические
методы расчета фундаментных балок и плит на упругом основании. М.: Стройиздат,
1947. 67 с.
54. Зволинский Н.В. К вопросу о деформации
плавающего ледяного слоя. Свердловск: Гидрометеоиздат, 1946. 56 с.
55. Зубов Н.Н. Основы
устройства дорог на ледяном покрове. М.: Гидрометеоиздат, 1946. 175 с.
56. Иванов К.Е., Кобеко
П.П., Шульман А.Р. Деформация ледового покрова при движении грузов // Журнал
технической физики. 1946. Т. XVI. Вып. 3.
57. Иванов
К.Е., Лавров В.В. Об одной особенности механизма пластической деформации льда//
Журнал технической физики. 1950. Т. XX. Вып. 2.
58. Иванов К.Е,
Песчанский И.С. Грузоподъемность ледяного покрова и устройство дорог на льду //
Труды Арктического НИИ Главсевморпути. Т. 23. М.: Изд-во Главсевморпуть, 1949.
59. Ильюшин А.А.
Пластичность. М.: ОГИЗ, 1948. Ч. I.
60. Инструкция по проектированию вспомогательных сооружений и
устройств для строительства мостов, ВСН 139-78. М.: Минтрансстрой, 1978. 300 с.
61. Исследование
ледового режима рек и водохранилищ / Под ред. А.Н. Чижова. М.: Гидрометеоиздат,
1971.
62. Ишлинский А.Ю.
Продольные колебания стержня при наличии линейного закона последействия и
релаксации // Прикладная математика
и механика. 1940. Т. IV.
63. Карташкин Б.Д.
Экспериментальные исследования физико-механических свойств льда / Труды ЦАГИ.
1947. № 607.
64. Качанов Л.М. Основы теории пластичности. М.:
Гостехтеориздат, 1956.
65. Киселев В.А.
Строительная механика. Специальный курс (динамика и устойчивость сооружений).
М., 1969.
66. Кистьян К.А. Определение частот колебаний
пластинок на упругом основании // Прикладная механика. 1965. Т. I. Вып. 5.
67. Китовер К. Круглые тонкие плиты. М.:
Госстройиздат, 1958.
68. Клишевич Г.В. Расчет балок на упругом основании.
Л., 1932.
69. Ключарев В., Изюмов С. Определение
грузоподъемности ледяных переправ // Военно-инженерный журнал. 1943. № 2-3.
70. Кобеко П.П., Шишкин Н.Т., Марей Ф.И.
Пластическая деформация и вязкость льда // Журнал технической физики. 1946. Т.
XVI. Вып. 3.
71. Комаровский А.Н. Структура и физические
свойства ледяного покрова пресных вод. М.-Л.: Госэнергоиздат, 1932.
72. Копп Н.С. Сооружение ледяных дорог и мостов
в Канаде // Транспортное строительство. 1976. № 7.
73. Коренев Б.Г. Вопросы
расчета балок и плит на упругом основании. М.: Госстройиздат, 1954.
74. Коренев Б.Г.
Движение силы по бесконечной балке на упругом основании // Строительная
механика и расчет сооружений. 1967. № 3.
75. Коренев Б.Г.
Некоторые задачи динамики балок на упругом основании // Научные сообщения
ЦНИПС. 1955. Вып. 20.
76. Коренев Б.Г. О расчете балок и плит с учетом
пластических деформаций // Инженерный сборник. 1948. Т. 5. Вып. 1.
77. Коренев Б.Г.,
Черниговская Е.И. Расчет плит на упругом основании. М.: Госстройиздат, 1962. *
78. Коржавин К.Н. Воздействие
льда на инженерные сооружения. Новосибирск: СО АН СССР, 1962. 203 с.
79. Коржавин К.Н.
Исследование механических свойств речного льда. Новосибирск: НИВИТ, 1940.
80. Коржавин К.Н. Особенности
физико-механических свойств пресноводного льда // Труды координационных
совещаний по гидротехнике. 1965. Вып. XXIII.
81. Коржавин К.Н., Бутягин И.П. Исследование
деформаций и прочности ледяных полей в натурных условиях // Труды ТЭИ СО АН
СССР. Новосибирск, 1961. Вып. XI.
82. Корунов М.М. Интенсивность образования
ледяного слоя из воды, налитой на лед // Метеорология и гидрология. 1940. № 9.
83. Корунов М.М. Расчет ледяных переправ. М.:
Гостехиздат, 1940.
84. Крицкий С.Н. Зимний термический режим
водохранилищ, рек и каналов. М.-Л.: Госэнергоиздат, 1947. 155 с.
85. Крылов А.Н. Вибрация
судов. М.: ОНТИ, 1936. 103 с.
86. Крылов А.Н. О расчете балок, лежащих на
упругом основании. Л., 1930. 154 с.
87. Кузнецов П.А. Действие льда на сооружения
морских портов и защита от него. Л., 1939.
88. Кузнецов В.И. Упругое основание. Расчеты балок, плит и рам.
М.: Госстройиздат, 1952. 296 с.
89. Кузуб Г.Я.
Температурный режим ледяного покрова // Труды ТЭИ СО АН СССР. Новосибирск,
1955. Вып. 5.
90. Кузуб Г.Я.
Температурные трещины в ледяном покрове // Труды ТЭИ СО АН СССР. Новосибирск,
1958. Вып. 7.
91. Лавров В.В. Природа масштабного эффекта у
льда и прочность ледяного покрова // ДАН СССР. 1958. Т. 122, № 4.
92. Ландау Л.Д., Лифшиц Е.Н. Теоретическая
физика. Т. 7. Теория упругости. М.: Наука, 1965. 203 с.
93. Лебедев П.И. Ледяные переправы.
М.: Воениздат, 1940.
94. Ледяные переправы /
Под ред. Г.Р. Брегмана и Б.В. Проскурякова. М.: Гидрометеоиздат, 1943. 97 с.
95. Лисер И.Я. Влияние условий замерзания на
толщину ледяного покрова рек // Труды ТЭИ СО АН СССР. Новосибирск, 1965. Вып.
15.
96. Ляв А. Математическая теория упругости. М.:
ОНТИ, 1935. 674 с.
97. Маслов А.И. Опыт расчета внешних усилий,
действующих на корпус судна в ледовых условиях // Труды ВИТО Судостроения.
1933. Т. II. Вып. 1П.
98. Марчук А.Н. Перекрытие рек под ледяным
покровом. М.: Энергия, 1973. 103 с..
99. Марчук А.Н., Митти СВ. Использование несущей
способности льда на строительстве Братской ГЭС // Гидротехническое
строительство. 1966. №7.
100. Матошко СИ. К несущей способности пластин
при изгибе // Прикладная механика. 1965. Т. I. Вып. П.
101. Москатов Н.А. О посадке самолетов на лед//
Труды Арктического института. 1938. Т. 110.
102. Муравский Г.Б.
Неустановившиеся колебания груза, лежащего на бесконечной плите, опирающейся на
упругое основание // Известия АН СССР. Механика. 1965. № 1.
103. Мучников В.М. О некоторых методах расчета
упругих систем на колебания при подвижной нагрузке. М.: Госстройиздат, 1953.
104. Найвельт В.В. Действие подвижной нагрузки
на бесконечную плиту, лежавшую на упругом основании // Известия вузов.
Строительство и архитектура. 1967. № 5.
105. Найвельт В.В.
Колебания бесконечной плиты, лежащей на упругом основании, при действии
подвижной нагрузки: Автореф. ... канд. техн. наук. М., 1967. 34 с.
106. Найвельт В.В.
Неустановившиеся колебания бесконечной плиты, лежащей на упругом основании, при
движении по ней инерционного груза // Прикладная механика. 1969. Т. 5. Вып. 8.
107. Некрасов СФ. Работа ледяного пути под
вагонной нагрузкой // Труды ГТИ. 1936. Т. XV.
108. Нечаев В.М. Экономическая эффективность
устройства ледяных переправ //Известия вузов. Строительство и архитектура.
1977. № 2.
109. Новиков Г.Л. Снеговые и ледовые дороги.
М.-Л.: Гострансиздат, 1935.
110. Палатников Е.А. Прямоугольная плита на
упругом основании. М.: Стройиздат, 1964. 236 с.
111. Пановко Я.Г. Введение в теорию механических
колебаний. М.: Наука, 1971. 223 с.
112. Пановко Я.Г. Исторический очерк развития
теории динамического действия подвижной нагрузки // Труды Ленинградской ВВИА.
1948. Вып. 17.
113. Пановко Я.Г. Основы
прикладной теории упругих колебаний. М.: Машиностроение, 1967. 316 с.
114. Панфилов Д.Ф.
Влияние поперечных сдвигов и анизотропии льда на деформацию ледяного слоя при
изгибе // Труды координационных совещаний по гидротехнике. 1965. Вып. ХХIII.
115. Панфилов Д.Ф.
Влияние характера распределения нагрузки на несущую способность льда //
Гидротехническое строительство. 1964. № 3.
116. Панфилов Д.Ф. Изгиб ледяного покрова
кратковременной статической нагрузкой // Труды координационных совещаний по
гидротехнике. М.: Энергия, 1964. Вып. X.
117. Панфилов Д.Ф. Изменение грузоподъемности
ледяного покрова при подходе грузов на кромку льда// Гидротехническое
строительство. 1966. №1.
118. Панфилов Д.Ф. О методах расчета
грузоподъемности льда // Гидротехническое строительство. 1963. № 4.
119. Панфилов Д.Ф.
Определение грузоподъемности ледяного покрова для целей производства работ по
перекрытию русел рек в зимнее время //
Труды ГИСИ им. Чкалова. Горький, 1958. Вып. 29.
120. Панфилов Д.Ф. Расчет грузоподъемности
ледяного покрова// Труды ГИСИ им. Чкалова. Горький, 1960. Вып. 35.
121. Панфилов Д.Ф. Экспериментальные
исследования грузоподъемности льда // Известия ВНИИГ. 1960. Т. 64.
122. Папкович В.Ф.
Строительная механика корабля. Л.: Оборонгиз, 1941.640 с.
123. Пастернак П.Л. Основы нового метода расчета
фундаментов на упругом основании при помощи двух коэффициентов
постели. М: Госстройиздат, 1954. 56 с.
124. Песчанский И.С. Ледоведение и ледотехника.
Л.: Гидрометеоиздат, 1967. 274 с.
125. Петров A.M. Расчет балок с учетом
пластических деформаций// Строительная механика и расчет сооружений. 1968. № 5.
126. Петруничев Н.Н. О динамическом давлении
льда// Ледотехнические вопросы в гидротехнике. М.: Госэнергоиздат, 1954.
127. Пинетин В.Н. Об
изменении модуля упругости и коэффициента Пуассона у речного льда при сжатии //
Наука и техника. 1927. № 3-4.
128.
Порожняков B.C. Ледяные переправы. М.: Автотрансиздат, 1963.88 с.
129. Птухин Ф.И. Исследование механических свойств намороженного
строительного льда // Труды координационных совещаний по гидротехнике. М.:
Энергия, 1965. Вып. XXIII.
130. Расчет пластин и оболочек/ Под общ. ред.
В.Г. Рекача. М.: Машгиз, 1963.
131. Рейнов Н.М.
Прогибограф // Журнал технической физики. 1943. Т.ХIII.Вып,
11-12.
132. Ржаницын А.Р. Расчет сооружений с учетом
пластических свойств материалов. М.: Госстройиздат, 1954. 288 с.
133. Ротенберг Р.В. Подвеска автомобиля и его
колебания. М.: Машгиз, 1960.355 с.
134. Ручимский М.Н. К
расчету конических и пологих сферических оболочек при осесимметричном загружении.
М.: Стройиздат, 1958.
135. Ручимский М.Н. О
вертикальных динамических усилиях, возникающих при движении мостового крана по подкрановым балкам // Исследования по динамике сооружений.
М.: Стройиздат, 1951.
136. Рымша В.А. Ледовые исследования на реках и
водохранилищах. Л.: Гидрометеоиздат, 1959. 191с.
137. Савельев Б.А. Изучение механических и
физических свойств льда. М.: Изд-во АН СССР, 1957.
138. Савельев Б.А.
Руководство по изучению свойств льда. М.: Изд-во МГУ, 1968.
139. Савельев Б.А.
Строение, состав и свойства ледяного покрова морских и пресных
водоемов. М.: Изд-во МГУ, 1968.
140. Савельев Б.А. Физика, химия и строение
природных льдов и мерзлых горных пород. М.: Изд-во МГУ, 1971.
141. Савинов A.M. Прочность строительного льда
при различной температуре // Труды координационных совещаний по гидротехнике.
1965. Вып. XXIII.
142. Сергеев Б.Н. Устройство зимней переправы
вагонов по льду и работа ледяного слоя под действием нагрузки // Ледяные
переправы: XVIII сборник отдела инженерных исследований НТК НКПС. М.:
Транспечать, 1939.
143. Синицын А.П. Расчет
балок и плит на упругом основании за пределом упругости. М.: Стройиздат, 1964.
144. Слепян Л.М. О взаимодействии пластинок с
жидкостью при ударе // Механика твердого тела. 1966. № 6.
145. СНиП 2.06.04-82*. Нагрузка и
воздействия на гидротехнические сооружения (волновые, ледовые и от судов). М.,
1989.
146. Снитко Н.К. Грузоподъемность ледяных переправ
(новые данные по расчету ледяных переправ) // Труды ВТА. 1945. Вып. II.
147. Снитко Н.К. Методы расчета сооружений на
вибрацию и удар. М.: Госстройиздат, 1958. 287 с.
148. Снитко Н.К. Некоторые новые задачи динамики
// Информационный бюллетень ВТА. 1955. № 55.
149. Соколова Е.М. Термический режим рек
Сибири// Труды ГТИ. 1951. Вып. 30.
150. Сорокин Е.С.
Замкнутое решение задачи о вынужденных колебаниях стержней с гистерезисом // Исследования по теории сооружений. Сборник № 4. М.:
Стройиздат, 1949.
151. Сорокин Е.С. К
вопросу неупругого сопротивления строительных материалов при колебаниях// Научные сообщения ЦНИПС. М.: Гос-стройиздат, 1954. Вып.
15.
152. Сорокин Е.С. К
теории внутреннего трения при колебаниях упругих систем. М.: Госстройиздат, 1960. 131 с.
153. Сорокин Е.С. Метод учета неупругого сопротивления материала
при расчете конструкций на колебания // Исследования по динамике
сооружений. М.: Стройиздат, 1951.
154. Телов В.И., Кануков
И.М. Наплавные мосты, паромные и ледяные переправы. М.: Транспорт, 1978. 384 с.
155. Тимошенко С.П.
История науки о сопротивлении материалов. М.: Гостехиздат, 1957. 536 с.
156. Тимошенко С.П.
Колебания в инженерном деле. М: Машиностроение, 1985. 472 с.
157. Тимошенко С.П. Курс теории упругости. Киев:
Наук, думка, 1972.544 с.
158. Тимошенко С.П. Прикладная теория упругости.
М.: ОНТИ, 1931.392 с.
159. Тимошенко С.П. Войновский-Кригер. Пластинки
и оболочки. М.: Физматгиз, 1966. 635 с.
160. Уманский А.А. О расчете балок на упругом
основании. М.: Стройиздат, 1933. 112 с.
161. Уманский А.А.
Специальный курс строительной механики.
М.: ОНТИ, 1935.4.1.238 с.
162. Ухов СБ. Методика
определения модуля упругости и коэффициента вязкости льда по изгибам // Труды
координационного совещания по гидротехнике. М.: Энергия, 1964. Вып. X.
163. Хейсин Д.Е. Влияние
неупругих свойств льда на изгибные колебания ледяного слоя // Труды
координационного совещания по гидротехнике. 1964. Вып. X.
164. Хейсин Д.Е.
Колебания плавающего ледяного покрова// Проблемы Арктики и Антарктики. 1963. №
12.
165. Хренов А.Ф. О ледяных переправах// Техника
и вооружение. 1939. № 12, №22.
166.
Фалькевич Б.С. Теория автомобиля. М.: Машгиз, 1963. 239 с.
167. Филиппов А.П.
Колебания деформируемых систем. М.: Машиностроение, 1970. 734 с.
168. Филиппов А.П.,
Кохманюк С.С. Динамическое воздействие подвижных нагрузок на стержни. Киев:
Наук, думка, 1967. 132 с.
169. Цейтлин А.И. Ударное загружение бесконечной
балки на упругом основании // Исследования по динамике сооружений и расчет
конструкций на упругом основании. М, 196 Г.
170. Шадрин Г.С. Экспериментальное исследование
динамического воздействия льда на сооружения. MV. ВНИИГ, 1952.
171. Шанкин П.А. К вопросу о расчете на
прочность бетонного покрытия откоса на воздействие ледяного припоя //
Гидротехническое строительство. 1961. № 3.
172. Шапиро Г.С. Изгиб полубесконечной плиты, на
упругом основании // Прикладная математика и механика. 1943. Т. VII. Вып. 4.
173. Шапиро Г.С. О расчете плиты, имеющей вид
бесконечной ленты, лежащей на упругом основании // ДАН. 1942. Т. XXXVII, № 7-8.
174. Шехтер О.Я., Винокурова А.В. Расчет плит на
упругом основании. М., 1936.
175. Шишов Н.Д. О прочности льда// Метеорология
и гидрология. 1946. №2.
176. Шулейкин В.В. Физика моря. М.: Наука, 1968.
432 с.
177. Шульман А.Р. К расчету грузоподъемности ледяных
переправ по теории центрального изгиба упругой плиты на упругом основании U
Материалы к вопросу о ледовых переправах. М.: Гидрометеоиздат, 1946.
178. Шульман А.Р., Казанский М.М. Теоретические
и опытные основания таблиц грузоподъемности ледяного покрова // Материалы к
вопросу о ледовых переправах. М.: Гидрометеоиздат, 1946.
179. Шумский П.А. Основы
структурного ледоведения. М.: Изд-во АН ССР, 1955.355 с.
180. Шушерина Е.П., Туликов А.Е. Механические
свойства льдов различного строения // Труды координационных совещаний по
гидротехнике. 1964. Вып. X.
181. Щапов Н.М. Удар льдин о сооружения//
Гидротехническое строительство. 1933. № 2.
182. Яковлев А.С. Вынужденные колебания
бесконечной балки с учетом инерции упругого основания // Строительная механика
и расчет сооружений. 1965. № 1.
183. Яковлев А.С. Учет-инерции упругого
основания в задачах о вынужденных колебаниях балок и плит// Строительная
механика и расчет сооружений. 1967. № 1.
184. Яковлев Г.Н. Тепловой баланс дрейфующего
ледяного покрова центральной Арктики // Проблемы Арктики. 1957. № 5.
185. Якунин А.Е.
Изучение несущей способности ледяного покрова// Труды координационных совещаний по вопросам гидротехники.
М.: Энергия, 1965. Вып. ХХШ.
186. Яровой В.Е. О
динамическом воздействии движущегося груза на плиту, лежащую на упругом
основании // Известия вузов. Строительство и архитектура. 1968. № 8.
187. Яценко Н.Н.
Нагруженность трансмиссии автомобиля и плавность дороги. М.: Транспорт, 1967.
164 с.
188. Яценко Н.Н.,
Прутчиков O.K. Плавность хода грузовых автомобилей. М.: Машиностроение, 1969.
220 с.
189.
Bodeau А.С. Can we measure riding comfort electronically? SAE annual Meet,
Preprints. 1959. N 34T.
190.
Devik O. Termische und Dynamische der Eisbildung auf Norwe-gische Verhmltnisse
angewand// Geophisike Publikasjoner. Oslo, 1931. V. DC № 1.
191.
Glen Z.W. The creep of polycrystalline ice// Proc. Roy. Soc. № 1175, London,
1955.
192.
Krummel O. Handbuch der Ozeanographie. Stutgart, 1923.
193.
Ringer W. bber die Verflnderungen in der Zusammensetzung des Meereswassersalzes
beim Ausfrieren, 1906.
194.
Royen N. Jstrick vid temperatur hoginner Hillnigsskifttiangned. Vieh Heusen,
Stokholm, 1922.
195.
Sleicher F. Kreisplatten auf elastischen unterlage, 1926.
196.
Tabata T. Ameasurement of viso-elastic constants of sea ice // J. Oceanograph.
Soc. Japan. Dec. 1955. Vol. II. № 4.
197.
Timoshenko S. Coolected Papers. Me Graw Hill. N.Y.
London, 1953.
Приложение
Значения характеристик ледяного покрова λ и l (см-1) в
зависимости от толщины и модуля упругости льда
|
Толщина льда h, см
|
Модуль упругости льда, кгс/см2
|
Толщина льда h, см
|
Модуль упругости льда, кгс/см2
|
|
60000
|
90000
|
60000
|
90000
|
|
λ×104
|
l×104
|
λ×104
|
l×104
|
λ×104
|
l×104
|
λ×104
|
l×104
|
|
10
|
25,972
|
36,724
|
23,468
|
33,184
|
46
|
8,269
|
11,692
|
7,472
|
10,565
|
|
11
|
24,180
|
34,191
|
21,849
|
30,895
|
47
|
8,136
|
11,505
|
7,352
|
10,396
|
|
12
|
22,653
|
32,031
|
20,469
|
28,943
|
48
|
8,009
|
11,244
|
7,237
|
10,161
|
|
13
|
21,333
|
30,165
|
19,276
|
27,257
|
49
|
7,886
|
11,151
|
7,126
|
10,076
|
|
14
|
20,179
|
28,533
|
18,234
|
25,782
|
50
|
7,767
|
10,983
|
7,018
|
9,924
|
|
15
|
19,495
|
27,566
|
17,616
|
24,909
|
51
|
7,653
|
10,821
|
9,915
|
9,778
|
|
16
|
18,256
|
25,814
|
16,496
|
23,326
|
52
|
7,542
|
10,665
|
6,815
|
9,637
|
|
17
|
17,445
|
24,667
|
15,763
|
22,289
|
53
|
7,435
|
10,513
|
6,718
|
9,499
|
|
18
|
16,713
|
23,632
|
15,102
|
21,354
|
54
|
7,332
|
10,367
|
6,624
|
9,368
|
|
19
|
16,049
|
22,693
|
14,502
|
20,505
|
55
|
7,232
|
10,225
|
6,535
|
9,240
|
|
20
|
15,443
|
21,836
|
13,954
|
19,731
|
56
|
7,135
|
10,088
|
6,447
|
9,116
|
|
21
|
14,888
|
21,052
|
13,453
|
19,022
|
57
|
7,040
|
9,955
|
6,361
|
8,995
|
|
22
|
14,378
|
20,329
|
12,992
|
18,371
|
58
|
6,949
|
9,826
|
6,279
|
8,879
|
|
23
|
13,906
|
19,663
|
12,565
|
17,768
|
59
|
6,861
|
9,701
|
6,199
|
8,766
|
|
24
|
13,469
|
19,046
|
12,171
|
17,209
|
60
|
6,775
|
9,579
|
6,122
|
8,656
|
|
25
|
13,063
|
18,471
|
11,804
|
16,691
|
61
|
6,691
|
9,461
|
6,046
|
8,549
|
|
26
|
12,684
|
17,936
|
11,461
|
16,207
|
62
|
6,610
|
9,347
|
5,973
|
8,446
|
|
27
|
12,330
|
17,435
|
11,141
|
15,754
|
63
|
6,531
|
9,235
|
5,901
|
8,345
|
|
28
|
11,999
|
16,966
|
10,842
|
15,331
|
64
|
6,455
|
9,127
|
5,833
|
8,247
|
|
29
|
11,687
|
16,525
|
10,560
|
14,932
|
65
|
6,379
|
9,021
|
5,764
|
8,152
|
|
30
|
11,394
|
16,111
|
10,296
|
14,558
|
66
|
6,307
|
8,919
|
5,699
|
8,059
|
|
31
|
11,117
|
15,719
|
10,045
|
14,204
|
67
|
6,237
|
8,819
|
5,636
|
7,968
|
|
32
|
10,855
|
15,349
|
9,809
|
13,869
|
68
|
6,168
|
8,722
|
5,573
|
7,881
|
|
33
|
10,608
|
14,999
|
9,585
|
13,553
|
69
|
6,101
|
8,626
|
5,513
|
7,795
|
|
34
|
10,373
|
14,667
|
9,373
|
13,253
|
70
|
6,035
|
8,534
|
5,453
|
7,711
|
|
35
|
10,150
|
14,352
|
9,172
|
12,968
|
71
|
5,971
|
8,443
|
5,395
|
7,629
|
|
36
|
9,937
|
14,052
|
8,979
|
12,697
|
72
|
5,909
|
8,305
|
5,339
|
7,549
|
|
37
|
9,735
|
13,766
|
8,797
|
12,439
|
73
|
5,848
|
6,269
|
5,284
|
7,472
|
|
38
|
9,543
|
13,493
|
8,623
|
12,192
|
74
|
5,789
|
8,185
|
5,231
|
7,396
|
|
39
|
9,358
|
13,232
|
8,456
|
11,957
|
75
|
5,731
|
8,103
|
5,178
|
7,322
|
|
40
|
9,182
|
12,983
|
8,297
|
11,732
|
76
|
5,674
|
8,023
|
5,127
|
7,250
|
|
41
|
9,014
|
12,746
|
8,145
|
11,517
|
77
|
5,619
|
7,945
|
5,077
|
7,179
|
|
42
|
8,852
|
12,517
|
7,999
|
11,311
|
78
|
5,565
|
7,868
|
5,029
|
7,110
|
|
43
|
8,698
|
12,298
|
7,859
|
11,113
|
79
|
5,512
|
7,793
|
4,981
|
7,042
|
|
44
|
8,549
|
12,088
|
7,725
|
10,923
|
80
|
5,460
|
7,720
|
4,934
|
6,976
|
|
45
|
8,406
|
11,986
|
7,596
|
10,740
|
81
|
5,409
|
7,649
|
4,888
|
6,911
|
|
82
|
5,360
|
7,579
|
4,843
|
6,848
|
117
|
4,105
|
5,805
|
3,709
|
5,246
|
|
83
|
5,311
|
7,510
|
4,799
|
6,786
|
118
|
4,079
|
5,767
|
3,6В6
|
5,212
|
|
84
|
5,264
|
7,443
|
4,757
|
6,725
|
119
|
4,054
|
5,732
|
3,663
|
5,179
|
|
85
|
5,217
|
7,337
|
4,714
|
6,666
|
120
|
4,028
|
5,696
|
3,639
|
5,147
|
|
86
|
5,172
|
7,313
|
4,673
|
6,608
|
121
|
4,003
|
5,661
|
3,617
|
5,115
|
|
87
|
5,127
|
7,250
|
4,633
|
5,551
|
122
|
3,979
|
5,626
|
3,595
|
5,083
|
|
88
|
5,083
|
7,188
|
4,593
|
6,495
|
123
|
3,954
|
5,591
|
3,573
|
5,052
|
|
89
|
5,040
|
7,127
|
4,554
|
6,440
|
124
|
3,931
|
5,558
|
3,552
|
5,022
|
|
90
|
4,998
|
7,068
|
4,516
|
6,386
|
125
|
3,907
|
5,524
|
3,530
|
4,992
|
|
91
|
4,957
|
7,009
|
4,479
|
6,334
|
126
|
3,884
|
5,491
|
3,509
|
4,962
|
|
92
|
4,917
|
6,952
|
4,443
|
6,282
|
127
|
3,861
|
5,459
|
3,489
|
4,933
|
|
93
|
4,877
|
6,896
|
4,407
|
6,231
|
128
|
3,838
|
5,427
|
3,468
|
4,904
|
|
94
|
4,838
|
6,841
|
4,372
|
6,181
|
129
|
3,816
|
5,395
|
3,443
|
4,875
|
|
95
|
4,801
|
6,788
|
4,338
|
6,132
|
130
|
3,794
|
5,364
|
3,428
|
4,847
|
|
96
|
4,762
|
6,734
|
4,303
|
6,085
|
131
|
3,772
|
5,334
|
3,408
|
4,819
|
|
97
|
4,725
|
6,681
|
4,296
|
6,037
|
132
|
3,750
|
5,303
|
3,389
|
4,792
|
|
98
|
4,689
|
6,630
|
4,237
|
5,991
|
133
|
3,729
|
5,273
|
3,370
|
4,765
|
|
99
|
4,653
|
6,580
|
4,204
|
5,946
|
134
|
3,708
|
5,244
|
3,351
|
4,738
|
|
100
|
4,619
|
6,531
|
4,174
|
5,901
|
135
|
3,688
|
5,214
|
3,332
|
4,712
|
|
101
|
4,584
|
6,482
|
4,142
|
5,857
|
136
|
3,667
|
5,186
|
3,314
|
4,6В6
|
|
102
|
4,550
|
6,434
|
4,111
|
5,814
|
137
|
3,647
|
5,157
|
3,295
|
4,660
|
|
103
|
4,517
|
6,387
|
4,082
|
5,772
|
138
|
3,627
|
5,129
|
3,277
|
4,625
|
|
104
|
4,487
|
6,341
|
4,054
|
5,730
|
139
|
3,608
|
5,101
|
3,260
|
4,609
|
|
105
|
4,453
|
6,296
|
4,024
|
5,689
|
140
|
3,588
|
5,074
|
3,242
|
4,585
|
|
106
|
4,421
|
6,251
|
3,995
|
5,649
|
141
|
3,569
|
5,047
|
3,225
|
4,561
|
|
107
|
4,390
|
6,207
|
3,967
|
5,609
|
142
|
3,551
|
5,020
|
3,209
|
4,536
|
|
108
|
4,359'
|
6,164
|
3,939
|
5,570
|
143
|
3,532
|
4,994
|
3,192
|
4,513
|
|
109
|
4,329
|
6,122
|
3,912
|
5,532
|
144
|
3,513
|
4,968
|
3,174
|
4,489
|
|
110
|
4,301
|
6,080
|
3,886
|
5,494
|
145
|
3,501
|
4,951
|
3,164
|
4,474
|
|
111
|
4,271
|
6,039
|
3,859
|
5,457
|
146
|
3,477
|
4,917
|
3,142
|
4,443
|
|
112
|
4,242
|
5,998
|
3,833
|
5,420
|
147
|
3,460
|
4,892
|
3,126
|
4,420
|
|
113
|
4,214
|
5,959
|
3,808
|
5,384
|
148
|
3,442
|
4,867
|
3,110
|
4,398
|
|
114
|
4,186
|
5,919
|
3,782
|
5,349
|
149
|
3,425
|
4,842
|
3,095
|
4,376
|
|
115
|
4,159
|
5,881
|
3,758
|
5,314
|
150
|
3,407
|
4,818
|
3,079
|
4,354
|
|
116
|
4,132
|
5,843
|
3,734
|
5,279
|
|
|
|
|
|
Содержание
|
ПРЕДИСЛОВИЕ
ВВЕДЕНИЕ
Часть первая
ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА ЛЕДЯНОГО ПОКРОВА
ГЛАВА 1. ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА ЛЬДА
1.1. Структура ледяного покрова
1.2. Основные закономерности деформирования льда
1.3. Упругие характеристики ледяного покрова, модуль
упругости и модуль сдвига льда
1.4. Коэффициент Пуассона
1.5. Пределы прочности, расчетные значения
нормативных сопротивлений и пределов текучести льда
1.6. Механические свойства намороженного
строительного льда
1.7. Сопротивление льда динамическим нагрузкам
1.8. Распределение напряжений по толщине ледяного
слоя при изгибе
1.9. Испытания ледяного слоя на изгиб
1.10. Температурный режим ледяного покрова
1.11. Температурные напряжения и трещины в ледяном
покрове
1.12. Ледовый режим рек и водохранилищ, расчетная
толщина ледяного покрова
1.13. Проведение транспортных и монтажных работ в
зимнее время при строительстве автодорожного моста через р. Обь у г. Сургута
ГЛАВА 2. УЧЕТ НЕУПРУГОГО СОПРОТИВЛЕНИЯ ЛЬДА ПРИ
РАСЧЕТЕ ЛЕДЯНОГО ПОКРОВА НА КОЛЕБАНИЯ
2.1. Общие сведения о природе поглощения энергии
колебаний в твердом материале
2.2. Теории внутреннего трения упругопластического
материала
2.3. Гипотеза внутреннего трения
2.4. Методика определения коэффициента поглощения
энергии колебаний
2.5. Экспериментальное определение коэффициента поглощения
энергии колебаний льда и логарифмического декремента затухания колебаний воды
как упругого основания ледяного покрова
2.6. Экспериментальное исследование динамического воздействия
движущегося автомобиля на ледяной покров
Часть вторая
РАСЧЕТ ЛЕДЯНОГО ПОКРОВА НА ДЕЙСТВИЕ СТАТИЧЕСКИХ
НАГРУЗОК
ГЛАВА 3. РАСЧЕТ КРАЕВОГО УЧАСТКА ЛЕДЯНОГО ПОКРОВА
3.1. Методы определения грузоподъемности ледяного
покрова
3.2. Состояние вопроса и цель исследования
3.3. Расчет полубесконечного ледяного слоя с
защемленной кромкой
3.4. Расчет полубесконечного ледяного слоя с
шарнирно-опертой кромкой
3.5. Расчет полубесконечного ледяного слоя со
свободной кромкой
3.6. Изгиб краевого участка ледяного покрова при
колебаниях уровня воды
3.7. Расчет ледяного слоя, ослабленного круговым
отверстием
3.8. Расчет ледяного слоя, имеющего жесткую вставку
3.9. Неосесимметричный изгиб ледяного слоя, имеющего
жесткую вставку
3.10. Изгиб ледяного слоя, имеющего жесткую вставку,
при колебаниях уровня воды
3.11. Условия применения результатов полученных,
решений
ГЛАВА 4 УСИЛЕНИЕ ЛЕДЯНОГО ПОКРОВА И ЕГО РАСЧЕТ
4.1. Состояние вопроса и цель исследования, конструкции
усиления ледяного покрова
4.2. Цилиндрический изгиб усиленного ледяного слоя
4.3. Определение напряжений в ледяном слое при
намораживании дополнительной полосы льда
4.4. Изгиб усиленного ледяного слоя равномерно
распределенной полосовой нагрузкой
4.5. Цилиндрический изгиб ледяного слоя, усиленного
комбинированным способом
4.6. Расчет одноступенчатой ледяной плиты на
сосредоточенную нагрузку
4.7. Центральный изгиб одноступенчатой ледяной плиты
равномерно распределенной по окружности нагрузкой
4.8. Расчет двухступенчатой ледяной плиты на
сосредоточенную нагрузку
4.9. Центральный изгиб двухступенчатой ледяной плиты
равномерно распределенной по окружности нагрузкой
ГЛАВА 5. РАСЧЕТ УСИЛЕННОГО ЛЕДЯНОГО СЛОЯ ПО
ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
5.1. Состояние вопроса и цель исследования
5.2. Расчет плит переменной толщины, лежащих на
упругом основании, с учетом упругопластических деформаций
5.3. Расчет усиленного ледяного слоя с учетом
упругопластических деформаций при загружении равномерно распределенной
нагрузкой
5.4. Расчет усиленного ледяного слоя при
цилиндрическом изгибе по предельным состояниям без учета упругопластических
деформаций
5.5. Расчет усиленного ледяного слоя при
цилиндрическом изгибе по предельным состояниям с учетом упругопластических
деформаций
5.6. Расчет усиленного ледяного слоя на
сосредоточенную нагрузку по предельным состояниям без учета
упругопластических деформаций
5.7. Расчет усиленного ледяного слоя на
сосредоточенную нагрузку с учетом упругопластических деформаций
Часть третья
РАСЧЕТ ЛЕДЯНОГО ПОКРОВА НА ДЕЙСТВИЕ ДИНАМИЧЕСКИХ
НАГРУЗОК
ГЛАВА 6. ДИНАМИЧЕСКИЙ РАСЧЕТ ГИБКИХ ЛЕДОВЫХ ПЛИТ,
ЛЕЖАЩИХ НА УПРУГОМ ОСНОВАНИИ. ДИНАМИЧЕСКИЕ НАГРУЗКИ ОТ ДВИЖУЩЕГОСЯ АВТОМОБИЛЯ
ПРИ ПРОЕЗДЕ ПО НЕРОВНОСТЯМ ЛЕДОВЫХ ПЕРЕПРАВ
6.1. Общие положения
6.2. Возмущающее воздействие неровностей дороги и
режимы движения грузовых автомобилей
6.3. Определение параметров свободных колебаний
подрессоренных и неподрессоренных масс грузовых автомобилей
6.4. Вынужденные колебания автомобиля при движении
по неровностям
ГЛАВА 7. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ЛЕДЯНОГО СЛОЯ ПРИ
ВОЗДЕЙСТВИИ ВИБРАЦИОННОЙ НАГРУЗКИ
7.1. Состояние вопроса и цели исследования покрова
7.2. Вынужденные колебания ледяного слоя при
цилиндрическом изгибе
7.3. Вынужденные колебания ледяного слоя при
центральном изгибе
7.4. Колебания плиты на упругом основании с учетом
массы действующего на нее груза
7.5. Колебания ледяного слоя при цилиндрическом и
центральном изгибе с учетом массы действующего на него груза
7.6. Колебания ледяного слоя с учетом инерции
упругого основания
ГЛАВА 8. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ЛЕДЯНОГО СЛОЯ ПОД
ДЕЙСТВИЕМ ДВИЖУЩЕЙСЯ НАГРУЗКИ
8.1. Состояние вопроса и цели исследования
8.2. Колебания плиты на упругом основании с учетом
массы движущегося по ней груза
8.3. Колебания ледяного слоя под действием
движущегося с постоянной скоростью сосредоточенного груза
8.4. Колебания ледяного слоя под действием
движущейся нагрузки, распределенной по окружности
8.5. Колебания ледяного слоя под действием груза,
движущегося с переменной скоростью
8.6. Колебания ледяного слоя под действием
движущейся сосредоточенной вибрационной нагрузки
8.7. Колебания ледяного слоя под действием
движущейся вибрационной нагрузки, распределенной по окружности
ГЛАВА 9. КОЛЕБАНИЯ ЛЕДЯНОГО ПОКРОВА ПОД ВОЗДЕЙСТВИЕМ
ДВИЖУЩЕЙСЯ НАГРУЗКИ С УЧЕТОМ ВОЛНОВОГО ПРОЦЕССА, РАЗВИВАЮЩЕГОСЯ В ВОДЕ
9.1. Состояние вопроса и цели исследования
9.2. Определение длины волны, периода колебаний и
скорости распространения ее под ледяным покровом
9.3. Колебания ледяного слоя постоянной толщины под действием
движущегося сосредоточенного груза
9.4. Колебания ледяного слоя переменной толщины под
действием движущегося сосредоточенного груза
ГЛАВА 10. МЕСТНЫЕ ИМПУЛЬСИВНЫЕ ВОЗДЕЙСТВИЯ НА
ЛЕДЯНОЙ СЛОЙ
10.1. Постановка задачи и цель исследования
10.2. Определение импульса сил
10.3. Колебания ледяного слоя, возникающие при
преодолении автомобилем вертикального препятствия
10.4. Учет взаимного влияния нескольких движущихся
нагрузок
ОБЩИЕ ВЫВОДЫ И РЕКОМЕНДАЦИИ
библиографический список
Приложение Значения характеристик ледяного покрова λ и l (см-1) в
зависимости от толщины и модуля упругости льда
|


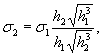 (1.1)
(1.1)![]() (1.3)
(1.3)![]() (1.4)
(1.4)![]() (1.5)
(1.5)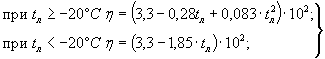 (1,6)
(1,6)![]() (1.7)
(1.7)![]() (1.8)
(1.8)![]() (1.9)
(1.9)![]()

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()




![]()
![]()
![]()
![]() (2.3)
(2.3)![]() дает знак скорости.
дает знак скорости.![]()
![]()
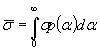 (2.6)
(2.6)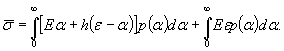 (2.7)
(2.7)![]() . (2.8)
. (2.8)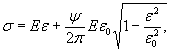 (2.10)
(2.10)![]() (2.12)
(2.12)![]()
![]() (2.13)
(2.13)![]() (2.14)
(2.14)![]() (2.15)
(2.15)![]() (2.16)
(2.16)
![]() (2.17)
(2.17)![]() (2.19)
(2.19)![]() (2.20)
(2.20)


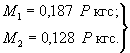
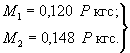

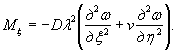
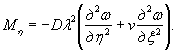
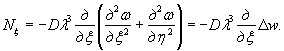


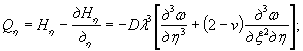
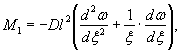











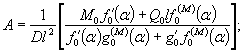
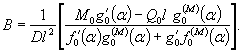



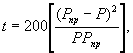

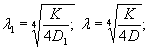










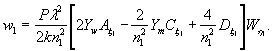

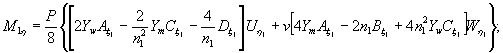






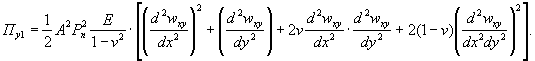
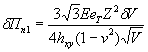

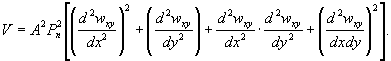

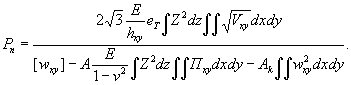
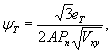

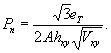
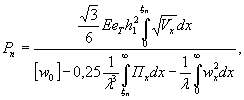
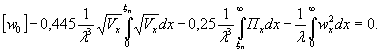

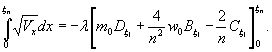

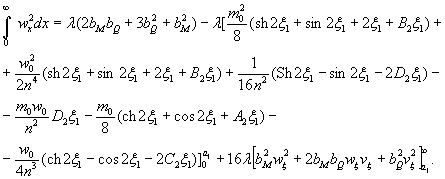







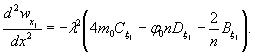








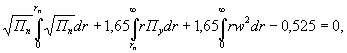
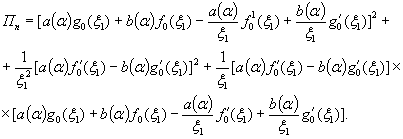

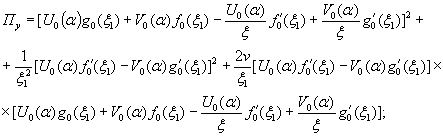

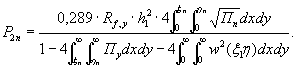



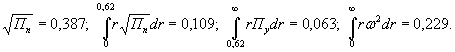

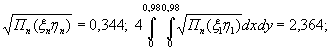


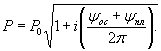
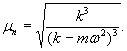
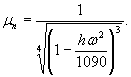
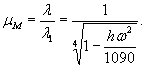
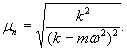
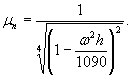
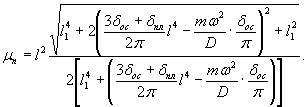
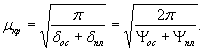


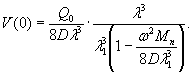
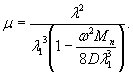
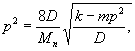
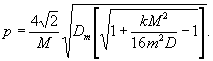


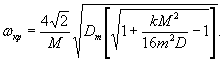
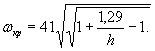
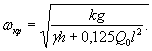



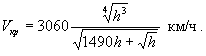
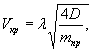
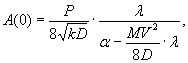


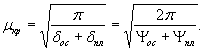



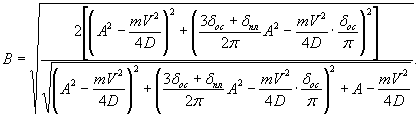
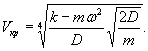
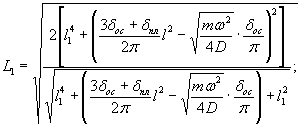
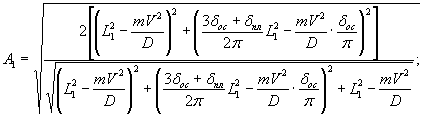
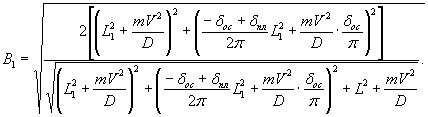





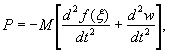
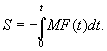


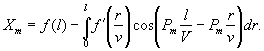

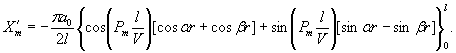
 (10.12)
(10.12)