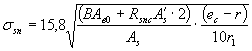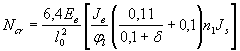МИНИСТЕРСТВО ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА
ВСЕСОЮЗНЫЙ ОРДЕНА ОКТЯБРЬСКОЙ РЕВОЛЮЦИИ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА
УТВЕРЖДАЮ
Зам. директора института
Г.Д. ХАСХАЧИХ
13 мая 1986 г.
РЕКОМЕНДАЦИИ
ПО РАСЧЕТУ НА ПРОЧНОСТЬ ИЗГИБАЕМЫХ И ВНЕЦЕНТРЕННО СЖАТЫХ ЖЕЛЕЗОБЕТОННЫХ
ЭЛЕМЕНТОВ КРУГЛОГО СЕЧЕНИЯ
Одобрены Главтранспроектом
Москва 1986
СОДЕРЖАНИЕ
|
2. РАСЧЕТ ПО ПРОЧНОСТИ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ 3. РАСЧЕТ ПО ПРОЧНОСТИ И УСТОЙЧИВОСТИ ВНЕЦЕНТРЕННО СЖАТЫХ ЭЛЕМЕНТОВ |
Предисловие
Настоящие Рекомендации разработаны в дополнение главы СНиП 2.05.03-84 и предназначены для использования при проектировании железобетонных элементов круглого сечения мостовых конструкций. В них изложен расчет по прочности и устойчивости внецентренно сжатых элементов круглого сечения из тяжелого бетона без предварительного напряжения с арматурой из стали классов А-II и А-III, расположенной равномерно по контуру сечения или сосредоточенно. В Рекомендациях приведены алгоритмы и примеры расчетов наиболее типичного случая армирования, встречающегося в настоящее время в практике проектирования железобетонных опор, столбов и свай мостов: арматура из стали класса А-II расположена равномерно по контуру сечения.
Рекомендации разработаны ЦНИИСом (канд. техн. наук В.В. Дегтерев и инж. А.С. Бизюков) при участии Гипротрансмоста (инж. Р.И. Цюрупа) и Харгипротранса (инж. В.Н. Сондар).
|
Зав. отделением строительных материалов, прочности и долговечности железобетонных конструкций |
Е.Н. Щербаков |
ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Усилия от внешних нагрузок в поперечном сечении элемента:
М = Мl + Мm - изгибающий момент от расчетных нагрузок;
Мl - то же от расчетной постоянной нагрузки;
Мm - то же от расчетной временной нагрузки;
N = Nl + Nm - полное расчетное продольное усилие;
Nl - продольное усилие от расчетной постоянной нагрузки;
Nm - то же от расчетной временной нагрузки.
Характеристики материалов:
В - нормативная кубиковая прочность, равная по величине классу бетона по прочности на сжатие;
Rв - расчетное сопротивление бетона осевому сжатию;
Rs - расчетное сопротивление ненапрягаемой арматуры растяжению;
Rsn - нормативное сопротивление ненапрягаемой арматуры растяжению;
Rsc - расчетное сопротивление ненапрягаемой арматуры сжатию;
Rsnc - нормативное сопротивление ненапрягаемой арматуры сжатию;
σsn - напряжение в растянутой арматуре, вычисленное по нормативным сопротивлениям;
σs - расчетное напряжение в растянутой арматуре;
Ев - модуль упругости бетона;
Es - модуль упругости арматуры;
n1 - отношение модулей упругости арматуры и бетона.
Геометрические характеристики:
d - диаметр бетонного сечения;
r1 - радиус бетонного сечения;
Aв - площадь сечения всего бетона;
Jв - момент инерции бетонного сечения относительно его центра тяжести;
Asi - площадь одного стержня;
Asn - площадь всех рабочих стержней в бетонном сечении;
n - количество всех рабочих стержней в бетонном сечении;
AS, A's - площадь сечения расчетной ненапрягаемой растянутой и сжатой продольной арматуры;
rs - радиус окружности, проходящей через центры сечения стержней продольной арматуры;
as, a's - расстояние от центра тяжести сечения расчетной растянутой и расчетной сжатой арматуры до соответствующей наиболее растянутой и сжатой грани сечения;
h0 = d - as - рабочая высота сечения;
hs = r1 - 0,5rs - высота расчетной растянутой зоны на первом этапе без учета сжатой арматуры;
hs = d - x - высота расчетной растянутой зоны на первом этапе при учете сжатой арматуры и на остальных этапах;
asi - расстояние от центра сечения i-го стержня до соответствующей оси 1-1 и 2-2;
a'si - расстояние от центра сечения расчетного сжатого i-го стержня до оси 2-2;
asc - расстояние от центра сечения наиболее близко расположенного рабочего стержня к оси 2-2 до этой же оси;
as0 и ds0 - соответственно расстояние от центра сечения менее растянутого стержня, расположенного в расчетной растянутой зоне, до оси 1-1 н диаметр этого стержня;
![]() - расстояние от центра сечения
дополнительного растянутого стержня, ближайшего к расчетной растянутой зоне, до
оси 1-1;
- расстояние от центра сечения
дополнительного растянутого стержня, ближайшего к расчетной растянутой зоне, до
оси 1-1;
x = ξr1 - высота сжатой зоны бетона;
ξ = х/r1 -относительная высота сжатой зоны;
![]() - относительная площадь сжатой зоны;
- относительная площадь сжатой зоны;
Авс - рабочая площадь сечения высотой h0;
Aвс - площадь сжатой зоны бетона;
с = 0,6x - расстояние от центра тяжести площади сжатой зоны бетона до наиболее сжатой грани сечения; высота расчетной сжатой зоны, в пределах которой производят учет расчетных сжатых стержней;
ξ = as/r1 - относительная высота части наиболее растянутой зоны бетона, расположенной за пределами рабочей площади сечения Aвo;
y - расстояние от центра тяжести приведенного сечения до наиболее растянутой грани;
еci = M/N - эксцентриситет продольной силы N относительно центра тяжести приведенного сечения, определяемый из статического расчета конструкции;
![]() - случайный эксцентриситет продольной силы N относительно центра тяжести
приведенного сечения;
- случайный эксцентриситет продольной силы N относительно центра тяжести
приведенного сечения;
![]() - расчетный начальный эксцентриситет
продольной силы относительно центра тяжести приведенного сечения;
- расчетный начальный эксцентриситет
продольной силы относительно центра тяжести приведенного сечения;
e0 - расчетное расстояние от точки приложения силы N до равнодействующей усилий в расчетной растянутой арматуре;
l0 - расчетная длина элемента;
η - коэффициент, учитывающий влияние прогиба на величину эксцентриситета продольного усилия ес;
Js - момент инерции арматуры относительно центра тяжести приведенного сечения;
l - радиус инерции поперечного сечения;
Arеd - площадь приведенного сечения;
Wred - момент сопротивления приведенного сечения;
![]() - ядровое расстояние;
- ядровое расстояние;
Jred - момент инерции приведенного сечения элемента;
φ - коэффициент продольного изгиба.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. В настоящих Рекомендациях приводится расчет по прочности железобетонных элементов круглого сечения с различным расположением арматурных стержней как по контуру сечения, так и сосредоточенно в местах наибольших напряжений.
1.2. Прочностные и деформативные характеристики бетона и арматуры, а также конструктивные решения и величины действующих усилий определяются в соответствии со СНиП 2.05.03-84.
1.3. По настоящим Рекомендациям проверяется прочность сечения. Необходимые геометрические размеры, количество арматуры и ее расположение назначаются из опыта проектирования железобетонных элементов круглого сечения с использованием типовых решений и с учетом имеющегося у строителей технологического оборудования.
При расчете сечений с направленным армированием основная масса растянутых рабочих стержней размешается в предполагаемой расчетной растянутой зоне высотой, равной примерно половине радиуса бетонного сечения; в предполагаемой сжатой зоне стержни устанавливаются в пределах ее высоты, равной четверти радиуса. Средняя часть армируется монтажными стержнями того же или меньшего диаметра.
1.4. Расчетные площади сечений растянутой As и сжатой A's арматуры и соответствующие им положения центров тяжести as и a's устанавливаются по фактической площади каждого стержня и его месту нахождения в бетонном сечении. Это позволяет расширить область проектирования железобетонных элементов круглого сечения с различными диаметрами рабочих стержней при любом их расположении.
1.5. Определение разрушения сечения по арматуре и бетону производится при отсутствии условной характеристики граничного значения ξR. Случаи разрушения и несущая способность устанавливаются прямым путем: по напряжению в растянутой арматуре σsn. Последнее вычисляется исходя из нормативных сопротивлений бетона и стали, что позволяет определять наиболее вероятное значение напряжений в растянутых стержнях в момент разрушения сжатой зоны и обеспечивать с помощью коэффициента аs необходимый запас прочности при расчете элементов с использованием расчетных сопротивлений, когда растянутая арматура работает в упругой стадии (переармированные сечения и случаи малых эксцентриситетов).
1.6. Изложенный расчет построен без применения гипотезы плоских сечений, не свойственной работе железобетона. Подбор расчетной площади арматуры производится методом последовательного приближения - поэтапным увеличением количества растянутых стержней. На каждом этапе выполняются следующие операции:
1) определяется в приближении расчетное количество растянутой арматуры;
2) находится расчетное количество сжатой арматуры в зависимости от высоты с;
3) устанавливается относительная площадь бетона сжатой зоны из условия равновесия внешних и внутренних сил системы, которым осуществляется связь между растянутой и сжатой зонами сечения на рассматриваемом этапе;
4) вычисляются параметры, которые определяют дальнейший путь расчета: или переход к следующему этапу - введению нового количества растянутой арматуры, или проверка условий прочности.
1.7. Расчет по прочности внецентренно сжатых элементов представлен формулами, отражающими случаи разрушения в зависимости от эксцентриситета: ес > r и ес ≤ r. В последнем случае на всем диапазоне изменения эксцентриситета несущая способность принимается постоянной при высоте с - 0,75r1 и количестве сжатых стержней, находящихся в пределах этой высоты.
2. РАСЧЕТ ПО ПРОЧНОСТИ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ
2.1. Несущая способность изгибаемых элементов круглого сечения определяется по формуле, выведенной из условия равновесия внешних и внутренних сил относительно равнодействующей усилий в растянутых стержнях, расположенных в пределах расчетной растянутой зоны (рис. 1):
2.2. Относительная площадь бетона сжатой зоны вычисляется из формулы, выведенной из условия равенства нулю суммы проекций всех внутренних сил на горизонтальную ось:
2.3. По значению ω, расположенному в определенных интервалах, определяется соответствующая величина ξ из формул:
при ω ≤ 0,055 ξ = 1,818ω; (3)
при 0,055 < ω ≤ 0,295 ξ = 0,833ω + 0,0542; (4)
при 0,295< ω ≤ 0,786 ξ = 0,612ω + 0,119; (5)
при ω > 0,786 ξ = 0,509ω + 0,199. (6)
По ξ устанавливаются значения:
x = ξr1, c = 0,6x и hs = d - x.
2.4. В зависимости от напряжения в растянутой арматуре условно различаются два расчетных случая:
случай 1 - разрушение по арматуре - характеризуется достижением растянутой арматурой ее расчетного сопротивления (σs = Rs);
случай 2 - разрушение по бетону, (переармированные сечения) - характеризуется достижением бетоном сжатой зоны своего расчетного сопротивления ранее достижения растянутой арматурой ее расчетного сопротивления (0 < σs < Rs).
Случаи 1 и 2 устанавливаются по величине напряжения в растянутой арматуре:
где Aв0 - рабочая площадь сечения, определяемая по формуле:
здесь значение ω находится по ξ = as/r1 из формул:
при ξ ≤ 0,1 ω = 0.55ξ (9)
при 0,1 < ξ ≤ 0,3 ω = 1,2ξ - 0,065; (10)
при 0,3 < ξ ≤ 0,6 ω = 1,633ξ - 0,195; (11)
при ξ > 0,6 ω = 1,965ξ - 0.392. (12)
Случай 1 соответствует условию σsn ≥ Rsn, в расчете принимается σs = Rs.
Случай 2 соответствует
условию σsn
< Rsn, в расчете принимается σs = asRs,
где ![]() .
.
2.5. Определение требуемого количества растянутой арматуры производится следующим образом.
Сначала, на первом этапе, расчетное количество арматуры определяется при As = 0 по числу стержней, расположенных в расчетной растянутой зоне высотой hs - r1 - 0,5rs, для которых выполняется условие аsi ≤ hs. После подбора необходимого количества сжатой арматуры на первом же этапе расчетная растянутая зона выражается высотой hs = d - x, которая принимается для определения растянутой арматуры на всех других этапах.
Переход к следующему этапу с введением в расчет нового дополнительного ряда растянутых стержней осуществляется при соблюдении четырех условий:
где
|
|
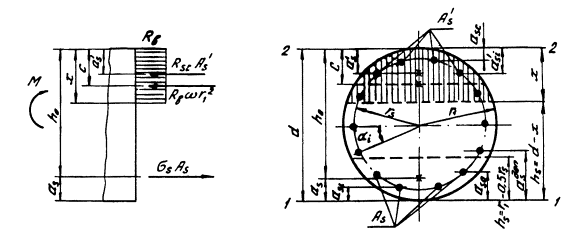
Рис. 1. Схема напряженного состояния поперечного сечения изгибаемого элемента круглого сечения с равномерно распределенной арматурой
Подбор растянутой арматуры заканчивается на этапе, где нарушается хотя бы одно из условий: (13), (14), (15), (16).
Для растянутой расчетной арматуры вычисляются значения:
as, as, as0
и ![]()
2.6. Определение требуемого количества сжатой арматуры производится следующим образом.
На первом этапе с начала принимается А's = 0, т.е. сечение рассчитывается как с одиночной арматурой; по формуле (2) с учетом формулы (7) находится ω и по формулам (3) - (6) вычисляется значение ξ, а по нему - значения x и c с проверкой условия:
|
c ≤ cm = 0,6(d - asm); |
при с > сm принимается с = сm.
В пределах части площади бетона сжатой зоны, ограниченной высотой с, определяются стержни, для которых соблюдается условие a'si ≤ c и устанавливаются соответствующие значения A's и a's. При σs = Rs выявленное количество сжатой арматуры принимается за расчетное на данном этапе; при σs = asRs определяются с использованием формулы (7) новая величина напряжения σs с учетом выявленной площади А's и по формуле (2) при А's = 0 значение ω и величины x и c. Если в пределах расчетной площади сжатой зоны, ограниченной новой высотой c количество сжатых стержней изменяется, то снова вычисляются σs и c при выявленной площади А's. Эта операция повторяется до тех пор, пока число сжатых стержней в пределах вычисленного с не будет изменяться, оно принимается за расчетное для данного этапа.
При с < a'sc или a'sc = 0 сечение рассчитывается без учета сжатой арматуры.
2.7. Определяются ω по
формуле (2) по п. 2.3,
а также соответствующие параметры ξ, x, с
и значение hs = d - x; проверяется выполнение условий (13), (14),
(15) и (16). При их соблюдении переходят к следующему этапу подбора растянутой арматуры
- вводится следующий ряд растянутых стержней и расчет производится при новых
значениях Аs, аs, аs0, ![]() и
установленных A's и a's.
и
установленных A's и a's.
При нарушении условия (13) принимается c = cm, а усилие в бетоне сжатой зоны вычисляется по формуле:
несущая способность сечения определяется по формуле (1).
При соблюдении условия (13) и нарушении хотя бы одного из условий (14), (15) и (16) проверяется условие:
|
c ≥ a's; |
если условие (19) соблюдается, несущая способность определяется по формуле (1); при нарушении условия (19) она определяется по формуле:
|
M ≤ σsAs(h0 - a's) |
2.8. Для расчета прочности изгибаемых элементов рекомендуется следующий алгоритм расчета (табл. 1).
Исходные данные: изгибающий момент от расчетных нагрузок M, геометрические характеристики сечения d, r1 и rs, класс бетона, класс арматурной стали, общее количество арматуры и диаметр стержней, характер их расположения по сечению (равномерно по контуру или сосредоточенно). Требуется проверить несущую способность элемента.
Таблица 1
|
Порядок действия |
Содержание действия |
|
1 |
Определяются В, Rв, Rs, Rsc, Rsnc, Rsn |
|
2 |
Устанавливаются для каждого стержня значение asi и параметр asc; определяется расчетная растянутая зона с высотой hs = r1 - 0,5 rs |
|
3 |
Определяются количество стержней в пределах
hs и значения A's,
as, as0,
|
|
4 |
Вычисляются ξ
= as/r1
и по формулам
(9) - (12) значение ω и величина Aв0 = |
|
5 |
Определяются по формуле (7) σsn при A's = 0 на первом этапе и напряжение σs |
|
6 |
Находятся по формуле (2) ω при A's = 0 на всех этапах и по п. 2.3 значения ξ, x и c; при asc = 0 или asc > c расчет производится по пп. 11 - 16 алгоритма при А's = 0; если asc > 0 и расчет осуществляется по п. 7 |
|
7 |
Проверяется условие (17); при его выполнении в расчет вводится вычисленная высота c; если условие не выполняется, принимается c = сm |
|
8 |
Определяется количество стержней в сжатой зоне высотой с и вычисляются значения A's и a's |
|
9 |
При σs = Rs значения a's и A's принимаются за расчетные; дальше расчет ведется по п. 11 алгоритма |
|
10 |
При σs = asRs определяется с использованием формулы (7) новое значение σs с учетом Аs и расчет повторяется по пп. 6 - 9 алгоритма до тех пор, пока количество выявленных сжатых стержней в пределах нового с перестанет изменяться или станет σs = Rs; это количество арматуры принимается за расчетное с определением A's и а's |
|
11 |
По формуле (2) вычисляется ω и по п. 2.3 определяются параметры ξ, x и c и устанавливается новое значение hs = d - x |
|
12 |
Проверяются условия (13), (14), (15) и (16). При их выполнении вводятся в
расчет дополнительный ряд растянутых стержней с определением новых значений As, as, |
|
13 |
При нарушении условия (13) принимается c = cm и вычисляется значение Конец |
|
14 |
При соблюдении условия (13) и нарушении хотя бы одного из условий (14), (15) и (16) проверяется условие (19) |
|
15 |
При выполнении условия (19) прочность определяется по формуле (1) Конец |
|
16 |
При нарушении условия (19) прочность определяется по формуле (20) Конец |
Пример расчета
Исходные данные: М = 800 кН·м, d = 80 см, r1 = 40 см, rs = 33,4 см, класс бетона В30, арматура из стали класса А-II, общее количество и расчетный диаметр арматуры 14 Ø 32. Требуется проверить несущую способность элемента при общем случае расположения арматуры - равномерном распределении по контуру сечения (рис. 2).
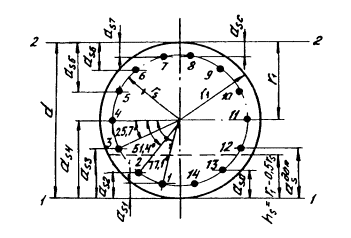
Рис.2. Сечение железобетонного элемента в примерах расчета (1 - 14 - стержни)
Решение. 1. Определяем В = 30 МПа, Rв - 15,5 МПа, Rs - Rsc - 250 МПа, Rsn = Rsnc - 295 МПа.
2. Устанавливаем для каждого стержня:
as1 = as14 = as7 = as8 = 40 - 33,4·sin 77,14° = 7,43 см;
as2 = as13 = as6 = as9 = 40 - 33,4·sin 51,42° = 13,89 см;
as3 = as12 = as5 = as10 = 40 - 33,4·sin 25,71° = 25,51 см;
as4 = as11 = 40 - 33,4·sin 0o = 40,0 см;
определяем значение asc = as7 = as8 = 7,43 см и hs = 40 - 0,5·33,4 = 23,3 см.
3. Поскольку as2 = 13,89 см < hs = 23,3 см < as3
= 25,51 см, принимаем стержни 1, 2, 13 и 14 в качестве растянутых и определяем Аs = (4 Ø 32) = 32,16 см2,
![]() .
.
as0
= 13,89 см, ![]() =25,51 см, asm = 13,89 + 3,2 = 17,09 см, cm = 0,6(80 - 17,09) = 37,75
см, ho - 80 - 10,66 = 69,34 см.
=25,51 см, asm = 13,89 + 3,2 = 17,09 см, cm = 0,6(80 - 17,09) = 37,75
см, ho - 80 - 10,66 = 69,34 см.
4. Вычисляем ξ = 10,66/40 = 0,266 и по формуле (10) определяем ω - 1,2·0,266 - 0,065 = 0,254,
Aв0 = 402(3,14 - 0,254) = 4617,6 см2.
5. По формуле (7) определяем
(при А's
= 0) напряжение σsn =
![]() = 1037 МПа; поскольку
σsn = 1037 МПа > Rsn = 295 МПа, принимаем σs = Rs - 250 МПа.
= 1037 МПа; поскольку
σsn = 1037 МПа > Rsn = 295 МПа, принимаем σs = Rs - 250 МПа.
6. По формуле (2)
находим (при A's = 0) значение ![]() и по формуле (5)
- ξ = 0,612·0,324 + 0,119 =
0,317; определяем x = 0,317·40 = 12,7 см и c = 0,6·12,7 = 7,6 см.
Поскольку asc = 7,43 см > 0 и аsс = 7,43см < с = 7,6 см, расчет производим по п. 7.
и по формуле (5)
- ξ = 0,612·0,324 + 0,119 =
0,317; определяем x = 0,317·40 = 12,7 см и c = 0,6·12,7 = 7,6 см.
Поскольку asc = 7,43 см > 0 и аsс = 7,43см < с = 7,6 см, расчет производим по п. 7.
7. Проверяем условие (17): c = 7,6 см < cm = 37,75 см, принимаем c = 7,6 см.
8. Поскольку ![]() = 7,43 см < c = 7,6 см < as6 = 13,89 см, в расчет вводим два
стержня 7 и 8, имеющих A's
= (2 Ø 32) = 16,08 см2, a's = 7,43 см.
= 7,43 см < c = 7,6 см < as6 = 13,89 см, в расчет вводим два
стержня 7 и 8, имеющих A's
= (2 Ø 32) = 16,08 см2, a's = 7,43 см.
9. Эти сжатые стержни принимаем за расчетные, так как σs = Rs и дальнейшие вычисления производим по п. 11.
11. По формуле (2) определяем
![]() = 0,162
и по формуле (4)
ξ = 0,833·0,162 + 0,0542 =
0,189, x = 0,189·40 = 7,6 см, c = 0,6·7,6 = 4,6 см и hs = 80 - 7,6 = 72,4 см.
= 0,162
и по формуле (4)
ξ = 0,833·0,162 + 0,0542 =
0,189, x = 0,189·40 = 7,6 см, c = 0,6·7,6 = 4,6 см и hs = 80 - 7,6 = 72,4 см.
12. Проверяем условия (13), (14), (15) и (16):
аsm - 17,09 см < h = 72,4 см, σsn = 1037 МПа > Rsn
- 295 МПа, ![]() = 25,51 см > 0,
= 25,51 см > 0, ![]() = 25,51 см < 0,9hs
= 0,9·72,4 = 65,2 см; условия выполняются, переходим к следующему этапу
подбора количества растянутой арматуры введением дополнительного ряда стержней:
= 25,51 см < 0,9hs
= 0,9·72,4 = 65,2 см; условия выполняются, переходим к следующему этапу
подбора количества растянутой арматуры введением дополнительного ряда стержней:
As = (6 Ø 32) = 48,24 см2,
![]() = 15,61 см,
= 15,61 см, ![]() = 40 см,
= 40 см,
as0 = 25,51, asm = 25,51 + 3,2 = 28,71 см,
cm = 0,6(80 - 28,7) = 30,77 см, А's - 16,08 см2,
а's = 7,43 см, h0 = 80 - 15,61 = 64,39 см; переходим к п. 4.
4. Вычисляем ξ = 15,61/40 = 0,39 и по формуле (11) определяем ω = 1,633·0,39 - 0,195 = 0,442;
Aв0 = 402(3,14 - 0,442) - 4316,8 см2.
5. По формуле (7) находим.
![]() = 848 МПа,
поскольку σsn = 848 МПа > Rsn = 295 МПа, принимаем σs - Rs = 250 МПа.
= 848 МПа,
поскольку σsn = 848 МПа > Rsn = 295 МПа, принимаем σs - Rs = 250 МПа.
6. По формуле (2)
вычисляем (при A's
= 0) значение ω = ![]() = 0,486 и по формуле
(5) ξ = 0,612·0,486 + 0,119 =
0,416, х = 0,416·40 = 16,6 см,
= 0,486 и по формуле
(5) ξ = 0,612·0,486 + 0,119 =
0,416, х = 0,416·40 = 16,6 см,
c = 0,6·16,6 = 10 см.
Поскольку asc = 7,43 см > 0 и asc = 7,43 см < c = 10 см, расчет производим по п. 7.
7. Проверяем условие (17): с = 10 см < cm = 30,77 см, оно выполняется; принимаем c = 10 см.
8. Поскольку a's7 = 7,43 см < c = 10 см < as6 = 13,89 см, в расчет вводим прежние два сжатых стержня 7 и 8, имеющих A's = (2 Ø 32) = 16,08 см2, a's = 7,43 см.
9. Эти сжатые стержни принимаем за расчетные на втором этапе, так как σs = Rs; переходим к п. 11.
11. По формуле (2) вычисляем
![]() = 0,324
и по формуле (5) - ξ = 0,612·0,324 + 0,119 = 0,317, x = 0,317·40 = 12,7 см, c =
0,6·12,7 = 7,6 см и hs = 80 - 12,7 = 67,3 см.
= 0,324
и по формуле (5) - ξ = 0,612·0,324 + 0,119 = 0,317, x = 0,317·40 = 12,7 см, c =
0,6·12,7 = 7,6 см и hs = 80 - 12,7 = 67,3 см.
12. Проверяем условия (13), (14), (15) и (16):
asm = 28,71 см < hs
= 67,3 см, σsn = 848 МПа > Rsn = 295 МПа, ![]() = 40 см > 0,
= 40 см > 0, ![]() = 40 см < 0,9hs
= 0,9·67,3 = 60,6 см - условия выполняются; переходим к третьему этапу
подбора расчетного количества растянутой арматуры введением дополнительного
ряда стержней As = (8 Ø 32) = 64,31 см2,
= 40 см < 0,9hs
= 0,9·67,3 = 60,6 см - условия выполняются; переходим к третьему этапу
подбора расчетного количества растянутой арматуры введением дополнительного
ряда стержней As = (8 Ø 32) = 64,31 см2,
![]() = 21,71 см,
= 21,71 см,
![]() = 54,49 см. as0 = 40 см, аsm = 40 + 3,2 = 43.2 см, с = 0,6(80 - 43,2) = 22,08 см, h0 = 80 - 21,71 = 58,29 см - при прежнем
количестве сжатой арматуры A's
- 16,08 см2, a's = 7,43см; переходим к п. 4.
= 54,49 см. as0 = 40 см, аsm = 40 + 3,2 = 43.2 см, с = 0,6(80 - 43,2) = 22,08 см, h0 = 80 - 21,71 = 58,29 см - при прежнем
количестве сжатой арматуры A's
- 16,08 см2, a's = 7,43см; переходим к п. 4.
4. Вычисляем ξ = 21,71/40 = 0,543 и по формуле (11) определяем ω = 1,633·0,543 - 0,195 = 0,692,
Aв0 = 402(3,14 - 0,692) = 3917 см2.
5. По формуле (7) находим
![]() = 702 МПа > Rsn = 295 МПа; к расчету принимаем σs
= Rs - 250 МПа.
= 702 МПа > Rsn = 295 МПа; к расчету принимаем σs
= Rs - 250 МПа.
6. По формуле
(2) определяем (при A's - 0)
значение ![]() = 0,648 и по формуле (5)
- ξ = 0,612·0,848 + 0,119 = 0,518, x = 0,516·40 = 20,8 см, c = 0,6·20,8 = 12,4 см. Поскольку asc =
7,43 см > 0 и asc = 7,43 см < с = 12,4 см, расчет производим по п. 7.
= 0,648 и по формуле (5)
- ξ = 0,612·0,848 + 0,119 = 0,518, x = 0,516·40 = 20,8 см, c = 0,6·20,8 = 12,4 см. Поскольку asc =
7,43 см > 0 и asc = 7,43 см < с = 12,4 см, расчет производим по п. 7.
7. Проверяем условие (17): c = 12,4 см < cm = 22,08 см - оно выполняется; в расчет вводим c = 12,4 см.
8. Поскольку a's7 = 7,43 см < с = 12,4 см < as6 = 13,89 см в расчете остается прежнее количество сжатой арматуры A's = 16,08 см, as = 7,43 см.
9. Это количество арматуры принимаем за расчетное на третьем этапе, так как σs = Rs; дальнейшие вычисления производим по п. 11.
11. По формуле (2) определяем
![]() и по
формуле (5) - ξ = 0,612·0,486 + 0,119 = 0,416, x = 0,416·40 = 16,6 см, с = 0,6·16,6 = 10 см, hs = 80 - 16,6 = 63,4 см.
и по
формуле (5) - ξ = 0,612·0,486 + 0,119 = 0,416, x = 0,416·40 = 16,6 см, с = 0,6·16,6 = 10 см, hs = 80 - 16,6 = 63,4 см.
12. Проверяем условия (13), (14), (15) и (16);
aсm = 43,2см < hs = 63,4 см, σsn = 702 МПа > Rsn =
295 МПа, ![]() = 54,49 см > 0.
= 54,49 см > 0. ![]() = 54,49 см < 0,9 hs
= 0,9·63,4 = 57,1 см - условия выполняются; переходим к четвертому этапу
подбора расчетного количества растянутой арматуры введением дополнительного
ряда стержней Аs
= (10 Ø 32) = 80,4 см2,
= 54,49 см < 0,9 hs
= 0,9·63,4 = 57,1 см - условия выполняются; переходим к четвертому этапу
подбора расчетного количества растянутой арматуры введением дополнительного
ряда стержней Аs
= (10 Ø 32) = 80,4 см2, ![]() = 28,26 см,
= 28,26 см, ![]() = 66, 11 см, aso = 54,48 см,
= 66, 11 см, aso = 54,48 см,
asm = 54,49 + 3,2 = 57,69 см, ![]() = 0,6(80 - 57,69) =
13,39 см, A's
- 16,08 см2, as = 7,43см, h0
= 80 - 28,26 = 51,74 см; переходим к п. 4.
= 0,6(80 - 57,69) =
13,39 см, A's
- 16,08 см2, as = 7,43см, h0
= 80 - 28,26 = 51,74 см; переходим к п. 4.
4. Вычисляем ![]() = 0,706 и по формуле (12)
определяем ω = 1,965·0,706 -
0,392 = 0,996,
= 0,706 и по формуле (12)
определяем ω = 1,965·0,706 -
0,392 = 0,996,
Aв0 = 402(3,14 - 0,996) = 3430,4 см2.
5. По формуле (7) определяем
![]() = 590,76 МПа;
= 590,76 МПа;
поскольку σsn = 590,76 МПа > Rsn = 295 МПа. принимаем σs = Rs = 250 МПа.
6. По формуле (2) находим (при А's = 0) значение ![]() = 0,81 и по формуле (6)
- ξ = 0,509·0,81 + 0,199 =
0,611, x = 0,611·40 = 24,44 см, c = 0,6·24,44 - 14,66 см.
= 0,81 и по формуле (6)
- ξ = 0,509·0,81 + 0,199 =
0,611, x = 0,611·40 = 24,44 см, c = 0,6·24,44 - 14,66 см.
Поскольку asc = 7,43 см > 0 asc = 7,43 см < 0 = 14,66 см, расчет производим по п. 7.
7. Проверяем условие (17): с = 14,66 см > cm = 13,39 см - оно не выполняется; принимаем с = сm = 13,39 см.
8. Поскольку a's7 = 7,43 см < c = 13,39 см < as6 = 13,89 см, в расчет вводим прежние два сжатых стержня 7 и 8, имеющих А's = (2 Ø 32) = 16,08 см2, a's = 7,43 см.
9. Эти сжатые стержни принимаем за расчетные на четвертом этапе, так как σs = Rs; переходим к п. 11.
11. По формуле (2) вычисляем
![]() = 0,648
и по формуле (5)
- значение ξ = 0,612·0,648 +
0,119 = 0,516, x = 0,516·40 = 20,63 см, c = 0,6·20,63 = 12,38 см,
= 0,648
и по формуле (5)
- значение ξ = 0,612·0,648 +
0,119 = 0,516, x = 0,516·40 = 20,63 см, c = 0,6·20,63 = 12,38 см,
hs = 80 - 20,63 = 59,37 см.
12. Проверяем условия (13), (14), (15) и (16):
asm
= 57,69 см < hs = 59,37 см, σsn =
590,76 МПа > Rsn = 295 МПа, ![]() = 66,11 см > 0,
= 66,11 см > 0, ![]() = 66,11 см > 0,9hs = 0,9·59,37 = 53,43 см, т.е. условие (16) не
соблюдается, расчетное количество сжатой и растянутой арматуры считаются
подобранным; переходим к п. 14, так как условие (13) выполняется.
= 66,11 см > 0,9hs = 0,9·59,37 = 53,43 см, т.е. условие (16) не
соблюдается, расчетное количество сжатой и растянутой арматуры считаются
подобранным; переходим к п. 14, так как условие (13) выполняется.
14. Проверяем условие (19): с = 12,38 см > a's = 7,43 см.
15. Условие (19) выполняется, прочность определяем по формуле (1).
80000 кН·см < (0,1)*·0,648·402·15,5(51,74 - 12,38) + (0,1)*·16,08·250(51,74 - 7,43) = 81065,7 кН·см; прочность сечения достаточна.
Множитель (0,1) введен для перехода от размерности МПа·см3 к кН·см.
3. РАСЧЕТ ПО ПРОЧНОСТИ И УСТОЙЧИВОСТИ ВНЕЦЕНТРЕННО СЖАТЫХ ЭЛЕМЕНТОВ
Расчет по прочности
3.1. Расчет по прочности внецентренно сжатых элементов круглого сечения с эксцентриситетом eс > r следует производить по формуле, выведенной из условия равновесия внешних и внутренних сил относительно равнодействующей усилий в растянутых стержнях, расположенных в пределах расчетной растянутой зоны (рис. 3):
|
|
Величина e0 определяется из уравнения
|
e0 = ecη + y - as. |
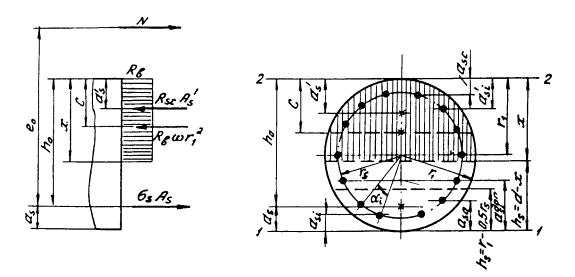
Рис. 3. Схема напряженного состояния поперечного сечения внецентренно сжатого элемента круглого сечения с равномерно распределенной арматурой
Относительная площадь бетона сжатой зоны вычисляется по формуле, выведенной из условия равенства нулю суммы проекций внешних и внутренних сил на горизонтальную ось:
По значению ω, расположенному в определенных интервалах, по п. 2.3 определяются соответствующая величина ξ, и значения x = ξr1, с = 0,6x и hs = d - x.
3.2. Расчет по прочности внецентренно сжатых элементов круглого сечения с эксцентриситетом еc ≤ r следует производить по формуле:
где площадь сечения сжатых стержней определяется в пределах высоты c = 0,75r1.
3.3. В зависимости от напряжения в растянутой арматуре условно различаются два расчетных случая:
случай 1 - разрушение по арматуре - характеризуется достижением растянутой арматурой ее расчетного сопротивления (σs = Rs);
случай 2 - разрушение по бетону - характеризуется достижением бетоном сжатой зоны его расчетного сопротивления ранее достижения растянутой арматурой ее расчетного сопротивления (0 < σs < Rs).
Случаи 1 и 2 устанавливаются по величине напряжения в растянутой арматуре по формуле:
|
|
где Ав0 определяется по формуле (8).
В формуле (25) должно соблюдаться условие:
ес - r ≤ 10r1; при ес - r > 10r1 принимается еc - r = 10r1.
Случай 1 соответствует условию σsn ≥ Rsn, в формулах принимается σs = Rs.
Случай 2 соответствует условию σsn < Rsn в формулах принимается σs = αsRs, где αs = σsn/Rsn.
3.4. Расчетное количество растянутой арматуры устанавливается по п. 2.5.
Требуемое количество сжатой арматуры определяется следующим образом.
На первом этапе сначала принимается A's = 0, т.е. сечение рассчитывается как с одиночной арматурой; по формуле (23) с учетом формулы (25) находится ω, по п. 2.3 - высота c, с проверкой условия (17). В пределах части площади бетона сжатой зоны, ограниченной высотой c, определяются стержни, для которых соблюдается условие a'si ≤ c, и устанавливаются соответствующие значения A's и a's.
При σs = Rs выявленное количество сжатой арматуры принимается за расчетное на данном этапе; при σs = αsRs определяются с использованием формулы (25) новая величина напряжения с учетом выявленной площади A's и по формуле (23) при A's = 0 значение ω и величины x и c.
Если в пределах расчетной площади сжатой зоны, ограниченной новой высотой с, количество сжатых стержней изменяется, то снова вычисляются σs и c при выявленной площади A's. Эта операция повторяется до тех пор, пока число сжатых стержней в пределах вычисленного c не будет изменяться; оно принимается за расчетное для данного этапа.
При c < asc или asc = 0 сечение рассчитывается без учета сжатой арматуры.
3.5. Определяются ω по формуле (23) и по п. 2.3 соответствующие
параметры ξ, x, c и значение hs = d - x; проверяется выполнение условий (13), (14), (15) и (16). При
их соблюдении переходят к следующему этапу подбора растянутой арматуры -
вводится следующий ряд растянутых стержней, и расчет производится при новых
значениях аs,
As, as0,
![]() и установленных A's и a's. При нарушении условия (13)
принимается с = ст, а усилие в бетоне сжатой зоны вычисляется по
формуле:
и установленных A's и a's. При нарушении условия (13)
принимается с = ст, а усилие в бетоне сжатой зоны вычисляется по
формуле:
несущая способность сечения определяется по формуле (21).
При выполнении условия (13) и нарушении хотя бы одного из условий (14), (15) и (16) проверяется условие (19); если оно соблюдается, несущая способность рассчитывается по формуле (21), если оно нарушается, по формуле:
|
|
3.6. Влияние прогиба на
несущую способность элемента следует определять, как правило, посредством
расчета конструкций по деформированной схеме. Допускается производить расчет по
недеформированной схеме, учитывая при гибкости элемента ![]() > 3,5 влияние его
прогиба на прочность, путем умножения эксцентриситета eс
на коэффициент η, согласно формуле (22).
> 3,5 влияние его
прогиба на прочность, путем умножения эксцентриситета eс
на коэффициент η, согласно формуле (22).
3.7. Коэффициент η определяется по формуле:
|
|
где Ncr - условная критическая сила:
|
|
Значение коэффициента φl, учитывающего влияние на прогиб длительного действия нагрузки, следует принимать равным:
|
|
(30) |
При этом моменты от постоянной и временной нагрузок принимаются относительно наиболее растянутого стержня или менее сжатого стержня в рассматриваемом сечении.
Значение коэффициента δ следует принимать равным ec/2r1, но не менее:
|
δmin = 0,5 + 0,01l0/2r1 - 0,01Rв, |
(31) |
где Rв - в МПа,
Сжатые железобетонные элементы должны иметь характеристики, при которых обеспечивается условие N/Ncr ≤ 0,7.
Для железобетонных элементов, имеющих несмещаемые опоры или опоры, одинаково перемещающиеся при вынужденных деформациях (например, при температурных удлинениях), значения коэффициента η принимаются:
а) для сечений в средней трети длины элемента - по формуле (28);
б) для сечений в пределах крайних третей длины элемента - по интерполяции между значениями, вычисленными для средней трети, и единицей, принимаемой для опорных сечений.
3.8. Для определения прочности внецентренно сжатых элементов рекомендуется следующий алгоритм расчета (табл. 2).
Исходные данные: действующие усилия Мm и Nm, Мl и Nl, геометрические характеристики сечения (d, r1 и rs, класс бетона, класс арматурной стали, общее количество арматуры в сечении, диаметр стержней, расчетная длина элемента, характер расположения стержней в сечении. Требуется проверить несущую способность элемента.
|
Порядок действия |
Содержание действия |
|
1 |
Определяются B, Rв, Rs, Rsn, Rsc, Rsnc, ES,
Eв,
M, N,
ec1, |
|
2 |
Устанавливаются для каждого стержня asi; и asc, а для первого этапа - hs = r1 - 0,5rs |
|
3 |
Определяются количество растянутых стержней
в зоне высотой hs и значения As, as, as0, |
|
4 |
Определяются значения n1, Aв, Asn, Ared, Jв, J8, Jred, y, r, φl, δ, δmin |
|
5 |
Вычисляется Ncr по формуле (29) |
|
6 |
Определяется η формуле (28) |
|
7 |
Вычисляется е0 по формуле (22) |
|
8 |
При ес ≤ r вычисляется высота с = 0,75r1 в пределах ее определяются расчетное количество сжатой арматуры и площадь A's; по формуле (24) устанавливается прочность сечения Конец |
|
9 |
При ec > r расчет ведется по п. 10 алгоритма |
|
10 |
Вычисляются ξ = as/r1 и по формулам (9)
- (12) значение ω и устанавливается Аво
= |
|
11 |
По формуле (25) определяется σsn (при A's на первом этапе) и устанавливается напряжение σ3 |
|
12 |
По формуле (23) находится ω (при A's = 0 на всех этапах) и по п. 2.3 определяются значения ξ, x и c; при asc = 0 или asc > с расчет ведется по пп. 17 - 20 алгоритма при A's = 0; если asc > 0 и asc < с, расчет производится по п. 13 |
|
13 |
Проверяется условие (17); при его выполнении в расчет вводится высота с; если нет, принимается с = сm |
|
14 |
Определяется количество стержней в сжатой зоне высотой с и вычисляются значения A's и a's |
|
15 |
При σs = Rs значения A's и a's принимаются за расчетные; дальше расчет осуществляется по п. 17 алгоритма |
|
16 |
При σs = αsRs с помощью формулы (25) устанавливается новое значение σs с учетом A's и расчет повторяется по пп. 12 - 15 алгоритма до тех пор, пока количество выявляемых сжатых стержней в пределах нового c перестанет изменяться или станет σs = Rs; это количество арматуры принимается за расчетное с определением A'c и a's |
|
17 |
По формуле (23) определяется ω; по п. 2.3 вычисляются ξ, x, c и устанавливается новое значение hs = d - x |
|
18 |
Проверяются условия (13), (14), (15) и (16). При их выполнении вводится в расчет
дополнительный ряд растянутых стержней с определением новых значений As, as |
|
19 |
При нарушении условия (13) принимается c = сm и вычисляется значение Конец |
|
20 |
При соблюдении условия (13) и нарушении хотя бы одного из условия (14), (15) и (16) проверяется условие (19); при его выполнении прочность определяется по формуле (21); при нарушении условия (19) она определяется по формуле (27) Конец |
Пример расчета
Исходные данные: действующие усилия Мт = 855 кН·м, Nm = 250 кН, Ml = 95 кН·м, Nl = 1000 кН; геометрические характеристики: d = 80см, r1 = 40 см, rs - 33,4 см, класс бетона В30, класс арматуры А-II, количество и диаметр стержней 14 Ø 32, l0 = 400 см. Требуется проверить несущую способность сваи при общем случае расположения арматуры - равномерном распределении по контуру сечения (см. рис. 2).
Решение 1. Определяем В = 30 МПа, Rв = 15,5 МПа, Rs = Rsc = 250 МПа, Rsn = Rsnc = 295 МПа, Es = 206000 МПа, Ев = 32500 МПа, М = 855 + 95 = 950 кН·м, N = 1000 + 250 = 1250 кН,
ес1 = 950/1250 = 0,76 м = 76 см, ![]() =
= ![]() ·400 = 1 см, ес
= 76 + 1 = 77 см.
·400 = 1 см, ес
= 76 + 1 = 77 см.
2. Устанавливаем для каждого стержня asi:
as1 = as14 = as7 = as8 = 40 - 33,4, sin 77,14° = 7,43 см;
as2 = as13 = as6 = as9 = 40 - 33,4·sin 51,42° = 13,89 см;
as3 - as12 = as5 = as10 = 40 - 33,4·sin25,71° =25,51 см;
as4 = as11 = 40 - 33,4·sin 0° = 40 см
и величину аsc = as7 = as8 = 7,43 см;
определяем для первого этапа расчетную растянутую зону высотой hs = 40 - 0,5·33,4 = 23,3 см.
3. Поскольку аs2 = 13,89см < hs = 23,3 см < as3 = 25,51 см, принимаем стержни 1, 2, 13 и 14 в качестве растянутых и определяем Аs = (4 Ø 32) = 32,16 см2.
![]() = 10,66
см.
= 10,66
см.
aso = 13,89
см, ![]() = 25,51 см, asm = 13,89 + 3,2 = 17,09 см, cm - 0,6(80 - 17,09) = 37,75 см, h0 = 80 - 10,66 =
69,34 см.
= 25,51 см, asm = 13,89 + 3,2 = 17,09 см, cm - 0,6(80 - 17,09) = 37,75 см, h0 = 80 - 10,66 =
69,34 см.
4. Определяем значения ![]() ,
,
Aв - 3,14·402 - 5024 см2, Asn = 14·8,04 = 112,56 см2, Ared = 5024 + 6,34·112,56 = 5738 см2.
![]() = 2009600 см4, Js
=
= 2009600 см4, Js
= ![]() = 62784 см4, Jred = 2009600 + 6,34·62784 = 2407650 см4,
= 62784 см4, Jred = 2009600 + 6,34·62784 = 2407650 см4,
![]() = 10,5 см;
= 10,5 см; ![]()
δ = 77/80 =
0,962, δmin = 0,5 - 0,01·![]() - 0,01·15,5 = 0,285; к расчету принимаем δ = 0,962, так как δ -
0,962 > δmin = 0,295.
- 0,01·15,5 = 0,285; к расчету принимаем δ = 0,962, так как δ -
0,962 > δmin = 0,295.
5. По формуле (29) вычисляем
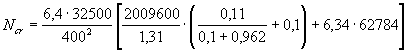 = 923453,3
МПа·см2 = 92345,33 кН.
= 923453,3
МПа·см2 = 92345,33 кН.
6. По формуле (28)
определяем 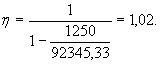
7. По формуле (22) вычисляем е0 = 77·1,02 + 40 - 10,66 = 107,9 см.
9. Так как ec = 77 см > r = 10,5 см, то расчет ведем по п. 10.
10. Вычисляем ξ = 10,66/40 = 0,266 и по формуле (10) ω = 1,2·0,266 - 0,065 = 0,254, Aв0 = 402(3,14 - 0,254) = 4617,6 см2.
11. По формуле (25) определяем при A's = 0 напряжение
![]() = 422,8 МПа
> Rsn - 295 МПа; принимаем σs = 250 МПа.
= 422,8 МПа
> Rsn - 295 МПа; принимаем σs = 250 МПа.
12. По формуле (23) находим ω при A's = 0
![]() и по п. 2.3 определяем
и по п. 2.3 определяем
ξ = 0,509·0,828 + 0,199 = 0,620, x = 0,62·40 = 24,8 см, c = 0,6·24,8 = 14,9 см, asc - 7,43 см < c = 14,9 см.
13. Проверяем условие (17): с = 14,9 см < сm = 37,75 см, оно выполняется, в расчет вводим c = 14,9 см.
14. В пределах высоты c = 14,9 см располагаются четыре сжатых стержня с A's = 32,16 см2 и a's = 10,66 см, эти стержни принимаем за расчетные, так как σs = Rs; расчет ведем по п. 17.
17. По формуле (23) определяем
![]() и по п. 2.3 находим ξ =
0,612·0,504 + 0,119 = 0,427, x = 0,427·40 = 17,1 см, c = 0,6·17,1 = 10,3 см,
и по п. 2.3 находим ξ =
0,612·0,504 + 0,119 = 0,427, x = 0,427·40 = 17,1 см, c = 0,6·17,1 = 10,3 см,
hs = 80 - 17,1 = 62,9 см.
18. Проверяем условия (13), (14), (15) и (16);
asm =
17,09 см < hs - 62,9 см, σsn =
422,8 МПа > Rsn - 295 МПа, ![]() - 25,51 см > 0,
- 25,51 см > 0,
![]() = 25,51 cм < 0,9hs =
0,9·62,9 = 56,61 см;
= 25,51 cм < 0,9hs =
0,9·62,9 = 56,61 см;
условия выполняются, переходим к следующему этапу подбора количества растянутой арматуры введением дополнительного ряда стержней: As = (6 Ø 32) = 48,24 см2,
![]() = 15,61 см, аs0 = 25,51 см,
= 15,61 см, аs0 = 25,51 см, ![]() = 40 см, asm = 25,51 + 3,2 = 28,71 см, сm =
0,6(80 - 28,7) - 30,78 см, A's =
32,16 см2 и а's - 10,66 см;
= 40 см, asm = 25,51 + 3,2 = 28,71 см, сm =
0,6(80 - 28,7) - 30,78 см, A's =
32,16 см2 и а's - 10,66 см;
расчет дальше ведем по п. 7.
7. Определяем по формуле (22) значение е0 = 77·1,02 + 40 - 15,61 = 102,9 см;
переходим к п. 10.
10. Вычисляем ξ = 15,61/40 = 0,39 и по формуле (11) находим значение ω = 1,633·0,39 - 0,195 = 0,442 и величину Aв0 = 402 (3,14 - 0,422) = 4316,8 см.
11. По формуле (25) определяем напряжение
![]() = 357,4 МПа; поскольку σsn = 357,4 МПа > Rsn =
295 МПа, принимаем σn = Rs = 250 МПа.
= 357,4 МПа; поскольку σsn = 357,4 МПа > Rsn =
295 МПа, принимаем σn = Rs = 250 МПа.
12. По формуле (23) находим ω при A's = 0
![]() = 0,990 и по формуле (6) ξ
- 0,509·0,99 + 0,199
= 0,703; определяем значения x = 0,703·40 - 28,1 см и c = 0,6·28,1
= 16,9 см;
= 0,990 и по формуле (6) ξ
- 0,509·0,99 + 0,199
= 0,703; определяем значения x = 0,703·40 - 28,1 см и c = 0,6·28,1
= 16,9 см;
asc = 7,43 см < с = 16,9 см.
13. Проверяем условие (17): с = 16,9 см < cm = 30,78 см, оно выполняется, в расчет вводим c = 16,9 см.
14. Поскольку as6 = 13,89 см < с = 16,8 см < as5 = 25,51 см, в расчет вводим прежние четыре сжатых стержня A's = (4 Ø 32) = 32,16 см2, a's = 10,66 см; эти стержни принимаем за расчетные, так как σs = Rs; переходим к п. 17.
17. По формуле (23) определяем
![]() и по формуле (5) ξ = 0,612·0,666 + 0,119 = 0,526;
и по формуле (5) ξ = 0,612·0,666 + 0,119 = 0,526;
определяем значения x = 0,526·40 = 21 см, с = 0,6·21 = 12,6 см и hs = 80 - 21 = 59 см.
18. Проверяем условия (13), (14), (15) и (16):
asm = 28,71
см < hs - 59 см, σs - 357,4 МПа > Rsn = 295 МПа, ![]() = 40 см > 0,
= 40 см > 0, ![]() = 40 см < 0,9hs = 0,9·59 = 53,1 см; условия выполняются,
переходим к третьему этапу подбора расчетного количества растянутой арматуры
введением дополнительного ряда стержней: As = 8 Ø 32 = 64,32 см2,
= 40 см < 0,9hs = 0,9·59 = 53,1 см; условия выполняются,
переходим к третьему этапу подбора расчетного количества растянутой арматуры
введением дополнительного ряда стержней: As = 8 Ø 32 = 64,32 см2,
![]() = 21,71 см, as0 - 40 см,
= 21,71 см, as0 - 40 см, ![]() = 54,49 см, asm = 40 + 3,2 = 43,2 см, cm
= 0,6(80 - 43,2) = 22,08 см, h0 = 80 -
21,71 = 58,29 см, при прежнем количестве сжатой арматуры А's = 32, 16 см2 и а's = 10,66 см; переходим к п.
7.
= 54,49 см, asm = 40 + 3,2 = 43,2 см, cm
= 0,6(80 - 43,2) = 22,08 см, h0 = 80 -
21,71 = 58,29 см, при прежнем количестве сжатой арматуры А's = 32, 16 см2 и а's = 10,66 см; переходим к п.
7.
7. По формуле (22) определяем е0 = 77·1,02 + 40 - 21,71 = 96,8 см, переходим к п. 10.
10. Вычисляем ξ = 21,7/40 = 0,542, по формуле (11) определяем ω = 1,633·0,542 - 0,195 = 0,690 и находим Ав0 - 402(3,14 - 0,690) = 3920 см2.
11. По формуле (25) определяем напряжение
![]() = 296,8 МПа;
поскольку σsn - 296,8 МПа > Rsn
= 295 МПа, принимаем σs =
Rs = 250 МПа.
= 296,8 МПа;
поскольку σsn - 296,8 МПа > Rsn
= 295 МПа, принимаем σs =
Rs = 250 МПа.
12. По формуле (23) вычисляем ω при A's = 0
![]() = 1,152, по формуле (6) - ξ = 0,509·1,152 + 0,199 = 0,785; устанавливаем
значения x = 0,785·40 = 31,4 см, c = 0,6·31,4 = 18,8 см.
= 1,152, по формуле (6) - ξ = 0,509·1,152 + 0,199 = 0,785; устанавливаем
значения x = 0,785·40 = 31,4 см, c = 0,6·31,4 = 18,8 см.
13. Проверяем условие (17): c = 18,8 см < cm = 22,08 см; принимаем с = 18,8 см.
14. Поскольку а's6 = 13,89 см < c = 18,8 см < as5 = 25,51 см, в расчете остается прежнее количество сжатых стержней A's = 32,16 см2 и a's = 10,66 см; переходим к п. 17.
17. По формуле (23) определяем
![]() = 0,828 и по формуле (6) ξ - 0,509·0,828 + 0,199 = 0,620, устанавливаем значения x = 0,620·40 = 24,8 см, c = 0,6·24,8 - 14,9 см, hs = 80 - 24,8 = 55,2 см.
= 0,828 и по формуле (6) ξ - 0,509·0,828 + 0,199 = 0,620, устанавливаем значения x = 0,620·40 = 24,8 см, c = 0,6·24,8 - 14,9 см, hs = 80 - 24,8 = 55,2 см.
18. Проверяем условия (13), (14), (15) и (16): asm = 43,2 см < hs = 55,2
см, σsn - 296,8 МПа > Rsn - 295
МПа, ![]() = 54,49 см > 0,
= 54,49 см > 0, ![]() = 54,49 см > 0,9hs = 0,9·55,2 = 49,68 см; условие (16)
нарушается при выполнении условия (13); переходим к п. 20.
= 54,49 см > 0,9hs = 0,9·55,2 = 49,68 см; условие (16)
нарушается при выполнении условия (13); переходим к п. 20.
20. Проверяем условие (19): с = 14,9 см > a's = 10,66 см - условие соблюдается, прочность сечения определяем по формуле (21): 1250·96,8 = 121000 кН·см < (0,1)·0,828·402·15,5(58,29 - 14,9) + (0,1)·250·32,16×(58,29 - 10,66) = 127393,3 кН·см; прочность сечения достаточна.
Расчет по устойчивости
3.9. Внецентренно сжатые железобетонные элементы с эксцентриситетом ес ≤ r следует рассчитывать по устойчивости по формуле:
|
N = φ(RвАв + RscAsn). |
Если площадь поперечного сечения арматуры превышает 3 %, то Ав заменяют на Ав - Asn.
3.10. Коэффициент продольного изгиба определяется по формуле:
|
|
где φm - коэффициент продольного изгиба, учитывающий воздействие временной нагрузки;
φl - коэффициент продольного изгиба, учитывающий воздействие постоянных нагрузок.
Значения коэффициентов φm и φl, при вычислении которых учтены также значения случайных эксцентриситетов, следует принимать по табл. 3.
|
Характеристика гибкости элементов l0/d |
Коэффициенты продольного изгиба |
||||
|
φm при относительном
эксцентриситете |
φl |
||||
|
0 |
0,25 |
0,50 |
1,0 |
||
|
3,5 |
1,00 |
0,90 |
0,81 |
0,69 |
1,00 |
|
8,6 |
1,00 |
0,86 |
0,77 |
0,65 |
0,84 |
|
10,4 |
0,95 |
0,83 |
0,74 |
0,62 |
0,79 |
|
12,1 |
0,90 |
0,79 |
0,70 |
0,58 |
0,70 |
|
13,8 |
0,86 |
0,75 |
0,66 |
0,55 |
0,65 |
|
15,6 |
0,82 |
0,71 |
0,62 |
0,51 |
0,56 |
|
17,3 |
0,78 |
0,67 |
0,57 |
0,48 |
0,47 |
|
19,1 |
0,72 |
0,60 |
0,52 |
0,43 |
0,41 |
|
20,8 |
0,67 |
0,55 |
0,47 |
0,38 |
0,32 |
|
22,5 |
0,62 |
0,51 |
0,44 |
0,35 |
0,25 |
|
24,3 |
0,58 |
0,49 |
0,43 |
0,34 |
0,20 |
|
26,0 |
0,53 |
0,45 |
0,39 |
0,32 |
0,16 |
|
27,7 |
0,48 |
0,41 |
0,36 |
0,31 |
0,14 |
|
29,0 |
0,43 |
0,36 |
0,31 |
0,25 |
0,10 |
|
33,0 |
0,38 |
0,32 |
0,28 |
0,24 |
0,08 |
|
34,6 |
0,35 |
0,29 |
0,25 |
0,21 |
0,07 |
|
37,5 |
0,33 |
0,28 |
0,24 |
0,21 |
0,08 |
3.11. При расчете железобетонных элементов на воздействие сжимающей продольной силы N при eс ≤ r за расчетное значение усилий принимается меньшее, полученное из расчетов по прочности по формуле (24) и по устойчивости по формуле (32).
3.12. Для расчета по устойчивости внецентренно сжатых элементов рекомендуется следующий алгоритм расчета (табл. 4).
Исходные данные: эксцентриситет eс, геометрические характеристики сечения d, r1, rs и r, класс бетона, класс арматурной стали, общее количество арматуры в сечении, диаметр стержней, величина αi или расстояние между стержнями, расчетная длина элемента, значения Ml, Nl, Mm и Nm. Требуется рассчитать элемент по устойчивости при равномерном расположении арматуры по контуру сечения.
Таблица 4
|
Порядок действия |
Содержание действия |
|
1 |
Определяются Rв, Rsс |
|
2 |
Последовательно находятся Aв, Asn, N, l0/d, ec/r |
|
3 |
По табл. 3 определяются φm и φl |
|
4 |
По формуле (33) вычисляется φ |
|
5 |
По формуле (32) производится расчет по устойчивости |
|
6 |
По формуле (24) с использованием алгоритма, приведенного в табл. 2 (пп. 1-8), определяется прочность сечения |
|
7 |
Принимается меньшее расчетное значение несущей способности, полученное по формулам (24) и (32) |
|
|
Конец |