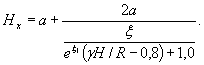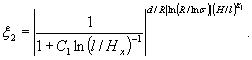МИНИСТЕРСТВО ТОПЛИВА И
ЭНЕРГЕТИКИ РФ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ГОРНОЙ ГЕОМЕХАНИКИ И МАРКШЕЙДЕРСКОГО ДЕЛА
(ВНИМИ)
РЕКОМЕНДАЦИИ
ПО ОПРЕДЕЛЕНИЮ МЕХАНИЧЕСКИХ СВОЙСТВ ТРЕЩИНОВАТОГО МАССИВА
С.-ПЕТЕРБУРГ
1992
Содержание
|
ПРОГНОЗИРОВАНИЕ МЕХАНИЧЕСКИХ СВОЙСТВ ТРЕЩИНОВАТОГО МАССИВА 1. ОПРЕДЕЛЕНИЕ ПРОЧНОСТНЫХ СВОЙСТВ МАССИВА, НАРУШЕННОГО ТРЕЩИНАМИ
|
В рекомендациях приведены принципы расчета коэффициента структурного ослабления массива горных пород для широкого круга горно-геологических условий. Рассмотрен вопрос определения реологических свойств массива, ослабленного системой трещин. Рекомендации составлены на основании многочисленных результатов исследований на моделях из эквивалентных материалов с использованием метода рационального планирования экспериментов. Помещены примеры конкретных расчетов коэффициентов структурного ослабления и реологического параметра трещиноватого массива. Рекомендации рассмотрены секцией Ученого совета ВНИМИ по горному давлению и рекомендованы к использованию в НИИ.
ВВЕДЕНИЕ
Общая тенденция к переходу на большие глубины при разработке полезных ископаемых требует дополнительных всесторонних исследований по изучению деформационных и прочностных свойств угольных пластов и вмещающего массива в постоянно усложняющихся геомеханических условиях.
Под влиянием высоких напряжений возрастает степень нарушенности массива горных пород. Это, в свою очередь, усложняет условия поддержания выработок и отработки полезного ископаемого. В связи с этим при постановке экспериментальных и аналитических исследований прежде всего встает вопрос о влиянии на процессы, протекающие в массиве горных пород, о характере и степени влияния нарушенности на проявление горного давления в выработках.
Прогнозирование прочностных и деформационных свойств трещиноватого массива также приобретает большое значение при строительстве подземных сооружений, особенно гидроэнергетических, имеющих площади поперечного сечения порядка 500 м2 и более [1]. В последние годы строится все больше подобных подземных сооружений.
Всестороннее изучение процессов, протекающих в трещиноватом массиве в условиях натуры, достаточно сложно. Хотя натурные опыты и являлись показательными в настоящих исследованиях, но постановка экспериментов была очень трудоемкой, а повторить исследования не представлялось возможным. К сложностям также следует отнести: установление параметров, необходимых для прогнозирования степени ослабления массива (в том числе величина сцепления на контактных поверхностях элементарных блоков, достаточно обоснованное расположение плоскостей ослабления и т. д.). Кроме того, как отметил Г.Н. Кузнецов [2], натурные исследования позволяют определить значение показателей свойств массива только для его локального участка и не могут вскрыть общих закономерностей и зависимостей свойств массива от различных видов его макроструктуры и напряженного состояния. В числе нерешенных до настоящего времени остается вопрос определения геометрических параметров участка трещиноватого массива, который был достаточно представительном с точки зрения геомеханических процессов при определении механических свойств такого массива, поскольку соотношение размеров элементарных блоков и исследуемого участка, при прочих равных условиях, может оказаться определяющим в процессе изучения степени влияния горно-геологических факторов на механические свойства массива.
К основным недостаткам широко практикуемых лабораторных испытаний образцов трещиноватых горных пород необходимо отнести необоснованность переноса их результатов на весь массив.
Аналитические исследования, связанные только с изменением прочностных свойств трещиноватого массива, проведенные Г.Н. Кузнецовым [2, 3], а впоследствии Л. Мюллером [4] и К. Ионом [5], открывают широкие возможности для оценки момента наступления предельного состояния пород. Несомненно, что они должны пройти всестороннюю экспериментальную проверку на моделях и в условиях производства при широком диапазоне изменения горно-геологической обстановки. Исследования реологических свойств трещиноватых образцов горных пород, а тем более трещиноватого массива в условиях натуры, немногочисленны. К наиболее известным можно отнести эксперименты над трещиноватыми образцами горных пород в лабораторных условиях, проведенные В.И. Глушко [6] Указанные образцы были получены после испытания монолитных образцов на прессах на сжатие, параметры трещиноватости не устанавливались, поэтому обоснованные выводы относительно изменения реологических свойств по результатам подобных экспериментов практически невозможны
Наиболее приемлемым для исследований (как показывают результаты анализа многочисленных данных) и позволяющим глубоко и всесторонне изучить процессы, протекающие в трещиноватом массиве горных пород, является один из методов физического моделирования. Это метод моделирования на эквивалентных материалах, открывающий широкие возможности для имитации массива горных пород с заранее заданными параметрами трещиноватости. Большое преимущество применения указанного метода - это возможность непосредственно моделировать и испытывать трещиноватый массив, а не трещиноватые образцы, как это имеет место при лабораторных испытаниях, и переносить результаты исследований с учетом масштаба моделирования непосредственно на условия натуры. В настоящей работе даны рекомендации по определению прочностных и реологических свойств массива горных пород, основанные на результатах экспериментальных исследований на моделях методом эквивалентных материалов.
ПРОГНОЗИРОВАНИЕ МЕХАНИЧЕСКИХ СВОЙСТВ ТРЕЩИНОВАТОГО МАССИВА
Прежде чем составить и предложить настоящие рекомендации для прогнозирования механических свойств трещиноватого массива были проанализированы результаты испытаний трещиноватых образцов горных пород и данные подобных испытаний на моделях из эквивалентных материалов.
На рис. 1 приведены результаты детального анализа процессов, протекающих в трещиноватом массиве в условиях натуры и модели, где по оси абсцисс отложены прочности элементарных блоков, образованных между плоскостями ослабления, и по оси ординат - значения прочности на сжатие массива, ослабленного трещинами (на графике пунктирные линии относятся к условиям модели, а сплошные - натуры). Около каждой кривой показана степень нарушенности массива l/Hx, (l - размер элементарного блока, образующего массив, Hx - размер структурного образца или модели массива). Как следует из графиков, чем выше степень нарушенности массива, при прочих равных условиях, тем меньше разница между прочностью Rстр и прочностью на сжатие элементарного блока. Например, для условий нарушенности массива l/Hx = 0,1, при прочности на сжатие элементарного блока R = 20 МПа и 100 МПа, прочность ослабленного трещинами, массива горных пород практически одного порядка, - соответственно, 9 и 12 МПа. В то же время при степени нарушенности l/Hx = 0,8 для R = 20 МПа; R = 17 МПа и для R = 100 МПа соответственно Rстр = 52 МПа. Общий же характер зависимостей Rстр = f(R) сохраняется для опытов, проведенных в условиях как натуры, так и моделей. Незначительное различие в количественном отношении между результатами экспериментов на моделях и в условиях натуры объясняется тем, что в процессе исследования на моделях из эквивалентных материалов была известна величина сцеплений на контактных поверхностях элементарных блоков, составляющих массив модели, и ряд других параметров, заранее заданных, в то время как при проведении экспериментов в условиях натуры подобные параметры не были установлены. Анализ приведенных зависимостей (см. рис. 1) позволил сделать вывод относительно правомерности результатов исследований на моделях из эквивалентных материалов, а также переноса этих результатов непосредственно на условия натуры.
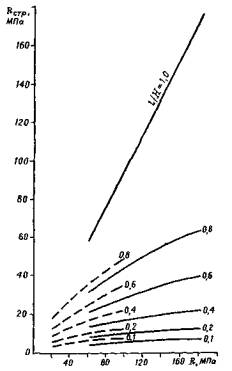
Рис. 1. Зависимость Rстр от R для условий натуры и модели
Прогнозирование механических свойств массива горных пород, ослабленного системой трещин, на моделях из эквивалентных материалов
Определяемые механические свойства трещиноватого массива делятся на две основные группы:
1) прочностные,
2) реологические.
1. ОПРЕДЕЛЕНИЕ ПРОЧНОСТНЫХ СВОЙСТВ МАССИВА, НАРУШЕННОГО ТРЕЩИНАМИ
1.1. В целях определения прочностных свойств трещиноватого массива с заранее заданными параметрами ослабления массива горных пород на моделях методом эквивалентных материалов воспроизводились, как правило, три плоскости ослабления: горизонтальная и две остальные - или взаимноперпендикулярные, или направленные под различными углами одна к другой. Три плоскости ослабления массива были приняты в результате анализа данных предыдущих исследований Г.Н. Кузнецова [3] и К. Иона [5]. Их опыты и аналитические решения показали, что уже при трех плоскостях ослабления среда в процессе деформирования ведет себя как квазиизотропное тело. Исходя из этого, принятая структурная система является в определенной степени оптимальным вариантом для исследований настоящего вопроса на моделях, результаты которых позволили, как это видно далее, установить ряд закономерностей, необходимых для прогнозирования механических свойств трещиноватого массива.
1.2. Оценка степени нарушенности массива, таким образом, основывалась во всех случаях на результатах исследований на моделях из эквивалентных материалов. В качестве примера на рис. 2 показаны результаты одной из серий опытов на моделях, где в функции отношения l/Hx приведены значения коэффициента структурного ослабления массива Kстр (l - размер элементарного блока, образованного между плоскостями ослабления; Hx - максимальный размер трещиноватой модели). Зависимости 1 и 2 получены для моделей, массив которых был образован элементарными блоками прочностью соответственно 30 и 45 МПа на сжатие в пересчете на условия натуры, и кривые 3 и 4 для прочности элементарных блоков 60 и 120 МПа. В результате обработки многочисленных данных экспериментов, подобных приведенным на рис. 2, получена зависимость, предлагаемая для оценки коэффициента структурного ослабления массива. Зависимость имеет следующий вид:
где ρ - угол внутреннего трения пород, C - сцепление на контактных поверхностях отдельностей, МПа, R - прочность на сжатие элементарного блока, МПа; m1, m2, n - коэффициенты, численные значения которых следующие: m1 = -0,447; m2 = 2,34·10-ζ и n = 2,73.
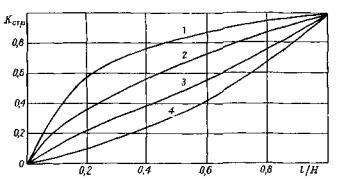
Рис. 2. Влияние степени нарушенности массива на величину коэффициента структурного ослабления
1.3. Как следует из анализа зависимости [1], на степень ослабления массива влияет ряд факторов. К наименее изученным из них следует отнести сцепление по контактным поверхностям элементарных блоков, величину которого практически невозможно установить в условиях натуры. В то же время этот фактор может заметно влиять на изменение коэффициента структурного ослабления.
1.4. В результате расчетов по формуле (1) построена номограмма (рис. 3). Пользуясь ею, можно производить предварительные прогнозные расчеты относительно изменения величины коэффициента структурного ослабления трещиноватого массива в зависимости от основных действующих геомеханических факторов.
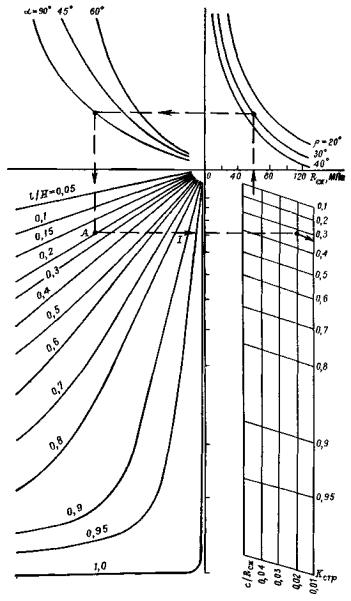
Рис. 3. Номограмма для определения коэффициента структурного ослабления массива
1.5. В связи с расчетами коэффициента структурного ослабления массива неизученным остается вопрос о параметрах участка массива, который необходимо учитывать при определении величины Kстр. Дело в том, что при различных параметрах Hx для тех же горно-геологических условий, для одной и той же величины элементарных блоков l, из которых состоит трещиноватый массив, величина l/Hx может быть, как следует из зависимости (1), различной. Например, для условий натуры при l = 1,0 м и Hx = 10 м степень нарушенности массива составит l/Hx = 0,1. При Hx = 20 м тот же параметр l/Hx будет равен 0,05 и при Hx = 50 м соответственно 0,02. Исходя из номограммы (см. рис. 3), для одинаковых геомеханических условий ρ = 30°, R = 60 МПа, α = 90°, C/R = 0,05 коэффициент структурного ослабления примет следующие значения: Kстр = 0,3; 0,2 и 0,07.
Поэтому для правильного прогнозирования степени ослабления массива системой трещин необходимо установить параметры той области массива «активной зоны», которая участвует в формировании характера геомеханического процесса, протекающего на определенном участке массива, т.е. следует найти величину некоторой зоны Hx. При определении этого параметра необходимо различать следующие случаи:
1) интересующий участок толщи не связан с массивом и является самостоятельным элементом системы разработки. Например, это целик породы полезного ископаемого. Для рассматриваемого случая его параметр Hx находят как максимальную величину целика, а для определения отношения l/Hx необходимо знать размер элементарного блока l, который образуется между плоскостями ослабления. Знание отношения l/Hx и других параметров будет достаточно для входа в номограмму (см. рис. 3) или в зависимость (1);
2) исследуемый участок является дальнейшим продолжением массива. Например, это часть массива, окружающая горную выработку, часть уступа при открытых работах или часть стенки выработки. В этом случае необходимо рассматривать ту часть массива, которая влияет на формирование геомеханических процессов.
Так, чтобы найти «активную зону» для участка трещиноватого массива с пройденной в нем выработкой, предлагается определять последнюю из условий напряженного состояния массива, окружающего выработку.
Общий характер распределения нормальных напряжений в боках выработки показан на рис. 4. Размер «активной зоны» предлагается определять как сумму двух величин a и Xm, где a - пролет выработки, Xm - расстояние от контура выработки до местоположения максимума напряжений (точка A, см. рис. 4).
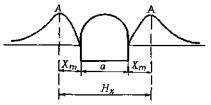
Рис. 4. Распределение напряжений в боках выработки
В пределах этой «активной зоны» возникают максимальные напряжения и на процессы, протекающие в выработке, влияет именно эта область массива. В зависимости (2) величина пролета выработки известна, а параметр Xm может быть получен по графику (рис. 5). Зависимость, приведенная на этом графике, выявлена в результате исследований на моделях из эквивалентных материалов (на оси абсцисс показана степень напряженного состояния массива γH/R, R - прочность элементарного блока на сжатие или прочность монолитного образца). Как следует из анализа зависимости (см. рис. 5), по мере возрастания степени напряженного состояния массива возрастает и расстояние максимума напряжений от контура выработки, т.е. максимум напряжений уходит вглубь массива, и при степени напряженности последнего γH/R = 0,8 зависимость постепенно начинает затухать.
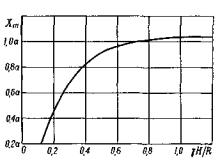
Рис. 5. График зависимости Xm от степени напряженного состояния массива
1.6. Приведенная зависимость (см. рис. 5) аппроксимируется функцией вида:
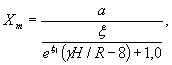 (3)
(3)
где ξ и ξ1 - коэффициенты, соответственно равные 0,25/ln15γH и ξ = 1,22; a - пролет выработки, γH/R - степень напряженного состояния массива.
Величину «активной зоны» Hx, в свою очередь, определяем из выражения:
Пример определения коэффициента структурного ослабления массива
Исходные данные: порода - глинистый сланец. Прочность элементарного блока, образованного между плоскостями ослабления R = 60 МПа. Угол наклона трещины к напластованию α = 90°.
Размер блока l = 1,0 м. Величина относительного сцепления на контактных поверхностях элементарных блоков C/R = 0,05. Угол внутреннего трения ρ = 30°. Глубина работ H = 1000 м. Размер целика 5´5´5 м. Пролет выработки 4 м. Степень напряженного состояния массива с учетом глубины 1000 м, среднего объемного веса 2,5 т/м3 и прочности 60 МПа на сжатие: γH/R = 0,42.
Расчет ведем для двух случаев:
1) для условий трещиноватого целика величина «активной зоны» Hx = 5 м. Степень нарушенности для этого случая l/Hx = 0,2, из номограммы (см. рис. 3) с учетом исходных данных и величины l/Hx получаем Kстр = 0,40;
2) для условий трещиноватого массива с пройденной в нем выработкой величину Kстр определяем следующим образом: находим Xm, из зависимости, приведенной на рис. 5 с учетом степени напряженного состояния массива γH/R = 0,42, которая после подстановки последнего указанного значения будет равна 0,83a.
Размер «активной зоны» составит после подстановки исходных данных в зависимость (2): Hx = 4,0 + 2,0´4,0´0,83 = 10,7 м.
Подставляя в номограмму (см. рис. 3) основное исходные данные и величину степени нарушенности массива l/Hx = 0,09, получим коэффициент структурного ослабления Kстр = 0,22. В данном случае коэффициент ослабления массива получился почти в два раза меньше, чем для условий целика при тех же основных исходных данных,
Несомненно, что при подстановке других данных, в номограмму получим соответственно иные значения коэффициентов структурного ослабления, которые будут в Значительной степени зависеть от параметров «активной зоны» Hx.
2. ПРОГНОЗИРОВАНИЕ РЕОЛОГИЧЕСКИХ СВОЙСТВ МАССИВА ГОРНЫХ ПОРОД, В РАЗЛИЧНОЙ СТЕПЕНИ ОСЛАБЛЕННОГО СИСТЕМОЙ ТРЕЩИН
2.1. Оценка степени пластичности трещиноватого массива горных пород является одним из ключевых и в то же время наименее изученных вопросов горной геомеханики. Точное прогнозирование реологических свойств массива в производственных условиях необходимо для правильного обоснования процессов проявления горного давления в выработках, для выбора параметров крепей, расчета несущей способности целиков и других элементов системы разработки.
Для обоснованного прогноза реологических параметров трещиноватого массива горных пород предварительно должны быть установлены основные параметры плоскостей ослабления, их количество, взаимное расположение в пространстве. Большое значение имеет также, как показали результаты многочисленных исследований на моделях, величина скопления на контактах между элементарными блоками, слагающими массив пород. Определить сцепление на контактных поверхностях отдельностей в условиях натуры практически не представляется возможным.
2.2. Горный массив, представленный хрупкими породами, характеризуется определенным численным значением реологических параметров, присущих соответственно хрупкому телу. При наличии плоскостей ослабления тот же самый массив изменит свои реологические свойства, и определять их будет, очевидно, при прочих равных условиях, степень его нарушенности, а именно величина отношения l/Hx.
В лабораторных условиях определяют, как указано, реологические параметры только сплошных образцов горных пород без учета существующих плоскостей ослабления. Методы, предлагаемые рядом авторов [6], суть которых в доведении образцов горных пород до разрушения и последующем вторичном испытании уже нарушенных образцов на прессах в режиме заданной нагрузки для определения их реологических параметров, нужно считать весьма приближенными. На таких параметрах практически невозможно базироваться при прогнозировании реологических свойств трещиноватого массива, имеющего вполне определенные характеристики нарушенности.
2.3. Для определения влияния степени нарушенности массива горных пород на изменение его реологических свойств были также проведены исследования на моделях из эквивалентных материалов. При этом заранее были известны достаточные для обоснованных прогнозов геомеханические параметры: прочность элементарных блоков, сцепление на контактных поверхностях отдельностей, геометрические размеры отдельностей.
2.4. Деформации массива моделей во времени замеряли при постоянном напряжении, равном 0,3; 0,5 и 0,65 от прочности на одноосное сжатие монолитных и трещиноватых моделей.
В процессе исследований на моделях имитировалась три плоскости ослабления так же, как это имело место при изучении на трещиноватых моделях прочностных свойств массива. Определяли модули деформаций массива моделей, монолитных и нарушенных трещинами, условно мгновенные Eмг, и значение модулей деформации Et в момент затухания процесса деформирования испытываемых моделей. В качестве основного параметра пластичности принято отношение этих двух модулей, а именно, Et/Eмг, предложенное Г.Н. Кузнецовым. Как показали многочисленные исследования образцов горных пород и эквивалентных материалов, этот параметр является в достаточной степени объективным показателем пластичности, пригодным для сравнения монолитных и нарушенных трещинами породных образцов и моделей.
2.5. Пример испытания модели без трещин для прочности в пересчете на условия натуры 30 МПа на сжатие приведен на рис. 6, а на рис. 7 показан результат испытания модели с той же прочностью элементарных блоков, но нарушенной трещинами (размеры элементарных блоков, образованных между плоскостями ослабления, составили 2´2´2 см). Подобные графики являются основой первичной обработки результатов исследований. На основании этих графиков строили зависимости изменения реологического параметра Et/Eмг от отношения l/Hx. Подобный график с прочностью элементарных блоков 30 МПа на сжатие (в пересчете на условия натуры) приведен на рис. 8. Как следует из анализа графика, с увеличением степени ослабления массива трещинами, при прочих равных условиях снижается численное значение реологического параметра Et/Eмг, т.е. массив становится более податливым.
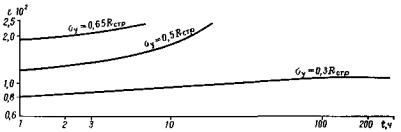
Рис. 6. Изменение деформации однородного массива модели во времени
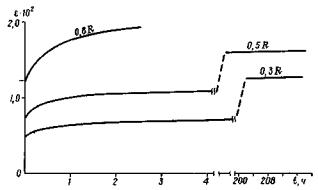
Рис. 7. Изменение деформаций структурной модели во времени
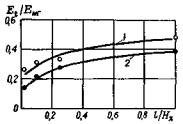
Рис. 8. Изменение реологического параметра Et/Eмг в зависимости от структурного строения массива
Так, для отношения l/Hx = 1,0, что соответствует ненарушенному трещинами массиву, значение Et/Eмг - 0,5 (кривая 1), т.е. это сравнительно хрупкая среда. При отношении l/Hx = 0,05 величина параметра Et/Eмг снижается до 0,2, что соответствует пластичной среде.
2.6. Необходимо отметить, что численное значение Параметра Et/Eмг зависит также, при прочих равных условиях, от степени напряженного состояния массива σ/R (или, что то же самое, от γH/R). Так, в числе зависимостей, приведенных на рис. 8, кривая 1 получена для условий напряженного состояния массива модели σ/R = 0,3. Зависимость 2 соответствует степени напряженного состояния массива модели σ/R = 0,5. Далее, в таблице, приведены численные значения реологических параметров Et/Eмг горных пород, полеченные в результате исследований в лабораторных условиях для сравнительной оценки степени пластичности. Поскольку Et/Eмг - величина безразмерная, то, как указано ранее, может характеризовать не только пластичные свойства горных пород, но и степень пластичности эквивалентных материалов. Здесь же качественно охарактеризована степень ползучести.
|
Породы |
R, МПа |
Et/Eмг |
Степень ползучести |
|
Известняки, песчаники |
80 - 120 |
0,8 - 0,9 |
Весьма слабая |
|
Песчанистые сланцы, алевролиты |
50 - 80 |
0,6 - 0,8 |
Слабая |
|
Песчаноглинистые сланцы, алевролиты |
30 - 50 |
0,4 - 0,5 |
Средняя |
|
Глинистые, углисто-глинистые сланцы |
15 - 30 |
0,3 - 0,4 |
Сильная |
|
Глинистые сланцы, глины уплотненные |
10 - 15 |
0,1 - 0,2 |
Весьма сильная |
2.7. После обработки результатов исследований по специальной программе, применяемой при планировании экспериментов [7], построена номограмма (рис. 9), на основании которой возможно прогнозировать величину реологического параметра Et/Eмг для массива горных пород, в различной степени нарушенного трещинами. Номограмма связывает между собой прочность на сжатие R (МПа) элементарных блоков, которые образуются в трещиноватом массиве между плоскостями ослабления, относительные размеры элементарных блоков l/Hx от 0,1 до 1,0, степень напряженного состояния массива σ/Rстр (где Rстр - прочность на сжатие массива, ослабленного трещинами, σ - действующее напряжение; предел изменения σ/Rстр от 0,2 до 0,6) и величину сцепления C на контактных поверхностях элементарных блоков, отнесенную к прочности последних на сжатие. (В номограмме значения Et/Eмг приведены для момента времени t, отвечающего затуханию деформаций массива моделей). Следует иметь в виду, что в номограмме значения R и Rстр, а также действующие напряжения пересчитаны на условия натуры. Предложенная номограмма может быть использована в производственных условиях для прогнозирования реологических параметров массива, ослабленного в различной степени трещинами.
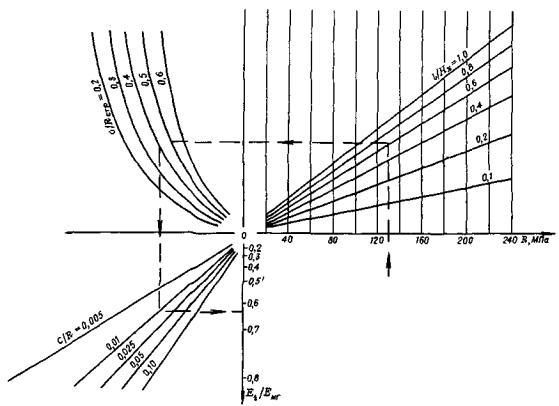
Рис. 9. Номограмма для определения реологического параметра Et/Eмг
Кроме этой основной задачи, с помощью номограммы возможно устанавливать степень влияния основных действующих факторов на реологические процессы, протекающие в массиве, и одновременно выявлять из целого комплекса факторов наиболее сильнодействующий.
Пример определения по номограмме реологического параметра Et/Eмг
Исходные данные: порода - песчаник, относительное сцепление C/R = 0,01; прочность на сжатие элементарного блока R = 80 МПа; степень нарушенности массива l/Hx = 0,2; степень напряженного состояния массива σ/Rстр = 0,5 (величину «активной доны» Hx определяем из тех же условий, что при расчетах коэффициента структурного ослабления Kстр из зависимости, приведенной на рис. 5, или на основании формулы (4).
После подстановки в номограмму (см. рис. 9) указанных данных получим Et/Eмг = 0,35, рассчитанное численное значение параметра Et/Eмг соответствует пластичной породе (см, таблицу). Для тех же исходных данных, но для более низкой степени нарушенности l/Hx = 0,8 из номограммы (см. рис. 9) получим численное значение параметра Et/Eмг = 0,55, отвечающее горной породе с более высокими хрупкими свойствами. Как следует из этих примеров, при одной и той же прочности элементарного блока уменьшение его геометрических размеров ведет к значительному возрастанию реологических свойств массива.
Определение параметра пластичности при расчетах несущей способности элементов системы разработки весьма важно. В производственных условиях подавляющую часть горных выработок проходят в массиве, нарушенном трещинами. Поэтому, если не учитывать ослабление массива трещинами, а также изменение реологических свойств, то в расчетах это может вызвать необоснованное занижение несущей способности крепи или неоправданный выбор способов охраны выработок. Это, в свою очередь, приведет к разрушению крепи и завалу выработок.
2.8. По номограмме, кроме определения параметра пластичности Et/Eмг, для интересующих исследователя конкретных геомеханических условий дополнительно возможна оценка степени влияния входящих в эту номограмму факторов на характер изменения реологических свойств массива.
Далее показаны результаты подобного анализа, так, на рис. 10 для постоянных значений напряженного состояния массива σ/R = 0,5 и степени нарушенности l/Hx = 0,5 приведен характер изменения величины C/R от сцепления и прочности. Изменение величины C/R от 0,005 до 0,05, т.е. увеличение в 10 раз, приводит к возрастанию реологического параметра (для прочности 120 МПа) от 0,42 до 0,84, т е. в два раза. В первом случае среда пластичная, во втором хрупкая.
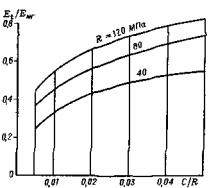
Рис. 10. График изменения реологического параметра Et/Eмг от сцепления C
Результаты дополнительного анализа номограммы приведены на рис. 11. По оси абсцисс здесь отложены значения прочности элементарного блока от 20 до 200 МПа для степени нарушенности l/Hx = 0,1; 0,5 и 1,0 (зависимости построены для постоянных значений C/K = 0,025 и σ/Rстр = 0,5). Из анализа графика следует, что, например, для диапазона Изменения прочности на сжатие от 20 до 200 МПа для степени нарушенности l/Hx = 0,1 реологические свойства возрастают от 0,16 до 0,47, т.е. почти в три раза. Графики, подобные приведенным на рис. 10 и 11, получены на основании обработки номограммы (см. рис. 9), могут быть построены для любых сочетаний факторов, влияющих на реологические процессы, протекающие в трещиноватом массиве.
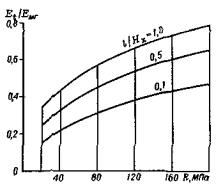
Рис. 11. График изменения реологического параметра Et/Eмг от прочности элементарного блока
Как следует из приведенных примеров, на основании номограммы (см. рис. 9) определяем значение реологического параметра Et/Eмг для трещиноватой среды в широком диапазоне изменения геомеханических факторов. В расчетах величины Et/Eмг для однородного массива горных пород следует принимать численное значение отношения l/Hx = 1,0.
2.9. Определение мгновенного модуля деформации массива, ослабленного трещинами, или трещиноватого целика часто необходимо в производственных условиях для оценки возможной податливости последних. На основании лабораторных испытаний монолитных образцов горных пород или элементарного блока, составляющего участок массива, предлагается модуль деформации определять на основании зависимости, полученной также в результате испытания трещиноватых и монолитных моделей из эквивалентных материалов. Формула имеет вид:
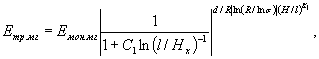 (5)
(5)
где C1, d, K1 - численные коэффициенты; C1 = 1,3; d = 4,0; K1 = 0,2; R - прочность на сжатие отдельного элементарного блока, составляющего массив, или монолитного образца горной породы, МПа; σ/Rстр - напряженное состояние трещиноватого массива; l/Hx - показатель степени нарушенности массива.
Величину в квадратных скобках для удобства расчетов обозначим параметром ξ2:
В результате рассчитываем параметр ξ2, на который следует умножить величину мгновенного модуля деформации монолитного образца для определения модуля деформации массива, нарушенного трещинами. Номограмма, рассчитанная по формуле (6), приведена на рис. 12. Номограмма связывает между собой величины R, σ/R и l/Hx.
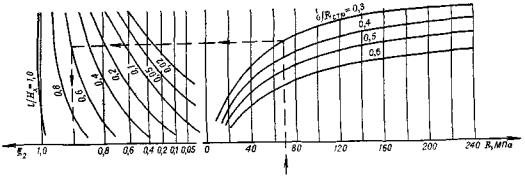
Рис. 12. Номограмма для определения параметра ξ2
2.10. Примеры определения величины Eмг.стр по известному модулю деформации монолитного образца породы.
1) Исходные данные: порода - песчанистый сланец, R = 30 МПа; степень напряженного состояния трещиноватого массива σ/Rстр = 0,3; модуль деформации Eмг.мон = 1,5·104 МПа; степень нарушенности массива l/Hx = 0,2; размер элементарного билона 2,0 м Величина «активной зоны» Hx = 0 м. Подставляя указанные значения в номограмму (см. рис. 12), получим величину параметра ξ2 = 0,62. Значение модуля деформации трещиноватого массива Eмг.стр получим умножением Eмг.мон на параметр ξ2.
Eмг.стр = 1,5·104·0,62 = 0,92·104 МПа.
2) Исходные данные, порода - известняк, R = 220 МПа, степень напряженного состояния трещиноватого массива σ/Rстр =0,5, модуль деформации Eмг.мон = 5,8·10 МПа; степень нарушенности l/Hx = 0,05. Размер элементарного блока l = 1,0 м. Величина «активной зоны» известна: Hx = 20 м. Подставляя исходные данные так же, как в примере 1, в номограмму (см. рис. 12), получим значение параметра ξ2 = 0,45. Искомый модуль мгновенной деформации трещиноватой среды будет равен:
Eмг.стр = 5,8·0,45·104 = 2,6·104 МПа.
2.11. Определим модуль длительной деформации трещиноватого массива по известному аналогичному модулю монолита.
Чтобы полнее учесть деформационные свойства реального массива, можно рассчитать модуль длительной деформации однородного образца той же горной породы, из которой состоит массив. Это, в свою очередь, позволит с большей достоверностью прогнозировать устойчивость горных выработок и трещиноватых целиков угля и породы.
Для расчетов предлагаем следующую зависимость, полученную при обработке результатов многочисленных опытов на моделях из эквивалентных материалов:
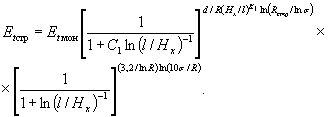 (7)
(7)
Первая часть формулы - это тот же параметр ξ2, определяемый на основании номограммы (см. рис. 12). Вторая часть зависимости (7) является также некоторым переменным параметром ξ3, определяемым на основании номограммы (рис. 13), построенной в результате расчетов по формуле:
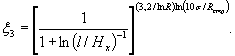 (8)
(8)
Чтобы получить интересующий модуль длительной деформации трещиноватого массива Et, следует найденные по номограммам (см. рис. 12, 13) параметры ξ2 и ξ3 перемножить и затем умножить на модуль длительной деформации монолитного образца породы или, что то же самое, - аналогичный модуль элементарных блоков, из которых состоит трещиноватый массив.
Etстр = Etмонξ2ξ3. (9)
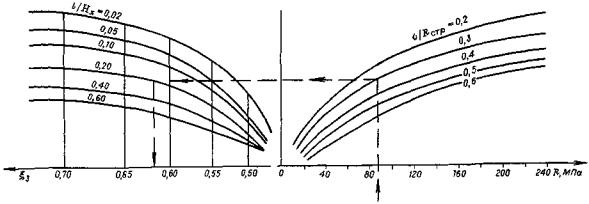
Рис. 13. Номограмма для определения параметра ξ3
2.12. Пример определения величины Etстр по известному модулю Etмон.
Исходные данные: порода - песчанистый сланец; R = 68 МПа: Etмон = 2,14·104 МПа.
Порядок расчета: а) определяем из номограммы (см. рис. 9) величину Etмон для условий l/Hx = 1,0 (монолит); σ/R = 0,3 и максимального значения C/R = 0,1, отношение Et/Eмг будет равно 0,78. Отсюда определяем Et, который составит, в свою очередь, Et = 0,78Eмг = 0,78·2,14·104 = 1,68·104 МПа;
б) из номограммы (см. рис. 12) определяем для рассматриваемых условий l/Hx = 0,1; σ/R = 0,3 и R = 68 МПа, а также величину параметра ξ2, который будет равен 0,65;
в) по номограмме (см. рис. 13) находим параметр ξ3, который для исходных данных l/Hx = 0,1, σ/R = 0,3 будет соответственно ξ3 = 0,56;
г) зная численные значения ξ2 и ξ3, определим модуль длительной деформации трещиноватого массива:
Etстр = 0,65·0,56·1,68·104 = 0,61·104 МПа.
ЗАКЛЮЧЕНИЕ
Приведенные в рекомендациях примеры определения коэффициента структурного ослабления и реологических параметров трещиноватого массива горных пород показали целесообразность применения настоящего метода для расчета указанных величин.
Особое внимание при составлении рекомендаций обращено на те геомеханические факторы, степень воздействия которых на процесс деформирования массива ранее не была установлена. К таким малоизученным факторам относится величина сцепления на контактных поверхностях элементарных блоков, образующих трещиноватый массив.
Предложенные в рекомендациях многофакторные зависимости, полученные в результате обработки экспериментальных данных на моделях, позволяют обоснованно устанавливать степень влияния основных геомеханических факторов на процесс деформирования трещиноватого массива во времени.
Дальнейшее совершенствование метода должно развиваться в направлении разработки прочностных и реологических параметров трещиноватого массива, работающего в условиях сложного напряженного состояния.
ЛИТЕРАТУРА
1. Мостков В.М. Подземные сооружения большого сечения. - М.: Недра, 1974. - 317 с.
2. Кузнецов Г.Н. Методические указания по определению прочности трещиноватого массива горных пород. - Л.: ВНИМИ, 1991. - 40 с.
3. Кузнецов Г.Н. Графические методы оценки предельных состояний трещиноватого массива вокруг горных выработок//Сб. Современные проблемы механики годных пород. - М.: Наука, 1972. - С. 30 - 40.
4. Muller L. Kriterien zur Erkennung der geklufteten Medien//Rock Mech., Suppl. 2. - 1973. - S. 71 - 92.
5. John K. Ein Ingenieurverfahren zur rechnerischen Abschatzung von Festigkeit und Verformbarkeit regelmassig geklufteten Felsens //Rock Mech., 1969, Nr. 1, S. 183 - 197.
6. Глушко В.И., Чередниченко В.П., Усатенко Б.С. Реология горного массива. - Киев: Наукова Думка, 1981. - 230 с.
7. Протодьяконов М.М., Тедер В.Н. Методика рационального планирования экспериментов. - М.: Наука, 1970. - 74 с.