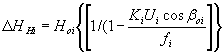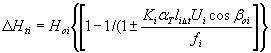министерство строительства предприятий
нефтяной и газовой промышленности

Всесоюзный научно-исследовательский институт
по строительству магистральных трубопроводов

ВНИИСТ

РЕКОМЕНДАЦИИ

ПО РАСЧЕТУ ВЕТРОВЫХ ТРОСОВ В ВИСЯЧИХ И ВАНТОВЫХ ТРУБОПРОВОДНЫХ ПЕРЕХОДАХ

Р 549-84

Москва 1985

Настоящие Рекомендации содержат методику учета, действия ветровой нагрузки при проектировании висячих трубопроводных переходов. Рекомендации разработаны в развитие действующих нормативных документов на основе теоретических и экспериментальных исследований, проведенных Всесоюзным научно-исследовательским институтом по строительству Магистральных трубопроводов (ВНИИСТом) Грозненским нефтяным институтом (ГНИ), и обобщения имеющегося опыта проектирования различных сооружений.

Рекомендации составлены кандидатами технических наук: В.В. Спиридоновым (ВНИИСТ, отдел трубопроводов, сооружаемых в особых условиях) и Л.А. Луневым. (Грозненский нефтяной институт.

Рекомендации предназначены для специалистов проектных и научных организаций, а также для работников, занятых на строительстве трубопроводов.

Содержание

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1 Настоящие Рекомендации распространяются на проектирование висячих и вантовых трубопроводных переходов (а именно расчет их на действие статической и динамической нагрузок ветра).

1.2 Модель воздействия ветра принимается в виде стационарного однородного процесса;

1.3 Ветровая нагрузка q действующая на конструкции перехода, определяется как сумма  - статической составляю щей, соответствующей усредненному скоростному напору, и  - динамической составляющей, вызываемой пульсациями скоростного напора ветра.

1.4 Динамическая составляющая ветра должна учитываться в конструкциях с периодом колебаний более 0,25 с [1].

1.5 Явление аэродинамической неустойчивости не рассматривается.

2. РАСЧЕТ ВЕТРОВЫХ ТРОСОВ В ВИСЯЧИХ И ВАНТОВЫХ ТРУБОПРОВОДНЫХ ПЕРЕХОДАХ НА ДЕЙСТВИЕ СТАТИЧЕСКОЙ НАГРУЗКИ ВЕТРА

2.1. Нормативную ветровую нагрузку , действующую на конструкции трубопроводных переходов, определяют по формуле:

где q₀ - скоростной напор ветра, принимают по СНиП II-6-74 [1] или по формуле

где α_n = 0,75 + S/V поправочный коэффициент, принимаемый не более единицы;

V - скорость ветра;

C_х - аэродинамический коэффициент, принимаемый по данным аэродинамических испытаний.

2.2. Расчетную ветровую нагрузку  находим по формуле

где n - коэффициент перегрузки;

d - диаметр трубы.

2.3. Уравнение изогнутой оси трубопровода определяют по формуле

где ξ=X/l

l - пролет трубопровода;

X - расстояние от левой опоры трубопровода до сечения X;

А - определяют из уравнений, указанных ниже, для различных конструкции трубопроводных переходов.

2.4. Висячий трубопроводный переход с ветровыми оттяжками

где .

l_i - длина хорды провисания i-й стяжки;

β_oi - угол наклона оттяжки;

μ, V_n, Р - линейная плотность, скорость и давление внутреннего потока;

α_Т - коэффициент линейного расширения трубы;

Δt - приращение температуры;

H_0i - первоначальный распор в i-й оттяжке;

α_K - вылет компенсатора;

f_i - стрела провисания ветрового i-го троса;

q_в - масса трубопровода с продуктом транспортирования;

h - расстояния от оголовка троса до оси трубопровода;

l - пролет трубопровода.

Распоры в i-x оттяжках в наветренных и заветренных тросах:

2.5. Висячий трубопроводный переход с ветровыми фермами

где f_T - стрела подъема ветрового троса в середине пролета;

Н₀ - распор в тросе от предварительного напряжения:

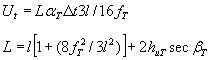
β_Т - угол наклона оттяжки;

EF - жесткость ветровых трос о, в при растяжении;

 - пролет трубопровода;

h_оT - высота консоли оттяжки.

Распоры в наветренных и заветренных тросах:

где n= (0,9 - 0,6), берется в зависимости от остаточного предварительного напряжения в заветренных тросах.

3. РАСЧЕТ ВЕТРОВЫХ ТРОСОВ В ВИСЯЧИХ И ВАНТОВЫХ ПЕРЕХОДАХ НА ДЕЙСТВИЕ ДИНАМИЧЕСКОЙ НАГРУЗКИ ВЕТРА

3.1. Максимальное смещение трубопровода в сечении Х определяется по формуле

где  - прогиб трубопровода при действии статической ветровой нагрузки, определяемой пп. 2.3, 2.4;

К_Т - число стандартов, принимаемое по СНиП II-6-74;

D_uj - дисперсия смещения трубопровода, определяемая по формуле

где S(ω) - нормированная спектральная плотность ветра;

 - средняя часовая скорость ветра на высоте 10 м;

ω_j - частота;

m - масса трубы с продуктом транспортировки;

K₀ - коэффициент шероховатости подстилающей поверхности, принимаемый в первом приближении для водной поверхности реки 0,003-0,004;

λ₁ = 4,73: λ₂ = 7,85; λ₃ = 10,99; λ_j > 4 = (2j+1)π/2

α₁ = 1,0178; α₂ = 0,99922; α₃ = 0,999; α_i > 3 = δ

δ - логарифмический декремент конструкции перехода.

3.2. Квадрат круговой частоты висячего трубопроводного перехода с ветровыми оттяжками

где Z_j(ξ_i) - функция Z при фиксированном значении ξ_i в местах прикрепления i-й оттяжки;

l - пролет трубопровода.

3.3. Квадрат круговой частоты висячего трубопроводного перехода с ветровыми фермами

где

3.4 Распор в ветровых тросах с учетом динамического воз действия ветра определяем по формулам (6) - (8), (10) - (12) с по мощью подстановки нового значения U (т.е, U_max).

ПРИЛОЖЕНИЯ

Приложение 1
пример расчета ветровых тросов висячего перехода с ветровыми оттяжками.

Параметры перехода:

трубопровод 377×12 мм,

l = 130 м,

P = 6 МПа,

q = 450 Па,

диаметр тросов 19 мм,

жесткость тросов EF = 2,65·10⁷ Па,

угол наклона коротких оттяжек 28°30'

длинных 47°20'

α_K = 600 см (рис. 1, 2)

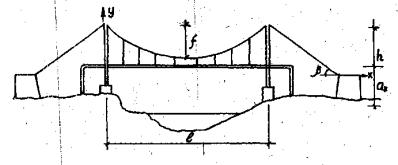
Рис. 1. Схема висячего перехода в вертикальной плоскости

Определяем А по формуле (5)

;

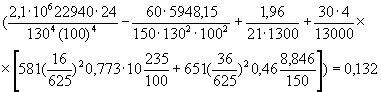А=143,3 см

;

.

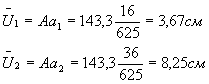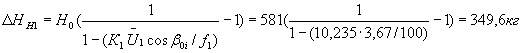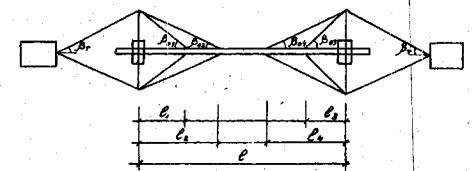
Рис. 2. Схема висячего перехода (в плане) с вантовыми ветровыми тросами

;

;

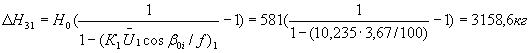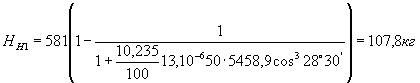Н_Н1=581+349,6-107,8=892,8 кг

;

;

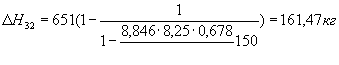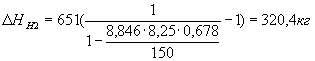Н_Н2=651+320,4-47,16=924,27 кг;

;

;

;

;

;

.

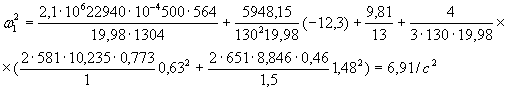Найдем распор в длинных наветренных оттяжках как самых напряженных с учетом динамического воздействия:

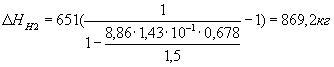
Н₂=Н₀+ΔН_Н2-ΔН_Нt=651+869,2-47,16=1473,05 кг

Разрывное усилие в канате 19450,0 кгс. В настоящее время для ветровых тросов коэффициент запаса прочности по рекомендациям [2] составляет:

1:(γ_cγ_кК/γ_uγ_mγ_n)=1:(1,05×0,95×0,85/1,3×1,2×1,1)=1:0,494=2,02

где γ_с - коэффициент общих условий работы канатного элемента;

γ_к - коэффициент условий работы, учитывающий влияние на прочность каната местных концентраторов напряжений;

К - коэффициент агрегатной прочности каната; |

γ_u - коэффициент надежности для элементов конструкций, рассчитываемых по временному сопротивлению разрыва;

γ_n - коэффициент надежности по назначению.

Фактический запас прочности составляет К = 19450,0/1473 = 13. Таким образом, сечение троса назначают с большим запасом прочности.

Приложение 2
ПРИМЕР РАСЧЕТА ВЕТРОВЫХ ТРОСОВ ВИСЯЧЕГО ПЕРЕХОДА С ВЕТРОВЫМИ ФЕРМАМИ.

Параметры перехода следующие:

630×8 мм,

l - 200 м,

Р = 6 МПа,

q₀ = 270 Па,

диаметр тросов 19 мм,

жесткость тросов EF = 2,65·10⁷ Па,

V = 2 м/с, продукт транспортировки - нефть (рис. 1, 3).

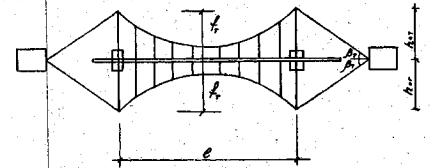
Рис. 3. Схема висячего перехода (в плане) с ветровыми тросами и растяжками

Определяем А по формуле (9):

;

;

Δр=4,386 см; Δt=12 см.

60×Ц/l²×105=4626,2×60/20000⁴ =6,6×10^-6 А;

;

;

;

;

;

;

;

;

После предварительных вычислений получаем:

1,24×10^-8 А²+1,16×10^-4 А-0,1322=0

откуда А = 1030,4 см,

Н₀ = 2,366×1030,4+2203,2 = 2438,06 + 2203,2 = 4641,26 кг ~ 46412,6 Н.

Определяем U_max no формулам пп. 3.1, 3.2, 3.3

;

;

;

;

;

.

После предварительных вычислений получаем:

;

ω₁ = 8,189×10^-1

U=1200×0,819/20,8 = 47,24 с^-2;

;

;

.

Определяем дисперсию перемещения для второй частоты:

;

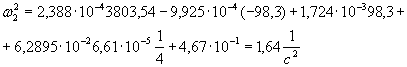ω₂ = 1,28 1/с;

U=1200×1,28/20,8=73,9;

;

.

Определяем дисперсию перемещения для третьей части:

;

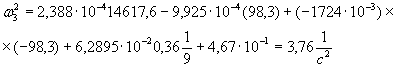ω₃ = 1,939 1/с;

U=1200×1,939/20,8=111,87;

;

;

;

;

;

.

Самым невыгодным загружением является отсутствие температурного воздействия:

Н_н = 7597,1 кг.

Разрывное усилие в канате диаметром 19 мм равно 10450,0 кгс. Фактический запас прочности составляет К = 19450,0/7597 = 2,56 > 2,02. Таким образом, сечение троса назначено правильно.

ЛИТЕРАТУРА

1 СНиП II-6-74. Нагрузки и воздействия. М., 1976.

2 Рекомендации по расчету прочности стальных канатов, применяемых в строительных металлических конструкциях. М., ЦНИИПСК, 1982.