РОСТОВСКИЙ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ ИНСТИТУТ
ПРИМЕРЫ РАСЧЕТА БАЛОЧНОГО ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОГО ЖЕЛЕЗОБЕТОННОГО АВТОДОРОЖНОГО ПРОЛЕТНОГО СТРОЕНИЯ
УЧЕБНОЕ ПОСОБИЕ
РОСТОВ НА ДОНУ
1971
Содержание
АННОТАЦИИ
В учебном пособии даны примеры расчета сборного балочного предварительно напряженного железобетонного автодорожного пролетного строения с натяжением полигональных и прямолинейных пучков до бетонирования.
Расчеты выполнены в соответствии с Указаниями по проектированию железобетонных и бетонных конструкций железнодорожных, автодорожных и городских мостов и труб - СH 365-67.
В расчетах наряду с основными усилиями учтено воздействие крутящих моментов от общей и местной временной нагрузки.
Учет кручения от общей нагрузки выполнен по способу, разработанному автором.
Примеры расчета снабжены подробными методическими указаниями.
Приведены уточненные способы расчета.
Учебное пособие рассчитано на студентов специальности "Автомобильные дороги", "Городское строительство" и "Мосты и тоннели", оно также может быть полезным студентам, специальности "Строительство железных дорог" и инженерам-проектировщикам.
§ 1. ИСХОДНЫЕ ДАННЫЕ, КОНСТРУКЦИЯ И ИЗГОТОВЛЕНИЕ ПРОЛЕТНОГО СТРОЕНИЯ С НАТЯЖЕНИЕМ ПОЛИГОНАЛЬНОЙ И ПРЯМОЛИНЕЙНОЙ АРМАТУРЫ ДО БЕТОНИРОВАНИЯ
Пролетное строение железобетонного сборное с натяжением полигональных и прямолинейных пучков до бетонирования.
Условный пролет в свету lсв = 20 м.
Расчетный пролет цельноперевозимых диафрагменных балок l = 21,50 м.
Расстояние от торца балки до оси опирания С = 0,33 м.
Расстояния между осями диафрагм d = 4,31 и 4,295 м.
Расстояние от торца балки до оси крайней диафрагмы d0 = 0,32 м.
Полная длина пролетного строения lп = 0,32 + 4,295 +4,31´3 + 4,295 + 0,32 = 22,16 м.
Опалубочные размеры балок приняты по типовому проекту сооружений на автомобильных дорогах выпуск 122-62.
ПРИМЕЧАНИЕ. Схемы и показатели типовых сборных железобетонных балочных пролетных строений приведены в приложениях I-V.
Габарит проезжей части Г-8 с тротуарами по Т = 1 м.
Расстояние между осями балок по ширине моста в = 1,66 м. Число балок по ширине моста для габарита Г-8 при Т = 1 м ... п = 6.
Нормативные нагрузки: H-30, HK-80 и толпа на тротуарах 400 кГ/м2.
Нормы проектирования
Расчеты выполнены в соответствии с нормами проектирования:
1. Технические условия проектирования железнодорожных, автодорожных и городских мостов и труб (СН 200-62), обозначенные в тексте сокращенно СН-200.
2. Мосты и трубы. Нормы проектирования. СНиП П-Д.7-62, обозначенные в тексте сокращенно СНиП.
3. Указания по проектирование железобетонных и бетонных конструкций железнодорожных, автодорожных и городских мостов и труб (СН-365-67), обозначенные в тексте сокращенно СН (с введением в действие в 1967 г. Указании СН-365-67 утратили силу разделы II и VI СН 200-62 в части, относящейся к железобетонным и бетонным конструкциям).
В тексте расчетов в необходимых случаях даны ссылки на соответствующие пункты СН, СН-200 и СНиП.
Материалы
Бетон для балок тяжелый проектной марки:
по прочности на сжатие - 400;
по морозостойкости - не менее Мрз200 по ГОСТ 4795-59 (пункт 1.6. СН).
ПРИМЕЧАНИЕ. Для климатических условий, соответствующих среднемесячной температуре наиболее холодного месяца ниже минус 15°С проектная марка бетона по морозостойкости - не менее Мрз300.
Бетон принят по группе А в соответствии с классификацией СН (пункт 1.3).
Предварительно напрягаемая
арматура балок - в виде пучков стальных высокопрочных холоднотянутых гладких
проводов класса В-П диаметром 5 мм с нормативным сопротивлением (пределом
прочности) ![]() по ГОСТ
7348-63 (пункт 1.10 и таблица 30 СН).
по ГОСТ
7348-63 (пункт 1.10 и таблица 30 СН).
Рабочая ненапрягаемая арматура консольных плит, ребра, диафрагм, нижнего уширения и опорного утолщения главных балок - периодического профиля из углеродистой горячекатаной стали класса А-II по ГОСТ 5881-61 марки Ст.5сп мартеновской или конверторной по ГОСТ 380-60 (пункт 1.8 СН).
Прочая ненапрягаемая арматура главных балок, каркасно-стержневые анкеры напрягаемых пучков, планки и накладки сварных стыков диафрагм - из углеродистой горячекатаной стали класса А-I по ГОСТ 5781-61 марки ВМСт.3сп мартеновской или марки ВКСт.3сп конверторной по ГОСТ 380-60 (пункт 1.8 СН).
Конструкция балок
В поперечном сечении пролетное строение состоит из двух крайних и четырех средних Т-образных балок с нижними уширениями ребер (нижними поясами).
Крайние балки отличаются от средних наличием односторонних диафрагм и большим количеством напрягаемых арматурных пучков.
ПРИМЕЧАНИЕ. В пособии рассчитаны более напряженные крайние балки.
Предварительно напряженная арматура балок состоит из полигональных и прямолинейных пучков, собранных из 24 параллельных проволок диаметром 5 мм.
Пучки на концах снабжены каркасно-стержневыми анкерами.
Ненапряженная арматура консольных плит, ребер и нижних уширений балок состоит из сварных сеток.
Диафрагмы соседних балок стыкуются путем приварки стальных накладок к планкам диафрагм.
Изготовление балок
Изготовление балок с напряжением арматуры до бетонирования принято по поточно-агрегатной технологии на передвижном упоре-стенде, перемещаемом для термовлажностной обработки в пропарочную камеру.
По этой причине не учтены потери предварительного напряжения от температурного перепада (разность между температурой напрягаемой арматуры и упоров стенда) при пропаривании и прогреве бетона (приложение 4 СН).
В расчетах не учтены возможные потери напряжения в напрягаемой арматуре из-за упругих деформаций стенда. Эти потери должен учитывать завод-изготовитель балок.
Контролируемое напряжение в
арматуре с учетом перетяжки на величину этих потерь должно быть не более 0,75
нормативного сопротивлении (предела прочности) ![]() .
.
Для уменьшения потерь от релаксации напряжений стали все пучки должны быть подвергнуты кратковременной (пятиминутной) перетяжке в размере 10% проектных значений контролируемых напряжении с последующим снижением напряжении (примечание к табл. 36 СН). При натяжении пучков обязательно должен осуществляться двойной контроль за величиной натяжения по манометру на домкрате и по замеру удлинения проволоки.
Отпуск арматуры производится после достижения бетоном балок 90% проектной марочной прочности и, как правило, достигается плавной передачей усилий с упора стенда на бетон балок путем перемещения упоров с закрепленной натянутой арматурой в сторону стенда при помощи плоских листовых гидродомкратов, песочниц или клиновых устройств.
Разрешается отпуск арматуры путем поочередного перерезывания пучков автогеном с предварительным разогревом докрасна свободного участка пучка между торцом балки и упором стенда.
§ 2. РАСЧЕТ КОНСОЛЬНОЙ ПЛИТЫ
1. ОПРЕДЕЛЕНИЕ УСИЛИИ ОТ ПОСТОЯННОЙ НАГРУЗКИ
Рассчитывают консольную плиту в сечении I-I у вута (рис. 1).

Рис. 1. К расчету плиты на постоянную нагрузку.
Расчетный пролет консоли l = 0,63 м.
Средняя толщина плиты ![]() Средняя толщина
бетонного сточного треугольника (см. рис. 1)
Средняя толщина
бетонного сточного треугольника (см. рис. 1)
![]()
Толщины и объемные веса:
асфальтобетон................................... h1 = 0,05 м; g1 = 2,3 т/м3;
защитный бетонный слой................. h2 = 0,04 м; g2 = 2,4 т/м3;
гидроизоляция................................... h3 = 0,01 м; g3 = 1,5 т/м3;
сточный бетонный треугольник...... h4 = 0,04 м; g4 = 2,4 т/м3;
железобетонная плита....................... hср = 0,10 м; gж.б = 2,5 т/м3.
Суммарная толщина четырех слоев дорожной одежды
h = h1 + h2 + h3 + h4 = 0,05 + 0,04 + 0,01 + 0,04 = 0,14 м.
Рассчитывается полоска плиты шириной в0 = 1 м (см. план на рис. 1).
Постоянная нагрузка на 1 п.м. полоски:
от веса четырех слоев дорожной одежды
![]()
от веса плиты
![]()
Коэффициент перегрузки (пункт 115 СН-200):
вес слоев одежды..........1,5;
вес плиты.......................1,1.
Изгибающий момент в сечении I-I плиты от постоянной нагрузки:
расчетный
![]()
нормативный
![]()
Нормативная поперечная сила в сечении I-I плиты от постоянной нагрузки
![]()
2. ОПРЕДЕЛЕНИЕ УСИЛИЙ ОТ ВРЕМЕННОЙ НАГРУЗКИ ПО СН 200-62
На основании исследовании С.П. Тимошенко (см. Н.А. Калашников и E.В. Тумас. Таблицы и графики для расчета плит проезжей части мостов. Автотрансиздат, 1956 стр. 6) давление от сосредоточенного в одной точке груза Р, расположенного на свободном краю, условно распределяется в плане консольной плиты под углом 45° от точки приложения груза (рис. 2), что определяет величину рабочей ширины плиты "а".
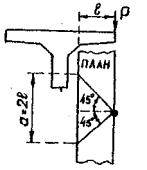
Рис. 2. Распределение давления от сосредоточенного груза в консольной плите на основе исследований С.П. Тимошенко.
Это распределение приближенно принимается в СН 200-62 (стр. 265) и при нагрузке равномерно распределенной по грузовой площадке со сторонами а1 и в1 (рис. 3), при этом рабочая ширина плити "а" определяется с учетом распределения влияния равномерной нагрузки в плане под углами в 45° от средней линии, проходящей через центр тяжести грузовой площадки.
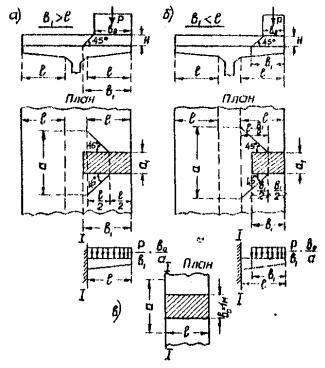
Рис. 3. К расчету плиты на временную нагрузку по СН 200-62.
Тяжелое колесо весом Р устанавливается на краю консольной плиты (рис. 3).
Размеры грузовой площадки (СН 200, стр. 265)
а1 = а2 + 2Н; в1 = в2 + Н,
где а2 = 0,2 м - длина соприкасания ската с покрытием проезжей части вдоль движения для любых нагрузок (СН 200, стр. 262);
в2 - ширина заднего ската колеса (СН 200, стр. 262 и 263);
в2 = 0,6 м........... Н-30;
в2 = 0,4 м........... Н-10;
в2 = 0,8 м.......... НК-80;
Н = 0,14 м (см. выше)
а1 = 0,2 + 2´0,14 = 0,48 м
Рабочая ширина плиты при в1 > l (рис. 3а)
а = а1 + l.
Рабочая ширина плиты при в1 < l (рис. 3б)
а = а1 + 2l - в1.
Расчетный изгибающий момент в сечении I-I плите от временной нагрузки при в1 > l (рис. 3а и в)
![]()
То же при в1 < l (рис. 3б и в)
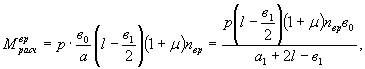
где (1 + m) - динамический коэффициент (пункт 126 СН 200);
1 + m = 1,3.......... Н-30 и Н-10;
1 + m = 1,0.......... НК-80;
пвр - коэффициент перегрузки (пункт 127 СН 200);
пвр = 1,4.......... Н-30 и Н-10;
пвр = 1,1......... НК-80.
Нагрузка Н-30
р = 6 т (СН 200, стр. 262);
в1 = в2 + Н = 0,6 + 0,14 = 0,74 м > l = 0,63 м;
![]()
Нагрузка НК-80
р = 10 т (СН 200, стр. 263);
в1 = в2 + Н = 0,8 + 0,14 = 0,94 м > l = 0,63 м;
![]()
Нагрузка Н-10
р = 4,75 т (СН 200, стр. 262);
в1 = в2 + Н = 0,4 + 0,14 = 0,54 м < l = 0,63 м;
![]()
Большее из трех значений (для
расчета плиты на прочность): ![]() (нагрузка Н-30)
(нагрузка Н-30)
Для расчетов на трещиностойкость вычисляем нормативные величины изгибающего момента и поперечной силы без динамического коэффициента (пункт 2.2 СН).
При расчетах на трещиностойкость нагрузка НК-80 принимается с коэффициентом 0,8 (пункт 116 СН 200).
Нормативный изгибающий момент в сечении I-I плиты от временной нагрузки:
Нагрузка Н-30
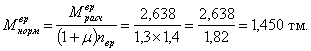
Нагрузка НК-80
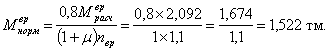
Нагрузка Н-10
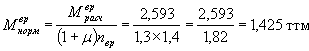
Большее из трех значений (для
расчета плиты на трещиностойкость) ![]() (нагрузка НК-80).
(нагрузка НК-80).
Нормативная поперечная сила в сечении I-I плиты от временной нагрузки без динамического коэффициента:
Нагрузка Н-30
в1 = 0,94 м > l = 0,63 м (рис. 3а);
![]()
Нагрузка НК-80
в1 = 0,94 м > l = 0,63 м;
![]()
Нагрузка Н-10
в1 = 0,54 м < l = 0,63 м (рис. 3б);
![]()
Большее из трех значений (для
расчета плиты на трещиностойкость) ![]() (нагрузка НК-80).
(нагрузка НК-80).
3. ОПРЕДЕЛЕНИЕ УСИЛИЙ ОТ ВРЕМЕННОЙ НАГРУЗКИ УТОЧНЕННЫМ СПОСОБОМ
При расположении равномерно-распределенной нагрузки по грузовой площадке со сторонами а1 и в1 более точно определять изгибающий момент в сечении I-I путем суммирования моментов от нагрузок с элементарных площадок а1dx (рис. 4), при этом нагрузка с каждой площадки распределяется под углом в 45°, что ближе к решению С.П. Тимошенко для сосредоточенных грузов.
Тогда получим


Рис. 4. К расчету плиты на временную нагрузку уточненным способом.
Откуда
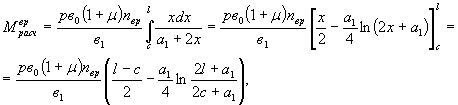
где С - расстояние от края грузовой площадки до корня консоли (см. рис. 4);
ln - символ натурального логарифма.
ПРИМЕЧАНИЕ. Эта формула, предложенная A.Ю. Гимельфарбом и М.Б. Фельдманом (см. "Автомобильные дороги", 1960, № 5), принята в типовых альбомах железобетонных мостов (выпуски 149-62, 122-62, 122-63 и 123-64), составленных Киевским филиалом Союздорпроекта.
Расчетные изгибающий момент в сечении I-I плиты от временной нагрузки при в1 > l (рис. 4 при С = 0)

То же при в1 < l (рис. 4, где С = l - в1)

Нагрузка Н-30
р = 6 т; в1 = 0,74 м > l = 0,63 м; а1 = 0,48;

ПРИМЕЧАНИЕ. По способу СН 200-62 ![]() уменьшение
величины момента при уточненном расчете
уменьшение
величины момента при уточненном расчете
![]()
![]()
Нагрузка НК-80
р = 10 т; в1 = 0,94 м > l = 0,63 м; а1 = 0,48;
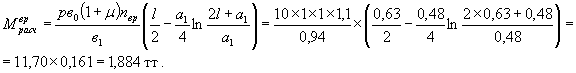
ПРИМЕЧАНИЕ. По способу СН 200-62 ![]() уменьшение
величины момента при уточненном расчете
уменьшение
величины момента при уточненном расчете
![]()
![]()
Нагрузка Н-10
р = 4,75 т; в1 = 0,54 м < l = 0,63 м; а1 = 0,48;
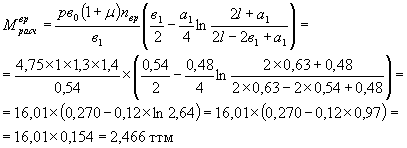
ПРИМЕЧАНИЕ. По способу СН 200-62 ![]() уменьшение
величины момента при уточненном расчете
уменьшение
величины момента при уточненном расчете ![]()
![]()
Большее из трех значений ![]() (нагрузка Н-10)
(нагрузка Н-10)
Это уточненное значение принято для расчета плиты на прочность.
ПРИМЕЧАНИЕ. При расчете по СН 200-62 (см. выше) максимальное значение ![]() (нагрузка Н-30)
больше уточненного значения на
(нагрузка Н-30)
больше уточненного значения на ![]()
Таким образом, при l = 0,63 и для расчета на прочность расчетной нагрузкой является H-10.
Нормативный изгибающий момент в сечении I-I плиты от временной нагрузки:
Нагрузка Н-30

Нагрузка НК-80
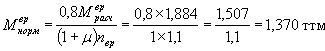
Нагрузка Н-10

Большее из трех значений ![]() (нагрузка НК-80).
(нагрузка НК-80).
Это уточненное значение принято для расчета плиты на трещиностойкость.
ПРИМЕЧАНИЕ. При расчете по СН200-62 (см. выше) максимальное
значение ![]() (нагрузка
НК-80).
(нагрузка
НК-80).
Нормативная поперечная сила в сечении I-I плиты от временной нагрузки без динамического коэффициента (см. рис. 4)

Нормативная поперечная сила в сечении I-I плиты от временной нагрузки при в1 > l (рис. 4 при С = 0)
![]()
То же при в1 < l (рис. 4, где С = l - в1)
![]()
Нагрузка Н-30
р = 6 т; в1 = 0,74 м > l = 0,63 м; а1 = 0,48;
![]()
ПРИМЕЧАНИЕ. По способу СН 200-62 ![]()
Нагрузка НК-80 (с коэффициентом 0,8)
р = 10 т; в1 = 0,94 м > l = 0,63 м; а1 = 0,48;
![]()
ПРИМЕЧАНИЕ. По способу СН 200-62 ![]()
Нагрузка Н-10
р = 4,75 т; в1 = 0,54 м < l = 0,63 м; а1 = 0,48;

ПРИМЕЧАНИЕ. По способу СН 200-62 ![]()
Большее из трех значении ![]() (нагрузка НК-80).
(нагрузка НК-80).
Это уточненное значение принято для расчета плиты на трещиностойкость.
ПРИМЕЧАНИЕ. При расчете по СН 200-62 максимальное значении ![]() (нагрузка НК-80) -
меньше уточненного значения на
(нагрузка НК-80) -
меньше уточненного значения на ![]()
Суммарные усилия от постоянной и временной нагрузки:
расчетный изгибающий момент
![]()
нормативный изгибающий момент
![]()
нормативная поперечная сила
![]()
ПРИМЕЧАНИЕ. Изгибающие моменты от временной нагрузки с учетом расстояния "d" между диафрагмами консольной плиты могут быть определены по упрощенному пространственному способу В.И. Руденко, основанному на теории пространственных расчетов Б.Е. Улицкого, по следующим формулам (см. Н.Л. Филимонова, В.И. Руденко. Особенности проектирования плитных мостов. Автотрансиздат, 1962):
при в1 > l
![]()
при в1 < l

где ![]()

x и b - коэффициенты, определяемые в зависимости
от ![]() по графикам рис. 5.
по графикам рис. 5.

Рис. 5 Графики коэффициентов распределения x
и b
для различных значений ![]() .
.
4. РАСЧЕТ НА ПРОЧНОСТЬ ПО ПЕРВОМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ (ПО ИЗГИБАЮЩЕМУ МОМЕНТУ)
Бетон марки 400 группы A c Ru = 205 кГ/см2 (пункт 1.13 СН).
Рабочая арматура периодического профиля из стали класса А-II (марки Ст.5сп) с Ra = 2400 кГ/см2 (пункт 1.14 СН).
Задаемся арматурой Æ 12 А-II с наружным диаметром по выступам d1 = 1,35 см (приложение VI).

Рис. 6. Поперечное сечение I-I плиты.
Толщина плиты в сечении I-I hп = 12 см (рис. 1 и 6).
Толщина защитного слоя бетона С = 2 см.
Полезная высота плиты (рис. 6).
![]()
Расчетная ширина плиты в0 = 100 см.
Табличный коэффициент
![]()
По приложению VII этому коэффициенту соответствует g0 = 0,916.
ПРИМЕЧАНИЕ. Допустимо, не вычисляя величины A0 вести расчет без использования таблицы приложения VII, приняв приближенно g0 = 0,9.
Потребная площадь сечения растянутой арматуры
![]()
Площадь сечения одного стержня f = 1,131 см (приложение VI).
Потребное число стержней
![]()
Принято 12 Æ 12А-II с Fa = 12 f = 12´1,131 = 13,57 cм2 > 13,25 cм2
Высота сжатой зоны
![]()
Условие, ограничивающее высоту
сжатой зоны (пункт 3.4 СН) ![]() - условие соблюдено (сечение не
переармировано).
- условие соблюдено (сечение не
переармировано).
Предельный момент,
воспринимаемый сечением плиты ![]() - прочность плиты
обеспечена.
- прочность плиты
обеспечена.
5. РАСЧЕТ НА ТРЕЩИНОСТОЙКОСТЬ ПО ТРЕТЬЕМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ ПО НАИБОЛЬШЕМУ РАСКРЫТИЮ НОРМАЛЬНЫХ ТРЕЩИН
Ширина раскрытия трещин в сечении I-I плиты (нормальной к оси арматуры) при арматуре периодического профиля класса А-II (пункт 3.23 СН)
![]()
где  - напряжение в растянутой арматуре (в соответствии с
пунктом 3.23 СН плечо внутренней пары сил z принято по результатам расчета сечения на
прочность);
- напряжение в растянутой арматуре (в соответствии с
пунктом 3.23 СН плечо внутренней пары сил z принято по результатам расчета сечения на
прочность);
Еa = 2100000 кГ/см2 - модуль упругости арматуры класса А-II (пункт 1.26 СН);
y2 = 0,5 - коэффициент, учитывающий влияние бетона растянутой зоны и деформации арматуры (для бетона марки 400 по пункту 3.24 СН);
![]() - радиус армирования;
- радиус армирования;
b = 1 - коэффициент при армировании одиночными стержнями (пункт 3.25 СН);
d = 1,2 см - расчетный диаметр принятой арматуры периодического профиля Æ 12 (см. выше);
n = 12 - принятое число стержней (cм. выше);
![]() - площадь зоны
взаимодействия (пункт 3.26 СН и выше рис. 5).
- площадь зоны
взаимодействия (пункт 3.26 СН и выше рис. 5).
![]()
ширина раскрытия трещины
![]() (пункт 3.23
СН) -трещиностойкость нормального к оси арматуры сечения I-I плиты обеспечена.
(пункт 3.23
СН) -трещиностойкость нормального к оси арматуры сечения I-I плиты обеспечена.
6. РАСЧЕТ НА ТРЕЩИНОСТОЙКОСТЬ ПО ТРЕТЬЕМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ ПО НАКЛОННЫМ ТРЕЩИНАМ (ПО ГЛАВНЫМ РАСТЯГИВАЮЩИМ НАПРЯЖЕНИЯМ) И ПРОВЕРКА НЕОБХОДИМОСТИ ХОМУТОВ И ОТОГНУТЫХ СТЕРЖНЕЙ
Тангенс угла наклона нижней грани плиты к горизонту (см. рис. 1)
![]()
Приведенная нормативная поперечная сила в сечении I-I плиты с учетом переменности ее толщины (пункт 3.27 СН)
![]()
Главные растягивающие напряжения (пункт 3.27 СН):

(пункт 1.13 СН для бетона марки 400).
Расчетное сопротивление на осевое растяжение для бетона марки 400 (пункт 1.13 СН) Rp.o = 11 кГ/см2. Так как главные растягивающие напряжения sгр = 5,8 кГ/см2 < 0,7Rp.o = 0,7´11 = 7,7 кГ/см2, то расчет на прочность наклонных сечений по поперечной силе можно не производить (пункт 3.9 СН), т.е. хомутов и отогнутых стержней в плите не требуется (наклонные трещины в плите не возникают).
Расчет плиты по второму предельному состоянию на деформации (прогиб) можно не производить, так как при малых пролетах железобетонных консольных плит величина прогиба от нормативной временной нагрузки (без динамического коэффициента) всегда будет меньше допускаемых величин (пункт 52 СН 200).
§ 3. РАСЧЕТ ГЛАВНОЙ БАЛКИ
1. ВЫЧИСЛЕНИЕ ПОСТОЯННЫХ НАГРУЗОК НА ГЛАВНУЮ БАЛКУ
Рассчитываем крайнюю главную балку.
Площадь поперечного сечения балки (рис. 7)

Рис. 7. К вычислению постоянной нагрузки на крайнюю главную балку.

Площадь боковой грани диафрагмы (см. рис. 6)
![]()
Расстояния между осями диафрагм d = 4,31 м.
Толщина диафрагмы d = 0,16 м.
Объемный вес железобетона gж.б = 2,5 т/м3 (приложение 5 СН 200).
Нормативная постоянная нагрузка на 1 п.м. крайней главной балки от ее собственного веса
![]()
Нормативная постоянная нагрузка на 1 п.м. типового тротуарного блока при ширине тротуара Т = 1 м ...... q2 = 0,550 т/м.
ПРИМЕЧАНИЕ. При Т = 1,5 м ....... q2 = 0,700 т/м.
Нормативная постоянная нагрузка на 1 п.м. типовых железобетонных перил q3 = 0,135 т/м.
Нормативная постоянная нагрузка на 1 п.м. моста от веса четырех слоев дорожной одежды с шириной габарита Г = 8 м (см. выше пункт 1 § 2 и рис. 7):
q4 = (h1g1 + h2g2 + h3g3 + h4g4)Г = (0,05´2,3 + 0,04´2,4 + 0,01´1,5 + 0,04´2,4)´8 = 0,322´8 = 2,576 т/м.
Нагрузки 2q2, 2q3 и q4 от веса двух тротуаров, двух перил и дорожной одежды прикладываются после стыкования диафрагм всех главных балок и равномерно распределяется между всеми "n" главными балками, расположенными по ширине моста.
При Г = 8 м и Т = 1 м ..... n = 6.
Постоянная нормативная нагрузка на 1 п.м. крайней главной балки:
от ее собственного веса
q1 = 1,115 т/м;
от веса перил и тротуаров
![]()
от веса дорожной одежды
![]()
2. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ ПОПЕРЕЧНОЙ УСТАНОВКИ БЕЗ УЧЕТА КРУЧЕНИЯ
Число балов n = 6.
Расстояния между симметричными балками (рис. 8):
в1 = 1,66´5 = 8,3 м;
в2 = 1,6´3 = 4,98 м;
в3 = 1,66 м.

Рис. 8. К вычисление коэффициентов поперечной установки.
Коэффициенты поперечной установки по методу внецентренного сжатия без учета кручения (см. рис. 8):
Нагрузка Н-30 (число полос nn = 2)

Нагрузка НК-80 (число полос nn = 1)
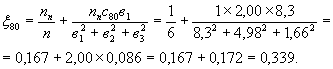
Толпа на одном тротуаре шириной T = 1 м
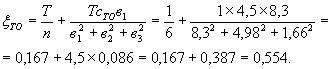
3. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ ПОПЕРЕЧНОЙ УСТАНОВКИ С УЧЕТОМ КРУЧЕНИЯ
Коэффициент поперечной установки по методу внецентренного сжатия с учетом кручения (см. Я.C. Файн. К расчету мостов с учетом кручения главных балок " Изд. Строительство и архитектура, 1963, № 8) определяется по формуле
![]()
где
![]() - поправка на
кручение балок;
- поправка на
кручение балок;
Е и G - модули упругости и сдвига бетона;
Jкр - момент инерции балки на кручение;
J - момент инерции балки при изгибе в вертикальной плоскости;
n = 6 - число балок в поперечном сечении моста;
nп, с, в1, в2 и в3 имеют прежние значения;
![]() - (для
разрезной балки с расчетным пролетом l)
- (для
разрезной балки с расчетным пролетом l)
ПРИМЕЧАНИЕ. Значение ![]() получено
автором в упомянутой работе при частом расположении диафрагмы. При наличии,
кроме опорных, лишь одной диафрагмы, расположенной в середине пролета,
получено
автором в упомянутой работе при частом расположении диафрагмы. При наличии,
кроме опорных, лишь одной диафрагмы, расположенной в середине пролета, ![]() .
.
Для бетона марки 400 (пункт 1.25 СН)
Е = 350000 кГ/cм2;
G = 140000 кГ/cм2.
l = 21,50 м (см. выше § 1)
![]()
Вычисление Jкр
Действительное сечение балки (рис. 9а) заменяем расчетным (рис. 9б).
Приведенная толщина плиты (с учетом вутов)
![]()
Толщина нижнего уширения
h1 = a + 0,5в = 30 + 0,5´10 = 35 см.
Высота ребра без плиты и нижнего уширения
h2 = h - hп - h1 = 120 - 10,96 - 35 = 74 ,01 см .
По СН 58-61 (Технические указания по расчету балочных плит проезжей части мостов) можно принять
![]()
где а и d - длины и толщины прямоугольников, из которых составлено сечение балки. По рис. 9б:

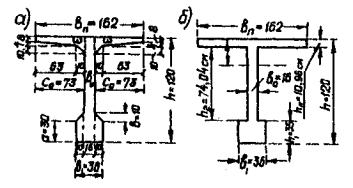
Рис. 9 К вычислению Jкр и J
а - действительное сечение; б - расчетное сечение.
Вычисление J
Расстояние до центра тяжести сечения от верхней грани балки (рис. 9б)

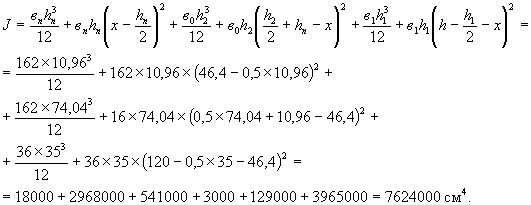
Поправка на кручение
![]()
Коэффициенты поперечной установки по методу внецентренного сжатия с учетом кручения (см. рис. 8):
Нагрузка Н-30 (число полос nn = 2)
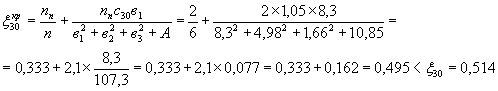
(без учета кручения) на ![]()
Нагрузка НК-80 (число полос nn = 1)
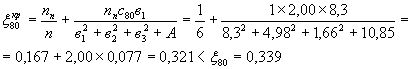
(без учета кручения) на ![]()
Толпа на одном тротуаре шириной T = 1 м
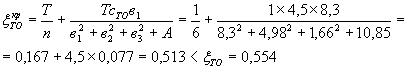
(без учета кручения) на ![]()
4. ВЫЧИСЛЕНИЕ НОРМАТИВНЫХ ИЗГИБАЮЩИХ МОМЕНТОВ В СЕРЕДИНЕ ПРОЛЕТА БАЛКИ БЕЗ УЧЕТА ДИНАМИКИ
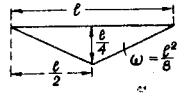
Рис. 10. Линия влияния ![]()
Расчетный пролет l = 21,50 м.
Площадь линии влияния изгибающего момента в середине пролета (рис. 10)
![]()
Коэффициент многополосности к нагрузке Н-30 (пункт 117 СН 200) при l = 21,5 м < 25 м: b = 1
ПРИМЕЧАНИЕ. При l > 25 м:
b = 0,9 для Г-7; Г-8 и Г-9;
b = 0,8 для Г-10,5
Коэффициенты поперечной установки (см. выше):
![]()
![]()
![]()
Нагрузка от толпы: KТО = 0,4 т/м2 (пункт 125 СН 200)
Нормативные постоянные нагрузки (см. выше):
q1 = 1,115 т/м;
![]()
![]()
Эквивалентные нагрузки (приложение 10 СН 200):
от Н-30...............К30 = 2,32 т/м;
от НК-80.......... К80 = 6,62 т/м.
Нормативные изгибающие моменты в середине пролета балки без учета динамики:
от собственного веса балки
М1 = q1w = 1,115´57,78 = 64,4 тм;
от веса тротуаров и перил
![]()
от веса дорожной одежды
![]()
от автомобильной нагрузки Н-30
![]()
от толпы на одном тротуаре
![]()
от колесной нагрузки HК-80
![]()
5. РАСЧЕТ БАЛКИ НА ПРОЧНОСТЬ ПО ПЕРВОМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ (ПО ИЗГИБАЮЩЕМУ МОМЕНТУ) ПОСЕРЕДИНЕ ПРОЛЕТА НА СТАДИИ ЭКСПЛУАТАЦИИ
Динамический коэффициент к временной нагрузке Н-30 по интерполяции при 5 м < l < 45 м (пункт 126 СН 200)
![]()
Коэффициенты перегрузки (пункты 115 и 127 СН 200):
для q1 и ![]() ...........1,1;
...........1,1;
для ![]() ...............1,5;
...............1,5;
для Н-30 .............1,4;
для НК-80 ..........1,1;
для толпы ..........1,4;
Расчетные изгибающие моменты в середине пролета балки:
от постоянной нагрузки, Н-30 и толпы
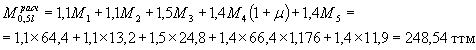
от постоянной нагрузки и НК-80
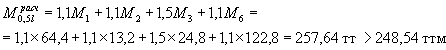
Принимаем
![]()
Действительное сечение балки (рис. 11а) заменяем расчетным (рис. 11б).

Рис. 11. Схемы к расчету балки на прочность посередине пролета.
Приведенная постоянная толщина сжатого пояса (плиты)
![]()
Толщина нижнего уширения балки
h1 = a + 0,5в = 30 + 0,5´1,0 = 35 см.
Полная высота балки h = 120 м.
Расчетная ширина сжатого пояса (плиты) по пунктам 4.10 и 3.6 СН (см.
рис. 11а и в) ![]() но не более вп, где учитываемая расчетом максимальная величина консольной части
плиты за вутом;
но не более вп, где учитываемая расчетом максимальная величина консольной части
плиты за вутом;
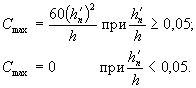
Имеем ![]()
Следовательно,
![]()
![]()
Принимаем ![]()
Предварительно принимаем
армирование балки 7 пучками (см. приложение II) по 24 высокопрочных гладких стальных
проволок класса В-П диаметром 5 мм с нормативным сопротивлением (пределом
прочности) ![]() (пункт 1.10 и табл.
30 СН).
(пункт 1.10 и табл.
30 СН).
Расчетное сопротивление растяжению такой напрягаемой арматуры при расчете на прочность в стадии эксплуатации (вторая стадия) RH2 = 9800 кГ/см2.
Размещение 7 напрягаемых арматурных пучков в 3 ряда по высоте показано на рис. 11а.
Расстояние от центра тяжести всех арматурных пучков до низа балки (см. рис. 11а и 11б):
![]()
ПРИМЕЧАНИЕ. При расположении пучков в растянутой зоне изгибаемого элемента более чем в три ряда по высоте при расчете на прочность к числу пучков четвертого ряда вводят коэффициент 0,9, а пятого и последующих рядов - 0,8 (см. пункт 2.23 СН).
Например,
для 10 пучков, размещенных в 4 ряда по высоте (см. рис. 11в), ![]()
Полезная высота балки (рис. 11б)
h0 = h - а0 = 120 - 15,1 = 104,9 см.
В первом приближении необходимая по прочности площадь поперечного сечения всех арматурных пучков
![]()
Площадь поперечного сечения одного пучка из 24 проволок диаметром d = 0,5 см
![]()
Необходимое число пучков
![]()
Принято с запасом для удовлетворения последующего расчета на трещиностойкость 7 пучков по 24Æ5В-П с Fн = 7f1 = 7´4,71 = 32,97 см2 > 26,44 см2. Бетон марки 400 группы А с Ru = 205 кГ/см2 (пункт 1.13 СН).
Предполагаем, что нейтральная ось проходит в плите (см. рис. 11б),
тогда расстояние до центральной оси ![]() т.е. нейтральная ось действительно проходит в
плите, сечение рассчитывается как прямоугольное шириной
т.е. нейтральная ось действительно проходит в
плите, сечение рассчитывается как прямоугольное шириной ![]() и высотой
и высотой ![]() .
.
Условие, ограничивающее высоту сжатой зоны (пункты 4.10 и 3.4 СН)
![]() - условие соблюдено.
- условие соблюдено.
ПРИМЕЧАНИЕ. При ![]() необходимо увеличить
высоту балки или повысить марку бетона, если
уменьшение Fн
невозможно.
необходимо увеличить
высоту балки или повысить марку бетона, если
уменьшение Fн
невозможно.
При ![]() коэффициент условий
работы m2 = 1 (пункт 2.24 СН). Предельный момент,
выдерживаемый сечением балки посередине пролета (пункт 4.10 СН)
коэффициент условий
работы m2 = 1 (пункт 2.24 СН). Предельный момент,
выдерживаемый сечением балки посередине пролета (пункт 4.10 СН)

- прочность балки посередине пролетf на стадии эксплуатации обеспечена.
ПРИМЕЧАНИЕ. Если расстояние x,
вычисленное по формуле ![]() окажется более
окажется более ![]() , то нейтральная ось проходит в ребре балки (рис. 11г), сечение рассчитывается
как тавровое и действительное расстояние до нейтральной оси (при
, то нейтральная ось проходит в ребре балки (рис. 11г), сечение рассчитывается
как тавровое и действительное расстояние до нейтральной оси (при ![]() ) определяется по формуле (пункт 4.10 СН)
) определяется по формуле (пункт 4.10 СН)
![]()
где Rnp = 165 кГ/cм2 - расчетное сопротивление на осевое сжатие бетона марки 400 группы А (пункт 1.13 СН);
в0 = 16 см - ширина ребра балки (см. рис. 11). Условие, ограничивающее высоту сжатой зоны (пункты 4.10 и 3.4 СН)
![]()
Предельный момент, выдерживаемый тавровым сечением балки посередине пролета (пункт 4.10 СН)
![]()
Проверка на прочность
![]()
Коэффициент условий работы (пункты 4.10 и 2.24 СН):
при ![]()
при  при этом принимают 0,8 £ m2 £ 1
при этом принимают 0,8 £ m2 £ 1
Здесь А = 0,00015 R0 £ 0,75;
![]()
![]() (см. выше);
(см. выше);
sН1 = sНК - Sпотерь - установившееся предварительное напряжение в пучковой арматуре (после всех потерь);
sНК - контролируемое напряжение в пучковой арматуре в момент ее натяжения;
принимаем предварительно
sНК = RН1,
RН1 = 11000 кГ/см2 - расчетное сопротивление растяжению напрягаемой арматуры из высокопрочных гладких проволок диаметром 5 мм в стадии создания предварительных напряжений (первая стадия) по пункту 1.16 СН;
потери принимают предварительно приближенно в количестве 20¸25% от контролируемого напряжения (Sпотерь = 0,2¸0,25sНК)
Например, принимаем
Sпотерь = 0,2sНК;
sН1 = sНК - Sпотерь = 0,8sНК =0,8´11000 = 8600 кГ/см2;
![]()
А = 0,00015 R0 = 0,00015´4800 = 0,72 < 0,75 - принимаем А = 0,72;
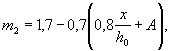 но не более 1 и не менее 0,8.
но не более 1 и не менее 0,8.
Проверяем прочность балки в сечении посередине пролета на стадии эксплуатации при воздействии только постоянных нагрузок, при этом расчетные сопротивления бетона понижают на 20% (пункт 1.13 СН), а расчетное сопротивление растяжению напрягаемой арматуры не изменяется (пункт 1.15 СН).
Расчетный изгибающий момент в середине пролета балки от постоянных нагрузок (см. выше)
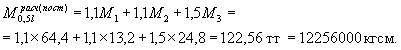
Предполагаем, что нейтральная ось проходит в плите, тогда расстояние до нейтральной оси
![]()
т.е. нейтральная ось проходит не в плите, а в ребре балки, сечение рассчитываем как тавровое.
Действительное расстояние до нейтральной оси
![]()
![]() (сечение не переармировано);
(сечение не переармировано);
![]() следовательно, вычисляем величину
коэффициента условий работы по пункту 2.24 СН.
следовательно, вычисляем величину
коэффициента условий работы по пункту 2.24 СН.
Принимаем приближенно суммарные потери напряжений в пучковой арматуре Sпотерь = 0,25sНК.
Контролируемое напряжение в напрягаемой арматуре принимаем предварительно sНК = RH1 = 11000 кГ/см2 (пункт 1.15 СH).
Установившееся предварительное напряжение:
sН1 = sНК - Sпотерь = 0,75sНК = 0,75´11000 = 8250 кГ/см2;
![]()
А° = 0,00015 R0 = 0,00015´5350 = 0,80 > 0,75;
принимаем А = 0,75.
 т2 = 0,93.
т2 = 0,93.
Предельный момент, выдерживаемый тавровым сечением балки посередине пролета при воздействии только постоянных нагрузок,
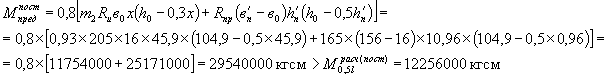
- прочность балки при действии только постоянных нагрузок обеспечена.
ПРИМЕЧАНИЕ. При ![]() предельный момент при
воздействии только постоянных нагрузок
предельный момент при
воздействии только постоянных нагрузок ![]()
6. ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЕЧЕНИЯ БАЛКИ ПОСЕРЕДИНЕ ПРОЛЕТА
Ен = 1,8´106 кГ/см2 - модуль упругости высокопрочной стальной проволоки (пункт 1.26 СН).
Еб = 350000 кГ/см2 - модуль упругости бетона марки 400 (пункт 1.25 СН)
Коэффициент приведения
![]()
ПРИМЕЧАНИЕ. Допускается приникать п1 = 5,2 по табл. 12 СН

Рис. 12. К определению геометрических характеристик расчетного сечения посередине пролета балки.
Площадь напрягаемой арматуры Fн = 32,97 см2 (см. выше).
Геометрические характеристики, учитываемые при расчетах по второму предельному состоянию на деформации (прогиб) и по третьему предельному состоянии на трещиностойкость, определяют с учетом работы сжатой и растянутой зон; при этой в расчет вводят приведённое сечение, т.е. полное сечение бетона и приведенную площадь арматуры (пункты 4.27 и 4.29 СН).
Расчетное сечение балки посередине пролета при расчетах по второму и третьему предельным состояниям (рис. 12) принимается таким же, как и при расчете на прочность по первому предельному состоянию (рис. 11б).
Площадь приведенного сечения (см. рис. 12)

Статический момент приведенного сечения относительно верха балки
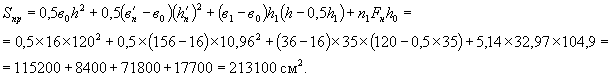
Расстояния центра тяжести приведенного сечения (см. рис. 12):
от верха балки
![]()
от низа балки
Ун = h - Ув = 120 - 49,3 = 70,70 см.
Момент инерции приведенного сечения относительно оси I-I (рис. 12), проходящей через его центр тяжести,

7. ОПРЕДЕЛЕНИЕ ПОТЕРЬ НАПРЯЖЕНИЙ И РАСЧЁТ БАЛКИ НА ТРЕЩИНОСТОЙКОСТЬ ПО ТРЕТЬЕМУ ПРЕДЕЛЬНОМУ СОСТОЯНИИ ПОСЕРЕДИНЕ ПРОЛЕТА НА СТАДИИ ЭКСПЛУАТАЦИИ (НА СТОЙКОСТЬ ПРОТИВ ОБРАЗОВАНИЯ ПОПЕРЕЧНЫХ НОРМАЛЬНЫХ ТРЕЩИН)
А. Определение потерь напряжений
Для пучковой напрягаемой арматуры из стальных высокопрочных проволок класса В-П диаметром 5 мм имеем:
![]() - нормативное сопротивление (предел
прочности) по пункту 1.10 и таблице 30 СН;
- нормативное сопротивление (предел
прочности) по пункту 1.10 и таблице 30 СН;
RН1 = 11000 кГ/см2 - расчетное сопротивление растяжению напрягаемой арматуры в стадии создания предварительных напряжений (первая стадия) по пункту 1.15 СН.
Контролируемое напряжение в пучковой арматуре в момент ее натяжения предварительно принято максимально допустимым
sНК = RН1 = 11000 кГ/см2.
В соответствии с пунктом 4.2 СН учитываем следующие потери предварительного напряжения при натяжении арматуры до бетонирования на упоры стенда:
а) к моменту окончания передачи на бетон натяжения арматуры (в момент отпуска арматуры)
s6 - потери от температурного перепада (разность между температурой напрягаемой арматуры и упоров стенда) при пропаривании и прогреве бетона;
s5 - потери от трения полигональных пучков об оттяжки в местах перегибов;
s4 - потери от деформации тяговых анкеров;
s3 - потери от релаксаций напряжений стали;
б) в стадии эксплуатации кроме потерь s3+s4+s5+s6, учитывают
s2 - Ds2 - потери от ползучести бетона с учетом постадийного приложения постоянной внешней нагрузки частями в разном возрасте;
s1 - потери от усадки бетона. Потери учитываются по приложении 4 СН.
Вычисление потерь s6
Изготовление балок с натяжением арматуры до бетонирования принято по поточно-агрегатной технологии на передвижном упоре-стенде, перемещаемом для термовлажностной обработки в пропарочную камеру.
По этой причине принимаем s6 = 0 (пункт 7 приложения 4 CH). При этом не учитываем потери от обжатия упорных устройств. Эти потери должен учитывать завод-изготовитель балок.
ПРИМЕЧАНИЕ, При изготовлении балок в стационарных железобетонных стендах потери s6 определяют в кГ/см2 по формуле
s6 = 20Трасч,
где

DТ - разность температуры внутри камеры стенда и наружного воздуха.
Вычисление потерь s5
Балка армирована посередине пролета 7 пучками (п пучков = 7), из них полигональных (пполиг. = 3) отогнутых к опорам (рис. 13).
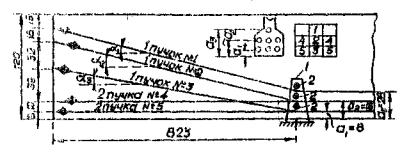
Рис. 13. Схема расположения пучков по длине
балки:
1 - общая оттяжка, жестко соединенная со стендом; 2 - трубки оттяжки.
Вычисляем углы наклона пучков.
Пучок № 1
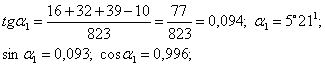
Пучок № 2

Пучок № 3

Средний угол наклона полигональных пучков
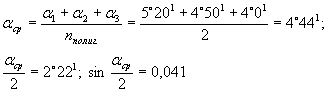
Площадь поперечного сечения всех пучков посередине пролета Fн = f1×п пучков, где f1 - площадь поперечного сечения одного пучка.

Рис. 14. К определении потерь s5:
1 - стальная трубка оттяжки
m = 0,3 - коэффициент трения полигонального пучка на перегибе стальной трубки оттяжки (рис. 14). Поперечное усилие от сил натяжения полигональных пучков, действующее на трубки оттяжки (рис. 14)
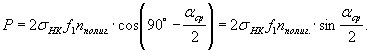
Потери от трения всех полигональных пучков в местах перегибов о трубки общей оттяжки, жестко соединенной со стендом (пункт 6 приложения 4 СН), отнесенные к площади всех пучков,


Рис. 15. Схематические варианты оттяжек, свободно перемещаемых
вдоль стенда:
а - с общей оттяжкой для всех полигональных пучков; б - с раздельными оттяжками
для каждого полигонального пучка;
1 - общая оттяжка; 2 - раздельная оттяжка; 3 - днище стенда.
ПРИМЕЧАНИЕ 1. При общей для всех полигональных пучков
оттяжке, свободно перемещаемой вдоль стенда (рис. 15а), ![]() (cм.
пункт 6 приложения 4 СН).
(cм.
пункт 6 приложения 4 СН).
ПРИМЕЧАНИЕ 2. При раздельных для каждого полигонального пучка оттяжках, свободно перемещаемых вдоль стенда (рис. 15б), s5 = 0 (пункт 6 приложения 4 СН).

Рис. 16. Схема передвижного стенда:
1 - упор стенда; 2 - конусный тяговый анкер; 3 - внутренний каркасно-стержневой
анкер; 4 - оттяжка полигональных пучков.
Вычисление потерь s4
Полная длина балки lп = 22,15 м (см. § 1 и рис. 16). Средняя длина арматурных пучков (см. рис. 16)
l1 » lп + 2 = 22,16 + 2 = 24,16 м.
Модуль упругости высокопрочной стальной проволоки Ен = 1,8´106 кГ/см2. Смещение (проскальзывание) пучка относительно конусных тяговых анкеров у упоров стенда (рис. 16) при запрессовке конических пробок (анкеры и натяжение с двух сторон) по пункту 4 приложения 4 СН
Dl1 = 2´0,2 = 0,4 см.
Потери от деформации тяговых анкеров
![]()
Вычисление потерь s3
Напряжения в арматуре с учетом начальных потерь s4, s5, s6
sН = sНК - s4 - s5 - s6 = 11000 - 298 - 116 - 0 = 10586 кГ/см2
Потери от релаксации напряжений стали (пункт 3 причинения 4 СН)

Вычисление потерь s1 и s2
Потери напряжения от усадки и ползучести бетона s1 и s2 определяем с момента передачи на бетон натяжения арматуры.
Усилие предварительного натяжения арматуры в момент ее отпуска с учетом первичных потерь
N0 = Fн(sНК - s3 - s4 - s5 - s6) = 32,97´(11000 - 721 - 298 - 116 - 0) = 32,97´9865 = 325300 кг
По пункту 6 § 3 для сечения посередине пролета имеем: Fпр = 4323 см2 - площадь приведенного сечения; Jпр = 8208000 см4 - момент инерции приведенного сечения.
Нормативный изгибающий момент в середине пролета балки от ее собственного веса, включаемого в работу балки в момент отпуска арматуры при изгибе балки кверху под воздействием эксцентрично приложенного усилия N0, М1 = 64,4 тм = 6440000 кгсм (см. выше пункт 4 § 3). Расстояние центра тяжести прямолинейных пучков от низа балки (см. рис. 13)
![]()

Рис. 17. Схема к определению s6 в момент отпуска арматуры.
Расстояние центра тяжести полигональных пучков от низа балки (см. там же)
![]()
Расстояние центра тяжести приведенного сечения от низа балки
Ун = 70,7 см (см. пункт 6 § 3).
Число пучков: полигональных..... ппол = 3;
прямолинейных..... ппр = 4.
Площадь сечения одного пучка f1 = 4,71 см2 (пункт 5 § 3). Эксцентриситет усилия предварительного натяжения N0 относительно центра тяжести приведенного сечения с учетом различных потерь в прямолинейных и полигональных пучках (см. рис. 12, 13 и 17)
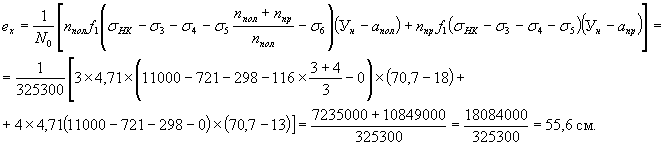
ПРИМЕЧАНИЕ. Если в балке имеются только прямолинейные пучки, то (см. рис. 12): ex = Ун - а0. Предположим, что все пучки прямолинейные, тогда ex = Ун - а0 = 70,7 - 15,1 = 55,6 см, т.е. получили значение ex, совпадающее с его значением, подсчитанным с учетом дополнительных потерь в полигональных пучках. По причине относительной малости потерь s5 допустимо и при полигональных пучках принимать ex = Ун - а0 (для сечения балки посередине пролета).
Сжимающее напряжение в бетоне от усилия N0 и момента М1 от собственного веса балки на уровне расположения усилия N0 (рис. 17)
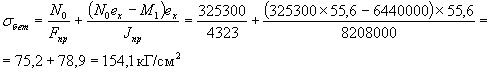
Принимаем бетон с осадкой конуса 5-6 см. Соответственно для бетона марки 400, подвергнутого тепловлажностной обработке в камере пропаривания по полному режиму (прочность после пропаривания не менее 80% проектной марочной прочности), принимаем по приложению 3 СН нормативные значения:
меры ползучести бетона ![]()
деформаций усадки бетона ![]()
Вводимые в расчет конечные (при t ® ∞) значения меры ползучести сt и деформаций усадки eу вычисляют в зависимости от их нормативных величин по формулам:
сt = снx1x2x3x4,
eу = eунx3x4,
где x1, x2, x3 и x4 - коэффициенты, учитывающие фактические условия работы конструкции и принимаемые по таблице 34 приложения 3 СН.
Принимаем возраст бетона балок в момент загружения (отпуска арматуры) менее 28 суток после достижения бетоном 80% проектной марочной прочности.
Соответственно по табл. 34 x1 = 1,25 и x2 = 1,0
При относительной влажности среды в 70% по табл. 34 принимаем x4 = 1,0.
ПРИМЕЧАНИЕ. Относительную влажность среды устанавливают по фактическим данным, а влажность воздуха - в зависимости от климатического района расположения сооружения как среднюю летнюю за многолетний период. При отсутствии таких данных, а также для типовых балок допускается принимать x4 = 1.
Площадь поперечного сечения балки (см. рис. 9б)
F = вnhn + h2в0 + h1вl = 152´10,96 + 74,04´16 + 35´36 = 4219 cм2.
Открытый периметр поперечного сечения балки (см. рис. 9б)
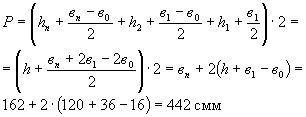
Открытая удельная поверхность ![]()
IIо табл. 34 приложения 3
CH при ![]() принимаем x3 = 0,73. Конечное значение меры ползучести бетона
принимаем x3 = 0,73. Конечное значение меры ползучести бетона
![]()
Конечное значение деформаций усадки бетона
![]()
Модуль упругости бетона марки 400 (см. табл. 10 СН) Еб = 350000 кГ/см2.
Кубиковая прочность бетона в момент загружения при достижении бетоном 80% проектной марочной прочности равняется 400´0,8 = 320 кГ/см2.
Модуль упругости бетона, соответствующий прочности 320 кГ/см2 (по интерполяции данных табл. 10 СН):
![]()
Характеристика ползучести бетона (см. пункт 8 приложения 3 СН)
![]()
Модуль упругости напрягаемой арматуры
Ен =1,8´106 кГ/см2.
Отношение модулей упругости напрягаемой арматуры и бетона
![]()
По приложении 4 СН вычисляем функцию Ф, учитывающую влияние длительности протекания усадки и ползучести бетона на величину потерь,
![]()
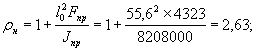
rп1mн = 2,63´5,14´0,0076 = 0,11.
В зависимости от величии rп1mн = 0,11 и jt = 2,05 по табл. 35 приложения 4 СН имеем Ф = 0,815.
Потери с момента предварительного обжатия (приложение 4 СН):
от усадки бетона
![]()
от ползучести бетона
s2 = s6п1jtФ = 154,1´5,14´2,05´0,815 = 1324 кГ/см2.
Вычисление уменьшения потерь Ds2
С момента приложения дополнительной постоянной нагрузки (вес тротуаров, перил и дорожной одежды), уменьшающей сжимающие напряжения в бетоне на уровне центра напрягаемой арматуры, происходит уменьшении потерь от ползучести бетона на величину Ds2.
Нормативные изгибающие моменты в середине пролета балки (см. выше пункт 4 § 3): от веса тротуаров и перил М2 = 13,2 тм; от веса дорожной одежды М3 = 24,8 тм.
М2 + М3 = 13,2 + 24,8 = 38,0 тм = 3800000 кгсм.
Растягивающее напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от моментов М2 + М3 (рис. 18)
![]()
Принимаем возраст бетона балок в момент их загружения весом тротуарных блоков, перил и дорожной одежды 90 суток. Соответственно по табл. 34 приложения 3 СН x2 = 0,75 и x1 = 1

Рис. 18. Схема к определению ![]() в момент
приложения дополнительной постоянной нагрузки.
в момент
приложения дополнительной постоянной нагрузки.
По предыдущему x3 = 0,73 и x4 = 1,0
Конечное значение меры ползучести бетона
![]()
Характеристика ползучести бетона
![]()
По предыдущему rп1mн = 0,11. В зависимости от величин rп1mн = 0,11 и jt = 1,40 по табл. 35 приложения 4 СН имеем: Ф = 0,842.
Уменьшение потерь от ползучести бетона с момента приложения дополнительной постоянной нагрузки
![]()
Б. РАСЧЕТ СЕЧЕНИЯ БАЛКИ ПОСЕРЕДИНЕ ПРОЛЕТА ПО ТРЕТЬЕМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ НА ТРЕЩИНОСТОЙКОСТЬ ПО ПОПЕРЕЧНЫМ НОРМАЛЬНЫМ ТРЕЩИНАМ НА СТАДИИ ЭКСПЛУАТАЦИИ
Сумма всех потерь
Sпотерь
= s1
+ s2
- Ds2
+ s3
+ s4
+ s5
+ s6
=
= 386 + 1324 - 156 + 721 + 298 + 116 +
0 = 2689 кГ/см2.
Минимальное усилие предварительного натяжения арматуры на стадии эксплуатации, т.е. с учетом всех потерь
N = (sНК - Sпотерь)Fн = (11000 - 2689)´32,97 = 8311´32,07 = 274263 кг.
Расчет на трещиностойкость производят на нормативные нагрузки без динамического коэффициента (пункт 2.2 СН). При этом нагрузка НК-80 принимается с коэффициентом 0,8 (пункт 116 СН 200).
Нормативные изгибающие моменты в середине пролета балки (см. выше пункт 4 § 3):
М1 = 34,4 тм - от собственного веса балки;
М2 = 13,2 тм - от веса тротуаров и перил;
М3 = 24,8 тм - от веса дорожной одежды;
М4 = 66,4 тм - от нагрузки Н-30;
М5 = 11,9 тм - от толпы на тротуаре;
М6 = 122,8 тм - от нагрузки НК-80.
Максимальный суммарный нормативный изгибающий момент:
Постоянная нагрузка, Н-30 и толпа
![]()
Постоянная нагрузка и НК-80
![]()
Принимаем большее из двух значений
норм
![]()
Рассматриваем работу балки при
действии N и момента ![]() (рис. 19).
(рис. 19).
При этом в нижнем волокне балки не должны возникать растягивающие напряжения (пункты 4.32 и 4.33 СН) .
Расстояние центра тяжести приведенного сечения от низа балки Ун = 70,7 см (см. выше пункт 6 § 3).
По предыдущему эксцентриситет ex » Ун - а0 = 55,6 см (см. примечание выше).
ПРИМЕЧАНИЕ. Точнее

Минимальные сжимающее напряжения в нижних волокнах балки посередине пролета на стадии эксплуатации (рис. 19)

- растяжение не возникает, трещиностойкость обеспечена (поперечные нормальные трещины посередине пролета на стадии эксплуатации не возникают).

Рис. 19. Схема к расчету сечения балки посередине пролета на трещиностойкость в стадии эксплуатации.
Однако при принятом максимально-допустимом значении sHК = RН1 = 11000 кГ/см2 полученный запас сжимающих напряжении в 21,9 кГ/см2 несколько велик. Поэтому уменьшим величину контролируемого напряжения sHК.
ПРИМЕЧАНИЕ. При sсж < 10-15 кГ/cм2 допустимо оставить предварительно принятое значение sHК = 11000 кГ/см2.
Для определения уменьшенного значения sHК вычисляем величину N из выражения
![]()
Откуда

Из выражения N = (sHК - Sпотерь)Fн получим окончательно значение контролируемого напряжения
![]()
Потери s1, Ds2, s4 и s6 не зависящие от sHК, имеют прежние величины:
s1 = 386 кГ/см2;
Ds2 = 156 кГ/см2;
s4 = 298 кГ/см2;
s6 = 0.
Уточняем величины потерь s2, s3 и s5 в соответствии с изменившимся значением sHК.
Потери s5
![]()
Потери s3
sН = sНК - s4 - s5 - s6 = 10100 - 298 - 107 - 0 = 9695 кГ/см2;

Потери s2
N0 = Fн(sНК - s3 - s4 - s5 - s6) = 32,97´(10100 - 524 - 298 - 107 - 0) = 32,97´9171 = 302600 кг

s2 = sбетп1jtФ = 141,2´5,14´2,05´0,815 = 1213 кГ/см2.
Sпотерь
= s1
+ s2
- Ds2
+ s3
+ s4
+ s5
+ s6
=
= 386 + 1213 - 136 + 524 + 298 + 107 +
0 = 2372 кГ/см2.
Окончательно минимальное усилие предварительного натяжения арматуры на стадии эксплуатации, т.е. с учетом всех потерь:
N = (sHК - Sпотерь)Fн = (10100 - 2372)´32,97 = 7728´32,97 = 255000 кг.
Окончательно минимальные сжимающие напряжения в нижних волокнах балки посередине пролета на стадии эксплуатации

- растяжение не возникает, трещиностойкость по поперечным трещинам по низу балки обеспечена.
ПРИМЕЧАНИЕ. Точнее ех определяется по формуле предыдущего примечания при уточненных значениях потерь и sHК.
ПРИМЕЧАНИЕ. Если условие sсж ³ 0 не удовлетворяется, необходимо увеличить N, т.е. увеличить площадь Fн напрягаемой арматуры.
В опытном порядке можно перейти к конструкции с частичным обжатием бетона (см. Г.К. Евграфов и Н.Н. Богданов. Проектирование мостов. М., "Транспорт", 1966 или Л.И. Иосилевский. Долговечность предварительно-напряженных железобетонных балочных пролетных строений мостов. М., "Транспорт", 1967).
Однако расчет балок с частичным предварительным напряжением в действующих нормах (СН и СНиП) не предусмотрен.
Проверяем стойкость против образования поперечных трещин на стадии эксплуатации по верху балки в сечении посередине пролета.
Рассматриваем работу балки при
действии момента от полной нормативной постоянной нагрузки ![]() и максимальной
величины силы предварительного обжатая, возможной в период эксплуатации, т.е. с
учетом наименьших возможных потерь.
и максимальной
величины силы предварительного обжатая, возможной в период эксплуатации, т.е. с
учетом наименьших возможных потерь.
При этом в верхнем волокне балки не должны возникать растягивающие напряжения (пункт 4.32 СН).
![]()
Выше принят возраст бетона балок в момент их загружения весом тротуарных блоков, перил и дорожной одежды 90 суток.
К этому времени проявилось только 50% потерь от усадки и ползучести бетона s1 + s2 и еще не проявилось уменьшение потерь от ползучести бетона Ds2 (см. табл. 37 приложения 4 СН).
Усилие обжатия бетона балки на начальной стадия эксплуатации в возрасте бетона 90 суток
N' = Fн[sНК - 0,5(s1
+ s2)
- s3
- s4
- s5
- s6] =
= 32,97´[10100 - 0,5´(386 + 1213) - 524 - 298 - 107 - 0]
= 32,97´8371 = 276000 кг.
Минимальные сжимающие напряжения в верхних волокнах балки посередине пролета на стадии эксплуатация
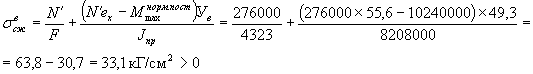
- растяжение не возникает, трещиностойкость по поперечным трещинам по верху балки обеспечена.
8. РАСЧЕТ БАЛКИ ПО ВТОРОМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ НА ДЕФОРМАЦИИ ПОСЕРЕДИНЕ ПРОЛЕТА НА СТАДИИ ЭКСПЛУАТАЦИИ (ОПРЕДЕЛЕНИЕ ПРОГИБА, ОБРАТНОГО ПРОГИБА-ВЫГИБА И СТРОИТЕЛЬНОГО ПОДЪЕМА)
Жесткость сечения (пункт 4.27 СН).
В1 = 0,85ЕбJпр = 0,85´350000´8208000 = 242´1010 кгсм2.
Нормативный изгибающий момент от временном нагрузки (кратковременной) без учета динамики (см. пункт 2.0 СН и выше пункт 4 § 3):
от автомобильной нагрузки Н-30 и толпы
М4 + М5 = 66,4 + 11,9 = 78,3 тм;
от колесной нагрузки НК-80
Мб = 125,8 тм > 78,3 тм (опаснее нагрузка HК-80).
Принимаем ![]()
Расчетный пролет балки l = 21,50 м = 2150 см.
Прогиб балки посередине пролета от максимальной нормативной временной нагрузки (кратковременного действия)
![]()
Допустимый прогиб от нормативной временной нагрузки (пункт 52 СН 200).
![]()
Нормативный изгибающий момент в середине пролета балки от постоянной нагрузки (см. выше)
М1 + М2 + М3 = 64,4 + 13,2 + 24,8 = 102,4 тм = 10240000 кгсм.
Прогиб балки посередине пролета от постоянной нагрузки длительного действия с учетом ползучести бетона (пункту 4.27 СН и 9.4 СНиП П-В.1-62)
![]()
где с - коэффициент, учитывающий увеличение деформации вследствие ползучести бетона от длительного действия нагрузки, который рекомендуется принимать равных: 2,0 - при нормальных температурно-влажностных условиях; 3,0 - при сухом климата; 1,5 - при влажном климате.
Принимаем с = 2.
![]()
Усилие предварительного натяжения арматуры с учетом всех потерь (см. выше)
N = (sНК - Sпотерь)Fн = 255000 кг.
Изгибающий момент от усилия N
М = Nl0 = 255000´55,6 = 14176000 кгсм.
Обратная прогиб - выгиб от предварительного обжатия бетона длительного действия с учетом ползучести бетона (пункты 4.27 СН и 9.4 СНиП П-В.1-62)
![]()
Суммарный прогиб
f = fвр + fпост - fпредв = 2,51 + 4,12 - 6,00 = 0,63 см.
Так как f =
0,63 см менее 1,5 см и менее ![]() то специального
строительного подъема балкам допустимо не придавать (пункт 58 СН 200).
то специального
строительного подъема балкам допустимо не придавать (пункт 58 СН 200).
Примем с = 3 (сухой климат).
Тогда суммарный прогиб
![]()
- (выгиб) - специального строительного подъема балкам подавно можно не предавать.
9. ПРОВЕРКА МАКСИМАЛЬНЫХ НАПРЯЖЕНИЙ В НАПРЯГАЕМОЙ АРМАТУРЕ ПОСЕРЕДИНЕ ПРОЛЕТА БАЛКИ НА СТАДИИ ЭКСПЛУАТАЦИИ
При натяжении арматуры на упоры стенда максимальное напряжение в напрягаемой арматуре посередине пролета балки на стадии эксплуатации (см. пункты 4.24, 4.25 и 5.2 СН)
sн.макс = sHК - Sпотерь - sуо +sн(п+в),
где sHК = 10100 кГ/см2 - контролируемые напряжения в арматуре в момент ее натяжения (см. пункт 7 § 3);
Sпотерь = s1 + s2 - Ds2 + s3 + s4 + s5 + s6 = 2372 кГ/см2 (см. там же) - сумма потерь;
sуо = п1sб - снижение напряжения в напрягаемой арматуре от упругого обжатия бетона усилием предварительного натяжения арматуры N;
sн(п+в) - растягивающее напряжение в напрягаемой арматуре от нормативной постоянной и временной нагрузки с учетом динамики;
![]() (см. выше);
(см. выше);
N = (sНК - Sпотерь)Fн = 255000 кг (см. пункт 7 § 3)
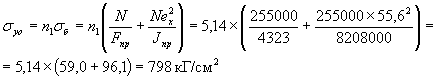
Динамический коэффициент для Н-30:
1 - m = 1,176 (см. пункт 5 § 3).
Максимальный суммарный нормативный изгибающий момент посередине пролета балки (см. пункт 4 § 3) с учетом динамики:
постоянная нагрузка, Н-30 и толпа
![]()
постоянная нагрузка и НК-80
![]()
Принимаем большее из двух значений
![]()
![]()
Максимальное напряжение в арматуре
sн.макс = sHК - Sпотерь - sуо +sн(п+в) = 10100 - 2372 - 798 + 784 = 7714 кГ/см2.
Расчетное сопротивление арматуры изв высокопрочной проволоки принимают равным (пункт 4.24 СН)
![]()
10. РАСЧЕТ БАЛКИ НА ПРОЧНОСТЬ ПО ПЕРВОМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ ПОСЕРЕДИНЕ ПРОЛЕТА НА СТАДИИ ПРЕДВАРИТЕЛЬНОГО НАПРЯЖЕНИЯ
Предварительное напряжение производим при достижении бетоном 80% проектной марочной прочности.
Расчетное сопротивление бетона марки 400 группы А при изгибе .... и осевому сжатию, соответствующие 80% прочности бетона к моменту натяжения арматуры с увеличением на 10%, как для случая строительных нагрузок в ста.... предварительного натяжения.

Расчетное продольное обжимающее усилие на стадии предварительного напряжения (пункт 4.19 и 4.20 СН)
Nн = [1,1(sНК - s3 - s4 - s5 - s6) - sсн]Fн,
где 1,1 - коэффициент перегрузки (пункт 115 СН 200);
sсн = 2700 кГ/см2 - расчетное снижение предварительного напряжения в арматуре от укорочения бетона в предельном состоянии при его обжатии напрягаемой арматурой (пункт 4.3 СН);
sНК = s3 - s4 - s5 - s6 = 10100 - 524 - 298 - 107 - 0 = 9171 кГ/см2 (см. выше пункт 7 § 3);
Fн = 32,97 см2.
Nн = [1,1(sНК - s3 - s4 - s5 - s6) - sсн]Fн = (1,1´9171 - 2700)´32,97 = 243800 кг.
Нормативный изгибающий момент посередине пролета балки от ее собственного веса М1 = 64,4 тм (см. выше пункт 4 § 3).
Расчетный изгибающий момент посередине пролета балки от ее собственного веса с минимальным коэффициентом перегрузки 0,9 (пункт 115 СН 200)
![]()
Размеры расчетного сечения посередине пролета балки (рис. 12 и 20):
h1 = 35 см; в1 = 36 см; в0
= 16 см; а0 = 15,1; h0 = 104,9 см; h =
120 см; ![]()
Рассчитываем сечение на
внецентренное сжатие под действием внешних нагрузок Nн и ![]() (см. рис. 20 пункт
4.19 СН).
(см. рис. 20 пункт
4.19 СН).
Высота сжатой зоны бетона хN, соответствующую внешнему усилию Nн, определится из условия (см. пункт 4.19 СН)
равенства нулю моментов внешних и внутренних сил (кроме силы ![]() ) относительно точки приложения силы Nн (знаки соответствуют расположению силы Nн на рис. 20)
) относительно точки приложения силы Nн (знаки соответствуют расположению силы Nн на рис. 20)

Рис. 20. Расчетная схема напряжений и усилий при расчете на прочность сечения посередине пролета на стадии предварительного напряжения.
![]()
откуда
![]()
Подставляя численные значения величин, входящих в уравнение, получаем:
![]()
![]()
![]()
откуда
![]()
0,55h = 0,55´120 = 66 см.
0,7h = 0,7´120 = 84 см.
Так как 84 > 78,9 > 66, т.е. 0,7h > хN > 0,55h имеем случай 2 (см. пункт 4.19 СН), для которого прочность сечения проверяем из условия:
![]()
где коэффициент условий работы
![]() и не менее 0,8 (см. пункт 2.24 СН).
и не менее 0,8 (см. пункт 2.24 СН).
принимаем ![]()

![]()
- прочность балки посередине пролета на стадии предварительного напряжения обеспечена.
ПРИМЕЧАНИЕ 1 При хN > 0,7h (случай 3) прочности сечения проверяется из условия (пункт 4.19 СН)
![]()
ПРИМЕЧАНИЕ 2 При хN £ 0,55h (случай 1) полную высоту сжатой зоны бетона х (см. рис. 20) определяют из уравнения (пункт 4.19 СН)
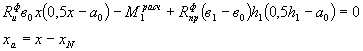
При х > hn прочность сечения проверяют из условия
![]()
При х £ hn прочность сечения проверяют из условия
![]()
Здесь m2 и ![]() определяются по
пункту 2.24 СН
определяются по
пункту 2.24 СН
![]() и не менее 0,8
и не менее 0,8
![]() при этом принимают 0,8 £ m2 £ 1;
при этом принимают 0,8 £ m2 £ 1;
А = 0,00015 R0 £ 0,75;
![]()
11. РАСЧЕТ БАЛКИ НА ТРЕЩИНОСТОЙКОСТЬ ПО ТРЕТЬЕМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ ПОСЕРЕДИНЕ ПРОЛЕТА НА СТАДИИ ПРЕДВАРИТЕЛЬНОГО НАПРЯЖЕНИЯ (НА СТОЙКОСТЬ ПРОТИВ ОБРАЗОВАНИЯ ПРОДОЛЬНЫХ И ПОПЕРЕЧНЫХ ТРЕЩИН)
Усилие предварительного натяжения арматуры в момент отпуска с учетом первичных потерь (см. выше пункт 8 § 3)
N0 = Fн(sНК - s3 - s4 - s5 - s6) = 32,97´(10100 - 524 - 298 - 107 - 0) = 302600 кг.
Нормативный изгибающий момент посередине пролета балки от ее собственного веса, включаемого в работу балки при ее выгибе кверху под воздействием эксцентрично приложенного усилия N0:
М1 = 64,4 тм = 6440000 кгсм (см. выше пункт 4 § 3).
Геометрические характеристики сечения (пункт 6 § 3)
Fnp = 4323 см2; Jпр = 8208000 см4;
ув = 49,3 см; Ун = 70,7 см; в1 = 36 см; в0 = 16 см; h1 =35 см
Эксцентриситет силы N0: ex » Ун - а0 = 55,6 см (см. пункт 7 § 3).
А. РАСЧЕТ НА СТОЙКОСТЬ ПРОТИВ ОБРАЗОВАНИЯ ПРОДОЛЬНЫХ ТРЕЩИН ПО НИЗУ БАЛКИ
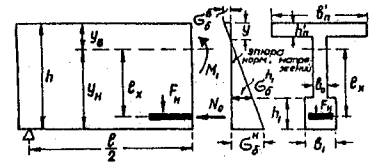
Рис. 21. Схемы к расчету балки посередине пролета на трещиностойкость на стадии предварительного напряжения.
Максимальные сжимающие напряжения в нижнем волокне балки (см. рис. 21) с их увеличением на 10% для учета воздействия стесненной усадки бетона и резких перепадов температур в пределах сечения (пункт 4.30 СН)

Расчет на стойкость против образования продольных трещин производится из условия (пункт 4.30 СН)
![]()
RT - расчетное сопротивление бетона сжатию, соответствующее прочности бетона к моменту обжатия.
Величину RT (пункт 4.31 СН) определяют в зависимости от двух критериев: градиента (перепада) напряжений и отношения толщины ребра балки в0 к ширине обжимаемого нижнего пояса балки в1 (см. рис. 21).
Определяем величину RT по первому критерию (по перепаду напряжений).
Предварительное напряжение производим при достижении бетоном 80% проектной марочной прочности.
Расчетные сопротивления батона марки 400 группы А при расчетах на трещиностойкость по продольным трещинам (пункт 1.13 СН), соответствующее 80% прочности бетона к моменту обжатия:
на сжатие при изгибе
![]()
на сжатие осевое
![]()
Сжимающее напряжение в бетоне на уровне верха нижнего пояса (нижней полки) балки, т.е. в волокнах на высоте h1 над низом балки (см. рис. 21):

![]()
Расчетное сопротивление RT по первому критерию принимают равным (пункт 4.31 СН):

Имеем:

Определяем величину RT по второму критерию (по отношению ![]() ).
).
![]()
Расчетное сопротивление RT по второму критерию принимают равным (пункт 4.31 СН):

Имеем:

Из двух значений RT = 183 кГ/см2 и RT = 174 кГ/см2, определенных двум критериям, принимаем согласно пункту 4.31 СН большее значение RT = 183 кГ/см2.
Проверка на трещиностойкость:
![]() -
стойкость против образования продольных трещин по низу балки на стадии
предварительного напряжения обеспечена.
-
стойкость против образования продольных трещин по низу балки на стадии
предварительного напряжения обеспечена.
ПРИМЕЧАНИЕ. Если условие ![]() не удовлетворяется,
то для увеличения RT можно произвести, если
производственные условия позволяют, предварительное напряжение при достижении
бетоном не 80% проектной марочной прочности, а 85, 90, 95 или 100%.
не удовлетворяется,
то для увеличения RT можно произвести, если
производственные условия позволяют, предварительное напряжение при достижении
бетоном не 80% проектной марочной прочности, а 85, 90, 95 или 100%.
Для этой же
цели можно повысить марку бетона. Если же отпуск арматуры производится при
достижении бетоном 80% марочной прочности, то избыточное обжатие нижних волокон
балки ![]() можно погасить
постановкой верхних съемных инвентарных пучков (рис. 22).
можно погасить
постановкой верхних съемных инвентарных пучков (рис. 22).
Для возможности многократной оборачиваемости инвентарных пучков в каждой линии устраивается цепочки из трех пучков: двух коротких однопетлевых (рис. 22) и одного длинного двухпетлевого инвентарного 2.
Два коротких пучка соединяются с длинным инвентарным посредством двухпетлевого замка с соединительным болтом.
Каждая цепочка пучков натягивается на бетон с торцов балки домкратами двойного действия до отпуска натяжения основных нижние пучков.
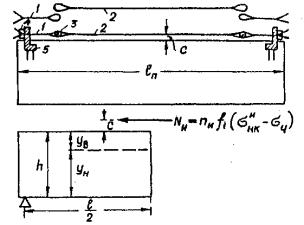
Рис 22. Схемы к расчету контролируемых
напряжений в инвентарных пучках в момент отпуска основных пучков:
1 - однопетлевое пучок из 24 Æ 5 мм; 2 - инвентарный двухпетлевой пучок из 24 Æ
5 мм; 3 - соединительный болт d
= 60 мм из Ст.5; 4 - конусный анкер; 5 - упор.
Верхние пучки
закрепляются конусными анкерами 4 за упоры 5 (см. рис. 22),
заделанные в ребре балки. После установки балок в пролет и укладки тротуарных
блоков и перил надобность в верхних пучках отпадает. Последние могут быть сняты
и до установки балок в пролет при 85, 90, 95 или 100% марочной прочности, при
которой соблюдается условие ![]() . В этом случае применяются съемные инвентарные упоры 5 (см.
типовой проект, вып. 122, Киевского Филиала Союздорпроекта). Короткие пучке
перерезываются автогеном, а двухпетлевые инвентарные пучки возвращаются для
повторного использования.
. В этом случае применяются съемные инвентарные упоры 5 (см.
типовой проект, вып. 122, Киевского Филиала Союздорпроекта). Короткие пучке
перерезываются автогеном, а двухпетлевые инвентарные пучки возвращаются для
повторного использования.
Выступающая часть заделанных упоров 5 обрезается автогеном.
Поверху поставлено два (пп = 2) инвентарных пучка каждый из 24 проволок d = 5 мм. Площадь сечения каждого пучка f1 = 4,71 см2.
Пучки возвышаются над плитой балки на величину «с» (см. рис. 22).
Потери напряжений в инвентарных пучках в момент отпуска основных пучков с достаточной точностью равны s4.
Сила натяжений двух инвентарных пучков
![]()
где ![]() - искомое
контролируемое напряжение в инвентарных пучках в момент их натяжения.
- искомое
контролируемое напряжение в инвентарных пучках в момент их натяжения.
Растягивающее напряжение в нижних волокнах балки от силы Nu равно (см. рис. 22)
![]()
Это растяжение должно погасить избыточное
сжатие ![]() Из уравнения
Из уравнения
![]()
учитывая, что ![]()
получаем
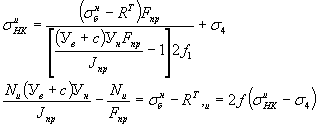
Например, по предыдущему RT = 183 кГ/см2
Допустим, что ![]()
Принимаем с = 7 см.
Тогда контролируемое напряжение в инвентарных пучках

Б. РАСЧЕТ НА СТОЙКОСТЬ ПРОТИВ ОБРАЗОВАНИЯ ПОПЕРЕЧНЫХ ТРЕЩИН ПО ВЕРХУ БАЛКИ
Максимальные растягивающие напряжения в верхней зоне балки на стадии предварительного напряжения (см. рис. 21)
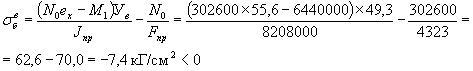
- растяжение не влияет, стойкость балки против образования поперечных трещин по верху балки на стадии предварительного напряжения обеспечена.
ПРИМЕЧАНИЕ 1. Растягивающие напряжения по верху балки допускаются не более расчетного сопротивления бетона растяжению Rp.n., т.е. должно быть соблюдено условие
![]()
При этой расчетом должна бить предусмотрена передача всего растягивающего усилия верхней зоны балки на ненапрягаемую арматуру (пункт 4.31 СН).
Для бетона марки 400 Rp.n. = 16 кГ/см2 (пункт 1.13 СН)
Допустим, что ![]() (растяжение)
< Rp.n. - стойкость балки против образования поперечных трещин по верху балки
обеспечена, при этом передаем все растягивающее усилие на распределительную
арматуру плиты. Сжимающее напряжения по низу балки
(растяжение)
< Rp.n. - стойкость балки против образования поперечных трещин по верху балки
обеспечена, при этом передаем все растягивающее усилие на распределительную
арматуру плиты. Сжимающее напряжения по низу балки ![]()
Высота растянутой зоны по верху балки (рис. 21)
![]()
Растягивающие усилив в верхней зоне балки (рис. 21)
![]()
В пределах расчетной ширины плиты вв уложены вдоль балки 8 стержней распределительной арматуры Æ 8 мм класса А (марки ВМ Ст.3сп) с расчетным сопротивлением Ra = 1900 кГ/см2 (пункт 1.1 СН). Площадь 8 стержней (приложение V) 8´0,503 = 4,02 см2.
Напряжение в арматуре
![]()
ПРИМЕЧАНИЕ 2. Если условие ![]() не удовлетворяется,
то избыточное растяжение верхних волокон балки
не удовлетворяется,
то избыточное растяжение верхних волокон балки ![]() можно оооо
постановкой верхних съемных инвентарных пучков (рис. 22),
состоящих каждый из 24 проволок d = 5 мм с площадью пучка 4,71
см2.
можно оооо
постановкой верхних съемных инвентарных пучков (рис. 22),
состоящих каждый из 24 проволок d = 5 мм с площадью пучка 4,71
см2.
Принимаем один пучок (пп = 1).
Инвентарной
пучок натягивается до отпуска натяжения основных нижних пучков и удаляется
после достижения бетоном 85-100% марочной прочности, при которой соблюдается
условие ![]() или после установки
балок в пролет и укладки тротуарных блоков и перил.
или после установки
балок в пролет и укладки тротуарных блоков и перил.
Сила натяжения инвентарного пучка
![]()
Сжимающее натяжение в верхних волокнах балки от силы Nu равно (см. рис. 22)
![]()
Этим сжатием погашаем избыточное
растяжение ![]() . Из уравнения
. Из уравнения ![]() учитывая, что
учитывая, что ![]() получаем
получаем
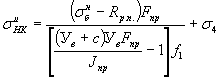
Например,
допустим, что ![]()
Принимаем с = 7 см (см. рис. 22).
Тогда контролируемое напряжение в инвентарном пучке в момент его натяжения
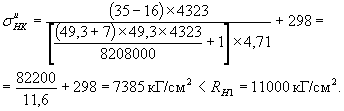
12. ВЫЧИСЛЕНИЕ НОРМАТИВНЫХ И РАСЧЕТНЫХ ПОПЕРЕЧНЫХ СИЛ В ПРИОПОРНОМ СЕЧЕНИИ БАЛКИ
Вычисляем поперечные силы в приопорном сечении балки А-А у начала опорного утолщения балки на расстоянии х от оси опирания балки (рис. 23).
х = 0,41 + 0,30 - 0,33 = 0,38 м
Расчетный пролет l = 21,50 м.
Площади участков линии влияния поперечной силы в сечении А-А (см. рис. 23б):
![]()
![]()
w1 + w2 = 10,372 - 0,003 = +10,369 м.
Коэффициент многополосности к нагрузке Н-30 (пункт 117 СН 200) при длине загружения l - x = 21,50 - 0,38 = 21,12 м < 25 м ....... b = 1.
ПРИМЕЧАНИЕ. При l - x > 25 м:
b = 0,9 для Г-7, Г-8 и Г-9;
b = 0,8 для Г-10,5.
Коэффициенты поперечной установки (см. выше пункты 2 и 3 § 3):
![]()

Рис. 23. К расчету поперечных сил в приопорном
сечении А-А балки:
а - фасад приопорного участке балки; б - линия влияния QA
Нагрузка от толпы: Кто = 0,4 т/м2 (пункт 125 СН 200). Нормативные постоянные нагрузки (см. выше пункт 1 § 3):
q1 = 1,155 т/м;
![]()
![]()
Эквивалентные нагрузки при загружении участка w1 линии влияния с длиной загружения l - x = 21,12 м (приложение 10 СН 200):
от Н-30 .............. ![]()
от НК-80 ........... ![]()
Нормативные поперечные силы в сечении А-А балки без учета динамики:
от собственного веса балки
Q1 = q1(w1 + w2) = 1,115´10,369 = 11,6 т;
от веса тротуаров и перил
![]()
от веса дорожной одежды
![]()
от автомобильной нагрузки H-30
![]()
от толпы на одном тротуаре
![]()
от колесной нагрузки НК-80
![]()
Нормативные поперечные силы в сечении А-А без учета динамики:
от постоянной нагрузки, Н-30 и толпы
![]()
от постоянной нагрузки и НК-80
![]()
Принимаем: ![]()
Динамический коэффициент к нагрузке Н-30 1 + m = 1,176 (см. выше пункт 6 § 3).
Коэффициенты перегрузки (пункты 115 и 127 СН 200):
для q1 и ![]() ................. 1,1;
................. 1,1;
для ![]() .................................... 1,5;
.................................... 1,5;
для Н-30 ................................. 1,4;
для НК-80 ............................... 1,1;
для толпы ............................... 1,4.
Расчетные поперечные силы в сечении А-А:
от постоянной нагрузки, Н-30 и толпы
![]()
от постоянной нагрузки и НК-80
![]()
Принимаем ![]()
13. ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПРИОПОРНОГО СЕЧЕНИЯ БАЛКИ
Размещение напрягаемых арматурных пучков в приопорном сечении А-А на расстоянии х = 38 см от оси опирания показано на рис. 24а и б.
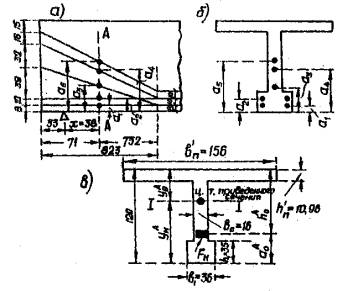
Рис. 24. К определению геометрических характеристик расчетного сечения А-А (приопорного)
Вычисляем расстояния пучков в сечении А-А от низа балки:
a1 = 8 см;
a2 = 18 см;
![]()
![]()
![]()
Расстояния от центра тяжести всех арматурных пучков в сечении А-А (рис. 24):
до низа балки
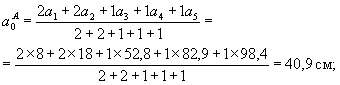
до верха балки
![]()
Коэффициент приведения
![]()
Площадь напрягаемой арматуры Fн = 32,97 см2 (см. выше).
Площадь приведенного сечения (см. рис. 24в)
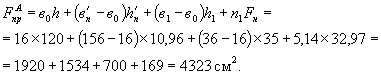
Статический момент приведенного сечения относительно верха балки

Расстояния центра тяжести приведенного сечения (см. рис. 24)
от верха балки
![]()
от низа балки
![]()
Момент инерции приведенного сечения относительно оси I-I (рис. 24), проходящей через его центр тяжести

14. РАСЧЕТ ПРИОПОРНОГО СЕЧЕНИЯ БАЛКИ ПО КАСАТЕЛЬНЫМ И ГЛАВНЫМ НАПРАВЛЕНИЯМ НА СТАДИИ ЭКСПЛУАТАЦИИ
Расчет по главным растягивающим напряжениям является расчетом на трещиностойкость и производится на нормативные нагрузки без учета динамики (пункты 4.35 и 2.2 СН).
Расчеты на главные сжимающие и касательные напряжения относят к расчетам на прочность (пункты 2.2 и 4.14 СН) и производят на расчетные нагрузки.

Рис. 25. Схемы к расчету приопорного сечения А-А на касательные и главные напряжения (пунктиром показан контур действительного сечения с вутами).
Число пучков: полигональных ........ ппол = 3
прямолинейных ....... ппр = 4
Средний угол наклона
равнодействующей всех полигональных пучков ![]() (см. выше пункт 7
§ 3).
(см. выше пункт 7
§ 3).
![]()
Площадь сечения одного пучка f1 =4 ,71 см2 (см. выше пункт 5 § 3).
По предыдущему (см. пункт 7 § 3):
sНК = 11000 кГ/см2; s3 = 524 кГ/см2;
s1 = 386 кГ/см2; s4 =298 кГ/см2;
s2 =1213 кГ/см2; s5 =107 кГ/см2;
Ds2 = 156 кГ/см2; s6 =0.
Усилия предварительного натяжения арматуры в приопорном сечении А-А (рис. 25) на стадии эксплуатации, т.е. с учетом всех потерь:
в полигональных пучках
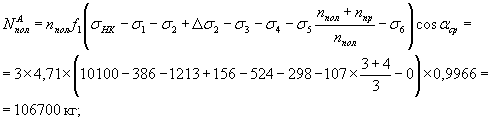
в прямолинейных пучках

в полигональных и прямолинейных пучках
![]()
Расчетная поперечная в сечении
А-А от постоянной и временной нагрузки ![]() (пункт 12
§ 3).
(пункт 12
§ 3).
Минимальная (с коэффициентом
перегрузки 0,9) поперечная сила от усилий в наклонных пучках равна ![]()
Геометрические характеристики приопорного сечения I-I (cм. выше пункт 13 § 3):
![]()
Приведенный к бетону статический момент отсечённой части сечения (заштрихована на рис. 25б) относительно нейтральной оси I-I (в пределах отсеченной части два пучка на расстояниях в'1 = 15 см и в0 = 31 см от верха балки)

Наибольшие касательные расчетные напряжения на уровне оси I-I, проходящей через центр тяжести приведенного сечения (пункт 4.14 СН)
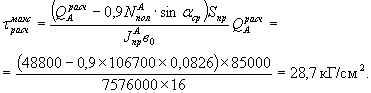
Расчетное сопротивление на
скалывание при изгибе для бетона марки 400 (пункт 1.13 СН) ![]()
- проверка на скалывающие напряжения удовлетворяется.
Главные сжимающие напряжения определяют по формуле (пункт 4.14 СН)
![]()
Главные растягивающие напряжения определяют по формуле (пункт 4.35 СН)
![]()
Вычисление ![]()
Нормальные сжимающие напряжения в бетоне вдоль оси балки на уровне нейтральной оси I-I (см. рис. 25):
расчетные с коэффициентом перегрузки 1,1
![]()
нормативные
![]()
Вычисление ![]()
Сжимающие напряжения в бетоне, нормальные к продольной оси балки, созданные напрягаемыми полигональными пучками при высоте балки h = 120 см (см. пункт 4.13 СН):
расчетные с коэффициентом перегрузки 1,1
![]()
нормативные
![]()
Вычисление tрасч и tнорм
Касательные напряжения на уровне нейтральной оси I-I (см. рис. 25):
расчетные с коэффициентом перегрузки 1,1
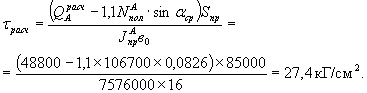
нормативные
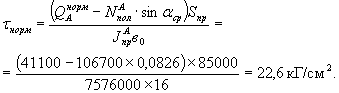
Вычисление ![]()
Dsу - сжимающие напряжения в бетоне, действующие в направлении, нормальном к продольной оси балки, и вызываемые опорной реакцией Б (см. рис. 26 и пункт 4.15 СН).
Вычисляем величину опорной реакции Б при загружении постоянной нагрузкой всего пролета l = 21,50 м, а временной нагрузкой (как и при вычислении QА) длины l - x (см. рис. 23).
Нормативная опорная реакция (используя данные пункта 12 § 3):
от постоянной нагрузки, Н-30 и толпы

от постоянной нагрузки и НК-80
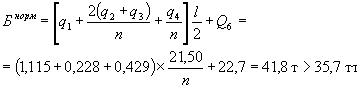
Принимаем: ![]()
Расчетная опорная реакции (используя данные пункта 12 § 3):
от постоянной нагрузки, Н-30 и толпы
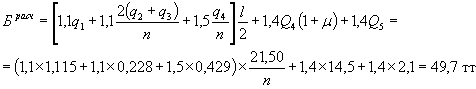
от постоянной нагрузки и НК-80

Принимаем: ![]()
Расстояние от низа балки до продольного сечения, в котором определяют напряжения Dsу (см. рис. 25 и 26),
![]()
Высота банки h = 120 см.
Расстояние приопорного сечения А-А от оси опирания балки х = 38 см (см. выше).
Так как У = 71,7 см > 0,4h = 48 см и х = 38 см < 0,7h = 84 см, то сжимающие напряжения по пункту 4.15 СН
![]()
ПРИМЕЧАНИЕ. При У > 0,4h
если х £ 0,7h
......... ![]()
если х = 0,8h
......... ![]()
если х = 0,9h
......... ![]()
если х = h .............. ![]()
При У £ 0,4h и х £ 2,5У
![]()
F - площадь продольного сечения (в пределах зоны, учитываемой в расчете), расположенного на высоте У от нива балки (площадь F заштрихована на рис. 26б). Так как У > 0,4h, то длина площади F (см. рис. 26) по пункту 4.15 СН
z = a + h = 33 + 120 = 153 см.

Рис. 26. К определению сжимающих напряжений Dsу:
а - фасад балки; б - горизонтальный разрез С-С (опорная диафрагма не показана).
ПРИМЕЧАНИЕ. При У > 0,4h
z = 5У при а ³ 2,5у;
z = 2,5У + а при а < 2,5у.
По рис. 26
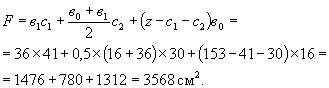
Сжимающие напряжения, вызываемые опорной реакцией:
расчетные
![]()
нормативные
![]()
Главные сжимающие напряжения по нейтральной оси

Главные растягивающие напряжения по нейтральной оси

Так как оба главные напряжения сжимающие, то главные сжимающие напряжения должны удовлетворять условии (пункт 4.15 СН)
sг.с £ Rnp
Для бетона марки 400 группы А расчетное сопротивление на осевое сжатие (пункт 1.13 СН)
![]()
(условие соблюдено).
ПРИМЕЧАНИЕ 1. Если sг.с > 0 (растяжение), то главные сжимающие напряжения должны удовлетворять условию (см. пункт 4.14 и 1.13 СН)
sг.с £ Rг.с.п
(для бетона марки 400 группы A Rг.с.п = 140 кГ/см2), а главные растягивающие напряжения должны удовлетворять условию (см. пункт 4.35 и 1.13 СН)
sг.р £ mpRг.р.п
(для бетона марки 400 группы А Rг.р.п = 24 кГ/см2),
где mp = 0,7, если sг.с £ 0,8Rг.с.п;
mp = 0,5, если sг.с = Rг.с.п
(для бетона марок 300-400) ;
mp = 0,55, если sг.с = Rг.с.п
(для бетона марок 500-600).
Для промежуточных значений sг.с величина коэффициента mp определяется по интерполяции.
ПРИМЕЧАНИЕ 2. При расчете на нагрузку НК-80 величину Rг.с.п допускается повышать до Rnp.
ПРИМЕЧАНИЕ 3. Главные напряжения по высоте балки надлежит определить не только на уровне нейтральной оси I-I, но и на уровне оси II-II (низ верхних вутов) и оси III-III (верх нижних вутов), показанных на рис. 25б (вуты действительного сечения балки показаны пунктиром). При определении главных напряжений на уровне осей II-II, и III-III (см. рис. 25) имеем:

где ![]() - суммарный момент в сечении А-II от
постоянной и временной нагрузки;
- суммарный момент в сечении А-II от
постоянной и временной нагрузки;
у0 - расстояние оси II-II или III-III от оси I-I;
Snp - приведенный статическиq момент, отсекаемой осями II-II или III-III части сечения, относительно оси I-I;
У (при определении Dsу) - расстояние от низа балки до уровня оси II-II или III-III.
15. РАСЧЕТ ПРИОПОРНОГО СЕЧЕНИЯ БАЛКИ НА ТРЕЩИНОСТОЙКОСТЬ ПО ТРЕТЬЕМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ НА СТАДИИ ПРЕДВАРИТЕЛЬНОГО НАПРЯЖЕНИЯ (НА СТОЙКОСТЬ ПРОТИВ ОБРАЗОВАНИЯ ПРОДОЛЬНЫХ И ПОПЕРЕЧНЫХ ТРЕЩИН)
Усилия предварительного натяжения аркатуры в приопорном сечении А-А (см. рис. 25) в момент ее отпуска с учетом первичных потерь (см. выше пункт 14 § 3):
в полигональных пучках

в прямолинейных пучках
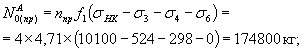
в прямолинейных и полигональных пучках
![]()
Расстояние центра тяжести прямолинейных пучков от низа балки (см. рис. 24 и 25а)
![]()
Расстояние центра тяжести полигональных пучков от низа балки (см. там же)
![]()
Расстояние центра тяжести
приведенного сечения от низа балки (см. пункт 13
§ 3)
![]()
Эксцентриситет усилия ![]() относительно центра
тяжести приведенного сечения (см. рис. 25)
относительно центра
тяжести приведенного сечения (см. рис. 25)
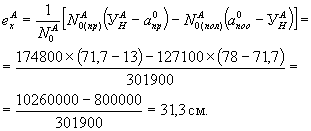
ПРИМЕЧАНИЕ. Приближенно (см. рис. 24):
![]()
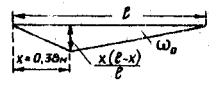
Рис 27. Линия влияния момента и приопорном сечении
Расчетный пролет l = 21,50 м.
Площадь линии влияния и вгибающего момента в приопорном сечении балки А-А на расстоянии = 0,38 м от оси опирания (рис. 27)
![]()
Нормативный изгибающий момент в сечении А-А от собственного веса балки
![]()
Геометрические характеристики сечения (пункт 13 § 3):
![]()
А. РАСЧЕТ НА СТОЙКОСТЬ ПРОТИВ ОБРАЗОВАНИЯ ПРОДОЛЬНЫХ ТРЕЩИН ПО НИЗУ БАЛКИ
Максимальные сжимающие напряжения в нижнем волокне приопорного сечения балки (см. по аналогии рис. 21) с их увеличением на 10% для учета воздействия стесненной усадки бетона и резких перепадов температур в пределах сечения (пункт 4.30 СН)

По предыдущему (см. пункт 11 § 3)
![]()
Определяем величину RT по первому критерию.
Сжимающее напряжение в бетона на уровне верха нижней полки балки, т.е. в волокнах на высоте h1 над низом балки (см. по аналогии рис. 21),
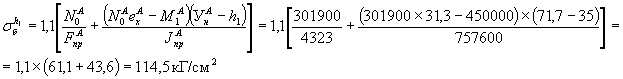
![]() По пункту 4.31 СН:
По пункту 4.31 СН:
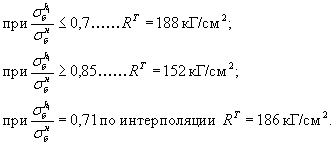
Определяем RT по второму критерию
![]()
по пункту 4.31 СН:
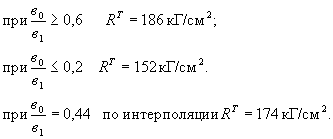
Из двух значений RT = 186 кГ/см2 и RT = 174 кГ/см2, определенных по двум критериям, принимаем согласно пункту 4.31 СН большее значение RT = 186 кГ/см2. Проверка на трещиностойкость:
![]() - стойкость против образования продольных
трещин по низу балки в приопорном сечении на стадии предварительного напряжения
обеспечена.
- стойкость против образования продольных
трещин по низу балки в приопорном сечении на стадии предварительного напряжения
обеспечена.
ПРИМЕЧАНИЕ. Если условие ![]() не соблюдается,
необходимо принять меры, указанные в примечании пункта 11
§ 3.
не соблюдается,
необходимо принять меры, указанные в примечании пункта 11
§ 3.
В. РАСЧЕТ НА СТОЙКОСТЬ ПРОТИВ ОБРАЗОВАНИЯ ПОПЕРЕЧНЫХ ТРЕЩИН ПО ВЕРХУ БАЛКИ
Максимальные растягивающие напряжения в верхнем волокне балки на стадии предварительного напряжения (см. по аналогии рис. 21)
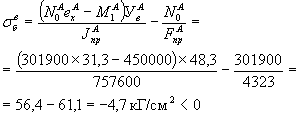
- растяжение не возникает, стойкость против образования поперечных трещин по верху приопорного сечения балки на стадия предварительного напряжения обеспечена.
ПРИМЕЧАНИЕ. При ![]() (растяжение) - см.
выше примечания 1
и 2
в конце пункта 11
§ 3.
(растяжение) - см.
выше примечания 1
и 2
в конце пункта 11
§ 3.
16. РАСЧЕТ ПРИОПОРНОГО СЕЧЕНИЯ БАЛКИ НА ПРОЧНОСТЬ ПО ПЕРВОМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ НА СТАДИИ ПРЕДВАРИТЕЛЬНОГО НАПРЯЖЕНИЯ
Расчетные сопротивления бетона при достижении бетоном марки 400 80% проектной прочности (см. выше пункт 10 § 3):
![]()
Расчетное снижение предварительного напряжения от укорочения бетона (пункт 4.3 СН): sсн = 2700 кГ/см2.
Площадь поперечного сечения всех пучков в сечении A-A: Fн = 32,97 см2 (см. выше).
Усилие предварительного
натяжения арматуры в приопорном сечении А-А в момент ее отпуска (см. выше пункт
15
§ 3): ![]()
Расчетное продольное обжимающее усилие на стадии предварительного напряжения (пункты 4.19 и 4.20 СН)
![]()
Расчетный изгибающий момент от собственного веса балки с минимальным коэффициентом перегрузки
![]()
Расстояния центра приложения
силы ![]() (см. выше пункт 15
§ 3):
(см. выше пункт 15
§ 3):
от низа балки
![]()
от верха балки
![]()
Размеры расчетного приопорного сечения (см. по аналогии рис. 20):
h1 = 35 см; в1 = 36 см; в0
= 16 см; ![]()
Рассчитываем сечение на
внецентренное сжатие под действием внешних нагрузок ![]() и
и ![]() (см. пункт 4.19 СН и
по аналогии рис. 20).
(см. пункт 4.19 СН и
по аналогии рис. 20).
Высота сжатой зоны бетона хN определится из уравнения (см. там же и выше пункт 10 § 3)
![]()
Подставляя численные значения величин, входящих в уравнение, получим:
![]()
![]()
![]()
откуда
![]()
0,7h = 0,7´120 = 84 см.
Так как 99,8 > 84 см, т.е. хN > 0,7h, имеем случай 3 (см. пункт 4.19 СН), для которого прочность сечения проверяем из условия:
![]()

![]()
- прочность приопорного сечения балки на стадии предварительного напряжения обеспечена.
ПРИМЕЧАНИЕ. Условия проверки прочности при 0,7h > хN > 0,55h (случай 2) и при хN £ 0,55h (случай 1) приведены выше в пункте 10 § 3 и в пункте 4.19 СН.
17. РАСЧЕТ ПО ПЕРВОМУ ПРЕДЕЛЬНОМУ СОСТОЯНИЮ НА ПРОЧНОСТЬ НАКЛОННЫХ СЕЧЕНИЙ ПО ПОПЕРЕЧНОЙ СИЛЕ НА СТАДИИ ЭКСПЛУАТАЦИИ (РАСЧЕТ ХОМУТОВ ПО ИЗГИБУ)
Шаг хомутов по изгибу рассчитываем в зоне 1 по расчетной поперечной силе в приопорном сечении А-А и в зоне II по расчетной поперечной силе в сечении B-В у места перегиба полигональных пучков (рис. 28).

Рис. 28. К расчету хомутов по изгибу.
А. РАСЧЕТ ШАГА ХОММУТОВ ПО ИЗГИБУ В ЗОНЕ I
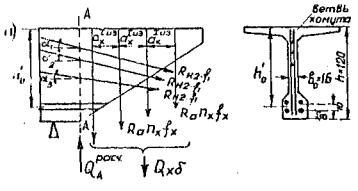
Рис. 29. К расчету шага хомутов по изгибу:
а - схема к расчету на поперечную силу по наклонному сечению;
б - поперечное сечение балки.
Расчет на прочность наклонного сечения балки, проходящего через нижнюю точку приопорного сечения А-А (см. рис. 29), производят из условия (пункт 4.13 СН)
![]()
где предельная поперечная сила, воспринимаемая бетоном сжатой зоны и хомутами в невыгоднейшем наклонном сечении
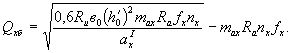
Подставляя в это условие значение Qхб, получаем требуемый максимальный шаг хомутов по изгибу в зоне I

где Rи = 205 кГ/см2 - расчетное сопротивление на осевое сжатие бетона марки 400 группы А (см. пункт 1.13 СH);
в0 = 16 см - толщина ребра балки;
![]() - расстояние от верха балки до центра тяжести
прямолинейных пучков (см. рис. 29б);
- расстояние от верха балки до центра тяжести
прямолинейных пучков (см. рис. 29б);
mах = 0,8 - коэффициент условий (неравномерности) работы стержневых хомутов (пункт 1.17 СН);
Ra = 2400 кГ/см2 - расчетное сопротивление стержней хомутов периодического профиля из стали класса А-II марки Ст5сп (пункт 1.14 СН);
fх = 0,785 см2 - площадь поперечного сечения одной ветви хомута номинальным диаметром 10 мм (см. приложение VI);
nх = 2 - число ветвей хомутов в одном поперечном сечении балки (см. рис. 29б);
![]() - расчетная поперечная сила в приопорном
сечении балки А-А (см. пункт 12
§ 3) ;
- расчетная поперечная сила в приопорном
сечении балки А-А (см. пункт 12
§ 3) ;
тн.о = 0,7 - коэффициент условий (неравномерности) работы пучков из высокопрочных проволок (пункт 1.17 СН);
RН2 = 9800 кГ/см2 - расчетное сопротивление высокопрочной гладкой проволоки диаметром 5 мм для пучков в стадии эксплуатации (пункт 1.15 СН);
f1 = 4,71 см2 - площадь поперечного сечении одного пучка (см. выше);
Ssina = sina1 + sina2 + sina3 = 0,093 + 0,004 + 0,070 = 0,243 - сумма синусов углов наклона пучков к горизонтали (см. рис. 29 и пункт 7 § 3).

Б. РАСЧЕТ ШАГА ХОМУТОВ ПО ИЗГИБУ В ЗОНЕ II
Начисляем расчетную поперечную силу в сечении В-В балки на расстоянии х1 = 7,90 и от оси опирания (см. рис. 28)

Рис. 30. Линия влияния Qв.
Расчетный пролет l = 21,50 м. Площади участков линии влияния поперечной силы в сечении В-В (рис. 30):
![]()
![]()
w1 + w2 = 4,31 - 1,45 = +2,86 м.
По предыдущему (см. пункт 12 § 3):

Эквивалентные нагрузки при загружении участка w1 линии влияния с длиной загружения l х1 = 21,50 - 7,90 = 13,6 м (приложение 10 СН 200):
от Н-30 .............. ![]()
от НК-80 ........... ![]()
Расчетные поперечные силы в сечении В-В:
от постоянной нагрузки, Н-30 и толпы

постоянной нагрузки и HK-80

Принимаем: ![]()
Полезная высота балки в сечении В-В h0 = 104,9 см (см. выше пункт 5 § 3).
Требуемый максимальный шаг хомутов по изгибу в зоне II

18. РАСЧЕТ ХОМУТОВ НА СТАДИИ ЭКСПЛУАТАЦИИ ПО КРУЧЕНИЮ БАЛКИ ОТ МЕСТНОЙ НАГРУЗКИ И ОПРЕДЕЛЕНИЕ СУММАРНОГО ШАГА ХОМУТОВ ПО ИЗГИБУ ОТ ОБЩЕЙ И КРУЧЕНИЮ ОТ МЕСТНОЙ НАГРУЗКИ. РАСЧЕТ ДОБАВОЧНОЙ ПРОДОЛЬНОЙ АРМАТУРЫ В БАЛКЕ ПО КРУЧЕНИЮ
Схема загружения в поперечной разрезе моста при расчете крайней балки на кручение показана на рис. 31.
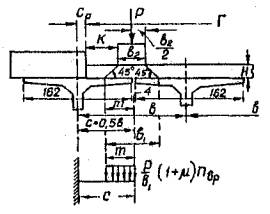
Рис. 31. Схема загружения в поперечном разрезе моста при расчете крайней балки на кручение.
Ширина проезжей части Г = 8 м.
Расстояние между осями балок по ширине моста в = 1,66 м.
Число балок по ширине моста п = 6.
Расстояние от оси крайней балки до края тротуара (рис. 31)
![]()
Ширина заднего ската колеса (приложение 10 СН 200):
в2 = 0,6 м ................Н-30;
в2 = 0,8 м ................НК-80.
Устанавливаем тяжелое колесо весом Р с минимально допустимым приближением к тротуару.
Минимальное расстояние от края ската до края тротуара (см. там же и рис. 31):
--0,50-0,5 в2 = 0,50 - 0,5´0,6 = 0,20 м ........... H-30;
--0,25 м ........................................................... HK-80.
Суммарная толщина четыpеx слоев дорожной одежды (см. пункт 1 § 2) Н = 0,14 м.
Длина соприкасания ската с покрытием проезжей части вдоль моста для любых нагрузок (приложение 10 СН 200)
а2 = 0,2 м.
Размеры грузовой площадки:
вдоль моста а1 = а2 + 2Н = 0,2 + 2´0,14 = 0,48 м;
поперек моста в1 = в2 + 2Н.
Длина консольного свеса плиты от оси крайней балки до оси шва (рис. 31)
![]()
Длина загружения консольного свеса (см. рис. 31)
т = с - (с0 + К - Н) = с - с0 - К + Н.
Динамический коэффициент (пункт 126 СН 200):
1 + m = 1,3 ..................Н-30;
1 + m = 1,0 ..................НК-80
Коэффициенты перегрузки:
пвр = 1,4 ................Н-30;
пвр = 1,1 ................HК-80
iiiiii крутящий момент от одного колеса (рис. 31)
![]()
Нагрузка Н-30
Р = 6 т (СН 200, приложение 10);
в1 = в2 + 2Н = 0,60 + 2´0,14 = 0,88 м;
т = с - с0 - К + Н = 0,83 - 0,15 - 0,20 + 0,14 = 0,62 м.
![]()
Нагрузка НК-80
Р = 10 т (СН 200, приложение 10)
в1 = в2 + 2Н = 0,80 + 2´0,14 = 1,04 м.
т = с - с0 - К + Н = 0,83 - 0,15 - 0,25 + 0,14 = 0,57 м;
![]()
Расстояние между диафрагмами d = 4,31 м.
Принимаем условно, что нагрузка, расположенная на концевых треугольных участках А (см. рис. 32а) отсека между диафрагмами, не вызывает кручение балки, а воздействует непосредственно на диафрагму.
Можно принять, что наибольшее кручение балки в отсеке между диафрагмами возникает в том случае, когда край грузовой площадки отстоит от оси диафрагмы на величину "с" (см. рис. 32). При приближении этой площадки и оси диафрагмы на расстояние менее величины "с" давление будет передаваться также и на диафрагму, уменьшая крутящий момент в главной балке.

Рис. 32. К расчету максимального крутящего момента
от местной нагрузки Н-30:
а - расположение нагрузки Н-30 в плане; б - расчетная схема; в - эпюра крутящих
моментов в балке.
При нагрузке Н-30 на отсеке размещается два колеса задних осей на взаимном расстоянии 1,6 м друг от друга (рис. 32).
Принимаем, что концы отсека балки заделаны в диафрагмах и балка в пределах отсека работает на чистое вручение.
Внешний крутящий момент равномерно распределен по длине (см. рис. 32а и пункт 2 § 2)
а = а1 + 2с - т = 0,48 + 2´0,83 - 0,62 = 1,52 м
Эпюру крутящих моментов в балке
строим по принципу построения эпюры поперечных сил в простой балке длиной
"d", загруженной
на участках длиной "а" равномерно распределенными нагрузками
![]() (рис. 32б).
(рис. 32б).
Расстояния центра нагрузок до диафрагмы (см. рис. 32а и б):
и1 = d - 1,60 - с - 0,5а1 = 4,31 - 1,60 - 0,83 - 0,5´0,48 = 1,64 м;
и2 = d - с - 0,5а1 = 4,31 - 0,83 - 0,5´0,48 = 3,24 м.
Максимальный опорный расчетный крутящий момент в балке от нагрузки Н-30 (см. рис. 32в)
![]()
При нагрузке НК-80 на отсеке размещаем три колеса на расстоянии 1,2 м друг от друга (см. рис. 33).
Колеса устанавливаем симметрично на отсеке длиной "d", пренебрегая несущественный заходом грузовых площадок крайних колес на концевые треугольные участки А отсека (см. рис. 33а).
Внешний крутящий момент от одного колеса равномерно распределен по длине а1 + 2с - т = 0,48 + 2´0,83 - 0,57 = 1,57 м > 1,2 м, т.е. длины распределения моментов от давления колес накладываются друг на друга.
Поэтому в расчет принимаем суммарный внешний крутящий момент от трех колес, равномерно распределенный по длине (см. приложение 10 СН 200 и рис. 33а)
a1 = 1,2´2+ а1 + 2с - т =2,40 + 1,57 = 3,97 м.

Рис. 33. К расчету крутящего момента от
местной нагрузки НК-80:
а - расположение нагрузки НК-80 в плане; б - расчетная схема; в - эпюра
крутящих моментов в балке.
Максимальный опорный расчетный крутящий момент в балке от нагрузки НК-80 (см. рис. 33в)
![]()
Момент инерции всей балки на кручение (см. пункт 3 § 3)
Jкр = 358000 см4.
Моменты инерции на кручение (см. там же и рис. 9б):
Плиты

Ребра балки

Нижней полки балки

![]()
Расчетный крутящий момент от нагрузки Н-30:
передаваемый ребру балки

передаваемый нижней полке балки

Расчетный крутящий момент от нагрузки НК-80:
передаваемый ребру балки

передаваемый нижней полке балки


Рис. 34. К подсчету пллощади ядра сечения ребра и нижней полки балки.
А. РАСЧЕТ ШАГА ХОМУТОВ ПО КРУЧЕНИЮ БАЛКИ ОТ МЕСТНОЙ НАГРУЗКИ В ЗОНЕ 1 И ОПРЕДЕЛЕНИЕ СУММАРНОГО ШАГА ХОМУТОВ
По предыдущему (пункт 17):
fx = 0,785 см2 - площадь поперечного сечения одной ветви хомута номинальным диаметром 10 мм;
Ra = 2400 кГ/см2 - расчетное сопротивление стержней хомутов периодического профиля из стали класса А-II Ст5сп. Наружный диаметр по выступам ветви хомута d1 = 1,13 см (приложение VI).
Боковой защитный слой ненапрягаемых хомутов с = 1,5 см (пункт 5.26 СН).
Ширина ядра сечения ребра балки (рис. 34а)
вя = в0 - 2c - d1 = 16 - 2´1,5 - 1,13 = 11,87 см.
Площадь ядра сечения ребра (рис. 34а)
![]()
Для расчета хомутов по кручению в ребре в зоне I принимаем нагрузку Н-30, соответствующую расчету хомута по изгибу в той же зоне.
Требуемый шаг дополнительных хомутов по кручению от местной нагрузки в зоне I
![]()
Требуемый шаг хомутов по изгибу
от общей нагрузки в зоне I (см. пункт 17
§ 3) ![]()
Требуемый суммарный шаг хомутов в зоне I ребра балки по изгибу от общей и кручению от местной нагрузки
![]()
Наибольший шаг ненапрягаемых хомутов в тонких ребрах (в0 = 16 см < 20 см) предварительно напряженных балок при условии расчета на совместное действие изгиба и кручения принимают независимо от расчета не более 00 см (см. пункт 5.84 СН).
Принимаем ![]()
ПРИМЕЧАНИЕ. При в0 > 20 см наибольший шаг хомутов принимают не более 1,5в0.
Объем стержней хомутов в процентах от объема ребра
![]()
(см. пункт 5.84 СН).
Нижнюю полку балки (рис. 34б) армируют хомутами периодического профиля номинальным диаметром 10 мм с площадью поперечного сечения fx = 0,785 см2 из стали класса А-II марки Ст5сп с Ra = 2400 кГ/см2.
Площадь ядра сечения нижней полки балки (заштрихована на рис. 34б)
![]()
Расчетный крутящий момент, передаваемый нижней полке балки (см. выше):
![]()
![]()
Принимаем большее значение ![]()
Требуемый шаг хомутов в нижней полке балки по кручению от местной нагрузки в зоне I и II
![]()
Наибольший шаг хомутов в нижней полке предварительно напряженных балок принимают не более 20 см.
ПРИМЕЧАНИЕ. При условии, если максимальные сжимающие напряжения в
нижнем волокне балки на стадии предварительного напряжения ![]() (см. выше пункт 11
§ 3 и пункт 5.85 СН), то наибольший шаг
хомутов допускается принимать равным 30 см.
(см. выше пункт 11
§ 3 и пункт 5.85 СН), то наибольший шаг
хомутов допускается принимать равным 30 см.
Принимаем ![]()
Полная длина хомута в нижней полке (см. рис. 34б), включая участи хомутов ребра в пределах нижней полки (пункт 5.85 СН)
lх = 31 + 27´2 + 26´2 + 37,5´2 = 212 см.
Площадь нижней полки (см. рис. 34б)
![]()
Объем стержней хомутов в процентах от объема нижней полки
![]()
(см. пункт 5.05 СН).
Б. РАСЧЕТ ШАГА ХОМУТОВ ПО КРУЧЕНИЮ БАЛКИ ОТ МЕСТНОЙ НАГРУЗКИ В ЗОНЕ II И ОПРЕДЕЛЕНИЕ СУММАРНОГО ШАГА ХОМУТОВ
Для расчета хомутов по кручению в ребре в зоне II принимаем нагрузку HK-80, соответствующую расчету хомутов по изгибу в той же зоне.
Требуемый шаг дополнительных хомутов по кручению от местной нагрузки в зоне II
![]()
Требуемый шаг хомутов по изгибу
от общей нагрузки в зоне II
(см. пункт 17 §
3) ![]()
Требуемый суммарный шаг хомутов в зоне II ребра балки по изгибу от общей и кручению от местной нагрузки
![]()
Принимаем ![]()
Объем стержней хомутов в процентах от объема ребра
![]()
В. РАСЧЕТ ДОБАВОЧНОЙ ПРОДОЛЬНОЙ АРМАТУРЫ В БАЛКЕ ПО КРУЧЕНИЮ
Добавочная продольная арматура в ребре балки принята периодического профиля номинальным диаметром 10 мм из стали класса А-II (марки Ст.5сп) с Ra = 2400 кГ/см2 (пункт 1.14 СН).
Площадь поперечного сечения одного стержня f = 0,785 см2 (приложение VI).
Периметр ядра сечения и ребре балки (см. рис. 34а):
![]()
![]()
![]()
Принимаем большее значение ![]()
Требуемая добавочная площадь поперечного сечения продольной арматуры в ребре балки
![]()
Потребное количество добавочных продольных стержней в ребре балки
![]()
Принято 8Æ10 А-II (рис. 34б).
Периметр ядра сечения в нижней
полке балки (см. рис. 34б) ![]()
Требуемая добавочная площадь поперечного сечения продольной арматуры в нижней полке балки
![]()
Потребное количество добавочных продольных стержней в нижней полке балки
![]()
Принято 10Æ10 А-II (рис. 34б).
19. УСКОРЕННЫЙ РАСЧЕТ ХОМУТОВ НА СТАДИИ ЭКСПЛУАТАЦИИ ПО КРУЧЕНИЮ БАЛКИ ОТ ОБЩЕЙ НАГРУЗКИ И ОПРЕДЕЛЕНИЕ СУММАРНОГО ШАГА ХОМУТОВ ПО ИЗГИБУ ОТ ОБЩЕЙ И КРУЧЕНИЮ ОТ ОБЩЕЙ И МЕСТНОЙ НАГРУЗКИ
Расчет хомутов на стадии эксплуатации по кручению балки от общей нагрузки может выполняться следующим образом.
При том же расположении общей нагрузки (Н-30 + толпа или НК-80), как и при определении коэффициента поперечной установки с учетом кручения (см. рис. 8), на крайнюю балку воздействует внешний погонный крутящий момент (см. Я.С. Файн. К расчету мостов с учетом кручения главных балок." Изд. вузов. Строительство и архитектура", 1963, № 8), определяемый по формуле
![]()
где ![]() - поправка на кручение (см. выше пункт 3 §
3);
- поправка на кручение (см. выше пункт 3 §
3);
n = 6 - число балок в поперечном сечении моста;
в1 = 8,3 м - расстояние между крайними балками (см. рис. 8);
R1 - погонная нагрузка на крайнюю балку, равная произведению эквивалентной нагрузки (с учетом коэффициентов динамики, многополосности и перегрузки) на второе слагаемое коэффициента поперечной установки.
Для нагрузки Н-30 и толпы на одной тротуаре
![]()
где пп = 2 - число полос движения и T = 1 м - ширина тротуара.
Для нагрузки НК-80
![]() где пп
= 1 - число полос движения.
где пп
= 1 - число полос движения.
Для расчета хомутов по кручению в ребре в зоне I принимаем нагрузку Н-30, соответствующую расчету хомутов по изгибу в той же зоне (по поперечной силе в сечении А-А).
По предыдущему (см. выше пункт 12 § 3):
![]() -
эквивалентная нагрузка при загружении участка w1, линии влияния QА с длиной загружения l - x = 21,50 - 0,38 =
21,12 м;
-
эквивалентная нагрузка при загружении участка w1, линии влияния QА с длиной загружения l - x = 21,50 - 0,38 =
21,12 м;

Нагрузка на 1 п.м. крайней балки от Н-30 и толпы:
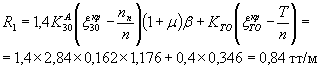
Внешний погонный крутящий момент
![]()
Расчетный крутящий момент в приопорном участке балки от общей нагрузки Н-30 и толпы (рис. 35), предполагая, что на концах балки невозможны повороты сечений относительно ее оси
![]()

Рис. 35. К расчету максимального крутящего момента в зоне I от общей нагрузки Н-30 и
толпы:
а - расчетная схема; б - эпюра крутящих моментов в балке.
Расчетный крутящий момент от общей нагрузки Н-30 и толпы, передаваемый ребру балки

Требуемый шаг дополнительных хомутов по кручению от местной и общей временной нагрузки в зоне I, учитывая разное направление крутящих моментов для крайней балки от этих нагрузок
![]()
Требуемый суммарный шаг хомутов в зоне I ребра балки (приопорный отсек) по изгибу от общей и кручению от общей и местной нагрузки
![]()
В соседнем отсеке приопорного участка балки, где местная нагрузка отсутствует:
![]()
![]()
Предложенный способ учета кручения от общей и временной нагрузки, по нашему мнению, существенно уточняет расчеты хомутов.
ПРИМЕЧАНИЕ. 1. Если на крайней балке местная временная нагрузка (колеса Н-30 или НК-80) отсутствует во всех отсеках между диафрагмами (например, для типовых балок при габарите Г-7 и тротуарах по 1,5 м), то хомуты должны быть рассчитаны по изгибу от общей нагрузки и кручении от общей временной нагрузки.
ПРИМЕЧАНИЕ. 2. Для средних балок расчетные крутящие моменты от местной и общей временной нагрузки могут совпадать по направлению.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ I
Схемы и показатели типовых сборных предварительно напряженных пролетных строений с диафрагмами с натяжением прямолинейной арматуры до бетонирования (выпуски 122-63 и 149-62 часть II) пролетами свету 10¸30 м под нагрузки Н-30 и НК-80).

Геометрические показатели (см. рис. 36) и число пучков в балке.
|
lсв, м |
lп, м |
l, м |
hб, м |
с, м |
hап, м |
d0, м |
d, м |
Число пучков |
|
10 |
11,36 |
11,10 |
0,80 |
0,13 |
0,00 |
0,28 |
2,70 |
4 по 20 Æ 5 мм |
|
12,5 |
14,06 |
13,70 |
0,85 |
0,18 |
0,07 |
0,28 |
2,70 |
4 по 24 Æ 5 мм |
|
15 |
16,76 |
16,30 |
1,00 |
0,23 |
0,08 |
0,28 |
2,70 |
5 по 24 Æ 5 мм |
|
20 |
22,16 |
21,50 |
1,20 |
0,33 |
0,41 |
0,31 |
4,31 |
7 по 24 Æ 5 мм |
|
30 |
32,96 |
32,32 |
1,70 |
0,32 |
0,44 |
0,32 |
4,04 |
10 по 24 Æ 5 мм |
lсв - условный пролет в свету;
lп - полная длина балки;
l - расчетный пролет;
с - расстояние от торца балки до оси опирания;
hап - высота опорных частей;
d0 - расстояние от торца балки до оси крайней диафрагмы;
d - расстояние между осями диафрагм;
№ 1 - крайние тротуарные блоки длиной 4,33 м;
№ 2 - средние тротуарные блоки длиной 2,70 м;
Количество балок на одно пролетное строение
|
Габарит |
Количество балов |
|
|
Т = 1 м |
Т = 1,5 м |
|
|
Г-7 |
5 |
6 |
|
Г-8 |
6 |
6 |
|
Г-9 |
7 |
7 |
|
Г-10,5 |
8 |
8 |
Т - ширина тротуара.
Таблица расхода бетона (в м3) на одно пролетное строение
|
lп, м |
Г-7 |
Г-8 |
Г-9 |
Г-10,5 |
||||
|
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
|
|
11,36 |
27,0 |
31,8 |
31,7 |
31,8 |
36,3 |
36,4 |
41,0 |
41,1 |
|
14,06 |
33,1 |
39,7 |
38,8 |
39,1 |
44,6 |
44,8 |
50,3 |
60,5 |
|
16,76 |
41,2 |
48,7 |
48,4 |
48,7 |
65,5 |
55,8 |
62,7 |
63,0 |
|
22,16 |
60,9 |
72,0 |
71,6 |
72,0 |
82,3 |
82,7 |
93,1 |
93,6 |
|
32,96 |
106,9 |
126,7 |
123,1 |
126,7 |
145,6 |
146,2 |
164,9 |
165,6 |
ПРИЛОЖЕНИЕ II
Схемы и показатели типовых сборных предварительно напряженных пролетных строений с диафрагмами с натяжением криволинейной арматуры до бетонирования (выпуски 122-62 и 149-62-часть 1) с пролетами в свету 10¸30 м под нагрузки Н-30 и НК-80
Геометрические показатели и число пучков в балке - см. приложение I и рис. 36.
Количество балок на одно пролетное строение - см. приложение I.
Таблица расхода бетона (в м3) на одно пролетное строение
|
lп, м |
Г-7 |
Г-8 |
Г-9 |
Г-10,5 |
||||
|
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
|
|
11,36 |
27,0 |
31,8 |
31,7 |
31,8 |
36,3 |
36,4 |
41,0 |
41,1 |
|
14,06 |
33,1 |
39,7 |
38,8 |
39,1 |
44,6 |
44,8 |
50,3 |
60,5 |
|
16,76 |
41,2 |
48,7 |
48,4 |
48,7 |
65,5 |
55,8 |
62,7 |
63,0 |
|
22,16 |
60,9 |
72,0 |
71,6 |
72,0 |
82,3 |
82,7 |
93,1 |
93,6 |
|
32,96 |
106,9 |
126,7 |
123,1 |
126,7 |
145,6 |
146,2 |
164,9 |
165,6 |
ПРИЛОЖЕНИЕ III
Схема и показатели типового сборного предварительно напряженного пролетного строения с диафрагмами с натяжением арматуры после бетонирования (выпуск 123-64) пролетом в свету 40 и под нагрузки Н-30 и НК-80
Геометрические показатели (см. рис. 36) и число пучков в балке
|
lсв, м |
lп, м |
l, м |
hб, м |
с, м |
hап, м |
d0, м |
d, м |
Число пучков |
|
40 |
43,2 |
42,6 |
2,3 |
0,35 |
0,49 |
0,35 |
5,005 и 6,235 |
14 по 20 Æ 5 мм или 8 по 48 Æ 5 мм |
ПРИМЕЧАНИЕ. Крайние тротуарные блоки № 1 - длиной 4,04 м; средние тротуарные блоки № 2 - длиной 2,7 м.
Количество балок на одно пролетное строение - см. приложение I.
Таблица расхода бетона (в м3) на одно пролетное строение
|
lп, м |
Г-7 |
Г-8 |
Г-9 |
Г-10,5 |
||||
|
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
|
|
43,2 |
204,6 |
242,4 |
241,7 |
242,3 |
278,8 |
279,5 |
315,9 |
316,5 |
ПРИЛОЖЕНИЕ IV
Схемы и показатели типовых унифицированных сборных балочных бездиафрагменных пролетных строений из предварительно напряженного железобетона полной длиной 12¸42 м под нагрузки Н-30 и НК-80 (выпуски 384/2¸384/11)

Геометрические показатели (см. рис. 37) и число пучков в балке
|
lп, м |
l, м |
hб, м |
с, м |
hап, м |
Число пучков |
|
12 |
11,4 |
0,9 |
0,30 |
0,20 |
4 по 24 Æ 5 мм |
|
15 |
14,4 |
0,9 |
0,30 |
0,20 |
6 по 24 Æ 5 мм |
|
18 |
17,4 |
1,2 |
0,30 |
0,20 |
6 по 24 Æ 5 мм |
|
24 |
23,4 |
1,2 |
0,30 |
0,20 |
9 по 24 Æ 5 мм |
|
33 |
32,2 |
1,5 |
0,40 |
0,35 |
13 по 24 Æ 5 мм |
|
42 |
41,2 |
2,1 |
0,40 |
0,36 |
15 по 24 Æ 5 мм |
Количество балок на одно пролетное строение
|
Габарит |
Количество балок при тротуарах шириной |
|
|
Т = 1 м |
Т = 1,5 м |
|
|
Г-7 |
4 |
5 |
|
Г-8 |
5 |
5 |
|
Г-9 |
5 |
6 |
|
Г-10,5 |
6 |
6 |
Таблица расхода бетона (в м3) на одно пролетное строение
|
lп, м |
Г-7 |
Г-8 |
Г-9 |
Г-10,5 |
||||
|
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
|
|
12 |
33,8 |
42,2 |
41,1 |
42,0 |
40,8 |
49,2 |
48,0 |
48,9 |
|
15 |
42,2 |
52,6 |
51,1 |
52,3 |
50,9 |
61,4 |
59,8 |
61,0 |
|
10 |
55,8 |
69,7 |
67,9 |
69,4 |
67,6 |
81,4 |
79,5 |
81,0 |
|
24 |
74,1 |
92,4 |
90,1 |
92,0 |
89,7 |
108,1 |
105,6 |
107,5 |
|
33 |
111,9 |
138,5 |
135,2 |
137,9 |
134,6 |
162,3 |
158,8 |
161,5 |
|
42 |
157,7 |
196,9 |
196,9 |
196,2 |
192,1 |
231,3 |
227,0 |
230,3 |
ПРИМЕЧАНИЕ. Балки с lп = 12¸33 м - цельноперевозимые, балка с lп = 42 м - поперечночлененная.
ПРИЛОЖЕНИЕ V
Схемы и показатели типовых унифицированных сборных плитных пролетных строений из предварительно напряженного железобетона полной длиной 6¸18 м под нагрузки Н-30, НК-80 (выпуски 304/1, 384-10 и 384/11)
Геометрические показатели (см. рис. 37)
|
lп, м |
l, м |
hб, м |
с, м |
hап, м |
|
6 |
5,60 |
0,30 |
0,20 |
0,028 |
|
9 |
8,60 |
0,45 |
0,20 |
0,028 |
|
12 |
11,40 |
0,60 |
0,30 |
0,028 |
|
15 |
14,40 |
0,60 |
0,30 |
0,128 |
|
18 |
17,40 |
0,75 |
0,30 |
0,128 |
Количество плит на одно пролетное строение
|
Габарит |
Количество балок при тротуарах шириной |
|
|
Т = 1 м |
Т = 1,5 м |
|
|
Г-7 |
9 |
10 |
|
Г-8 |
10 |
11 |
|
Г-9 |
11 |
12 |
|
Г-10,5 |
12 |
13 |
Таблица расхода бетона (в м3) на одно пролетное строение
|
lп, м |
Г-7 |
Г-8 |
Г-9 |
Г-10,5 |
||||
|
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
Т = 1 м |
Т = 1,5 м |
|
|
6 |
15,2 |
17,0 |
16,0 |
18,3 |
17,8 |
19,7 |
19,1 |
20,9 |
|
9 |
27,2 |
30,6 |
29,7 |
33,1 |
32,2 |
35,8 |
34,8 |
38,2 |
|
12 |
41,7 |
46,9 |
45,7 |
51,0 |
49,8 |
55,0 |
53,7 |
58.9 |
|
15 |
52,1 |
58,6 |
57,2 |
63,7 |
62,3 |
68,7 |
67,1 |
73,7 |
|
18 |
70,6 |
78,0 |
78,5 |
86,3 |
84,5 |
93,3 |
91,3 |
100,1 |
ПРИЛОЖЕНИЕ VI
Сортамент горячекатанных арматурных сталей
|
Номера сечений (номинальный диаметр), мм |
Класс А-I |
Класс А-II |
Площадь f, см2 |
|
диаметр d, мм |
диаметр d1, по выступам, мм |
||
|
6 |
6 |
- |
0,283 |
|
7 |
7 |
- |
0,385 |
|
8 |
8 |
- |
0,503 |
|
9 |
9 |
- |
0,636 |
|
10 |
10 |
11,3 |
0,785 |
|
12 |
12 |
13,5 |
1,131 |
|
14 |
14 |
15,5 |
1,539 |
|
16 |
16 |
18,0 |
2,011 |
|
18 |
18 |
20,0 |
2,545 |
|
20 |
20 |
22,0 |
3,142 |
|
22 |
22 |
24,0 |
3,801 |
|
25 |
25 |
27,0 |
4,909 |
|
28 |
28 |
30,5 |
6,153 |
|
32 |
32 |
34,5 |
8,043 |
|
36 |
36 |
39,5 |
10,179 |
|
40 |
40 |
43,5 |
12,561 |
ПРИЛОЖЕНИЕ VII
Коэффициенты для расчета прямоугольных сечений железобетонных элементов на изгиб
|
a |
r0 |
g0 |
A0 |
|
a |
r0 |
g0 |
A0 |
|
0,01 |
10,00 |
0,995 |
0,010 |
|
0,29 |
2,01 |
0,855 |
0,248 |
|
0,02 |
7,12 |
0,990 |
0,020 |
|
0,30 |
1,98 |
0,650 |
0,255 |
|
0,03 |
5,82 |
0,985 |
0,030 |
|
0,31 |
1,95 |
0,845 |
0,262 |
|
0,04 |
5,05 |
0,980 |
0,039 |
|
0,32 |
1,93 |
0,840 |
0,269 |
|
0,05 |
4,53 |
0,975 |
0,048 |
|
0,33 |
1,90 |
0,835 |
0,275 |
|
0,06 |
4,15 |
0,970 |
0,058 |
|
0,34 |
1,88 |
0,830 |
0,282 |
|
0,07 |
3,85 |
0,955 |
0,067 |
|
0,35 |
1,86 |
0,825 |
0,289 |
|
0,08 |
3,61 |
0,960 |
0,077 |
|
0,36 |
1,84 |
0,820 |
0,295 |
|
0,09 |
3,41 |
0,955 |
0,085 |
|
0,37 |
1,82 |
0,815 |
0,301 |
|
0,10 |
3,24 |
0,950 |
0,095 |
|
0,38 |
1,80 |
0,810 |
0,309 |
|
0,11 |
3,11 |
0,945 |
0,104 |
|
0,39 |
1,78 |
0,805 |
0,314 |
|
0,12 |
2,96 |
0,940 |
0,113 |
|
0,40 |
1,77 |
0,800 |
0,320 |
|
0,13 |
2,88 |
0,935 |
0,121 |
|
0,41 |
1,75 |
0,795 |
0,326 |
|
0,14 |
2,77 |
0,930 |
0,130 |
|
0,42 |
1,74 |
0,790 |
0,332 |
|
0,15 |
2,68 |
0,925 |
0,139 |
|
0,43 |
1,72 |
0,785 |
0,337 |
|
0,16 |
2,61 |
0,920 |
0,147 |
|
0,44 |
1,71 |
0,780 |
0,343 |
|
0,17 |
2,53 |
0,915 |
0,155 |
|
0,45 |
1,69 |
0,775 |
0,349 |
|
0,18 |
2,47 |
0,910 |
0,164 |
|
0,46 |
1,68 |
0,770 |
0,354 |
|
0,19 |
2,41 |
0,905 |
0,172 |
|
0,47 |
1,67 |
0,765 |
0,359 |
|
0,20 |
2,36 |
0,900 |
0,180 |
|
0,48 |
1,66 |
0,760 |
0,365 |
|
0,21 |
2,31 |
0,895 |
0,188 |
|
0,49 |
1,64 |
0,755 |
0,375 |
|
0,22 |
2,26 |
0,890 |
0,196 |
|
0,50 |
1,63 |
0,750 |
0,370 |
|
0,23 |
2,22 |
0,885 |
0,203 |
|
0,51 |
1,62 |
0,745 |
0,380 |
|
0,24 |
2,18 |
0,880 |
0,211 |
|
0,52 |
1,61 |
0,740 |
0,385 |
|
0,25 |
2,14 |
0,875 |
0,219 |
|
0,53 |
1,80 |
0,735 |
0,390 |
|
0,26 |
2,10 |
0,870 |
0,226 |
|
0,54 |
1,59 |
0,730 |
0,394 |
|
0,27 |
2,07 |
0,865 |
0,234 |
|
0,55 |
1,58 |
0,726 |
0,400 |
|
0,28 |
2,04 |
0,860 |
0,241 |
|
|
|
|
|