|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО |
||
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р ИСО |
Контроль состояния и диагностика машин
ВИБРАЦИОННЫЙ КОНТРОЛЬ СОСТОЯНИЯ МАШИН
Часть 2
Обработка, анализ и представление результатов измерений вибрации
ISO
13373-2:2005
Condition monitoring and diagnostics of machines - Vibration condition
monitoring - Part 2: Processing, analysis and presentation of vibration data
(IDT)
|
|
Москва Стандартинформ 2010 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией «Научно-исследовательский центр контроля и диагностики технических систем» (АНО «НИЦ КД») на основе собственного аутентичного перевода на русском языке стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 183 «Вибрация, удар и контроль технического состояния»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 15 декабря 2009 г. № 858-ст
4 Настоящий стандарт является идентичным по отношению к международному стандарту ИСО 13373-2:2005 «Контроль состояния и диагностика машин. Вибрационный контроль состояния машин. Часть 2. Обработка, анализ и представление результатов измерений вибрации» (ISО 13373-2:2005 «Condition monitoring and diagnostics of machines - Vibration condition monitoring - Part 2: Processing, analysis and presentation of vibration data»).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные и межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
|
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов национальным стандартам Российской Федерации (и действующим в этом качестве межгосударственным стандартам)
|
Введение
Измерения вибрации в широкой полосе частот позволяют получить общую оценку вибрационного состояния машины, а отслеживание изменений параметров широкополосной вибрации - сформировать сигнал, предупреждающий обслуживающий персонал машины об изменении ее технического состояния. Обработка и анализ сигналов вибрации в соответствии с методами, установленными настоящим стандартом, позволяют пользователю выявить возможные причины изменений технического состояния и наблюдать за их развитием.
Достоинством контроля состояния по сигналам вибрации является не только возможность получения информации о предполагаемом отказе машины к определенному моменту времени и планирования мер по предотвращению этого отказа, но также поступление ценной информации для последующего планирования и выполнения операций по техническому обслуживанию. Анализ вибрации позволяет выявить такие характерные неисправности машины, как нарушение в сопряжениях кинематических пар, дисбаланс, ускоренный износ, нестабильность потока, дефекты смазки.
Общее руководство по вибрационному контролю состояния машин установлено ИСО 13373-1 [8]. В настоящем стандарте приведены рекомендации по обработке, анализу и представлению данных, полученных в процессе вибрационного контроля состояния, которые могут быть использованы для углубленного диагностирования причин появления неисправностей.
Обработка сигналов, их анализ и методы диагностирования могут различаться в зависимости от контролируемых технологических процессов, необходимой точности диагноза, имеющихся ресурсов и т.п. Правильно спланированная и внедренная система мониторинга учитывает влияние многих факторов, таких как приоритетность выполняемой машиной операции, критичность и сложность технологической системы, потери от простоя, вероятности отказов разных видов и наличие диагностических признаков зарождающихся неисправностей.
Выбор данных, необходимых для контроля состояния машины, требует проведения соответствующего анализа.
Специалист в области вибрационного анализа должен собрать максимальное количество значимой информации о контролируемой машине. Например, знание резонансных и возбуждаемых частот машины позволяет определить ожидаемые частотные составляющие в спектре вибрации и диапазон частот анализа. Знание вибрационного состояния машины при ее вводе в эксплуатацию, истории машины, режимов работы также может быть использовано специалистом в процессе анализа.
Проведение предварительного анализа при построении системы мониторинга позволяет правильно выбрать типы датчиков, определить места их установки, способы формирования сигналов, методы их обработки и установить критерии оценки состояния.
ГОСТ Р ИСО 13373-2-2009
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Контроль состояния и диагностика машин
ВИБРАЦИОННЫЙ КОНТРОЛЬ СОСТОЯНИЯ МАШИН
Часть 2 Обработка, анализ и представление результатов измерений вибрации
Condition monitoring and diagnostics of
machines. Vibration condition monitoring.
Part 2. Processing, analysis and presentation of vibration data
Дата введения 2011-01-01
1 Область применения
Настоящий стандарт устанавливает методы обработки и представления результатов измерений вибрации, анализа вибрационных характеристик в целях вибрационного контроля состояния машин вращательного действия и их диагностирования. Рассмотрены методы фильтрации и анализа сигналов при исследовании характерных типов динамического поведения машины. Многие из установленных методов могут быть распространены и на машины других видов, включая машины возвратно-поступательного действия. Приведены примеры представления параметров, которые обычно используют для оценки технического состояния машин и ее диагностирования.
В настоящем стандарте рассмотрены два основных подхода к анализу вибрации: в частотной и временной областях. Рассмотрены также возможности уточнения диагноза посредством изменения режима работы машины.
Настоящий стандарт распространяется на методы вибрационного контроля состояния машин, нашедшие широкое практическое применение. Существует много других методов исследования поведения машины посредством углубленного анализа вибрации и диагностирования, выходящие за пределы обычных процедур мониторинга. Эти методы не описаны в настоящем стандарте, но некоторые из них указаны (для сведения) в разделе 5.
Руководства по использованию результатов измерений широкополосной вибрации для машин разных классов и размеров установлены в международных стандартах серий ИСО 7919 [4] и ИСО 10816 [5], а также в других документах (например, [11], [12]), где приведена дополнительная информация в отношении специфических неисправностей, которые могут быть обнаружены методами вибрационной диагностики.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ИСО 1683, Акустика. Рекомендуемые опорные значения при определении уровней шума (ISO 1683, Acoustics - Preferred reference quantities for acoustic levels)
3 Обработка сигналов
3.1 Общие положения
Вибрационные измерения осуществляют с помощью датчиков, производящих аналоговый электрический сигнал, пропорциональный мгновенному значению ускорения, скорости или перемещения. Сигнал может быть записан для последующего анализа или отображен, например, на осциллографе. Для получения действительного значения измеряемого параметра вибрации выходное напряжение умножают на коэффициент преобразования измерительной цепи, включающей датчик, усилитель и устройство записи. Наиболее распространен анализ вибрации в частотной области, но часто полезным является представление сигнала как функции времени.
|
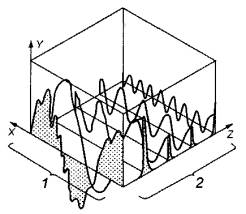
X - время; Y -
значение сигнала (амплитуда); Z - частота; 1 - осциллограмма во временной области; 2 -
спектр в частотной области |
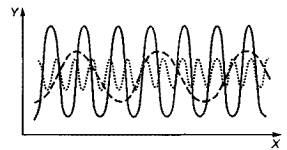
X - время; Y - значение сигнала |
На рисунке 1 показано одновременное представление сигнала во временной и частотной областях. В данном примере сигнал является суперпозицией четырех составляющих. Суммарный временной сигнал, наблюдаемый на экране анализатора, выделен на рисунке темным цветом. Посредством преобразования Фурье анализатор выделяет из исходного временного сигнала четыре частотные компоненты.
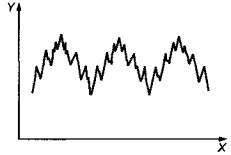
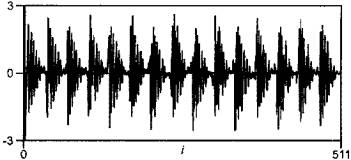
На рисунке 2 показан аналогичный пример сложного сигнала с датчика вибрации, наблюдаемый на экране анализатора. В данном случае сигнал образован тремя составляющими, показанными на рисунке 3, с частотами, показанными на рисунке 4.
|
X - время; Y - значение сигнала |
X - частота; Y - значение сигнала |
Часто соотношения между параметрами вибрации в разных точках конструкции или в разных направлениях не менее важны, чем сам сигнал вибрации. По этой причине на практике используют многоканальные анализаторы сигналов с функциями сопоставления сигналов по двум каналам. Для проведения подобного анализа важно иметь информацию об амплитудных и фазовых соотношениях в сопоставляемых сигналах.
3.2 Аналоговые и цифровые системы
3.2.1 Общие положения
Аналоговый сигнал с датчика может быть обработан с помощью как аналоговой, так и цифровой системы. Обычно аналоговые системы включают в себя фильтры, усилители, записывающие устройства, интеграторы и другие устройства, которые преобразуют сигнал без изменения его аналоговой природы. Однако в последнее время все более очевидными становятся преимущества цифровой обработки сигналов. Аналого-цифровой преобразователь (АЦП) осуществляет многократные выборки аналогового сигнала и преобразует их в последовательности чисел. После этого для выполнения операций фильтрации, интегрирования, вычисления спектра (см. 4.3.2), построения гистограмм и др. используют стандартные компьютерные программы. Оцифрованный сигнал также может быть отображен как функция времени. При правильном выборе частоты дискретизации цифровой сигнал будет содержать в себе ту же исходную информацию, что и аналоговый.
При любом способе обработки сигнала необходимо знать коэффициент преобразования измерительной цепи (отношение напряжения сигнала на выходе к истинному значению измеряемого параметра). Анализируемый сигнал должен существенно превышать уровень фонового шума, но не быть чрезмерным, чтобы не допускать его искажения в измерительной цепи (например, в результате клиппирования).
3.2.2 Оцифровка сигнала
Наиболее важными параметрами, характеризующими процесс оцифровки аналогового сигнала, являются частота дискретизации и разрешение. Важно убедиться, что в сигнале не содержатся частотные составляющие на частоте выше половинной частоты дискретизации. В противном случае форма оцифрованного временного сигнала будет искажена, а при реализации процедуры быстрого преобразования Фурье (БПФ) в спектре вибрации вследствие эффекта наложения спектров появятся ложные составляющие (см. 4.3.7). Частота дискретизации зависит от вида выполняемого анализа и ожидаемого частотного состава сигнала. Если целью является построение временной функции сигнала, то рекомендуется, чтобы частота дискретизации примерно в 10 раз превышала максимальную частоту сигнала. Если анализ проводят в частотной области, то для реализации процедуры БПФ необходимо, чтобы частота дискретизации была в два раза выше максимальной частоты сигнала. Для защиты от наложения спектров используют фильтр нижних частот, подавляющий высокочастотный шум или другие высокочастотные составляющие с частотами выше половины частоты дискретизации. Разрядность АЦП должна быть достаточной для представления оцифрованного сигнала с требуемой точностью.
3.3 Предварительное формирование сигнала
3.3.1 Общие положения
Вибрационные сигналы с датчиков до их передачи на устройства записи обычно должны пройти еще ряд устройств для достижения необходимого уровня электрического напряжения, подавления шумов и других нежелательных сигналов. Устройства предварительного формирования сигналов включают в себя источник питания датчика вибрации, предусилитель, усилитель, интегратор и фильтры разных видов. Фильтрация сигналов рассмотрена в 3.4.
3.3.2 Интегрирование и дифференцирование
Вибрация может быть выражена через величины перемещения, скорости или ускорения. Обычно выбор предпочтительной величины обусловлен диапазоном частот анализа (в низкочастотной области выше уровень сигнала перемещения, а в высокочастотной - сигнала ускорения) или применяемым критерием оценки вибрации. Преобразование одной величины в другую может быть осуществлено посредством операций интегрирования и дифференцирования. Интегрирование ускорения по времени позволяет получить сигнал скорости, а интегрирование сигнала скорости - перемещение. Двойное интегрирование ускорения позволяет получить сигнал перемещения непосредственно, без промежуточных операций. Дифференцирование является операцией, обратной интегрированию.
Для гармонических сигналов справедливы следующие математические соотношения между перемещением х, скоростью v и ускорением а:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
где w - угловая частота гармонического сигнала, w = 2pf.
Примечание - См. также 4.3.12.
Обычно в качестве датчика вибрации используют акселерометр, поэтому операция интегрирования является более употребительной, чем операция дифференцирования. Технически операцию интегрирования реализовать проще, чем дифференцирование. Однако особого внимания требует интегрирование низкочастотного сигнала. Перед операцией интегрирования следует использовать фильтр верхних частот для подавления составляющих на частотах ниже диапазона частот анализа.
3.3.3 Среднеквадратичное значение
В стандартах, посвященных оценке вибрационного состояния машин, критерии оценки, как правило, построены для среднеквадратичного значения одной из величин, характеризующих вибрацию, в определенном диапазоне частот. Данный параметр наиболее часто используют для количественного описания вибрации на заданном интервале времени. Применение других параметров может вызвать трудности, если сигнал вибрации содержит множественные частотные составляющие или модуляционные компоненты. Среднеквадратичное значение может быть получено для любого сигнала, и большинство средств измерений вибрации обеспечивают его непосредственное измерение (см. рисунок 5). Кроме того, среднеквадратичное значение сигнала может быть получено с помощью анализатора спектра интегрированием по всем частотным составляющим в диапазоне частот анализа.
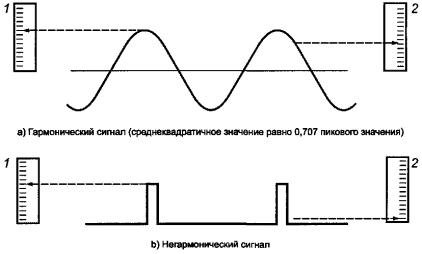
1 - пиковое значение; 2 - среднеквадратичное значение
Рисунок 5 - Среднеквадратичное значение сигнала
Отфильтрованный сигнал вибрации может быть подан на показывающее устройство, откалиброванное для считывания среднеквадратичных значений, если эти показания не изменяются значительно за короткий промежуток времени. В противном случае сигнал должен быть усреднен на некотором интервале времени. Для этого может использоваться средство измерений с достаточно большой постоянной времени.
3.3.4 Динамический диапазон
Динамический диапазон представляет собой отношение максимального значения сигнала к его минимальному значению, которые могут быть измерены данным средством измерений при данных настройках. Значения сигналов пропорциональны выходным напряжениям датчиков и измеряются обычно в милливольтах.
Динамический диапазон аналоговых систем обычно ограничен их внутренним электрическим шумом, создаваемым в таких элементах измерительной цепи, как фильтры, усилители, записывающие устройства и т.д.
В цифровых системах динамический диапазон зависит от реализации процедуры дискретизации. Частота дискретизации должна соответствовать частотам анализируемого сигнала. Соотношение между разрядностью АЦП N, в битах, и динамическим диапазоном D, в дБ, (если учесть, что один разряд используют для обозначения знака сигнала) определяют по формуле
D = 6(N - 1). (4)
Таким образом, 16-разрядный анализатор имеет динамический диапазон 90 дБ, однако этот динамический диапазон будет уменьшен при наличии любых факторов, искажающих результат оцифровки аналогового сигнала.
3.3.5 Калибровка
Калибровка датчиков вибрации рассмотрена в ряде стандартов (см., например, [9]). Эту операцию проводят в специализированной лаборатории перед применением датчика в процессе измерений. Рекомендуется проводить калибровку каждый раз до начала измерений. Обычно калибровку выполняют для измерительной цепи в целом, включающей в себя помимо датчика усилители, фильтры, интеграторы и устройства записи. Как правило, калибровку осуществляют подачей на вход измерительной цепи известного тестового сигнала с наблюдением сигнала на выходе. В зависимости от типа измерений тестовый сигнал может представлять собой ступенчатую функцию, гармонический или случайный сигнал.
Датчики некоторых типов, например, бесконтактные датчики перемещений, даже будучи предварительно калиброванными, требуют подтверждения характеристик в условиях измерений для учета влияния чистоты обработки и физических свойств поверхности, вибрацию которой измеряют. Калибровку таких датчиков проводят на месте измерений с помощью микрометра.
Для калибровки на месте датчиков инерционного типа используют вибростенд.
Датчики деформации также часто калибруют на месте после их установки. Если известна нагрузка, прилагаемая к элементу конструкции, на котором проводят измерения, то калибровку рекомендуется проводить, прилагая эту нагрузку. Если это неосуществимо, то калибровку датчика деформации проводят, соединив его параллельно с шунтирующим сопротивлением, что позволяет изменить электрический импеданс на известную величину, которая эквивалентна определенной деформации, измеряемой датчиком.
Для предварительной обработки сигнала и его последующего анализа применяют фильтры трех основных типов:
- фильтры нижних частот;
- фильтры верхних частот;
- полосовые фильтры.
Фильтр нижних частот пропускает низкочастотные составляющие сигнала, подавляя составляющие на частотах выше граничной частоты фильтра (частоты среза). Примером применения таких фильтров является фильтрация для защиты от наложения спектров (см. 4.3.7), а также подавление нежелательных высокочастотных составляющих в задачах определенного вида (например, подавление зубцовой частоты при балансировке машины).
Фильтры верхних частот в основном используют для исключения собственного низкочастотного шума датчиков вибрации (тепловые шумы) или других нежелательных частотных составляющих сигнала перед проведением анализа. Эти составляющие, хотя и не представляют интереса с точки зрения проводимого анализа, могут существенно перегрузить измерительную систему, вызывая уменьшение ее динамического диапазона.
Полосовые фильтры при анализе вибрации применяют для выделения определенных полос частот. Наиболее употребительными полосовыми фильтрами являются октавные фильтры и фильтры с шириной полосы в долю октавы, применяемые особенно часто при совместных измерениях вибрации и шума.
Применение фильтрации особенно важно, если измерения проводят в широком динамическом диапазоне значений сигнала. Если в спектре сигнала, например, присутствуют составляющие как с большими, так и с малыми амплитудами, то их нельзя оценить с одинаковой точностью ввиду ограничений на динамический диапазон измерительной системы. В таких случаях может потребоваться «вырезать» составляющие с большой амплитудой, чтобы повысить точность анализа оставшихся компонент сигнала.
Фильтрацию часто применяют для отделения информативного сигнала от возмущений (электронного шума в высокочастотной области, сейсмических колебаний в области очень низких частот).
Если фильтры используют для выделения конкретной частотной составляющей, то следует убедиться, что фильтрация обеспечивает достаточное подавление составляющих на других частотах. Фильтры простой конструкции (низких порядков) не обеспечивают подавление всех составляющих вне анализируемой области частот вследствие пологого спада их частотной характеристики.
Пример - Фильтр, крутизна спада частотной характеристики которого составляет 24 дБ/октава, будет пропускать 15 % сигнала на удвоенной частоте среза и 45% сигнала на полуторной частоте среза. Чтобы улучшить подавление нежелательных составляющих, применяют каскад из нескольких фильтров простой конструкции или используют фильтры более высоких порядков.
4 Обработка и анализ данных
4.1 Общие положения
Обработка данных включает сбор исходных данных, фильтрацию нежелательного шума и других сигналов, не представляющих интерес для последующего анализа, и представление сигналов в форме, требуемой для диагностирования. Поэтому обработка данных является важным этапом в процессе постановки диагноза. Сборщики данных с датчиков вибрации должны обеспечивать достаточное разрешение как по амплитуде, так и по времени. Если собираемые данные представляют в цифровом виде, то разрядность устройства должна быть достаточно высока для обеспечения требуемого разрешения по амплитуде. Устройства высокой разрядности позволяют проводить анализ с более высокой точностью, но имеют большую стоимость и предъявляют более высокие требования к быстродействию.
После того, как данные собраны, следующий этап состоит в их обработке и представлении, в максимальной степени облегчающему пользователю постановку диагноза. Примерами форматов представления данных являются диаграмма Найквиста, диаграмма Боде, диаграмма Кэмпбелла, каскадный спектр. В данном разделе приведены разные методы представления данных, используемые при определении технического состояния машин.
4.2 Анализ во временной области
4.2.1 Временная форма сигналов
Исследование временной формы сигналов ранее являлось основным способом вибрационного анализа. График зависимости мгновенного значения величины, характеризующей вибрацию, от времени или осциллограмма процесса подвергали визуальному анализу с выделением пиков широкополосной вибрации. Простое исследование формы сигнала с применением более современных средств измерений по-прежнему позволяет получить ценную информацию о техническом состоянии машины. Например, задиры на цапфе обнаруживают по сигналам с датчика перемещения, клиппирование (ограничение) сигнала свидетельствует о наличии таких дефектов как износ, ослабление в механических соединениях и т.д.
Хотя характерные особенности временных сигналов служат признаками определенных изменений в техническом состоянии машины, в ряде случаев может потребоваться дополняющий их анализ в частотной области (см. 4.3).
Основой анализа сигналов является то, что любой периодический процесс может быть представлен в виде суммы синусоид с кратными частотами. Некоторые примеры таких сигналов показаны на рисунках 6-9.
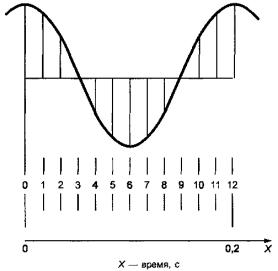
Рисунок 6 - Временная форма сигнала
На рисунке 6 показан один период гармонического сигнала постоянной амплитуды. Размах величины, характеризующей вибрацию, получают, измеряя удвоенную амплитуду сигнала и умножая на коэффициент преобразования измерительного тракта, определенный при калибровке. Частоту сигнала определяют по числу циклов на определенном интервале времени. Время определяют по временным меткам на осциллографе или по скорости протяжки ленты самописца. В изображенном на рисунке 6 примере одной секунде соответствуют 60 временных отсечек, из которых 12 отсечек приходятся на один период сигнала. Таким образом, период сигнала Т равен 0,2 с, а его частота f = 1/Т равна 5 Гц. Точность определения периода и частоты можно повысить, увеличив длину записи и, соответственно, число рассматриваемых периодов сигнала.
На рисунке 7 показана суперпозиция двух гармонических сигналов, причем на длине записи помещаются три периода сигнала с более низкой частотой. Эти сигналы можно разделить, если провести две огибающие по вершинам пиков разной полярности. Амплитуда и частота низкочастотной составляющей будут теми же, что и у построенных таким образом огибающих. Расстояние между огибающими в вертикальном направлении равно размаху высокочастотной составляющей, а ее частоту получают подсчетом пиков. В данном примере можно увидеть, что частота высокочастотной составляющей в три раза выше, чем у низкочастотной. Если отношение между частотами велико, то его можно определить визуально по графику сигнала. Во всех других случаях обычно используют Фурье-анализ.
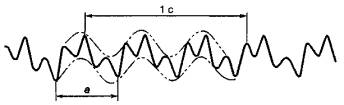
а - один период
Рисунок 7 - Суперпозиция сигналов
4.2.2 Биения
Часто сигналы имеют вид, как показано на рисунке 8, где верхняя и нижняя огибающие не совпадают по фазе. При этом совокупность верхней и нижней огибающей образует ясно различимые места пучностей и сужений. Это частный случай суперпозиции двух сигналов, которые близки и по частоте, и по амплитуде. Временные сигналы такого вида называют биениями. На практике примером биений может служить суперпозиция двух лопастных частот сдвоенного корабельного винта. Максимальные значения двух составляющих сигналов попеременно то складываются, то вычитаются. Это определяет местоположение пучностей и сужений. Расстояние между огибающими в пучностях и сужениях равно, соответственно, сумме и разности размахов составляющих сигнала. Другим примером оборудования, создающего вибрацию такого же вида, являются две спаренные машины (например, компрессоры) с приводом от асинхронного электродвигателя.
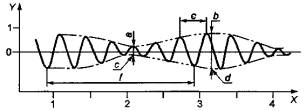
X - время, с; Y - значение сигнала; а - размах в сужении (0,2); b - размах в пучности (0,7); с
- сужение; d - пучность; е - период
вибрации (0,33 с, что соответствует 3 Гц); f - период биений (2 с, что соответствует 0,5 Гц)
Рисунок 8 - Биения
Пример - Если амплитуда большей составляющей - Хт, а меньшей составляющей - Хп, и измерения показали значение сигнала в пучности Хт + Хп = 0,7, а в сужении - Хт - Хп = 0,2, то амплитуды составляющих, соответственно, равны Хт = 0,45, Хп = 0,25. Для получения амплитуд величин, характеризующих вибрацию, эти значения нужно умножить на коэффициент преобразования измерительной цепи. Частота большей составляющей может быть определена подсчетом числа пиков, как указано выше (в примере на рисунке 8 эта частота равна 3 Гц). Данная частота может быть получена умножением частоты биений на число пиков на периоде сигнала (в данном случае на 6). Частоту меньшей составляющей получают умножением частоты биений на целое число, которое либо на единицу больше (в данном случае равно 7), либо на единицу меньше (в данном случае равно 5) числа пиков на периоде. Какой вариант следует выбрать, показывает расположение пиков в месте сужения. В примере на рисунке 8 расстояние между пиками по мере приближения к области сужения уменьшается. Это означает, что большая составляющая имеет более высокую частоту (и, наоборот, если бы большая составляющая имела более низкую частоту, то к области сужения расстояние между пиками сигнала должно было бы возрастать). По рисунку 8 можно определить, что частота биений равна 0,5 Гц. Таким образом, частоту меньшей составляющей получают умножением частоты биений на 5, и она равна 2,5 Гц.
Частота биений равна разности частот составляющих, т.е.
fb = fm - fn, (5)
где fb -частота биений;
fm - частота большей составляющей;
fn - частота меньшей составляющей.
Средняя частота появления сигналов равна полусумме частот составляющих.
Подсчет пиков для сигнала, изображенного на рисунке 8, показывает, что в интервале 2 с содержится 6 пиков, т.е. fm = 3 Гц. Интервал 2 с соответствует одному периоду биений, т.е. fb = 0,5 Гц. Из формулы (5) следует, что fn = fm - fb = 3 - 0,5 = 2,5 Гц.
Модулированный сигнал вибрации показан на рисунке 9. По форме он похож на биения, но в нем есть только одна составляющая вибрации, амплитуда которой изменяется со временем (модулирована). Существенным отличием от биений является то, что в модулированном сигнале расстояние между пиками сохраняется постоянным - ив областях пучностей, и в областях сужений. Примером модулированного сигнала является вибрация на частоте вращения шестерни с частотой изменения амплитуды вибрации, равной зубцовой частоте зубчатой передачи.

Рисунок 9 - Модуляция
Реальные сигналы вибрации могут иметь сложную форму и включать в себя одновременно как модуляцию, так и биения. Такие сигналы трудны для анализа, однако можно попытаться выделить область сигнала, где один из эффектов (и соответствующие ему частоты) временно отсутствует, и по данной области определить амплитуду и частоту интересующей составляющей сигнала.
4.2.4 Анализ огибающей
Анализ огибающей состоит в демодуляции низкочастотных составляющих в узкой полосе частот, которые плохо различимы на фоне широкополосной вибрации высокого уровня (свободные колебания ударного происхождения, вибрация на зубцовой частоте и др.). Анализ огибающей является надежным средством распознавания дефектов на ранней стадии их зарождения. Наиболее часто данный метод обработки сигнала используют при анализе вибрации зубчатых передач и подшипников качения, где низкочастотные процессы, как правило, малой мощности (например, вхождение в зацепление дефектного зуба или соударение сколотого элемента качения с дорожкой качения) возбуждают высокочастотные резонансы, что приводит к модуляции высокочастотного сигнала сигналом на частоте проявления дефекта. Пример выделения огибающей показан на рисунке 10.

Рисунок 10 - Анализ огибающей
Необходимо отметить, что перед выполнением демодуляции модулированный сигнал следует отфильтровать с помощью узкополосного фильтра.
4.2.5 Спектральные маски
Амплитуды составляющих вибрации контролируют, сопоставляя их с опорными спектральными масками - линиями предварительно установленных в полосах частот предельных значений по всему диапазону частот анализа. Превышение предельного значения какой-либо составляющей обычно вызывает появление сигнала предупреждения о возможной неисправности.
При установлении предельных значений для отдельной составляющей спектра обычно усредняют несколько спектров с высоким разрешением по частоте и определяют выборочное среднее значение и стандартное отклонение. Уровень ПРЕДУПРЕЖДЕНИЕ устанавливают выше среднего значения на 2,5-2,8 стандартных отклонений.
4.2.6 Орбита прецессии вала
Анализ траектории движения вала может быть проведен для любой машины, где есть возможность установить датчики перемещения, обычно под углом 90° друг к другу. На крупных машинах с подшипниками скольжения анализ орбиты прецессии вала является обычной практикой, поскольку он позволяет контролировать положение вала внутри подшипника и зазор между подшипником и валом. При этом необходимо убедиться, что показываемая траектория движения вала не искажена механическими и электрическими биениями. Правильная интерпретация орбиты прецессии вала позволяет понять природу вынуждающих сил. Кроме того, она позволяет определить направление прецессии вала - по направлению или против направления вращения ротора. Орбита прецессии вала может быть представлена в исходном или сглаженном виде. В последнем случае сигнал вибрации подвергают фильтрации, оставляя только составляющую на частоте вращения. Типичные графики исходной и сглаженной орбит представлены на рисунке 11.
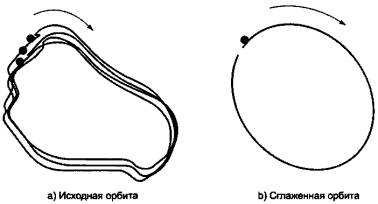
Рисунок 11 - Орбита прецессии вала
Обычно используют представление траектории движения вала, синхронизированное с оборотной составляющей, однако учет других гармоник и субгармоник вибрации при построении орбиты может быть полезен для описания источников прецессии. Отметка на валу позволяет получить сигнал синхронизации (один импульс за один оборот вала) для установления соотношения между частотой вращения и другими частотами, присутствующими в сигнале.
Орбита прецессии вала представляет собой траекторию движения центра вала в плоскости измерений. Датчики, измеряющие движение, должны быть разнесены на угол 90°, в противном случае орбита будет выглядеть сплющенной. Если на валу имеется шпоночная канавка, то по умолчанию на графике орбиты ей соответствует участок разрыва (начало канавки) и яркое пятно, показанное на рисунке темным кружком, (конец канавки). По этой информации можно судить о направлении прецессии. Из рисунка 11 следует, что прецессионное движение вала происходит по часовой стрелке.
Направление прецессии вала - по ходу или против хода часовой стрелки - зависит от точки наблюдения. Если направление прецессии совпадает с направлением вращения вала, то такую прецессию называют прямой, если не совпадает - то обратной. Из рисунка 11 видно, что имеет место прямая прецессия.
4.2.7 Среднее положение вала
Датчики перемещения часто используют для определения среднего положения вала, что позволяет оценить нагруженность подшипника скольжения. Высота положения цапфы ротора в подшипнике, измеренная по постоянной составляющей сигнала с датчика перемещения, - полезный диагностический признак при контроле состояния крупных машин. По нему можно судить, насколько точно выполнена установка подшипника и вала. При измерениях следует обращать внимание на возможный дрейф со временем постоянной составляющей сигнала, что вносит ошибку в результат измерений.
4.2.8 Переходный процесс
Измерение вибрации при изменении частоты вращения ротора обычно связано с режимами разгона и выбега. Вибрацию в этих режимах представляют в виде каскадного спектра, диаграммы Боде, диаграммы Найквиста и диаграммы Кэмпбелла.
Переходные процессы, как правило, возникают при возбуждении конструкции кратковременным силовым воздействием. Оно может представлять собой единичный импульс или колебания короткой длительности. Такое воздействие побуждает конструкцию совершать колебания на собственных частотах, но присущее системе демпфирование приводит к экспоненциальному затуханию колебаний.
Таким образом, после прекращения действия вынуждающей силы отклик конструкции представляет собой комбинацию затухающих гармонических колебаний. Пример таких колебаний показан на рисунке 12. Следует отметить, что кратковременное силовое воздействие вызывает одновременное возбуждение всех собственных мод конструкции. Обычно составляющие на высоких частотах затухают быстро, поэтому форма переходного процесса стремится к затухающей синусоиде на частоте низшей собственной моды.
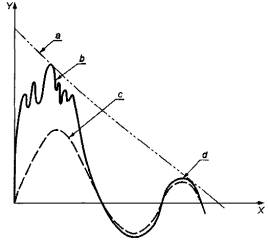
X - время; Y
- значение сигнала; а - экспоненциально затухающая огибающая пиков
сигнала; b -
сложный состав колебаний в начале переходного процесса; с - колебания на
низшей собственной моде; d - затухающие колебания
Рисунок 12 - Переходный процесс
По наличию повторяющихся переходных процессов в сигнале вибрации подшипников часто судят о наличии дефектов дорожек или элементов качения.
4.2.9 Импульс
Импульс механической системы является ее реакцией на импульсное силовое воздействие Fb приложенное в течение очень короткого промежутка времени Dt, и количественно может быть представлен в виде интеграла от F1dt по времени (в пределах от t до t + Dt) - см. рисунок 13.
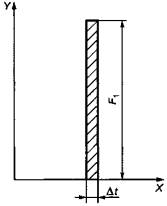
X - время; Y - сила
Рисунок 13 - Импульс
Часто импульсное воздействие используют для обнаружения резонансных частот стационарных конструкций.
4.2.10 Демпфирование
Демпфирование - это механизм преобразования колебательного движения в другую форму энергии (обычно тепловую), приводящий к затуханию колебаний. Коэффициент демпфирования с чаще всего пропорционален скорости. Если в реальной конструкции эта зависимость не соблюдается, то ее, тем не менее, часто используют для приближенных расчетов. Если коэффициент демпфирования минимальный из возможных, при которых система возвращается в состояние равновесия без колебаний относительно точки равновесия (переколебаний), то его называют коэффициентом критического демпфирования сс.
Если коэффициент демпфирования системы ниже критического, то при возвращении в положение равновесия будут наблюдаться колебания с затухающей амплитудой (см. рисунок 14). В системах со многими степенями свободы для одних собственных мод демпфирование может быть выше критического, а для других - ниже.
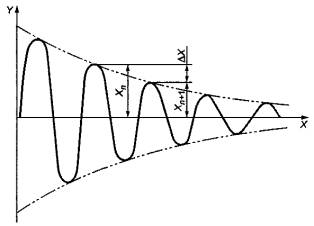
X - время; Y - значение сигнала
Рисунок 14 - Затухание сигнала вследствие демпфирования в системе
Если на графике отложена зависимость от времени затухающих колебаний собственной моды X, то логарифмический декремент колебаний d может быть рассчитан по формуле:
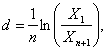 (6)
(6)
где п - число циклов затухания амплитуды от X1 до Хп+1.
Мерой относительного демпфирования в колебательной системе является коэффициент потерь h, который связан с логарифмическим декрементом колебаний зависимостью h = d/p.
Примечание - В технической литературе для обозначения коэффициента потерь обычно используют символы h, z или h, а для логарифмического декремента колебаний - a и L.
Коэффициент потерь может быть выражен через скорость затуханий X', дБ/с, по формуле
h = X'/(27,3fn), (7)
где fn - частота собственных колебаний, Гц.
Демпфирование в колебательной системе описывают также через ее добротность Q, которая представляет собой значение амплитудно-частотной характеристики системы с одной степенью свободы на собственной частоте при отсутствии затухания. Амплитудно-частотная характеристика системы представляет собой отношение амплитуды перемещения под действием динамической силы с амплитудой F к статическому перемещению под действием постоянной силы F. В предположении отсутствия существенного взаимодействия между модами добротность каждой моды может быть рассчитана по формуле
Q = 1/(2с/сс), (8)
где с - коэффициент линейного демпфирования системы;
сс - коэффициент критического демпфирования.
Если известна амплитудно-частотная характеристика системы в окрестности некоторой моды колебаний, то добротность Q для данной моды может быть приближенно рассчитана по формуле:
![]() (9)
(9)
где fr - резонансная частота;
Df = f2 - f1 - ширина полосы резонансного пика на уровне 0,707 (частоты f1 и f2, на которых значение амплитудно-частотной характеристики спадает до уровня 0,707, лежат соответственно по левую и правую стороны от пика).
Добротность связана с логарифмическим декрементом колебаний следующей приближенной формулой:
Q » p/d. (10)
Примечание - В случае малого демпфирования Q = 1/h.
В качестве примера на рисунке 15 показан способ определения добротности по амплитудно-частотной характеристике, называемой также диаграммой Боде.
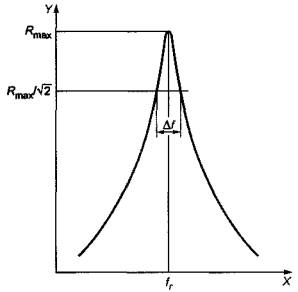
X - частота; Y -
отклик (амплитудно-частотная характеристика)
Рисунок 15 - Определение добротности Q
Аналогичный результат можно получить по графику амплитудно-фазовой частотной характеристики в полярных координатах, называемой также диаграммой Найквиста.
Характеристики демпфирования системы несут полезную информацию при исследовании причин и следствий вибрации машин вращательного действия. Допустимо, чтобы машина имела собственные моды вибрации вблизи рабочей частоты вращения, если эти моды сильно демпфированы и не способны значительно влиять на вибрацию. Кроме того, если моды слабо демпфированы, то отклик машины может быть настолько высок, что она будет неспособна пройти через область резонанса.
4.2.11 Синхронное усреднение (накопление)
Сигнал вибрации содержит как составляющие, синхронные с процессами, проходящими в машине, так и несинхронные составляющие. Разделить синхронные и несинхронные составляющие можно с помощью анализа в частотной области (см. 4.3). Другим распространенным способом анализа синхронных составляющих является синхронное усреднение по времени. При данном способе выборку данных осуществляют синхронно сдвижением отдельных частей машины посредством сигналов (импульсов) синхронизации. Усреднение по выборкам, число которых может варьироваться от нескольких единиц до нескольких сотен, проводят во временной области, а для последующего спектрального представления используют сглаженный временной сигнал. В процессе синхронного усреднения несинхронные составляющие взаимно подавляются. Чем большее число реализаций используют для усреднения, тем более гладким получается сигнал. Число реализаций зависит от конкретной ситуации.
При синхронном усреднении значения сигнала, соответствующие одной и той же фазе движения конкретной части машины, суммируют, после чего полученный результат делят на число усредняемых реализаций. В результате сохраняется только та часть сигнала, которая синхронна с рассматриваемым движением, а все остальные составляющие (в том числе, регулярной природы, но связанные с другими, несинхронизованными движениями) стремятся с ростом числа реализаций к нулю. Скорость стремления к нулю равна квадратному корню из числа реализаций.
Примечание - Усреднение по 100 реализациям уменьшает нежелательные составляющие сигнала в 10 раз, по 10 000 реализациям - в 100 раз.
Метод синхронного усреднения применяют, например, при необходимости определить, какой ротор в машине с несколькими роторами является источником повышенной вибрации. Его используют при обнаружении неисправностей, например, подшипников, лопаток или валков каландра.
Пример 1 - На каждом валу турбонасосного агрегата с приводом через редуктор установлен датчик сигнала синхронизации. Сигнал с акселерометра, установленного на редукторе, анализируют методом синхронного усреднения, позволяющим выделить сигнал, синхронизованный с каждым валом. Усреднение по времени, синхронизованное с вращением вала турбины, позволяет преобразовать исходный сигнал сложной формы в почти гармонический сигнал, амплитуда которого зависит от дисбаланса исследуемого вала. Использование сигнала синхронизации с вала насоса позволяет привести исходный сигнал к почти периодическому, соответствующему лопастной частоте насоса. По усредненному сигналу судят о радиальном смещении вала насоса в подшипнике.
Пример 2 - На две лопатки крупного гидротурбинного агрегата установлены мостовые датчики деформаций. Прием сигналов с датчиков осуществляют средствами телеметрии. Для синхронного усреднения используют сигнал синхронизации с вращением ротора турбины. После нескольких усреднений, позволяющих подавить шум водяного потока, появляются накопленные сигналы сложной формы, идентичные для каждой лопатки турбины, но сдвинутые по времени в соответствии с угловым шагом лопаток. При диагностировании требуется определить неоднородность потока через направляющие аппараты гидротурбины. Усредненные сигналы используют для регулировки направляющих аппаратов гидротурбины, чтобы улучшить характеристики потока и снизить динамические напряжения в лопатках турбины.
Хотя синхронное усреднение является эффективным средством обнаружения ряда неисправностей, оно не может быть использовано для диагностирования нерегулярных процессов, например, связанных с дефектами подшипников качения.
Для усреднения сигналов со сложными спектрами обычно необходимо, чтобы вибрация представляла собой стационарный процесс. При наличии нестационарных частотных составляющих или при изменяющейся частоте вращения простое усреднение во временной области не применяют. В этих случаях выборку значений сигнала необходимо осуществлять через интервалы, синхронизованные с нестационарным процессом (например, через интервалы, соответствующие повороту ротора на некоторый заданный угол). При преобразовании накопленного сигнала в частотную область получают вместо частотного спектра порядковый спектр. Если сигнал вибрации представляет собой реакцию на последовательность импульсных возмущений, то усреднение во временной области может быть синхронизовано с началом каждого импульса возбуждения.
Источником сигнала синхронизации не обязательно должна быть вращающаяся часть машины. Для синхронизации могут быть использованы движущиеся ремни бумагоделательных машин или конвейерных лент. Усредняемый сигнал не обязательно должен быть сигналом вибрации. Это может быть любой процесс, связанный с обследуемой машиной, по которому можно судить о ее неправильном функционировании. Кроме того, чтобы не устанавливать датчики синхронизации на каждом валу (например, при диагностировании зубчатой передачи), можно установить его на одном валу и использовать умножитель частоты для получения сигнала синхронизации с вращением других валов.
4.3 Анализ в частотной области
4.3.1 Общие положения
Широкое распространение анализа вибрации в частотной области объясняется тем, что, как правило, каждому источнику вибрации можно поставить в соответствие некоторые спектральные компоненты. Информативным является даже одноканальный анализ вибрации, однако часто бывает важно использовать второй канал для сравнения фаз или амплитуд частотных составляющих.
Основным методом преобразования широкополосного временного сигнала в отдельные частотные составляющие является преобразование Фурье - математическая операция, позволяющая разложить сигнал вместе с присутствующим в нем механическим или электрическим шумом на синусоидальные составляющие. Для реализации метода используют компьютер с соответствующей программой обработки данных, специальное измерительное устройство (Фурье-анализатор) или микропроцессор. В современных средствах анализа преобразование Фурье выполняется посредством эффективного математического алгоритма быстрого преобразования Фурье (БПФ).
Посредством БПФ временной сигнал преобразуют в отдельные синусоидальные составляющие, зависящие от частоты (см. рисунок 16). При выборе анализатора БПФ необходимо принимать во внимание несколько важных факторов. Существует соотношение между числом спектральных линий (разрешением по частоте), диапазоном анализируемых частот и длиной исходной временной реализации. В примере на рисунке 16 разрешение по частоте составляет 2 Гц, что дает 100 спектральных линий в диапазоне от 0 до 200 Гц.
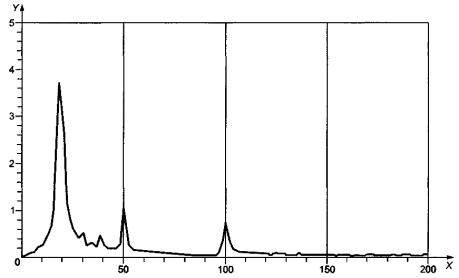
X - частота, Гц; Y -
амплитуда
Рисунок 16 - Амплитудный спектр
Указанные параметры должны быть выбраны так, чтобы обеспечить максимальное разрешение в диапазоне частот анализа.
Вследствие эффекта наложения спектров (см. 4.3.7) некоторые высокочастотные составляющие сигнала могут быть ложно истолкованы как низкочастотные составляющие. Чтобы избежать этого, используют специальный фильтр нижних частот.
Результатом преобразования Фурье является комплексный спектр, который может быть представлен в виде:
- амплитуд и фаз частотных составляющих;
-действительной и мнимой части каждой частотной составляющей.
Как правило, амплитудный спектр является более информативным для целей диагностики, поэтому фазовым спектром в анализе зачастую пренебрегают.
4.3.3 Эффект просачивания энергии и применение оконных функций
При оцифровке временного сигнала может наблюдаться эффект перераспределения энергии между частотными составляющими (эффект просачивания), если длина выборки содержит нецелое число циклов сигнала. Результатом такого неточного представления реализацией исходного временного сигнала является размывание частотных пиков. Уменьшить эффект просачивания помогает применение соответствующих оконных функций. Наиболее употребительным является окно Ханна (хэннинг), которое дает хорошие результаты для стационарных процессов, однако возможно применение и окон другого вида.
Для переходных процессов наилучший результат может быть получен при использовании окна прямоугольной формы. Окно Хэмминга позволяет получить более острые пики, чем в случае применения хэннинга, но при этом увеличивает уровень боковых лепестков (просачивания энергии). Наоборот, окно Блэкмана и его модификация, окно Блэкмана-Харриса, обеспечивают пониженный уровень боковых лепестков, но при увеличенной размытости центрального пика. Плосковершинное окно позволяет получить более точную оценку амплитуд, чем хэннинг, но при этом невозможно различить слабые сигналы в окрестности мощного частотного пика. Плосковершинное окно дает наиболее широкий пик с боковыми лепестками, аналогичными хэннингу, но гладкая вершина пика позволяет наиболее точно определить соотношение между амплитудами при изменении частоты. Сглаживая погрешности выборки, оконные функции улучшают и спектральное представление нестационарных сигналов (например, каскадный спектр). Плосковершинное окно, как сохраняющее наиболее точные соотношения между амплитудами разных гармонических сигналов, может использоваться в процедурах калибровки.
Примечание - Оконные функции, применяемые совместно с преобразованием Фурье, рассмотрены в [10].
4.3.4 Разрешение по частоте
Применение БПФ требует, чтобы исследуемый диапазон частот был разбит на конечное число поддиапазонов, вибрация в каждом из которых отображается в виде вертикальной линии. Число поддиапазонов соответствует числу линий разрешения NLOR. Поддиапазон может включать в себя более одной частотной составляющей сигнала. В этом случае анализатор отобразит суммарную энергию этих составляющих в виде одной спектральной линии на центральной частоте поддиапазона.
Чтобы различить близкорасположенные частотные составляющие сигнала, число линий разрешения спектра должно быть достаточно велико. В то же время диапазон анализа должен включать все интересующие исследователя частотные составляющие. Обычно используют не менее 400 линий разрешения, но диагностирование многих машин требует еще более высокого разрешения. Рассматриваемые параметры связаны следующей формулой:
NLOR = fmax/В, (11)
где NLOR - число линий разрешения;
fmax - максимальная частота анализируемого диапазона частот;
В - ширина поддиапазона (расстояние между соседними спектральными линиями).
Как видно из формулы (11), для одного и того же анализируемого диапазона частот лучшее разрешение по частоте обеспечивается при меньшем расстоянии между спектральными линиями.
4.3.5 Длина записи
Для реализации преобразования Фурье достаточно короткой записи сигнала длительностью Т, но при заданном разрешении по частоте В длину записи определяют по формуле
Т = 1/В. (12)
Если длина записи сигнала ограничена, то это может наложить ограничение на разрешение по частоте. Например, если диапазон частот анализа составляет 100 Гц с разрешением 400 спектральных линий, то расстояние между линиями должно быть 1/4 Гц, а длина записи сигнала - 4 с. Если при том же числе спектральных линий анализируемый диапазон частот увеличить в несколько раз, то во столько же раз будет больше расстояние между линиями, и, соответственно, во столько же раз уменьшится необходимая длина записи.
Если частота вращения части машины медленно изменяется в ходе обследования, то важно обеспечить такое расстояние между спектральными линиями, чтобы каждой частотной составляющей сигнала соответствовала одна спектральная линия. Если изменение частоты вращения значительно, то выборка должна быть синхронизована с изменениями углового положения вращающейся части машины и применен порядковый анализ сигнала (см. 4.2.11 и 4.3.8).
4.3.6 Амплитудная модуляция (боковые полосы)
Представление амплитудно-модулированного сигнала во временной области рассмотрено в 4.2.3. БПФ модулированного гармонического сигнала представляет собой составляющую на частоте гармонического сигнала и боковые полосы по обе стороны от этой частоты на расстоянии, равном частоте модулирующего сигнала. Если модулирующий сигнал тоже представляет собой гармонический процесс, то в боковой полосе будет одна частотная компонента. Таким может быть вид спектра зубчатой передачи, если зубцовая частота модулирована сигналом, обусловленным эксцентриситетом или износом одной из шестерен. Если модуляция является периодической, но не гармонической, то боковые полосы содержат по нескольку частотных составляющих. Если модуляция непериодическая, то боковые полосы будут размыты.
Наличие боковых полос является хорошим диагностическим признаком обрыва стержня ротора асинхронного двигателя. Отношение боковых составляющих к составляющей основной частоты LD, дБ, может быть получено по формуле
LD = 20lg(l1/lref), (13)
где l1 - амплитуда боковой составляющей;
lref - амплитуда составляющей на частоте сети (50 или 60 ГЦ).
Как видно по рисунку 17, спектр вибрации исправного двигателя содержит выраженный пик на сетевой частоте и размытые боковые полосы, уровень которых ниже уровня основного пика (в данном случае, на частоте 60 Гц) на 60 дБ.
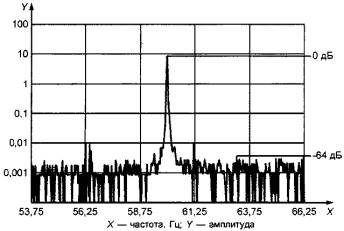
Рисунок 17 - Спектр вибрации исправного электродвигателя
На рисунке 18 показан спектр вибрации неисправного двигателя. На нем отчетливо виден пик сетевой частоты и увеличившиеся боковые пики, появление которых обусловлено обрывом стержня ротора.

X - частота, Гц; Y - амплитуда
Рисунок 18 - Спектр вибрации неисправного электродвигателя
Следует отметить, что вид боковых полос несет ту же информацию, что и спектр огибающей сигнала при его анализе во временной области.
Эффект наложения спектров заключается в появлении в спектре ложных частотных составляющих, что имеет место, когда частота дискретизации цифрового анализатора ниже необходимой, чтобы адекватно описать анализируемый сигнал. Это похоже на то, как вращающийся диск кажется неподвижным, если частота стробоскопа (аналогичная частоте дискретизации сигнала) точно совпадает с частотой вращения, а если совпадение неточное, то диск кажется медленно вращающимся. Аналогично, если выборки сигнала брать через слишком большие интервалы времени, то в спектре сигнала появится несуществующая в действительности составляющая низкой частоты. Данный эффект устраняется, если перед процедурой выборки сигнал пропустить через фильтр нижних частот, подавляющий составляющие сигнала с частотами выше половины частоты дискретизации (антиалайзинговый фильтр).
Сказанное проиллюстрировано на рисунке 19. Из рисунка видно, что частота дискретизации менее половины частоты высокочастотного сигнала. В результате вместо реального высокочастотного сигнала анализу будет подвергнут его «двойник» в низкочастотной области, построенный по тем же выборочным значениям сигнала (на графике они обозначены светлыми кружками).
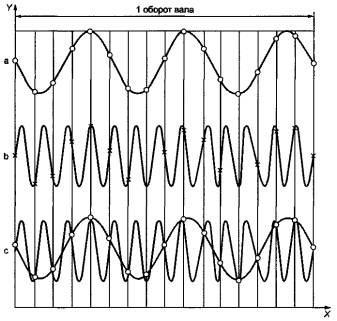
X - время; Y - значение сигнала; а - 3-я гармоника оборотной частоты; b - 13-я гармоника оборотной частоты; с
- 3-я и 13-я гармоники оборотной частоты с совпадающими выборочными значениями
сигнала
Рисунок 19 - Эффект наложения спектров
Если половинная частота дискретизации, называемая частотой Найквиста, точно совпадает с максимальной частотой реального сигнала, то, теоретически, выборка несет полную информацию об исходном сигнале. На практике, как правило, частоту дискретизации выбирают более высокой (обычно в 2,56 раза выше максимальной частоты сигнала), принимая во внимание, что антиалайзинговый фильтр имеет неидеально резкую характеристику спада.
Современные цифровые анализаторы содержат встроенные фильтры для защиты от наложения спектров, позволяющие подавлять все частотные составляющие выше 40 % частоты дискретизации до выполнения процедуры оцифровки сигнала, тем самым исключая эффект наложения спектров. Тем не менее, специалист должен перед началом исследования убедиться в том, что такой проблемы действительно не существует.
Многие анализаторы сигналов не ограничиваются проведением выборки на фиксированных частотах дискретизации, но позволяют варьировать эту частоту синхронно с внешним сигналом. Обычно частоту дискретизации выбирают кратной частоте внешнего сигнала. Особенно часто данный прием применяют при анализе сигналов машин вращательного действия, где для определения частоты дискретизации используют отметчик числа оборотов. Частота дискретизации должна более чем в два раза превосходить частоту наивысшей гармоники оборотной частоты, принимаемой во внимание при анализе.
Фурье-преобразование синхронизованной выборки значений сигнала представляет собой порядковый спектр Х(п). Порядок п = 1 соответствует оборотной частоте.
Получение синхронной выборки и применение порядкового спектра имеют следующие основные достоинства:
a) при изменении частоты вращения машины большинство частотных составляющих, связанных с оборотной частотой (лопастные, зубцовые частоты и т.п.), остаются в порядковом спектре на своих местах, и их энергия не размывается по нескольким спектральным линиям;
b) все гармоники точно совпадают с положением одной из спектральных линий порядкового спектра (попадают в середину поддиапазона, определяющего спектральную линию), благодаря чему их амплитуды измеряют с большей точностью;
c) можно провести усреднение по нескольким измерениям, не принимая во внимание изменения частоты вращения машины;
d) все гармоники вибрации будут сохранять один и тот же фазовый угол по отношению к внешнему сигналу синхронизации. Это означает, что при усреднении все составляющие сигнала, связанные с вращением вала, будут сохраняться, в то время как несинхронные случайные составляющие, пусть даже и на частоте гармоник оборотной частоты, будут стремиться к нулю.
Порядковый анализ является одним из широко применяемых методов исследования сигнала (см. 4.6).
Проводя синхронное усреднение сигнала, следует помнить, что при этом подавляются несинхронные составляющие, которые могут иметь важное значение для диагностирования.
4.3.9 Усреднение спектров
В зависимости от частотного состава сигнала для получения одной реализации спектра (преобразования Фурье) требуется реализация сигнала длительностью от долей секунды до нескольких секунд. Однако для модулированного сигнала надежное определение средней амплитуды может потребовать большего времени. Поэтому очень важной функцией анализатора является усреднение нескольких полученных подряд спектров. При наличии одного канала передачи данных (канала измерений) усреднение проводят по амплитудам частотных составляющих без учета фазовых соотношений. Чтобы провести усреднение комплексного спектра (действительной и мнимой частей), необходима синхронизация спектров посредством дополнительного сигнала, связанного с фазами движения частей машины.
Существует ряд модификаций метода усреднения в частотной области, но ввиду сложности их математического аппарата они используются только в особых случаях.
Тем не менее, многие анализаторы способны дополнительно проводить экспоненциальное усреднение спектров. При этом усредняемым спектрам присваиваются экспоненциально убывающие веса, так что большие веса имеют спектры, рассчитанные последними. Данный метод часто применяют при анализе переходных процессов, в которых сигнал спадает со временем по экспоненциальному закону.
Еще одним применяемым в анализаторах методом усреднения является удержание пиковых значений. Этот метод состоит в том, что в течение заданного временного интервала для каждой спектральной линии находят ее максимальное значение по всем спектрам, снятым за данный период, и эти максимальные значения отображаются в усредненном спектре.
4.3.10 Логарифмический масштаб представления данных
Сигналы вибрации часто содержат много частотных составляющих с существенно разными амплитудами. Составляющие с малыми амплитудами могут быть важны для вибрационного контроля состояния машин, но на графике в линейном масштабе плохо различимы. Построение графика в логарифмическом масштабе приводит к уменьшению больших составляющих и подчеркиванию малых, что позволяет представить в удобном виде все нужные компоненты сигнала, а также уровень шумового пьедестала. При представлении данных в логарифмическом масштабе амплитуду X преобразуют в ее уровень L, дБ, по формуле
L = 20lg(X/Xref), (14)
где Xref - опорное значение.
Иногда логарифмический масштаб используют для оси частот. Это позволяет лучше распознать отдельные области или подчеркнуть низкочастотный диапазон. Однако при этом сохраняют представление частот в абсолютных, а не относительных единицах (см. 4.7).
Примеры отношений двух величин в абсолютных единицах и в децибелах приведены в таблице 1.
Таблица 1 - Отношения двух величин в абсолютных единицах и в децибелах
|
Отношение в децибелах |
Отношение в абсолютных единицах |
Отношение в децибелах |
Отношение в абсолютных единицах |
|
0 |
1 |
26 |
20 |
|
6 |
2 |
40 |
100 |
|
20 |
10 |
60 |
1 000 |
Если отношение двух величин менее единицы, то соответствующее ему значение в децибелах будет отрицательной величиной. Например, отношению 1/2 соответствует минус 6 дБ.
Опорные значения для уровней разных величин приведены в ИСО 1683. В целях анализа вибрации рекомендуется использовать опорные значения, приведенные в таблице 2.
Таблица 2 - Опорные значения для уровней величин
|
Величина |
Опорное значение |
Величина |
Опорное значение |
|
Ускорение |
10-6 м/с2 |
Перемещение |
10-12 м |
|
Скорость |
10-9 м/с |
Мощность |
10-12 Вт |
4.3.11 Увеличение масштаба («лупа»)
Часто отображаемые частотные составляющие спектра (содержащего, как правило, 400 линий) расположены слишком близко друг к другу, что затрудняет их распознавание. Некоторые анализаторы обладают функцией увеличения разрешения (числа спектральных линий), но чаще для лучшего различения частотных составляющих используют режим увеличения масштаба, называемый также «лупой». В данном режиме начало спектра совпадает не с 0 Гц, а с любой заданной частотой, так что в произвольно выбранном анализируемом диапазоне частот содержится одинаковое число спектральных линий. Необходимо отметить, что при сужении полосы анализа длина записи должна соответствующим образом возрастать. Применение режима увеличения масштаба предъявляет повышенное требование к стабильности частотных составляющих сигнала.
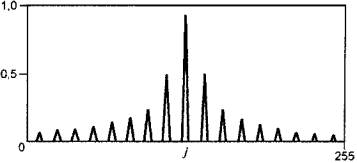
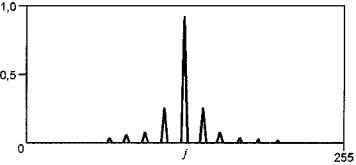
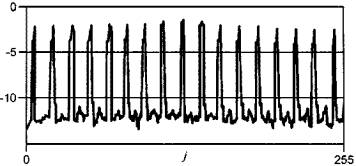
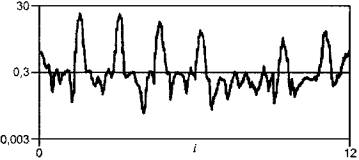
Примером использования режима увеличения масштаба является диагностирование зубчатой передачи. Дефект зубчатой передачи проявляется в появлении боковых полос по обе стороны от зубцовой частоты, а расположение боковых полос указывает на дефектную шестерню. Режим увеличения масштаба может быть также полезен при диагностировании подшипников качения. На рисунке 20 видны преимущества такого анализа. Частотные составляющие, не различимые в первоначальном спектре, после увеличения масштаба становятся отчетливо видимыми.
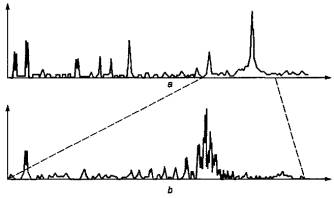
a -
участок исходного спектра; b - тот же участок спектра
после увеличения масштаба
Рисунок 20 - Увеличение масштаба
4.3.12 Дифференцирование и интегрирование
Операции дифференцирования и интегрирования используют в анализе вибрации при необходимости преобразовать друг в друга сигналы перемещения, скорости и ускорения. У машин вращательного действия часто доминирует составляющая на частоте вращения, а сигнал близок к гармоническому. Для таких сигналов справедливы следующие формулы для перемещения х, скорости v и ускорения а:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
или
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
где ![]() - амплитуды,
соответственно, перемещения, скорости и частоты;
- амплитуды,
соответственно, перемещения, скорости и частоты;
w - угловая частота;
t - время.
Фаза перемещения опережает фазу скорости на 90°, а фаза скорости на 90° опережает фазу ускорения. В частотной области преобразование величин друг в друга при дифференцировании и интегрировании осуществляется, соответственно, умножением и делением каждой составляющей спектра на ее собственную угловую частоту. Большинство анализаторов позволяет осуществить операции дифференцирования и интегрирования в частотной области.
Следует подчеркнуть, что применение формул (15)-(20) предполагает, что сигнал является преимущественно гармоническим, т.е. необходимо убедиться, что доля составляющей оборотной частоты в исходном сигнале составляет не менее 90 %. В противном случае преобразование одной величины в другую следует осуществлять для каждой частотной составляющей в отдельности.
4.4 Представление результатов измерений для переходных режимов работы машины
4.4.1 Амплитуда и фаза сигнала
Если гармонический сигнал описывают в терминах амплитуды и фазы, то необходим дополнительный опорный сигнал для определения фазы. Такой сигнал может быть получен с помощью отметчика числа оборотов; с датчиков, измеряющих вибрацию в другой точке или в другом направлении; с устройств измерения силы и т.п. Частоту (частоты) опорного сигнала соотносят с анализируемой частотой сигнала вибрации. Например, отметчик числа оборотов может быть использован для получения опорного значения фазы составляющей на частоте вращения или фаз ее гармоник. Фаза может изменяться в диапазоне от 0 до 360° или в диапазоне ±180°.
Если сигналы соответствуют разным физическим величинам (например, силе, скорости, ускорению), то их интерпретация должна быть проведена с учетом особенностей этих величин. Например, для гармонического сигнала скорость запаздывает по отношению к перемещению на 90°, и также на 90° запаздывает ускорение по отношению к скорости. Фаза сигнала может быть искажена при его прохождении по измерительной цепи. Поэтому в результаты измерений необходимо корректировать с учетом сдвига фазы, вносимого измерительной цепью.
Амплитуда и фаза гармонического сигнала могут быть представлены как функции времени. Если же аргументом амплитуды и фазы вибрации машины выбирают частоту вращения, то график в этих координатах называют диаграммой Боде (см. рисунок 21).
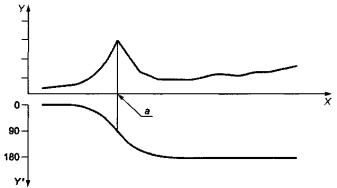
X - частота вращения; Y - амплитуда; Y' - фаза (в градусах); а - резонанс
Рисунок 21 - Диаграмма Боде
4.4.2 Диаграмма в полярных координатах (диаграмма Найквиста)
На диаграмме в полярных координатах (см. рисунок 22) каждой частоте поставлен в соответствие вектор частотной составляющей (длина вектора - амплитуда, угол поворота вектора - фаза). Если параметром является частота вращения, и концы векторов, соответствующих разным частотам вращения, соединены линией, то такой график называют диаграммой Найквиста.

Примечание - Параметром (точки на кривой) является частота вращения ротора, мин-1.
Рисунок 22 - Диаграмма Найквиста
Диаграмма в полярных координатах построена относительно опорного значения фазы (по сигналу с датчика синхронизации). Диаграммы Найквиста и Боде используют для определения частот вращения, на которых имеют место резонансы системы «ротор - подшипник-опора».
4.4.3 Каскадный спектр
Каскадный спектр обеспечивает проведение сравнительного анализа поведения нескольких частотных составляющих. Он представляет собой трехмерный график, на котором показано изменение частотных составляющих в зависимости от выбранного параметра (частоты вращения, нагрузки, температуры), измеряемого в фиксированные моменты времени.
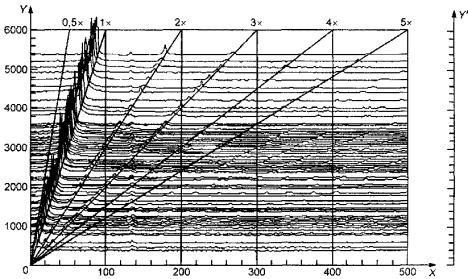
X - частота, Гц; Y - частота вращения, мин-1;
Y' - амплитуда
Рисунок 23 - Каскадный спектр
Пример каскадного спектра, изображенного на рисунке 23, иллюстрирует, каким образом изменяются спектры вибрации машины в режиме разгона (выбега). Каскадный спектр показывает зависимость амплитуды от частоты (выраженной в герцах или в порядковом номере гармоники) частотных составляющих при разных значениях частоты вращения. Иногда частоту вращения заменяют другой переменной (временем, нагрузкой). Если каскадный спектр строят для разных значений частоты вращения, то необходимо иметь запись сигнала синхронизации с частотой вращения ротора.

X - частота, Гц; Y - время суток; Y' - частота вращения, мин-1;
Y'' - амплитуда
Рисунок 24 - Каскадный спектр вибрации турбины
На рисунке 24 показано изменение оборотной частоты и других существенных гармоник сигнала. Если каскадный спектр отражает поведение ротора в переходном режиме, то на нем отчетливо видны критические частоты вращения ротора.
Вид каскадного спектра зависит от типа и режима работы машины. На рисунке 24 показан каскадный спектр вибрации паровой турбины с номинальной частотой вращения 3 000 мин-1 (50 Гц) при разгоне и выбеге.
Если форма спектра зависит от времени, то альтернативным представлением сигнала является спектрограмма процесса (см. рисунок 25). На спектрограмме изменение амплитуд частотных составляющих во времени или в соответствии с изменением частоты вращения показано изменением оттенка серого цвета.
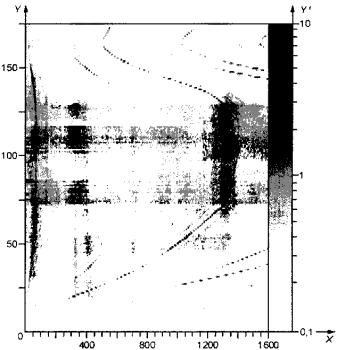
X - частота, Гц; Y - время, с; Y' - амплитуда ускорения, м/с2 (показана оттенками
серого цвета)
Рисунок 25 - Двумерная спектрограмма
Примечание - Графики на рисунках 23, 24 и 25 относятся к разным машинам.
4.4.4 Диаграмма Кэмпбелла
Диаграмма Кэмпбелла (см. рисунок 26) является частным случаем каскадного спектра. Она показывает, как изменяются характерные частотные составляющие (на лопастной, зубцовой частотах) с изменением частоты вращения. Амплитуду показывают высотой соответствующего столбика. Диаграмма Кэмпбелла особенно полезна для обнаружения самовозбуждения собственных колебаний.
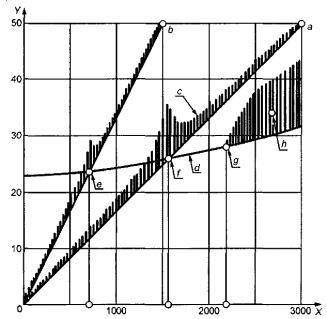
X - частота вращения, мин-1; Y -
частота, Гц; а - 1-я гармоника частоты вращения; b - 2-я
гармоника частоты вращения; с - амплитуда; d - собственная частота; е - резонансная частота вращения;
f - резонансная частота
вращения; g - граница области
нестабильности; h - субгармоники,
появляющиеся при нестабильном поведении ротора
Рисунок 26 - Диаграмма Кэмпбелла
4.5 Анализ в реальном масштабе времени
Анализом в реальном масштабе времени называют исследования, при которых результат отображается в момент измерений. Часто под этим понимают, что данные отображаются сразу же после их записи, что позволяет оператору проводить наблюдение данных в процессе их сбора. Однако в настоящем подразделе понятие анализа в реальном масштабе времени основано на сопоставлении затрат времени на сбор данных и на их обработку. Если время, требуемое на обработку блока данных, превышает время их сбора, т.е. не все данные могут быть обработаны в момент их поступления, то такую процедуру нельзя назвать анализом в реальном масштабе времени. Иногда обработка данных предполагает предварительное формирование всего массива данных, а иногда в процессе анализа происходит неоднократное обращение к одному и тому же массиву данных. С другой стороны, некоторое количество данных может быть собрано сверх необходимого для обработки, т.е. в процессе обработки их не используют.
В аналоговых системах анализатор в реальном масштабе времени обычно состоит из набора фильтров, через которые входные сигналы пропускаются одновременно. Ранее в таких анализаторах применяли преимущественно октавные и третьоктавные фильтры.
В цифровых системах сигнал вибрации оцифровывают для получения последовательностей записей. Каждая запись обрабатывается для получения соответствующей характеристики, например, спектра. Перед обработкой записи выборка должна быть завершена. Однако выборка текущей записи и обработка предыдущей записи могут проводиться одновременно. Если процедура формирования записи занимает больше времени, чем ее обработка, то за время сбора данных может быть проведен анализ всех сигналов. Такой анализ считают выполненным в реальном масштабе времени. Если же время обработки записи превышает время записи, то часть сигналов остается необработанной, и такой анализ нельзя рассматривать как выполненный в реальном масштабе времени. Различные анализаторы обладают разной скоростью обработки данных, поэтому для каждого анализатора существует свой диапазон частот, в котором анализ может быть выполнен в реальном масштабе времени. Такой диапазон частот называют полосой частот реального масштаба времени.
Для машин с постоянной частотой вращения проведение анализа в реальном масштабе времени, как правило, не является необходимым. Но в переходных режимах работы, таких как разгон и выбег, слишком узкая полоса частот реального масштаба времени может привести к пропуску существенной информации.
Чтобы избежать этого, рекомендуется записать временной сигнал для всего переходного режима, после чего проводить анализ не в реальном масштабе времени с той скоростью, которую позволяет измерительная аппаратура
Если машина работает с изменяющейся частотой вращения, то процедура усреднения спектров вибрации затруднена, поскольку энергия отдельных гармоник оборотной частоты может быть сосредоточена (в зависимости от реализации) в разных спектральных линиях. В результате полученная при усреднении амплитуда гармоники будет более низкой, чем если бы частота вращения машины оставалась постоянной. Управляя частотой выборки синхронно с частотой вращения машины посредством дополнительного сигнала синхронизации (см. 4.3.8), можно добиться того, чтобы энергия каждой гармоники была сосредоточена в единственной спектральной линии. Обычно дополнительный сигнал синхронизован с оборотной частотой вращения ротора. Полученный при этом спектр гармоник оборотной частоты называют порядковым.
Первоначально порядковый спектр был получен с помощью следящих фильтров, используемых для защиты от наложения спектров, у которых частота среза (в 2,56 раза превышающая максимальную частоту диапазона анализа) изменялась синхронно с вращением ротора и в соответствии с изменением диапазона анализа изменялась частота дискретизации. Повышенный шум и невысокая точность аналоговых систем вместе с ограничениями на скорость управления изменением частоты дискретизации привели к использованию цифровых систем вычисления порядкового спектра.
В цифровых системах оцифровке с одной и той же фиксированной частотой дискретизации подлежат как сигнал вибрации, так и сигнал синхронизации с датчика оборотов. Оцифрованный сигнал синхронизации используют для восстановления частоты оборотов и определения интервала дискретизации для каждого оборота вала, а сигнал вибрации подлежит интерполяции для взятия повторных выборочных значений через полученные интервалы дискретизации. Интервалы дискретизации могут изменяться скачкообразно от оборота к обороту или плавно с использованием алгоритма полиноминальной интерполяции.
Как указано в 4.3.8, выборка сигнала через равные угловые положения вала имеет по сравнению с выборкой через равные интервалы времени два преимущества. Во-первых, вся энергия гармоники оборотной частоты сосредоточена в середине поддиапазона данной спектральной линии (погрешность определения амплитуды частотной составляющей, которая находится не в середине, а на границе поддиапазона, может достигать 15 %).
Другое достоинство заключается в возможности усреднения по нескольким реализациям выборочных значений, соответствующих одному и тому же углу поворота вала (аналогично усреднению оцифрованных временных реализаций), с последующим расчетом порядкового спектра, содержащего только гармоники оборотной частоты. Все несинхронные составляющие при этом будут стремиться к нулю. При получении порядкового спектра усреднение происходит без размывания отдельных составляющих.
Октава представляет собой меру относительного изменения частоты. Изменение в одну октаву соответствует увеличению (уменьшению) частоты в два раза. Например, увеличение частоты 100 Гц на октаву дает частоту 200 Гц, а уменьшение ее на октаву - 50 Гц. Таким образом, если децибел является широко применяемой единицей для описания соотношений амплитуд, то октава - для описания соотношений частот. При необходимости более подробного описания шкалы частот октава может быть по логарифмическому закону разделена на доли (например, третьоктавы).
4.8 Анализ кепстров
Кепстр представляет собой обратное преобразование Фурье логарифма спектра мощности исходного временного сигнала. Кепстр представляют аналогично спектру, но по вертикальной оси откладывают амплитуды, а по горизонтальной - псевдовремя, называемое кьюфренси или сачтота. Кепстр можно рассматривать как спектр от спектра. При этом энергия всех гармоник одной частоты концентрируется в одной составляющей кепстра.
Кепстр является удобным инструментом для анализа сложных сигналов, содержащих несколько рядов гармоник, например, генерируемых зубчатыми передачами или подшипниками качения. Способность выделить и сосредоточить в дискретных составляющих периодические процессы для определения соотношений между ними является основным достоинством кепстров. Этапы вычисления кепстра показаны в таблице 3.
Таблица 3 - Вычисление кепстра
|
Этап |
Результат |
|
|
Измерение временного сигнала |
Оцифрованный сигнал х(t) |
|
|
БПФ оцифрованного сигнала |
Амплитудный спектр X(f) |
|
|
Вычисление квадратов составляющих амплитудного спектра |
Спектр мощности SXx(f) = X2(f) |
|
|
Вычисление логарифма спектра мощности и умножение на 10 |
10lgSXx(f), дБ |
|
|
Обратное БПФ от IfJlgSxxCf) |
Кепстр мощности SXx(t) |
|
5 Другие методы
В настоящей части ИСО 13373 рассмотрены наиболее широко применяемые методы обработки, анализа и представления данных в целях вибрационного контроля состояния и диагностирования машин. Однако в отдельных случаях используют методы, специально разработанные для решения конкретных задач. Объектами исследования в этих методах, могут быть, например:
- пик-фактор;
- функция автокорреляции;
- функция взаимной корреляции;
- коэффициент эксцесса;
- композитный спектр;
- высокочастотная вибрация;
- интенсивность вибрации;
- тренды нескольких параметров (среднеквадратичных значений, частотных составляющих);
- форма пиков сигнала;
- ударные импульсы;
- разложение по вейвлетам;
- векторы составляющих вибрации;
- энергия импульсов в подшипнике качения.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам Российской Федерации (и действующим в этом качестве межгосударственным стандартам)
Таблица А.1
|
Обозначение ссылочного международного стандарта |
Степень соответствия |
Обозначение и наименование межгосударственного стандарта |
|
ИСО 1683:2008 |
- |
* |
|
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов. |
||
Библиография
|
[1] |
ISO 2041, Mechanical vibration, shock and condition monitoring -Vocabulary |
|
[2] |
ISO 2954, Mechanical vibration of rotating and reciprocating machinery - Requirements for instruments for measuring vibration severity |
|
[3] |
ISO 5348, Mechanical vibration and shock - Mechanical mounting of accelerometers |
|
ISO 7919 (all parts), Mechanical vibration - Evaluation of machine vibration by measurements on rotating shafts |
|
|
ISO 10816-1 (all parts), Mechanical vibration - Evaluation of machine vibration by measurements on non-rotating parts |
|
|
[6] |
ISO 10817-1, Rotating shaft vibration measuring systems - Part 1: Relative and absolute sensing of radial vibration |
|
[7] |
ISO 13372, Condition monitoring and diagnostics of machines - Vocabulary |
|
ISO 13373-1, Condition monitoring and diagnostics of machines - Vibration condition monitoring - Part 1: General procedures |
|
|
ISO 16063-21, Methods for the calibration of vibration and shock transducers - Part 21: Vibration calibration by comparison to a reference transducer |
|
|
ISO 18431 (all parts), Mechanical vibration and shock - Signal processing |
|
|
VDI3839 Blatt 1, Hinweise zur Messung und Interpretation der Schwingungen von Maschinen-Allgemeine Grundlagen (Instructions on measuring and interpreting the vibrations of machine - General principles) (Bilingual edition) |
|
|
VDI 3841, Schwingungstiberwachung von Maschinen - Erforderliche Messungen (Vibration monitoring of machinery - Necessary measurements) (Bilingual edition) |
|
|
[13] |
Mitchell, J. S. An introduction to machinery analysis and monitoring. Pennwell Publishing, 1993 |
|
[14] |
Неразрушающий контроль: Справочник в 7 т. под общ. ред. В.В. Клюева /Т.7 в 2 кн./ Кн. 2: Ф.Я. Балицкий, А.В. Барков, И.А. Баркова и др. Вибродигностика. - М: - Машиностроение, 2005, 829 стр.1) |
1) Добавлен по сравнению с оригиналом (ИСО 13373-2:2005).
Ключевые слова: контроль технического состояния, диагностирование, вибрация, сигнал, обработка данных, анализ, представление, временная область, частотная область