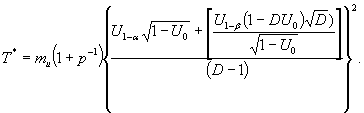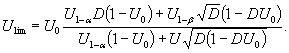|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО |
||
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р |
Надежность в технике
ПЛАНЫ ИСПЫТАНИЙ ДЛЯ КОНТРОЛЯ
КОЭФФИЦИЕНТА ГОТОВНОСТИ
|
|
Москва Стандартинформ 2010 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря
Сведения о стандарте
1 РАЗРАБОТАН Федеральным государственным предприятием «Всероссийский научно-исследовательский институт стандартизации и сертификации в машиностроении» (ФГУП «ВНИИНМАШ»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 119 «Надежность в технике»
3
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 15 декабря
4 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Содержание
|
3 Термины, определения и обозначения 5 Распределения временных характеристик Приложение А (справочное) Примеры
|
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
|
Надежность в технике ПЛАНЫ ИСПЫТАНИЙ ДЛЯ КОНТРОЛЯ КОЭФФИЦИЕНТА ГОТОВНОСТИ Dependability in technics. Compliance test plans for steady-state availability |
Дата введения - 2010-09-01
1 Область применения
Настоящий стандарт распространяется на восстанавливаемые (ремонтируемые) изделия, распределения наработок между отказами которых аппроксимируют экспоненциальным распределением, и устанавливает планы контрольных испытаний для проверки соответствия коэффициента готовности заданным требованиям. Требования стандарта применимы при испытании одного изделия.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ 27.002-89 Надежность в технике. Основные понятия, термины и определения
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочного стандарта в информационной системе общего пользования - на официальном сайте федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины, определения и обозначения
3.1 В настоящем стандарте применены термины по ГОСТ 27.002, а также следующие термины с соответствующими определениями:
3.1.1 план испытаний: Совокупность правил, определяющих продолжительность испытаний и принятие решений в зависимости от суммарного учитываемого числа наблюдений (проб, опытов) и учитываемого числа отказов (неудач), достигнутых (накопленных) к данному моменту испытаний.
3.1.2 приемочный уровень: Пороговое значение коэффициента готовности для принятия решения о приемке изделий.
Примечание - Решение о приемке принимают, если истинное значение коэффициента готовности равно или более приемочного уровня.
3.1.3 браковочный уровень: Пороговое значение коэффициента готовности для принятия решения о браковке изделий.
Примечание - Решение о браковке принимают, если истинное значение коэффициента готовности равно или менее браковочного уровня.
3.1.4 риск поставщика (изготовителя): Вероятность принятия решения о браковке изделий при условии, что истинное значение коэффициента готовности равно приемочному уровню.
3.1.5 риск потребителя: Вероятность принятия решения о приемке изделий при условии, что истинное значение коэффициента готовности равно браковочному уровню.
3.2 В настоящем стандарте применены следующие обозначения:
α - номинальный (заданный) риск поставщика;
β - номинальный (заданный) риск потребителя;
А0 - приемочный уровень;
А1 - браковочный уровень;
U0 - приемочный уровень коэффициента простоя; U0 = 1 - А0;
U1 - браковочный уровень коэффициента простоя; U1 = 1 - A1;
D - разрешающий коэффициент; D = U1/U0;
Ас(r) - граница приемки в последовательных испытаниях;
Re(r) - граница браковки в последовательных испытаниях;
Ulim - критерий принятия решения;
U1-α - квантиль уровня (1 - α) нормированного нормального распределения;
F1-α(v1, v2) - квантиль уровня (1 - α) F-распределения с (v1, v2) степенями свободы;
mα - среднее время пребывания изделия в неработоспособном состоянии;
mu - наработка на отказ;
n - объем выборки; число отказов (восстановлений) изделия за время испытаний ограниченной продолжительности;
r - число отказов в последовательных испытаниях;
T - суммарное время пребывания изделия в работоспособном состоянии; ![]() ;
;
Т* - продолжительность испытаний;
ti - наработка между отказами; i = 1, 2, 3,...;
Y - суммарное время пребывания изделия в неработоспособном состоянии; ![]() ;
;
уi - время пребывания изделия в неработоспособном состоянии; i = 1, 2, 3,...;
f(t), E(t), E(t2) - плотность, математическое ожидание (среднее значение) и дисперсия распределений случайных величин;
гамма-распределение:
f(t) = S(st)p-1exp(-st)/Г(p),
E(t) = p/s,
E(t2) = p/s2;
p - параметр формы;
s - параметр масштаба;
Г(р) - гамма-функция:
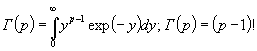 при целых р;
при целых р;
экспоненциальное распределение (частный случай гамма-распределения при р = 1):
f(t) = sexp(-st),
E(t) = 1/s,
E(t2) = 1/s2.
4 Основные положения
4.1 Контролируемыми показателями готовности являются стационарный коэффициент готовности или стационарный коэффициент технического использования (далее - коэффициент готовности).
Методы контроля, установленные в настоящем стандарте, в качестве контролируемого показателя используют также коэффициент простоя, дополняющий значения коэффициента готовности и коэффициента технического использования до единицы.
4.2 По результатам испытаний в отношении контролируемого показателя принимают одно из следующих решений:
- соответствие установленным требованиям (приемка);
- несоответствие установленным требованиям (браковка).
4.3 При испытаниях высоконадежного изделия отказ может не наступить, поэтому не могут быть получены количественные данные о готовности изделия. В подобных случаях заинтересованные стороны должны прийти к согласованному решению.
4.4 Исходными данными для выбора плана испытаний являются номинальный риск поставщика α и риск потребителя β, а также приемочный и браковочный коэффициенты простоя (разрешающий коэффициент D).
4.5 Планы испытаний, установленные в настоящем стандарте, предназначены для непрерывно работающих изделий, готовность которых определяют относительно суммарного времени их эксплуатации.
При использовании планов испытаний для изделий с прерывающимся режимом работы должны быть приняты соответствующие решения в отношении учета числа восстановлений изделия в перерывах между рабочими периодами.
4.6 Методы испытаний, установленные в настоящем стандарте, применимы только для изделий, которые могут находиться в двух состояниях - работоспособном и неработоспособном.
Для сложных изделий могут быть установлены несколько режимов работы. В этом случае планы испытаний следует применять раздельно для каждого режима работы изделия. При получении противоречащих друг другу результатов контроля готовности для разных режимов работы должны быть установлены требования к принятию решений.
4.7 В зависимости от вида контролируемого показателя, составляющие времени пребывания изделия в неработоспособном состоянии подразделяют на учитываемые и неучитываемые. Классификация составляющих времени пребывания в неработоспособном состоянии должна быть установлена до начала испытаний.
5 Распределения временных характеристик
5.1 Испытаниям подвергают работоспособное изделие. По истечении интервала времени возникает первый отказ и изделие переходит в неработоспособное состояние. После восстановления изделие возвращается в работоспособное состояние. Затем начинается новый цикл «работоспособность - отказ - неработоспособность - восстановление». Реализация этого процесса представлена на рисунке 1.
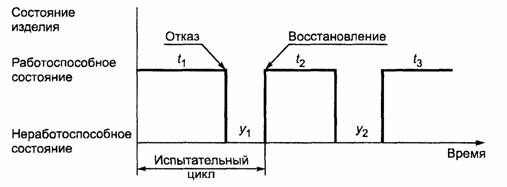
Рисунок 1 - Типовая реализация процесса функционирования изделий при испытаниях в виде испытательных циклов
5.2 В основе планов испытаний лежит предположение, что наработка изделия между отказами представляют собой выборку из экспоненциального распределения, а продолжительность пребывания в неработоспособном состоянии - выборку из гамма-распределения. Значение параметра формы р определяют по согласованию между поставщиком и потребителем до начала испытаний (по результатам испытаний аналогичных изделий или оценивают по статистическим данным, полученным в процессе испытаний.
Примечание - При отсутствии информации допускается по согласованию между поставщиком и потребителем принимать р = 1 (экспоненциальное распределение пребывания изделия в неработоспособном состоянии).
6 Виды планов испытаний
6.1 План испытаний с ограниченным числом отказов
Определяют число отказов n, которое должно быть получено в ходе испытаний как минимальное из возможных чисел, для которых выполняется неравенство
Вычисляют значение критерия принятия решения Ulim по формуле
По результатам испытаний после получения n отказов вычисляют значение Y/Т.
Решение о приемке изделий принимают в случае, если Y/Т ≤ Ulim.
В противном случае принимают решение о браковке.
Значения F1-α(v1, v2) и F1-β(v1, v2) приведены в таблице 1.
Таблица 1 - Квантили F-распределения с (v1, v2) степенями свободы
|
v2 |
v1 |
|||||||||
|
2 |
4 |
6 |
8 |
10 |
20 |
30 |
40 |
60 |
120 |
|
|
0,80 квантиля |
||||||||||
|
2 |
4,00 |
4,24 |
4,32 |
4,36 |
4,38 |
4,43 |
4,45 |
4,46 |
4,46 |
4,47 |
|
4 |
2,47 |
2,48 |
2,47 |
2,47 |
2,46 |
2,44 |
2,44 |
2,44 |
2,43 |
2,43 |
|
6 |
2,13 |
2,09 |
2,06 |
2,04 |
2,03 |
2,00 |
1,98 |
1,98 |
1,97 |
1,96 |
|
8 |
1,98 |
1,92 |
1,88 |
1,86 |
1,84 |
1,80 |
1,78 |
1,77 |
1,76 |
1,75 |
|
10 |
1,90 |
1,83 |
1,78 |
1,75 |
1,73 |
1,68 |
1,66 |
1,65 |
1,64 |
1,63 |
|
12 |
1,85 |
1,77 |
1,72 |
1,69 |
1,66 |
1,61 |
1,59 |
1,58 |
1,56 |
1,55 |
|
14 |
1,81 |
1,73 |
1,67 |
1,65 |
1,62 |
1,56 |
1,53 |
1,52 |
1,51 |
1,49 |
|
16 |
1,78 |
1,70 |
1,64 |
1,61 |
1,58 |
1,52 |
1,49 |
1,48 |
1,47 |
1,45 |
|
18 |
1,76 |
1,67 |
1,62 |
1,58 |
1,55 |
1,49 |
1,46 |
1,45 |
1,43 |
1,42 |
|
20 |
1,75 |
1,65 |
1,60 |
1,56 |
1,53 |
1,47 |
1,44 |
1,42 |
1,41 |
1,39 |
|
30 |
1,70 |
1,60 |
1,54 |
1,50 |
1,47 |
1,39 |
1,36 |
1,35 |
1,33 |
1,31 |
|
40 |
1,68 |
1,57 |
1,51 |
1,47 |
1,44 |
1,36 |
1,33 |
1,31 |
1,29 |
1,26 |
|
60 |
1,65 |
1,55 |
1,48 |
1,44 |
1,41 |
1,32 |
1,29 |
1,27 |
1,24 |
1,22 |
|
120 |
1,63 |
1,52 |
1,45 |
1,41 |
1,37 |
1,29 |
1,25 |
1,23 |
1,20 |
1,17 |
|
0,90 квантиля |
||||||||||
|
2 |
9,00 |
9,24 |
9,33 |
9,37 |
9,39 |
9,44 |
9,46 |
9,47 |
9,47 |
9,48 |
|
4 |
4,32 |
4,11 |
4,01 |
3,96 |
3,92 |
3,84 |
3,82 |
3,80 |
3,79 |
3,78 |
|
6 |
3,46 |
3,18 |
3,05 |
2,98 |
2,94 |
2,84 |
2,80 |
2,78 |
2,76 |
2,74 |
|
8 |
3,11 |
2,81 |
2,67 |
2,59 |
2,54 |
2,42 |
2,38 |
2,36 |
2,34 |
2,32 |
|
10 |
2,92 |
2,61 |
2,46 |
2,38 |
2,32 |
2,20 |
2,16 |
2,13 |
2,11 |
2,08 |
|
12 |
2,81 |
2,48 |
2,33 |
2,24 |
2,19 |
2,06 |
2,01 |
1,99 |
1,96 |
1,93 |
|
14 |
2,73 |
2,39 |
2,24 |
2,15 |
2,10 |
1,96 |
1,91 |
1,89 |
1,86 |
1,83 |
|
16 |
2,67 |
2,33 |
2,18 |
2,09 |
2,03 |
1,89 |
1,84 |
1,81 |
1,78 |
1,75 |
|
18 |
2,62 |
2,29 |
2,13 |
2,04 |
1,98 |
1,84 |
1,78 |
1,75 |
1,72 |
1,69 |
|
20 |
2,59 |
2,25 |
2,09 |
2,00 |
1,94 |
1,78 |
1,74 |
1,71 |
1,68 |
1,64 |
|
30 |
2,49 |
2,14 |
1,98 |
1,88 |
1,82 |
1,67 |
1,61 |
1,57 |
1,54 |
1,50 |
|
40 |
2,44 |
2,09 |
1,93 |
1,83 |
1,76 |
1,61 |
1,54 |
1,51 |
1,47 |
1,42 |
|
60 |
2,39 |
2,04 |
1,87 |
1,77 |
1,71 |
1,54 |
1,48 |
1,44 |
1,40 |
1,35 |
|
120 |
2,35 |
1,99 |
1,82 |
1,72 |
1,65 |
1,48 |
1,41 |
1,37 |
1,32 |
1,26 |
|
0,95 квантиля |
||||||||||
|
2 |
19,00 |
19,25 |
19,33 |
19,37 |
19,40 |
19,45 |
19,46 |
19,47 |
19,48 |
19,49 |
|
4 |
6,94 |
6,39 |
6,16 |
6,04 |
5,96 |
5,80 |
5,75 |
5,72 |
5,69 |
5,66 |
|
6 |
5,14 |
4,53 |
4,28 |
4,15 |
4,06 |
3,87 |
3,81 |
3,77 |
3,74 |
3,71 |
|
8 |
4,46 |
3,84 |
3,58 |
3,44 |
3,35 |
3,15 |
3,08 |
3,04 |
3,01 |
2,97 |
|
10 |
4,10 |
3,48 |
3,22 |
3,07 |
2,98 |
2,77 |
2,70 |
2,66 |
2,62 |
2,58 |
|
12 |
3,89 |
3,26 |
3,0 |
2,85 |
2,75 |
2,54 |
2,47 |
2,43 |
2,38 |
2,34 |
|
14 |
3,74 |
3,11 |
2,85 |
2,70 |
2,60 |
2,39 |
2,31 |
2,27 |
2,22 |
2,18 |
|
16 |
3,63 |
3,01 |
2,74 |
2,59 |
2,49 |
2,28 |
2,19 |
2,15 |
2,11 |
2,06 |
|
18 |
3,55 |
2,93 |
2,66 |
2,51 |
2,41 |
2,19 |
2,11 |
2,06 |
2,02 |
1,97 |
|
20 |
3,49 |
2,87 |
2,60 |
2,45 |
2,35 |
2,12 |
2,04 |
1,99 |
1,95 |
1,90 |
|
30 |
3,32 |
2,69 |
2,42 |
2,27 |
2,16 |
1,93 |
1,84 |
1,79 |
1,74 |
1,68 |
|
40 |
3,23 |
2,61 |
2,34 |
2,18 |
2,08 |
1,84 |
1,74 |
1,69 |
1,64 |
1,58 |
|
60 |
3,15 |
2,53 |
2,25 |
2,10 |
1,99 |
1,75 |
1,65 |
1,59 |
1,53 |
1,47 |
|
120 |
3,07 |
2,45 |
2,17 |
2,02 |
1,91 |
1,66 |
1,55 |
1,50 |
1,43 |
1,35 |
6.2 План испытаний с ограниченной продолжительностью (превышающей пятнадцати кратное значение наработки на отказ)
Определяют продолжительность испытаний T* по формуле
Значение критерия принятия решения Ulim вычисляют по формуле
По результатам испытаний вычисляют значения Y; Т.
Решение о приемке принимают в том случае, если Y/(Y + Т) ≤ Ulim.
В противном случае принимают решение о браковке.
Значения U1-α и U1-β приведены в таблице 2.
Таблица 2 - Квантили нормированного нормального распределения
|
1 - α |
U1-α |
|
0,80 |
0,842 |
6.3 План испытаний с ограниченной продолжительностью (U < 0,05)
Этот план применяют, если mα/mu менее 0,05.
Продолжительность испытаний - Т*.
Критерий принятия решения Ulim является функцией продолжительности испытаний и его значение определяют по таблице 3 с учетом соотношения между продолжительностью испытаний T* и разрешающим коэффициентом D.
По результатам испытаний определяют значения Y, Т.
Решение о приемке принимают в том случае, если Y/(Y = T) < Ulim.
В противном случае принимают решение о браковке.
Таблица 3 - Разрешающие коэффициенты D и браковочные пределы Ulim для плана испытаний
|
Т*/mu |
α = β = 0,05 |
α = β = 0,10 |
α = β = 0,20 |
|||
|
D |
Ulim/U0 |
D |
Ulim/U0 |
D |
Ulim/U0 |
|
|
p = 1 |
||||||
|
1,0 |
24,72 |
3,92 |
15,01 |
2,91 |
7,37 |
1,86 |
|
1,2 |
20,01 |
3,64 |
12,39 |
2,75 |
6,30 |
1,83 |
|
1,4 |
16,88 |
3,42 |
10,64 |
2,63 |
5,56 |
1,80 |
|
1,6 |
14,66 |
3,24 |
9,38 |
2,52 |
5,03 |
1,77 |
|
1,8 |
13,01 |
3,10 |
8,44 |
2,44 |
4,63 |
1,74 |
|
2,0 |
11,73 |
2,98 |
7,70 |
2,36 |
4,31 |
1,71 |
|
2,5 |
9,52 |
2,75 |
6,42 |
2,22 |
3,74 |
1,65 |
|
3,0 |
8,12 |
2,58 |
5,59 |
2,11 |
3,37 |
1,61 |
|
3,5 |
7,15 |
2,45 |
5,01 |
2,03 |
3,10 |
1,57 |
|
4,0 |
6,44 |
2,34 |
4,58 |
1,96 |
2,90 |
1,54 |
|
5,0 |
5,46 |
2,19 |
3,98 |
1,86 |
2,61 |
1,49 |
|
6,0 |
4,82 |
2,07 |
3,58 |
1,78 |
2,42 |
1,45 |
|
7,0 |
4,36 |
1,99 |
3,29 |
1,72 |
2,28 |
1,42 |
|
8,0 |
4,02 |
1,92 |
3,07 |
1,67 |
2,17 |
1,40 |
|
9,0 |
3,75 |
1,86 |
2,90 |
1,63 |
2,08 |
1,37 |
|
10,0 |
3,53 |
1,81 |
2,76 |
1,60 |
2,01 |
1,36 |
|
15,0 |
2,88 |
1,65 |
2,33 |
1,49 |
1,78 |
1,29 |
|
20,0 |
2,53 |
1,56 |
2,10 |
1,42 |
1,65 |
1,26 |
|
р = 2 |
||||||
|
1,0 |
18,94 |
3,47 |
11,74 |
2,59 |
6,01 |
1,87 |
|
1,2 |
15,43 |
3,22 |
9,78 |
2,54 |
5,19 |
1,81 |
|
1,4 |
13,11 |
3,04 |
8,46 |
2,42 |
4,63 |
1,76 |
|
1,6 |
11,45 |
2,89 |
7,52 |
2,33 |
4,22 |
1,72 |
|
1,8 |
10,22 |
2,77 |
6,80 |
2,25 |
3,91 |
1,69 |
|
2,0 |
9,26 |
2,67 |
6,25 |
2,18 |
3,66 |
1,66 |
|
2,5 |
7,62 |
2,47 |
5,28 |
2,06 |
3,22 |
1,60 |
|
3,0 |
6,56 |
2,33 |
4,65 |
1,96 |
2,93 |
1,55 |
|
3,5 |
5,83 |
2,22 |
4,20 |
1,89 |
2,72 |
1,51 |
|
4,0 |
5,29 |
2,13 |
3,84 |
1,83 |
2,56 |
1,48 |
|
5,0 |
4,54 |
2,00 |
3,40 |
1,74 |
2,33 |
1,44 |
|
6,0 |
4,05 |
1,91 |
3,09 |
1,67 |
2,17 |
1,40 |
|
7,0 |
3,70 |
1,84 |
2,87 |
1,62 |
2,06 |
1,37 |
|
8,0 |
3,43 |
1,78 |
2,70 |
1,58 |
1,97 |
1,35 |
|
9,0 |
3,22 |
1,73 |
2,56 |
1,54 |
1,90 |
1,33 |
|
10,0 |
3,06 |
1,69 |
2,45 |
1,51 |
1,84 |
1,31 |
|
15,0 |
2,54 |
1,56 |
2,10 |
1,42 |
1,65 |
1,26 |
|
20,0 |
2,26 |
1,48 |
1,92 |
1,36 |
1,55 |
1,22 |
|
р = 5 |
||||||
|
1,0 |
15,37 |
3,14 |
9,64 |
2,52 |
5,05 |
1,83 |
|
1,2 |
12,72 |
2,93 |
8,19 |
2,38 |
4,48 |
1,77 |
|
1,4 |
10,87 |
2,77 |
7,15 |
2,27 |
4,04 |
1,72 |
|
1,6 |
9,54 |
2,64 |
6,38 |
2,19 |
3,71 |
1,68 |
|
1,8 |
8,55 |
2,54 |
5,80 |
2,11 |
3,45 |
1,61 |
|
2,0 |
7,78 |
2,45 |
5,36 |
2,05 |
3,25 |
1,61 |
|
2,5 |
6,47 |
2,28 |
4,57 |
1,94 |
2,89 |
1,55 |
|
3,0 |
5,62 |
2,16 |
4,06 |
1,85 |
2,65 |
1,51 |
|
3,5 |
5,03 |
2,07 |
3,70 |
1,79 |
2,47 |
1,47 |
|
4,0 |
4,59 |
1,99 |
3,43 |
1,73 |
2,34 |
1,44 |
|
5,0 |
3,98 |
1,88 |
3,04 |
1,65 |
2,15 |
1,40 |
|
6,0 |
3,58 |
1,80 |
2,79 |
1,60 |
2,02 |
1,36 |
|
7,0 |
3,29 |
1,73 |
2,60 |
1,55 |
1,92 |
1,34 |
|
8,0 |
3,07 |
1,68 |
2,46 |
1,51 |
1,84 |
1,32 |
|
9,0 |
2,90 |
1,64 |
2,34 |
1,48 |
1,78 |
1,30 |
|
10,0 |
2,76 |
1,61 |
2,25 |
1,46 |
1,73 |
1,28 |
|
15,0 |
2,32 |
1,49 |
1,96 |
1,37 |
1,57 |
1,23 |
|
20,0 |
2,09 |
1,42 |
1,80 |
1,32 |
1,48 |
1,20 |
6.4 Последовательные испытания
Продолжительность испытаний изделий по этому плану зависит от коэффициента готовности.
После очередного восстановления в соответствии с приведенными ниже правилами принимают решение о завершении испытаний или об их продолжении. Границы приемки и браковки зависят от числа циклов (отказов и восстановлений) изделия, произошедших на данный момент времени.
Изделие бракуют, если Y/T > Rе(r)U0/(1 - U0).
Изделие принимают, если Y/Т < Aс(r)U0/(1 - U0).
Испытания продолжают, если Aс(r)U0/(1 - U0) ≤ Y/T ≤ Rе(r)U0/(1 - U0).
Границы областей приемки и браковки рассчитывают по формулам:
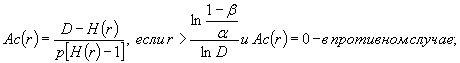 ;
;
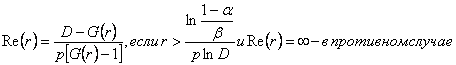 ,
,
где
![]()
![]()
Значения Aс(r) и Re(r) приведены в таблице 4.
Пример плана последовательных испытаний для исходных данных р = 1, D = 5, α = β = 0,1 приведен на рисунке 2.
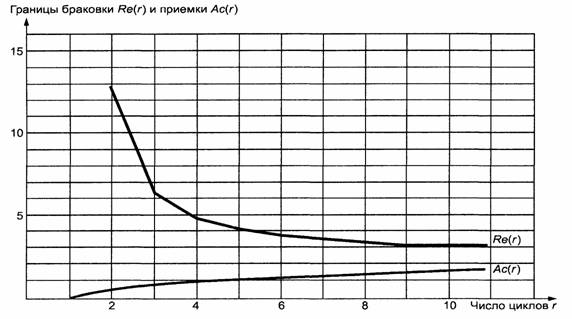
Рисунок 2 - Пример плана испытаний
Таблица 4 - Границы областей приемки Ас(r) и браковки Re(r) для последовательного плана испытаний
|
r |
α = β = 0,05 |
α = β = 0,10 |
α = β = 0,20 |
|||
|
Ас(r) |
Re(r) |
Ac(r) |
Re(r) |
Ac(r) |
Re(r) |
|
|
D = 2, p = 1 |
||||||
|
1 |
0,00 |
- |
0,00 |
- |
0,00 |
- |
|
2 |
0,00 |
- |
0,00 |
- |
0,00 |
- |
|
3 |
0,00 |
- |
0,00 |
- |
0,28 |
7,17 |
|
4 |
0,00 |
- |
0,16 |
12,41 |
0,47 |
4,29 |
|
5 |
0,11 |
17,69 |
0,31 |
6,39 |
0,60 |
3,33 |
|
6 |
0,24 |
8,39 |
0,43 |
4,63 |
0,70 |
2,85 |
|
7 |
0,34 |
5,85 |
0,53 |
3,79 |
0,78 |
2,56 |
|
8 |
0,43 |
4,67 |
0,61 |
3,30 |
0,84 |
2,37 |
|
9 |
0,50 |
3,98 |
0,67 |
2,97 |
0,90 |
2,23 |
|
10 |
0,57 |
3,53 |
0,73 |
2,74 |
0,94 |
2,13 |
|
11 |
0,62 |
3,22 |
0,78 |
2,57 |
0,98 |
2,05 |
|
12 |
0,67 |
2,99 |
0,82 |
2,44 |
1,01 |
1,99 |
|
13 |
0,71 |
2,81 |
0,86 |
2,34 |
1,03 |
1,93 |
|
14 |
0,75 |
2,66 |
0,89 |
2,25 |
1,06 |
1,89 |
|
15 |
0,79 |
2,55 |
0,92 |
2,18 |
1,08 |
1,85 |
|
16 |
0,82 |
2,45 |
0,94 |
2,12 |
1,10 |
1,82 |
|
17 |
0,84 |
2,37 |
0,97 |
2,07 |
1,11 |
1,80 |
|
18 |
0,87 |
2,30 |
0,99 |
2,03 |
1,13 |
1,77 |
|
19 |
0,89 |
2,24 |
1,01 |
1,99 |
1,14 |
1,75 |
|
20 |
0,91 |
2,19 |
1,02 |
1,95 |
1,15 |
1,73 |
|
D = 2, p = 2 |
||||||
|
1 |
0,00 |
- |
0,00 |
- |
0,00 |
- |
|
2 |
0,00 |
- |
0,11 |
- |
0,35 |
- |
|
3 |
0,17 |
- |
0,32 |
- |
0,56 |
5,75 |
|
4 |
0,32 |
- |
0,47 |
9,68 |
0,71 |
3,58 |
|
5 |
0,44 |
13,64 |
0,59 |
5,17 |
0,81 |
2,86 |
|
6 |
0,53 |
6,66 |
0,68 |
3,84 |
0,89 |
2,50 |
|
7 |
0,61 |
4,76 |
0,75 |
3,21 |
0,95 |
2,29 |
|
8 |
0,68 |
3,87 |
0,81 |
2,84 |
0,99 |
2,14 |
|
9 |
0,73 |
3,35 |
0,86 |
2,60 |
1,03 |
2,04 |
|
10 |
0,78 |
3,02 |
0,91 |
2,42 |
1,06 |
1,96 |
|
11 |
0,82 |
2,78 |
0,94 |
2,30 |
1,09 |
1,90 |
|
12 |
0,86 |
2,61 |
0,97 |
2,20 |
1,12 |
1,85 |
|
13 |
0,89 |
2,47 |
1,00 |
2,12 |
1,14 |
1,82 |
|
14 |
0,92 |
2,36 |
1,03 |
2,05 |
1,15 |
1,78 |
|
15 |
0,95 |
2,28 |
1,05 |
2,00 |
1,17 |
1,76 |
|
16 |
0,97 |
2,20 |
1,07 |
1,96 |
1,18 |
1,73 |
|
17 |
0,99 |
2,14 |
1,09 |
1,92 |
1,20 |
1,71 |
|
18 |
1,01 |
2,09 |
1,10 |
1,88 |
1,21 |
1,69 |
|
19 |
1,03 |
2,04 |
1,12 |
1,86 |
1,22 |
1,68 |
|
20 |
1,05 |
2,01 |
1,13 |
1,83 |
1,23 |
1,66 |
|
D = 2, p = 5 |
||||||
|
1 |
0,04 |
- |
0,12 |
- |
0,28 |
- |
|
2 |
0,26 |
- |
0,37 |
- |
0,57 |
- |
|
3 |
0,42 |
- |
0,55 |
- |
0,74 |
4,89 |
|
4 |
0,54 |
- |
0,67 |
8,04 |
0,86 |
3,16 |
|
5 |
0,64 |
11,21 |
0,76 |
4,43 |
0,94 |
2,59 |
|
6 |
0,72 |
5,63 |
0,84 |
3,37 |
1,00 |
2,30 |
|
7 |
0,78 |
4,10 |
0,89 |
2,87 |
1,05 |
2,13 |
|
8 |
0,83 |
3,39 |
0,94 |
2,57 |
1,09 |
2,01 |
|
9 |
0,88 |
2,98 |
0,98 |
2,37 |
1,12 |
1,93 |
|
10 |
0,92 |
2,71 |
1,02 |
2,24 |
1,15 |
1,87 |
|
11 |
0,95 |
2,52 |
1,05 |
2,13 |
1,17 |
1,82 |
|
12 |
0,99 |
2,38 |
1,07 |
2,05 |
1,19 |
1,78 |
|
13 |
1,01 |
2,27 |
1,09 |
1,99 |
1,20 |
1,75 |
|
14 |
1,03 |
2,19 |
1,11 |
1,94 |
1,22 |
1,72 |
|
15 |
1,05 |
2,12 |
1,13 |
1,90 |
1,23 |
1,70 |
|
16 |
1,07 |
2,06 |
1,15 |
1,86 |
1,24 |
1,68 |
|
17 |
1,09 |
2,01 |
1,16 |
1,83 |
1,25 |
1,66 |
|
18 |
1,10 |
1,97 |
1,17 |
1,80 |
1,26 |
1,65 |
|
19 |
1,12 |
1,93 |
1,19 |
1,78 |
1,27 |
1,64 |
|
20 |
1,13 |
1,90 |
1,20 |
1,76 |
1,28 |
1,63 |
|
D = 5, р = 1 |
||||||
|
1 |
0,00 |
- |
0,00 |
- |
0,15 |
32,89 |
|
2 |
0,09 |
55,32 |
0,39 |
12,75 |
0,85 |
5,86 |
|
3 |
0,51 |
9,84 |
0,80 |
6,27 |
1,20 |
4,16 |
|
4 |
0,79 |
6,31 |
1,06 |
4,72 |
1,41 |
3,54 |
|
5 |
1,00 |
5,01 |
1,24 |
4,03 |
1,55 |
3,23 |
|
6 |
1,15 |
4,34 |
1,37 |
3,64 |
1,65 |
3,03 |
|
7 |
1,27 |
3,93 |
1,48 |
3,39 |
1,72 |
2,90 |
|
8 |
1,37 |
3,65 |
1,56 |
3,21 |
1,78 |
2,81 |
|
9 |
1,45 |
3,45 |
1,62 |
3,09 |
1,83 |
2,74 |
|
10 |
1,51 |
3,30 |
1,67 |
2,99 |
1,86 |
2,68 |
|
11 |
1,57 |
3,18 |
1,72 |
2,91 |
1,90 |
2,64 |
|
12 |
1,62 |
3,09 |
1,76 |
2,84 |
1,92 |
2,60 |
|
13 |
1,66 |
3,01 |
1,79 |
2,79 |
1,94 |
2,57 |
|
14 |
1,70 |
2,95 |
1,82 |
2,75 |
1,96 |
2,55 |
|
15 |
1,73 |
2,89 |
1,84 |
2,71 |
1,98 |
2,52 |
|
16 |
1,76 |
2,85 |
1,87 |
2,68 |
2,00 |
2,50 |
|
17 |
1,78 |
2,81 |
1,89 |
2,65 |
2,01 |
2,49 |
|
18 |
1,80 |
2,77 |
1,91 |
2,62 |
2,02 |
2,47 |
|
19 |
1,82 |
2,74 |
1,92 |
2,60 |
2,03 |
2,46 |
|
20 |
1,84 |
2,71 |
1,94 |
2,58 |
2,04 |
2,45 |
|
D = 5, р = 2 |
||||||
|
1 |
0,06 |
- |
0,28 |
- |
0,67 |
25,40 |
|
2 |
0,62 |
42,23 |
0,86 |
10,27 |
1,23 |
5,10 |
|
3 |
0,96 |
8,09 |
1,19 |
5,39 |
1,51 |
3,79 |
|
4 |
1,19 |
5,42 |
1,40 |
4,22 |
1,68 |
3,32 |
|
5 |
1,35 |
4,44 |
1,54 |
3,69 |
1,78 |
3,08 |
|
6 |
1,47 |
3,93 |
1,65 |
3,39 |
1,86 |
2,93 |
|
7 |
1,57 |
3,61 |
1,73 |
3,20 |
1,92 |
2,83 |
|
8 |
1,64 |
3,40 |
1,79 |
3,07 |
1,96 |
2,76 |
|
9 |
1,71 |
3,25 |
1,84 |
2,97 |
2,00 |
2,70 |
|
10 |
176 |
3,14 |
1,88 |
2,89 |
2,03 |
2,66 |
|
11 |
1,80 |
3,05 |
1,92 |
2,83 |
2,05 |
2,63 |
|
12 |
1,84 |
2,97 |
1,95 |
2,79 |
2,07 |
2,60 |
|
13 |
1,87 |
2,92 |
1,97 |
2,75 |
2,09 |
2,58 |
|
14 |
1,90 |
2,87 |
1,99 |
2,71 |
2,11 |
2,56 |
|
15 |
1,92 |
2,82 |
2,01 |
2,68 |
2,12 |
2,54 |
|
16 |
1,94 |
2,79 |
2,03 |
2,66 |
2,13 |
2,52 |
|
17 |
1,96 |
2,76 |
2,05 |
2,64 |
2,14 |
2,51 |
|
18 |
1,98 |
2,73 |
2,06 |
2,62 |
2,15 |
2,50 |
|
19 |
2,00 |
2,71 |
2,07 |
2,60 |
2,16 |
2,49 |
|
20 |
2,01 |
2,68 |
2,08 |
2,58 |
2,17 |
2,48 |
|
D = 5, р = 5 |
||||||
|
1 |
0,50 |
- |
0,70 |
- |
1,04 |
20,91 |
|
2 |
0,99 |
34,38 |
1,20 |
8,80 |
1,51 |
4,65 |
|
3 |
1,28 |
7,05 |
1,48 |
4,88 |
1,74 |
3,60 |
|
4 |
1,47 |
4,91 |
1,65 |
3,94 |
1,88 |
3,21 |
|
5 |
1,61 |
4,11 |
1,77 |
3,52 |
1,97 |
3,02 |
|
6 |
1,71 |
3,70 |
1,85 |
3,27 |
2,03 |
2,90 |
|
7 |
1,79 |
3,45 |
1,92 |
3,12 |
2,08 |
2,82 |
|
8 |
1,85 |
3,28 |
1,97 |
3,01 |
2,11 |
2,76 |
|
9 |
1,90 |
3,16 |
2,01 |
2,93 |
2,14 |
2,71 |
|
10 |
1,94 |
3,06 |
2,04 |
2,87 |
2,17 |
2,68 |
|
11 |
1,98 |
2,99 |
2,07 |
2,82 |
2,19 |
2,64 |
|
12 |
2,01 |
2,93 |
2,10 |
2,78 |
2,20 |
2,63 |
|
13 |
2,03 |
2,89 |
2,12 |
2,75 |
2,22 |
2,61 |
|
14 |
2,06 |
2,85 |
2,14 |
2,72 |
2,23 |
2,59 |
|
15 |
2,08 |
2,81 |
2,15 |
2,70 |
2,24 |
2,58 |
|
16 |
2,10 |
2,78 |
2,17 |
2,68 |
2,25 |
2,57 |
|
17 |
2,11 |
2,76 |
2,18 |
2,66 |
2,26 |
2,56 |
|
18 |
2,13 |
2,74 |
2,19 |
2,64 |
2,26 |
2,55 |
|
19 |
2,14 |
2,72 |
2,20 |
2,63 |
2,27 |
2,54 |
|
20 |
2,15 |
2,70 |
2,21 |
2,62 |
2,28 |
2,53 |
|
Примечание - Знак «-» в таблице означает, что принятие решения о браковке в данном случае невозможно. |
||||||
Приложение А
(справочное)
Примеры
А.1 Пример 1
План с ограниченным числом отказов
Исходные данные для определения плана испытаний: U0 = 0,01; U1 = 0,05; α = 0,10; β = 0,05; р = 2.
Определяют необходимое число отказов изделия в соответствии с неравенством (1), в том числе:
- вычисляют значение D(1 - U0)/(1 - DU0) = 5(0,99)/0,95 = 5,2105;
- вычисляют значения F1-α(2pn; 2n)F1-β(2n; 2pn) для различных значений n до получения неравенства (1).
Результаты вычислений приведены в таблице.
|
n |
10 |
4 |
5 |
|
F1-α(2pn; 2n)F1-β(2n; 2pn) |
3,15 |
6,40 |
5,17 |
Например, для n = 10 в таблице
F1-α(2pn; 2n)F1-β(2n; 2pn) = F09(40; 20)F095(40; 20) = 1,71×1,84 = 3,15.
Таким образом, испытания изделия продолжают до наступления пятого отказа и последующего восстановления.
Вычисляют значение критерия принятия решения по формуле (2)
Ulim = F1-α(2pn; 2n)U0/(1 - U0) = F09(20; 10)U0/(1 - U0) = 2,20×0,01/0,99 = 0,0222.
Если отношение Y/T, вычисленное по результатам испытаний, не превышает значение Ulim = 0,0222, то изделие принимают.
В противном случае изделие бракуют.
Пример 2
План с ограниченной продолжительностью испытаний
Исходные данные для определения плана испытаний: U0 = 0,10; U1 =0,20 (D = 2); α = β = 0,05; р = 1 (продолжительность неработоспособного состояния изделия предполагают распределенной экспоненциально).
Вычисляют продолжительность испытаний T* по формуле (3) и таблице 2
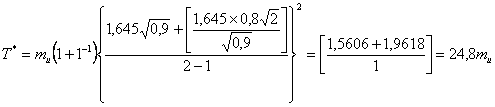
и значение критерия принятия решения Ulim по формуле (4)
![]()
Если отношение Y/Y + Т, вычисленное по результатам испытаний, не превышает Ulim = 0,2288, то изделие принимают.
В противном случае изделие бракуют.
Ключевые слова: надежность и безотказность техники, коэффициент готовности, коэффициент технического использования, планы контрольных испытаний