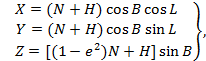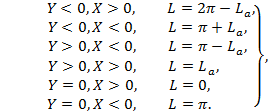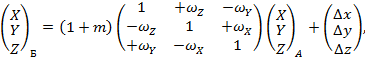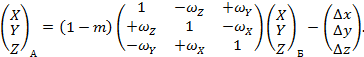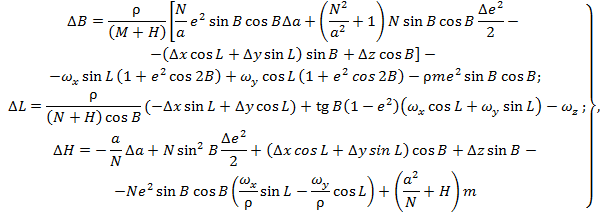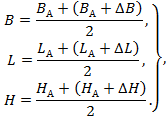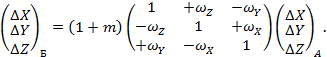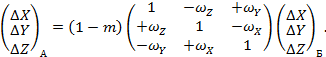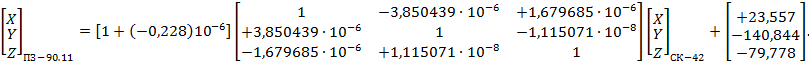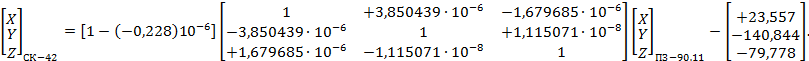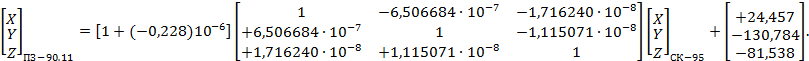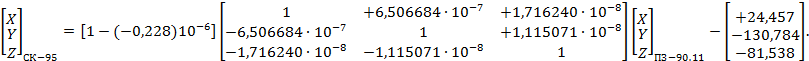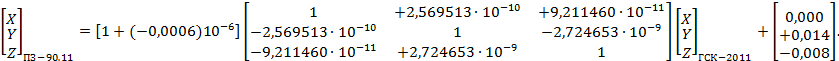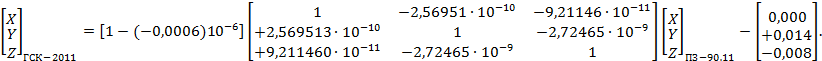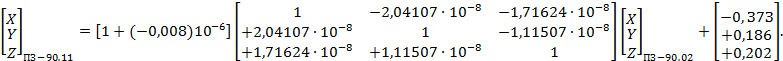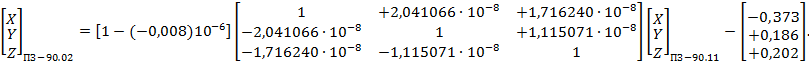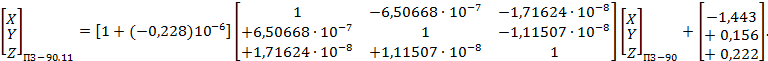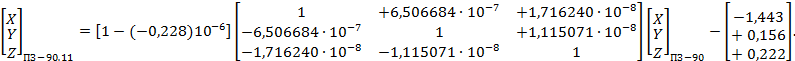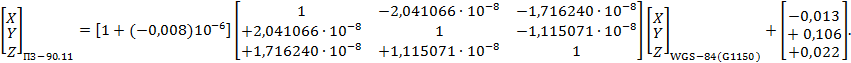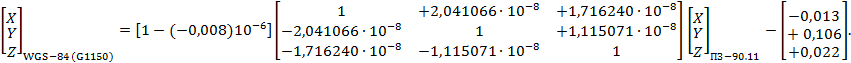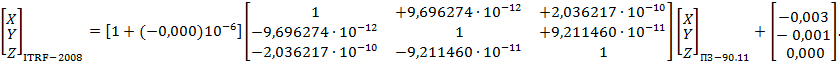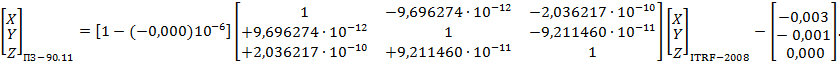|
МЕЖГОСУДАРСТВЕННЫЙ СОВЕТ ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И
СЕРТИФИКАЦИИ |
|
|
ГОСТ |
|
Глобальная навигационная спутниковая система
Методы преобразований координат
определяемых точек
|
|
Москва |
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-2015 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены»
1 РАЗРАБОТАН Акционерным обществом «Научно-технический центр современных навигационных технологий «Интернавигация» (АО «НТЦ «Интернавигация»)
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 Принят Межгосударственным советом по стандартизации, метрологии и сертификации по результатам голосования (протокол от 30 августа 2017 г. № 102-П)
За принятие проголосовали:
|
Краткое
наименование страны |
Код страны
по МК |
Сокращенное
наименование национального органа |
|
Азербайджан |
AZ |
Азстандарт |
|
Армения |
AM |
Минэкономики Республики Армения |
|
Беларусь |
BY |
Госстандарт Республики Беларусь |
|
Казахстан |
KZ |
Госстандарт Республики Казахстан |
|
Киргизия |
KG |
Кыргызстандарт |
|
Молдова |
MD |
Молдова-Стандарт |
|
Россия |
RU |
Росстандарт |
|
Таджикистан |
TJ |
Таджикстандарт |
|
Туркменистан |
TM |
Главгосслужба «Туркменстандартлары» |
|
Узбекистан |
UZ |
Узгосстандарт |
|
Украина |
UA |
Минэкономразвития Украины |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 12 сентября 2017 г. № 1055-ст межгосударственный стандарт ГОСТ 32453-2017 введен в действие в качестве национального стандарта с 1 июля 2018 г.
5 ВЗАМЕН ГОСТ 32453-2013
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
ГОСТ 32453-2017
Глобальная навигационная спутниковая система
СИСТЕМЫ КООРДИНАТ
Методы преобразований координат определяемых точек
Global navigation satellite system. Coordinate systems. Methods of transformations for determinated points coordinates
Дата введения - 2018-07-01
1 Область применения
Настоящий стандарт распространяется на системы координат, входящие в состав систем геодезических параметров «Параметры Земли 1990 года» и референцные системы координат Российской Федерации.
Настоящий стандарт устанавливает методы преобразований координат и их приращений из одной системы в другую, а также порядок использования параметров преобразования систем координат при выполнении геодезических, навигационных, картографических работ с применением аппаратуры потребителей глобальных навигационных спутниковых систем.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 большая полуось эллипсоида а: Параметр, характеризующий размер эллипсоида.
2.2 высокоточная геодезическая сеть; ВГС: Спутниковая геодезическая сеть со средним расстоянием между смежными пунктами 150 - 300 км, координаты которой определяются относительно пунктов фундаментальной астрономо-геодезической сети.
2.3 геоид: Эквипотенциальная поверхность, совпадающая с поверхностью Мирового океана в состоянии полного покоя и равновесия и продолженная под материками.
2.4 геодезическая высота: Высота точки над поверхностью отсчетного эллипсоида, отсчитываемая по нормали к эллипсоиду.
2.5 геодезическая долгота: Двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического меридиана.
2.6 геодезическая широта: Угол между нормалью к поверхности отсчетного эллипсоида, проходящей через заданную точку, и плоскостью его экватора.
2.7 гравитационное поле Земли; ГПЗ: Поле силы тяжести на поверхности Земли и во внешнем пространстве, обусловленное силой притяжения Земли и центробежной силой, возникающей в результате суточного вращения Земли.
2.8 квазигеоид: Геометрическое место точек, получаемых путем откладывания нормальных высот от точек физической поверхности Земли по нормали к эллипсоиду. Математическая поверхность, близкая к геоиду, и являющаяся отсчетной для установления системы нормальных высот.
2.9 космическая геодезическая сеть; КГС: Сеть геодезических пунктов, закрепляющих геоцентрическую систему координат, положение которых на земной поверхности определено по наблюдениям искусственных спутников Земли.
2.10 модель гравитационного поля Земли: Математическое описание характеристик гравитационного поля Земли.
2.11 нормальная высота: Измеренная разность геопотенциала в данной точке и начале счета высот, деленная на среднее значение нормальной силы тяжести.
2.12 нормальное гравитационное поле Земли: Модель гравитационного поля Земли, представляемая нормальным потенциалом силы тяжести уровенного эллипсоида вращения и фундаментальными геодезическими параметрами, однозначно определяющими отсчетную систему.
2.13 общеземной эллипсоид; ОЗЭ: Эллипсоид вращения, который характеризует фигуру и размеры Земли и применяется для обработки геодезических измерений на всей поверхности Земли в общеземной (геоцентрической) системе координат.
2.14 отсчетный эллипсоид: Эллипсоид вращения, который характеризует фигуру и размеры Земли и определенным образом ориентирован в теле Земли.
2.15 планетарная модель гравитационного поля Земли: Модель гравитационного поля Земли, отражающая гравитационные особенности Земли в целом.
2.16 плоскость астрономического меридиана: Плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.
2.17 плоскость геодезического меридиана: Плоскость, проходящая через нормаль к поверхности отсчетного эллипсоида в данной точке и параллельная его малой оси.
2.18 плоскость начального меридиана: Плоскость меридиана, от которого ведется счет долгот.
2.19 плоские прямоугольные координаты: Линейные величины, определяющие положение точек на плоскости, на которой отображена в заданной картографической проекции ограниченная часть поверхности отсчетного эллипсоида. Осями координат являются прямолинейные изображения экватора эллипсоида и осевого меридиана соответствующей зоны, пересекающиеся под прямым углом.
2.20 сжатие эллипсоида α: Разность между большой или малой осями эллипсоида, выраженная в единицах большой полуоси и вычисляемая по формуле
![]()
2.21 первый (второй) эксцентриситет e (eʹ)
эллипсоида: Фокальное расстояние с, выраженное в единицах большой
(малой) полуоси эллипсоида и вычисляемое по формуле ![]() ,
где
,
где ![]() .
.
2.22 геодезические координаты: Параметры, два из которых (геодезическая широта и геодезическая долгота) характеризуют направление нормали к поверхности отсчетного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третий (геодезическая высота) представляет собой высоту точки над поверхностью отсчетного эллипсоида.
2.23 система геодезических параметров Земли: Совокупность параметров и точностных характеристик фундаментальных геодезических постоянных, общеземного эллипсоида, модели гравитационного поля Земли, геоцентрической системы координат и параметров трансформирования ее в другие системы координат.
2.24 спутниковая геодезическая сеть 1-го класса; СГС-1: Спутниковая геодезическая сеть со средним расстоянием между соседними пунктами 15 - 20 км, координаты которых определяются относительно высокоточной геодезической сети.
2.25 фундаментальная астрономо-геодезическая сеть; ФАГС: Спутниковая геодезическая сеть со средним расстоянием между соседними пунктами 650 - 1000 км, координаты которых определяются в геоцентрической системе координат.
2.26 фундаментальные геодезические постоянные: Взаимосогласованные геодезические постоянные, однозначно определяющие параметры общеземного эллипсоида и нормальное гравитационное поле Земли.
2.27 эквипотенциальная поверхность: Поверхность, в каждой точке которой потенциал остается постоянным.
2.28 параметры трансформирования систем координат: Параметры, с помощью которых выполняется преобразование координат из одной системы координат в другую.
3 Сокращения
В настоящем стандарте применены следующие сокращения:
|
ВГС |
- высокоточная геодезическая сеть; |
|
ГГС |
- государственная геодезическая сеть; |
|
ГЛОНАСС |
- глобальная навигационная спутниковая система Российской Федерации; |
|
ГНСС |
- глобальная навигационная спутниковая система; |
|
ГПЗ |
- гравитационное поле Земли; |
|
ПЗ-90, ПЗ-90.02, ПЗ-90.11 |
- системы геодезических параметров «Параметры Земли 1990 года» Российской Федерации; |
|
ГСК-2011 |
- геодезическая система координат 2011 года Российской Федерации, эпоха 2011 года; |
|
СГС-1 |
- спутниковая геодезическая сеть 1-го класса; |
|
СК |
- система координат; |
|
ФАГС |
- фундаментальная астрономо-геодезическая сеть; |
|
BIH |
- Международное бюро времени; |
|
GPS |
- глобальная навигационная спутниковая система Соединенных Штатов Америки; |
|
IERS |
- Международная служба вращения Земли; |
|
ITRF |
- практическая реализация системы координат TRS, осуществляемая IERS; |
|
IRM |
- референцный меридиан, установленный IERS; |
|
IRP |
- референцный полюс, установленный IERS; |
|
TRS |
- земная система координат, участвующая вместе с Землей в ее суточном вращении вокруг оси; |
|
TRF |
- практическая реализация системы координат TRS; |
|
aWGS-84 |
- большая полуось общеземного эллипсоида в системе WGS-84; |
|
аКр |
- большая полуось эллипсоида Красовского; |
|
αКр |
- сжатие эллипсоида Красовского; |
|
WGS-84 |
- система геодезических параметров «Мировая геодезическая система 1984 года» Соединенных Штатов Америки. |
4 Земная система координат и ее практические реализации
Земная система координат предназначена для количественного описания положения и движения объектов, находящихся на поверхности Земли и в околоземном пространстве.
Количественными характеристиками положения точки в земной системе координат являются координаты, имеющие вариации во времени, вызванные геофизическими явлениями (тектоническими или приливными деформациями).
Практическая реализация TRS, осуществляемая IERS, получила наименование ITRF и заключается в определении координат пунктов (и их скоростей изменения во времени), закрепляющих ITRF на поверхности Земли.
Начало и направление осей системы координат ITRF определены следующим образом:
- начало - в центре масс Земли;
- ось Z направлена в IRP;
- ось X направлена в точку пересечения плоскости IRM с плоскостью, проходящей через начало системы координат TRF и перпендикулярную к оси Z;
- ось Y дополняет систему до правой ортогональной координатной системы.
Точность последних практических реализаций TRS находится на субсантиметровом уровне точности определения координат пунктов.
Практические реализации земной системы координат TRS, используемые в глобальных навигационных спутниковых системах ГЛОНАСС (ПЗ-90) и GPS (WGS-84), а также референцные системы координат Российской Федерации (СК-42, СК-95, ГСК-2011) приведены в 4.1.
Примечание - В настоящее время Международной службой вращения Земли получена практическая реализация TRS, обозначаемая как ITRF-2014 на эпоху 2010 года.
4.1 Системы геодезических параметров
4.1.1 Система геодезических параметров «Параметры Земли 1990 года»
4.1.1.1 Система геодезических параметров ПЗ-90 включает в себя:
- фундаментальные геодезические постоянные;
- параметры ОЗЭ;
- систему координат ПЗ-90, закрепляемую координатами пунктов космической геодезической сети;
- характеристики модели ГПЗ;
- параметры трансформирования геоцентрической системы координат ПЗ-90 в референцные системы координат России и зарубежные системы координат.
Параметры трансформирования между системой координат ПЗ-90 и референцными системами координат России и порядок их использования при преобразовании систем координат приведены в приложении А.
Примечание - В соответствии с [1] в настоящее время установлена государственная геоцентрическая система координат «Параметры Земли 1990 года» (ПЗ-90), отнесенная к эпохе 2010.0 и обозначаемая как ПЗ-90.11.
Числовые значения элементов трансформирования между системами координат ПЗ-90, ПЗ-90.02 и ПЗ-90.11, а также порядок их использования при преобразовании систем координат приведены в приложениях Б и В.
4.1.1.2 Теоретическое определение системы координат ПЗ-90 основывается на следующих положениях:
- начало системы координат расположено в центре масс Земли;
- ось Z направлена к условному земному полюсу (международному условному началу);
- ось X лежит в плоскости начального астрономического меридиана, установленного IERS и Международным бюро времени;
- ось Y дополняет систему до правой системы координат.
4.1.1.3 Положения точек в системе ПЗ-90 могут быть получены в виде пространственных прямоугольных или геодезических координат.
Геодезические координаты относятся к ОЗЭ, размеры и форма которого определяются значениями большой полуоси и сжатия.
Центр ОЗЭ совпадает с началом системы координат ПЗ-90, ось вращения эллипсоида - с осью Z, а плоскость начального меридиана - с плоскостью XOZ.
Примечание - За отсчетную поверхность в системах геодезических параметров ПЗ-90, ПЗ-90.02 и ПЗ-90.11 принят общеземной эллипсоид с большой полуосью aПЗ = 6378136 м и сжатием αПЗ = 1/298,25784.
4.1.2 Система геодезических параметров «Мировая геодезическая система 1984 года»
4.1.2.1 Система параметров WGS-84 включает в себя:
- фундаментальные геодезические постоянные;
- систему координат WGS-84, закрепляемую координатами пунктов глобальной геодезической сети;
- параметры ОЗЭ;
- характеристики модели ГПЗ;
- параметры элементов трансформирования между геоцентрической системой координат WGS-84 в различные национальные системы координат.
Параметры элементов трансформирования между геоцентрическими системами координат ПЗ-90 и WGS-84, а также порядок использования элементов трансформирования приведены в приложении Г.
Примечание - В настоящее время действует шестая версия системы координат WGS-84, отнесенная к эпохе 2005.0 и обозначаемая как WGS-84(G1762). В приведенных обозначениях версий системы координат WGS-84 литера «G» означает «GPS», а «730», «873», «1150» и «1762» указывают на номер GPS-недели, соответствующей дате, к которой отнесены эти версии системы координат WGS-84.
По оценкам зарубежных специалистов система координат WGS-84(G1762) согласована с системой координат ITRF-2008 на субмиллимитровом уровне.
4.1.2.2 Теоретическое определение системы координат WGS-84 основывается на следующих положениях:
- начало системы координат расположено в центре масс Земли;
- ось Z направлена в IERS Reference Pole (IRP);
- ось X направлена в точку пересечения плоскости (IRM) с плоскостью, проходящей через начало системы координат WGS-84 и перпендикулярную к оси Z;
- ось Y дополняет систему до правой системы координат.
4.1.2.3 Положения точек в системе WGS-84 могут быть получены в виде пространственных прямоугольных или геодезических координат.
Геодезические координаты относятся к ОЗЭ, размеры и форма которого определяются значениями большой полуоси и сжатия.
Центр эллипсоида совпадает с началом системы координат WGS-84, ось вращения эллипсоида совпадает с осью Z, а плоскость начального меридиана - с плоскостью XOZ.
Примечание - За отсчетную поверхность в WGS принят общеземной эллипсоид с большой полуосью aWGS-84 , равным 6378137 м, и сжатием αWGS-84 равным 1/298,257223563.
4.2 Референцные геодезические системы координат Российской Федерации
4.2.1 Геодезическая система координат Российской Федерации ГСК-2011
4.2.1.1 В соответствии с [1] в качестве государственной установлена также ГСК-2011, отнесенная к эпохе 2011 года.
ГСК-2011 - государственная геодезическая система координат, предназначенная для осуществления геодезической, картографической, навигационной и других видов деятельности для текущих и перспективных потребностей экономики, науки, обороны и безопасности Российской Федерации и обеспечивающая преемственность существующих геодезических систем координат СК-95 и СК-42.
4.2.1.2 Теоретическое определение системы координат ГСК-2011 основывается на следующих положениях:
- начало системы координат расположено в центре масс Земли;
- ось Z направлена к Условному земному полюсу, как определено рекомендациями IERS и BIH;
- ось X направлена в точку пересечения плоскости экватора и начального меридиана, установленного BIH;
- ось Y дополняет систему до правой системы координат.
4.2.1.3 ГСК-2011 закрепляется на поверхности Земли пунктами ФАГС, ВГС, СГС-1, а также пунктами ГГС Российской Федерации общим числом около 300000.
4.2.1.4 Положения точек в системе ГСК-2011 могут быть получены в виде пространственных прямоугольных или геодезических координат.
Геодезические координаты относятся к ОЗЭ, размеры и форма которого определяются значениями большой полуоси и сжатия.
Центр ОЗЭ совпадает с началом системы координат ГСК-2011, ось вращения эллипсоида совпадает с осью Z, а плоскость начального меридиана - с плоскостью XOZ.
Примечание - За отсчетную поверхность в ГСК-2011 принят общеземной эллипсоид с большой полуосью aГСК-2011 равной, 6 378 136,5 м, и сжатием αГСК-2011 равным 2564151.
4.2.2 Референцные системы координат СК-95 и СК-42
Кроме ГСК-2011 координатная основа Российской Федерации представлена референцной системой координат, реализованной в виде ГГС, закрепляющей систему координат на территории страны, и государственной нивелирной сети, распространяющей на всю территорию страны систему нормальных высот (Балтийская система), исходным началом которой является нуль Кронштадтского футштока.
Положения определяемых точек относительно координатной основы могут быть получены в виде пространственных прямоугольных или геодезических координат либо в виде плоских прямоугольных координат и высот.
Геодезические координаты в референцных системах координат Российской Федерации СК-95 и СК-42 относятся к эллипсоиду Красовского, размеры и форма которого определяются значениями большой полуоси aКр равной 6378245 м, и сжатия αКр равного 1/298,3.
Центр эллипсоида Красовского совпадает с началом референцной системы координат, ось вращения эллипсоида параллельна оси вращения Земли, а плоскость нулевого меридиана определяет положение начала счета долгот.
Примечание - В соответствии [1] система геодезических координат 1995 года (СК-95) и единая система геодезических координат 1942 года (СК-42), введенная в соответствии с [2], применяются до 1 января 2021 г. в отношении материалов (документов), созданных с их использованием.
5 Методы преобразований координат определяемых точек
5.1 Преобразование геодезических координат в прямоугольные пространственные координаты и обратно
5.1.1 Преобразование геодезических координат в прямоугольные пространственные координаты осуществляют по формулам:
где Х, Y, Z- прямоугольные пространственные координаты точки;
В, L - геодезические широта и долгота точки соответственно, рад;
Н - геодезическая высота точки, м;
N- радиус кривизны первого вертикала, м;
е - эксцентриситет эллипсоида.
Значения радиуса кривизны первого вертикала и квадрата эксцентриситета эллипсоида вычисляют соответственно по формулам:
|
|
(2) |
|
|
где а - большая полуось эллипсоида, м;
α - сжатие эллипсоида.
5.1.2 Для преобразования пространственных прямоугольных координат в геодезические необходимо проведение итераций при вычислении геодезической широты.
Для этого используют следующий алгоритм:
1 - вычисляют вспомогательную величину D по формуле
|
|
(4) |
2 - анализируют значение D:
а) если D = 0, то
|
|
(5) |
|
|
(6) |
б) если D ≠ 0, то при
|
(7) |
|
|
где |
3 - анализируют значение Z:
а) если Z = 0, то
|
|
(9) |
б) во всех других случаях вычисления выполняют следующим образом:
- вычисляют значения вспомогательных величин r, c, p по формулам:
|
|
(10) |
|
|
(11) |
|
|
(12) |
- реализуют итеративный процесс, используя вспомогательные величины s1 и s2:
|
|
(13) |
|
(14) |
|
|
|
(15) |
|
(16) |
если значение d, определяемое по формуле (16), меньше установленного значения допуска, то
|
|
(17) |
|
|
(18) |
если значение d не менее установленного значения допуска, то
|
|
(19) |
и вычисления повторяют, начиная с формулы (14).
5.1.3 При преобразованиях координат в качестве допуска прекращения итеративного процесса принимают значение d, равное 10-4.
В этом случае погрешность вычисления геодезической высоты не превышает 0,003 м.
5.2 Преобразование пространственных прямоугольных координат
Пользователям ГНСС ГЛОНАСС и GPS необходимо выполнять преобразования координат из системы ПЗ-90 в систему WGS-84 и обратно, а также из ПЗ-90 и WGS-84 в референцные системы координат Российской Федерации, используя семь элементов трансформирования, точность которых определяет точность преобразований.
Параметры трансформирования между системами координат указаны в соответствии с приложениями А - Д:
- ПЗ-90.11 и СК-42, СК-95, ГСК-2011 (см. приложение А);
- ПЗ-90.11 и ПЗ-90.02 (см. приложение Б);
- ПЗ-90.11 и ПЗ-90 (см. приложение В);
- ПЗ-90.11 и WGS-84(G1150) (см. приложение Г);
- ПЗ-90.11 и ITRF-2008 - (см. приложение Д);
Приложения А, Б и Д содержат эпоху параметров преобразования.
Это обстоятельство необходимо учитывать при преобразовании координат в соответствии с процедурой, приведенной в приложении Е.
Если данные об эпохе параметров преобразования отсутствуют, то преобразование координат выполняют стандартным образом.
Преобразование координат из системы WGS-84 в координаты референцных систем Российской Федерации осуществляют последовательным преобразованием координат сначала в систему ПЗ-90, а затем - в координаты референцных систем.
Преобразование пространственных прямоугольных координат выполняют по формуле
|
|
(20) |
где ∆х, ∆у, ∆z - линейные параметры трансформирования при переходе из системы А в систему Б, м;
ωх, ωу, ωz - угловые параметры трансформирования при переходе из системы А в систему Б, рад;
m - масштабный параметр трансформирования при переходе из системы А в систему Б.
Обратное преобразование прямоугольных координат выполняют по формуле
|
|
(21) |
5.3 Преобразование геодезических координат
Преобразование геодезических координат из системы А в систему Б выполняют по формулам
|
(22) |
где B, L - геодезические широта и долгота, выраженные в единицах плоского угла;
H - геодезическая высота, м;
∆B, ∆L, ∆Н - поправки к геодезическим координатам точки.
Поправки к геодезическим координатам вычисляют по формулам: