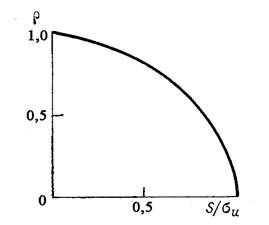
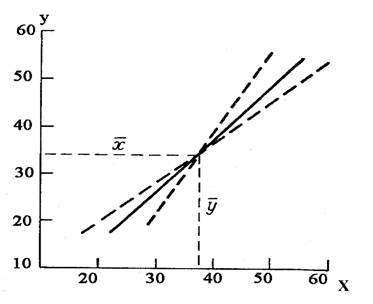
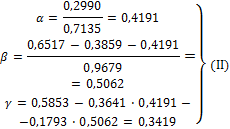
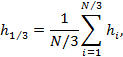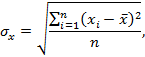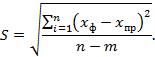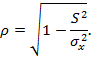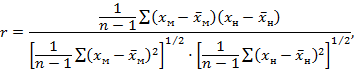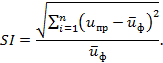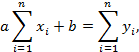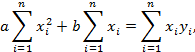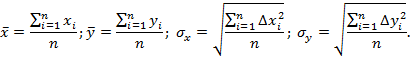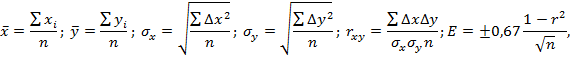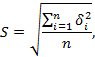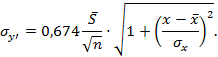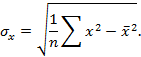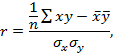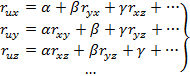|
МИНИСТЕРСТВО
ПРИРОДНЫХ РЕСУРСОВ И ЭКОЛОГИИ Федеральная
служба по гидрометеорологии и мониторингу окружающей среды |
|
|
РУКОВОДЯЩИЙ ДОКУМЕНТ |
РД 52.27.759-2011 |
НАСТАВЛЕНИЕ
ПО СЛУЖБЕ ПРОГНОЗОВ
Раздел 3
Часть III
Служба морских гидрологических прогнозов
Место
Издательская организация
2011
Предисловие
|
1 РАЗРАБОТАН |
Федеральным государственным бюджетным учреждением «Гидрометеорологический научно-исследовательский центр Российской Федерации» (ФГБУ «Гидрометцентр России») |
|
2 РАЗРАБОТЧИКИ |
З.К. Абузяров, канд. геогр. наук; Е.С. Нестеров, д-р геогр. наук (научный редактор); В.А. Мартыщенко (руководитель разработки) |
|
3 СОГЛАСОВАН |
УМЗА Росгидромета |
|
4 УТВЕРЖДЕН |
руководителем Росгидромета А.В. Фроловым |
|
5 ВВЕДЕН В ДЕЙСТВИЕ |
приказом Росгидромета |
|
6 ОДОБРЕН |
Центральной методической комиссией по гидрометеорологическим и гелиогеофизическим прогнозам Росгидромета 25 июня 2010 г. |
|
7 ЗАРЕГИСТРИРОВАН |
ЦМТР ФГБУ «НПО «Тайфун», за номером РД 52.27.759-2011 от 21.11.2011 г. |
|
8 ВЗАМЕН |
«Наставление по службе прогнозов. Раздел 3. Часть III. Служба морских гидрологических прогнозов». Изд. 3-е. 1982 г. и «Наставление по службе прогнозов. Раздел 2. Служба метеорологических прогнозов. Части III, IV, V», разделы 8, 9, 10. Изд. 1981 г. |
СОДЕРЖАНИЕ
|
РУКОВОДЯЩИЙ ДОКУМЕНТ |
|
НАСТАВЛЕНИЕ
Раздел 3 Часть III СЛУЖБА МОРСКИХ ГИДРОЛОГИЧЕСКИХ ПРОГНОЗОВ |
Дата введения 01.03.2012 г.
1 Область применения
1.1 Настоящий руководящий документ устанавливает общие требования к подготовке и выпуску морских гидрологических прогнозов (далее - прогнозы) и штормовых предупреждений различной заблаговременности общего и специализированного назначения и оценке эффективности методов прогнозов и качества предоставляемой потребителям морской гидрометеорологической информации (далее - гидрометеорологическая информация).
1.2 Настоящий руководящий документ предназначен для службы морских гидрологических прогнозов, функционирующей на базе научно-исследовательских учреждений и территориальных управлений Росгидромета морской направленности и осуществляющих гидрометеорологическое обеспечение различных видов морской деятельности.
2 Нормативные ссылки
В настоящем руководящем документе использованы ссылки на следующие нормативные документы:
ГОСТ 18458-84 Приборы, оборудование и плавсредства наблюдений в морях и океанах. Термины и определения
РД 52.04.316-1992 Наставление гидрометеорологическим станциям и постам. Выпуск 9. Гидрометеорологические наблюдения на морских станциях. Часть II. Гидрометеорологические наблюдения на судовых станциях, производимые штатными наблюдателями. Книга 1. Общие методические требования к организации и обеспечению гидрометеорологических и актинометрических наблюдений на судах. Книга 2. Методики выполнения гидрометеорологических наблюдений на судах
РД 52.04.567-2003 Положение о государственной наблюдательной сети
РД 52.04.614-2000 Наставление гидрометеорологическим станциям и постам. Выпуск 3. Часть II. Обработка материалов метеорологических наблюдений
РД 52.04.663-2005 Наставление гидрометеорологическим станциям и постам. Выпуск 9. Гидрометеорологические наблюдения на морских станциях. Часть II. Гидрометеорологические наблюдения на судовых станциях, производимые штатными наблюдателями. Книга 3. Общие требования к программному обеспечению первичной обработки и архивации результатов судовых наблюдений гидрометеорологических и актинометрических величин. Журнал КГМ-15 для записи судовых гидрометеорологических наблюдений
РД 52.14.642-2005 Текстовые документы. Общие требования к построению, изложению, оформлению, содержанию и обозначению
РД 52.19.143-2010 Перечень документов архивного фонда данных о состоянии окружающей среды, ее загрязнении
РД 52.27.723-2009 Базовые требования к технологии подготовки краткосрочных прогнозов погоды
РД 52.27.724-2009 Наставление по краткосрочным прогнозам погоды общего назначения
РД 52.88.699-2008 Положение о порядке действий учреждений и организаций при угрозе возникновения и возникновении опасных природных явлений
3 Термины, определения и сокращения
3.1 В настоящем руководящем документе использованы следующие термины с соответствующими определениями:
3.1.1 автоматизированное рабочее место; АРМ: Индивидуальный комплекс технических и программных средств, предназначенный для автоматизации профессионального труда специалиста и обеспечивающий подготовку, редактирование, поиск и выдачу (на экран и печать) необходимых ему документов и данных, АРМ может быть реализован в виде автономной автоматизированной системы на ПЭВМ или являться терминалом автоматизированной системы.
3.1.2 банк данных; БД: Система программных, языковых, организационных и технических средств, предназначенных для централизованного накопления и коллективного многоаспектного использования данных.
3.1.3 береговая земная станция; БЗС: Стационарное наземное радиоустройство, действующее как соединительное звено между наземной сетью и спутниками ИНМАРСАТ в Морской подвижной спутниковой связи.
3.1.4 внутренние морские воды Российской Федерации: Воды, расположенные в сторону берега от исходных линий, от которых отмеряется ширина территориального моря Российской Федерации [1].
Внутренние морские воды являются составной частью территории Российской Федерации.
3.1.5 гидрометеорологическое обеспечение: Совокупность работ по своевременному и наиболее полному удовлетворению запросов потребителей гидрометеорологической информацией.
3.1.6 государственная наблюдательная сеть: Система стационарных и подвижных пунктов наблюдений, в том числе постов, станций, лабораторий, центров, бюро, обсерваторий, предназначенных для наблюдений за физическими и химическими процессами, происходящими в окружающей природной среде.
3.1.7 информационная продукция: Полученная в результате обработки сведений (данных) обобщенная информация, предназначенная для распространения или реализации [2].
Примечание - информационная продукция является конечным результатом деятельности по сбору и обработке полученных в результате наблюдений данных и включает в себя специализированную, экстренную информацию и информацию общего назначения.
3.1.8 информация о состоянии окружающей среды, ее загрязнении: Сведения (данные), полученные в результате мониторинга окружающей среды, ее загрязнения.
3.1.9 информация общего назначения: Полученная и обработанная в порядке, установленном федеральным органом исполнительной власти в области гидрометеорологии и смежных с ней областях, предоставляемая пользователям (потребителям) бесплатно информация о фактическом и прогнозируемом состоянии окружающей природной среды, ее загрязнении.
3.1.10 информация по обеспечению безопасности на море: Навигационные и метеорологические предупреждения, метеорологические прогнозы и другие срочные сообщения, относящиеся к обеспечению безопасности, передаваемые на суда [3].
3.1.11 координатор НАВТЕКС: Полномочный орган, которому поручено эксплуатировать и осуществлять управление одной или более станциями НАВТЕКС радиопередачи информации для обеспечения безопасности на море в качестве части Международной службы НАВТЕКС [4].
3.1.12 координатор МЕТЗОНЫ: Полномочный орган, которому поручено координировать радиопередачу информации для обеспечения безопасности на море посредством одной или нескольких национальных метеорологических служб, действующих в качестве подготавливающих или выпускающих служб для данной МЕТЗОНЫ [4].
3.1.13 Международная служба НАВТЕКС: Система для координированной радиопередачи и автоматического приема на частоте 518 кГц информации по безопасности на море с помощью узкополосной буквопечатающей телеграфии с использованием английского языка [3].
Примечание - национальная служба НАВТЕКС использует язык по решению соответствующего органа.
3.1.14 Международная служба SafetyNET: Система для координируемой передачи и автоматизированного приема информации по обеспечению безопасности на море через систему расширенного группового вызова ИНМАРСАТа с использованием английского языка и в соответствии с положениями Международной конвенции по обеспечению безопасности жизни на море (СОЛАС) 1974 г. с учетом поправок к ней [4].
3.1.15 МЕТЗОНА: Географическая морская зона, определенная для целей координирования радиопередач морской гидрометеорологической информации. Термин МЕТЗОНА сопровождается римской цифрой, которая используется для обозначения конкретной области моря. Границы таких областей не имеют отношение и не должны ставить под сомнение любые границы между государствами [4].
3.1.16 морская гидрометеорологическая информация: Совокупность сведений, включающих данные морских метеорологических и гидрологических наблюдений наземного и космического базирования, и информационная продукция.
3.1.17 морские гидрологические прогнозы: Научно обоснованное предсказание изменений гидрологических характеристик - представляют собой предвычисление во времени определенного явления или элемента гидрологического режима моря, основанное на знании законов физики океана и атмосферы и учитывающие местные физико-географические условия.
3.1.18 НАВАРЕА/МЕТАРЕА: Географический морской район, установленный для координации передачи по радио навигационных и метеорологических предупреждений.
3.1.19 обработка результатов наблюдений: Совокупность процедур и правил по подготовке гидрометеорологической информационной продукции для передачи ее потребителям и (или) в фонды постоянного хранения данных для дальнейшего использования (по РД 52.04.614).
3.1.20 опасное природное явление (ОЯ): Гидрометеорологическое явление, которое по интенсивности развития, продолжительности или моменту возникновения могут представлять угрозу жизни или здоровью граждан, а также могут наносить значительный материальный ущерб (по РД 52.88.699).
К гидрометеорологическим явлениям относятся морские метеорологические и гидрологические явления или их сочетания, возникающие на акватории морей и океанов.
3.1.21 оправдываемость морских гидрологических прогнозов: Степень соответствия прогнозируемых гидрометеорологических величин и явлений фактически наблюдавшимся.
3.1.22 оправдываемость штормовых предупреждений: Степень соответствия прогнозируемых характеристик ОЯ фактически наблюдавшимся значениям морских метеорологических и гидрологических величин) (по РД 52.27.724).
3.1.23 пользователь (потребитель) информации: Субъект, обращающийся к информационной системе или посреднику за получением необходимой ему информации и пользующийся ею.
3.1.24 порт: Участок берега и прилегающий район и акватория, где размещен комплекс сооружений и устройств для полного обслуживания судов.
3.1.25 прогноз общего назначения: прогноз, публикуемый для общего сведения и не имеющий определенного потребителя.
3.1.26 служба информации по безопасности на море: Координационная служба навигационных предупреждений и морских метеорологических и гидрологических прогнозов и оповещений о бедствии.
3.1.27 специализированная информация; СИ: Информация, которая предоставляется по заказу пользователя (потребителя) и за счет его средств.
3.1.28 специализированный прогноз: прогноз, составленный по заказу определенного потребителя, на договорной основе.
3.1.29 территориальное море Российской Федерации: Примыкающий к сухопутной территории или к внутренним морским водам морской пояс шириной 12 морских миль, отмеряемых от исходных линий, указанных в статье 4 Федерального закона (внешняя граница территориального моря является государственной границей Российской Федерации) [1].
3.1.30 Центр ЕСИМО: Организация, наделенная полномочиями выполнять функции ЕСИМО в соответствии с документом «Порядок и регламент деятельности центра ЕСИМО» [5].
3.1.31 штормовое предупреждение: Информация о прогнозируемом ОЯ (по РД 52.88.699).
3.1.32 штормовое оповещение: Информация о начавшемся ОЯ (по РД 52.88.699).
3.1.33 экстренная информация: Незамедлительно передаваемые штормовые предупреждения и/или штормовые оповещения, а также незамедлительно передаваемая информация о фактических и прогнозируемых резких изменениях погоды и загрязнения окружающей среды, которые могут угрожать жизни или здоровью граждан и наносить ущерб окружающей среде [2].
3.1.34 эффективность прогноза или штормового предупреждения: Комплексная характеристика успешности прогноза или штормового предупреждения, учитывающая его оправдываемость и заблаговременность.
3.2 В настоящем руководящем документе применены следующие сокращения:
АРГО - Международный проект по размещению в Мировом океане системы всплывающих буев;
АРМ - автоматизированное рабочее место;
АСПД - автоматизированная система передачи данных;
БД - база данных;
БЗС - береговая земная станция;
ВМО - Всемирная метеорологическая организация;
ВНИРО - Всероссийский научно-исследовательский институт рыбного хозяйства и океанографии;
ГМБ - гидрометеорологическое бюро;
ГМЦ - гидрометеорологический центр;
ГМССБ - Глобальная морская система связи при бедствии и для обеспечения безопасности;
ГСТ - Глобальная система телесвязи;
ЕСИМО - Единая система информации об обстановке в Мировом океане;
ИБМ - информация по обеспечению безопасности на море;
ИНМАРСАТ - международная система подвижной спутниковой связи;
КРС - кустовые радиостанции;
МИНКОМСВЯЗЬ - Министерство связи и массовых коммуникаций Российской Федерации;
МИНТРАНС - Министерство транспорта Российской Федерации;
ММЦ - Мировой метеорологический центр;
МОК - Международный олимпийский комитет;
МО РФ - Министерство обороны Российской Федерации;
МПР РФ - Министерство природных ресурсов Российской Федерации;
МСКЦ - морской спасательный координационный центр;
МЧС России - Министерство Российской Федерации по делам гражданской обороны, чрезвычайным ситуациям и ликвидации последствий стихийных бедствий;
НИИ - научно-исследовательский институт;
НИС - научно-исследовательское судно;
НИЦ ГОСНИНГИ МО ГУП РФ - Государственный научно-исследовательский навигационный и гидрографический институт Минобороны РФ;
НМЦ - Национальный метеорологический центр;
НПО - научно-производственное объединение;
ОНС - организация наблюдательной сети;
РГВ - расширенный групповой вызов;
РМЦ - радиометеорологический центр;
РОСГИДРОМЕТ - Федеральная служба России по гидрометеорологии и мониторингу окружающей среды;
РОСРЫБОЛОВСТВО - Федеральное агентство по рыболовству;
РСЧС - Единая государственная система предупреждения и ликвидации чрезвычайных ситуаций;
СБД - специализированная база данных;
СИ - специализированная информация;
СМГП - служба морских гидрологических прогнозов;
СМГМО - специализированное морское гидрометеорологическое обеспечение;
СОЛАС - Международная конвенция по охране человеческой жизни на море;
СРБД - система распределенных баз данных;
ТПО - температура поверхности океана;
УГМК - Управление гидрометеорологии и кадров Росгидромета;
УГМАВ - Управление геофизического мониторинга активных воздействий и государственного надзора Росгидромета;
УГМС - Управление по гидрометеорологии и мониторингу окружающей среды;
УМЗА - Управление мониторинга загрязнения окружающей среды, полярных и морских работ Росгидромета;
ФГУ «Дальневосточный РЦПОД» - Федеральное государственное учреждение «Дальневосточный региональный центр приема и обработки данных»;
ФГБУ «ААНИИ» - Федеральное государственное бюджетное учреждение «Арктический и антарктический научно-исследовательский институт»;
ФГБУ «Авиаметтелеком Росгидромета» - Главный центр информационных технологий и метеорологического обслуживания авиации;
ФГБУ «ВНИИГМИ-МЦД» - Всероссийский научно-исследовательский институт гидрометеорологической информации - Мировой центр данных;
ФГБУ «Гидрометцентр России» - Гидрометеорологический научно-исследовательский центр Российской Федерации;
ФГБУ «ГОИН» - Государственный океанографический институт имени Н.Н. Зубова;
ФГБУ «ДВНИГМИ» - Дальневосточный региональный научно-исследовательский гидрометеорологический институт;
ФГБУ «РФИ Минприроды России» - Главный научно-исследовательский и информационно-вычислительный центр Министерства природных ресурсов Российской Федерации;
ФГУП «ВНИРО» - Федеральное государственное унитарное предприятие «Всероссийский научно-исследовательский институт рыбного хозяйства и океанографии»;
ЦБМД - централизованная база метаданных;
ЦГМС - областной (республиканский, краевой, окружной и др.) центр по гидрометеорологии и мониторингу окружающей среды Росгидромета;
ЦМКП - Центральная методическая комиссия по гидрометеорологическим и гелиофизическим прогнозам Росгидромета;
ЦРС - центральная радиостанция;
ЧС - чрезвычайная ситуация;
SafetyNET - система передачи и автоматизированного приема информации по обеспечению безопасности на море через расширенный групповой вызов ИНМАРСАТА с использованием английского языка для удовлетворения требований КОНВЕНЦИИ СОЛАС;
UTS - всемирное скоординированное время.
4 Служба морских гидрологических прогнозов
4.1 Общие положения
4.1.1 Служба морских гидрологических прогнозов (СМГП) функционирует на базе научно-исследовательских учреждений и территориальных управлений Росгидромета морской направленности и осуществляет гидрометеорологическое обеспечение различных видов морской деятельности.
4.1.2 Гидрометеорологическое обеспечение согласно [6] включает в себя:
- предоставление прогнозов и штормовых предупреждений в форме морских метеорологических бюллетеней, карт, таблиц и т.д.;
- осуществление гидрометеорологической поддержки морских операций по поиску и спасению;
- предоставление специализированной информации;
- предоставление консультаций и экспертных заключений.
4.1.3 Объектами гидрометеорологического обеспечения являются федеральные и региональные органы власти, население, государственные и коммерческие производственные предприятия и организации, связанные морем [2].
4.1.4 В функциональные обязанности СМГП входит:
- регулярное получение гидрометеорологической информации о текущем гидрометеорологическом состоянии морей и океанов, включая сведения об опасных природных явлениях (ОЯ);
- обработка, контроль и оперативный анализ гидрометеорологической информации, поступающей по различным каналам связи;
- составление прогнозов различной заблаговременности и доведение их до потребителя;
- разработка новых и усовершенствование существующих методов и технологий диагноза и прогноза гидрометеорологических характеристик моря и оценка их качества;
- ведение фонда научно-оперативных материалов СМГП;
- анализ результатов прогнозов и штормовых предупреждений;
- составление и оформление методической записки, на основании которой составляются морские гидрологические прогнозы.
4.1.5 Организации СМГП должны обеспечивать современные требования к оперативности, информативности и качеству предоставляемой потребителю информационной продукции, в том числе по РД 52.27.723.
4.1.6 Деятельность организаций СМГП регламентируется нормативными правовыми актами и рекомендациями ВМО/МОК согласно [1 - 5, 7]
4.2 Морская гидрометеорологическая наблюдательная сеть
4.2.1 Морская гидрометеорологическая наблюдательная сеть (далее наблюдательная сеть) состоит из систем наземных и дистанционных пунктов наблюдений в соответствии с РД 52.04.567.
Элементами системы наземных пунктов наблюдений являются прибрежные и островные гидрометеорологические станции и посты (далее станции и посты), судовые станции, организованные на судах Росгидромета и судах зарубежных стран, выполняющие добровольные наблюдения по программе ВМО согласно РД 52.04.316, корабли погоды, экспедиционные суда, автоматические стационарные и дрейфующие буйковые станции.
Элементами дистанционных пунктов наблюдений являются спутники, самолеты, радиолокаторы.
Основным назначением наблюдательной сети является проведение систематических наблюдений за состоянием морской среды в открытых, прибрежных и устьевых районах морей и океанов.
4.2.2 Поступающие данные используются для:
- подготовки оперативных диагностических и прогностических материалов;
- выполнения научных исследований по разработке математических моделей и методов расчета и прогноза основных параметров морской природной среды, включая загрязнение моря;
- расчета климатических характеристик и для получения необходимых расчетных параметров, из которых исходят при проектировании судов, платформ, портовых сооружений и т.д.
4.2.3 Наблюдательная сеть организуется и развивается таким образом, чтобы обеспечить нормальную работу по гидрометеорологическому обеспечению.
Она должна удовлетворять следующим основным принципам:
- максимально полное и своевременное удовлетворение запросов потребителей;
- репрезентативность (надежность наблюдений) наблюдательных пунктов;
- объективная характеристика особенностей гидрометеорологического режима морей с учетом их размеров и конфигурации, наличия островов, заливов и проливов;
- наличие каналов связи (телеграф, телефон, радио и др.).
4.2.4 Размещение наземных станций и постов следует производить с таким расчетом, чтобы обеспечить всестороннее изучение гидрометеорологического режима, а также выполнение задач по оперативному гидрометеорологическому обеспечению потребителей.
Станции и посты организуются с учетом следующих факторов:
- степени изменчивости наблюдаемых гидрометеорологических величин и явлений, геофизических характеристик и уровня загрязнения природной среды;
- точности измерения (наблюдения), необходимой для обслуживания потребителей;
- необходимости иметь сведения о состояния окружающей среды по данному району.
4.2.5 Основным источником информации о гидрометеорологическом состоянии открытых районов морей и океанов являются данные наблюдений судовых станций, которые передаются в береговые центры сбора четыре раза в сутки (за 00, 06, 12 и 18 ч UTC). Дополнительно, вне очереди, они также передают информацию об ОЯ.
4.2.6. Значительная часть информации поступает с океанских дрейфующих и стационарных буев, автоматически измеряющих метеорологические и гидрологические параметры (ветер, температуру, соленость и т.д.) и передающих их через спутник на береговые центры сбора информации.
4.2.7 Наблюдения по международной программе АРГО являются специфическим видом глубоководных океанографических наблюдений, охватывающих всю толщу мирового океана. Буи АРГО передают через спутниковые системы в береговые центры информацию о вертикальном распределении температуры и электропроводности/солености морской воды, а также позволяют получать данные о течениях на поверхности моря и глубине дрейфа.
4.2.8 Важную роль играют сведения, регулярно получаемые с ИСЗ. Снимки с ИСЗ в первую очередь используются для составления карт ледовых условий, карт распределения температуры поверхности моря, для определения зон штормового волнения и положения тропических циклонов, зон подъема глубинных холодных вод (апвеллинга), положения гидрологических фронтов и т.д.
С помощью спутниковых снимков также определяют положение береговой линии, положение кромки неподвижного льда, границы различной сплоченности льда, положение крупных разводий, полыней, а также форму и размеры больших ледяных полей.
4.2.9 Значительная часть информации поступает в СМГП в рамках международного сотрудничества по линии ВМО/МОК. Порядок международного обмена и процедуры обработки осуществляются через кооперацию всех морских стран, членов ВМО, участвующих в этом процессе на бесплатной основе. Международный обмен информацией регламентируется соответствующими решениями ВМО/МОК [8, 9].
4.2.10 Предоставление информации частным фирмам и компаниям осуществляется на договорных условиях за плату с пересчетом на цены мирового рынка.
4.3 Порядок сбора, обработки и распространения гидрометеорологической информации
4.3.1 Результаты гидрометеорологических наблюдений, полученные с наблюдательной сети в соответствии с РД 52.04.614 и РД 52.04.663, составляют основу баз данных (БД) различных видов и назначений, которые используются для составления прогнозов и штормовых предупреждений, а также для описания гидрометеорологического режима и климата морей и океанов.
4.3.2 Сбор данных наблюдений осуществляется в «Оперативном режиме» и «Задержанном режиме».
4.3.3 «Оперативный режим» предполагает передачу по каналам телесвязи данных наблюдений, прошедших первичную обработку, в ближайший установленный регламентом срок после производства наблюдений.
4.3.4 Система сбора в «Задержанном режиме» осуществляется в соответствии с ведомственными схемами и с применением программно-технологических средств занесения на носитель, контроля и данных наблюдений в ведомственные Центры данных: ФГБУ «Гидрометцентр России» (оперативная информация), ФГБУ «ВНИИГМИ-МЦД» (гидрометеорология, океанография и загрязнение морей и океанов), ФГБУ «ААНИИ», НИЦ ГОСНИНГИ МО РФ, ФГУП «ВНИРО» Федерального Агентства по рыболовству (биология), ФГБУ «РФИ Минприроды России» (морская геология и геофизика).
4.3.5 Система сбора и распространения гидрометеорологической информации включает следующие центры и узлы связи:
- ФГБУ «Авиаметтелеком Росгидромета» в Москве, выполняющее функции регионального узла глобальной сети телесвязи ВМО и Главного центра национальной сети по обмену оперативной гидрометеорологической информацией;
- службы АСПД в Новосибирске, Хабаровске, выполняющие функции регионального узла телесвязи ВМО;
- службы АСПД, выполняющие функции территориальных центров по зонам ответственности соответствующих территориальных управлений Росгидромета;
- центральные радиостанции и кустовые радиостанции), установленные на труднодоступных и полярных гидрометеорологических станциях;
- центры сбора гидрометеорологической информации по видам наблюдений (физическая океанография и гидрометеорология - ФГБУ «ВНИИГМИ-МЦД»); (загрязнение морской среды - ФГБУ «ГОИН»); (морские льды - ФГБУ «ААНИИ»); (спутниковые наблюдения - ФГБУ «НИЦ «Планета»).
Эти системы обеспечивают оперативное доведение информации до прогностических центров и потребителей, а также неоперативное доведение данных до Центров сбора и Госфонда.
4.3.6 Гидрометеорологическая информация подразделяются на регулярную и эпизодическую:
а) к регулярной гидрометеорологической информации относятся ежедневные сводки погоды и состояния поверхности моря, поступающие в течение всего года с береговых и судовых станций, с океанских буев, а также с ИСЗ.
б) к эпизодической гидрометеорологической информации относятся сведения об ОЯ, а также специально запрашиваемые сведения, необходимые для обслуживания специальных морских операций, непредусмотренных текущими планами обслуживания.
4.3.7 Регулярная гидрометеорологическая информация передаются в закодированном виде, эпизодические данные об ОЯ открытым текстом.
4.3.8 Передача осуществляется по национальным и международным кодам ВМО.
4.3.9 Для передачи сообщений морских наблюдений с береговых станций внутри России используется национальный код КН-02. Судовые наблюдения кодируются в международном коде КН-01с.
4.3.10 Данные спутниковых наблюдений принимаются и обрабатываются пунктами приема спутниковой информации, после чего по каналам связи передаются в прогностические центры для использования в оперативной практике.
4.3.11 Данные о ледовой обстановке в районах Крайнего Севера и Арктики поступает с судов, самолетов ледовой разведки, береговых станций в центр сбора ледовой информации - ФГБУ «AАНИИ», где она используется для составления ледовых карт, накапливается и хранится.
4.3.12 Данные с НИС Росгидромета для оперативных целей передаются по радиосвязи в ФГБУ «Авиаметтелеком Росгидромета» в виде телеграмм, а по окончании рейсов оформляются в виде отчетов о рейсах и массивов данных, которые сдаются в Единый государственный фонд данных по гидрометеорологии и загрязнению природной среды, функционирующий на базе ФГБУ «ВНИИГМИ-МЦД». Единый фонд данных составляет документы, содержащие информацию общего назначения и специализированную информацию.
4.3.13 Данные наблюдений с судов передаются по каналам радиосвязи через соответствующие радиостанции пароходств.
4.3.14 Капитаны и штурманский состав российских судов, находящихся в открытых водах Мирового океана и прибрежных зонах, для упрощения работы с полученной гидрометеорологической информации от прогностических организаций Росгидромета должны использовать Атлас [10].
Цифровой индекс, присвоенный каждому району, позволяет сократить и упростить текст сообщения, а, следовательно, и время доведения гидрометеорологической информации до потребителя. Капитаны судов, поевшая запрос в оперативные подразделения НМС на получение гидрометеорологической информации по интересующему их району моря или океана, должны указать местонахождение судна или цифровое обозначение района, по которому необходимо передать гидрометеорологическую информацию.
4.3.15 Достоверность наблюдений, поступающих с сети, обеспечивается единообразием средств измерений, эффективностью процедур контроля, используемых для выявления ошибок, возникающих на разных стадиях обработки данных.
4.3.16 Поступающая с морской наблюдательной сети информация проходит несколько этапов обработки:
- первичная обработка, сортировка, контроль и комплектация данных;
- объективный анализ гидрометеорологических полей;
- подготовка и выпуск прогнозов.
4.3.17 Современная технология обработки данных основана на автоматизированной обработке результатов гидрометеорологических наблюдений. При необходимости вычисление обобщенных характеристик может выполняться вручную непосредственно на станции.
4.3.18 Основными средствами доведения гидрометеорологической информации до потребителя являются радио, почта, электронная почта, Интернет, телефакс, телефон, радио и телевидение, а также мобильные средства связи.
4.3.19 Для передачи штормовых предупреждений об ОЯ используется общегосударственный «горячий» радиотелефонный канал, предоставляемый прогностическим службам Росгидромета Минкомсвязи РФ, для передачи в приоритетном порядке предупреждений в местные административные органы.
4.3.20 Информирование о погоде и состоянии морей и океанов по телевидению производится метеорологами, находящимися на службе у телекомпаний по материалам, предоставляемым им прогностическими учреждениями Росгидромета. Они включаются в сводки новостей и транслируются один раз в сутки.
4.3.21 Международной системой связи для целей морского метеорологического и связанного с ней океанографического обслуживания является ГСТ ВМО. В соответствии с [8] основными функциями ГСТ являются:
- сбор данных наблюдений,
- передача гидрометеорологической информации в ММЦ, РМЦ и НМЦ.
4.3.22 Гидрометеорологическая информация передается на суда в соответствии с положениями ГМССБ с использованием системы НАВТЕКС для прибрежных районов и спутниковой системы SeftyNET для открытых районов морей и океанов, а также для прибрежных районов, не охваченных системой НАВТЕКС. Этими системами в настоящее время пользуются на практике подавляющее большинство мирового коммерческого судоходства.
4.3.23 Вопросы обеспечения морских прогностических подразделений гидрометеорологической информацией координируются УГМК Росгидромета.
4.3.24 Контроль за качеством гидрометеорологической информации, поступившей в СМГП, производится дежурным специалистом отдела морских гидрологических прогнозов. Контроль должен обеспечивать исключение (или исправление) обнаруживаемых ошибочных данных.
4.3.25 Наиболее эффективным является комплексный контроль.
Решение по каждой обнаруженной ошибке при комплексном контроле принимается на основе сопоставления показателей различных видов контроля, таких как:
- проверка взаимной согласованности данных о различных гидрометеорологических элементах, в пределах одного сообщения;
- сравнение с предыдущими данными (или с прогностическим значением гидрометеорологического элемента на рассматриваемый срок);
- проверка сообщаемых координат в судовых сводках принадлежности их акваториям морей и др.
4.3.26 О качестве поступающих данных с наблюдательной сети следует информировать соответствующие отделы морских УГМС, ведающие вопросами работы наблюдательной сети. Сведения о задержках телеграмм следует доводить до начальников узлов связи УГМС для принятия соответствующих мер.
4.4 Фонд научно-оперативных материалов СМГП
4.4.1 Содержание материалов, составляющих научно-оперативный фонд СМГП
4.4.1.1 Оперативная работа СМГП основывается на детальном изучении гидрометеорологического режима моря, на анализе условий формирования гидрологических явлений и научно-обоснованных методах их прогноза. Для этого в каждой организации СМГП должен быть создан свой фонд научно-оперативных материалов (фонд), включающий материалы многолетних гидрологических и метеорологических наблюдений, дополнительные материалы по гидрографии, геологии, режиму устьев рек, материалы специальных исследований, аналитические обзоры состояния погоды и моря, методики прогноза и методические записки и т.д. Создание фонда научно-оперативных материалов является одной из первостепенных работ организаций СМГП.
4.4.1.2 Формирование фонда осуществляется:
- путем сбора, систематизации и соответствующей обработки накопленных материалов (например, составление специальных таблиц, графиков, карт и т.д.),
- путем ежегодного систематического пополнения новыми данными наблюдений и новыми материалами, полученными в результате научно-исследовательской и оперативной работы.
4.4.1.3 К фонду научно-оперативных материалов СМГП должны предъявляться следующие основные требования:
- в состав фонда должны входить данные наблюдений всех элементов гидрологического режима моря и все необходимые для составления прогнозов метеорологические данные, которые должны быть надежными и репрезентативными;
- материалы фонда должны наиболее полно освещать гидрометеорологический режим морей, должны быть обработаны в соответствии с требованиями методик прогноза с соблюдением единообразия форм и методов обработки материалов наблюдений;
- материалы фонда должны храниться так, чтобы обеспечивалась их полная сохранность.
Важным требованием является также учет и простота нахождения нужных материалов. Фонд не должен подменять архив или библиотеку. В нем должны находиться только те материалы, которые необходимы для оперативной и научно-методической работы СМГП.
4.4.1.4 В связи с большим разнообразием как гидрометеорологического режима морей, так и запросов потребителей на информационную продукцию, невозможно разработать единые требования к составу научно-оперативных материалов, подлежащих включению в фонд. Поэтому право решать вопрос о составе фонда и его ведении должно принадлежать самой организация СМГП.
4.4.1.5 Содержание и объем фонда должны определяться:
- особенностями гидрологического режима моря и степенью его изученности;
- потребностью обслуживаемых государственных и коммерческих организаций;
- потребностью в разработке той или иной методики прогноза.
4.4.1.6 Все материалы фонда можно разделить на три основные группы:
- материалы гидрометеорологических наблюдений;
- графические и картографические материалы;
- научно-методические и научно-оперативные материалы.
4.4.1.6.1 Материалы фонда, относящиеся к гидрометеорологическим наблюдениям, должны содержать Морские гидрометеорологические ежегодники и ежемесячники, а также журналы и таблицы с данными срочных наблюдений, данными многолетних наблюдений, а также материалы с выборками за год, сезон, месяц и декаду.
Кроме таблиц с основными гидрометеорологическими элементами, содержащимися в морских гидрометеорологических ежегодниках и ежемесячниках, в фонде СМГП целесообразно хранить дополнительно таблицы, в которые могут быть включены, например, даты перехода температуры воды через определенные градации, суммы проекций ветра на эффективное направление и др.
Материалы ледовых наблюдений должны включать данные по распределению и сплоченности льда по акватории морей, данные о сроках наступления ледовых явлений (первое появление льда, дата полного замерзания льда, даты вскрытия и полного очищения моря ото льда), о возрасте, форме и толщине льда, о высоте и плотности снега на льду, о положении кромок и границ льда и др.
Материалы о ледовом режиме моря должны оформляться в виде специальных таблиц, включающих в себя основные ледовые характеристики. По окончании каждого ледового сезона эти таблицы должны пополняться.
4.4.1.6.2 Графические и картографические материалы, включаемые в научно-оперативный фонд СМГП, делятся на три вида:
- материалы, составляемые на основе данных гидрометеорологических наблюдений после их специальной обработки. Эти материалы включают ежедневные гидросиноптические карты, составляемые по судовым данным (за четыре срока), атласы, построенные на основе многолетних наблюдений и работ отдельных экспедиций, карты состояния льдов, построенные по данным ИСЗ и судовым и береговым наблюдениям, карты распределения температуры поверхности океана (ТПО), составленные по данным ИСЗ, данным судовых и буйковых наблюдений.
- материалы, характеризующие гидрографические и другие физико-географические условия района деятельности СМГП должны включать административную карту обслуживаемой территории, физическую карту обслуживаемой территории, морские навигационные карты, батиметрические карты.
- материалы оперативного значения должны включать карты информационной морской сети е указанием на них береговых гидрометеорологических станций и постов, карты-схемы расположения хозяйственных объектов на территории, обслуживаемой данной СМГП.
4.4.1.6.3 К научно-методическим материалам относятся материалы, полученные при разработке методов прогнозов и методических указаний, а также каталоги литературы по морским гидрометеорологическим прогнозам, а также труды научно-исследовательских институтов, должны использоваться в оперативной работе как справочный материал.
4.4.1.6.4 К научно-оперативным материалам относятся:
- журналы учета успешности морских гидрологических прогнозов и штормовых предупреждений об ОЯ;
- журналы для регистрации прогнозов;
- каталог опасных отметок уровня воды и опасных градаций других гидрологических явлений;
- картотека морских информационных станций и постов;
- руководящие документы по вопросам СМГП, включающие важнейшие приказы и распоряжения Росгидромета, регламентирующие деятельность СГМП.
4.4.1.7 Основной формой учета материалов фонда является ведение каталога, в котором указываются номера, шифры материалов и место их хранения, сведения о содержании каждого вида материалов, периоде наблюдений.
4.4.1.8 Пополнение каталога должно вестись систематически, по мере поступления новых материалов. Рекомендуется иметь бумажные и компьютерные варианты каталогов, где каталожные карточки или соответствующие им файлы могут быть упорядочены по видам информации, по типам носителя и др.
4.4.1.9 Все прогнозы и составленные на основе их штормовые предупреждения подлежат учету и должны регистрироваться в специальных журналах и храниться.
4.4.1.10 Сроки хранения материалов документальных административных и технических материалов регламентируются РД 52.19.143 и относятся к подлинным документам, оригиналам, подлежащим официальному учету и передаче на хранение в архив учреждения.
4.4.2 Каталог опасных морских гидрометеорологических явлений
4.4.2.1 На станциях и постах составляется каталог опасных морских гидрометеорологических явлений (каталог ОЯ). Типовой перечень опасных природных явлений (в том числе морских гидрологических) приведен в РД 52.88.699.
4.4.2.2 Назначение каталога ОЯ - способствовать быстрому и точному определению хозяйственных объектов, которым угрожает опасность при ожидаемом по прогнозу развитии гидрометеорологического явления.
4.4.2.3 Каталог ОЯ представляет собой систематизированные сведения об ОЯ или сочетании гидрометеорологических явлений, которые образуют ОЯ, и о морских объектах, которым угрожают ОЯ.
4.4.2.4 Каталог ОЯ состоит из карточек морской гидрометеорологической станции (поста), карточек опасного морского гидрометеорологического явления, карточек хозяйственных объектов, альбомов распространения ОЯ и альбомов типовых ситуаций, вызывающих ОЯ, с приложением описания ОЯ.
4.4.2.5 Форма карточки морской гидрометеорологической станции (поста), приведенная в приложении А, содержит сведения о местоположении, типе станции (поста), дальности видимости горизонта и т.п.. Карточка станции (поста) включает в себя наименование всех хозяйственных объектов, для которых установлены опасные отметки уровня воды, тягуна и др. В графе «критерий опасности» в случае, если хозяйственный объект имеет несколько опасных отметок, помещается наименьшее значение.
4.4.2.6 Карточка морской гидрометеорологической станции (поста) имеет свой порядковый номер. Порядок нумерации осуществляется в последовательности, принятой в морских гидрологических ежемесячниках и ежегодниках.
4.4.2.7 Карточка опасного морского гидрометеорологического явления составляется по форме, приведенной в приложении Б. В карточке указываются название ОЯ, водный объект, перечень хозяйственных объектов, которым угрожает ОЯ, а также номера карточек этих хозяйственных объектов и других обособленных акваторий моря и т.п.
4.4.2.8 Карточка хозяйственного объекта (населенные пункты, склады, причалы, гидротехнические сооружения и другие объекты прибрежной инфраструктуры) составляется по форме, приведенной в приложении В. В ней должны указываться название хозяйственного объекта, а также конкретные данные о характере угрозы объекту. В эту же карточку должны заноситься сведения об имевших место вредных воздействиях опасных явлений на конкретный объект.
4.4.2.9 Альбом распространения ОЯ состоит из карт морей и океанов различного масштаба (приложение Г) и планов с нанесенными на них хозяйственными объектами и границами распространения ОЯ по прибрежной территории (например, границей затопления прибрежной территории во время штормовых нагонов, зонами воздействия наката волн во время штормового волнения и т.п.). Основное назначение этих карт - определение границ распространения опасного явления по территории. К альбому прилагается записка, в которой перечисляются исходные материалы и степень их надежности, характеристика наблюдавшихся ОЯ и другие необходимые пояснения. Записка составляется на основе отчетов о каждом прошедшем ОЯ и представляет полезное методическое пособие, в котором обобщаются синоптические и гидрологические условия, предшествующие развитию ОЯ.
4.4.2.10 Альбом типовых ситуаций, вызывающих ОЯ, является полезным методическим разделом каталога ОЯ. Он должен содержать различные гидросиноптические карты, освещающие гидрометеорологические условия, предшествующие и сопутствующие развитию ОЯ. Все необходимые пояснения на этих картах, учитывая оперативный характер их использования, должны быть предельно краткими и ясными [11]. К альбому должны быть приложены описания условий возникновения, интенсивности и последствий различных ОЯ.
4.4.2.11 Карточки каталога ОЯ должны систематически проверяться и пополняться на основании уточненных или новых сведений об опасных гидрометеорологических явлениях. В случае ликвидации какого-либо хозяйственного объекта, сведения о котором имеются в каталоге ОЯ, карточка этого хозяйственного объекта изымается и уничтожается. Одновременно все сведения о данном объекте вычеркиваются из карточек опасного морского гидрометеорологического явления с указанием причин изъятия. Все материалы об изменениях в карточках, копии новых карточек, относящихся к каталогу ОЯ, а также сведения об изъятии из каталога карточек с указанием причин изъятия пересылаются в ФГБУ «Гидрометцентр России». Обо всех изменениях в каталогах ОЯ сообщается в УГМС (ЦГМС).
4.4.2.12 Для учета всех карточек каталога ОЯ ведется журнал (форма журнала показана в приложении Д), в который заносятся все без исключения карточки каталога ОЯ сразу же после их заполнения или получения. При замене карточки с устаревшими сведениями на новую, в журнале отмечается только дата замены, а место и номер карточки в журнале и каталоге ОЯ остаются прежними.
4.4.2.13 Для ведения каталога ОЯ выделяется ответственное лицо, которое вносит в каталог ОЯ необходимые исправления и дополнения.
5 Порядок составления и выпуска прогнозов и штормовых предупреждений
5.1 Виды прогнозов
5.1.1 Прогнозы классифицируют по следующим признакам:
а) условное деление всех видов прогнозов;
б) деление:
- по содержанию;
- по времени действия;
- по продолжительности действия;
- по месту действия;
- по целевому назначению.
5.1.2 Все прогнозы условно делят на две группы: прогнозы явлений и прогнозы величин:
а) к прогнозам явлений относятся прогнозы ОЯ, например, прогноз возникновения цунами, сильного тягуна в портах, прогнозы сгонно-нагонных явлений, обледенения рыболовных судов, сильного тумана на море т.д.;
б) к прогнозам величин относятся прогнозы, которые могут быть выражены количественно - в градусах Цельсия (температура воды моря), в метрах (высота волны, уровень), метрах в секунду (скорость ветра, течения) и т.д., и которые отнесены к определенному моменту времени и к некоторой фиксированной точке.
В действительности, необходимую информацию можно получить, прогнозируя одновременно как само явление, так и его количественные характеристики. Например, можно прогнозировать факт возникновения тягуна в порту, с одновременным указанием его количественных характеристик (интенсивности, продолжительности, амплитуды колебаний и т.д.).
5.1.3 По содержанию прогнозы можно разделить на две группы:
а) прогнозы, характеризующие динамические процессы. К ним относятся прогнозы волнения, течений, сгонно-нагонных колебаний уровня моря, дрейфа льда и т.д.;
б) прогнозы, характеризующие тепловые процессы. К ним относятся прогнозы температуры воды и ледовых явлений.
5.1.4 По времени действия различают прогнозы на заданный промежуток или момент времени, выпускаемые по расписанию в установленное время суток, и выпускаемые независимо от времени суток при угрозе возникновения ОЯ.
5.1.5 По продолжительности действия прогнозы делятся на:
|
- краткосрочные |
от нескольких часов до 3 сут; |
|
- среднесрочные |
от 3 до 15 сут; |
|
- долгосрочные |
от 15 сут до 6 мес; |
|
- сверхдолгосрочные |
свыше 6 мес. |
5.1.6 По месту действия различают прогнозы:
- для пункта (порт, местонахождение судна, приморский населенный пункт и др.);
- для отдельных районов и для моря в целом, вдоль маршрута плавания судна или буксировки каких-либо несамоходных объектов (кранов, плавучих доков и др.);
- для больших акваторий океанов (например, прогнозы ТПО по Северным частям Атлантического и Тихого океанов) и в целом по Мировому океану (глобальные прогнозы волнения).
5.1.7 По целевому назначению прогнозы делятся на прогнозы общего назначения и специализированные:
а) к прогнозам общего назначения относятся прогнозы, не имеющие определенной специфики по месту и времени проведения морских операций. Прогнозы общего назначения в соответствии с [2] предоставляются потребителям на регулярной основе. Органам государственной власти Российской Федерации, органам государственной власти субъектов РФ, органам единой государственной системы предупреждения и ликвидации чрезвычайных ситуаций (МЧС России), органам МО РФ гидрометеорологическая информация и прогнозы предоставляются бесплатно. Другим пользователям (потребителям) прогнозы общего назначения предоставляются за плату в размерах, возмещающих расходы на их подготовку, тиражирование и передачу по каналам связи. В примерный перечень информационных услуг общего назначения входит:
- прогностическая и фактическая информация об ОЯ в соответствии с типовым перечнем ОЯ согласно РД 52.88.699;
- прогнозы погоды и состояния моря до 2 суток при проведении аварийно-спасательных и восстановительных работ в районах стихийных бедствий, аварий и катастроф;
- предупреждения об угрозе цунами;
б) к специализированным прогнозам относятся прогнозы, составляемые по заявкам потребителей, как правило, на договорной основе за плату, стоимость которой определяется договором. В договоре четко оговариваются обязанности исполнителя и заказчика. В ориентировочный перечень специализированной информации входит:
- данные о текущем состоянии погоды и моря;
- краткосрочные прогнозы погоды и состояния моря по районам проведения морских операций, рекомендуемым курсам, морским портам;
- среднесрочные прогнозы погоды и состояния моря по районам проведения морских операций, судоходным трассам, морским портам;
- прогнозы погоды, температуры воды в океанах и морях на месяц;
- прогнозы ледовых условий на месяц и зимний период по акваториям морей и судоходным трассам;
- прогнозы ОЯ в соответствии с типовым перечнем по РД 52.88.699;
- анализы (доклады, справки, консультации) метеорологических условий и состояния моря по заданным районам проведения морских операций.
5.1.8 Предоставление информационных услуг и выполнение работ в рамках ГМССБ определяется [12 - 17] и осуществляется в рамках договоров, заключаемых организациями и предприятиями Минтранса России с предприятиями, организациями - владельцами гидрометеорологической информации в порядке, установленном Минтрансом России. Порядок взаимодействия сторон при выполнении работ в рамках ГМССБ регламентируется совместно разработанным и утвержденным Сторонами договором.
5.1.9 При заключении договоров (соглашений) стороны должны исходить из действующего законодательства РФ, обязательств РФ, вытекающих из Международной Конвенции по охране человеческой жизни на море СОЛАС 74/78, руководящих документов ВМО и Росгидромета.
5.2 Порядок составления и выпуска прогнозов
5.2.1 Прогнозы составляют организации СМГП по закрепленным за ними зонам ответственности в соответствии с [10]. По акваториям океанов и морей, не входящих в зоны ответственности УГМС (ЦГМС) Росгидромета, обеспечение осуществляется на оперативной основе по специальным запросам потребителей и отдельным поручениям Росгидромета.
5.2.2 Подготовленная в организациях СМГП информационная продукция доводится до потребителей (пользователей) по различным каналам связи (радио, телевидение, Интернет, ГСТ ВМО, электронная почта, мобильная связь и т.д.).
Передача и доведение информационной продукции до портов и судов в море осуществляется предприятиями морского транспорта и рыбного хозяйства по принадлежности.
5.2.3 Составление и выпуск прогнозов производится по заранее разработанным планам. Вне плана составляются и выпускаются только штормовые предупреждения и оповещения, уточнения прогнозов, справки и консультации по специальным запросам.
5.2.4 Порядок сбора, обработки и распространения гидрометеорологической информации, регламентируется нормативными документами, указаниями Росгидромета и соответствующих отделов УГМС, а также решениями и рекомендациями Центральной методической комиссии по гидрометеорологическим и гелиофизическим прогнозам Росгидромета (ЦМКП) и технических советов УГМС или учеными советами региональных НИИ.
5.2.5 Краткосрочные прогнозы в зависимости от продолжительности действия и назначения составляют на 12 ч, сутки, последующие двое суток и период (в виде консультации). Конкретное время составления прогнозов устанавливает УГМС. Для детализации времени суток следует использовать его характеристики в соответствии с РД 52.27.724.
5.2.6 В прогнозах и штормовых предупреждениях, передаваемых для судов по радио, указывается местное время. В прогнозах, выпускаемых в рамках международных обязательств, указывается всемирное скоординированное время (UTS).
5.2.7 Прогнозы общего назначения выпускаются циркулярно, согласно расписанию, прогнозы специализированного назначения выпускают в соответствии с условиями, оговоренными договорами, штормовые предупреждения - немедленно по получении информации об ОЯ.
5.2.8 Для циркулярных передач по радио гидрометеорологическая информация (в пределах зоны ответственности УГМС) предоставляется в следующем порядке (по форме, принятой ВМО [9, 12]):
- штормовые предупреждения;
- обзор синоптической обстановки по приземной синоптической карте;
- прогноз на текущий день, сутки и последующие двое суток.
5.2.9 В прогнозах по акватории моря указываются:
- период действия прогноза, дата;
- район, для которого составлен прогноз;
- направление и скорость ветра, м/с;
- видимость, км или в морских милях;
- явления, ухудшающие видимость (туман, дымка, осадки и др.);
- высота ветровых волн и волн зыби, м;
- параметры обледенения судов;
- температура воды и воздуха, °С;
- ледовые условия.
Кроме того, в прогнозы, составляемые по акватории порта, должна включаться информация о тягуне, сгонно-нагонных явлениях, а также о таких явлениях, как шквал, град, гроза и др.
5.2.10 Прогнозы погоды и состояния моря на сутки и текущий день для района моря и расположенного в нем населенного пункта передают, как правило, общим текстом.
Если предполагается, что в некоторых частях акватории моря, прогнозируемые гидрометеорологические величины и явления будут значительно различаться, то рекомендуется выделить эти части, применив для этой цели характеристики географического положения: запад, юг, северная половина, центральные районы, правобережье, прибрежные районы и т.д.
5.2.11 Прогнозы погоды и состояния моря на сутки уточняют полусуточным прогнозом на текущий день. Если в уточнении нет необходимости, то формулировку суточного прогноза повторяют в полусуточном прогнозе на день. Полусуточный прогноз погоды составляют не позднее 7 ч местного времени и распространяют по согласованным схемам обслуживания.
5.2.12 Учет, обоснование и все исходные данные для составления долгосрочных прогнозов должны фиксироваться в специальном журнале, в который специалист записывает результаты анализа предшествующей гидрометеорологической обстановки, результаты вычислений исходных для прогноза величин, обоснования всех отклонений от метода, допущенных при составлении прогноза, а также окончательно принятые значения ожидаемых величин. Все эти записи делаются в процессе работы по составлению прогноза вплоть до выпуска последнего.
Подготовка исходных материалов и их анализ должны выполняться в соответствии с требованиями, изложенными в методической записке.
5.2.13 Результаты долгосрочных прогнозов на сезон, год и более рекомендуется обсуждать с привлечением специалистов-синоптиков. Такое обсуждение целесообразно не только с целью корректировки прогноза, но и с целью ознакомления других специалистов с ожидаемыми условиями погоды и гидрологического состояния моря.
После обсуждения составляется окончательный текст прогноза, который подписывается лицом, ответственным за его выпуск.
5.2.14 Если явление развивалось не так, как ожидалось по прогнозу, подготавливается и выпускается его уточнение.
5.2.15 Первый долгосрочный прогноз, составленный в соответствии с годовым планом, считается основным. Все последующие прогнозы того же элемента рассматриваются как уточнения. В прогнозе-уточнении четко указывается, какой ранее выпущенный прогноз уточняется и в какой его части он утратил силу.
5.2.16 Прогнозы ледовых фаз составляются по порту, бухте, заливу, проливу, участку побережья и т.п., при этом, как правило, указывается пункт ледовых наблюдений. В прогнозах ледовых фаз для участков побережья при необходимости указывается район действия прогноза.
5.2.17 Срок ожидаемого ледового явления в долгосрочном прогнозе указывается двумя числами - датами. Отрезок времени, заключенный между этими датами, не должен превышать допустимую погрешность данного прогноза и составлять более 10 дней. Например, если в тексте прогноза появления льда указаны даты 14 - 18 ноября, то это означает, что появление льда ожидается в пределах 14 - 18 ноября.
В прогнозах с заблаговременностью до 15 дней отрезок времени, в пределах которого ожидается предсказываемое явление, составляет:
|
- при заблаговременности 13 - 15 дней |
4 дня; |
|
- при заблаговременности 9 - 12 дней |
3 дня; |
|
- при заблаговременности 5 - 8 дней |
2 дня; |
|
- при заблаговременности менее 5 дней |
1 - 2 дня (в зависимости от условий района). |
5.2.18 Прогноз толщины льда дается по пунктам, участкам или отдельным районам моря. В прогнозах указывают толщину льда в см и время, к которому лед достигает ожидаемой толщины. В прогнозах могут также указываться максимальная, минимальная и средняя толщина льда. Когда сообщается минимальная толщина льда, это специально оговаривается в тексте прогноза. Ожидаемая толщина льда относится к концу прогностического периода, все отступления от этого правила должны оговариваться.
Толщина льда в долгосрочных прогнозах сообщается двумя числами, разность между которыми должна быть не более 10 см. В среднесрочных прогнозах ожидаемая толщина сообщается одним числом с добавлением слова «около» или двумя с разностью 2 - 3 см.
5.2.19 Прогнозы сплоченности, торосистости льда, сжатий и разрежений льдов, раздробленности и разрушенности льда могут даваться как по районам моря, так и по всей акватории моря. Районы определяются по особенностям их ледового режима с учетом запросов потребителей. Характеристика ледового состояния сообщается в баллах в заданном интервале.
5.2.20 Прогнозы температуры поверхности моря могут даваться как в виде карт изотерм, так и в виде конкретных значений температуры или ее аномалии, ожидаемой в конкретном пункте, районе открытого моря или побережья за определенный период времени (пятидневка, декада, месяц).
5.2.21 Кроме прогнозов распределения температуры воды по акватории морей, могут составляться прогнозы сроков перехода температуры воды через определенные значения, за разные периоды осреднений, а именно: за сутки, за пятидневку, за декаду и т.д. Поэтому всегда необходимо указывать, за какой период произведено осреднение.
5.2.22 Прогнозы высоты ветровых волн и зыби могут составляться по пункту, по отдельным участкам морей и океанов и по глобусу. В последних случаях прогноз волнения выпускается в виде карты с изолиниями равных высот волн.
Прогнозы высоты ветровых волн и волн зыби даются в метрах, а направление их распространения в румбах. В прогнозах должна сообщаться обеспеченность прогнозируемой высоты волны.
Прогнозы высоты ветровых волн и зыби могут совмещаться с прогнозом ветра. Прогнозы длины и периода волн выпускаются, как правило, только по запросам потребителей.
Примеры
1 Ветер западный, умеренный, высота волн 1,5 - 2 м.
2 Ветер слабый, зыбь высотой 2 - 3 м от юго-востока.
5.2.23 Краткосрочные прогнозы непериодических колебаний уровня могу даваться как по пунктам (в см над нулем поста), так и по акватории моря виде изолиний на карте.
5.3 Порядок составления и выпуска штормовых предупреждений и оповещений
5.3.1 При составлении и выпуске штормовых предупреждений и оповещений следует руководствоваться требованиями РД 52.88.699 с учетом морской специфики.
5.3.1 Во всех случаях, когда ожидаемое по прогнозу гидрометеорологическое явление и его числовые значения представляют опасность для населенных пунктов и хозяйственных объектов на берегу, а также после получения штормовых предупреждений от других УГМС (ЦГМС), СМГП обязана немедленно предупредить об этом все заинтересованные организации.
5.3.2 Штормовые предупреждения по акватории моря и порта составляются в тех случаях, когда ожидаются ОЯ гидрометеорологического характера. По акватории порта, составляются также штормовые предупреждения, предусмотренных для сухопутных районов, если они являются опасными для работ, проводимых в порту, и указаны в планах-схемах.
5.3.3 Перечень организаций, которым необходимо передавать штормовые предупреждения, и порядок действий, определен в РД 52.88.699.
5.3.4 Степень опасности ожидаемого по прогнозу гидрометеорологического явления для конкретных населенных пунктов и хозяйственных объектов устанавливается в соответствии с Каталогом ОЯ.
5.3.5 Штормовое предупреждение составляется независимо от того, предусматривалось или не предусматривалось ОЯ в ранее составленном прогнозе погоды. Штормовое предупреждение составляют с максимально возможной заблаговременностью.
5.3.6 Штормовое предупреждение должно содержать:
- порядковый номер штормового предупреждения (с начала года);
- дату, время возникновения и, по возможности, продолжительность ожидаемого ОЯ (комплекса неблагоприятных гидрометеорологических явлений);
- район возникновения (распространения) ОЯ;
- название и максимальную интенсивность ОЯ;
- подпись лица, выпустившего штормовое предупреждение.
Для более полной характеристики гидрометеорологических условий наряду с ОЯ штормовые предупреждения могут содержать прогноз явлений, к ОЯ не относящихся или не достигающих критериев ОЯ.
5.3.7 Штормовые предупреждения составляют и передают по РД 52.88.699. На основании данного документа в УГМС (ЦГМС) и ФГУ «Калининградский ЦГМС» разрабатывается «Порядок действий дежурных смен ОНС и НПО УГМС при угрозе возникновения ОЯ». В нем содержится перечень и критерии ОЯ по обслуживаемой территории, перечень и последовательность действий дежурного прогнозиста и наблюдателя, а также порядок передачи штормовых предупреждений и оповещений.
5.3.8 УГМС совместно с ЦГМС разрабатывают (уточняют) региональные перечни и критерии ОЯ по обслуживаемым территориям (субъектам РФ), которые могут служить источниками чрезвычайной ситуации, с учетом местных природно-климатических и экономических особенностей обслуживаемой территории и включают его в перечень ОЯ.
5.3.9 При разработке региональных перечней и критериев морских гидрометеорологических ОЯ следует учитывать, что повторяемость и интенсивность явлений (критические значения гидрометеорологической величины) должны быть достаточно редкими для данной территории (климатическая повторяемость должна составлять не более 10 % по РД 52.88.699) и что эти явления представляют угрозу безопасности людей и могут нанести значительный ущерб большинству морских отраслей экономики.
5.3.10 Разработанные УГМС и ФГУ «Калининградское ЦГМС» региональные перечни и критерии ОЯ по территории обслуживания направляются в Росгидромет для утверждения, и с момента их утверждения вступают в силу.
5.3.11 Штормовые предупреждения подаются наблюдательными подразделениями в соответствии с критериями ОЯ, установленными соответствующими УГМС (ЦГМС). Обобщение результатов наблюдений за ОЯ в центрах обработки ведется по единым критериям ОЯ.
5.3.12 Критерии ОЯ устанавливаются либо по вероятности возникновения явлений, либо «директивно» с учетом результатов анализа данных гидрометеорологических наблюдений за многолетний период. При этом критерии ОЯ либо принимаются едиными для всей территории страны, либо устанавливаются дифференцированно для различных физико-географических и природно-климатических районов.
5.3.13 Перечень и критерии ОЯ, а также адреса подачи штормовых сообщений доводятся до сведения каждого сетевого наблюдательного подразделения.
5.3.14 Если ОЯ возникло внезапно (не было предусмотрено), то немедленно составляется штормовое оповещение, в котором указывается время начала ОЯ, его интенсивность, а также штормовое предупреждение о прогнозируемой продолжительности, максимальных значениях характеристик и о возможности распространения ОЯ на другие районы.
5.3.15 В случае необходимости уточнения времени возникновения, интенсивности, района распространения ОЯ, составляют уточнение к штормовому предупреждению.
5.3.16 Если ОЯ прекратилось (ослабело), а затем вновь возникло (усилилось) и перерыв (ослабление) продолжался менее 6 ч, то считается, что ОЯ продолжается, и новое штормовое предупреждение не составляют. Если перерыв (ослабление) продолжался 6 ч и более, то следует составить новое штормовое предупреждение.
5.3.17 После окончания ОЯ УГМС (ЦГМС) обязаны немедленно доложить в УГМК Росгидромета сведения об интенсивности, продолжительности, заблаговременности и районе распространения ОЯ. Структура формализованного сообщения о прогнозируемом ОЯ (штормового предупреждения) и структура формализованного оперативного донесения о наблюдавшемся ОЯ и ущербе от него представлена в РД 52.88.699.
5.3.18 Если ожидается возникновение одновременно или друг за другом нескольких ОЯ, в штормовом предупреждении указывается время возникновения, название и интенсивность каждого из них.
5.3.19 Если последующий анализ гидрометеорологического материала или данных наблюдений показывает, что ожидавшее ранее ОЯ не возникло то дают отмену штормового предупреждения с максимально возможной заблаговременностью.
5.3.20 Дежурные прогнозисты ФГБУ «Гидрометцентр России» и ФГБУ «ААНИИ» обязаны:
- при получении из УГМС (ЦГМС) и ФГУ «Калининградский ЦГМС» штормового предупреждения продублировать его текст и передать в Росгидромет (УГМК, УМЗА, УГМАВ), а по окончании рабочего дня - ответственному дежурному Росгидромета;
- передать его по Схеме штормового предупреждения и штормового оповещения об ОЯ в соответствии с РД 52.88.699, используя имеющиеся каналы и средства связи;
- в журнале записать время передачи и фамилию принявшего информацию.
5.3.21 При необходимости уточнения интенсивности, времени возникновения или распространения по территории ОЯ, предусмотренных в штормовом предупреждении, составляют дополнение к штормовому предупреждению.
5.3.22 При возникновении ОЯ ФГБУ «НИЦ «Планета», ФГБУ «Дальневосточный РЦПОД» и УГМС (ЦГМС), исходя из имеющихся технических возможностей, обеспечивают материалами космических съемок ОНС и заинтересованные организации, министерства и ведомства (по их запросу).
Для обеспечения материалами космических съемок по району возникновения ОЯ и ЧС ОНС Росгидромета направляют заявку в ФГБУ «НИЦ «Планета», в которой указывается вид ОЯ или ЧС, географические координаты района ОЯ или ЧС, названия населенных пунктов, рек и других объектов, период выполнения съемки и виды необходимой информации.
5.3.23 Ежегодно до 10 января УГМС (ЦГМС) и ФГУ «Калининградский ЦГМС» представляют в Росгидромет (УГМК, УМЗА, УГМАВ), ФГБУ «Гидрометцентр России» и ФГБУ «ВНИИГМИ-МЦЦ» сведения обо всех наблюдавшихся в течение прошедшего года ОЯ. В случае возникновения уникального, редко повторяющегося ОЯ составляется более подробный отчет, е описанием условий возникновения и развития явления, с приложением картографического материала, данных метеорологических спутников и радиолокаторов.
5.3.24 Штормовые предупреждения и оповещения об ОЯ, составляемые по обслуживаемой территории, выпускаются за подписью соответствующего руководителя территориального органа, начальника учреждения или лица его замещающего.
5.3.25 Текст переданного потребителям штормового предупреждения и/или оповещения фиксируется в специальном журнале с указанием времени его передачи, а также фамилии, принявшего данное штормовое предупреждение и/или оповещение (форма журнала показана в приложении Е).
5.3.26 В случае объявления на территории субъекта Российской Федерации чрезвычайной ситуации, связанной с ОЯ, территориальный орган (УГМС (ЦГМС) или ФГУ «Калининградский ЦГМС») немедленно информирует об этом Росгидромет (УГМК, УМЗА, УГМАВ) и в донесении (телеграмме) представляет информацию о сложившейся гидрометеорологической обстановке и ее ожидаемом развитии.
5.3.27 Наблюдательные подразделения составляют штормовое оповещение (штормовое сообщение) при возникновении ОЯ или при достижении значений гидрометеорологических величин критериев ОЯ, передают его потребителям и в учреждения Росгидромета в соответствии со Схемой штормового предупреждения и штормового оповещения об ОЯ по РД 52.88.699.
5.3.28 Наблюдательные пункты, расположенные в городах или в районных центрах, при получении из вышестоящей организации штормового предупреждения, обязаны немедленно довести эту информацию до городской (районной) дежурной службы РСЧС в соответствии со Схемой штормового предупреждения и штормового оповещения об ОЯ.
5.3.29 После окончания ОЯ территориальные УГМС и ФГУ «Калининградский ЦГМС» обязаны немедленно доложить телеграммой в УГМК и/или УМЗА Росгидромета обобщенные сведения о виде, интенсивности (значении характеристик), продолжительности и районе распространения ОЯ, заблаговременности штормового предупреждения о нем в соответствии с РД 52.88.699.
5.3.30 Выпуск экстренной информации (штормовых предупреждений и оповещений) об ОЯ осуществляет Росгидромет и его территориальные органы через подведомственные им организации. Экстренная информация заносится в специальный журнал, форма которого приведена в приложении Ж.
5.3.31 Порядок представления оперативных и итоговых донесений об ОЯ осуществляется в соответствии с РД 52.88.699. Сведения об ОЯ за месяц (год) представляются в соответствии с приложением И.
5.4 Подготовка и передача гидрометеорологической информации для ГМССБ
5.4.1 Общие положения
5.4.1.1 Глобальная морская система связи при бедствии и для обеспечения безопасности (ГМССБ) создана в рамках реализации требований Конвенции СОЛАС 74/78 [3] и в соответствии с [13]. В соответствии с этими документами, в портах Российской Федерации построены, введены в эксплуатацию и внесены в реестр Международной морской организации около 60 объектов ГМССБ.
5.4.1.2 Функции головной организации, ответственной за функционирование ГМССБ в России возложены на Министерство транспорта. Информационное обеспечение этой системы гидрометеорологической информацией возложено на Росгидромет.
5.4.1.3 Суда, подпадающие под действие СОЛАС, должны быть оборудованы соответствующей приемной аппаратурой. При этом гидрометеорологическое обеспечение должно осуществляться в соответствии с [4].
5.4.1.4 Предоставление предупреждений, метеорологических и морских бюллетеней в рамках ГМССБ осуществляется через международную службу НАВТЕКС для прибрежных районов морей и океанов [15] и международную службу SafetyNet ИНМАРСАТ для открытых районов морей и океанов в соответствии с [16].
5.4.1.5 Подготовку гидрометеорологической информации для пунктов НАВТЕКС и национальных координаторов подсистемы SafetyNet осуществляют территориальные учреждения Росгидромета. Обобщение и передачу метеорологической информации национальным координаторам подсистемы SafetyNet осуществляют уполномоченные организации Росгидромета (таблица 1).
5.4.1.6 Метеорологические и морские бюллетени должны содержать части:
Часть I - Штормовые предупреждения;
Часть II - Краткий обзор основных характеристик приземной карты погоды и в максимально возможной степени особые характеристики состояния поверхности моря;
Часть III - Прогнозы.
Метеорологические и морские бюллетени для открытого моря должны дополнительно включать следующие части:
Часть IV - Анализы и/или прогнозы в кодовой форме IAC FLEET;
Часть V - Подборка сводок с морских станций;
Часть VI - Подборка сводок с наземных станций.
Части IV, V и VI допускается выпускать в отдельный срок.
Таблица 1 - Расположение объектов ГМССБ по районам и обслуживающие их учреждения Росгидромета
|
Подсистема |
Район расположения объектов ГМССБ |
Учреждение Росгидромета |
Море Российской Федерации |
|
НАВТЕКС |
Европейская часть РФ |
Северо-Кавказское УГМС |
Каспийское море |
|
ГУ «Астраханский ЦГМС» |
|
||
|
ГУ «Краснодарский ЦГМС» |
Черное, Азовское моря |
||
|
ГУ «Мурманское УГМС» |
Баренцево море |
||
|
Северное УГМС |
Белое море Юго-восток Баренцева моря |
||
|
Северо-Западное УГМС (через координатора в Швеции) |
Балтийское море |
||
|
ГУ «Колымское УГМС» |
Охотское море |
||
|
Дальний Восток |
ГУ «Сахалинское УГМС» |
Охотское море |
|
|
ГУ «Приморское УГМС» |
Японское море |
||
|
SafetyNet |
Северо-западная часть |
ГУ «Приморское УГМС» |
Японское море |
|
Тихого океана |
ГУ «Сахалинское УГМС» |
Охотское море |
|
|
ГУ «Колымское УГМС» |
Охотское море |
||
|
НАВАРЕА XIII |
ГУ «Камчатское УГМС» |
Охотское море |
|
|
ГУ «Чукотское УГМС» |
Берингово море |
||
|
Западный район СМП |
ГУ «ААНИИ» |
Карское море |
|
|
Северное УГМС (Архангельский ЦГМС) |
Карское море, море Лаптевых, Новоземельские проливы |
||
|
Восточный район СМП |
ГУ «ААНИИ» |
Море Лаптевых |
|
|
ГУ «Якутское УГМС» (Тиксинский ЦГМС) |
Восточно-Сибирское море |
||
|
ГУ «Чукотское УГМС» |
Чукотское море |
5.4.2 Подготовка и передача гидрометеорологической информации по системе НАВТЕКС
5.4.2.1 Порядок передачи гидрометеорологической информации по системе НАВТЕКС определен в [14].
5.4.2.2 Информация о сообщениях службы НАВТЕКС группируется по видам, каждому из которых присваивается буквенный указатель, раскрывающий характер передаваемого сообщения. Для штормовых предупреждений используется буква В. Для прогноза погоды - буква Е, для ледового обзора - буква С. Буква Z означает, что сообщений для передачи нет.
5.4.2.3 Для установления очередности передачи сообщений в службе НАВТЕКС используется три степени приоритета. В убывающем порядке срочности приоритеты следующие:
VITAL warnings (Особо важное) - для немедленной передачи по радио;
IMPORTANT warnings (Важное) - для передачи по радио в ближайший возможный промежуток времени, когда частота не занята;
ROUTINE warnings (Обычное) - для передачи по радио в очередной срок по расписанию.
5.4.2.4 Гидрометеорологическое обеспечение для ГМССБ осуществляется на основании договора (соглашения) между представителем Минтранса, который выступает как Заказчик в лице морской администрации порта и представителем Росгидромета в лице начальника УГМС (ЦГМС), который выступает как Исполнитель.
В договоре должен быть отражен предмет договора, обязанности Исполнителя и Заказчика, срок договора, стоимость работ и порядок расчета, ответственность сторон и т.д. К договору прилагается протокол соглашения о договорной цене. Исполнитель ежесуточно в круглогодичном режиме обеспечивает по закрепленному морскому району (радиусом 300 морских миль относительно порта) подготовку на английском языке гидрометеорологической информации по безопасности судоходства.
5.4.2.5 Гидрометеорологическая информация в виде формализованного текста, пригодного передаче в эфир, подготавливается в строгом соответствии с [14] и передается по телефону (или по электронной почте) на радиостанцию порта для трансляции в эфир мореплавателям по установленному расписанию.
Штормовые предупреждения подаются на передающие радиостанции по получении и в очередной срок по расписанию.
Прогнозы погоды на морские районы НАВТЕКС передаются дважды в сутки. Эти передачи должны тщательно координироваться в тех случаях, когда передатчики находятся на близком расстоянии друг от друга. Важно, чтобы прогнозы предназначались для конкретных районов, обслуживаемых НАВТЕКС.
Ледовые обзоры обычно передаются службой НАВТЕКС один раз в сутки.
Предупреждения об опасности обледенения должны включаться в ледовые обзоры службы НАВТЕКС, но если они объявляются отдельно, то рассматриваются как метеорологические предупреждения и должны передаваться по получении и в очередной срок по расписанию.
5.4.2.6 Исполнитель должен вести журнал учета гидрометеорологической информации по безопасности мореплавания, передаваемой радиостанциям, с указанием в них фамилий ответственных исполнителей и получателей информации, дат и времени ее передач, а также обеспечивать сохранность переданной информации. Для этого информация, переданная на радиостанцию порта для трансляции в эфир, должна быть перенесена на бумажный носитель при передаче по электронной почте и подписана лицом, ответственным за ее достоверность и хранится в течение года.
Пример - метеорологическое сообщение для НАВТЕКС
ZCZC ААОО
NOVOROSSIISK 279458 21.11 1315-
WEATHER FORECASTS FROM 21.00 TILL 21.00 22.11
ON AREA ANAPA-TUAPSE
WIND NE 6 - 11 ONNORTH IMPULSES 14 m/sec
WITHOUT DEPOSITS VISIBILITY OF 10 - 20 kms, PLACES IN THE SEA
MIST VISIBILITY OF 1 - 2 kms, HEIGHT OF WA VES OF 0,7 – 1,2 m
TEMPERATURE OF AIR AT THE NIGHT 4 - 9, DAY OF 12 - 17 DEGREES
NNNN (конец сообщения)
5.4.3 Подготовка и передача гидрометеорологической информации по системе SafetyNET
5.4.3.1 Передача гидрометеорологической информации по обеспечению безопасности на море (ИБМ) по сети SafetyNet осуществляется, в основном, по районам МЕТАРЕА в соответствии с действующим расписанием передач и в соответствии с [15].
5.4.3.2 Метеорологические и морские бюллетени для открытого моря передаются через спутник ИНМАРСАТ с расширенным групповым вызовом (РГВ). РГВ открытого моря обеспечивает передачу бюллетеня всем судам, имеющим соответствующее приемное оборудование. Суда получают информацию с помощью аппаратуры, которая автоматически отслеживает соответствующие частоты, и передает стандартным текстом на английском языке только ту информацию, которая относится к судну.
5.4.3.3 Гидрометеорологическая информация по трассе Северного морского пути, передаваемая в рамках ГМССБ, подготавливается в арктических УГМС и ЦГМС (Архангельск, Амдерма, Диксон, Тикси, Певек) в соответствии с [13].
5.4.3.4 Штормовые предупреждения по трассе Северного морского пути передаются немедленно, а информация о фактическом состоянии погоды и моря и прогнозе передается по расписанию в виде адресных телеграмм по каналам автоматизированной сети передачи данных Росгидромета в ФГБУ «ААНИИ» (адрес службы АСПД ААНИИ 5850/AASF/).
ФГБУ «ААНИИ» обобщает полученную информацию и подготавливает на английском языке гидрометеорологический бюллетень (формат) ИБМ и передает его в адрес национального координатора Российской Федерации сети SafetyNet (ГУГП).
5.4.3.5 В соответствии с согласованными международными правилами по сети SafetyNet по трассе Северного морского пути должна передаваться следующая гидрометеорологическая информация:
- штормовые предупреждения;
- фактическая погода;
- прогнозы погоды;
- ледовые обзоры.
При передаче гидрометеорологических бюллетеней необходимо использовать следующий адрес формата сообщения:
- Западный район Арктики: 1:04:67N044E16081:01:00;
- Восточный район Арктики: 1:04:63N125E17070:01:00.
5.4.3.6 Текст метеорологических и морских бюллетеней составляется в соответствии с требованиями и с использованием терминологии, приведенных в [13].
5.4.3.7 Метеорологическому и морскому бюллетеню должно предшествовать слово «SECURITE», за исключением срочных предупреждений, которым должно предшествовать слово «PANPAN».
5.4.3.8 Все метеорологические и морские бюллетени после слов «SECURITE» или «PANPAN» должна включаться информация по соответствующей Метзоне и выпускающей службе.
Пример - SECURITE
Marine weather bulletin for Metarea II issued by Meteo-France.
5.4.3.9 Штормовые предупреждения, краткие обзоры и прогнозы должны передаваться открытым текстом на английском языке.
5.4.3.10 Штормовые предупреждения о сильных ветрах, штормах и тропических циклонах должны иметь следующее содержание и порядок пунктов:
- тип штормового предупреждения;
- дата и время;
- тип атмосферного возмущения (т.е. область низкого давления, ураган и т.д.) с указанием давления в центре в гектопаскалях;
- местоположение атмосферного возмущения по широте и долготе или по отношению к хорошо известным береговым ориентирам;
- направление и скорость движения атмосферного возмущения;
- протяженность района воздействия;
- скорость и направление ветра в районах воздействия;
- ветровое волнение моря и зыбь в районах воздействия;
- другая информация, например будущее положение атмосферного возмущения.
5.4.3.11 Когда штормовое предупреждение включает более одного атмосферного возмущения (системы), оно должно описываться в порядке, начиная с наиболее опасной.
5.4.3.12 Штормовое предупреждение должно быть как можно более кратким, но в то же время четким и полным.
5.4.3.13 Время последнего положения каждого тропического циклона или нового тропического шторма должно указываться в штормовом предупреждении.
5.4.3.14 Штормовые предупреждения выпускаются при возникновении необходимости в них и передаются не по расписанию, а сразу по получении с повтором 6 мин.
Штормовое предупреждение, выпущенное как часть I бюллетеня по расписанию, не нуждается в повторе через 6 минут.
5.4.3.15 Штормовое предупреждение должно оставаться в силе до тех пор, пока в него не будет внесено уточнение или оно не будет отменено.
5.4.3.16 Краткий обзор, даваемый в части II бюллетеня о состоянии погоды и моря, должен иметь следующее содержание и порядок пунктов:
- дата и время (UTC);
- краткий обзор основных характеристик приземной синоптической карты;
- направление и скорость движения значительных барических систем и тропических возмущений.
Важные характеристики состояния моря (волнение и зыбь) включаются в обзор всегда, когда имеется такая информация, как и других характеристик (дрейфующий лед, течения и т.п.), если это возможно и имеет значение.
5.4.3.17 Прогнозы, даваемые в части III бюллетеней о состоянии погоды и моря, должны иметь следующее содержание и порядок пунктов:
- период действия прогноза;
- название или обозначение района(ов) прогноза в пределах основного района действия информации по безопасности на море;
- описание: скорости и направления ветра, видимости, когда по прогнозу она менее шести морских миль (10 км), обледенения, волн.
Прогнозы должны включать ожидаемые значительные изменения в период действия прогноза таких важных явлений, как осадки, вызывающие обледенение, выпадение снега или дождя, перспективы на период вне пределов обычного охвата прогнозов. Единицы измерения при оценке характеристик состояния погоды и моря должны указываться.
Пример - принятый на судне гидрометеорологический бюллетень, переданный по сети SafetyNet ИНМАРСАТ
|
EGC.003 |
Page 1 |
UTC Time: 00-07-27 |
10:36:20 |
LES 322 MSG 14675 MetWarn/Fore Safety Call to Areas: to NO
HIGH SEAS FORECAST FROM ВUREOU OF METEOROLOGY FORWARDED 00072710
IDF15WOO
40:0:1:31:10:01:00
SECURITE
HIGH SEAS FORECAST FOR METAREA 10
WESTERN AREA 12/30S 90/125E, 30/50S 80/129E
ISSUED BY THE AUSTRALIAN BUREAU OF METEOROLOGY, PERTH
FOR 24 HOURS COMMENCING 1100 UTC 27 JULY 2000
IMPORTANT INFORMATION. Understand the definitions and terminology in the
Bureau's pamphlet «MARINE WEATHER SERVICES». A few of them follow:
* Wind speed mentioned in forecasts and coastal observations refers to the average speed over a 10-minute period at a height of 10 metres above the surface.
* Gusts may be up to 40 per cent stronger then the average wind speed.
* The wave and swell heights given refer to significant wave heights which represent the average of the highest one third of the waves. The probable maximum wave height can be up to twice the significant wave height.
PART 1 WARNINGS
Gale warning south of line 42S080E 42S110E 50S125E.
PART2 SITUATION AT 0600UTS
Refer to latest warning.
Cold front 27S100E 40S116E 50S127E moving ESE 25 knots.
Second cold front 33S090E 40S102E 50S101E moving E 35 knots.
Low 1014 HPa near 30S101E, moving southeast 25 knots.
Ridge 30S090E 27S115E.
PART 3 FORECAST
Within 120nm of ridge:
SW/SE winds 10/20 knots. Moderate seas, low to moderate swell.
North of 21S, east of 115E;
E/SE winds 20/30 knots. Rough seas, low to moderate swell.
Remainder north of Ridge:
E/SE winds 15/25 knots. Moderate to rough seas, low to moderate swell
Within 180 nm of low:
Clockwice winds 20/25 knots, increasing to 20/30 knots northern semicircle.
Rough seas, moderate swell
Remainder south of ridge outside warning area:
NW/SW winds 15/25 knots. Moderate to rough seas moderate swell,
increasing to 25/33 knots rough seas m.oderate to heavy swell within
of warning area.
WEATHER PERTH
NNNN (конец сообщения)
EGC.003
5.5 Подготовка и распространение гидрометеорологической информации в центрах ЕСИМО
5.5.1 Центры ЕСИМО организованы в соответствии с [17]. Порядок подготовки и выпуска гидрометеорологической информации в центрах ЕСИМО показан ниже на примере работы центра ЕСИМО ФГБУ «Гидрометцентр России».
5.5.2 Центр ЕСИМО - ФГБУ «Гидрометцентр России» - осуществляет деятельность в области подготовки и распространения оперативной диагностической и прогностической информации о состоянии атмосферы и морской среды. Производимая центром информационная продукция предназначена для широкого круга пользователей ЕСИМО в целях обеспечения хозяйственной, оборонной и других видов деятельности в океанах и морях. Предоставление информации потребителям производится непосредственно из центра и через систему распределенных баз данных (СРБД) ЕСИМО.
5.5.3 Выпуск прогнозов штормовых предупреждений в центре ЕСИМО определен порядком и регламентом, утвержденным Руководителем Росгидромета 21.03.2006 г.
5.5.4 Функции центра ЕСИМО выполняются научными и оперативными подразделениями ФГБУ «Гидрометцентр России», осуществляющие деятельность в соответствии с предметной областью деятельности центра.
5.5.5 Нормативной основой деятельности центра являются документы [5, 16, 17].
5.5.6 Оперативная продукция - информация о текущем состоянии морской среды и прогнозе ее развития - строится на базе использования систем объективного анализа и усвоения гидрометеорологических данных, прогностических расчетов по гидродинамическим моделям, работающим в оперативном режиме. В технологическом отношении деятельность центра состоит в реализации информационно-вычислительной системы, действующей в автоматизированном режиме и обеспечивающей регулярный выпуск и распространение регламентированной оперативной продукции ЕСИМО.
5.5.7 Центр ЕСИМО ФГБУ «Гидрометцентр России» осуществляет свою деятельность с использованием следующих общесистемных средств и ресурсов:
- единых кодификаторов и кодов ЕСИМО;
- централизованной базы метаданных (ЦБМД) ЕСИМО;
- системы распределенных баз данных (СРБД) ЕСИМО;
- виртуальной сети ЕСИМО;
- портала ЕСИМО и комплексных АРМов пользователей системы.
5.5.8 Средства и ресурсы реализуются при создании и эксплуатации технологий, характеристики которых даны в таблице (Приложение К), и предполагает выполнение следующих работ:
- архивация и хранение исходных текстов программных комплексов и эксплуатационной документации, обновление их версий в соответствии с планами развития общесистемных информационных технологий;
- взаимодействие с центром ЕСИМО ФГБУ «ВНИИГМИ-МЦД» и другими организациями-разработчиками ЕСИМО по вопросам уточнения и развития общесистемных средств и технологий;
- обеспечение консультаций и другой методической помощи пользователям данными и других ресурсов центра;
- проверка работоспособности телекоммуникационных узлов и ресурсов центра (один раз в сутки) и их соответствия обязательствам центра (один раз в квартал), взаимодействие с центром ЕСИМО ФГБУ «ВНИИГМИ-МЦД» для обеспечения устойчивого функционирования системы;
- представление справочных сведений о технических средствах, информационных технологиях и ресурсах центра в ЕСИМО ФГБУ «ВНИИГМИ-МЦД» по итогам каждого года деятельности центра;
- подготовка и представление в междуведомственный научно-технический совет ЕСИМО и Росгидромет планов и предложений по функционированию и развитию центра;
- участие в подготовке общесистемных справочных и информационных материалов в части сведений о состоянии и использовании ресурсов центра;
- участие в проведении конференций (семинаров) пользователей ЕСИМО.
5.5.9 В зависимости от категории пользователей устанавливается несколько видов комплексного информационного обеспечения в рамках ЕСИМО:
- предоставление информации по запросу пользователей;
- предоставление регламентированной по составу и срокам информации об обстановке в Мировом океане органам государственной власти России, другим юридическим и физическим лицам, осуществляющим морскую деятельность;
- информационное сопровождение морской деятельности по специальным программам, определяющим информационные, технологические и другие условия обслуживания.
5.5.10 К задачам центра ЕСИМО ФГБУ «Гидрометцентр России» относятся:
- обеспечение функционирования оперативных технологий по приему и обработке данных гидрометеорологических наблюдений и прогностической продукции, поступающих по международным каналам ГСТ ВМО и АСПД, а также через сеть Интернет;
- обеспечение функционирования оперативных технологий по подготовке диагностических и прогностических продуктов и их распространению;
- интеграция информационных ресурсов центра с применением общесистемных технологий и ресурсов ЕСИМО;
- подготовка специализированных информационно-аналитических материалов о гидрометеорологических условиях в морях и океанах;
подготовка и поддержание в актуальном состоянии информационных ресурсов СРБД ЕСИМО в соответствии с профилем центра;
- архивация и обеспечение хранения массивов и баз данных, технологий и нормативно-методической документации по профилю центра;
- разработка (модернизация) и внедрение новых видов диагностической и прогностической информационной продукции по мере развития наблюдательных систем, средств моделирования морской среды и прогностических методов.
5.5.11 Центр ЕСИМО осуществляет информационное обеспечение организаций Росгидромета, федеральных органов исполнительной власти Российской Федерации, юридических лиц диагностической и прогностической информацией о погодных условиях и состоянии вод океана и морей:
- обзор текущей обстановки в океанах и морях - ежедневно, за исключением выходных и праздничных дней;
- прогноз метеорологических условий в Мировом океане и на акватории отдельных морей - два раза в сутки;
- метеорологические анализы и прогнозы зарубежных центров - два раза в сутки;
- прогноз параметров ветровых волн в Мировом океане и отдельных морях - два раза в сутки;
- прогнозы погоды в портовых и других городах - ежедневно;
- интерактивный доступ к полям метеорологических прогнозов - ежедневно;
- анализ состояния ледового покрова в Арктике и Антарктике - еженедельно;
- объективный анализ полей температуры поверхности океана и морей - ежедневно;
- анализ текущего состояния верхнего слоя Мирового океана на базе усвоения данных по температуре и солености воды в океане - ежедневно;
- прогноз штормовых нагонов в Каспийском море - два раза в сутки;
- месячный прогноз ледовых условий для неарктических морей (в холодный период года).
5.5.12 Центр ЕСИМО осуществляет ведение Web-сайта центра, на котором размещается диагностическая и прогностическая информация о состоянии атмосферы и морской среды. Адрес Web-сайта; http://hmc.hydromet.ru/sea/ind.html. Материалы сайта обновляются ежедневно.
6 Терминология, применяемая в морских гидрологических прогнозах и штормовых предупреждениях
6.1 Общие положения
6.1.1 При составлении морских гидрологических прогнозов и штормовых предупреждений должны применяться термины гидрометеорологических величин и явлений, принятые в системе Росгидромета [18, 19], а также термины вошедшие в ГОСТ 18458.
6.1.2 В морских гидрологических прогнозах следует использовать терминологию, понятную для потребителя и в наибольшей степени отражающую ожидаемое развитие гидрологических процессов. Не допускается применять термины, вызывающие неопределенность толкования прогноза, например, «возможно», «вероятно», «местами» и «в отдельных районах». При наличии методик вероятностного прогноза явлений их вероятность указывают в процентах.
6.1.3 В прогнозах метеорологических явлений, а также в штормовых предупреждениях, составляемых по акватории порта и моря, применяются те же термины, что и для сухопутных районов (по РД 52.27.724 и РД 52.88.699).
6.2 Термины и определения, применяемые в прогнозах волнения, течений, уровня и температуры воды
6.2.1 В практике прогнозирования волнения часто используется термин «значительная высота волны». Математически «значительная высота волны» определяется как средняя из 1/3 наибольших волн из числа наблюденных. Ее можно определить по формуле
|
|
(1) |
где N - число наблюденных волн;
i - порядковый номер.
Таким образом, если все волны, зафиксированные в процессе наблюдения, расположить в понижающем порядке и затем взять 1/3 часть, содержащую самые высокие волны, то средняя из них и будет характеризоваться как «значительная высота волны».
6.2.2 В прогнозах волнения указываются параметры волн следующих типов волнения: ветрового волнения, смешанного волнения и зыби. При прогнозе только лишь ветрового волнения слово «ветровое» в тексте опускается. В случае прогноза смешанного волнения отдельно указываются параметры ветрового волнения и параметры зыби и их результирующая величина.
6.2.3 Ветровое волнение - процесс формирования, развития и распространения вызванных ветром волн на акватории океанов, морей и других бассейнов.
6.2.4 Зыбь - вызванные ветром волны, распространяющиеся в области волнообразования после ослабления ветра и (или) изменения его направления или вызванные ветром волны, пришедшие из области волнообразования в другую область, где дует ветер с другой скоростью и (или) другим направлением;
6.2.5 Мертвая зыбь - вызванные ветром волны, распространяющиеся при отсутствии ветра
6.2.6 Смешанное волнение - волнение, образующееся в результате взаимодействия ветровых волн и зыби.
6.2.7 Генеральное направление распространения волн - среднее направление распространения волн, определяемое по многим волнам.
6.2.8 Ретроспективный прогноз - диагностический расчет параметров волнения, основанный на исторических данных о ветре.
6.2.9 Расчеты, основанные на текущих данных о ветре, в общем случае являются анализом волнения.
6.2.10 Течения в зависимости от вызывающих их причин подразделяются на:
- ветровые течения, вся совокупность непериодических движений воды, вызванных непосредственным влекущим воздействием ветра, а также наклоном водной поверхности и перераспределением плотности воды, обусловленных ветром;
- дрейфовые течения, возникающие в результате влекущего действия ветра;
- градиентные течения, обусловленные горизонтальным градиентом гидростатического давления, возникающим при наклоне поверхности моря относительно изопотенциальной поверхности;
- стоковые течения, образующиеся под влиянием впадающих в море рек;
- приливные течения, вызванные приливными волнами;
- периодические течения, изменение которых происходит с определенным периодом;
- инерционные течения, наблюдаемые после прекращения действия силы, вызвавшей течения.
6.2.11 Уровень моря - высота поверхности моря, свободной от ветровых волн и зыби, измеренная относительно условного горизонта.
6.2.12 Колебание уровня моря - разность между наибольшим и наименьшим значением уровня моря за определенный интервал времени.
6.2.13 Ход уровня - изменение уровня за определенный интервал времени.
6.2.14 Эвстатические колебания уровня моря - изменения уровня Мирового океана, связанные с изменениями объема воды в нем, а также с изменениями емкости морей и океанов.
6.2.15 Цунами - долгопериодные морские гравитационные волны, возникающие в результате подводных землетрясений, извержений подводных вулканов, подводных и береговых обвалов и оползней, приводящие к затоплению прибрежных населенных пунктов, береговых сооружений и народнохозяйственных объектов.
6.2.16 Сгонно-нагонные колебания уровня моря - изменения уровня морей и океанов под воздействием ветра и атмосферного давления.
6.2.17 Критические отметки уровня моря - отметки уровня моря, превышение которых или падение ниже которых влечет за собой опасные в данном районе последствия.
6.2.18 Температура поверхностного слоя моря - температура поверхностного слоя моря толщиной не более 1 м.
6.3 Термины, применяемые в прогнозах ледовых фаз и ледового состояния морей
6.3.1 Под ледовым явлением понимают совокупность ледовых фаз и процессов, сменяющихся в течение года на замерзающих акваториях. К ледовым явлениям относят: появление льда, установление льда на всей видимой водной поверхности, разрушение неподвижного льда на этой акватории, его окончательное исчезновение, очищение акватории ото льдов всех форм и возрастных характеристик.
Исходя из характера перехода из одного состояния в другое, различают следующие фазы: начало ледообразования, полное замерзание, установление припая или ледостава, начало таяния, полное очищение ото льда.
К дрейфующему льду относится любой вид морского льда, который не связан с берегом или дном и находится в движении под воздействием ветра и течений,
6.3.2 Днем первого появления льда (без уточнения формы льда) считается день, когда в осенне-зимний период (а на арктических морях после окончательного очищения) впервые на наблюдаемом пространстве появляется лед независимо от вида, количества и места образования (образовался ли он на месте или перенесен из других районов). Случаи обмерзания свай или камней во внимание не принимаются. Когда это целесообразно, в прогнозах отмечается:
- «ожидается первое появление местного льда»;
- «ожидается первое появление льда, внесенного из устья реки»;
- «ожидается первое появление льда, дрейфующего с ...».
6.3.3 Днем первого появления льда первичных форм (сала, шуги, снежуры), битого льда или ледяных полей считается день, когда впервые на наблюдаемом пространстве появляется лед этих форм, независимо от его количества или сплоченности».
6.3.4 Днем первого появления дрейфующего льда сплоченностью четыре балла и более (восемь баллов и более) считается день, когда впервые появляются дрейфующие льды сплоченностью более четырех баллов (более восьми баллов), независимо от форм. Если в день первого появления дрейфующего льда появился лед сплоченностью восемь баллов и более, независимо от его формы, то этот день следует считать и днем первого появления дрейфующего льда сплоченностью четыре и восемь баллов.
6.3.5 Днем устойчивого появления льда считается день, когда впервые появился лед и больше не исчезал. Если впервые появившийся лед исчез, а затем появился вновь, устойчивому появлению льда отвечают условия, при которых промежуток времени со льдом был больше или равен промежутку времени безо льда.
6.3.6 Днем первого замерзания моря, бухты и др. считается день, когда впервые неподвижный лед (береговой припай) занял не менее половины наблюдаемого пространства.
6.3.7 Днем первого полного замерзания моря считается день, когда впервые в данную зиму на видимом пространстве установился неподвижный ледяной покров.
6.3.8 Днем устойчивого полного замерзания считается день, после которого вплоть до начала весеннего разрушения ледяного покрова в пределах наблюдаемого пространства не происходит уменьшения площади неподвижного льда или эти изменения несущественны (менее одного балла).
6.3.9 Днем первого взлома неподвижного ледяного покрова считается день, когда впервые площадь неподвижного льда на видимом пространстве становится меньше 10 баллов и ледяной покров приобретает четкие признаки слабого или умеренного весеннего разрушения (образование отдельных сквозных трещин, появление озерков и отдельных проталин, водяных заберегов и др.).
6.3.10 Днем устойчивого взлома считается день, когда впервые количество плавучего льда или чистой воды в пределах видимой поверхности моря становится около 5 баллов. Припай находится в стадии весеннего разрушения.
6.3.11 Днем полного разрушения неподвижного льда считается день, когда на наблюдаемом участке моря неподвижный лед оказывается полностью взломанным и оторванным от берега. Случаи, когда на берегу и береговых отмелях осталась часть подошвы, во внимание не принимаются.
6.3.12 Днем исчезновения дрейфующих льдов количеством восемь баллов и более (четыре балла и более) считается день, когда впервые весной на наблюдаемом пространстве количество льда менее восьми баллов (четыре балла и менее) стало устойчиво.
6.3.13 Днем полного очищения моря ото льда считается первый день безо льда или день, когда на видимом пространстве моря наблюдаются отдельные льдины (менее 1 балла); наличие стамух и остатков льда на берегу и отмелях во внимание не принимается.
6.4 Термины, применяемые в прогнозах обледенения рыболовных судов
В прогнозах указывается возможность обледенения и его интенсивность. Интенсивность обледенения характеризуется следующими терминами:
- медленное: скорость отложения льда на судне менее 0,7 см/ч;
- быстрое: скорость обледенения от 0,7 до 1,3 см/ч (характеризуется как ОЯ);
- очень быстрое: скорость обледенения 1,4 см/ч и более (характеризуется как ОЯ).
6.5 Термины, применяемые в прогнозах тягуна
Слабый тягун - периодически усиливающееся натяжение и ослабление швартовых концов (оценивается в 1 балл).
Умеренный тягун - происходит обрыв швартовых; погрузочно-разгрузочные работы прекращаются (оценивается в 2 балла).
Сильный тягун - суда отводят от причала и выводят на внешний рейд (оценивается в 3 балла) - характеризуется как ОЯ.
7 Оценка качества методов прогноза и успешности прогнозов и штормовых предупреждений
7.1 Оценка качества методов прогноза
7.1.1 Общие положения
7.1.1.1 Под оценкой качества метода прогноза обычно понимают весь процесс сравнения предсказанных значений величин с фактическими значениями и с результатами прогнозов по другим аналогичным методам.
7.1.1.2 Качество метода определяется эффективностью и заблаговременностью прогноза. При этом, чем больше заблаговременность, тем с большим эффектом, при равной степени его точности, можно пользоваться данным методом.
7.1.1.3 Для оценки качества метода прогноза устанавливается некоторый интервал (допуск) предельного значения допустимой ошибки прогноза δдоп, в котором будет находиться прогнозируемое явление. Точность прогноза определяется путем сравнения ошибки прогноза δ с допустимой ошибкой δдоп, которая составляет долю среднеквадратичного (стандартного) отклонения предсказываемого явления от нормы σх.
7.1.1.4 Для оценки качества метода большое значение имеют объективность определения допустимой ошибки δдоп и сравнимость метода с результатами других альтернативных методов, в качестве которых обычно используются климатический или инерционный метод прогноза. Методические прогнозы имеют смысл лишь в том случае, если они являются более точными (в статистическом смысле), чем климатические или инерционные прогнозы.
7.1.2 Критерии качества методов прогноза
7.1.2.1 Количественные критерии, используемые при оценке качества методов прогноза должны правильно отражать вероятностный характер и природную изменчивость прогнозируемого явления. Эти критерии не должны предъявлять чрезмерных требований в отношении точности прогнозов. Разнообразие прогнозов и методов их составления требует дифференциального подхода к выбору критериев оценки качества прогнозов. При установлении критериев следует исходить из знания показателей природной вариации прогнозируемых величин, а именно: среднего квадратичного отклонения от нормы или многолетней амплитуды.
7.1.2.2 Если распределение ошибок прогнозов и распределение отклонений гидрологических величин от средней многолетней (нормы) близки к нормальному распределению или отличаются от него незначительно, за критерий качества метода прогноза принимается отношение S/σx, в котором σх - среднее квадратичное отклонение предсказываемого явления от нормы, вычисляемое по формуле
|
|
a S - средняя квадратичная ошибка проверочных прогнозов, определяемая по формуле
|
|
(3) |
В формулах (2) и (3):
х - данное значение явления в многолетнем ряду наблюдений;
![]() - среднее
многолетнее значение явления (норма);
- среднее
многолетнее значение явления (норма);
хф и хпр - фактическое и прогнозируемое значения соответственно;
n - число членов ряда;
m - число степеней свободы, характеризующее вид уравнения регрессии и равно количеству постоянных величин в нем. Для линейного уравнения вида у = ах + b m равно 2. В случае нелинейной зависимости т принимается равным числу постоянных величин уравнении связи (если последнее задано), а при графическом построении кривой - равным числу постоянных величин такого уравнения, которому близка по виду кривая связи.
7.1.2.3 Средняя квадратичная ошибка проверочных прогнозов S связана с коэффициентом корреляции r и величиной σх соотношением
|
|
(4) |
Зная отношение S/σх, легко перейти к стандартному выражению корреляционного отношения (индексу корреляции ρ), характеризующему степень нелинейности связи
|
|
(5) |
Для линейных зависимостей корреляционное отношение ρ численно совпадает с коэффициентом корреляции (ρ = r). При нелинейной связи ρ будет отличаться от коэффициента корреляции r тем больше, чем сильнее выражена нелинейность связи.
7.1.2.4 Отношение S/σх является характеристикой эффективности метода, т.е. показывает выигрыш в распределении ошибок, который дает метод прогноза по сравнению с распределением ошибок в случае принятия ожидаемой величины, равной ее норме. Чем меньше отношение S/σх, тем надежнее корреляционная связь, так как оно является мерой независимости вариации функции от вариации аргумента. При функциональной зависимости отношение S/σх равно нулю, а если оно равно единице, то корреляционная связь между переменными отсутствует, т.е. функция не зависит от вариации аргумента.
7.1.2.5 Таким образом, критериями качества корреляционной связи являются: отношение S/σх, коэффициент корреляции r (или корреляционное отношение ρ).
7.1.2.6 Коэффициенты уравнения регрессии, определенные из условий оптимальности по выборочным оценкам единственным образом, не будут оптимальными ни для какой другой выборки, кроме той, для которой они определены. Поэтому важным является вопрос надежности коэффициента корреляции ограниченной выборки.
В больших выборках распределение корреляций имеет тенденцию быть нормальным, и вероятная (стандартная) ошибка частного коэффициента корреляции Еr для линейных зависимостей между двумя переменными может быть приближенно оценена по формуле
|
|
(6) |
7.1.2.7 Для определения вероятной ошибки общего коэффициента множественной корреляции ER служит формула
|
|
(7) |
7.1.2.8 Вероятная ошибка индекса корреляции для криволинейных функций Еρ вычисляется по формуле
|
|
(8) |
7.1.2.9 Предельные значения основных критериев применимости уравнения регрессии S и σх будут разными при разном числе членов ряда, использованного при установлении прогностических зависимостей. Как известно, любая статистическая характеристика, вычисленная по данным ограниченной выборки, отличается от ее истинного значения для генеральной совокупности и тем больше, чем меньше объем этой выборки. Отсюда следует, что критерий качества метода должен учитывать число членов ряда n.
7.1.3 Оценка эффективности методов прогноза
7.1.3.1 Основным критерием оценки эффективности метода прогноза является выигрыш обеспеченности метода Pi по сравнению с природной или инерционной обеспеченностью. Обеспеченность метода зависит от допустимой ошибки δдоп и связана с величиной S/σх, являющейся показателем качества прогноза.
7.1.3.2 Характерные значения отношения S/σх
и соответствующие им значения коэффициента корреляции r
(или ρ) и обеспеченность Рi при различных допустимых погрешностях для нормального
распределения приведены в таблице 3. Они
справедливы для длины ряда ![]() .
.
Таблица 2 позволяет определить выигрыш в обеспеченности при заданной допустимой ошибке, который дает метод прогноза при данном значении S/σх по сравнению с обеспеченностью прогноза по норме. Для этого из обеспеченности, указанной в таблице 2, при принятых допустимых ошибках 0,674σх, 0,8σх и σх необходимо вычесть соответственно 50 %, 58 % и 68 %, что характеризует теоретическую обеспеченность климатического прогноза при различных допустимых ошибках.
Таблица 2
|
Показатели успешности метода прогноза |
Обеспеченность метода прогноза Pi при допустимой ошибке |
Показатели успешности метода прогноза |
Обеспеченность метода прогноза Pi при допустимой ошибке |
||||||
|
S/σх |
r(ρ) |
0,674σх |
0,8σх |
σх |
S/σх |
r(ρ) |
0,674σх |
0,8σх |
σх |
|
0,05 |
0,995 |
100 |
100 |
100 |
0,60 |
0,80 |
74 |
82 |
90 |
|
0,10 |
0,993 |
100 |
100 |
100 |
0,65 |
0,76 |
70 |
78 |
88 |
|
0,15 |
0,99 |
100 |
100 |
100 |
0,67 |
0,74 |
68 |
77 |
86 |
|
0,20 |
0,98 |
100 |
100 |
100 |
0,70 |
0,72 |
67 |
75 |
85 |
|
0,25 |
0,97 |
100 |
100 |
100 |
0,75 |
0,67 |
64 |
72 |
82 |
|
0,30 |
0,95 |
95 |
99 |
100 |
0,80 |
0,60 |
60 |
68 |
79 |
|
0,35 |
0,94 |
94 |
98 |
100 |
0,85 |
0,54 |
58 |
66 |
77 |
|
0,40 |
0,92 |
91 |
96 |
99 |
0,90 |
0,45 |
55 |
63 |
74 |
|
0,45 |
0,90 |
87 |
93 |
98 |
0,95 |
0,32 |
52 |
60 |
71 |
|
0,50 |
0,87 |
83 |
90 |
96 |
1,00 |
0,00 |
50 |
58 |
68 |
|
0,55 |
0,84 |
79 |
86 |
94 |
|
|
|
|
|
Следовательно, теоретически метод прогноза может считаться эффективным уже тогда, когда обеспеченность его при заданных допустимых ошибках будет несколько больше обеспеченности прогноза по норме при тех же ошибках.
Однако на практике зависимости с коэффициентом корреляции, близким к нулю, и обеспеченностью допустимых ошибок, близких к 50 %, 58 % и 68 %, не могут считаться удовлетворительными. Для получения практически эффективного и надежного метода его обеспеченность должна значительно превосходить минимальную теоретическую, установленную для абсолютно случайных корреляционных связей с коэффициентом корреляции, равным нулю.
Следовательно, для получения действительной эффективности метода необходимо из его обеспеченности вычесть действительную обеспеченность климатического прогноза Ркл, %, которая определяется формулой
|
|
(9) |
где т - число случаев, когда отличие климатической величины (нормы) от действительных величин не превышает принятой допустимой ошибки;
n - число членов ряда.
7.1.3.4 Применение метода краткосрочного прогноза в
оперативную практику допускается лишь в том случае, если обеспеченность
допустимой ошибки ![]() не менее чем на 18 % превышает
обеспеченность вероятного отклонения от нормы.
не менее чем на 18 % превышает
обеспеченность вероятного отклонения от нормы.
7.1.3.5 Предельными значениями основного критерия применимости методов прогнозов S/σх являются:
|
S/σх ≤ 0,57 |
для n ≤ 15; |
|
S/σх ≤ 0,62 |
для 15 ≤ n ≤ 25; |
|
S/σх ≤ 0,67 |
для n ≥ 25. |
Здесь n - число членов ряда, использованного при установлении прогностической зависимости или число проверочных прогнозов.
7.1.3.6 Применение метода долгосрочного прогноза с заблаговременностью от 2 до 6 месяцев и выше в практике является целесообразным, если обеспеченность допустимой ошибки δдоп = ±0,8σх не менее, чем на 10 % превышает обеспеченность допустимой ошибки отклонения от нормы. Метод прогноза в этом случае считается применимым для выпуска оперативных прогнозов при следующих отношениях S/σх:
|
S/σх ≤ 0,7 |
для n ≤ 15; |
|
S/σх ≤ 0,75 |
для 15 ≤ n ≤ 25; |
|
S/σх ≤ 0,80 |
для n ≥ 25. |
7.1.3.7 Для методов сверхдолгосрочных прогнозов, где допустимая ошибка δдоп = σх, конкретное превышение обеспеченности метода над обеспеченностью допустимой ошибки отклонения от нормы не устанавливается. В общем случае, чем эта величина больше, тем метод эффективнее.
7.1.3.8 Для определения эффективности метода краткосрочных прогнозов обеспеченность метода сравнивается не с природной обеспеченностью, рассмотренной выше, а с обеспеченностью инерционных прогнозов, в которых предыдущее значение элемента приравнивается к его последующему значению.
Указанным способом устанавливается эффективность всех методов краткосрочных прогнозов морских гидрометеорологических явлений, повторяющихся систематически (уровень, течение, волнение и др.).
7.1.3.9 Обеспеченность инерционных прогнозов Рин, %, определяется по формуле
|
|
(10) |
где тин - количество оправдавшихся инерционных прогнозов;
п - общее число всех инерционных прогнозов.
7.1.3.10 Для установления качества корреляционной зависимости, можно также воспользоваться формулой
|
|
(11) |
где Р - обеспеченность допустимой ошибки для данной зависимости;
PN - обеспеченность допустимой ошибки природной обеспеченности.
Зависимость, для которой γ ≤ 0,8, можно считать хорошей, для 0,8 ≥ γ ≥ 0,5 -удовлетворительной, для 0,5 ≥ γ ≥ 0,2 - слабой и для γ ≤ 0,2 - непригодной.
7.1.4 Особые случаи оценки методов прогноза
7.1.4.1 Изложенные выше способы определения достоверности методов прогноза, а также способы оценки их эффективности, могут быть использованы для оценки большинства методов морских гидрологических прогнозов.
Имеются, однако, случаи, когда использование указанных критериев затруднено и возникает необходимость учета специфических особенностей методов. К числу таких случаев относятся:
- оценка методов, по которым прогнозы составляются в сроки, находящиеся в пределах многолетней амплитуды явления;
- оценка методов прогноза гидрологических элементов, базирующихся на прогнозах элементов погоды;
- оценка методов прогноза полей гидрологических элементов;
- оценка методов прогноза гидрологических элементов, допустимая погрешность которых не связана со средней квадратичной величиной ряда σс;
- оценка численных методов прогноза;
- оценка методов, не имеющих фиксированной даты составления прогноза, т.е. таких, дата составления прогнозов по которым определяется сроком наступления тех или иных факторов, учет которых положен в основу метода. К этой группе относятся методы краткосрочных прогнозов и методы уточнения долгосрочных. Оценка этих методов прогноза производится по величине средней квадратичной ошибки проверочных прогнозов в зависимости от допустимой ошибки для данного метода (таблица 3).
Таблица 3 - Оценка методов, не имеющих фиксированной даты составления прогноза
|
Оценка метода прогноза |
Допустимая ошибка, дни, при S |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
Хорошая, при S ≤ |
0,7 |
1,5 |
2,2 |
3,0 |
3,7 |
4,5 |
5,2 |
|
Удовлетворительная, при S ≤ |
1,2 |
2,4 |
3,6 |
4,8 |
5,9 |
7,1 |
8,2 |
7.1.4.2 Оценка методов, по которым прогнозы составляются в сроки, находящиеся в пределах многолетней амплитуды явления, производится по отношению S/σc, σс -среднее квадратичное отклонение явления от его среднего значения, установленного для членов ряда n', находящегося в пределах сокращенной амплитуды Ас, т.е. от даты составления прогноза до самой поздней даты явления.
Величина σс определяется по формуле (2), где число членов многолетнего ряда п заменяется числом ряда n' для сокращенной амплитуды Ас. Дальнейшее определение применимости подобных зависимостей производится изложенным выше способом.
7.1.4.3 При оценках методов морских гидрологических прогнозов, базирующихся на прогнозах элементов погоды (температуры воздуха, ветра, давления и т.д.), следует учитывать обеспеченность методов, использованных для прогноза метеорологических элементов. При этом общая обеспеченность метода будет равна произведению обеспеченности обоих методов при условии сопоставимости допустимых ошибок прогнозов.
Общая обеспеченность метода Робщ, %, может быть установлена непосредственно по данным ряда проверочных прогнозов, составленных по прогнозируемым значениям метеорологических элементов по формуле
|
|
(12) |
где т - число оправдавшихся проверочных прогнозов;
п - общее число проверочных прогнозов.
7.1.4.4 Общая обеспеченность методов прогноза средней заблаговременности может быть установлена в течение одного-двух сезонов при достаточно большом числе проверочных прогнозов. Полученная общая обеспеченность Робщ позволяет уточнить предварительное решение о применимости метода в оперативной работе и определить обеспеченность метода прогноза метеорологических элементов Рмет, %, в сравнении с обеспеченностью гидрологического прогноза Ргидр, %, по формуле
|
|
(13) |
7.1.4.5. Оценка методов прогнозов полей морских гидрометеорологических элементов производится путем определения только обеспеченности метода Р, %, по формуле
|
|
(14) |
где т - число оправдавшихся проверочных прогнозов;
п - общее число проверочных прогнозов в постоянных узлах сеток.
Удовлетворительным считается метод, обеспеченность которого не ниже 68 %.
7.1.4.6 Оценка методов прогноза морских гидрологических элементов, выраженных кривыми (в тех случаях, когда кривые, как границы, отделяющие разные гидрологические среды, имеют самостоятельное значение, например, расположение кромки дрейфующего льда в море), производится аналогично оценке прогнозов полей, т.е. путем определения обеспеченности метода. Критерий удовлетворительной обеспеченности равен или больше 68 %.
7.1.4.7 К числу методов, допустимая ошибка которых не связана со средней квадратичной величиной ряда σх, относятся:
- методы прогноза времени наступления гидрометеорологических явлений с условным значением допустимых ошибок;
- методы прогноза волнения и ряд других.
7.1.4.8 Отличительной особенностью перечисленных методов является возможность получения расчетных формул теоретическим путем. Последнее затрудняет использование для оценки подобных методов установленных выше критериев, основанных на комплексном применении статистических величин r, S и σх. В таких случаях для оценки методов используются результаты определения успешности проверочных прогнозов. На основе этих материалов устанавливается только обеспеченность метода по формуле (12).
Удовлетворительной, т.е. применимой для составления оперативных прогнозов, считается метод с обеспеченностью 68 % и выше.
7.2 Оценка успешности прогнозов и штормовых предупреждений
7.2.1 Допустимые ошибки и оценка прогнозов
7.2.1.1 Оценка успешности прогнозов заключается в сопоставлении прогнозируемых хпр и фактических хф значений элементов гидрометеорологического режима моря.
7.2.1.2 Ошибка прогноза δ определяется как разность между значениями фактической величины хф и ожидаемой по прогнозу хпр
|
δ = хф - хпр. |
(15) |
Ожидавшаяся по прогнозу величина, сложенная с ошибкой, должна быть равна фактической величине. Чем меньше δ, тем точнее прогноз.
Ошибка выражается в тех же величинах, что и само прогнозируемое явление: для сроков наступления гидрологических явлений - в днях, для высоты волны - в м, для температуры - в градусах Цельсия и т.д.
7.2.1.3 Для оценки успешности прогноза устанавливается некоторый интервал (допуск) предельного значения ошибки прогноза δдоп, в котором будет находиться прогнозируемое явление.
7.2.1.4 Точность прогноза определяется путем сравнения ошибки прогноза δ с допустимой ошибкой δдоп, которая составляет долю среднеквадратичного (стандартного) отклонения предсказываемого явления от нормы σх.
7.2.1.5 В практике опенки прогнозов используется два различных способа.
Наиболее распространенный способ, по которому прогнозу дается одна из двух возможных оценок: 100 %, если прогноз оправдался, или 0 %, если прогноз не оправдался. Оценку 100 % по этому способу получает прогноз, ошибка которого была меньше или равнялась допустимой ошибке δдоп. Оценку 0 % получает прогноз, ошибка которого превышает δдоп.
7.2.1.6 Допустимая ошибка прогноза должна быть пропорциональной среднему квадратичному отклонению от нормы ошибок стандартного прогноза, в качестве которого обычно берется прогноз по норме. Ошибки такого стандартного прогноза будут фактические аномалии Δ.
Если оценку такого стандартного прогноза производить, исходя из допуска, равного среднему квадратичному отклонению от нормы σх фактических аномалий, то при условии нормального распределения величин, систематически прогнозируя норму при допустимой ошибке σх, прогнозист обеспечит среднюю оправдываемость прогнозов около 68 %. Использование критерия 0,674σх для оценки климатического прогноза обеспечит среднюю оправдываемость 50 %.
7.2.1.7 Другой способ оценки прогноза дает оценку в зависимости от ошибки прогноза. Эта оценка характеризуется следующими особенностями:
- при малых ошибках прогноза оценка высока;
- небольшое увеличение ошибки прогноза влечет за собой небольшое уменьшение оценки;
- при значительных ошибках, близких к критериям допустимых ошибок, когда удовлетворительный прогноз переходит в неудовлетворительный, снижение оценки прогноза при дальнейшем возрастании ошибок будет происходить наиболее быстро;
- при очень большой ошибке прогноза оценка будет близка к нулю, так что дальнейшее возрастание ошибки не сможет вызвать сколько-нибудь значительного уменьшения оценки.
7.2.1.8 Оценка прогноза F в зависимости от ошибки прогноза вычисляется по формуле [20]
|
|
(16) |
где δ - ошибка прогноза;
с и а - коэффициенты, определяемые дополнительными условиями.
Из формулы (16) видно, что чем больше коэффициент а, тем строже оценка F, так как с возрастанием ошибки прогноза δ оценка F быстро стремится к нулю. При безошибочном прогнозе (δ = 0 и с = 1) оценка равна 1.
Численное значение коэффициента а определяется из
условия задания средней оценки какого-либо стандартного вида прогноза ![]() . При этом средняя оценка вычисляется
не по произвольно назначенному числу случаев, а является теоретической средней,
т.е. математическим ожиданием, и может быть найдена с помощью интеграла
вероятности Гаусса, характеризующего нормальное распределение величин.
. При этом средняя оценка вычисляется
не по произвольно назначенному числу случаев, а является теоретической средней,
т.е. математическим ожиданием, и может быть найдена с помощью интеграла
вероятности Гаусса, характеризующего нормальное распределение величин.
7.2.1.9 Выражение для коэффициента а записывается в следующем виде:
|
|
(17) |
где величина ![]() характеризует
меру строгости оценки прогнозов.
характеризует
меру строгости оценки прогнозов.
Учитывая, что оценка прогнозов F меняется от 0 до 1
(от 0 до 100 %), то при условии ![]() = 50 % (т.е. половина всех прогнозов
оправдывается, а половина не оправдывается), что соответствует допустимой
ошибке ±0,674σх, величина k
= 3,0.
= 50 % (т.е. половина всех прогнозов
оправдывается, а половина не оправдывается), что соответствует допустимой
ошибке ±0,674σх, величина k
= 3,0.
При k = 3,0 формула (16) примет вид
|
|
(18) |
При условии ![]() = 58 %, что в среднем обеспечивается
при допустимой ошибке, равной ±0,80σх, при k = 1,94 оценка прогноза имеет вид
= 58 %, что в среднем обеспечивается
при допустимой ошибке, равной ±0,80σх, при k = 1,94 оценка прогноза имеет вид
|
|
(19) |
При условии ![]() = 68 %, что в среднем обеспечено при
допустимой ошибке ±σх, при k = 1,17 оценка прогноза имеет вид
= 68 %, что в среднем обеспечено при
допустимой ошибке ±σх, при k = 1,17 оценка прогноза имеет вид
|
|
(20) |
7.2.1.10 Для определения оценки конкретных прогнозов по формулам (18 - 20) существуют таблицы (приложение Л), в которых даны значения оценок прогноза F при допустимой ошибке δдоп от 1 до 30 и σx в пределах значений от 5 до 24.
Как видно из таблиц Л.1 - Л.3, снижение оценки при увеличении ошибки прогноза на одну и ту же величину будет происходить быстрее в случае малой изменчивости природного явление (при малых значениях σx), и медленнее в случае большой изменчивости явления (при больших значениях σx).
Расчеты по формулам (18 - 20) показывают, что успешность прогнозов высока при малых ошибках прогноза, близка к природной обеспеченности при ошибках прогноза, равных допустимой ошибке, и ниже природной обеспеченности при ошибках прогноза, превышающих допустимую ошибку прогноза.
7.2.2 Критерии, используемые при оценке прогнозов
7.2.2.1 Для краткосрочных и среднесрочных прогнозов за критерий допустимой ошибки принимается величина, равная ±0,674σx; для долгосрочных прогнозов с заблаговременностью до двух месяцев за критерий допустимой ошибки принимается величина, равная ±0,8σx; для сверхдолгосрочных прогнозов принимается величина, равная ±σx.
7.2.2.2 В
тех случаях, когда на предсказываемую величину в значительной мере оказывают
влияние начальные условия, за допустимую ошибку принимается величина ![]() , где
, где ![]() - среднее квадратичное отклонение от
среднего изменения гидрологического элемента за период заблаговременности
прогноза, вычисляемое по формуле
- среднее квадратичное отклонение от
среднего изменения гидрологического элемента за период заблаговременности
прогноза, вычисляемое по формуле
|
|
(21) |
где Δх - разность между начальным и конечным значениями элемента (явления) за период заблаговременности прогноза;
![]() - среднее значение этой разности;
- среднее значение этой разности;
n - число членов ряда.
7.2.2.3 Допустимые ошибки долгосрочных прогнозов с заблаговременностью до двух месяцев определяются следующим образом:
- если долгосрочный прогноз составляется раньше самой ранней даты наступления предсказываемого явления, допустимая ошибка принимается равной вероятному отклонению от нормы (допустимой ошибке)
|
δдоп = ±0,674σx; |
(22) |
- если долгосрочный прогноз составляется позже самой ранней даты наступления предсказываемого явления в многолетнем ряду, допустимая ошибка принимается вероятному отклонению от нормы в пределах сокращенной амплитуды
|
|
(23) |
Величина ![]() может быть получена обычным путем или
взята из таблицы 4.
может быть получена обычным путем или
взята из таблицы 4.
Таблица 4 - Определение величины δдоп
= ±0,674σx по данным σх
и ![]()
|
σx |
Значение δдоп при Ас/Ам |
||||||
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
3 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
|
4 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
5 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
|
6 |
2 |
3 |
3 |
3 |
4 |
4 |
4 |
|
7 |
2 |
3 |
4 |
4 |
5 |
5 |
5 |
|
8 |
3 |
3 |
4 |
4 |
5 |
5 |
5 |
|
9 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
|
10 |
4 |
4 |
5 |
6 |
6 |
6 |
7 |
|
11 |
4 |
5 |
6 |
6 |
6 |
7 |
7 |
|
12 |
4 |
5 |
6 |
6 |
7 |
7 |
8 |
|
13 |
5 |
6 |
6 |
7 |
8 |
8 |
9 |
|
14 |
5 |
6 |
7 |
8 |
8 |
9 |
9 |
|
15 |
5 |
6 |
8 |
8 |
9 |
9 |
10 |
7.2.2.4 Для нахождения допустимой ошибки при сокращенной амплитуде необходимо знать среднее квадратичное отклонение от нормы многолетнего ряда σх и отношение сокращенной амплитуды к многолетней амплитуде Ас/Ам. Величина допустимой погрешности, равная вероятной ошибке средней величины явления в пределах сокращенной амплитуды, находится при пересечении соответствующей графы и строки таблицы 4.
7.2.2.5 Критериями качества корреляционной связи являются отношение S/σх, коэффициент корреляции r (или корреляционное отношение ρ), и обеспеченность метода Рi, выражаемая в процентах (таблица 5).
Таблица 5 - Критерии качества применимости корреляционной связи при числе проверочных прогнозов п ≥ 25 и δдоп = ±0,674σх
|
Оценка качества |
S/σх |
r(ρ) |
Рi, % |
|
Хорошая |
≤0,5 |
≥0,9 |
≥80 |
|
Удовлетворительная |
≤0,8 |
≥0,7 |
≥75 |
|
Неудовлетворительная |
>0,9 |
<0,6 |
<75 |
7.2.2.6 Все оценки, приведенные в таблице 5 справедливы для выборки, по которой построена корреляционная связь (зависимый ряд). Однако для ряда, не входящего в эту выборку (независимый ряд), оценки прогнозов, полученные в результате применения этой корреляционной связи, обычно ухудшаются.
7.3 Оценка прогнозов различных морских гидрологических элементов
7.3.1 Общие положения
7.3.1.1 Оценке подлежат все прогнозы, составленные по закрепленной за оперативным подразделением Росгидромета зоной ответственности. Прогнозы по акватории моря и по порту и их уточнения оцениваются отдельно.
7.3.1.2 При оценке прогнозов по акватории порта используются данные наблюдений береговых, островных, устьевых станций и постов, расположенных в районе порта или вблизи него.
7.3.1.3 Специализированные прогнозы оцениваются так же, как и прогнозы по акватории моря, если они составлялись для района моря или по маршруту, и так же, как прогнозы по акватории порта, если они составлялись для работ, проводимых в порту.
7.3.1.4 Существенным условием для успешности оценки прогнозов является условие объективности, требующее, чтобы прогнозы были четко сформулированы в числовых или качественных характеристиках и их терминология должна быть общепринятой. Это необходимо для того, чтобы при сравнении прогнозов с данными наблюдений исключить элементы субъективности. Только те прогнозы, которые выражены в объективных терминах, могут быть удовлетворительно оценены как прогнозы.
7.3.1.5 Оценка оправдываемости каждого прогноза производится специалистами СМГП после истечения срока его действия при наличии фактических данных наблюдений о тех характеристиках и показателях, которые содержаться в прогнозе. Если такие данные отсутствуют, то прогноз не оценивается.
7.3.1.6 Успешность морских гидрологических прогнозов в значительной мере зависит от качества исходных данных и, прежде всего, от точности метеорологических прогнозов. При отсутствии исходной информации начальные условия определяют иногда с помощью диагностических расчетов с учетом фактических гидрометеорологических условий моря за предшествующий прогнозу период.
7.3.2 Оценка прогнозов полей распределения морских гидрологических элементов
7.3.2.1 Оценка прогнозов полей распределения гидрологических элементов производится путем сопоставления прогностических и фактических величин в ряде точек, выбранных на акватории моря (если отсутствует объективный анализ). Для каждой точки определяются показатели вариации гидрологического элемента и допустимые ошибки прогнозов δдоп, которыми и следует пользоваться при оценке оправдываемости прогнозов.
7.3.2.2 Для оценки прогнозов полей гидрометеорологических элементов рассчитываются следующие статистические характеристики:
- средняя абсолютная ошибка прогноза - по формуле
|
|
(24) |
где п - общее число составленных прогнозов;
хпр и хф - прогностическое и фактическое значение элемента; соответственно;
- средняя арифметическая (систематическая) ошибка прогноза
|
|
(25) |
Систематическая
ошибка позволяет судить о фоновой ошибке, т.е. о методическом среднем смещении
прогноза. При ![]() > 0 имеет место систематическое
завышение прогностических значений, при
> 0 имеет место систематическое
завышение прогностических значений, при ![]() < 0 - систематическое занижение.
< 0 - систематическое занижение.
7.3.2.3 Значения относительной ошибки прогноза можно рассчитать по формуле
|
ε = δ/δф, |
(26) |
где ![]() - средняя абсолютная фактическая
изменчивость в конкретном пункте;
- средняя абсолютная фактическая
изменчивость в конкретном пункте;
![]() - значение элемента в пункте, для
которого производится сравнение.
- значение элемента в пункте, для
которого производится сравнение.
Чем меньше δ и ε, тем лучше прогноз. При значении ε = 1 качество методических прогнозов находится на уровне инерционных прогнозов, а при ε > 1 методические прогнозы хуже инерционных.
Коэффициент корреляции между фактическими и рассчитанными величинами определяется по формуле
|
|
(27) |
где хм - результаты расчетов по модели;
хн - наблюденные данные.
В таблице 6 приведены доверительные интервалы для различных значений r и ε в зависимости от количества расчетных точек n.
Таблица 6 - Доверительный интервал коэффициента корреляции Δr и относительной ошибки Δε
|
r |
εтеор |
Значение Δr, при п |
Значение Δε, при п |
||||
|
30 |
143 |
841 |
30 |
143 |
841 |
||
|
0,3 |
0,95 |
0,17 |
0,08 |
0,03 |
0,05 |
0,02 |
0,01 |
|
0,4 |
0,92 |
0,15 |
0,07 |
0,03 |
0,06 |
0,03 |
0,01 |
|
0,5 |
0,87 |
0,14 |
0,06 |
0,02 |
0,08 |
0,03 |
0,01 |
|
0,6 |
0,80 |
0,12 |
0,05 |
0,02 |
0,09 |
0,04 |
0,02 |
|
0,7 |
0,71 |
0,09 |
0,04 |
0,02 |
0,09 |
0,04 |
0,02 |
|
0,8 |
0,60 |
0,06 |
0,03 |
0,01 |
0,08 |
0,04 |
0,02 |
|
0,9 |
0,44 |
0,03 |
0,02 |
0,01 |
0,06 |
0,04 |
0,02 |
7.3.2.4 Снижение ошибки методического прогноза по сравнению с ошибкой инерционного прогноза (для прогнозов на срок до трех суток) или с ошибкой климатического прогноза (для прогнозов на срок более трех суток) можно определить по формуле
|
|
(28) |
где Xм - мера ошибки методического прогноза; X - мера ошибки инерционного или климатического прогноза.
В качестве меры ошибки могут быть приняты также значения среднеквадратичной ошибки прогноза S и показатель рассеяния ошибки прогноза SI.
Средняя квадратичная ошибка прогноза рассчитывается по формуле
|
|
(29) |
Чем меньше S, тем выше качество прогноза.
Показатель рассеяния ошибок прогноза SI можно рассчитать по формуле
|
|
(30) |
7.3.2.5 Перечисленные показатели рассчитываются как по области в целом, так и по отдельным ее частям.
Наряду с этими данными следует рассчитывать и накапливать осредненные за различные периоды поля значений ошибок прогнозов в точках сетки (относительных, абсолютных и с учетом знаков). Такие сведения необходимы для вычисления систематических ошибок и для других работ по совершенствованию методик прогноза.
7.3.2.6 При оценке полей распределения гидрологических элементов может рассматриваться оправдываемость прогноза по знаку и числовому значению.
7.3.2.7 При оценке оправдываемости прогнозов поля по знаку подсчитывается число точек, в которых знак ожидаемой и действительной аномалии совпал, затем находится отношение числа этих точек т к общему числу выбранных точек п, по которым велась проверка оправдываемости прогнозов. При несовпадении знака прогнозируемой и действительной аномалии прогноз считается оправдавшимся в тех случаях, когда абсолютное значение расхождения не превышает допустимую ошибку.
7.3.2.8 При оценке оправдываемости прогноза поля по числовому значению подсчитывается число точек, в которых ошибка прогноза не превышала допустимую ошибку, затем находится отношение числа точек т к общему числу выбранных точек п, по которым велась проверка оправдываемости прогнозов.
7.3.2.9 Общая оправдываемость поля распределения гидрологического элемента по знаку или по числовому значению Р, %, определяется по формуле (16).
7.3.3 Особые случаи оценки прогнозов
7.3.3.1 Ориентировочные прогнозы и консультации не оцениваются.
7.3.3.2 Качество прогнозов за месяц, квартал и год оценивается в зависимости от их заблаговременности.
7.3.3.3 Значение и оценка оправдываемости прогнозов приведена в таблице 7.
Таблица 7 - Оценки краткосрочных, среднесрочных и долгосрочных прогнозов
|
Оценка |
Значение оправдываемости прогноза, % |
||
|
Краткосрочный |
Среднесрочный |
Долгосрочный |
|
|
Отлично |
Свыше 93 |
Свыше 90 |
Свыше 90 |
|
Хорошо |
Менее 93 до 87 включительно |
Менее 90 до 84 включительно |
Менее 90 до 80 включительно |
|
Удовлетворительно |
Менее 87 до 80 включительно |
Менее 84 до 75 включительно |
Менее 75 |
|
Неудовлетворительно |
Менее 80 |
Менее 75 |
Менее 70 |
7.3.4 Оценка краткосрочных и среднесрочных прогнозов
7.3.4.1 Прогнозы ледовых условий
Толщина льда
7.3.4.1.1 Оценка прогнозов толщины льда может производиться как для отдельного пункта (порта), так и для района моря. В прогнозе должны указываться как ожидаемая толщина льда, так и изменение толщины льда за период заблаговременности. Поэтому независимо от формы самого прогноза (в нем может указываться ожидаемая толщина льда) оценка толщины льда должна производиться по ее изменению за период заблаговременности.
7.3.4.1.2 При оценке прогнозов толщины льда допустимая ошибка прогноза устанавливается равной 30 % от фактического ее изменения за период заблаговременности прогноза (таблица 8).
Если прогноз толщины льда не выходит за пределы допустимой ошибки, он считается оправдавшимся.
Таблица 8 - Допустимые ошибки прогноза толщины льда
|
Фактическое изменение толщины льда, см |
>10 |
11 - 15 |
16 - 20 |
21 - 25 |
26 - 30 |
>30 |
|
Допустимая ошибка, см |
±3 |
±4 |
±6 |
±7 |
±8 |
±10 |
Сплоченность, зоны сжатия и разрежения
7.3.4.1.3 Допустимая ошибка прогнозов сплоченности, разрушения льдов, торосистости, сжатия льдов и других показателей состояния ледового режима, определяемых в баллах, принимается равной ±1 балл.
Указанные рядом на карте фактические сжатия объединяются в зоны, и общая оправдываемость зон сжатия и разрежения Р, %, определяется по формуле
|
|
(31) |
где т - количество оправдавшихся зон сжатия;
п - общее количество поддающихся оценке зон сжатия на карте.
Любой прогноз зон сжатия считается оправдавшимся при фактической зоне сжатия менее 2 баллов.
Эффективность оценивается путем сравнения результатов методического прогноза с инерционными прогнозами.
Сроки наступления ледовых фаз
7.3.4.1.4 Допустимые ошибки прогнозов сроков наступления ледовых явлений (вскрытие и очищение моря ото льда, первое появление льда, замерзание) приведены в таблице 9.
Таблица 9 - Допустимые ошибки прогнозов сроков наступления ледовых явлений в зависимости от заблаговременности прогноза
|
Заблаговременность, сутки |
Допустимая ошибка, сутки |
|
3 |
±1 |
|
5 |
±2 |
|
9 |
±3 |
|
13 |
±4 |
|
15 |
±5 |
Знак минус указывает ошибку в сторону более ранних сроков наступления ледовых явлений, а знак плюс - в сторону более поздних сроков.
Дрейф льда
7.3.4.1.5 В качестве допустимой ошибки δдоп прогноза дрейфа льда принимается величина равная ±0,674σΔ, где σΔ - среднее квадратичное отклонение изменения скорости (направления) дрейфа от среднего изменения за период заблаговременности прогноза в данном районе моря. Если данных для определения природной вариации дрейфа льда недостаточно, можно использовать в качестве допустимой ошибки δдоп величину, соответствующую 20 % амплитуды изменения величины за период заблаговременности прогноза.
Положение кромки льда
7.3.4.1.6 В качестве допустимой ошибки положения кромки льда принимается величина δкр = 0,674σкр, где σкр среднеквадратическое значение изменчивости положения кромки льда. Оправдываемость прогноза положения кромки льда Р, %, определяется по формуле
|
|
(32) |
где l1 - общая длина участков предсказанной кромки, на которой отклонение от фактического положения кромки не превышает величину допустимой ошибки δкр;
ls - длина прогностической кромки, обеспеченной фактическими данными.
Положение полыней
7.3.4.1.7 Оценке подлежат только полыньи, продолжительность существования которых соизмерима с заблаговременностью прогноза. Полностью оправдавшиеся полыньи получают оценку 1, полностью не оправдавшиеся - оценку 0, а оправдавшиеся частично могут получать оценку от 0 до 1 в соответствии с долей относительной длины полыней, оправдавшихся при прогнозе. Общая оправдываемость полыней Р, %, вычисляется по формуле
|
|
(33) |
где т - сумма оценок оправдавшихся полыней;
п - общее количество полыней, подлежащих оценке.
При отсутствии полыней на фактической и прогностической карте общая оправдываемость прогноза составляет 100 %.
Прогнозы высоты ветровых волн и зыби
7.3.4.1.8 Оценка оправдываемости прогноза высоты волн производится как для отдельных пунктов прибрежных районов моря, так и по акватории морей и океанов.
7.3.4.1.9 При оценке оправдываемости прогнозов высот волн по данным судовых визуальных наблюдений в качестве допустимой ошибки прогноза высоты волн принимается величина равная 30 % от наблюденной высоты волны, приблизительно соответствующей обеспеченности 12 %. Прогноз считается оправдавшимся, если выполняется условие
|
|
где hф - фактически наблюденная высота волны;
hпр - предсказанная высота волны.
7.3.4.1.10 Допустимая ошибка не устанавливается для оценки прогнозов волн с высотой до 0,25 м в бухтах, небольших заливах, портах и на мелководье прибрежных зон, до 1 м в открытых морских районах и до 2 м в океанах.
Во всех этих случаях соответствующие прогнозы считаются оправдавшимися при любой действительной высоте волн от 0 до 0,25; 1,0; 2,0 м (в зависимости от размеров водного бассейна).
7.3.4.1.11 Оценка оправдываемости и прогнозов полей высот волн, составленных численным или синоптическим методом, производится путем сравнения предсказанных высот волн с высотами волн, снятых с карт волнения проанализированных по данным судовых наблюдений, на которых поле волнения представлено в виде изолиний, соединяющих точки с равными высотами волн.
С этой целью на прогностической карте выбирается ряд контрольных точек (порядка 20 - 30), равномерно распределенных по области прогноза и в каждой из них снимаются прогностические значения высот волн. В этих же точках с проанализированных карт волнения снимаются путем интерполяции значения высот волн, принимаемых в качестве фактических. Полученные данные сопоставляются друг с другом. Прогноз высоты волны в каждой из выбранных точек считается оправдавшимся, если выполняется условие (34).
7.3.4.1.12 Общая оправдываемость прогноза Р, %, определяется по формуле:
|
|
(35) |
где т - количество точек, в которых прогноз оправдался;
п - общее количество точек.
7.3.4.1.13 Направление ветровых волн не оценивается. Оценка прогноза высот ветровых волн и высот волн зыби, если они составлены отдельно производится раздельно. При прогнозе зыби должно оцениваться также и направление, откуда зыбь распространяется.
7.3.4.2 Прогнозы уровня, течений и температуры воды
7.3.4.2.1 За допустимую ошибку δдоп прогноза уровня принимается величина, равная ±0,674σΔ, где σΔ - средне квадратичное отклонение изменения уровня от нормы изменения уровня в данном пункте за период заблаговременности прогноза.
Среднее квадратичное отклонение приращений уровня σΔh рассчитывается на основе фактических приращений уровня за время заблаговременности по формуле
|
|
(36) |
где Δh - изменение уровня за интервал времени, равный заблаговременности прогноза;
![]() - среднее значение этих изменений для
данной станции или поста;
- среднее значение этих изменений для
данной станции или поста;
n - длина ряда наблюдений.
Прогноз считается оправдавшимся, если ошибка прогноза δ ≤ δдоп.
7.3.4.2.2 Аналогичным образом оцениваются прогнозы течений и температуры воды. Только в этих случаях устанавливаются свои средние квадратичные отклонения σΔ.
13.4.23 Общая оправдываемость прогнозов этих элементов выражается процентным отношением числа оправдавшихся прогнозов к общему числу прогнозов.
7.3.4.2.4 Учет и оценка краткосрочных и среднесрочных морских гидрологических прогнозов ведется в специальном журнале (приложение М).
7.3.5 Оценка штормовых предупреждений
7.3.5.1 Показателями успешности штормовых предупреждений являются их оправдываемость, предупрежденность, заблаговременность и эффективность, которые рассчитываются по факту наличия или отсутствия явления.
7.5.3.2 Оценка успешности штормовых предупреждений, составленных для всего моря или его части, производят по всей территории моря (пункт включается в территорию). Успешность штормовых предупреждений, составленных только для пункта, оценивают по пункту.
7.3.5.3 Оценке успешности подлежат все штормовые предупреждения с учетом «пропущенных» ОЯ, которые не спрогнозированы, но наблюдались. Оценка оправдываемости метеорологических явлений по пункту (порту) и территории моря производится в соответствии с РД 52.27.724.
7.3.5.4 Штормовое предупреждение о сохранении успешно предусмотренного ранее явления (продление срока действия штормового предупреждения) не оценивают.
7.3.5.5 Если предусмотренное в штормовом предупреждении ОЯ не наблюдалось, но штормовое предупреждение было отменено не позднее, чем за 2 ч до ожидаемого возникновения ОЯ, то данное штормовое предупреждение не оценивают.
7.3.5.6 Не предусмотренное прогнозом, но наблюдавшееся ОЯ интерпретируют как прогноз отсутствия ОЯ, а не составленное штормовое предупреждение об этом ОЯ учитывают как не оправдавшееся.
7.3.5.7 Оправдываемость штормовых предупреждений, составленных с заблаговременностью до трех суток, оценивается как по пункту, так и по территории, а с заблаговременностью до 10 суток - только по территории.
7.3.5.8 Оценка оправдываемости штормовых предупреждений производится по двум градациям: «оправдалось» (Роя = 100 %) и «не оправдалось» (Роя = 0 %) - в зависимости от правильности предсказания интенсивности явления, акватории распространения явления, времени возникновения явления, продолжительности явления.
7.3.5.9 Заблаговременность штормового предупреждения определяется:
- для пункта - интервалом времени, определяемым от момента первого доведения штормового предупреждения до обслуживаемых организаций до момента возникновения ОЯ в данном пункте;
- для территории - интервалом времени, определяемым от момента первого доведения предупреждения до обслуживаемых организаций до момента возникновения ОЯ на одной из станций, если оно наблюдалось только на одной станции, или на второй станции, если оно наблюдалось на нескольких станциях.
7.3.5.10 Оценка штормовых предупреждений по акватории распространения ОЯ должна производиться с учетом следующих условий:
- штормовое предупреждение, составленное для всей акватории моря (в пределах зоны ответственности оперативного органа), считается оправдавшимся, если ожидаемое ОЯ наблюдалось не менее чем на трети этой территории;
- ОЯ (или комплекс явлений, близких к ОЯ), возникновение которого не было предусмотрено штормовым предупреждением, считается непредупрежденным, если оно наблюдалось более чем на трети обслуживаемой территории;
- штормовое предупреждение, составленное по какой-то части акватории моря, считается оправдавшимся, если оно отмечалось, хотя бы одной береговой или судовой станцией на данной части акватории моря;
- если возникновение ОЯ предусматривалось штормовым предупреждением на одной части акватории моря, а оно наблюдалось на другой, для которой штормовое предупреждение не выпускалось, такое предупреждение оценивается как неоправдавшееся, а явление - как непредусмотренное;
- если штормовое предупреждение было дано по одной части акватории моря, а ОЯ наблюдалось и на других ее частях, штормовое предупреждение считается оправдавшимся, если ОЯ наблюдалось не более чем на трети той части акватории, по которой предупреждение не давалось;
- если ОЯ наблюдалось более чем на трети акватории моря, по которой штормовое предупреждение не выпускалось, то ОЯ считается непредупрежденным, а оценка «оправдалось» относится только к той части, для которой составлялось штормовое предупреждение.
7.3.5.11 Оценка штормовых предупреждений по времени начала возникновения ОЯ и его продолжительности производится с учетом следующих условий:
- штормовое предупреждение считается оправдавшимся по времени, если разница между предсказанным и фактическим временем возникновения ОЯ не превышает величину, указанную в таблице 10.
Таблица 10 - Допустимая разница между предсказанным и фактическим временем возникновения ОЯ
|
Заблаговременность предупреждения, ч |
Допустимая разница между предсказанным и фактическим временем возникновения ОЯ, ч |
|
|
Раньше на |
Позже на |
|
|
От 2 до 6 включительно |
1 |
2 |
|
От 7 до 24 включительно |
2 |
3 |
|
От 25 до 48 включительно |
3 |
4 |
|
Более 48 |
4 |
6 |
- штормовое предупреждение не оценивается, если ожидавшееся ОЯ не наблюдалось и потребителям была передана отмена этого предупреждения не позднее, чем за 2 ч до ожидаемого срока начала явления. Если отмена предупреждения дана позднее этого срока, штормовое предупреждение считается неоправдавшимся;
- штормовые предупреждения, содержащие уточнение ранее сообщенного времени начала или границ распространения ОЯ, оцениваются как новое предупреждение.
7.3.5.12 Штормовое предупреждение считается оправдавшимся, если ОЯ было отмечено на одном пункте наблюдения или более и по силе (интенсивности) достигали установленного критерия ОЯ по РД 52.88.699.
7.3.5.13 Штормовое предупреждение считается оправдавшимся, если наблюдалось, хотя бы одно ОЯ из нескольких, указанных в штормовом предупреждении ОЯ.
7.3.5.14 Штормовое предупреждение считается оправдавшимся, если одновременно наблюдалось несколько ОЯ, а предусмотрено - хотя бы одно из них.
7.3.5.15 Штормовое предупреждение, содержащее комплекс гидрометеорологических явлений, считается оправдавшимся, если не менее двух перечисленных в нем явлений достигли установленных для обслуживаемой территории значений гидрометеорологических величин и наблюдались в одном пункте наблюдений и более.
Примеры
1 Дано штормовое предупреждение об усилении ветра от 20 до 25 м/с, начиная с 18 ч (критерий ОЯ по ветру равен 25 м/с)
Фактически в 19 ч ветер усилился на станциях от 14 до 18 м/с, на одной станции - до 25 м/с. Штормовое предупреждение оправдалось (Роя = 100 %).
2 В прогнозе ожидалась скорость ветра от 18 до 23 м/с (критерий ОЯ равен 25 м/с), штормовое предупреждение не выпускалось.
Фактически по территории моря (десять станций) скорость ветра на трех станциях было от 14 до 16 м/с, на шести станциях - от 19 до 22 м/с, на одной станции - 26 м/с (ОЯ).
В данном случае ОЯ оказалось не предусмотренным, т.к. штормовое предупреждение не составлено и поэтому учитывается как неоправдавшееся (Роя = 0 %).
7.3.5.16 Штормовое предупреждение считается неоправдавшимся (Роя = 0 %), если:
- прогнозировалось одно ОЯ, а наблюдалось другое ОЯ;
- ОЯ не было предусмотрено штормовым предупреждением, а наблюдалось в одном или нескольких пунктах наблюдений;
- указанные в штормовом предупреждении ОЯ фактически не наблюдались (значения гидрометеорологических величин не достигли установленных критериев ОЯ или комплекса ОЯ).
7.3.5.17 Штормовое предупреждение считается эффективным (Роя = 100 %), если оно оправдалось и выпущено (доведено до потребителя) с заблаговременностью 2 ч и более.
Оправдавшиеся, но переданные с заблаговременностью менее 2 ч, а также не оправдавшиеся (включая «пропущенные») штормовые предупреждения считаются не эффективными (Роя = 0 %).
Пример - Оценка оправдываемости прогноза тягуна
Оценка прогноза тягуна производится по трем показателям:
- по времени начала явления;
- по интенсивности;
- по продолжительности.
Срок начала явления оценивается только для умеренного, сильного «тягуна», практически влияющего на работу порта.
Прогноз считается оправдавшимся:
- если умеренный до сильного тягун ожидался в ближайшие 6 ч, а фактически явление началось не ранее чем в ближайшие 2 чине позднее чем через 8 ч с момента составления прогноза;
- если умеренный до сильного тягун ожидался в ближайшие 12 - 24 ч, а фактически явление начиналось не раньше ближайших 10 ч и не позднее 24 ч с момента составления прогноза.
По интенсивности прогноз считается оправдавшимся:
- если при ожидаемом очень слабом до слабого тягуне не наблюдался умеренный тягун (даже кратковременно);
- если дан прогноз от умеренного до сильного тягуна и фактически явление осуществилось.
По продолжительности прогноз считается оправдавшимся, если фактическая продолжительность от умеренного до сильного тягуна соответствует данным таблицы.
Таблица - Оценка оправдываемости прогноза продолжительности тягуна
|
Продолжительность тягуна, ч |
||||
|
Ожидаемая |
до 6 |
до 12 |
до 24 |
36 |
|
Фактическая |
6 ± 2 |
12 ± 4 |
24 ± 6 |
36 ± 10 |
Примечание - В случае отсутствия данных по акватории моря или его части, где ожидалось ОЯ, допустимо использовать рассчитанные данные, полученные на основе фактической погоды и состояния моря за соответствующие сроки наблюдений, с учетом типовых синоптических ситуаций.
7.3.6 Оценка долгосрочных ледовых прогнозов по арктическим морям
7.3.6.1 Основные критерии и принципы оценки
7.3.6.1.1 Долгосрочные прогнозы ледовых явлений включают прогнозы сроков наступления ледовых явлений и их количественных характеристик (первого и устойчивого появления льда, замерзания, вскрытия и очищения, толщины льда, ледовитости, положения кромки льда). Для морей арктического бассейна, кроме указанных видов прогнозов, составляются также прогнозы сроков взлома и разрушения припая, площадей ледовых массивов, полыней и др.
При оценке оправдываемости прогнозов сроков наступления ледовых явлений, не имеющих резко выраженного годового хода, за допустимую ошибку δдоп принимается величина, равная ±σ, ±0,8σ или ±0,674σ в зависимости от заблаговременности прогноза. Величина σ вычисляется по формуле (2), как среднее квадратичное отклонение прогнозируемого элемента от нормы за многолетний период в данном районе моря или океана.
При оценке прогнозов тех элементов ледового режима, которые имеют годовой ход (ледовитость, толщина льда, положение кромки льда), значения допустимых погрешностей δдоп = σΔ вычисляются как средние квадратичные отклонения изменений от среднего изменения прогнозируемого элемента за период заблаговременности прогноза.
7.3.6.1.2 Работа по оценке оправдываемости долгосрочных ледовых прогнозов начинается со сбора фактического материала по тем элементам, которые были включены в прогноз (таблицы Л.4 - Л.6).
Исходным материалом для этого служат данные фактических наблюдений за состоянием льдов с самолетов, ИСЗ, судов и полярных станций, данные радиовех и дрейфующих станций, а также сведения о ходе навигации в арктических морях.
Оценивается оправдываемость всех элементов ледового прогноза и его уточнений.
Оценка прогнозов производится по группам элементов, в которые объединяются прогнозируемые показатели, имеющие режимное сходство; по районам моря или для моря в целом: по заблаговременности прогнозов.
7.3.6.1.3 Все прогнозируемые элементы режима объединены в пять групп.
Группа 1. Взлом и окончательное разрушение припая, куда включаются сведения о сроках взлома и разрушения припая в бухтах, проливах или в районе полярных станций.
Группа 2. Ледовитость морей и площади ледовых массивов, куда включаются сведения о ледовитости моря в целом, о ледовитости отдельных районов моря, о площади ледовых массивов в море.
Группа 3. Распределение льда, куда входят следующие сведения: широта и долгота положения кромки, тип распределения массива, сплоченность, время образования заприпайных полыней или прогалин, время разделения или разрыва массивов и т.д.
Группа 4. Устойчивое ледообразование и нарастание молодого льда, куда включены сведения о сроках начала устойчивого образования льда в бухтах, проливах и в море, а также данные о сроках достижения молодым льдом толщины 5 - 10, 20 - 25 см и т.д., лимитирующей плавание транспортных судов и ледоколов в арктических морях осенью.
Группа 5. Навигационные рекомендации.
Данные этой группы элементов ледового прогноза имеют наибольшее практическое значение, так как дают сведения о возможных сроках начала и окончания ледокольного и безледокольного плавания на различных участках трассы Северного морского пути (СМП), сроках выхода последних судов из арктических портов, а также указывают наиболее благоприятное время прохождения судами лимитирующих участков трассы и подхода судов к труднодоступным (по ледовым условиям) пунктам Арктики.
В качестве единого показателя условий плавания на арктических трассах принято отношение эксплуатационной скорости хода судна в одиночном плавании во льду на заданной трассе к эксплуатационной скорости хода судна на чистой воде. Это отношение, называемое коэффициентом трудности плавания KТ, является безразмерным показателем, позволяющим объективно сравнивать условия ледового плавания в различных физико-географических районах и в разные навигационные периоды
|
|
(37) |
где V0 - техническая скорость хода судна на чистой воде;
S0 - общая протяженность рассматриваемой трассы;
Sпр, S9-10, Sч.в. - протяженность участков в припае, во льдах протяженностью 9 - 10 баллов и на чистой воде;
Vпр, V9-10 - техническая ледовая скорость хода судна в припае, во льду сплоченностью 9 - 10 баллов и т.д.
7.3.6.1.4 Оценка прогнозов по элементам ледового режима производится для следующих районов:
- по морям северо-западной Атлантики;
- по Баренцеву морю в целом и по его районам, а также по району Земли Франца-Иосифа;
- по юго-западной и северо-восточной части Карского моря, включая пролив Вилькицкого;
- по морю Лаптевых в целом и отдельно по западной и восточной его части;
- для района Новосибирских островов, куда включается восточная часть моря Лаптевых и западная часть Восточно-Сибирского моря;
- по Восточно-Сибирскому морю в целом и отдельно по западной и восточной его части;
- по району Анадырского залива.
7.3.6.1.5 Оценка по заблаговременности производится для следующих плановых прогнозов и уточнений:
- долгосрочного прогноза, составленного в январе на первую половину навигации (заблаговременность более 6 - 8 мес);
- основного долгосрочного прогноза, составленного в марте на первую половину навигации (заблаговременность 4 - 6 мес);
- уточнение ледового прогноза, составляемого в мае (заблаговременность 3 - 6 мес);
- уточнение ледового прогноза, составляемого в июне (заблаговременность 1 - 3 мес.);
- долгосрочного прогноза, составляемого в августе на вторую половину навигации (заблаговременность 2 - 4 мес);
- долгосрочного прогноза, составляемого в сентябре на вторую половину навигации (заблаговременность 1 - 3 мес).
7.3.6.1.6 Для оценки январского прогноза по элементам режима для всех районов, которые указаны в тексте официального прогноза ФГБУ «ААНИИ», заполняется таблица Л.4.
7.3.6.1.7 Для оценки прогноза, составленного в марте, и последующих его уточнений, а также для прогнозов, выпущенных в августе и в сентябре по элементам режима для всех районов, заполняются таблицы Л.5 и Л.6.
7.3.6.1.8 В соответствующие графы таблиц Л.4 - Л.6 в записываются необходимые для проверки прогнозов сведения:
- фактическое состояние элемента в текущем году хф;
- среднее многолетнее значение данного элемента ![]() ;
;
- многолетняя амплитуда Ам;
- среднее квадратичное отклонение от нормы σх;
- прогнозируемое числовое значение элемента хпр;
- допустимая ошибка δдоп, выраженная либо в долях многолетней амплитуды, либо в долях σх.
Сведения о среднем многолетнем значении приводятся для того, чтобы было видно, на каком уровне относительно нормы происходило явление фактически и по прогнозу. Многолетняя амплитуда Ам и среднее квадратичное отклонение от нормы σх даются для подсчета значения допустимых ошибок, выраженных в долях Ам или σх.
Показатели Ам, ![]() и σх должны
быть получены на одном ряде наблюдений, чтобы имелась полная возможность их
сопоставления. Ряд наблюдений за элементом гидрологического режима моря, по
которому вычислены значения нормы, амплитуды и σх должны
быть указаны в тексте. Если ряды наблюдений для различных пунктов неодинаковы,
следует указать преобладающую для района или моря длину ряда наблюдений, по
которым получены Ам,
и σх должны
быть получены на одном ряде наблюдений, чтобы имелась полная возможность их
сопоставления. Ряд наблюдений за элементом гидрологического режима моря, по
которому вычислены значения нормы, амплитуды и σх должны
быть указаны в тексте. Если ряды наблюдений для различных пунктов неодинаковы,
следует указать преобладающую для района или моря длину ряда наблюдений, по
которым получены Ам, ![]() и σх.
и σх.
В соответствующие графы таблиц Л.4 - Л.6 записывается допустимая ошибка, выраженная либо в процентах многолетней амплитуды, либо в долях σх (δдоп.1 или δдоп.2).
Ошибка прогноза находится из сопоставления фактически наблюдавшегося значения элемента хф и ожидавшегося по прогнозу хпр.
7.3.6.1.9 Оценка оправдываемости прогноза производится путем сопоставления ошибки прогноза δ с допустимой ошибкой δдоп.1 или δдоп.2. В случае, когда δ ≤ δдоп.1 и δ ≤ δдоп.2, прогноз считается оправдавшимся и получает оценку 100 %. В случае, когда δ > δдоп.1 или δ > δдоп.2, прогноз считается неоправдавшимся и получает оценку 0 %.
7.3.6.1.10 Кроме общепринятой оценки оправдываемости прогноза, когда ошибка прогноза сравнивается с допустимой ошибкой и прогнозу дается одна их двух возможных оценок (100 % или 0 %), производится оценка этого же прогноза в зависимости от ошибки прогноза.
7.3.6.1.11 Оценка прогноза в зависимости от ошибки прогноза выражается в процентах и изменяется в диапазоне от 100 до 0 %.
Оценка прогноза F находится по допустимой ошибке прогноза δдоп и среднему квадратичному отклонению от нормы σx (таблицы Л.1 - Л.3).
7.3.6.1.12 Сопоставление значений многолетней амплитуды Ам и среднего квадратичного отклонения от нормы σx по материалам для арктических морей, где ряды наблюдений в среднем составляют порядка 30 - 50 лет, дало следующие соотношения:
|
0,25Ам = σх; |
0,2Ам = 0,8σх, |
0,17Ам = 0,674σх. |
7.3.6.1.13 На основе обработки многолетних рядов наблюдений в Арктике приняты следующие значения допустимых ошибок для оценки долгосрочных прогнозов, выраженные в долях среднего квадратичного отклонения от нормы:
а) при заблаговременности прогнозов более 6 мес. за критерий допустимой ошибки принимается ±σх;
б) при заблаговременности прогнозов менее 6 мес. за критерий допустимой ошибки принимается ±0,8σх;
в) при заблаговременности прогнозов менее 6 мес. для рядов, приближающихся к 100 годам, за критерий допустимой ошибки берется ±0,674σх.
7.3.6.2 Оценка прогнозов взлома и окончательного разрушения припая
7.3.6.2.1 Оценка прогнозов срока взлома и разрушения припая начинается с подготовки исходного материала. В таблицу Л.4 из прогноза, составленного в январе, и в таблицу Л.5 из прогноза, составленного в марте, и его уточнений вписываются пункты или районы моря, для которых давался прогноз, прогнозируемые сроки, данные о средних многолетних значениях, данные природной изменчивости и значения допустимых погрешностей.
7.3.6.2.2 По данным полярных станций, ледовых авиаразведок, судовых и спутниковых данных, а также в результате анализа ледово-гидрологических процессов в морях устанавливаются сроки взлома припая в текущем году для всех пунктов, вписанных в таблицы Л.4, Л.5. Из сравнения сроков фактического взлома припая и ожидавшегося по прогнозу находят ошибку каждого прогноза δ.
7.3.6.2.3 Оценка оправдываемости и оценка прогноза в зависимости от ошибки прогноза производится последовательно для всех пунктов, после чего подсчитываются средние оценки прогнозов, составленных в январе и в марте и их уточнений по каждому морю. Результаты подсчета средних оценок вносятся в соответствующие графы сводной таблицы Л.7.
7.3.6.2.4 После заполнения таблиц Л.4, Л.5 и Л.7 следует приступить к анализу результатов проверки прогнозов сроков взлома и окончательного разрушения припая в текущем году.
7.3.6.3 Оценка прогнозов ледовитости моря и площадей ледяных массивов
7.3.6.3.1 Работа по оценке прогнозов ледовитости арктических морей начинается со сбора материалов. Отдельно для каждого моря (Баренцева, Карского, Лаптевых, Восточно-Сибирского и Чукотского), для района Новосибирских островов и Анадырского залива заполняются таблицы Л.4 и Л.5, в которые из официальных прогнозов, составленных в январе и марте (с уточнением в апреле и июне), записываются периоды прогноза ледовитости на первую половину навигации.
В таблицу Л.6 из официальных прогнозов, составленных в августе и сентябре, записываются периоды прогноза ледовитости на вторую половину навигации.
Прогнозы площадей ледовых массивов - Новоземельского, Северо-Земельского, Таймырского, Янского, Айонского и Врангелевского - на первую и вторую половину навигации записываются в таблицы Л.4 - Л.6 после прогноза ледовитости того моря, в пределах которого располагался данный массив. В этих таблицах заполняются все графы, содержащие сведения о прогнозируемой ледовитости или площади массива, норма, данные о природной изменчивости, многолетней амплитуде и допустимые погрешности δдоп.
7.3.6.3.2 Сведения о фактически наблюдавшейся ледовитости моря или площади массива в текущем году вписываются в соответствующие графы таблиц Л.4 - Л.6 на основании данных планиметрирования ежедекадных обзорных карт ледовой обстановки в моря, которое производится научно-оперативными группами при штабах морских операций.
7.3.6.3.3 Фактические значения ледовитости за определенные промежутки времени, указанные в прогнозе, определяются путем осреднения или интерполяции данных, полученных из непосредственного планиметрирования обзорных карт за каждую декаду. Из сопоставления фактически наблюдавшихся значений ледовитости и площади массивов с ожидаемыми по прогнозу соответственно заблаговременности находят ошибку прогноза δ.
7.3.6.3.4 Оценка оправдываемости прогноза и оценка прогноза в зависимости от ошибки прогноза производится последовательно для всех показателей ледовитости и площадей массивов по каждому морю и по каждому прогнозу, после чего подсчитываются средние оценки для прогнозов, составленных в январе, марте (с уточнениями), августе и сентябре и полученные данные вписываются в сводную таблицу Л.7.
7.3.6.3.5 После заполнения всех граф таблиц Л.4 - Л.7 необходимо тщательно проанализировать материалы, которые были заложены в обоснование прогнозов ледовитости или площади массивов; при этом следует кратко охарактеризовать методику долгосрочных прогнозов данного элемента ледового режима конкретно по морю или району.
В анализе ошибочных прогнозов следует указать, на какой материал по фактическим наблюдениям и на какой материал из долгосрочного метеорологического прогноза опирались при составлении ледового прогноза в текущем году.
7.3.6.3.6 В заключение следует рассмотреть средние оценки оправдываемости и оценки в зависимости от значений ошибок прогноза ледовитости в среднем для каждого моря и для различных по заблаговременности прогнозов.
7.3.6.4 Оценка прогнозов распределения льда
7.3.6.4.1 Оценка прогноза распределения льда может быть произведена количественно и качественно (в зависимости от вида прогноза).
Количественная оценка прогнозов распределения льда производится в том случае, если прогноз дается в виде конкретных цифровых характеристик на основании разработанной методики (например, положение кромки на определенном меридиане или параллели), а также при наличии сведений о природной изменчивости самого явления, показателей этой изменчивости - многолетней амплитуде или средней квадратичной ошибки и определенной по ним допустимой ошибки.
В таблицы Л.4 - Л.6 вписываются прогнозы распределения льда с количественными характеристиками, дается оценка оправдываемости и определяется оценка в зависимости от ошибки прогноза.
7.3.6.4.2 Качественную оценку получают прогнозы положения массива, образования прогалины, разрежений льда и разрывов между ледяными массивами.
Прогнозы положения массивов Новоземельского, Таймырского, Айонского и Врангелевского, а также прогнозы взаимного положения массивов могут быть выписаны их текстов прогноза и представлены в виде таблицы, где в соответствующих графах дается оценка оправдываемости каждого прогноза.
7.3.6.4.3 Оценка прогноза появления чукотской заприпайной прогалины, составляемого в марте с последующим уточнением в мае и июне, производится путем сравнения ожидаемого состояния прогалины, выраженного в виде площади чистой воды за припаем, с фактически наблюдавшейся в этом районе ледовой обстановкой, с учетом природной изменчивости или многолетней амплитуды, а также допустимой погрешности прогноза.
7.3.6.4.4 К элементу распределения льда относится также прогноз времени полного очищения района ото льда и прогноз наличия остаточного льда при осеннем ледообразовании в районе пролива, бухты или полярной станции.
7.3.6.4.5 После проверки и оценки всех пунктов ледового прогноза, касающегося распределения льда в арктических морях, результаты проверки заносятся в виде средних оценок в соответствующие графы сводной таблицы Л.7.
7.3.6.4.6 При анализе результатов оценки прогнозов распределения льда необходимо наиболее подробно разобрать случаи плохой оправдываемости прогноза и выявить причины.
7.3.6.5 Оценка прогнозов устойчивого ледообразования и нарастания молодого льда
7.3.6.5.1 Проверка прогнозов устойчивого ледообразования и нарастания льда начинается с подбора исходного материала. В таблице Л.6 из текста прогнозов, составленных в августе и сентябре, вписываются пункты, для которых давался прогноз данного элемента, прогнозируемые сроки, данные о средних многолетних сроках, данные об Ам, σх и допустимой ошибки δдоп. Критерии допустимых ошибок для прогнозов, составленных в августе и сентябре принимаются 0,8σх, или 20 % от Ам.
Отдельно проверяется численный прогноз устойчивого ледообразования или других ледовых фаз по всему морю или отдельным его районам путем сравнения прогностических данных с фактическими данными, снятыми с проанализированных карт в узлах стандартной сетки.
7.3.6.5.2 По данным полярных станций, судовых наблюдений, ледовых авиаразведок и спутниковых снимков, а также в результате анализа ледово-гидрологических процессов в арктических морях, устанавливаются сроки фактического начала устойчивого ледообразования и сроки достижения молодым льдом определенной толщины в текущем году; полученные результаты для каждого пункта записываются в таблицу. На основании сопоставления фактического начала устойчивого ледообразования (или нарастания льда) с ожидавшимся по прогнозу, находят ошибку прогноза δ.
7.3.6.5.3 После определения оценок оправдываемости и оценок в зависимости от ошибки прогноза по каждому пункту и численного прогноза осенних ледовых явлений по акватории моря подсчитываются средние оценки для моря по прогнозам, составленным в августе и сентябре. Результаты подсчета средних оценок вносятся в соответствующие графы сводной таблицы Л.7.
После заполнения всех граф таблиц Л.6 и Л.7 следует приступить к анализу результатов проверки прогнозов сроков устойчивого ледообразования и нарастания молодого льда в текущем году. При анализе необходимо увязать оправдываемость ледового прогноза с оправдываемостью долгосрочного метеорологического прогноза (главным образом оправдываемость аномалий температуры воздуха).
7.3.6.6 Оценка прогнозов навигационных рекомендаций
7.3.6.6.1 Оценка прогнозов навигационных рекомендаций начинается с заполнения таблиц. В таблицы Л.4 - Л.5 из прогнозов, составленных в январе и марте, и их уточнений, а также из прогнозов, составленных в августе и сентябре (таблица Л.6), выписываются участки трассы в каждом из арктических морей, для которых давался прогноз навигационных рекомендаций.
7.3.6.6.2 Для отдельных участков Северного морского пути составляются следующие навигационные рекомендации:
а) в Баренцевом море - сроки начала и окончания плавания к архипелагу Земля Франца-Иосифа весной и осенью;
б) в Карском море - сроки начала и окончания плавания с ледоколами и без ледоколов на участках: пр. Карские Ворота - о. Диксон, Баренцево море (вокруг мыса Желания) - о. Диксон, о. Диксон - пр. Велькицкого, о. Диксон - о. Белый - Енисейский залив;
в) в море Лаптевых - сроки начала и окончания плавания с ледоколами и без ледоколов на участках: пр. Вилькицкого - порты моря Лаптевых, б. Тикси - Колыма (через пр. Санникова или через пр. Д. Лаптева), каботажное плавание на участках б. Кожевниково - пос. Тикси, б. Тикси - р. Яна; в навигационных рекомендациях для моря Лаптевых могут указываться сроки проводки единичных судов через Таймырский массив осенью, сроки вывода судов из устьев рек Анабара, Хатанги и Оленька;
г) в Восточно-Сибирском и Чукотском морях - сроки начала и окончания плавания с ледоколами и без ледоколов на участках: б. Певек - Берингов пр., б. Певек - Амбарчик; сроки вывода судов из Колымы и Идигирки осенью; сроки грузовых операций у побережья Чукотки; в Анадырском заливе - сроки плавания на участках м. Наварин - б. Провидения, в заливе Креста сроки грузовых операций в районе б. Угольной, сроки вывода судов осенью из б. Провидения.
7.3.6.6.3 В таблицы, куда вписаны участки по каждому морю, в
соответствии с текстом прогноза записываются ожидаемые сроки навигационных
рекомендаций, средние многолетние сроки ![]() , амплитуда и среднеквадратичное
отклонение от нормы Ам и σх, а также
допустимые погрешности, выраженные либо в долях σх, либо
в долях Ам.
, амплитуда и среднеквадратичное
отклонение от нормы Ам и σх, а также
допустимые погрешности, выраженные либо в долях σх, либо
в долях Ам.
Возможные сроки начала и окончания ледокольной проводки и безледокольного плавания на конкретных участках в текущем году устанавливаются, исходя из критериев и фактических ледовых условий на этих участках.
7.3.6.6.4 Ошибка прогноза δ находится при сопоставлении возможного срока с ожидаемым по прогнозу. Оценка оправдываемости получается при сопоставлении ошибок прогноза с допустимой ошибкой δдоп: при δ ≤ δдоп принимается оценка 100 % (прогноз оправдался), при δ > δдоп принимается оценка 0 % (прогноз не оправдался).
7.3.6.6.5 Оценка прогноза F в зависимости от ошибки прогноза дается согласно формулам (19), (20) или находится из таблиц Л.2 и Л.3.
7.3.6.6.6 После определения оценок каждого конкретного прогноза подсчитываются средние оценки для прогноза по каждому морю. Результаты прогноза средних оценок вносятся в соответствующие графы сводной таблицы Л.7.
7.3.6.6.7 Результаты проверки прогнозов навигационных рекомендаций подвергаются анализу; наиболее подробно следует остановиться на причинах плохой оправдываемости прогнозов конкретно по каждому морю.
После окончания работы по определению оправдываемости конкретных прогнозов и определения оценки прогнозов в зависимости от ошибки по данным таблиц Л.1 - Л.3 подсчитываются средние значения оценок прогнозов для каждой группы элементов ледового режима по морям или отдельным районам моря и для прогнозов различной заблаговременности.
7.3.6.6.8 Средняя оправдываемости прогнозов получается в результате деления суммы всех оценок таблицы Л.6 на число всех слагаемых.
7.3.6.6.9 Средняя оценка прогнозов в зависимости от ошибки прогнозов получается в результате деления суммы всех оценок F на число всех слагаемых.
7.3.6.6.10 Средние оценки прогнозов позволяют сопоставлять количественные результаты прогностической работы от года к году и показывают успешность прогнозов.
Среднее значение оправдываемости прогнозов указывает, какая часть прогностических показателей в процентах от общего числа показателей (за исключением непроверенных) оправдалась, т.е. ошибки таких прогнозов были меньше или равны δдоп, а какая часть не оправдалась (100 % минус средняя оценка оправдываемости в процентах).
7.3.6.6.11 Средняя оценка, определенная в зависимости от ошибок прогноза, дает представление о преобладании ошибок прогноза по значению. При высоких значениях средних оценок (80 - 100 %) преобладают ошибки прогноза значительно меньше δдоп; при значениях средних оценок, равных 60 - 70 %, ошибки прогноза в большинстве случаев близки к δдоп; при низких значения оценок преобладают ошибки, превышающие δдоп.
7.3.6.6.12 Между средней оценкой оправдываемости и средней оценкой прогнозов в зависимости от ошибки прогнозов возможны следующие соотношения.
Средняя оценка оправдываемости прогнозов будет выше средней оценки этих же прогнозов, определенных в зависимости от ошибок прогнозов, в тех случаях, когда преобладают ошибки прогноза меньше δдоп, т.е. всем этим прогнозам дается оценка оправдываемости 100 %, в то время как оценку 100 % в зависимости от ошибки прогноза получают только безошибочные прогнозы (δ = 0).
7.3.6.6.13 В результате всей работы по проверке прогнозов составляется сводная таблица Л.7 и проводится анализ средних ошибок прогноза по морям, элементам, заблаговременности и в целом для всех арктических морей по данным таблицы. Здесь же производится сопоставление результатов прогностической работы за текущий год с результатами предыдущего года и т.д.
В заключение приводятся выводы, в которых отмечаются недостатки долгосрочных ледовых прогнозов.
Результаты проверки и оценки долгосрочных ледовых прогнозов обсуждаются на совещании специалистов-прогнозистов.
7.3.7 Оценка долгосрочных ледовых прогнозов по неарктическим морям
7.3.7.1 К неарктическим морям окружающим территорию России традиционно отнесены Каспийское, Черное, Азовское, Балтийское, Белое, Берингово, Охотское и Японское моря.
7.3.7.2 Для долгосрочных ледовых прогнозов по неарктическим морям устанавливаются следующие значения допустимых ошибок:
- при заблаговременности прогнозов до двух месяцев за критерий допустимой ошибки принимается ошибка, равная ±0,674σx;
- при заблаговременности от двух до шеста месяцев за критерий допустимой ошибки принимается ошибка ±0,8σx;
- при заблаговременности прогнозов более шести месяцев за критерий допустимой ошибки принимается ошибка, равная ±σx.
7.3.7.3 Допустимые ошибки долгосрочных прогнозов ледовых явлений на неарктических морях с заблаговременностью до двух месяцев определяются в соответствии с правилами, изложенными в пункте 7.2.1.
7.3.7.4 Допустимые ошибки для малой заблаговременности времени наступления ледовых явлений принимаются в зависимости от заблаговременности этих прогнозов по таблице 10.
7.3.7.5 Допустимые ошибки прогнозов толщины льда определяются по табл. 9 в зависимости от величины фактического ее изменения за период от даты выпуска прогнозов, до даты, на которую составлялись прогнозы.
7.3.8 Оценка долгосрочных прогнозов аномалий температуры поверхности океана
7.3.8.1 Поскольку температура морской воды имеет хорошо выраженный годовой ход, величины допустимых ошибок δдоп для всех видов прогнозов вычисляются как средние квадратичные отклонения изменений температуры от среднего изменения ее за период заблаговременности прогноза.
7.3.8.2 Для долгосрочных прогнозов температуры воды (Tw) в зависимости от заблаговременности устанавливаются следующие критерии допустимой ошибки:
|
|
при заблаговременности больше 6 месяцев; |
|
|
при заблаговременности от 2 до 6 месяцев; |
|
|
при заблаговременности до 2 месяцев, |
где ![]() - среднее квадратичное отклонение Tw от среднего
многолетнего значения.
- среднее квадратичное отклонение Tw от среднего
многолетнего значения.
7.3.8.3 Для районов океана с малой изменчивостью температуры поверхности воды (например в экваториальных областях океанов или центрах областей высоко давления) значение допустимой ошибки принимается равным 0,5 °С.
7.3.8.4 Для характеристики аномальности температурного поля применяется критерий
|
|
(38) |
где ΔTw - аномалия температуры воды ![]() ;
;
σi - дисперсия аномалий в соответствующих точках.
7.3.8.5 Критерий K характеризует степень аномальности температурного поля, но не дает информации о знаке аномалии. О преобладании положительной или отрицательной аномалии можно судить по параметру ρ, вычисляемому по формуле [21]
|
|
(39) |
где n+ - число квадратов с положительной аномалией температуры воды;
n- - число квадратов с отрицательной аномалией.
Оправдываемость прогноза ТПО, по знаку можно определить по формуле
|
Р = 50·(1 + ρ), |
(40) |
где параметр ρ вычисляется по формуле
|
|
(41) |
Здесь nопр - количество оправдавшихся по знаку прогнозов;
nнеопр - количество неоправдавшихся по знаку прогнозов;
N - общее количество составленных прогнозов.
Метод прогноза считается хорошим при Р > 50 % и |δТ| < σТ, удовлетворительным при Р > 50 % и |δТ| > σТ или Р < 50 % и |δТ| < σТ, неудовлетворительным при Р < 50 % и |δТ| > σТ.
7.3.8.6 Для оценки качества прогноза ТПО также используется соотношение S/σТ, где S - среднеквадратичная ошибка прогноза, а σТ - среднеквадратичное отклонение от нормы. Прогноз считается оправдавшимся, если его ошибка δ < δдоп и не оправдавшимся, если δ > δдоп.
Средняя квадратичная ошибка прогнозов ST определяется по формуле
|
|
(42) |
где п - число членов ряда, для которого определяется ошибка;
m - число степеней свободы, определяемое количеством постоянных величин в прогностическом уравнении.
Оправдываемость Р, %, каждого прогноза поля температуры воды определяется процентным отношением числа точек m, в которых прогноз оправдался, к общему числу точек п, по которым составлялись прогнозы
|
|
(43) |
При оценке прогнозов сроков перехода температуры воды через определенные градации, допустимая ошибка выражается в днях и принимается равной среднему квадратичному отклонению от средней многолетней даты перехода температуры воды через заданные градации.
7.3.9 Оценка сверхдолгосрочных прогнозов уровня Каспийского моря
7.3.9.1 Долгосрочные и сверхдолгосрочные прогнозы изменений уровня на сроки до одного года и более разрабатываются, как правило, для замкнутых морей (типа Каспийского или Аральского морей), в которых уровень моря подвержен существенным колебаниям в многолетнем ходе.
7.3.9.2 Существование векового хода уровня Каспийского моря не позволяет рассматривать колебания уровня моря как случайный стационарный процесс. Поэтому для оценки оправдываемости прогноза применяется следующий способ.
7.3.9.3 По материалам годового хода среднего уровня моря в базовых пунктах: Махачкала, Форт-Шевченко, Баку, Туркменбаши, Куули-Маяк, Кара-Богаз-Гол и Жилой определяются величины средних многолетних приращений уровня моря от месяца к месяцу, и статистические характеристики рассчитываются для каждого месяца.
7.3.9.4 Величины допустимых ошибок прогнозов уровня
составляют: при заблаговременности до двух месяцев ![]() , при заблаговременности от двух до
шести месяцев
, при заблаговременности от двух до
шести месяцев ![]() и при заблаговременности более шести
месяцев
и при заблаговременности более шести
месяцев ![]() , где
, где ![]() - вариации среднего уровня моря, σΔH - вариации превышений
уровня в данном пункте над средним уровнем моря.
- вариации среднего уровня моря, σΔH - вариации превышений
уровня в данном пункте над средним уровнем моря.
7.3.10 Оценка прогнозов, выраженных в вероятностной форме
7.3.10.1 В ряде случаев использование прогнозов в практике связано со знанием отклонений более редкой повторяемости, чем вероятностная погрешность, в связи с чем обычная форма прогноза становится для потребителей недостаточной. Тогда прогноз дается в вероятностной форме.
Вопрос выдачи прогноза в вероятностной форме решается по договоренности с заинтересованными организациями, которые на основании этих прогнозов могут самостоятельно решать свои практические задачи.
7.3.10.2 Под вероятностным прогнозом понимается прогноз, в котором ожидаемая величина дается рядом ее значений с указанием обеспеченности (вероятности) появления каждого из этих значений. Обычно прогноз выражается в табличной форме с указанием ожидаемой величины, обеспеченной на 10 %, 25 %, 50 %, 75 % и 90 %. Расширение диапазона ожидаемой величины за пределы 5 % и 95 % обеспеченности не рекомендуется.
7.3.10.3 Ожидаемая величина заданной обеспеченности определяется по формуле
|
|
(44) |
где ![]() - среднее значение ожидаемой величины
по прогнозу; δпр - ошибка прогноза заданной
обеспеченности.
- среднее значение ожидаемой величины
по прогнозу; δпр - ошибка прогноза заданной
обеспеченности.
7.3.10.4 Ошибка прогноза заданной обеспеченности определяется по формуле
|
|
(45) |
где ![]() - средняя квадратичная ошибка
прогноза;
- средняя квадратичная ошибка
прогноза;
kн - нормированное отклонение, соответствующее заданной обеспеченности, значение которого можно получить из таблицы 11.
Таблица 11
|
Обеспеченность, % |
10 |
25 |
50 |
75 |
90 |
|
kн |
1,28 |
0,674 |
0,000 |
-0,674 |
-1,28 |
7.3.10.5 Если используемая для прогноза зависимость установлена без учета резко отклонившихся случаев от линии регрессии, то погрешность прогноза заданной обеспеченности определяется по эмпирическим кривым распределения погрешности. Для этого все погрешности располагаются в убывающем порядке (от наибольшей положительной через нулевое значение к наибольшей отрицательной) и для каждой погрешности определяется ее обеспеченность Р, %, по формуле
|
|
(46) |
где m - порядковый номер ошибки в убывающем ряду;
п - общее число членов ряда.
7.3.11 Учет и оценка долгосрочных морских гидрологических прогнозов ведется в специальном журнале (приложение Н).
7.3.12 Более полное освещение некоторых вопросов, связанных с оценкой вариации статистических переменных и зависимостей между ними приведены в приложении П.
7.4 Оценка эффективности специализированных прогнозов
7.4.1 При специализированном гидрометеорологическом обеспечении морской деятельности важное значение имеет не столько оправдываемость прогнозов, сколько их эффективность. Для оценки эффективности гидрометеорологического обслуживания наибольший интерес представляют данные, характеризующие ту часть ущерба, которая оказывается предотвращенной в результате гидрометеорологического обслуживания.
7.4.2 К специализированным прогнозам относятся прогнозы выпускаемые по заказам потребителей. В заказах обычно конкретизируются требования к району или пункту, где выполняются специальные морские операции производственного или другого характера, пространственно-временному разрешению, заблаговременности и допустимых пороговых значений гидрологических явлений, ограничивающих те или иные виды морских работ. Оценка оправдываемости и эффективности специализированных прогнозов оценивается по тем же критериям, что и прогнозы общего назначения.
7.4.3 Основными видами специализированного гидрометеорологического обеспечения являются:
- обеспечение рыбопромысловых операций;
- проводка судов рекомендуемыми курсами;
- проводка и буксировка плавсредств с ограниченной мореходностью;
- обслуживания морских портов;
- доставка рабочего персонала, грузов и оборудования на геологоразведочные платформы в море и др.
7.4.4 Оценка эффективности проводки судов рекомендуемыми курсами
7.4.4.1 Обслуживание судов рекомендуемыми курсами состоит в выдаче капитанам судов рекомендаций о путях наиболее благоприятного плавания с точки зрения погодных и навигационных условий [22 - 24]. Вместе с рекомендацией капитану судна передается прогноз ветра и волнения вдоль рекомендованного маршрута.
7.4.4.2 Оценка оправдываемости прогнозов ветра и высот волн вдоль маршрута осуществляются методами, описанными выше.
7.4.4.3 Эффективность плавания судов рекомендуемыми курсами оценивается по следующим показателям:
- по продолжительности плавания;
- по пройденному расстоянию;
- по числу штормовых дней на переходе через океан;
- по количеству израсходованного топлива;
- по скорости хода судна;
- по выдерживанию запланированного времени рейса
- по количеству часов прерывания погрузо-разгрузочных работ в порту.
7.4.4.4 Для оценки эффективности проводки судов рекомендуемыми курсами может быть применено несколько методов, в зависимости от наличия исходных данных, например, технических данных о судне (водоизмещении, технической скорости, положения метацентрической высоты и др.), видов и характера размещения грузов на судне, графиков потерь скорости хода судна на волнении, гидрометеорологических данных и т.д.
Наиболее распространенными среди них являются:
- сопоставление времени, затраченного на фактическом переходе судна с временем перехода условного судна, следующего кратчайшим расстоянием (дугой большого круга) или по климатическому пути [23];
- сопоставление фактически затраченного времени на переход с плановым временем;
- сопоставление средней путевой скорости хода судна с технической скоростью судна;
- расчет числа штормовых дней на переходе.
7.4.4.5 Количественной характеристикой условий безопасности плавания судна на волнении может служить коэффициент безопасности K, рассчитываемый по формуле
|
|
(47) |
где hm - максимальная высота волны, м, за время перехода;
h0 - максимальная допустимая высота, м, (ограничение, сообщаемое капитаном);
τ1 и τ2 - повторяемость неблагоприятных, близких к опасным, высот (h0) и опасных высот волн (8 м и более), соответственно, для судна за период перехода.
Чем больше значение K, тем более трудны и опасны условия плавания. Выбрав некоторые критические значения K, можно разделить условия волнения по пути судна на опасные и безопасные. При использовании коэффициента K предлагается руководствоваться следующими правилами:
- если K ≤ 1, условия безопасные для судна, имеющего ограничение по высоте волны;
- если K ≤ 2, условия благоприятны для судна, не имеющего ограничений на высоту волны;
- если K > 2, условия плавания неблагоприятны.
Относительная эффективность плавания по рекомендованному пути KO вычисляется как отношение коэффициента безопасности (KР) на рекомендованном пути к коэффициенту безопасности (KА) на альтернативном пути
|
|
(48) |
В качестве единого показателя условий плавания судов на арктических трассах рекомендуется использовать коэффициент трудности плавания KТ как отношение
|
|
(49) |
где VЛ - эксплуатационная ледовая скорость судна в одиночном плавании на заданной трассе;
V0 - скорость хода судна на чистой воде.
Коэффициент трудности плавания KТ можно рассматривать как отношение затрат времени на переход судна по трассе в конкретных ледовых условиях к затратам времени на переход судна по чистой воде по этой же трассе.
7.4.5 Оценка эффективности обслуживания проводок и буксировок плавсредств с ограниченной мореходностью
7.4.5.1 Эффективность проводок и буксировок плавсредств с ограниченной мореходностью определяется двумя показателями:
- сокращением убытков от аварий и повреждений, вызванных гидрометеорологическими причинами;
- выигрышем ходового времени, затраченного на перегон или буксировку.
7.4.5.2 Выигрыш ходового времени в результате гидрометеорологического обслуживания проводок и буксировок плавсредств с ограниченной мореходностью может быть определен двумя способами.
7.4.5.3 Первый способ основан на сопоставлении фактически затраченного времени на данный перегон или буксировку с плановым временем, которое принято эксплуатационниками для данного типа операции по рассматриваемой трассе на основании имеющегося опыта проводок.
7.4.5.4 Второй, более сложный способ, основан на сравнении фактического времени, затраченного на данную операцию и среднего приведенного времени, которое затрачивалось на аналогичные операции в прошлом.
7.4.5.5 Для определения влияния гидрометеорологических условий на проводку каравана рассчитывается фактическая скорость хода судна Vф по соотношению
|
|
(50) |
где S - путь пройденный караваном;
Тф - фактическое время, затраченное на переход.
Зная Vф и техническую скорость VТ, рассчитывается коэффициент K, показывающий, в какой степени по времени гидрометеорологические условия увеличили продолжительность данного перегона по сравнению со временем, которое понадобилось бы в случае идеальных гидрометеорологических условий, т.е.
|
|
(51) |
Имея данные о нескольких таких перегонах, можно найти средний приведенный коэффициент потерь времени Kпривед по формуле:
|
|
(52) |
где i - номер каждой конкретной операции;
п - общее число операций.
Разделив время, фактически затраченное на конкретную операцию, Тф на Kпривед, можно получить время Тпривед, которое потребовалось бы на данный перегон или буксировку
|
|
(53) |
7.4.6 Оценка эффективности обслуживания морских портов
7.4.6.1 Влияние гидрометеорологических условий на производственную деятельность портов выражается в убытках, которые несут порты в результате прекращения погрузочно-разгрузочных работ и аварий судов, портовых сооружений и техники из-за неблагоприятных погодных условий.
Опыт гидрометеорологического обеспечения работ в портах показывает, что основные убытки порты несут в результате внезапно возникающих ОЯ, таких как:
- резкие подъемы и падения уровня воды в порту выше или ниже критических отметок;
- ураганные ветры;
- тягун;
- цунами;
- напоры льда на оградительные сооружения порта;
- обледенение судов у причалов и т.д.
Поэтому важным показателем нормальной работы портов являются штормовые предупреждения об угрозе возникновения ОЯ, учет которых позволяет заблаговременно принять необходимые предупредительные меры и, тем самым, сократить причиняемые убытки.
7.4.6.2 Эффективность работы порта оценивается путем сравнения убытков, которые понес порт в случае не предсказанных ОЯ, или в случае, когда ОЯ было предсказано, но, по тем или иным причинам, штормовое предупреждение не было использовано, с убытками, которые понес порт в случае использования штормового предупреждения. При этом базой для сравнения служат средние убытки, которые мог бы понести порт в случае непредсказанных ОЯ.
Для того, чтобы определить среднюю величину убытков, необходимо произвести осреднение по возможно большему числу случаев. При этом исследуемые случаи должны быть сравнимы с точки зрения вида штормового явления, его интенсивности, объема работ в порту, количества находившихся в порту судов и т.д.
7.4.6.3 Экономическая эффективность определяется как разность между средними убытками при не предсказанных штормовых явлениях и убытками, которые понес порт, когда явление было предсказано. Следует иметь в виду, что в большинстве случаев в результате наличия непредотвратимого ущерба, убытки в портах возникают даже, когда штормовое явление предсказано с большой заблаговременностью. Общая эффективность обслуживания портов штормовыми предупреждениями за месяц или какой-то другой период времени определяется как результат суммирования всех случаев штормовых явлений за рассматриваемый период.
7.4.6.4 Другим важным показателем эффективности обслуживания портов является уменьшение простоев в работе порта по гидрометеорологическим причинам. Непроизводительные потери рабочего времени в портах складываются из простоев судов из-за не оправдавшихся прогнозов, что обычно происходит в тех случаях, когда по прогнозу предсказывалось штормовое явление, а на самом деле оно не осуществилось. Непроизводительные простои в этих случаях увеличиваются, когда несвоевременно дается отмена не оправдавшегося штормового предупреждения или несвоевременно оповещаются портовые службы о прекращении действия штормового явления.
Указанные непроизводительные потери времени целесообразно выражать в судосутках простоя судов, а затем путем умножения этой величины на стоимость стояночных судосуток, определить убыток в денежном выражении.
Убытки в результате неоправданного сокращения производственных операций в порту определяются не только простоями судов, они могут выражаться также дополнительной потерей скоропортящихся грузов, издержками, связанными с задержкой в сроках поставки грузов потребителями и т.п. Однако все эти дополнительные издержки трудно учитываемы и поэтому при практической оценке ущерба ими часто пренебрегают.
7.4.6.5 Общая эффективность определяется как разность между средними убытками от простоев из-за не оправдавшихся прогнозов за прошлые годы и текущими убытками по тем же причинам. Результирующая эффективность гидрометеорологического обслуживания портов определяется как сумма экономического выигрыша, полученного в результате сокращения аварийности и экономического эффекта, связанного с уменьшением убытков по простоям судов.
7.5 Анализ оправдываемости прогнозов и штормовых предупреждений
7.5.1 Анализ оправдываемости прогнозов является завершающим этапом работы специалиста над прогнозом. Он осуществляется в целях определения эффективности обслуживания потребителей, с одной стороны и выявления и устранения причин ошибок и разработки рабочей гипотезы усовершенствования метода прогноза, с другой.
7.5.2 Анализу подлежат все долгосрочные прогнозы элементов гидрометеорологического режима моря с ошибкой, превышающей 0,674σдоп, краткосрочные прогнозы ОЯ, ошибка которых превышает допустимую, и краткосрочных прогнозов независимо от величины ошибки, если они привели к значительному ущербу морским отраслям экономики.
7.5.3 Оправдавшиеся прогнозы в зависимости от величины ошибки прогноза подразделяются на:
- отличные, при допустимой ошибке меньше 0,30σх;
- хорошие, при допустимой ошибке от 0,30σх до 0,674σх;
- удовлетворительные, при допустимой ошибке от 0,674σх до σх.
7.5.4 Прогнозы уровня воды с ошибкой 5 см и меньше, прогнозы дат характерных явлений с ошибкой ±1 день считаются отличными независимо от допустимой ошибки.
7.5.5 Основным исходным материалом для анализа оправдываемости долгосрочных прогнозов является журнал обоснования этих прогнозов. Он дает возможность проверить весь процесс составления прогноза (анализ предшествующей гидрометеорологической обстановки и ее особенностей в данном году, вычисление исходных для прогноза гидрометеорологических и других данных, обоснование всех отклонений от методики), убедиться в правильности или ошибочности отдельных этапов этого процесса и сделать вывод о причине больших погрешностей прогноза. Выявленные в результате этого анализа причины ошибок прогнозов, а также предложения по их устранению и усовершенствованию метода прогноза должны записываться в журнал обоснований прогнозов.
7.5.6 Анализ оправдываемости краткосрочных морских гидрологических прогнозов строится на тщательной проверке использования метода прогноза и подготовки исходных для прогноза данных. Результат анализа оправдываемости краткосрочных прогнозов гидрологических явлений (величин) записывается в соответствующий журнал анализа оправдываемости краткосрочных прогнозов.
7.5.7 Результат анализа оправдываемости краткосрочных прогнозов должен содержать:
- сущность метода и порядок составления прогноза;
- содержание прогноза и его оправдываемость;
- выявленные или предполагаемые причины погрешностей прогнозов;
- предложения по устранению выявленных причин погрешностей прогноза, усовершенствованию метода и другие предложения.
7.5.8 Результат анализа оправдываемости прогнозов, сразу же после его завершения, обсуждается на совещании специалистов органа СМГП.
7.5.9 Оценка качества прогнозов морских гидрологических величин и явлений и штормовых предупреждений заключается в вычислении их средней оправдываемости РΔТ за календарный период ΔТ (месяц, квартал, год) по формуле
|
|
(54) |
где Рс - оправдываемость прогнозов за каждые сутки (полусутки, вторые и третьи сутки) данного месяца, квартала, года.
7.5.10 Характеристики качества штормовых предупреждений за период времени (месяц, квартал, год) содержат следующие показатели:
- оправдываемость ОЯ;
- эффективность ОЯ;
- предупрежденность ОЯ.
Указанные показатели рассчитывают только для акватории моря или части акватории. Вычисление оправдываемости и предупрежденности за период времени (месяц, квартал, год) можно произвести с помощью сокращенной таблицы сопряженности (таблица 12).
Таблица 12 - Сокращенная таблица сопряженности для расчета оправдываемости штормовых предупреждений
|
Штормовое предупреждение |
Число дней |
Сумма |
|
|
с ОЯ |
без ОЯ |
||
|
Дано |
k11 |
k12 |
k10 |
|
Не дано |
k21 |
|
|
|
Сумма |
k01 |
||
В таблице 12 введены следующие обозначения:
k11 - число оправдавшихся штормовых предупреждений;
k12 - число «ложных» штормовых предупреждений, когда они давались, но ОЯ не наблюдались;
k10 - общее число составленных штормовых предупреждений за период времени (месяц, квартал, год);
k21 - число пропущенных штормовых предупреждений, когда ОЯ наблюдалось, но штормовое предупреждение составлено не было;
k01 - число наблюдавшихся ОЯ за период времени (месяц, квартал, год).
7.5.11 Оправдываемость штормовых предупреждений ОЯ за период времени (месяц, квартал, год) РОЯ, %, рассчитывают как отношение числа оправдавшихся штормовых предупреждений к общему числу штормовых предупреждений, в том числе пропущенных, за рассматриваемый промежуток времени:
|
|
(55) |
7.5.12 Эффективность штормовых предупреждений, в том числе с допусками, за период времени (месяц, квартал, год) с учетом их заблаговременности ЭОЯ, %, рассчитывают как отношение числа эффективных штормовых предупреждений к числу оправдавшихся штормовых предупреждений за рассматриваемый промежуток времени:
|
|
(56) |
где kОЯ≥2ч - число оправдавшихся штормовых предупреждений по территории, переданных с заблаговременностью 2 ч и более.
7.5.13 Предупрежденность случаев ОЯ за период времени (месяц, квартал, год) ПОЯ, %, рассчитывают как отношение числа оправдавшихся штормовых предупреждений к общему числу наблюдавшихся ОЯ за рассматриваемый промежуток времени
|
|
(57) |
7.5.14 Качество предупреждений об ОЯ за месяц, квартал год оценивается по таблице 13.
Таблица 13 - Оценка качества штормовых предупреждений
|
Оценка |
Отлично |
Хорошо |
Удовлетворительно |
Неудовлетворительно |
|
Оправдываемость предупреждений, % |
95 |
Менее 95 до 90 |
Менее 90 до 80 |
Менее 80 |
8 Составление и оформление методической записки
8.1 Работа по созданию метода прогноза гидрологического элемента завершается методической запиской, на основании которой составляются морские гидрологические прогнозы.
8.2 В соответствии со своим целевым назначением методическая записка должна давать полное представление о физической сущности, достоинствах и недостатках метода прогноза и содержать исчерпывающие указания в отношении его практического применения. Другими словами, содержание методической записки должно быть таким, чтобы любой специалист, работающий в области морских гидрологических прогнозов, пользуясь методической запиской, мог самостоятельно составлять прогнозы.
8.3 Объем и содержание методической записки зависит в каждом конкретном случае от характера прогнозируемого явления и степени сложности метода прогноза.
8.4 Методическая записка должна быть оформлена по РД 52.14.642 и должна содержать предисловие и следующие разделы:
1) краткая характеристика рассматриваемого явления и физико-географические условия;
3) характеристика исходных данных и приемов их обработки;
4) физические основы и теоретические предпосылки методики прогноза;
5) расчетные приемы и построение корреляционных связей и их оценка;
6) порядок составления прогнозов;
7) допустимые ошибки;
8) приложения;
8.5 В предисловии к методической записке должны содержаться сведения о практическом значении метода прогноза, общая характеристика и оценка предшествующих разработок, если таковые были, и другие пояснительные сведения по усмотрению автора методической записки. Кроме того, должны быть отмечены, имевшие место при разработке метода прогноза трудности и проблемы, а также перечислены исполнители, разрабатывающие методику прогноза.
8.6 В разделе «Краткая характеристика рассматриваемого явления и физико-географические условия» дается краткое физико-географическое описание района. Оно должно быть проиллюстрировано схематической картой района моря с указанием гидрометеорологических станций, стандартных разрезов и рейдовых точек, маршрутов авиаразведок и экспедиций, материалы наблюдений которых были использованы при разработке метода прогноза.
8.7 В третьем разделе кратко описываются исходные материалы, использованные для разработки метода, их полнота и качество, методы обработки.
8.8 В четвертом разделе записки излагаются основные особенности гидрометеорологического режима моря, основные факторы, формирующие рассматриваемое явление, а также теоретические предпосылки и рабочая гипотеза, положенные в основу разработки данного метода прогноза.
8.9 В пятом разделе описываются расчетные приемы и построение корреляционных связей и статистическая оценка параметров уравнений регрессии.
8.10 В шестом разделе в четкой и ясной форме описывается весь порядок составления прогноза по разработанному методу с обязательной иллюстрацией использования каждой зависимости на практике. При этом должны быть указаны:
- дата составления прогноза;
- объем исходных материалов, использованных для составления прогноза;
- порядок подсчета всех аргументов, входящих в зависимость, с обязательным указанием, по каким пунктам и каким образом они подсчитываются.
8.11 Если метод включен в общую технологию прогноза, то в методической записке должно быть дано описание технических особенностей системы, а также результаты проведенных прогностических экспериментов. Должна быть представлена вычислительная блок-схема численного прогноза, включающая:
1) блок подготовки исходных данных:
- базы объективного анализа;
- архивы;
- локальная и глобальная сеть;
2) вычислительный блок:
- подготовка начальных данных;
- интегрирование численной модели;
- формирование набора выходных полей;
3) блок выходной продукции, который должен связывать базы прогностических характеристик, полученных в результате работы схемы с программами статистических оценок и с системой визуализации результатов прогноза.
8.12 Обязательными приложениями к методической записке являются:
- карта-схема района прогноза;
- систематизированные и обобщенные данные гидрометеорологических наблюдений (в виде таблиц, графиков, номограмм и т.д.), использованные при разработке метода;
- графические и аналитические зависимости для расчета и прогноза;
- таблицы допустимых ошибок прогнозов;
- таблицы проверочных прогнозов.
8.13 Методическая записка рассматривается соответствующим научно-техническим советом УГМС или Ученым советом НИУ, и на основе принятого решения дается рекомендация о практическом использовании методики прогноза. Выписка из решения прикладывается к каждому экземпляру методической записки.
8.14 После одобрения методической записки методическим органом какие-либо исправления ее текста не допускаются. К исправлениям не относятся обязательные дополнения графических зависимостей и таблиц новыми данными (по мере появления новых случаев прогнозируемого явления).
8.15 После того, как принято решение о внедрении метода в практику, должна регулярно оцениваться успешность оперативных прогнозов.
8.16 Систематическая количественная оценка успешности оперативных прогнозов дается с целью:
- установления общего уровня успешности оперативной работы;
- определения эффективности, как различных уточнений метода и прогностических уравнений, так и текущих усовершенствований технологии прогноза в целом;
- накопления средних ошибок и иных показателей успешности прогноза для их использования при выборе способов корректировки прогнозов.
Приложение А
(обязательное)
Карточка морской гидрометеорологической станции (поста)
|
Форма |
|||||||||||||||||||||||||
|
№ ______________ Карточка морской гидрометеорологической станции (поста) Море ______________________ станция (пост) _____________________________ Отметка нуля графика ____________________________ м абс. Система отметок моря
|
|||||||||||||||||||||||||
Приложение Б
(обязательное)
Карточка опасного морского гидрометеорологического явления
|
Форма |
||||||||||||||||||||
|
№ ______________ Карточка опасного морского гидрометеорологического явления Наименование явления ___________________________________________________
|
Приложение В
(обязательное)
Карточка хозяйственного объекта
|
Форма |
||||||||||||||||||
|
№ ___________ Карточка хозяйственного объекта Море _____________________________ Наименование хозяйственного объекта _________________________________________ ___________________________________________________________________________ Гидрометеорологическая станция (пост) ________________________________________ Ведомственная принадлежность _______________________________________________ Расстояние от гидрометеорологической станции (поста) ______________________ км
|
||||||||||||||||||
|
|
||||||||||||||||||
|
Сведения о вредных воздействиях на объект
|
Приложение Г
(рекомендуемое)
Бланковые карты морей и океанов
Г.1 В повседневной оперативной работе СМГП используются бланки карт морей и океанов. В целях их унификации и стандартизации рекомендуется пользоваться стандартными проекциями:
а) для карт мира:
- конформной конической проекцией Ламберта при пересечении со сферой по стандартным параллелям 10° и 40° или 30° и 60°;
- проекцией Меркатора для стандартной параллели 0°;
б) для карт Атлантического, Тихого и Индийского океанов:
- стереографической проекцией на плоскость сечения земного шара по стандартной параллели 60°;
- проекцией Меркатора для стандартной параллели 40°;
в) для карт отдельных районов океанов и морей:
- проекцией Меркатора для стандартной параллели 22°30'.
Г.2 Для морских бланков карт рекомендуется использовать стандартные масштабы:
а) для карт мира - 1:40000000, 1:50000000, 1:30000000; альтернатива - 1:60000000;
б) для полусферных карт - 1:30000000, 1:40000000; альтернатива - 1:60000000;
в) для карт Атлантического, Тихого и Индийского океанов - 1:15000000, 1:20000000; альтернатива - 1:30000000;
г) для карт части океана или моря - 1:75000000, 1:10000000; альтернатива -1:15000000.
Примечание. Для незначительных частей океана и морей, окружающих территорию России используются более крупные масштабы карт от 1:5000000 до 1:500000.
Г.3 Наименование проекции, масштабы следует указывать на каждом бланке карты.
Приложение Д
(обязательное)
Журнал учета карточек каталога ОЯ
|
Форма |
|||||||||||||||||||||||||||||
|
Журнал учета карточек каталога ОЯ
|
|||||||||||||||||||||||||||||