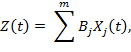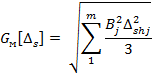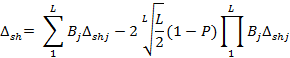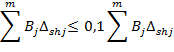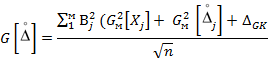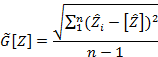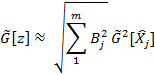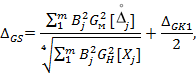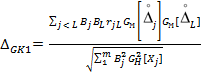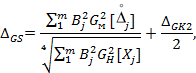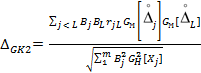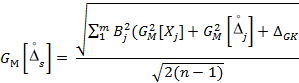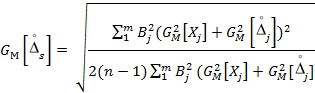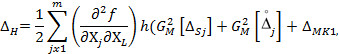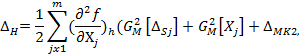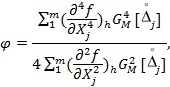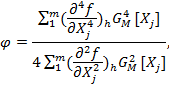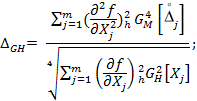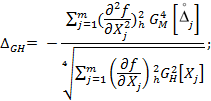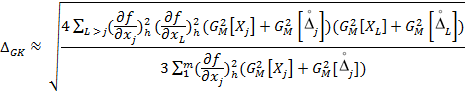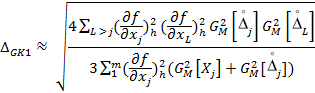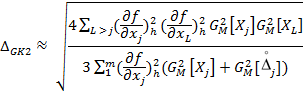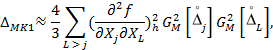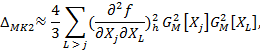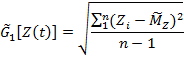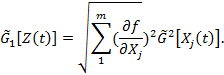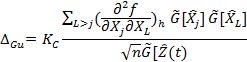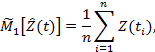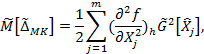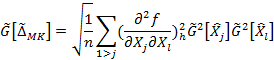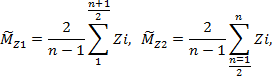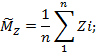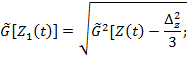ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ

Всесоюзный научно-исследовательский институт метрологической службы
(ВНИИМС)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Государственная система обеспечения единства измерений.

ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ ХАРАКТЕРИСТИК ПРОЦЕССОВ.

МЕТОДЫ РАСЧЕТА.

МИ 1730-87

Москва 1987 г.

Настоящие методические указания распространяются на нормативно-техническую документацию, регламентирующую проведение аттестации методик выполнения косвенных измерений (МВИ) математического ожидания и среднего квадратического отклонения случайных стационарных эргодических процессов, и устанавливает основные положения определения характеристик погрешности измерений при условии, что параметры исследуемого процесса определяются путем обработки результатов прямых измерений мгновенных значений процессов, функционально связанных с исследуемым процессом.

1.ОБЩИЕ ПОЛОЖЕНИЯ.

1.1 Определение характеристик погрешности МВИ при ее аттестации производятся с целью установления значений характеристик погрешности МВИ, либо с целью проверки нахождения характеристик погрешности МВИ в допускаемых пределах.

1.2 Вычисление результатов измерений параметров процесса Z(t) производится с использованием установленной для МВИ функциональной зависимости

где Z(t) - процесс, параметры которого определяются путем обработки результатов прямых измерений мгновенных значений процессов Х_j(t).

1.3 При проведении косвенных измерений обычно используются два метода определения результата измерений:

- метод при котором значение параметра процесса Z(t) определяют по мгновенным значениям этого процесса, вычисляемым в соответствии с (1), по результатам синхронных измерений мгновенных значений процессов Х_j(t) - метод 1;

- метод, при котором значение параметра процесса Z(t) определяют по оценкам аналогичных параметров процессов Х_j(t) - метод 2.

1.4 В качестве характеристик погрешности МВИ используются следующие характеристики, регламентированные МИ 1317-86:

- наибольшее возможное значение среднего квадратичного отклонения не исключенной систематической составляющей погрешности измерений G_м[∆_з] или

- границы ± ∆_sh, в которых не исключенная систематическая составляющая погрешности измерений находится с заданной вероятностью;

- наибольшее возможное значение среднего квадратического отклонения случайной составляющей погрешности измерений G_м[∆];

- наибольшее возможное значение среднего квадратического отклонения случайной составляющей погрешности измерений G_м[∆] или

- границы ± ∆_h, в которых погрешность измерений находится с заданной вероятностью.

1.5 Оценивание характеристик погрешности МВИ производится на основании функциональной зависимости, учитывающей влияние погрешностей ∆Х_j(t) прямых измерений мгновенных значений процессов Х_j(t)

1.6 Для расчета характеристик погрешности МВИ в общем случае необходимо располагать следующими данными:

- значениями характеристик погрешностей прямых измерений мгновенных значений процессов X_i (t);

- значениями математических ожиданий и средних квадратических отклонений процессов X_j(t), при которых погрешность МВИ для объектов измерений определенного типа имеет максимальное значение;

необходимо располагать следующими данными:

- значением составляющей погрешности МВИ, обусловленной влиянием взаимной корреляции процессов , при котором погрешность МВИ принимает максимальное значение.

Примечание: 1. Предполагается, что для объектов измерений определенного типа, являющихся источниками процессов X_i(t), известны диапазоны возможных значений математических ожиданий и средних квадратических отклонений процессов X_j(t).

2. Проверка необходимости учета влияния взаимной корреляции процессов X_i(t) при расчете характеристик погрешности МВИ проводится в соответствии с Приложением 1.

1.6.1. В качестве характеристик погрешностей прямых измерений мгновенных значений процессов X_j(t) используются:

- наибольшее возможное значение среднего квадратического отклонения неисключенной систематической составляющей погрешности измерений G_м[∆_si] или

- границы ± ∆_{s hj}, в которых находится неисключенная систематическая составляющая погрешности измерений;

- наибольшее возможное значение среднего квадратического отклонения случайной составляющей погрешности измерений .

1.7 Расчет характеристик неисключенной систематической составляющей погрешности МВИ производится исходя из предположения с равновероятном распределении неисключенных систематических составляющих погрешностей измерений мгновенных значений процессов X_j(t) в пределах границ ± ∆_shj.

1.8 Метод расчета интервальных характеристик погрешности МВИ, рекомендуемый МИ может применяться если имеется основание считать, что законы распространения мгновенных значений процессов  являются симметричными, одномодальными и усеченными.

1.9 При наличии тренда процесса Z(t) оценивание характеристик тренда и проверка необходимости учета тренда при определении характеристики тренда и проверка необходимости учета тренда при определении характеристик погрешности измерений производится в соответствии с Приложением 2.

1.10 Необходимым условием правильности оцениваемых в соответствии с МИ характеристик погрешности МВИ является набор интервала дискретизации процессов Х_j(t) большим или равным интервалу корреляции процесса . Методика экспериментального определения интервала дискретизации процессов Х_j(t) приведена в Приложении 3.

1.11 По виду функциональной зависимости (1) МИ разграничивают косвенные измерения на линейные и нелинейные. Учет составляющей погрешности, обусловленной нелинейностью зависимости (1) , производится в случае существенности этой составляющей по сравнению с результирующей других составляющих погрешности, либо по сравнению с нормой, заданной на погрешность МВИ.

1.12 По наличию взаимной корреляции между процессами  МИ разграничивают косвенные измерения на коррелированные и некоррелированные. Учет влияния корреляции производится в случае существенности корреляционной погрешности измерений, либо по сравнению с заданной нормой на погрешность МВИ.

1.13 При аттестации МВИ допускается применение других методов расчета характеристик погрешности МВИ при условии, что эти методы позволяют оценить характеристики погрешности с требуемой достоверностью.

2. РАСЧЕТ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИЙ МЕТЕМАТИЧЕСКОГО ОЖИДАНИЯ ПРОЦЕССА ПРИ ЛИНЕЙНОЙ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ.

2.1 Процесс Z(t) связан с процессами Х_j(t), мгновенные значения которых определяются прямыми измерениями, линейной зависимостью

где В_j - постоянные коэффициенты.

2.2 Характеристики погрешности измерений для обоих методов определения результата измерений (п. 1.3) имеют одинаковые значения и вычисляются по одним и тем же формулам независимо от степени взаимной корреляции процессов

2.3 Расчет наибольшего возможного значения среднего квадратического отклонения неисключенной систематической составляющей погрешности измерений производится по формуле

2.3.1 Расчет границ, в которых неисключенная систематическая составляющая погрешности измерений находится с вероятностью Р, производится по формуле

При вычислении ∆_sh, необходимо учитывать лишь L ≤ m наибольших по значению составляющих (В₁∆_sh1 ³ В₂∆_sh2. ³…В_L∆_shL).Число L составляющих В_L∆_shj, учитываемых в (5), определяется исходя из выполнения неравенства.

Примечание. При L ≤ 8 относительная погрешность оценивания ∆_shj по п. 2.3.1 для любых соотношений между ∆_shj не превышает 5 % при Р = 0,9 = 0,99 и 10 % при Р > 0,99.

2.4 Расчет наибольшего возможного значения среднего квадратического отклонения случайной составляющей погрешности измерений производится по формуле

где G[X_j] - наибольшие возможные для объектов измерений определенного типа значения средних квадратических отклонений процессов Х_j(t);

G[_j] - наибольшие возможные значения средних квадратических отклонений случайных составляющих погрешностей измерений мгновенных значений процессов Х_j(t);

∆_GK - значение составляющей среднего квадратического отклонения погрешности измерений, обусловленной взаимной корреляцией процессов

n - объем выборки, используемой для оценивания математического ожидания процесса Z(t).

Примечание. Оценивание составляющей погрешности ∆_GK и поверка необходимости ее учета производится в соответствии с Приложением 1, либо с помощью других методов, позволяющих сделать вывод о необходимости учета корреляции погрешности, и в случае необходимости оценить ее значение.

2.5 Расчет наибольшего возможного значения среднего квадратического отклонения погрешности измерений производится по формуле

2.6 Расчет границ, в которых погрешность измерений находится с вероятностью Р, производится по формуле

где К - квантиль нормированной интегральной функции нормального распределения, соответствующий вероятности Р (К = 1,96 при Р = 0,95, К = 2,58 при Р = 0,99).

3. РАСЧЕТ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИЙ СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ ПРОЦЕССА ПРИ ЛИНЕЙНОЙ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ.

3.1 Вычисление результата измерений среднего квадратического отклонения процесса Z(t) производится по приближенной формуле

- при использовании метода 1 (п. 1.3)

где  - оценка мгновенного значения процесса Z(t) в момент времени t_i;

 - оценка математического ожидания процесса Z(t)

- при использования метода 2

где      - оценка среднего квадратического отклонения процесса Х_j(t).

3.1.1 Результаты измерений, вычисляемые по п. 3.1, содержат систематическую погрешность д обусловленную пренебрежением случайной составляющей погрешности измерений мгновенных значений процессов Х_j(t) и влиянием взаимной корреляции процессов Х_j(t).

Расчет систематической составляющей погрешности результата измерений производится по формуле:

- для метода 1

 

G_H[X_j] - наименьшее возможное для объектов измерений определенного типа значение среднего квадратического отклонения процессов ∆Х_j(t);

r_jL - коэффициент корреляции процессов ∆Х_j(t)), ∆X_L(t).

-для метода 2

 

R_jL - коэффициент корреляции процессов Х_j(t), Х_L(t).

Примечание. Учет систематической погрешности ∆_GS в виде поправки в результатах измерений целесообразно производить в том случае, если значение ∆_GS существенно по сравнению с граничным значением случайной составляющей погрешности измерений при используемом объеме выборки n.

3.2 Расчет наибольшего возможного значения среднего квадратического отклонения неисключенной систематической составляющей погрешности измерений производится по формуле:

3.3 Расчет наибольшего возможного значения среднего квадратического отклонения случайной составляющей погрешности измерений производится по формуле:

- для метода 1

Примечание. Оценивание корреляционной погрешности и проверка необходимости ее учета производится в соответствии с Приложением, либо с помощью других методов, позволяющих сделать вывод о необходимости учета корреляционной погрешности и в случае необходимости оценить ее значение.

3.4 Расчет наибольшего возможного значения среднего квадратического отклонения погрешности измерений производится по формуле:

3.5 Расчет границ, в которых погрешность измерений находится с вероятностью Р, производится по формуле:

где К - коэффициент, определяемый в соответствии с МИ 1317-86.

4. РАСЧЕТ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИЙ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ПРОЦЕССА ПРИ НЕЛИНЕЙНОЙ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ.

4.1 При расчете характеристик погрешности косвенных измерений с нелинейной функциональной зависимостью применяется метод линеаризации (использование в разложении нелинейной функциональной зависимости в ряд Тейлора только членов первого порядка) с оцениванием и учетом в случае необходимости составляющей погрешности, связанной с пренебрежением членов разложения более высокого порядка.

4.2 В случае несущественности составляющей погрешности, обусловленной пренебрежением нелинейных членов разложения, по сравнению с результирующей других составляющих погрешности, либо с заданной нормой на погрешность МВИ, характеристики погрешности измерений математического ожидания процесса вычисляются в соответствии с формулами раздела 2, в которых вместо коэффициентов В используются первые производные нелинейной функциональной зависимости по соответствующим аргументам Х_j.

4.3 Расчет наибольшего возможного значения составляющей систематической погрешности, обусловленной использованием при расчете характеристик погрешности измерений метода линеаризации производится по формуле:д

- для метода 1

r_jL - коэффициент взаимной корреляции между погрешностями измерений мгновенных значений процессов Х_j(t), Х_L(t)

- для метода 2

Индекс h в (19), (20) показывает, что в выражениях для частных производных в качестве аргументов Х_j используются те значения математических ожиданий процессов Х_j(t) в диапазоне их возможных значений, при которых значение систематической составляющей погрешности измерений принимает наибольшее значение.

4.4 Относительная погрешность оценивания ∆_H при симметричных законах распределения мгновенных значений процессов Х_L(t) и погрешностей их измерений определяется по формуле:

- для метода 1

- для метода 2

ПРИМЕЧАНИЕ. Условием допускающим применение метода линеаризации при оценивании характеристик погрешностей измерений является j ≤ 0,2.

4.5 В тех случаях, когда составляющая систематической погрешности измерений или по сравнению с другими характеристиками погрешности измерений или по сравнению с другими характеристиками погрешности измерений или по сравнению с заданной нормой на погрешность измерений, в результате измерений математического ожидания процесса Х(t) вводится поправка l = -∆_H/2. При этом в качестве дополнительной составляющей среднего квадратического отклонения неисключенной систематической составляющей погрешности используется

5. РАСЧЕТ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИЙ СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ ПРОЦЕССА ПРИ НЕЛИНЕЙНОЙ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ.

5.1 При расчете характеристик погрешности измерений среднего квадратического отклонения процесса при нелинейной функциональной зависимости применяется метод линеаризации с оцениванием и учетом в случае необходимости составляющей погрешности, обусловленной пренебрежением членов разложения более высокого порядка.

5.2 В случае несущественности составляющей погрешности, обусловленной линеаризацией нелинейной зависимости, по сравнению с другими составляющими погрешности, либо с заданной нормой на погрешность МВИ характеристики погрешности измерений среднего квадратического отклонения процесса вычисляются в соответствии с формулами раздела 3, в которых вместо коэффициентов В_j используется первые производные нелинейной функциональной зависимости по соответствующими аргументами X_j.

5.3 Расчет необходимости возможного значения составляющей систематической погрешности измерений, обусловленной использованием метода линеаризации производится по формуле:

- для метода 2

5.4 В тех случаях, когда ∆_GH существенна по сравнению с результирующей других составляющих погрешности, или по сравнению с заданной нормой на погрешность измерений, в результат измерений, вводится поправка l = -∆_GH/2. При этом в качестве дополнительной составляющей среднего квадратического отклонения неисключенной погрешности измерений используется Gg

ПРИЛОЖЕНИЕ 1
Справочное.

ПРОВЕРКА НЕОБХОДИМОСТИ УЧЕТА ВЛИЯНИЯ КОРРЕЛЯЦИЙ ПРИ РАСЧЕТЕ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ПРОЦЕССА.

Проверка необходимости учета влияния корреляции при расчете характеристик погрешности измерений, параметров процесса проводится в тех случаях, когда есть основания полагать, что имеется взаимная корреляция между процессами  функциональной зависимости (2). В общем случае такая проверка проводится в два этапа: ориентированный расчет корреляционной погрешности и, в случае необходимости, экспериментальное определение корреляционной погрешности. Необходимость проведения экспериментальное определение корреляционной погрешности. Необходимость проведения экспериментального определения корреляционной погрешности устанавливается в зависимости от результата ориентировочного расчета.

При ориентировочном расчете корреляционной погрешности предполагается, что каждый коэффициент взаимной корреляции коррелированных процессов ,  при L > о может с равной вероятностью иметь значение в диапазоне ± 1. Экспериментальное определение корреляционной погрешности проводится в том случае, если характеристики МВИ, вычисленные с учетом ориентировочного значения корреляционной погрешности, существенно отличается от характеристик погрешности МВИ, вычисленных без учета влияния взаимной корреляции, либо превышают заданные нормы на характеристики погрешности измерений.

Экспериментальное определение корреляционной погрешности производится по результатам экспериментального исследования N объектов измерений определенного типа. Количество N исследуемых объектов измерений устанавливается в каждом конкретном случае в зависимости от степени существенности корреляционной составляющей погрешности измерений, а также от степени разброса оценок корреляционной погрешности при экспериментальном исследовании объектов измерений определенного типа.

Ориентировочный расчет составляющей погрешности ∆_GK отражающей в (7), (15) влияние взаимной корреляции процессов , производится по формуле

Ориентировочный расчет составляющих ∆_GK1, ∆_GK2, отраженных в (12), (13) влияние взаимной корреляции соответствующих процессов, производится по формулам:

Ориентировочный расчет составляющих ∆_MK1, ∆_MK2, отраженных в (19), (20) влияние взаимной корреляции соответствующих процессов, производится по формулам:

В приведенных формулах учитываются характеристики только тех процессов  и тех погрешностей прямых измерений, между которыми предполагается наличие взаимной корреляции.

В том случае, когда заданы нормы на характеристики погрешности МВИ, экспериментальное определение корреляционной погрешности производится в том случае, если учет ориентировочного значения корреляционной погрешности приводит к существенному увеличению расчетных значений характеристик погрешности МВИ и превышению ими заданных норм. В том случае, когда нормы на характеристики погрешности МВИ не заданны и установление значений характеристик погрешности, приписывается МВИ, производится в том случае, если характеристики погрешности МВИ, вычисленные с учетом и без учета ориентировочного значения корреляционной погрешности отличаются друг от друга более чем на 15 ¸ 20 %.

Экспериментальное определение корреляционной погрешности для конкретного объекта измерений основано на получении для одной и той же реализации случайного процесса Z(t) двух оценок среднего квадратического отклонения мгновенных значений процесса. Одна из оценок определяется с использованием оценочной функции

где

Вторая оценка определяется по формуле

Полученная разность

где К_C - коэффициент Стьюдента, соответствующий вероятности Р = 0,95 и объему выборки n.

В том случае, когда экспериментально полученное значение  не выходит за границы интервала ± ∆_Gr, при расчете характеристик погрешности измерений влиянием взаимной корреляции можно пренебречь. В противном случае влиянием корреляции можно пренебречь, лишь в том случае, если учет ее интервальной оценки  не приводит к существенному изменению характеристик погрешности.

Экспериментальное определение корреляционной погрешности  для конкретного образца объекта измерений основано на получении для одной и той же реализации случайного процесса Z(t) двух оценок  математического ожидания процесса Z(t). Одна из оценок определяется с использованием

а вторая с использованием оценочной функции

Полученная разность

сравнивается с расчетной интервальной оценкой, полученной без учета влияния корреляции между процессами Х_j(t),

где

В том случае, когда экспериментально полученное значение ∆_MK не выходит за границы интервала ∆_МКР, при расчете характеристик погрешности измерений влиянием взаимной корреляции можно пренебречь. В противном случае влиянием корреляции можно пренебречь, если учет ее интервальной оценки приводит к существенному изменению характеристик погрешности МВИ.

Определение наибольшей возможной корреляционной погрешности для объектов измерений определенного типа производится по результатам экспериментального исследования нескольких объектов измерений. Количество исследуемых объектов измерений должно устанавливаться в каждом конкретном случае в зависимости от степени существенности корреляционной погрешности у объектов измерений одного и того же типа.

ПРИЛОЖЕНИЕ 2.
Справочное

ПРОВЕРКА ОТСУТСТВИЯ ТРЕНДА НА ИНТЕРВАЛЕ ИЗМЕРЕНИЯ.

При проверке отсутствия тренда процесса Z(t) и оценивании характеристик тренда принимается следующая модель процесса

где Z₁(t) - стационарный процесс, обладающий эргодическим свойством;

В - крутизна тренда, аппроксимируемого линейной функцией.

Проверка отсутствия тренда процесса Z(t) на интервале измерения Т=∆Т(n - 1) производится по п результатам значений Z_i используемых для оценивания параметров М[Z(t)], G[Z(t)] процесса Z(t).

Процедура обработки результатов измерений Z_i, с целью проверки отсутствия тренда заключается в следующем:

- измерительный интервал Т делится на два равных участка, и на каждом участке оцениваются средние значения процесса по формулам:

в которых предполагается нечетное значение n;

- вычисляется разность

- оценивается крутизна тренда

- оценивается среднее квадратическое отклонение процесса Z(t) на участке Т

где

- оценивается среднее квадратическое отклонение оценки крутизны тренда

- где в качестве среднего квадратического отклонения процесса Z₁(t) модели (2.1) принимается

- определяется интервальная оценка для крутизны линейной аппроксимации тренда

где К_C - коэффициент Стьюдента, соответствующий вероятности Р ± 0,95 и числу степеней свободы к  = (n - 2).

В том случае, если в пределах интервальной оценки (2.8) находится значение В = 0, то при оценивании параметров М[Z(t)], G[Z(t)] принимается, что тренд отсутствует. В том случае, когда интервальная оценка (2.8) не накрывает значение В = 0, в качестве оценки параметров G[Z(t)] используется оценка G[Z₁(t)], а в качестве оценки параметра М[Z(t)] используется

В этом случае процесс [Z(t)] дополнительно должен характеризоваться крутизной тренда с указанием интервальной оценки погрешности ее определения. Если погрешность оценивания крутизны тренда не удовлетворяет требованиям к погрешности измерений параметров процесса Z(t), то оценивание крутизны тренда производится на интервале T₁ > T, выбираемом исходя из требуемой точности оценивания крутизны тренда.

СОДЕРЖАНИЕ