СССР
МИНИСТЕРСТВО ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА
ВСЕСОЮЗНЫЙ
ОРДЕНА ОКТЯБРЬСКОЙ РЕВОЛЮЦИИ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА
|
УТВЕРЖДАЮ Зам. директора института ________Г.Д. ХАСХАЧИХ 12 ноября 1987 г. |
РУКОВОДСТВО
ПО АВТОМАТИЗИРОВАННОМУ РАСЧЕТУ ОБДЕЛОК
ПОДЗЕМНЫХ ТРАНСПОРТНЫХ
СООРУЖЕНИЙ
Одобрено Главтранспроектом
Москва 1987
Научный редактор канд. техн. наук В.А. Гарбер
ПРЕДИСЛОВИЕ
Руководство разработано в развитие глав СНиП II-40-80, ч. II. «Нормы проектирования. Метрополитены» и СНиП II-44-78, ч. II «Нормы проектирования. Тоннели железнодорожные и автодорожные».
В Руководстве рассмотрены вопросы классификации методик расчета подземных конструкций на основе заложенных в них предпосылок, классификации подземных сооружений по условиям их работы, сравнения расчетов подземных конструкций по различным методикам и программам. Даны рекомендации по применению конкретного программного обеспечения ЭВМ для статического и динамического расчетов конкретных видов подземных транспортных сооружений.
Работа выполнена на основе сравнительных расчетов всей номенклатуры постоянных подземных конструкций транспортных сооружений по всем существующим в СССР методикам и программам для ЭВМ, а также на основе анализа результатов многочисленных экспериментальных стендовых и натурных исследований тоннельных конструкций.
Руководство разработано канд. техн. наук В.А. Гарбером, инженерами Ю.Е. Лысенко (ЦНИИС), В.И. Гульбе (Метрогипротранс), канд. техн. наук А.А. Лянда (Ленметрогипротранс) при участии канд. физ.-мат. наук С.Ю. Хазанова, инженеров М.Б. Евдокимовой, Л.А. Муриной, Г.Б. Медведевой (ЦНИИС).
Руководство предназначено для проектировщиков транспортных тоннелей и метрополитенов при расчетах несущих конструкций.
|
Зав. отделением тоннелей и метрополитенов |
В.Е. Маркин |
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Настоящее Руководство составлено в развитие СНиП II-40-80, ч. II «Нормы проектирования. Метрополитены» (пп. 5.56 - 5.59, 5.61, 5.63) и СНиП II-44-78, ч. II «Нормы проектирования. Тоннели железнодорожные и автодорожные» (пп. 5.24, 5.30, 5.34, 5.35) и предназначено для использования при выборе конкретных методик и программ для ЭВМ при статических и динамических расчетах постоянных несущих конструкций транспортных тоннелей и метрополитенов. Рассмотрены существующие в практике проектирования подземных конструкций расчетные методики и программы, области их применения в конкретных горно-геологических условиях и видах сооружений.
Применение Руководства должно способствовать обоснованному выбору метода расчета подземных конструкций, наиболее соответствующему условиям их работы и обеспечивающему надежные данные для проверки прочностных и деформативных характеристик этих конструкций.
1.2. В качестве источников для разработки Руководства использованы результаты сравнительных расчетов всей номенклатуры постоянных подземных конструкций транспортных сооружений по всем существующим в СССР методикам и программам для ЭВМ, которые были собраны на вычислительном центре ЦНИИСа. Использованы также результаты анализа методик расчета на основе заложенных в них предпосылок, результаты анализа подземных сооружений по условиям их работы и результаты многочисленных экспериментальных стендовых и натурных исследований по измерению напряженно-деформированного состояния конструкций тоннелей и метрополитенов, проводимых сотрудниками ЦНИИСа.
1.3. Развивая отдельные положения указанных выше документов (разд. 1, п. 1.1), настоящее Руководство определяет классификацию методик расчета подземных конструкций на основе заложенных в них предпосылок (разд. 2) и классификацию подземных сооружений по условиям их работы (разд. 3). В Руководстве приведены результаты сравнительных расчетов подземных конструкций по различным программам (разд. 4) и даны рекомендации по применению конкретного программного обеспечения ЭВМ для статического и динамического расчета конкретных видов подземных транспортных сооружений (разд. 5).
1.4. Настоящее Руководство содержит систему исходных данных для программ по методикам ЦНИИСа.
2. КЛАССИФИКАЦИЯ МЕТОДИК РАСЧЕТА НА ОСНОВЕ ЗАЛОЖЕННЫХ В НИХ ПРЕДПОСЫЛОК
общие методы строительной механики;
методы механики сплошных сред;
инженерные методы, базирующиеся на уравнениях равновесия системы абсолютно жестких блоков и на дифференциальных уравнениях, отражающих свойства вмещающей среды.
2.3. По программам второй группы теоретически возможно рассчитывать только замкнутые односвязные подземные конструкции глубокого заложения круговой или эллиптической формы, имеющие постоянную жесткость по всему контуру конструкции. При этом можно производить расчет конструкций, находящихся только в однородном изотропном горном массиве. Расчет может осуществляться только в упругой стадии работы системы «порода - обделка».
2.4. По программам третьей группы теоретически можно рассчитывать только односводчатые сборные многошарнирные подземные конструкции глубокого заложения как замкнутые, так и разомкнутые. Расчет проводится в упругой стадии работы конструкции с учетом реологических свойств породного массива.
2.5. Известны следующие программы, относящиеся к первой группе:
«SRTSEC», реализующая метод перемещений для статического расчета конструкций в упругой стадии (держатель программы - Метрогипротранс);
«РК-6», являющаяся модификацией программы «SRTSEC» в части ввода исходных данных, решения системы уравнений и адаптации на СМ ЭВМ (держатель программы - Ленметрогипротранс);
«T1GG2», реализующая метод сил для статического расчета конструкций в упругой стадии (держатель программы ЦНИИС);
«T1GNL», реализующая метод линеаризации при пошаговом нагружении для статического расчета конструкций в нелинейной стадии работы системы «порода - обделка» (держатель программы ЦНИИС);
«СПРИНТ», реализующая метод конечных элементов для расчета плоских и пространственных конструкций (держатель программы - МИИТ);
«ЛИРА», реализующая метод конечных элементов для расчета плоских и пространственных конструкций (держатель программы - Киевский НИИАСС Госстроя УССР).
2.6. Программы «СПРИНТ» и «ЛИРА» не имеют блоков, реализующих работу односторонних связей подземных конструкций с породным массивом. Эти программы целесообразно использовать для моделирования напряженного состояния сложных плоских и пространственных конструкций (торцевые камеры, пересадочные узлы и т.п.).
2.7. Известны следующие программы, относящиеся ко второй группе и реализующие:
«РК-1» - решение плоской задачи теории упругости однородной изотропной среды для плоскости с круговым или эллиптическим вырезом, подкрепленным кольцом постоянной толщины (держатель программы - Ленметрогипротранс);
«РК-2» - решение плоской задачи теории упругости однородной изотропной среды для плоскости с круговым вырезом, подкрепленным многослойным кольцом постоянной толщины (держатель программы - Ленметрогипротранс);
«METRO» - решение плоской задачи теории упругости однородной изотропной среды для плоскости с круговым вырезом, подкрепленным однослойным кольцом, жесткость которого может меняться во времени (держатель программы - КАДИ).
2.8. Программа «РК-1» теоретически предназначена для расчета замкнутых монолитных круговых и эллипсообразных обделок, вытянутых вертикально, на статические нагрузки и сейсмические воздействия.
2.9. Программа «РК-2» теоретически предназначена для расчета кольцевых многослойных монолитных и комбинированных обделок на статические нагрузки и сейсмические воздействия.
2.10. Программа «METRO» предназначена для статического расчета монолитно-прессованной обделки с учетом технологических стадий твердения бетона.
2.11. Известны следующие программы, относящиеся к третьей группе и реализующие:
«РК-3» - метод Антонова-Айвазова для расчета односводчатых сборных многошарнирных станций метрополитена глубокого заложения с массивными круговыми опорами верхнего свода (держатель программы - Ленметрогипротранс);
«CAT» - метод Антонова-Айвазова для расчета односводчатых сборных многошарнирных станций метрополитена глубокого заложения коробового очертания (держатель программы - ЦНИИС);
«STATION» - метод Антонова-Айвазова для расчета односводчатых сборных многошарнирных станций метрополитена глубокого заложения с массивными опорами произвольного очертания: штольневыми и круговыми (держатель программы - КАДИ).
2.12. Программа «STATION» не прошла апробации в практике проектирования и является экспериментальной.
2.13. Помимо перечисленных в пп. 2.5, 2.7 и 2.11 программ прочностного расчета подземных конструкций известна программа «CBK» (держатель программы - Метрогипротранс), предназначенная для расчета сечений железобетонных элементов по предельным состояниям 1 и 2 групп: проверки на прочность и подбора арматуры (для СМ ЭВМ аналог программы РК-7 выполнен и поддерживается Ленметрогипротрансом).
3. КЛАССИФИКАЦИЯ ПОДЗЕМНЫХ СООРУЖЕНИЙ ПО УСЛОВИЯМ ИХ РАБОТЫ
3.1. По условиям работы с позиций прочностного расчета конструкции подземных сооружений делятся на конструкции мелкого заложения и конструкции глубокого заложения.
3.2. К конструкциям мелкого заложения относятся цельносекционная и сборная обделки перегонных тоннелей метрополитенов прямоугольного очертания, колонная станция метрополитена открытого способа работ, монолитная односводчатая станция метрополитена открытого способа работ. Сюда же относятся конструкции пешеходных переходов и входов на станции метрополитена мелкого заложения.
3.3. Статический и динамический расчеты конструкций мелкого заложения теоретически могут осуществляться только с использованием программ для ЭВМ первой группы (пп. 2.1, 2.2, 2.5).
3.4. Конструкции глубокого заложения с позиций прочностного расчета подразделяются на монолитные конструкции и многошарнирные блочные конструкции.
3.5. Монолитные конструкции глубокого заложения подразделяются на односвязные, многосвязные и разомкнутые.
3.6. К односвязным монолитным конструкциям глубокого заложения относятся обделки кругового очертания, замкнутые подковообразные обделки и монолитные большепролетные односводчатые конструкции типа односводчатой станции.
3.7. Статический и динамический расчеты односвязных монолитных конструкций глубокого заложения теоретически могут осуществляться только с использованием программ для ЭВМ, указанных в пп. 2.5 и 2.7.
3.8. К многосвязным монолитным конструкциям глубокого заложения относятся колонные и пилонные станции метрополитена.
3.9. Статический и динамический расчеты многосвязных конструкций глубокого заложения теоретически могут осуществляться только с использованием программ для ЭВМ, указанных в п. 2.5.
3.10. К разомкнутым монолитным конструкциям глубокого заложения относятся подковообразные обделки горных тоннелей без лотка или обратного свода и односводчатые большепролетные конструкции без лотка или обратного свода.
3.11. Статический и динамический расчеты разомкнутых монолитных конструкций глубокого заложения теоретически могут осуществляться только с использованием программ для ЭВМ, указанных в п. 2.5.
3.12. К многошарнирным блочным конструкциям относятся необжатые и обжатые в породу круговые блочные шарнирные обделки и односводчатые станции метрополитенов глубокого заложения с многошарнирными сводами.
3.13. Статический расчет многошарнирных блочных конструкций теоретически может осуществляться с использованием программ, указанных в пп. 2.5 и 2.11. Однако расчет этих конструкции по программам первой группы (см. пп. 2.1 и 2.5) практически нецелесообразен при наличии специализированных программ третьей группы (см. пп. 2.1 и 2.11).
4. РЕЗУЛЬТАТЫ СРАВНИТЕЛЬНЫХ РАСЧЕТОВ ПОДЗЕМНЫХ КОНСТРУКЦИЙ ПО РАЗЛИЧНЫМ ПРОГРАММАМ
4.1. Сравнительные статические расчеты монолитной кольцевой обделки проводились по программам «РК-6», «T1GG2», «РК-1», «METRO».
Результаты расчетов по программам первой группы («РК-6» и «T1GG2») в качественном отношении идентичны между собой.
Результаты расчетов по программам второй группы («РК-1» и «METRO») в качественном отношении идентичны между собой.
Результаты расчетов по программам первой группы в качественном отношении резко отличаются от результатов расчетов по программам второй группы.
Практика строительства и эксплуатации монолитных кольцевых тоннелей подтверждает качественную картину, получаемую при расчетах по программам первой группы («РК-6» и «T1GG2»): обделка разрушается в первую очередь в верхней части тоннеля, а в лотке трещины наблюдаются редко, что соответствует наличию экстремальных значений изгибающего момента в сводовой части тоннеля.
Результаты расчетов монолитной кольцевой обделки по программам «РК-6» и «T1GG2» имеют следующие количественные различия:
максимальный положительный изгибающий момент 9 - 10 %;
максимальный отрицательный изгибающий момент до 0,5 %;
максимальное осевое усилие 1 - 5 %.
4.2. Сравнительные статические расчеты подковообразной обделки замкнутого очертания проводились по программам «РК-6», «T1GG2» и «РК-1».
Результаты расчетов по программам первой группы («РК-6» и «T1GG2») в качественном отношении идентичны между собой.
Результаты расчета по программам первой группы («РК-6» и «T1GG2») в качественном отношении принципиально отличаются от результата расчета по программе второй группы («РК-1»).
Практика строительства и эксплуатации горных тоннелей подковообразного очертания подтверждает качественную картину, получаемую при расчете замкнутой подковообразной обделки на преобладающее вертикальное горное давление по программам первой группы «РК-6» и «T1GG2»: обделка разрушается в первую очередь в своде, а не в лотке; в боковых стенах появляются продольные трещины с внутренней стороны тоннеля, а не со стороны породы.
Результаты расчетов замкнутой подковообразной обделки по программам «РК-6» и «T1GG2» имеют следующие количественные различия:
максимальный положительный изгибающий момент в шелыге свода 3,4 %;
максимальный положительный изгибающий момент в стене или пяте 2,3 %;
максимальный положительный изгибающий момент в обратном своде 2,2 %;
максимальный отрицательный изгибающий момент 0,7 %;
максимальное осевое усилие 0,2 %.
4.3. Сравнительные статические расчеты разомкнутой подковообразной обделки (без обратного свода) проводились по программам «РК-6» и «T1GG2».
Результаты расчетов разомкнутой подковообразной обделки (без обратного свода) по программам «РК-6» и «T1GG2» практически полностью совпадают как качественно, так и количественно.
4.4. Сравнительные статические расчеты монолитной односводчатой станции метрополитена глубокого заложения проводились по программам «РК-6» и «T1GG2».
Результаты расчетов монолитной односводчатой станции метрополитена глубокого заложения по программам «РК-6» и «T1GG2» полностью совпадают качественно и практически количественно.
4.5. Сравнительные статические расчеты колонной станции метрополитена глубокого заложения проводились по программам «РК-6» и «T1GG2».
Результаты расчетов колонной станции метрополитена глубокого заложения по программам «РК-6» и «T1GG2» имеют следующие качественные сравнительные показатели:
верхний свод среднего тоннеля - полная идентичность;
боковые тоннели - полная идентичность;
обратный свод среднего тоннеля - существенное различие.
Результаты расчетов колонной станции метрополитена глубокого заложения по программам «РК-6» и «T1GG2» имеют следующие количественные различия:
максимальный положительный изгибающий момент в верхнем своде среднего тоннеля в 2,5 раза;
максимальный отрицательный изгибающий момент в верхнем своде среднего тоннеля 15 %;
положительный изгибающий момент в надколонном узле 2,5 %;
положительный изгибающий момент в своде боковых тоннелей 39 %;
максимальный отрицательный изгибающий момент в своде боковых тоннелей 34 %;
максимальное осевое усилие в верхнем своде среднего тоннеля 5,5 %;
максимальное осевое усилие в боковом тоннеле до 2 %;
осевое усилие в колонне до 1 %;
прогиб шелыги свода среднего тоннеля в 7 раз;
прогиб шелыги свода боковых тоннелей 42 %.
4.6. Сравнительные статические расчеты семиблочной сборной круговой обделки перегонного тоннеля метрополитена проводились по программам «РК-6», «T1GG2» и «BATON» (КАДИ-ЦНИИС).
Результаты расчетов по программам первой группы («РК-6» и «T1GG2») в качественном отношении идентичны между собой.
Результаты расчетов по программам первой группы («РК-6» и «T1GG2») в качественном отношении принципиально отличаются от результата расчета по программе третьей группы («BATON»).
Практика строительства и эксплуатации унифицированной круговой семиблочной сборной обделки подтверждает качественную картину, получаемую при расчете этой конструкции по программам первой группы («РК-6» и «T1GG2»): разрушение в первую очередь верхних блоков, а не лотка.
Результаты расчетов семиблочной круговой сборной обделки по программам «РК-6» и «T1GG2» имеют следующие количественные различия:
максимальный изгибающий момент в расчетном блоке № 1 1 - 6 %;
максимальное осевое усилие в кольце 2 - 4 %;
перемещение шелыги свода 5 - 6 %.
4.7. Сравнительные статические расчеты цельносекционной обделки перегонного тоннеля метрополитена открытого способа работ проводились по программам «РК-6» и «T1GG2».
Результаты расчетов цельносекционной обделки по программам «РК-6» и «T1GG2» полностью совпадают качественно и практически количественно,
4.8. Сравнительные статические расчеты монолитной односводчатой станции метрополитена открытого способа работ проводились по программам «РК-6» и «T1GG2».
Результаты расчетов по программам «РК-6» и «T1GG2» в качественном отношении идентичны между собой.
Результаты расчетов монолитной односводчатой станции метрополитена открытого способа работ по программам «РК-6» и «T1GG2» имеют следующие количественные различия:
максимальный положительный изгибающий момент в своде 42 %;
отрицательный изгибающий момент в пяте свода 39 %;
максимальный положительный изгибающий момент в стене до 6 %;
осевое усилие в шелыге свода 13 %;
осевое усилие в пяте свода 14 %;
максимальное осевое усилие в стене до 1 %;
осевое усилие в лотке до 20 %;
прогиб шелыги свода до 23 %.
4.9. Сравнительные статические расчеты колонной станции метрополитена открытого способа работ проводились по программам «РК-6» и «T1GG2».
Результаты расчетов по программам «РК-6» и « T1GG2» в качественном отношении идентичны между собой.
Результаты расчетов колонной станции метрополитенов открытого способа работ по программам «РК-6» и «T1GG2» имеют следующие количественные различия:
максимальный положительный изгибающий момент по ригелю среднего зала 3 %;
максимальный положительный изгибающий момент по ригелю боковых тоннелей до 15 %;
максимальный отрицательный изгибающий момент над колонной до 4 %;
максимальный отрицательный изгибающий момент в верхнем вуте до 18 %;
максимальный положительный изгибающий момент по боковой стене до 26 %;
максимальный отрицательный изгибающий момент в нижнем вуте до 6 %;
осевое усилие в колонне до 3 %;
максимальное осевое усилие в ригеле среднего свода до 1,5 %;
максимальное осевое усилие в ригеле бокового тоннеля 5 %;
максимальное осевое усилие в боковой стене до 7 %.
5. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ РАСЧЕТА ОБДЕЛОК ПОДЗЕМНЫХ ТРАНСПОРТНЫХ СООРУЖЕНИЙ
5.1. Расчет монолитных кольцевых обделок в упругой стадии на статические нагрузки следует производить по одной из следующих программ: «T1GG2» (обязательное приложение), «SRTSEC», «РК-6».
5.2. Расчет монолитных кольцевых обделок глубокого заложения на сейсмические воздействия следует производить по программе «РК-1».
5.3. Расчет монолитных круговых многослойных и комбинированных обделок глубокого заложения на статические нагрузки и сейсмические воздействия следует производить по программ «РК-2».
5.4. Расчет монолитных кольцевых обделок на статические нагрузки в нелинейной стадии следует производить по программе «T1GNL» (см. обязательное приложение).
5.5. Расчет монолитных подковообразных замкнутых обделок в упругой стадии на статические нагрузки следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2».
5.6. Расчет монолитных подковообразных замкнутых обделок на сейсмические воздействия следует производить по программе «РК-1».
5.7. Расчет монолитных подковообразных замкнутых обделок на статические нагрузки в нелинейной стадии следует производить по программе «T1GNL».
5.8. Расчет монолитных односводчатых станций метрополитена закрытого способа работ в упругой стадии на статические нагрузки следует производить по одной из следующих программ: «SRTSEC» «РК-6», «T1GG2».
5.9. Расчет монолитных односводчатых станций метрополитена закрытого способа работ на сейсмические воздействия следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2». При этом расчет должен осуществляться на приведенные статические нагрузки, вычисляемые в соответствии с ВСН 193-81.
5.10. Расчет монолитных односводчатых станций метрополитена закрытого способа работ на статические нагрузки в нелинейной стадии следует производить по программе «T1GNL».
5.11. Расчет монолитных подковообразных разомкнутых (без лотка или без обратного свода) обделок в упругой стадии на статические нагрузки следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2».
5.12. Расчет монолитных подковообразных разомкнутых (без лотка или без обратного свода) обделок на сейсмические воздействия следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2». При этом расчет должен осуществляться на приведенные статические нагрузки, вычисляемые в соответствии с ВСН 193-81.
5.13. Расчет монолитных подковообразных разомкнутых (без лотка или без обратного свода) обделок на статические нагрузки в нелинейной стадии следует производить по программе «T1GNL».
5.14. Расчет колонных станций метрополитена закрытого способа работ в упругой стадии на статические нагрузки следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2»
5.15. Расчет колонных станций метрополитена закрытого способа работ на сейсмические воздействия следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2» При этом расчет должен осуществляться на приведенные статические нагрузки, вычисляемые в соответствии с ВСН 193-81.
5.16. Расчет колонных станций метрополитена закрытого способа работ на статические нагрузки в нелинейной стадии следует производить по программе «T1GNL».
5.17. Расчет пилонных станций метрополитена в упругой стадии на статические нагрузки следует производить по программе «SRTSEC» или «РК-6».
5.18. Расчет пилонных станций метрополитена на сейсмические воздействия следует производить по программе «SRTSEC» или «РК-6». При этом расчет должен осуществляться на приведенные статические нагрузки, вычисляемые в соответствии с ВСН 193-81.
5.19. Расчет сборных (шарнирных) кольцевых обделок в упругой стадии на статические нагрузки следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2»
5.20. Расчет сборных (шарнирных) кольцевых обделок на сейсмические воздействия следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2». При этом расчет должен осуществляться на приведенные статические нагрузки, вычисляемые в соответствии с ВСН 193-81.
5.21. Расчет сборных (шарнирных) кольцевых обделок на статические нагрузки в нелинейной стадии следует производить по программе «T1GNL».
5.22. Расчет цельносекционных и сборных обделок прямоугольного очертания в упругой стадии на статические нагрузки следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2».
5.23. Расчет цельносекционных и сборных обделок прямоугольного очертания на сейсмические воздействия следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2». При этом расчет должен осуществляться на приведенные статические нагрузки, вычисляемые в соответствии с ВСН 193-81.
5.24. Расчет цельносекционных и сборных обделок прямоугольного очертания на статические нагрузки в нелинейной стадии следует производить по программе «T1GNL».
5.25. Расчет монолитных односводчатых и колонных станций метрополитена открытого способа работ в упругой стадии на статические нагрузки следует производить по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2».
5.26. Расчет монолитных односводчатых и колонных станций метрополитена открытого способа работ на сейсмические воздействия должен осуществляться по одной из следующих программ: «SRTSEC», «РК-6», «T1GG2». При этом расчет должен осуществляться на приведенные статические нагрузки, вычисляемые в соответствии с ВСН 193-81.
5.27. Расчет монолитных односводчатых и колонных станций метрополитена открытого способа работ на статические нагрузки в нелинейной стадии должен осуществляться по программе «T1GNL».
5.28. Расчет односводчатых сборных многошарнирных станций метрополитена глубокого заложения следует производить по программам «РК-3» и «САТ» в соответствии с типом опорных частей верхнего свода.
5.29. Расчет сечений железобетонных элементов (проверка на прочность и подбор арматуры) следует производить по программе «РК-7».
Приложение
Обязательное
ПРИМЕНЕНИЕ МЕТОДА ЦНИИС ДЛЯ РАСЧЕТА ПОДЗЕМНЫХ КОНСТРУКЦИЙ НА ЕС ЭВМ
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
Настоящее обязательное приложение посвящено статическому расчету подземных конструкций тоннелей и метрополитенов на ЕС ЭВМ в упругой стадии, а также с учетом нелинейности работы системы «порода - обделка».
За основу обязательного приложения приняты разработанные в отделении «Тоннели и метрополитены» в 1973 - 1983 гг. методики расчета подземных конструкций произвольного очертания на воздействие произвольно заданного загружения.
В обязательном приложении отражены 2 методики расчета:
расчет в упругой стадии работы системы «порода - обделка»;
расчет конструкций с учетом следующих видов нелинейности системы «порода - обделка»:
нелинейность работы материала обделки - учет истинных физико-механических свойств материалов, из которых возводится собственно конструкция;
нелинейность работы вмещающего породного массива - учет истинной зависимости коэффициента упругого отпора породы от величины контактного давления между обделкой и породой;
геометрическая нелинейность расчетной схемы - учет общих деформаций конструкции на каждом этапе загружения (расчет по деформированной схеме);
конструктивная нелинейность расчетной схемы - учет изменения физико-механических характеристик расчетных сечений конструкций в процессе ее загружения.
Обязательное приложение является инструктивным материалом к программам расчета, написанным на стандартной версии языка «ФОРТРАН 4».
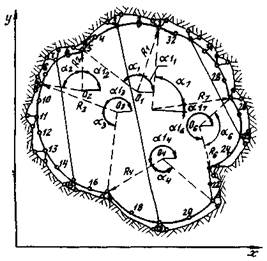
Расчетная схема подземной конструкции с многосвязным (в общем случае) поперечным сечением (рис. 1) включает в себя следующие элементы:
массив грунта с выработкой;
собственно несущую подземную конструкцию с внутренними связями (или без них);
контактный слой между несущей конструкцией и контуром выработки.
Методика расчета подземной конструкции в упругой стадии предусматривает определение:
а) внутренних усилий в стержневой системе, которой моделируется несущая подземная конструкция;
б) усилий в стержневых опорных элементах: нормальных и тангенциальных к контуру конструкции, которыми моделируется контактный слой;
в) продольных (осевых) и изгибных (угловых) деформаций стержневой системы, моделирующей несущую конструкцию;
г) продольных деформаций нормальных и тангенциальных опорных стержневых элементов, моделирующих контактный слой. Эти деформации определяют общие перемещения основного контура конструкции;
Рис. 1. Расчетная схема подземного сооружения
д) осевых усилий во внутренних связях.
Перечисленные компоненты напряженно-деформированного состояния подземной конструкции являются результатом воздействия силовых факторов, возникающих при взаимодействии подземной конструкции с грунтовым массивом. Эти силовые факторы могут определяться различными методами:
а) натурными измерениями;
б) решением контактной задачи механики сплошных сред;
в) применением различных теорий горного давления;
г) применением нормативных документов.
Данная методика не включает в себя определения силовых факторов, воздействующих на конструкцию. Это силовое воздействие считается заданным и может иметь произвольные количественные и качественные характеристики.
В качестве метода решения принят метод сил. Основная система получена из расчетной схемы введением шарниров в представляющих конструкцию точках расчетной оси. Наличие шарниров компенсируется приложением в каждом из них парных внешних взаимно уравновешенных изгибающих моментов.
Специфическая особенность использованного метода решения состоит в том, что опорные стержневые элементы, моделирующие контактный слой, расположены только в нечетных вершинах расчетной схемы. Эта особенность позволила разделить на уровне основной системы решение сложной контактной задачи для произвольного контура на две более простые задачи: о деформациях неподкрепленного выреза в плоскости и о напряженно-деформированном состоянии стержневой системы под действием этих деформаций. Излагаемая методика относится только ко второй задаче.
Расчетная ось конструкции представляет собой совокупность криволинейных и прямолинейных участков, каждый из которых имеет постоянную кривизну. Так, расчетная ось конструкции, схема которой представлена на рис. 1, состоит из 7 участков, каждый из них имеет характеристики, указанные в табл. 1.
Таблица 1
|
Вершины, входящие в участок |
Координаты центра кривизны участка |
Радиус кривизны участка |
Центральный угол участка |
Направляющий угол нормали к контуру участка в его начальной точке |
|
|
1 |
От 1 до 5 |
Xо1, Yо1 |
R1 |
a1 |
a11 |
|
2 |
От 5 до 9 |
Xо2, Yо2 |
R2 |
a2 |
a12 |
|
3 |
От 9 до 17 |
Xо3, Yо3 |
R3 |
a3 |
a13 |
|
4 |
От 17 до 21 |
Xо4, Yо4 |
R4 |
a4 |
a14 |
|
5 |
От 21 до 23 |
X21, Y21 |
0 |
0 |
a14 + a4 |
|
6 |
От 23 до 27 |
Xо6; Yо6 |
R6 |
a6 |
a16 |
|
7 |
От 27 до 1 |
Xо7, Yo7 |
R7 |
a7 |
a17 |
Направляющие углы нормалей к контуру отсчитываются от положительного направления оси 0X против часовой стрелки.
Для прямолинейных участков в качестве центра кривизны принимается начальная точка участка. Соответственно радиус кривизны и центральный угол прямолинейного участка принимаются нулевыми, а направляющий угол нормали к контуру равен направляющему углу отрезка, соединяющего центр кривизны предыдущего участка с начальной точкой прямолинейного участка.
При расчете незамкнутых конструкций участок размыкания моделируется следующим образом: участок фиктивно замыкается прямолинейным отрезком, который имеет по концам нечетные вершины расчетной схемы, а в середине - четную фиктивную вершину; во всех трех вершинах фиктивного участка вводятся шарнирные связи. Таким образом, получается трехшарнирный двухзвенник, который является механизмом и, свободно деформируясь, не передает усилий с одного своего конца на другой, так как на средней (безопорной) его вершине нагрузки нет, потому что эта вершина фиктивная. Поскольку через этот фиктивный участок в конструкции не передается внутренних усилий, то он в статическом смысле эквивалентен разомкнутому участку. Необходимость в введении такого фиктивного участка продиктована требованием стандартизации и однотипности вычислительного процесса.
Физико-механические свойства фиктивного участка должны задаваться произвольными положительными ненулевыми величинами.
Данная методика допускает расчет подземных конструкций при наличии до 15 внутренних связей, не пересекающихся между собой. Предусмотрена работа внутренних связей только на восприятие центрального осевого усилия. Такая работа внутренних связей в натуре должна обеспечиваться конструктивными мероприятиями, например, введением шарниров по концам связи.
Методика предусматривает только такие внутренние связи, которые соединяет нечетные вершины расчетной схемы, находящиеся в зоне активной нагрузки (на рис. 1 вершины 7, 3, 31), с нечетными вершинами расчетной схемы, расположенными в зоне пассивного отпора породы (на рис. 1 вершины, 15, 19, 25).
Внутренние связи моделируются следующим образом:
а) в вершинах расчетной схемы, к которым примыкают внутренние связи в зоне активной нагрузки, жесткость опорных нормальных стержневых элементов назначается равной жесткости соответствующей внутренней связи на осевое воздействие;
б) одновременно направляющий угол этого нормального опорного элемента задается равным направляющему углу внутренней связи;
в) в вершинах расчетной схемы, к которым примыкают соответствующие внутренние связи в зоне пассивного отпора породы, направляющий угол нормального опорного элемента также задается равным направляющему углу внутренней связи;
г) после этого статическая работа внутренней связи заменяется эквивалентным воздействием опорного элемента в зоне активной нагрузки, непосредственно передающего свое опорное усилие на опорный элемент в зоне пассивного отпора породы.
Получаемое в результате такого расчета конструкции усилие в нормальном опорном элементе, расположенном в месте примыкания внутренней связи в зоне активной нагрузки, равно искомому усилию во внутренней связи, возникающему от воздействия нагрузки на 1 м тоннеля.
Методика расчета подземной конструкции в нелинейной стадии имеет следующие предпосылки:
все предпосылки расчета подземной конструкции в упругой стадии сохраняются и для нелинейного расчета;
помимо учета нелинейностей системы «порода - обделка», перечисленных в основных положениях, расчет включает в себя анализ конструкции по предельным состояниям и учет наследственности напряженно-деформированного состояния в процессе загружения;
расчету подлежат конструкции монолитные и сборные; в общую модель входит математическая модель стыка элементов сборной конструкции;
могут быть рассчитаны многослойные конструкции из различных материалов;
расчет осуществляется автоматически на ЭВМ до достижения конструкцией одного из предельных состояний;
при расчете на ЭВМ выдается полная количественная и качественная информация о процессе разрушения и структурных изменениях конструкции;
максимальное число вершин расчетной схемы 110;
конструкция может состоять из четырех различных материалов, тип материала может меняться как по контуру конструкции, так и по высоте сечения;
при поэтапном загружении конструкции применяется гипотеза плоских сечений (правомерность такого подхода обоснована в работах А.С. Городецкого);
конструкция описывается совокупностью расчетных сечений, каждое из которых рассматривается состоящим из К слоев; К = const по контуру конструкции и может назначаться в пределах от 1 до 20 т.е. может быть рассчитана 20-слойная конструкция; все К слоев в одном сечении имеют одинаковую высоту h1:
![]()
где i - номер слоя;
hj - общая высота j-го сечения.
В каждом сечении слои нумеруются от наружной грани обделки к внутренней и соответственно имеют номера от 1 до К;
в j-м расчетном сечении каждый i-й слой рассматривается как условно прямоугольный с шириной bi.
При этом в ширине bi учитываются только те части слоя расчетного сечения, в котором есть неразрушенный материал, т.е. bi не чисто геометрическая характеристика слоя, а физическая (условно-геометрическая);
деформативные свойства материалов, из которых состоит конструкция, характеризуются диаграммами их испытания. Каждая диаграмма «s - e» задается в виде двух таблиц: значения напряжений s (тс/м2) и соответствующие значения относительных деформаций e.
Напряжения и деформации сжатия считаются положительными, а компоненты растяжения - отрицательными;
предельными деформативными характеристиками принимаются максимальные по абсолютной величине значения таблицы относительных деформаций e. Слой считается разрушенным при выходе его деформаций за пределы диаграммы «s - e» для материала, его составляющего;
осью расчетной схемы конструкции считается геометрическое место центров тяжести ненарушенного материала расчетных сечений. Под этим понимается корректировка положения расчетной оси на каждом этапе загружения в соответствии с изменением высоты ненарушенного материала в сечении и величиной общих деформаций (перемещений) расчетных сечений по нормали и касательной к контуру конструкции;
величина поэтапного приращения нагрузки может быть неравномерной; однако качественный характер загружения, т.е. вид нагрузки, остается постоянным;
поскольку каждый i-й слой каждого j-го расчетного сечения характеризуется своей диаграммой «s - e» то для каждого этапа загружения введено понятие «приведенного условного модуля деформации расчетного сечения» Ej.
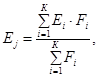
где Ei - условный модуль деформаций i-го слоя;
Fi = bi · h1 - площадь i-го слоя в j-м сечении, м2.
Условным модулем деформации i-го слоя Ei названо отношение напряжений s к деформации e для материала слоя на рассматриваемом этапе загружения. Ei вычисляется по соответствующей диаграмме «s - e» и может быть только положительным ненулевым числом.
При нелинейном расчете рассматриваются 3 предельные состояния подземных конструкций в соответствии с положениями СНиПов по проектированию автодорожных, железнодорожных тоннелей и метрополитенов. Однако первое предельное состояние сформулировано следующим образом: конструкция достигает предельного состояния по несущей способности (прочности) при разрушении материала какого-либо из ее линейных участков. Линейным участком конструкции считаются какие-либо три последовательных ее расчетных сечения. Разрушение таких трех последовательных сечений адекватно образованию трех соседних шарниров, что ведет к появлению мгновенно изменяемого участка в расчетной схеме конструкции.
Естественно, что при достижении подземной конструкцией такого состояния дальнейшая эксплуатация ее невозможна по двум причинам:
а) потеря устойчивости одним из участков расчетной схемы неизбежно должна повлечь за собой недопустимые общие деформации всей расчетной схемы;
б) разрушение материала обделки на линейном участке вызовет проникновение в тоннель породы и грунтовых вод, что недопустимо для подземного сооружения.
Все основные аналитические зависимости, используемые в нелинейной модели работы системы «порода - обделка», приведены в сборнике научных трудов [3].
2. АЛГОРИТМ
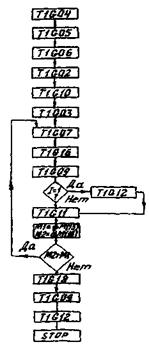
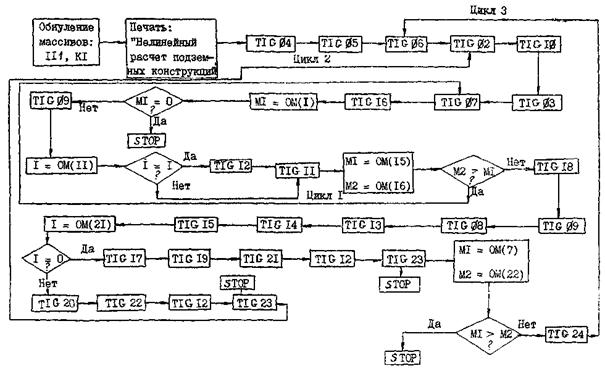
На рис. 2 приведена блок-схема программы расчета подземных конструкций в упругой (линейной) стадии работы; а на рис. 3 - блок-схема программы нелинейного расчета подземных конструкций.
Из сравнения этих рисунков видно, что линейная модель работы подземной конструкции является составной частью нелинейной модели. Алгоритмы нелинейной и линейной моделей и программы, их реализующие, имеют модульную структуру, включающую в себя функциональные модули и управляющие операторы.
Рис. 2. Блок-схема программы для расчета произвольной конструкции на произвольно заданное загружение в упругой стадии
Функциональные модули имеют 5-символьный префикс, начинающийся с символов Т1G, и выполняют следующие действия:
|
T1G04 |
- ввод, обработка и оптимизация исходной информации о параметрах первоначального состояния системы «обделка - порода»; |
|
T1G05 |
|
|
T1G06 |
- вычисление компонент матриц единичных состояний основной системы метода сил; |
|
T1G02 |
- вычисление компонент вектора грузового состояния основной системы метода сил; |
|
T1G10 |
|
|
T1G03 |
- вычисление характеристик жесткости на действие продольной силы и изгибающего момента расчетных сечений конструкции; |
|
T1G07 |
- формирование матрицы коэффициентов левой части системы канонических уравнений метода сил и грузового столбца системы; |
Рис. 3. Блок-схема программы T1GNL
|
T1G16 |
- решение системы канонических уравнений метода сил; |
|
T1G09 |
- вычисление компонент напряженно-деформированного состояния конструкции; |
|
T1G12 |
- печать на АЦПУ таблицы напряженно-деформированного состояния системы «обделка - порода» на очередном этапе загружения; |
|
T1G11 |
- анализ состояния контактного слоя системы «обделка - порода»; в случае необходимости корректировки «зоны отлипания» проводится корректировка матрицы коэффициентов левой части системы канонических уравнений метода сил и грузового столбца системы; |
|
T1G18 |
- оценка и «разбрасывание» погрешности метода решения системы уравнений; |
|
T1G08 |
- ввод, обработка и «запоминание» информации о количестве слоев в расчетных сечениях, о ширине каждого слоя во всех сечениях, о диаграммах «s - e»; |
|
T1G13 |
- анализ напряженно-деформированного состояния монолитных (не стыковых) расчетных сечений с целью уточнения жесткостных характеристик, выявления разрушений материала и структурных изменений; |
|
T1G14 |
- анализ напряженно-деформированного состояния стыков сборных конструкций и «пластических шарниров», образовавшихся в результате разрушения материала в монолитных расчетных сечениях; |
|
Т1G15 |
- проверка окончания итерационного процесса по уточнению жесткостных характеристик конструкции на очередном этапе ее загружения; вычисление нагрузки следующего этапа в случае завершения итерационного процесса; |
|
T1G17 |
- вычисление новых геометрических характеристик расчетной схемы для перехода к следующему этапу загружения - завершающий этап реализации геометрической нелинейности расчетной схемы; |
|
T1G19 |
- учет наследственности деформированного состояния контактного слоя между обделкой и породой с запоминанием дифференциальных и интегральных компонент этого состояния; |
|
T1G20 |
- то же, что и T1G19, но с запоминанием только дифференциальных компонент деформаций контактного слоя; |
|
T1G21 |
- учет наследственности деформированного состояния расчетных сечений и конструкции в целом с запоминанием дифференциальных и интегральных компонент этого состояния; |
|
T1G22 |
- то же, что и Т1G21, но с запоминанием только дифференциальных компонент осевых и изгибных деформаций конструкций; |
|
T1G23 |
- анализ конструкции для выявления возможности достижения ею одного из предельных состояний; |
|
T1G24 |
- учет нелинейности деформативных свойств породы. |
Из рис. 3 видно, что алгоритм нелинейного расчета включает в себя 3 циклических процесса. В первом цикле реализован итерационный процесс по уточнению «зоны отлипания». Это уточнение проводится на каждом этапе загружения конструкции. Критерием завершения данного итерационного процесса является стабилизация деформированного состояния контактного слоя между породой и обделкой в соответствии с теорией местных деформаций.
Второй цикл реализует итерационный процесс уточнения жесткостных характеристик конструкции на каждом этапе ее загружения. Поскольку модули T1G13 и T1G14 в результате анализа напряженно-деформированного состояния расчетных сечений могут изменить их физико-механические характеристики, то модуль T1G15 проверяет, изменилась ли жесткость конструкции в целом относительно предыдущей итерации.
В случае расхождения между соседними итерациями, превышающего допустимую погрешность, управление передается последовательно блокам: T1G20, T1G22, T1G12 и T1G23, которые, осуществив свои вышеуказанные функции, либо передают управление модулю T1G02, либо прекращают расчет в случае достижения конструкцией одного из предельных состояний. Критерием окончания итерационного процесса во втором цикле является стабилизация жесткости конструкции. В случае достижения стабилизации управление передается третьему циклу. В этом цикле осуществляется учет геометрической нелинейности расчетной схемы (T1G17), учет наследственности деформированного состояния контактного слоя и самой конструкции (T1G19 и TIG21), анализируется конструкция по предельным состояниям (T1G23), учитывается нелинейность деформативных свойств породного массива (T1G24), вычисляется нагрузка следующего этапа загружения (T1G15), печатается таблица напряженно-деформированного состояния системы «порода - обделка» на данном этапе загружения (T1G12) и передается управление на анализ следующего этапа загружения (T1G06). Если модуль T1G23 выявит достижение конструкцией одного из предельных состояний, то расчет прекращается. Расчет прекращается и при достижении заданного в исходных данных максимального количества этапов загружения.
3. ПОДГОТОВКА ИСХОДНЫХ ДАННЫХ К РАСЧЕТУ
В настоящем обязательном приложении приводится единая инструкция: для расчета подземных конструкций в упругой (линейной) стадии и для нелинейного их расчета. При линейном расчете при подготовке исходных данных следует использовать первые 21 позицию общей инструкции: нумерация файлов ведется в первом левом столбце инструкции, представленной в табл. 2.
Для подготовки исходных данных необходимо знакомство с оператором «FORMAT» языка «ФОРТРАН». В частности, требуется знание описателей полей ввода для преобразования информации от внешнего представления к внутреннему.
Описание исходных данных приводится в последовательности их ввода в читающее устройство ЭВМ. Следует обратить особое внимание на нумерацию вводимых массивов (первая левая колонка таблицы - инструкции) - каждый номер в одном расчете может встречаться только один раз.
4. ФОРМИРОВАНИЕ ЗАДАНИЯ НА РАСЧЕТ
Расчет подземных конструкций по методу ЦНИИС производится на ЕС ЭВМ (ЕС-1033, ЕC-1045) по следующим двум программам:
T1GG2 - линейный расчет;
T1GNL - нелинейный расчет.
Для проведения линейного расчета на перфокартах формируется колода, включающая в себя следующие составные части:


Для проведения нелинейного расчета на перфокартах формируется колода, включающая в себя следующие составные части:

Таблица 2
|
Идентификатор |
Размерность |
Формат ввода |
Содержательный смысл |
Примечание |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
ОМ |
30 |
10F6.0 |
Общий массив |
Смысл каждой компоненты поясняется ниже |
|
OM(1) |
Количество нечетных точек расчетной схемы |
3 £ OM(1) £ 55 |
|||
|
OM(2) |
Признак режима работы блока Т1G08: |
При подготовке исходных данных надо задавать OM(2) = 0 |
|||
|
при OM(2) = 0 блок T1G08 вводит с перфокарт массивы K10, K30, КВ, SC, ЕР; |
|||||
|
при OM(2) ¹ 0 блок Т1G08 не вводит эти массивы, так как они уже находятся в области «COMMON» |
|||||
|
OM(3) |
Признак режима работы блока T1G23: |
При подготовке исходных данных надо задавать OM(3) = 0 |
|||
|
при OM(3) = 0 блок T1G23 вводит с перфокарт массивы NB и PR; |
|||||
|
при OM(3) ¹ 0 блок T1G23 не вводит эти массивы, так как они уже находятся в области «COMMON» |
|||||
|
OM(4) |
Признак наличия внутренних связей в конструкции: |
||||
|
при OM(4) = 0 в конструкции нет внутренних связей; |
|||||
|
при OM(4) = 1 в конструкции есть внутренние связи |
|||||
|
OM(5) |
Номер точки, лежащей на вертикальной оси симметрии нагрузки и конструкции |
Если симметрии нет, то OM(5) = 0 |
|||
|
OM(6) |
Номер точки, лежащей на горизонтальной оси симметрии конструкции и нагрузки |
Если симметрии нет, то OM(6) = 0 |
|||
|
OM(7) |
Номер этапа загружения |
При подготовке исходных данных для нелинейного расчета OM(7) = 1; для линейного расчета OM(7) = 0 |
|||
|
OM(8) |
Номер этапа загружения, с которого приращение нагрузки размельчается |
При линейном расчете OM(8) = 0 |
|||
|
OM(9) |
Число, во сколько раз размельчается приращение нагрузки с этапа, указанного в OM(8) |
При линейном расчете OM(9) = 0 |
|||
|
OM(10) |
Количество внутренних связей в конструкции |
||||
|
OM(11) |
Признак печати напряженно-деформированного состояния конструкции на промежуточных этапах итерационного процесса по уточнению «зоны отлипания»: |
||||
|
при OM(11) = 1 печать нужна; |
|||||
|
при OM(11) = 0 печать не нужна |
|||||
|
OM(12) |
Число участков, на которые разбита расчетная схема, с равномерным распределением расчетных сечений на них. Учитываются только нечетные точки |
Если расчетная ось задана координатами своих вершин, то OM(12) равно количеству нечетных вершин OM(1) |
|||
|
OM(13) |
Параметр оптимизации исходных данных |
Надо всегда задавать OM(13) = 90 |
|||
|
OM(14) |
Признак, указывающий тип нагрузки на подземную конструкцию: |
Задана только сосредоточенная в нечетных вершинах нагрузка: обязательно и вертикальная и горизонтальная |
|||
|
OM(14) = 1 |
|||||
|
OM(14) = 2 |
Задана только интенсивность нагрузки между нечетными вершинами: обязательно и вертикальная и горизонтальная |
||||
|
OM(14) = 3 |
Задана совместно нагрузка, которая указана для OM(14) = 1 и OM(14) = 2. Сначала вводится узловая нагрузка (вертикальная и горизонтальная), затем интенсивность |
||||
|
OM(14) = 4 |
Задана только узловая вертикальная нагрузка, т.е. горизонтальной нагрузки нет |
||||
|
OM(14) = 5 |
Задана только узловая горизонтальная нагрузка, т.е. вертикальной нагрузка нет. |
||||
|
OM(14) = 6 |
Задана только интенсивность вертикальной нагрузки между нечетными вершинами, т.е. горизонтальной нагрузки нет |
||||
|
OM(14) = 7 |
Задана только интенсивность горизонтальной нагрузки между нечетными вершинами, т.е. вертикальной нагрузки нет |
||||
|
OM(14) = 8 |
Задана совместно нагрузка, указанная при OM(14) = 4 и при OM(14) = 6 |
||||
|
OM(14) = 9 |
Задана совместно нагрузка, указанная при OM(14) = 5 и при OM(14) = 7 |
||||
|
OM(14) = 10 |
Задана совместно нагрузка, указанная при OM(14) = 4 и при OM(14) = 7 |
||||
|
OM(14) = 11 |
Задана совместно нагрузка, указанная при OM(14) = 5 и при OM(14) = 6 |
||||
|
OM(15) |
Количество опорных элементов Винклеровского основания, в которых допускается растяжение - точность определения «зоны отлипания» |
При абсолютной точности определения «зоны отлипания» надо задавать OM(15) = 0 |
|||
|
OM(16) |
Рабочая ячейка (ее занимать нельзя) |
Задавать OM(16) = 0 |
|||
|
OM(17) |
Признак режима работы блока T1G24: |
При нелинейном расчете задавать OM(17) = 0, если учитывается нелинейность работы породы по нормали к контуру, и OM(17) = 1, если не учитывается эта нелинейность. При линейном расчёте задавать OM(17) = 0 |
|||
|
при OM(17) = 0 блок T1G24 вводит с перфокарт массивы HK1 и SH1 (см. пп. 29 и 30); |
|||||
|
при OM(17) ¹ 0 эти массивы не вводятся, так как они уже находятся в области «COMMON» или их вообще нет |
|||||
|
OM(18) |
Второй признак режима работы блока T1G24: |
При нелинейном расчете задавать OM(18) = 0, если учитывается нелинейность работы породы по касательной к контуру, и OM(18) = 1, если не учитывается эта нелинейность. При линейном расчете задавать OM(18) = 0 |
|||
|
при OM(18) = 0 блок T1G24 вводит с перфокарт массивы GK1 и SK1 (см. пп. 31 и 32); |
|||||
|
при 0М(18) ¹ 0 эти массивы не вводятся, так как они уже находятся в области «COMMON» или их вообще нет |
|||||
|
OM(19) |
Рабочая ячейка |
Задавать OM(19) = 0 |
|||
|
OM(20) |
Признак работы блока T1G15: |
||||
|
при OM(20) = 1 расчет ведется на полную нагрузку; |
При нелинейном расчете задавать OM(20) = 1 |
||||
|
при OM(20) = 0 расчет ведется на приращение нагрузки |
При линейном расчете задавать OM(20) = 0 |
||||
|
OM(21) |
Признак бокового выхода блока T1G15: |
Задавать всегда OM(21) = 0 |
|||
|
при OM(21) = 0 блок T1G15 работает в обычной последовательности, т.е. передает управление блоку T1G17 (прямой выход); |
|||||
|
при OM(21) ¹ 0 блок T1G15 передает управление блоку T1G20 (боковой выход) |
|||||
|
OM(22) |
Максимальное число ступеней (этапов) загружения конструкции |
Это число регулирует максимальное время счета |
|||
|
OM(23) |
Признак печати выходной информации о состоянии четных вершин расчетной схемы: |
||||
|
при OM(23) = 0 надо печатать; |
|||||
|
при OM(23) = 1 не надо печатать |
|||||
|
OM(24) - OM(30) |
Резервные ячейки |
Задавать их равными 0 |
Продолжение таблицы
|
Порядковый номер файла |
Идентификатор |
Размерность |
Формат ввода |
Содержательный смысл |
Примечание |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
2 |
№ 2 |
OM(12) |
3012 |
Количество равных подучастков на каждом участке расчетной схемы с постоянным радиусом (учитываются только нечетные точки) |
Если расчетная ось задана координатами, то все компоненты массива № 2 задавать, равными 1. Вообще для i-го прямолинейного участка № 2 (i) = 1 |
|
3 |
RO |
OM(12) |
9Е7.3 |
Радиусы кривизны участков расчетной схемы. Размерность - метры |
Если расчетная ось задана координатами своих вершин, то все компоненты массива RO задавать равными 0. |
|
Вообще для i-го прямолинейного участка R0(i) = 0 |
|||||
|
4 |
X |
OM(12) |
9Е7.3 |
Абсциссы центров кривизны участков расчетной схемы. Размерность - метры |
Если расчетная ось задана координатами своих вершин, то массивы X и Y - массивы координат нечетных вершин расчетной схемы |
|
5 |
Y |
OM(12) |
9Е7.3 |
Ординаты центров кривизны участков расчетной схемы. Размерность - метры |
|
|
6 |
L (логический массив)» |
3´OM(1) |
60L1 |
Признаки наличия шарниров в конструкции и отсутствия упругих опор в нечетных вершинах расчетной схемы: |
|
|
L(1) = T - при отсутствии шарнира в 1-й вершине; |
|||||
|
L(1) = F - при наличии шарнира в 1-й вершине; |
|||||
|
L[2´OM(1) + J] = Т - при наличии Винклеровской опоры в J-й нечетной вершине: |
|||||
|
L[2´OM(1) + J] = F - при отсутствии Винклеровской опоры в J-й нечетной вершине |
|||||
|
7 |
№ 22 |
8 |
811 |
Признаки для последующей информации (см. пп. 8 - 15) |
Смысловое значение дается по каждой компоненте этого массива |
|
№ 22(1) |
№ 22(1) = 1, если массив AL весь нулевой, кроме признака размерности; |
См. п. 8 |
|||
|
№ 22(1) = 2, если массив AL не нулевой: вводится полностью, а перед ним признак размерности |
|||||
|
№ 22(2) |
№ 22(2) = 1, если массив Е постоянный по контуру конструкции; |
См. п. 10 |
|||
|
№ 22(2) = 2, если массив Е переменный по контуру конструкции |
|||||
|
№ 22(3) |
№ 22(3) = 1, если массив R постоянный по контуру конструкции; |
См. п. 11 |
|||
|
№ 22(3) = 2, если массив R переменный по контуру конструкции |
|||||
|
№ 22(4) |
№ 22(4) = 1, если массив F постоянный по контуру конструкции; |
См. п. 12 |
|||
|
№ 22(4) = 2, если массив F переменный по контуру конструкции |
|||||
|
№ 22(5) |
№ 22(5) = 1, если массив НК постоянный по контуру конструкции и не равен 0; |
См. п. 13 |
|||
|
№ 22(5) = 2, если массив НК переменный по контуру и ни одна из его компонент не равен 0 |
|||||
|
№ 22(6) |
№ 22(6) = 1, если массив GK постоянный по контуру и не равен 0 |
См. п. 14 |
|||
|
№ 22(6) = 2, если массив GK переменный по контуру и ни одна из его компонент не равна 0 |
|||||
|
№ 22(7) |
№ 22(7) = 1, если массив F1 не нулевой: |
См. п. 15 |
|||
|
№22(7) = 2, если массив F1 весь нулевой и вводить его не надо |
|||||
|
№ 22(8) |
№ 22(8) = 1, если нужна отладочная печать по исходной информации; |
||||
|
№ 22(8) = 2, если не нужна отладочная печать |
|||||
|
8 |
Если № 22(1) = 1, то AL(1) |
1 |
F2.0 |
Это число является признаком размерности массивов AL и AL1: |
|
|
AL(1) = 1, если углы задаются в градусах, минутах, секундах; |
|||||
|
AL(1) = 2, если углы задаются в радианах |
|||||
|
Если № 22(1) = 2, то AL (массив) |
OM(12) + 1 |
6F10.0 |
Центральные углы участков расчетной схемы. |
Первая компонента этого массива задается по вышеуказанному правилу |
|
|
Первая компонента этого массива - признак размерности, в которой задаются остальные компоненты этого массива. |
|||||
|
При AL(1) = 1 остальные компоненты этого массива задаются в условном формате: |
|||||
|
+ a1 a2 a3 a4 a5 a6 a7 a8 a9, |
|||||
|
где a1 - сотни градусов |
|||||
|
a2 - десятки градусов |
|||||
|
a3 - градусы |
|||||
|
a4 - десятки минут |
|||||
|
a5 - минуты |
|||||
|
a6 - десятки секунд |
|||||
|
a7 - секунды |
|||||
|
a8 - десятые доли секунд |
|||||
|
a9 - сотые доли секунд |
|||||
|
При AL(1) = 2, остальные компоненты массива задаются в радианах как вещественные десятичные числа в формате, указанном в столбце 4 |
|||||
|
9 |
AL1 |
OM(12) |
6F10.0 |
Углы направления нормалей к контуру конструкции в начальных точках каждого участка расчетной схемы |
Массив AL1 обязательно задается в тех же единицах, что и массив AL |
|
10 |
Если № 22(2) = 1 то E(1) |
1 |
P8.3 |
Постоянный по контуру приведенный модуль деформации сечений, вычисляемый по формуле
где I - номер расчетного сечения; J - номер слоя в сечении; K - число слоев в сечении (см. массив K30); Е(J) - модуль деформации J-го слоя; |
При линейном расчете Е(I) - постоянный по контуру конструкции модуль упругости ее материала |
|
Размерности: Е(I) и Е(J) - тс/м2 |
|||||
|
F(J) - м2 |
|||||
|
Если № 22(2) = 2 то Е (массив) |
2´OM(1) |
8F8.3 |
F(J) - площадь J-го слоя |
Вычисляются по вышеприведенной формуле. |
|
|
Значения переменного по контуру приведенного модуля деформаций расчетных сечений |
|||||
|
В случае линейного расчета - это массив значений переменного по контуру конструкции модуля упругости материала, ее составляющего |
Продолжение таблицы 2
|
11 |
Если № 22(3) = 1, то R(1) |
1 |
F10.5 |
Постоянный по контуру конструкции момент инерции расчетного сечения относительно его центра тяжести, вычисляемый по формуле
где I - номер расчетного сечения; J - номер слоя в сечении; K - число слоев в сечении (см. массив K30); Y(J) - расстояние J-го слоя от центра тяжести сечения; F(J) - площадь J-го слоя |
При линейном расчете R(I) - постоянный по контуру момент инерции сечения, вычисляемый по обычным формулам сопромата. |
|
|
Размерности: |
||||||
|
R(I) - м4 |
||||||
|
|
||||||
|
|
||||||
|
Координаты центра тяжести сечения вычисляются по формулам:
|
||||||
|
где |
координаты j-го слоя относительно нижней грани сечения; |
|||||
|
F(I) - площадь всего i-го сечения |
||||||
|
Если № 22(3) = 2, то R (массив) |
2´OM(1) |
6P10.5 |
Значения переменного по контуру момента инерции расчетных сечений относительно их центров тяжести |
Вычисляются по вышеприведенным формулам. Размерность - м4 |
||
|
12 |
Если № 22(4) = 1, то P(1) |
1 |
P10.5 |
Постоянная по контуру конструкции площадь расчетных сечений |
Размерность - м2 |
|
|
Если № 22(4) = 2, то P (массив) |
2´OM(1) |
6F10.5 |
Значения переменной по контуру конструкции площади поперечного сечения расчетных сечений конструкции |
Размерность - м2 |
||
|
13 |
Если № 22(5) = 1, то HK(1) |
1 |
F7.1 |
Постоянный по контуру конструкции коэффициент упругого отпора породы по нормали к контуру, не равный нулю |
Размерность - тс/м3. В случае отсутствия отпора на отдельных участках контура конструкции информация об этом задается в массиве L (см. п. 6) |
|
|
Если № 22(50) = 2, то HK(массив) |
OM(1) |
10P7.1 |
Значения переменного по контуру конструкции коэффициента упругого отпора породы по направлению нормали, не равного нулю |
Размерность - тс/м3. |
||
|
В случае отсутствия отпора на отдельных участках контура конструкции информация об этом задается в массиве L, а в массиве HK на этих участках задается значение отпора так же, как на соседних участках, где есть отпор |
||||||
|
Другой способ: |
||||||
|
в массиве L никакой информации об отсутствии отпора не давать |
||||||
|
в массиве НК соответствующие компоненты задавать равными 10 (условный нуль) |
||||||
|
14 |
Если № 22(6) = 1, то GK(1) |
1 |
F7.1 |
Постоянный по контуру конструкции коэффициент упругого отпора породы по направлению касательной к контуру, не равный нулю |
Размерность - тс/м3. В случае отсутствия отпора по касательному направлению надо задавать GK(1) = 10 |
|
|
Если № 22(6) = 2, то GK (массив) |
OM(1) |
10P7.1 |
Значения переменного по контуру коэффициента упругого отпора породы по направлению касательной к контуру конструкции, не равного нулю |
Размерность - тс/м3. В случае отсутствия отпора по касательной на отдельных участках контура, соответствующие компоненты массива GK надо задавать равными 10 |
||
|
15 |
Если № 22(7) = 1, то F1 |
OM(1) |
6P11.10 |
Угол отклонения нормальных опорных стержней от направления нормали при наличии трения обделки по породе. |
Размерность - радианы |
|
|
Значения компонент массива FI вычисляются по формуле |
||||||
|
FI(I) = 0,5´arctg(Ktp), где Ktp - коэффициент трения обделки по породе. |
||||||
|
Массив FI можно использовать в тех случаях, когда надо изменить направление нормальных опорных стержней в отдельных или во всех нечетных вершинах. Например, при расчете многосвязной конструкции может понадобиться изменить направление нормальных опорных стержней в местах примыкания внутренних связей к основному контуру конструкции |
||||||
|
Если № 22(7) = 2, то массив FI вводить не надо |
||||||
|
Если OM(14) = 1 |
||||||
|
16 |
P1 |
OM(1) |
8Е8.2 |
Вертикальные узловые нагрузки в нечетных вершинах расчетной схемы. |
Размерность - тонны. |
|
|
В нечетных вершинах расчетной схемы, в которых нагрузка отсутствует, надо задавать Р1(1) = 0 |
||||||
|
Правило знаков: сила считается положительной, если она направлена против положительного направления координатной оси 0Y; сила считается отрицательной, если она направлена вдоль положительного направления координатной оси 0Y |
||||||
|
17 |
Q1 |
OM(1) |
8Е8.2 |
Горизонтальные узловые нагрузки в нечетных вершинах расчетной схемы. |
Размерность - тонны. |
|
|
В нечетных вершинах расчетной схема, в которых нагрузка отсутствует, надо задавать Q1(1) = 0 |
||||||
|
Правило знаков: сила считается положительной, если она направлена против положительного направления координатной оси 0X; сила, направленная вдоль положительного направления оси 0X, считается отрицательной |
||||||
|
Если OM(14) = 2 |
||||||
|
16 |
Р2 |
OM(1) |
8Е8.2 |
Интенсивность вертикальной нагрузки на участках между нечетными вершинами расчетной схемы. |
Размерность - тс/м2. |
|
|
На участках без нагрузки надо задавать Р2(1) = 0 |
||||||
|
Правило знаков то же, что для P1 (см. выше) |
||||||
|
17 |
Q2 |
OM(1) |
8E8.2 |
Интенсивность горизонтальной нагрузки на участках между нечетными вершинами расчетной схемы. |
Размерность - тс/м2 |
|
|
На участках без нагрузки надо задавать Q2(1) = 0 |
||||||
|
Правило знаков то же, что для Q1 (см. выше) |
||||||
|
Если OM(14) = 3 |
||||||
|
16 |
P1 |
OM(1) |
8E8.2 |
см. P1 при OM(14) = 1 |
||
|
17 |
Q1 |
OM(1) |
8E8.2 |
см. Q1 при OM(14) = 1 |
||
|
18 |
P2 |
OM(1) |
8E8.2 |
см. Р2 при OM(14) = 2 |
||
|
19 |
Q2 |
OM(1) |
8E8.2 |
см. Q2 при OM(14) = 2 |
||
|
Если OM(14) = 4 |
||||||
|
16 |
P1 |
OM(1) |
8Е8.2 |
см. P1 при OM(14) = 1 |
||
|
Если OM(14) = 5 |
||||||
|
16 |
Q1 |
OM(1) |
8E8.2 |
см. Q1 при OM(14) = 1 |
||
|
Если OM(14) = 6 |
||||||
|
16 |
P2 |
OM(1) |
8E8.2 |
см. Р2 при OM(14) = 2 |
||
|
Если OM(14) = 7 |
||||||
|
16 |
Q2 |
OM(1) |
8E8.2 |
см. Q2 при OM(14) = 2 |
||
|
Если OM(14) = 8 |
||||||
|
16 |
P1 |
OM(1) |
8E8.2 |
см. P1 при OM(14) = 1 |
||
|
17 |
P2 |
OM(1) |
8E8.2 |
см. Р2 при OM(14) = 2 |
||
|
Если OM(14) = 9 |
||||||
|
16 |
Q1 |
OM(1) |
8E8.2 |
см. Q1 при OM(14) = 1 |
||
|
17 |
Q2 |
OM(1) |
8E8.2 |
см. Q2 при OM(14) = 2 |
||
|
Если OM(14) = 10 |
||||||
|
16 |
P1 |
OM(1) |
8E8.2 |
см. P1 при OM(14) = 1 |
||
|
17 |
Q2 |
OM(1) |
8E8.2 |
см. Q2 при OM(14) = 2 |
||
|
Если OM(14) = 11 |
||||||
|
16 |
Q1 |
OM(1) |
8E8.2 |
см. Q1 при OM(14) = 1 |
||
|
17 |
P2 |
OM(1) |
8E8.2 |
см. Р2 при OM(14) = 2 |
||
|
Если OM(10) ≠ 0 и OM(4) = 1 |
||||||
Продолжение таблицы 2
|
20 |
II1 |
OM(10) |
1513 |
Компоненты массива вычисляются по формуле |
||||||
|
II1(К) = (I + 1)/2, где К - порядковый номер компоненты массива II1 I - номер нечетной вершины, к которой примыкает внутренняя связь со стороны активной нагрузки |
||||||||||
|
21 |
K1 |
OM(10) |
1513 |
Компоненты массива K1 вычисляются по формуле K1(K) = (I1 + l)/2, где К - порядковый номер компоненты массива K1, совпадающий с номером К компоненты массива II1 |
||||||
|
I1 - номер нечетной вершины, к которой примыкает внутренняя связь со стороны пассивного отпора |
Компоненты массивов II1 и K1 с одинаковым порядковым номером должны относиться к одной и той же внутренней связи |
|||||||||
|
Если OM(10) = 0 и OM(4) = 0, то массивы II1 и K1 вводить не надо |
||||||||||
|
Дополнительная информация для нелинейного расчета |
||||||||||
|
22 |
K30 |
11 |
1114 |
K30(1) - число слоев, на которые разбиты расчетные сечения 1 ≠ K30(1) ≤ 20 |
Все компоненты этого массива располагать на одной перфокарте |
|||||
|
K30(2) - число вводимых диаграмм 1 ≤ K30(2) ≤ 4 |
||||||||||
|
K30(3) - количество компонент в диаграмме «σ - ε» с номером 1 |
||||||||||
|
K30(4) - количество компонент в диаграмме «σ - ε» с номером 2 |
||||||||||
|
K30(5) - количество компонент в диаграмме «σ - ε» с номером 3 |
||||||||||
|
K30(6) - количество компонент в диаграмме «σ - ε» с номером 4 |
||||||||||
|
K30(7) - количество компонент массива K10 5 ≤ K30(7) ≤ 2200 |
Подсчитывается при подготовке массива K10 |
|||||||||
|
K30(8) - количество компонент массива KB 5 ≤ K30(8) ≤ 2200 |
Подсчитывается при подготовке массива KB |
|||||||||
|
K30(9) - количество компонент массивов NB и РR 2 ≤ K30(9) ≤ 30 |
Подсчитывается при подготовке массивов NB и PR |
|||||||||
|
K30(10) - количество компонент массивов HK1 и SH1 0 ≤ K30(10) ≤ 20 |
Подсчитывается при подготовке массивов HK1 и SH1 |
|||||||||
|
K30(11) - количество компонент массивов GK1 и SK1 0 ≤ K30(11) ≤ 20 |
Подсчитывается при подготовке массивов GK1 и SK1 |
|||||||||
|
23 |
Sg |
K30(3) + K30(4) + K30(5) + K30(6), но не более 160 |
8P9.1 |
Значения напряжений σ для всех вводимых диаграмм «σ - ε». вводятся подряд (без перерыва) значения всех имеющихся диаграмм (от № 1 до № 4). Каждая диаграмма записывается слева направо: от максимальных по модулю отрицательных значений до максимальных положительных значений |
Размерность - тс/м2. |
|||||
|
Растягивающие напряжения должны иметь знак минус. |
||||||||||
|
Если проводится нелинейный расчет конструкции при линейной работе материала обделки, то надо вводить линейную диаграмму «σ - ε» |
||||||||||
|
24 |
Ep |
K30(3) + K30(4) + K30(5) + K30(6), но не более 160 |
8P9.1 |
Значения относительных деформаций Е для всех вводимых диаграмм «σ - ε». |
Безразмерные величины - доли единицы. |
|||||
|
Растягивающие деформации должны иметь знак минус. Если проводится нелинейный расчёт конструкции при линейной работе материала обделки, то надо вводить относительные деформации из линейной диаграммы «σ - ε». |
||||||||||
|
Вводятся подряд (без перерыва) значения всех имеющихся диаграмм (от № 1 до № 4) в строгом соответствии с последовательностью компонент массива Sg |
||||||||||
|
25 |
K10 |
K30(7) |
2014 |
Информация о номерах диаграмм «s - e» для всех слоев всех сечений. Может задаваться в виде двух форматов: Формат № 1 (5 целых положительных последовательных чисел) |
Форматом № 1 можно описать участки обделки, в которых номер диаграммы «s - e» постоянен по всей высоте сечения или его части. |
|||||
|
№ компоненты массива K10 |
Содержательный смысл |
Диапазон значений |
Содержательный смысл формата № 1: |
|||||||
|
на участке обделки от сечения a1 до сечения a2 слои от номера a3 до номера a4 имеют диаграмму«s - e» номер a5 |
||||||||||
|
1 |
2 |
3 |
||||||||
|
i |
Номер сечения начала участка a1 |
1 - 110 |
||||||||
|
i + 1 |
Номер сечения конца участка a2 |
1 - 110 |
||||||||
|
i + 2 |
Номер начального слоя в сечении a3 |
1 - 20 |
||||||||
|
i + 3 |
Номер конечного слоя в сечении a4 |
1 - 20 |
||||||||
|
i + 4 |
Номер диаграммы «s - e» a5 |
1 - 4 |
||||||||
|
Формат № 2 (3 последовательных целых числа, из которых первое - отрицательное) |
Форматом № 2 можно задавать номер диаграммы «s - e» в одном любом слое любого сечения обделки |
|||||||||
|
Содержательный смысл формата № 2: |
||||||||||
|
1 |
2 |
3 |
||||||||
|
i |
Номер сечения a1 |
от - 1 до - 110 |
в сечении a1, слой a2 имеет диаграмму «s - e» номер a3 |
|||||||
|
i + 1 |
Номер слоя a2 |
1 - 20 |
||||||||
|
i + 2 |
Номер диаграммы «s - e» a3 |
1 - 4 |
||||||||
|
26 |
KB |
K30(8) |
2014 |
Информация о ширине слоев всех сечении. Может задаваться в виде двух форматов. |
Форматом № 3 можно описать участки обделки, в которых ширина постоянна по всей высоте сечения или по его части |
|||||
|
Формат № 3 (5 целых положительных последовательных чисел). |
||||||||||
|
Содержательный смысл формата № 3: |
||||||||||
|
Первые четыре числа по форме и содержанию идентичны первым четырем числам формата № 1 для массива K10 |
||||||||||
|
на участке обделки от сечения a1 до сечения a2 слои от номера a3 до номера a4, имеют ширину a5, см |
||||||||||
|
Пятое число |
||||||||||
|
1 |
2 |
3 |
||||||||
|
i + 4 |
Ширина слоя в сантиметрах a5 (округлять до целого) |
1 - 999 |
||||||||
|
Формат № 4 (3 последовательных числа, из которых первое отрицательное) |
Форматом № 4 можно задать ширину одного любого слоя в любом сечении обделки |
|||||||||
|
Первые два числа по форме и содержанию идентичны первым двум числам формата № 2 для массива K10 |
||||||||||
|
Третье число |
Содержательный смысл формата № 4: |
|||||||||
|
1 |
2 |
3 |
в сечении a1 слой a2 имеет ширину a3, см |
|||||||
|
L + 2 |
a3 - ширина слоя в сантиметрах (округлять до целого) |
1 - 999 |
||||||||
|
27 |
NB |
K30(9) |
2613 |
Пары номеров вершин расчетной схемы, между которыми надо измерять расстояние и сравнивать с предельными величинами Структура массива NB |
Если при нелинейном расчете нет надобности проверять предельные общие деформации конструкции, то в массиве NB надо задать одну любую пару номеров вершин |
|||||
|
Номер компоненты массива |
Номер вершины расчетной схемы |
Примечания |
||||||||
|
X |
i |
} |
пара № 1 |
|||||||
|
X + 1 |
j |
|||||||||
|
X + 2 |
k |
} |
пара № 2 |
|||||||
|
X + 3 |
l |
|||||||||
|
... |
... |
... |
||||||||
|
K30(9) - 1 |
h |
} |
пара
|
|||||||
|
K30(9) |
g |
|||||||||
|
28 |
PR |
K30(9) |
13F6.3 |
Пары предельных величин (МАХ и MIN) для измерений расстояний между парами вершин, указанных в массиве NB |
Размерность: |
|||||
|
метры и их доли с точностью до тысячных. |
||||||||||
|
Значения МАХ задаются положительными, a MIN - отрицательными. Если МАХ или MTN не может быть задан, то их значения надо задавать равными нулю или очень большому числу (например 1000) |
||||||||||
|
Структура массива PR |
||||||||||
|
Номер компоненты массива PR |
Значение чисел |
Примечания |
||||||||
|
r |
a |
МАХ для пары № 1 |
||||||||
|
r + 1 |
b |
MIN для пары № 1 |
||||||||
|
r + 2 |
c |
МАХ для пары № 2 |
||||||||
|
r + 3 |
d |
MIN для пары № 2 |
||||||||
|
K30(9)-1 |
m1 |
МАХ
для пары |
||||||||
|
K30(9) |
n1 |
MIN для пары |
||||||||
|
29 |
HK1 |
K30(10) |
10P8.0 |
Таблица значений коэффициентов упругого, отпора по нормали к контуру в диаграмме «kн - sн» |
Размерность - тс/м3. |
|||||
|
Числа записывать с десятичной точкой |
||||||||||
|
Массив HK1 не может содержать нулей и располагается в порядке возрастания контактных давлений |
||||||||||
|
30 |
SH1 |
K30(10) |
10P8.0 |
Таблица значений контактных удельных давлений по нормали к контуру, соответствующих значениям массива HK1, массив SH1 не может содержать нулей |
Размерность - тс/м2. |
|||||
|
Записывать с десятичной точкой в порядке возрастания контактных давлений |
||||||||||
|
31 |
GK1 |
K30(11) |
10P8.0 |
Таблица значений коэффициента упругого отпора по касательной к контуру конструкции в диаграмме «KK - sk» |
Размерность - тс/м3 |
|||||
|
Правила задания массива с K1 те же, что у массива HK1 |
||||||||||
|
32 |
SK1 |
K30(11) |
10P8.0 |
Таблица значений контактных удельных давлений по касательной к контуру, соответствующих значениям массива GK1 |
Размерность - тс/м2. |
|||||
|
Правила задания массива SK1 те же, что у массива SH1 |
||||||||||
СПИСОК ЛИТЕРАТУРЫ
1. Волков В.П. и др. Тоннели и метрополитены М., Транспорт, 1975.
2. Тоннели и метрополитены. Методические указания по использованию ЭВМ при курсовом и дипломном проектировании для студентов специальности «Мосты и тоннели». М., ВЗИИТ, 1979.
СОДЕРЖАНИЕ