ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
РЕКОМЕНДАЦИИ |
Р 50.1.073-2010 |
Статистические методы
ПРИМЕРЫ ПРИМЕНЕНИЯ
Часть 2
Анализ данных на соответствие
установленным требованиям
|
|
Москва Стандартинформ 2011 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о рекомендациях
1 РАЗРАБОТАНЫ Автономной некоммерческой организацией «Научно-исследовательский центр контроля и диагностики технических систем» (АНО «НИЦ КД»)
2 ВНЕСЕНЫ Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»
3 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 12 ноября 2010 г. № 438-ст
4 ВВЕДЕНЫ ВПЕРВЫЕ
Информация об изменениях к рекомендациям публикуется в ежегодном указателе «Руководящие документы, рекомендации и правила», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящих рекомендаций соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Содержание
Введение
Серия рекомендаций по стандартизации «Статистические методы. Примеры применения» включает разъяснения по применению статистических методов в простой и доступной форме.
В рекомендациях представлены способы применения простых статистических методов и приемов, показано, как знание процесса производства может способствовать его улучшению, повышению эффективности, производительности и повышению качества изготавливаемой продукции.
Термин «статистический» обычно применяют по отношению к методам, связанным с обработкой числовых данных, относящихся к контролю качества продукции, управлению технологическими процессами, увеличению выпуска продукции и продаж, снижению затрат, и как следствие, стоимости продукции, а также к заработной плате. До применения конкретного статистического метода необходимо четко понимать его назначение, а также знать ответы на следующие вопросы: Зачем нужны статистические методы вообще? Что они собой представляют? Какую пользу может дать их применение? Где и когда может быть применен данный статистический метод и следует ли его применять? Ответы на эти вопросы целесообразно получить на конкретных примерах.
В настоящих рекомендациях показаны основные направления исследований при отборе выборки для проверки соответствия установленным требованиям. Показано практическое использование теоретических выводов математической статистики.
Р 50.1.073-2010
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
Статистические методы
ПРИМЕРЫ ПРИМЕНЕНИЯ
Часть 2
Анализ данных на соответствие установленным требованиям
Statistical methods. Examples of application. Part 2. Data analysis for compliance to requirements
Дата введения -2011-12-01
1 Область применения
В серии рекомендаций «Статистические методы. Примеры применения» приведены пояснения к использованию статистических методов, применяемых в менеджменте, контроле и улучшении процессов, с учетом требований ГОСТ Р ИСО/ТО 10017. В настоящих рекомендациях рассмотрены особенности отбора выборки продукции и анализа ее на соответствие установленным требованиям.
2 Нормативные ссылки
В настоящих рекомендациях использованы нормативные ссылки на следующие документы:
ГОСТ Р 50779.10-2000 Статистические методы. Вероятность и основы статистики. Термины и определения
ГОСТ Р 50779.11-2000 Статистические методы. Статистическое управление качеством. Термины и определения
Р 50.1.040-2002 Статистические методы. Планирование экспериментов. Термины и определения
ГОСТ Р ИСО 9000-2008 Системы менеджмента качества. Основные положения и словарь
ГОСТ Р ИСО/ТО 10017-2005 Статистические методы. Руководство по применению в соответствии с ГОСТ Р ИСО 9001
3 Термины и определения
В настоящих рекомендациях применены термины по ГОСТ Р 50779.10, ГОСТ Р 50779.11, Р 50.1.040 и ГОСТ Р ИСО 9000.
4 Общее описание задачи
В настоящих рекомендациях рассмотрены проблемы, возникающие при отборе выборки продукции для проверки их соответствия установленным требованиям. В этом случае является важным соотношение между объемом выборки и требованиями правил приемки к точности результатов измерений или испытаний.
Установленные требования могут быть заданы в виде минимального или максимального значения или в виде двух значений: минимального и максимального. Выполняя последовательные измерения в условиях устойчивого и точного процесса, нельзя быть уверенным, что результаты измерений или наблюдений будут идентичны. Отклонения результатов измерений во многом определяют свойства измерительного прибора. Следовательно, для получения адекватной оценки характеристики должно быть получено достаточно много результатов измерений, по которым получают не только выборочное среднее результатов, но и оценивают их однородность по разбросу данных вокруг этого среднего.
Из этого следует, что при проверке соответствия установленным требованиям на основе результатов измерений необходимо:
а) учитывать соотношение между выборочным средним, минимальным установленным значением и диапазоном значений результатов измерений;
б) использовать методы определения необходимого количества результатов наблюдений.
5 Результаты наблюдений и установленные предельные значения характеристики
Связь результатов наблюдений с установленными предельными значениями показана на следующем примере. В таблице 1 представлены результаты измерений массы одинаковых по размеру образцов, взятых из рулона ткани. Они сгруппированы в 32 пробы по 4 образца в каждой.
Таблица 1 - Масса образцов ткани (нижняя граница поля допуска составляет 98 г)
Единица измерения = 0,1 г
|
Масса образца, г |
№ выборки |
Масса образца, г |
№ выборки |
Масса образца, г |
№ выборки |
Масса образца, г |
|
|
1 |
101 99 100 102 |
5 |
96 97 100 96 |
9 |
104 102 95 100 |
13 |
95 94 97 100 |
|
2 |
106 98 101 99 |
6 |
101 96 97 97 |
10 |
98 101 99 107 |
14 |
102 100 100 95 |
|
3 |
98 101 102 100 |
7 |
109 100 106 101 |
11 |
99 98 99 99 |
15 |
97 101 102 98 |
|
4 |
103 104 95 96 |
8 |
92 97 100 95 |
12 |
109 101 105 102 |
16 |
103 101 99 100 |
Окончание таблицы 1
|
№ выборки |
Масса образца, г |
№ выборки |
Масса образца, г |
№ выборки |
Масса образца, г |
№ выборки |
Масса образца, г |
|
17 |
100 97 91 92 |
21 |
100 101 95 103 |
25 |
102 100 105 98 |
29 |
100 97 100 98 |
|
18 |
106 100 102 100 |
22 |
101 99 99 99 |
26 |
99 98 103 97 |
30 |
104 103 104 100 |
|
19 |
97 97 94 99 |
23 |
94 96 94 98 |
27 |
97 98 106 104 |
31 |
105 99 103 103 |
|
20 |
99 101 100 101 |
24 |
99 100 104 108 |
28 |
97 101 108 99 |
32 |
98 104 102 103 |
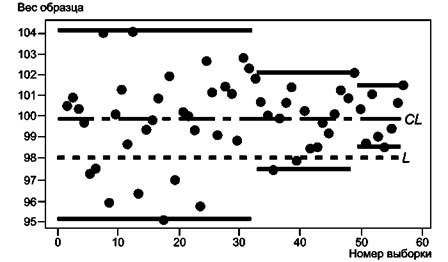
На рисунке 1 представлены данные таблицы 1 для трех способов формирования выборок:
а) 32 выборки по 4 образца в каждой (см. таблицу 1);
б) 6 выборок (33-48) по 8 образцов в каждой (составлены по данным таблицы 1);
в) 8 выборок(49-56) по 6 образцов в каждой (составлены поданным таблицы 1).
Примечание 1 - Отрезки горизонтальной прямой показывают максимальный диапазон изменения выборочных средних для объемов выборки 4, 8 и 16.
Примечание 2 - L - минимальное установленное значение характеристики.
Примечание 3 - CL - общее выборочное среднее.
Рисунок 1 - Выборочное среднее для трех объемов выборок (4, 8, 16).
На рисунке 2 показан размах для трех вариантов формирования выборок (см. таблицу 2) по данным таблицы 1:
а) выборки с номерами 1-32 включают в себя по 4 данных таблицы 1 (см. таблицу 2);
б) выборки с номерами 33-48 включают в себя по 8 данных таблицы 1 (см. таблицу 2);
в) выборки с номерами 49-56 включают в себя по 16 данных таблицы 1 (см. таблицу 2).
Пунктиром показан средний размах выборок с одинаковым объемом
Рисунок 2 - График размаха массы образца в выборке для трех вариантов объема выборок
Значения выборочных средних и размахов для трех вариантов формирования выборки приведены в таблице 2.