Статистические методы

СТАТИСТИКИ ПРИГОДНОСТИ
И ВОСПРОИЗВОДИМОСТИ ПРОЦЕССА
ДЛЯ КОЛИЧЕСТВЕННЫХ ХАРАКТЕРИСТИК
КАЧЕСТВА

ISO 21747:2006

Statistical methods - Process performance and capability statistics
for measured quality characteristics

(IDT)

Предисловие

Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»

Сведения о стандарте

1 ПОДГОТОВЛЕН Автономной некоммерческой организацией «Научно-исследовательский центр контроля и диагностики технических систем» (АНО «НИЦ КД») на основе собственного аутентичного перевода на русский язык международного стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 12 ноября 2010 г. № 439-ст

4 Настоящий стандарт идентичен международному стандарту ИСО 21747:2006 «Статистические методы. Статистики пригодности и воспроизводимости процесса для количественных характеристик качества» (ISO 21747:2006 «Statistical methods - Process performance and capability statistics for measured quality characteristics»).

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА

5 ВЗАМЕН ГОСТ Р 50779.44-2001

Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет

СОДЕРЖАНИЕ

Введение

Существует много стандартов, относящихся к оценке воспроизводимости и пригодности процессов. Однако все они предполагают, что процесс находится в состоянии статистической управляемости, а соответствующая характеристика качества подчиняется стационарному нормальному распределению. Анализ производственных процессов показывает, что процессы очень редко имеют нормальное распределение и стационарное состояние. Настоящий стандарт позволяет оценить воспроизводимость и пригодность производственного процесса для большой группы процессов, у которых первые и вторые моменты распределения постоянны или изменяются монотонно, или случайным образом. Анализ воспроизводимости и пригодности процесса может быть проведен для очень разных распределений, изменяющихся во времени.

Международный стандарт ИСО 21747 подготовлен ИСО/ТК 69 «Применение статистических методов».

ГОСТ Р ИСО 21747-2010

Статистические методы

СТАТИСТИКИ ПРИГОДНОСТИ И ВОСПРОИЗВОДИМОСТИ ПРОЦЕССА
ДЛЯ КОЛИЧЕСТВЕННЫХ ХАРАКТЕРИСТИК КАЧЕСТВА

Statistical methods.
Process performance and capability statistics for measured quality characteristics

1 Область применения

Настоящий стандарт устанавливает процедуру определения статистик, используемых для оценки характеристик качества процесса и продукции. Для результатов наблюдений рассмотрено восемь возможных моделей распределений. Приведены формулы вычисления статистик для каждой модели распределения.

Процедуры определения статистик распространяются только на непрерывные характеристики качества. Настоящий стандарт применим к любым процессам в сфере экономики или производственным процессам.

Примечание - Статистики воспроизводимости и пригодности процесса обычно применяют при наличии большого количества данных наблюдений, но они могут быть использованы и при наличии небольшого количества результатов измерений характеристик процесса.

2 Нормативные ссылки

В настоящем стандарте использована нормативная ссылка на следующий стандарт ИСО 9000:2005 Системы управления качеством. Основные принципы и словарь (ISO 9000:2005, Quality management systems - Fundamentals and vocabulary)

3 Термины и определения

В настоящем стандарте применены термины по ИСО 9000, а также следующие термины с соответствующими определениями.

3.1 характеристика качества (quality characteristic): Присущая продукции, процессу или системе характеристика, относящаяся к требованию.

Примечание 1 - Слово «присущая» означает «имеющаяся».

Примечание 2 - Назначенные характеристики продукции, процесса или системы (например, цена или владелец продукции) не являются характеристикой качества продукции, процесса или системы.

[ИСО 9000:2005, пункт 3.5.2]

3.1.1 Понятия, связанные с изменчивостью данных

3.1.1.1 изменчивость (variation): Свойство характеристики принимать различные значения.

Примечание - Изменчивость характеризуют среднеквадратическим отклонением.

[ИСО 3534-2:2006, пункт 2.2.1]

3.1.1.2 собственная изменчивость процесса (inherent process variation): Изменчивость (3.1.1.1), присущая наблюдаемой характеристике процесса¹⁾, когда он функционирует в состоянии статистической управляемости.

_____________

¹⁾ Часть наблюдаемой характеристики процесса является характеристика качества поставляемой процессом продукции.

Примечание 1 - Если в качестве показателя собственной изменчивости процесса используют среднеквадратическое отклонение (стандартное отклонение) наблюдаемой характеристики, его обозначают с индексом w (например, s_w, S_w или s_w).

Примечание 2 - Собственная изменчивость процесса отражает «изменчивость внутри подгруппы».

[ИСО 3534-2:2006, пункт 2.2.2]

3.1.1.3 полная изменчивость процесса (total process variation): Изменчивость процесса (3.1.1.1), вызванная как специальными (3.1.1.4), так и случайными причинами (3.1.1.5).

Примечание 1 - Если в качестве показателя полной изменчивости процесса используют среднеквадратическое отклонение, его обозначают с индексом t (например, s_t, S_t или s_t) (см. 3.1.3.1, примечание 3).

Примечание 2 - Полная изменчивость процесса отражает комбинацию «изменчивости в подгруппе» и «изменчивости между подгруппами».

[ИСО 3534-2:2006, пункт 2.2.3]

3.1.1.4 специальная причина (special cause): Причина изменчивости процесса, не являющаяся причиной собственной изменчивости процесса (3.1.1.2).

Примечание 1 - Иногда термин «специальная причина» используют в качестве синонима термину «устанавливаемая причина». Однако различие очевидно. Специальную причину вводят только, если она идентифицирована.

Примечание 2 - Специальная причина возникает вследствие конкретных обстоятельств, которые не всегда имеют место. Таким образом, под воздействием специальной причины изменчивость процесса время от времени может быть непредсказуемой.

[ИСО 3534-2:2006, пункт 2.2.4]

3.1.1.5 случайная причина, общая причина, непредсказуемая причина (random cause, common cause, chance cause): Причина, которая является причиной собственной изменчивости процесса в течение продолжительного интервала времени.

Примечание 1 - Для процесса изменчивость, вызванную случайными причинами, можно спрогнозировать в виде статистически установленных пределов.

Примечание 2 - Сокращение количества случайных причин способствует улучшению процесса. Идентификация, сокращение количества и устранение случайных причин является объектом анализа прибыли/затрат в технических и экономических аспектах.

[ИСО 3534-2:2006, пункт 2.2.5]

3.1.1.6 стабильный процесс, процесс в состоянии статистической управляемости (stable process, process in a state of statistical control): Процесс с постоянным средним, изменчивость которого вызвана только случайными причинами (3.1.1.5).

Примечание 1 - Для стабильного процесса выборки из процесса в любой момент времени являются случайными выборками из одной и той же генеральной совокупности.

Примечание 2 - Стабильность процесса не предполагает, что случайная изменчивость больше, меньше или соответствует требованиям, а лишь означает, что изменчивость (3.1.1.1) может быть спрогнозирована с помощью статистических методов.

Примечание 3 - Показатель воспроизводимости стабильного процесса (3.1.4.1) может быть улучшен за счет сокращения или устранения части случайных причин и/или корректировки среднего в сторону предпочтительного значения.

Примечание 4 - У некоторых процессов среднее контролируемой характеристики может иметь дрейф, а ее среднеквадратическое отклонение может возрастать, например, в случае износа инструмента или уменьшения концентрации раствора. Изменение среднего или среднеквадратического отклонения такого процесса рассматривают как следствие систематических, а не случайных причин. В этом случае результаты наблюдений не являются простыми случайными выборками из одной и той же генеральной совокупности.

[ИСО 3534-2:2006, пункт 2.2.7]

3.1.1.7 специальный критерий (out-of-control criteria): Набор правил, позволяющих принимать решение о наличии специальных причин (3.1.1.4)

Примечание - Правила принятия решения могут использовать наличие точек за пределами контрольных границ в серии данных, тренда контролируемых величин, наблюдаемых циклов и периодичности концентрации точек около центральной оси или контрольных границ, особенностей в расположении точек в пределах контрольных границ (большой или малый разброс) и соотношения значений характеристик разброса внутри подгрупп.

[ИСО 3534-2:2006, пункт 2.2.8]

3.1.2 Термины, относящиеся к воспроизводимости и пригодности процесса

3.1.2.1 распределение характеристики (distribution): Распределение вероятностей наблюдаемой характеристики, описывающее ее вероятностное поведение.

Примечание 1 - Распределение вероятностей наблюдаемой характеристики может быть представлено, например, в виде ранжированных результатов наблюдений или гистограммы, построенной по результатам наблюдений. Распределение вероятностей позволяет описать все свойства наблюдаемой характеристики за исключением последовательности, в которой получены данные.

Примечание 2 - Распределение характеристики зависит от преобладающих условий получения данных. Таким образом, для получения достоверной информации о распределении характеристики необходимо установить условия получения данных.

Примечание 3 - Важно знать вид распределения (нормальное, лог-нормальное и т.п.) до прогнозирования или оценки показателя воспроизводимости процесса, показателей его функционирования (пригодности), индексов или доли несоответствующих единиц продукции.

[3534-2:2006, пункт 2.5.1]

3.1.2.2 вид распределения (class of distributions): Группа распределений (3.1.2.1), имеющих общие параметры, полностью определяющие данную группу распределений.

Пример 1 - Двухпараметрическое симметричное унимодальное нормальное распределение с параметрами среднего и среднеквадратического отклонения.

Пример 2 - Распределение Вейбулла с тремя параметрами положения, формы и масштаба.

Пример 3 - Унимодальные непрерывные распределения.

Примечание - Часто вид распределения полностью определяется значениями параметров распределения.

[3534-2:2006, пункт 2.5.2]

3.1.2.3 модель распределения (distribution model): Конкретное распределение (3.1.2.1) или вид распределений (3.1.2.2).

Пример 1 - Моделью распределения такой характеристики продукции, как диаметр болта, может быть нормальное распределение со средним 15 мм и среднеквадратическим отклонением 0,05 мм. В данном случае модель полностью определена.

Пример 2 - Моделью распределения диаметра болта (см. пример 1) может быть нормальное распределение без указания конкретных параметров распределений. Здесь моделью является вся совокупность нормальных распределений.

[3534-2:2006, пункт 2.5.3]

3.1.2.4 верхняя доля несоответствующих единиц продукции; р_U (upper fraction nonconforming, р_U): Часть распределения (3.1.2.1), которой соответствуют значения характеристики больше верхней границы поля допуска (3.2.1.3) U.

Пример - Для нормального распределения со средним m и среднеквадратическим отклонением s:

                                               (1)

р_U - верхняя доля несоответствующих единиц продукции;

Ф - функция распределения нормированного нормального распределения;

U - верхняя граница поля допуска.

Примечание 1 - Использование таблицы или соответствующего пакета компьютерных программ для нормированного нормального распределения, позволяющих определить значения доли процесса вне установленного значения, например, границы поля допуска (3.2.1.2) в зависимости от среднеквадратического отклонения и среднего процесса, позволяет отказаться от построения функции распределения, данной в примере.

Примечание 2 - Функция распределения описывает теоретическое распределение. На практике эмпирическое распределение получают путем замены параметров распределения на их оценки.

[ИСО 3534-2:2006, пункт 2.5.4]

3.1.2.5 нижняя доля несоответствующих единиц продукции; p_L (lower fraction nonconforming, p_L): Часть распределения (3.1.2.1), которой соответствуют значения характеристики меньше нижней границы поля допуска L. (3.2.1.4).

Пример - Для нормального распределения (3.1.2.1) со средним m и среднеквадратическим отклонением s:

                                                             (2)

где p_L - нижняя доля несоответствующих единиц продукции;

Ф - функция распределения нормированного нормального распределения;

L - нижняя граница поля допуска.

Примечание 1 - Использование таблицы или соответствующего пакета компьютерных программ для нормированного нормального распределения, позволяющих определить значения доли процесса вне установленного значения, например, границы поля допуска (3.2.1.2) в зависимости от среднеквадратического отклонения и среднего процесса, позволяет отказаться от построения функции распределения, данной в примере.

Примечание 2 - Функция распределения описывает теоретическое распределение. На практике эмпирическое распределение получают путем замены параметров распределения на их оценки.

[3534-2:2006, пункт 2.5.5]

3.1.2.6 общая доля несоответствующих единиц продукции; p_t (total fraction nonconforming): Сумма верхней и нижней долей несоответствующих единиц продукции.

Пример - Для нормального распределения со средним m и среднеквадратическим отклонением s:

                                                    (3)

где p_t - общая доля несоответствующих единиц продукции;

Ф - функция распределения нормированного нормального распределения;

L - нижняя граница поля допуска;

U - верхняя граница поля допуска.

Примечание 1 - Использование таблицы или соответствующего пакета компьютерных программ для нормированного нормального распределения, позволяющих определить значения средней доли процесса вне установленного значения, например, границы поля допуска (3.2.1.2) в зависимости от среднеквадратического отклонения и среднего процесса, позволяет отказаться от построения функции распределения, данной в примере.

Примечание 2 - Функция распределения описывает теоретическое распределение. На практике эмпирическое распределение получают путем замены параметров распределения на их оценки.

[3534-2:2006, пункт 2.5.6]

3.1.2.7 опорный интервал (reference interval): Интервал, границами которого являются квантили X_99,865% и X_0,135% уровней значимости 99,865 % и 0,135 % соответственно.

Примечание 1 - Интервал представляют в виде (X_99,865%, X_0,135%), длина интервала равна разности (X_99,865% - X_0,135%).

Примечание 2 - Опорный интервал используют только для определения индекса пригодности процесса (3.1.3.2) и индекса воспроизводимости процесса (3.1.4.2).

Примечание 3 - Для нормального распределения (3.1.2.1) длина опорного интервала равна шести среднеквадратическим отклонениям (6s) или (6S), если оценку s определяют по выборке.

Примечание 4 - Для других распределений длину опорного интервала можно оценить с помощью соответствующей вероятностной бумаги (например, лог-нормальной) или на основе выборочных оценок коэффициентов эксцесса и асимметрии.

Примечание 5 - Квантиль указывает точку деления функции распределения в долях единицы или процентах. Определение квантили приведено в ИСО 3534-1.

[ИСО 3534-2:2006, пункт 2.5.7]

3.1.2.8 нижний опорный интервал (lower reference interval): Интервал, границами которого являются 50 %-ая и 0,135 %-ая квантили распределения X_50% и X_0,135%.

Примечание 1 - Нижний опорный интервал имеет вид (X_0,135%, Х_50%), а длина интервала равна разности (Х_50% - Х_0,135%).

Примечание 2 - Нижний опорный интервал используют только для определения нижнего индекса пригодности процесса (3.1.3.3) и нижнего индекса воспроизводимости процесса (3.1.4.3).

Примечание 3 - Для нормального распределения (3.1.2.1) длина нижнего опорного интервала равна трем среднеквадратическим отклонениям (3s) или, при неизвестном s, 3S, a Х_50% равна среднему и медиане.

Примечание 4 - Для других распределений 50 %-ная квантиль Х_50%, т.е. медиана, и 0,135 %-ная квантиль Х_0,135% могут быть оценены с помощью соответствующей вероятностной бумаги (например, лог-нормальной) или на основе выборочных оценок коэффициентов эксцесса и асимметрии.

[ИСО 3534-2:2006, пункт 2.5.8]

3.1.2.9 верхний опорный интервал (upper reference interval): Интервал, границами которого являются 99,865 %-ная - X_99,865%, и 50 %-ная - Х_50% квантили распределения.

Примечание 1 - Верхний опорный интервал имеет вид (Х_50%, X_99,865%), а длина интервала равна (X_99,865% - Х_50%).

Примечание 2 - Верхний опорный интервал используют только для определения верхнего индекса пригодности процесса (3.1.3.4) и верхнего индекса воспроизводимости процесса (3.1.4.4).

Примечание 3 - Для нормального распределения (3.1.2.1) длина верхнего опорного интервала равна трем среднеквадратическим отклонениям 3s или, при неизвестном s, 3S, а Х_50% равна среднему и медиане.

Примечание 4 - Для других распределений 50 %-ная квантиль распределения Х_50%, т.е. медиана, и 99,865 %-ная квантиль распределения Х_99,865% могут быть оценены с помощью соответствующей вероятностной бумаги (например, лог-нормальной) или на основе выборочных оценок коэффициентов эксцесса и асимметрии.

[ИСО 3534-2:2006, пункт 2.5.9]

3.1.3 Пригодность процесса по результатам измерений

3.1.3.1 показатель пригодности процесса (process performance): Статистический показатель выходной характеристики процесса, используемый для описания процесса, пребывание которого в состоянии статистической управляемости не подтверждено.

Примечание 1 - Выходная характеристика процесса - случайная величина, для которой необходимо определить вид распределения (3.1.2.1) и оценить его параметры.

Примечание 2 - При использовании данного показателя необходимо учитывать, что он может быть подвержен изменчивости, вызванной специальными причинами (3.1.1.4), размах которой, как правило, неизвестен.

Примечание 3 - Для нормального распределения оценка среднеквадратического отклонения S_t по одной выборке размера N имеет вид:

                                                                      (4)

где                                                                                                                                                                 (5)

Оценка S_t учитывает изменения, вызванные случайными причинами (3.1.1.5), а также любыми имеющимися специальными причинами. Оценку S_t используют вместо s_t для статистического описания изменчивости процесса. Объем выборки N может быть составлен из m более мелких выборок объемом п каждая.

Примечание 4 - В случае нормального распределения показатель пригодности процесса оценивают по формуле:

Показатель пригодности процесса =  ± (zS_t).

Значение z зависит от требуемого значения показателя пригодности процесса в единицах продукции на миллион. Обычно значение z равно 3, 4 или 5. Если показатель пригодности процесса соответствует установленным требованиям, значение z = 3 показывает, что в среднем 2700 объектов на миллион не соответствуют требованиям. Аналогично z = 4 показывает, что в среднем 64 объекта на миллион, а z = 5, что в среднем 0,6 объекта на миллион не соответствуют требованиям.

Примечание 5 - Для других распределений показатель пригодности процесса может быть оценен с помощью соответствующей вероятностной бумаги или по параметрам распределения соответствующих данных. Выражение для показателя пригодности процесса в этом случае имеет вид:

Показатель пригодности процесса =

Обозначение  имеет тот же смысл, что и допуски по отношению к номиналу или предпочтительному значению для контролируемой характеристики. Данное обозначение эквивалентно обозначению «+» для симметричных границ поля допуска. Это обозначение дает возможность проводить сравнение показателя пригодности процесса с установленными требованиями в терминах параметров положения и изменчивости.

[ИСО 3534-2:2006, пункт 2.6.1]

3.1.3.2 индекс пригодности процесса; Р_р (process performance index, P_р): Индекс, отражающий устойчивость процесса, стабильность которого не подтверждена относительно установленных границ.

Примечание 1 - Часто индекс пригодности процесса выражают в виде значения разности установленных границ поля допуска, деленного на длину опорного интервала (3.1.2.7):

                                                                            (6)

Примечание 2 - Для нормального распределения (3.1.2.1) длина опорного интервала равна 6S_t (см. 3.1.3.1, примечание 3).

Примечание 3 - Для других распределений длину опорного интервала можно оценить, используя выборочные оценки коэффициентов эксцесса и асимметрии.

[ИСО 3534-2:2006, пункт 2.6.2]

3.1.3.3 нижний индекс пригодности процесса; P_pkL (lower process performance index, P_pkL): Индекс, отражающий устойчивость процесса, стабильность которого не подтверждена относительно нижней границы поля допуска (3.2.1.4), L.

Примечание 1 - Обычно нижний индекс пригодности процесса выражают в виде разности 50 %-ной квантили распределения Х_50% и нижней границы поля допуска (3.2.1.4), деленной на длину нижнего опорного интервала (3.1.2.8):

                                                                       (7)

Примечание 2 - Для симметричного нормального распределения (3.1.2.1) длина нижнего опорного интервала равна 3S_t (см. 3.1.3.1, примечание 3), а Х_50% представляет собой среднее и медиану распределения.

Примечание 3 - Для других распределений длину нижнего опорного интервала можно оценить, используя выборочные оценки коэффициентов эксцесса и асимметрии, а Х_50% представляет собой медиану распределения.

[ИСО 3534-2:2006, пункт 2.6.3]

3.1.3.4 верхний индекс пригодности процесса; P_pkU (upper process performance index, P_pkU): Индекс, отражающий устойчивость процесса, стабильность которого не подтверждена по отношению к верхней границе поля допуска (3.2.1.3), U.

Примечание 1 - Обычно верхний индекс пригодности процесса выражают в виде разности верхней границы поля допуска и 50 %-ной квантили распределения Х_50%, деленной на длину верхнего опорного интервала (3.1.2.9):

                                                                          (8)

Примечание 2 - Для нормального распределения (3.1.2.1) длина верхнего опорного интервала равна 3S_t (см. 3.1.3.1, примечание 3), а Х_50% представляет собой среднее и медиану распределения.

Примечание 3 - Для других распределений длину верхнего опорного интервала можно оценить, используя выборочные оценки коэффициентов эксцесса и асимметрии, а Х_50% представляет собой медиану распределения.

[ИСО 3534-2:2006, пункт 2.6.4]

3.1.3.5 меньший индекс пригодности процесса; Р_рk (minimum process performance index, P_рk): Наименьший из верхнего (3.1.3.4) и нижнего (3.1.3.3) индексов пригодности процесса.

[ИСО 3534-2:2006, пункт 2.6.5]

3.1.4 Воспроизводимость процесса и результаты измерений

3.1.4.1 показатель воспроизводимости процесса (process capability): Статистический показатель процесса, находящегося в состоянии статистической управляемости, который позволяет оценить способность процесса поддерживать выходную характеристику качества процесса на уровне установленных для нее требований.

Примечание 1 - Для выходной характеристики необходимо определить вид распределения (3.1.2.1), которому она подчиняется, и оценить его параметры.

Примечание 2 - В случае нормального распределения оценку полного среднеквадратического отклонения процесса s_t можно определить по формуле для S_t (см. 3.1.3.1, примечание 3).

В некоторых случаях среднеквадратическое отклонение S_w, представляющее изменчивость в пределах только подгруппы, может быть использовано вместо S_t.

 или  или                                                      (9)

где  - среднее арифметическое размаха, вычисленное по т размахам подгрупп;

S_i - выборочная оценка среднеквадратического отклонения i-й подгруппы;

т - количество подгрупп объема п каждая;

d₂, с₄ - константы, соответствующие подгруппе объема п (см. ИСО 8258).

Для процесса в состоянии статистической управляемости оценки S_t и S_w сходятся. Таким образом, сравнение этих двух оценок позволяет оценить уровень стабильности процесса. Для неконтролируемого процесса с постоянным средним или для процесса с систематически изменяющимся средним (см. 3.1.1.6, примечание 4) значение S_w существенно занижает среднеквадратическое отклонение процесса.

Следовательно, оценку S_w необходимо использовать с большой осторожностью. Иногда оценка S_t является более предпочтительной, чем S_w из-за своих статистических свойств (например, более простого вычисления границ доверительного интервала).

Примечание 3 - В случае нормального распределения показатель воспроизводимости процесса можно оценить по формуле:

Показатель воспроизводимости процесса =  ± (zS_t),                                                                                  (10)

где                                                                                                                                                             (11)

- выборочное среднее i-й подгруппы. Оценка  аналогична  (см. 3.1.3.1, примечание 3).

Выбор значения z зависит от требуемого значения показателя воспроизводимости процесса в единицах продукции на миллион. Обычно z присваивают значения 3, 4 или 5. Если показатель воспроизводимости процесса соответствует установленным требованиям, z = 3 означает наличие в среднем 2700 единиц продукции на миллион за пределами требований.

Аналогично z = 4 означает наличие в среднем 64 единиц продукции, не соответствующих установленным требованиям, на миллион, a z = 5 означает наличие в среднем 0,6 таких единиц продукции на миллион.

Примечание 4 - Для других распределений показатель воспроизводимости процесса можно оценить, используя, например, соответствующую вероятностную бумагу или параметры распределения, соответствующие данным. Выражение для оценки показателя воспроизводимости процесса принимает в этом случае асимметричную форму:

показатель воспроизводимости процесса =

Обозначение  имеет тот же смысл, что и допуски по отношению к номиналу или предпочтительному значению для характеристики, когда верхние и нижние допуски различны. Данное обозначение эквивалентно обозначению «+» для симметричных границ поля допуска. Это обозначение дает возможность проводить сравнение показателя процесса с установленными требованиями в терминах параметров положения и разброса.

Примечание 5 - При использовании формулы  необходимо помнить, что оценка S_w:

- становится менее эффективной при увеличении объема подгрупп;

- чрезвычайно чувствительна к особенностям распределения;

- не позволяет легко определять границы доверительного интервала.

[ИСО 3534-2:2006, пункт 2.7.1]

3.1.4.2 индекс воспроизводимости процесса; С_р (process capability index, С_p): Индекс, отражающий устойчивость стабильного процесса (3.1.4.1) относительно установленных границ поля допуска.

Примечание 1 - Часто индекс воспроизводимости процесса выражают в виде разности границ установленного поля допуска, деленной на длину опорного интервала (3.1.2.7) для процесса в состоянии статистической управляемости (3.1.1.6):

                                                                     (12)

Примечание 2 - Для нормального распределения (3.1.2.1) длина опорного интервала равна 6S (см. 3.1.4.1, примечания).

Примечание 3 - Для других распределений длину опорного интервала можно оценить, используя выборочные оценки коэффициентов эксцесса и асимметрии.

[ИСО 3534-2:2006, пункт 2.7.2]

3.1.4.3 нижний индекс воспроизводимости процесса; C_pkL (lower process capability index, C_pkL): Индекс, отражающий устойчивость стабильного процесса относительно нижней границы поля допуска (3.2.1.4), L.

Примечание 1 - Часто нижний индекс воспроизводимости процесса выражают в виде разности 50 %-ной квантили распределения Х_50% и нижней границы поля допуска, деленной на длину нижнего опорного интервала (3.1.2.8) для процесса в состоянии статистической управляемости (3.1.1.6):

                                                                       (13)

Примечание 2 - Для нормального распределения (3.1.2.1) длина нижнего опорного интервала равна 3S (см. 3.1.4.1, примечания), а Х_50% представляет собой среднее и медиану.

Примечание 3 - Для других распределений нижний опорный интервал можно оценить, используя выборочные оценки коэффициентов эксцесса и асимметрии, а Х_50% представляет собой медиану.

[ИСО 3534-2:2006, пункт 2.7.3]

3.1.4.4 верхний индекс воспроизводимости процесса; C_pkU (upper process capability index, С_pkU): Индекс, отражающий устойчивость стабильного процесса относительно верхней границы поля допуска, (7(3.2.1.3).

Примечание 1 - Обычно, верхний индекс воспроизводимости процесса выражают в виде разности верхней границы поля допуска и 50 %-ной квантили распределения Х_50%, деленной на длину верхнего опорного интервала (3.1.2.9) для процесса в состоянии статистической управляемости (3.1.1.6):

                                                                    (14)

Примечание 2 - Для нормального распределения (3.1.2.1) длина верхнего опорного интервала равна 3S (см. 3.1.4.1, примечания), а Х_50% представляет собой среднее и медиану.

Примечание 3 - Для других распределений длину верхнего опорного интервала можно оценить, используя выборочные оценки коэффициентов эксцесса и асимметрии, а Х_50% представляет собой медиану.

[ИСО 3534-2:2006, пункт 2.7.4]

3.1.4.5 меньший индекс воспроизводимости процесса; C_pk (minimum process capability index): Наименьший из верхнего (3.1.4.4) и нижнего (3.1.4.3) индексов воспроизводимости процесса.

[ИСО 3534-2:2006, пункт 2.7.5]

3.2 Требования, значения и результаты испытаний

3.2.1 Понятия, относящиеся к требованиям

3.2.1.1 спецификация (specification): Документ, устанавливающий требования.

[ИСО 9000:2005, пункт 3.7.3]

Примечание 1 - Документ, содержащий информацию о требованиях, может быть размещен на бумажном носителе, компьютерном диске или представлять собой образец изделия.

Примечание 2 - Обычно для этого термина необходимы уточнения. Примерами спецификаций являются спецификации на продукцию, процесс и функциональная спецификация.

Примечание 3 - В выборочном контроле при приемке партия может быть принята, поскольку она соответствует критериям приемки партии, но некоторые единицы продукции в выборке или партии могут не соответствовать требованиям к продукции.

Примечание 4 - По возможности требования необходимо выражать количественно в соответствующих единицах с границами поля допуска. В противном случае необходимо устанавливать критерий, применяемый для экспертизы и принятия решения при контроле. Критерий может быть задан в виде эталонного экземпляра продукции, эталонной выборки или фотографии. Критерий показывает минимально приемлемую или неприемлемую продукцию, вид и/или степень несоответствия, которые недопустимы.

3.2.1.2 граница поля допуска (specification limit): Предельное значение, установленное для характеристики.

[ИСО 3534-2:2006, пункт 3.1.3]

3.2.1.3 верхняя граница поля допуска; U (upper specification limit, U): Граница поля допуска (3.2.1.2), определяющая верхнее предельно допустимое значение.

[ИСО 3534-2:2006, пункт 3.1.4]

3.2.1.4 нижняя граница поля допуска; L (lower specification limit, L): Граница поля допуска (3.2.1.2), определяющая нижнее предельно допустимое значение.

[ИСО 3534-2:2006, пункт 3.1.5]

3.2.1.5 поле допуска (specified tolerance): Зона между верхней (3.2.1.3) и нижней границами поля допуска (3.2.1.4).

[ИСО 3534-2:2006, пункт 3.1.6]

4 Обозначения и сокращения

В настоящем стандарте применены следующие обозначения и сокращения:

а - дополнительные флуктуации;

С_р - индекс воспроизводимости процесса;

С_рк - меньший индекс воспроизводимости процесса;

C_pkL - нижний индекс воспроизводимости процесса;

С_рkU - верхний индекс воспроизводимости процесса;

с₄ - константа, соответствующая подгруппе объема п (см. ИСО 8258);

D - характеристика изменчивости процесса (см. раздел 7);

d₂ - константа, соответствующая подгруппе объема п (см. ИСО 8258);

т - количество подгрупп объема п каждая;

m - параметр положения процесса (см. раздел 7);

L - нижняя граница поля допуска;

N - объем выборки;

p_L - нижняя доля несоответствующих единиц продукции;

p_t - общая доля несоответствующих единиц продукции;

p_U - верхняя доля несоответствующих единиц продукции;

Р_р - индекс пригодности процесса;

Р_рk - меньший индекс пригодности процесса;

P_pkL - нижний индекс пригодности процесса;

Р_pkU - верхний индекс пригодности процесса;

R - размах;

s - оценка среднеквадратического отклонения по результатам наблюдений;

s - среднеквадратическое отклонение совокупности (истинное);

S - выборочная оценка среднеквадратического отклонения, выборочная статистика;

S_i - выборочная оценка среднеквадратического отклонения i-й подгруппы;

S_t - оценка среднеквадратического отклонения, характеризующая полную изменчивость процесса (см. 3.1.1.3);

S_w - оценка среднеквадратического отклонения, характеризующая собственную изменчивость процесса (см. 3.1.1.2);

SPC - статистическое управление процессом;

U - верхняя граница поля допуска;

Х_L - нижняя контрольная граница;

Х_U - верхняя контрольная граница;

Х_50% - 50 %-ная квантиль распределения;

z_a - квантиль нормированного нормального распределения уровня a;

Ф - функция распределения нормированного нормального распределения.

5 Анализ процесса

Целью анализа процесса является получение знаний о процессе, которые необходимы для эффективного управления процессом и обеспечения требуемого качества продукции, для изготовления которой предназначен процесс. В настоящем стандарте предполагается, что анализ процесса выполнен, и необходимые улучшения процесса осуществлены.

Значения исследуемых характеристик обычно определяют на основе выборок, отобранных при функционировании процесса. Объем и частота отбора выборок должны быть установлены в зависимости от особенностей процесса и продукции таким образом, чтобы все важные изменения были обнаружены вовремя. Выборки должны быть представительными для исследуемой характеристики.

Поведение исследуемой характеристики может быть описано распределением и параметрами положения, изменчивости и формы, которые в общем случае являются функциями времени. Различные модели распределений, параметры которых являются функциями времени, рассмотрены в разделах 6 и 7. Для проверки соответствия модели распределения, зависящего от времени, результатам наблюдений используют статистические методы [например методы оценки параметров, дисперсионный анализ (ANOVA)], включая графические (например, вероятностную бумагу, контрольные карты).

6 Модели распределений, зависящих от времени

Для определения мгновенного состояния параметров распределения исследуют поведение характеристики за короткий интервал времени. Обычно это интервал времени, в течение которого отбирают выборку (например, подгруппу). Наблюдение процесса в течение более продолжительного интервала времени позволяет получить распределение объединенной выборки продукции для соответствующего процесса и описать его моделью зависимости распределения от времени, которая отражает:

- мгновенное распределение исследуемой характеристики;

- изменение параметров положения, изменчивости и формы за период наблюдения процесса. На практике это распределение может быть представлено целым набором данных, например при применении SPC всеми подгруппами, отобранными за период наблюдения процесса.

Модели зависимости распределений от времени могут быть отнесены к одной из четырех групп в зависимости от того, являются ли параметры положения¹⁾ и изменчивости постоянными или меняющимися.

_____________

¹⁾ Параметр распределения, характеризующий положение функции распределения на числовой оси. Часто параметром положения являются математическое ожидание или медиана. Для нормального распределения параметром положения является математическое ожидание.

a) Модель А описывает процесс, у которого параметры положения и изменчивости являются постоянными во времени. Только в этом случае все мгновенные распределения совпадают с распределением объединенной выборки.

b) Модель В описывает процесс, у которого параметр изменчивости процесса изменяется во времени, а параметр положения остается постоянным.

c) Модель С описывает процесс, у которого параметр изменчивости является постоянным, а параметр положения изменяется во времени.

d) Все остальные процессы описывает модель D.

Модели могут быть далее классифицированы по типу изменения моментов распределения в зависимости от того, являются ли изменения случайными и/или систематическими.

В таблице 1 приведены основные характеристики моделей зависимости распределений от времени. Их графические представления приведены на рисунках 1 - 8. Существуют подклассы моделей распределений А и С, которые введены из-за их широкого практического применения. Они отличаются по виду распределения и наличием/отсутствием состояния статистической управляемости.

На приведенных ниже рисунках для каждой модели зависимости распределения от времени показано несколько мгновенных распределений и соответствующее распределение объединенной выборки. Эти распределения изображены без учета масштаба.

Таблица 1 - Основные характеристики моделей зависимости распределений от времени

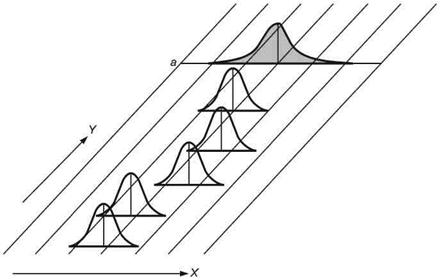
Для модели А1 (см. рисунок 1) характерны следующие особенности (например, распределение результатов измерений характеристики качества единицы продукции, процесс изготовления которой находится в состоянии статистической управляемости):

- параметр положения постоянен;

- параметр изменчивости постоянен;

- мгновенное распределение нормальное;

- распределение объединенной выборки нормальное.

Данный процесс находится в состоянии статистической управляемости.

X - контролируемая характеристика; Y - время; а - распределение объединенной выборки

Рисунок 1 - Графическое представление зависимости распределения от времени (модель А1)

Для модели А2 (см. рисунок 2) характерны следующие особенности (например, определение шероховатости поверхности в качестве контролируемой характеристики):

- параметр положения постоянен;

- параметр изменчивости постоянен;

- мгновенное распределение унимодальное (не нормальное);

- распределение объединенной выборки унимодальное (не нормальное).

Данный процесс находится в состоянии статистической управляемости.

X - контролируемая характеристика; Y - время; а - распределение объединенной выборки

Рисунок 2 - Графическое представление зависимости распределения от времени (модель А2)

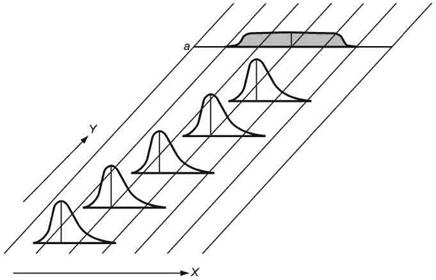
Для модели В (см. рисунок 3) характерны следующие особенности (например, различный износ шпинделей на автомате с несколькими шпинделями и общей осью вращения):

- параметр положения постоянен;

- параметр изменчивости изменяется систематически или случайным образом;

- мгновенное распределение нормальное;

- распределение объединенной выборки унимодальное (не нормальное).

X - контролируемая характеристика; Y - время; а - распределение объединенной выборки

Рисунок 3 - Графическое представление зависимости распределения от времени (модель В)

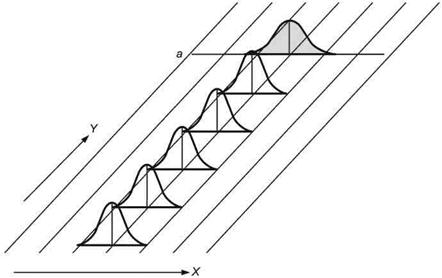
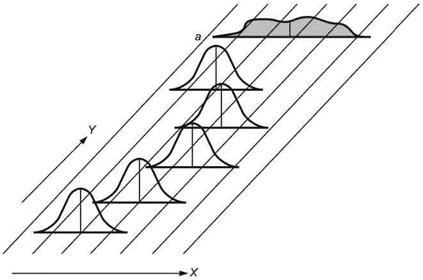
Для модели С1 (см. рисунок 4) характерны следующие особенности (например, при различном центрировании заготовки):

- параметр положения случайный (нормальное распределение);

- параметр изменчивости постоянный;

- мгновенное распределение нормальное;

- распределение объединенной выборки нормальное.

X - контролируемая характеристика; Y - время; а - распределение объединенной выборки

Рисунок 4 - Графическое представление зависимости распределения от времени (модель С1)

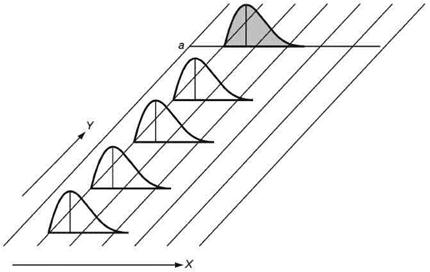
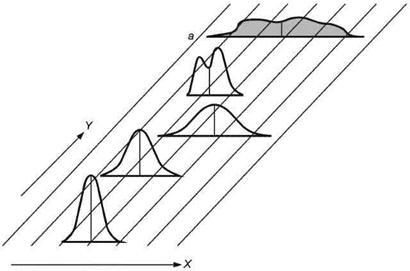
Для модели С2 (см. рисунок 5) характерны следующие особенности (например, невращающийся инструмент):

- параметр положения случайный (распределение не нормальное, унимодальное);

- параметр изменчивости постоянный;

- мгновенное распределение нормальное;

- распределение объединенной выборки (не нормальное, унимодальное).

X - контролируемая характеристика; Y - время; а - распределение объединенной выборки

Рисунок 5 - Графическое представление зависимости распределения от времени (модель С2)

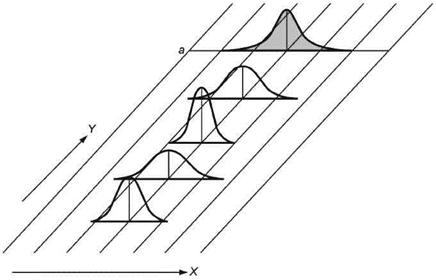
Для модели С3 (см. рисунок 6) характерны следующие особенности:

- параметр положения является функцией времени (например, при изнашивании инструмента или в случае циклических процессов);

- параметр изменчивости постоянен;

- мгновенное распределение любое;

- распределение объединенной выборки любое.

X - контролируемая характеристика; Y - время; а - распределение объединенной выборки

Рисунок 6 - Графическое представление зависимости распределения от времени (модель С3)

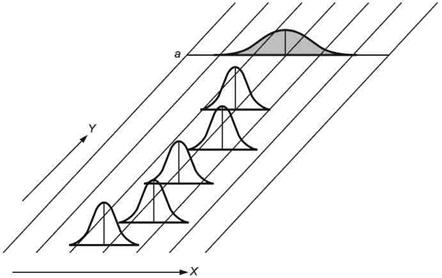
Для модели С4 (см. рисунок 7) характерны следующие особенности:

- параметр положения изменяется систематически и случайным образом (например, смена партий);

- параметр изменчивости постоянен;

- мгновенное распределение любое;

- распределение объединенной выборки любое.

X - контролируемая характеристика; Y - время; а - распределение объединенной выборки

Рисунок 7 - Графическое представление зависимости распределения от времени (модель С4)

Для модели D (см. рисунок 8) характерны следующие особенности (например, многопоточные процессы):

- параметр положения изменяется систематически и случайным образом;

- параметр изменчивости изменяется систематически и случайным образом;

- мгновенное распределение любое;

- распределение объединенной выборки любое.

X - контролируемая характеристика; Y - время; а - распределение объединенной выборки

Рисунок 8 - Графическое представление зависимости распределения от времени (модель D)

7 Индексы воспроизводимости и пригодности процесса

7.1 Методы определения индексов воспроизводимости и пригодности процесса. Краткий обзор

Определение индексов воспроизводимости и пригодности процесса основано на информации о распределении контролируемой характеристики продукции.

При вычислении индексов воспроизводимости и пригодности процесса учитывают положение контролируемой характеристики относительно границ поля допуска. Для вычислений индексов применяют четыре метода вычислений (см. таблицу 2).

Таблица 2 - Методы определения индексов воспроизводимости и пригодности процессов

7.2 Общий геометрический метод (М1_l,d)

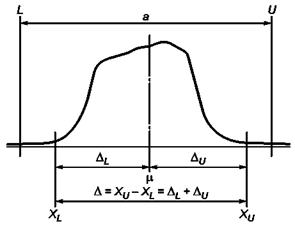
а - поле допуска шириной (U - L)

Рисунок 9 - Графическое представление общего геометрического метода М1

На рисунке 9m - параметр положения процесса, D - параметр изменчивости процесса. Их точные определения в зависимости от метода будут приведены ниже. Параметр изменчивости связан с границами поля допуска и значениями контролируемой характеристики X_L и Х_U:

D_L = m - X_L,                                                              (15)

D_U = Х_U - m.                                                               (16)

Индексы пригодности процесса представляют собой дробь.

Индекс пригодности процесса:                                                                  (17)

Нижний индекс пригодности процесса:                                                 (18)

Верхний индекс пригодности процесса:                                               (19)

Меньший индекс пригодности процесса: P_pk = min(P_pkL, P_pkU).                                 (20)

Если доказано, что процесс находится в состоянии статистической управляемости, может быть применен индекс воспроизводимости процесса. Формулы для определения индекса воспроизводимости процесса аналогичны (17) - (20).

Индекс воспроизводимости процесса:                                                    (21)

Нижний индекс воспроизводимости процесса:                                   (22)

Верхний индекс воспроизводимости процесса:                                  (23)

Меньший индекс воспроизводимости процесса: C_pk = min (C_pkL, C_pkU).                   (24)

Существуют различные оценки для параметров положения μ и изменчивости А на основе имеющегося набора данных.

ВНИМАНИЕ - Следует помнить, что количественное сравнение индексов пригодности и воспроизводимости процесса, вычисленных в соответствии с различными методами, невозможно.

Оценка  параметра положения процесса может быть получена одним из приведенных ниже способов:

Способ 1 (в обозначении метода l = 1)

                                                          (25)

где х_i - i-ое наблюдаемое значение;

п - количество наблюдений.

Способ 2 (в обозначении метода l = 2)

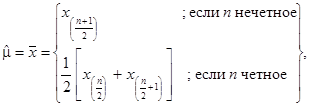                                 (26)

где х_(j) - j-я порядковая статистика.

Способ 3 (в обозначении метода l = 3)

                                                               (27)

Способ 4 (в обозначении метода l = 4)

                                                           (28)

где  - среднее арифметическое i-й подгруппы;

т - количество подгрупп объема п.

Способ 5 (в обозначении метода l = 5)

                                                        (29)

где  - медиана i-й подгруппы;

т - количество подгрупп объема п.

Оценку  параметра изменчивости процесса D можно определить одним из приведенных ниже способов:

Способ 1 (в обозначении метода d = 1)

                                                    (30)

где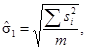

 - оценка дисперсии i-й подгруппы;

m - количество подгрупп объема п.

Способ 2 (в обозначении метода d = 2)

                                                  (31)

где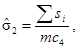

s_i - оценка среднеквадратического отклонения i-й подгруппы;

m - количество подгрупп объема п.

Значения с₄ определяют по таблице ИСО 8258.

Способ 3 (в обозначении метода d = 3)

                                                   (32)

где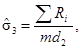

R_i - размах i-й подгруппы;

R = X_U - X_L;

m - число подгрупп объема п.

Значения d₂ определяют по таблицам ИСО 8258.

Способ 4 (в обозначении метода d = 4)

                                                   (33)

где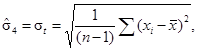

s_t - среднеквадратическое отклонение всего набора данных.

Способ 5 (в обозначении метода d = 5)

                                     (34)

Способ 6 (в обозначении метода d = 6)

                          (35)

Примечание 1 - Оценки  при использовании формул (30) - (32) учитывают только разброс в подгруппе, но не учитывают разброс между подгруппами. Эти оценки следует использовать только для модели А1.

Примечание 2 - Оценки  при использовании формул (30) - (33) предполагают, что данные подчиняются нормальному распределению. В случае других распределений оценка  является смещенной.

Примечание 3 - Оценка  при использовании формулы (34) является смещенной. Смещение зависит от вида распределения и объема подгруппы.

Примечание 4 - Оценка  при использовании формулы (35) является наиболее общей и может быть использована во всех случаях,  является длиной опорного интервала.

7.3 Учет дополнительной изменчивости (M2_l,d,а)

Метод является модификацией первого метода, но позволяет учесть дополнительные изменения среднего m_add. Оценки D при использовании формул (30), (31), (32) позволяют учесть только собственную изменчивость в подгруппах. Данный метод позволяет оценить дополнительную изменчивость между подгруппами (модели процесса С и D).

Индекс пригодности процесса:                                                            (36)

Нижний индекс пригодности процесса: 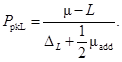                                     (37)

Верхний индекс пригодности процесса: 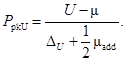                                   (38)

Меньший индекс пригодности процесса: P_pk = min(P_pkL, P_pkU).                               (39)

Методы оценки параметров положения и изменчивости D те же, что и в подходе М1. Кроме того, имеется возможность оценить дополнительную изменчивость:

- определить оценки  для m_add;

- оценить изменчивость между различными подгруппами.

Данный метод должен быть использован только в комбинации с одной из оценок D при использовании формул (30), (31), (32), которая не учитывает изменчивость между подгруппами

а = 1,                                               (40)

где  - выборочное среднее i-й подгруппы.

а = 2,  вычисляют методами дисперсионного анализа (ANOVA).                     (41)

7.4 Альтернативный метод учета дополнительной изменчивости (М3_l,d,a)

Данный метод аналогичен предыдущему, но дополнительную изменчивость учитывает иначе. Индекс пригодности процесса:     (42)

Нижний индекс пригодности процесса: 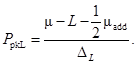                                  (43)

Верхний индекс пригодности процесса: 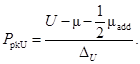                                 (44)

Меньший индекс пригодности процесса: P_pk = min(P_pkL, P_pkU).                                (45)

7.5 Вычисление доли несоответствующих единиц продукции (М4)

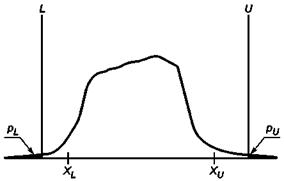
Для данных вычислений модель зависимости распределения от времени должна быть известна (см. рисунок 10).

Рисунок 10 - Графическое представление метода вычислений М4

Нижняя (p_L) и верхняя (р_U) доли несоответствующих единиц продукции представляют собой площадь под плотностью распределения левее нижней и правее верхней границ поля допуска.

Нижний индекс пригодности процесса:                                               (46)

Верхний индекс пригодности процесса:                                              (47)

Меньший индекс пригодности процесса: Р_рк = min(P_pkL, P_pkU),                                (48)

где z_a - квантиль нормированного нормального распределения уровня a.

Если процесс находится в состоянии статистической управляемости, может быть применен индекс воспроизводимости процесса. Соответствующие формулы аналогичны (46) - (48).

Нижний индекс воспроизводимости процесса:                                 (49)

Верхний индекс воспроизводимости процесса:                                (50)

Меньший индекс воспроизводимости процесса: C_pk = min(C_pkL, C_pkU).                  (51)

Вычислить индексы Р_р или С_р этим методом невозможно.

7.6 Односторонние границы поля допуска

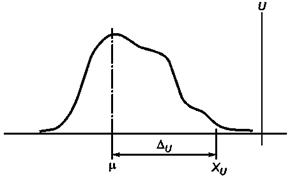
В случае односторонних границ поля допуска расчеты выполняют аналогичным образом (см. рисунок 11).

Рисунок 11 - Графическое представление метода вычисления D_U

В случае одностороннего поля допуска с установленной верхней границей применяют формулы (52) - (55).

Верхний индекс пригодности процесса:                                            (52)

Меньший индекс пригодности процесса: P_pk = Р_рkU.                                                 (53)

Если процесс находится в состоянии статистической управляемости, может быть применен индекс воспроизводимости процесса. Формулы - аналогичны:

Верхний индекс воспроизводимости процесса:                               (54)

Меньший индекс воспроизводимости процесса: C_pk = C_рkU.                                     (55)

Оценки Х_U и m определяют в соответствии с методом М1.

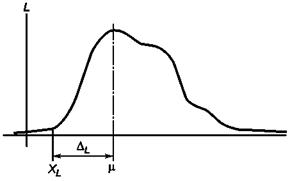
Рисунок 12 - Графическое представление метода вычисления D_L

В случае одностороннего поля допуска с установленной нижней границей применяют формулы (56) - (59).

Нижний индекс пригодности процесса:                                             (56)

Меньший индекс пригодности процесса: P_pk = P_pkL.                                                  (57)

Если процесс находится в состоянии статистической управляемости, может быть применен индекс воспроизводимости процесса. Формулы - аналогичны:

Нижний индекс воспроизводимости процесса:                                 (58)

Меньший индекс воспроизводимости процесса: C_pk = C_pkL.                                     (59)

Оценки X_L и m определяют в соответствии с методом М1.

8 Записи индексов воспроизводимости и пригодности процесса

Если статистические данные о пригодности/воспроизводимости процесса используют для квалификации процесса, они должны быть зафиксированы в соответствии с настоящим стандартом. В записях должны быть указаны методы вычислений и количество используемых данных. Пример записей приведен в таблице 3.

Таблица 3 - Пример индексов воспроизводимости процесса

Приложение ДА
(справочное)

Сведения о соответствии ссылочных международных стандартов
ссылочным национальным стандартам Российской Федерации

Таблица ДА.1

Библиография

[1] ИСО 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics¹⁾

[2] ИСО 8258, Shewhart control charts²⁾.

____________

¹⁾ Стандарт ИСО 3534-2:1993 соответствует ГОСТ Р 50779.11-2000 «Статистические методы. Статистическое управление качеством. Термины и определения».

²⁾ Стандарт ИСО 8258:1991 соответствует ГОСТ Р 50779.42-99 (ИСО 8258:1991) «Статистические методы. Контрольные карты Шухарта».