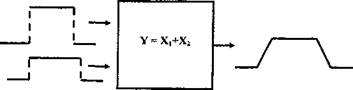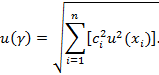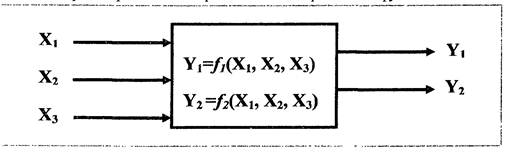Федеральное
государственное унитарное предприятие
«Всероссийский научно-исследовательский институт
метрологической службы»
ФГУП «ВНИИМС»
Рекомендация
Государственная система обеспечения единства измерений
Оценка результатов измерений -
Пояснения к «Руководству по выражению
неопределенности измерений»
МИ 3281-2010
Москва
2010
1 РАЗРАБОТАНА ФГУП «ВНИИМС»
ИСПОЛНИТЕЛЬ: Левин Е.В., Лукашов Ю.Е., Сковородников Б.В.
2 УТВЕРЖДЕНА ФГУП «ВНИИМС» 10.06.2010 г.
3 ЗАРЕГИСТРИРОВАНА ФГУП «ВНИИМС» 10.06.2010 г.
4 ВВЕДЕНА ВПЕРВЫЕ
Содержание
Предисловие к изданию МОЗМ
В 1997 году семь международных организаций, которые в 1993 году разработали «Руководство по выражению неопределенности результатов измерений» (GUM) и «Международный метрологический словарь - основные термины и определения» (VIM), учредили Объединенный комитет по подготовке руководств в метрологии (JCOM), возглавляемый директором МБМВ. К JCGM отошли обязанности по обеспечению внедрения двух указанных документов, ранее возлагавшиеся на Группу технических консультантов № 4 ИСО.
Настоящий документ разработан на основе Руководства G 1-104 «Оценка результатов измерений - Пояснения к «Руководству по выражению неопределенности измерений» и другим действующим документам», подготовленного Рабочей группой № 1 JCGM на основании заключений организаций - членов JCGM.
Упомянутое Руководство является составной частью серии под общим названием Оценка результатов измерений. Кроме него в состав серии также входят:
JCGM 100-2008 «Оценка результатов измерений - Руководство к выражению неопределенности измерений (GUM)»;
JCGM 101-2008 «Оценка результатов измерений - Дополнение 1 к «Руководству по выражению неопределенности измерений» - оценка с использованием метода Монте-Карло»;
JCGM 102 «Оценка результатов измерений - Дополнение 2 к «Руководству по выражению неопределенности измерений» - Модели с произвольным числом выходных величин»;
JCGM 103 «Оценка результатов измерений - Дополнение 3 к «Руководству по выражению неопределенности измерений» - Создание измерительных моделей»;
JCGM 105 «Оценка результатов измерений - Основные понятия и базовые принципы»;
JCGM 106 «Оценка результатов измерений - Значение неопределенности измерений для оценки соответствия»;
JCGM 107 «Оценка результатов измерений - Применение метода наименьших квадратов».
Если опыт подготовки настоящего документа окажется удачным, то, видимо, будет целесообразно подготовить рекомендации на основании части или всех перечисленных документов.
РЕКОМЕНДАЦИЯ
|
Государственная система обеспечения единства измерений Оценка
результатов измерений - Пояснения к |
МИ 3281-2010 |
Введение
Понятие неопределенности играет важную роль при определении соответствия результатов проводимого измерения его целям. Покупатель в овощном магазине будет полностью удовлетворен, если при покупке 1 кг фруктов отклонение реального веса от значения, полученного при взвешивании, составит, к примеру, 2 грамма. В то же время параметры компоненты гироскопов, применяемых в навигационной системе гражданских воздушных судов, должны измеряться с точностью до миллионных долей от их номинальных значений.
Неопределенность - это общее понятие, связанное с любыми измерениями и используемое при принятии решений в производственной и во многих других областях теоретической и практической деятельности. По мере повышения требований к допускам в промышленности возрастает значение неопределенности измерений применительно к оценке соответствия указанным требованиям. Неопределенность измерений играет важную роль при оценке качества продукции, что находит отражение в соответствующих нормативных документах.
Практически все виды жизнедеятельности человека в той или иной степени связаны с измерениями, в том числе производственная, коммерческая, научная деятельность, деятельность по защите окружающей среды, охране здоровья и обеспечению безопасности. В любом из них измерения крайне важны для принятия обоснованных решений. Неопределенность измерений создает возможность для сравнения результатов измерений и оценки их соответствия решаемой задаче, что, в свою очередь, позволяет на их основе определять вероятность принятия некорректных решений и, как следствие, управлять возникающими рисками.
Настоящий документ содержит пояснения к понятию неопределенности измерений и является введением к GUM и другим документам, перечисленным в Предисловии к изданию МОЗМ. Для оценки неопределенности измерений используется вероятностный подход. Оценка результатов измерений - Пояснения к «Руководству по выражению неопределенности измерений»
1 Область применения
1.1 Настоящий документ разработан с целью проведения объективной оценки неопределенности измерений на основе GUM и может быть использован как введение к Приложениям к GUM и другим документам, издаваемым JCGM [3, 4, 5, 6, 7].
1.2 Настоящий документ, как и GUM, в основном рассматривает вопросы, связанные с выражением неопределенности в процессе измерений величины, характеризуемой условным истинным значением (JCGM 200:2008 (VIM) 2.11 Примечание 3). GUM предлагает отказаться от использования термина «истинное значение», тем не менее, во избежание возможных разночтений и путаницы, в настоящем документе данный термин применяется.
1.3 Дополнения к GUM и другие документы JCGM в первую очередь предназначены для интерпретации положений Руководства. Кроме того, они являются основой для расширения области применения GUM и стимулируют его внедрение.
1.4 Настоящий документ вводит понятие неопределенности измерений, дает разъяснения по применению GUM, дополнений к GUM и других, имеющих отношение к GUM документов. Преимущественно рассматриваются вопросы, относящиеся к измерениям величин, характеризуемых непрерывными переменными, таких как длина, температура, время и количество вещества.
1.5 Настоящий документ применим при осуществлении, например, следующих видов деятельности:
- научные исследования и смежные виды деятельности;
- производство и смежные виды деятельности;
- деятельность калибровочных и испытательных лабораторий, деятельность по обеспечению безопасности, охраны здоровья и окружающей среды;
- деятельность органов по аккредитации и органов метрологического надзора.
1.6 Предполагается, что настоящий документ может быть полезен для разработчиков различных видов продукции. Очевидно, что если при разработке продукции учтены все требования (в том числе применительно к измерениям), предъявляемые в рамках государственного метрологического надзора, то это упрощает контроль продукции в процессе производства. Кроме того, документ может представлять интерес для научного сообщества, принимая во внимание постоянный рост числа университетов, включающих в свои учебные планы модули (дисциплины), имеющие отношение к оценке неопределенности результатов измерений. Вследствие этого можно ожидать, что последующие поколения студентов будут лучше понимать смысл понятия неопределенности измерений и измерений в целом.
1.7 Настоящий документ, GUM, приложения к GUM и другие действующие документы можно рассматривать как дополнения к «Международному метрологическому словарю - Основные термины и определения» и стандарту ИСО 3534 (три части), устанавливающему основные статистические понятия, используемые в статистике и теории вероятностей, в том числе в прикладной статистике и экспериментальном моделировании. Это обусловлено тем, что теоретической основой оценки результатов измерений и оценки неопределенности измерений являются математическая статистика и теория вероятностей.
2 Нормативные ссылки
Настоящий документ тесно связан со следующими документами, разработанными в рамках Объединенного комитета по подготовке руководств в области метрологии - JCGM и ИСО. Если документ датирован, то речь идет о данном конкретном издании. Если дата не указана, то подразумевается последнее издание документа (с учетом всех имевших место изменений).
JCGM 100:2008. Оценка результатов измерений - Руководство по выражению неопределенности измерений (GUM). Объединенный комитет по подготовке руководств в области метрологии.
JCGM 101:2008. Оценка результатов измерений - Дополнение 1 к «Руководству по выражению неопределенности измерений» - оценка с использованием метода Монте-Карло. Объединенный комитет по подготовке руководств в области метрологии.
JCGM 200:2008. Международный метрологический словарь - Основные понятия и термины, Издание 3. Объединенный комитет по подготовке руководств в области метрологии.
ИСО 3534-1:2006. Статистика - Словарь и символы - Часть 1: Основные статистические термины и термины, используемые в теории вероятностей.
ИСО 3534-2:2006. Статистика - Словарь и символы - Часть 2: Прикладная статистика.
ИСО 3534-3:1999. Статистика - Словарь и символы - Часть 3: Экспериментальное моделирование.
3 Что такое неопределенность измерений?
3.1 Целью измерения является получение информации об интересующей нас величине - измеряемой величине (JCGM 200:2008 (VIM) 2.3). Измеряемой величиной может быть объем сосуда, разность потенциалов на клеммах аккумуляторной батареи или концентрация свинца в колбе с водой.
3.2 Ни одно измерение не является абсолютно точным. Результат измерения зависит от измерительной системы (JCGM 200:2008 (VIM) 3.2), метода измерения, квалификации специалиста, выполняющего измерение, внешних условий и других факторов [1]. Если одна и та же величина измерена несколько раз с помощью одного и того же метода и при одинаковых условиях, то можно увидеть, если измерительная система обладает соответствующей разрешающей способностью, что результаты измерений отличаются друг от друга. Каждый из этих результатов можно считать действительным значением измеренной величины.
3.3 Разброс результатов при измерении одной и той же величины зависит от ряда факторов. Среднее значение результатов измерений можно условно назвать действительным значением измеряемой величины (JCGM 200:2008 (VIM) 2.11), которое является более точным по сравнению с результатами отдельных измерений. Объем выборки и конкретные значения результатов измерений являются той информацией, которая позволяет получить среднее значение, представляющее собой условно действительное значение измеренной величины. Однако и эта информация не является полной.
3.4 Результаты измерений, полученные с помощью измерительной системы, отличаются от истинного значения измеряемой величины. Разница между истинным значением и полученной оценкой результата измерения иногда называется систематической погрешностью измерения. В качестве примера можно взять домашние весы. Предположим, что весы неправильно установлены на ноль, т.е. показывают некий отличный от нуля результат при отсутствии нагрузки. В этом случае при любом числе измерений такая систематическая погрешность будет оказывать определяющее воздействие на среднее значение результатов измерений. При этом под систематической погрешностью, являющейся некой величиной, понимают составную часть погрешности измерения, которая остается неизменной или закономерно изменяющейся в зависимости от другой величины.
3.5 Существуют два вида погрешности: систематическая и случайная (JCGM 200:2008 (VIM) 2.19). Систематическая погрешность (составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся) обусловлена неточностью градуировки шкалы средства измерений. Проявлением случайной погрешности является то, что при неоднократных измерениях одной и той же величины полученные результаты отличаются друг от друга. Случайность такой погрешности состоит в том, что результат измерения не может быть предсказан на основании предыдущих результатов измерений (если бы это было возможно, то было бы также возможно применить соответствующую поправку). Существует много причин, обусловливающих наличие каждого из видов погрешностей.
3.6 Главная проблема, связанная с измерением, заключается в необходимости наилучшим образом выразить то, что известно об измеряемой величине.
Определение величины систематической и случайной погрешностей, наряду с наилучшей возможной оценкой значений измеряемой величины, представляют собой подход, который широко применялся до введения в действие GUM. GUM предлагает другой подход к измерению, в частности, через оценку качества результатов измерений. Согласно GUM, результатом измерения не является наиболее точная оценка значения измеряемой величины с учетом систематической и случайной погрешностей, а наиболее точная оценка значений измеряемой величины с учетом соответствующей неопределенности измерений.
3.7 Одним из базовых положений подхода, определяемого GUM, является возможность оценки качества результатов измерений, выполняемой по методике, предлагаемой GUM (см. 7.2), с учетом систематической и случайной погрешностей.
Такой подход позволяет очистить информацию, получаемую путем «анализа погрешности», и провести ее последующую обработку с использованием вероятностного метода и понятия неопределенности измерений.
3.8 Другое важное положение GUM связано с невозможностью абсолютно точно определить истинное значение измеряемой величины. Фактически определяется степень нашей уверенности в том, насколько точно мы можем это сделать. Неопределенность измерения может быть определена как мера того, насколько мы уверены в том, что знаем истинное значение измеренной величины. Такая неопределенность является отражением неполного знания измеряемой величины. Понятие «уверенность» является крайне важным, поскольку оно переводит метрологию в область, где результаты измерений рассматриваются количественно и оцениваются с помощью вероятностного подхода, отражающего степень «уверенности».
3.9 Все вышесказанное относится к прямым измерениям, которые на практике встречаются достаточно редко. Например, весы в ванной комнате показывают величину растяжения пружины, преобразованную в условное значение измеряемой величины, т.е. массы человека, стоящего на весах. Соотношение величины растяжения пружины и массы человека определяется калибровкой (JCGM 200:2008 (VIM) 2.39).
3.10 Описанное в пункте 3.9 соотношение представляет собой модель, позволяющую преобразовать определенную величину в результат измерения. Эта модель называется измерительной моделью (JCGM 200:2008 (VIM) 2.48) или просто моделью. На практике существует много видов измерений и соответствующих им измерительных моделей. Даже для одного вида измерений может использоваться несколько измерительных моделей. Простой модели (например, пропорциональная модель, когда масса пропорциональна степени растяжения пружины) может быть достаточно для измерений, производимых на бытовом уровне. В то же время для промышленных и научных целей используются гораздо более совершенные модели измерений веса, учитывающие множество дополнительных факторов, к примеру, таких, как воздушные потоки. Обычно приходится учитывать сразу несколько таких факторов, например, температуру, влажность, месторасположение объекта, влияющих на результат измерений и принимаемых во внимание при проведении измерений.
3.11 Если не удается обеспечить требуемые условия проведения измерений, модель предусматривает возможность применения соответствующих поправок. Поправки должны учитывать величину систематической погрешности (JCGM 100:2008 (GUM) 3.2.4). Всегда существует неопределенность, связанная с оценкой систематической погрешности, даже если она равна нулю. Примером систематической погрешности может быть погрешность при измерении высоты, обусловленная отклонением средства измерений от вертикальной оси, а также отличием температуры окружающего воздуха при проведении измерения от предписанной. Величина отклонения от вертикали, как и разница температур, не могут быть точно определены, однако некоторая информация о них все-таки имеется. Например, известно, что отклонение от вертикали должно составлять не более 0,001 градуса, а температура воздуха в момент измерения не должна отличаться от требуемой более, чем на 2 °С.
3.12 Результат измерения может зависеть от времени его проведения, как, например, в случае с радионуклидами, распадающимися с определенной скоростью. Измерительная модель должна учитывать данное явление с тем, чтобы соотносить результаты измерений с временем их проведения.
3.13 Наряду с оцениваемыми значениями измеряемой величины модель также использует и другие виды данных. Отдельные виды данных относятся к величинам, представляющим физические константы, которые пока еще недостаточно изучены. Например, константы эластичности или температурные константы. Часто в калибровочных сертификатах, справочной и другой литературе приводятся данные, которые могут использоваться как оценочные значения измеряемых величин.
3.14 Данные, используемые измерительной моделью для определения значений измеряемой величины, называются исходными данными (JCGM 200-2008 (VIM) 2.50). Модель представляет собой образец «функциональных отношений» (JCGV 100:2008 (GUM) 4.1). Значения величин на выходе измерительной модели (JCGM 200:2008 (VIM) 2.51) являются значениями измеряемых величин.
3.15 Формально, выходная величина U, информацию о которой требуется получить, связана со значениями исходных величин, обозначаемых Х1, …, Хn, информация о которых доступна измерительной модели (JCGV 100:2008 (GUM) 4.1.1), выражаемой функцией (JCGM 200:2008 (VIM) 2.49)
3.16 В общем виде измерительная модель (JCGM 200:2008 (VIM) 2.48 примечание 1) представляет собой
Предполагается, что Y зависит от X1, …, Хn, его значение может быть рассчитано и полностью определяется уравнением (2).
3.17 Если предположить, что истинные значения исходных величин Х1, ..., Хn не известны, но могут характеризоваться с помощью распределения вероятностей этих величин (JCGM 100:2008 (GUM) 3.3.5, ИСО 3534-1:2006 2.11), то такие величины, с точки зрения математики, могут считаться случайными переменными (ИСО 3534-1: 2006 2.10). Распределение вероятности позволяет получить представление о значении величины, основанное на знании истинных значений Х1, ..., Хn и соответствующих им интервалов. В некоторых случаях все или отдельные из Х1, ..., Хn являются взаимозависимыми, тогда распределения соответствующих им значений называются «совместными» (т.е. описываются многомерными функциями распределения вероятности). Ниже рассматриваются требования, в большей степени относящиеся к несвязанным (независимым) величинам, которые в некоторых случаях могут быть применимы и для взаимозависимых величин.
3.18 Рассмотрим оценки x1, ..., хn исходных величин Х1, ..., Хn, которые можно найти в соответствующих сертификатах, протоколах испытаний, спецификациях изготовителя, аналитических материалах и измерительных данных. Распределения вероятности, характеризующие Х1, ..., Хn, выбираются такие, чтобы оцененные значения x1, ..., хn, совпадали с центрами группирования Х1, ..., Хn (JCGM 101:2008 3.6, ИСО 3534-1:2006 2.12). Для i-ой исходной величины рассмотрим так называемую неопределенность условного истинного значения (JCGM 200:2008 (VIM) 2.30), обозначаемого символом u(хi), определяемым как стандартная неопределенность (JCGM 101:2008 3.8, ИСО 3534-1:2006 2.37) исходной величины Xi. Данная стандартная неопределенность называется ассоциированной с оценочным значением хi. Это значение хi представляет собой наилучшую оценку в том случае, если u2(хi) меньше, чем средняя сумма квадратов разностей значений Xi и любого другого оцененного значения данной величины.
3.19 Использование имеющихся знаний в целях определения распределения вероятности, характеризующего каждую из рассматриваемых величин, применимо как в отношении Хi, так и Y. В последнем случае распределение вероятности, характеризующее Y, определяется с помощью функции (1) или (2) одновременно с распределением вероятностей для Xi. Мера рассеяния для Y, оцененная с помощью указанных знаний о распределениях всех указанных величин, называется «дисперсией» распределений (JCGM 101:2008 5.2).
3.20 Должны приниматься во внимание и исходные знания об истинном значении выходной величины Y. Применительно к весам в ванной комнате к исходным знаниям может быть отнесена информация о том, что масса человека является положительной величиной и что она отличается, к примеру, от массы автомашины. Такая вспомогательная информация может быть необходима при определении распределения вероятности для Y и позволяет получить меньшее значение стандартного отклонения и, как следствие, меньшее значение неопределенности условного истинного значения Y, являющегося оценочным значением [2, 13, 24].
4 Основные понятия и принципы
4.1 Помимо раздела 3 настоящего документа, фундаментальные понятия и принципы теории вероятностей, определяющие подходы к оценке и выражению неопределенности результатов измерений, приведены в JCGM 105:2008 [4].
4.2 Неопределенность результатов измерений определяется (JCGM 200:2008 (VIM) 2.26) как «не отрицательная» величина, характеризующая, с учетом имеющихся сведений, распределение значений измеряемой величины. Такое определение не противоречит пунктам 3.8, 3.17 - 3.20 настоящего документа.
4.3 Могут применяться два способа оценки неопределенности значений независимой переменной X (JCGM 101:2008 3.1, ИСО 3534- 1:2006 2.11):
- с использованием функции распределения (JCGM 101:2008 3.2, ИСО 3534-1:2006 2.7), позволяющей для любого значения независимой переменной установить вероятность того, что X будет меньше или равно этому значению;
- с использованием функции плотности распределения вероятности (JCGM 101: 2008 3.3, ИСО 3534-1:2006 2,26), являющейся производной функции распределения.
4.4 Знания об исходной величине Xi измерительной модели способствуют наилучшей оценке значений хi и соответствующей неопределенности условного истинного значения и(Хi) измеряемой величины (см. 3.18). Если два любых значения исходной величины Xi и Xj взаимосвязаны (зависимы), то обобщенная информация о величине должна включать данные о степени такой зависимости, часто называемой корреляцией (ИСО 3534-1:2006 2.43). Если Xi и Xj являются независимыми (не связаны), то для них коэффициент корреляции равен нулю1.
______________
1 Строго говоря, равенство нулю коэффициента корреляции свидетельствует о независимости случайных величин только в случае линейной зависимости.
4.5 Оценка измерительных данных применительно к измерительной модели (1) или (2) заключается в использовании имеющихся знаний о значениях исходных величин Х1, ..., Хn, представленных в виде распределений вероятности, характеризующих эти величины, с целью оценки распределения вероятности для выходной величины Y. В некоторых случаях оценка результатов измерений позволяет получить только приблизительные данные о распределении вероятности для Y.
4.6 Знания об исходной величине Xi могут быть получены на основании результатов повторных измерений (оценка неопределенности типа A) [JCGM 100:2008 (GUM) 4.2, JCGM 200:2008 (VIM) 2.28], научных исследований или другой информации о возможном значении данной величины (оценка неопределенности типа В) [JCGM 100:2008 (GUM) 4.3, JCGM 200:2008 (VIM) 2.29].
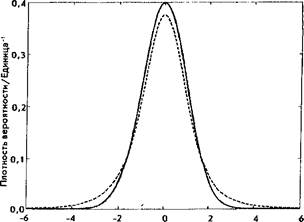
4.7 Оценка неопределенности типа A [JCGM 200:2008 (VIM) 2.28] предполагает, что распределение значений исходной величины X, полученное на основании многократных измерений (независимых), является распределением Гаусса [ИСО 3534-1-2006 2.50]. При этом ожидаемое значение X будет равно среднему арифметическому результатов измерений этой величины, а стандартное отклонение результата - стандартному отклонению этого среднего арифметического.
Величина/Единица
Рис. 1 Распределение Гаусса (сплошная линия) и /-распределение с четырьмя степенями свободы (пунктирная линия)
Оценка неопределенности при небольшом числе измерений (рассматриваются как отдельные измерения, описываемые распределением Гаусса) характеризуется t - распределением2 [ИСО 3534-1:2006 2.53]. На рис. 1 показаны распределение Гаусса (сплошная линия) и /-распределение с четырьмя степенями свободы (пунктирная кривая).
Если получаемые результаты измерений не могут считаться независимыми, то применяются другие методы измерений.
____________
2 t - распределение или распределение Стьюдента используется в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения
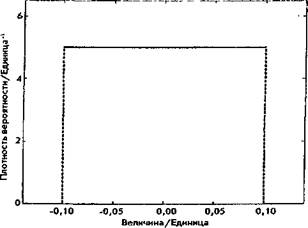
4.8 При оценке неопределенности типа В [JCGM 200:2008 (V1M) 2.29] часто единственной информацией о распределении X является то, что ее значения находятся в границах интервала [а, b]. В этом случае знание величины можно описать с помощью прямоугольного (равномерного) распределения вероятности [JCGM 100:2008 (GUM) 4.3.7, ИСО 3534-1:2006 2.60] с границами а и b (рис. 2). При наличии других знаний используются соответствующие им виды распределения вероятности [26].
4.9 Когда значения исходных величин X1, ... , Хn определяются с помощью соответствующих распределений вероятности и разработана соответствующая измерительная модель, то распределение вероятности для значений измеряемой величины Y можно считать полностью определенным в рамках имеющихся возможностей (также см. 3.19). В частности, ожидаемое значение Y может считаться оценкой Y, а стандартное отклонение Y - стандартной неопределенностью этой оценки.
Рис. 2 Функция плотности вероятности для равномерного распределения с границами а = -0,1 и b = 0,1
4.10 На рис. 3 изображена вспомогательная измерительная функция Y = X1 + Х2, где X1 и Х2 характеризуются с помощью методов (разных) прямоугольного распределения вероятности. В этом случае распределение вероятности для Y будет иметь форму симметричной трапеции.
Рис. 3 Плотность распределения вероятностей суммы двух независимых равномерно распределенных величин X1 и Х2
4.11 Часто возникает потребность в определении интервала, в пределах которого с заданной вероятностью будут находиться значения Y. Данный интервал, называемый доверительным интервалом [JCGM 200:2008 (VIM) 2.36], может быть определен на основании распределения вероятности Y. Соответствующая вероятность называется доверительной вероятностью [JCGM 200:2008 (VIM) 2.37].
4.12 Каждой доверительной вероятности соответствует несколько доверительных интервалов.
а) вероятностно-симметричный доверительный интервал [JCGM 101:2008 3.15], для которого величины вероятности (сумма которых равна единице минус доверительная вероятность), расположенные справа и слева от интервала, равны.
b) наименьший доверительный интервал [JCGM 101:2008 3.16], имеющий наименьшую длину из всех интервалов с одинаковой доверительной вероятностью.
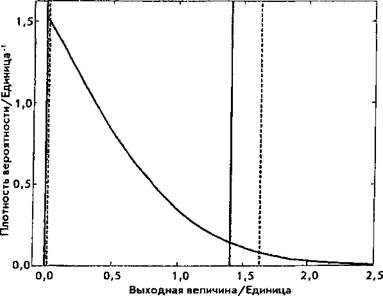
4.13 На рис. 4 показано распределение вероятности (распределение асимметричное в виде убывающей кривой) для случайной величины, а также наименьший доверительный интервал (ограничен точками, расположенными на непрерывных вертикальных синих линиях) и вероятностно симметричный доверительный интервал (ограничен прерывистыми вертикальными линиями) с 95 % доверительной вероятностью.
Распределение асимметрично, два доверительных интервала различаются (наиболее заметно в конечных точках справа). Наименьший доверительный интервал имеет левую граничную точку, совпадающую с нулем, являющимся наименьшим возможным значением величины. Вероятностно-симметричный доверительный интервал в данном случае на 15 % длиннее, чем наименьший доверительный интервал.
Рис. 4 Вероятностно-симметричный и наименьший доверительные интервалы
4.14 Коэффициенты чувствительности с1, ..., сn, [JCGM 100:2008 (GUM) 5.1.3] показывают, как оценка у величины Y меняется при незначительных изменениях оценочных значений х1, …, хn исходных величин Х1, …, Хn. Для измерительной функции (1) с1 равен частной производной первого порядка функции f от Хi, оцениваемой при X1 = x1, Х2 = х2 и т.д. Для линейной измерительной функции
Y = с1Х1+...+сnХn,
где Х1,
…, Хn независимы, а
изменение хi равное u(хi), вызывает изменение у, равное сiu(хi).
В целом в отношении измерительных моделей (1)
и (2) данное заключение можно считать
условно применимым (см. 7.2.4).
Относительная величина выражения [сi]u(xi) важна для оценки
степени влияния исходной величины на стандартную неопределенность ![]() , относящуюся к
, относящуюся к ![]() .
.
4.15 Стандартная
неопределенность ![]() , связанная с оценкой у выходной
величины Y, зависит не от суммы значений [сi]u(xi), а от суммы их
квадратов [JCGM 100:2008 (GUM) 5.1.3.] и выражается (для измерительных моделей
(1) и (2)
приблизительно) в виде
, связанная с оценкой у выходной
величины Y, зависит не от суммы значений [сi]u(xi), а от суммы их
квадратов [JCGM 100:2008 (GUM) 5.1.3.] и выражается (для измерительных моделей
(1) и (2)
приблизительно) в виде
Если исходные
величины X, имеют зависимые значения, формула (4) должна быть дополнена
соответствующими поправками [JCGM 100:2008 (GUM) 5.2/2], которые могут привести
к уменьшению или увеличению ![]() .
.
4.16 В соответствии с Резолюцией 10 22-го CGPM (2003), «... для отделения десятичной доли от целой части числа может использоваться как точка, так и запятая...». В документах JCGM на английском языке в качестве такого символа используется точка. В отечественных документах принято использовать запятую.
5 Стадии оценки неопределенности
5.1 Основными стадиями оценки неопределенности являются определение и расчет. Последняя стадия включает оценку дисперсии и суммирование.
5.2 Стадия определения (см. пункт 6) включает:
а) определение значений выходной величины Y (объект измерения);
b) идентификацию исходных величин, от которых зависит значение Y
с) разработку измерительной модели, определяющей зависимость Y от. исходных величин;
d) на основании полученной информации описание распределения вероятности для исходных величин - распределение Гаусса, прямоугольное и т.д. (или совместное распределение вероятности для исходных величин, не являющихся независимыми).
5.3 Стадия расчета (см. пункт 7) включает оценку среднего значения и дисперсии распределения вероятности для значений исходных величин с помощью измерительной модели, а также оценку распределения вероятности для значений выходной величины Y и суммирование на базе данного распределения оценок характеристик исходных распределений с целью определения:
а) ожидаемого значения величины Y в виде оценки у значения Y;
b)
стандартного отклонения значения Y, рассматриваемого как стандартная
неопределенность ![]() значения v [JCGM 100:2008 (GUM)
Е.3.2];
значения v [JCGM 100:2008 (GUM)
Е.3.2];
с) доверительного интервала для Y, соответствующего заданной доверительной вероятности.
6 Стадия определения: разработка измерительной модели
6.1 Эта стадия оценки неопределенности включает разработку измерительной модели, в том числе поправок и параметров. Для некоторых видов измерений данная стадия является наиболее сложной. Она подразумевает применение имеющихся знаний для характеристики исходных величин измерительной модели посредством распределения вероятности. JCGM 103 [6] содержит соответствующие рекомендации по разработке и применению измерительных моделей. JCGM 101 [JCGM 101:2008 6) и JCGM 102 [5] устанавливают связь распределения вероятности с исходными величинами измерительной модели.
6.2 В первую очередь разрабатывается измерительная модель, устанавливающая связь исходных величин с выходной величиной. Допускается возможность наличия нескольких выходных величин в измерительной модели (см. 6.5). Измерительная модель создается на базе теоретических разработок, с учетом результатов предыдущих измерений, или одновременно того и другого в зависимости от характера метрологической деятельности: электрические измерения, геометрические измерения, измерения массы, измерения температуры и пр. В последующем модель может дополняться другими исходными величинами, что приводит к изменению процесса измерений. JCGM 103 [6] содержит рекомендации по проведению измерений при наличии погрешностей, обусловленных влиянием на результат измерений дополнительных исходных величин, которые могут вызывать систематические или случайные изменения результатов измерений.
6.3 В отличие от GUM, JCGM 103 устанавливает более широкие классы измерительных моделей, разделяя их по категориям в зависимости от того:
а) являются ли подлежащие измерению величины простыми или составными;
b) соответствует ли измерительная модель форме (2) или выражена в виде измерительной функции (1);
с) имеет измерительная модель одну или несколько выходных величин (см. 6.5).
6.4 Применительно к категории (а) составные величины чаще используются при проведении электрических, акустических и оптических измерений. Применительно к измерительной функции, упомянутой в категории (b), выходная величина выражается через формулу, включающую исходные величины, а применительно к общей измерительной модели выходная величина рассчитывается с помощью соответствующего алгоритма, позволяющего выразить ее через исходные величины (см. 6.5).
6.5 Как в GUM, так и в JCGM 101:2008 большое внимание уделяется измерительным моделям в форме измерительных функций с одной выходной величиной Y. Серьезные проблемы возникают при использовании измерительной модели с несколькими выходными величинами, зависящими от набора одних и тех же исходных величин. Данные выходные величины обозначаются Yb ...,Ym. К ним могут быть отнесены: (а) сложная выходная величина, выраженная посредством действительных и мнимых составляющих (амплитуда или фаза); (b) величина, определяющая параметры функции калибровки, и (с) величина, определяющая геометрию поверхности объекта. GUM рассматривает подобные случаи на примерах: при одновременном измерении величины активного и реактивного сопротивления [JCGM 100:2008 (GUM) Н.2] или при калибровке термометров [JCGM 100:2008 (GUM) Н.З].
6.6 Фаза определения применительно к оценке неопределенности, при наличии нескольких измеряемых величин, сравнима с соответствующей фазой измерительной модели с одной измеряемой величиной: она включает разработку модели и соотносит
распределение вероятности Y с соответствующими исходными величинами с использованием имеющихся знаний. При применении измерительной модели с одной выходной величиной производится оценка значений каждой исходной величины и определяется связанная с ней стандартная неопределенность результата (а также возможные поправки, касающиеся взаимозависимости пар исходных оценок). Поскольку каждая выходная величина обычно зависит от всех исходных величин, помимо оценок значений выходных величин и стандартных неопределенностей, связанных с этими оценками, также необходимо определить поправки для всех пар таких оценок.
6.7 Измерительная функция (1), когда число выходных величин равняется ш, может быть выражена:
Y1 = f1(X1 ...,Хn), Y2 = f2(Xi ...,Хn), ..., Ym = fm(Xi,..., Хn),
где число функций f1, ..., fm равно m.
На рис. 5 представлен образец такой измерительной функции.
Рис. 5 Измерительная функция с тремя исходными величинами X1, Х2 и Х3 и двумя выходными величинами Y1 и Y2
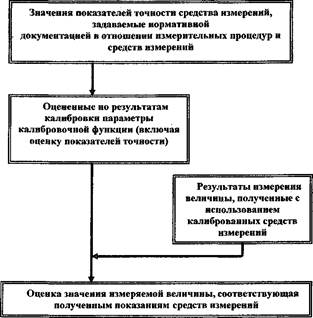
6.8 Многоэтапные измерительные модели, где выходные величины предыдущих этапов являются исходными величинами последующих, рассматриваются в JCGM 103. Примером многоэтапной измерительной модели можно считать процедуру разработки и применения функции калибровки [JCGM 200:2008 (VIM) 2.39] (см. рис. 6):
а) На основании значений величины, устанавливаемых требованиями соответствующих нормативных документов, и показаний измерительной системы определяются соответствующие оценочные значения параметров калибровочной функции. Стандартные неопределенности, относящиеся к значениям измеряемых величин, и показания средств измерений увеличивают стандартные неопределенности оценочных значений, что обусловливает корреляцию всех пар значений оценки величины.
б) На основании показаний средства измерений производится оценка калибровочной функции применительно к возможности получения требуемых результатов измерений. Для выполнения данной операции используется обратная калибровочная функция. Стандартные неопределенности и поправки, относящиеся к оценкам значений параметров калибровочной функции, вместе со стандартной неопределенностью последующих показаний средства измерений увеличивают стандартную неопределенность результата измерений.
7 Расчетная стадия (дисперсия и суммирование) оценки неопределенности
7.1 Общие положения
7.1.1 Стадия определения дисперсии в рамках оценки неопределенности, называемая «дисперсией распределений» [JCGM 101:2008 5.2], предполагает:
а) использование методов оценки неопределенности, приведенных в GUM, что обусловливает применение закона распределения неопределенности и оценку выходной величины Y с помощью распределения Гаусса или t - распределения (см. 7.2);
Рис. 6 Двухэтапная измерительная модель получения калибровочной функции, где величины, определяемые нормативными документами, и соответствующие показания средств измерений используются для определения оценочных значений параметров калибровочной функции, которые, с учетом последующих показаний, применяются для оценки значения измеряемой величины
б) использование аналитических методов, основанных на математическом анализе, что позволяет выразить в алгебраической форме распределение вероятности для Y (см. 7.3);
c) использование метода Монте-Карло, что позволяет выразить в числовой форме приближенное значение функции распределения значений Y с помощью метода произвольных выборок из распределений вероятности исходных величин и оценки измерительной модели через выходные величины (см. 7.4).
7.1.2 При решении задачи, связанной с оценкой неопределенности, используются методики а), b) или с) (или другие), при этом методика а) рассчитана на получение приблизительных значений, методика b) - сравнительно точных, а методика с) - математически точных значений, допускающих возможность контроля.
7.1.3 Применение методик а) и с) в отношении измерительных функций с произвольным числом выходных величин, а также общие измерительные модели рассматриваются в п. 7.5.
7.2 Описание неопределенности GUM
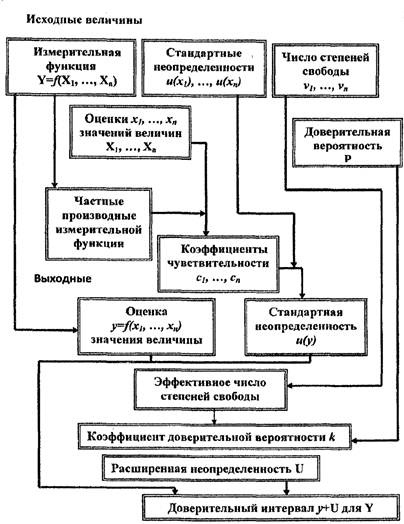
7.2.1 Применительно к описанию неопределенности, введенному GUM [JCGM 100:2008 (GUM) 3.4.8, 5.1] (схематично показано на рис. 7), определяются:
а) наиболее точные оценки хi исходных величин Xi,
б) стандартные неопределенности u(хi) значений хi
c)
коэффициенты чувствительности сi (см. 4.14) для получения значений оценки у
выходной величины Y и значений ассоциированной с ней неопределенности ![]() .
.
7.2.2 Вариант,
описанный в пункте 7.2.1, применим и
в том случае, если исходные величины взаимозависимы (на рис. 7 этот случай не представлен) [JCGM 100:2008 (GUM) 5.2]. Если
распределение вероятности для Y соответствует распределению Гаусса, то для Y
можно определить доверительный интервал, соответствующий заданной доверительной
вероятности [JCGM 100:2008 (GUM) G.2]. Если число степеней свободы [ИСО
3534-1:2006 2.54] для u(xi) ограничено, то
число степеней (эффективное) свободы ![]() может быть определено, а распределение
вероятности для Y рассматривается как t -
распределение.
может быть определено, а распределение
вероятности для Y рассматривается как t -
распределение.
7.2.3 Установленные GUM методы оценки неопределенности [JCGM 100:2008 (GUM) 5] применимы при определении достоверных значений неопределенности. Если измерительная функция исходных величин является линейной, а распределение вероятности для значений этих величин является распределением Гаусса, методы оценки неопределенности, приведенные в GUM, позволяют получить максимально точные результаты оценки неопределенности измерений [JCGM 101:2008 5.7]. Практическое использование данного метода возможно [JCGM 101: 2008 5.8] даже в случае несоблюдения указанных условий.
7.2.4 В некоторых случаях использование методов оценки неопределенности, приведенных в GUM, не представляется возможным, например, когда:
a) измерительная функция не является линейной;
b) распределение вероятности для значений исходных величин является асимметричным;
c) неопределенности [c1]u(x1), ..., [сn]u(хn) (см. 4.14) различаются по степени влияния [JCGM 100:2008 (GUM) G.2.2];
d) распределение вероятности для значений выходной величины является либо асимметричным, либо t - распределением, но не распределением Гаусса.
Не всегда можно предвидеть возникновение подобных проблем.
Рис. 7 Оценка неопределенности результатов измерений с помощью методов, описанных в GUM
7.2.5 Возникают трудности при использовании рамок неопределенности GUM применительно к частным производным (или их приблизительным числовым значениям) сложных измерительных моделей, получаемым в соответствии с требованиями закона распределения неопределенности [JCGM 100:2008 (GUM) 5]. В отдельных случаях наиболее предпочтительным является применение метода Монте-Карло (см. 7.4).
7.3 Аналитические методы
7.3.1 Аналитические методы, позволяющие получить алгебраическое выражение для описания распределения вероятности значений выходной величины, не применимы для оценки значений и могут использоваться только для сравнительно простых измерительных моделей. Руководство по использованию подобных аналитических методов приведено в [8, 12]. К ним можно отнести линейные измерительные функции с числом исходных величин равным N (выражение (3)), если распределение вероятности для всех исходных величин является распределением Гаусса или прямоугольным распределением с одинаковыми границами. Пример с двумя исходными величинами (N = 2), где распределение вероятности значений исходной величины имеет прямоугольную форму, а распределение вероятности для выходной величины имеет форму трапеции [10], приведен на рис. 3.
7.3.2 В случае с одной исходной величиной (N = 1) часто применяются аналитические методы с использованием соответствующей формулы [25, стр. 57 - 61] для определения распределения вероятности значений выходной величины. Данные методы используются при преобразовании единиц измерений, например, линейных в логарифмические [10, стр. 95 - 98].
7.3.3 Преимущество алгебраического метода заключается в том, что он дает понимание зависимости распределения вероятности значений выходной величины от параметров распределения вероятности для исходных величин.
7.4 Метод Монте-Карло
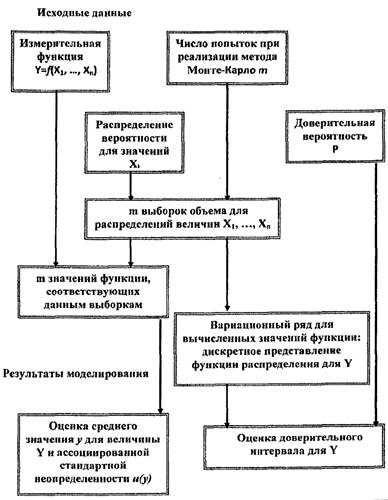
7.4.1 JCGM 101:2008 дает подробное разъяснение по использованию метода Монте-Карло применительно к дисперсии распределений [JCGM 101:2008 5.9]. По сравнению с рамками неопределенности GUM, применение метода Монте-Карло ограничено значительно меньшим числом условий [JCGM 101:2008 5.10]. Рис. 8 иллюстрирует применение данного метода. Приведенные в JCGM 101: 2008 примеры позволяют сравнить метод Монте-Карло с методами, приведенными в рамках оценки неопределенности GUM [JCGM 101:2008 9].
7.4.2 JCGM 101:2008 содержит адаптированную методику применения метода Монте-Карло с числом попыток, автоматически определяемым посредством меры сходимости процесса [JCGM 101: 2008 7.9].
7.4.3 В JCGM 101:2008 приводится методика применения метода Монте-Карло для определения применимости рамок неопределенности GUM в каждом конкретном случае [JCGM 101:2008 8].
7.5 Измерительные модели с произвольным числом выходных величин
7.5.1 Для оценки неопределенностей и поправок, относящихся к выходным величинам измерительных моделей с произвольным числом выходных величин, рамки неопределенности GUM, как и метод Монте-Карло, с точки зрения JCGM 101:2008, требуют определенного расширения.
GUM [JCGM 100:2008 (GUM) F. 1.2.3] рассматривает вопросы, связанные с таким расширением, на конкретных примерах.
Рис. 8 Оценка неопределенности результатов измерений с применением метода Монте-Карло
7.5.2 JCGM 102 [5] отмечает, что закон распределения неопределенности, составляющий основу оценки неопределенности GUM, применительно к измерительной модели с одной исходной величиной в краткой форме может быть выражен в виде соответствующей матрицы. Матричная форма имеет преимущество в том плане, что она может быть использована как база для программного обеспечения, а также как основа для расширения применительно к другим измерительным моделям.
7.5.3 Расширение, применимое для измерительной функции с произвольным числом выходных величин, приведено в JCGM 102. Кроме того, JCGM 102 рассматривает случай, связанный с увеличением количества выходных величин у стандартной измерительной модели (см. 3.16).
7.5.4 JCGM 102 допускает возможность использования метода Монте-Карло применительно к измерительной модели с произвольным числом выходных величин. При этом может быть получено достоверное изображение распределения вероятности для значений выходных величин. На основании данного изображения могут быть произведены оценки значений выходных величин, связанных с ними стандартных неопределенностей, а также определены соответствующие поправки, относящиеся к парам оценок значений.
7.5.5 Помимо оценок значений выходных величин, соответствующих им стандартных неопределенностей и поправок, иногда требуется определить «область», в которую с заданной вероятностью попадали бы значения выходных величин. Как следствие, возникает необходимость в расширении до размеров «области» вероятностно симметричного доверительного интервала и наименьшего доверительного интервала. Вместе с тем, не существует естественного аналога вероятностно симметричного доверительного интервала покрытия в виде доверительной «области», в то время как для наименьшего доверительного интервала такой аналог возможен. В целом, определение наименьшей доверительной «области» является достаточно сложной задачей.
7.5.6 При определенных обстоятельствах бывает достаточно определить приблизительную доверительную область, имеющую простую геометрическую форму. В качестве примера можно рассмотреть две формы доверительных областей, у одной из которых выходные величины характеризуются распределением Гаусса, например, с использованием центральной предельной теоремы [JCGM 100:2008 (GUM) G.2], когда наименьшая доверительная область ограничена гиперэллипсом. Другой такой формой области покрытия может быть гиперпрямоугольник.
7.5.7 Методы получения указанных форм приведены в JCGM 102.
8 Неопределенность измерений при оценке соответствия
8.1 Оценка соответствия является важным аспектом в системе контроля качества, сфере законодательной метрологии, в области обеспечения безопасности и охраны здоровья. В рамках системы контроля качества на производстве принимаются решения о соответствии продукции требованиям конструкторской документации. Аналогичные действия производятся в рамках осуществления количественного контроля (уровень радиации и загрязнения окружающей среды, состав лекарственных препаратов и пр.) с целью выявления случаев превышения установленных норм. Соответствующее руководство приведено в JCGM 106 [7]. Также см. [18].
8.2 Измерение неотделимо от оценки соответствия, в частности, при принятии решения относительно соответствия выходной или измеряемой величины установленным требованиям. Применительно к отдельной величине такие требования могут выражаться в виде заданных пределов допустимых значений этой величины. Без учета неопределенности измерений значение измеренной величины считается соответствующим, если оно находится в заданном интервале, в противном случае - несоответствующим. С точки зрения метрологического обеспечения решения подобных задач, неопределенность измерений позволяет обеспечить сбалансированное распределение рисков между изготовителем и потребителем продукции.
8.3 Для характеристики возможных значений измеряемой величины Y может использоваться распределение вероятности. Вероятность того, что Y соответствует установленным требованиям, может быть определена исходя из распределения вероятности с учетом заданного спецификацией интервала.
8.4 Вследствие недостаточности знаний о величине Y (что обусловлено дисперсией результата наблюдений) существует риск принятия ошибочных решений относительно соответствия данной величины установленным спецификацией требованиям. Подобные ошибочные решения бывают двух видов: когда значение величины считается соответствующим, но в действительности таковым не является; и наоборот, когда оно считается несоответствующим, на самом деле, будучи соответствующим. Эти риски распространяются как на потребителя, так и изготовителя продукции (см. JCGM 106).
8.5 Устанавливая «интервал допустимых значений» измеряемой величины, можно уменьшить риски принятия ошибочных решений относительно соответствия или несоответствия продукции, что, в свою очередь, позволяет минимизировать связанные с этим потери [19]. JCGM 106 рассматривает вопросы определения вероятности соответствия и вероятности принятия ошибочных решений обоих типов исходя из распределения вероятности, задаваемых спецификацией пределов и границ интервала. Границы интервала устанавливаются с учетом возможных последствий принятия ошибочных решений.
8.6 В пунктах 8.3 - 8.5 настоящего документа рассматриваются общие принципы распределения вероятности, а в JCGM 106 - их специфические особенности на примере наиболее типичных случаев, в частности, при распределении вероятности по закону Гаусса.
9 Применение метода наименьших квадратов
9.1 Руководство по применению метода наименьших квадратов при решении метрологических задач, связанных с оценкой результатов измерений, приведено в JCGM 107 [3]. В основе таких задач часто лежат взаимозависимость независимой и зависимой переменных, составляющих базу для приведения в соответствие параметров искомой зависимости или кривой в целом. Исходные величины измерительной модели - это значения независимых переменных и зависимых переменных, которые являются выходными величинами. Выходные величины - это величины, представляющие заданные параметры. Способ получения значений выходных величин на основании задания исходных величин посредством метода наименьших квадратов является основой, определяющей измерительную модель.
9.2 Применяемое в калибровочной терминологии (см. 6.8) понятие значения измеряемой величины (независимой переменной) в полной мере соответствует метрологическим нормативным документам. Значение зависимой переменной - это значение соответствующей независимой переменной, преобразованное с помощью измерительной системы. В этой связи приведение в соответствие значению независимой переменной значения выходной величины, представленное в виде кривой, особым случаем которого является калибровка, можно рассматривать как часть рассматриваемой в JCGM 107 обобщенной версии метода наименьших квадратов.
9.3 Задача заключается в оценке параметров кривой, описывающей искомую зависимость (в том числе количественной), на основании пар значений измеряемой величины и соответствующих показаний средства измерений. Данные пары вместе с соответствующими стандартными неопределенностями и, если необходимо, поправками составляют исходные величины, подлежащие последующей обработке.
9.4 Основные измерительные задачи, подпадающие под действие JCGM 107, связаны с (а) отысканием линейной или нелинейной зависимости, в том числе при отсутствии полной информации о значениях независимой переменной, и (b) использованием простых измерительных моделей применительно к оценке параметров физических процессов. Применение JCGM 107 не сводится к отысканию зависимости в узком смысле этого слова. JCGM 107 применимо, к примеру, при решении сложных измерительных задач [21], определении фундаментальных констант [22], проведении сличения в целях оценки результатов измерений [9].
9.5 Применительно к задачам типа (а), указанным в пункте 9.4, если оценка параметров калибровочной функции, стандартных неопределенностей и поправок проводится методом наименьших квадратов, то за ней должны последовать соответствующие измерения с использованием измерительной системы. В этом случае оценки значений параметров калибровочной функции вместе с показаниями средства измерений используются для оценки значений измеряемой величины. Стандартная неопределенность данной оценки определяется с учетом стандартных неопределенностей и поправок, относящихся к оценкам параметров калибровочной функции, и стандартной неопределенности показаний средства измерений.
9.6 Как отмечается в JCGM 107, «структура неопределенности» должна в полной мере учитываться при постановке и решении измерительных задач, осуществляемых с помощью метода наименьших квадратов. Понятие «структура неопределенности» распространяется на стандартные неопределенности, показания и любые поправки, относящиеся к парам входных и выходных величин.
9.7 В рамках задач типа (b), рассматриваемых в пункте 9.4, или при определении параметров, предусмотренном задачами типа (а), отыскание зависимости обычно применяется в отношении не одной, а сразу нескольких выходных величин, математическое представление которых допускает их выражение в матричной форме. В JCGM 107 уделяется большое внимание матричным формам, поскольку они дают возможность использования компьютера для получения численных решений (см. 7.5).
10 Библиография
[1] Bell S. Measurement Good Practice Guide No. 11. A Beginners Guide to Uncertainty of Measurement. Tech, rep., National Physical Laboratory, 1999. 3.2
[2] Bernardo J., AND SMITH A. Bayesian Theory. John Wiley & Sons, New York, USA, 2000. 3.20
[3] BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, AND OIML. Evaluation of measurement data - Applications of the least-squares method. Joint Committee for Guides in Metrology, JCGM 107, in preparation. 1, 9.1
[4] BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, AND OIML. Evaluation of measurement data - Concepts and basic principles. Joint Committee for Guides in Metrology, JCGM 105, in preparation. 1,4.1
[5] BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, AND OIML. Evaluation of measurement data - Supplement 2 to the «Guide to the expression of uncertainty in measurement» - Models with any number of output quantities. Joint Committee for Guides in Metrology, JCGM 102, in preparation. 1, 6.1, 7.5.2
[6] BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, AND OIML. Evaluation of measurement data - Supplement 3 to the «Guide to the expression of uncertainty in measurement» - Modelling. Joint Committee for Guides in Metrology, JCGM 103, in preparation. 1, 6.1,6.2
[7] BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, AND OIML. Evaluation of measurement data - The role of measurement uncertainty in conformity assessment. Joint Committee for Guides in Metrology, JCGM 106, in preparation. 1, 8.1
[8] Casella G.C., AND Berger, R. L. Statistical Inference. Duxbury Press, Pacific Grove, 2001. Second Edition. 7.3.1
[9] Cox M.G. The evaluation of key comparison data. Metrologia 39 (2002), 589-595. 9.4
[10] Cox M.G., AND Harris P.M. SS/M Best Practice Guide No. 6, Uncertainty evaluation. Tech. Rep. DEM-ES-011, National Physical Laboratory, Teddington, UK, 2006. 7.3.1, 7.3.2
[11] Cox M.G. AND Harris P.M. Software specifications for uncertainty evaluation. Tech. Rep. DEM-ES-010, National Physical Laboratory, Teddington, UK, 2006
[12] Dietrich C.F. Uncertainty, Calibration and Probability. Adam Hilger, Bristol, UK, 1991.7.3.1
[13] Elster С. Calculation of uncertainty in the presence of prior knowledge. Metrologia 44 (2007), 111-116. 3.20
[14] EURACHEM/CITAC. Quantifying uncertainty in analytical measurement. Tech. Rep. Guide CG4, EURACHEM/CITEC,[EURACHEM/CITAC Guide], 2000. Second edition. (Руководство ЕВРФХИМ/СИТАК Количественное описание неопределенности в аналитических измерениях. 2-е издание, 2000, перевод с английского Р.Л. Кадиса, Г.Р. Нежиховского, В.Б. Симина, под общей редакцией Л.А. Конопелько, Санкт-Петербург, ВНИИМ им. Д.И. Менделеева, 2002. - 149 с.)
[15] Feller W. An Introduction to Probability Theoty and its Applications, Volume 1. Wiley, 1968.
[16] Feller W. An Introduction to Probability Theoty and its Applications, Volume II. Wiley, 1971
[17] HiBBert D. B. Quality Assurance for the Analytical Chemistry Laboratoiy. Oxford University Press, Oxford, UK,2007.
[18] IEC. IEC Guide 115. Application of uncertainty of measurement to conformity assessment activities in the electrotechnical sector. International Electrotechnical Commission, Geneva, Switzerland, 2007. 8.1
[19] ISO. ISO 10576-1. Statistical methods - Guidelines for the evaluation of conformity with specified requirements - Part 1: General principles, 2003. International Standards Organization, Geneva. 8.5
[20] ISO/IEC. ISO/IEC 17025. General requirements for the competence of testing and calibration laboratories, 2005. International Standards Organization, Geneva.
[21] KorczynsKi M. J., Cox M. G. AND Harris P. M. Convolution and uncertainty evaluation. In Advanced Mathematical Tools in Metrology VII (Singapore, 2006), P. Ciarlini, E. Felipe, A. B. Forbes, and F. Pavese, Eds., World Scientific, pp. 188-195. 9.4
[22] Mohr P. J. AND Taylor B. N. CODATA recommended values of the fundamental physical constants: 2002. Rev. Mod. Phys. 76 (2004), 4.9.4
[23] NIST. Uncertainty of measurement results.
[24] Possolo A., AND Toman B. Assessment of measurement uncertainty via observation equations. Metrologia 44 (2007), 464-475. 3.20
[25] Rice J. R. Mathematical Statistics and Data Analysis, second ed. Duxbury Press, Belmont, Ca., USA, 1995. 7.3.2
[26] Weise К. AND Woger W. A Bayesian theory of measurement uncertainty. Meas. Sci. Technol. 3 (1992), 1-11. 4.8
Дополнительная литература
ГОСТ P 51318.16.4.2-2006. Совместимость технических средств электромагнитная. Неопределенность измерений в области электромагнитной совместимости.
ГОСТ Р ИСО 11222-2006. Качество воздуха. Оценка неопределенности измерений характеристик качества воздуха, полученных усреднением по времени.
ГОСТ Р ИСО 13752-2005. Качество воздуха. Оценка неопределенности метода измерений в условиях применения с использованием референтного метода.
Ефремова Н.Ю. Оценка неопределенности в измерениях. Практическое пособие / БелГИМ - Минск, 2003.
МИ 1317-2004. Рекомендация. Государственная система обеспечения единства измерений. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров.
Походун А.И. Экспериментальные методы исследований. Погрешности и неопределенности измерений / Учебное пособие. - СПб: СПбГУ ИТМО, 2006. - 112 с.
Р 50.1.060-2006. Статистические методы. Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений.
Р 50.1.062-2007. Статистические методы. Неопределенность при повторных измерениях и иерархических экспериментах.
Р 50.2.038-2004. Государственная система обеспечения единства измерений. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений.
РМГ 43-2001. Государственная система обеспечения единства измерений. Применение Руководства по выражению неопределенности измерений.
РМГ 91-2009. Государственная система обеспечения единства измерений. Совместное использование понятий «погрешность измерения» и «неопределенность измерения». Общие принципы.
РМГ 93-2009. Государственная система обеспечения единства измерений. Оценивание неопределенностей аттестованных значений стандартных образцов.
Руководство ИСО/МЭК 2:1996. Стандартизация и смежные виды деятельности. Общий словарь. ISO/IEC Guide 2:1996) (Standardization and related activities - General vocabulary).
Руководство по выражению неопределенности измерений (GUM: 1993) / Перевод с английского ВНИИМ им. Д.И. Менделеева,- СПб.
СТ РК 7.13-2008. Система аккредитации. Оценка неопределенности результатов измерений при калибровке.