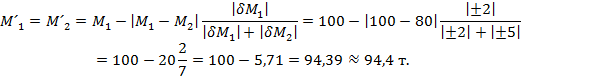ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ УНИТАРНОЕ ПРЕДПРИЯТИЕ
«ВСЕРОССИЙСКИЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
ИНСТИТУТ МЕТРОЛОГИЧЕСКОЙ СЛУЖБЫ»
(ФГУП ВНИИМС)
ГОССТАНДАРТА РОССИИ
РЕКОМЕНДАЦИЯ
Государственная система обеспечения единства измерений.
Объем и масса нефти и
нефтепродуктов.
Методика оценки точности измерений (определения)
количества нефти и нефтепродуктов при распределении
небаланса между поставщиками и потребителями в
ОАО «ЛУКОЙЛ»
МИ 2772-2002
Москва
2002
|
РАЗРАБОТАНА |
ФГУП ВНИИМС |
|
ИСПОЛНИТЕЛИ |
Б.М. Беляев Ю.А. Богданов (рук. темы) А.И. Вересков |
|
УТВЕРЖДЕНА |
ФГУП ВНИИМС 16 декабря 2002 г. |
|
ЗАРЕГИСТРИРОВАНА |
ФГУП ВНИИМС 17 декабря 2002 г. |
|
ВВЕДЕНА |
ВПЕРВЫЕ |
СОДЕРЖАНИЕ
РЕКОМЕНДАЦИЯ
|
Государственная система обеспечения единства измерений. Объем и масса нефти и нефтепродуктов. |
МИ 2772-2002 |
1. Введение
1.1. Настоящая рекомендация распространяется на объем и массу нефти и нефтепродуктов и устанавливает методику оценки точности измерений (определения) количества нефти и нефтепродуктов при распределении небаланса между поставщиками и потребителями в ОАО «ЛУКОЙЛ».
1.2. Исходные положения, принятые при решении задачи распределения небаланса, и особенности её постановки приведены в приложении А.
1.3. Рекомендация разработана с учетом требований МИ 2525-99 «ГСИ. Рекомендации по метрологии, утверждаемые Государственными научными метрологическими центрами Госстандарта России».
2. Классификация систем передачи и распределения продукта
К типовым системам «поставщики-потребители (получатели)», применяемым в практике [4], отнесены следующие:
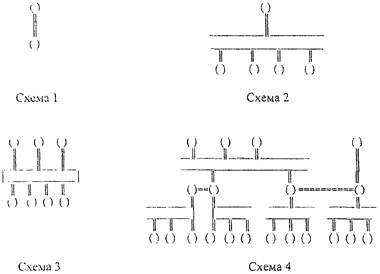
2.1. Простейшая система «один поставщик, один получатель» представлена схемой 1 на рис. 1. Этот случай соответствует, например, отпуску нефти в танкер, когда количество измеряют дважды - вначале береговыми узлами учета, затем судовыми средствами измерений.
Рисунок 1
Схемы связей в системах «поставщики-потребители». Обозначения: () - участники учетной операции; двумя горизонтальными чертами обозначены пункты передачи продукта; двойными вертикальными - направления передачи продукта с выполнением измерений его количества (на схеме 3 прямоугольником обозначен промежуточный участник учетной операции)
2.2. Система «один поставщик, несколько получателей» представленная схемой 2 на рис. 1, реализуется при передаче нефти по нефтепроводу. Отпускаемое количество измеряют узлом учета, затем части этого количества измеряют получатели.
2.3. Система «несколько поставщиков, несколько получателей» представлена схемой 3 на рис. 1. Примером служит работа нефтебазы.
2.4. Система с достаточно общей структурой связей представлена схемой 4 на рис. 1. Например, это может быть система транспортировки и поставки нефти от исходных поставщиков к конечным потребителям через промежуточные звенья.
Схема 4 наглядно демонстрирует возможное многообразие связей в системах «поставщики-потребители». Вторая из рассмотренных систем является частным случаем четвертой и входит в нее как подсистема. Отличительная особенность систем 3 и 4 - наличие в них промежуточных участников учетных операций, которые одновременно являются получателями и поставщиками продукта.
3. Метод решения
3.1. Задачу многомерного статистического анализа решают путем выполнения операций, приведенных ниже.
3.2. Постановка математической задачи определения учетных значений и сведения баланса в системе со структурой связей общего вида.
Известны значения следующих величин: v = (v1 …, vn) - результаты измерений количества, Δ = (Δ1, …, Δn) - пределы допускаемых абсолютных погрешностей, n - число участников, m - число пунктов передачи продукта.
Структуру связей в системе задают с помощью матрицы (таблицы) А размера m×n, элементы которой определяют по следующему правилу (см. пример в приложении Б):
aij = 1, если j-й участник является поставщиком в i-м пункте,
aij = -1, если j-й участник является получателем в i-м пункте,
aij = 0, если j-й участник не участвует в i-м пункте передачи продукта, где aij - элемент, находящийся на пересечении i-й строки и j-го столбца.
Требуется определить учетные значения u = (u1 …, un).
3.3. Метод определения учетных значений при условном
распределении небаланса Учетные значения определяют в оптимизационной задачи результате решения
|
||v - u|| + ||Au|| → min |
(1) |
при ограничениях в виде неравенств
Двойные вертикальные черты в (1) обозначают норму вектора [3], определенную равенством
|
||w|| = (Σ|wj|p)1/p, где p ≥1. |
(3) |
Примечание - Метод решения задачи, как и его модификация, описанная в п. 3.8, соответствует статистическому методу оценки параметров, который позволяет получать как традиционные, так и робастные оценки [2]. В соответствии с теорией математической статистики значение р в (3) следует выбирать в зависимости от вида распределения погрешностей измерений. В частности, при нормальном законе распределения оценки с оптимальными статистическими свойствами получают при р = 2 по методу наименьших квадратов.
Все расчеты проводят с помощью программы, разработанной ВНИИМС, в автоматическом режиме.
3.4. Рассчитывают вектор d (размерности m) исходного небаланса измеренных значений:
|
(4) |
Таким образом, i-я компонента вектора равна разности между суммой измерений поставщиков и суммой измерений получателей в i-м пункте передачи продукта (см. пример в приложении Б).
3.5. Алгоритм расчета учетных значений по методу п. 3.3 основан на итерационной процедуре, на каждом шаге которой определяют вектор приближенных значений ũq, где q - номер итерации.
3.5.1. Проверяют выполнение неравенств (2), подставляя в них u = ũq, и при необходимости корректируют значения ũq.
3.5.2. Рассчитывают вектор разности между измеренными и приближенными значениями v - ũq.
3.5.3. Рассчитывают вектор небаланса приближенных значений, в соответствии с формулой (4), равный Аũ (вектор размерности m).
3.5.4. Полученные значения векторов v - ũq и Аũ подставляют в (1). Вектор приближенных значений ũq определяют так, чтобы значение левой части (1) на текущей итерации было меньше соответствующего значения на предыдущей итерации.
Наличие первого слагаемого в (1) обеспечивает близость учетных значений к измеренным. Второе слагаемое включено в (1) для минимизации величины остаточного небаланса учетных значений, равного Аu.
3.6. Учитывают, что ограничения (2) связаны с тем, что назначение учетного значения uj, отличного от результата измерений vj более чем на величину предела допускаемой абсолютной погрешности Δj, может вызвать несогласие j-го участника учетной операции (см. п. 3.12).
3.7. Полученное решение удовлетворяет ограничениям (2), однако при этом распределение небаланса может оказаться либо полным, либо частичным - в зависимости от конкретных числовых значений исходных данных. Исходя из практических потребностей пользователя и стоящей перед ним задачи, актуальным может оказаться полное распределение небаланса. В связи с этим предусмотрен второй вариант решения задачи.
3.8. Метод определения учетных значений при полном распределении небаланса. В условиях, сформулированных в п. 3.2, учетные значения определяют в результате решения оптимизационной задачи
|
||v - u|| → min |
(5) |
при ограничениях в виде равенств
|
(6) |
3.9. Алгоритм расчета учетных значений по методу п. 3.8 основан на итерационной процедуре, на каждом шаге которой определяют вектор приближенных значений ũq, где q - номер итерации.
3.9.1. Проверяют выполнение равенств (6), подставляя в них u = ũq, и при необходимости корректируют значения ũq (левая и правая часть (6) представляют собой векторы размерности m).
3.9.2. Рассчитывают вектор разности между измеренными и приближенными значениями v - ũq.
3.9.3. Полученные значения вектора v - ũq подставляют в (5). Вектор приближенных значений ũq определяют так, чтобы значение левой части (5) на текущей итерации было меньше соответствующего значения на предыдущей итерации.
Соотношение (5) обеспечивает близость учетных значений к измеренным, (6) - равенство нулю величины остаточного небаланса учетных значений во всех пунктах передачи продукта.
3.10. Полученное решение удовлетворяет условию полного распределения небаланса (6), однако при этом ограничения (2) могут оказаться выполненными либо нарушенными - в зависимости от конкретных числовых значений исходных данных. Выбор того или другого варианта решения задачи - по методу п. 3.3 или п. 3.8 -предоставлен пользователю программы.
3.11. Анализ условий полного распределения небаланса. Наилучшим вариантом решения задачи является равенство нулю остаточного небаланса во всех пунктах передачи продукта при соблюдении ограничений (2). Математически это выражается одновременным выполнением соотношений (2), (5), (6). В программе предусмотрено исследование такой возможности.
3.11.1. Рассчитывают теоретический предел допускаемого исходного небаланса по результатам измерений - вектор dn (размерности m), i-я компонента которого равна сумме пределов допускаемых абсолютных погрешностей измерений Δj участников учетной операции в i-м пункте передачи продукта.
3.11.2. Проверяют необходимое условие полного сведения баланса при ограничениях (2): компоненты вектора исходного небаланса d, рассчитанного по п. 3.4, по абсолютной величине не превосходят соответствующих компонент вектора dn.
3.11.3. Если условие п. 3.11.2 выполнено, определяют учетные значения по методу п. 3.8. Для полученного решения проверяют выполнение соотношений (2). Если (2) выполнены, решение найдено. В противоположном случае определяют учетные значения по методу п. 3.3. Выбирают наиболее подходящее из двух найденных решений.
3.11.4. Если условие п. 3.11.2 нарушено, соотношения (2), (5), (6) не могут быть выполнены вместе. Могут быть получены решения задачи определения учетных значений по методу п. 3.3 и по методу п. 3.8, но при этом полученные решения не совпадают.
3.12. Учитывают, что нарушение условия п. 3.11.2 может произойти вследствие неучтенных потерь и убыли продукта, нарушений требований методик выполнения измерений (МВИ) и других причин. В отсутствие подобных причин МВИ гарантирует, что с вероятностью 0,95 измеренные значения у отличаются от истинных значений не более чем на величину предела допускаемой абсолютной погрешности Δj. В этом случае указанное условие, как правило, оказывается выполненным, и баланс может быть сведен полностью с соблюдением ограничений (2).
3.13. В программе предусмотрена возможность выбора значения управляющего параметра р (см. п. 3.3), который влияет на решение задачи следующим образом: его значение определяет, будет ли небаланс распределен в большей степени между «крупными» участниками учетной операции или его распределение будет более равномерным. Исходя из этого, пользователь может выбрать наиболее подходящее значение параметра в диапазоне, указанном в п. 3.3. В другом варианте можно использовать результаты анализа данных и рекомендацию по выбору значения р, полученные программой.
3.13.1. Программой проводится проверка статистической гипотезы о соответствии погрешностей результатов измерений нормальному распределению. В случае принятия гипотезы рекомендовано значение р = 2, что соответствует методу наименьших квадратов.
3.13.2. По договоренности с заказчиком при разработке программы может быть выбрано и зафиксировано определенное значение параметра, либо его значение может варьировать оператор. В последнем случае при расчете по методу п. 3.3 можно рекомендовать следующую последовательность действий. Проводят расчет по программе при значении р = 2. Если небаланс оказался распределенным полностью, решение получено. Если нет, постепенно изменяя значение параметра, добиться по возможности полного сведения баланса.
3.14. Используемый метод статистической обработки данных помимо самих оценок истинных значений позволяет получать величины стандартных отклонений оценок [1] (см. выдачу программы в приложении Б). На основании этих величин с учетом известных значений пределов допускаемых погрешностей измерений рассчитывают показатели точности определения количества нефти и нефтепродуктов.
3.15. Из общих теоретических результатов [1, 2] следует, что полученные по данной методике оценки являются более точными по сравнению с исходными результатами измерений (обладают меньшей дисперсией).
4. Алгоритмическая и программная реализация
Сформулированная задача решена в алгоритме и реализующей его программе «Баланс нефти и нефтепродуктов в ОАО «ЛУКОЙЛ», разработанных ВНИИМС. Математическое обеспечение учитывает специальный вид и структуру данных конкретных задач. Структура связей в системе «поставщики-потребители» должна быть задана заказчиком в виде схемы (рисунка) и матрицы (таблицы) и согласована с разработчиком.
В программе сведения баланса предусмотрены дополнительные возможности. Для определенных участников учетной операции (например, для некоторых из поставщиков) могут быть зафиксированы исходные измеренные значения, остающиеся неизменными в результате решения задачи. Может быть предусмотрена возможность учета естественной убыли и потерь продукта в пределах установленной нормы, которые в этом случае не будут влиять на величину исходного небаланса по результатам измерений.
В приложении Б приведен пример определения учетных значений и распределения небаланса количества продукта по результатам измерений за отчетный период в системе с заданной структурой связей.
5. Требования к квалификации операторов
Выполнение расчетов количества нефти и нефтепродуктов при распределении небаланса с использованием ЭВМ проводят сотрудники, изучившие настоящую рекомендацию и инструкцию пользователя программы.
6. Подготовка к выполнению расчетов
При подготовке к выполнению расчетов формируют информацию в соответствии с п. 3.2.
6.1. Задают числовые значения следующих величин:
n - число участников учетной операции,
m - число пунктов передачи продукта,
v1, …, vn - результаты измерений количества,
Δ1, …, Δn - пределы допускаемых абсолютных погрешностей измерений.
6.2. Структуру связей в системе задают с помощью матрицы (таблицы) А размера m×n, элементы которой определяют по правилу, сформулированному в п. 3.2.
7. Выполнение расчетов
7.1. Для получения учетных значений количества продукта, корректирующих количеств (равных разности между учетным и измеренным значениями) и коэффициентов коррекции (равных отношению учетного значения к измеренному) к измеренным значениям, величины остаточного небаланса (если таковой имеется), данные, перечисленные в разделе 6, обрабатывают по методу, описанному в разделе 3.
7.2. Расчет проводят по программе «Баланс нефти и нефтепродуктов в ОАО «ЛУКОЙЛ».
8. Инженерная методика расчета
8.1. Алгоритмы сведения балансов между поставщиками и потребителями, описанные в предыдущих разделах, позволяют оптимизировать эту процедуру для большого количества участников учетно-расчетных операций. Поэтому в их основе используют методы последовательных итерационных процедур. В то же время в практике часто встречаются задачи сведения небаланса между двумя участниками сделки: поставщиком и потребителем. При этом можно использовать более простые методы, основанные на применении коэффициентов весомости распределения небаланса в зависимости от соотношения погрешностей измерений количества у поставщика и потребителя. Ниже рассмотрена методика распределения небаланса для такой задачи.
8.2. Условия задачи
Поставщик измерил количество отпущенного товара М1 с абсолютной погрешностью δМ1 Это значение зафиксировано в накладной.
Потребитель, получив товар, измерил его количество М2 с абсолютной погрешностью δМ2. Это значение отражено в акте приемки.
Поставлена задача: получить откорректированные значения Mʹ1 и Мʹ2 которые должны быть зафиксированы у поставщика и потребителя, исходя из условия Mʹ1 = Мʹ2 (принимают, что естественная убыль при поставке товара отсутствует).
8.3. Решение задачи
Проводят ранжирование полученных значений М1; δМ1 и М2; δМ2 по величине погрешности.
1 вариант
Пусть |δМ1| < |δМ2|, тогда имеем при М1 > М2:
при М1 < М2:
|
|
(8) |
2 вариант
Пусть |δМ2| < |δМ1|, тогда имеем при М2 > М1:
|
|
(9) |
при М2 < М1:
|
|
(10) |
При наличии естественной убыли, равной Е, значение М2 заменяют на М2 + Е.
8.4. Применение полученных соотношений на конкретном примере Пусть M1 = 100 т; М2 = 80 т; δM1 = 2 т; δМ2 = 5 т.
Проведем ранжирование.
Так как |δМ1| < |δМ2|, a M1 > M2, расчет ведем для Мʹ1, с использованием соотношения (7).
Имеем
|
|
|
Таким образом, накладную отгрузки и акт приемки следует откорректировать на величину 94,4 т.
Приложение А
Обработка результатов измерений количества нефти и нефтепродуктов при их передаче от поставщиков к потребителям требует использования специальной статистической процедуры. Это связано, во-первых, со сложной структурой связей в системе «поставщики-потребители», характерной для большинства таких систем, а во-вторых, с часто имеющим место на практике значительным отклонением результатов измерений отдельными участниками учетных операций от истинных значений, происходящим из-за нарушений условий, регламентированных МВИ, потерь и других причин. Вследствие этого распределение погрешности результатов измерений может не соответствовать нормальному закону и являться причиной возникновения больших значений небаланса (разницы между результатами измерений поставщиков и потребителей), существенно превосходящих значения, которые могут быть обусловлены погрешностями средств измерений.
При обработке результатов измерений необходимо принимать во внимание перечисленные особенности задачи, целью которой является определение значений количества нефти и нефтепродуктов (далее - продукта) при учетных операциях (далее - учетных значений).
Оптимальная статистическая процедура должна использовать всю имеющуюся информацию, в частности, условие баланса, т.е. равенства значений отпущенного и полученного количеств продукта. Такая процедура служит для коррекции результатов измерений с учетом условия баланса в качестве дополнительной информации.
Скорректированные таким способом результаты измерений должны удовлетворять условию баланса, что свидетельствует о повышении точности измерений и позволяет решать задачу распределения небаланса между поставщиками и потребителями.
Проблема статистической обработки данных при постановке задачи имеет следующие особенности. Во-первых, в общем случае требуется решить задачу многомерного статистического анализа с ограничением на переменные [1], которое является математическим выражением условия баланса. Например, в системе 2 на рис. 1 - это равенство значений количества продукта, отпущенного поставщиком, и полученного потребителями.
Другая особенность связана с отмеченным выше возможным отклонением от нормального закона распределения погрешностей измерений отдельными участниками учетных операций. В случаях, когда это происходит, необходимо привлечение робастных методов статистической обработки данных, т.е. методов, устойчивых по отношению к отклонениям от нормального закона [2].
Исходными данными для решения задачи служат результаты измерений, значения пределов погрешностей измерений и структура связей в системе «поставщики-потребители». При нормальном законе распределения погрешностей измерений для некоторых частных видов систем с несложной структурой решение может быть получено аналитически. В общем случае решение носит алгоритмический характер и реализуется с помощью специальной программы, разработанной ВНИИМС.
Приложение Б
Пример определения учетных значений и распределения
небаланса
количества продукта
Пример расчета основан на программе «Баланс нефти и нефтепродуктов в ОАО «ЛУКОЙЛ», разработанной ФГУП ВНИИМС.
Определены учетные значения и сведен баланс количества продукта, измеренного в м3, по результатам измерений за отчетный период в системе со структурой связей, показанной на рис. Б.1. Номера с 1 по 10 соответствуют номерам участников учетной операции на этом рисунке.
Исходные числовые данные измерений vj и пределов погрешностей Δj содержатся в выдаче программы, представленной ниже.
Проиллюстрируем некоторые этапы методики на этом примере.
В соответствии со схемой на рис. Б.1 и правилом в п. 3.2 матрица А имеет вид
|
1 |
1 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
-1 |
-1 |
-1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
-1 |
По формуле (4) вектор исходного небаланса d равен
68500 + 33600 - 51000 - 29900 - 20100 = 1100
51000 - 22400 - 13900 - 13500 = 1200
29900 - 21000 - 8400 = 500.
Предел допускаемого исходного небаланса, вектор dn равен
1027 + 604 + 1020 + 747 + 502 = 3900
1020 + 560 + 403 + 391 = 2374
747 + 525 + 243 = 1515.
Сопоставляя соответствующие компоненты векторов d и dn, убеждаемся, что сформулированное в п. 3.11.2 условие полного сведения баланса выполнено. В результате проверки статистической гипотезы убеждаемся, что нет оснований сомневаться в соответствии погрешностей результатов измерений нормальному распределению (эта проверка, как и все приводимые здесь вычисления, выполняются программой в автоматическом режиме.)
В представленном фрагменте выдачи программы корректирующее количество равно разности между учетным и измеренным значениями, коэффициент коррекции - отношению этих величин. Решение получено при значении параметра р = 2, что соответствует нормальному закону распределения погрешностей результатов измерений. Можно убедиться, что для полученных учетных значений выполнены соотношения (6), то есть баланс сведен полностью.
Таблица взаимного влияния факторов (справочная) характеризует степень статистической связи между участниками учетной операции в соответствии с принятой нумерацией.
Рисунок Б.1
Схема связей в системе «поставщики-потребители». Обозначения: (1), (2) - поставщики; (3), (4) - промежуточные участники учетной операции; (5) - (10) - потребители; двумя горизонтальными чертами обозначены пункты передачи продукта; двойными вертикальными - направления передачи продукта с выполнением измерений его количества
|
Число участников операции |
10 |
|
Число пунктов передачи продукта |
3 |
|
Единица измерения количества |
м3 |
Пункт передачи продукта 1 (* поставщики отмечены звездочкой)
|
№ |
Измеренное значение |
Предел погр. отн., %, абс |
Учетное значение |
Корректир. количество |
Коэффициент коррекции |
|
|
1* |
68500 |
1,50 |
1027 |
67497 |
-1002 |
0,9854 |
|
2* |
33600 |
1,80 |
604 |
33252 |
-347 |
0,9897 |
|
3 |
51000 |
2,00 |
1020 |
50624 |
-375 |
0,9926 |
|
4 |
29900 |
2,50 |
747 |
29786 |
-113 |
0,9962 |
|
5 |
20100 |
2,50 |
502 |
20339 |
239 |
1,0119 |
Измерено: поставщики 102100, получатели 101000, исходный небаланс 1100
Учтено: поставщики 100750, получатели 100750, остаточный небаланс 0
Пункт передачи продукта 2
|
№ |
Измеренное значение |
Предел погр. отн., %, абс |
Учетное значение |
Корректир. количество |
Коэффициент коррекции |
|
|
3* |
51000 |
2,00 |
1020 |
50624 |
-375 |
0,9926 |
|
6 |
22400 |
2,50 |
560 |
22810 |
410 |
1,0183 |
|
7 |
13900 |
2,90 |
403 |
14112 |
212 |
1,0153 |
|
8 |
13500 |
2,90 |
391 |
13700 |
200 |
1,0149 |
Измерено: поставщики 51000, получатели 49800, исходный небаланс 1200
Учтено: поставщики 50624, получатели 50624, остаточный небаланс 0
Пункт передачи продукта 3
|
№ |
Измеренное значение |
Предел погр. отн., %, абс |
Учетное значение |
Корректир. количество |
Коэффициент коррекции |
|
|
4* |
29900 |
2,50 |
747 |
29786 |
-113 |
0,9962 |
|
9 |
21000 |
2,50 |
525 |
21317 |
317 |
1,0151 |
|
10 |
8400 |
2,90 |
243 |
8468 |
68 |
1,0081 |
Измерено: поставщики 29900, получатели 29400, исходный небаланс 500
Учтено: поставщики 29786, получатели 29786, остаточный небаланс 0
Сводная информация
|
Число участников операции |
10 |
|
Число поставщиков, не являющихся получателями |
2 |
|
Число получателей, не являющихся поставщиками |
6 |
|
Число поставщиков, являющихся получателями |
2 |
|
№ |
Измеренное значение |
Погрешность отн., % абс |
Учетное значение |
Корректир. количество |
Коэффициент коррекции |
Станд. откл. учетного знач. |
|
|
1 |
68500 |
1,50 |
1027 |
67497 |
-1002 |
0,9854 |
776 |
|
2 |
33600 |
1,80 |
604 |
33252 |
-347 |
0,9897 |
571 |
|
3 |
51000 |
2,00 |
1020 |
50624 |
-375 |
0,9926 |
587 |
|
4 |
29900 |
2,50 |
747 |
29786 |
-113 |
0,9962 |
449 |
|
5 |
20100 |
2,50 |
502 |
20339 |
239 |
1,0119 |
488 |
|
6 |
22400 |
2,50 |
560 |
22810 |
410 |
1,0183 |
503 |
|
7 |
13900 |
2,90 |
403 |
14112 |
212 |
1,0153 |
388 |
|
8 |
13500 |
2,90 |
391 |
13700 |
200 |
1,0149 |
379 |
|
9 |
21000 |
2,50 |
525 |
21317 |
317 |
1,0151 |
434 |
|
10 |
8400 |
2,90 |
243 |
8468 |
68 |
1,0081 |
241 |
Таблица взаимного влияния факторов (справочная)
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1,00 |
|
|
|
|
|
|
|
|
2 |
-0,41 |
1,00 |
|
|
|
|
|
|
|
3 |
0,42 |
0,20 |
1,0 |
|
|
|
|
|
|
4 |
0,30 |
0,14 |
-0,15 |
1,00 |
|
|
|
|
|
5 |
0,33 |
0,15 |
-0,16 |
-0,11 |
1,0 |
|
|
|
|
6 |
0,25 |
0,12 |
0,58 |
-0,08 |
-0,09 |
1,00 |
|
|
|
7 |
0,17 |
0,08 |
0,39 |
-0,06 |
-0,06 |
-0,21 |
1,00 |
|
|
8 |
0,16 |
0,08 |
0,38 |
-0,05 |
-0,06 |
-0,21 |
-0,14 |
1,0 |
|
9 |
0,25 |
0,12 |
-0,12 |
0,85 |
-0,1 |
-0,07 |
-0,05 |
-0,05 |
|
10 |
0,1 |
0,05 |
-0,05 |
0,33 |
-0,04 |
-0,03 |
-0,02 |
-0,02 |
Приложение В
[1]. Себер Дж. Линейный регрессионный анализ. М.; Мир, 1980.
[2]. Хьюбер П. Робастность в статистике. М.; Мир, 1984.
[3]. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.; Наука, 1992.
[4]. Контроль количества и качества нефтепродуктов//А.М. Несговоров и др.; Под ред. В.Ф. Новоселова. М,; Недра, 1995.