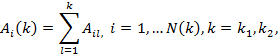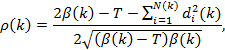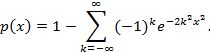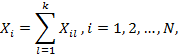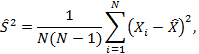ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ УНИТАРНОЕ ПРЕДПРИЯТИЕ
ВСЕРОССИЙСКИЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
МЕТРОЛОГИЧЕСКОЙ СЛУЖБЫ
(ФГУП ВНИИМС)
ГОССТАНДАРТА РОССИИ
РЕКОМЕНДАЦИЯ
ГОСУДАРСТВЕННАЯ
СИСТЕМА
ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
ИГРОВЫЕ АВТОМАТЫ С ДЕНЕЖНЫМ ВЫИГРЫШЕМ.
МЕТОДИКА ОБРАБОТКИ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ
ПРИ ИСПЫТАНИЯХ С ЦЕЛЬЮ УТВЕРЖДЕНИЯ ТИПА
МИ 2562-2001
Москва
2001
ПРЕДИСЛОВИЕ
РАЗРАБОТАНА ФГУП ВНИИМС Госстандарта России
ИСПОЛНИТЕЛИ Ю.В. Стефанов (руководитель темы); Ю.А. Кудеяров, д.ф.-м.н.; А.Г. Спроге
УТВЕРЖДЕНА ФГУП ВНИИМС Госстандарта России 24 декабря 2001 г.
ЗАРЕГИСТРИРОВАНА ФГУП ВНИИМС Госстандарта России 25 декабря 2001 г.
ВВЕДЕНА ВЗАМЕН МИ 2562-99
РЕКОМЕНДАЦИЯ
|
ГОСУДАРСТВЕННАЯ
СИСТЕМА ИГРОВЫЕ АВТОМАТЫ С
ДЕНЕЖНЫМ |
МИ 2562-2001 |
Настоящая рекомендация распространяется на игровые автоматы с денежным выигрышем (далее - игровые автоматы) и содержит описание методики обработки статистической информации при испытаниях с целью утверждения типа в соответствии с ПР 50.2.023.
При разработке настоящей рекомендации использованы следующие нормативные и законодательные документы:
1. Закон РФ от 27.04.1993 г. № 4871-1 «Об обеспечении единства измерений».
2. ПР 50.2.023-2000 «ГСИ. Правила проведения испытаний игровых автоматов с денежным выигрышем с целью утверждения типа и контроля за их соответствием утвержденному типу»
3. Правила испытаний РТВ (ФРГ).
1 ОПРЕДЕЛЕНИЯ
1.1 Игровой автомат с денежным выигрышем - специальное устройство, которое после внесения в него денежной ставки предоставляет пользователю (игроку) право на проведение игры с возможностью получения денежного выигрыша.
1.2 Тип игрового автомата - совокупность игровых автоматов, основанных на одном и том же принципе, имеющих одинаковые центральные блоки управления, одни и те же игровые программы, одну и ту же конструкцию, и выполненные по одной и той же технической документации и технологии.
1.3 Игровая программа - средство, обеспечивающее совокупность ответных действий игрового автомата, обусловленных действиями игрока.
1.4 Начало игры - момент времени, в который игрок приводит в действие игровую программу.
1.5 Окончание игры - момент времени, в который игровая программа заканчивает свои действия.
1.6 Игра - последовательность происходящих между началом и окончанием игры событий, включающих в себя действия игрока в рамках правил игры и ответные действия игрового автомата, обусловленные игровой программой.
1.7 Основная игра - игра, право на проведение которой дает ставка, вносимая в автомат в виде денежной суммы или ее эквивалента.
1.8 Дополнительная игра - игра, в которой в качестве ставки используется выигрыш в основной игре в виде права на проведение игры, предоставляющей возможность игроку либо увеличить выигрыш, либо его потерять.
1.9 Ставка - вносимая в игровой автомат сумма, выраженная в рублях или средствах их заменяющих (например, в жетонах) и позволяющая провести игру. Ставкой может быть и выигрыш в основной игре, который может быть использован для проведения дополнительной игры.
1.10 Результат игры - результат взаимодействия в процессе игры игрока и игрового автомата, возникающий после окончания игры, выраженный либо в рублях, либо в средствах, их заменяющих. Результат каждой игры может быть как положительным, так и нулевым.
1.11 Выигрыш - положительный результат игры; при этом игрок имеет возможность либо перевести выигрыш в выплату, либо использовать его полностью или частично в качестве ставки.
1.12 Проигрыш - результат игры, при котором выигрыш равен нулю, т.е. отсутствует.
1.13 Выплата - денежная сумма, выплачиваемая игроку по окончании игры в случае выигрыша.
1.14 Процент выигрыша - отношение выигрыша к значению ставки, выраженное в процентах.
2 ЗАДАЧИ ОБРАБОТКИ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ ПРИ ИСПЫТАНИЯХ ИГРОВЫХ АВТОМАТОВ С ЦЕЛЬЮ УТВЕРЖДЕНИЯ ТИПА
Задачи обработки статистической информации при испытаниях игровых автоматов с целью утверждения типа определяются следующими основными требованиями, предъявляемыми к ним существующей законодательной и нормативной документацией:
- на игровых автоматах разрешается применять лишь те игровые программы, которые обеспечивают получение выигрыша только в зависимости от случая;
- технологически заложенный процент выигрыша не может быть ниже определенного значения, устанавливаемого, как правило, в законодательном порядке. Так в Российской Федерации это значение установлено на уровне 75 %, в Венгрии - 80 %, в Германии - 60 % и т.д.
Соответствие свойств игровых программ игровых автоматов упомянутым требованиям подтверждают в ходе их испытаний с целью утверждения типа на основе соответствующей обработки и анализа статистической информации.
3 МЕТОДЫ ОБРАБОТКИ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ ПРИ ИСПЫТАНИЯХ ИГРОВЫХ АВТОМАТОВ С ЦЕЛЬЮ УТВЕРЖДЕНИЯ ТИПА
Проверку соответствия игрового автомата требованиям раздела 2 настоящей рекомендации осуществляют с помощью методики обработки статистической информации, описанной в этом разделе. Для реализации методики необходимо иметь исходный массив статистических данных, обработку которых проводят по алгоритмам, описываемым ниже.
Примечание - Поскольку при испытаниях игровых автоматов устанавливают соответствие игровых программ требованию получения выигрыша только в зависимости от случая, то при формировании числового массива результатов игр необходимо добиваться, чтобы эти результаты были максимально независимы от действий игрока и определялись главным образом соответствующей игровой программой. Например, для slot - автоматов необходимыми свойствами обладает массив результатов основной игры. В игровых автоматах покерного типа соответствующий числовой массив может быть получен при игре с использованием типовой стратегии (п. 3.4.1), при которой индивидуальные особенности оператора (игрока) нивелируются, и в этом смысле реальные результаты игры можно считать в значительной степени определяющимися только игровой программой.
Значение контрольного параметра р' (см. ниже) устанавливают таким образом, чтобы суммарная вероятность ошибки первого рода всех статистических испытаний не превышала 1 %.
В данной методике используют метод ранговых корреляций Спирмена, позволяющий обнаруживать в хронологической последовательности результатов игр тенденцию к возрастанию значений выигрышей. В общем случае этот метод позволяет с заданной вероятностью установить отсутствие каких - либо детерминированных закономерностей в хронологической последовательности результатов игр, а также их независимость от результатов предшествующих игр.
3.1.1 Метод ранговых корреляций Спирмена
3.1.1.1 Определение необходимого количества игр
В настоящей рекомендации определение необходимого количества игр основывают на результатах статистических экспериментов, проведенных в ФРГ на slot - автоматах, которые показали, что зависимость относительной частоты появления различных результатов игр от значений соответствующей квоты выплаты становится устойчивой (т.е. не меняется при увеличении количества игр) при числе игр не менее 35000. В настоящей рекомендации по результатам проведенных численных экспериментов принято, что числом игр М, обеспечивающим достоверные заключения статистического анализа результатов игр на игровых автоматах, является рекомендуемое значение M = 100000.
3.1.1.2 Разбиение результатов игр на блоки
Хронологический ряд результатов игр
|
А1, A2,..., Am |
разбивают на N блоков одинаковой длины k (т.е. k - количество игр в блоке). Разбиение исходного числового массива результатов игр (1) проводят дважды, например, для k = k1 = 150 и k = k2 = 1500, при этом значения N составляют N(k1) = 1000 и N(k2) = 100 соответственно.
Далее формируют ряд
где Аil - результат l - ой игры i - го блока. Таким образом, каждое значение Ai(k) означает суммарный результат для i-го блока игр, и вместо исходного ряда (1) используют ряд суммарных результатов игр (2), пронумерованных натуральным рядом чисел, при этом каждому члену натурального ряда соответствует как момент времени, когда был получен результат игры, так и значение этого результата. Одновременно каждый номер результата игр именуют рангом, т.е. числом, показывающим место результата в упорядоченном ряде. При этом такая характеристика результата, как его значение, изменяется случайным образом при переходе от одного члена хронологического (упорядоченного во времени) ряда результатов к другому. После такой нумерации ряд (2) принимают упорядоченным, а числа натурального ряда рассматривают как ранги.
3.1.1.3 Ранжирование по признаку возрастания значения выигрыша
Ряд суммарных результатов игр (2) выстраивают по признаку возрастания их значений, формируя новый ряд суммарных результатов игр, в котором члены ряда расположены по признаку возрастания значений этих результатов (либо по какому-то другому признаку). После нумерации членов нового ряда каждый его член Ai характеризуют новым рангом Rang(Ai). Так, например, 327-й член исходного ряда после ранжирования по рассматриваемому признаку в новом ряду может оказаться на 961-м месте, т.е. теперь Rang(A327) = 961, и при вычислении коэффициента корреляции сравнивают этот новый ранг с прежним, равным 327.
В общем случае в ряде суммарных результатов (2) могут встретиться результаты с одинаковыми значениями. В этом случае каждому такому значению результата приписывают усредненный ранг по правилу, описанному в приведенном ниже примере, а сами ранги называются связанными. При этом сумма всех связанных рангов результатов остается точно такой, как и при ранжировании без связей. Например, суммарный результат игр в 10 условных единиц в исходном ряду (2) встретился в 4-м, 20-м, 101-м, 463-м, 622-м, 623-м, 752-м и 934-м блоках. В новом ряду всем результатам игр, равным 10 условным единицам, независимо от того, в каком блоке они находились ранее, присваивают усредненный ранг Rang10 , который вычисляют по формуле
|
|
(3) |
Количество блоков с одинаковыми значениями суммарных результатов игр, которым был присвоен связанный ранг по описанному выше правилу, называют длиной связи t. В приведенном примере длина связи t = 8. Каждой длине связи присваивают номер j, по мере того, как они встречаются в новом ряду суммарных результатов игр.
3.1.1.4 Вычисление коэффициента ранговой корреляции
Коэффициент ранговой корреляции Спирмена ρ(k) вычисляют по формуле
|
|
(4) |
где
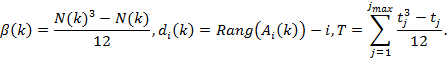
Результат
испытаний считают положительным, если для обоих значений k = k1
и k = k2 асимптотический коэффициент ранговой
корреляции Спирмена ![]() удовлетворяет
условию
удовлетворяет
условию
|
|
(5) |
где χ1-ρ'/2 - квантиль нормального распределения для уровня вероятности ρ' = 0,0025. При таком значении параметра ρ' условие (5) выполняется с вероятностью 0,9987. Это означает, что с такой же вероятностью результаты игры можно считать не проявляющими возрастание значений с течением времени. Для выявления других закономерностей и независимости результатов игр от предшествующих игр и игр других игроков проводят соответствующее ранжирование.
Данной проверкой устанавливают, что во временной последовательности игр отсутствуют тенденции в частоте выпадения больших и малых сумм денежных выигрышей.
3.2.1 Разбиение результатов игр на блоки
Как и в п. 3.1.1.2, все результаты игр, расположенные хронологически, разбивают на блоки и формируют ряд суммарных результатов игр в соответствии с формулой (2). Члены этого ряда образуют выборку суммарных результатов игр
|
А1, A2,..., AN(k) |
(6) |
3.2.2 Оценка медианы распределения и его преобразование в двоичную последовательность
Т.к. для дискретного ряда (6) понятие медианы не является определенным, его ранжируют по признаку возрастания. В том случае, если число членов ряда m является нечетным, медиану а1/2 принимают равной среднему (по нумерации) значению в ранжированном ряде. При четном числе членов ряда медиану вычисляют по формуле
![]()
где А'i и А'i+1 - два соседних средних значения суммарных результатов в ранжированном ряде.
Выборку (6) для Аi(k) преобразуют в двоичную последовательность A'i(k) по следующему правилу:
|
A'i(k) = 0, для Аi(k) < a1/2, A'i(k) = 1, для Аi(k) > a1/2. |
(7) |
В новой последовательности A'i, состоящей из нулей и единиц, подсчитывают количество итераций (последовательностей) r0 членов с нулевыми значениями и количество итераций r1 членов с единичными значениями. Полное число итераций r(k) = r0 + r1. При фиксированном числе результатов игр распределение 0 - итераций и 1 - итераций в общем случае может быть разным, а вероятность получения r0 0 - итераций при n0 событий 0 - вида и r1 1 - итераций при n1 событий 1 - вида можно оценить комбинаторными методами, вычисляя соответствующее число сочетаний.
3.2.3 Вычисление асимптотической частоты итераций
При большом объеме выборки, т.е. когда n → ∞ да, распределение вероятностей различных значений полного числа r итераций (их частоты) является нормальным, среднее значение этого распределения имеет вид
|
|
(8) |
Как и в п. 3.1.1.5 вводят асимптотическую частоту (общее число) итераций с помощью соотношения
|
|
(9) |
а дисперсию определяют формулой
|
|
(10) |
Выражение (10) используют как критерий (5) для оценки достоверности найденной из ряда (6) частоты итераций.
3.2.4 Результат испытаний
Результат испытаний считают положительным, если для обоих значений k = k1 и k = k2 выполнено условие (5). Это означает, что с вероятностью 0,9987 частоты выпадения больших и малых сумм денежных выигрышей являются случайными величинами.
3.3 Проверка по критерию согласия Колмогорова-Смирнова ограничения последовательностей проигрышей.
Данной проверкой устанавливают, что последовательности проигрышных игр не превышают определенного значения, установленного настоящей рекомендацией. Разбиения результатов игр на блоки при данной проверке не проводят.
3.3.1 Нахождение вероятности выигрыша
Из общего числа М игр выделяют число Na игр с выигрышем. Вероятность выигрыша p читывают по формуле
|
|
(11) |
3.3.2 Вычисление функции распределения последовательностей с проигрышными играми
Вероятность P(s) появления хотя бы одного выигрыша в серии результатов из s игр (s ≥ 1) определяют биномиальным законом распределения и вычисляют по формуле
|
P(s) = 1 - (1 - p)s, s = 1, 2…., |
(12) |
где p - вероятность выигрыша, определяемая формулой (11).
В частности, P(1) = p, P(2) = р(2 - р) и т. д.
3.3.3 Разбиение хронологического ряда результатов игр на серии основных игр с проигрышами и вычисление вероятности выигрыша для каждой серии
Хронологический ряд результатов основных игр (1) разбивают на серии таким образом, чтобы каждая серия включала в себя последовательность игр с проигрышем до появления первого выигрыша. Если ряд результатов игр (1) начинается с проигрыша, то в первую серию включают все игры до первой выигрышной игры, результат которой включают в эту серию. Минимальный размер серии в этом случае s = 2. Следующую серию начинают с первого результата последующей основной игры. Если этот результат является выигрышным, то в серию включают все выигрышные и проигрышные результаты вплоть до появления первого выигрышного результата после серии проигрышей. В этом случае минимальная серия состоит из трех игр. Если же первый результат следующей после первой серии является проигрышным, то серию образуют по такому же правилу, как и первую. Если же ряд (1) начинается с выигрышной игры, то в первую серию включают все выигрышные и проигрышные игры, вплоть до появления первого выигрыша после последовательности проигрышей, а далее разбиение ведут так, как описано выше. При таком способе разбиения исходной последовательности на серии отсутствуют серии с s = 1, так как выделение таких серий является неоднозначным. Их отсутствием пренебрегают, так как нахождение контрольного параметра происходит при больших размерах серий.
Для зафиксированной длины s полученных серий число выигрышей nr(s) в каждой r-ой серии будет разным. Вероятность выигрыша pRs в играх с длиной серий s определяют по формуле
|
|
(13) |
где Rs - число серий, содержащих последовательности игр длиной s;
Ns - общее число основных игр, отвечающих сериям длиной s (Ns = s × Rs).
3.3.4 Нахождение эмпирической функции распределения последовательностей игр с проигрышами
Эмпирическую функцию распределения последовательностей игр с проигрышами FRs(s) вычисляют по формуле
|
FRs(s) = 1 - (1 - pRs(s))s, s = 1, 2…., |
(14) |
где вероятность pRs определяют формулой (13).
3.3.5 Использование асимптотической формы критерия согласия Колмогорова-Смирнова для контроля последовательностей проигрышных игр
По формуле
|
|
(15) |
вычисляют контрольный параметр DR асимптотической формы критерия согласия Колмогорова-Смирнова.
3.3.6 Результат испытаний
Результат испытаний считают положительным, если контрольный параметр DR удовлетворяет условию
|
|
(16) |
где R - число серий, в которых число последовательных проигрышных игр соответствует максимальному различию между вычисленной и эмпирической функциями распределения длин последовательностей проигрышей,
χ1-р' - квантиль асимптотического распределения Колмогорова
|
|
(17) |
В частности, если p' = 0,0025, то условие (16) выполняется с вероятностью 0,9975, и, соответственно, с этой же вероятностью последовательности результатов игр с проигрышем в исходном хронологическом ряде результатов (1) не превышают значений, разрешенных условием (16).
3.4 Проверка ограничения снизу среднего процента выигрыша
Данной проверкой устанавливают, что средний процент денежного выигрыша не превышает определенного значения, установленного в ПР 50.2.023.
Эту проверку осуществляют с использованием числового массива результатов, полученного при игре, проводимой по типовой стратегии.
При этом центр испытаний игровых автоматов контролирует значение квоты выплаты двумя способами.
Первый способ основан на использовании показаний счетчиков ставок и выплат, которые установлены на игровых автоматах. Так как выплата игрокам за достаточно длительный период времени суммирована из наличных денег С, выплаченных им по результатам игр с выигрышем, и из кредита С', который использован игроками в качестве ставок, уменьшенного на величину В ставок в виде денег, квоту выплаты К определяют выражением
|
|
(18) |
Если ставки сделаны только в виде денег, то С' = В и выражение (18) принимает вид
|
|
(19) |
Второй метод контроля квоты выплаты основан на использовании статистических методов обработки информации о результатах игр, полученных при типовой стратегии.
3.4.1 Определение типовой стратегии, применяемой при испытаниях игровых автоматов покерного типа
В типовой стратегии используют следующую терминологию:
выигрышная комбинация карт - комбинация карт, возникающая после любой раздачи, которая совпадает с одной из комбинаций в таблице выигрышей игрового автомата;
предвыигрышная комбинация карт - комбинация, когда после первой раздачи возникает одна из следующих ситуаций:
- две одинаковые карты (либо один джокер); такой комбинации присваивается низший приоритет;
- straights без одной карты (в колоде без джокера), либо без двух карт, но с джокером (в колоде с джокером); средний приоритет (straights - комбинация, в которой карты различных мастей можно расположить по порядку возрастания без пропуска, например - 10, D, 9, J, 8);
- четыре карты одной масти (в колоде без джокера), либо 3 карты одной масти и джокер (в колоде с джокером); высший приоритет.
Типовая стратегия игры представляет следующую последовательность действий:
1. После первой раздачи производят идентификацию (распознавание) карт.
2. Если выпадает любая выигрышная комбинация, то ее удерживают, остальные карты меняют.
3. Если выпадает хотя бы одна предвыигрышная комбинация, то ее удерживают, остальные карты меняют.
4. Если одновременно выпадают несколько предвыигрышных комбинаций, то удерживают ту, которая имеет больший приоритет.
5. Если отсутствуют выигрышные и предвыигрышные комбинации, то меняют все карты.
3.4.2 Формирование массива результатов игр
С помощью методики, описанной в п. 3.4.1, формируют массив результатов игр. Результаты игр разбивают на N = 100 блоков одинаковой длины k = 50 игр и для каждого i-го блока (i - индекс блока разбиения) вычисляют сумму процентов выигрышей
|
|
(20) |
где l - индекс игры,
Хil - процент выигрыша в l-ой игре i-го блока, т.е
![]()
где Bil - ставка в соответствующей игре.
3.4.3 Вычисление коэффициента Стьюдента
Оценку среднего значения процента выигрыша вычисляют по формуле
|
|
(21) |
где под N понимают число блоков, на которые происходит разбиение исходной хронологической последовательности игр.
Коэффициент Стьюдента ts вычисляют с помощью выражения
|
|
(22) |
где Ŝ - оценка дисперсии полученного t - распределения (распределения Стьюдента), вычисленная по формуле
|
|
(23) |
Xmin - заданное минимальное значение процента выигрыша.
3.4.4 Результат испытаний
Результат испытаний считают положительным, если выполнено неравенство
|
|
(24) |
где tN-1,1-p' - квантиль порядка (1-р') t - распределения с N-1 степенями свободы, р = 0,0025.
При выполнении данного условия с
вероятностью 0,9975 среднее значение процента выигрыша превышает Xmin,
т.е. ![]() ≥ Хmin.
≥ Хmin.
СОДЕРЖАНИЕ
|
3.3 Проверка по критерию согласия Колмогорова-Смирнова ограничения последовательностей проигрышей. 6 3.4 Проверка ограничения снизу среднего процента выигрыша. 8
|