ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ

ВСЕСОЮЗНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ЦЕНТР ПО ИЗУЧЕНИЮ
СВОЙСТВ ПОВЕРХНОСТИ И ВАКУУМА (ВНИЦ ПВ)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ОЦЕНКА ДОСТОВЕРНОСТИ ДАННЫХ О МОДУЛЯХ
УПРУГОСТИ МЕТАЛЛОВ И СПЛАВОВ

МИ 668-84

Москва
ИЗДАТЕЛЬСТВО СТАНДАРТОВ
1985

РАЗРАБОТАНЫ Тульским политехническим институтом, Всесоюзным научно-исследовательским центром по материалам и веществам Госстандарта (ВНИЦ MB Госстандарта)

ИСПОЛНИТЕЛИ:

канд. техн. наук Д.М. Левин (руководитель темы), д-р техн. наук С.А. Головин, Л.В. Кобликова, В.В. Зубец

ПОДГОТОВЛЕНЫ К УТВЕРЖДЕНИЮ Всесоюзным научно-исследовательским институтом метрологической службы (ВНИИМС)

Нач. отдела стандартизации Г.П. Сафаров

УТВЕРЖДЕНЫ секцией № 3 научно-технического совета Всесоюзного научно-исследовательского центра по изучению свойств поверхности и вакуума 11 декабря 1984 г. (протокол № 13)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Оценка достоверности данных о модулях упругости металлов и сплавов

МИ 668-84

Настоящие методические указания устанавливают принципы оценки достоверности результатов измерений модулей нормальной упругости металлов и сплавов динамическим методом на цилиндрических образцах. Достоверность результатов измерений модулей нормальной упругости динамическим методом на призматических образцах, а также результатов измерений модулей сдвига следует оценивать аналогичным образом.

Методические указания разработаны в дополнение к ГОСТ 25156-82.

1. ТРЕБОВАНИЯ К ИЗМЕРЕНИЮ МОДУЛЕЙ УПРУГОСТИ

1.1. Методика измерения модулей нормальной упругости и модулей сдвига металлов и сплавов в диапазоне температур от 4,2 до 700 К, требования к способу обработки и исходному состоянию образцов для измерений регламентирует ГОСТ 25156-82.

1.2. Для повышения точности измерений необходимо использовать образцы, для которых отношение длины к диаметру должно быть не менее 20. Отношение длины к максимальному значению стрелы прогиба изогнутых образцов - не ниже 400.

1.3. Значение модуля нормальной упругости рассчитывают по формуле

                                                (1)

где r = m/V - плотность металла, кг/м³; т, V, l и d - масса, кг, объем, м³, длина, м, и диаметр, м, образца соответственно; v_p - резонансная частота первой гармоники изгибных колебаний образца, Гц.

1.4. Для исключения систематической погрешности измерения модулей нормальной упругости, обусловленной изменением геометрических размеров образцов при измерениях в широком диапазоне температур, в формулу (1) следует вводить безразмерный поправочный коэффициент

                                                          (2)

где DT = T - T₀, Т - температура измерения, Т₀ - температура, при которой измерены значения длины l и диаметра d образца; a - термический коэффициент линейного расширения исследуемого материала при температуре Т.

1.5. Для исключения систематической погрешности измерения модулей нормальной упругости, обусловленной влиянием сдвигов и инерции вращения сечений цилиндрических образцов при изгибных колебаниях, в формулу (1) следует вводить поправочный коэффициент

                                                    (3)

где G - модуль сдвига.

1.6. Для исключения систематической погрешности измерения модулей нормальной упругости, обусловленной неупругим характером деформации образцов под действием напряжения измерения в исследуемом температурном интервале, в формулу (1) следует вводить безразмерный поправочный коэффициент

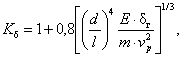                                                   (4)

где d_г = d - d₀, d - логарифмический декремент колебаний при напряжениях измерения, d₀ - логарифмический декремент колебаний, соответствующий уровню фона внутреннего трения.

2. МЕТОДИКА РАСЧЕТА ПОГРЕШНОСТИ ИЗМЕРЕНИЙ МОДУЛЕЙ НОРМАЛЬНОЙ УПРУГОСТИ ДИНАМИЧЕСКИМ МЕТОДОМ

2.1. В соответствии с ГОСТ 8.207-76 статистическая обработка результатов измерений модулей нормальной упругости состоит из следующих операций:

исключения известных систематических погрешностей из результатов наблюдений и получение их исправленных значений;

вычисления результатов измерения, за которые принимают среднее арифметическое значение массива исправленных результатов параллельных наблюдений, проводимых при неизменном комплексе основных факторов;

вычисления оценки среднего квадратического отклонения результата измерения;

проверки гипотезы о нормальном характере функции распределения результатов наблюдений;

вычисления доверительных границ случайной составляющей погрешности измерения;

вычисления границы неисключенной систематической погрешности результата измерения;

вычисления доверительной границы суммарной погрешности результата измерения.

2.1.1. Проверку гипотезы о нормальном характере функции распределения наблюдений модулей нормальной упругости следует производить с уровнем значимости 5 %.

2.1.2. Для определения доверительных границ суммарной погрешности результата измерения модулей нормальной упругости доверительную вероятность Р следует принимать равной 0,95.

2.2. Результат измерения модулей нормальной упругости Е и среднее квадратическое отклонение результата измерения S(Е) рассчитывают по формулам

                                                              (5а)

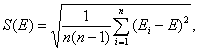                                             (5б)

где Е_i - i-й исправленный результат наблюдений; Е - результат измерения модуля нормальной упругости; п - число результатов наблюдений; S(E) - оценка среднего квадратического отклонения результата измерения.

2.3. Доверительные границы случайной погрешности результата измерения модуля нормальной упругости следует находить для результатов наблюдений, принадлежащих нормальному распределению.

2.3.1. Принадлежность результатов наблюдений модулей нормальной упругости к нормальному распределению для числа результатов наблюдений больше 50 следует проверять, согласно ГОСТ 11.006-74, с помощью одного из двух критериев: c² - Пирсона и w² - Мизеса-Смирнова. При числе результатов наблюдений 50 > n > 15 следует использовать составной критерий, приведенный в ГОСТ 8.207-76.

2.3.2. Доверительные границы e случайной погрешности результата измерения модуля нормальной упругости находят по формуле

e = t(P, n) × S(E),                                                       (6)

где t(P, n) - коэффициент распределения Стьюдента, соответствующий принятому уровню доверительной вероятности Р и числу наблюдений п.

2.4. Неисключенная систематическая погрешность результата измерения модуля нормальной упругости образуется из частных неисключенных систематических погрешностей результатов измерения факторов т, V, l, d, v_p, T, а также погрешностей величин d, d₀, a, E/G, используемых для расчета безразмерных поправочных коэффициентов K_т, K_ц и K_d. Расчет границ частных погрешностей D(m), D(V), D(l), D(d), D(Т), D(v_p), D(d), D(a), D(E/G) следует производить по значениям первичных частных погрешностей результатов измерений этих факторов D^*(Т), D^*(v_p), D^*(d), D^*(a), D^*(E/G).

Рекомендации по расчету границ частных погрешностей результатов измерений приведены в приложении 1.

2.4.1. Для учета отклонений формы образца от идеальной цилиндрической, связанных с бочкообразностью и огранкой, границы первичных частных неисключенных систематических погрешностей измерения диаметра d рассчитывают по формуле

                                               (7)

где d _max и d _min - наибольшее и наименьшее значения диаметра образца. Определение d _max и d _min необходимо производить по результатам не менее пяти измерений диаметра в сечениях образца, равно расположенных по его длине. Полученное по формуле (7) значение границы погрешности соответствует доверительной вероятности Р = 0,95.

Если рассчитанное по формуле (7) значение границы погрешности измерения диаметра окажется меньше предела допускаемой погрешности используемого средства измерения, то последнее следует использовать в качестве оценки границы первичной частной погрешности D^*(d).

2.4.2. В качестве границ первичных частных неисключенных систематических погрешностей D^*(m), D^*(l), D^*(V), D^*(v_p), D^*(d) с доверительной вероятностью Р = 0,997 следует принимать пределы допускаемых погрешностей средств измерений.

2.4.3. Границы первичных частных неисключенных систематических погрешностей D^*(a) и D^*(E/G) должны быть указаны в литературном источнике, откуда берутся числовые значения a и E/G.

2.4.4. При автоматическом регулировании температуры образца в качестве границы первичной частной неисключенной систематической погрешности берут

                                            (8)

где T_max и T_min - наибольшее и наименьшее значения температуры.

Определение T_max и T_min необходимо производить по результатам не менее пяти последовательных измерений температуры образца, выполняемых с интервалом не менее 15 мин. Полученное по формуле (8) значение границы погрешности соответствует доверительной вероятности Р = 0,95.

Если рассчитанное по формуле (8) значение границы погрешности измерения температуры образца окажется меньше предела допускаемой погрешности используемого средства измерений, то последнее следует использовать в качестве оценки границы первичной частной погрешности D^*T.

2.4.5. В случае отсутствия сведений о виде распределения первичных частных неисключенных систематических погрешностей границы первичных частных погрешностей следует считать симметричными, а функцию распределения равномерной.

2.5. Границы частных неисключенных систематических погрешностей результатов измерения D_i рассчитывают по известным с доверительной вероятностью P_i значениям первичных частных погрешностей i-го фактора по формулам

                                           (9)

Если при измерении плотности вещества V объем образца определяют по результатам измерений l и d как V = (p/4)d²l, то границы частных погрешностей рассчитывают по формулам

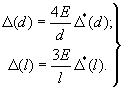                                                      (10a)

Если объем V определяют независимым образом, то границы частных погрешностей D(V), D(l) и D(d) рассчитывают по формулам

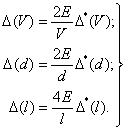                                                     (10б)

2.6. Если частные погрешности результатов измерений D_i характеризуются несколькими различными функциями распределения, то среднее квадратическое отклонение и границу неисключенной систематической погрешности результатов измерения модуля нормальной упругости при доверительной вероятности Р₀ определяют по формулам

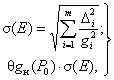                                                       (11)

где D_i - граница частной погрешности измерения i-го фактора; т - общее количество факторов; g_i - коэффициент, зависящий от вида функции распределения и вероятности P_i, с которой известны ее границы; g_н(Р₀) - коэффициент стандартного нормального распределения. Значения коэффициентов g_i для стандартных аппроксимаций некоторых функций распределения при доверительной вероятности 0,997 приведены в ГОСТ 8.011-72 и в приложении 1.

2.6.1. Если все частные погрешности характеризуются равномерной функцией распределения, то среднее квадратическое отклонение и границу неисключенной систематической погрешности измерения модуля нормальной упругости для доверительной вероятности Р определяют по формулам

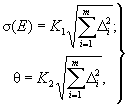                                                    (12)

где K₁ = 2,6 и K₂ = 1,1 при Р₀ = 0,95; K₁ = 2,9 и K₂ = 1,4 при Р₀ = 0,99; K₁ = 3 при Р₀ = 0,997.

2.7. Границу суммарной погрешности результата измерения модуля нормальной упругости для доверительной вероятности Р₀ рассчитывают по формуле

D = K × S,                                                             (13)

где оценку суммарного среднего квадратического отклонения результата измерения и коэффициента K определяют по формулам

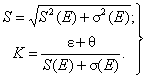                                                 (14)

2.7.1. Доверительную вероятность Р₀, с которой рассчитывают границу суммарной погрешности результата измерения, а также доверительную вероятность Р₀, с которой рассчитывают границу неисключенной систематической погрешности результата измерения q, следует брать равной или ниже каждой из вероятностей P_i, с которыми известны границы первичных частных погрешностей D^*_i.

2.8. Результат измерения модуля нормальной упругости в соответствии с ГОСТ 8.011-72 представляют в виде E ± D, Р₀. Пример расчета границы суммарной погрешности результата измерения модуля Е приведен в приложении 2.

2.9. Значения статических (изотермических) модулей нормальной упругости Е_ст по результатам измерений значений динамических (адиабатических) модулей нормальной упругости Е_дин рассчитывают по формуле

Е_ст = р × Е_дин,

где значения коэффициента р статического (изотермического) и динамического (адиабатического) модулей нормальной упругости металлов:

Приведенные значения коэффициента р для чистых металлов могут быть использованы для оценки отношения Е_ст/Е_дин и в низколегированных сплавах.

ПРИЛОЖЕНИЕ 1

МЕТОДИКА ОЦЕНКИ НЕИСКЛЮЧЕННОЙ СИСТЕМАТИЧЕСКОЙ ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

Неисключенная систематическая погрешность результата измерения образуется из составляющих, связанных с неисключенными систематическими погрешностями метода измерений, средств измерений и другими источниками. Можно выделить три этапа оценки границ неисключенной систематической погрешности результата измерения:

выявление частных неисключенных систематических погрешностей, образуемых действием независимых источников;

оценка границ частных погрешностей;

оценка границ общей неисключенной систематической погрешности результата измерения.

На первом этапе следует провести анализ аналитической формулы z = f(x₁, х₂, ..., х_п), используемой для вычисления результата косвенных измерений z по значениям факторов x_i. В число факторов x_i входят как значения параметров, характеризующих условия проведения измерений, так и независимые переменные факторы, величинами которых можно управлять в ходе измерений.

Неисключенная систематическая погрешность результата измерения D(z) складывается из D(x_i) - частных неисключенных систематических погрешностей измерения или воспроизведения величин х_i, а также погрешности D(f), обусловленной отличием формулы измерений от идеально точной, включая зависимость от ряда факторов, которые принятой формулой измерений не учитываются.

Границы частных неисключенных систематических погрешностей D(x_i) определяют на основе значений первичных частных погрешностей результатов прямых измерений каждого фактора D^*(x_i). Обозначения частных погрешностей факторов, формирующих общую неисключенную систематическую погрешность D(x_i), должны быть внесены в графу 1 таблицы. Для оценки границ частных погрешностей D(x_i) необходимо определить математическое ожидание М^*(х_i) и среднее квадратическое отклонение (СКО) s^*(х_i) каждой из первичных частных погрешностей D^*(x_i). Значения M^*(x_i) и s^*(x_i) могут быть получены:

из обработки результатов специально проведенных измерений эталонов или стандартных образцов, соответствующих требованиям ГОСТ 8.315-78;

на основе априорных сведений;

из значений погрешностей применяемых средств измерений, указанных в паспортах или технических описаниях приборов. В последнем случае обычно указывают нижнюю  и верхнюю  границы первичной частной погрешности D^*(x_i), соответствующие некоторой доверительной вероятности Р. В некоторых случаях приводятся сведения о характере функции распределения возможных значений погрешности. Если распределение погрешности в заданных границах можно считать симметричным, то ее математическое ожидание и СКО можно оценить как

                                               (1а)

                                               (1б)

где g_i - коэффициент, зависящий от вида функции распределения погрешности и доверительной вероятности P_i, с которой известны значения границ погрешности. Значения для стандартных аппроксимаций распределений при доверительной вероятности 0,997 приведены в ГОСТ 8.011-72. Если значение P_i не указано, то в соответствии с ГОСТ 8.207-76 следует считать P_i = 0,95. Для определения числовых значений коэффициентов g_i следует иметь представление о функциях распределения величин D^*(x_i). Отсутствие сведений о характере распределения или их неопределенность вынуждает при оценке s^*(x_i) исходить из наименее благоприятного из всех возможных распределений, которое характеризуется наименьшим из возможных значений параметра g_i.

Если источником погрешности являются средства измерений, регулируемые в процессе работы человеком или автоматом, то распределение первичной частной погрешности следует считать антимодальным II рода (а. м. II): g = l,2 при Р = 0,95, Р = 0,99 и Р = 0,997. Если первичная частная погрешность возникает из-за естественного, не регулируемого человеком или автоматом процесса, то в этом случае, а также в случае неопределенности, распределение первичной частной погрешности следует считать равномерным: g = 1,6 при Р = 0,95 и g = 1,7 при Р = 0,99 и Р = 0,997.

Если распределение первичной частной погрешности несимметрично, то в качестве аппроксимирующей функции следует брать функцию распределения Рэлея. При этом СКО вычисляют по формуле

                                           (2)

математическое ожидание - по формуле

                                  (3а)

если более вероятны значения погрешности вблизи , в противном случае

                                  (3б)

Верхний и нижний пределы измерения погрешности  и , вероятность P_i, с которой известны границы изменения первичной частной погрешности, рассчитанные значения математического ожидания M^*(x_i) и СКО s^*(х_i) и вид распределения первичной частной погрешности следует внести в графы 2 - 7 таблицы.

На следующем этапе следует определить весовые множители  соответствующие полученным в результате измерений значениям факторов x_i. Если известны приращения Dz, вызванные приращениями отдельных факторов Dx_i при сохранении постоянного уровня остальных факторов, то можно использовать оценку W(x_i) » Dz/Dx_i. Результаты расчета весовых множителей W(x_i) следует внести в графу 8 таблицы. На основании вычисленных значений M^*(x_i), g^*(x_i) и W(x_i) следует определить и внести в графы 9 и 10 таблицы значения математических ожиданий М(х_i) и СКО s(х_i) соответствующих частных неисключенных систематических погрешностей

M(x_i) = W(x_i) × M^*(x_i);                                                       (4а)

                                                      (4б)

Для оценки математического ожидания M(f) первичной частной погрешности D(f), связанной с использованием приближенной формулы измерений, оценивают:

разность значений измеряемой величины, вычисленных по приближенной и уточненной формулам измерений;

разность значений измеряемой величины, полученной в ходе испытания при существенно различающихся уровнях действующих факторов или условиях проведения испытания, когда возможно изменение величин вкладов неучтенных факторов в результат измерения.

При необходимости можно определить верхнюю (нижнюю) границу частных погрешностей

                                               (5)

которые заносят в графы 11 и 12 таблицы.

Числовые характеристики систематической погрешности результата измерения вычисляют по формулам

                                                      (6а)

                                                      (6б)

Окончательно доверительную верхнюю (нижнюю) границу неисключенной систематической погрешности результата измерения при заданной доверительной вероятности Р₀ рассчитывают по формуле

D_в(н) = M(z) ± g_нs(z),                                                       (7)

где для получения оценки коэффициент g_н принимают наибольшим, соответствующим наименее благоприятному нормальному распределению: g_н = 2 для Р₀ = 0,95; g_н = 2,6 для Р₀ = 0,99 и g_н = 3 для Р₀ = 0,997. Если распределение всех частных погрешностей является равномерным, то доверительную верхнюю (нижнюю) границу неисключенной систематической погрешности результата измерения оценивают по формуле, рекомендованной в ГОСТ 8.207-76.

                                                          (8)

где обозначено D_i = (D_в - D_н)/2, а коэффициент K = 1,1 при Р₀ = 0,95. Метод расчета K при больших значениях доверительной вероятности приведен в ГОСТ 8.207-76. Вероятность Р₀, при которой определяют доверительные границы неисключенной систематической погрешности результата измерения, должна быть равна или ниже каждой из доверительных вероятностей Р_i, определяющих границы первичных частных неисключенных систематических погрешностей D^*(х_i).

Для предотвращения необоснованного завышения оценки доверительной границы систематической погрешности результата измерения следует производить поверочный расчет границ. Для этого необходимо вычислить значения  и  Если полученные таким образом границы определяют более узкий интервал, чем рассчитанные по формуле (8), то именно значения  и  должны быть приняты в качестве окончательно установленных значений доверительных границ неисключенной систематической погрешности результата измерения.

Характеристики частных погрешностей результатов измерения

___________

¹ Характеристики первичных частных погрешностей имеют размерности соответствующих факторов.

² Характеристики частных погрешностей имеют размерность результата измерения.

ПРИЛОЖЕНИЕ 2

ПРИМЕР ИСПОЛЬЗОВАНИЯ МЕТОДИКИ ОЦЕНКИ ДОСТОВЕРНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ МОДУЛЯ НОРМАЛЬНОЙ УПРУГОСТИ МАТЕРИАЛА

Изучали модуль нормальной упругости стали 30 при температуре 200 °С. Модуль упругости измеряли динамическим методом на резонансной установке с автоматической регулировкой температуры. Использовали цилиндрические образцы длиной l = 0,2 м, диаметром d = 0,008 м, массой m = 0,08 кг. При комнатной температуре первая гармоника резонансной частоты колебаний образца v_p составляла 920 Гц, амплитуда деформации образца в ходе измерений не превосходила 3×10^-6. Статистическую обработку проводили по результатам измерений модулей упругости двадцати идентичных образцов из стали 30 различных плавок и партий. Значение модуля нормальной упругости каждого образца определяли по серии из пяти наблюдений. При вычислении значений модулей упругости плотности стали рассчитывали по формуле r = 4m/(pd²×l), измерение длины l и диаметра d производили при температуре 20 °С. Для расчета поправочного коэффициента K_ц использовали оценку E/G ≈ 8/3, первичная частная неисключенная систематическая погрешность которой D^*(E/G) = 0,2 при Р = 0,95. Термический коэффициент линейного расширения K^-1 стали 30 при температуре 200 °С рассчитывали с помощью аппроксимирующего соотношения

a = [11,7 - 1,9С + 10^-2×T(1 - 0,43C)]×10^-6,

где С - массовая доля углерода в стали, %; Т - температура измерения, °С.

Первичная частная неисключенная систематическая погрешность значения D^*(a), рассчитанного с помощью аппроксимирующего соотношения, составляет D^*(a) = 2×10^-6 К^-1 при Р = 0,95. При температуре 200 °С и амплитуде деформации 3×10^-6 внутреннее трение в стали 30 имеет амплитудно независимый характер, т.е. d_г = 0. Поэтому при расчете значения модуля нормальной упругости поправочный коэффициент K_d не учитывают.

При статической обработке данных измерения получены следующие результаты: модуль нормальной упругости оказался равным E = 199000 МПа, среднее квадратическое отклонение случайной составляющей погрешности результата измерения S(E) = 600 МПа, результаты наблюдений при уровне значимости 5 % характеризуются нормальной функцией распределения. Первичные частные погрешности факторов, вносящих вклад в неисключенную систематическую погрешность результата измерения модуля нормальной упругости, весовые множители и частные погрешности приведены в таблице. По этим данным рассчитаны значения СКО s(E) = 680 МПа, доверительная граница неисключенной систематической погрешности результата измерения q = 1360 МПа, P₀ = 0,95, доверительная граница суммарной погрешности D = 1800 МПа, Р₀ = 0,95.

Окончательное значение модуля нормальной упругости стали 30 при температуре 200 °С составило Е = (189000 ± 1800) МПа при Р₀ = 0,95.

Характеристики частных погрешностей измерения модуля нормальной упругости

СОДЕРЖАНИЕ