ГОСУДАРСТВЕННЫЙ
КОМИТЕТ СССР ПО УПРАВЛЕНИЮ КАЧЕСТВОМ
ПРОДУКЦИИ И СТАНДАРТАМ НАУЧНО-ПРОИЗВОДСТВЕННОЕ
ОБЪЕДИНЕНИЕ «СИСТЕМА»
ВСЕСОЮЗНЫЙ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
МЕТРОЛОГИИ ИЗМЕРИТЕЛЬНЫХ И УПРАВЛЯЮЩИХ СИСТЕМ
(ВНИИМИУС)
|
УТВЕРЖДАЮ Генеральный директор НПО «Система» Удовиченко Е.Т. «__» _________ 1991 г. |
РЕКОМЕНДАЦИЯ
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
СИСТЕМЫ ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ.
МЕТОДИКА РАСЧЕТА МЕТРОЛОГИЧЕСКИХ
ХАРАКТЕРИСТИК
ИЗМЕРИТЕЛЬНЫХ КАНАЛОВ ПО МЕТРОЛОГИЧЕСКИМ
ХАРАКТЕРИСТИКАМ ЛИНЕЙНЫХ АНАЛОГОВЫХ
КОМПОНЕНТОВ
МИ 2168-91
Львов - 1991
1. РАЗРАБОТАНА Всесоюзным научно-исследовательским институтом измерительных и управляющих систем (ВНИИМИУС) HПO «Система»
2. ВНЕСЕНА НПО «Система»,
ИСПОЛНИТЕЛИ:
Б.А. Грановский, канд.тех.наук (руководитель темы); С.Л. Васильева, А.Н. Винниченко, Т.М. Иванцюк
3. УТВЕРЖДЕНА НПО «Система»
4. ЗАРЕГИСТРИРОВАНА ВНИИМС
Настоящий руководящий документ по метрологии устанавливает способы расчета метрологических характеристик (MX) измерительных каналов (ИК) измерительных информационных систем (ИИС) по MX компонентов.
Методика может быть использована в качестве исходной при разработке частных методик и программ, реализующих расчеты для конкретных ИИС.
Методика распространяется на ИК ИИС, которые, как законченное изделие, комплектуются из серийных агрегатных средств при монтаже на месте эксплуатации и характеризуются отсутствием доступа ко входу ИК.
Регламентированные методикой способы расчета МХ ИК ИИС могут быть использованы:
при проектной оценке MX ИК ИИС на стадии создания;
при метрологической аттестации ИК ИИС на этапе ввода ИИС в эксплуатацию (при экспериментально-расчетном методе ее проведения);
при поверке ИК ИИС поэлементным способом в процессе эксплуатации.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1 Методика соответствует простейшему варианту расчета MX ИК ИИС и является первой из совокупности рекомендаций, охватывающей, различные направления, связанные с усложнением расчетных методов.
1.2. В методике рассматриваются ИК с двухкомпонентной структурой, т.е. ИК, состоящие по меньшей мере, из двух конструктивно обособленных частей, одна из которых - первичная - вырабатывает в результате воздействия измеряемой величины сигнал, поступающий во вторичную часть, завершающую измерительное преобразование в ИК.
MX компонентов предполагаются известными. Как правило, в качестве первого компонента выбирают датчик, второго - электроизмерительную цепь.
Примечание. Допускается использование настоящей методики для расчета МХ ИК с более, чем двумя компонентами за счет последовательного применения метода расчета для двухкомпонентной структуры.
1.2. В настоящей методике приняты следующие допущения:
1/. Компоненты ИК предполагаются линейными аналоговыми элементами с сосредоточенными параметрами.
2/. Форма представления и способы нормирования MX компонентов одинаковы и согласованы по размерности. Форма представления результирующей MX ИК, получаемой в результате расчета, совпадает с формой представления MX компонентов.
3/. Диапазоны измерений компонентов, характеристики компонентов, отряжающие их взаимодействия во входу и выходу, характеристики влияющих величин м условий эксплуатации ИК в целом и его компонентов известны и согласованы. Взаимное влияние компонента на компонент ИК и влияние других ИК на рассматриваемый ИК в ИИС не учитывают.
1.3. Форма представления исходных данных оговаривается при описании расчета конкретных МХ в разделе 3.
1.4. Исходные данные, необходимые для расчета, следует брать из нормативно-технической документации, в тех случаях, корда исходные данные в требуемой форме не заданы или представлены неполно, недостающие данные должны быть определены на основании экспериментальных данных.
1.5. Выражения используемые для расчета характеристик погрешности согласно п.п. 3.3 - 3.6, могут быть использованы для расчета характеристик как основой, так и дополнительной погрешностей. Исходными данными для расчета характеристик основной допускаемой погрешности ИК является характеристики основой допускаемой погрешности компонентов. Исходными данными для характеристик дополнительной допускаемой погрешности ИК являются характеристики дополнительной допускаемой погрешности компонентов.
1.6. МХ ИК выбраны из числа регламентируемых ГОСТ 8.009-84 и МИ 302-80 при различных формах представления и способах нормирования согласно ГОСТ 8.009-84, ГОСТ 8.401-80 и ГОСТ 8.256-77.
1.7. Терминология, используемая в настоящей методике соответствует ГОСТ 16263-70, ГОСТ 8.009-84 и МИ 1951-88.
2. ПЕРЕЧЕНЬ РАССЧИТЫВАЕМЫХ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
2.1. Статические характеристики
2.1.1 Коэффициенты номинальной функции преобразования К, а.
2.1.2. Номинальный статический коэффициент преобразования
2.1.3. Пределы (положительный и. отрицательный) допускаемой погрешности - Δр.
2.1.4. Предел допускаемой систематической составляющей погрешности - Δsр.
2.1.5. Предел допускаемого среднего квадратического отклонения (СКО)
случайной составлявшей погрешности - ![]()
2.1.6. Математическое ожидание систематической составляющей абсолютной погрешности М[Δs].
2.1.7. СКО систематической составляющей абсолютной погрешности ![]()
2.2. Полные динамические характеристики
2.2.1. Порядок и коэффициенты дифференциального уравнения (ДУ).
2.2.2. Приведенная импульсная характеристика (ИХ) - q(t)
2.2.3. Приведенная переходная характеристика (ПХ) - h(t)
2.2.4. Приведенная передаточная функция (ПФ) - W(p)
2.2.5. Приведенная амплитудно-частотная (АЧХ) - (ω) и фазочастотная (ФЧХ) Ф(ω) характеристики.
3. РАСЧЕТ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ИЗМЕРИТЕЛЬНОГО КАНАЛА
3.1. Коэффициенты номинальной статической функции преобразования f(x), задаваемой в виде линейной функции входного сигнала
f(x) = кх + а (3.1)
где кх - мультипликативная составляющая номинальной статической функции преобразования; а - аддитивная составляющая статической функции преобразования; х - измеряемая величина (информативный параметр входного сигнала), рассчитывают по формулам
Исходными данными для расчета являются:
кi, i = 1, 2 - коэффициент мультипликативной составляющей номинальной статической функции преобразования i-го компонента;
ai, i = 1, 2 - аддитивная составляющая номинальной статической функции преобразования i-го компонента.
Результатом расчета по формулам (3.2), (3.3) являются значения коэффициентов к и а номинальной статической функции преобразования f(x).
3.2. Пределы (нижний и верхний) допускаемого значения абсолютной погрешности - Δр рассчитывают по формуле
Исходными данными для расчета являются:
Δрi, i = 1, 2 - пределы (положительный и отрицательный) допускаемой абсолютной погрешности, приведенной ко входу 1-го компонента;
к1 - номинальный статический коэффициент преобразования 1-го компонента.
Результатом расчета, по формуле (3.4) является абсолютное значение погрешности Δр, приведенной ко входу ИК.
В случае, если Δрi заданы в форме пределов допускаемой приведенной погрешности γi; в процентах, носящей чисто аддитивный характер в диапазоне измерений и устанавливаемой по формуле
![]() (3.5)
(3.5)
где р - отвлеченное положительное число, выбираемое из ряда согласно разделу 2 ГОСТ 8.401-80, то пределы (нижний и верхний) допускаемой погрешности ИК рассчитывают по формуле
Исходными данными для расчета являются:
γi, i = 1, 2 - предел (нижний и верхний, соответственно) допускаемой приведенной погрешности i-го компонента, задаваемые в процентах и обозначаемые как класс точности согласно ГОСТ 8.401-80;
![]() , i
= 1, 2 - нормирующее значение, принятое для i-го
компонента, выраженное в единицах измеряемой величины на входе i-го компонента;
, i
= 1, 2 - нормирующее значение, принятое для i-го
компонента, выраженное в единицах измеряемой величины на входе i-го компонента;
XN - нормирующее значение,
принятое для ИК, выраженное в единицах измеряемой величины на входе ИК, т.е. в
единицах ![]() .
.
Результатом расчета по формуле (3.6) является значение предела допускаемое приведенной погрешности ИК в процентах. При необходимости значение предела допускаемой абсолютной погрешности может быть получено по формуле
![]() (3.7)
(3.7)
В случае, если Δрi заданы в относительной форме в виде пределов допускаемой относительной погрешности δMi в процентах, носящей чисто мультипликативный характер в диапазоне измерений и задаваемой во формуле
![]() (3.8)
(3.8)
где q - отвлеченное положительное число, выбираемое согласно разделу 2 ГОСТ 8.401-80, то пределы допускаемой относительной погрешности ИК рассчитывают по формуле
Исходными данными для расчета являются:
δMi, i = 1,2 - пределы допускаемой относительной погрешности i-го компонента, задаваемые в процентах, обозначаемые как класс точности δMi согласно ГОСТ 8.401-80.
Результатом расчета по формуле (3.9) является значение предела допускаемой относительной погрешности ИК δM в процентах. При необходимости может быть получено значение пределов допускаемой абсолютной погрешности для значения диапазона измерений ИК по формуле
![]() (3.10)
(3.10)
В случае, если Δрi заданы в относительной форме в виде пределов допускаемой относительной погрешности δi(х) в процентах, задаваемой согласно ГОСТ 8.401-80 по формуле
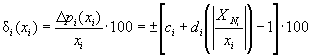 (3.11)
(3.11)
где сi, di - положительные числа, выбираемые из ряда согласно разделу 2 ГОСТ 8.401-80, то пределы допускаемой относительной погрешности ИК δ(х) в процентах рассчитывают по формуле
Исходными данными для расчета является:
сi, di - числа, установленные в документации для i-го компонента и связанные с числами, проводимыми в обозначении класса точности Сi/Дi согласно ГОСТ 8.401-80, следующими соотношениями:
![]() (3.13)
(3.13)
![]() (3.14)
(3.14)
Результатом расчета по формуле (3.12) является значение предела допускаемой относительной погрешности δ(х) в процентах для значений х диапазона измерений.
При этом предел допускаемой относительной погрешности ИК устанавливают по формуле
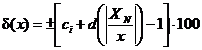 (3.15)
(3.15)
где d - минимальное положительное число, выбираемое из ряда, согласно разделу 2 ГОСТ 8.401-80 и для которого выполняется условие d* £ d; d* - число, определяемое по формуле
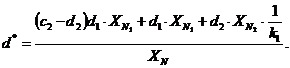 (3.16)
(3.16)
с - минимальное положительное число, которое выбирают из ряде согласно разделу 2 ГОСТ 8.401-80 и для которого выполняется условие с* £ с; с* - число, определяемое по формуле
![]() (3.17)
(3.17)
При необходимости может быть пожучено значение пределов допускаемой абсолютной погрешности для значения х диапазона измерений ИК по формуле
![]() (3.18)
(3.18)
3.3. Предел допускаемой систематической составляющей абсолютной погрешности Δsр рассчитывают по формуле
Исходными данными для расчета являются:
Δsрi, i = 1, 2 - предел допускаемой систематической составлявшей абсолютной погрешности на входе i-го компонента ИК;
к1 - номинальный статический коэффициент преобразования 1-го компонента.
Результатом расчета по формуле (3.19) является значение предела допускаемой систематической составляющей абсолютной погрешности Δsр на входе ИК.
3.4. Предел допускаемого СКО случайной составляющей абсолютной
погрешности ![]() рассчитывают по формуле
рассчитывают по формуле
Исходными данными для расчета являются:
![]() ,
i = 1, 2 - предел допускаемого
СКО случайной составляющей абсолютной погрешности i-го
компонента ИК;
,
i = 1, 2 - предел допускаемого
СКО случайной составляющей абсолютной погрешности i-го
компонента ИК;
к1 - номинальный статический коэффициент преобразования 1-го компонента.
Результатом расчета по формуле (3.20) является значение предела допускаемого СКО случайной составляющей абсолютной погрешности на входе ИК.
3.5. Математическое ожидание систематической составляющей абсолютной погрешности М[Δ] рассчитывают по формуле
Исходными данными для расчета являются:
М[Δi], i = 1, 2 - математическое ожидание абсолютной погрешности на входа i-го компонента ИК;
к1 - номинальный статический коэффициент преобразования 1-го компонента.
Результатом расчета по формуле (3.21) является значение математического ожидания абсолютной погрешности М[Δ] на входе ИК.
3.6. СКО систематической составляющей абсолютной погрешности σ[Δ] рассчитывают по формуле
Исходными данными для расчета являются:
σ[Δi], i = 1, 2 - CKО абсолютной погрешности на входе i-го компонента
к1 - номинальный статический коэффициент преобразования 1-гo компонента.
Результатом расчета по формуле (3.22) является значение CKО абсолютной погрешности σ[Δ] на входе ИК
3.8. Расчет полных динамических характеристик ИК по характеристикам компонентов, заданным в аналитической форме
3.8.1. Расчет полной динамической характеристики ИК в виде ДУ заключается в определении порядка и коэффициентов уравнения.
Расчет проводится по формулам (3.34) - (3.48).
Исходными данными являются характеристики компонентов, заданные в виде ДУ:
Для первого компонента ИК
![]() (3.23)
(3.23)
для второго компонента ИК
где x1(t) - измеряемая величина, информативный параметр входного сигнала 1-го компонента ИК;
x2(t) - информативный параметр выходного сигнала 1-го компонента;
x3(t) - информативный параметр выходного сигнала 2-го компонента;
к1, к2 - номинальные значения статических коэффициентов преобразования компонентов;
аi, вк, dj, cr - коэффициенты ДУ.
Исходные данные заданы в форме:
номинальных значений коэффициентов ДУ а1ном, вкном, djном, crном и границ допускаемых отклонений от них ± Δаi, ± Δвк, ± Δdj, ± Δcr для нормальных условий (3.25), а также границ допускаемых отклонений от них, обусловленных изменением влияющих величин (т.е. в виде дополнительных погрешностей коэффициентов)
± Δаiдоп, ± Δвкдоп, ± Δdjдоп, ± Δcrдоп
для рабочих условий (3.26) либо пределов допускаемых значений коэффициентов
аiниж, аiверх, вкниж, вкверх, djниж, djверх, crниж, crверх
для нормальных условий (3.27) и дополнительных погрешностей для рабочих условий (3.28)
Общий вид результирующего ДУ:
где k - номинальный статический коэффициент преобразования ИК, значение которого получают по формуле (3.2).
Коэффициенты es, fv для нормальных условий определяются в виде
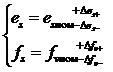 (3.30)
(3.30)
где Des+, -Des-, Dfv+, -Dfv- - положительный и отрицательный пределы отклонений коэффициентов от номинальных; либо в виде предельных значений коэффициентов
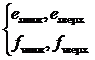 (3.31)
(3.31)
Для рабочих условий соответственно
 (3.32)
(3.32)
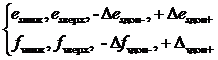 (3.33)
(3.33)
где Desдоп+, -Desдоп-, Dfvдоп+, -Dfvдоп- дополнительные погрешности коэффициентов.
Если коэффициенты ДУ компонентов заданы в виде (3.25), (3.26), то коэффициенты результирующего ДУ рассчитывают по формулам:
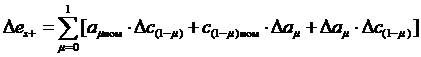 (3.35)
(3.35)
 (3.36)
(3.36)
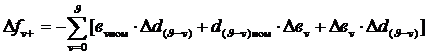 (3.37)
(3.37)
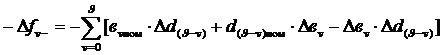 (3.38)
(3.38)
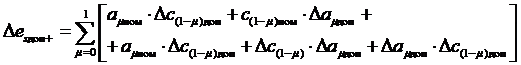 (3.39)
(3.39)
 (3.40)
(3.40)
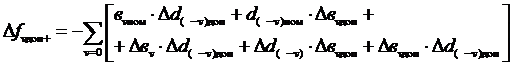 (3.41)
(3.41)
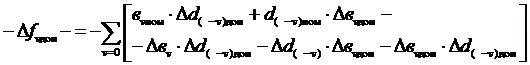 (3.42)
(3.42)
Если коэффициенты ДУ компонентов заданы в виде (3.27), (3.28), то коэффициенты результирующего рассчитывают по формулам:
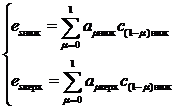 (3.43)
(3.43)
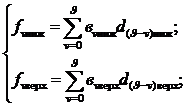 (3.44)
(3.44)
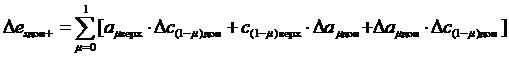 (3.45)
(3.45)
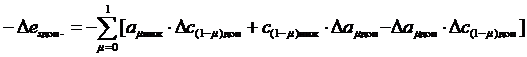 (3.46)
(3.46)
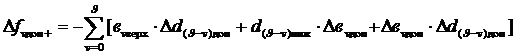 (3.47)
(3.47)
3.8.2. Расчет приведенной импульсной характеристики
3.8.2.1. Для расчета приведенной ИХ ИК исходными данными являются приведенные ИХ компонентов. Рассчитывается приведенная ИХ для ИК, состоящего из компонентов, описываемых звеньями первого или второго порядка.
Исходные данные заданы в формуле: аналитических выражений функций q1(g1, T1, t), q2(g2, T2, t) с параметрами g, T в виде номинальных значений gном, Tном и пределов допускаемых отклонений от них ± Δg, ± ΔТ для нормальных условий (3.49), а также пределов допускаемых отклонений от них, обусловленных изменением влияющих величин (дополнительных погрешностей) параметров ± Δgдоп, ± ΔТдоп для рабочих условий (3.50), либо в виде пределов допускаемых параметров gниж, gверх, Tниж, Tверх для нормальных (3.51), а также дополнительных погрешностей для рабочих условий (3.52):
3.8.2.2. Моделью каждого компонента является звено первого порядка:
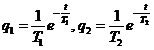
Результирующая приведенная ИХ
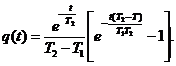 (3.53)
(3.53)
где T1, T2 записываются в виде (3.49) ¸ (3.52).
3.8.2.3. Моделью одного из компонентов является звено первого, а другого - звено второго порядка:

Результирующая приведенная ИХ

где параметры g, T1, T2 записываются в виде (3.49) ¸ (3.52).
3.8.3. Расчет приведенной переходной характеристики
3.8.3.1. Исходными данными для расчета приведенной ПХ ИК являются приведенные ПХ компонентов h1(t) и h2(t).
Аналитическая форма представления приведенных ПХ используется для тех же компонентов, что в п. 3.8.2.
Исходные данные заданы в форме:
аналитических выражений функций h1(t), h2(t) с параметрами g, T в виде (3.49) ¸ (3.52).
Результирующую приведенную ПХ ИК получают в результате свертки ПХ компонентов: h(g1, g2, T1, T2) = h1(g1, T1, t) ´ h2(g2, T2, t), где параметры g1, g2, T1, T2 заданы в виде (3.49) ¸ (3.52).
3.8.3.2. Моделью каждого компонента является звено первого порядка
![]()
Результирующая приведенная ПХ
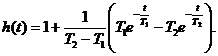 (3.54)
(3.54)
3.8.3.3. Моделью одного из компонентов является звено первого, другого - звено второго порядка

Результирующая приведенная ПХ
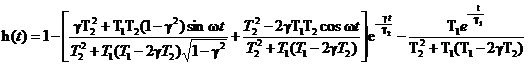 (3.55)
(3.55)
3.8.4. Расчет приведенной передаточной функции При расчете приведенной ПХ ИК W(p) исходными данными являются приведенные ПФ компонентов W1(p), W2(p). Исходные данные заданы в форме:
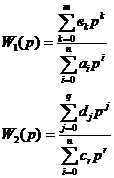 (3.57)
(3.57)
где аi, вк, dj, cr - коэффициенты, соответствующие коэффициентам в ДУ п. 3.8.1, формулы (3.25) ¸ (3.28).
Результирующая приведенная ПФ
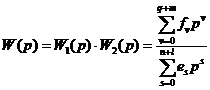 (3.58)
(3.58)
Коэффициенты fv и es соответствует коэффициентам ДУ в формуле (3.29) п. 3.8.1 и определяется по формулам (3.24) ¸ (3.48).
3.8.5. Расчет приведенной амплитудночастотной и фазочастотной характеристик
Исходными данными для расчета приведенной АЧХ и ФЧХ являются приведенные АЧХ и ФЧХ компонентов.
Исходные данные заданы в форму:
аналитических выражений приведенных АЧХ А1(g1, T1, ω), А2(g2, T2, ω) и ФЧХ Ф1(g1, T1, t), Ф2(g2, T2, t) с параметрами g, T теми же, что в п. 3.8.2, формулы (3.49) ¸ (3.52).
Результирующая приведенная АЧХ
А(ω) = А1(ω) · А2(ω) (3.59)
Результирующая ФЧХ
Ф(ω) = Ф1(ω) + Ф2(ω) (3.60)
3.9. Расчет полных динамических характеристик по полным динамическим характеристикам компонентов, заданным в табличной форме
3.9.1. Расчет приведенной импульсной характеристики
Исходными данными для расчета приведенной ИХ ИК являются приведенные ИХ компонентов.
Исходные данные заданы в форме:
номинальных функций q1ном(m), q2ном(m) и границ допускаемых отклонений от них ± Δq1(m), ± Δq2(m) нормальных условий (3.61), а также пределов допускаемых отклонений от них, обусловленных изменением влияющих величин (дополнительные погрешности) ± Δq1доп(m), ± Δq2доп(m) для рабочих условий (3.62), либо в виде граничных функций q1ниж(m), q1верх(m), q2ниж(m), q2верх(m) для нормальных условий (3.63), а также дополнительных погрешностей ± Δq1доп(m), ± Δq2доп(m) для рабочих условий (3.64):
Для нормальных условий, если q1(m), q2(m) заданы в виде (3.61), результирующая приведенная ИХ
![]() (3.65)
(3.65)
где
![]() (3.66)
(3.66)
![]() (3.67)
(3.67)
![]() (3.68)
(3.68)
Примечания: 1. m - номер отсчета характеристики компонента.
2. n - номер отсчета результирующей характеристики ИК.
3. Отсчеты исходных характеристик компонентов берутся в одни и те же моменты времени с одинаковым периодом дискретизации. Количество отсчетов исходных характеристик компонентов одинаково и равно М + 1, где М максимальное значение m. Количество отсчетов N результирующей характеристики равно 2 М + 1.
Для рабочих условий, когда приведенные ИК компонентов заданы в виде (3.62), результирующая приведенная ИК:
![]() (3.69)
(3.69)
где qном(n), Δq+(n), - Δq-(n) - вычисляют по формулам (3.71) ¸ (3.72).
![]() (3.71)
(3.71)
![]() (3.72)
(3.72)
Если исходные приведенные ИХ заданы в виде (3.63) или (3.64), то результирующая приведенная ИХ соответственно записывается в виде (3.73) или (3.74).
где
![]() (3.75)
(3.75)
![]() (3.76)
(3.76)
![]() (3.77)
(3.77)
![]() (3.78)
(3.78)
3.9.2. Расчет приведенной переходной характеристики
Исходными данными для расчета приведенной ПХ ИК являются приведенные ПХ компонентов.
Исходные данные заданы в форме:
номинальных функций h1ном(m), h2ном(m) и границ допускаемых отклонений от них ± Δh1(m), ± Δh2(m) для нормальных условий (3.79), а также границ допускаемых отклонений, обусловленных изменением внешних влияющих величин (т.е. в виде дополнительных погрешностей), для рабочих условий ± Δh1доп(m), ± Δh2доп(m) (3.80), либо граничных функций (3.81) h1ниж(m), h1верх(m), h2ниж(m), h2верх(m) для нормальных условий, а также дополнительных погрешностей ± Δh1доп(m), ± Δh2доп(m) для рабочих условий (3.82)
Если h1(m), h2(m) для нормальных и рабочих условий заданы по (3.79), (3.80), расчет результирующей приведенной ПХ ведется по формулам:
![]() (3.83)
(3.83)
![]() (3.84)
(3.84)
где
![]() (3.85)
(3.85)
![]() (3.86)
(3.86)
![]() (3.87)
(3.87)
![]() (3.88)
(3.88)
![]() (3.89)
(3.89)
Если h1(m), h2(m) заданы по (3.81), (3.82), результирующая приведенная ИХ определяются соответственно по формулам (3.90) и (3.91).
для нормальных условий:
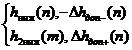 для рабочих
условий, (3.91)
для рабочих
условий, (3.91)
где
![]() (3.92)
(3.92)
![]() (3.93)
(3.93)
Для приведенных ПХ компонентов и приведенной ПХ ИК справедливо Примечание п. 3.9.1.
3.9.3. Расчет приведенной амплитудночастотной и фазочастотной характеристик.
Исходными данными для расчета приведенной АЧХ и ФЧХ являются приведенные АЧХ и ФЧХ компонентов.
Исходные данные заданы в форме:
номинальных функций А1ном(ωi), А2ном(ωi), Ф1ном(ωi), Ф2ном(ωi) и границ допускаемых отклонений от них ± DА1(ωi), ± DА2(ωi), ± DФ1(ωi), ± DФ2(ωi) для нормальных условий
а также границ допускаемых отклонений от них, обусловленных изменением внешних влияющих величин (т.е. в виде дополнительных погрешностей
![]()
для рабочих условий, т.е.
либо
граничных функций А1ниж(ωi), А1верх(ωi), А2ниж(ωi), А2верх(ωi), Ф1ниж(ωi), Ф1верх(ωi), Ф2ниж(ωi), Ф2верх(ωi)
для нормальных условий
а также дополнительных погрешностей ± DА1доп(ωi), ± DА2доп(ωi), ± DФ1доп(ωi), ± DФ2доп(ωi) для рабочих условий, т.е.
Если приведенные АЧХ и ФЧХ компонентов заданы в виде (3.94), (3.95), то результирующие характеристики записываются в виде
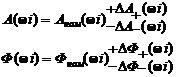 (3.98)
(3.98)
для нормальных условий;
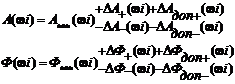 (3.99)
(3.99)
для рабочих условий,
где
![]() (3.100)
(3.100)
![]() (3.101)
(3.101)
![]() (3.102)
(3.102)
![]() (3.103)
(3.103)
![]() (3.104)
(3.104)
![]() (3.105)
(3.105)
![]() (3.106)
(3.106)
![]() (3.107)
(3.107)
![]() (3.108)
(3.108)
Если приведенные АЧХ и ФЧХ компонентов заданы по (3.96), (3.97), результирующие характеристики записываются в виде:
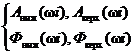 (3.109)
(3.109)
для нормальных; условий;
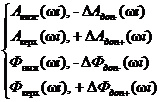 (3.110)
(3.110)
для рабочих условий, где
![]() (3.111)
(3.111)
![]() (3.112)
(3.112)
![]() (3.113)
(3.113)
![]() (3.114)
(3.114)
![]() (3.115)
(3.115)
![]() (3.116)
(3.116)
![]() (3.117)
(3.117)
![]() (3.118)
(3.118)
Примечание: Отсчеты приведенных АЧХ и ФЧХ компонентов и значения результирующих характеристик берутся и получены для одних и тех же частот wi
СОДЕРЖАНИЕ
|
2. Перечень рассчитываемых метрологических характеристик. 2 3. Расчет метрологических характеристик измерительного канала. 3 |
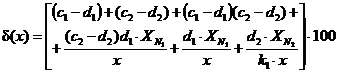
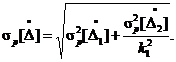 (3.20)
(3.20) (3.22)
(3.22) (3.25)
(3.25) (3.26)
(3.26)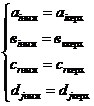 (3.27)
(3.27)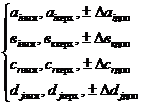 (3.28)
(3.28)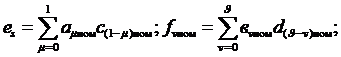 (3.34)
(3.34)
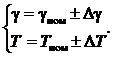 (3.49)
(3.49)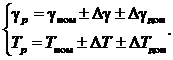 (3.50)
(3.50)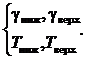 (3.51)
(3.51)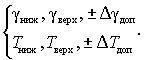 (3.52)
(3.52)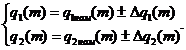 (3.61)
(3.61)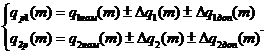 (3.62)
(3.62)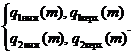 (3.63)
(3.63)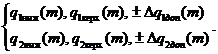 (3.64)
(3.64)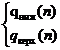 (3.73)
(3.73)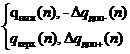 (3.74)
(3.74)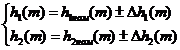 (3.79)
(3.79) (3.80)
(3.80)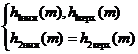 (3.81)
(3.81)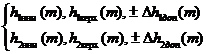 (3.82)
(3.82)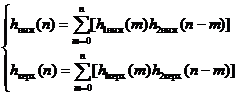 (3.90)
(3.90) (3.94)
(3.94)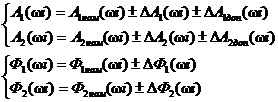 (3.95)
(3.95)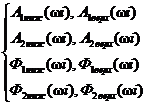 (3.96)
(3.96) (3.97)
(3.97)