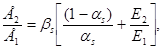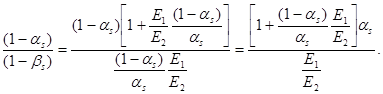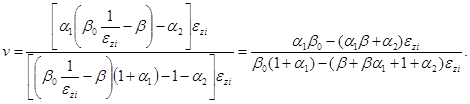СТАНДАРТ ОРГАНИЗАЦИИ

Выявление
самонапряженного состояния
горной породы

СТО 36554501-019-2009

Москва 2010

Предисловие

Сведения о стандарте:

1 РАЗРАБОТАН И ВНЕСЕН отделом натурных испытаний и автоматизации экспериментальных исследований НИИОСП им. Н.М. Герсеванова - института ОАО «НИЦ «Строительство» и группой специалистов (зам. начальника отдела, канд. техн. наук А.И. Мороз, начальник отдела, канд. техн. наук Л.Н. Репников при участии научного сотрудника А.А. Аникина).

2 РЕКОМЕНДОВАН К ПРИНЯТИЮ секцией механики грунтов и исследования свойств грунтов НТС НИИОСП им. Н.М. Герсеванова.

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ приказом генерального директора ОАО «НИЦ «Строительство» от 25 декабря 2009 г № 24.

4 ВВЕДЕН ВПЕРВЫЕ

СОДЕРЖАНИЕ

Введение

При освоении подземного пространства в настоящее время одной из актуальных проблем остается полнота и достоверность описания напряженно-деформированного состояния (НДС) массива и его механических характеристик в процессе проведения горных работ, в результате которых в массиве образуются полости (тоннели, штольни, фурнели, лавы и др.). При проходке горных выработок происходит изменение внешних нагрузок (разгрузка), т.е. с контура выработки снимаются действовавшие до этого нагрузки, и порода, находящаяся вблизи контура, оказывается разгруженной.

Такие же процессы претерпевает и образец при извлечении его из скважины при разведочном бурении, и экспериментатор, как правило, не знает не только о фактическом напряженном состоянии исследуемого образца, но и о влиянии истории формирования его НДС на результирующее состояние после разгрузки.

Вместе с тем при определении механических свойств пород по изъятым из массива кернам (особенно с больших глубин) в них обнаруживают деформации упругого последействия, снижение прочности, остаточные напряжения, являющиеся следствием перехода образцов в самонапряженное состояние после разгрузки по аналогии с краевой дислокацией в металлах.

Результаты выполненных в НИИОСП им. Н.М. Герсеванова исследований показали, что одной из причин возникновения самонапряженного состояния в горных породах является предшествующая история формирования НДС и связанное с ней возникновение внутренних полей напряжений в период генезиса.

На стадии разгрузки в компонентах такой породы реализуются биполярные самоуравновешенные напряжения, характерные для самонапряженного состояния, показателями которых являются проявляющиеся и поддающиеся регистрации эффекты в виде снижения прочности, самопроизвольного приращения деформаций, образования дефектов и т.п.

Эти признаки свидетельствуют о том, что в породе имеются причины, сдерживающие полную мгновенную реализацию потенциальной энергии упругих деформаций в процессе снятия внешних сил, что дает основание сформулировать концепцию частичного связывания упругой энергии при разгрузке.

Явление возникновения самонапряженного состояния горной породы, сформировавшейся под действием внешних сил, получило статус открытия (№ 162 РФ, 2001) с выдачей свидетельства НИИОСП им. Н.М. Герсеванова, авторам - дипломов.

СТО 36554501-019-2009

СТАНДАРТ ОРГАНИЗАЦИИ

Дата введения 2009-12-15

1 Область применения

1.1 Настоящий стандарт разработан на основе результатов теоретических и экспериментальных исследований, которые показали, что при определенных естественных или искусственных условиях, связанных с предыдущей историей формирования НДС, существует большая вероятность при последующей разгрузке перехода материала в самонапряженное состояние, характеризуемое наличием остаточных напряжений. К таким условиям относится, например, способ формирования НДС при генезисе породы по схеме «нагружение-цементирование», при которой эффективные напряжения в скелете (матрице) превышают давление в цементирующем заполнителе.

1.2 Настоящий стандарт разработан для обнаружения возможного перехода в основном естественных природных образований (горных пород) и, в меньшей степени, искусственных материалов в самонапряженное состояние в условиях снятия внешних силовых воздействий (далее - разгрузки) и составления паспорта прочности материала.

1.3 Данный стандарт рекомендуется применять для оценки влияния образования самонапряженного состояния на уменьшение прочности пород вмещающего массива в эксплуатационный период, возникновения наведенной анизотропии, проявления деформаций упругого последействия и для минимизации влияния техногенного воздействия на изменение начального (природного) НДС и уменьшения несущей способности массива горных пород на контуре выработки, а также для повышения устойчивости выработок и предотвращения образования возникновения опасных горно-геологических явлений, с помощью, например, «активных» способов.

1.4 К техногенным воздействиям на массив пород применительно к настоящему стандарту следует относить проведение горных выработок, строительство подземных сооружений, эксплуатацию месторождений полезных ископаемых, вызывающих изменение НДС вмещающего массива, согласно СНиП 3.02.03 и СНиП II-94.

1.5 Настоящий стандарт предназначен для изыскательских, научно-исследовательских, проектных и строительных организаций, связанных с освоением подземного пространства при проходке горных выработок, сложенных породами, склонных к образованию самонапряженного состояния, разработкой методов управления горным давлением для повышения техники безопасности производства подземных работ в добывающих отраслях.

1.6 Стандарт организации может быть применен в основном при проходке горных выработок в породах осадочного происхождения (песчаниках, алевролитах, аргиллитах и т.п.) с эпигенетической (последующей) цементацией [5, 7], склонных к возникновению в них самонапряженного состояния.

1.7 Данный стандарт может быть распространен и на случаи разработки материалов для крепления горных выработок с использованием новых технологий изготовления крепей, приводящих к возникновению двух систем напряжений в материале.

1.8 Настоящий стандарт распространяется на определение механических свойств и НДС породы непосредственно на контуре выработки, в глубине массива и из выработки или с дневной поверхности и на образцах, изъятых из массива.

2 Нормативные ссылки

В настоящем стандарте использованы ссылки на следующие нормативные документы:

3 Определение принадлежности горной породы к самонапряженному состоянию

3.1 Методики определения принадлежности породы к самонапряженному состоянию должны включать прямые испытания в полевых и лабораторных условиях на образцах, изъятых из кровли, стенок и подошвы выработки, или непосредственно в массиве пород, в том числе и склонных к опасным явлениям, в соответствии со СНиП 22-01.

3.2 При разгрузке породы, образованной по схеме «нагружение-цементирование», один из структурных элементов испытывает растяжение, что отражает (3.1) для текущего значения результирующего напряжения:

s_i = s^(I) - s^(II),                                                                  (3.1)

где s^(I), s^(II) - соответственно напряжения в скелете и заполнителе.

Растягивающие напряжения при этом являются потенциальным источником образования структурных дефектов.

3.3 Основными критериями, которые определяют принадлежность породы к самонапряженному состоянию, следует принимать следующие:

«самопроизвольное» приращение относительных деформаций De_с после разгрузки, которое можно трактовать как эффект самонапряженного состояния, позволяющее записать закон Гука в виде:

                                                            (3.2)

где e - относительные деформации;

s - начальное напряжение;

Е - обобщенный модуль упругости (вывод формулы (3.3) приведен в приложении В), зависящий от долевого вклада упругих констант, составляющих среду:

Е = a_sE₂ + (1 - a_s)E₁,                                                      (3.3)

где Е₁ и Е₂ - соответственно модули упругости минералов скелета и заполнителя;

a_s и (1 - a_s) - соответственно коэффициенты, учитывающие долевой вклад цементирующего заполнителя пор и скелета в объеме среды;

образование дефектов после разгрузки, характеризующееся различными признаками: выделением звуковой энергии (акустической эмиссии), выделением тепла, магнитными эффектами и др.;

несовпадение ветвей повторных нагружений и разгрузок;

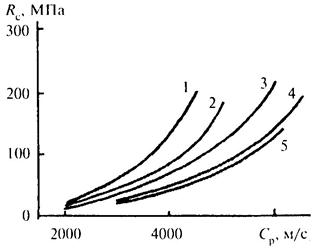
снижение механических свойств после разгрузки, определяемое различными, в том числе и косвенными, методами (например, сейсмоакустическим), позволяющими определять скорости распространения упругих волн в породе на основе корреляционной зависимости между прочностью на одноосное сжатие R_c и скоростью распространения упругих волн С_р [5] (рис. 3.1).

Рисунок 3.1 - Графики связи величин прочности на сжатие (R_с) и скорости
распространения продольных упругих волн для пород:

1 - алевриты; 2 - песчаники; 3 - базальты; 4 - известняки; 5 - интрузивные породы [5]

3.4 При определении принадлежности породы к самонапряженному состоянию предпочтение следует отдавать неразрушающим способам:

определять приращения относительных деформаций разгруженных образцов во времени;

выполнять анализ сигналов акустической (АЭ) или электромагнитной (ЭМЭ) эмиссии, представляющих собой регистрацию образования дефектов;

измерять изменение скорости прохождения ультразвука во времени, являющейся показателем прочности породы на сжатие, измеренной в первый день разгрузки и далее, в течение одного месяца, с частотой замеров не реже одного раза в три дня, с накоплением базы данных.

3.5 Для выявления самонапряженного состояния проводить мониторинг состояния образцов:

привлекая методы, инспирирующие появление новых или развитие существовавших дефектов с регистрацией реакции образца на действующие факторы по заданному параметру (помещая образцы в вакуум-камеру с фиксацией с помощью специальной аппаратуры возможных процессов саморазрушения, создавая воздействия вибрации и т.п.), поскольку даже незначительное дополнительное растягивающее воздействие на образец, находящийся в самонапряженном состоянии, может привести к изменению его НДС;

выполнять визуальный мониторинг динамики поврежденности, например, наведенной физической анизотропии, которая может проявляться в различных формах: открытая форма обнаруживается визуально при осмотре извлеченных из скважин образцов в виде расслоений монолитного образца; скрытая - регистрируется с помощью геофизических методов.

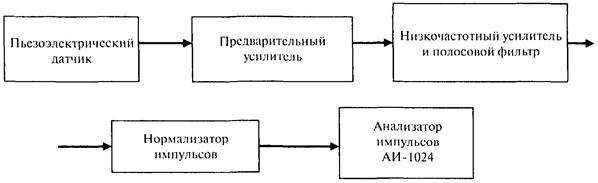
3.6 При использовании метода акустической эмиссии для определения сигналов АЭ целесообразно применять разработанный в НИИОСП им. Н.М. Герсеванова блок измерительного комплекса (рис. 3.2) с анализатором АИ-1024, обеспечивающим регистрацию импульсов по 1024 каналам [10, 14].

3.7 Для регистрации сигналов АЭ во времени анализатор импульсов целесообразно использовать в режиме работы восьми групп со 128 каналами в каждой группе, что дает возможность записывать поступающие сигналы порциями за выбранный интервал времени и получать результат наблюдения в виде ступенчатой эпюры в координатах «количество дефектов - время».

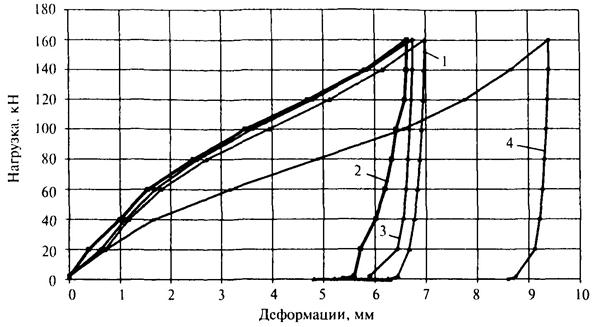
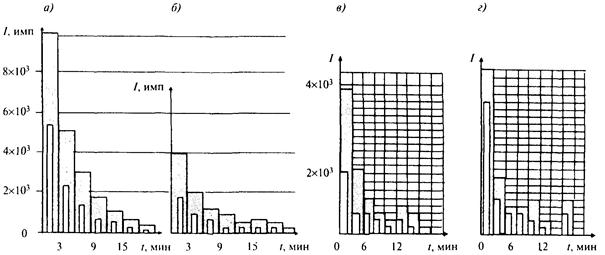
3.8 Учет вклада каждого импульса и, в частности, с высоким уровнем АЭ, которые располагаются в верхних каналах АИ-1024, выполнять нормированием сигналов, принимая в качестве нормы одиночный сигнал первого канала, т.е. один импульс 128-го канала равен 128 нормированным импульсам. В качестве примера регистрации сигналов АЭ после разгрузки несвязной породы [14] в условиях декомпрессии (рис. 3.3) на рис. 3.4, 3.5 представлены данные продолжительности затухания АЭ, где количество нормированных импульсов показано темными столбцами, ненормированных (арифметической суммы) - в виде белых столбцов.

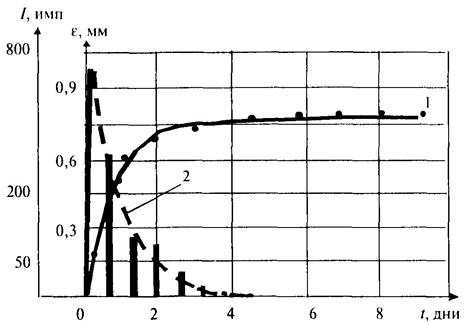
3.9 В скальных породах изменение НДС целесообразно определять комбинированным способом, например тензометрией и АЭ. В качестве примера на рис. 3.6 приведен результат синхронного измерения деформаций и импульсов АЭ искусственного образца породы с различными по величине системами напряжений в его элементах во времени, качественно совпадающий с натурными данными измерения деформаций образцов песчанистого сланца после разгрузки при колонковом бурении с глубины 945 м [15].

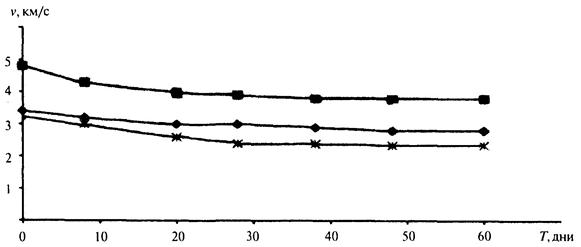
3.10 Среди геофизических способов целесообразно определять изменение скорости прохождения волн во времени ультразвуковым методом, например серийно выпускаемым прибором УК-14П, с измерением скорости в двух перпендикулярных направлениях. График изменения скорости прохождения ультразвуковых волн для образцов песчаника и алевролита, измеренных сразу после извлечения из забоя и в течение 60 дней через каждые десять суток, приведен на рис. 3.7.

Рисунок 3.2 - Блок-схема измерительного комплекса сигналов акустической эмиссии

Рисунок 3.3 - Графики деформаций при нагрузке и разгрузке песка в условиях компрессии:

1 - 3 - опыты № 2, 1, 3; 4 - влажный песок
(деформации после разгрузки выделены на оси деформаций толстой линией)

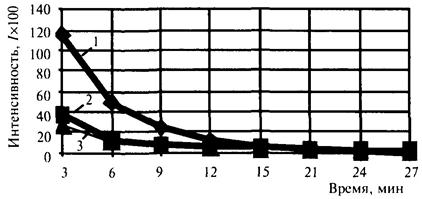
Рисунок 3.4 - Изменения интенсивности АЭ песчаных сред,
сформированных давлениями:

а, б, в - 2,27 МПа; г - 5,54 МПа, после разгрузки

Рисунок 3.5 - Затухание сигналов АЭ после разгрузки для несвязных сред различных фракций, мм:

1 - щебень 30; 2 - песок 5; 3 - песок 2

Рисунок 3.6 - Изменение деформаций (1) и сигналов АЭ (2) после разгрузки
песчано-цементного образца, сформированного под давлением на скелет,
равным 10 МПа

Рисунок 3.7 - Изменение скорости ультразвука во времени для образцов
песчаника (верхняя зависимость) и алевролита (нижние кривые)
во времени после извлечения их из забоя

3.11 При использовании ультразвукового способа целесообразно исследовать породу в массиве, после чего - на образцах, извлеченных из этого массива.

3.12 Допускается применение разрушающих методов с определением прочности образцов на растяжение R_р и сжатие R_сж. Критерием принадлежности породы к самонапряженному состоянию может быть сравнение результатов отношений R_р/R_сж для аналогичной породы, находящейся в несамонапряженном состоянии.

3.13 В расчетах для породы в самонапряженном состоянии величину остаточных напряжений рекомендуется принимать равной 10 - 12 % начальных напряжений, величину модуля упругости (3.3) допускается принимать по справочным данным.

3.14 Сравнение полученных значений остаточных напряжений рекомендуется проводить с данными прочности породы на растяжение, приведенными, например, в табл. 3.1 [5].

Таблица 3.1

Временное сопротивление растяжению скальных пород [5]

4 Отбор проб для испытаний

4.1 Отбор проб и их доставка для испытаний производятся в соответствии с ГОСТ 12071 в упаковке, обеспечивающей сохранность образцов при транспортировании, в прочных дощатых ящиках с ручками, без щелей, с досыпкой стружкой, опилками или иными материалами, смягчающими удары и толчки.

4.2 Количество образцов и скважин согласно ГОСТ 20522 должно быть представительным, высота образца должна не менее чем вдвое превышать его диаметр, который допускается от 30 мм и более.

4.3 Отбор проб производят из забоя путем вращательного выбуривания кернов из скважин, допускается отбирать керны по трассе будущей выработки из скважин, например, с дневной поверхности.

4.4 Извлечение кернов осуществляется из типичной части слоя горной породы, не допускается отбор с места перехода или контакта с соседними слоями.

4.5 Не допускается в процессе отделения проб прилагать механические усилия и производить динамические воздействия (удары, выкайливание, взрывы).

4.6 При бурении легкоразмокающих пород немедленно удалить механическим способом намокший слой керна.

4.7 Допускается в соответствии с ГОСТ 25100 в качестве проб использовать монолиты, отделяемые от массива сразу же после обнажения забоя или обуренные шпурами, позволяющими их отделение без значительных усилий.

4.8 Отобранные образцы во избежание их пересыхания или увлажнения надежно консервируют известными способами, например обертыванием в смоченную расплавленным парафином ткань, которая плотно прижимается к образцу во избежание зазора между образцом и тканью.

4.9 Консервация образцов с целью сохранения ими естественной влажности производится немедленно после их извлечения.

4.10 Для сведения к минимуму изменения природного напряженного состояния образцы породы после извлечения из массива целесообразно поместить в низкотемпературную камеру, например с сухим льдом (температура сухого льда составляет -80 °С), до момента испытания.

4.11 Одновременно с отбором проб должна производиться их маркировка в журнале и на этикетке, на которой указываются дата и время отбора пробы, номер пробы, наименование породы, номер разведочной скважины, ее ориентировка, наименование места отбора (выработка, место в выработке, время после обнажения забоя, глубина заложения выработки от дневной поверхности).

4.12 Ведомость регистрации проб доставляется вместе с пробами в лабораторию для проведения испытаний.

5 Испытание образцов

5.1 Первые регистрации информативного параметра целесообразно проводить в забое сразу же после извлечения образца из массива, поскольку в породе в самонапряженном состоянии происходит изменение механических свойств уже при разгрузке и транспортировке ее из забоя в лабораторию.

5.2 При невозможности организовать начало испытаний в забое и дальнейшие лабораторные испытания вблизи от выработки допускается транспортирование образцов в лабораторию в оборудованном для испытаний различными методами транспорте, предусмотрев обязательно возможность при транспортировании испытание образцов хотя бы одним из геофизических методов (УЗ, АЭ и др.).

5.3 При испытаниях образцов разрушающими методами необходимо выполнять требования ГОСТ 24452 относительно геометрических размеров и чистоты поверхности образцов, параметров нагрузки, захватных приспособлений и др.

5.4 Для испытаний образцов в соответствии с ГОСТ 30416 на сжатие необходимо предварительно подготовить плоскости торцов, которые должны быть параллельными, «заглаживанием» на них неровностей цементным раствором марки не ниже предполагаемой прочности образца на сжатие с точностью 0,02 мм [6].

5.5 Скорость нагружения допускается принимать равной 0,5 - 1,0 МПа/с [6] до заданного уровня нагрузки.

5.6 При испытании образцов на растяжение целесообразно применять системы захватов на разрыв конструкции «Оргэнергостроя» (рис. 5.1).

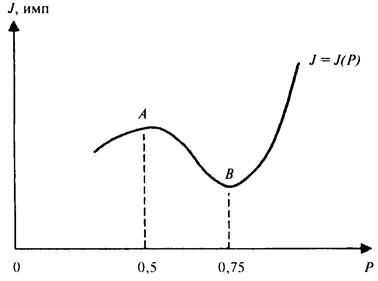
5.7 Испытание образцов на сжатие, растяжение, срез в режиме линейного (во времени) увеличения нагрузки от нуля до разрушающей целесообразно проводить совместно с АЭ-измерениями. Экспериментально установлено, что в процессе изменения НДС во всем интервале действующих нагрузок существует специфическая форма зависимости между интенсивностью АЭ и уровнем действующих напряжений [10, 16], совпадающая с данными испытаний других материалов [17]. При нагрузках 0,5 - 0,6 разрушающей имеет место максимум функции (рис. 5.2), далее идет спад до минимума (точка В) при уровне нагрузки примерно 0,65 - 0,75 разрушающей. Участок, находящийся между этими экспериментальными значениями, предшествует стадии разрушения. Начало стадии разрушения породы определяется по экстремальному значению функции - минимуму. На участке кривой от минимума и далее на прогрессирующем подъеме интенсивности АЭ происходит разрушение породы.

5.8 Испытания на повторные нагружения и разгрузку рекомендуется проводить с учетом экспериментальной зависимости, представленной на рис. 5.2, на участке графика от 0 до 0,75P (точка В).

Рисунок 5.1 - Захваты для испытания призм породы или бетона на растяжение

Рисунок 5.2 - Экспериментальная зависимость интенсивности АЭ от нагрузки
вплоть до разрушающей (Р = 1) при лабораторных испытаниях каменных образцов

Приложение А

Термины и определения

Активные способы - технические мероприятия, выполняемые до начала, в процессе или после техногенного воздействия по сохранению или улучшению существовавшего НДС массива или по крайней мере минимизации его изменения.

Акустическая эмиссия (АЭ) - выделение энергии звуковых колебаний в процессе образования дефектов в материале (породе).

Генетические напряжения - природные механические напряжения на момент их рассмотрения, сформированные различными способами в процессах генезиса массива, постгенетических преобразований или изменений его координатно-пространственного положения.

Горная выработка - общее название полостей в породном массиве или углублений на его поверхности, произведенных горными работами.

Двухсистемное напряженное состояние - одновременное действие в элементах породы двух разных по величине систем напряжений (совмещенных или локальных), например эффективных - в скелете, воспринимающих основную силовую нагрузку, и нейтральных - в заполнителе пор.

Деформации упругого последействия - деформации, возникающие после окончания разгрузки.

Забой - фрагмент выработки, подлежащий проходке.

Мониторинг - процесс наблюдения (комплекс операций) за приращением изменения состояния объекта по выбранному i-му параметру (или m-параметрам), вызванного различными причинами, анализ этих приращений с определением их динамики и т.д. и оценка результатов наблюдения по принятому критерию (или критериям) с целью выявления тенденций в изменениях состояния объекта. Границами интервала мониторинга являются моменты его начала и окончания регистрации. Начальное состояние объекта определяется в общем случае n-параметрами, по отношению к которым выполняется мониторинг информативных m-параметров, причем, как правило, n >> m.

Наведенная анизотропия - появление различий, носящих ориентированный характер, в прочностных и деформационных свойствах в материале (породе) в процессе разгрузки.

Начальное НДС - результирующее напряженно-деформированное состояние массива до начала всякого рода воздействий техногенного характера, сложившееся в гравитационном поле от действия природных факторов (механических, магнитных, температурных, химических и др.).

Открытая схема формирования НДС - характеризуется возможностью свободного выхода жидкой фазы из пор при увеличении внешних силовых воздействий, в этой схеме при приложении внешних сил основная силовая нагрузка передается на скелет.

Остаточные напряжения - внутренние напряжения, возникающие в породе или грунте после снятия внешних сил, характеризуемые не реализованной при разгрузке потенциальной энергией упругих деформаций.

Проходка - процесс разработки и удаления породы из горной выработки в пределах ее проектного очертания.

Разгрузка - процесс уменьшения внешних силовых воздействий, действовавших ранее на породу, приводящий к перераспределению ее НДС.

Самонапряженное состояние - характеризуется наличием внутренних остаточных напряжений разных знаков (сжимающих и растягивающих) в структурных элементах породы после частичного или полного снятия внешних сил.

Техногенное воздействие на массив пород - вторжение в природную среду при освоении подземного пространства, приводящее, в частности, к изменению начального НДС вмещающего массива пород.

Приложение Б

Графическая интерпретация образования самонапряженного состояния породы

1 Графическое построение результирующей зависимости

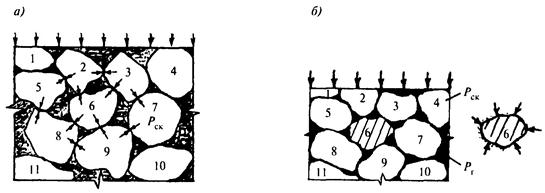
Цель построения состоит в наглядной иллюстрации зависимости между изменением внешней нагрузки и перераспределением усилий в элементах, образующих эту среду, при разгрузке. Это построение выполнено с учетом предыдущей истории формирования НДС при генезисе осадочной обломочной породы с последующей цементацией. Известная из курсов геологии [5, 7] последовательность сводится к тому, что отложившиеся осадки из обломочного материала в течение длительного времени (геологических эпох) сначала постепенно сдавливались вышележащими, более поздними, слоями осадков (рис. Б.1, а) с выжиманием жидкой фазы из пор, уплотнением элементов скелета и уменьшением пористости. Далее в процессах фильтрации природных растворов вода в порах замещалась цементирующим раствором. В таком состоянии происходило омоноличивание среды (рис. Б.1, б) за счет твердения различных растворов в порах уплотненного высоким давлением и деформированного скелета.

Рисунок Б.1 - Механический процесс образования эффективных напряжений
в осадочной породе в условиях открытой схемы:

а - сжатие и деформирование зерен (1 - 11 и т.д.) скелета внешней нагрузкой с вытеснением жидкой фазы из пор; б - последующее твердение раствора в порах сжатого скелета (показано темным цветом)

Рассмотрим эту последовательность с точки зрения концепции механики грунтов о двух системах напряжений [8, 9], согласно которой в грунтовых массах - средах, состоящих из скелета и полностью заполненных водой пор, в условиях открытой схемы одновременно действуют две системы напряжений: эффективные - в скелете, которые эффективно воздействуют на частицы грунта, передают давление нижележащим слоям скелета, воспринимая основную силовую нагрузку, и нейтральные, в этом процессе не участвующие. При этом полное напряжение в среде [8, 9] равно:

s = s₀ + p_w,                                                                (Б.1)

где s₀, p_w - эффективные и нейтральные (гидростатические) напряжения.

Аналогия процесса образования породы с данной концепцией состоит в том, что на начальном этапе генезиса порода состояла из скелета, нагруженного и деформированного вышележащими, более «молодыми», слоями, и жидкой фазы. Эта среда являлась не чем иным, как грунтовой массой, в элементах которой действовали свои системы напряжений.

Продолжив анализ грунтовой массы применительно к образованию осадочной сцементированной породы и вместо жидкой фазы рассмотрев цементный заполнитель, можно обнаружить, что в основных чертах генезис происходил по схеме: нагружение скелета (образование одного поля напряжений) с последующим цементированием (второе поле напряжений).

Образовавшийся материал с прочными связями между отдельными частицами можно рассматривать сплошным, изотропным и однородным, являющимся носителем двух совмещенных полей напряжений. Следовательно, для любой точки новой среды результирующее напряжение определится, как и в [8, 9], суммой напряжений в системах (I и II):

s = s^(I) + s^(II).                                                          (Б.2)

Вместе с тем, как следует из известных компрессионных зависимостей, отражающих процесс нагружения скелета [5, 6 и др.], грунт, независимо от цикла нагружения, является накопителем упругих деформаций, реализация которых происходит при разгрузке.

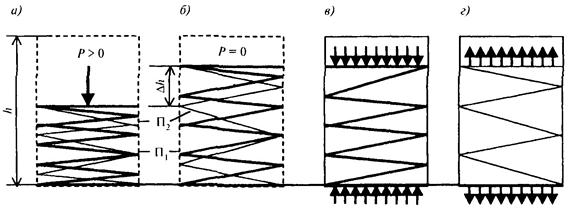
Учитывая вышеизложенное, процесс образования осадочной сцементированной породы можно представить механической моделью, где упругий элемент П₁, сжатый силой Р (показан толстой линией), моделирующий скелет, скреплен с несжатым элементом П₂ (рис. Б.2, а). Второй элемент моделирует цементный заполнитель. При снятии нагрузки сжатый элемент начинает деформировать несжатый элемент, после чего - удерживать его в новом положении (рис. Б.2, б).

В результате после снятия нагрузки в элементах будут существовать остаточные напряжения разных знаков: сжимающие (рис. Б.2, в) и растягивающие (рис. Б.2, г).

Рисунок Б.2 - Механическая модель, иллюстрирующая образование
остаточных напряжений в элементах среды после снятия внешних сил

Подтверждением возможности консервации ранее сжатой структуры песка при разгрузке цементным заполнителем являются результаты экспериментов (рис. Б.3). Связывающее влияние затвердевшего раствора выражается в существенном уменьшении величины упругих деформаций (примерно в два раза) образцов при полной разгрузке.

Рассмотренная схема одновременного действия двух совмещенных систем механических напряжений, образованных в результате последовательности «нагружение-цементирование», показывает принципиальное отличие начального НДС пород от напряженного состояния искусственных материалов, а также пород, образованных в условиях закрытой схемы (компрессии). Сформированное НДС при эпигенетической цементации проявляется только при разгрузке образованием самонапряженного состояния. Подтверждением являются исследования Н.М. Герсеванова и Д.Е. Польшина [8] процесса разгрузки грунтовой массы на механической модели, сформулировавшие положение о возможности при разгрузке консервации эффективных напряжений нейтральными с сохранением первоначального напряженного состояния скелета.

Рисунок Б.3 - Экспериментальные результаты разгрузки образцов с различной
прочностью цементирующего раствора: АЕ₁ и АЕ₂ - составов 6:1 и 3:1
(песок : цемент); АВ - с незатвердевшим («сырым») раствором

В общем случае процессы сжатия и растяжения двух элементов породы (скелета и цементирующего заполнителя), представленных на модели на рис. Б.2, если рассматривать их по отдельности, отражаются зависимостями P = f(Dl) (рис. Б.4).

Рисунок Б.4 - Зависимости между усилиями и деформациями при сжатии и
разгрузке для первого элемента - скелета (а);
растяжении и разгрузке для второго элемента (б)

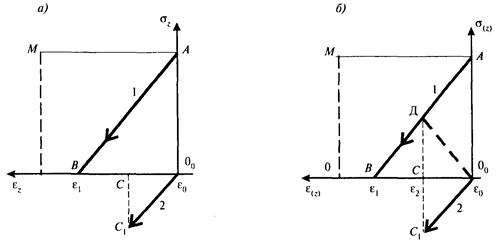
Поскольку после образования породы она стала единым материалом, необходимо соединить эти зависимости для элементов породы в одно целое с общим началом координат 0₀ (рис. Б.5, а). В этом случае при снятии внешних сил элементы скелета и заполнителя, будучи объединенными в одном объеме общим омоноличивающим материалом, вовлекают в деформации друг друга [18]. Деформации прекратятся, когда усилия в элементах сравняются (рис. Б.5, б).

Рисунок Б.5 - Совмещение зависимостей s = f(e) для элементов,
составляющих модель, с общим началом координат

Примечание - На графике Б.5 приведена только ветвь разгрузки для первого структурного элемента (1), поскольку для анализа процесса снятия внешних сил необходимо лишь начальное состояние перед разгрузкой (точка А).

Для удобства определения результатов взаимодействия элементов строится зеркальное отражение зависимости при нагружении (растяжении) для второго элемента относительно оси деформаций 0₀Д.

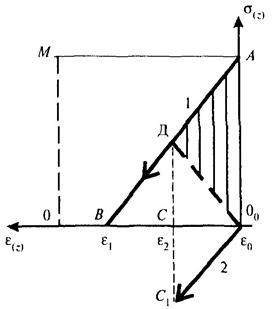
Это построение дает возможность определить ординаты внешней нагрузки, которые находятся между зеркальным отображением ветви нагружения второго и ветвью разгрузки первого элемента (в заштрихованном треугольнике 0₀ДА на рис. Б.6). Точка пересечения этих ветвей Д соответствует полному снятию внешней нагрузки.

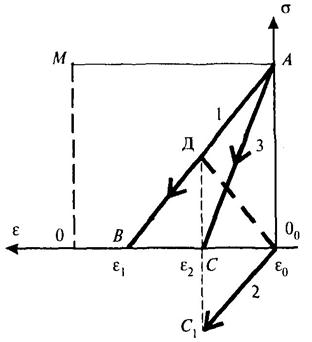
Если эти ординаты отложить от одной горизонтальной оси или спроектировать точку Д на ось e, то определим точку С зависимости (3) (рис. Б.7) для породы, пришедшей в самонапряженное состояние после разгрузки, между внешней нагрузкой (на весь материал) и деформацией АС, которую получил бы экспериментатор в «привычном» виде, если значения внешней нагрузки как обычно откладывались бы от оси деформаций, но без фактических ординат внутренних напряжений ДС, которые без знания истории образования НДС среды оказываются неизвестны.

Рисунок Б.6 - Изменение внешней нагрузки на графике совмещенных зависимостей (1) и (2)

Рисунок Б.7 - Зависимости s = f(e) для элементов, составляющих модель, при разгрузке:

1 - s^(I) = f_I(e₀ - e₁); 2 - s^(II) = f_II(e₀ - e₂); 3 - s = f(e₀ - e₂);

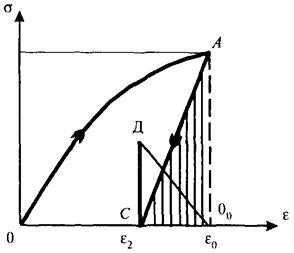
Таким образом, получаем привычную формальную зависимость с указанием присутствия скрытых от экспериментатора остаточных напряжений. Оставим за кадром построения, отражающие внутренний механизм перераспределения напряжений в элементах этого материала при уменьшении полной внешней нагрузки на этот материал; на рис. Б.8 приведен график, на котором в привычном виде отражена ветвь разгрузки, однако с ординатами остаточных напряжений ДС.

Эффективные боковые напряжения после снятия внешней нагрузки в общем случае после разгрузки будут создавать остаточные напряжения в горизонтальной плоскости. При испытании такого образца, например на одноосное сжатие, горизонтальные остаточные напряжения до приложения нагрузки будут способствовать образованию в нем вертикальных трещин.

Рисунок Б.8 - Результирующая зависимость s = f(e) в «привычном» виде с
дополнением остаточными напряжениями (равными отрезку ДС) после разгрузки

2 Возможные случаи самонапряженного состояния при разгрузке

В зависимости от уровня давлений формирования породы, прочностных характеристик «скелетной» структуры и омоноличивающего материала, режима разгрузки и других факторов при разгрузке возможны различные случаи изменения НДС.

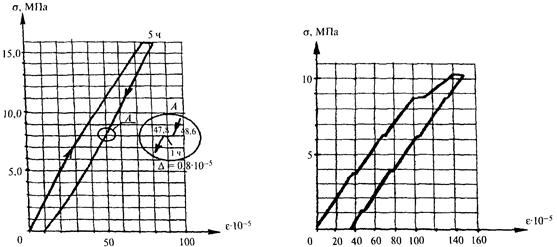
Например, влияние режима разгрузки иллюстрируется на графиках испытаний искусственных образцов породы [10]. При достаточно быстром снятии нагрузки ветвь разгрузки - близкая к линейной. Выдержка под давлением на каких-либо ступенях приводит к деформациям ползучести (рис. Б.9).

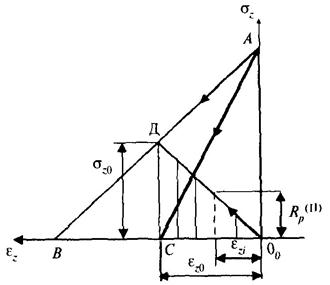
Нереализованную потенциальную энергию, т.е. работу упругих деформаций, обусловленную остаточными напряжениями (пояснение об остаточной потенциальной энергии приведено в приложении Д), необходимо рассматривать в связи с прочностными свойствами связующего материала . В соответствии с этим всю область деформаций целесообразно разделить на два интервала: e_zi и e_z0 (рис. Б.10).

Рисунок Б.9 - Результаты испытаний бетонных призм с приостановкой разгрузки (в точке А)

Рисунок Б.10 - Изменение НДС породы с генетическими напряжениями при разгрузке

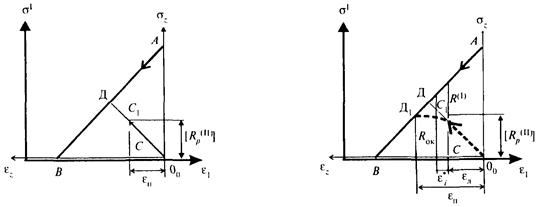
Случай 1. Омоноличивающий материал характеризуется высокой прочностью на растяжение (в т.ч. после разгрузки)  (рис. Б.11) с устойчивым равновесием. После разгрузки образец породы (например, в виде керна) будет сохранять стабильность свойств при последующем хранении и, скорее всего, не обнаружит в течение длительного времени приращений дополнительных деформаций, снижения прочности и т.п.

Рисунок Б.11 - Графическая интерпретация разгрузки с устойчивым равновесием

С практической точки зрения, порода может быть исследована в лаборатории после доставки ее из забоя, с другой стороны - при оценке устойчивости выработки и вмещающего массива вопрос учета самонапряженного состояния теряет остроту. Случай, когда прочностные характеристики цементирующего материала очень высоки и не проявляются известные факторы при полной разгрузке, является наиболее сложным, поскольку к настоящему времени, к сожалению, не разработано способов идентификации такого состояния и, насколько известно, исследований в этом направлении не ведется.

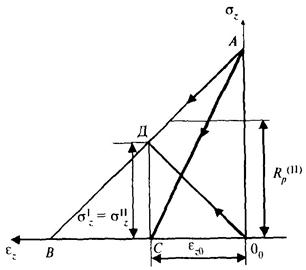
Случай 2. Связующий материал является хрупким и его прочность на растяжение равна уровню напряжений в самонапряженном образце после разгрузки  (рис. Б.12), причем . Его состояние характеризуется неустойчивым равновесием, и в зависимости от каких-либо дополнительных факторов воздействия (вибрация, температура и т.п.) упругое последействие может произойти, а может и не произойти.

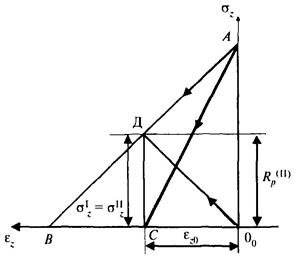
В области значений деформаций e_i < e_z0 он будет находиться в допредельном состоянии и, следовательно, без снижения прочности. В случае если он обладает пластическими или вязкопластическими свойствами и предел пластичности , то при извлечении из забоя образец в первое время будет сохранять стабильность свойств. Это позволит доставить образцы в лабораторию для исследования изменения их прочностных свойств во времени.

Рисунок Б.12 - Графическая интерпретация разгрузки для случая

Случай 3. При  образец, будучи извлеченным из массива, уже изменит свою прочность, и величина этого понижения будет зависеть от соотношения . Когда это отношение значительно, например 1,5 - 2,0 и более, произойдет нарушение природной прочности и, скорее всего, разрушение породы. Реализация упругого последействия будет зависеть от многих факторов, в том числе от изменения прочности во времени и режима разгрузки, т.е. . При быстрой разгрузке упругое последействие выразится в дополнительных деформациях во времени, которые будут происходить, пока прочность на растяжение не сравняется с остаточными напряжениями. Если материал хрупкий, то при мгновенном характере разрушения уже никаких дополнительных деформаций упругого последействия не произойдет.

Следует отметить, что на практике в кернах породы обнаруживают деформации упругого последействия, снижение прочности вплоть до саморазрушения, остаточные напряжения [2 - 4, 15 и др.].

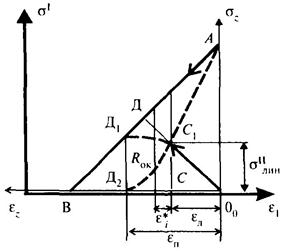
Случай 4. Уровень напряжений, передаваемых при реализации упругих деформаций скелетной структуры, приближается к прочности на растяжение омоноличивающего материала. Особенность этого случая будет состоять в том, что в процессе разгрузки действующие биполярные напряжения достигнут уровня напряжений, при которых начинается образование дефектов, что приведет к началу изменения (уменьшения) прочности. Изменение соотношений биполярных напряжений и внешних усилий уже в процессе разгрузки будет определяться зависимостями в соответствии с графиком Б.13.

Следует отметить, что под дефектами во второй структуре подразумеваются не обязательно трещины, дефекты могут быть в результате «искривления» решетки, дислокаций и т.д. Результаты испытаний (рис. 5.2) показывают, что массовое образование дефектов начинается при превышении уровня нагрузки примерно .

Рисунок Б.13 - Изменение самонапряженного состояния при разгрузке
при приближении действующих напряжений к пределу прочности
омоноличивающего материала

Изменение зависимости между напряжениями и деформациями для омоноличивающей структуры показано на рис. Б.13 пунктирной линией. Деформация при разгрузке равна:

                                                                (Б.3)

где e_п - полная относительная деформация при разгрузке до начала упругого последействия;

e_л - участок линейной относительной деформации, определяемый выражением:

                                                   (Б.4)

где  - текущее значение относительной деформации после линейного участка, которая является функцией разности напряжений в структурах на нелинейном участке и времени, т.е.:

                                                        (Б.5)

где t - время.

Текущее значение полной деформации будет определяться формулой:

                                 (Б.6)

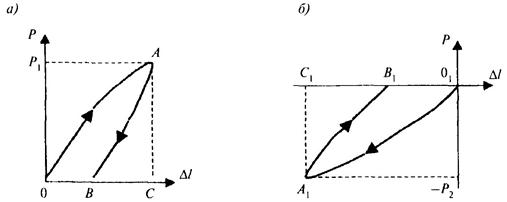
Если продолжить дальнейшее построение рис. Б.13, то результирующая зависимость разгрузки для этого случая будет отражена ветвью АД₂ на рис. Б.14.

Рисунок Б.14 - Результирующая зависимость между напряжениями и
деформациями при разгрузке для случая 4

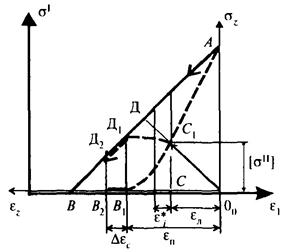
После полного снятия внешних сил возникшее состояние может оказаться неустойчивым из-за воздействия остаточных упругих напряжений на омоноличивающую структуру, например, с продолжением процесса образования дефектов и уменьшением прочности, которые приведут к приращению деформаций, пока не наступит равновесие биполярных остаточных напряжений. Если это равновесие неустойчиво, то со временем начнется новый процесс образования дефектов, сопровождающийся дополнительными приращениями деформаций. На рис. Б.15 снижение прочности после разгрузки из-за дефектов показано отрезком Д₁Д₂, общая деформация будет равна e = e_п + De_с, при этом величина приращения деформаций De_с может трактоваться как упругое последействие. Результирующая зависимость разгрузки в этом случае отразится ветвью AB₁B₂.

Рисунок Б.15 - Графическая интерпретация упругого последействия
после разгрузки среды с двумя системами напряжений

Для учета эффекта самонапряженного состояния формула (Б.4) для традиционного случая, при котором остаточных напряжений нет, может быть записана [10] в следующем виде:

                                                         (Б.7)

где De_с, как и в формуле Б.5, является функцией разности напряжений в структурах, времени и, возможно, других факторов.

Примечание - При определении результирующей зависимости между напряжениями и деформациями можно ограничиться этими случаями, которые дают наглядное представление о динамике образования самонапряженного состояния. Некоторые другие условия проявления De_с рассмотрены в [10].

Приложение В

Определение результирующего модуля упругости породы, образованной по схеме «нагружение-цементирование»

В качестве исходных данных приняты: F - общая площадь; a_sF - площадь сечения пор; (1 - a_s)F - эффективная площадь сечения минералов скелета; Е₁ и Е₂ - соответственно модули упругости минералов скелета и заполнителя. При увеличении внешней нагрузки после заполнение пор твердеющим раствором дополнительная нагрузка DР (или напряжения Ds) воспринимается как скелетом, так и заполнителем:

DР₁ + DР₂ = DP,                                                       (В.1)

причем условие, отражающее сохранность среды, будет состоять в том, что относительные деформации первой и второй составляющих будут равны, т.е.:

De_1: = De₂ = De,                                                        (В.2)

где

                                                             (В.3)

Деформации составляющих структурных элементов будут определяться долями нагрузки, приходящимися на скелет и цементирующий раствор:

                                              (В.4)

Введя коэффициент b_s, определяющий долевое участие общего приращения нагрузки на соответствующие элементы 1 и 2, имеем:

DР₁ = (1 - b_s)DР; DР₂ = b_sDР                                          (В.5)

 или                     (В.6)

Из (В.6) определим неизвестную величину b_s:

                                                       (B.7)

 или

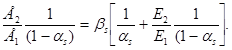
После преобразования получаем:

откуда 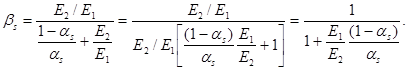                          (В.8)

Определим результирующий модуль упругости. Приравнивая, например, De₁ = De₂, с учетом (В.2) - (В.4) имеем:

                                                    (В.9)

Учитывая (В.5), из (В.9) получим:

 откуда  или

                                                      (В.10)

Учитывая значение для коэффициента b_s (В.8), найдем:

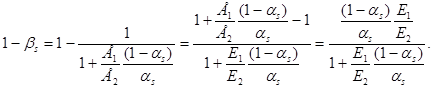        (В.11)

Далее определим дробь в правой части формулы (В.10):

                 (В.12)

Теперь, учитывая (В.12), из (В.10) определим значение Е:

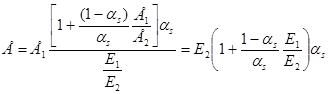 или

Е = a_sЕ₂ + (1 - a_s)Е₁.                                                  (В.13)

Проверка предельных переходов показывает корректность (В.13):

а) при a_s = 0,5                                     Е = 0,5(Е₁ + Е₂);                                                (В.14)

б) при a_s = 0                                       Е = Е₁;                                                                (В.15)

в) при a_s = 1                                       Е = Е₂.                                                                (В.16)

Полученная формула (В.13) дает представление о долевом вкладе упругих констант, составляющих среду, при различных соотношениях объемов скелета и цементирующего заполнителя пор. Результат (В.14) показывает, что при равном количестве минералов и заполнителя в общем объеме среды результирующий модуль упругости равен среднеарифметическому значению модулей упругости составляющих среду элементов.

Приложение Г

Определение результирующего коэффициента Пуассона v при разгрузке в горной породе с двухсистемным напряженным состоянием

Определение вида функции v = f(v₁, v₂) для среды, образованной по схеме «нагружение-цементирование», выполнено в [19] для разгрузки в условиях декомпрессии в допредельном напряженно-деформированном состоянии. Задача решалась в линейной постановке с учетом выполнения условий: совместности перемещений во всем диапазоне изменения напряжений De₁ = De₂ = De при отсутствии горизонтальных деформаций породы:

e_х = e_у = 0.                                                             (Г.1)

Касательные напряжения полагаем равными нулю.

Соотношение для относительной деформации системы в плоскости х, у:

                                               (Г.2)

Принимая во внимание

                                                   (Г.3)

с учетом (Г.1) из (Г.2) получим:

                                                           (Г.4)

Согласно (3.1) и (Г.3) для полных напряжений и напряжений в системах имеем:

                                (Г.5)

где  и

v₁, v₂ - соответственно коэффициенты Пуассона скелета и заполнителя. Преобразуем (Г.4) с учетом (Г.5):

                           (Г.6)

где

В частности, при v₁ = v₂ получается, что a₁ = a₂ = a, следовательно:

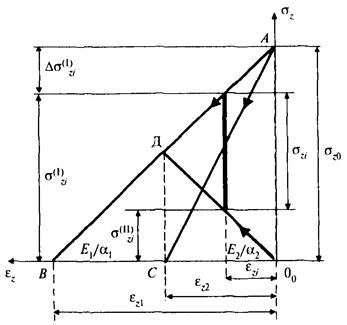
Таким образом, результирующий коэффициент Пуассона v в этом случае не зависит от коэффициента k, что подтверждает корректность формулы (Г.6). Учитывая зависимости между напряжениями в системах и соответствующими относительными деформациями в условиях декомпрессии в виде на рис. Г.1

Рисунок Г.1 - Изменение НДС горной породы при разгрузке

                                   (Г.7)

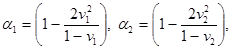где                                                                          (Г.8)

получим:

                           (Г.9)

Введя обозначения

                                                 (Г.10)

из (Г.6) находим:

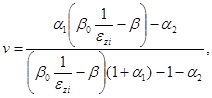                                        (Г.11)

откуда

     (Г.12)

Формула (Г.12) дает возможность проследить за изменением результирующего коэффициента Пуассона в предельных переходах:

а) при e_zi ® 0 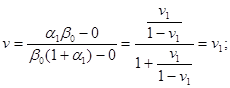                                                   (Г.12, а)

б) при e_zi ® e_z1                                                                      (Г.12, б)

в) при e_zi ® e_z2 напряжения  (сжатия) и  (растяжения), отличающиеся друг от друга по знаку, станут равными по абсолютной величине. Это соответствует полной разгрузке, при которой остаточные напряжения (сжимающие и растягивающие) равны между собой, но отличаются знаком, поэтому k = -1. В этом случае из (Г.6) получаем:

                                (Г.12, в)

Результат (Г.12, а) является очевидным и отражает в процессе разгрузки особенности такого напряженного состояния среды с совмещенными системами напряжений, когда нагрузку несет первая система, а вторая система напряжений является инертной.

Результат (Г.12, б) показывает, что инертной является первая система напряжений. Результат (Г.12, в), менее очевидный, свидетельствует о том, что в процессе разгрузки (при e_zi > 0) в результате суперпозиции систем напряжений результирующие поперечные деформации характеризуются обобщенным коэффициентом Пуассона, величина которого при полной разгрузке определяется по полученной формуле.

Рассмотрим (Г.12, в) или (Г.6) более подробно.

При k ® 0                                   

что совпадает с результатом (Г.12, б).

При k ® ¥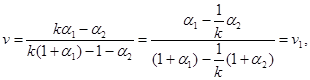                    

что совпадает с результатом (Г.12, a).

При k ® -1 имеем:                               или

                                             (Г.13)

Ниже в таблице для примера приведены некоторые результаты расчетов для реальных коэффициентов Пуассона систем из [19] по формуле (Г.6).

Таблица Г.1

Результаты расчета обобщенного коэффициента Пуассона по формуле (Г.6)

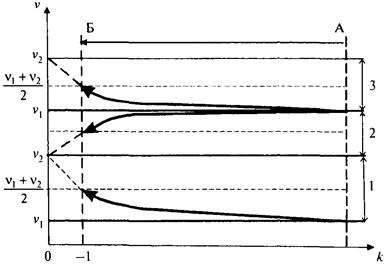
На основании вычисленных данных (для случая, когда v₁ ¹ v₂) обнаруживается закономерность диапазона изменения результирующего коэффициента Пуассона v в процессе разгрузки породы с двухсистемным напряженным состоянием - от величины коэффициента Пуассона первой системы в начале разгрузки к практически среднеарифметическому значению коэффициентов первой и второй систем (рис. Г.2) при полном снятии внешних силовых воздействий. Как следует из приведенных материалов, в диапазоне реальных значений коэффициентов Пуассона для горных пород такое изменение результирующего коэффициента Пуассона (увеличение в интервалах 1 и 3 или уменьшение в диапазоне 2) является незначительным.

При равенстве соответствующих коэффициентов Пуассона систем напряжений между собой одновременное действие этих систем при снятии внешней нагрузки приводит к тому, что результирующий коэффициент Пуассона такой горной породы остается постоянным.

Рисунок Г.2 - Изменение результирующего коэффициента Пуассона при разгрузке
среды с различными коэффициентами Пуассона в элементах породы
(в диапазонах 1, 2, 3):

А - начало разгрузки; Б - полное снятие внешней нагрузки

Таким образом, в процессе снятия внешней нагрузки одновременное действие (суперпозиция) генетических полей напряжений приводит к тому, что коэффициент Пуассона такой породы зависит от коэффициентов Пуассона слагающих ее структурных элементов и определяется по формуле (Г.13).

Приложение Д

Определение остаточной потенциальной энергии при разгрузке породы, образованной по схеме «нагружение-цементирование»

Разгрузка приводит к образованию остаточной потенциальной энергии упругих деформаций в горной породе с двухсистемным напряженным состоянием [20].

В работе [20] приведен анализ одной из причин неполной реализации накопленной энергии упругой деформации при уменьшении внешних сил с позиции существования перед разгрузкой совмещенного двухсистемного напряженного состояния породы. В результате после разгрузки в первой системе частично «консервируется» ранее накопленная энергия упругой деформации, во второй - заново аккумулируется энергия, и порода в целом обладает внутренней энергией, равной сумме энергий в двух системах.

При традиционной постановке вопроса в рамках положений теории упругости (при доказательстве единственности решения) считается, что накопленная потенциальная энергия, зависящая от модуля упругости, уровня действовавших внешних нагрузок, при разгрузке исчезает (полностью реализуется) так же, как и внутренние напряжения [1].

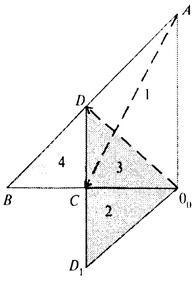
Зависимости между напряжениями и деформациями в системах, слагающих горную породу, при уменьшении начальных напряжений в цикле разгрузки в общем случае могут быть нелинейными. Следовательно, нелинейной будет и результирующая зависимость между внешними напряжениями s_z и соответствующими деформациями e_z в цикле разгрузки. При совместной деформации систем в условиях рассматриваемой задачи эти зависимости могут быть представлены функциями 1 - f_I(e) для первой системы, 2 - f_II(e) для второй системы и 3 - f_III(e) для результирующей зависимости (рис. Д.1). Начало координат принято в точке 0₀, соответствующей начальному напряженному состоянию. При уменьшении внешней нагрузки начнется реализация энергии упругой деформации в первой системе, от воздействия которой во второй системе начнется изменение усилий (растяжения) (2).

Рисунок Д.1 - График совмещения зависимостей между напряжениями
и деформациями при разгрузке для элементов, слагающих породу

Следует отметить, что площади полученных фигур, ограниченных зависимостями 1 - 3, отражают не что иное, как удельную работу деформации [21], а значит, потенциальную энергию, накапливаемую в материале в результате упругой деформации, вызванной действием внешних сил. Запасенная энергия первой системы, которая может быть реализована при снятии внешних нагрузок, отражается криволинейным треугольником АВ0₀, если пренебречь другими видами энергии (тепловой, магнитной и др.) [21]. Однако, затратив часть своей энергии на растяжение второй системы, которая при этом сама накапливает потенциальную энергию, равную площади треугольника 0₀ДС, и удержание ее в таком состоянии, первая система часть своей потенциальной энергии, ограниченной площадью треугольника ДВС, не реализует. Таким образом, после полного снятия внешних сил среда обладает потенциальной энергией, некоторое количество которой сохранила первая система (площадь треугольника ДВС), другая часть энергии вновь накоплена второй системой (площадь треугольника 0₀ДС).

Площадь, ограничиваемая результирующей зависимостью 3 в интервале изменения деформаций от e₀ до e₁, определяется зависимостями для отдельных систем в этом же интервале. Поэтому можно записать:

                               (Д.1)

Для случая, когда эти зависимости являются линейными (что в данном случае можно принять без ущерба для определения фактического перераспределения внутренних усилий), уравнения линий разгрузки запишутся в следующем виде, если угловые коэффициенты для функций f_I, f_II, f_III обозначить через K_I, K_II и K_III:

f_I(e₀ - e) = K_I(e₀ - e), f_II(e₀ - e) = K_II(e₀ - e), f_III(e₀ - e) = K_III(e₀ - e).             (Д.2)

Тогда интегралы, входящие в уравнение (Д.1), могут быть выражены:

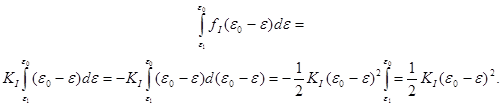    (Д.3)

Аналогично:

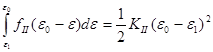 и

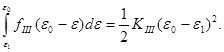                                         (Д.4)

Из рис. Д.1 видно, что начальное вертикальное напряжение s_ZH отражено линией А0₀, результирующее напряжение R равно отрезку ДС, и далее можно записать:

Тогда:

       (Д.5)

Для рассмотренных линейных зависимостей диаграмма распределения энергии после разгрузки в допредельном состоянии отражена на рис. Д.2. Из этой диаграммы видно, что порода после разгрузки обладает внутренней потенциальной энергией, равной сумме площадей треугольников 4 (остаточная энергия первого поля) и 2 (или то же самое 3 - эту часть энергии накопило в процессе разгрузки второе поле):

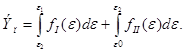                                           (Д.6)

Рисунок Д.2 - Схема распределения составных частей потенциальной
энергии после разгрузки породы:

1 - израсходованной; 3(2) - вновь накопленной; 4 - остаточной

Анализ приведенного графика показывает, что с увеличением модуля упругости второй системы и возможностью ее воспринимать большие растягивающие напряжения возрастает доля нереализованной внутренней потенциальной энергии после разгрузки.

Приложение Е

Список литературы

1. Тимошенко С.П., Гудьер Дж. Теория упругости. - М.: Наука, 1979.

2. Барон Л.И., Турчанинов И.А., Ключников А.В. Нарушения горных пород при контурном взрывании. - Л.: Наука, 1975. - С.61 - 62.

3. Усков В.А. Саморазрушение пород вокруг подземных выработок // Горный журнал. - 2000. - № 10. - С. 16.

4. Гамсахурдия Г.Р. Система геофизических и петрофизических исследований земной коры океанического типа при глубоководном научном бурении // Автореф. дисс. д-ра техн. наук. - Тверь, 2000.

5. Грунтоведение / Трофимов В.Т., Королев В.А., Вознесенский Е.А. и др. Под ред. Трофимова В.Т. - 6-е изд., переработ. и доп. - М.: Изд-во МГУ, 2005.

6. Болдырев Г.Г. Методы определения механических свойств грунтов. Состояние вопроса. - Пенза: ПГУАС, 2008.

7. Горшков Г.П., Якушова А.Ф. Общая геология. - М.: Изд-во МГУ, 1973.

8. Герсеванов Н.М., Польшин Д.Е. Теоретические основы механики грунтов и их практическое применение. - М.: Госстройиздат, 1948.

9. Терцаги К., Пек Р. Механика грунтов в инженерной практике / Перевод с англ. - М.: Госстройиздат, 1958.

10. Мороз А.И. Самонапряженное состояние горных пород. - М.: Изд-во Московского государственного горного университета, 2004.

11. Шрейнер Л.А., Байдюк Б.В., Павлова Н.Н. и др. Деформационные свойства горных пород при высоких давлениях и температурах. - М.: Недра, 1968.

12. Открытие № 162 РФ. Явление возникновения самонапряженного состояния горной породы, сформировавшейся под действием внешних сил // Репников Л.Н., Картозия Б.А., Мороз А.И. // Научные открытия, М.: РАЕН, 2001.

13. Репников Л.Н., Мороз А.И., Аникин А.А. Совершенствование средств мониторинга дефектов в практике обследований зданий и сооружений // Труды института «НИИОСП им. Н.М. Герсеванова - 70 лет». - М.: НИИОСП, 2001.

14. Мороз А.И. Изменение напряженно-деформированного состояния несвязного грунта после разгрузки. В сб. научных трудов НИИОСП им. Н.М. Герсеванова. Выпуск 99. - М.: Изд-во «ЭСТ», 2008.

15. Николин В.И., Подкопаев С.В., Колесников В.Т. О новой теории горного давления в угольных шахтах // Безопасность труда в промышленности. - 2002. - № 11.

16. Способ обработки сигналов акустической эмиссии при разрушении каменных материалов / А.с. № 1762287 СССР. Репников Л.Н., Аникин А.А., Ковальчук С.Л., Мороз А.И., Четыркин Н.С. // Б.И. - 1992. - № 34.

17. Козинкина А.И. Моделирование и оценка накопления повреждений в конструкционных материалах на базе данных акустической эмиссии // Автореф. дисс. д-ра техн. наук. - М., 2008.

18. Сахновский К.В. Железобетонные конструкции. - М.: Госстройиздат, 1960.

19. Мороз А.И. К вопросу об определении коэффициента Пуассона осадочных горных пород // ФТПРПИ. - 2006. - № 4. - С. 59 - 68.

20. Мороз А.И. Образование остаточной потенциальной энергии в горной породе с двухсистемным напряженным состоянием после ее разгрузки / Геодинамика и напряженное состояние недр Земли. Труды международной конф. (10 - 13 октября 2005 г.). - Новосибирск: Ин-т горного дела СО РАН, 2006. - С. 302 - 308.

21. Беляев Н.М. Сопротивление материалов. - М.: Наука, 1976.