|
МИНИСТЕРСТВО ПРИРОДНЫХ РЕСУРСОВ И ЭКОЛОГИИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
|
|
ФЕДЕРАЛЬНАЯ СЛУЖБА ПО ЭКОЛОГИЧЕСКОМУ,
ТЕХНОЛОГИЧЕСКОМУ И АТОМНОМУ НАДЗОРУ
|
|
УТВЕРЖДЕНО
|
|
приказом Федеральной службы
|
|
по экологическому,
|
|
технологическому
|
|
и атомному надзору
|
|
от 20 июля 2009 г. № 641
|
РУКОВОДСТВО ПО БЕЗОПАСНОСТИ
«РАСЧЕТНЫЕ СООТНОШЕНИЯ И МЕТОДИКИ РАСЧЕТА
ГИДРОДИНАМИЧЕСКИХ И ТЕПЛОВЫХ ХАРАКТЕРИСТИК
ЭЛЕМЕНТОВ И ОБОРУДОВАНИЯ ВОДООХЛАЖДАЕМЫХ
ЯДЕРНЫХ ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК»
РБ-040-09
|
Введено в действие
|
|
с 1 сентября 2009 г.
|
Настоящее руководство по
безопасности носит рекомендательный характер и не является нормативным правовым
актом.
Руководство
по безопасности содержит рекомендации по реализации требований федеральных норм
и правил в области использования атомной энергии.
Руководство
по безопасности содержит расчетные соотношения и методики расчета
гидродинамических и тепловых характеристик элементов и оборудования водоохлаждаемых
ядерных энергетических установок (ЯЭУ), включая:
■
коэффициенты гидравлического сопротивления трения и местных касательных
напряжений, расходов;
■
коэффициенты теплоотдачи;
■
температуры поверхностей теплообмена;
■
параметры кризиса теплоотдачи при кипении воды;
■
погрешности этих характеристик, рекомендуемых расчетных соотношений.
Выпускается
впервые*.
____________
* В
1991 г. ГНЦ РФ ФЭИ разработал руководящий технический материал (РТМ) под
названием «Рекомендации, правила, методики расчета гидродинамических и тепловых
характеристик элементов и оборудования энергетических установок». Однако за
прошедшее время в стране и за рубежом накоплено и опубликовано много материалов
по различным аспектам теплогидравлики ЯЭУ, которые могут быть использованы в
проектных и конструкторских расчетах, при разработке, верификации и экспертизе
программных средств, применяемых при обосновании и обеспечении безопасности
ЯЭУ.
В 2006 г. разработан
Методический документ ФГУ НТЦ ЯРБ «Расчетные соотношения и методики расчета
гидродинамических и тепловых характеристик элементов оборудования
водоохлаждаемых ЯЭУ», в котором были учтены новые научные данные и требования
существующей системы рекомендательных документов. Этот документ в 2007 г.
проходил опытную эксплуатацию в ФГУ НТЦ ЯРБ и организациях отрасли, результаты
которой учтены при разработке настоящего РБ.
СОДЕРЖАНИЕ
1. НАЗНАЧЕНИЕ И ОБЛАСТЬ ПРИМЕНЕНИЯ
1.1.
Настоящее руководство по безопасности носит рекомендательный характер и не
является нормативным правовым актом.
1.2.
Руководство по безопасности содержит рекомендации по реализации требований
федеральных норм и правил в области использования атомной энергии.
1.3.
В руководстве по безопасности приводятся расчетные соотношения и методики
расчета гидродинамических и тепловых характеристик элементов и оборудования
водоохлаждаемых ядерных энергетических установок (ЯЭУ), включая:
■
коэффициенты гидравлического сопротивления трения и местных касательных
напряжений, расходов;
■
коэффициенты теплоотдачи и температур поверхностей теплообмена;
■
параметры кризиса теплоотдачи при кипении воды;
■
а также погрешности этих характеристик, рекомендуемых расчетных соотношений.
1.4.
Для режимов без кипения воды в руководстве по безопасности приводятся
рекомендации, относящиеся только к стационарным процессам.
1.5.
Настоящее руководство по безопасности (далее - РБ) рекомендуется использовать
при создании, верификации и экспертизе программных средств (далее - ПС),
применяемых при обосновании и обеспечении безопасности ЯЭУ.
1.6.
В случае использования других соотношений и методик, чем те, которые указаны в
настоящем РБ, следует показать, что расчет теплогидравлических параметров
выполнен с погрешностями, дающими возможность сделать обоснованные заключения о
безопасности ЯЭУ.
2. ОБЩИЕ ПОЛОЖЕНИЯ
2.1.
При составлении РБ учтен опыт Федерального государственного учреждения «Научно
технический центр по ядерной и радиационной безопасности» (далее - ФГУ НТЦ ЯРБ)
и других организаций по разработке, верификации и экспертизе ПС, применяемых
при обосновании и обеспечении безопасности ЯЭУ, а также по применению расчетных
соотношений и методик расчета гидродинамических и тепловых характеристик
активных зон и оборудования циркуляционных контуров водоохлаждаемых ЯЭУ при их
проектировании, конструктруировании и эксплуатации.
2.2.
РБ разработано с использованием Международной системы единиц СИ. В РБ
использована единая терминология и система обозначений, принятая в «Сборнике
рекомендуемых терминов, выпуск 83, Теория теплообмена, Терминология, изд. «Наука»,
М. 1971». Однако в ряде случаев разработчики РБ вынуждены были сохранять
предложенные некоторыми авторами обозначения, поэтому ряд символов имеет
несколько значений, отличных от рекомендуемых, что оговорено по тексту.
2.3.
В каждой из рекомендованных методик приводятся погрешности, как правило, в виде
авторских оценок, такие как:
■
Δ (в % или абсолютных величинах) - среднеарифметическая погрешность
описания данной методикой использованного массива экспериментальных данных;
■
σ (в % или абсолютных величинах) - среднеквадратичная погрешность
описания данной методикой использованного массива экспериментальных данных;
■
δ (±δ в % или абсолютных величинах) - максимальное
отклонение рекомендованной методики от использованного массива
экспериментальных данных.
2.4.
Для каждой методики приводятся пределы применимости по определяющим параметрам
в использованном массиве экспериментальных данных, а также из общефизических
соображений.
3. РЕКОМЕНДАЦИИ ПО РАСЧЕТУ ГИДРОДИНАМИЧЕСКИХ И
ТЕПЛОВЫХ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ И ОБОРУДОВАНИЯ
ЯЭУ С ВОДООХЛАЖДАЕМЫМИ РЕАКТОРАМИ
3.1. ГИДРОДИНАМИКА
Гидравлическая
система ЯЭУ состоит из насосов, трубопроводов, коллекторов, каналов активной
зоны и предназначена для прокачки теплоносителя. Дополнительными устройствами,
входящими в гидравлическую систему, являются теплообменные аппараты,
парогенераторы, арматура, дроссельные и сепарирующие устройства. Замкнутая
гидравлическая система подводящих и отводящих трубопроводов, распределительных
устройств внутри корпуса реактора и каналов (кассет) с тепловыделяющими
элементами называется циркуляционным контуром.
Большинство
гидродинамических расчетов в ядерной энергетике связано с течениями в каналах.
Главными задачами при расчете таких течений являются определение гидравлических
сопротивлений каналов различной геометрии и местных сопротивлений, расчет
распределения по каналам расходов, скоростей и касательных напряжений. Цель
расчета гидравлических сопротивлений - определение потерь давления в каналах и
затрат мощности на прокачку теплоносителя.
При
проведении гидравлических расчетов используются следующие величины,
характеризующие поток в каналах: геометрические параметры канала (площадь
поперечного сечения, гидравлический диаметр, длина, абсолютная шероховатость и
т.д.), скорость, плотность и вязкость среды.
Средняя
плотность среды определяется по средней температуре среды в канале на данном
участке.
Все
теплоносители, используемые в атомной энергетике, включая жидкие металлы,
являются ньютоновскими жидкостями и, таким образом, подчиняются общим закономерностям.
3.1.1.
РЕЖИМЫ ОДНОФАЗНОГО ТЕЧЕНИЯ
3.1.1.1. РЕЖИМЫ ТЕЧЕНИЯ В КАНАЛАХ С БЕЗОТРЫВНЫМ ОБТЕКАНИЕМ
Ламинарный,
или слоистый, режим течения характеризуется отсутствием пульсаций
гидродинамических величин. Критическое число Рейнольдса Reкр,
(Re = wd/v) при достижении которого происходит потеря
устойчивости и разрушения ламинарного режима течения в трубах круглого
поперечного сечения, обычно принимается равным 2300. За счет устранений
возмущений на входе в канал можно существенно затянуть существование
ламинарного режима течения до Reкр = (5 ÷ 7)·104.
Наличие шероховатости на стенках трубы уменьшает значение критического числа
Рейнольдса. Неизотермичность потока также влияет на критическое число
Рейнольдса. При совпадении направлений свободного и вынужденного движений у
стенки критическое число Рейнольдса возрастает в зависимости от величины числа
Релея (Ra = gβl3Δt/va) (табл. 3.1.1.1).
Таблица 3.1.1.1
Зависимость критического числа Рейнольдса от числа Релея при
совпадении
направлений свободного и вынужденного движений в круглой гладкой трубе
|
Ra·10-6
|
0
|
1,6
|
4,7
|
11,6
|
15,8
|
|
Reкр
|
2300
|
3500
|
5200
|
6200
|
7100
|
При противоположном
направлении естественной конвекции и вынужденного движения у стенки критическое
число Рейнольдса уменьшается, снижаясь при Ra = 105 до
значения Reкр = 103.
Критическое
число Рейнольдса для каналов некруглого поперечного сечения имеет примерно
такое же значение, как и для круглой трубы (табл. 3.1.1.2). Для каналов с
узкими угловыми областями критическое число Рейнольдса является условной
величиной, поскольку турбулентность сначала возникает в широкой части канала, а
затем распространяется на узкую.
Таблица 3.1.1.2
Критическое число Рейнольдса для каналов различной геометрии
при продольном обтекании
|
Тип
канала
|
Reкр
|
|
Кольцевой
|
2000 ÷ 2800
|
|
Прямоугольный
|
2000 ÷ 2300
|
|
Треугольный
с αmin >
45°
|
≈ 2000
|
|
Сборки
стержней различной упаковки
|
≈ 2000
|
В змеевиках и других
криволинейных каналах, где возникают значительные центробежные силы, граница
перехода к турбулентному режиму течения сдвигается в область более высоких
значений чисел Рейнольдса.
Критическое число Рейнольдса при ламинарном течении в змеевиках
рассчитывается по формуле [1]:
|

|
(3.1.1.1)
|
где dзм -
диаметр змеевиков, м;
dвн -
внутренний диаметр трубы змеевика, м.
Критическое число Рейнольдса
при ламинарном течении в спирально-навитых (витых) трубах диаметром dсн,
меньшим их внутреннего диаметра (рис. 3.1.1.1) и в локально-навитых трубах, у которых
навитые участки чередуются с прямолинейными длиной L, рассчитываются по
формуле [1]:
|

|
(3.1.1.2)
|
где dсн = dцп - dвн,
м.
Пределы
применимости формулы: S/d = 12 ÷ 40; 0,2 < dцп/dвн
< 0,7.
Переходный
к турбулентному режим течения характеризуется чередованием областей с
ламинарным и турбулентным течениями. На величину чисел Рейнольдса, в диапазоне
изменения которых наблюдается указанный режим течения, сильно влияют
шероховатость поверхности, интенсивность турбулентности потока на входе в
канал, которые сдвигают начало переходного режима течения в область более
низких чисел Рейнольдса, и величина температурного фактора, определяющая
взаимодействие между вынужденной и естественной конвекциями.
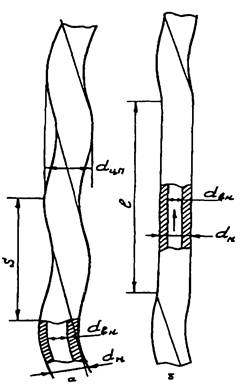
а - спирально-навитая труба; б - локально спирально-навитая
труба;
dцп - диаметр цилиндрической поверхности, описанной около
спирально-навитой трубы, м;
dвн - внутренний диаметр исходной гладкой трубы, м; S
- шаг навивки трубы, м;
dн - наружный диаметр, м.
Рис. 3.1.1.1. Геометрия
спирально-навитых труб
При
переходном режиме течения возникают низкочастотные пульсации параметров потока
и наблюдается резкое изменение интенсивности переноса тепла и импульса с
возрастанием числа Рейнольдса.
Принимается,
что переход от переходного режима течения к турбулентному в трубах происходит
при Re = (5 ÷ 7)·103, а в сборках стержней треугольной
и квадратной упаковок при Re = (10 ÷ 15)·103.
Турбулентный
режим течения характеризуется наличием интенсивных пульсаций параметров потока
(скорости, плотности, температуры и т.д.), что связано с существованием вихрей,
имеющих широкий диапазон пространственных и временных масштабов. Особенностью
турбулентного режима течения является также наличие вязкого подслоя у стенки, в
котором происходит затухание пульсаций.
3.1.1.2. РЕЖИМЫ ТЕЧЕНИЯ В КАНАЛАХ С ОТРЫВНЫМ ОБТЕКАНИЕМ СТЕНОК
Структура
течения в каналах с повышенной шероховатостью стенок, с турбулизирующими поток
вставками, с поперечным расположением труб и в засыпках определяется характером
развития и отрыва пограничных слоев, которые формируются на стенках обтекаемых
тел. Процесс отрыва сопровождается возникновением турбулентных вихрей и
интенсификацией теплообмена. Наличие по ходу потока большого количества
дискретных элементов (выступы, шероховатости, трубы, песчинки) приводит к
постоянному чередованию зон отрыва и областей, где происходит восстановление
пограничного слоя, и препятствует образованию устойчивой структуры течения
(ламинарной, турбулентной).
Ламинарное (безотрывное)
течение в таких каналах имеет место при более низких числах Рейнольдса.
Относительная величина шероховатости, начиная с которой проявляется ее влияние
на переход к турбулентному течению в трубах, рассчитывается по формуле [1]:
|

|
(3.1.1.3)
|
При течении среды в трубах с
интенсификаторами теплосъема критическое число Рейнольдса в зависимости от
степени шероховатости изменяется в пределах 500 ÷ 2000. Особо низкие
значения (Reкр ≈ 50) наблюдаются при поперечном
обтекании труб и в засыпках.
При
числах Рейнольдса, больших критического, имеет место течение со смешанной структурой
пограничных слоев. Например, при поперечном обтекании труб в диапазоне чисел
Рейнольдса 2·103 < Re < 2·105 на фронтальной
части трубы образуется ламинарный пограничный слой, а на тыловой -
турбулентный.
3.1.1.3. ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ КАНАЛОВ
ПРИ ТЕЧЕНИИ ОДНОФАЗНОЙ СРЕДЫ (ОБЩИЕ ПОЛОЖЕНИЯ)
Расчет
гидравлических сопротивлений проводится для определения полного перепада
давления в теплообменном аппарате и затрат мощности на прокачку теплоносителей.
Общий
перепад давления между двумя сечениями канала, в котором движется однофазный
стабилизированный поток, складывается из потерь давления на трение ΔРтр,
потерь давления, возникающих при движении потока через местные сопротивления ΔРм,
нивелирного напора ΔРнив и перепада давления, связанного
с ускорением потока ΔРуск.
Общий перепад давления,
таким образом, рассчитывается по формуле [1]:
|
ΔР =
ΔРтр + ΔРм + ΔРнив
+ ΔРуск
|
(3.1.1.4)
|
Сопротивление
трения при стабилизированном течении однофазного потока в трубах, каналах
различного сечения при продольном обтекании пучков труб для изотермического и
неизотермического потоков при практически применяемых величинах температурного
напора рассчитывается по формуле [1,
2]:
|

|
(3.1.1.5)
|
где ξ - коэффициент гидравлического сопротивления
трения, зависящий от геометрии канала, числа Рейнольдса и относительной
шероховатости поверхности Δ/dг;
L -
длина канала, м;
dг -
гидравлический диаметр канала, м;
ρ -
плотность среды, кг/м3;
 - средняя скорость
теплоносителя в канале, м/с.
- средняя скорость
теплоносителя в канале, м/с.
Потери давления на местном
сопротивлении рассчитываются по формуле [1, 2]:
где ξм - коэффициент местного
гидравлического сопротивления;
 - средняя скорость потока,
к которой отнесен коэффициент местного гидравлического сопротивления, м/с.
- средняя скорость потока,
к которой отнесен коэффициент местного гидравлического сопротивления, м/с.
Местные
сопротивления возникают при резком изменении поперечного сечения канала или
направления движения теплоносителя и считаются сосредоточенными.
Нивелирный напор на данном
участке рассчитывается по формуле [2]:
где ρ - среднее значение плотности среды, кг/м3;
h - высота канала, м;
g -
ускорение силы тяжести, м/с2.
Потери напора на ускорение
потока при постоянных проходном сечении и расходе теплоносителя рассчитываются
по формуле [2]:
|

|
(3.1.1.8)
|
где ρк, ρн -
плотности среды в конце и начале канала, кг/м3.
Погрешность
расчета δ общего гидравлического сопротивления по формуле (3.1.1.4) определяется в основном
погрешностью расчета гидравлического сопротивления трения и местного
сопротивления и составляет ±(10 ÷ 25) %.
Конкретные
формулы для расчета коэффициентов гидравлического сопротивления трения и
местного сопротивления приведены в последующих разделах РБ.
Список литературы к разделу 3.1.1
1. Тепловой и гидравлический расчет теплообменного оборудования
АЭС. РД.24.035.05-89, - Л.: НПО ЦКТИ, 1991.
2. Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по
теплогидравлическим расчетам (ядерные реакторы, теплообменники,
парогенераторы). - М.: Энергоатомиздат, 1984, 1990.
3.1.2.
ЛАМИНАРНЫЕ ТЕЧЕНИЯ
3.1.2.1. ЛАМИНАРНЫЕ СТАБИЛИЗИРОВАННЫЕ ТЕЧЕНИЯ В КАНАЛАХ
В
разделе приведены формулы для расчета коэффициентов гидравлического
сопротивления трения, распределения скоростей и касательных напряжений при
ламинарном течении в каналах разной геометрии.
Тепло
физические характеристики, если иное не оговаривается, относятся к средней
массовой температуре потока в заданном сечении канала. Формулы получены как
результат точных решений и аппроксимации этих решений простыми формулами.
3.1.2.1.1. Ламинарное течение в трубах
Коэффициент гидравлического
сопротивления трения при ламинарном течении в трубе круглого поперечного
сечения рассчитывается по формуле [1]:
где  (
( - средняя по сечению
скорость).
- средняя по сечению
скорость).
Пределы
применимости формулы: Re ≤ 2300.
Погрешность
δ расчета ξ составляет ±5 %.
Распределение скорости при
ламинарном течении в трубе круглого поперечного сечения подчиняется
параболическому закону и рассчитывается по формуле [1]:
|

|
(3.1.2.2)
|
Пределы применимости
формулы: Re ≤ 2300.
Погрешность
Δ расчета w составляет ±10 %.
Касательное напряжение на
стенке трубы круглого поперечного сечения при ламинарном течении рассчитывается
по формуле [1]:
|

|
(3.1.2.3)
|
Пределы применимости
формулы: Re ≤ 2300.
Погрешность
Δ расчета τст составляет ±10 %.
Коэффициент гидравлического
сопротивления трения при ламинарном течении между двумя плоскими параллельными
пластинами бесконечных размеров (плоская труба) рассчитывается по формуле [1]:
где Re = (2wH)/ν;
Н -
расстояние между пластинами, м.
Пределы
применимости формулы: Re ≤ 2300.
Погрешность
δ расчета ξ составляет ±5 %.
Распределение скорости при
ламинарном течении в плоской трубе рассчитывается по формуле [1]:
|

|
(3.1.2.5)
|
где у - расстояние по нормали от оси трубы до
рассматриваемой точки.
Пределы
применимости формулы: Re ≤ 2300 (где  ; dг = 4F/П
- гидравлический диаметр, м; F - площадь, м2; П - периметр,
м).
; dг = 4F/П
- гидравлический диаметр, м; F - площадь, м2; П - периметр,
м).
Погрешность
δ расчета w составляет ±10 %.
Коэффициент гидравлического
сопротивления трения при ламинарном течении в трубе эллиптического поперечного
сечения рассчитывается по формуле [1]:
|
ξRe = 8[dг / b2]2[1+(b2 / b1)2],
|
(3.1.2.6)
|
где  ; dг = 4F/П
- гидравлический диаметр, м;
; dг = 4F/П
- гидравлический диаметр, м;
F -
площадь, м2;
П -
смоченный периметр, м;
b1, b2 - большая и малая полуоси эллипса, м.
Пределы
применимости формулы: Re ≤ 2300.
Погрешность
Δ расчета ξ составляет ±5 %.
Распределение скорости при
ламинарном течении в трубах эллиптического поперечного сечения рассчитывается
по формуле [1]:
|

|
(3.1.2.7)
|
где у - координата точки от центра эллипса вдоль оси b1;
z -
координата точки от центра вдоль оси b2.
Пределы
применимости формулы: Re ≤ 2300.
Погрешность
δ расчета w составляет ±10 %.
Коэффициент
гидравлического сопротивления трения при ламинарном течении в трубах
прямоугольного поперечного сечения определяется по таблице 3.1.2.1 [1].
Таблица 3.1.2.1
Коэффициент гидравлического сопротивления трения труб
прямоугольного поперечного сечения
|
b/h
|
1,00
|
1,25
|
1,50
|
2,00
|
2,50
|
3,00
|
4,00
|
5,00
|
10,00
|
∞
|
|
ξRe
|
56,90
|
57,47
|
58,82
|
62,14
|
64,00
|
68,35
|
72,90
|
76,29
|
84,61
|
96,00
|
b, h -
стороны прямоугольника; определяющий размер при расчете Re -
гидравлический диаметр.
Пределы
применимости: Re ≤ 2300.
Погрешность
δ определения ξ по таблице составляет ±5 %;
Данные
таблицы со среднеквадратичной погрешностью 0,6 % описываются формулой:
ξRe =
95,9 - 123,31х + 135,14х2 - 50,89х3,
где x = h/b.
Коэффициент гидравлического
сопротивления трения при ламинарном течении в трубах с поперечным сечением в
форме равнобедренного треугольника рассчитывается по формуле [2]:
где β - половина угла при вершине равнобедренного
треугольника;
В -
параметр, который рассчитывается по формуле [2]:
|

|
(3.1.2.9)
|
Определяющий размер при
расчете Re - гидравлический диаметр.
Пределы
применимости формулы (3.1.2.8):
Re ≤ 2300.
Для
равностороннего треугольника, когда β = 30°, ξRe =
53,33; для прямоугольного равнобедренного треугольника, когда β =
45°, ξRe = 52,71.
Погрешность
δ расчета ξ составляет ±5 %.
3.1.2.1.2. Ламинарное течение в кольцевых каналах
В
разделе приведены формулы для расчета коэффициентов гидравлического
сопротивления трения и распределения скорости при ламинарном течении в
концентрических кольцевых каналах.
Для
эксцентрических кольцевых каналов даны приближенные формулы расчета
коэффициентов гидравлического сопротивления трения и касательных напряжений.
Коэффициент
гидравлического сопротивления трения при ламинарном течении в кольцевых каналах
определяется числом Re и отношением радиусов кольцевого канала θ
= R1/R2,
где R1 -
внутренний радиус зазора кольцевого канала, м;
R2 -
наружный радиус зазора кольцевого канала, м.
Коэффициент гидравлического
сопротивления трения при ламинарном течении в концентрических кольцевых каналах
рассчитывается по формуле [3]:
где Kф - коэффициент формы, который рассчитывается по формуле [3]:
|

|
(3.1.2.11)
|
где определяющий размер при расчете числа Re -
гидравлический диаметр кольцевого канала dг = d2
- d1.
Пределы
применимости формулы (3.1.2.10):
Re ≤ 2300.
Погрешность
δ расчета ξ составляет ±5 %.
Распределение скорости при
ламинарном течении в концентрических кольцевых каналах рассчитывается по
формуле [3]:
|

|
(3.1.2.12)
|
где R - текущий радиус зазора кольцевого канала, R1
< R < R2.
Пределы
применимости формулы: Re ≤ 2300.
Погрешность
δ расчета w составляет ±10 %.
Коэффициент гидравлического
сопротивления трения при ламинарном течении в эксцентрических кольцевых каналах
рассчитывается по формуле [3, 4]:
где A = 3 - 4,5(1 - θ)
+ 2(1 - θ)2;
е -
относительный эксцентриситет кольцевого канала, е = a / (R2
- R1);
а -
эксцентриситет кольцевого канала, м;
ξо -
коэффициент гидравлического сопротивления трения при ламинарном течении в
трубах, рассчитывается по формуле (3.1.2.1).
Определяющий
размер при расчете Re по формуле (3.1.2.13) - гидравлический диаметр
эксцентрического кольцевого канала.
Пределы
применимости формулы: Re ≤ 2300; 0,3 < 0,1 + 0,5е < θ.
Погрешность
δ расчета ξ составляет ±8 %.

Рис. 3.1.2.1. Схема
поперечного сечения эксцентрического кольцевого канала
Распределение касательных
напряжений по периметру внутренней и внешней стенок эксцентрического кольцевого
канала при ламинарном течении рассчитывается по формуле [3, 4]:
|
 , ,
|
(3.1.2.14)
|
где
при i = 1
|

|
(3.1.2.15)
|
при i = 2
|

|
(3.1.2.16)
|
|

|
(3.1.2.17)
|
индексы i = 1, 2
относятся к внутренней и внешней поверхностям кольцевого канала соответственно;
углы
φ1 и φ2 отсчитываются от узкой
части эксцентрического кольцевого канала (рис. 3.1.2.1).
Пределы
применимости формулы: Re ≤ 2300.
Погрешность
δ расчета τi
составляет ±10 %.
3.1.2.1.3.
Ламинарное продольное течение в сборках стержней
В
разделе рассматриваются правильные упаковки стержней. Стержни (твэлы)
располагаются по вершинам равностороннего треугольника или квадрата.
Соответственно такие системы называются треугольными или квадратными упаковками
стержней. Схемы ячеек показаны на рис. 3.1.2.2.

Рис. 3.1.2.2. Схемы
треугольной и квадратной упаковки стержней
Коэффициент гидравлического
сопротивления трения при ламинарном течении в сборках стержней треугольной и
квадратной упаковок рассчитывается по формуле [3]:
где  ;
;
ξ⁎ -
относительный радиус эквивалентной окружности, которой заменяется шестигранная
или квадратная граница ячейки вокруг стержней;
где R* - радиус эквивалентного по площади
сектора круга;
dн -
наружный диаметр стержня, м;
dг -
гидравлический диаметр сборки стержней, который рассчитывается:
для треугольной упаковки
стержней по формуле:
для квадратной упаковки стержней по формуле:
где X - относительный шаг расположения стержней в решетке.
Определяющий
размер при расчете Re - гидравлический диаметр сборки стержней.
Пределы
применимости формулы (3.1.2.18):
Re ≤ 2000; X = S/dн > 1,40.
Погрешность
δ расчета ξ по формуле (3.1.2.18) составляет ±8 %.
Коэффициенты гидравлического
сопротивления трения для сборок стержней треугольной и квадратной упаковок с
погрешностью, большей, чем по формуле (3.1.2.18), рассчитываются по формуле [3]:
где Kф -
коэффициент формы, значения которого приведены в таблице 3.1.2.2 [2].
Таблица 3.1.2.2
Коэффициент формы для сборок стержней треугольной
и квадратной упаковок
|
X = S/dн
|
1,00
|
1,02
|
1,05
|
1,10
|
1,20
|
1,30
|
1,40
|
1,50
|
2,00
|
|
Треугольная
упаковка стержней
|
0,407
|
0,663
|
0,966
|
1,274
|
1,560
|
1,715
|
1,834
|
1,940
|
2,462
|
|
Квадратная
упаковка стержней
|
0,406
|
0,518
|
0,679
|
0,913
|
1,264
|
1,510
|
1,699
|
1,858
|
2,518
|
Пределы применимости формулы
(3.1.2.19): Re ≤
2000; S/dн = 1,0 ÷ 2,0.
Погрешность
δ расчета ξ по формуле составляет:
при S/dн
= 1,0 ÷ 1,4 - ±12 %;
при
1,4 < S/dн < 2,0 - ±8 %.
Оценочные
расчеты коэффициентов гидравлического сопротивления трения в сборках стержней
допускается проводить по формуле (3.1.2.19),
если принять:
для треугольной упаковки
стержней [1, 2]
|

|
(3.1.2.20)
|
для квадратной упаковки стержней [1, 2]
|

|
(3.1.2.21)
|
В этом случае погрешность δ
расчета ξ составляет ±15 %.
3.1.2.2. НЕСТАБИЛИЗИРОВАННОЕ ЛАМИНАРНОЕ ТЕЧЕНИЕ НА
ВХОДНОМ УЧАСТКЕ КАНАЛОВ
Под
влиянием трения о стенки гидродинамические характеристики ламинарного потока в
прямолинейных каналах изменяются на некоторой длине, называемой входным или
начальным участком. Развитие характеристик потока сопряжено с дополнительными
затратами энергии на прокачивание жидкости через канал.
При
расчете теплообменных аппаратов с малой относительной длиной целесообразно
учитывать особенности течения жидкости на начальном участке по сравнению с
участком стабилизированного течения.
Длина
входного участка и профиля гидродинамических характеристик в его различных
сечениях зависят от конфигурации входных устройств.
Формирование
профиля скорости на гидродинамическом входном участке осуществляется через
молекулярный механизм обмена. Это приводит к тому, что длина входного участка
при выбранной конфигурации входного устройства не зависит от характеристик
поверхности каналов, т.е. для каналов с гладкими или шероховатыми стенками
длина входных участков практически одинакова при фиксированном числе
Рейнольдса.
3.1.2.2.1. Нестабилизированное ламинарное течение на входном
участке круглой трубы
Длина входного участка
(участка стабилизации потока) при ламинарном течении в круглых трубах с плавным
профилированным входом рассчитывается по формуле [5, 6]:
|
Lст/dвн =
0,055Re,
|
(3.1.2.25)
|
где Lст - длина входного участка, м;
dвн -
внутренний диаметр, м.
Пределы
применимости формулы: Re ≤ 2300.
Погрешность
δ расчета Lст составляет ±10 калибров трубы.
Падение
давления по длине входного участка круглой трубы вызывается поверхностным
трением и изменением количества движения потока жидкости.
Перепад давления на участке
между входным и произвольными поперечными сечениями входного участка трубы
рассчитывается по формуле [5, 6]:
|

|
(3.1.2.26)
|
где X = x/(Redвн) - безразмерное расстояние
между входным и произвольным поперечными сечениями входного участка трубы.
Пределы
применимости формулы: Re ≤ Reкр.
Погрешность
δ расчета  составляет ±6 %.
составляет ±6 %.
Перепад давления на всей
длине входного участка трубы рассчитывается по формуле:
При стабилизированном ламинарном течении перепад давления на длине
трубы, равной длине входного участка, равен:
|

|
(3.1.2.28)
|
Средняя скорость задаётся.
Из
отношения перепадов давления, найденных по формулам (3.1.2.27) и (3.1.2.28),
следует, что на всей длине входного участка затраты энергии на прокачивание
ламинарного потока жидкости в 1,33 раза больше, чем на соответствующей длине
стабилизированного ламинарного течения.
Пределы
применимости формулы (3.1.2.27):
Re ≤ Reкр;
погрешность
δ расчета ΔРвх составляет ± 6 %.
Профиль
скорости при ламинарном течении жидкости на входном участке круглой трубы
рассчитывается [5, 6]:
■ в пограничном слое
по формуле:
|

|
(3.1.2.29)
|
где  - относительная толщина
пограничного слоя, зависящая от продольной координаты х;
- относительная толщина
пограничного слоя, зависящая от продольной координаты х;
Y -
расстояние от стенки трубы;
■ в центральной части
трубы за пределами пограничного слоя по формуле [5, 6]:
|

|
(3.1.2.30)
|
Пределы применимости формул
(1.2.29), (1.2.30): Re ≤ Reкр.
Погрешность
δ расчета u
составляет ±10 %.
Толщина пограничного слоя
при заданном числе Рейнольдса связана с продольной координатой зависимостью [5, 6]:
|

|
(3.1.2.31)
|
При фиксированных
расстояниях х и Re толщина пограничного слоя находится
итерационно.
3.1.2.2.2. Нестабилизированное ламинарное течение на
входном участке плоской трубы
Плоская
труба - канал, образованный двумя плоскими параллельными пластинами бесконечных
размеров. Плоская труба является предельным случаем кольцевого канала.
Длина входного
гидродинамического участка в плоских трубах с гладкой и шероховатой
поверхностями рассчитывается по формуле [5, 6]:
|

|
(3.1.2.32)
|
где Re = 2wH/ν; H -
расстояние между параллельными пластинами, характерный размер при расчете Re.
Пределы
применимости: пластины с регулярной шероховатостью в форме выступов
прямоугольного поперечного сечения; относительная высота элементов
шероховатости изменяется от 0 до H/3; Re
≤ Reкр.
Погрешность
расчета Lст составляет 10H.
Список литературы к разделу 3.1.2
1. Петухов Б.С. Теплообмен и сопротивление при ламинарном течении
жидкости в трубах. - М.: Энергия, 1967.
2. Мигай В.К. Гидравлическое сопротивление треугольных каналов в
ламинарном потоке. - Известия вузов, сер. Энергетика, 1963, № 5.
3. Субботин В.И., Ибрагимов М.Х., Ушаков П.А. и др. Гидродинамика и
теплообмен в атомных энергетических установках. - М.: Атомиздат, 1975.
4. Ушаков П.А. Влияние эксцентриситета на гидродинамические
характеристики кольцевых каналов. Теплофизика высоких температур, 1976, том 14,
№ 1.
5. Шах. Корреляция решений для гидродинамического начального
участка каналов круглого и некруглого сечений при ламинарном режиме.
Теоретические основы инженерных расчетов, 1978, т. 100, № 2.
6. Кэмпбелл, Слэттерн. Течение на начальном участке трубы. Техническая
механика, 1963, т. 85, сер. Д., № 1.
3.1.3.
ОДНОФАЗНЫЕ ТУРБУЛЕНТНЫЕ ТЕЧЕНИЯ
3.1.3.1
СТАЦИОНАРНОЕ СТАБИЛИЗИРОВАННОЕ ТУРБУЛЕНТНОЕ
ТЕЧЕНИЕ В КАНАЛАХ
Помимо
ламинарного наблюдаются также следующие режимы течения [1]:
■
турбулентный режим без проявления шероховатости при у+ ≤
5, где у+ = yv⁎/v;  , у - расстояние от
стенки, м.
, у - расстояние от
стенки, м.
В
этом режиме гидравлическое сопротивление такое же, как и в гладких трубах:
■
переходный режим при 5 < у+ ≤ 70; в этом режиме
течения гидравлическое сопротивление зависит от Re и отношения dвн/k,
где k - абсолютная высота бугорков шероховатости;
■
автомодельный режим при у+ > 70, при котором коэффициент
гидравлического сопротивления не зависит (или слабо зависит) от Re и
зависит от отношения dвн/k.
Трубы
с неравномерной шероховатостью считаются гладкими, если Δ/dг
< 15/Re,
где Δ -
эквивалентная абсолютная шероховатость, м; Re = Wdг/v
[2].
Таблица 3.1.3
Значения Δ для различных материалов [2]
|
Материал
|
Значение
Δ, м
|
|
Нержавеющая
сталь
|
1·10-5
|
|
Алюминий
|
1,5·10-5
|
|
Углеродистая
сталь:
|
|
|
новые
трубы при тщательной очистке воды
|
8·10-5
|
|
трубы
для насыщенного пара или воды с незначительной коррозией
|
2·10-4
|
|
водопроводы,
находящиеся в эксплуатации
|
2·10-3
|
Все рекомендации раздела
получены для изотермического течения или случаев слабой зависимости
теплофизических свойств от температуры.
Теплофизические
свойства, если особо не оговаривается, относятся к средней массовой температуре
потока в заданном сечении канала.
3.1.3.1.1. Стационарное стабилизированное турбулентное течение в
трубах
В
разделе приведены соотношения для расчета коэффициентов гидравлического
сопротивления трения, касательных напряжений и полей скорости.
Коэффициент гидравлического
сопротивления трения при турбулентном течении в круглой трубе рассчитывается по
формуле Филоненко:
|
ξ = 1/(1,82lgRe - 1,64)2,
|
(3.1.3.1)
|
где 
Пределы
применимости формулы: Re = 4·103 ÷ 108.
Погрешность
δ расчета ξ составляет ±5 %.
Касательное напряжение на
стенке трубы круглого поперечного сечения при турбулентном течении
рассчитывается по формуле:
|
τст =
(ξ/8)ρw2.
|
(3.1.3.2)
|
Пределы применимости
формулы: Re = 4·103 ÷ 108.
Погрешность
δ расчета τст составляет ±10 %.
Распределение скорости при
турбулентном течении в трубе круглого поперечного сечения рассчитывается по
формулам универсального закона [1]:
|
u+ = y+
|
при
y+ < 5;
|
(3.1.3.3)
|
|
u+ = 11,5lgy+ - 3,05
|
при y+ =
5 ÷ 30;
|
(3.1.3.4)
|
|
u+ = 5,75lgy+ + 5,5
|
при
y+
> 30,
|
(3.1.3.5)
|
где u+ = w/v⁎;
у+ = yv⁎/v;  ; у - расстояние от
стенки трубы, м.
; у - расстояние от
стенки трубы, м.
Пределы
применимости формул: Re = 4·103 ÷ 108.
Погрешность
δ расчета w по формулам (3.1.3.3), (3.1.3.4), (3.1.3.5)
составляет ±5 %.
Распределение скорости в
трубе круглого поперечного сечения может также рассчитываться по единой по всем
диапазонам изменения у+ формуле [3]:
где  .
.
Пределы
применимости формулы: Re = 4·103 ÷ 108.
Погрешность
δ расчета w по формуле составляет (+3 %; -5 %).
Отношение средней скорости к
максимальной при турбулентном течении в трубе круглого поперечного сечения
рассчитывается по формулам [1]:
|

|
(3.1.3.7)
|
Пределы применимости формул:
Re = 4·103 ÷ 108.
Погрешность
δ = ±10 %.
Коэффициент турбулентного
переноса количества движения при турбулентном течении в трубе круглого
поперечного сечения рассчитывается по формуле [4]:
где 
wmax -
максимальная скорость потока;
Y = y/rвн
- относительное расстояние от стенки трубы;
rвн - внутренний радиус трубы;
распределение
скорости рассчитывается по ранее приведенным формулам.
Пределы
применимости формулы: Re = 104 ÷ 105.
Погрешность
δ расчета ξν
составляет ±20 %.
Интенсивность пульсаций
скорости при турбулентном течении в трубе круглого поперечного сечения
рассчитывается по формуле [4]:
где i = 1,
2, 3 - индекс, обозначающий направление пульсаций:
i = 1 - вдоль среднего движения;
i = 2 - перпендикулярно стенке;
i = 3 - в тангенциальном направлении;
А1 =
0,95; А2 = 0,40; А3 = 0,60;
B1 =
1,8; В2 = 0,7; В3 = 1,17;
w
рассчитывается по формулам (3.1.3.5),
(3.1.3.6).
Пределы
применимости формулы: Re = 7,5·103 ÷ 2,5·105;
у+ > 10.
Погрешность
δ расчета Gi
составляет ±10 %.
3.1.3.1.2. Стационарное стабилизированное турбулентное течение
в концентрических кольцевых каналах
В
раздел включены соотношения для расчета коэффициентов гидравлического
сопротивления трения, касательных напряжений и полей скорости при турбулентном
течении в гладких кольцевых каналах. Схема кольцевого канала приведена на рис. 3.1.3.1.
Коэффициент гидравлического
сопротивления трения при турбулентном течении в кольцевых каналах
рассчитывается по формуле [5]:
|

|
(3.1.3.11)
|
где θ = R1/R2;
ξо -
коэффициент гидравлического сопротивления трения круглой трубы диаметром,
равным гидравлическому диаметру кольцевого канала, ξо
рассчитывается по формуле (3.1.3.1).
Пределы
применимости формулы: Re = 2,3·103 ÷ 4·106;
θ = 0,06 ÷ 1,00.
Погрешность
δ расчета ξ составляет ±8 %.
Для приближенных расчетов в
диапазоне θ = 0,1 ÷ 0,80 можно использовать формулу [6]:
|
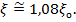
|
(3.1.3.12)
|
Касательное напряжение на
стенках концентрического кольцевого канала при турбулентном течении
рассчитывается [7]:
■ на внутренней стенке
по формуле:
|

|
(3.1.3.13)
|
■ на наружной стенке по формуле:
|

|
(3.1.3.14)
|
где ξ - рассчитывается по формуле (3.1.2.10).
Пределы
применимости формул (3.1.3.13), (3.1.3.14):
Re =
2,3·103 ÷ 4·106; θ = 0,06 ÷
1,00.
Погрешность
δ расчета τ1 и τ2 по
формулам составляет ±10 %.
Распределение
скорости при турбулентном течении в кольцевом канале, при R1/R2
> 0,50 рассчитывается по формулам (3.1.3.3) ÷ (3.1.3.5), (3.1.3.6) для круглой трубы. Линия максимальной
скорости при этом условии считается равноудаленной от стенок кольцевого канала.
Положение линии максимальной
скорости в кольцевых каналах при θ < 0,50 рассчитывается по
формуле [5]:
|

|
(3.1.3.15)
|
где rо -
радиус линии максимальной скорости, м.

Рис. 3.1.3.1 Схема
кольцевого канала
3.1.3.1.3. Стационарное стабилизированное турбулентное течение в
эксцентрических кольцевых каналах
Коэффициенты гидравлического
сопротивления трения при турбулентном течении в эксцентрических кольцевых
каналах рассчитываются по формуле [8]:
где ξo -
рассчитывается по формуле (3.1.2.10);
В = 0,577 - 0,866(1 - θ) + 0,46(1 - θ)2;
f = 1
+ 0,35е(1 - θ)4;
е = a/(R1 - R2);
а -
эксцентриситет, м.
Пределы
применимости формулы: Re = 6·103 ÷ 2,5·105;
θ > (0,1 + 0,5е) > 0,3.
Погрешность
расчета ξ в первоисточнике не указана, но проиллюстрирована на
рисунке сравнением с экспериментальными данными.
Относительное распределение
касательного напряжения на стенках кольцевого канала с эксцентриситетом
рассчитывается по формуле [8]:
|

|
(3.1.3.17)
|
где i = 1 для внутреннего и i = 2 для внешнего периметров
кольцевого зазора;
|

|
(3.1.3.18)
|
|

|
(3.1.3.19)
|
|

|
(3.1.3.20)
|
Пределы применимости
формулы: θ = 0,25 ÷ 1,00.
Погрешность
δ расчета τi
составляет ±15 %.
Средние по периметру
касательные напряжения на стенках кольцевого канала с эксцентриситетом
рассчитываются по формулам [8]:
|

|
(3.1.3.21)
|
|

|
(3.1.3.22)
|
где ξ - рассчитывается по формуле (3.1.3.16),  - средняя скорость среды в
канале.
- средняя скорость среды в
канале.
Пределы
применимости формул: θ = 0,25 ÷ 1,00;  - для внешней стенки
кольцевого канала;
- для внешней стенки
кольцевого канала;
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
Средние по радиусу
кольцевого канала с эксцентриситетом локальные скорости рассчитываются по
формуле [8]:
|

|
(3.1.3.23)
|
где ξ - рассчитывается по формуле (3.1.2.10); ξo - рассчитывается по формуле (3.1.3.16).
Пределы
применимости формулы: Re = 6·103 ÷ 2,5·105;
θ ≥
0,1 + 0,5е ≥ 0,3, где е - значение эксцентриситета, 0 ≤
е ≤ 1.
Погрешность
δ расчета  составляет ±20 %.
составляет ±20 %.
3.1.3.1.4. Стационарное стабилизированное турбулентное течение
в сборках стержней треугольной упаковки
В
раздел включены соотношения для расчета коэффициентов гидравлического
сопротивления трения, касательных напряжений и полей скорости при турбулентном
стабилизированном течении вдоль сборок гладких цилиндрических стержней
треугольной упаковки. Так как гидродинамика жидких металлов и воды одинакова,
то формулы для жидких металлов справедливы и для воды.
Стержни
сборки треугольной упаковки образуют три типа ячеек (рис. 3.1.3.2).
Коэффициент гидравлического
сопротивления трения при турбулентном течении в сборках гладких стержней
треугольной упаковки рассчитывается по формуле [9]:
где ξo =
0,210/Re0,25;  .
.
Определяющий размер при
расчете числа Re - гидравлический диаметр треугольной упаковки стержней,
рассчитывается, как (см. раздел 3.1.2.1.3):
Пределы применимости
формулы: S/dн = 1,0 ÷ 1,5; Re = 6·103
÷ 105.
Погрешность
δ расчета ξ составляет ±6 %.

Рис. 3.1.3.2. Расположение
ячеек внутри сборки гладких стержней
треугольной упаковки:
1 - центральная ячейка; 2 - боковая ячейка; 3 - угловая ячейка
Среднее по периметру стержня
в сборке гладких стержней касательное напряжение рассчитывается по формуле [1, 10]:
|

|
(3.1.3.25)
|
где ξ - рассчитывается по формуле (3.1.3.24).
Пределы
применимости формулы: S/dн = 1,0 ÷ 1,5; Re =
6·103 ÷ 105.
Погрешность
δ расчета τ составляет ±10 %.
Распределение касательных
напряжений по периметру стержня центральной ячейки рассчитывается по формуле [1, 10]:
где φ - угол, отсчитываемый от узкого сечения
центральной ячейки в радианах;
коэффициенты
А1 ÷ А4 приведены в таблице 3.1.3.1.
Пределы
применимости формулы: S/dн = 1,0 ÷ 1,5; Re =
6·103 ÷ 105.
Погрешность
δ расчета τφ составляет ±15 %.
Таблица 3.1.3.1
Значения коэффициентов А1 ÷ А4
в формуле (3.1.3.26)
|
S/dн
|
A1
|
А2
|
А3
|
A4
|
|
1,00
|
-1,0073
|
-0,1059
|
0,0991
|
0,0318
|
|
1,05
|
-0,2522
|
0,0043
|
-0,0410
|
-0,0002
|
|
1,10
|
-0,1277
|
-0,0098
|
0,0028
|
0,0014
|
|
1,20
|
-0,0143
|
0
|
0
|
0
|
|
1,25
|
0
|
0
|
0
|
0
|
Расчет расходов в
элементарных ячейках между стержнями часто производится по методу «изобарных
сечений». Для учета обмена массой и количеством движения между ячейками
стержневой сборки вводят коэффициенты межканального обмена.
Коэффициент
межканального обмена массой представляет собой отношение расхода теплоносителя
через единицу длины зазора между стержнями к продольному расходу теплоносителя.
Коэффициент межканального обмена количеством движения указывает, какую долю от
разности количества движения в двух смежных ячейках составляет поперечный
перенос количества движения, отнесенный к единице длины зазора между ячейками.
Показано, что коэффициент межканального обмена массой равен коэффициенту
межканального обмена количеством движения, если оперировать лишь средними
скоростями потока в ячейках. В дальнейшем не делается различия между этими
двумя коэффициентами перемешивания.
Межканальный обмен
количеством движения осуществляется за счет молекулярного и турбулентного
переноса ( ), а также за счет
направленной конвекции (
), а также за счет
направленной конвекции ( ), поэтому суммарный
коэффициент межканального обмена выглядит следующим образом [6]:
), поэтому суммарный
коэффициент межканального обмена выглядит следующим образом [6]:
|

|
(3.1.3.27)
|
Коэффициент межканального обмена количеством движения за счет
молекулярных и турбулентных процессов для сборок гладких стержней треугольной
упаковки бесконечной длины рассчитывается по формуле [6]:
где  .
.
Отношение между средними
скоростями теплоносителя в боковой и центральной ячейках сборки гладких
стержней треугольной упаковки при турбулентном течении рассчитывается по
формуле [6]:
|

|
(3.1.3.29)
|
где  ;
;  ;
;
dг = 4ω/Р
- гидравлический диаметр ячейки, м;
ω -
площадь проходного сечения ячейки, м2;
Р -
смоченный периметр ячейки, м;
 - коэффициент межканального
обмена количеством движения, рассчитывается по формуле (3.1.3.28).
- коэффициент межканального
обмена количеством движения, рассчитывается по формуле (3.1.3.28).
Скорость в заданной точке
внутри ячейки рассчитывается по соотношениям для круглых труб (формулы 3.1.3.3 ÷ 3.1.3.6) с использованием локальных
масштабов [6]:
|

|
(3.1.3.30)
|
где  ; τφ
рассчитывается по формуле (3.1.3.26),
уi -
координата по нормали к стенке.
; τφ
рассчитывается по формуле (3.1.3.26),
уi -
координата по нормали к стенке.
Отношение средней скорости к
максимальной в ячейке сборки гладких стержней треугольной упаковки при
турбулентном течении рассчитывается по формуле [6, 10]:
|

|
(3.1.3.31)
|
где  ; dн - наружный диаметр стержней.
; dн - наружный диаметр стержней.
Пределы
применимости формулы: Re = 4·103 ÷ 105.
Погрешность
δ расчета  составляет ±10 %.
составляет ±10 %.
3.1.3.1.5. Стационарное стабилизированное турбулентное течение
в сборках стержней квадратной упаковки
Коэффициент гидравлического
сопротивления трения при турбулентном течении в сборках гладких стержней
квадратной упаковки рассчитывается по формуле [10]:
|

|
(3.1.3.32)
|
где β = 10(S/dн - 1); ξо - коэффициент гидравлического
сопротивления трения при турбулентном течении в трубе, внутренний диаметр
которой равен гидравлическому диаметру сборки стержней квадратной упаковки; ξо
рассчитывается по формуле (3.1.3.1).
Определяющий размер при
расчете числа Re по формуле (3.1.3.1)
- гидравлический диаметр сборки стержней квадратной упаковки, который
рассчитывается по формуле (см. раздел 3.1.2.1.3):
Пределы применимости
формулы: 1< S/dн < 2.
Погрешность
δ расчета ξ составляет ±10 %.
3.1.3.1.6. Стационарное стабилизированное турбулентное течение
внутри трубы змеевика
Коэффициент гидравлического
сопротивления трения при турбулентном течении внутри трубы змеевика
рассчитывается по формуле [11]:
где ξо - коэффициент гидравлического
сопротивления трения в прямой трубе того же внутреннего диаметра, что и труба
змеевика;
Kф -
коэффициент формы змеевика;
где dвн - внутренний диаметр трубы змеевика, м;
dзм -
диаметр навивки змеевика, м;
пределы
применимости:  .
.
Погрешность
δ расчета ξ составляет ±10 %.
Коэффициент
гидравлического сопротивления при течении внутри труб змеевиков с большим
радиусом гиба  рассчитывается по
зависимостям для прямых труб.
рассчитывается по
зависимостям для прямых труб.
3.1.3.1.7. Местные гидравлические сопротивления при стационарном
турбулентном течении в каналах
Потери давления на местном
сопротивлении рассчитываются по формуле (3.1.1.6) [6]:
где ΔРм в [Па];
ξм -
коэффициент местного сопротивления;  - средняя скорость потока,
к которой отнесен коэффициент местного сопротивления, м/с. Обычно это скорость
в наименьшем проходном сечении канала.
- средняя скорость потока,
к которой отнесен коэффициент местного сопротивления, м/с. Обычно это скорость
в наименьшем проходном сечении канала.
Местные
гидравлические сопротивления возникают при резком изменении поперечного сечения
канала и направления движения потока теплоносителя и считаются
сосредоточенными.
Коэффициенты
местного гидравлического сопротивления рассчитываются [11]:
■
при внезапном расширении канала по формуле:

где  - отношения площади
проходного сечения канала за расширением к площади канала до расширения;
определяющая скорость - скорость потока до расширения;
- отношения площади
проходного сечения канала за расширением к площади канала до расширения;
определяющая скорость - скорость потока до расширения;
■ при внезапном
сужении канала по формулам:

|

|
при
m > 0,20,
|
(3.1.3.35б)
|
где  - отношение площади за
сужением к площади канала перед сужением, определяющая скорость - скорость
потока за сужением;
- отношение площади за
сужением к площади канала перед сужением, определяющая скорость - скорость
потока за сужением;
■ при выходе
турбулентного потока из канала в большой объем по формуле:
■ при входе турбулентного потока в трубу, заделанную
заподлицо со стенкой по формуле:
■ при входе турбулентного потока в трубу с выступающими
кромками с помощью таблицы:

|
δ/dвн
|
b/dвн
|
ξм
|
|

|
0,20
|
1,00
|
|

|
0,05 ÷
0,20
|
0,85
|
|
>
0,4
|
-
|
0,50
|
■ при входе турбулентного потока в трубу с закругленными
кромками с помощью таблицы:

|
r/dвн
|
ξм
|
Примечания
|
|
0,05
|
0,40
|
при
выступающих кромках
|
|
0,05
|
0,25
|
при
кромках заподлицо
|
|
0,10
|
0,12
|
со
стенкой
|
|
0,20
|
0
|
-
|
■ при входе турбулентного потока в трубу через решетку или
диафрагму по формуле:

|
ξм =
(1,707n - 1)2,
|
(3.1.3.38)
|
где n = f2/f1;
f2 - площадь проходного сечения решетки или диафрагмы;
f1 - площадь сечения трубы;
определяющая
скорость - скорость потока до решетки или диафрагмы;
■ выход турбулентного
потока через решетку или диафрагму по формуле:

|

|
(3.1.3.39)
|
где n = f1/f2;
определяющая
скорость - скорость потока за решеткой или диафрагмой;
■
при течении турбулентного потока через решетку или диафрагму, расположенную
внутри трубы по формуле и схематически:

|

|
(3.1.3.40)
|
где n = f1/f2;
определяющая
скорость - скорость потока до решетки или диафрагмы;
■
при входе турбулентного потока в трубу через боковые отверстия (m - число отверстий) - с помощью таблицы и схематически:

|
f1/f2
|
ξm
|
|
т =
1
|
m = 2
|
|
0,20
|
65,0
|
65,0
|
|
0,30
|
30,0
|
36,5
|
|
0,40
|
14,9
|
17,0
|
|
0,50
|
9,0
|
12,0
|
|
0,60
|
6,3
|
8,7
|
|
0,70
|
4,5
|
6,9
|
|
0,80
|
3,5
|
5,5
|
|
0,90
|
2,7
|
4,5
|
|
1,00
|
2,3
|
3,8
|
|
1,20
|
1,6
|
2,8
|
|
1,40
|
-
|
2,0
|
Определяющая скорость -
скорость в наименьшем проходном сечении;
■ выход турбулентного
потока из трубы через боковые отверстия - с помощью таблицы (m - число отверстий) и схематически:

|
f1/f2
|
ξm
|
|
т =
1
|
т
= 2
|
|
0,20
|
66,0
|
68,0
|
|
0,30
|
30,0
|
33,0
|
|
0,40
|
16,0
|
16,0
|
|
0,50
|
10,0
|
12,0
|
|
0,60
|
7,3
|
8,5
|
|
0,70
|
5,5
|
6,8
|
|
0,80
|
4,5
|
5,9
|
|
0,90
|
3,7
|
5,0
|
|
1,00
|
3,2
|
4,4
|
|
1,20
|
2,4
|
3,5
|
Определяющая скорость -
скорость в наименьшем проходном сечении.
Гидравлический коэффициент
местного сопротивления при течении турбулентного потока через дистанционирующие
решетки и решетки-интенсификаторы теплосъема при равномерном распределении
расхода по ячейкам проходного сечения рассчитывается по формуле [11]:
где  - коэффициент сужения;
- коэффициент сужения;
f - площадь проходного сечения канала, м2;
fp - площадь проходного сечения дистанционирующей решетки, м2;

wp -
скорость потока через отверстие решетки, м/с;
dг -
гидравлический диаметр решетки, м;
Lp -
высота решетки, м;
kш - абсолютная шероховатость материала решетки-интенсификатора, м.
Пределы
применимости формулы: Re = 105 ÷ 106.
Погрешность
δ расчета ξм составляет ±10 %.
Коэффициент местного
гидравлического сопротивления при течении турбулентного потока через
дистанционирующие решетки и решетки-интенсификаторы теплосъема с неравномерным
распределением расхода по ячейкам рассчитывается по формуле [10]:
|

|
(3.1.3.42)
|
где ξ1 - рассчитывается по формуле (3.1.3.41);
dгi -
гидравлический диаметр i-й
ячейки, м;
 - доля проходного сечения i-ой ячейки в общем проходном сечении дистанционирующей решетки;
- доля проходного сечения i-ой ячейки в общем проходном сечении дистанционирующей решетки;
 ;
;  - средняя скорость потока в
канале, м/с;
- средняя скорость потока в
канале, м/с;
dгo -
гидравлический диаметр канала, м.
Пределы
применимости формулы: Re = 105 ÷ 106.
Погрешность
δ расчета ξм составляет ±10 %.
Гидравлическое сопротивление
при турбулентном течении потока в поворотах рассчитывается по формуле [10]:
|

|
(3.1.3.43)
|
где ΔР в [Па];
ξм =
0,73KN;
ξтр -
коэффициент гидравлического сопротивления трения о стенки гиба рассчитывается
по формулам раздела 3.1.3.1;
L -
длина гиба, м;
dвн -
внутренний диаметр гиба, м;
K - коэффициент, зависящий от угла поворота потока в канале,
определяется по чертежу (3.1.3.3);
N -
коэффициент, зависящий от относительного радиуса закругления гиба, r - определяется по рис. (3.1.3.4).
Пределы
применимости формулы: Re = 104 ÷ 106.
Погрешность
δ расчета ΔР составляет ±20 %.

Рис. 3.1.3.3. Зависимость
коэффициента K от угла поворота
Эта кривая со
среднеквадратичной погрешностью 0,5 % описывается формулой:
|
K = - 1 - 0,393074·104 / (δ
- 0,139532·104) - 0,170774·103 / (δ + 0,934155·102)
|
|
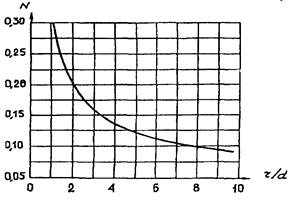
Рис. 3.1.3.4. Зависимость
коэффициента N от относительного
радиуса закругления гиба
Эта кривая со
среднеквадратичной погрешностью 0,9 % описывается формулой:
|
N =
0,05684 + 0,364 / (r/d +
0,4925).
|
|
3.1.3.2. НЕСТАБИЛИЗИРОВАННОЕ ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ НА
ВХОДНЫХ УЧАСТКАХ КАНАЛОВ
3.1.3.2.1. Нестабилизированное турбулентное течение
на входном участке трубы
Длина входного участка при
турбулентном течении в круглых гладких трубах с плавным профилированным входом
рассчитывается по формуле [12, 13]:
где 
Погрешность
в определении Lст при плавном входе в круглую трубу
составляет ±7 калибров трубы.
Схема
развития пограничного слоя при течении жидкости на начальном участке круглых
труб с плавным входом приведена на рис. 3.1.3.5.

Рис. 3.1.3.5. Схема
развитого пограничного слоя при течении жидкости
на начальном участке круглых труб с плавным входом (карта устойчивости)
Длина входного участка при
турбулентном течении в круглых гладких трубах с турбулизирующими входными
устройствами (внезапное сужение, конфузор, диффузор, диафрагмирующие шайбы и
т.д.) рассчитывается по формуле [12,
13]:
Из сравнения формул (3.1.3.44) и (3.1.3.44а) следует,
что гидродинамические возмущения турбулентного потока на входе в круглые трубы
значительно уменьшают длину входного участка.
Пределы
применимости формул (3.1.3.44)
и (3.1.3.44а):
Re = 5·103 ÷ 106.
Погрешность
δ в определении Lст составляет ±3 калибра трубы.
При
турбулентном течении жидкости энергия на перестройку гидродинамических
характеристик потока затрачивается, в основном, на первой половине входного
участка круглой трубы.
Падение давления на длине ΔL
= 0,5Lст при турбулентном течении в трубах с плавным
профилированным входом рассчитывается по формуле [12, 13]:
|

|
(3.1.3.45)
|
где wст - скорость на оси трубы при
стабилизированном турбулентном течении;
величина
 зависит от числа Рейнольдса
и вычисляется по формуле (3.1.3.9).
зависит от числа Рейнольдса
и вычисляется по формуле (3.1.3.9).
Пределы
применимости формулы: Re = 104 ÷ 105.
Погрешность
δ расчета ΔРвх составляет ±20 %.
3.1.3.2.2. Нестабилизированное турбулентное течение
на входном участке стержневых сборок
Длина
входного участка зависит от конструктивного оформления входа в стержневую
сборку.
Максимальная
относительная длина входного участка принимается [14]:
■ при плавном
профилированном входе в сборку:
■ при остроугольном входе, или иначе, входе из большого объема:
■ при наличии трубной решетки на входе в стержневую сборку:
Пределы применимости формул:
S/dн = 1; Re = 1,5·104 ÷ 7,5·104.
Погрешность
δ определения Lст составляет ±5dг.
3.1.3.3. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ В КАНАЛАХ С ШЕРОХОВАТЫМИ
СТЕНКАМИ
3.1.3.3.1. Турбулентное течение в трубах с регулярной
шероховатостью стенки
Падение давления при
турбулентном течении в трубе с регулярно расположенными на стенке элементами
шероховатости (выступы прямоугольного сечения, рис. 3.1.3.6) рассчитывается по формуле [15]:
|

|
(3.1.3.49)
|
где dэ - эффективный внутренний диаметр трубы с
регулярной шероховатостью стенки, который рассчитывается с учетом объема
вихревых зон потока при обтекании элементов шероховатости.
Эффективный
внутренний диаметр рассчитывается:
■ при  по формуле:
по формуле:
|

|
(3.1.3.50)
|
■ при 
|

|
(3.1.3.51)
|
где 
Средняя эффективная скорость потока в трубе с регулярной
шероховатостью стенки рассчитывается по формуле:
|

|
(3.1.3.52)
|
где М - массовый расход жидкости, кг/с; ρ -
средняя на длине ΔL плотность, кг/м3.

Рис.
3.1.3.6. Линейные размеры трубы и элемента регулярной шероховатости:
Do = dвн - внутренний диаметр трубы без выступов,
м;
m - продольный размер выступа, м; k -
высота выступа, м;
S - шаг расположения элементов регулярной шероховатости, м;
dэ - эффективный диаметр трубы с регулярной шероховатостью
стенки, м;
Dпр = dпp - приведенный диаметр
трубы с регулярной шероховатостью стенки, м.
Эффективное число Рейнольдса
при турбулентном течении в трубе с регулярной шероховатостью стенки
рассчитывается по формуле:
|

|
(3.1.3.53)
|
Эффективный коэффициент гидравлического сопротивления трения при
турбулентном течении в трубе с регулярной шероховатостью стенки рассчитывается
по формуле:
где ξв - вихревой коэффициент
гидравлического сопротивления трения;
ΔLв -
длина трубы, занятая вихревыми зонами;
ΔLв =
1,7k - до элемента шероховатости, ΔLв = 5k - после элемента шероховатости, общая ΔLв
= 1,7k + 5k = 6,7k;
ξo - коэффициент гидравлического сопротивления трения при
турбулентном течении в гладкой трубе внутренним диаметром dэ
рассчитывается по формуле (3.1.3.1).
Вихревой коэффициент
гидравлического сопротивления трения рассчитывается по формуле:
где
А = 1,19, когда 0,3 < Х < 1,8;
А = -0,52X +
1,34, когда -2,7 < Х < 0,3;
kэ - эффективная высота шероховатости, kэ = k - (Rвн - Rэ);
 - средний масштаб вихрей
при турбулентном течении в трубе с регулярной шероховатостью стенки;
- средний масштаб вихрей
при турбулентном течении в трубе с регулярной шероховатостью стенки;
где Rпp - приведенный радиус трубы с регулярной шероховатостью стенки:
Пределы применимости формулы (3.1.3.55):
Погрешность δ
расчета ΔР составляет ±25 %.
При
расчете профиля скорости труба внутренним диаметром dвн с
регулярной шероховатостью стенки условно заменяется на трубу с гладкими
стенками с внутренним диаметром dэ.
Профиль скорости при
турбулентном течении в трубе с внутренним диаметром dэ
рассчитывается по формуле:
|

|
(3.1.3.57)
|
где
|
FI(ξэ) = 0,8925 -
0,2325lg(100ξэ)
|
(3.1.3.58)
|
- соотношение между средней
эффективной и максимальной скоростями турбулентного потока в трубе с регулярной
шероховатостью стенки;
ξэ -
рассчитывается по формуле (3.1.3.54);
w = U+V⁎;
уэ = ηэv/v⁎
- для безразмерных расстояний по нормали от стенки трубы диаметром dэ,
которые измеряются в пределах:
|

|
(3.1.3.59)
|
|

|
(3.1.3.60)
|
где ηэ
- безразмерное расстояние от стенки трубы диаметром dэ,
которое рассчитывается по формуле:
 - скорость трения на стенке
трубы диаметром dэ;
- скорость трения на стенке
трубы диаметром dэ;
τo - касательное напряжение
трения на стенке трубы диаметром dэ, которое рассчитывается
по формуле:
уэ -
расстояние от стенки трубы диаметром dэ,
ηоэ -
безразмерный эффективный радиус трубы с регулярной шероховатостью стенки;
|

|
(3.1.3.61)
|
Пределы применимости формулы (3.1.3.61):
Погрешность δ
расчета локальных скоростей w составляет ±10 %.
3.1.3.3.2. Турбулентное течение в кольцевых каналах
с регулярной шероховатостью стенок
Коэффициент гидравлического
сопротивления трения при турбулентном течении в кольцевых каналах с регулярной
шероховатостью (прямоугольные выступы, рис. 3.1.3.7) на поверхности внутреннего стержня
рассчитываются по формуле:
|
ξ =
(0,53 + 1,85k/dэ)Re-0,07,
|
(3.1.3.62)
|
где k - высота прямоугольного
выступа, м;
dэ = d2
- d1 - эквивалентный диаметр зазора кольцевого канала (рис. 3.1.3.7), м;
d1 -
внутренний диаметр зазора кольцевого канала с учетом шероховатости;
dэ -
определяющий размер при расчете числа Рейнольдса.
Пределы
применимости формулы: Re = 5·103 ÷ 5·105;
k/dэ =
0,0028 ÷ 0,021; k/b =
0,3 ÷ 0,8, b - ширина выступа;
S/k =
10; d1/d2 = 0,40.
Погрешность
δ расчета ξ составляет ±4 %.

Рис.3.1.3.7. Линейные
размеры кольцевого канала и элементов
регулярной шероховатости:
а) - прямоугольные выступы; б) - закругленные трапецеидальные выступы
Коэффициенты гидравлического
сопротивления трения при турбулентном течении в кольцевых каналах с регулярной
шероховатостью (закругленные трапецеидальные выступы, рис. 3.1.3.7) на
поверхности внутреннего стержня рассчитываются по формуле:
|
ξ =
(0,063 + 5k/dэ)Re-0,11,
|
(3.1.3.63)
|
где k - высота закругленного
трапецеидального выступа;
dэ = d2
- d1 - эквивалентный диаметр кольцевого канала (рис. 3.1.3.7);
dэ -
определяющий размер при расчете числа Рейнольдса.
Пределы
применимости формулы:
Re = 5·103 ÷ 5·105;
k/dэ = 0,0028 ÷ 0,021;
k/b = 0,3 ÷ 0,8; S/k ~ 10; d1/d2
~ 0,40.
Погрешность
δ расчета ξ составляет ±4 %.
3.1.3.4. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ В ТРУБАХ С ПЕСОЧНОЙ
И ТЕХНИЧЕСКОЙ ШЕРОХОВАТОСТЯМИ
Турбулентное
течение в трубах с песочной и технической шероховатостями приведено в
соответствии с [15].
3.1.3.4.1 Турбулентное течение в трубе с песочной
шероховатостью стенки
Коэффициент гидравлического
сопротивления трения при турбулентном течении в трубе с песочной шероховатостью
стенки (рис. 3.1.3.8)
рассчитывается по формуле:
где ks - абсолютный размер песочной
шероховатости, м;
Rпр -
приведенный внутренний радиус трубы с песочной шероховатостью стенки (рис. 3.1.3.8);
Rпр -
определяющий размер при расчете числа Рейнольдса;

Предел применимости формулы:
Re > 6000.
Погрешность
δ расчета ξ составляет ±7 %.

Рис. 3.1.3.8. Схема песочной
и технической шероховатости стенки трубы
3.1.3.4.2. Турбулентное течение в трубе с технической
шероховатостью стенки
Песочная
шероховатость стенок в теплотехнических и гидротехнических устройствах
реализуется редко. На практике имеют место случаи нерегулярной шероховатости
стенок, которая является следствием либо технологической обработки материала,
либо появляется в процессе эксплуатации в результате осаждения на стенках
твердых примесей потока, в результате коррозии, эрозии материалов. Такую
шероховатость называют технической. Размеры технической шероховатости
определить достаточно сложно.
В
связи с этим вводится величина шероховатости, эквивалентной песочной
шероховатости технического канала. Эквивалентная шероховатость устанавливается
в опытах из равенства гидравлических сопротивлений технического канала и канала
с песочной шероховатостью.
Коэффициент гидравлического
сопротивления трения при турбулентном течении в трубе с технической
шероховатостью стенки (рис. 3.1.3.8)
рассчитывается по формуле
|

|
(3.1.3.65)
|
где ks/Rпр
- техническая шероховатость эквивалентная песочной;
эквивалентная
песочная техническая шероховатость, определяется по таблицам 2 и 3 справочника
[2];
Rпр -
приведенный внутренний диаметр трубы с технической шероховатостью стенки;
Rпр -
определяющий размер при расчете числа Рейнольдса.
Пределы
применимости формулы: Re > 6000.
Погрешность
δ расчета ξ из-за неопределенностей в классификации
характера поверхности составляет ±25 %.
Профиль
скорости при турбулентном течении в трубе с песочной и технической
шероховатостями рассчитывается по формулам (3.1.3.56) ÷ (3.1.3.58), в которых ξэ
рассчитывается по формуле (3.1.3.64).
При
расчетах принимается Rэ = Rпp, что для
случаев песочной и технической шероховатостей стенок трубы не вносит заметной
погрешности в результаты расчета скорости.
3.1.3.5. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ТУРБУЛЕНТНЫМ ПОТОКОМ
ЦИЛИНДРИЧЕСКИХ ТЕЛ И ПУЧКОВ ТРУБ
3.1.3.5.1 Поперечное обтекание турбулентным потоком цилиндрических
тел
Полное
гидравлическое сопротивление при поперечном обтекании изотермическим
турбулентным потоком цилиндрических тел равно равнодействующей сил трения и
давления, приложенных к поверхности тел.
Безразмерный коэффициент
полного гидравлического сопротивления рассчитывается по формуле [16]:
|

|
(3.1.3.66)
|
|
или
ξ = ξтр + ξд,
|
(3.1.3.67)
|
где ΔРд - потери давления, обусловленные
неполным восстановлением давления;
wнп -
скорость набегающего потока, м/с;
dн -
наружный диаметр трубы, цилиндра, м.
При
малых значениях Re основную часть полного сопротивления составляет
сопротивление трения, которое с увеличением Re уменьшается так, что  .
.
Коэффициент гидравлического
сопротивления трения при поперечном обтекании потоком круглого цилиндра при Re
< 30 рассчитывается по формуле [17]:
|

|
(3.1.3.68)
|
а в
диапазоне Re = 30 ÷ 104 - по формуле [17]:
Коэффициент полного
гидравлического сопротивления при поперечном обтекании турбулентным потоком (Re
= 104 ÷ 2·105) [18]:
■ круглого цилиндра
■ эллиптического цилиндра вдоль большой оси
■ эллиптического цилиндра вдоль малой оси
При Re > 103
основной вклад в коэффициент полного гидравлического сопротивления вносит
коэффициент сопротивления давления, на который влияют степень турбулентности
потока Тu, загромождение канала kзгр и шероховатость обтекаемых тел.
Коэффициент
сопротивления давления при обтекании потоком одиночного цилиндра рассчитывается
[16]:
■ при Ret = 40
÷ 103 по формуле [16, 18]:
где Ret = ReTu
- турбулентное число Рейнольдса;
 - степень турбулентности,
доли единицы при расчетах;
- степень турбулентности,
доли единицы при расчетах;
 - интенсивность пульсаций
скорости рассчитывается, например, по формуле (3.1.3.10);
- интенсивность пульсаций
скорости рассчитывается, например, по формуле (3.1.3.10);
■ при Ret = 103
÷ 104, Тu =
(0,3 ÷ 10) % рассчитывается по формуле [18]:
|
ξд =
45,3Re-0,5;
|
(3.1.3.74)
|
■ при Ret =
4·103 ÷ 105, Тu =
(0,3 ÷ 12) %, kзгр =
0,25 по формуле [18]:
|

|
(3.1.3.75)
|
■ при Ret =
104 ÷ 2·105, kзгр = 0
÷ 0,90 рассчитывается по формуле [19]:
|

|
(3.1.3.76)
|
где ξдо
- коэффициент сопротивления давления при поперечном обтекании цилиндра
безграничным потоком, при Ret =
105 ÷ 106, kзгр =
0,3 ÷ 0,7 рассчитывается по формуле [16]:
|

|
(3.1.3.77)
|
Значения констант формулы
(3.1.3.77) приведены в таблице 3.1.3.2.
Погрешность
δ расчета ξ, ξтр, ξд
составляет ±10 %.
Таблица 3.1.3.2
Значения констант в формуле (3.1.3.77) для расчета коэффициента
сопротивления давления при поперечном обтекании турбулентным
потоком одиночного цилиндра
|
kзгр
|
Ао
|
А1
|
В1
|
С1
|
А2
|
В2
|
С2
|
|
0
|
0,10
|
1,11
|
1,80
|
3,95
|
0,25
|
0,80
|
6,00
|
|
0,30
|
0,22
|
1,58
|
2,50
|
2,06
|
0,30
|
1,10
|
4,50
|
|
0,50
|
0,88
|
1,62
|
5,80
|
1,78
|
1,50
|
1,20
|
4,30
|
|
0,70
|
2,25
|
4,80
|
6,00
|
1,58
|
1,90
|
1,22
|
4,20
|
Шероховатость поверхности
влияет на коэффициент сопротивления давления при поперечном обтекании потоком
цилиндрических тел в случае, если ее высота превышает безразмерную критическую
величину, которая рассчитывается по формуле ukкр/v и
равна 15-ти для ламинарного пограничного слоя и 70-ти для турбулентного
пограничного слоя.
3.1.3.5.2. Поперечное обтекание турбулентным потоком пучков труб
Схема
расположения труб и обозначение геометрических параметров для коридорных и
шахматных пучков приведены на рис. 3.1.3.9.

Рис. 3.1.3.9. Схема
расположения труб в шахматном и коридорном пучках:
S1 - поперечный шаг пучка; S2 - продольный
шаг пучка
Гидравлическое сопротивление
многорядных (для рядов с номера 4 и далее) коридорных и шахматных пучков
гладких, наклонных и шероховатых труб при поперечном обтекании их турбулентным
потоком рассчитывается по формуле [16]:
|

|
(3.1.3.78)
|
где ξ1 = (ξ/χ)χ -
коэффициент гидравлического сопротивления одного глубинного ряда коридорных и
шахматных пучков труб при поперечном обтекании;
ξ/χ - для коридорных пучков труб определяется по рис. 3.1.3.10 в зависимости от
продольного относительного шага b и числа Рейнольдса, b = s2/dн;
ξ/χ - для шахматных пучков труб определяется по рис. 3.1.3.10 в зависимости от
поперечного относительного шага а и числа Рейнольдса, а = s1/dн;
χ -
для коридорных и шахматных пучков труб определяется по вспомогательным графикам
на рис. 3.1.3.10 (а) и (б);
w -
средняя скорость в минимальном проходном сечении пучка, используется для
расчета числа Рейнольдса;
z -
количество рядов в пучке труб;
cz -
коэффициент, учитывающий зависимость гидравлического сопротивления от
количества рядов пучка. Значения cz для малорядных коридорных
и шахматных пучков труб определяются на рис. 3.1.3.11. Принимается, что cz =
1 при z ≥ 3;
cβ -
коэффициент, учитывающий уменьшение гидравлического сопротивления пучка
вследствие уменьшения угла атаки. Значения cβ
определяются на рис. 3.1.3.12;
ск -
коэффициент, учитывающий увеличение гидравлического сопротивления из-за
шероховатости труб пучка. Значения ск для шахматных пучков
труб определяется на рис. 3.1.3.13.
При
расчете гидравлического сопротивления за определяющую температуру потока
принимается средняя на глубине пучка температура, за определяющую скорость -
средняя скорость в наименьшем проходном сечении пучка, за определяющий размер -
наружный диаметр трубы пучка, т.е. 
Пределы
применимости формулы (1.3.97) определяются рис. 3.1.3.10 ÷ 3.1.3.13.
Погрешность
δ расчета ΔР составляет ±20 %.
Коэффициент
гидравлического сопротивления одного ряда при поперечном обтекании турбулентным
потоком шахматных пучков шероховатых труб рассчитывается [16]:
■ при Re = 103
÷ 2·105, а = S1/dн = 1,25 ÷ 2,00, b = S2/dн ≥ 0,395, k/dн = 6·10-3 ÷ 40·10-3 по формуле:
|
ξ1ш = 14,4(а - 1)-0,40Re-0,30(k/dн)0,15,
|
(3.1.3.79)
|
где 
■
при Re = 2·105 ÷ 107, а = 1,25
÷ 2,00, b =
1,25 ÷ 2,00,
k/dн = 10-3 ÷
8·103 по формуле:
|
ξ1ш = 0,450(а - 1)-0,45(k/dн)0,07,
|
(3.1.3.80)
|
где k - высота элементов
шероховатости, м;
dн -
наружный диаметр трубы пучка, несущей шероховатость, м.

Рис. 3.1.3.10. Нормограммы
для определения коэффициентов гидравлического
сопротивления коридорных и шахматных пучков труб при поперечном обтекании
их турбулентным потоком: а) - коридорные пучки труб, б) - шахматные пучки труб

Рис. 3.1.3.11. Поправочные
коэффициенты для расчета гидравлического сопротивления
малорядных коридорных и шахматных пучков труб при поперечном обтекании их
турбулентным потоком: а) коридорные пучки труб, б) шахматные пучки труб

Рис. 3.1.3.12. Поправочный
коэффициент ср для расчета гидравлического
сопротивления шахматных и коридорных пучков труб при поперечном
обтекании их турбулентным потоком:
1 - шахматные пучки труб, 2 - коридорные пучки труб

Рис. 3.1.3.13. Поправочный
коэффициент ск для расчета гидравлического сопротивления
шахматных пучков труб при поперечном обтекании их турбулентным потоком: k/dн -
относительная высота элементов шероховатости
При
расчете ξ1ш за определяющую температуру принимается
средняя температура жидкости, за определяющую скорость - средняя скорость в
наименьшем проходном сечении пучка, за определяющий размер - наружный диаметр
трубы пучка, т.е.  .
.
Погрешность
δ расчета ξ1ш составляет ±10 %.
Коэффициент
гидравлического сопротивления одного глубинного ряда шахматных пучков
оребренных труб (спиральное оребрение) при поперечном обтекании их турбулентным
потоком рассчитывается [20, 21]:
■ при Re = 102
÷ 103, ε = 1,5 ÷ 6,0; а = 1,13
÷ 2,00; b = 1,06 ÷ 2,00 по формуле:
|
ξ1ор =
135,2ε0,50Re-0,70a-0,55b0,50,
|
(3.1.3.81)
|
где ε - коэффициент оребрения - отношение полной
внешней поверхности оребренной трубы к наружной поверхности трубы без
оребрения;
■ при Re = 103
÷ 105, ε = 1,9 ÷ 6,0, а = 1,60
÷ 4,13, b = 1,20 ÷ 2,35 по формуле:
|
ξ1ор =
6,4ε0,50Re-0,25a-0,55b-0,50,
|
(3.1.3.82)
|
■ при Re = 105 ÷ 1,4·106,
ε = 1,9 ÷ 16,0, а = 1,60 ÷ 4,13, b = 1,20 ÷ 2,35 по формуле:
|
ξ1ор =
0,36ε0,50a-0,55b-0,50.
|
(3.1.3.83)
|
Погрешность δ
расчета ξ1ор составляет ±10 %.
Коэффициент гидравлического
сопротивления одного глубинного ряда коридорных пучков оребренных труб
(спиральное и круглое оребрение) при поперечном обтекании их турбулентным
потоком рассчитывается по формуле [20,
21]:
|
ξ1ор =
0,13ε0,50η-0,40,
|
(3.1.3.84)
|
где η = (а -
1)(b - 1).
Пределы
применимости формулы: Re = 103 ÷ 105; ε
= 1,9 ÷ 16,3;
а =
2,38 ÷ 3,13; b = 1,20 ÷ 2,35.
Погрешность
δ расчета ξ1ор составляет ±10 %.
3.1.3.6. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ В КАНАЛАХ
С ИНТЕНСИФИКАТОРАМИ ТЕПЛОСЪЕМА
3.1.3.6.1. Турбулентное течение в трубах с интенсификаторами
Теплосъема
Коэффициент
гидравлического сопротивления при турбулентном течении однофазной среды в
одиночных трубах с поперечными кольцевыми гофрами (рис. 3.1.3.14) рассчитывается [22]:
■ при dвн/Dвн
= 0,90 ÷ 0,97; t/Dвн = 0,5 ÷ 10 по формуле:
■ при dвн/Dвн = 0,88
÷ 0,98; t/Dвн = 0,50 по формуле:
■ при dвн/Dвн = 0,90
÷ 0,98; t/Dвн = 0,25 по формуле:
где  - при расчетах по формуле
(3.1.3.87);
- при расчетах по формуле
(3.1.3.87);
n = 1/3 - при нагревании жидкостей;
ξгл =
0,185Re-0,20 - коэффициент гидравлического сопротивления в гладкой трубе при
расчетах по формулам (3.1.3.86),
(3.1.3.87).
Пределы применимости формул
(3.1.3.85) - (3.1.3.87):

где ν рассчитывается по среднемассовой температуре
потока;
w -
скорость потока в гладкой трубе, м/с.
Погрешность
δ расчета ξ составляет ±12 %.

Рис. 3.1.3.14. Труба с
поперечными кольцевыми гофрами-интенсификаторами
теплосъема:
Dвн - внутренний диаметр гладкой трубы; dвн
- внутренний диаметр трубы с
кольцевыми гофрами; dн - наружный диаметр трубы с кольцевыми
гофрами;
h - высота кольцевой гофры; t - шаг расположения кольцевых гофр
Коэффициент гидравлического
сопротивления трения при стабилизированном течении газов внутри одиночной витой
трубы (рис. 3.1.3.15)
рассчитывается по формуле [22]:
|

|
(3.1.3.88)
|
где dг - гидравлический диаметр витой трубы, м; D
- диаметр кривизны канала, м.
Пределы применимости
формулы:


Погрешность δ
расчета ξ составляет ±15 %.

Рис.
3.1.3.15. Схема пучка из витых труб:
S - шаг закрутки витой трубы; dов - максимальный
размер овала,
Δ - толщина витой трубы, dн -
наружный диаметр исходной гладкой трубы
Коэффициент гидравлического
сопротивления трения при турбулентном течении внутри одиночной
спирально-навитой трубы (рис. 3.1.1.1)
рассчитывается по формуле [11]:
где dсн = dцп
- dвн, м,
dцп -
диаметр цилиндрической поверхности, описанной около спирально навитой трубы, м;
dвн - внутренний диаметр исходной трубы, м.
Пределы применимости
формулы: Reкp < Re ≤ 8·104; S/dсн
= 12 ÷ 40;

Погрешность δ
расчета ξ составляет ±15 %.
Коэффициент гидравлического
сопротивления трения при турбулентном течении внутри одиночной
локально-спирально-навитой трубы (рис. 3.1.1.1) рассчитывается по формуле [11]:
|
ξ = ξo[1
- 0,035(L/S)1,42],
|
(3.1.3.90)
|
где ξo -
рассчитывается по формуле (3.1.3.89).
Пределы
применимости формулы те же, что и формулы (3.1.3.89), а также L/S = 2 ÷ 5.
Погрешность
δ расчета ξ составляет ±15 %.
Коэффициент гидравлического
сопротивления при турбулентном течении внутри трубы с трехзаходным внутренним
спиральным оребрением рассчитывается по формуле [11]:
|

|
(3.1.3.91)
|
где ξo -
коэффициент гидравлического сопротивления трения исходной гладкой трубы;


w -
скорость потока в исходной гладкой трубе;
dвн -
внутренний диаметр исходной трубы;
h -
высота оребрения, м;
S -
шаг оребрения, м;
Пределы применимости
формулы:

Погрешность δ расчета
ξ составляет ±15 %.
3.1.3.6.2. Турбулентное течение в кольцевых каналах
с интенсификаторами теплосъема
Коэффициент
гидравлического сопротивления трения при турбулентном течении в кольцевых
каналах с внутренней спирально-навитой трубой (рис. 3.1.3.16) рассчитывается [11]:
■ при S/dцп
= 3 ÷ 5 по формуле:
■ при S/dцп > 5 по формуле:
где 
dн -
наружный диаметр исходной гладкой трубы, м.
Пределы
применимости формулы: Re = Reкр ÷ 5·104;
Reкр = 2000(S/dсн)-0,30; dсн = dцп - dн; θ = 0,5 ÷ 0,95.
Погрешность
δ расчета ξ составляет ±15 %.
Коэффициент гидравлического
сопротивления трения при турбулентном течении в кольцевых каналах с внутренней
локально спирально-навитой трубой (рис. 3.1.3.16) рассчитывается по формуле [11]:
|
ξ = ξo[1
- 0,065(L/S)1,2],
|
(3.1.3.94)
|
где ξo -
рассчитывается по формулам (3.1.3.92),
(3.1.3.93).
Пределы
применимости формулы: S/dцп = 1,2 ÷ 1,6; L/S =2
÷ 5.
Погрешность
δ расчета ξ составляет ±15 %.
3.1.3.6.3. Турбулентное течение в пучках труб
с интенсификаторами теплосъема
Коэффициент
гидравлического сопротивления при турбулентном продольном течении среды в
межтрубном пространстве шахматных пучков труб с поперечными кольцевыми гофрами
(рис. 3.1.3.14)
рассчитывается [11]:

Рис. 3.1.3.16. Кольцевой
канал с внутренней спирально-навитой трубой:
а - кольцевой канал с внутренней спирально-навитой трубой;
б - кольцевой канал с внутренней локально-спирально-навитой трубой
■ при Re <
3,1·103 по формуле:
■ при Re = 3,1·103 ÷ 2·104
по формуле:
|

|
(3.1.3.96)
|
■ при Re = 2·104 ÷ 105
по формуле:
|

|
(3.1.3.97)
|
где

 - коэффициент
гидравлического сопротивления трения в гладкой трубе исходного диаметра.
- коэффициент
гидравлического сопротивления трения в гладкой трубе исходного диаметра.
Пределы
применимости формул: S/Dн = 1,02 ÷ 10.
Погрешность
δ расчета ξ составляет ±15 %.
Коэффициент
гидравлического сопротивления при продольном стабилизированном течении
однофазной среды в межтрубном пространстве теплообменников из витых труб (рис. 3.1.3.15) рассчитывается [11]:
■ при Frм
> 100 по формуле:
|
ξ =
0,3164Re-0,25(1 + 3,6Frм-0,357);
|
(3.1.3.98)
|
■ при Frм < 100 по формуле:
|
ξ =
0,3164Re-0,25(1 + 3,1·106Frм-3,38),
|
(3.1.3.99)
|
где Frм -
модифицированное число Фруда, характеризующее соотношение между инерционными и
центробежными силами,  - для пучка витых труб;
- для пучка витых труб;
Re -
рассчитывается по среднемассовой температуре потока в рассматриваемом сечении;
S -
шаг закрутки витых труб, м.
Пределы
применимости формул: Re = 3·103 ÷ 5·104; S/dов=
6 ÷ 12;
tст/tж
= 11,42; dов/Δ =
1,7.
Погрешность
δ расчета ξ составляет ±15 %.
3.1.3.6.4. Поперечное обтекание турбулентным потоком
пучков труб с интенсификаторами теплосъема
Гидравлическое
сопротивление пучков поперечно омываемых витых труб (рис. 3.1.3.15) рассчитывается [11]:
■ при Re = 103
÷ 4,7·103; S/dов = 12,2 по формуле:
|

|
(3.1.3.100)
|
■ при Re = 4,7·103 ÷ 3·104;
S/dов = 12,2 по формуле:
|
Eu = 8,0Re-0,17;
|
(3.1.3.101)
|
■ при Re = 103 ÷ 3,7·103;
S/dов = 6,1 по формуле:
■ при Re = 3,7·103 ÷ 3·104;
S/dов = 6,1 по формуле:
|
Eu = 5,78Re-0,13;
|
(3.1.3.103)
|
где Z
- число рядов в пучке витых труб;

ψ -
пористость пучка витых труб по теплоносителю (отношение объёма пространства
между трубами к полному объёму);
Vтр -
объем витой трубы, м3;
F -
поверхность витой трубы, м2;
L' -
половина периметра витой трубы;
S -
шаг закрутки витой трубы;
 - определяющая скорость,
м/с;
- определяющая скорость,
м/с;
wo - скорость набегающего потока, м/с.
Пределы
применимости формул, кроме указанных выше:
tст/tж =
1,1 ÷ 1,5.
Погрешность
δ расчета ΔР составляет ±25 %.
Коэффициент гидравлического
сопротивления при поперечном обтекании шахматных пучков плоско-овальных
спирально-оребренных труб (рис. 3.1.3.17)
рассчитывается по формуле [22]:
|
ξ =
20,8Re-0,42(δ1/δ2)-0,65Z,
|
(3.1.3.104)
|
где 
Z -
число рядов в пучке;
f - площадь сжатого сечения (задаётся), м2;
L -
глубина пучка (задаётся), м;
Fп -
площадь теплоотдающей поверхности пучка, м2;
w -
скорость в сжатом сечении пучка, м/с;

S1 - поперечный шаг пучка, м (рис. 3.1.3.11);

S2 -
продольный шаг пучка, м, (рис. 3.1.3.11);
d1, d2 - параметры плоско-овальной трубы (рис. 3.1.3.17).
Пределы
применимости формулы: Re = 4·102 ÷ 4·103; δ1/δ2
= 1,5 ÷ 2,5;
Sp =
2,0 мм; hр = 2,9 мм; d1d2 = 5,5×13,5 мм.
Погрешность
δ расчета ξ
составляет ±10 %.

Рис. 3.1.3.17.
Геометрические характеристики плоско-овальных
спирально-оребренных труб
Список литературы к разделу 3.1.3
1. Субботин В.И., Ибрагимов М.Х., Ушаков П.А., Бобков В.П., Жуков
А.В., Юрьев Ю.С. Гидродинамика и теплообмен в атомных энергетических
установках. М.: Атомиздат, 1975.
2. Идельчик И.Е. Справочник по гидравлическим сопротивлениям. Изд.
2. М.: Машиностроение, 1975, 559 с.
3. Ушаков П.А., Левченко Ю.Д. Новая формула турбулентного профиля
скорости для потока жидкости в круглых трубах. - Препринт ФЭИ-561, Обнинск,
1975.
4. Бобков В.П., Ибрагимов М.Х., Сабелев Г.И. Обобщение
экспериментальных данных по интенсивности пульсаций скорости при турбулентном
течении жидкости в каналах различной формы. - Известия АН СССР, МЖГ, 1968, № 2,
с. 20 - 25.
5. Ушаков П.А., Субботин В.И. Приближенные расчеты гидравлических
характеристик потока жидкости в кольцевых каналах. - Теплофизика высоких
температур, 1972, т. 10, № 5, с. 1025 - 1030.
6. Кириллов П.Л, Юрьев Ю.С., Бобков В.П. Справочник по
теплогидравлическим расчетам (ядерные реакторы, теплообменники,
парогенераторы). М.: Энергоатомиздат, 1984, 1990.
7. Brighton J.A. Jones J.B. Fully
Developed Turbulent Flow in Annuli. - Trans. ASME, ser. D., 1964, v. 86, n. 4, p. 842 - 847.
8. Ушаков П.А. Влияние эксцентриситета на гидродинамические
характеристики кольцевых каналов. - Теплофизика высоких температур, 1976, т.
14, № 1, с. 106 - 111.
9. Жуков А.В., Сорокин А.П., Титов П.А., Ушаков П.А. Гидравлическое
сопротивление ТВС быстрых реакторов. Препринт ФЭИ-1707, Обнинск, 1985.
10. Ушаков П.А. Расчет гидродинамических характеристик при
продольном обтекании жидкостью правильных решеток стержневых твэлов.
Теплофизика высоких температур, 1974, т. 12, № 1, с. 103 - 110.
11. Тепловой и гидравлический расчет теплообменного оборудования
АЭС. РД.24.035.05-89. Л.: НПО ЦКТИ, 1991.
12. Трубаков Ю.П., Габрианович Б.Н., Левченко Ю.Д. Исследование
турбулентного потока жидкости на входном участке круглой трубы. - Известия АН
БССР, сер. Физико-энергетических наук, 1976, № 2.
13. Трубаков Ю.П. Экспериментальное исследование турбулентного
потока на входных участках круглых труб. Кандидатская диссертация, ФЭИ, 1978.
14. Бибиков Л.Н., Левченко Ю.Д., Субботин В.И., Ушаков П.А. Профили
скорости жидкости на входном участке плотно упакованного пучка стержней.
Атомная энергия, 1973, т. 35, вып. 1, с. 19
- 24.
15. Webb R.L., Eckert E.R.G., Goldstein
R.J. Heat Transfer and Friction in Tubes with Repeated - Rib Roughness. - Int.
J.Heat and Mass Transfer, 1971, v. 14, N. 4, p. 601 - 618.
16. Жукаускас А.А. Конвективный перенос в теплообменниках. М.:
Наука, 1982.
17. Жукаускас А.А., Жюгжда И. Теплоотдача цилиндра в поперечном
потоке жидкости. Вильнюс: Мокслас, 1979.
18. Дыбан Е.П., Эпик Э.Я., Козлова Л.Г. Совместное влияние степени,
продольного масштаба турбулентности и ускоренности воздушного потока на
теплообмен круглого цилиндра. Теплообмен-1974. Советские исследования. М.:
Наука, 1975, с. 21 - 25.
19. Акылбаев Ж.С., Исатаев С.И., Тарасов С.Б. Структура течения в
следе за цилиндром в канале. В сб.: Вопросы общей и прикладной физики.
Алма-Ата. 1969.
20. Юдин В.Ф. Теплообмен поперечно-оребренных труб. Л.: Машиностроение,
1982.
21. Жукаускас А.А., Макарявичус В.В., Шланчаускас А. Теплоотдача
пучков труб в поперечном потоке жидкости. Вильнюс: Минтис, 1968.
22. Локшин В.А., Фомина В.Н. Обобщение материалов по
экспериментальному исследованию сопротивления ребристых пучков труб. -
Теплоэнергетика, 1978, № 6.
23. Дрейцер Г.А. Компактные теплообменные аппараты. М.: МАИ, 1986.
3.1.4.
ДВУХФАЗНЫЕ ТЕЧЕНИЯ
Под
двухфазными течениями понимается совместное течение жидкости и пара (газа).
Формы движения двухфазных потоков значительно многообразнее и их законы
существенно сложнее, чем для однофазных сред. Во-первых, это связано с наличием
второй фазы, а во-вторых, с тем, что силовые и тепловые взаимодействия
возникают не только на границах потока с твердой стенкой, но также и на
поверхности раздела фаз внутри потока. В-третьих, сжимаемость пара или газа
значительно больше, чем сжимаемость жидкости. Двухфазный поток характеризуется
большим количеством параметров, чем однофазный поток.
Двухфазные
потоки являются гомогенными, если фазы распределены равномерно по объему. В
противном случае поток является гетерогенным.
Двухфазные
потоки являются адиабатными, если отсутствует теплообмен между потоком,
поверхностью канала и между фазами. Если фазы имеют одинаковую температуру,
поток является термодинамически равновесным. Режим кипения жидкости, недогретой
до температуры насыщения, и режим закризисного теплообмена являются примерами
термодинамически неравновесных потоков.
В
условиях работы каналов активной зоны реактора и парогенераторов при значениях
относительной энтальпии, близких к нулю или единице, двухфазный поток при
подводе тепла может быть термодинамически неравновесным. Пар может
присутствовать в жидкости, которая в среднем не догрета до температуры насыщения.
В закризисной зоне пар может быть перегрет, несмотря на присутствие влаги. Эти
обстоятельства усложняют точные расчеты таких режимов.
3.1.4.1. РЕЖИМЫ ТЕЧЕНИЯ ДВУХФАЗНОГО ПОТОКА В КАНАЛАХ
В
парогенерирующих установках поток теплоносителя претерпевает изменения в
процессе превращения его из жидкого состояния в пар. В вертикально
расположенном канале наблюдаемые режимы течения можно условно разделить на пять
зон, каждая из которых достаточно четко отличается от других, как по внешним
признакам, так и по физическим законам описания течения в этих зонах.
Первая
зона - зона течения недогретой до температуры насыщения воды, в которой течение
описывается зависимостями для однофазного потока.
Вторая
зона - зона перехода от начала поверхностного кипения до начала дисперсно-кольцевого
режима течения. В этой области на гидродинамику потока существенное влияние
оказывает количество паровой фазы. Зона охватывает пузырьковый, снарядный,
эмульсионный (пенный, полукольцевой) режимы течения двухфазного потока.
Третья
зона - зона дисперсно-кольцевого режима течения, в которой закон сопротивления,
кроме того, определяется взаимодействием парового ядра потока с пристенной
пленкой жидкости.
Четвертая
зона - зона дисперсного режима течения до массового паросодержания X ≥
1. В этой зоне поток пара испытывает влияние мелкодисперсных капель воды.
Пятая
зона - зона течения перегретого пара, в которой поток можно считать однофазным.
Граница
начала интенсивного роста истинного паросодержания в трубах рассчитывается по
формуле [1].
Относительная энтальпия, при
которой начинается интенсивный рост истинного паросодержания в трубах
рассчитывается по формуле [1]:
|

|
(3.1.4.1)
|
где 
q -
тепловой поток, Вт/м2;
ρw -
массовая скорость, кг/м2·с;
r - теплота парообразования, Дж/кг;
d -
диаметр трубы, м;
μ' -
вязкость воды, Па с.
Формула
проверена в диапазоне параметров: Р = 3 ÷ 15 МПа;
q =
0,4 ÷ 2,5 МВт/м2; ρw = 400 ÷ 3000 кг/м2·с;
d = 12 мм.
Погрешность
расчета Xφ составляет ±20 %.
Граница начала
дисперсно-кольцевого режима течения двухфазного потока в трубах рассчитывается
по формуле [2, 3]:
|

|
(3.1.4.2)
|
где
|
a10 = 0,200 - 10,88dвн - 3,5·10-5ρw;
|
|
при dвн ≥ 17·10-3 м а10 = 0;
Р -
давление, МПа;
q -
плотность теплового потока, МВт/м2;
ρw -
массовая скорость, кг/(м2·с).
Пределы
применимости формулы (1.4.2):
Р =
6,9 ÷ 14 МПа; ρw = 500 ÷ 1000 кг/(м2·с).
Погрешность
δ расчета Хндк составляет ±10 %.
Граница начала дисперсного
режима течения в трубах рассчитывается по формуле [2, 3]:
|

|
(3.1.4.6)
|
где а1 рассчитывается по формуле (3.1.4.3);
а2
рассчитывается по формуле (3.1.4.4);
а9
рассчитывается по формуле (3.1.4.5).
Пределы
применимости формулы: q = 0; P =
6,9 ÷ 14 МПа;
ρw =
500 ÷ 1000 кг/(м2·с).
Погрешность
δ расчета Хнд составляет ±10 %.
3.1.4.2. ИСТИННОЕ ОБЪЕМНОЕ ПАРОСОДЕРЖАНИЕ
ПРИ ТЕЧЕНИИ ДВУХФАЗНЫХ ПОТОКОВ
3.1.4.2.1.
Истинное объемное паросодержание при течении двухфазного
потока в трубе
Истинное объемное
паросодержание при течении двухфазного потока в трубе рассчитывается по формуле
[4]:
|

|
(3.1.4.7)
|
где s - коэффициент скольжения фаз;
s = w''/w'.
Коэффициент скольжения фаз
при течении двухфазного потока в необогреваемой трубе рассчитывается по формуле
[4]:
где Fr
- критерий Фруда, Fr = (ρw)2/g(ρ')2D;
ρw -
массовая скорость, кг/м2 с;
μ' -
коэффициент динамической вязкости на линии насыщения;
ρ' -
плотность воды на линии насыщения;
ρ" -
плотность сухого насыщенного пара.
Пределы
применимости формулы: Р = 1 ÷ 22 МПа;
(ρw)
= 400 ÷ 3340 кг/м2·с.
Погрешность
δ расчета s составляет ±10 %.
В размерном виде формула (3.1.4.8) записывается в виде:
|

|
(3.1.4.9)
|
где dвн в [м]; ρw в [кг/м2·с];
ρ' в [кг/м3].
Для вертикально
расположенных труб при  не замечено влияния
массовой скорости и геометрических размеров на величину коэффициента скольжения
фаз, поэтому s рассчитывается по формуле [4]:
не замечено влияния
массовой скорости и геометрических размеров на величину коэффициента скольжения
фаз, поэтому s рассчитывается по формуле [4]:
|

|
(3.1.4.10)
|
Пределы применимости
формулы:  ;
;
ρw =
400 ÷ 3340 кг/м2·с; Р = 1 ÷ 22 МПа.
Погрешность
δ расчета s составляет ±10 %.
Коэффициент скольжения фаз
при течении двухфазного потока в наклонных необогреваемых трубах рассчитывается
по формуле [4]:
|
s = sokα
= so[1 + (1 - 5·10-6Re)(1 - α/90°)],
|
(3.1.4.11)
|
где kα - поправочный коэффициент на угол наклон трубы к горизонту, kα = 1 при Re > 2·105;
so - рассчитывается по формулам (3.1.3.8), (3.1.3.9);
v' -
коэффициент кинематической вязкости на линии насыщения. При расчете истинного
объемного паросодержания в вертикальной парогенерирующей трубе выделяются три
области [5, 6]:
■
область, в которой Хотн ≤ Хнп,
где Хотн -
относительная энтальпия потока (массовое балансовое паросодержание);
Хнп -
массовое паросодержание, соответствующее началу интенсивного парообразования,
которое рассчитывается по формуле:
|
Хнп =
Хгк + ΔХотн,
|
(3.1.4.12)
|
где
Хгк - массовое паросодержание, соответствующее границе кипения,
|

|
(3.1.4.13)
|
iгк = f(Р, tгк) -
определяется по таблицам термодинамических свойств;
tгк
определяется путем решения системы уравнений:
|

|
(3.1.4.14)
|
|
(3.1.4.15)
|
|
(3.1.4.16)
|
■ область, в которой Хнп ≤ Хотн
≤ Хр (область термически неравновесного двухфазного
потока), где Хр - равновесное массовое паросодержание:
|

|
(3.1.4.17)
|
■ область, в которой Хотн
≥ Хр (область термически равновесного двухфазного
потока).
Истинное
объемное паросодержание рассчитывается:
■ в области Хотн
≤ Хнп по формуле:
■ в области Хнп ≤ Хотн
≤ Хр по формуле:
|

|
(3.1.4.19)
|
где Хист
- истинное паросодержание:
|

|
(3.1.4.20)
|
S -
коэффициент скольжения фаз:
|

|
(3.1.4.21)
|
Sp - коэффициент скольжения фаз в равновесной области двухфазного
потока:
|

|
(3.1.4.23)
|
Теплофизические параметры жидкости, входящие в формулу (3.1.4.23),
принимаются по температуре, соответствующей теплосодержанию:
|

|
(3.1.4.24)
|
■ в области Хотн ≥ Хр
по формуле:
|

|
(3.1.4.25)
|
где Sp
рассчитывается по формуле (3.1.4.22);
Пределы применимости
расчетной методики:
Р =
3,0 ÷ 19,5 МПа; ρw = 500 ÷ 3000 кг/м2·с; q
= 0,25 ÷ 3,00 МВт/м2; dвн =
12 ÷ 22 мм; обогрев равномерный и косинусоидальный по длине трубы.
Погрешность
δ расчета φ составляет ±10 %.
В
формулах этого раздела:
Р -
давление, МПа;
t -
температура, °С;
i -
теплосодержание, Дж/кг;
r - теплота парообразования, Дж/кг;
ρ -
плотность, кг/м3;
λ -
коэффициент теплопроводности, Вт/(м·К);
dвн - внутренний диаметр трубы, м;
ρw -
массовая скорость, кг/(м2·с);
q -
плотность теплового потока, МВт/м2;
 - критерий Рейнольдса;
- критерий Рейнольдса;
 - критерий Прандтля;
- критерий Прандтля;
 - критерий Нуссельта;
- критерий Нуссельта;
 - критерий Вебера;
- критерий Вебера;
α -
коэффициент теплоотдачи, Вт/м2·К;
Хотн -
относительное теплосодержание потока;
β -
объемное расходное паросодержание;
S -
коэффициент скольжения фаз.
Индексы:
' -
относится к воде на линии насыщения;
"
- относится к пару на линии насыщения;
s - на
линии насыщения;
бал
- рассчитано по тепловому балансу;
ГК -
граница кипения;
Нп -
начало интенсивного парообразования;
Р -
равновесное;
Кр -
критическое значение;
Ж -
жидкость.
3.1.4.2.2. Истинное объемное паросодержание при течении
двухфазного потока в стержневых сборках
Истинное объемное
паросодержание при течении двухфазного потока в необогреваемых стержневых
сборках рассчитывается по формуле [4]:
|

|
(3.1.4.26)
|
где s
- коэффициент скольжения фаз в стержневых сборках,
|

|
(3.1.4.27)
|
ρw в
[кг/м2·с].
Пределы
применимости формулы (3.1.4.27): Р = 2 ÷ 10 МПа;
n = 3 ÷ 19 (n -
число стержней); ρw = 100 ÷ 1000 кг/м2·с;
dг =
6,7 ÷ 17,7 мм.
Погрешность
δ расчета φ составляет ±10 %.
Истинное объемное
паросодержание при течении двухфазного потока в обогреваемых стержневых сборках
рассчитывается по формуле [4]:
где
В формулах (3.1.4.28) ÷ (3.1.4.30):
q в
[Вт/м2]; r в
[Дж/кг];
σ в
[Н/м]; ρw в [кг/м2·с]; ρ' и ρ"
в [кг/м3]; g в [м/с2];
μ' в
[кг/м·с].
Пределы
применимости формулы (3.1.4.28):
Р = 2 ÷ 10 МПа;
n = 3 ÷ 9 шт; ρw = 100 ÷ 1000 кг/м2·с;
dг = 6,7 ÷ 17,7 мм.
Погрешность
расчета φ составляет ±10 %.
Пределы
применимости формул (3.1.4.29)
и (3.1.4.30):
ρw =
200 ÷ 1000 кг/м2·с; q = (0,6 ÷ 1,8)·106
Вт/м2.
3.1.4.2.3. Модель потока дрейфа
В большинстве современных
теплогидравлических расчетных кодов истинное объемное паросодержание при
течении двухфазного потока в каналах рассчитывается с использованием модели
потока дрейфа, согласно которой:
|

|
(3.1.4.31)
|
где j' и j'' - приведенные скорости жидкой и паровой фаз;
Со -
параметр распределения;
 - скорость дрейфа.
- скорость дрейфа.
Для
эмпирических параметров Со и  модели потока дрейфа
существует множество рекомендаций, из которых наибольший диапазон применимости
для пароводяного потока имеют рекомендации Chexal-Lellouche [7]. Поскольку эти рекомендации чаще
всего используются в теплогидравлических расчетных кодах, именно они и
приводятся ниже.
модели потока дрейфа
существует множество рекомендаций, из которых наибольший диапазон применимости
для пароводяного потока имеют рекомендации Chexal-Lellouche [7]. Поскольку эти рекомендации чаще
всего используются в теплогидравлических расчетных кодах, именно они и
приводятся ниже.
3.1.4.2.3.1. Параметр распределения
Для двухфазной смеси,
текущей в трубе, наклоненной под произвольным углом θ,
отсчитываемым от вертикали, параметр распределения Со
задается соотношением:
|
Со =
FСов + (1 - F)Сог,
|
(3.1.4.32)
|
где Сов и Сог - параметры
распределения для вертикального и горизонтального потока, a F - параметр
ориентации потока.
Для Re" > 0:
|
F =
(90° - θ) / 90° для 0° ≤ θ ≤ 90°.
|
(3.1.4.33а)
|
Для Re" < 0:
|

|
(3.1.4.33б)
|
где Re" = (ρw)xdг/μ"
- число Рейнольдса для пара.
3.1.4.2.3.1.1. Вертикальный поток
Для
вертикальной трубы (θ = 0°) приведенные скорости j' и j'' считаются
положительными для подъемного течения обеих фаз и отрицательными - для
опускного.
Для
противоточного течения скорость пара всегда положительна (направлена вверх), а
скорость жидкости всегда отрицательна (направлена вниз):
для Re" ≥
0
для Re" < 0
|

|
(3.1.4.34б)
|
где
|

|
(3.1.4.36)
|
где
|

|
(3.1.4.37)
|
Параметры С2,
С3 и С4 будут определены ниже.
Другие переменные в
корреляции для параметра распределения имеют вид:
|

|
(3.1.4.38)
|
|

|
(3.1.4.39)
|
|
B1 = min(0,8; A1);
|
(3.1.4.40)
|
|

|
(3.1.4.41)
|
|

|
(3.1.4.42)
|
|

|
(3.1.4.43)
|
|

|
(3.1.4.44)
|
Знаки у чисел Рейнольдса
совпадают со знаками приведенных скоростей фаз.
3.1.4.2.3.1.2. Горизонтальный поток со спутным течением фаз
Для горизонтального потока (θ
= 90°) со спутным течением фаз приведенные скорости фаз считаются всегда
положительными. Параметр распределения для такого потока задается соотношением:
|
Cог = [1 + φ0,05(1 - φ)2]Cов,
|
(3.1.4.45)
|
где Cов
находится по формуле (3.1.4.34а).
Все
другие параметры находятся по формулам для вертикального потока с
использованием положительных значений приведенных скоростей фаз.
Следует
подчеркнуть, что поскольку параметр распределения в рекомендациях Chexal-Lellouche
является функцией паросодержания, расчет истинного объемного паросодержания по
модели потока дрейфа следует проводить итерационным способом.
3.1.4.2.3.2. Скорость дрейфа
Скорость дрейфа  для спутного подъемного
течения фаз в трубе с произвольным углом наклона рассчитывается по формуле:
для спутного подъемного
течения фаз в трубе с произвольным углом наклона рассчитывается по формуле:
|

|
(3.1.4.46)
|
где  и
и  - скорости дрейфа для
вертикального и горизонтального потока, a F - параметр ориентации
потока, определяемый соотношениями (1.4.33а) и (1.4.33б).
- скорости дрейфа для
вертикального и горизонтального потока, a F - параметр ориентации
потока, определяемый соотношениями (1.4.33а) и (1.4.33б).
Для спутного опускного
течения скорость дрейфа определяется соотношением:
|

|
(3.1.4.47)
|
3.1.4.2.3.2.1. Вертикальный поток
Скорость дрейфа для
вертикального потока находится по формуле:
где  определяется соотношением (3.1.4.35);
определяется соотношением (3.1.4.35);
|

|
(3.1.4.49)
|
|

|
(3.1.4.50)
|
Другие параметры определены следующим образом:
|

|
(3.1.4.51)
|
|

|
(3.1.4.52)
|
где
|

|
(3.1.4.53)
|
|

|
(3.1.4.54)
|
|
C7 = (d2/dг)0,6;
|
(3.1.4.55)
|
|

|
(3.1.4.56)
|
|
d2 = 0,09144 м.
|
(3.1.4.57)
|
Параметр С3
определяется с учетом направления течения потоков пара и жидкости.
Для спутного подъемного
течения фаз:
|

|
(3.1.4.58)
|
Для спутного опускного течения фаз, противотока (опускное течение
воды и подъемное течение пара) и режима захлебывания параметр С3
задается единым соотношением:
где
|

|
(3.1.4.60)
|
|

|
(3.1.4.61)
|
d1 = 0,0381 м.
Для ясности, общее выражение
для С10 разбивается на три члена, которые в сумме и дают С10:
|

|
(3.1.4.62)
|
|

|
(3.1.4.63)
|
|

|
(3.1.4.64)
|
где
|

|
(3.1.4.65)
|
и
|

|
(3.1.4.66)
|
Здесь  - приведенная скорость
жидкости в режиме захлебывания и
- приведенная скорость
жидкости в режиме захлебывания и
|

|
(3.1.4.67)
|
3.1.4.2.3.2.2. Противоточное движение
|

|
(3.1.4.68)
|
где
С3N = C3 по
формуле (3.1.4.59);
|
XT = (dг - d1) /
(0,3048 - d1).
|
|
3.1.4.2.3.2.3. Горизонтальный поток
Для
горизонтального потока рассматривается только спутное течение фаз. Скорость
дрейфа при этом оценивается по соотношению (3.1.4.48) с использованием положительных значений
скоростей фаз.
Пределы
применимости расчетной методики: по давлению - 0,7 ÷ 10,3 МПа, по
массовой скорости - 173 ÷ 2050 кг/м2·сек, по массовому
расходному паросодержанию - от 0 ÷ 0,38, по гидравлическому диаметру -
6,1 ÷ 49,3 мм.
Погрешности
расчета φ составляют: Δ = 5,1 % (расчет выше), σ
= 22,74 %.
3.1.4.3. ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ ПРИ ТЕЧЕНИИ
ДВУХФАЗНЫХ ПОТОКОВ В КАНАЛАХ
Полное гидравлическое
сопротивление при течении двухфазного потока в каналах складывается из
гидравлического сопротивления трения, местных сопротивлений, потери давления от
ускорения потока и нивелирного перепада давления и рассчитывается по формуле:
|
ΔP = ΣΔPтр +
ΣΔPм ±
ΔPуск ±
ΔPнив.
|
(3.1.4.69)
|
3.1.4.3.1. Гидравлические сопротивления трения при течении
двухфазного потока в трубах
Потери давления на трение
при течении двухфазного потока в не-обогреваемых трубах с внутренним диаметром dвн
≥ 17·10-3 м рассчитываются по формуле [4]:
ΔPтр/ΔPо) - определяется по
таблицам 3.1.4.1 для заданных значений давления и массовой скорости;
ΔPо -
потери давления на трение при течении в трубах воды, нагретой до температуры
насыщения, ΔPо рассчитывается по
формуле [2]:
где 
Пределы
применимости формулы (3.1.4.70):
dвн ≥ 17·103 м;
Р =
6,86 ÷ 22 МПа; ρw = 500 ÷ 3000 кг/м2·с; Х
= 0 ÷ 1,0.
Погрешность
δ расчета ΔPтр
составляет ±25 %.
Таблица 3.1.4.1(a)
Таблицы для определения относительных потерь давления на трение
при подъемном течении пароводяного потока в трубах
ρw = 500 кг/м2с
|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
|
6,86
|
0,0
|
1,27
|
10,8
|
0,01
|
1,22
|
14,7
|
0,02
|
1,17
|
|
|
0,09
|
3,8
|
|
0,12
|
2,29
|
|
0,12
|
1,31
|
|
|
0,21
|
6,86
|
|
0,2
|
3,26
|
|
0,2
|
1,46
|
|
|
0,3
|
9,54
|
|
0,3
|
4,28
|
|
0,3
|
1,51
|
|
|
0,4
|
12,3
|
|
0,4
|
5,26
|
|
0,39
|
1,41
|
|
|
0,49
|
14,9
|
|
0,5
|
6,18
|
|
0,47
|
1,22
|
|
|
0,6
|
17,1
|
|
0,6
|
6,67
|
|
0,59
|
1,75
|
|
|
0,7
|
18,8
|
|
0,7
|
6,81
|
|
0,68
|
2,53
|
|
|
0,8
|
19,9
|
|
0,79
|
6,62
|
|
0,79
|
3,41
|
|
|
0,89
|
19,5
|
|
0,89
|
7,4
|
|
0,88
|
4,28
|
|
|
0,93
|
18,5
|
|
1,0
|
8,13
|
|
0,99
|
5,06
|
|
|
0,95
|
17,4
|
11,8
|
0,01
|
1,27
|
15,7
|
0,55
|
1,17
|
|
|
0,99
|
15,4
|
|
0,11
|
1,95
|
|
0,69
|
2,29
|
|
7,85
|
0,0
|
1,17
|
|
0,21
|
2,58
|
|
0,78
|
2,97
|
|
|
0,12
|
3,75
|
|
0,4
|
3,94
|
|
0,89
|
3,8
|
|
|
0,21
|
5,64
|
|
0,51
|
4,48
|
|
0,99
|
4,38
|
|
|
0,29
|
7,59
|
|
0,6
|
4,48
|
16,7
|
0,57
|
1,22
|
|
|
0,39
|
9,83
|
|
0,68
|
4,33
|
|
0,69
|
2,19
|
|
|
0,5
|
12,0
|
|
0,79
|
5,06
|
|
0,79
|
2,73
|
|
|
0,6
|
13,7
|
|
0,9
|
6,13
|
|
0,89
|
3,36
|
|
|
0,69
|
15,2
|
|
0,99
|
7,01
|
|
0,99
|
3,84
|
|
|
0,79
|
15,8
|
12,8
|
0,0
|
1,27
|
17,6
|
0,57
|
1,12
|
|
|
0,9
|
15,0
|
|
0,11
|
1,75
|
|
0,7
|
1,95
|
|
|
1,0
|
13,2
|
|
0,21
|
2,19
|
|
0,79
|
2,34
|
|
8,83
|
0,01
|
1,36
|
|
0,31
|
2,58
|
|
0,89
|
2,87
|
|
|
0,12
|
3,11
|
|
0,4
|
2,92
|
|
0,99
|
3,31
|
|
|
0,21
|
4,67
|
|
0,5
|
2,82
|
18,6
|
0,57
|
1,12
|
|
|
0,3
|
6,28
|
|
0,59
|
2,53
|
|
0,7
|
1,85
|
|
|
0,39
|
7,74
|
|
0,7
|
3,55
|
|
0,79
|
2,14
|
|
|
0,5
|
9,34
|
|
0,78
|
4,28
|
|
0,89
|
2,53
|
|
|
0,6
|
10,8
|
|
0,89
|
5,5
|
|
0,99
|
2,82
|
|
|
0,7
|
11,9
|
|
0,99
|
6,42
|
19,6
|
0,57
|
1,17
|
|
|
0,79
|
12,2
|
13,7
|
0,01
|
1,27
|
|
0,7
|
1,65
|
|
|
0,89
|
11,4
|
|
0,11
|
1,51
|
|
0,78
|
1,75
|
|
|
1,0
|
10,7
|
|
0,2
|
1,75
|
|
0,89
|
2,04
|
|
9,81
|
0,01
|
1,27
|
|
0,29
|
1,85
|
|
0,99
|
2,24
|
|
|
0,12
|
2,73
|
|
0,39
|
1,7
|
20,6
|
0,57
|
1,31
|
|
|
0,2
|
3,89
|
|
0,5
|
1,56
|
|
0,71
|
1,46
|
|
|
0,3
|
5,06
|
|
0,6
|
2,14
|
|
0,79
|
1,61
|
|
|
0,39
|
6,33
|
|
0,7
|
2,97
|
|
0,89
|
1,7
|
|
|
0,5
|
7,59
|
|
0,79
|
3,89
|
|
0,99
|
1,95
|
|
|
0,6
|
8,42
|
|
0,88
|
4,72
|
21,6
|
0,57
|
1,17
|
|
|
0,7
|
8,95
|
|
0,99
|
5,6
|
|
0,71
|
1,27
|
|
|
0,79
|
9,1
|
|
|
|
|
0,76
|
1,22
|
|
|
0,9
|
8,95
|
|
|
|
|
0,9
|
1,31
|
|
|
0,99
|
9,2
|
|
|
|
|
0,99
|
1,31
|
Таблица 3.1.4.1(б)
ρw = 1000 кг/м2с
|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
|
6,86
|
1,0
|
15,4
|
10,8
|
0,7
|
5,22
|
15,7
|
0,69
|
3,0
|
|
|
0,9
|
13,7
|
|
0,62
|
4,35
|
|
0,61
|
2,51
|
|
|
0,8
|
12,1
|
|
0,49
|
3,43
|
|
0,5
|
2,03
|
|
|
0,71
|
10,7
|
|
0,4
|
3,33
|
|
0,39
|
1,4
|
|
|
0,61
|
10,2
|
|
0,3
|
3,09
|
16,7
|
1,0
|
4,01
|
|
|
0,49
|
9,52
|
|
0,21
|
2,8
|
|
0,9
|
3,62
|
|
|
0,4
|
8,6
|
|
0,11
|
2,27
|
|
0,81
|
3,24
|
|
|
0,3
|
7,15
|
|
0,02
|
1,45
|
|
0,69
|
2,71
|
|
|
0,21
|
5,65
|
11,8
|
0,99
|
7,1
|
|
0,61
|
2,37
|
|
|
0,12
|
3,77
|
|
0,89
|
6,23
|
|
0,5
|
1,98
|
|
|
0,01
|
1,3
|
|
0,8
|
5,51
|
|
0,39
|
1,35
|
|
7,85
|
1,0
|
13,1
|
|
0,69
|
4,49
|
17,6
|
0,99
|
3,43
|
|
|
0,89
|
11,4
|
|
0,61
|
3,86
|
|
0,9
|
3,19
|
|
|
0,8
|
10,1
|
|
0,49
|
2,95
|
|
0,8
|
2,8
|
|
|
0,71
|
8,84
|
|
0,41
|
2,46
|
|
0,68
|
2,37
|
|
|
0,61
|
7,68
|
|
0,29
|
2,37
|
|
0,61
|
2,17
|
|
|
0,5
|
7,39
|
|
0,21
|
2,27
|
|
0,5
|
1,88
|
|
|
0,41
|
6,91
|
|
0,1
|
1,93
|
|
0,39
|
1,4
|
|
|
0,32
|
6,04
|
|
0,01
|
1,3
|
18,6
|
0,99
|
3,0
|
|
|
0,21
|
4,54
|
12,8
|
0,99
|
6,52
|
|
0,89
|
2,71
|
|
|
0,11
|
3,04
|
|
0,89
|
5,75
|
|
0,8
|
2,46
|
|
|
0,01
|
1,35
|
|
0,81
|
5,02
|
|
0,69
|
2,17
|
|
8,83
|
1,0
|
10,7
|
|
0,69
|
4,11
|
|
0,6
|
1,88
|
|
|
0,9
|
9,42
|
|
0,61
|
3,48
|
|
0,5
|
1,79
|
|
|
0,81
|
8,45
|
|
0,49
|
2,61
|
|
0,38
|
1,3
|
|
|
0,7
|
7,2
|
|
0,41
|
1,88
|
19,6
|
0,99
|
2,51
|
|
|
0,61
|
6,14
|
|
0,29
|
1,45
|
|
0,9
|
2,27
|
|
|
0,52
|
5,7
|
|
0,21
|
1,64
|
|
0,8
|
2,13
|
|
|
0,41
|
5,46
|
|
0,11
|
1,64
|
|
0,7
|
1,93
|
|
|
0,3
|
4,73
|
|
0,01
|
1,4
|
|
0,61
|
1,79
|
|
|
0,21
|
3,96
|
13,7
|
0,99
|
5,75
|
|
0,49
|
1,59
|
|
|
0,11
|
2,75
|
|
0,88
|
5,02
|
|
0,38
|
1,4
|
|
|
0,02
|
1,4
|
|
0,8
|
4,44
|
20,6
|
1,0
|
2,13
|
|
9,81
|
0,99
|
9,23
|
|
0,69
|
3,57
|
|
0,89
|
1,98
|
|
|
0,9
|
8,36
|
|
0,61
|
3,0
|
|
0,81
|
1,84
|
|
|
0,81
|
7,2
|
|
0,5
|
2,22
|
|
0,69
|
1,59
|
|
|
0,7
|
6,09
|
|
0,39
|
1,4
|
|
0,6
|
1,64
|
|
|
0,61
|
5,17
|
14,7
|
1,0
|
5,22
|
|
0,49
|
1,55
|
|
|
0,5
|
4,11
|
|
0,88
|
4,44
|
|
0,38
|
1,35
|
|
|
0,41
|
4,06
|
|
0,8
|
3,96
|
21,6
|
1,0
|
1,59
|
|
|
0,3
|
3,91
|
|
0,69
|
3,29
|
|
0,89
|
1,59
|
|
|
0,21
|
3,38
|
|
0,61
|
2,8
|
|
0,8
|
1,55
|
|
|
0,11
|
2,66
|
|
0,5
|
2,08
|
|
0,69
|
1,45
|
|
|
0,02
|
1,45
|
|
0,39
|
1,45
|
|
0,6
|
1,5
|
|
10,8
|
0,99
|
8,31
|
15,7
|
1,0
|
4,64
|
|
0,49
|
1,4
|
|
|
0,89
|
7,25
|
|
0,91
|
4,15
|
|
0,39
|
1,35
|
|
|
0,8
|
6,38
|
|
0,81
|
3,57
|
|
|
|
Таблица 3.1.4.1(в)
ρw = 1500 кг/м2с
|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
|
6,86
|
0,01
|
1,23
|
10,8
|
0,5
|
3,57
|
16,7
|
0,3
|
1,35
|
|
|
0,11
|
2,85
|
|
0,59
|
4,41
|
|
0,43
|
1,71
|
|
|
0,21
|
4,05
|
|
0,7
|
5,49
|
|
0,52
|
2,19
|
|
|
0,31
|
5,31
|
|
0,78
|
6,39
|
|
0,59
|
2,43
|
|
|
0,4
|
5,97
|
|
0,88
|
7,4
|
|
0,7
|
2,97
|
|
|
0,5
|
6,45
|
|
0,99
|
8,42
|
|
0,78
|
3,27
|
|
|
0,59
|
7,64
|
11,8
|
0,02
|
1,23
|
|
0,89
|
3,75
|
|
|
0,68
|
9,2
|
|
0,12
|
1,53
|
|
0,99
|
4,17
|
|
|
0,79
|
11,1
|
|
0,21
|
1,77
|
17,6
|
0,3
|
1,29
|
|
|
0,9
|
13,0
|
|
0,31
|
2,13
|
|
0,43
|
1,65
|
|
|
0,99
|
14,7
|
|
0,41
|
2,49
|
|
0,52
|
2,01
|
|
7,85
|
0,01
|
1,29
|
|
0,51
|
3,27
|
|
0,59
|
2,31
|
|
|
0,11
|
2,49
|
|
0,59
|
4,05
|
|
0,7
|
2,61
|
|
|
0,21
|
3,57
|
|
0,69
|
4,95
|
|
0,78
|
2,97
|
|
|
0,31
|
4,47
|
|
0,78
|
5,85
|
|
0,9
|
3,39
|
|
|
0,4
|
5,07
|
|
0,89
|
6,63
|
|
0,99
|
3,63
|
|
|
0,51
|
5,55
|
|
0,99
|
7,52
|
18,6
|
0,3
|
1,29
|
|
|
0,59
|
6,33
|
12,8
|
0,29
|
1,17
|
|
0,43
|
1,59
|
|
|
0,69
|
7,94
|
|
0,41
|
2,19
|
|
0,53
|
1,89
|
|
|
0,79
|
9,44
|
|
0,51
|
2,97
|
|
0,59
|
2,01
|
|
|
0,89
|
11,2
|
|
0,59
|
3,69
|
|
0,71
|
2,31
|
|
|
0,99
|
12,9
|
|
0,7
|
4,53
|
|
0,78
|
2,49
|
|
8,83
|
0,02
|
1,29
|
|
0,78
|
5,31
|
|
0,9
|
2,79
|
|
|
0,11
|
2,19
|
|
0,89
|
6,09
|
|
0,99
|
3,09
|
|
|
0,21
|
2,97
|
|
0,99
|
6,81
|
19,6
|
0,3
|
1,23
|
|
|
0,31
|
3,57
|
13,7
|
0,3
|
1,23
|
|
0,43
|
1,47
|
|
|
0,4
|
3,87
|
|
0,42
|
2,07
|
|
0,52
|
1,65
|
|
|
0,5
|
4,35
|
|
0,51
|
2,73
|
|
0,59
|
1,77
|
|
|
0,59
|
5,49
|
|
0,59
|
3,33
|
|
0,71
|
2,01
|
|
|
0,68
|
6,69
|
|
0,71
|
4,11
|
|
0,78
|
2,07
|
|
|
0,79
|
8,0
|
|
0,78
|
4,59
|
|
0,89
|
2,31
|
|
|
0,89
|
9,44
|
|
0,9
|
5,31
|
|
0,98
|
2,55
|
|
|
0,99
|
10,9
|
|
0,99
|
5,91
|
20,6
|
0,3
|
1,29
|
|
9,81
|
0,02
|
1,23
|
14,7
|
0,3
|
1,29
|
|
0,45
|
1,47
|
|
|
0,12
|
2,01
|
|
0,42
|
1,95
|
|
0,53
|
1,65
|
|
|
0,21
|
2,49
|
|
0,52
|
2,61
|
|
0,6
|
1,65
|
|
|
0,31
|
2,85
|
|
0,59
|
3,03
|
|
0,71
|
1,77
|
|
|
0,41
|
3,15
|
|
0,7
|
3,69
|
|
0,78
|
1,77
|
|
|
0,51
|
3,81
|
|
0,79
|
4,17
|
|
0,9
|
2,01
|
|
|
0,59
|
4,89
|
|
0,9
|
4,83
|
|
0,99
|
2,01
|
|
|
0,69
|
6,09
|
|
0,99
|
5,43
|
21,6
|
0,3
|
1,23
|
|
|
0,78
|
7,1
|
15,7
|
0,29
|
1,23
|
|
0,44
|
1,29
|
|
|
0,89
|
8,36
|
|
0,42
|
1,77
|
|
0,52
|
1,35
|
|
|
0,99
|
9,68
|
|
0,52
|
2,37
|
|
0,59
|
1,35
|
|
|
|
|
|
|
|
|
|
|
|
10,8
|
0,02
|
1,29
|
|
0,58
|
2,73
|
|
0,71
|
1,47
|
|
|
0,12
|
1,83
|
|
0,7
|
3,21
|
|
0,79
|
1,41
|
|
|
0,21
|
2,19
|
|
0,78
|
3,63
|
|
0,9
|
1,53
|
|
|
0,32
|
2,43
|
|
0,89
|
4,17
|
|
0,99
|
1,53
|
|
|
0,4
|
2,79
|
|
0,99
|
4,53
|
|
|
|
Таблица 3.1.4.1(г)
ρw = 2000 кг/м2с
|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
|
6,86
|
0,99
|
14,8
|
10,8
|
0,49
|
3,65
|
16,7
|
1,0
|
4,01
|
|
|
0,9
|
12,9
|
|
0,39
|
2,64
|
|
0,89
|
3,71
|
|
|
0,81
|
11,3
|
|
0,27
|
2,28
|
|
0,8
|
3,35
|
|
|
0,71
|
9,29
|
|
0,2
|
2,1
|
|
0,69
|
2,94
|
|
|
0,61
|
7,37
|
|
0,08
|
1,74
|
|
0,6
|
2,64
|
|
|
0,5
|
5,57
|
|
0,01
|
1,44
|
|
0,49
|
2,16
|
|
|
0,4
|
5,09
|
11,8
|
0,98
|
7,49
|
|
0,39
|
1,86
|
|
|
0,29
|
4,43
|
|
0,88
|
6,65
|
|
0,26
|
1,32
|
|
|
0,19
|
3,53
|
|
0,81
|
5,93
|
17,6
|
0,99
|
3,59
|
|
|
0,09
|
2,52
|
|
0,7
|
5,03
|
|
0,89
|
3,29
|
|
|
0,01
|
1,44
|
|
0,61
|
4,25
|
|
0,81
|
3,0
|
|
7,85
|
1,0
|
12,8
|
|
0,5
|
3,29
|
|
0,69
|
2,7
|
|
|
0,9
|
11,1
|
|
0,4
|
2,52
|
|
0,61
|
2,4
|
|
|
0,81
|
9,64
|
|
0,27
|
1,92
|
|
0,49
|
2,04
|
|
|
0,7
|
8,03
|
|
0,19
|
1,8
|
|
0,39
|
1,8
|
|
|
0,61
|
6,35
|
|
0,08
|
1,74
|
|
0,26
|
1,32
|
|
|
0,5
|
4,73
|
|
0,02
|
1,44
|
18,6
|
0,99
|
3,0
|
|
|
0,4
|
4,07
|
12,8
|
1,0
|
6,77
|
|
0,89
|
2,7
|
|
|
0,29
|
3,59
|
|
0,9
|
5,99
|
|
0,81
|
2,52
|
|
|
0,2
|
3,06
|
|
0,81
|
5,39
|
|
0,69
|
2,28
|
|
|
0,09
|
2,4
|
|
0,7
|
4,55
|
|
0,61
|
2,1
|
|
|
0,01
|
1,44
|
|
0,61
|
3,89
|
|
0,49
|
1,86
|
|
8,83
|
1,0
|
10,9
|
|
0,49
|
3,06
|
|
0,39
|
1,68
|
|
|
0,9
|
9,52
|
|
0,39
|
2,28
|
|
0,27
|
1,26
|
|
|
0,81
|
8,33
|
|
0,26
|
1,26
|
19,6
|
1,0
|
2,4
|
|
|
0,69
|
6,77
|
13,7
|
1,0
|
5,81
|
|
0,89
|
2,34
|
|
|
0,61
|
5,81
|
|
0,9
|
5,27
|
|
0,81
|
2,16
|
|
|
0,5
|
4,19
|
|
0,8
|
4,73
|
|
0,69
|
1,98
|
|
|
0,4
|
3,47
|
|
0,7
|
4,07
|
|
0,58
|
1,86
|
|
|
0,28
|
3,12
|
|
0,61
|
3,47
|
|
0,49
|
1,68
|
|
|
0,19
|
2,7
|
|
0,49
|
2,7
|
|
0,39
|
1,62
|
|
|
0,09
|
2,16
|
|
0,39
|
2,16
|
|
0,27
|
1,26
|
|
|
0,01
|
1,44
|
|
0,26
|
1,26
|
20,6
|
1,0
|
1,98
|
|
9,81
|
1,0
|
9,58
|
14,7
|
1,0
|
5,27
|
|
0,89
|
1,92
|
|
|
0,89
|
8,51
|
|
0,9
|
4,85
|
|
0,8
|
1,86
|
|
|
0,81
|
7,43
|
|
0,8
|
4,31
|
|
0,69
|
1,68
|
|
|
0,71
|
6,35
|
|
0,69
|
3,65
|
|
0,6
|
1,68
|
|
|
0,61
|
5,21
|
|
0,61
|
3,23
|
|
0,48
|
1,5
|
|
|
0,49
|
3,83
|
|
0,48
|
2,64
|
|
0,39
|
1,5
|
|
|
0,4
|
3,12
|
|
0,39
|
2,1
|
|
0,26
|
1,26
|
|
|
0,28
|
2,64
|
|
0,26
|
1,26
|
21,6
|
1,0
|
1,62
|
|
|
0,19
|
2,4
|
15,7
|
1,0
|
4,55
|
|
0,9
|
1,56
|
|
|
0,09
|
1,92
|
|
0,9
|
4,19
|
|
0,8
|
1,5
|
|
|
0,01
|
1,44
|
|
0,81
|
3,71
|
|
0,69
|
1,44
|
|
10,8
|
1,0
|
8,33
|
|
0,69
|
3,29
|
|
0,61
|
1,44
|
|
|
0,9
|
7,55
|
|
0,61
|
2,88
|
|
0,48
|
1,44
|
|
|
0,81
|
6,77
|
|
0,49
|
2,28
|
|
0,39
|
1,38
|
|
|
0,72
|
5,81
|
|
0,39
|
1,92
|
|
0,26
|
1,32
|
|
|
0,61
|
4,73
|
|
0,26
|
1,32
|
|
|
|
Таблица 3.1.4.1(д)
ρw = 2000 кг/м2с
|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
|
6,86
|
0,99
|
14,8
|
10,8
|
0,49
|
3,65
|
16,7
|
1,0
|
4,01
|
|
|
0,9
|
12,9
|
|
0,39
|
2,64
|
|
0,89
|
3,71
|
|
|
0,81
|
11,3
|
|
0,27
|
2,28
|
|
0,8
|
3,35
|
|
|
0,71
|
9,29
|
|
0,2
|
2,1
|
|
0,69
|
2,94
|
|
|
0,61
|
7,37
|
|
0,08
|
1,74
|
|
0,6
|
2,64
|
|
|
0,5
|
5,57
|
|
0,01
|
1,44
|
|
0,49
|
2,16
|
|
|
0,4
|
5,09
|
11,8
|
0,98
|
7,49
|
|
0,39
|
1,86
|
|
|
0,29
|
4,43
|
|
0,88
|
6,65
|
|
0,26
|
1,32
|
|
|
0,19
|
3,53
|
|
0,81
|
5,93
|
17,6
|
0,99
|
3,59
|
|
|
0,09
|
2,52
|
|
0,7
|
5,03
|
|
0,89
|
3,29
|
|
|
0,01
|
1,44
|
|
0,61
|
4,25
|
|
0,81
|
3,0
|
|
7,85
|
1,0
|
12,8
|
|
0,5
|
3,29
|
|
0,69
|
2,7
|
|
|
0,9
|
11,1
|
|
0,4
|
2,52
|
|
0,61
|
2,4
|
|
|
0,81
|
9,64
|
|
0,27
|
1,92
|
|
0,49
|
2,04
|
|
|
0,7
|
8,03
|
|
0,19
|
1,8
|
|
0,39
|
1,8
|
|
|
0,61
|
6,35
|
|
0,08
|
1,74
|
|
0,26
|
1,32
|
|
|
0,5
|
4,73
|
|
0,02
|
1,44
|
18,6
|
0,99
|
3,0
|
|
|
0,4
|
4,07
|
12,8
|
1,0
|
6,77
|
|
0,89
|
2,7
|
|
|
0,29
|
3,59
|
|
0,9
|
5,99
|
|
0,81
|
2,52
|
|
|
0,2
|
3,06
|
|
0,81
|
5,39
|
|
0,69
|
2,28
|
|
|
0,09
|
2,4
|
|
0,7
|
4,55
|
|
0,61
|
2,1
|
|
|
0,01
|
1,44
|
|
0,61
|
3,89
|
|
0,49
|
1,86
|
|
8,83
|
1,0
|
10,9
|
|
0,49
|
3,06
|
|
0,39
|
1,68
|
|
|
0,9
|
9,52
|
|
0,39
|
2,28
|
|
0,27
|
1,26
|
|
|
0,81
|
8,33
|
|
0,26
|
1,26
|
19,6
|
1,0
|
2,4
|
|
|
0,69
|
6,77
|
13,7
|
1,0
|
5,81
|
|
0,89
|
2,34
|
|
|
0,61
|
5,81
|
|
0,9
|
5,27
|
|
0,81
|
2,16
|
|
|
0,5
|
4,19
|
|
0,8
|
4,73
|
|
0,69
|
1,98
|
|
|
0,4
|
3,47
|
|
0,7
|
4,07
|
|
0,58
|
1,86
|
|
|
0,28
|
3,12
|
|
0,61
|
3,47
|
|
0,49
|
1,68
|
|
|
0,19
|
2,7
|
|
0,49
|
2,7
|
|
0,39
|
1,62
|
|
|
0,09
|
2,16
|
|
0,39
|
2,16
|
|
0,27
|
1,26
|
|
|
0,01
|
1,44
|
|
0,26
|
1,26
|
20,6
|
1,0
|
1,98
|
|
9,81
|
1,0
|
9,58
|
14,7
|
1,0
|
5,27
|
|
0,89
|
1,92
|
|
|
0,89
|
8,51
|
|
0,9
|
4,85
|
|
0,8
|
1,86
|
|
|
0,81
|
7,43
|
|
0,8
|
4,31
|
|
0,69
|
1,68
|
|
|
0,71
|
6,35
|
|
0,69
|
3,65
|
|
0,6
|
1,68
|
|
|
0,61
|
5,21
|
|
0,61
|
3,23
|
|
0,48
|
1,5
|
|
|
0,49
|
3,83
|
|
0,48
|
2,64
|
|
0,39
|
1,5
|
|
|
0,4
|
3,12
|
|
0,39
|
2,1
|
|
0,26
|
1,26
|
|
|
0,28
|
2,64
|
|
0,26
|
1,26
|
21,6
|
1,0
|
1,62
|
|
|
0,19
|
2,4
|
15,7
|
1,0
|
4,55
|
|
0,9
|
1,56
|
|
|
0,09
|
1,92
|
|
0,9
|
4,19
|
|
0,8
|
1,5
|
|
|
0,01
|
1,44
|
|
0,81
|
3,71
|
|
0,69
|
1,44
|
|
10,8
|
1,0
|
8,33
|
|
0,69
|
3,29
|
|
0,61
|
1,44
|
|
|
0,9
|
7,55
|
|
0,61
|
2,88
|
|
0,48
|
1,44
|
|
|
0,81
|
6,77
|
|
0,49
|
2,28
|
|
0,39
|
1,38
|
|
|
0,72
|
5,81
|
|
0,39
|
1,92
|
|
0,26
|
1,32
|
|
|
0,61
|
4,73
|
|
0,26
|
1,32
|
|
|
|
Таблица 3.1.4.1(e)
ρw = 2500 кг/м2с
|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
|
6,86
|
0,01
|
1,32
|
10,8
|
0,31
|
1,85
|
16,7
|
0,38
|
1,26
|
|
|
0,12
|
1,91
|
|
0,41
|
2,21
|
|
0,52
|
1,91
|
|
|
0,21
|
2,56
|
|
0,51
|
3,16
|
|
0,6
|
2,33
|
|
|
0,31
|
3,33
|
|
0,6
|
3,99
|
|
0,7
|
2,74
|
|
|
0,41
|
3,87
|
|
0,7
|
5,11
|
|
0,79
|
3,16
|
|
|
0,5
|
4,58
|
|
0,79
|
6,18
|
|
0,89
|
3,57
|
|
|
0,59
|
5,83
|
|
0,89
|
7,43
|
|
1,0
|
4,05
|
|
|
0,7
|
8,08
|
|
1,0
|
8,56
|
17,6
|
0,38
|
1,32
|
|
|
0,8
|
10,2
|
11,8
|
0,02
|
1,32
|
|
0,52
|
1,79
|
|
|
0,9
|
12,6
|
|
0,13
|
1,5
|
|
0,6
|
2,09
|
|
|
1,0
|
14,8
|
|
0,21
|
1,5
|
|
0,7
|
2,44
|
|
7,85
|
0,02
|
1,38
|
|
0,32
|
1,55
|
|
0,79
|
2,8
|
|
|
0,12
|
1,79
|
|
0,41
|
1,91
|
|
0,89
|
3,1
|
|
|
0,21
|
2,21
|
|
0,51
|
2,8
|
|
1,0
|
3,51
|
|
|
0,31
|
2,74
|
|
0,6
|
3,57
|
18,6
|
0,38
|
1,38
|
|
|
0,41
|
3,45
|
|
0,7
|
4,64
|
|
0,53
|
1,79
|
|
|
0,5
|
4,11
|
|
0,79
|
5,53
|
|
0,6
|
2,03
|
|
|
0,6
|
5,29
|
|
0,89
|
6,54
|
|
0,7
|
2,33
|
|
|
0,7
|
7,13
|
|
0,99
|
7,73
|
|
0,79
|
2,56
|
|
|
0,79
|
8,91
|
12,8
|
0,37
|
1,38
|
|
0,89
|
2,8
|
|
|
0,9
|
11,0
|
|
0,51
|
2,56
|
|
1,0
|
3,1
|
|
|
1,0
|
12,8
|
|
0,6
|
3,33
|
19,6
|
0,38
|
1,32
|
|
8,83
|
0,02
|
1,32
|
|
0,7
|
4,05
|
|
0,51
|
1,61
|
|
|
0,12
|
1,79
|
|
0,79
|
4,94
|
|
0,6
|
1,85
|
|
|
0,21
|
2,09
|
|
0,89
|
5,83
|
|
0,7
|
2,09
|
|
|
0,32
|
2,39
|
|
1,0
|
6,72
|
|
0,78
|
2,21
|
|
|
0,41
|
2,86
|
13,7
|
0,38
|
1,32
|
|
0,89
|
2,44
|
|
|
0,51
|
3,75
|
|
0,52
|
2,39
|
|
1,0
|
2,68
|
|
|
0,6
|
4,94
|
|
0,6
|
2,98
|
20,6
|
0,38
|
1,38
|
|
|
0,7
|
6,36
|
|
0,7
|
3,81
|
|
0,51
|
1,61
|
|
|
0,79
|
7,84
|
|
0,79
|
4,34
|
|
0,6
|
1,61
|
|
|
0,9
|
9,56
|
|
0,89
|
5,11
|
|
0,71
|
1,85
|
|
|
0,99
|
10,9
|
|
1,0
|
5,89
|
|
0,78
|
1,97
|
|
9,81
|
0,02
|
1,26
|
14,7
|
0,38
|
1,32
|
|
0,89
|
2,09
|
|
|
0,13
|
1,67
|
|
0,52
|
2,27
|
|
1,0
|
2,21
|
|
|
0,22
|
1,79
|
|
0,6
|
2,8
|
21,6
|
0,38
|
1,38
|
|
|
0,31
|
2,15
|
|
0,7
|
3,33
|
|
0,51
|
1,5
|
|
|
0,41
|
2,62
|
|
0,79
|
3,99
|
|
0,6
|
1,5
|
|
|
0,51
|
3,45
|
|
0,89
|
4,64
|
|
0,7
|
1,55
|
|
|
0,6
|
4,46
|
|
1,0
|
5,29
|
|
0,78
|
1,61
|
|
|
0,7
|
5,89
|
15,7
|
0,39
|
1,26
|
|
0,89
|
1,67
|
|
|
0,79
|
7,07
|
|
0,52
|
2,15
|
|
0,99
|
1,91
|
|
|
0,9
|
8,56
|
|
0,61
|
2,56
|
|
|
|
|
|
1,0
|
9,86
|
|
0,7
|
3,04
|
|
|
|
|
10,8
|
0,01
|
1,26
|
|
0,79
|
3,51
|
|
|
|
|
|
0,12
|
1,55
|
|
0,89
|
4,11
|
|
|
|
|
|
0,22
|
1,79
|
|
1,0
|
4,58
|
|
|
|
Таблица 3.1.4.1(ж)
ρw = 3000 кг/м2с
|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
P, МПа
|
X
|

|
|
6,86
|
1,0
|
14,9
|
10,8
|
0,68
|
5,77
|
16,7
|
0,99
|
3,93
|
|
|
0,88
|
12,9
|
|
0,61
|
4,64
|
|
0,88
|
3,45
|
|
|
0,79
|
10,9
|
|
0,49
|
2,5
|
|
0,8
|
3,1
|
|
|
0,7
|
8,73
|
|
0,4
|
1,67
|
|
0,69
|
2,56
|
|
|
0,61
|
6,72
|
|
0,29
|
1,5
|
|
0,61
|
2,21
|
|
|
0,49
|
4,46
|
|
0,2
|
1,55
|
|
0,48
|
1,67
|
|
|
0,4
|
3,57
|
|
0,01
|
1,2
|
|
0,41
|
1,32
|
|
|
0,29
|
3,04
|
11,8
|
0,99
|
7,73
|
17,6
|
0,99
|
3,51
|
|
|
0,2
|
2,5
|
|
0,88
|
7,07
|
|
0,88
|
3,1
|
|
|
0,0
|
1,26
|
|
0,81
|
6,54
|
|
0,8
|
2,8
|
|
7,85
|
0,99
|
12,8
|
|
0,69
|
5,29
|
|
0,69
|
2,44
|
|
|
0,89
|
11,1
|
|
0,61
|
3,99
|
|
0,61
|
2,03
|
|
|
0,79
|
9,45
|
|
0,49
|
2,09
|
|
0,48
|
1,61
|
|
|
0,69
|
7,55
|
|
0,41
|
1,26
|
|
0,4
|
1,26
|
|
|
0,61
|
5,89
|
12,8
|
0,99
|
6,66
|
18,6
|
0,99
|
3,04
|
|
|
0,5
|
3,93
|
|
0,88
|
6,3
|
|
0,89
|
2,8
|
|
|
0,4
|
3,16
|
|
0,8
|
5,89
|
|
0,8
|
2,5
|
|
|
0,29
|
2,56
|
|
0,69
|
4,94
|
|
0,69
|
2,21
|
|
|
0,2
|
2,21
|
|
0,61
|
3,87
|
|
0,61
|
1,91
|
|
|
0,0
|
1,26
|
|
0,48
|
1,91
|
|
0,47
|
1,55
|
|
8,83
|
0,99
|
10,9
|
|
0,4
|
1,32
|
|
0,4
|
1,38
|
|
|
0,89
|
9,68
|
13,7
|
0,99
|
5,89
|
19,6
|
0,99
|
2,62
|
|
|
0,8
|
8,44
|
|
0,88
|
5,59
|
|
0,89
|
2,39
|
|
|
0,69
|
6,78
|
|
0,79
|
5,06
|
|
0,8
|
2,21
|
|
|
0,61
|
5,23
|
|
0,68
|
4,11
|
|
0,69
|
1,91
|
|
|
0,49
|
3,28
|
|
0,61
|
3,45
|
|
0,6
|
1,79
|
|
|
0,4
|
2,56
|
|
0,48
|
1,73
|
|
0,47
|
1,5
|
|
|
0,3
|
2,21
|
|
0,41
|
1,32
|
|
0,4
|
1,26
|
|
|
0,2
|
1,97
|
14,7
|
0,99
|
5,17
|
20,6
|
0,99
|
2,21
|
|
|
0,01
|
1,32
|
|
0,88
|
4,94
|
|
0,88
|
2,03
|
|
9,81
|
0,99
|
9,8
|
|
0,8
|
4,34
|
|
0,8
|
1,85
|
|
|
0,89
|
8,79
|
|
0,69
|
3,51
|
|
0,7
|
1,73
|
|
|
0,79
|
7,73
|
|
0,61
|
2,92
|
|
0,6
|
1,61
|
|
|
0,69
|
6,24
|
|
0,48
|
1,67
|
|
0,47
|
1,44
|
|
|
0,61
|
4,88
|
|
0,4
|
1,26
|
|
0,4
|
1,2
|
|
|
0,5
|
2,92
|
15,7
|
0,99
|
4,52
|
21,6
|
0,99
|
1,73
|
|
|
0,4
|
2,09
|
|
0,88
|
3,93
|
|
0,89
|
1,61
|
|
|
0,29
|
1,79
|
|
0,8
|
3,45
|
|
0,8
|
1,61
|
|
|
0,2
|
1,67
|
|
0,68
|
2,86
|
|
0,69
|
1,5
|
|
|
0,01
|
1,26
|
|
0,61
|
2,44
|
|
0,61
|
1,44
|
|
10,8
|
0,99
|
8,62
|
|
0,47
|
1,67
|
|
0,47
|
1,38
|
|
|
0,88
|
7,9
|
|
0,41
|
1,26
|
|
0,4
|
1,26
|
|
|
0,79
|
7,01
|
|
|
|
|
|
|
Потери давления на трение при течении двухфазного потока в
необогреваемых трубах с внутренним диаметром dвн ≤
17·10-3 м рассчитываются по формуле [2]:
где (ΔРтр/ΔРо)
находится по таб. 3.1.4.1;
ΔРо
рассчитывается по формуле (3.1.4.71);
а = -4(b -
1)X2 + 4(b -
1)X + 1;
b = 3,10 - 124dвн;
а = 1
при Р ≥ 17,7 МПа.
Пределы
применимости формулы: Р = 6,86 ÷ 22 МПа;
ρw =
500 ÷ 3000 кг/м2·с; X = 0
÷ 1,0; dвн = (4 ÷ 17)·10-3 м.
Погрешность
δ расчета ΔР составляет ±25 %.
Потери давления на трение
при течении двухфазного потока в обогреваемых трубах рассчитываются по формуле
[8]:
где  - рассчитывается по
формулам (3.1.4.70) и (3.1.4.72).
- рассчитывается по
формулам (3.1.4.70) и (3.1.4.72).
Пределы
применимости формулы (3.1.4.73):
Р = 6,86 ÷ 22 МПа;
ρw =
500 ÷ 3000 кг/м2·с; q = (0 ÷ 1,5)·106
Вт/м2; Х = 0 ÷ 1,0;
dвн = (4 ÷ 30)·10-3 м.
Погрешность
δ расчета ΔРтр составляет ±25 %.
В
формулах (3.1.4.71), (3.1.4.72) и (3.1.4.73):
ΔР в
[МПа]; Р в [МПа]; ΔL в [м]; ρw в [кг/(м2·с)];
X -
массовое паросодержание; dвн в [м]; q в [Вт/м2];
v' -
коэффициент кинематической вязкости воды на линии насыщения, м2/с;
ρ' -
плотность воды на линии насыщения, кг/м3.
3.1.4.3.2. Гидравлические сопротивления трения при течении
двухфазного потока в стержневых сборках
Потери давления на трение
при течении двухфазного потока в сборках гладких необогреваемых стержней
(адиабатное течение) рассчитываются по формуле [9]:
где ξо =
0,86Re-0,36, ξсм = f1f2f3f4;
f1 = 1,50s/dвн - 0,73;
f2 = 0,25 + 1,7{1 - 10(P - 1)[16,4 + 9,15(P - 1)]-1};
f3 = 3,1X(1 - Х)-1, f4 = wо0,60;
wо = ρw/ρ'
- скорость циркуляции;
Re = wоdг/v'.
В
формуле (3.1.4.74): P
в [МПа]; ρw в [кг/м2·с]; dг в [м]; L
в [м]; v' в [м2/с]; μ' в [кг/(м·с)]; ρ'
в [кг/м3]; dн в [м]; v', μ', ρ'
- на линии насыщения.
Пределы
применимости формулы (3.1.3.74): Р = 1 ÷ 12 МПа;
ρw =
500 ÷ 3000 кг/м2·с; Х = 0 ÷ 0,90; s/dн
= 1,077 ÷ 1,308.
Погрешность
δ расчета ΔРтр составляет ±25 %.
Потери давления на трение
при течении двухфазного потока в сборках гладких обогреваемых стержней
рассчитываются по формуле [10]:
|

|
(3.1.4.76)
|
|

|
(3.1.4.77)
|
ξ = ξоη;
ξо рассчитывается по формуле (3.1.3.1), в которой
Re = wоdг/v';
|

|
(3.1.4.78)
|
|

|
(3.1.4.79)
|
|

|
(3.1.4.80)
|
ε = sc/(f + sc) - плотность пучка, доля площади канала, занятая трубами
(стержнями, твэлами);
f - проходное сечение стержневой сборки;
sc - сечение сборки, занятое
стержнями;
wо = ρw/ρ'
- скорость циркуляции, м/с;
 - для стержневых сборок, в
которых s/dн > 1,20;
- для стержневых сборок, в
которых s/dн > 1,20;
для стержневых сборок, в
которых ε → 1:
|

|
(3.1.4.81)
|
Пределы применимости формулы
(3.1.4.75) не указаны.
Погрешность
δ расчета ΔРтр составляет ±25 %.
3.1.4.3.3. Местные гидравлические сопротивления при течении
двухфазных потоков
Гидравлическое сопротивление
дистанционирующих решеток (оценочные расчеты) рассчитывается по формуле из [11]:
|
ξп =
ξкв + 3400m-1,50Re-1;
|
|
|
ξкв =
[(1 - m)/2m2]
+ [(1/m) - 1]2 + ξр(hр/dр)m-2 - 0,036;
|
|
|
ξр = [1,74 - 2lg(3,5·10-2/dр)]2;
|
|
dp = 4fp/P
- гидравлический диаметр решетки, м;
m = fз/fп;
fз = fп - fp - сечение
загромождения;
fр - проходное сечение решетки;
fп - проходное сечение пучка стержней;
hр - высота решетки.
Влияние интенсификаторов
теплосъема на ΔРдр проявляется через ξкв.
При отсутствии в решетке интенсификаторов теплосъема ξкв
= 0,5. В формуле (3.1.4.82):
Пределы применимости
формулы: Р = 2 ÷ 13 МПа;
ρw =
500 ÷ 3000 кг/м2·с.
Погрешность
δ расчета ΔРдр составляет ±30 %.
Оценочные расчеты потерь
давления при течении пароводяного потока высокого давления через местные
сопротивления (диафрагмы, внезапные сужения, расширения, вход из большого объем
в канал, выход из канала в большой объем) рекомендуется проводить по формуле [12]:
где ΔРм - потери давления двухфазного
потока при течении через местное сопротивление, МПа;
Ро -
потери давления при течении воды, нагретой до температуры насыщения, через
местное сопротивление при таких же режимах (Р, ρw) и
геометрических размерах, как и при течении двухфазного потока;
Р -
давление, МПа;
X -
массовое паросодержание;
к -
параметр, зависящий от вида местного сопротивления:
к =
1,20 - для местных сопротивлений типа «диафрагма»;
к =
0,62 - для местных сопротивлений типа «сужение потока»;
к =
1,80 - для местных сопротивлений типа «расширение потока»;
к =
0,72 - для местных сопротивлений типа «вход из большого объема в канал»;
к
=1,60 - для местных сопротивлений типа «выход из канала в большой объем»;
ΔРо
рассчитывается по формуле:
|

|
(3.1.4.84)
|
где ξм - коэффициент потерь давления на
местном сопротивлении;
ξм =
(1 - n2) - для местного сопротивления типа «расширение потока»;
n = d12/d22;
d1 -
диаметр канала до местного сопротивления, м;
d2 -
диаметр канала после местного сопротивления, м;
ξм = 1
- для местного сопротивления типа «выход из канала в большой объем».
Коэффициент потерь давления ξм
для местного сопротивления типа «диафрагма» рассчитывается по формуле:
|

|
(3.1.4.85)
|
|
τ =
0,4exp(-bо)
+ 0,93exp(-bо3,5/0,44)
- 0,001exp[1,566bо2(1
- 0,1033bо2)];
|
|
λ =
0,02 - приведенный коэффициент сопротивления трения о стенки отверстия;
bо = Lо/dо
- относительная глубина отверстия диафрагмы;
dо -
эквивалентный гидравлический диаметр отверстия диафрагмы, м;
Lо -
толщина диафрагмы, м;
 - отношение площадей
проходного сечения каналов в местном сопротивлении и перед ним.
- отношение площадей
проходного сечения каналов в местном сопротивлении и перед ним.
Пределы
применимости формулы (3.1.4.83):
Р = 4,91 ÷ 19,62 МПа.
Погрешность
δ расчета ΔРм составляет ±30 %.
3.1.4.3.4. Гидравлическое сопротивление на ускорение
и нивелирный напор при течении двухфазного потока
Потерями
давления на ускорение при течении двухфазного потока в необогреваемых каналах,
как правило, пренебрегают.
Потери давления на ускорение
при течении двухфазного потока в обогреваемых каналах рассчитываются по формуле
[4]:
|
ΔРуск =
(ρw)(wсм,вых - wсм,вх),
|
(3.1.4.86)
|
где wсм,вых = ρw/ρсм,вых;
wсм,вх = ρw/ρсм,вх;
ρсм = (1 - φ)ρ'
+ φρ";
φ
рассчитывается по формулам раздела 3.1.4.2.1.
При P > 13,0 МПа влияние плотности теплового потока не учитывается и
φ рассчитывается по формуле:
|

|
(3.1.4.87)
|
где
dвн -
внутренний диаметр трубы, м.
Погрешность
δ расчета ΔРуск составляет ±25 %.
Нивелирный напор при течении
двухфазного потока в каналах рассчитывается по формуле [4]:
|
ΔРнив =
ΔL[(1 - φ)ρ' +
φρ'']g
|
(3.1.4.88)
|
где φ рассчитывается для трубы по формулам раздела 3.1.4.2.1.
Погрешность
δ расчета ΔРнив составляет ±20 %.
Перепад давления на
дроссельной шайбе в двухфазном потоке рассчитывается по формуле [13]:
где
ξ -
коэффициент гидравлического сопротивления для однофазного потока.
3.1.4.4. ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ ПРИ ПЛЕНОЧНОЙ
КОНДЕНСАЦИИ ПАРА В КАНАЛАХ
3.1.4.4.1. Гидравлические сопротивления при пленочной конденсации
пара в горизонтальных трубах
При пленочной конденсации
пара в горизонтальных трубах величина гидравлического сопротивления [14] рассчитывается по формуле:
где ΔРтр - потери давления на трение, МПа;
ΔРуск -
потери давления на ускорение, МПа.
Потери давления на трение
рассчитываются по формуле:
где
ξ -
коэффициент гидравлического сопротивления трения при пленочной конденсации пара
в горизонтальных трубах.
Коэффициент
гидравлического сопротивления трения рассчитывается:
■ при Re ≤
7·104 по формуле:
|

|
(3.1.4.91)
|
где  ; wо -
скорость циркуляции в трубе, м/с;
; wо -
скорость циркуляции в трубе, м/с;
■ при Re ≥
7·104 по формуле:
|

|
(3.1.4.92)
|
C1 =
0,0091; С2 = 0,45 при входе в горизонтальную трубу сухого
насыщенного пара (Хвх = 1);
C1 =
0,0121; С2 = 0,60 при входе в трубу пароводяной смеси (0,86
> Хвх > 0,26);
ξо -
коэффициент гидравлического сопротивления трения при течении в трубе однофазной
среды на линии насыщения, рассчитывается:
при 4·103 < Re
≤ 105 по формуле:
|

|
(3.1.4.93)
|
при 4·103 < Re ≤
1012 по формуле:
|

|
(3.1.4.94)
|
где 
Пределы применимости
формулы: dвн = 10 ÷ 17мм; L = 2,5 ÷ 12м;
q =
(140 ÷ 1300)·103 Вт/м2; ρw > 100
кг/м2·с; 1,0 > Хвх > 0,26.
Погрешность
δ расчета ΔРтр составляет ±15 %.
Потери давления на ускорение
рассчитываются по формуле:
|

|
(3.1.4.95)
|
где  ,
,  - скорости циркуляции на
входе и выходе из трубы, м/с.
- скорости циркуляции на
входе и выходе из трубы, м/с.
Погрешность
δ расчета ΔРуск составляет ±10 %.
Погрешность
δ расчета полного гидравлического сопротивления по формуле (3.1.4.89) составляет ±25 %.
Пределы
применимости формулы те же, что и формулы (3.1.4.90).
3.1.4.4.2. Гидравлические сопротивления при пленочной
конденсации пара в вертикальных трубах
Гидравлическое сопротивление
при полной пленочной конденсации пара в вертикальной трубе рассчитывается по
формуле [14]:
где ΔРнив - нивелирная составляющая
сопротивления, Па;
ΔРуск -
потери давления на ускорение, Па;
ΔРтр -
потери давления на трение, Па.
Нивелирная составляющая
сопротивления рассчитывается по формуле:
где  - среднее по длине трубы
истинное объемное паросодержание;
- среднее по длине трубы
истинное объемное паросодержание;
 - средняя по длине трубы
толщина пленки конденсата, м;
- средняя по длине трубы
толщина пленки конденсата, м;
 - средний по длине трубы
коэффициент теплоотдачи при конденсации пара рассчитывается по формуле, Вт/м2·К:
- средний по длине трубы
коэффициент теплоотдачи при конденсации пара рассчитывается по формуле, Вт/м2·К:
где  - число Рейнольдса пленки
конденсата в выходном сечении трубы;
- число Рейнольдса пленки
конденсата в выходном сечении трубы;
А -
безразмерный параметр, определяемый по формуле:
 - число Галилея;
- число Галилея;
q = qп
+ qф - плотность теплового потока на стенке трубы, Вт/м2;
 - плотность теплового
потока за счет теплоты фазового перехода, Вт/м2;
- плотность теплового
потока за счет теплоты фазового перехода, Вт/м2;
 - плотность теплового
потока за счет перегрева пара, Вт/м2;
- плотность теплового
потока за счет перегрева пара, Вт/м2;
 - относительная величина
плотности теплового потока за счет перегрева пара;
- относительная величина
плотности теплового потока за счет перегрева пара;
Δiпп = iпп - i' - энтальпия перегрева пара на входе в трубу, Дж/кг;
iпп - энтальпия перегретого пара на входе в трубу, Дж/кг;
i' -
энтальпия насыщенного пара на входе в трубу, Дж/кг;
Xвых - массовое расходное паросодержание в выходном сечении трубы;
G -
массовый расход пара на входе в трубу, кг/с.
Теплофизические
свойства определяются при температуре насыщения пара на входе в трубу.
Пределы
применимости формулы (3.1.4.97):
Р =
0,1 ÷ 9 МПа; L = 0,5 ÷ 7 м; dвн = 5
÷ 30 мм;
Хвх =
1; Хвых = 0 ÷ 0,7; Δiпп/r = 0 ÷ 0,20; tст ≤
tнаc.
Погрешность
δ расчета ΔРнив составляет ±15 % .
Потери давления на ускорение
рассчитываются по формуле:
|

|
(3.1.4.99)
|
где  - истинное объемное
паросодержание в выходном сечении трубы;
- истинное объемное
паросодержание в выходном сечении трубы;
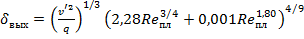 - толщина пленки конденсата
в выходном сечении трубы при полной конденсации пара, м.
- толщина пленки конденсата
в выходном сечении трубы при полной конденсации пара, м.
Погрешность
δ расчета ΔРуск составляет ± 10%.
Потери давления на трение
рассчитываются по формуле:
|

|
(3.1.4.100)
|
где τст = KNu⁎-1 при τстK
< 7,50;
τст =
1163KNu⁎2,50 при τстK = 7,5
÷ 485;
τст =
976,5KNu⁎2 при τстK
> 485;
 рассчитывается по формуле (3.1.4.98);
рассчитывается по формуле (3.1.4.98);
K = ρ'(v'g)2/3(Рr')-1/2.
Пределы
применимости формулы:
K = 0,084 ÷ 0,150; Р/Ркр = 4·10-3
÷ 3,5·10-1;
dвн = 5
÷ 30 мм, Хвх = 1, Хвых = 0.
Погрешность
δ расчет ΔРтр составляет ±15 %.
Погрешность
δ расчета ΔР по формуле (3.1.4.96) составляет ±25 %.
Гидравлическое сопротивление
при полной пленочной конденсации пара в вертикальной трубе (оценочные расчеты) рассчитывается
по формуле:
|

|
(3.1.4.101)
|
где  - критерии Эйлера;
- критерии Эйлера;
 ; ρw в [кг/м2·с];
ΔР в [Па].
; ρw в [кг/м2·с];
ΔР в [Па].
Пределы
применимости формулы:
Р = 1
÷ 5 МПа; ρw = 10 ÷ 500 кг/м2·с;
dвн = 10 ÷ 13,2 мм; L = 3 м.
Погрешность
δ расчета ΔР составляет ±30 %.
Гидравлическое сопротивление
при конденсации быстродвижущегося пара (ρw > 400 кг/м2
с) внутри вертикальных труб на участке длиной ΔL = Lвх
- Lвых, где X изменяется от Хвх до Хвых,
рассчитывается по формуле (3.1.4.96),
в которой:
|

|
(3.1.4.102)
|
|
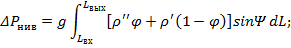
|
(3.1.4.103)
|
|

|
(3.1.4.104)
|
ξо -
коэффициент гидравлического сопротивления трения при течении в трубе
однофазного потока при температуре насыщения и заданной массовой скорости;
ξо -
рассчитывается по формулам раздела 3.1.3;
Ψ -
угол наклона трубы к горизонту.
Истинное
объемное паросодержание рассчитывается по формулам адиабатического течения
пароводяной смеси в трубах.
Пределы
применимости формул: Р = 0,4 ÷ 21,6 МПа;
ρw =
400 ÷ 4000 кг/м2·с; dвн = 2,85 ÷
10,0 мм; q = 2·104 ÷ 107 Вт/м2.
Погрешность
δ расчета ΔР составляет ±25 %.
Список литературы к разделу 3.1.4
1. Кириллов П.Л., Смогалев И.П., Дорошенко В.А. Графический метод
расчета потерь давления на трение при подъемном течении пароводяного потока в
круглых трубах. - Теплоэнергетика, 1982, № 3, с. 73 - 75.
2. Кириллов П.Л., Смогалев И.П., Дорошенко В.А., Суворов М.Я.
Методика гидравлического расчета вертикального парогенерирующего канала. -
Теплоэнергетика, 1980, № 2, с. 71 - 74.
3. Ивашкевич А.А. Начало интенсивного парообразования в трубе.
Теплоэнергетика. 1992, № 1, с. 66 - 67.
4. Миропольский З.Л., Шнеерова Р.И., Карамышева А.И. Паросодержание
при напорном движении пароводяной смеси с подводом тепла и в адиабатических
условиях. - Теплоэнергетика, 1971, № 5, с. 60 - 63.
5. Громова И.И., Есиков В.И., Карамыслов А.В., Смолин В.Н. Методика
расчета истинного объемного паросодержания в парогенерирующих трубах. -
Теплофизика-86. Теплотехническая безопасность ядерных реакторов ВВЭР. В сб.:
Доклады семинара СЭВ. Росток, ГДР, 1986, том 1, с. 410 - 415.
6. Громова И.И., Есиков В.И., Смолин В.Н. Границы и средняя
температура жидкой фазы термически неравновесного потока в парогенерирующих
трубах. В кн.: Теплофизика-84. Сборник докладов семинара СЭВ. Варна, НРБ, 1984.
М.: 1985, т. 2, с. 166 - 168.
7. Thermohydraulic Relationships for
advanced water cooled reactors. Vienna: IAEA. 2001.
IAEA-TECDOC-1203.
8. Тарасова H.B. Гидродинамическое сопротивление при кипении воды и
пароводяной смеси в трубах и кольцевых каналах. - Труды ЦКТИ, 1965, № 59, с. 47
- 58.
9. Методика и зависимости для теоретического расчета теплообмена и
гидравлического сопротивления теплообменного оборудования АЭС.
РТМ-24.031.05-72. М.: 1972.
10. Осмачкин В.С. Исследование теплогидравлических характеристик
топливных сборок реакторов в ИАЭ им. И.В. Курчатова Сб. докладов СЭВ:
Исследование критических тепловых потоков в пучках стержней в стационарных и
нестационарных режимах теплообмена. - М.: 1974, с. 9 - 41.
11. Боришанский В.М. и др. К расчету гидравлики местных сопротивлений
в двухфазном потоке. - Труды ЦКТИ, 1975, вып. 139.
12. Смогалев И.П., Дорошенко В.А. Расчет потерь давления при течении
пароводяного потока через местные сопротивления. - Теплоэнергетика, 1984, № 5,
с. 72 - 74.
13. Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по
теплогидравлическим расчетам (ядерные реакторы, теплообменники,
парогенераторы). М.: Энергоатомиздат, 1990.
14. Тепловой и гидравлический расчет теплообменного оборудования АЭС.
РД 24.035.05-89. Л.: НПО ЦКТИ, 1991.
3.2. ТЕПЛООБМЕН
3.2.1.
КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
В ОДНОФАЗНОЙ СРЕДЕ
Коэффициенты
теплообмена (числа Нуссельта) в каналах с проходным сечением сложного профиля в
общем случае зависят от характеристик конструкции твэла (внутренней «начинки»
твэла). Это: толщина и теплопроводность оболочки, толщина и теплопроводность
различных промежуточных слоев, геометрия и теплопроводность тепловыделяющего
материала, схемы расположения твэла в сборке и др. Особенно это важно для
тесных сборок (пучков) при (Х < 1,1) или для эксцентричных кольцевых
каналов, где проходное сечение сильно неоднородно по периметру и тепловой поток
вынужден перераспределяться по периметру теплообмена. Эти факторы определяют
эффективную теплопроводность твэла. Количественно эффективную теплопроводность
твэла или его модели в эксперименте отражает параметр приближенного теплового
моделирования εko, введенный Ушаковым П.А. [1]. В настоящем документе этот
параметр широко (см. раздел 3.2.2) используется в формулах для чисел Нуссельта.
Его влияние существенно. Его использование позволяет перенести результаты
экспериментальных исследований (которые проводятся на моделях твэлов,
выполненных в виде труб, через которые пропускается электрический ток) на
натурные сборки твэлов любой конструкции. Основное условие, которое следует
соблюдать, εko = idem. Поэтому в
разделе 3.2.2
приводится подробная информация по расчету этого параметра для многих случаев.
3.2.1.1. ТЕПЛООБМЕН ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ В КАНАЛАХ
Задачи
о теплообмене при ламинарном течении рассматриваются в предположении, что:
■
течение и теплообмен стационарные;
■
жидкость несжимаема, ее физические свойства не зависят от температуры;
■
течение жидкости гидродинамически стабилизировано;
■
во входном сечении теплообменного участка температура жидкости постоянна по
сечению;
■
на поверхности теплообмена задана постоянная плотность теплового потока;
■
в потоке отсутствуют внутренние источники тепла;
■
изменение плотности теплового потока вдоль оси за счет теплопроводности мало по
сравнению с изменением плотности вдоль оси, обусловленной конвекцией.
Интенсивность
конвективной теплоотдачи жидкостей и газов при ламинарном течении определяется
коэффициентом теплоотдачи, который, как правило, относится к разнице температур
стенки и средней температуры среды: α = q/(tст
- tж). Коэффициент теплоотдачи обычно определяется через число
Нуссельта: α = Nuλ/dг, где dг
- гидравлический диаметр канала. Теплофизические свойства относятся, как
правило, к среднемассовой температуре потока в данном сечении. При вычислении
среднего по длине коэффициента теплоотдачи свойства относят к средней
температуре потока: tж = (tвх + tвых)/2.
3.2.1.1.1. Теплообмен при ламинарном течении в трубах
Теплообмен при ламинарном
течении в трубах [2] при
постоянном тепловом потоке на стенке рассчитывается по формуле (для Re
< Reкр):
Погрешность Δ
расчета Nu практически равна нулю.
Теплообмен в плоских трубах
при постоянном тепловом потоке с двух сторон рассчитывается по формуле (для Re
< Reкр):
Погрешность расчета Nu
практически равна нулю.
3.2.1.1.2. Теплообмен при ламинарном течении в кольцевых каналах
Теплообмен при ламинарном
течении в кольцевых каналах при двухстороннем постоянном по длине тепловом
потоке (или с одной стороны подвод тепла, а с другой отвод, или наоборот) с
произвольным отношением плотностей тепловых потоков q1 и q2
рассчитывается по формуле [3]:
где i - номер поверхности кольцевого канала;
i = 1 - относится к внутренней поверхности зазора кольцевого
канала;
i = 2 - к наружной поверхности;
Q = q2/q1;
 - число Нуссельта для
внутренней поверхности кольцевого зазора при отсутствии теплового потока на
противоположной поверхности;
- число Нуссельта для
внутренней поверхности кольцевого зазора при отсутствии теплового потока на
противоположной поверхности;
|
Nu1q = 4,25 + 1,13θ-0,083.
|
|
Пределы применимости
формулы: θ = 0,1 ÷ 1,0.
Погрешность
δ расчета Nu1q составляет ±2 %.
 - число Нуссельта для
внешней поверхности зазора кольцевого канала при отсутствии теплового потока на
внутренней поверхности, Nu2q = 4,36 + θ-0,20.
- число Нуссельта для
внешней поверхности зазора кольцевого канала при отсутствии теплового потока на
внутренней поверхности, Nu2q = 4,36 + θ-0,20.
Пределы
применимости формулы: θ = 0
÷ 1,00.
Погрешность
δ расчета Nu2q составляет ±5 %.
Пределы
применимости формулы (3.2.1.3):
θ = 0 ÷ 1,00.
Погрешность
δ расчета Nui
составляет ±5 %.
3.2.1.2.
ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ
В КАНАЛАХ ПРИ PR ≥ 1
(НЕКИПЯЩАЯ ВОДА, КАПЕЛЬНЫЕ ЖИДКОСТИ)
В
разделе приводятся соотношения для расчета температурных режимов при
стационарном стабилизированном турбулентном течении теплоносителей (газы, вода,
водяной пар и др.) в гладких каналах различного поперечного сечения. В
стержневых сборках средние числа Нуссельта и температурные неравномерности
зависят не только от чисел Рейнольдса, Прандтля, степени неизотермичности
потока, но и от параметра приближенного теплового моделирования.
Интенсивность
конвективной теплоотдачи, как и при ламинарном течении, определяется
коэффициентом теплоотдачи, который, как правило, относится к разнице температур
стенки и средней температуры среды:  . Коэффициент теплоотдачи
определяется обычно через число Нуссельта: α = Nuλ/dг,
где dг - гидравлический диаметр канала. Теплофизические
характеристики относятся, если иное не предусмотрено, к средней массовой
температуре потока в данном сечении канала. При вычислении среднего по длине
коэффициента теплоотдачи свойства относятся к средней температуре потока: tж = (tвх + tвых)/2.
. Коэффициент теплоотдачи
определяется обычно через число Нуссельта: α = Nuλ/dг,
где dг - гидравлический диаметр канала. Теплофизические
характеристики относятся, если иное не предусмотрено, к средней массовой
температуре потока в данном сечении канала. При вычислении среднего по длине
коэффициента теплоотдачи свойства относятся к средней температуре потока: tж = (tвх + tвых)/2.
3.2.1.2.1. Теплообмен при турбулентном течении в трубах
Теплообмен при турбулентном
течении и небольших плотностях тепловых потоков (когда еще нет влияния на
теплообмен неизотермичности через естественную конвекцию и переменность свойств
теплоносителя) в трубах рассчитывается по формуле [4]:
где
K1 = 1 + 900/Re; K2
= 12,7.
Коэффициент гидравлического
сопротивления трения рассчитывается:
Пределы применимости
формулы: Re = 4·103 ÷ 5·106; Рr = 0,5 ÷ 5,0.
Погрешность
расчета Nu составляет σ = 3 - 5 %.
Формула
(3.2.1.4) применима также для
расчета среднего по длине теплообмена при турбулентном течении в трубах с
относительной длиной L/dвн > 50.
Коэффициент турбулентного
переноса тепла по сечению трубы рассчитывается по формуле [5]:
|

|
(3.2.1.6)
|
где Y = y/rвн; у -
расстояние от стенки трубы по нормали; wо - максимальная по
сечению трубы скорость теплоносителя, м/с;  - средняя по сечению трубы
скорость теплоносителя, м/с; rвн -
внутренний радиус трубы, м.
- средняя по сечению трубы
скорость теплоносителя, м/с; rвн -
внутренний радиус трубы, м.
Пределы
применимости формулы: Re = 3·103 ÷ 5·105; Рr = 0 ÷ 100.
Погрешность
δ расчета αТ составляет ±8 %.
Турбулентное число Прандтля
по сечению трубы рассчитывается по формуле [6]:
|

|
(3.2.1.7)
|
Пределы применимости
формулы: Re = 104 ÷ 105; Рr = 0 ÷ 100.
Погрешность
δ расчета РrТ
составляет ±7 %.
3.2.1.2.2. Теплообмен при турбулентном течении
в концентрических кольцевых каналах при Рr~ > 1
Теплообмен
при турбулентном течении в концентрических кольцевых каналах с двусторонним
обогревом рассчитывается [7]:
■ на внутренней стенке
зазора кольцевого канала по формуле:
■ на наружной стенке зазора кольцевого канала по формуле:
где Nu1q
и Nu2q - значения чисел Нуссельта при одностороннем
обогреве:
 и
и  - значения температур
адиабатных (необогреваемых) поверхностей при одностороннем обогреве:
- значения температур
адиабатных (необогреваемых) поверхностей при одностороннем обогреве:
θ = r1/r2 -
отношение внутреннего радиуса зазора кольцевого канала к внешнему;
Q = q2/q1;
Nu -
число Нуссельта при турбулентном течении в трубе с внутренним диаметром dвн
= dг = 2(r2 - r1) и
такими же, как в кольцевом канале, значениями Re и Pr; Nu
- рассчитывается по формуле (3.2.1.4).
Пределы
применимости формул:
θ =
0,03 ÷ 1,00; Рr =
0,7 ÷ 100; Rе =
104 ÷ 106.
Погрешность
σ расчета Nu1, Nu2 составляет 3
%.
3.2.1.2.3. Теплообмен при турбулентном течении в сборках
стержней треугольной упаковки при Pr ≥ 1
Теплообмен при турбулентном
течении в стержневых сборках при Х = 1,1 ÷ 1,8 рассчитывается по
формуле [8]:
|
где А1 =
0,0165 + 0,02[1 - 0,91/X2]X0,15; X = S/dн.
|
(3.2.1.11)
|
Пределы применимости
формулы:
Х =
1,1 ÷ 1,8; Рr =
0,7 ÷ 20; Re = 5·103 ÷ 5·105.
Погрешность
расчета Nu составляет σ = 5 %.
Теплообмен
при турбулентном течении в сборках твэлов с малыми шагами: Х = 1,015
÷ 1,06.
В этом случае имеется
существенная зависимость теплообмена от параметра приближенного теплового
моделирования, рассчитывается по формуле [9]:
|
Nu = A2Re0,8Pr0,4,
|
(3.2.1.12)
|
где A2 = A1(1 + 0,103lgεкo); А1 рассчитывается по формуле (3.2.1.11).
Пределы
применимости формулы: Х = 1,015 ÷ 1,06; Re = 5·103
÷ 5·105;
Рr = 0,7 ÷ 20,0; εкo = 7 ÷ 600.
Погрешность
σ расчета Nu
составляет 10 %.
Теплообмен при турбулентном
течении в стержневых сборках в широком диапазоне изменения X с учетом
влияния параметра приближенного теплового моделирования рассчитывается по
формуле [10]:
|
Nu = ARe0,8Pr0,4,
|
(3.2.1.13)
|
где 
Пределы
применимости формулы: Re = 104 ÷ 5·105; εкo = 7 ÷ 600;
X = 1
÷ 2.
Погрешность
δ расчета Nu составляет ±20 %.
Максимальная неравномерность
температуры оболочки твэла в сборке стержней плотной упаковки рассчитывается по
формуле [10]:
|

|
(3.2.1.14)
|
где  в [К];
в [К];  в [Вт/м2]; rн в [м]; λ в [Вт/м·К].
в [Вт/м2]; rн в [м]; λ в [Вт/м·К].
Пределы
применимости формулы:
Х =
1,00 ÷ 1,06; εкo = 7
÷ 600; Re = 6·103 ÷ 4·104.
Погрешность
расчета σ = 7 %.
Параметр
приближенного теплового моделирования твэлов рассчитывается [1]:
■ для цилиндрического
твэла с тремя оболочками (рис. 3.2.1.1)
по формуле:
где 
K = 6 - для сборки твэлов треугольной упаковки;
K = 4 - для сборки твэлов квадратной упаковки;
■ для цилиндрического
твэла с двумя оболочками (рис. 3.2.1.2)
по формуле:
|

|
(3.2.1.16)
|
где 

Рис. 3.2.1.1. Поперечное
сечение цилиндрического твэла с тремя оболочками

Рис. 3.2.1.2. Поперечное
сечение цилиндрического твэла с двумя оболочками

Рис. 3.2.1.3. Поперечное
сечение цилиндрического твэла с одной оболочкой
■ для цилиндрического
твэла с одной оболочкой (рис. 3.2.1.3) по формуле:
|

|
(3.1.1.17)
|
где 
■ для цилиндрического твэла без оболочки (рис. 3.2.1.4) по формуле:
|

|
(3.2.1.18)
|
■ для кольцевого твэла с оболочкой и контактным термическим
сопротивлением Ф (рис. 3.2.1.5)
по формуле:
|

|
(3.2.1.19)
|
где 
■ для цилиндрического
твэла с оболочкой и контактным термическим сопротивлением Ф (рис. 3.2.1.6) по формуле:
где 
В
формулах (3.2.1.15) ÷
(3.2.1.20):
λi (i
= 1, 2, 3, 4) - коэффициенты теплопроводности оболочек твэла, Вт/м·°С;
λ -
коэффициент теплопроводности теплоносителя, Вт/м·°С;
Ф -
контактное термическое сопротивление, Вт/м2·°С;
Ri (i = 1, 2, 3, 4) - внутренние радиусы оболочек твэла, м;
rо - радиус внутреннего кольца, м;
k = 6 - для сборки стержней треугольной упаковки;
k = 4- для сборки стержней квадратной упаковки;
λо -
коэффициент теплопроводности топлива, Вт/м·°С.

Рис. 3.2.1.4. Поперечное
сечение цилиндрического твэла без оболочки

Рис. 3.2.1.5. Поперечное
сечение кольцевого твэла с оболочкой и контактным
термическим сопротивлением

Рис. 3.2.1.6. Поперечное
сечение цилиндрического твэла с оболочкой и контактным
термическим сопротивлением
3.2.1.3. ТЕПЛООБМЕН НА ВХОДНОМ УЧАСТКЕ ТРУБЫ ПРИ
ТУРБУЛЕНТНОМ ТЕЧЕНИИ
Длина
входного теплового участка при турбулентном течении некипящей воды, газов в
трубе рассчитывается [11]:
■ при Re = 104
÷ 5·104; Рr =
0,7 ÷ 10 по формуле:
|

|
(3.2.1.21)
|
■ при Re = 5 104 ÷ 1,2·105,
Рr = 0,7 ÷ 10 по формуле:
|

|
(3.2.1.22)
|
Погрешность Δ
расчета Lст составляет ±20 %.
Теплообмен на входном
участке круглой трубы при турбулентном течении некипящей воды, газов
рассчитывается по формуле [11]:
Nu
рассчитывается по формуле (3.2.1.4);
Сст -
поправочный коэффициент, который рассчитывается:
■ при L/dвн
≥ 0,6; Re = 4·103 ÷ 5·104; Рr = 0,7 ÷ 1,0 по формуле:
|

|
(3.2.1.24)
|
где L - текущая длина (расстояние от начала обогрева), м;
■ при L/dвн
> 2; Re = 3·10 ÷ 5·104;  по формуле:
по формуле:
|

|
(3.2.1.25)
|
■ при L/dвн > 1; Re = 5·103
÷ 5·104; Pr = 5 ÷ 10 по формуле:
|

|
(3.2.1.26)
|
Погрешность δ
расчета Nuвх составляет ±15 %.
3.2.1.4. ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ ТЕПЛОНОСИТЕЛЕЙ
ОКОЛОКРИТИЧЕСКИХ ПАРАМЕТРОВ СОСТОЯНИЯ
Особенности
теплообмена при околокритических параметрах состояния связаны с сильным
изменением теплофизических свойств среды и температуры а, в первую очередь,
плотности и теплоемкости. Температура, соответствующая максимуму теплоемкости,
называется псевдокритической и обозначается Тm [K].
Роль
естественной конвекции при теплообмене учитывается критериями GrRe-2
или критерием K = (1 - ρст/ρ)GrRe-2,
где 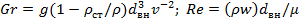 .
.
При K < 0,40 или GrRe-2 < 0,6 имеет место
снижение (ухудшение) теплоотдачи, а при больших значениях этих критериев -
улучшение теплоотдачи.
Теплообмен
при течении теплоносителей околокритических параметров в трубах при нагревании
рассчитывается [10, 11]:
■ при K < 0,01 по формуле:
■ при K > 0,01 по формуле:
где Nuо рассчитывается по формулам (3.2.1.4), (3.2.1.5) при среднемассовой температуре Тж
в сечении канала;
 - среднеинтегральная
теплоемкость в диапазоне (Tст -
Тж);
- среднеинтегральная
теплоемкость в диапазоне (Tст -
Тж);
Ср -
теплоемкость среды, кДж/кг·К;
i -
энтальпия, кДж/кг;
m = 0,30 - для горизонтальных труб и опускного течения в
вертикальных трубах;
m = 0,40 - для подъемного течения в вертикальных трубах;
n = 0,70 при  для подъемного течения в
вертикальных трубах.
для подъемного течения в
вертикальных трубах.
Для  значения показателя степени
n приведены в таблице 3.2.1.1 в зависимости от отношений Tж/Tm;
Tст/Tm.
значения показателя степени
n приведены в таблице 3.2.1.1 в зависимости от отношений Tж/Tm;
Tст/Tm.
Таблица 3.2.1.1
Значения показателя степени п в формулах (3.2.1.27), (3.2.1.28)
|
Область
|
Значения
|
|
Tст/Tm <
1; Tж/Tm >
1,20
|
0,40
|
|
2,6
> Tст/Tm > 1; Tж/Tm < 1
|
0,22 + 0,18(Tст/Tm)
|
|
2,6
> Tст/Tm >
1; 1 < Tж/Tm <
1,20
|
0,9Tж/Tm(1
- Tст/Tm)
+ 1,08Tст/Tm - 0,68
|
Таблица 3.2.1.2
Значения функции (K) в
формуле (3.2.1.34) в
зависимости от величины K
|
K
|
0,01
|
0,02
|
0,04
|
0,06
|
0,08
|
0,10
|
0,20
|
0,40
|
|
φ(K)
|
1,0
|
0,88
|
0,72
|
0,67
|
0,65
|
0,65
|
0,74
|
1,00
|
φ(K) = 140K0,37 при
K > 0,40.
Пределы
применимости формул:
Re =
2·104 ÷ 8·105; ρст/ρ
= 0,09 ÷ 1,00; Pr =
0,85 ÷ 55;
Tж/Tm = 1,0 ÷ 1,2; Tст/Tm = 0,6 ÷ 2,6; 
q = 2,3·104 ÷ 2,6·106
Вт/м2; Р/Ркр = 1,01 ÷ 1,33; L/dвн > 15.
Погрешность
σ расчета Nu составляет 10 %.
При K < 0,01 формула (3.2.1.27)
обобщает режимы с ухудшением теплоотдачи вне зависимости от величины K. Максимальную температуру стенки можно наблюдать в сечениях трубы
с температурой жидкости ниже псевдокритической на несколько градусов.
Вероятно
ухудшение теплоотдачи при K
< 0,01 связано с влиянием переменности теплофизических свойств по сечению
потока на процессы турбулентного переноса.
При K = 0,01 ÷ 0,40 под влиянием естественной конвекции
происходит дополнительное снижение теплоотдачи. Максимальную температуру стенки
можно наблюдают в сечениях трубы, где средняя температура ниже
псевдокритической на 15 ÷ 20 °С и более.
При K ≥ 0,40 снижение
теплоотдачи под влиянием естественной конвекции вырождается и может наступить
улучшение теплоотдачи.
Теплообмен при течении
теплоносителей околокритических параметров в трубах при охлаждении
рассчитывается по формуле [11]:
где Nuо
- рассчитывается по формулам (3.2.1.4),
(3.2.1.5) при среднемассовой
температуре Тж в сечении трубы;
Таблица 3.2.1.3
Значения коэффициентов В, S, m1 в
формуле (3.2.1.29)
|
P/Pкр
|
1,06
|
1,08
|
1,15
|
1,22
|
1,35
|
1,63
|
|
m1
|
0,300
|
0,380
|
0,540
|
0,610
|
0,680
|
0,800
|
|
В
|
0,680
|
0,750
|
0,850
|
0,910
|
0,970
|
1,000
|
|
S
|
0,210
|
0,180
|
0,104
|
0,066
|
0,040
|
0
|
Пределы применимости
формулы:
Re =
9·104 ÷ 4,5·105; q
= 1,4·104 ÷ 1,1·106
Вт/м2;
P/Pкр =
1,06 ÷ 1,63; Tж/Tm = 0,95 ÷ 1,50; Tст/Tm =
0,9 ÷ 1,2.
Погрешность
σ расчета Nu составляет 10 %.
При
расчетах температуры стенки по формулам (3.2.1.27) ÷ (3.2.1.29) приходится прибегать к методу
последовательных приближений. Расчеты упрощаются, если построить зависимости q
= f(Тст) при разных Тж для
заданного давления, диаметра и массовой скорости.
Теплообмен при турбулентном
течении среды в трубе при сверхкритическом давлении при нормальных и ухудшенных
режимах теплосъема рассчитывается по формуле [11]:
|

|
(3.2.1.30)
|
где  - число Стентона.
- число Стентона.
При расчете по формуле
используются две определяющие температуры t1 и t2.
Температура t1 (энтальпия i1),
являющаяся первым приближением к температуре стенки трубы tст,
рассчитывается по формуле [11]:
Температура t2 рассчитывается по формуле [11]:
При температуре t1
определяются ρ1, μ1, β1,
Рr1, а при температуре t2 - Рr, ρ2, i2.
Критерии и коэффициенты
рассчитываются по формулам:
 - параметр ускорения;
- параметр ускорения;
tж -
среднемассовая температура в сечении трубы, °С;
b = 800 - при подъемном течении в обогреваемых трубах;
b = 100 - при опускном течении;
β1 -
коэффициент объемного расширения при температуре;
ξ1 -
коэффициент гидравлического сопротивления трения, который рассчитывается по
формуле (3.1.2.1) при
температуре t1;
g -
кВт/м2.
Влияние
подъемных сил на теплообмен является существенным при Gr > 104PrRe2,8,
а при А > PrRe2,8 104 существенно и
ускорение потока.
Пределы
применимости формулы: L/dвн > 50; Gr/PrRe2,8
≤ 2·10-5.
При Gr/PrRe2,8
= 10-4 ÷ 2·10-5 формула применима для расчета
теплообмена при течении воды, гелия, углекислоты при подъемном и опускном
течении в обогреваемых трубах.
Погрешность
σ расчета St составляет 15 %.
3.2.1.5. ТЕПЛООБМЕН В КАНАЛАХ ПРИ СОВМЕСТНОМ ВЛИЯНИИ
СВОБОДНОЙ И ВЫНУЖДЕННОЙ КОНВЕКЦИИ
При
вынужденном подъёмном течении жидкости в каналах свободная конвекция уменьшает
интенсивность теплоотдачи при малых скоростях движения, заметных разностях
температур и высоких плотностях теплового потока.
Граница
влияния свободной конвекции определяется конкретным значением комплекса Gr/Re2.
Для
описания теплоотдачи при смешанной конвекции используется система безразмерных
критериев Gr/Re2, Re, Pr, L/dвн.
Граница начала влияния
свободной конвекции на теплообмен при вынужденном течении воды в трубах
рассчитывается по формуле [11]:
|

|
(3.2.1.31)
|
где
a -
температуропроводность теплоносителя;
β -
коэффициент объёмного расширения.
При
расчете критериев все теплофизические параметры определяются при температуре
воды на входе в трубу.
Погрешность
δ расчета Kн
составляет ±15 %.
При
указанных ниже значениях комплекса GrA/Re2
и безразмерного расстояния от входа в трубу (L/dвн)ст
теплообмен стабилизируется.
В
этих условиях теплообмен рассчитывается:
■ при K = GrA/Re2 < 2·10-6
по формуле:
|
(Nu/Nuв)ст =
1,
|
(3.2.1.32)
|
где Nuв -
число Нуссельта для чисто вынужденного течения;
■ при 2·10-6 <
K < 10-4 по формуле:
|

|
(3.2.1.33)
|
■ при K
> 10-4 по формуле:
В условиях смешанной
конвекции появляются максимумы в распределении температуры теплоотдающей
поверхности по длине трубы при значениях комплекса K ≥ Kгр.
Комплекс Kгр рассчитывается по формуле:
|
Kгр = 7·10-5[exp(1,1·10-3A)
- 1].
|
(3.2.1.35)
|
При значениях K = Kгр первый максимум температуры находится на безразмерном расстоянии
от входа в трубу:
|

|
(3.2.1.36)
|
При K > Kгр первый максимум температуры смещается к входу в трубу и
рассчитывается по формуле:
|

|
(3.2.1.37)
|
Теплообмен по длине трубы от
сечения с максимальной температурой рассчитывается по формуле:
■ при L/dвн
> Lо/dвн по формуле:
|

|
(3.2.1.38)
|
где T
= 8,56(Lо/dвн)0,46;
■ при L/dвн ≤ Lо/dвн
по формуле:
|

|
(3.2.1.39)
|
где 
Значение безразмерного расстояния от входа в трубу, с которого
наступает установившийся теплообмен рассчитывается по формуле:
|
(L/dвн)ст
= (Lо/dвн) + Т.
|
(3.2.1.40)
|
Пределы применимости
методики: Р = 6 ÷ 18 МПа;
ρw =
150 ÷ 1000 кг/м2·с; dвн = 10 ÷ 25
мм; L ≤ 20 м.
Погрешность
δ расчета Nu составляет ±15 %.
3.2.1.6. ТЕПЛООБМЕН ПРИ ПОПЕРЕЧНОМ ОБТЕКАНИИ ТЕЛ
ТУРБУЛЕНТНЫМ ПОТОКОМ
3.2.1.6.1. Теплообмен при поперечном обтекании турбулентным
потоком одиночного цилиндра и шара
Средний по периметру
коэффициент теплоотдачи при поперечном обтекании одиночного цилиндра (угол
атаки φ = 90°) рассчитывается по формуле [12]:
где
wзгр -
скорость набегающего потока с учетом поправки на степень загромождения
цилиндром канала (скорость потока в самом узком сечении канала, м/с);
 при Kзгр = 0 ÷ 0,827; Reнп = 103
÷ 2·105;
при Kзгр = 0 ÷ 0,827; Reнп = 103
÷ 2·105;
wзгр = wнп(1 + Kзгр)
при Kзгр = 0 ÷ 0,70; Reнп = 105
÷ 2·106;
wнп -
скорость набегающего потока, м/с;

Kзгр = Fзгр/Fкан
- степень загромождения канала цилиндром. Теплофизические свойства определяются
при температуре набегающего потока. Определяющий размер - наружный диаметр
цилиндра.
Таблица 3.2.1.4
Значения констант С и n
формуле (3.2.1.41) для
расчета теплообмена
при поперечном обтекании одиночного цилиндра
|
Reнп
|
С
|
n
|
|
1 ÷ 40
|
0,76
|
0,40
|
|
40 ÷ 1000
|
0,52
|
0,50
|
|
103 ÷ 2·105
|
0,26
|
0,60
|
|
2·105
÷ 107
|
0,023
|
0,80
|
Пределы применимости
формулы:
 ; Тu - степень турбулентности потока,
; Тu - степень турбулентности потока,  .
.
Погрешность
Δ расчета  составляет ±30 %.
составляет ±30 %.
При уменьшении угла атаки (β
= 30° ÷ 90°) средний по периметру коэффициент теплоотдачи при поперечном
обтекании одиночного цилиндра уменьшается и рассчитывается по формуле [12]:
где β - угол атаки;  рассчитывается по формуле (3.2.1.41).
рассчитывается по формуле (3.2.1.41).
Пределы
применимости формулы:  ; β = 30°
÷ 90°.
; β = 30°
÷ 90°.
Погрешность
δ расчета  составляет ±30 %.
составляет ±30 %.
При возрастании степени
турбулентности набегающего потока свыше 1 % средний коэффициент теплоотдачи при
поперечном обтекании одиночного цилиндра рассчитывается по формуле [12]:
где  рассчитывается по формуле (3.2.1.42);
рассчитывается по формуле (3.2.1.42);
K(Тu) -
поправочный коэффициент, значение которого определяется с помощью рис. 3.2.1.7.
Пределы
применимости определяются рис. 3.2.1.7.
Погрешность
δ расчета  составляет ±30 %.
составляет ±30 %.
Средний по периметру
коэффициент теплоотдачи при поперечном обтекании потоком одиночного
эллиптического цилиндра параллельно большой или малой осям рассчитывается по
формуле [12]:
|

|
(3.2.1.44)
|

Рис. 3.2.1.7. Зависимость
коэффициента K(Тu) от степени турбулентности
потока в формуле (3.2.1.43)
Теплофизические
свойства определяются при температуре набегающего потока. Определяющий размер -
диаметр эллиптического цилиндра, параллельный набегающему потоку.
Пределы
применимости формулы: Re = 103 ÷ 2·105.
Погрешность
Δ расчета  составляет ±30 %.
составляет ±30 %.
Средний коэффициент
теплоотдачи при обтекании потоком одиночного шара рассчитывается по формуле [13]:
|

|
(3.2.1.45)
|
где 
wнп - скорость набегающего потока, м/с;
dш -
диаметр шара, м.
Пределы
применимости формулы: Re = 0,3 ÷ 3·105; Рr = 0,7 ÷ 8.
Погрешность
δ расчета  составляет ±10 %.
составляет ±10 %.
3.2.1.6.2.
Теплообмен при поперечном обтекании турбулентным потоком
пучков стержней
Средняя теплоотдача всего
пучка труб (сборки стержней) при поперечном обтекании потоком рассчитывается по
формуле [12]:
где  - средняя теплоотдача одной
трубы в глубинном ряду поперечно обтекаемого пучка труб при β =
90°, где β - угол атаки;
- средняя теплоотдача одной
трубы в глубинном ряду поперечно обтекаемого пучка труб при β =
90°, где β - угол атаки;
Сβ -
коэффициент, учитывающий уменьшение средней теплоотдачи пучка труб из-за
уменьшения угла атаки;
CZ -
коэффициент, учитывающий зависимость средней теплоотдачи пучка труб от числа
рядов пучка.
Средняя
теплоотдача одной трубы в глубинном ряду поперечно обтекаемого шахматного пучка
гладких труб рассчитывается [12]:
■ при Рr ≥ 0,50; Re = 2
÷ 40 по формуле:
■ при Рr ≥ 0,5; Re = 40 ÷ 5·102 по формуле:
|

|
(3.2.1.48)
|
■ при Рr ≥ 0,5; Re = 5·102 ÷ 2·105;
а/b < 2 по формуле:
|

|
(3.2.1.49)
|
■ при Рr ≥ 0,5; Re = 5·102 ÷ 2·105;
а/b > 2 по формуле:
|

|
(3.2.1.50)
|
■ при Рr ≥ 0,5; Re > 2·105 по формуле:
|

|
(3.2.1.51)
|
где а = S1/dн -
поперечный относительный шаг пучка;
b = S2/dн продольный
относительный шаг пучка.
Схема
размещения труб в пучке приведена на рис. 3.1.3.9.
Средняя
теплоотдача одной трубы в глубинном ряду поперечно обтекаемого коридорного
пучка гладких труб рассчитывается [12]:
■ при Рr ≥ 0,5; Re = 2
÷ 102 по формуле:
|

|
(3.2.1.52)
|
■ при Рr ≥ 0,5; Re = 102 ÷ 7·102
по формуле:
|

|
(3.2.1.53)
|
■ при Рr ≥ 0,5; Re = 7·102 ÷ 2·105
по формуле:
|

|
(3.2.1.54)
|
■ при Рr ≥ 0,50; Re > 2·105 по формуле:
|

|
(3.2.1.55)
|
При расчетах по формулам (3.2.1.47) - (3.2.1.55) за
характерный размер принимается наружный диаметр трубы; за расчетную скорость -
средняя скорость в наименьшем проходном сечении пучка (поперечном для
коридорных пучков, поперечном или диагональном для шахматных пучков), за
определяющую температуру - средняя температура теплоносителя в пучке; за
температуру стенки - средняя температура поверхности труб пучка.
Погрешность
δ расчета  составляет ±30 %.
составляет ±30 %.
Коэффициент
Сβ, учитывающий уменьшение средней теплоотдачи всего
пучка из-за уменьшения угла атаки (косое обтекание пучка труб), рассчитывается:
■
при β = 30° ÷ 90°; Рr ≥ 0,5 с помощью рис. 3.2.1.8;
■
при β = 0 ÷ 90°, Рr ≈ 1, S/dн = 1,2 ÷ 1,50,
Re =
103 ÷ 105 по формуле [14]:
где 

Рис. 3.2.1.8. Поправка на
влияние угла атаки при расчете средней
теплоотдачи всего пучка стержней при поперечном обтекании
Светлые и зачерченные символы - первый и глубинные ряды
труб, соответственно
Коэффициент
CZ , учитывающий зависимость средней теплоотдачи всего пучка
труб от числа рядов, определяется с помощью рис. 3.2.1.9.
Погрешность
δ расчета  по формуле (3.2.1.46) составляет ±30 %.
по формуле (3.2.1.46) составляет ±30 %.
Средняя теплоотдача всего
шахматного пучка шероховатых труб рассчитывается по формуле [12]:
где  - средняя теплоотдача одной
шероховатой трубы в глубинном ряду поперечно обтекаемого шахматного пучка,
которая рассчитывается:
- средняя теплоотдача одной
шероховатой трубы в глубинном ряду поперечно обтекаемого шахматного пучка,
которая рассчитывается:
■
при Re = 103 ÷ 105; а = 1,25
÷ 2,0; b = 0,935 ÷ 2;
K/dн =
6,67·10-3 ÷ 40·10-3 по формуле:
где K - высота элементов шероховатости, м;
■ при Re = 105
÷ 2·106 по формуле:
Коэффициенты Сβ
и CZ в формуле (3.2.1.57)
определяются по рис. 3.2.1.8, 3.2.1.9 и формуле (3.2.1.56).
Погрешность
δ расчета  составляет ±30 %.
составляет ±30 %.
Погрешность
Δ расчета  по формуле (3.2.1.57) составляет ±30 %.
по формуле (3.2.1.57) составляет ±30 %.
Средняя теплоотдача всего
пучка при поперечном обтекании шахматных и коридорных пучков оребренных труб
потоком вязких жидкостей рассчитывается по формуле [12]:
где  - средняя теплоотдача одной
трубы в глубинном ряду шахматных или коридорных пучков труб при поперечном
обтекании.
- средняя теплоотдача одной
трубы в глубинном ряду шахматных или коридорных пучков труб при поперечном
обтекании.

Рис. 3.2.1.9. Поправка на
число рядов при расчете средней теплоотдачи
пучков труб при поперечном обтекании

Рис. 3.2.1.10.
Геометрические характеристики оребренных труб
Средняя
теплоотдача одной трубы в глубинном ряду шахматного пучка оребренных труб при
поперечном обтекании потоком рассчитывается [15, 16]:
■
при Re = 102 ÷ 2·104; Рr ≥ 0,7; а = 1,1
÷ 4;
b = 1,03 ÷ 2,05; hр/dн =
0,07 ÷ 0,715;
Sp/dн
= 0,06 ÷ 0,36 по формуле:
■ при Re = 2·104 ÷ 2·105;
Pr ≥ 0,7; a = 1,1 ÷ 4; b = 1,03 ÷ 2,50
и параметрах оребрения hр/dн =
0,07 ÷ 0,715; Sp/dн = 0,06 ÷
0,36 по формуле:
|

|
(3.2.1.64)
|
■ при Re = 2·105
÷ 1,4·106; Pr ≥ 0,7;
a =
2,2 ÷ 4,2; b = 1,27 ÷ 2,2; Sp/dн = 0,125
÷ 0,28
hр/dн =
0,125 ÷ 0,60 по формуле:
где a = S1/dн; dн
- наружный диаметр трубы, несущей оребрение, м;
b = S2/dн - относительные шаги,
которые вычисляются с помощью рис. 3.1.3.9.
Параметры
оребрения вычисляются с помощью рис. 3.2.1.10.
Погрешность
δ расчета  по формулам (3.2.1.63) - (3.2.1.65) составляет ±30 %.
по формулам (3.2.1.63) - (3.2.1.65) составляет ±30 %.
Средняя теплоотдача одной
трубы в глубинном ряду коридорного пучка оребренных труб при поперечном
обтекании рассчитывается по формуле [12]:
где ε - коэффициент оребрения, равный отношению полной
внешней поверхности оребренной трубы к наружной поверхности трубы без ребер.
Пределы
применимости формулы: Re = 5·103 ÷ 105 ; а
= 1,72 ÷ 3;
b = 1,80 ÷ 4; ε
= 5 ÷ 12; Рr ≥ 0,7.
Погрешность
σ расчета  составляет 20 %.
составляет 20 %.
Коэффициент
Сβ рассчитывается по формуле (3.2.1.56) и с помощью рис. 3.2.1.8.
При
расчетах по формулам (3.2.1.58),
(3.2.1.59), (3.2.1.63) ÷ (3.2.1.66) за определяющий размер
принимается наружный диаметр трубы, несущей оребрение (шероховатость), за
расчетную скорость - средняя скорость в наименьшем проходном сечении пучка; за
определяющую температуру - средняя температура теплоносителя в пучке, за
температуру стенки - средняя температура поверхности труб пучка.
Погрешность
δ расчета  по формуле (3.2.1.63) составляет ±30 %.
по формуле (3.2.1.63) составляет ±30 %.
3.2.1.7. ТЕПЛООБМЕН В КАНАЛАХ С ШЕРОХОВАТЫМИ СТЕНКАМИ
ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ
Шероховатость
поверхности стенок каналов используется для интенсификации теплообмена.
Применение шероховатых поверхностей особенно целесообразно при больших числах
Прандтля, так как эффект интенсификации достигается благодаря дополнительному
вихреобразованию, приводящему к повышению турбулентной диффузии в переходной
зоне, турбулентном ядре потока и снижению устойчивости и толщины слоя
молекулярной теплопроводности у стенки.
Элементы
шероховатости интенсифицируют теплообмен, но, с другой стороны, создают
условия, при которых перенос тепла уменьшается. Причиной снижения теплообмена
являются застойные зоны перед и за выступами шероховатости. Условия, при
которых теплообмен уменьшается, определяются геометрией шероховатости и
значением критериев Re и Рr.
Таким образом, при выборе геометрии шероховатости для каждого конкретного
условия возникает необходимость инженерной оптимизации теплоотдающей
поверхности.
3.2.1.7.1. Теплообмен при турбулентном течении в трубах
с регулярной шероховатостью стенки
Теплообмен при турбулентном
течении в трубах с двумерной шероховатостью стенки (прямоугольные выступы) при
развитом ее проявлении рассчитывается по формуле [17]:
|

|
(3.2.1.67)
|
где ξ рассчитывается по формуле (3.1.3.54);
Ks+ = Ks*wD/v;
Ks -
абсолютная высота элемента шероховатости, м;
wD -
динамическая скорость;
Rэ -
эффективный радиус шероховатой трубы, который рассчитывается по формуле (3.1.3.62);
 - средняя по сечению трубы
скорость потока, м/с2.
- средняя по сечению трубы
скорость потока, м/с2.
В
формуле: Rэ в [м]; v в [м2/с]; λ
в [Вт/м·К]; Ks в [м].
Пределы
применимости формулы: Re = 3·103 ÷ 2·105;
Рr = 0,7 ÷ 4600; Ks = 10 ÷ 4·103;
S/Ks = 4 ÷ 40; S - расстояние между элементами
шероховатости, м.
Погрешность
δ расчета Nu
составляет ±30 %.
3.2.1.7.2. Теплообмен при турбулентном течении в кольцевых каналах
с шероховатыми стенками
Теплообмен
при турбулентном течении в кольцевых каналах с регулярной шероховатостью на
внутренней стенке (двумерная шероховатость прямоугольной или закругленной трапецеидальной
формы, рис. 3.2.1.11)
рассчитывается [18, 19]:
■
при частичном проявлении шероховатости (Re < Reп),
когда
K/dэ ≥
0,0025, по формуле:
где K - высота элемента шероховатости, м;
dэ -
эффективный наружный диаметр внутренней стенки зазора кольцевого канала,
который рассчитывается, например, по формуле (3.1.3.62);
Tст, Тж
в [К];
■ при полном
проявлении шероховатости (Re > Reп) по формуле:
Граница перехода частичного влияния шероховатости на теплообмен к
полному рассчитывается по формуле:
|
Reп = exp(12,2 - 126K/dэ).
|
|
В формулах:
Пределы применимости формул
(3.2.1.68), (3.2.1.69):
Re = 5·103 ÷ 5·105; d1/d2  0,4; Тст/Тж
= 1 ÷ 2,8;
0,4; Тст/Тж
= 1 ÷ 2,8;
K/dэ =
0,0028 ÷ 0,021; K/b = 0,3 ÷ 0,8; s/K ~
1.
Погрешность
δ расчета Nu1
составляет ±30 %.

Рис. 3.2.1.11. Формы
регулярной шероховатости на внутренней
стенке кольцевого канала:
а) прямоугольные выступы, б) закругленные трапецеидальные выступы
3.2.1.8. ТЕПЛООБМЕН ПРИ ЕСТЕСТВЕННОЙ КОНВЕКЦИИ
Естественная
конвекция вызывается различием плотности неодинаково нагретых частей среды.
3.2.1.8.1. Теплоотдача от вертикальных пластин и цилиндров
Средний
по длине коэффициент теплоотдачи при естественной конвекции от вертикальных
пластин и цилиндров рассчитывается [14,
20]:
■ при ламинарном
режиме течения по формуле:
|

|
((3.2.1.70)
|
где  ;
;
Ra -
число Рэлея, характеризующее меру отношения подъемных сил, обусловленных
градиентом плотности и сил вязкости:
L -
высота пластин или цилиндра (характерный линейный размер).
Теплофизические
характеристики рассчитываются по средней температуре:
где tст - температура теплоотдающей поверхности,
°С;
tо -
температура окружающей среды, °С.
Пределы
применимости формулы: GrPr = 5·102 ÷ 2·107.
Погрешность
Δ расчета  составляет ±15 %;
составляет ±15 %;
■ при турбулентном
режиме течения по формуле:
|

|
(3.2.1.71)
|
Пределы применимости
формулы: GrPr > 2·107.
Погрешность
δ расчета  составляет
±15 %.
составляет
±15 %.
3.2.1.8.2. Теплоотдача от горизонтальных пластин и цилиндров
Средний
по длине коэффициент теплоотдачи при естественной конвекции от горизонтальных
пластин, обращенных греющей стороной вверх, и цилиндров при ламинарном режиме
течения рассчитывается [20]:
■ для горизонтальных
пластин, обращенных греющей стороной вверх, по формуле:
где
Lmin -
наименьшая длина пластины, м.
Пределы
применимости формулы: GrPr < 2·107.
Погрешность
Δ расчета  составляет ±15 %;
составляет ±15 %;
■ для горизонтально
расположенных цилиндров по формуле:
где 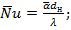

dн -
наружный диаметр цилиндра, м.
Пределы
применимости формулы: GrPr < 2·107.
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
Средний по длине коэффициент
теплоотдачи при естественной конвекции от горизонтальных пластин, обращенных
греющей стороной вверх, и цилиндров при турбулентном режиме течения
рассчитывается по формуле [20]:
где  , GrPr -
рассчитываются как в формулах (3.2.1.72),
(3.2.1.73).
, GrPr -
рассчитываются как в формулах (3.2.1.72),
(3.2.1.73).
Пределы
применимости формулы: GrPr > 2·107.
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
Теплофизические
свойства в формулах (3.2.1.72)
- (3.2.1.74) рассчитываются
по средней температуре t = 0,5(tст + tо).
Средний по длине коэффициент
теплоотдачи от горизонтальных пластин, обращенных греющей поверхностью вверх, и
цилиндров при Ra < 103, когда тепло распространяется лишь
теплопроводностью, рассчитывается по формуле [2]:
|

|
(3.2.1.75)
|
где  - рассчитывается также как
в формулах (3.2.1.72) - (3.2.1.74).
- рассчитывается также как
в формулах (3.2.1.72) - (3.2.1.74).
Теплофизические
свойства принимаются при температуре стенки трубы.
При
расчете чисел Gr в качестве температурного напора принимается разность
между температурой стенки и температурой жидкости у открытого конца трубы.
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
3.2.1.8.4. Теплообмен в прослойках
В
горизонтальных слоях, нагреваемых снизу, при Ra = GrPr <
1,7·103 = Rакр слой остается неподвижным и тепло
распространяется только теплопроводностью.
Коэффициент
теплоотдачи в горизонтальных слоях, нагреваемых снизу, рассчитывается [11]:
■ при Ra = 103
÷ 4·103 (область малой надкритичности) по формуле:
|
Nu = 1 + 1,4(1 - Rакр/Rа),
|
(3.2.1.81)
|
где  ;
;

δ -
толщина прослойки, м;
■ при Ra = 4·103
÷ 105 (квазиячеистое ламинарное течение) по формуле:
|
Nu = 0,23Ra1/4;
|
(3.2.1.82)
|
■ при Ra = 105 ÷ 109
(турбулентный режим течения) по формуле:
Погрешность δ
расчета Nu составляет ±15 %.
Коэффициент
теплоотдачи в вертикальных и наклонных слоях рассчитывается [11]:
■ при Ra <
103 по формуле:
■ при Ra = 104 ÷ 7·108; Рr = 0,02 ÷ 1,1·104; Н/δ = 5 ÷
18,5 по формуле:
где Н - высота слоя, м;
δ -
толщина слоя, м;
С(φ)
- коэффициент, зависящий от угла наклона слоя (табл. 3.2.1.5);
φ = 0
- горизонтальный слой.
Погрешность
δ расчета Nu составляет ±15 %.
Таблица 3.2.1.5
Значения коэффициента С(φ) в формуле (3.2.1.84)
|
φ°
|
0
|
30
|
45
|
60
|
90
|
|
С(φ)
|
0,07
|
0,065
|
0,06
|
0,057
|
0,05
|
В вертикальных и наклонных
слоях при значениях GrPr2 ≤ 124(1 + Рr)Н/b перенос тепла вычисляется по уравнению теплопроводности, и
распределение температур в слое линейное.
3.2.1.8.5. Теплопередача через плоские горизонтальные и
цилиндрические прослойки
Расчет
теплопередачи при естественной конвекции через плоские горизонтальные и
цилиндрические прослойки проводится с использованием коэффициента конвекции Е,
учитывающего интенсифицирующее воздействие естественной конвекции на процесс
передачи тепла.
Количество тепла,
передаваемое через 1 м2 поверхности плоских горизонтальных и
вертикальных прослоек, рассчитывается по формуле [20]:
где λ - коэффициент теплопроводности среды прослойки,
Вт/м·°С;
tгор - температура теплоотдающей поверхности, °С;
tхол - температура тепловоспринимающей поверхности, °С;
δ -
толщина прослойки, м;
Е -
коэффициент конвекции.
Коэффициент
конвекции рассчитывается [20]:
■ при (GrPr)
< 103 по формуле:
■ при 103 < (GrPr) < 106
по формуле:
|
Е
= 0,105(GrPr)0,3;
|
(3.2.1.87)
|
■ при lg(GrPr) > 106 по формуле:
|
Е
= 0,4(GrPr)0,2.
|
(3.2.1.88)
|
За характерный линейный размер принимается толщина слоя δ,
теплофизические свойства определяются при средней температуре прослойки:
Погрешность Δ
расчета q составляет ±10 %.
Количество тепла,
передаваемое через 1 погонный метр высоты цилиндрической прослойки,
рассчитывается по формуле [20]:
|

|
(3.2.1.89)
|
где dн - наружный диаметр цилиндрической
прослойки, м;
dвн -
внутренний диаметр цилиндрической прослойки, м;
Коэффициент
конвекции Е, характерный линейный размер, теплофизические характеристики
определяются также как при расчетах по формуле (3.2.1.85).
Погрешность
δ расчета qL составляет ±10 %.
Количество тепла,
передаваемое через 1 погонный метр длины горизонтальных цилиндрических
прослоек, рассчитывается по формуле [20]:
где коэффициент конвекции Е рассчитывается [20]:
■ при (GrPr)
> 103 по формуле:
|
Е
= 0,20(GrPr)0,25;
|
(3.2.1.91)
|
■ при (GrPr) < 103 по формуле:
где
Теплофизические свойства
определяются как при расчете по формуле (3.2.1.85).
Пределы
применимости формул (3.2.1.85),
(3.2.1.90):
Рr = 0,7 ÷ 800; dвн/dн =
0,12 ÷ 0,84.
Погрешность
δ расчета qL составляет ±10 %.
Теплопередача в гладком
заполненном жидкостью вертикальном канале внутренним диаметром dвн
от горячего с температурой tгop к холодному с температурой tхол
торцу (по всей высоте канала L имеется тепловая изоляция),
рассчитывается по формуле [20]:
|

|
(3.2.1.93)
|
где 

Δt = tгор - tхол,
°С.
Теплофизические
свойства в формуле для расчета коэффициента конвекции Е принимаются при
температуре:
t = 0,5(tгор + tхол).
Пределы
применимости формулы:
dвн =20
÷ 90 мм; L/dвн = 4 ÷ 50; GrPr(dвн/L) = 4·105 ÷ 2·1011.
Погрешность
δ расчета q составляет ±10 %.
3.2.1.9. ТЕПЛООБМЕН ПРИ ЕСТЕСТВЕННОЙ КОНВЕКЦИИ
В ЗАМКНУТОМ ПРОСТРАНСТВЕ
Естественная
конвекция, возникающая в жидкости, заключенной в замкнутых объемах, оказывает
значительное влияние на теплообмен и на возникновение тепловой стратификации,
при которой верхние слои жидкости имеют температуру выше средней. Стратификация
может быть значительной в зависимости от подогрева стенки, физических свойств
жидкости и тепломассообмена на свободной поверхности.
3.2.1.9.1. Теплообмен при естественной конвекции в шаровой емкости
Теплообмен
в шаровой емкости рассчитывается [21,
22]:
■ при ламинарной
свободной конвекции по формуле:
где 

dвн -
внутренний диаметр шара, м.
Пределы
применимости формулы:
Pr = 1
÷ 20; Rad= 106 ÷ 109.
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
Время прогрева жидкости в
шаровой емкости рассчитывается по формуле:
|

|
(3.2.1.95)
|
■ при переходном режиме от ламинарной свободной конвекции к
турбулентной по формуле:
Пределы применимости
формулы:
Pr = 2
÷ 10; Rad = 108 ÷ 1011.
Погрешность
δ расчета  составляет ±15 %;
составляет ±15 %;
■ при турбулентной
свободной конвекции по формуле:
Пределы применимости
формулы:
Рr = 1
÷ 20; Rad > 1010.
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
Время прогрева жидкости
рассчитывается по формуле:
|

|
(3.2.1.98)
|
При расчете по формулам (3.2.1.94), (3.2.1.96), (3.2.1.97) теплофизические параметры вычисляются
при t = 0,5(tст + tо),
где а -
температуропроводность шаров;
tст - температура стенки, °С;
tо -
температура окружающей среды, °С.
Эксперименты
показали, что при охлаждении в нижней части шаровой емкости накапливается
холодная жидкость и образуется застойная зона. При разогреве застойная зона
образуется в верхней части емкости. Наличие застойной зоны ухудшает теплообмен.
3.2.1.9.2. Теплообмен при естественной конвекции
в вертикальном цилиндре
Теплообмен при мгновенном
увеличении температуры боковой стенки цилиндра рассчитывается по формуле [23, 24]:
где 

dвн -
внутренний диаметр цилиндра, м;
Н -
высота цилиндра, м.
Пределы
применимости формулы:
H/dвн
= 0,25 ÷ 5; Р = 5 ÷ 80000; Rad = 8·105
÷ 4·1010.
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
Теплообмен при внезапном
подводе к боковой стенке цилиндра теплового потока, величина которого затем
остается неизменной во времени, рассчитывается по формуле [23, 24]:
где 

q -
плотность теплового потока, Вт/м2.
Пределы
применимости формулы:
H/dвн =
1; Pr = 1; Rad ≥ 105.
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
При
расчетах по формулам (3.2.1.99),
(3.2.1.100) физические
параметры вычисляются при t = 0,5(tст + tо).
При
числах  стремится к постоянному
значению, что соответствует квазистационарному режиму, где преобладает
температурное расслоение жидкости.
стремится к постоянному
значению, что соответствует квазистационарному режиму, где преобладает
температурное расслоение жидкости.
Разности
температур по вертикали вначале возрастают, достигая максимального значения при
 , затем уменьшаются. С
увеличением
, затем уменьшаются. С
увеличением  перемешивание преобладает
над расслоением.
перемешивание преобладает
над расслоением.
При
увеличении высоты цилиндра перемешивание становится менее интенсивным, что
приводит к большему температурному расслоению.
3.2.1.10. ИНТЕНСИФИКАЦИЯ ТЕПЛОСЪЕМА ПРИ ТУРБУЛЕНТНОМ
ТЕЧЕНИИ ОДНОФАЗНОГО ПОТОКА В КАНАЛАХ
К
теплообменным аппаратам часто предъявляются повышенные требования по
компактности, габаритам и массе. При заданных значениях тепловой мощности,
расходов теплоносителей и гидравлических сопротивлений можно уменьшить габариты
и массу аппаратов за счет увеличения коэффициентов теплоотдачи или за счет
более плотной компоновки (уменьшение диаметра труб пучка, расстояния между
трубами). Уменьшение диаметра труб и расстояния между ними ограничивается
технологическими требованиями, поэтому практические возможности этого пути
исчерпаны. Остается единственный путь уменьшения габаритных размеров и массы
-интенсификация теплосъема.
Известны
различные способы интенсификации теплосъема. Среди них видное место занимают
различные способы закрутки потока в трубах с помощью различного рода винтовых
вставок (закрученные ленты, шнеки) на всей длине трубы или на ее части,
тангенциального подвода теплоносителя в трубу, лопаточных завихрителей,
расположенных на входе. С целью интенсификации теплосъема используются также
криволинейные каналы (змеевиковые, спиральные).
Однако,
наиболее реальным и доступным путем интенсификации теплосъема является
искусственная турбулизация потока. Искусственная турбулизация потока
рассматривается как наиболее просто осуществимый и высокоэффективный метод
интенсификации теплосъема, так как она позволяет при умеренном росте
гидравлического сопротивления получить значительное увеличение коэффициентов
теплоотдачи.
3.2.1.10.1. Интенсификация теплосъема при турбулентном течении
однофазной среды в трубах
Одним
из способов искусственной турбулизации потока в трубчатых теплообменных
аппаратах является нанесение на внутреннюю поверхность труб поперечных
кольцевых гофр с плавной конфигурацией (рис. 3.1.3.14).
Образующиеся
гофры и кольцевые канавки турбулизируют поток в пристенном слое и обеспечивают
интенсификацию теплосъема как снаружи, так и внутри труб. При этом не
увеличивается наружный диаметр труб, что позволяет использовать такие трубы в
тесных пучках труб и не менять существующую технологию сборки трубчатых
теплообменных аппаратов. Данные поверхности применимы для теплообменных
аппаратов, работающих на газах и жидкостях.
Средний по длине коэффициент
теплоотдачи при турбулентном течении капельных жидкостей в одиночных трубах с
поперечными кольцевыми гофрами рассчитывается по формуле [25]:
|

|
(3.2.1.101)
|
|

|
(3.2.1.102)
|
|
Nuгл =
0,216Re0,80Pr0,445;
|
(3.2.1.103)
|
|

|
(3.2.1.104)
|
w -
скорость потока в гладкой трубе, м/с;
 , Nuгл, Re, Рr рассчитываются по среднемассовой температуре жидкости по длине
трубы.
, Nuгл, Re, Рr рассчитываются по среднемассовой температуре жидкости по длине
трубы.
Пределы
применимости формулы:
Pr ≥ 1; Re ≥ Re⁎;
Re⁎ - значение Re, при котором прекращается
возрастание отношения
Re ≥ Re⁎;
Re⁎ - значение Re, при котором прекращается
возрастание отношения  с ростом Re:
с ростом Re:
|

|
(3.2.1.105)
|
Погрешность δ расчета  составляет ±15 %.
составляет ±15 %.
Коэффициент теплоотдачи при
турбулентном течении воды в спирально-навитых трубах (рис. 3.1.1.1) рассчитывается по формуле [20]
где 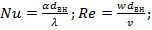
dвн -
внутренний диаметр исходной трубы, м;
dсн = dцп
- dвн, м;
dцп -
диаметр цилиндрической поверхности, описанной около спирально-навитой трубы, м;
S -
шаг навивки трубы, м;
Пределы
применимости формулы:
S/dсн =
12 ÷ 40; dсн/dвн = 0,2 ÷ 0,7; Rекр
< Re < 8·104;
Rекр = 2200(S/dсн)-0,30.
Погрешность
Δ расчета Nu составляет ±15 %.
Коэффициент теплоотдачи при
турбулентном течении воды в локально спирально-навитых трубах (рис. 3.1.1.1), у которых навитые
участки периодически чередуются с прямолинейными длиной L, рассчитывается
по формуле [20]:
|
Nu = Nuо[1 - 0,005(L/S)2,6],
|
(3.2.1.107)
|
где Nuо
рассчитывается по формуле (3.2.1.106).
Пределы
применимости формулы те же, что и формулы (3.2.1.106), а также L/S = 2 ÷ 5.
Погрешность
δ расчета Nu составляет ±15 %.
Коэффициент теплоотдачи при
турбулентном течении воды в трубах с внутренними спиральными трехзаходными
выступами, образованными накаткой на наружной поверхности, рассчитывается по
формуле [20]:
|

|
(3.2.1.108)
|
где 

dвн -
внутренний диаметр исходной трубы, м;
h -
высота выступов, м;
S -
осевой шаг выступов;
t -
осевое расстояние между соседними выступами;
S = 3t
- для труб с трехзаходными выступами.
Пределы
применимости формулы:
Re = 2·104 ÷ 1,6·105; Рr = 2 ÷ 10; h/S = 0,008 ÷ 0,04; h/dвн = 0,01 ÷ 0,08;
S/dвн =
0,75 ÷ 4,5.
Погрешность
δ расчета Nu составляет ±15 %.
3.2.1.10.2. Интенсификация теплосъема при турбулентном течении
однофазной среды в кольцевых каналах
Теплоотдача
от внутренней и наружной стенок плоских винтообразных каналов (рис. 3.2.1.12) зависит от значения
параметра D/h, где D = 0,5(d1 + d2)sin2φ,
φ = arctg[0,5(d1 + d2/S)].
При
развитом турбулентном течении газа с уменьшением параметра D/h
теплоотдача от наружной стенки кольцевого канала увеличивается, а от внутренней
уменьшается, все больше отличаясь от теплоотдачи в гладком кольцевом канале.
Коэффициент
теплоотдачи в винтообразных каналах с односторонним обогревом при турбулентном
течении газа (воздуха) рассчитывается [20]:
■ от внутренней
выпуклой стенки кольцевого канала по формуле:
|

|
(3.2.1.109)
|
где  ;
;
Nuо1
рассчитывается по формуле (3.2.1.8);
h -
ширина зазора кольцевого канала.
Пределы
применимости формулы:
D/h =
10 ÷ 75; b/h ≥ 5;  .
.
Погрешность
δ расчета Nu1 составляет ±20 %;
■ от наружной,
вогнутой стенки кольцевого канала по формуле:
где 
Nuo2 рассчитывается
по формуле (3.2.1.9).
Пределы
применимости формулы:
b/h ≥
5; Re ≥ 105.
Погрешность
δ расчета Nu2 составляет ±20 %.

Рис. 3.2.1.12. Геометрия
плоского винтообразного канала
Теплоотдачи
при турбулентном течении воды и перегретого пара в каналах, образованных
гладкой наружной трубой с внутренним диаметром dцп (рис. 3.1.3.16) и вставленной внутрь
спирально-навитой или локально спирально-навитой трубой, с двухсторонним
теплоподводом рассчитываются [20]:
■ в кольцевом канале с
внутренней спирально-навитой трубой по формуле:
где 
dн -
наружный диаметр исходной гладкой трубы, м.
Пределы
применимости формулы:
dн/dцп =
0,5 ÷ 0,95; S/dцп = 3 ÷ 5; Re = Reкр ÷ 5·104;
Reкp = 2200(S/dсн)-0,30; dсн = dцп - dн.
Погрешность
δ расчета Nu1 и Nu2 составляет
±20 %;
■ в кольцевом канале с
внутренней локально спирально-навитой трубой по формуле:
|
Nu1 = Nu2 = Nu[1 - 0,0012(L/S)4,4],
|
(3.2.1.111)
|
где Nu - рассчитывается по формуле (3.2.1.110);
L -
длина прямых участков, м.
Пределы
применимости формулы:
dн/dцп =
0,5 ÷ 0,95; S/dцп = 2 ÷ 5; Re = Reкр ÷ 5·104.
Погрешность
δ расчета Nu1 и Nu2 составляет
±20 %.
3.2.1.10.3. Интенсификация теплосъема при продольном турбулентном
течении однофазной среды в сборках стержней
Средний
по длине коэффициент теплоотдачи при продольном турбулентном течении среды в
межтрубном пространстве шахматных пучков труб с поперечными кольцевыми гофрами
(рис. 3.1.3.17)
рассчитывается [25]:
■ при Re < Re1
по формуле:
■ при Re1 < Re
< Re2 по формуле:
|

|
(3.2.1.113)
|
■ при Re1 < Re
< 105 по формуле:
где 
dг -
гидравлический диаметр шахматного пучка при бесконечно большом числе труб, м;
S -
шаг расположения труб в пучке, м;
Re1 -
значение числа Рейнольдса, до значения которого поперечные кольцевые диафрагмы
не оказывают влияния на теплоотдачу;
Re1 = (3,6 - 33,8h/dг)·104;
Re2 -
значение числа Рейнольдса, при превышении которого теплоотдача не зависит от
числа Рейнольдса;
Re2 = (4,7 - 18,85h/dг)·104;
h -
высота кольцевых гофр, м;
t -
шаг расположения кольцевых гофр, м.
Определяющая температура при
расчете  , Re - среднемассовая
температура среды.
, Re - среднемассовая
температура среды.
Nuгл, Recр, Рrср
рассчитываются по средней температуре:
где tст - температура наружной стенки трубы, °С;
tж -
среднемассовая температура среды в рассматриваемом сечении, °С.
Пределы
применимости формулы (3.2.1.115):
-
при Re > 1,3·104, S/Dн = 1,1 ÷ 1,2;
- при Re > 2·104,
S/Dн = 1,2 ÷ 1,4;
- при Re > 3·104,
S/Dн = 1,4 ÷ 1,5.
Пределы
применимости формул (3.2.1.112)
÷ (3.2.1.114):
Re = 1,3·104 ÷ 105; S/Dн =
1,1 ÷ 1,5; h/dг = 0 ÷ 0,1; t/dг = 0,25 ÷ 2.
Погрешность
δ расчета  составляет ±15 %.
составляет ±15 %.
Локальный
коэффициент теплоотдачи при продольном течении среды в межтрубном пространстве
теплообменника, пучок которого собран из витых труб (рис. 3.1.3.15) рассчитывается [25]:
■ при  .
.
tст/tж = 1 ÷ 1,75 по формуле:
где Frм - модифицированное число Фруда,
характеризующее соотношение между инерционными и центробежными силами;
tст -
температура наружной стенки трубы, °С;
tж - среднемассовая температура среды в рассматриваемом сечении,
dг -
гидравлический диаметр пучка витых труб, м;
■ при Frм
> 30; Re = 6·103 ÷ 105; tст/tж = 1
÷ 1,40 по формуле:
|

|
(3.2.1.117)
|
где  при Frм =
30 ÷ 270;
при Frм =
30 ÷ 270;
n =
0,55 при Frм > 270;
■ при  по
формуле:
по
формуле:
|

|
(3.2.1.118)
|
В формулах (3.2.1.116) ÷
(3.2.1.118) критерии Nu, Re, Рr
рассчитываются по среднемассовой температуре потока в рассматриваемом сечении.
Пределы
применимости формул:
N ≥
37, где N - число витых труб в пучке.
Погрешность
Δ расчета Nu составляет ±20 %.
Коэффициент теплоотдачи при
продольном обтекании турбулентным потоком пучков спирально-навитых труб (рис. 3.1.1.1) рассчитывается по формуле
[20]:
где 
dг = 4F/П;
F -
площадь проходного сечения по теплоносителю;
П -
смоченный периметр, м;
 ;
;
V -
объемный расход, м3/с;
dcн = dцп - dн.
Пределы
применимости формулы:
Re =1,7·104 ÷ 9·104;
Рr = 0,7 ÷ 2,0; X = S/dн = 1,2 ÷ 1,5; dсн/dн =
0,1 ÷ 0,7;
S/dсн =
12 ÷ 40.
Погрешность
δ расчета Nu составляет ±15 %.
Коэффициент теплоотдачи при
продольном обтекании турбулентным потоком пучков локально спирально навитых
труб, расположенных по треугольной решетке (рис. 3.1.1.1) рассчитывается по формуле [20]:
где Nuо -
рассчитывается по формуле (3.2.1.119).
Пределы
применимости формулы (3.2.1.120)
те же, что и формулы (3.2.1.119),
а также L/S = 2 ± 5.
Погрешность
δ расчета Nu составляет ±15 %.
Теплофизические
свойства теплоносителя при расчетах по формулам (3.2.1.119), (3.2.1.120) относятся к средней температуре
теплоносителя.
3.2.1.10.4. Интенсификация теплосъема при поперечном обтекании
однофазным турбулентным потоком пучков витых труб
При
проектировании теплообменников с поперечным обтеканием пучка витых труб следует
иметь в виду, что такой аппарат будет эффективным, если трубы овального профиля
в каждом поперечном ряду пучка устанавливаются с образованием щелевых зазоров
примерно постоянной ширины для прохода теплоносителя и имеют касание только с
трубами соседних рядов. Такая установка витых труб обеспечивает оптимальную
интенсификацию теплосъема и уменьшение неравномерности теплоотдачи по периметру
труб в 2 - 3 раза по сравнению с пучками гладких труб.
Средняя
теплоотдача пучков поперечно обтекаемых витых труб (рис. 3.1.3.15) рассчитывается [25]:
■ при отношении S/dов
= 12,2 по формуле:
|
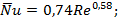
|
(3.2.1.121)
|
■ при отношении S/dов = 6,1 по формуле:
|

|
(3.2.1.122)
|
где 
dp -
определяющий размер [м], 
Ψ -
пористость пучка витых труб по теплоносителю;
Vтр - объем витой трубы;
Fтр - поверхность витой трубы;
L' - половина периметра трубы;
S -
шаг закрутки трубы;
w -
определяющая скорость, м/с, w = wнп/Ψ;
wнп - скорость набегающего потока, м/с;
определяющая
температура - температура набегающего потока.
Пределы
применимости формул: Re = 103 - 3·104; tст/tж =
1,1 ÷ 1,5.
Погрешность
δ расчета  составляет ±20 %.
составляет ±20 %.
Расчет
средней теплоотдачи всего пучка при поперечном обтекании шахматных и коридорных
пучков оребренных труб потоком вязких жидкостей приведен в разделе 3.2.1.6.2 (формулы 3.2.1.62 ÷ 3.2.1.66).
Список литературы к разделу 3.2.1
1. Ушаков П.А. Приближенное тепловое моделирование цилиндрических
тепловыделяющих элементов. - В сб. Жидкие металлы. М.: Атомиздат, 1967.
2. Петухов Б.С. Теплообмен и сопротивление при ламинарном течении
жидкости в трубах. М.: Энергия, 1967.
3. Бобков В.П., Ибрагимов М.Х., Саванин Н.К. Теплообмен при
турбулентном течении теплоносителей в кольцевых зазорах. Теплофизика высоких
температур, 1975, т. 13, № 4.
4. Петухов Б.С., Кириллов В.В. К вопросу о теплообмене при
турбулентном течении жидкости в трубах. - Теплоэнергетика, 1958, № 4.
5. Бобков В.П., Ибрагимов М.Х. Диффузия тепла при турбулентном
течении жидкости с различными числами Прандтля. - Теплофизика высоких
температур, 1970, т. 8, № 1.
6. Бобков В.П., Ибрагимов М.Х. Применение модели однофазной
диффузии к расчету касательного напряжения и поля скорости в турбулентном
потоке жидкости. - Теплофизика высоких температур, 1970, т. 8, № 2.
7. Петухов Б.С., Ройзен Л.И. Обобщенные зависимости для теплоотдачи
при турбулентном течении газа в трубах кольцевого сечения. - Теплофизика высоких
температур, 1964, т. 2, № 1.
8. Ушаков П.А., Жуков А.В., Титов П.А. Обобщение экспериментальных
данных по теплоотдаче к воде в шахматных пучках стержней. - Препринт ФЭИ-526,
Обнинск, 1974.
9. Жуков А.В., Мужанов А.Б., Ушаков П.А. Исследование температурных
полей и теплоотдачи в тесных решетках имитаторов твэлов, охлаждаемых водой. -
Препринт ФЭИ-1203, Обнинск, 1981.
10. Ибрагимов М.Х., Субботин В.И., Бобков В.П., Сабелев Г.И.,
Таранов Г.С. Структура турбулентного потока и механизм теплообмена в каналах.
М.: Атомиздат, 1978.
11. Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по
теплогидравлическим расчетам (ядерные реакторы, теплообменники,
парогенераторы). М.: Энергоатомиздат), 1984.
12. Жукаускас А.А. Конвективный перенос в теплообменниках. М.: Наука,
1982.
13. Achenbach Е. Heat transfer from spheres up to Re = 6·106. Heat
Transfer, 1978, vol 5, № 3.
14. Юрьев Ю.С., Ефанов А.Д. Коэффициент теплоотдачи при косом обтекании твэлов и труб. - Атомная энергия, 1985, т. 59, вып. 1.
15. Юдин В.Ф. Теплообмен поперечно-оребренных труб. Л.:
Машиностроение, 1982.
16. Локшин В.А., Фомина В.Н. Обобщение материалов по
экспериментальному исследованию сопротивления ребристых пучков труб. -
Теплоэнергетика, 1978, № 6.
17. Кадер Б.А., Яглом А.М. Турбулентный тепло- и массоперенос от
стенки, покрытой двумерной шероховатостью. - В кн.: Пристенное пристенное
турбулентное течение. Новосибирск: Изд. СО АН СССР, 1975.
18. Шимонис В.М., Вилемас Ю.В. Влияние переменности физических
свойств газа на теплообмен в шероховатых кольцевых каналах. В кн.: Проблемы
турбулентного переноса. Минск, ИТМО АН БССР, 1979.
19. Шимонис В.М., Вилемас Ю.В. Теплообмен и гидравлическое
сопротивление шероховатых кольцевых каналов при течении газов с переменными
физическими свойствами. - Труды АН Лит. ССР, сер. Б. 1984, т. 3.
20. Тепловой и гидравлический расчет теплообменного оборудования
АЭС. РД 24.035.05-89. Л.: НПО ЦКТИ, 1991.
21. Hiddink J. Natural convection heating
of liquids with reference to sterilization of canned food. - Agr. Res. Repts,
1975, № 839.
22. Hiddink J., Schenk J., Bruin S.
Natural convection heating of liquids in closed containers. - Appl.Sci.Res.,
1976, V.32, N3.
23. Полежаев В.И. Численное решение системы двумерных нестационарных
уравнений Навье-Стокса для сжимаемого газа в замкнутой области. - Механика
жидкости и газов, 1967, № 2.
24. Полежаев В.И. Нестационарная ламинарная тепловая конвекция в
заданной области при заданном потоке тепла. - Механика жидкостей и газов, 1970,
№ 4.
25. Дрейцер Г.А. Компактные теплообменные аппараты. М.: МАИ, 1986.
3.2.2.
ТЕПЛООБМЕН ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО СОСТОЯНИЯ
Превышение
температуры теплоотдающей поверхности, погруженной в жидкость или омываемой
жидкостью, над температурой насыщения на определенную величину (Δtнк) приводит к образованию пара на поверхности - кипению жидкости.
Значение перепада температуры, при котором начинается кипение, зависит от
большого количества факторов (давления, скорости движения жидкости, недогрева
до температуры насыщения, материала поверхности, ее шероховатости, краевого
угла смачиваемости, количества растворимых в жидкости газов и т.д.).
В
зависимости от плотности теплового потока и ряда других факторов на поверхности
нагрева образуются или отдельные паровые пузыри, или сплошной слой пленки пара,
и кипение называется пузырьковым или пленочным. Кроме того, кипение различается
по типу конвекции (кипение при свободной конвекции в большом объеме и кипение
при вынужденной конвекции) и по отношению средней температуры жидкости Тж
к температуре насыщения Ts (кипение жидкости, недогретой до
температуры насыщения, - поверхностное кипение при Тж < Ts
и кипение жидкости, нагретой до температуры насыщения при Тж ≈
Ts).
Пузырьковое
кипение может быть развитым (при большом количестве центров парообразования) и
неразвитым (при малом количестве центров парообразования). В последнем случае
значительная доля тепла снимается конвекцией жидкости. Неустойчивым кипением
называется случай кипения, когда пузырьковое кипение сменяется режимом
конвекции и наоборот. Зависимость q = f(Δt)
называется кривой кипения (рис. 3.2.2.1), где Δt = tст - ts.

Рис. 3.2.2.1. Кривая кипения
3.2.2.1. Теплообмен при кипении жидкостей в каналах
3.2.2.1.1. Теплообмен при пузырьковом кипении жидкостей в большом
объеме
Теплообмен при развитом
пузырьковом кипении воды на поверхности, погруженной в большой объем,
рассчитывается по формулам [1, 2]:
|
α =
4,34q0,70(P0,14 + 1,35·10-2P2),
|
(3.2.2.1)
|
или
|

|
(3.2.2.2)
|
где q в [Вт/м2]; Р в [МПа]; α
в [Вт/м2·К]; Ts в [К].
Пределы
применимости формул: Р = 0,1 ÷ 20 МПа.
Погрешность
Δ расчета α составляет ±25 %.
Формула
(3.2.2.1) используется также
для расчета теплообмена при кипении воды, недогретой до температуры насыщения.
Температурный напор определяется в этом случае как разница между температурой
поверхности и температурой насыщения. Пределы применимости формулы и
погрешность расчета а остаются прежними.
Теплообмен при развитом
пузырьковом кипении неметаллических жидкостей на поверхности, погруженной в
большой объем, рассчитываются по формуле [2]:
|
Nu = CRenPr1/3,
|
(3.2.2.3)
|
где при Re ≤ 0,01 С = 0,0625, n = 0,50;
при Re > 0,01 С
= 0,125, n = 0,65;

λ', Ср',
Ts, ρ' - параметры на линии насыщения;
ρ" -
плотность сухого насыщенного пара.
Пределы
применимости формулы: Рr =
0,86 ÷ 7,6;
Re
< 104 ÷ 105; при кипении воды: Р = 0,45
÷ 17,5 МПа.
Погрешность
Δ расчета Nu составляет ±25 %.
3.2.2.1.2. Теплообмен при пленочном кипении жидкостей в большом
объеме
При
пленочном кипении теплоотдающая поверхность окружена сплошным слоем пара и ее
температура, как правило, значительно превышает температуру насыщения
окружающей жидкости.
Теплообмен
при пленочном кипении жидкости определяется граничными условиями на
теплоотдающей поверхности. Различают два предельных случая теплообмена:
■
теплообмен при постоянной плотности теплового потока (q = const);
■
теплообмен при постоянном температурном напоре (T =
const).
В
первом случае пленочный режим кипения возникает при значении плотности
теплового потока, равной  , а прекращается при
, а прекращается при  .
.
Переход
от пузырькового режима кипения к пленочному и обратно сопровождается скачкообразным
изменением температурного напора.
Возникновение
и прекращение пленочного режима кипения на изотермической поверхности (при ΔТ
= const) имеет место при температурном напоре, равном  .
.
При пленочном кипении
передача энергии через низко проводную паровую пленку осуществляется конвекцией
и излучением, поэтому суммарный коэффициент теплоотдачи рассчитывается по
формуле:
где αк - конвективная составляющая
коэффициента теплоотдачи;
αр -
радиационная составляющая коэффициента теплоотдачи:
|

|
(3.2.2.7)
|
εпр -
приведенная степень черноты;
s =
5,67·10-8 Вт/м2К2 - постоянная
Стефана-Больцмана;

εгр, εст
- степень черноты границы раздела жидкость-пар и поверхности теплообмена;
εпр  1,0 и εст
1,0 и εст  0,75 - для металлических
поверхностей.
0,75 - для металлических
поверхностей.
Конвективная составляющая
теплоотдачи зависит от гидродинамических характеристик течения паровой пленки.
При ламинарном течении пленки пара интенсивность конвективной теплоотдачи
связана с теплопроводным механизмом в пленке. Возникновение и развитие
колебаний границы жидкость-пар происходит на участке, равном двум длинам волн,
после которого формируется волновой режим течения паровой пленки (развитое
пленочное кипение). Сечение возникновения развитого пленочного кипения
совпадает с координатой конца участка развития волны, которая определяется как Xv,кр ≈
200/Rej, где
Теплоотдача на участке
развития волны определяется как среднее между значениями теплоотдачи при
развитом пленочном кипении и в конце ламинарного участка. В волновом режиме
течения паровой пленки теплоотдача автомодельна относительно длины
теплоотдающей поверхности.
Теплофизические
свойства пара в формулах этого раздела для расчета конвективной теплоотдачи
берутся при температуре  .
.
Локальный коэффициент
теплоотдачи при пленочном кипении жидкости на вертикальной поверхности (q
= const) и ламинарном течении паровой пленки рассчитывается по формуле [3, 4]:
|
Nu* =
0,437(RejXv)-1/3,
|
(3.2.2.8)
|
где 
Пределы
применимости формулы:
Xv ≤ Xv,b; Rej ≥ 0,10;  ;
;
Погрешность Δ
расчета Nu* составляет ±10 %.
Средний
по длине коэффициент теплоотдачи при пленочном кипении жидкости на вертикальной
поверхности (q-const) рассчитывается [3, 4]:
■ при ламинарном
течении паровой пленки по формуле:
Пределы применимости
формулы:
Xv = 0 ÷ Xv,b;
Rej > 0,10;  .
.
Погрешность
Δ расчета  составляет ±12 %;
составляет ±12 %;
■ на участке развития
волны в паровой пленке по формулам:
где  рассчитывается по формуле (3.2.2.10);
рассчитывается по формуле (3.2.2.10);
 - средние по длине
коэффициенты теплоотдачи при развитом пленочном кипении.
- средние по длине
коэффициенты теплоотдачи при развитом пленочном кипении.
Пределы применимости формул:
Погрешность Δ
расчета  составляет ±12 %;
составляет ±12 %;
■ при развитом
пленочном кипении по формулам:
Выбор формулы (3.2.2.12) или
(3.2.2.13) для расчета определяется из условия:


Пределы
применимости формул:
Хv ≥
200/Rej, Rej = 200 ÷ 1·104;
 .
.
Погрешность
Δ расчета  составляет ±12 %;
составляет ±12 %;
■ по всей длине
теплоотдающей поверхности по формуле:
где  рассчитывается по формуле (3.2.2.10);
рассчитывается по формуле (3.2.2.10);
 рассчитывается по формуле (3.2.2.11);
рассчитывается по формуле (3.2.2.11);
 рассчитывается по формулам
(3.2.2.12), (3.2.2.13);
рассчитывается по формулам
(3.2.2.12), (3.2.2.13);
Lv = L/Lv;
L -
длина поверхности;
Xv,кр = 200/Rej.
Погрешность
Δ расчета  составляет ±12 %.
составляет ±12 %.
Пределы
применимости формулы:
Rej =
0,1 ÷ 1·104;  .
.
Средний
по длине коэффициент теплоотдачи при пленочном кипении жидкости на вертикальных
цилиндрах (q = const) рассчитывается [3, 4]:
■ при ламинарном
течении паровой пленки по формуле:
|

|
(3.2.2.15)
|
где 
|

|
(3.2.2.16)
|
Xv,R = x/Lv,
где х - текущая координата, м;
Xv,b рассчитывается по формуле (3.2.2.9);
 рассчитывается по формуле (3.2.2.10);
рассчитывается по формуле (3.2.2.10);
Rv = R/Lv - безразмерный радиус цилиндра.
Пределы
применимости формулы:
Xv ≤
Xv,b, Rej ≥ 0,10; Rv =
10 ÷ ∞;  ;
;
■
на участке развития волны в паровой пленке по формуле (3.2.2.11);
■ при развитом
пленочном кипении по формуле:
|

|
(3.2.2.17)
|
где  рассчитывается по формуле (3.2.2.13).
рассчитывается по формуле (3.2.2.13).
Пределы
применимости формулы:
Xv ≥
200/Rej, Rej =
200 ÷ 1·104;  ; Rv = 10 ÷ ∞.
; Rv = 10 ÷ ∞.
Погрешность
Δ расчета  составляет ±12 %;
составляет ±12 %;
Средний
по длине коэффициент теплоотдачи при пленочном кипении жидкости на одиночном
горизонтальном цилиндре (q = const) рассчитывается [5]:
■ при Re ≤
2Reв по формуле:
|

|
(3.2.2.18)
|
где
D - наружный диаметр цилиндра, м;
■ при 2Reв < Re ≤ 200 по
формуле:
|

|
(3.2.2.19)
|
Локальный коэффициент
теплоотдачи рассчитывается [5]:
■ при Re >
200, Dv = D/Lv
< 271 по формуле:
|

|
(3.2.2.20)
|
где
 - критерий фазового
перехода;
- критерий фазового
перехода;
 - число Прандтля;
- число Прандтля;
■ при Re > 200, Dv
> 271 по формуле:
|

|
(3.2.2.21)
|
где
Погрешность Δ
расчета  и Nu*
составляет ±15 %.
и Nu*
составляет ±15 %.
Локальный
коэффициент теплоотдачи при пленочном кипении жидкости на вертикальной
изотермической поверхности (ΔТ = const) (ламинарное течение
паровой пленки) рассчитывается [6]:
■ при NuR* = 0 по формуле:
|

|
(3.2.2.22)
|
■ при NuR* ≠ 0 по
формуле:
|

|
(3.2.2.23)
|
где
R -
радиус кривизны поверхности, м;
δ(Xv) определяется из трансцендентного уравнения:
Пределы применимости формул:
Xv = 0
÷ Хv,b; KРr = 0,4 ÷ 10;  ; NuR* = 0
÷ 0,04.
; NuR* = 0
÷ 0,04.
 .
.
Погрешность Δ
расчета Nu* составляет ±15 %.
Средний
по длине коэффициент теплоотдачи при пленочном кипении жидкостей на
вертикальной изотермической поверхности (ΔТ = const)
рассчитывается [6]:
■ при ламинарном
течении паровой пленки по формулам:
|

|
(3.2.2.24)
|
|

|
(3.2.2.25)
|
Пределы применимости формул:
Xv = 0 ÷ Xv,b; Pr = 0,4 ÷ 10;
 ; NuR*
= 0 ÷ 0,04.
; NuR*
= 0 ÷ 0,04.
Погрешность
Δ расчета  составляет ±15 %;
составляет ±15 %;
■
на участке развития волны (Xv = Xv,b ÷ 200/Rej) по формуле: (2.2.11);
■ при развитом
пленочном кипении по формулам:
|

|
(3.2.2.26)
|
или
|
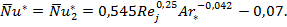
|
(3.2.2.27)
|
Выбор формулы (2.2.26) или
(2.2.27) для расчета  определяется из условия:
определяется из условия:


Пределы
применимости формул:
Xv
> 200/Rej, KРr = 0,4 ÷ 10;  ; NuR* = 0
÷ 0,04.
; NuR* = 0
÷ 0,04.
Погрешность
Δ расчета  составляет ±15 %;
составляет ±15 %;
■
по всей длине теплоотдающей поверхности по формуле (3.2.2.14).
При
пленочном режиме кипения жидкость отделена от поверхности нагрева пленкой пара.
Теплообмен зависит от режима течения пара в пленке, который определяется
размером и формой поверхности нагрева, ее ориентацией в поле силы тяжести.
3.2.2.1.3. Теплообмен при кипении воды в трубах
Начало поверхностного
кипения (появление первых пузырьков пара на стенке канала) при вынужденном
течении воды в трубах рассчитывается по формуле [2]:
где i в [кДж/кг]; q в [Вт/м2]; dвн
в [м]; ρw в [кг/м2·с].
Пределы
применимости формулы:
Р =
4,9 ÷ 19,6 МПа;
ρw =
1300 ÷ 11000 кг/м2·с; q = 0,43 ÷ 1,3 МВт/м2;
dвн = 2,9 ÷ 6,3 мм.
Погрешность
Δ расчета Δiнк
составляет ±15 %.
Коэффициент теплоотдачи при
кипении в трубах воды, недогретой до температуры насыщения, рассчитывается по
формуле [7]:
|

|
(3.2.2.29)
|
где αо рассчитывается по формуле (3.2.2.1);
α1
рассчитывается по формуле (3.2.1.10);
 - при расчете α1;
- при расчете α1;
wо -
скорость циркуляции воды, м/с;
q -
Вт/м2;
tж -
средняя температура воды в заданном сечении трубы, °С;
ts
- tж - недогрев воды до температуры насыщения, °С.
Пределы
применимости формулы:
Р =
0,10 ÷ 18 МПа; ts - tж = 1 ÷ 260 °С.
Погрешность
Δ расчета α составляет ±30 %.
Коэффициент
теплоотдачи при развитом пузырьковом кипении в трубах рассчитывается [8]:
■ при  по формуле:
по формуле:
|

|
(3.2.2.30)
|
где 
■ при  по формуле:
по формуле:
|

|
(3.2.2.31)
|
где α в [Вт/м2·К]; q в [кВт/м2];
αо
рассчитывается по формуле (3.2.2.1);
α2
рассчитывается по формуле (3.2.1.10);
 - при расчете α2;
- при расчете α2;
wо -
скорость циркуляции, м/с;
wо = Gв/fρ';
Gв -
расход воды в трубе, кг/с;
f - площадь поперечного сечения трубы, м2;
wсм -
средняя скорость пароводяной смеси, м/с;

х -
массовое паросодержание.
Пределы
применимости формул:
Р =
0,20 ÷ 17,0 МПа;
q =
0,8·105 ÷ 6·106 Вт/м2; wсм
= 1 ÷ 300 м/с; х < хкр.
Погрешность
Δ расчета α составляет ±30 %.
Коэффициент теплоотдачи при
развитом пузырьковом кипении в трубах (небольшие скорости пароводяной смеси)
рассчитывается по упрощенной формуле [9]:
|

|
(3.2.2.32)
|
где α в [Вт/м2·°С]; q в [Вт/м2].
Пределы
применимости формулы: Р = 0,10 ÷ 20 МПа.
Погрешность
Δ расчета α составляет ±35 %.
3.2.2.1.4. Теплообмен при кипении воды в кольцевых каналах
Коэффициент теплоотдачи при
кипении воды в кольцевых каналах рассчитывается по формуле [9]:
|

|
(3.2.2.32)
|
где α в [Вт/м2·°С]; q в [Вт/м2].
Пределы
применимости формулы: Р = 10 ÷ 20 МПа;
ρw =
500 ÷ 3000 кг/м2·с; δ = 1 ÷ 3 мм;
δ -
ширина зазора кольцевого канала; q1/q2 = 0
÷ 1.
Погрешность
Δ расчета α составляет ±30 %.
3.2.2.1.5. Теплообмен при кипении воды в сборках стержней
Коэффициент
теплоотдачи при кипении воды в сборках стержней рассчитывается [2]:
■ при  по формуле:
по формуле:
|

|
(3.2.2.33)
|
■ при  по формуле:
по формуле:
|

|
(3.2.2.34)
|
где 
x -
массовое парocoдержание;
f - площадь проходного сечения сборки стержней, м2;
Gв -
расход воды через сборку стержней, кг/с;
αо
рассчитывается по формуле (3.2.2.1);
α1 -
коэффициент теплоотдачи при течении через сборку стержней однофазной среды на
линии насыщения, который рассчитывается по формуле:
|
Nu = 0,023Re0,80Pr0,40εсt;
|
|
dг -
гидравлический диаметр сборки стержней, м;
dн -
наружный диаметр стержня, м;
 wо = Gв/fρ'
- скорость циркуляции, м/с;
wо = Gв/fρ'
- скорость циркуляции, м/с;
q в
[кВт/м2]; α в [Вт/м2·К]; Pr = v'/a.
Пределы
применимости формулы: Re = 104 ÷ 106; Рr = 0,7 ÷ 20.
Погрешность
Δ расчета Nu составляет ±15 %.
Пределы
применимости формул:
Р =
0,20 ÷ 17,0 МПа; q = 0,08 ÷ 6,00 МВт/м2; wсм
= 1 ÷ 300 м/с.
Погрешность
Δ расчета α составляет ±30 %.
3.2.2.2
ТЕПЛОМАССООБМЕН ПРИ КОНДЕНСАЦИИ И ФАЗОВЫХ
ПРЕВРАЩЕНИЯХ С УЧАСТИЕМ ТВЕРДОЙ ФАЗЫ
Поверхностная
конденсация пара возникает при температуре твердой стенки, которая несколько
меньше температуры насыщения. Возможны три вида конденсации:
■
пленочная конденсация пара, которая характеризуется стеканием с
тепломассообменной поверхности сплошной пленки жидкости. Пленочная конденсация
пара возникает на поверхностях, для которых силы молекулярного взаимодействия
жидкость-стенка (силы адгезии) превосходят аналогичные силы внутри жидкости
(силы когезии);
■
капельная конденсация пара характеризуется скатыванием отдельных капель
жидкости с теплообменной поверхности. Капельная конденсация пара возникает на
не смачиваемых жидкостью поверхностях (силы когезии превосходят силы адгезии);
■
смешанная конденсация пара, свойственная поверхностям, для которых в разных
частях одновременно выполняются условия, определяющие существование пленочной и
капельной конденсации пара.
Интенсивность
теплоотдачи при капельной конденсации пара значительно выше, чем при пленочной.
Однако в энергооборудовании трудно обеспечить длительное существование
капельной конденсации.
При
пленочной конденсации пара интенсивность теплоотдачи определяется
гидродинамическими характеристиками течения конденсата. Начиная от места
возникновения пленки конденсата, происходит развитие ламинарного течения.
Теплоотдача при этом связана только с теплопроводным механизмом в жидкости
(теория Нуссельта). При достижении некоторого критического числа Рейнольдса на
межфазной границе начинают развиваться волны, которые интенсифицируют тепло- и
массообмен. После завершения формирования волн теплоотдача становится
автомодельной относительно длины теплообменной поверхности. Такая
консервативность термического сопротивления связана с интенсивным
перемешиванием за счет волновых движений и, как следствие, с возникновением
термического сопротивления только в невозмущенном пристенном слое. Дальнейший
рост числа Рейнольдса приводит к развитию хаотических пульсаций,
соответствующих турбулентности.
При пленочной конденсации
коэффициент теплоотдачи от пара к твердой поверхности рассчитывается по
формуле:
|

|
(3.2.2.35)
|
где Rф -
термическое сопротивление на границе пар-конденсат (сопротивление фазового
перехода), м2·К/Вт;
Rк -
термическое сопротивление на границе конденсат-поверхность охлаждения
(контактное термическое сопротивление), м2·К/Вт;
Rпл -
термическое сопротивление пленки конденсата, м2·К/Вт;
Rпо -
термическое сопротивление, обусловленное наличием в паре неконденсирующихся
газов, м2·К/Вт.
Основным
термическим сопротивлением при пленочной конденсации чистого, т.е. не
содержащего примесей неконденсирующихся газов, пара неметаллических жидкостей,
является термическое сопротивление пленки конденсата. Для этих условий
суммарное сопротивление переносу тепла R ≈ Rпл.
Величина термического сопротивления Rпл зависит от режима
течения пленки конденсата (ламинарный, ламинарно-волновой, турбулентный),
скорости движения парового потока, ориентации поверхности конденсации в
пространстве.
Режим течения пленки характеризуется
числом Рейнольдса пленки конденсата:
|

|
(3.2.2.36)
|
где 
 - вязкостная постоянная;
- вязкостная постоянная;
δ -
толщина пленки конденсата, м;
G -
массовый расход конденсата, кг/с;
П -
смоченный периметр канала, м;
L -
длина (высота поверхности конденсации), м;
ΔТ -
перепад температур на пленке конденсата, К;
 - число фазового перехода;
- число фазового перехода;
Pr = v/a
- критерий Прандтля.
При
пленочной конденсации чистых паров жидких металлов, имеющих высокую
теплопроводность, термическое сопротивление Rпл относительно
мало. В этих условиях при определении коэффициента теплоотдачи наряду с Reпл,
необходимо учитывать и другие виды термических сопротивлений.
3.2.2.2.1
Теплоотдача при пленочной конденсации неподвижного пара
на вертикальной поверхности
Средняя
по длине теплоотдача при пленочной конденсации неподвижного насыщенного пара на
вертикальной теплообменной поверхности рассчитывается [10, 11]:
■ при Reпл ≤ Reв по формуле:
где 
Pr' = v'/a';

■ при Reв < Reпл ≤
Reкр по формуле:
|

|
(3.2.2.38)
|
где 
 - критерий Архимеда;
- критерий Архимеда;
 - капиллярная составляющая;
- капиллярная составляющая;
■ при Reкр
< Reпл ≤ 4·103 по формуле:
Формулы применимы при
конденсации чистых паров воды, фреона-12, фреона-22, углекислого газа,
четыреххлористого углерода, дефинила, ацетона, бензина, этанола, смеси
гептанов, аммиака, кислорода, азота, аргона.
Пределы
применимости формул:
5
< KPr' < 103;
103
< Ar⁎ < 5·106; L/Lσ
> 5.
Погрешность
Δ расчета  составляет ±10 %.
составляет ±10 %.
При
значениях KPr' ≤ 5 полученные по формулам (3.2.2.37) ÷ (3.2.2.39) значения  умножаются на поправки,
учитывающие конвективные перемешивания εi и переменность теплофизических свойств конденсата εt.
умножаются на поправки,
учитывающие конвективные перемешивания εi и переменность теплофизических свойств конденсата εt.
Поправка
εi
определяется по графику.

Рис. 3.2.2.2. Поправка εi, учитывающая конвективные перемещения при пленочной
конденсации неподвижного пара на вертикальной поверхности
Поправка
εt
рассчитывается по формуле:

Локальная
теплоотдача при пленочной конденсации неподвижного пара на вертикальной
теплообменной поверхности рассчитывается [10, 11]:
■ при Re < 5
по формуле:
где


L -
высота поверхности конденсации, м;
 - средний тепловой поток на
поверхности конденсации, Вт/м2;
- средний тепловой поток на
поверхности конденсации, Вт/м2;
■ при Reпл = 5 ÷ Re⁎ по
формуле:
где  - поправка на волновое
движение пленки конденсата;
- поправка на волновое
движение пленки конденсата;
Re⁎ = 2,3Ar⁎1/5;

■ при Reпл = Re⁎
÷ Reкр по формуле:
|
 , ,
|
(3.2.2.42)
|
где Reкр =
35Ar⁎1/5;
Reкр соответствует
переходу ламинарно-волнового течения пленки конденсата к турбулентному.
Средняя по длине теплоотдача
при пленочной конденсации неподвижного пара на вертикальной поверхности при
смешанном (ламинарно-волновом-турбулентном) режиме течения пленки конденсата
рассчитывается по формуле [10, 11]:
|
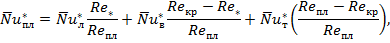
|
(3.2.2.43)
|
где 
Nuл*
рассчитывается по формуле (3.2.2.40);
 рассчитывается по формуле (3.2.2.41);
рассчитывается по формуле (3.2.2.41);
 характеризует
среднюю по длине теплоотдачу при турбулентном режиме течения пленки конденсата.
характеризует
среднюю по длине теплоотдачу при турбулентном режиме течения пленки конденсата.
Средняя по длине теплоотдача
при пленочной конденсации неподвижного пара на вертикальной поверхности при
турбулентном режиме течения пленки конденсата рассчитывается по формуле:
где
Nuт*
характеризует локальную теплоотдачу при турбулентном течении пленки конденсата;
η - безразмерная толщина пленки конденсата, связанная с Reпл
соотношением:
|

|
(3.2.2.46)
|
где





μт -
коэффициент турбулентной динамической вязкости:
 при 0 < η
< 6,80;
при 0 < η
< 6,80;
 ; при 6,8 < η
<0,2(ηδ - 6,8);
; при 6,8 < η
<0,2(ηδ - 6,8);
 при 0,2(ηδ
- 6,8) < η < ηδ;
при 0,2(ηδ
- 6,8) < η < ηδ;
δ -
толщина пленки конденсата, м;
τст -
касательное напряжение на стенке.
Результаты
численного расчета  приведены в таблице
3.2.2.1.
приведены в таблице
3.2.2.1.
Пределы
применимости формул (3.2.2.40)
÷ (3.2.2.45):
чистые
пары воды, хладонов 12, 21, 22; углекислого газа, четыреххлористого углерода,
аммиака, ацетона, этанола, азота, аргона.
Погрешность
Δ расчета Nuпл*,  ,
,  , Nuт*
составляет ±15 %.
, Nuт*
составляет ±15 %.
Таблица 3.2.2.1
Результаты численного расчета Nuт* по
формуле (3.2.2.44)
|
ηδ
|
|
εРr
|
60
|
100
|
200
|
300
|
1000
|
4000
|
|
1
|
0,157
|
0,160
|
0,168
|
0,176
|
0,213
|
0,285
|

|
|
2
|
0,212
|
0,223
|
0,245
|
0,262
|
0,332
|
0,452
|
|
3
|
0,252
|
0,270
|
0,300
|
0,324
|
0,416
|
0,572
|
|
5
|
0,307
|
0,332
|
0,377
|
0,410
|
0,532
|
0,735
|
|
7
|
0,344
|
0,374
|
0,428
|
0,467
|
0,607
|
0,841
|
|
10
|
0,382
|
0,418
|
0,479
|
0,523
|
0,682
|
0,948
|
Данная таблица определяет,
приблизительно, пределы применимости формулы (3.2.2.28).
3.2.2.2.2. Теплоотдача при пленочной конденсации пара на наружной
поверхности труб, отклоненных от вертикали
Средняя
по длине теплоотдача при пленочной конденсации неподвижного насыщенного пара на
наружной поверхности одиночных труб, отклоненных от вертикали на угол менее
10°, рассчитывается по формулам раздела 3.2.2.2.1.
Средняя теплоотдача при
пленочной конденсации пара, движущегося вдоль оси одиночных труб, отклоненных
от вертикали на угол φ, рассчитывается по формуле [12]:
|

|
(3.2.2.47)
|
где 
Пределы
применимости формулы:
Р = 0,005 ÷ 0,20 МПа; φ = 0 ÷ 35°; 
Погрешность
Δ расчета Nuпл составляет ±15 %.
3.2.2.2.3. Теплоотдача при пленочной конденсации пара на
внутренней
поверхности вертикальных труб
Средний по длине трубы
коэффициент теплоотдачи при медленном опускном движении насыщенного или
перегретого пара и пленки конденсата внутри вертикальной трубы при ламинарном
режиме течения пленки конденсата и полной конденсации пара рассчитывается по
формуле [10, 11, 13]:
где 
εt - поправка на переменность теплофизических свойств конденсата,

Рr' - число Прандтля воды на линии насыщения;
 - вязкостная постоянная.
- вязкостная постоянная.
Пределы
применимости формулы:
Reвх" =
104 ÷ 5·104; ρ"/ρ' ≤
10-3; μ"/μ' ≥ 0,10; L/Lv
≥ 104.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
Локальный
и средний по длине коэффициенты теплоотдачи при опускном движении насыщенного
пара и пленки конденсата и турбулентном режиме течения пара и пленки конденсата
рассчитываются [10, 11, 13, 14]:
■ локальный - по
формуле:
|

|
(3.2.2.49)
|
■ средний по длине - по формуле:
где  - критерий Рейнольдса
циркуляции пароконденсатной смеси;
- критерий Рейнольдса
циркуляции пароконденсатной смеси;
Gсм = G'
+ G" - массовый расход пароконденсатной смеси;
 - массовое расходное
паросодержание;
- массовое расходное
паросодержание;

С =
0,024 - для трубы из нержавеющей стали;
С =
0,032 - для трубы из меди;
С =
0,026 - для трубы из латуни.
Пределы
применимости формулу Reц > 103.
Погрешность
Δ расчета Nuпл и  составляет ±15 %.
составляет ±15 %.
3.2.2.2.4. Теплоотдача при пленочной конденсации пара на
внутренней
поверхности горизонтальных труб
Средний по длине коэффициент
теплоотдачи при полной конденсации практически неподвижных паров холодильных
агентов на внутренней поверхности горизонтальных труб рассчитывается по формуле
[12]
|

|
(3.2.2.51)
|
где 
 - число Рейнольдса парового
потока во входном сечении трубы;
- число Рейнольдса парового
потока во входном сечении трубы;



L -
длина горизонтальной трубы, м;
а =
0,215, т = 0 при Reвх" < 7·104;
а =
4,35·10-3, т = 0,35 при Reвх" =
7·104 ÷ 2·105.
Пределы
применимости формулы:
Хладоагенты
- Х-11; Х-22; Х-113; Х-142; Х-502, аммиак;
Р =
0,75 ÷ 1,95 МПа; dвн = 10 ÷ 20 мм; L = 1
÷ 6,4 м.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
Средний
по длине коэффициент теплоотдачи при пленочной конденсации движущегося водяного
пара на внутренней поверхности горизонтальных труб рассчитывается [12]:
■ при Reпл
≤ Reгр по формуле:
■ при Reпл
> Reгр; Reц
> 5·103 по формуле:
где 




C1 =
0,02 - для труб из углеродистых сталей;
C1 =
0,031 - для труб из меди и латуни;
С2 =
0,024 - для труб из углеродистых и нержавеющих сталей;
С2 =
0,032 - для труб из меди и латуни.
Пределы
применимости формулы (3.2.2.52):
Рr' = 0,88 ÷ 1,78; Reпл = 20 ÷ 14700;
q =
(2,3 ÷ 1350)·102 Вт/м2; L = 1 ÷ 4 м;
dвн = 10 ÷ 38 мм.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
Пределы
применимости формулы (3.2.2.53):
Рr' = 0,86 ÷ 0,96; Rец =
5·103 ÷ 3·105; Р = 1,2 ÷ 9 МПа;
 = (160 ÷ 1600)·103
Вт/м2; L = 2,2 ÷ 12,0 м;
= (160 ÷ 1600)·103
Вт/м2; L = 2,2 ÷ 12,0 м;
dвн = 10 ÷ 17 мм; 0,26 ≤ Xвх ≤
1; 0 ≤ Хвых ≤ 0,069.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
3.2.2.2.5. Теплоотдача при пленочной конденсации пара на
поверхности
внутренней трубы кольцевого канала
Локальный коэффициент
теплоотдачи при конденсации водяного пара на поверхности внутренней трубы
кольцевого канала (опускное движение насыщенного пара) рассчитывается по
формуле [12]:
|

|
(3.2.2.54)
|
где 

X -
паросодержание;
d2 -
внутренний диаметр наружной трубы кольцевого канала, м;
d1 -
наружный диаметр внутренней трубы кольцевого канала, м;
С =
0,024 - для внутренней трубы кольцевого канала из углеродистой и нержавеющей
стали;
С =
0,026 - для внутренней трубы кольцевого канала из меди и латуни.
Пределы
применимости формулы:
dг = 3,7 ÷ 9,0 мм; Р = 1 ÷ 10 МПа; ρw
= 100 ÷ 600 кг/м2·с.
Погрешность
Δ расчета Nuпл составляет ±15 %.
3.2.2.2.6. Теплоотдача при пленочной конденсации пара на
внутренней
поверхности канала прямоугольного поперечного сечения
Средний по длине коэффициент
теплоотдачи при полной и частичной конденсации водяного пара, движущегося
сверху вниз внутри каналов прямоугольного поперечного сечения, расположенных
вертикально или горизонтально, с неполным охлаждением по периметру (охлаждение
боковой или потолочной стенки) рассчитывается по формуле [12]:
|

|
(3.2.2.55)
|
где 
dг -
гидравлический диаметр канала, м;
 - приведенная скорость
конденсата в выходном сечении канала, м/с;
- приведенная скорость
конденсата в выходном сечении канала, м/с;
f = ab
- площадь поперечного сечения канала, м2;

d -
диаметр гиба канала в случае изогнутых каналов, м.
Пределы
применимости формулы: а/b =
0,34; L = 0,8 ÷ 1,5 м;
 = 0,01; Р = 0,15
÷ 2 МПа;
= 0,01; Р = 0,15
÷ 2 МПа; 
Погрешность
Δ расчета Nu составляет ±15 %.
3.2.2.2.7. Теплоотдача при пленочной конденсации пара на пластинах
Средний
по длине коэффициент теплоотдачи при конденсации неподвижного пара на
поверхности вертикально расположенной пластины, а также пластиной, отклоненной
от вертикали на угол менее 10°, рассчитывается по формулам раздела 3.2.2.2.1.
Средний по длине коэффициент
теплоотдачи при конденсации неподвижного пара на нижней и верхней поверхностях
пластины, отклоненной от вертикали на угол более 10°, и ламинарном режиме
течения пленки конденсата, рассчитывается по формуле [10, 11,
13, 14]:
|

|
(3.2.2.56)
|
где 
θ -
угол наклона пластины к горизонтальной плоскости, градус;
εt - поправка на переменность теплофизических свойств конденсата,

а =
0,65, т = 1/5 при θ = 6 ÷ 23°;
а =
0,74, т = 1/3 при θ = 23 ÷ 80°.
Пределы
применимости формулы:
 = 0,5 ÷ 2,0;
= 0,5 ÷ 2,0;  = 0,1 ÷ 1,0; θ
= 6 ÷ 80°; Reпл
< Reв;
= 0,1 ÷ 1,0; θ
= 6 ÷ 80°; Reпл
< Reв;
где


Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
Средний по длине коэффициент
теплоотдачи при пленочной конденсации неподвижного водяного пара на нижней
поверхности пластины, отклоненной от горизонтали на угол 0 < θ ≤
6°, при ламинарном течении пленки конденсата рассчитывается по формуле [12]:
|

|
(3.2.2.57)
|
где 

Ra = KPr'Ar⁎cosθ;

r' = r + 0,68Cp'Δt.
Пределы
применимости формулы: Δt < 40K; 0
< θ < 6°.
Погрешность
Δ расчета Nuпл составляет ±15 %.
Средний по длине коэффициент
теплоотдачи при пленочной конденсации чистого водяного пара на нижней
поверхности горизонтальной пластины рассчитывается по формуле [12]:
|

|
(3.2.2.58)
|
где 
с =
0,66, т = 0,193 при 1010 > Ra
> 108;
с =
0,58, т = 0,200 при 108 > Ra
> 106.
Погрешность
Δ расчета Nuпл составляет ±15 %.
3.2.2.2.8. Теплоотдача при пленочной конденсации пара на внешней
поверхности одиночного горизонтального цилиндра
Средний
по длине коэффициент теплоотдачи при конденсации неподвижного насыщенного пара
на внешней поверхности одиночного горизонтального цилиндра рассчитывается [13]:
■ при Reпл
< Reв по формуле:
где 

εt - поправка на переменность теплофизических свойств конденсата:

εi
определяется по рис. 2.2.2;



■ при Reпл > Reв по
формуле:
|

|
(3.2.2.60)
|
Пределы применимости
формулы:  > 3.
> 3.
Погрешность
Δ расчета  составляет ±10 %.
составляет ±10 %.
Средний по длине коэффициент
теплоотдачи при пленочной конденсации движущегося сверху вниз пара на внешней
поверхности одиночного горизонтального цилиндра рассчитывается по формуле [15 - 17]:
где 

wо - скорость пара вдали от цилиндра, м/с;
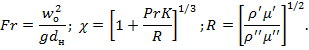
Пределы применимости
формулы:
Reпл = 1
÷ 106; KPr'/Fr = 10-5 ÷ 105.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
В
настоящее время отсутствуют общепринятые формулы для расчета теплоотдачи при
конденсации пара на горизонтальном цилиндре.
Средний
по длине коэффициент теплоотдачи при пленочной конденсации практически
неподвижного пара на внешней поверхности одиночного горизонтального цилиндра
рассчитывается поэтому по равноправным с формулами (3.2.2.59) ÷ (3.2.2.61) формулам [15 - 17]:
■ при Reпл
= Reв ÷ 40 по формуле:
где 

εv - поправка на волновое
течение пленки конденсата,  ,
,

■ при  = 2 ÷ 10, Reпл = Reв
÷ 40 по формуле:
= 2 ÷ 10, Reпл = Reв
÷ 40 по формуле:
где 
Пределы
применимости формулы: dн = 3 ÷ 45 мм.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
Средний по длине коэффициент
теплоотдачи при пленочной конденсации движущегося сверху вниз пара на внешней
поверхности одиночного горизонтального цилиндра рассчитывается по формулам [15 - 17]:
|

|
(3.2.2.64)
|
или
по аналогичной зависимости:
|

|
(3.2.2.65)
|
где 
w" -
скорость пара в узком проходном сечении канала, где расположена труба
(цилиндр);



Пределы применимости
формулы:
 для чистых паров воды,
хладонов 12 и 21;
для чистых паров воды,
хладонов 12 и 21;
dн =
2,5 ÷ 25 мм.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
Относительное изменение
коэффициента теплоотдачи при Δt = idem по сравнению с
конденсацией неподвижного пара рассчитывается по формуле:
|

|
(3.2.2.66)
|
где  рассчитывается по формулам
(3.2.2.62), (3.2.2.63).
рассчитывается по формулам
(3.2.2.62), (3.2.2.63).
3.2.2.2.9. Теплоотдача при пленочной конденсации пара на наружной
поверхности
оребренных снаружи вертикальных труб
Средний по длине коэффициент
теплоотдачи при пленочной конденсации пара на наружной поверхности вертикальных
труб с мелким продольным оребрением трапецеидальной формы рассчитывается по
формуле [12]:
|

|
(3.2.2.67)
|
где 
 = 0,7n-0,4We0,1
при β < 1, nWe0,25
≥ 1;
= 0,7n-0,4We0,1
при β < 1, nWe0,25
≥ 1;
 = 0,77β-0,07(nWe0,25)m
при β ≥ 1, nWe0,25 ≥ 1, m
= -0,4β-0,15;
= 0,77β-0,07(nWe0,25)m
при β ≥ 1, nWe0,25 ≥ 1, m
= -0,4β-0,15;
 = 1 - 0,23β-0,36(nWe0,25)1,2
при β ≥ 1, nWe0,25 < 1;
= 1 - 0,23β-0,36(nWe0,25)1,2
при β ≥ 1, nWe0,25 < 1;


b -
половина толщины ребра на торце, м;
h -
высота ребра, м;
Н -
длина трубы, м;
а -
половина ширины межреберной канавки, м;
S -
шаг ребер, м;
φ -
острый угол между боковой поверхностью ребра и его осевой плоскостью, град.;
Δtо -
температурный напор в основании ребра, К.
Значения
 относятся к поверхности
гладкой трубы с наружным диаметром по основанию ребер.
относятся к поверхности
гладкой трубы с наружным диаметром по основанию ребер.
Пределы
применимости формулы:
We ≥
10; 
Погрешность Δ
расчета  u
составляет ±20 %.
u
составляет ±20 %.
Средний по длине коэффициент
теплоотдачи при пленочной конденсации пара на наружной поверхности вертикальных
труб с мелким продольным оребрением, имеющим треугольный профиль со скругленной
вершиной, рассчитывается по формуле [12]:
|

|
(3.2.2.68)
|
где  H -
длина трубы, м;
H -
длина трубы, м;
L -
ширина боковой поверхности ребра, м.
Значение параметра (0 ≤
у ≤ 1) определяется из уравнения:

где 
R -
радиус кривизны вершины ребра, м.
Значения
 относятся к полной наружной
поверхности трубы с учетом оребрения.
относятся к полной наружной
поверхности трубы с учетом оребрения.
Пределы
применимости формулы: А ≤ 0;
Погрешность
Δ расчета  составляет ±20 %.
составляет ±20 %.
3.2.2.2.10. Теплоотдача при пленочной конденсации пара на наружной
поверхности профилированных вертикальных труб
Средний
по длине коэффициент теплоотдачи при пленочной конденсации практически
неподвижного пара на наружной поверхности одиночных вертикальных труб с внутренними
поперечными гофрами (кольцевое профилирование, рис. 3.1.3.14) рассчитывается [12]:
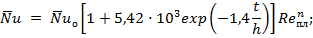
■ при Reпл = 30 ÷ 3000,  по формуле:
по формуле:
где 
■ при Reпл < 400,  по формуле:
по формуле:
|

|
(3.2.2.70)
|
В формулах:

H -
высота трубы, м;
h -
высота кольцевой гофры, м;
t -
шаг расположения кольцевых гофр, м;
Dн - наружный диаметр гладкой трубы, м;
 - средний коэффициент
теплоотдачи при пленочной конденсации пара на наружной поверхности исходной
гладкой одиночной трубы,
- средний коэффициент
теплоотдачи при пленочной конденсации пара на наружной поверхности исходной
гладкой одиночной трубы,  рассчитывается по формуле [12]:
рассчитывается по формуле [12]:
где 
C = Reпл0,04Et при
Reпл ≤ 100;
C = 1 + 0,04Reпл0,2 + 2,27·10-3Reпл0,8(Pr')0,5;

 - физические свойства
конденсата при температуре стенки трубы;
- физические свойства
конденсата при температуре стенки трубы;
 - физические свойства
конденсата при температуре насыщения.
- физические свойства
конденсата при температуре насыщения.
Погрешность
Δ расчета  составляет ±20 %.
составляет ±20 %.
Средний
по длине коэффициент теплоотдачи при пленочной конденсации практически
неподвижного пара на наружной поверхности вертикальных труб с внутренним
трехзаходным спиральным оребрением (спиральное профилирование) рассчитывается [12]:
■
для труб из нержавеющей стали при Reпл = 80 ÷ 400,
h/S = 0,048 ÷ 0,20, S/dн = 0,33 ÷ 0,91 по формуле:
|

|
(3.2.2.72)
|
■ для труб из латунных и медноникелевых сплавов,
углеродистой стали при Reпл =
30 ÷ 2500, S/h ≥ 7, S/dн ≤ 0,90 по
формуле:
В формулах: 
 - рассчитывается по формуле
(2.2.71);
- рассчитывается по формуле
(2.2.71);
Н -
высота трубы, м;
S -
шаг закрутки ребра, м;
h -
высота ребра, м;
dн -
наружный диаметр исходной гладкой трубы, м.
Погрешность
Δ расчета  составляет ±20 %.
составляет ±20 %.
Средний по длине коэффициент
теплоотдачи при пленочной конденсации движущегося пара, который поперечно
обтекает вертикальную профильную трубу из нержавеющей стали с внутренним
трехзаходным спиральным оребрением рассчитывается по формуле [12]:
|

|
(3.2.2.74)
|
где  ;
;

 рассчитывается по формуле (3.2.2.71), где C = Reпл0,04Еt.
рассчитывается по формуле (3.2.2.71), где C = Reпл0,04Еt.
Пределы
применимости формулы:
П1
= 14 ÷ 1000; Reпл ≤
500;
h/S =
0,057 ÷ 0,122;  = 0,438 ÷ 1,0.
= 0,438 ÷ 1,0.
Погрешность
Δ расчета  составляет ±25 %.
составляет ±25 %.
3.2.2.2.11. Теплоотдача при пленочной конденсации пара на пакете
горизонтальных труб
Особенностью
теплообмена при конденсации пара на пакете (пучке расположенных друг над
другом) горизонтальных труб является конденсация пара на переохлажденных каплях
и струях в межтрубном пространстве. На каждую нижерасположенную трубу жидкость
поступает при температуре, равной температуре насыщения. На каждой трубе
пакета, кроме первой, формируется начальный участок теплового пограничного
слоя. Точка выхода теплового пограничного слоя, развивающегося от стенки на
поверхность пленки, определяет длину начального участка хн
или угол φ.
Средний по длине коэффициент
теплоотдачи при пленочной конденсации практически неподвижного пара на i-той трубе пакета рассчитывается по формуле [15 - 17]:
где 
 описывает теплообмен на
начальном участке теплового пограничного слоя на i-той
трубе пакета, расположенной ниже первой, начиная сверху;
описывает теплообмен на
начальном участке теплового пограничного слоя на i-той
трубе пакета, расположенной ниже первой, начиная сверху;
где Reпл
- число Рейнольдса пленки конденсата, вычисленное на предыдущей трубе пакета, 

n -
номер трубы при отсчете сверху;
 -
плотность теплового потока на данной трубе пакета, Вт/м2;
-
плотность теплового потока на данной трубе пакета, Вт/м2;
φ -
значение угла, при котором тепловой пограничный слой достигает толщины пленки
конденсата, определяется соотношением [15 - 17]:
Значения функций Q(φ),  , Р(φ) приведены в таблице 3.2.2.2.
, Р(φ) приведены в таблице 3.2.2.2.
Таблица 3.2.2.2
Значения функций Q(φ),
 , Р(φ) в формулах (3.2.2.76), (3.2.2.77)
, Р(φ) в формулах (3.2.2.76), (3.2.2.77)
|
Град.
|
Р(φ)
|
Q(φ)
|
Q(φ)
|
Град.
|
Р(φ)
|
Q(φ)
|
Q(φ)
|
|
0
|
0
|
0
|
0
|
100
|
1,469
|
1,939
|
1,111
|
|
10
|
0,073
|
0,260
|
1,490
|
110
|
1,641
|
2,088
|
1,088
|
|
20
|
0,184
|
0,489
|
1,401
|
120
|
1,810
|
2,229
|
1,064
|
|
30
|
0,315
|
0,697
|
1,331
|
130
|
1,974
|
2,361
|
1,040
|
|
40
|
0,479
|
0,896
|
1,283
|
140
|
2,129
|
2,483
|
1,016
|
|
50
|
0,615
|
1,088
|
1,247
|
150
|
2,273
|
2,594
|
0,991
|
|
60
|
0,779
|
1,272
|
1,215
|
160
|
2,404
|
2,696
|
0,965
|
|
70
|
0,948
|
1,449
|
1,186
|
170
|
2,515
|
2,777
|
0,936
|
|
80
|
1,120
|
1,619
|
1,160
|
180
|
2,589
|
2,824
|
0,899
|
|
90
|
1,295
|
1,783
|
1,135
|
|
|
|
|
При  рассчитывается по формуле [15 - 17]:
рассчитывается по формуле [15 - 17]:
В формуле (3.2.2.75):
 - число Нуссельта на той
части трубы, где происходит конденсация пара,
- число Нуссельта на той
части трубы, где происходит конденсация пара,  рассчитывается:
рассчитывается:
при Reпл < 2,3Аr⁎1/5 по
формуле (3.2.2.62);
при Reпл > 2,3Аr⁎1/5 по
формуле (3.2.2.62)
подстановкой в нее Reпл = 2,3Аr⁎1/5.
Пределы
применимости формул (3.2.2.75)
÷ (3.2.2.78):
Re =
10 ÷ Reкр, где Reкр = 353Аr⁎1/5.
При Reпл
< 10 расчет 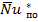 производится по формуле (3.2.2.62) для одиночного
цилиндра без учета плотности орошения.
производится по формуле (3.2.2.62) для одиночного
цилиндра без учета плотности орошения.
Погрешность
Δ расчета 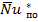 ,
,  ,
,  составляет ±20 %.
составляет ±20 %.
При конденсации пара на
пакете труб диаметром  = 2 ÷ 10 значение
= 2 ÷ 10 значение 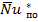 , рассчитанное по формуле (3.2.2.75), умножается на
коэффициент εσ.
, рассчитанное по формуле (3.2.2.75), умножается на
коэффициент εσ.
|

|
(3.2.2.79)
|
Средний по длине коэффициент теплоотдачи при пленочной конденсации
нисходящего потока пара на пучке расположенных друг над другом горизонтальных
труб рассчитывается по формуле [16,
18]:
где 
n - номер трубы при отсчете сверху.
Пределы
применимости формулы: K
> 1/2.
Погрешность
Δ расчета 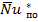 составляет ±15 %.
составляет ±15 %.
3.2.2.2.12. Теплоотдача при пленочной конденсации пара в
поперечно-обтекаемых
шахматных и коридорных пучках горизонтальных труб
Средний по длине коэффициент
теплоотдачи первого ряда шахматных и коридорных поперечно-обтекаемых пучков
горизонтальных труб при пленочной конденсации нисходящего потока пара
рассчитывается по формуле [16, 18]:
где 
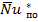 рассчитывается по формуле (3.2.2.80);
рассчитывается по формуле (3.2.2.80);
 - средняя скорость пара в
узком сечении горизонтального ряда труб, м/с.
- средняя скорость пара в
узком сечении горизонтального ряда труб, м/с.
Пределы
применимости формулы:
Р =
(0,032 ÷ 0,89)·105 Па; Δt = 0,6 ÷ 12 °С;  .
.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
Средний по длине коэффициент
теплоотдачи всего пучка при пленочной конденсации в поперечно-обтекаемом пучке
горизонтальных труб, имеющем постоянное по высоте пучка проходное сечение для
пара, рассчитывается по формуле [16,
18]:
|

|
(3.2.2.82)
|
где 
 рассчитывается по формуле (3.2.2.81);
рассчитывается по формуле (3.2.2.81);

n -
число рядов труб по высоте коридорного пучка труб или половина числа рядов труб
шахматного пучка.
Пределы
применимости формулы: Р = (0,032 ÷ 0,89)·105 Па;
Δt =
0,6 ÷ 12 °С;  .
.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
3.2.2.2.13. Теплоотдача при пленочной конденсации нисходящего
потока пара
на внутренней поверхности трубы змеевика с вертикальной осью навивки
Средний по длине коэффициент
теплоотдачи при пленочной конденсации нисходящего потока пара на внутренней
поверхности трубы змеевика с вертикальной осью навивки рассчитывается по
формуле [12]:
|

|
(3.2.2.83)
|
где 
 внутренний диаметр трубы
змеевика, м;
внутренний диаметр трубы
змеевика, м;

dзм -
диаметр змеевика, м;
h -
шаг навивки змеевика, м;

 - приведенная скорость
конденсата в выходном сечении трубы, м/с;
- приведенная скорость
конденсата в выходном сечении трубы, м/с;
L -
длина трубы змеевика, м,
С =
160, n = -0,27 при Fr0 = 1,6·10-3 ÷
7·10-2;
С =
425, n = 0,20 при Fr0 = 7·10-2 ÷ 10.
Пределы
применимости формулы:
Р =
0,5 ÷ 4,0 МПа;  = (60 ÷ 950)·103
Вт/м2; Xвых =
0,03 ÷ 0,50;
= (60 ÷ 950)·103
Вт/м2; Xвых =
0,03 ÷ 0,50;
Хвх =
1,0; L = 2,3 ÷ 4,0 м; dзм = 130 ÷ 210 мм;
h =
100 ÷ 200 мм; dвн = 10 ÷ 16 мм.
Погрешность
Δ расчета  составляет ±15 %.
составляет ±15 %.
Локальный коэффициент
теплоотдачи при пленочной конденсации нисходящего потока пара на внутренней
поверхности трубы змеевика с вертикальной осью навивки рассчитывается по
формуле [12]:
|

|
(3.2.2.84)
|
где 
Nu⁎ -
безразмерный коэффициент теплоотдачи при течении внутри змеевика воды при
температуре насыщения с массовой скоростью конденсирующегося пара,
|

|
(2.2.85)
|
где Nu0 = 0,023Reц0,80(Pr')0,40;

A = 1 - 0,334(lgK - 3,40) при K > 2,5·103;
A = 1 при K < 2,5·103;
 - число фазового перехода.
- число фазового перехода.
Пределы
применимости формулы:
Р =
0,7 ÷ 10 МПа; Х = 0 ÷ 1,0; ρw = 200 ÷
1200 кг/м2·с;
dвн = 2,2 ÷ 10 мм; dзм = 115 ÷ 510
мм.
Погрешность
Δ расчета Nuпл составляет ±15 %.
3.2.2.2.14. Тепломассообмен при пленочной конденсации парогазовой
смеси на твердой поверхности
Водяной
пар, поступающий в конденсаторы ядерных энергетических установок, содержит
кислород, водород, азот и другие газы. В процессе конденсации концентрация газа
в паре повышается, что приводит к ухудшению теплоотдачи, так как скапливающийся
в зоне охлаждения газ препятствует притоку пара к поверхности теплообмена.
Возможны
два режима работы поверхностей теплообмена с конденсацией пара из парогазовой
смеси:
■
с продувкой части парогазовой смеси из зоны с максимальной концентрацией
неконденсирующегося газа;
■
с полной конденсацией пара и удалением газа за счет растворимости в конденсате.
Количество продувочного пара
при удалении неконденсирующихся газов продувкой паром рассчитывается по
формуле:
|

|
(3.2.2.86)
|
где  -
отношение массового расхода продувочного пара к общему расходу греющего пара Gпп;
-
отношение массового расхода продувочного пара к общему расходу греющего пара Gпп;
 - массовая концентрация
газа в продувочном паре на входе в конденсатор, кг/кг;
- массовая концентрация
газа в продувочном паре на входе в конденсатор, кг/кг;
 - массовая концентрация
газа в продувочном паре на выходе из конденсатора, кг/кг;
- массовая концентрация
газа в продувочном паре на выходе из конденсатора, кг/кг;
 - равновесная концентрация
газа паре;
- равновесная концентрация
газа паре;
 - массовый расход газа,
удаляемого из конденсатора с продувочным паром, кг/с;
- массовый расход газа,
удаляемого из конденсатора с продувочным паром, кг/с;
 - массовый расход газа,
растворяющегося в конденсате, кг/с;
- массовый расход газа,
растворяющегося в конденсате, кг/с;
Gконд - массовый расход пара, сконденсировавшегося в конденсаторе,
кг/с;
Gпп - массовый расход продувочного пара, кг/с;
Kг - константа Генри, зависящая от температуры и рода газа, м2/Н;
Рг -
парциальное давление газа в парогазовой смеси, Н/м2.
Массовая
концентрация газа в продувочном паре на входе в конденсатор Свх
выбирается по условиям работы установки. Массовая концентрация газа в
продувочном паре на выходе из конденсатора Свых принимается с
учетом максимально возможной недовыработки электроэнергии, с одной стороны, и с
учетом максимально возможного увеличения поверхности конденсации, с другой
стороны.
При
работе с полной конденсацией парогазовой смеси удаление неконденсирующихся
газов происходит за счет растворимости в конденсате. При этом выполняется
условие:
Свх = Сконд.
Теплоотдача
при пленочной конденсации пара из парогазовой смеси определяется диффузионным
термическим сопротивлением и термическим сопротивлением пленки конденсата.
При
разработке расчетных рекомендаций используются два метода [12]:
- первый метод состоит в
использовании эмпирических зависимостей для эквивалентного термического
сопротивления:
|
q = αг(Ts -
Tст),
|
(3.2.2.87)
|
где αг -
суммарный коэффициент теплоотдачи при конденсации из парогазовой смеси, Вт/(м2К);
Ts, Tст в [К];
- второй метод заключается в
раздельном описании этих термических сопротивлений с привлечением уравнений
диффузии. При таком подходе величина плотности теплового потока, переданного от
парогазовой смеси к пленке конденсата и от пленки конденсата к стенке должна
удовлетворять одновременно двум уравнениям:
где Рп - парциальное давление пара в парогазовой
смеси, Н/м2;
 - парциальное давление пара
в парогазовой смеси на границе пар-пленка конденсата, Н/м2;
- парциальное давление пара
в парогазовой смеси на границе пар-пленка конденсата, Н/м2;
 - температура насыщения
пара на границе пар-пленка конденсата, К;
- температура насыщения
пара на границе пар-пленка конденсата, К;
βр -
коэффициент массоотдачи из парогазовой смеси к пленке конденсата, м/с;
Δi -
теплота перегрева пара в парогазовой смеси относительно температуры насыщения
при парциальном давлении, Дж/кг;
α -
коэффициент теплоотдачи от пленки конденсата к стенке, Вт/м2К.
Рассматривая уравнение (3.2.2.88) и уравнение,
описывающее способ отвода тепла:
где Тохл - средняя температура охлаждающей воды,
К; Rохл - термическое сопротивление теплоотдачи от внутренней стенки
трубы к охлаждающей воде, м2·К/Вт, получают систему трех нелинейных
уравнений с тремя неизвестными: Тст, Тпгр,
q, определив которые методом последовательных приближений рассчитывают
теплоотдачу при конденсации парогазовой смеси.
Суммарный локальный
коэффициент теплоотдачи при пленочной конденсации парогазовой смеси
рассчитывается по эмпирической формуле из [12]:
где  - объемное газосодержание
смеси;
- объемное газосодержание
смеси;
Рг -
парциальное давление газа, Н/см2;
Рcм - общее давление парогазовой смеси, Н/см ;
m - эмпирический показатель, значения которого в зависимости от
режимных параметров приведены в таблице 3.2.2.3;
α
рассчитывается по формулам раздела 3.2.2.2.
Погрешность
Δ расчета αг составляет 20 %.
Таблица 3.2.2.3
Значения эмпирического показателя m в формуле (3.2.2.90)
в зависимости от режимных параметров
|
Р,
МПа
|
εг
|
q, кВт/м2
|
Re
|
т
|
|
7,85
|
0 ÷ 0,24
|
123 ÷ 172
|
700 ÷ 1200
|
1,30
|
|
7,85
|
0 ÷ 0,24
|
51 ÷ 63
|
1800 ÷ 10000
|
0,71
|
|
3,92
|
0 ÷ 0,12
|
79 ÷ 124
|
2900 ÷ 8800
|
0,60
|
|
1,96
|
0 ÷ 0,12
|
93 ÷ 113
|
2600 ÷ 9400
|
0,49
|
|
1,96
|
0 ÷ 0,12
|
35 ÷ 52
|
2900 ÷ 4300
|
0,40
|
Средний коэффициент теплоотдачи при конденсации водяного пара из
движущейся внутри вертикальной трубы парогазовой смеси рассчитывается по
эмпирической формуле [12]:
где  - объемное газосодержание
на входе в конденсатор;
- объемное газосодержание
на входе в конденсатор;
 рассчитывается по формулам
(3.2.2.48) ÷ (3.2.2.50).
рассчитывается по формулам
(3.2.2.48) ÷ (3.2.2.50).
Пределы
применимости формулы:
Р =
0,8 ÷ 3,0 МПа; L ≤ 3 м;  ≤ 2,5 %.
≤ 2,5 %.
Погрешность
Δ расчета αг составляет 20 %.
Система
уравнений (3.2.2.88), (3.2.2.89) является нелинейной,
поскольку все входящие в нее параметры представляют собой функции искомых
величин:
-
коэффициент теплоотдачи от пленки конденсата к стенке зависит от q, Тст,
Тпгр и рассчитывается по формулам для конденсации
чистого насыщенного пара, которые приведены в разделе 3.2.2.2;
-
термические сопротивления Roxл и Rст
зависят от q и Тст. Они рассчитываются по формулам раздела
3.2.1.2 и по формулам для
расчета термического сопротивления цилиндрических стенок;
- коэффициент массоотдачи βр
зависит от Тпгр и рассчитывается по формуле [12]:
|

|
(3.2.2.92)
|
где L - характерный размер, м;
Dp -
коэффициент диффузии для пара, отнесенный к градиенту парциального давления;
NuD -
диффузионное число Нуссельта с учетом влияния поперечного потока массы.
Коэффициент диффузии Dp
рассчитывается по формуле:
|

|
(3.2.2.93)
|
где R = 8,31·103 Дж/(кмоль·град) - универсальная
газовая постоянная;
Мп -
молекулярная масса пара, кг/кмоль;
Тсм -
температура парогазовой смеси, К;
D1-2 -
коэффициент взаимной диффузии компонентов парогазовой смеси, который
рассчитывается по формуле [12],
м2/с:
|

|
(3.2.2.94)
|
где D0 - коэффициент взаимной диффузии при
нормальных условиях, м2/с;
Р0 =
1,013·105 Н/м2;
T =273K.
Диффузионное число Нуссельта
с учетом влияния поперечного потока массы определяется соотношением [12]:
|

|
(3.2.2.95)
|
где NuD = βpL/Dp,
 - диффузионное число
Нуссельта без учет влияния поперечного потока массы, определяемое по аналогии
между тепло- и массообменом путем замены в критериальных формулах теплового
числа Прандтля на диффузионное;
- диффузионное число
Нуссельта без учет влияния поперечного потока массы, определяемое по аналогии
между тепло- и массообменом путем замены в критериальных формулах теплового
числа Прандтля на диффузионное;
РrD = vсм/D1-2;
 - коэффициент динамической
вязкости парогазовой смеси, Н с/м2;
- коэффициент динамической
вязкости парогазовой смеси, Н с/м2;
μг, μп
- коэффициент динамической вязкости газа и пара при tсм и ρсм,
(Н·с)/м2;
ρсм = ρп
+ ρг - плотность парогазовой смеси, кг/м3;
ρп, ρг
- плотность пара и газа при парциальном давлении пара Рп и
газа Рг и температуре смеси, кг/м3;
 - объемное газосодержание
парогазовой смеси;
- объемное газосодержание
парогазовой смеси;
Rп/Rг = Mг/Mп -
отношение газовых постоянных газа и пара;
Mг, Mп -
молекулярные массы газа и пара, кг/кмоль;
Gп, Gг
- массовые расходы пара и газа, кг/с;
 - относительный перепад
давлений.
- относительный перепад
давлений.
Характер течения парогазовой
смеси определяется числом Рейнольдса [12]:
|

|
(3.2.2.96)
|
где  - массовая скорость
парогазовой смеси, кг/(м2·с);
- массовая скорость
парогазовой смеси, кг/(м2·с);
f - площадь поперечного сечения канала, м2.
Диффузионное
число Нуссельта с учетом поперечного потока массы рассчитывается [12]:
■ при турбулентном
течении парогазовой смеси (Reсм > 1000) по формулам:
|

|
(3.2.2.98)
|
■ при ламинарном течении парогазовой смеси (Reсм
< 1000) по формулам:
|

|
(3.2.2.99)
|
|

|
(3.2.2.100)
|
Диффузионное число Нуссельта
с учетом поперечного потока массы при εг < πD
< 0,1 рассчитывается [12]:
■ для турбулентного
пограничного слоя по формулам:
■ для ламинарного пограничного слоя по формулам:
где Rп/Rсм = 1 + εг[Rп/Rг
- 1] - отношение газовых постоянных пара и парогазовой смеси;
b -
параметр отсоса, учитывающий поперечный поток массы.
В
процессе конденсации парогазовой смеси параметр отсоса является искомой
величиной. Приведенные зависимости (3.2.2.101), (3.2.2.102) и (3.2.2.103), (3.2.2.104) представляют собой систему
алгебраических уравнений с неизвестными NuD/ и b. Таким образом, для определения искомой величины NuD/
и b. Таким образом, для определения искомой величины NuD/ из второго уравнения
системы рассчитывается параметр b и
подставляется в первое уравнение.
из второго уравнения
системы рассчитывается параметр b и
подставляется в первое уравнение.
Погрешность
Δ расчета NuD по формулам (3.2.2.97 ÷ 3.2.2.103) составляет ±20 %.
Система
уравнений (3.2.2.88), (3.2.2.89) решается следующим
образом:
-
задается температура охлаждающей воды на выходе из рассчитываемого ряда труб
теплообменника ( )1;
)1;
-
определяется средняя температура охлаждающей воды в первом приближении  ;
;
-
задается температура наружной стенки труб теплообменника в первом приближении  ;
;
-
рассчитываются термические сопротивления Roxл и Rст;
- рассчитывается
передаваемая плотность теплового потока в первом приближении:

- задается  в первом приближении,
рассчитывается α, и рассчитывается
в первом приближении,
рассчитывается α, и рассчитывается  во втором приближении:
во втором приближении:

- расчет продолжается, когда
|

|
(3.2.2.105)
|
если это условие не выполняется, то  уточняется еще раз:
уточняется еще раз:
- по
известному значению  рассчитывается
рассчитывается  ;
;
- по
известным  ,
,  рассчитывается коэффициент
массоотдачи βр;
рассчитывается коэффициент
массоотдачи βр;
- рассчитывается
передаваемая при этом коэффициенте массоотдачи плотность теплового потока:

- расчет продолжается, если выполняется условие:
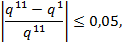
если это условие не выполняется, то задается новая температура:

и расчет повторяется:
-
рассчитывается количество тепла, передаваемого охлаждающей воде:
Q = qF;
- рассчитывается температура
охлаждающей воды на выходе во втором приближении:

где  - температура охлаждающей
воды на входе в теплообменник, К;
- температура охлаждающей
воды на входе в теплообменник, К;
Gохл -
массовый расход охлаждающей воды, кг/с;
Ср -
теплоемкость охлаждающей воды, Дж/(кг·К);
- расчет продолжается, если
|

|
(3.2.2.106)
|
если это условие не выполняется, то расчет повторяется сначала.
В
результате проведенного расчета определяется:
-
количество тепла Q, передаваемого охлаждающей воде, массовый расход
сконденсировавшегося пара Gк = Q/r, где r - теплота парообразования при Рп, Дж/кг;
- объемная концентрация газа
на выходе:

Погрешность Δ
расчета Q составляет ±15 %; Gк - ±20 %.
3.2.2.2.15. Теплоотдача при пленочной конденсации пара из
паровоздушной
смеси на наружной поверхности вертикальных профилированных труб
Средний по длине коэффициент
теплоотдачи при конденсации практически неподвижного водяного пара из
паровоздушной смеси на наружной поверхности вертикальной трубы с внутренними
кольцевыми поперечными гофрами и трехзаходным спиральным оребрением
рассчитывается по формуле [12]:
|

|
(3.2.2.107)
|
где  - средний по длине
коэффициент теплоотдачи при конденсации водяного пара из паровоздушной смеси на
наружной поверхности вертикальной гладкой трубы;
- средний по длине
коэффициент теплоотдачи при конденсации водяного пара из паровоздушной смеси на
наружной поверхности вертикальной гладкой трубы;
 рассчитывается по формуле (3.2.2.91);
рассчитывается по формуле (3.2.2.91);
εг -
объемное газосодержание;
 при εг
≤ 0,025;
при εг
≤ 0,025;
С = 1
при εг > 0,025;
 рассчитывается по формулам
(3.2.2.69) ÷ (3.2.2.73).
рассчитывается по формулам
(3.2.2.69) ÷ (3.2.2.73).
Пределы
применимости формулы:
трубы
из латунных и медных сплавов;
εг = 0
÷ 1; Р = 0,1 ÷ 0,7 МПа.
Погрешность
Δ расчета  составляет ±25 %.
составляет ±25 %.
3.2.2.2.16. Теплоотдача при конденсации пара на спутной струе воды
Средний по длине коэффициент
теплоотдачи от конденсирующего пара к охлаждающей струе воды при спутном
течении рассчитывается по формуле [12]:
|

|
(3.2.2.108)
|
где 
L -
длина струи, м;
d0 -
диаметр сопла, м;
w0 -
скорость воды в выходном срезе сопла, м/с;
t0 -
среднемассовая температура воды на входе в сопло, °С;
t', r - температура насыщения и
скрытая теплота парообразования при давлении в конденсаторе;
vв, αв,
λв, Cpв - физические свойства воды,
определяются при температуре:

 отнесен к
среднеарифметическому температурному напору:
отнесен к
среднеарифметическому температурному напору:

tL -
среднемассовая температура струи в сечении на расстоянии от выходного среза
сопла.
Пределы
применимости формулы:
Р =
0,01 ÷ 0,098 МПа; w0 = 5 ÷ 26 м/с; L =
20 ÷ 1200 мм; d = 2 ÷ 20 м;
wп = 0,4 ÷ 30 м/с; n = 1
÷ 46;
wп - скорость пара в сечении среза сопла;
Р -
абсолютное давление в конденсаторе;
n - число струй воды.
Погрешность
Δ расчета  составляет ±30 %.
составляет ±30 %.
3.2.2.2.17. Тепломассообмен при конденсации пара из паровоздушной
среды на водяных каплях
Охлаждение
паровоздушной смеси, образующейся при аварии с разуплотнением контура водяного
теплоносителя, происходит в гермозоне АС на диспергированных водяных струях
спринклерной системы, представляющих собой конгломерат капель.
Зависимость степени прогрева
капли воды, движущейся в паровоздушной среде, от режимных параметров и
безразмерный эффективный коэффициент теплоотдачи рассчитываются по формулам [19, 20]:
|

|
(3.2.2.109)
|
|

|
(3.2.2.110)
|
где Рс - давление паровоздушной среды, МПа;
wк -
скорость капли относительно паровоздушной среды, м/с;
т0 -
начальная масса капли, кг;
εп -
мольная концентрация пара в паровоздушной среде;
τ
- время, с;
Lрко - число Лапласа,  ;
;
σк, ρк
и vк - коэффициент поверхностного натяжения, плотность и
коэффициент кинематической вязкости.
Индексы
«с», «п» и «к» относятся к паровоздушной смеси, пару и капле, «ко» - к
начальной температуре капли при нормальных условиях (Р = 0,1 МПа);
Пределы
применимости формулы:
dк = 0,9 ÷ 1,8 мм; tко = 20 ÷ 100
°С; Рс = 0,1 ÷ 0,5 МПа;
tc =
40 ÷ 140 °С; wк =
0,8 ÷ 15 м/с; εп = 0,09 ÷ 0,85.
Погрешность
Δ расчета θ составляет 6,1 %.
Погрешность
Δ расчета Nuэ составляет 13 %.
3.2.2.3. ЗАКРИЗИСНЫЙ ТЕПЛООБМЕН ПРИ КИПЕНИИ ВОДЫ В КАНАЛАХ
При
течении кипящей жидкости в обогреваемом канале в некотором его сечении может
произойти резкое ухудшение теплоотдачи (кризис теплоотдачи), проявляющееся либо
в увеличении температуры теплоотдающей поверхности, либо в снижении теплового
потока в месте возникновения кризиса теплоотдачи и ниже по потоку. Участок
канала между сечением, где возник кризис теплоотдачи и сечением, ниже которого
по течению поток становится однофазным (зона перегрева пара), называют
закризисной областью или областью ухудшенного теплообмена, а режим теплообмена
в ней закризисным (пленочное кипение).
В
общем случае двухфазный поток в закризисной зоне является термически
неравновесным, а температура теплоотдающей поверхности определяется несколькими
одновременно протекающими процессами: конвективной теплоотдачей к пару,
испарением капель и излучением. При этом истинные параметры потока зависят от
испарения влаги, как на теплоотдающей поверхности, так и в паре, температура
которого может значительно превышать температуру насыщения. В расчетной
практике часто используется допущение о термическом равновесии между жидкой и
паровой фазами. В этом случае границей между закризисной зоной и зоной
перегрева пара считается сечение канала с относительной энтальпией потока,
равной 1. Часто закризисную зону дополнительно разбивают на области переходного
и развитого пленочного кипения, однако такое разбиение также весьма условно.
В
зависимости от сочетания режимных параметров и геометрии канала режим течения в
закризисной зоне может быть либо обратнокольцевым, когда жидкость отделена от
теплоотдающих поверхностей паровой прослойкой, либо дисперсным, когда жидкость
распределена в паровом потоке в виде капель. Надежных рекомендаций для расчета
теплоотдачи при обратно-кольцевом режиме течения в настоящее время нет, однако
эта структура двухфазного потока весьма неустойчива: жидкое ядро довольно
быстро распадается на капли, и поток становится дисперсным. Таким образом,
преобладающим режимом течения в закризисной зоне является дисперсный. Большие
значения температуры стенки в этой зоне объясняются тем, что теплоотдающая
поверхность омывается, в основном, перегретым паром.
3.2.2.3.1. Закризисный теплообмен при дисперсном режиме
Закризисный
теплообмен при кризисе теплоотдачи, обусловленном сменой дисперсно-кольцевой
структуры потока дисперсной в условиях подъемного течения парожидкостной смеси
в цилиндрических каналах, рассчитывается по методике [21, 22],
учитывающей термическую неравновесность потока.
Основные
допущения:
■
двухфазный поток в закризисной области представляет собой однородную смесь
перегретого пара и капель жидкости;
■
тепло от греющей поверхности передается конвекцией к пару и от него к каплям,
т.е. испарением капель на теплоотдающей поверхности и излучением
пренебрегается;
■
коэффициент теплоотдачи от стенки к пару и критическое паросодержание (Xкр) считаются известными.
Область
применения:
■
геометрия каналов: трубы, кольцевые каналы, пучки стержней с дистанционирующими
решетками;
■
гидравлический диаметр каналов 4 ÷ 20 мм;
■
режимные параметры: Р = 1,1 ÷ 19,6 МПа,
ρw = 70 ÷ 2000 кг/м2·с, q ≤ 1 МВт/м2;
■
tст - ts ≤ 500 °C, Xб > Xкр ≥
0,1.
При этих допущениях
изменение истинного паросодержания в закризисной зоне канала определяется
следующим дифференциальным уравнением:
где С - эмпирическая константа;
Пг
- смоченный периметр канала, м;
Птi - - обогреваемый периметр i-ой
теплоотдающей поверхности, м;
qi(Хб) - осевое
распределение плотности теплового потока на i-ой
теплоотдающей поверхности, Вт/м2;
X -
истинное массовое паросодержание;
Хб -
балансовое (равновесное) паросодержание;
m и n - коэффициенты в степенной
аппроксимации калорического уравнения состояния перегретого пара.
Для
водяного пара:
при Р
< 6 МПа
т = 1149,1 - 28,2534р + 0,995р2 -
1,8421·10-2р3 + 1,213·10-4р4,
°С;
п = 1,0003 + 4,3389·10-3р - 2,5466·10-5p2;
при Р
≥ 6 МПа
т = 864,664 - 4,0128p,
°С;
n = 1,0861 + 8,6654·10-4р
+ 1,0772·10-5p2,
где Р
- давление в МПа, р = Р/10 - давление в барах.
Для
труб и пучков стержней С = 1,5.
Для
кольцевых каналов с односторонним обогревом С = 3. Для кольцевых каналов
с двухсторонним обогревом [23]
до сечения возникновения кризиса теплоотдачи на второй теплоотдающей
поверхности канала плотность теплового потока принимается равной нулю, а
константа С = 3. Ниже этого сечения по ходу потока принимается С
= 1,5.
Интегрирование
уравнения (3.2.2.3.1)
ведется от сечения возникновения кризиса теплоотдачи, в котором принимается,
что Хкр = (Хб)кр и tпп = ts.
При n = 1 (большие перегревы пара) уравнение (3.2.2.3.1) имеет аналитическое решение:
где 
В -
константа, определяемая из условия Хкр = (Хб)кр;

Ф(ξ)
- интеграл вероятности.
Формулу
(3.2.2.3.2) можно
использовать для тестирования схемы численного интегрирования уравнения (3.2.2.3.1).
Порядок
расчета теплообмена в закризисной области:
■
путем решения дифференциального уравнения (3.2.2.3.1) либо по формуле (3.2.2.3.2) находится истинное паросодержание
потока X при заданном балансовом паросодержании Хб;
■
по формуле  рассчитывается энтальпия
перегретого пара iпп в
заданном сечении канала;
рассчитывается энтальпия
перегретого пара iпп в
заданном сечении канала;
■
по найденной энтальпии перегретого пара и термодинамическим таблицам водяного
пара либо по приближенному соотношению  определяется температура
перегретого пара tпп;
определяется температура
перегретого пара tпп;
■
далее рассчитывается температура i-ой
теплоотдающей поверхности  ,
,
где αпп
- коэффициент конвективной теплоотдачи к перегретому пару.
Соотношения
для расчета теплоотдачи к пару
В трубах при q
≤ 0,5 МВт/м2 коэффициент теплоотдачи к перегретому пару αпп
рассчитывается по формуле [24]:
|

|
(3.2.2.3.3)
|
где 
При q > 0,5 МВт/м2
для расчета теплоотдачи к пару используется среднеарифметическое значение αпп
из результатов расчета по формулам (2.2.3.3) и (2.2.3.4):
|

|
(3.2.2.3.4)
|
где Тпп - температура перегретого пара, К;
Тст -
температура стенки, К.
Теплофизические
свойства берутся при температуре перегретого пара tпп;
В
кольцевых каналах коэффициент теплоотдачи αпп рассчитывается
[25]:
■
при тепловыделении на внутренней стенке кольцевого канала по
формуле:
Nu1пп =
0,86Nuпп(d1/d2)-0,16;
■
при тепловыделении в наружной стенке кольцевого канала по формуле:
Nu2пп =
Nuпп [1 - 0,14(d1/d2)0,6];
■
при двухстороннем тепловыделении в кольцевом канале:
для
внутренней стенки Nu*1пп =
Nu1пп/[1 + Nu1ппθ1q2/q1];
для
наружной стенки кольцевого канала
Nu*2пп =
Nu2пп/[1 + Nu2ппθ2q1/q2],
где 
θ1 = 32[0,16(d1/d2)2
- 1]Reпп-0,88;
θ2 = θ1d1/d2;


Индексы 1 и 2 относятся к
внутренней и наружной стенкам кольцевого канала, соответственно.
Теплофизические
свойства определяются при температуре перегретого пара tпп.
В пучках стержней
коэффициент теплоотдачи αпп рассчитывается по формуле [26]:
|

|
(3.2.2.3.5)
|
где С = 0,0165 + 0,02[1 - 0,91/(s/d)2](s/d)0,15;
s/d -
относительный шаг расположения стержней.
Учет
нестабилизированного теплообмена на входном участке закризисной зоны
Теплоотдача к перегретому
пару на участке формирования теплового пограничного слоя на расстояниях до 15
гидравлических диаметров от сечения возникновения кризиса теплоотдачи
рассчитывается по эмпирическому соотношению [27]:
|
Nu = 1,38(dг/Δz)0,12Nuо,
|
(3.2.2.3.6)
|
где Nuо - число Нуссельта для стабилизированного
теплообмена, a Δz -расстояние от сечения кризиса теплоотдачи.
Учет
влияния дистанционирующих элементов [28]
При интегрировании уравнения
(3.2.2.3.1) в каждом
сечении дистанционирования налагается новое граничное условие в соответствии с
формулой (3.2.2.3.7), учитывающее возрастание паросодержания из-за
дополнительного испарения влаги в результате взаимодействия с дистанционирующим
элементом (ДЭ) на величину:
|
ΔХ =
(1 - X)kΔF/F,
|
(3.2.2.3.7)
|
где ΔF/F - степень блокировки проходного сечения
канала дистанционирующим элементом;
k -
эмпирический коэффициент эффективности ДЭ, который может зависеть от геометрии
дистанционирующего элемента и режимных параметров (0 < k < 1). Для простых (без завихрителей) ДЭ при ρw < 500 кг/м2 с для оценки величины k можно использовать соотношение:
|
k = (1 - ρw/3000)
± 0,15.
|
(3.2.2.3.8)
|
Если паросодержание в сечении расположения ДЭ, рассчитанное с
учетом (2.2.3.7), превышает значение относительной энтальпии в этом же сечении,
то считается, что разница (X - Хб) обусловлена
испарением жидкой пленки, образовавшейся в результате взаимодействия потока с
ДЭ и покрывающей теплоотдающую поверхность на отрезке длиной:
|

|
(3.2.2.3.9)
|
На этом отрезке теплоотдача
определяется по формулам для кипения, после чего описанная выше процедура
решения уравнения (2.2.3.1) повторяется, начиная от сечения, удаленного от ДЭ
на Δzp, где принимается термическое равновесие.
Интенсификация однофазного
теплообмена дистанционирующим элементом учитывается с помощью формулы [29]:
|

|
(3.2.2.3.10)
|
где Nuо - число Нуссельта для канала без ДЭ;
Nu -
число Нуссельта для канала с ДЭ;
z -
расстояние от ДЭ;
dг -
эквивалентный гидравлический диаметр канала.
Учет
излучения
Суммарный теплоотвод
конвекцией к пару и излучением к каплям определяется выражением [21, 22]:
|

|
(3.2.2.3.11)
|
где σ - постоянная Больцмана;
ε -
приведенная степень черноты системы стенка-капли.
Температура
стенки находится по вышеописанной методике путем совместного решения уравнений
(3.2.2.3.1) и (3.2.2.3.11).
По найденной температуре стенки вычисляется приведенный коэффициент
теплоотдачи:
αi = qi/(tппi - ts).
В
формулах этого раздела:
α в
[Вт/м2 °С]; t в [°С]; q в [Вт/м2]; Р
в [МПа];
i
[Дж/кг]; ρw в [кг/м2 с]; r в
[Дж/кг]; μ в [Н с/м2];
dг =(d2
- d1) в [м]; dвн в [м]; λ в
[Вт/м °С];
σ в
[Н/м]; т в [°С]; ρ в [кг/м3]; T в [К].
Пределы
применимости методики:
Р =
1,1 ÷ 19,6 МПа; tст - tж ≤ 500 °С; ρw = 70 ÷ 2000 кг/м2
с;
q ≤
1 МВт/м2; Хб > Хкр ≥
0,1; dг = 4 ÷ 20 мм.
Погрешность
σ расчета α для круглых труб с равномерным и
косинусоидальным тепловыделением составляет 10 %.
3.2.2.3.2. Эмпирические соотношения для закризисного теплообмена в
трубах
Теплообмен
в закризисной области при течении воды в трубах рассчитывается [30]:
■ при Р ≤
14,5 МПа по формуле:
|

|
(3.2.2.3.12)
|
пределы применимости
формулы:
Р =
6,9 ÷ 14,5 МПа; ρw = 330 ÷ 760 кг/м2·с; q
= 2·105 ÷ 6·105 Вт/м2;
Xкр < Xб ≤
1; dвн = 10 мм;
погрешность
δ расчета α составляет ±25 %;
■ при Р ≥ 16 МПа
по формуле:
|

|
(3.2.2.3.13)
|
Пределы применимости
формулы:
Р =
16,0 ÷ 18,0 МПа; ρw = 500 ÷ 1050 кг/м2·с;
q = 2·105 ÷ 6·105 Вт/м2; Xкр < Xб ≤
1; dвн = 10 мм.
Погрешность
δ (максимальная) расчета α составляет ±35 %.
В
формулах этого раздела:
q в
[Вт/м2]; ρw в [кг/м2·с]; dвн
в [мм];
Хб -
относительная энтальпия;
Хкр -
относительная энтальпия в сечении возникновения кризиса теплоотдачи;
ρ в
[кг/м3]; λ в [Вт/м·°С]; μ в [Н·с/м2];
α = q/(tcт
- ts) в [Вт/м2·°С].
3.2.2.3.3. Скелетная таблица для коэффициента теплоотдачи в
закризисной
зоне при течении воды в равномерно обогреваемых трубах
Для
оценочных расчетов теплоотдачи в равномерно обогреваемых трубах диаметром 10 мм
могут быть использованы значения коэффициента теплоотдачи из таблицы 3.2.2.3.1 [31]. Эта таблица охватывает следующий диапазон
изменения параметров: давление 0,1 - 20 МПа, массовая скорость 250 - 3000 кг/м2
с, относительная энтальпия от -0,2 до 2,0, тепловой поток 0,2 - 1 МВт/м2,
диаметр трубы 10 мм.
Приведенные в таблице 3.2.2.3.1 значения
коэффициента теплоотдачи отнесены к разности температур tcт -
ts. Выбор в качестве определяющей температуры ts
значительно упрощает расчет температуры стенки, которая рассчитывается:

где α - коэффициент теплоотдачи берется из таблицы 3.2.2.3.1. Приведенные в
таблице 3.2.2.3.1 значения
коэффициента теплоотдачи снабжены индексами, которые указывают на способ их
получения:
е -
среднеарифметическое значение опытных данных из банка данных [32];
s -
рассчитанное по модели [33];
q -
значения из скелетной таблицы, предложенной в работе [34];
α -
значения полученные интерполяцией и экстраполяцией.
Погрешность
расчета а по таблице составляет не более δ ±35 %.
В
таблице 3.2.2.3.1 проведены
вертикальные линии, делящие каждую строчку на X < Хкр
и Х > Хкр, где Хкр - критическое
паросодержание для равномерно обогреваемых труб. Значения Хкр
были рассчитаны на основании скелетной таблицы для критических тепловых потоков
при вынужденном течении воды в равномерно обогреваемых трубах диаметром 8 мм [35]. Значения коэффициента
теплоотдачи при X < Хкр были получены в работе [34] на основании опытов с «горячим
пятном». Значения коэффициента теплоотдачи при X > Хкр,
были получены по экспериментальным данным из банка [32] и расчетом по модели [33].
Таблица 3.2.2.3.1
Скелетная таблица для коэффициента теплоотдачи (кВт/м2·К)
в закризисной области в трубе диаметром 10 мм
|
P,
МПа
|
G,
кг/м2 сек
|
q,
МВт/м2
|
x
|
|
-0,2
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,4
|
1,6
|
1,8
|
2,0
|
|
0,1
|
250
|
0,2
|
0,42g
|
0,24g
|
0,19g
|
0,19g
|
0,25g
|
0,32g
|
0,28s
|
0,14a
|
0,10a
|
0,08a
|
0,07a
|
0,06a
|
0,05a
|
|
|
|
0,6
|
0,60g
|
0,50g
|
0,45g
|
0,43g
|
0,47g
|
0,52g
|
0,61g
|
0,43a
|
0,29a
|
0,22a
|
0,18a
|
0,15a
|
0,13a
|
|
|
|
1,0
|
1,18g
|
0,75g
|
0,71g
|
0,72g
|
0,72g
|
0,76g
|
0,82g
|
0,71a
|
0,49a
|
0,37a
|
0,30a
|
0,25a
|
0,22a
|
|
0,1
|
500
|
0,2
|
0,42g
|
0,24g
|
0,21g
|
0,26g
|
0,42g
|
0,18s
|
0,11a
|
0,09a
|
0,08a
|
0,07a
|
0,07a
|
0,06a
|
0,06a
|
|
|
|
0,6
|
0,60g
|
0,50g
|
0,45g
|
0,46g
|
0,60g
|
0,52a
|
0,29a
|
0,21a
|
0,17a
|
0,15a
|
0,13a
|
0,12a
|
0,12a
|
|
|
|
1,0
|
1,18g
|
0,75g
|
0,72g
|
0,72g
|
0,78g
|
0,85a
|
0,47a
|
0,33a
|
0,26a
|
0,22a
|
0,20a
|
0,18a
|
0,17a
|
|
0,1
|
1000
|
0,2
|
0,42g
|
0,24g
|
0,32g
|
0,53g
|
0,18s
|
0,14s
|
0,14s
|
0,14s
|
0,14s
|
0,13s
|
0,12a
|
0,10a
|
0,09a
|
|
|
|
0,6
|
0,60g
|
0,50g
|
0,47g
|
0,66g
|
0,44a
|
0,26a
|
0,22a
|
0,21a
|
0,21a
|
0,21a
|
0,21a
|
0,20a
|
0,19a
|
|
|
|
1,0
|
1,18g
|
0,75g
|
0,72g
|
0,82g
|
0,70a
|
0,38a
|
0,30a
|
0,28a
|
0,27a
|
0,26a
|
0,26a
|
0,26a
|
0,25a
|
|
0,1
|
3000
|
0,2
|
0,43g
|
0,24g
|
0,34a
|
0,44s
|
0,65s
|
0,72s
|
0,66s
|
0,51s
|
0,34s
|
0,22s
|
0,15s
|
0,12s
|
0,09a
|
|
|
|
0,6
|
0,60g
|
0,50g
|
0,55a
|
0,62s
|
0,74s
|
0,88s
|
0,91s
|
0,84s
|
0,71s
|
0,57s
|
0,44s
|
0,35a
|
0,28a
|
|
|
|
1,0
|
1,18g
|
0,74g
|
0,73a
|
0,73a
|
0,79a
|
0,95s
|
1,03s
|
1,02s
|
0,93s
|
0,81s
|
0,68s
|
0,56a
|
0,47a
|
|
0,2
|
250
|
0,2
|
0,41g
|
0,27g
|
0,23g
|
0,19g
|
0,26g
|
0,32g
|
0,42g
|
0,23s
|
0,14a
|
0,11a
|
0,08a
|
0,07a
|
0,06a
|
|
|
|
0,6
|
0,66g
|
0,52g
|
0,45g
|
0,44g
|
0,47g
|
0,52g
|
0,62g
|
0,70a
|
0,43a
|
0,31a
|
0,24a
|
0,20a
|
0,17a
|
|
|
|
1,0
|
0,95g
|
0,77g
|
0,72g
|
0,73g
|
0,73g
|
0,77g
|
0,83g
|
0,94g
|
0,71a
|
0,51a
|
0,40a
|
0,33a
|
0,28a
|
|
0,2
|
500
|
0,2
|
0,41g
|
0,27g
|
0,24g
|
0,30g
|
0,43g
|
0,35s
|
0,16s
|
0,11a
|
0,09a
|
0,08a
|
0,08a
|
0,07a
|
0,07a
|
|
|
|
0,6
|
0,66g
|
0,52g
|
0,45g
|
0,47g
|
0,51g
|
0,76g
|
0,44a
|
0,29a
|
0,22a
|
0,19a
|
0,17a
|
0,15a
|
0,14a
|
|
|
|
1,0
|
0,95g
|
0,77g
|
0,72g
|
0,72g
|
0,78g
|
0,96g
|
0,72a
|
0,47a
|
0,35a
|
0,29a
|
0,25a
|
0,22a
|
0,20a
|
|
0,2
|
1000
|
0,2
|
0,41g
|
0,27g
|
0,33g
|
0,54g
|
0,30s
|
0,18s
|
0,17s
|
0,16s
|
0,15s
|
0,14s
|
0,13s
|
0,11a
|
0,09a
|
|
|
|
0,6
|
0,66g
|
0,52g
|
0,47g
|
0,68g
|
0,78s
|
0,36a
|
0,28a
|
0,26a
|
0,25a
|
0,24a
|
0,23a
|
0,23a
|
0,21a
|
|
|
|
1,0
|
0,95g
|
0,77g
|
0,73g
|
0,82g
|
1,17g
|
0,54a
|
0,40a
|
0,34a
|
0,32a
|
0,31a
|
0,30a
|
0,29a
|
0,29a
|
|
0,2
|
3000
|
0,2
|
0,56a
|
0,27g
|
0,40a
|
0,54s
|
0,77s
|
0,85s
|
0,77s
|
0,58s
|
0,38s
|
0,24s
|
0,16s
|
0,12s
|
0,10a
|
|
|
|
0,6
|
0,66g
|
0,52g
|
0,60a
|
0,68a
|
0,87s
|
1,03s
|
1,05s
|
0,96s
|
0,79s
|
0,62s
|
0,47s
|
0,37s
|
0,30a
|
|
|
|
1,0
|
0,95g
|
0,77g
|
0,81a
|
0,85a
|
0,95s
|
1,11s
|
1,19s
|
1,16s
|
1,05s
|
0,89s
|
0,73s
|
0,59a
|
0,49a
|
|
0,5
|
250
|
0,2
|
0,34g
|
0,29g
|
0,26g
|
0,20g
|
0,27g
|
0,34g
|
0,44g
|
0,49a
|
0,29s
|
0,18s
|
0,13a
|
0,10a
|
0,09a
|
|
|
|
0,6
|
0,57g
|
0,46g
|
0,46g
|
0,45g
|
0,49g
|
0,54g
|
0,64g
|
0,82g
|
0,74a
|
0,54a
|
0,39a
|
0,31a
|
0,25a
|
|
|
|
1,0
|
0,87g
|
0,75g
|
0,74g
|
0,74g
|
0,75g
|
0,79g
|
0,85g
|
0,96g
|
0,97g
|
0,89a
|
0,65a
|
0,51a
|
0,42a
|
|
0,5
|
500
|
0,2
|
0,38g
|
0,31g
|
0,26g
|
0,34g
|
0,45g
|
0,58g
|
0,53s
|
0,23s
|
0,16s
|
0,12a
|
0,10a
|
0,09a
|
0,08a
|
|
|
|
0,6
|
0,62g
|
0,46g
|
0,46g
|
0,48g
|
0,64g
|
0,82g
|
1,04g
|
0,65a
|
0,42a
|
0,32a
|
0,26a
|
0,22a
|
0,20a
|
|
|
|
1,0
|
0,94g
|
0,75g
|
0,74g
|
0,74g
|
0,81g
|
0,99g
|
1,21g
|
1,07a
|
0,69a
|
0,51a
|
0,41a
|
0,35a
|
0,31a
|
|
0,5
|
1000
|
0,2
|
0,38g
|
0,31g
|
0,36g
|
0,58g
|
0,87g
|
0,36s
|
0,24s
|
0,21s
|
0,19s
|
0,17s
|
0,14s
|
0,12a
|
0,10a
|
|
|
|
0,6
|
0,62g
|
0,47g
|
0,48g
|
0,70g
|
1,07g
|
0,92s
|
0,50a
|
0,39a
|
0,34a
|
0,31a
|
0,29a
|
0,27a
|
0,25a
|
|
|
|
1,0
|
0,94g
|
0,75g
|
0,75g
|
0,84g
|
1,23g
|
1,47a
|
0,75a
|
0,55a
|
0,47a
|
0,42a
|
0,39a
|
0,37a
|
0,35a
|
|
0,5
|
3000
|
0,2
|
0,81g
|
0,31g
|
0,50a
|
0,70a
|
1,03s
|
1,13s
|
1,00s
|
0,71s
|
0,43s
|
0,25s
|
0,17s
|
0,13s
|
0,10a
|
|
|
|
0,6
|
0,79g
|
0,49g
|
1,12g
|
1,16a
|
1,23a
|
1,33s
|
1,32s
|
1,17s
|
0,93s
|
0,69s
|
0,51s
|
0,39s
|
0,31a
|
|
|
|
1,0
|
0,94g
|
0,76g
|
1,22g
|
1,26a
|
1,35s
|
1,45s
|
1,51s
|
1,42s
|
1,24s
|
1,01s
|
0,80s
|
0,64a
|
0,52a
|
|
1,0
|
250
|
0,2
|
0,55g
|
0,36g
|
0,32g
|
0,25g
|
0,31g
|
0,36g
|
0,48g
|
0,70g
|
0,39s
|
0,23s
|
0,16s
|
0,12a
|
0,10a
|
|
|
|
0,6
|
0,71g
|
0,52g
|
0,50g
|
0,47g
|
0,50g
|
0,56g
|
0,67g
|
0,81g
|
0,79g
|
0,67a
|
0,47a
|
0,36a
|
0,30a
|
|
|
|
1,0
|
0,88g
|
0,78g
|
0,77g
|
0,77g
|
0,76g
|
0,81g
|
0,87g
|
0,99g
|
1,01g
|
0,95a
|
0,78a
|
0,60a
|
0,49a
|
|
1,0
|
500
|
0,2
|
0,84g
|
0,40g
|
0,33g
|
0,44g
|
0,50g
|
0,61g
|
0,69a
|
0,37s
|
0,21s
|
0,16a
|
0,13a
|
0,11a
|
0,09a
|
|
|
|
0,6
|
0,82g
|
0,59g
|
0,52g
|
0,57g
|
0,67g
|
0,85g
|
1,10g
|
1,06s
|
0,59a
|
0,42a
|
0,33a
|
0,28a
|
0,24a
|
|
|
|
1,0
|
1,02g
|
0,82g
|
0,77g
|
0,80g
|
0,83g
|
1,02g
|
1,27g
|
1,35a
|
0,98a
|
0,68a
|
0,53a
|
0,44a
|
0,38a
|
|
1,0
|
1000
|
0,2
|
0,84g
|
0,44g
|
0,46g
|
0,66g
|
0,92g
|
0,81s
|
0,33s
|
0,26s
|
0,23s
|
0,19s
|
0,16s
|
0,13s
|
0,11a
|
|
|
|
0,6
|
0,82g
|
0,59g
|
0,56g
|
0,75g
|
1,23g
|
1,20a
|
0,74s
|
0,52s
|
0,43a
|
0,38a
|
0,34a
|
0,31a
|
0,28a
|
|
|
|
1,0
|
1,02g
|
0,83g
|
0,81g
|
0,89g
|
1,30g
|
1,62g
|
1,15a
|
0,76a
|
0,61a
|
0,53a
|
0,48a
|
0,44a
|
0,41a
|
|
1,0
|
3000
|
0,2
|
0,84g
|
0,44g
|
1,19g
|
1,21a
|
1,34s
|
1,46s
|
1,26s
|
0,87s
|
0,48s
|
0,27s
|
0,18s
|
0,14s
|
0,11a
|
|
|
|
0,6
|
0,82g
|
0,66g
|
1,18g
|
1,58a
|
1,56s
|
1,69s
|
1,65s
|
1,40s
|
1,07s
|
0,76s
|
0,54s
|
0,41s
|
0,33a
|
|
|
|
1,0
|
1,02g
|
0,86g
|
1,26g
|
2,10g
|
1,84s
|
1,85s
|
1,87s
|
1,72s
|
1,45s
|
1,14s
|
0,88s
|
0,68a
|
0,55a
|
|
4
|
250
|
0,2
|
1,08g
|
0,63g
|
0,50g
|
0,36g
|
0,44g
|
0,49g
|
0,76g
|
0,80a
|
0,76s
|
0,36s
|
0,23s
|
0,17s
|
0,14a
|
|
|
|
0,6
|
1,22g
|
0,75g
|
0,68g
|
0,59g
|
0,61g
|
0,64g
|
0,78g
|
0,85g
|
0,88a
|
1,07a
|
0,70a
|
0,52a
|
0,41a
|
|
|
|
1,0
|
1,42g
|
0,92g
|
0,88g
|
0,84g
|
0,85g
|
0,88g
|
1,00g
|
1,08g
|
1,32a
|
1,78a
|
1,16a
|
0,86a
|
0,68a
|
|
4
|
500
|
0,2
|
1,10g
|
0,65g
|
0,53g
|
0,50g
|
0,66g
|
0,89g
|
1,00a
|
1,47s
|
0,47s
|
0,28s
|
0,21s
|
0,16s
|
0,14a
|
|
|
|
0,6
|
1,22g
|
0,82g
|
0,73g
|
0,72g
|
0,86g
|
0,96g
|
1,17g
|
1,55g
|
1,35s
|
0,79s
|
0,57a
|
0,45a
|
0,37a
|
|
|
|
1,0
|
1,46g
|
1,01g
|
0,93g
|
0,92g
|
1,01g
|
1,12g
|
1,20a
|
1,59g
|
1,52g
|
1,30a
|
0,93a
|
0,73a
|
0,60a
|
|
4
|
1000
|
0,2
|
1,30g
|
0,70g
|
0,70g
|
0,82g
|
1,08g
|
1,50a
|
1,18s
|
0,60s
|
0,44s
|
0,32s
|
0,23s
|
0,18s
|
0,14a
|
|
|
|
0,6
|
1,22g
|
0,82g
|
0,78g
|
0,96g
|
1,60a
|
1,68g
|
1,81a
|
1,23s
|
0,87s
|
0,70s
|
0,58s
|
0,48a
|
0,41a
|
|
|
|
1,0
|
1,46g
|
1,03g
|
1,05g
|
1,11g
|
1,67g
|
1,70g
|
2,14g
|
1,85s
|
1,26s
|
1,00a
|
0,85a
|
0,73a
|
0,63a
|
|
4
|
3000
|
0,2
|
1,30g
|
0,84g
|
1,40a
|
2,35a
|
4,19s
|
4,37s
|
3,55s
|
2,04s
|
0,80s
|
0,38s
|
0,24s
|
0,18s
|
0,14s
|
|
|
|
0,6
|
1,22g
|
0,90g
|
1,45a
|
2,40a
|
4,35a
|
4,80s
|
4,33s
|
3,19s
|
1,94s
|
1,11s
|
0,72s
|
0,53s
|
0,42a
|
|
|
|
1,0
|
1,46g
|
1,07g
|
1,50g
|
2,46g
|
4,45g
|
5,04s
|
4,75s
|
3,85s
|
2,71s
|
1,77s
|
1,20s
|
0,89s
|
0,70a
|
|
10
|
250
|
0,2
|
3,16g
|
0,86g
|
0,77g
|
0,46g
|
0,50g
|
0,58g
|
0,75g
|
0,90a
|
0,82a
|
0,68s
|
0,40s
|
0,28s
|
0,22s
|
|
|
|
0,6
|
2,39g
|
0,93g
|
0,82g
|
0,59g
|
0,61g
|
0,62g
|
0,71g
|
0,95g
|
0,86g
|
0,86a
|
0,86a
|
0,84a
|
0,64a
|
|
|
|
1,0
|
2,06g
|
1,07g
|
1,00g
|
0,88g
|
0,90g
|
0,93g
|
0,99g
|
1,17g
|
1,18g
|
1,18a
|
1,18a
|
1,18a
|
1,07a
|
|
10
|
500
|
0,2
|
3,16g
|
1,08g
|
0,87g
|
0,77g
|
0,86g
|
0,89a
|
0,90a
|
1,20a
|
1,02a
|
0,57s
|
0,38s
|
0,27s
|
0,22s
|
|
|
|
0,6
|
2,39g
|
1,29g
|
1,03g
|
0,88g
|
0,90g
|
0,88a
|
0,95g
|
1,29g
|
1,04g
|
1,04a
|
1,03s
|
0,78s
|
0,62a
|
|
|
|
1,0
|
2,06g
|
1,36g
|
1,19g
|
1,08g
|
1,14g
|
1,16a
|
1,29g
|
1,69g
|
1,64g
|
1,64a
|
1,64a
|
1,24a
|
1,00a
|
|
10
|
1000
|
0,2
|
3,16g
|
1,08g
|
1,10g
|
1,42g
|
1,74g
|
2,16g
|
2,50a
|
1,83s
|
1,14s
|
0,67s
|
0,41s
|
0,29s
|
0,22s
|
|
|
|
0,6
|
2,39g
|
1,38g
|
1,26g
|
1,32g
|
1,62g
|
1,98g
|
2,42g
|
3,12g
|
2,15s
|
1,55s
|
1,13s
|
0,84s
|
0,65s
|
|
|
|
1,0
|
2,06g
|
1,47g
|
1,23g
|
1,29g
|
1,63g|
|
2,07g
|
2,62g
|
3,16g
|
2,94s
|
2,19s
|
1,70s
|
1,34s
|
1,07s
|
|
10
|
3000
|
0,2
|
3,16g
|
1,26g
|
2,89g
|
4,56g
|
6,99g
|
15,0s
|
12,0s
|
6,43s
|
1,83s
|
0,71s
|
0,41s
|
0,29s
|
0,22s
|
|
|
|
0,6
|
2,39g
|
1,38g
|
2,40g
|
3,39g
|
5,86g
|
11,0g
|
15,6s
|
10,3s
|
4,85s
|
2,13s
|
1,23s
|
0,86s
|
0,66s
|
|
|
|
1,0
|
2,06g
|
1,47g
|
2,26g
|
2,88g
|
5,76g
|
9,52g
|
14,0g
|
12,6s
|
7,06s
|
3,52s
|
2,06s
|
1,43s
|
1,09s
|
|
16
|
250
|
0,2
|
6,41g
|
1,44g
|
1,12g
|
0,55g
|
0,70g
|
1,14g
|
1,16g
|
1,11g
|
1,05g
|
1,05a
|
0,94s
|
0,60s
|
0,43s
|
|
|
|
0,6
|
4,63g
|
0,96g
|
0,93g
|
0,64g
|
0,64g
|
0,86g
|
0,98g
|
1,06g
|
0,97g
|
0,97a
|
0,97a
|
0,97a
|
0,97a
|
|
|
|
1,0
|
3,29g
|
1,39g
|
1,21g
|
0,90g
|
0,95g
|
1,06g
|
1,14g
|
1,25g
|
1,27g
|
1,27a
|
1,27a
|
1,27a
|
1,27a
|
|
16
|
500
|
0,2
|
6,41s
|
1,44g
|
1,13g
|
1,03g
|
1,46g
|
1,91g
|
2,00e
|
2,00e
|
1,90e
|
1,60e
|
1,20e
|
0,61s
|
0,43s
|
|
|
|
0,6
|
4,63g
|
0,97g
|
0,96g
|
0,81g
|
0,88g
|
1,24g
|
1,63g
|
2,00a
|
1,58g
|
1,58a
|
1,58a
|
1,58a
|
1,28s
|
|
|
|
1,0
|
3,29g
|
1,39g
|
1,21g
|
1,06g
|
1,20g
|
1,34g
|
1,63g
|
2,01g
|
1,82g
|
1,82a
|
1,82a
|
1,82a
|
1,82a
|
|
16
|
1000
|
0,2
|
6,41g
|
1,44g
|
2,00a
|
2,11g
|
3,13g
|
4,04g
|
5,20g
|
5,75g
|
3,80s
|
1,86s
|
0,98s
|
0,61s
|
0,43s
|
|
|
|
0,6
|
4,63g
|
1,06g
|
1,08a
|
1,10g
|
1,49g
|
2,53g
|
4,11g
|
5,75g
|
4,14g
|
4,14a
|
2,89s
|
1,84s
|
1,30s
|
|
|
|
1,0
|
3,29g
|
1,39g
|
1,47g
|
1,52g
|
1,80g
|
2,90g
|
4,27g
|
5,82g
|
4,70g
|
4,70a
|
4,59s
|
3,04s
|
2,16s
|
|
16
|
3000
|
0,2
|
6,41g
|
1,80g
|
9,04g
|
12,3g
|
16,6g
|
22,2g
|
27,0a
|
17,0s
|
4,94s
|
1,89s
|
0,98s
|
0,61s
|
0,43
|
|
|
|
0,6
|
4,63g
|
1,63g
|
6,31g
|
6,54g
|
14,4g
|
20,5g
|
26,1g
|
31,5s
|
14,2s
|
5,68s
|
2,95s
|
1,84s
|
1,30s
|
|
|
|
1,0
|
3,29g
|
1,72g
|
3,90a
|
6,12g
|
11,6g
|
19,8g
|
28,6g
|
35,0g
|
19,6g
|
9,46s
|
4,92s
|
3,07s
|
2,17s
|
|
20
|
250
|
0,2
|
8,40g
|
2,56g
|
1,80g
|
0,97g
|
0,99g
|
1,24g
|
1,40g
|
1,76g
|
1,59g
|
1,59a
|
1,70e
|
1,40e
|
1,40a
|
|
|
|
0,6
|
6,31g
|
1,46g
|
1,17g
|
0,79g
|
0,84g
|
1,06g
|
1,26g
|
1,48g
|
1,49g
|
1,49a
|
1,49a
|
1,49a
|
1,49a
|
|
|
|
1,0
|
6,25g
|
1,38g
|
1,20g
|
1,00g
|
1,07g
|
1,19g
|
1,29g
|
1,46g
|
1,47g
|
1,47a
|
1,47a
|
1,47a
|
1,47a
|
|
20
|
500
|
0,2
|
8,41g
|
2,56g
|
2,00g
|
2,28g
|
2,52g
|
3,24g
|
3,71g
|
4,21g
|
4,10e
|
3,30e
|
2,40e
|
2,40a
|
1,67s
|
|
|
|
0,6
|
7,79g
|
1,46g
|
1,26g
|
1,16g
|
1,21g
|
1,87g
|
2,50g
|
3,35g
|
2,82g
|
2,82a
|
2,82a
|
2,82a
|
2,82a
|
|
|
|
1,0
|
6,67g
|
1,38g
|
1,28g
|
1,25g
|
1,40g
|
1,76g
|
2,12g
|
2,58g
|
2,27g
|
2,27a
|
2,27a
|
2,27a
|
2,27a
|
|
20
|
1000
|
0,2
|
8,41g
|
2,56g
|
3,36a
|
4,15g
|
7,82g
|
11,7g
|
16,2g
|
19,2g
|
14,8g
|
12,3s
|
5,64s
|
2,87s
|
1,67s
|
|
|
|
0,6
|
7,79g
|
1,46g
|
1,90a
|
2,35g
|
4,18g
|
6,43g
|
9,71g
|
12,5g
|
10,4g
|
10,4a
|
10,4a
|
8,60s
|
5,02s
|
|
|
|
1,0
|
6,67g
|
1,38g
|
2,30g
|
2,64g
|
4,38g
|
6,05g
|
6,68g
|
11,1g
|
9,68g
|
9,68a
|
9,68a
|
9,68a
|
8,36s
|
|
20
|
3000
|
0,2
|
8,41g
|
2,56g
|
15,8g
|
20,8g
|
28,4g
|
34,4g
|
37,4g
|
41,0g
|
26,7s
|
12,4s
|
5,66s
|
2,88s
|
1,68s
|
|
|
|
0,6
|
7,79g
|
2,39g
|
14,4g
|
26,1g
|
34,4g
|
44,3g
|
51,4g
|
52,4g
|
41,1g
|
37,1s
|
17,0s
|
8,63s
|
5,03s
|
|
|
|
1,0
|
6,67g
|
2,41g
|
10,3g
|
17,7g
|
23,8g
|
33,8g
|
45,1g
|
45,3g
|
34,0g
|
34,0a
|
28,3s
|
14,4s
|
8,38s
|
Список литературы к разделу 3.2.2
1. Боришанский В.М., Козырев А.П., Светлова Л.С. Изучение
теплообмена при пузырьковом кипении жидкости. - В сб.: Конвективная
теплопередача в двухфазном и однофазном потоках. М.: Энергия, 1964.
2. Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по
теплогидравлическим расчетам (ядерные реакторы, теплообменники,
парогенераторы). М.: Энергоатомиздат, 1990.
3. Будов В.М., Самойлов О.Б., Соколов В.А., Шемагин И.А. Теплообмен
при пленочном кипении у вертикальной поверхности с постоянным тепловым потоком.
Атомная энергия, 1989, т. 65, вып. 3.
4. Будов В.М., Шемагин И.А., Соколов В.А. Влияние изменения толщины
паровой пленки на развитие неустойчивости при пленочном кипении у вертикальной
поверхности. Изв. ВУЗов СССР. Энергетика, 1983, № 7.
5. Клименко В.В. Теплоотдача при свободно конвективном пленочном
кипении насыщенной жидкости на одиночном горизонтальном цилиндре.
Теплоэнергетика, 1984, № 8.
6. Клименко В.В., Снытин С.Ю. Расчетное соотношение для пленочного
кипения на вертикальной поверхности. Теплоэнергетика, 1983, № 3.
7. Похвалов Ю.Е., Кронин И.В., Мурганова И.В. Обобщение
экспериментальных данных по теплоотдаче при пузырьковом кипении недогретой
жидкости в трубах. Теплоэнергетика, 1966, № 5.
8. Боришанский В.М., Андриевский А.А., Фокин В.М. Теплоотдача при
движении двухфазного потока в каналах. Теплоэнергетика, 1971, № 11.
9. Лабунцов Д.А. Вопросы теплообмена при пузырьковом кипении
жидкости. Теплоэнергетика, 1972, № 9.
10. Будов В.М., Кирьянов В.А., Шемагин И.А. Неустойчивость при
пленочной конденсации на поверхности цилиндра. Изв. АН СССР. Энергетика и
транспорт, 1984, № 6.
11. Будов В.М., Кирьянов В.А., Шемагин И.А. Теплоотдача на
ламинарно-волновом участке конденсации неподвижного пара. Инженерно-физический
журнал, 1987, т. 52, № 6.
12. Тепловой и гидравлический расчет теплообменного оборудования
АЭС. РД 24.035.05-89. Л.: НПО ЦКТИ.
13. Будов В.М., Шемагин И.А. Волновые характеристики межфазной
поверхности при конденсации пара на горизонтальном цилиндре. Изв. СО АН СССР,
Серия технических наук, 1988, вып. 2.
14. Будов В.М., Кирьянов В.А., Шемагин И.А. О неустойчивости при
конденсации движущегося пара. Изв. АН СССР. Энергетика и транспорт, 1984, № 5.
15. Гогонин И.И., Дорохов А.Р., Сосунов В.И. Теплоотдача при
конденсации неподвижного пара на пучке гладких горизонтальных труб.
Теплоэнергетика, 1977, № 4.
16. Гогонин И.И., Сосунов В.И., Лазарев С.И., Кабов О.А.
Исследование теплообмена при конденсации неподвижного пара на пакетах
горизонтальных труб разного диаметра. Теплоэнергетика, 1983, № 3.
17. Кутателадзе С.С., Гогонин И.И., Дорохов А.Р., Сосунов В.И.
Пленочная конденсация движущегося пара на пучке гладких горизонтальных труб.
Теплоэнергетика, 1979, № 5.
18. Гогонин И.И., Сосунов В.И., Лазарев С.И., Кабов О.А. Теплообмен
при конденсации неподвижного пара на пакетах горизонтальных труб различной
геометрии. Теплоэнергетика, 1982, № 3.
19. Уголева И.Р., Гордон Б.Г., Григорьев А.С. Тепло- и массообмен
движущейся паровоздушной смеси с каплями воды. Теплоэнергетика, 1989, № 6.
20. Уголева И.Р., Гордон Б.Г., Григорьев А.С. Обобщение опытных
данных по тепло- и массообмену движущейся паровоздушной смеси с каплями воды.
Теплоэнергетика, 1989, № 7.
21. Сергеев В.В. Закризисный теплообмен в элементах ЯЭУ. Обнинск.
2004.
22. Сергеев В.В. Верификация модели закризисного теплообмена для
дисперсного режима течения // Труды 3-й Российской нац. конф. по теплообмену.
М.: Изд-во МЭИ. 2002. Т. 4
23. Сергеев В.В., Гальченко Э.Ф., Ремизов О.В. Инженерный расчет
теплообмена в закризисной зоне кольцевых каналов / Физикоэнергетический
институт: Препринт ФЭИ-1649. Обнинск. 1985.
24. Миропольский З.Л. Теплоотдача к перегретому пару с подводом и
отводом тепла // Теплоэнергетика. 1975, № 3.
25. РТМ 24.031.05-72. Методика и зависимости для теоретического
расчета теплообмена и гидравлического сопротивления теплообменного оборудования
АЭС. М.: 1974.
26. Гидродинамика и теплообмен в атомных энергетических установках /
В.И. Субботин. и др. М.: Атомиздат. 1975.
27. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. М.:
Энергоиздат. 1981.
28. Сергеев В.В., Гонин А.И., Ремизов О.В. Закризисный теплообмен в
каналах с дистанционирующими элементами // Атомная энергия. 1990. Т. 68, вып.
6.
29. Яо, Хохрейтер, Лич. Интенсификация теплообмена в стержневых
сборках вблизи дистанционирующих решеток // Теплопередача. 1982. Т. 107, № 1.
30. Ремизов О.В. Исследование температурных условий работы
парогенерирующей поверхности при кризисе теплоотдачи // Теплоэнергетика. 1978.
№ 2.
31. Ефанов А.Д., Кириллов П.Л., Смогалев И.П., Ивашкевич А.А.,
Виноградов В.Н., Сергеев В.В. Скелетная таблица для коэффициента теплоотдачи в
закризисной области при течении воды в тубе (версия 1997 г.) // Труды
международной конференции «Теплофизические аспекты безопасности ВВЭР».
Теплофизика-98. Обнинск: ФЭИ, 1998. Т. 1.
32. Бобков В.П., Виноградов В.Н., Кириллов П.Л., Смогалев И.П.
Базовый Центр теплофизических данных Минатома Российской Федерации. // Атомная
энергия. 1996. Т. 80, вып. 5.
33. Сергеев В.В. Расчет теплообмена в закризисной зоне вертикальных
цилиндрических каналов / Физико-энергетический институт: Препринт ФЭИ-1836.
Обнинск. 1987.
34. Leung L.K.H., Hammouda N., Groeneveld
D.C. A look-up table for film-boiling heat transfer coefficients in tubes with
upward flow. // 8th Int. Topical Meeting on Nuclear Reactor
Thermal-Hydraulics. NURETH-8. Kyoto. 1997. V.2.
35. Groeneveld D.C., Leung L.K.H.,
Kirillov P.L., Bobkov V.P., Smogalev I.P., Vinogradov V.N., Huang X.C., Rover
E. The 1995 Look-up Table for Critical Heat Flux in Tubes. // Nuclear
Engineering and Design. 1996. V.163. N1.
3.2.3.
ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ
ГАЗОЖИДКОСТНОЙ СМЕСИ В ТРУБАХ
Эксперименты
показали, что при течении газожидкостной смеси в трубах коэффициенты
теплоотдачи имеют более высокие значения, чем при течении однофазной среды.
Возрастание коэффициентов теплоотдачи сопровождается уплощением полей
температуры, указывающим на изменение турбулентных свойств потока. Замечено,
что коэффициенты теплоотдачи возрастают более интенсивно в области небольших
объемных газосодержаний (φ ≤ 10 %), уменьшаются при
возрастании расхода теплоносителя. Кроме того, эффект повышения теплоотдачи
зависит от направления потока и диаметра трубы.
Средний
коэффициент теплоотдачи при течении газожидкостной смеси в круглых гладких
трубах рассчитывается [1]:
■ при φ
< 10 % по формуле:
|

|
(3.2.3.1)
|
где f(Re) = 3,3 + 78,2(Rе·10-4)-1,75;
■ при φ
> 10 % по формуле:
|

|
(3.2.3.2)
|
где A = - 0,13 + 10,5(Rе·10-4)-1,8;
В =
8,0 + 0,08(Rе·10-4)1,7.
В
формулах  ,
,  - числа Нуссельта при
наличии и отсутствии газовой фазы в потоке; критерии
- числа Нуссельта при
наличии и отсутствии газовой фазы в потоке; критерии  ,
,  , Re, Рr рассчитываются по параметрам однофазного потока;
, Re, Рr рассчитываются по параметрам однофазного потока;
β -
объемное расходное газосодержание, доли единицы при расчетах;

Vг, Vж - объемы, занимаемые газом и жидкостью;
dвн -
внутренний диаметр трубы, м.
Пределы
применимости формулы (2.3.1):
Re =
104 ÷ 3,6·104 - для восходящего течения воды;
Re =
1,5·104 ÷ 3,6·104 - для нисходящего течения воды
dвн =
21,96 ÷ 50,0 мм.
Погрешность
σ расчета  составляет 6 %.
составляет 6 %.
Пределы
применимости формулы (2.3.2.):
Re =
104 ÷ 3 104 - для восходящего течения воды;
dвн =
21,96 ÷ 50 мм.
Погрешность
σ расчета  составляет 8 %.
составляет 8 %.
Эффективный коэффициент
турбулентного переноса тепла при течении газожидкостной смеси рассчитывается на
основе принципа суперпозиции по формуле [2]:
|
аэф =
ам + ат + аг,
|
(3.2.3.3)
|
где ам - коэффициент турбулентного переноса
тепла за счет молекулярной температуропроводности;
ат -
за счет турбулентной температуропроводности;
аг -
коэффициент турбулентного переноса тепла за счет дополнительной турбулизации
потока газовой фазой;
|

|
(3.2.3.4)
|
n = 4,5 + 1,5exp(-0,07Pr);
 - локальная относительная
скорость теплоносителя;
- локальная относительная
скорость теплоносителя;

r -
текущий радиус трубы, м.
Коэффициенты
турбулентного переноса тепла за счет дополнительной турбулизации потока газовой
фазой рассчитываются [1, 2]:
■ при φ
< 10 % по формуле:
|

|
(3.2.3.5)
|
где A(Re) =
2,9 + 62,0exp(0,7Re·10-4);
пределы
применимости формулы:
Re =
104 ÷ 3,6·104 - при восходящем течении воды;
Re =
1,5·104 ÷ 3,6·104 - при нисходящем течении воды;
dвн =
21,96 ÷ 50,0 мм.
Погрешность
σ расчета аг составляет 4 % для описания средней
теплоотдачи и 20 % для описания температурных полей;
■ при φ
> 0,10 % по формуле:
|

|
(3.2.3.6)
|
где A(Re) =
5,6 + 162,0exp(-0,63Re·10-4).
Пределы
применимости формулы:
Re =
104 ÷ 3·104 - при восходящем течении воды;
Re =
5,5·104 ÷ 12·104 - при восходящем течении ртути;
d =
21,96 ÷ 50,0 мм.
Погрешность
σ расчета аг составляет 6 % для описания средней
теплоотдачи и 15 % для описания температурных полей.
Список литературы к разделу 3.2.3
1. Козина Н.В., Бобков В.П. О влиянии газовых пузырей на теплообмен
в каналах. - Препринт ФЭИ-1991, Обнинск, 1989.
2. Бобков В.П., Ибрагимов М.Х., Субботин В.И. Расчет коэффициента
турбулентного переноса тепла при течении жидкости в трубе. - Атомная энергия,
1968, т. 24, вып. 5.
3.3.
РАСЧЕТ КРИТИЧЕСКОГО ТЕПЛОВОГО ПОТОКА ПРИ КИПЕНИИ
ВОДЫ В КАНАЛАХ ЯДЕРНЫХ ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК
Под
кризисом теплоотдачи при кипении понимается (КТП) достаточно резкое снижение
интенсивности теплообмена при повышении плотности теплового потока вследствие
изменения механизма переноса тепла от стенки. Это явление обычно связывают с
изменением структуры пристенного слоя при достижении определенных критических
условий. При этом происходит уменьшение контакта жидкости со стенкой, что и
вызывает резкий рост температуры обогреваемой поверхности.
Характер
движения жидкости и интенсивность теплоотдачи при кипении в большом объеме
определяются, в основном, свойствами кипящей жидкости и плотностью теплового
потока или температурой поверхности. Возникновение кризиса теплоотдачи в этом
случае связывается с переходом пузырькового кипения в пленочное.
При
вынужденном движении жидкости, недогретой до температуры насыщения, или
парожидкостной смеси с небольшим паросодержанием, поверхность нагрева перегревается
вследствие недостаточного поступления к ней жидкости, оттесняемой образующимся
паром.
При
положительных паросодержаниях смеси, начиная с X ≈ 0,05, наступает
дисперсно-кольцевой режим течения (в ядре потока течет пар с каплями жидкости,
а по стенке - пленка жидкости). В этом случае возникновение кризиса теплоотдачи
связывается с высыханием или срывом пристенной пленки жидкости и образованием
сухой поверхности.
Кризис
теплоотдачи при течении кипящей воды в каналах является сложнейшим процессом,
обусловленным большим количеством определяющих параметров. Этим объясняется
возникновение большого количества предложенных многими авторами эмпирических и
полуэмпирических подходов, которые позволили дать рекомендации к расчету КТП
лишь в узких областях параметров. Очевидно, что использование подходов,
основанных на фундаментальных уравнениях [1],
в случае их реализации, было бы наиболее оправданным, предпочтительным и
вызывало бы максимальное доверие. Но пока нет надежды на их реализацию. В связи
с этим исследователи вынуждены основывать свои разработки и рекомендации на
полуэмпирических методах, используя массивы экспериментальных данных,
накопленных в различных научных центрах. Наиболее представительным является
массив данных по КТП, имеющийся в Отраслевом базовом Центре теплофизических
данных Физико-энергетического института [2].
На
примере описания КТП в круглых трубах можно убедиться [3], что вполне удобной формой обобщения данных по КТП
является их табличное представление. Такая форма позволяет избавиться от
основных недостатков традиционного аналитического описания КТП: узкий диапазон
режимных и геометрических параметров, сложность перехода от одних расчетных
соотношений к другим с учетом необходимости сшивки на границах, необходимость
вычисления теплофизических свойств теплоносителя и др. Табличное описание КТП,
названное в России «методом скелетной таблицы», а в зарубежной литературе - «Look-Up
Table», сейчас превратилось в надежный универсальный метод расчета КТП.
Преимущества табличного описания КТП следующие: широкий диапазон определяющих
параметров, отсутствие сшивок и скачков описания, наглядность представления.
Именно широкий диапазон режимных и геометрических параметров позволяет
использовать табличный метод в рамках единого подхода для описания КТП как в
номинальных, так и в переходных и аварийных режимах работы ЯЭУ.
Более
сложной проблемой является описание КТП при неравномерном аксиальном и/или
радиальном тепловыделении. Случай неравномерного радиального тепловыделения в
пучках твэлов требует привлечения методов поячеечного расчета и в данном
Руководстве не рассматривается.
При
проведении опытов с неравномерным аксиальным обогревом появляются
дополнительные источники погрешностей, которые следует рассматривать как
абсолютно объективные.
1)
Основной дополнительный источник погрешностей связан с определением координаты
кризиса. Локализация кризиса теплообмена определяется скачком (подъемом)
температуры, зафиксированным термопарами в одном из сечений. В связи с этим
координата кризиса и, следовательно, значение критического теплового потока
определяются с неопределенностью, зависящей от расстояния между термопарами и
от локального градиента теплового потока. Эта неопределенность не имеет
статистической природы.
2)
На погрешность в значениях параметров кризиса в пучках твэлов влияет и
взаиморасположение термопар и дистанционирующих решеток.
3)
Особенно велика погрешность в экспериментальном определении критического
теплового потока вблизи выходного конца рабочего участка, где толщина стенки
трубок максимальна, а сам тепловой поток минимален. Здесь же максимальны
растечки тепла и концевые эффекты (токоподводы) и минимальна чувствительность
термопар к изменению температуры теплоотдающей поверхности (относительно велик
перепад температуры в стенке).
Для
описания КТП при неравномерном аксиальном тепловыделении часто используется
метод формфактора. В литературе имеется достаточно много формул для определения
формфактора (см. [4]). Как правило,
все они не являются универсальными, т.к. получены эмпирическим или
полуэмпирическим способом и используются как поправки к вполне определенным
формулам и методикам для равномерного обогрева. Очевидно, что результаты
использования этих формфакторов жестко связаны с использованием исходных формул
или методик для определения qкр при
равномерном обогреве. Более того, сам способ получения этих поправок
подразумевает, что они пригодны для описания конкретного набора данных, на
котором они получены. Их использование для иных наборов данных требует
дополнительного обоснования и проверки.
Для
пучков твэлов геометрии ВВЭР можно упомянуть два метода описания КТП при
неравномерном аксиальном тепловыделении [5
- 8]. В первом из них [5, 6] используется эмпирический формфактор и корреляция
ОКБ «Гидропресс» для описания КТП при равномерном аксиальном обогреве. Во
втором [7] - эмпирический формфактор
и скелетная таблица для треугольных пучков твэлов [8].
Также
можно рассчитать критическую мощность пучка твэлов с неравномерным аксиальным
обогревом, если использовать давно отмеченный [9 - 15]
экспериментальный факт: полная мощность канала (труба, пучок стержней) с
плавным профилем тепловыделения по длине (Loб > 2 м) с
точностью около 10 % совпадает с критической мощностью такого же канала с
равномерным обогревом при близких значениях режимных параметров (Р, G,
Хвх).
Следует
признать, что для выбора надежного общепризнанного метода описания КТП при
неравномерном аксиальном тепловыделении следует провести дополнительную работу.
При этом нужно, во-первых, сделать выбор из двух методов описания (по полной
мощности или по локальному потоку), во-вторых, построить и верифицировать саму
методику.
При
разработке методов описания и определении ошибок описания в качестве методов
анализа используются два подхода:
1)
по входным параметрам,
2)
по локальным параметрам в месте кризиса.
Оцененные
по этим двум методам погрешности различаются в 1,5 - 3,5 раза в зависимости от
области режимных параметров. Погрешность по локальным параметрам много больше.
Каждый из этих методов обработки имеет свои преимущества и недостатки. Поэтому
в данной работе использовались и представлены оба метода обобщения. Таблицы для
КТП и все поправочные функции даны для выходных (локальных) параметров.
Результаты оценки точности даются по обоим методам.
3.3.1. КРИТИЧЕСКИЕ ТЕПЛОВЫЕ ПОТОКИ В БОЛЬШОМ ОБЪЕМЕ
При
кипении жидкости с увеличением плотности теплового потока на стенке
(температурного напора) число центров парообразования и частота отрыва паровых
пузырей растут. Вместо одиночных пузырей от поверхности нагрева движутся струи
пара, а между ними навстречу жидкость. Образующийся пар затрудняет доступ
жидкости к поверхности нагрева. При критической плотности теплового потока
устойчивость встречных потоков пара и жидкости нарушается, что ведет к
нарушению структуры пристенного слоя, уменьшению времени и поверхности контакта
между жидкостью и стенкой. Это приводит к резкому снижению коэффициента
теплоотдачи, повышению температуры поверхности нагрева.
Критическая плотность
теплового потока при кипении жидкости в большом объеме (горизонтальная плоская
поверхность, обращенная вверх) при температуре насыщения рассчитывается по
формуле [4]:
Таблица 3.3.1
Значения С и соотношения для k
|
Авторы
|
С
|
K
|
|
Кутателадзе
С.С. [16]
|
0,16
|
1
|
|
Зубер
и др. [17]
|
π/24
|
[ρ'/(ρ" - ρ')]0,5
|
|
Боришанский
В.М. [18]
|
1
|
0,13 + 4[{g(μ'2)(ρ' -
ρ")0,5}/(ρ'σ1,5)]
|
|
Чанг
и Снайдер [19]
|
0,145
|
[(ρ' + ρ")/ρ']0,5
|
|
Маленков
И.Г. [20]
|
1
|
30M2/3, М = (ρ'/ρ")0,5[gσ/(ρ' - ρ")0,25
|
|
Мойссис
и Беренсон [21]
|
0,18
|
[(ρ'
+ ρ")/(ρ'ρ")0,5][1
+ 2(ρ"/ρ')0,5
+ (ρ"/ρ')](1/ρ"0,5)
|
Пределы применимости
формулы: Р = 0,1 ÷ Pкр
МПа.
Погрешность
Δ расчета qкр не превышает ±10 %.
Критическая плотность
теплового потока при кипении в большом объеме жидкости, температура которой
вдали от поверхности нагрева меньше температуры насыщения, рассчитывается по
формуле:
|
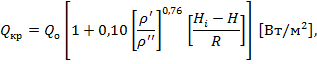
|
(3.3.1.2)
|
где Hi - энтальпия воды на линии насыщения, Дж/кг;
Н -
энтальпия недогретой до температуры насыщения воды, Дж/кг;
Qо
рассчитывается по формуле (3.3.1.1).
Пределы
применимости формулы: горизонтальные поверхности;
Р/Ркр
< 0,50; (Hi - H)/R
< 0,60.
Погрешность
Δ расчета Qкр
составляет ±10 %.
3.3.2. КРИТИЧЕСКИЕ ТЕПЛОВЫЕ ПОТОКИ ПРИ ТЕЧЕНИИ
В КРУГЛЫХ ТРУБАХ
По
установившимся представлениям кризис теплоотдачи при кипении воды в трубах
вызывается уменьшением контакта жидкости с поверхностью нагрева. Кризис
теплоотдачи возникает в результате двух основных процессов.
1.
Гидродинамическое и тепловое разрушение пристенного парожидкостного слоя и
образование паровой пленки. Это характерно для недогретой до температуры
насыщения жидкости или малого паросодержания;
2.
Испарение (высыхание) пленки жидкости, текущей вдоль теплоотдающей поверхности
(дисперсно-кольцевой режим течения). Высыхание пленки жидкости связано с
процессами испарения, механического уноса жидкости и недостаточного выпадения
капель из парожидкостного ядра потока на стенку.
Эти
два вида кризиса теплоотдачи получили название кризисов теплоотдачи 1-го и 2-го
рода.
При
больших паросодержаниях, соответствующих дисперсному режиму течения, тепло от
стенки трубы отводится выпадающими на нее каплями жидкости. Возникновение
кризиса теплоотдачи в этом режиме связывается с недостаточным орошением стенки
каплями жидкости (кризис орошения).
Механизмы
кризиса теплоотдачи в трубах в значительной мере определяется режимами течения
двухфазной смеси, недогревом жидкости до температуры насыщения и плотностью
теплового потока. Между всеми механизмами кризиса теплоотдачи, по-видимому,
отсутствуют резкие границы и существуют области одновременного влияния двух и
более механизмов. В связи с этим интерпретация опытных данных и форма описания
их эмпирическими уравнениями вызывают значительные трудности. Традиционным
является представление опытных данных в координатах Qкр(Xкр) или Nкр(Xвх). При разных G, dh, Р, X
наблюдаются три вида зависимостей
Кризис
теплоотдачи при дисперсно-кольцевом режиме течения двухфазного потока связан с
истощением пристенной пленки жидкости и переходом в дисперсную структуру
потока. Когда истощение пристенной пленки жидкости происходит в условиях
отсутствия ее подпитки каплями из ядра потока, кризис теплоотдачи, согласно
Дорощуку В.Е. [22],
характеризуется величиной так называемого граничного паросодержания,
соответствующего началу резкого увеличения наклона зависимости КТП от потока.
Почти вертикальные зависимости КТП от паросодержания на выходе наблюдаются в
трубах при G ≈ 500 ÷ 2000 кг/м2·с и Р = 5
÷ 15 МПа. Значения граничного паросодержания для трубы с внутренним
диаметром 8 мм приведены в таблице 3.2.
Значение граничного
паросодержания также может быть определено по формуле [23, 24]:
|

|
(3.3.2.1)
|
где We = dh(G)2/(σρ')
- число Вебера, определенное по внутреннему диаметру трубы.
Таблица 3.3.2
Значения граничного паросодержания для трубы с внутренним
диаметром 8 мм [4]
|
Р,
МПа
|
Массовая
скорость G,
кг/м2·с
|
|
350
|
500
|
700
|
1000
|
1500
|
2000
|
|
5
|
0,95 ± 0,02
|
0,91 ± 0,04
|
0,78 ± 0,05
|
0,65 ± 0,03
|
|
|
|
7
|
0,95 ± 0,02
|
0,92 ± 0,05
|
0,85 ± 0,03
|
0,69 ± 0,03
|
|
|
|
10
|
0,89 ± 0,09
|
0,81 ± 0,05
|
0,67 ± 0,09
|
0,54 ± 0,09
|
0,40 ± 0,04
|
0,39 ± 0,05
|
|
12
|
0,83 ± 0,06
|
0,62 ± 0,03
|
0,51 ± 0,03
|
0,41 ± 0,06
|
0,35 ± 0,04
|
0,32 ± 0,03
|
|
14
|
0,70 ± 0,10
|
0,59 ± 0,07
|
0,49 ± 0,06
|
0,40 ± 0,06
|
0,32 ± 0,06
|
0,28 ± 0,05
|
|
16
|
0,63 ± 0,03
|
0,56 ± 0,04
|
0,49 ± 0,04
|
0,39 ± 0,06
|
0,30 ± 0,06
|
0,26 ± 0,04
|
Пределы применимости
формулы: 2,4 ≤ Р ≤ 17,7 МПа;
55 ≤ G
≤ 5000 кг/(м2·с); L > 1 м; dh =
3,84 ÷ 32,2 мм; Хвх < 0;
1
> Xкр ≥ 0,05.
Среднеквадратичная
погрешность формулы 11,8 %.
Интенсивность
выпадения капель (орошение) из ядра потока увеличивается с ростом массовой
скорости и давления. При Р > 16 МПа и G > 2500 кг/м2·с
интенсивность орошения является основным фактором, определяющим отвод тепла от
стенки и ее температурный режим.
3.3.2.1. КРИТИЧЕСКИЕ ТЕПЛОВЫЕ ПОТОКИ ПРИ КИПЕНИИ ВОДЫ
В ТРУБАХ С РАВНОМЕРНЫМ ТЕПЛОВЫДЕЛЕНИЕМ ПО ДЛИНЕ
В
разделе представлены: табличный метод расчета критических тепловых потоков и
традиционный аналитический метод расчета.
3.3.2.1.1. Табличный метод расчета КТП в трубах
Величину
критической плотности теплового потока для гладкой, достаточно длинной (при Lh/dh ≥
300), трубы диаметром 8 мм при равномерном энерговыделении рекомендуется
определять по таблице 1 Приложения (международная версия) [3]. Для получения КТП в трубе диаметром
8 мм используются следующие параметры в месте кризиса (при равномерном
энерговыделении - на выходе из трубы): давление, массовая скорость и балансное
паросодержание. Если параметры не совпадают с параметрами узлов таблицы,
следует использовать метод трехмерной линейной интерполяции.
Для получения КТП в трубе
другого диаметра (от 2 мм до 40 мм) необходимо ввести поправку на величину
диаметра F(dh):
|
Qdh = Q8F(dh)
= Q8(8/dh)(1/3).
|
(3.3.2.2)
|
Поправка на относительное расстояние от места кризиса до входа
(отношение расстояния от места кризиса до входа Zh к диаметру
трубы) имеет вид:
|
F(zh/dh) = 1 + 0,4exp(-0,02Zh/dh)
для Zh/dh ≥ 40.
|
(3.3.2.3)
|
Расчет критической мощности трубчатого твэла с обогреваемой длиной
можно произвести по формуле:
Относительную энтальпию на входе в обогреваемую зону вычисляют по
формуле:
|
Хвх =
X - 4N/(Gπdо2R).
|
(3.3.2.5)
|
Погрешности Δ и σ
описания данных по локальным параметрам 2 - 3 % и 16 %, по входным
параметрам - не более 1 - 2 % и не более 8 %. Эти погрешности относятся к
областям параметров, обеспеченным экспериментальными данными и обозначенным в
таблице 3.3.1 полужирным шрифтом.
3.3.2.1.2. Расчетный метод НИКИЭТ
Критическая
плотность теплового потока при кипении воды в трубах в соответствии с
характером зависимостей Qкр(Xкр) рассчитывается по соотношениям [25, 26]:
а) при Х ≤ Х0
по формуле:
где Q0
= 0,18R(ρ")0,50[σg(ρ' - ρ")]0,25[(v"/v')0,50
- 1];
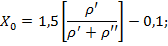
б) при Xкр = Х0
÷ Х1 по формуле:
|
Q = Qкр{exp -
[0,2[d/ρ'σ]0,333G0,667[Xжт -
X0]]}-1,
|
(3.3.2.7)
|
где 
в) при Xкр > X1 по формуле:
При G = const и P
= const критическая плотность теплового потока рассчитывается по приведенным
формулам до взаимного пересечения кривых Qкр(Xкр). Область над кривыми Qкр(Xкр) характеризуется как кризисная.
Если результаты расчетов
критической плотности теплового потока по формуле (3.3.2.8) окажутся выше, чем по формуле (3.3.2.7), то при Xкр > X1 для данного режима:
где Qкр рассчитывается
по формуле (3.3.2.8).
В
формулах (3.3.2.6 - 3.3.2.9) dh в
[м]; g в [м/с2]; Н в [Дж/кг];
R в
[Дж/кг]; G в [кг/м2·с]; Q в [Вт/м2]; v
в [м2/с]; ρ в [кг/м3]; σ в [Н/м];
μ в [Па·с].
Пределы
применимости формул (3.3.2.6 - 3.3.2.9): Р = 4 ÷ 18
МПа;
G =
500 ÷ 7500 кг/м2·с; Lh = 0,5 ÷ 6 м; dh = 4 ÷ 16 мм.
Погрешность
σ расчета Qкр по
входным параметрам, указанная авторами и полученная на ограниченном массиве
данных, составляет 8 %.
3.3.3. КРИТИЧЕСКИЙ ТЕПЛОВОЙ ПОТОК В КОЛЬЦЕВЫХ КАНАЛАХ
С РАВНОМЕРНЫМ ЭНЕРГОВЫДЕЛЕНИЕМ ПО ДЛИНЕ
В
разделе представлены два метода определения КТП в кольцевых каналах: первый -
на основе скелетной таблицы для КТП в кольцевых каналах, второй - на основе
эмпирических расчетных соотношений.
Значения граничного
паросодержания в кольцевых каналах определяются по формуле [24, 27]:
|

|
(3.3.3.1)
|
где We = dэ(G)2/(σρ')
- число Вебера, определенное по эквивалентному диаметру кольцевого канала dэ
= dтПг/По. Здесь Пг и По,
соответственно, - смоченный и обогреваемый периметры канала, dт = 4S/По -
эквивалентный тепловой диаметр, S - проходное сечение канала.
Пределы
применимости формулы: 3,4 ≤ Р ≤ 16,7 МПа;
350 ≤
G ≤ 4500 кг/м2с; L > 1 м; dэ = 14,06 ÷ 151,65 мм;
Хвх
< 0; 1 > Xкр ≥
0,05.
Среднеквадратичная
погрешность формулы около 10 %.
3.3.3.1. РАСЧЕТ КТП В КОЛЬЦЕВЫХ КАНАЛАХ ПО СКЕЛЕТНОЙ ТАБЛИЦЕ
Имеющаяся
методика описания КТП в одиночных каналах различного поперечного сечения [28] позволила сформировать таблицу
для численного описания КТП в кольцевых каналах [29] (Приложение,
таблица 2). На основе экспериментальных
данных [30] получена базовая
таблица, позволяющая рассчитывать КТП в различных кольцевых каналах. С целью
соблюдения традиции таблица для кольцевых каналов была сформирована для
теплового диаметра, равного 8 мм и соотношением диаметров d1/d2
= 1 (плоская щель как предельный случай кольцевого канала).
3.3.3.1.1. Концентричные кольцевые каналы, односторонний обогрев
В
качестве исходных данных нужно иметь Р, G, Хвых, d1,
d2, lh.
Необходимые
геометрические параметры находим по соотношениям:
■
для внутреннего обогрева:
dh1 = (d22 - d12)/d1;
Со1 = (d2 - d1)/d1;
■
для наружного обогрева:
dh2 = (d22 - d12)/d2;
Со2 = (d2 - d1)/d2.
Определяется КТП по
соотношению:
|
Q =
Qt(P,
G, Xо, dh)F(dh)F(lh),
|
(3.3.3.2)
|
где Хо1 = Х - 0,05Со12;
Хо2 = Х + 0,05Со22;
F(dh) =
(dh/8)(-1/3) при dh ≤
16;
F(dh) =
(16/8)(-1/3) при dh
> 16;
F(lh) =
1 + 0,4exp(-0,02lh/dh).
3.3.3.1.2. Концентричные кольцевые каналы, двусторонний обогрев
В
качестве исходных данных нужно иметь Р, G, Хвых, d1,
d2, lh, Q1,
Q2.
Определяем диаметр - границу
охлаждающих слоев по соотношению:
|
dо2 = [Q1d1(d22)
+ Q2d2(d12)]/(Q1d1
+ Q2d2),
|
(3.3.3.3)
|
где для каждой поверхности из определения имеем:
■
для внутренней стенки:
dh1 = (dо2 - d12)/d1;
Со1 = (dо - d1)/d1;
■
для наружной стенки:
dh2 = (d22 - dо2)/d2;
Со2 = (dо - d2)/d2.
Хо1, Хо2
- определяются по формулам предыдущего раздела.
Определяется КТП по
соотношению:
|
Q =
Qtab(P, G, Хо, dh)F(dh)F(lh);
|
(3.3.3.4)
|
F(dh) = (dh/8)(-1/3)
при dh ≤
16;
F(dh) =
(16/8)(-1/3) при dh > 16,2;
F(lh) =
1 + 0,4exp(-0,02lh/dh).
В
результате имеем две величины КТП, соответственно, для двух поверхностей.
Сравнение с заданными величинами тепловых потоков на обеих поверхностях покажет
близость к кризису на обеих поверхностях.
3.3.3.1.3. Эксцентричные каналы, односторонний обогрев
В
качестве исходных данных нужно иметь Р, G, Хвых, d1,
d2, lh и е -эксцентриситет.
Необходимые геометрические параметры находим по соотношениям:
■
для внутреннего обогрева:
dh1 = (d22 - d12)/d1;
Yo1 = (d2 - d1 - e)/(d2
- d1);
Cо1 = (d2 - d1)/d1;
Lо1 = (πd1)/(d2 - d1);
■
для наружного обогрева:
dh2 = (d22 - d12)/d2;
Yo2 = (d2 - d1 - e)/(d2
- d1);
Cо2 = (d2 - d1)/d2;
Lо2 = (πd2)/(d2 - d1);
Для
обеих поверхностей находим параметры:
п = 0,5 + 0,0015(G)(Co)2;
А = K1K2K3K4K5;
K1 = K(Lо) = 1,15[1 - exp(-Lо/8,5)];
K2 = K(G,Cо) = Gα;
α = (- 0,37|Со|0,5);
K3 = K(Lmm, Со) = (Lmm)β;
β =
(0,29|Со|0,33);
K 4 = K(Х) = 1 - 0,3Х;
K5 = K(Еk) =
0,5.
Определяется КТП по
соотношению:
|
Q =
Qtab(P, G, Хо, dh)F(Yо, Cо, Lо, Еk)F(dh)F(lh),
|
(3.3.3.5)
|
где F(Yо, Cо, Lо, Еk) =
[1 - А(1 - Yо)n];
F(dh) = (dh/8)(-1/3)
при dh ≤
16;
F(dh) =
(16/8)(-1/3) при dh > 16;
F(lh) =
1 + 0,4exp(-0,02lh/dh).
Xо1, Xо2 -
по формулам предыдущего раздела.
3.3.3.1.4. Эксцентричные каналы, двусторонний обогрев
В
качестве исходных данных имеем: Q1, Q2, Р,
G, Хвых, d1, d2, lh, е
- эксцентриситет.
Определяем диаметр
окружности - границу нулевого обмена:
|
dо2 = [Q1d1(d22)
+ Q2d2(d12)]/(Q1d1
+ Q2d2).
|
(3.3.3.6)
|
Xо1, Xо2 - находим по формулам предыдущего раздела.
Необходимые
геометрические параметры находим по соотношениям:
■
для внутреннего обогрева:
dh1 = (d22 - d12)/d1;
Yo1 = (d2 - d1 - e)/(d2
- d1);
Cо1 = (d2 - d1)/d1;
Lо1 = (πd1)/(d2 - d1);
■
для наружного обогрева:
dh2 = (d22 - d12)/d2;
Yo2 = (d2 - d1 - e)/(d2
- d1);
Cо2 = (d2 - d1)/d2;
Lо2 = (πd2)/(d2 - d1);
Для
обеих поверхностей находим параметры:
п = 0,5 + 0,0015(G)(C)2;
А = K1K2K3K4K5;
K1 = K(Lо) =
1,15[1 - exp(-Lо/8,5)];
K2 = K(G,Cо) = Gα;
α = (-0,37|Со|0,5);
K3 = K(Lmm, Со) = (Lmm)β;
β =
(0,29|Со|0,33);
K4 = K(Х) = 1 - 0,3Х;
K5 = K(Еk) =
0,5.
Определяем КТП по
соотношению:
|
Q =
Qtab(P, G, Хо, dh)F(Yо, Cо, Lо, Еk)F(dh)F(lh),
|
(3.3.3.7)
|
где F(Yо, Cо, Lо, Еk) =
[1 - А(1 - Yо)n];
F(dh) =
(dh/8)(-1/3) при dh ≤
16;
F(dh) =
(16/8)(-1/3) при dh > 16;
F(lh) =
1 + 0,4exp(-0,02lh/dh).
В
результате имеем две величины КТП для двух поверхностей. Сравнение с заданными
величинами тепловых потоков на обеих поверхностях покажет близость к кризису на
обеих поверхностях.
О погрешностях табличного метода
В
таблице 2 Приложения выделены области параметров, которые обеспечены
экспериментальными данными. Эти области узкие, особенно, при малых давлениях.
Поэтому требуется проверка данных таблицы в областях, полученных экстраполяцией
по определенной методике.
Табличный
метод был проверен на экспериментальных данных для концентрических каналов [30]:
■
для внутреннего обогрева: число точек - 5564, тепловой диаметр от 6 мм до 96
мм, длина lh > 0,04 м. Среднее отклонение экспериментов от
расчетов по таблице по входным параметрам не более 3 %, среднеквадратичный
разброс не более 17 %;
■
для наружного обогрева: число точек - 2271, тепловой диаметр от 3,84 мм до 22
мм, L от 0,5 до 1,5 м; средняя ошибка 1 %, среднеквадратичная ошибка 9 %
по входным параметрам.
Максимальный диапазон применимости метода:
■
давление от 0,1 до 20 МПа,
■
массовая скорость от 50 до 6000 кг/м2·с,
■
балансное паросодержание от -0,5 до 0,9,
■
тепловой диаметр от 3,8 до 97 мм,
■
обогреваемая длина от 0,04 до 2,8 м,
■
соотношение радиусов от 0 до 1 для наружного обогрева и от 0,3 до 1 для
внутреннего обогрева.
Для
концентрических каналов с двусторонним обогревом и для эксцентрических каналов
данных для надежного определения погрешности метода недостаточно, поэтому
приведенные выше алгоритмы расчета для этих случаев следует считать как
оценочные.
3.3.3.2 ЭМПИРИЧЕСКАЯ МЕТОДИКА
Данная методика для
одностороннего обогрева разработана Судницыным О.А. [29] на основе экспериментальных данных для гладких
кольцевых каналов с односторонним, внутренним или наружным, обогревами (в
количестве 2906 опытных точек, находящихся в банке ФЭИ [30]). Она создавалась в 70-х годах, усовершенствована
в 80-х годах и применима в относительно узком диапазоне параметров и
геометрических размеров (см. ниже). Система зависимостей для КТП имеет вид:
|
Qкк = K1gm[KXgmX -
X]KdKL;
|
(3.3.3.8)
|
K1 = а1р2
+ a2p + а3;
Kx = а7р2
+ a8p + а9;
mх = a10p + а11; т = а4р2
+ a5p + а6;
р = Р/Рcr - давление воды; g = G/1000; G - массовая
скорость потока в кг/м2·с;
Kd =
(0,007/dm)0,17(0,93 - 0,07dh/0,0175) -
поправка на тепловой диаметр;
KL = 1
+ 1,28ехр(-3,6Lh/Lбв) - поправка на
длину обогрева Lh;
Lбв =
0,87 - 0,59Р.
В
формулах данного раздела константы имеют различные значения в различных
областях X:
для X
< Xгр см. первую строчку таблицы 3.3.1;
для X
> Xгр см. вторую строчку этой таблицы.
Здесь
|
Xгр =
(0,75р2 - 1,275р + 0,7)g - 0,4.
|
(3.3.3.9)
|
Таблица 3.3.3.1
Значения коэффициентов аi
|
a1
|
a2
|
a3
|
a4
|
a5
|
a6
|
а7
|
a8
|
a9
|
a10
|
a11
|
|
0,17
|
-13,1
|
9,41
|
0
|
0
|
0,7
|
-0,97
|
1,0
|
0,47
|
0,41
|
-0,8
|
|
4,48
|
-16,5
|
12,9
|
-0,88
|
1,79
|
-0,20
|
0
|
0
|
0,6
|
0
|
-0,44
|
Приведенная здесь методика
рекомендуется для давлений от 7 до 20 МПа, массовых скоростей от 250 до 3500
кг/м2·с, величин паросодержаний в месте кризиса от -1,1 до 0,5,
обогреваемых диаметров от 0,004 до 0,045 м и обогреваемых длин от 0,1 до 1,5 м.
При этом среднеквадратичный разброс данных по выходным параметрам не превышает
17 % при нулевом среднем отклонении, по входным параметрам - 10 %. Проверка
методики на массиве данных в широком диапазоне параметров (Р > 70
атм, Х от -1,1 до 0,9, G от 150 до 6000 кг/м2·с)
показала, что она описывает экспериментальные данные с погрешностями (по
входным параметрам): при наружном обогреве (число точек 1721) - среднее
отклонение 0 %, среднеквадратичный разброс - 10 %; для внутреннего обогрева
(число точек 3094) - 4 и 15 %, соответственно.
3.3.4. КРИЗИС ТЕПЛООТДАЧИ ПРИ КИПЕНИИ ВОДЫ В СБОРКАХ
ЦИЛИНДРИЧЕСКИХ ТВЭЛОВ
Кризис
теплоотдачи в стержневых сборках - явление более сложное, чем в одиночных
каналах более простой формы, рассмотренных ранее. Сложность определяется не
только формой сечения ячеек пучков, но и фактом взаимного влияния потоков в
ячейках. Играют роль и периферийные каналы, и наличие необогреваемых
поверхностей, и неравномерность обогрева по сечению и длине, и наличие
дистанционирующих решеток, и тепловая развертка между периферийными и стандартными
ячейками. Под стандартными ячейками понимается часть проходного сечения сборки,
заключенная между соседними одинаково обогреваемыми стержнями.
В
данном разделе приводятся как табличные методы расчета КТП в сборках, так и
традиционные методы (на основе аналитических соотношений).
3.3.4.1. ТАБЛИЧНЫЙ МЕТОД РАСЧЕТА КТП В СБОРКАХ ТРЕУГОЛЬНОЙ
ГЕОМЕТРИИ ПРИ РАВНОМЕРНОМ ЭНЕРГОВЫДЕЛЕНИИ
В
качестве основы для получения скелетной таблицы (Приложение, таблица 3)
использованы данные, полученные на 47 сборках (5240 точек) в широком диапазоне
режимных и геометрических параметров: давление - от 0,1 МПа до 20 МПа, массовая
скорость - от 25 до 4960 кг/м2·с; балансное паросодержание - от -0,5
до 1,0; обогреваемая длина стержней - от 0,45 до 3,54 м; диаметр стержней - от
5 до 13,5 мм; тепловой диаметр ячеек - от 2,81 до 20,9 мм; относительный шаг
стержней - от 1,16 до 1,52; количество стержней в сборках - 7 и 19. Степень
«несбалансированности» использованных для анализа сборок (отношение тепловых
диаметров dh/dh1) составляла от
0,42 до 0,93. Указаны крайние пределы, охватывающие все данные, полученные в
разных областях параметров и включенные в базу данных ФЭИ.
3.3.4.1.1. Метод ФЭИ расчета КТП в сборках по осредненным
по сечению параметрам
Метод
изложен в [31], там же приведена
история создания серии скелетных таблиц. В этом случае в качестве исходных
данных, кроме геометрии (длина, диаметры стержней, относительный шаг
расположения стержней, количество стержней, конструкция обечайки, наличие или
отсутствие направляющих стержней, расположение дистанционирующих решеток и их
коэффициенты сопротивления) необходимо знать средние по сечению режимные
параметры сборки в каждом сечении сборки: Р - давление, G
-массовая скорость, X - балансное паросодержание в месте кризиса.
Согласно
исходной геометрии (конструкции сборки) определяются (задаются или
рассчитываются) все безразмерные и размерные геометрические определяющие
параметры: dh/dh1, s/d, L/dh,
Kf, Z/dh, где dh -
тепловой диаметр внутренней ячейки сборки, dh1 -
тепловой диаметр всего сечения сборки, s/d - относительный шаг стержней,
L/dh - относительное расстояние от места кризиса до
входа в сборку, Kf - коэффициент, учитывающий влияние
дистанционирующей решетки, Z/dh - относительное
расстояние от места кризиса до ближайшей дистанционирующей решетки в сторону
входа.
КТП по табличному методу
рассчитывается по соотношению:
где Qт - критические тепловые потоки согласно
таблице, которая дана для стандартной идеальной ячейки сборки со следующими
параметрами: s/d = 1,4; dh = 9,36 мм, dh/dh1
= 1, L/dh > 300. Под стандартными ячейками
подразумеваются ячейки между одинаковыми и одинаково обогреваемыми твэлами.
Еще
раз следует подчеркнуть, что табличные значения Qт даны для
локальных параметров ячеек сборок в отсутствии каких-либо влияний, т.е. при K1 = K2 = K3 = K4 = K5 = K6 = K7 = 1.
В
формуле (3.3.4.1) содержится
система поправок, учитывающих влияние различных значимых факторов. Эти факторы
следующие:
■ поправка на величину
теплового диаметра стандартной ячейки:
|
K1 = F(dh) = (dh/9,36)-1/3,
где dh =
d[1,103(s/d)2 - 1];
|
(3.3.4.2)
|
■ поправка на относительный шаг расположения стержней
|
K2 = F(s/d) = 0,82 - 0,7exp[-35(s/d -
1)] для s/d ≤ 1,1
(до 1,02);
|
(3.3.4.3)
|
K2 = F(s/d) = 0,2 + 0,57s/d для s/d > 1,1 (до 1,52);
■ поправка на влияние
входных условий сборки (относительного расстояния от места кризиса до входа в
сборку L, которая совпадает с длиной обогрева Lh при
равномерном по длине энерговыделении):
|
K3 = F(L/dh) = 1,0 + 0,6exp(-0,01L/dh);
|
(3.3.4.4)
|
■ поправка на турбулизирующее влияние дистанционирующих или
смесительных решеток:
|
K4 = F(Kf) = 1 + Aexp(-0,1Z/dh),
|
(3.3.4.5)
|
где А = 1,5Kf0,5(G/1000)0,2,
Kf -
коэффициент местного сопротивления решетки (относится к сечению вдали от
решетки);
Z -
расстояние от места кризиса до ближайшей дистанционирующей решетки в сторону
входа;
■ поправка на
теплогидравлическую неравноценность экспериментальной сборки:
|
K5 = F(dh/dh1)
= dh/dh1,
|
(3.3.4.6)
|
где dh1 - тепловой диаметр сечения
сборки в целом.
3.3.4.1.2. Метод ФЭИ расчета локальных величин КТП при поканальном
анализе сборок
Табличный
метод расчета КТП, разработанный в ФЭИ и представленный в [31] (таблица и необходимые поправочные функции),
наиболее пригоден к расчёту КТП при поячеечном (поканальном) методе анализа.
Как известно, поячеечный
теплогидравлический расчет сборки дает значения режимных параметров по длине в
каждой ячейке проходного сечения сборки. Эти значения и используются для
расчета КТП в ячейках сборки. Рекомендуется рассчитывать КТП по соотношению (3.3.4.1), но без поправки K5:
|
Q =
QтK1K2K3K4,
|
(3.3.4.7)
|
где Qт - критические тепловые потоки согласно
таблице, которая дана для «идеальной ячейки» сборки со следующими параметрами: s/d
= 1,4; dh = 9,36 мм; dh/dh1
= 1; L/dh > 300. Под «идеальными ячейками» подразумеваются
ячейки между одинаковыми по геометрии и одинаково обогреваемыми твэлами.
При
поячеечном анализе возникает также проблема описания КТП и в ячейках,
существенно отличающихся от «идеальных ячеек» сборки. В сборке могут оказаться
ячейки около необогреваемой обечайки или около необогреваемых стержней (НК),
или около стержней с другим энерговыделением, или в углу сборки, или ячейки
другого размера и т.д.
В
этих случаях КТП рассчитывается по нижеприведенной схеме.
1.
По таблице определяем Qт по известным по ячейкам режимным
параметрам, используя линейную или квадратичную интерполяцию.
2.
Определяем K1 = (dh/9,36)-1/3 - поправочную
функцию на величину теплового диаметра каждой ячейки. Обращаем внимание, что в
качестве определяющего диаметра при расчете КТП в ячейках следует использовать
тепловой диаметр ячейки (четыре площади проходного сечения ячейки S,
поделенные на обогреваемый периметр ячейки Ро: dh
= 4S/Pо).
3.
Поправочная функция на относительный шаг K2
получена как для «идеальных ячеек». Для других ячеек в качестве относительного
шага следует использовать величину (некий эквивалент относительного шага): s/d
= 1 + δ/D, где
δ - средняя величина минимального зазора между стержнями, D
- средний диаметр ближайших тепловыделяющих стержней, ограничивающих данную
ячейку.
Другие
поправочные функции не требуют пояснения.
Области применения табличного метода
Метод
используется для расчета КТП в треугольных пучках в следующих диапазонах
параметров:
■
сборки с тепловыми диаметрами ячейки от 2,8 до 21 мм;
■
сборки с относительными шагами от 1,16 до 1,52;
■
в диапазоне давлений от 0,1 до 20 МПа;
■
в диапазоне массовых скоростей от 25 до 5000 кг/м2с;
■
в диапазоне локальных балансных паросодержаний от -0,5 до 1;
■
в диапазоне относительных длин от 40 до 350 и более.
Ошибки при использовании табличных методов для расчета КТП
в треугольных сборках
Метод
описывает экспериментальные данные со среднеквадратичной погрешностью около 17
% по локальным параметрам (оценка по данным, полученным на 47 экспериментальных
моделях, 5240 точек).
В
таблице 3 Приложения обозначены выделенные жирным шрифтом области,
обеспеченные экспериментальными данными. Упомянутая ранее погрешность описания
относится именно к этим областям режимных параметров или к промежуточным
областям параметров. В связи с наличием «белых пятен» использование расчетных
результатов в таких областях требует должной осторожности. По мнению авторов, в
таких областях использование данного метода, как и любого другого,
целесообразно ограничить только стадией предварительных, оценочных расчетов.
3.3.4.2. МЕТОД РНЦ КИ РАСЧЕТА КТП
Метод РНЦ КИ предназначен
для расчета КТП в треугольных и квадратных сборках. Основы метода были заложены
В.С. Осмачкиным [32], в настоящее
время метод реализован в виде следующих зависимостей [33, 34]:
|

|
(3.3.4.8)
|
где qcr(z)
- критический тепловой поток для «горячего» твэла, Вт/м2;
f1 = rp'[g(ga')1/3(v'/а')d]1/3(d/μ')1/5/345;


f4 = 1
+ 0,7ехр[-11,4(1 - p/pcr)2];
х(z)
- относительная энтальпия (равновесное массовое паросодержание);
R -
скрытая теплота парообразования, Дж/кг;
ρ' и ρ"
- плотность воды и пара на линии насыщения, кг/м3;
v' и μ'
- кинематическая [м2/сек] и динамическая [кг/м·сек] вязкость воды на
линии насыщения;
а' -
коэффициент температуропроводности воды на линии насыщения, м2/сек;
σ -
поверхностное натяжение, кг/сек2;
Fr = (G/r')2/(gd)
- критерий Фруда;
g =
9,81 м/сек2 - ускорение свободного падения;
d = 0,0115 м - размерная
константа;
kn - коэффициент, учитывающий
теплогидравлическую неравноценность ячеек пучка; в одномерных расчетах равен 1,
в поячейковых расчетах равен 1,21 (см. ниже).
В
практических расчетах функции f1 и f2
удобно аппроксимировать зависимостями от давления. Для определения значений f1 и f2 в области давлений р ≤ 20 МПа
используются полиномы вида:
у = а0 + а1(ts/tcr) + a2(ts/tcr)2 + ...,
где ts - температура насыщения при давлении Р, °С;
tcr
= 374,12 °С - критическая температура.
Таблица 3.3.3.2
Значения коэффициентов полиномов
|
y
|
Интервал
ts, °С
|
a0
|
a1
|
a2
|
a3
|
a4
|
a5
|
a6
|
a7
|
|
f1(p)·10-10
|
10 ÷ 270
|
0,8535617
|
-1,815439
|
4,213829
|
-7,457705
|
7,159704
|
-2,917067
|
|
|
|
f1(p)·10-10
|
270 ÷ 370
|
-4,206398
|
23,49028
|
-44,47373
|
36,96860
|
-11,69473
|
|
|
|
|
f2
|
10 ÷ 270
|
0,4200931
|
0,08186843
|
-0,08173943
|
0,843390
|
-1,459060
|
1,093261
|
|
|
|

|
270 ÷ 370
|
-92,09139
|
388,6714
|
-412,5018
|
-301,4595
|
628,3313
|
187,7497
|
-683,35
|
285,34
|
Метод РНЦ КИ для расчета
критических тепловых потоков может использоваться как в одномерных, так и в
поячейковых расчетах. Переход от «одномерного» или «пучкового» вида к
«ячейковому» виду связан с заданием соответствующего значения kn. Коэффициент kn определяется поперечной
теплогидравлической неоднородностью той части поперечного сечения активной
зоны, к которой применяется формула (элементарной ячейки, доли кассеты, целой
кассеты, области из нескольких кассет). Он учитывает отличие параметров
теплоносителя в самой «горячей» ячейке в пределах рассматриваемой части
поперечного сечения от средних для этой части параметров.
Выбор
коэффициента kn
производится следующим образом. Если рассматриваемая часть поперечного сечения
активной зоны выделена так, что обеспечивается идентичность средних по ее
сечению параметров теплоносителя и параметров в «горячей» ячейке, то
принимается kn =
1,21. Проще всего это условие удовлетворяется, если выполнено разбиение
поперечного сечения пучка на элементарные ячейки. В противном случае
принимается: kn =
1. Значение kn
принимается равным 1, в частности, при одномерном расчете тепловыделяющей
сборки или активной зоны в целом.
Физический
смысл коэффициента kn
заключается в том, что он предназначен учитывать (хотя и грубо)
теплогидравлическую неравноценность сборок.
При
подстановке kn =
1,21 учитывается отличие параметров теплоносителя в «горячей» ячейке от средних
по сечению пучка параметров для тех экспериментальных участков, эксперименты на
которых были использованы при получении «одномерной» корреляции. Значение kn = 1,21 было получено на основании
сравнения результатов поячейковых и одномерных расчетов критических тепловых
потоков с экспериментальными данными для этих пучков [33].
Рекомендуемый
диапазон применения метода РНЦ КИ:
■
давление 30 ÷ 190 бар;
■
массовая скорость 200 ÷ 4500 кг/м2·с;
■
массовое паросодержание -0,2 ÷ +0,8.
В
этом диапазоне параметров в поячейковых расчетах критического теплового потока
для 55 пучков (2614 экспериментальных точек) получена среднеквадратичная
ошибка, составляющая 21,9 %. В одномерных расчетах для того же массива данных
получена значительно меньшая среднеквадратичная ошибка - всего 13 %. Этот
результат говорит о том, что для поячейковых расчетов следует создавать
специальные методики для определения критического теплового потока.
3.3.4.3. МЕТОД РАСЧЕТА КТП ПРИ ДИСПЕРСНО-КОЛЬЦЕВОМ
РЕЖИМЕ ТЕЧЕНИЯ
Кризис теплоотдачи при этом режиме
течения двухфазного потока связан с истощением пристенной пленки жидкости и
переходом дисперсно-кольцевой структуры потока в дисперсную. Соответствующее
этому переходу значение критического паросодержания (относительной энтальпии)
потока определяется по формуле [24,
35]:
где We = dэ(G)2/(σρ")
- число Вебера, определенное по эквивалентному диаметру сборки dэ
= 4dh1;
dh1 = 4S/Pо
- эквивалентный тепловой диаметр сборки;
S -
проходное сечение сборки;
Ро -
её обогреваемый периметр.
Критическая
мощность или критическая плотность теплового потока находятся далее из
теплового баланса.
Пределы
применимости формулы: 0,1 ≤ Р ≤ 16,8 МПа;
50 ≤
G ≤ 3800 кг/м2с; Lh > 1 м; dh1
= 5,5 ÷ 25,3 мм; Хвх < 0,1; Хвх ≥
0,05.
Среднеквадратичная
погрешность определения КТП по локальным параметрам с помощью формулы (3.3.4.9) для сборок треугольной
упаковки в указанном диапазоне параметров составляет 17,1 % (среднее отклонение
- 1,4 %).
3.3.4.4. КРИТИЧЕСКАЯ ПЛОТНОСТЬ ТЕПЛОВОГО ПОТОКА ПРИ КИПЕНИИ
ВОДЫ В СБОРКАХ СТЕРЖНЕЙ ВВЭР-440 И ВВЭР-1000 ПРИ РАВНОМЕРНОМ
ЭНЕРГОВЫДЕЛЕНИИ (МЕТОД ОКБ «ГИДРОПРЕСС»)
Согласно [36] для проектов ВВЭР-440 и ВВЭР-1000 рекомендуется
метод расчёта ОКБ «Гидропресс» 1976 г.:
|
Q =
7,95·105(1 - X)n(G)m(1 - 0,0185·10-6P),
|
(3.3.4.10)
|
где n = 0,105·10-6Р - 0,5;
т =
0,311(1 - X) - 0,127;
G в
[кг/м2·с];
Р в
[Па]; Q в [Вт/м2].
Пределы
применимости формулы: Р = 7,45 ÷ 16,7 МПа;
G =
700 ÷ 3800 кг/м2·с; относительная энтальпия X в месте
кризиса от -0,1 до 0,4; L = 1,7 ÷ 3,5 м; d = 9 мм; s/d
= 1,34 ÷ 1,385; d - наружный диаметр стержня, м; s - шаг расположения стержней в сборке, м.
Погрешность
а описания и расчета Q (по локальным параметрам) составляет 13 % - по
верификации на полном современном массиве данных и 10 % - по верификации на
массиве данных, имевшихся на 1974 г.
Условные обозначения к разделу 3
d -
диаметр;
dо -
внутренний диаметр трубы, наружный диаметр твэла в сборке; диаметр адиабатной
линии при двустороннем обогреве в кольцевом канале;
dг -
гидравлический диаметр;
 - тепловой диаметр канала
(трубы, кольцевого канала, сборки);
- тепловой диаметр канала
(трубы, кольцевого канала, сборки);
dh1 -
тепловой диаметр сечения сборки;
d1 -
внутренний диаметр кольцевого канала;
d2 -
внешний диаметр кольцевого канала;
e - эксцентриситет кольцевого канала;
Ek - параметр приближенного теплового
моделирования твэлов;
F -
площадь сечения;
F1 и F2
- площади сечения охлаждающих слоёв в кольцевом канале;
G -
массовая скорость, кг/м2 с, (g = G/1000);
g -
ускорение свободного падения;
Н -
энтальпия;
Ph -
обогреваемый периметр сечения ячейки;
Ро -
обогреваемый периметр,
Р -
давление в МПа или в КПа;
Ркр -
давление в критической точке;
Рсм -
смоченный периметр микроячейки сложного сечения;
Q, q -
плотность теплового потока, Qтаб - табличное значение;
Q1 и Q2
- тепловой поток на внутренней и наружной поверхностях кольцевого канала;
Q(z)
- изменение Q вдоль канала;
Qcp -
среднее по длине значение теплового потока;
Q(z)*
= Q(z)/Qcp - относительная эпюра теплового
потока вдоль канала;
ΔQ* = Q(z)*
- 1; ΔQ*макс - максимальное значение относительной
эпюры;
Kf -
коэффициент местного сопротивления решетки;
Lh,
lh - обогреваемая длина;
Lо = Рсм/Yср - продолговатость сечения охлаждающего слоя;
Lh -
обогреваемая длина канала;
N -
мощность;
R -
теплота парообразования;
r - радиус гиба трубы;
S -
площадь сечения;
s -
шаг расположения стержней;
X -
балансное паросодержание;
Хо -
условное балансное паросодержание в кольцевом канале;
Y = Yмин/Yср
- параметр неравномерности толщины охлаждающего слоя, или отношение
минимального значения толщины теплового слоя к среднему его значению (для
кольцевых каналов);
Yср -
средняя толщина теплового пограничного слоя,
Z, z -
координата от начала обогрева,
Zp -
расстояние от места кризиса до ближайшей дистанционирующей решетки в сторону
входа;
Zкр -
координата кризиса от начала обогрева;
ρ -
плотность;
ρ' -
плотность жидкости на линии насыщения;
ρ"
- плотность пара на линии насыщения;
v -
кинематическая вязкость;
μ -
динамическая вязкость;
π = Р/Ркр;
Δ -
средняя ошибка;
σ -
среднеквадратичная ошибка; поверхностное натяжение.
Список литературы к разделу 3.3
1. Зейгарник Ю.А. Об универсальной модели кризиса кипения
недогретой жидкости в каналах. Теплофизика высоких температур, 1996, том 34,
N1.
2. Ефанов А.Д., Кириллов П.Л., Смогалев И.П., Бобков В.П., Анисимов
В.А., Ивашкевич А.А. Теплогидравлическая база знаний для решения задач анализа
и управления тяжелыми авариями. Сборник трудов конференции «Теплофизика-98».
1998.
3. Groeneveld D.C., Leung L.K.H., Kirillov P.L., Bobkov V.P.,
Vinogradov V.N., Smogalev I.P, Royer E. The 1996 look-up table for critical
heat flux in tubes. Nuclear Engineering and Design, 163, 1996.
4. Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по
теплогидравлическим расчетам (ядерные реакторы, теплообменники,
парогенераторы). М.: Энергоатомиздат, 1990. Издание второе, исправленное и дополненное.
5. Астахов В.И., Безруков Ю.А., Логвинов С.А., Брантов В.Г.
Исследование влияния профиля тепловыделения по длине на кризис теплообмена в
пучках стержней. Семинар ТФ-78, «Теплофизические исследования для обеспечения
надежности и безопасности ядерных реакторов водо-водяного типа», Будапешт,
1978, т. 2.
6. Безруков Ю.А., Астахов В.И., Трушин А.М. и др. Исследование
кризиса теплообмена применительно к реальным аксиальным профилям
тепловыделения. Доклад на 3-ю научно-техническую конференцию «Обеспечение
безопасности АЭС с ВВЭР», Подольск, 26 - 30 мая 2003.
7. Виноградов В.Н., Смогалев И.П., Сергеев В.В. Анализ кризиса
теплообмена при неравномерном аксиальном обогреве применительно к реакторам
ВВЭР-1000. Доклад на 2-ую Всероссийскую конф. «Обеспечение безопасности АЭС с
ВВЭР», Подольск, ОКБ «Гидропресс», 2001.
8. Бобков В.П., Виноградов В.Н., Кириллов П.Л., Смогалев И.П.
Табличный метод расчета критического теплового потока в водоохлаждаемых
треугольных сборках стержней. Атомная энергия, т 87, № 1, 1999.
9. Зенкевич Б.А., Песков О.Л., Петрищева Г.А., Сергеев Н.Д.,
Субботин В.И. Анализ и обобщение опытных данных по кризису теплоотдачи при
вынужденном течении кипящей воды в трубах. М., Атомиздат, 1969.
10.
Ремизов О.В., Воробьев В.А., Шуркин Н.Г., Подгорный К.К. Кризис теплоотдачи и
динамика его развития в трубе с косинусным тепловыделением по длине при
вынужденном течении воды. Препринт ФЭИ-481, Обнинск, ФЭИ, 1974.
11.
Тонг Л. Кризис кипения и критический тепловой поток. Москва, Атомиздат, 1976.
12.
Смолин В.Н., Шпанский С.В., Есиков В.И., Седова Т.К. Экспериментальные данные и
методика расчета кризиса теплоотдачи при кипении воды, циркулирующей в трубах с
равномерным и неравномерным тепловыделением. ВАНТ, Сер.: Физика и техника
ядерных реакторов, вып. 5(9), 1979.
13.
Астахов В.И., Безруков Ю.А., Логвинов С.А. Учет аксиальной неравномерности
тепловыделения при определении запасов по кризису теплообмена в реакторе типа
ВВЭР. ВАНТ, Сер.: Физика и техника ядерных реакторов, вып. 5(9), 1979.
14.
Толубинский В.И. Теплообмен при кипении. Киев, Наукова думка, 1980, с. 270.
15. Ли Д. Расчет кризиса кипения. Статья в сб. «Теплопередача в
двухфазном потоке». М., Энергия, 1980.
16. Кутателадзе С.С. Основы теории теплообмена. 5-е изд., доп. М.: Атомиздат, 1979.
17. Zuber N. Hydrodynamic Aspects of
Boiling Heat Transfer. USAEC Report AECU-4439, 1959.
18. Боришанский B.M., Арефьев K.M., Гнедина И.А. Обобщение опытных
данных по критическим нагрузкам при кипении в большом объеме с помощью
термодинамического подобия физических свойств рабочих сред // Т.р. ЦКТИ. 1965.
Вып. 62.
19. Chung Y.Р., Snyder N.W. Heat Transfer in Saturated Boiling // Chem. Eng. Progr.,
Symp. Ser. 1960. Vol. 56. № 3.
20. Маленков И.Г. Критические явления в процессах барботажа и
кипения // Журн. прикл. механики и техн. физики. 1963. № 6.
21. Мойссис, Беренсон. К вопросу о гидродинамических переходах при
пузырьковом кипении // Тр. американского общества инженеров - механиков. Сер.
С. Теплопередача. 1963. № 3.
22. Дорощук В.Е. Кризисы теплообмена при кипении воды в трубах. М.:
Энергоатомиздат, 1983.
23. Гальченко Э.Ф., Сергеев В.В. К обобщению данных по граничным
паросодержаниям. Теплоэнергетика, 1983, № 3.
24. Сергеев В.В. Закризисный теплообмен в элементах ЯЭУ. Дисс. канд.
техн. наук, Обнинск, ГНЦ РФ - ФЭИ, 2004.
25. Смолин В.Н., Шпанский С.В., Есиков В.И., Седова Т.К. Методика
расчета кризиса теплоотдачи в трубчатых твэлах при охлаждении их водой и
пароводяной смесью Теплоэнергетика, 1977, № 12.
26. Смолин В.Н., Шпанский С.В., Есиков В.И., Седова Т.К.
Экспериментальные данные и методика расчета кризиса теплоотдачи при кипении
воды, циркулирующей в трубах с равномерным и неравномерным тепловыделением
Вопросы атомной науки и техники. Сер. Физика и техника ядерных реакторов, 1979,
вып. 5(9).
27. Сергеев В.В., Ремизов О.В., Гальченко Э.Ф. Закризисный
теплообмен в кольцевом канале с двусторонним обогревом. Атомная энергия, 1986,
т. 60, вып. 3.
28. Бобков В.П., Виноградов В.Н., Зятнина О.А., Козина Н.В. Метод
оценки кризиса в каналах сложного профиля сечения. Теплоэнергетика, 1995, № 3.
29. Бобков В.П., Судницын О.А., Судницына М.О. Численное и
аналитическое описание критических тепловых потоков в каналах. Атомная энергия,
1998, № 3.
30. Судницын О.А., Кириллов П.Л., Бобков В.П., Болтенко Э.А.,
Виноградов В.Н. Обзор экспериментальных данных по критическим тепловым потокам
в концентричных и эксцентричных кольцевых каналах. Препринт ФЭИ-2318, Обнинск.
1993.
31. Бобков В.П., Ефанов А.Д., Пометько Р.С., Смогалев И.П.
Модифицированная таблица для критических тепловых потоков в сборках
тепловыделяющих стержней в треугольной упаковке. Теплоэнергетика (в печати).
32. Осмачкин В.С., Лысцова Н.Н. Сравнение опытных данных по условиям
кризиса теплообмена в моделях топливных сборок реакторов типа ВВЭР с
результатами расчета по методике ИАЭ. Препринт ИАЭ-2558, 1975.
33. Иванов В.К., Кобзарь Л.Л., Лысцова Н.Н., Суслов А.И. Результаты
исследований кризиса теплоотдачи, выполненных в Институте атомной энергии им.
И.В. Курчатова. В сб. «Теплофизика-86. Теплотехническая безопасность ядерных
реакторов ВВЭР». Росток, 1986.
34. Котрнох Й., Голоуш В., Щеттина Я. (ЗЭМ «Шкода»), Кобзарь Л.Л.,
Иванов В.К. (ИАЭ), Логвинов С.А., Безруков Ю.А., Трушин А.М. (ОКБ ГП).
Исследование кризиса теплоотдачи в пучках стержней на Большом водяном стенде
ЗЭМ «Шкода». В сб. «Теплофизика-88. Теплотехническая безопасность ядерных
реакторов ВВЭР». Варшава, 1988.
35. Сергеев В.В. Обобщение данных по кризису кипения при подъемном
движении воды в каналах. Теплоэнергетика, 2000, № 3.
36. Безруков Ю.А., Астахов В.И., В.Г. Брантов и др.
Экспериментальные исследования и статистический анализ данных по кризису
теплообмена в пучках стержней для реакторов ВВЭР, Теплоэнергетика № 2, 1976.
ПРИЛОЖЕНИЕ
Таблица 1
Критический тепловой поток в трубах диаметром 8 мм.
Обозначения: КТП в кВт/м2, в левой колонке - массовая скорость в
кг/м2с
Р = 0,1 МПа
|
x:
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
4593
|
3419
|
2247
|
1066
|
421
|
298
|
207
|
158
|
142
|
130
|
120
|
111
|
103
|
99
|
84
|
74
|
68
|
67
|
|
50
|
4940
|
3881
|
2618
|
1526
|
787
|
754
|
683
|
635
|
620
|
609
|
600
|
591
|
582
|
570
|
513
|
401
|
288
|
253
|
|
100
|
5206
|
4124
|
2942
|
1947
|
1159
|
1137
|
1123
|
1107
|
1093
|
1084
|
1078
|
1070
|
1060
|
1037
|
961
|
747
|
550
|
416
|
|
300
|
5232
|
4206
|
3475
|
2792
|
1693
|
1665
|
1651
|
1598
|
1536
|
1502
|
1475
|
1378
|
1243
|
1151
|
979
|
751
|
626
|
550
|
|
500
|
5261
|
4305
|
3768
|
3204
|
2040
|
1887
|
1883
|
1875
|
1798
|
1725
|
1714
|
1615
|
1486
|
1463
|
1188
|
752
|
558
|
415
|
|
1000
|
5387
|
4626
|
4129
|
3527
|
2528
|
2286
|
2280
|
2211
|
2129
|
2028
|
1870
|
1655
|
1632
|
1631
|
1434
|
850
|
428
|
206
|
|
1500
|
5432
|
4734
|
4216
|
3606
|
2652
|
2427
|
2405
|
2292
|
2195
|
2084
|
1905
|
1857
|
1856
|
1856
|
1597
|
839
|
|
|
|
2000
|
5434
|
4739
|
4218
|
3616
|
2693
|
2487
|
2446
|
2333
|
2212
|
2054
|
1950
|
1918
|
1889
|
1815
|
1466
|
|
|
|
|
2500
|
5443
|
4745
|
4220
|
3631
|
2743
|
2548
|
2505
|
2367
|
2217
|
1985
|
1846
|
1779
|
1693
|
1582
|
|
|
|
|
|
3000
|
5452
|
4751
|
4239
|
3651
|
2795
|
2606
|
2572
|
2418
|
2245
|
1941
|
1738
|
1596
|
1472
|
|
|
|
|
|
|
3500
|
5504
|
4827
|
4277
|
3662
|
2843
|
2652
|
2624
|
2470
|
2282
|
1937
|
1684
|
|
|
|
|
|
|
|
|
4000
|
5660
|
4908
|
4310
|
3688
|
2947
|
2727
|
2685
|
2530
|
2327
|
|
|
|
|
|
|
|
|
|
|
4500
|
5902
|
5006
|
4338
|
3707
|
3060
|
2820
|
2738
|
|
|
|
|
|
|
|
|
|
|
|
|
5000
|
6242
|
5266
|
4412
|
3738
|
3157
|
2893
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5500
|
6513
|
5487
|
4529
|
3813
|
3242
|
2952
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6000
|
6772
|
5668
|
4684
|
3933
|
3349
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6500
|
7060
|
5876
|
4856
|
4103
|
3439
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7000
|
7349
|
6087
|
5029
|
4223
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7500
|
7643
|
6288
|
5181
|
4300
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8000
|
7939
|
6507
|
5370
|
4375
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение таблицы 1
Р =0,3 МПа
|
х:
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
5024
|
4349
|
3432
|
2433
|
1596
|
1575
|
1029
|
665
|
467
|
317
|
234
|
194
|
178
|
171
|
170
|
149
|
143
|
143
|
90
|
|
50
|
5644
|
4951
|
3882
|
2842
|
2003
|
1987
|
1443
|
1123
|
938
|
813
|
745
|
708
|
686
|
660
|
642
|
601
|
472
|
391
|
300
|
|
100
|
6174
|
5211
|
4235
|
3225
|
2431
|
2076
|
1574
|
1291
|
1258
|
1230
|
1211
|
1190
|
1168
|
1118
|
1081
|
1026
|
857
|
669
|
473
|
|
300
|
6403
|
5447
|
4544
|
3889
|
3371
|
2433
|
2095
|
2071
|
1995
|
1895
|
1828
|
1771
|
1636
|
1494
|
1418
|
1203
|
866
|
695
|
564
|
|
500
|
6414
|
5498
|
4667
|
4234
|
3832
|
2863
|
2479
|
2435
|
2333
|
2185
|
2072
|
1869
|
1700
|
1539
|
1447
|
1155
|
764
|
574
|
521
|
|
1000
|
6430
|
5590
|
4931
|
4585
|
4189
|
3285
|
2845
|
2750
|
2553
|
2388
|
2283
|
1968
|
1766
|
1586
|
1545
|
1174
|
677
|
439
|
288
|
|
1500
|
6438
|
5610
|
4985
|
4609
|
4209
|
3339
|
2922
|
2834
|
2570
|
2424
|
2301
|
2021
|
1834
|
1615
|
1525
|
1103
|
568
|
220
|
131
|
|
2000
|
6454
|
5629
|
4995
|
4615
|
4210
|
3370
|
2948
|
2863
|
2590
|
2462
|
2320
|
2066
|
1771
|
1571
|
1410
|
1029
|
490
|
|
|
|
2500
|
6547
|
5663
|
5004
|
4622
|
4225
|
3415
|
2979
|
2869
|
2610
|
2444
|
2282
|
1916
|
1700
|
1524
|
1327
|
|
|
|
|
|
3000
|
6735
|
5786
|
5087
|
4656
|
4239
|
3462
|
3021
|
2879
|
2630
|
2426
|
2245
|
1806
|
|
|
|
|
|
|
|
|
3500
|
7036
|
6024
|
5320
|
4744
|
4249
|
3515
|
3073
|
2895
|
2650
|
2407
|
2154
|
1692
|
|
|
|
|
|
|
|
|
4000
|
7495
|
6343
|
5601
|
4851
|
4254
|
3520
|
3102
|
2908
|
2670
|
2389
|
|
|
|
|
|
|
|
|
|
|
4500
|
8034
|
6702
|
5832
|
4927
|
4266
|
3525
|
3110
|
2926
|
|
|
|
|
|
|
|
|
|
|
|
|
5000
|
8435
|
7062
|
6098
|
5000
|
4275
|
3530
|
3141
|
2959
|
|
|
|
|
|
|
|
|
|
|
|
|
5500
|
8809
|
7372
|
6360
|
5090
|
4277
|
3536
|
3178
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6000
|
9216
|
7692
|
6645
|
5211
|
4287
|
3543
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6500
|
9605
|
8015
|
6908
|
5346
|
4308
|
3577
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7000
|
9975
|
8325
|
7175
|
5592
|
4450
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7500
|
10356
|
8630
|
7427
|
5870
|
4662
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8000
|
10747
|
8936
|
7656
|
6117
|
4840
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение таблицы 1
Р = 0,5 МПа
|
х:
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
4879
|
4200
|
3469
|
2595
|
1783
|
1697
|
1174
|
786
|
535
|
374
|
278
|
226
|
207
|
191
|
183
|
151
|
150
|
149
|
140
|
|
50
|
5568
|
4962
|
3983
|
3168
|
2424
|
2249
|
1728
|
1380
|
1145
|
1005
|
921
|
865
|
826
|
793
|
754
|
611
|
493
|
476
|
359
|
|
100
|
6195
|
5267
|
4489
|
3688
|
2975
|
2478
|
1780
|
1683
|
1623
|
1566
|
1525
|
1492
|
1440
|
1391
|
1292
|
1158
|
1045
|
875
|
539
|
|
300
|
6589
|
5783
|
5098
|
4547
|
4089
|
3396
|
2921
|
2801
|
2679
|
2527
|
2409
|
2050
|
1799
|
1552
|
1489
|
1188
|
1049
|
919
|
607
|
|
500
|
6629
|
5876
|
5250
|
4853
|
4452
|
3784
|
3247
|
3074
|
2888
|
2695
|
2498
|
2187
|
1887
|
1593
|
1414
|
959
|
774
|
622
|
554
|
|
1000
|
6650
|
5991
|
5531
|
5273
|
4873
|
4075
|
3452
|
3256
|
2975
|
2923
|
2629
|
2277
|
1911
|
1547
|
1385
|
962
|
635
|
445
|
301
|
|
1500
|
6664
|
5994
|
5576
|
5323
|
4909
|
4093
|
3456
|
3313
|
3293
|
3154
|
2782
|
2260
|
1811
|
1453
|
1268
|
911
|
|
|
|
|
2000
|
6677
|
6037
|
5601
|
5327
|
4911
|
4104
|
3460
|
3407
|
3406
|
3261
|
2790
|
2184
|
1696
|
1383
|
|
|
|
|
|
|
2500
|
6839
|
6141
|
5645
|
5331
|
4913
|
4138
|
3605
|
3545
|
3527
|
3335
|
2696
|
1991
|
|
|
|
|
|
|
|
|
3000
|
7189
|
6430
|
5789
|
5366
|
4915
|
4182
|
3750
|
3725
|
3662
|
3428
|
|
|
|
|
|
|
|
|
|
|
3500
|
7654
|
6789
|
6006
|
5430
|
4939
|
4271
|
3726
|
3712
|
3652
|
|
|
|
|
|
|
|
|
|
|
|
4000
|
8155
|
7143
|
6293
|
5553
|
4951
|
4152
|
3593
|
3578
|
|
|
|
|
|
|
|
|
|
|
|
|
4500
|
8688
|
7556
|
6584
|
5670
|
4963
|
4006
|
3513
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5000
|
9138
|
7969
|
6877
|
5748
|
4922
|
3913
|
3408
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5500
|
9580
|
8334
|
7180
|
5765
|
4815
|
3863
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6000
|
10022
|
8690
|
7517
|
5754
|
4632
|
3880
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6500
|
10439
|
9036
|
7799
|
5735
|
4402
|
3899
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7000
|
10822
|
9366
|
8112
|
6026
|
4577
|
3945
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7500
|
11192
|
9675
|
8411
|
6441
|
4962
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8000
|
11571
|
9969
|
8642
|
6746
|
5268
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение таблицы 1
Р = 1
МПа
|
х:
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
5619
|
4685
|
4058
|
3564
|
2859
|
2175
|
1910
|
1438
|
1030
|
717
|
519
|
389
|
312
|
286
|
270
|
256
|
198
|
188
|
181
|
175
|
|
50
|
6371
|
5523
|
4991
|
4436
|
3928
|
3323
|
2944
|
2469
|
2071
|
1752
|
1559
|
1414
|
1307
|
1230
|
1157
|
1076
|
876
|
806
|
804
|
700
|
|
100
|
6981
|
6252
|
5685
|
5281
|
4851
|
4268
|
3386
|
2799
|
2651
|
2531
|
2415
|
2292
|
2184
|
2041
|
1891
|
1703
|
1312
|
1291
|
1250
|
732
|
|
300
|
7492
|
7295
|
7089
|
6901
|
6766
|
6620
|
6215
|
5289
|
4760
|
4456
|
4120
|
3432
|
2600
|
2151
|
1924
|
1708
|
1343
|
1289
|
1215
|
660
|
|
500
|
7577
|
7464
|
7327
|
7177
|
7110
|
7048
|
6818
|
5771
|
5094
|
4660
|
4233
|
3856
|
2754
|
2284
|
1979
|
1659
|
1035
|
825
|
767
|
589
|
|
1000
|
7594
|
7466
|
7329
|
7192
|
7124
|
7022
|
6705
|
5694
|
5042
|
4634
|
3953
|
3264
|
2670
|
2035
|
1741
|
1516
|
958
|
592
|
452
|
338
|
|
1500
|
7700
|
7468
|
7349
|
7230
|
7153
|
7013
|
6604
|
5532
|
4989
|
4422
|
3952
|
3236
|
2429
|
1557
|
1145
|
930
|
637
|
411
|
370
|
266
|
|
2000
|
8187
|
7552
|
7424
|
7281
|
7192
|
7012
|
6401
|
5196
|
4720
|
4404
|
3952
|
3143
|
2259
|
1373
|
980
|
713
|
541
|
343
|
137
|
86
|
|
2500
|
8962
|
7788
|
7544
|
7314
|
7202
|
6979
|
6100
|
5028
|
4668
|
4397
|
3924
|
2999
|
2081
|
1281
|
925
|
690
|
512
|
306
|
84
|
25
|
|
3000
|
9731
|
8149
|
7728
|
7370
|
7206
|
6966
|
5900
|
4920
|
4647
|
4391
|
3898
|
2880
|
1955
|
1234
|
908
|
701
|
510
|
|
|
|
|
3500
|
10456
|
8659
|
8005
|
7450
|
7179
|
6910
|
5800
|
4849
|
4628
|
4385
|
3865
|
2765
|
1797
|
1252
|
1059
|
1000
|
|
|
|
|
|
4000
|
11146
|
9203
|
8342
|
7591
|
7143
|
6778
|
5752
|
4757
|
4584
|
4380
|
3794
|
2723
|
1891
|
1484
|
1292
|
|
|
|
|
|
|
4500
|
11816
|
9746
|
8754
|
7750
|
7141
|
6500
|
5537
|
4627
|
4477
|
4304
|
3715
|
2689
|
1953
|
|
|
|
|
|
|
|
|
5000
|
12447
|
10239
|
9182
|
7859
|
6988
|
5900
|
5107
|
4361
|
4211
|
3924
|
3338
|
2581
|
|
|
|
|
|
|
|
|
|
5500
|
13033
|
10745
|
9599
|
8124
|
6794
|
5800
|
4822
|
4239
|
4085
|
3729
|
3112
|
|
|
|
|
|
|
|
|
|
|
6000
|
13573
|
11285
|
10064
|
8595
|
6647
|
5530
|
4654
|
4096
|
3966
|
3625
|
|
|
|
|
|
|
|
|
|
|
|
6500
|
14101
|
11770
|
10479
|
8933
|
6351
|
5228
|
4460
|
3913
|
3804
|
|
|
|
|
|
|
|
|
|
|
|
|
7000
|
14608
|
12172
|
10857
|
9325
|
6654
|
4850
|
4232
|
3734
|
3547
|
|
|
|
|
|
|
|
|
|
|
|
|
7500
|
15109
|
12524
|
11194
|
9725
|
7272
|
5409
|
4227
|
3683
|
3525
|
|
|
|
|
|
|
|
|
|
|
|
|
8000
|
15629
|
12866
|
11463
|
9958
|
7773
|
6039
|
4447
|
3684
|
3536
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение таблицы 1
Р = 3 МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
6583
|
5927
|
5252
|
4544
|
4205
|
3891
|
3536
|
3022
|
2429
|
2009
|
1564
|
1145
|
892
|
699
|
568
|
502
|
452
|
413
|
321
|
275
|
266
|
256
|
|
50
|
7307
|
6575
|
5972
|
5386
|
5107
|
4857
|
4570
|
4135
|
3478
|
3061
|
2653
|
2266
|
2041
|
1865
|
1722
|
1614
|
1521
|
1418
|
1409
|
1400
|
1392
|
1000
|
|
100
|
7888
|
7106
|
6580
|
6114
|
5897
|
5708
|
5479
|
5057
|
4121
|
3502
|
3326
|
3186
|
3051
|
2926
|
2796
|
2625
|
2475
|
2367
|
2191
|
1936
|
1587
|
1015
|
|
300
|
8463
|
7476
|
7307
|
7303
|
7302
|
7300
|
7298
|
7255
|
6954
|
5922
|
5380
|
5211
|
4936
|
4635
|
3997
|
3322
|
3177
|
3173
|
2865
|
2078
|
1536
|
953
|
|
500
|
8655
|
7674
|
7578
|
7560
|
7554
|
7541
|
7627
|
7621
|
7496
|
7000
|
6400
|
5660
|
5269
|
4807
|
4297
|
3392
|
3376
|
3324
|
2745
|
1841
|
1320
|
835
|
|
1000
|
9003
|
7776
|
7660
|
7598
|
7560
|
7548
|
7518
|
7512
|
7444
|
6846
|
6208
|
5620
|
4728
|
4200
|
3745
|
3079
|
2910
|
2618
|
1925
|
1242
|
830
|
471
|
|
1500
|
9523
|
8313
|
7824
|
7647
|
7578
|
7560
|
7471
|
7436
|
7250
|
6661
|
5980
|
5043
|
4364
|
3792
|
3422
|
2691
|
2130
|
1728
|
1080
|
626
|
499
|
312
|
|
2000
|
10680
|
9563
|
8427
|
7706
|
7640
|
7567
|
7453
|
7298
|
6723
|
6026
|
5315
|
4507
|
3991
|
3485
|
2958
|
2279
|
1686
|
1211
|
608
|
373
|
330
|
216
|
|
2500
|
11975
|
10928
|
9397
|
8034
|
7681
|
7634
|
7441
|
7158
|
6226
|
5599
|
4880
|
4175
|
3702
|
3152
|
2369
|
1726
|
1252
|
867
|
431
|
308
|
89
|
25
|
|
3000
|
12932
|
11900
|
10414
|
8640
|
7947
|
7643
|
7439
|
7069
|
5966
|
5339
|
4712
|
4094
|
3619
|
2963
|
2085
|
1423
|
1037
|
772
|
520
|
374
|
129
|
45
|
|
3500
|
13887
|
12661
|
11230
|
9396
|
8434
|
7824
|
7437
|
6995
|
5829
|
5131
|
4586
|
4067
|
3540
|
2705
|
1715
|
1329
|
1127
|
1020
|
678
|
431
|
137
|
44
|
|
4000
|
14813
|
13379
|
11939
|
10174
|
9013
|
8028
|
7418
|
6832
|
5753
|
4966
|
4471
|
4021
|
3424
|
2463
|
1474
|
1234
|
1228
|
1118
|
699
|
440
|
147
|
54
|
|
4500
|
15714
|
14077
|
12608
|
10862
|
9586
|
8292
|
7365
|
6566
|
5570
|
4792
|
4348
|
3945
|
3273
|
2302
|
1514
|
1311
|
1306
|
1145
|
713
|
445
|
163
|
63
|
|
5000
|
16584
|
14778
|
13200
|
11500
|
10262
|
8818
|
7348
|
6039
|
5258
|
4610
|
4242
|
3867
|
3121
|
2196
|
1610
|
1505
|
1405
|
1173
|
766
|
466
|
179
|
72
|
|
5500
|
17426
|
15454
|
13765
|
12044
|
10824
|
9249
|
7402
|
6188
|
5134
|
4431
|
4136
|
3794
|
3006
|
2155
|
1712
|
1650
|
1500
|
1252
|
846
|
493
|
|
|
|
6000
|
18238
|
16101
|
14321
|
12489
|
11385
|
10063
|
7735
|
6382
|
5070
|
4332
|
4061
|
3753
|
3042
|
2265
|
1853
|
1738
|
1542
|
1311
|
876
|
|
|
|
|
6500
|
19035
|
16814
|
14849
|
12926
|
11946
|
10878
|
8193
|
6446
|
5002
|
4181
|
3931
|
3693
|
3067
|
2360
|
2043
|
1876
|
1622
|
1388
|
|
|
|
|
|
7000
|
19813
|
17464
|
15350
|
13332
|
12053
|
11351
|
8542
|
6507
|
4694
|
3888
|
3705
|
3557
|
3084
|
2530
|
2209
|
2008
|
1755
|
|
|
|
|
|
|
7500
|
20584
|
18107
|
15834
|
13724
|
12429
|
11527
|
8891
|
6526
|
4644
|
3817
|
3643
|
3459
|
3103
|
2699
|
2390
|
2073
|
|
|
|
|
|
|
|
8000
|
21353
|
18730
|
16299
|
14090
|
12789
|
11585
|
9157
|
7075
|
4971
|
3980
|
3715
|
3548
|
3291
|
2904
|
2413
|
|
|
|
|
|
|
|
Продолжение таблицы 1
Р = 5 МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
5951
|
5460
|
4941
|
4459
|
4230
|
4011
|
3762
|
3360
|
2628
|
2234
|
1791
|
1346
|
1083
|
877
|
731
|
638
|
571
|
515
|
405
|
345
|
341
|
323
|
|
50
|
6644
|
6095
|
5629
|
5224
|
5030
|
4840
|
4626
|
4294
|
3606
|
3225
|
2837
|
2450
|
2224
|
2047
|
1896
|
1774
|
1666
|
1553
|
1532
|
1512
|
945
|
830
|
|
100
|
7234
|
6636
|
6223
|
5891
|
5734
|
5573
|
5387
|
5065
|
4165
|
3609
|
3458
|
3315
|
3174
|
3061
|
2936
|
2803
|
2655
|
2476
|
2300
|
2148
|
1757
|
1080
|
|
300
|
7680
|
6990
|
6769
|
6737
|
6722
|
6686
|
6677
|
6619
|
6280
|
5401
|
5007
|
4907
|
4741
|
4509
|
4202
|
3881
|
3659
|
3315
|
7973
|
2543
|
1823
|
1215
|
|
500
|
7918
|
7164
|
6943
|
6900
|
6882
|
6819
|
6812
|
6739
|
6395
|
5734
|
5296
|
5178
|
5027
|
4588
|
4244
|
3975
|
3803
|
3503
|
3040
|
2459
|
1769
|
1118
|
|
1000
|
8364
|
7454
|
7171
|
7014
|
6944
|
6829
|
6743
|
6595
|
6107
|
5662
|
5289
|
4957
|
4676
|
4166
|
3759
|
3447
|
3322
|
3086
|
2066
|
1433
|
1034
|
763
|
|
1500
|
9068
|
8009
|
7470
|
7142
|
7025
|
6859
|
6707
|
6441
|
5779
|
5317
|
4899
|
4530
|
4074
|
3623
|
3337
|
2983
|
2569
|
2134
|
1194
|
913
|
899
|
744
|
|
2000
|
10362
|
9287
|
8159
|
7346
|
7139
|
6944
|
6593
|
6110
|
5262
|
4779
|
4405
|
3984
|
3610
|
3206
|
2865
|
2557
|
1973
|
1332
|
668
|
650
|
650
|
526
|
|
2500
|
11531
|
10599
|
9179
|
7837
|
7458
|
7195
|
6565
|
5849
|
4915
|
4515
|
3981
|
3594
|
3401
|
3067
|
2474
|
1861
|
1301
|
921
|
401
|
313
|
117
|
53
|
|
3000
|
12458
|
11530
|
10191
|
8483
|
7761
|
7353
|
6543
|
5664
|
4750
|
4321
|
3782
|
3428
|
3268
|
2855
|
2024
|
1406
|
948
|
793
|
584
|
420
|
132
|
53
|
|
3500
|
13348
|
12271
|
10990
|
9196
|
8178
|
7551
|
6527
|
5421
|
4581
|
4144
|
3693
|
3380
|
3109
|
2510
|
1688
|
1195
|
958
|
874
|
645
|
441
|
149
|
55
|
|
4000
|
14214
|
12958
|
11651
|
9917
|
8669
|
7764
|
6476
|
5139
|
4421
|
3916
|
3540
|
3317
|
2945
|
2221
|
1437
|
1140
|
1108
|
1049
|
688
|
441
|
151
|
58
|
|
4500
|
15045
|
13625
|
12254
|
10566
|
9102
|
7980
|
6502
|
5044
|
4317
|
3784
|
3457
|
3260
|
2799
|
2059
|
1425
|
1247
|
1242
|
1187
|
734
|
453
|
167
|
61
|
|
5000
|
15844
|
14283
|
12804
|
11186
|
9669
|
8443
|
6655
|
4986
|
4255
|
3723
|
3454
|
3251
|
2745
|
1990
|
1470
|
1385
|
1295
|
1205
|
786
|
472
|
164
|
66
|
|
5500
|
16626
|
14896
|
13352
|
11741
|
10379
|
8952
|
6807
|
5334
|
4253
|
3656
|
3421
|
3240
|
2717
|
1992
|
1583
|
1504
|
1459
|
1234
|
804
|
481
|
182
|
76
|
|
6000
|
17388
|
15495
|
13856
|
12319
|
11076
|
9876
|
7558
|
5744
|
4314
|
3627
|
3415
|
3239
|
2688
|
2091
|
1812
|
1679
|
1529
|
1296
|
850
|
500
|
211
|
94
|
|
6500
|
18126
|
16100
|
14340
|
12662
|
11773
|
10800
|
8118
|
5954
|
4356
|
3603
|
3397
|
3235
|
2711
|
2303
|
2034
|
1869
|
1611
|
1370
|
913
|
531
|
239
|
110
|
|
7000
|
18845
|
16707
|
14796
|
12961
|
11971
|
11295
|
8492
|
6049
|
4363
|
3613
|
3445
|
3291
|
2801
|
2510
|
2189
|
1951
|
1689
|
1444
|
989
|
592
|
282
|
130
|
|
7500
|
19549
|
17296
|
15245
|
13320
|
12236
|
11413
|
8865
|
6189
|
4478
|
3749
|
3547
|
3350
|
3051
|
2667
|
2329
|
2021
|
1764
|
1519
|
1064
|
656
|
328
|
154
|
|
8000
|
20238
|
17880
|
15671
|
13711
|
12701
|
11561
|
9151
|
6556
|
4717
|
3975
|
3695
|
3482
|
3290
|
2882
|
2405
|
2074
|
1829
|
1588
|
1130
|
717
|
379
|
178
|
Продолжение таблицы 1
Р = 6 МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
5626
|
5219
|
4798
|
4387
|
4185
|
3995
|
3777
|
3415
|
2669
|
2291
|
1859
|
1416
|
1150
|
941
|
787
|
686
|
608
|
547
|
439
|
348
|
344
|
327
|
|
50
|
6300
|
5838
|
5443
|
5092
|
4920
|
4760
|
4575
|
4272
|
3564
|
3191
|
2812
|
2431
|
2204
|
2023
|
1871
|
1749
|
1645
|
1537
|
1229
|
989
|
942
|
823
|
|
100
|
6873
|
6366
|
5999
|
5708
|
5567
|
5434
|
5273
|
4973
|
4079
|
3530
|
3377
|
3237
|
3089
|
2966
|
2854
|
2724
|
2598
|
2431
|
1833
|
1647
|
1511
|
1070
|
|
300
|
7318
|
6710
|
6451
|
6395
|
6379
|
6330
|
6310
|
6255
|
5942
|
5126
|
4783
|
4679
|
4496
|
4269
|
4066
|
3800
|
3584
|
3283
|
2663
|
2330
|
1766
|
1193
|
|
500
|
7573
|
6883
|
6586
|
6512
|
6480
|
6364
|
6316
|
6261
|
5978
|
5371
|
5005
|
4822
|
4683
|
4333
|
4077
|
3812
|
3707
|
3468
|
2874
|
2374
|
1636
|
1061
|
|
1000
|
8080
|
7185
|
6742
|
6576
|
6502
|
6256
|
6114
|
6008
|
5633
|
5334
|
4857
|
4429
|
4177
|
3788
|
3528
|
3418
|
3263
|
2964
|
1965
|
1257
|
803
|
735
|
|
1500
|
8817
|
7758
|
7023
|
6667
|
6585
|
6331
|
6146
|
5787
|
5138
|
4703
|
4326
|
3964
|
3637
|
3309
|
3056
|
2839
|
2550
|
2068
|
1029
|
785
|
714
|
707
|
|
2000
|
10109
|
9053
|
7842
|
6970
|
6796
|
6559
|
6167
|
5531
|
4716
|
4227
|
3875
|
3532
|
3229
|
2919
|
2640
|
2383
|
1789
|
1096
|
532
|
518
|
439
|
435
|
|
2500
|
11237
|
10324
|
8947
|
7698
|
7356
|
7038
|
6235
|
5383
|
4543
|
4030
|
3545
|
3244
|
3054
|
2797
|
2311
|
1632
|
930
|
519
|
370
|
305
|
107
|
52
|
|
3000
|
12123
|
11219
|
9913
|
8360
|
7693
|
7264
|
6241
|
5237
|
4449
|
3882
|
3340
|
3043
|
2876
|
2560
|
1887
|
1093
|
571
|
477
|
472
|
353
|
122
|
52
|
|
3500
|
12969
|
11949
|
10669
|
8979
|
7986
|
7458
|
6243
|
4962
|
4218
|
3651
|
3219
|
2961
|
2696
|
2235
|
1522
|
871
|
582
|
576
|
505
|
382
|
145
|
57
|
|
4000
|
13791
|
12626
|
11288
|
9594
|
8324
|
7679
|
6245
|
4590
|
3787
|
3318
|
3038
|
2893
|
2570
|
1995
|
1376
|
988
|
952
|
952
|
580
|
384
|
146
|
59
|
|
4500
|
14582
|
13274
|
11857
|
10119
|
8549
|
7682
|
6247
|
4578
|
3624
|
3133
|
2922
|
2814
|
2470
|
1863
|
1358
|
1154
|
1133
|
1124
|
622
|
386
|
147
|
60
|
|
5000
|
15341
|
13920
|
12372
|
10555
|
8820
|
7811
|
6336
|
4701
|
3674
|
3115
|
2918
|
2795
|
2432
|
1792
|
1319
|
1237
|
1183
|
1130
|
650
|
390
|
148
|
64
|
|
5500
|
16091
|
14489
|
12910
|
11165
|
9671
|
8416
|
6533
|
4793
|
3751
|
3148
|
2936
|
2816
|
2475
|
1877
|
1459
|
1363
|
1345
|
1149
|
698
|
411
|
167
|
74
|
|
6000
|
16823
|
15039
|
13396
|
12151
|
10623
|
9568
|
7356
|
5118
|
3824
|
3169
|
2946
|
2843
|
2506
|
2049
|
1755
|
1621
|
1405
|
1192
|
756
|
438
|
196
|
90
|
|
6500
|
17524
|
15635
|
13826
|
12525
|
11575
|
10720
|
8043
|
5370
|
3900
|
3211
|
2979
|
2886
|
2586
|
2247
|
2026
|
1760
|
1468
|
1250
|
818
|
472
|
223
|
105
|
|
7000
|
18210
|
16212
|
14268
|
12743
|
11838
|
11239
|
8441
|
5556
|
4010
|
3305
|
3095
|
2988
|
2795
|
2492
|
2169
|
1822
|
1545
|
1314
|
887
|
528
|
260
|
123
|
|
7500
|
18884
|
16771
|
14706
|
13013
|
12063
|
11299
|
8839
|
5779
|
4287
|
3660
|
3411
|
3187
|
2980
|
2635
|
2268
|
1901
|
1632
|
1394
|
960
|
587
|
299
|
142
|
|
8000
|
19548
|
17309
|
15140
|
13347
|
12447
|
11537
|
9144
|
6019
|
4481
|
3966
|
3675
|
3423
|
3262
|
2860
|
2359
|
1981
|
1717
|
1479
|
1034
|
646
|
341
|
162
|
Продолжение таблицы 1
Р = 7
МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
5361
|
5010
|
4651
|
4293
|
4118
|
3954
|
3762
|
3426
|
2692
|
2336
|
1918
|
1485
|
1212
|
996
|
834
|
723
|
641
|
575
|
466
|
369
|
357
|
339
|
|
50
|
6002
|
5599
|
5236
|
4926
|
4778
|
4644
|
4483
|
4198
|
3498
|
3137
|
2769
|
2397
|
2165
|
1981
|
1826
|
1706
|
1604
|
1501
|
1200
|
984
|
940
|
774
|
|
100
|
6539
|
6094
|
5738
|
5474
|
5355
|
5245
|
5105
|
4818
|
3957
|
3401
|
3239
|
3093
|
2941
|
2820
|
2707
|
2595
|
2489
|
2302
|
1710
|
1515
|
1479
|
1060
|
|
300
|
6998
|
6441
|
6104
|
6015
|
6002
|
5947
|
5886
|
5865
|
5582
|
4834
|
4494
|
4247
|
4046
|
3862
|
3632
|
3430
|
3318
|
3065
|
2402
|
2144
|
1735
|
1179
|
|
500
|
7264
|
6617
|
6233
|
6123
|
6088
|
5953
|
5940
|
5887
|
5690
|
5134
|
4682
|
4316
|
4157
|
3900
|
3634
|
3469
|
3366
|
3157
|
2596
|
2213
|
1587
|
1029
|
|
1000
|
7798
|
6930
|
6386
|
6216
|
6135
|
5799
|
5604
|
5505
|
5318
|
5070
|
4472
|
3892
|
3626
|
3347
|
3136
|
3031
|
3028
|
2838
|
1774
|
1121
|
735
|
613
|
|
1500
|
8557
|
7520
|
6715
|
6339
|
6253
|
5886
|
5603
|
5145
|
4673
|
4301
|
3874
|
3486
|
3189
|
2964
|
2735
|
2523
|
2250
|
1728
|
805
|
488
|
273
|
259
|
|
2000
|
9793
|
8774
|
7597
|
6676
|
6480
|
6142
|
5684
|
4952
|
4275
|
3785
|
3407
|
3122
|
2890
|
2731
|
2451
|
2023
|
1445
|
844
|
432
|
322
|
196
|
190
|
|
2500
|
10882
|
9986
|
8709
|
7496
|
7142
|
6690
|
5806
|
4876
|
4104
|
3537
|
3147
|
2922
|
2723
|
2445
|
1983
|
1367
|
789
|
424
|
261
|
204
|
99
|
51
|
|
3000
|
11730
|
10850
|
9620
|
8170
|
7523
|
6953
|
5816
|
4724
|
3981
|
3369
|
2940
|
2714
|
2491
|
2133
|
1570
|
967
|
553
|
425
|
346
|
263
|
112
|
52
|
|
3500
|
12535
|
11558
|
10344
|
8740
|
7757
|
7135
|
5848
|
4567
|
3834
|
3199
|
2786
|
2565
|
2294
|
1896
|
1323
|
782
|
519
|
490
|
409
|
317
|
135
|
57
|
|
4000
|
13317
|
12216
|
10929
|
9320
|
8041
|
7398
|
5938
|
4372
|
3469
|
2928
|
2645
|
2490
|
2201
|
1730
|
1228
|
840
|
734
|
732
|
470
|
317
|
136
|
58
|
|
4500
|
14070
|
12839
|
11469
|
9769
|
8188
|
7399
|
6061
|
4410
|
3347
|
2743
|
2515
|
2418
|
2139
|
1640
|
1200
|
930
|
872
|
854
|
492
|
317
|
137
|
59
|
|
5000
|
14792
|
13465
|
11954
|
10124
|
8354
|
7427
|
6225
|
4552
|
3378
|
2696
|
2458
|
2380
|
2105
|
1591
|
1193
|
1010
|
949
|
888
|
521
|
326
|
138
|
63
|
|
5500
|
15509
|
14000
|
12474
|
10713
|
9223
|
8025
|
6409
|
4682
|
3454
|
2710
|
2471
|
2382
|
2146
|
1673
|
1308
|
1154
|
1102
|
952
|
582
|
348
|
153
|
70
|
|
6000
|
16208
|
14521
|
12931
|
11464
|
10460
|
9338
|
7226
|
4752
|
3483
|
2714
|
2470
|
2415
|
2213
|
1869
|
1539
|
1385
|
1228
|
1032
|
655
|
379
|
179
|
84
|
|
6500
|
16875
|
15091
|
13336
|
12214
|
11432
|
10650
|
7804
|
4867
|
3535
|
2784
|
2519
|
2466
|
2330
|
2140
|
1879
|
1599
|
1311
|
1108
|
725
|
422
|
210
|
99
|
|
7000
|
17529
|
15640
|
13763
|
12432
|
11718
|
11183
|
8065
|
5055
|
3745
|
3006
|
2708
|
2595
|
2464
|
2260
|
2014
|
1687
|
1401
|
1186
|
795
|
476
|
243
|
116
|
|
7500
|
18170
|
16174
|
14182
|
12682
|
11740
|
11185
|
8202
|
5208
|
3974
|
3339
|
3032
|
2913
|
2779
|
2541
|
2199
|
1773
|
1489
|
1269
|
866
|
530
|
277
|
132
|
|
8000
|
18806
|
16673
|
14610
|
12995
|
12067
|
11187
|
8424
|
5405
|
4172
|
3727
|
3483
|
3384
|
3259
|
2846
|
2288
|
1851
|
1576
|
1353
|
936
|
581
|
312
|
149
|
Продолжение таблицы 1
Р = 8 МПа
|
х:
|
-0,05
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
5101
|
4795
|
4484
|
4175
|
4022
|
3883
|
3716
|
3403
|
2547
|
2044
|
1674
|
1295
|
1195
|
994
|
838
|
731
|
653
|
591
|
542
|
456
|
423
|
364
|
|
50
|
5714
|
5359
|
5025
|
4744
|
4615
|
4503
|
4362
|
4081
|
3170
|
2622
|
2374
|
2169
|
2006
|
1871
|
1761
|
1667
|
1579
|
1490
|
1183
|
980
|
938
|
720
|
|
100
|
6229
|
5834
|
5487
|
5235
|
5132
|
5039
|
4916
|
4650
|
3796
|
3239
|
3086
|
2969
|
2837
|
2708
|
2601
|
2507
|
2417
|
2281
|
1678
|
1457
|
1449
|
1050
|
|
300
|
6685
|
6179
|
5792
|
5654
|
5637
|
5577
|
5512
|
5484
|
5250
|
4549
|
4207
|
3911
|
3759
|
3642
|
3458
|
3328
|
3212
|
2893
|
2144
|
1877
|
1538
|
1083
|
|
500
|
6958
|
6354
|
5920
|
5763
|
5718
|
5605
|
5597
|
5544
|
5324
|
4784
|
4306
|
3829
|
3583
|
3411
|
3248
|
3096
|
2964
|
2629
|
2068
|
1858
|
1427
|
917
|
|
1000
|
7518
|
6668
|
6144
|
5919
|
5765
|
5314
|
5072
|
5040
|
4997
|
4755
|
4106
|
3452
|
3103
|
2847
|
2749
|
2560
|
2331
|
2069
|
1413
|
944
|
554
|
511
|
|
1500
|
8280
|
7266
|
6556
|
6124
|
5911
|
5334
|
5042
|
4774
|
4459
|
4066
|
3562
|
3137
|
2863
|
2639
|
2355
|
2001
|
1661
|
1209
|
643
|
364
|
205
|
195
|
|
2000
|
9465
|
8470
|
7416
|
6490
|
6179
|
5626
|
5178
|
4623
|
4015
|
3483
|
3039
|
2749
|
2551
|
2345
|
2014
|
1559
|
1068
|
656
|
388
|
250
|
154
|
134
|
|
2500
|
10508
|
9633
|
8457
|
7323
|
6937
|
6335
|
5386
|
4575
|
3816
|
3144
|
2769
|
2551
|
2319
|
1899
|
1514
|
1099
|
655
|
396
|
237
|
178
|
96
|
49
|
|
3000
|
11320
|
10465
|
9316
|
7976
|
7376
|
6702
|
5426
|
4348
|
3609
|
2906
|
2535
|
2340
|
2093
|
1694
|
1253
|
811
|
524
|
397
|
307
|
225
|
111
|
50
|
|
3500
|
12091
|
11136
|
10017
|
8489
|
7576
|
6794
|
5461
|
4205
|
3479
|
2798
|
2381
|
2179
|
1947
|
1616
|
1128
|
696
|
501
|
470
|
385
|
258
|
122
|
55
|
|
4000
|
12839
|
11763
|
10584
|
9021
|
7836
|
7014
|
5626
|
4145
|
3241
|
2592
|
2238
|
2084
|
1893
|
1528
|
1063
|
702
|
603
|
577
|
401
|
258
|
122
|
56
|
|
4500
|
13559
|
12361
|
11093
|
9494
|
8078
|
7215
|
5921
|
4248
|
3137
|
2403
|
2116
|
2037
|
1867
|
1475
|
1066
|
783
|
738
|
676
|
425
|
259
|
122
|
57
|
|
5000
|
14251
|
12945
|
11568
|
9938
|
8351
|
7424
|
6106
|
4394
|
3169
|
2420
|
2120
|
2031
|
1821
|
1450
|
1147
|
923
|
859
|
756
|
470
|
275
|
125
|
59
|
|
5500
|
14934
|
13466
|
12056
|
10488
|
9083
|
7990
|
6213
|
4479
|
3283
|
2478
|
2177
|
2070
|
1878
|
1570
|
1300
|
1076
|
988
|
850
|
535
|
304
|
139
|
65
|
|
6000
|
15597
|
13983
|
12477
|
11140
|
10142
|
9265
|
6851
|
4526
|
3352
|
2510
|
2237
|
2159
|
1998
|
1721
|
1519
|
1256
|
1136
|
938
|
607
|
346
|
165
|
77
|
|
6500
|
16235
|
14521
|
12879
|
11791
|
10678
|
9903
|
7172
|
4629
|
3419
|
2556
|
2432
|
2391
|
2207
|
2027
|
1794
|
1514
|
1225
|
1025
|
678
|
396
|
197
|
93
|
|
7000
|
16859
|
15043
|
13288
|
12019
|
11214
|
10542
|
7253
|
4766
|
3593
|
2843
|
2558
|
2466
|
2287
|
2179
|
1832
|
1585
|
1316
|
1111
|
747
|
447
|
228
|
108
|
|
7500
|
17470
|
15550
|
13689
|
12260
|
11235
|
10544
|
7292
|
4874
|
3748
|
3136
|
2935
|
2820
|
2611
|
2287
|
1980
|
1654
|
1402
|
1193
|
814
|
498
|
260
|
124
|
|
8000
|
18075
|
16026
|
14098
|
12584
|
11555
|
10546
|
7482
|
4967
|
3931
|
3490
|
3380
|
3376
|
3257
|
2798
|
2157
|
1718
|
1479
|
1272
|
881
|
548
|
295
|
140
|
Продолжение таблицы 1
Р = 9 МПа
|
х:
|
-0,05
|
-0,04
|
-0,03
|
-0,02
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
4836
|
4571
|
4301
|
4034
|
3902
|
3783
|
3639
|
3352
|
2503
|
1977
|
1637
|
1290
|
1179
|
992
|
843
|
739
|
660
|
608
|
560
|
471
|
431
|
349
|
|
50
|
5422
|
5114
|
4813
|
4547
|
4432
|
4335
|
4213
|
3960
|
3071
|
2528
|
2304
|
2110
|
1945
|
1810
|
1699
|
1610
|
1536
|
1457
|
1152
|
971
|
938
|
650
|
|
100
|
5916
|
5571
|
5251
|
4988
|
4892
|
4811
|
4704
|
4462
|
3658
|
3134
|
2976
|
2841
|
2697
|
2575
|
2458
|
2373
|
2317
|
2165
|
1554
|
1306
|
1300
|
1040
|
|
300
|
6366
|
5916
|
5527
|
5300
|
5260
|
5239
|
5236
|
5194
|
4944
|
4270
|
3692
|
3478
|
3344
|
3257
|
3065
|
2894
|
2713
|
2334
|
1672
|
1380
|
1197
|
899
|
|
500
|
6641
|
6100
|
5668
|
5412
|
5332
|
5205
|
5147
|
5114
|
4925
|
4243
|
3625
|
3364
|
3160
|
2999
|
2887
|
2741
|
2351
|
1983
|
1583
|
1282
|
904
|
626
|
|
1000
|
7221
|
6432
|
5947
|
5625
|
5398
|
4936
|
4705
|
4703
|
4697
|
4204
|
3520
|
3118
|
2854
|
2661
|
2545
|
2118
|
1553
|
1143
|
984
|
729
|
346
|
311
|
|
1500
|
7976
|
7023
|
6356
|
5856
|
5535
|
4958
|
4693
|
4467
|
4189
|
3730
|
3227
|
2850
|
2712
|
2495
|
2034
|
1429
|
1081
|
892
|
546
|
350
|
131
|
119
|
|
2000
|
9111
|
8171
|
7160
|
6258
|
5863
|
5299
|
4835
|
4196
|
3569
|
3097
|
2746
|
2448
|
2312
|
1931
|
1428
|
1027
|
745
|
603
|
345
|
186
|
97
|
48
|
|
2500
|
10108
|
9252
|
8185
|
7162
|
6749
|
6025
|
5004
|
4119
|
3339
|
2797
|
2521
|
2241
|
1942
|
1373
|
1028
|
809
|
570
|
348
|
211
|
136
|
96
|
48
|
|
3000
|
10887
|
10041
|
8998
|
7755
|
7210
|
6399
|
5097
|
4045
|
3240
|
2604
|
2289
|
2038
|
1724
|
1354
|
967
|
708
|
508
|
393
|
282
|
169
|
103
|
49
|
|
3500
|
11622
|
10683
|
9660
|
8227
|
7395
|
6453
|
5140
|
3995
|
3155
|
2487
|
2124
|
1896
|
1643
|
1276
|
952
|
650
|
457
|
419
|
305
|
184
|
107
|
54
|
|
4000
|
12336
|
11283
|
10200
|
8756
|
7669
|
6674
|
5266
|
3983
|
3066
|
2349
|
1931
|
1750
|
1604
|
1375
|
982
|
664
|
558
|
499
|
331
|
190
|
108
|
55
|
|
4500
|
13022
|
11857
|
10680
|
9235
|
7924
|
6936
|
5469
|
4047
|
3026
|
2245
|
1827
|
1719
|
1631
|
1385
|
1037
|
771
|
670
|
615
|
381
|
205
|
109
|
56
|
|
5000
|
13683
|
12418
|
11127
|
9685
|
8259
|
7305
|
5645
|
4183
|
3080
|
2249
|
1836
|
1755
|
1663
|
1416
|
1152
|
908
|
816
|
717
|
445
|
239
|
116
|
57
|
|
5500
|
14332
|
12927
|
11580
|
10180
|
8872
|
7818
|
5764
|
4272
|
3210
|
2355
|
1963
|
1856
|
1760
|
1542
|
1290
|
1071
|
935
|
801
|
512
|
281
|
130
|
62
|
|
6000
|
14961
|
13402
|
11998
|
10758
|
9759
|
8777
|
6149
|
4331
|
3303
|
2421
|
2126
|
2045
|
1937
|
1699
|
1500
|
1219
|
1072
|
892
|
578
|
329
|
157
|
73
|
|
6500
|
15570
|
13909
|
12387
|
11336
|
10230
|
9257
|
6353
|
4416
|
3344
|
2492
|
2346
|
2317
|
2197
|
1985
|
1710
|
1431
|
1170
|
977
|
646
|
378
|
186
|
88
|
|
7000
|
16165
|
14403
|
12779
|
11578
|
10702
|
9737
|
6355
|
4542
|
3482
|
2788
|
2527
|
2402
|
2245
|
2070
|
1785
|
1497
|
1258
|
1058
|
712
|
426
|
216
|
103
|
|
7500
|
16748
|
14881
|
13166
|
11824
|
10747
|
9739
|
6394
|
4637
|
3660
|
3076
|
2877
|
2745
|
2567
|
2142
|
1800
|
1557
|
1339
|
1140
|
778
|
475
|
248
|
118
|
|
8000
|
17323
|
15340
|
13551
|
12107
|
10954
|
9741
|
6556
|
4714
|
3838
|
3419
|
3342
|
3299
|
3162
|
2736
|
2042
|
1620
|
1420
|
1218
|
842
|
525
|
281
|
134
|
Продолжение таблицы 1
Р = 10 МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
4568
|
4337
|
4103
|
3874
|
3760
|
3658
|
3534
|
3274
|
2464
|
1922
|
1596
|
1276
|
1163
|
991
|
849
|
748
|
680
|
625
|
562
|
474
|
410
|
282
|
|
50
|
5126
|
4857
|
4591
|
4336
|
4230
|
4146
|
4040
|
3814
|
3002
|
2482
|
2256
|
2057
|
1890
|
1750
|
1641
|
1555
|
1482
|
1415
|
1139
|
965
|
886
|
645
|
|
100
|
5597
|
5296
|
5007
|
4734
|
4637
|
4565
|
4472
|
4253
|
3512
|
3015
|
2865
|
2728
|
2582
|
2457
|
2347
|
2266
|
2213
|
2105
|
1551
|
1296
|
1211
|
897
|
|
300
|
6039
|
5642
|
5266
|
4961
|
4891
|
4870
|
4868
|
4832
|
4636
|
4016
|
3506
|
3393
|
3315
|
3233
|
2987
|
2781
|
2593
|
2240
|
1383
|
1076
|
1021
|
674
|
|
500
|
6318
|
5831
|
5417
|
5074
|
4965
|
4855
|
4800
|
4765
|
4599
|
4013
|
3353
|
3165
|
3038
|
2871
|
2644
|
2239
|
2002
|
1651
|
1137
|
848
|
796
|
522
|
|
1000
|
6912
|
6184
|
5732
|
5328
|
5073
|
4676
|
4463
|
4376
|
4328
|
3822
|
3225
|
2936
|
2680
|
2484
|
2171
|
1342
|
1033
|
802
|
636
|
460
|
298
|
250
|
|
1500
|
7650
|
6747
|
6118
|
5570
|
5212
|
4712
|
4476
|
4178
|
3843
|
3402
|
2958
|
2559
|
2393
|
2102
|
1655
|
938
|
647
|
547
|
451
|
253
|
127
|
86
|
|
2000
|
8720
|
7826
|
6896
|
6030
|
5591
|
5000
|
4575
|
3974
|
3349
|
2872
|
2468
|
2106
|
1912
|
1402
|
972
|
677
|
480
|
355
|
303
|
155
|
95
|
46
|
|
2500
|
9664
|
8829
|
7895
|
7010
|
6589
|
5726
|
4678
|
3901
|
3191
|
2623
|
2258
|
1901
|
1601
|
1035
|
666
|
533
|
399
|
280
|
195
|
126
|
95
|
47
|
|
3000
|
10400
|
9580
|
8648
|
7587
|
7077
|
6149
|
4779
|
3891
|
3089
|
2444
|
2030
|
1701
|
1419
|
1001
|
647
|
478
|
388
|
300
|
256
|
147
|
97
|
48
|
|
3500
|
11099
|
10200
|
9259
|
8008
|
7253
|
6254
|
4797
|
3830
|
3005
|
2327
|
1877
|
1591
|
1361
|
1062
|
723
|
525
|
414
|
364
|
274
|
151
|
99
|
51
|
|
4000
|
11783
|
10775
|
9774
|
8533
|
7582
|
6503
|
4841
|
3728
|
2909
|
2178
|
1686
|
1470
|
1345
|
1147
|
870
|
641
|
492
|
429
|
291
|
160
|
101
|
53
|
|
4500
|
12444
|
11327
|
10230
|
8989
|
7824
|
6787
|
4940
|
3754
|
2892
|
2087
|
1605
|
1476
|
1410
|
1262
|
1016
|
768
|
590
|
545
|
359
|
188
|
105
|
54
|
|
5000
|
13081
|
11867
|
10655
|
9402
|
8114
|
7092
|
5116
|
3898
|
2977
|
2088
|
1612
|
1562
|
1539
|
1383
|
1130
|
876
|
686
|
639
|
430
|
229
|
112
|
56
|
|
5500
|
13694
|
12355
|
11078
|
9834
|
8616
|
7476
|
5265
|
4034
|
3114
|
2208
|
1742
|
1692
|
1663
|
1496
|
1261
|
993
|
796
|
703
|
490
|
274
|
126
|
59
|
|
6000
|
14268
|
12772
|
11467
|
10320
|
9342
|
8224
|
5687
|
4147
|
3227
|
2286
|
1927
|
1902
|
1821
|
1641
|
1440
|
1183
|
993
|
842
|
553
|
317
|
150
|
70
|
|
6500
|
14835
|
13236
|
11837
|
10808
|
9713
|
8600
|
5912
|
4241
|
3275
|
2378
|
2206
|
2200
|
2098
|
1895
|
1687
|
1382
|
1133
|
942
|
620
|
363
|
179
|
85
|
|
7000
|
15399
|
13708
|
12204
|
11028
|
10083
|
8975
|
5926
|
4267
|
3390
|
2707
|
2422
|
2309
|
2182
|
2003
|
1720
|
1432
|
1212
|
1021
|
686
|
410
|
208
|
99
|
|
7500
|
15952
|
14166
|
12567
|
11253
|
10103
|
8977
|
5940
|
4279
|
3559
|
2995
|
2729
|
2594
|
2483
|
2092
|
1733
|
1484
|
1287
|
1097
|
750
|
459
|
240
|
114
|
|
8000
|
16496
|
14588
|
12938
|
11536
|
10351
|
8979
|
5955
|
4484
|
3783
|
3325
|
3120
|
2988
|
2864
|
2621
|
2015
|
1596
|
1393
|
1182
|
812
|
507
|
272
|
129
|
Продолжение таблицы 1
Р = 11
МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
4294
|
4095
|
3891
|
3694
|
3599
|
3513
|
3407
|
3175
|
2437
|
1880
|
1560
|
1270
|
1146
|
989
|
854
|
757
|
693
|
643
|
565
|
493
|
389
|
267
|
|
50
|
4821
|
4588
|
4356
|
4124
|
4017
|
3938
|
3844
|
3646
|
2917
|
2416
|
2184
|
1985
|
1820
|
1673
|
1579
|
1510
|
1451
|
1375
|
1101
|
938
|
837
|
565
|
|
100
|
5267
|
5006
|
4752
|
4492
|
4379
|
4303
|
4217
|
4027
|
3358
|
2892
|
2727
|
2589
|
2441
|
2299
|
2230
|
2182
|
2146
|
2048
|
1471
|
1039
|
960
|
741
|
|
300
|
5694
|
5346
|
5002
|
4672
|
4560
|
4526
|
4505
|
4452
|
4236
|
3709
|
3392
|
3301
|
3207
|
2996
|
2872
|
2516
|
2259
|
1687
|
1316
|
963
|
652
|
548
|
|
500
|
5966
|
5534
|
5145
|
4765
|
4640
|
4516
|
4468
|
4393
|
4218
|
3706
|
3250
|
3083
|
2957
|
2761
|
2395
|
1926
|
1663
|
1311
|
959
|
728
|
550
|
344
|
|
1000
|
6553
|
5906
|
5430
|
4911
|
4665
|
4365
|
4197
|
4035
|
3837
|
3389
|
2981
|
2693
|
2389
|
2153
|
1682
|
919
|
791
|
696
|
477
|
363
|
245
|
189
|
|
1500
|
7281
|
6484
|
5794
|
5105
|
4739
|
4389
|
4171
|
3806
|
3390
|
2982
|
2564
|
2201
|
1934
|
1567
|
1212
|
675
|
458
|
361
|
295
|
209
|
124
|
65
|
|
2000
|
8285
|
7469
|
6600
|
5732
|
5270
|
4675
|
4221
|
3695
|
3122
|
2619
|
2195
|
1772
|
1484
|
972
|
738
|
554
|
345
|
305
|
228
|
135
|
94
|
46
|
|
2500
|
9166
|
8371
|
7589
|
6807
|
6361
|
5371
|
4332
|
3676
|
3005
|
2461
|
1970
|
1537
|
1265
|
818
|
529
|
399
|
283
|
241
|
192
|
115
|
90
|
47
|
|
3000
|
9861
|
9055
|
8268
|
7343
|
6854
|
5785
|
4446
|
3668
|
2920
|
2257
|
1695
|
1311
|
1109
|
802
|
457
|
322
|
277
|
276
|
237
|
126
|
90
|
48
|
|
3500
|
10518
|
9636
|
8798
|
7680
|
7019
|
5939
|
4491
|
3619
|
2843
|
2127
|
1570
|
1251
|
1101
|
820
|
524
|
407
|
349
|
331
|
247
|
129
|
92
|
49
|
|
4000
|
11153
|
10169
|
9265
|
8151
|
7358
|
6242
|
4605
|
3503
|
2761
|
1952
|
1471
|
1266
|
1160
|
962
|
733
|
572
|
434
|
359
|
274
|
151
|
97
|
50
|
|
4500
|
11765
|
10675
|
9696
|
8592
|
7672
|
6551
|
4757
|
3566
|
2765
|
1999
|
1476
|
1336
|
1256
|
1133
|
922
|
699
|
489
|
408
|
338
|
186
|
104
|
51
|
|
5000
|
12351
|
11158
|
10092
|
8934
|
7863
|
6753
|
4892
|
3707
|
2890
|
2004
|
1540
|
1491
|
1440
|
1299
|
1057
|
804
|
550
|
462
|
397
|
226
|
112
|
53
|
|
5500
|
12922
|
11622
|
10478
|
9284
|
8203
|
7035
|
5020
|
3849
|
2985
|
2108
|
1677
|
1645
|
1578
|
1416
|
1181
|
936
|
664
|
534
|
450
|
272
|
126
|
57
|
|
6000
|
13495
|
12064
|
10871
|
9741
|
8840
|
7663
|
5414
|
4024
|
3128
|
2210
|
1846
|
1823
|
1716
|
1518
|
1326
|
1115
|
920
|
780
|
529
|
307
|
146
|
68
|
|
6500
|
14034
|
12509
|
11220
|
10197
|
9174
|
7996
|
5637
|
4157
|
3262
|
2360
|
2118
|
2112
|
2032
|
1743
|
1521
|
1302
|
1104
|
922
|
602
|
351
|
173
|
82
|
|
7000
|
14562
|
12953
|
11560
|
10403
|
9509
|
8328
|
5655
|
4188
|
3347
|
2669
|
2349
|
2256
|
2110
|
1824
|
1591
|
1396
|
1178
|
994
|
666
|
399
|
203
|
97
|
|
7500
|
15082
|
13381
|
11899
|
10634
|
9563
|
8334
|
5673
|
4209
|
3497
|
2915
|
2635
|
2511
|
2375
|
2020
|
1689
|
1451
|
1248
|
1061
|
729
|
447
|
233
|
111
|
|
8000
|
15594
|
13784
|
12241
|
10923
|
9825
|
8435
|
5692
|
4231
|
3680
|
3152
|
2836
|
2703
|
2634
|
2467
|
1976
|
1595
|
1383
|
1159
|
790
|
493
|
265
|
126
|
Продолжение таблицы 1
Р = 12
МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
4022
|
3849
|
3671
|
3501
|
3419
|
3349
|
3259
|
3053
|
2397
|
1859
|
1535
|
1258
|
1130
|
988
|
859
|
766
|
706
|
660
|
565
|
494
|
376
|
224
|
|
50
|
4511
|
4309
|
4111
|
3909
|
3809
|
3729
|
3634
|
3462
|
2826
|
2360
|
2111
|
1910
|
1745
|
1598
|
1505
|
1436
|
1383
|
1309
|
1069
|
933
|
818
|
507
|
|
100
|
4924
|
4699
|
4488
|
4261
|
4147
|
4058
|
3957
|
3791
|
3213
|
2789
|
2599
|
2447
|
2293
|
2152
|
2088
|
2036
|
2008
|
1916
|
1415
|
985
|
946
|
708
|
|
300
|
5311
|
5011
|
4728
|
4435
|
4333
|
4239
|
4176
|
4057
|
3775
|
3401
|
3187
|
3099
|
2966
|
2695
|
2591
|
2227
|
2034
|
1389
|
1132
|
820
|
636
|
545
|
|
500
|
5533
|
5172
|
4848
|
4467
|
4300
|
4185
|
4097
|
3919
|
3659
|
3254
|
3004
|
2866
|
2685
|
2402
|
2057
|
1673
|
1341
|
940
|
716
|
537
|
263
|
228
|
|
1000
|
6063
|
5518
|
5083
|
4489
|
4119
|
3776
|
3577
|
3372
|
3118
|
2733
|
2496
|
2232
|
1947
|
1675
|
1318
|
815
|
619
|
514
|
338
|
262
|
128
|
96
|
|
1500
|
6852
|
6169
|
5458
|
4626
|
4129
|
3854
|
3569
|
3177
|
2823
|
2464
|
2101
|
1764
|
1474
|
1094
|
793
|
536
|
408
|
320
|
235
|
175
|
114
|
54
|
|
2000
|
7804
|
7104
|
6246
|
5206
|
4596
|
4089
|
3659
|
3172
|
2712
|
2281
|
1898
|
1497
|
1168
|
747
|
568
|
474
|
345
|
257
|
221
|
119
|
91
|
44
|
|
2500
|
8606
|
7926
|
7227
|
6161
|
5502
|
4523
|
3768
|
3225
|
2688
|
2203
|
1707
|
1262
|
949
|
640
|
457
|
363
|
275
|
221
|
176
|
107
|
87
|
44
|
|
3000
|
9263
|
8483
|
7798
|
6682
|
6060
|
4884
|
3885
|
3274
|
2659
|
2064
|
1477
|
1064
|
850
|
620
|
402
|
310
|
263
|
253
|
209
|
113
|
87
|
48
|
|
3500
|
9873
|
8929
|
8209
|
7076
|
6416
|
5166
|
4024
|
3319
|
2654
|
1983
|
1395
|
1053
|
900
|
682
|
485
|
376
|
335
|
309
|
220
|
116
|
88
|
49
|
|
4000
|
10395
|
9339
|
8589
|
7553
|
6877
|
5668
|
4293
|
3390
|
2687
|
1935
|
1384
|
1160
|
1038
|
867
|
687
|
559
|
419
|
342
|
260
|
145
|
94
|
50
|
|
4500
|
10866
|
9735
|
8953
|
7997
|
7296
|
6103
|
4504
|
3487
|
2735
|
1952
|
1450
|
1285
|
1176
|
1020
|
863
|
684
|
462
|
363
|
318
|
181
|
101
|
51
|
|
5000
|
11303
|
10049
|
9228
|
8306
|
7473
|
6374
|
4628
|
3605
|
2874
|
2068
|
1598
|
1465
|
1359
|
1211
|
995
|
777
|
540
|
433
|
376
|
226
|
109
|
52
|
|
5500
|
11820
|
10479
|
9563
|
8588
|
7674
|
6576
|
4720
|
3697
|
2952
|
2165
|
1738
|
1625
|
1501
|
1343
|
1135
|
914
|
650
|
518
|
424
|
265
|
123
|
55
|
|
6000
|
12614
|
11227
|
10153
|
9051
|
8222
|
7070
|
5076
|
3873
|
3098
|
2268
|
1877
|
1799
|
1673
|
1456
|
1281
|
1109
|
894
|
749
|
513
|
299
|
142
|
66
|
|
6500
|
13206
|
11751
|
10530
|
9514
|
8530
|
7357
|
5290
|
3991
|
3239
|
2429
|
2116
|
2091
|
2020
|
1664
|
1445
|
1280
|
1076
|
903
|
588
|
343
|
169
|
80
|
|
7000
|
13689
|
12152
|
10841
|
9715
|
8838
|
7643
|
5346
|
4035
|
3319
|
2652
|
2326
|
2225
|
2106
|
1800
|
1576
|
1390
|
1150
|
973
|
652
|
390
|
198
|
94
|
|
7500
|
14161
|
12534
|
11149
|
9952
|
8942
|
7712
|
5403
|
4054
|
3404
|
2855
|
2556
|
2423
|
2286
|
1948
|
1653
|
1433
|
1223
|
1037
|
714
|
437
|
228
|
109
|
|
8000
|
14662
|
12943
|
11474
|
10247
|
9213
|
7919
|
5460
|
4075
|
3533
|
3020
|
2664
|
2570
|
2496
|
2307
|
1914
|
1594
|
1374
|
1140
|
774
|
484
|
260
|
123
|
Продолжение таблицы 1
Р = 13 МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
3766
|
3617
|
3465
|
3317
|
3247
|
3184
|
3111
|
2935
|
2352
|
1850
|
1530
|
1255
|
1115
|
987
|
865
|
775
|
720
|
677
|
588
|
518
|
373
|
187
|
|
50
|
4208
|
4039
|
3883
|
3712
|
3624
|
3555
|
3463
|
3302
|
2728
|
2293
|
2039
|
1827
|
1658
|
1496
|
1404
|
1326
|
1237
|
1143
|
1005
|
926
|
752
|
444
|
|
100
|
4575
|
4391
|
4236
|
4030
|
3947
|
3870
|
3762
|
3597
|
3067
|
2675
|
2463
|
2279
|
2106
|
1909
|
1830
|
1749
|
1618
|
1446
|
1234
|
940
|
933
|
636
|
|
300
|
4843
|
4613
|
4448
|
4050
|
4030
|
4018
|
3934
|
3831
|
3536
|
3175
|
2868
|
2663
|
2492
|
2124
|
1896
|
1746
|
1454
|
1179
|
931
|
746
|
622
|
506
|
|
500
|
4923
|
4655
|
4500
|
4070
|
4000
|
3803
|
3654
|
3560
|
3358
|
3019
|
2708
|
2485
|
2193
|
1864
|
1584
|
1320
|
1069
|
716
|
473
|
397
|
245
|
208
|
|
1000
|
5355
|
4921
|
4614
|
4095
|
3769
|
3369
|
3032
|
2832
|
2644
|
2307
|
1992
|
1724
|
1540
|
1361
|
1136
|
721
|
471
|
351
|
254
|
202
|
122
|
72
|
|
1500
|
6344
|
5777
|
5070
|
4197
|
3817
|
3594
|
3201
|
2766
|
2390
|
2013
|
1697
|
1396
|
1182
|
937
|
699
|
476
|
361
|
293
|
229
|
162
|
112
|
50
|
|
2000
|
7337
|
6773
|
5836
|
4656
|
4124
|
3820
|
3363
|
2852
|
2361
|
1983
|
1637
|
1277
|
962
|
638
|
455
|
387
|
307
|
243
|
206
|
113
|
86
|
44
|
|
2500
|
8056
|
7515
|
6896
|
5685
|
4865
|
4126
|
3471
|
2940
|
2403
|
1965
|
1567
|
1149
|
797
|
504
|
362
|
290
|
231
|
192
|
161
|
105
|
84
|
44
|
|
3000
|
8688
|
7876
|
7317
|
6269
|
5533
|
4509
|
3631
|
3022
|
2449
|
1962
|
1434
|
1031
|
777
|
562
|
385
|
309
|
235
|
228
|
186
|
111
|
84
|
45
|
|
3500
|
9210
|
8021
|
7365
|
6395
|
5766
|
4775
|
3802
|
3091
|
2491
|
1978
|
1413
|
1065
|
874
|
681
|
462
|
364
|
331
|
287
|
201
|
112
|
86
|
46
|
|
4000
|
9436
|
8108
|
7419
|
6533
|
5984
|
5113
|
4060
|
3223
|
2622
|
2024
|
1493
|
1222
|
1050
|
882
|
695
|
586
|
452
|
342
|
244
|
139
|
90
|
47
|
|
4500
|
9495
|
8197
|
7536
|
6741
|
6225
|
5464
|
4230
|
3342
|
2784
|
2106
|
1604
|
1362
|
1188
|
1023
|
866
|
712
|
526
|
387
|
298
|
178
|
97
|
48
|
|
5000
|
9545
|
8199
|
7622
|
7067
|
6480
|
5834
|
4420
|
3429
|
2879
|
2232
|
1789
|
1532
|
1324
|
1139
|
950
|
769
|
530
|
403
|
355
|
218
|
105
|
49
|
|
5500
|
10034
|
8609
|
7982
|
7400
|
6731
|
6064
|
4489
|
3515
|
2935
|
2324
|
1949
|
1726
|
1520
|
1303
|
1094
|
904
|
640
|
473
|
403
|
255
|
119
|
54
|
|
6000
|
11456
|
10012
|
9157
|
8347
|
7605
|
6635
|
4586
|
3609
|
3029
|
2384
|
2027
|
1894
|
1714
|
1449
|
1265
|
1098
|
890
|
735
|
499
|
292
|
139
|
65
|
|
6500
|
12458
|
11078
|
9915
|
8897
|
8120
|
6995
|
4727
|
3679
|
3121
|
2471
|
2174
|
2110
|
2016
|
1658
|
1431
|
1278
|
1053
|
882
|
578
|
336
|
165
|
78
|
|
7000
|
12882
|
11431
|
10179
|
9113
|
8280
|
7180
|
4812
|
3703
|
3206
|
2607
|
2298
|
2192
|
2090
|
1791
|
1573
|
1369
|
1137
|
955
|
641
|
383
|
194
|
93
|
|
7500
|
13246
|
11713
|
10405
|
9314
|
8405
|
7305
|
4870
|
3742
|
3310
|
2761
|
2431
|
2305
|
2191
|
1898
|
1640
|
1434
|
1217
|
1022
|
703
|
431
|
225
|
107
|
|
8000
|
13772
|
12145
|
10756
|
9606
|
8630
|
7448
|
4957
|
3776
|
3396
|
2923
|
2537
|
2427
|
2360
|
2161
|
1859
|
1592
|
1365
|
1126
|
763
|
477
|
257
|
122
|
Продолжение таблицы 1
Р = 14 МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
3493
|
3365
|
3232
|
3106
|
3046
|
2994
|
2930
|
2779
|
2271
|
1812
|
1510
|
1248
|
1089
|
963
|
851
|
767
|
714
|
695
|
598
|
509
|
351
|
175
|
|
50
|
3895
|
3750
|
3620
|
3476
|
3402
|
3343
|
3266
|
3123
|
2618
|
2211
|
1958
|
1756
|
1588
|
1423
|
1327
|
1253
|
1168
|
1070
|
974
|
807
|
632
|
355
|
|
100
|
4229
|
4072
|
3948
|
3794
|
3708
|
3641
|
3551
|
3403
|
2933
|
2560
|
2336
|
2169
|
2005
|
1804
|
1708
|
1636
|
1509
|
1300
|
992
|
764
|
615
|
350
|
|
300
|
4448
|
4260
|
4142
|
3958
|
3862
|
3800
|
3706
|
3630
|
3411
|
3099
|
2800
|
2552
|
2404
|
1967
|
1669
|
1554
|
1263
|
986
|
757
|
563
|
378
|
246
|
|
500
|
4497
|
4278
|
4181
|
3970
|
3832
|
3618
|
3453
|
3399
|
3267
|
2963
|
2612
|
2295
|
1941
|
1605
|
1318
|
1124
|
950
|
626
|
381
|
322
|
224
|
164
|
|
1000
|
4928
|
4533
|
4349
|
4004
|
3659
|
3197
|
2864
|
2705
|
2530
|
2189
|
1791
|
1508
|
1359
|
1209
|
980
|
627
|
434
|
334
|
223
|
190
|
116
|
70
|
|
1500
|
5911
|
5399
|
4821
|
4046
|
3724
|
3394
|
3020
|
2650
|
2255
|
1886
|
1534
|
1287
|
1089
|
877
|
629
|
396
|
307
|
273
|
205
|
150
|
93
|
47
|
|
2000
|
6752
|
6229
|
5421
|
4413
|
3994
|
3672
|
3200
|
2739
|
2230
|
1847
|
1520
|
1188
|
902
|
629
|
425
|
316
|
248
|
220
|
195
|
109
|
80
|
41
|
|
2500
|
7369
|
6879
|
6351
|
5379
|
4639
|
4017
|
3363
|
2826
|
2300
|
1938
|
1477
|
1078
|
782
|
529
|
351
|
266
|
200
|
170
|
148
|
104
|
82
|
43
|
|
3000
|
8033
|
7236
|
6834
|
6001
|
5227
|
4390
|
3551
|
2931
|
2372
|
1959
|
1498
|
1089
|
826
|
589
|
388
|
285
|
218
|
202
|
166
|
108
|
83
|
43
|
|
3500
|
8543
|
7311
|
6865
|
6069
|
5420
|
4584
|
3679
|
3013
|
2439
|
2039
|
1546
|
1190
|
943
|
696
|
496
|
383
|
312
|
257
|
185
|
111
|
84
|
44
|
|
4000
|
8724
|
7332
|
6886
|
6137
|
5545
|
4794
|
3790
|
3086
|
2620
|
2184
|
1688
|
1356
|
1106
|
871
|
702
|
596
|
471
|
330
|
227
|
135
|
87
|
44
|
|
4500
|
8731
|
7377
|
6942
|
6292
|
5734
|
5054
|
3846
|
3189
|
2929
|
2368
|
1828
|
1489
|
1240
|
1067
|
874
|
746
|
586
|
394
|
282
|
172
|
94
|
45
|
|
5000
|
8733
|
7394
|
6999
|
6618
|
6103
|
5568
|
4075
|
3321
|
3081
|
2520
|
1993
|
1648
|
1390
|
1164
|
988
|
840
|
685
|
480
|
338
|
210
|
101
|
47
|
|
5500
|
9100
|
7685
|
7266
|
6926
|
6363
|
5822
|
4241
|
3364
|
3088
|
2583
|
2156
|
1850
|
1596
|
1343
|
1148
|
985
|
803
|
568
|
382
|
246
|
116
|
53
|
|
6000
|
10544
|
9148
|
8464
|
7715
|
7010
|
6223
|
4288
|
3456
|
3126
|
2613
|
2254
|
1996
|
1776
|
1472
|
1280
|
1152
|
942
|
721
|
484
|
286
|
136
|
64
|
|
6500
|
11595
|
10306
|
9186
|
8230
|
7474
|
6512
|
4416
|
3503
|
3132
|
2665
|
2333
|
2149
|
2002
|
1646
|
1413
|
1270
|
1053
|
866
|
568
|
332
|
163
|
77
|
|
7000
|
11986
|
10624
|
9429
|
8450
|
7655
|
6686
|
4467
|
3523
|
3169
|
2673
|
2344
|
2172
|
2079
|
1741
|
1567
|
1364
|
1136
|
942
|
633
|
379
|
192
|
91
|
|
7500
|
12314
|
10864
|
9636
|
8641
|
7821
|
6853
|
4610
|
3613
|
3242
|
2682
|
2356
|
2240
|
2133
|
1870
|
1623
|
1444
|
1217
|
1012
|
695
|
427
|
222
|
106
|
|
8000
|
12821
|
11286
|
9967
|
8893
|
8043
|
7029
|
4837
|
3735
|
3362
|
2870
|
2481
|
2313
|
2243
|
2034
|
1810
|
1588
|
1357
|
1116
|
757
|
474
|
255
|
121
|
Продолжение таблицы 1
Р = 15
МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
3196
|
3087
|
2976
|
2868
|
2815
|
2772
|
2720
|
2595
|
2165
|
1750
|
1456
|
1221
|
1047
|
923
|
831
|
745
|
694
|
693
|
645
|
501
|
297
|
172
|
|
50
|
3566
|
3437
|
3319
|
3207
|
3149
|
3098
|
3033
|
2910
|
2485
|
2114
|
1873
|
1695
|
1514
|
1341
|
1223
|
1152
|
1073
|
968
|
900
|
712
|
520
|
332
|
|
100
|
3874
|
3730
|
3611
|
3497
|
3434
|
3373
|
3295
|
3163
|
2768
|
2430
|
2229
|
2087
|
1906
|
1686
|
1537
|
1472
|
1355
|
1123
|
871
|
648
|
494
|
327
|
|
300
|
4082
|
3878
|
3747
|
3630
|
3543
|
3442
|
3358
|
3274
|
3111
|
2884
|
2667
|
2393
|
2193
|
1807
|
1514
|
1251
|
1128
|
866
|
644
|
482
|
351
|
227
|
|
500
|
4184
|
3933
|
3790
|
3638
|
3517
|
3315
|
3195
|
3115
|
3003
|
2739
|
2384
|
1923
|
1657
|
1425
|
1191
|
1038
|
895
|
597
|
368
|
299
|
213
|
134
|
|
1000
|
4678
|
4287
|
4068
|
3724
|
3482
|
3068
|
2708
|
2468
|
2251
|
1897
|
1523
|
1286
|
1204
|
1147
|
927
|
606
|
420
|
312
|
200
|
174
|
108
|
60
|
|
1500
|
5402
|
4961
|
4532
|
3891
|
3586
|
3155
|
2674
|
2312
|
1955
|
1649
|
1367
|
1179
|
1025
|
850
|
595
|
368
|
259
|
233
|
176
|
135
|
92
|
43
|
|
2000
|
5890
|
5387
|
4879
|
4196
|
3805
|
3351
|
2833
|
2464
|
2071
|
1843
|
1501
|
1178
|
918
|
664
|
424
|
281
|
202
|
190
|
163
|
107
|
76
|
39
|
|
2500
|
6438
|
5806
|
5478
|
4946
|
4365
|
3686
|
3083
|
2705
|
2224
|
1912
|
1559
|
1171
|
891
|
618
|
395
|
272
|
193
|
149
|
139
|
103
|
80
|
41
|
|
3000
|
7244
|
6348
|
6122
|
5596
|
4858
|
4010
|
3336
|
2854
|
2322
|
1974
|
1595
|
1225
|
954
|
675
|
461
|
344
|
257
|
180
|
154
|
107
|
81
|
42
|
|
3500
|
7886
|
6597
|
6342
|
5765
|
5039
|
4226
|
3459
|
2904
|
2340
|
2055
|
1670
|
1339
|
1062
|
769
|
557
|
454
|
360
|
266
|
185
|
116
|
82
|
42
|
|
4000
|
8278
|
6675
|
6445
|
5899
|
5239
|
4502
|
3517
|
2916
|
2615
|
2270
|
1815
|
1483
|
1217
|
939
|
750
|
673
|
549
|
377
|
231
|
132
|
83
|
42
|
|
4500
|
8512
|
6767
|
6565
|
6179
|
5561
|
4808
|
3552
|
3057
|
2953
|
2472
|
1951
|
1607
|
1355
|
1103
|
934
|
841
|
676
|
455
|
291
|
164
|
88
|
43
|
|
5000
|
8629
|
6956
|
6681
|
6504
|
5999
|
5383
|
3789
|
3255
|
3188
|
2657
|
2131
|
1774
|
1495
|
1250
|
1083
|
944
|
762
|
524
|
352
|
204
|
95
|
45
|
|
5500
|
8926
|
7284
|
6913
|
6707
|
6217
|
5673
|
3984
|
3297
|
3216
|
2744
|
2295
|
1947
|
1676
|
1419
|
1232
|
1065
|
855
|
605
|
406
|
244
|
113
|
52
|
|
6000
|
9942
|
8684
|
7860
|
7163
|
6512
|
5863
|
4029
|
3339
|
3221
|
2785
|
2397
|
2063
|
1838
|
1539
|
1321
|
1180
|
967
|
739
|
484
|
283
|
135
|
63
|
|
6500
|
10615
|
9447
|
8361
|
7475
|
6767
|
5984
|
4103
|
3419
|
3228
|
2823
|
2440
|
2165
|
2010
|
1656
|
1421
|
1300
|
1079
|
855
|
558
|
328
|
162
|
77
|
|
7000
|
10992
|
9718
|
8592
|
7676
|
6946
|
6098
|
4135
|
3443
|
3286
|
2826
|
2450
|
2179
|
2030
|
1754
|
1570
|
1400
|
1160
|
938
|
623
|
375
|
191
|
91
|
|
7500
|
11337
|
9941
|
8797
|
7866
|
7112
|
6222
|
4282
|
3522
|
3297
|
2831
|
2461
|
2194
|
2120
|
1845
|
1610
|
1458
|
1230
|
1013
|
689
|
424
|
221
|
105
|
|
8000
|
11774
|
10337
|
9087
|
8074
|
7319
|
6455
|
4633
|
3670
|
3309
|
2836
|
2470
|
2218
|
2166
|
1988
|
1784
|
1576
|
1349
|
1111
|
753
|
471
|
253
|
121
|
Продолжение таблицы 1
Р = 16
МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
2883
|
2793
|
2700
|
2612
|
2571
|
2530
|
2489
|
2380
|
2020
|
1647
|
1379
|
1162
|
997
|
873
|
769
|
674
|
614
|
612
|
537
|
383
|
260
|
167
|
|
50
|
3213
|
3103
|
3009
|
2911
|
2857
|
2816
|
2759
|
2664
|
2329
|
1998
|
1756
|
1586
|
1404
|
1228
|
1076
|
975
|
888
|
791
|
693
|
482
|
383
|
319
|
|
100
|
3486
|
3359
|
3268
|
3163
|
3101
|
3054
|
2983
|
2888
|
2593
|
2295
|
2072
|
1940
|
1741
|
1521
|
1333
|
1226
|
1114
|
907
|
695
|
550
|
360
|
311
|
|
300
|
3649
|
3441
|
3336
|
3210
|
3159
|
3080
|
3009
|
2934
|
2818
|
2597
|
2432
|
2194
|
2016
|
1688
|
1438
|
1124
|
978
|
747
|
508
|
428
|
325
|
210
|
|
500
|
3683
|
3473
|
3359
|
3236
|
3112
|
2886
|
2775
|
2673
|
2545
|
2268
|
1963
|
1580
|
1362
|
1198
|
1051
|
934
|
803
|
574
|
333
|
272
|
203
|
127
|
|
1000
|
4042
|
3623
|
3491
|
3323
|
3149
|
2725
|
2366
|
2089
|
1853
|
1528
|
1251
|
1076
|
992
|
948
|
804
|
587
|
407
|
288
|
190
|
154
|
102
|
59
|
|
1500
|
4726
|
4312
|
4002
|
3586
|
3329
|
2901
|
2360
|
1945
|
1655
|
1419
|
1235
|
1071
|
907
|
743
|
541
|
357
|
228
|
172
|
125
|
115
|
80
|
39
|
|
2000
|
5241
|
4790
|
4395
|
3873
|
3538
|
3050
|
2500
|
2166
|
1841
|
1688
|
1477
|
1188
|
943
|
704
|
462
|
312
|
201
|
147
|
120
|
105
|
72
|
36
|
|
2500
|
5901
|
5360
|
5038
|
4546
|
4031
|
3307
|
2724
|
2446
|
2112
|
1888
|
1628
|
1298
|
1031
|
754
|
495
|
339
|
244
|
197
|
165
|
120
|
76
|
37
|
|
3000
|
6667
|
5912
|
5709
|
5190
|
4449
|
3540
|
2937
|
2617
|
2282
|
2058
|
1745
|
1408
|
1139
|
849
|
597
|
465
|
370
|
271
|
190
|
123
|
78
|
39
|
|
3500
|
7252
|
6155
|
5907
|
5393
|
4622
|
3772
|
3075
|
2660
|
2440
|
2199
|
1859
|
1554
|
1254
|
947
|
698
|
588
|
485
|
369
|
247
|
129
|
79
|
39
|
|
4000
|
7734
|
6288
|
6048
|
5561
|
4834
|
4052
|
3170
|
2824
|
2668
|
2401
|
2011
|
1691
|
1412
|
1104
|
867
|
763
|
634
|
476
|
297
|
136
|
80
|
39
|
|
4500
|
8088
|
6346
|
6193
|
5888
|
5220
|
4407
|
3270
|
2980
|
2932
|
2554
|
2118
|
1807
|
1543
|
1240
|
1026
|
901
|
736
|
543
|
343
|
163
|
81
|
40
|
|
5000
|
8350
|
6494
|
6277
|
6217
|
5695
|
4991
|
3561
|
3223
|
3209
|
2774
|
2307
|
1979
|
1684
|
1391
|
1174
|
990
|
803
|
597
|
395
|
201
|
89
|
42
|
|
5500
|
8669
|
6857
|
6463
|
6376
|
5903
|
5268
|
3783
|
3344
|
3321
|
2940
|
2470
|
2116
|
1814
|
1519
|
1289
|
1084
|
885
|
667
|
449
|
244
|
109
|
50
|
|
6000
|
9148
|
7890
|
7094
|
6537
|
5988
|
5386
|
3873
|
3367
|
3321
|
2993
|
2586
|
2242
|
1942
|
1627
|
1389
|
1211
|
1009
|
765
|
499
|
283
|
134
|
63
|
|
6500
|
9555
|
8478
|
7462
|
6654
|
6074
|
5402
|
3928
|
3388
|
3321
|
3003
|
2611
|
2301
|
2033
|
1704
|
1481
|
1339
|
1121
|
857
|
557
|
328
|
161
|
76
|
|
7000
|
9926
|
8738
|
7682
|
6811
|
6188
|
5423
|
3952
|
3406
|
3395
|
3020
|
2629
|
2340
|
2040
|
1774
|
1572
|
1405
|
1199
|
940
|
618
|
373
|
190
|
90
|
|
7500
|
10287
|
8963
|
7885
|
6963
|
6314
|
5492
|
4090
|
3520
|
3414
|
3039
|
2650
|
2359
|
2110
|
1830
|
1598
|
1473
|
1249
|
1018
|
686
|
422
|
220
|
105
|
|
8000
|
10652
|
9312
|
8130
|
7145
|
6495
|
5785
|
4413
|
3660
|
3434
|
3050
|
2669
|
2380
|
2141
|
1969
|
1749
|
1554
|
1342
|
1107
|
751
|
470
|
253
|
120
|
Продолжение таблицы 1
Р = 17
МПа
|
x:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
2551
|
2479
|
2406
|
2335
|
2300
|
2276
|
2235
|
2146
|
1849
|
1547
|
1327
|
1144
|
993
|
866
|
761
|
672
|
608
|
598
|
494
|
354
|
257
|
156
|
|
50
|
2800
|
2707
|
2619
|
2530
|
2485
|
2439
|
2398
|
2319
|
2046
|
1734
|
1473
|
1299
|
1154
|
1022
|
922
|
858
|
798
|
726
|
581
|
407
|
347
|
292
|
|
100
|
2998
|
2886
|
2789
|
2685
|
2631
|
2566
|
2521
|
2439
|
2196
|
1878
|
1584
|
1423
|
1286
|
1150
|
1054
|
1007
|
946
|
806
|
587
|
490
|
350
|
258
|
|
300
|
2970
|
2769
|
2607
|
2439
|
2347
|
2260
|
2175
|
2102
|
1972
|
1755
|
1532
|
1399
|
1286
|
1107
|
1000
|
941
|
821
|
659
|
429
|
390
|
295
|
192
|
|
500
|
2817
|
2549
|
2374
|
2227
|
2138
|
2044
|
1917
|
1774
|
1661
|
1487
|
1308
|
1151
|
1048
|
958
|
868
|
802
|
685
|
534
|
291
|
243
|
194
|
118
|
|
1000
|
3054
|
2719
|
2452
|
2318
|
2233
|
2074
|
1850
|
1597
|
1407
|
1205
|
1045
|
912
|
839
|
744
|
635
|
483
|
354
|
273
|
180
|
136
|
95
|
52
|
|
1500
|
3874
|
3538
|
3124
|
2722
|
2518
|
2320
|
2043
|
1753
|
1526
|
1305
|
1187
|
1020
|
859
|
685
|
527
|
361
|
223
|
155
|
104
|
83
|
74
|
39
|
|
2000
|
4639
|
4218
|
3790
|
3214
|
2860
|
2568
|
2288
|
2018
|
1757
|
1533
|
1448
|
1223
|
993
|
780
|
567
|
405
|
273
|
180
|
125
|
108
|
69
|
33
|
|
2500
|
5565
|
5074
|
4638
|
3963
|
3416
|
2911
|
2529
|
2283
|
1991
|
1790
|
1637
|
1408
|
1148
|
885
|
618
|
462
|
358
|
288
|
218
|
136
|
72
|
35
|
|
3000
|
6358
|
5769
|
5238
|
4406
|
3758
|
3197
|
2726
|
2415
|
2218
|
2081
|
1832
|
1562
|
1289
|
1006
|
719
|
568
|
483
|
407
|
302
|
148
|
73
|
36
|
|
3500
|
6917
|
6047
|
5368
|
4467
|
3874
|
3398
|
2844
|
2588
|
2526
|
2337
|
1993
|
1685
|
1399
|
1114
|
831
|
694
|
609
|
533
|
462
|
193
|
76
|
36
|
|
4000
|
7403
|
6224
|
5569
|
4621
|
4012
|
3528
|
2931
|
2765
|
2746
|
2519
|
2134
|
1807
|
1533
|
1246
|
978
|
832
|
702
|
615
|
489
|
212
|
77
|
37
|
|
4500
|
7593
|
6226
|
5723
|
4953
|
4355
|
3694
|
3017
|
2902
|
2863
|
2619
|
2245
|
1935
|
1681
|
1380
|
1120
|
947
|
775
|
646
|
499
|
216
|
80
|
37
|
|
5000
|
7689
|
6228
|
5814
|
5285
|
4769
|
3933
|
3247
|
3128
|
3110
|
2821
|
2406
|
2092
|
1833
|
1539
|
1273
|
1048
|
849
|
685
|
508
|
242
|
89
|
40
|
|
5500
|
7871
|
6397
|
5943
|
5432
|
4936
|
4086
|
3463
|
3458
|
3330
|
3024
|
2545
|
2203
|
1931
|
1643
|
1365
|
1135
|
938
|
743
|
530
|
275
|
109
|
49
|
|
6000
|
8132
|
6991
|
6277
|
5506
|
4986
|
4123
|
3557
|
3471
|
3370
|
3080
|
2673
|
2311
|
1984
|
1694
|
1457
|
1277
|
1069
|
821
|
577
|
307
|
135
|
62
|
|
6500
|
8472
|
7405
|
6535
|
5600
|
5049
|
4154
|
3656
|
3485
|
3374
|
3087
|
2708
|
2349
|
2037
|
1733
|
1526
|
1395
|
1174
|
872
|
597
|
340
|
161
|
76
|
|
7000
|
8820
|
7664
|
6746
|
5718
|
5133
|
4169
|
3754
|
3498
|
3415
|
3116
|
2719
|
2357
|
2050
|
1785
|
1580
|
1435
|
1237
|
947
|
629
|
376
|
189
|
90
|
|
7500
|
9163
|
7907
|
6947
|
5876
|
5271
|
4622
|
3853
|
3517
|
3434
|
3135
|
2738
|
2367
|
2100
|
1825
|
1593
|
1490
|
1269
|
1023
|
683
|
420
|
219
|
104
|
|
8000
|
9480
|
8235
|
7110
|
6148
|
5620
|
5075
|
4230
|
3649
|
3455
|
3155
|
2757
|
2388
|
2120
|
1952
|
1722
|
1537
|
1334
|
1104
|
748
|
468
|
251
|
120
|
Продолжение таблицы 1
Р = 18 МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
2189
|
2133
|
2078
|
2022
|
1997
|
1976
|
1950
|
1885
|
1647
|
1398
|
1213
|
1060
|
930
|
812
|
726
|
657
|
595
|
577
|
444
|
315
|
228
|
139
|
|
50
|
2382
|
2308
|
2239
|
2172
|
2137
|
2103
|
2070
|
2004
|
1782
|
1532
|
1325
|
1183
|
1062
|
937
|
849
|
796
|
752
|
691
|
525
|
400
|
314
|
248
|
|
100
|
2524
|
2435
|
2357
|
2282
|
2239
|
2192
|
2152
|
2077
|
1880
|
1632
|
1410
|
1278
|
1168
|
1040
|
940
|
892
|
865
|
757
|
542
|
478
|
340
|
233
|
|
300
|
2378
|
2223
|
2101
|
2002
|
1936
|
1854
|
1777
|
1693
|
1600
|
1481
|
1325
|
1192
|
1112
|
991
|
871
|
759
|
688
|
580
|
392
|
375
|
271
|
174
|
|
500
|
2137
|
1930
|
1790
|
1698
|
1657
|
1582
|
1487
|
1377
|
1275
|
1210
|
1096
|
964
|
895
|
854
|
749
|
653
|
545
|
457
|
274
|
231
|
184
|
115
|
|
1000
|
2484
|
2220
|
1960
|
1832
|
1759
|
1689
|
1587
|
1399
|
1195
|
1049
|
979
|
854
|
747
|
652
|
543
|
420
|
350
|
269
|
170
|
126
|
88
|
47
|
|
1500
|
3354
|
3048
|
2648
|
2304
|
2097
|
2004
|
1862
|
1606
|
1377
|
1204
|
1165
|
1011
|
849
|
695
|
554
|
383
|
229
|
198
|
112
|
73
|
71
|
35
|
|
2000
|
4160
|
3773
|
3358
|
2874
|
2589
|
2408
|
2176
|
1855
|
1637
|
1484
|
1435
|
1259
|
1077
|
897
|
675
|
447
|
288
|
234
|
138
|
115
|
66
|
31
|
|
2500
|
5115
|
4671
|
4271
|
3613
|
3118
|
2736
|
2410
|
2108
|
1885
|
1730
|
1680
|
1431
|
1241
|
1010
|
757
|
532
|
413
|
352
|
268
|
147
|
68
|
32
|
|
3000
|
5776
|
5147
|
4697
|
3919
|
3353
|
2939
|
2529
|
2224
|
2092
|
2088
|
1863
|
1569
|
1328
|
1104
|
860
|
653
|
513
|
465
|
368
|
158
|
69
|
33
|
|
3500
|
6200
|
5263
|
4751
|
3952
|
3428
|
3073
|
2613
|
2476
|
2473
|
2291
|
1953
|
1645
|
1395
|
1186
|
966
|
764
|
640
|
606
|
526
|
209
|
72
|
34
|
|
4000
|
6698
|
5557
|
5016
|
4100
|
3547
|
3146
|
2683
|
2602
|
2600
|
2432
|
2107
|
1808
|
1584
|
1341
|
1080
|
881
|
705
|
643
|
583
|
238
|
74
|
34
|
|
4500
|
6863
|
5589
|
5164
|
4349
|
3817
|
3236
|
2917
|
2828
|
2795
|
2504
|
2176
|
2020
|
1761
|
1486
|
1188
|
1000
|
777
|
664
|
585
|
239
|
76
|
35
|
|
5000
|
6894
|
5600
|
5215
|
4608
|
4132
|
3365
|
3148
|
3069
|
2992
|
2578
|
2354
|
2132
|
1877
|
1636
|
1342
|
1113
|
887
|
720
|
628
|
260
|
88
|
39
|
|
5500
|
6982
|
5726
|
5328
|
4726
|
4258
|
3473
|
3458
|
3348
|
3313
|
2865
|
2532
|
2295
|
2023
|
1768
|
1410
|
1167
|
983
|
817
|
635
|
291
|
109
|
49
|
|
6000
|
7157
|
6118
|
5497
|
4754
|
4297
|
3667
|
3478
|
3399
|
3334
|
2885
|
2620
|
2357
|
2031
|
1778
|
1494
|
1312
|
1126
|
869
|
651
|
324
|
135
|
62
|
|
6500
|
7437
|
6468
|
5657
|
4756
|
4302
|
3860
|
3524
|
3399
|
3355
|
2904
|
2640
|
2363
|
2038
|
1789
|
1535
|
1417
|
1227
|
898
|
654
|
356
|
162
|
75
|
|
7000
|
7750
|
6724
|
5829
|
4805
|
4340
|
4053
|
3580
|
3437
|
3374
|
2924
|
2659
|
2383
|
2060
|
1799
|
1580
|
1451
|
1261
|
965
|
667
|
387
|
190
|
89
|
|
7500
|
8065
|
6948
|
6031
|
5039
|
4556
|
4247
|
3770
|
3511
|
3393
|
2945
|
2680
|
2404
|
2090
|
1809
|
1590
|
1464
|
1275
|
1034
|
697
|
423
|
218
|
104
|
|
8000
|
8347
|
7225
|
6182
|
5286
|
4858
|
4441
|
3952
|
3525
|
3414
|
2965
|
2701
|
2423
|
2114
|
1934
|
1710
|
1515
|
1321
|
1103
|
746
|
468
|
249
|
120
|
Продолжение таблицы 1
Р = 20
МПа
|
х:
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
-0,15
|
-0,10
|
-0,05
|
0,00
|
0,05
|
0,10
|
0,15
|
0,20
|
0,25
|
0,30
|
0,35
|
0,40
|
0,45
|
0,50
|
0,60
|
0,70
|
0,80
|
0,90
|
|
0
|
1367
|
1333
|
1304
|
1277
|
1261
|
1255
|
1235
|
1193
|
1092
|
988
|
921
|
846
|
761
|
665
|
573
|
522
|
472
|
418
|
321
|
228
|
154
|
90
|
|
50
|
1628
|
1593
|
1576
|
1552
|
1522
|
1477
|
1396
|
1314
|
1222
|
1094
|
1001
|
951
|
881
|
747
|
623
|
547
|
476
|
421
|
345
|
270
|
215
|
152
|
|
100
|
1806
|
1774
|
1772
|
1752
|
1715
|
1633
|
1508
|
1394
|
1310
|
1165
|
1044
|
1014
|
957
|
797
|
651
|
553
|
480
|
424
|
371
|
369
|
224
|
187
|
|
300
|
1524
|
1476
|
1461
|
1461
|
1449
|
1379
|
1253
|
1173
|
1072
|
904
|
721
|
667
|
652
|
609
|
547
|
432
|
400
|
318
|
292
|
291
|
223
|
140
|
|
500
|
1167
|
1090
|
1024
|
997
|
978
|
962
|
905
|
858
|
750
|
685
|
592
|
572
|
572
|
539
|
487
|
430
|
375
|
269
|
210
|
185
|
165
|
72
|
|
1000
|
1538
|
1403
|
1259
|
1142
|
1086
|
996
|
936
|
873
|
781
|
713
|
712
|
711
|
667
|
610
|
485
|
393
|
330
|
259
|
150
|
103
|
77
|
31
|
|
1500
|
2411
|
2193
|
1966
|
1766
|
1640
|
1468
|
1328
|
1194
|
1161
|
1161
|
1096
|
949
|
769
|
681
|
611
|
533
|
385
|
250
|
139
|
102
|
63
|
29
|
|
2000
|
3269
|
2881
|
2536
|
2229
|
2049
|
1812
|
1633
|
1469
|
1396
|
1360
|
1198
|
1153
|
1029
|
939
|
825
|
593
|
411
|
283
|
167
|
129
|
62
|
27
|
|
2500
|
3945
|
3350
|
2983
|
2597
|
2338
|
2012
|
1864
|
1692
|
1534
|
1369
|
1252
|
1250
|
1153
|
1124
|
939
|
808
|
611
|
428
|
291
|
159
|
64
|
28
|
|
3000
|
4169
|
3514
|
3182
|
2767
|
2442
|
2077
|
1949
|
1770
|
1566
|
1380
|
1294
|
1293
|
1292
|
1227
|
1033
|
905
|
672
|
558
|
390
|
184
|
65
|
29
|
|
3500
|
4171
|
3606
|
3286
|
2850
|
2522
|
2154
|
2014
|
1854
|
1763
|
1669
|
1581
|
1522
|
1331
|
1253
|
1128
|
962
|
813
|
671
|
582
|
232
|
70
|
29
|
|
4000
|
4173
|
3765
|
3426
|
2954
|
2639
|
2294
|
2174
|
2013
|
1960
|
1959
|
1870
|
1720
|
1371
|
1264
|
1188
|
1035
|
856
|
690
|
601
|
272
|
72
|
29
|
|
4500
|
4233
|
4009
|
3596
|
3034
|
2742
|
2472
|
2308
|
2123
|
2096
|
2096
|
2008
|
1892
|
1473
|
1425
|
1280
|
1044
|
871
|
695
|
611
|
278
|
75
|
31
|
|
5000
|
4436
|
4270
|
3812
|
3193
|
2893
|
2659
|
2489
|
2485
|
2256
|
2120
|
2038
|
1927
|
1576
|
1571
|
1374
|
1150
|
900
|
750
|
692
|
300
|
88
|
37
|
|
5500
|
4687
|
4581
|
4048
|
3320
|
3002
|
2825
|
2661
|
2657
|
2428
|
2146
|
2068
|
1962
|
1678
|
1669
|
1519
|
1230
|
1021
|
857
|
693
|
302
|
109
|
48
|
|
6000
|
4915
|
4686
|
4148
|
3416
|
3109
|
2950
|
2733
|
2728
|
2611
|
2172
|
2100
|
1999
|
1832
|
1671
|
1521
|
1335
|
1178
|
935
|
694
|
333
|
135
|
60
|
|
6500
|
5129
|
4688
|
4157
|
3492
|
3206
|
3018
|
2820
|
2815
|
2697
|
2220
|
2116
|
2040
|
1891
|
1674
|
1534
|
1438
|
1273
|
958
|
696
|
366
|
163
|
74
|
|
7000
|
5338
|
4706
|
4158
|
3532
|
3242
|
3051
|
2840
|
2835
|
2717
|
2260
|
2147
|
2083
|
1937
|
1725
|
1548
|
1463
|
1287
|
998
|
700
|
399
|
190
|
88
|
|
7500
|
5548
|
4808
|
4185
|
3586
|
3298
|
3110
|
2861
|
2854
|
2736
|
2329
|
2179
|
2114
|
1983
|
1776
|
1561
|
1478
|
1296
|
1053
|
726
|
433
|
220
|
103
|
|
8000
|
5757
|
4976
|
4232
|
3614
|
3338
|
3135
|
2882
|
2876
|
2755
|
2443
|
2255
|
2164
|
2075
|
1912
|
1697
|
1493
|
1304
|
1102
|
744
|
467
|
247
|
119
|
Таблица 2
Критический тепловой поток в кольцевых каналах (кВт/м2)
для: dh = 8 мм,
d1/d2 = 1,0, Lh/dh
≥ 300, давление Р [кПа], массовая скорость G [кг/м2сек]
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
100
|
50
|
|
|
|
|
2385
|
745
|
644
|
588
|
569
|
552
|
512
|
429
|
322
|
224
|
126
|
|
100
|
100
|
|
|
|
|
2702
|
1099
|
1065
|
1038
|
1023
|
1005
|
945
|
801
|
607
|
414
|
221
|
|
100
|
200
|
|
|
|
|
2970
|
1352
|
1314
|
1247
|
1208
|
1089
|
975
|
806
|
628
|
428
|
228
|
|
100
|
300
|
|
|
|
|
3237
|
1606
|
1563
|
1456
|
1392
|
1172
|
1004
|
811
|
648
|
|
|
|
100
|
500
|
|
|
|
|
3527
|
1924
|
1788
|
1701
|
1619
|
1410
|
1246
|
901
|
|
|
|
|
100
|
750
|
|
|
|
|
3697
|
2151
|
1974
|
1857
|
1688
|
1480
|
1347
|
|
|
|
|
|
100
|
1000
|
|
|
|
|
3866
|
2379
|
2160
|
2013
|
1756
|
|
|
|
|
|
|
|
100
|
1500
|
|
|
|
|
3948
|
2498
|
2274
|
2075
|
1805
|
|
|
|
|
|
|
|
100
|
2000
|
|
|
|
|
3951
|
2539
|
2313
|
2087
|
|
|
|
|
|
|
|
|
100
|
3000
|
|
|
|
|
3972
|
2638
|
2429
|
|
|
|
|
|
|
|
|
|
100
|
4000
|
|
|
|
|
4036
|
2779
|
|
|
|
|
|
|
|
|
|
|
100
|
5000
|
|
|
|
|
4128
|
|
|
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
200
|
50
|
|
|
|
|
2507
|
1292
|
847
|
677
|
620
|
589
|
550
|
467
|
364
|
252
|
140
|
|
200
|
100
|
|
|
|
|
2849
|
1513
|
1144
|
1102
|
1076
|
1032
|
972
|
844
|
662
|
451
|
240
|
|
200
|
200
|
|
|
|
|
3146
|
1728
|
1453
|
1364
|
1304
|
1162
|
1046
|
867
|
676
|
460
|
244
|
|
200
|
300
|
|
|
|
|
3444
|
1943
|
1762
|
1625
|
1531
|
1293
|
1120
|
890
|
691
|
470
|
249
|
|
200
|
500
|
|
|
|
|
3758
|
2305
|
2045
|
1884
|
1690
|
1432
|
1235
|
898
|
620
|
423
|
|
|
200
|
750
|
|
|
|
|
3926
|
2518
|
2212
|
2010
|
1747
|
1479
|
1298
|
928
|
|
|
|
|
200
|
1000
|
|
|
|
|
4094
|
2731
|
2377
|
2136
|
1804
|
1527
|
1361
|
|
|
|
|
|
200
|
1500
|
|
|
|
|
4147
|
2817
|
2472
|
2184
|
1854
|
1645
|
|
|
|
|
|
|
200
|
2000
|
|
|
|
|
4150
|
2852
|
2504
|
2207
|
1893
|
|
|
|
|
|
|
|
200
|
3000
|
|
|
|
|
4180
|
2944
|
2571
|
2197
|
|
|
|
|
|
|
|
|
200
|
4000
|
|
|
|
|
4297
|
3043
|
|
|
|
|
|
|
|
|
|
|
200
|
5000
|
|
|
|
|
4408
|
|
|
|
|
|
|
|
|
|
|
|
200
|
6000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
300
|
50
|
|
|
|
4612
|
2628
|
1841
|
1051
|
767
|
671
|
625
|
589
|
504
|
406
|
280
|
154
|
|
300
|
100
|
|
|
|
4867
|
2995
|
1929
|
1224
|
1167
|
1129
|
1059
|
998
|
887
|
717
|
487
|
258
|
|
300
|
200
|
|
|
|
4982
|
3323
|
2106
|
1592
|
1481
|
1400
|
1236
|
1117
|
928
|
725
|
493
|
261
|
|
300
|
300
|
|
|
|
5097
|
3650
|
2282
|
1961
|
1794
|
1671
|
1413
|
1236
|
968
|
734
|
499
|
264
|
|
300
|
500
|
|
|
|
5152
|
3988
|
2687
|
2304
|
2066
|
1761
|
1454
|
1223
|
895
|
627
|
428
|
|
|
300
|
750
|
|
|
|
5203
|
4155
|
2885
|
2450
|
2163
|
1807
|
1479
|
1249
|
876
|
574
|
|
|
|
300
|
1000
|
|
|
|
5254
|
4322
|
3083
|
2596
|
2260
|
1852
|
1503
|
1276
|
|
|
|
|
|
300
|
1500
|
|
|
|
5276
|
4344
|
3136
|
2670
|
2292
|
1904
|
1527
|
|
|
|
|
|
|
300
|
2000
|
|
|
|
5293
|
4349
|
3165
|
2696
|
2327
|
1937
|
|
|
|
|
|
|
|
300
|
3000
|
|
|
|
5437
|
4387
|
3251
|
2714
|
2289
|
|
|
|
|
|
|
|
|
300
|
4000
|
|
|
|
5962
|
4557
|
3308
|
2742
|
|
|
|
|
|
|
|
|
|
300
|
5000
|
|
|
|
6626
|
4688
|
3320
|
|
|
|
|
|
|
|
|
|
|
300
|
6000
|
|
|
|
7217
|
4871
|
|
|
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
400
|
50
|
|
|
|
4624
|
2790
|
1968
|
1172
|
857
|
745
|
688
|
616
|
512
|
433
|
298
|
163
|
|
400
|
100
|
|
|
|
4905
|
3222
|
2114
|
1409
|
1326
|
1271
|
1186
|
1078
|
965
|
811
|
550
|
289
|
|
400
|
200
|
|
|
|
5087
|
3594
|
2425
|
1857
|
1709
|
1535
|
1314
|
1163
|
989
|
822
|
557
|
293
|
|
400
|
300
|
|
|
|
5269
|
3967
|
2735
|
2306
|
2093
|
1799
|
1441
|
1248
|
1013
|
832
|
564
|
296
|
|
400
|
500
|
|
|
|
5343
|
4283
|
3119
|
2605
|
2305
|
1907
|
1477
|
1166
|
856
|
642
|
438
|
|
|
400
|
750
|
|
|
|
5399
|
4467
|
3286
|
2719
|
2406
|
1950
|
1478
|
1177
|
829
|
578
|
|
|
|
400
|
1000
|
|
|
|
5455
|
4650
|
3452
|
2833
|
2506
|
1993
|
1480
|
1187
|
|
|
|
|
|
400
|
1500
|
|
|
|
5469
|
4684
|
3487
|
2908
|
2629
|
2007
|
1446
|
|
|
|
|
|
|
400
|
2000
|
|
|
|
5497
|
4689
|
3506
|
2967
|
2693
|
1987
|
|
|
|
|
|
|
|
400
|
3000
|
|
|
|
5748
|
4725
|
3595
|
3124
|
2740
|
|
|
|
|
|
|
|
|
400
|
4000
|
|
|
|
6340
|
4893
|
3604
|
3067
|
|
|
|
|
|
|
|
|
|
400
|
5000
|
|
|
|
7055
|
5042
|
3499
|
|
|
|
|
|
|
|
|
|
|
400
|
6000
|
|
|
|
7690
|
5124
|
|
|
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
500
|
50
|
|
|
|
5637
|
2951
|
2096
|
1293
|
948
|
819
|
750
|
643
|
520
|
460
|
316
|
172
|
|
500
|
100
|
|
|
|
5943
|
3448
|
2299
|
1594
|
1484
|
1413
|
1314
|
1158
|
1042
|
905
|
613
|
321
|
|
500
|
200
|
|
|
|
5191
|
3866
|
2744
|
2123
|
1938
|
1671
|
1392
|
1209
|
1050
|
918
|
621
|
325
|
|
500
|
300
|
|
|
|
5440
|
4284
|
3189
|
2651
|
2391
|
1928
|
1469
|
1260
|
1057
|
930
|
629
|
329
|
|
500
|
500
|
|
|
|
5533
|
4579
|
3553
|
2906
|
2545
|
2054
|
1499
|
1109
|
816
|
657
|
448
|
238
|
|
500
|
750
|
|
|
|
5594
|
4778
|
3688
|
2988
|
2649
|
2094
|
1478
|
1104
|
781
|
|
|
|
|
500
|
1000
|
|
|
|
5655
|
4978
|
3822
|
3071
|
2754
|
2134
|
1457
|
|
|
|
|
|
|
500
|
1500
|
|
|
|
5662
|
5024
|
3838
|
3146
|
2967
|
2112
|
|
|
|
|
|
|
|
500
|
2000
|
|
|
|
5701
|
5028
|
3848
|
3237
|
3061
|
|
|
|
|
|
|
|
|
500
|
3000
|
|
|
|
6058
|
5062
|
3939
|
3534
|
|
|
|
|
|
|
|
|
|
500
|
4000
|
|
|
|
6719
|
5228
|
3901
|
|
|
|
|
|
|
|
|
|
|
500
|
5000
|
|
|
|
7485
|
5396
|
|
|
|
|
|
|
|
|
|
|
|
500
|
6000
|
|
|
|
8164
|
|
|
|
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
600
|
50
|
|
|
5667
|
4653
|
3101
|
2230
|
1423
|
1053
|
902
|
819
|
698
|
575
|
521
|
357
|
193
|
|
600
|
100
|
|
|
6273
|
5031
|
3673
|
2476
|
1777
|
1645
|
1544
|
1408
|
1211
|
1081
|
966
|
653
|
341
|
|
600
|
200
|
|
|
6496
|
5364
|
4193
|
3098
|
2399
|
2165
|
1787
|
1473
|
1253
|
1088
|
973
|
658
|
343
|
|
600
|
300
|
|
|
6719
|
5698
|
4712
|
3720
|
3021
|
2686
|
2030
|
1538
|
1295
|
1096
|
981
|
664
|
346
|
|
600
|
500
|
|
|
6777
|
5818
|
5014
|
4124
|
3287
|
2835
|
2160
|
1571
|
1139
|
828
|
677
|
461
|
|
|
600
|
750
|
|
|
6785
|
5867
|
5175
|
4221
|
3348
|
2890
|
2183
|
1532
|
1125
|
785
|
590
|
|
|
|
600
|
1000
|
|
|
6793
|
5916
|
5336
|
4319
|
3410
|
2945
|
2220
|
1493
|
1110
|
742
|
|
|
|
|
600
|
1500
|
|
|
6837
|
5925
|
5378
|
4311
|
3456
|
3115
|
2139
|
1308
|
964
|
|
|
|
|
|
600
|
2000
|
|
|
7047
|
5971
|
5387
|
4279
|
3481
|
3189
|
2047
|
1220
|
|
|
|
|
|
|
600
|
3000
|
|
|
7957
|
6311
|
5417
|
4259
|
3706
|
3283
|
1756
|
|
|
|
|
|
|
|
600
|
4000
|
|
|
9066
|
6952
|
5536
|
4200
|
3582
|
3054
|
|
|
|
|
|
|
|
|
600
|
5000
|
|
|
10127
|
7716
|
5631
|
3903
|
3178
|
|
|
|
|
|
|
|
|
|
600
|
6000
|
|
|
11086
|
8425
|
5552
|
3802
|
|
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
700
|
50
|
|
|
5656
|
4668
|
3250
|
2365
|
1555
|
1158
|
986
|
888
|
754
|
631
|
582
|
397
|
213
|
|
700
|
100
|
|
|
6271
|
5118
|
3899
|
2653
|
1961
|
1805
|
1674
|
1502
|
1263
|
1120
|
1026
|
693
|
361
|
|
700
|
200
|
|
|
6533
|
5537
|
4519
|
3452
|
2676
|
2393
|
1904
|
1554
|
1297
|
1127
|
1029
|
696
|
362
|
|
700
|
300
|
|
|
6794
|
5956
|
5139
|
4251
|
3392
|
2981
|
2133
|
1607
|
1331
|
1134
|
1033
|
698
|
363
|
|
700
|
500
|
|
|
6869
|
6103
|
5449
|
4695
|
3668
|
3126
|
2267
|
1643
|
1170
|
840
|
696
|
474
|
251
|
|
700
|
750
|
|
|
6876
|
6140
|
5571
|
4755
|
3708
|
3131
|
2273
|
1587
|
1146
|
789
|
598
|
408
|
218
|
|
700
|
1000
|
|
|
6883
|
6176
|
5693
|
4816
|
3748
|
3136
|
2279
|
1530
|
1122
|
738
|
500
|
343
|
|
|
700
|
1500
|
|
|
6928
|
6188
|
5731
|
4785
|
3767
|
3263
|
2167
|
1249
|
907
|
602
|
374
|
|
|
|
700
|
2000
|
|
|
8150
|
6240
|
5747
|
4710
|
3727
|
3318
|
2057
|
1144
|
804
|
492
|
|
|
|
|
700
|
3000
|
|
|
8080
|
6564
|
5771
|
4580
|
3879
|
3372
|
1770
|
1026
|
658
|
|
|
|
|
|
700
|
4000
|
|
|
9202
|
7184
|
5844
|
4500
|
3772
|
3175
|
1716
|
1176
|
|
|
|
|
|
|
700
|
5000
|
|
|
10274
|
7948
|
5866
|
4128
|
3379
|
2815
|
1811
|
|
|
|
|
|
|
|
700
|
6000
|
|
|
11250
|
8686
|
5726
|
3948
|
3401
|
2683
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
800
|
50
|
|
|
5646
|
4682
|
3398
|
2500
|
1686
|
1262
|
1070
|
957
|
810
|
686
|
643
|
438
|
233
|
|
800
|
100
|
|
|
6269
|
5205
|
4124
|
2829
|
2144
|
1966
|
1805
|
1596
|
1315
|
1158
|
1086
|
733
|
381
|
|
800
|
200
|
|
|
6569
|
5709
|
4845
|
3806
|
2953
|
2622
|
2020
|
1636
|
1341
|
1165
|
1085
|
733
|
381
|
|
800
|
300
|
|
|
6869
|
6212
|
5566
|
4783
|
3762
|
3278
|
2236
|
1676
|
1367
|
1172
|
1084
|
732
|
380
|
|
800
|
500
|
|
|
6960
|
6386
|
5884
|
5268
|
4049
|
3416
|
2374
|
1716
|
1200
|
853
|
716
|
487
|
258
|
|
800
|
750
|
|
|
6966
|
6411
|
5967
|
5290
|
4068
|
3372
|
2363
|
1641
|
1167
|
793
|
607
|
414
|
221
|
|
800
|
1000
|
|
|
6972
|
6436
|
6050
|
5313
|
4087
|
3390
|
2352
|
1567
|
1134
|
733
|
497
|
341
|
|
|
800
|
1500
|
|
|
7019
|
6451
|
6083
|
5259
|
4079
|
3412
|
2196
|
1191
|
850
|
565
|
373
|
|
|
|
800
|
2000
|
|
|
7253
|
6508
|
6105
|
5142
|
3972
|
3447
|
2069
|
1068
|
733
|
|
|
|
|
|
800
|
3000
|
|
|
8203
|
6817
|
6125
|
4901
|
4052
|
3462
|
1784
|
968
|
|
|
|
|
|
|
800
|
4000
|
|
|
9338
|
7416
|
6151
|
4801
|
3962
|
3296
|
1735
|
|
|
|
|
|
|
|
800
|
5000
|
|
|
10420
|
8179
|
6101
|
4354
|
3581
|
2918
|
|
|
|
|
|
|
|
|
800
|
6000
|
|
|
11414
|
8948
|
5900
|
4094
|
3517
|
2744
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
1000
|
50
|
6654
|
6195
|
5624
|
4708
|
3696
|
2769
|
1948
|
1472
|
1237
|
1094
|
921
|
797
|
765
|
519
|
274
|
|
1000
|
100
|
7215
|
6756
|
6264
|
5377
|
4574
|
3182
|
2511
|
2287
|
2066
|
1785
|
1420
|
1236
|
1206
|
813
|
421
|
|
1000
|
200
|
7400
|
6960
|
6641
|
6050
|
5496
|
4515
|
3508
|
3080
|
2255
|
1800
|
1429
|
1242
|
1196
|
807
|
418
|
|
1000
|
300
|
7584
|
7164
|
7018
|
6723
|
6419
|
5849
|
4504
|
3873
|
2443
|
1815
|
1438
|
1249
|
1187
|
801
|
415
|
|
1000
|
500
|
7710
|
7243
|
7141
|
6952
|
6751
|
6415
|
4813
|
3999
|
2588
|
1861
|
1261
|
877
|
754
|
512
|
270
|
|
1000
|
750
|
7804
|
7272
|
7145
|
6953
|
6756
|
6362
|
4790
|
3857
|
2544
|
1751
|
1210
|
801
|
623
|
425
|
227
|
|
1000
|
1000
|
7898
|
7301
|
7150
|
6954
|
6762
|
6310
|
4766
|
3714
|
2499
|
1641
|
1159
|
725
|
492
|
337
|
|
|
1000
|
1500
|
8414
|
7584
|
7198
|
6974
|
6787
|
6210
|
4706
|
3712
|
2256
|
1075
|
736
|
491
|
370
|
|
|
|
1000
|
2000
|
9536
|
8352
|
7457
|
7044
|
6822
|
6009
|
4465
|
3706
|
2093
|
915
|
591
|
414
|
|
|
|
|
1000
|
3000
|
11705
|
10168
|
8446
|
7320
|
6831
|
5547
|
4399
|
3643
|
1814
|
850
|
|
|
|
|
|
|
1000
|
4000
|
13271
|
11526
|
9608
|
7880
|
6764
|
5405
|
4343
|
3541
|
1772
|
|
|
|
|
|
|
|
1000
|
5000
|
14719
|
12772
|
10710
|
8644
|
6574
|
4807
|
3983
|
3126
|
|
|
|
|
|
|
|
|
1000
|
6000
|
16130
|
13937
|
11739
|
9473
|
6248
|
4388
|
3747
|
|
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
2000
|
50
|
6627
|
6077
|
5515
|
4788
|
4025
|
3041
|
2236
|
1707
|
1437
|
1270
|
1134
|
1066
|
1045
|
706
|
367
|
|
2000
|
100
|
7171
|
6628
|
6151
|
5495
|
4896
|
3553
|
2836
|
2594
|
2362
|
2071
|
1796
|
1597
|
1438
|
968
|
498
|
|
2000
|
200
|
7376
|
6861
|
6566
|
6164
|
5787
|
4893
|
3824
|
3442
|
2742
|
2246
|
1975
|
1696
|
1444
|
972
|
500
|
|
2000
|
300
|
7580
|
7093
|
6981
|
6834
|
6678
|
6234
|
4811
|
4291
|
3121
|
2421
|
2155
|
1795
|
1450
|
976
|
502
|
|
2000
|
500
|
7736
|
7244
|
7167
|
7067
|
6999
|
6782
|
5447
|
4504
|
3334
|
2540
|
2075
|
1525
|
1126
|
760
|
394
|
|
2000
|
750
|
7837
|
7281
|
7183
|
7069
|
6977
|
6743
|
5390
|
4307
|
3184
|
2372
|
1867
|
1320
|
931
|
630
|
329
|
|
2000
|
1000
|
7938
|
7318
|
7199
|
7071
|
6954
|
6703
|
5333
|
4110
|
3033
|
2204
|
1660
|
1115
|
737
|
501
|
265
|
|
2000
|
1500
|
8448
|
7628
|
7275
|
7089
|
6945
|
6563
|
5194
|
3936
|
2762
|
1549
|
1034
|
650
|
452
|
311
|
|
|
2000
|
2000
|
9581
|
8455
|
7562
|
7153
|
6953
|
6213
|
4754
|
3759
|
2461
|
1258
|
726
|
441
|
280
|
|
|
|
2000
|
3000
|
11755
|
10395
|
8754
|
7438
|
6950
|
5619
|
4436
|
3552
|
1904
|
919
|
592
|
415
|
|
|
|
|
2000
|
4000
|
13338
|
11788
|
10065
|
8225
|
6906
|
5446
|
4294
|
3407
|
1591
|
1193
|
813
|
|
|
|
|
|
2000
|
5000
|
14817
|
13042
|
11233
|
9206
|
6784
|
4908
|
4008
|
3050
|
1699
|
1310
|
|
|
|
|
|
|
2000
|
6000
|
16230
|
14206
|
12249
|
10158
|
6805
|
4605
|
3806
|
2880
|
1856
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
3000
|
50
|
6600
|
5965
|
5400
|
4856
|
4346
|
3315
|
2527
|
1943
|
1638
|
1446
|
1343
|
1334
|
1326
|
894
|
461
|
|
3000
|
100
|
7129
|
6505
|
6033
|
5606
|
5209
|
3930
|
3163
|
2901
|
2658
|
2354
|
2166
|
1962
|
1676
|
1127
|
578
|
|
3000
|
200
|
7354
|
6764
|
6487
|
6271
|
6071
|
5271
|
4141
|
3797
|
3233
|
2687
|
2519
|
2158
|
1699
|
1142
|
585
|
|
3000
|
300
|
7579
|
7023
|
6940
|
6937
|
6933
|
6611
|
5120
|
4694
|
3808
|
3021
|
2871
|
2354
|
1721
|
1157
|
593
|
|
3000
|
500
|
7764
|
7245
|
7191
|
7176
|
7244
|
7123
|
6090
|
5012
|
4090
|
3207
|
2887
|
2186
|
1506
|
1013
|
521
|
|
3000
|
750
|
7872
|
7289
|
7219
|
7180
|
7193
|
7098
|
5999
|
4759
|
3828
|
2987
|
2526
|
1848
|
1247
|
841
|
435
|
|
3000
|
1000
|
7980
|
7333
|
7248
|
7183
|
7143
|
7073
|
5908
|
4506
|
3565
|
2767
|
2164
|
1510
|
988
|
668
|
348
|
|
3000
|
1500
|
8482
|
7669
|
7350
|
7200
|
7099
|
6891
|
5692
|
4157
|
3257
|
2033
|
1339
|
814
|
535
|
366
|
|
|
3000
|
2000
|
9625
|
8555
|
7669
|
7259
|
7082
|
6396
|
5061
|
3800
|
2819
|
1611
|
869
|
468
|
334
|
|
|
|
3000
|
3000
|
11804
|
10611
|
9065
|
7561
|
7070
|
5686
|
4487
|
3446
|
1995
|
991
|
616
|
426
|
|
|
|
|
3000
|
4000
|
13403
|
12038
|
10518
|
8581
|
7057
|
5483
|
4256
|
3263
|
1416
|
1167
|
866
|
|
|
|
|
|
3000
|
5000
|
14912
|
13302
|
11746
|
9769
|
7005
|
5008
|
4036
|
2977
|
1539
|
1336
|
|
|
|
|
|
|
3000
|
6000
|
16328
|
14465
|
12750
|
10834
|
7386
|
4838
|
3862
|
2901
|
1767
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
5000
|
50
|
6076
|
5590
|
5174
|
4796
|
4414
|
3489
|
2731
|
2134
|
1815
|
1593
|
1466
|
1447
|
1193
|
805
|
417
|
|
5000
|
100
|
6616
|
6127
|
5769
|
5462
|
5135
|
4040
|
3299
|
3028
|
2801
|
2536
|
2277
|
2120
|
1873
|
1258
|
643
|
|
5000
|
200
|
6808
|
6336
|
6093
|
5925
|
5739
|
5018
|
4046
|
3774
|
3410
|
3016
|
2640
|
2380
|
1990
|
1336
|
682
|
|
5000
|
300
|
7000
|
6546
|
6417
|
6387
|
6344
|
5997
|
4793
|
4519
|
4020
|
3496
|
3003
|
2640
|
2107
|
1414
|
721
|
|
5000
|
500
|
7199
|
6711
|
6577
|
6540
|
6472
|
6107
|
5072
|
4790
|
4063
|
3629
|
3129
|
2639
|
2040
|
1370
|
699
|
|
5000
|
750
|
7377
|
6835
|
6661
|
6571
|
6443
|
5977
|
5065
|
4629
|
3836
|
3398
|
2812
|
2165
|
1615
|
1086
|
557
|
|
5000
|
1000
|
7555
|
6960
|
6745
|
6603
|
6414
|
5847
|
5059
|
4468
|
3609
|
3167
|
2494
|
1691
|
1190
|
803
|
416
|
|
5000
|
1500
|
8160
|
7377
|
6956
|
6685
|
6386
|
5551
|
4693
|
3912
|
3196
|
2479
|
1624
|
1014
|
861
|
584
|
|
|
5000
|
2000
|
9383
|
8339
|
7402
|
6801
|
6296
|
5077
|
4219
|
3464
|
2753
|
1928
|
981
|
627
|
617
|
|
|
|
5000
|
3000
|
11437
|
10379
|
8949
|
7439
|
6290
|
4597
|
3643
|
3119
|
1999
|
943
|
664
|
484
|
|
|
|
|
5000
|
4000
|
12965
|
11749
|
10325
|
8350
|
6271
|
4266
|
3398
|
2832
|
1437
|
1056
|
842
|
|
|
|
|
|
5000
|
5000
|
14382
|
12934
|
11470
|
9325
|
6487
|
4110
|
3306
|
2654
|
1444
|
1239
|
|
|
|
|
|
|
5000
|
6000
|
15707
|
14017
|
12504
|
10637
|
7394
|
4230
|
3264
|
2604
|
1747
|
|
|
|
|
|
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
6000
|
50
|
5796
|
5384
|
5027
|
4696
|
4370
|
3478
|
2721
|
2123
|
1797
|
1576
|
1334
|
1069
|
920
|
623
|
326
|
|
6000
|
100
|
6321
|
5897
|
5580
|
5307
|
5030
|
3991
|
3228
|
2954
|
2726
|
2484
|
2064
|
1665
|
1509
|
1015
|
522
|
|
6000
|
200
|
6512
|
6083
|
5843
|
5685
|
5514
|
4838
|
3908
|
3624
|
3307
|
2959
|
2464
|
2029
|
1746
|
1173
|
601
|
|
6000
|
300
|
6703
|
6268
|
6105
|
6062
|
5997
|
5686
|
4588
|
4295
|
3889
|
3433
|
2865
|
2393
|
1982
|
1331
|
680
|
|
6000
|
500
|
6911
|
6417
|
6226
|
6160
|
6006
|
5716
|
4802
|
4467
|
3906
|
3535
|
3051
|
2525
|
1953
|
1311
|
670
|
|
6000
|
750
|
7110
|
6531
|
6282
|
6173
|
5917
|
5558
|
4739
|
4234
|
3646
|
3328
|
2729
|
2051
|
1480
|
996
|
512
|
|
6000
|
1000
|
7309
|
6644
|
6337
|
6187
|
5827
|
5400
|
4676
|
4001
|
3385
|
3120
|
2406
|
1576
|
1008
|
681
|
355
|
|
6000
|
1500
|
7942
|
7069
|
6526
|
6266
|
5863
|
4965
|
4159
|
3498
|
2936
|
2460
|
1539
|
878
|
717
|
487
|
258
|
|
6000
|
2000
|
9171
|
8104
|
7092
|
6479
|
5910
|
4586
|
3727
|
3107
|
2544
|
1777
|
810
|
500
|
460
|
316
|
172
|
|
6000
|
3000
|
11146
|
10123
|
8781
|
7395
|
6062
|
4329
|
3243
|
2754
|
1880
|
610
|
451
|
400
|
241
|
170
|
99
|
|
6000
|
4000
|
12624
|
11446
|
10029
|
8073
|
6119
|
3702
|
2922
|
2483
|
1388
|
909
|
752
|
471
|
267
|
188
|
108
|
|
6000
|
5000
|
13991
|
12589
|
11008
|
8604
|
6211
|
3624
|
2798
|
2358
|
1315
|
1131
|
877
|
511
|
271
|
190
|
109
|
|
6000
|
6000
|
15250
|
13613
|
12216
|
10290
|
7276
|
3801
|
2828
|
2424
|
1705
|
1363
|
954
|
588
|
317
|
221
|
125
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
8000
|
50
|
5296
|
4967
|
4669
|
4411
|
4173
|
3199
|
2306
|
1939
|
1696
|
1518
|
1301
|
1048
|
915
|
620
|
324
|
|
8000
|
100
|
5771
|
5413
|
5119
|
4897
|
4696
|
3782
|
2963
|
2722
|
2493
|
2315
|
1943
|
1512
|
1381
|
930
|
479
|
|
8000
|
200
|
5967
|
5570
|
5285
|
5128
|
4973
|
4409
|
3515
|
3162
|
2908
|
2695
|
2206
|
1725
|
1519
|
1022
|
525
|
|
8000
|
300
|
6162
|
5726
|
5451
|
5359
|
5250
|
5036
|
4067
|
3602
|
3323
|
3075
|
2470
|
1937
|
1657
|
1114
|
571
|
|
8000
|
500
|
6385
|
5875
|
5566
|
5441
|
5319
|
5103
|
4189
|
3454
|
3119
|
2843
|
2289
|
1886
|
1605
|
1079
|
554
|
|
8000
|
750
|
6606
|
6007
|
5659
|
5475
|
5093
|
4930
|
4112
|
3237
|
2875
|
2552
|
2005
|
1527
|
1178
|
795
|
412
|
|
8000
|
1000
|
6826
|
6140
|
5753
|
5508
|
4868
|
4756
|
4034
|
3020
|
2632
|
2262
|
1721
|
1168
|
752
|
511
|
270
|
|
8000
|
1500
|
7489
|
6638
|
6067
|
5659
|
4850
|
4301
|
3488
|
2776
|
2296
|
1648
|
938
|
507
|
287
|
201
|
115
|
|
8000
|
2000
|
8621
|
7654
|
6701
|
5934
|
5011
|
3939
|
2978
|
2464
|
1981
|
1116
|
523
|
317
|
202
|
144
|
86
|
|
8000
|
3000
|
10436
|
9514
|
8352
|
7131
|
5417
|
3581
|
2485
|
2039
|
1281
|
557
|
344
|
261
|
171
|
124
|
76
|
|
8000
|
4000
|
11797
|
10736
|
9473
|
7688
|
5630
|
3265
|
2199
|
1838
|
1106
|
593
|
483
|
328
|
194
|
139
|
84
|
|
8000
|
5000
|
13052
|
11785
|
10383
|
8260
|
6072
|
3263
|
2076
|
1773
|
1152
|
829
|
612
|
374
|
205
|
146
|
87
|
|
8000
|
6000
|
14217
|
12723
|
11356
|
9840
|
7005
|
3426
|
2181
|
1931
|
1485
|
1104
|
768
|
480
|
261
|
184
|
106
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
10000
|
50
|
4780
|
4525
|
4276
|
4048
|
3868
|
3080
|
2207
|
1843
|
1590
|
1428
|
1252
|
1024
|
890
|
603
|
316
|
|
10000
|
100
|
5217
|
4935
|
4665
|
4432
|
4275
|
3545
|
2764
|
2494
|
2261
|
2117
|
1815
|
1388
|
1203
|
811
|
420
|
|
10000
|
200
|
5410
|
5084
|
4783
|
4549
|
4450
|
4002
|
3119
|
2833
|
2584
|
2317
|
1828
|
1300
|
1103
|
745
|
387
|
|
10000
|
300
|
5604
|
5234
|
4901
|
4666
|
4625
|
4459
|
3474
|
3171
|
2907
|
2516
|
1842
|
1211
|
1004
|
679
|
354
|
|
10000
|
500
|
5839
|
5401
|
5032
|
4747
|
4575
|
4416
|
3371
|
2922
|
2576
|
1969
|
1397
|
984
|
788
|
535
|
282
|
|
10000
|
750
|
6081
|
5562
|
5171
|
4819
|
4438
|
4270
|
3301
|
2770
|
2363
|
1518
|
1052
|
764
|
586
|
400
|
214
|
|
10000
|
1000
|
6323
|
5724
|
5310
|
4891
|
4300
|
4125
|
3232
|
2618
|
2151
|
1068
|
706
|
545
|
383
|
265
|
147
|
|
10000
|
1500
|
6966
|
6199
|
5629
|
5052
|
4319
|
3745
|
2935
|
2320
|
1698
|
697
|
488
|
362
|
198
|
142
|
85
|
|
10000
|
2000
|
7985
|
7124
|
6262
|
5435
|
4466
|
3357
|
2458
|
1871
|
1044
|
511
|
320
|
238
|
127
|
94
|
61
|
|
10000
|
3000
|
9606
|
8789
|
7861
|
6867
|
4926
|
3160
|
2045
|
1427
|
714
|
394
|
270
|
207
|
123
|
91
|
60
|
|
10000
|
4000
|
10857
|
9902
|
8871
|
7471
|
5067
|
2994
|
1740
|
1313
|
904
|
509
|
361
|
233
|
132
|
98
|
63
|
|
10000
|
5000
|
12021
|
10869
|
9703
|
8071
|
5416
|
3087
|
1665
|
1469
|
1145
|
705
|
537
|
341
|
178
|
128
|
78
|
|
10000
|
6000
|
13055
|
11697
|
10510
|
9150
|
6117
|
3325
|
1932
|
1753
|
1425
|
997
|
703
|
446
|
245
|
173
|
101
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
12000
|
50
|
4226
|
4035
|
3846
|
3654
|
3486
|
2912
|
2094
|
1717
|
1463
|
1333
|
1172
|
975
|
852
|
578
|
303
|
|
12000
|
100
|
4611
|
4402
|
4196
|
3980
|
3795
|
3259
|
2537
|
2233
|
2006
|
1918
|
1672
|
1217
|
924
|
626
|
327
|
|
12000
|
200
|
4784
|
4539
|
4301
|
4067
|
3892
|
3473
|
2821
|
2549
|
2253
|
1959
|
1458
|
1100
|
824
|
559
|
294
|
|
12000
|
300
|
4957
|
4677
|
4405
|
4153
|
3990
|
3687
|
3104
|
2865
|
2499
|
2001
|
1243
|
983
|
724
|
492
|
260
|
|
12000
|
500
|
5149
|
4817
|
4493
|
4145
|
3924
|
3569
|
2943
|
2615
|
2077
|
1393
|
827
|
627
|
429
|
295
|
162
|
|
12000
|
750
|
5374
|
4965
|
4573
|
4095
|
3696
|
3311
|
2699
|
2283
|
1729
|
1025
|
631
|
463
|
319
|
222
|
125
|
|
12000
|
1000
|
5598
|
5113
|
4653
|
4045
|
3469
|
3053
|
2456
|
1951
|
1380
|
658
|
436
|
299
|
209
|
149
|
89
|
|
12000
|
1500
|
6307
|
5650
|
4939
|
4100
|
3492
|
2808
|
2126
|
1504
|
861
|
433
|
279
|
205
|
148
|
108
|
68
|
|
12000
|
2000
|
7206
|
6495
|
5625
|
4584
|
3630
|
2741
|
1940
|
1227
|
604
|
374
|
233
|
180
|
105
|
79
|
54
|
|
12000
|
3000
|
8569
|
7856
|
7077
|
5979
|
4048
|
2746
|
1613
|
884
|
460
|
267
|
227
|
170
|
100
|
76
|
52
|
|
12000
|
4000
|
9562
|
8650
|
7853
|
6775
|
4570
|
2804
|
1512
|
1030
|
717
|
448
|
301
|
213
|
123
|
91
|
60
|
|
12000
|
5000
|
10366
|
9303
|
8493
|
7397
|
5020
|
2991
|
1686
|
1329
|
1022
|
598
|
394
|
313
|
180
|
130
|
79
|
|
12000
|
6000
|
11572
|
10347
|
9319
|
8107
|
5535
|
3220
|
1923
|
1634
|
1279
|
926
|
642
|
424
|
238
|
168
|
98
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
14000
|
50
|
3663
|
3529
|
3402
|
3264
|
3136
|
2706
|
1970
|
1581
|
1302
|
1146
|
992
|
882
|
721
|
490
|
259
|
|
14000
|
100
|
3977
|
3836
|
3711
|
3560
|
3412
|
2990
|
2316
|
1976
|
1664
|
1489
|
1155
|
883
|
687
|
468
|
248
|
|
14000
|
200
|
4077
|
3926
|
3799
|
3635
|
3487
|
3163
|
2553
|
2162
|
1689
|
1407
|
1016
|
776
|
587
|
401
|
215
|
|
14000
|
300
|
4177
|
4017
|
3887
|
3710
|
3561
|
3335
|
2789
|
2348
|
1715
|
1326
|
878
|
669
|
487
|
334
|
181
|
|
14000
|
500
|
4216
|
4039
|
3917
|
3700
|
3352
|
3161
|
2633
|
1997
|
1376
|
978
|
531
|
347
|
281
|
197
|
113
|
|
14000
|
750
|
4398
|
4149
|
3980
|
3663
|
3108
|
2820
|
2254
|
1676
|
1203
|
737
|
410
|
275
|
221
|
157
|
93
|
|
14000
|
1000
|
4580
|
4259
|
4042
|
3625
|
2865
|
2479
|
1874
|
1356
|
1030
|
496
|
289
|
203
|
161
|
117
|
73
|
|
14000
|
1500
|
5483
|
4980
|
4380
|
3677
|
3031
|
2313
|
1610
|
1120
|
705
|
330
|
242
|
181
|
128
|
95
|
62
|
|
14000
|
2000
|
6279
|
5709
|
4889
|
3976
|
3244
|
2339
|
1586
|
981
|
492
|
265
|
203
|
163
|
96
|
74
|
51
|
|
14000
|
3000
|
7425
|
6770
|
6277
|
5301
|
3737
|
2495
|
1623
|
899
|
456
|
236
|
183
|
143
|
96
|
74
|
51
|
|
14000
|
4000
|
7928
|
6850
|
6348
|
5524
|
4035
|
2691
|
1818
|
1159
|
740
|
502
|
287
|
192
|
116
|
87
|
58
|
|
14000
|
5000
|
7950
|
6922
|
6551
|
6021
|
4518
|
3031
|
2122
|
1432
|
1015
|
718
|
419
|
288
|
171
|
124
|
76
|
|
14000
|
6000
|
9656
|
8514
|
7847
|
6965
|
4912
|
3113
|
2297
|
1782
|
1299
|
986
|
624
|
409
|
233
|
165
|
97
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
16000
|
50
|
3028
|
2927
|
2837
|
2742
|
2650
|
2383
|
1791
|
1426
|
1100
|
888
|
730
|
612
|
436
|
300
|
164
|
|
16000
|
100
|
3284
|
3171
|
3081
|
2977
|
2870
|
2613
|
2082
|
1755
|
1362
|
1115
|
815
|
628
|
481
|
330
|
179
|
|
16000
|
200
|
3352
|
3208
|
3111
|
3002
|
2882
|
2675
|
2238
|
1880
|
1428
|
1059
|
736
|
547
|
432
|
298
|
163
|
|
16000
|
300
|
3421
|
3246
|
3141
|
3027
|
2895
|
2736
|
2394
|
2006
|
1493
|
1003
|
657
|
465
|
384
|
265
|
147
|
|
16000
|
500
|
3453
|
3274
|
3164
|
3019
|
2693
|
2483
|
2020
|
1405
|
1073
|
830
|
492
|
303
|
243
|
172
|
100
|
|
16000
|
750
|
3600
|
3343
|
3222
|
3050
|
2562
|
2182
|
1675
|
1195
|
955
|
654
|
372
|
238
|
189
|
136
|
82
|
|
16000
|
1000
|
3747
|
3413
|
3279
|
3080
|
2430
|
1880
|
1329
|
985
|
837
|
478
|
252
|
173
|
135
|
99
|
64
|
|
16000
|
1500
|
4398
|
4028
|
3710
|
3293
|
2517
|
1720
|
1267
|
945
|
617
|
282
|
153
|
117
|
102
|
77
|
53
|
|
16000
|
2000
|
4879
|
4463
|
4060
|
3532
|
2655
|
1914
|
1511
|
1021
|
562
|
247
|
134
|
111
|
92
|
71
|
50
|
|
16000
|
3000
|
6167
|
5572
|
5309
|
4604
|
3097
|
2338
|
1817
|
1219
|
695
|
400
|
240
|
166
|
107
|
81
|
55
|
|
16000
|
4000
|
7028
|
5921
|
5638
|
4962
|
3460
|
2614
|
2109
|
1483
|
944
|
668
|
413
|
247
|
117
|
87
|
58
|
|
16000
|
5000
|
7523
|
6121
|
5950
|
5676
|
4111
|
3056
|
2429
|
1750
|
1226
|
858
|
523
|
332
|
166
|
120
|
74
|
|
16000
|
6000
|
8413
|
7320
|
6616
|
5968
|
4449
|
3178
|
2664
|
1998
|
1441
|
1061
|
668
|
426
|
236
|
167
|
98
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
18000
|
50
|
2249
|
2180
|
2115
|
2051
|
1986
|
1823
|
1380
|
1080
|
858
|
740
|
626
|
476
|
364
|
252
|
140
|
|
18000
|
100
|
2382
|
2299
|
2225
|
2152
|
2068
|
1901
|
1469
|
1174
|
951
|
838
|
680
|
503
|
429
|
295
|
162
|
|
18000
|
200
|
2306
|
2194
|
2102
|
2015
|
1900
|
1738
|
1410
|
1139
|
925
|
766
|
598
|
436
|
383
|
265
|
147
|
|
18000
|
300
|
2231
|
2090
|
1978
|
1878
|
1733
|
1574
|
1350
|
1103
|
898
|
695
|
517
|
369
|
337
|
234
|
131
|
|
18000
|
500
|
1992
|
1808
|
1684
|
1598
|
1468
|
1271
|
1108
|
891
|
773
|
581
|
401
|
252
|
211
|
150
|
89
|
|
18000
|
750
|
2152
|
1935
|
1761
|
1656
|
1518
|
1263
|
1039
|
831
|
676
|
477
|
319
|
203
|
162
|
117
|
73
|
|
18000
|
1000
|
2312
|
2061
|
1839
|
1714
|
1567
|
1255
|
971
|
772
|
580
|
373
|
237
|
153
|
113
|
85
|
57
|
|
18000
|
1500
|
3130
|
2823
|
2453
|
2113
|
1852
|
1442
|
1130
|
901
|
609
|
308
|
172
|
99
|
69
|
55
|
42
|
|
18000
|
2000
|
3881
|
3509
|
3102
|
2626
|
2203
|
1683
|
1392
|
1130
|
771
|
367
|
205
|
127
|
100
|
76
|
52
|
|
18000
|
3000
|
5372
|
4807
|
4320
|
3516
|
2642
|
2065
|
1901
|
1402
|
960
|
569
|
424
|
311
|
134
|
99
|
64
|
|
18000
|
4000
|
6155
|
5180
|
4598
|
3693
|
2820
|
2471
|
2192
|
1636
|
1179
|
773
|
600
|
491
|
196
|
140
|
84
|
|
18000
|
5000
|
6313
|
5250
|
4843
|
4204
|
3117
|
2887
|
2367
|
1932
|
1447
|
975
|
667
|
529
|
216
|
153
|
91
|
|
18000
|
6000
|
6609
|
5699
|
5086
|
4349
|
3415
|
3205
|
2644
|
2120
|
1585
|
1178
|
786
|
559
|
273
|
192
|
110
|
|
Р
|
G/X
|
-0,5
|
-0,4
|
-0,3
|
-0,2
|
-0,1
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
|
20000
|
50
|
1542
|
1511
|
1494
|
1466
|
1380
|
1222
|
1012
|
883
|
674
|
499
|
389
|
317
|
249
|
175
|
102
|
|
20000
|
100
|
1711
|
1685
|
1681
|
1654
|
1515
|
1300
|
1072
|
947
|
715
|
504
|
395
|
352
|
330
|
229
|
129
|
|
20000
|
200
|
1576
|
1543
|
1534
|
1519
|
1394
|
1193
|
939
|
788
|
638
|
453
|
347
|
315
|
298
|
208
|
118
|
|
20000
|
300
|
1441
|
1400
|
1388
|
1384
|
1274
|
1085
|
806
|
629
|
561
|
401
|
298
|
277
|
267
|
187
|
108
|
|
20000
|
500
|
1098
|
1026
|
969
|
942
|
897
|
784
|
624
|
543
|
497
|
393
|
247
|
196
|
173
|
125
|
77
|
|
20000
|
750
|
1270
|
1169
|
1074
|
1005
|
913
|
793
|
650
|
603
|
520
|
374
|
239
|
166
|
133
|
98
|
63
|
|
20000
|
1000
|
1442
|
1312
|
1179
|
1069
|
929
|
803
|
677
|
663
|
543
|
355
|
230
|
136
|
94
|
72
|
50
|
|
20000
|
1500
|
2259
|
2050
|
1839
|
1641
|
1354
|
1125
|
1084
|
849
|
627
|
463
|
221
|
127
|
91
|
70
|
49
|
|
20000
|
2000
|
3049
|
2687
|
2365
|
2065
|
1670
|
1374
|
1245
|
1059
|
859
|
511
|
252
|
153
|
113
|
85
|
57
|
|
20000
|
3000
|
3866
|
3290
|
2963
|
2535
|
1936
|
1622
|
1286
|
1228
|
1109
|
792
|
506
|
341
|
158
|
115
|
72
|
|
20000
|
4000
|
3905
|
3528
|
3186
|
2715
|
2145
|
1897
|
1835
|
1533
|
1179
|
931
|
643
|
523
|
229
|
162
|
95
|
|
20000
|
5000
|
4190
|
3990
|
3532
|
2946
|
2477
|
2294
|
1990
|
1729
|
1435
|
1020
|
704
|
601
|
254
|
179
|
104
|
|
20000
|
6000
|
4636
|
4374
|
3835
|
3156
|
2740
|
2558
|
2043
|
1851
|
1544
|
1223
|
853
|
607
|
288
|
201
|
115
|
Таблица 3
Таблица по КТП (кВт/м2) в идеальных ячейках сборок
твэлов в треугольной
упаковке с параметрами: dh = 9,36 мм, s/d = 1,4, L/dh
> 300, без влияния
дистанционирующих решеток
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
|
100
|
25
|
-
|
-
|
-
|
370
|
140
|
72
|
70
|
70
|
68
|
67
|
67
|
53
|
49
|
46
|
43
|
42
|
|
100
|
50
|
-
|
-
|
-
|
596
|
227
|
118
|
114
|
113
|
111
|
110
|
109
|
89
|
68
|
68
|
68
|
68
|
|
100
|
100
|
-
|
-
|
-
|
661
|
304
|
189
|
196
|
205
|
215
|
221
|
214
|
174
|
134
|
132
|
132
|
132
|
|
100
|
200
|
-
|
-
|
-
|
937
|
519
|
324
|
334
|
343
|
342
|
323
|
299
|
243
|
200
|
185
|
189
|
|
|
100
|
300
|
-
|
-
|
-
|
1418
|
910
|
573
|
587
|
590
|
569
|
504
|
450
|
365
|
321
|
|
|
|
|
100
|
500
|
-
|
-
|
-
|
1930
|
1386
|
859
|
911
|
898
|
884
|
846
|
716
|
479
|
|
|
|
|
|
100
|
750
|
-
|
-
|
-
|
2188
|
1601
|
1038
|
1084
|
1061
|
981
|
977
|
|
|
|
|
|
|
|
100
|
1000
|
-
|
-
|
-
|
2416
|
1795
|
1210
|
1249
|
1213
|
1061
|
|
|
|
|
|
|
|
|
100
|
1500
|
-
|
-
|
-
|
2813
|
2093
|
1462
|
1472
|
1418
|
1358
|
|
|
|
|
|
|
|
|
100
|
2000
|
-
|
-
|
-
|
3181
|
2377
|
1689
|
1689
|
1588
|
|
|
|
|
|
|
|
|
|
100
|
3000
|
-
|
-
|
-
|
3951
|
2981
|
2196
|
2163
|
|
|
|
|
|
|
|
|
|
|
100
|
4000
|
-
|
-
|
-
|
4963
|
3687
|
2799
|
|
|
|
|
|
|
|
|
|
|
|
100
|
5000
|
-
|
-
|
-
|
6307
|
4481
|
3525
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
200
|
25
|
-
|
-
|
-
|
357
|
162
|
100
|
77
|
72
|
72
|
73
|
69
|
57
|
47
|
46
|
46
|
45
|
|
200
|
50
|
-
|
-
|
-
|
575
|
263
|
164
|
126
|
117
|
117
|
119
|
114
|
93
|
76
|
74
|
72
|
70
|
|
200
|
100
|
-
|
-
|
-
|
645
|
336
|
212
|
200
|
209
|
216
|
216
|
212
|
179
|
142
|
132
|
133
|
116
|
|
200
|
200
|
-
|
-
|
-
|
925
|
563
|
358
|
351
|
357
|
350
|
331
|
309
|
251
|
208
|
188
|
190
|
160
|
|
200
|
300
|
-
|
-
|
-
|
1417
|
975
|
620
|
632
|
627
|
597
|
541
|
480
|
376
|
323
|
292
|
288
|
227
|
|
200
|
500
|
-
|
-
|
-
|
1930
|
1476
|
951
|
976
|
940
|
868
|
806
|
678
|
462
|
364
|
327
|
|
|
|
200
|
750
|
-
|
-
|
-
|
2180
|
1696
|
1128
|
1136
|
1092
|
964
|
921
|
780
|
505
|
|
|
|
|
|
200
|
1000
|
-
|
-
|
-
|
2396
|
1895
|
1298
|
1287
|
1230
|
1045
|
1022
|
870
|
|
|
|
|
|
|
200
|
1500
|
-
|
-
|
-
|
2773
|
2187
|
1540
|
1494
|
1425
|
1282
|
1237
|
|
|
|
|
|
|
|
200
|
2000
|
-
|
-
|
-
|
3140
|
2479
|
1768
|
1709
|
1613
|
1448
|
|
|
|
|
|
|
|
|
200
|
3000
|
-
|
-
|
-
|
3926
|
3102
|
2266
|
2165
|
1893
|
|
|
|
|
|
|
|
|
|
200
|
4000
|
-
|
-
|
-
|
5089
|
3816
|
2856
|
|
|
|
|
|
|
|
|
|
|
|
200
|
5000
|
-
|
-
|
-
|
6518
|
4600
|
3518
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
300
|
25
|
-
|
-
|
-
|
344
|
182
|
127
|
90
|
76
|
74
|
73
|
72
|
60
|
53
|
52
|
50
|
49
|
|
300
|
50
|
-
|
-
|
-
|
554
|
294
|
206
|
145
|
123
|
121
|
119
|
117
|
97
|
85
|
84
|
83
|
80
|
|
300
|
100
|
-
|
-
|
-
|
630
|
365
|
234
|
206
|
210
|
215
|
211
|
210
|
184
|
149
|
136
|
136
|
98
|
|
300
|
200
|
-
|
-
|
-
|
915
|
601
|
386
|
370
|
368
|
359
|
339
|
318
|
259
|
213
|
194
|
194
|
185
|
|
300
|
300
|
-
|
-
|
-
|
1416
|
1032
|
662
|
672
|
660
|
622
|
571
|
507
|
386
|
326
|
293
|
286
|
211
|
|
300
|
500
|
-
|
-
|
-
|
1932
|
1554
|
1035
|
1038
|
978
|
853
|
769
|
643
|
450
|
357
|
321
|
|
|
|
300
|
750
|
-
|
-
|
-
|
2173
|
1780
|
1211
|
1188
|
1121
|
949
|
866
|
704
|
460
|
341
|
|
|
|
|
300
|
1000
|
-
|
-
|
-
|
2378
|
1981
|
1377
|
1319
|
1245
|
1029
|
950
|
753
|
|
|
|
|
|
|
300
|
1500
|
-
|
-
|
-
|
2736
|
2271
|
1613
|
1513
|
1433
|
1212
|
1066
|
|
|
|
|
|
|
|
300
|
2000
|
-
|
-
|
-
|
3097
|
2568
|
1838
|
1723
|
1636
|
1326
|
|
|
|
|
|
|
|
|
300
|
3000
|
-
|
-
|
-
|
3902
|
3210
|
2327
|
2163
|
1938
|
|
|
|
|
|
|
|
|
|
300
|
4000
|
-
|
-
|
-
|
5203
|
3931
|
2908
|
2665
|
|
|
|
|
|
|
|
|
|
|
300
|
5000
|
-
|
-
|
-
|
6708
|
4705
|
3507
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
400
|
25
|
-
|
-
|
-
|
336
|
194
|
135
|
94
|
83
|
78
|
76
|
70
|
60
|
56
|
55
|
53
|
50
|
|
400
|
50
|
-
|
-
|
-
|
541
|
312
|
217
|
154
|
133
|
128
|
125
|
113
|
95
|
90
|
86
|
84
|
80
|
|
400
|
100
|
-
|
|
-
|
626
|
389
|
242
|
226
|
229
|
231
|
223
|
215
|
196
|
166
|
150
|
150
|
120
|
|
400
|
200
|
-
|
-
|
-
|
921
|
644
|
425
|
411
|
403
|
371
|
344
|
313
|
276
|
237
|
213
|
208
|
153
|
|
400
|
300
|
-
|
-
|
-
|
1447
|
1105
|
759
|
757
|
727
|
625
|
561
|
486
|
411
|
360
|
320
|
311
|
217
|
|
400
|
500
|
-
|
-
|
-
|
1974
|
1627
|
1144
|
1114
|
1036
|
861
|
726
|
566
|
434
|
356
|
319
|
308
|
|
|
400
|
750
|
-
|
-
|
-
|
2218
|
2156
|
1310
|
1255
|
1170
|
951
|
803
|
619
|
437
|
|
|
|
|
|
400
|
1000
|
-
|
-
|
-
|
2426
|
2068
|
1461
|
1375
|
1287
|
1023
|
863
|
659
|
|
|
|
|
|
|
400
|
1500
|
-
|
-
|
-
|
2786
|
2369
|
1685
|
1659
|
1514
|
1153
|
937
|
|
|
|
|
|
|
|
400
|
2000
|
-
|
-
|
-
|
3161
|
2681
|
1919
|
1919
|
1719
|
1242
|
|
|
|
|
|
|
|
|
400
|
3000
|
-
|
-
|
-
|
4008
|
3339
|
2510
|
2486
|
2008
|
|
|
|
|
|
|
|
|
|
400
|
4000
|
-
|
-
|
-
|
5311
|
4089
|
3024
|
2954
|
|
|
|
|
|
|
|
|
|
|
400
|
5000
|
-
|
-
|
-
|
6863
|
4854
|
3508
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
500
|
25
|
-
|
-
|
466
|
330
|
202
|
141
|
101
|
87
|
83
|
80
|
68
|
58
|
58
|
54
|
53
|
52
|
|
500
|
50
|
-
|
-
|
749
|
530
|
327
|
228
|
163
|
140
|
134
|
129
|
110
|
94
|
94
|
92
|
91
|
90
|
|
500
|
100
|
-
|
-
|
862
|
622
|
412
|
248
|
244
|
244
|
244
|
232
|
220
|
207
|
180
|
163
|
158
|
98
|
|
500
|
200
|
-
|
-
|
1239
|
929
|
682
|
460
|
450
|
437
|
382
|
347
|
311
|
291
|
258
|
231
|
222
|
145
|
|
500
|
300
|
-
|
-
|
1902
|
1473
|
1173
|
849
|
834
|
791
|
629
|
552
|
467
|
434
|
394
|
349
|
330
|
202
|
|
500
|
500
|
-
|
-
|
2527
|
2009
|
1689
|
1245
|
1184
|
1086
|
868
|
688
|
495
|
420
|
356
|
318
|
312
|
243
|
|
500
|
750
|
-
|
-
|
2766
|
2257
|
1931
|
1403
|
1317
|
1217
|
952
|
744
|
540
|
416
|
331
|
293
|
|
|
|
500
|
1000
|
-
|
-
|
2950
|
2468
|
2145
|
1537
|
1426
|
1327
|
1016
|
782
|
574
|
397
|
292
|
|
|
|
|
500
|
1500
|
-
|
-
|
3366
|
2833
|
2459
|
1756
|
1793
|
1588
|
1097
|
818
|
|
|
|
|
|
|
|
500
|
2000
|
-
|
-
|
3812
|
3214
|
2782
|
1993
|
2095
|
1794
|
|
|
|
|
|
|
|
|
|
500
|
3000
|
-
|
-
|
5078
|
4103
|
3454
|
2677
|
2783
|
|
|
|
|
|
|
|
|
|
|
500
|
4000
|
-
|
-
|
7005
|
5410
|
4235
|
3127
|
3217
|
|
|
|
|
|
|
|
|
|
|
500
|
5000
|
-
|
-
|
9345
|
7004
|
4990
|
3506
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
600
|
25
|
-
|
-
|
449
|
325
|
210
|
148
|
107
|
93
|
88
|
84
|
70
|
63
|
63
|
62
|
61
|
54
|
|
600
|
50
|
-
|
-
|
721
|
524
|
337
|
240
|
174
|
150
|
143,
|
135
|
116
|
102
|
101
|
98
|
96
|
95
|
|
600
|
100
|
-
|
-
|
833
|
621
|
431
|
266
|
261
|
259
|
256
|
238
|
218
|
211
|
189
|
168
|
162
|
137
|
|
600
|
200
|
-
|
-
|
1210
|
944
|
729
|
505
|
487
|
458
|
389
|
350
|
306
|
293
|
267
|
237
|
225
|
158
|
|
600
|
300
|
-
|
-
|
1874
|
1522
|
1275
|
947
|
909
|
824
|
630
|
547
|
461
|
437
|
404
|
357
|
333
|
192
|
|
600
|
500
|
-
|
-
|
2500
|
2078
|
1823
|
1383
|
1278
|
1154
|
873
|
684
|
485
|
410
|
359
|
317
|
310
|
238
|
|
600
|
750
|
-
|
-
|
2733
|
2318
|
2056
|
1538
|
1413
|
1258
|
942
|
735
|
524
|
402
|
328
|
290
|
|
|
|
600
|
1000
|
-
|
-
|
2915
|
2519
|
2255
|
1668
|
1519
|
1337
|
994
|
767
|
550
|
379
|
282
|
|
|
|
|
600
|
1500
|
-
|
-
|
3322
|
2890
|
2579
|
1888
|
1840
|
1577
|
1027
|
745
|
|
|
|
|
|
|
|
600
|
2000
|
-
|
-
|
3773
|
3280
|
2914
|
2104
|
2130
|
1770
|
1076
|
|
|
|
|
|
|
|
|
600
|
3000
|
-
|
-
|
5024
|
4169
|
3603
|
2732
|
2781
|
2036
|
|
|
|
|
|
|
|
|
|
600
|
4000
|
-
|
-
|
6921
|
5428
|
4379
|
3199
|
3252
|
|
|
|
|
|
|
|
|
|
|
600
|
5000
|
-
|
-
|
9218
|
6946
|
5005
|
3564
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
700
|
25
|
-
|
-
|
432
|
322
|
215
|
155
|
113
|
98
|
92
|
87
|
74
|
68
|
69
|
68
|
66
|
65
|
|
700
|
50
|
-
|
-
|
693
|
517
|
346
|
250
|
183
|
158
|
149
|
141
|
121
|
110
|
112
|
104
|
108
|
97
|
|
700
|
100
|
-
|
-
|
804
|
621
|
448
|
284
|
276
|
272
|
264
|
242
|
215
|
212
|
197
|
174
|
165
|
94
|
|
700
|
200
|
-
|
-
|
1182
|
959
|
772
|
547
|
520
|
477
|
396
|
351
|
303
|
296
|
276
|
243
|
228
|
126
|
|
700
|
300
|
-
|
-
|
1846
|
1565
|
1366
|
1039
|
975
|
855
|
629
|
542
|
458
|
439
|
412
|
362
|
336
|
178
|
|
700
|
500
|
-
|
-
|
2473
|
2143
|
1945
|
1508
|
1366
|
1217
|
874
|
682
|
474
|
401
|
360
|
319
|
306
|
210
|
|
700
|
750
|
-
|
-
|
2704
|
2376
|
2171
|
1664
|
1500
|
1298
|
933
|
727
|
507
|
390
|
325
|
288
|
276
|
212
|
|
700
|
1000
|
-
|
-
|
2878
|
2564
|
2356
|
1791
|
1604
|
1347
|
971
|
753
|
530
|
360
|
274
|
|
|
|
|
700
|
1500
|
-
|
-
|
3281
|
2941
|
2688
|
2012
|
1882
|
1567
|
958
|
678
|
|
|
|
|
|
|
|
700
|
2000
|
-
|
-
|
3731
|
3340
|
3035
|
2207
|
2163
|
1748
|
993
|
|
|
|
|
|
|
|
|
700
|
3000
|
|
-
|
4972
|
4228
|
3740
|
2782
|
2779
|
2001
|
|
|
|
|
|
|
|
|
|
700
|
4000
|
-
|
-
|
6841
|
5444
|
4512
|
3266
|
3283
|
|
|
|
|
|
|
|
|
|
|
700
|
5000
|
-
|
-
|
9097
|
6888
|
5018
|
3619
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
800
|
25
|
-
|
-
|
416
|
317
|
221
|
161
|
119
|
103
|
96
|
90
|
77
|
76
|
75
|
68
|
67
|
65
|
|
800
|
50
|
-
|
-
|
668
|
511
|
356
|
260
|
193
|
167
|
156
|
146
|
125
|
117
|
121
|
110
|
113
|
95
|
|
800
|
100
|
-
|
-
|
779
|
620
|
465
|
299
|
291
|
284
|
273
|
247
|
213
|
213
|
204
|
181
|
171
|
110
|
|
800
|
200
|
-
|
-
|
1154
|
971
|
812
|
587
|
553
|
496
|
402
|
352
|
300
|
297
|
283
|
250
|
234
|
144
|
|
800
|
300
|
-
|
-
|
1820
|
1606
|
1452
|
1126
|
1040
|
885
|
631
|
537
|
451
|
441
|
420
|
369
|
340
|
170
|
|
800
|
500
|
-
|
-
|
2446
|
2201
|
2060
|
1626
|
1447
|
1276
|
877
|
679
|
465
|
393
|
361
|
322
|
304
|
200
|
|
800
|
750
|
-
|
-
|
2672
|
2427
|
2276
|
1781
|
1583
|
1335
|
924
|
719
|
493
|
375
|
321
|
283
|
271
|
203
|
|
800
|
1000
|
-
|
-
|
2847
|
2608
|
2449
|
1903
|
1687
|
1357
|
950
|
740
|
512
|
343
|
264
|
|
|
|
|
800
|
1500
|
-
|
-
|
3243
|
2988
|
2789
|
2127
|
1923
|
1559
|
898
|
614
|
|
|
|
|
|
|
|
800
|
2000
|
-
|
-
|
3694
|
3395
|
3149
|
2304
|
2193
|
1727
|
918
|
|
|
|
|
|
|
|
|
800
|
3000
|
-
|
-
|
4922
|
4283
|
3869
|
2829
|
2778
|
1969
|
|
|
|
|
|
|
|
|
|
800
|
4000
|
-
|
-
|
6765
|
5459
|
4638
|
3327
|
|
|
|
|
|
|
|
|
|
|
|
800
|
5000
|
-
|
-
|
8983
|
6835
|
5028
|
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
1000
|
25
|
-
|
448
|
387
|
310
|
232
|
171
|
130
|
112
|
103
|
96
|
84
|
84
|
83
|
76
|
74
|
50
|
|
1000
|
50
|
-
|
721
|
622
|
499
|
373
|
275
|
210
|
182
|
167
|
155
|
133
|
133
|
132
|
123
|
119
|
81
|
|
1000
|
100
|
-
|
819
|
731
|
619
|
494
|
328
|
318
|
306
|
288
|
255
|
208
|
216
|
217
|
190
|
178
|
88
|
|
1000
|
200
|
-
|
1184
|
1106
|
995
|
885
|
658
|
611
|
529
|
414
|
355
|
294
|
301
|
298
|
262
|
242
|
122
|
|
1000
|
300
|
-
|
1824
|
1775
|
1680
|
1606
|
1279
|
1156
|
938
|
631
|
529
|
443
|
446
|
435
|
381
|
348
|
168
|
|
1000
|
500
|
-
|
2437
|
2398
|
2306
|
2263
|
1840
|
1596
|
1388
|
883
|
676
|
447
|
377
|
366
|
322
|
302
|
187
|
|
1000
|
750
|
-
|
2662
|
2618
|
2521
|
2463
|
1997
|
1733
|
1404
|
911
|
707
|
468
|
352
|
316
|
279
|
262
|
185
|
|
1000
|
1000
|
-
|
2835
|
2787
|
2685
|
2616
|
2110
|
1836
|
1374
|
913
|
717
|
476
|
311
|
249
|
220
|
211
|
177
|
|
1000
|
1500
|
-
|
3273
|
3173
|
3073
|
2969
|
2336
|
1999
|
1544
|
787
|
501
|
|
|
|
|
|
|
|
1000
|
2000
|
-
|
3926
|
3627
|
3497
|
3350
|
2482
|
2251
|
1691
|
|
|
|
|
|
|
|
|
|
1000
|
3000
|
-
|
5761
|
4834
|
4381
|
4102
|
2917
|
2779
|
|
|
|
|
|
|
|
|
|
|
1000
|
4000
|
-
|
8037
|
6633
|
5484
|
4864
|
3442
|
|
|
|
|
|
|
|
|
|
|
|
1000
|
5000
|
-
|
10688
|
8783
|
6737
|
5049
|
|
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
2000
|
25
|
369
|
344
|
303
|
259
|
207
|
153
|
118
|
104
|
95
|
89
|
86
|
87
|
91
|
81
|
74
|
38
|
|
2000
|
50
|
594
|
553
|
488
|
415
|
333
|
247
|
192
|
167
|
154
|
143
|
138
|
140
|
146
|
130
|
123
|
62
|
|
2000
|
100
|
667
|
630
|
575
|
511
|
433
|
293
|
283
|
276
|
263
|
243
|
220
|
213
|
196
|
172
|
158
|
95
|
|
2000
|
200
|
953
|
918
|
872
|
815
|
751
|
567
|
533
|
491
|
398
|
372
|
338
|
312
|
270
|
236
|
215
|
111
|
|
2000
|
300
|
1449
|
1422
|
1403
|
1366
|
1334
|
1079
|
996
|
886
|
639
|
602
|
549
|
462
|
396
|
344
|
311
|
130
|
|
2000
|
500
|
1949
|
1923
|
1906
|
1868
|
1861
|
1620
|
1403
|
1256
|
875
|
814
|
651
|
482
|
396
|
344
|
311
|
148
|
|
2000
|
750
|
2143
|
2107
|
2085
|
2041
|
2023
|
1754
|
1528
|
1278
|
908
|
811
|
627
|
445
|
350
|
300
|
273
|
152
|
|
2000
|
1000
|
2295
|
2248
|
2220
|
2173
|
2142
|
1850
|
1620
|
1257
|
916
|
783
|
576
|
385
|
282
|
244
|
221
|
134
|
|
2000
|
1500
|
2789
|
2605
|
2536
|
2481
|
2424
|
2047
|
1702
|
1348
|
866
|
573
|
390
|
248
|
218
|
184
|
167
|
122
|
|
2000
|
2000
|
3613
|
3153
|
2894
|
2816
|
2714
|
2131
|
1811
|
1438
|
841
|
468
|
294
|
193
|
|
|
|
|
|
2000
|
3000
|
5570
|
4735
|
3946
|
3527
|
3297
|
2412
|
2136
|
1571
|
759
|
444
|
|
|
|
|
|
|
|
2000
|
4000
|
7625
|
6610
|
5549
|
4473
|
3896
|
2785
|
2577
|
1700
|
|
|
|
|
|
|
|
|
|
2000
|
5000
|
10011
|
8748
|
7415
|
5692
|
4074
|
3061
|
2847
|
|
|
|
|
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
3000
|
25
|
340
|
310
|
278
|
251
|
215
|
159
|
126
|
110
|
105
|
100
|
99
|
98
|
97
|
93
|
89
|
48
|
|
3000
|
50
|
547
|
498
|
448
|
404
|
346
|
256
|
203
|
177
|
162
|
152
|
158
|
164
|
172
|
152
|
142
|
70
|
|
3000
|
100
|
616
|
570
|
530
|
494
|
440
|
306
|
295
|
290
|
276
|
263
|
257
|
239
|
207
|
181
|
164
|
100
|
|
3000
|
200
|
889
|
844
|
815
|
790
|
749
|
580
|
548
|
526
|
443
|
432
|
416
|
350
|
287
|
250
|
226
|
95
|
|
3000
|
300
|
1367
|
1329
|
1327
|
1326
|
1319
|
1091
|
1017
|
967
|
744
|
741
|
709
|
548
|
424
|
367
|
330
|
134
|
|
3000
|
500
|
1876
|
1856
|
1841
|
1826
|
1787
|
1614
|
1445
|
1319
|
1078
|
977
|
827
|
648
|
488
|
418
|
374
|
158
|
|
3000
|
750
|
2092
|
2073
|
2050
|
2027
|
1979
|
1805
|
1616
|
1396
|
1166
|
982
|
806
|
601
|
441
|
371
|
331
|
165
|
|
3000
|
1000
|
2267
|
2301
|
2261
|
2225
|
2157
|
1950
|
1708
|
1440
|
1155
|
941
|
714
|
510
|
362
|
304
|
275
|
162
|
|
3000
|
1500
|
2803
|
2740
|
2618
|
2537
|
2416
|
2124
|
1807
|
1485
|
1109
|
796
|
545
|
365
|
273
|
231
|
206
|
115
|
|
3000
|
2000
|
3685
|
3561
|
3247
|
3015
|
2763
|
2317
|
1925
|
1529
|
1051
|
669
|
415
|
277
|
195
|
162
|
141
|
|
|
3000
|
3000
|
5758
|
5107
|
4405
|
3814
|
3269
|
2616
|
2141
|
1605
|
1011
|
630
|
419
|
276
|
155
|
129
|
|
|
|
3000
|
4000
|
7964
|
7082
|
6068
|
4933
|
3888
|
2998
|
2474
|
1748
|
1127
|
819
|
570
|
369
|
184
|
|
|
|
|
3000
|
5000
|
10534
|
9408
|
8206
|
6339
|
4360
|
3306
|
2961
|
1842
|
1303
|
1086
|
753
|
483
|
|
|
|
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
5000
|
25
|
340
|
313
|
291
|
269
|
240
|
182
|
148
|
131
|
120
|
112
|
114
|
119
|
82
|
74
|
71
|
47
|
|
5000
|
50
|
546
|
504
|
467
|
433
|
387
|
294
|
240
|
211
|
194
|
179
|
183
|
192
|
134
|
120
|
116
|
67
|
|
5000
|
100
|
628
|
588
|
556
|
526
|
482
|
351
|
336
|
330
|
321
|
303
|
295
|
290
|
252
|
220
|
201
|
78
|
|
5000
|
200
|
929
|
881
|
854
|
829
|
793
|
630
|
597
|
588
|
555
|
512
|
488
|
458
|
375
|
325
|
290
|
134
|
|
5000
|
300
|
1431
|
1381
|
1375
|
1371
|
1361
|
1139
|
1066
|
1033
|
875
|
823
|
781
|
659
|
508
|
439
|
391
|
153
|
|
5000
|
500
|
1998
|
2005
|
1982
|
1961
|
1907
|
1738
|
1625
|
1498
|
1371
|
1195
|
1044
|
835
|
636
|
541
|
479
|
180
|
|
5000
|
750
|
2278
|
2288
|
2251
|
2210
|
2137
|
1984
|
1801
|
1676
|
1458
|
1277
|
1038
|
797
|
580
|
486
|
425
|
164
|
|
5000
|
1000
|
2515
|
2587
|
2524
|
2460
|
2351
|
2144
|
1939
|
1736
|
1483
|
1227
|
944
|
673
|
483
|
399
|
347
|
158
|
|
5000
|
1500
|
3165
|
3141
|
2970
|
2834
|
2639
|
2338
|
2047
|
1781
|
1442
|
1066
|
725
|
500
|
368
|
315
|
283
|
155
|
|
5000
|
2000
|
4203
|
4161
|
3770
|
3423
|
3029
|
2525
|
2137
|
1785
|
1310
|
858
|
540
|
366
|
273
|
231
|
222
|
111
|
|
5000
|
3000
|
6558
|
5925
|
5138
|
4361
|
3557
|
2805
|
2290
|
1791
|
1200
|
758
|
491
|
336
|
208
|
147
|
122
|
77
|
|
5000
|
4000
|
9003
|
8087
|
6952
|
5589
|
4190
|
3170
|
2580
|
1896
|
1270
|
909
|
655
|
430
|
226
|
145
|
111
|
55
|
|
5000
|
5000
|
11755
|
10521
|
9199
|
7090
|
4611
|
3415
|
3096
|
2042
|
1420
|
1251
|
879
|
563
|
234
|
169
|
105
|
34
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
6000
|
25
|
351
|
327
|
306
|
285
|
259
|
195
|
162
|
141
|
127
|
119
|
102
|
86
|
83
|
75
|
71
|
41
|
|
6000
|
50
|
565
|
526
|
493
|
460
|
417
|
315
|
260
|
227
|
207
|
192
|
165
|
139
|
134
|
121
|
118
|
74
|
|
6000
|
100
|
654
|
615
|
584
|
555
|
514
|
375
|
356
|
348
|
340
|
323
|
265
|
242
|
232
|
203
|
184
|
95
|
|
6000
|
200
|
974
|
922
|
893
|
869
|
833
|
667
|
629
|
616
|
593
|
553
|
467
|
425
|
373
|
323
|
289
|
120
|
|
6000
|
300
|
1538
|
1466
|
1447
|
1433
|
1417
|
1216
|
1139
|
1120
|
1065
|
980
|
846
|
768
|
628
|
540
|
473
|
153
|
|
6000
|
500
|
2199
|
2164
|
2109
|
2062
|
1987
|
1842
|
1679
|
1613
|
1471
|
1327
|
1126
|
952
|
749
|
646
|
604
|
320
|
|
6000
|
750
|
2578
|
2510
|
2420
|
2337
|
2237
|
2052
|
1889
|
1730
|
1570
|
1367
|
1138
|
897
|
673
|
566
|
511
|
274
|
|
6000
|
1000
|
2898
|
2877
|
2746
|
2613
|
2442
|
2223
|
2000
|
1807
|
1604
|
1327
|
1027
|
748
|
535
|
439
|
377
|
174
|
|
6000
|
1500
|
3697
|
3537
|
3273
|
3030
|
2733
|
2370
|
2114
|
1887
|
1548
|
1167
|
796
|
542
|
395
|
334
|
344
|
171
|
|
6000
|
2000
|
4913
|
4678
|
4181
|
3690
|
3084
|
2524
|
2135
|
1829
|
1406
|
913
|
566
|
390
|
287
|
241
|
242
|
154
|
|
6000
|
3000
|
7339
|
6467
|
5593
|
4632
|
3576
|
2689
|
2177
|
1757
|
1210
|
758
|
487
|
336
|
219
|
160
|
123
|
103
|
|
6000
|
4000
|
9554
|
8407
|
7188
|
5692
|
4076
|
2890
|
2317
|
1765
|
1206
|
862
|
608
|
408
|
229
|
153
|
115
|
74
|
|
6000
|
5000
|
11669
|
10409
|
8945
|
6708
|
4305
|
2716
|
2504
|
1880
|
1264
|
1215
|
812
|
507
|
229
|
166
|
103
|
38
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
8000
|
25
|
415
|
389
|
366
|
346
|
321
|
218
|
185
|
168
|
158
|
149
|
128
|
111
|
107
|
95
|
87
|
41
|
|
8000
|
50
|
666
|
625
|
589
|
558
|
517
|
352
|
296
|
271
|
254
|
240
|
208
|
178
|
172
|
152
|
144
|
76
|
|
8000
|
100
|
772
|
726
|
690
|
662
|
622
|
456
|
422
|
411
|
404
|
392
|
321
|
280
|
283
|
245
|
221
|
82
|
|
8000
|
200
|
1159
|
1085
|
1040
|
1013
|
973
|
794
|
718
|
700
|
683
|
655
|
531
|
466
|
435
|
376
|
331
|
99
|
|
8000
|
300
|
1838
|
1717'
|
1659
|
1635
|
1605
|
1425
|
1267
|
1232
|
1202
|
1142
|
919
|
808
|
707
|
607
|
529
|
148
|
|
8000
|
500
|
2645
|
2508
|
2395
|
2305
|
2224
|
2030
|
1868
|
1706
|
1575
|
1355
|
1125
|
942
|
764
|
671
|
680
|
394
|
|
8000
|
750
|
3110
|
2916
|
2752
|
2609
|
2457
|
2283
|
2018
|
1818
|
1600
|
1340
|
1086
|
862
|
656
|
560
|
544
|
442
|
|
8000
|
1000
|
3493
|
3351
|
3124
|
2892
|
2649
|
2351
|
2077
|
1836
|
1544
|
1251
|
941
|
684
|
483
|
395
|
359
|
216
|
|
8000
|
1500
|
4432
|
4100
|
3718
|
3335
|
2870
|
2457
|
2108
|
1809
|
1476
|
1058
|
707
|
467
|
319
|
253
|
169
|
297
|
|
8000
|
2000
|
5748
|
5316
|
4706
|
4017
|
3229
|
2526
|
2105
|
1753
|
1302
|
835
|
500
|
327
|
223
|
178
|
134
|
123
|
|
8000
|
3000
|
8074
|
7004
|
6065
|
4956
|
3639
|
2644
|
2071
|
1622
|
1140
|
676
|
421
|
285
|
186
|
137
|
108
|
100
|
|
8000
|
4000
|
9753
|
8494
|
7310
|
5772
|
4036
|
2700
|
2037
|
1566
|
1059
|
721
|
497
|
335
|
201
|
139
|
106
|
72
|
|
8000
|
5000
|
10797
|
9690
|
8409
|
6405
|
4238
|
2259
|
1808
|
1513
|
1016
|
842
|
593
|
372
|
195
|
143
|
91
|
38
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
10000
|
25
|
503
|
475
|
450
|
428
|
402
|
285
|
237
|
213
|
198
|
189
|
168
|
146
|
138
|
120
|
109
|
47
|
|
10000
|
50
|
808
|
764
|
722
|
686
|
646
|
459
|
381
|
342
|
319
|
305
|
271
|
237
|
222
|
195
|
179
|
76
|
|
10000
|
100
|
934
|
883
|
835
|
799
|
760
|
576
|
522
|
501
|
487
|
483
|
405
|
339
|
321
|
279
|
248
|
82
|
|
10000
|
200
|
1395
|
1311
|
1235
|
1187
|
1156
|
966
|
841
|
831
|
792
|
743
|
573
|
454
|
426
|
368
|
327
|
88
|
|
10000
|
300
|
2207
|
2061
|
1936
|
1870
|
1858
|
1686
|
1420
|
1437
|
1353
|
1212
|
856
|
640
|
595
|
512
|
449
|
140
|
|
10000
|
500
|
3159
|
2920
|
2738
|
2590
|
2427
|
2234
|
1924
|
1787
|
1556
|
1281
|
971
|
762
|
614
|
536
|
484
|
205
|
|
10000
|
750
|
3691
|
3366
|
3118
|
2883
|
2668
|
2375
|
2106
|
1811
|
1516
|
1164
|
882
|
671
|
503
|
431
|
386
|
192
|
|
10000
|
1000
|
4128
|
3840
|
3510
|
3161
|
2792
|
2456
|
2085
|
1744
|
1386
|
1001
|
724
|
512
|
361
|
297
|
260
|
123
|
|
10000
|
1500
|
5138
|
4638
|
4131
|
3579
|
2995
|
2444
|
2033
|
1648
|
1217
|
814
|
534
|
357
|
235
|
189
|
150
|
110
|
|
10000
|
2000
|
6473
|
5846
|
5124
|
4285
|
3277
|
2541
|
1985
|
1538
|
1073
|
642
|
398
|
260
|
173
|
137
|
115
|
97
|
|
10000
|
3000
|
8536
|
7315
|
6355
|
5111
|
3674
|
2591
|
1940
|
1418
|
939
|
556
|
350
|
244
|
160
|
122
|
103
|
80
|
|
10000
|
4000
|
9604
|
8252
|
7175
|
5691
|
3893
|
2575
|
1822
|
1354
|
916
|
589
|
416
|
282
|
176
|
126
|
92
|
57
|
|
10000
|
5000
|
9564
|
8616
|
7649
|
6038
|
3640
|
2065
|
1332
|
1320
|
981
|
670
|
525
|
325
|
173
|
128
|
83
|
38
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
12000
|
25
|
588
|
559
|
532
|
507
|
481
|
364
|
295
|
260
|
241
|
233
|
210
|
188
|
172
|
150
|
133
|
42
|
|
12000
|
50
|
942
|
898
|
856
|
814
|
772
|
585
|
475
|
419
|
387
|
377
|
338
|
302
|
276
|
242
|
216
|
77
|
|
12000
|
100
|
1081
|
1033
|
982
|
932
|
886
|
705
|
620
|
584
|
569
|
576
|
493
|
372
|
324
|
281
|
250
|
80
|
|
12000
|
200
|
1595
|
1514
|
1431
|
1358
|
1299
|
1096
|
988
|
950
|
896
|
802
|
620
|
480
|
402
|
347
|
309
|
104
|
|
12000
|
300
|
2499
|
2358
|
2216
|
2101
|
2022
|
1799
|
1653
|
1618
|
1486
|
1186
|
815
|
655
|
516
|
446
|
397
|
223
|
|
12000
|
500
|
3505
|
3219
|
3005
|
2789
|
2548
|
2207
|
1948
|
1694
|
1479
|
1134
|
825
|
612
|
461
|
395
|
296
|
207
|
|
12000
|
750
|
4036
|
3639
|
3343
|
3011
|
2645
|
2321
|
1926
|
1657
|
1319
|
969
|
685
|
495
|
354
|
299
|
243
|
142
|
|
12000
|
1000
|
4459
|
4093
|
3690
|
3235
|
2737
|
2303
|
1925
|
1549
|
1150
|
766
|
524
|
370
|
258
|
216
|
180
|
137
|
|
12000
|
1500
|
5543
|
4885
|
4275
|
3599
|
2889
|
2347
|
1868
|
1423
|
978
|
591
|
391
|
269
|
189
|
155
|
148
|
133
|
|
12000
|
2000
|
6789
|
5987
|
5206
|
4195
|
3223
|
2444
|
1893
|
1348
|
864
|
493
|
312
|
227
|
156
|
128
|
117
|
101
|
|
12000
|
3000
|
8389
|
7120
|
6146
|
4908
|
3517
|
2567
|
1855
|
1281
|
788
|
461
|
311
|
219
|
149
|
118
|
101
|
83
|
|
12000
|
4000
|
8736
|
7451
|
6515
|
5221
|
3635
|
2504
|
1750
|
1216
|
802
|
506
|
358
|
252
|
162
|
120
|
92
|
63
|
|
12000
|
5000
|
7687
|
6964
|
6321
|
5276
|
3213
|
1969
|
1225
|
1105
|
839
|
484
|
393
|
295
|
168
|
124
|
81
|
37
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
14000
|
25
|
647
|
623
|
601
|
576
|
552
|
439
|
353
|
304
|
271
|
253
|
233
|
213
|
179
|
157
|
139
|
42
|
|
14000
|
50
|
1039
|
1001
|
964
|
925
|
887
|
705
|
568
|
490
|
436
|
406
|
375
|
343
|
290
|
253
|
227
|
78
|
|
14000
|
100
|
1176
|
1136
|
1097
|
1050
|
1005
|
825
|
706
|
645
|
586
|
545
|
437
|
352
|
290
|
252
|
226
|
84
|
|
14000
|
200
|
1690
|
1631
|
1573
|
1504
|
1441
|
1253
|
1089
|
993
|
812
|
701
|
539
|
432
|
342
|
297
|
267
|
101
|
|
14000
|
300
|
2581
|
2492
|
2402
|
2290
|
2198
|
2015
|
1771
|
1612
|
1198
|
951
|
695
|
554
|
413
|
359
|
327
|
152
|
|
14000
|
500
|
3439
|
3240'
|
3069
|
2840
|
2536
|
2223
|
1853
|
1600
|
1272
|
975
|
691
|
502
|
366
|
315
|
262
|
179
|
|
14000
|
750
|
3867
|
3577
|
3316
|
2975
|
2510
|
2113
|
1781
|
1431
|
1143
|
815
|
573
|
390
|
282
|
239
|
224
|
163
|
|
14000
|
1000
|
4190
|
3957
|
3607
|
3084
|
2541
|
2086
|
1698
|
1336
|
974
|
633
|
417
|
295
|
212
|
183
|
173
|
135
|
|
14000
|
1500
|
5384
|
4686
|
4087
|
3366
|
2639
|
2125
|
1686
|
1258
|
841
|
493
|
314
|
228
|
169
|
146
|
144
|
139
|
|
14000
|
2000
|
6453
|
5596
|
4795
|
3830
|
2900
|
2298
|
1771
|
1259
|
800
|
443
|
287
|
204
|
150
|
125
|
117
|
120
|
|
14000
|
3000
|
7550
|
6328
|
5454
|
4252
|
3166
|
2406
|
1828
|
1256
|
786
|
480
|
308
|
217
|
147
|
116
|
102
|
92
|
|
14000
|
4000
|
7084
|
6131
|
5386
|
4360
|
3185
|
2393
|
1763
|
1228
|
819
|
539
|
368
|
246
|
156
|
115
|
89
|
66
|
|
14000
|
5000
|
5339
|
4781
|
4523
|
4040
|
2680
|
2027
|
1405
|
1046
|
790
|
574
|
364
|
256
|
152
|
114
|
77
|
40
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
16000
|
25
|
654
|
633
|
614
|
592
|
572
|
489
|
394
|
335
|
273
|
237
|
209
|
175
|
133
|
118
|
109
|
43
|
|
16000
|
50
|
1051
|
1017
|
985
|
951
|
919
|
783
|
632
|
539
|
438
|
381
|
335
|
282
|
217
|
191
|
174
|
79
|
|
16000
|
100
|
1174
|
1137
|
1103
|
1064
|
1025
|
898
|
767
|
688
|
561
|
495
|
376
|
307
|
237
|
208
|
188
|
86
|
|
16000
|
200
|
1644
|
1580
|
1530
|
1476
|
1414
|
1284
|
1145
|
1020
|
803
|
639
|
462
|
369
|
298
|
259
|
236
|
103
|
|
16000
|
300
|
2455
|
2344
|
2264
|
2184
|
2081
|
1953
|
1810
|
1603
|
1225
|
879
|
596
|
465
|
393
|
343
|
316
|
137
|
|
16000
|
500
|
3178
|
2868
|
2714
|
2527
|
2255
|
1950
|
1694
|
1400
|
1128
|
854
|
601
|
433
|
334
|
295
|
264
|
161
|
|
16000
|
750
|
3460
|
3075
|
2864
|
2566
|
2172
|
1817
|
1493
|
1224
|
964
|
714
|
488
|
341
|
250
|
222
|
219
|
194
|
|
16000
|
1000
|
3652
|
3351
|
3053
|
2672
|
2145
|
1764
|
1440
|
1108
|
833
|
549
|
360
|
247
|
187
|
166
|
162
|
159
|
|
16000
|
1500
|
4455
|
3910
|
3456
|
2852
|
2287
|
1834
|
1473
|
1098
|
760
|
437
|
267
|
192
|
147
|
131
|
140
|
131
|
|
16000
|
2000
|
5018
|
4583
|
4015
|
3223
|
2533
|
2044
|
1639
|
1208
|
786
|
455
|
268
|
190
|
137
|
119
|
114
|
122
|
|
16000
|
3000
|
6024
|
5140
|
4450
|
3544
|
2738
|
2211
|
1754
|
1277
|
862
|
522
|
347
|
233
|
152
|
117
|
106
|
94
|
|
16000
|
4000
|
5835
|
4900
|
4322
|
3557
|
2705
|
2198
|
1742
|
1296
|
890
|
617
|
415
|
277
|
165
|
115
|
86
|
67
|
|
16000
|
5000
|
4467
|
3805
|
3717
|
3417
|
2199
|
1909
|
1498
|
1163
|
861
|
627
|
407
|
259
|
133
|
102
|
71
|
41
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
18000
|
25
|
573
|
556
|
538
|
522
|
505
|
446
|
358
|
302
|
255
|
237
|
206
|
165
|
132
|
117
|
107
|
44
|
|
18000
|
50
|
920
|
892
|
864
|
838
|
811
|
718
|
575
|
486
|
411
|
382
|
333
|
266
|
214
|
189
|
173
|
81
|
|
18000
|
100
|
989
|
956
|
926
|
894
|
859
|
766
|
623
|
542
|
465
|
445
|
363
|
293
|
253
|
221
|
200
|
101
|
|
18000
|
200
|
1283
|
1221
|
1171
|
1120
|
1055
|
947
|
807
|
708
|
602
|
539
|
428
|
343
|
304
|
265
|
241
|
126
|
|
18000
|
300
|
1771
|
1663
|
1576
|
1491
|
1373
|
1240
|
1117
|
988
|
836
|
692
|
526
|
420
|
385
|
335
|
309
|
158
|
|
18000
|
500
|
1937
|
1941
|
1844
|
1735
|
1555
|
1369
|
1181
|
1029
|
869
|
690
|
505
|
375
|
306
|
276
|
254
|
165
|
|
18000
|
750
|
2102
|
2035
|
1901
|
1741
|
1503
|
1273
|
1108
|
935
|
781
|
599
|
411
|
288
|
221
|
199
|
200
|
174
|
|
18000
|
1000
|
2217
|
2215
|
2040
|
1796
|
1513
|
1253
|
1057
|
882
|
695
|
479
|
310
|
211
|
159
|
142
|
147
|
132
|
|
18000
|
1500
|
2941
|
2693
|
2387
|
2039
|
1652
|
1371
|
1161
|
916
|
673
|
424
|
249
|
168
|
142
|
129
|
131
|
124
|
|
18000
|
2000
|
3548
|
3216
|
2834
|
2342
|
1907
|
1585
|
1333
|
1055
|
769
|
457
|
280
|
189
|
150
|
125
|
121
|
115
|
|
18000
|
3000
|
4450
|
3624
|
3134
|
2566
|
2061
|
1719
|
1445
|
1155
|
834
|
567
|
381
|
264
|
161
|
118
|
108
|
99
|
|
18000
|
4000
|
4316
|
3474
|
3036
|
2510
|
2032
|
1732
|
1482
|
1179
|
887
|
628
|
461
|
328
|
182
|
112
|
92
|
71
|
|
18000
|
5000
|
3349
|
2851
|
2607
|
2222
|
1672
|
1573
|
1349
|
1159
|
898
|
634
|
485
|
365
|
152
|
106
|
76
|
43
|
|
Р,
кПа
|
G, кг/м2с
|
Х =
-0,5
|
Х =
-0,4
|
X =
-0,3
|
X =
-0,2
|
Х =
-0,1
|
Х = 0,0
|
Х = 0,1
|
Х = 0,2
|
Х = 0,3
|
Х = 0,4
|
Х = 0,5
|
Х = 0,6
|
Х = 0,7
|
Х = 0,8
|
Х = 0,9
|
Х =
1,0
|
|
20000
|
25
|
445
|
438
|
431
|
422
|
393
|
346
|
306
|
285
|
224
|
178
|
148
|
126
|
103
|
90
|
85
|
45
|
|
20000
|
50
|
716
|
702
|
694
|
678
|
632
|
556
|
492
|
459
|
360
|
286
|
237
|
204
|
167
|
149
|
142
|
83
|
|
20000
|
100
|
796
|
785
|
782
|
766
|
691
|
596
|
518
|
496
|
381
|
289
|
244
|
233
|
215
|
190
|
176
|
90
|
|
20000
|
200
|
951
|
933
|
929
|
915
|
824
|
707
|
581
|
538
|
447
|
341
|
279
|
271
|
256
|
225
|
210
|
150
|
|
20000
|
300
|
1207
|
1176
|
938
|
911
|
842
|
728
|
611
|
601
|
555
|
423
|
335
|
332
|
323
|
285
|
265
|
167
|
|
20000
|
500
|
1160
|
1192
|
941
|
914
|
859
|
735
|
625
|
605
|
571
|
472
|
314
|
266
|
246
|
221
|
220
|
196
|
|
20000
|
750
|
1146
|
1054
|
972
|
908
|
819
|
699
|
623
|
623
|
549
|
419
|
279
|
209
|
178
|
162
|
160
|
159
|
|
20000
|
1000
|
1196
|
1087
|
978
|
885
|
767
|
653
|
608
|
624
|
518
|
363
|
243
|
153
|
121
|
117
|
111
|
102
|
|
20000
|
1500
|
1631
|
1478
|
1327
|
1176
|
962
|
818
|
836
|
669
|
538
|
396
|
204
|
135
|
110
|
105
|
100
|
98
|
|
20000
|
2000
|
1946
|
1714
|
1508
|
1309
|
1051
|
878
|
834
|
760
|
651
|
382
|
207
|
136
|
110
|
99
|
96
|
93
|
|
20000
|
3000
|
2016
|
1732
|
1551
|
1306
|
1014
|
835
|
721
|
748
|
683
|
499
|
348
|
237
|
111
|
96
|
95
|
90
|
|
20000
|
4000
|
1854
|
1678
|
1503
|
1267
|
1016
|
906
|
934
|
790
|
676
|
545
|
412
|
328
|
144
|
115
|
91
|
60
|
|
20000
|
5000
|
1995
|
1880
|
1650
|
1370
|
1164
|
1067
|
1008
|
893
|
802
|
584
|
452
|
372
|
160
|
119
|
80
|
37
|
![]() - средняя скорость
теплоносителя в канале, м/с.
- средняя скорость
теплоносителя в канале, м/с.![]() - средняя скорость потока,
к которой отнесен коэффициент местного гидравлического сопротивления, м/с.
- средняя скорость потока,
к которой отнесен коэффициент местного гидравлического сопротивления, м/с.![]() (
(![]() - средняя по сечению
скорость).
- средняя по сечению
скорость).![]() ; dг = 4F/П
- гидравлический диаметр, м; F - площадь, м2; П - периметр,
м).
; dг = 4F/П
- гидравлический диаметр, м; F - площадь, м2; П - периметр,
м).![]() ; dг = 4F/П
- гидравлический диаметр, м;
; dг = 4F/П
- гидравлический диаметр, м;![]() ;
;![]() составляет ±6 %.
составляет ±6 %.![]() - относительная толщина
пограничного слоя, зависящая от продольной координаты х;
- относительная толщина
пограничного слоя, зависящая от продольной координаты х;