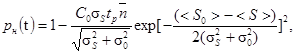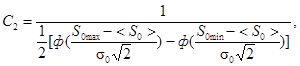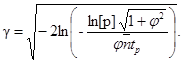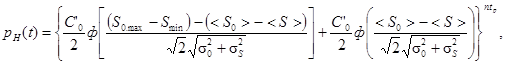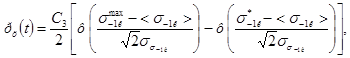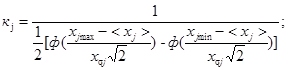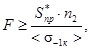РУКОВОДЯЩИЙ ТЕХНИЧЕСКИЙ МАТЕРИАЛ
КРАНЫ ГРУЗОПОДЪЕМНЫЕ
РАСЧЕТ ВЕРОЯТНОСТИ
БЕЗОТКАЗНОЙ РАБОТЫ ЭЛЕМЕНТОВ
РТМ 24.090.25-76
РАЗРАБОТАН И ВНЕСЕН Всесоюзным научно-исследовательским и проектно-конструкторским институтом подъемно-транспортного машиностроения, погрузочно-разгрузочного и складского оборудования и контейнеров (ВНИИПТмаш)
Директор ВНИИПТмаш А.X. Комашенко
Заведующий отделом стандартизации А.С. Оболенский
Руководитель темы И.О. Спицына
Руководитель и исполнитель В.И. Брауде (Ленинградский институт водного транспорта)
Исполнитель Е.Н. Андрианов (Ленинградский институт водного транспорта)
ПОДГОТОВЛЕН К УТВЕРЖДЕНИЮ Главным управлением подъемно-транспортного машиностроения
Главный инженер В.К. Пирогов
УТВЕРЖДЕН Министерством тяжелого и транспортного машиностроения
ВВЕДЕН В ДЕЙСТВИЕ Распоряжением Министерства тяжелого и транспортного машиностроения от 9 февраля 1976 г. № ГС-002/1086.
РУКОВОДЯЩИЙ ТЕХНИЧЕСКИЙ МАТЕРИАЛ
|
КРАНЫ
ГРУЗОПОДЪЕМНЫЕ. |
РТМ 24.090.25-76 |
|
Вводится впервые |
Распоряжением Министерства тяжелого и транспортного машиностроения от 9 февраля 1976 г. № ГС 002/1086 данный руководящий технический материал утвержден в качестве рекомендуемого.
Настоящий РТМ распространяется на механизмы и металлоконструкции кранов и содержит описание методов расчета вероятности безотказной работы отдельных элементов и их групп.
Вероятность безотказной работы определяется по условию непревышения нагрузкой (напряжением) опасного уровня и по условию сохранения циклической прочности. Расчет выполняется на основе полученных в результате натурных тензометричёских испытаний или статистического моделирования данных о представительных реализациях или статистических распределениях действующих нагрузок (напряжений), а также необходимых данных о законах распределения опасного уровня нагрузок (напряжений). Статистические характеристики действующих нагрузок (напряжений) могут быть определены аналитически.
Расчетная вероятность безотказной работы сопоставляется с нормативной. Время, в течение которого должна обеспечиваться вероятность безотказной работы, устанавливается на основе минимизации средней суммы приведенных годовых затрат или по данным эксплуатации лучших образцов кранов.
1. ОБЩИЕ ПОЛОЖЕНИЯ РАСЧЕТА
1.1. Эксплуатационные нагрузки (напряжения) и опасный уровень нагрузок (напряжений) элементов кранов представляют собой случайные процессы или случайные величины, поэтому показатели надежности элементов имеют вероятностный характер.
1.2. Элементы кранов в зависимости от степени ответственности делятся на две группы. К первой группе относятся элементы, отказ которых имеет аварийные последствия. В качестве их показателя надежности принимается вероятность безотказной работы p (t) за расчетное время tp. Остальные элементы образуют вторую группу. Их отказ приводит к экономическим потерям, и в качестве показателя надежности этих элементов принимается средний ресурс.
1.3. Для элементов первой группы должно выполняться условие:
p (t = tp) ³ [p], (1)
где t - текущее время;
[p] - нормированное значение вероятности безотказной работы, которое устанавливается путем анализа надежности элементов лучших образцов кранов и сопоставления с нормированными показателями надежности элементов машин других типов.
При отсутствии этих данных рекомендуется принимать для кранов общего назначения:
[р] ³ 0,99. (2)
1.4. Отказ системы, состоящей из последовательно соединенных элементов, происходит при отказе любого из них.
Вероятность безотказной работы системы, состоящей из к последовательно соединенных элементов определяется по формуле
![]() (3)
(3)
где pj (t) - вероятность безотказной работы элемента j.
Отказ системы, состоящей из параллельно соединенных элементов, происходит в случае отказа всех элементов. При параллельном соединении п элементов и неизменной вероятности безотказной работы оставшихся элементов (после отказа части из них), общая вероятность безотказной работы системы определяется по зависимости
![]() (4)
(4)
где pj - вероятность безотказной работы элемента j.
1.5. Вероятность безотказной работы j-того элемента, отказ которого может возникнуть из-за превышения нагрузкой (напряжением) опасного уровня или накопления усталостных повреждений определяется по формуле
pj(t) = pн(t)pц(t), (5)
где рн(t) - вероятность безотказной работы по условию непревышения нагрузкой (напряжением) опасного уровня;
рц(t) - вероятность безотказной работы по условию сохранения циклической прочности.
1.6. Расчетное определение вероятности безотказной работы ограничивается областью
р(t) £ 0,9999. (6)
1.7. Расчет вероятности безотказной работы элементов и систем выполняется на стадии технического проектирования.
В случае отсутствия статистических данных по нагрузкам и напряжениям допускается расчетное определение вероятности безотказной работы по результатам натурных испытаний опытных образцов кранов и их элементов.
2. РАСЧЕТ ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ ЭЛЕМЕНТОВ КРАНОВ рн(t) ПО УСЛОВИЮ НЕПРЕВЫШЕНИЯ ДЕЙСТВУЮЩЕЙ НАГРУЗКОЙ (НАПРЯЖЕНИЕМ) ОПАСНОГО УРОВНЯ
2.1. Отказ из-за превышения нагрузкой (напряжением) опасного уровня может возникнуть в связи с разрушением, недопустимо большой упругой или пластической деформацией элемента.
2.2. Для определения вероятности безотказной работы необходимы вероятностные характеристики процессов нагружения (изменения напряжений) и величины опасного уровня нагрузки (напряжения).
Возможны два расчетных случая:
А - действующая нагрузка (напряжение) - случайный процесс S(t) (черт, 1); опасный уровень нагрузки (напряжения) - случайная величина Sо (черт, 2);
Б - действующие нагрузки (напряжения) - совокупность независимых случайных величин S (черт. 3); опасный уровень нагрузки (напряжения) - случайная величина So.
Действующая нагрузка - случайный процесс
Реализация процесса
Черт. 1
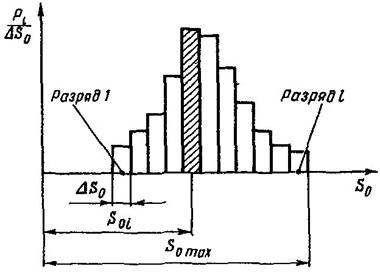
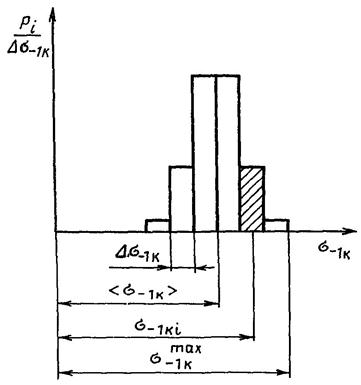
Опасный уровень нагрузки - случайная величина
Гистограмма опасных нагрузок
Черт. 2
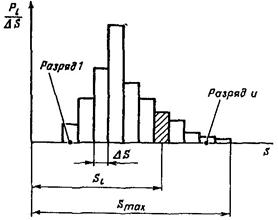
Действующие нагрузки - случайные величины
Гистограмма действующих нагрузок
Черт. 3
Случай А характерен для большинства элементов механизмов и металлоконструкций кранов, нагрузки и напряжения /S(t)/, в которых меняются в процессе работы непрерывно. Случайный характер изменения S(t) предопределяется случайностью таких факторов, как уровень и частота динамических нагрузок, скорость и направление ветра, значения коэффициентов трения и т.п.
Случай Б имеет место тогда, когда нагрузки могут рассматриваться как совокупность независимых случайных величин. Например, нагрузки от сил тяжести поднимаемых грузов случайной массы, пиковые, независящие друг от друга нагрузки, возникающие при соударениях в зазорах или в результате наложения упругих колебаний и т.п.
где ![]() - среднее число пересечений в единицу
времени уровня процессом S(t);
- среднее число пересечений в единицу
времени уровня процессом S(t);
tp - расчетное время работы элемента;
Со = С1С2. (8)
где ф - табулированная функция Лапласа (см. таблицу и черт. 4);
Smax, Smin - максимальное и минимальное значения нагрузки (напряжения);
S0.max, S0.min - максимальное и минимальное значения опасного уровня нагрузки (напряжения);
σS, σ0 - средние квадратические отклонения нагрузки (напряжения) и ее опасного уровня;
График функции Лапласа
Черт. 4
<S>, <S0>- математические ожидания нагрузки (напряжения) и ее опасного уровня.
Если нормальные распределения имеют неусеченный характер, то С0 = 1.
В том случае, когда Smax ³ <S> + 2σS и Smin £ <S> - 2σS, можно полагать С1 = 1. Если S0max ³ <S0> + 2σ0 и S0min £ <S0> - 2σ0, то можно полагать С2 = 1.
Пример расчета приведен в приложении справочном.
2.4. При условиях, оговоренных в пункте 2.3 нормированная вероятность безотказной работы в течение расчетного времени tp будет обеспечена, если
где Smax - максимальное расчетное напряжение, кгс/см2,
Smax = <S>(1 + кφ); (12)
S0min - минимальное расчетное опасное напряжение, кгс/см2,
S0min = <S0>(1 - zv); (13)
Значения функции Лапласа 
|
x |
Ф(х) |
x |
Ф(х) |
|
1,00 |
0,8427 |
||
|
1,05 |
0,8624 |
1,95 |
0,9942 |
|
1,10 |
0,8802 |
2,00 |
0,9953 |
|
1,15 |
0,8961 |
2,05 |
0,9963 |
|
1,20 |
0,9103 |
2,10 |
0,9970 |
|
1,25 |
0,9228 |
2,15 |
0,9976 |
|
1,30 |
0,9340 |
2,20 |
0,9981 |
|
1,35 |
0,9438 |
2,25 |
0,9985 |
|
1,40 |
0,9523 |
2,30 |
0,9988 |
|
1,45 |
0,9597 |
2,35 |
0,9991 |
|
1,50 |
0,9661 |
2,40 |
0,9993 |
|
1,55 |
0,9716 |
2,45 |
0,9995 |
|
1,60 |
0,9766 |
2,50 |
0,9996 |
|
1,65 |
0,9804 |
2,55 |
0,9997 |
|
1,70 |
0,9838 |
2,60 |
0,9998 |
|
1,75 |
0,9867 |
2,65 |
0,9998 |
|
1,80 |
0,9891 |
2,70 |
0,9009 |
|
1,85 |
0,9911 |
2,75 |
0,9999 |
|
1,90 |
0,9928 |
2,80 |
0,9999 |
|
3,00 |
1,0000 |
n1 - коэффициент запаса прочности;
В этих зависимостях обозначены: ![]()
![]() -
коэффициент вариации напряжений S(t);
-
коэффициент вариации напряжений S(t);
к - количество средних квадратических отклонений между средним <S> и максимальным расчетным напряжением Smax;
![]() -
коэффициент вариации опасного напряжения S0;
-
коэффициент вариации опасного напряжения S0;
z - количество средних квадратических отклонений между средним <S0> и минимальным опасным напряжением S0min;
g - характеристика безопасности
Пример расчета приведен в приложении.
2.5. Выбор геометрической характеристики F (площадь, момент сопротивления и т.п.) сечения элемента, при условиях, оговоренных в пункте 2.3, выполняется по формуле
где SH.max - расчетное значение максимальной нагрузки, кгс.
SH.max = <SH>(1 + кНφН); (17)
<SH> - среднее значение нагрузки, кгс;
![]() - коэффициент вариации нагрузки;
- коэффициент вариации нагрузки;
кН - количество средних квадратических отклонений между средней <SH> и расчетной максимальной SH.max нагрузкой.
Минимальное расчетное опасное напряжение S0.min вычисляется по формуле (13), а коэффициент запаса прочности n1 по формуле (14), в которой все значения <S> и σS заменяются соответственно на <SH> и σSH.
Пример расчета приведен в приложении.
2.6. Расчет вероятности безотказной работы в случае А при условии, что имеется представительная реализация S(t) действующих нагрузок (напряжений) и гистограмма (см. черт. 1, 2) их опасного уровня, осуществляется по формуле
pH(t) = 1 - n*tp, (18)
где ![]() - среднее число выбросов за опасный
уровень в единицу времени;
- среднее число выбросов за опасный
уровень в единицу времени;
pi - частота попадания случайного значения опасного уровня в i-тый разряд гистограммы;
l - общее количество разрядов в гистограмме S0;
tp - расчетное время работы элемента;
ni - среднее число выбросов в единицу времени за опасный уровень i;
где nH -
среднее число выбросов в единицу времени за относительный уровень ![]()
Smax - максимальная нагрузка в реализации;
<S> - среднее значение нагрузок в реализации (при определении <S> нулевые участки не учитываются, нагрузки берутся по модулю);
![]() -
относительный уровень, соответствующий среднему значению i-того
разряда опасного уровня S0i;
-
относительный уровень, соответствующий среднему значению i-того
разряда опасного уровня S0i;
![]() (20)
(20)
nк - среднее число
выбросов в единицу времени за относительный уровень ![]() .
.
Пример расчета приведен в приложении.
2.7. Расчет вероятности безотказной работы pH(t) в случае Б при условии, что действующие нагрузки (напряжения) и их опасные уровни распределяются по усеченным нормальным законам, выполняется по формуле
где п - количество нагружений в единицу времени;
tp - расчетное время работы элемента
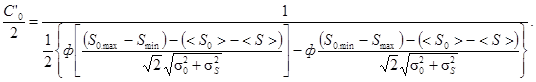 (22)
(22)
Формулу (21) рекомендуется использовать для инженерных расчетов, основанных на использовании обычных таблиц функции ф(x) - в том случае, когда общее количество нагружений за время работы - ntp находится в пределах от 1 до 200. При больших ntp предпочтительно использовать представление о нагрузке, как случайном процессе.
Пример расчета приведен в приложении.
2.8. При условиях, оговоренных в пунктах 2.7, и когда С'0 » 1,0, нормированная вероятность безотказной работы в течение времени tp будет обеспечена, если выполняется неравенство (11).
В формуле запаса прочности (14) характеристика безопасности g заменяется величиной
где x определяется с помощью таблицы или черт. 4 по расчетному значению
Пример расчета приведен в приложении.
2.9. Выбор геометрической характеристики F (площадь, момент сопротивления и т.п.) сечения элемента, при условиях, оговоренных в пункте 2.7., и когда С'0 » 1, выполняется по формуле (16).
При вычислении запаса прочности g заменяется на g1 в соответствии с пунктом 2.8.
Пример расчета приведен в приложении.
3. РАСЧЕТ ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ ЭЛЕМЕНТОВ
КРАНОВ рц(t)
ПО УСЛОВИЮ СОХРАНЕНИЯ ЦИКЛИЧЕСКОЙ ПРОЧНОСТИ
3.1. Отказ из-за потери циклической прочности возникает в связи с накоплением усталостных повреждений и образованием макроскопической трещины в элементе.
3.2. Для определения вероятности безотказной работы требуются вероятностные характеристики амплитуд действующих напряжений, приведенных к симметричному циклу, и неограниченного предела выносливости элемента.
где <σ-1к>, σσ-1к,
![]() кгс/см2
- математическое ожидание, среднее квадратическое отклонение и максимальное
значение неограниченного предела выносливости элемента (черт. 5);
кгс/см2
- математическое ожидание, среднее квадратическое отклонение и максимальное
значение неограниченного предела выносливости элемента (черт. 5);
С3 - определяется по формуле, аналогичной (10) при условии замены характеристик величины So характеристиками величины σ-1к;
σ*-1к - пороговое значение неограниченного предела выносливости, кгс/см2 (см. следующие пункты);
ф - табулированная функция Лапласа (см. черт. 4, таблицу).
Предел выносливости - случайная величина.
Гистограмма пределов выносливости
Черт. 5
3.4. Пороговое значение неограниченного предела выносливости σ*-1к, при известной гистограмме действующих напряжений (аналогичной приведенной на черт. 3 при условии замены S на σпр), приведенных к симметричному циклу определяется по формуле
 (26)
(26)
где N0 - базовое число циклов;
m - показатель кривой усталостной прочности;
N - количество циклов изменения напряжений за расчетный срок службы элемента;
сумма относительных повреждений, которая при a < 0,2 принимается равной 0,2; если все амплитуды σпр.i превышают значение σ*-1к и нет значительных кратковременных перегрузок (σпр.max £ (1,5 - 2)σ*-1к), то следует принимать а = 1.
σ'np.i, pi - напряжение, кгс/см2 (середина разряда) и частность i-того разряда гистограммы приведенных напряжений (см. черт. 3).
Если σ*-1к £ σmin-1к, то рц(t) = 1, если σ*-1к > σmax-1к, то рц(t) = 0.
Распределение приведенных напряжений σпр2 может быть заменено распределением амплитуд - σа кгс/см2. В этом случае σ*-1к определяется по формуле
где
 (29)
(29)
п - коэффициент чувствительности к асимметрии цикла;
к - эффективный коэффициент концентрации;
<r> - средний коэффициент асимметрии.
Уравнения (26), (23) решаются графически или методом последовательных приближений, однако, при выполнении расчетов с точностью до 10 % можно полагать в правых частях формул (26), (27), (28)
σ*-1к » <σ-1к>.
При этом сопоставляются значения σ*-1к, вычисленные по формуле (26) и принятые в первом приближении по формуле (28), в результате чего принимается решение о необходимости уточненного вычисления порогового значения неограниченного предела выносливости.
Пример расчета приведен в приложении.
3.5. Расчет порогового значения неограниченного предела выносливости σ*-1к в том случае, когда распределение амплитуд представлено в виде суммы п нормальных усеченных законов выполняется по формуле
где
или при условиях, оговоренных в пункте 3.4, принимается a = l;
pj - вероятность появления усеченного нормального закона j в общем суммарном распределении амплитуд;
qj - находится по черт. 6 в зависимости от <xj> и xσ j;
<xj> - относительное значение математического ожидания распределения амплитуд j-того закона;
xσ j - относительное значение среднего квадратического отклонения j-того закона.
![]()
<σj> - математическое ожидание j-того закона распределения амплитуд;
σσj - среднее квадратическое отклонение j-того закона распределения амплитуд.
Значение коэффициента qj в зависимости от <xj> и xσj
а - при т = 6; б - при т = 9
Черт. 6
![]() (32)
(32)
![]() (33)
(33)
Cj = кj(f3j - f4j); (36)
f1,2,3,4 j - определяются по графикам (черт. 7) в зависимости от hjmax и hj
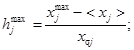 (37)
(37)
![]() (38)
(38)
![]()
Пример расчета приведен в приложении.
3.6. При условиях, оговоренных в пункте 3.3, нормированная вероятность безотказной работы [р] за период, соответствующий N нагружениям, будет обеспечена, если
Расчетные коэффициенты
Черт. 7
где σ*-1к определяется в соответствии с пунктами 3.4 или 3.5.
Коэффициент запаса циклической прочности
где x определяется с помощью таблицы или черт. 4 по расчетному значению
![]() -
коэффициент вариации предела выносливости элемента в расчетном сечении.
-
коэффициент вариации предела выносливости элемента в расчетном сечении.
Пример расчета приведен в приложении.
3.7. Выбор геометрической характеристики F (площадь, момент сопротивления и т.п.) сечения элемента, при условиях, оговоренных в пункте 3.3, выполняется по формуле
где пороговое значение нагрузки S*пр определяется по формулам (26), или (28), или (30), при условии замены σпр на Sпр. Коэффициент запаса циклической прочности находится по формуле (40).
Пример расчета приведен в приложении.
4. ОПРЕДЕЛЕНИЕ ИСХОДНЫХ ДАННЫХ ДЛЯ РАСЧЕТА ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ ЭЛЕМЕНТОВ КРАНА
4.1. Экспериментальные значения
статистических характеристик действующих нагрузок (напряжений), <S>,
σS, ![]() , Smax,
Smin, nн, nк и распределения приведенных напряжений определяются по
результатам испытаний кранов аналогичной конструкции или опытного образца
проектируемой машины. Обработка статистической информации о нагруженности
элементов должна проводиться в соответствии с РТМ 24.090.07-75.
, Smax,
Smin, nн, nк и распределения приведенных напряжений определяются по
результатам испытаний кранов аналогичной конструкции или опытного образца
проектируемой машины. Обработка статистической информации о нагруженности
элементов должна проводиться в соответствии с РТМ 24.090.07-75.
4.2. Все характеристики действующих нагрузок (напряжений) могут быть определены на стадии проектирования с помощью ЭВМ методом статистического моделирования.
4.3. Аналитическое определение <S>,
σS, ![]() и
характеристик распределений приведенных
напряжений выполняется в процессе проектирования методами статистической
динамики машин циклического действия.
и
характеристик распределений приведенных
напряжений выполняется в процессе проектирования методами статистической
динамики машин циклического действия.
4.4. Характеристики опасного уровня нагрузок (напряжений) <S0>, σ0 и циклической прочности элементов <σ-1>, <t-1>, r, m, N0, kσ (d), kr (d) определяются на основе испытаний образцов материала (деталей) и содержатся в справочной литературе.
4.5. Расчетное время tp задается на основе обобщения опыта эксплуатации лучших образцов кранов. Возможно определение tp, исходя из минимизации годовых приведенных эксплуатационных и капитальных затрат.
ПРИЛОЖЕНИЕ
Справочное
ПРИМЕРЫ РАСЧЕТА
Пример 1. Расчет вероятности безотказной работы оси механизма подъема по условию непревышения нагрузкой опасного уровня (случай А п. 2.3).
Исходные данные:
dв = 15,0 см - диаметр оси в опасном сечении;
Wи = 335 см3 - момент сопротивления сечения;
материал - сталь 34ХН3М (НВ = 270);
<σт> = 6,7 · 103 кгс/см2 - математическое ожидание предела текучести;
<S0> = <σт> Wи = 6,7 · 103 · 335 = 22,5 · 105 кгс · см - математическое ожидание опасного уровня нагружения;
v = 0,06 - коэффициент вариации опасного уровня нагружения материала;
σ0 = v <S0> = 0,06 · 22,5 = 1,3 · 10 кгс · см - среднее квадратическое отклонение опасного уровня;
Smax = 9 · 105 кгс · см; Smin = 0; <S> = 3 · 105
кгс · см; σS = 2,2 · 105
кгс · см; ![]() =
11 1/с - характеристики процесса нагружения в опасном сечении вала;
=
11 1/с - характеристики процесса нагружения в опасном сечении вала;
tр = 2 · 108 с - расчетное время работы вала за 20-летний период эксплуатации крана;

С2 » 1;
C0 = C1 · C2 = 1,097.
Решение:
Исходные данные подставляются в формулу (7) для определения значения рн(t) - вероятности безотказной работы по условию непревышения нагрузкой опасного уровня*
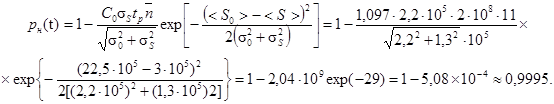
______________
* Здесь и далее вероятность неразрушении определяется с точностью до четырех знаков.
Пример 2. Расчет прочности оси барабана механизма подъема по заданной нормированной величине безотказной работы, когда нагрузка является случайным процессом (случай А п. 2.4).
Исходные данные:
Материал оси - сталь 34ХН3М;
<S> = 0,45 · 103 кгс/см2 - математическое ожидание процесса действующих напряжений;
φ = 0,75 - коэффициент вариации процесса напряжений;
k = 3 - количество средних квадратических отклонений между <S> и Smax;
<S0> = 7,6 · 10 кгс/см2 - математическое ожидание опасного уровня напряжений;
v = 0,06 - коэффициент вариации опасного уровня напряжений;
l = 2 - количество средних квадратических отклонений между <S0> и S0min;
φ = 0,75; ![]() = 5 · 10-2
1/с; tp = 2
· 108 с; [р] = 0,99.
= 5 · 10-2
1/с; tp = 2
· 108 с; [р] = 0,99.
Решение:
1. По формуле (12) определяется максимальное расчетное напряжение
Smax = <S>(1 + kφ) = 0,45 · 103 (1 + 3 · 0,75) = 1,46 · 103 кгс/см2.
2. По формуле (13) определяется минимальное расчетное опасное напряжение
S0.min = <S0>(1 - lv) = 7,6 · 103 (1 - 2 · 0,06) = 6,7 · 103 кгс/см2.
3. По формуле (15) определяется характеристика безопасности
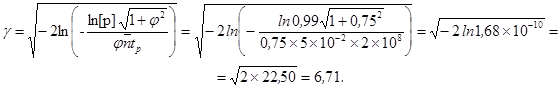
4. По формуле (14) определяется коэффициент запаса прочности
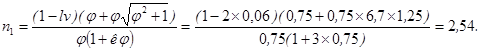
5. По формуле (11) производится проверка прочности оси барабана
![]()
Прочность оси обеспечена.
Пример 3. Определение диаметра расчетного сечения оси барабана при условии, что нагрузка является случайным процессом (случай А п. 2.5).
Исходные данные аналогичны предыдущему примеру.
Дополнительные данные:
<Sн> = 3 · 105 кгс · см - математическое ожидание опасного уровня нагружения;
кн = 3 - количество средних квадратических отклонений между <Sн> и Sн.max;
φн = 0,75 - коэффициент вариации нагрузки.
Решение:
1. По формуле (17) определяется расчетное значение максимальной нагрузки
Sн.max = <Sн>(l + kнφн) = 3 · 105(1 + 3 · 0,75) = 9,75 · 105 кгс · см.
2. По формуле (16) определяется момент сопротивления оси барабана
![]()
и следовательно,
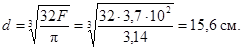
Пример 4. Расчет вероятности безотказной работы вала механизма подъема по условию непревышения нагрузкой опасного уровня (случай А п. 2.6.).
Исходные данные:
dв = 15 см - диаметр вала в опасном сечении;
<S0> = 22,5 · 105 кгс · см; DS0 = 1,3 · 105 кгс · см - среднее значение и цена разряда гистограммы уровня опасного нагружения (по аналогии с примером по п. 2.3);
материал вала - сталь 34ХН3М (НВ = 270);
р1 = 0,02; р2 = 0,14; р3 = 0,34; р4 = 0,34; p5 = 0,14; p6 = 0,02; - частости появления нагрузок в соответствующих разрядах гистограммы опасного уровня нагружения (см. черт. 2).
S0.min = <S0> - 3DS0 = 18,6 · 105 кгс·см;
S0.max = <S0> + 3DS0 = 26,4 · 105 кгс·см - минимальное и максимальное значения опасного уровня нагружения;
<S> = 3 · 105 кгс·см; Smax = 9 · 105 кгс·см - математическое ожидание и максимальное значение процесса нагружения;
tp = 2 · 108 с - время работы вала;
nк = 2,55 · 10-1 1/с; nн = 1,1 1/с - среднее число выбросов в единицу времени за уровни Rк и Rн, полученное по осциллограммам.
Решение:
1. В соответствии с пунктом 2.6 определяются значения уровней R0i, Rк, Rн и коэффициент g;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. По формуле (19) определяется среднее число выбросов в единицу времени за каждый из уровней i.
n1 = 1,1exp{-0,91[(6,20 - 1)2 - (2,55 - 1)2} = 1,1exp(-22,5) = 1,1 · 4,5 · 10-5 · 4,5 · 10-5 · 8,2 · 10-2 = 1,83 · 10-10 1/c;
n2 = 1,1exp{-0,91[(6,64 - 1)2 - (2,55 - 1)2} = 1,1exp(-29,4) = 1,1 · 4,5 · 10-5 · 4,5 · 10-5 · 1,11 · 10-3 = 2,5 · 10-12 1/c;
n3 = 1,1exp{-0,91[(7,06 - 1)2 - (2,55 - 1)2} = 1,1exp(-31,3) = 1,1 · 4,5 · 10-5 · 4,5 · 10-5 · 4,5 · 10-5 · 0,273 = 2,74 · 10-14 1/c;
n4 = 1,1exp{-0,91[(7,50 - 1)2 - (2,55 - 1)2} = 1,1exp(-36,4) = 1,1 · 4,5 · 10-5 · 4,5 · 10-5 · 4,5 · 10-5 · 1,67 · 10-3 = 1,68 · 10-16 1/c;
n5 = 1,1exp{-0,91[(7,94 - 1)2 - (2,55 - 1)2} = 1,1exp(-41,6) = 1,1 · 4,5 · 10-5 · 4,5 · 10-5 · 4,5 · 10-5 · 4,5 · 10-5 2,02 · 10-1 = 9,12 · 10-19 1/c;
n6 = 1,1exp{-0,91[(8,36 - 1)2 - (2,55 - 1)2} = 1,1exp(-47) = 1,1 · (4,5 · 10-6) · 4 · 9,1 · 10-4 = 4,12 · 10-21 1/c.
3. Определяется среднее число выбросов в единицу времени за опасный уровень
n* = Snipi = 1,83 · 10-10 · 0,02 + 2,5 · 10-12 · 0,14 + 2,74 · 10-14 · 0,34 + 1,68 · 10-16 · 0,34 + 9,12 · 10-19 · 0,14 + 4,12 · 10-21 · 0,02 » 4,02 · 10-12.
4. По формуле (18) определяется вероятность неразрушения вала из условия непревышении нагрузкой опасного уровня.
рн(t) = l - n*tp = 1 - 4,02 · 10-12 · 2 · 108 » 0,9992.
При совместном действии кручения и изгиба характеристики процесса нагружения можно определить по следующим зависимостям
![]()
![]()
где <Sн>, <Sк> - математические ожидания процесса нагружения при изгибе и кручении;
Sн.max, Sк.max - максимальные значения процесса нагружения при изгибе и кручении.
Количество выбросов в единицу времени приведенного момента S за уровни Sн и Sк определяется непосредственно по осциллограммам.
Пример 5. Расчет вероятности безотказной работы вала механизма подъема по условию непревышения нагрузкой опасного уровня (случай Б п. 2.7.).
Исходные данные:
dв = 12,0 см - диаметр вала;
Wи = 169,6 см3 - момент сопротивления сечения;
<σт> = 6,7 · 103 кгс/см2 - математическое ожидание предела текучести для стали 34ХН3М;
<S0> = <σт> Wи = 11,4 × 105 кгс·см - математическое ожидание опасного уровня нагружения;
σ0 = 0,7 · 105 кгс·см - среднее квадратическое отклонение опасного уровня нагружения;
S0.max = <S0> + 3σ0 = 11,4 · 105 + 3 · 0,7 · 105 = 13,5 · 105 кгс·см;
S0.min = <S0> - 3σ0 = 11,4 · 105 - 3 · 0,7 · 105 = 9,3 · 105 кгс·см,
максимальное и минимальное значения опасного уровня нагружения;
Smax = 9 · 105 кгс·см; Smin = 0; <S> = 3 · 105 кгс·см;
σS = 2,2 · 105 кгс·см - характеристики процесса нагружения в опасном сечении вала;
tp = 2 · 108 с - расчетное время работы вала;
n = 7,5 · 10-7 1/с - количество нагружений в единицу времени.
Решение:
В соответствии с п. 2.7. и формулой (21) определяется


Пример 6. Расчет прочности вала механизма подъема по заданной нормированной величине безотказной работы, когда нагрузка является случайной величиной (случай Б, п. 2.8). Исходные данные:
<S> = 0,77 · 103 кгс/см2 - математическое ожидание уровня напряжений;
φ = 0,73 - коэффициент вариации действующих напряжений;
к = 2,7 - количество средних квадратических отклонений между <S> и Smax;
v = 0,06 - коэффициент вариации опасного уровня напряжений;
<S0> = 6,7 · 103 кгс/см2 - математическое ожидание опасного уровня напряжений,
С'0
» 1,0; l = 2; φ = 1,4; [р]
= 0,99; tp = 2 ×
102 с; ![]() = 7,5 × 10-7 1/c.
= 7,5 × 10-7 1/c.
Решение:
1. По формуле (12) определяется максимальное расчетное напряжение.
Smax = <S>(1 + kφ) = 0,77 · 103(1 + 2,7 · 0,73) = 2,3 · 103 кгс/см2.
2. По формуле (13) определяете я минимальное расчетное опасное напряжение
S0.min = <S0>(1 - lv) = 6,7 · 103(1 - 2 · 0,06) = 5,9 · 103 кгс/см2.
3. По формуле (24) определяется значение функции Лапласа
![]()
4. По таблице устанавливается, что данному значению ф (x) соответствует величина
x = 3,0.
5. По формуле (23) определяется характеристика безопасности
![]()
6. По формуле (14) определяется коэффициент запаса прочности

7. По формуле (11) производится проверка прочности вала
![]()
Прочность вала обеспечена.
Пример 7. Определение диаметра расчетного сечения оси барабана механизма подъема, при условии, что нагрузка является случайной величиной (п. 2.9).
Исходными данными являются данные предыдущих примеров 5 и 6. Помимо этого
kн = 2,7; φн = 0,73; <Sн> = 3 · 105 кгс·см.
Решение:
1. По формуле (17) определяется расчетное значение максимальной нагрузки
Sн.max = <Sн>(1 + kнφн) = 3 · 105(1 + 2,7 · 0,73) = 9 · 105 кгс·см.
2. По формуле (16) определяется момент сопротивления оси
![]()
откуда
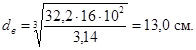
Пример 8. Расчет вероятности безотказной работы по условию сохранения циклической прочности оси барабана механизма подъема при изгибе.
Исходные данные:
материал оси - сталь 34ХН3М (НВ = 270);
do = 20,0 см - диаметр оси в опасном сечении;
Wи = 785 см3 - момент сопротивления сечения;
kσ(d) = 2,9 - эффективный коэффициент концентрации в расчетном сечении;
<σ-1> = 3,7 · 103 кгс/см2 - средняя величина предала выносливости материала по изгибу;
r = 0,12 - коэффициент вариации предела выносливости материала;
![]()
- минимальное, максимальное значения и цена разряда гистограммы приведенных напряжений;
np = 12 - число разрядов гистограммы приведенных напряжений;
р1 = 0,01; р2 = 0,05; р3 = 0,10; р4 = 0,18; р5 = 0,20; р6 = 0,12; p7 = 0,11; р8 = 0,09; р9 = 0,07; р10 = 0,03; р11 = 0,01; р12 = 0,01 - частости разрядов гистограммы приведенных напряжений;
N = 2 · 106 - количество нагружений вала за 20 лет эксплуатации крана;
N0 = 2 · 106 - базовое число циклов нагружения;
m = 9 - показатель степени кривой усталости.
Решение:
1. Определяются характеристики предела выносливости оси при изгибе.
![]()
![]()
![]()
![]()
2. Выбирается начальная величина порогового значения неограниченного предела усталости
σ*-1к = 0,5 · <σ-1 к> = 0,5 · 1,3 · 103 = 0,65 · 103 кгс/см2;
0,5σ*-1к = 0,5 · 0,65 · 103 = 0,32 · 103 кгс/см2.
3. Определяется значение сумм в формуле (27) и устанавливается значение корректирующего коэффициента а.
а) 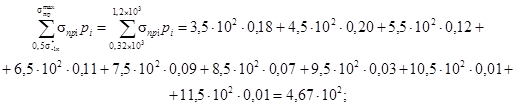
б) 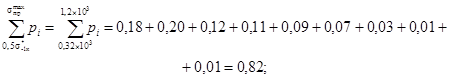
в) 
4. Определяется значение суммы подкоренного выражения в формуле (26)
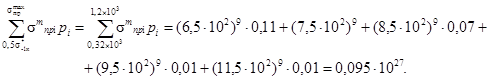
5. По формуле (26) определяется первое приближение значения неограниченного предела выносливости

6. Производится расчет сумм в формуле (27) и устанавливается новое значение коэффициента а из условия, что
![]()
В этом случае
а) 
б) 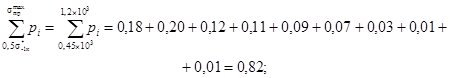
в) 
7. Определяется значение суммы в формуле (26)
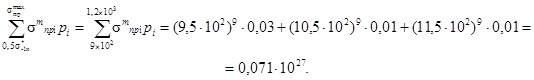
8. Определяется второе приближенное значение неограниченного предела выносливости

Это значение ![]() приемлемо, так как нижний
порог суммирования в формуле (26) был равным 0,9 · 103 кгс/см2.
приемлемо, так как нижний
порог суммирования в формуле (26) был равным 0,9 · 103 кгс/см2.
9. По формуле (9) с учетом замены величины S на величину ![]() определяется
значение коэффициента С3
определяется
значение коэффициента С3

10. По формуле (25) определяется вероятность неразрушения оси при изгибе по условию сохранения циклической прочности:
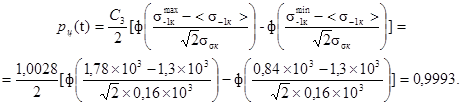
11. Расчет приближенного значения неограниченного предела выносливости производится по формулам, аналогичным (26), (27). При этом принимается начальное значение σ-1к = <σ-1к>.
В том случае, когда <σ-1к> > σmax-1к, допускается нижний предел интегрирования в формуле (26) принимать равным σmin-1к.
![]()
![]()
12. Определяются значения сумм в формуле (26)
а) 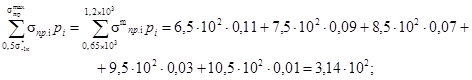
б) 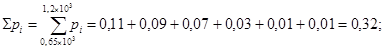
в) 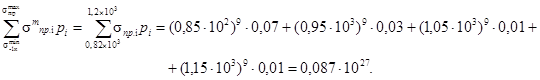
13. По формуле (27) определяется сумма относительных повреждений

14. Вычисляется пороговое значение неограниченного предела выносливости по формуле (26)
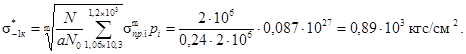
15. Относительная величина погрешности по эквивалентному напряжению вычисляется как
![]()
16. При подстановке значения ![]() в формулу
(25)
аналогично пункту 10 определяется вероятность неразрушения оси
в формулу
(25)
аналогично пункту 10 определяется вероятность неразрушения оси ![]() .
.
Относительная погрешность по вероятности неразрушения оси при изгибе определится как
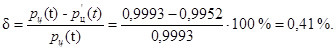
Пример 9. Расчет вероятности безотказной работы по условию сохранения циклической прочности вала механизма подъема при кручении (пункт 3.5.).
Исходные данные:
Материал вала - сталь 34ХН3М;
kt(d) = 2,7 - эффективный коэффициент концентрации вала в расчетном сечении;
<t-1> = 2,2 · 103 кгс/см2 - средняя величина предела выносливости материала по кручению;
r = 0,14 - коэффициент вариации предела выносливости материала;
<t1> = 6 · 102 кгс/см2; σt1 = 0,8 · 102 кгс/см2 - математическое ожидание и среднее квадратическое отклонение при обработке нагрузки по огибающей (обработка по амплитудам низкочастотной составляющей);
<t2> = 2,5 · 102 кгс/см2; σt2 = 2 · 102 кгс/см2 - математическое ожидание и среднеквадратическое отклонение при обработке по максимальным и минимальным значениям нагрузки;
N = 2 · 106 - количество нагружений вала;
N0 = 2 · 106 - базовое число нагружений;
m = 9 - показатель степени кривой усталости;
р1 = 0,15 - вероятность появления 1-го закона (обработка по огибающей);
р2 = 0,85 - вероятность появления 2-го закона (обработка по максимальным и минимальным значениям);
С3 = 1,0028.
Решение:
1. Определяются характеристики предела выносливости вала по кручению
![]()
![]()
![]()
![]()
2. Определяются относительные характеристики законов распределения приведенных амплитуд
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3. Определяется значение коэффициента kj по п. 3.5, формула (34); k1 = 1,0;
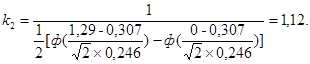
4. Определяются значения функций hj и hjmax
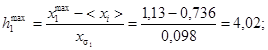
![]()
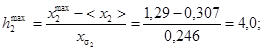
![]()
5. По черт. 7 определяются значения функций
f11 = fa(h1max) = fa(4,02) = 0,45;
f21 = fa(h1) = fa(-2,41) = - 0,42;
f31 = fв(h1max) = fa(4,02) = 0,50;
f41 = fв(h1) = fa(-2,41) = - 0,48;
f12 = fa(h2max) = fa(4,0) = 0,45;
f22 = fa(h2) = fa(2,485) = 0,18;
f32 = fa(h2max) = fa(4,0) = 0,50;
f42 = fa(h2) = fa(2,485) = 0,29.
6. Определяется значение коэффициентов bj; cj по формулам (35), (36)
b1 = 0,098(0,45 + 0,42) + 0,736(0,50 + 0,48) = 0,085 + 0,725 = 0,840;
С1 = 0,98;
b2 = 1,12 · 0,246(0,45 - 0,18) + 0,307(0,50 - 0,29) = 0,147;
С2 = 1,12(0,50 - 0,29) = 0,235.
7. По формуле (31) определяется значение коэффициента a

8. По черт. 6, б при m = 9 определяется значение
q1 = 0,61 (при <x1> = 0,736; xσ1 = 0,098);
q2 = 0,52 (при <x2> = 0,307; xσ2 = 0,246).
9. Определяется пороговое значение неограниченного предела выносливости вала при кручении согласно выражению (30)
![]()
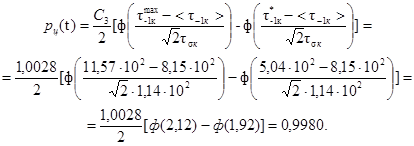
11. В случае совместного действия изгиба
и кручения устанавливаются пороговые значения при изгибе ![]() (см. пример 10) и
кручении
(см. пример 10) и
кручении ![]() .
.
Эквивалентное напряжение определяется согласно следующей зависимости

Дальнейший расчет вероятности безотказной
работы по условию сохранения циклической прочности осуществляется по формуле (25) при
условии замены величины ![]() на
на ![]() .
.
Пример 10. Расчет циклической прочности оси барабана механизма подъема (пункт 3.6.).
Исходные данные аналогичны примеру 9. Помимо этого
<σ-1к> = 1,3 · 103 кгс/см2; σ*-1к = 0,84 · 103 кгс/см2; С3 » 1,0; [p] = 0,99; S*пр = 6,6 · 105 кгс · см; r = 0,12.
Решение:
1. По формуле (41) определяется значение функции Лапласа
![]()
2. По таблице или графику на черт. 4 устанавливается, что этому значению ф(х) соответствует величина
х = 1,68.
3. По формуле (40) определяется коэффициент запаса прочности
![]()
4. По формуле (39) производится проверка прочности оси
![]()
Пример 11. Определение диаметра расчетного сечения оси барабана по условию сохранения циклической прочности (пункт 3.7.).
На основании данных примеров 9 и 10 по формуле (42) определяется момент сопротивления оси барабана

откуда диаметр оси
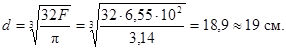
СОДЕРЖАНИЕ