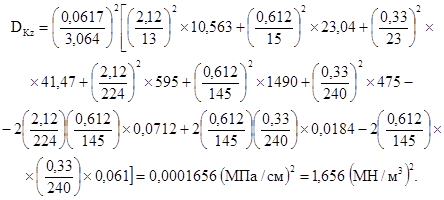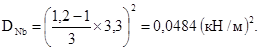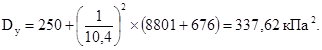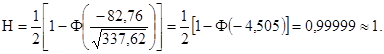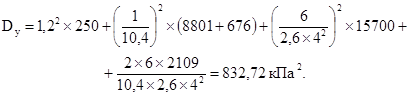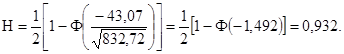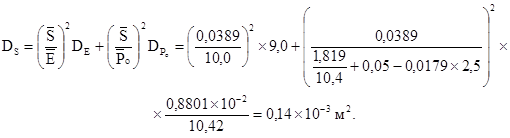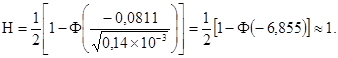ОРДЕНА ТРУДОВОГО
КРАСНОГО ЗНАМЕНИ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ОСНОВАНИЙ И ПОДЗЕМНЫХ СООРУЖЕНИЙ
имени Н.М. ГЕРСЕВАНОВА
ГОССТРОЯ СССР
РЕКОМЕНДАЦИИ
ПО ВЕРОЯТНОСТНОМУ
РАСЧЕТУ ОСНОВАНИЙ
И ФУНДАМЕНТОВ
КАРКАСНЫХ ЗДАНИЙ
(Методика
и алгоритм)
Москва 1985
Настоящие Рекомендации подготовлены в качестве вспомогательного материала для проектирования промышленных каркасных зданий с отдельно стоящими фундаментами на естественном основании.
Целью создания настоящих Рекомендаций является выявление в результате вероятностных расчетов с применением теории надежности неиспользованных резервов получения оптимальных проектных решений фундаментов и их реализация.
В Рекомендациях содержатся методика и алгоритм оценки проектного уровня надежности оснований и фундаментов каркасных зданий на основе учета случайной изменчивости характеристик грунтов и нагрузок на здание. Предусмотрен совместный расчет здания и податливого статистически неоднородного основания.
Предназначены для использования в проектных организациях, обслуживающих строительство промышленных зданий.
Рекомендации подготовлены в лаборатории методов исследования грунтов кандидатами технических наук И.В. Маевской и О.И. Игнатовой, одобрены секцией Ученого совета института и рекомендованы к изданию.
Замечания и предложения по содержанию Рекомендаций просим направлять по адресу: 109389, Москва, 2-я Институтская ул., д. 6, НИИОСП.
ВВЕДЕНИЕ
Совершенствование применяемого в настоящее время метода расчета строительных конструкций и оснований по предельным состояниям возможно путем использования методов теории вероятностей и положений теории надежности. Вероятностный подход является более общим по сравнению с детерминированным и позволяет учесть в расчетах случайную природу целого ряда факторов без существенного усложнения расчетных моделей.
Модель статистически неоднородного основания более точно отражает свойства грунтового массива, а расчет с использованием такой модели более соответствует действительной работе системы основание-сооружение.
Для каркасных промышленных зданий с отдельностоящими фундаментами на естественном основании разработана методика оценки проектного уровня надежности основании и фундаментов на основе учета случайной изменчивости характеристик грунтов и нагрузок на здание. Для оснований зданий рассмотрен их расчет по второму предельному состоянию.
Исследования, проведенные в НИИОСП, показали, что расчетный уровень надежности оснований и фундаментов при проектировании по действующим нормам может быть существенно различным в зависимости от исходных параметров проектирования.
При переходе к вероятностным методам расчета в качестве основной нормированной величины принимается некоторая заданная вероятность отказа конструкции или основания (нормативный уровень надежности). Выбор нормируемого уровня вероятности появления предельных состояний дифференцируется в зависимости от назначения элемента системы основание-здание и от выбранного критерия возникновения предельного состояния, т.е. каждому предельному состоянию предписывается своя допустимая вероятность его наступления.
Величины нормативных уровней надежности, рекомендуемые для проектирования, получены на основе анализа результатов многочисленных расчетов по разработанной методике для зданий, запроектированных в соответствии с действующими нормативными документами. Переход к расчету на заданный уровень надежности позволяет получать в случаях, когда проектный уровень надежности выше нормативного, более экономичные решения.
1. основные положения расчета
1.1. Настоящие Рекомендации распространяются на проектирование оснований и отдельностоящих железобетонных фундаментов промышленных каркасных зданий.
1.2. Под уровнем надежности при проектировании основания или фундамента понимается вероятность выполнения соответствующего предельного неравенства метода предельных состояний.
1.3. Любое предельное неравенство может быть сведено к виду
У1 ³ У2 (1.1)
или
У = У1 - У2 ³ 0, (1.2)
где У1 - внутренний фактор системы здание-основание, характеризующий ее несущую способность или предельно допустимую деформацию;
У2 - внешний фактор, характеризующий нагрузки и воздействия на систему;
У - совокупный фактор, являющийся функцией случайных аргументов, определяющих числовые характеристики как внутреннего фактора У1, так и внешнего фактора У2.
1.4. Соотношение для получения количественного показателя надежности рассматриваемого элемента (основания или фундамента) имеет вид
Н = Р [У ³ 0] = Р [(У1 - У2) ³ 0], (1.3)
где Н - уровень надежности элемента системы (начальная безотказность);
Р - вероятность события, заключающегося в ненаступлении предельного состояния элемента системы.
1.5. Совокупный фактор У рассматривается как случайная величина, имеющая нормальный закон распределения. В этом случае вероятность безотказной работы элемента системы определяется по формуле
где ![]() -
математическое ожидание, а Ду - дисперсия совокупного фактора У;
-
математическое ожидание, а Ду - дисперсия совокупного фактора У;
Ф - интеграл вероятности Гаусса, определяемый по статистическим таблицам [1].
При определении интеграла вероятности Гаусса по таблицам [2] необходимо вместо (1.4) использовать
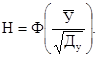 (1.4a)
(1.4a)
1.6. Статистические
характеристики совокупного фактора (математическое ожидание ![]() и дисперсию Ду)
определяют методом линеаризации функций случайных величин по статистическим
характеристикам параметров, функцией которых является У [3].
и дисперсию Ду)
определяют методом линеаризации функций случайных величин по статистическим
характеристикам параметров, функцией которых является У [3].
1.7. Для основания сооружения методика предусматривает расчет его по второму предельному состоянию (по деформациям) в соответствии с [4].
В качестве предельных неравенств рассматриваются
P £ R; (1.5)
S £ Su, (1.7)
где Р, Ркр и Ругл - соответственно среднее, краевое и угловое давление под подошвой фундамента;
R - расчетное сопротивление грунта;
S и Su - соответственно деформация основания и ее предельно допустимая величина.
1.8. При определении вероятности безотказной работы (уровня надежности) основания в качестве критерия отказа рассматривается каждое из предельных неравенств (1.5) - (1.7). За уровень надежности принимается меньший из полученных по разным критериям.
Примечание. Неравенства (1.5) и (1.6) как критерий отказа являются условными, так как и в случае их невыполнения отказ может не наступить. Принятие условий (1.5) и (1.6) в качестве критерия отказа обеспечивает дополнительный запас надежности, а сам отказ будет параметрическим, т.е. характеризующим лишь выход параметра за допустимый предел R.
1.9. Расчет фундаментов по прочности с целью определения его минимальных размеров и необходимого количества арматуры производят в соответствии с указаниями [5].
1.10. При расчетах фундамента на продавливание плитной части в качестве критерия отказа рассматривается предельное неравенство
Р £ кRpbcpHo, (1.8)
где Р - продавливающая сила, принимаемая равной величине продольной силы N, действующей на пирамиду продавливания, за вычетом нагрузок, приложенных к большему основанию пирамиды продавливания (считая до плоскости расположения растянутой арматуры) и сопротивляющихся продавливанию;
к - коэффициент, принимаемый равным 1 для тяжелых и ячеистых бетонов и 0,8 для бетонов на пористых заполнителях;
bср - среднее арифметическое величин периметров верхнего и нижнего основания пирамиды продавливания в пределах рабочей высоты сечения Но;
Rр - расчетное сопротивление бетона осевому растяжению.
При расчетах фундаментов на изгиб консольного выступа в качестве критерия отказа рассматривается предельное неравенство
Mi-i £ 0,9HoRaFа, (1.9)
где Mi-i - изгибающий момент в одном из сечений фундамента;
Rа - расчетное сопротивление продольной растянутой арматуры;
Fa - площадь сечения арматуры на 1 м ширины фундамента.
1.11. В качестве случайных величин при расчете уровней надежности рассматриваются характеристики грунтов основания и нагрузки на здания. Делается допущение о нормальном законе распределения всех рассматриваемых случайных величин.
1.12. Для описания статистической неоднородности грунтового массива применяется следующая модель. Грунтовый массив разделяется на инженерно-геологические элементы, в пределах которых статистические характеристики того или иного параметра грунта можно считать постоянными. При переходе от одного инженерно-геологического элемента к другому статистические характеристики параметра скачкообразно изменяются. Для учета неоднородности напластований грунтов вводится величина изменчивости толщин слоев грунта.
1.13. Расчет оснований и фундаментов, как правило, должен производиться из условия совместной работы здания и основания с учетом перераспределения нагрузок надфундаментной конструкцией.
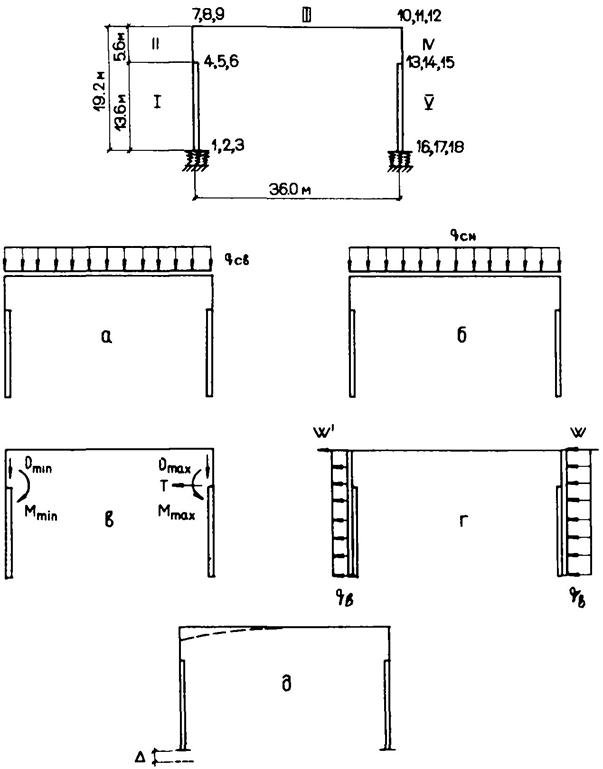
Для рассматриваемой системы (каркасные здания с отдельностоящими фундаментами на естественном основании) совместный расчет здания и основания представляет собой расчет рамы с опорами на податливом основании.
1.14. Податливость основания задается с помощью коэффициентов жесткости при осадке Кz, повороте Кφ и сдвиге Кx фундамента, определяемыми по формулам, предложенным в [6]:
где: N - центральная сила;
А - площадь подошвы фундамента;
S - осадка фундамента;
wz, wφ, wx - безразмерные коэффициенты, зависящие от соотношения сторон подошвы фундамента;
n - коэффициент Пуассона грунта.
Осадка фундамента определяется по методу послойного суммирования [4].
Коэффициенты жесткости (1.10) определяются для каждого из фундаментов рамы в соответствии с инженерно-геологическим разрезом по этому фундаменту. Если несколько фундаментов находятся в аналогичных инженерно-геологических условиях, то для расчета осадок и коэффициентов жесткости основания выбирается наиболее характерный инженерно-геологический разрез.
1.15. Дня учета податливости основания применяется итерационный подход, заключающийся в следующем:
1 этап. Ведется расчет рамы при предпосылке, что основание несжимаемо. По результатам расчета собираются нагрузки на фундаментные опоры. Далее, в строгом соответствии со СНиП проектируются и рассчитываются фундаменты и устанавливаются коэффициенты жесткости основания для каждой из опор рамы:
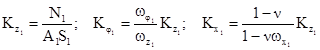 (1.11)
(1.11)
2 этап. Ведется расчет
рамы в предположении, что они имеют податливые опоры, при коэффициентах
жесткости основания ![]() ,
, ![]() ,
, ![]() . По результатам расчета собираются
нагрузки на фундаменты (по величине они отличаются от прежних нагрузок,
вычисленных на первом этапе). Снова (согласно СНиП) проектируют и рассчитывают
фундаменты и определяют новые значения коэффициентов жесткости:
. По результатам расчета собираются
нагрузки на фундаменты (по величине они отличаются от прежних нагрузок,
вычисленных на первом этапе). Снова (согласно СНиП) проектируют и рассчитывают
фундаменты и определяют новые значения коэффициентов жесткости:
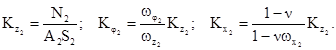 (1.12)
(1.12)
Эти
величины сравниваются с соответствующими результатами по первому этапу. Если ![]() (ε -
заданная точность), то последовательный расчет можно завершить, в противном
случае нужен третий вариант счета (по результатам второго этапа) и т.д. Процесс
достаточно быстро сходится (2 - 3 итерации).
(ε -
заданная точность), то последовательный расчет можно завершить, в противном
случае нужен третий вариант счета (по результатам второго этапа) и т.д. Процесс
достаточно быстро сходится (2 - 3 итерации).
1.16. После расчета основания и фундаментов по нагрузкам последнего этапа производится оценка их уровня надежности.
2. МЕТОДИКА ОЦЕНКИ УРОВНЯ НАДЕЖНОСТИ ОСНОВАНИЙ И ФУНДАМЕНТОВ
2.1. Оценка уровня надежности производится для всех различных фундаментов данной рамы. Если имеется несколько фундаментов одинакового размера и с одинаковой глубиной заложения, то уровни надежности оцениваются для наиболее характерного из них.
2.2. Расчет уровня надежности для данного фундамента производится на сочетание нагрузок, наиболее опасное для этого фундамента. Рассматриваются нормативные значения нагрузок с учетом коэффициентов сочетаний и их дисперсии в отличие от детерминированного расчета, когда учитываются их расчетные значения.
2.3. Уровень надежности основания под данным фундаментом оценивается по критериям (1.5), (1.6) и (1.7). Для центрально нагруженных фундаментов рассматриваются предельные неравенства (1.5) и (1.7) Для внецентренно нагруженных фундаментов уровень надежности определяется по обоим предельным неравенствам (1.5) и (1.6), а также по неравенству (1.7). Окончательно принимается меньшая из полученных величин.
Для отдельностоящих фундаментов условие (1.5) будет иметь вид
а условие (1.6)
где: N и М - соответственно центральная сила и изгибающий момент на уровне обреза фундамента;
G - вес фундамента и грунта на его уступах;
A, W - соответственно площадь и момент сопротивления подошвы фундамента.
Для приведения неравенств (2.1) и (2.2) к виду (1.2) обозначим:
У1 = R для неравенства (2.1);
У1 = 1,2R для неравенства (2.2);
![]() для
неравенства (2.1);
для
неравенства (2.1);
![]() для неравенства
(2.2).
для неравенства
(2.2).
Тогда для (2.1) и (2.2) соответственно имеем:
Математическое ожидание и дисперсия совокупного фактора определяется по формулам:
для (2.3)
для (2.4)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - математические
ожидания соответствующих параметров, численно равные их нормативным значениям;
- математические
ожидания соответствующих параметров, численно равные их нормативным значениям;
DR, DN, DG, DM - дисперсии соответствующих параметров;
mM,N - корреляционный момент величин изгибающего момента и центральной силы, действующих на фундамент.
Порядок определения дисперсий и корреляционных моментов нагрузок на фундамент изложен в разделах 3 и 5 настоящих Рекомендаций.
Математическое ожидание и дисперсию расчетного сопротивления грунта получают по формулам:
где ![]()
gC1 - коэффициент условий работы грунтового основания, определяемый по [4]; gC2 = K = 1;
![]() ,
, ![]() ,
, ![]() - безразмерные
коэффициенты, принимаемые по [4];
- безразмерные
коэффициенты, принимаемые по [4];
b - меньшая сторона (ширина) подошвы фундамента, м;
d1 - глубина заложения фундамента бесподвальных сооружений от уровня планировки или приведенная глубина заложения фундамента от пола подвала, определяемая по [4], м;
![]() -
осредненное (по слоям) нормативное значение удельного веса грунта, залегающего
вне отметки заложения фундамента, кН/м3;
-
осредненное (по слоям) нормативное значение удельного веса грунта, залегающего
вне отметки заложения фундамента, кН/м3;
![]() - то же
кН/м3, но залегающего ниже подошвы фундамента;
- то же
кН/м3, но залегающего ниже подошвы фундамента;
![]() - нормативное
значение удельного сцепления грунта, залегающего непосредственно под подошвой
фундамента, кПа;
- нормативное
значение удельного сцепления грунта, залегающего непосредственно под подошвой
фундамента, кПа;
db - глубина до пола подвала, м;
Dtgφ, Dc, Dg - дисперсии соответствующих параметров;
ma, tg φ - корреляционный момент удельного сцепления и тангенса угла внутреннего трения.
Порядок определения дисперсий и корреляционных моментов характеристик грунтов изложен в разд. 3 настоящих Рекомендаций.
Уровень
надежности, используя ![]() и ДУ, определяют по формуле
(1.4).
и ДУ, определяют по формуле
(1.4).
2.4.
Под
величинами S и Su в условии (1.7)
при расчете каркасных зданий с отдельностоящими фундаментами в соответствии с [4]
понимается максимальная абсолютная осадка Si и Siu или
относительная разность осадок ![]() и
и ![]() , где DS - разность
вертикальных перемещений фундаментов, L - расстояние между ними. Оценивать
уровень надежности следует для обоих случаев.
, где DS - разность
вертикальных перемещений фундаментов, L - расстояние между ними. Оценивать
уровень надежности следует для обоих случаев.
В случае, когда под S и Su понимается максимальная абсолютная осадка, условие (1.7) преобразуется к виду (1.2) следующим образом
У = Siu - Si ³ 0 (2.11)
Математическое ожидание и дисперсию У определяют по формулам:
Dу = DSi, (2.13)
где: ![]() - математическое
ожидание (или нормативное значение) максимальной абсолютной осадки;
- математическое
ожидание (или нормативное значение) максимальной абсолютной осадки;
DSi - ее дисперсия.
Дисперсия абсолютной осадки фундамента DSi определяется по формуле
где k - число различных слоев грунта в пределах сжимаемой толщи;
![]() ,
, ![]() ,
, ![]() - осадка, модуль
деформации и толщина j-го слоя грунта соответственно;
- осадка, модуль
деформации и толщина j-го слоя грунта соответственно;
![]() - полная
осадка;
- полная
осадка;
Рo - дополнительное давление на грунт по подошве фундамента, определяемое по указаниям [4];
DCj, DAj - дисперсии модуля деформации (п. 3.5) и толщины j-го слоя (п. 3.6);
![]() - дисперсия
дополнительного давления на грунт, здесь DN - дисперсия
центральной силы, действующей на фундамент (пп. 3.10 - 3.12), А - площадь подошвы
фундамента;
- дисперсия
дополнительного давления на грунт, здесь DN - дисперсия
центральной силы, действующей на фундамент (пп. 3.10 - 3.12), А - площадь подошвы
фундамента;
![]() - корреляционный
момент толщин слоев в пределах сжимаемой толщи (п. 3.6).
- корреляционный
момент толщин слоев в пределах сжимаемой толщи (п. 3.6).
Уровень
надежности осадки определяют по формуле (1.4), используя ![]() (2.12)
и Dу (2.13).
(2.12)
и Dу (2.13).
2.5. Для относительной разности осадок условие (1.7) принимает вид
где DS - разность осадок двух соседних фундаментов;
L - расстояние между этими фундаментам;
![]() - предельная
величина относительной разности осадок, определяемая по указаниям [4].
- предельная
величина относительной разности осадок, определяемая по указаниям [4].
Условие (2.15), преобразованное к виду (1.2), имеет вид
Математическое ожидание и дисперсию У определяют по формулам
![]() (2.17)
(2.17)
где ![]() и
и ![]() - математические
ожидания осадок двух фундаментов;
- математические
ожидания осадок двух фундаментов;
DS1 и DS2 - их дисперсии, определяемые по формуле (2.14);
σS1 и σS2 - среднеквадратичные
отклонения осадок двух фундаментов ![]() ;
;
r - коэффициент корреляции осадок двух фундаментов, назначаемый по табл. 2.1.
Таблица 2.1.
|
6 |
12 |
18 |
24 |
30 |
|
|
Коэффициент корреляции r |
0,85 |
0,8 |
0,7 |
0,65 |
0,6 |
Вероятность выполнения неравенства (2.16) определяют по формуле (1.4).
2.10. Уровень надежности данного фундамента при расчетах на продавливание плитной части оценивается по критерию (1.8).
Условие (1.8), преобразованное к виду (1.2), для центрально нагруженных квадратных железобетонных фундаментов имеет вид
У = kRpbcpHo - N ³ 0, (2.19)
а для центрально нагруженных прямоугольных и внецентренно нагруженных квадратных и прямоугольных железобетонных фундаментов:
![]() (2.20)
(2.20)
где Fo определяется по геометрическим параметрам фундамента [5].
Математическое ожидание и дисперсию У определяют для центрально нагруженных квадратных фундаментов:
DУ = DN, (2.22)
а для центрально нагруженных прямоугольных и внецентренно нагруженных квадратных и прямоугольных фундаментов:
Уровень надежности определяют по формуле (1.4).
2.11. Уровень надежности данного фундамента при расчетах на изгиб консольного выступа оценивается по критерию (1.9).
Изгибающий момент Mi-i в произвольном сечении фундамента определяется в соответствии с [5] по формуле:
где l, li - соответственно длина подошвы и ступени фундамента, по грани которой проводится расчетное сечение;
давления Р2 и Р3 получаются по формулам:
Условие (1.9), преобразованное к виду (1.2), имеет вид
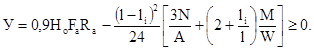 (2.27)
(2.27)
Математическое ожидание и дисперсию определяют по формулам
Уровень надежности определяют по формуле (1.4).
3. ПОЛУЧЕНИЕ НЕОБХОДИМЫХ ДЛЯ РАСЧЕТА ИСХОДНЫХ ПАРАМЕТРОВ
3.1. Необходимыми для расчета уровня надежности параметрами, кроме всех параметров, необходимых для детерминированного расчета, являются статистические характеристики свойств грунтов основания и нагрузок на здание (нормативные значения, дисперсии и корреляционные моменты).
3.2. Нормативные значения характеристик грунта и их средние квадратические отклонения σ вычисляют по результатам непосредственных определений, выполняемых в лабораторных или полевых условиях, по указаниям [7].
Дисперсии тангенса угла внутреннего трения, удельного сцепления и удельного веса грунта определяют по формулам
![]() (3.1)
(3.1)
3.3. В случае многослойного основания дисперсия удельного веса грунта определяется по формуле
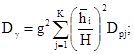 (3.2)
(3.2)
где k - количество различных слоев грунта выше границы сжимаемой толщи;
g - ускорение свободного падения;
hj - толщина j-го слоя грунта;
Н - общая толщина грунта до границы сжимаемой толщи;
Dpj - дисперсия плотности грунта j-го слоя.
3.4. Корреляционный момент удельного сцепления и тангенса угла внутреннего трения mc, tg φ определяется по формуле
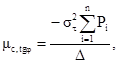 (3.3)
(3.3)
где στ, D, ![]() определяют по
указаниям [7].
определяют по
указаниям [7].
3.5. Дисперсию модуля деформации вычисляет по формуле
![]() (3.4)
(3.4)
где n - число определений модуля деформации;
Еn и Ei - соответственно нормативное и частное значение модуля деформации;
Если число определений модуля деформации n < 6, то дисперсию DE определяют по формуле
DE = (VE · En)2, (3.5)
где VE - коэффициент вариации Е, принимаемый равным 0,3.
3.6. Статистические характеристики слоев грунта, залегающих в пределах сжимаемой толщи основания, определяют на основе анализа инженерно-геологических разрезов площадки строительства.
Если напластования грунтов являются практически горизонтальными и толщины слоев обладают только случайной изменчивостью, то под толщиной j-го слоя понимается его средняя толщина, а дисперсия определяется по формуле
![]() (3.6)
(3.6)
где N - количество скважин, прорезающих данный слой грунта;
hji - толщина слоя по отдельной скважине;
![]() - средняя толщина
слоя.
- средняя толщина
слоя.
Корреляционный
момент толщин слоев в пределах сжимаемой толщи ![]() определяется для всех
сочетаний из двух слоев по формуле (3.7). Так, например, для
трехслойного основания определяются три корреляционных момента:
определяется для всех
сочетаний из двух слоев по формуле (3.7). Так, например, для
трехслойного основания определяются три корреляционных момента: ![]() ,
, ![]() и
и ![]()
где ![]() и
и ![]() - средняя толщина
слоев j и t соответственно;
- средняя толщина
слоев j и t соответственно;
hji и hti - толщина слоев j и t по отдельной скважине;
N - количество скважин, прорезающих слои j и t.
Если напластования грунтов является сложными (наличие линз, выклиниваний), то для определения уровня надежности основания и фундаментов выбирают рамы с наиболее неблагоприятными инженерно-геологическими разрезами. В этом случае под толщиной j-го слоя понимается его толщина непосредственно под данным фундаментом, а дисперсия толщины слоя и корреляционные моменты принимаются равными нулю.
3.7.
Дисперсию коэффициента жесткости основания ![]() под каждым из
фундаментов рамы определяют по формуле
под каждым из
фундаментов рамы определяют по формуле
где ![]() и
и ![]() - нормативные
значения коэффициента жесткости основания и полной осадки;
- нормативные
значения коэффициента жесткости основания и полной осадки;
k - число различных слоев грунта в пределах сжимаемой толщи;
![]() ,
, ![]() ,
, ![]() - осадка, модуль
деформации и толщина j-го слоя грунта соответственно;
- осадка, модуль
деформации и толщина j-го слоя грунта соответственно;
![]() и
и ![]() - дисперсия модуля
деформации (п. 3.5)
и толщины j-го слоя (п. 3.6);
- дисперсия модуля
деформации (п. 3.5)
и толщины j-го слоя (п. 3.6);
![]() - то же, что и
в формуле (3.7).
- то же, что и
в формуле (3.7).
3.8. Математическое ожидание каждой из нагрузок на здание принимается равным ее нормативному значению, определенному в соответствии с главой СНиП по нагрузкам и воздействиям.
3.9. Поперечник здания может быть загружен несколькими вариантами загружения. Под вариантом загружения понимается несколько одновременно действующих на конструкции силовых факторов (сосредоточенных сил или моментов, равномерно распределенных нагрузок), от которых при статическом расчете рамы здания строится одна эпюра. Вариантом загружения может быть постоянная нагрузка, снеговая, крановая, ветровая, полезная временная и т.д.
3.10. Дисперсия
нагрузок определяются по одной на каждый вариант загружения. Для этого для
каждого варианта загружения выбирается одна приведенная нагрузка. За
приведенную нагрузку может быть принят любой из силовых факторов заданного варианта
загружения ![]() (его нормативное значение). Например,
для крановой нагрузки за приведенную нагрузку может быть принято максимальное
давление от колеса крана в одном из пролетов. Дисперсия для каждого конкретного
варианта загружения DNi определяется из следующих соотношений
(его нормативное значение). Например,
для крановой нагрузки за приведенную нагрузку может быть принято максимальное
давление от колеса крана в одном из пролетов. Дисперсия для каждого конкретного
варианта загружения DNi определяется из следующих соотношений
при
gfi > 1 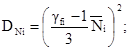 при gfi < 1
при gfi < 1 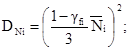 (3.9)
(3.9)
где gfi - коэффициент надежности по нагрузке заданного варианта загружения.
3.11. Нагрузки на фундаменты при совместной работе системы здание-основание представляют собой внутренние усилия в опорных сечениях надфундаментной конструкции. Определение дисперсий и корреляционных моментов внутренних усилий в раме, включая опорные сечения, производится по алгоритму, описанному в разделе 5.3 Рекомендаций.
Примечание. Знак корреляционного момента mMN, полученный при расчете (разд. 5.3), сохраняется, если изгибающий момент М и центральная сила N имели одинаковые знаки, и меняется на противоположный, если М и N имели разные знаки. Знак mMN учитывается в формулах (2.8), (2.24) и (2.29).
3.12. В случае, когда нагрузки на фундаменты определяют без учета перераспределения надфундаментной конструкцией в соответствии со статической схемой здания, дисперсию нагрузки на фундамент DN определяют по следующей формуле
где Nварj - суммарная нагрузка на фундамент от всех силовых факторов j-го варианта загружения;
![]() -
приведенная нагрузка j-го варианта загружения;
-
приведенная нагрузка j-го варианта загружения;
DNj - дисперсия приведенной нагрузки (п. 3.10);
k - количество вариантов загружения, входящих в рассматриваемое сочетание нагрузок.
4. ПОРЯДОК РАСЧЕТА
4.1. В первом варианте система основание-здание проектируется в соответствии с указаниями норм [4, 5, 8, 9, 10] и использованием расчетных значений величин нагрузок на здание и характеристик грунтов. Определение внутренних усилий в системе ведется с учетом совместной работы здания и основания методом итерации (см. пп. 1.13 - 1.15).
4.2. Оцениваются статистические характеристики свойств грунтов и напластований под фундаментами и нагрузок на здание по указаниям разд. 3.
4.3. Для оценки надежности основания и фундаментов по критериям (1.5) - (1.9) для каждого из фундаментов здания выбирается наиболее опасное сочетание нагрузок (вариантов загружения). В статистическом расчете используются нормативные значения этих нагрузок с учетом коэффициентов сочетаний.
4.4. Производится статистический расчет каркаса здания совместно с деформирующимся основанием по алгоритму, изложенному в разд. 5, с целью получения корреляционных матриц и математических ожиданий (нормативных значений) внутренних усилий в системе. В результате расчета имеем математические ожидания, дисперсии и корреляционные моменты нагрузок на фундаменты.
4.5. В случае, когда нагрузки на фундаменты определяют без учета их перераспределения надфундаментной конструкцией в соответствии со статической схемой здания, дисперсию нагрузок на фундаменты определяют по формуле (3.10).
4.6. Используя полученные результаты, оценивают уровень надежности основания и фундаментов по формуле (1.4) с использованием формул (2.5) - (2.18) для оснований и (2.21) - (2.24), (2.28), (2.29) для фундаментов.
4.7. Проверяют выполнение условия
Н ³ Нн, (4.1)
где Н - расчетный уровень надежности основания или фундамента, оцененный по формуле (1.4);
Нн - нормативный уровень надежности, принимаемый по указаниям п. 4.8.
4.8. За нормативный уровень надежности при расчете оснований по условию непревышения расчетного давления на основание и по условию непревышения предельно допустимых деформаций основания принимается величина Нн = 0,85. За нормативный уровень надежности при расчете прочности тела фундамента при продавливании и прочности рабочей арматуры при изгибе консольного выступа фундамента принимается величина Нн = 0,98.
4.9. Если расчетное значение Н значительно превосходит нормативное, то производят снижение размеров фундамента или количества рабочей арматуры, вычисляет новое значение Н и снова производят проверку условия (4.1).
4.10. В случае, если при проектировании фундаментов не выполняется расчет каркаса здания (привязка типовых проектов, расчет оснований зданий и сооружений III класса) или нет возможности произвести полный расчет уровней надежности, то обеспечение уровня надежности основания H = 0,85 может производиться по указаниям п. 4.11.
4.11. При коэффициенте вариации модуля деформации подстилающих грунтов, не превышающем 0,3, рекомендуется определять коэффициент безопасности КR по расчетному сопротивлению грунта.
![]() (4.2)
(4.2)
где Rn = ![]() - определяется по
формуле (2.9);
- определяется по
формуле (2.9);
R - расчетное сопротивление грунта, определяемое по [4].
Если КR превышает значения, приведенные в табл. 4.2, то в расчет принимается значения, указанные в этой таблице. В этом случае расчетное сопротивление R, используемое для назначения размеров подошвы фундамента, определяется по формуле
![]() (4.3)
(4.3)
KR
принимается
по табл. 4.2
в зависимости от относительного эксцентриситета приложенной на уровне подошвы
фундамента нагрузки ![]() и коэффициента вариации удельного
сцепления Vc
грунта,
залегающего непосредственно под подошвой фундамента.
и коэффициента вариации удельного
сцепления Vc
грунта,
залегающего непосредственно под подошвой фундамента.
Таблица 4.2
|
Коэффициент безопасности КR |
|||
|
Пылевато-глинистые грунты |
Песчаные грунты |
||
|
Vc £ 0,25 |
Vc > 0,25 |
||
|
|
1,15 |
1,20 |
1,30 |
|
|
1,20 |
1,25 |
1,35 |
Значение относительного эксцентриситета нагрузки на основание определяется по формуле
![]() (4.4)
(4.4)
где N - продольная сила, кН;
М - больший из изгибающих моментов, действующих вдоль каждой из осей фундамента, кН·м;
l - длина стороны подошвы фундамента, вдоль которой действует больший изгибающий момент, м.
Коэффициент вариации удельного сцепления Vc определяется по указаниям [7].
5. ОЦЕНКА СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ВНУТРЕННИХ УСИЛИЙ В СИСТЕМЕ ОСНОВАНИЕ - КАРКАСНОЕ ЗДАНИЕ
5.1. Общие указания.
5.1.1. Определение внутренних усилий в системе основание-каркасное здание и их статистических характеристик является одним из этапов вероятностного расчета оснований и фундаментов, необходимым для оценки нагрузок на фундаменты, их дисперсий и корреляционных моментов с учетом перераспределения усилий каркасом здания. Совместный расчет здания и деформируемого основания требует большого объема вычислений и в большинстве случаев предполагает применение ЭВМ. В настоящем разделе изложен алгоритм такого расчета, имеющий целью получение не только эпюр внутренних усилий и деформаций в системе, но и их статистических характеристик (дисперсий и корреляционных моментов).
5.1.2. Рассматривается плоская расчетная схема здания (рама). Податливость основания учитывается путем введения коэффициентов жесткости (см. п. 1.14) для каждого из фундаментов. Рама здания может быть загружена несколькими вариантами загружения (см. раздел 3).
5.1.3. Для расчета каркаса (рамы) здания принят метод перемещений строительной механики как наиболее удобный для реализации в программах для ЭВМ. Метод предусматривает учет влияния всех трех интегралов усилий на перемещения.
5.1.4. Внутренние усилия и деформации каркаса здания находятся путем решения системы линейных алгебраических уравнений метода перемещений.
RlZ + Rp = 0, (5.1)
где Rl - матрица реакций в узлах каркаса от единичных перемещений узлов;
Rp - матрица реакций в узлах нагрузок на раму;
Z - матрица перемещений узлов.
Введены следующие допущения:
а) задача рассматривается в геометрически и физически линейной постановке;
б) связь медку податливым основанием и фундаментной конструкцией, находящейся с ним в контакте, считается двусторонней;
5.1.5. Стержни надфундаментного каркаса могут быть произвольным образом ориентированы в пространстве. Поверхность основания всегда предполагается расположенной в горизонтальной плоскости.
Предполагается, что все сооружение целиком располагается в 1 квадрате правосторонней декартовой системы координат. В дальнейшем она называется общей системой координат; в ней вычисляются координаты всех узлов конструкции. Кроме того, с каждым элементом связывается местная система координат, такая, чтобы матрица жесткости этого элемента имела в ней наиболее простой и удобный вид. Местная система координат также является правосторонней декартовой. Для прямолинейного стержня она имеет свое начало в начальном узле стержня, одна ее ось совпадает с продольной осью стержня и направлена в сторону конечного узла. Две другие оси совпадают с главными осями инерции поперечного сечения стержня. Для столбчатого фундамента начало местной системы координат совпадает с центром его подошвы, одна ось направлена вертикально, а две другие совпадают с главными осями инерции подошвы фундамента. Перемещения узлов вычисляются в общей системе координат, а эпюры усилий в местной.
5.1.6. Перемещения считаются положительными, если они направлены вдоль положительного направления осей координат. При этом перемещения всех видов рассматриваются как векторы. Реакция каждой связи, вызываемая ее положительным перемещением, считается положительной.
5.1.7. В каждый узел конструкции вводится три связи: на вертикальное перемещение, горизонтальное и поворот. Виды эпюр усилий соответствуют количеству степеней свободы узлов конструкции, т.е. вычисляются значения изгибающих моментов, продольных и поперечных сил.
Для удобства построения расчетных зависимостей принимается стандартный порядок следования перемещений в узлах конструкции: Dx, Dz, φу, где D - линейное смещение; φ - поворот.
В общем векторе перемещений Z группы перемещений каждого узла из трех чисел идут подряд друг за другом в порядке нумерации узлов. Предполагается, что нумерация узлов начинается с единицы и не имеет пропущенных и повторяющихся номеров.
5.1.8. Матрица перемещений узлов находится из соотношения
путем обращения матрицы реакций в узлах каркаса от единичных перемещений узлов.
Переводя
матрицу перемещений узлов из общей системы координат в местную и используя лишь
те перемещения, которые относятся к одному элементу, можно вычислить матрицу
реакций в узлах каждого элемента от фактических перемещений ![]()
Здесь и в дальнейшем индексом «м» обозначены матрицы в местной системе координат, индексом «о» - соответствующие матрицы в общей системе координат, индексом «э» - матрицы, относящиеся к одному элементу.
Матрицы, относящиеся ко всей раме в целом, привязаны к общей системе координат.
Знак * обозначает операцию жордановых исключений (см. разд. 5.3).
5.1.9. Основным результатом расчета по программе являются усилия (с их статистическими характеристиками) в узлах, находящихся на поверхности основания (фундаментных узлах), поэтому алгоритм не предусматривает определения усилий в промежуточных сечениях стержней надфундаментной конструкции, а ограничивается определением узловых реакций с учетом того, что они численно равны усилиям в узлах. Статистические характеристики узловых реакций также будут численно равны статистическим характеристикам внутренних усилий в узлах.
В случае необходимости усилия в промежуточных сечениях стержней надфундаментной конструкции можно определить по известным соотношениям метода начальных параметров, используя в качестве начальных параметров узловые реакции. Статистические характеристики внутренних усилий в промежуточных сечениях стержней надфундаментной конструкции находят методом линеаризации соотношений метода начальных параметров по статистическим характеристикам узловых реакций.
5.1.10. Корреляционные матрицы узловых реакций находятся для каждого элемента (стержня) в местной системе координат по формуле
где ![]() ,
, ![]() ,
, ![]() - корреляционные
матрицы реакций от фактических перемещений в узлах элемента, перемещений узлов
и реакций в узлах от нагрузок на элемент.
- корреляционные
матрицы реакций от фактических перемещений в узлах элемента, перемещений узлов
и реакций в узлах от нагрузок на элемент.
На главных диагоналях корреляционных матриц располагаются дисперсии соответствующих усилий или перемещений, все остальные элементы представляет собой корреляционные моменты соответствующих усилий или перемещений;
![]() - смешанные корреляционные
матрицы перемещений узлов и реакций от нагрузок на элемент;
- смешанные корреляционные
матрицы перемещений узлов и реакций от нагрузок на элемент;
Символ «-» над обозначением матрицы соответствует математическому ожиданию или нормативному значению элементов матрицы.
Знак «/» обозначает операцию транспонирования матрицы.
5.1.11.
Корреляционная матрица перемещений узлов элемента ![]() получается из
общей корреляционной матрицы перемещений узлов Kz:
получается из
общей корреляционной матрицы перемещений узлов Kz:
где ![]() - корреляционная
матрица коэффициентов жесткости основания размером m×m, где m - количество
перемещений во всей раме.
- корреляционная
матрица коэффициентов жесткости основания размером m×m, где m - количество
перемещений во всей раме.
Коэффициенты жесткости под каждым из фундаментов рассматриваются как статистически независимые случайные величины, поэтому корреляционные моменты между коэффициентами жесткости соседних опор принимаются равными нулю, а изменчивость коэффициентов жесткости определяется только их дисперсиями, задаваемыми по формуле (3.8).
Матрица
![]() имеет
следующую структуру:
имеет
следующую структуру:
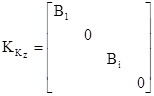
Здесь
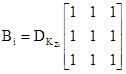
(![]() - дисперсия коэффициента
жесткости основания i-го фундамента)
- дисперсия коэффициента
жесткости основания i-го фундамента)
Блоки
Bi располагаются в
матрице ![]() в
местах, соответствующих номерам связей (перемещений) i-го фундамента:
в
местах, соответствующих номерам связей (перемещений) i-го фундамента:
![]() - корреляционная
матрица j-го варианта
загружения размерностью m×m, все элементы
которой равны дисперсии j-го варианта загружения
- корреляционная
матрица j-го варианта
загружения размерностью m×m, все элементы
которой равны дисперсии j-го варианта загружения ![]() ;
;
V - матрица, определяемая по указаниям п. 5.1.12;
Di - матрица, определяемая по указаниям п. 5.1.13;
к - количество вариантов загружения.
5.1.12. Матрица V, имеющая размерность m×m вычисляется по формуле
где I - квадратная матрица размером m×m, имеющая вид
Здесь
![]()
(![]() - матрица реакций
столбчатого фундамента от единичных перемещений)
- матрица реакций
столбчатого фундамента от единичных перемещений)
![]() - диагональная
матрица размером m×m, элементами главной диагонали
которой являются элементы вектора перемещений от всех вариантов
загружения (
- диагональная
матрица размером m×m, элементами главной диагонали
которой являются элементы вектора перемещений от всех вариантов
загружения (![]() ).
).
5.1.13. Матрица Di размером m´m вычисляется по формуле
где ![]() - диагональная
матрица размером m×m, элементами главной диагонали
которой являются элементы столбца матрицы реакций в узлах от нагрузок на раму RP, соответствующего
j-му варианту
загружения, деленные на приведенную нагрузку этого варианта загружения
- диагональная
матрица размером m×m, элементами главной диагонали
которой являются элементы столбца матрицы реакций в узлах от нагрузок на раму RP, соответствующего
j-му варианту
загружения, деленные на приведенную нагрузку этого варианта загружения ![]() .
.
5.1.14. Корреляционная
матрица реакций в узлах элемента стержня от нагрузок на элемент ![]() находится
по формуле
находится
по формуле
где к - количество вариантов загружения;
![]() - диагональная
матрица размером 6×6, элементами главной диагонали которой являются
элементы столбца матрицы реакций в узлах стержня от нагрузок на него RPэм, соответствующего
j-му варианту
нагружения, деленные на приведенную нагрузку
- диагональная
матрица размером 6×6, элементами главной диагонали которой являются
элементы столбца матрицы реакций в узлах стержня от нагрузок на него RPэм, соответствующего
j-му варианту
нагружения, деленные на приведенную нагрузку ![]() ;
; ![]() - корреляционная матрица j-го варианта
загружения, представляющая собой квадратную матрицу размером 6×6, все
элементы которой равны дисперсии j-го варианта загружения
- корреляционная матрица j-го варианта
загружения, представляющая собой квадратную матрицу размером 6×6, все
элементы которой равны дисперсии j-го варианта загружения ![]() ;
;
5.1.15. Смешанные корреляционные
матрицы перемещений узлов и нагрузок на элемент ![]() и
и ![]() находят по формуле
находят по формуле
где к - количество вариантов загружения;
Dэj - матрица размером 6×m, составленная из строк матрицы соответствующих данному элементу (стержню);
![]() - корреляционная
матрица j-го варианта
загружения размером m×6, все элементы которой равны дисперсии j-го варианта
загружения
- корреляционная
матрица j-го варианта
загружения размером m×6, все элементы которой равны дисперсии j-го варианта
загружения ![]() ;
;
![]() - определяется по
указаниям п. 5.1.14.
- определяется по
указаниям п. 5.1.14.
5.2. Подготовка исходной информации для ввода в ЭВМ.
5.2.1. Исходная информация для ввода в ЭВМ представляет собой ряд исходных чисел и исходных массивов. Исходными числами для рассматриваемого расчета является:
а) количество участков рамы n; разделение рамы на участки производится в соответствии с правилами метода перемещений;
б) количество перемещений в раме m; так как в каждый узел рамы вводится три связи, то количество перемещений равно утроенному количеству узлов;
в) количество фундаментов f;
г) количество нулевых перемещений в узлах рамы mo; равно количеству отсутствующих связей по направлению обобщенных перемещений (наличие шарниров, ползунов, свободных концов);
д) количество вариантов загружения в рассматриваемом сочетании к.
5.2.2. Исходные массивы чисел, относящиеся к геометрическим и жесткостным параметрам стержней рамы. Эти массивы является одномерными и имеют размерность n;
а) жесткости стержней при расчете на изгиб E Ji (i = 1, ..., n);
б) жесткости стержней при расчете на растяжение-сжатие E Fi (i = 1, ..., n);
в) длины стержней Li (i = 1, ..., n);
г) коэффициенты, учитывающие форму сечения стержней рамы ηi (i = 1, ..., n)
д) косинусы угла наклона оси стержней к оси абсцисс общей системы координат cos li (i = 1, ..., n);
е) синусы угла наклона оси стержней к оси абсцисс общей системы координат sin li (i = 1, ..., n).
Кроме того для каждого стержня вводится специальный массив из шести чисел, включающий в себя номера перемещений, соответствующих данному стержню три числа для начала стержня и три числа для конца стержня в порядке, предусмотренном п. 5.1.7.
5.2.3. Одномерный массив NO размером mo включает в себя номера нулевых перемещений узлов.
5.2.4. Исходные массивы чисел, относящиеся к фундаментам. Массивы одномерные размером f:
а) длина фундаментов li (i = 1, ..., f);
б) ширина фундаментов bi (i = 1, ..., f);
в) коэффициенты жесткости основания под каждым из фундаментов КZi (i = 1, ..., f);
г) корректирующие
множители для получения коэффициентов жесткости при повороте фундаментов yφi (i = 1, ..., f). 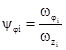 по формуле
(1.10);
по формуле
(1.10);
д) корректирующие
множители для получения коэффициентов жесткости при сдвиге фундаментов yxi (i = 1, ..., f). ![]() по формуле
(1.10);
по формуле
(1.10);
е) дисперсии
коэффициентов жесткости под каждым из фундаментов ![]() (i = 1, ..., f), получаемые по
формуле (4.6).
(i = 1, ..., f), получаемые по
формуле (4.6).
Кроме того, для каждого фундамента вводится специальный массив из трех чисел ТФi, включающий в себя номера перемещений, соответствующих данному фундаменту, в порядке, предусмотренном п. 5.1.7.
5.2.5. Массив RV, включающий в себя реакции в узлах элементов от действия пролетных нагрузок в местной системе координат. Массив трехмерный, имеет размерность 6×n×к. Реакции вычисляются для каждого варианта загружения.
5.2.6. Массив RO, включающий реакции в узлах рамы от действия узловых нагрузок в общей системе координат. Массив двумерный имеет размерность m×к. Реакции вычисляются для каждого варианта загружения.
5.2.7. Одномерные массивы, размерностью к, включающие в себя:
а) приведенные
нагрузки вариантов загружения ![]() (i = 1, ..., к);
(i = 1, ..., к);
б) дисперсии вариантов загружения DNi (i = 1, ..., к).
5.3. Алгоритм расчета.
5.3.1. Построение
матриц реакций элементов надфундаментной конструкции (стержневой) от единичных перемещений
узлов в местной системе координат Rэмi. Матрицы
строятся для каждого стержня в цикле по i = 1, 2, ..., n. Матрицы Rэмi имеют
размерность 6×6 и вычисляются по табл. 5.1. В таблице 5.1
введены обозначения ![]() ,
, ![]() . Индексы «u», «v», «w» указывают на ось
местной системы координат, относительно которой подсчитывается жесткость.
. Индексы «u», «v», «w» указывают на ось
местной системы координат, относительно которой подсчитывается жесткость.
5.3.2. Построение матриц реакций фундаментов (местная система координат для фундаментов совпадает с общей) от единичных перемещений Rфундi. Матрицы строятся для каждого фундамента в цикле по i = 1, 2, ..., f. Для прямоугольного фундамента матрица реакций
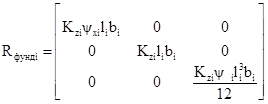 (5.12)
(5.12)
Для круглого фундамента радиуса r:
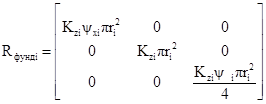 (5.12)
(5.12)
5.3.3. Построение матрицы реакций элементов надфундаментной конструкции от пролетных нагрузок в местной системе координат Rpэмi. Матрицы строятся для каждого стержня в цикле по i = 1, 2, ..., n. Матрицы Rpэмi имеют размерность 6×к и получается путем выбора соответствующих данному стержню элементов из исходного массива RV.
5.3.4. Производят операцию жордановых исключений для тех элементов, в узлах которых имеются нулевые перемещения в следующем порядке:
а) если mo = 0, то операция жордановых исключений не требуется и переходят к дальнейшему расчету;
б) для каждого элемента организуют сравнение его номеров перемещений из массива Ti с номерами имеющихся в раме нулевых перемещений из массива NO.
Если Tij = NOii (j = 1, ... 6; ii = 1, ... mo), то для номера j производят операцию жордановых исключений в матрицах Rэмi и Rpэмi.
Если произвольный элемент матрицы Rэмi обозначить rmn (m = 1, ... 6; n = 1, ... 6), а произвольный элемент матрицы Rpэмi - Pmn (m = 1,...6; с = 1,...к), то в соответствии с [10] один шаг жордановых исключений с разрешающим элементом rij (номеру j соответствует нулевое перемещение) выполняется для каждого элемента матриц Rэмi и Rpэмi по формулам:
![]() (5.14)
(5.14)
Таблица 5.1
Матрица реакций защемленного по концам стержня от единичных перемещений его концов
|
Rэм = |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
В операции жордановых исключений выполняется столько шагов, сколько нулевых перемещений окажется в узлах стержня.
В результате выполнения операции жордановых исключений вместо матриц Rэмi и Rpэмi имеем матрицы R*эмi и R*pэмi.
5.3.5. Перевод матриц реакций элементов (стержней) в общую систему координат. Производится по формулам
![]() (5.15)
(5.15)
где С - матрица направляющих косинусов, имеющая вид
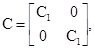
где
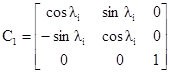 (5.16)
(5.16)
5.3.6. Формирование общей матрицы реакций от единичных перемещений узлов R1.
Элементы матриц Rэоi накапливаются на поле общей матрицы реакций путем присвоения строкам и столбцам матриц Rэоi номеров, соответствующих номерам перемещений i-го стержня из исходного массива Ti.
Таким же образом накапливаются на поле матрицы R1 элементы матриц Rфундi, но с использованием исходных массивов ТФi. Матрица R1 является симметричной.
5.3.7. Формирование общей матрицы реакций в узлах рамы от нагрузок Rp.
Элементы матриц Rрэоi накапливаются на поле общей матрицы реакций Rp по тому же принципу, что и для матрицы R1 с той лишь разницей, что номера перемещений i-го стержня из исходного массива Ti присваивается только строкам матриц Rрэоi. Номера столбцов соответствуют рассматриваемым вариантам загружения.
После этого необходимо добавить в матрицу Rp реакции от узловых нагрузок из массива RO. Это легко делается путем сложения матриц Rp и RO. Результаты сложения записываются на месте матрицы Rp.
5.3.8. Производится обращение матрицы R1. Получаем матрицу R1-1.
5.3.9. Вычисляются матрицы перемещений узлов Z по формуле (5.2).
5.3.10. Из общей матрицы перемещений Z составляются матрицы перемещений элементов (стержней) путем отбора строк, относящихся к данному элементу с использованием массивов Ti. в результате имеем n матриц Zэоi.
5.3.11. Перевод матриц Zэоi в местную систему координат производят по формуле
Zэмi = C Zэоi (5.17)
5.3.12. Вычисляются
матрицы реакций в узлах элементов от фактических перемещений ![]() по формуле
(5.3).
Эти матрицы являются результирующими для статической части расчета рамы (см. п.
5.1.9)
и выводятся на печать.
по формуле
(5.3).
Эти матрицы являются результирующими для статической части расчета рамы (см. п.
5.1.9)
и выводятся на печать.
5.3.13. Формируется матрица I по формуле (5.7). Элементы матриц Rфундi делятся на соответствующие коэффициенты жесткости основания KZi и накапливаются на поле матрицы I путем присвоения строкам и столбцам соответствующих номеров перемещений из массивов ТФi.
Матрица I является диагональной.
5.3.14. Формируется диагональная матрица LZo размером m×m. Для этого получают вектор перемещений от всех вариантов загружения Zо путем сложения всех столбцов матрицы Z (каждый столбец соответствует одному варианту загружения). Элементы вектора Zo становятся элементами главной диагонали матрицы LZo.
5.3.15. Вычисляется матрица V по формуле (5.6).
5.3.16. Формируется матрица KKz по формуле (5.5). Матрицы Bi размером 3×3, все элементы которых равны дисперсии соответствующего коэффициента жесткости основания DKzi, накапливаются на поле матрицы KKz путем присвоения строкам и столбцам соответствующих номеров перемещений из массивов ТФi.
5.3.17. В цикле по
количеству вариантов загружения для каждого из вариантов загружения формируются
матрицы KNi и Di. Все элементы квадратной
матрицы КNj равны дисперсии j-го варианта
загружения DNj. А матрицу Dj
получат
по формуле (5.8),
предварительно сформировав диагональную матрицу ![]() .
.
Элементами
главной диагонали матрицы ![]() являются элементы j-го столбца
матрицы RP, деленные на
приведенную нагрузку j-го варианта загружения Nj.
являются элементы j-го столбца
матрицы RP, деленные на
приведенную нагрузку j-го варианта загружения Nj.
5.3.18. Формирование из общих матриц V и Dj (в цикле по количеству вариантов загружения) матриц для каждого элемента (стержня) надфундаментной конструкции Vэi и Dэji.
Матрицы Vэi и Dэji имеют размерность 6×m и образуются из матриц V и Dj путем отбора строк, соответствующих номерам перемещений i-го элемента, записанных в массивах Ti.
5.3.19. Вычисление корреляционных матриц перемещений узлов элементов в общей системе координат KZэоi размером 6×6 по формуле
![]() (5.18)
(5.18)
5.3.20. Перевод матриц KZэоi из обшей системы координат в местную производится по формуле
KZэмi = C KZэоi C’. (5.19)
5.3.21. Организуется цикл по j (j = 1 ... к) для вычисления корреляционных матриц реакций в узлах элементов (стержней) от нагрузок на них KRpэмi (для каждого стержня отдельно) по формуле (5.9).
Для
формирования диагональной матрицы ![]() из матрицы Rэм выписывается в j-й столбец, его
элементы делятся на приведенную нагрузку
из матрицы Rэм выписывается в j-й столбец, его
элементы делятся на приведенную нагрузку ![]() и устанавливаются по главной диагонали
матрицы
и устанавливаются по главной диагонали
матрицы ![]() .
.
5.3.22. Организуется цикл по j (j = 1 .... к) для вычисления смешанных корреляционных матриц перемещений узлов и нагрузок на элемент KZэмi,Rpэмi (для каждого элемента отдельно) по формуле (5.10).
5.3.23. Для получения матрицы KRpэмi,Zэмi производится транспонирование матрицы KZэмi,Rpэмi (см. формулу 5.11).
5.3.24. Вычисляются корреляционные матрицы узловых реакций для каждого элемента (стержня) в местной системе координат по формуле (5.4).
Полученные
по формуле (5.4)
матрицы ![]() для
каждого элемента надфундаментной конструкции являются результирующими и
выводятся на печать.
для
каждого элемента надфундаментной конструкции являются результирующими и
выводятся на печать.
По главной диагонали этих матриц в порядке, принятом в п. 5.1.7 следуют дисперсии внутренних усилий: продольной силы, поперечной силы и изгибающего момента в начале и в конце стержня.
Все остальные элементы являются корреляционными моментами между соответствующими усилиями.
6. ПРИМЕРЫ РАСЧЕТА
Пример 1. Определение коэффициентов жесткости основания и их дисперсий.
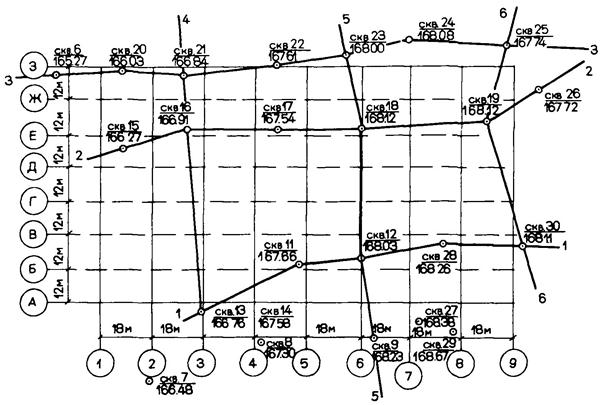
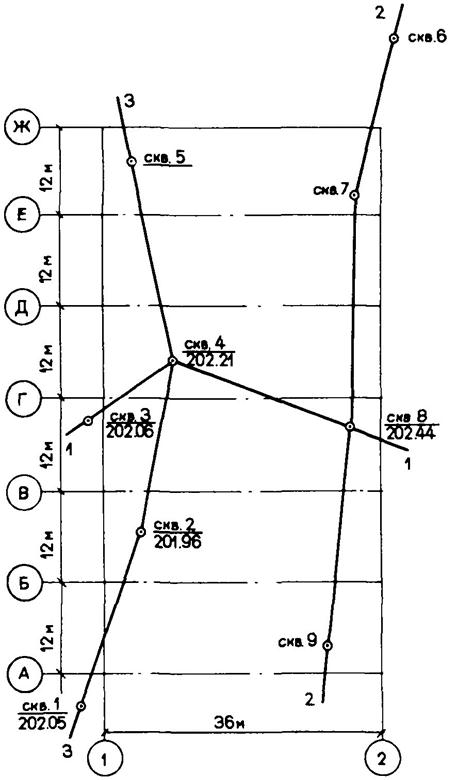
Дано: одноэтажное восьмипролетное промышленное здание; схематический план здания и план расположения скважин, пробуренных на площадке строительства, приведены на рис. 6.1.
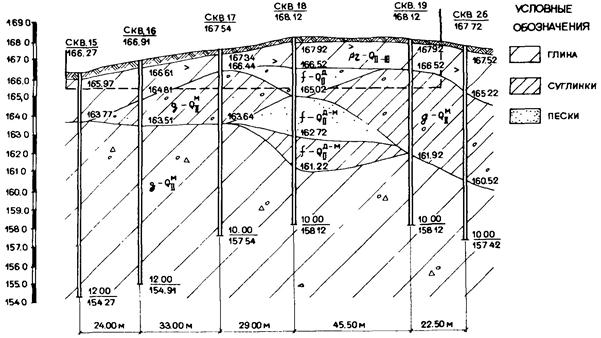
фундаменты столбчатые с глубиной заложения для всего здания на отметке 165,4 м. Для расчета выбрана поперечная рама по оси Е, где наблюдается наибольшая неоднородность напластований (рис. 6.2). Результаты статистической обработки материалов по определению модуля деформации грунтов, слагающих площадку, приведены в табл. 6.1.
Таблица 6.1.
|
Е, МПа |
DE, МПа2 |
|
|
1. Глина пылеватая, тугопластичная, p z - QII-III |
18 |
51,8 |
|
2. Суглинок с прослоями песка, с редким мелким гравием, тугопластичный, g - QIIM |
25 |
64 |
|
3. Глина с гравием и щебнем, g - QIID |
39 |
136,9 |
|
4. Глина с прослойками песка, тугопластичная, f - QIIM |
21 |
67,08 |
|
5. Суглинок с прослойками пылеватого песка, тугопластичный, f - QIID-M |
27 |
122,55 |
|
6. Песок пылеватый, глинистый с линзами суглинка средней плотности, f - QIID-M |
34 |
176 |
Для примера рассмотрим определение коэффициентов жесткости и их дисперсий для некоторых фундаментов рамы по оси Е.
1. Фундамент E-1.
По последнему этапу итерационного расчета рамы совместно с деформирующимся основанием площадь подошвы фундамента А = 2,1 × 2,4 = 5,04 м2. Дополнительное давление на уровень подошвы фундамента ro = 0,123 МПа.
Определяем осадку фундамента по методу послойного суммирования. Разбиваем сжимаемую толщу основания на горизонтальные слои, однородные по сжимаемости высотой не более 0,4b = 0,84 м. Результаты расчетов представлены в табл. 6.2. Осадка фундамента, равная сумме Si, составила 0,00846 м.
Коэффициент жесткости основания вычисляем по формуле (1.10), подставляя вместо N/А давление Ро
![]()
Дисперсию коэффициента жесткости определяем по указаниям пп. 3.6 и 3.7. Так как напластования грунтов под сооружением являются сложными (наличие выклиниваний, линз), то в соответствии с п. 3.6 за толщину j-го слоя грунта принимается его толщина непосредственно под данным фундаментом, а дисперсии толщин слоев и их корреляционные моменты полагаются равными нулю. Тогда по формуле (3.8)
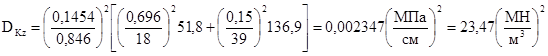
2. Фундаменты Е-5, Е-6, Е-7.
Площадь подошвы фундаментов А = 2,1 × 2,1 = 4,41 м2. Дополнительное давление на уровне подошвы фундаментов Ро = 0,193 МПа. Результаты расчета осадки фундаментов представлены в табл. 6.2.
Осадка фундаментов составила 0,00987 м. Коэффициент жесткости основания
![]()
Дисперсия коэффициента жесткости
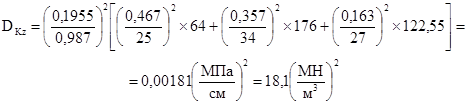
Аналогичным образом находятся коэффициенты и их дисперсии других фундаментов.
Пример 2. Определение коэффициентов жесткости основания и их дисперсий.
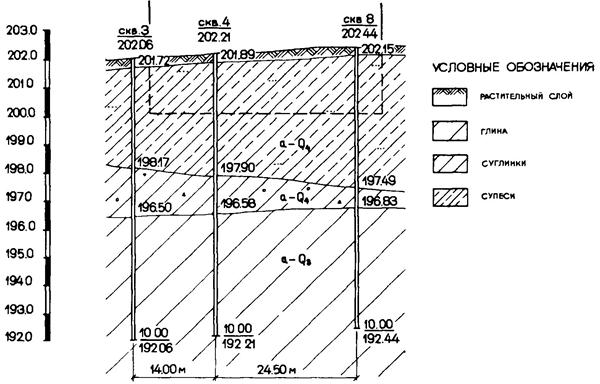
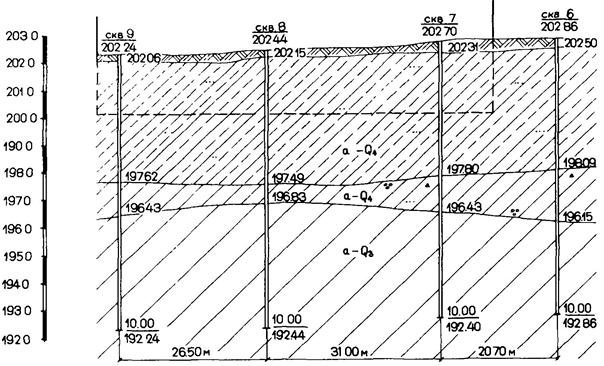
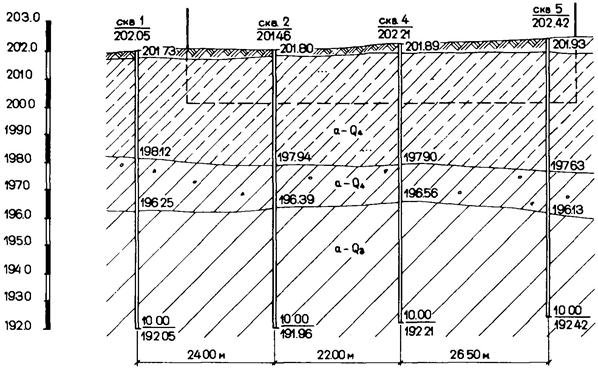
Дано: одноэтажное однопролетное промышленное здание расположено на площадке, геологические разрезы которой показаны на рис. 6.4 - 6.6. Схематический план здания и план расположения скважин приведены на рис. 6.3. Результаты статистической обработки материалов по определению модуля деформации грунтов, слагающих площадку, приведены в табл. 6.3.
Фундаменты столбчатые, на естественном основании. Глубина заложения фундаментов для всего здания принята на отметке 200,1.
Так как напластования грунтов является практически горизонтальными и все фундаменты находятся в аналогичных инженерно-геологических условиях, то для расчета выбираем одну из средних рам здания, например по оси Е.
Рама здания однопролетная, нагрузки на нее не имеют закономерной асимметрии, поэтому фундаменты рамы проектируем одинаковыми.
По последнему этапу итерационного расчета рамы совместно с деформирующимся основанием площадь подошвы фундамента А = 3,0 × 3,9 = 11,7 м2. Дополнительное давление на уровне подошвы фундамента rо = 0,189 МПа.
Определяем осадку фундамента по методу послойного суммирования. Напластования грунтов практически горизонтальны, поэтому под толщиной слоя понимаем его среднюю толщину по девяти скважинам.
Статистическая обработка значений толщин слоев сведена в табл. 6.4.
Средняя толщина слоя супеси ниже подошвы фундамента составляет
![]()
Средняя толщина слоя суглинка составляет
Таблица 6.2
|
Е, МПа |
|
Z, м |
|
l |
σzp, МПа |
σzg,o, МПа |
Si, м |
|
|
Фундамент E-1 |
||||||||
|
Глина p z - QII-III |
18 |
19,6 |
0,84 |
0,80 |
0,816 |
0,100 |
0,033 |
0,00417 |
|
1,63 |
1,55 |
0,477 |
0,059 |
0,049 |
0,00279 |
|||
|
Глина g - QIIM |
39 |
20,4 |
2,10 |
2,00 |
0,362 |
0,044 |
0,059 |
0,00050 |
|
2,94 |
2,80 |
0,220 |
0,027 |
0,076 |
0,00062 |
|||
|
3,78 |
3,60 |
0,142 |
0,018 |
0,093 |
0,00038 |
|||
|
Фундаменты В-5, Е-6, Е-7 |
||||||||
|
Суглинок g - QIIM |
25 |
20,8 |
0,84 |
0,80 |
0,800 |
0,154 |
0,071 |
0,00467 |
|
Песок f - QIID-M |
34 |
18,0 |
1,68 |
1,60 |
0,449 |
0,087 |
0,086 |
0,00238 |
|
2,40 |
2,29 |
0,279 |
0,054 |
0,099 |
0,00119 |
|||
|
Суглинок f - QIID-M |
27 |
20,8 |
3,24 |
3,09 |
0,170 |
0,033 |
0,117 |
0,00108 |
|
3,90 |
3,71 |
0,124 |
0,024 |
0,131 |
0,00055 |
|||
Таблица 6.3
|
Е, МПа |
DE, (МПа)2 |
||
|
1. |
Супесь с маломощными линзами песка, мягкопластичная, а - Q4 |
13 |
10,563 |
|
2. |
Суглинок мягкопластичная, а - Q4 |
15 |
23,04 |
|
3. |
Глина тугопластичная, а - Q3 |
23 |
41,47 |
![]()
Результаты расчета осадки приведены в табл. 6.5
Таблица 6.5
|
Е, МПа |
|
Z, м |
|
l |
σzp, МПа |
σzg,o, МПа |
Si, м |
|
|
Супесь а - Q4 |
13 |
18,1 |
1,20 |
0,80 |
0,836 |
0,1580 |
0,0670 |
0,01281 |
|
2,24 |
1,49 |
0,553 |
0,1045 |
0,0858 |
0,00840 |
|||
|
Суглинок а - Q4 |
15 |
17,9 |
3,04 |
2,03 |
0,395 |
0,0747 |
0,1001 |
0,00382 |
|
3,69 |
2,46 |
0,308 |
0,0582 |
0,1117 |
0,00230 |
|||
|
Глина а - Q3 |
23 |
19,0 |
4,89 |
3,26 |
0,197 |
0,0372 |
0,1345 |
0,00199 |
|
6,09 |
4,06 |
0,135 |
0,0255 |
0,1573 |
0,00131 |
Как следует из табл. 6.5, нижняя граница сжимаемой толщи находится на глубине 6,09 м от подошвы фундамента или на отметке 194,01.
Исходя из этой отметки вычислены толщины слоев глины h3i в табл. 6.4. Средняя толщина слоя глины составляет
![]()
Осадка фундамента, как сумма осадок Si (табл. 6.5) составляет 0,03064 м. Коэффициент жесткости основания
![]()
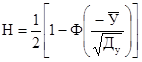 (1.4)
(1.4)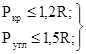
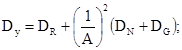 (2.6)
(2.6)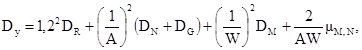 (2.8)
(2.8)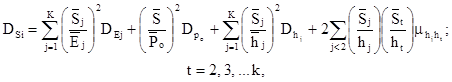
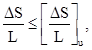
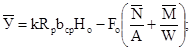
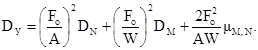 (2.24)
(2.24)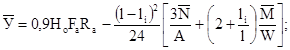 (2.28)
(2.28)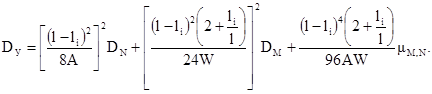 (2.29)
(2.29)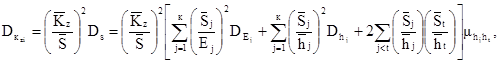
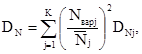
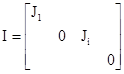
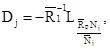
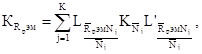 (5.9)
(5.9)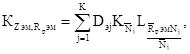 (5.10)
(5.10)