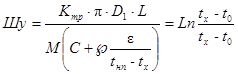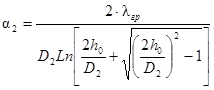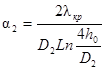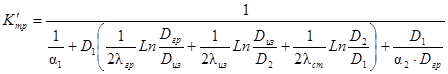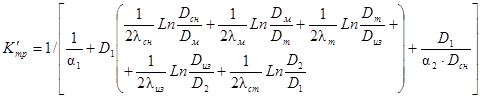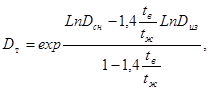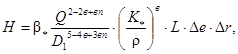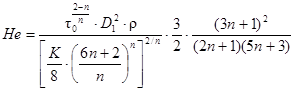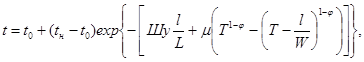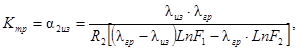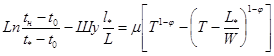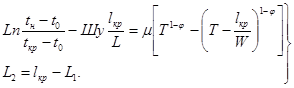МИНИСТЕРСТВО НЕФТЯНОЙ ПРОМЫШЛЕННОСТИ

ВНИИСПТнефть

УТВЕРЖДЕНА Первым заместителем Министра нефтяной промышленности В.И. Кремневым 5 февраля 1979 года

 

 

МЕТОДИКА
ТЕПЛОВОГО И ГИДРАВЛИЧЕСКОГО РАСЧЕТА
МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ ПРИ
СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ
РЕЖИМАХ ПЕРЕКАЧКИ НЬЮТОНОВСКИХ И
Неньютоновских нефтей в различных
КЛИМАТИЧЕСКИХ УСЛОВИЯХ

РД 39-30-139-79

«Методика теплового и гидравлического расчета магистральных трубопроводов при стационарных и нестационарных режимах перекачки ньютоновских и неньютоновских нефтей в различных климатических условиях» является универсальной для расчета трубопроводов, перекачивавших как нелинейно-вязкопластичные, так и псевдопластичные, бингамовские и ньютоновские жидкости, а также дегазированные нефти. Методика предназначена для теплогидравлических расчетов действующих и проектируемых трубопроводов. Методика охватывает области ламинарного и турбулентного режимов движения жидкостей в трубопроводе.

Базой для составления методики явились теоретические и экспериментальные исследования отдела трубопроводного транспорта ВНИИСПТнефть и литературные рекомендации.

Вычисления по методике могут выполняться вручную или по разработанным программам на языке ФОРТРАН-IV для ЭВМ серии ЕС.

Методика составлена к.т.н. Тонкошкуровым Б.А., Гостевым Н.М. и Шутовым А.А.

 

 

РУКОВОДЯЩИЙ ДОКУМЕНТ

РД 39-30-139-79

Вводится взамен:

«Методики теплового и гидравлического расчета трубопроводов при установившемся режиме перекачки подогретых вязкопластичных нефтей и нефтепродуктов», ВНИИСПТнефть, 1974.

«Методики определения безопасного времени остановки «горячих» трубопроводов при перекачке вязкопластичных нефтей».

«Методики теплового и гидравлического расчета пуска и вывода на стационарный режим «горячих» нефтепроводов при перекачке линейно-вязкопластичных нефтей», ВНИИСПТнефть, 1978, РД 39-30-41-78.

«Методики гидравлического расчета трубопроводов при изотермическом режиме течения нелинейно-вязкопластичных нефтей», ВНИИСПТнефть, 1978, РД 39-30-40-78.

Приказом министерства нефтяной промышленности

от 22.02.79 г. № 114 Срок введения с 25.04.79 г. Срок действия до

 

Настоящая методика предназначена для теплогидравлических расчетов действующих и проектируемых нефтепроводов.

Методика позволяет:

1. При известной начальной и конечной температурах жидкости в трубопроводе рассчитать длину участка, на которой происходит падение температуры и потери напора на трение.

2. По начальной температуре подогрева и длине участка определять конечную температуру на участке и потери напора на трение.

3. Произвести тепловой и гидравлический расчеты пускового участка трубопровода.

4. Варьирование исходных параметров определить условия пуска «горячего» нефтепровода в эксплуатацию.

5. Произвести тепловой расчет остановленного трубопровода.

6. Произвести гидравлический расчет трубопровода в период возобновления перекачки.

7. Определить безопасное время остановки трубопровода.

1. ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ

1.1. Индексы

в - величина относится к воздуху;

вгм - величина относится к верхней границе мерзлоты;

вмг - величина относится к вечномерзлому грунту;

вн - величина берется на внутренней поверхности;

гр - величина относится к грунту;

ж - величина относится к жидкости;

из - величина относится к изоляции;

изот - величина относится к изотермическим условиям;

о - величина относится к окружающей среде;

к - конечное значение величины на участке;

кп - величина относится к концу кристаллизации парафина;

кр - критическое значение величины, соответствующее условиям смены режима движения;

лам - величина относится к ламинарному течению;

м - величина относится к мерзлому грунту;

н - начальное значение величины на участке;

нар - величина берется на наружной поверхности;

нп - величина относится к началу кристаллизации парафина;

п - величина относится к поверхности грунта;

пр - предельное значение величины;

сн - величина относится к снегу;

ст - величина относится к стенке трубы;

ср - среднее значение величины;

т - величина относится к талому грунту;

тур - величина относится к турбулентному режиму;

тр. - величина относится к трубопроводу;

ф.в. - фиктивная величина, эквивалентная сопротивлению теплоотдачи от грунта в воздух;

ф.сн - фиктивная величина, эквивалентная сопротивлению снежного покрова;

f - параметр взят при средней температуре потока;

W - параметр взят при средней температуре стенки;

x - величина берется при температуре t_x, при которой из нефти выделилось ε парафина (в частях единицы);

эф - величина, относящаяся к эффективному показателю;

^* - величина, характеризующая проявление неньютоновских свойств жидкости;

20 - величина берется при температуре 20 °C;

15 - величина берется при температуре 15 °C;

1.2. Обозначения

а) техническая характеристика трубопровода:

D₁ - внутренний диаметр трубопровода, м;

R₁ - внутренний радиус трубопровода, м;

D₂ - наружный диаметр трубопровода, м;

R₂ - наружный радиус трубопровода, м;

L - полная длина участка, м;

l - текущая длина участка, м;

h₀ - глубина заложения оси трубопровода, м;

h'₀ - приведенная глубина заложения, м;

β' - конструктивный угол насыпи, градус;

б) тепловая и гидравлическая характеристика перекачиваемой жидкости:

M - массовый расход, кг/с;

Q - объемный расход, м³/с;

W - скорость течения, м/с;

ρ - плотность, кг/м³;

β - коэффициент объемного расширения, 1/°C;

ξ - коэффициент гидравлического сопротивления;

η - динамическая вязкость, Н.с/м²;

v - кинематическая вязкость, м²/с;

 - градиент скорости, 1/с;

k - мера консистенции, Н×сⁿ/м²;

t - температура, °С;

τ₀ - предельное напряжение сдвига, Н/м²;

n - показатель поведения жидкости, 0 < n ≤ 1;

П - общее содержание парафина в нефти (в частях единицы);

ε - количество парафина (в частях единицы), выпавшее из нефти в интервале температур t_fмп ÷ t_fкп;

æ - скрытая теплота кристаллизации парафина:

æ = (2,26 - 2,3) · 10⁵ Дж/кг;

a' - коэффициент температуропроводности, м²/с;

С - весовая теплоемкость, Дж/кг°С;

λ - коэффициент теплопроводности, Вт/м°C;

θ - безразмерная температура, характеризующая темп остывания;

Т - время, с;

T_ост - продолжительность процесса остывания трубы, с;

α₁ - внутренний коэффициент теплоотдачи от жидкости к стенке, Вт/м²×°С;

H - потери напора на трение, м;

р - потери давления на трение, Н/м²;

Z_н = t_н - t₀; Z_* = t_* - t₀;

Z_к = t_к - t₀; Δt = t_f - t_w

в) характеристика окружающей среды:

t₀ - температура окружающей среды в ненарушенном тепловом состоянии в плоскости (горизонтальной) расположения оси трубопровода, °С;

v - скорость ветра, м /с;

δ - толщина слоя, м;

α₂ - внешний коэффициент теплоотдачи от наружной поверхности трубы в окружающую среду, Вт/м²×°С;

K_тр - полный коэффициент теплопередачи трубы, Вт/м²×°С;

1.3. Константы

а - константа в формуле для коэффициента гидравлического сопротивления;

в - показатель степени в формуле для коэффициента гидравлического сопротивления;

B - константа в формуле для предельного напряжения сдвига, 1/°С;

τ"₀ - коэффициент в формуле для определения напряжения сдвига;

u - показатель крутизны вискограммы, 1/°С;

g - ускорение земного притяжения

g = 9,81 м/с²;

Δr - поправка на неизотермичность по радиусу трубы;

Δe - поправка на неизотермичность по длине трубы;

β_* - коэффициент в формуле для определения потерь напора при движении неньютоновской нефти.

A_L - числа Чебышева

А₁ = 0,08375; А₂ = 0,31273; А₃ = 0,5.

А₄ = 0,68727; А₅ = 0,91625.

1.4. Параметры

Ньютоновская жидкость

 - число Рейнольдса;

 - параметр Прандтля;

 - параметр Грасгофа;

Псевдопластичная жидкость

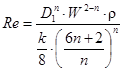 - число Рейнольдса;

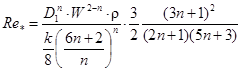 - обобщенный параметр Рейнольдса;

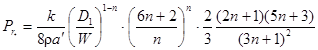 - обобщенный параметр Прандтля;

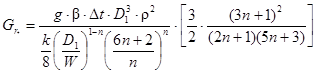 - обобщенный параметр Грасгофа;

Бингамовская жидкость

 - параметр Ильюшина;

 - число Рейнольдса;

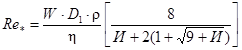 - обобщенное число Рейнольдса

 - число Прандтля;

 - параметр Грасгофа;

 - параметр Хедстрема;

Нелинейно-вязкопластичная жидкость

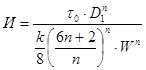 - параметр Ильюшина;

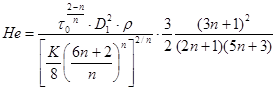 - критерий Хедстрема;

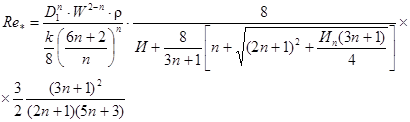 - обобщенный параметр Рейнольдса;

 - обобщенный параметр Прандтля;

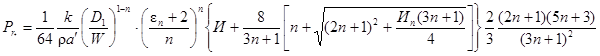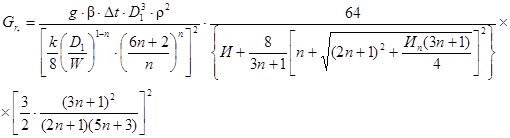 - обобщенный параметр Грасгофа.

2. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА

Исходные данные должны включать в себя:

1) Техническую характеристику трубопровода:

а) производительность перекачки - M;

б) внутренний и наружный диаметр трубопровода - D₁, D₂;

в) длину трубопровода - L;

г) глубину заложения трубопровода, считая по оси - h₀;

д) материал и толщину изоляции - λ_из и δ_из;

е) начальную температуру жидкости - t_н;

ж) конечную температуру жидкости - t_к;

Величины по пунктам в) и ж) могут совместно не задаваться.

2) Характеристику перекачиваемой жидкости - зависимости плотности ρ, коэффициентов теплопроводности λ, удельной теплоемкости C от температуры t; зависимости меры консистенции k, показателя поведения жидкости n, вязкости η и предельного (динамического) напряжения сдвига τ₀ от температуры, температуру проявления неньютоновских свойств жидкости t_*, значение коэффициента объемного расширения.

3) Характеристику внешней среды:

а) сведения о распределении грунтов по трассе трубопровода;

б) данные о температуре, влажности, теплоемкости, объемном весе и коэффициенте теплопроводности грунтов на глубине заложения по месяцам года;

в) данные по срокам выпадания и толщине снегового покрова в районах прохождения трассы трубопровода;

Определение характеристики жидкости необходимо провести в лаборатории непосредственно на нефти (нефтепродукте), предназначенной для перекачки.

Значения τ₀, k, n, η, t_* определяются по методике реологических исследований ВНИИСПТнефть.

Определение плотности производится в соответствии с действующим ГОСТом при температуре 20 °С. Пересчет плотности на плотность при других температурах производится по формуле

                                                             (1)

где β - коэффициент объемного расширения, величина которого выбирается в соответствии с табл. 3 (см. приложение).

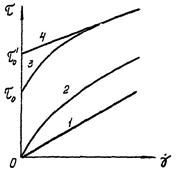
Определение реологических свойств жидкости позволяет установить, к каким моделям следует отнести данную среду при различных температурах (ньютоновской, псевдопластичной, нелинейно-вязкопластичной или бингамовской модели жидкости). Зависимость напряжения от скорости сдвига приведена на рис. 1. Обобщающей моделью всех этих кривых является модель Балкли-Гершеля

                                                                (2)

описывающая нелинейно-вязкопластичную жидкость.

Рис. 1. Зависимость напряжения сдвига от скорости сдвига для различных жидкостей:

1 - ньютоновская, 2 - псевдопластичная, 3 - нелинейно-вязкопластичная, 4 - бингамовская.

При n = 1 уравнение (2) принимает вид:

                                                                    (3)

Это модель Шведова-Бингама, описывающая бингамовскую жидкость.

При τ₀ = 0 уравнение (2) описывает псевдопластичную жидкость

                                                                    (4)

При n = 1 и τ₀ = 0 уравнение (2) переходит в уравнение Ньйтона для описания ньютоновских жидкостей

                                                                 (5)

Определение меры консистенции k и показателя поведения жидкости n производится с помощью кривых  для различных температур. При этом составляется система уравнений для одной кривой

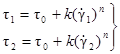
и решается относительно k и n.

Значения градиентов скорости  и  выбирается в рабочей диапазоне режима работы трубопровода .

Параметр консистенции k с повышением температуры уменьшается , приближаясь по численному значению к вязкости обычной ньютоновской жидкости (при t > t_*).

Параметр n с повышением температуры до значения t_* - температуры проявления неньютоновских свойств жидкости возрастает (n = A_N + S_N · t), приближаясь к единице.

Остальные реологические характеристики также определяются в лабораторных условиях. Если такое определение по каким-либо причинам окажется невозможным, то часть их характеристик можно рассчитать.

Весовая теплоемкость рассчитывается по формуле Крего [1]:

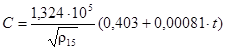                                        (6)

Коэффициент теплопроводности также рассчитывается по формуле Крего [1]:

                                             (7)

Особенностью нелинейно-вязкопластичных нефтей и нефтепродуктов является высокое содержание парафина. Поэтому для них дополнительно необходимо иметь лабораторные данные о температуре начала и конца кристаллизации парафина t_нп и t_кп, а также о количестве парафина в частях единицы ε, выпадающем при температуре t_x < t_нп.

Темп выделения ε/(t_нп - t_x) можно приближенно оценить по следующему выражению:

                                                       (8)

При ориентировочных расчетах интервал (t_нп - t_кп) можно принимать равный 40 - 50 °C, а температуру t_нп выбирать в пределах 40 - 50 °C [3]. Содержание парафина в некоторых нефтях по данным Ашумова, Павловой к др. [4], [5], [6], представлено в табл. 4 (см. приложение).

Теплофизические свойства (коэффициенты теплопроводности и температуропроводности и теплоемкость) грунтов в мерзлом и талом состоянии являются важными параметрами при тепловом расчете трубопровода. Необходимо определять теплофизические свойства грунтов непосредственно в полевых условиях на трассах трубопроводов. При этом можно методом статистической обработки более обоснованно выбрать значения их коэффициентов теплопроводности и температуропроводности, определить длину расчетных участков трубопровода, на которых теплофизические свойства грунтов можно принять постоянными.

В качестве основного метода полевых определений теплофизических свойств вечномерзлых грунтов рекомендуется метод регулярного режима [7].

При определении теплофизических свойств грунтов, не относящихся к категориям вечномерзлых, наиболее простым является зондовый.

При отсутствии возможности определения теплофизических свойств грунтов в полевых условиях необходимые параметры могут быть приняты по действующим СНиПам (СНиП II-18-76, СНиП II-A.6-72 и др.) и «Справочникам по климату СССР».

3. ТЕПЛОВОЙ РАСЧЕТ НЕФТЕПРОВОДА ПРИ УСТАНОВИВШЕМСЯ РЕЖИМЕ ПЕРЕКАЧКИ ЖИДКОСТИ

Тепловой расчет ставит своей задачей установить распределение средней температуры потока по длине «горячего» трубопровода в пределах участка с одинаковыми теплофизическими свойствами грунта (окружающей среды).

Поскольку выделение парафина из нефти оценивается пропорционально понижению температуры, то расчет распределения температуры по длине «горячего» трубопровода проводится по формуле Шухова-Черникина [2]:

                                          (9)

При перекачке подогретых нелинейно-вязкопластичных жидкостей в результате падения температуры изменяются физические свойства нефти по длине трубопровода. Вследствие этого в трубопроводе может иметь место несколько режимов течения. Каждому из них соответствует свой закон изменения температуры и давления.

В общем случае на начальном участке наблюдается турбулентный режим течения, на конечном - ламинарный. Кроме того, при температуре t_* в результате выпадения парафина начинается проявление неньютоновских свойств нефти. Картина изменения температуры нефти по длине трубопровода показана на рис. 2 [8].

Рис. 2. Изменение температуры жидкости по длине трубопровода

При этом могут иметь место два случая:

1) При t_* > t_кр на участке L - l_кр наблюдается ламинарный режим течения неньютоновской жидкости, на участке 0 - l_* - ньютоновское турбулентное и на участке l_кр - l_* - неньютоновское турбулентное.

2) при t_* = t_кр на участке 0 - l_кр будет иметь место турбулентный режим течения ньютоновской жидкости, а на участке l_кр - L - ламинарный режим течения неньютоновской жидкости.

Здесь t_кр - критическая температура, определяющая границу перехода турбулентного режима течения в ламинарный (см. разд. 5).

В параметр Шухова входит полный коэффициент теплопередачи, величина которого определяется в зависимости от способа прокладки.

3.1. Подземная прокладка

Полный коэффициент теплопередачи следует рассчитывать из выражения:

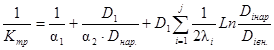                            (10)

Коэффициент внутренней теплоотдачи от жидкости к стенке (α₁) определяется по следующей зависимости:

                                                        (11)

Число Нуссельта при ламинарном течении нелинейно-вязкопластика находится по формуле:

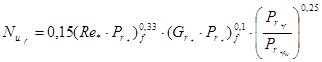                            (12)

При турбулентном режиме течения внутренний коэффициент теплоотдачи определяется по формуле:

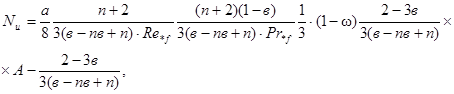          (13)

где a и в - коэффициенты, определяемые графически (см. разд. 4.2)

ω = τ₀/τ_w,

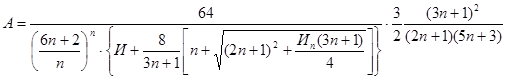
В переходной области значения α₁ можно по рекомендации М.А. Михеева приближенно находить интерполяцией между формулами для ламинарного и турбулентного режимов течения.

Наружный коэффициент теплоотдачи от стенки трубопровода в грунт определяется по формуле Форхгеймера-Гребера:

                                           (14)

В практических расчетах формула (14) заменяется с точностью до 1 % формулой

                                                      (15)

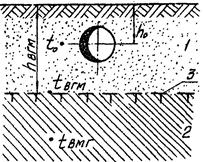
В формулах (14) и (15) α₂ относится к разности температур внешней поверхности трубы и температуры грунта в ненарушенном тепловом состоянии на глубине заложения трубопровода. Эти формулы применимы при h₀/D₂ ≥ 3. При меньшей относительной глубине заложения, а также при глубине засыпки трубы меньше 0,7 м необходимо учитывать тепловое сопротивление на границе «грунт-воздух» [16]. Это сопротивление можно заменить сопротивлением фиктивного слоя грунта толщиной

                                                         (16)

где α_в - коэффициент теплоотдачи от грунта в воздух (11,63 ÷ 17,45 Вт /м²×°С). Коэффициент α_в можно также определить в зависимости от скорости ветра по данным Фокина [17] (табл. 8, приложения).

Сведения по величине скорости ветра по месяцам года для различных районов содержатся в СНиП II-А.6-72 и [18].

При наличии снегового покрова его теплоизолирующее влияние учитывается введением в расчет толщины фиктивного слоя грунта, заменяющего по тепловому сопротивлению снежный покров

                                                   (17)

Значения коэффициента теплопроводности снега λ_сн [Вт/м°C] можно назначить, ориентируясь данными [18], или приближенно принимать для рыхлого снега -0,23, плотного -0,58.

Таким образом, при малой глубине заложения трубопровода и наличии снегового покрова в формулу (15) необходимо вводить приведенную глубину заложения

h'₀ = h₀ + δ_ф.в + δ_ф.сн.                                                 (18)

Значение глубины заложения (h₀) трубопровода выбирается в соответствии с СНиП II-45-75.

При малой глубине заложения трубопровода (h₀/D₂ < 3) α₂ относят к разности температур внешней поверхности трубы и воздуха. Для подземного трубопровода с концентрической тепловой изоляцией коэффициент внешней теплоотдачи определяется по формуле

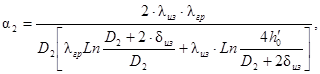                         (19)

где λ_из и δ_из - соответственно коэффициент теплопроводности и толщина изоляции.

При подземной прокладке трубопровода в районе распространения вечномерзлых грунтов значение параметра Шухова определяется по зависимости

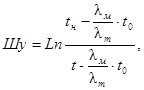                                                   (20)

здесь λ_м и λ_т - соответственно коэффициенты теплопроводности мерзлого и талого грунтов, значения которых выбираются по табл. 5 (см. приложение).

t₀ - температура грунта в слое сезонного оттаивания на глубине заложения оси трубопровода (рис. 3)

Значение t₀ определяется линейной интерполяцией, используя табл. 1, при известных значениях глубины залегания и температуры верхней границы мерзлоты.

Рис. 3. Вид залегания вечномерзлых грунтов (сливающаяся криолитозона)

1 - слой сезонного оттаивания; 2 - вечномерзлая толща грунтов; 3 - верхняя граница вечномерзлых грунтов.

Таблица 1

Температурный градиент в слое сезонного оттаивания на глубине ниже 1 м от поверхности земли

Месяцы

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

Температурный градиент °С/м

-4

-4

-4

-2,5

+2

+3

+4

+3

+3

-0,5

-3

-4

Примечание. Знак градиента показан в направлении к дневной поверхности.

Для определения температуры грунта в метровом слое от поверхности необходимо вычислить температуру на глубине 1 м и температуру дневной поверхности грунта, а затем путем интерполяции по этим двум значениям определить температуру на заданной глубине.

Глубина залегания верхней границы вечномерзлой толщи грунтов определяется расчетным путем на момент максимального оттаивания с поверхности (сентябрь, а в южных районах области вечномерзлых грунтов - начало октября) в наиболее теплое лето за срок 10 - 15 лет. Расчет ведется по формуле:

h_вгм = k_w · S,                                                                (21)

где S - глубина оттаивания грунта, взятая по карте глубины сезонного оттаивания [19] для данного географического района.

k_w - поправочный коэффициент для перехода на фактическую влажность [19].

Температура грунта на уровне верхней границы мерзлоты определяется по формуле:

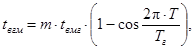                                              (22)

где m - коэффициент, зависящий от периода года (для периода октябрь-май m = 1,5, а для периода июнь-сентябрь m = 1,0);

t_вмг - температура вечномерзлой толщи грунтов;

Т_г - время, равное году (8760 ч);

Т - время, отсчитываемое вперед (через 1 января) от момента начала осеннего замерзания грунта до момента, для которого ведется расчет температуры, ч.

Температура вечномерзлой толщи грунтов может быть получена непосредственным измерением температуры грунта на глубине 10 м от поверхности или по карте изолиний температуры криолитозоны [19]. В местах перехода через водотоки, где термический режим вечномерзлых грунтов под влиянием тепла в массах воды нарушается, этой картой пользоваться нельзя.

Для расчета α₁ и α₂ необходимо знать соответствующие температуры стенки трубы. Они находятся методом последовательных приближений с проверкой по уравнению теплового баланса:

α₁ · D₁ · (t_f - t_v) = α₂ · D₂ · (t_w - t₀)                                          (23)

При расчетах удобнее пользоваться следующим методом.

Задаются рядом значений t_w (тремя или четырьмя). Для каждого из значений по соответствующим формулам рассчитываются α₁ и α₂. Затем составляются произведения α₁ · D₁ · (t_f - t_w) и α₂ · D₂ · (t_w - t₀), которые наносятся на график в зависимости от t_w. Точка пересечения кривых определит значение температуры стенки t_w в данном сечении трубопровода.

3.2. Прокладка в насыпи

Полный коэффициент теплопередачи определяется по-разному для различных участков периметра трубы и в зависимости от периода (зимнего или летнего) года. Для верхней части трубы коэффициент теплопередачи K'_тр определяется следующим образом:

Для летнего периода:

           (24)

Величины коэффициентов теплопроводности различных типов тепловой изоляции, по данным С.В. Хижнякова [13], приведены в приложении (табл. 6) в зависимости от средней температуры слоя изоляции, определяемой по табл. 7 (приложение).

Для зимнего периода:

   (25)

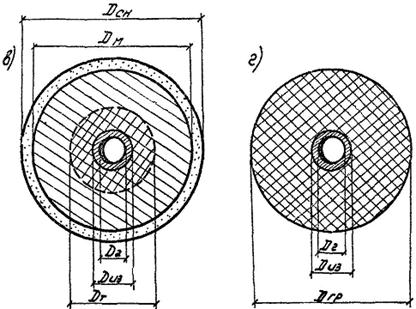
Диаметры, входящие в формулы (24) и (25), находятся из предположения, что теплоизоляция трубы состоит из ряда концентрических слоев (рис. 4).

Для зимнего периода:

D_сн = D₂ + 2 · (δ_из + δ_гр + δ_сн)                                                (26)

D_м = D₂ + 2 · (δ_из + δ_м)                                                     (27)

D_из = D₂ + 2 · δ_из                                                               (28)

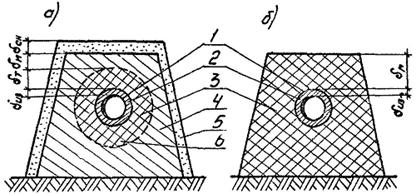
Рис. 4. Расчетные схемы для трубопроводов, уложенных в насыпи

а) и в) - для зимнего периода; б) и г) - для летнего периода; 1 - трубопровод; 2 - теплоизоляция; 3 - грунт насыпи в талом состоянии; 4 - грунт в насыпи в мерзлом состоянии; 5 - снежный покров; 6 - граница ореола оттаивания вокруг трубы.

Для летнего периода:

D_гр = D₂ + 2 · (δ_из + δ_т)                                               (29)

D_из = D₂ + 2 · δ_из                                                   (30)

Входящую в формулы расчета K'_тр величину α₂ (коэффициент теплоотдачи на поверхности насыпи) определяют по формуле:

α₂ = 6,16 + 4,19 · V, Вт /м² · °C                                       (31)

где V - скорость ветра, м /с.

Величина D_т - диаметр ореола протаивания (талика) в слое вечномерзлого грунта рассчитывается по формуле:

                                           (32)

где t_в - расчетная температура наружного воздуха;

t_ж - температура жидкости в трубопроводе.

Диаметр талика вокруг трубы в данном случае будет величиной переменной, т.к. зависит от постоянно меняющейся по длине трубопровода температуры жидкости. Однако для инженерных расчетов нет необходимости идти на такие осложнения. Для участков, где температура жидкости будет изменяться от начальной положительной до 0 °C, можно принимать среднюю температуру жидкости.

Ошибка при этом не будет превышать 5 %. При этом формула (32) примет вид:

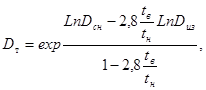                                            (33)

здесь t_н - начальная температура жидкости на участке.

Коэффициент теплопередачи для нижней части трубы определяется по формуле:

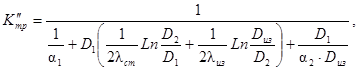                        (34)

где α₂ определяется по формуле (15) с заменой λ_гр на λ_м - зимой и λ_т - летом.

Величина h'₀, входящая в формулу (15), в данном случае определяется по следующей зависимости:

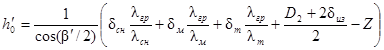                   (35)

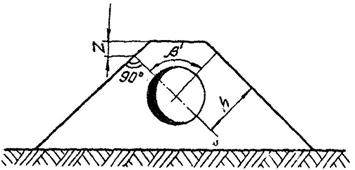
Угол β' и Z берутся по чертежу конструкции насыпи (рис. 5). В окончательном виде для подстановки в формулу (9) величину K_тр следует определять по формуле:

                                          (36)

Рис. 5 Схема конструкции насыпи

Параметр Шухова определяется по зависимости:

                                                         (37)

здесь t_o - температура внешней среды вокруг трубопровода;

                                     (38)

Для зимнего периода, когда температуру на поверхности насыпи можно принимать равной температуре воздуха, формула (38) записывается так:

                                       (39)

где t_в - температура воздуха на расчетный период, °С;

t_п - температура поверхности насыпи, °С;

t_вмг - температура вечномерзлой толщи грунтов, °C.

Для летнего периода можно принимать t_п = 2 + 1,15 · t_в.

3.3. Надземная прокладка

Для трубопровода, проложенного надземно с теплоизоляцией, коэффициент теплопередачи определяется по формуле:

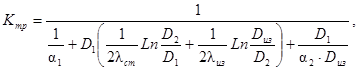                        (40)

Здесь α₂ - коэффициент теплоотдачи на наружной поверхности трубы

                                              (41)

где V - скорость ветра, м /с.

3.4. Подводная прокладка

При прокладке «горячего» трубопровода в воде коэффициент теплоотдачи от стенки трубопровода к воде определяется по формуле (15):

а) непроточная вода:

                                                     (42)

где значения m₁ и n₁ выбирайся по табл. 9 (см. приложение).

При этом физические характеристики для вычисления произведения (G_r · P_r) относят к средней температуре

                                                        (43)

за линейный размер в параметре Грасгофа принимается наружный диаметр трубы;

б) проточная вода (поперечное обтекание):

                                                         (44)

где значения m₂ и n₂ выбираются по табл. 10 (см. приложение).

4. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДА ПРИ УСТАНОВИВШЕМСЯ РЕЖИМЕ ПЕРЕКАЧКИ НЕЛИНЕЙНО-ВЯЗКОПЛАСТИЧНОЙ ЖИДКОСТИ

Гидравлический расчет трубопроводов, перекачивающих нелинейно-вязкопластичную жидкость, для всех режимов течения проводится по формуле [32]:

                                  (45)

где

                           (46)

Значения a, в, n и ρ определяется при среднеарифметической температуре потока жидкости на рассматриваемом участке.

4.1. Ламинарный режим

Для ламинарного режима течения нелинейно-вязкопластичных жидкостей а = 64, в = 1 и формула (45) с учетом (46) примет вид:

                       (47)

Поправку на неизотермичность по длине трубопровода в уравнении (47) следует рассчитывать по следующей зависимости:

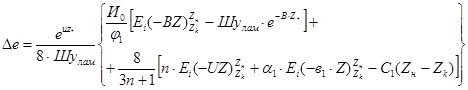                (48)

Здесь e^х - показательная функция, значения которой приведены в [36]

e - основание натуральных логарифмов

E_i(z) - интегральная показательная функция, значения которой приведены в [35]

                                  (49)

                           (50)

                                       (51)

                                                        (52)

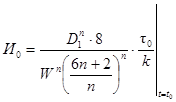                                         (53)

Показатель крутизны вискограммы определяется по следующей зависимости:

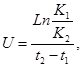                                                          (54)

где K₁ и K₂ - значения меры консистенции, соответствующие произвольным температурам t₁ и t₂, входящим в рабочий интервал температур.

Предельное напряжение сдвига в зависимости от температуры определяется по формуле:

                                                    (55)

где τ^"₀ - величина, определяемая опытным путем;

B - постоянный для данной жидкости коэффициент;

t_* - температура появления предельного напряжения сдвига.

Поправка на неизотермичность по радиусу трубопровода определяется по формуле М.А. Михеева с учетом нелинейно-вязкопластичных свойств жидкости:

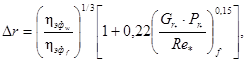                                  (56)

где η - эффективная вязкость, определяемая следующим образом:

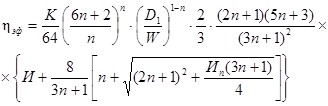                       (57)

Индексы W и f обозначает, что реологические параметры принимаются при среднеарифметической температуре стенки и потока нефти по длине трубопровода:

                                                       (58)

                                                        (59)

4.2. Турбулентный режим

Коэффициент гидравлического сопротивления, входящий в формулу Дарси-Вейсбаха

                                                         (60)

определяется по эмпирической формуле

                                                           (61)

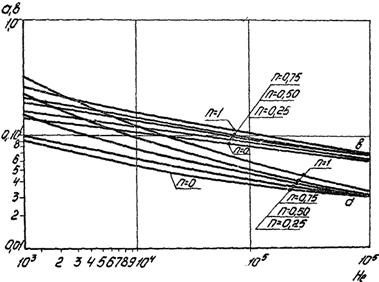
Значения коэффициента a и показателя степени в, зависящие от числа Хедстрема (Не) и показателя поведения жидкости (n), определяют графически (рис. 6) или в интервалах изменения 0,25 < n ≤ 1 и 10³ < He ≤ 10⁶ по зависимостям

a = (0,521 - 1,75n + 4,409n²) · He^{-(0,137 + 0,212n)}                                    (62)

                                    (63)

здесь

                                   (64)

При He > 10⁶ ξ не зависит от n, , Не и равно ξ = 0,0156; при Не < 10³ а и в выбираются для значений He < 10³ в зависимости от n.

Для турбулентного режима течения нелинейно-вязкопластичных жидкостей расчетными формулами являются формулы (45) и (46).

Поправка на неизотермичность по длине трубопровода определяется

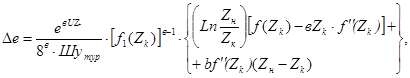                     (65)

где

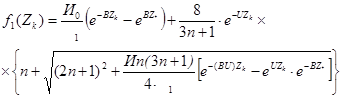                            (66)

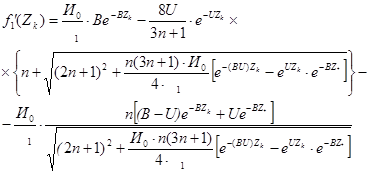                     (67)

Рис. 6. Значения коэффициента a и показателя степени в в формуле для определения коэффициента ξ
в зависимости от параметра Хедстрема и показателя поведения жидкости.

Поправку на неизотермичность по радиусу трубы при турбулентном течении нелинейно-вязкопластичных жидкостей следует определять по формуле М.А. Михеева с учетом нелинейно-вязкопластичных свойств жидкости:

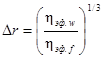                                                           (68)

При перекачке подогретой нелинейно-вязкопластичной жидкости на начальных участках до момента значительного выделения парафина и проявления нелинейно-вязкопластичных свойств имеет место течение ньютоновской жадности. Для этого участка имеем a = 0,3164, в = 0,25 (турбулентный режим течения в области действия закона Блазиуса) и формула (45) с учетом (46) переходит в формулу В.И. Черникина для ньютоновской жидкости

                                       (69)

Поправка на неизотермичность по длине трубопровода в формуле (69) рассчитывается по зависимости:

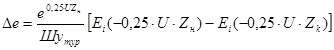                           (70)

Поправка на неизотермичность по радиусу трубы по формуле (69) определяется следующим образом:

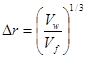                                                         (71)

Для расчета трубопроводов, перекачивающих нелинейно-вязкопластичную жидкость при изотермическом режиме используются те же формулы (45), (46), (47), (69) без учета поправок Δe и Δr.

5. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ПОТОКА ЖИДКОСТИ

Переход от турбулентного режима течения жидкости в трубопроводе в ламинарный наступает при определенном числе Рейнольдса и критической температуре.

Для нелинейно-вязкопластичных жидкостей значение критического обобщенного числа Рейнольдса определяется по формуле:

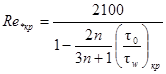                                                      (72)

и изменяется в пределах от 2100 до 4200.

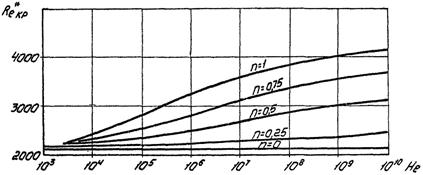
Исследования [22] позволили получить графическую зависимость критического обобщенного числа Рейнольдса от параметра Хедстрема и показателя поведения жидкости (рис. 7).

Для определения критической температуры рассчитывается обобщенное число Рейнольдса в рабочем диапазоне температур по формуле:

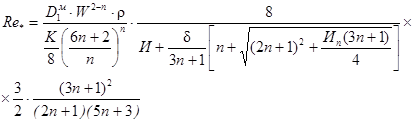               (73)

и строится график зависимости обобщенного числа Рейнольдса от температуры

Затем по формуле (64) рассчитывается параметр Хедстрема в интервале температур, при которых перекачивается жидкость. Значение критического обобщенного числа Рейнольдса определяется по рис. 7 в зависимости от параметра Хедстрема и показателя поведения жидкости.

При изменении параметра Хедстрема от 10³ до 10⁶ и показателя поведения жидкости от 0,25 до 1,0 значение критического обобщенного числа Рейнольдса можно определить по формуле:

                                        (74)

Рис. 7. График зависимости значения критического обобщенного числа Рейнольдса
от параметра Хедстрема и показателя поведения жидкости

Построив график зависимости обобщенного критического числа Рейнольдса от температуры, находим точку пересечения кривых  и , которая и даст значение критической температуры.

6. ТЕПЛОВОЙ РАСЧЕТ ПУСКА НЕФТЕПРОВОДА

(нестационарный режим перекачки)

В отличие от стационарной работы в пусковой период значительно возрастают потери тепла, в связи с этим ухудшаются реологические свойства нефти и увеличиваются потери на трение. Чрезмерный рост их может привести к замораживанию трубопровода. Поэтому большое значение имеет проведение теплогидравлических расчетов в период пуска.

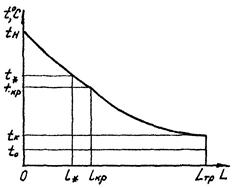
Тепловой расчет при пуске нефтепровода ставит своей задачей установить распределение средней по сечению температуры потока по длине нефтепровода в зависимости от времени с начала его заполнения. Эта температура описывается следующим уравнением:

                     (75)

где

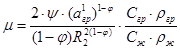
Коэффициенты ψ и φ зависят от глубины заложения и диаметра трубопровода и определяются по табл. 11 (см. приложение)

 - параметр Шухова;

В период пуска, значение полного коэффициента теплопередачи принимается равным внешнему коэффициенту теплоотдачи трубопровода (K_тр = α₂). Если трубопровод имеет тепловую изоляцию, общий вид формулы следующий:

                                    (76)

где

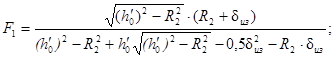
Если трубопровод не имеет тепловой изоляции (δ_из = 0), то формула (76) переходит в формулу Форхгеймера-Гребера.

Значение приведенной глубины заложения h'₀ определяется аналогично, как для стационарного режима (см. раздел 3.1), по формуле (18).

При Т → ∞ формула (75) дает распределение температуры по длине неизотерического трубопровода по закону Шухова (стационарный режим)

                                                (77)

В результате падения температуры нефти, закачиваемой в нефтепровод, ее физические свойства изменяется по длине трубопровода. Вследствие этого в трубопроводе может быть несколько режимов течения.

При заполнении нефтепровода неньютоновской (псевдопластичной, нелинейно-вязкопластичной, вязкопластичной) жидкостью будут те же режимы течения, что и при стационарной перекачке:

а) в случае, если t_* > t_кр, то будет три типа течения: турбулентный режим течения ньютоновской жидкости, турбулентный и ламинарный режимы течения неньютоновской жидкости.

Длина участка с турбулентным режимом течения ньютоновской жидкости l₁ определяется из следующего уравнения: (l₁ = l_*)

                                   (78)

Длина участка с турбулентным режимом течения неньютоновской жидкости l₂ определяется из системы уравнений:

                                   (79)

Длина участка с ламинарным режимом течения неньютоновской жидкости l₃ определяется следующим образом:

l₃ = W · T - l_кр при W · T < L

l₃ = L - l_кр при W · T ≥ L                                                      (80)

б) в случае, если t_* = t_кр, то будет два типа течения: турбулентный режим течения ньютоновской жидкости и ламинарный режим течения неньютоновской жидкости.

Длины участков данных типов течения определяются из уравнений (78, 80). В этом случае l₂ = 0.

В связи с тем, что уравнения (78, 79) являются трансцендентными, l_кр и l_* определяются при помощи графоаналитических методов или метода последовательных приближений.

Если при расчете длины первого участка получится, что l₁ > W · T(W· T < L) или l₁ > W · T(W · T ≥ L), то следует за l₁ принять, соответственно, W · T или L, a l₂ и l₃ приравнять к нулю. Если при расчете (l₁ + l₂) получится, что (l₁ + l₂) > W · T(W · T < L) или (l₁ + l₂) > L(W · T ≥ L), то следует (l₁ + l₂) приравнять соответственно, W · T или L.

7. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ПУСКА НЕФТЕПРОВОДА

Потери напора на трение на участке нефтепровода при любом режиме течения жидкости, подчиняющейся реологическому закону Балкли-Гершеля, определяются по следующей формуле [32]:

H_j = H_изот · Δl, τ,                                                          (81)

где

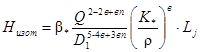                                      (82)

β_* - коэффициент, определяемый по формуле (46)

Δl, τ - поправка на неизотермичность и нестационарность процесса в период пуска нефтепровода.

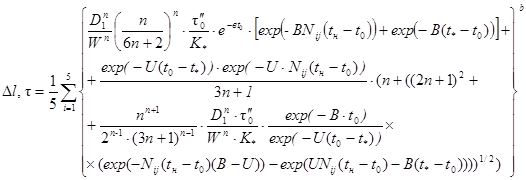  (83)

Здесь

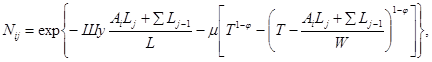
где ΣL_j-1 - сумма длин участков течения жидкости, предшествующих расчетному; j - индекс, обозначающий порядковый номер участка, A_i - числа Чебышева (см. 1.3).

При расчете потерь напора на трение в формулах значения коэффициентов a и b следует принимать в соответствии с табл. 2.

Таблица 2

Значение коэффициентов a и в в зависимости от вида жидкости и режима течения

Полные потери напора на трение на заполняемом нефтью трубопроводе составляется из потерь напора на трение на отдельных участках с соответствующим режимом течения.

8. ВЫХОД «ГОРЯЧЕГО» НЕФТЕПРОВОДА НА СТАЦИОНАРНЫЙ РЕЖИМ

При заполнении трубопровода горячим нефтепродуктом с постоянным расходом полные потери напора на трение будут возрастать и достигнут максимального значения в момент, когда жидкость заполнит весь трубопровод (участок нефтепровода между насосными станциями). Максимальные потери напора на трение и будут тем критерием, по которому выбирается вариант пуска нефтепровода. В случае, если заполнение осуществляется высоковязкой высокозастывающей нефтью, то пусковое давление может превысить возможности насосно-силового оборудования и прочность трубопровода. Снижение пускового давления достигается как предварительным подогревом трубопровода и окружающего его грунта маловязким нефтепродуктом или водой, так и повышением температуры закачиваемой нефти или введением в нее депрессатора, снижающего вязкость и прочность структуры.

При дальнейшей работе трубопровода (после его заполнения) грунт вокруг трубопровода будет постепенно прогреваться, температура нефтепродукта повысится, а вязкость понизится. В связи с этим потери напора на трение снизятся, а при достаточно длительной работе нефтепровода станут близкими к постоянным - наступит гидравлический стационарный режим.

При этом давление значительно раньше приближается к значению, близкому к стационарному, чем наступает стационарный тепловой режим.

Время выхода «горячего» нефтепровода на тепловой стационарный режим определяется по формуле:

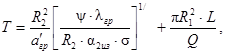                                            (84)

где

В расчетах σ - можно принимать равной 0,1.

9. ТЕПЛОВОЙ РАСЧЕТ БЕЗОПАСНОГО ВРЕМЕНИ ОСТАНОВКИ НЕФТЕПРОВОДА

Процесс остывания характеризуется темпом охлаждения или безразмерной температурой, определяемой по следующей формуле:

                                         (85)

Здесь

 - параметр Фурье

При h₀ /R₂ ≥ 4 величина  практически стремится к нулю. При таком допущении из (85)

                                                   (86)

Изменение температуры нефти по длине трубопровода в процессе остывания описывается зависимостью

                                                (87)

Если время остановки Т_ост = 0, то Θ = 1 и имеем закон Шухова для распределения температуры нефти по длине трубопровода для стационарного режима.

Значение коэффициента теплоотдачи от трубы в грунт в процессе остывания описывается формулой:

                                                      (88)

где  - коэффициент теплоотдачи от наружной поверхности трубопровода в окружающую среду при стационарном режиме теплообмена, определяемый по формуле (15).

10. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ БЕЗОПАСНОГО ВPEМЕНИ ОСТАНОВКИ НЕФТЕПРОВОДА

Расчет критической температуры и определение потерь напора на трение при возобновлении перекачки по нефтепроводу производится по формулам стационарного режима с учетом изменения температуры жидкости и ее свойств в результате остывания.

11. ОПРЕДЕЛЕНИЕ БЕЗОПАСНОГО ВРЕМЕНИ ОСТАНОВКИ «ГОРЯЧЕГО» НЕФТЕПРОВОДА

При возобновлении перекачки после остановки потери на трение в трубопроводе будут складываться из потерь на трение по перекачке остывшего и вновь закачиваемого нефтепродукта.

Максимальные потери на трение будут наблюдаться в момент пуска, когда весь трубопровод заполнен остывшим нефтепродуктом. Эти потери можно определить по вышеприведенной методике.

Пуск нефтепровода после остановки необходимо производить при максимально допустимом напоре, исходя из механической прочности трубы.

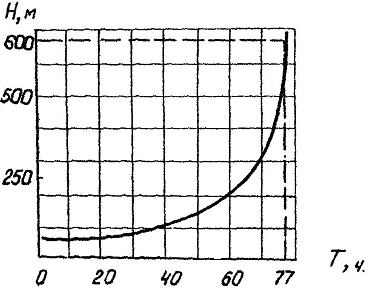
Определение безопасного времени остановки производится следующим образом. Строится график изменения потерь на трение в момент пуска в зависимости от продолжительности остановки, т.е. H = f(T) (рис. 8)

Рис. 8 Определение времени безопасной остановки трубопровода

Откладывается на графике допустимый напор и проводится параллельная оси абсцисс до пересечения с кривой H = f(T). Из точки пересечения опускается перпендикуляр на ось абсцисс. Точка пересечения дает отсчет безопасного времени остановки с учетом возможности насосно-силового оборудования и несущей способности трубопровода.

12. ПРОГРАММА ВЫЧИСЛЕНИЙ ПО МЕТОДИКЕ НА ЭВМ EС-1020, 1022

Методика запрограммирована на языке ФОРТРАН-IV для ЭВМ серии ЕС с использованием операционной системы ДОС/ЕС и состоит из трех индивидуальных программ.

Программирование осуществлялось в ВЦ ВНИИСПТнефть программистами Нуретдиновой Р.Л. и Яканиной Т.В. при научной консультации Телкошкурова Б.А., Гостева H.М., Титова Н.С., Шутова А.А.

12.1. Программа RASNEF

Программа RASNEF составлена для теплового и гидравлического расчета нефтепровода при установившемся режиме перекачки неньютоновских жидкостей.

В программе используются стандартные модули системы управления вводом-выводом и стандартные программы из библиотеки ФОРТРАНА. Время счета контрольного примера - 5 минут.

На АЦПУ распечатываются исходные данные и выводятся результаты по трем участкам нефтепровода: турбулентный ньютоновский, турбулентный неньютоновский и ламинарный неньютоновский.

Исходными данными являются: D₁, D₂, W, t_н, t_к, t_о, h_о, n, K, ρ, C, λ_ж, λ_гр, λ_м, α_в, δ_сн, λ_сн, D_из, λ_из, λ_т, τ'₀;

Таблица А (28,5), R_k (55,5)

Выходная информация:

- критическая температура;

- критический параметр Рейнольдса;

- критический параметр Хедстрема;

- длина участка;

- потери давления на участке.

Пример 1: Произвести тепловой и гидравлический расчет стационарного режима нефтепровода при следующих исходных данных:

Прокладка подземная

D₁ = 0,996 м; D₂ = 1,02 м; h_о = 1,3 м; t_н = 57,4 °C;

t_k = 34,02 °C; t_о = 13,2 °C; t_* = 41 °C; W = 0,42 м/с;

η = 1,03 · e^-0,08t, Нс/м², при t > t_*;

K = 25,898 · e^-0,155t, Нсⁿ/м², при t < t_*;

τ₀ = 97610,813 · e^-0,318t, Н/м², при t < t_*;

n = 0,526 · 0,0114 · t, при t < t_*

ρ = 863,4 - 0,557 · t, кг/м³

С = 1822,65 + 0,00367 · t, Дж/кг · °C

λ = 0,137 - 0,000074t, Вт/м · °C (нефть)

λ_гр = 0,812 Вт/ м · °C

β = 0,0006 1/°C;

Выходной документ программы RASNEF приведен на стр. 41.

12.2. Программа TOPAZ

Программа TOPAZ разработана для теплового и гидравлического расчета пуска нефтепровода. В программе использованы стандартные программы LINEX, SEARCH из пакета научных прикладных программ на ФОРТРАНЕ.

Время решения контрольного примера 7 минут.

Для эксплуатации программы используется следующая исходная информация:

L, D₁, D₂, h_о, ψ, φ, M, C, ρ, W, t_н, t_*, T [30], t_о, λ_гр,  λ_из, δ_сн, α_в, a'_гр, B [2], τ"₀ [2], K [2], U [2], A_k, S_k, A_N, S_N;

Таблица значений a и

Выходная информация:

- время остывания нефти;

ВЫХОДНОЙ ДОКУМЕНТ ПРОГРАММЫ RASNEF

37,90 RE = 2041,16 HE = 125080,50

выходной докУМЕНТ программы TIME

ВРЕМЯ ОСТАНОВКИ 5,0 (час)

Т = 37,90 RE = 2841,16 НЕ = 125080,50

выходной докУМЕНТ программы TOPAZ

L = 139000 (м), 01 = 0,998 (м) тн = 69,00 (град) ТО = 13,2 (град)

- потери напора на участке;

- температура нефти на конце участка;

- длина участка.

Пример 2: Произвести тепловой и гидравлический расчет пуска нефтепровода при следующих исходных данных:

D₁ = 0,938 м; D₂ = 1,02 м; h_о = 1,3 м; t_о = 18 °C;

t_н = 65 °C; t_* = 42 °C; t_* = 41 °C; L = 139000 м;

K = 25,898 · e^-0,155t, Нсⁿ/м²;

h = 0,525 + 0,0114 · t;

τ_о = 14789,547e^-0,247t, Н/м²;

φ = 0,346; ψ = 0,574;

λ_гр = 0,814 Вт/м · °C

a'_гр = 0,56 · 10^-6 м²/c;

С = 1884 Дж/кг · °C

ρ = 835 кг/м³;

W = 0,51 м/с.

Выходной документ программы TOPAZ приведен на стр. 42.

12.3. Программа TIME

Программа TIME предназначена для теплового расчета остановленного трубопровода и гидравлического расчета трубопроводов в период возобновления перекачки.

В программе определяется безопасное время остановки трубопровода.

В программе использованы стандартные модули системы управления вводом - выводом и стандартные программы из библиотеки ФОРТРАНА.

На АЦПУ распечатываются исходные данные и выводятся результаты по трем участкам нефтепровода.

Исходными данными являются:

D₁, D₂, W, t_н, t_k, t_о, h_о, n, K, ρ, C, λ_н, λ_гр, λ_м, α_в, δ_сн, λ_сн, D_из, λ_из, λ_т, τ_о, a'_гр, T_ост, Х53 (шаг расчета). INNN (число шагов); таблица A (28,5),  (55)

Выходная информация:

- время остановки;

- критическая температура;

- параметр Рейнольдса;

- критерий Хедстрема;

- длина участка;

- потери давления на участке.

Пример 3. Произвести тепловой расчет остановленного трубопровода и гидравлический расчет трубопровода в период возобновления перекачки при следующих исходных данных:

T_ост = 5 ч;            a'_гр = 0,002 м²/ч;

остальные исходные данные - по условиям примера 1.

Выходной документ программы TIME приведен на стр. 41.

список литературы

1. Кусаков М.М. Методы определения физико-химических характеристик нефтяных продуктов. М-Л., ОНТИ, НКТП, СССР, 1936.

2. Черникин В.И. Перекачка вязких и застывающих нефтей. М., Гостоптехиздат, 1959.

3. Нежевенко В.Ф., Кедрова Р.И. Состав твердых парафинов нефтей Куйбышевской области. В сб. Борьба с отложениями парафина М., «Недра», 1965.

4. Ашумов Г.Г. Азербайджанские нефти. Баку, АН АзССР, 1961.

5. Павлова С.Н. и др. Нефти восточных районов СССР, М., Гостоптехиздат, 1962.

6. Павлова С.Н. и др. Новые нефти восточных районов СССР. М., «Химия», 1967.

7. Методика исследования взаимодействия трубопроводов с окружающей средой на опытных участках трубопроводов, ОНТИ, ВНИИСТа, М., 1973.

8. Губин В.Е., Скрипников Ю.В. Неизотермическое течение вязкопластичных нефтей по трубопроводу. Труды ВНИИСПТнефть, вып. 9, 1972.

9. Михеев М.А. Средняя теплоотдача при движении жидкости в трубах. Теплопередача и тепловое моделирование. Изд. АН СССР, 1959.

10. Михеев М.А. Основы теплопередач. Изд. 3-е, Госэнергоиздат, 1956.

11. Петухов Б.С. Теплообмен и сопротивление при ламинарном течении жидкости в трубах. «Энергия», 1967.

12. Мизушина Т., Куриваки Е. Турбулентный перенос тепла в неньютоновских жидкостях. «Инж. физ. Журнал», 12, № 2, 1967.

13. Хижняков С.В. Практические расчеты тепловой изоляции. М-Л., Госэнергоиздат, 1959.

14. Зеликсон Н.М., Шпеер М.Г. Тепловая изоляция трубопроводов тепловых сетей. М-Л., Госэнергоиздат, 1962.

15. Кутателадзе С.С., Боришанский В.М. Справочник по теплопередаче. М-Л., Госэнергоиздат, 1958.

16. Кутателадзе С.С. Основы теории теплообмена. М., Машгиз, 1962.

17. Яблонский В.С., Белоусов В.Д. Проектирование нефтегазопроводов. М., Гостоптехиздат, 1959.

18. Велли Ю.Я., Докучаев В.И., Федоров Н.Ф. Справочник по строительству на вечномерзлых грунтах. Л., Стройиздат, 1977.

19. Ястребов А.Л. Инженерные коммуникации на вечномерзлых грунтах. Л., Стройиздат, 1972.

20. Корн Г., Корн Т. Справочник по математике, «Наука», 1970.

21. Губин В.Е., Гостев Н.М., Тонкошкуров Б.А. Гидравлический расчет трубопроводов при неизотермическом течении вязкопластичных нефтей. Труды ВНИИСПТнефть, вып. 12, 1975.

22. Губин В.Е., Тонкошкуров Б.А. Критические параметры потока при течении нелинейно-вязкопластичных нефтей и нефтепродуктов по трубопроводам. Труды ВНИИСПТнефть, вып. 12, 1975.

25. Тонкошкуров Б.А. Расчет трубопроводов при турбулентном течении нелинейно-вязкопластичных нефтей. Труды ВНИИСПТнефть, вып. 16, 1976.

24. Тугунов П.И., Новоселов В.Ф. Определение температурного поля грунта вокруг трубопровода при циклической его работе. Сб. «Проектирование, строительство и эксплуатация магистральных газонефтепроводов и нефтебаз», вып. 1» М., «Недра», 1966.

25. Тугунов П.И., Новоселов В.Ф. Изменение температуры нефтепродукта по длине трубопровода при возобновлении перекачки после остановки. Сб. «Проектирование, строительство и эксплуатация магистральных газонефтепроводов и нефтебаз», Уфа, УНИ 1968.

26. Тугунов П.И. Неустановившиеся режимы работы «горячих» магистральных трубопроводов. Тематический научно-технический обзор. ВНИИОЭНГ, М., 1971.

27. Тугунов П.И., Яблонский B.C. Прогрев грунта линейным источником при граничных условиях 3-го рода. «Нефть и газ», № 4, 1963.

28. Методика теплового и гидравлического расчета трубопроводов при установившемся режиме перекачки подогретых вязкопластичных нефтей и нефтепродуктов. ВНИИСПТнефть, 1974.

29. Методика теплового и гидравлического расчета пуска и вывода на стационарный режим «горячих» нефтепроводов при перекачке линейно-вязкопластичных нефтей. ВНИИСПТнефть, 1978, РД 39-30-41-78.

30. Методика определения безопасного времени остановки «горячих» трубопроводов при перекачке вязкопластичных нефтей. ВНИИСПТнефть, 1975.

31. Методика гидравлического расчета трубопроводов при изотермическом режиме течения нелинейно-вязкопластичных нефтей. ВНИИСПТнефть, 1978, РД 39-30-40-78.

32. Тонкошкуров Б.А., Шутов А.А., Мироненко Н.Я., Гостев Н.м. Стародубцева Р.А. Гидравлические параметры неизотермических трубопроводов при перекачке неньютоновских нефтей. Труды ВНИИСПТнефть, вып. 18, 1977.

33. Уилкинсон У.Д. Неньютоновские жидкости, «Мир», 1964.

34. Шульман З.П. Конвективный тепломассоперенос реологически сложных жидкостей, М., Энергия; 1975.

35. Таблицы интегральной показательной функции, АН СССР, М., 1954.

36. Сегал Б.И. Сенендяев К.А. Пятизначные математические таблицы, М., Физматгиз, 1962.

37. Herschell W.H., Bulkley R., Kolloid-Zeitsen, 39, 291, 1926.

Приложение

СПРАВОЧНЫЕ ТАБЛИЦЫ

Таблица 3

Коэффициенты объемного расширения в зависимости от плотности при 20 °C

Таблица 4

Содержание парафина в некоторых нефтях

Таблица 5

Расчетные значения теплофизических характеристик талых и мерзлых грунтов

Таблица 6

Коэффициент теплопроводности различных типов изоляции

Таблица 7

Средняя температура изоляционного слоя

Таблица 8

Значение коэффициента теплоотдачи от грунта в воздух в зависимости от скорости ветра

Таблица 9

Значения коэффициентов в уравнении (42)

Таблица 10

Значения коэффициентов в уравнении (44)

Таблица 11

Зависимость апроксимационных коэффициентов от параметров заполнения трубопровода

СОДЕРЖАНИЕ