ОТРАСЛЕВОЙ СТАНДАРТ
|
ОТРАСЛЕВАЯ АВТОМАТИЗИРОВАННАЯ СИСТЕМА УПРАВЛЕНИЯ. Методика прогнозирования показателей |
ОСТ 1 00320-78Введен впервые Проверено в 1982 г. |
Распоряжением Министерства от 26 декабря 1978 г. № 087-16 срок введения установлен с 1 июля 1979 г.
Настоящий стандарт распространяется на теоретические методы прогнозирования показателей, закладываемых в отраслевой автоматизированной системе управления (ОАСУ).
Стандарт устанавливает способ определения значений показателей, представленных в виде временных рядов.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Временные ряды показателей строятся по результатам контроля изделий на этапах производства и эксплуатации. При этом считается, что временные ряды являются случайными реализациями процессов изменения показателей.
1.2. Стандарт позволяет осуществлять прогноз как стационарных, так и нестационарных со стационарными n-ми приращениями временных рядов.
1.3. Методы, используемые при прогнозировании, инвариантны к видам показателей и этапам «жизненного цикла» изделий.
1.4. Процесс прогнозирования включает:
- вычисление прогнозируемых значений;
- корректирование прогноза;
- определение доверительных интервалов прогнозируемых значений.
2. МЕТОД ПРОГНОЗИРОВАНИЯ ВРЕМЕННЫХ РЯДОВ
2.1. Прогнозирование будущих значений временных рядов осуществляется на основании представления их в виде параметрических моделей:
- для стационарных временных рядов
![]() (1)
(1)
где ф - параметры авторегрессии;
θ - параметры скользящего среднего;
![]() - отклонение значений временного ряда от его среднего значения μ;
- отклонение значений временного ряда от его среднего значения μ;
аt - импульсы «белого шума»;
В - оператор сдвига назад.
ВкРt = Рt-к, к = 0, 1, ..., i, ..., n;
- для нестационарных временных рядов
![]() (2)
(2)
где d - число процедур взятия разностей временного ряда для приведения его к стационарному виду.
2.2. Определение вида модели и значений ее параметров осуществляется согласно ОСТ 1 00321-78.
2.3. Представление модели в виде разностного уравнения осуществляется следующим образом:
если обобщенный оператор авторегрессии обозначить
![]() (3)
(3)
то получается
![]() (4)
(4)
Тогда общая модель представляется в виде
![]() (5)
(5)
где r - число параметров авторегрессии;
q - число параметров скользящего среднего.
Такое представление модели называется разностным уравнением и используется для прогнозирования временных рядов
![]() (6)
(6)
где l - упреждение прогноза в момент t.
2.4. Корректирование прогноза производится с помощью оператора авторегрессии
![]() (7)
(7)
значение ![]() может быть, в свою очередь,
выражено как
может быть, в свою очередь,
выражено как
![]() (8)
(8)
Исключая таким же образом ![]() и т.д., получаем
бесконечный ряд из импульсов а, т.е. модель
и т.д., получаем
бесконечный ряд из импульсов а, т.е. модель
![]() (9)
(9)
принимает вид
![]() (10)
(10)
при ψ(В) = Ф-1(В).
Такое представление модели
через текущее и предшествующие значения импульсов а используется для
корректирования прогноза. На основании того, что прогнозы ![]() и
и ![]() будущего значения
будущего значения ![]() , сделанные в моменты (t + 1) и t,
выражаются как
, сделанные в моменты (t + 1) и t,
выражаются как
![]()
![]() (11)
(11)
определяется прогнозируемое значение
![]() (12)
(12)
2.5. Доверительные интервалы прогнозируемых значений определяются из предположения, что импульсы а подчиняются нормальному закону распределения; вычисление доверительных интервалов прогнозируемых значений осуществляется по формуле
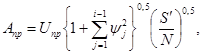 (13)
(13)
при S’ = 0,25S,
где Uпр - квантиль уровня (1 - ε/2) стандартного нормального распределения;
S - безусловная сумма квадратов последовательности импульсов а;
N - число наблюдений стационарного временного ряда.
3. АЛГОРИТМ ПРОГНОЗИРОВАНИЯ
3.1. Входные данные:
- число наблюдений временного ряда N;
- значения временного ряда ![]() , t = 1, 2,…, N;
, t = 1, 2,…, N;
- вид и порядок модели временного ряда r, q, d;
- значения параметров модели
Фi, i = 1, ..., r; θj, j = 1, ..., q;
- интервал прогнозирования Lпр;
- квантиль уровня (1 - ε/2) стандартного нормального распределения Uпр.
3.2. Определение последовательности импульсов аt
3.2.1. Вычисление последовательности случайных импульсов еt производится по формуле
![]() (14)
(14)
при t = 1, 2, ..., N - r.
3.2.2. Вычисление значений
временного ряда ![]() для
t ≤ 0 производится по формуле
для
t ≤ 0 производится по формуле
![]() (15)
(15)
при t = 0, -1, -2, ..., Т; еt = 0,
где Т - момент времени, при котором
![]() ≤
0,01.
≤
0,01.
3.2.3. Вычисление последовательности случайных импульсов аt производится по формуле
![]() (16)
(16)
при t = T, ..., 0, 1, ..., N - r; a-t = 0, t > Т - 1.
3.3. Вычисление прогноза из разностного уравнения производится по формуле
![]() (17)
(17)
для l = 1,
2, ..., Lпр, ![]() (0) = 1.
(0) = 1.
3.4. Вычисление доверительных интервалов прогнозируемых значений
3.4.1. Вычисление суммы квадратов последовательности случайных импульсов производится по формуле
![]() (18)
(18)
3.4.2. Вычисление доверительных интервалов производится по формулам
 (19)
(19)
![]()
![]() (20)
(20)
3.5. Корректирование прогноза
3.5.1. Вычисление поправки производится по формуле
![]() (21)
(21)
3.5.2. Вычисление подправленных значений прогнозов производится по формуле
![]() (22)
(22)
при i = 1, 2, ..., (Lпр - 1).
3.6. Выходные данные:
- прогнозируемые значения
временного ряда, полученные из разностного уравнения ![]() ;
;
- прогнозируемые значения,
полученные подправлением ![]() ;
;
- доверительные интервалы прогнозируемых значений в зависимости от интервала прогнозирования (σt+l)1, (σt+l)2.
3.7. Блок-схема алгоритма прогнозирования приведена в рекомендуемом приложении 1.
3.8. Пример прогнозирования временных рядов приведен в справочном приложении 2.
ПРИЛОЖЕНИЕ 1
Рекомендуемое
Блок-схема алгоритма прогнозирования

ПРИЛОЖЕНИЕ 2
Справочное
ПРИМЕР ПРОГНОЗИРОВАНИЯ ВРЕМЕННЫХ РЯДОВ
1. ИСХОДНАЯ ИНФОРМАЦИЯ ДЛЯ РАСЧЕТА
1.1. Входные данные:
- число значений временного ряда N = 24;
- значения временного ряда, сведенные в табл. 1.
Таблица 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Pt |
0,92 |
0,90 |
0,88 |
0,87 |
0,92 |
0,91 |
0,91 |
0,94 |
0,92 |
0,92 |
|
t |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Pt |
0,90 |
0,94 |
0,93 |
0,94 |
0,94 |
0,92 |
0,93 |
0,93 |
0,94 |
0,91 |
|
t |
21 |
22 |
23 |
24 |
|
Pt |
0,92 |
0,94 |
0,94 |
0,94 |
1.2. Для данного временного ряда была получена модель вида
![]()
с параметрами:
- порядок нестационарности d = 0;
- порядок авторегрессии r = 1;
- порядок скользящего среднего q = 1;
- параметр авторегрессии Ф = 0,6;
- параметр скользящего среднего θ = 0,2.
1.3. Для вычисления доверительных интервалов прогнозов необходимы значения квантилей (1 - ε/2) % стандартного нормального распределения, представленные в табл. 2.
Таблица 2
|
50 |
90 |
95 |
|
|
Квантили |
0,674 |
1,650 |
1,960 |
1.4. В результате расчета нужно получить:
- прогнозируемые значения ряда на Lпр = 1, 2, 3, 4;
- скорректированные значения на Lпр = 1, 2, 3;
- вероятностные пределы прогнозов.
1.5. Результаты расчета удобно представить в виде таблицы, графы которой соответствуют времени упреждения, а строки - моментам времени, на которые осуществляется прогноз. Таким образом, прогнозируемые значения располагаются по диагонали таблицы, скорректированные значения располагаются в таблице под соответствующими прогнозируемыми значениями.
2. ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА
2.1. Приведение ряда к стационарному виду
2.1.1. В данном случае процесс стационарен (d = 0), следовательно, приводить его к стационарному виду не надо.
2.2. Вычисление последовательности случайных импульсов
2.2.1. Вычисление приведенных значений временного ряда (если имели место процедуры взятия разностей вследствие нестационарности исходного ряда, этот пункт не нужен) производится по формуле
![]()
при t = 1, ..., N,
где μ - математическое ожидание ряда, вычисляемое по формуле
![]()
μ = 0,042 · (0,92 + 0,90 + 0,88 + ... + 0,94) = 0,921;
![]() = 0,920 - 0,921 = -0,001;
= 0,920 - 0,921 = -0,001;
![]() = 0,900 - 0,921 = -0,021;
= 0,900 - 0,921 = -0,021;
..............................................
![]() = 0,940 - 0,921 = 0,019.
= 0,940 - 0,921 = 0,019.
Приведенные значения ряда сведены в табл. 3.
Таблица 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
-0,001 |
-0,021 |
-0,041 |
-0,051 |
-0,001 |
-0,011 |
-0,011 |
0,019 |
-0,001 |
|
t |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
-0,001 |
-0,021 |
0,019 |
0,009 |
0,019 |
0,019 |
-0,001 |
0,009 |
0,009 |
|
t |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
0,019 |
-0,011 |
-0,001 |
0,019 |
0,019 |
0,019 |
2.2.2. Вычисление последовательности et производится по формуле:
![]()
при t = 23, 22, ..., 1.
е24 = 0;
е23 = 0,019 - 0,6·0,019 = 0,0076;
е22 = 0,019 - 0,6·0,019 + 0,2·0,0076 = 0,0078;
е21 = -0,001 - 0,6·0,019 + 0,2·0,0078 = -0,0084.
…………………………………………………
е1 = ...
Результаты расчета еt сведены в табл. 4.
Таблица 4
|
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
|
|
еt |
0,0076 |
0,0078 |
-0,0084 |
-0,0118 |
0,0232 |
0,0220 |
0,0080 |
0,0048 |
|
t |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
|
еt |
0,0197 |
0,0115 |
-0,0001 |
0,0136 |
-0,0297 |
0,0055 |
0,0007 |
0,0197 |
|
t |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
еt |
-0,0185 |
-0,0081 |
0,0040 |
-0,0412 |
-0,0461 |
-0,0056 |
0,0105 |
2.2.3. Вычисление значений временного ряда Рt для t ≤ 0 производится по формуле
![]()
при еt = 0 и t = 0, -1, ..., Г;
где Г - время, при котором ![]() ≤ 0,01;
≤ 0,01;
![]() = 0,6 · (-0,001) - 0,2 · 0,0105 = -0,003.
= 0,6 · (-0,001) - 0,2 · 0,0105 = -0,003.
Вследствие этого получаем Г = 0.
2.2.4. Вычисление последовательности аt производится по формуле
![]()
при t = 0, ..., 23,
а0 = -0,0027,
а1 = -0,001 - 0,6(-0,0027) + 0,2(-0,0027) = -0,0013,
а2 = -0,021 - 0,6(-0,001) + 0,2(-0,0013) = -0,0206.
Результаты вычислений сведены в табл. 5.
Таблица 5
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
at |
-0,0027 |
-0,0013 |
-0,0206 |
-0,0325 |
-0,0311 |
0,0234 |
-0,0078 |
-0,0106 |
|
t |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
at |
0,0235 |
-0,0078 |
-0,0006 |
-0,0205 |
0,0275 |
0,0031 |
0,0142 |
0,0104 |
|
t |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
at |
-0,0099 |
0,0076 |
0,0051 |
0,0146 |
-0,0195 |
0,0017 |
0,0199 |
0,0116 |
0,0099 |
2.3. Вычисление прогнозов из разностного уравнения
2.3.1. Производится вычисление коэффициентов φi
![]()
![]()
![]()
2.3.2. Вычисляются коэффициенты ψj
![]()
![]()
ψj = …
Результаты вычислений сведены в табл. 6.
Таблица 6
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
ψj |
0,40 |
0,24 |
0,144 |
0,086 |
0,052 |
0,031 |
0,019 |
0,011 |
2.3.3. Для осуществления корректирования прогноза необходимо иметь для одного и того же момента времени спрогнозированное и реальное значения временного ряда, поэтому прогноз осуществляется с момента t = 23.
Разностное уравнение имеет вид:
![]()
Вычисление прогнозов приведенного ряда проводится следующим образом:
![]() (1) =
0,6·0,0190 + 0,0116 - 0,2·0,0199 = 0,0191;
(1) =
0,6·0,0190 + 0,0116 - 0,2·0,0199 = 0,0191;
![]() (2) =
0,6·0,0191 - 0,2·0,0116 = 0,0091;
(2) =
0,6·0,0191 - 0,2·0,0116 = 0,0091;
![]() (3) =
0,6·0,0091 = 0,0054;
(3) =
0,6·0,0091 = 0,0054;
![]() (4) = 0,6·0,0054 = 0,0032.
(4) = 0,6·0,0054 = 0,0032.
Вычисление прогнозов ряда проводится следующим образом:
![]() (1) =
0,921 + 0,0191 = 0,9401;
(1) =
0,921 + 0,0191 = 0,9401;
![]() (2) =
0,921 + 0,0091 = 0,9301;
(2) =
0,921 + 0,0091 = 0,9301;
![]() (3)
= 0,921 + 0,0054 = 0,9264;
(3)
= 0,921 + 0,0054 = 0,9264;
![]() (4) = 0,921 + 0,0032
= 0,9242.
(4) = 0,921 + 0,0032
= 0,9242.
2.4. Вычисление доверительных интервалов
2.4.1. Вычисление суммы квадратов последовательности случайных импульсов проводится по формуле
![]()
S = (-0,0027)2 + (-0,0013)2 + ... + 0,00992 = 0,0114; S´ = 0,0028.
2.4.2. Из таблицы квантилей стандартного нормального распределения выбирается значение, соответствующее требуемым пределам в процентах, например:
Uпр = 1,960 для пределов 95 %-ной вероятности.
Вычисление доверительной области прогнозируемых значений проводится следующим образом:
Апр (1) = 1,96(0,0028/24)0,5 = 0,0216;
Апр (2) = 1,96(1 + 0,402)0,5(0,0028/24)0,5 = 0,0230;
Апр (3) = 1,96(1 + 0,402 + 0,242)0,5 (0,0028/24)0,5 = 0,0234;
Апр (4) = 1,96(1 + 0,402 + 0,242 + 0,1442)0,5(0,0028/24)0,5 = 0,0236.
2.4.3. Вычисление доверительных интервалов проводится следующим образом:
(σ24)1 = 0,9401 + 0,0216 = 0,9612;
(σ24)2 = 0,9401 - 0,0216 = 0,8760;
(σ25)1 = 0,9301 + 0,0230 = 0,9532;
(σ25)2 = 0,9301 - 0,0230 = 0,8620;
(σ26)1 = 0,9264 + 0,0234 = 0,9500;
(σ26)2 = 0,9264 - 0,0234 = 0,8561;
(σ27)1 = 0,9242 + 0,0236 = 0,9474;
(σ27)2 = 0,9242 - 0,0236 = 0,8533.
2.5. Корректирование прогноза
2.5.1. Вычисление поправки производится следующим образом:
![]()
а24 = 0,0190 - 0,0191 = -0,0001.
2.5.2. Вычисление скорректированных значений прогнозов приведенного ряда производится следующим образом:
![]() (1) = 0,0091 + 0,40(-0,0001) = 0,00896;
(1) = 0,0091 + 0,40(-0,0001) = 0,00896;
![]() (2) =
0,0054 + 0,24(-0,0001) = 0,00538;
(2) =
0,0054 + 0,24(-0,0001) = 0,00538;
![]() (3)
= 0,0032 + 0,14(-0,0001) =
0,00319.
(3)
= 0,0032 + 0,14(-0,0001) =
0,00319.
2.5.3. Вычисление скорректированных значений ряда производится следующим образом:
![]() (1) = 0,921 + 0,00896 = 0,9300;
(1) = 0,921 + 0,00896 = 0,9300;
![]() (2) = 0,9264;
(2) = 0,9264;
![]() (3) = 0,9242.
(3) = 0,9242.
Результаты расчета сведены в табл. 7 и 8.
Таблица 7
|
1 |
2 |
3 |
4 |
|
|
95 %-ный предел вероятности |
0,0216 |
0,0230 |
0,0234 |
0,0236 |
Таблица 8
|
Pt |
at |
Время упреждения |
||||
|
1 |
2 |
3 |
4 |
|||
|
23 |
0,94 |
- |
- |
- |
- |
- |
|
24 |
0,94 |
-0,0001 |
0,9401 |
- |
- |
- |
|
25 |
- |
- |
0,9300 |
0,9301 |
- |
- |
|
26 |
- |
- |
- |
0,9264 |
0,9264 |
- |
|
27 |
- |
- |
- |
- |
0,9242 |
0,9242 |
Результаты прогноза приведены на черт. 1
Обозначения:
![]() - прогноз
- прогноз
![]() - доверительные интервалы
- доверительные интервалы
Черт. 1
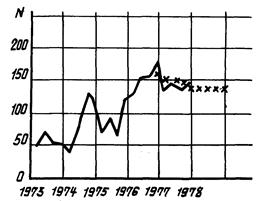
2.5.4. На черт. 2 - 9 представлены примеры прогнозирования реальных временных рядов таких показателей, как наработка на отказ (N) и процент брака (δ).
Черт. 2

Черт. 3
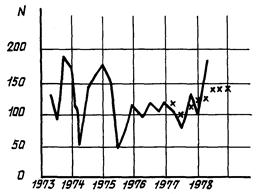
Черт. 4
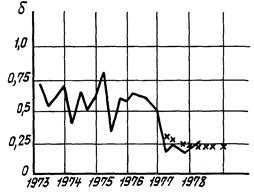
Черт. 5
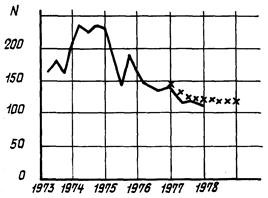
Черт. 6
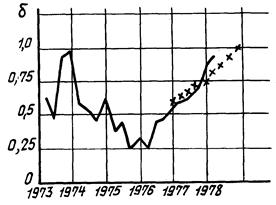
Черт. 7
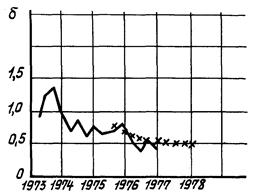
Черт. 8
Черт. 9
СОДЕРЖАНИЕ
|
2. Метод прогнозирования временных рядов. 1 3. Алгоритм прогнозирования. 3 |