ОТРАСЛЕВОЙ СТАНДАРТ
|
ПЕРЕДАЧИ
ЗУБЧАТЫЕ ЦИЛИНДРИЧЕСКИЕ ПРЯМОЗУБЫЕ Расчет геометрических параметров |
ОСТ 1 00319-78 Взамен 150МТ |
Распоряжением Министерства от 19 декабря 1978 г. № 087-16/5 срок введения установлен с 1 января 1980 г.
1. Настоящий стандарт устанавливает расчет геометрических параметров зубчатой передачи, а также расчет номинальных размеров сопряженных зубчатых колес без поднутрения у основания зуба, с модулем более 1 мм, со смещенным и несмещенным исходным контуром или исходными производящими контурами по ГОСТ 13755-81 и ОСТ 1 00219-76.
2. Термины и обозначения, применяемые в стандарте, - по ГОСТ 16530-83 и ГОСТ 16531-83.
3. Схема расчета геометрии приведена на черт. 1.
Черт. 1
4. Расчет по формулам должен производиться с погрешностью измерения:
- линейные размеры - не менее 0,001 мм;
- угловые размеры - не менее 0,01°;
- тригонометрические величины - не менее 0,00001;
- коэффициенты смещений - не менее 0,01.
5. Исходные данные для расчета приведены в табл. 1.
Таблица 1
|
Обозначение |
|
|
Число зубьев: |
|
|
шестерни........................................................................................ |
z1 |
|
колеса............................................................................................ |
z2 |
|
Модуль |
m |
|
Исходный контур или исходный производящий контур: |
|
|
угол профиля.................................................................................. |
α |
|
коэффициент высоты головки............................................................ |
h*a |
|
коэффициент радиального зазора...................................................... |
c* |
|
коэффициент радиуса кривизны переходной кривой............................ |
ρ*f |
|
Межосевое расстояние |
aw |
|
Коэффициент смещения: |
|
|
шестерни........................................................................................ |
х1 |
|
колеса………………………………………………………………………. |
х2 |
|
Коэффициент глубины модификации профиля головки зуба: |
|
|
шестерни........................................................................................ |
Δ*1 |
|
колеса............................................................................................ |
Δ*2 |
|
Коэффициент высоты модификации профиля головки зуба: |
|
|
шестерни........................................................................................ |
h*g1 |
|
колеса............................................................................................ |
h*g2 |
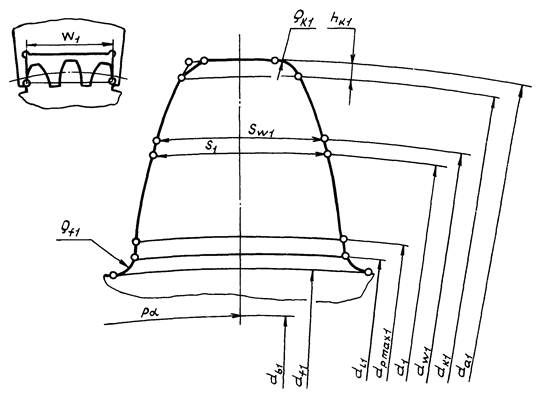
6. Геометрические параметры зубчатых передач и колес приведены на черт. 2 и 3.
Черт. 2
Черт. 3
7. Формулы расчета основных геометрических параметров зубчатых передач и колес приведены в табл. 2, дополнительных геометрических параметров - в справочном приложении 1.
Таблица 2
|
Обозначение |
Расчетная формула |
|
|
Угол зацепления |
αw |
|
|
Коэффициент разности смещений |
xd |
|
|
Коэффициент смещения при заданном межосевом расстоянии aw: |
При исходном контуре по ГОСТ 13755-81 разбивку значения xd на составляющие х1 и х2 рекомендуется производить по блокировочным контурам |
|
|
шестерни................................... |
х1 |
|
|
колеса....................................... |
х2 |
|
|
Коэффициент разности смещений |
xd |
xd = х2 - х1 |
|
Угол зацепления |
αw |
|
|
Межосевое расстояние при заданных х1 и х2 |
аw |
|
|
Передаточное число |
u |
|
|
Делительный диаметр |
d |
d = mz |
|
Начальный диаметр: |
||
|
шестерни................................... |
dw1 |
|
|
колеса....................................... |
dw2 |
dw2 = udw1 |
|
Диаметр впадин: |
||
|
шестерни................................... |
df1 |
df1 = d1 - 2m(h*a + c* - x1) |
|
колеса....................................... |
df2 |
df2 = d2 + 2m(h*a + c* + x2) |
|
Диаметр вершин зубьев: |
||
|
шестерни................................... |
da1 |
da1 = df2 - 2aw - 2mc* |
|
колеса....................................... |
da2 |
da2 = 2aw + df1 + 2mc* |
|
Окружная толщина зуба на делительном диаметре: |
||
|
шестерни................................... |
S1 |
S1 = m(0,5π + 2x1tgα) |
|
колеса....................................... |
S2 |
S2 = m(0,5π - 2x2tgα) |
Примечания: 1. Допускается изменение значений диаметров вершин зубьев и расчет их по другим формулам для получения требуемых качеств зацепления по геометрическим параметрам.
2. Расчет диаметров вершин зубчатых колес при окончательной обработке внутренних зубьев зуборезным долбяком приведен в справочном приложении 1.
8. Формулы расчета геометрических параметров, необходимых для сведения и расчета на прочность зубчатых колес, приведены в табл. 3.
Таблица 3
|
Обозначение |
Расчетная формула |
|
|
Основной диаметр |
db |
db = dcosα |
|
Угол профиля у вершины зуба |
αa |
|
|
Радиус кривизны профиля у вершины зуба |
ρa |
ρa = 0,5dbtgαa |
|
Радиус кривизны активного профиля зуба в нижней точке: |
||
|
шестерни..................................... |
ρp1 |
ρp1 = ρa2 - awsinαw |
|
колеса......................................... |
ρp2 |
ρp2 = ρa1 + awsinαw |
|
Диаметр окружности начала активного профиля в нижней точке |
dp |
|
|
Радиус кривизны профиля в начале модификации головки зуба: |
||
|
шестерни..................................... |
ρg1 |
|
|
колеса......................................... |
ρg2 |
|
|
Диаметр окружности модификации головок зубьев |
dg |
|
|
Угол профиля в начальной точке модификации головки |
αg |
|
|
Угол профиля в середине активной части зуба |
αc |
|
|
Угол профиля модификации головки зуба |
αм |
|
|
Диаметр основной окружности участка профиля зуба модифицированного по эвольвенте |
dbм |
dbм = dcosαм |
|
Половина угловой толщины зуба на основной окружности: |
||
|
шестерни..................................... |
ψb1 |
|
|
колеса......................................... |
ψb2 |
|
|
Толщина зуба по дуге на окружности dy: |
||
|
шестерни..................................... |
Sy1 |
|
|
колеса......................................... |
Sy2 |
|
Примечание. При наличии притупления продольной кромки зуба радиусом ρк угол αк следует определять по формуле
![]()
где dk1 = da1 - 2hk1 ≈ da1 - 2ρk1,
dk2 = da2 - 2hk2 ≈ da2 + 2ρk2,
![]()
9. Формулы расчета размеров для контроля одноименных и разноименных поверхностей зуба приведены в табл. 4.
Таблица 4
|
Обозначение |
Расчетная формула |
|
|
Длина общей нормали шестерни |
w1 |
Должно выполняться условие: 2ρa1 > w1 > 2ρp1, а при наличии модификации профиля головки зуба - условие: 2ρg1 > w1 > 2ρp1. |
|
Если условия не выполняются, то w пересчитать, уменьшив zw на 1 при 2ρa1 ≤ w1(2ρg ≤ w) или увеличив zw1 на 1 при w1 ≤ 2ρp1 |
||
|
Угол профиля зуба на окружности, проходящей через центр ролика (шарика) колеса |
αD2 |
Должно выполняться условие:
а при наличии модификации профиля головки зуба - условие:
|
|
Диаметр концентрической окружности зубчатого колеса, проходящей через центр ролика (шарика) колеса |
dD2 |
|
|
Размер по роликам (шарикам) колеса: с четным числом зубьев с нечетным числом зубьев |
м2 |
м2 = dD2 - D
Должны выполняться условия м2 < dD2 dD2 + D < df2 |
|
Шаг зацепления |
pα |
pα = πmcosα |
|
Радиус кривизны переходной кривой (наименьший) |
ρfmin |
|
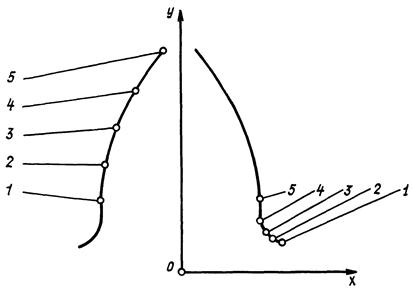
10. Формулы расчета длины линии зацепления и расшифровки диаграмм для шестерни (черт. 4) и колеса (черт. 5) приведены в табл. 5.
Черт. 4
Черт. 5
Таблица 5
|
Обозначение |
Расчетная формула |
|
|
Длина активной линии зацепления (по эвольвентограмме): |
||
|
шестерни.................................... |
gα1 |
gα1 = ρa1 - ρg1 |
|
колеса........................................ |
gα2 |
gα2 = ρg2 - ρa2 |
|
Длина модификации головки зуба по эвольвентограмме: |
||
|
шестерни.................................... |
lg1 |
lg1 = ρa1 - ρg1, |
|
колеса........................................ |
lg2 |
lg2 = ρa2 - ρg2, |
|
Диаметр окружности модификации головок зуба |
dg |
|
11. Формулы проверки качества зацепления по геометрическим показателям приведены в табл. 6.
Таблица 6
|
Обозначение |
Расчетная формула |
|
|
Коэффициент наименьшего смещения у шестерни |
xmin1 |
Должно выполняться условие: x1 > x1min |
|
Толщина зуба на поверхности вершин: |
||
|
шестерни.................................... |
Sa1 |
Sa1 = da1(ψb1 - invαa1) |
|
колеса........................................ |
Sa2 |
Sa2 = da2(ψb2 + invαa2) рекомендуется Sa ≥ 0,3m - без химико-термической обработки, Sa ≥ 0,4m - с химико-термической обработкой |
|
Коэффициент перекрытия (геометрический) |
εα |
|
|
Радиус кривизны в граничной точке профиля зуба: |
||
|
шестерни.................................... |
ρL1 |
|
|
колеса........................................ |
ρL2 |
Должны выполняться условия: ρL1 ≤ ρp1; ρL2 ≥ ρp2. При подрезании зубьев ρL1 < 0 |
|
Параметры, определяющие отсутствие интерференции |
δ |
Должны выполняться условия: δ ≥ 0; ρL1 ≤ ρp1; ρL2 ≥ ρp2 |
Примечания: 1. При необходимости расчета коэффициента перекрытия с учетом притупления продольных кромок зубьев, в расчетные формулы подставляются вместо значений αа значения αк.
2. При уточненном расчете радиусов кривизны в граничных точках следует учитывать вид переходной поверхности и параметры производящих поверхностей.
12. Пример расчета геометрических параметров приведен в справочном приложении 2.
ПРИЛОЖЕНИЕ 1
Справочное
РАСЧЕТ ДОПОЛНИТЕЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
1. Исходные параметры инструмента реечного типа приведены в табл. 1
Таблица 1
|
Обозначение |
|
|
Угол профиля |
α0 |
|
Толщина по хорде |
|
|
Высота до хорды |
|
|
Радиус кривизны линии притупления |
ρк0 |
2. Исходные параметры зуборезного долбяка приведены в табл. 2
Таблица 2
|
Обозначение |
|
|
Число зубьев |
z0 |
|
Модуль |
m0 |
|
Диаметр вершин |
da0 |
|
Номинальная толщина зуба |
S0 |
|
Радиус кривизны линии притупления |
ρк0 |
3. Формулы расчета диаметра колеса, окончательно обработанного зуборезным долбяком, приведены в табл. 3.
Таблица 3
|
Обозначение |
Расчетная формула |
|
|
Коэффициент смещения у долбяка |
x0 |
|
|
Угол станочного зацепления с долбяком |
αw02 |
|
|
Межосевое расстояние в станочном зацеплении |
aw02 |
|
|
Диаметр вершин зубьев колеса |
da2 |
da2 = d2 - 2(h*a - x2 - к2)m1, где к2 = c*(1 - 0,5x2) при x2 < 2 для α = 20°, при x2 ≤ 1 для α ≥ 25° |
|
Диаметр впадин колеса |
df2 |
df2 = 2aw02 + da0 |
4. Формулы расчета координат точек эвольвенты приведены в табл. 4
Таблица 4
|
Обозначение |
Расчетная формула |
|
|
Половина угловой толщины |
ψ |
|
|
Координаты точек эвольвенты |
x |
|
|
y |
|
Примечание. Для определения координат использована прямоугольная система координат X0Y с центром на оси зубчатого колеса и осью Y, совпадающей с осью симметрии зуба.
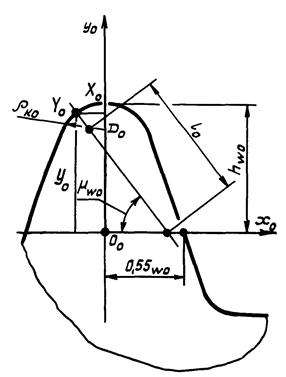
5. Формулы расчета параметров переходной кривой у впадины зуба шестерни, указанных на черт. 1 и 2, приведены в табл. 5.
Черт. 1
Черт. 2
Таблица 5
|
Обозначение |
Расчетная формула |
|
|
Текущий угол станочного зацепления |
μw0 |
90° ≥ μw0 ≥ α0 |
|
Модуль производящего контура |
m0 |
|
|
Начальный диаметр шестерни в станочном зацеплении |
dw01 |
dw01 = m0z1 |
|
Начальная толщина зуба шестерни в станочном зацеплении |
Sw01 |
Sw01 = dw01(ψb1 - invα0) |
|
Начальная толщина зуба инструмента |
Sw0 |
Sw0 = πm - Sw01 |
|
Высота начальной головки инструмента |
hw0 |
|
|
Координаты центра округления кромки инструмента |
xD0 |
|
|
yD0 |
yD0 = hw0 - ρк0 |
|
|
Координаты контактной точки кромки инструмента |
x0 |
x0 = xD0 + ρк0cosμw0 |
|
y0 |
y0 = yD0 - ρк0sinμw0 |
|
|
Расстояние от центра округления кромки зуба инструмента до полюса станочного зацепления |
l0 |
|
|
Угол профиля в точке на окружности заданного диаметра dy |
μy |
при μw0 = 90° μy = 90° |
|
Диаметр окружности, проходящей через точку у |
dy |
при μw0 = 90° dy = dw01 - 2yD0 - 2ρк0 |
|
Полярный угол точки у |
δу |
|
|
Радиус кривизны переходной кривой |
ρf |
|
|
Координаты точки переходной кривой |
x |
x = 0,5dysin(ψb1 - δy) |
|
y |
y = 0,5dycos(ψb1 - δy) |
6. Формулы расчета параметров переходной кривой у впадины зуба колеса, указанных на черт. 3 и 4, приведены в табл. 6.
Черт. 3
Черт. 4
Таблица 6
|
Обозначение |
Расчетная формула |
|
|
Текущий угол станочного зацепления |
μw0 |
αw02 ≤ μw0 ≤ 90° |
|
Диаметр окружности, проходящий через центр округления кромки зуба долбяка |
dD0 |
dD0 = da0 - 2ρк0 |
|
Угол профиля эвольвенты в точке на окружности, проходящей через центр округления кромки долбяка |
αD0 |
|
|
Угловая координата центра округления |
δD0 |
|
|
Начальный диаметр долбяка в станочном зацеплении |
dw0 |
|
|
Угол профиля эвольвенты в точке на окружности dy0 |
τy0 |
при μw0 = 90°, τy0 = 90°. |
|
μy0 |
|
|
|
Расстояние от центра округления кромки долбяка до полюса станочного зацепления |
l0 |
при μw0 = 90°, l0 = 0,5(dD0 - dw0) |
|
Угол профиля в точке на окружности диаметра dy |
μy |
при μw0 = 90°, μy = 90° |
|
Диаметр окружности, проходящей через точку у |
dy |
при μw0 = 90°, dy = df = 2aw0 + da0 |
|
Угловая координата точки y |
δy |
|
|
Радиус кривизны переходной кривой |
ρf |
|
|
Координаты точки переходной кривой |
x y |
x = 0,5dysin(δy + ψb2) y = 0,5dycos(δy + ψb2) |
7. Формулы расчета диаметров граничных точек зон зацепления приведены в табл. 7.
Таблица 7
|
Обозначение |
Расчетная формула |
|
|
Радиус кривизны профиля зуба в верхней граничной точке однопарного зацепления: |
||
|
шестерни.................................... |
ρu1 |
ρu1 = ρp1 + pα |
|
колеса........................................ |
ρu2 |
ρu2 = ρp2 - pα |
|
Угол профиля зуба в верхней граничной точке однопарного зацепления |
αu |
|
|
Диаметр окружности верхних граничных точек однопарного зацепления |
du |
|
|
Радиус кривизны профиля зуба в нижней граничной точке однопарного зацепления: |
||
|
шестерни.................................... |
ρv1 |
ρv1 = ρк1 - pα |
|
колеса........................................ |
ρv2 |
Ρv2 = ρк2 + pα |
|
Угол профиля зуба в нижней граничной точке однопарного зацепления |
αv |
|
|
Диаметр окружности нижних граничных точек однопарного зацепления |
dv |
|
8. Формулы расчета кинематических параметров приведены в табл. 8.
Таблица 8
|
Обозначение |
Расчетная формула |
|
|
Удельное скольжение в нижней точке активного профиля: |
||
|
шестерни..................................... |
υp1 |
|
|
колеса......................................... |
υp2 |
|
ПРИЛОЖЕНИЕ 2
Справочное
ПРИМЕР РАСЧЕТА ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
1. Исходные данные для расчета приведены в табл. 1.
Таблица 1
|
Обозначение |
Номинальный размер |
|
|
Число зубьев: |
||
|
шестерни...................................................................... |
z1 |
11 |
|
колеса.......................................................................... |
z2 |
53 |
|
Модуль, мм |
т |
3 |
|
Исходный контур: |
||
|
угол профиля, град........................................................ |
α |
20 |
|
коэффициент высоты головки.......................................... |
h*a |
1 |
|
коэффициент радиального зазора.................................... |
c* |
0,25 |
|
коэффициент радиуса кривизны переходной кривой |
ρ*f |
0,4 |
|
Межосевое расстояние, мм |
aw |
64,5 |
|
Коэффициент смещения: |
||
|
шестерни...................................................................... |
x1 |
+0,39 |
|
колеса.......................................................................... |
x2 |
- |
|
Коэффициент глубины модификации профиля головки зуба: |
||
|
шестерни...................................................................... |
Δ*1 |
- |
|
колеса.......................................................................... |
Δ*2 |
- |
|
Коэффициент высоты модификации профиля головки зуба: |
||
|
шестерни...................................................................... |
h*g1 |
- |
|
колеса.......................................................................... |
h*g2 |
- |
2. Номинальные размеры основных геометрических параметров, подсчитанные по формулам, приведены в табл. 2.
Таблица 2
|
Расчетная формула |
Номинальный размер |
|
|
Угол зацепления, град |
|
23,39 |
|
Коэффициент разности смещений |
|
+0,54 |
|
Коэффициент смещения: |
||
|
у шестерни.................................... |
Значение x1 принято по блокировочному контуру |
|
|
у колеса........................................ |
x2 = xd + x1 |
+0,93 |
|
Передаточное число |
|
4,82 |
|
Делительный диаметр, мм: |
||
|
шестерни...................................... |
d1 = mz1 |
33 |
|
колеса.......................................... |
d2 = mz2 |
159 |
|
Начальный диаметр, мм: |
||
|
шестерни...................................... |
|
33,770 |
|
колеса.......................................... |
dw2 = udw1 |
162,770 |
|
Диаметр впадин, мм: |
||
|
шестерни...................................... |
df1 = d1 - 2m(h*a + c* - x1) |
27,840 |
|
колеса.......................................... |
df2 = d2 + 2m(h*a + c* + x2) |
172,080 |
|
Диаметр вершин зубьев, мм: |
||
|
шестерни...................................... |
da1 = df2 - 2aw - 2c*m |
41,580 |
|
колеса.......................................... |
da2 = 2aw + df1 + 2c*m |
158,340 |
|
Толщина зуба, мм: |
||
|
шестерни...................................... |
S1 = m(0,5π + 2x1tgα) |
5,564 |
|
колеса.......................................... |
S2 = m(0,5π - 2x2tgα) |
2,681 |
3. Номинальные размеры геометрических параметров, необходимых для сведения и расчета на прочность зубчатых колес, приведены в табл. 3.
Таблица 3
|
Расчетная формула |
Номинальный размер |
|
|
Основной диаметр, мм: |
||
|
шестерни....................................... |
db1 = d1cosα |
31,010 |
|
колеса........................................... |
db2 = d2cosα |
149,411 |
|
Угол профиля у вершины зуба, град: |
||
|
шестерни....................................... |
|
41,77 |
|
колеса........................................... |
|
19,33 |
|
Радиус кривизны профиля у вершины зуба, мм: |
||
|
шестерни....................................... |
ρa1 = 0,5db1tgαa1 |
13,848 |
|
колеса........................................... |
ρa2 = 0,5db2tgαa2 |
26,205 |
|
Радиус кривизны активного профиля зуба в нижней точке, мм: |
||
|
шестерни....................................... |
ρp1 = ρa2 - awsinαw |
0,599 |
|
колеса........................................... |
ρp2 = ρa1 + awsinαw |
39,454 |
|
Диаметр окружности начала активного профиля в нижней точке, мм: |
||
|
шестерни....................................... |
|
31,033 |
|
колеса........................................... |
|
168,968 |
|
Радиус кривизны профиля в начале модификации головки зуба, мм: |
||
|
шестерни....................................... |
|
- |
|
колеса........................................... |
|
- |
|
Диаметр окружности модификации головки зуба, мм: |
||
|
шестерни....................................... |
|
- |
|
колеса........................................... |
|
- |
|
Угол профиля в начальной точке модификации головки колеса, град: |
||
|
шестерни....................................... |
|
- |
|
колеса........................................... |
|
- |
|
Угол профиля в середине активной части зуба, град: |
||
|
шестерни....................................... |
|
31,34 |
|
колеса........................................... |
|
24,08 |
|
Угол профиля модификации головки зуба, град |
|
- |
|
Диаметр основной окружности участка профиля зуба модифицированного по эвольвенте, мм: |
||
|
шестерни....................................... |
dbм1 = d1cosαм1 |
- |
|
колеса........................................... |
dbм2 = d2cosαм2 |
- |
|
Половина угловой толщины зуба на основной окружности, рад: |
||
|
шестерни....................................... |
|
0,18351 |
|
колеса........................................... |
|
0,00196 |
4. Номинальные размеры для контроля приведены в табл. 4.
Таблица 4
|
Расчетная формула |
Номинальный размер |
|
|
Длина общей нормали шестерни, мм |
|
14,547 |
|
Угол профиля на окружности, проходящей через центр ролика, град |
При D2 = 4,773 мм
|
23,71 |
|
Размер по роликам (шарикам) на колесе, мм |
|
158,340 |
|
Шаг зацепления, мм |
pα = πmcosα |
8,856 |
|
Радиус кривизны переходной кривой (наименьший), мм |
|
1,519 |
|
|
1,536 |
5. Номинальные размеры длины линии зацепления и диаметра окружности модификации головок зубьев приведены в табл. 5
Таблица 5
|
Расчетная формула |
Номинальный размер |
|
|
Длина активной линии зацепления (по эвольвентограмме), мм: |
||
|
шестерни........................................ |
gα1 = ρa1 - ρр1 |
13,249 |
|
колеса............................................ |
gα2 = ρр2 - ρa2 |
13,249 |
|
Радиус кривизны профиля зуба в начале модификации головки зуба, мм: |
При lg1 = 2,5 мм и lg2 = 2,5 мм (из эвольвентограммы) |
|
|
шестерни........................................ |
ρg1 = ρa1 - lg1 |
11,348 |
|
колеса............................................ |
ρg2 = ρa2 + lg2 |
28,705 |
|
Диаметр окружности модификации головки зуба, мм: |
||
|
шестерни........................................ |
|
38,873 |
|
колеса............................................ |
|
160,060 |
6. Номинальные размеры для проверки качества зацепления по геометрическим показателям приведены в табл. 6.
Таблица 6
|
Расчетная формула |
Номинальный размер |
|
|
Коэффициент наименьшего смещения шестерни |
Должно выполняться условие: x1 > x1min |
0,36 |
|
Толщина зуба на поверхности вершин шестерни, мм: |
||
|
шестерни........................................ |
Sa1 = (ψb1 - invαa1)da1 |
0,805 |
|
колеса............................................ |
Sa2 = (ψb2 + invαa2)da2 |
2,433 |
|
Коэффициент перекрытия (геометрический) |
|
1,496 |
|
Радиус кривизны в граничной точке профиля зуба колеса, мм: |
||
|
шестерни........................................ |
|
0,293 |
|
колеса............................................ |
|
44,119 |
|
Параметр, определяющий наличие интерференции |
|
0,193 |
7. Исходные параметры фрезы червячной правой m3×112АА-1 ГОСТ 9324-79 приведены в табл. 7.
Таблица 7
|
Обозначение |
Номинальный размер |
|
|
Угол профиля, град |
α0 |
20 |
|
Толщина по хорде, мм |
|
4,85 |
|
Высота до хорды, мм |
|
3,75 |
|
Радиус кривизны линии притупления, мм |
ρк0 |
0,90 |
8. Исходные параметры зуборезного долбяка чашечного прямозубого m3×50А-Ш ГОСТ 9323-79 приведены в табл. 8.
Таблица 8
|
Обозначение |
Номинальный размер |
|
|
Число зубьев |
z0 |
17 |
|
Модуль, мм |
m0 = m |
3,000 |
|
Диаметр вершин, мм |
da0 |
59,140 |
|
Номинальная толщина зуба, мм |
S0 |
4,943 |
|
Радиус кривизны линии притупления (принятый), мм |
ρк0 |
1,100 |
9. Номинальные размеры диаметров колеса, окончательно обработанного зуборезным долбяком, приведены в табл. 9.
Таблица 9
|
Расчетная формула |
Номинальный размер |
|
|
Коэффициент смещения у долбяка |
|
0,11 |
|
Угол станочного зацепления колеса с долбяком, град |
|
25,39 |
|
Межосевое расстояние в станочном зацеплении колеса с долбяком, мм |
|
56,168 |
|
Вспомогательная величина |
к2 = 0,25 - 0,125х2 |
0,134 |
|
Диаметр вершин зубьев колеса, мм |
da2 = d2 - 2(h*a - x2 + Δу - к2)m |
159,143 |
|
Диаметр впадин колеса, мм |
df2 = 2aw02 + da0 |
171,477 |
10. Профили зубьев шестерни и колеса построены по координатам, указанным в табл. 10 - 13, и приведены на черт. 1 и 2.
Черт. 1
Черт. 2
11. Номинальные размеры координат точек эвольвенты зуба шестерни приведены в табл. 10.
Таблица 10
|
Расчетная формула |
Номинальный размер для точки |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
Диаметр окружности, мм |
dy1 |
27,84 < db1 |
31,010 |
33,500 |
36,000 |
38,500 |
41,100 |
|
Угол профиля в точке на окружности диаметра dy, град |
|
- |
0 |
22,23 |
30,53 |
36,35 |
41,02 |
|
Половина угловой толщины зуба на окружности диаметра dy, град |
ψys1 = ψb1 - invαy1 |
- |
10,52 |
9,33 |
7,25 |
4,70 |
1,69 |
|
Координаты точки эвольвенты, мм |
x = 0,5dy1sinψy1 |
- |
2,831 |
2,715 |
2,272 |
1,577 |
0,606 |
|
y = 0,5dy1cosψy1 |
- |
15,244 |
16,528 |
17,856 |
19,185 |
20,541 |
|
12. Номинальные размеры координат точек эвольвенты зуба колеса приведены в табл. 11.
Таблица 11
|
Расчетная формула |
Номинальный размер для точки |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
Диаметр окружности, мм |
dy2 |
159,540 |
163,000 |
165,500 |
168,000 |
170,500 |
172,080 |
|
Угол профиля в точке на окружности диаметра dy, град |
|
20,53 |
23,56 |
25,47 |
27,21 |
28,80 |
29,74 |
|
Половина угловой толщины зуба на окружности диаметра dy, град |
ψys2 = ψb2 + invαy2 |
1,04 |
1,54 |
1,93 |
2,36 |
2,81 |
3,11 |
|
Координаты точки эвольвенты, мм |
x = 0,5dy2sinψy2 |
1,448 |
2,190 |
2,787 |
3,459 |
4,179 |
4,668 |
|
y = 0,5dy2cosψy2 |
79,757 |
81,471 |
82,703 |
83,929 |
85,148 |
85,225 |
|
13. Номинальные размеры параметров переходной кривой зуба шестерни, окончательно обработанной червячной фрезой, приведены в табл. 12.
Таблица 12
|
Расчетная формула |
Номинальный размер для точки |
|||||
|
1 |
2 |
3 |
4 |
5 |
||
|
Текущий угол станочного зацепления, град |
μw0 |
20,00 |
37,50 |
55,00 |
72,50 |
90,00 |
|
Модуль производящего контура, мм |
|
3 |
||||
|
Начальный диаметр шестерни в станочном зацеплении, мм |
dw01 = m0z1 |
33 |
||||
|
Начальная толщина зуба шестерни в станочном зацеплении, мм |
Sw01 = dw01(ψb1 - invα0) |
5,564 |
||||
|
Начальная толщина зуба инструмента, мм |
Sw0 = πm0 - Sw01 |
3,861 |
||||
|
Высота начальной головки инструмента, мм |
|
2,391 |
||||
|
Координаты центра округления кромки инструмента, мм |
|
0,430 |
||||
|
yD0 = hw0 - ρк0 |
1,491 |
|||||
|
Координаты контактной точки кромки инструмента, мм |
x0 = xD0 - ρк0cosμw0 |
1,276 |
1,144 |
0,946 |
0,701 |
0,430 |
|
y0 = yD0 + ρк0sinμw0 |
1,799 |
2,039 |
2,228 |
2,349 |
2,391 |
|
|
Полярный угол точки у |
|
0 |
-0,01255 |
-0,03039 |
-0,05215 |
-0,07603 |
|
Радиус кривизны переходной кривой, мм |
|
2,800 |
1,380 |
1,116 |
1,049 |
1,024 |
|
Координаты переходной кривой, мм |
x = 0,5dysin(ψb1 - δy) |
2,832 |
2,8658 |
3,048 |
3,310 |
3,621 |
|
y = 0,5dycos(ψb1 - δy) |
15,249 |
14,421 |
14,029 |
13,776 |
13,636 |
|
|
Расстояние от центра округления кромки зуба инструмента до полюса станочного зацепления, мм |
|
4,359 |
2,449 |
1,820 |
1,563 |
1,491 |
|
Угол профиля в точке на окружности заданного диаметра dy, град |
при μw0 = 90° μy = 90° |
1,42 |
27,09 |
48,76 |
69,50 |
90,00 |
|
Диаметр окружности, проходящей через точку у, мм |
при μw0 = 90° dy = dw01 - 2yD0 - 2ρк0 |
31,019 |
29,407 |
28,713 |
28,336 |
28,218 |
14. Номинальные размеры параметров переходной кривой зуба колеса, окончательно обработанного зуборезным долбяком, приведены в табл. 13.
Таблица 13
|
Расчетная формула |
Номинальный размер для точки |
|||||
|
1 |
2 |
3 |
4 |
5 |
||
|
Текущий угол станочного зацепления, град |
μw0 |
25,39 |
42,00 |
58,00 |
74,00 |
90,00 |
|
Диаметр окружности, проходящей через центр округления кромки зуба долбяка, мм |
dD0 = da0 - 2ρк0 |
56,94 |
||||
|
Угол профиля эвольвенты в точке на окружности, проходящей через центр округления кромки долбяка, град |
|
32,68 |
||||
|
Угловая координата центра округления, рад |
|
0,11703 |
||||
|
Начальный диаметр долбяка в станочном зацеплении, мм |
|
53,048 |
||||
|
Угол профиля эвольвенты в точке на окружности, град |
При μw0 = 90°, τy0 = 90°
|
34,51 |
47,67 |
61,48 |
75,67 |
- |
|
Расстояние от центра округления кромки долбяка до полюса станочного зацепления, мм |
при μw0 = 90° l0 = 0,5(dD0 - dw0) |
3,999 |
2,792 |
2,269 |
2,019 |
1,946 |
|
Угол профиля в точке на окружности заданного диаметра dy, град |
при μw0 = 90°, μy = 90° |
28,50 |
43,94 |
59,20 |
74,57 |
90,00 |
|
Диаметр окружности, проходящей через точку у, мм |
При μw0 = 90° dy = df = 2aw0 + da0 |
170,013 |
170,684 |
171,160 |
171,340 |
171,477 |
|
Угловая координата точки у, рад |
|
0,04546 |
0,04846 |
0,05153 |
0,05524 |
0,05892 |
|
Радиус кривизны переходной кривой, мм |
|
1,871 |
1,370 |
1,245 |
1,203 |
1,192 |
|
Координаты переходной кривой, мм |
x = 0,5dysin(δy + ψb2) |
4,019 |
4,302 |
4,568 |
4,901 |
5,219 |
|
y = 0,5dycos(δy + ψb2) |
84,911 |
85,233 |
85,458 |
85,530 |
85,579 |
|
16. Номинальные размеры диаметров граничных точек зон зацепления приведены в табл. 14.
Таблица 14
|
Расчетная формула |
Номинальный размер |
|
|
Радиус кривизны профиля зуба в верхней граничной точке однопарного зацепления, мм |
ρu1 = ρp1 + pα |
11,226 |
|
ρu2 = ρp2 - pα |
30,232 |
|
|
Угол профиля зуба в верхней граничной точке однопарного зацепления, град |
|
35,91 |
|
|
22,03 |
|
|
Диаметр окружности верхних граничных точек однопарного зацепления, мм |
|
38,281 |
|
|
161,200 |
|
|
Радиус кривизны профиля зуба в точке на окружности выступа, мм |
ρа1 = 0,5dа1sinαa1 |
13,485 |
|
ρа2 = 0,5dа2sinαa2 |
27,975 |
|
|
Радиус кривизны профиля зуба в нижней граничной точке однопарного зацепления, мм |
ρv1 = ρa1 - pα |
4,628 |
|
Ρv2 = ρa2 + pα |
36,832 |
|
|
Угол профиля зуба в нижней граничной точке однопарного зацепления, град |
|
16,62 |
|
|
26,25 |
|
|
Диаметр окружности нижних граничных точек однопарного зацепления, мм |
|
32,363 |
|
|
166,550 |
17. Номинальные величины кинематических параметров приведены в табл. 15
Таблица 15
|
Расчетная формула |
Номинальная величина |
|
|
Удельные скольжения в нижней точке активного профиля зуба |
|
8,81 |
|
|
-0,691 |
СОДЕРЖАНИЕ







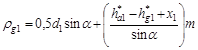


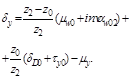 При μw0 = 90°
При μw0 = 90°