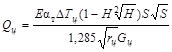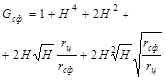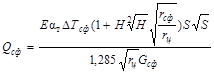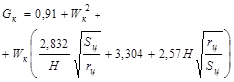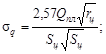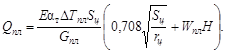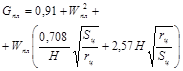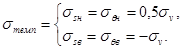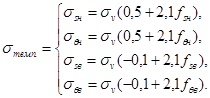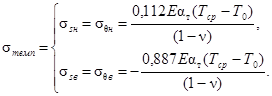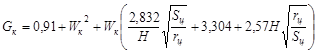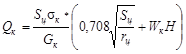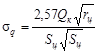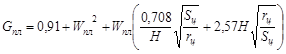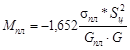|
УТВЕРЖДАЮ
Руководитель
предприятия
С.И. Косых
«21» 10 1988 г.
|
Руководящий
документ
|
Осесимметричные
элементы корпусов трубопроводной арматуры.
Методические указания по расчету температурных напряжений
|
РДМУ
26-07-270-88
Вводится
впервые
|
Дата введения
01.01.89
Настоящий
руководящий документ распространяется на корпуса трубопроводной арматуры,
работающей в условиях температурных воздействий и устанавливает методики
расчета температурных напряжений в осесимметричных элементах корпуса, представляющих
собой цилиндрические и сферические тонкостенные оболочки, кольцевые пластины и
узкие кольца прямоугольного сечения, и узлах сопряжения указанных элементов.
1.1.
Для расчета температурных напряжений осесимметричных элементов и узлов корпуса
трубопроводной арматуры используются основные положения и методы
квазистатической задачи термоупругости тонких оболочек вращения, пластин и
стержней. При нестационарных тепловых режимах время играет роль параметра.
1.2.
Рассматриваются цилиндрические и сферические тонкостенные оболочки
вращения, кольцевые пластины, узкие кольца прямоугольного сечения и узлы
сопряжения указанных элементов.
1.2.1.
Формулы справедливы при следующих условиях с погрешностью порядка 10 %:
-
для оболочек вращения
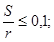
-
для пластин
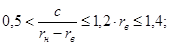
-
для колец
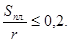
Указанные
пределы могут быть расширены, что приводит к снижению, точности расчета.
1.3.
Температурная нагрузка - осесимметричное температурное поле расчетного
элемента.
1.4.
Исходными данными для расчета являются:
-
геометрические размеры;
-
физические и механические характеристики материала корпуса;
-
температурная нагрузка расчетного элемента.
2.1.
Температурные нагрузки при расчете отдельных осесимметричных элементов корпуса
выбраны следующие:
-
для оболочек вращения - изменение температуры по толщине оболочки;
- для
пластин и колец - изменение температуры по радиусу элемента.
2.2.
Температурные напряжения в цилиндрической и сферической оболочках определяются
вдали от края на наружной и внутренней поверхности оболочки, для колец и
пластин температурные напряжения определяются на наружном или внутреннем крае
элемента.
2.3.
Для цилиндрической и сферической оболочек температурные напряжения на наружной
и внутренней поверхности равны:
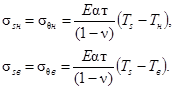 (1)
(1)
2.4.
Температурные напряжения на наружном или внутреннем крае кольцевой пластины
равны:
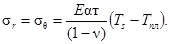 (2)
(2)
2.5.
Температурные напряжения на наружном или внутреннем крае кольца с радиусом r равны:
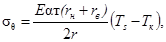 (3)
(3)
2.6.
Алгоритм, форма расчета и пример расчета приведены в приложении 2,
таблица 2.
3.1.
Температурные напряжения определяются для наиболее распространенных в корпусе
арматуры сочетаний осесимметричных элементов: двух цилиндрических оболочек
различной толщины, цилиндрической и сферической оболочек, цилиндрической
оболочки с пластиной или кольцом.
Расчетные
схемы узлов сопряжения осесимметричных элементов корпуса представлены на рис. 1 - 4.
3.2.
В качестве температурных нагрузок при расчете узлов сопряжения выбрана разность
средних температур сопрягаемых элементов.
3.2.1.
В качестве средней температуры расчетного элемента выбирается
среднеинтегральная температура по толщине оболочки или по площади поперечного
сечения кольца, пластины.
3.3.
Расчет температурных напряжений в узлах сопряжений при наличии разности средних
температур осесимметричных элементов корпуса выполняется в месте стыка
сопрягаемых элементов по формулам, представленным в таблице 1.
3.4.
Алгоритм, форма и пример расчета приведены в приложении 2, таблица 3.
3.5.
Температурные напряжения в узлах сопряжения от действия различных видов
нагрузок определяются как сумма напряжений по методике раздела 2 и п. 3.3.
Расчетные схемы узлов сопряжения осесимметричных
элементов корпуса
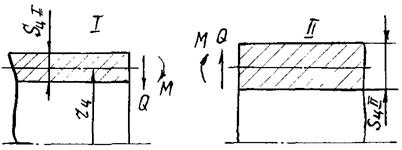
Рис.
1. Узел сопряжения двух цилиндрических оболочек
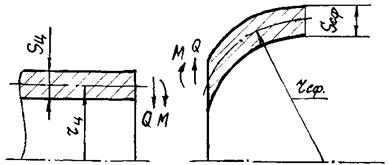
Рис. 2. Узел сопряжения цилиндрической и сферической
оболочек
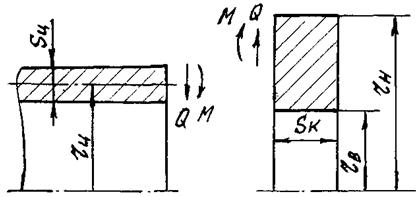
Рис.
3. Узел сопряжения цилиндрической оболочки с кольцом
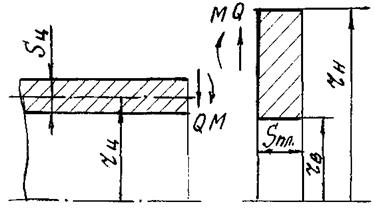
Рис.
4 Узел сопряжения цилиндрической оболочки с пластиной
Таблица 1
4.1.
С целью сокращения времени проведения прочностных расчетов при оценке
температурных напряжений в корпусе арматуры предлагается упрощенная методика
расчета модельного узла корпуса арматуры на температурные воздействия для двух
предельных тепловых режимов.
4.1.
Модельный узел корпуса арматуры представляет собой узел сопряжения двух
полубесконечных тонкостенных цилиндрических оболочек различной толщины.
4.2.
Предельными тепловыми режимами работы арматуры являются:
а)
квазистационарные режимы;
б)
термоудары.
4.3.
Температурные напряжения определяются вдали от зоны сопряжения расчетных
элементов и в зоне сопряжения расчетных элементов.
4.4.
Упрощенная методика расчета температурных напряжений при квазистационарных
режимах работы арматуры.
4.4.1.
Исходными данными для расчета являются:
-
тепловые параметры режима;
-
геометрические размеры;
-
физические и механические характеристики материала корпуса.
Коэффициент
температуропроводности определяется по справочнику [6] или по формуле 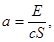 в которой
входящие величины находятся по теплофизическим справочникам.
в которой
входящие величины находятся по теплофизическим справочникам.
4.4.2.
Если тепловые параметры режима удовлетворяют условию
Fo* ³ 3, (4)
где 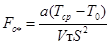 -
предельное число Фурье для квазистационарных режимов, выполняется упрощенный
расчет температурных
напряжений.
-
предельное число Фурье для квазистационарных режимов, выполняется упрощенный
расчет температурных
напряжений.
4.4.3.
Расчет температурных напряжений не производится, если
sv < sусл, (5)
где 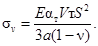
4.4.3.1.
В качестве sусл может быть
выбрано значение напряжения составляющего 5 - 10 % от предела текучести.
4.4.4.
Температурные напряжения вдали от зоны сопряжения расчетных элементов
определяются по формулам:
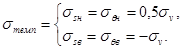 (6)
(6)
4.4.5.
Температурные напряжения в зоне сопряжения расчетных элементов определяются по
формулам:
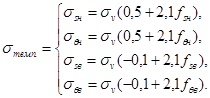 (7)
(7)
4.4.5.1.
Коэффициенты fsн, fθн, fsв, fθв, зависящие от соотношения
толщин сопрягаемых элементов, находят по графику на рис. 5.
4.5.
Упрощенная методика расчета температурных напряжений при термоударах.
4.5.1.
Исходными данными для расчета являются:
-
начальная и конечная температуры рабочей среды;
-
физические и механические характеристики материала корпуса.
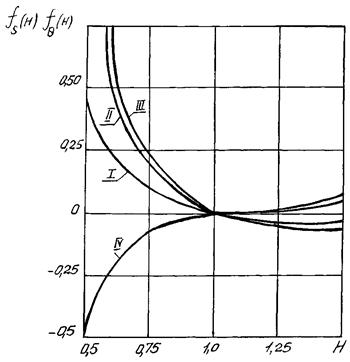
Рис. 5. Коэффициенты в модельном узле корпуса
арматуры
I - fsн на наружной поверхности
оболочки; II - fθн на наружной поверхности
оболочки; III - fsв на внутренней поверхности
оболочки; IV - fθв на внутренней поверхности
оболочки.
4.5.2.
Расчет температурных напряжений вдали от зоны сопряжения и в самой зоне
сопряжения расчетных элементов выполняется в момент времени близкой к
начальному, когда температурная нагрузка максимальна, по следующим формулам:
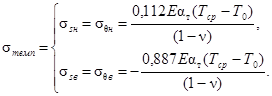 (10)
(10)
4.6.
Алгоритм, форма и пример расчета приведены в приложении 2, таблица 4.
Главный
инженер предприятия п/я А-7899 М.И. Власов
Заместитель
руководителя В.А. Айриев
Начальник
отдела 161 Р.И. Хасанов
Начальник
отдела 118 Р.А.
Азарашвили
Руководитель
темы, ответственный исполнитель О.П. Котельникова
(Обязательное)
a - коэффициент
температуропроводности, м2/сек;
Е - модуль
упругости материала расчетного элемента, МПа;
fsн, fθн, fsв, fθв - коэффициенты
на рис. 5;
Fo* - предельные
значения числа Фурье для квазистационарных режимов;
M, O - краевые
усилия и моменты;
rц,сф - радиус
срединной поверхности оболочки, мм;
rн, rв - наружный и
внутренний радиусы кольца или пластины;
rк - наружный или
внутренний радиус кольца, мм;
S - толщина
оболочки, мм;
Sк, Sпл - толщина кольца
или пластины, мм;
Т0 - начальная
температура рабочей среды, °С;
Тср - конечная
температура рабочей среды, °С;
Ts - средняя
температура расчетного элемента, °С;
Тн - температура на
наружной поверхности оболочки, °С
Та
-
температура на внутренней поверхности оболочки, °С;
Тк - температура
на наружном или внутреннем крае кольца с радиусом r, °С;
Тпл - температура
на наружном или внутреннем крае пластины, °С;
Vт - скорость
изменения температуры рабочей среды, °C/сек;
aт - коэффициент
линейного расширения материала;
ν - коэффициент
Пуассона;
sтемп. - температурные
напряжения расчетного элемента, МПа;
- условное минимальное
значение температурного напряжения,
МПа;
ssн, ssв -
меридиональные температурные напряжения на наружной и внутренней поверхности
оболочки, МПа;
sθн, sθв - кольцевые
температурные напряжения на наружной и внутренней поверхности оболочки, МПа;
sθ - кольцевые
температурные напряжения, МПа;
sr - радиальные
температурные напряжения, МПа;
sv - температурные
напряжения при квазистационарном режиме, МПа;
λ - коэффициент
теплопроводности, вт/м °С;
c - удельная
теплоемкость, кДж/кг °С;
ρ - плотность,
кг/м3.
(Справочное)
1.
Задача расчета.
Задачей
расчета является определение следующих температурных напряжений в
осесимметричных элементах и узлах корпуса:
ssн, ssв - меридиональные
температурные напряжения на наружной и внутренней поверхности оболочек;
sθн, sθв - кольцевые
температурные напряжения на наружной и внутренней поверхности оболочек;
sr - радиальные
напряжения в пластине;
sθ - кольцевые
напряжения в пластине или кольце.
Индексы
ц, сф, А, пл относятся соответственно к цилиндрической, сферической
оболочке, кольцу и пластине.
2.
Исходные данные:
S, r, rн, rв -
геометрические размеры (см. рис. 1 - 4);
E, aт, w - модуль
упругости, коэффициент линейного расширения, коэффициент Пуссона;
Тн,
Та
- температуры на наружной и внутренней поверхности оболочки;
Ts - средняя
температура расчетного элемента;
Тк,
Тпл -
температура в расчетной точке кольца или пластины.
3.
Расчет температурных напряжений в корпусе арматуры выполнен по методике РДМУ
26-07-270-88.
4.
Расчет выполнен для распространенных узлов корпуса арматуры (рис. 6).
5.
Алгоритм расчета, форма и пример расчета приведены на таблицах 2, 3, 4.
Узел I
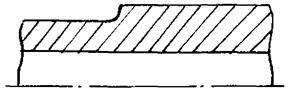
Расчетная
схема п. 2.3.
и табл. 1
п.п. 1 (Рис. 1)
Узел II
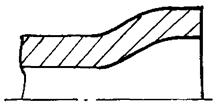
Расчетная
схема п. 2.3.
и табл. 1
п.п. 2 (рис. 2)
Узел III
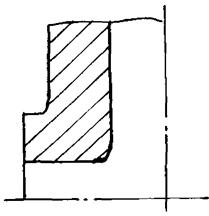
Расчетная схема п. 2.4. и табл. 1 п.п. 3
(Рис. 3)
Узел
IV
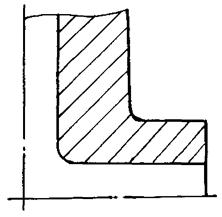
Расчетная
схема п. 2.5.
и табл. 1
п.п. 4 (Рис. 4)
Рис. 6.
Расчетные узлы корпуса трубопроводной арматуры.
Отдельные
осесимметричные элементы корпуса арматуры
Таблица 2
|
Расчетные
величины и формулы
|
|
|
Исходные данные
|
|
Материал
|
12Х18Н10Т
|
|
См. п. 1.4.
|
E, МПа
|
1,97 · 105
|
|
aт, 1/°С
|
1,77 · 10-5
|
|
ν, °С
|
0,3
|
|
См. п. 2.3.
|
Тн, °С
|
20
|
|
Тв, °С
|
300
|
|
(Ts)ц, °С
|
100
|
|
(Ts)к, °С
|
60
|
|
(Ts)пл, °С
|
80
|
|
Тк, °С
|
300
|
|
Тпл, мм
|
300
|
|
См. рис. 1 - 4
|
rн, мм
|
140
|
|
rв, мм
|
90
|
|
rк, мм
|
90
|
|
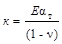 , МПА/°С , МПА/°С
|
4,981
|
|
Цилиндрическая и сферическая
оболочка
|
|
ssн = sθн = к(Тs - Тн), МПа
|
398
|
|
ssв = sθв = к(Тs - Тв), мПа
|
-996
|
|
Пластина
|
|
sθ
= sr = к(Тs - Тпл), МПа
|
-1096
|
|
Кольцо
|
|
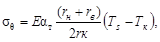 МПа МПа
|
-1069
|
Узлы сопряжения, состоящие из двух элементов корпуса
арматуры
Таблица 3
|
Расчетные
величины и формулы
|
|
|
Узел I (см. рис. 6)
|
|
Узел сопряжения двух
цилиндрических оболочек различной толщины (см.
рис. 1)
|
|
Исходные данные
|
|
См. п. 1.4.
|
Материал
|
12Х18Н10Т
|
|
E, МПа
|
1,97 · 105
|
|
aт, 1/°С
|
1,77 · 10-5
|
|
r, мм
|
100
|
|
См. рис. 1
|
SцI, мм
|
20
|
|
SцII, мм
|
30
|
|
См. п. 3.3
|
(Ts)цI, °С
|
100
|
|
(Ts)цII, °С
|
80
|
|
Вспомогательные величины
|
|
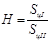
|
0,667
|
|
K1 = 1 - Н2
|
0,555
|
|
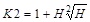
|
1,363
|
|
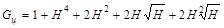
|
3,9
|
|
DТц = (Тs)цI - (Тs)цII, °C
|
20
|
|
sц* = EaтDТц, МПа
|
70
|
|
М1 = -1,816sц*К1/Gц
|
-18,09
|
|
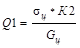
|
24,46
|
|
Температурные напряжения в
цилиндрической оболочке I
|
|
ssн
= М1, МПа
|
-18
|
|
sθн
= 2Q1 - 0,25М1, МПа
|
54
|
|
ssв
= -М1, МПа
|
18
|
|
sθв
= 2Q1 - 0,85М1, МПа
|
64
|
|
Температурные напряжения в
цилиндрической оболочке II
|
|
|
ssн
= Н2М1, МПа
|
-8
|
|
sθн
= 2Н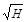 Q1 - 0,25Н2М1,
МПа Q1 - 0,25Н2М1,
МПа
|
30
|
|
ssв
= -Н2М1, МПа
|
8
|
|
sθв
= 2Н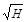 Q1 - 0,85Н2М1,
МПа Q1 - 0,85Н2М1,
МПа
|
37
|
|
Узел II (см. рис. 6)
|
|
Узел сопряжения цилиндрической
оболочки со сферической (см. рис. 2)
|
|
Исходные данные
|
|
См. п. 1.4
|
Материал
|
12Х18Н10Т
|
|
E, МПа
|
1,97 · 105
|
|
aт, 1/°С
|
1,77 · 10-5
|
|
См. рис. 2
|
Sц, мм
|
20
|
|
Sсф, мм
|
30
|
|
rц, мм
|
100
|
|
rсф, мм
|
150
|
|
См. п. 3.3
|
(Ts)ц, °С
|
100
|
|
(Ts)сф, °С
|
80
|
|
Вспомогательные величины
|
|
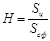
|
0,555
|
|
K1 = 1 - Н2
|
0,691
|
|
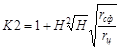
|
1,667
|
|
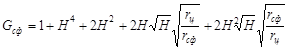
|
3,6
|
|
DТсф = (Тs)ц - (Тs)сф, °C
|
20
|
|
sсф* = EaтDТсф, МПа
|
70
|
|
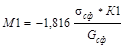
|
-24,4
|
|
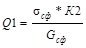
|
32,41
|
|
Температурные напряжения в
цилиндрической оболочке
|
|
ssн
= М1, МПа
|
-24
|
|
ssв
= -ssн, МПа
|
71
|
|
sθн
= 2Q1 - 0,25М1, МПа
|
24
|
|
sθв
= 2Q1 - 0,85М1, МПа
|
85
|
|
Температурные напряжения в
сферической оболочке
|
|
ssн
= Н2М1, МПа
|
-11
|
|
ssв
= -ssн, МПа
|
38
|
|
sθн
= 2Н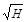 Q1 - 0,25Н2М1,
МПа Q1 - 0,25Н2М1,
МПа
|
11
|
|
sθв
= 2Н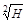 Q1 - 0,85Н2М1,
МПа Q1 - 0,85Н2М1,
МПа
|
44
|
|
Узел I (см. рис. 6)
|
|
Узел сопряжения цилиндрической
оболочки с кольцом (Рис. 3)
|
|
Исходные данные
|
|
См. п. 1.4
|
Материал
|
12Х18Н10Т
|
|
E, МПа
|
1,97 · 105
|
|
aт, 1/°С
|
1,77 · 10-5
|
|
Sц, мм
|
20
|
|
См. рис. 3
|
Sк, мм
|
50
|
|
rн, мм
|
140
|
|
rв, мм
|
90
|
|
rц, мм
|
100
|
|
См. п. 3.3
|
(Ts)ц, °С
|
100
|
|
(Ts)к, °С
|
60
|
|
Вспомогательные величины
|
|
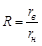
|
0,643
|
|
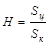
|
0,4
|
|
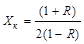
|
2,3
|
|
Wк = XкН2
|
0,368
|
|
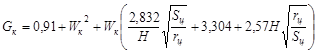
|
4,272
|
|
DТк = (Тs)ц - (Тs)к, °C
|
40
|
|
sсф* = EaтDТсф, МПа
|
140
|
|
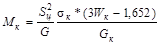 , МПа мм , МПа мм
|
-1197
|
|
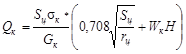 , МПа мм , МПа мм
|
304
|
|
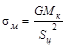 , МПа , МПа
|
-18
|
|
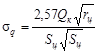 , МПа , МПа
|
87
|
|
Температурные напряжения в
цилиндрической оболочке
|
|
ssн
= sм, МПа
|
-18
|
|
ssв
= -ssн, МПа
|
92
|
|
sθн
= sq - 0,25sм, МПа
|
18
|
|
sθв
= sq - 0,85sм, МПа
|
102
|
|
Температурные напряжения в
кольце
|
|
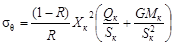 , МПа , МПа
|
9,4
|
|
Узел IV (см. рис. 6)
|
|
Узел сопряжения цилиндрической
оболочки с пластиной (см. рис. 4)
|
|
Исходные данные
|
|
Материал
|
12Х18Н10Т
|
|
См. п. 1.4
|
E, МПа
|
1,97 · 105
|
|
aт, 1/°С
|
1,77 · 10-5
|
|
См. рис. 3
|
Sц, мм
|
20
|
|
rц, мм
|
100
|
|
Sпл, мм
|
20
|
|
rн, мм
|
140
|
|
rв, мм
|
90
|
|
rпл, мм
|
90
|
|
См. п. 3.3
|
(Ts)ц, °С
|
100
|
|
(Ts)пл, °С
|
80
|
|
Вспомогательные величины
|
|
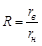
|
0,643
|
|
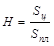
|
1,0
|
|
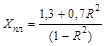
|
0,932
|
|
Wпл = XплН2
|
0,932
|
|
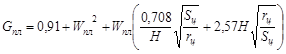
|
7,42
|
|
DТпл = (Тs)ц - (Тs)пл, °C
|
20
|
|
sпл* = EaтDТпл, МПа
|
70
|
|
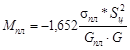 , МПа мм2 , МПа мм2
|
-1039
|
|
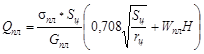 , МПа мм , МПа мм
|
235
|
|
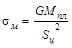 , МПа , МПа
|
-16
|
|
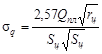 , МПа , МПа
|
68
|
|
Температурные напряжения в
цилиндрической оболочке
|
|
ssн
= sм, МПа
|
-16
|
|
ssв
= -ssн, МПа
|
72
|
|
sθн
= sq - 0,25sм, МПа
|
16
|
|
sθв
= sq - 0,85sм, МПа
|
82
|
|
Температурные напряжения в
пластине
|
|
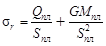
|
3,8
|
|
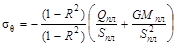 , МПа , МПа
|
9,2
|
|
|
|
|
Упрощенный расчет температурных напряжений в
модельном узле корпуса для предельных тепловых режимов
Таблица 4
|
Расчетные
величины и формулы
|
|
|
Упрощенный расчет температурных
напряжений при квазистационарных режимах
|
|
Исходные данные
|
|
См. п. 1.4
|
Материал
|
12Х18Н10Т
|
|
E, МПа
|
1,95 · 105
|
|
aт, 1/°С
|
1,74 · 10-5
|
|
v
|
0,3
|
|
п. 4.4.1.2
|
a, мм2/сек
|
4,7
|
|
См. рис. 1
|
SцI, мм
|
20
|
|
SцII, мм
|
30
|
|
См. п. 4.4.1
|
T0, мм
|
20
|
|
Tср, °С
|
300
|
|
Vт, °С/сек
|
0,084
|
|
Предельное число Фурье
|
|
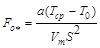
|
39
|
|
Условие Fo* ³
3 (выполнено, не
выполнено)
|
выполнено
|
|
Температурные напряжения
|
|
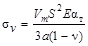 , МПа , МПа
|
11,6
|
|
Расчетные величины и формулы
|
|
|
См. п. 4.4.5.1
|
sусл, МПа
|
9,4
|
|
Условие sv < sусл (выполнено, не выполнено)
|
выполнено
|
|
Температурные напряжения вдали
от зоны сопряжения
|
|
ssн
= sθн = 0,5sν, МПа
|
5,6
|
|
ssв
= sθв = -sν, МПа
|
-11,6
|
|
Вспомогательные величины
|
|
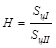
|
0,667
|
|
См. п. 4.4.5.1
|
fsн
|
0,13
|
|
fsв
|
-0,13
|
|
fθн
|
0,3
|
|
fθв
|
0,36
|
|
Температурные напряжения в зоне
сопряжения
|
|
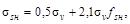 МПа МПа
|
8,4
|
|
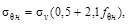 МПа МПа
|
13,1
|
|
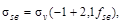 МПа МПа
|
-14,8
|
|
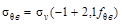 МПа МПа
|
-2,8
|
|
Упрощенный расчет температурных
напряжений при термоударах
|
|
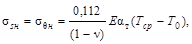 МПа МПа
|
152
|
|
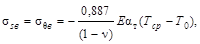 МПа МПа
|
-1204
|
|
|
|
|
(Справочное)
1.
Отчеты п/я А-7899, 1987 - 88 гг. по исследованию температурных напряжений в
осесимметричных элементах корпусов трубопроводной арматуры.
2.
«Нормы расчета на прочность оборудования и трубопроводов атомных энергетических
установок», ПиН АЭ Г-7-002-86.
3.
Основы термоупругости. А.Д. Коваленко - Киев, Наукова Думка, 1970 г., с. 307.
4.
Прочность, устойчивость, колебания: Справочник, том I, под редакцией
И.А. Биргера и Л.Г. Пановко. - М., Машиностроение, 1986 г., с. 831.
5.
Klečkova.
Nestasionárni teplotni
pole a napjatost ve strginich částech. - SNTa, Praha, 1979.
6.
Физические свойства сталей и сплавов, применяемых в энергетике. Справочник под
ред. Б.Е. Неймарк. - М. - Л., Энергия 1967.
СОДЕРЖАНИЕ
![]()
![]()
![]()
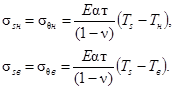 (1)
(1)![]() (2)
(2)![]() (3)
(3)