ФЕДЕРАЛЬНЫЙ НАДЗОР РОССИИ
ПО ЯДЕРНОЙ И РАДИАЦИОННОЙ БЕЗОПАСНОСТИ
(ГОСАТОМНАДЗОР РОССИИ)

ПОСТАНОВЛЕНИЕ

Об утверждении и введении в действие руководства по безопасности «Методика оценки выбросов соединений йода в атмосферу при авариях на АЭС с реакторами ВВЭР-1000»

Федеральный надзор России по ядерной и радиационной безопасности

ПОСТАНОВЛЯЕТ:

Утвердить и ввести в действие с 1 марта 2002 г. прилагаемое руководство по безопасности «Методика оценки выбросов соединений йода в атмосферу при авариях на АЭС с реакторами ВВЭР-1000» (РБ-020-01).

Начальник
Госатомнадзора России                                                                           Ю.Г. Вишневский

Федеральный надзор России по ядерной и радиационной безопасности
(Госатомнадзор России)

МЕТОДИКА ОЦЕНКИ ВЫБРОСОВ СОЕДИНЕНИЙ ЙОДА В АТМОСФЕРУ ПРИ АВАРИЯХ НА АЭС С РЕАКТОРАМИ ВВЭР-1000

РБ-020-01

МЕТОДИКА ОЦЕНКИ ВЫБРОСОВ СОЕДИНЕНИЙ ЙОДА В АТМОСФЕРУ ПРИ АВАРИЯХ НА АЭС С РЕАКТОРАМИ ВВЭР-1000. РБ-020-01

Госатомнадзор России

Москва, 2001

Методика устанавливает порядок расчета массопереноса соединений йода в герметичных помещениях системы локализации аварий на энергоблоке с реактором ВВЭР-1000 и их выброса в окружающую среду при аварии с выходом продуктов деления.

В Методике изложены общие подходы к математическому моделированию переноса продуктов деления, в том числе соединений йода. Представлены рекомендуемые к использованию значения эффективности абсорбции, значения коэффициентов, характеризующих скорости реакций соединений йода в воде, а также другие параметры, необходимые для решения системы дифференциальных уравнений.

Методика выпускается впервые.

Разработчики: Степнов В.Д., Ткаченко А.В., Клементьева Е.М., Казаков В.А. (НТЦ ЯРБ Госатомнадзора России).

При разработке Методики рассмотрены и учтены замечания и предложения специалистов Балаковской АЭС, НИКИЭТ, РФ «ФЭИ», ВНИИ ГО ЧС, ИБРАЭ.

СОДЕРЖАНИЕ

Термины и определения

Применительно к настоящей Методике приняты следующие термины и определения.

1. Абсорбция - поглощение вещества из газовой или жидкой среды всей массой другого вещества (абсорбента).

2. Адсорбция - поглощение вещества из газовой или жидкой среды поверхностным слоем твердого тела или жидкости (адсорбента).

3. Авария^* - нарушение эксплуатации АЭС, при котором произошел выход радиоактивных веществ и/или ионизирующего излучения за предусмотренные проектом^** для нормальной эксплуатации границы в количествах, превышающих установленные пределы безопасной эксплуатации. Авария характеризуется исходным событием, путями протекания и последствиями.

^* Под термином «авария» здесь и далее по тексту всегда понимается событие, связанное с радиационными последствиями.

^** Определение термина «проект» устанавливается действующей нормативной документацией.

4. Авария проектная - авария, для которой проектом определены исходные события и конечные состояния и предусмотрены системы безопасности, обеспечивающие с учетом принципа единичного отказа систем безопасности или одной, независимой от исходного события ошибки персонала ограничение ее последствий установленными для таких аварий пределами.

5. Активность (А) - мера радиоактивности какого-либо количества радионуклида, находящегося в данном энергетическом состоянии в данный момент времени: А = dN/dt, где dN - ожидаемое число спонтанных ядерных превращений из данного энергетического состояния, происходящих за промежуток времени dt. Единицей активности является беккерель (Бк).

6. Аэрозольные частицы (аэрозоли) - дисперсные системы, состоящие из частиц твердого тела или капель жидкости, находящихся во взвешенном состоянии в газовой среде (обычно в воздухе).

7. Группа продуктов деления - продукты деления, объединенные по сходству физико-химических свойств. В настоящей Методике рассматриваются три группы продуктов деления:

радиоактивные благородные газы и трудноулавливаемые соединения йода, представителем которых следует принимать йодистый метил CH₃I;

неорганические соединения йода, представителем которых следует принимать наиболее химически стабильное соединение элементарный йод I₂;

продукты деления на аэрозолях.

Все другие продукты деления, кроме инертных газов и элементарного йода, следует полагать находящимися в аэрозольной форме.

8. Десорбция - процесс регенерации абсорбентов и адсорбентов, заключающийся в удалении поглощенных ими веществ.

9. Запроектная авария - авария, вызванная не учитываемыми для проектных аварий исходными событиями или сопровождающаяся дополнительными по сравнению с проектными авариями отказами систем безопасности сверх единичного отказа, реализацией ошибочных решений работников (персонала).

10. Массоперенос - самопроизвольный необратимый процесс переноса массы данного вещества в пространстве с неоднородным полем химического потенциала этого вещества (в простейшем случае - с неоднородным полем концентрации или парциального давления данного вещества).

11. Продукты деления - простые или сложные вещества, содержащие радионуклиды.

12. Радионуклиды - ядра радиоактивных элементов, образующиеся в топливе в результате деления тяжелых ядер.

13. Среда распространения продуктов деления - область пространства, заполненная веществом, в которой распространяются продукты деления. В настоящей Методике рассматриваются три вида сред:

газовая среда (обозначается индексом G),

жидкая среда (обозначается индексом W),

поверхность (обозначается индексом S).

Газообразные и летучие продукты деления в процессе аварии могут переходить из одной среды в другую в результате работы систем локализации аварии, осаждения на поверхностях и десорбции с них.

14. Термодинамические потенциалы - определенные функции объема, давления, температуры, энтропии и других макроскопических параметров, характеризующих состояние термодинамической системы.

15. Функционал - математическое понятие, обозначающее переменную величину, заданную на множестве функций и зависящую от выбора одной или нескольких функций.

16. Химический потенциал - термодинамическая функция состояния, определяющая изменение термодинамических потенциалов при изменении числа частиц в системе и необходимая для описания свойств системы.

Перечень сокращений

АЭС - атомная электрическая станция

СЛА - системы локализации аварии

РБГ - радиоактивные благородные газы (Kr, Xe, Ar)

1. НАЗНАЧЕНИЕ И ОБЛАСТЬ ПРИМЕНЕНИЯ

1.1. Методика оценки выбросов соединений йода в окружающую среду при авариях на АЭС с реакторами ВВЭР-1000 (далее - Методика) содержит способы и методы проверки положений и выполнения требований, установленных в пунктах 1.2.2, 1.2.18 и 4.8.1 федеральных норм и правил в области использования атомной энергии «Общие положения обеспечения безопасности атомных станций (ОПБ-88/97)».

1.2. Методика предназначена в качестве руководства при разработке алгоритма расчета массопереноса продуктов деления и анализа радиационных последствий проектных аварий на конкретном реакторном блоке.

1.3. Она описывает способ моделирования и расчетного исследования массопереноса соединений йода в герметичных помещениях СЛА на реакторном блоке и их утечки в окружающую среду при аварии с выходом продуктов деления.

1.4. Методику следует использовать для реакторного блока ВВЭР-1000 с учетом его особенностей. В ней изложены общие положения по математическому моделированию переноса продуктов деления в аварийном реакторном блоке, в том числе йода и его соединений.

1.5. В Методике представлены рекомендуемые исходные данные для выполнения расчетных анализов (значения эффективности абсорбции, адсорбции, десорбции, коэффициентов, характеризующих скорости реакций соединений йода в воде, и другие параметры), а также предложения по проведению оценок выбросов для проектных аварий.

1.6. Методику не следует применять для запроектных аварий с плавлением активной зоны, так как в этих условиях характеристики процессов переноса и взаимодействия продуктов деления со средами недостаточно обоснованы экспериментально.

2. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ ПО ОЦЕНКЕ ВЫБРОСОВ СОЕДИНЕНИЙ ЙОДА В АТМОСФЕРУ ПРИ АВАРИЯХ НА АЭС С РЕАКТОРАМИ ВВЭР-1000

2.1. При проведении численных анализов распространения радионуклидов и определения их концентраций в помещениях реакторного блока следует принимать возможность разделения продуктов деления на группы. Это необходимо в связи с тем, что группы продуктов деления имеют отличающиеся физико-химические свойства и ведут себя по-разному при одних и тех же параметрах среды. В Методике рассматриваются три группы продуктов деления: радиоактивные благородные газы и трудноулавливаемые соединения йода, неорганические соединения йода, продукты деления на аэрозолях.

2.2. Для анализа массопереноса необходимо с учетом особенностей компоновки реакторного блока, параметров СЛА обеспечивать подготовку достоверных исходных данных.

2.3. Исходными данными являются:

·    параметры СЛА реакторного блока (объемы, площади поверхностей, расходы воды и другие параметры спринклерной или других систем);

·    конфигурация СЛА;

·    экспериментальные данные о свойствах используемых типов форсунок спринклерных систем (если эти системы присутствуют на реакторном блоке);

·    расход и распределение капель воды по размерам;

·     функции утечки радионуклидов в аварийное помещение;

·     функции изменения теплофизических параметров среды (температуры, давления, влажности) в помещениях СЛА, полученные в результате расчета.

2.4. Для решения задачи следует математически описывать процессы массопереноса продуктов деления в помещениях аварийного реакторного блока с помощью системы дифференциальных уравнений, которая учитывает баланс k-го радионуклида i-й группы. Особое внимание следует уделять корректной записи функционалов, описывающих переходы различных групп радионуклидов из газовой среды в жидкую среду, из жидкой среды на поверхность, из газовой среды на поверхность, из группы в группу, из жидкой среды в газовую среду, с поверхности в газовую среду.

2.5. Следует обеспечивать консерватизм оценок переноса продуктов деления по помещениям СЛА аварийного блока и утечки в окружающую среду за счет управления точностью используемых эмпирических коэффициентов в уравнениях.

2.6. Конечным результатом расчетов должно быть определение концентрации радионуклида каждой группы в СЛА реакторного блока, а также утечек радионуклидов в окружающую среду.

3. РЕКОМЕНДАЦИИ ПО МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ ПРОЦЕССОВ ПЕРЕНОСА ПРОДУКТОВ ДЕЛЕНИЯ

3.1. В каждом случае определения концентрации радионуклидов как функции параметров среды составляются системы дифференциальных уравнений баланса радионуклидов.

3.2. Для построения системы дифференциальных уравнений, описывающей баланс k-го радионуклида i-й группы, следует руководствоваться разделом 1 приложения 1.

3.3. Для построения функционала, описывающего переходы различных групп радионуклидов из газовой среды в жидкую среду, следует использовать раздел 2 приложения 1.

3.4. Для построения функционала, описывающего переходы различных групп радионуклидов из газовой среды на поверхность (адсорбция), следует использовать раздел 3 приложения 1.

3.5. Для построения функционала, описывающего переходы радионуклидов и группы в группу, следует использовать раздел 4 приложения 1.

3.6. Для построения функционала, описывающего переходы радионуклидов различных групп из жидкой среды в газовую среду, следует использовать раздел 5 приложения 1.

3.7. Для построения функционала, описывающего переходы радионуклидов различных групп из жидкой среды на поверхность и с поверхности в жидкую среду, следует использовать раздел 6 приложения 1.

3.8. Для построения функционала, описывающего переход радионуклидов различных групп с поверхности в газовую среду (десорбция), следует использовать раздел 7 приложения 1.

3.9. Решение системы дифференциальных уравнений следует выполнять с учетом заданных начальных и граничных условий.

3.10. Пример построения уравнений для СЛА, состоящей из двух помещений и барботера, представлен в разделе 8 приложения 1.

Приложение 1

Методика расчета переноса и концентраций соединений йода в помещениях аварийного реакторного блока и утечки в атмосферу окружающей среды

1. Общие положения для расчетного анализа

Радиационная обстановка на местности при авариях на АЭС обусловливается вышедшими в атмосферу окружающей среды радиоактивными продуктами деления, при этом часть продуктов деления будет находиться в газообразном виде, а часть - на аэрозольных частицах.

Выход продуктов деления в атмосферу технологических помещений и окружающую среду, как правило, связан с истечением теплоносителя из первого контура. Активность теплоносителя контура циркуляции реактора ВВЭР-1000 составляет около 3,7 · 10⁸ Бк/м³. В случае разрывов трубопроводов малого диаметра происходит выход продуктов деления, накопившихся в теплоносителе первого контура, а при обрыве трубопровода большого диаметра дополнительно к этому количеству могут выйти продукты деления, накопившиеся под оболочками твэлов (от 1 до 3 % от накопленного количества продуктов деления в топливе [1]). Массовая доля аэрозольных частиц в полном балансе продуктов деления, находящихся в воздухе под защитной оболочкой реакторного блока, при проектных авариях составляет не более 10 % [2].

В таблице показано, какие функционалы и в каких случаях следует использовать в Методике для анализа проектных аварий. Частица «Нет» означает, что данный функционал не используется в расчетах переноса приведенной в колонках 2, 3, 4, 5 таблицы группы продуктов деления. Частица «Да» означает, что данный функционал используется в расчетах переноса группы продуктов деления, приведенной в колонках 2, 3, 4, 5 таблицы.

Значения соответствующих функционалов должны быть определены для следующего диапазона изменения теплогидравлических параметров при проектных авариях:

Температура, °С                                           От    20       до     150

Давление паровоздушной среды, МПа     От    0,05    до     0,5

Парциальное давление воздуха, МПа       От    0,0      до     0,15

Перечень рассматриваемых функционалов

Обозначим NGⁱ_k(t), NWⁱ_k(t), NSⁱ_k(t) - количество продуктов деления i-й группы в объеме герметичного помещения СЛА в газовой и жидкой средах и на поверхности соответственно. Тогда, если поступление k-го радионуклида i-й группы продуктов деления в помещение составляет G_enAⁱ_k(t) (где G_en - расход среды, поступающей в помещение; Aⁱ_k(t) - удельная активность k-го радионуклида i-й группы продуктов деления), а утечка осуществляется за счет утечки паровоздушной среды с расходом G_en(t), то система, описывающая баланс k-го радионуклида i-й группы, будет иметь вид:

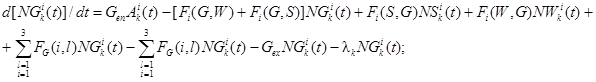
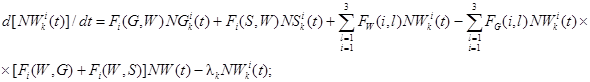
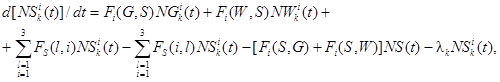          (1)

где F_i(G, W) - функционал, описывающий переход продуктов деления i-й группы из газовой среды в жидкую среду, где i изменяется от 1 до 3 (количество групп продуктов деления);

F_i(W, G) - функционал, описывающий переход продуктов деления i-й группы из жидкой среды в газовую среду;

F_i(G, S) - функционал, описывающий переход продуктов деления i-й группы из газовой среды на поверхность;

F_i(S, G) - функционал, описывающий переход продуктов деления i-й группы с поверхности в газовую среду;

F_i(W, S) - функционал, описывающий переход продуктов деления i-й группы из жидкой среды на поверхность;

F_i(S, W) - функционал, описывающий переход продуктов деления i-й группы с поверхности в жидкую среду;

F_G(i, l) - функционал, описывающий переход продуктов деления i-й группы в l-ю группу в газовой среде;

F_W(i, l) - функционал, описывающий переход продуктов деления i-й группы в l-ю группу в жидкой среде;

F_S(i, l) - функционал, описывающий переход продуктов деления i-й группы в l-ю группу на поверхности;

λ_k - постоянная распада k-го радионуклида, 1/с.

В случае если в результате распада некоторого радионуклида образуется заметное количество k-го радионуклида, то это учитывается с помощью дополнительного члена в каждом уравнении.

2. Функционал, описывающий переходы различных групп радионуклидов из газовой среды в жидкую среду

Функционал, описывающий переход i-го радионуклида k-й группы из газовой среды в жидкую среду, в зависимости от используемых технических средств может иметь различный вид. Переход из газовой среды в жидкую среду может осуществляться при работе спринклерной системы, водоэжекционных охладителей, при барбортаже, а также за счет диффузии из газовой среды в жидкую. Последний процесс, как правило, незначителен и им пренебрегают.

Из-за слабой растворимости в воде в рассматриваемом диапазоне температур и давлений переход РБГ в воду также не рассматривается.

Спринклерная система

В соответствии с рекомендациями [3] функционал F_i(G, W) для первой и второй группы радионуклидов может быть записан в виде:

F_1,2(G, W) = E_1,2(t)H_1,2(t)L/V,                                               (2)

где L - расход водного раствора, подаваемого на форсунки спринклерной системы;

V - объем помещения, где происходит разбрызгивание раствора;

H_1,2(t) - коэффициенты распределения радионуклидов первой и второй группы соответственно, определяемые согласно рекомендациям, изложенным в приложении 3;

E_1,2(t) - эффективность абсорбции радионуклидов первой и второй группы соответственно спринклерной системы (определяется согласно рекомендациям, изложенным в приложении 2).

Для третьей группы радионуклидов этот функционал будет иметь вид:

F₃(G, W) = E₃(t)L/V.                                                             (3)

Значение E₃(t) для радионуклидов третьей группы можно определить в соответствии с рекомендациями, изложенными в приложении 2.

Водоэжекционные охладители

Величины F_1,2(G, W) для водоэжекционных охладителей находятся по тем же соотношениям (2), (3), что и для спринклерной системы. Значения промежуточных параметров, используемых в соотношениях, приведены в таблице приложения 2 и в приложении 3.

Барботажные устройства

Переход из газовой среды в жидкую среду и обратно может происходить при барботаже. Тогда барботер может быть представлен как помещение без газовой среды, т.е. только с жидкой средой. Если принять, что концентрация соединений йода, относящихся к первой и второй группе, в паровоздушной смеси внутри пузырька при всплытии в воде барботера приходит в равновесие с концентрацией их в воде барботера, то уравнение расчета взаимодействия соединений йода, растворенных в паровоздушной смеси, с водой барботера будет иметь вид:

d[NW^1,2_i/(t, 2)]/dt = NG^1,2_i(t, 1)G_en(G + S_t)/V(1) - G_en(G)NW^1,2_i(t, 2)/[V(2)Н^1,2_i(t)],           (4)

где NW^1,2_i(t, 2) - количество i-го радионуклида первой и второй группы в воде барботера;

NG^1,2_i(t, 1) - количество i-го радионуклида первой и второй группы в газовой среде помещения перед барботером;

G_en(G + S_t) - расход пара и воздуха на барботер;

G_en(G) - расход воздуха на барботер;

V(1) - объем помещения до барботера;

V(2) - объем воды в барботере.

Таким образом, при принятом допущении функционал F_i(G, W) для барботажа имеет вид:

F_1,2(G, W) = G_en(G)/[V(2)H_1,2(t)].                                         (5)

В случае если равновесие между концентрацией соединений йода в паровоздушной смеси внутри пузырька и в воде барботера не достигается, то необходимо в формуле (5) использовать коэффициент абсорбции, который может быть определен расчетным или экспериментальным путем. С учетом этого формула (5) будет иметь вид:

F_1,2(G, W) = F_1,2(t)G_en(G)/[V(2)H_1,2(t)].                                (6)

Для третьей группы этот функционал будет иметь вид:

F₃(G, W) = E₃(t).                                                       (7)

3. Функционал, описывающий переход радионуклидов из газовой среды на поверхность (адсорбция)

Как следует из таблицы, скорость осаждения радионуклидов первой группы (РБ и органические соединения йода) из газовой среды на поверхность считается незначительной, т.е. F_i(G, S) = 0.

Скорость осаждения радионуклидов второй группы определяется по формуле [4]

F₂(G, S) = 10^-2S/V,                                                                (8)

где S - площадь внутренних поверхностей, м²;

V - объем помещения, м³;

10^-2 - численный коэффициент, м/с.

Выведение радионуклидов третьей группы из объема на поверхность может осуществляться за счет различных процессов. В частности, в условиях перемешивания модель выведения аэрозолей хорошо известна [5]. Изменение счетной концентрации аэрозолей dN(t) за время dt за счет осаждения на поверхность:

dN(r)/dt = -N(r)u(r)S/V,                                                        (9)

где V - объем, в котором содержатся аэрозоли;

S - площадь, на которую осаждаются частицы;

u(t) - скорость осаждения, равная:

u(r) = FB(r),                                                            (10)

которой обладает частица радиуса r и подвижности В(r) под воздействием действующей силы F. Для сферической частицы подвижность В(r) определяется законом Стокса:

B(r) = C(r)/(6pvr),                                                        (11)

где v - вязкость газа-носителя;

C(r) - эмпирический поправочный коэффициент Каннингхэма, равный:

C(r) = 1 + 1,246Kn ехр(-0,87/Kn),                                      (12)

где Kn - число Кнудсена.

Скорость гравитационного осаждения в стационарном состоянии получается подстановкой силы тяжести F в уравнение (10):

u_s(r) = 2ρ_effg/(9v)r²C(r),                                                        (13)

где g - гравитационная постоянная;

ρ_eff - эффективная плотность (сферической) частицы.

Для гравитационного осаждения площадь поверхности S в уравнении (9) нужно брать в виде суммы всех направленных вверх проекций поверхностей в объеме V. Для всех других процессов ориентация поверхности не важна.

Для диффузионного осаждения используется уравнение:

u_s(r) = D(r)/δD,                                                              (14)

где D(r) - коэффициент диффузии;

D(r) = kTB(r),                                                              (15)

где k - постоянная Больцмана;

T - абсолютная температура;

δD - толщина диффузионного пограничного слоя, в котором концентрация частиц спадает до нуля с постоянным градиентом. В большинстве случаев принимаемая величина δD равна 0,01 см.

Для рассматриваемых случаев выражение для F₃(G, S) будет иметь вид:

F₃(G, S) = Σu(r)S/V,                                                        (16)

а значение u(r) выбирается в зависимости от описываемого процесса.

Для оценки скорости осаждения, когда трудно оценивать влияние тех или иных процессов, часто используются эмпирические соотношения, полученные экспериментально в условиях, приближенных к проектной аварии. В качестве такого эмпирического соотношения используется выражение для постоянной скорости осаждения следующего вида [4]:

F₃(G, S) = 5 · 10^-2S/V.                                                      (17)

4. Функционал, описывающий переход радионуклидов из группы в группу

Из-за разнообразия механизмов, обусловливающих переход радионуклидов из группы в группу, описывать этот процесс наиболее трудно. Переход может осуществляться как за счет механизмов физической природы (распад продуктов деления, испарение и т.д.), так и за счет химических реакций. В результате распада некоторых радионуклидов инертных радиоактивных газов (первая группа) могут образовываться аэрозоли цезия или рубидия (третья группа). Взаимодействие неорганических соединений йода (вторая группа) с органическими примесями в атмосфере может приводить к образованию органических соединений (первая группа). В Методике принимается, что:

·     переход радионуклидов из одной группы в другую группу за счет радиоактивного распада незначителен и им можно пренебречь;

·     переход радионуклидов инертных радиоактивных газов в другие группы не происходит F_{G, W, S}(i, l) = 0;

·     возможное образование органических соединений йода (первая группа) в результате химических реакций в газовой среде соединений йода первой и второй группы учитывается с помощью введения доли йодистого метила (первая группа).

Газовая среда

Как следует из таблицы, скорость перехода радионуклидов в газовой среде F_G(i, l) из одной группы в другую не учитывается, т.е. принимается равной нулю. Таким образом, в расчетах последствий проектных аварий считается, что в газовой среде не происходит никаких физико-химических реакций, приводящих к изменению свойств веществ.

Жидкая среда

Переход радионуклидов органических соединений йода (первая группа) в группу неорганических соединений (вторая группа) осуществляется за счет реакций гидролиза и других реакций с химическими добавками в воде. В этом случае F_W(1, 2) равно сумме констант скоростей реакций первого и псевдопервого порядка.

Значения некоторых констант скоростей для различных условий приведены в приложении 4.

Образование нерастворимых и нелетучих соединений йода (третья группа) за счет химических реакций с соответствующими добавками как органических, так и неорганических соединений можно учитывать с помощью констант скоростей реакций первого и псевдопервого порядка. Следовательно, и F_W(1, 3), и F_W(2, 3) равно сумме констант скоростей реакций первого и псевдопервого порядка.

В настоящее время нет достаточно надежных сведений, которые можно было использовать для проектных расчетов химических реакций неорганических соединений йода (вторая группа) и йода, осевшего на аэрозольных частицах, с образованием органических соединений. Есть лишь косвенные сведения о таких возможностях. В дальнейшем этот переход не учитывается, а значения F_W(2, 1) и F_W(3, 1) принимаются равными нулю: F_W(2, 1) = F_W(3, 1) = 0. Аналогично принимается, что и F_W(1, 3) = F_W(2, 3) = F_W(3, 2) = 0.

Поверхности

Принято, что радионуклиды первой группы не осаждаются на поверхности. Отсюда: F_S(1, 2) = F_S(1, 3) = 0.

При взаимодействии соединений второй группы с химическими соединениями на поверхностях могут образовываться органические соединения (первая группа). Аналогичные реакции могут иметь место для радионуклидов третьей группы. Эксперименты показывают [6], что при десорбции йода с поверхностей часть его соединений находится в «летучей», скорее в органической форме (первая группа), а часть в виде хорошо улавливаемых соединений (скорее, неорганических, т.е. второй группы). Поскольку эти процессы в достаточной степени не изучены, то переход радионуклидов второй и третьей группы в первую и вторую группу учитывается с помощью коэффициентов при функционале, описывающем переход радионуклидов различных групп с поверхности в газовую среду, полученных экспериментально.

5. Функционал, описывающий переход радионуклидов различных групп из жидкой среды в газовую среду

Соединения первой и второй группы

При описании процессов перехода соединений первой и второй группы из жидкой среды в газовую среду предполагается, что процесс растворения газов и газообразных веществ является обратимым. Поэтому при превышении отношения концентрации химических веществ в жидкости к соответствующей концентрации в газе некоторого предела NW_k(t)/NG_k(t) = H_k(t) происходит обратное поступление соединений из жидкой среды в газовую. Например, при работе спринклерной системы раствор, поступающий в газовую среду помещения в виде капель, имеет некоторую начальную концентрацию NW_ko(t)/V(W) = A₀. В процессе падения капля раствора поглощает (или отдает) некоторое количество соединений k-й группы и средняя концентрация в капле становится равной A_m. Если обозначить равновесную концентрацию [когда NW_k(r)/NG_k(t) = H_k(t)] через A_eq, то соотношение, определяющее направление процесса массопереноса, будет иметь вид: (A_m - A₀)/(A_eq - A₀). Из соотношения видно, что если начальная концентрация в растворе меньше произведения концентрации в газовой среде на коэффициент распределения NG_k(t)H_k(t), то массоперенос направлен внутрь капли; если они равны, то массоперенос не происходит; если больше, то идет массоперенос из капли, т.е. из жидкой среды в газовую среду.

В Методике принимается, что массоперенос происходит в однородной среде, т.е. скорость массопереноса одинакова, вне зависимости от направления переноса. С учетом этого предположения функционал, описывающий перенос радионуклидов первой и второй группы, будет иметь следующий вид:

для спринклерной системы и водоэжекционных охладителей значение F_i(G, W) может быть рассчитано по формуле (1);

для барботажа, значение F_i(G, W) может быть рассчитано по формуле (5).

Значения параметров F_i(t) и H_i(t) могут быть рассчитаны с помощью уравнения (2) приложения 2 и соотношения (1) приложения 3.

Третья группа

При проектных авариях выход аэрозолей из жидкой среды в основном определяется образованием мелкодисперсной влаги при работе водоразбрызгивающих систем (спринклерной системы и водоэжекционных охладителей). Все используемые для водоразбрызгивающих систем форсунки дают определенное распределение капель по размерам. Тогда левый край этого распределения может быть использован для оценки количества мелкодисперсной влаги, образующейся при работе систем. В качестве минимального размера выбирается минимальный размер капель для используемой форсунки. В качестве правой границы распределения мелкодисперсных капель может быть выбран размер, при котором капля может находиться в стабильной паровоздушной среде заданное время, например, 30 мин. По известным границам и форм распределения может быть легко найдено количество мелкодисперсной влаги, образующейся при работе системы. Практически все форсунки для водоразбрызгивающих систем имеют логнормальное распределение капель по размерам.

6. Функционал, описывающий переход радионуклидов из жидкой среды на поверхность и с поверхности в жидкую среду

В настоящее время нет достаточно надежных экспериментальных данных о процессах осаждения различных групп соединений на поверхности из водного раствора поведения этих соединений на поверхностях и выхода с поверхностей в жидкую среду. Поэтому в Методике рекомендуется использовать значение F_i(W, S) = F_i(S, W) = 0. Использование других значений должно быть обосновано.

7. Функционал, описывающий переход радионуклидов с поверхности в газовую среду (десорбция)

Процесс десорбции с поверхности - процесс сложный, меняющийся во времени. В приложении 5 дан краткий анализ некоторых экспериментальных исследований по десорбции и обоснование предлагаемого способа математического моделирования этого процесса. Переход радионуклидов йода с поверхности в газовую среду следует учитывать с помощью постоянного коэффициента, который не зависит от времени, температуры и концентрации на поверхности и равен 10^-7 1/c.

Следует считать, что половина десорбированного йода находится в молекулярной форме (вторая группа), а половина - в органической форме (первая группа). Таким образом, F₁(S, G) = 5 · 10^-8, 1/с, а F₂(S, G) = 5 · 10^-8, 1/с.

Описанные выше функционалы следует использовать для составления системы дифференциальных уравнений массопереноса, решив которую можно определят концентрации продуктов деления в средах для каждой группы, а также утечку продуктов деления в окружающую среду.

8. Пример построения уравнений для системы локализации аварии, состоящего из двух помещений и барботера

Рассмотрим СЛА, состоящую из помещения, в которое происходит истечение теплоносителя, бассейна-барботера и помещения ловушек, куда передавливается через барботер паровоздушная среда в процессе аварии. Работает спринклерная система, забор воды для которой производится из бассейна-барботера. Задача состоит в определении содержания радиоактивных продуктов (в этой задаче рассмотрим соединение радиоактивных изотопов йода) в помещениях СЛА в различных формах в воде бассейна-барботера и утечку их в окружающую среду.

Для выполнения поставленной задачи следует решить систему из 13 дифференциальных уравнений. Она включает в себя по четыре уравнения для каждого помещения и два уравнения для утечки разных форм радиоактивного йода, являющихся представителями трех групп соединений по принятой классификации. Исходя из построения общей системы уравнений для одного помещения и учитывая методики расчета функционалов и коэффициентов, входящих в функционалы, получим следующую систему дифференциальных уравнений:

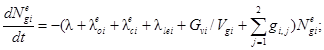
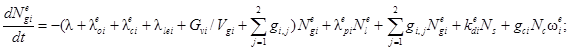
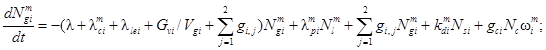
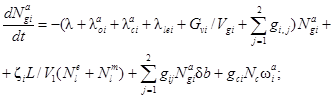
где l = 1, 2;

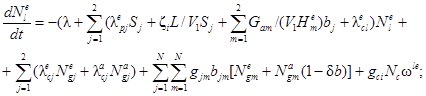
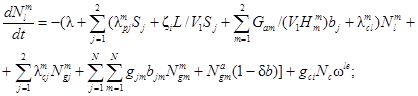
где N_gi^e, N_gi^m, N_gi^a - количество радиоактивного йода в каждой из трех форм в i-м помещении СЛА, Бк;

N_l^e, N_l^m - количество радиоактивного йода в виде I₂ и CH₃I соответственно в объеме воды, Бк;

N_le^e, N_le^m, N_le^a - количество йода в каждой из форм, вышедшего в атмосферу вне АЭС к моменту времени t, Бк;

λ - постоянная распада, 1/с;

λ_oi^e, λ_oi^m - коэффициенты осаждения йода для элементарной и аэрозольной форм в i-м помещении, 1/с;

λ_ci^e, λ_ci^m, λ_ci^a - начальные коэффициенты выведения разных форм йода из воздуха водоразбрызгивающими системами, 1/с;

λ_lei - коэффициент утечки паровоздушной среды из i-го помещения СЛА через неплотности в окружающую среду, 1/с;

G_vi - расход паровоздушной среды из i-го помещения через вентиляционную трубку, м³/с;

V_gi - объем i-го помещения СЛА, м³;

g_ij - коэффициент перетечек паровоздушной среды из i-го в j-е помещение СЛА, 1/с;

λ_pi^e, λ_pi^m - коэффициенты перехода I₂ и CH₃I из воды в паровоздушную среду j-го помещения СЛА при работе водоразбрызгивающих систем, 1/с;

k_di^e, k_di^m - коэффициенты десорбции радиоактивного йода в формах I₂ и CH₃I соответственно в i-м помещении, 1/с;

g_ci - расход течи теплоносителя в i-е помещение, м³/с;

N_c -удельная активность теплоносителя, Бк/м³;

ω_i^e, ω_i^m, ω_i^a, ω^le, ω^lm - коэффициенты выхода разных форм радиоактивного йода в атмосферу ω_i i-го помещения и в воду ω^l объема при истечении теплоносителя, безразмерные;

ω_i^e + ω_i^m + ω_i^a + ω^le + ω^lm = 1,

ζ_i - коэффициент дробления капель (перехода их в разряд аэрозолей), безразмерный;

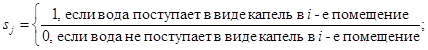
V_i - объем воды, м³;

G_am - расход паровоздушной среды через барботер из m-го помещения в объем воды, м³/с;

H_m^e, H_m^m - равновесные коэффициенты распределения элементарного йода и йодистого метила соответственно между водой и воздухом, безразмерные;

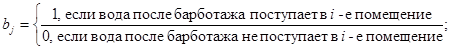
λ_cl^e, λ_cl^m - коэффициенты очистки воды от элементарного йода и йодистого метила соответственно на ионообменных фильтрах, 1/с;

δb - коэффициент проскока аэрозолей при барботаже.

Для решения задачи, приведенной в разделе 8 приложения 1, следует создавать соответствующий компьютерный код.

Литература к приложению 1

1. Reactor Safety Study WASH-1400, NUREG 75/014, October, 1975 Appendix VII.

2. Антропов В.Н., Федулов В.Ф., Степнов В.Д., Ткаченко А.В. и др. Отчет о НИР «Расчетное обоснование выполнения критериев радиационной безопасности окружающей среды при проектных и запроектных авариях с обрывом главного циркуляционного трубопровода Ду 850 для АЭС с ВВЭР-1000 (проект АЭС-91 для третьих стран)». Договор № 25/Д-92/94-361 с ЛИАЭП. Инв. № 400-07-21. НТЦ ЯРБ, Москва, 1991.

3. Parsly L.F. Pilot Plant Studies of Nethyl Iodide Clieanup by Sprays, Nucl. Appl. Technol., 1970, 8, p. 13.

4. Павленко В.И. Оценка радиационных последствий крупных аварий на АЭС с ВВЭР. Отчет ИАЭ инв. № 10/826, Москва, 1973.

5. Bunz H., Schock M. NAUA Mod4: A Code for Calculating Aerozol Behaviour in LWR Core Melt Accidents, KFK-3554, August, 1983.

6. Экспериментальное исследование выхода радиоактивного йода в технологические помещения атомной электростанции при истечении теплоносителя i-го контура. Тезисы докладов Всесоюзной конференции «Радиационная безопасность населения и защита окружающей среды в связи с эксплуатацией атомных электростанций». Казаков В.А., Ткаченко А.В., Федулов В.Ф. и др. Димитровград, 26 - 29 мая 1981 г.

Приложение 2

Расчет эффективности абсорбции летучих соединений и аэрозолей водоразбрызгивающими и барботажной системами

Спринклерная система

Процесс поглощения растворимого газообразного соединения каплями спринклерного раствора в общем виде может быть представлен как процесс массопереноса из свободного объема через газовую пленку капли, растворение на поверхности (жидкой пленки) и процесс массопереноса в объем капли.

Эффективность абсорбции E соединений первой и второй группы каплей определяется путем решения уравнения диффузии в капле для каждого соединения. Диффузионный поток у поверхности капли со стороны газовой и жидкой сред должен быть одинаков:

D₁dC/dN = k_g + 1/(C_g + C_gi),                                                (1)

где dC/dN - градиент концентрации в жидкости у поверхности капли;

k_g - коэффициент массопереноса через газовую пленку, м/с;

H - равновесный коэффициент распределения соединения между водой и воздухом (см. приложение 3);

C_g - концентрация соединения в основной массе газа;

C_gi - концентрация соединения в газе у поверхности капли.

Общий вид уравнения диффузии для описания поведения соединения, растворенного в капле с учетом химических реакций:

D₁(d²C/dr² + 2/rdC/dr) - kC = dC/dt,                                   (2)

где r - радиус капли на данный момент времени;

k - константа реакции первого или псевдопервого порядка;

t - текущее время.

Решение этого уравнения для начальных и граничных условий в связи с (1) будет иметь вид:

C(r, 0) = C₀;

t = C(r, 0) = C;

dC(R, t)/dr = k_g/(HD₁)(C^* - С),

что дает следующее выражение для E(t):

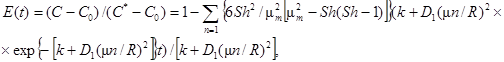
где С^* - равновесная концентрация соединения в капле у поверхности капли;

C₀ - начальная концентрация соединения в капле;

Sh = k_gd/D_g - число Шервуда;

μn - корни уравнения tg(μn) = μn/(1 - Sh);

R - радиус капли.

Коэффициент массопереноса через газовую пленку k_g определяется следующей формулой [1]:

k_g = D_g(2 + 0,6Re^1/2Sc^1/3)/d,                                                  (3)

где Re = Dρ/μ - число Рейнольдса;                                       (4)

Sc = μ/(ρD_g) - число Шмидта;                                            (5)

ρ - плотность паровоздушной среды, кг/м³;

μ - вязкость среды, кг/(м · с);

D_g - коэффициент диффузии в паровоздушной среде, м²/с;

v - скорость падения капли, м/с;

d - диаметр капли, м;

μ = 10^-6[0,85ε^{(0,6εε - 0,62ε + 0,884)} + 0,00385(T - 273,15)];

D_g = 1/[D_gaP_a/P + 1/D_g,vP_v/P);

D₁ = 7,4 · 10^-8(XM_v)^1/2T_w/(μ1v_M^0,6), [2, 3],

где D_ga,gv = BT^1/6(1/M + 1/M_a,v)^1/2/[Pσs,(a,v)ωD] - коэффициент диффузии соединения в воздухе (a) или в паре (v);

ε = P_a/P - отношение парциального давления воздуха к полному давлению;

B = 0,00214 - 0,000492(1/M + 1/M_a,v)^0,5;

P_a,v - парциальные давления воздуха и пара;

P - полное давление в атмосфере;

T - температура паровоздушной среды;

T_w - температура воды;

X - степень диссоциации жидкости (для воды - 2,6);

M - молекулярный вес соединения;

M_w,a,v - молекулярный вес воды, воздуха или пара;

μ1 = 241,4 · 10^{[247,8/(Tw - 140)]} - вязкость воды;

v_M - молекулярный объем соединения (для I₂ - v_M = 71,5, для CH₃I - v_M = 62,9);

σs,(a,v) = (1/2) · (σs + σa,v) - диаметр соударения молекул соединения с молекулами воздуха или пара;

ωD = (ωs, ωa,v)^1/2 - интеграл столкновений.

Значения основных параметров для расчета коэффициентов диффузии соединений в паровоздушной среде приведены в таблице [4, 5].

^* k - постоянная Больцмана.

Описанный выше расчет эффективности абсорбции E можно использовать для первых двух групп соединений, приведенных в таблице настоящего раздела.

Для аэрозолей эффективность прямого захвата каплями определяется выражением [6]:

E = (1 + d_a/d)² - 1/(1 + d_a/d),

где d_a - средний аэродинамический диаметр аэрозольных частиц.

Эжекционный охладитель

Методика определения эффективности абсорбции E для эжекционных установок аналогична методике для спринклерной системы. Однако приведенные формулы нельзя использовать ввиду того, что в них не учитывается внутренняя циркуляция в каплях и изменение дисперсности в процессе дробления капель. В эжекционном охладителе данный процесс будет иметь существенное значение из-за сильной турбулизации водовоздушного потока в камере смешения. Указанные значения можно получать экспериментально. Например, эксперименты [7] показали, что рассматриваемые выше эффекты могут увеличивать значения эффективности абсорбции E на порядок по сравнению со значениями эффективности абсорбции, рассчитанными по методике для спринклерной системы. В соответствии с полученными экспериментальными данными значение эффективности абсорбции E для CH₃I (первая группа) составляет 0,49, а для I₂ (вторая группа) E равно 6 · 10^-3. Эффективность улавливания аэрозолей со средним диаметром 2,3 мкм в камере смешения оказалась равной 0,2. При экспертизе проектных расчетов должно быть уделено внимание экспериментальному подтверждению значений эффективности абсорбции Е для используемых в проекте типов эжекционных охладителей.

Барботер

Эффективность абсорбции соединений при барботаже может быть рассчитана для известного начального диаметра пузырька парогазовой смеси. Однако на практике это выполнить довольно трудно, поскольку образующиеся в процессе барботажа пузырьки имеют распределение по размерам, которое часто неизвестно. Поэтому используются экспериментальные значения. Например, по данным [8] эффективность абсорбции при барботаже для аэрозолей составляет примерно 0,98. В процессе экспертизы проектных расчетов должно быть уделено внимание экспериментальному подтверждение значений эффективности абсорбции различных групп радионуклидов при барботаже для используемых в проекте типов барботажных устройств.

Выбор формы аэрозольных частиц

Наиболее важным результатом экспериментальных исследований было подтверждение процесса сферификации. Частицы, подвергающиеся процессам конденсации-испарения, сжимаются до почти сферической формы. Необъясненное отклонение от идеальной сферы мало, и нет необходимости учитывать его в модели. За счет этого процесса могут подвергаться дальнейшему сжатию скоагулированые совокупности ранее сжатых частиц. Эффект, экспериментально установленный для негигроскопических частиц, будет сильнее для растворимых гидроскопичных частиц. Тогда очевидно предположить, что процесс сферификации имеет место при аварии в водяном реакторе для очень коротких периодов времени или в очень маленьких пространствах здания. Поэтому можно принять, что сферическая форма будет сохраняться в процессе расчета.

Литература к приложению 2

1. Sideman S. Direct Contact Heat Transfer Beetween Innescible Liguids. Adv. Chem. Eng., 6, p. 207 - 296, (1966).

2. Методика и зависимости для теоретического расчета теплообмена и гидравлического сопротивления теплообменного оборудования АЭС. РТМ 24.031.05-72. Москва, 1972.

3. Методика расчета распространения радиоактивных продуктов на АЭС при авариях (применительно к количественному анализу безопасности), Казаков В.А., Скачков В.С., Ткаченко А.В., Федулов В.Ф., отчет ВТИ, арх. № 11171, 1978.

4. Knudsen J.G. Properties of air-steam mixtures containing small emounts of iodine. BNWL - 1326, 1970.

5. Svehla R.A. Viscosities and Thermoconductivities of Gases at High Temperatures Suitable for Heat Transfer Calculations, NASA-ТВ-R-132. National Aeronautics and Space Administration, 1962.

6. Parsly L.F. Removal of Radioactive Particles by Sprays, ORNL - 4671, 1971.

7. Экспериментальное исследование очистки воздуха от соединений радиоактивного йода на модели водоструйного эжектора. Казаков В.А., Ткаченко А.В., Федулов В.Ф. и другие, отчет ВТИ, арх. № 12951, 1985.

8. Reactor Safety Study WASH-1400, NUREG 75/014, October, 1975 Appendix VII.

Приложение 3

Распределение соединений йода между водной и газовой фазами

Органические соединения йода (первая группа)

Среди наиболее распространенных органических соединений йода, оказывающие при проектных авариях заметное влияние на радиационную безопасность, йодистый метил CH₃I наименее химически активен, т.е. способен вступать в физико-химические реакции. Как правило, для описания поведения соединений йода, относящихся к первой группе, в качестве представителя группы выбирается CH₃I.

Среди известных работ по исследованию коэффициента распределения H для CH₃I наиболее консервативные (наименьшие) значения H даны в [1]. Они экспериментально обоснованы в диапазоне температур от 5 до 70 °С (наиболее широкий исследуемый диапазон температур, известных авторам). Наблюдаемые значения хорошо описываются эмпирической функцией, зависящей от температуры, которую предполагается использовать для расчета Н, моль/л раств./моль/л газа:

lgH = -4,82 + 1597/T,                                                           (1)

где Т - температура, К.

Неорганические соединения йода (вторая группа)

При проектных авариях в качестве представителя неорганических соединений йода рассматривают элементарный йод I₂, являющийся наименее химически активных соединением этой группы.

Распределение элементарного йода между водной и газовой средами будет определяться его физическим состоянием, образующимися химическими соединениями или гидролизом в воде. Полный или видимый коэффициент распределения Р элементарного йода между водной и газовой средами зависит от отношения концентрации йода в воде к концентрации элементарного йода в газовой среде:

Р = масса йода в 1 м³/масса йода в 1 м³ газа.

Элементарный йод, попадая в водный раствор, подвергается гидролизу с образованием других соединений йода. Таким образом, количество йода, растворяющееся в водном растворе, становится значительно большим, чем это следует из закона Генри для I₂. Степень гидролиза I₂ зависит от температуры и рН раствора. Реакции гидролиз обратимы. Эгглетон [2] предложил следующий набор реакций для описания процесса:

                                        K₁

1) I₂ (газовая среда) ↔ I₂ (водная среда),

K₁ = [I₂]_{в водной среде}/[I₂]_{в газовой среде},                                                                                         (2)

где [I₂]_{в водной среде} - концентрация молекулярного йода в водной среде;

[I₂]_{в газовой среде} - концентрация концентрацию молекулярного йода в газовой среде (например, грамм-моль на литр);

2) в водной среде:

                                                                                 K₂

I₂ + I^- ↔ I^-₃;

K₂ = [I^-₃]_{в водной среде}/([I₂]_{в водной среде} [I^-]);                                        (3)

3) в водной среде:

                                                                           K₃

I₂ + H₂O ↔ H⁺ + I^- + HIO;

K₃ = [I^-][H⁺][HIO]/[I₂]_{в водной среде};                                             (4)

4) в водной среде:

                                                                          K₄

I₂ + H₂O ↔ H⁺ + H₂OI⁺ + I^-;

K₄ = [H₂OI⁺][I^-]/[I₂]_{в водной среде};                                                   (5)

5) в водной среде:

                                                                            K₅

3I₂ + 3H₂O ↔ IO₃ + 5I^- + 6H⁺;

K₅ = [IO₃][I^-]⁵[H⁺]⁶/[I₂]_{в водной среде};                                              (6)

6) в водной среде:

                                                                           K₆

HIO ↔ H⁺ + IO^-;

K₆ = ([H⁺][IO])/[HIO];                                                         (7)

7) в водной среде:

                                                                                 K₇

IO^- + I^- + H₂O ↔ I₂OH + OH;

K₇ = [I₂OH][OH]/([OI] + [I^-]);                                                  (8)

8) в водной среде:

                                                                                 K₈

IO^- + I^- ↔ I₂O^-;

K₈ = [I₂O^-]/([OI^-] + [I^-]).                                                       (9)

При оценке концентрации йода в воздушной среде считается, что любое соединение йода, присутствующее в растворе, имеет ненулевое значение летучести. Исследование различных реакций йода в воде позволило выделить первых четыре «быстрые» реакции, определяющие равновесие между элементарным йодом и продуктами его гидролиза. Предполагая, что только четыре первые реакции имеют место и только I₂ является летучим соединением, коэффициент распределения Р будет выражаться следующим уравнением [2]:

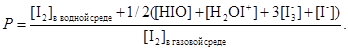                               (10)

Поскольку в реакциях гидролиза равновесия (3) (4) и (5) устанавливаются в свежеполученных растворах йода и в случае отсутствия йодид-иона, обусловливаемого примесями, то концентрация образующегося йодид-иона должна быть эквивалентна сумме концентраций гипойодной кислоты и катиона Н₂ОI⁺:

[I^-] + [I^-₃] = [H₂OI⁺] + [HIO].                                              (11)

Подставляя в уравнение (11) значения [I^-₃], [HIO] и [H₂OI⁺], получаемые из уравнений реакций (3), (4) и (5) соответственно, и решая относительно [I^-], может быть показано, что

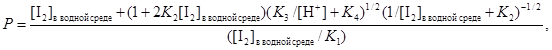     (12)

из которого видно, что коэффициент распределения Р может быть рассчитан для различных значений [I₂]_{в водной среде}, [Н⁺] и констант равновесия K₁, K₂, K₃, K₄.

Коэффициент K₁ (коэффициент распределения I₂ между водой и воздухом) можно определить, используя закон Генри для идеальных газов и данные по растворимости [3] и парциальному давлению [4] I₂ в воде и воздухе. С учетом зависимости парциального давления и растворимости от температуры (T, К) получена зависимость K₁ от T в диапазоне температур от 283 до 423 К, которая имеет следующий вид:

lgK₁ = -92,6 + 5760,0/T + 30,37lgT.                                    (13)

Отклонение значений K₁, рассчитанных по формуле (13), от значений, рассчитанных по значениям растворимости и парциального давления, не превышает ±5 %. В [5] приведены результаты измерения величины K₁ при температуре 20 °С. Среднее из шести экспериментов значение K₁ равно 117, а расчетное по формуле (10) составляет 95,1. Для расчета значений K₂ предлагается использовать формулу, приведенную в [6], поскольку она дает наименьшие значения коэффициента в зависимости от температуры из известных соотношений:

lgK₂ = 550,0/T + 7,355 - 2,5751lgT.                                    (14)

Значение K₃ предлагается рассчитывать также по формуле, приведенной в [7], по той же причине. Эта формула имеет вид:

lgK₃ = -13929/T - 44,764 + 0,070692T.                                  (15)

Константу K₄ в уравнении (5) следует рассчитывать с учетом [2, 7]. В [7] получено значение K₄, равное 1,2 · 10^-11 при температуре 25 °С. В [2] на основе подхода, изложенного в [6], получено значение K₄, равное 3,9 · 10^-11 для температуры 100 °С. С помощью этих двух значений можно получить коэффициенты для уравнения Аррениуса:

K₄ = 4,226 · 10^-9ехр(-3474/RT).                                           (16)

Литература к приложению 3

1. Beahm Е.С., Shockley W.E., Weber С.F. Chemistry and Transport of Iodine in Containment Proc. Symp. Source Term Evaluation for Accident Conditions, Columbus U.S.A. IAEA-SM-281/41, p. 479 (1986)

2. Eggleton A.E.J. A Theoretical Examination of Iodine-Water Partition Coefficients. AERE-R4887;

3. Справочник по растворимости. Академия наук СССР, Москва-Ленинград, 1961;

4. Несмеянов А.Н. Давление паров химических экспериментов. Из-во Академии наук СССР, Москва, 1961, с. 314 - 318;

5. Taylor R.F. Absorption of iodine vapour by aqueous solutions. Chemical Engineering science, vol. 10, p. 68 - 79, 1959;

6. Palmer D.A., Ramette R.W. and Mesmer R.E. The Hydrolysis of Iodine: Equilibria at High Temperature. Journal of Nuclear Materials 130 (1985), p. 280 - 286.

7. Bell R.P., Gelles E. The Helogen cation in Aqueons Solution. J. Chem. Soc., p. 2734 - 2740, oct. 1951;

Приложение 4

Взаимодействие соединений йода с химическими примесями

Органические (первая группа) и неорганические (вторая группа) соединения йода в водном растворе могут вступать в химические реакции с образованием соединений, относящихся к другим группам. Эти реакции могут быть достаточно медленными и не оказывать влияние на эффективность улавливания соединений в процессе работы активных и пассивных систем (спринклерной системы, водоэжекционных охладителей, барботажных устройств). Однако даже медленные изменения в химических группах могут приводить в конечном счете к значительному влиянию на радиационные последствия аварии. Особый интерес представляют необратимые химические реакции органических соединений йода с образованием неорганических. В настоящем приложении даются примеры таких реакций и возможные значения констант скоростей этих реакций.

Органические соединения йода (первая группа)

Представителем органических соединений йода является йодистый метил CH₃I. Поэтому в дальнейшем будут рассмотрены примеры реакций CH₃I в водном растворе с химическими примесями.

Гидролиз CH₃I в водном растворе

Реакция гидролиза CH₃I в водном растворе описывается уравнением (1):

                                                                                      

                                         (1)

В [2 - 5] обобщены данные об экспериментальных значениях K₁ и приведены некоторые собственные значения. В [3] дано эмпирическое соотношение, описывающее изменение K₁ в зависимости от температуры:

lgK₁ = 111,859 - 10534/T - 33,821lgT,                                       (2)

где Т - температура, К. Расчетные, выполненные по формуле (2), и экспериментальные значения K₁ приведены в таблице.

Константы скорости реакции первого порядка для гидролиза CH₃I в воде

Как видно из таблицы, наблюдается хорошее соответствие между имеющимися в распоряжении авторов экспериментальными данными и расчетными значениями, полученными по формуле (2).

Реакция CH₃I с ионами ОН^-

Реакция CH₃I с ионом гидроксила OH^- имеет следующий вид:

                                                                                                  (3)

В [6 - 8] приведены экспериментальные данные о константе скорости второго порядка бимолекулярной реакции CH₃I с OH^- в диапазоне температур от 288,16 до 347,96 К, достаточно хорошо описывающиеся уравнением Аррениуса:

K₂ = Qехр(-E/RT),                                                                (4)

где Q - коэффициент, равный 425 л/моль/с;

E - энергия активации, равная 23050, кал/моль;

R - газовая постоянная, равная 1,987 кал/моль/град, К;

T - температура, К.

Концентрация ионов OH^- при неизвестном рН в зависимости от температуры чистой воды может быть получена из [10]. В диапазоне температур от 0 до 140 °С значение концентрации может быть определено по соотношению:

lg[OH] = -(6,266 · 10^-5 · T² - 1,965 · 10^-2 · T + 7,399),                           (5)

где [ОН] - концентрация ОН^-, г-ион/л;

Т - температура, °С.

При известном pH концентрация ионов OH^- может быть определена из очевидного соотношения lg[OH^-] = рН - 14.

Реакция CH₃I с гидразином

Реакция между CH₃I и гидразингидратом протекает по следующей схеме:

                                                                                                                        (6)

Образующийся в результате реакции монометилгидразин также может вступать в реакцию с CH₃I. Однако было показано, что скорости этой и последующих реакций значительно меньшие, чем скорость реакции (6). В [11] экспериментально получены значения константы скорости второго порядка для указанной реакции при температурах 24,6, 34,7, 49,3 и 64,7 °С. Методом наименьших квадратов были получены следующие значения параметров уравнения Аррениуса для константы K₃:

K₃ = 7,26 · 1011ехр(-20200/RT),                                         (7)

где R и Т определены в формуле (4) приложения 4, а K₃ имеет размерность литр/моль/с.

Реакция CH₃I с тиосульфатом натрия

Реакция йодистого метила с тиосульфатом натрия (реакция Слайтора) протекает по следующей схеме:

                                                                                              (8)

Выполнен ряд экспериментальных работ по определению K₄ [7, 10, 12]. В результате обработки полученных экспериментальных данных методом наименьших квадратов с учетом их весов получено следующее выражение для определения K₄ в зависимости от температуры:

K₄ = 1,35 · 1013ехр(-20000/RT),                                         (9)

где R и Т определены в формуле (4) приложения 4, а K₄, имеет размерность литр/моль/с.

Литература к приложению 4

1. The Kinetics of Certain Reaction between Methyl Halids and Anions in Water by Moelwyn-Hughes. Proceeding of Royal Society A-196, p. 540 - 553, 1949.

2. Richard A., Ogg Jr. The Hydrolysis of Methyl Iodide. Journal of Am. Chem. Soc. Vol. 6, p. 2000 - 2001.

3. Moelwyn-Hughes E.A. The Hydrolysis of the Methyl Halids, Proceeding of Royal Society A-164, pp. 295 - 306, 1938.

4. Moelwyn-Hughes E.A. The Kinetics of Hydrolysis. Proceeding of Royal Society A-220, p. 386 - 396, 1953.

5. Heppoletty R.L., Robertson R.E. The Neutral Hydrolysis of the Methyl Halides. Proceeding of Royal Society A-252, p. 273 - 285, 1955.

6. Edwards J.O. Correlation of Relative Rates and Equlibrio with a Double Basicity Scale. J. Amer. Chem. Soc., № 76, p. 1540, 1954.

7. Seltzar S., Zavitsas A.A. Correlation of Isotope Effects in Substitution Reactions with Nucleophilicitites - secondary Alpha-Deuterium Isotope Effect in the Iodide-131 Exchange of Methyl - d3 iodide. Can. J. Chem., 45, p. 2023 - 2031, 1967.

8. Gand E. Ionic Disociation of Alkyl Halides in Aqueous Solution. Am. Far. Sci., Narseille, 2, p. 134 - 239, 1939.

9. Hasty R.A., Sutter S.L. Kinetics of the Reaction of Methyl iodide with Sulfite and Thiosulfite Ions in Aqueous Solution. Can. J. Chem., 47, p. 4537 - 4571, 1960.

10. Гороновский И.Т. и другие. Краткий справочник по химии, Наукова Думка, Киев, 1974, с. 768.

11. Hasty R.A. The Rate of the Reaction of Methyl iodide and Hydrazine in Aqueous Solution. The Journal of Physical Chemistry, vol. 73, № 2, p. 317 - 321, 1969.

12. Willi A.Y., Won C.M. Kinetic deuterium isotopic effect in the reaction of methyl iodide with thiosulfate ion in aqueous solution. Canadian Journal of Chemictry, 48, p. 1452 - 1455, 1970.

Приложение 5

Выбор коэффициента десорбции K_д йода

Имеющиеся в литературе экспериментальные данные [1 - 3] указывают на широкий диапазон коэффициента десорбции K_д, зависимость этого коэффициента от типа поверхности, температуры и относительной влажности, а также от концентрации радиоактивного йода на поверхности. Кроме того, в процессе экспериментов обнаруживается снижение коэффициента десорбции во времени с выходом на постоянное значение через 10 - 15 ч после начала опытов [3]. Значения K_д на плато отличаются от начальных в 8 - 10 раз.

На основании анализа экспериментальных данных в [2] предлагается аналитическое выражение зависимости коэффициента десорбции K_д от поверхностной концентрации и температуры:

K_д = (0,1/а^0,27)ехр(-5330/T),                                                 (1)

где а - поверхностная концентрация, Ки/см²;

T - температура поверхности, К.

В таблице представлены экспериментальные значения коэффициента десорбции K_д по данным [1, 3] и расчетные значения, вычисленные по формуле (1).

Значения K_д для различных температур и поверхностной концентрации

Сопоставление расчетных и экспериментальных значений коэффициента десорбции K_д обнаруживает удовлетворительное согласие для температуры 50 °С в диапазоне поверхностной концентрации от 10^-5 до 10^-7 Ки/см². Для более высоких температур 100 - 200 °С расчетные значения K_д превышают экспериментальные на один - два порядка. Причины такого расхождения можно объяснить методическими особенностями экспериментальных исследований, в результате которых авторы [2] предложили формулу (1). В отличие от [1, 3] в [2] при определении коэффициента десорбции K_д применялся интегральный метод, причем продолжительность экспериментов для температур 100 - 200 °С не превышала нескольких десятков минут. По данным [1, 3] именно в конце этого периода резко снижается коэффициент десорбции, а установившееся значение K_д наблюдается лишь через несколько часов. Использование формулы (1) может привести к неоправданному завышению расчетной величины утечки радиоактивного йода в окружающую среду в послеаварийный период.

Оценочное значение концентрации радиоактивного йода на поверхности в послеаварийный период находится в пределах 10^-6 - 10^-2 Ки/см². Для таких концентраций скорость десорбции, если использовать зависимость K_д = 1/а^0,27, должна быть в 5 - 10 раз ниже экспериментальных данных [2].

Из-за отсутствия экспериментального подтверждения значений коэффициент десорбции K_д при высоких концентрациях (10^-3 - 10^-2) в расчетах рекомендуется использовать постоянное значение K_д, равное 10^-7 с^-1. Эксперименты показывают, что с консервативным запасом можно считать, что 50 % йода будет находиться в органической (первая группа), а 50 % - в молекулярной форме (вторая группа).

Литература к приложению 5

1. Изучение десорбции различных форм йода с разных конструктивных материалов. Отчет по контракту ЭГУ - ВТИ № 70451/200072. Научно-исследовательский институт энергетики, Прага, ЧССР, Ясловске Богунице, сентябрь 1980.

2. Изучение десорбции радиоактивного йода в зависимости от температуры и поверхностной концентрации. Отчет ИАЭ, инв. № 32/107479, 1979.

3. Исследование десорбции радиоактивного йода с различных конструктивных материалов после испарения теплоносителя ВВЭР. Отчет ВТИ, арх. № 11635, Москва, 1980.