Статистические методы

РУКОВОДСТВО ПО ОЦЕНКЕ СООТВЕТСТВИЯ
УСТАНОВЛЕННЫМ ТРЕБОВАНИЯМ

Часть 1

Общие принципы

(ISO 10576-1:2003, Guidelines for the evaluation of conformity with specified
requirements - Part 1: General principles, IDT)

Предисловие

1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») и Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4

2 ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 17 октября 2006 г. № 229-ст

4 Настоящий стандарт идентичен международному стандарту ИСО 10576-1:2003 «Руководство по оценке соответствия установленным требованиям. Часть 1. Общие принципы» (ISO 10576-1:2003 «Guidelines for the evaluation of conformity with specified requirements - Part 1: General principles», IDT).

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов и документа соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА

5 ВВЕДЕН ВПЕРВЫЕ

6 ИЗДАНИЕ (март 2020 г.) с Поправкой (ИУС 7-2011)

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок - в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

Содержание

Введение

Цель оценки соответствия состоит в подтверждении соответствия установленным требованиям в форме декларации поставщика или свидетельства третьего лица (ИСО/МЭК Руководство 2:2004 «Стандартизация и смежные виды деятельности. Общий словарь»). Обычно в требованиях указывают для измеряемой характеристики единственное предельное значение LV или два предельных значения (верхнее и нижнее). Если требования имеют отношение к характеристикам, связанным со здоровьем, предельные значения иногда называют предельно допустимыми значениями TLV или предельно допустимыми воздействиями PEL.

Когда оценка соответствия связана с оценкой неопределенности измерений, обычно применяют элементы теории статистической проверки гипотез. Зная процедуры измерений и соответствующую неопределенность, можно оценить и минимизировать риск принятия ошибочных решений о соответствии или несоответствии установленным требованиям. На практике обычно понимают, что если объект объявлен соответствующим требованиям, его статус не должен изменяться в результате последующих измерений на объекте, даже при использовании более точных методов или технологий измерений. С позиций анализа риска это означает, что риск ошибочного решения о несоответствии объекта требованиям должен быть небольшим. Следовательно, необходимо допустить (большой) риск, что объект, характеристики которого несколько лучше требований, не будет признан соответствующим. Применение двухэтапной процедуры вместо одноэтапной процедуры в общем случае приводит к уменьшению риска.

Аналогичные соображения справедливы и в том случае, если испытания проводят для оценки несоответствия.

Настоящий стандарт задачу оценки соответствия рассматривает применительно к разработке требований и проверке продукции или услуг на соответствие или несоответствие установленным требованиям.

Из-за очевидной аналогии с процедурами приемочного выборочного контроля иногда планы приемочного выборочного контроля используют при оценке соответствия. Приемочный выборочный контроль и оценка соответствия используют элементы проверки гипотез (например, ИСО 2854 «Статистическое представление данных. Методы оценки и проверки гипотез о средних и дисперсиях»). Однако важно понимать, что цели этих процедур существенно различны, в частности они подразумевают различные подходы к оценке риска ошибочного решения (см. ИСО 2854).

ГОСТ Р ИСО 10576-1-2006

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

РУКОВОДСТВО ПО ОЦЕНКЕ СООТВЕТСТВИЯ УСТАНОВЛЕННЫМ ТРЕБОВАНИЯМ

Часть 1

Общие принципы

Дата введения - 2007-01-01

1 Область применения

Настоящий стандарт является руководством в следующих ситуациях:

a) при разработке требований к объекту оценки, которые могут быть сформулированы в виде предельных значений для количественных параметров объекта;

b) при оценке соответствия упомянутым требованиям, когда результаты измерений или испытаний указаны вместе с неопределенностью.

Стандарт применим в случаях, когда неопределенность может быть оценена количественно в соответствии с принципами, изложенными в GUM [1]. Термин [1] «неопределенность» используют для описания всех элементов изменчивости результатов измерений, включая неопределенность, связанную с отбором выборки.

В настоящем стандарте не приведены правила для ситуации, когда получен неокончательный результат оценки соответствия.

Примечание - Стандарт не содержит ограничений на объект и требований к измеряемой характеристике. Примеры объектов и измеряемых характеристик приведены в таблице A.1 (приложение А).

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты и документ. Для датированных ссылок применяют только указанное издание ссылочного стандарта и документа, для недатированных - последнее издание (включая все изменения):

ISO 2602, Statistical interpretation of test results - Estimation of the mean - Confidence interval (Статистическое представление результатов испытаний. Оценка среднего. Доверительный интервал)

ISO 2854, Statistical interpretation of data - Techniques of estimation and tests relating to means and variances (Статистическое представление данных. Методы оценки и проверки гипотез о средних и дисперсиях)

ISO 3534-1:1993¹⁾, Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability (Статистика. Словарь и условные обозначения. Часть 1. Вероятность и основные статистические термины)

__________

¹⁾ Заменен на ISO 3534-1:2006.

ISO 3534-2:1993²⁾, Statistics - Vocabulary and symbols - Part 2: Statistical quality control (Статистика. Словарь и условные обозначения. Часть 2. Статистическое управление качеством)

__________

²⁾ Заменен на ISO 3534-2:2006.

ISO 5725-1, Accuracy (trueness and precision) of measurement methods and results - Part 1: General principles and definitions [Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения]

ISO 5725-2¹⁾, Accuracy (trueness and precision) of measurement methods and results - Part 2: Basic methods for the determination of repeatability and reproducibility of a standard measurement method [Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений]

__________

¹⁾ Заменен на ISO 5725-2:2019.

ISO 5725-3, Accuracy (trueness and precision) of measurement methods and results - Part 3: Intermediate measures of the precision of a standard measurement methods [Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений]

ISO 5725-4, Accuracy (trueness and precision) of measurement methods and results - Part 4: Basic methods for the determination of the trueness of a standard measurement methods [Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений]

ISO 5725-5, Accuracy (trueness and precision) of measurement methods and results - Part 5: Alternative methods for the determination of the precision of a standard measurement methods [Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений]

ISO 5725-6, Accuracy (trueness and precision) of measurement methods and results - Part 6: use in practice of accuracy values [Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике]

ISO/TS 14253-2:1999²⁾, Geometrical Product Specifications (GPS) - Inspection by measurement of workpieces and measuring equipment - Part 2: Guide to the estimation of uncertainty in GPS measurement, in calibration of measuring equipment and in product verification [Спецификации на геометрические размеры продукции (GPS). Контроль измерений заготовок и измерительного оборудования. Часть 2. Руководство по оценке неопределенности измерений GPS при калибровке измерительного оборудования и верификации продукции]

__________

²⁾ Заменен на ISO 14253-2:2011.

3 Термины и определения

В настоящем стандарте применены термины по ИСО 3534-1 и ИСО 3534-2, а также следующие термины с соответствующими определениями:

3.1 предельные значения, пределы поля допуска (limiting values, specification limits) L: Установленные значения параметра, представляющие собой верхнюю и/или нижнюю границы допустимых значений.

[ИСО 3534-2:1993, пункт 1.4.3]

3.2 нижняя граница поля допуска (lower specification limit) L_SL: Нижняя граница допустимых значений параметра.

3.3 верхняя граница поля допуска (upper specification limit) U_SL: Верхняя граница допустимых значений параметра.

3.4 оценка соответствия (conformity test): Систематическая оценка соответствия продукции, процесса или услуги установленным требованиям посредством испытаний.

3.5 область допустимых значений (region of permissible values): Интервал или интервалы всех допустимых значений параметра.

Примечание - Если иначе не установлено, предельные значения считают принадлежащими области допустимых значений.

3.6 область недопустимых значений (region of non-permissible values): Интервал или интервалы всех недопустимых значений параметра.

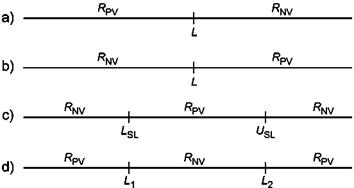
Примечание - На рисунке 1 показаны возможные ситуации разделения области возможных значений параметра на область допустимых и недопустимых значений.

R_PV - область допустимых значений; R_NV - область недопустимых значений;
L, L_SL, U_SL, L₁ и L₂ - пределы поля допуска

Рисунок 1 - Разделение области значений параметра

3.7 интервал неопределенности (uncertainty interval): Интервал, получаемый на основе измерений параметра и оценки его неопределенности, накрывающий область возможных значений, которые обоснованно могут быть приписаны измеряемому параметру.

Примечания

1 Интервал неопределенности может быть симметричным интервалом с центром в точке значения результата измерений, как определено в пункте 6.2.1 GUM [1].

2 В случае, когда неопределенность получают путем оценки типа А для компонентов неопределенности, интервалом неопределенности может быть доверительный интервал для параметра (см. например, пункт 2.57 ИСО 3534-1:1993 и пункт G.3 GUM [1]).

3.8 двусторонний доверительный интервал (two-sided confidence interval): Если T₁ и T₂ - две функции наблюдаемых значений, таких что для оценки параметра распределения совокупности Θ вероятность Pr (T₁ ≤ T₂) равна (1 - α), где (1 - α) - константа положительная и меньше 1, то интервал между T₁ и T₂ - это двусторонний доверительный интервал для Θ при доверительной вероятности (1 - α).

Примечания

1 Границы T₁ и T₂ доверительного интервала - это статистики (ИСО 3534-1:1993, пункт 2.45), которые в общих предположениях принимают различные значения от выборки к выборке.

2 В длинном ряду выборок относительная частота случаев, когда доверительный интервал накрывает истинное значение параметра совокупности Θ, больше или равна (1 - α).

[ИСО 3534-1:1993, пункт 2.57]

3.9 доверительная вероятность, уровень доверия (confidence coefficient, confidence level): Величина (1 - α) - вероятность, связанная с доверительным интервалом или со статистически накрывающим интервалом.

Примечание - Величину (1 - α) часто выражают в процентах.

[ИСО 3534-1:1993, пункт 2.59]

4 Требования

4.1 Общие требования при установлении предельных значений

4.1.1 Объект должен быть четко и однозначно определен.

4.1.2 Количественный параметр объекта должен быть четко и однозначно определен. Процедуры измерений или испытаний, выполняемые для определения значения параметра, должны позволять получать оценку неопределенности измерений.

4.1.3 Процедура измерений или испытаний должна быть стандартизованной процедурой¹⁾.

__________

¹⁾ Стандартизованная процедура - это процедура, соответствующая требованиям Государственной системы обеспечения единства измерений и стандартов на методы измерений и испытаний.

4.1.4 Устанавливаемые предельные значения не должны включать в себя (в явном или неявном виде) неопределенность измерений.

4.2 Особенности предельных значений

Предельные значения должны быть установлены при выполнении требований 4.1.1 и 4.1.2. Область допустимых значений количественного параметра может быть ограничена только с одной стороны или с двух сторон. Границы области поэтому бывают двух видов: двусторонние, состоящие из верхней и нижней границ, и односторонние, состоящие из верхней или нижней границы.

Примеры

1 Двусторонние границы

Для единственной единицы продукции - барреля моторного масла (объект) требования к кинематической вязкости масла (параметр) могут быть заданы в следующем виде:

- кинематическая вязкость должна быть не менее 0,5 · 10^-7 мм²/с и не более 1,0 · 10^-7 мм²/с.

2 Двусторонние границы

Для одной партии бутылок растительного масла (объект) требования к средней температуре кипения при атмосферном давлении 101,6 кПа для масла в бутылках (параметр) могут быть заданы в следующем виде:

- средняя температура кипения должна находиться внутри интервала от 105,0 °С до 115,0 °С.

3 Односторонняя верхняя граница

Для отгрузки сырой нефти (объект) требования к массовой доле серы (параметр) могут быть заданы в следующем виде:

- массовая доля серы должна быть не более 2 %.

4 Односторонняя граница

Для индивидуума (объект) требования к молярной концентрации свинца в крови (параметр) могут быть заданы в следующем виде:

- молярная концентрация свинца в крови должна быть не более 0,96 мкмоль/л.

5 Односторонняя нижняя граница

Для партии битума (объект) требования к растворимости битума в керосине при 20 °С (параметр) могут быть заданы в следующем виде:

- растворимость битума в керосине при 20 °С должна быть не менее 99 % массы.

6 Односторонняя верхняя граница

Для отгрузки яблок (объект) требования к доле яблок, зараженных вредителями (параметр), могут быть заданы в следующем виде:

- доля яблок, зараженных вредителями, должна быть менее 0,2 %.

Из-за различий в массе отдельных яблок доля зараженных яблок по массе будет отличаться от доли зараженных яблок по количеству.

Примечание - Во многих случаях (например, в экологии) дополнительный подразумеваемый предел, такой как 0 %, 0,0 кг/л и 100 %, может быть не указан вследствие его очевидности. В этом случае может быть установлено единственное предельное значение.

5 Неопределенность результатов

5.1 Общие положения

При сравнении результатов измерений или испытаний с предельными значениями необходимо учитывать неопределенность результатов измерений. Неопределенность должна быть оценена в соответствии с [1]. Для идентификации некоторых составляющих неопределенности могут быть использованы ИСО 5725-1 - ИСО 5725-6.

Примечание - Должны быть учтены вклады в неопределенность всех стадий процедуры измерений, а также неопределенности, связанной с отбором выборки.

5.2 Регистрация неопределенности результатов измерений

Результаты измерений параметра и неопределенность измерений должны быть зарегистрированы. Неопределенность измерений следует представлять в виде интервала неопределенности. Если этот интервал является доверительным интервалом, необходимо указывать доверительную вероятность (1 - α), соответствующую интервалу (см. пункты 2.57 и 2.59 ИСО 3534-1:1993). В противном случае следует указывать коэффициент охвата интервала неопределенности (см. [1], пункт 6.2.1).

6 Оценка соответствия требованиям

6.1 Общие положения

Оценка соответствия - это систематическая экспертиза (посредством измерений) соответствия объекта установленным требованиям. Цель оценки соответствия - обеспечить уверенность в том, что объект соответствует установленным требованиям. Настоящий стандарт рекомендует выполнять оценку соответствия как двухэтапную процедуру. В случаях, когда двухэтапная процедура не может быть выполнена или по каким-то причинам не должна быть выполнена, необходимо выполнять одноэтапную процедуру. При выполнении двухэтапной процедуры должна быть применена соответствующая процедура оценки результатов измерений.

Примечание - Преимущество двухэтапной процедуры по сравнению с одноэтапной процедурой состоит в том, что двухэтапной процедуре присуща значительно более высокая вероятность соответствия для объектов с допустимыми значениями количественного параметра, близкими к предельному значению. Недостаток двухэтапной процедуры состоит в том, что для нее характерна несколько более высокая вероятность решения о соответствии объекта с недопустимыми значениями контролируемого параметра, близкими к предельному значению. Если эта вероятность решения о соответствии несоответствующих объектов не может быть принята, должна быть применена одноэтапная процедура.

6.2 Двухэтапная процедура оценки соответствия

6.2.1 Этап 1

Проводят измерения и рассчитывают неопределенность результатов измерений.

Решение о соответствии требованиям может быть принято тогда и только тогда, когда интервал неопределенности, построенный по результатам измерений, находится внутри области допустимых значений. Второй этап должен быть выполнен тогда и только тогда, когда границы интервала неопределенности, рассчитанные после первого этапа, выходят за пределы поля допуска.

6.2.2 Этап 2

Проводят измерения еще раз и получают соответствующую комбинацию результатов измерений двух этапов, чтобы определить окончательный результат измерений и вычислить его неопределенность.

Решение о соответствии требованиям может быть принято только в том случае, если интервал неопределенности окончательного результата измерений находится внутри области допустимых значений.

Если после первого или после второго этапа принимают решение о соответствии, его формулируют согласно 7.2.

Примечание - Если интервал неопределенности находится внутри области допустимых значений и одна из границ интервала неопределенности совпадает с предельным значением, считают, что интервал неопределенности находится в области допустимых значений.

Если интервал неопределенности результатов измерений полностью лежит в области недопустимых значений, после первого или после второго этапа принимают решение о несоответствии требованиям, которое формулируют согласно 7.3.

Примечание - Если интервал неопределенности находится в области недопустимых значений и одна из границ интервала неопределенности совпадает с границей поля допуска, считают, что интервал неопределенности находится в области недопустимых значений.

Если интервал неопределенности, рассчитанный после этапа 2, включает в себя границу поля допуска, результат оценки соответствия является неокончательным. Решение формулируют согласно 7.4.

Примечание - Процедуры измерений, используемые на этих двух этапах, могут быть неидентичны. Соответствующая комбинация результатов первого и второго этапов, отнесенная к этапу 2, включает в себя также ситуацию, когда, например, только результат этапа 2 используют как окончательный результат измерений.

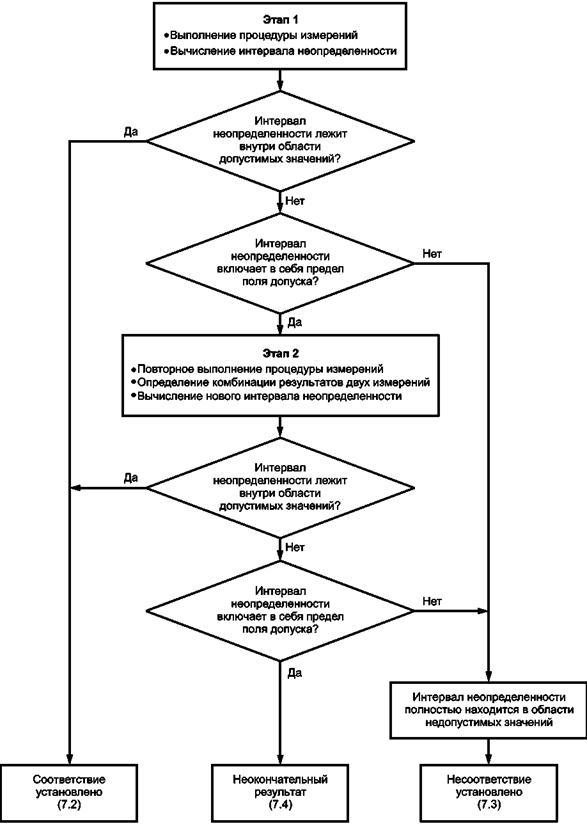
Схема двухэтапной процедуры оценки соответствия приведена на рисунке 2.

Рисунок 2 - Схема двухэтапной процедуры оценки соответствия

6.3 Одноэтапная процедура оценки соответствия

Проводят измерения и вычисляют неопределенность результатов измерений.

Решение о соответствии требованиям может быть принято в том случае, если интервал неопределенности результатов измерений находится внутри области допустимых значений.

Примечание - Если интервал неопределенности находится в области допустимых значений и одна из границ интервала неопределенности совпадает с пределом поля допуска, считают, что интервал неопределенности находится в области допустимых значений.

Если интервал неопределенности результатов измерений целиком лежит в области недопустимых значений, то может быть принято решение о несоответствии требованиям. Решение формулируют согласно 7.3.

Примечание - Если интервал неопределенности находится в области недопустимых значений и одна из границ интервала неопределенности совпадает с пределом поля допуска, считают, что интервал неопределенности находится в области недопустимых значений.

Если интервал неопределенности включает в себя границу поля допуска, оценка соответствия является неокончательной. Решение формулируют согласно 7.4.

6.4 Интервал неопределенности, заданный в форме доверительного интервала

В настоящем подразделе рассмотрена ситуация, когда интервал неопределенности задан в форме доверительного интервала с доверительной вероятностью (1 - α) (см. 5.2). Если в требованиях указана единственная граница поля допуска [случай a) или b) на рисунке 1], то вероятность ошибочного решения о соответствии составляет не более α/2 для одноэтапной процедуры и не более (α - α²/2) для двухэтапной процедуры. В случае с двумя пределами поля допуска [случай c) или d) на рисунке 1] вероятность ошибочного решения о соответствии зависит от математического ожидания длины доверительного интервала. Однако если средняя длина доверительного интервала составляет часть разности между пределами поля допуска, то вышеупомянутое выражение для вероятности ошибочного решения о соответствии все же можно использовать.

(Поправка, ИУС 7-2011)

Если можно предположить, что неопределенность измерений известна (т.е. неопределенность не рассчитана по наблюдениям), вероятность решения о соответствии требованиям и вероятность получения неокончательного решения при оценке соответствия могут быть рассчитаны.

6.5 Неокончательный результат оценки соответствия

Если значение параметра находится в окрестности предела поля допуска, существует большая вероятность того, что результат оценки соответствия будет неокончательным. Это ситуация в принципе неудовлетворительная, но она неизбежна, если декларация о соответствии требованиям должна содержать доказательство утверждения, приведенного в 7.2.

7 Составление отчета о результатах оценки соответствия

7.1 Общие положения

Поскольку результаты измерений являются случайными величинами, основанное на них утверждение может быть неверным. Программа измерений и испытаний должна предусматривать это в расчетах, результаты которых приведены в отчете об оценке соответствия.

В отчете о результатах оценки соответствия утверждения для соответствия, несоответствия или неокончательной оценки, приведенные в 7.2, 7.3 и 7.4, должны быть дополнены всеми свидетельствами, которые удостоверяют использованное утверждение.

7.2 Решение о соответствии

Если интервал неопределенности результатов измерений находится внутри области допустимых значений (см. 6.1 и 6.2), принимают решение о соответствии. Решение о соответствии должно быть сформулировано следующим образом: оценка соответствия продемонстрировала, что значение контролируемого параметра соответствует требованиям.

7.3 Решение о несоответствии

Если интервал неопределенности результатов измерений находится внутри области недопустимых значений (см. 6.1 и 6.2), то принимают решение о несоответствии.

Решение о несоответствии должно быть сформулировано следующим образом: оценка соответствия продемонстрировала, что значение контролируемого параметра не соответствует требованиям.

7.4 Неокончательный результат

Если в соответствии с 6.1 или 6.2 не может быть принято решение ни о соответствии, ни о несоответствии требованиям, результат оценки соответствия является неокончательным. Результат неокончательной оценки должен иметь следующую формулировку: оценка соответствия не способна продемонстрировать, что значение контролируемого параметра соответствует или не соответствует требованиям.

Приложение A
(справочное)
Примеры объектов и количественных параметров

Таблица A.1 - Примеры объектов с соответствующими количественными параметрами

Объект	Количественный параметр объекта
	Параметр единицы продукции	Среднее	Параметр гомогенности	Относительная частота
Различимая единица продукции или отдельный ее представитель	×	-	-	-
{гиря для весов}	{масса}	-	-	-
Группа различимых единиц продукции (партия или совокупность)	-	×	×	×
{партия мешков сахара}	-	{средняя масса мешка}	{стандартное отклонение массы мешка}	{процент мешков с соответствующей массой}
Процесс	-	×	×	×
{продукция в бутылках}	-	{средний объем продукции в бутылке}	{стандартное отклонение объема продукции в бутылке}	{процент бутылок с соответствующим объемом продукции}
Партия нештучной продукции (сыпучий, жидкий или газообразный материал)	-	×	×	×
{партия доломита}	-	{доля массы асбестовых волокон}	{стандартное отклонение массовой доли асбестовых волокон по отобранным образцам}	{массовая доля асбестовых волокон соответствующей длины}
Услуги	-	×	×	×
{лечение конкретной болезни}	-	{среднее время от появления болезни до начала ее лечения}	{стандартное отклонение времени от появления болезни до начала ее лечения}	{процент времени от появления болезни до начала ее лечения соответствующей продолжительности}
Примечание - Символ «×» означает то, что параметр может соответствовать указанному объекту. Конкретные примеры приведены в фигурных скобках. Приведенные в таблице виды объектов и перечень параметров не являются исчерпывающими.

Приложение B
(справочное)
Примеры

B.1 Общие положения

Следующие примеры охватывают только некоторые из комбинаций объектов и количественных параметров, указанных в таблице A.1¹⁾.

___________

¹⁾ В примерах использована различная разрядность результатов вычисления. Обычно в промежуточных вычислениях сохраняют на две значащие цифры больше, чем в исходных данных. Это позволяет гарантировать, что в числовом значении результата вычислений ошибка округления может повлиять лишь на последнюю значащую цифру, если окончательный результат вычислений и исходные данные приводятся с одинаковым количеством значащих цифр.

B.2 Пример 1

Для ряда чисто выточенных стальных стержней, имеющих номинальные размеры Ø 25 мм × 150 мм, пределы поля допуска для диаметра L_SL = 24,9 мм и U_SL = 25,0 мм. Таким образом, объектом является стержень, а параметром - диаметр стержня.

Измерения выполнены с использованием аналогового внешнего микрометра, имеющего диапазон измерений от 0 до 25 мм с ценой деления верньерной шкалы 10^-2 мм. Стандартная неопределенность измерений u_c = 3,79 · 10^-3 мм рассчитана с учетом нескольких источников неопределенности (см. пункт A.2 ISO/TS 14253-2:1999). По экономическим причинам была выполнена одноэтапная проверка для каждого стержня ряда. Интервалы неопределенности были рассчитаны в соответствии с пунктом 6.2.1 GUM [1] для коэффициента охвата k = 2. Интервалы неопределенности для размеров трех стержней: (24,857 ± 0,0076) мм; (24,907 ± 0,0076) мм и (24,962 ± 0,0076) мм. В соответствии с 6.3 первый стержень является несоответствующим, а третий стержень соответствует требованиям. Оценка соответствия второго стержня дает неокончательный результат.

B.3 Пример 2

Установленное предельно допустимое значение концентрации свинца в крови человека составляет 0,97 мкмоль/л. Таким образом, объектом является кровь человека. Параметром является молярная концентрация свинца в крови на время отбора крови. Если применяют двухэтапную процедуру, пробу крови делят на две пробы. При этом вторую пробу анализируют только в том случае, если интервал неопределенности после первого этапа включает в себя значения границы допуска (см. 6.2). Измерения выполнены в соответствии со стандартной методикой измерений, для которой неопределенность σ_Y = 0,048 мкмоль/л ([2], [3]). Интервал неопределенности может быть выражен в форме доверительного интервала для параметра с доверительной вероятностью (1 - α) ([4], [5]). Если выполнено n независимых измерений (определения содержания свинца в пробе) с неопределенностью σ_Y каждое и средним арифметическим измерений Y₁ то доверительный интервал определяют по формуле

__________

²⁾ Здесь (так же, как и в примере B.4) неявно предполагается, что систематическими погрешностями, связанными с действиями лаборанта, средством измерений и пр., можно пренебречь. Справедливость такого предположения требует проверки в каждой конкретной задаче.

где u_{1 - α/2} - квантиль уровня (1 - α/2) стандартного нормального распределения (ИСО 2602).

Измерена концентрация свинца в крови конкретного человека, для которого источником свинца являются ежедневный рацион питания и выхлопные газы автомашин. Оценка концентрации свинца по измерениям первой пробы крови (n = 1) составила Y₁ = 0,60 мкмоль/л. Интервал неопределенности, заданный в форме доверительного интервала (с доверительной вероятностью 0,95), включает в себя значения от 0,504 до 0,693 мкмоль/л. Так как этот интервал полностью попадает в допустимую область, согласно 6.3 принято решение о соответствии установленным требованиям.

Измерена концентрация свинца в крови другого человека, который подвергается дополнительному воздействию свинца по дороге на работу. Измерение первой пробы (n = 1) дает Y₁ = 1,06 мкмоль/л, а соответствующий доверительный интервал для концентрации свинца включает в себя значения от 0,96 до 1,15 мкмоль/л. Так как этот интервал содержит предельное значение, измерена вторая проба (n = 1). Результат измерений составил 1,00 мкмоль/л. Измерения двух этапов объединены: Y_* = (1,06 + 1,00)/2 мкмоль/л = 1,03 мкмоль/л. Доверительный интервал для среднего арифметического двух оценок концентрации свинца, рассчитанный для n = 2, включает в себя значения от 0,96 до 1,10 мкмоль/л. Предельное значение находится в этом интервале. Таким образом, решение о том, что концентрация свинца соответствует требованиям, не может быть принято. Также не может быть принято решение о том, что концентрация свинца не соответствует требованиям. Согласно 6.3 результат двух этапов оценки соответствия является неокончательным¹⁾.

__________

¹⁾ Необходимо подчеркнуть, что приведенная процедура оценки соответствия концентрации свинца в крови человека не эквивалентна обычно используемой процедуре.

B.4 Пример 3

Определено, что полная масса кадмия в сбрасываемой воде электростанции не должна превышать ежедневную массу 5 г в более чем 20 % дней за период измерений. Таким образом, объектом является процесс ежедневного сброса воды электростанцией. Параметром является 80 %-ный процентиль (т.е. квантиль уровня 0,8) распределения ежедневного сброса кадмия. Верхним пределом допуска для процентиля являются 5 г. Измерение ежедневного количества кадмия в сбрасываемой воде показало, что оно может быть описано логнормальным распределением. Верхняя доверительная граница U_CL, соответствующая доверительной вероятности (1 - α) для p-квантиля логнормального распределения, основанная на выборке из n независимых измерений, имеет вид

где  - среднее арифметическое n логарифмов наблюдений;

s_x - соответствующее выборочное стандартное отклонение;

t_{1 - α} [δ, (n - 1)] - квантиль уровня (1 - α) нецентрального t-распределения с (n - 1) степенями свободы и параметром нецентральности δ.

Если u_p означает квантиль уровня p стандартного нормального распределения, то для δ справедлива формула .

Одноэтапная оценка соответствия была выполнена на 10 образцах сбрасываемой воды. Образцы выбирали последовательно с интервалом в 14 дней. Измеряли содержание кадмия в каждом образце и оценивали ежедневный выход кадмия. Предполагалась однородность содержания кадмия в сбрасываемой воде. Неопределенность отдельных результатов измерений (т.е. ежедневного выхода кадмия) незначительна по сравнению с отклонениями в выходе кадмия по дням. Ежедневные наблюдения содержания кадмия (в граммах) в сбрасываемой воде составили

0,3486; 0,1408; 0,0890; 1,1417; 0,7524; 0,6262; 3,7560; 0,5520; 0,2304; 1,7226.

Среднее арифметическое и стандартное отклонение натурального логарифма наблюдений составили

 и s_x = 1,14379.

Поскольку p = 0,80, то u_p = 0,841621 и, таким образом, δ = -2,66144. Для 95%-ного доверительного интервала (т.е. α = 0,05) для 80 %-ного процентиля

t_{1 - α} [δ, (n - 1)] = t_0,95 (2,66144; 9) = 5,38687.

Верхний предел одностороннего 95 %-ного доверительного интервала для 80 %-ного процентиля распределения ежедневного количества кадмия в сбрасываемой воде

U_CL = exp (-0,624837 + 1,14379 · 5,38687/) = exp (1,32358) = 3,7569.

Так как U_CL < 5, можно подтвердить соответствие требованиям.

B.5 Пример 4

Скандинавский доломит обычно содержит незначительную долю волокон асбеста, которые могут нанести вред здоровью людей, работающих с доломитом. Поэтому был определен верхний предел доли асбеста в массе скандинавского доломита, используемого в промышленности. Пределами допуска являются массовые доли 0,001 % и 0,1 %. Перед обработкой партий доломита проводят оценку их соответствия этим требованиям. Таким образом, объектом является партия доломита, а исследуемым параметром - массовая доля w волокон асбеста в партии. Измерения проводят для проверки требования w ≤ 0,1 %.

Для оценки исследуемого параметра из партии отбирают несколько первичных образцов. Из каждого образца формируют заданное количество лабораторных проб и используют их для анализа. Для каждого образца подсчитывают выборочное среднее  массовой доли по соответствующим лабораторным пробам. Известно, что если количество лабораторных проб является большим, распределение (по первичным образцам) выборочных средних хорошо описывается нормальным распределением со средним w и дисперсией σ². Дисперсия σ² включает в себя вклад отклонений между первичными образцами, вклад отклонений в пределах первичных образцов и неопределенность измерений, связанную с анализом лабораторных проб. Если проанализировано n первичных проб и из каждого первичного образца сформировано одинаковое количество лабораторных проб, массовую долю волокон асбеста в партии оценивают с помощью среднего арифметического  по результатам измерений первичных образцов, т.е.

Предполагая, что наблюдения являются независимыми с одинаковой дисперсией, оценку дисперсии s² можно получить по формуле

Доверительный интервал для среднего с доверительной вероятностью (1 - α) имеет вид

где t_{1 - α/2} (n - 1) - квантиль t-распределения уровня (1 - α/2) с (n - 1) степенями свободы в соответствии с ИСО 2602.

Партия скандинавского доломита была представлена для оценки соответствия требованиям к содержанию асбеста. Так как процедура измерений требует очень много времени, было принято решение выполнять оценку соответствия как двухэтапную процедуру с пятью образцами на первом этапе и четырьмя образцами на втором этапе. Были сформированы для анализа 10 лабораторных проб от каждого образца.

На первом этапе были получены следующие результаты в массовых долях асбеста: 0,152 %; 0,0704 %; 0,0772 %; 0,0731 %; 0,0551 %.

На основе наблюдений первого этапа для α = 0,05 был получен следующий доверительный интервал для w

0,0856 % ± (2,776 · 0,0381 %)/ = (0,038 %; 0,133 %).

Так как граница поля допуска 0,1 % лежит в этом интервале, было принято решение о переходе ко второму этапу оценки соответствия и анализу 10 лабораторных проб от каждого из четырех образцов. Были получены следующие результаты

0,0828 %; 0,0671 %; 0,0743 %; 0,0561 %.

С использованием приведенных выше процедур получен следующий доверительный интервал

0,0787 % ± 2,306 · 0,0290/ % = (0,056 %; 0,101 %).

Поскольку этот интервал также содержит границу поля допуска, принимают решение о несоответствии установленным требованиям.

Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов и документа
национальным стандартам

Таблица ДА.1

Обозначение ссылочного международного стандарта и документа	Степень соответствия	Обозначение и наименование соответствующего национального стандарта
ISO 2602:1980	IDT	ГОСТ Р 50779.22-2005 (ИСО 2602:1980) «Статистические методы. Статистическое представление данных. Точечная оценка и доверительный интервал для среднего»
ISO 2854:1976	IDT	ГОСТ Р 50779.21-2004 «Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение»
ISO 3534-1:1993	IDT	ГОСТ Р ИСО 3534-1-2019 «Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей»
ISO 3534-2:1993	IDT	ГОСТ Р ИСО 3534-2-2019 «Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика»
ISO 5725-1:1994	IDT	ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения»
ISO 5725-2:1994	IDT	ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»
ISO 5725-3:1994	IDT	ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»
ISO 5725-4:1994	IDT	ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений»
ISO 5725-5:1994	IDT	ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений»
ISO 5725-6:1994	IDT	ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике»
ISO/TR 14253-2:1999	-	*
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты.

Библиография

[1] Guide to the expression of uncertainty in measurement (GUM), 1995

[2] Christensen J.M., Poulsen O.M. and Anglov T. Protocol for the design and interpretation of method evaluation in ASS analysis. Application to the determination of lead and manganese in blood. Journal of Analytical Atomic Spectroscopy, 1992, vol. 7, p. 329 - 334

[3] Christensen J.M. Human Exposure to Toxic Metals. Factors influencing Interpretation of Biomonitoring Results, Science of the Total Environment, 1995, vol. 166, p. 89 - 135

[4] Kristiansen J., Christensen J.M. and Nielsen J.L. Uncertainty of atomic absorption spectrometry: Applications to the determination of lead in blood. Mikrochimica Acta, 1996, vol. 123, p. 241-249

[5] Kristiansen J. and Christensen J.M. Traceability and uncertainty in analytical measurements. Annals of Clinical Biochemistry, 1998, vol. 35, p. 371 - 379