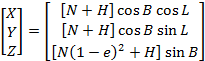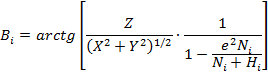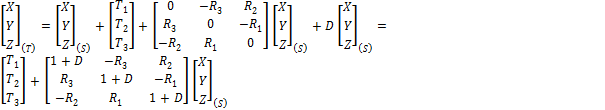ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р |
ГЕОГРАФИЧЕСКИЕ ИНФОРМАЦИОННЫЕ
СИСТЕМЫ
Координатная основа.
Общие требования
|
|
Москва |
Предисловие
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Государственный научно-внедренческий центр геоинформационных систем и технологий» (ФГУП «ГОСГИСЦЕНТР»), Федеральным государственным унитарным предприятием «Центральный ордена «Знак Почета» научно-исследовательский институт геодезии, аэросъемки и картографии им. Ф.Н. Красовского» (ФГУП «ЦНИИГАиК») и Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт стандартизации и сертификации в машиностроении» (ВНИИНМАШ)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 394 «Географическая информация/геоматика»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 28 августа 2006 г. № 215-ст
4 Настоящий стандарт соответствует международному стандарту ИСО 19111:2003 «Географическая информация. Пространственное описание с использованием координат» (ISO 19111:2003 «Geographic information - Spatial referencing by coordinates», NEQ) в части требований к определению концептуальной схемы координатных систем отсчета и основных операций с координатами
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Октябрь 2018 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок - в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Содержание
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГЕОГРАФИЧЕСКИЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
Координатная основа. Общие требования
Geographical information systems. Coordinate frame. General requirements
Дата введения - 2007-01-01
1 Область применения
Настоящий стандарт распространяется на координатную основу географических информационных систем (далее - ГИС) и устанавливает минимальное количество данных, требуемых для определения одно-, двух- и трехмерных координатных систем отсчета, а также рекомендует информацию, необходимую для изменения значений координат при переходе от одной координатной отсчетной системы к другой.
Стандарт предназначен для применения организациями и предприятиями, создающими ГИС различного назначения, базы и банки пространственных данных.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 52438-2005 Географические информационные системы. Термины и определения
ГОСТ 8.417 Государственная система обеспечения единства измерений. Единицы величин
ГОСТ 22268 Геодезия. Термины и определения
ГОСТ Р 57773 (ИСО 19157:2013) Пространственные данные. Качество данных
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ 22268, ГОСТ Р 52438-2005, а также следующие термины с соответствующими определениями:
3.1 абсцисса X: Линейное расстояние в системе координат картографической сетки от отсчетной линии восток - запад, к северу положительное и к югу отрицательное.
3.2 большая полуось а: Максимальный радиус эллипсоида.
Примечание - Для эллипсоида, представляющего Землю, это радиус экватора.
3.3 высотные (вертикальные) даты: Набор параметров, описывающих отнесение высот, связанных с гравитационным полем, к поверхности Земли.
Примечание - В большинстве случаев высотные даты будут отнесены к уровню моря. Геодезические высоты связаны с геодезическими датами. Высотные даты, использующие акустические данные (в гидрографических задачах), имеют отрицательные высоты или положительные глубины.
3.4 высота: Расстояние от отсчетной поверхности до выбранной точки по нормали к этой поверхности.
Примечание - Высота точки, расположенная выше отсчетной поверхности, является положительной, а ниже нее - отрицательной.
3.5 нормальная высота Нγ: Разность геопотенциала в данной точке и в начале отсчета высот, деленная на среднее значение нормальной силы тяжести на отрезке силовой линии нормального поля, соответствующем определяемой высоте.
3.6 высота квазигеоида: Разность между геодезической высотой и нормальной высотой.
3.7 геодезическая высота Н: Расстояние от эллипсоида до точки на физической поверхности Земли по нормали к его поверхности.
3.8 геодезическая долгота L: Двугранный угол между плоскостями начального меридиана и меридиана данной точки, положительный при направлении на восток.
3.9 геодезическая отсчетная основа (геодезическая основа): Совокупность геодезических пунктов (или иных объектов - носителей координат) и соответствующих значений координат.
3.10 геодезическая система координат: Система координат, в которой положение объекта описывается геодезическими широтой и долготой, а в трехмерном пространстве - геодезической высотой.
3.11 геодезическая широта В: Острый угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью экватора, положительный по направлению к северу и отрицательный - к югу.
3.12 геодезические даты: Набор параметров, описывающих связь координатной системы с Землей.
3.13 геоид: Уровенная поверхность, наилучшим образом аппроксимирующая уровень моря как в локальном, так и в глобальном случаях.
Примечание - Уровенная поверхность является эквипотенциальной поверхностью земного гравитационного поля, которая везде перпендикулярна к направлению отвесной линии.
3.14 геопотенциал: Реальный потенциал силы тяжести Земли.
3.15 Гринвичский меридиан: Меридиан, проходящий через плоскость большого круга пассажного инструмента в Королевской обсерватории Гринвича Соединенного королевства Великобритании.
3.16 исходные даты: Термин, обобщающий геодезические, высотные и местные даты.
Примечание - Даты определяют положение начала, масштаб и ориентировку осей системы координат по отношению к Земле.
3.17 картографическое проектирование: Перевычисление координат, когда одна координатная система является геодезической, а другая - плоской.
3.18 квазигеоид: Геометрическое место точек, получаемых путем откладывания нормальных высот по силовым линиям нормального гравитационного поля от точек физической поверхности Земли; высоты квазигеоида отсчитывают от поверхности эллипсоида.
3.19 координата: Число из упорядоченного набора N чисел, описывающих положение пункта в N-мерном пространстве.
3.20 координатная основа: Совокупность данных, обеспечивающих описание местоположения с использованием координат.
3.21 координатная система отсчета: Система координат, связанная (для задач, регламентируемых настоящим стандартом) с Землей исходными датами.
3.22 малая полуось b: Полярная ось эллипсоида.
Примечание - Для эллипсоида, представляющего Землю, это расстояние от его центра до любого из полюсов.
3.23 меридиан: Сечение эллипсоида плоскостью, содержащей малую полуось эллипсоида.
Примечание - Этот термин чаще используется для дуги от полюса до полюса, чем для полного сечения.
3.24 местные даты: Даты с местной привязкой начальной точки.
3.25 начальный меридиан: Меридиан, от которого отсчитывают долготы или другие меридианы.
Примечание - Большинство геодезических дат используют Гринвичский меридиан в качестве начального.
3.26 нормальный потенциал: Потенциал силы тяжести нормального эллипсоида.
3.27 нормальный эллипсоид: Эллипсоид вращения, создающий гравитационное поле, максимально близкое к гравитационному полю Земли.
3.28 операции с координатами: Изменение координат пространственных объектов с использованием их математической связи при переходе от одной системы координат к другой.
Примечание - Общий случай трансформирования или перевычисления.
3.29 ордината Y: Линейное расстояние в системе координат или картографической сетки по направлениям на восток (положительное) или запад (отрицательное) от отсчетной линии север - юг.
3.30 отсчетная линия: В системе координат линия, от которой отсчитывают координаты.
3.31 отсчетная поверхность: В системе координат геометрическая поверхность, от которой отсчитывают координаты.
3.32
перевычисление координат: Операция с координатами пространственных объектов, основанная на математически строго определенной связи, при переходе из одной системы координат в другую, используя одни и те же исходные геодезические даты.
Примечание - При перевычислении координат используют параметры, являющиеся постоянными величинами.
[ГОСТ Р 52438-2005, статья 44]
3.33 полярная система координат: Система координат, в которой положение объекта задается расстоянием и направлением от ее начала.
3.34 прямоугольная система координат: Система координат, определяющая положение точек по отношению к N взаимно перпендикулярным осям, исходящим из одной точки.
Примечание - N - 1, 2 или 3.
3.35 сжатие α: Отношение разности между большой и малой полуосями к большой полуоси эллипсоида, вычисляемое по формуле α = (а - b)/а.
Примечание - Иногда применяют обратное сжатие 1/α = а/(а - b).
3.36 составная система координат: Описание местоположения с использованием двух независимых систем координат.
Пример - Одна координатная отсчетная система, основанная на двух- или трехмерной системе координат, и другая, основанная на системе высот, связанной с гравитационным полем Земли.
3.37 система координат: Набор математических правил, описывающих, как координаты должны быть соотнесены сточками пространства.
3.38 система координат проекции: Двухмерная система координат, образованная в результате картографического проектирования.
3.39 средний уровень моря: Средний уровень морской поверхности для всех стадий прилива.
Примечание - Средний уровень моря обычно означает средний уровень для региона, определенный по измерениям на одном или нескольких уровенных постах в заданный период времени.
3.40
трансформирование координат: Операция с координатами пространственных объектов при переходе от одной координатной системы отсчета к координатной системе отсчета, основанной на других датах.
Примечание - При трансформировании координат используют параметры, которые могут быть определены опытным путем с использованием набора пунктов, общих для обеих координатных систем отсчета.
[ГОСТ Р 52438-2005, статья 45]
3.41 точность трансформирования: Близость значений трансформированных координат к принятым за истинные в целевой координатной отсчетной системе.
Примечание - Трансформирование часто применяется для географических данных с целью преобразовать их в желаемую отсчетную систему, но если параметры трансформирования определены опытным путем, то для такого преобразования характерны соответствующие ошибки.
3.42 точность перевычисления: Близость преобразованных значений координат к их точным значениям.
3.43 эллипсоид: Поверхность, полученная при вращении эллипсоида вокруг собственной оси.
Примечание - Параметры каждого эллипсоида определяются измерениями формы и размеров Земли, чтобы аппроксимировать геоид с наиболее возможно высокой точностью.
4 Системы координат и их реализации
Для описания пространственного положения объектов в геоинформационных задачах используют системы пространственных прямоугольных, плоских прямоугольных и геодезических координат. Для картографической основы мелких масштабов применяют географические координаты на сферической поверхности.
Наиболее часто применяют составные системы координат, объединяющие систему плоских прямоугольных координат в картографической проекции и высот, связанных с гравитационным полем Земли. В настоящее время применяют систему геодезических координат 1995 года (СК-95) на эллипсоиде Красовского, перевычисленных в плоские прямоугольные координаты проекции Гаусса-Крюгера, и Балтийскую систему нормальных высот 1977 года.
Реализацией системы координат является совокупность пунктов геодезической сети и значений координат, присвоенных этим пунктам. Для территории Российской Федерации такой реализацией являются государственные геодезическая и нивелирная сети, а также каталоги значений координат и высот.
Для геодезического обеспечения орбитальных полетов и решения навигационных задач используют геоцентрическую систему координат «Параметры Земли 1990 года» (ПЗ-90).
Реализацией системы координат ПЗ-90 является совокупность пунктов космической геодезической сети с пространственными геоцентрическими координатами.
5 Концептуальная схема координатных систем отсчета
5.1 Общие положения
Положение объекта на (или вблизи) поверхности Земли определяют координатами. Каждое положение объекта должно быть описано набором координат, отнесенных к определенной координатной системе отсчета.
Координаты помещают в наборы пространственных данных, в которых все значения координат должны принадлежать одной и той же координатной системе отсчета. Каждый набор данных должен содержать описание одной системы координат, которая применена ко всем координатам в наборе данных. Если пространственные данные отнесены более чем к одной системе координат, то они должны быть разделены на две или более соответствующие группы, каждая со своим собственным описанием системы.
5.2 Координатные системы отсчета
5.2.1 Типы координатных систем отсчета
В настоящем стандарте рассматривают два типа координатных систем отсчета:
- координатную систему отсчета (общий случай);
- составную координатную систему отсчета (особый случай).
Координатная система отсчета определена в 6.2.2, а составная - в 6.2.3.
5.2.2 Координатная система отсчета
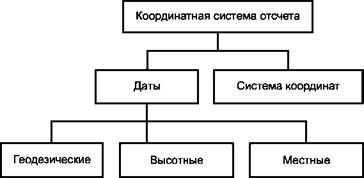
Положение объекта может быть задано набором координат. Координатная система отсчета реализуется набором координат, отнесенных к их физическим носителям. Такая реализация именуется отсчетной основой. Координатная система отсчета должна быть определена одним вариантом дат и одной системой координат, как показано на рисунке 1.
|
|
|
Рисунок 1 - Координатная система отсчета |
5.2.3 Составная координатная система отсчета
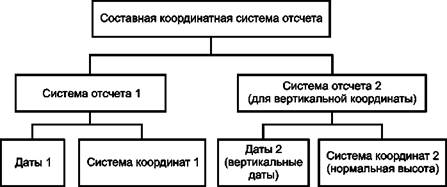
Горизонтальные и вертикальные компоненты положения объекта в трехмерном физическом пространстве, как правило, могут быть выбраны из разных координатных систем отсчета. Таким является описание положений объектов с использованием высот, отнесенных к уровню моря, и горизонтальных координат, отнесенных к другой системе. При этом применяют составную координатную систему отсчета, которая объединяет две используемые координатные системы отсчета в соответствии с рисунком 2.
|
|
|
Рисунок 2 - Составная координатная система отсчета |
5.3 Исходные даты
5.3.1 Типы исходных дат
Даты могут быть геодезическими, высотными и местными. Геодезические даты обеспечивают связь координатной системы с Землей и используются для двух- или трехмерных систем отсчета. Они должны включать определение эллипсоида. Высотные даты обеспечивают связь нормальных высот с поверхностью квазигеоида. Местные даты применяют для локальных геодезических задач. Связь местных дат с Землей может быть неопределенной. Местные даты применимы к местным геодезическим отсчетным основам.
Для геоинформационных задач необходимо идентифицировать даты, но определение дат является необязательным.
5.3.2 Описание исходных дат
Описание исходных дат является обязательным, если не приведена ссылка на документы по применяемой координатной системе отсчета.
5.3.3 Начальный меридиан
Начальный меридиан определяет начало отсчета долгот.
Описание начального меридиана необязательно при использовании вертикальных и местных дат, и когда начальный меридиан является Гринвичским. Для геодезических дат и при использовании в качестве начального иного меридиана описание начального меридиана обязательно.
5.4 Система координат
Для системы координат набор данных должен включать: название, единицы измерения, направление и взаимное чередование осей. Координаты в соответствующих наборах данных представляют в соответствии с этим чередованием. Координаты, основанные на координатных системах отсчета картографических проекций, являются результатом перевычисления. Операция перевычисления в 6.5.
Описание системы координат в ГИС должно быть обязательным, если не даны ссылки на соответствующий документ, содержащий ее описание.
Каждая ось системы координат должна быть описана, последовательность описания осей соответствует порядку расположения координат в наборе данных.
5.5 Операции - перевычисление и трансформирование
5.5.1 Общие положения
Информация об операциях должна быть представлена, если наборы данных, содержащие координаты, использующие разные координатные системы отсчета, должны быть объединены.
Различаются два типа операций:
- перевычисление координат из одной координатной системы в другую при неизменных датах; в этой операции значения параметров являются точными;
- трансформирование координат из одной системы в другую при их различных геодезических датах. При этом трансформирование отличается от перевычисления тем, что значения параметров трансформирования определяются опытным путем, поэтому они могут иметь несколько различных оценок или реализаций.
Изменения координат одной координатной системы отсчета при переходе к другой происходят в результате операций, состоящих из одного или более трансформирований и одного или более пересчетов.
Описание операций является обязательным, если координатные системы являются проекционными и не приведены ссылки на описание координатной системы отсчета и системы координат.
Операции должны быть описаны в наборе данных в порядке их следования.
5.5.2 Перевычисление координат
Перевычисление геодезических координат в плоские прямоугольные координаты широко используют при картографическом проектировании. Перевычисление также используют для изменения единиц измерения или сдвига начала отсчета плановых координат для создания локальной картографической сетки. Перевычисление координат не изменяет значения дат, так как оно использует математические функции, не влияющие на точность значений координат.
Перевычисление координат должно включать:
- картографическое проектирование, которое является методом, использующим математические функции для перевычисления геодезических координат (исключая высоты) в двухмерные плановые координаты и наоборот;
- перевычисление геодезических координат (включая высоты) в трехмерные прямоугольные координаты и наоборот;
- перевод единиц из одной системы в другую с помощью коэффициентов или алгоритма (например, радианов в градусы, минут в секунды, метров в футы);
- параллельный сдвиг начала координат для получения местной координатной основы.
Картографическая проекция является особым случаем перевычисления координат с эллипсоида на плоскость. Для координат, принадлежащих к системе координат, полученных путем проектирования, описание перевычисления должно быть обязательным.
5.5.3 Трансформирование координат
Координаты допускается трансформировать путем приведения их к другим датам. При этом системы координат имеют один и тот же тип (например, обе геодезические или обе прямоугольные). Трансформирование проводят посредством метода, имеющего определенный алгоритм. Каждый алгоритм имеет соответствующий набор параметров. Так как значения параметров могут быть определены опытным путем, они зависят от измерений и их погрешностей. Допустимы разные варианты трансформирования между двумя датами.
Описание трансформирования не является необходимым для описания координатной системы отсчета. Может быть полезным описание трансформирования, которое уже было применено к координатам, или трансформирования из прежней системы в определяемую пользователем стандартную координатную систему отсчета.
5.5.4 Операция объединения
Преобразование координат из одной системы отсчета в другую может сопровождаться операциями, состоящими из одного или более трансформирований и/или одного или более перевычислений. Объединение приводит к изменению координат вследствие нескольких трансформирований и/или перевычислений.
5.6 Точность координат, операций и параметров
Координатная система отсчета реализуется набором геодезических пунктов. Точность пространственного описания зависит от точности реализации координатной системы отсчета, как и точность координат последующего сгущения координатной основы.
Точность трансформирования зависит от точности реализации обеих координатных систем отсчета. Перевычисления являются математически точными без погрешностей измерений или параметров дат.
Информация о точности и надежности значений координат или операций и их параметров должна быть представлена в соответствии с ГОСТ Р 57773. Характеристика точности должна быть дана для каждого местоположения объекта, каждой координаты, каждого трансформирования или параметра трансформирования либо одновременно для всех компонентов набора данных.
Числовые значения координат приводят в соответствии с международной системой единиц по ГОСТ 8.417.
Операции перевычисления и трансформирования координат представлены в приложении А.
Приложение А
(справочное)
Геодезические взаимосвязи
А.1 Координатная система отсчета - перевычисление и трансформирование
На рисунке А.1 приведены три разные координатные системы отсчета:
- координатная система отсчета 1 (даты 1, система координат А),
- координатная система отсчета 2 (даты 1, система координат В),
- координатная система отсчета 3 (даты 2, система координат А).
|
|
|
Рисунок А.1 - Перевычисление и трансформирование |
Перевычисление приводит к изменению координат при переходе из системы отсчета 1 в систему отсчета 2, имеющих одни и те же даты. Трансформирование применено для перевычисления координат из системы отсчета 1 в систему отсчета 3 при использовании одной и той же системы координат. Трансформирование 2 использовано для перевычисления координат непосредственно из системы отсчета 2 в систему отсчета 3, имеющих также различные даты. Перевычисление координат из системы отсчета 2 в систему отсчета 3 может быть так же описано, как операция объединения, состоящая из перевычисления плюс трансформирование 1.
А.2 Перевычисление - соотношение между геодезическими и прямоугольными координатами
Для определения положения пункта в пространстве необходима трехмерная координатная отсчетная система. Системы координат устанавливают упорядоченную связь между физическими пунктами в пространстве и действительными числами (координатами). Перевычисление координат из одной системы координат в другую является математическим действием. Между разными системами координат существует однозначно определенная математическая связь.
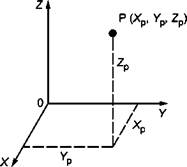
В геодезии трехмерную систему прямоугольных координат применяют для решения глобальных задач. Она задается тремя ортогональными осями, сориентированными в правой системе координат. Координатные оси X, Y, и Z исходят из одной точки 0, находящейся в начале системы координат (рисунок А.2).
|
|
|
Рисунок А.2 - Прямоугольные координаты |
Координатные оси называются параллелями для постоянной широты В и меридианами для постоянной долготы L.
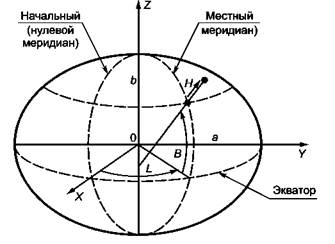
Когда эллипсоид является связанным с Землей, эллипсоидальные координаты называют геодезическими координатами (рисунок А.З).
|
|
|
Рисунок А.3 - Прямоугольные и геодезические координаты |
Если начало правой прямоугольной системы координат совпадает с центром эллипсоида, ось Z совпадает с осью вращения эллипса и положительное направление оси X проходит через точку В = 0, L = 0, тогда следующие формулы преобразуют эллипсоидальные координаты в геоцентрические прямоугольные:
|
|
(А.1) |
где N - радиус кривизны первого вертикала, перпендикулярный к меридиану, вычисляемый по формуле
|
|
(А.2) |
где е - первый эксцентриситет эллипсоида, вычисляемый по формуле
|
|
(А.3) |
Преобразование геоцентрических прямоугольных координат в эллипсоидальные координаты выполняют по формулам:
|
|
(А.4) |
и
|
|
(А.5) |
Вычисление Нi и Вi осуществляют последовательными приближениями по формулам:
|
|
(А.6) |
|
|
(А.7) |
|
|
(А.8) |
где i - номер приближения.
А.З Трансформирование геодезических дат
В общем случае параметры трансформирования определяют по координатам совокупности пунктов, принадлежащих реализациям обеих координатных систем отсчета. Они являются приближенными, и их применимость может быть ограничена определенным регионом.
Наиболее широко применяют трансформирование подобия, когда две координатные системы отсчета различаются только их взаимным расположением, ориентировкой в пространстве и масштабом.
Трансформирование подобия является конформным. Оно может быть выполнено как в прямоугольных, так и в эллипсоидальных координатах.
В некоторых случаях при трансформировании используются только три параметра (как правило, параметры вращения) из семи. Основная формула трансформирования:
|
|
(А.9) |
где X, Y, Z - три сдвига вдоль координатных осей;
R1, R2, R3 - три угла поворота вокруг осей;
D - масштабная поправка.
Три сдвига вдоль координатных осей X, Y, Z, три угла поворота вокруг осей R1, R2, R3 и масштабную поправку D, как правило, определяют под условием минимизации квадратов разностей координат одноименных пунктов в координатных системах S и Т. Одноименные пункты являются идентичными в пространстве и времени. При трансформировании подобия смещениями пунктов пренебрегают, эти смещения отражаются в остаточных отклонениях после уравнивания. Отношения прямоугольных координат, используемые в трансформировании к эллипсоидальным координатам, представлены в А.2.
Особым случаем трансформирования является долготный сдвиг. Он происходит между датами, которые являются идентичными, за исключением различных начальных меридианов. Например, некоторые европейские государства используют одни и те же даты, но разные начальные меридианы: Гринвичский или Парижский.
А.4 Перевычисление - картографическое проектирование
Геодезические координаты отнесены к криволинейной поверхности эллипсоида. Проектирование, необходимое для получения плоских прямоугольных координат, может быть произведено с использованием разных типов проекций. При изображении на плоскости искривленные поверхности искажаются. Проектирование с эллипсоида на плоскость должно быть конформным и не искажающим площади. Проектирование, сохраняющее масштаб во всех направлениях, является невозможным. Картографическая проекция является математическим отображением эллипсоида или его части на плоскости. Проекция будет иметь соответствующую точку отсчета, называемую началом проекции для картографируемого региона. Это будет нулевой (начальный) пункт отсчетной основы на плане.
Картографическая проекция определяется двумя функциями:
|
X = f(B; L), Y = g(B; L), |
|
где X - абсцисса;
Y - ордината;
В и L - геодезические широта и долгота.
Каждая точка в пространстве может быть представлена трехмерными координатами (X, Y, Н), основанными на датах и картографической проекции. Они применимы только для продольных и поперечных проекций.
А.5 Геоид и высоты
Для описания гравитационного поля Земли используют потенциал силы тяжести W, который складывается из потенциала силы гравитационного притяжения и потенциала центробежной силы. Вектор силы тяжести определяют как градиент потенциала W по формуле:
|
|
(А.10) |
Геоидом называют эквипотенциальную поверхность гравитационного поля Земли, наиболее близко аппроксимирующую невозмущенную поверхность морей и океанов. На практике в качестве геоида принимают эквипотенциальную поверхность, проходящую через начальный пункт отсчета высот. Из-за того, что в различных регионах Земли используют свои начальные пункты отсчета высот, поверхности геоида, принятые в этих регионах, немного отличаются друг от друга.
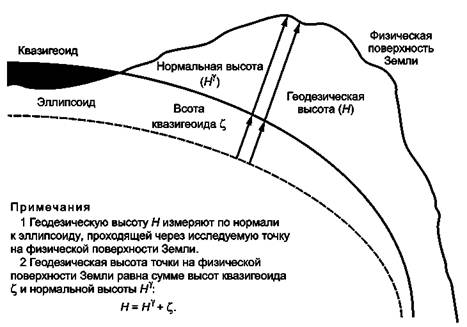
Поверхность геоида отличается от поверхности эллипсоида вращения или поверхностей подобных простых геометрических фигур (рисунок А.4). Сложность математического описания поверхности геоида возрастает по мере увеличения описываемой территории и возрастания детальности этого описания.
Разность потенциалов силы тяжести между поверхностью геоида
и эквипотенциальной поверхностью, проходящей через некоторую точку Р,
называют геопотенциальным числом ![]() ,
которое вычисляют по формуле:
,
которое вычисляют по формуле:
|
|
(А.11) |
Для описания пространственного положения точки в дополнение к двум плановым координатам достаточно указать значение ее геопотенциального числа. Однако на практике в качестве третьей координатной компоненты принято использовать высоту. Распространены три типа высот, связанных с геопотенциальными числами:
- ортометрическая высота ![]() ,
,
где ![]() -
среднее значение силы тяжести вдоль отвесной линии между точкой и геоидом;
-
среднее значение силы тяжести вдоль отвесной линии между точкой и геоидом;
- нормальная высота ![]() ,
,
где ![]() -
среднее значение нормальной силы тяжести на отрезке силовой линии нормального
поля, равном значению нормальной высоты,
-
среднее значение нормальной силы тяжести на отрезке силовой линии нормального
поля, равном значению нормальной высоты,
- динамическая высота ![]() ,
,
где ![]() -
некоторая постоянная величина, численно близкая значению силы тяжести.
-
некоторая постоянная величина, численно близкая значению силы тяжести.
|
|
|
Рисунок А.4 - Взаимосвязь геодезической высоты, высоты квазигеоида и нормальной высоты |
Ключевые слова: системы координат, координатные системы отсчета, исходные даты, перевычисление координат, трансформирование координат