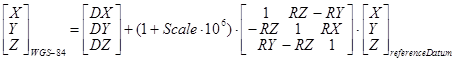ФЕДЕРАЛЬНАЯ
СЛУЖБА ГЕОДЕЗИИ И КАРТОГРАФИИ
РОССИИ
Геодезические и
картографические инструкции,
нормы и правила
РУКОВОДСТВО
пользователя по выполнению работ
в системе координат 1995 года (СК-95)
ГКИНП (ГНТА)-06-278-04
Обязательно для исполнения всеми
субъектами геодезической и
картографической деятельности.
Утверждено руководителем Федеральной службы
геодезии
и картографии России от 1 марта 2004
г. № 29-пр.
Москва
ЦНИИГАиК
2004
Настоящий нормативно-технический акт (НТА)
разработан в соответствии с «Законом о геодезии и картографии» от 26 декабря
1995 г. № 209-ФЗ (с изменениями), постановлением Правительства Российской
Федерации от 28 июля 2000 года № 586 «Об установлении единых государственных
систем координат» в рамках организационно-технических мероприятий, необходимых
для перехода к системе координат 1995 года, а также в соответствии с «Основными
положениями о государственной геодезической сети Российской Федерации».
В «Руководстве пользователя по выполнению
работ в системе координат 1995 года» дано представление о системе геодезических
координат 1995 года (СК-95), ее особенностях и преимуществах перед системой
координат 1942 года (СК-42), о возможных затруднениях, возникающих при переходе
к применению СК-95, особенно на начальной стадии, когда большинство
существующих геодезических материалов и топосъемок еще связаны с СК-42 и носят
на себе отпечаток ее недостатков.
В «Руководстве пользователя» даны общие
рекомендации по работе с СК-95 и конкретные указания по порядку и содержанию
действий при решении различных типовых задач и использовании
специализированного программного обеспечения, описание автоматизированного
каталога, его содержания, функционирования, состава и формы информации, представляемой
пользователям.
Общее содержание руководства и рекомендации
рассчитаны на различную квалификацию пользователей.
Настоящий НТА подготовлен в соответствии с
требованиями Инструкции ГКИНП (ГНТА)-119-94.
«Руководство пользователя по выполнению
работ в системе координат 1995 года» составлено в развитие основных положений,
инструкций, норм и правил по выполнению работ в системе геодезических координат
1995 года на территории Российской Федерации.
Руководство разработали: к.т.н. Н.А.
Бовшин, д.т.н. Б.В. Бровар, к.т.н. Г.В. Демьянов, к.т.н. В.И. Зубинский, А.Н.
Майоров, Н.В. Майорова.
Утверждено приказом руководителя
Федеральной службы геодезии и картографии России от 1 марта 2004 г. № 29-пр.
Вводится в действие с 1 марта 2004 года.
|
АГП КГС
|
астрономо-геодезические пункты космической геодезической сети
|
|
АГП
|
аэрогеодезическое предприятие
|
|
АГС
|
астрономо-геодезическая сеть
|
|
ВГС
|
высокоточная геодезическая сеть
|
|
ГВО
|
главная высотная основа
|
|
ГГС
|
государственная геодезическая сеть
|
|
ГЛОНАСС
|
глобальная навигационная спутниковая система
|
|
ГСВЧ
|
государственная служба времени и частоты
|
|
ДГС
|
доплеровская геодезическая сеть
|
|
КВО
|
координатно-временное обеспечение
|
|
КГС
|
космическая геодезическая сеть
|
|
ПВЗ
|
параметры вращения Земли
|
|
ПЗ-90
|
система геодезических параметров Земли 1990 года («Параметры
Земли 1990 года»)
|
|
ПЭВМ
|
персональная электронно-вычислительная машина
|
|
РАН
|
Российская Академия наук
|
|
СГС-1
|
спутниковая геодезическая сеть 1 класса
|
|
СК-42
|
система координат 1942 года
|
|
СК-95
|
система координат 1995 года
|
|
СКО
|
среднеквадратическая ошибка
|
|
ФАГС
|
фундаментальная астрономо-геодезическая сеть
|
|
ФГП
|
фундаментальные геодезические параметры
|
|
GPS
|
Global Positional System (глобальная навигационная система)
|
|
ICRS
|
International Celestial Reference System (международная небесная опорная
система)
|
|
ITRF
|
International Terrestrial Reference
Frame (международная общеземная
пространственная система координат)
|
|
ITRS
|
International Terrestrial Reference
System (новая международная земная опорная система)
|
|
UTM
|
Universal Transverse Mercator (поперечно-цилиндрическая
проекция Меркатора)
|
|
WGS-84
|
Wold Geodetic System (мировая геодезическая система 1984
года)
|
Совместным решением Главного управления
геодезии и картографии (ГУГК) и Военно-топографического управления Генерального
Штаба Министерства Обороны (ВТУ ГШ МО) от 4 июня 1942 года в качестве
референц-эллипсоида при уравнивании астрономо-геодезической сети СССР был
принят эллипсоид с параметрами: а = 6378245, a = 298,3 (в последующем получившего имя
Красовского), а систему координат, в которой велись вычисления, было решено
именовать системой координат 1942 года. Единая система геодезических координат
1942 года была введена постановлением Совета Министров СССР от 7 апреля 1946
года № 760 и прослужила около 50 лет. Однако в настоящее время система
координат 1942 года во многом уже не отвечает современным требованиям науки и
практики.
Единая государственная система
геодезических координат 1995 года (СК-95) введена постановлением Правительства
Российской Федерации от 28 июля 2000 года № 586 «Об установлении единых
государственных систем координат» для использования при осуществлении
геодезических и картографических работ начиная с 1 июля 2002 года.
Указанным постановлением Правительства
Российской Федерации Роскартографии было поручено осуществить
организационно-технические мероприятия, необходимые для перехода к
использованию системы координат 1995 года. До завершения этих мероприятий
Правительство Российской Федерации постановило использовать единую систему
геодезических координат 1942 года.
Целесообразность введения системы координат
1995 года состоит в повышении точности, оперативности и экономической
эффективности решения задач геодезического обеспечения, отвечающего современным
требованиям экономики, науки и обороны страны.
Полученная в 1995 году в результате
совместного уравнивания координат пунктов космической геодезической сети (КГС),
доплеровской геодезической сети (ДГС) и астрономо-геодезической сети (АТС),
система координат 1995 года закреплена пунктами государственной геодезической
сети (ГГС).
Система координат 1995 года строго согласована
с единой государственной геоцентрической системой координат ПЗ-90 (см. документ
«Параметры Земли 1990 года»).
Система координат ПЗ-90 закреплена пунктами
космической геодезической сети. Точность отнесения системы к центру масс Земли
характеризуется средней квадратической ошибкой порядка 1 м. За отсчетную
поверхность в государственной геоцентрической системе координат (ПЗ-90) принят
общий земной эллипсоид со следующими геометрическими параметрами:
• большая полуось 6378136 м;
• сжатие 1:298,257839.
Центр этого эллипсоида совмещен с началом
геоцентрической системы координат; плоскость начального (нулевого) меридиана
совпадает с плоскостью 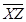 этой системы.
этой системы.
Геометрические параметры общего земного
эллипсоида приняты равными соответствующим параметрам уровенного эллипсоида
вращения. При этом за уровенный эллипсоид вращения принята внешняя поверхность
нормальной Земли, масса и угловая скорость вращения которой задаются равными
массе и угловой скорости вращения Земли.
Масса Земли М, включая массу ее
атмосферы, умноженная на постоянную тяготения f, составляет геоцентрическую гравитационную постоянную fM = 39860044´107 м3/с2, угловая
скорость вращения Земли w принята равной 7292115´10-11 рад/с, гармонический
коэффициент геопотенциала второй степени J2, определяющий сжатие общего земного
эллипсоида, принят равным 108263´10-8.
За отсчетную поверхность в СК-95 принят
референц-эллипсоид Красовского с параметрами:
• большая полуось 6378245
м;
• сжатие 1:298,3.
Главные оси отсчетного эллипсоида
параллельны пространственным осям системы координат ПЗ-90. Положение начала
СК-95 задано таким образом, что значения координат пункта ГГС Пулково в
системах СК-95 и СК-42 совпадают.
Переход от геоцентрической системы координат
к СК-95 выполняется по формулам, приведенным в прил. 1.
Положение пунктов в принятой системе
координат задается следующими координатами:
• пространственными прямоугольными
координатами X, Y, Z (направление оси Z совпадает с
осью вращения отсчетного эллипсоида, ось X лежит в
плоскости нулевого меридиана, а ось Y дополняет систему
до правой; началом системы координат является
центр отсчетного эллипсоида);
• геодезическими координатами:
широтой - В, долготой - L, высотой - Н;
• плоскими прямоугольными координатами
х и у, вычисляемыми в проекции Гаусса
- Крюгера.
Геодезическая высота Н образуется
как сумма нормальной высоты и высоты квазигеоида над отсчетным эллипсоидом.
Нормальные высоты геодезических пунктов
определяются в Балтийской системе высот 1977 года, исходным началом которой
является нуль Кронштадтского футштока, а высоты квазигеоида вычисляются над
эллипсоидом Красовского.
При решении специальных задач могут
применяться и другие проекции поверхности эллипсоида на плоскость.
Точность СК-95 характеризуется следующими
средними квадратическими ошибками взаимного положения пунктов по каждой из
плановых координат:
• 2 - 4 см - для
смежных пунктов АГС;
• 0,3 - 0,8 м
- при расстояниях от 1 до 9 тысяч
км.
Точность нормальных высот, в зависимости от
метода их определения, характеризуется следующими средними квадратическими
ошибками:
• 6 - 10 см - в
среднем по стране из уравнивания нивелирных
сетей I u II классов;
• 0,2 - 0,3 м
- из астрономо-геодезических определений при
создании АГС.
Точность превышений высот квазигеоида
астрономо-гравиметрическим методом характеризуется следующими средними
квадратическими ошибками:
• 6 - 9 см - при
расстояниях 10 - 20 км;
• 0,3 - 0,5 м
- при расстоянии 1000 км.
Система координат СК-95 отличается от
системы координат СК-42:
• повышением точности передачи
координат на расстояния свыше 1000 км
в 10 - 15 раз и точности взаимного
положения смежных пунктов в государственной геодезической
сети в среднем в 2 - 3 раза;
• одинаковой точностью распространения
системы координат для всей территории Российской
Федерации и стран, входивших в состав
СССР;
• отсутствием региональных деформаций
государственной геодезической сети, достигающих в
системе координат 1942 года нескольких метров;
• возможностью создания высокоэффективной
системы геодезического обеспечения на основе
использования глобальных навигационных спутниковых систем
ГЛОНАСС u
GPS.
К настоящему времени разработан ряд
документов [1
- 5, 7 - 11, 13], предназначенных для различных
потребителей для более успешного перехода от СК-42 к СК-95.
Настоящее «Руководство пользователя по
выполнению работ в системе координат СК-95» содержит более полную информацию об
СК-95 и ее отличии от СК-42, а также рекомендации по решениям задач,
возникающих перед пользователем в связи с переходом от СК-42 к СК-95.
Руководство рассчитано на пользователей, работающих как в ведомстве
Роскартографии, так и в других министерствах и ведомствах.
Руководство включает пять разделов и десять
приложений.
В разделе 1 «Общая часть» дано общее представление об
основных понятиях в геодезии, взаимосвязях геодезических данных, получаемых
различными методами, основных системах координат, используемых в геодезии. Дано
описание СК-42 и СК-95 и методов, использованных при создании этих систем
координат. Приведено описание современных работ, направленных на
совершенствование государственной геодезической основы, уже сейчас обеспечивающих
возможность контроля СК-95 и ее более эффективного использования в связи с
широким использованием спутниковых методов при выполнении геодезических работ.
В разделе 2 рассматриваются общие рекомендации по
решению задач, связанных с переходом от СК-42 к СК-95.
Раздел 3 посвящен сравнительному анализу
деформаций СК-42 и СК-95 в представлении их в виде деформаций ГГС в этих
системах.
В разделе 4 дано общее описание средств хранения
геодезических данных федерального уровня, обеспечивающих исходную основу
практического использования СК-95, и структуры банка геодезических данных.
В разделе 5 дано описание стандартных возможностей
использования СК-95 и данных вновь создаваемых точных государственных
геодезических сетей при выполнении геодезических работ различного назначения с
применением современных спутниковых GPS/ГЛОНАСС
технологий.
В прил. 1 даны параметры связи между системами
координат СК-95 и ПЗ-90.
В прил. 2 приведен удобный для реализации на ПЭВМ
алгоритм прямого и обратного перехода от геодезических координат к
пространственным прямоугольным координатам.
В прил. 3 и 4 дано описание процедур получения и
использования цифровых моделей преобразования координат с использованием
специальных программных средств общего пользования и приведены практические
примеры применения таких моделей для преобразования координат между системами
СК-42 и СК-95.
В прил. 5 и 6 дано описание процедур получения и
использования параметров ортогонального преобразования координат и приведены
практические примеры использования преобразований такого вида применительно к
задачам перехода между системами СК-42 и СК-95.
В прил. 7 приведена карта-схема зон деятельности
ответственности АГП на территории Российской Федерации.
В прил. 8 приведена схема расположения регионов,
для которых требуется корректировка карт масштабов 1:10000, 1:125000, 1:50000.
В прил. 9 приведена карта-схема высот квазигеоида
над эллипсоидом Красовского на территорию России.
В прил. 10 приведена карта-схема высот квазигеоида
над общим земным эллипсоидом на территорию России.
1. ОБЩАЯ ЧАСТЬ
Геодезические измерения служат для
математического описания физической поверхности Земли в единой системе
координат. Результаты геодезических измерений, как исходные данные для решения
геодезических задач такого рода, относятся к поверхности эллипсоида. Параметры
земного эллипсоида выводились многократно учеными разных стран на основании
астрономо-геодезических, гравиметрических, а позднее и спутниковых данных
измерений. В разных странах используют различные эллипсоиды.
На рис. 1 показан эллипсоид вращения с центром О,
осью вращения Z, экваториальным эллипсом, проходящим
через плоскость OXY, и меридианным эллипсом, проходящим через
точку начала счета долгот и через плоскость OXZ. К параметрам земного эллипсоида относятся:
а - большая (экваториальная)
полуось эллипсоида;
b - малая (полярная) полуось эллипсоида;
a - полярное сжатие эллипсоида: a = (а - b)/a;
е - первый
эксцентриситет меридианного эллипса: е2 = (а2
- b2)/а2 = 2a - a2.
Система геодезических (географических)
координат определяется геодезическими широтой В, долготой L и геодезической высотой Н.
Геодезическая широта В - угол между
нормалью к поверхности эллипсоида в исследуемой точке и плоскостью экватора.
Геодезическая долгота L - двугранный угол, образованный плоскостью начального меридиана и
плоскостью меридиана исследуемой точки.
Геодезическая высота Н - расстояние
от исследуемой точки по нормали к эллипсоиду до его поверхности.
Широты точек, расположенных в северном
полушарии от 0° на экваторе до +90° на Северном полюсе, называют северными,
широты точек южного полушария от 0° на экваторе до +90° на Южном полюсе - южными.
Долготы точек, расположенных восточнее нулевого меридиана до меридиана 180°,
называются восточными, долготы точек, расположенных западнее начального
меридиана от 0° на начальном меридиане до 180° на противоположном меридиане - западными.
Чтобы избежать смену направлений отсчета
координат в полушариях, наряду с указанными выше, применяют оцифровки координат,
изменяющихся по широте от -90° на Южном полюсе до +90° на Северном полюсе, и по
долготе - от 0° до 360°: в Восточном полушарии от 0° до 180°, и далее в
Западном полушарии от 180° до 360°. При этом отпадает необходимость пояснений в
каких полушариях находится исследуемая точка.
Астрономические координаты, относящиеся к
уровенной поверхности, определяются астрономическими широтой и долготой.
Отвесная линия - нормаль к уровенной
поверхности.
Астрономическая широта j - угол между отвесной линией в исследуемой точке и плоскостью
экватора.
Астрономическая долгота l - двугранный угол, образованный плоскостью начального меридиана и
плоскостью астрономического меридиана исследуемой точки, при этом под
плоскостью астрономического меридиана понимается плоскость, проходящая через
отвесную линию в этой точке и параллельная оси мира.
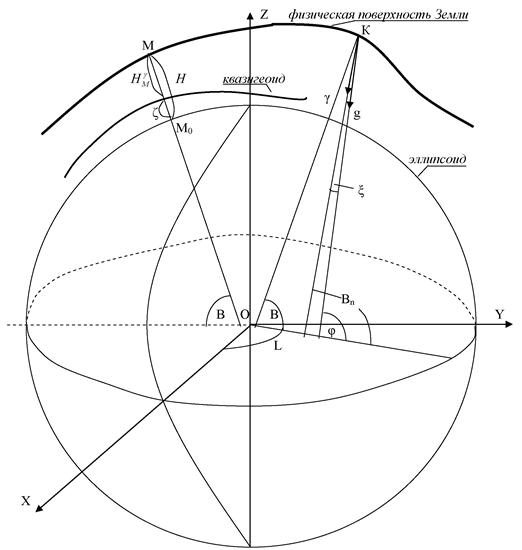
Рис. 1.
Геодезические широта В, долгота L, высота Н
и прямоугольные пространственные координаты X, Y, Z.
На рис. 1 обозначено:
Вп - нормальная геодезическая широта;
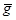 - направление силы тяжести в точке К на поверхности Земли;
- направление силы тяжести в точке К на поверхности Земли;
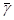 - направление
касательной к силовой линии нормального поля в точке К.
- направление
касательной к силовой линии нормального поля в точке К.
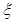 - составляющая
уклонения отвесной линии в плоскости меридиана;
- составляющая
уклонения отвесной линии в плоскости меридиана;
j, l - астрономические
широта и долгота;
Н - геодезическая высота в точке М, равная 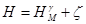 ,
,
где
Нg -
нормальная высота в точке М;
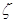 - высота
квазигеоида (аномалия высоты) в точке М.
- высота
квазигеоида (аномалия высоты) в точке М.
В геодезических работах обязательно
учитываются различия между геодезическими и астрономическими координатами,
обусловленные влиянием выбора размеров и ориентировки референц-эллипсоида и
уклонениями отвесных линий.
Астрономо-геодезическое уклонение отвесной
линии (в геометрическом определении) - угол между направлениями отвесной линии
и нормали к референц-эллипсоиду.
Составляющие астрономо-геодезического
уклонения в плоскости меридиана xАГ и в плоскости первого вертикала hАГ определяются
из сравнения геодезических В, L и астрономических j, l координат:
xАГ = j - B - 0,171²Hsin2B,
hАГ = (l - L)cosВ.
Разность геодезического АГ
и астрономического азимутов aАСТР некоторого направления в данной точке определяется из выражения:
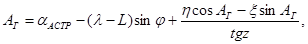
где z - зенитное расстояние направления в данной точке.
Полное уклонение отвесной линии (в
физическом определении) и - угол между касательными к силовым линиям
реального и нормального полей силы тяжести, то есть угол между направлением
действительной силой тяжести g
и направлением нормальной
силы тяжести у в исследуемой точке.
Составляющие уклонения отвесной линии в
первом вертикале в физическом и геометрическом определении совпадают, так как
силовые линии нормального поля силы тяжести - плоские кривые, лежащие в
меридиональных плоскостях.
Составляющая уклонения отвесной линии в
плоскости меридиана x¢ (в физическом определении) - угол между
касательной к силовой линии нормального поля и проекцией силовой линии
реального поля силы тяжести на меридиональную плоскость.
x¢ = j - Вп
= j - В - dВ,
где Вп - нормальная широта;
dВ = Вп
- В = 0,171² × H
× sin2B;
Н - геодезическая высота.
Абсолютное уклонение отвесной линии -
уклонение отвесной линии, определяемое относительно нормали к общему земному
эллипсоиду.
Относительное уклонение отвесной линии -
уклонение отвесной линии, определяемое относительно нормали к референц-эллипсоиду.
Разности между относительными x¢, h и абсолютными 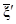 ,
, 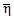 составляющими
уклонения отвесной линии вычисляют следующим образом:
составляющими
уклонения отвесной линии вычисляют следующим образом:
(x¢ - 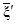 ) = exsinL - eycosL,
) = exsinL - eycosL,
(h - 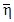 ) = (excosL + eysinL)sinL + ezcosB,
) = (excosL + eysinL)sinL + ezcosB,
где sx, sy, sz - угловые элементы ориентирования референцной системы относительно
общеземной.
Геодезическая высота Н равна сумме
нормальной высоты Нg и высоты квазигеоида x:
Н = Нg + z.
Нормальная высота Нg определяется следующим выражением:
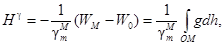
где WO, WM - значения потенциалов силы тяжести для уровенных поверхностей,
проходящих начальный пункт (футшток) на уровне моря (точку О) и через
точку М. Разность потенциалов WO
- WM называют геопотенциальной отметкой точки М;
g - значения силы тяжести в пунктах нивелирного хода;
dh - элементарное измеренное превышение;
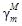 - среднее
значение нормальной силы тяжести на отвесной линии ММ1:
- среднее
значение нормальной силы тяжести на отвесной линии ММ1:
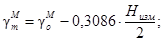
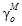 у1 - нормальная сила тяжести на поверхности относимости, вычисленная по
нормальной формуле как функции широты ВM.
у1 - нормальная сила тяжести на поверхности относимости, вычисленная по
нормальной формуле как функции широты ВM.
Практически расчет нормальной высоты 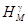 в точке М
относительно точки K
выполняют с использованием
следующей формулы:
в точке М
относительно точки K
выполняют с использованием
следующей формулы:
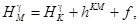
где 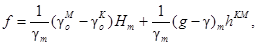
hKM - измеренное превышение репера М над репером K;
Нт - средняя высота реперов K и М;
(g - g)т
- среднее арифметическое из
аномалий силы тяжести в точках K и М.
Определение общего земного эллипсоида
(абсолютного земного эллипсоида) и нормального потенциала выполняется при
следующих условиях:
1. Масса М0 эллипсоида
равна массе Мз Земли.
2. Центр эллипсоида совпадает с центром
масс Земли.
3. Разность (АЭ - СЭ)
между экваториальным и полярным моментами инерции эллипсоида равна С02
- разности между средним из экваториальных и полярных моментами инерции Земли.
4. Координатная ось Z совпадает с осью вращения Земли.
5. Потенциал U0 на эллипсоиде равен потенциалу Земли на уровне
моря W0.
Референц-эллипсоид (относительный
эллипсоид) - эллипсоид определенных размеров, таким образом ориентированный в
теле Земли, что геодезические координаты какого-либо одного пункта поверхности
Земли оказываются равными наперед заданным величинам и при этом малая ось
эллипсоида параллельна оси вращения Земли.
После установления параметров
ориентирования референц-эллипсоида задача определения геодезических координат
других пунктов, расположенных на территории данного государства, формально
сводится к определению приращений этих координат относительно исходного пункта.
Для определения этих приращений координат изучаемая территория покрывается
триангуляционными и спутниковыми сетями,
полигонометрическими ходами и нивелирными
полигонами.
Системы координат СК-42 и СК-95 формально
являются плановыми системами координат. Однако во многих случаях результаты
геодезических определений бывают представлены одновременно и плановыми
координатами и высотами. При использовании спутниковых методов пространственное
представление положений пунктов является стандартным. Во многих программных
приложениях при обработке координат в системах СК-42 и СК-95 пространственное
представление положений пунктов может быть обязательным.
1.1.
Система координат 1942 года
1.1.1. Началом истории построения в нашей
стране единой геодезической системы координат можно считать 1816 год. С этого
года начались работы под руководством академика Петербургской Академии Наук,
основателя и первого директора Пулковской обсерватории В.Я. Струве и генерала
от инфантерии, почетного члена Петербургской Академии Наук К.И. Теннера по
проложению триангуляционного ряда по территории России от устья Дуная до
Северного Ледовитого океана через Финляндию с включением территорий Швеции и
Норвегии. Этот ряд триангуляции, протяженностью 25°20¢, получил в последствии название дуги
Струве.
В 1898 году Корпусом Военных Топографов под
руководством генерала К.В. Шарнгорста было начато уравнивание разрозненных
«губернских триангуляции», покрывавших страну от западных границ до Урала,
включая Кавказ. Завершена эта работа была только в 1926 году изданием силами
Военнно-топографической службы каталога Шарнгорста. Референц-эллипсоидом служил
эллипсоид Бесселя, а исходными пунктами являлись астрономическая обсерватория в
Дерпте и пункты триангуляции меридианной дуги Струве.
1.1.2. Началом следующего этапа построения
единой системы координат на всю территорию России является 1928 год, когда
Главным геодезическим управлением СССР была утверждена единая схема и программа
развития государственной триангуляции страны, предложенная Ф.Н. Красовским. В
схеме Ф.Н. Красовского передача координат на большие расстояния осуществляется
проложением по возможности вдоль меридианов и параллелей звеньев (рядов)
триангуляции 1 класса, образующих при взаимном пересечении полигоны с
периметром 800 - 1000 км. Звено триангуляции 1 класса длиной обычно не более
200 км состоит из треугольников, близких к равносторонним, или из комбинации
треугольников, геодезических четырехугольников и центральных систем. Длины
сторон в звеньях триангуляции 1 класса составляют, как правило, не менее 20 км.
На концах звеньев триангуляции 1 класса измерялись базисные стороны
непосредственно прибором Едерина (инварными проволоками) или светодальномером.
На обоих концах базисных сторон (в вершинах полигонов) определялись пункты
Лапласа (астрономические определения широт, долгот и азимутов). Звено
полигонометрии 1 класса вытянуто и состоит не более чем из 10 сторон длиною 20
- 25 км. На обоих концах крайних сторон звена (в вершинах полигонов)
определяются пункты Лапласа с целью исключения накопления ошибок от полигона к
полигону и решения редукционных задач высшей геодезии. Для решения редукционных
задач необходимо знать составляющие уклонения отвесных линий в плоскости меридиана
x и в плоскости первого вертикала h.
Государственная геодезическая сеть
подразделялась на сети 1, 2, 3 и 4 классов, различающихся между собой точностью
измерений углов и расстояний, длиной сторон сети и порядком последовательного
развития. Основные характеристики построения астрономо-геодезической сети
приведены в табл. 1
в соответствии с [6,
9, 13], [12, с. 360].
В 1930 году под общим руководством Ф.Н.
Красовского вычислительное бюро Главного геодезического управления приступило к
уравниванию 8 полигонов 1 класса для Европейской части СССР. Позднее к этим
полигонам был присоединен Уральский полигон. Вычисления велись относительно
эллипсоида Бесселя методом развертывания, за начальный пункт принимался пункт
Саблино. Основная особенность и главный недостаток метода развертывания состоит
в том, что результаты измерений, выполненные на земной поверхности и
редуцированные к уровню моря при дальнейшей обработки считались выполненными на
поверхности референц-эллипсоида без каких либо поправок за несовпадение поверхности
эллипсоида и уровенной поверхности нулевой высоты.
Работы по уравниванию триангуляции были
завершены в 1932 году и принятая система координат получила название системы
1932 года.
В те же годы в ЦНИИГАиК под руководством
Ф.Н. Красовского и А.А. Изотова начались работы по выводу референц-эллипсоида,
наилучшим образом подходившего для территории СССР. Под руководством и участием
М.С. Молоденского велись работы по определению высот геоида по данным
астрономо-гравиметрического нивелирования.
1.1.3. В 1942 году начались работы по
переуравниванию АГС. Совместным решением Главного управления геодезии и
картографии (ГУГК) и Военно-топографического управления Генерального Штаба
Министерства Обороны (ВТУ ГШ МО) от 4 июня 1942 года в качестве
референц-эллипсоида при уравнивании был принят эллипсоид (в последующем
получившего имя Красовского) со следующими параметрами:
большая полуось а = 6378245,0 м и обратное
сжатие a = 298,3,
а систему координат, в которой велись вычисления, было решено
именовать системой координат 1942 года.
Установление системы координат 1942 года
предполагало также вывод значений исходных геодезических дат в исходном пункте
геодезической сети Пулково. В состав исходных геодезических дат входят
геодезические широта и долгота исходного пункта на референц-эллипсоиде
Красовского, геодезический азимут исходного направления, составляющие уклонения
отвесной линии и высота квазигеоида над эллипсоидом Красовского в исходном
пункте. Эти данные в совокупности определяют пространственную ориентировку осей
референц-эллипсоида в теле Земли при выполнении следующих теоретически строгих
условий:
- малая ось эллипсоида параллельна
направлению к положению среднего полюса;
- плоскость нулевого меридиана параллельна
плоскости начального астрономического меридиана;
- поверхность референц-эллипсоида имеет в
среднем наименьшие уклонения от поверхности геоида на всей территории
расположения обрабатываемой геодезической сети.
Реальная строгость выполнения перечисленных
условий определяется точностью всех использованных астрономо-геодезических
данных и не зависит от конкретного выбора исходного пункта. Значения исходных
геодезических дат устанавливают систему отсчета координат, но не определяют
внутреннюю точность самой геодезической сети. Точность взаимного положения геодезических
пунктов в сети также не зависит от местоположения исходного пункта, а также от
значений исходных геодезических дат.
Подобное установление по существу
референцных систем координат был единственно возможным в то время при использовании
традиционных астрономо-геодезических измерений, выполняемых на земной
поверхности. Исходные геодезические даты лишь частично определяют
пространственное положение референцной системы в теле Земли через взаимное
положение поверхности референц-эллипсоида и геоида для данной территории.
Однако положение центра референц-эллипсоида относительно центра масс Земли
остается неизвестным без привлечения дополнительной информации. Например, высот
геоида над общим земным эллипсоидом или координат некоторого количества
пунктов, известных в референцной и общеземной геоцентрической системе
координат.
При установлении системы координат 1942
года в уравнивание вошли 87 полигонов АТС, покрывавших большую часть
Европейской территории СССР и узкой полосой распространяющих координаты до
Дальнего Востока. Обработка выполнялась на эллипсоиде Красовского с
использованием метода проектирования. Метод проектирования в отличие от метода
развертывания предполагал редуцирование данных геодезических измерений с земной
поверхности через поверхность уровня моря на поверхность референц-эллипсоида.
Определение высот квазигеоида и составляющих уклонений отвесных линий,
необходимых для такого редуцирования, выполнялось с использованием
гравиметрических данных: сначала для повышения точности интерполяции
астрономо-геодезических уклонений отвеса и для расчета приращений высот
квазигеоида, а затем с развитием гравиметрического метода высоты квазигеоида и
составляющие уклонений отвесных линий определялись независимо от
астрономо-геодезических данных.
Постановлением Совета Министров СССР от 7
апреля 1946 года № 760 на основе результатов выполненного уравнивания была
введена единая система геодезических координат и высот на территории СССР -
система координат 1942 года.
Дальнейшее распространение системы
координат 1942 года на территорию СССР проводилось последовательно несколькими
крупными блоками полигонов триангуляции и полигонометрии 1 класса. При
присоединении каждого очередного блока координаты пунктов на границах блоков
уравненной сети принимались за жесткие. Для сгущения АГС, сформированной в виде
системы полигонов, выполнялось их заполнение сплошными сетями триангуляции 2
класса (рис. 2)
[6]. Реальная схема полигонов рядов
триангуляции 1 класса часто существенно отличалась от приведенной на этом
рисунке.
Сплошные сети триангуляции 2 класса
уравнивались в пределах отдельных полигонов с использованием уравненных
координат пунктов триангуляции 1 класса в качестве исходных.
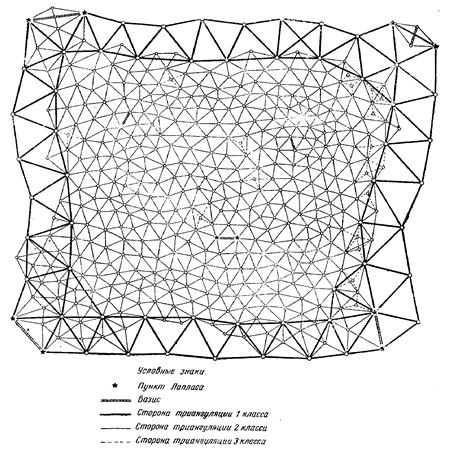
Рис. 2. Схема
полигона триангуляции 1 класса и заполняющей сети триангуляции 2 класса
1.2. Система координат 1995 года
1.2.1. Развитие традиционной
астрономо-геодезической сети для всей территории СССР было завершено к началу
80-х годов.
К этому времени стала очевидной
необходимость выполнения общего уравнивания АТС без разделения на ряды
триангуляции 1 класса и сплошные сети 2 класса. Раздельное уравнивание
полигонов 1 класса и последующая вставка в них сплошных сетей 2 класса
приводили, как к недопустимо большим ошибкам в координатах самих пунктов 1
класса, так и к значительным деформациям сплошных сетей 2 класса вблизи рядов 1
класса и особенно вблизи углов полигонов [1, 7,
9, 13]. В то же время было показано, что
сплошная сеть пунктов 1 - 2 классов потенциально представляет собой значительно
более жесткое построение.
В целях подготовки к сплошному уравниванию
в 80-х годах было выполнено несколько вариантов общего полигонального
уравнивания АТС. С учетом результатов этого уравнивания выполнялось повторное
уравнивание линий астрономо-гравиметрического нивелирования с соответствующим
последовательным уточнением карт высот квазигеоида над эллипсоидом Красовского.
Уточненная карта высот квазигеоида была составлена в 1987 году, данные которой
были использованы затем в общем уравнивании АТС как свободной сети.
В мае 1991 года общее уравнивание АТС было
завершено. По результатам уравнивания получены следующие основные характеристики
точности АТС [7,
9]:
• средняя квадратическая ошибка
направления - 0,7²;
• средняя квадратическая ошибка
измеренного азимута - 1,3²;
• относительная средняя квадратическая
ошибка измеренных базисных сторон - 1:260000;
• средняя квадратическая ошибка
взаимного положения смежных пунктов - 2 - 4
см;
• средняя квадратическая ошибка
передачи координат от исходного пункта на
пункты на краях сети по каждой координате
- 1 м.
Уравненная астрономо-геодезическая сеть
включала в себя 164306 пунктов 1 и 2 классов, 3,6 тысяч геодезических азимутов,
определенных из астрономических наблюдений, и 2,8 тысяч базисных сторон,
расположенных через 170 - 200 км.
1.2.2. К моменту завершения общего уравнивания
АТС на территории нашей страны независимо были созданы две спутниковые
геодезические сети: космическая геодезическая сеть ВТУ ГШ МО и доплеровская
геодезическая сеть ГУГК.
Космическая геодезическая сеть (КГС) ВТУ ГШ
МО на территории бывшего СССР включала в себя 26 стационарных
астрономо-геодезических пунктов при расстояниях между смежными пунктами от 500
до 1500 тыс. км. Координаты пунктов КГС были определены по фотографическим,
доплеровским, дальномерным радиотехническим и лазерным наблюдениям ИСЗ системы
ГЕОИК. Точность определения взаимного положения любых пунктов КГС
характеризовалась средними квадратическими ошибками, равными 0,3 - 0,4 м.
Использованные при построении КГС орбитальные методы космической геодезии
обеспечивали определение координат непосредственно в геоцентрической системе
координат с началом координат, теоретически совпадающим с центром масс Земли, и
осью Z, направленной к положению среднего
полюса. Система координат КГС, практически реализованная координатами ее
пунктов, является составной частью более широкого набора фундаментальных
геодезических параметров, получивших название «Параметры Земли 1990 года»
(ПЗ-90). Этот же шифр получила и сама система координат.
Доплеровская геодезическая сеть ГУГК (ДГС)
состояла из 131 пункта, координаты которых определялись по доплеровским
наблюдениям ИСЗ системы TRANSIT.
Точность определения взаимного положения пунктов при среднем расстоянии между
ними 500 - 700 км характеризовалась средними квадратическими ошибками, равными
0,4 - 0,6 м. ДГС строилась в своей собственной системе координат WGS-84, близкой к геоцентрической, но по ряду
причин точно не совпадающей с системой координат ПЗ-90, и существенно
отличающейся по точности от системы координат с тем же наименованием WGS-84, которая фактически существует сейчас
на время написания данного руководства.
1.2.3. Для использования потенциала всех трех
перечисленных сетей, как независимых построений, и достижения максимально
высокой точности распространения государственной системы координат на всю
территорию бывшего СССР было выполнено совместное уравнивание АТС, ДГС и КГС. В
совместное уравнивание были включены все указанные пункты КГС и ДГС и общие с
ними (совмещенные или близко расположенные и привязанные) пункты АТС.
Дополнительно в общее уравнивание были
включены значения геоцентрических радиусов-векторов для части пунктов
объединенной сети и сеть из семи пунктов, построенная по наблюдениям спутников GPS для точной привязки о. Сахалин к АТС на
материке.
Географическое положение пунктов
геодезических сетей, включенных в совместное уравнивание показано на рис. П5.2 Приложения 5.
Значения геоцентрических радиусов-векторов
вычислялись с использованием параметров общеземного эллипсоида и высот пунктов
над этим эллипсоидом как суммы высот квазигеоида и нормальных высот. Высоты
квазигеоида вычислялись с использованием гравиметрических данных и планетарной
модели гравитационного поля Земли. Начало системы координат, к которой
относятся получаемые радиусы вектора, теоретически совпадает с центром масс
Земли. Радиусы-вектора были вычислены для 35 пунктов КГС или ДГС, расположенных
не ближе 1000 км друг от друга, чтобы можно было считать эти значения
независимыми друг от друга.
Уравнивание выполнялось в пространственной
системе координат. Поэтому данные о плановых координатах по результатам общего
уравнивания АТС были дополнены данными о геодезических высотах пунктов над
эллипсоидом Красовского. Значения этих высот получались как сумма нормальных
(нивелирных высот) пунктов и высот квазигеоида. Последние получались по данным
обработки астрономо-гравиметрического нивелирования, выполненного в ЦНИИГАиК в
1993 г. с использованием данных общего уравнивания АТС 1991 г. В процессе
совместного уравнивания было проведено дополнительное уточнение этих данных для
территории Дальнего востока, Чукотки и Камчатки.
Все данные включались в общее уравнивание с
учетом их ковариационных матриц, которые или были получены непосредственно при
построении уравниваемых сетей (КГС и ДГС) или специально моделировались
(плановые координаты и высоты для АТС, геоцентрические радиусы-вектора пунктов,
сеть привязки о. Сахалин). Совместное уравнивание выполнялось в несколько
этапов (приближений) с последовательной корректировкой используемых
ковариационных матриц.
За опорную систему, в которой получались
окончательные уравненные значения координат, была выбрана система координат
КГС. В качестве определяемых неизвестных в уравнивание входили поправки в три
пространственные координаты пунктов и дополнительные параметры координатных
преобразований, обеспечивающих преобразование каждой из других групп данных в
систему координат КГС. При включении в уравнивание данных ДГС и АТС
дополнительно определялось по семь параметров ортогонального координатного
преобразования (три смещения, три разворота и масштабная поправка). При
включении в уравнивание геоцентрических радиусов векторов определялись
дополнительно три параметра смещения и масштабная поправка. Включение сети
привязки Сахалина дополнялось определением трех параметров смещения.
1.2.4. В результате такого совместного
уравнивания была построена геодезическая сеть, содержащая 134 пункта при
среднем расстоянии между смежными пунктами 400 - 500 км. При этом уравненные
координаты были получены в системе ПЗ-90, точнее в ее частной реализации
совокупностью координат всех пунктов КГС, вошедших в уравнивание. Для
использования этих данных для окончательного общего уравнивания АТС уравненные
координаты были предварительно переведены в референцную систему, достаточно
близкую к СК-42. Из большого числа возможных способов формирования референцной
системы был выбран следующий вариант. Направление осей и масштаб референцной
системы совпадает с таковыми в упомянутой выше реализации системы координат
ПЗ-90, а положение начала системы выбирается так, чтобы в результате координаты
пункта Пулково во вновь создаваемой референцной системе были равны его
координатам в системе СК-42. Такому выбору новой референцной системы,
получившей название «Система координат 1995 года», соответствуют три параметра
связи с ПЗ-90, значения которых приведены в Приложении 1.
Сеть из 134 пунктов с согласованной системой
плановых координат в СК-95 и геодезических высот была использована как жесткая
исходная основа в последующем заключительном уравнивании всех 164306 пунктов
триангуляции и полигонометрии 1 и 2 классов.
Точность определения взаимного планового
положения пунктов, полученная из заключительного уравнивания АГС 1995 года,
характеризуется средними квадратическими ошибками:
• 0,02 - 0,04 м
- при расстояниях до нескольких десятков
километров;
• 0,2 - 0,5 м
- при расстояниях от 1 до 9 тысяч
км.
Объем измерительной астрономо-геодезической
информации, обработанной при совместном уравнивании АГС, ДГС и КГС для
установления системы координат 1995 года, превышает на порядок объем
измерительной информации, использованной для установления системы координат
1942 года.
Оценка точности уравненных координат,
полученная в процессе выполнения общего уравнивания, основана на оценках
внутренней согласованности всех включенных в уравнивание данных и имеет
обобщенный характер. Более объективная и детальная оценка может быть получена
только сравнением положений пунктов в СК-95 с какими-либо более точными и
независимо полученными результатами. Реально такую возможность представляют
данные, получаемые в процессе выполняемых в настоящее время работ по построению
ФАГС и ВГС. Такое сравнение показывает, что внутренние деформации СК-95 в целом
по всей сети могут быть оценены их средними квадратическими значениями, равными
примерно 30 см по координатам «х» и около 20 см по координатам «у». Под
внутренними деформациями в данном случае понимаются те ошибки координат
пунктов, которые не могут быть исключены в результате ортогонального
преобразования. Более подробно информация о сетях ФАГС и ВГС и оценках
деформаций СК-95 дана в подразделах 1.3.3 и 1.3.4, разделе 3 и Приложении 5.
1.2.5. Геодезические высоты пунктов ГГС
определяют или как сумму нормальной высоты и высоты квазигеоида над отсчетным
эллипсоидом, или непосредственно методами космической геодезии, или путем
привязки к пунктам с известными геоцентрическими координатами.
Нормальные высоты пунктов ГГС определяются
в Балтийской системе высот 1977 года, исходным началом которой является нуль
Кронштадтского футштока.
Карты высот квазигеоида над общим земным
эллипсоидом и референц-эллипсоидом Красовского на территории Российской
Федерации издаются Роскартографией и Топографической службой ВС РФ.
КГС создавалась при метрологическом
обеспечении эталонными средствами Госстандарта СССР. Масштаб задавался Единым
государственным эталоном времени-частоты-длины при длине метра как расстояния,
проходимого светом в вакууме за 1:299792458-ую долю секунды, в соответствии с
резолюцией XVII Генеральной конференции по мерам и весам
(октябрь 1983 г.). При построении КГС в системе координат ПЗ-90 использовались
шкалы атомного ТА (SU) и координированного UTC (SU) времени, задаваемые существующей эталонной базой Российской
Федерации, а также параметры вращения Земли и поправки для перехода к
международным шкалам времени, периодически публикуемые Госстандартом России в
специальных бюллетенях Государственной службы времени и частоты (ГСВЧ).
Соответствующие эталонные масштаб и ориентировка переданы на ГГС косвенным
образом через масштаб и ориентировку КГС.
1.3. Основные
положения дальнейшего развития государственной геодезической сети Российской
Федерации
1.3.1. О концепции развития
системы геодезического обеспечения
Обеспечивая многие практические потребности
экономики и обороны страны, существующие наземные геодезические методы по
точности, оперативности, экономической эффективности не соответствуют некоторым
крайне важным современным требованиям науки и практики. В частности
требованиям, возникающим при крупномасштабных съемках городов и поселков, при
строительных изысканиях, при геодезическом обеспечении обороны страны, решении
задач морской и авиационной навигации и изучении природной среды. Эти задачи на
современном уровне требований могут быть решены только с использованием
спутниковых методов. Ядром современных геодезических спутниковых методов
являются технологии оперативных координатных определений (в том числе и
высотных), основанные на использовании глобальных навигационных спутниковых
систем ГЛОНАСС и GPS [7, 9].
Задание, поддержание и воспроизведение
системы координат на уровне требований, обеспечивающих решение фундаментальных
перспективных задач в области геодезии, геофизики, геодинамики и космонавтики,
обусловливает необходимость создания геодезической сети на качественно новом,
более высоком, уровне точности.
Система координат СК-95 и существующая сеть
ГГС, созданная главным образом традиционными методами геодезии, не могут, в
качестве исходной геодезической основы, в полной мере обеспечить возможности
для реализации всего потенциала современных спутниковых методов. В данном
случае имеется в виду не только реальная точность пунктов ГГС в СК-95, но и
недостаточная их доступность и возможность обеспечения благоприятных условий
для спутниковых наблюдений. Современные спутниковые ГЛОНАСС/GPS технологии даже в оперативном режиме
обеспечивают возможность передачи координат на большие расстояния и с меньшими
относительными ошибками, чем в мы имеем сейчас в ГГС. Еще в большей мере
подобное точностное несоответствие имеет место при решении задач геодинамики.
Использование современных спутниковых технологий при решении различных
практических и научных задач требует и развития соответствующей им высокоточной
и легко доступной исходной геодезической основы.
Построение таких опорных сетей - составная
часть работ по созданию новой высокоэффективной государственной системы
геодезического обеспечения территорий Российской Федерации, основанной на
применении методов космической геодезии и использовании глобальных
навигационных спутниковых систем ГЛОНАСС и GPS.
Использование методов космической геодезии
определения координат принципиально изменяет решение задач всей системы
геодезического обеспечения [3].
В сравнении с традиционными методами ГЛОHACC/GPS-технологии
обладают следующими основными преимуществами:
- возможностью передачи координат
практически на любые расстояния с оперативностью и точностью, недоступными для
традиционных наземных методов;
- значительным снижением затрат в связи с
отсутствием необходимости сооружения геодезических знаков;
- уменьшением риска при выполнении работ,
особенно в труднодоступных и климатически сложных районах;
- отсутствием требования к взаимной
видимости между пунктами, позволяющим без сооружения геодезических знаков располагать
пункты в местах, более благоприятных для их сохранности и последующего
использования;
- резким понижением требований к плотности
исходной геодезической основы, позволяющим на 2 порядка сократить количество
геодезических пунктов, как при создании Государственных геодезических сетей
нового поколения, так опорных пунктов при выполнении геодезических съемок
широким кругом пользователей;
- большей простотой в организации и
выполнении работ, особенно в труднодоступных и климатически сложных районах;
- большим уровнем автоматизации на всех
стадиях проведения работ, отсутствием технической зависимости от времени суток,
года, погодных условий;
- более высоким уровнем культуры труда при
исполнении геодезических работ;
- лучшими возможностями для объединения точной
плановой и высотной геодезической основы на базе использования единой
технологии, совмещения пунктов носителей координат и высот и связи существующих
плановых и высотных сетей.
Открываются перспективы для создания и
использования автоматизированных систем оперативных съемок, основанных на
совместном использовании ГЛОHACC/GPS-технологий и цифровых наземных, воздушных
и космических оптико-электронных, радиолокационных и других съемочных систем
цифрового картографирования. Применение таких систем может быть особенно
эффективно при проведении городских съемок многоцелевого назначения с
последующей (по мере возникновения потребностей) выборочной целевой обработкой
и при выполнении съемок в чрезвычайных ситуациях в режиме, приближенном к
режиму реального времени.
Одним из наиболее перспективных направлений
оперативного навигационного и геодезического обеспечения потребителя является
создание сетей активных пунктов спутниковых систем координатных определений
реального времени.
Чрезвычайно важной особенностью геодезических
спутниковых технологий является возможность одновременного
определения с сопоставимыми точностями, как плановых
координат, так и геодезических высот.
Появляется вполне реальная возможность
реализации метода спутникового нивелирования, как альтернативы геометрическому
нивелированию, но в значительно более оперативном и дешевом варианте. Однако
для практического применения такого метода необходимо составление по
гравиметрическим и спутниковым данным точных детальных карт высот квазигеоида
на соответствующих территориях - по существу нового точного вида исходного
геодезического обеспечения.
При традиционных видах геодезических
измерений система высотного обеспечения развивалась обособленно от системы
планового обеспечения: высотное и плановое обеспечение создавалось путем
развития двух разных видов геодезических сетей. Плановое обоснование
развивалось на основе плановых геодезических сетей триангуляции и
полигонометрии, а высотное - на основе сетей геометрического нивелирования.
Система нормальных высот на территории
России реализована сетью высокоточного геометрического нивелирования I и II классов -
главной высотной основы (ГВО) страны. Сеть геометрического нивелирования I и II классов общей
протяженностью около 400 тысяч км имеет один исходный пункт Кронштадт, в
котором значение нормальной высоты принимается равным нулю.
Вся сеть нивелирования образует порядка
тысячи замкнутых полигонов, по которым производится уравнивание сети как
свободной с опорой на один исходный пункт. Поэтому система нормальных высот на
всей протяженности нивелирной сети не имеет внешнего контроля, несмотря на то,
что территория России имеет береговую линию протяженностью около 12000 км,
омываемую морями трех океанов, и в каждом из этих морей расположено по
несколько уровнемерных постов, имеющих высокоточную связь с главной высотной
основой. Так как отличие уровня одного моря от другого может достигать метра и
более, то уровнемерные данные не могут служить контролем точности
нивелирования.
Применение ГЛОНАСС/GPS технологий позволяет развивать плановое и высотное обоснование с
помощью одной и той же совокупности геодезических сетей. Для согласования
измеренных величин (нормальных и геодезических высот), получаемых
соответственно по данным нивелирования и данным ГЛОНАСС/GPS измерений, необходимо точное знание высот
квазигеоида.
Новая структура системы геодезического
обеспечения показана на рис. 3.
Применение современных спутниковых
технологий оптимальным образом развивает систему геодезического обеспечения,
создавая условия, в том числе, и для реализации потенциала плановых и высотных
опорных сетей, созданных на основе традиционных методов геодезических
измерений.
Высшим звеном в иерархии опорных
геодезических сетей в системе геодезического обеспечения является одна и та же
совокупность геодезических пунктов спутниковых геодезических сетей ФАГС, ВГС и
СГС-1, которые являются физической реализацией одновременно высокоточной
системы координат и системы нормальных высот.
Структура и технология построения
спутниковых геодезических сетей, создаваемых Роскартографией, определяется,
во-первых, - необходимостью создания единой системы геодезических координат и
поддержания ее на уровне современных требований науки, экономики и обеспечения
безопасности, и, во-вторых, - задачами, возложенными на Роскартографию, по
ведению Службы деформации земной коры, входящей в состав Федеральной системы
сейсмологических наблюдений и прогноза землетрясений.
Существующая геодезическая основа,
созданная с помощью традиционных методов геодезических измерений не
обеспечивает на должном уровне возможности эффективного использования
современных высокоэффективных спутниковых технологий по следующим основным причинам:
- точность существующих геодезических
сетей не отвечает современных требованиям экономики и обороны страны;
- пункты опорных геодезических сетей, как
правило, располагаются в труднодоступных местах, неблагоприятных для их
последующего использования в системе геодезического обеспечения с аппаратурой
ГЛОНАСС/GPS;
- большой объем геодезических пунктов,
существующих опорных геодезических сетей, и места их расположения делают задачу
их поддержания в рабочем состоянии практически трудно выполнимой в современных
условиях.
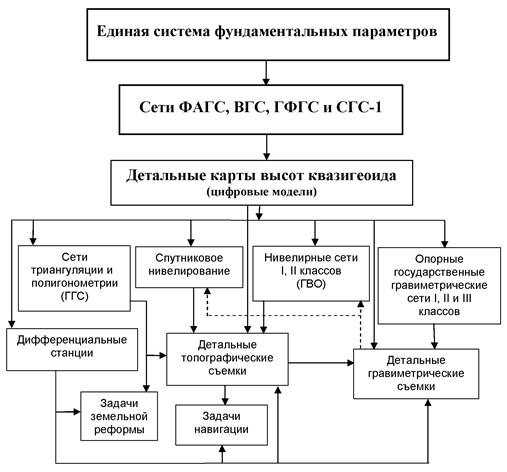
Рис. 3.
Иерархическая структура системы геодезического обеспечения
Государственная геодезическая сеть,
создаваемая в соответствии «Концепцией перехода топографо-геодезического
производства на автономные спутниковые методы координатных определений» (1995
г.) и с «Основными положениями о построении государственной геодезической сети
Российской Федерации» (2003 г.), структурно формируется по принципу перехода от
общего к частному и включает в себя геодезические построения различных классов
точности:
- фундаментальную астрономо-геодезическую
сеть (ФАГС), состоящую из 50 - 70 пунктов, включая пункты космической
геодезической сети, при расстояниях между пунктами, равных 650 - 1000 км. Из
всех пунктов ФАГС 10 - 15 должны быть постоянно действующими, а остальные -
периодически переопределяться группами с цикличностью, зависящей от
геодинамической активности региона;
- высокоточная геодезическая сеть (ВГС),
состоящая из 500 - 700 пунктов, при расстояниях между смежными пунктами, равных
150 - 300 км;
- спутниковая геодезическая сеть 1 класса
(СГС-1) при расстояниях между смежными пунктами, равных 30 - 35 км в обжитых
районах и 40 - 50 км и более - в малообжитых. В экономически развитых районах
пункты СГС-1 могут располагаться и с большей плотностью, в зависимости от
требований министерств и ведомств.
Часть пунктов ФАГС интегрируется в мировую
спутниковую сеть в рамках международных программ.
В первую очередь СГС-1 будет развиваться в
районах с интенсивной хозяйственной деятельностью.
Необходимо особо отметить, что пункты ФАГС
и ВГС связываются не менее чем с 2-мя пунктами ГГС и с 2-мя пунктами ГВО, тем
самым, реализуя и преумножая потенциал старой ГГС, и что пункты ФАГС, ВГС и
СГС-1 располагаются в легко доступных местах.
Таким образом, для создания указанной новой
высокоэффективной государственной системы геодезического обеспечения территории
Российской Федерации, основанной на применении глобальной навигационной
спутниковой системы ГЛОНАСС/GPS и других
средств и технологий, должны выполняться:
1. Высокоточные геодезические измерения с
наземной спутниковой аппаратурой на пунктах создаваемых фундаментальной
астрономо-геодезической сети (ФАГС), высокоточной геодезической сети (ВГС) и спутниковой
геодезической сети 1 класса (СГС-1);
2. Абсолютные измерения значений ускорения
силы тяжести g с помощью высокоточной гравиметрической аппаратуры и
определения нормальных высот на пунктах ФАГС и ВГС;
3. Работы по построению высокоточных карт
высот квазигеоида z гравиметрическим методом, необходимых при
определении нормальных высот Нg с
использованием глобальных навигационных спутниковых систем;
4. Работы по согласованию на
соответствующем уровне точности геоцентрической системы координат, задаваемой
пунктами ФАГС, с международной небесной опорной системой (ICRS - International Celestial Reference System), не связанной более с экватором и
эклиптикой, а зафиксированной относительно системы направлений на 212 квазаров,
принимаемых за неподвижные в пространстве и распределенных по всему небу со
средней плотностью 1 квазар на 194,6 квадратных градуса.
Высокая точность слежения за положениями
инструментов, с которыми наблюдаются и определяются координаты квазаров, и
одновременно за параметрами вращения Земли (ПВЗ), обеспечивающими связь
небесной (ICRS) и новой международной земной опорной
системой (ITRS - International Terresrial Reference System), позволяет успешно решать целый ряд
практических задач.
По измерениям, указанным в п. 1, определяются геодезические координаты:
широта В, долгота L
и высота Н в принятой
системе координат.
По измерениям, указанным в п.п. 1 и 2, осуществляется задание абсолютной
гравиметрической системы. Эти измерения, в частности, позволят в дальнейшем
выявлять возможные причины изменений координат пунктов ФАГС и ВГС во времени.
По высокоточным высотам квазигеоида z (п. 3)
и геодезическим высотам Н (п. 1)
определяются нормальные высоты Нg, ранее определяемые с высокой точностью только из геометрического
нивелирования.
По астрометрическим данным (п. 4) геоцентрическая система координат,
задаваемая пунктами ФАГС, согласовывается на соответствующем уровне точности с
фундаментальными астрономическими (небесными) системами координат.
1.3.2. Основные принципы дальнейшего
развития государственной геодезической сети
Государственная геодезическая сеть,
создаваемая в соответствии с «Основными положениями о построении
государственной геодезической сети Российской Федерации» (2003 г.), структурно
формируется по принципу перехода от общего к частному и включает в себя
геодезические построения различных классов точности:
• фундаментальную астрономо-геодезическую сеть (ФАГС),
• высокоточную геодезическую сеть (ВГС),
• спутниковую геодезическую сеть 1 класса (СГС-1).
На основе этих пунктов создаются системы
постоянно действующих пунктов спутниковых наблюдений с целью обеспечения
возможностей определения координат потребителями в режиме реального времени или
близком к реальному времени.
В указанную систему построений вписываются
также существующие сети триангуляции и полигонометрии 1 ... 4 классов.
По мере развития сетей ФАГС, ВГС и СГС-1
выполняется уравнивание всей ГТС или ее отдельных участков с целью более полной
и быстрой реализации накапливаемой геодезической информации.
1.3.3. Фундаментальная астрономо-геодезическая
сеть
Высший уровень в структуре координатного
обеспечения территории России занимает фундаментальная астрономо-геодезическая
сеть. Она служит исходной геодезической основой для дальнейшего повышения
точности пунктов государственной геодезической сети. ФАГС практически реализует
геоцентрическую систему координат в рамках решения задач координатно-временного
обеспечения (КВО).
Фундаментальная астрономо-геодезическая
сеть состоит из постоянно действующих и периодически определяемых пунктов
Роскартографии, формирующих единую сеть на территории Российской Федерации.
В состав постоянно действующих пунктов ФАГС
по согласованию могут включаться пункты службы вращения Земли Госстандарта
России, пункты спутниковых наблюдений РАН и пункты радиоинтерферометрических
измерений со сверхдлинной базой, а также часть АГП КГС, расположенных на
территории страны. На стадии обработки измерений в состав постоянно действующих
пунктов в ФАГС может также включаться часть пунктов, входящих в международную
геодинамическую сеть пунктов (IGS).
В состав периодически определяемых пунктов
ФАГС могут быть включены пункты Роскартографии, РАН и АГП КГС на территории
страны, не вошедшие в число постоянно действующих пунктов ФАГС, пункты
наблюдений ГЛОНАСС, а также пункты службы вращения Земли Госстандарта России и
пункты, периодически участвующие в программах лазерной локации спутников и
длиннобазисной радиоинтерферометрии.
Расположение остальных пунктов ФАГС
определяется, исходя из решения задач геодинамики и требования равномерного
покрытия всей территории страны.
Расстояние между смежными пунктами ФАГС -
650 ... 1000 км.
Количество, расположение постоянно
действующих и периодически определяемых пунктов ФАГС, состав аппаратуры и
программы наблюдений определяются научно-технической программой построения и
функционирования ФАГС с учетом проектов международного сотрудничества.
Все пункты ФАГС должны быть фундаментально
закреплены с обеспечением долговременной стабильности их положения как в плане,
так и по высоте.
Пространственное положение пунктов ФАГС
определяется методами космической геодезии в геоцентрической системе координат
относительно центра масс Земли со средней квадратической ошибкой 10 ... 15 см,
а средняя квадратическая ошибка взаимного положения пунктов ФАГС должна быть не
более 2 см по плановому положению и 3 см по высоте с учетом скоростей их
изменения во времени. В число основных задач построения ФАГС входит достижение
требуемой точности и достоверное оценивание точности создаваемой новой геоцентрической
системы координат и определение изменений координат пунктов ФАГС во времени.
На пунктах ФАГС выполняются определения
нормальных высот и абсолютных значений ускорений силы тяжести. Определения
нормальной высоты производится нивелированием не ниже II класса точности, абсолютные определения силы тяжести - по
программе определения фундаментальных гравиметрических пунктов.
Периодичность этих определений на пунктах
ФАГС устанавливается в пределах 5 ... 8 лет и уточняется в зависимости от
ожидаемых изменений измеряемых характеристик.
Задаваемая пунктами ФАГС геоцентрическая
система координат согласовывается на соответствующем уровне точности с
фундаментальными астрономическими (небесными) системами координат и надежно
связывается с аналогичными пунктами различных государств в рамках согласованных
научных проектов международного сотрудничества.
Параметры связи между земной системой
координат, задаваемой пунктами ГГС, с фундаментальными астрономическими
(небесными) координатами на адекватном уровне точности устанавливаются
оперативными наблюдениями ГСВЧ и публикуются в специальных бюллетенях этой
службы.
1.3.4. Высокоточная геодезическая
сеть
Второй уровень в современной структуре ГГС
занимает высокоточная геодезическая сеть, основные функции которой состоят в дальнейшем
распространении на всю территорию России геоцентрической системы координат и
уточнении параметров взаимного ориентирования геоцентрической системы и системы
геодезических координат.
ВГС, наряду с ФАГС, служит основой для
развития геодезических построений последующих классов, а также используется для
создания высокоточных карт высот квазигеоида совместно с гравиметрической
информацией и данными нивелирования.
ВГС представляет собой опирающееся на пункты
ФАГС, однородное по точности пространственное геодезическое построение,
состоящее из системы пунктов, удаленных один от другого на 150 ... 300 км.
Пункты ВГС определяются относительными
методами космической геодезии, обеспечивающими точность взаимного положения со
средними квадратическими ошибками, не превышающими 3 мм + 5´10-8 D (где D - расстояние между пунктами) по каждой из
плановых координат и 5 мм + 7´10-8
D по геодезической высоте. Каждый пункт ВГС
должен быть связан измерениями со смежными пунктами ВГС и не менее чем с тремя
ближайшими пунктами ФАГС. В исключительных случаях на труднодоступных
территориях допускается отсутствие связей между смежными пунктами ВГС при
условии их связи с большим количеством близких пунктов ФАГС и использовании
наблюдений большей продолжительности.
На пунктах ВГС нормальные высоты
определяются нивелированием не ниже II класса
точности, абсолютные определения силы тяжести - по программе определения
фундаментальных гравиметрических пунктов. Периодичность этих определений
устанавливается Роскартографией в зависимости от ожидаемых изменений измеряемых
характеристик. Для связи существующей сети с вновь создаваемыми геодезическими
построениями определяется взаимное положение пунктов ФАГС и ВГС с ближними
пунктами АТС со средней квадратической ошибкой, не превышающей 2 см по каждой
координате. Для связи с главной высотной основой пункты ВГС привязываются к
реперам нивелирной сети I ... II классов или совмещаются с реперами
соответствующих линий нивелирования. Существующая сеть пунктов ФАГС и ВГС на
территории России создана в период с 1999 года по 2003 год. Спутниковая
геодезическая сеть на 2003 г. состоит из 212 пунктов, в том числе:
- 19 постоянно действующих пунктов ФАГС;
- 15 периодически определяемых пунктов
ФАГС;
- 178 пунктов ВГС.
Существующая сеть пунктов ФАГС и ВГС на
территории Российской Федерации по состоянию на 2003 год показана на рис. 4.
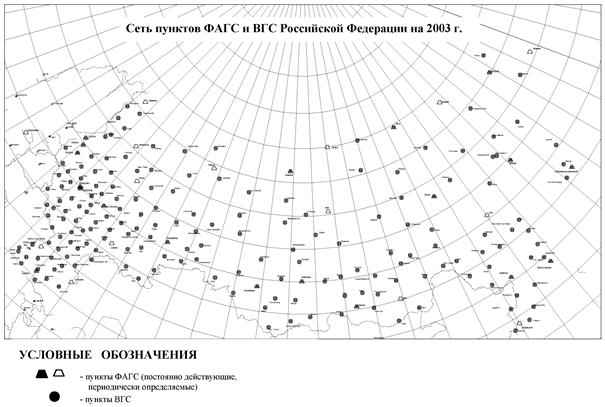
Рис. 4.
Существующая сеть пунктов ФАГС и ВГС на территории Российской Федерации по
состоянию на 2003 год.
1.3.5. Спутниковая геодезическая сеть
I класса, астрономо-геодезическая сеть и
геодезические сети сгущения
Третий уровень в современной структуре ГГС
занимает спутниковая геодезическая сеть 1-го класса, основная функция которой
состоит в обеспечении оптимальных условий для реализации точностных и
оперативных возможностей спутниковой аппаратуры при переводе геодезического
обеспечения территории России на спутниковые методы определения координат.
СГС-1 представляет собой пространственное
геодезическое построение, создаваемое по мере необходимости, в первую очередь,
в экономически развитых районах страны, состоящее из системы легко доступных
пунктов с плотностью, достаточной для эффективного использования всех
возможностей спутниковых определений потребителями, как правило, со средними
расстояниями между смежными пунктами около 25 ... 35 км.
СГС-1 создается относительными методами
космической геодезии, обеспечивающими определение взаимного положения ее
смежных пунктов со средними квадратическими ошибками 3 мм + 1´10-7 D по каждой из плановых координат и 5 мм + 2´10-7 D по геодезической высоте.
СГС-1 может строиться отдельными фрагментами.
Создаваемый фрагмент должен опираться на окружающие пункты ВГС и включать в
себя пункты ФАГС, и ВГС, расположенные на территории фрагмента СГС-1.
Средняя квадратическая ошибка определения положения
пунктов СГС-1 относительно ближайших пунктов ВГС и ФАГС не должна превышать 1
... 2 см в районах с сейсмической активностью 7 и более баллов и 2 ... 3 см в
остальных регионах страны.
Нормальные высоты должны определяться на
всех пунктах СГС-1, либо из геометрического нивелирования с точностью,
соответствующей требованиям к нивелирным сетям II, III классов, либо из спутникового
нивелирования как разности геодезических высот, определяемых относительными
методами космической геодезии, и высот квазигеоида.
Окончательная точность положения пунктов
СГС-1 определяется по материалам обработки в соответствии с методиками по
построению СГС-1, утверждаемыми Роскартографией.
Для связи СГС-1 с АТС и нивелирной сетью
часть пунктов СГС-1 должна быть совмещена или связана с существующими пунктами
АТС и реперами нивелирной сети не ниже III класса. Связь, как правило, должна определяться методами
космической геодезии со средними квадратическими ошибками не более 2 см для
плановых координат при привязке пунктов АТС и 1 см для геодезических высот при
привязке нивелирных реперов. При высотной привязке использование пунктов АТС с
известными нормальными высотами вместо нивелирных реперов не допускается.
Расстояние между пунктами АТС, совмещенными с пунктами СГС-1 или привязанными к
ним, не должно быть больше 70 км при средней плотности СГС-1 и 100 км при
построении разреженной сети СГС-1 в необжитых районах. Расстояние между
нивелирными реперами для связи с пунктами СГС-1 должно быть не более 100 км.
В случае необходимости могут создаваться
геодезические спутниковые сети сгущения в соответствии с методиками,
утверждаемыми Роскартографией.
Повторные определения координат пунктов ГГС
и высот реперов должны планироваться в необходимом объеме и с требуемой
точностью для выявления деформаций земной поверхности и изучения
закономерностей их изменений.
При необходимости повторных определений
координат пунктов в сейсмоактивном регионе построение СГС-1 планируется с
повторным определением пунктов ВГС на этой и смежной территориях.
В районах происшедших землетрясений с
магнитудой 5 и более повторное определение координат пунктов геодезических
сетей проводится в возможно короткие сроки. Протяженность создаваемых
фрагментов СГС-1, включая пункты ВГС, на которые опираются фрагменты СГС-1, должна
обеспечивать опору на пункты, не затронутые влиянием произошедшего
землетрясения. Необходимость повторных определений координат пунктов
геодезических сетей, обусловленная деформациями техногенного происхождения,
обосновывается маркшейдерскими и другими геолого-геофизическими данными.
Пункты СГС-1, совмещенные или связанные с
реперами нивелирной сети I ... III классов, используются для уточнения высот
квазигеоида.
В исключительных случаях в районах, не
обеспеченных необходимыми данными о высотах квазигеоида, для определения
нормальных высот допускается применение тригонометрического нивелирования. В
последнем случае средняя квадратическая ошибка взаимного положения смежных
пунктов по высоте должна быть не более 20 см.
1.3.6. Геодезические сети специального
назначения
Существующая плотность ГГС при условии
применения современных спутниковых и аэросъемочных технологий обеспечивает
решение задач картографирования и обновления карт всего масштабного ряда до
1:500 для городов и 1:2000 для остальной территории.
Геодезические сети специального назначения
создаются в тех случаях, когда дальнейшее сгущение пунктов ГГС экономически
нецелесообразно или когда требуется особо высокая точность геодезической сети.
Геодезические сети специального назначения
создаются в единых государственных системах координат или в местных системах
координат, устанавливаемых для отдельных участков местности.
Учет и хранение исходных данных,
раскрывающих переход от этих местных систем координат к государственным
системам координат (ключи перехода) осуществляется органами государственного
геодезического надзора (госгеонадзора).
1.3.7. Организация работ и
проектирование сетей
Производственный цикл построения
геодезических сетей состоит из следующих основных видов работ: проектирование,
рекогносцировка и закрепление геодезических пунктов, выполнение измерений,
математическая обработка, составление каталогов и технических отчетов.
ФАГС и ВГС создаются в соответствии с
научно-техническим проектом и специальным руководством.
Проектирование геодезических сетей
выполняется с учетом всех ранее исполненных работ после обследования
сохранности геодезических пунктов.
Выбор места расположения геодезического
пункта и типа центра должен обеспечивать долговременную сохранность и
устойчивость пунктов в плане и по высоте в течение длительного периода времени
и удобства его использования.
Пункты СГС-1 располагаются, как правило, в
легко и круглогодично доступных местах с условиями, благоприятными для
спутниковых наблюдений. При соблюдении указанных требований пункты СГС-1 могут
совмещаться с существующими пунктами АТС или реперами нивелирной сети I - III классов.
В геодинамически активных регионах при
выборе местоположения пунктов учитываются данные о вертикальных движениях земной
поверхности, а также данные о структуре разломов земной коры. СГС-1 на
территориях существующих геодинамических и техногенных полигонов проектируется
с учетом уже созданных на них плановых и высотных геодезических построений.
Типы центров устанавливаются в зависимости
от физико-географических условий района работ, глубины промерзания и оттаивания
грунтов, гидрогеологического режима и других особенностей местности.
В целях обеспечения длительной сохранности
центров геодезических пунктов, они подлежат периодическому обследованию и при
необходимости восстановлению.
Геодезический пункт считается утраченным,
если не сохранился ни верхний, ни нижний центр и утрата центра подтверждена
данными инструментально-геодезического поиска.
Предприятия Роскартографии несут
ответственность за поддержание в рабочем состоянии пунктов ФАГС, ВГС и СГС-1 в
пределах закрепленной за ними территории.
1.3.8. Математическая обработка измерений
в ГГС
Математическая обработка измерений в
государственной геодезической сети выполняется поэтапно по мере накопления
материалов.
Математическая обработка геодезических
измерений, выполняемых при построении и модернизации ГГС, включает полевые
вычисления, предварительные вычисления и уравнивание сетей.
Полевые вычисления выполняются с целью контроля
измерений на их соответствие допускам, установленным действующими
нормативно-техническими актами и техническими предписаниями на выполнение
работ. При выполнении работ традиционными геодезическими методами полевые
вычисления выполняются непосредственно на каждом пункте наблюдений.
При использовании спутниковых методов
космической геодезии соответствующие контрольные вычисления должны быть
выполнены до завершения полевых работ на объекте. Объемы и состав полевых
вычислений устанавливаются в технических проектах на выполнение работ и в
соответствующих методических указаниях и инструкциях. При построении ФАГС, ВГС
и СГС-1 полевой контрольной обработке подвергаются, как правило, материалы
наблюдений по взаимной связи пунктов вновь создаваемых и существующих сетей.
Целью предварительных вычислений является
вероятностно-статистический анализ результатов измерений, выявление и
исключение грубых ошибок, вычисление рабочих координат, оценка качества и
подготовка всей измерительной информации к окончательной обработке.
Необходимость выполнения предварительной обработки результатов спутниковых
наблюдений и ее содержание определяются при техническом проектировании работ.
Результаты измерений, прошедших
предварительную обработку, передаются в архивы и банки данных.
Результаты наблюдений ФАГС обрабатываются в
соответствии с программой ее построения. Порядок обработки ВГС, СГС-1, а также
совместной обработки ФАГС, ВГС, СГС-1 и АТС определяется соответствующими
методическими указаниями.
В результате совместной обработки ФАГС,
ВГС, СГС-1 и АТС должны быть получены значения координат пунктов в системах
геодезических и геоцентрических координат, а также параметры перехода,
устанавливающие связь между координатами пунктов в обеих системах.
При уравнивании геодезических сетей 3 и 4
классов в качестве исходных используются уравненные координаты пунктов высших
классов. Измерения, выполненные в сетях 3 и 4 классов, редуцируются методом
проектирования на поверхность отсчетного эллипсоида, а затем, при
необходимости, на плоскость в проекции Гаусса-Крюгера. Для редуцирования
используются нормальные высоты и высоты квазигеоида над эллипсоидом, полученные
в результате совместной обработки ФАГС, ВГС, СГС-1 и АТС.
По результатам совместной обработки ГГС,
данных нивелирования и гравиметрической информации составляется карта высот
квазигеоида на соответствующую территорию.
1.3.9. Каталогизация и хранение
информации
Уравнивание сетей завершается составлением
каталогов координат и высот геодезических пунктов и составлением
научно-технических отчетов. При уравнивании сетей по объектам работ каталоги
координат и технические отчеты составляются отдельно по каждому объекту.
На территорию страны составляются и
издаются каталоги пунктов ГГС, в основной раздел которых помещаются плоские
прямоугольные координаты пунктов 1 ... 4 классов.
Плоские прямоугольные координаты приводятся
в проекции Гаусса-Крюгера с шестиградусными зонами. Осевыми меридианами
шестиградусных зон являются: 21, 27, 33, ..., 177°. Началом координат в каждой зоне является точка пересечения
осевого меридиана с экватором; значение ординаты на осевом меридиане
принимается равным 500 км.
Наряду с плановыми координатами в банках
данных ГГС помещаются нормальные высоты пунктов и высоты квазигеоида.
Уравненные пространственные координаты
пунктов ФАГС, ВГС и СГС-1, скорости их изменения и характеристики точности
хранятся в специальных каталогах на машинных носителях в геоцентрической и
геодезической системах координат с указанием эпох.
Каталоги пространственных прямоугольных
координат пунктов ФАГС, совмещенных с пунктами наблюдений параметров вращения
Земли ГСВЧ, ежегодно публикуются с указанием эпохи в специальных бюллетенях
ГСВЧ.
Порядок и особенности каталогизации пунктов
ГГС регламентируются действующей Инструкцией по составлению и изданию каталогов
геодезических пунктов ГКИНП (ГНТА)-06, утвержденной 6.02.2002 г. руководителем
Федеральной службы геодезии и картографии России и согласованной 4.02.2002 г.
ВРИД начальника Военно-топографического управления Генерального Штаба
Вооруженных Сил Российской Федерации.
Результаты измерений и уравнивания сетей,
координаты геодезических пунктов, другие количественные характеристики
элементов ГГС, сведения о геодезических знаках и центрах пунктов хранятся:
• на всю территорию страны
- в банках геодезических данных при Роскартографии;
• на территорию регионов
Российской Федерации - в региональных банках
геодезических данных аэрогеодезических предприятий Роскартографии
и геодезических частей Топографической службы
ВС РФ, а также в территориальных инспекциях
государственного геодезического надзора.
Структура и специальное программное
обеспечение региональных банков геодезических данных должны быть идентичны и
сопряжены с банками геодезических данных при Роскартографии.
2. ПЕРЕХОД ОТ СИСТЕМЫ
КООРДИНАТ 1942 ГОДА К СИСТЕМЕ КООРДИНАТ 1995 ГОДА
2.1.
Перевод геодезических координат 1942 года в СК-95 методом уравнивания и методом
трансформирования
Уравнивание является традиционным методом
определения координат по результатам геодезических измерений. В отличие от
других методов уравнивание позволяет не только получить координаты, но и
проконтролировать результаты, и достаточно строго оценить индивидуальную
точность координат каждого пункта. Поэтому наиболее целесообразно вычислять
координаты в системе СК-95 с помощью уравнивания измерений относительно
геодезических пунктов в этой системе. Если геодезические пункты, координаты
которых известны в СК-42, необходимо определить в СК-95, то в случае
сохранности измерений метод уравнивания должен рассматриваться как
приоритетный.
Преобразование координат из системы СК-42 в
систему СК-95 методами трансформирования выполняют в тех случаях, когда
координаты в СК-42 известны, а информация о геодезических измерениях, на основе
которых эти координаты были получены, утрачена. Все методы трансформирования
используют один и тот же прием. На пунктах, для которых известны координаты и в
СК-42 и в СК-95, предварительно получают их разности. Разности по существу
отражают отличия систем координат в дискретных точках. Поэтому необходимо
каким-либо образом распространить информацию об отличии систем координат с
точек на окружающую их территорию, т.е. построить непрерывное поле разностей
координат между СК-42 и СК-95. Когда поле разностей построено, по известным
координатам в одной системе легко получить координаты в другой.
Отличия методов трансформирования
заключаются в том, какая математическая модель выбирается для формирования
непрерывного поля разностей координат. В настоящее время в геодезической практике
широко распространен аналитический метод трансформирования, использующий
ортогональное преобразование координат. Математическая модель этого метода
подразумевает, что одна и та же точка имеет различные значения в двух
пространственных прямоугольных системах координат из-за того, что:
Ø существует сдвиг между началами этих
систем, описываемый параметрами х, у, z;
Ø существуют углы между одноименными осями
этих систем, учитываемые с помощью параметров wх,
wу, wz;
Ø существуют отличия в масштабах длин, учитываемые масштабным
коэффициентом т.
Дополнительные различия, вызванные любыми
иными причинами достаточно малы, и могут не учитываться.
Формула преобразования координат в этом
случае имеет вид
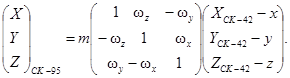
Использование модели ортогонального
преобразования координат для трансформирования координат из СК-42 в СК-95 может
быть затруднено (особенно на значительных территориях) в связи с тем, что:
• обе системы координат, строго говоря, не
являются пространственными, а реализованы на поверхности эллипсоида
Красовского. Плановые координаты могут быть дополнены
высотной составляющей относительно этого же эллипсоида. Но ее точность
значительно ниже, чем точность плановых координат. Этот фактор имеет, однако,
значение только при попытках преобразования координат на значительных
территориях с использованием одного набора параметров преобразования.
• малое количество параметров не может адекватно описать все
многообразие существенных деформаций системы координат СК-42 относительно
СК-95. Поэтому сами ошибки преобразования могут оказаться недопустимыми. В
любом практическом случае такого преобразования на всех пунктах с координатами,
известными в обеих системах, координаты СК-95, полученные трансформированием,
будут отличаться от оригинальных координат в СК-95.
Для преодоления указанных недостатков
метода ортогонального преобразования координат, возможно применение численного
метода трансформирования, использующего цифровые модели разностей координат в
системах СК-42 и СК-95. В цифровые модели входит информация о геодезических
пунктах, на которых эти разности известны. Для определения поправки за переход
от СК-42 к СК-95 (и наоборот) в этом случае достаточно проинтерполировать
разности с исходных пунктов в нужную точку.
Такой подход позволяет выполнять
трансформирование координат более точно, чем метод ортогонального
преобразования в том смысле, что поправки в координаты, вычисленные для опорных
пунктов, совпадают с исходными разностями. А для промежуточных точек ошибки
трансформирования координат, по крайней мере, не превышают аналогичных ошибок
ортогонального преобразования.
2.2. Общие
рекомендации по использованию методов перевода геодезических координат 1942
года в СК-95
Переход к применению СК-95 при выполнении
большинства видов геодезических работ, выполнявшихся ранее в СК-42, не должен
вызывать каких-либо проблем. Поскольку между СК-42 и СК-95 не существует
формальных различий, переход к использованию системы СК-95 во вновь выполняемых
работах сводится по существу к замене координат исходных пунктов, задававшихся
ранее в СК-42, на их координаты в СК-95. Все остальные процедуры, необходимые
для получения результатов геодезических определений в государственной системе,
остаются без изменений.
Более того, при выполнении геодезических
работ современными спутниковыми методами переход к СК-95 значительно упрощает
получение результатов именно в этой системе по сравнению с использованием СК-42.
Существенно меньшие деформации ГГС в СК-95 обеспечивают возможность более
эффективной реализации высокой точности ГЛОНАСС/GPS методов. При этом для получения результатов спутниковых
координатных определений в государственной системе СК-95 будет достаточна
существенно менее плотная сеть опорных пунктов в этой системе. Это обеспечивает
большую свободу и возможности в выборе соответствующих пунктов. С другой
стороны требуемая точность геодезических определений при малом количестве
опорных пунктов может быть обеспечена на территории существенно больших
размеров, чем при использовании СК-42.
Основные проблемы промежуточного этапа
перехода от СК-42 к СК-95 связаны с задачами, требующими приведения в СК-95
результатов геодезических определений или топографических съемок, ранее
выполненных в СК-42 или иных системах, однозначно с ней связанных. Такие же
проблемы будут и при необходимости представления новых данных, получаемых в
СК-95, в системе координат ранее выполненных съемок с адекватным
воспроизведением их фактических деформаций.
По существу возникающие при этом проблемы
во многом аналогичны проблемам, имеющим место при переводе координат точных
спутниковых определений в деформированную систему СК-42. С той лишь
существенной разницей, что для перехода от СК-42 к СК-95 (или наоборот) в
большинстве случаев уже имеется необходимые исходные данные в виде координат
достаточно плотной ГГС, известных в обеих системах координат, по которым могут
быть заблаговременно получены модели преобразования координат необходимого
вида. При этом для их использования с целью решения такой задачи нет никаких
ограничений, связанных с невозможностью выполнять на каких-то пунктах реальные
наблюдения или даже с их физической утратой. Вся задача решается лишь на основе
уже имеющихся каталогов координат и уже выполненных ранее измерений.
2.2.1. Уравнивание
Перевод координат пунктов из системы в
систему методом уравнивания является наиболее корректным из всех вычислительных
методов такого преобразования. Получение координат в СК-95 методом уравнивания
естественно может быть использовано только при наличии результатов измерений
между пунктами с уже известными координатами в СК-95 и пунктами, координаты
которых должны быть определены в этой же системе. Этот метод наиболее
трудоемок, требует сбора и анализа результатов прежних измерений. Но при этом
он дает результаты, наиболее адекватно отражающие данные непосредственных
измерений на местности, и сами эти результаты не содержат в себе каких либо
следов деформаций сети, свойственных системе координат СК-42. Получаемые
результаты в этом смысле эквивалентны результатам вновь выполняемых
геодезических определений в СК-95. Это единственный способ модернизации уже
существующих геодезических построений на тех территориях, где из-за
значительных нерегулярных деформаций ГГС в СК-42 не применимы какие-либо другие
интерполяционные методы преобразования (трансформирования) координат.
Как правило, метод уравнивания применяется
для определения в СК-95 положений пунктов ГГС 3 - 4 классов. Однако, применение
метода уравнивания может быть связано со значительными трудностями в задачах,
целью которых является взаимное согласование результатов геодезических и
топографических съемок, выполненных ранее в СК-42 и вновь выполняемых на той же
территории в СК-95. Проблемы могут быть связаны как с значительной
трудоемкостью подготовки к уравниванию материалов соответствующих полевых
измерений, так и с отсутствием таковых вообще. В тоже время сгущение ГГС в
СК-95, получаемое по результатам уравнивания пунктов 3 - 4 классов, а иногда и
более низких классов, дает дополнительные данные, во многих случаях облегчающие
применение интерполяционных методов взаимного преобразования координат для
более локальных геодезических построений на конкретных территориях. Упомянутое
выше дополнительное сгущение ГГС в СК-95 позволяет либо выявить более детальную
картину местных деформаций сети в СК-42 для применения нелинейных методов
трансформации, либо уменьшить участки сети и соответственно величины внутренних
ее деформаций на этих участках до величин, допускающих применение
ортогонального преобразования координат.
Для обеспечения работ по уравниванию
пунктов 3 - 4 классов в СК-95, выполняемых геодезическими предприятиями
Роскартографии, в ЦНИИГАиК по заданию Роскартографии разработан пакет программ
под общим названием «ГЕОМАСТЕР». Программы пакета обеспечивают, в частности,
импорт из геодезических банков данных координат пунктов ГГС, результатов
геодезических измерений, выполненных в ГГС 3 - 4 классов и в разрядных сетях,
их последующее уравнивание и каталогизацию результатов уравнивания.
2.2.2. Нелинейное преобразование координат
с использованием цифровых моделей.
Под нелинейным преобразованием здесь и
далее понимается преобразование координат с использованием цифровых моделей,
учитывающие в совокупности различие двух сопоставляемых систем координат и их
дифференциальные нелинейные (нерегулярные) деформаций. С точки зрения
построения и использования цифровых моделей любые деформации геодезических
построений могут рассматриваться как следствие деформаций соответствующих им
систем координат. И наоборот, деформации систем координат, независимо от причин
их появления, могут интерпретироваться как деформации геодезических построений,
выполненных в недеформированных системах. Если предположить существование двух
систем координат с разным характером и уровнем деформаций, для которых по
координатам общих пунктов построена цифровая модель преобразования координат,
то такое преобразование будет обладать следующим свойством. В результатах
преобразования будут воспроизводиться деформации той системы, в которую
выполняется преобразования, и исключаться деформации исходной системы
координат.
Степень воспроизведения деформаций будет
зависеть от того, насколько координаты общих пунктов, использованных для построения
модели, адекватно отражаются «рельеф» дифференциальных деформаций двух
сопоставляемых систем координат.
Таким образом, преобразование координат
методом нелинейного трансформирования наиболее адекватно задачам, требующим
согласования результатов съемок, ранее выполненных в СК-42 (или в местных
системах, основанных на СК-42) и вновь выполняемых съемок на основе СК-95. При
этом предполагается, что данные съемок представлены в цифровом виде.
Соответствующие цифровые модели трансформирования могут быть построены заранее
с использованием, например, координат пунктов ГГС от 1 - 2 до 3 - 4 классов.
Применительно к задачам перехода между
системами координат СК-42 и СК-95 нелинейное трансформирование является
наилучшим способом получения данных новых съемок, в системе ранее выполненных
съемок, пусть даже значительно деформированных. Возможна и может быть
необходима обратная процедура приведения результатов старых съемок, выполненных
в местной деформированной реализации СК-42, в новую недеформированную систему
СК-95. Такая процедура перехода к СК-95 обеспечит одновременно и устранение
деформаций и согласование результатов при условии, что данные съемки, ранее
выполненные на основе СК-42, представлены в цифровом виде.
Для участков ГГС, не имеющих значительных
резко выраженных деформаций нелинейное трансформирование может быть эффективным
и для вычисления координат пунктов 3 - 4 классов в СК-95 по их координатам в
СК-42. При этом не существенно, имеются ли еще эти пункты реально на местности.
Нелинейное трансформирование является
оптимальным, в смысле метода наименьших квадратов, способом воспроизведения или
исключения влияния локальных деформаций геодезических и топографических данных.
Однако этот метод в той же схеме аппроксимирует и грубые ошибки в координатах
опорных пунктов, не имеющие отношения собственно к деформациям сети в СК-42, а
вызванные любыми другими причинами, вплоть до ошибок подготовки исходных данных
или отнесением координат к физически различным центрам. При этом влияние этой
ошибки распределяется и на ближайшее окружение таких пунктов, искажая их
преобразованные координаты.
Наличие таких ошибок естественно
проявляется при построении числовых моделей, но в значительно завуалированном
сглаженном виде, а возможности их анализа в процессе построения самой цифровой
модели ограничены принципиальными свойствами таких моделей. Поэтому при
применении этого метода возможности анализа характера деформаций ГГС и
возможности отбраковки аномальных (в упомянутом выше смысле) данных могут быть
недостаточными. Недостаточно корректная формальная отбраковка может приводить к
ухудшению точности преобразования. Во многих случаях может потребоваться
дополнительный анализ данных с использованием метода ортогонального
преобразования координат, а возможно и проверка всех данных, связанных с
историей определения отдельных пунктов ГГС.
Пакет программ ГЕОМАСТЕР обеспечивает как
построение цифровых моделей преобразования координат по данным ГГС 1 - 4 класса
в обеих системах, так и преобразование координат с использованием полученных
моделей. Единая цифровая модель может быть построена на территорию практически
любой протяженности. В прил. 3
дано общее описание порядка работы с программой при построении цифровых
моделей. Более подробные инструкции по работе с программным пакетом даны в его
собственном руководстве. Конкретные рекомендации по построению цифровых моделей
даны на конкретных примерах в прил. 4.
При построении цифровых моделей в границах
некоторого участка территории, используемые для этого пункты должны выбираться
не только внутри этих границ, но и по всей длине границы за пределами этой
территории. Такое расширение должно быть не менее двух рядов пунктов. Оно необходимо
как для построения надежной модели, так и для обеспечения согласованности
моделей, создаваемых для смежных территорий. Использование построенной таким
образом модели допускается лишь в пределах границ участка без расширения.
2.2.3. Преобразование координат методом
ортогонального преобразования.
В смысле переноса ошибок свойства
ортогонального преобразования во многом противоположны свойствам преобразования
с использованием цифровых моделей.
Напомним, что при преобразовании с
использованием цифровых моделей воспроизводятся все деформации в положениях
опорных сетей, существующие в конечной системе координат. Поэтому при
использовании цифровых моделей возможно преобразование из менее точной системы
в более точную систему при сохранении основных точностных свойств последней.
Однако, при переходе из более точной системы в менее точную, неизбежно
воспроизведение и деформаций последней.
При ортогональном преобразовании на
преобразованные координаты переносятся внутренние (в пределах самого участка)
не ортогональные деформации исходной системы координат. Однако, при этом
ортогональное преобразование позволяет «вписать» преобразованные положения
пунктов в конечную систему координат наилучшим образом. Иными словами, такое
преобразование приводит к наименьшим (в смысле способа наименьших квадратов)
смешениям пунктов относительно координатной сетки конечной системы.
При использовании ортогонального
преобразования для перехода от менее точной системы к более точной исходная
точность взаимного положения пунктов не улучшается. Однако при переходе из
более точной системы в менее точную в преобразованных координатах сохраняется
высокая внутренняя точность исходной системы при одновременно наилучшем
встраивании преобразованных положений всех совокупности пунктов в сетку координат
конечной системы. Дополнительное преимущество ортогонального преобразования
состоит в том, что для его применения может быть достаточно существенно меньшее
количество опорных пунктов, чем это необходимо для построения цифровых моделей.
Прежде всего, здесь имеется в виду не сама процедура преобразования координат,
а возможность оценки его достоверности.
Таким образом, при помощи ортогонального
преобразования результаты новых съемок, выполненных в более точной системе
координат СК-95, могут быть преобразованы в систему координат 1942 года (или в
местную систему, с ней связанную) с наименьшими общими смещениями и
одновременно с наименьшими внутренними деформациями, свойственными СК-95. Это
невозможно при преобразовании с использованием цифровых моделей.
В тоже время при ортогональном
преобразовании из СК-42 в СК-95 в преобразованных координатах сохраняются все
внутренние не ортогональные деформации исходной системы в пределах участка
территории, для которой были определены используемые параметры преобразования.
Однако, во многих случаях такое преобразование может быть достаточным даже для
относительно больших участков ГГС вплоть до размеров трапеций масштаба
1:200000. Как показывает совместный анализ данных построения ГГС в СК-42 и
СК-95 примерно для 30 % таких трапеций ортогональное преобразование
обеспечивает среднюю квадратическую погрешность перевычисления координат не
более 5 см. Это означает, что при сопоставлении данных геодезических
определений, выполненных ранее в СК-42, и новых определений на основе СК-95
расхождение сведенных в одну и ту же систему результатов не будет превышать 10
см с вероятностью 95 % на территории около 500 км.
Одновременно с определением параметров
может быть обеспечен анализ дифференциальных неортогональных деформаций
соответствующих сопоставляемых фрагментов сети в разных системах и выполнена
отбраковка аномальных данных по величинам остаточных расхождений в значениях
координат и характеру их распределения на участке сети.
При использовании цифровых моделей
возможности анализа и отбраковки существенно более ограничены. Поэтому
процедура анализа и отбраковки с использованием ортогональных преобразований
может быть рекомендована перед построением или в процессе построения цифровых
моделей нелинейного трансформирования. Однако, при этом максимально аномальные
величины остаточных расхождений по формальным критериям метода наименьших
квадратов во многих случаях могут быть достаточным основанием для отбраковки
лишь при условии их явной несогласованности с остаточными расхождениями
координат для ближайших окружающих пунктов.
Средние квадратические значения остаточных
расхождений в координатах, полученные при определении параметров ортогонального
преобразования, могут быть достаточно надежным критерием для оценки
приемлемости такого преобразования, исходя из требований к точности выполняемых
работ. Или, в противном случае, для принятия решения либо об уменьшении
размеров территории, обеспечиваемых одним набором параметров ортогонального
преобразования, либо о переходе к использованию нелинейного трансформирования.
Ортогональное преобразование систем
координат в настоящее время применяется достаточно широко при выполнении
геодезических работ спутниковыми методами. Соответственно и многие
геодезические пакеты программ обработки спутниковых наблюдений имеют в своем
составе программные инструменты для выполнения соответствующих координатных
преобразований, начиная с определения самих значений параметров.
2.2.4. СК-95 и местные
системы координат.
Местные системы координат, как правило,
основаны на координатах в СК-42 и связаны с ними непосредственно
преобразованием с использованием ключей. Проблема перехода к СК-95 в связи с
применением местных систем координат имеет, таким образом, несколько аспектов.
Местные системы координат несут на себе
отпечаток всех локальных деформаций ГГС в СК-42 на соответствующей территории.
Переход к менее деформированной системе СК-95 должен, как следствие, обеспечить
и возможность уменьшения внутренних локальных деформаций местных геодезических
сетей в местных системах координат. Такая модернизация местных геодезических
сетей может быть выполнена как их переуравниванием с использованием обновленной
геодезической основы, так и одним из выше описанных методов трансформирования.
Однако, такая процедура модернизации не может быть проведена непосредственно с
координатами в местной системе. С другой стороны при такой модернизации крайне
желательно обеспечить минимальные изменения местной системы координат в целом,
чтобы по возможности в максимальной мере сохранить преемственность
(согласованность) результатов прежних и вновь выполняемых съемок на данной
территории.
Рекомендуется следующий порядок действий
при переходе к использованию системы координат СК-95. Для всей территории
применения конкретной местной системы из каталогов выбираются все пункты ГГС 1
- 2 классов и по их координатам в СК-42 и СК-95 определяются значения семи
параметров ортогонального пространственного координатного преобразования.
Количество пунктов, по координатам которых выполняется определение этих
параметров, не должно быть меньше пяти. При меньшем количестве выбираются
дополнительные пункты уже за пределами соответствующей территории. Параметры
определяются в топоцентрической системе с топоцентром в точке, соответствующей
началу координат местной системы. Одновременно по величинам остаточных
расхождений в значениях координат, полученным после преобразования, выполняется
оценка внутренних деформаций СК-42, и соответственно местной системы, по
отношению к СК-95 на данной территории.
Дополнительно к пунктам ГГС могут
использоваться и другие пункты, составляющие основу местной геодезической сети,
и, соответственно, местной системы координат. Для таких пунктов координаты в
СК-42 вычисляются по их координатам в местной системе, а координаты в СК-95
определяются одним из описанных ранее способов по координатам в СК-42.
Если деформации существующей местной
системы координат невелики, т.е. удовлетворяют требованиям к точности исходной
геодезической основы для проведения планируемых геодезических работ на данной
территории, то следующая, и последняя, необходимая операция состоит только в
корректировке ключей перехода от государственной к местной системе координат.
При этом определенные в топоцентрической системе значения параметров
ортогонального преобразования, соответствующие компонентам сдвига в плане,
азимутальному развороту и масштабу, будут эквивалентны поправкам к
соответствующим значением ключа перехода.
Невозможно заранее определить правило
назначения знаков этим поправкам, поскольку для индивидуальных местных систем
координат могут быть и индивидуальные программы преобразования координат из
государственной в местную систему. Поэтому знаки поправок должны также
устанавливаться индивидуально с проведением контрольных преобразований.
Использование старых ключей при преобразовании координат СК-42 должно давать
тот же результат, что и использование новых ключей при преобразовании координат
СК-95. При этом для контрольных вычислений должны браться координаты в СК-95,
полученные из СК-42 в результате семипараметрического пространственного
преобразования.
Если в компонентах ключа перехода
отсутствует масштабная поправка, то предварительно необходимо выполнить оценку
погрешности преобразования, вызываемую этим фактором. Для этого параметры
ортогонального шестипараметрического преобразования между двумя
государственными системами определяются также без использования масштабной
поправки. Если сравнение результатов 6-ти и 7-ми параметрического
преобразования показывают допустимость пренебрежения масштабной поправкой, то
нет и необходимости вводить ее в состав ключа перехода, а значения поправок к
остальным элементам ключа берутся по данным 6-ти параметрического
пространственного преобразования. В противном случае добавление масштабного коэффициента
в состав элементов ключа перехода к местной системе обязательно.
В выше описанной ситуации в процессе
перехода к использованию СК-95 нет обязательной необходимости пересчета
координат всех пунктов, уже имеющихся в местной системе, или в каких-либо
преобразованиях уже существующих материалов геодезических и топографических
съемок. Однако координаты пунктов ГГС в СК-95, включая координаты пунктов
триангуляции 3 - 4 классов, должны быть пересчитаны в местную систему уже с
использованием скорректированных ключей.
Для контроля координаты этих пунктов должны
быть получены в двух вариантах. Непосредственным перевычислением уравненных
координат СК-95 в местную систему по скорректированным ключам и таким же
пересчетом по тем же ключам координат пунктов в СК-95, которые получены
ортогональным преобразованием из координат в системе СК-42. Расхождения
полученных таким образом двух наборов координат одних и тех пунктов будут
характеризовать различие двух реализаций одной и той же местной системы,
основанных на СК-95 и СК-42.
В случае, когда 7-ми параметрическое
преобразование не обеспечивает достаточную точность перехода между СК-42 и
СК-95 для данной территории, необходимо дополнительное использование
нелинейного трансформирования. В этом случае может использоваться следующая
схема корректировки координат в местной системе.
Определяются параметры ортогонального 7-ми
параметрического преобразования для перехода от СК-95 к СК-42 для требуемой
территории. Параметры определяются по всему составу пунктов ГГС 1 - 4 классов
на этой территории с добавлением равномерно распределенных пунктов в ее
ближайшей окрестности по всей границе территории. С использованием этих
параметров координаты пунктов из СК-95 перевычисляются в СК-42. В результате
соответствующего преобразования получаем некоторую модернизированную реализацию
системы координат СК-42 в среднем согласованную с уже существующей реализацией
этой же системы, но не содержащую тех значительных внутренних деформаций,
которые были ранее присущи ГГС на данной территории. По всему составу опорных
пунктов формируется цифровая модель, обеспечивающая перевычисление существующих
координат СК-42 в полученную модернизированную реализацию этой же системы.
Требующие корректировки координаты пунктов
в существующей местной системе с использованием существующих (старых) ключей
перехода переводятся в СК-42. Далее с применением полученной цифровой модели
они преобразуются в модернизированную СК-42 и с использованием тех же ключей
вновь преобразуются в местную систему. В результате получаются
скорректированные координаты в модернизированной местной системе, в
совокупности обладающие тем свойством, что при более высокой точности они в
среднем наилучшим образом согласованы с прежними координатами в ранее
использовавшейся местной системе. Корректировка ключей выполняется, как описано
раньше, но при этом параметры ортогонального преобразования определяются с
использованием координат в СК-95 и координат в модернизированной реализации
СК-42.
Подобная же схема преобразования может
использоваться и для сведения в ту или другую единую систему результатов
топографических съемок, выполненных до и после перехода к новой системе
координат, при условии, что данные съемок могут быть представлены в цифровой
форме.
3. ДЕФОРМАЦИИ СК-42 и
СК-95
В системе координат 1942 года геодезическая
сеть, сформированная последовательным присоединением уравниваемых блоков, не
является однородным геодезическим построением. Эти блоки имеют различный
уровень систематических и случайных ошибок координат геодезических пунктов. Поэтому
использование единой системы параметров преобразования координат из СК-42 в
СК-95 не удовлетворяет современным требованиям к точности перехода в том или
ином регионе. В целом по сети деформации СК-42 могут быть оценены величинами
средних квадратических ошибок координат, равными примерно 3,5 - 4 м. Именно с
такой точностью (СКО) в среднем могут быть преобразованы координаты СК-42 в
СК-95 при использовании единого для всей ГГС набора параметров ортогонального
преобразования. При этом абсолютные величины ошибок могут достигать 10 и более
метров. Для обеспечения более высокой требуемой точности преобразования
координат на всей территории страны необходимо использовать либо системы
локальных параметров преобразования, либо картосхемы поправок в координаты по
листам карт масштаба 1:200000, определенных по данным заключительного
уравнивания АГС.
Определение локальных параметров
ортогонального координатного преобразования основано на сопоставлении координат
пунктов АГС в системах СК-42 и СК-95 в некоторой локальной области. Точность
преобразования координат с использованием локальных параметров, оцениваемая по
величинам остаточных деформаций, в разных регионах страны неодинакова. Для 60 %
трапеций масштаба 1:200000 средние квадратические ошибки преобразования координат
с использованием локальных параметров не превышают 5 см, для 30 % - 10 см. В
остальных случаях ошибки преобразования координат могут достигать 30 см и
более. Потенциальная точность преобразования с использованием картосхемы
поправок, всегда будет хуже, поскольку последние соответствуют частному случаю
ортогонального преобразования, в котором используются только параметры смещения
начала координат и игнорируются возможные местные угловые развороты участка
сети и местные масштабные ошибки.
В основном повышенный уровень ошибок
преобразованных координат, полученных с использованием локальных параметров,
свойственен участкам на краях геодезической сети, на стыках раздельно
уравненных блоков сети, для пунктов ГГС 1 класса и пунктов 2 класса,
расположенных вблизи таких пунктов 1 класса. Даже для трапеций с относительно
небольшим средним уровнем остаточных деформаций для отдельных пунктов или их
групп возможны аномальные величины остаточных ошибок, значительно превышающие
средний уровень и достигающие нескольких дециметров.
При увеличении участков, для которых
определяются локальные параметры, возможности их использования и точность
преобразования быстро уменьшаются. Примеры, показывающие величины и характер
локальных деформаций СК-95 и возможностей использования локальных
преобразований можно найти в приложении 6.
Переход к СК-95 означает изменение
положения координатной сетки по всей территории и смещение положений углов
рамок трапеций. Чтобы определить вызванную этим необходимость корректировки
карт масштабов 1:10000, 1:25000, 1:50000 при их издании и обновлении в СК-95,
необходимо сопоставить конкретную для данного листа карты величину суммарного
влияния 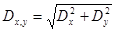 поправок
Dx и Dy в плановые
координаты системы 1942 года со следующими её допустимыми значениями:
поправок
Dx и Dy в плановые
координаты системы 1942 года со следующими её допустимыми значениями:
для листа карты масштаба 1:10000 3
м;
для листа карты масштаба 1:25000 7,5
м;
для листа карты масштаба 1:50000 15
м.
Если величина Dx,y превышает её допустимое значение, то этот лист карты
требует корректировки. Схема расположения регионов, для которых требуется
корректировка карт масштабов 1:10000, 1:25000, 1:50000 приведена в приложении 8.
Детальные карты поправок находятся в
аэрогеодезических предприятиях Роскартографии в соответствии с зонами их
деятельности, а также в территориальных инспекциях и отделах государственного
геодезического надзора. Аэрогеодезические предприятия располагают также
соответствующим программно-математическим обеспечением для автоматизированного
преобразования координат из СК-42 в СК-95.
Оценка деформации самой системы координат
СК-95 может быть выполнена на основе сравнения с более точными и независимо
полученными данными о положениях пунктов. Такое сравнение было выполнено с
использованием координат пунктов АТС, определенных с более высокой точностью в
системе координат ITRF в процессе построения ФАГС и ВГС по
наблюдениям спутников GPS. Сравнение
этих данных после их приведения ортогональным преобразованием в единую систему
показало, что внутренние деформации СК-95 составляют 20 - 30 см. Указанные
оценки имеют следующее содержание. Это средние квадратические значения
остаточных расхождений координат указанных выше пунктов в СК-95, содержащихся в
каталоге и полученных 7-параметрическим преобразованием из более точных
определений в системе ITRF. Более
полная и детальная картину деформаций СК-95 показана на рисунке П5.1 приложения 5. На рисунке показаны вектора смещения
пунктов от положений, соответствующих каталогу в СК95, к более точным их
положениям в этой же системе, полученным в результате общего для всей сети
7-параметрического ортогонального преобразования координат из системы ITRF.
4. АВТОМАТИЗИРОВАННЫЙ
БАНК ГЕОДЕЗИЧЕСКИХ ДАННЫХ И КАТАЛОГИ КООРДИНАТ ПУНКТОВ ГГС В СК-95.
В процессе реализации мер по введению
системы координат СК-95 в Роскартографии создана сеть автоматизированных банков
данных геодезической основы, предназначенных для автоматизации процессов
геодезического и картографического обеспечения в системе координат СК-95.
Структура сети автоматизированных банков
геодезической основы и система их функционирования в системе
топографо-геодезического и картографического производства показана на рис. 5.
На верхней ступени общей иерархической
структуры банковской сети располагается Федеральный банк Роскартографии,
состоящий из двух филиалов в МАГП и ДВАГП и координационно-методического и
вычислительного центра (КМИВЦ) в ЦНИИГАиК. На следующей ступени этой структуры
расположены региональные банки данных геодезической основы аэрогеодезических
предприятий Роскартографии (АГП).
Региональные банки предназначены для
непосредственного обслуживания соответствующих территорий АГП при реализации
геодезической основы в топографо-геодезическом и картографическом производстве
отрасли и при обеспечении запросов потребителей из других министерств и
ведомств, ведущих геодезическую и картографическую деятельность. Для этих целей
в Региональные банки данных, кроме пунктов ГГС в системе координат СК-95,
заносятся данные о пунктах опорных сетей низших классов, сетей сгущения,
разрядных сетей и т.п.
Одной из задач, решаемых при помощи
Региональных банков, является создание каталогов координат в СК-95 на листы
карты масштаба 1:200000 на всю территорию Российской Федерации. Для этих целей
в Региональных банках разработана специальная процедура экспорта практически
полностью автоматизирующая процесс создания каталогов. На базе Региональных
банков формируются геодезические данные для экспорта в банки ТИГГН. Банки ТИГГН
разработаны в формате совместимом с форматами Региональных банков данных, что
позволяет осуществлять всесторонний обмен данными между этими банками.
В задачу Федерального банка геодезической
основы входит хранение, обновление и контроль данных государственной геодезической
сети (ГГС 1 - 4 классов). Состав геодезических данных и форматы их
представления в банках данных разрабатывались с учетом современных требований
экономики и в тесном взаимодействии с ВТУ ГШ.
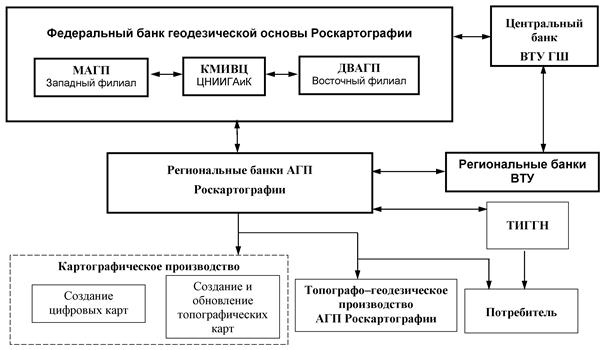
Рис. 5. Структура
функционирования банков геодезической основы Роскартографии в системе
топографо-геодезического и картографического производства
Потребитель информации в установленном
порядке может получить необходимые данные о координатах пунктов опорных
геодезических сетей в аэро-геодезических предприятиях (АГП) Роскартографии, в
соответствии с их зоной деятельности. Схема территориального деления зон
деятельности АГП Роскартографии приведена приложении 7.
5. ВЫПОЛНЕНИЕ НОВЫХ
ГЕОДЕЗИЧЕСКИХ РАБОТ В СИСТЕМЕ КООРДИНАТ 1995 ГОДА
Переход к системе государственных
геодезических координат 1995 года не вносит каких-либо принципиальных или
существенных изменений в технологию выполнения геодезических работ
традиционными геодезическими методами. Но при выполнении геодезических работ
или топосъемки с использованием спутниковых методов переход к СК-95 позволяет
снять многие ограничения или проблемы в обработке таких измерений, имеющих
целью получение окончательных результатов геодезических определений также в
СК-95.
Основные проблемы получения координат в
государственной системе СК-42 на основе данных спутниковых определений были
связаны с ее недостаточной точностью по сравнению с потенциальной точностью спутниковых
определений. Это существенно ограничивало возможности использования спутниковых
методов при передаче координат на большие расстояния или получения высокоточных
результатов на ограниченных территориях в значительно деформированной системе
координат СК-42. В результате при выполнении спутниковых определений для
обеспечения перехода к СК-42 требовалось использование существенно более
плотной сети опорных пунктов с координатами в этой же системе, чем это было бы
на самом деле необходимо, исходя из возможностей высокой точности и
значительной дальности передачи координат спутниковыми методами. Часто
возникали проблемы, связанные со значительными, практически грубыми ошибками
координат в СК-42.
Из-за недостаточной точности СК-42 и
соответственно ограниченных возможностей преобразования результатов спутниковых
определений в государственную систему координат и основанные на них местные
системы во всех случаях требовалось одновременной использование не менее трех
опорных пунктов в непосредственной близости от района выполняемых работ. Были
существенно ограничены возможности получения и использования единого набора
заблаговременно определенных параметров преобразования координат на достаточно
обширные регионы. Это обстоятельство также затрудняет полноценное использование
систем постоянно действующих опорных пунктов спутниковых наблюдений
коллективного использования.
Введение более точной и внутренне
существенно лучше согласованной системы координат СК-95 позволяет в
значительной мере снять эти проблемы и открывает возможности применения более
общих методов решения задач перевода результатов спутниковых определений в
государственную или местные системы координат. В результате будет
обеспечиваться и более высокая точность и большая однородность конечных данных.
Как показывают данные сравнения ГГС в СК-95
и высокоточных спутниковых определений, выполненных при построении ФАГС и ВГС
по наблюдениям спутников GPS/ГЛОНАСС,
внутренние деформации СК-95 на обширных территориях протяженностью в несколько
сотен километров не выходят за пределы 3 - 5 см в их представлении в величинах
средних квадратических ошибок. Это позволяет при преобразовании данных
спутниковых определений к системе СК-95 ограничиваться единым набором
параметров ортогонального координатного преобразования для территорий целых
административных единиц или их групп.
Наиболее эффективно задача точного
преобразования координат для значительных территорий может быть решена по
результатам построения Спутниковой геодезической сети первого класса (СГС-1) на
соответствующей территории или фрагментов этой сети на наиболее необходимые
районы в единой общеземной системе координат ФАГС/ВГС.
Построение такой, первоначально даже очень
разреженной сети позволит определить единый для всей этой территории набор
параметров преобразования координат спутниковой сети в СК-95. Далее для
обеспечения геодезических работ на любом объекте на этой территории достаточно
по спутниковым наблюдениям определить даже один опорный пункт на этом объекте в
той же системе координат ФАГС/ВГС, чтобы иметь возможность создавать на этом
объекте спутниковыми же методами любые геодезические построения с последующим
переводом этих координат в СК-95 по единому для всей территории набору
параметров координатного преобразования. В перспективе одновременно может
решаться задача передачи по этим же наблюдениям и нормальных высот в единой
государственной системе. Соответствующие наборы параметров координатного
преобразования становятся по существу составляющими элементами геодезического
обеспечения страны, наряду с координатами ГГС в СК-95, собственными
координатами ФАГС/ВГС и ключами перехода к местным системам координат.
До построения СГС-1 эти же задачи, но с
несколько меньшей точностью и надежностью, могут решаться только на основе
координат пунктов ВГС. В этом случае для определения параметров координатного
преобразования необходимо использование большего количества пунктов ВГС,
находящихся вокруг обеспечиваемой территории. Кроме того, при таком варианте
должно быть рекомендовано определение на объекте работ или на удалении не более
20 - 30 км от него контрольного пункта с координатами, известными в СК-95 с
достаточной для выполняемых работ точностью. Как опорный, так и контрольный
пункты могут быть определены относительно ближайших пунктов постоянных спутниковых
наблюдений с использованием двухчастотной спутниковой аппаратуры или от уже
существующих пунктов ВГС (СГС-1). Необходимая продолжительность таких
наблюдений зависит от удаленности от опорных пунктов спутниковых наблюдений в
предположении, что на всех пунктах для таких наблюдений обеспечены хорошие
условия. Даже при удалении в несколько сотен километров от этих пунктов для
обеспечения точности привязки 2 - 3 см (СКО) достаточно суточных наблюдений при
условии использования при обработке точных эфемерид спутников.
До создания подобной системы геодезического
обеспечения для получения результатов спутниковых определений в СК-95 с
точностями 2 - 3 см (СКО) необходимо использование не менее трех опорных
пунктов, равномерно расположенных вокруг объекта работ на возможно меньшем
удалении, но не более 20 - 30 км от него. В качестве опорных пунктов могут
использоваться как непосредственно пункты ГГС с координатами в СК-95, так и
пункты ранее созданных спутниковых сетей при условии, что точность их координат
в СК-95 соответствует требованиям к точности исходной основы для выполняемого
на объекте вида работ. По результатам спутниковых координатных определений на
исходных пунктах и известным их координатам в СК-95 должны быть определены
параметры координатного преобразования для пересчета всех результатов
спутниковых определений на объекте в СК-95. При этом все спутниковые
определения могут быть выполнены в относительно произвольной системе координат,
но обязательно одной и той же для всех результатов определений на объекте. В
качестве исходных координат для спутниковых определений рекомендуется
использовать координаты вычисленные даже по непродолжительным определениям
относительно какого-либо пункта постоянных спутниковых наблюдений. Для
небольших объектов в качестве координат исходного пункта, используемых для
обработки и уравнивания спутниковых определений, достаточно получить на этом
пункте результаты автономных определений по наблюдениям продолжительностью 1 -
3 часа.
Задача перехода к СК-95 от результатов
спутниковых определений в большинстве случаев может быть решена с
использованием программно-математического обеспечения, закупаемого вместе со
спутниковой аппаратурой для полевой и камеральной обработки. Применительно к
полевой обработке спутниковых определений, продаваемыми коммерческими пакетами
программ, процедура обеспечения требуемого автоматического преобразования
координат (как к государственной, так и к любой местной системе координат)
называется калибровкой.
1. Бовшин
Н.А., Зубинский В.И., Остач О.М.
Совместное уравнивание общегосударственных опорных геодезических сетей.
Геодезия и картография, № 8, 1995, 6 - 17.
2. Галазин В.Ф., Каплан
Б.Л., Лебедев М.Г., Максимов В.Г.,
Петров Н.В., Сидорова-Бирюкова Т.Л.
Система геодезических параметров Земли «Параметры Земли 1990 года» (ПЗ-90),
(Справочный документ). Под общей редакцией Хвостова В.В. Москва, 1998, 37 с.
3. Демьянов Г.В. Концепция
современного развития системы нормальных высот. Известия ВУЗов, «Геодезия и
аэрофотосъемка», № 3, 2003, 3 - 20.
4. Дражнюк А.А., Лазарев
С.А., Макаренко Н.Л., Демьянов Г.В.,
Зубинский В.И., Ефимов Г.А., Максимов
В.Г. Завершение уравнивания ГГС и введение новой государственной
системы геодезических координат. Материалы юбилейной научно-технической
конференции «Современное состояние и перспективы развития геодезии,
фототопографии, картографии и геоинформационных систем», посвященной 850-летию
г. Москвы (Москва, ЦНИИГАиК, сентябрь 1997 г.) Часть 1, М.: ЦНИИГАиК, 1998, 11
- 20.
5. Ефимов Г.Н. Результаты
уравнивания астрономо-геодезической сети. Геодезия и картография, № 8, 1995, 17
- 22.
6. Инструкция о построении государственной
геодезической сети Союза ССР. М., Недра, 1966.
7.
Концепция перехода топографо-геодезического производства на автономные
спутниковые методы координатных определений. ЦНИИГАиК, М., 1995.
8. Макаренко Н.Л., Демьянов
Г.В., Е.В. Новиков, Бровар Б.В.,
Ефимов Г.Н., Зубинский В.И., Майоров
А.Н., Назарова Н.Г. Единая государственная
система геодезических координат 1995 года (СК-95). Справочный документ. Под
общей редакцией А.А. Дражнюка. М.:
ЦНИИГАиК, 2000, 34 с.
9.
Основные положения о государственной геодезической сети Российской Федерации.
ГКИНП (ГНТА)-01-006-03. Утверждены приказом Федеральной службы геодезии и
картографии России от 17.06.2003 г. № 101-пр. Согласованы начальником ВТУ ГШ ВС
Российской Федерации 16.06.2003 г. М., 2004 г., 28 с.
10. Параметры общего земного эллипсоида и
гравитационного поля Земли (Параметры Земли 1990 года). РИО ВТУ ГШ, М., 1991,
68 с.
11. Плешаков И.Я., Макаренко
Н.Л., Демьянов Г.В., Бровар Б.В.,
Зубинский В.И. Состояние и перспективы развития системы
геодезического обеспечения страны в условиях перехода на спутниковые методы. Материалы
юбилейной НТК «Современное состояние и перспективы развития геодезии,
фототопографии, картографии и ГИС», посвященной 850-летию г. Москвы (Москва,
ЦНИИГАиК, сентябрь 1997 г.). Часть 1. М.: ЦНИИГАиК, 1998, 21 - 30.
12. Справочник геодезиста. Под редакцией
В.Д. Большакова и Г.П. Левчука. «Недра»,
М., 1966. 984 с.
13. Технико-экономический доклад «Введение новой государственной
референцной системы геодезических координат 1995 года (СК-95)». ЦНИИГАиК, М.,
1998, 72 с.
14. Федеральный закон «О геодезии и
картографии» от 26 декабря 1995 г. № 209-ФЗ (с изменениями).
ПРИЛОЖЕНИЯ
Приложение 1.
Параметры связи между системами координат СК-95 и ПЗ-90
Переход от системы геодезических координат
1995 года к геоцентрической системе координат ПЗ-90 выполняется по следующим
формулам:
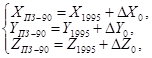 (1.1)
(1.1)
где DХ0, DY0, DZ0 - линейные элементы ориентирования, задающие положение начала
системы координат 1995 года в геоцентрической системе координат ПЗ-90.
Численные значения элементов ориентирования
составляют:
DХ0 = +25,90 м; DY0 = -130,94 м; DZ0 = -81,76 м.
Приложение 2. Прямой и обратный
переход от геодезических координат к пространственным прямоугольным координатам
Вычисление пространственных прямоугольных
координат X, Y, Z по геодезическим координатам B, L, H, заданным в
системе СК-95 относительно эллипсоида Красовского или в системе ПЗ-90
относительно общего земного эллипсоида, осуществляется по формулам:
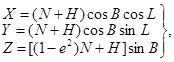 (2.1)
(2.1)
где B, L, H - геодезические широта, долгота и высота;
Н = Нg + z;
Нg, z - нормальная высота и высота квазигеоида над отсчетным эллипсоидом;
N - радиус кривизны первого вертикала;
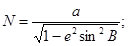
е2 -
квадрат первого
эксцентриситета эллипсоида;
е2 =
2a - a2;
а, a - большая
полуось и сжатие, соответственно равные:
для эллипсоида Красовского 6378245 м и 1:298,3;
для общего земного эллипсоида
6378136 м и 1:298,257839303.
Для вычисления геодезических координат B, L, H по пространственным прямоугольным координатам X, Y, Z используется следующий алгоритм:
а) вычисляется вспомогательная величина D
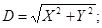 (2.2)
(2.2)
б) выполняется анализ величины D:
Если D = 0, то
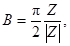 L = 0, (2.3)
L = 0, (2.3)
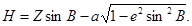 (2.4)
(2.4)
Если D > 0, то
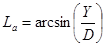 (2.5)
(2.5)
при этом
если Y < 0, Х > 0, то L = 2p - La;
если Y < 0, Х < 0, то L = 2p + La; (2.6)
если Y > 0, Х < 0, то L = p - La;
если Y > 0, Х > 0, то L = La.
в) анализируют значение Z:
если Z = 0, то
В = 0, H = D
- a, (2.7)
иначе выполняются следующие вычисления:
- вычисляются вспомогательные величины r, с, р по формулам:
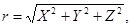 (2.8)
(2.8)
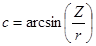 , (2.9)
, (2.9)
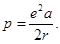 (2.10)
(2.10)
- присваивают величине s1 значение нуль и
реализуют итеративный процесс вычисления геодезической широты В:
b = c + s1, (2.11)
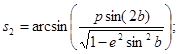 (2.12)
(2.12)
если модуль 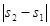 меньше заданного e, то
меньше заданного e, то
В = b, Н
= DcosB + ZsinB - a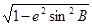 . (2.13)
. (2.13)
В противном случае величине s1 присваивается
значение величины s2 и вычисления повторяют, начиная с вычисления величины b по формуле (2.11).
Точность вычислений геодезической широты В
и высоты Н зависит от значения e. При задании e = 1´10-10 погрешность вычисления
широты В не превысит 0,0001², а высоты - 0,001 м.
Приложение 3. Создание и использование цифровых моделей преобразования
координат между СК-42 в СК-95 в программном пакете ГЕОМАСТЕР.
Программный пакет ГЕОМАСТЕР ориентирован в
основном на использование данных о ГГС и как основной способ ввода данных
использует автоматический импорт данных из геодезических банков данных или из
файловых каталогов сформированных программными средствами базы данных или из
самого программного пакета в виде бинарных файлов. Предусмотрена также
возможность ручного ввода координат пунктов.
Программный пакет состоит из четырех
основных взаимосвязанных компонентов:
- библиотеки систем координат и координатных
преобразований (блок Фундаментальных геодезических параметров
- ФГП);
- библиотеки каталогов;
- блока построения цифровых моделей преобразования
координат;
- блока уравнивания координат пунктов.
Для работы с программным пакетом имеется
достаточно подробное руководство. В настоящем приложении отражены только те
моменты, которые имеют непосредственное и обязательное отношение к построению и
использованию цифровых моделей и основным этапам этого процесса, но без
детального описания всех действий с интерфейсом программы. Описание деталей
выполнения операций и дополнительных возможностей программы, в частности в
отношении преобразования координат можно найти в руководстве по работе с
программой.
П.3.1.
Создание описаний свойств систем координат и ФГП
Использование программного пакета
начинается с формирования используемых систем координат: их наименований,
параметров и основных свойств.
На рис. П3.1 показано главное окно этого блока с
несколькими закладками.

Рис. П3.1 Главное
окно «Фундаментальные Геодезические Параметры», закладка «Эллипсоид»
В окне открыта закладка назначения
параметров эллипсоидов, используемых для формирования требуемых систем
координат. На рис. П3.1 схематически показана последовательность действий по добавлению в
библиотеку ФГП нового референцного эллипсоида с параметрами эллипсоида Красовского
в том случае, если он отсутствует в библиотеке. Этот эллипсоид будет
использоваться для работы и с СК-42, и с СК-95.
На рис. П3.1 в главном окне эллипсоид Красовского
показан как уже зарегистрированный в библиотеке. В действительности он
появляется в списке только после выполнения команды «Сохранить». Подобная
некорректность рисунков будет встречаться и в дальнейшем с целью сокращения
объема документа. Но соответствующие разъяснения в последующем делаться не
будут.
Далее с использованием закладки «Система
координат/высот» должны быть указана информация о необходимых системах
координат.
На рис. П3.2 показано введение данных для системы
координат СК-95.
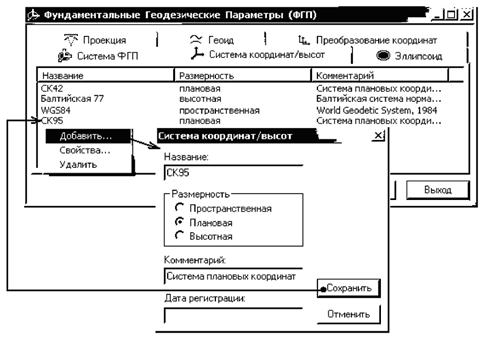
Рис. П3.2 Главное
окно «Фундаментальные Геодезические Параметры», закладка «Система
координат/высот»
В окне, вызываемом командой «Добавить»,
вводится название системы координат и ее тип (размерность). По имеющемуся
содержанию главного окна предполагается, что аналогичным образом ранее была
введена и информация о системе координат СК-42.
Если предполагается использование координат
в виде координат в проекции Гаусса-Крюгера, эквивалентной
поперечно-цилиндрической проекции Меркатора (UTM) с единичным масштабным коэффициентом на осевом меридиане, то
заранее должны быть заданы и свойства этой проекции:
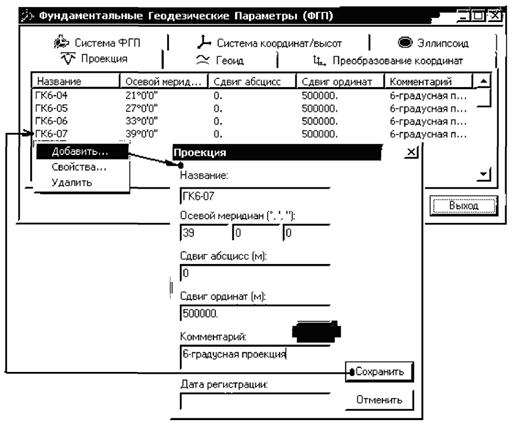
Рис. П3.3 Главное
окно «Фундаментальные Геодезические Параметры», закладка «Проекция»
На рис. П3.3 показано формирование данных проекции для
37 колонки при использовании 6-ти градусных зон.
Отметим, что для решения рассматриваемых
задач преобразования координат безразлично, в каком виде будут представлены
координаты пунктов в используемых каталогах: в виде геодезических координат
(широт и долгот на референц-эллипсоиде) или в виде плоских координат в проекции
Гаусса-Крюгера. Это замечание относится как процедуре построения цифровых
моделей преобразования координат, так и к их последующему использованию для
выполнения такого преобразования.
Последним шагом является формирование так
называемых фундаментальных параметров систем координат. Фундаментальные
параметры объединяют в себе их уникальное название; сформированное ранее
название соответствующей системы координат (СК-42 или СК-95) и ее размерность
(плановая); и ее вид (в нашем случае работы с координатами в СК-42 и СК-95 это
планово-высотная система).
Вся информация о ФГП, за исключением
параметров эллипсоида и параметров проекции, фактически служит для однозначной
идентификации свойств данных, содержащихся в конкретных каталогах и указания
программе правил действия с этими данными.
На рис. П3.4 показана последовательность действий и
содержание всех подокон при формировании ФГП для системы координат СК-95.
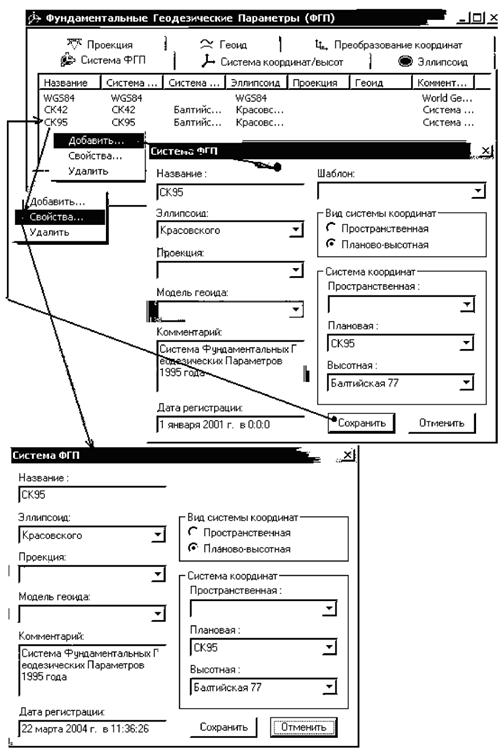
Рис. П3.4 Порядок
действий и содержание всех подокон при формировании ФГП для СК-95
В состав ФГП в данном программном пакете
намеренно не включены данные о положении конкретных систем координат в теле Земли.
Точнее говоря о ее положении относительно некоторой системы координат, принятой
в конкретном приложении за «эталонную» общеземную геоцентрическую систему
координат. К этим данным относятся: положение начала системы координат по
отношению к положению центра масс Земли (или относительно начала
геоцентрической системы), развороты системы относительно осей XYZ геоцентрической системы и масштабный
коэффициент. Заметим, что наборы этих параметров для конкретной системы,
именуемые термином «Datum», используются практически во всех
программных пакетах обработки спутниковых ГЛОНАСС/GPS наблюдений. В этих пакетах за некоторую идеальную (опорную)
систему принимается система WGS-84.
В этих параметрах в данном программном
пакете нет специальной необходимости, а их недостаточно грамотное использование
может приводить к грубым ошибкам. Однако, они всегда могут быть введены
пользователем в виде параметров преобразования координат.
Как правило, программный пакет ГЕОМАСТЕР
передается пользователям с уже подготовленными ФГП для СК-42 и СК-95. В этом
случае, а также когда пользователь уже сам сформировал соответствующие ФГП, они
могут выбираться в качестве шаблона для формирования ФГП с аналогичными
свойствами, но с другими названиями. При этом могут быть добавлены ранее отсутствующие
свойства (например, указание на использование проекции). Но уже существующие
свойства, за исключением названия ФГП отредактированы быть не могут. Уже
созданные ФГП, а также любые другие элементы библиотеки ФГП, тоже не подлежат
редактированию, а могут быть только удалены. При этом из библиотеки ФГП
удаляются все другие элементы, которые в своем составе содержат ссылки на
удаляемые. Одновременно и уже введенные, и используемые в пакете каталоги
утрачивают необходимые ссылки на эти элементы и становятся частично или
полностью непригодными для последующей работы с ними.
Ниже показан вид окон при использовании
шаблона для формирования ФГП, аналогичного ФГП СК-95.
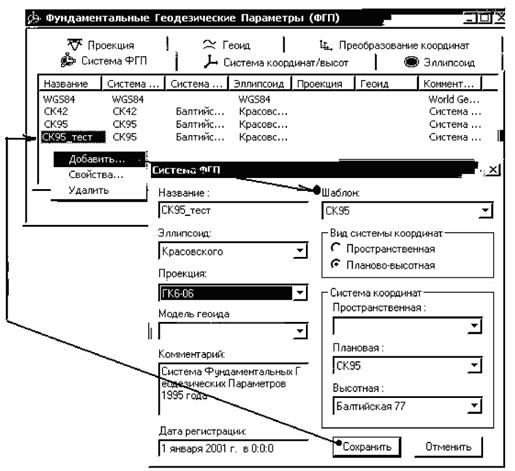
Рис. П3.5 Вид окон
при использовании шаблона для формирования ФГП, аналогичного ФГП СК-95
Использование шаблонов удобно для
формирования новых ФГП, формально воспринимаемых программным пакетом как
относящихся к разным системам координат с идентичными свойствами. При этом
сохраняется возможность их взаимного преобразования при фактическом отсутствии
параметров преобразования так, как будто соответствующие параметры имеют
нулевые значения. Такая возможность удобна для работы с каталогами, содержащими
различные (по любым известным пользователю причинам) данные, но формально (за
исключением названия ФГП) относящихся к одной и той же системе координат.
Например, для работы с координатами в СК-95, содержащимися в каталоге, и
координатами в этой же системе, полученными в результате какого-либо
преобразования из другой системы.
Все конкретные свойства систем координат и
ФГП обязательно содержатся в каталогах координат создаваемых внутри пакета
ГЕОМАСТЕР и экспортируемых из него в специальном формате. Эти же свойства
должны обязательно содержаться и в каталогах, импортируемых в базу данных
программного пакета из файла такого формата.
П.3.2. Формирование каталогов координат
Координаты пунктов могут быть импортированы
в базу данных программного пакета только из специальных файлов с расширением «.ctg», которые в свою очередь создаются
программными средствами геодезических банков данных ГГС.
Окно каталогов с открытым каталогом и
развернутым меню, обеспечивающим работу с данными одного выделенного пункта
этого каталога показано на следующем рисунке. Некоторые из этих функций могут
быть выполнены для всех пунктов каталога.
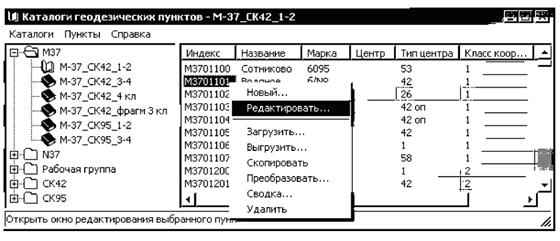
Рис. П3.6 Окно каталогов
с открытым каталогом и развернутым меню с выделенным пунктом этого каталога
В базу данных новые каталоги могут быть
импортированы лишь в том случае, если в библиотеке фундаментальных параметров
уже создана группа ФГП, соответствующая аналогичным свойствам каталога, уже
указанным в импортируемом файле и занесенным в него во время его создания. В
базу данных может быть добавлен новый первоначально пустой каталог. В этом
случае программа предложит назначить ему ФГП из числа уже имеющихся в соответствующей
библиотеке ФГП. В дальнейшем в любой каталог, в том числе и пустой,
автоматической загрузкой могут быть добавлены новые данные при условии
совпадения ФГП каталога и добавляемых координат пунктов. Проверка
согласованности ФГП выполняется автоматически. Пункты в каталог могут быть
добавлены и вручную. Возможно и ручное редактирование данных о пунктах, уже
содержащихся в каталогах. Более детальное описание всех операций с каталогами
можно найти в руководстве к программному пакету ГЕОМАСТЕР.
П.3.3. Построение цифровых моделей
преобразования координат
Построение цифровых моделей начинается с
создания проекта. В каждом проекте может быть построена только одна модель при
любом возможном количестве ее последующих изменений и уточнений. Ниже на рис. П3.7 показан процесс создания нового проекта.
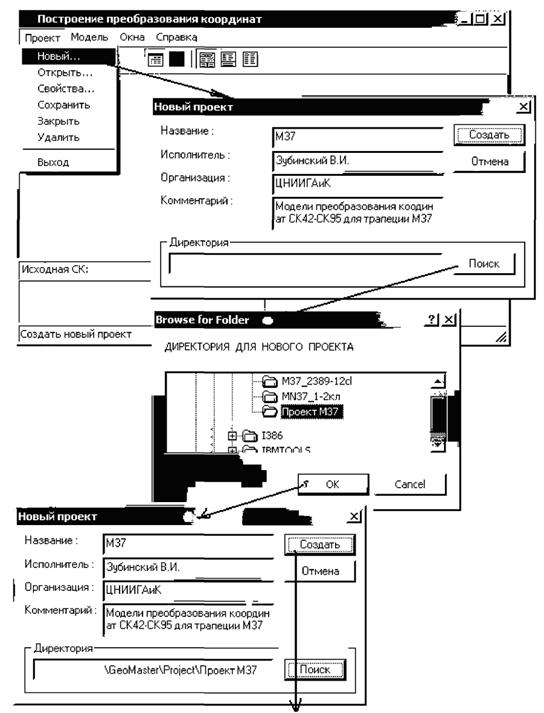
Рис. П3.7 Вид
окон при создании нового проекта модели преобразования координат
На рис. П3.8 показано главное окно нового проекта в
процессе задания свойств модели и импорта в проект координат пунктов для данной
территории в двух системах координат для построения цифровой модели. Задание
свойств цифровой модели включает в частности указание территориальных границ
создаваемой модели, глубины примыкающей территории и критериев отбраковки
аномальных данных. Использование пунктов на примыкающей территории по всей
границе необходимо, как для повышения надежности построения модели для
определения координат граничных пунктов, так и для обеспечения согласованности
модели, создаваемой на данной территории и моделей, которые будут строиться или
уже построены для смежных или перекрывающихся участков сети.
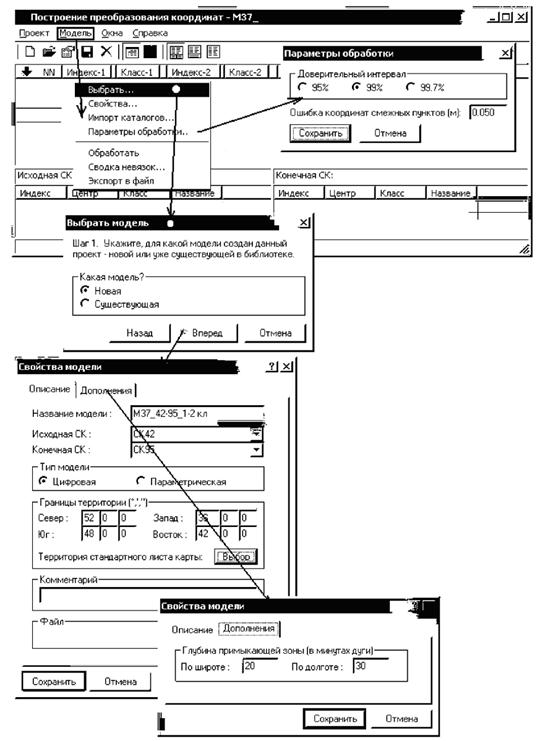
Рис. П3.8 Порядок
действий задания свойств модели для данной территории в двух системах координат
Импорт координат в проект схематически
показан на следующем рисунке. Импорт может осуществляться последовательно из
нескольких каталогов для каждой из систем координат. При этом каталоги для
импорта могут выбираться в произвольном порядке. Первоначально импортируемые
данные помещаются в нижних таблицах, в левой или правой ее половине в
зависимости от системы координат, к которой относятся импортируемые координаты.
В процессе импорта выполняется отождествление данных, представленных в разных
системах, но относящихся к одному и тому же пункту. Данные об отождествленных
пунктах переносятся в верхнюю объединенную таблицу.
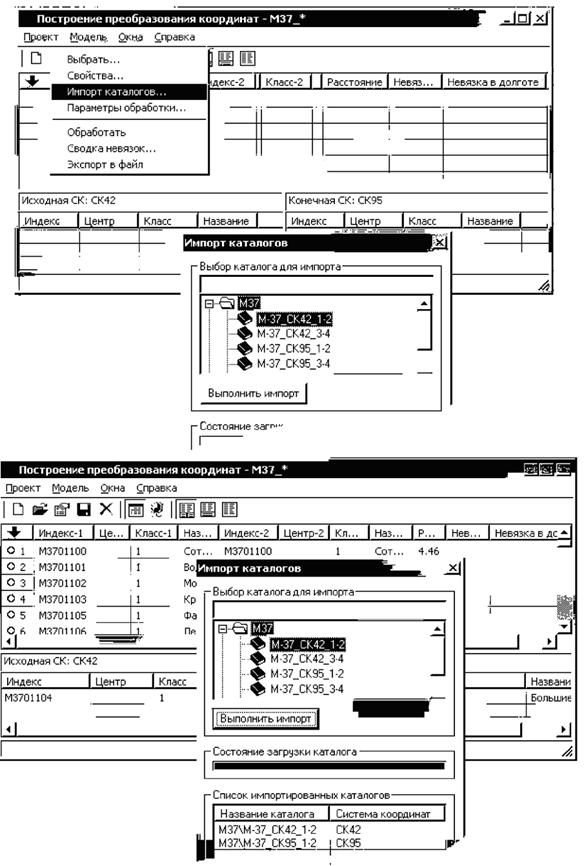
Рис. П3.9 Вид
окон при импорте координат из каталогов в проект из каждой из систем координат
Отождествление выполняется по совпадению
индексов пунктов, а если пункт имел более одного центра и у этих центров в
каталогах заданы номера, то и по одновременному совпадению этих номеров.
Неотождествленные пункты остаются в нижних таблицах.
По команде «Модель/Обработать» начинается
построение цифровой модели с одновременным анализом качества данных и
отбраковкой. Результаты анализа в виде значений невязок для обеих плановых
координат по всему списку общих пунктов выводятся в табличном виде в верхнюю
часть окна программы и в виде протокола отбраковки в его нижней части.
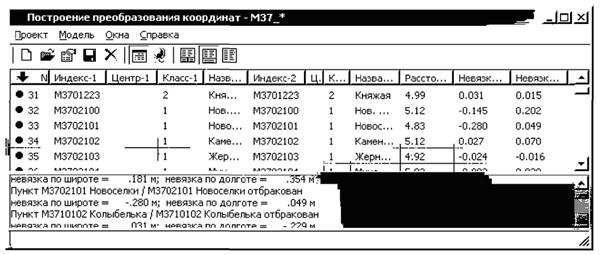
Рис. П3.10 Вид
окон со значениями невязок для обеих плановых координат по всему списку общих
пунктов и протокола отбраковки
Смысл получаемых невязок в данной задаче
построения цифровых моделей преобразования координат требует дополнительного
пояснения. Одно из свойств создаваемой цифровой модели состоит в том, что в так
называемых узлах этой модели, совпадающих с положениями пунктов, использованных
для ее построения, невязки при преобразовании отсутствуют. Иными словами
полученная модель при ее использовании точно воспроизводит координаты пунктов в
узлах, независимо от того, имеются в этих координатах какие-либо ошибки, каковы
их свойства и источник происхождения.
Невязки, оцениваемые при построении модели,
получаются как разность между двумя парами координат: координатами пункта в
каталоге конечной системы координат и его координатами, полученными из исходной
системы посредством координатного преобразования по модели, которая построена
без использования этого пункта. Получаемая невязка показывает, с какой
точностью возможна интерполяция поправок координат в районе данного пункта,
если данные этого пункта для интерполяции не используется. Получаемая невязка
может быть как следствием реальных деформаций сети в окрестностях данного
пункта, которые не могут быть учтены без использования координат этого пункта
для такой интерполяции, так и следствием каких либо других ошибок, не имеющих
отношения собственно к деформациям сети. Например, просто ошибок ввода
координат или отнесения координат не к тому центру. В первом случае отбраковка
конкретного пункта приведет лишь к ухудшению качества интерполяции в его
окрестностях. Более актуальны в таком случае меры по привлечению к построению
модели дополнительных пунктов в данном районе. Во втором случае отбраковка
пункта с аномальными значениями невязок реально необходима.
Таким образом процедура, именуемая
отбраковкой, при построении модели не является таковой в ее общепринятом
понимании. Это лишь инструмент, облегчающий оценку качества сравниваемых сетей
и одновременно возможности создаваемой модели воспроизводить взаимные
деформации сравниваемых сетей и учитывать их при преобразовании координат. Это
указание пользователю на те пункты и участки сети, которые могут потребовать
дополнительного анализа исходных материалов, а возможно и дополнительных данных
для построения качественной модели.
При анализе необходимо принимать во
внимание и то обстоятельство, что оцениваемые невязки получаются при
использовании модели, в определенном смысле неполноценной вследствие исключения
из нее гипотетически проблемного пункта. При этом остается, вообще говоря,
неизвестным, каковы будут ошибки преобразования координат для пунктов, расположенных
в пространстве между ним и ближайшими окружающими пунктами, если пункт с
аномальной невязкой не будет отбракован. В некоторых сложных случаях только
дополнительные пункты сгущения, не использовавшиеся при построении модели могут
дать возможность такой оценки. Величины рассогласования координат для этих
пунктов с учетом их территориального распределения могут дать основания для
окончательного решения о необходимости исключения пункта или целесообразности
его сохранения в модели (возможно и в совокупности с этими дополнительными
пунктами или их частью).
Не исключается и вероятность того, что на
части территории с аномально большими и быстро меняющимися деформациями ГГС
задача преобразования координат в СК-95 невозможно будет решить иначе, чем
переуравниванием прежних измерений или даже проведением полевых работ.
Положение пунктов с аномальными невязками
могут быть просмотрены в совокупности с положениями остальных пунктов сети, как
показано на рис. П3.11.
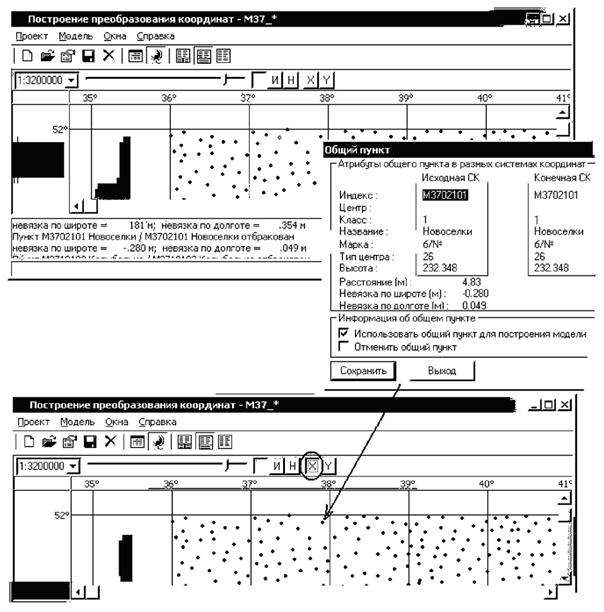
Рис. П3.11 Вид
окон с различными невязками координат пунктов
Пункты с аномальными невязками могут быть
показаны без учета их дифференциации по величинам невязок в широтах или
долготах (первая часть приведенного выше рисунка), так и порознь для каждой из
координат (нижняя часть рисунка). В этом случае разными цветами показываются
пункты с невязками разных знаков, а такими же, но более бледными цветами
показываются пункты с невязками, не выходящие за предельные значения, но по
абсолютной величине превышающие 2/3 предела. Предельно допустимые величины
невязок определяются двумя параметрами, задаваемыми пользователем при
подготовке к обработке. Требованием к ошибке координат смежных пунктов и
требованием к доверительному интервалу этой оценки. Первый параметр может
выбираться произвольно по желанию пользователя. Второй параметр может иметь три
значения: 95 %, 99 % и 99,7 %. Не останавливаясь на деталях выбора доверительного
интервала, укажем, что выбор 95 % интервала означает выбор более жесткого
критерия отбраковки при одинаковых требованиях к точности взаимного положения
смежных пунктов.
Непосредственно с плана сети можно
просмотреть индивидуальную информацию о любом выбранном на плане пункте. Окно с
соответствующей информацией показано в середине рис. П3.11. Это окно может быть вызвано не только из
окна плана сети, но и из таблицы невязок, показанной на предшествующем рисунке.
В окне с индивидуальной информацией о пунктах можно, используя переключатели в
его нижней части, исключить данный пункт из процесса построения модели,
независимо от соответствующих ему величин невязок.
П.3.4. Сохранение и использование цифровой модели
После получения окончательного варианта
цифровой модели последняя может быть сохранена в виде файла.
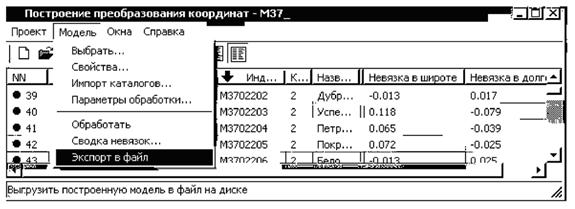
Рис. П3.12 Вид
окон при сохранении цифровой модели как файла
Для использования цифровой модели она
должна быть внесена в раздел «Преобразование координат» библиотеки
фундаментальных геодезических параметров.
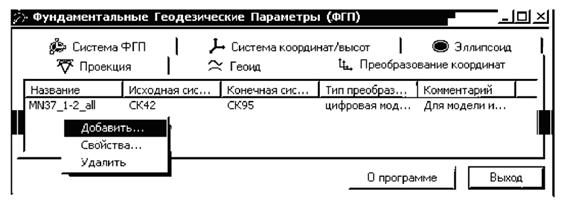
Рис. П3.13 Вид
окна ФГП, раздел «Преобразование координат» при внесении цифровой модели в
библиотеку фундаментальных параметров
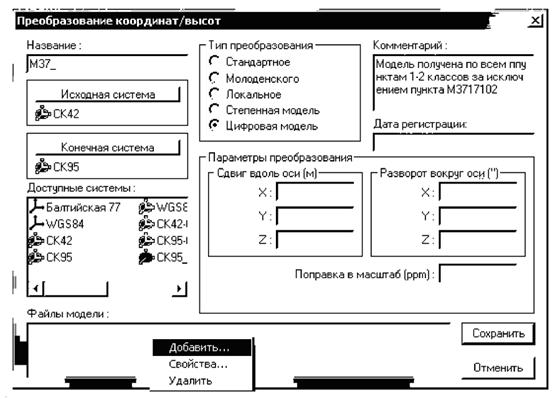
Рис. П3.14 Вид
окон при заполнении паспорта вносимой цифровой модели
По команде «Добавить» открывается окно,
показанное на рис. П3.14, в котором нужно указать название модели; из числа доступных
систем выбрать названия исходной и конечной систем, для которых строилась
модель; тип преобразования (цифровая модель); комментарий (рекомендуется) и в
области «файлы модели» по команде «добавить» указать путь к файлу с данной
моделью на диске. После этого по команде «Сохранить» соответствующая модель
регистрируется в библиотеке ФГП и доступна для использования.
Для выполнения координатного преобразования
необходимо в библиотеке каталогов открыть каталог пунктов на соответствующей
территории, координаты которых заданы в исходной системе и вызвать команду
«Преобразовать».
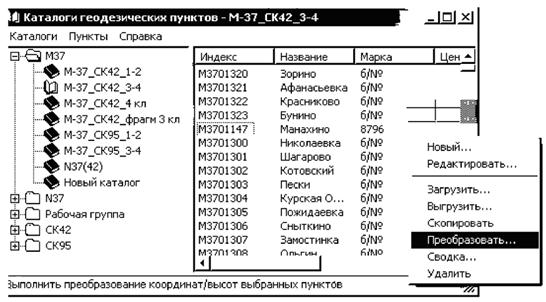
Рис. П3.15 Вид
окон при выполнении координатного преобразования на выбранной территории в
библиотеке каталогов
По команде «Преобразовать» вызывается окно
назначения режимов преобразования координат.

Рис. П3.16 Вид
окон назначения режимов преобразования координат
В окне преобразования координат (рис. П3.16) достаточно указать имя каталога, в
который должны быть помещены преобразованные координаты, название системы ФГП,
в которую должны бать преобразованы координаты пунктов открытого каталога.
После этого из всех преобразований, доступных для данной пары систем координат,
необходимо выбрать нужное координатное преобразование и дать команду
«Выполнить». После преобразования новый полученный каталог можно сохранить в
базе данных в желаемом месте под ранее выбранным именем. В любое время каталоги
могут быть переименованы без нарушения каких-либо связей, свойств или функций
каталога.
Приложение 4. Практические примеры создания и использования цифровых
моделей преобразования координат между СК-42 в СК-95 в программном пакете
ГЕОМАСТЕР.
Для практических примеров был выбран
участок ГГС России на территории двух листов М37 и N37 масштаба 1:1000000. В
границах листа N37 были использованы только пункты ГГС 1 и 2 классов. В
границах листа М37 использовались также и пункты 3 и 4 классов. Цифровые модели
составлялись как для объединенной территории двух листов (только по координатам
пунктов 1 - 2 классов), так и отдельно для листа М37 (по пунктам 1 - 2 классов
и с привлечением пунктов 3 класса).
Схема расположения пунктов 1 - 2 классов
показана на рисунке П.4.1. На схеме четко видны пункты рядов триангуляции 1 класса и
достаточно легко дешифрируются базисные сети. Реальная схема рядов и полигонов
1 класса существенно отличается от идеальной. На юго-западе отсутствие пунктов
объясняется тем, что это уже территория Украины. В центре пункты отсутствуют
из-за элементарного пропуска данных одной трапеции масштаба 1:200000 м-ба,
допущенного при формировании объединенного каталога на территорию миллионных
листов.
Цифровая модель строилась без
дополнительных полос уширения за внешними границами листов миллионного
масштаба. В качестве критерия для оценки аномальных величин невязок была
выбрана предельная величина ошибки взаимного положения смежных пунктов, равная
7 см при уровне доверительной вероятности 95 %.
При этих установках количество пунктов с
аномальными величинами невязок получилось равным 35. В их числе было 25 пунктов
1 класса и 10 пунктов второго класса, в подавляющем большинстве смежных с
забракованными пунктами 1 класса. Как уже говорилось раньше, такая ситуация объясняется
схемой уравнивания, принятой при установлении СК-42 и последующем развитии ГГС
в этой системе. Сначала уравнивались полигоны первого класса, и лишь потом
полигоны заполнялись сплошными сетями 2 класса. Сети 2 класса уравнивали,
принимая координаты пунктов 1 класса за твердые. Поскольку в действительности
полигоны триангуляции 1 класса являются существенно менее жесткими
построениями, чем сплошные сети 2 класса, то и наибольшие деформации сети в
большей мере связаны именно с пунктами 1 класса. Следует обратить внимание и на
то обстоятельство, что большинство аномальных невязок относится к нескольким
относительно компактным группам пунктов.
Типичные величины аномальных невязок при
выбранных критериях отбраковки находятся в интервале 20 - 30 см. Однако
величина одной невязки достигает 1 метра. Как будет видно позднее, эта невязка
является не результатом деформации сети, а скорее всего, вызвана тем, что
координаты пункта в СК-42 и СК-95 по какой-то причине отнесены к разным центрам
пункта.
На рис. П4.2 в виде векторов показаны величины и
распределение в сети остаточных расхождений в координатах пунктов, полученных
после преобразования с использованием цифровой модели, в которой не использованы
все пункты, имевшие аномальные невязки при ее построении. Напомним, что для
использованных пунктов остаточные расхождения координат всегда равны нулю.
Вектора смещения отражают расхождения координат пунктов в СК-95 из каталога и
координат в этой же системе, полученных по координатам в СК-42 в результате
преобразования с использованием цифровой модели.
Величины этих остаточных расхождений и
величины невязок, оцениваемых при построении модели не равны между собой, но,
как правило, эти различия не очень велики. Эти различия объясняются тем, что
невязки при построении модели вычисляются при исключении из модели только
одного, оцениваемого пункта, даже если для смежных пунктов невязки также имеют
аномальные величины.
Рис. П4.1 Пункты ГГС 1 и 2 классов, использованные
при построении цифровой модели преобразования координат из СК42 в СК95 на
трапеции М37 и N37
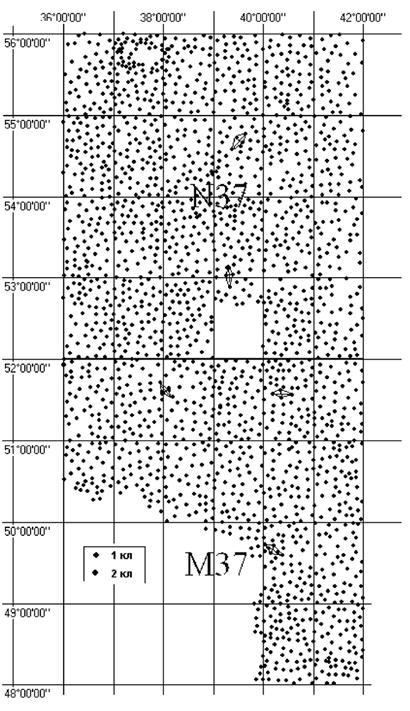
Рис. П4.2 Пункты ГГС 1 и 2 классов, отбракованные при построении цифровой
модели преобразования координат из СК-42 в СК-95 на трапеции М37 и N37
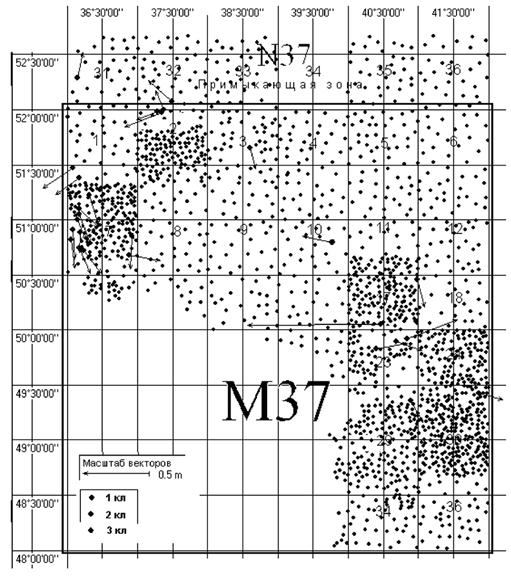
Рис. П4.3 Пункты ГГС 1, 2 и 3 классов, использованные при построении
цифровой модели преобразования координат из СК-42 в СК-95 на трапецию М37 и
вектора остаточных расхождений в положениях пунктов, данных в каталогах СК-95 и
полученных преобразованием по цифровой модели
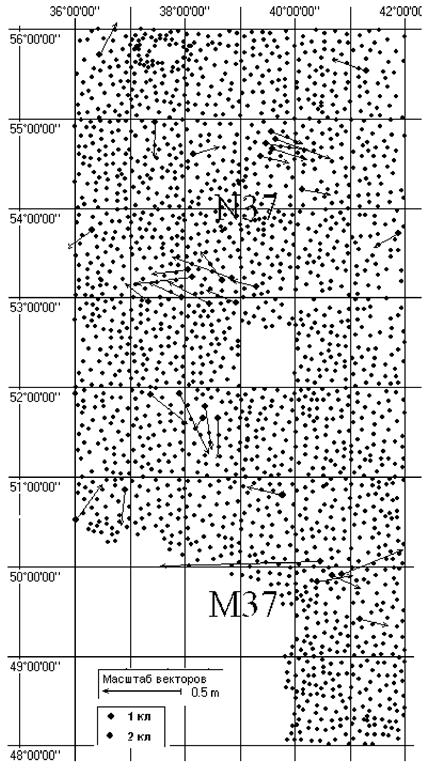
На рисунке П4.3 показаны пункты 1 - 3 классов,
использованные при построении цифровой модели для территории только одного
листа М37 карты масштаба 1:1000000, и полученные остаточные расхождения в
координатах пунктов, исключенных при построении модели.
Пункты 3 класса добавлены лишь на тех
трапециях масштаба 1:200000, на которых были проблемные пункты 1 класса с
большими невязками координат. Имеются как совпадения, так и различия в
сравнении с результатами, полученными только по пунктам 1 - 2 классов и
отраженными на рис. П4.2. На рис. П4.4, на котором показаны только пункты с остаточными расхождениям в
координатах для обоих вариантов построения модели на одну и ту же территорию,
сходства и различия этих двух результатов видны более четко.
Рис. П4.4. Вектора остаточных расхождений в
положениях пунктов из каталога СК-95 и полученных преобразованием из СК-42 по
цифровой модели.
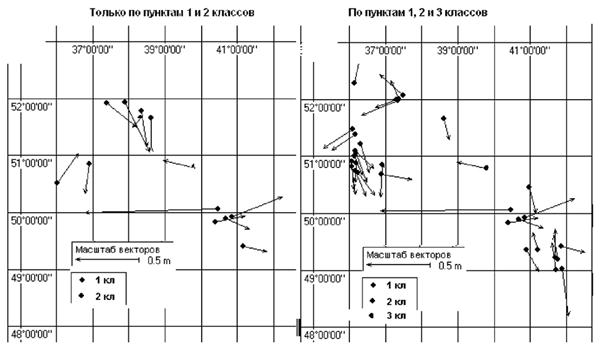
Для некоторых пунктов 1 и 2 классов
ситуация не изменилась после добавления в модель данных о пунктах 3 класса. У
некоторых из этих пунктов невязки уменьшились до допустимых и они исключены из
числа забракованных. Но в числе забракованных появилось три новых пункта 1
класса и пять новых пунктов 2 класса. К числу забракованных добавились и пункты
3 класса. Внешне общая ситуация скорее ухудшилась.
На рисунках П4.5а и П4.5б показаны результаты использования
построенных цифровых моделей при преобразовании координат пунктов 3 класса.
Использовались две версии модели, обе построенные по координатам пунктов 1 - 2
классов на территорию объединенных трапеций М37 и N37: версия модели с
включением данных о всех пунктах 1 - 2 классов и версия, построенная с
отбраковкой пунктов исходя из значения пороговой ошибки взаимного положения
смежных пунктов, равной 7 см при доверительной вероятности 95 %. Оценивалась
точность преобразования координат для пунктов 3 класса на двух трапециях м-ба
1:200000: для трапеции М37-II (рис П4.5а) и M37-XVII (рис П4.5б). При работе в программных пакетах из-за
неудобства использования римских цифр трапеции обозначены как М3702 и М3717.
Такие же обозначения использовались и в тексте.
На обеих трапециях при построении моделей
встретились пункты с значительными невязками. Фрагменты сети 1 - 2 класса на
соответствующих участках с векторами невязок показаны на этих же рисунках на
врезках. На рисунках показаны разности положений пунктов 3 класса по каталогу в
системе СК-95 и положений этих же пунктов, полученных преобразованием из
системы СК-42 с использованием упомянутых выше моделей. Помимо графического
представления остаточных расхождений координат на рисунках даны таблички с
оценками средних квадратических значений для получаемых расхождений координат,
а также минимальные и максимальные величины полученных расхождений.
Для разных трапеций результаты оценок
приводят к различным выводам. На трапеции М3702 включение в модель данных о
пунктах с аномальными невязками приводит к некоторому улучшению точности
преобразования вблизи мест расположения этих пунктов. Но уже в некотором
удалении от них остаточные уклонения остаются относительно большими. Общая
точность, вообще говоря, невелика и для получения более достоверного
преобразования необходимо привлечение к построению модели дополнительных
данных.
Рис. П4.5. Сравнение результатов
преобразования координат двумя вариантами цифровых моделей, построенных по
пунктам 1 - 2 классов. Слева без отбраковки, справа с отбраковкой.
Рис.
П4.5а Трапеция М3702 (м-б 1:200000)
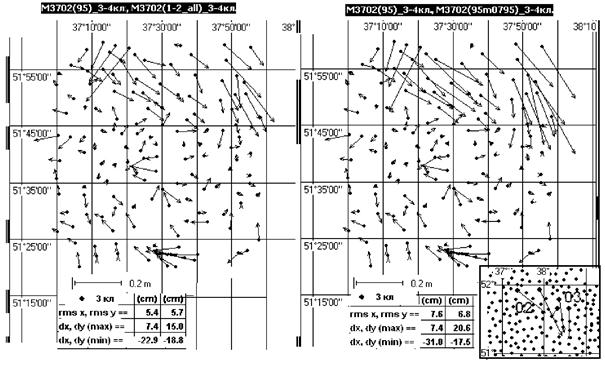
Рис. П4.5б Трапеция М3717 (м-б 1:200000)
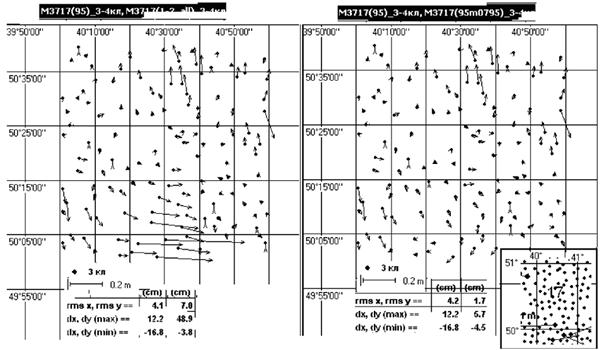
На трапеции М3717 включение в модель данных
о единственном пункте с аномальными невязками приводит к прямо противоположному
результату.
Точность преобразования резко ухудшается
при включении в модель данных единственного пункта с аномальной невязкой. Это
указывает на то, что эта невязка вызвана причинами, на имеющими отношения к
деформациям сети на этой территории. Скорее всего это результат какой-либо
грубой ошибки при подготовке данных об этом пункте и эта ошибка никак не
повлияла на точность координат окружающих пунктов.
Приложение 5. Определение и использование параметров ортогонального
преобразования координат
Возможности построения и использования
ортогональных преобразований координат предусмотрены в большинстве прикладных
программных пакетов обработки результатов геодезических спутниковых ГЛОНАСС/GPC определений. Соответствующие инструменты
в разных программных пакетах естественно различаться по интерфейсу пользователя
и порядку работы, но основаны на применении одинаковых принципов. Эти
инструменты в первую очередь предназначены для преобразования результатов
построения спутниковых геодезических сетей из системы координат WGS84 в систему координат пользователя. В
частности, в СК-95 или СК-42. Однако, они применимы и для выполнения
координатных преобразований между этими двумя системами. В настоящем приложении
использование ортогонального параметрического преобразования показано на
примере программного пакета PINNACLE фирмы Toрcon.
Для работы с этим программным пакетом
имеется достаточно подробное руководство. В данном приложении будут отражены
только те моменты, которые имеют непосредственное и обязательное отношение к
построению и использованию моделей ортогонального преобразования для связи
между СК-42 и СК-95, основным этапам этого процесса, но без детального описания
всех действий с интерфейсом программы. Описание деталей выполнения операций и
дополнительных возможностей программы, в частности в отношении преобразования
координат можно найти в руководстве по работе с программой.
Любые координатные преобразования, как и в
программном пакете ГЕОМАСТЕР начинаются с задания основных свойств используемых
систем координат. Однако, в отличие от пакета ГЕОМАСТЕР в программных пакетах
обработки спутниковых наблюдений системы координат определяются заданием двух
наборов свойств:
• параметрами используемого референц-эллипсоида
(для СК-42 и СК-95 это параметры
эллипсоида Красовского) и
• параметрами ориентирования,
определяющими положение необходимой системы координат
в мировой геодезической системе координат WGS84.
Таким образом, система координат WGS84 играет роль опорной системы при задании
любых других систем координат. При переходах между какими-либо другими
системами координат она служит промежуточной системой. Если необходимо,
например, перевести координаты из системы «А» в систему «Б», то автоматически
выполняется следующая цепочка преобразований:
«А» → WGS84 → «Б».
Естественно, что параметры ориентирования
обеих систем в системе WGS84 должны
быть заранее заданы или определены. В качестве параметров ориентирования
используются значения коэффициентов 7-ми параметрического ортогонального
координатного преобразования. Соответственно и преобразование между системами
«А» и «Б» будет обладать теми же свойствами ортогональности и будет
эквивалентно непосредственному преобразованию с коэффициентами, равными
разности соответствующих параметров ориентирования каждой из этих систем в WGS84. В качестве параметров ориентирования
используются 3 параметра линейного смещения DX, DY, DZ по каждой из осей X, Y и Z
геоцентрической системы, три значения малых углов вращения RX, RY, RZ вокруг каждой
из этих осей и общая поправка Scale к
единичному масштабному множителю.
К параметрам ориентирования какой-либо
системы в системе WGS84 применяется общий термин «Datum» системы. Выбранные параметры
соответствуют следующей форме координатного преобразования:
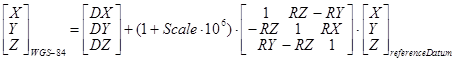
Для вновь вводимой системы параметры
ориентирования могут быть заранее не специфицированы и определены в
последующем.
На рис. П5.1 показан фрагмент главного окна программы Pinnacle с открытым окном редактора координатных
систем. В окне редактора открыта закладка с уже заданными параметрами
ориентирования системы СК-95 и указанием эллипсоида Красовского как
референц-эллипсоида этой системы. Обычно параметры эллипсоида Красовского уже
заданы в программных пакетах. Однако, при их отсутствии они могут быть введены
как параметры нового эллипсоида в закладке Ellipsoid.

Рис. П5.1
Фрагмент главного окна программы Pinnacle с открытым
окном редактора координатных систем
В формальном названии SK95, видном в строке, выделенной синим
цветом, использован латинский шрифт, чтобы избежать путаницы с кодировкой букв
разного алфавита, имеющих одинаковое изображение.
На закладке показаны значения параметров
системы СК-95. Ниже эти же значения повторены в текстовом формате:
DX = +24,653 м; DY = -129,136 м; DZ = -83,057 м;
RX = -0,06696²; RY = +0,00391,
RZ = -0,12902²;
Scale = -0,175´106.
Как вводятся параметры для нового Datum будет показано ниже.
Указанные выше значения параметров для
СК-95 (SK95) получены как параметры связи между
координатами пунктов ГГС в СК-95 и координатами этих же пунктов в системе ITRF. В свою очередь практическая реализация ITRF получена при построении фундаментальной
астрономо-геодезической сети (ФАГС) и высокоточной геодезической сети (ВГС) по
наблюдениям спутников GPS в результате
привязки к международной сети постоянно действующих пунктов спутниковых
наблюдений. Координаты в системе ITRF вычислены
по результатам предварительной обработки наблюдений ФАГС и ВГС 1999, 2001 и
2002 годов. Погрешности этих координат в целом по сети не превышают нескольких
сантиметров, а сама сеть имеет протяженность от западных границ до Дальнего
востока, но не покрывает северные территории Западной и Восточной Сибири,
Чукотки. Фактические различия между WGS84 и ITRF находятся в пределах дециметра.
Внутренние деформации СК-95 на всей протяженности ГГС составляют несколько
дециметров. Поэтому для преобразования между СК-95 и WGS84 систему ITRF можно
считать идентичной системе WGS84. Точность
такого преобразования в целом по всей ГГС будет находиться в пределах
нескольких дециметров и в основном определяться внутренними деформациями ГГС в
СК-95.
На рис. П5.2 показаны вектора остаточных расхождений
координат пунктов АТС в СК95 и координат этих же пунктов, полученных выше
приведенным преобразованием из координат в системе ITRF, полученных при построении ВГС. Средние квадратические значения
остаточных расхождений по координате х равны 27 см и по координате у
- 20 см. Показанные на схеме пункты АТС обычно расположены не дальше 10 - 15 км
от пунктов ВГС (по два или одному пункту АТС возле каждого пункта ВГС). На этом
же рисунке показано расположение пунктов Космической и Доплеровской
геодезических сетей, использовавшихся при установлении СК-95.
Указанная точность будет обеспечиваться,
если координаты в исходной системе, будь то СК-95 или WGS84 (ITRF), получены в результате привязки к физическим
пунктам, носителям соответствующей системы. В большинстве обычных работ с
использованием GPS, система координат, получаемая из
непосредственной обработки спутниковых наблюдений и называемая WGS84, лишь по ориентировке и масштабу
действительно достаточно точно соответствует этой системе. Положение же ее
начала может быть произвольным в пределах нескольких метров. Это связано с тем,
что при отсутствии реальных исходных пунктов с координатами в системе WGS84 абсолютное положение совокупности
пунктов создаваемой сети определяются фактически по автономным спутниковым
определениям, точность которых обычно не лучше нескольких метров. Фактически
имеется лишь три способа получения более точных абсолютных положений пунктов в WGS84:
- использование наблюдений исходных
пунктов, реальных носителей системы;
- использование глобальных систем
дифференциальных кодовых спутниковых определений;
- использование исходных пунктов с
координатами в СК-95 с последующим их преобразованием в WGS84 с использованием указанных выше
значений параметров.
Это обстоятельство необходимо всегда иметь
в виду при выполнении координатных преобразований в практических работах по
спутниковым определениям.
В задачах преобразования между СК-95 и
СК-42 сделанные выше замечания не имеют принципиального значения, поскольку в
таких задачах речь фактически идет о различиях в этих системах или, в более
конкретной форме о разностях параметров (Datum’ов) этих двух систем. Поэтому, для одной из этих систем,
например, для СК-95, параметры могут быть назначены относительно произвольно, в
частности, нулевыми.
Система СК-42 имеет значительные внутренние
деформации, как в целом, так и на отдельных территориях. Для обеспечения
достаточной точности преобразования координат между системами СК-95 и СК-42
размеров фрагмента сети, для которых преобразование выполняется по одному
набору параметров, должны быть существенно ограничены.
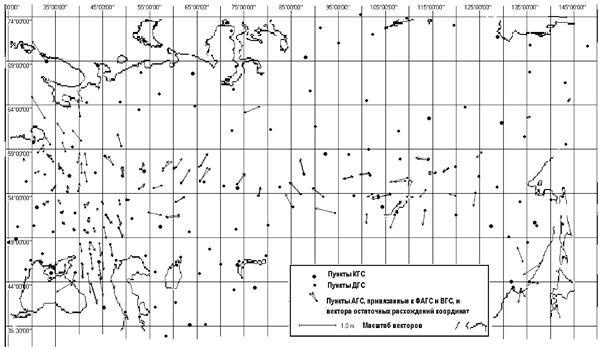
Рис.
П5.2. Схема
расположения пунктов Космической геодезической сети (КГС), Доплеровской
геодезической сети (ДГС) и пунктов АГС в местах расположения пунктов ФАГС и
ВГС.
(Данные о ФАГС и ВГС по состоянию наблюдений 1999 - 2002
гг.)
Фактически координаты пунктов ГГС на
некоторой ограниченной территории необходимо рассматривать как некоторую
частную практическую реализацию общей системы СК-42. Соответственно для каждого
из этих участков должен быть назначен свой набор параметров (свой Datum) в библиотеке координатных систем в
программе Pinnacle. При это систему СК-95 удобнее, в данном
случае, рассматривать как единую систему с одним набором параметров
ориентирования относительно системы WGS84.
Ниже показан пример начального задания
частной реализации СК-42, которая будет в последующем использована при работе с
координатами на всей трапеции М37.
Фактически сначала для системы назначается
только используемый эллипсоид, название и, возможно примечание. Сами значения
параметров можно определить как не специфицированные, поставив отметку в
соответствующем переключателе. Можно оставить их нулевыми, поскольку имеется
возможность последующего изменения их значений.
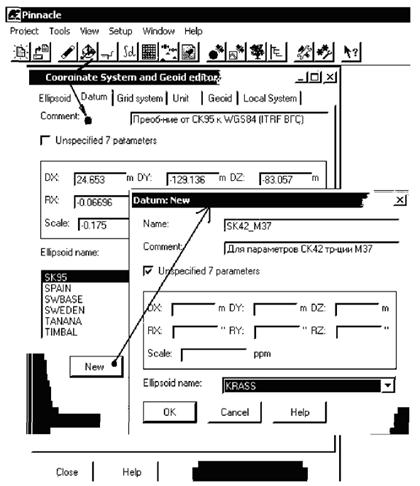
Рис. П5.3 Вид
окна начального задания частной реализации СК-42
После такого начального задания необходимых
систем координат можно начинать определение связи между СК-95 и реализацией
СК-42 для выбранного участка территории. Для этих целей используется Табличный
координатный калькулятор Pinnacle.
Предварительно должны быть подготовлены
файлы со списками координат одних и тех же пунктов в обеих системах координат в
текстовом формате. Рекомендуется, по крайней мере, до получения необходимого
опыта пользоваться координатами не в проекции Гаусса-Крюгера, а геодезическими
эллипсоидальными координатами. В обоих списках пункты должны располагаться в
одном и том же порядке. Совпадение имен пунктов не обязательно. У некоторых
пунктов в каталогах могут отсутствовать значения высот. Для работы в Табличном
координатном калькуляторе это недопустимо. Отсутствующие высоты могут быть
заменены нулевыми значениями. Желательно, чтобы высоты в обоих списках были
примерно одинаковыми. Для подготовки файлов может быть использована функция
экспорта координат пунктов из каталогов средствами программного пакета
ГЕОМАСТЕР. Имеется в виду составление списка координат по команде «Сводка». В
сводку должны включаться только названия пунктов, их координаты и высоты.
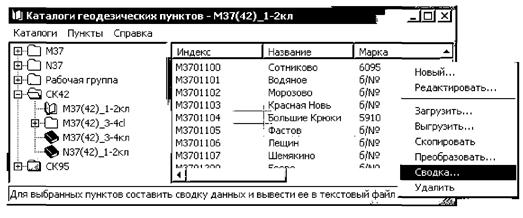
Рис. П5.4 Вид
окон при составлении списка координат по команде «Сводка»
Форматы соответствующих текстовых
экспортных файлов и файлов, импортируемых в Табличный координатный калькулятор Pinnacle, полностью совместимы. Различие состоит
лишь в том, что при экспорте из каталогов выдается лишь список пунктов с
координатами. А для импорта в калькулятор этому списку должен предшествовать
заголовок, содержащий информацию о представленной в списке системе координат.
Название системы координат должно строго соответствовать ее названию,
заданному, как указано выше, в библиотеке систем координат программного пакета Pinnacle. Имя файла может быть произвольным,
удобным для пользователя.
Образец текста импортируемого файла показан
ниже.
Table calculator
Left pane:
Geodetic: SK-42_M37
Unit name: Meters
Name Latitude Longitude Height, m
M3701100 51°51¢05,379200² 36°08¢43,950000² 262,334
M3701101 51°50¢52,932400² 36°30¢35,967400² 259,549
M3701102 51°46¢07,044700² 36°58¢19,644500² 259,500
...
M3701103 51°28¢24,000400² 36°04¢55,929500² 266,962
Точно запоминать формат нет необходимости,
поскольку он всегда может быть воспроизведен экспортом подходящих данных,
занесенных любым удобным способом в список координат табличного калькулятора.
Табличный координатный калькулятор имеет две панели (левую и правую) для
выполнения операций с двумя наборами координат одновременно. При экспорте в
заголовке текстового файла указывается, данные какой панели были
экспортированы. При импорте в Табличный координатный калькулятор наличие
соответствующей строки также необходимо, однако при этом импорт возможен и в
левую и в правую панель, независимо от того, какая именно панель указана в
текстовом файле.
Далее дано несколько последовательных
рисунков, показывающих импорт в калькулятор координат пунктов ГГС 1 - 2 классов
трапеции М37 на листе карты масштаба 1:1000000.
Перед импортом нет необходимости указывать
тип и название системы вводимых координат. Поскольку вводимая система описана и
в импортируемом файле и в библиотеке программного пакета, то ее идентификация
при импорте выполняется автоматически.
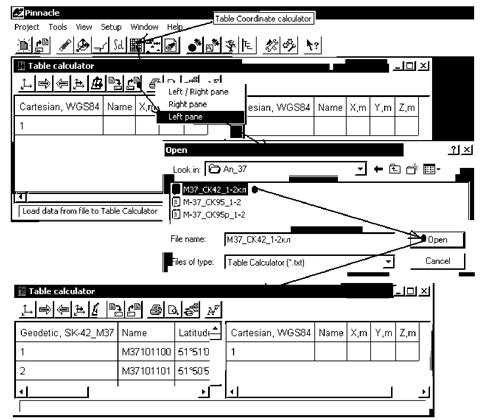
Рис. П5.5 Ввод
координат СК-42 в левую панель из файла М-37_СК-42_1-2.
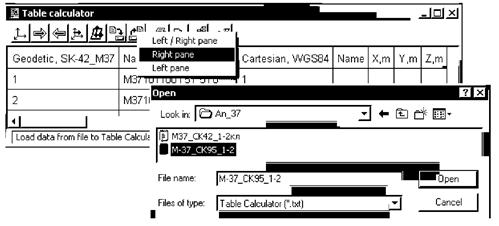
Рис. П5.6 Ввод
координат СК-95 в правую панель из файла М-37_СК-95_1-2.
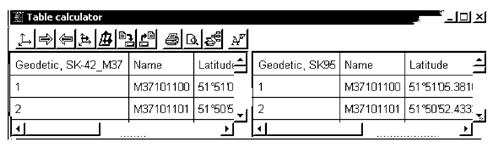
Рис. П5.7 Вид
панелей координатного калькулятора после импорта.
После этого программа готова к вычислению
параметров координатного преобразования из системы координат левой панели в
систему координат правой панели. Однако, поскольку в идеологию координатных
преобразований заложено использование для этих целей системы WGS84 как опорной или промежуточной, то
координаты в правой панели должны быть предварительно преобразованы в систему WGS84. Соответствующие параметры
преобразования были уже заданы, как показано ранее.
Соответствующее преобразование может быть
выполнено простым назначением требуемой системы координат для левой панели.
Вызов окна назначения систем координат для
любой из двух панелей выполняется самой левой кнопкой меню.
Соответствующее окно уже после выбора для
правой панели системы координат WGS84, а также окно
с уже преобразованными координатами правой панели показаны на двух следующих
рисунках.
На втором из этих рисунков показана кнопка
управления, запускающая процесс вычисления параметров координатного
преобразования.
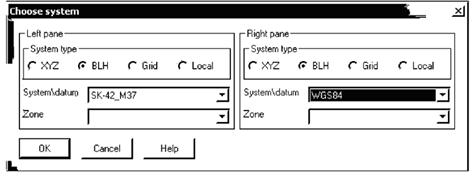
Рис. П5.8 Вид
окна после выбора для правой панели системы координат WGS84
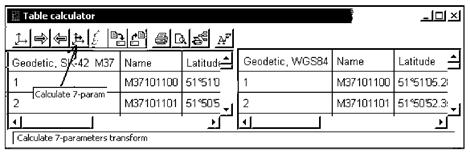
Рис. П5.9 Вид
окна с преобразованными координатами WG 84
правой панели
На рис. П5.10 показано окно с результатами вычислений
параметров и графиками величин остаточных невязок в плановых координатах в
соответствии с порядком следования пунктов в списке (самой правой кнопкой меню
может быть вызвана таблица с величинами невязок). Параметры определяются под
обычным условием метода наименьших квадратов. При обработке никакой отбраковки
не производится. Отбраковка возможна только вручную исключением из обоих
списков пунктов в панелях отбраковываемых пунктов. Полученные параметры можно
сохранить, используя специальную кнопку меню, указанную на рис. П5.10. Определенные параметры могут быть
сохранены под тем же именем для Datum, под которым
соответствующая реализация SK-42_M37 системы СК-42 была предварительно определена в
библиотеке с неспецифицированным значениями параметров. При этом параметрам
присваиваются полученные значения. Полученные параметры могут быть сохранены и
как новый Datum под другим именем. Полученные параметры
могут быть в любое время переопределены с использованием измененного состава
исходных данных или отредактированы вручную, если из какого-либо источника
известны более подходящие параметры.
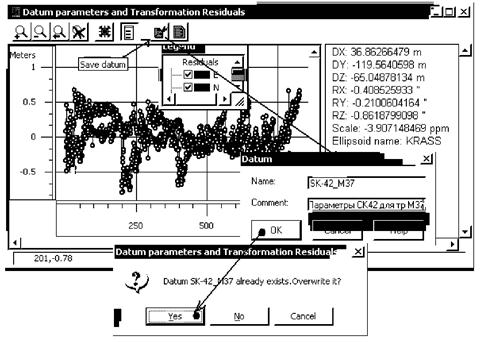
Рис. П5.10 Вид
окна с результатами расчета параметров и графики величин остаточных невязок в
плановых координатах пунктов
На рис. П5.11 показан вид окна с
обновленными данными для параметров преобразования локальной реализации СК-42
на участке трапеции М37.

Рис. П5.11 Вид
окна с обновленными данными для параметров преобразования локальной реализации
СК-42 на участке трапеции М37
Для использования полученных параметров с
целью преобразования координат из СК-42 в СК-95 в том же табличном координатном
калькуляторе достаточно импортировать исходные координаты, как заданные в
системе координат SK-42_M37 в любую из панелей и переназначить для этой панели систему
координат с SK-42_M37 на SK95. Подобным же образом выполняется и
обратное преобразование.
Приложение 6. Практические примеры использования параметров
ортогонального координатного преобразования.
Для практических примеров был выбран один
из участков ГТС, для которого в прил. 4 приводились примеры использования
цифровых моделей. Параметры ортогонального преобразования определялись как по
всем пунктам ГТС 1 - 2 классов в границах листа М37 масштаба 1:1000000, так и
для более ограниченных участков площадью в 1 - 2 листа карты масштаба 1:200000.
Небольшие участки выбирались там, где возникали какие-либо особенности при
использовании цифровых моделей. Для оценки полученных преобразований использовались
также и пункты ГГС 3 класса. С учетом результатов, полученных при построении
цифровых моделей, из исходных данных сразу же был исключен пункт 1 класса на
листе М3717, дававший метровую величину невязки вследствие явно грубой ошибки в
подготовки исходных данных в каталоге.
Рис. П6.1. Деформации СК42 на участке листа
карты М37 м-ба 1:1000000
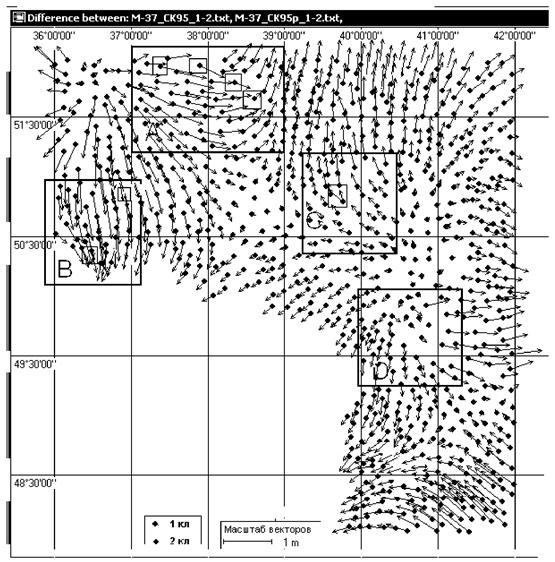
На рис. П.6.1 в виде векторов показаны величины
нелинейных деформаций ГГС 1 - 2 классов в системе СК-42 по отношению к данным
по ГГС в СК-95 в границах листа карты М37.
Вектора смещений (нелинейных деформаций)
получены как разности координат пунктов в СК-95 и координат этих же пунктов в
этой же системе координат, но полученных в результате преобразования из СК-42.
Использовалось 7-ми параметрическое ортогональное преобразование с параметрами,
полученными в Табличном координатном калькуляторе Pinnacle по координатам пунктов 1 - 2 классов на этой трапеции.
На рисунках П.6.2А, В, С и D показаны в увеличенном масштабе отдельные фрагменты рис. П.6.1 на те участки ГТС, на которых были
получены аномальные невязки при построении цифровой модели преобразования
координат (см. рис. П4.2 приложения 4).
На рисунках видно, что аномальные невязки получались в двух случаях: когда
величины остаточных расхождений координат для отдельных пунктов не
соответствовали общему характеру деформаций координат окружающих пунктов
(фрагменты А и D) или когда у одного пункта имелось два
центра, отнесенных к разным классам с несогласованными между собой
координатами. В обоих случаях до получения окончательной модели преобразования
координат (либо цифровой, либо 7-ми параметрической) необходимо проведение
анализа для выявления причин таких расхождений и их учета.
Рис. П6.2А, В, С, D Деформации ГГС в СК42 на отдельных
участках листа М37.
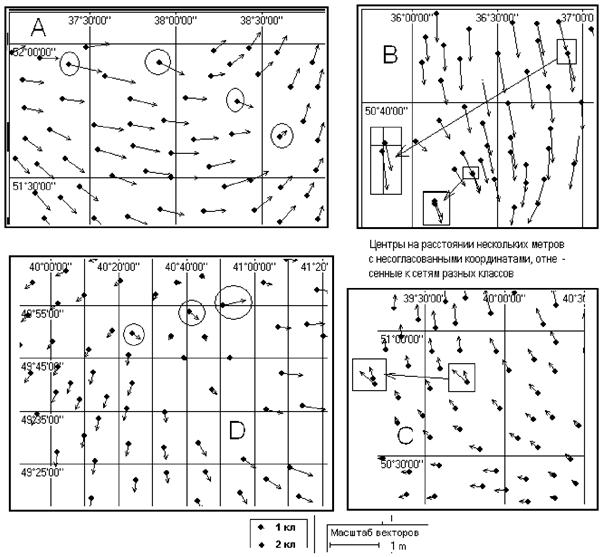
Рис. П6.3а. Определение параметров преобразования для трапеций M37D2 и M37D3
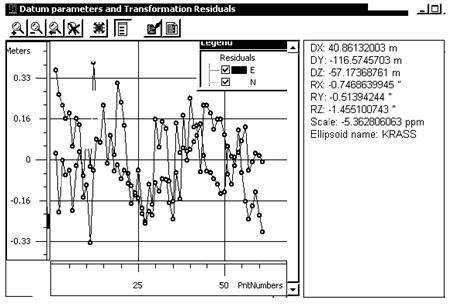
На рис. П6.3а показаны результаты определения
параметров по координатам пунктов 1 - 2 классов на участок объединенных
трапеций М37-II и М37-III листов карты
м-ба 1:200000. Этот участок соответствует фрагменту «А» на рисунках П.6.1 и П.6.2. Подчеркнем, что параметры, определяемые
по координатам пунктов ГГС на ограниченной территории, являются по существу
интерполяционными коэффициентами и не имеют четкого геометрического смысла,
ассоциируемого с понятием элементов ориентирования системы координат. Их можно
рассматривать как параметры локального преобразования координат.
На рис. П6.3б для этих же трапеций показаны величины
остаточных разностей координат пунктов в СК-95 и координат этих же пунктов,
пересчитанных из СК-42 с использованием параметров локального координатного
преобразования. Противоречия между векторами остаточных расхождений более
наглядны, чем на рисунке П.6.2а. Сами величины остаточных расхождений еще остаются излишне
большими, чтобы применить единый набор параметров ортогонального преобразования
одновременно для всех пунктов на этой территории.
Рис. П6.3б. Остаточные расхождения
координат на тр. М3702 и М3703
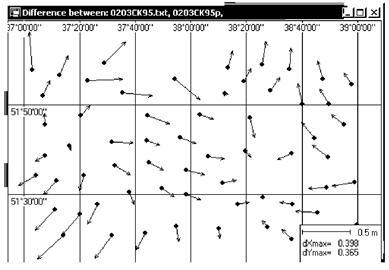
Рис. П6.4. Остаточные уклонения координат. Трапеция М3702
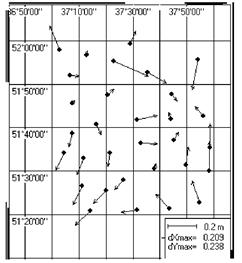
Из-за заметных локальных ошибок координат
остаточные расхождения остаются большими и при ограничении территории преобразования
координат только одной трапецией М3702 (см. рис. П6.4).
Рис. П6.5. Определение параметров
преобразования для тр-ции М3717 и остаточные уклонения.
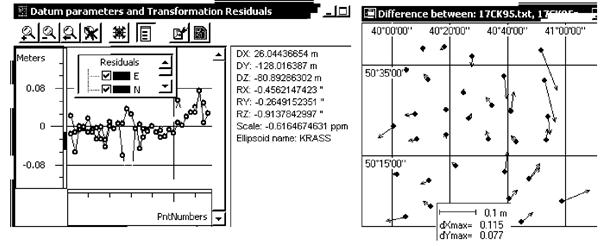
Для трапеции М3717 ортогональное
преобразование дает заметно лучшие результаты. Как видно на рис.
П6.5 остаточные
уклонения лишь для двух пунктов 2 класса близки к 10 см. Для большинства
остальных пунктов они заметно меньше.
Используя параметры преобразования,
полученные по координатам 1 - 2 классов для трапеции М3717, было выполнено
преобразование координат СК-42 в СК-95 для пунктов ГГС 3 класса на той же
трапеции.
На рис. П6.6 показаны величины остаточных расхождений
в значениях оригинальных координат пунктов 1 - 3 классов в СК-95 и координат
этих пунктов, полученных в результате ортогонального преобразования из СК-42. В
основном получены достаточно удовлетворительные результаты. Исключение
составляют несколько пунктов в северо-восточном углу трапеции.
Рис. П6.6. Остаточные расхождения координат
пунктов ГГС 1 - 3 классов при ортогональном преобразовании для трапеции М3717.
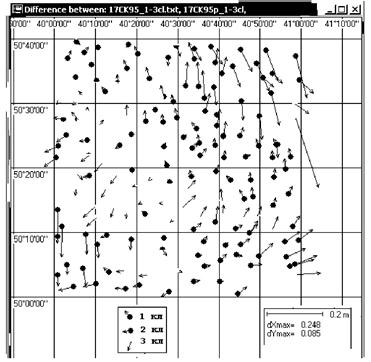
Рис. П4.6б. Остаточные расхождения координат п-тов 3 класса при
преобразовании координат по цифровой модели.
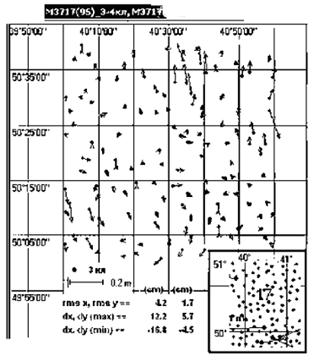
Для сравнения рядом на рис.
П4.6б, взятом из
приложения 4
показаны остаточные расхождения координат при использовании для преобразования
цифровой модели для всей трапеции М37. Общий характер поведения остаточных
расхождений (с учетом разницы масштабов изображения векторов) практически
одинаков на обоих рисунках. Однако общий уровень остаточных расхождений при
использовании преобразования координат по цифровой модели ниже. Меньше и
количество остаточных расхождений, заметно превышающих общий уровень.
В отличие от использования цифровых моделей
дополнение состава опорных пунктов пунктами 3 и (или) 4 классов не приведет к
повышению точности ортогонального преобразования на одной и той же территории,
но может способствовать более эффективному анализу проблемных ситуаций. При
недостаточной точности ортогонального преобразования может быть рекомендовано
лишь уменьшение размеров территории, для которой эти параметры определяются.
При этом, однако, количество используемых опорных пунктов не должно быть очень
малым, чтобы сохранилась возможность обнаружения грубых ошибок. При
необходимости ограничения размеров территории использование дополнительных
пунктов 3 - 4 классов может дать заметный эффект в повышении достоверности
преобразования координат.
Необходимо дополнительно подчеркнуть два
основных свойства ортогонального преобразования. При таком преобразовании с
одной стороны полностью сохраняется внутренняя точность (конфигурация)
положений пунктов исходной системы координат, а с другой стороны
преобразованные координаты наилучшим образом «вписываются» в конечную систему по
совокупному положению пунктов, ориентировке и масштабу. Иными словами, такое
преобразование приводит к минимизации изменений в положении координатной сетки
конечной системы. Таким образом, ортогональное преобразование может
использоваться как инструмент модернизации используемой системы координат на
основе использования новых более точных геодезических данных по всей сети или
на ее отдельных участках.
Приведенные примеры позволяют очертить круг
основных задач, решение которых рационально выполнять с использованием
ортогонального трансформирования координат при переходе к применению системы
координат СК-95.
1. Общий анализ характера локальных и
региональных деформаций ГГС и данных геодезических съемок, выполненных в СК-42.
2. Выявление проблемных данных в каталогах
координат пунктов ГГС. Проведение соответствующего анализа исходных данных
рекомендуется, прежде всего, в окрестностях тех пунктов, для которых возникают
большие невязки при построении цифровых моделей преобразования координат между
системами СК-42 и СК-95 перед получением окончательной модели.
3. Модернизация результатов геодезических и
топографических съемок, выполненных ранее в СК-42, в тех случаях, когда
ставиться задача повышения их точности при одновременном выполнении условия
минимизации общих расхождений с СК-42 (минимальных смещений сетки координат
ранее выполненных съемок).
4. Преобразование координат из СК-42 в
СК-95 на территориях с небольшими нелинейными деформациями ГГС в СК-42 и на
ограниченных территориях с небольшим количеством данных, недостаточных для
построения надежных цифровых моделей преобразования координат.
В противоположность ортогональному
преобразованию при использовании цифровых моделей обеспечивается сохранение
точности той системы координат, в которую они преобразуются, вплоть до точного
совпадения значений координат для общих пунктов обеих систем. Поэтому этот
метод, эффективный при перевычислении координат из менее точной системы СК-42 в
более точную систему СК-95, не пригоден непосредственно для обратной задачи
модернизации ранее использовавшейся системы координат, будь то СК-42 или
основанные на ней местные системы.
Использование для преобразования координат
цифровых моделей более эффективно при условии использования достаточно большого
количества опорных пунктов с координатами, известными в обеих системах. Однако
этот метод обладает ограниченными возможностями выявления и анализа аномальных
данных. При малом количестве опорных пунктов обнаружить даже явно грубые ошибки
при построении цифровых моделей практически невозможно.
Примечание: Программные
средства, использованные при подготовке данного
отчета для отображения на схемах плановых
положений пунктов сети и векторов остаточных
расхождений координат, не входят в состав
программных пакетов Геомастер и Pinnacle.
Приложение 7. Схема зон ответственности аэрогеодезических предприятий
Роскартографии на территории Российской Федерации
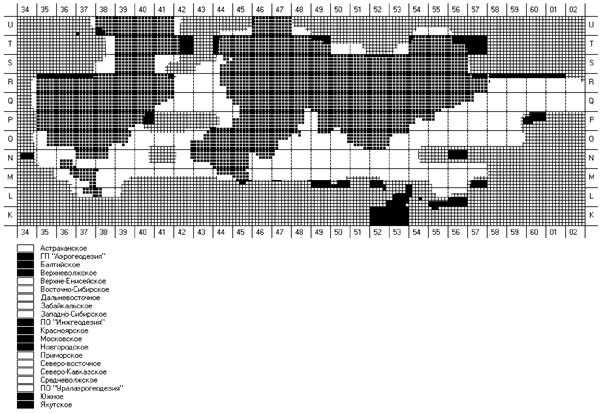
Приложение 8. Схема расположения
регионов, для которых требуется корректировка карт масштабов 1:10000, 1:25000,
1:50000
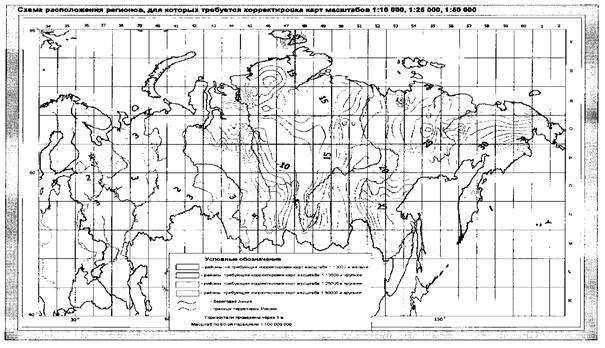
Приложение 9. Карта-схема высот
квазигеоида над эллипсоидом Красовского на территорию России
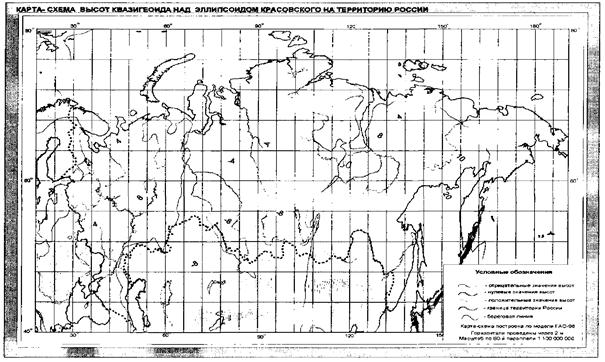
Приложение 10 Карта-схема высот квазигеоида над общим земным эллипсоидом
на территорию России
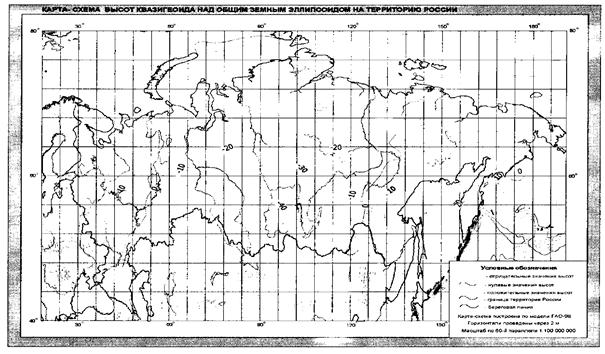
СОДЕРЖАНИЕ
![]() этой системы.
этой системы.![]() - направление силы тяжести в точке К на поверхности Земли;
- направление силы тяжести в точке К на поверхности Земли;![]() - направление
касательной к силовой линии нормального поля в точке К.
- направление
касательной к силовой линии нормального поля в точке К.![]() - составляющая
уклонения отвесной линии в плоскости меридиана;
- составляющая
уклонения отвесной линии в плоскости меридиана;![]() ,
,![]() - высота
квазигеоида (аномалия высоты) в точке М.
- высота
квазигеоида (аномалия высоты) в точке М.![]()
![]() ,
, ![]() составляющими
уклонения отвесной линии вычисляют следующим образом:
составляющими
уклонения отвесной линии вычисляют следующим образом:![]() ) = exsinL - eycosL,
) = exsinL - eycosL,![]() ) = (excosL + eysinL)sinL + ezcosB,
) = (excosL + eysinL)sinL + ezcosB,![]()
![]() - среднее
значение нормальной силы тяжести на отвесной линии ММ1:
- среднее
значение нормальной силы тяжести на отвесной линии ММ1:![]()
![]() у1 - нормальная сила тяжести на поверхности относимости, вычисленная по
нормальной формуле как функции широты ВM.
у1 - нормальная сила тяжести на поверхности относимости, вычисленная по
нормальной формуле как функции широты ВM.![]() в точке М
относительно точки K
выполняют с использованием
следующей формулы:
в точке М
относительно точки K
выполняют с использованием
следующей формулы:![]()
![]()





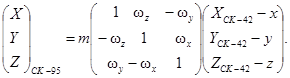

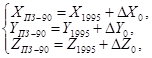 (
(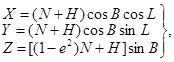 (
(