ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
(ГОССТАНДАРТ СССР)
ВСЕСОЮЗНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ПО НОРМАЛИЗАЦИИ В МАШИНОСТРОЕНИИ
(ВНИИНМАШ)
Утверждены
Приказом
ВНИИНМАШ
№ 91 от 06.04.1988 г.
МЕТОДЫ ОЦЕНИВАНИЯ ТОЧНОСТИ РЕЗУЛЬТАТОВ
ИСПЫТАНИЙ ПРОМЫШЛЕННЫХ РОБОТОВ
РЕКОМЕНДАЦИИ
Р 50-54-53-88
МОСКВА 1988
РЕКОМЕНДАЦИИ
Дата введения 01.01.89
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Среди всех видов испытаний, проводимых на различных стадиях жизненного цикла промышленных роботов (ПР), одно из важнейших мест занимают испытания, выполняемые с целью оценки технического уровня и качества выпускаемых ПР. Задачей испытаний такого вида является получение оценок количественных характеристик свойств ПР, определяющих их техническое совершенство и качество, причем эти характеристики рассматриваются применительно к определенным условиям эксплуатации ПР. При такой постановке задачи, понятие «испытание» определим как организованное взаимодействие объекта испытаний со средой с целью прогнозирования его состояния в типовых условиях эксплуатации. В дальнейшем будем рассматривать испытания именно такого вида.
1.2. Объектом испытаний может служить единичный образец ПР, партия или тип ПР. В двух последних случаях объект испытаний представляет собой соответственно конечную и бесконечную совокупность единичных образцов ПР. При этом непосредственному экспериментальному исследованию, как правило, подвергаются не все образцы, а лишь часть, выборка, полученная из соответствующей совокупности методом случайного отбора.
1.3. Условия испытаний представляют собой совокупность воздействующих на объект испытаний факторов внешней среды и режимов функционирования объекта.
Для промышленных роботов условия испытаний описываются следующими факторами: температура, влажность, давление окружающей среды, напряженность электромагнитного и электростатического полей, уровень вибрации, колебания напряжения питания электрической сети, колебания давления гидравлической и/или/ пневматической сети, масса рабочего органа и/или/ переносимого груза, величина и скорость перемещения конечного звена робота.
1.4. Результат испытаний в данном случае составляют оценки количественных характеристик свойств объекта, соответствующих типовым условиям эксплуатации. При этом для ПР возможны следующие виды характеристик свойств:
- детерминированная (постоянная) величина;
- случайная величина.
1.5. Точность результатов испытаний - свойство, характеризуемое близостью результатов испытаний к действительным значениям характеристик объекта, соответствующих типовым условиям его эксплуатации. Действительное значение физической величины - это найденное экспериментальным путем значение, настолько приближающееся к истинному, что для выбранной цели может быть использовано вместо него.
1.6. На точность результатов определительных испытаний ПР существенное влияние оказывают:
- степень адекватности статистических свойств совокупности отобранных образцов ПР для испытаний статистическим свойствам объекта (см. п.п. 1.2);
- степень адекватности воспроизведенных условий испытаний типовым условиям эксплуатации ПР;
- точность определения (измерения) данных испытаний;
- точность обработки данных испытания.
1.7. Весомость перечисленных факторов в формировании погрешности результатов испытаний не одинакова. Основное влияние оказывают первые три фактора. А вклад последнего в общую погрешность результатов, как правило, составляет 0,1 ... 1,0 %. Поэтому в настоящих рекомендациях рассмотрены такие случаи, когда влиянием этого фактора на точность результатов испытаний ПР можно пренебречь.
2. ОБЩИЕ ПРИНЦИПЫ ОЦЕНИВАНИЯ ТОЧНОСТИ РЕЗУЛЬТАТОВ ОПРЕДЕЛИТЕЛЬНЫХ ИСПЫТАНИЙ ПРОМЫШЛЕННЫХ РОБОТОВ
2.1. Будем считать, что объект испытаний представляет собой совокупность из N экземпляров ПР. При этом, если испытаниям подвергается партия ПР, то N - любое положительное целое число, если же тип ПР, то N = ¥. Как известно, для случайной выборки объема NB из конечной генеральной совокупности, оценка дисперсии среднего отличается от одноименной оценки для выборки из бесконечной генеральной совокупности лишь на величину множителя (N - NB)/(N - 1), который называется поправкой на конечность совокупности. Поэтому без потери общности все дальнейшие рассуждения будем проводить для случая N = ¥.
2.2. При функционировании в типовых условиях эксплуатации объект проявляет свои свойства и находится в состояниях, которые можно описать многомерным случайным вектором Y0 = (Y1, Y2, ..., Yk,)T, где Yi - i-й показатель качества объекта (ПР). Примем, что целью испытаний является получение оценок статистических характеристик (математического ожидания и дисперсии) этих показателей качества, что соответствует задаче определительных испытаний.
2.3. Учитывая, что ПР представляют собой сложные технические объекты, можно утверждать, что разброс реализаций вектора параметров Y0 обусловлен неидентичностью свойств единиц ПР, составляющих объект испытаний, и в некоторых случаях, случайным характером входных воздействующих факторов.
2.4. В дальнейшем предположим, что в процессе оценивания статистических характеристик вектора Y0 допускаются погрешности, обусловленные неадекватностью статистических свойств совокупности отобранных для испытаний образцов свойствам объекта, неточностью методов и средств определения (измерения) свойств образцов ПР, в некоторых случаях неадекватностью воспроизведенных условий испытаний типовым условиям эксплуатации ПР. Будем считать, что неисключенные систематические погрешности измерений настолько малы, что ими можно пренебречь.
2.5. Точность точечных оценок статистических характеристик вектора Y0, представляющих собой результаты испытаний, оцениваем с учетом перечисленных факторов. При этом, в зависимости от степени адекватности условий испытаний типовым условиям эксплуатации, возможны следующие четыре случая:
2.5.1. Случай 1. Типовые условия эксплуатации характеризуются детерминированными внешними воздействиями и режимами функционирования объекта. Испытания проводятся как подконтрольная эксплуатация NB образцов ПР.
2.5.2. Случай 2. Типовые условия эксплуатации характеризуются детерминированными внешними воздействиями и режимами функционирования объекта. Испытания проводятся в лабораторных и/или полигонных условиях. При воспроизведении вектора параметров, характеризующих типовые условия эксплуатации, допускаются систематические и случайные погрешности.
2.5.3. Случай 3. Типовые условия эксплуатации определяются случайными внешними воздействиями и детерминированными режимами функционирования объекта. Испытания проводятся как подконтрольная эксплуатация NB образцов ПР.
2.5.4. Случай 4. Типовые условия эксплуатации характеризуются случайными внешними воздействиями и детерминированными режимами функционирования объекта. Испытания проводятся в лабораторных или полигонных условиях. При воспроизведении вектора параметров, определяющих типовые условия эксплуатации, допускаются систематические и случайные погрешности.
2.6. Оценивание точности результатов испытаний ПР в условиях п.п. 2.5.1.
2.6.1. Результат a-го наблюдения каждой i-ой компоненты вектора параметров j-го образца можно представить в следующем виде:
![]()
![]()
![]() (2.1)
(2.1)
где ![]() - математическое ожидание
вектора параметров объекта испытаний;
- математическое ожидание
вектора параметров объекта испытаний;
![]() - нормально
распределенная случайная величина, характеризующая разброс j-x реализаций вектора Y0
относительно среднего (m0) за счет
неидентичности свойств образцов;
- нормально
распределенная случайная величина, характеризующая разброс j-x реализаций вектора Y0
относительно среднего (m0) за счет
неидентичности свойств образцов;
![]() - нормально
распределенная случайная погрешность a-го
наблюдения j-ой реализации вектора Y0;
- нормально
распределенная случайная погрешность a-го
наблюдения j-ой реализации вектора Y0;
n - число наблюдений i-ой компоненты вектора параметров объекта испытаний (предполагается одинаковым для всех i).
При этом
задачей испытаний является нахождение оценок ![]() и
и ![]() .
.
2.6.2. Несмещенная состоятельная оценка m0 определяется как среднеарифметическое по всей совокупности результатов измерений:
2.6.3. Доверительные границы
погрешностей оценки ![]() могут быть построены следующим образом:
могут быть построены следующим образом:
![]() (2.3)
(2.3)
![]() (2.4)
(2.4)
где DВ и DН
- соответственно верхняя и нижняя доверительные границы оценки ![]() ;
;
tb - квантиль распределения Стьюдента с (NB - 1) степенями свободы при доверительной вероятности b;
S1 - статистика, определяемая по формуле
 (2.5)
(2.5)
В итоге доверительный интервал для неизвестного математического ожидания вектора Y0 будет иметь вид
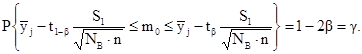 (2.6)
(2.6)
2.6.4. Несмещенной оценкой дисперсии ![]() является
является
![]() (2.7)
(2.7)
где ![]() - статистика, определяемая
выражением (2.5);
- статистика, определяемая
выражением (2.5);
![]() -
статистика, определяемая по формуле
-
статистика, определяемая по формуле
 (2.8)
(2.8)
2.6.5. Доверительные границы
погрешности оценки ![]() требуют применения различных
аппроксимаций. Наилучшей является аппроксимация, согласно которой приближенным g = 1 - 2b
доверительным интервалом для
требуют применения различных
аппроксимаций. Наилучшей является аппроксимация, согласно которой приближенным g = 1 - 2b
доверительным интервалом для ![]() является:
является:
![]() (2.9)
(2.9)
где
![]()
![]()
F0 - наблюдаемое значение отношения ![]() ;
;
F1-b и Fb - квантили F - распределения с NB - 1 и NB(n - 1) степенями свободы;
F¢1-b и F¢b - квантили F - распределения со степенями свободы NB - 1 и ¥.
Если
получится, что наблюдаемое значение F0
меньше, чем ![]() , то в качестве нижней границы
доверительного интервала следует принять ноль, так как дисперсия не может быть
отрицательной.
, то в качестве нижней границы
доверительного интервала следует принять ноль, так как дисперсия не может быть
отрицательной.
2.6.6. В случае, когда дисперсия
погрешности измерений известна, может быть получен точный доверительный
интервал для ![]()
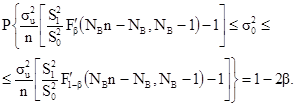 (2.10)
(2.10)
Заметим, что в отличие от (2.9) для построения данного доверительного интервала не требуется получения точечной оценки искомой дисперсии.
Таким образом, в случае определительных испытаний как подконтрольной эксплуатации NB экземпляров ПР при детерминированных внешних воздействиях и режимах функционирования, результаты испытаний описываются выражениями (2.2) и (2.7). Точность полученных результатов характеризуется формулами (2.3), (2.5) и (2.9), (2.10) соответственно.
2.7. Оценивание точности результатов испытаний ПР в условиях п.п. 2.5.2.
2.7.1. Первый этап решения задачи в данном случае - приведение результатов наблюдений i-х компонент вектора параметров каждого из NB экземпляров ПР к нормальным условиям. В результате выполнения этой процедуры устраняется смещение результата испытаний, обусловленное наличием систематической составляющей погрешности воспроизведения типовых условий эксплуатации объекта.
2.7.2. Выбор способа приведения результатов наблюдений к номинальным условиям зависит от наличия информации о модели взаимодействия объекта испытаний со средой.
2.7.3. Если модель определена, т.е. известна функциональная зависимость
Y = F(x, l*),
где x - вектор параметров, описывающих состояние среды и режимы функционирования объекта;
l - параметр, принадлежащий множеству L, конкретное значение которого l = l* определяет конкретную функцию F(x, l*) класса F(x, l), то для приведения результатов целесообразно воспользоваться разложением функции F(x, l*) в ряд Тейлора в окрестностях точки x4. В этом случае систематическое смещение результатов наблюдений определяется по соотношению:
 (2.11)
(2.11)
где m - определяется тем, каким остаточным членом ряда можно пренебречь;
xн - вектор x, соответствующий номинальным условиям (типовым условиям эксплуатации ПР).
2.7.4. Если функциональная зависимость Y = F(x, l*) неизвестна, то для приведения результатов наблюдений к номинальным условиям необходимо воспользоваться другим способом, который заключается в следующем. Пусть задано множество
x1, ..., xl, xl+1, ..., xl+k. (2.12)
состоящее из l + k векторов. При этом известно, что существует функция y = j(x), которая ставит в соответствие каждому вектору x множества (2.12) число y.
Для l векторов множества (2.12) определены соответствующие реализации ya. Таким образом, имеется множество пар
которые будем называть обучающей выборкой.
Множество векторов
назовем рабочей выборкой.
Требуется по элементам обучающей выборки найти реализации ya, соответствующие элементам рабочей выборки, то есть восстановить значения функции y = j(x) в точках xl+1, ..., xl+k.
Наилучшее решение задачи восстановления значений функции в заданных точках обеспечивает метод упорядоченной минимизации суммарного риска, суть которого состоит в следующем. По элементам обучающей и рабочей выборок среди заданного множества функций F(x, l) необходимо найти такую функцию F(x, l*), которая с заданной вероятностью 1 - h минимизирует суммарный риск прогноза значений функции ya = j(xa) на элементах рабочей выборки, т.е. с заданной вероятностью 1 - h доставляет функционалу
![]() (2.15)
(2.15)
значение, близкое к минимальному.
2.7.5. После приведения, результат a-го наблюдения каждой i-ой компоненты вектора параметров j-го образца можно представить в следующем виде:
![]()
![]() (2.16)
(2.16)
где ![]() - нормально распределенная
случайная величина, характеризующая разброс a-ых
наблюдений j-ой реализации вектора Y0
относительно среднего (m0 + tj), за
счет случайной погрешности воспроизведения условий испытаний.
- нормально распределенная
случайная величина, характеризующая разброс a-ых
наблюдений j-ой реализации вектора Y0
относительно среднего (m0 + tj), за
счет случайной погрешности воспроизведения условий испытаний.
2.7.6. Дальнейший ход решения задачи полностью соответствует п.п. 2.6.2 - 2.6.5 предыдущего случая при условии, что частота наблюдений j-х реализаций i-х компонент вектора параметров объекта испытаний соизмерима с частотой изменения случайной погрешности воспроизведения условий испытаний.
2.8. Оценивание точности результатов испытаний ПР в условиях п.п. 2.5.3.
2.8.1. Математическая модель
результата a-го наблюдения вектора
параметров j-го образца может быть представлена
выражением (2.16) (см. п.п. 2.7.5), с той лишь разницей, что
здесь ![]() -
нормально распределенная случайная величина, характеризующая разброс a-ых наблюдений j-ой
реализации компонент вектора Y0 относительно
среднего (m0 + tj), за счет случайного
характера внешних воздействующих факторов. Поэтому цель испытаний, в данном
случае, состоит в нахождении оценок
-
нормально распределенная случайная величина, характеризующая разброс a-ых наблюдений j-ой
реализации компонент вектора Y0 относительно
среднего (m0 + tj), за счет случайного
характера внешних воздействующих факторов. Поэтому цель испытаний, в данном
случае, состоит в нахождении оценок ![]() и
и ![]() .
.
2.8.2. Решение этой задачи двумя способами. Первый предполагает выполнение 2 n наблюдений j-х реализаций компонент вектора Y0. Причем первые n наблюдений выполняется с частотой изменения значений внешних воздействующих факторов, а вторые n наблюдений c частотой, значительно превышающей последнюю.
После этого
для каждой серии наблюдений производится расчет среднеарифметических оценок ![]() , а также
статистик
, а также
статистик ![]() и
и
![]() (cм. п.п. 2.6.2, 2.6.3 и 2.6.4).
(cм. п.п. 2.6.2, 2.6.3 и 2.6.4).
В качестве
несмещенной состоятельной оценки математического ожидания m0
следует принять оценку ![]() , рассчитанную для первой серии
наблюдений.
, рассчитанную для первой серии
наблюдений.
Несмещенной
оценкой дисперсии ![]() в данном случае будет
в данном случае будет
![]() (2.17)
(2.17)
где ![]() - статистика
- статистика ![]() , полученная
для первой серии наблюдений (см. выражение (2.5));
, полученная
для первой серии наблюдений (см. выражение (2.5));
![]() и
и ![]() - статистика
- статистика
![]() ,
рассчитанная для первой и второй серии наблюдений соответственно (см. выражение
(2.8)).
,
рассчитанная для первой и второй серии наблюдений соответственно (см. выражение
(2.8)).
2.8.3. Если дисперсия ![]() или ее
оценка
или ее
оценка ![]() априорно
известны, целесообразно воспользоваться вторым способом получения несмещенной
оценки дисперсии (
априорно
известны, целесообразно воспользоваться вторым способом получения несмещенной
оценки дисперсии (![]() +
+ ![]() ), который предусматривает
следующее. По результатам n наблюдений j-х реализаций компонент вектора Y0,
выполненных с частотой изменения значений внешних воздействующих факторов,
формируются статистики
), который предусматривает
следующее. По результатам n наблюдений j-х реализаций компонент вектора Y0,
выполненных с частотой изменения значений внешних воздействующих факторов,
формируются статистики ![]() и
и ![]() . После этого определяются
несмещенная оценка дисперсии
. После этого определяются
несмещенная оценка дисперсии ![]() :
:
![]()
и несмещенная оценка дисперсии ![]() :
:
![]()
где ![]() - оценка дисперсии
погрешности измерений
- оценка дисперсии
погрешности измерений ![]() .
.
В итоге,
несмещенная оценка искомой дисперсии (![]() +
+ ![]() ) определяется следующим
образом:
) определяется следующим
образом:
![]() (2.18
(2.18
Полученное
выражение (2.18)
совпадает с выражением (2.17), с той лишь разницей, что ![]() -
представляет собой апостериорную, а
-
представляет собой апостериорную, а ![]() - априорную оценку дисперсии
- априорную оценку дисперсии ![]() .
.
2.8.4. Доверительные границы
погрешности оценок m0 и ![]() определяются
соответственно по п.п. 2.6.3 и 2.6.5.
определяются
соответственно по п.п. 2.6.3 и 2.6.5.
2.9. Оценивание точности результатов испытаний ПР в условия п.п. 2.5.4.
2.9.1. Необходимо привести результаты наблюдений i-х компонент вектора параметров каждого из NB экземпляров ПР к типовым условиям эксплуатации объекта испытаний. При этом, если при переходе от воспроизведенных условий испытаний к типовым условиям эксплуатации теоретическая модель взаимодействия объекта испытаний со средой не претерпевает изменений, то рассматриваемую задачу можно интерпретировать как задачу распространения результатов экспериментального исследования образцов на вероятностных мерах.
Приведение результатов наблюдений осуществляется по следующей формуле:
![]()
где xa - a-я реализация вектора x, характеризующего типовые условия эксплуатации ПР, при которой был получен результат a-го наблюдения yia;
![]() -
производная Радона-Никодима Pн по Pв;
-
производная Радона-Никодима Pн по Pв;
Pн(x) - закон распределения вектора параметров, характеризующих типовые условия эксплуатации объекта;
Pв(x) - закон распределения вектора параметров, характеризующих воспроизведенные условия испытаний.
Если законы распределения Pн(x) и Pв(x) - нормальные, то справедливо следующее выражение:

где K - ковариационная матрица вектора x, а |K| - ее детерминант.
2.9.2. Дальнейший ход решения задачи оценивания точности результатов испытаний ПР для данного случая совпадает c п.п. 2.8.
3. ОЦЕНИВАНИЕ ТОЧНОСТИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ ПРОМЫШЛЕННЫХ РОБОТОВ С УЧЕТОМ АПРИОРНОЙ ИНФОРМАЦИИ.
3.1. Если при построении доверительных границ погрешности результатов испытаний предполагается, что i-е компоненты вектора параметров объекта испытаний имеют нормальное распределение, то в условиях малой выборки, характерной для испытаний промышленных роботов, точность оценивания результатов крайне низка: доверительные границы погрешности превышают физически реализуемый диапазон значений показателей качества. Это обусловлено тем, что одной из особенностей нормального закона распределения является бесконечный диапазон возможных значений аргумента.
3.2. Один из путей повышения точности оценивания результатов испытаний ПР - использование априорной информации двух следующих видов:
- о предельном диапазоне возможных значений показателей качества;
- о предельной величине дисперсии данных испытаний.
3.3. Наличие в процессе испытаний априорной информации первого вида не вызывает сомнений. Так, при проведении приемо-сдаточных испытаний - это границы диапазона физически возможных значений показателей. При проведении периодических, аттестационных, сертификационных и других испытаний ПР, прошедших приемо-сдаточные испытания, - это границы одностороннего или двустороннего допуска, установленные в стандартах и технических условиях на ПР. И в том, и в другом случае - это границы усечения законов распределения значений показателей объекта испытаний. Поэтому объединение априорной информации такого вида с апостериорными данными испытания выражается в переходе к усеченным законам распределения исходной генеральной совокупности значений оцениваемых показателей качества. То есть в выражениях (2.3), (2.4), (2.9) или (2.10) доверительных границ погрешностей результатов испытаний необходимо использовать квантили соответствующих «усеченных» распределений Стьюдента и Фишера.
В таблицах 1 и 2 приведены квантили указанных распределений, соответствующие стандартным уровням вероятности при типовых вариантах симметричного усечения исходной генеральный совокупности.
Квантили «усеченного» распределения Стьюдента
|
t(¦) |
1 - b |
|
|||
|
1,282 |
1,96 |
2,807 |
|
||
|
t(1) |
0,950 |
5,623 |
6,0 |
6,309 |
6,314 |
|
0,975 |
10,965 |
12,023 |
12,612 |
12,706 |
|
|
0,990 |
25,119 |
29,512 |
31,261 |
31,821 |
|
|
0,995 |
46,774 |
57,544 |
62,374 |
63,657 |
|
|
t(2) |
0,950 |
2,40 |
2,667 |
2,906 |
2,920 |
|
0,975 |
3,44 |
3,838 |
4,20 |
4,303 |
|
|
0,990 |
5,333 |
6,0 |
6,667 |
6,965 |
|
|
0,995 |
6,667 |
8,0 |
9,335 |
9,925 |
|
Квантили «усеченного» F - распределения
|
F(¦1; ¦2) |
1 - b |
|
|||
|
1,282 |
1,96 |
2,807 |
|
||
|
F(1; 1) |
0,9 |
31,618 |
36,0 |
39,804 |
39,86 |
|
0,95 |
120,23 |
144,55 |
159,06 |
161,4 |
|
|
0,975 |
470,4 |
562,3 |
631,2 |
647,8 |
|
|
0,99 |
2188 |
3311 |
3890 |
4052 |
|
|
F(1; 2) |
0,95 |
11,834 |
14,73 |
17,64 |
18,51 |
|
0,975 |
22,91 |
29,6 |
36,0 |
38,51 |
|
|
0,990 |
44,45 |
64,0 |
87,142 |
98,50 |
|
В последнем столбце каждой таблицы указаны значения квантилей, соответствующие «неусеченному» случаю.
Значения квантилей при других вариантах симметричного усечения могут быть получены при помощи соответствующей аппроксимации.
3.4. Степень усечения исходного закона распределения может быть определена одним из следующих способов.
3.4.1. Пусть объект испытаний представляет собой некоторую совокупность из N образцов (экземпляров) ПР, не прошедших еще технического контроля. Такую совокупность ПР, включающую в себя как «годные» так и «дефектные» изделия, будем называть исходной генеральной совокупностью. Примером испытаний такого объекта могут служить приемо-сдаточные испытания продукции. В этом случае: границы усечения исходной генеральной совокупности не заданы, а определяются как границы диапазона физически возможных значений показателей качества испытываемого объекта; информация о степени усечения отсутствует, однако существует способ ее получения. Суть его заключается в следующем.
Пусть ![]() -
результаты экспериментального исследования NB
образцов ПР (j-е реализации вектора Y0
параметров объекта испытаний, j = [1, NB]).
А в качестве верхней и нижней границ диапазона физически возможных значений yj приняты точки yв
= b; yн = a, соответственно. Чтобы оценить степень усечения закона
распределения, необходимо найти значения функции распределения в этих точках, а
для этого получить оценки соответствующих квантилей ub
и ua нормированного нормального закона. С
этой целью следует воспользоваться зависимостью
-
результаты экспериментального исследования NB
образцов ПР (j-е реализации вектора Y0
параметров объекта испытаний, j = [1, NB]).
А в качестве верхней и нижней границ диапазона физически возможных значений yj приняты точки yв
= b; yн = a, соответственно. Чтобы оценить степень усечения закона
распределения, необходимо найти значения функции распределения в этих точках, а
для этого получить оценки соответствующих квантилей ub
и ua нормированного нормального закона. С
этой целью следует воспользоваться зависимостью ![]() , где
, где ![]() - оценка
нормированной точки усечения закона распределения, а m подсчитывается по следующей формуле:
- оценка
нормированной точки усечения закона распределения, а m подсчитывается по следующей формуле:
где ![]() - значение
- значение ![]() ,
центрированное относительно точки усечения.
,
центрированное относительно точки усечения.
Значения функции ![]() для m от 0,550 до 0,910 с шагом 0,001 приведены в
таблице 3.
для m от 0,550 до 0,910 с шагом 0,001 приведены в
таблице 3.
Таким
образом, для оценок ![]() и
и ![]() будем иметь
будем иметь
![]()
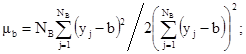
![]()
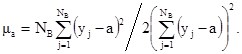
После этого, воспользовавшись данными для функции распределения нормированного нормального закона, можно легко найти искомую степень усечения.
3.4.2. При проведении периодических, аттестационных, сертификационных испытаний промышленных роботов объект испытаний представляет собой совокупность только «годных» изделий, т.е. совокупность ПР, прошедших приемо-сдаточные испытания. В этом случае информацию о степени усечения исходной генеральной совокупности можно получить в отделе технического контроля, проводившем приемо-сдаточные испытания ПР. Границы усечения, в отличие от предыдущего случая, заданы и представляют собой соответствующие границы допусков на контролируемые параметры объекта испытаний. Доля изделий не прошедших допусковой контроль (приемо-сдаточные испытания) по нижней границе допуска, может служить оценкой степени усечения слева, а доля изделий у которых, по результатам приемосдаточных испытаний значения контролируемых параметров превышают верхнюю границу допуска, - оценкой степени усечения справа. Если же допуск односторонний, то при ограничении «снизу» или «сверху» оценка степени усечения также представляет собой долю дефектных изделий. Однако, при построении доверительных границ погрешности здесь может быть принято допущение о двустороннем усечении закона распределения исходной генеральной совокупности. При этом в качестве второй границы (верхней или нижней, в зависимости от вида одностороннего допуска) используется соответствующая граница диапазона физически возможных значений контролируемого параметра. Значение функции распределения в этой точке определяется описанным выше способом.
Таким образом в обоих из рассмотренных случаев степень усечения исходной генеральной совокупности может быть определена.
Оценки нормированной точки усечения нормальной генеральной совокупности
|
|
m |
|
m |
|
m |
|
m |
|
|
|
0,550 |
-3,145 |
0,565 |
-2,727 |
0,580 |
-2,410 |
0,595 |
-2,151 |
0,610 |
-1,928 |
|
,551 |
-3,113 |
,566 |
-2,703 |
,581 |
-2,391 |
,596 |
-2,135 |
,611 |
-1,914 |
|
,552 |
-3,081 |
,567 |
-2,680 |
,582 |
-2,373 |
,597 |
-2,119 |
,612 |
-1,900 |
|
,553 |
-3,050 |
,568 |
-2,657 |
,583 |
-2,355 |
,598 |
-2,104 |
,613 |
-1,886 |
|
,554 |
-3,019 |
,569 |
-2,635 |
,584 |
-2,336 |
,599 |
-2,089 |
,614 |
-1,872 |
|
,555 |
-2,990 |
,570 |
-2,613 |
,585 |
-2,319 |
,600 |
-2,073 |
,615 |
-1,659 |
|
,556 |
-2,961 |
,571 |
-2,591 |
,586 |
-2,301 |
,601 |
-2,058 |
,616 |
-1,845 |
|
,557 |
-2,933 |
,572 |
-2,570 |
,587 |
-2,284 |
,602 |
-2,043 |
,517 |
-1,832 |
|
,558 |
-2,905 |
,573 |
-2,549 |
,588 |
-2,266 |
,603 |
-2,028 |
,618 |
-1,819 |
|
,559 |
-2,878 |
,574 |
-2,528 |
,589 |
-2,249 |
,604 |
-2,014 |
,619 |
-1,806 |
|
,560 |
-2,851 |
,575 |
-2,508 |
,590 |
-2,232 |
,605 |
-1,999 |
,620 |
-1,792 |
|
,561 |
-2,826 |
,576 |
-2,488 |
,591 |
-2,216 |
,606 |
-1,984 |
,621 |
-1,779 |
|
,562 |
-2,800 |
,577 |
-2,468 |
,592 |
-2,199 |
,607 |
-1,970 |
,622 |
-1,766 |
|
,563 |
-2,775 |
,578 |
-2,448 |
,593 |
-2,183 |
,608 |
-1,956 |
,623 |
-1,754 |
|
,564 |
-2,751 |
,579 |
-2,429 |
,594 |
-2,167 |
,609 |
-1,942 |
,624 |
-1,741 |
|
|
|
|
|
|
|
|
|
|
|
|
,625 |
-1,728 |
,640 |
-1,545 |
,655 |
-1,373 |
,670 |
-1,209 |
,685 |
-1,051 |
|
,626 |
-1,715 |
,641 |
-1,533 |
,656 |
-1,362 |
,671 |
-1,199 |
,686 |
-1,040 |
|
,627 |
-1,703 |
,642 |
-1,521 |
,657 |
-1,351 |
,672 |
-1,188 |
,687 |
-1,030 |
|
,628 |
-1,690 |
,643 |
-1,510 |
,658 |
-1,340 |
,673 |
-1,177 |
,688 |
-1,020 |
|
,629 |
-1,678 |
,644 |
-1,498 |
,659 |
-1,329 |
,674 |
-1,167 |
,689 |
-1,009 |
|
,630 |
-1,665 |
,645 |
-1,486 |
,660 |
-1,318 |
,675 |
-1,156 |
,690 |
-0,999 |
|
,631 |
-1,653 |
,646 |
-1,475 |
,661 |
-1,307 |
,676 |
-1,145 |
,691 |
-0,989 |
|
,632 |
-1,641 |
,647 |
-1,463 |
,662 |
-1,296 |
,677 |
-1,135 |
,692 |
-0,978 |
|
,633 |
-1,629 |
,648 |
-1,452 |
,663 |
-1,285 |
,678 |
-1,124 |
,693 |
-0,968 |
|
,634 |
-1,616 |
,649 |
-1,441 |
,664 |
-1,274 |
,679 |
-1,114 |
,694 |
-0,958 |
|
,635 |
-1,604 |
,650 |
-1,429 |
,665 |
-1,263 |
,680 |
-1,103 |
,695 |
-0,947 |
|
,636 |
-1,592 |
,651 |
-1,418 |
,666 |
-1,252 |
,681 |
-1,093 |
,696 |
-0,937 |
|
,637 |
-1,580 |
,652 |
-1,407 |
,667 |
-1,242 |
,682 |
-1,082 |
,697 |
-0,927 |
|
,638 |
-1,568 |
,653 |
-1,395 |
,668 |
-1,231 |
,683 |
-1,072 |
,698 |
-0,917 |
|
,639 |
-1,557 |
,654 |
-1,384 |
,669 |
-1,220 |
,684 |
-1,061 |
,699 |
-0,906 |
|
|
|
|
|
|
|
|
|
|
|
|
,700 |
-0,896 |
,715 |
-0,743 |
,730 |
-0,589 |
,745 |
-0,435 |
,760 |
-0,277 |
|
,701 |
-0,886 |
,716 |
-0,732 |
,731 |
-0,579 |
,746 |
-0,424 |
,761 |
-0,267 |
|
,702 |
-0,875 |
,717 |
-0,722 |
,732 |
-0,569 |
,747 |
-0,414 |
,762 |
-0,256 |
|
,703 |
-0,865 |
,718 |
-0,712 |
,733 |
-0,559 |
,748 |
-0,404 |
,763 |
-0,245 |
|
,704 |
-0,855 |
,719 |
-0,702 |
,734 |
-0,548 |
,749 |
-0,393 |
,764 |
-0,235 |
|
,705 |
-0,845 |
,720 |
-0,692 |
,735 |
-0,538 |
,750 |
-0,383 |
,765 |
-0,224 |
|
,706 |
-0,835 |
,721 |
-0,681 |
,736 |
-0,528 |
,751 |
-0,372 |
,766 |
-0,213 |
|
,707 |
-0,824 |
,722 |
-0,671 |
,737 |
-0,517 |
,752 |
-0,362 |
,767 |
-0,203 |
|
,708 |
-0,814 |
,723 |
-0,661 |
,738 |
-0,507 |
,753 |
-0,351 |
,768 |
-0,192 |
|
,709 |
-0,804 |
,724 |
-0,651 |
,739 |
-0,497 |
,754 |
-0,341 |
,769 |
-0,181 |
|
,710 |
-0,794 |
,725 |
-0,641 |
,740 |
-0,487 |
,755 |
-0,330 |
,770 |
-0,170 |
|
-711 |
-0,783 |
,726 |
-0,630 |
,741 |
-0,476 |
,756 |
-0,320 |
,771 |
-0,159 |
|
,712 |
-0,773 |
,727 |
-0,620 |
,742 |
-0,466 |
,757 |
-0,309 |
,772 |
-0,148 |
|
,713 |
-0,763 |
,728 |
-0,610 |
,743 |
-0,455 |
,758 |
-0,299 |
,773 |
-0,137 |
|
,714 |
-0,753 |
,729 |
-0,600 |
,744 |
-0,445 |
,759 |
-0,288 |
,774 |
-0,127 |
|
|
|
|
|
|
|
|
|
|
|
|
,775 |
-0,116 |
,790 |
0,052 |
,805 |
0,228 |
,820 |
0,414 |
,835 |
0,613 |
|
,776 |
-0,105 |
,791 |
0,064 |
,806 |
0,240 |
,821 |
0,427 |
,836 |
0,627 |
|
,777 |
-0,094 |
,792 |
0,075 |
,807 |
0,252 |
,822 |
0,439 |
,837 |
0,641 |
|
,778 |
-0,083 |
,793 |
0,087 |
,808 |
0,264 |
,823 |
0,452 |
,838 |
0,655 |
|
,779 |
-0,071 |
,794 |
0,098 |
,809 |
0,276 |
,824 |
0,466 |
,839 |
0,669 |
|
,780 |
-0,060 |
,795 |
0,110 |
,810 |
0,289 |
,825 |
0,479 |
,840 |
0,683 |
|
,781 |
-0,049 |
,796 |
0,121 |
,811 |
0,301 |
,826 |
0,492 |
,841 |
0,697 |
|
,782 |
-0,028 |
,797 |
0,133 |
,812 |
0,313 |
,827 |
0,505 |
,842 |
0,711 |
|
,783 |
-0,027 |
,798 |
0,145 |
,813 |
0,326 |
,828 |
0,518 |
,843 |
0,726 |
|
,784 |
-0,018 |
,799 |
0,157 |
,814 |
0,338 |
,829 |
0,531 |
,844 |
0,740 |
|
,785 |
-0,004 |
,800 |
0,168 |
,815 |
0,351 |
,830 |
0,545 |
,845 |
0,754 |
|
,786 |
0,007 |
,801 |
0,180 |
,816 |
0,363 |
,831 |
0,558 |
,846 |
0,769 |
|
,787 |
0,018 |
,802 |
0,192 |
,817 |
0,376 |
,832 |
0,572 |
,847 |
0,784 |
|
,768 |
0,029 |
,803 |
0,204 |
,818 |
0,388 |
,833 |
0,585 |
,848 |
0,799 |
|
,789 |
0,041 |
,804 |
0,216 |
,819 |
0,401 |
,834 |
0,599 |
,846 |
0,814 |
|
|
|
|
|
|
|
|
|
|
|
|
,850 |
0,829 |
,865 |
1,006 |
,880 |
1,332 |
,895 |
1,636 |
,910 |
1,994 |
|
,851 |
0,844 |
,866 |
1,083 |
,881 |
1,351 |
,896 |
1,658 |
|
|
|
,852 |
0,859 |
,867 |
1,100 |
,882 |
1,370 |
,897 |
1,680 |
|
|
|
,853 |
0,874 |
,868 |
1,117 |
,883 |
1,389 |
,898 |
1,703 |
|
|
|
,854 |
0,889 |
,869 |
1,134 |
,884 |
1,409 |
,899 |
1,726 |
|
|
|
,855 |
0,905 |
,870 |
1,151 |
,885 |
1,428 |
,900 |
1,749 |
|
|
|
,856 |
0,921 |
,871 |
1,168 |
,886 |
1,448 |
,901 |
1,772 |
|
|
|
,857 |
0,936 |
,872 |
1,186 |
,887 |
1,469 |
,902 |
1,795 |
|
|
|
,858 |
0,952 |
,873 |
1,204 |
,888 |
1,489 |
,903 |
1,819 |
|
|
|
,859 |
0,968 |
,874 |
1,221 |
,889 |
1,509 |
,904 |
1,843 |
|
|
|
,860 |
0,984 |
,875 |
1,240 |
,890 |
1,530 |
,905 |
1,868 |
|
|
|
,861 |
1,000 |
,876 |
1,258 |
,891 |
1,551 |
,906 |
1,892 |
|
|
|
,862 |
1,016 |
,877 |
1,276 |
,892 |
1,572 |
,907 |
1,917 |
|
|
|
,863 |
1,033 |
,878 |
1,295 |
,893 |
1,593 |
,908 |
1,943 |
|
|
|
,864 |
1,049 |
,879 |
1,313 |
,894 |
1,615 |
,909 |
1,968 |
|
|
3.5. Наличие априорной информации о предельной величине дисперсии D[yj] данных испытаний, представляющих собой оценки j-ых компонент вектора параметров испытуемого объекта (j = [1, NB], i = [1, K]) позволяет использовать квантили усеченного нормального распределения в выражениях (2.3) и (2.4) доверительных границ погрешности результатов испытаний.
Однако эффективность такого подхода зависит от точности априорной информации о величине дисперсии D[yj]. Может оказаться, что априорная оценка дисперсии настолько превышает её истинное значение, что доверительные границы погрешности, построенные с использованием квантилей усеченного нормального распределения, будут шире соответствующих доверительных границ, построенных с использованием квантилей распределения Стьюдента и апостериорной оценки дисперсии D[yj].
Поэтому применение априорной информации о предельной величине дисперсии данных испытаний целесообразно лишь в том случае, когда исключено возникновение такой ситуации.
Условие, при котором выполняется это требование, эквивалентно следующему неравенству:
где sa - априорная предельная оценка среднеквадратического отклонения данных испытаний;
S2 - апостериорная оценка среднеквадратического отклонения данных испытаний;
tg - квантиль распределения Стьюдента с (NB - 1) степенями свободы, соответствующая вероятности g;
zg - квантиль усеченного нормального распределения, соответствующая вероятности g.
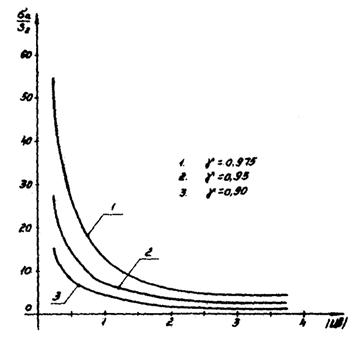
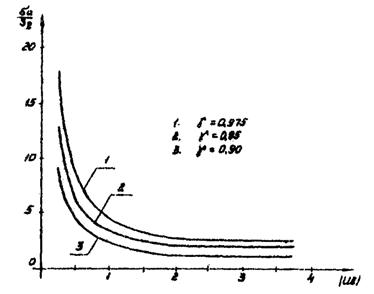
3.6. Правая часть неравенства (3.2) представляет собой граничное
значение отношения ![]() .
.
На рис. 1 и 2 представлены кривые зависимости этого граничного значения от степени усечения при симметричном усечении исходной совокупности для уровней вероятности g = 0,9; 0,95; 0,975 и числе степеней свободы 1 и 2 соответственно.
Представленные кривые позволяют оценить целесообразность использования априорной информации о предельной величине дисперсии данных испытаний при оценивании точности результатов испытаний ПР.
3.7. Квантили усеченного нормального распределения, соответствующие уровням вероятности g, равным 0,025 и 0,975 при различных вариантах усечения исходной генеральной совокупности, представлены в таблицах 4 и 5 соответственно.
3.8. Применение усеченных законов распределения позволяет существенно сократить доверительные границы погрешности результатов определительных испытаний ПР, что приводит к значительному повышению объективности принимаемых на их основе решений.
Рис.
1. Зависимость граничного значения отношения ![]() от степени усечения при
симметричном усечении исходной генеральной совокупности и числе степеней
свободы ¦ = 1.
от степени усечения при
симметричном усечении исходной генеральной совокупности и числе степеней
свободы ¦ = 1.
Рис. 2. Зависимость граничного значения отношения ![]() от степени усечения
при симметричном усечении исходной генеральной совокупности и числе степеней
свободы ¦ = 2.
от степени усечения
при симметричном усечении исходной генеральной совокупности и числе степеней
свободы ¦ = 2.
Квантили усеченного нормального распределения при g = 0,025
Квантили усеченного нормального распределения при g = 0,975
ПРИЛОЖЕНИЕ
ОЦЕНИВАНИЕ ТОЧНОСТИ РЕЗУЛЬТАТОВ ОПРЕДЕЛИТЕЛЬНЫХ ИСПЫТАНИЙ ПРОМЫШЛЕННЫХ РОБОТОВ АМ-80
С целью определения абсолютной погрешности позиционирования промышленных роботов АМ-80 были проведены определительные испытания. При этом непосредственному экспериментальному исследованию подвергались 3 образца ПР: АМ 80-01, АМ 80-02, АМ 80-04.
Типовые условия эксплуатации ПР этого типа характеризуются детерминированными внешними воздействиями (температура, влажность, давление, уровень вибрации и т.д.) и режимами функционирования (масса переносимых грузов, скорость и величина перемещения по степеням подвижности).
Испытания проводились как подконтрольная эксплуатация трех отобранных образцов ПР.
Результаты наблюдений погрешности позиционирования на каждом из трех экземпляров ПР приведены в таблице 6.
В соответствии с п.п. 2.6 настоящих рекомендаций результаты наблюдений погрешности позиционирования имеют разброс, обусловленный неидентичностью свойств образцов для испытаний и погрешностью средств измерений.
До получения
результатов испытаний ПР необходимо предварительно рассчитать статистики ![]() и
и ![]() , после чего
воспользоваться выражениями (2.2) и (2.7).
, после чего
воспользоваться выражениями (2.2) и (2.7).
Результаты расчета приведены в таблице 7.
Для
построения доверительных границ погрешности результатов испытаний воспользуемся
следующей априорной информацией: априорная оценка дисперсии данных испытаний не
превышает ![]() ,
абсолютная погрешность позиционирования промышленных роботов АМ-80 не может
превышать значения, равного ± 0,2.
Исходя из этого находим нормированные точки симметричного усечения законов
распределения погрешности позиционирования по каждой координате:
,
абсолютная погрешность позиционирования промышленных роботов АМ-80 не может
превышать значения, равного ± 0,2.
Исходя из этого находим нормированные точки симметричного усечения законов
распределения погрешности позиционирования по каждой координате:

Проверяем
целесообразность использования априорной информации о предельной величине
дисперсии данных испытаний, используя кривые, изображенные на рис. 2, и
расчетные значения отношения ![]() : для доверительной вероятности g = 0,95 критическое значение этого отношения
при расчетных степенях усечения составляет 2,5. Расчетные значения этого
отношения по координатам x, y, z соответственно равны 1,67; 2,22; 1,786, т.е. меньше
критического.
: для доверительной вероятности g = 0,95 критическое значение этого отношения
при расчетных степенях усечения составляет 2,5. Расчетные значения этого
отношения по координатам x, y, z соответственно равны 1,67; 2,22; 1,786, т.е. меньше
критического.
Результаты наблюдений погрешности позиционирования.
|
По координате X |
По координате Z |
По координате Y |
|||||||
|
номер экземпляра ПР |
|||||||||
|
01 |
02 |
04 |
01 |
02 |
04 |
01 |
02 |
04 |
|
|
1 |
0,04 |
0,006 |
0,04 |
0,052 |
-0,00 |
0,07 |
-0,001 |
-0,093 |
0,02 |
|
2 |
0,013 |
0,024 |
0,02 |
0,052 |
0,034 |
0,04 |
-0,005 |
-0,110 |
0,02 |
|
3 |
0,009 |
0,023 |
0,02 |
0,036 |
0,024 |
0,02 |
-0,009 |
-0,101 |
0,02 |
|
4 |
0,023 |
0,032 |
0,02 |
0,044 |
0,059 |
0,02 |
-0,095 |
-0,123 |
0,02 |
|
5 |
0,029 |
0,012 |
0,03 |
0,049 |
0,036 |
0,01 |
-0,021 |
-0,089 |
0,02 |
|
6 |
0,003 |
0,025 |
0,04 |
0,075 |
0,022 |
0,01 |
-0,142 |
-0,074 |
0,02 |
|
7 |
0,009 |
0,077 |
-0,04 |
0,056 |
0,031 |
0,02 |
-0,150 |
-0,084 |
0,02 |
|
8 |
0,018 |
0,046 |
-0,02 |
0,048 |
0,061 |
0,02 |
-0,127 |
-0,116 |
0,02 |
|
9 |
0,025 |
0,014 |
-0,05 |
0,070 |
-0,019 |
-0,02 |
0,008 |
-0,059 |
0,02 |
|
10 |
0,041 |
0,063 |
-0,05 |
0,089 |
0,066 |
-0,01 |
-0,004 |
-0,136 |
0,02 |
|
11 |
0,056 |
0,026 |
-0,06 |
0,102 |
0,070 |
-0,01 |
-0,024 |
-0,080 |
0,02 |
|
12 |
0,027 |
0,017 |
-0,06 |
0,098 |
0,055 |
-0,01 |
-0,082 |
-0,107 |
0,02 |
|
13 |
0,030 |
0,019 |
-0,09 |
0,062 |
-0,005 |
-0,02 |
-0,082 |
-0,044 |
0,02 |
|
14 |
0,058 |
0,021 |
-0,08 |
0,093 |
0,051 |
-0,03 |
0,039 |
-0,126 |
0,02 |
|
15 |
0,098 |
0,029 |
-0,09 |
0,098 |
0,045 |
-0,03 |
-0,133 |
-0,122 |
0,01 |
|
16 |
0,072 |
0,009 |
-0,07 |
0,074 |
-0,027 |
-0,02 |
-0,072 |
-0,026 |
0,02 |
|
17 |
0,077 |
0,039 |
-0,09 |
0,061 |
-0,015 |
-0,02 |
-0,056 |
-0,039 |
0,02 |
|
18 |
0,113 |
0,004 |
-0,09 |
0,088 |
0,020 |
-0,03 |
-0,164 |
-0,063 |
0,02 |
|
19 |
0,064 |
0,025 |
-0,08 |
0,122 |
-0,005 |
-0,03 |
0,064 |
-0,062 |
0,02 |
|
20 |
0,071 |
0,001 |
-0,09 |
0,086 |
0,011 |
-0,03 |
0,009 |
-0,034 |
0,02 |
|
21 |
0,070 |
0,055 |
-0,08 |
0,091 |
-0,051 |
-0,04 |
0,009 |
-0,057 |
0,02 |
|
22 |
0,076 |
0,000 |
-0,08 |
0,113 |
-0,001 |
-0,03 |
-0,045 |
-0,102 |
0,03 |
|
23 |
0,094 |
0,034 |
-0,08 |
0,073 |
-0,013 |
-0,03 |
-0,073 |
-0,102 |
0,02 |
|
24 |
0,120 |
0,017 |
-0,09 |
0,036 |
-0,051 |
-0,03 |
-0,0724 |
-0,068 |
0,02 |
|
25 |
0,100 |
0,031 |
-0,08 |
0,089 |
-0,087 |
-0,04 |
-0,075 |
-0,057 |
0,02 |
|
26 |
0,118 |
0,011 |
-0,08 |
0,043 |
-0,011 |
-0,03 |
-0,210 |
-0,086 |
0,03 |
|
27 |
0,121 |
0,063 |
-0,08 |
0,040 |
0,024 |
-0,03 |
-0,216 |
-0,123 |
0,02 |
|
28 |
0,122 |
0,012 |
-0,05 |
0,077 |
-0,029 |
-0,03 |
-0,158 |
-0,068 |
0,03 |
|
29 |
0,102 |
0,006 |
-0,09 |
0,118 |
-0,010 |
-0,03 |
-0,064 |
-0,081 |
0,02 |
|
30 |
0,116 |
0,031 |
-0,05 |
0,101 |
-0,046 |
-0,04 |
-0,193 |
-0,060 |
0,03 |
Результаты испытаний ПР АМ-80
|
№ экземпляра ПР |
|
|
|
|
|
|
X |
01 |
0,001485 |
0,09930 |
0,008843 |
0,003261 |
|
02 |
|||||
|
04 |
|||||
|
Z |
01 |
0,000948 |
0,05802 |
0,021764 |
0,0019024 |
|
02 |
|||||
|
04 |
|||||
|
Y |
01 |
0,002269 |
0,096360 |
-0,04400 |
0,003136 |
|
02 |
|||||
|
04 |
Этот факт подтверждает целесообразность использования априорной информации о предельной величине дисперсии данных испытаний и позволяет применять квантили усеченного нормального распределения при построении доверительных границ погрешности результатов испытаний ПР.
На основе данных, приведенных в таблицах 4 и 5, находим доверительные границы погрешности по каждой координате:
по координате X:
![]()
![]()
по координате Z и Y:
![]()
![]()
В итоге получаем, что с вероятностью g = 0,95 погрешность позиционирования промышленных роботов АМ-80 находится в интервале
по координате x:
-0,087 £ Dx £ 0,104,
по координате z:
-0,0624 £ Dz £ 0,106,
по координате y;
-0,128 £ Dx £ 0,040.
Наличие достоверной априорной информации о предельной величине дисперсии данных испытаний исключило необходимость построения доверительных границ апостериорной оценки дисперсии погрешности позиционирования, поскольку при оценке технического уровня и качества ПР используется лишь верхняя доверительная граница дисперсии оцениваемого показателя, которая в рассматриваемом случае априорно известна.
1. РАЗРАБОТАНЫ И ВНЕСЕНЫ Всесоюзным научно-исследовательским институтом по нормализации в машиностроении.
ИСПОЛНИТЕЛИ Александровская Л.Н., Гринфельдт А.Г., Евсеева Е.Б., Крупнов В.В. (ответственный исполнитель), Манзон М.М.
2. УТВЕРЖДЕНЫ Приказом ВНИИНМАШ № 91 от 6 апреля 1988 г.
3. ВВЕДЕНЫ ВПЕРВЫЕ.
СОДЕРЖАНИЕ
 (
(