ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
(Госстандарт СССР)
Всесоюзный научно-исследовательский институт по
нормализации в машиностроении
(ВНИИНМАШ)
Утверждены
Приказом ВНИИНМАШ
№ 12 от 13 января 1988 г.
Расчеты и испытания на прочность
МЕТОД ТЕНЗОМЕТРИЧЕСКИХ МОДЕЛЕЙ ИЗ
НИЗКОМОДУЛЬНЫХ МАТЕРИАЛОВ
Рекомендации
Р 50-54-46-88
Москва 1988
Рекомендации
|
Расчеты и испытания на прочность Метод тензометрических моделей из низкомодульных материалов |
Р 50-54-46-68 |
Рекомендации (Р) распространяются на методику моделирования и проведения исследований деформаций, напряжений, усилий и перемещений в конструкциях, работающих в пределах упругости, на тензометрических моделях из низкомодульных материалов. В Р обобщается опыт Института машиноведения им. А.А. Благонравова АН СССР и ряда других организаций по применению метода тензометрических моделей из низкомодульных материалов (таких, в которых деформации измеряют с применением тензорезисторов) для решения вопросов проектирования и оценки прочности сложных конструкций. Учитывая, что в качества материала моделей применяются пластмассы типа органического стекла (полиметилметакрилат), эпоксидной смолы и др., обладающие упругими свойствами и малым (Е = 2 + 5,103 МПа) модулем продольной упругости, данный метод носит название метода тензометрических моделей из полимерных материалов.
1. ЗАДАЧИ, РЕШАЕМЫЕ С ПРИМЕНЕНИЕМ МЕТОДА.
1.1. Задачи экспериментальных исследований.
Метод тензометрических моделей из материалов с низким модулем упругости применяется для решения следующих основных задач: а) определение напряжений, усилий и перемещений в сложных конструкциях при заданных нагрузках; б) экспериментальное выяснение и проверка расчетных схем и методов расчета напряжений и перемещений; в) сопоставление вариантов конструкций при проектировании по условиям прочности и жесткости, улучшение формы (оптимизация) деталей и узлов; г) выявления зависимостей между деформациями (напряжениями) и усилиями в деталях в связи с определением нагрузок на натурных конструкциях при их работе; д) выбор типа нагружения и расположения точек измерений при исследовании натурных конструкций в условиях стендовых и эксплуатационных испытаний; е) оценка по данным натурной тензометрии напряжений в натурной конструкции в местах, где не проводились измерения деформаций.
Метод применяется также для определения нагрузки при потере устойчивости элементов и для исследования формы и частоты собственных колебаний конструкций.
Метод тензометрических моделей из низкомодульных материалов может быть использован также для исследования напряжений от натяга и температурных напряжений. Так как исследования на моделях и переход к натуре при этих нагрузках имеют ряд особенностей по сравнению с моделированием при силовых воздействиях, которому посвящены настоящие рекомендации (Р), то они здесь не рассматриваются.
Вопросы моделирования и проведения измерений в этом случае приведены в работе [17].
1.2. Область применения и погрешность метода.
Область применения метода упругих тензометрических моделей из низкомодульных материалов ограничивается исследованием деформаций, напряжений, усилий и перемещений в конструкциях, материал которых деформируется в пределах упругости. Приведенные ниже (см. п. 2.4) способы получения упруго-пластических деформаций и напряжений по результатам исследования упругих моделей носят оценочный характер. Кроме того, рассматриваются такие упругие конструкции, где применяется принцип суперпозиции сил. Контактные задачи с применением этого метода в общем виде не решаются.
Метод моделирования динамических напряжений на полимерных моделях не разработан в полном объеме, как это имеет место в случае статических нагрузок. Это связано с большим, чем у металлов, внутренним трением и необходимостью учета зависимости модуля упругости и коэффициента Пуассона материала моделей от частоты деформирования. В настоящее время этот вопрос разрабатывается.
Относительная погрешность определения на моделях деформаций, напряжений, усилий и перемещений оценивается в большинстве случаев величиной 5 - 15 %. Эта погрешность складывается из ошибок измерения (до 5 % [1]), ошибок определения модуля упругости и его изменения по объему модели (до 5 % [2]) и погрешностей моделирования.
Погрешность моделирования в основном определяется различием в величинах коэффициента Пуассона материала натуры (μн = 0,28 - сталь) и модели (μм = 0,35 - полимерный материал). Величины возникающих при этом погрешностей даны в табл. п. 3.1. Необходимо отметить, что в ряде случаев эта погрешность может быть существенно уменьшена. Методы внесения поправки на различие в величинах коэффициента Пуассона модели и натуры рассмотрены в работах [1, 3, 4]. (См. также п. 2.5).
Оценка точности моделирования может быть выполнена или на основании сравнения данных модельных исследований с результатами натурных исследований, или путем оценки величины отклонения от равенства критериев, по которым ведется моделирование [1, 3]. Применение последнего метода рассмотрено в работе [5]. При этом необходимо учитывать, что выбор способа оценки точности моделирования и адекватности модели зависит от конкретной ситуации исследования.
2. МОДЕЛИРОВАНИЕ НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ
2.1. Условные обозначения.
Н - индекс при величинах, характеризующих натурную конструкцию;
М - индекс при величинах, характеризующих модель;
m - с индексом - масштаб подобия; без индекса - показатель степени при степенной аппроксимации диаграммы деформирования;
l, x, у, z - соответственно длина, линейные размеры в направлении осей координат;
σ, t - соответственно нормальное и касательное напряжения;
[σ], [t] - допускаемое напряжение;
q - погонная нагрузка;
p - внутреннее давление, поверхностные силы;
Р - сосредоточенная нагрузка, продольная сила;
M - изгибающий момент;
Q - поперечная сила;
μ - коэффициент Пуассона;
γ - деформация сдвига;
ε - относительная линейная деформация;
δ - абсолютная линейная деформация; толщина;
Dl - перемещение;
u, υ, ω - соответственно перемещения в направлении осей x, у, z;
f - прогиб;
E, G - соответственно модуль продольной упругости и модуль сдвига;
ν - частота;
F - площадь поперечного сечения;
W - момент сопротивления;
I - момент инерции при изгибе;
Ik - момент инерции при кручении;
![]() -
цилиндрическая жесткость;
-
цилиндрическая жесткость;
r - радиус кривизны;
ρ - удельная плотность
2.2. Основные положения теории моделирования
Исследования напряжений и перемещений в натурных конструкциях с применением моделей из материала с низким модулем продольной упругости основаны на условиях подобия. Условия подобия, по которым выполняют механическую модель и переходят от данных измерений на модели к искомым величинам для натуры, получают из анализа размерностей или по общим для натуры и модели функциональным зависимостям. При этом предполагается, что в исследуемой натурной конструкции (натуре), воспринимающей рабочие нагрузки, и в модели напряжения и деформации меняются в пределах пропорциональности.
Различают полное (строгое) и неполное (приближенное) подобие.
При полном подобии все безразмерные величины (коэффициент Пуассона, коэффициент трения, относительная деформация) в модели и натуре соответственно равны, а модель в некотором масштабе ml полностью воспроизводит натурный объект. На практике возможность осуществления такого моделирования весьма затруднительна, и, как будет показано ниже, не всегда необходима.
В связи c этим часто применяется приближенное моделирование, при котором в зависимости от задачи исследования в модели в полном масштабе выполняется лишь тот элемент или узел, который подлежит исследованию. Упрощению могут подвергаться и нагрузки. Остальные элементы, связанные с исследуемым и оказывающие на него влияние, соответствующим образом макетируются. Неполное подобие имеет место и при неравенстве коэффициентов Пуассона модели (μм = 0,35) и натуры (μн= 0,28 - сталь), т.е. когда mμ ≠ 1.
При моделировании, основанном на приближенном подобии, надо в каждом отдельном конкретном случае правильно оценивать относительную степень влияния некоторых факторов, чтобы достаточно обоснованно пренебречь ими. Кроме того, вследствие получения приближенных, а не точных результатов, необходимо знать возникающие при этом погрешности.
2.3. Условия подобия.
При полном подобии необходимо выполнить следующие требования: модель и натура должны быть геометрически подобны; влияющие на модель нагрузки должны отвечать нагрузкам, действующим на натурную конструкцию, т.е. прилагаться в сходных точках и находиться в том же соотношении между собой; коэффициенты Пуассона материала модели и натуры должны быть равны между собой; материал модели и натуры может быть разным, но в исследуемой области должен подчиняться закону Гука.
Рассмотрим связь между масштабами подобия. Масштаб модулей упругости mε зависит от выбора материала модели. Произвольно может быть назначен только один из двух масштабов - геометрического mе или силового ml подобия.
При назначении ml имеем:
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
При назначении mp
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
![]() (2.12)
(2.12)
mμ = 1;
mγ = mε = 1
Неполное подобие определяет подобие относительно некоторой части (а не всех) величин, характеризующих исследуемое явление. При воспроизведении упругих моделей изменением величин масштабов ml и mp не нарушаются условия подобия, и масштабный фактор нагрузок и размеров не сказывается прямым образом на погрешностях моделирования.
Масштаб ml геометрического подобия как в случае полного, так и приближенного подобия модели выбирается с учетом ряда факторов: величины нагрузки модели, которая может быть применена, сложности конфигурации исследуемой натуры и ее размеров, применяемых измерительных приборов, а также размера наличного материала для изготовления модели, времени и средств для испытания и требуемой точности. При изучении конкретной детали или конструкции форма натуры должна в модели воспроизводиться более точно. При обосновании или проверке метода расчета напряжений и перемещений модель рассматривается как сама натурная конструкция, причем создается серия моделей с диапазоном соотношения размеров, для которого разрабатывается метод расчета. В этом случае модели могут быть более простые с сохранением основной конфигурации, которую должен оценить расчет. При малых размерах натуры модель выполняют с меньшим ml; в некоторых случаях модель может быть выполнена больше натурной детали.
Масштаб mр силового подобия в тех же случаях определяется из условия создания в модели достаточных для измерения величин деформаций, которые должны быть в пределах пропорциональности и не вызывать заметной ползучести. В целях точности измерений получаемые в модели деформации Ем могут превышать соответствующие деформации Ен в натурной конструкции, т.е. mε < 1.
Связь между масштабами при независимых ml и mp следующая
![]() (2.13)
(2.13)
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
2.4. Переход от объемной модели к натурной конструкции.
Пересчет измеренных в объемной упругой модели величин на натурную конструкцию осуществляется с использованием выражений для масштабов подобия.
При полном подобии:
напряжения σнат = mE · σмод; (2.19)
относительные деформации Eнат = Eмод; γнат = γмод; (2.20)
при назначении mp
![]() (2.23)
(2.23)
при назначении ml
перемещения fн = ml · fм. (2.28)
При неполном подобии (при независимых масштабах ml и mp)
![]() (2.34)
(2.34)
В том случае, если модель нагружается
внутренним давлением, переход на натуру удобнее осуществлять, принимая во
внимание, что ![]() (2.16), по следующей
формуле
(2.16), по следующей
формуле
В том случае, если переход по приведенным выше формулам на натурную конструкцию показывает, что напряжения превышают предел текучести в зонах относительно малых размеров, когда влияние окружающей упругой области является преобладающим, пересчет деформации и напряжений на натурную конструкцию можно производить двумя способами по приближенным зависимостям, носящим оценочный характер.
Первый способ следует из предположения, что деформации в этих зонах распределяются так же, как в упругой области модели, и для натурной конструкции могут быть определены по формулам (2.20) или (2.30), а напряжения σн.пласт. в упругопластической области по этим деформациям необходимо определять из диаграммы σ - Е, полученной для материала натурной конструкции.
Второй способ использует выводы о связи коэффициентов концентрации деформаций и напряжений в упругой и упруго-пластической области, содержащиеся в работе [7]. Эти зависимости
Здесь KE, Кσ - соответственно коэффициенты концентрации деформаций и напряжений в упруго-пластической области и aσ - коэффициент концентрации напряжений (деформаций) в упругой области, определяемый на модели; m - показатель степени при степенной аппроксимации диаграммы деформирования f(σn, En) материала натуры; n - постоянная, определяемая на расчета или эксперимента для данных величин aσ, σn, обычно принимается равной n = 0,5; σn - номинальное напряжение в натурной конструкции.
Номинальное напряжение σн.n в натурной конструкции определяется выражениями (2.19), (2.29) или (2.36), а деформации - выражениями (2.20), (2.30). При этом в качестве номинального в модели принимается напряжение σм.n в зоне вне концентратора, где изменение напряжений имеет плавный характер, а сами напряжения при пересчете на натуру не превышают предел упругости. Коэффициент aσ рассчитывают на модели как отношения aσ = σм.max/σм.n, где σм.max - наибольшее напряжение в зоне концентрации.
В натурной конструкции наибольшие напряжения и деформации в упруго-пластической зоне вычисляются по формулам
где Ен - модуль продольной упругости материала натуры.
2.5. Частные случаи моделирования
2.5.1. Плоское напряженное состояние.
Деталь и модель имеют форму пластины постоянной толщины; нагрузка приложена в плоскости пластины равномерно по ее толщине. В этом случае распределение напряжений не зависит от толщины детали и модели. Толщина модели tм (масштаб толщины mt) может быть выбрана из условий удобства выполнения модели и измерений (нагружения) независимо от масштаба ml размеров в плоскости детали.
Переход на натуру в этом случае осуществляется по следующим формулам
![]() (2.41)
(2.41)
![]() (2.42)
(2.42)
![]() (2.43)
(2.43)
![]() (2.44)
(2.44)
Qн = mp · Qм;
![]()
В плоскости детали, имеющей односвязный контур, нагруженной внешними силами, прилагаемыми к контуру, распределение напряжений не зависит от материала, т.е. от его упругих постоянных E и μ. В случае многосвязного контура этот вывод также справедлив, если равны нулю главные векторы нагрузок, приложенных к каждому замкнутому контуру в отдельности. В противном случае оно зависит от величины коэффициента Пуассона μ.
2.5.2. Плиты и оболочки.
Определение напряжений в плитах с учетом всех особенностей их формы, влияющих на распределение напряжений (изменение толщины ребра, форма и устройство опорных частей и др.), должно выполняться на модели, полностью воспроизводящей деталь. Такого же типа модель применяется и для исследования оболочечных конструкций, если в исследуемой модели в правильном соотношении должна воспроизводиться деформация от изгиба и продольных сил в срединной поверхности оболочки.
Рассмотрим случай, когда натурная конструкция может рассматриваться в виде плиты или оболочки, нагруженной по нормали к срединной поверхности. При этом в натуре и модели сохраняется подобие по форме срединной поверхности, нагрузкам и условиям опирания. Толщина tм модели по нормали к срединной поверхности может выполняться по отношению к толщине tн натурной детали с другим масштабом mt толщин, чем размеры срединной поверхности (чем масштаб ml). Такое упрощение допускается, если при выбранных масштабах ml и mt модель и натура удовлетворяют требованиям теории тонких плит и оболочек.
Переход на натуру осуществляется при независимых масштабах mp и ml и mμ = 1 по следующим формулам
При μн ≠ μм выражение для прогиба fн имеет вид
Изгибающие моменты Мх и Му и крутящие моменты Мху в натуре и модели связаны зависимостями
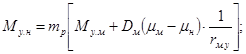 (2.49)
(2.49)
Поперечные силы Q и опорные реакции R на единицу ширины
2.5.3. Рамные и стержневые конструкции.
Для определения напряжений в узле рамы модель узла должна быть геометрически подобна натурному узлу.
При исследовании усилий в сечениях рамы или стержневой конструкции можно использовать или модель, полностью воспроизводящую натурную конструкцию, или модель, в которой сохранено то же соотношение жесткости отдельных элементов, что и в натурной конструкции. При этом возможно дальнейшее упрощение моделирования: если деформации от продольных сил существенно меньше деформаций от кручения и изгиба элементов конструкции, то должно сохраняться одно и то же соотношение жесткостей на изгиб в обеих главных плоскостях сечений рамы, на кручение и по жесткости узловых соединений.
В этом случае должно выполняться равенство
где mi - масштабный множитель для i-го элемента.
Если влияние изгибающих и крутящих моментов незначительно и преобладают деформации от продольных сил, то подобие можно соблюдать только по жесткости на сжатие - растяжение, и масштаб mEF можно назначить произвольным.
В сложных конструкциях, где трудно оценить соотношение всех указанных жесткостей, целесообразно тензометрическую модель выполнять с полным подобием по размерам и форме натурной конструкции.
2.5.4. Моделирование узла уплотнения корпусов энергетического оборудования.
Одной из особенностей корпусов энергетического оборудования является то, что напряжения в шпильках узлов уплотнения существенно выше, чем напряжения в других зонах корпуса [8, 9]. Поэтому при моделировании напряженного состояния этих конструкций на моделях из полимерных материалов может иметь место случай, когда напряжения в шпильках модели, выполненных по геометрическому подобию с натурой, превысят допускаемое при измерениях напряжений в модели. Это требует применения для шпилек в моделях материала с более высоким пределом прочности. При этом для таких полимерных материалов модуль упругости также выше, чем для органического стекла или эпоксидной смолы.
Для модели, выполненной с полным геометрическим подобием, а также с измененным материалом в шпильках (обозначения со штрихом), должны соблюдаться требования по условиям равенства деформаций от продольных сил и от изгибающих моментов в шпильках.
При этом, если шпилька в натурной
конструкции имеет сплошное сечение, то шпилька в модели из материала с ![]() должна
иметь кольцевое сечение. Из условия (2.54) получаем
должна
иметь кольцевое сечение. Из условия (2.54) получаем
![]()
где ![]() - наружный, внутренний диаметры и
толщина стенки шпильки кольцевого сечения; А1, А2,
А3 - коэффициенты, зависящие от отношения
- наружный, внутренний диаметры и
толщина стенки шпильки кольцевого сечения; А1, А2,
А3 - коэффициенты, зависящие от отношения ![]() ; dм - диаметр
шпильки сплошного сечения из материала с модулем упругости Eм. Растягивающие
напряжения в такой шпильке
; dм - диаметр
шпильки сплошного сечения из материала с модулем упругости Eм. Растягивающие
напряжения в такой шпильке
![]()
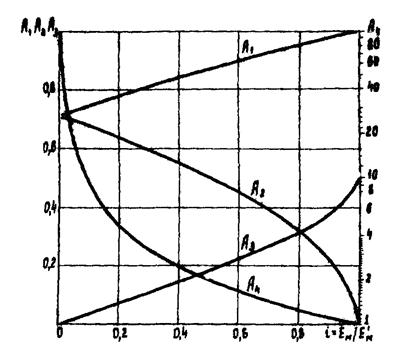
Величины коэффициентов А1 - А4 находятся по выражению:
На рис. П.3.1. приведены графики зависимостей (2.55) для случая 0 < i £ 1.
2.5.5. Устойчивость в пределах упругости.
При исследовании вопросов устойчивости модель выполняется в полном масштабе геометрического подобия ml. Потеря устойчивости в модели наблюдается по показаниям тензорезисторов. За критическую в модели принимается нагрузка Рм.кр., при превышении которой зависимость между деформациями и нагрузкой становится нелинейной. Величину критической нагрузки Рн.кр. в натурной конструкции рассчитывают в соответствии с (2.25) по формуле:
При этом необходимо убедиться, что в модели и получаемые по формуле (2.19) напряжения в натуре не превышают пределов упругости.
2.5.6. Моделирование частот и форм колебаний.
Связь между масштабными коэффициентами при исследовании частот и форм колебаний на моделях определяется выражением
Основная трудность применения моделей из полимерных материалов для исследования частот и форм колебаний заключается в зависимости модуля упругости материала модели от частоты ее колебаний и в большей, чем в натурной конструкции, величине логарифмического декремента затухания колебаний (соответственно в большей величине внутреннего трения). Известно [1, 10], что для ряда полимеров, используемых в качестве материала тензометрических моделей, динамический модуль продольной упругости Ед, модуль сдвига Gд монотонно увеличиваются с ростом частоты нагружения, достигая при определенной частоте f0 своих равновесных значений. Динамический коэффициент Пуассона μд с ростом частоты монотонно уменьшается, и его равновесное значение также имеет место при частоте f0.
В связи с этим масштабы mf и ml в формуле (2.57) определяются не только требованиями точности моделирования, размерами и типом тензорезисторов, технологией изготовления моделей, а также и условием обеспечения в модели частот колебаний fм > f0.
При наличии в конструкции сосредоточенных масс их вес в модели получают из соотношения
На несущих элементах натурной конструкции часто размещаются распределенные массы (например, теплоизоляция энергетического оборудования), которые, не изменяя существенно жесткости элементов, увеличивают уровень действующих на эти элементы инерционных сил. В этом случае плотность ρн для натурной конструкции, определяющая масштаб mρ в выражениях (2.57) и (2.58), должна учитывать как вес материала конструкции, так и вес находящихся на ней распределенных масс. Считая, что подобные массы размещены равномерно по объему исследуемой конструкции, получим
Здесь Gн.доп. - вес дополнительных распределительных масс; Gн.осн. и ρн.осн. - вес натурной конструкции и плотность ее материала.
3. ИЗГОТОВЛЕНИЕ МОДЕЛЕЙ
3.1. Материалы моделей и их физико-механические свойства.
Основным применяемым материалом для упругих тензометрических моделей служит органическое стекло (полиметилметакрилат). Кроме того, тензометрические модели выполняются из эпоксидной смолы без наполнителя или с наполнителем в виде алюминиевой пудры. Органическое стекло наиболее удобно использовать в качестве материала тензометрических моделей, так как оно выпускается промышленностью в виде готовых листов и блоков с большим диапазоном типоразмеров. В связи с этим ниже рассмотрены физико-механические свойства органического стекла как материала модели. Технология изготовления моделей из эпоксидной смолы и ее свойства описаны в [6] и в Р не приводятся.
Основные характеристики и типы применяемого органического стекла приведены в табл. П.3.2. Отметим, что стандарты на органическое стекло не нормируют однородность величины его модуля продольной упругости по плоскости листа или объему блока. Его изменение по объему блочного стекла составляет ± 10 + 15 % [2]. В связи с этим при принятии решения о допустимости использования листов или блоков органического стекла в качестве материала моделей необходима проверка величины их модуля упругости и его изменения по объему заготовок. Наиболее удобно это делать по методике, изложенной в П.1.3. Приложения I.
Коэффициент линейного расширения органического стекла составляет в среднем величину a = 110 · 10-6 град-1 и может меняться по объему блоков технического стекла на величину ± 15 %.
Блоки технического стекла, наиболее часто используемого для изготовления моделей, имеют в момент поставки начальные напряжения величиной до 10 МПа. Значительная часть (70 - 80 %) этих напряжений снимается отжигом. Температура, при которой происходит отжиг начальных напряжений, должна превышать на 5 ÷ 10° температуру размягчения всех частей объема блока.
В интервале температур 15 - 30 °С существует линейная зависимость величины модуля продольной упругости органического стекла от температуры [2]
Здесь Et - модуль упругости при температуре t опыта (тензоизмерений); Ет - модуль упругости при температуре T тарировки материала модели; φ = 25 МПа/град - средняя величина изменения величины модуля упругости на 1 °С для разных марок органического стекла, имеющих при 20 °С модуль упругости Е = 2,5 ÷ 3,0 · 103 МПа.
3.2. Изготовление моделей.
Наиболее часто тензометрические модели изготавливают путем механической или ручной обработки заготовок из листового или блочного стекла и последующей их склейки между собой.
В случае изготовления массивных моделей (особенно составных) из блочного органического стекла перед его механической обработкой необходимо выполнить отжиг начальных напряжений. Режим отжига для блоков толщиной до 200 мм следующий: разогрев со скоростью 5 град/час до температуры 95 ÷ 100 °С (для блоков технического стекла) и до температуры 115 ÷ 120 °С (для блоков конструкционного стекла); выдержка при этой температуре 8 ÷ 10 часов, медленное охлаждение со скоростью 2 ÷ 3 град/час до температуры 50 ÷ 55 °С, затем естественное охлаждение вместе с печью до комнатной температуры. Отжиг для лучшего прогрева блока и выравнивание температуры внутри него рекомендуется выполнять в термостате с жидкостной средой.
При применении блоков технического стекла время выдержки на предельной температуре можно увеличить до 25 - 40 час. В этом случае наряду с некоторым увеличением (на 4 - 5 %) модуля продольной упругости материала уменьшается его разброс по объему блока за счет некоторой деполимеризации его отдельных слоев.
При проведении отжига необходимо учитывать, что заготовки уменьшаются в плане на 2 - 3 % и увеличиваются по толщине на 4 - 5 %.
К режущему инструменту и режимам резания предъявляются следующие основные требования: шероховатость поверхностей (особенно тонкостенных элементов) должна быть минимальной; при чистовой обработке элементов модели температура поверхностных слоев не должна превышать 60 °С, а сама обработка должна выполняться без применения масла, так как органическое стекло обладает значительной маслоемкостью. Режимы резания и геометрии режущего инструмента рассмотрены в работах [1, 2].
Склейку заготовок моделей между собой наиболее удобно выполнять с помощью дихлорэтанового клея (5 - 6 % органического стекла в дихлорэтане ЧДА). Перед склейкой склеиваемые части заготовок обезжириваются в начале бензином «калоша», а затем этиловым спиртом и погружаются в зависимости от толщины склеиваемых деталей на 5 - 10 мин, в ванну с чистым дихлорэтаном. Далее на поверхность кистью наносится слой клея и склеиваемые поверхности соединяются; производится пригрузка склеиваемых частей для создания в клеевом шве давлений порядка 0,05 МПа для тонкостенных моделей; 0,1 ÷ 0,2 МПа - для толстостенных. Для выхода паров дихлорэтана из внутренних закрытых полостей модели в ее стенках выполняются одиночные отверстия диаметром 5 мм. Для уменьшения скорости испарения дихлорэтана, что может приводить к образованию пузырьков и непроклейкам, наружный контур шва заклеивается клейкой лентой. Нагрузка выдерживается на модели 4 - 6 часов, затем снимается, модель освобождается от клейкой ленты и подвергается обдуву воздухом 2 - 3 часа. Тензометрические исследования склеенных таким образом толстостенных моделей можно выполнять не ранее чем через 10 суток после склейки. Все операции по склейке дихлорэтановым клеем ведутся в вытяжном шкафу. Неплоскостность склеиваемых поверхностей не должна превышать 0,1 мм.
В тех зонах модели, которые после ее склейки окажутся недоступными, необходимо выполнить установку тензорезисторов и монтаж соединительных линий заранее до их склейки.
4. ПРОВЕДЕНИЕ ИЗМЕРЕНИЙ ДЕФОРМАЦИЙ И ПЕРЕМЕЩЕНИЙ
4.1. Нагружение моделей
В моделях воспроизводятся два вида нагрузок: а) нагрузки, прикладываемые к поверхности детали от других соприкасающихся с ней элементов или от действия давления жидкости или газа; б) силы, приложенные по объему детали (силы инерции, тяжести и т.д.).
Масштаб силового подобия mp (соответственно нагрузку на модель Pм) выбирают таким образом, чтобы при нагружении модели иметь деформации достаточной для их измерений величины, не вызывающие ползучести материала модели. Для органического стекла, эпоксидной смолы этому соответствуют максимально допустимые в модели напряжения [σ] = 5 ÷ 6 МПа. При этом вне зоны концентрации средняя величина напряжений составит 2 ÷ 3 МПа, что может быть измерено с достаточной степенью точности.
Величина сосредоточенной нагрузки Рм или давления рн в модели определяется одним из следующих способов:
а) для существующей или спроектированной конструкции по выражениям
б) для вновь разрабатываемой конструкции при отсутствии точных данных по напряжениям и условиям в натурной конструкции путем приближенного расчета наибольших напряжений или путем пробных испытаний.
Нагружение моделей осуществляется в специальных нагрузочных устройствах, которые должны удовлетворять следующим требованиям:
а) нагрузка на исследуемую модель должна без искажений воспроизводить соответствующую нагрузку на деталь, причем следует обеспечить возможность ступенчатого или плавного увеличения нагрузки;
б) при нагружении модели несколькими нагрузками необходимо достичь как одновременного, так и раздельного приложения нагрузок;
в) при деформации модели величины и направления прилагаемых сил не должны меняться, а также возникать дополнительные нагрузки;
г) нагрузочное устройство должно быть простым по конструкции, удобным для монтажа модели и ее осмотра.
Поверхностные нагрузки на модель могут создаваться грузами, пружинами, винтовыми тягами (механические нагрузочные устройства) и давлением газа или жидкости (пневматические и гидравлические устройства). Объемные нагрузки (собственный вес и центробежные силы) создаются вращением модели на центрифуге.
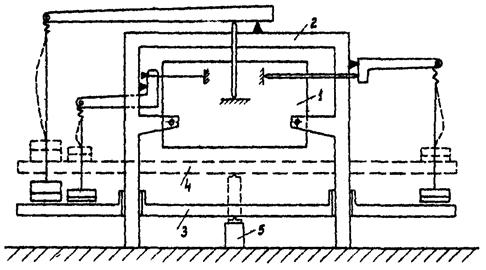
Наиболее часто при нагружении моделей применяются рычажные нагрузочные устройства. Их целесообразно применять при нагрузках, не превышающих 15 · 103 Н. При большом количестве рычагов (точек приложения нагрузки) грузы, действующие на рычаги через посредство гибких или жестких тяг и пружин, целесообразно размещать на общей платформе, которая с помощью гидравлического или механического домкратов может перемещаться в вертикальном направлении. Перемещение платформы может быть отрегулировано так, что в ее крайнем нижнем положении вес гирь действует на рычаги, а в крайнем верхнем положении гири опираются на платформу, и модель не нагружается. Такая схема нагружения может быть легко автоматизирована, и управление нагружением осуществляется оператором или управляющей ЭВМ. Это особенно важно для обеспечения равенства интервалов времени между нагружением (разгрузкой) и снятием отсчета по тензорезисторам и датчикам перемещений (см. п. 4.2.4). Принципиальная схема такого стенда приведена на рис. П.3.2.
Нагружение моделей конструкций, для которых рабочими нагрузками являются внутреннее или внешнее давление, осуществляется сжатым воздухом (газом) или жидкостью. При этом для создания внешнего для модели давления она помещается внутрь резервуара (нагрузочного устройства), в котором создается необходимая величина давления газа или жидкости.
Наиболее удобно осуществлять нагружение моделей с использованием сжатого азота, подаваемого в модель из промышленных баллонов, где он первоначально находится под давлением 150 ати. Применение сжатого азота определяется его относительно низкой стоимостью и малым содержанием в нем водяного конденсата. Для уменьшения расхода газа и рабочего объема, что важно с точки зрения требований техники безопасности, в модель необходимо помещать вытеснитель. В качестве материала вытеснителя можно использовать легкие, достаточно прочные и жесткие материалы типа пенопласта. Для лучшей стабилизации давления внутри модели вытеснитель необходимо помещать в оболочку из тонкой резины или прокрасить в 3 - 4 слоя нитрокраской.
Герметизация внутреннего объема моделей осуществляется тонкими резиновыми манжетами. При этом надо следить за обеспечением подобия местностей стыков. Требование абсолютной герметичности модели не всегда необходимо, так как при малых утечках газа через стыки достаточно легко достигается равновесие между его притоком из баллона и утечкой, при постоянном давлении внутри модели.
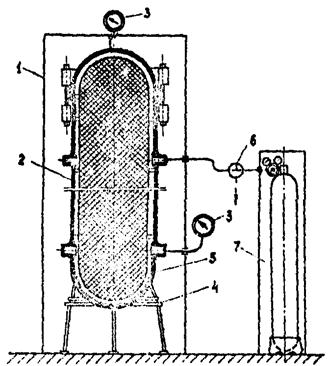
Сжатый газ должен поступать в модель по шлангам высокого давления через редуктор и тройной кран. Контроль давления газа в модели следует выполнять двумя (для контроля показаний) образцовыми манометрами. Обычно величина давления в модели не превышает 0,4 Мпа. Органы регулирования и управления подачей газа в модель и измерительная аппаратура должны быть выведены за специальное ограждение. Схема стенда для нагружения модели сосуда внутренним давлением приведена на рис. П.3.3.
С целью обеспечения безопасности эксперимента перед измерениями модель необходимо подвергнуть гидравлическим испытаниям на действие давления Р = 1,5 Рм. Эти испытания выполняются при нагружении модели водой (до установки тензорезисторов) или сжатым воздухом (азотом).
Нагружение моделей давлением можно также осуществлять при применении в качестве рабочей жидкости трансформаторного масла, обладающего диэлектрическими свойствами. При этом, однако, повышаются требования к обеспечению герметичности модели. Кроме того, учитывая значительную маслоемкость материала модели (у органического стекла маслоемкость достигает 3 %), ухудшается качество наклейки тензорезисторов на поверхностях, которые до этого смачивались маслом. Создание давления производится поршневым насосом или сжатым газом, действующим на свободную поверхность рабочей жидкости.
При нагружении модели в центрифуге с целью температурной компенсации и исключения дополнительных температурных или силовых (от трения о воздух и давления встречного потока) напряжений нужно обеспечить вакуум в объеме, где вращается модель, или поместить ее в теплоизоляционный герметичный контейнер.
Наиболее полно типы нагрузочных устройств и способы нагружения моделей изложены в работе [1].
При нагружении модели сжатым газом необходимо учитывать его нагрев (при нагружении) или охлаждение (при сбросе давления). Время стабилизации температуры при этом составляет ~ 2 мин. Учитывая это, а также некоторую ползучесть материала при проведении тензометрии моделей, нагружаемых как сосредоточенными нагрузками, так и внутренним давлением, следует выдерживать интервал времени величиной 2 мин. между моментом нагружения (разгрузки) и снятием отсчета по тензорезисторам и датчикам перемещений.
4.2. Измерение деформаций и перемещений
4.2.1. Выбор типа тензорезисторов и их монтаж на модели.
Наклеиваемые в различных местах модели тензорезисторы позволяют проводить измерения по точкам поверхности модели. Количество измерительных точек, а также число устанавливаемых в каждой точке поверхности модели тензорезисторов определяется типом напряженного состояния и числом компонент напряжений, которые должны быть определены в каждой точке. В целях достоверной проверки правильности показаний тензорезисторов необходимо устанавливать контрольные дублирующие тензорезисторы в идентичных местах модели. Учитывая, что в основном размеры модели меньше их оригиналов, наибольшая длина базы устанавливаемых на модели тензорезисторов редко превышает 10 мм. Высокие градиенты напряжений в зонах концентрации требуют применения малобазных тензорезисторов (база 0,5 - 2 мм).
Для выявления наиболее напряженных зон, направлений главных напряжений, а такие выбора мест установки тензорезисторов целесообразно вначале на модели проводить изучение полей деформаций с применением хрупких покрытий.
В таблице П.3.3. приведены рекомендуемые типы выпускаемых серийно тензорезисторов выбираемых в зависимости от геометрии исследуемой зоны моделей, типа напряженного состояния и исследуемых величин.
Более полные данные по типам тензорезисторов, выпускаемых промышленностью, см. [11, 12].
При тензометрии на моделях, особенно в зонах концентрации напряжений, необходимо учитывать, что измеренная деформация и подсчитанное по ней напряжение являются усредненными на базе тензорезисторов. В зонах с большим градиентом напряжений это усреднение может заметно сказываться на точности определения наибольших напряжений.
Для случая широкой полосы с отверстием (рис. П.3.4) выражение для вычисления погрешности из-за усреднения на базе тензорезистора имеет вид
Для пластины с отверстием, находящейся в условиях чистого сдвига (рис. П.3.4), выражение для погрешности b
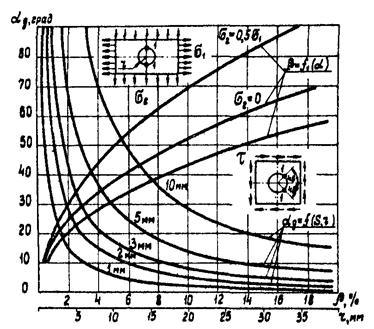
В формулах (4.3 - 4.5) aд - центральный угол в радианах, соответствующий тензорезистору с базой Sд, установленному по контуру отверстия с радиусом r. Таким образом, aд = f(Sд, r).
Приведенные выше выражения могут быть использованы как для приближенной оценки погрешности измерений при заданных типе напряженного состояния, базе тензорезисторов и радиусе отверстия, так и для выбора базы тензорезистора при заданной величине погрешности и радиусе отверстия. На рис. П.3.4. приведены графики зависимости aд = f(Sд, r), а также величины погрешности b = f(aд) для трех рассмотренных случаев.
Форма эпюры напряжений на контуре отверстия в пластине, нагруженной чистым сдвигом, является одной из наиболее неблагоприятных с точки зрения величины усреднения на базе тензорезистора. Оценка погрешности для этого случая, а также для других форм концентраторов, имеющих круговое очертание, может определяться с превышением по формуле (4.5).
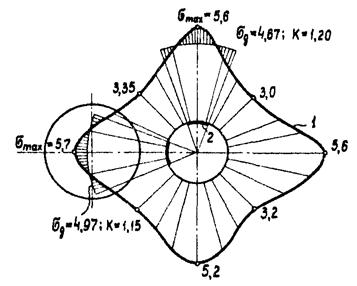
Погрешность в определении наибольших напряжений в зонах концентрации может иметь место также из-за того, что тензорезистор не будет установлен в точке с максимальными напряжениями. В этом случае точки с максимальными напряжениями выбираются по результатам предварительного исследования с помощью хрупких покрытий, оптически чувствительных наклеек или расчетом. Применяется также установка в зоне концентрации цепочки тензорезисторов или наклейка нескольких тензорезисторов с обеспечением взаимного перекрытия их баз. На рис. П.3.5, дан пример графических построений при оценке усреднения на базе тензорезистора.
Для наклейки тензорезисторов на модель применяют клеи холодного отверждения: ацетоно-целлулоидный (6 ÷ 8 % целлулоида в ацетоне ЧДА) для тензорезисторов на бумажной подложке и «циакрин» - на бумажной и полимерной подложке. Технология наклейки тензорезисторов и рекомендуемый тип клея указываются в инструкции завода-изготовителя.
В качестве коммуникационных проводов, учитывая высокие диэлектрические свойства материала модели, наиболее удобно применить провод марки ПЭЛШО Æ 0,22 - 0,28 мм. К поверхности модели соединительные провода прикрепляются в нескольких точках тем же клеем, что и тензорезисторы, или клейкой лентой. Жгут проводов от модели к разъему помещается в хлорвиниловую трубку Æ 4 ÷ 6 мм. К модели жгут проводов в трубке крепится с помощью металлической скрутки, которая двумя концами при нагреве паяльником погружается в тело модели в зоне, где не исследуются напряжения. Порядок коммутации тензорезисторов с измерительными приборами и количество соединительных проводов указываются в паспортах на эти приборы.
4.2.2. Измерительные приборы.
Аппаратура для измерения деформаций на моделях из полимерных материалов должна обеспечивать многоточечность измерений, регистрировать информацию в виде, удобном для автоматической обработки на ЭВМ, иметь малое напряжение питания на измерительный полумост. Последнее требование особенно важно в связи с низкой теплопроводностью полимерных материалов, что может приводить к перегреву тензорезисторов и появлению значительных температурных погрешностей.
В настоящее время серийно выпускаются промышленностью следующие типы и марки приборов: многоточечные автоматические цифровые мосты ЦТМ-5 и К-732, в состав которых входят тензоизмеритель, коммутатор, устройства вывода информации (цифропечатающие устройства и перфоратор); малогабаритные измерительные мосты с ручным переключателем каналов и визуальным отсчетом деформаций ИСД-3 и ИДЦ-1. Основные параметры указанных приборов приведены в работах [12, 13]. Коммутация тензорезисторов осуществляется в соответствии с паспортными данными.
К недостаткам приборов ЦТМ-5 и К-732, несколько затрудняющих их применение при тензоизмерениях на моделях из полимерных материалов, следует отнести высокое напряжение питания (соответственно 6 В и 5 В) и отсутствие возможности применения групповой и смешанной схем компенсации тензорезисторов. При применении тензорезисторов МПБ, допускающих максимальный ток питания тензорезисторов 1 ÷ 8 мА [2], необходимо использовать прибор ИСД-3, который обеспечивает измерения при напряжении на измерительный полумост 0,1 В.
4.2.3. Измерение линейных и угловых перемещений.
Измерение линейных и угловых перемещений выполняют с применением индикаторов часового типа и упругих тензометрических скоб.
Индикаторы перемещений стрелочного типа выпускаются на диапазоны измерений перемещений от 1 до 10 мм и имеют цену деления 0,001; 0,002 и 0,01 мм в зависимости от типа индикатора. Для крепления индикаторов к металлическим поверхностям удобно использовать штативы на магнитном основании.
Упругие тензометрические скобы используются для измерения перемещений в тех местах, где неприменимы стрелочные индикаторы, а также для дистанционного измерения, что особенно важно для моделей, нагруженных внутренним давлением, и измерений в замкнутых, недоступных визуальному контролю местах модели.
На рис. П.3.6. приведены некоторые типы упругих скоб. Тип а) состоит из металлической жесткой линейки, по которой в соответствии с размерами модели могут перемещаться по направляющим два металлических кронштейна с упругими элементами, выполненными из органического стекла. Тип б) полностью выполнен из органического стекла. Измерительные скобы этих типов не ужесточают существенно исследуемую модель и не искажают величины регистрируемых перемещений. На модель скобы устанавливаются с некоторым натягом для возможности замера перемещений обоих знаков и обеспечения надежного контакта. При установке скоба своей жесткой частью упруго закрепляется. Схема коммутации тензорезисторов приведена на рис. П.3.6, в.
Измеряемое перемещение f, пропорционально приращениям D показаний тензометрического прибора, снимаемых с тензорезисторов, установленных на упругих элементах
f = с · D.
Здесь С - постоянная упругой скобы, определяемая ее градуировкой на микрометре. Постоянная С численно равна величине взаимного перемещения опорных точек упругих элементов, вызвавшего приращение отсчета по прибору на одно деление.
4.2.4. Порядок нагружения моделей и проведения измерений.
Проведение статического тензометрирования сводится к снятию показаний (отсчетов) по тензорезисторам до нагружения - нулевое состояние и снятию показаний при наличии нагрузки - грузовое состояние. По величине приращений D показаний датчиков (деформаций и перемещений) определяются искомые величины деформаций, напряжений, усилий и перемещений в модели, а затем по формулам, приведенным в разделе 2.4, осуществляется переход на натурную конструкцию.
За нулевое состояние целесообразно принимать состояние модели при действии на нее нагрузки величиной 5 - 10 % от рабочей. При этом выбираются возможные зазоры в узлах сопряжения, в опорных устройствах модели и нагрузочных элементах, что приводит к более стабильной и линейной работе модели. При нагружении модели внутренним давлением такая ее предварительная пригрузка обеспечивает более точное определение давления в модели по шкале манометра. Модель перед измерениями необходимо подвергнуть трехкратному нагружению нагрузкой, равной рабочей. Такая «тренировка» материала модели повышает его упругие свойства и обеспечивает стабильность показаний тензорезисторов.
Для исключения грубых промахов и повышения точности измерений приращение показаний D определяется как среднее для нескольких независимых циклов нагружения. Обычно выполняют 3 ÷ 5 циклов нагружения. В каждом из них производится ступенчатое увеличение до наибольшей величины нагрузки с проведением на каждой ступени измерений по всем измерительным точкам. При этом необходимо точно выдержать двухминутный интервал между моментами нагружения (разгрузки) и снятия отсчета. При ступенчатом нагружении модели легко обнаружить повреждения тензосхемы, разрушение элементов модели, неисправность нагрузочного устройства, выражающиеся, как правило, в нелинейности показаний. При этом также можно установить нелинейную работу модели вследствие потери устойчивости ее элементов или в результате ее упругого нелинейного деформирования (например, при наличии продольно-поперечного изгиба).
При проведении тензоизмерений на моделях из полимерных материалов необходимо регулярно измерять температуру материала модели и помещения, где проводятся исследования. При необходимости в результаты измерений следует вносить поправки на температуру, как это показано в Приложении 1 (см. П.1.5)
4.3. Обработка результатов с применением ЭВМ
Применение при исследованиях на моделях автоматической цифровой аппаратуры и ЭВМ дает по сравнению с ручным способом измерения и обработки экспериментальных данных следующие преимущества: ускорение в 5 - 10 раз процесса измерения и обработки цифровой информации; повышение надежности тензоизмерений в результате устранения субъективных ошибок и проведения оценки средних значений по ряду измерений; учет воздействия на показания тензорезисторов влияющих факторов (см. П.1) и исключение влияния ползучести за счет стабильности и сокращения интервала времени между нулевым и грузовым отсчетами в одном цикле нагружения и между началом и концом измерения по всем тензорезисторам, установленным на модели; возможность анализа и оценки результатов в процессе эксперимента.
Блок-схема обработки экспериментальных данных, приведенная на рис. П.3.7, включает следующие основные блоки:
1. Ввод массива экспериментальных данных, состоящего из i строк (общее количество отсчетов по каждому тензорезистору) и j столбцов (количество обрабатываемых тензорезисторов).
2. Анализ сохранности тензосхемы и исключение грубых промахов на основании критериев отброса из так называемых профессиональных соображений (обрыв компенсационного или рабочего тензорезистора, плохой контакт и др.). Осуществляется проверка на наличие в массиве отсчетов, указывающих на обрыв рабочего или компенсационного тензорезисторов (например, в ЦТМ-3 соответственно 999 и 000).
3. При обнаружении такого рода анормальных отсчетов на печать выводится номер тензорезистора Nтр, номер цикла нагружения Nцн, величина анормального отсчета.
4. Тензорезистор, имеющий анормальный отсчет, из дальнейшей обработки исключается.
5. По каждому тензорезистору для данных циклов нагружения подсчитываются приращения показаний Di.
6. По каждому тензорезистору по приращениям показаний вычисляется среднее значение Diср.
7. В соответствии с правилами оценки анормальности результатов наблюдений наибольшее по величине приращение показания Dmax сравнивается с величиной КР, равной произведению среднеквадратического отклонения, характеризующего погрешность аппаратуры, и величиной b (взятой из табл. 2 ГОСТ 11.002.78). Если приращение показания Dmax меньше величины КР, то подозреваемый в анормальности результат считают нормальным и не исключают из обработки, в противном случае его считают анормальным и исключают из обработки. Число приращений показаний уменьшается на единицу и по оставшимся показаниям определяются новые величины Dср, Dmax. Эти операции повторяются до выполнения условия Dmax < КР.
8. Определяется количество приращений показаний тензорезисторов n1, оставшихся в результате отбраковки.
9. На печать выводится номер тензорезистора Nтр, средняя величина, подсчитанная по всем приращениям показаний Dср и элементы массива экспериментальных данных, соответствующие данному тензорезистору Эi. В этом блоке предусматривается оператор «СТОП», позволяющий работать в режиме - «ожидание» для осуществления задач блока 10.
10. Экспериментатором принимается решение об исправлении тензосхемы, модели, нагружающего устройства, внесение исправлений в массив средних значений Dср и повторении измерений при продолжении обработки результатов.
11. После получения массива средних значений Dср,j производится подсчет деформаций и напряжений с учетом влияющих факторов (температура, ужесточение).
12. Вычисление внутренних усилий и прогибов в модели; проверка полученных результатов по равновесию и сопоставлению экспериментальных и расчетных усилий. Переход от величин модели к натурной конструкции.
13. Вывод на печать таблицы результатов обработки: номера тензорезистора, величин деформации и напряжений для модели и натуры и т.д.
ПРИЛОЖЕНИЯ
1. РАСЧЕТНЫЕ ФОРМУЛЫ И СПОСОБЫ УЧЕТА ВЛИЯЮЩИХ ФАКТОРОВ
П.1.1. Расчетные формулы.
При тензоизмерениях на моделях из полимерных материалов вычисление напряжений наиболее удобно выполнять по приращениям D показаний тензорезисторов и тарировочным коэффициентам С, С′ и С′′ (см. П.1.2). Приращение этих коэффициентов позволяет учесть действительные величины модуля упругости Е, коэффициента Пуассона μ материала модели, поперечную чувствительность тензорезисторов, а также эффект уменьшения (ужесточающее влияние) показаний тензорезисторов, наклеиваемых на полимерные материалы. Приведенные в табл. П.1 расчетные формулы (П.1.1 ÷ П.1.13) учитывают кроме того влияние на показания тензорезисторов третьей компоненты, действующей при нагружении моделей внутренним (или внешним) давлением (см. П.1.4).
П.1.2. Определение тарировочных коэффициентов С, С′ и С′′.
Определение коэффициентов С, С′ и С′′ выполняется на тарировочной балке равного сопротивления на изгиб, выполненной из материала модели. Рекомендуемые размеры балки: длина от заделки до места приложения силы - 300 мм, высота в заделке 20 мм, ширина в заделке - 30 мм. Если такая балка не может быть получена (например, из листового органического стекла), то же изготовляют из материала подходящего размера с величиной модуля упругости Е, близкого к модулю упругости материала модели. Способ учета различия в величинах Е тарировочной балки и модели приведен в П.1.6.
Таблица 1
|
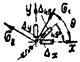
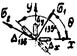
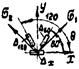
Эскиз розетки |
Расчетные формулы |
|
|
Главное напряжение σ (линейное напряженное состояние) |
Главные направления известны |
|
|
|
||
|
Главные напряжения σ1 и σ2 |
||
|
Нормальные напряжения σх и σу |
Главные направления неизвестны |
|
|
Направление θ и главные напряжения σ1 и σ2 |
|
|
|
|
||
|
|
||
|
Для розеток всех типов |
||
|
Нормальные напряжения σх, σу и касательное напряжение tху |
Для розеток всех типов |
|
На тарировочной балке для двух выборок тензорезисторов, по 5 - 10 тензорезисторов в каждой, наклеенных вдоль (направление 0°) и поперек (направление 90°) продольной оси образца [9, 14], определяют тарировкой коэффициенты
Здесь D0 и D90 - соответственно среднее приращение отсчета по тензорезисторам для каждой выборки; σ - нормальное напряжение на поверхности балки, одинаковой для всех тензорезисторов. По коэффициентам n1 и n2 подсчитываются коэффициенты С, C′ и C′′
![]() (П.1.17)
(П.1.17)
При подсчете коэффициентов С, C′ и C′′ по формулам (П.1.15) ÷ (П.1.17) коэффициенты n1 и n2 равны полусумме их значений, определенных для тензорезисторов, установленных со стороны сжатых и растянутых волокон. Это достигается путем переворачивания балки в заделке таким образом, что при одном и том же направлении действия силы тензорезисторы могут подвергаться и сжатию и растяжению. При этом также проверяется качество приклейки тензорезисторов к балке и их решетки к подложке.
Изложенный метод определения коэффициентов С, C′ и C′′ рекомендуется при применении малобазных (5 мм и менее) тензорезисторов (исключая тензорезисторы типа МПБ и аналогичные им без поперечной чувствительности) и при отсутствии достоверных данных о величине коэффициента Пуассона материала модели.
В случае применения тензорезисторов с базой более 5 мм, а также без поперечной чувствительности при известной величине μ процедура определения коэффициентов С, C′ и C′′ может быть упрощена. На балке равного сопротивления на изгиб или на консольной балке постоянного сечения (длина - 200 ÷ 250 мм, ширина - 20 мм, высота - 10 ÷ 20 мм) для совокупности в 5 - 10 тензорезисторов, наклеенных вдоль продольной оси образца, аналогично изложенному определяется коэффициент n1.
При применении балки постоянного сечения в формуле (П.1.14) D0 и σ - соответственно приращения показаний тензорезистора и величина напряжения в месте его установки. Коэффициент С определяется по формуле (П.1.15), а C′ и C′′ по формуле
Для органического стекла коэффициент Пуассона может быть принят равным μ = 0,85.
П.1.3. Определение модуля продольной упругости.
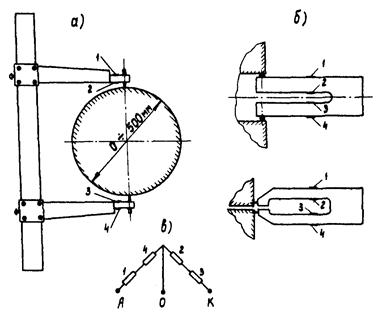
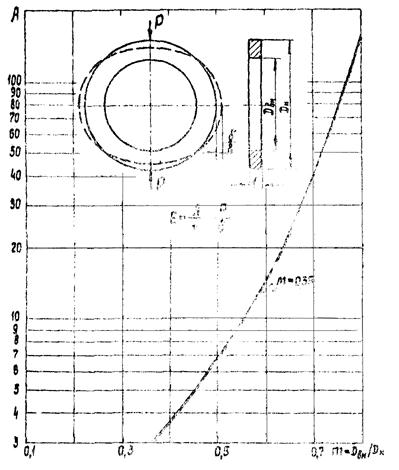
Модуль упругости Е материала наиболее удобно определять на кольцевых образцах [9, 15], сжимаемых силой Р в направлении вертикального диаметра (см. рис. П.1.1). Увеличение δ горизонтального диаметра связано с величиной Е и геометрическими размерами образца зависимостью
Здесь коэффициент ![]() , где
, где
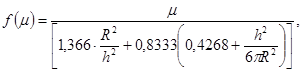 (П.1.22)
(П.1.22)
![]() (П.1.23)
(П.1.23)
Величина А, подсчитанная для μ = 0,35 (органическое стекло) и 0,8 £ m = Dвн/Dн £ 0,8, приведена на рис. П.11. Размеры образцов, исходя из требований точности и удобства измерений, необходимо принять следующими: Dн = 40 ÷ 60 мм, m = 0,60 ÷ 0,75, t = 3 ÷ 6 мм. При измерении увеличение диаметра δ образца цена деления индикатора часового типа должна быть не более 0,002 мм.
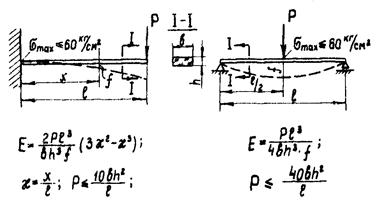
Схема определения модуля Е на балочных образцах приведена на рис. П.1.2. Величина наибольших напряжений, как в балочных, так и в кольцевых образцах из органического стекла и эпоксидной смолы не должна превышать 6 МПа. При испытании образцов необходимо также выдержать двухминутный интервал между моментом нагружения (разгрузки) и снятием отсчета по измерительному устройству. Перед проведением испытаний образцы подвергаются трехкратной «тренировке» рабочей нагрузкой.
Рис. П.1.1. Схема нагружения и зависимость параметра А от соотношения размеров кольцевого образца
Рис. П.1.2. Схема определения модуля упругости на балочных образцах
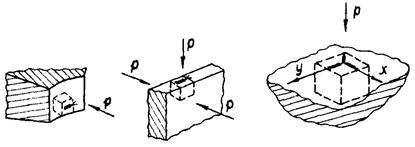
Рис. П.1.3. Варианты размещения тензорезисторов на элементах модели
П.1.4. Учет особенностей тензоизмерений на моделях сосудов давления.
Тензорезисторы, устанавливаемые на поверхностях модели, нагружаемых распределенной нагрузкой в виде давления Р газовой среды, находятся в условиях трехосного напряженного состояния, которое должно соответствующим образом учитываться.
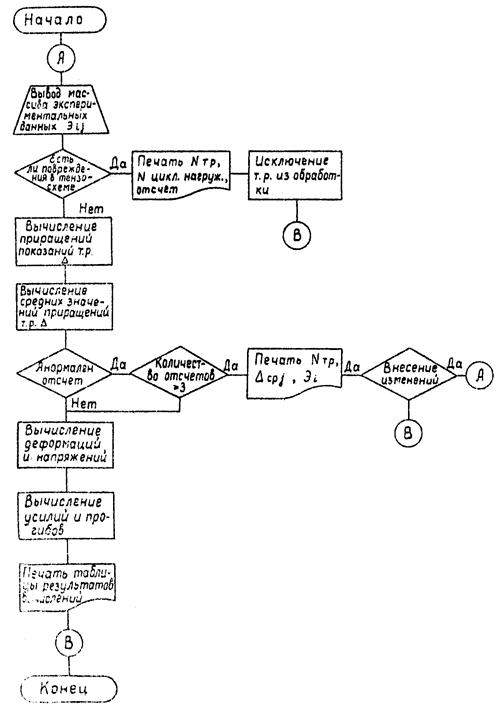
Возможны три характерных варианта установки тензорезисторов на элементах модели: одиночный тензорезистор на кромке массивной детали или на торце тонкой детали (рис. П.1.3, а, б) и розетка из двух или трех тензорезисторов на поверхности детали (рис. П.1.3, в). При этом применяются два способа размещения компенсационных тензорезисторов: вне модели (вне действия давления Р) и внутри модели (в зоне давления р).
Коэффициенты K* и ![]() в формулах
табл. П.1 учитывают взаимное расположение
рабочих и компенсационных тензорезисторов и воздействие на них давления:
в формулах
табл. П.1 учитывают взаимное расположение
рабочих и компенсационных тензорезисторов и воздействие на них давления:
K* = ![]() = 0 - на
рабочие и компенсационные тензорезисторы не действует давление Р;
= 0 - на
рабочие и компенсационные тензорезисторы не действует давление Р;
K* = 2μ,
![]() =
μ/(1 - μ) - на рабочие тензорезисторы действует
давление Р, на компенсационные тензорезисторы - нет;
=
μ/(1 - μ) - на рабочие тензорезисторы действует
давление Р, на компенсационные тензорезисторы - нет;
K* = ![]() = 1 на
рабочие и на компенсационные тензорезисторы действует давление Р.
= 1 на
рабочие и на компенсационные тензорезисторы действует давление Р.
П.1.5. Учет влияния температуры на результаты тензоизмерений.
Температура в лабораторном помещении может меняться не только в зависимости от времени года, но и в течение рабочего дня. Эти колебания могут достигать 5 - 10 °С. Учитывая большую величину коэффициента линейного расширения полимерных материалов и зависимость их упругих (в основном модуля упругости Е) свойств от температуры, исследования на тензометрических моделях целесообразно проводить в термостатированном помещении.
При отсутствии такого помещения необходимо при проведении тензоизмерений на моделях выполнять ряд мероприятий.
1. Контроль и обеспечение постоянства температуры помещения:
а) модель должна быть удалена от нагревательных и осветительных приборов; в помещении не должно быть воздушных потоков из-за открытых окон и дверей;
б) во время тензоизмерений нужно регулярно измерять температуру материала модели и регистрировать ее в журнале измерений или на перфоленте для последующего учета в величине постоянных С, С′ и С′′ и модуля упругости Е.
2. Обеспечение температурной компенсации:
а) толщины компенсационной пластины и элементов модели должны быть примерно одинаковы; для массивных деталей минимальная толщина компенсационной пластины 10 мм;
г) коэффициенты линейного расширения материала компенсационной пластины и модели должны быть одинаковы (разброс ± 5 %);
д) рабочие и компенсационные тензорезисторы должны быть из одной партии;
е) компенсационная пластина для тензорезисторов, установленных во внутренних полостях модели, также должна быть помещена внутри модели; на наружной поверхности - снаружи, вблизи модели;
ж) для исключения прогрева тензорезисторов током питания тензометрические приборы, применяемые для измерения на полимерных моделях, должны иметь напряжение питания 1 - 2 В (автоматические приборы) и 0,5 - 1 В (приборы с ручной балансировкой).
Модуль упругости материала модели
(назовем его Еt) и тарировочной
балки (назовем его Ет) могут быть различны не только из-за
того, что неодинаковы температура при тензоизмерениях на модели t и температура Т
при определении тарировочных коэффициентов, но и из-за того, что даже при
равенстве температур t = T тарировочная
балка может быть выполнена из материала с отличной от материала модели
величиной модуля упругости (см. П.1.2). Постоянные,
полученные тарировкой на балке c модулем упругости Ет
при температуре Т и вычисленные по формулам (П.1.15) ÷ (П.1.19), обозначим ![]()
Тогда для материала модели с модулем упругости Et при температуре t постоянные С, С′ и С′′, используемые в выражениях (П.1.1.) ÷ (П.1.13), вычисляются следующим образом
φ = 25 МПа · град. (для органического стекла, см. п. 3.1); К - чувствительность тензорезисторов примененного типа; μ - коэффициент Пуассона.
П.1.6. Учет ужесточающего влияния тензорезисторов.
При применении тензорезисторов на моделях из полимерных материалов необходимо учитывать возможность снижения показаний тензорезисторов из-за эффекта упрочнения поверхности модели в места их наклейки (ужесточающее влияние тензорезистора). Даже на толстостенных моделях напряжения, вычисленные по показаниям тензорезисторов, с использованием паспортного значения К чувствительности тензорезисторов и обычно применяемых в тензометрии формул типа
σ = Е · ε, (линейное напряженное состояние)
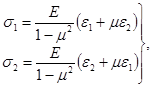 (плоское
напряженное состояние)
(плоское
напряженное состояние)
получаются заниженными на 2 - 4 % [2]. Применение коэффициентов С, С′ и С′′ автоматически учитывает эффект ужесточения.
Однако, на элементах моделей с толщинами 1 - 3 мм нельзя для вычисления напряжений пользоваться величинами С, С′ и С′′, полученными на толстых (10 - 20 мм) образцах. Расчетные оценки ужесточающего влияния тензорезисторов в этом случае отсутствуют, и постоянные С, С′ и С′′ необходимо определять на образцах, имеющих такую же толщину, что и элементы модели, создавая в них аналогичное напряженное состояние.
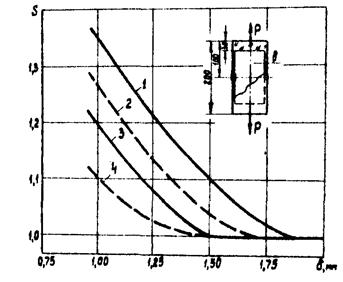
На рис. П.1.4 приведены экспериментальные данные по коэффициенту ужесточения S для некоторых типов тензорезисторов, определяемые как отношение постоянных С, полученных по формуле (П.1.15) на центрально растягиваемом или сжимаемом образце при толщине δ ³ 2,5 мм - С2 и δ < 2,5 мм - С1, т.е. S = С1/С2. Данные рис. П.1.4, полученные для органического стекла с Е = 2,8 · 103 МПа, показывают, что при толщине элемента 1 мм ошибка тензоизмерений из-за неучета эффекта ужесточения достигает 37 %. Для тонкостенных элементов, испытывающих поперечный изгиб, эта погрешность еще выше.
Рис. П.1.4. Коэффициент ужесточения для тензорезисторов, установленных с одной (пунктирные линии) и с двух (сплошные линии) сторон растягиваемого или сжимаемого образца из органического стекла
1 и 2 - тензорезисторы 2ФКПА-5-100; 3 и 4 - тензорезисторы 2ПКБ-5-50, 2ПКБ-5-100, 2ПКБ-10-100
2. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ, ПРИМЕНЯЕМЫЕ СОВМЕСТНО С МЕТОДОМ ТЕНЗОМЕТРИЧЕСКИХ МОДЕЛЕЙ
Возможности метода тензометрических моделей из полимерных материалов существенно повышаются при совместном применении с ним поляризационно-оптического метода [4, 6] и метода хрупких тензочувствительных покрытий. Наибольший эффект от совместного применения указанных методов получается при исследовании концентрации напряжений.
В сложных конструкциях метод хрупких покрытий достаточно просто и быстро выявляет нагруженные зоны и ориентацию главных напряжений. Такие исследования, выполняемые до установки тензорезисторов, позволяют существенно уменьшить количество устанавливаемых на модель тензорезисторов, что приводит к сокращению времени и средств на проведение и анализ результатов тензоизмерений [16].
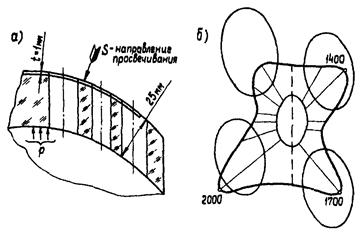
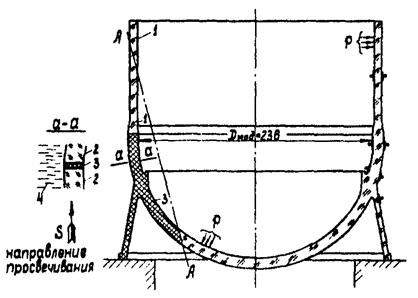
Поляризационно-оптический метод исследования напряжений на тензометрических моделях из полимерных материалов применяется в виде оптически-чувствительных наклеек и вклеек. Измерения на тензометрических моделях с применением таких наклеек на поверхности модели позволяет определять напряжения в зонах концентрации (например, на участках поверхности, имеющих отверстия, см. рис. П.2.1). При исследовании напряжений в зонах конструкции, где концентрация вызвана изменением формы элемента (например, резким искривлением меридиональной кривой стенки сосуда давления), применяются тензометрические модели с оптически чувствительными вклейками. Пример такой модели дан на рис. П.2.2.
Для исследования напряжений и усилий в моделях сложных пространственных конструкций в некоторых случаях целесообразно ряд задач решать на моделях поляризационно-оптического метода при прямом просвечивании или с применением метода «замораживания - размораживания» [6]. Обычно выполняют в модели не всю конструкцию, а только ее исследуемую часть (зону). Нагрузки на такую зональную модель (граничные условия) определяются по результатам исследования полной тензометрической модели из полимерного материала.
Рис. П.2.1. Оптически-чувствительная наклейка на тензометрической модели сферической крышки корпуса
а - расположение наклейки; б - напряжение на контуре малого косого отверстия.
Рис. П.2.2. Тензометрическая модель фланца корпуса с оптически-чувствительной вклейкой
1 - серийное органическое стекло; 2 - СНС (оптически нечувствительное органическое стекло); 3 - смола ЭД6-М; 4 - иммерсия.
3. ТАБЛИЦЫ И РИСУНКИ К ТЕКСТУ
Таблица П.3.1
Примерная величина изменения главных напряжений (%) при переходе от μ = 0,28 к μ = 0,35 [4]
|
Тип напряженного состояния |
|||||
|
Балки, плиты, оболочки |
Полоса с нагруженным отверстием |
Вал с надрезом |
Плоская контактная задача |
Объемная контактная задача |
|
|
Наибольшие главные напряжения |
0 - 5 |
2 |
0 - 10 |
2 |
5 - 15 |
|
Вторые компоненты главных напряжений |
0 - 10 |
7 |
0 - 20 |
10 |
10 - 40*) |
*) В центре площадки контакта.
Таблица П.3.2
Характеристики органического стекла, применяемого в качестве материала тензометрических моделей
|
Для остекления самолетов, ГОСТ 10667-74 |
Конструкционное, ГОСТ 15809-70 |
Техническое, ГОСТ 17622-72 |
||||||
|
СО-95 |
СО-120 |
СО-140 |
СОЛ |
ст-1 |
2-55 |
ТОСП |
ТОСН |
|
|
Температура размягчения, °С |
95 |
120 |
140 |
92 |
113 |
133 |
- |
110 - 113 |
|
Ударная вязкость, кгс. см/см2: |
||||||||
|
для толщин 1 - 4 мм |
9 |
9 |
9 |
9,5 |
10 |
8 |
- |
12 - 15 |
|
для толщин 5 мм и выше |
16 |
16 |
16 |
16,5 |
16,5 |
15 |
|
|
|
Предел прочности при растяжении, кгс/см2, не менее |
650 |
670 |
780 |
670 |
790 |
850 |
600 |
700 |
|
Модуль упругости при растяжении, кгс/см2, не менее |
27000 |
29000 |
35000 |
29000 |
29500 |
35000 |
- |
- |
|
Относительное удлинение при разрыве, %, не менее |
2,5 |
3,0 |
2,5 |
2,8 |
3,3 |
2,5 |
2 |
2,5 |
|
Размеры, мм: |
|
|
|
|
|
|
|
|
|
в плане |
от 500´400 |
до 1600´1400 |
от 300´400 до 600´400 |
|||||
|
толщин |
от 0,8 до 30 |
от 0,8 до 24 |
от 1 до 250 |
|||||
Таблица П.3.3
|
Рекомендуемый тип тензорезистора |
Примечание |
|
|
Линейное напряженное состояние |
||
|
Наибольшие напряжения (деформации) в элементах модели толщиной 1 ÷ 3 мм. |
МПБ-1, МПБ-2, МПБ-3 |
Тензорезисторы устанавливаются по толщине элемента (отверстия и галтели в плоских элементах) |
|
То же при толщине элементов более 3 мм. |
Те же типы, 2ФКПА - база 1 мм, КФ4П1 и КФ4П3 с базой 0,5 ÷ 1 мм |
Тензорезисторы устанавливаются на кромке в месте стыка двух элементов |
|
Распределение напряжений по линии при условии их плавного изменения |
Те же типы и ФКПА, КФ4П1 и КФ4П3 с базой 3 - 5 мм; 2ПКБ с базой 5 мм |
- '' - |
|
Плоское напряженное состояние |
||
|
Напряжения в сечении элемента при высоком градиенте их изменения |
2-х и 3-х-комнонентные розетки типа 2ФК-РВ, КФ4Р2, КФ4Р4, КФ4Р5 с базой 1 - 3 мм |
При исследовании изгиба элементов из их плоскости или для получения средних по толщине напряжений тензорезисторы устанавливаются в одной точке на обеих поверхностях элемента |
|
То же при плавном изменении напряжений |
Те же типы с базами до 5 мм, а также 2-х-и 3-х-компонентные розетки, составленные из одиночных тензорезисторов с базой 1 - 5 мм, типа 2ПКБ, 2ФКПА, КФ4П1, КФ4П3 |
|
Рис. П.3.1. Графики зависимостей А1 - А4 (2.55)
Рис. П.3.2. Схема нагрузочного стенда
1 - модель; 2 - опорная конструкция с рычагами; 3 - опорная платформа с грузами в нижнем положении (нагрузка действует на модель); 4 - опорная платформа в верхнем положении (нагрузка не действует на модель); 5 - гидравлический или винтовой домкрат.
Рис. П.3.3. Стенд для нагружения модели внутренним давлением
1 - защита; 2 - модель; 3 - образцовый манометр; 4 - опора; 5 - вытеснитель; 6 - тройной кран; 7 - баллон
Рис. П.3.4. Оценка усреднения напряжений на базе тензорезистора, установленного на контуре отверстия
1 - место установки тензорезистора
Рис. П.3.5. Графическая оценка усреднения на базе тензорезистора
1 - опора напряжений, полученная поляризационно-оптическим методом; 2 - тензорезистор, коэффициент усреднения
Рис. П.3.6. Упругие тензометрические скобы
Рис. П.3.7. Блок-схема обработки информации при тензоизмерениях на упругих моделях из полимерных материалов
Литература
1. Пригоровский Н.И., Прейсс А.К. Исследование напряжений и жесткости деталей машин на тензометрических моделях. - М.: Изд-во АН СССР, 1958.
2. Никитин С.В., Пригоровский Н.И., Хуршудов Г.Х. Тензометрические модели из полимерных материалов при исследовании напряжений и перемещений в тонкостенных конструкциях.
// Экспериментальные исследования и расчет напряжений в конструкциях. - М.: Наука, 1975.
3. Поляков Л.П., Файнбурд В.М. Моделирование строительных конструкций. - Киев; Будивельник, 1975.
4. Напряжения и деформации в деталях и узлах машин. / Ред. Н.И. Пригоровский. - М.: машгиз, 1961.
5. Рекомендации по определению напряженного и деформированного состояния пространственных металлоконструкций на моделях из низкомодульных материалов. - М.: ВНИИНМАШ, 1975.
6. Метод фотоупругости. / Ред. д.т.н. Г.Л. Хесин. - М.: Стройиздат, 1975. - Т. 1 - 3.
7. Махутов Н.А. Концентрация напряжений в упруго-пластической области детали. // Машиноведение. - 1971, - № 6.
8. Исследование напряжений и прочности корпуса реактора: Сб. статей. / ред. С.В. Серенсен, Я. Немец, Н.И. Пригоровский. - м.: Атомиздат, 1968.
9. Буянова Т.Е., Кукшинов А.И., Никитин С.В., Пригоровский Н.Н., Куршудов Г.х. Тензометрические модели из полимерных материалов для исследования напряжений и перемещений в корпусах энергетического оборудования // Экспериментальные методы исследования деформаций и напряжений в конструкциях. - м.: Наука, 1977.
10. Кукшинов А.И., Никитин С.В., Хуршудов Г.Х. Анализ возможностей исследования динамических напряжений и перемещений на тензометрических моделях из полимерных материалов // Методы исследования напряжений на моделях и натурных конструкциях. - М.: Наука, 1980.
11. Тензорезисторы КФ4 и КФ5. Техническое описание и инструкция по наклейке. - Киевское ПО «Веда».
12. Серьезнов А.Н. Измерения при испытаниях авиационных конструкций на прочность. - М.: машиностроение, 1976.
13. Расчеты и испытания на прочность в машиностроении. Экспериментальные методы определения напряженно-деформированного состояния элементов машин и конструкций. Методы и средства высокотемпературной тензометрии. - м.: ГосНИИмаш, 1979.
14. Звягинцев А.Д., Шабаров В.В. Испытания прочности судов на подводных крыльях. - Л.: Судостроение, 1965.
15. Durelli A.J., Ferrer L. New Methods to Derermine Elastic Constants // Materials and Standarts. - 1963. - V3, № 12.
16. Пригоровский Н.И., Панских В.К. метод хрупких тензочувствительных покрытий. - М.: Наука, 1978.
17. Шусторович В.м. Расчет на прочность кольцевых деталей металлургического оборудования. - М.: Машиностроение, 1976.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНЫ Институтом машиноведения им. А.А. Благонравова АН СССР
ИСПОЛНИТЕЛИ: д.т.н. Г.Х. Хуршудов, к.т.н. С.В. Никитин, А.И. Кукшинов.
2. ОДОБРЕНЫ научно-методической комиссией по стандартизации «Методы и средства экспериментального определения напряженно-деформированного состояния и эксплуатационной нагруженности машин на прочность» секции «Расчеты и испытания на прочность» НТС Госстандарта СССР.
3. Утверждены Приказом ВНИИНМАШ Госстандарта СССР № 12 от 13 января 1988 г.
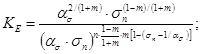 (
(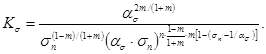 (
(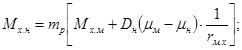 (
(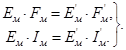 (
(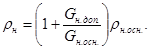 (
(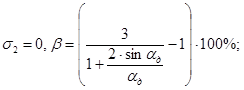 (
(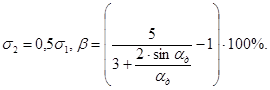 (
( (
(
 (
(
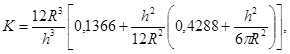 (
(
 (
(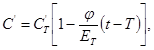 (
(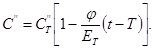 (
(