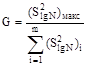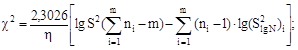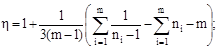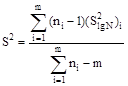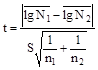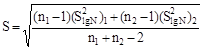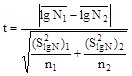ГОСУДАРСТВЕННЫЙ
КОМИТЕТ СССР
ПО СТАНДАРТАМ
Утверждены
Приказом ВНИИНМШ
№ 379 от 8.12.1987 г.
РАСЧЕТЫ
и испытАния нА прочность
МЕТОДЫ ИСПЫТАНИЙ
НА КОНТАКТНУЮ УСТАЛОСТЬ
Рекомендации
Р 50-54-30-87
Москва, 1988
Рекомендации
|
РАСЧЕТЫ И ИСПЫТАНИЯ НА ПРОЧНОСТЬ МЕТОДЫ ИСПЫТАНИЙ НА КОНТАКТНУЮ УСТАЛОСТЬ |
Р 50-54-30-87 Взамен ГОСТ 25.501-78 |
В настоящих рекомендациях (Р) описываются методы контрольных испытаний машиностроительных материалов на контактную усталость при нормальной и повышенной температурах и способы обработки их результатов.
Р не устанавливают методов испытаний на контактную усталость деталей машин и испытаний в условиях пониженной температуры окружающей среды, вакуума и лучевого воздействия.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Предлагаемые Р включают методы испытаний на контактную усталость по четырем схемам нагружения:
качение без проскальзывания (черт. 1);
качение с проскальзыванием (черт. 2);
качение с внешней касательной нагрузкой (черт. 3);
пульсирующий контакт (черт. 4).
1.2. Методы предусматривают испытания на контактную усталость в условиях:
нормальной температуры и влажности окружающей среды в соответствии с ГОСТ 15150-69* (исполнение У, категория 4.2) при наличии или отсутствии смазки;
повышенной температуры (до 673 °К) для схем нагружения, предусмотренных черт. 1 и 3, и наличия смазки.
1.3. Термины, определения и обозначения, применяемые в рекомендациях, указаны в приложении 1.
1.4. Сущность методов испытаний на контактную усталость:
определение главных (нормальных) и эквивалентных напряжений;
расчет предела контактной выносливости при ограниченном объеме партии;
оценка параметров функции распределения контактно-усталостного ресурса на заданном уровне напряжения;
получение среднего значения предела контактной выносливости и его среднего квадратического отклонения;
построение кривой контактной усталости;
построение группы кривых контактной усталости по параметру вероятности разрушения.
1.5. Контактно-усталостные характеристики, определяемые в Р, могут применяться при:
обосновании конструктивно-технологических решений;
расчетах на этапе проектирования деталей машин, работающих в условиях циклического контактного нагружения;
выборе металлов и сплавов для узлов и деталей машин, работавших в режиме контактного нагружения;
контроле свойств и качества металлов и сплавов;
выборе смазочных материалов и присадок к ним;
контроле качества (противопиттинговых свойств) смазочных материалов.
d - схема нагружения; δ - цикл напряжений; 1 - образец; 2 - контртела; 3 - приводные элементы; Тц - период цикла.
![]() -
относительная величина проскальзывания;
-
относительная величина проскальзывания;
![]()
![]()
![]()
d1 = d2; n1 = n2; w1 = w2; ![]()
d1, d2, d3 - диаметры рабочей части контртел и образца, мм;
n1, n2, n3 - скорости вращения контртел и образца, мин-1;
w1, w2, w3 - угловые скорости контртел и образца, рад/с;
v1, v2, v3 - окружные скорости рабочей части контртел и образца, м/с.
Черт. 1. Качение без проскальзывания
Привод на контртела осуществляется через дифференциальное устройство.
a - схема нагружения; δ - цикл напряжений; 1 - образец; 2 - контртела; 3 - приводные элементы; Tц - период цикла;
![]()
d1
= d2; n1 = n2; w1 = w2; ![]()
![]()
![]()
![]()
Черт. 2. Качение с проскальзыванием

а - схема нагружения; б - цикл напряжений; 1 -
образец; 2 - контртела; 3 - приводной элемент; Тц - период цикла; d1 = d2; ![]() - тормозной момент; Т -
касательная нагрузка
- тормозной момент; Т -
касательная нагрузка
Черт. 3. Качение с внешней касательной нагрузкой
d - схема нагружения; δ - цикл напряжений; 1 - образцы; Тц - период цикла
Черт. 4. Пульсирующий контакт
1.6. Расчет максимальных нормальных напряжений в зоне контакта.
1.6.1. Максимальное нормальное напряжение вычисляют по формулам:
для круговой площадки контакта (черт. 5а)
для эллиптической площадки контакта (черт. 5б)
для контакта по полоске (черт. 5в)
где Р - нормальная нагрузка, кгс, (см. приложение 1);
a и b - размеры большой и малой полуоси площадки контакта, соответственно, мм;
l - длина полоски контакта, мм.
1.6.2. Формулы для вычисления полуосей площадки контакта а и b и максимального нормального напряжения szмакс для основных случаев контактирования образцов и контртел с одинаковыми упругими характеристиками (одинаковые модули нормальной упругости Е1 = Е2 = 2,15∙104 кгс/мм2 = 21,08∙104 МПа и коэффициенты Пуассона μ1 = μ2 = 0,3) приведены в рекомендуемом приложении 2.
1.6.3. При неодинаковых упругих характеристиках образцов и контртел размеры полуосей площадки контакта a и b и максимальное нормальное напряжение вычисляют по формулам, приведенным в п.п. 1.6.4 - 1.6.6.
1.6.4. Для круговой и эллиптической площадок контакта
 (4)
(4)
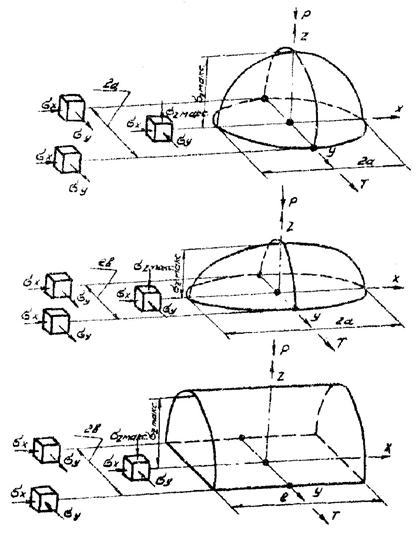
Черт. 5. Распределение напряжений на площадках контакта
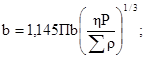 (5)
(5)
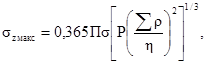 (6)
(6)
где η - коэффициент, учитывающий упругие характеристики материалов контактирующих тел, вычисляемый по формуле
![]()
где μ1 и μ2 - коэффициенты Пуассона материалов образца и контртела;
Е1 и Е2 - модули нормальной упругости материалов образца и контртела;
∑ρ =
ρ11 + ρ12 + ρ21 + ρ22
- сумма главной кривизны поверхностей соприкасающихся тел в точке
первоначального контакта, то есть величин, обратных радиусам кривизны: ![]()
ρ11 и ρ12 - главная кривизна первого тела (черт. 6) в двух взаимно перпендикулярных плоскостях;
ρ21 и ρ22 - главная кривизна второго тела (см. черт. 6).
Кривизна ρ положительна, если поверхность выпуклая, и отрицательна - если поверхность вогнутая;
Па, Пb, Пs - коэффициенты, учитывающие кривизну поверхностей упругих тел в районе касания и определяемые по табл. 3 справочного приложения 3 в зависимости от величины Ω.
Величину Ω определяют по приложению 2 или по формуле
1.6.5. Для контакта по полоске при сжатии цилиндра диаметром d с плоскостью величины b и szмакс вычисляют по формулам
Черт. 6. Контакт поверхностей двойной кривизны
y = f(x); x = 0; y = yмакс = bмакс; x = x; y = bx;
Черт. 7 . Площадка контакта сложной формы
1.6.6. Для контакта по полоске при сжатии цилиндра диаметром d с выпуклой («плюс») и охватывающей («минус») цилиндрической поверхностью диаметром D величины b и szмакс вычисляют по формулам
1.6.7. При контактировании поверхностей переменной кривизны, когда площадка контакта имеет сложную форму, отличную от эллиптической, но симметричную относительно оси Х, максимальное нормальное напряжение szмакс вычисляют по формуле
где Р - см. п. 1.6.1 и приложение 1;
а, bx, bмакс - см. п. 1.6.1 и черт 7.
Значение
интеграла ![]() определяют
методами численного интегрирования по экспериментально полученному отпечатку
площадки контакта.
определяют
методами численного интегрирования по экспериментально полученному отпечатку
площадки контакта.
Примечание. Пример расчета напряжений szмакс с учетом формоизменений, вызванных пластическими деформациями, приведен в рекомендуемом приложении 4.
1.6.8. Для материалов с неизвестными упругими характеристиками Е, μ значение коэффициента η вычисляют по формуле
где Р - см. п. 1.6.1 и приложение 1;
а - размер полуоси площадки контакта, полученный для данного сочетания материалов при сжатии шара радиусом R с плоскостью.
При одинаковом материале обоих тел (μ1 = μ2 = 0,3) значение модуля нормальной упругости Е вычисляют по формуле
1.7. Расчет эквивалентных напряжений.
1.7.1. Для схемы нагружения при качении с внешней касательной нагрузкой определяют эквивалентное напряжение sэкв в точке, лежащей на конце малой полуоси площадки контакта, направленной в сторону, обратную направлению вращения контактирующих тел (см. черт. 5).
Определение эквивалентного напряжения производят для наиболее напряженной точки, лежащей на конце малой полуоси площадки контакта (см. черт. 5).
1.7.2. При совместном действии нормальной
нагрузки и касательной нагрузки относительные напряжения на поверхности
площадки контакта ![]() и
и ![]() вычисляют по формулам
вычисляют по формулам
где ![]() - относительные напряжения от
действия нормальной нагрузки Р;
- относительные напряжения от
действия нормальной нагрузки Р;
![]() -
относительные напряжения от действия касательной нагрузки Т.
-
относительные напряжения от действия касательной нагрузки Т.
1.7.3. Относительные напряжения для точки, совпадающей с концом малой полуоси, вычисляют по формулам:
для круговой площадки контакта
![]() (18)
(18)
![]() (19)
(19)
для эллиптической площадки контакта
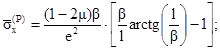 (21)
(21)
![]() (22)
(22)
для контакта по полоске
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
μ - коэффициент Пуассона;
![]() - см.
справочное приложение 1;
- см.
справочное приложение 1;
![]() -
интегральная функция;
-
интегральная функция;
![]() -
интегральная функция;
-
интегральная функция;
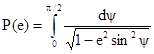 -
эллиптический интеграл первого рода, определяемый по табл. 4
приложения 3;
-
эллиптический интеграл первого рода, определяемый по табл. 4
приложения 3;
 -
эллиптический интеграл второго рода, определяемый там ;е.
-
эллиптический интеграл второго рода, определяемый там ;е.
1.7.4. При заданной величине szмакс значения нормальных напряжений sх и sy вычисляют по формулам
1.7.5. Для двухосного состояния определяют главные напряжения
![]()
1.7.6. Расчет эквивалентного напряжения, разработанный Институтом проблем прочности АН УССР, выполняют по формуле
где ![]() - коэффициент,
характеризующий степень участия сдвиговой деформации в микроразрушении
материала;
- коэффициент,
характеризующий степень участия сдвиговой деформации в микроразрушении
материала;
sВ - временное сопротивление материала при растяжении, определяемое по ГОСТ 1497-84;
sАс - временное сопротивление материала при сжатии, определяемое по ГОСТ 25.500-80;
![]() -
интенсивность напряжения;
-
интенсивность напряжения;
![]() - параметр
напряженного состояния;
- параметр
напряженного состояния;
А - параметр
структуры материала, вычисляемый по формуле ![]()
где ![]() - предел прочности материла
при кручении, определяемый по ГОСТ 3565-80.
- предел прочности материла
при кручении, определяемый по ГОСТ 3565-80.
1.7.7. Пример расчета напряженного состояния в зоне контакта и аналитического описания левой ветви кривой контактной усталости для схемы качения с внешней касательной нагрузкой приведен в рекомендуемом приложении 5.
2. ИСПЫТАТЕЛЬНОЕ ОБОРУДОВАНИЕ
2.1. Оборудование для испытаний на контактную усталость должно удовлетворять следующим основным требованиям:
моделировать схемы нагружения (п. 1.1, черт. 1 - 4);
обеспечивать постоянство температуры испытаний);
обеспечивать постоянство подачи смазочного материала;
автоматически выключаться при резком увеличении или уменьшении нагрузки или при прекращении подачи смазочного материала;
автоматически выключаться и фиксировать, согласно принятому критерию разрушения, момент выкрашивания на рабочей поверхности образца.
2.2. Погрешность фиксации момента разрушения не должна превышать ± 0,5 % значения измеряемой величины.
2.3. Суммарная погрешность нормальной нагрузки Р не должна превышать:
+ 3 % значения измеряемой величины - для схем нагружения, предусмотренных п. 1.1, черт. 1 - 3;
± 5 % значения измеряемой величины - для схемы пульсирующий контакт (п. 1.1, черт. 4).
2.4. Суммарная погрешность касательной нагрузки Т не должна превышать ± 5 % значения измеряемой величины.
2.5. Погрешность заданного коэффициента проскальзывания λц не должна превышать ± 5 % значения измеряемой величины.
2.6. Погрешность задания частоты нагружения образца не должна превышать ± 5 % значения измеряемой величины.
2.7. Погрешность заданной температуры испытаний не должна превышать ± 5 К.
2.8. Допускается тарировка испытательного оборудования в статике с расчетной оценкой динамической погрешности (до введения государственного стандарта на методы проверки метрологических характеристик при динамических режимах).
2.9. Для проведения контрольных испытаний образцов на контактную усталость применяют следующее испытательное оборудование:
для схем нагружения, предусмотренных п. 1.1, черт. 1 и 3, при нормальной температуре - машина МКВ-КМ (рекомендуемое приложение 6), при повышенных температурах - машина МКВ-ТМ (см. рекомендуемое приложение 7);
для пульсирующего контакта (п. 1.1, черт. 4) - гидропульсационные и резонансные усталостные машины;
для качения с проскальзыванием (п. 1.1, черт. 2) - машины для испытаний на трение и износ моделей СМЦ-2 и СМТ-1 в пределах характеристик, указанных в сопроводительной документации на машины.
Примечания. Требования настоящего раздела на машины моделей СМЦ-2 и СМТ-1 не распространяются.
2.10. При исследовательских испытаниях образцов на контактную усталость допускается применять другие испытательные машины, удовлетворяющие целям и условиям испытания.
3. УСЛОВИЯ ИСПЫТАНИЯ
3.1. Нагружение образцов при испытаниях производят:
при постоянных заданных амплитудах напряжений цикла
sа = szмакс - для схем нагружения, предусмотренных п. 1.1, черт. 1, 2;
sа = (sэкв)макс - для качения с внешней касательной нагрузкой (п. 1.1, черт, 3);
для схемы пульсирующий контакт (п. 1.1, черт 4) - при соблюдении подобия циклов, то есть при одновременном пропорциональном изменении среднего напряжения цикла (szмакс)m, и амплитуды (szмакс)n или при постоянном для вcех образцов среднем напряжении цикла (szмакс)m;
при постоянном
заданном коэффициенте ![]() - для схемы касания с внешней
касательной нагрузкой (п. 1.1, черт. 3);
- для схемы касания с внешней
касательной нагрузкой (п. 1.1, черт. 3);
при постоянной заданной относительной величине проскальзывания - для схемы качения с проскальзыванием (п. 1.1, черт. 2).
3.2. В пределах намеченной серии испытаний схема нагружения, способ подвода, температура, количество смазочного материала и критерий разрушения должны быть одинаковыми.
3.3. Испытание каждого образца проводится на новой дорожке обкатывающего цилиндрического контртела.
3.4. В пределах намеченной серии испытаний смазывание образцов должно осуществляться маслом одной марки с периодической проверкой соответствия масла требованиям стандартов или технических условий на него.
Выбор сорта смазки и температуры испытаний определяется задачами исследования, при этом температура вспышки масла должна быть выше максимальной температуры испытаний не менее чем на 20 °К.
В соответствии с условиями работы моделируемой детали выбирают один из 3-х вариантов подвида смазки в зону контакта;
1 - погружением;
2 - капельный;
3 - фитильный (польстерный).
3.5. Частота циклов нагружения в пределах намеченной серии испытаний должна быть постоянной.
Если при заданной частоте температура в зоне контакта вызывает изменение структуры и физико-механических свойств металла, то частоту необходимо уменьшить.
3.6. Для построения кривой контактной усталости и определения предела контактной выносливости число образцов в партии должно быть не менее 12.
В интервале напряжений 0,95 - 1,05 от значения предела контактной выносливости испытывают не менее трех образцов, причем не менее двух из них не должно разрушаться до базового числа циклов.
3.7. Минимальное число образцов при оценке параметров функции распределения контактно-усталостного ресурса на заданном уровне напряжения при логарифмически нормальном законе определяют следующим образом:
задают ожидаемое
значение среднего квадратического отклонения логарифма числа циклов SlnN (разд. 6) и
определяют коэффициент вариации VlnN из соотношения ![]()
по значению VlnN находят соответствующее значение R по таблице 1 справочного приложения 3;
задают величину относительной погрешности δ среднего значения lnN с доверительной вероятностью b;
по значениям δ и b находят значение Q по табл. 2 приложения 3;
по найденным значениям R и Q вычисляют минимальное число образцов n по формуле
Если по результатам испытания получен коэффициент вариации, меньший или равный заданному, то испытания прекращают. Если же коэффициент более заданного, то точность недостаточна, и необходимо провести дополнительные испытания.
На черт. 8, 9 приведены графики выбора числа образцов для наиболее распространенных значений SlgN, δ и b.
3.8. Число образцов для построения кривой контактной усталости в статистическом аспекте определяют на основе п. 3.7 и числа уровней напряжений.
3.9. Число образцов при оценке параметров функции распределения предела контактной выносливости находят по ГОСТ 27.502-83, исходя из нормального закона распределения.
Число образцов должно быть не менее 30.
3.10. В случаях, предусмотренных пп. 3.6 и 3.9, база испытаний при определении предела контактной выносливости должна быть не ниже:
107 циклов - для металлов и сплавов с твердостью НВ 200, имеющих горизонтальный участок на кривой контактной усталости;
5,0 ∙ 107 циклов - для металлов и сплавов с твердостью HRСэ £ 40, имеющих горизонтальный участок на кривой контактной усталости;
108 циклов - для металлов и сплавов с НRСэ > 40, имеющих горизонтальный участок на кривой контактной усталости;
2 ∙ 102 циклов - для металлов и сплавов, не имеющих горизонтального участка на кривой контактной усталости.
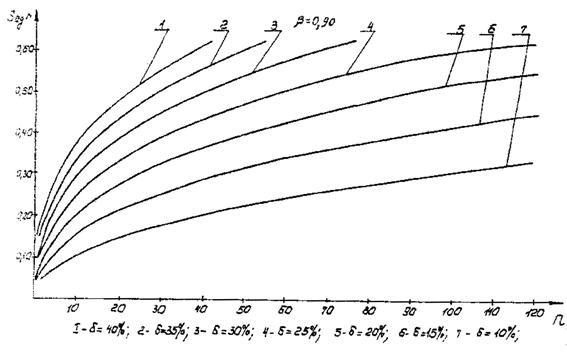
Черт. 8. График выбора числа образцов
Черт. 9. График выбора числа образцов
3.11. При оценке параметров функции распределения контактно-усталостного ресурса на заданном уровне напряжения допускается проводить испытания образцов на ограниченной базе.
Значения базы испытаний Ns вычисляют по формуле
где ![]() - среднее ожидаемое значение
числа циклов нагружения для заданного уровня напряжений.
- среднее ожидаемое значение
числа циклов нагружения для заданного уровня напряжений.
3.12. В качестве расчетного напряжения в зоне контакта принято максимальное нормальное напряжение szмакс для схем нагружения, предусмотренных п. 1.1, черт. 1, 2 и 4.
При испытании образцов по схеме качения с внешней касательной нагрузкой (пп. 1.1, черт. 3) в качестве расчетного принято эквивалентное напряжение sэкв.
Вычисление szмакс и sэкв производят по формулам, приведенным в разд. 1.
3.13. Выбор уровней напряжений должен обеспечивать в процессе испытаний постоянство размеров и формы площадки контакта. Если этого достигнуть не удается, то уточненный расчет напряжений szмакс производят по п. 1.6.7, исходя из переменной кривизны контактных поверхностей.
3.14. Выбор ориентированного значения szмакс при испытании образцов на верхнем уровне кривой контактной усталости осуществляют по априорной информации о результатах испытаний аналогичных образцов или по рекомендуемому приложению 8.
3.15. Выбор коэффициента К при испытании образцов по схеме качения с внешней касательной нагрузкой (п. 1.1, черт. 3) выполняют из условия обеспечения минимального проскальзывания между образцом и контртелом.
Рекомендуемый диапазон значений коэффициента К составляет от 0,02 до 0,05.
3.16. Основные критерии разрушения при определении пределов контактной выносливости и построения кривых контактной усталости:
для схем нагружения, предусмотренных п. 1.1, черт. 1 - 3 - наличие на контактной поверхности нескольких ямок выкрашивания или единичного выкрашивания диаметром, превышающим 50 % малой полуоси пятна контакта;
для схемы «пульсирующий контакт» - наличие на контактной поверхности усталостных трещин, возникающих у контура пятна контакта. Форма контура усталостных трещин зависит от геометрических размеров образца и контртела.
3.17. За момент разрушения принимают момент резкого изменения площади выкрашивания контактной поверхности.
Момент разрушения фиксируют или при помощи специальной аппаратуры или по результатам обработки графика изменения площади выкрашивания в функции наработки (числа циклов нагружения).
Измерение длины усталостной трещины или диаметра выкрашивания (в случаях, когда применение специальной аппаратуры не представляется возможным) производят оптическими средствами измерений.
3.18. При исследовательских испытаниях допустимо применять критерии разрушения, отличные от приведенных в пп. 3.16 и 3.17.
3.19. Нагружение образцов при испытаниях на контактную усталость производят по одной из схем, указанных на черт. 1 - 4.
4. МЕТОДЫ ОТБОРА ОБРАЗЦОВ
4.1. Контрольные испытания на контактную усталость.
4.1.1. Для проведения одной серии испытаний образцы должны быть изготовлены из металла одной марки и плавки по одному технологическому процессу.
4.1.2. Технологический процесс получения заготовки, маркировки и изготовления образцов не должен оказывать существенного влияния на контактно-усталостные свойства исходного материала.
4.1.3. В пределах одной серии испытаний макро- и микроструктура, а также твердость образцов должны быть близкими. Предельное отклонение по твердости не должно превышать ± 25 НВ или ± 1,5 НRСэ.
4.1.4. Термическая обработка металла должна производиться до финишных операций изготовления образцов.
Поверхностному упрочнению следует подвергать окончательно изготовленные образцы.
4.1.5. Точность изготовления образцов и контртел должна быть не ниже 6-го квалитета СТ СЭВ 145-75.
4.1.6. Шероховатость поверхности рабочей части образцов - Ra £ 0,32 мкм по ГОСТ 2789-73, на поверхности не должно быть следов коррозии, окалины, литейных корок, вальцовочный хлопьев, цветов побежалости, трещин и других дефектов.
4.1.7. Рабочую часть образца измеряют с погрешностью не более 0,01 мм.
4.1.8. Выбор типов образцов, контртел производят по табл. 1.
|
Условия испытаний |
Верхний уровень напряжения szмакс МПа (кгс/мм2) |
Тип образца и контртела |
|
|
Качение без проскальзывания |
Нормальная температура |
до 3000 (до 300) |
I |
|
Качение с внешней касательной нагрузкой |
|
до 6000 (до 600) |
II |
|
Качение с проскальзыванием |
То же |
|
III |
|
Пульсирующий контакт |
То же |
|
IV |
|
Качение без проскальзывания |
Повышенные температуры |
|
|
|
Качение с внешней касательной нагрузкой |
|
до 4000 (до 400) |
V |
4.1.9. Примеры рабочих чертежей образцов и контртел типов I - V приведены в рекомендуемом приложении 9.
4.2. При исследовательских испытаниях форма и размеры образцов и контртел, шероховатость поверхности, отклонение по твердости и другие параметры настоящими рекомендациями не регламентируются.
5. ПРОВЕДЕНИЕ ИСПЫТАНИЙ И ОБРАБОТКА РЕЗУЛЬТАТОВ
5.1. В пределах намеченной серии:
образцы испытывают на однотипных машинах;
последовательность установки, закрепления и нагружения образцов должна быть одинаковой.
5.2. Установка и закрепление образцов в испытательной машине не должны вызывать больших дополнительных напряжений от биения и несоосности образцов и захватов.
5.3. Нагружение образцов производят плавно после того, как будет достигнута заданная частота нагружения.
5.4. Испытание образцов рекомендуется проводить непрерывно до разрушения или до базового числа циклов.
5.5. В процессе испытаний контролируется стабильность задаваемых нагрузок, температуры и подачи смазочного материала.
5.6. Перед испытаниями производится настройка аппаратуры для фиксации момента разрушения. Критерий разрушения для настройки аппаратуры определяется в соответствии требованиям пп. 3.16 и 3.17.
5.7. Исходные данные и результаты испытаний каждого образца записывают в протокол испытаний (рекомендуемое приложение 10), а результаты испытаний партии образцов - в сводный протокол испытаний (рекомендуемое приложение 11).
Протоколы испытаний являются обязательными первичными документами, не подлежащими уничтожению в пределах установленных сроков хранения документации.
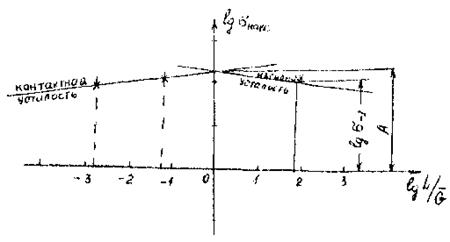
5.8. Кривые контактной усталости строят в полулогарифмических координатах; ординаты - наибольшие значения напряжений цикла szмакс, абсциссы - логарифмы чисел циклов до разрушения lgN (черт. 10) или в двойных логарифмических координатах
lg(szмакс), -lgN.
59. Кривые контактной усталости при пульсирующем контакте строят по результатам испытаний двух партий одинаковых образцов при одинаковых средних напряжениях цикла szмакс/n или одинаковых коэффициентах асимметрии.

Черт. 10. Кривая контактной усталости
5.10. При построении кривой контактной усталости при ограниченном объеме партии на 3 - 4 уровнях напряжений, превышающих предел контактной выносливости, испытывают партию одинаковых образцов (см. п. 3.6) до разрушения или базового числа циклов (см. п. 3.10).
Результаты испытаний подвергают регрессионному анализу (см. рекомендуемое приложение 12).
5.11. Для оценки параметров функции распределения контактно-усталостного ресурса на заданном уровне напряжения испытывают партию одинаковых образцов (см. п. 3.7) до разрушения или базового числа циклов (см. п.п. 3.10, 3.11). Результаты испытаний подвергают статистической оценке (см. раздел 6).
5.12. Для построения кривой контактной усталости в статистическом аспекте на 3 - 5 уровнях напряжений, превышающих предел контактной выносливости, испытывают партию одинаковых образцов (см. п. 3.8) до разрушения или базового числа циклов (см. пп. 3.10, 3.11). Результаты испытаний подвергают статистической оценке (см. раздел 6) и регрессионному анализу (см. приложение 12).
5.13. Для оценки среднего значения предела контактной выносливости и его среднего квадратического отклонения испытывают методом ступенчатого увеличения напряжений партию одинаковых образцов (см. п.3.9) до разрушения или до базового числа циклов (см. п. 3.10). Последовательность проведения испытаний методом ступенчатого увеличения напряжений приведена в рекомендуемом приложении 13.
5.14. При обработке результатов рекомендуется учитывать накопленную пластическую деформацию следующим образом:
по п. 1.6.7 уточняют значения szмакс, вызванные пластическими изменениями формы контактной площадки. Форму контактной площадки определяют с помощью сажевых отпечатков (см. приложение 4) путем замера измененных размеров контактных поверхностей профилографом или на измерительном микроскопе (см. приложение 4);
по уточненным значениям szмакс строят дополнительную кривую контактной усталости с учетом пластической деформации.
6. СТАТИСТИЧЕСКАЯ ОЦЕНКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
6.1. Оценка параметров функции распределения контактно-усталостного ресурса на заданном уровне напряжения.
6.1.1. Данный метод устанавливает оценку параметров, основанную на логарифмически нормальном распределении.
В обоснованных случаях допускается применять распределение Вейбулла, экспоненциальное, гамма-распределение и др.
6.1.2. Для заданного уровня напряжений составляют вариационный ряд ресурсов (чисел циклов) и производят первичную статистическую обработку, порядок которой указан в табл. 2.
|
Pj |
|
|
Nj |
lgNj |
|
|
|
1 |
Р1 |
|
|
N1 |
lgN1 |
|
|
2 |
р2 |
|
|
N2 |
lgN2 |
|
|
∙ |
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
n |
Pn |
|
|
Nn |
lgNn |
|
|
|
|
|
|
|
|
|
Примечание. j - номер образца в вариационном ряду ресурсов (чисел циклов), причем
N1 £ N2 £ ... £ Nj-1 £ Nj £ Nj+1 £ ... Nn;
Pj - выборочная вероятность, вычисляемая по формуле
![]()
или по табл. 5 приложения 3 (при n £ 20);
n - число образцов, испытанных на заданном уровне напряжения;
![]() - квантиль нормального
распределения, определяемый по табл. 6 приложения 3;
- квантиль нормального
распределения, определяемый по табл. 6 приложения 3;
Nj - число циклов до разрушения j-го образца.
6.1.3. Определяют параметры эмпирического
распределения величины lgNj, среднее
значение логарифма чисел циклов ![]() соответствующее выборочной вероятности
разрушения Р = 0,50, и среднее квадратическое отклонение SlgN.
соответствующее выборочной вероятности
разрушения Р = 0,50, и среднее квадратическое отклонение SlgN.
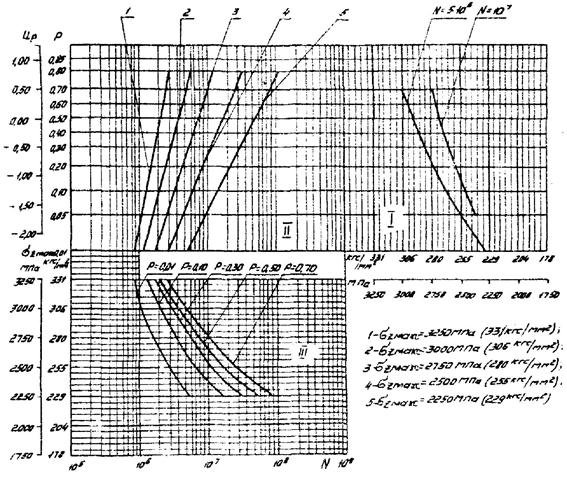
Порядок определения этих величин следующий: прямую, аппроксимирующую функцию распределения логарифмов чисел циклов, выражают уравнением
Используя данные
табл. 2,
методом наименьших квадратов определяют ![]() и SlgN в уравнении
(33).
и SlgN в уравнении
(33).
При разрушении
всех образцов на заданном уровне напряжения ![]() и SlgN вычисляют по формулам
и SlgN вычисляют по формулам
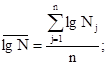 (34)
(34)
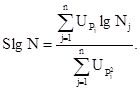 (35)
(35)
При неразрушении
части партии образцов (испытания на ограниченной базе) на заданном уровне
напряжения, ![]() и SlgN вычисляют по
формулам
и SlgN вычисляют по
формулам
где l - число образцов, испытанных на заданном уровне напряжения до разрушения.
6.1.4. Если в вариационном ряду ресурсов (чисел циклов) один или несколько результатов вызывают сомнение в принадлежности их к рассматриваемой выборке, используют 3s-критерий для непринятия резко выделяющихся наблюдений.
Если значения
ресурсов выходят за пределы интервала ![]() , то с доверительной вероятностью b = 0,997 можно утверждать, что
эти значения не принадлежат к рассматриваемой выборке.
, то с доверительной вероятностью b = 0,997 можно утверждать, что
эти значения не принадлежат к рассматриваемой выборке.
6.1.5. Проверку нормальности распределения логарифмов чисел циклов производят по критерию χ2 Пирсона.
6.1.6. Определяют доверительные интервалы, то
есть находят по выборочным значениям ![]() и SlgN наименьшие
интервалы, в которых
с заранее заданной вероятностью или надежностью будут находиться значения
математического ожидания а и дисперсии s2.
и SlgN наименьшие
интервалы, в которых
с заранее заданной вероятностью или надежностью будут находиться значения
математического ожидания а и дисперсии s2.
Доверительный интервал для математического ожидания вычисляют по формуле
где ![]() и
и ![]() - нижняя и верхняя
границы доверительного интервала для математического ожидания, соответственно;
- нижняя и верхняя
границы доверительного интервала для математического ожидания, соответственно;
tbk - критерий Cтьюдента, определяемый по табл. 7 приложения 3, для доверительной вероятности b и числа степеней свободы к = n - 1. Уровни доверительной вероятности принимают обычно равными 0,90 или 0,95.
Нижнюю и верхнюю границы доверительного интервала для стандартного отклонения вычисляют по выражениям
где ![]() - нижняя и верхняя
границы доверительного интервала для стандартного отклонения, соответственно;
- нижняя и верхняя
границы доверительного интервала для стандартного отклонения, соответственно;
ψ1 и ψ2 - коэффициенты, определяемые по табл. 8 приложения 3 в зависимости от заданной доверительной вероятности и числа степеней свободы.
Границы доверительного интервала для дисперсии находят по формуле
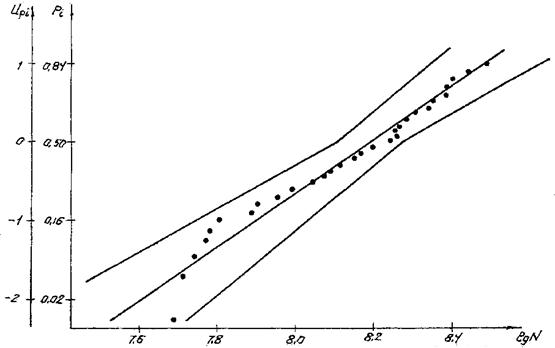
6.1.7. Значение координат для построения доверительных интервалов функции распределения ресурса приведены в табл. 3, расположение точек показано на черт. 11.
6.1.8. Для заданных уровней напряжений, зная параметры функций распределения и доверительные интервалы, строят на нормальной вероятностной бумаге графики функций распределения с доверительными интервалами (см. черт. 11).
|
Значение ординаты |
Значение абсциссы |
||
|
Pj |
|
||
|
1 |
84,10 |
1,00 |
|
|
2 |
50,00 |
0,00 |
|
|
3 |
15,90 |
1,00 |
|
|
4 |
84,10 |
1,00 |
|
|
5 |
50,00 |
0,00 |
|
|
6 |
15,90 |
-1,00 |
|
6.1.9. Пример оценки параметров функции распределения контактно-усталостного ресурса на заданном уровне напряжения приведен в рекомендуемом приложении 14.
6.1.10. Статистический анализ результатов сравнительных испытаний приведен в рекомендуемом приложении 15.
6.2. По графикам (черт. 12, квадрант II), задаваясь определенной вероятностью разрушения, находят числа циклов, соответствующие заданной вероятности разрушения и напряжению, и строят кривые контактной усталости для различных уровней вероятности разрушения (черт. 12, квадрант III).
Уровни вероятности разрушения принимают равными: 0,01; 0,10; 0,30; 0,50; 0,70.
6.3. По графикам (см. черт. 12, квадранты II и III), задаваясь определенными числами циклов, получают данные для построения кривых, характеризующих зависимости вероятности разрушения от уровня напряжений (черт. 12, квадрант I).
Черт. 11. График функции распределения с доверительными интервалами
6.4. Аналитическое описание левой ветви кривой контактной усталости методом регрессионного анализа приведено в приложении 12.
6.5. Методика статистической обработки результатов испытаний методом ступенчатого увеличения напряжений для оценки среднего значения предела контактной выносливости и его среднего квадратического отклонения приведена в приложении 13.
6.6. Методика оценки масштабного фактора на основе подобия контактно-усталостного разрушения приведена в рекомендуемом приложении 16.
Черт. 12. Вероятностная диаграмма контактной усталости
ПРИЛОЖЕНИЯ
1. Справочное
ТЕРМИНЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
1. Цикл напряжений, выносливость, база испытаний, кривая усталости, предел выносливости, функция распределения долговечности, кривая усталости равной вероятности разрушения, функция распределения предела выносливости, номинальное напряжение - по ГОСТ 2660-77.
2. Вариационный ряд, нормальное и логарифмически нормальное распределение, среднее значение и среднее квадратическое отклонение, математическое ожидание, стандартное отклонение, дисперсия, выборочная вероятность, доверительный интервал, уровень доверительной вероятности, уровень значимости, квантиль нормального распределения - по СТ СЭВ 3404-61.
3. Контактная усталость - процесс накопления повреждений и развития разрушения поверхностных слоев материала под действием переменных контактных напряжений, вызывающих образование ямок выкрашивания (питтинг) или трещин и снижение долговечности.
4. Основные обозначения величин, необходимых для проведения испытаний на контактную усталость, приведены в таблице.
|
Обозначение |
Единица |
Примечание |
|
|
Нормальная нагрузка |
Р |
Н (кгc) |
|
|
Касательная нагрузка |
Т |
Н (кгс) |
|
|
Средняя нормальная нагрузка цикла |
Рm |
Н (кгc) |
Черт, 4 |
|
Амплитуда нормальной нагрузки цикла |
Ра |
H (кгс) |
Черт. 4 |
|
Коэффициент, учитывающий соотношение между нормальной и касательной нагрузками на контакте |
|
- |
Черт. 3 |
|
Относительная величина проскальзывания между образцом и контртелом |
|
- |
|
|
Максимальное нормальное напряжение (давление) в центре зоны контакта |
szмакс |
МПа (кгс/мм2) |
Разд. 1 |
|
Нормальные напряжения в зоне контакта |
sx; sy; sz |
МПа (кгс/мм2) |
Разд. 1 |
|
Главные напряжения в зоне контакта |
s1; s2; s3 |
МПа (кгс/мм2) |
Разд. 1 |
|
Эквивалентное напряжение - нормальное растягивающее напряжение, создающее в материале напряженное состояние, равнозначное сложному по характеристикам контактной усталости |
sэкв |
МПа (кгс/мм2) |
Разд. 1 |
|
Амплитуда напряжений цикла |
sа |
МПа (кгс/мм2) |
sа = szмакс - п. 1.1, черт. 1 - 2; sа = (sэкв)макс - п. 1.1.3, черт. 3; |
|
Среднее напряжение цикла |
sm |
МПа (кгс/мм2) |
|
|
Наибольшее напряжение цикла |
sнаиб |
МПа (кгс/мм2) |
sнаиб = szмакс - п. 1.1, черт. 1 - 2; sнаиб = (sэкв)макс - п. 1.1.3, черт. 3; |
|
Наименьшее напряжение цикла |
sнаим |
МПа (кгс/мм2) |
|
|
Коэффициент асимметрии |
Rs |
- |
|
|
Абсцисса точки перегиба кривой контактной усталости |
No |
Цикл |
Черт. 9 |
|
Предел контактной выносливости |
sR |
МПа (кгс/мм2) |
|
|
Максимальная температура испытаний |
|
к |
Разд. 3 |
|
Температура вспышки масла |
|
К |
Разд. 3 |
2. Рекомендуемое
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ПОЛУОСЕЙ ПЛОЩАДКИ КОНТАКТА И МАКСИМАЛЬНОГО НОРМАЛЬНОГО НАПРЯЖЕНИЯ
|
Основные геометрические поверхности, образующие рабочую часть образца и контртела |
Чертеж |
Расчетные формулы |
Ω |
|
|
|
Е1 = Е2 = 21,02∙104 МПа Р, Н |
|||
|
Шар с шаром |
|
|
|
0 |
|
Шар с плоской плитой |
|
|
|
0 |
|
Шар с охватывающей сферой |
|
|
0 |
|
|
Шар с тороидальной поверхностью (знак - минус применяется в случае охватывающей поверхности радиусом R) |
|
|
|
|
|
Шар с цилиндром |
|
|
|
|
|
Шар с прямолинейным желобом |
|
|
|
|
|
Бочкообразное
тело с охватывающей сферой (при контакте с выпуклой сферой знак при |
|
|
|
|
|
Цилиндр с цилиндром со взаимоперпендикулярными осями |
|
|
|
|
|
Цилиндр с тороидом |
|
|
|
|
|
Цилиндр с плоскостью |
|
|
|
|
|
Цилиндр с выпуклой (+) и охватывающей (-) цилиндрическими поверхностями |
|
|
|
|
Примечание. Значения коэффициентов na(b), ns необходимо брать по табл. 3 справочного приложения 3 в соответствии со значением Ω: na(b) = na - для а; na(b) = nb - для b.
3. Справочное
ТАБЛИЦЫ
Таблица 1
Соотношение коэффициента вариации V и R
|
R |
V |
R |
|
|
0,10 |
0,01005 |
0,49 |
0,23399 |
|
0,11 |
0,01217 |
0,50 |
0,24529 |
|
0,12 |
0,01450 |
0,51 |
0,25694 |
|
0,13 |
0,01704 |
0,52 |
0,26892 |
|
0,14 |
0,01979 |
0,53 |
0,28125 |
|
0,16 |
0,02593 |
0,54 |
0,29893 |
|
0,17 |
0,02932 |
0,56 |
0,30696 |
|
0,18 |
0,03292 |
0,57 |
0,32035 |
|
0,19 |
0,03675 |
0,58 |
0,33412 |
|
0,20 |
0,04080 |
0,59 |
0,34825 |
|
0,21 |
0,04507 |
0,61 |
0,36277 |
|
0,22 |
0,04967 |
0,62 |
0,37768 |
|
0,23 |
0,05429 |
0,63 |
0,39298 |
|
0,24 |
0,05926 |
0,65 |
0,40869 |
|
0,25 |
0,06445 |
0,67 |
0,44133 |
|
0,26 |
0,06988 |
0,68 |
0,45828 |
|
0,27 |
0,07556 |
0,70 |
0,47566 |
|
0,28 |
0,08147 |
0,71 |
0,49849 |
|
0,29 |
0,08764 |
0,73 |
0,51175 |
|
0,31 |
0,09405 |
0,74 |
0,53047 |
|
0,32 |
0,10072 |
0,75 |
0,54966 |
|
0,33 |
0,10764 |
0,77 |
0,56931 |
|
0,34 |
0,11483 |
0,78 |
0,58944 |
|
0,35 |
0,12228 |
0,79 |
0,61005 |
|
0,36 |
0,13000 |
0,81 |
0,63116 |
|
0,37 |
0,13799 |
0,82 |
0,65277 |
|
0,38 |
0,14627 |
0,84 |
0,67489 |
|
0,39 |
0,15483 |
0,85 |
0,69753 |
|
0,40 |
0,16367 |
0,87 |
0,72070 |
|
0,42 |
0,17280 |
0,88 |
0,74410 |
|
0,43 |
0,18223 |
0,90 |
0,76367 |
|
0,44 |
0,19196 |
0,92 |
0,79348 |
|
0,45 |
0,20199 |
0,93 |
0,81885 |
|
0,46 |
0,21234 |
0,95 |
0,84480 |
|
0,47 |
0,22300 |
0,96 |
0,87133 |
Значения Q в зависимости от b и s
|
Значения Q при b равном |
||
|
0,90 |
0,95 |
|
|
0,01 |
16420,0 |
27060,0 |
|
0,02 |
4110,0 |
6760,0 |
|
0,03 |
1825,0 |
3010,0 |
|
0,04 |
1030,0 |
1690,0 |
|
0,05 |
657,0 |
1080,0 |
|
0,06 |
456,0 |
752,0 |
|
0,07 |
335,0 |
552,0 |
|
0,08 |
257,0 |
464,0 |
|
0,09 |
203,0 |
334,4 |
|
0,10 |
164,0 |
271,0 |
|
0,11 |
136,0 |
224,0 |
|
0,12 |
114,0 |
188,0 |
|
0,13 |
97,2 |
160,0 |
|
0,14 |
83,8 |
138,0 |
|
0,15 |
73,0 |
120,0 |
|
0,16 |
64,2 |
106,0 |
|
0,17 |
56,8 |
93,6 |
|
0,18 |
50,7 |
83,5 |
|
0,19 |
45,5 |
74,9 |
|
0,20 |
41,1 |
67,6 |
|
0,21 |
37,2 |
61,3 |
|
0,22 |
33,9 |
55,9 |
|
0,23 |
31,0 |
51,1 |
|
0,24 |
28,5 |
47,0 |
|
0,25 |
26,3 |
43,3 |
|
0,26 |
24,3 |
40,0 |
|
0,27 |
22,5 |
37,1 |
|
0,28 |
20,9 |
34,5 |
|
0,29 |
19,5 |
32,2 |
|
0,30 |
18,2 |
30,1 |
|
0,31 |
17,1 |
28,2 |
|
0,32 |
16,0 |
26,4 |
|
0,33 |
15,1 |
24,8 |
Значения коэффициентов na, nb, ns
|
е2 |
Ω |
na |
nb |
ns |
|
0,050 |
0,01923 |
1,013 |
0,9873 |
0,9999 |
|
0,100 |
0,03949 |
1,027 |
0,9742 |
0,9997 |
|
0,150 |
0,06087 |
1,042 |
0,9606 |
0,9992 |
|
0,200 |
0,08350 |
1,058 |
0,9465 |
0,9985 |
|
0,250 |
0,1075 |
1,076 |
0,9318 |
0,9974 |
|
0,300 |
0,1330 |
1,095 |
0,9165 |
0,9960 |
|
0,350 |
0,1602 |
1,117 |
0,9005 |
0,9942 |
|
0,400 |
0,1894 |
1,141 |
0,8837 |
0,9919 |
|
0,450 |
0,2207 |
1,168 |
0,8660 |
0,9890 |
|
0,500 |
0,2545 |
1,193 |
0,8472 |
0,9853 |
|
0,550 |
0,2913 |
1,233 |
0,8271 |
0,9805 |
|
0,600 |
0,3314 |
1,274 |
0,8056 |
0,9746 |
|
0,650 |
0,3755 |
1,322 |
0,7822 |
0,9669 |
|
0,700 |
0,4245 |
1,381 |
0,7565 |
0,9571 |
|
0,750 |
0,4795 |
1,456 |
0,7278 |
0,9440 |
|
0,760 |
0,4914 |
1,473 |
0,7216 |
0,9409 |
|
0,770 |
0,5036 |
1,491 |
0,7152 |
0,9376 |
|
0,780 |
0,5161 |
1,511 |
0,7086 |
0,9340 |
|
0,790 |
0,5291 |
1,532 |
0,7019 |
0,9302 |
|
0,800 |
0,5423 |
1,554 |
0,6949 |
0,9262 |
|
0,810 |
0,5560 |
1,578 |
0,6876 |
0,9219 |
|
0,820 |
0,5702 |
1,603 |
0,6801 |
0,9172 |
|
0,830 |
0,5848 |
1,631 |
0,6723 |
0,9121 |
|
0,840 |
0,5999 |
1,660 |
0,6642 |
0,9067 |
|
0,850 |
0,6155 |
1,693 |
0,6557 |
0,9008 |
|
0,860 |
0,6317 |
1,729 |
0,6468 |
0,8944 |
|
0,870 |
0,6486 |
1,768 |
0,6374 |
0,8873 |
|
0,880 |
0,6662 |
1,812 |
0,6276 |
0,8766 |
|
0,890 |
0,6845 |
1,861 |
0,6171 |
0,8710 |
|
0,900 |
0,7037 |
1,916 |
0,6059 |
0,8614 |
|
0,910 |
0,7238 |
1,979 |
0,5938 |
0,8507 |
|
0,920 |
0,7449 |
2,053 |
0,5808 |
0,8386 |
|
0,930 |
0,7673 |
2,141 |
0,5665 |
0,8246 |
|
0,940 |
0,7911 |
2,248 |
0,5505 |
0,8082 |
|
0,950 |
0,8166 |
2,381 |
0,5325 |
0,7887 |
|
0,955 |
0,8300 |
2,463 |
0,5224 |
0,7774 |
|
0,960 |
0,8441 |
2,557 |
0,5114 |
0,7647 |
|
0,965 |
0,8587 |
2,669 |
0,4993 |
0,7504 |
|
0,970 |
0,8741 |
2,805 |
0,4858 |
0,7338 |
|
0,975 |
0,8904 |
2,975 |
0,4704 |
0,7144 |
|
0,980 |
0,9077 |
3,199 |
0,4524 |
0,6909 |
|
0,981 |
0,9113 |
3,253 |
0,4484 |
0,6856 |
|
0,982 |
0,9150 |
3,311 |
0,4442 |
0,6799 |
|
0,983 |
0,9187 |
3,373 |
0,4398 |
0,6740 |
|
0,984 |
0,9225 |
3,441 |
0,4352 |
0,6678 |
|
0,965 |
0,9264 |
3,514 |
0,4304 |
0,6612 |
|
0,986 |
0,9303 |
3,594 |
0,4253 |
0,6542 |
|
0,987 |
0,9342 |
3,683 |
0,4199 |
0,6467 |
|
0,988 |
0,9383 |
3,781 |
0,4142 |
0,6387 |
|
0,989 |
0,9425 |
3,890 |
0,4080 |
0,6300 |
|
0,990 |
0,9467 |
4,014 |
0,4014 |
0,6206 |
|
0,991 |
0,9511 |
4,156 |
0,3942 |
0,6104 |
|
0,992 |
0,9556 |
4,320 |
0,3864 |
0,5990 |
|
0,993 |
0,9601 |
4,515 |
0,3777 |
0,5864 |
|
0,994 |
0,9649 |
4,750 |
0,3680 |
0,5721 |
|
0,996 |
0,9698 |
5,046 |
0,3568 |
0,5555 |
|
0,996 |
0,9749 |
5,432 |
0,3436 |
0,5358 |
|
0,997 |
0,+803 |
5,976 |
0,3273 |
0,5112 |
|
0,988 |
0,9861 |
8,837 |
0,3058 |
0,4783 |
|
0,999 |
0,9923 |
8,609 |
0,2722 |
0,4267 |
Примечание: ![]() - относительный
эксцентриситет контурного эллипса площадки контакта:
- относительный
эксцентриситет контурного эллипса площадки контакта:
![]()
Полные эллиптические интегралы
|
е2 |
F(e) |
Е(е) |
е2 |
F(e) |
Е(е) |
|
0,00000 |
1,5708 |
1,57080 |
0,47093 |
1,8302 |
1,36514 |
|
0,00030 |
1,5709 |
1,57068 |
0,48837 |
1,8443 |
1,35648 |
|
0,00122 |
1,5713 |
1,57032 |
0,50582 |
1,8530 |
1,34771 |
|
0,00274 |
1,5719 |
1,56972 |
0,52326 |
1,8743 |
1,33884 |
|
0,00487 |
1,5727 |
1,56888 |
0,54068 |
1,8902 |
1,32987 |
|
0,00760 |
1,5737 |
1,56781 |
0,55226 |
1,9011 |
1,32384 |
|
0,01093 |
1,5751 |
1,56650 |
0,56959 |
1,9180 |
1,31473 |
|
0,01485 |
1,5767 |
1,56495 |
0,58682 |
1,9356 |
1,30554 |
|
0,01937 |
1,5785 |
1,56316 |
0,60396 |
1,9539 |
1,29628 |
|
0,02447 |
1,5805 |
1,56114 |
0,62096 |
1,9729 |
1,28695 |
|
0,03015 |
1,5828 |
1,55889 |
0,63782 |
1,9927 |
1,27757 |
|
0,03641 |
1,5854 |
1,55640 |
0,65451 |
2,0133 |
1,26815 |
|
0,04323 |
1,5882 |
1,55368 |
0,67101 |
2,0347 |
1,25868 |
|
0,05060 |
1,5913 |
1,55073 |
0,68730 |
2,0571 |
1,24918 |
|
0,05853 |
1,5946 |
1,54755 |
0,70337 |
2,0804 |
1,23966 |
|
0,06699 |
1,5381 |
1,54415 |
0,71919 |
2,1047 |
1,23013 |
|
0,07598 |
1,6020 |
1,54052 |
0,73473 |
2,1333 |
1,22059 |
|
0,07909 |
1,6033 |
1,53926 |
0,75000 |
2,1565 |
1,21106 |
|
0,08226 |
1,6047 |
1,53798 |
0,76496 |
2,1842 |
1,20154 |
|
0,09210 |
1,6090 |
1,53398 |
0,77960 |
2,2132 |
1,19205 |
|
0,10244 |
1,6135 |
1,52976 |
0,79389 |
2,2435 |
1,18259 |
|
0,11326 |
1,6184 |
1,52533 |
0,80783 |
2,2754 |
1,17318 |
|
0,12456 |
1,6235 |
1,52068 |
0,81239 |
2,2863 |
1,17006 |
|
0,13631 |
1,6289 |
1,51581 |
0,81916 |
2,3031 |
1,16538 |
|
0,14851 |
1,6346 |
1,51074 |
0,82583 |
2,3203 |
1,16073 |
|
0,16113 |
1,6405 |
1,50547 |
0,83240 |
2,3379 |
1,15609 |
|
0,17417 |
1,6488 |
1,49999 |
0,83887 |
2,3560 |
1,15147 |
|
0,18761 |
1,6534 |
1,49431 |
0,84523 |
2,3746 |
1,14687 |
|
0,20142 |
1,6603 |
1,48843 |
0,85149 |
2,3936 |
1,14230 |
|
0,21560 |
1,6676 |
1,48236 |
0,85764 |
2,4132 |
1,13775 |
|
0,23012 |
1,6751 |
1,47610 |
0,86369 |
2,4333 |
1,13323 |
|
0,24498 |
1,6830 |
1,47695 |
0,86962 |
2,4540 |
1,12874 |
|
0,26014 |
1,6313 |
1,46302 |
0,87544 |
2,4752 |
1,12428 |
|
0,27560 |
1,6999 |
1,45622 |
0,88115 |
2,4971 |
1,11985 |
|
0,28606 |
1,7058 |
1,45158 |
0,88674 |
2,5196 |
1,11545 |
|
0,30196 |
1,7150 |
1,44449 |
0.89221 |
2,5428 |
1,11109 |
|
0,31810 |
1,7246 |
1,43722 |
0,89756 |
2,5668 |
1,10677 |
|
0,33447 |
1,7346 |
1,42980 |
0,90279 |
2,5914 |
1,10248 |
|
0,35103 |
1,7450 |
1,42222 |
0,90621 |
2,6083 |
1,09965 |
|
0,36778 |
1,7558 |
1,41448 |
0,91124 |
2,6343 |
1,09543 |
|
0,38469 |
1,7670 |
1,40660 |
0,91614 |
2,6612 |
1,09127 |
|
0,40174 |
1,7787 |
1,39857 |
0,92091 |
2,6890 |
1,08715 |
|
0,41891 |
1,7909 |
1,39040 |
0,92556 |
2,7178 |
1,08307 |
|
0,43618 |
1,8035 |
1,38211 |
0,93007 |
2,7476 |
1,07905 |
|
0,45353 |
1,8166 |
1,37368 |
0,93446 |
2,7785 |
1,07509 |
|
0,93871 |
2,8106 |
1,07118 |
0,98907 |
3,6519 |
1,01724 |
|
0,94283 |
2,8439 |
1,06733 |
0,98967 |
3,6796 |
1,01644 |
|
0,94662 |
2,8786 |
1,06355 |
0,99053 |
3,7228 |
1,01527 |
|
0,95066 |
2,9148 |
1,05983 |
0,99136 |
3,7680 |
1,01413 |
|
0,95438 |
2,9525 |
1,05617 |
0,99215 |
3,8154 |
1,01302 |
|
0,95795 |
2,9919 |
1,05259 |
0,99290 |
3,8653 |
1,01195 |
|
0,96138 |
3,0331 |
1,04908 |
0,99361 |
3,9178 |
1,01092 |
|
0,96467 |
3,0764 |
1,04565 |
0,99429 |
3,9734 |
1,00992 |
|
0,96782 |
3,1218 |
1,04230 |
0,99493 |
4,0323 |
1,00896 |
|
0,96985 |
3,1534 |
1,04011 |
0,99553 |
4,0950 |
1,00804 |
|
0,97132 |
3,1778 |
1,03850 |
0,99609 |
4,1620 |
1,00716 |
|
0,97276 |
3,2029 |
1,03691 |
0,99662 |
4,2338 |
1,00631 |
|
0,97416 |
3,2287 |
1,03534 |
0,99711 |
4,3114 |
1,00552 |
|
0,97553 |
3,2553 |
1,03379 |
0,99756 |
4,3956 |
1,00476 |
|
0,97686 |
3,2826 |
1,03227 |
0,99797 |
4,4876 |
1,00405 |
|
0,97815 |
3,3108 |
1,03077 |
0,99834 |
4,5890 |
1,00339 |
|
0,97941 |
3,3399 |
1,02929 |
0,99868 |
4,7020 |
1,00278 |
|
0,98063 |
3,3699 |
1,02784 |
0,99888 |
4,7852 |
1,00240 |
|
0,98182 |
3,4008 |
1,02642 |
0,99915 |
4,9247 |
1,00187 |
|
0,98296 |
3,4329 |
1,02502 |
0,99939 |
5,0869 |
1,00140 |
|
0,98408 |
3,4651 |
1,02365 |
0,99959 |
5,2809 |
1,00099 |
|
0,98515 |
3,5004 |
1,02231 |
0,99970 |
5,4349 |
1,00075 |
|
0,98616 |
3,5361 |
1,02100 |
0,99983 |
5,7224 |
1,00045 |
|
0,98719 |
3,5731 |
1,01972 |
0,99992 |
6,1278 |
1,00021 |
|
0,98815 |
3,6117 |
1,01846 |
1,00000 |
∞ |
1,00000 |
Значение выборочной вероятности Pj для выборок малого объема
|
j (j £ n) |
Значение выборочной вероятности Pj для выборок малого объема при n, равном |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
0,5000 |
0,2929 |
0,2063 |
0,1591 |
0,1294 |
0,1091 |
0,0943 |
0,0830 |
0,0741 |
0,0670 |
|
2 |
- |
0,7071 |
0,5000 |
0,3864 |
0,3147 |
0,2655 |
0,2295 |
0,2021 |
0,1806 |
0,1632 |
|
3 |
- |
- |
0,7937 |
0,6136 |
0,5000 |
0,4218 |
0,3648 |
0,3213 |
0,2871 |
0,2594 |
|
4 |
- |
- |
- |
0,8409 |
0,6853 |
0,5782 |
0,5000 |
0,4404 |
0,3935 |
0,3557 |
|
5 |
- |
- |
- |
- |
0,8706 |
0,7345 |
0,6352 |
0,5596 |
0,5000 |
0,4519 |
|
6 |
- |
- |
- |
- |
- |
0,8909 |
0,7705 |
0,6787 |
0,6065 |
0,5484 |
|
7 |
- |
- |
- |
- |
- |
- |
0,9057 |
0,7979 |
0,7129 |
0,6443 |
|
8 |
- |
- |
- |
- |
- |
- |
- |
0,9170 |
0,8194 |
0,7406 |
|
9 |
- |
- |
- |
- |
- |
- |
- |
- |
0,9259 |
0,8368 |
|
10 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,9330 |
Продолжение таблицы
|
j (j £ n) |
Значение выборочной вероятности Pj для выборок малого объема при n, равном |
|||||||||
|
11 |
12 |
13 1 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
0,0611 |
0,0561 |
0,0519 |
0,0483 |
0,0452 |
0,0424 |
0,0400 |
0,0378 |
0,0358 |
0,0341 |
|
2 |
0,1489 |
0,1368 |
0,1266 |
0,1178 |
0,1101 |
0,1034 |
0,0975 |
0,0922 |
0,0874 |
0,0831 |
|
3 |
0,2366 |
0,2175 |
0,2013 |
0,1873 |
0,1751 |
0,1644 |
0,1550 |
0,1465 |
0,1390 |
0,1322 |
|
4 |
0,3244 |
0,2982 |
0,2760 |
0,2568 |
0,2401 |
0,2254 |
0,2125 |
0,2009 |
0,1905 |
0,1812 |
|
5 |
0,4122 |
0,3789 |
0,3506 |
0,3263 |
0,3051 |
0,2865 |
0,2700 |
0,2553 |
0,2421 |
0,2302 |
|
6 |
0,5000 |
0,4596 |
0,4253 |
0,3958 |
0,3700 |
0,3475 |
0,3275 |
0,3097 |
0,2937 |
0,2793 |
|
7 |
0,5878 |
0,5404 |
0,5000 |
0,4653 |
0,4350 |
0,4085 |
0,3850 |
0,3641 |
0,3453 |
0,3283 |
|
8 |
0,6756 |
0,6211 |
0,5747 |
0,5347 |
0,5000 |
0,4695 |
0,4425 |
0,4184 |
0,3968 |
0,3774 |
|
9 |
0,7634 |
0,7018 |
0,6494 |
0,6042 |
0,5650 |
0,5305 |
0,5000 |
0,4728 |
0,4484 |
0,4264 |
|
10 |
0,8511 |
0,7825 |
0,7240 |
0,6737 |
0,6300 |
0,5915 |
0,5575 |
0,5272 |
0,5000 |
0,4755 |
|
11 |
0,9389 |
0,8632 |
0,7987 |
0,7432 |
0,6949 |
0,6525 |
0,6150 |
0,5816 |
0,5516 |
0,5245 |
|
12 |
- |
0,9439 |
0,8734 |
0,8125 |
0,7599 |
0,7135 |
0,6725 |
0,6359 |
0,6032 |
0,5736 |
|
13 |
- |
- |
0,9481 |
0,8822 |
0,8249 |
0,7746 |
0,7300 |
0,6903 |
0,6547 |
0,6226 |
|
14 |
- |
- |
- |
0,9517 |
0,8899 |
0,8356 |
0,7875 |
0,7447 |
0,7063 |
0,6717 |
|
15 |
- |
- |
- |
- |
0,9548 |
0,8966 |
0,8450 |
0,7991 |
0,7579 |
0,7207 |
|
16 |
- |
- |
- |
- |
- |
0,9576 |
0,9025 |
0,8535 |
0,8095 |
0,7698 |
|
17 |
- |
- |
- |
- |
- |
- |
0,9600 |
0,9078 |
0,8610 |
0,8188 |
|
18 |
- |
- |
- |
- |
- |
- |
- |
0,9622 |
0,9126 |
0,8678 |
|
19 |
- |
- |
- |
- |
- |
- |
- |
|
0,9642 |
0,9169 |
|
20 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,9659 |
Квантили
нормального распределения ![]()
|
Квантили нормального
распределения |
||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0,50 |
0,0000 |
0,00251 |
0,00501 |
0,00752 |
0,01002 |
0,01253 |
0,01504 |
0,01755 |
0,02005 |
0,02256 |
|
0,51 |
0,02507 |
0,02758 |
0,03008 |
0,03259 |
0,03510 |
0,03761 |
0,04012 |
0,04263 |
0,04513 |
0,04764 |
|
0,52 |
0,05015 |
0,05266 |
0,05517 |
0,05768 |
0,06020 |
0,06271 |
0,06522 |
0,06773 |
0,07024 |
0,07276 |
|
0,53 |
0,01527 |
0,07778 |
0,08030 |
0,08281 |
0,08533 |
0,08764 |
0,09036 |
0,09288 |
0,09540 |
0,09791 |
|
0,54 |
0,1004 |
0,1030 |
0,1055 |
0,1080 |
0,1105 |
0,1130 |
0,1156 |
0,1181 |
0,1206 |
0,1231 |
|
0,55 |
0,1257 |
0,1282 |
0,1307 |
0,1332 |
0,1358 |
0,1383 |
0,1408 |
0,1434 |
0,1459 |
0,1484 |
|
0,56 |
0,1510 |
0,1535 |
0,1560 |
0,1586 |
0,1611 |
0,1637 |
0,1662 |
0,1687 |
0,1713 |
0,1738 |
|
0,57 |
0,1764 |
0,1789 |
0,1815 |
0,1840 |
0,1866 |
0,1891 |
0,1917 |
0,1942 |
0,1968 |
0,1993 |
|
0,58 |
0,2019 |
0,2045 |
0,2070 |
0,2096 |
0,2121 |
0,2147 |
0,2173 |
0,2198 |
0,2224 |
0,2250 |
|
0,59 |
0,2275 |
0,2301 |
0,2327 |
0,2353 |
0,2378 |
0,2404 |
0,2430 |
0,2456 |
0,2482 |
0,2508 |
|
0,60 |
0,2533 |
0,2559 |
0,2585 |
0,2611 |
0,2637 |
0,2663 |
0,2689 |
0,2715 |
0,2741 |
0,2767 |
|
0,61 |
0,2793 |
0,2819 |
0,2845 |
0,2871 |
0,2898 |
0,2924 |
0,2950 |
0,2976 |
0,3002 |
0,3029 |
|
0,62 |
0,3055 |
0,3081 |
0,3107 |
0,3134 |
0,3160 |
0,3186 |
0,3213 |
0,3239 |
0,3266 |
0,3292 |
|
0,63 |
0,3319 |
0,3345 |
0,3372 |
0,3398 |
0,3425 |
0,3451 |
0,3478 |
0,3505 |
0,3531 |
0,3558 |
|
0,64 |
0,3585 |
0,3611 |
0,3638 |
0,3665 |
0,3692 |
0,3719 |
0,3745 |
0,3772 |
0,3799 |
0,3826 |
|
0,65 |
0,3853 |
0,3880 |
0,3907 |
0,3934 |
0,3961 |
0,3989 |
0,4016 |
0,4043 |
0,4070 |
0,4097 |
|
0,66 |
0,4125 |
0,4152 |
0,4179 |
0,4207 |
0,4234 |
0,4261 |
0,4289 |
0,4316 |
0,4344 |
0,4372 |
|
0,67 |
0,4399 |
0,4427 |
0,4454 |
0,4482 |
0,4510 |
0,4538 |
0,4565 |
0,4593 |
0.4621 |
0,4649 |
|
0,68 |
0,4677 |
0,4705 |
0,4733 |
0,4761 |
0,4789 |
0,4817 |
0,4845 |
0,4874 |
0,4902 |
0,4930 |
|
0,69 |
0,4969 |
0,4987 |
0,5015 |
0,5044 |
0,5072 |
0,5101 |
0,5129 |
0,5158 |
0,5187 |
0,5215 |
|
0,70 |
0,5244 |
0,5273 |
0,5302 |
0,5330 |
0,5359 |
0,5388 |
0,5417 |
0,5446 |
0,5476 |
0,5506 |
|
0,71 |
0,5634 |
0,5563 |
0,5592 |
0,5622 |
0,5651 |
0,5681 |
0,5710 |
0,5740 |
0,5769 |
6,5799 |
|
0,72 |
0,5828 |
0,5858 |
0,5888 |
0,5918 |
0,5948 |
0,5978 |
0,6008 |
0,6038 |
0,6068 |
6,6098 |
|
0,73 |
0,6128 |
0,6158 |
0,6189 |
0,6219 |
0,6250 |
0,6280 |
0,6311 |
0,6341 |
0,6372 |
0,6403 |
|
0,74 |
0,6433 |
0,6464 |
0,6495 |
0,6526 |
0,6557 |
0,6588 |
0,6620 |
0,6651 |
0,6682 |
0,6713 |
|
0,75 |
0,6745 |
0,6776 |
0,6808 |
0,6840 |
0,6871 |
0,6903 |
0,6935 |
0,6967 |
0,6999 |
0,7031 |
|
0,76 |
0,7063 |
0,7095 |
0,7128 |
0,7160 |
0,7192 |
0,7225 |
0,7257 |
0,7290 |
0,7323 |
0,7356 |
|
0,77 |
0,7388 |
0,7421 |
0,7454 |
0,7488 |
0,7521 |
0,7554 |
0,7588 |
0,7621 |
0,7655 |
0,7686 |
|
0,78 |
0,7722 |
0,7756 |
0,7790 |
0,7624 |
0,7858 |
0,7892 |
0,7926 |
0,7961 |
0,7995 |
0,8030 |
|
0,79 |
0,8064 |
0,8099 |
0,8134 |
0,8169 |
0,8204 |
0,8239 |
0,8274 |
0,8310 |
0,8345 |
0,8381 |
|
0,80 |
0,8416 |
0,8452 |
0,8488 |
0,8524 |
0,8560 |
0,8596 |
0,8633 |
0,8669 |
0,8705 |
0,8742 |
|
0,81 |
0,8779 |
0,8816 |
0,8853 |
0,8890 |
0,8927 |
0,8965 |
0,9002 |
0,9040 |
0,9078 |
0,9116 |
|
0,82 |
0,9154 |
0,9192 |
0,9230 |
0,9269 |
0,9307 |
0,9346 |
0,9385 |
0,9424 |
0,9463 |
0,9502 |
|
0,83 |
0,9542 |
0,9581 |
0,9621 |
0,9661 |
0,9701 |
0,9741 |
0,9782 |
0,9822 |
0,9863 |
0,9904 |
|
0,84 |
0,994 |
0,999 |
1,003 |
1,007 |
1,011 |
1,015 |
0,019 |
1,024 |
1,026 |
1,032 |
|
0,85 |
1,036 |
1,041 |
1,045 |
1,049 |
1,054 |
1,058 |
1,063 |
1,067 |
1,071 |
1,076 |
|
0,86 |
1,080 |
1,085 |
1,089 |
1,094 |
1,098 |
1,103 |
1,108 |
1,112 |
1,117 |
1,122 |
|
0,87 |
1,126 |
1,131 |
1,136 |
1,141 |
1,146 |
1,150 |
1,155 |
1,160 |
1,165 |
1,170 |
|
0,88 |
1,175 |
1,180 |
1,185 |
1,190 |
1,195 |
1,200 |
1,206 |
1,211 |
1,216 |
1,221 |
|
0,89 |
1,227 |
1,232 |
1,237 |
1,243 |
1,248 |
1,254 |
1,259 |
1,265 |
1,270 |
1,276 |
|
0,90 |
1,282 |
1,287 |
1,293 |
1,299 |
1,305 |
1,311 |
1,317 |
1,323 |
1,329 |
1,335 |
|
0,91 |
1,341 |
1,347 |
1,353 |
1,359 |
1,366 |
1,372 |
1,379 |
1,385 |
1,392 |
1,398 |
|
0,92 |
1,406 |
1,412 |
1,419 |
1,426 |
1,433 |
1,440 |
1,447 |
1,454 |
1,461 |
1,468 |
|
0,93 |
1,476 |
1,483 |
1,491 |
1,499 |
1,506 |
1,514 |
1,522 |
1,530 |
1,538 |
1,546 |
|
0,94 |
1,555 |
1,563 |
1,572 |
1,580 |
1,589 |
1,598 |
1,607 |
1,612 |
1,626 |
1,635 |
|
0,95 |
1,645 |
1,655 |
1,665 |
1,675 |
1,685 |
1,695 |
1,706 |
1,717 |
1,728 |
1,739 |
|
0,96 |
1,751 |
1,762 |
1,774 |
1,787 |
1,799 |
1,812 |
1,825 |
1,838 |
1,852 |
1,866 |
|
0,97 |
1,861 |
1,896 |
1,911 |
1,927 |
1,943 |
1,960 |
1,977 |
1,995 |
2,014 |
2,034 |
|
0,98 |
2,054 |
2,075 |
2,097 |
2,120 |
2,144 |
2,170 |
2,197 |
2,226 |
2,257 |
2,290 |
|
0,99 |
2,236 |
2,366 |
2,409 |
2,457 |
2,512 |
2,576 |
2,652 |
2,748 |
2,878 |
3,090 |
|
0,991 |
2,366 |
2,370 |
2,374 |
2,373 |
2,382 |
2,387 |
2,391 |
2,395 |
2,400 |
2,404 |
|
0,992 |
2,409 |
2,414 |
2,418 |
2,423 |
2,428 |
2,432 |
2,437 |
2,442 |
2,447 |
2,452 |
|
0,993 |
2,457 |
2,462 |
2,468 |
2,473 |
2,478 |
2,484 |
2,489 |
2,495 |
2,501 |
2,506 |
|
0,994 |
2,512 |
2,518 |
2,524 |
2,530 |
2,535 |
2,543 |
2,549 |
2,656 |
2,562 |
2,569 |
|
0,995 |
2,576 |
2,583 |
2,590 |
2,597 |
2,605 |
2,612 |
2,52б |
2,628 |
2,636 |
2,644 |
|
0,996 |
2,652 |
2,661 |
2,669 |
2,678 |
2,687 |
2,697 |
2,708 |
2,716 |
2,727 |
2,737 |
|
0,997 |
2,748 |
2,759 |
2,770 |
2,782 |
2,794 |
2,807 |
2,820 |
2,834 |
2,848 |
2,863 |
|
0,998 |
2,878 |
2,894 |
2,911 |
2,929 |
2,948 |
2,968 |
2,989 |
3,011 |
3,036 |
3,062 |
|
0,999 |
3,090 |
3,121 |
3,156 |
3,195 |
3,239 |
3,291 |
3,353 |
3,432 |
3,540 |
3,719 |
Примечание: В таблице приведены
значения квантилей ![]() для Pj ³
0,50. При Pj < 0,50 следует пользоваться
выражением U(-P) = U(1 - P). Например, для Pj = 0,20 находим U0,20 = U(1-0,80) = U(0,80) = -0,8416.
для Pj ³
0,50. При Pj < 0,50 следует пользоваться
выражением U(-P) = U(1 - P). Например, для Pj = 0,20 находим U0,20 = U(1-0,80) = U(0,80) = -0,8416.
Значения tBK зависимости от доверительной вероятности b и числа степеней свободы К
|
Значения tBK при b, равном |
||||
|
0,90 |
0,95 |
0,98 |
0,99 |
|
|
1 |
6,314 |
12,706 |
31,821 |
63,657 |
|
2 |
2,920 |
4,303 |
6,965 |
9,925 |
|
3 |
2,353 |
3,182 |
4,541 |
5,841 |
|
4 |
2,132 |
2,776 |
3,747 |
4,604 |
|
5 |
2,015 |
2,571 |
3,365 |
4,032 |
|
6 |
1,943 |
2,447 |
3,143 |
3,707 |
|
7 |
1,895 |
2,365 |
2.998 |
3,499 |
|
8 |
1,860 |
2,306 |
2,896 |
3.355 |
|
9 |
1,833 |
2,262 |
2,821 |
3,250 |
|
10 |
1,812 |
2,228 |
2,764 |
3,169 |
|
12 |
1,782 |
2,179 |
2,681 |
3,055 |
|
14 |
1,761 |
2,145 |
2,624 |
2,977 |
|
16 |
1,746 |
2,120 |
2,583 |
2,921 |
|
18 |
1,734 |
2,101 |
2,552 |
2,878 |
|
20 |
1,725 |
2,086 |
2,528 |
2,845 |
|
22 |
1,717 |
2,074 |
2,508 |
2,819 |
|
24 |
1,711 |
2,064 |
2,492 |
2,797 |
|
26 |
1,706 |
2,056 |
2,479 |
2,779 |
|
28 |
1,701 |
2,048 |
2,467 |
2,763 |
|
30 |
1,697 |
2,042 |
2,457 |
2,750 |
|
∞ |
1,645 |
1,960 |
2,326 |
2,576 |
Значения Ψ1 и Ψ2 в зависимости от доверительной вероятности b и числа степеней свободы K
|
b = 0,99 |
b = 0,98 |
b = 0,95 |
b = 0,90 |
|||||
|
Ψ1 |
Ψ2 |
Ψ1 |
Ψ2 |
Ψ1 |
Ψ2 |
Ψ1 |
Ψ2 |
|
|
1 |
0,356 |
159,000 |
0,388 |
79,800 |
0,446 |
31,900 |
0,510 |
15,900 |
|
2 |
0,434 |
14,100 |
0,466 |
9,970 |
0,521 |
6,280 |
0,578 |
4,400 |
|
3 |
0,483 |
6,470 |
0,514 |
5,110 |
0,566 |
3,730 |
0,620 |
2,920 |
|
4 |
0,519 |
4,390 |
0,549 |
3,670 |
0,599 |
2,870 |
0,649 |
2,370 |
|
5 |
0,546 |
3,480 |
0,576 |
3,000 |
0,624 |
2,450 |
0,672 |
2,090 |
|
6 |
0,569 |
2,980 |
0,597 |
2,620 |
0,644 |
2,202 |
0,690 |
1,916 |
|
7 |
0,588 |
2,660 |
0,616 |
2,376 |
0,661 |
2,035 |
0,705 |
1,797 |
|
8 |
0,604 |
2,440 |
0,631 |
2,205 |
0,675 |
1,916 |
0,718 |
1,711 |
|
9 |
0,618 |
2,277 |
0,644 |
2,076 |
0,688 |
1,826 |
0,729 |
1,645 |
|
10 |
0,630 |
2,154 |
0,656 |
1,977 |
0,699 |
1,755 |
0,739 |
1,593 |
|
11 |
0,641 |
2,056 |
0,667 |
1,898 |
0,708 |
1,698 |
0,748 |
1,550 |
|
12 |
0,651 |
1,976 |
0,677 |
1,833 |
0,717 |
1,651 |
0,755 |
1,515 |
|
13 |
0,660 |
1,910 |
0,685 |
1,779 |
0,725 |
1,611 |
0,762 |
1,485 |
|
14 |
0,669 |
1,854 |
0,693 |
1,733 |
0,732 |
1,577 |
0,769 |
1,460 |
|
15 |
0,676 |
1,806 |
0,700 |
1,694 |
0,739 |
1,548 |
0,775 |
1,437 |
|
16 |
0,683 |
1,764 |
0,707 |
1,659 |
0,745 |
1,522 |
0,780 |
1,418 |
|
17 |
0,690 |
1,727 |
0,713 |
1,629 |
0,750 |
1,499 |
0,785 |
1,400 |
|
18 |
0,696 |
1,695 |
0,719 |
1,602 |
0,756 |
1,479 |
0,790 |
1,385 |
|
19 |
0,702 |
1,666 |
0,725 |
1,578 |
0,760 |
1,460 |
0,794 |
1,370 |
|
20 |
0,707 |
1,640 |
0,730 |
1,556 |
0,765 |
1,444 |
0,798 |
1,358 |
|
21 |
0,712 |
1,617 |
0,734 |
1,536 |
0,769 |
1,429 |
0,802 |
1,346 |
|
22 |
0,717 |
1,595 |
0,739 |
1,519 |
0,773 |
1,416 |
0,805 |
1,335 |
|
23 |
0,722 |
1,576 |
0,743 |
1,502 |
0,777 |
1,402 |
0,809 |
1,326 |
|
24 |
0,726 |
1,558 |
0,747 |
1,487 |
0,781 |
1,391 |
0,812 |
1,316 |
|
25 |
0,730 |
1,541 |
0,751 |
1,473 |
0,784 |
1,380 |
0,815 |
1,308 |
|
26 |
0,734 |
1,526 |
0,755 |
1,460 |
0,788 |
1,371 |
0,818 |
1,300 |
|
27 |
0,737 |
1,512 |
0,756 |
1,448 |
0,791 |
1,361 |
0,820 |
1,293 |
|
28 |
0,741 |
1,499 |
0,762 |
1,436 |
0,794 |
1,352 |
0,823 |
1,286 |
|
29 |
0,744 |
1,487 |
0,765 |
1,426 |
0,796 |
1,344 |
0,825 |
1,279 |
|
30 |
0,748 |
1,475 |
0,768 |
1,417 |
0,799 |
1,337 |
0,828 |
1,274 |
|
40 |
0,774 |
1,390 |
0,792 |
1,344 |
0,821 |
1,279 |
0,847 |
1,228 |
|
50 |
0,793 |
1,336 |
0,810 |
1,297 |
0,837 |
1,243 |
0,861 |
1,199 |
|
60 |
0,808 |
1,299 |
0,824 |
1,265 |
0,849 |
1,217 |
0,871 |
1,179 |
|
70 |
0,820 |
1,272 |
0,835 |
1,241 |
0,858 |
1,198 |
0,879 |
1,163 |
|
80 |
0,829 |
1,250 |
0,844 |
1,222 |
0,866 |
1,183 |
0,886 |
1,151 |
|
90 |
0,838 |
1,233 |
0,852 |
1,207 |
0,873 |
1,171 |
0,892 |
1,141 |
|
100 |
0,845 |
1,219 |
0,858 |
1,195 |
0,878 |
1,161 |
0,897 |
1,133 |
|
120 |
0,887 |
1,150 |
0,897 |
1,130 |
0,912 |
1,110 |
0,925 |
1,106 |
Значения F-критерия Фишера при 5 %-ном уровне значимости
|
K2 |
Значения F при K1, равном |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
12 |
24 |
∞ |
|
|
1 |
161,4 |
199,5 |
215,7 |
224,6 |
230,2 |
234,0 |
244,9 |
249,0 |
254,3 |
|
2 |
18,5 |
19,2 |
19,2 |
19,3 |
19,3 |
19,3 |
19,4 |
19,4 |
19,5 |
|
3 |
10,1 |
9,6 |
9,3 |
9,1 |
9,0 |
8,9 |
8,7 |
8,6 |
8,5 |
|
4 |
7,7 |
6,9 |
6,6 |
6,4 |
6,3 |
6,2 |
5,9 |
5,8 |
5,6 |
|
5 |
6,6 |
5,8 |
5,4 |
5,2 |
5,1 |
5,0 |
4,7 |
4,5 |
4,4 |
|
6 |
6,0 |
5,1 |
4,8 |
4,5 |
4,4 |
4,3 |
4,0 |
3,8 |
3,7 |
|
7 |
5,5 |
4,7 |
4,4 |
4,1 |
4,0 |
3,9 |
3,6 |
3,4 |
3,2 |
|
8 |
5,3 |
4,5 |
4,1 |
3,8 |
3,7 |
3,6 |
3,3 |
3,1 |
2,9 |
|
9 |
5,1 |
4,3 |
3,9 |
3,6 |
3,5 |
3,4 |
3,1 |
2,9 |
2,7 |
|
10 |
5,0 |
4,1 |
3,7 |
3,5 |
3,3 |
3,2 |
2,9 |
2,7 |
2,5 |
|
11 |
4,8 |
4,0 |
3,6 |
3,4 |
3,2 |
3,1 |
2,8 |
2,6 |
2.4 |
|
12 |
4,8 |
3,9 |
3,5 |
3,3 |
3,1 |
3,0 |
2,7 |
2,5 |
2,3 |
|
13 |
4,7 |
3,8 |
3,4 |
3,2 |
3,0 |
2,9 |
2,6 |
2,4 |
2,2 |
|
14 |
4,6 |
3,7 |
3,3 |
3,1 |
3,0 |
2,9 |
2,5 |
2,3 |
2,1 |
|
15 |
4,5 |
3,7 |
3,3 |
3,1 |
2,9 |
2,8 |
2,5 |
2,3 |
2,1 |
|
16 |
4,5 |
3,6 |
3,2 |
3,0 |
2,9 |
2,7 |
2,4 |
2,2 |
2.0 |
|
17 |
4,5 |
3,6 |
3,2 |
3,0 |
2,8 |
2,7 |
2,4 |
2,2 |
2,0 |
|
18 |
4,4 |
3,6 |
3,2 |
2,9 |
2,8 |
2,7 |
2,3 |
2,1 |
1,9 |
|
19 |
4,4 |
3,5 |
3,1 |
2,9 |
2,7 |
2,6 |
2,3 |
2,1 |
1,9 |
|
20 |
4,4 |
3,5 |
3,1 |
2,9 |
2,7 |
2,6 |
2,3 |
2,1 |
1,9 |
|
22 |
4,3 |
3,4 |
3,1 |
2,8 |
2,7 |
2,6 |
2,2 |
2,0 |
1,8 |
|
24 |
4,3 |
3.4 |
3,0 |
2,8 |
2,6 |
2,5 |
2,2 |
2,0 |
1,7 |
|
26 |
4,2 |
3,4 |
3,0 |
2,7 |
2,6 |
2,5 |
2,2 |
2,0 |
1,7 |
|
28 |
4,2 |
3,3 |
3,0 |
2,7 |
2,6 |
2,4 |
2,1 |
1,9 |
1,7 |
|
30 |
4,2 |
3,3 |
2,9 |
2,7 |
2,5 |
2,4 |
2,1 |
1,9 |
1,6 |
|
40 |
4,1 |
3,2 |
2,9 |
2,6 |
2,5 |
2,3 |
2,0 |
1,8 |
1,5 |
|
60 |
4,0 |
3,2 |
2,8 |
2,5 |
2,4 |
2,3 |
1,9 |
1,7 |
1,4 |
|
120 |
3,9 |
3,1 |
2,7 |
2,5 |
2,3 |
2,2 |
1,8 |
1,6 |
1,3 |
|
∞ |
3,8 |
3,0 |
2,6 |
2,4 |
2,2 |
2,1 |
1,8 |
1,5 |
1,0 |
Значения F-критерия Фишера при 1 %-ном уровне значимости
|
K2 |
Значения F при K1, равном |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
12 |
24 |
∞ |
|
|
1 |
4052,0 |
4999,0 |
5625,0 |
5764,0 |
5889,0 |
5928,0 |
6106,0 |
6234,0 |
6366,0 |
|
2 |
98,5 |
99,0 |
99,2 |
99,3 |
99,3 |
99,4 |
99,5 |
99,5 |
99,5 |
|
3 |
34,1 |
30,8 |
29,5 |
28,7 |
28,2 |
27,9 |
27,1 |
26,6 |
26,1 |
|
4 |
21,2 |
18,0 |
16,6 |
16,0 |
15,5 |
15,2 |
14,4 |
13,9 |
13,5 |
|
5 |
16,3 |
13,3 |
12,1 |
11,4 |
11,0 |
10,7 |
9,9 |
9,5 |
9,0 |
|
6 |
13,7 |
10,9 |
9,8 |
9,2 |
8,8 |
8,5 |
7,7 |
7,3 |
6,9 |
|
7 |
12,3 |
9,6 |
8,5 |
7,9 |
7,5 |
7,2 |
6,5 |
6,1 |
5,7 |
|
8 |
11,3 |
8,7 |
7,6 |
7,1 |
6,6 |
6,4 |
5,7 |
5,3 |
4,9 |
|
9 |
10,6 |
8,0 |
9,0 |
6,4 |
6,1 |
5,8 |
5,1 |
4,7 |
4,3 |
|
10 |
10,0 |
7,6 |
6,6 |
6,0 |
5,6 |
5,4 |
4,7 |
4,3 |
3,9 |
|
11 |
9,9 |
7,2 |
6,2 |
5,9 |
5,3 |
5,1 |
4,4 |
4,0 |
3,6 |
|
12 |
9,3 |
6,9 |
6,0 |
5,4 |
5,1 |
4,8 |
4,2 |
3,8 |
3,4 |
|
13 |
9,1 |
6,7 |
5,7 |
5,2 |
4,9 |
4,6 |
4,0 |
3,6 |
3,2 |
|
14 |
8,9 |
6,5 |
5,6 |
5,1 |
4,7 |
4,5 |
3,8 |
3,4 |
3,0 |
|
15 |
8,7 |
6,4 |
5,4 |
4,9 |
4,6 |
4,3 |
3,7 |
3,3 |
2,9 |
|
16 |
8,6 |
6,3 |
5,3 |
4,8 |
4,4 |
4,2 |
3,6 |
3,2 |
2,8 |
|
17 |
8,4 |
6,1 |
5,2 |
4,7 |
4,3 |
4,1 |
3,5 |
3,1 |
2,7 |
|
16 |
8,2 |
6,0 |
5,1 |
4,6 |
4,3 |
4,0 |
3.4 |
3,0 |
2,6 |
|
20 |
8,1 |
5,9 |
4,9 |
4,4 |
4,1 |
3,9 |
3,2 |
2,9 |
2,4 |
|
22 |
7,9 |
5,7 |
4,8 |
4,3 |
4,0 |
3,8 |
3,1 |
2,8 |
2,3 |
|
24 |
7,8 |
5,6 |
4,7 |
4,2 |
3,9 |
3,7 |
3,0 |
2,7 |
2,2 |
|
26 |
7,7 |
5,5 |
4,6 |
4,1 |
3,8 |
3,6 |
3,0 |
2,6 |
2,1 |
|
28 |
7,6 |
5,5 |
4,6 |
4,1 |
3,8 |
3,5 |
2,9 |
2,5 |
2,1 |
|
30 |
7,6 |
5,4 |
4,5 |
4,0 |
3,7 |
3,5 |
2,8 |
2,5 |
2,0 |
|
40 |
7,3 |
5,2 |
4,3 |
3,8 |
3,5 |
3,3 |
2,7 |
2,3 |
1,8 |
|
60 |
7,1 |
5,0 |
4,1 |
3,7 |
3,3 |
3,1 |
2,6 |
2,1 |
1,6 |
|
120 |
6,8 |
4,8 |
3,9 |
3,5 |
3,2 |
3,0 |
2,3 |
1,9 |
1,4 |
|
∞ |
6,6 |
4,6 |
3,8 |
3,3 |
3,0 |
2,8 |
2,2 |
1,8 |
1,1 |
Значения критерия Кохрена при 5 %-ном уровне значимости
|
Значения критерия Кохрена при К1, равном |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
∞ |
|
|
2 |
0,999 |
0,973 |
0,939 |
0,906 |
0,877 |
0,853 |
0,833 |
0,916 |
0,801 |
0,788 |
0,734 |
0,660 |
0,581 |
0,500 |
|
3 |
0,967 |
0,871 |
0,798 |
0,746 |
0,707 |
0,677 |
0,653 |
0,653 |
0,617 |
0,603 |
0,547 |
0,475 |
0,403 |
0,333 |
|
4 |
0,907 |
0,768 |
0,684 |
0,629 |
0,590 |
0,560 |
0,537 |
0,518 |
0,502 |
0,488 |
0,437 |
0,372 |
0,309 |
0,250 |
|
5 |
0,841 |
0,684 |
0,598 |
0,544 |
0,507 |
0,478 |
0,456 |
0,439 |
0,424 |
0,412 |
0,365 |
0,307 |
0,251 |
0,200 |
|
6 |
0,781 |
0,616 |
0,532 |
0,480 |
0,445 |
0,418 |
0,398 |
0,382 |
0,368 |
0,357 |
0,314 |
0,261 |
0,212 |
0,167 |
|
7 |
0,727 |
0,561 |
0,480 |
0,431 |
0,397 |
0,373 |
0,354 |
0,338 |
0,326 |
0,315 |
0,276 |
0,228 |
0,183 |
0,143 |
|
8 |
0,680 |
0,516 |
0,438 |
0,391 |
0,360 |
0,336 |
0,319 |
0,304 |
0,293 |
0,283 |
0,246 |
0,202 |
0,162 |
0,125 |
|
9 |
0,639 |
0,478 |
0,403 |
0,358 |
0,329 |
0,307 |
0,290 |
0,277 |
0,266 |
0,257 |
0,223 |
0,182 |
0,145 |
0,111 |
|
10 |
0,602 |
0,445 |
0.373 |
0,331 |
0,303 |
0,282 |
0,267 |
0,254 |
0,244 |
0,235 |
0,203 |
0,166 |
0,131 |
0,100 |
|
12 |
0,541 |
0,392 |
0,326 |
0,288 |
0.262 |
0,244 |
0,230 |
0,219 |
0,210 |
0,202 |
0,174 |
0,140 |
0,110 |
0,083 |
|
15 |
0,471 |
0,335 |
0,276 |
0,242 |
0,220 |
0,202 |
0,191 |
0,182 |
0,174 |
0,167 |
0,143 |
0,114 |
0,089 |
0,067 |
|
20 |
0,389 |
0,271 |
0,221 |
0,192 |
0,174 |
0,160 |
0,150 |
0,142 |
0,136 |
0,130 |
0,111 |
0,088 |
0,068 |
0,050 |
|
24 |
0,343 |
0,255 |
0,191 |
0,166 |
0,149 |
0,137 |
0,129 |
0,122 |
0,116 |
0,111 |
0,094 |
0,074 |
0,057 |
0,042 |
|
30 |
0,293 |
0,198 |
0,159 |
0,138 |
0,124 |
0,114 |
0,106 |
0,100 |
0,096 |
0,092 |
0,077 |
0,060 |
0,046 |
0,033 |
Значения критерия Кохрена при 1 %-ном уровне значимости
|
Значения критерия Кохрена при K1, равном |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
∞ |
|
|
2 |
0,999 |
0,995 |
0,979 |
0,959 |
0,937 |
0,917 |
0,899 |
0,882 |
0,867 |
0,854 |
0,795 |
0,707 |
0,606 |
0,500 |
|
3 |
0,993 |
0,942 |
0,883 |
0,834 |
0,793 |
0,761 |
0,734 |
0,711 |
0,691 |
0,674 |
0,606 |
0,515 |
0,423 |
0,333 |
|
4 |
0,968 |
0,864 |
0,781 |
0,721 |
0,676 |
0,641 |
0,613 |
0,590 |
0,570 |
0,554 |
0,488 |
0,406 |
0,325 |
0,250 |
|
5 |
0,928 |
0,789 |
0,696 |
0,633 |
0,588 |
0,553 |
0,526 |
0,504 |
0,485 |
0,470 |
0,409 |
0,335 |
0,264 |
0,200 |
|
6 |
0,883 |
0,722 |
0,626 |
0,564 |
0,520 |
0,487 |
0,461 |
0,440 |
0,423 |
0,408 |
0,353 |
0,286 |
0,223 |
0,167 |
|
7 |
0.838 |
0,664 |
0,596 |
0,508 |
0,466 |
0,435 |
0,411 |
0,391 |
0,375 |
0,362 |
0,311 |
0,249 |
0,193 |
0,143 |
|
8 |
0,795 |
0,615 |
0,520 |
0,463 |
0,423 |
0,393 |
0,370 |
0,352 |
0,337 |
0,325 |
0,278 |
0,221 |
0,170 |
0,125 |
|
9 |
0,754 |
0,573 |
0,481 |
0,425 |
0,387 |
0,359 |
0,338 |
0,320 |
0,307 |
0,295 |
0,251 |
0,199 |
0,152 |
0,111 |
|
10 |
0,718 |
0,536 |
0,447 |
0,393 |
0,357 |
0,331 |
0,311 |
0,295 |
0,281 |
0,270 |
0,230 |
0,181 |
0,138 |
0,100 |
|
12 |
0,653 |
0,475 |
0,392 |
0,333 |
0,310 |
0,286 |
0,268 |
0,254 |
0,242 |
0,232 |
0,196 |
0,154 |
0,116 |
0,083 |
|
15 |
0,575 |
0,407 |
0,332 |
0,288 |
0,259 |
0,239 |
0,223 |
0,210 |
0,200 |
0,192 |
0,161 |
0,125 |
0,093 |
0,067 |
|
20 |
0,480 |
0,330 |
0,265 |
0,229 |
0,205 |
0,188 |
0,175 |
0,165 |
0,157 |
0,150 |
0,125 |
0,096 |
0,071 |
0,050 |
|
24 |
0,425 |
0,287 |
0,230 |
0,197 |
0,176 |
0,161 |
0,150 |
0,140 |
0,134 |
0,128 |
0,106 |
0,081 |
0,060 |
0,042 |
|
30 |
0,363 |
0,241 |
0,191 |
0,164 |
0,145 |
0,133 |
0,123 |
0,116 |
0,110 |
0,105 |
0,077 |
0,066 |
0,048 |
0,033 |
Значения ![]() в
зависимости от доверительной вероятности b
и числа степеней свободы К
в
зависимости от доверительной вероятности b
и числа степеней свободы К
|
Значения |
||||
|
0,90 |
0,95 |
0,98 |
0,99 |
|
|
2 |
0,211 |
0,103 |
0,040 |
0,020 |
|
3 |
0,584 |
0,352 |
0,185 |
0,115 |
|
4 |
1,064 |
0,711 |
0,429 |
0,297 |
|
5 |
1,610 |
1,145 |
0,752 |
0,554 |
|
6 |
2,204 |
1,635 |
1,134 |
0,872 |
|
7 |
2,883 |
2,167 |
1,564 |
1,239 |
|
8 |
3,490 |
2,733 |
2,032 |
1,646 |
|
9 |
4,168 |
3,325 |
2,532 |
2,088 |
|
10 |
4,865 |
3,940 |
3,059 |
2,558 |
|
11 |
5,578 |
4,575 |
3,609 |
3,053 |
|
12 |
6,304 |
5,226 |
4,178 |
3,571 |
|
13 |
7,042 |
5,892 |
4,765 |
4,107 |
|
14 |
7,790 |
6,571 |
5,368 |
4,660 |
|
15 |
8,547 |
7,261 |
5,985 |
5,229 |
|
16 |
9,312 |
7,962 |
6,614 |
5,812 |
|
17 |
10,085 |
8,672 |
7,255 |
6,408 |
|
18 |
10,865 |
9,390 |
7,906 |
7,015 |
|
19 |
11,651 |
10,117 |
8,567 |
7,633 |
|
20 |
12,443 |
10,851 |
9,237 |
8,260 |
|
21 |
13,240 |
11,591 |
9,915 |
8,897 |
|
22 |
14,041 |
12,338 |
10,600 |
9,542 |
|
23 |
14,848 |
13,091 |
11,293 |
10,196 |
|
24 |
14,659 |
13,848 |
11,992 |
10,856 |
|
25 |
16,473 |
14,611 |
12,097 |
11,524 |
|
26 |
17,292 |
15,379 |
12,409 |
12,198 |
|
27 |
18,114 |
16,151 |
14,125 |
12,879 |
|
28 |
18,939 |
16,928 |
14,847 |
13,565 |
|
29 |
19,768 |
17,708 |
15,574 |
14,256 |
|
30 |
20,599 |
18,493 |
16,306 |
14,953 |
4. Рекомендуемое
ПРИМЕР РАСЧЕТА НАПРЯЖЕНИЙ szмакс С УЧЕТОМ ФОРМОИЗМЕНЕНИЙ, ВЫЗВАННЫХ ПЛАСТИЧЕСКИМИ ДЕФОРМАЦИЯМИ
1. Цель испытаний - определение значений действительных контактных напряжений при воздействии факторов, наиболее ответственных за процесс пластического формоизменения рабочих поверхностей.
2. Требования к испытательному оборудованию - по разд. 2 настоящих рекомендаций.
Оборудование - испытательная машина типа МИД, моделирующая схему нагружения без проскальзывания.
3. Условия проведения испытаний соответствуют разд. 3 настоящих рекомендаций.
Частота нагружения - 500 Гц.
Число образцов - по три образца на каждом режиме нагружения.
Смазочный материал - масло «Индустриальное 20».
Способ подвода смазочного материала - фитильный.
4. Отбор образцов - по разд. 5 настоящих рекомендаций.
Образец - шар диаметром 12,66 мм.
Контртело - цилиндрический диск диаметром 150 мм.
Материал образцов и контртел - подшипниковая сталь марки ШХ15.
Твердость образцов и контртел - 57 HRСэ и 63 НRСэ.
Шероховатость поверхности рабочей части образца - Ra £ 0,32 мкм по ГОСТ 2789-73.
5. Независимыми переменными являются следующие факторы: szмакс; N - число циклов нагружения шара, вращающегося между двумя контртелами; твердость шара и цилиндрического диска (контртела).
В качестве зависимых переменных (откликов) приняты максимальное (szмакс)g и среднее (Pср)g напряжения в центре зоны контакта, которые определяют с учетом изменения геометрии рабочих поверхностей в зоне контакта. Уровни факторов и матрица планирования полного факторного эксперимента класса 23 приведены в табл. 1, 2.
|
szмакс МПа |
lgN цикл |
Твердость шара и контртела НRСэ |
|
|
Основной уровень |
5000 |
4 |
60 |
|
Интервал изменения |
1000 |
2 |
3 |
|
Верхний уровень |
6000 |
6 |
63 |
|
Нижний уровень |
4000 |
2 |
57 |
Перевод действительных значений факторов в кодированные переменные производят по формулам
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
|
X0 |
X1 |
Х2 |
X3 |
Х1X2 |
Х1Х3 |
X2X3 |
х1х2X3 |
Зависимые переменные |
||
|
(szмакс)g, МПа (кгс/мм2) |
(Pср)g, (кгс/мм2) |
|||||||||
|
1 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
3322 (338,6) |
2257 (230,1) |
|
2 |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
4267 (435,0) |
3072 (313,1) |
|
3 |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
3037 (309,6) |
2090 (213,0) |
|
4 |
+ |
+ |
+ |
- |
+ |
- |
- |
- |
3720 (379,2) |
2732 (278,5) |
|
5 |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
3865 (343,0) |
2294 (233,8) |
|
6 |
+ |
+ |
- |
+ |
- |
+ |
+ |
- |
5214 (531,5) |
3589 (365,9) |
|
7 |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
3241 (330,4) |
2205 (224,8) |
|
8 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
5147 (524,7) |
3569 (363,8) |
Примечание. Х0 - кодовое обозначение основного уровня зависимой переменной; Х1 - Х3 - кодовые обозначения факторов.
6. На заданных режимах испытаний шарам задаст наработку. После проведения эксперимента жар снимают с испытательной машины и дорожку качения покрывают тонким слоем сажевого покрытия. Далее этот же шар ставят в машину и на нагрузке, при которой проводят эксперимент на дорожке качения шара, получают 6 - 8 отпечатков пятна контакта шара с цилиндрическим диском. Измеряют на микроскопе ширину этих площадок (2у) в различных сечениях (X) и определяют средние значения координат контура пятна контакта.
Для всех режимов испытаний контур пятна отличается от эллиптического.
7. Значения зависимых переменных (szмаск)g (Pср)g оценивают следующим образом. Контур полученных в эксперименте пятен контакта аппроксимируют зависимостью
Дли определения элементов А, В, С, D и К решают систему пяти уравнений с использованием осредненных координат контура.
Площадь пятна контакта вычисляют по формуле
Исходя из полученной площади, действительное значение среднего контактного напряжения вычисляют по формуле
Контур площади контакта (черт. 1 и 2) разбивают на ряд полос, параллельных оси y, и рассматривают их как участки линейного контакта цилиндра с цилиндром. Для данного вида контакта формула для вычисления полуоси имеет вид (см. п. 1.6.6 настоящих рекомендаций)
где g - погонная
нагрузка ![]()
η - см. п. 1.6.4.
Из формулы (7) имеем
Общая нагрузка на контакте

Подставив с в формулу (8), получим
Полагаем эллиптический закон распределения напряжений по оси Y (черт. 1), при этом справедливо соотношение.
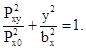
Общая нагрузка на полоске единичной ширины

Половина площади
эллипса с полуосями Рх0 и bx равна ![]()
Приравнивая формулы (9) и (10), имеем
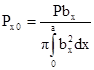
или
Для
эллиптической площадки контакта 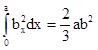 и
и ![]() то есть получаем формулу
Герца, что свидетельствует о достаточной точности расчета. Используя
зависимость (4) и подставляя формулу (11),
окончательно получаем
то есть получаем формулу
Герца, что свидетельствует о достаточной точности расчета. Используя
зависимость (4) и подставляя формулу (11),
окончательно получаем
Расчеты по аппроксимации контура пятна контакта, вычислению площадей и распределению напряжений проведены на ЭЦВМ «Наири-2».
В качестве примера на черт. 1 и 2 приведены распределение напряжений и профиль пятна контакта для четвертого режима нагружения.
Из полученных значений (Рср)g и (szмакс)g (см. табл. 2) следует, что для всех режимов испытаний (szмакс)g < 1,5 (Рср)g.
1 - рассчитанный по формулам теории упругости; 2 - полученный экспериментально
Черт. 1. Профиль пятна контакта для четвертого режима нагружения
Черт. 2. Распределение напряжений на площадке контакта для четвертого режима нагружения
С первого по восьмой режим отличия от точечного контакта, выражающиеся величиной szмаксg/Рсрg, соответственно составляют 1,47; 1,39; 1,45; 1,36; 1,47; 1,45; 1,47; 1,44.
8. Обработку результатов эксперимента, производят следующим образом.
Перед расчетом коэффициентов регрессии полиномиальной модели проводят проверку однородности дисперсий в параллельных опытах. Однородность дисперсий проверяют по критерию Кохрена (см. рекомендуемое приложение 15). Полиномиальная модель, описывающая влияние факторовных взаимодействий на отклик (szмакс)g, имеет вид
|
(szмакс)g = 9,81(396,982 + 68,613X1 - 13,034Х2 + 33,383Х3 - 2,587Х1X2 + 27,097Х1X3 + 8,180Х2Х3 + 4,082Х1X2Х3) |
(13) |
Проверка значимости коэффициентов регрессии выполнена построением доверительного интервала.
Незначимы оказались три коэффициента регрессии (b12, b23; b123).
Окончательно полиномиальная модель запишется в виде
(szмакс)g = 9,81(398,982 + 68,613Х1 - 13,034X2 + 33,383Х3 + 27,097Х1Х3). (14)
Из полученной модели видно, что на процесс формоизменения рабочих поверхностей существенно влияют все факторы, а также одно взаимодействие. В порядке убывания значимости факторы располагаются в такой последовательности: уровень нагружения, твердость материала, число циклов нагружения.
9. Измерения профиля дорожек качения производят следующим образом.
Измерения проведены на профилографе типа «Тэлисерф-4» (фирма «Rank Taylor Hobson», Англия) с записью на электротермическую бумагу (черт. 3). При этом радиус кривизны дорожек качения вычисляют по формуле
R = a2/2h,
где a - половина хорды, стягивающей дугу;
h - глубина отпечатка (стрела прогиба данного участка дуги).
Профилограммы показали, что кривизна дорожек качения непостоянна на различных участках, поэтому радиус вычислялся для 1/3, 2/3 и для всей ширины дорожки качения. Значения радиусов кривизны дорожек качения шара и контртела, соответствующие 2/3 ширины пятна контакта, приведены в табл. 3. Размеры радиусов кривизны для другой плоскости равны R12 = 6,35 мм (шар); R22 = 75,00 мм (контртело).
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Шар R12, мм |
6,933 |
9,625 |
8,820 |
10,10 |
6,933 |
7,628 |
7,888 |
10,100 |
|
Контртело R22, мм |
55,13 |
37,35 |
23,13 |
19,60 |
68,75 |
41,63 |
81,43 |
46,20 |
10. Эксперименты показали, что на рабочих поверхностях, несущих контактные нагрузки, имеют место весьма существенные пластические деформации. Для уточнения расчетов на долговечность и статическую прочность при контактном нагружении кроме упругих деформаций необходимо учитывать также и пластические, так как в результате формоизменения рабочих поверхностей происходит значительное изменение условий контактирования по сравнению с исходными. На всех режимах испытаний рабочие поверхности прирабатываются и контакт шара с цилиндром преобразуется в контакт бочкообразного тела с желобом; при этом уменьшается разница кривизны, площадка контакта имеет большие отличия от эллипса и увеличивается по площади, распределение давлений становится промежуточным между точечным и линейным контактом, уменьшается уровень максимальных и средних контактных напряжений.
а - профилограмма дорожек качения для второго режима; б - профилограмма дорожек качения для четвертого режима; 1 - желоб; 2 - бочкообразное тело (шар после испытания); 3 - шар до испытания
Черт. 3. Профилограмма дорожек качения
5. Рекомендуемое
ПРИМЕР РАСЧЕТА НАПРЯЖЕННОГО СОСТОЯНИЯ В ЗОНЕ КОНТАКТА И АНАЛИТИЧЕСКОГО ОПИСАНИЯ ЛЕВОЙ ВЕТВИ КРИВОЙ КОНТАКТНОЙ УСТАЛОСТИ ДЛЯ СХЕМЫ КАЧЕНИЯ С ВНЕШНЕЙ КАСАТЕЛЬНОЙ НАГРУЗКОЙ
1. Требования к испытательному оборудованию - по разд. 2 настоящих рекомендаций.
Оборудование - испытательная машина МКВ-КМ, моделирующая схему нагружения качения с внешней касательной нагрузкой (см. рекомендуемое приложение 6).
2. Условия испытаний - по разд. 3 рекомендаций. Частота нагружения образца - 1000 Гц.
Смазочный материал образца и контртел - масло «Индустриальное-20». На каждом режиме испытаний исследовали 18 образцов. Испытания проводились на ограниченной базе. Значения баз испытаний определяли по п. 3.11 рекомендаций. Режимы испытаний образцов приведены и табл. 1. В качестве расчетного напряжения в зоне контакта принято эквивалентное напряжение (см. п. 1.7.6 рекомендаций). Критерием разрушения служило наличие на контактной поверхности единичного выкрашивания диаметром, повышающим 50 % малой полуоси пятна контакта (см. п. 3.16 настоящих Р). Момент разрушения фиксировался электронным автоматическим выпрямителем.
3. Отбор образцов и контртел - по разд. 4 рекомендаций. Образец (рабочая часть) - сфера диаметром 6 мм. Контртело - цилиндрический диск диаметром 150 мм.
Твердость образцов и контртел - 62 НRСэ.
Шероховатость поверхности рабочей части образца - Ra £ 0,32 мкм по ГОСТ 2789-73.
4. Расчет максимальных нормальных напряжений в зоне контакта проведен по разд. 1 настоящих Р и рекомендуемому приложению 2.
Для контакта сферы с цилиндром (при Е1 = Е2 = 21,08 ∙ 104 МПа = 2,15 ∙ 104 кгс/мм2 и μ1 = μ2 = 0,3) формулы для расчета напряжения szмакс имеют вид (см. рекомендуемое приложение 2)
|
Р, Н (кгс) |
Т, Н (кгс) |
szмакс, МПа (кгс/мм2) |
s1 = sy, МПа (кгс/мм2) |
s3 = sx, МПа (кгс/мм2) |
sэкв, МПа (кгс/мм2) |
|
|
1 |
396,2 (40,40) |
0,0 (0,00) |
4905,0 (500,00) |
650,4 (66,30) |
-650,4 (-66,30) |
821,1 (82,70) |
|
2 |
396,2 (40,40) |
14,7 (1,50) |
4905,0 (500,00) |
945,1 (96,34) |
-569,0 (-58,00) |
1037,3 (105,74) |
|
3 |
396,2 (40,40) |
19,6 (2,00) |
4905,0 (500,00) |
1043,3 (106,35) |
-541,8 (-55,23) |
1120,0 (114,17) |
|
4 |
396,2 (40,40) |
38,1 (3,88) |
4905,0 (500,00) |
1412,6 (144,00) |
-439,7 (-44,82) |
1417,3 (144,48) |
|
5 |
527,9 (53,81) |
27,5 (2,80) |
5395,5 (550,00) |
1169,7 (119,24) |
-589,9 (-60,13) |
1250,0 (127,42) |
|
6 |
871,1 (88,80) |
21,6 (2,20) |
6376,5 (650,00) |
1111,0 (113,25) |
-774,9 (-78,99) |
1258,3 (128,27) |
|
7 |
871,1 (88,60) |
38,1 (3,88) |
6376,5 (650,00) |
1296,3 (132,14) |
-720,9 (-73,49) |
1407,9 (143,52) |
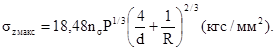 (2)
(2)
5. Расчет напряжений с учетом касательных нагрузок проведен по разд. 1 для наиболее напряженной точки, лежащей на конце малой полуоси площадки контакта.
Для
эллиптической площадки контакта по формулам п. 1.7.3 данных рекомендаций
вычисляем относительные напряжения ![]() и
и ![]() .
.
В окончательном
виде формулы для расчета ![]() и
и ![]() имеют вид
имеют вид
![]() = 0,1326 + 0,4473
= 0,1326 + 0,4473 ![]() (3)
(3)
![]() = 0,1326 +
1,6180
= 0,1326 +
1,6180 ![]() (4)
(4)
По п. 1.7.4 настоящих Р определяем напряжения sх и sy
sx = (-0,1326 +
0,4473![]() )szмакс; (5)
)szмакс; (5)
sy = (0,1326 +
1,6180![]() )szмакс. (6)
)szмакс. (6)
Для двухосного напряженного состояния имеем
s1 = sy; s2 = 0; s3 = sх.
По п. 1.7.6 рекомендаций определяем значения эквивалентных напряжений sэкв. При расчете эквивалентных напряжений значения коэффициента χ и параметра А определяли по результатам испытаний образцов на растяжение, сжатие и кручение. Образцы изготовлены из стали марки ШХ15 и термообработаны по стандартному режиму твердости (61 ÷ 62)HRCэ. Значения временных сопротивлений материала при растяжении и сжатии составляли
sвр = 1903 МПа (194 кгс/мм2); sвс = 2943 МПа (300 кгс/мм2).
Значение χ равнялось 0,65.
Значения предела прочности материала при кручении tпч = 2256 МПа (230 кгс/мм2), а значение А = 0,431.
Значение напряжений szмакс; s1 = sy; s3 = sх; sэкв для каждого режима испытаний приведены в табл. 1.
6. Результаты испытаний образцов на
контактную усталость подвергали статистической оценке. По разд. 6 рекомендаций для каждого режима
испытаний оценивали параметры функций распределения контактно-усталостных
ресурсов (![]() и SlgN). Параметры
функций распределения и графики функции приведены в табл. 2 и на черт. 1.
и SlgN). Параметры
функций распределения и графики функции приведены в табл. 2 и на черт. 1.
|
|
N ∙ 10-6 (цикл) |
SlgN |
S2lgN |
|
|
1 |
8,5185 |
329,98 |
0,334 |
0,112 |
|
2 |
7,6745 |
47,26 |
0,286 |
0,082 |
|
3 |
7,4576 |
28,68 |
0,258 |
0,067 |
|
4 |
6,4546 |
2,85 |
0,158 |
0,025 |
|
5 |
6,9559 |
9,04 |
0,247 |
0,061 |
|
6 |
7,0914 |
12,34 |
0,228 |
0,052 |
|
7 |
6,6567 |
4,54 |
0,184 |
0,034 |
7. Аналитическое описание левой ветви кривой контактной усталости методом регрессивного анализа.
7.1. По рекомендуемому приложению 15 проверяем однородность дисперсий в заданных режимах испытаний. Проверку однородности дисперсий проводили по критерию Кохрена
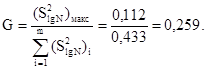
Задаваясь уровнем значимости a = 0,05 при числах степеней свободы К1 = n - 1 = 18 - 1 = 17 и К2 = m = 7), по табл. 11 справочного приложения 3 определяем G0,05 = 0,274. G < G0,05 - гипотеза об однородности дисперсий принимается.
7.2. По п. 5 рекомендуемого приложения 12 методом наименьших квадратов оцениваем параметры уравнения эмпирической линии регрессии. Последовательность вычисления параметров приведена в табл. 3.
При расчете параметров уравнения принимаем w = 1, так как дисперсии однородны.

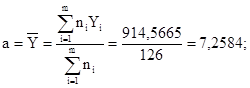
1 - sэкв = 811,29 МПа (82,70 кгс/мм2); 2 - sэкв = 1037,31 МПа (105,74 кгс/мм2); 3 - sэкв = 1120 МПа (714,17 кгс/мм2); 4 - sэкв = 1417,35 МПа (114,48 кгс/мм2); 5 - sэкв = 1250 МПа (127,42к/мм2); 6 - sэкв = 1258,33 МПа (128,27 кгс/мм2); 7 - sэкв = 1407,93 МПа (143,52 кгс/мм2)
Черт. 1. Графики функций распределения контактно-усталостного ресурса
|
|
ni |
|
niXi |
|
|
|
|
|
|
|
1 |
82,70 |
18 |
8,5185 |
1488,5959 |
153,3330 |
-5857,3207 |
223749,6542 |
0,0517 |
1,7043 |
|
2 |
105,74 |
18 |
7,6745 |
1903,3199 |
138,1410 |
-2094,2176 |
31748,3417 |
0,0708 |
1,2515 |
|
3 |
114,17 |
18 |
7,4576 |
2055,0599 |
134,2367 |
-903,4138 |
6079,9765 |
0,0032 |
1,2246 |
|
4 |
144,48 |
18 |
6,4546 |
2600,6399 |
116,1827 |
2739,5903 |
64599,5361 |
0,0629 |
0,4887 |
|
5 |
127,42 |
18 |
6,9559 |
2293,5599 |
125,2061 |
816,3442 |
5322,5632 |
0,1681 |
0,9600 |
|
6 |
128,27 |
18 |
7,0914 |
2308,8599 |
127,6451 |
940,7448 |
6933,2877 |
0,0777 |
0,8270 |
|
7 |
143,52 |
18 |
6,6567 |
2583,3599 |
119,8205 |
2710,3417 |
61307,9243 |
0,2285 |
0,5583 |
![]() = 846,3000;
= 846,3000;
![]() =
126;
=
126; ![]() =
50,8092;
=
50,8092; ![]() = 15233,4000;
= 15233,4000; ![]() = 914,5656;
= 914,5656; ![]() = -1647,9311;
= -1647,9311; ![]() =
399741,2851;
=
399741,2851;
![]() = 0,6629;
= 0,6629; ![]() = 7,0144.
= 7,0144.
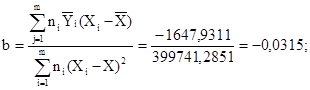
![]() = 7,2564 -
0,0315 (Хi - 120,9000).
= 7,2564 -
0,0315 (Хi - 120,9000).
7.3. По п. 6 рекомендуемого приложения 12 проверяем адекватность уравнения регрессии
![]()
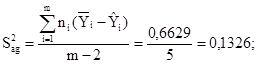

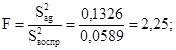
Задаваясь
уравнен значимости a = 0,05, при
числах степеней свободы ![]() и К2 = m - 2 = 7 - 2 = 5
по табл. 9
справочного приложения 3 определяем
F0,05 = 2,30.
и К2 = m - 2 = 7 - 2 = 5
по табл. 9
справочного приложения 3 определяем
F0,05 = 2,30.
F < F0,05 - гипотеза об адекватности уравнения регрессии принимается.
7.4. По п. 6 рекомендуемого приложения 12 объединяем дисперсии в общую оценку
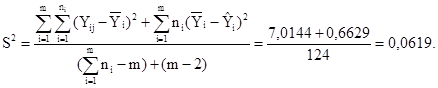
7.5. По п. 7 рекомендуемого приложения 12 проводим оценку дисперсий параметров уравнения эмпирической линии регрессии и величины
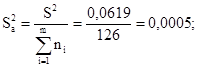
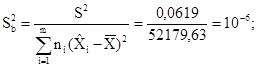
![]()
Для уровня доверительной вероятности b = 0,95 по п. 8 рекомендуемого приложения 12 определяем доверительные интервалы для параметров уравнения теоретической линии регрессии
7,2151 < a < 7,3017
0,0295 < b < 0,0335.
7.6. Кривая контактной усталости с доверительными интервалами для вероятности разрушения Р = 50 % приведена на черт. 2.
Черт. 2. Кривая контактной усталости
6. Рекомендуемое
ОПИСАНИЕ ИСПЫТАТЕЛЬНОЙ МАШИНЫ МКВ-КМ
1. Испытательная машина МКВ-КМ отвечает требованиям, изложенным в разделе 2 настоящих рекомендаций.
2. Испытательная машина МКВ-КМ моделирует
схемы качения без проскальзывания и качения с внешней касательной нагрузкой.
Кинематическая схема испытательной машины приведены на чертеже. Испытания
проводят путам обкатки образца между двумя контртелами по принципу фрикционной
передачи с двухцикличным нагружением за один оборот образца. Вращение ведущего
контртела, испытуемого образца, ведомого контртела осуществляется от
электродвигателя переменного тока через клиноременную передачу. Нормальная
нагрузка Р задается при помощи пружинного механизма. Касательная нагрузка Т в
зоне контакта образца задается торможением ведомого контртела от
электродвигателя постоянного тока с параллельным возбуждением, работающего в
режиме динамического торможения. Задание различных значений тормозных моментов ![]() достигается
изменением тока в обмотке возбуждения.
достигается
изменением тока в обмотке возбуждения.
Передача тормозного момента от электродвигателя постоянного тока к валу ведомого контртела осуществляется через упругую втулочно-пальцевую муфту. Устройство, измеряющее тормозной момент, встроено между валом ведомого контртела и электродвигателем постоянного тока и включает в себя полую балочку с двумя наклеенными под углом 45° фольговыми тензодатчиками и токосъемник с ртутным контактом. При передаче тормозного момента тензометрическая балочка деформируется и от тензодатчиков выдается электрический сигнал, пропорциональный внешней касательной нагрузке.
Электрический сигнал при установке соответствующего уровня касательной нагрузки Т регистрируется универсальным измерительным устройством.
Испытательная машина МКВ-КМ оснащена:
электронным автоматическим выключателем, фиксирующим момент выкрашивания на рабочей поверхности образца (см. приложение 9); фитильной системой смазки образца и контртел;
счетчиком числа циклов нагружения;
приспособлением для проверки точности установки образца и контртел;
приспособлениями для проверки точности нагружения образца нормальной Р и касательной нагрузкой Т.
3. Технические данные:
максимальная нормальная нагрузка Р - 2 кН (≈ 200 кгс);
максимальная касательная нагрузка Т - 50 Н (≈ 5 кгс);
мощность электродвигателя (кВт):
переменного тока - 0,50;
постоянного тока - 0,50;
частота вращения электродвигателя (мин-1):
переменного тока - 1410;
постоянного тока - 1410;
габаритные размеры (мм):
длина - 900;
ширина - 490;
высота - 1050.
1 - ведущее контртело; 2 - образец; 3 - ведомое контртело; 4 - пружинный механизм; 5 - тензометрическая балочка; 6 - токосъемник; 7 - упругая втулочно-пальцевая муфта; 8 - электродвигатель постоянного тока; 9 - клиноременная передача; 10 - электродвигатель переменного тока
Кинематическая схема
7. Рекомендуемое
ОПИСАНИЕ ИСПЫТАТЕЛЬНОЙ МАШИНЫ МКВ-ТМ
1 Испытательная машина МКВ-ТМ изготовлена на базе машины МКВ-КМ и отвечает требованиям, изложенным в разд. 2 настоящих рекомендаций.
Испытательная машина МКВ-ТМ моделирует схемы качения без проскальзывания и качения с внешней касательной нагрузкой при повышенной температуре. Кинематическая схема машины приведена на чертеже. Испытания проводят путем обкатки образца 4 между двумя «горячими» контртелами 3 и 6, температура которых контролируется датчиками температуры 1. Нагрев контртел 3 и 6 осуществляется с помощью нагревателей 2, установленных в кольцевые проточки вращающихся ступиц 8 неподвижно и с зазором относительно последних. Для охлаждения подшипников вала, на котором закреплена ступица 8 контртела, на валу установлен вентилятор 7.
Контртела изготовлены из сталей ЭИ347Ш, Р9, Р18, термообработанных на вторичную твердость и обеспечивающих проведение испытаний при температурах до 673 К. Подача смазки в зону контакта осуществляется через капельницу 5.
Технические данные:
Пределы изменения рабочих температур, К 293 - 673
Мощность нагревателей, кВт 2´1
Напряжение, В 220
1 - датчики температуры; 2 - нагреватели; 3 - ведущее контртело; 4 - образец; 5 - капельница; 6 - ведомое контртело; 7 - вентилятор; 8 - ступица контртела
Кинематическая схема
8. Рекомендуемое
МЕТОДИКА ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ ПРЕДЕЛЬНОГО СРЕДНЕГО КОНТАКТНОГО НАПРЯЖЕНИЯ
1. Предельное среднее контактное напряжение q* - равномерно распределенное на поверхности пятна контакта напряжение, соответствующее началу пластического течения металла. Экспериментально его определяют методом вдавливания шара в плоскую плиту с последующим построением графика зависимости диаметра отпечатка (d = 2a) от среднего контактного напряжения q, которое вычисляют по формуле
где Р - нормальная нагрузка, Н (кгс), (см. приложение 1);
aэ - размер полуоси площадки контакта, определяемый экспериментально.
Экспериментальная зависимость диаметра отпечатка от среднего контактного напряжения является ломаной линией, состоящей из двух участков (см. чертеж). Первый участок соответствует или только упругим, или упругим и микропластическим деформациям. При отсутствии погрешностей измерений участок практически совпадает с теоретической зависимостью, представляющей прямую линию. Второй линейный участок соответствует макропластическим деформациям. Угловые коэффициенты обоих участков существенно различаются, точка перегиба соответствует предельному контактному напряжению q*.
Определение ориентировочного szмакс при испытании образцов на верхнем уровне кривой контактной усталости для схем нагружения, предусмотренных п. 1.1 настоящих Р, производят по формулам:
szмакс = 2,57 ∙ q* - при качении без проскальзывания, пульсирующем контакте и наличии смазки;
szмакс = 2,24 ∙ q* - при качении с проскальзыванием, при качении с внешней касательной нагрузкой, при неудовлетворительной смазке;
szмакс = 1,29 · q* - при качении с проскальзыванием, при отсутствии смазки и локальном схватывании контактирующих поверхностей.
2. Методика экспериментального определения предельного среднего контактного напряжения распространяется на конструкционные материалы, работающие при контактном нагружении, поведение которых при нормальной температуре описывается моделями идеально упругого и идеально жесткопластического тел.
2.1. Методы отбора образцов.
Плоскую плиту изготавливают из металла той же марки, плавки и по идентичному технологическому процессу, что и образцы для испытаний на контактную усталость. Толщина плиты должна быть не менее 6,0 ∙ d. Рекомендуемая величина площади плиты - 2000 мм2. Шероховатость поверхности плиты Ra £ 0,32 мкм.
Твердость материала шара должна превышать твердость плиты не менее чем на 5 единиц по шкале НRСэ. Рекомендуемый диаметр шара D = 10 - 20 мм. Шероховатость поверхности шара Ra £ 0,04 мкм.
2.2. Оборудование.
При вдавливании шара в плиту используют машины всех систем, отвечающие ГОСТ 7855-84, а также специально изготовленные машины. Периодичность проверки испытательного оборудования проводят в соответствии с ГОСТ 8.043-72. Нагружаемое устройство должно обеспечивать:
плавное возрастание нагрузки до заданного значения;
постоянство приложенной нагрузки в течение установленного времени;
относительную погрешность нагрузки на образец не более ± 1 %.
Испытуемая плита должна лежать на основании испытательной машины устойчиво, чтобы не могло произойти ее прогиба или смещения во время нагружения.
2.3. Испытания.
Расстояние от центра отпечатка до края плиты должно быть не менее 3,0 ∙ d, а интервал между центрами двух соседних отпечатков не менее 6,0 ∙ d. Перед испытаниями рекомендуется наносить на исследуемую поверхность плиты сажевое или гальваническое покрытие толщиной до 2 мкм.
Диаметр отпечатков измеряют на инструментальном микроскопе или профилографе. Погрешность измерения диаметра отпечатка не более ± 0,02 мм.
В плиту вдавливают шар и выдерживают под нагрузкой 5 - 10 с. Испытания рекомендуется проводить при 10 - 12 значениях среднего контактного напряжения q, равного (0,03 - 0,12) НКСэ (ГПа), где HRСэ - твердость исследуемой поверхности плиты. После снятия нагрузки измеряют диаметр отпечатка, оставшегося на поверхности плиты. Диаметр отпечатка измеряют в двух взаимно-перпендикулярных направлениях и определяют как среднее арифметическое из двух измерений.
2.4. Пример экспериментального определения предельного среднего контактного напряжения.
Материал плоской плиты - сталь ШХ15.
Модуль упругости стали Ес = 21,5 ∙ 104 МПа.
Коэффициент Пуассона стали μс = 0,3.
Твердость плиты 40 НRСэ.
Шероховатость поверхности Ra £ 0,32 мкм.
Вид покрытия - гальваническое меднение толщиной 1,5 мкм.
Материал шара - твердый сплав 307.
Модуль упругости ЕТС = 38,0 ∙ 104 МПа.
Коэффициент Пуассона μТС = 0,23.
Твердость 71 НRСэ.
Диаметр D = 15,1 мм.
Экспериментальные и теоретические (герцевские) значения диаметров отпечатков пятен контакта (d = 2a) приведены в табл. 1. Значения q, приведенные в табл. 1, определены по формуле 1 настоящего приложения, а значения d = 2 ∙ a из расчета по Герцу (разд. 1 настоящих Р для случая шар-плоскость). График зависимости, построенный по данным табл. 1, приведен на чертеже. Из него видно, что перегиб, соответствующий предельному контактному напряжению q*, приходится на 3000 МПа.
|
Р, Н |
d = 2 ∙ aэ, мм |
d = 2 ∙ a, мм |
|
|
|
1 |
359,7 |
0,55 |
0,48 |
2000 |
|
2 |
702,5 |
0,64 |
0,60 |
2500 |
|
3 |
1213,9 |
0,72 |
0,72 |
3000 |
|
4 |
1927,6 |
0,97 |
0,84 |
3500 |
|
5 |
2877,4 |
1,12 |
0,96 |
4000 |
|
6 |
4096,9 |
1,34 |
1,08 |
4500 |
|
7 |
5619,9 |
1,57 |
1,20 |
5000 |
|
8 |
7480,0 |
1,80 |
1,32 |
5500 |
|
9 |
9711,1 |
2,01 |
1,44 |
6000 |
|
10 |
12346,8 |
2,23 |
1,56 |
6500 |
3. Для большого числа машиностроительных материалов выбор ориентировочного значения szмакс на верхнем уровне кривой контактной усталости при нормальной температуре рекомендуется проводить также по табл. 2.
Зависимость диаметра отпечатка от среднего контактного напряжения для стали марки ШХ 15
----- теоретическая зависимость
------- экспериментальная зависимость
|
szмакс, МПа (кгс/мм2) |
||
|
От НВ200 до НRCэ30 включ. |
2000 (200) |
1500 (150) |
|
Св. НRCэ30 » НRСэ35 |
3000 (300) |
2000 (200) |
|
» НRCэ35 » НRCэ40 |
3500 (350) |
2300 (230) |
|
» НRCэ40 » НRCэ45 |
4000 (400) |
2600 (260) |
|
» НRCэ45 » НRCэ50 |
4500 (450) |
3000 (300) |
|
» НRCэ50 » НRCэ55 |
5000 (500) |
3300 (330) |
|
» НRCэ55 » НRCэ60 |
5500 (550) |
3600 (360) |
|
» НRCэ60 » НRCэ65 |
6000 (600) |
4000 (400) |
Примечание. Значения szмакс, приведенные в табл. 2, справедливы для круговой и эллиптической площадок контакта. Для контакта по полоске значения szмакс уменьшают на 20 %.
9. Рекомендуемое
ПРИМЕРЫ РАБОЧИХ ЧЕРТЕЖЕЙ ОБРАЗЦОВ ДЛЯ ИСПЫТАНИЙ НА КОНТАКТНУЮ УСТАЛОСТЬ
1. Неуказанные предельные отклонения валов h12.
2. Отверстие центровое А1,6, ГОСТ 14034-74.
3. Механическая обработка с охлаждением.
4. Шлифование без ожогов.
5. Твердость: HRCэ ___________, НВ _____________
6. Острые кромки притупить R0,3.
1. Неуказанные предельные отклонения валов h12.
2. Отверстие центровое А1, ГОСТ 14034-74.
3. Острые кромки притупить R0,3.
4. Механическая обработка с охлаждением.
5. Шлифование без ожогов.
6. Твердость: HRCэ ___________, НВ _____________
1. Неуказанные предельные отклонения валов h12.
2. Острые кромки притупить R0,3.
3. Механическая обработка с охлаждением.
4. Шлифование без ожогов.
5. Твердость: HRCэ ___________, НВ _____________
1. Неуказанные предельные отклонения валов h12.
2. Механическая обработка с охлаждением.
3. Шлифование без ожогов.
- Твердость: HRCэ ___________, НВ _____________
- Острые кромки притупить.

1. Неуказанные предельные отклонения валов h12.
2. Отверстие центровое А1 ГОСТ 14034-74.
3. Острые кромки притупить R0,3.
4. Механическая обработка с охлаждением.
5. Шлифование без ожогов.
6. Твердость: HRCэ ___________, НВ _____________
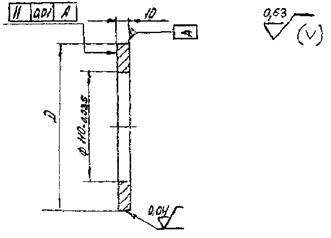
|
D, мм |
|
|
I |
138 |
|
II |
150 |
1. Неуказанные предельные отклонения валов h12.
2. Механическая обработка с охлаждением.
3. Шлифование без ожогов.
4. Твердость: HRCэ ___________, НВ _____________
5. Острые кромки притупить R0,3.
1. Неуказанные предельные отклонения валов h12.
2. Острые кромки притупить R0,3.
3. Механическая обработка с охлаждением.
4. Шлифование без ожогов.
5. Твердость: HRCэ ___________, НВ _____________

1. Шарик II 25,4 мм ГОСТ 3722-81.
2. Механическая обработка охлаждением.
3. Твердость HRCэ _______________
10. Рекомендуемое
ПРОТОКОЛиспытаний образца на контактную усталость (приложение к сводному протоколу № ____________________________) Назначение испытаний: Образец: Шифр _______________ основные размеры __________________________ Машина: тип ______________________, частота _______________________________ Амплитуда напряжений цикла (szмакс), (sэкв), (szмакс)а ___________________________ ___________________________________________________________________________ Среднее напряжение цикла (szмакс)m _________________________________________ Наибольшее напряжение цикла (szмакс), (sэкв)макс, (szмакс)а + (szмакс)m ______________ Наименьшее напряжение цикла (szмакс)а - (szмакс)m _____________________________ Нормальная нагрузка цикла (Р) _____________________________________________ Касательная нагрузка цикла (Т) _____________________________________________ Средняя нормальная нагрузка цикла (Рm)_____________________________________ Амплитудная нормальная нагрузка цикла (Рa) _________________________________ Температура испытаний (Т, К) ______________________________________________ Биение (в мм): образца ____________________, контртела ______________________
Испытания проводил _____________ (подпись) Зав. лабораторией ________________ (подпись) |
||||||||||||||||||
11. Рекомендуемое
СВОДНЫЙ ПРОТОКОЛЦель испытаний __________________________________________________________ ________________________________________________________________________ Материал: марка и состояние ________________________________________________________ направление волокон _____________________________________________________ тип заголовки (при сложной форме прилагается план вырезки образцов) ________________________________________________________________________ Условия испытаний: схема нагружения ________________________________________________________ частота циклов нагружения ________________________________________________ база испытаний___________________________________________________________ коэффициент, учитывающий соотношение между нормальной и касательной нагрузками на контакте (К) ___________________________________________________ Относительная
величина проскальзывания между образцом и контртелом ( Температура испытаний (Т, К) ______________________________________________ Смазка: наименование ________________________ ГОСТ или ТУ _______________________ способ подвода ___________________________________________________________ температура _____________________________________________________________ Форма и основные размеры: образцов ________________________________________________________________ контртел ________________________________________________________________ Состояние поверхности: образцов ________________________________________________________________ контртел ________________________________________________________________ Твердость по шкалам Бринелля или Роквелла образцов ________________________________________________________________ контртел ________________________________________________________________ Испытательная машина Тип _______________________________, № _______________________________
Испытания проводил _____________ (подпись) Зав. лабораторией ________________ (подпись) |
12. Рекомендуемое
АНАЛИТИЧЕСКОЕ ОПИСАНИЕ ЛЕВОЙ ВЕТВИ КРИВОЙ КОНТАКТНОЙ УСТАЛОСТИ МЕТОДОМ РЕГРЕССИОННОГО АНАЛИЗА
1. Метод регрессионного анализа позволяет получить:
параметры уравнения левой ветви кривой контактной усталости, соответствующие вероятности разрушения Р = 50 %, при ограниченном объеме партии образцов для испытаний;
параметры уравнений левых ветвей кривых контактной усталости с доверительными интервалами для различных уровней разрушения, при испытаниях в статистическом аспекте.
При регрессионном анализе за независимую величину принимают х = f1(sнаиб), зависимой величиной является y = f2(N).
Вид функции х = f1(sнаиб) выбирают из условия линейности зависимости у = f(х). Условию линейности обычно удовлетворяют экспоненциальное и степенное уравнения кривой контактной усталости. При этом функция х = f1(sнаиб) выражается как х = sнаиб, или z = lgsнаиб.
2. В основе регрессионного анализа лежат следующие постулаты:
при каждом значении х = sнаиб или х = lgsнаиб величина y = lgN распределена нормально;
среднее значение
логарифма чисел циклов ![]() соответствующее данному значению х,
является линейной функцией х.
соответствующее данному значению х,
является линейной функцией х.
При этом уравнение теоретической линии регрессии имеет вид
зависимость дисперсии величины у от уровня напряжения должна быть известна.
Дисперсии на заданных уровнях напряжений могут быть однородны. Дисперсия может быть обратно пропорциональна напряжению:
где ![]() - параметр.
- параметр.
Зависимость w(х) устанавливается на основании опытных данных и может быть представлена в аналитической и графической формах.
Оценкой уравнения теоретической линии регрессии является уравнение эмпирической линии
3. По п. 6.1.3 настоящих Р оцениваем параметры функций распределения контактно-усталостных ресурсов lgN, SlgN для заданных уровней напряжения.
4. По рекомендуемому приложению 15 проверяется однородность дисперсий на заданных уровнях напряжения. При независимости дисперсий от уровня напряжения в формулах (4 - 6; 8 - 13) принимается wi = 1.
5. Методом наименьших квадратов оценивают параметры уравнения эмпирической линии регрессии
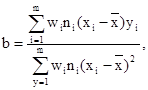 (6)
(6)
где wini - «веса» точек;
m - число уровней напряжений;
ni - число образцов, испытанных на заданном уровне напряжения (i = 1, 2, 3 ..., m);
![]() - см. п. 6.1.3
настоящих рекомендаций,
- см. п. 6.1.3
настоящих рекомендаций,
- Адекватность уравнения регрессии проверяют по F-критерию Фишера:
где ![]() - дисперсия адекватности;
- дисперсия адекватности;
![]() - дисперсия
воспроизводимости;
- дисперсия
воспроизводимости;
ni - число образцов, испытанных на i-ом уровне напряжения;
![]() - значение
логарифма чисел циклов j-го образца, испытанного на i-ом уровне
напряжения;
- значение
логарифма чисел циклов j-го образца, испытанного на i-ом уровне
напряжения;
![]() - значение
логарифма чисел циклов на i-ом режиме нагружения, рассчитанное по
уравнению регрессии.
- значение
логарифма чисел циклов на i-ом режиме нагружения, рассчитанное по
уравнению регрессии.
При проведении
испытаний на ограниченной базе (см. п. 3.11 настоящих Р) при расчете
дисперсии воспроизводимости ![]() значения yij, превышающие
значения ограниченной базы испытаний, определяют экстраполяцией прямых,
аппроксимирующих функции распределения контактно-усталостных ресурсов.
значения yij, превышающие
значения ограниченной базы испытаний, определяют экстраполяцией прямых,
аппроксимирующих функции распределения контактно-усталостных ресурсов.
Если
рассчитанное значение F-критерия не превышает указанного в
табл. 9
приложения 3 для уровня
значимости a (обычно a = 0,05) и чисел степеней свободы
![]() и
К2 = m - 2, то регрессионное уравнение
адекватно. При этом дисперсии объединяют в общую оценку
и
К2 = m - 2, то регрессионное уравнение
адекватно. При этом дисперсии объединяют в общую оценку
7. Оценку дисперсий параметров уравнения
эмпирической линии регрессии
и величины ![]() производят по формулам
производят по формулам
8. Доверительные интервалы для параметров уравнения теоретической линии регрессии и генерального среднего значения вычисляют по формулам
![]() (16)
(16)
где tbk - критерий
Стьюдента, определяемый по табл. 7, приложения 3 для доверительной вероятности
b и числа
степеней свободы ![]()
9. Используя регрессионное уравнение и зависимость дисперсии величины у от уровня напряжения, строят кривые контактной усталости для различных уровней вероятности разрушения. Оценку ресурса при заданных sнаиб и уровне вероятности разрушения производят по формуле
10. Примеры расчета регрессионного уравнения кривой контактной усталости приведены в рекомендуемом приложении 5.
13. Рекомендуемое
ПРОВЕДЕНИЕ ИСПЫТАНИЙ МЕТоДОМ СТУПЕНЧАТОГО ИЗМЕНЕНИЯ НАПРЯЖЕНИЙ
1. Метод ступенчатого увеличения нагрузки
(см. чертеж) применяют для определения среднего значения предела контактной
выносливости ![]() и его среднего квадратического
отклонения
и его среднего квадратического
отклонения ![]() .
.
2. Метод предусматривает испытания образцов до разрушения или базового числа циклов. Число образцов и базы испытаний выбирают по пп. 3.9 и 3.10.
3. Последовательность испытаний образцов приведена на чертеже и заключается в следующем.
Первый образец испытывают на уровне ожидаемого значения предела контактной выносливости;
при разрушении первого образца второй испытывает при более низком значении напряжения, а если образец не разрушится - при более высоком значении;
уровень напряжения для каждого последующего образца понижается, если предыдущий образец разрушается, и повышается - если предыдущий образец не разрушился.
4. Разность между уровнями напряжений составляет 2 % от ожидаемого значения предела контактной выносливости.
5. Составляют таблицу, в которой указывают для каждого значения напряжений число разрушенных и неразрушенных образцов.
|
Напряжение s и i |
Число разрушенных образцов |
Число неразрушенных образцов |
Общее число образцов |
|
|
1 |
(sа)1 |
n'1 |
n''1 |
n'1 + n''1 |
|
2 |
(sа)2 |
n'2 |
n''2 |
n'2 + n''2 |
|
3 |
(sа)3 |
n'3 |
n''3 |
n'3 + n''3 |
|
l |
(sа)l |
n'l |
n''l |
n'l + n''l |
|
|
|
|
|
M' + M'' |
- Среднее значение предела контактной выносливости вычисляют по формуле
где d - разность между уровнями напряжения (см. чертеж);
i - порядковый номер уровня напряжения;
M - общее число разрушений (или неразрушений) образцов:
если М' > М'', то М = М'',
если М' < М'', то М = М'';
ni - число разрушений (или неразрушений) образцов на i-ом уровне:
если n'i > n''i, то ni = n''i;
если n'i < n'' то ni = n'i.
Примечание. Знак «плюс» в формуле (1) принимается в том случае, когда М' > М'', а знак «минус» при М' < М''.
Последовательность испытания образцов методом ступенчатого изменения напряжения
7. Среднее квадратическое отклонение предела контактной выносливости вычисляют по формуле
8. Прямую, аппроксимирующую функцию распределения предела контактной выносливости, выражают уравнением
9. Методика определения доверительных интервалов для математического ожидания, стандартного отклонения, дисперсии, аналогична изложенной в пп. 6.1.6 и 6.1.7 настоящих рекомендаций.
10. Зная параметры функции распределения предела контактной выносливости и доверительные интервалы, строят на нормальной вероятностной бумаге график функции распределения с доверительными интервалами.
14. Рекомендуемое
ПРИМЕР ОЦЕНКИ ПАРАМЕТРОВ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ КОНТАКТНО-УСТАЛОСТНОГО РЕСУРСА НА ЗАДАННОМ УРОВНЕ НАПРЯЖЕНИЙ
1. Оборудование - испытательная машина МКВ-КМ, моделирующая схему нагружения качения без проскальзывания (см. рекомендуемое приложение 6).
2. Условия испытаний - по разд. 3 настоящих рекомендаций.
Частота нагружения образца - 1000 Гц.
Смазочный материал образцов и контртел - масло «Индустриальное 20».
Задаваясь ожидаемым значением SlgN = 0,35, доверительной вероятностью b = 0,90 и относительной погрешностью δ = 20 %, по черт. 8 п. 3.7 данных Р определяют минимальное число образцов n = 35.
Уровень напряжения - 6000 МПа (≈ 600 кгс/мм2).
Испытания проводились на ограниченной базе. Значение базы испытаний Ns = 350 ∙ 106 циклов определялось по п. 3.11 настоящих рекомендаций.
Критерием разрушения служило наличие на контактной поверхности единичного выкрашивания диаметром, превышающим 50 % малой полуоси пятна контакта (см. п. 3.16 настоящих рекомендаций).
Момент разрушения фиксировался электронным автоматическим выключателем (см. рекомендуемое приложение 8).
3. Отбор образцов и контртел - по разд. 4 настоящих рекомендаций.
Образец со сферической рабочей частью диаметром 6 мм.
Контртело - цилиндрический диск диаметром 150 мм.
Материал образцов и контртел - подшипниковая сталь марки ШХ15.
Твердость образцов и контртел - 62 HRСэ.
Шероховатость поверхности рабочей части образца - Ra £ 0,32 мкм по ГОСТ 2789-73.
4. Проведение испытаний - по разд. 5 настоящих рекомендаций.
5. Оценка параметров функции распределения контактно-усталостного ресурса основана на логарифмически нормальном распределении.
Вариационный ряд ресурсов образцов и первичная статистическая обработка приведены в табл. 1.
По п. 6.1.3
настоящих Р, используя данные табл. 1, определяем методом наименьших
квадратов ![]() и
SlgN:
и
SlgN:
![]()
![]()
![]()
Задаваясь доверительной вероятностью b = 0,90, по п. 6.1.6 рекомендаций находим доверительные интервалы для математического ожидания а, стандартного отклонения s и дисперсии s2:
8,1069 < а < 8,2746;
0,243 < s 0,362;
0,059 < s2 < 0,131.
|
Pj |
|
|
Nj∙10-6 |
lgNj |
|
|
|
1 |
0,014 |
-2,197 |
4,827 |
49,30 |
7,6928 |
-16,9011 |
|
2 |
0,043 |
-1,717 |
2,948 |
51,60 |
7,7126 |
-13,2426 |
|
3 |
0,071 |
-1,468 |
2,155 |
55,00 |
7,7403 |
-11,3628 |
|
4 |
0,100 |
-1,282 |
1,644 |
58,70 |
7,7686 |
-9,9593 |
|
5 |
0,129 |
-1,131 |
1,279 |
60,40 |
7,7810 |
-8,8003 |
|
6 |
0,157 |
-1,007 |
1,014 |
63,80 |
7,8048 |
-7,8594 |
|
7 |
0,196 |
-0,893 |
0,805 |
76,60 |
7,8836 |
-7,0716 |
|
8 |
0,214 |
-0,793 |
0,629 |
80,10 |
7,9036 |
-6,2675 |
|
9 |
0,243 |
-0,697 |
0,486 |
89,90 |
7,9537 |
-5,5437 |
|
10 |
0,271 |
-0,610 |
0,372 |
97,70 |
7,9898 |
-4,8738 |
|
11 |
0,300 |
-0,524 |
0,275 |
110,20 |
8,0421 |
-4,2141 |
|
12 |
0,329 |
-0,443 |
0,196 |
117,30 |
8,0692 |
-3,5746 |
|
13 |
0,357 |
-0,367 |
0,135 |
121,40 |
8,0842 |
-2,9669 |
|
14 |
0,386 |
-0,290 |
0,084 |
129,60 |
8,1126 |
-2,3526 |
|
15 |
0,414 |
-0,217 |
0,047 |
141,30 |
8,1501 |
-1,7685 |
|
16 |
0,443 |
-0,143 |
0,020 |
146.80 |
8,1666 |
-1,1678 |
|
17 |
0,471 |
-0,073 |
0,005 |
157,00 |
8,1958 |
-0,5983 |
|
18 |
0,500 |
0,000 |
0,000 |
173,40 |
8,2390 |
0,0000 |
|
19 |
0,529 |
0,073 |
0,005 |
179,40 |
8,2538 |
0,6025 |
|
20 |
0,557 |
0,143 |
0,020 |
180,30 |
8,2559 |
1,1606 |
|
21 |
0,586 |
0,217 |
0,047 |
182,10 |
8,2603 |
1,7924 |
|
22 |
0,614 |
0,290 |
0,084 |
189,70 |
8,2780 |
2,4006 |
|
23 |
0,643 |
0,367 |
0,135 |
202,60 |
8,3066 |
3,0485 |
|
24 |
0,671 |
0,443 |
0,196 |
217,40 |
8,3372 |
3,6934 |
|
25 |
0,700 |
0,524 |
0.275 |
222,50 |
8,3473 |
4,3740 |
|
26 |
0,729 |
0,610 |
0,372 |
241,90 |
8,3836 |
5,1140 |
|
27 |
0,757 |
0,697 |
0,486 |
243,70 |
8,3868 |
5,8456 |
|
28 |
0,786 |
0,793 |
0,629 |
252,10 |
8,4015 |
6,6624 |
|
29 |
0,814 |
0,893 |
0,805 |
274,60 |
8,4387 |
7,5357 |
|
30 |
0,843 |
1,007 |
1,014 |
311,00 |
8,4927 |
8,5522 |
|
31 |
- |
- |
- |
База |
- |
- |
|
32 |
- |
- |
- |
База |
- |
- |
|
34 |
- |
- |
- |
База |
- |
- |
|
35 |
- |
- |
- |
База |
- |
- |
![]()
По п. 6.1.7 рекомендаций определяем значения координат для построения доверительных интервалов функции распределения контактно-усталостного ресурса. Полученные значения координат приведены в табл. 2.
|
Значение ординаты |
Значение абсциссы |
||
|
Рj |
|
||
|
1 |
84,10 |
1,00 |
8,3499 |
|
2 |
50,00 |
0,00 |
8,1069 |
|
3 |
15,90 |
-1,00 |
7,7454 |
|
4 |
84,10 |
1,00 |
8,6461 |
|
5 |
50,00 |
0,00 |
8,2746 |
|
6 |
15,90 |
-1,00 |
8,0317 |
График функции распределения контактно-усталостного ресурса с доверительными интервалами приведен на чертеже.
Функция распределения контактно-усталостного ресурса с доверительными интервалами
15. Рекомендуемое
СТАТИСТИЧЕСКИЙ АНАЛИЗ РЕЗУЛЬТАТОВ СРАВНИТЕЛЬНЫХ ИСПЫТАНИЙ
1. Для проведения статистического анализа необходимо:
по п. 6.1.2 настоящих рекомендаций построить вариационные ряды ресурсов (чисел циклов) для сравнительных партий и произвести первичную статистическую обработку;
по п. 6.1.3 определить параметры эмпирических распределений для каждой сравниваемой партии;
по п. 6.1.4 выявить грубые ошибки при испытании отдельных образцов;
по п. 6.1.5 проверить соответствие распределения, если имеется сомнение в правильности выбора закона распределения.
2. Порядок проверки однородности дисперсий и равенства средних в сравниваемых партиях приведен в табл. 1 и 2.
3. При проведении статистического анализа уровни значимости принимают равными a = 0,05 или a = 0,10, уровни доверительной вероятности b = 0,95 или b = 0,90.
|
Критерий проверки гипотезы |
Число степеней свободы |
Гипотеза принимается, если удовлетворяется неравенство |
Примечание |
|
|
|
|
К1 = n1 - 1 К2 = n2 - 1 |
F < Fa Fa - табл. 9, 10 приложения 3; a - уровень значимости |
Критерий Фишера применим при неодинаковом числе образцов (n1 и n2) в сравниваемых партиях |
|
|
|
К1 = n1 - 1 К2 = m, m - число сравниваемых дисперсий |
Критерий Кохрена применим при одинаковом числе образцов n в сравниваемых партиях |
|
|
|
|
К = m - 1 ni - число образцов в i-й партии |
|
Критерий Бартлета применим при неодинаковом числе образцов в сравниваемых партиях |
|
Критерий проверки гипотезы |
Число степеней свободы |
Гипотеза принимается, если удовлетворяется неравенстве |
Примечание |
|
|
а1 = а2 |
|
К = n1 + n2 - 2 |
t < tbk b - уровень доверительной вероятности |
Критерий применим при |
|
а1 = а2 |
|
|
t < tbk
|
Критерий применим при |
16. Рекомендуемое
АНАЛИЗ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ НА ОСНОВЕ ПОДОБИЯ КОНТАКТНО-УСТАЛОСТНОГО РАЗРУШЕНИЯ
1. Анализ проводят на основе уравнения подобия контактно-усталостного разрушения для вероятности разрушения Р = 50 %:
где sмакс - наибольшее значение первого главного напряжения на поверхности контакта, МПа (кгс/мм2);
А, В - безразмерные коэффициенты уравнения подобия;
![]() - критерий
подобия контактно-усталостного разрушения, мм2.
- критерий
подобия контактно-усталостного разрушения, мм2.
2. Значение величин ![]() и sмакс для материалов
с коэффициентом Пуассона μ = 0,3 вычисляют
по формулам:
и sмакс для материалов
с коэффициентом Пуассона μ = 0,3 вычисляют
по формулам:
при качении для площадки контакта любой формы
где d - диаметр дорожки качения образца (детали), на которой происходит разрушение, мм;
b - размер малой полуоси контактной площадки по полоске или эллиптической площадки контакта, радиус круговой площадки контакта, мм;
при пульсирующей контактной нагрузке для круговой площадки контакта, контакта по полоске длиной l ³ 10 и эллиптической площадки контакта с соотношением полуосей b/a £ 0,2
для эллиптической площадки контакта с соотношением полуосей b/a > 0,4
![]() (4)
(4)
при качении и при пульсирующей контактной нагрузке для круговой и эллиптической площадок контакта с соотношением полуосей b/a > 0,9 и b/a < 0,4
для эллиптической площадки контакта с соотношением полуосей 0,9 > b/a > 0,4
для контакта по полоске длиной l ³ 10b
3. Коэффициент А уравнения (1) одинаков и для контактной усталости и для усталости при изгибе с вращением, поскольку прямые подобия усталости материала при качении и при изгибе с вращением для вероятности разрушения Р = 50 % пересекаются на оси ординат (см. чертеж).
При этом свойства материала и твердость поверхности образцов в обоих видах испытаний одинаковы.
Приближенное значение А вычисляют по формуле
А = lg(1,05s-1),
где s-1 - предел выносливости гладкого образца
диаметром 7,5 мм (![]() = 88,3 мм2,
= 88,3 мм2,
![]() = 1,946) для
вероятности разрушения Р = 50 % и базы испытания Ns, для которой
строится прямая подобия.
= 1,946) для
вероятности разрушения Р = 50 % и базы испытания Ns, для которой
строится прямая подобия.
4. Коэффициент В уравнения подобия определяется тангенсом угла наклона прямой подобия контактно-усталостного разрушения к оси абсцисс. Для конструкционных сталей с твердостью поверхности от 36 НRСэ до 62 HRСэ приближенное значение В находят по эмпирической формуле
где Н - число твердости по Роквеллу (шкала С) материала образца (детали) на поверхности контакта.
6. Оценку масштабного фактора проводят на основе испытания не менее двух партий образцов разного диаметра с определением значения szмакс для вероятности разрушения Р = 50 % и одной и той же базы испытании согласно п. 3.10 и вычислением размеров площадки контакта согласно п. 1.6 настоящих рекомендаций.
По полученным
значениям szмакс и размерам
площадок контакта вычисляют значения ![]() и sмакc и наносят на
график в координатах (lgszмакс,
и sмакc и наносят на
график в координатах (lgszмакс, ![]() ) точки для
каждого размера испытанных образцов. Через полученные точки проводят прямую
линию (см. чертеж).
) точки для
каждого размера испытанных образцов. Через полученные точки проводят прямую
линию (см. чертеж).
6. Для расчетного определения значений ![]() и sмакc площадок
контакта сложной формы проводят их аппроксимацию круговой или эллиптической
площадкой или площадкой контакта по полоске, исходя из условия наименьшего
искажения первоначальной формы и площади поверхности контакта после
аппроксимации.
и sмакc площадок
контакта сложной формы проводят их аппроксимацию круговой или эллиптической
площадкой или площадкой контакта по полоске, исходя из условия наименьшего
искажения первоначальной формы и площади поверхности контакта после
аппроксимации.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНЫ И ВНЕСЕНЫ ВНИИНМАШ Государственного комитета СССР по стандартам
ИСПОЛНИТЕЛИ:
В.М. Нестеров, к.т.н.; Л.В. Пушин; Р.Н. Рыньков, к.т.н.; А.В. Великанов, к.т.н.; Е.А. Шур, к.т.н; Н.Я. Бычкова; А.В. Орлов, к.т.н.; О.Н. Черменский, к.т.н.; И.Н. Спицына; А.И. Вильчек, к.т.н.; Р.В. Суворов, к.т.н.; Б.С. Гутенев, к.т.н.; С.В. Степаненко.
2. УТВЕРЖДЕНЫ Приказом ВНИИНМАШ № 379 от 8.12.1987 г.
СОДЕРЖАНИЕ
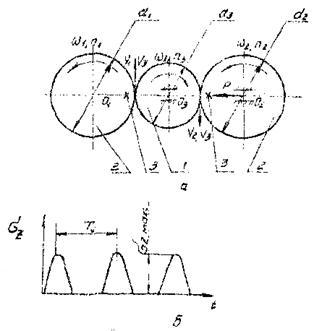
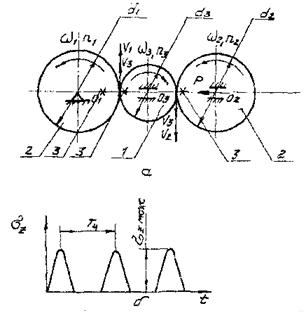
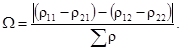 (
(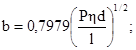 (
(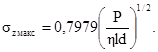 (
(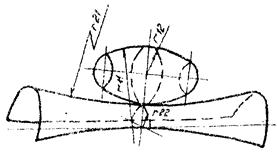
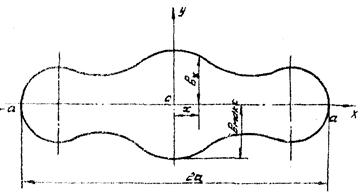
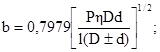 (
(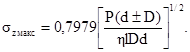 (
(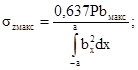 (
(
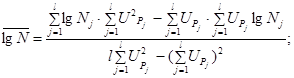 (
(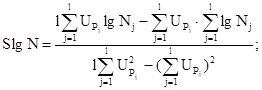 (
(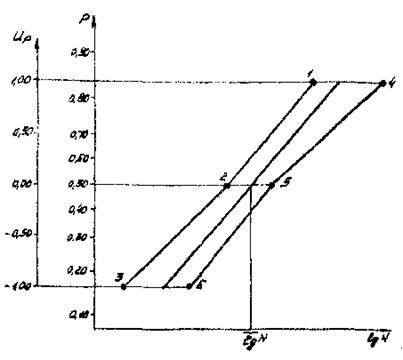
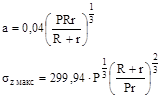
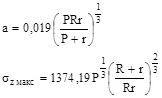

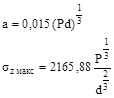
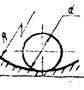
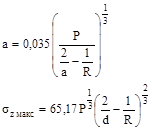
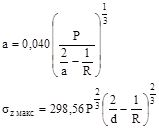
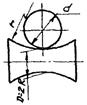

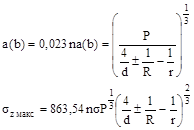
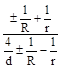
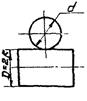
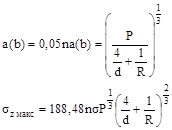

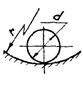
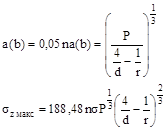

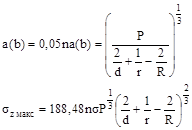
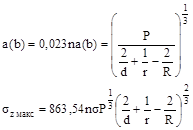
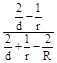
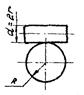
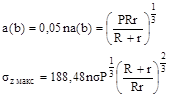
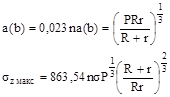
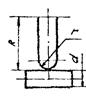
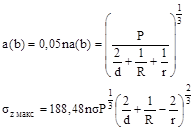

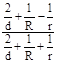
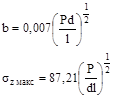
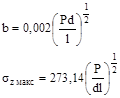
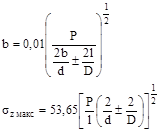
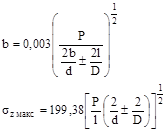
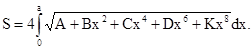 (
(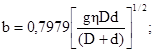 (
(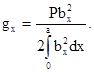 (
(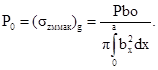 (
(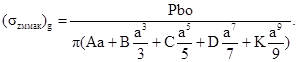 (
(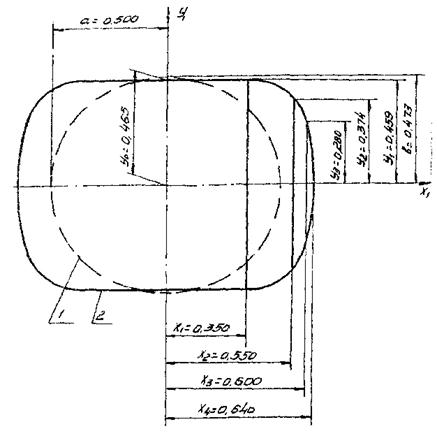
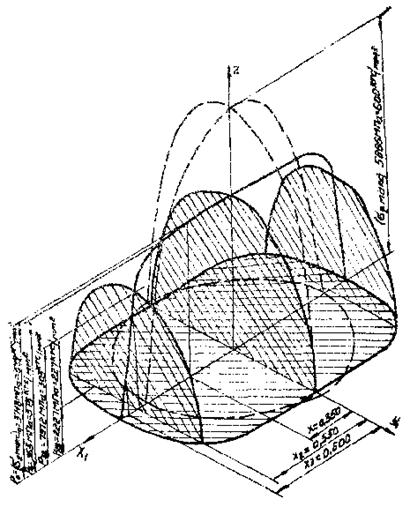
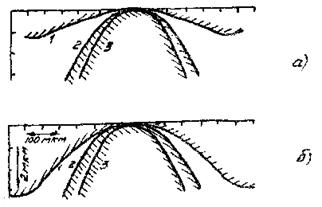
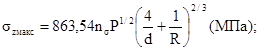 (
(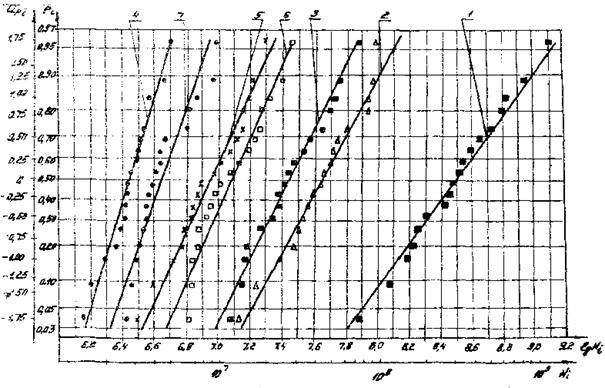
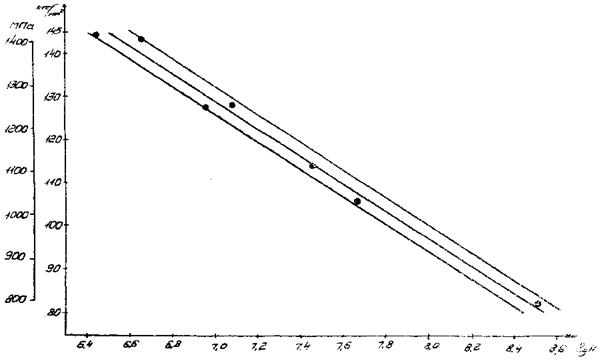
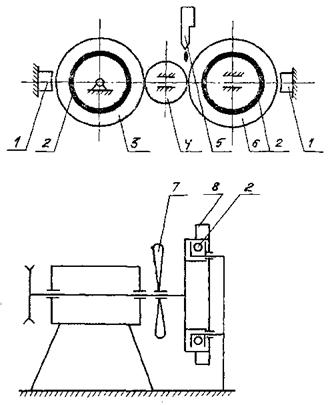
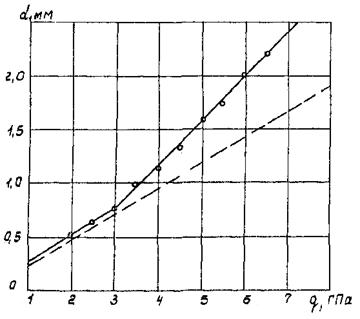
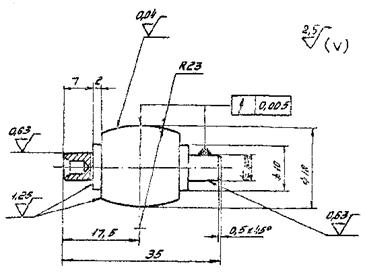



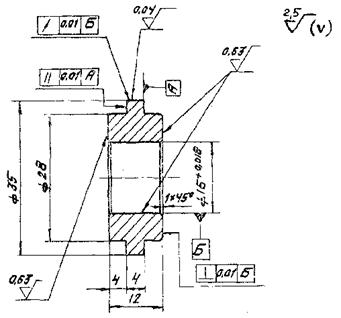
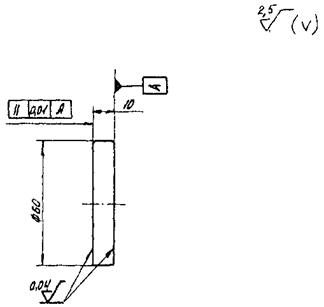
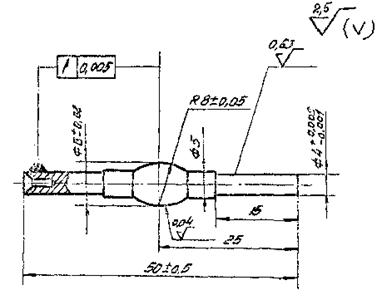


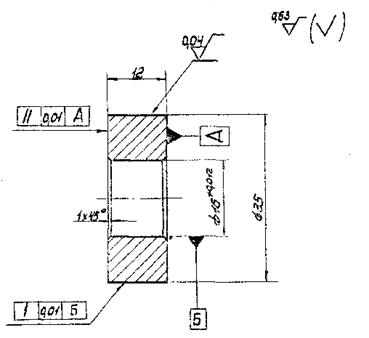


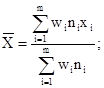 (
(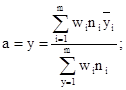 (
(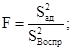 (
(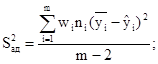 (
(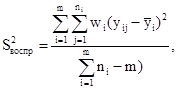 (
(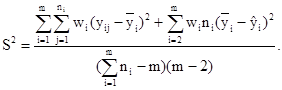 (
(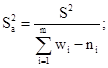 (
(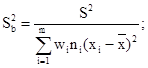 (
(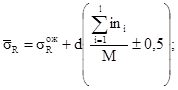 (
(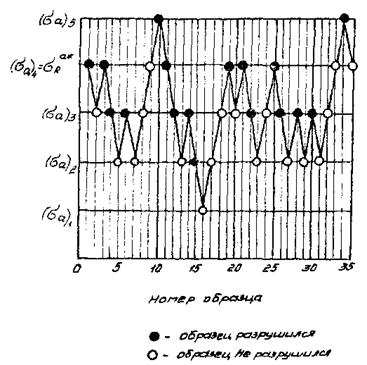
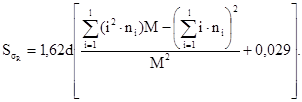 (
(