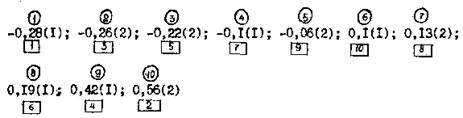ГОСУДАРСТВЕННЫЙ
КОМИТЕТ СССР ПО СТАНДАРТАМ
(Госстандарт СССР)
Всесоюзный научно-исследовательский институт
по нормализации в машиностроении
(ВНИИНМАШ)
Утверждены
Приказом ВНИИНМАШ
№ 274 от 3.9.87.
Расчеты и испытания на прочность
Методы статистического
анализа
полей начальных
несовершенств и полных
прогибов оболочек
Рекомендации
Р 50-54-19-87
Москва 1987
РЕКОМЕНДАЦИИ
|
Р 50-54-19-87 |
Рекомендации направлены на унификацию статистических методов анализа случайных несовершенств и полных прогибов тонких оболочек, склонных к потере устойчивости, выпучиванию и другим видам отказов, при решении детерминированных и стохастических задач устойчивости, динамики и надежности пластин и оболочек. Распространяются на результаты экспериментальных замеров и моделирования геометрических начальных несовершенств и полных прогибов гладких, ребристых, многослойных оболочек нулевой, положительной и отрицательной гауссовой кривизны в условиях эксплуатации.
Рекомендации содержат методы и алгоритмы:
нахождения параметров и построения плотности распределения ординат начальных несовершенств и полных прогибов оболочек как случайных величин;
нахождения оценок их вероятностных характеристик или случайных функций;
предварительной фильтрации результатов экспериментальных замеров полей и выделения неслучайной составляющей, а также методы;
проверки двумерных случайных полей прогибов оболочек на однородность, изотропность, нормальность;
выявления скрытых периодичностей и построения оценок двумерных корреляционных функций и спектральных плотностей;
построения совместной плотности вероятности ординат поля прогибов, его первых и вторых производных.
Предлагаемые в Р методы анализа распространяются на однородные в широком смысле эргодичные случайные функции и поля. Приводятся таблицы, наиболее часто используемые для обработки результатов экспериментальных замеров. Разработанные алгоритмы реализованы в программах расчета для ЕС ЭВМ. Держатель программ - лаборатория надежности ОКПМ ИМет УНЦ АН СССР.
Рекомендации предназначены для работников НИИ, вузов, КБ и заводских лабораторий, занимающихся анализом начальных несовершенств с позиций точности изготовления и процессов выпучивания тонкостенных пространственных элементов машин и конструкций.
1. ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
![]() , D, s, R -
математическое ожидание, дисперсия, стандарт, размах выборки соответственно;
, D, s, R -
математическое ожидание, дисперсия, стандарт, размах выборки соответственно;
V, А, Е - коэффициенты вариации, асимметрии, эксцесса соответственно;
![]() - К-й начальный
момент;
- К-й начальный
момент;
μк - К-й центральный момент;
Xmax, Xmin - максимальное и минимальное значение ординат в выборке;
p(x) - плотность распределения ординат;
T - число заданных эмпирических моментов;
с, d - границы интервала изменения ординат;
n2 - число реализаций замеров ординат;
L - длина реализации;
k - волновое число спектра;
kmax - наибольшее волновое число, содержащееся в спектре;
h - интервал дискретизации;
![]() - значения замеров
ординат случайной функции прогибов оболочки;
- значения замеров
ординат случайной функции прогибов оболочки;
N - объем реализации;
Р - доверительная вероятность;
K(jh) - значение корреляционной функции в точке jh;
![]() - значение
нормированной корреляционной функции;
- значение
нормированной корреляционной функции;
m - число точек, в которых вычисляется корреляционная функция;
S(Kj) - значение спектральной плотности для Кj;
![]() - значение
нормированной спектральной плотности;
- значение
нормированной спектральной плотности;
Sc(Kj) - значение сглаженной спектральной плотности;
![]() - значение
нормированной сглаженной спектральной плотности;
- значение
нормированной сглаженной спектральной плотности;
a, b - размеры оболочки в плане;
![]() - значения замеров
ординат случайного поля прогибов оболочки;
- значения замеров
ординат случайного поля прогибов оболочки;
NX, NY - номера граничных узлов сетки;
S1(nDk1, mDk2) - несмещенная спектральная плотность случайного поля прогибов оболочки;
S(nDk1, mDk2) - несмещенная состоятельная спектральная плотность случайного поля прогибов оболочки;
Р(ξ1, ..., ξn) - совместная плотность вероятности переменных ξ1, ..., ξn;
f(x) - непрерывная случайная функция ординат прогибов оболочки;
f(x, y) - непрерывное случайное поле ординат прогибов оболочки;
θ(V1, ..., Vn) - характеристическая функция n-мерной случайной величины V1, ..., Vn);
ρx, ρy - масштабы корреляция по осям x, y соответственно;
W1, W2 - значения критериев при проверке случайной функции на однородность;
ha, hb - интервалы дискретизации по осям x и y соответственно;
kamax, kbmax - наибольшие волновые числа, содержащиеся, в спектре по осям x и b соответственно;
Ucos(k1, k2), Usin(k1, k2) - периодограммы реализаций случайных полей.
2. ПОСТАНОВКА ЗАДАЧИ
2.1. Общие положения
Главная причина отказов тонкостенных оболочек и пластин - ведущей конструктивной формы - потеря устойчивости. Поэтому критерии недопустимости их предельного состояния формулируются в терминах теории устойчивости, а надежность определяется методами статистической динамики; квазистатическими при наличии информации о несовершенствах и прогибах оболочек как о случайных величинах, корреляционными и методами кинетических уравнений при наличии информации о них как о случайных функциях и полях.
Наибольшее влияние на устойчивость оболочек оказывают начальные геометрические несовершенства формы, формально представляемые в виде случайных величин или разложений в одномерный или двумерный ряд Фурье со случайными коэффициентами. Эти ряды усекаются с учетом предпосылок. Однако реальные поля начальных несовершенств, зависящие, как правило, от конечного числа возмущений, могут иметь прерывистый или узкополосный спектр частот. Отсюда важная практическая задача установления реальной структуры экспериментальных полей начальных несовершенств по результатам их измерений, то есть проведение не формально-математического, а физического анализа.
Случайные несовершенства и прогибы оболочек, пластин и конструкций из них должны рассматривать как случайные величины, функции и поля. Исходная информация о результатах замеров ординат поля прогибов может быть представлена в виде вариационного ряда, последовательности замеров, таблиц, графиков или осциллограмм. Она должна быть репрезентативной и отражать основные закономерности исследуемого поля прогибов. При сборе исходных данных следует стремиться к тому, чтобы выборки (длина реализаций) были одинаковыми. Это упростит обработку информации и обеспечит одинаковую достоверность вычисленных статистических характеристик.
Ниже приводятся постановки задач, возникающих при анализе результатов экспериментальных замеров ординат поля начальных несовершенств или полных прогибов оболочек.
2.2. Постановка задачи анализа начальных несовершенств и полных прогибов оболочек как случайных величин
В этих условиях результаты замеров ординат начальных и полных прогибов оболочек должны быть представлены в виде вариационного ряда. Задача состоит в полном статистическом анализе полученных результатов, то есть по имеющемуся дискретному набору значений (выборке) х1, х2, ..., хn1 объемом n1 произвести оценивание статистических характеристик случайной величины (математического ожидания, дисперсии, стандарта, асимметрии, эксцесса и т.д.) и найти плотность ее распределения.
2.3. Постановка задачи анализа начальных несовершенств и полных прогибов оболочек как случайных функций
В этом классе задач результаты замеров ординат начальных и полных прогибов оболочек должны быть представлены в виде графиков, осциллограмм или дискретных последовательностей с заданным шагом. Набор реализаций образует ансамбль.
Задача ставится следующим образом - получить дискретный аналог непрерывной реализации случайной функции; отфильтровать неслучайную составляющую; проверить статистические гипотезы об основных свойствах случайных функций (однородности, эргодичности, нормальности); по имеющемуся дискретному набору значений произвести оценивание статистических характеристик случайной функции и найти плотность распределения ее ординат, а также первых и вторых производных; вычислить корреляционную функцию и определить масштаб корреляции; построить спектральную плотность случайной функции прогибов оболочки.
2.4. Постановка задачи анализа начальных несовершенств и полных прогибов оболочек как случайных двумерных полей
Здесь результаты экспериментальных замеров ординат начальных несовершенств и полных прогибов оболочек должны быть представлены в виде непрерывных или дискретных реализаций с заданным шагом по осям х и y.
Задача ставится следующим образом: получить дискретный аналог непрерывной реализации случайного поля; отфильтровать неслучайную составляющую; проверить статистические гипотезы об основных свойствах случайных полей (однородности, эргодичности, изотропности, нормальности); по имеющемуся дискретному набору значений произвести оценивание статистических характеристик случайного поля и построить плотность распределения его ординат; построить совместную плотность распределения ординат поля и его первых и вторых производных; определить истинную спектральную структуру поля прогибов; построить спектральную плотность случайного поля; вычислить корреляционную функцию и определить масштабы пространственной корреляции поля.
3. МЕТОДЫ И АЛГОРИТМЫ РЕШЕНИЯ ЗАДАЧ
3.1. Анализ начальных несовершенств и полных прогибов оболочек как случайных величин
Пусть имеется выборка (объемом n1) значений ординат начальных или полных прогибов оболочек x1, x2, ..., xn1. Выборка может состоять из набора измеренных ординат в одной и той же точке разных экземпляров оболочек или из набора разных ординат одной и той же оболочки. Сначала производится «отбраковка» значений, резко отличающихся от остальных, по следующему правилу.
Если известно, что значение ординаты получено вследствие грубой ошибки, то его необходимо отбросить, не подвергая никаким статистическим оценкам. В тех случаях, когда имеется лишь подозрение, что одна или несколько ординат получены ошибочно, применяется критерий для непринятия резко выделяющихся («выскакивающих») значений Xk* [1].
Пусть их будет r штук (k = 1, 2, ..., r). Вычислим для остальных ординат следующие величины:
Затем для каждого Хk* найдем
и сравним его с критической величиной tn(P) из табл. 3.1.
Если при данном числе ![]() приемлемых ординат tk
³ tn(P) табличного, то
с доверительной вероятностью Р можно считать, что «выскакивающее» значение
содержит грубую ошибку и его следует исключить. Если tk < tn(P), то Хk* исключать из
дальнейшей обработки не следует.
приемлемых ординат tk
³ tn(P) табличного, то
с доверительной вероятностью Р можно считать, что «выскакивающее» значение
содержит грубую ошибку и его следует исключить. Если tk < tn(P), то Хk* исключать из
дальнейшей обработки не следует.
Для оставшихся в выборке n значений ординат вычисляются следующие характеристики [2]:
начальные моменты по формуле
центральные моменты по формуле
В инженерных расчетах для описания случайной величины обычно достаточно первых четырех моментов. Кроме этого в случае необходимости вычисляются
математическое ожидание и дисперсия
стандарт
размах выборки
коэффициент вариации
коэффициент асимметрии
коэффициент эксцесса
Е = μ4/s4 - 3. (3.10)
Критические величины tn(P) для отбраковки «выскакивающих» значений
|
n\P |
0,95 |
0,99 |
0,999 |
n\P |
0,95 |
0,99 |
0,999 |
|
5 |
3,04 |
5,04 |
9,43 |
30 |
2,079 |
2,802 |
3,719 |
|
6 |
2,78 |
4,36 |
7,41 |
35 |
2,061 |
2,768 |
3,682 |
|
7 |
2,62 |
3,96 |
6,37 |
40 |
2,048 |
2,742 |
3,602 |
|
8 |
2,51 |
3,71 |
5,73 |
45 |
2,038 |
2,722 |
3,565 |
|
9 |
2,43 |
3,54 |
5,31 |
50 |
2,03 |
2,707 |
3,532 |
|
10 |
2,37 |
3,41 |
5,01 |
60 |
2,018 |
2,683 |
3,482 |
|
11 |
2,33 |
3,31 |
4,79 |
70 |
2,009 |
2,667 |
3,462 |
|
12 |
2,29 |
3,23 |
4,62 |
80 |
2,003 |
2,655 |
3,439 |
|
15 |
2,22 |
3,08 |
4,28 |
90 |
1,993 |
2,646 |
3,423 |
|
20 |
2,145 |
2,932 |
3,979 |
100 |
1,994 |
2,639 |
3,409 |
|
25 |
2,105 |
2,852 |
3,819 |
>100 |
1,96 |
2,576 |
3,291 |
Значения aom, ρ´m для построения плотности распределения малой выборки
|
Вид предполагаемого закона распределения |
||||||
|
Нормальный |
Экспоненциальный |
Вейбулла |
||||
|
aom |
ρ´m |
aom |
ρ´m |
aom |
ρ´m |
|
|
3 |
0,6 |
0,45 |
0,45 |
0,45 |
0,075 |
0,57 |
|
4 |
0,37 |
0,42 |
0,41 |
0,4 |
0,041 |
0,525 |
|
5 |
0,22 |
0,405 |
0,38 |
0,375 |
0,025 |
0,5 |
|
6 |
0,11 |
0,395 |
0,36 |
0,36 |
0,016 |
0,485 |
|
7 |
0,05 |
0,385 |
0,34 |
0,345 |
0,015 |
0,475 |
|
8 |
0,02 |
0,375 |
0,33 |
0,33 |
0,012 |
0,465 |
|
9 |
0,01 |
0,371 |
0,32 |
0,32 |
0,012 |
0,46 |
|
10 |
0 |
0,37 |
0,31 |
0,31 |
0,012 |
0,455 |
Далее строится аналитическое выражение для плотности распределения ординат поля прогибов оболочки. Различают несколько случаев.
Выборка малая (n £ 10). Плотность распределения записывается в виде [3]
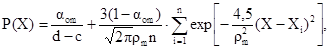 (3.11)
(3.11)
где ρm = ρ´m(d - c), (d - c) - теоретический интервал изменения изучаемой случайной величины; Xi - известные из выборки значения случайной величины; aom, ρ´m - коэффициенты, принимаемые по табл. 3.2 в зависимости от вида предполагаемого закона распределения.
Выборка большая (n > 10). Сначала проверяется на нормальность по критерию X2 [4]. Для этого ее члены объединяются по группам в К интервалов. Длина интервала определяется по формуле
Число К выбирается таким образом, чтобы в каждый интервал попадало не менее пяти членов ряда. При n ³ 200 для выбора К можно использовать рекомендации, изложенные в работе [4].
|
200 |
400 |
600 |
800 |
1000 |
1500 |
2000 |
|
|
к |
16 |
20 |
24 |
27 |
30 |
35 |
39 |
Подсчитывается число членов ряда, попавших в i-й интервал (наблюдаемая частота Vi). Затем для каждого интервала находится ожидаемая частота V´i по формуле
V´i = n[Ф(z2i) - Ф(z1i)], (3.13)
где Ф(z) - функция
Лапласа [2],
а ![]() X1i, X2i - начало и
конец i-го интервала
соответственно. Вычисляется наблюдаемое значение критерия
X1i, X2i - начало и
конец i-го интервала
соответственно. Вычисляется наблюдаемое значение критерия
По таблице
критерия согласия X2 [4] находится величина ![]() где P - доверительная
вероятность. Если
где P - доверительная
вероятность. Если
то искомая плотность распределения подчиняется нормальному закону и она записывается в виде
Если плотность распределения не является гауссовской, то она записывается в виде [5]
Коэффициенты λi определяются из решения вариационной задачи
при условии
Решение задачи возможно только численным методом.
3.2. Анализ начальных несовершенств и полных прогибов оболочек как случайных функций
3.2.1. Предварительная обработка
Пусть имеется n2 непрерывных реализаций (длины - l) замеров значений случайной функции ординат начальных несовершенств или полных прогибов оболочек. Интервал дискретизации определяется по формуле [6]
где kmax - наибольшее волновое число, которое может содержаться в спектре изучаемой случайной функции, причем на длине полуволны гармоники с наибольшим волновым числом, содержащимся в реализациях, должно укладываться не менее 3 - 5 точек дискретизации. Если число замеров велико, то шаг дискретизации выбирается с учетом следующих соображений: 1) наличия аппаратуры с необходимой разрешающей способностью; 2) возможности осуществления нужного количества замеров; 3) экономических критериев.
Для каждой реализации ординаты, замеренные в точках дискретизации, образуют выборку (X*i1, Х*i2, ..., X*iN, i = 1, 2, ..., N) объемом
Из полученной дискретной реализации нужно выделить неслучайную составляющую, то есть представить каждый член выборки в виде
где неизвестные коэффициенты Аi, Bi и Сi находятся из решения системы уравнений
NAi
+ H1Bi + H2Ci = ![]()
H2Ai + H12Bi + H3Ci = ![]()
В уравнениях (3.23)
Таким образом, в результате предварительной обработки будет получено n2 дискретных реализаций случайной функции ординат начальных или полных прогибов оболочек вида (Хi1, Хi2, ..., XiN, i = 1, 2, ..., n2).
3.2.2. Проверка на однородность и эргодичность
Проверка на
однородность.
Каждая реализация проверяется одновременно по двум критериям: Вилкоксона и
Сиджела-Тьюки [7]. Для этого она делится на две части, каждая
объемом N/2 (при N нечетном крайняя точка исключается). Затем ординаты,
входящие в каждую из частей, располагают в возрастающем порядке, т.е. в виде
одного вариационного ряда. Каждому из членов этого вариационного ряда
приписывается определенный ранг: для первого критерия ранг отсчета ![]() равен
номеру его позиции в общем вариационном ряду; для второго критерия ранг
равен
номеру его позиции в общем вариационном ряду; для второго критерия ранг ![]() приписывается
наименьшему члену, ранг
приписывается
наименьшему члену, ранг ![]() - наибольшему члену, ранг
- наибольшему члену, ранг ![]() -
наименьшему оставшемуся, ранг
-
наименьшему оставшемуся, ранг ![]() - наибольшему оставшемуся в общем
вариационном ряду и так далее. Если величины элементов совпадают, то им
приписывается одинаковый ранг, равный среднему арифметическому их рангов. Затем
составляем два критерия W1 и W2, равные сумме
рангов членов, входящих только в одну из частей реализации. W1 подсчитывается
для первого способа назначения рангов:
- наибольшему оставшемуся в общем
вариационном ряду и так далее. Если величины элементов совпадают, то им
приписывается одинаковый ранг, равный среднему арифметическому их рангов. Затем
составляем два критерия W1 и W2, равные сумме
рангов членов, входящих только в одну из частей реализации. W1 подсчитывается
для первого способа назначения рангов:
а W2 - для второго:
![]()
Затем вычисляем
где mw = N(N + 1)/4 и сравниваем эти значения с величиной zw (N/2, Р) из табл. 3.3. При одновременном выполнении неравенств
реализация считается однородной. Если неравенства типа (3.27) выполняются для всех реализаций, то случайная функция ординат начальных несовершенств для полных прогибов оболочек считается однородной в широком смысле, в противном случае гипотеза об однородности отвергается и изучаемые результаты следует обрабатывать методами анализа неоднородных случайных функций [4], [8].
Проверка на эргодичность. Для возможности дальнейшего упрощения всех статистических расчетов реализации однородной случайной функции проверяются на эргодичность, поскольку статистические характеристики эргодических функций можно вычислять по одной реализации, т.е. осреднять не по ансамблю, а по координатам. На практике случайные функции, соответствующие стационарным или однородным физическим явлениям, как правило, обладают свойством эргодичности [4]. Для проверки эргодичности используют следующий критерий:
который обычно нарушается, если исследуемая функция содержит периодические составляющие. Условие (3.28) служит достаточным, но не необходимым условием эргодичности, и поэтому на практике усреднение по координатам можно производить даже при наличии периодических компонент [6].
Критические значения функции Zw (N/2, Р) дли проверки однородности случайных функций
|
P\N/2 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
14 |
16 |
18 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
0,8 |
0,26 |
0,23 |
0,21 |
0,19 |
0,18 |
0,17 |
0,16 |
0,15 |
0,14 |
0,13 |
0,12 |
0,11 |
0,09 |
0,06 |
0,07 |
0,06 |
0,055 |
0,05 |
0,045 |
0,04 |
|
0,9 |
0,31 |
0,28 |
0,25 |
0,23 |
0,22 |
0,21 |
0,2 |
0,19 |
0,18 |
0,17 |
0,16 |
0,13 |
0,115 |
0,1 |
0,09 |
0,08 |
0,075 |
0,07 |
0,065 |
0,06 |
|
0,95 |
0,37 |
0,34 |
0,32 |
0,30 |
0,28 |
0,26 |
0,24 |
0,22 |
0,205 |
0 |
0,18 |
0,16 |
0,14 |
0,12 |
0,11 |
0,1 |
0,09 |
0,085 |
0,08 |
0,075 |
|
0,99 |
0,45 |
0,42 |
0,39 |
0,36 |
0,34 |
0,32 |
0,3 |
0,28 |
0,26 |
0,25 |
0,24 |
0,22 |
0,2 |
0,17 |
0,15 |
0,14 |
0,13 |
0,12 |
0,15 |
0,11 |
3.2.3. Вычисление статистических характеристик, корреляционной функции и спектральной плотности
Сначала полученная последовательность значений ординат случайной функции прогибов оболочки рассматривается как выборка объемом N, к которой применяются методы обработки случайных величин, изложенные в п. 3.1, т.е. вычисляются статистические характеристики и строится плотность распределения ординат.
Затем
вычисляются корреляционная функция К и нормированная корреляционная функция ![]() по формулам
[9]
по формулам
[9]
![]() (3.30)
(3.30)
где m £ [N/10] - число точек, в которых вычисляется корреляционная функция; x(ih) - значение ординаты случайной функции прогибов в точке ih, K(0) = D. По корреляционной функции находится масштаб корреляции по формуле
или вычисляется как расстояние от начала координат до той точки, где корреляционная функция становится в первый раз равной К(0)/e [≈0,37 К(0)].
Спектральная плотность S рассчитывается для m + 1 волновых чисел
![]()
по формуле [4]
Состоятельная сглаженная по Хеммингу спектральная плотность вычисляется по формуле [9]
Нормированные спектральные плотности вычисляются по формулам
![]() (3.34)
(3.34)
3.3. Анализ начальных несовершенств и полных прогибов оболочек как случайных полей
3.3.1. Предварительная обработка
Пусть имеется n2 прямоугольных в плане непрерывных реализаций (размером а´b) замеров значений случайного поля ординат начальных несовершенств или полных прогибов оболочек. Дискретные значения ординат замеряются в узлах прямоугольной сетки, линии которой параллельны сторонам оболочки. Расстояния между координатными линиями по каждому из направлений (шаги дискретизации) вычисляются по формулам
где Каmах, Kbmах - наибольшие волновые числа, которые могут содержаться в спектре изучаемого случайного поля по каждому из направлений. Если величины Каmах, Kbmах заранее неизвестны, то шаг дискретизации выбирается из тех же соображений, что и для случайной функции (см. п. 3.2.1).
Для каждой r-й реализации ординаты, замеренные в точках дискретизации, образуют массив
![]() (3.36)
(3.36)
(r = 1, 2, ..., n2)
объемом
![]()
Из полученной дискретной реализации выделяется неслучайная составляющая, то есть каждый член массива представляется в виде [10]
где коэффициенты А, B, С, D, E, F вычисляются по формулам
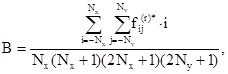
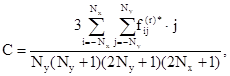
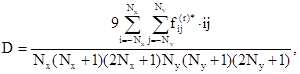
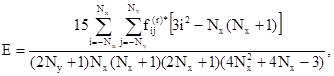 (3.38)
(3.38)
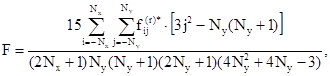
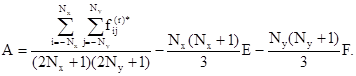
В (3.38) A - математическое ожидание реализации. Таким образом, в результате предварительной обработки будет получено n2 дискретных реализаций случайного поля ординат начальных или полных прогибов оболочек вида
3.3.2. Проверка на однородность, эргодичность, изотропность, нормальность
Проверка на
однородность.
Дискретные реализации, полученные в результате предварительной обработки,
проверяются на однородность одновременно по двум критериям: тренда и серий [4].
Для этого каждая реализация разбивается сеткой на R прямоугольников
(R
³ 4 ÷ 20).
Для каждого прямоугольника вычисляются математическое ожидание m1(r) и дисперсия ![]() содержащихся
в нем ординат прогибов по формулам (3.3) и (3.4). Полученные
значения образуют две последовательности
содержащихся
в нем ординат прогибов по формулам (3.3) и (3.4). Полученные
значения образуют две последовательности
![]() и
и ![]() (r´ = 1,
..., R).
(r´ = 1,
..., R).
Для R значений первой последовательности подсчитывается общее число инверсий А∑ по формуле
Затем по табл. 3.4
находят значения критерия ![]() и
и ![]()
Если
то члены последовательности независимы и монотонный тренд отсутствует. Вторая последовательность проверяется на отсутствие монотонного тренда аналогично.
Далее для обеих
последовательностей ![]() и
и ![]() вычисляются величины
вычисляются величины
Каждому из
членов первой последовательности ставится в соответствие знак (+), если ![]() и (-) в
противном случае. Для членов второй последовательности знак (+) берется при
и (-) в
противном случае. Для членов второй последовательности знак (+) берется при ![]() и (-) - при
и (-) - при
![]() .
Полученные для первой последовательности знаки записываются по порядку и
вычисляется число серий υ, т.е. количество групп из одного или нескольких
одинаковых подряд расположенных знаков, до и после которых имеются группы
других знаков либо знаки вообще отсутствуют. По табл. 3.5 находят значения критерия
.
Полученные для первой последовательности знаки записываются по порядку и
вычисляется число серий υ, т.е. количество групп из одного или нескольких
одинаковых подряд расположенных знаков, до и после которых имеются группы
других знаков либо знаки вообще отсутствуют. По табл. 3.5 находят значения критерия ![]() и
и ![]() .
.
Значения критерия инверсий при ![]() ,
, ![]()
|
Р |
||||||
|
0,99 |
0,975 |
0,95 |
0,05 |
0,025 |
0,01 |
|
|
10 |
9 |
11 |
13 |
31 |
33 |
35 |
|
12 |
16 |
18 |
21 |
44 |
47 |
49 |
|
14 |
24 |
27 |
30 |
60 |
63 |
66 |
|
16 |
34 |
38 |
41 |
78 |
81 |
85 |
|
18 |
45 |
50 |
54 |
98 |
102 |
107 |
|
20 |
59 |
64 |
69 |
120 |
125 |
130 |
|
30 |
152 |
162 |
171 |
263 |
272 |
282 |
|
40 |
290 |
305 |
319 |
460 |
474 |
489 |
|
50 |
473 |
495 |
514 |
710 |
729 |
751 |
|
60 |
702 |
731 |
756 |
1013 |
1038 |
1067 |
|
70 |
977 |
1014 |
1045 |
1369 |
1400 |
1437 |
|
80 |
1299 |
1344 |
1382 |
1777 |
1815 |
1860 |
|
90 |
1668 |
1721 |
1766 |
2238 |
2283 |
2336 |
|
100 |
2083 |
2145 |
2198 |
2751 |
2804 |
2866 |
Значения
критерия серий ![]() и
и ![]()
|
R/2 |
Р |
|||||
|
0,99 |
0,975 |
0,95 |
0,05 |
0,025 |
0,01 |
|
|
5 |
2 |
2 |
3 |
8 |
9 |
9 |
|
6 |
2 |
3 |
3 |
10 |
10 |
11 |
|
7 |
3 |
3 |
4 |
11 |
12 |
12 |
|
8 |
4 |
4 |
5 |
12 |
13 |
13 |
|
9 |
4 |
5 |
6 |
13 |
14 |
15 |
|
10 |
5 |
6 |
6 |
15 |
15 |
16 |
|
11 |
6 |
7 |
7 |
16 |
16 |
17 |
|
12 |
7 |
7 |
8 |
17 |
18 |
18 |
|
13 |
7 |
8 |
9 |
18 |
19 |
20 |
|
14 |
8 |
9 |
10 |
19 |
20 |
21 |
|
15 |
9 |
10 |
11 |
20 |
21 |
22 |
|
16 |
10 |
11 |
11 |
22 |
22 |
23 |
|
18 |
11 |
12 |
13 |
24 |
25 |
26 |
|
20 |
13 |
14 |
15 |
26 |
27 |
28 |
|
25 |
17 |
18 |
19 |
32 |
33 |
34 |
|
30 |
21 |
22 |
24 |
37 |
39 |
40 |
|
35 |
25 |
27 |
28 |
43 |
44 |
46 |
|
40 |
30 |
31 |
33 |
48 |
50 |
51 |
|
45 |
34 |
36 |
37 |
54 |
55 |
57 |
|
50 |
38 |
40 |
42 |
59 |
61 |
63 |
|
55 |
43 |
45 |
46 |
65 |
66 |
68 |
|
60 |
47 |
49 |
51 |
70 |
72 |
74 |
|
65 |
52 |
54 |
56 |
75 |
77 |
79 |
|
70 |
56 |
58 |
60 |
81 |
83 |
85 |
|
75 |
61 |
63 |
65 |
86 |
88 |
90 |
|
80 |
65 |
68 |
70 |
91 |
93 |
96 |
|
85 |
70 |
72 |
74 |
97 |
99 |
101 |
|
90 |
74 |
77 |
79 |
102 |
104 |
107 |
|
95 |
79 |
82 |
84 |
107 |
109 |
112 |
|
100 |
84 |
86 |
88 |
113 |
115 |
117 |
Если
то члены последовательности независимы и колебательный тренд отсутствует. Аналогично проверяется вторая последовательность.
Если в результате проверки окажется, что числа серий и инверсий для обеих последовательностей одновременно попадают в границы найденных интервалов, то поле является однородным.
Проверка на эргодичность. Выполняется так же, как и для случайной функции (см. п. 3.2.2). Критерий эргодичности поля имеет вид
При a → ∞, b → ∞.
Проверка на изотропность. Из центральной точки поля проводится 8 лучей, четыре из которых совпадают с координатными линиями, а четыре с диагоналями прямоугольника. Значения ординат поля прогибов оболочки, замеренные в узлах сетки, лежащие на каждом из лучей, образуют восемь последовательностей вида
![]()
где n3 - число точек на каждом луче.
К каждой паре
последовательностей применяется процедура проверки на однородность (см. п. 3.2.2).
Всего выполняется ![]() = 28 проверок. Если для всех возможных
пар неравенства (3.27) выполнены, то поле изотропно.
= 28 проверок. Если для всех возможных
пар неравенства (3.27) выполнены, то поле изотропно.
Если поле изотропно, то все его характеристики можно вычислить по ординатам прогибов, замеренным только в одном (любом) диагональном сечении оболочки (как для случайных функций). Если поле неизотропно, то его характеристики вычисляются методами, изложенными в п. 3.3.3.
Проверка на нормальность. Проверка нормальности поля производится по критерию согласия χ2. При этом весь имеющийся массив ординат поля прогибов рассматривается как набор значений некоторой случайной величины. Порядок проверки изложен в п. 3.1.
3.3.3. Вычисление статистических характеристик, спектральной плотности и корреляционной функции случайного поля прогибов оболочки
Сначала к полученной дискретной реализации случайного поля применяются методы обработки случайных величин, изложенные в п. 3.1, т.е. вычисляются статистические характеристики и строится плотность распределения ординат. Затем вычисляется несмещенная спектральная плотность для N точек дискретизации по формуле [11]
где n = 0, ±1, ..., ±Nx; m = 0, ±1, ..., ±Ny; a, b - размеры
оболочки в плане; ![]() - периодограммы, вычисляемые с шагами
дискретности
- периодограммы, вычисляемые с шагами
дискретности ![]() в N точках по формулам
в N точках по формулам
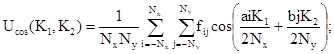 (3.48)
(3.48)
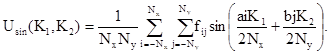 (3.49)
(3.49)
Несмещенная и состоятельная спектральная плотность определяется с использованием окна Пугачева-Даниэля по формуле [11]
где r = -1, 0, 1; S = -1, 0, 1.
Нормированная спектральная плотность вычисляется по формуле (3.34).
Разрешающая способность спектрального анализа для случая прямоугольного спектрального окна определяется величиной [12]
где DK1э, DК2э - эквивалентная полоса частот спектрального анализа. Формула (3.51) устанавливает фундаментальную связь между разрешением и размерами реализации поля при заданной статистической точности:
«Соотношение неопределенности» (3.52) играет основную роль в спектральном анализе. Для улучшения разрешения при сохранении ошибки e следует соответствующим образом увеличивать размер реализации, если это невозможно, то приходится делать выбор между разрешающей способностью окна и точностью определения спектральной плотности мощности.
Корреляционная функция случайного поля вычисляется по формуле
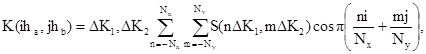
![]()
где ![]()
Нормированная корреляционная функция вычисляется по формуле (3.30).
Масштабы корреляции определяются по формулам [13]
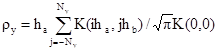 (3.55)
(3.55)
Масштаб корреляции, усредненный по всем направлениям, определяется по формуле
3.3.4. Выявление скрытых периодичностей
Выявление скрытых периодичностей производится следующим образом. Вычисляются периодограммы в N точках по формулам [10, 14]
n = 0, ± 1, ..., ± Nx; m = 0, ± 1, ..., ± Ny.
Находятся все точки, при которых нарушается чередование знаков периодограммы Ucos(n, m). Для этого каждая такая точка (n*, m*) проверяется на выполнение следующего условия;
![]() (3.59)
(3.59)
Если оно
выполняется, то ![]() где e1, e2 вычисляются методами квадратичного
интерполирования по формулам
где e1, e2 вычисляются методами квадратичного
интерполирования по формулам
Затем определяются амплитуды А´i и B´i периодограмм Ucos(n, m) и Usin(n, m) соответственно с волновыми числами (Ki´1, Кi´2) где Ki´1 = a1DK1, Ki´2 = a2DK2 (a1, a2 - нецелые числа), методом наименьших квадратов из системы 2υ линейных неоднородных уравнений относительно искомых амплитуд:
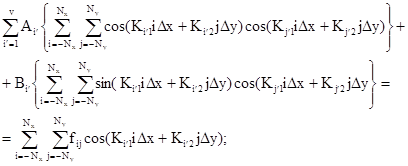
j´ = 1, 2, ..., υ.
Решение системы (3.62) требует большого времени счета на ЭВМ. Поэтому амплитуды можно находить приближенно по формулам
Далее случайное поле прогибов представляется в виде
![]() (3.64)
(3.64)
где Аi´, Вi´ - амплитуды периодограмм Ucos(n, m), Usin(n, m); Ki´1, Ki´2 - волновые числа по x и по y соответственно; υ - количество волновых чисел и задача выявления скрытых периодичностей решена.
3.4. Построение совместной плотности вероятности случайного поля (функции) ординат прогибов оболочки и его первых и вторых производит (СПП)
Знание совместной плотности вероятности распределения ординат поля, его первых и вторых производных (угловых коэффициентов и кривизн) позволяет определять все характеристики случайного поля (функции) прогибов оболочки (среднее число выбросов за заданный уровень, среднее число максимумов и т.д.).
Совместная плотность находится методом характеристических функций и записывается в виде
где ![]() обозначают соответственно
обозначают соответственно ![]() и
вычисляются по формулам
и
вычисляются по формулам
![]()
![]()
![]()
![]()
Совместная плотность вероятности случайной функции ординат прогибов и ее первой и второй производной определяется по аналогичной формуле
где ![]() обозначают
соответственно f(x),
обозначают
соответственно f(x), ![]() и
вычисляют по формулам
и
вычисляют по формулам
Для гауссовского изотропного случайного поля СИП можно находить методом спектральных моментов [16, 17]:
Спектральные моменты m0, m2, m4 определяются по формулам
где H0, He - число нулей и экстремумов (максимумов и минимумов) соответственно на единице длины сечения поля.
ПРИЛОЖЕНИЕ
1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
1.1. Пояснение основных формул Р
Предварительная обработка. Полученный после дискретизации массив точек поля оболочки М{fij*} может включать начальные несовершенства детерминированного типа, которые необходимо предварительно отфильтровать, то есть подготовить его к анализу как чисто случайного [10, 18]. Для реальных пластин, оболочек и их моделей - это низкочастотные составляющие, возникающие при их изготовлении и монтаже конструкций. Так, например, действительный радиус реального изделия отличается от проектного, что можно учесть, вычитая из массива М{fij*} некоторую константу А. Возможен поворот плана оболочки относительно горизонтальной плоскости, который учитывается членами Вx и Cy. Скручивание пластин и оболочек в плане учитывается членом Dxy. Из-за погрешностей монтажа опор оболочки плоскость опорного контура может быть приподнятой или опущенной относительно базовой проектной плоскости, что устраняется учетом элементов Ех2 и Fy2. Таким образом, неслучайные составляющие поля оболочки записываются в виде
z = А + Bx + Сy + Вxу + Еx2 + Fx2. (1.1)
Коэффициенты A ÷ F подбираются так, чтобы поверхность z приближала массив М{fij*} в среднеквадратичном, то есть
Дифференцируя функцию U по А, В, C, D, Е, F и приравнивая производные нулю, получим систему линейных уравнений для нахождения неизвестных коэффициентов А ÷ F. Аналогичные рассуждения для случайных функций приводят к системе уравнений (3.23).
Выявление скрытых периодичностей. Основная идея метода состоит в использовании нелинейного преобразования исходной функции, позволяющего осуществить селекцию по различию в волновых числах и амплитудах [19]. Общий подход и метод распознавания истинной спектральной структуры полей начальных и полных прогибов оболочек дан в [18]. Зарегистрированное поле f(х, y) может быть представлено в виде (3.62) или
 (1.3)
(1.3)
Отличие (3.62)
от (1.3)
состоит в том, что в первом случае рассматривается случай двумерного, почти
периодического поля, разлагающегося по двумерным гармоникам, а второе
представление справедливо для полей вида ![]() [10, 14, 20]. Представление (3.62)
применяется в тех случаях, когда поля начальных несовершенств или полных
прогибов содержат «косые» волны [11].
[10, 14, 20]. Представление (3.62)
применяется в тех случаях, когда поля начальных несовершенств или полных
прогибов содержат «косые» волны [11].
Рассматривается случайное поле ординат начальных или полных прогибов оболочки
где ![]() Для него косинус и синус -
периодограммы имеют вид
Для него косинус и синус -
периодограммы имеют вид
и с учетом разрешающей способности дискретного преобразования Фурье [21]
![]()
представляются формулами (3.57), (3.58).
Для выявления реально присутствующих в поле пространственных гармоник с частотами a1DК1, a2DК2 применяется двумерный аналог Ланцоша [22].
Максимумы
функций Ucos(n, m) и Usin(n, m) указывают
местоположение существенных пар волновых чисел, представляющих собой искомые
частоты ![]() Значения
Значения
![]() получаются
из решения линейной системы уравнений [18]
получаются
из решения линейной системы уравнений [18]
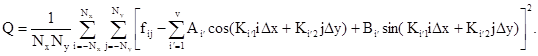 (1.8)
(1.8)
Построение
совместной плотности ![]() Основано на построении предварительной
оценки характеристической функции (ХФ) n-мерной
случайной величины (СВ)
Основано на построении предварительной
оценки характеристической функции (ХФ) n-мерной
случайной величины (СВ) ![]() заданной дискретно, с последующим
обращением ХФ по Фурье в пространстве волновых чисел. Оператор математического
ожидания выражения, определяющего ХФ, заменяется оператором усреднения СВ
заданной дискретно, с последующим
обращением ХФ по Фурье в пространстве волновых чисел. Оператор математического
ожидания выражения, определяющего ХФ, заменяется оператором усреднения СВ ![]() по полю
оболочки G (x, y)
по полю
оболочки G (x, y)
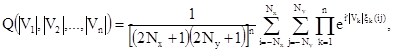 (1.9)
(1.9)
где ![]() i´ - мнимая единица.
Суммирование ведется по всем узлам прямоугольной сетки размером
i´ - мнимая единица.
Суммирование ведется по всем узлам прямоугольной сетки размером ![]() наброшенной
на оболочку. Тогда плотность вероятности распределения СВ
наброшенной
на оболочку. Тогда плотность вероятности распределения СВ ![]() получается как n-кратное
преобразование Фурье для ХФ (1.9):
получается как n-кратное
преобразование Фурье для ХФ (1.9):
Формула (1.10)
определения совместной плотности вероятности распределения ординат случайного
поля прогибов оболочки и его первых и вторых производных является
окончательной. Пределы интегрирования в (1.10) для ![]() определяются исходя из
преобразования Фурье
определяются исходя из
преобразования Фурье
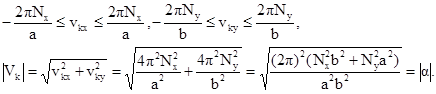
Метод характеристических функций для построения совместной плотности ординат случайного поля и его первых и вторых производных в отличие от метода спектральных моментов (пригодного только для изотропных гауссовских полей) применим для однородных и негауссовских полей.
Литература
1. Румшиский Л.З. Статистическая обработка результатов эксперимента. - М.: Наука, 1969. - 251 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1977. - 479 с.
3. Гаскаров Д.В., Шаповалов В.И. Малая выборка. - М.: Статистика, 1978. - 247 с.
4. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. - М.: Мир, 1971. - 407 с.
5. Плетнев И.Л., Рембеза А.И., Соколов Ю.А., Чалый-Прилуцкий В.А. Эффективность и надежность сложных систем. - М.: Машиностроение, 1977. - 216 с.
6. Вендат Дж., Пирсол А. Применения корреляционного и спектрального анализа. - М.: Мир, 1963. - 312 с.
7. Жовинский А.Н., Жовинский В.Н. Инженерный экспресс-анализ случайных процессов. - М.: Энергия, 1978. - 119 с.
8. Цветков Э.И. Нестационарные случайные процессы и их анализ. - М.: Энергия, 1973. - 128 с.
9. Грибанов Ю.И., Мальков В.Л. Спектральный анализ случайных процессов. - М.: Энергия, 1973. - 238 с.
10. Кантор С.Л. Влияние случайных геометрических начальных несовершенств на устойчивость гибких пологих оболочек. - Дисс. на соискание уч. ст. канд. тех. наук. - Свердловск, 1981. - 160 с.
11. Тимашев С.А., Кантор С.Л. Стохастическая устойчивость и надежность подкрепленных оболочек. - 3 кн.: Доклады Международной конференции по облегченным пространственным конструкциям покрытий для строительства в обычных и сейсмических районах. - М.: Стройиздат, 1977, с. 421 - 428.
12. Тимашев С.А. Методы расчета надежности оболочек как распределенных систем. - В кн.: Исследования пространственных конструкций. Свердловск: Урал. политехн. ин-т, 1981, с. 25 - 36.
13. Басс Ф.Г., Фукс И.М. Рассеяние волн на статически неровной поверхности. - М.: Наука, 1973. - 287 с.
14. Тимашев С.А., Кантор С.Л. Анализ случайных полей на основе двумерного преобразования Фурье. - В кн.: Пути повышения прочности, надежности и долговечности выпускаемых машин и оборудования. - Свердловск: УПИ им. С.М. Кирова. 1976, с. 26 - 32.
15. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1969. - 400 с.
16. Найак П.Р. Применение модели случайного поля для исследования шероховатых поверхностей. - Проблемы трения и смазки. Мир, 1971, № 3, 85 - 95 с.
17. Лонге-Хиггинс М.С. Статистическая геометрия случайных поверхностей. - В кн.: Гидродинамическая неустойчивость. - Мир, 1964. - 371 с.
18. Тимашев С.А. Устойчивость подкрепленных оболочек. - М.: Стройиздат, 1974. - 256 с.
19. Серебренников М.Г., Первозванский А.А. Выявление скрытых периодичностей. - М.: Наука, 1965. - 244 с.
20. Тимашев С.А. Стохастическая устойчивость и надежность подкрепленных оболочек: Дисс. на соиск. уч. ст. докт. техн. наук. - Свердловск, 1975. - 500 с.
21. Коняев К.В. Спектральный анализ случайных процессов и полей. - М.: Наука, 1973. - 237 с.
22. Ланцош К. Практические методы прикладного анализа. - М.: Физматгиз, 1961. - 524 с.
23. Гольдберг Н.И. К оценке многомерной характеристической функции случайного процесса - Техн. кибернетика, 1972, № 4, с. 162 - 167.
24. Математическое обеспечение ЕС ЭВМ. Вып. 18. - Минск, ИМ БССР, 1979. - 62 с.
2. ПРОГРАММНАЯ ДОКУМЕНТАЦИЯ
Часть программ по обработке полученных статистических данных входит в пакет научных подпрограмм «Библиотека Института математики» (ПНП-БИМ). Пакет написан на алгоритмическом языке ФОРТРАН и предназначен для использования на ЕС ЭВМ, работающих под управлением операционной системы ДОС ЕС, ОС ЕС или ДОС АСВТ (для М-4030) [24]. Программы, не вошедшие в данный пакет, приводятся ниже.
2.1. Программа определения масштаба корреляции
2.1.1. Описание программы
Подпрограмма МАСКОR предназначена для определения масштаба корреляции корреляционной функции. Программа написана на языке ПЛ/1 в среде ОС ЕС ЭВМ, содержит около 100 операторов языка ПЛ/1. Объем оперативной памяти зависит от количества заданных дискретных значений корреляционной функции.
Обращение к подпрограмме:
САLL MАRКOR (КORF, КFN1, KFN2, MKOR) (КFN1 < KFN2),
где:
KORF (KFN1 : KFN2) FLOAT DEC (6) CTL - исходный массив значений корреляционной функции;
KFN1 FIXED BIN (15) - нижний индекс массива KORF;
KFN2 FIXED BIN (15) - верхний индекс массива KORF;
МKOR FLOAT DЕС (6) - выходное значение масштаба корреляции.
2.1.2. Формуляр
Подпрограмма МАСКОR составлена для ЭВМ ЕС-1033. Время выполнения программы от 1 до 4 мин в зависимости от значений KFN1 и KFN2. Используемый тип машинного носителя - ленты или перфокарты.
2.2. Программа выявления скрытых периодичностей
2.2.1. Описание программы
Программа РЕRIOD предназначена для отыскания скрытых периодичноcтей и случайной компоненты обрабатываемой функции, заданной дискретно. В результате определяется случайная компонента.
Программа написана на языке ПЛ/1 в среде ОС ЕС ЭВМ, содержит около 200 операторов языка ПЛ/1.
Объем оперативной памяти зависит от количества заданных дискретных значений обрабатываемой функции.
Обращение к программе:
САLL РЕRIOD (МАS, N1, N2, D1, D2, РЕRMAS) (![]() ),
),
где
МАS (N1:N2) FLOАТ DEC (6) СTL - исходный массив значений функции;
N1 FIXED BIN (15) - нижний индекс массива МАS;
N2 FIXED BIN (15) верхний индекс массива МАS;
D1 FIXED BIN (15) - нижний индекс массива РЕRМАS (D1 = N1),
D2 FIXED BIN (15) - верхний индекс массива РЕRМАS (D2 = N2);
PERMAS (D1:D2) FLOAT DEC (6) CTL - выходной массив значений случайной компоненты.
2.2.2. Формуляр
Программа PERIOD составлена для ЭВМ ЕС-1033.
Время выполнения программы от 1 до 10 мин в зависимости от N1 и N2. Используемый тип машинного носителя - ленты или перфокарты.
2.3. Программа вычисления совместной плотности вероятности случайной функции ординат прогибов оболочки и ее первой и второй производных (СПФ)
2.3.1. Описание программы
Подпрограмма SPBF12, предназначенная для определения СПФ, написана на языке ПЛ/1 в среде ОС ЕС ЭВМ и содержит около 300 операторов языка ПЛ/1. Объем оперативной памяти зависит от количества заданных дискретных значений функции ординат прогибов.
Обращение к подпрограмме на языке ПЛ/1:
CALL SРВF (ISМF, IFN1, IFN2, SНD, SPBF, SРBFN1, SРBFN2),
где
ISMF (IFN1:IFN2) FLOAT DEC (6) CTL - исходный массив значений функции ординат прогибов;
IFN1 FIXED BIN (15) - нижний индекс массива ISMF;
IFN2 FIXED BIN (15) - верхний индекс массива ISMF;
IHD FIXED BIN (15) - шаг дискретизации;
SPBF (SPFN1:SPFN2) FLOAT DEC (6) CTL - выходной массив значений СПФ;
SPFN1 FIXED BIN (15) - нижний индекс массива SРBF;
SРFN2 FIXED BIN (15) - верхний индекс массива SPBF.
2.3.2. Формуляр
Подпрограмма SРBF12 составлена для ЭВМ ЕС-1033. Время выполнения программы от 1 до 10 мин в зависимости от значений IFN1 и IFN2. Используемый тип машинного носителя - ленты или перфокарты.
2.4. Программа вычисления совместной плотности вероятности случайного поля ординат прогибов оболочки и его первых и вторых производных (СПП)
2.4.1. Описание программы
Подпрограмма SРBР12, предназначенная для определения СПП, написана на языке ПЛ/1 в среде ОС ЕС ЭВМ и содержит около 400 операторов языка ПЛ/1. Объем оперативной памяти зависит от количества заданных дискретных значений поля ординат прогибов.
Обращение к подпрограмме:
CALL SPBP12 (ISМР, IРGN1, IРGN2, IРWN1, IРWN2, SHDG, SHDW,
SРВР, SРGN1, SРGN2, SРWN1, SPWN2),
где
ISMP (IРGN1:IРGN2, IРWN1:IPWN2) FLOAT DEC (6) CTL - исходный массив значений поля ординат прогибов; IPGN1 FIXED BIN (15) - нижний индекс первого измерения массива ISMP; IPGN2 FIXED BIN (15) - второй индекс первого измерения массива ISМР; IPWN1 FIXED BIN (15) - нижний индекс второго измерения массива ISМР; IPWN2 FIXED BIN (15) - верхний индекс второго измерения массива ISMP; SHDG FIXED BIN (15) - шаг дискретизации первого измерения массива ISМР; SHDW FIXED BIN (15) - шаг дискретизации второго измерения массива ISМР; SPBP (SPGN1:SPGN2, SPWN1:SPWN2) FLOAT DEC (6) CTL - выходной двумерный массив значений СПП; SРGN1 FIXED BIN (15) - нижний индекс первого измерения массива SPBP; SРGN2 FIXED BIN (15) - верхний индекс первого измерения массива SPBP; SРWN1 FIXED BIN (15) - нижний индекс второго измерения массива SРBР; SРWN2 FIXED BIN (15) - верхний индекс второго измерения массива SРВР.
2.4.2. Формуляр
Подпрограмма SРBР12 составлена для ЭВМ ЕС-1033. Время выполнения программы от 1 до 15 мин в зависимости от значений IРGN1, IPGN2, IРWN1, IРWN2. Используемый тип машинного носителя - ленты или перфокарты.
3. ПРИМЕРЫ РАСЧЕТА
3.1. Анализ начальных несовершенств оболочки как случайной величины
Путем экспериментальных замеров были получены данные об отклонениях от проекта ординат поля железобетонных оболочек, собираемых из плоских плит размером 3´6 м. Гистограмма отклонений, оставшихся в выборке после отбраковки «выскакивающих» значений, приведена на рис. 1. Результаты расчета (по формулам 3.5 - 3.10 Р) статистических характеристик замеренных отклонений даны в табл. 1.
Статистические характеристики отклонений поля оболочки из железобетонных плит размером 3´6 м
|
|
D, мм3 |
s, мм |
R, мм |
А |
Е |
|
|
Величина |
0 |
641,2 |
25,3 |
160 |
0,09 |
-0,01 |
Проверим выборку на нормальность по критерию χ2. Результаты расчетов приведены в табл. 2. Эмпирическое значение статистики χ2 равно 1,327. Критическое значение для гипотезы о нормальности при уровне значимости 0,05 и трех степенях свободы, равно 7,815. Так как 1,327 < 7,815, то это распределение можно считать нормальным и плотность распределения отклонений от проекта ординат поля исследуемых оболочек записать в виде
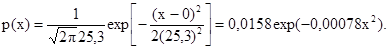
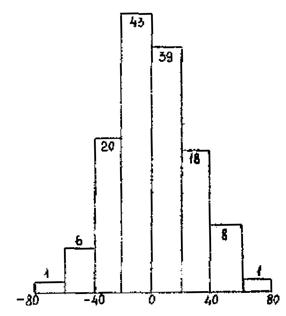
Рис. 1. Гистограмма отклонений поля оболочки из железобетонных плит размером 3´6 м
Результаты проверки выборки на нормальность по критерию χ2
|
Наблюдаемые частоты vi |
zi |
Ф(zi) |
Ф(zi) - Ф(zi-1) |
Теоретические частоты v´i |
vi - v´i |
|
|
|
-80 |
|
-3,16 |
0,01 |
|
|
|
|
|
|
7 |
|
|
0,056 |
7,6 |
0,6 |
0,047 |
|
-40 |
|
-1,58 |
0,057 |
|
|
|
|
|
|
20 |
|
|
0,157 |
21,3 |
1,3 |
0,079 |
|
-20 |
|
-0,79 |
0,214 |
|
|
|
|
|
|
43 |
|
|
0,286 |
38,9 |
4,1 |
0,432 |
|
0 |
|
0 |
0,5 |
|
|
|
|
|
|
39 |
|
|
0,283 |
38,9 |
0,1 |
0 |
|
20 |
|
0,79 |
0,784 |
|
|
|
|
|
|
18 |
|
|
0,157 |
21,3 |
3,3 |
0,511 |
|
40 |
|
1,58 |
0,943 |
|
|
|
|
|
|
9 |
|
|
0,056 |
7,6 |
1,4 |
0,258 |
|
80 |
|
3,16 |
0,999 |
|
|
|
|
|
∑ |
136 |
|
|
0,998 |
135,6 |
|
1,327 |
3.2. Анализ начальных несовершенств оболочки как случайной функции
Пример 1. Путем экспериментальных замеров собраны данные об отклонениях от проекта площади поперечного сечения двух подкрепляющих ребер оболочки размером 18´18 м. Данные о величинах отклонений приведены в табл. 3.
Полученные данные проверим на однородность, для чего воспользуемся методикой, изложенной в п. 3.2.2. Сначала разделим обе реализации на две равные части объемом N = 5. Затем для каждой реализации составим вариационный ряд. Для первой реализации этот ряд имеет следующий вид (цифра в скобках означает, к какой части реализации принадлежит данный замер):
Для второй реализации:
Найдем значения критериев W1 и W2 для каждой реализации. Цифры, обведенные кружком, означают ранг отсчета при первом способе назначения рангов. Цифры в квадратах равны рангу отсчета при втором способе назначения рангов. Тогда:
Величины отклонений от проекта площади поперечного сечения подкрепляющих ребер оболочки (в см2)
|
№ ребра |
№ сечения |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
0,16 |
0,3 |
-0,08 |
-0,58 |
-0,1 |
-0,04 |
0,1 |
0,32 |
0,01 |
0,1 |
|
2 |
0,1 |
-0,1 |
0,19 |
-0,28 |
0,42 |
0,13 |
-0,26 |
-0,06 |
0,56 |
-0,22 |
Статистические характеристики отклонений от проекта площади поперечного сечения подкрепляющих ребер
|
m, см2 |
D, см4 |
s, см2 |
А |
Е |
R, см2 |
|
|
0,1 |
1,4 |
1,18 |
-0,63 |
0,1 |
7,4 |
Рис. 2. Односторонняя корреляционная функция отклонений от проекта площади поперечного сечения подкрепляющих ребер оболочек
W´1 = 1 + 2 + 3 + 8 + 9 = 23, W´2 = 1 + 3 + 5 + 6 + 4 = 19.
W21 = 1 + 4 + 6 + 8 + 9 = 28, W22 = 1 + 7 + 10 + 6 + 4 = 28.
Для обеих
реализаций mw = 10 (10 + 1)/4
= 22,5. Следовательно, ![]() = 0,02;
= 0,02; ![]() 0,16;
0,16; ![]() = 0,24;
= 0,24; ![]() = 0,24.
Зададимся Р = 0,9, тогда z (5; 0,9) = 0,31 (см. табл. 3.3).
Так как одновременно
= 0,24.
Зададимся Р = 0,9, тогда z (5; 0,9) = 0,31 (см. табл. 3.3).
Так как одновременно ![]() < z и
< z и ![]() < z, то первая
реализация однородна. Аналогичными рассуждениями приходим к выводу, что вторая
реализация также однородна.
< z, то первая
реализация однородна. Аналогичными рассуждениями приходим к выводу, что вторая
реализация также однородна.
Пример 2. Результаты замеров отклонений от проектного размера площади поперечного сечения подкрепляющих ребер оболочек размером 18´18 м были обработаны по предлагаемой в п. 3.3.2 методике. Вычисленные статистические характеристики распределения приведены в табл. 4. Проверка показала, что это распределение не является нормальным, а его плотность распределения записывается в виде (3.17)
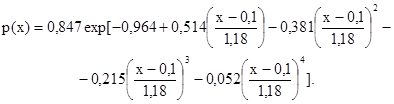
Коэффициенты λi найдены из решения вариационной задачи (3.18). Затем вычислялась корреляционная функция и спектральная плотность по формулам (3.29) - (3.30) и (3.32) - (3.34). Так, например, график односторонней нормированной корреляционной функции приведен на рис. 2.
3.3. Исследование начальных несовершенств и полных прогибов пластин и оболочек как случайных полей
В изложенных ниже примерах массивы чисел замеренных полей не приводятся в силу их громоздкости.
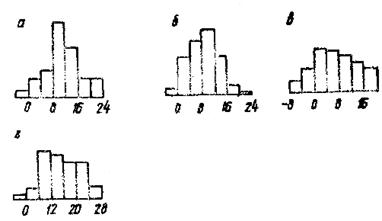
Пример 1. Рассмотрим модель подкрепленной тонкой сферической на квадратном плане оболочки, выполненную из алюминиевого сплава AMц - М с а = b = 300 мм с пологостью 1/7,5 [10]. Толщина оболочки 0,4 мм, высота, ширина и шаг ребер соответственно 0,4 мм, 5 мм и а/8, а/6, а/5. Замер поля начальных несовершенств и полей прогибов производился при двух - трех ступенях нагрузки на профилографе [18]. На рис. 3 приведены гистограммы значений ординат случайных полей начальных и полных прогибов оболочки.
После предварительной обработки поля проверялись на однородность, нормальность, строились периодограммы, вычислялись двумерные спектральная плотность и корреляционная функция.
Величины X2, вычисленные по формуле (3.14) для этих трех полей, равны соответственно: 35,77; 14,44; 10,13. По таблице критерия согласия χ2 [4] находится величина χ2к-3,р. В данном случае χ2к-3,р - χ233;0б95 = 4377. Сравнивая χ2 с χ233;0б95, приходим к выводу, что гипотеза нормальности полей начальных и предкритических прогибов с доверительной вероятностью Р = 0,95 может быть принята.
Предполагая, что
масштаб корреляции исследуемых полей на порядок меньше размера оболочки в
плане, разобьем каждую их реализацию сеткой на 100 прямоугольников и вычислим
для каждого прямоугольника математическое ожидание ![]() и дисперсию
и дисперсию ![]() содержащихся
в нем ординат прогибов по формулам (3.3) и (3.4).
Результаты проверки однородности полей начальных и полных прогибов оболочки по
математическому ожиданию и дисперсии доказывают отсутствие монотонного и
колебательного тренда в исследуемых случайных полях.
содержащихся
в нем ординат прогибов по формулам (3.3) и (3.4).
Результаты проверки однородности полей начальных и полных прогибов оболочки по
математическому ожиданию и дисперсии доказывают отсутствие монотонного и
колебательного тренда в исследуемых случайных полях.
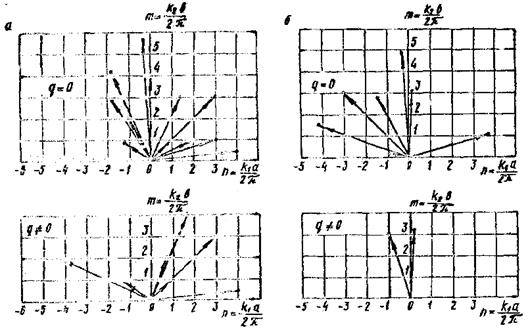
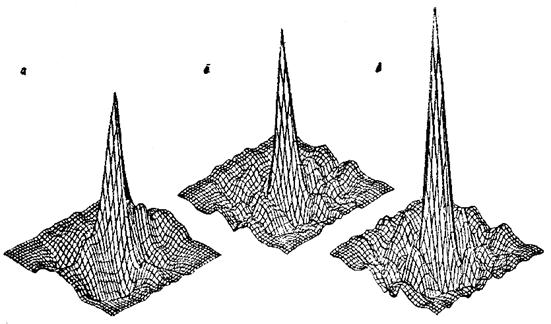
Вычисление периодограмм позволило выделить в полях начальных прогибов 15 ÷ 20 двумерных существенных (амплитуды, большие 0,03 мм) гармоник. Частотные пары гармоник с существенными амплитудами для поля прогибов оболочки представлены на рис. 4, из которого следует, что, во-первых, под действием нагрузки преобладающее развитие получают низкочастотные гармоники, а во-вторых, возникают новые волны, отсутствующие в поле начальных несовершенств. Сечения спектральных плотностей полей прогибов оболочки на различных уровнях нагрузки представлены на рис. 5. Видно, что энергия полей сосредоточена в окрестности нескольких пар волновых чисел.
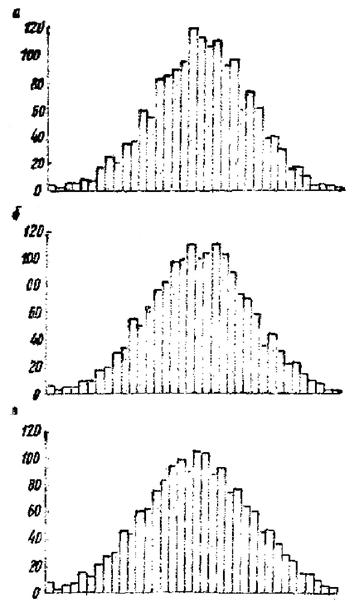
Рис. 3. Гистограммы распределения ординат полей прогибов оболочки:
а - начальных; б, в - полных (j = 0,42qкр, q = 0,8qкр)
Корреляционные функции представлены на рис. 6. Масштабы корреляции для начальных прогибов равны соответственно ρх = 0,038 и ρy = 0,026 м, ρх = ρy = D = 0,012 м; при q = 0,42qкр ρх = 0,033 м, ρy = 0,027 м, D = 0,006 м; при q = 0,8qкр ρх = 0,029 м, ρy = 0,027 м, D = 0,002 м.
Пример 2. Рассмотрим начальную геометрию плоских плит 3´3 м. Гистограммы отклонений точек поверхности плоских плит разных типов представлены на рис. 7 - 9. Здесь чаще всего справедлив нормальный закон. Вычисления статистических характеристик их геометрических несовершенств приводятся в табл. 5.
|
Число замеров |
Математическое ожидание |
Стандарт |
Коэффициент вариации |
Асимметрия |
Эксцесс |
|
|
7а |
69 |
5,3 |
4,5 |
85,7 |
0,1 |
-0,35 |
|
7б |
67 |
6,1 |
7,0 |
114,3 |
0,6 |
0,11 |
|
7в |
211 |
5,5 |
5,7 |
104,9 |
-0,2 |
0,58 |
|
8а |
72 |
11,2 |
5,9 |
52,7 |
-0,01 |
-0,3 |
|
8б |
72 |
8,6 |
5,1 |
59,5 |
-0,02 |
-0,3 |
|
8в |
71 |
7,2 |
6,9 |
96,2 |
-0,06 |
-0,9 |
|
8г |
70 |
11,6 |
6,3 |
54,2 |
-0,05 |
-0,8 |
|
9 |
449 |
7,3 |
6,8 |
92,9 |
-0,25 |
0,25 |
Спектральные плотности поля начальных прогибов и поля отклонений толщины от номинальной плиты 3´3 м представлены на рис. 10. Судя по рисунку, энергия полей сосредоточена в окрестности нескольких волновых чисел.
Рис. 4. Волновые векторы основных двумерных гармоник поля начальных несовершенств и поля дополнительных прогибов оболочек:
а - косинусоиды; б - синусоиды
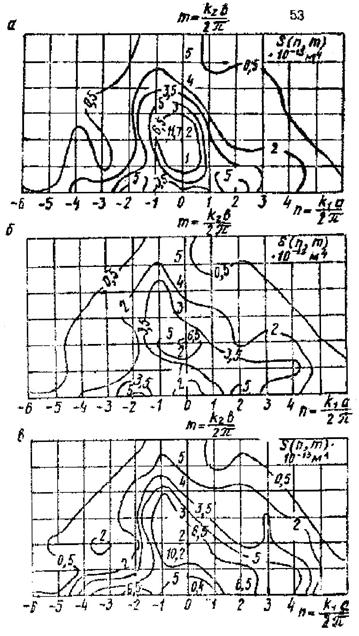
Рис. 5. Сечение двумерных спектральных плотностей полей прогибов оболочки:
а - начальных; б, в - полных (q = 0,42qкр, q = 0,8qкр)
Рис. 6. Двумерные корреляционные функции полей прогибов оболочки:
а - начальных; б, в - полных (q = 0,42qкр, q = 0,8qкр)
Рис. 7. Гистограмма отклонений отметок поля плит типа ПК-3 от номинальных:
а, б - для каждой плиты в отдельности; в - общая по всем плитам
Рис. 8. Гистограмма отклонений отметок поля плит ПК-7 от номинальных:
в - г - разные плиты
Рис. 9. Общая гистограмма отклонений отметок поля плит всех типов от номинальных
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНЫ ОКПМ ИМет УНЦ АН СССР
ИСПОЛНИТЕЛИ: С.А. Тимашев (руководитель темы), Я.М. Зильбер, Л.В. Полуян
2. ОДОБРЕНЫ научно-методической комиссией Госстандарта СССР по стандартизации методов расчета и испытаний на устойчивость секции «Расчеты и испытания на прочность»
УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом ВНИИНМАШ № 274 от 03.09.87.
3. РАЗРАБОТАНЫ ВПЕРВЫЕ
СОДЕРЖАНИЕ
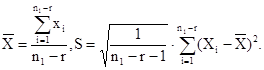 (
(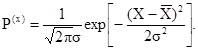 (
(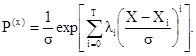 (
(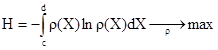 (
(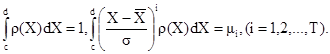 (
(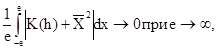 (
(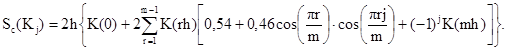 (
(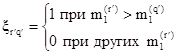 (
( (
( (
( (
( (
(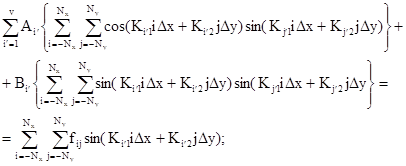 (
(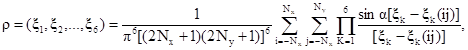 (
(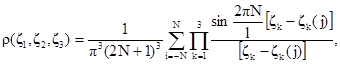 (
(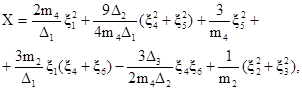 (
( (
(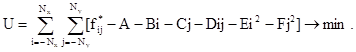 (
(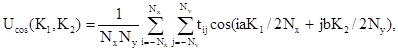 (
(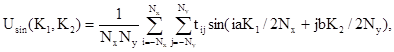 (
(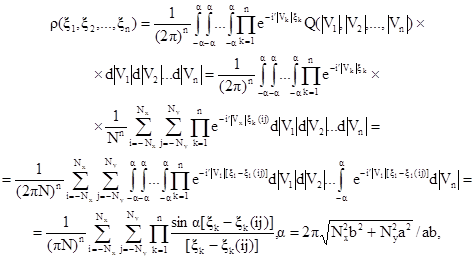 (1.10)
(1.10)