ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ

 

СТАТИСТИЧЕСКИЕ МЕТОДЫ

СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ

СРАВНЕНИЕ ДВУХ СРЕДНИХ В ПАРНЫХ НАБЛЮДЕНИЯХ

ISO 3301:1975

Statistical interpretation of data - Comparison of two means
in the case of paired observations
(MOD)

 

 

Москва

Стандартинформ

2005

 

Предисловие

Задачи, основные принципы и правила проведения работ по государственной стандартизации в Российской Федерации установлены ГОСТ Р 1.0-92 «Государственная система стандартизации Российской Федерации. Основные положения» и ГОСТ Р 1.2-92 «Государственная система стандартизации Российской Федерации. Порядок разработки государственных стандартов»

Сведения о стандарте

1 ПОДГОТОВЛЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» и Научно-исследовательским центром контроля и диагностики технических систем на основе собственного аутентичного перевода стандарта, указанного в пункте 4

2 ВНЕСЕН Управлением технического регулирования и стандартизации Федерального агентства по техническому регулированию и метрологии

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 31 мая 2005 г. № 112-ст

4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 3301:1975 «Статистическое представление данных. Сравнение двух средних в парных наблюдениях» (ISO 3301:1975 «Statistical interpretation of data - Comparison of two means in the case of paired observations», MOD) путем включения отдельных фраз, которые выделены в тексте курсивом, с целью гармонизации с национальными стандартами.

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ 1.5 (подраздел 3.6)

5 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в указателе «Национальные стандарты», а текст изменений - в информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе «Национальные стандарты»

 

ГОСТ Р 50779.23-2005

(ИСО 3301:1975)

Статистические методы

СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ

Сравнение двух средних в парных наблюдениях

Дата введения - 2005-07-01

1 Область применения

Настоящий стандарт устанавливает метод проверки статистической гипотезы о равенстве среднего распределения (далее - среднее) разностей парных наблюдений нулю (предположение о несущественности расхождения между рядами наблюдений) или какому-либо другому заданному значению.

2 Нормативные ссылки

В настоящем стандарте использована нормативная ссылка на следующий стандарт:

ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения (ИСО 3534-1:1993, IDТ)

Примечания

1 Настоящий раздел является дополнительным по отношению к содержанию международного стандарта ИСО 3301:1975 (ISO 3301:1975) и включен для учета основополагающих национальных стандартов в области статистических методов.

2 При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов по указателю «Национальные стандарты», составленному по состоянию на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться замененным (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяют в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены термины по ГОСТ Р 50779.10, а также следующий термин с соответствующим определением:

парные наблюдения (paired observations): Два результата наблюдений определенных свойств или характеристик объекта х_i и у_i называются парными, если они получены:

- как результаты наблюдений над одним и тем же объектом i (из совокупности), причем данные наблюдения относятся к различным условиям получения этих наблюдений (например, сравнение двух методов анализа свойств одного и того же объекта);

- как результаты наблюдений над объектами, идентичными во всех отношениях, кроме предполагаемого систематического различия в некотором интересующем аспекте; в отношении значимости этого различия проводят проверку статистической гипотезы (например, сравнение урожайности двух соседних участков, засеянных семенами различных сортов).

Во втором случае эффективность проверки гипотез зависит от степени уверенности в отсутствии каких-либо других систематических различий между объектами, кроме некоторого возможного различия, в отношении которого проверяют гипотезу.

4 Применение метода для сравнения двух способов обработки экспериментальных данных

Установленный в настоящем стандарте метод проверки статистической гипотезы может быть применен с целью подтвердить различие двух способов обработки. В этом случае можно считать, что результаты наблюдений х_i получены одним способом обработки, а результаты наблюдений y_i - некоторым другим способом. Две серии результатов наблюдений не являются независимыми, поскольку каждому х_i первой серии (первый способ обработки) ставится в соответствие вполне определенное y_i второй серии (второй способ обработки). Термин «способ обработки» понимают в широком смысле. При выявлении возможного систематического расхождения два сравниваемых способа обработки могут относиться к двум методам испытаний, к двум измерительным устройствам или к двум лабораториям. Два способа обработки, выполненные над одним и тем же экспериментальным материалом, могут влиять друг на друга, и полученное значение может зависеть от последовательности обработки. Оптимальный план эксперимента должен устранять возможные систематические смещения. В качестве альтернативы сравнению способов обработки можно рассмотреть воздействие одного способа обработки по сравнению со случаем полного отсутствия обработки.

5 Условия применения метода

Для корректного применения метода необходимо выполнение следующих двух условий:

- последовательность разностей d_i = x_i - y_i является выборкой независимой случайной величины;

- распределение величин d_i = x_i - y_i является нормальным или близким к нормальному.

Если распределение разностей отклоняется от нормального, метод проверки гипотез применим при условии, что объем выборки достаточно велик. При больших отклонениях от нормальности требуется соответственно большая выборка. Однако даже в предельных случаях отклонения от нормальности выборки объемом 100 могут быть достаточными для корректного применения метода в большинстве прикладных задач.

6 Расчетные формулы и правила принятия решения

Примечание - t_1-a(n) - квантиль уровня 1 - a статистики Стьюдента с (n) степенями свободы. Значения t_1-a(n) /  приведены в таблице 1.

Таблица 1 - Значения отношения t_1-a(n) /  для n = n - 1

Пример - Приведенные в таблице 2 данные собраны в процессе исследований, спланированных с целью определить, зависит ли скорость изнашивания шеек коленчатого вала двигателя внутреннего сгорания от типа материала металлических вкладышей подшипников скольжения этого вала.

Таблица 2 - Износ шеек коленчатых валов в течение заданной наработки, измеренный в стотысячных долях дюйма

 

7 Ошибка второго рода

Вероятность отклонения нулевой гипотезы, когда она верна, равна уровню значимости a. Отклонение нулевой гипотезы, когда она верна, называется ошибкой первого рода, и поэтому выбор значения a ограничивает риск такой ошибки.

С другой стороны, можно совершить ошибку второго рода, то есть проверить нулевую гипотезу, когда она неверна. Вероятность 1 - b отклонения нулевой гипотезы, когда она неверна, называется мощностью критерия статистической проверки гипотезы. Вероятность ошибки второго рода в таком случае равна b.

Для заданной выборки п и ошибки первого рода вероятность b зависит не только от истинного среднего D наблюдаемых разностей d_i = x_i - y_i, для которых устанавливают различные альтернативные гипотезы, но также и от стандартного отклонения s_d этих разностей. Это стандартное отклонение неизвестно, и, если п мало, выборка может обеспечить только плохую оценку. В результате невозможно устанавливать верхний предел вероятности ошибки второго рода.

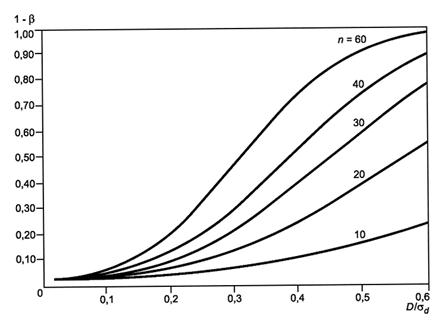
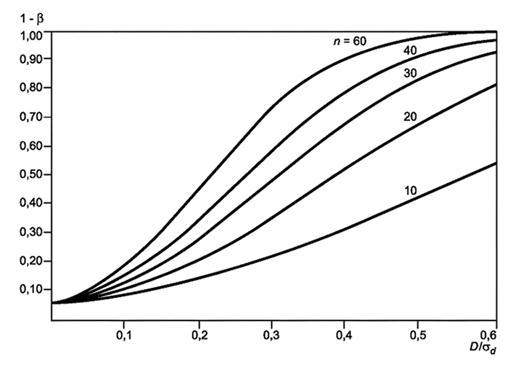
На графиках (рисунки 1 и 2) показаны зависимости между мощностью 1 - b критерия проверки гипотез и истинным средним совокупности, деленным на соответствующее стандартное отклонение (D/s_d) для случая односторонней гипотезы Н₀: D £ 0, различных значений n и уровней значимости 0,05 и 0,01 соответственно.

На основании этих графиков можно сделать следующие заключения:

1) Мощность критерия проверки гипотез однозначно определяется истинным средним D совокупности разностей, измеренных в единицах стандартного отклонения s_d, уровнем значимости a и объемом выборки.

2) Функция мощности является монотонно возрастающей функцией истинного среднего совокупности разностей. Она также монотонно возрастает с ростом объема выборки и уровня значимости a при условии, что D > 0 и a отличается от 0 и 1.

3) Для уровня значимости 0,05 и при объеме выборки 50 достигается мощность 0,95, если истинное среднее разностей превышает половину стандартного отклонения разностей. Для n = 20 такая мощность достигается для D/s_d = 0,78 и больших значений.

Рисунок 1 - Мощность критерия для одной выборки (односторонний критерий), a = 0,01

Рисунок 2 - Мощность критерия для одной выборки (односторонний критерий), a = 0,05

СОДЕРЖАНИЕ