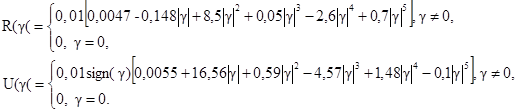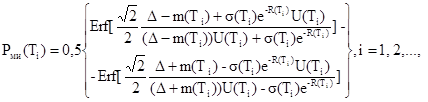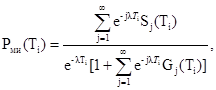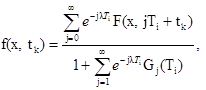ГОССТАНДАРТ РОССИИ
РЕКОМЕНДАЦИЯ
Государственная
система обеспечения единства измерений
Методы
определения межповерочных и
межкалибровочных интервалов средств измерений
МИ 2187-92
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНА И ВНЕСЕНА НПО «ВНИИМ им. Д.И. Менделеева»
2. исполнитель А.Э. Фридман, канд. техн. наук
3. УТВЕРЖДЕНА НПО «ВНИИМ им. Д.И. Менделеева»
4. ЗАРЕГИСТРИРОВАНА ВНИИМС, 10 февраля 1992 г.
Настоящая рекомендация распространяется на средства измерений /далее - СИ/, в том числе рабочие СИ и эталоны, подлежащие государственной или ведомственной поверке, калибровке, сличениям или градуировке /далее - поверке/.
Рекомендация содержит методы определения межповерочных и межкалибровочных интервалов /далее - МПИ/, основанные на предположении о непрерывном /с конечной случайной скоростью/ изменении метрологических характеристик СИ в процессе эксплуатации или хранения.
Рекомендация устанавливает критерии определения МПИ, зависимости от МПИ показателей, соответствующих этим критериям, и алгоритмы вычисления МПИ.
В приложениях 1 и 2 даны рекомендации по способам получения исходных данных о нестабильности СИ, необходимых для определения МПИ, а также примеры расчетов МПИ.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. МПИ называется промежуток времени или наработка между двумя последовательными поверками СИ.
1.2. По порядковому номеру поверки с начала эксплуатации различают 1-й МПИ, 2-й МПИ и т.д.
При определении МПИ для совокупностей однотипных СИ, как правило, назначают единый МПИ для всех СИ, вне зависимости от их возраста и порядкового номера поверки.
1.3. Первичное значение МПИ определяется разработчиком СИ, вносится в эксплуатационную документацию и утверждается при проведении сертификации /государственных приемочных испытаний типа/.
В процессе эксплуатации оно корректируется организациями, осуществляющими поверку СИ, с учетом результатов поверок.
Их значения целесообразно выбирать в месяцах /эксплуатации или наработки/ из ряда: 0,25; 0,5; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 15; 18; 21; 24; 30 и т.д. через 6 месяцев.
При определении интервала между градуировками СИ в других единицах времени /часах, сутках и др./ рекомендуется пользоваться этим же числовым рядом.
1.5. Назначение МПИ осуществляется на основании моделирования зависимости показателей точности или метрологической надежности СИ от времени /наработки/, прошедшего с момента последней поверки.
1.6. При моделировании изменения метрологических характеристик /далее MX/ СИ рекомендуется руководствоваться следующими положениями.
1.6.1. Определение MX и их формы выражения должны соответствовать ГОСТ 8.009.
1.6.2. При определении МПИ выбирается MX, определяющая состояние метрологической исправности данного типа СИ, т.е. та МХ, которая соответствует критерию исправности СИ при поверке /например, основная погрешность СИ; среднее квадратическое отклонение случайной составляющей основной погрешности, если последняя существенна, и т.д./.
1.6.3. Если состояние метрологической исправности определяют несколько MX, выбирают ту из них, по которой обеспечивается наибольший процент забракования при поверке.
1.6.4. Если выбрать одну MX в соответствии с пп. 1.6.2 и 1.6.3 невозможно, то рекомендуется определить ряд МПИ с учетом нестабильности каждой MX и затем выбрать из них наименьший.
1.6.5. Моделирование изменений MX многозначных мер и измерительных приборов в зависимости от диапазона измерений приводит к неоправданному усложнению расчетов. Поэтому для таких СИ рекомендуется переходить к обобщенным характеристикам точности диапазона в целом. В качестве этих характеристик рекомендуются:
при оценке первичного МПИ на этапе разработки СИ по исходным данным о нестабильности комплектующих элементов - характеристики аддитивной и мультипликативной погрешностей СИ;
при корректировке МПИ на этапе эксплуатации с учетом результатов поверок СИ данного типа - максимальная по абсолютному значению относительная или приведенная погрешность СИ, соответствующая рассматриваемому моменту времени; погрешность в граничной точке диапазона или другой «опасной» точке /точке диапазона, в которой сравнительно велика вероятность превышения предела допускаемых значений погрешности/.
После выбора одной или нескольких обобщенных характеристик точности СИ следует определить значения МПИ, соответствующие процессам дрейфа каждой из этих характеристик, и в качестве МПИ СИ взять наименьший из них.
1.7. При определении МПИ следует учитывать способ поверки СИ. В рекомендации рассмотрены следующие основные способы поверки.
1.7.1. Установление действительных значений или градуировка /далее - градуировка/ всех СИ, поступивших на поверку /далее - первый способ поверки/.
1.7.2. Определение пригодности СИ к применению по нормам стабильности /с забракованием тех СИ, изменение действительного значения или градуировочной характеристики которых за МПИ превысило предел допускаемой нестабильности, установленный для СИ данного типа/ и градуировка СИ, признанных годными /далее - второй способ поверки/.
2. Критерии для определения межповерочных интервалов
2.1. Применяются критерии назначения МПИ двух видов - нормируемые показатели метрологической надежности /нестабильности/ СИ и экономический критерий оптимальности МПИ, обеспечивающий максимальный экономический эффект эксплуатации СИ.
2.2.1. Предел допускаемых
значений доверительных границ нестабильности MX СИ ![]() за МПИ при заданной доверительной вероятности Р.
за МПИ при заданной доверительной вероятности Р.
2.2.2. Предел допускаемых
значений вероятности метрологической исправности СИ ![]() в момент
очередной поверки /либо предел средней доли СИ, забракованных при поверке,
в момент
очередной поверки /либо предел средней доли СИ, забракованных при поверке, ![]()
Рми является аналогом показателя надежности - вероятности безотказной работы.
2.2.3. Предел допускаемых
значений коэффициента метрологической исправности СИ ![]() , равного средней доле МПИ, в
течение которой СИ находилось в метрологически исправном состоянии.
, равного средней доле МПИ, в
течение которой СИ находилось в метрологически исправном состоянии.
Кми является аналогом показателя надежности - коэффициента готовности.
2.3. Экономическим критерием оптимальности МПИ является условный минимум экономических издержек эксплуатации СИ, зависящих от значения МПИ. Эти издержки складываются из убытков из-за нестабильности СИ и расходов, связанных с проведением поверок и ремонтов СИ, забракованных при поверке.
2.4. Критерий ![]() применяется при первом способе поверки.
применяется при первом способе поверки.
Критерии ![]() и
и ![]() применяются при втором и третьем способах поверки.
применяются при втором и третьем способах поверки.
При этом метрологическая исправность СИ определяется как соответствие установленному в техдокументации пределу допускаемых значений:
нестабильности MX СИ - при втором способе,
MX СИ - при третьем способе.
Экономический критерий можно применять при любом способе поверки СИ.
2.5. Численные значения критериев назначает орган государственной или ведомственной метрологической службы, проводящий поверку СИ, по согласованию с предприятием /организацией/, применяющим это СИ. При этом рекомендуется руководствоваться следующим.
2.6. При
поверке СИ первым способом значение ![]() следует устанавливать с учетом значения
предела допускаемых значений доверительной погрешности СИ, указанного в
поверочной схеме, а именно: значение доверительной вероятности Р должно
равняться доверительной вероятности, которой соответствует доверительная погрешность СИ; значение
предела допускаемых значений нестабильности MX должно обеспечивать предел доверительной погрешности с учетом
других ее составляющих.
следует устанавливать с учетом значения
предела допускаемых значений доверительной погрешности СИ, указанного в
поверочной схеме, а именно: значение доверительной вероятности Р должно
равняться доверительной вероятности, которой соответствует доверительная погрешность СИ; значение
предела допускаемых значений нестабильности MX должно обеспечивать предел доверительной погрешности с учетом
других ее составляющих.
2.7. При
поверке СИ вторым способом значение ![]() рекомендуется принимать равным пределу
допускаемых значений доверительной вероятности, указанному в поверочной схеме,
значение
рекомендуется принимать равным пределу
допускаемых значений доверительной вероятности, указанному в поверочной схеме,
значение ![]() - равным
0,5 /1 + Р/.
- равным
0,5 /1 + Р/.
2.8. Как следует из пп. 2.6 и 2.7 и ГОСТ 8.381, для первичных и вторичных эталонов
![]()
![]() при определении
при определении ![]() Р = 0,99.
Р = 0,99.
2.9. При поверке рабочих эталонов /образцовых СИ/ способом, указанным в пп. 1.7.3, рекомендуются значения критериев, указанные в табл. 1.
Таблица 1
|
|
|
|
|
Поверка СИ, применяемых в здравоохранении, экологии, при учете материальных ценностей, а также СИ, метрологический отказ которых может привести к значительным экономическим потерям |
0,95 ¸ 0,99 |
0,975 ¸ 0,995 |
|
Поверка СИ, не связанных со здоровьем и жизнью людей, и СИ, метрологический отказ которых не вызывает большого ущерба |
0,90 ¸ 0,95 |
0,95 ¸ 0,975 |
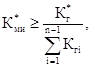 (1)
(1)
где Кгi, i = 1, ..., n - 1 - коэффициент готовности i-го технического средства.
2.10.1. При проведении обоснований по п. 2.10 рекомендуется учитывать, что погрешность измерений включает в себя не только основную погрешность СИ, но и другие составляющие /методическую погрешность, дополнительные погрешности и т.д./, и, следовательно, измерительная задача может быть выполнена правильно и неисправным СИ.
Тогда
![]() (2)
(2)
где: ![]() - нормируемое значение вероятности выполнения измерительной
задачи,
- нормируемое значение вероятности выполнения измерительной
задачи,
Рз/и, Рз/н - условные вероятности выполнения измерительной задачи при условии, что СИ метрологически исправно и неисправно.
2.11. Если МПИ определяется
по статистическим данным о нестабильности одной MX из нескольких нормируемых, либо в одной наиболее опасной точке
диапазона измерений, значение критерия, определенное в соответствии с пп. 2.6 ¸ 2.10, должно быть
скорректировано с учетом средней доли учитываемых метрологических отказов СИ. В
этом случае ![]() определится следующим образом
определится следующим образом
![]() (3)
(3)
где ![]() - значение критерия, определенное в соответствии с пп. 2.6 ¸ 2.10,
- значение критерия, определенное в соответствии с пп. 2.6 ¸ 2.10,
æ - средняя доля учитываемых метрологических отказов, % /определяется при статистической обработке результатов поверок СИ данной группы/.
3. исходные ДАННЫЕ ДЛЯ определения МПИ
3.1. Статистические характеристики процесса дрейфа MX СИ.
3.1.1. Зависимость математического ожидания нестабильности MX СИ за время /наработку/ t в виде
3.1.2. Зависимость СКО нестабильности MX СИ за время /наработку/ t в виде
s(t) = so∙ert. (5)
3.1.3. Зависимость коэффициента асимметрии распределения нестабильности MX СИ за время /наработку/ t в виде
3.1.4. Рекомендации по определению m(t), s(t) и g(t) приведены в Приложении 1.
3.2. При проведении поверки вторым и третьим способами - предел D допускаемой нестабильности MX /второй способ/ или допускаемых значений MX /третий способ/.
3.3. При проведении поверки третьим способом - интенсивность l явных отказов СИ, контрольный допуск при поверке Dс (Dс £ D).
3.4. При определении МПИ по критерию метрологической надежности /нестабильности/ - значение критерия /n*, Р*ми или К*ми, в соответствии с п. 2.2/.
3.5. При определении МПК по экономическому критерию - следующие данные.
3.5.1. Средние экономические потери из-за погрешности измерений, отнесенные к единице времени, C1 (х) при условии, что МХ СИ равна х.
С1 (х) = С1 ∙ xl. (7)
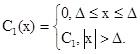 (8)
(8)
3.5.4. При применении СИ для контроля качества продукции или поверки СИ вторым и третьим способами
С1(х) = qпб ∙ Рпб(х) + qлб ∙ Рлб(х), (9)
где qпб, qлб - средний экономический ущерб в единицу времени из-за пропущенного брака /признания годными бракованных деталей, неисправных СИ/ и ложного брака /забракования годных деталей, СИ/ соответственно,
Рпб(х), Рлб(х) - условные вероятности пропущенного и ложного браков соответственно при условии, что MX СИ равна х.
Для определения Рпб(х), Рлб(х) должны быть заданы:
sд - СКО распределения погрешности контролируемого параметра детали, СИ,
Dд - предел допускаемых значений контролируемого параметра детали, СИ.
3.5.5. Переменная часть /не зависящая от числа поверок/ С2 средних расходов потребителя СИ, понесенных в связи с проведением одной поверки.
3.5.6. Переменная часть С3 средних расходов потребителя СИ, понесенных в связи с проведением одного ремонта.
Примечания.
1. При проведении поверки /ремонта/ в сторонней организации С2 (С3) складывается из цены поверки /ремонта/, транспортных расходов и недополученной прибыли из-за изъятия СИ из производственного процесса на период проведения поверки /ремонта/.
При проведении поверки /ремонта/ силами своей организации С2 (С3) складывается из части себестоимости поверки /ремонта/, не зависящей от числа поверок /ремонтов/ /заработная плата при сдельной оплате труда, расходуемые материалы, электроэнергия и т.д./, и недополученной прибили из-за изъятия СИ.
2. При проведении поверки первым способом принимают С3 = 0.
4. Методы определения МПИ ПО нормируемым показателям метрологической надежности /нестабильности/
4.1. Поверка первым способом
4.1.1. Выбирают значение t1 из членов ряда, приведенного в п. 1.4.
4.1.2. Вычисляют m(Т1), s(Т1), g(Т1) по формулам (4) ¸ (6), находят R(T1) и U(T1) по формулам
4.1.3. Вычисляют nр(Т1) по формуле
nр(Тi) = max {np1(Ti), np2(Ti)}, i = 1, 2, ..., (11)
где
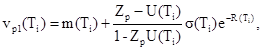
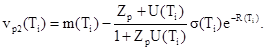
Zp - квантиль нормального распределения при доверительной вероятности Р.
4.1.4. Выбирают из членов ряда, приведенного в п. 1.4, значение Т2, ближайшее к Т1. Если np (T1) > v*p, то Т2 < Т1, если np (T1) < v*p, то Т2 > Т1.
4.1.5. Повторяют операции, указанные в пп. 4.1.2, 4.1.3. Если после этого окажется, что для n = 2
то приближения заканчиваются, и принимают равным min (T1, T2).
4.1.6. Если (11а) не выполняется, принимают Т3, ближайшее к Т2, и повторяют операции, указанные в пп. 4.1.2 ¸ 4.1.5, и т.д.
Приближения заканчиваются на n-м шаге, при котором впервые будет выполнено (11а). МПИ принимают равным
T = min ∙ (Tn-1, Tn). (12)
4.2.
Поверка вторым способом, нормируется ![]()
4.2.1. Выполняют операции, описанные в пп. 4.1.1 и 4.1.2. Вычисляют Рми(Т1) по формуле
где 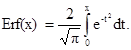
4.2.2.
Выбирают из членов ряда, приведенного в п. 1.4, значение Т2, ближайшее к Т1.
Если ![]() , то Т2 > Т1; если
, то Т2 > Т1; если ![]() , то Т2 < Т1.
, то Т2 < Т1.
4.2.3. Повторяют операции, указанные в пп. 4.2.1 и 4.2.2, для i = 2, 3, ...., до n, удовлетворяющего условию
МПИ определяют в соответствии с (12).
4.3. Поверка вторым способом,
нормируется ![]()
4.3.1. Выбирают значение Т1 из членов ряда, приведенного в п. 1.4.
4.3.2. Для каждого tк = 0,01k T1, k = 0,1, ..., 100, вычисляют Рми (tк) по формуле (13), в соответствии с п. 4.2.1.
4.3.3. Вычисляют Кми (Т1) по формуле
4.3.4.
Выбирают из членов ряда, приведенного в п. 1.4, значение Т2, ближайшее к T1. Если ![]() , то Т2 > T1; если
, то Т2 > T1; если ![]() , то Т2 < Т1.
, то Т2 < Т1.
4.3.5. Повторяют операции, указанные в пп. 4.3.1 ¸ 4.3.3, для i = 2, 3, ..., до n, удовлетворяющего условию
МПИ определяют в соответствии с (12).
4.4.
Поверка третьим способом, нормируется ![]()
4.4.1. Выполняют операции, описанные в пп. 4.1.1.
4.4.2. Вычисляют Pми(T1) по формуле
где
Gi(Ti) = max {0,5[Erf(Bj (Ti)) - Erf (-Aj (Ti))]; 0},
Si(Ti) = max {0,5[Erf(Dj (Ti)) - Erf(-Cj (Ti))]; 0},
Aj (Ti), Bj (Ti), Cj (Ti), Dj (Ti) - вычисляется последовательно для j = 1, 2, 3, ... по формулам
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4.4.3. Выбирают Т2 аналогично п. 4.2.2.
4.4.4. Повторяют операции, описанные в п.п. 4.4.1 ¸ 4.4.3, для i = 2, 3, ..., до n, удовлетворяющего условию (14). МПИ определяют в соответствии с (12).
4.5. Поверка третьим
способом, нормируется ![]()
4.5.1. Выполняют операции, описанные в п. 4.4.1.
4.5.2. Для каждого tk = 0,01kТ1, k = 0, 1, ... 100, вычисляют Рми (tk) по формуле
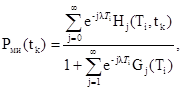 (18)
(18)
где
Hj (Ti, tk) = max {0,5 [Erf (Lj (Ti, tk)) - Erf (-Ej (Ti, tk))]; 0},
Ej (Ti, tk), Lj (Ti, tk) - вычисляются последовательно для j = 0, 1, 2, ... по формулам
![]()
![]()
![]()
![]() (19)
(19)
Aj (Ti), Bj (Ti), Cj (Ti) - как в (17).
4.5.3. Вычисляют Кми (Т1) по формуле (15).
4.5.4. Выбирают T2 аналогично п. 4.3.4.
4.5.5. Повторяют операции, описанные в пп. 4.5.1 ¸ 4.5.4, для i = 2, 3, ..., до n, удовлетворяющего (16).
МПИ определяют в соответствии с (12).
5. метод определения мпи по экономическому критерию оптимальности
5.1. Применение СИ в соответствии с п. 3.5.2
5.1.1. Выбирают значение T1 из членов ряда, приведенного в п. 1.4.
5.1.2. Вычисляют Рбр (Т1) в соответствии с п. 5.4.
5.1.3. Для каждого tk = 0,01 kT1, k = 0, 1, ..., 100, вычисляют Вl (tk) по формуле (20)
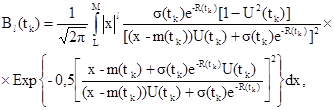 (20)
(20)
где
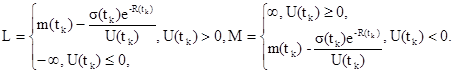
При поверке СИ третьим способом
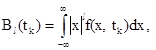
где
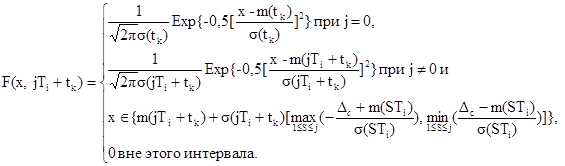
5.1.4. Вычисляют средние экономические издержки эксплуатации СИ в единицу времени W(T1) при МПИ, равном T1, по формуле
![]() (22)
(22)
5.1.5. Повторяют операции, описанные в пп. 5.1.2 ¸ 5.1.4, для значений Т2 и Т3 ближайших к Т1 членов ряда, приведенного в п. 1.4 /Т2 < Т1, T3 > Т1/. Если при этом W(T1) < W(T2) и W(T1) < W(T3), то МПИ равно T1. Если W(T1) > W(T2) и W(T1) < W(T3), выбирают Т4, ближайшее к T2, из членов ряда, приведенных в п. 1.4 /Т4 < Т2/. Если W(T1) < W(T2) и W(T1) > W(T3), выбирают Т4, ближайшее к Т3 /Т4 > Т3/.
5.1.6. Повторяют операции, описанные в пп. 5.1.2 ¸ 5.1.4, для значения Т4. Затем сравнивают W(T1), W(T2) (W(T3)) и W(T4) и аналогично п. 5.1.5. выносят решение о назначении МПИ, либо выборе T5.
Приближения продолжают до выполнения условий
W(Tn-1) < W(Tn-2), W(Tn) > W(Tn-1). (23)
МПИ принимают равным Т = Тn-1.
5.2. Применение СИ в соответствия с п. 3.5.3
5.2.1. Выбирают значение T1 из членов ряда, приведенного в п. 1.4.
5.2.2. Вычисляют Рми /T1/ в соответствии с п. 5.1.2.
5.2.3. Вычисляют Кми /T1/ в соответствии с пп. 4.3.2, 4.3.3, если поверка СИ проводится первым или вторым способом и в соответствии с пп. 4.5.1 ¸ 4.5.3, если поверка проводится третьим способом.
5.2.4. Вычисляют W (T1) по формуле
![]() (24)
(24)
5.2.5. Повторяют операции, описанные в пп. 5.2.1 ¸ 5.2.4, для значений T2 и Т3, выбранных в соответствии с п. 5.1.5. Сравнивают W(T1), W(T2) и W(T3), выбирают Т4 и т.д., в соответствии с пп. 5.1.5, 5.1.6 до выполнения (23) и определения МПИ.
5.3. Применение СИ в соответствии с п. 3.5.4
5.3.1. Выбирают значение T1 из членов ряда, приведенного в п. 1.4.
5.3.2. Вычисляют Рми /T1/ в соответствии с п. 5.1.2.
5.3.3. Для каждого tk = 0,01 k Т1, k = 0,1 ..., 100, вычисляют f (x, tk).
Если поверка СИ проводится первым или вторым способом, при МПИ, равном Ti,
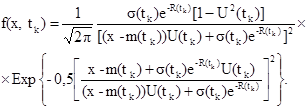 (25)
(25)
Если поверка СИ проводится третьим способом, f(x, tk) определяется (21).
5.3.4. Зачисляют средние вероятности ошибок измерений при МПИ, равном T1 в момент tк, по формулам
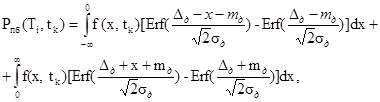 (26)
(26)
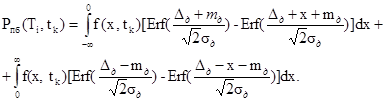
5.3.5. Вычисляют средние за МПИ вероятности ошибок измерений при МПИ, равном T1, по формулам
![]() (27)
(27)
![]() (28)
(28)
5.3.6. Вычисляют W(Т1) по формуле
![]() (29)
(29)
5.3.7. Повторяют операции, описанные в пп. 5.3.1 ¸ 5.3.6, для значений Т2 и Т3, выбранных в соответствии с п. 5.1.5. Сравнивают W(T1), W(Т2) и W(Т3). выбирают Т4 и т.д., в соответствии с рекомендациями п. 5.1.5, до выполнения (23) и определения МПИ.
5.4. Вероятность забракования СИ при поверке Рбр (Ti) определяется следующим образом:
при поверке первым способом Рбр (Ti) = 0;
при поверке вторым способом Рбр (Ti) = 1 - Рми (Ti);
при поверке третьим способом
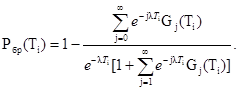
ПРИЛОЖЕНИЕ 1
ИСХОДНЫЕ ДАННЫЕ ДЛЯ определения межповерочных ИНТЕРВАЛОВ
Как следует из настоящих рекомендаций, основными исходными данными, необходимыми для определения МПИ, являются параметры распределения нестабильности СИ за время /наработку/ t, указателе в п. 3.1, - mk (k = 0, ..., P), s0, r, gk (k = 1, ..., q). Оценки этих параметров должны быть получены из имеющихся в распоряжении разработчика СИ или его владельца материалов - проектной документации, технических условий, протоколов испытаний, поверки и т.д. В принципе возможны следующие источники информации:
испытания СИ или его отдельных блоков,
данные о нестабильности элементов СИ,
показатели надежности СИ, нормируемые или подтвержденные испытаниями,
результаты поверок СИ.
Точность прогнозирования МПИ прежде всего обусловлена точностью исходных данных. Поэтому, рассматривая возможные источники информации о нестабильности СИ, следует установить для них шкалу предпочтения.
При назначении первичного значения МПИ на этапе разработки СИ или организации его серийного производства в принципе могут быть использованы три из перечисленных выше источников информации. Наиболее предпочтительными представляются испытания партии СИ с целью оценки их нестабильности. Такие испытания могут быть проведены специально, совмещены с контрольными испытаниями на надежность, либо проведены в виде подконтрольной эксплуатации первых партий СИ, выпущенных из производства.
Нередко отсутствует возможность проведения таких испытаний до момента назначения первичного МПИ, но имеется информация о результатах испытаний /в процессе разработки СИ/ отдельных элементов СИ, существенно влияющих на нестабильность СИ в целом /измерительные преобразователи, опорные элементы систем компенсации при настройке и др./, либо информация изготовителей комплектующих элементов об их нестабильности. В этом случае целесообразна расчетная оценка показателей нестабильности СИ по данным о нестабильности элементов СИ. /Соотношение этих способов примерно такое же, как методов поэлементной поверки и поверки сличением - поверка сличением предпочтительнее, но иногда приходится ограничиваться поэлементной поверкой, которая в принципе тоже может быть достаточно достоверной/.
В тех случаях, когда нет возможности оценки нестабильности СИ этими способами, рекомендуется использовать показатели надежности СИ, нормируемые в ТУ или фактические, подтвержденные испытаниями. Если же нет и такой информации, МПИ может быть назначен экспертным методом, исходя из опыта эксплуатации аналогичных СИ или интуиции разработчиков СИ.
В процессе эксплуатации СИ первичное значение МПИ может быть уточнено с учетом результатов поверок. Это идеальная информация: с одной стороны, она отражает не только конструктивные особенности СИ, но и специфику эксплуатации каждого экземпляра /интенсивность применения, условия измерения, качество обслуживания и т.д./; с другой стороны, получение этой информации не связано с дополнительными расходами, следует только организовать ее регистрацию. Поэтому на этапе эксплуатации СИ результаты поверки - единственный вид информации, который следует принимать во внимание при анализе нестабильности СИ.
1. испытания на нестабильность
1.1. Формируют партию СИ для проведения испытаний. Объем партии N должен быть не менее 30.
1.2. Отобранную партию СИ подвергают испытаниям в обычном или форсированном режиме (с известным коэффициентом ускорения). Через равные промежутки времени или наработки Dt поводят измерения контролируемых параметров. Промежуток должен быть такой, чтобы приращение МХ за Dt xj (Dt) могло быть измерено с приемлемой достоверностью. Это обеспечивается соблюдением следующих условий - не менее, чем у половины партии xj (Dt) должны быть: значимы на фоне случайных погрешностей СИ; не менее чем в 3 раза больше предела допускаемой погрешности СИ, применяемого для оценки нестабильности. Длительность испытаний должна быть не менее 3Dt.
1.3. По результатам измерений нестабильности xj (iDt), j=1, 2, ..., N за интервалы Dt, 2Dt, 3Dt и т.д., до nDt включительно, находят выборочные характеристики распределения нестабильности СИ
![]()
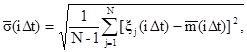 (30)
(30)
![]()
Все три характеристики оценивают, если N ³ 100.
При 30 £ N < 100 по (25) оценивают только ![]() и
и ![]() , и
принимают
, и
принимают ![]() .
.
1.4.
Подбирают аппроксимирующие полиномы для функций m(t), g(t), а
также значения s0 и ![]()
![]()
s(t) = s0 ∙ ert.
Постоянные коэффициенты mk, gk, s0 и r подбирают методом наименьших квадратов для функций m(t), g(t) и lns(t). Порядки полиномов lm и lg выбирают следующим образом:
при первом и втором способах поверки - оптимальными по критерию малости погрешности из ряда 1 ¸ 5;
при третьем способе поверки - lm = 1 ¸ 5, g(t) = 0.
На этом заканчивается экспериментальная оценка характеристик нестабильности СИ.
2. Оценка нестабильности СИ по известным характеристикам нестабильности комплектующих элементов
2.1. Аналитическим или экспериментальным способом определяют функцию преобразования СИ
Y = j [X, h1, ..., hn], (32)
где: X - измеряемая величина,
Y - результат измерения,
hi - i-й параметр элементов СИ,
n - общее число параметров элементов СИ, влияющих на Y.
Коэффициент влияния i-го параметра одного из элементов СИ определяется как
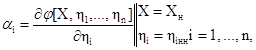 (33)
(33)
где Хн, hiн - номинальные значения X и hi.
2.2. Характеристики нестабильности СИ находят по формулам (31), где
![]()
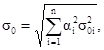
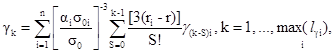
mki, s0i, ri, gki - характеристики нестабильности i-го параметра элемента СИ.
2.3. Формулы (34) предполагает взаимную независимость влияния нестабильности элементов на нестабильность СИ. Это допущение приемлемо для оценки первичного МПИ, т.к. дает оценку нестабильности СИ сверху, а МПИ - снизу. Если разработчик СИ может определить корреляционные зависимости параметров элементов СИ, это допущение может быть снято, а формулы (34) - уточнены.
3. Ориентировочная оценка нестабильности СИ по известным характеристикам его надежности
3.1. Известна /или нормируется/ вероятность безотказной работы СИ P(t) за время t
3.1.1. Если удается оценить, хотя бы ориентировочно, средний процент q метрологических отказов в общем потоке отказов СИ, оценивают вероятность работы СИ без метрологических отказов Pм(t) за время t
![]()
Если q не известно, принимают Pм(t) = P(t).
3.1.2. Минимальный объем информации вынуждает принять допущение о нормальном распределения MX. Поэтому полагают g(t) = 0.
При этом m (t) = 0, а СКО распределения нестабильности
s(t) = s0еrt,
где s0 - СКО распределения погрешности градуировки СИ.
![]() - скорость
приращения логарифма СКО нестабильности СИ,
- скорость
приращения логарифма СКО нестабильности СИ,
lp - квантиль нормального распределения при вероятности
![]()
t - время /наработка/, на которое нормируется Pм(t),
D - предел допускаемых значений погрешности /нестабильности/ СИ.
3.1.4. Принимают допущение о том, что дрейф MX СИ заключается в линейном изменении m(t) при неизменном СКО s0.
При этом s(t) = s0,
m(t) = m1 ∙ t,
где
![]()
P = Pм (t),
s0, t, lp, D - как в п. 3.1.3.
3.1.5. Находят два значения МПП:
Т1, соответствующее
m(T1) = 0, s(T1) = ![]() ,
,
где
![]()
T2, соответствующее
m(T2) = m1T2, s(T2) = s0,
где
![]()
В качестве МПИ принимают Т = min [Т1, Т2].
3.2. Известна /или нормируется/ средняя наработка до отказа Тср
3.2.1. Как и в п. 3.1, полагают l(t) = 0.
3.2.2. Принимают допущение о симметричности распределения нестабильности СИ относительно нуля.
При этом m(t) = 0, s(t) = s0ert, где ![]() , s0 - как в п. 3.1.
, s0 - как в п. 3.1.
3.2.3. Принимают допущение о том, что дрейф MX СИ заключается в линейном изменении m(t) при неизменном СКО s0.
При этом s(t) = s0, m(t) = m1 ∙ t, где ![]() , s0 и D - как в п. 3.1.
, s0 и D - как в п. 3.1.
3.2.4. Находят два значения МПИ:
T1, соответствующее
m(T1) = 0, ![]() где
где ![]()
и Т2, соответствующее
m(T2) = m1T2, s(T2) = s0, где ![]()
В качестве МПИ принимают Т = min [T1, T2].
4. Оценка нестабильности СИ по результатам поверок
4.1. При проведении поверок регистрируют значения MX каждого экземпляра СИ.
4.1.2. Проводят статистическую обработку сгруппированных результатов поверок в соответствии с пп. 1.3 ¸ 1.4.
4.2.1. Группируют результаты поверок аналогично п. 4.1.1. Далее проводят статистическую обработку сгруппированных результатов поверок в следующем порядке.
4.2.2. Формируют 4 области значений Wj MX СИ х следующим образом
W1 = (-¥, -D), W2 = [-D, 0),
W3 = [0, D], W4 = (D, ¥).
4.2.3.
Подсчитывают статистические вероятности ![]() попадания значения МХ СИ в j-ю область при проведении i-й поверки
попадания значения МХ СИ в j-ю область при проведении i-й поверки
![]()
4.2.4.
Определяет для каждого i квантили ![]() , j = 1, 2, 3, нормального распределения,
соответствующие статистическим вероятностям
, j = 1, 2, 3, нормального распределения,
соответствующие статистическим вероятностям ![]() .
.
4.2.5. Для каждого ti находят статистические оценки характеристик распределения нестабильности
![]()
![]()
![]() (35)
(35)
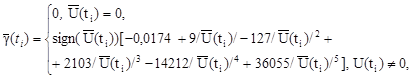
![]() - по формуле /10/ в зависимости от
- по формуле /10/ в зависимости от ![]() , где D - предел допускаемых значений MX.
, где D - предел допускаемых значений MX.
4.2.6. Подбирают аппроксимирующие полиномы для функций m(t), g(t), и параметры s(t) - s0 и r в соответствии с п. 1.4.
4.3. При проведении поверок регистрируют только альтернативный признак годности СИ и знак значения MX СИ, признанных негодными в результате поверки.
4.3.1. Группируют результаты поверок аналогично п. 4.1.1. Далее проводят статистическую обработку сгруппированных результатов поверок в следующем порядке.
4.3.2. Формируют 3 области значений Wj МХ СИ х
W1 = (-¥, -D), W2 = [-D, D], W3 = (D, ¥).
4.3.3. Определяют
статистические вероятности ![]() и квантили
и квантили ![]() аналогично пп. 4.2.3 и 4.2.4.
аналогично пп. 4.2.3 и 4.2.4.
4.3.4. Находят статистические
оценки ![]() и
и ![]() по следующим формулам
по следующим формулам
![]()
![]() (36)
(36)
4.3.5. Подбирают аппроксимирующий полином для функций m(t) и параметры s(t) - s0, r в соответствии с п. 1.4.
4.4. При проведении поверок регистрируют только альтернативный признак годности СИ, поверка первым или вторым способом.
4.4.1. Группируют результаты поверок аналогично п. 4.1.1. Далее проводят статистическую обработку сгруппированных результатов поверок в следующем порядке.
4.4.2.
Аналогично п. 3.1.3 принимают допущение о симметричности относительно нуля
распределения погрешности СИ, для каждого ti находят ![]() и подбирают аппроксимирующее значение r для функции s(t).
и подбирают аппроксимирующее значение r для функции s(t).
4.4.3.
Аналогично п. 3.1.4 принимают допущение о линейном дрейфе m(t) при неизменном ![]() находят
находят ![]() и аппроксимирующий полином m(t).
и аппроксимирующий полином m(t).
4.4.4. Аналогично п. 3.1.5 находят два значения МПИ, соответствующие п. 4.4.2 и 4.4.3.
В качестве МПИ, соответствующего результатам поверок и принятому значения критерия, принимают наименьший из них.
4.5. Третий способ поверки, известна только средняя доля СИ, забракованных при поверке.
4.5.1. Определяют статистическую оценку интенсивности явных отказов СИ l
![]() (37)
(37)
где ![]() - средняя доля СИ, забракованных из-за явных отказов в процессе
эксплуатации и при поверке /по признакам, не связанным со значениями
метрологических характеристик/,
- средняя доля СИ, забракованных из-за явных отказов в процессе
эксплуатации и при поверке /по признакам, не связанным со значениями
метрологических характеристик/,
Т - МПИ, принятый до корректировки.
4.5.2. Определяют статистическую оценку Рми /Т/
![]() (38)
(38)
где ![]() - средняя доля
СИ, забракованных при поверке по значениям метрологических характеристик.
- средняя доля
СИ, забракованных при поверке по значениям метрологических характеристик.
4.5.3. Принимают ![]()
4.5.4. Аналогично п. 3.1.3 принимают допущение о симметричном дрейфе погрешности СИ.
По формуле (17) определяют значение r, соответствующее
T, ![]()
4.5.5. Аналогично п. 3.1.4 принимают допущение о линейном дрейфе m(t)=m1t при неизменном s(t) = s0.
По формуле (17) определяют значение m1, соответствующее
Т, ![]()
4.5.6. Аналогично п. 3.1.5 находят два значения МПИ, соответствующие принятому значению критерия, при выполнении пп. 4.5.4 и 4.5.5.
В качестве МПИ, соответствующего результатам поверок, принимают наименьший из них.
Приложение 2
примеры расчетов межповерочных интервалов
1. Пример 1. (к п. 4.2 и п. 3 Приложения 1)
Поверка вторым способом.
Информация о нестабильности отсутствует. Известно только среднее время до наступления отказа Тср = 2 г. СКО погрешности градуировки СИ s0 = 0,3D. Найти МПИ, соответствующий условию Рми (Т) = 0,9.
В соответствии с п. 3.2 Приложения ![]()
В соответствии с п. 3.1.3
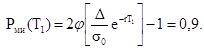
Отсюда ![]() и
и
![]()
Далее,
![]()
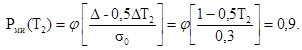
Отсюда
![]()
Т = min [T1, T2] = 1,2 г.
В соответствии с п. 1.4 Т = 15 мес.
2. Пример 2 (к п. 4.4)
Поверка третьим способом.
D = 1 %, m0 = -0,1
%, s0 = 0,3 %, ![]() Dс = 1 %,
Dс = 1 %, ![]()
![]()
Найти МПИ, соответствующий условию Рми(T) = 0,9.
2.1. Положим T1 = 1 г.
2.1.1. В соответствии с п. 4.4.2 Рми(Т) вычисляется по формуле (17), слагаемые которой для расчетов без использования ЭВМ удобно представить в виде
![]()
![]()
![]()
![]()
где
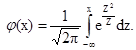
Расчет слагаемых (17) для T1 приведен в таблице 2.1. Как следует из таблицы,
![]()
![]()
Следовательно, ![]()
2.2. Так как Pми(T1) > 0,9, в соответствии с п. 1.4 примем T2 = 1,25 г.
Расчет слагаемых (17) для Т2 приведен в таблице 2.2. Как следует из таблицы,
![]()
![]()
Следовательно, ![]()
Таблица 2.1
|
m(jT1) |
s(jT1) |
aj |
bj |
cj |
dj |
Gj(T1) |
Sj(T1) |
|
ZGj(T1) |
ZSj(T1) |
|
|
1 |
-0,3 |
0,366 |
1,64 |
3,28 |
1,91 |
3,55 |
0,949 |
0,972 |
0,741 |
0,703 |
0,720 |
|
2 |
-0,5 |
0,448 |
0,89 |
3,12 |
1,12 |
3,35 |
0,813 |
0,869 |
0,549 |
0,446 |
0,477 |
|
3 |
-0,7 |
0,546 |
0,37 |
2,93 |
0,55 |
3,11 |
0,642 |
0,709 |
0,407 |
0,261 |
0,289 |
|
4 |
-0,9 |
0,668 |
0 |
2,69 |
0,15 |
2,84 |
0,496 |
0,558 |
0,301 |
0,149 |
0,168 |
|
5 |
-1,1 |
0,815 |
-0,245 |
2,45 |
-0,12 |
2,58 |
0,396 |
0,447 |
0,223 |
0,088 |
0,100 |
|
6 |
-1,3 |
0,997 |
-0,40 |
2,21 |
-0,30 |
2,31 |
0,331 |
0,372 |
0,165 |
0,055 |
0,061 |
|
7 |
-1,5 |
1,214 |
-0,49 |
1,98 |
-0,41 |
2,06 |
0,288 |
0,324 |
0,122 |
0,035 |
0,040 |
|
8 |
-1,7 |
1,485 |
-0,54 |
1,75 |
-0,49 |
1,82 |
0,255 |
0,302 |
0,091 |
0,023 |
0,027 |
|
9 |
-1,9 |
1,818 |
-0,55 |
1,54 |
-0,54 |
1,59 |
0,229 |
0,239 |
0,067 |
0,015 |
0,016 |
|
10 |
-2,1 |
2,222 |
то же |
1,35 |
-0,55 |
1,39 |
0,202 |
0,209 |
0,050 |
0,010 |
0,010 |
|
11 |
-2,3 |
2,703 |
" |
1,18 |
то же |
1,22 |
0,172 |
0,180 |
0,037 |
0,006 |
0,007 |
|
12 |
-2,5 |
3,297 |
" |
1,03 |
" |
1,06 |
0,139 |
0,146 |
0,027 |
0,004 |
0,004 |
|
13 |
-2,7 |
4,054 |
" |
0,89 |
" |
0,91 |
0,104 |
0,110 |
0,020 |
0,002 |
0,002 |
|
14 |
-2,9 |
4,918 |
" |
0,77 |
" |
0,79 |
0,070 |
0,104 |
0,015 |
0,001 |
0,001 |
|
15 |
-3,1 |
6,000 |
" |
0,67 |
" |
0,68 |
0,040 |
0,042 |
0,011 |
- |
- |
|
16 |
-3,3 |
7,317 |
" |
0,57 |
" |
0,59 |
0,007 |
0,014 |
0,008 |
- |
- |
|
17 |
-3,5 |
9,091 |
" |
0,55 |
" |
0,55 |
0 |
0 |
0,006 |
- |
- |
|
18 |
-3,7 |
11,111 |
" |
то же |
" |
то же |
то же |
то же |
0,004 |
- |
- |
|
|
1,798 |
1,922 |
Таблица 2.2
|
m(jT2) |
s(jT2) |
aj |
bj |
cj |
dj |
Gj(T2) |
Sj(T2) |
|
ZGj(T2) |
ZSj(T2) |
|
|
1 |
-0,35 |
0,385 |
1,43 |
3,24 |
1,69 |
3,50 |
0,924 |
0,954 |
0,687 |
0,635 |
0,655 |
|
2 |
-0,60 |
0,495 |
0,61 |
3,03 |
0,81 |
3,23 |
0,728 |
0,791 |
0,472 |
0,344 |
0,373 |
|
3 |
-0,85 |
0,636 |
0,08 |
2,75 |
0,24 |
2,91 |
0,529 |
0,593 |
0,325 |
0,172 |
0,193 |
|
4 |
-1,10 |
0,815 |
-0,24 |
2,45 |
-0,12 |
2,58 |
0,398 |
0,447 |
0,223 |
0,089 |
0,100 |
|
5 |
-1,35 |
1,049 |
-0,43 |
2,14 |
-0,33 |
2,24 |
0,318 |
0,358 |
0,153 |
0,049 |
0,055 |
|
6 |
-1,60 |
1,345 |
-0,52 |
1,86 |
-0,45 |
1,93 |
0,271 |
0,299 |
0,105 |
0,028 |
0,031 |
|
7 |
-1,85 |
1,724 |
-0,55 |
1,59 |
-0,52 |
1,65 |
0,235 |
0,252 |
0,072 |
0,017 |
0,018 |
|
8 |
-2,10 |
2,222 |
то же |
1,35 |
-0,55 |
1,39 |
0,202 |
0,209 |
0,050 |
0,010 |
0,010 |
|
9 |
-2,35 |
2,857 |
" |
1,14 |
то же |
1,17 |
0,164 |
0,170 |
0,034 |
0,006 |
0,006 |
|
10 |
-2,60 |
3,658 |
" |
0,96 |
" |
0,98 |
0,122 |
0,127 |
0,023 |
0,003 |
0,003 |
|
11 |
-2,85 |
4,687 |
" |
0,80 |
" |
0,82 |
0,079 |
0,085 |
0,016 |
0,001 |
0,001 |
|
12 |
-3,10 |
6,000 |
" |
0,67 |
" |
0,68 |
0,040 |
0,043 |
0,011 |
- |
- |
|
13 |
-3,35 |
7,769 |
" |
0,55 |
" |
0,56 |
0 |
0,003 |
0,008 |
- |
- |
|
14 |
-3,60 |
10,000 |
" |
то же |
" |
0,55 |
то же |
0 |
0,006 |
- |
- |
|
15 |
-3,85 |
13,044 |
" |
" |
" |
то же |
" |
то же |
0,004 |
- |
- |
|
|
1,354 |
1,445 |
Таким образом,
условию ![]() удовлетворяет МПИ Т =1,25 г.
удовлетворяет МПИ Т =1,25 г.
Поверка вторым способом.
D = 1 %, m(0) = 0, s0 = 0,1 %,
![]()
C2 = 40 руб., С3 = 100 руб.
![]()
3.1. Найти оптимальный МПИ.
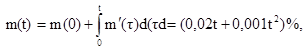
![]()
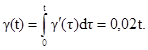
Для Ti Î [0,27] мес. с интервалом 3 мес. найдем значения m(Ti), s(Ti), g(ti), R(Ti), U(Ti).
3.2. Найдем значения W(Ti)
![]()
для Ti = 12, 15, 18 мес.
Результаты расчета приведены в таблице 3.
Таблица 3
|
Ti, мес |
Рми (ti) |
Кми (Ti) |
|
|
|
1 |
12 |
1,0 |
1,0 |
3,33 |
|
2 |
15 |
0,9998 |
0,99998 |
2,73 |
|
3 |
18 |
0,9950 |
0,9995 |
3,75 |
Из таблицы 3 следует, что ![]() при i
= 2.
при i
= 2.
Следовательно, оптимальный МПИ Т = 15 мес.
СОДЕРЖАНИЕ