РЕКОМЕНДАЦИЯ
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ
ЕДИНСТВА ИЗМЕРЕНИЙ
ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКИХ
ХАРАКТЕРИСТИК ЛИНЕЙНЫХ АНАЛОГОВЫХ
СРЕДСТВ ИЗМЕРЕНИЙ С СОСРЕДОТОЧЕННЫМИ
ПАРАМЕТРАМИ
ОБЩИЕ ПОЛОЖЕНИЯ
МИ 2090-90
КОМИТЕТ СТАНДАРТИЗАЦИИ И МЕТРОЛОГИИ СССР
Москва
1991
РЕКОМЕНДАЦИЯ
|
ГСИ.
ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКИХ
ХАРАКТЕРИСТИК ЛИНЕЙНЫХ АНАЛОГОВЫХ
СРЕДСТВ ИЗМЕРЕНИЙ С СОСРЕДОТОЧЕННЫМИ
ПАРАМЕТРАМИ
Общие положения
|
МИ 2090-90
|
Дата введения 01.08.91
Настоящая рекомендация распространяется
на методы определения динамических характеристик линейных аналоговых средств
измерений с сосредоточенными параметрами (далее - исследуемых средств
измерений) и устанавливает основные правила выбора и реализации методов. Методы
определения динамических характеристик
соответствуют одному из следующих общих методов по ГОСТ
8.061:
прямое измерение исследуемым средством
измерений испытательного сигнала, воспроизводимого образцовым генератором;
косвенные измерения испытательного
сигнала, воспроизводимого генератором.
Настоящий документ рекомендуется
применять при контроле выполнения требований ГОСТ
8.256. Термины, используемые в настоящей рекомендации, и пояснения к ним по
МИ 1951.
1.1. Для определения динамической
характеристики исследуемого средства измерений необходимо (см. рис. 1 а, б):
выбрать испытательный сигнал;
выбрать генератор испытательного сигнала
и средство измерений, предназначенное для определения выходного сигнала
исследуемого средства измерений;
подать на вход исследуемого средства
измерений испытательный сигнал;
определить выходной сигнал исследуемого
средства измерений, представляющий собой отклик на испытательный сигнал;
обработать данные по известному алгоритму
с целью нахождения оценки требуемой динамической характеристики и погрешности
ее определения.
Примечания:
1. При отсутствии необходимого генератора
допускается использовать в совокупности источник сигнала, не являющийся мерой,
и средство измерений, предназначенное для определения испытательного сигнала. В
указанном случае, кроме перечисленных выше операций, необходимо определить
испытательный сигнал.
2. Если исследуемое средство измерений -
управляемая мера, то генератором испытательного сигнала служит источник
управляющих воздействий (задающих кодов).
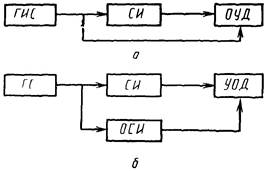
Рис. 1. Структурные схемы определения
динамических характеристик средств измерений:
ГИС -
образцовый генератор испытательного сигнала (образцовая динамическая мера); СИ
- исследуемое средство измерений; УОД - устройство обработки данных, включающее
средство измерений, предназначенное для определения выходного сигнала
исследуемого средства измерений; ГС - генератор сигнала; ОСИ - образцовое
(быстродействующее) средство измерений
1.2. В качестве данных
для нахождения динамической характеристики и погрешности ее определения следует
использовать:
совокупность оценок испытательного и
выходного сигналов исследуемого средства измерений и погрешностей указанных
оценок;
сведения об условиях эксперимента по
определению динамической характеристики исследуемого средства измерений;
предварительные сведения об исследуемом
средстве измерений.
1.2.1. Оценка испытательного сигнала
должна быть представлена либо:
номинальным аналитическим выражением и погрешностью
его воспроизведения,
номинальными значениями в известные
моменты времени и пределами допускаемых отклонений от указанных значений,
пределами допускаемых значений в
известные моменты времени (аналитическими выражениями предельных значений),
значениями в известные моменты времени и
погрешностями определения указанных значений.
1.2.2. Оценка выходного сигнала
исследуемого средства измерений должна быть представлена либо значениями в
известные моменты времени и погрешностями измерений указанных значений, либо
аппроксимирующим аналитическим выражением и погрешностью аппроксимации.
1.2.3. Предварительные сведения об
исследуемом средстве измерений могут включать:
нормы на статический коэффициент
преобразования;
структуру модели динамических свойств
исследуемого средства измерений (структуру дифференциального уравнения или
передаточной функции);
нормы на динамическую характеристику;
данные о возможных входных сигналах;
любые другие данные о средстве измерений
и условиях его применения.
2.1. Выбор метода определения
динамической характеристики должен быть обусловлен следующими качественными и
количественными факторами.
2.1.1. Качественные
факторы:
цель исследования;
требуемая динамическая характеристика;
требуемая форма представления
динамической характеристики;
предварительная информация об исследуемом
средстве измерений;
имеющиеся в наличии средства измерений
(генераторы и источники испытательных сигналов, средства определения и
регистрации испытательного сигнала и отклика исследуемого средства измерений);
имеющиеся в наличии средства
вычислительной техники и их математическое обеспечение.
2.1.1.1. Цель исследования может состоять
в следующем:
контроле нормированной динамической
характеристики;
определении динамической характеристики
типа средств измерений;
определении динамической характеристики
экземпляра средств измерений данного типа.
2.1.1.2. Требуемая динамическая
характеристика может быть полной или частной.
2.1.1.3. Испытательные сигналы могут быть
характеристическими и нехарактеристическими; соответственно, методы определения
динамических характеристик могут быть прямыми и
косвенными.
2.1.1.4. В зависимости от объема
предварительной информации косвенные методы определения полных динамических
характеристик могут быть структурно-параметрическими и параметрическими.
2.1.2. Количественные
факторы:
требуемая точность определения
динамической характеристики;
требуемый диапазон частот, в котором
должно быть исследовано средство измерений.
2.2. Выбор метода определения
динамических характеристик при контроле обусловлен следующими требованиями.
2.2.1. Контроль следует
производить преимущественно по частным динамическим характеристикам.
2.2.2. Контроль полных
динамических характеристик допускается производить путем сравнения отклика
исследуемого средства измерений на известный испытательный сигнал с
допускаемыми откликами. Допускаемые отклики определяют
(рассчитывают) с использованием нормированных динамических характеристик.
2.2.3. В качестве
испытательных следует использовать преимущественно характеристические сигналы.
2.3. Выбор метода определения
динамических характеристик типа средств измерений обусловлен следующими
требованиями.
2.3.1. Типовую частную динамическую характеристику
следует определять преимущественно с использованием характеристических
сигналов.
В случае выполнения указанного требования
частную динамическую характеристику следует находить по усредненному отклику
группы исследуемых средств измерений.
2.3.2. Типовую полную динамическую
характеристику следует определять по динамическим характеристикам экземпляров
группы исследуемых средств измерений.
2.4. Выбор метода определения
динамической характеристики экземпляра средств измерений данного типа
обусловлен следующими требованиями.
2.4.1. Динамическую характеристику
экземпляра средства измерений следует определять преимущественно путем
уточнения известной типовой характеристики указанного средства измерений.
2.4.2. При
необходимости представить полную динамическую характеристику исследуемого
экземпляра средства измерений в аналитической форме следует использовать преимущественно параметрические
методы.
2.5. При отсутствии требований к форме
представления полной динамической характеристики исследуемого средства
измерений следует определять указанную характеристику преимущественно прямым
методом.
2.6. При необходимости
представить полную динамическую характеристику исследуемого средства измерений
в аналитической форме следует определять указанную характеристику косвенным
методом с использованием преимущественно характеристических испытательных
сигналов.
Соотношения для пересчета динамических
характеристик из одной в другие для распространенных
моделей динамических свойств средств измерений приведены в приложении 1.
2.7. В том случае, когда при выборе
метода определения динамической характеристики исследуемого средства измерений
требования, обусловленные указанными в п. 2.1.1 качественными факторами,
противоречат друг другу, следует считать преимущественными те факторы, которые
связаны с наличием технических средств (преимущественно средств измерений).
2.8. Метод определения динамической
характеристики должен удовлетворять каждому из требований, обусловленных
указанными в п. 2.1.2 количественными факторами.
2.9. В зависимости от требуемой точности
определения динамической характеристики метод ее определения должен выбираться
таким, чтобы погрешность определения
динамической характеристики не превышала допускаемой погрешности.
2.9.1. При определении частной
динамической характеристики V характеристика погрешности De, V ее определения должна
удовлетворять условию
De,V £ DVпр, (1)
где DVпр -
предел допускаемой погрешности определения V.
2.9.2. При определении полной
динамической характеристики в известной аналитической форме выбранный метод
должен обеспечивать выполнение условий
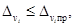 i = 1, ..., m, (2)
i = 1, ..., m, (2)
где 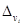 -
характеристика погрешности определения коэффициента vi,
входящего в аналитическое выражение динамической характеристики;
-
характеристика погрешности определения коэффициента vi,
входящего в аналитическое выражение динамической характеристики;
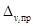 - предел допускаемой погрешности определения коэффициента vi; m - число определяемых
коэффициентов.
- предел допускаемой погрешности определения коэффициента vi; m - число определяемых
коэффициентов.
2.9.3. При определении полной
динамической характеристики в табличной или графической форме характеристика
погрешности определения De должна удовлетворять условию
De £ Dпр, (3)
где Dпр - предел допускаемой погрешности определения
динамической характеристики.
2.9.4. Погрешности методов следует
вычислять в форме, аналогичной пределу допускаемой погрешности.
2.10. В зависимости от требуемого
диапазона частот, в котором должно быть исследовано средство измерений, метод
определения динамической характеристики следует выбирать в соответствии с
требованиями разд. 3 настоящей рекомендации.
2.11. В зависимости от требуемых
метрологических характеристик средств измерений, используемых для определения
динамической характеристики исследуемого
средства измерений, метод определения динамической характеристики следует
выбирать в соответствии с требованиями разд. 4 настоящей рекомендации.
3.1. Испытательный сигнал для определения
динамической характеристики исследуемого средства измерений следует выбирать в
зависимости от определяемой характеристики, требуемого диапазона частот, в
котором должно быть исследовано средство измерений, и требуемой точности
определения динамической характеристики в указанном диапазоне, либо требуемой
точности измерений, которые должны проводиться
с помощью исследуемого средства измерений.
3.2. В зависимости от определяемой
динамической характеристики испытательный сигнал должен выбираться
преимущественно следующим:
для определения переходной характеристики
и (или) ее параметров (функционалов) - ступенчатый испытательный сигнал,
описываемый функцией, достаточно близкой по форме к
единичной ступенчатой функции 1(t);
для определения импульсной
характеристики и (или) ее параметров (функционалов) - импульсный испытательный сигнал, описываемый
функцией, достаточно близкой по форме к дельта-функции δ0 (t)
или двоичный псевдослучайный испытательный сигнал;
для определения частотных характеристик и
(или) их параметров (функционалов) - сигналы, достаточно близкие к
гармоническим.
В случае, если указанные сигналы не могут
быть воспроизведены (определены) с требуемой точностью, допускается выбор в
качестве испытательных других сигналов, удовлетворяющих требованиям пп. 3.3 - 3.7.
Примечание. Испытательные сигналы аппроксимируют
упрощенными функциями (модели сигналов), примеры которых приведены в приложении
3.
Точность воспроизведения (определения) испытательного сигнала обусловлена
отклонением модели сигнала по форме от характеристического сигнала (далее -
неидеальностью испытательного сигнала) и отклонением испытательного сигнала от
его модели.
3.3. В зависимости от
требуемого диапазона частот, в котором должно быть исследовано средство
измерений, амплитудный спектр X(f)
испытательного сигнала должен удовлетворять условию
f01 ³ fв, (4)
где f01 - частота, представляющая собой наименьший не равный
нулю корень уравнения X(f) = Dв (где f - частота);
Dв -
верхняя граница погрешности определения амплитудного спектра;
fв -
верхняя граничная частота требуемого диапазона.
Аналитические выражения f01 и Dв для
распространенных испытательных сигналов приведены в приложении 2.
3.4. В зависимости от требуемого
диапазона частот, в котором должно быть исследовано
средство измерений, максимальная скорость 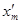 изменений во времени
(производная) импульсного испытательного сигнала хg(t) с длительностью tи должна удовлетворять условию
изменений во времени
(производная) импульсного испытательного сигнала хg(t) с длительностью tи должна удовлетворять условию
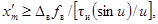 (5)
(5)
где u = pfв · tи.
Условие (5) заведомо удовлетворяется, если
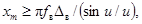 (6)
(6)
где xm
- максимальное значение сигнала xg(t).
3.5. При определении
динамической характеристики средства измерений прямым методом испытательный сигнал
должен быть выбран таким, чтобы предварительная оценка погрешности определения
динамической характеристики, складывающаяся из составляющих, обусловленных
неидеальностью испытательных сигналов и ожидаемой неточностью измерений и
вычислений, не превышала установленного предела:
для импульсной характеристики g(t)
Dgч £ Dgпр, (7)
где Dgч -
числовая характеристика погрешности Dg(t)
определения импульсной характеристики;
Dgпр -
предел допускаемой погрешности определения импульсной характеристики;
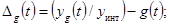

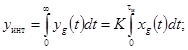
K - статический коэффициент преобразования исследуемого
средства измерений,
для переходной характеристики h(t)
Dhч £ Dhпр, (8)
где Dhч -
числовая характеристика погрешности Dh(t) определения переходной характеристики;
Dhпр -
предел допускаемой погрешности определения переходной характеристики;
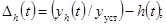
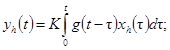
yуст -
установившееся значение выходного сигнала, yуст = Kxуст;
xуст -
установившееся значение ступенчатого испытательного сигнала;
для амплитудно-частотной характеристики A(f)
DAч £ DAпр, (9)
где DAч -
числовая характеристика погрешности DA(f) определения амплитудно-частотной характеристики, DAпр - предел допускаемой погрешности определения
амплитудно-частотной характеристики;

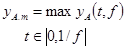

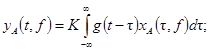
xA(t, f) - периодический испытательный сигнал,
близкий к гармоническому с периодом повторений, равным 1/f;
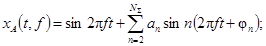
n - номер гармонической составляющей сигнала;
an - коэффициент гармонической составляющей с номером n ³ 2;
NΣ - общее число
гармонических составляющих (включая основную);
jn - фазовый сдвиг гармонической составляющей с номером n ³ 2 относительно основной,
для фазочастотной характеристики Ф(f)
DФч £ DΦпр, (10)
где DФч - числовая характеристика погрешности DΦ(f), определения
фазочастотной характеристики;
DΦпр - предел допускаемой погрешности определения фазочастотной
характеристики;
DΦ(f) = e0 - ζ0 - Φ(f);
e0, ζ0
- соответственно, корни уравнений
 (11)
(11)

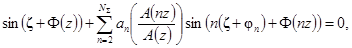 (12)
(12)
которым соответствуют положительные
производные по времени сигналов хА(t,
f) и уА(t, f);
z = 2pfT;
T - коэффициент или среднее геометрическое двух
коэффициентов передаточной функции исследуемого средства измерений.
Выражения z для
наиболее распространенных моделей динамических свойств исследуемых средств
измерений приведены в приложении 1.
Примечание. Допускается определять фазочастотную
характеристику прямым методом по ненулевым синфазным значениям испытательного
сигнала и отклика на него с использованием соотношений, отличных от
приведенных.
Составляющие погрешности определения
прямыми методами переходной, импульсной, амплитудно-частотной, фазочастотной
характеристик, обусловленные неидеальностью испытательных сигналов, в
зависимости от параметров указанных сигналов и коэффициентов передаточной функции исследуемого средства
измерений для распространенных моделей динамических свойств средств измерений и
испытательных сигналов приведены в приложениях 3 - 8.
3.6. В зависимости от требуемой точности
определения косвенными методами динамических характеристик исследуемых средств
измерений испытательные сигналы должны выбираться на основе соотношений для
оценивания погрешностей, входящих в состав конкретных алгоритмов обработки
данных. Примеры алгоритмов приведены в приложении 8.
3.7. В зависимости от
требуемой точности измерений, которые должны проводиться с помощью исследуемого
средства измерений, испытательный сигнал должен быть выбран таким, чтобы
удовлетворялись следующие неравенства:
во временной области
Dч ³ KзDn,t, (13)
где Dч - числовая характеристика временной зависимости D(t) искажений испытательного сигнала x(t);
Dn,t -
предел допускаемой погрешности измерений;
D(t) = (у(t)/K)
- x(t);
y(t) - выходной
сигнал исследуемого средства измерений;
Kз - коэффициент
запаса;
в частотной
области
Dfч ³ KзDn,f, (14)
где Dfч -
числовая характеристика частотной зависимости Df(f)
искажений испытательного сигнала x(t);
Dn,f - предел допускаемой погрешности
измерений;
Df(f) = (Y(f)/K) - X(f); Y(/) - амплитудный спектр выходного сигнала
исследуемого средства измерений.
Коэффициент запаса следует установить в
диапазоне Kз = 3 -
10, имея в виду, что при исследованиях более точных средств измерений Kз должно быть большим.
При необходимости уточнения коэффициент
запаса Kз для
конкретного метода определения динамических характеристик средств измерений
следует устанавливать путем последовательных приближений в соответствии с
приложением 9.
4.1. Генераторы испытательных сигналов
должны обеспечивать требуемые согласно разд. 3 характеристики испытательных
сигналов.
4.2. Погрешности
средств измерений, используемых для воспроизведения или определения
испытательного сигнала и для регистрации выходного сигнала исследуемого
средства измерений, должны удовлетворять условию
µч £ 0,2Dч, (15)
где µч - числовая
характеристика погрешности µ(t);
µ(t) = Dx(t)+Dу(t)/K;
Dx(t) - погрешность генератора испытательного сигнала
(исключая неидеальность испытательного сигнала) или регистрирующего прибора,
используемого для определения испытательного сигнала;
Dу(t)
- погрешность регистрирующего прибора, используемого для определения выходного
сигнала исследуемого средства измерений.
4.3. Импульсная характеристика gр(t)
регистрирующего прибора, используемого для определения испытательного сигнала
или выходного сигнала исследуемого средства измерений, должна удовлетворять
условию
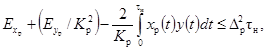 (16)
(16)
где  ;
;
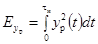 ;
;
Kp
- статический коэффициент преобразования регистрирующего прибора;
tн - длительность интервала времени наблюдений выходного
сигнала.
При регистрации испытательного сигнала xр(t)
= x(t);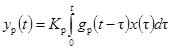 - результат регистрации x(t);
Dp
= Dxч.
- результат регистрации x(t);
Dp
= Dxч.
При регистрации выходного сигнала xp(t)
= y(t); 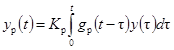 - результат регистрации y(t);
Dр = Dyч.
- результат регистрации y(t);
Dр = Dyч.
4.3.1. Известные номинальная импульсная
характеристика регистрирующего прибора gр.ном(t) и предел Dg допускаемого
отклонения от указанной характеристики должны удовлетворять условиям:
при выборе прибора
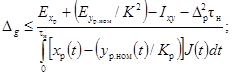 (17)
(17)
при проверке после
регистрации
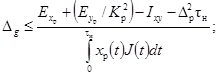 (18)
(18)
где 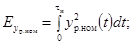
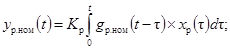
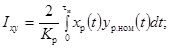
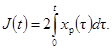
4.4. Частотные
характеристики Aр(f),
Φp(f) регистрирующего прибора, используемого для
определения испытательного сигнала или выходного сигнала исследуемого средства
измерений, должны удовлетворять условию
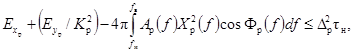 (19)
(19)
где fн - нижняя граница требуемого диапазона частот, в
котором исследуется средство измерений,
Xр(f) - амплитудный спектр сигнала xр(t).
4.4.1. Известные номинальные частотные
характеристики Aр.ном(f),
Φр.ном(f) регистрирующего прибора и пределы допускаемых
отклонений DA, DΦ от указанных характеристик должны удовлетворять
условиям:
при выборе прибора
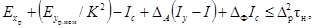 (20)
(20)
при проверке после
регистрации
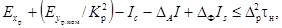 (21)
(21)
где 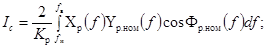
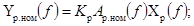
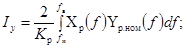


5.1. Алгоритм обработки данных при
определении динамической характеристики обусловлен определяемой характеристикой
и испытательным сигналом. Исходными данными служат испытательный и выходной
сигналы исследуемого средства измерений и предварительные сведения об
исследуемом средстве измерений, представленные в соответствии с требованиями п.
1.2.
5.2. При определении прямым методом
переходной и импульсной характеристик исследуемого средства измерений оценки
указанных характеристик следует находить с помощью соотношений:
переходной характеристики
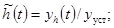 (22)
(22)
импульсной характеристики
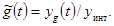 (23)
(23)
5.3. При определении прямым методом
амплитудно-частотной и фазочастотной характеристик исследуемого средства
измерений оценки указанных характеристик при частоте f
следует находить с помощью соотношений:
амплитудно-частотной характеристики
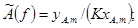 (24)
(24)
фазочастотной характеристики
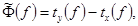 (25)
(25)
где ty(f),
tx(f) - значения времени, представляющие собой наименьшие
по модулю корни уравнений уA(ty, f) = 0 и xA(tx, f) = 0, удовлетворяющие условию tу(f)
- tx(f) < 1/f.
Примечание. Допускается в случае определения
фазочастотной характеристики прямым методом по ненулевым синфазным значениям
испытательного сигнала и отклика на него использовать соотношения, отличные от
приведенных.
5.4. В том случае, когда либо не задана
требуемая точность определения динамической характеристики или требуемая
точность измерений с помощью исследуемого средства измерений, либо отсутствует
возможность воспроизвести выбранный в соответствии с требованиями разд. 3
испытательный сигнал, кроме указанных в пп. 4.2 - 4.4 операций, следует также
оценивать погрешность определения найденной
динамической характеристики.
5.4.1. Оценивание погрешностей
определения динамических характеристик, найденных прямыми методами, должно
производиться в соответствии с требованиями разд. 6 рекомендаций.
5.5. Обработка данных с
целью определения динамических характеристик косвенным методом с использованием
испытательных сигналов, достаточно близких к характеристическим,
должна включать:
регистрацию отклика исследуемого средства
измерений на испытательный сигнал и отсчитывание значений отклика;
пересчет отсчитанных значений в значения
требуемой динамической характеристики (в аналитическое выражение требуемой
характеристики);
оценивание погрешностей рассчитанных значений (погрешностей
коэффициентов рассчитанного аналитического выражения).
Соотношения для пересчета для
распространенных моделей динамических свойств средств измерений приведены в
приложении 1.
5.6. Обработка данных с целью определения
динамических характеристик с использованием испытательных сигналов, отличных от
указанных в п. 5.5,
должна включать:
расчет по совокупности испытательного и
выходного сигналов требуемой динамической характеристики в форме таблицы
значений или аналитического выражения;
оценивание погрешностей рассчитанных
значений или коэффициентов аналитического выражения.
При определении динамической
характеристики в аналитической форме по совокупности рассчитанных значений,
кроме указанных выше операций, должны быть также произведены аппроксимация
указанной совокупности аналитическим выражением и оценивание погрешностей
найденных коэффициентов этого выражения.
5.7. Алгоритм обработки данных при
определении динамической характеристики средства измерений косвенным методом
должен удовлетворять следующим требованиям:
обеспечивать получение возможно более
простых аналитических выражений для динамических характеристик;
предусматривать возможность упрощений
вычислений и получаемого результата за счет использования предварительных
сведений об исследуемом средстве измерений;
включать в себя методику оценивания
погрешностей найденной динамической характеристики, учитывающую неидеальность
испытательного сигнала, погрешности регистрации отклика (выходного сигнала)
средства измерений и погрешности вычислений;
обеспечивать регулярную зависимость
найденной характеристики от исходных данных (при уменьшении погрешностей
определения испытательного сигнала и отклика на него исследуемого средства
измерений погрешность оценки характеристики не должна возрастать).
Алгоритмы обработки данных при
определении полных динамических характеристик косвенными методами приведены в
приложении 8.
6.1. При оценивании погрешностей
определения динамических характеристик следует учитывать:
погрешность определения испытательного
сигнала, в том числе погрешность, обусловленную неидеальностью испытательного
сигнала, и погрешность генератора испытательного сигнала или
погрешность источника сигнала и
регистрирующего прибора и погрешность отсчитывания значений зарегистрированного
сигнала (при аналоговой регистрации);
погрешность, обусловленную
взаимодействием генератора (источника) испытательного сигнала и исследуемого
средства измерений;
погрешность определения выходного сигнала
исследуемого средства измерений, в том числе:
погрешность регистрирующего прибора,
предназначенного для регистрации выходного сигнала, и погрешность отсчитывания
зарегистрированных значений (при аналоговой регистрации);
погрешность, обусловленную
взаимодействием регистрирующего прибора и исследуемого средства измерений,
погрешность, обусловленную помехами,
воздействующими на выход исследуемого средства измерений и на вход
регистрирующего прибора;
погрешность обработки данных, в том
числе:
погрешность, обусловленную
неадекватностью принятой модели исследуемому средству измерений,
погрешность, вызванную несовершенством
выбранного критерия сравнения экспериментальных и расчетных данных,
погрешность, обусловленную приближенным
характером используемых формул,
погрешность округления чисел,
погрешность аппроксимации
экспериментальных данных,
погрешности используемых средств
обработки.
6.2. Погрешность
определения переходной (импульсной) характеристики прямым методом следует
оценивать путем суммирования составляющих на основе следующего выражения,
представляющего структуру модели указанной погрешности:
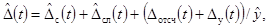 (26)
(26)
где при определении h(t):
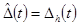 ;
; 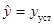 ;
;
при определении g(t): 
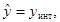
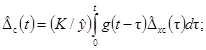
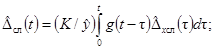
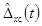 - систематическая составляющая
погрешности
- систематическая составляющая
погрешности 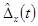 ;
;
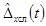 - случайная составляющая
погрешности
- случайная составляющая
погрешности 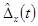 ;
;
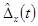 - погрешность определения испытательного
сигнала;
- погрешность определения испытательного
сигнала;
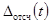 - погрешность отсчитывания значений
выходного сигнала (при аналоговой регистрации).
- погрешность отсчитывания значений
выходного сигнала (при аналоговой регистрации).
При известных характеристиках
составляющих границы погрешности 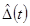 следует находить по ГОСТ
8.207.
следует находить по ГОСТ
8.207.
Выражения и числовые характеристики
систематической составляющей 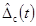 погрешности
погрешности 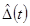 , обусловленной неидеальностью
испытательного сигнала, для средств измерений с распространенными моделями
динамических свойств и распространенных испытательных сигналов приведены в
приложениях 3
- 5.
, обусловленной неидеальностью
испытательного сигнала, для средств измерений с распространенными моделями
динамических свойств и распространенных испытательных сигналов приведены в
приложениях 3
- 5.
6.3. Погрешности
определения частотных характеристик прямым методом следует оценивать путем
суммирования составляющих на основе следующих выражений, отражающих структуру
указанных погрешностей:
для амплитудно-частотной характеристики
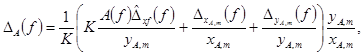 (27)
(27)
где Dx,f(f)
- частотная зависимость погрешности воспроизведения (определения) испытательного сигнала;
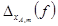 - погрешность определения xA.т при частоте f;
- погрешность определения xA.т при частоте f;
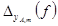 - погрешность определения yA.т при частоте f.
- погрешность определения yA.т при частоте f.
для фазочастотной
характеристики
 (28)
(28)
где DΦс(f)
- систематическая составляющая, обусловленная неидеальностью испытательного сигнала, при частоте f;
DΦсл(f)
- суммарная случайная составляющая, обусловленная случайными погрешностями
определения испытательного и выходного сигналов, при частоте f;
DΦ,x(f),
DΦ,y(f)
- соответственно, погрешности, обусловленные неточностью фиксации нулевых
уровней (при определении фазочастотной характеристики по ненулевым синфазным
значениям - уровней, соответствующих указанным значениям) испытательного и
выходного сигналов, при частоте f.
Числовые характеристики составляющих
погрешностей, обусловленных неидеальностью испытательных сигналов, для
распространенных моделей динамических свойств средств измерений и
распространенных испытательных сигналов приведены в приложениях 6, 7.
6.4. Погрешности определения динамических
характеристик косвенными методами следует оценивать с помощью операций,
входящих в состав конкретных алгоритмов обработки данных.
Примеры алгоритмов обработки данных при
определении полных динамических характеристик косвенными методами приведены в
приложении 8.
6.5. Погрешность определения динамической
характеристики косвенным методом с использованием испытательных сигналов,
достаточно близких к характеристическим, следует оценивать путем суммирования
составляющих погрешности, указанных в пп. 6.2, 6.3, и погрешности пересчета
значений отклика исследуемого средства измерений в значения требуемой
характеристики (в аналитическое выражение требуемой
характеристики).
Примеры определения динамических
характеристик средств измерений приведены в приложении 10.
АНАЛИТИЧЕСКИЕ
ВЫРАЖЕНИЯ f01
И Dв
ДЛЯ РАСПРОСТРАНЕННЫХ ИСПЫТАТЕЛЬНЫХ СИГНАЛОВ
|
Испытательный
сигнал
|
Уравнение
для определения f01
|
Выражение
для Dв
|
|
Наименование
|
Аналитическое
выражение
|
|
Сигнал с линейным нарастанием до
установившегося значения
|
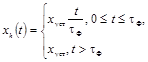
|
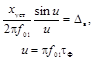
|
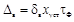
|
|
Сигнал с экспоненциальным нарастанием до установившегося значения
|
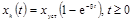
|
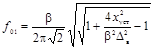
|
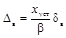
|
|
Сигнал с косинусоидальным нарастанием до установившегося значения
|
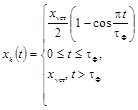
|
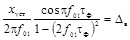
|
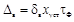
|
|
Импульсный сигнал прямоугольной формы
|
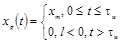
|
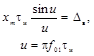
|
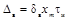
|
|
Импульсный сигнал симметричной треугольной
формы
|
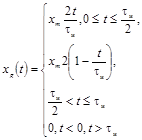
|
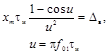
|
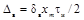
|
|
Импульсный сигнал синусоидальной формы
|
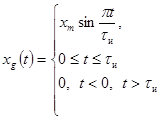
|
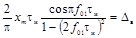
|
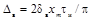
|
|
Импульсный сигнал косинусоидальной формы
|
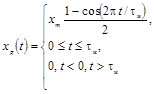
|
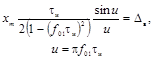
|
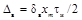
|
xуст -
установившееся значение испытательного сигнала xh(t) с ненулевым установившимся значением;
xm - максимальное значение
импульсного сигнала xg(t);
tΦ - длительность
фронта нарастания сигнала хh(t);
tи - длительность
сигнала xg(t);
δв - безразмерная величина, изменяющаяся в диапазоне от
0 до 1.
ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ ПРЯМЫМИ МЕТОДАМИ ПЕРЕХОДНОЙ И
ИМПУЛЬСНОЙ ХАРАКТЕРИСТИК ИССЛЕДУЕМОГО СРЕДСТВА ИЗМЕРЕНИЯ, ОБУСЛОВЛЕННЫЕ
НЕИДЕАЛЬНОСТЬЮ ИСПЫТАТЕЛЬНЫХ СИГНАЛОВ, В ЗАВИСИМОСТИ ОТ ПАРАМЕТРОВ УКАЗАННЫХ
СИГНАЛОВ, ВИДА И КОЭФФИЦИЕНТОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СРЕДСТВА ИЗМЕРЕНИЯ (СИГНАЛ
С ЛИНЕЙНЫМ НАРАСТАНИЕМ ДО УСТАНОВИВШЕГОСЯ ЗНАЧЕНИЯ ВМЕСТО СИГНАЛА, ОПИСЫВАЕМОГО
ФУНКЦИЕЙ 1(t), - ДЛЯ ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ; ИМПУЛЬСНЫЙ СИГНАЛ
ПРЯМОУГОЛЬНОЙ ФОРМЫ ВМЕСТО СИГНАЛА, ОПИСЫВАЕМОГО ФУНКЦИЕЙ δ0(t), - ДЛЯ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ)
ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ ПРЯМЫМ МЕТОДОМ ПЕРЕХОДНОЙ
ХАРАКТЕРИСТИКИ ИССЛЕДУЕМОГО СРЕДСТВА ИЗМЕРЕНИЙ, ОБУСЛОВЛЕННЫЕ НЕИДЕАЛЬНОСТЬЮ
ИСПЫТАТЕЛЬНОГО СИГНАЛА, В ЗАВИСИМОСТИ ОТ ПАРАМЕТРА УКАЗАННОГО СИГНАЛА, ВИДА И
КОЭФФИЦИЕНТОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СРЕДСТВА ИЗМЕРЕНИЯ (СИГНАЛ С
ЭКСПОНЕНЦИАЛЬНЫМ НАРАСТАНИЕМ xh(t) = 1 - е-bt ВМЕСТО СИГНАЛА, ОПИСЫВАЕМОГО ФУНКЦИЕЙ 1(t)
Погрешности Dhc(t)
определения переходной характеристики или их числовые характеристики
представляются следующими выражениями в зависимости от передаточных функций W(p):
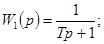
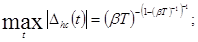
при bT ³ 10
можно пользоваться выражением
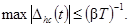
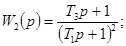
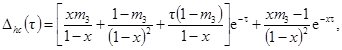
где 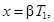

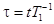
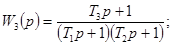
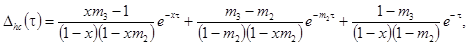
где 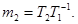
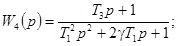
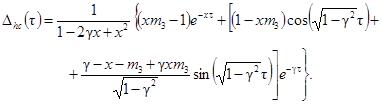
Для W2(p), W3(p),
W4(p)
отсутствуют аналитические выражения для 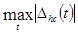 , поэтому даны графические зависимости
приведенных максимального модуля погрешности
, поэтому даны графические зависимости
приведенных максимального модуля погрешности 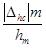 , среднего квадратического
значения
, среднего квадратического
значения 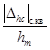 и среднего модуля
и среднего модуля 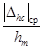 от параметра сигнала x, полученные численным способом. Здесь
от параметра сигнала x, полученные численным способом. Здесь 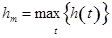 .
Указанные характеристики рассчитаны на интервале времени с длительностью 5T1, разделенном на 100 частей.
.
Указанные характеристики рассчитаны на интервале времени с длительностью 5T1, разделенном на 100 частей.
Указанные зависимости числовых
характеристик погрешности представлены: для W3(p) - на рис. 1 - 3, для W4(p)
- на рис. 4
- 6.
Зависимости для W2(p)
отдельно не представлены, так как последняя является частным случаем W3(p)
при m2 = 1.
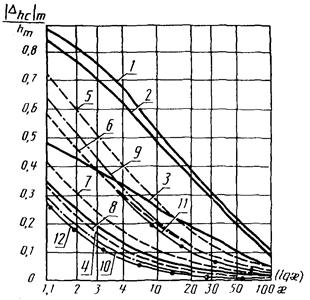
Рис. 1. Зависимость 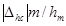 от x для W3(p):
от x для W3(p):
1 - 3 - т2 = 0,06; m3 = 30; 1; 0,5; 4 - m3 = m2 и
m2 = 0,05; m2
= 0; 5, 6, 8 - m2
= 0,3; m2 = 30; 1; 0; 7 - т2
= 0,03; m2 = 0,5 и m2 = 0,7; m3
= 1; 9, 8, 10 - m2
= 0,7; m3 = 30; 0,5; 0; 11, 12
- m2 = 1; m3
= 30; 0
Для получения оценок  при m3 £ 0,5 и g - 0,05; 0,9 (для W4(p))
можно пользоваться приближенным соотношением
при m3 £ 0,5 и g - 0,05; 0,9 (для W4(p))
можно пользоваться приближенным соотношением
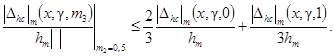
Значения hm приведены
в табл. 1
и 2.
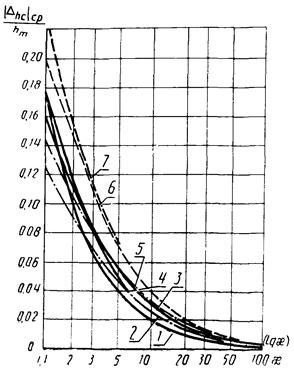
Рис. 2. Зависимость 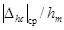 от x для W3(p):
от x для W3(p):
1
- m2 = 0; 1; m2
= 0,03; 0,3; 1; 2 - m2 = 0,03;
m2 = 3; 3 - m2 = 3; m2
= 0,3; 4 - m3 = 3; m2 = 1; 5 - m2
= 30; m2 = 0,03; 6 - m2 = 10; т2 = 1 и m3 = 30; m2
= 0,3; 7 - m2 = 30; m2 = 1
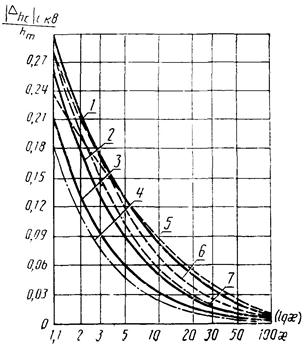
Рис. 3. Зависимость 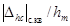 от x для W3(p):
от x для W3(p):
1,
2 - m3 = 1; m2 = 0,03; 0,3; 3 - m3 = 1; m2
= 1 и m3 = 0; m2
= 0,03; 0,3; 4 - m1 = 0; m2 = 1; 5, 6, 7 - m3 = 30; m2
= 0,03; 0,3; 1

Рис. 4. Зависимость  от x
для W4(p):
от x
для W4(p):
1,
2 - m3 = l;
g = 0,05; 0,9; 3, 4 -
т3 = 0; g
= 0,05; 0,9; 5, 6 - m3
= 30; g = 0,05; 0,9

Рис. 5. Зависимость 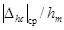 от x для W4(p):
от x для W4(p):
1
- т3 = 1; g
= 0,05 и m3 = 30; g = 0,7; 2 - т3 = 0;
1; g = 0,7; 3 - т3
= 0; g = 0,05; 4
- m3 = 30; g = 0,05
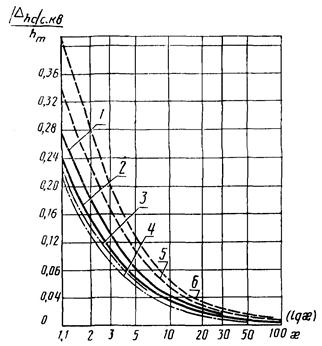
Рис. 6. Зависимость 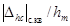 от x для W4(p):
от x для W4(p):
1,
2 - m3 = 1; g = 0,05; 0,03; 3, 4 - т3
= 0; g = 0,05; 0,3; 5,
6 - m3 = 30; g = 0,05; 0,3
Таблица 1
Значения hm в зависимости от параметров W3(p)
m2 и m3
|
m2
|
m3
|
|
0
|
0,03
|
0,05
|
0,1
|
0,3
|
0,5
|
1
|
3
|
5
|
10
|
30
|
|
0,03
|
0,993
|
0,993
|
0,993
|
0,994
|
0,995
|
0,996
|
1,000
|
2,756
|
4,549
|
9,029
|
26,950
|
|
0,05
|
0,993
|
0,993
|
0,993
|
0,994
|
0,995
|
0,996
|
1,000
|
2,667
|
4,365
|
8,633
|
25,705
|
|
0,1
|
0,993
|
0,993
|
0,993
|
0,993
|
0,995
|
0,996
|
1,000
|
2,486
|
4,021
|
7,835
|
23,369
|
|
0,3
|
0,990
|
0,991
|
0,991
|
0,991
|
0,993
|
0,995
|
1,000
|
2,050
|
3,227
|
6,302
|
18,119
|
|
0,5
|
0,987
|
0,987
|
0,987
|
0,988
|
0,991
|
0,993
|
1,000
|
1,800
|
2,778
|
5,263
|
15,253
|
|
0,7
|
0,978
|
0,980
|
0,980
|
0,981
|
0,985
|
0,989
|
0,999
|
1,628
|
2,470
|
4,627
|
13,317
|
|
0,9
|
0,967
|
0,968
|
0,969
|
0,970
|
0,976
|
0,982
|
0,996
|
1,499
|
2,241
|
4,157
|
11,890
|
|
1,0
|
0,960
|
0,961
|
0,961
|
0,963
|
0,970
|
0,976
|
0,993
|
1,446
|
2,146
|
3,963
|
11,306
|
Таблица 2
Значения hm в зависимости от параметров W4 (р) g и m3
|
g
|
m3
|
|
0
|
0,03
|
0,05
|
0,1
|
0,3
|
0,5
|
1
|
3
|
5
|
10
|
30
|
|
0,03
|
1,910
|
1,910
|
1,911
|
1,915
|
1,951
|
2,019
|
2,298
|
3,963
|
5,811
|
10,538
|
29,594
|
|
0,05
|
1,854
|
1,855
|
1,856
|
1,859
|
1,893
|
1,958
|
2,226
|
3,839
|
5,632
|
10,218
|
28,723
|
|
0,1
|
1,729
|
1,729
|
1,730
|
1,733
|
1,763
|
1,821
|
2,064
|
3,558
|
5,226
|
9,495
|
26,718
|
|
0,3
|
1,372
|
1,372
|
1,373
|
1,374
|
1,391
|
1,426
|
1,592
|
2,728
|
4,024
|
7,345
|
20,754
|
|
0,5
|
1,163
|
1,163
|
1,163
|
1,164
|
1,172
|
1,191
|
1,298
|
2,192
|
3,243
|
5,944
|
16,851
|
|
0,7
|
1,045
|
1,046
|
1,046
|
1,046
|
1,049
|
1,056
|
1,112
|
1,822
|
2,701
|
4,967
|
14,123
|
|
0,9
|
0,988
|
0,988
|
0,989
|
0,990
|
0,994
|
0,998
|
1,011
|
1,554
|
2,305
|
4,252
|
12,117
|
ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ
ПРЯМЫМ МЕТОДОМ ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ
ИССЛЕДУЕМОГО СРЕДСТВА ИЗМЕРЕНИЙ, ОБУСЛОВЛЕННЫЕ
НЕИДЕАЛЬНОСТЬЮ ИСПЫТАТЕЛЬНОГО СИГНАЛА,
В ЗАВИСИМОСТИ ОТ ПАРАМЕТРА СИГНАЛА, ВИДА И
КОЭФФИЦИЕНТОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СРЕДСТВА ИЗМЕРЕНИЙ
[СИГНАЛ С КОСИНУСОИДАЛЬНЫМ ФРОНТОМ
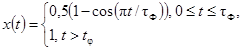
ВМЕСТО СИГНАЛА, ОПИСЫВАЕМОГО ФУНКЦИЕЙ 1(t)]
В настоящем приложении приведены
полученные расчетным путем зависимости следующих числовых характеристик
погрешности Dhc(t):
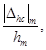
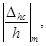
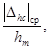
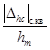
от параметра сигнала x1 = tΦ/T1.
Указанные характеристики рассчитаны на
интервале времени с длительностью 5T1, разделенном на 100 частей. Зависимости характеристик
погрешности представлены на рис. 1 - 4 для
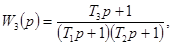
а на рис. 5 - 9 для
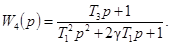
Значения hm
приведены в табл. 1 и 2 приложения 4.
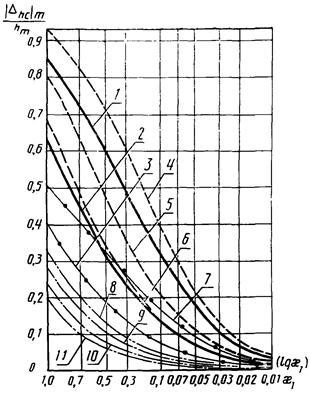
Рис. 1. Зависимость  от x1 для W3(p):
от x1 для W3(p):
1 - m3 = 1; m2
= 0,1; 2 - m3 = 1; m2 = 0,3 и m3
= 30; m2 = 1; 3 - m3 = 1; m2
= 0,7 и m3 = 0,5; m2 = 0,1; 4 - m3
= 30; m2 = 0,1; 5 - m3 = 30; m2
= 0,3; 6 - m3 = 30; m2 = 0,7; 7 - m3
= 0,5; m2 = 0,1; 8 - m3 = 0; m2
= 0,1 и m3 = 0,1; 9, 10,
11 - т3 = 0; m2
= 0,3; 0,7; 1
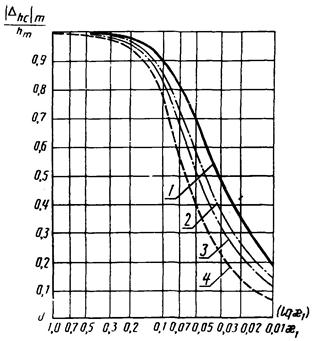
Рис. 2. Зависимость 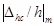 от x1 для W3(p):
от x1 для W3(p):
1
- m3 = 0; m2
£ 1; 2 - m3 = 0,03; m2
= 1; 3 - m3 = 30; m2 = 1 и m3
= 0,3; m2 = 0,05; 4 - m3 = 30; m2
= 0,05
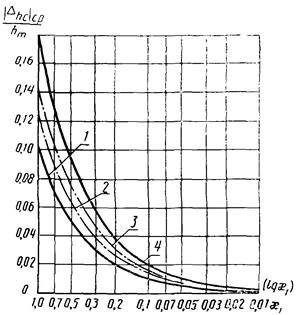
Рис. 3. Зависимость 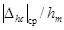 от x1 для W3(p):
от x1 для W3(p):
1 - 0 £ m3 £
1; 0 < m2 £ 1; 2 - m3
= 3; m2 = 1; 3 - m3 = 3; m2
= 0,3 и m3 = 5; m2
= 1; 4 - m3 = 30; 0 < m2 £
1
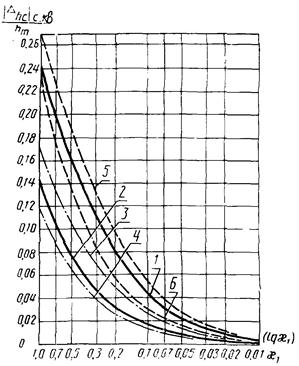
Рис. 4. Зависимость 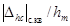 от x1 для W3(p):
от x1 для W3(p):
1
- m3 = 1; m2
= 0,1; 2 - m3 = 1; m2 = 1 и m3
£ 0,1; m2
= 0,1; 3 - m3 = 0,5; m2 = 0,1; 4 - m3
£ 0,5; m2
= 1; 5 - m3 = 30; m2 = 0,1; 6 - m3
= 30; m2 = 1
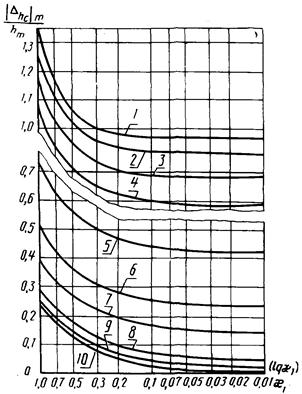
Рис. 5. Зависимость  от x1 для W4(p):
от x1 для W4(p):
1 - 10 - g = 0,3; m3
= 30; 10; 5; 3; 1; 0,5; 0,3; 0,1; 0,05; 0
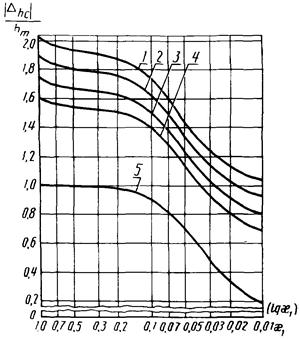
Рис. 6. Зависимость  от x1 для W4(p):
от x1 для W4(p):
1
- 5 - g = 0,03; m3 = 0,3; 0,1; 0,05; 0,03; 0
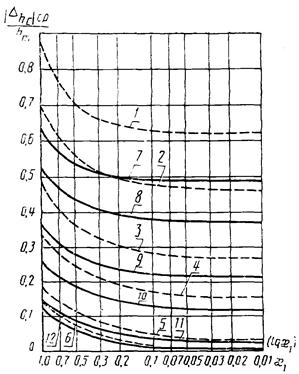
Рис. 7. Зависимость  от x1 для W4(p):
от x1 для W4(p):
1
- 6 - g = 0,03; m3 = 30; 3; 1; 0,5; 0,1; 0; 7 - 12
- g = 0,3; m3 = 30; 3; 1; 0,5; 0,1; 0
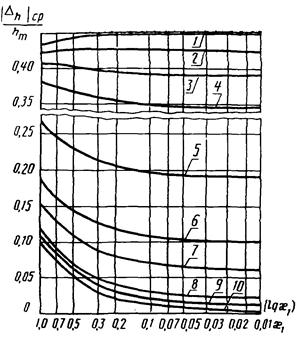
Рис. 8. Зависимость 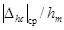 от x1 для
W4(p):
от x1 для
W4(p):
1
- 10 - g = 0,7; m3 = 30; 10; 5; 3; 1;
0,5; 0,3; 0,1; 0,05; 0
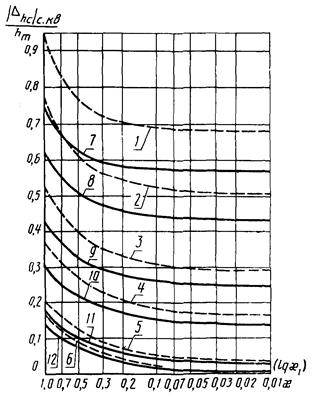
Рис. 9. Зависимость 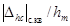 от x1 для W4(p):
от x1 для W4(p):
1
- 6 - g = 0,03; m2 = 30; 3; 1; 0,5; 0,1; 0; 7 - 12
- g = 0,3; m3 = 30; 3; 1; 0,5; 0,1; 0
ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ
ПРЯМЫМ МЕТОДОМ АМПЛИТУДНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
ИССЛЕДУЕМОГО СРЕДСТВА ИЗМЕРЕНИЙ, ОБУСЛОВЛЕННЫЕ
НЕИДЕАЛЬНОСТЬЮ ИСПЫТАТЕЛЬНОГО СИГНАЛА В ЗАВИСИМОСТИ
ОТ ПАРАМЕТРОВ СИГНАЛА, ВИДА И КОЭФФИЦИЕНТОВ
ПЕРЕДАТОЧНОЙ ФУНКЦИИ СРЕДСТВА ИЗМЕРЕНИЙ
(СУММА ОСНОВНОЙ И ВТОРОЙ ГАРМОНИЧЕСКИХ СОСТАВЛЯЮЩИХ
 0
£ a2 £ 0,2,
0
£ a2 £ 0,2,
ВМЕСТО ГАРМОНИЧЕСКОГО СИГНАЛА)
Погрешность DA(f)
по определению представляет собой разность между максимальным значением
приведенного ко входу отклика исследуемого средства измерений на неидеальный
испытательный сигнал, отнесенный к своему максимальному значению, и значением
искомой амплитудно-частотной характеристики указанного средства при частоте f
(см. п. 3.5).
Для испытательного сигнала,
представляющего собой сумму гармонических функций с частотами f
и 2f, соответственно, максимальные значения сигнала и
отклика на него имеют вид:
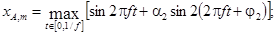
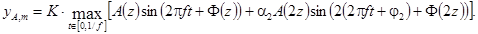
В данном приложении представлены
зависимости приведенных средней квадратической и максимальной погрешностей и
максимальной относительной погрешности:
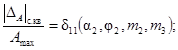
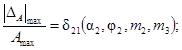
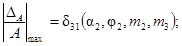 для
для
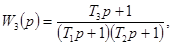
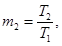
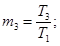
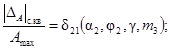

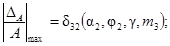 для
для
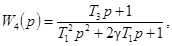
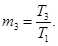
Значения сдвига j2 между
гармоническими составляющими испытательного сигнала приняты равными: 0, -p/8, -p/4.
Значения A(z)
и Φ(z) для указанных передаточных функций рассчитывались по
соотношениям, приведенным в приложении 1. Указанные выше числовые
характеристики погрешности определялись в диапазоне изменений безразмерной
частоты z от 0,01 до 100. Для коэффициентов передаточных функций
были приняты следующие значения: m2 = 0; 0,1; 0,3; m3 = 0; 0,1; 0,3; 1,0 для W3(p);
g =
0,1; 0,7; 0,9; 1,0; m3 = 0; 0,1; 0,3; 1,0 для W4(p).
Построенные по результатам расчетов
графики зависимостей числовых характеристик погрешностей проанализированы и
обобщены следующим образом. Близкие кривые, отличающиеся не более чем на 30 %,
заменены мажорантными; большая часть кривых аппроксимирована кусочно-линейными
функциями, зависящими от параметра a2 и состоящими из двух отрезков прямых.
Ниже приведены приближенные
аналитические выражения указанных характеристик и таблицы значений входящих в
них коэффициентов, а также графические зависимости.
1. 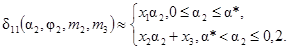
Значения a*, x1 x2, x3 приведены в табл. 1.
Таблица 1
|
a*, xj
|
m3
|
m2
|
j2
|
|
0
|
0,1
|
0,3
|
1,0
|
|
a*
|
0,075
|
0,075
|
0,075
|
0,075
|
0,1
|
0
|
|
x1
|
0,047
|
0,055
|
0,077
|
0,149
|
|
x2
|
0,064
|
0,072
|
0,097
|
0,202
|
|
x3
|
-0,0013
|
-0,0013
|
-0,0015
|
-0,004
|
|
a*
|
0,075
|
0,075
|
0,075
|
0,075
|
0,3
|
|
x1
|
0,041
|
0,041
|
0,055
|
0,092
|
|
x2
|
0,054
|
0,058
|
0,072
|
0,123
|
|
x3
|
-0,001
|
-0,0013
|
-0,0013
|
-0,0023
|
|
a*
|
0,070
|
0,070
|
0,075
|
0,075
|
0,9
|
|
x1
|
0,032
|
0,032
|
0,037
|
0,057
|
|
x2
|
0,047
|
0,078
|
0,054
|
0,076
|
|
x3
|
-0,0011
|
-0,0032
|
-0,0013
|
-0,0014
|
|
a*
|
0,138
|
0,138
|
0,090
|
0,100
|
0,1
|

|
|
x1
|
0,068
|
0,076
|
0,100
|
0,215
|
|
x2
|
0,052
|
0,055
|
0,076
|
0,169
|
|
x3
|
0,0022
|
0,0026
|
0,0022
|
0,0046
|
|
a*
|
0,125
|
0,125
|
0,120
|
0,116
|
0,3
|
|
x1
|
0,060
|
0,064
|
0,076
|
0,130
|
|
x2
|
0,053
|
0,053
|
0,059
|
0,103
|
|
x3
|
0,0009
|
0,0014
|
0,002
|
0,0031
|
|
a*
|
0,125
|
0,125
|
0,125
|
0,100
|
0,9
|
|
x1
|
0,054
|
0,054
|
0,060
|
0,081
|
|
x2
|
0,046
|
0,047
|
0,049
|
0,066
|
|
x3
|
0,001
|
0,0009
|
0,0014
|
0,0015
|
|
a*
|
0,100
|
0,100
|
0,088
|
0,076
|
0,1
|
|
|
x1
|
0,060
|
0,064
|
0,075
|
0,184
|
|
x2
|
0,046
|
0,044
|
0,055
|
0,128
|
|
x3
|
0,0014
|
0,002
|
0,0018
|
0,0043
|
|
a*
|
0,088
|
0,089
|
0,075
|
0,075
|
0,3
|
|
x1
|
0,057
|
0,060
|
0,067
|
0,113
|
|
x2
|
0,044
|
0,045
|
0,048
|
0,082
|
|
x3
|
0,0011
|
0,0013
|
0,0014
|
0,0023
|
|
a*
|
0,750
|
0,750
|
0,750
|
0,750
|
0,9
|
|
x1
|
0,056
|
0,056
|
0,056
|
0,070
|
|
x2
|
0,038
|
0,039
|
0,042
|
0,049
|
|
x3
|
0,0014
|
0,013
|
0,0011
|
0,0016
|
2. δ21н(a2, j2) £ δ21(a2; j2; m2; m3) £ δ21в(a2, j2); 0 £ a2 £ 0,2; m2 = 0,1; 0,3; 0,9; m3 = 0; 0,1; 0,3; 1,0; j2 = 0; -p/8; -p/4.
Зависимости δ21н(a2, j2) и
δ21в(a2, j2)
представлены: для j2 = 0 на
рис. 1,
для j2 = -p/8 на рис. 2, для j2 = -p/4 на рис. 3.
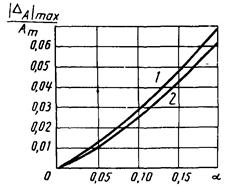
Рис. 1. Зависимость 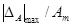 от a2 для W3(p):
от a2 для W3(p):
1
- δ21в(a2,
0); 2 - δ21н(a2,
0)
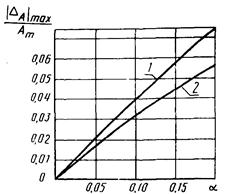
Рис. 2. Зависимость 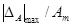 от a2 для W3(p):
от a2 для W3(p):
1
- δ21в(a2, -p/8); 2 - δ21н(a2, -p/8)
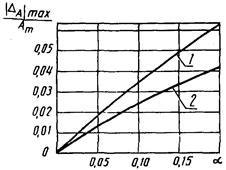
Рис. 3. Зависимость 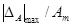 от a2 для W3(p):
от a2 для W3(p):
1 - δ21в(a2, -p/4);
2 - δ21н(a2,
-p/4)
3. Зависимости 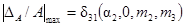 для m2 = 0,1; 0,3; 0,9 при 0,1 £ m3 £ 1,0 представлены на рис. 4.
для m2 = 0,1; 0,3; 0,9 при 0,1 £ m3 £ 1,0 представлены на рис. 4.
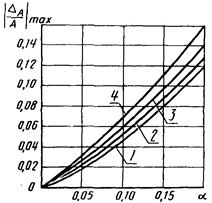
Рис. 4. Зависимость 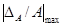 от a2 для W3(p):
от a2 для W3(p):
1 - δ31(a2,
0; 0,1; 0); 2 - δ31(a2,
0; 0,3; 0); 3 - δ31(a2,
0; 0,9; 0); 4 - δ31(a2,
0; m2; m3)
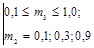
4. δ31н(a2, -p/8) £ δ31(a2, -p/8) £ δ31в(a2, -p/8),
где
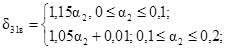
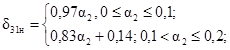
m2 = 0,1;
0,3; 0,9; m3 = 0;
0,1; 0,3; 1,0.
5. 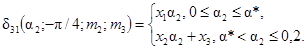
Значения a*, x1, x2, x3 приведены в табл. 2.
Таблица 2
|
a*, xj
|
m2
|
m2
|
|
0
|
0,1
|
0,3
|
1,0
|
|
a*
|
0,063
|
0,075
|
0,075
|
0,1
|
|
x1
|
1,23
|
0,947
|
0,893
|
|
x2
|
0,982
|
0,655
|
0,616
|
|
x3
|
0,016
|
0,022
|
0,021
|
|
a*
|
0,063
|
0,063
|
0,050
|
0,3
|
|
x1
|
1,23
|
1,17
|
1,02
|
|
x2
|
0,989
|
0,880
|
0,717
|
|
x3
|
0,015
|
0,018
|
0,015
|
|
a*
|
0,075
|
0,075
|
0,063
|
0,9
|
|
x1
|
1,24
|
1,07
|
0,992
|
|
x2
|
0,96
|
0,752
|
0,669
|
|
x3
|
0,021
|
0,024
|
0,020
|
6. 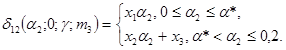
Значения a*, x1, x2, x3 приведены в табл. 3.
Таблица 3
|
a*, xj
|
m2
|
v
|
|
0
|
0,1
|
0,3
|
1,0
|
|
a*
|
0,100
|
0,100
|
0,1
|
|
x1
|
0,034
|
0,034
|
|
x2
|
0,051
|
0,048
|
|
x3
|
-0,0017
|
-0,0014
|
|
a*
|
0,075
|
0,070
|
0,075
|
0,7
|
|
x1
|
0,032
|
0,036
|
0,053
|
|
x2
|
0,052
|
0,057
|
0,074
|
|
x3
|
-0,0015
|
-0,0015
|
-0,0016
|
|
a*
|
0,070
|
0,063
|
0,070
|
0,9
|
|
x1
|
0,031
|
0,035
|
0,054
|
|
x2
|
0,048
|
0,052
|
0,075
|
|
x3
|
-0,0012
|
-0,0011
|
-0,0015
|
|
a*
|
0,075
|
0,075
|
0,090
|
0,100
|
1,0
|
|
x1
|
0,032
|
0,032
|
0,038
|
0,059
|
|
x2
|
0,046
|
0,047
|
0,052
|
0,073
|
|
x3
|
-0,0011
|
-0,0011
|
-0,0013
|
-0,0014
|
7. 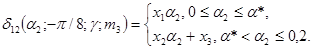
Значения a*, x1, x2, x3 приведены в табл. 3.
Таблица 4
|
a*, xj
|
m3
|
v
|
|
0
|
0,1
|
0,3
|
1,0
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
a*
|
0,145
|
0,150
|
0,1
|
|
x1
|
0,076
|
0,072
|
|
x2
|
0,070
|
0,068
|
|
x3
|
0,0009
|
0,0006
|
|
a*
|
0,130
|
0,128
|
0,115
|
0,125
|
0,7
|
|
x1
|
0,063
|
0,064
|
0,069
|
0,082
|
|
x2
|
0,056
|
0,057
|
0,060
|
0,069
|
|
x3
|
0,0009
|
0,0009
|
0,001
|
0,0016
|
|
a*
|
0,113
|
0,125
|
0,115
|
0,105
|
0,9
|
|
x1
|
0,055
|
0,056
|
0,061
|
0,081
|
|
x2
|
0,049
|
0,049
|
0,052
|
0,067
|
|
x3
|
0,0007
|
0,0009
|
0,001
|
0,0015
|
|
a*
|
0,125
|
0,125
|
0,125
|
0,110
|
1,0
|
|
x1
|
0,052
|
0,054
|
0,058
|
0,076
|
|
x2
|
0,045
|
0,045
|
0,047
|
0,062
|
|
x3
|
0,0009
|
0,0011
|
0,0014
|
0,0015
|
8. 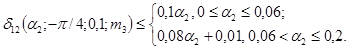
9. 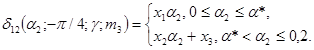
Значения a*, x1, x2, x3 приведены в табл. 5.
Таблица 5
|
a*, xj
|
m3
|
v
|
|
0
|
0,1
|
0,3
|
1,0
|
|
a*
|
0,075
|
0,075
|
0,065
|
0,7
|
|
x1
|
0,068
|
0,071
|
0,081
|
|
x2
|
0,054
|
0,055
|
0,059
|
|
x3
|
0,0011
|
0,0012
|
0,0014
|
|
a*
|
0,075
|
0,063
|
0,9
|
|
x1
|
0,059
|
0,073
|
|
x2
|
0,041
|
0,054
|
|
x3
|
0,0014
|
0,0012
|
|
a*
|
0,075
|
0,050
|
1,0
|
|
x1
|
0,056
|
0,072
|
|
x2
|
0,041
|
0,051
|
|
x3
|
0,0011
|
0,0011
|
10. 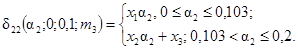
Значения x1, x2, x3 приведены в табл. 6.
Таблица 6
|
xj
|
m3
|
|
0;
0,1; 0,3
|
1,0
|
|
x1
|
0,956
|
0,937
|
|
x2
|
0,790
|
0,739
|
|
x3
|
0,017
|
0,0204
|
11. δ22н(a2, 0) £ δ22 (a2, 0, g, m3) £ δ22в(a2, 0).
0,7 £ g £ 1,0
Зависимости δ22в(a2, 0) и δ22н(a2, 0) представлены
на рис. 5.
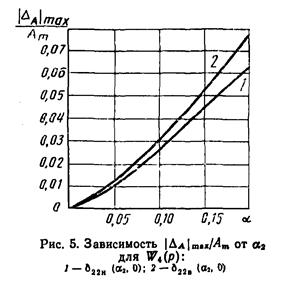
12. 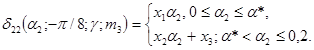
Значения a*, x1, x2, x3
приведены в табл. 7.
13. 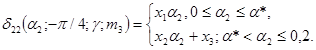
Значения a*, x1, x2, x3
приведены в табл. 8.
Таблица 7
|
a*, xj
|
m3
|
g
|
|
0;
0,1; 0,3
|
1,0
|
|
a*
|
0,075
|
0,075
|
0,1
|
|
x1
|
0,747
|
0,760
|
|
x2
|
0,632
|
0,668
|
|
x3
|
0,009
|
0,007
|
|
a*
|
0,125
|
0,088
|
0,7
|
|
x1
|
0,500
|
0,423
|
|
x2
|
0,453
|
0,373
|
|
x3
|
0,006
|
0,004
|
|
a*
|
0,125
|
0,075
|
0,9
|
|
x1
|
0,416
|
0,387
|
|
x2
|
0,353
|
0,327
|
|
x3
|
0,008
|
0,0045
|
|
a*
|
0,120
|
0,090
|
1,0
|
|
x1
|
0,396
|
0,356
|
|
x2
|
0,330
|
0,290
|
|
x3
|
0,008
|
0,006
|
Таблица 8
|
a*, xj
|
m3
|
g
|
|
0; 0,1; 0,3
|
1,0
|
|
a*
|
0,070
|
0,1
|
|
x1
|
0,910
|
|
x2
|
0,735
|
|
x3
|
0,0012
|
|
a*
|
0,070
|
0,070
|
0,7
|
|
x1
|
0,521
|
0,432
|
|
x2
|
0,408
|
0,344
|
|
x3
|
0,008
|
0,006
|
|
a*
|
0,080
|
0,080
|
0,9
|
|
x1
|
0,403
|
0,334
|
|
x2
|
0,394
|
0,252
|
|
x3
|
0,007
|
0,007
|
|
a*
|
0,075
|
0,075
|
1,0
|
|
x1
|
0,373
|
0,297
|
|
x2
|
0,290
|
0,220
|
|
x3
|
0,006
|
0,006
|
14. 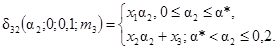
Значения a*, x1, x2, x3 приведены
в табл. 9.
15. Зависимости δ32(a2; 0; g, m3) для g = 0,7; 0,9; 1,0 и m3 = 0; 0,1; 0,3; 1,0 представлены на рис. 6.
16. 
Значения a*, x1, x2, x3 приведены
в табл. 10.
Таблица 9
|
a*, xj
|
m3
|
|
0; 0,1; 0,3
|
1,0
|
|
a*
|
0,075
|
0,06
|
|
x1
|
3,80
|
4,96
|
|
x2
|
3,14
|
3,93
|
|
x3
|
0,05
|
0,06
|
Таблица 10
|
a*, xj
|
m3
|
|
0; 0,1
|
0,3
|
1,0
|
|
a*
|
0,090
|
0,090
|
0,113
|
|
x1
|
2,89
|
3,00
|
3,65
|
|
x2
|
2,27
|
2,64
|
3,03
|
|
x3
|
0,055
|
0,032
|
0,07
|
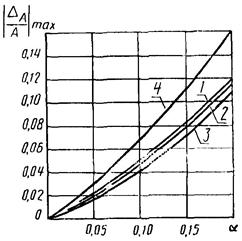
Рис. 6. Зависимость |DA/A|max от a2 для W4(p);
1 - δ32(a2; 0; 0,7; 0); 2 - δ32(a2; 0; 0,9; 0); 3 - δ32(a2; 0; 1,0; 0); 4 - δ32(a2; 0; g; m3) 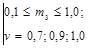
17. δ32н(a2, -p/8) £ δ32 (a2, -p/8, g, m3) £ δ32в(a2, -p/8);
0,7 £ g £ 1,0
0 £ m3 £ 1,0,
где
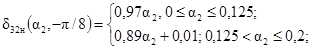
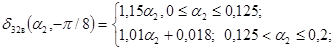
18. 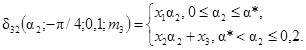
Значения a*, x1, x2, x3 приведены в табл. 11.
Таблица 11
|
a*, xj
|
m3
|
|
0; 0,1
|
0,3
|
1,0
|
|
a*
|
0,030
|
0,070
|
0,070
|
|
x1
|
1,92
|
2,00
|
2,47
|
|
x2
|
1,97
|
2,02
|
2,73
|
|
x3
|
-0,0015
|
-0,0014
|
-0,018
|
Таблица 12
|
g
|
m3
|
|
0
|
0,1
|
0,3
|
1,0
|
|
0,1
|
5,025
|
5,050
|
5,242
|
7,080
|
|
0,7
|
1,000
|
1,000
|
1,002
|
1,107
|
|
0,9
|
1,000
|
1,000
|
1,000
|
1,000
|
|
1,0
|
1,000
|
1,000
|
1,000
|
1,000
|
19. Зависимости δ32
(a2, -p/4, g, m3) для g = 0,7; 0,9; 1,0 представлены на рис. 7.
Пересчет приведенных погрешностей в
абсолютные для передаточных функций W3(p) не требуется, поскольку для этих функций Amax = 1. Пересчет для передаточных
функций W4(p)
может быть сделан на основе значений Amax, приведенных в табл. 12.
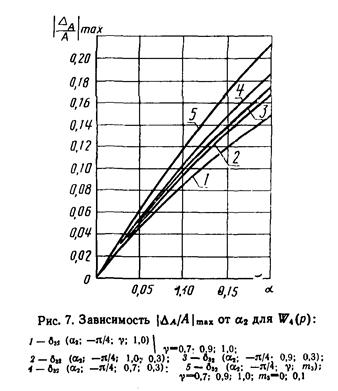
ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ
ПРЯМЫМ МЕТОДОМ ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
ИССЛЕДУЕМОГО СРЕДСТВА ИЗМЕРЕНИЯ, ОБУСЛОВЛЕННЫЕ
НЕИДЕАЛЬНОСТЬЮ ИСПЫТАТЕЛЬНОГО СИГНАЛА, В ЗАВИСИМОСТИ
ОТ ПАРАМЕТРОВ СИГНАЛА, ВИДА И КОЭФФИЦИЕНТОВ
ПЕРЕДАТОЧНОЙ ФУНКЦИИ СРЕДСТВА ИЗМЕРЕНИЙ
(СУММА ОСНОВНОЙ И ВТОРОЙ ГАРМОНИЧЕСКИХ СОСТАВЛЯЮЩИХ
 0 < a2
< 0,2,
0 < a2
< 0,2,
ВМЕСТО ГАРМОНИЧЕСКОГО СИГНАЛА)
Погрешность DΦ(f)
в соответствии с п. 3.5 представляет собой разность между корнями e0 и ζ0
уравнений (11)
и (12)
(которым соответствуют положительные производные по времени испытательного и
выходного сигналов исследуемого средства измерений) и искомой фазочастотной
характеристикой при частоте f.
Для испытательного сигнала,
представляющего собой сумму гармонических функции с частотами f
и 2f, соответственно, уравнения (11) и (12)
имеют вид: sine + a2 · sin2(e + j2) = 0, 0 £ e < 2p; sin(ζ + Φ(z)) + a2(A(2z)/A(z))
· sin(2ζ + j2) + Φ(2z)) = 0, 0 £ ζ < 2p.
В данном приложении
представлены полученные расчетным путем зависимости максимальной погрешности:
|DΦ|max = D1(a2, j2, m2, m3) для  ,
,
и 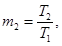

|DΦ|max = D2(a2, j2, g, m3) для 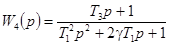 ,
,

Значения сдвига j2 между
гармоническими составляющими сигнала приняты равными: 0, -p/8, -p/4.
Указанная выше характеристика погрешности
определялась в диапазоне изменений безразмерной частоты z
от 0,01 до 100: 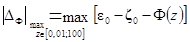 .
.
Частотные характеристики A(z)
и Φ(z), соответствующие передаточным функциям W3(p)
и W4(p),
рассчитывались по соотношениям, приведенным в справочном приложении 2.
Для коэффициентов передаточных функций
были приняты значения: m2 = 0,1;
0,3; 0,7; m3 = 0;
0,1; 0,3; 0,7; 1,0 для W3(p)
и v = 0,1; 0,3; 0,5; 0,7; 1,0; m3 = 0; 0,1; 0,3; 0,7; 1,0
для W4(p).
Большая часть построенных по результатам
расчетов зависимостей максимальной погрешности определения фазочастотной
характеристики была аппроксимирована кусочно-линейными функциями, зависящими от
параметра a2 и
состоящими из двух отрезков прямых.
Ниже приведены приближенные аналитические
выражения и таблицы значений входящих в них коэффициентов, а также графики
указанных выше зависимостей.
1. 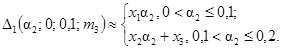
Значения x1, x2, x3 приведены в табл. 1.
Таблица 1
|
xj
|
m3
|
|
0
|
0,1
|
0,3
|
0,7; 1,0
|
|
x1
|
0,48
|
0,58
|
0,56
|
0,48
|
|
x2
|
0,4275
|
0,495
|
0,4775
|
0,4275
|
|
x3
|
0,005225
|
0,0085
|
0,00825
|
0,00525
|
2. 
3. 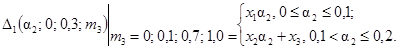
Значения x1, x2, x3 приведены в табл. 2.
Таблица 2
|
xj
|
m3
|
|
0
|
0,1
|
0,7;
1,0
|
|
x1
|
0,45
|
0,5
|
0,495
|
|
x2
|
0,4
|
0,485
|
0,466
|
|
x3
|
0,005
|
0,0015
|
0,003
|
Таблица 3
|
xj
|
m3
|
|
0
|
0,1;
0,3
|
0,7;
1,0
|
|
x1
|
0,43
|
0,517
|
0,495
|
|
x2
|
0,375
|
0,483
|
0,475
|
|
x3
|
0,0055
|
0,0034
|
0,002
|
4. 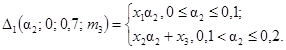
Значения x1, x2, x3 приведены в табл. 3.
5. 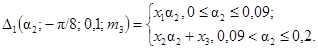
Значения x1, x2, x3 приведены в табл. 4.
Таблица 4
|
xj
|
m3
|
|
0
|
0,1
|
0,3;
0,7; 1,0
|
|
x1
|
0,965
|
0,934
|
0,8945
|
|
x2
|
0,711
|
0,6904
|
0,645
|
|
x3
|
0,023
|
0,022
|
0,02201
|
Таблица 5
|
xj
|
m3
|
|
0
|
0,1
|
0,3;
0,7; 1,0
|
|
x1
|
0,9445
|
1,0334
|
0,9445
|
|
x2
|
0,7545
|
0,7364
|
0,7545
|
|
x3
|
0,0171
|
0,0268
|
0,0171
|
6. 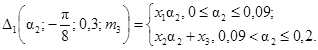
Значения x1, x2, x3 приведены в табл. 5.
7. 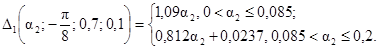
8. 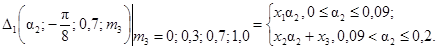
Значения x1, x2, x3
приведены в табл. 6.
Таблица 6
|
xj
|
m3
|
|
0
|
0,3;
0,7: 1,0
|
|
x1
|
0,9612
|
1,0
|
|
x2
|
0,67
|
0,714
|
|
x3
|
0,0235
|
0,0258
|
9. 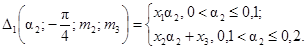
Значения x1, x2, x3 приведены в табл. 7.
Таблица 7
|
xj
|
m3
|
m2
|
|
0
|
0,1
|
0,3; 0,7; 1,0
|
|
x1
|
1,26
|
0,93
|
0,87
|
0,1
|
|
x2
|
1,09
|
0,795
|
0,79
|
|
x3
|
0,017
|
0,0135
|
0,008
|
|
x1
|
1,25
|
1,045
|
0,96
|
0,3
|
|
x2
|
1,13
|
0,895
|
0,87
|
|
x3
|
0,012
|
0,015
|
0,009
|
|
x1
|
1,27
|
1,17
|
0,99
|
0,7
|
|
x2
|
1,10
|
1,03
|
0,88
|
|
x3
|
0,017
|
0,014
|
0,011
|
10. Зависимость |DΦ|max(a2) = D2(a2; 0; 0,1;
m3) для 0
< a2 £ 0,1, m3 = 0; 0,1 представлена на рис. 1.
11. Зависимости |DΦ|max(a2) = D2(a2; 0; 0,3;
m3) для 0
< a2 £ 0,2, m3 = 0; 0,1, 0,3 представлены на рис. 2.
12. Зависимости |DΦ|max(a2) = D2(a2; 0; 0,5;
m3) для 0 £ m3 £ 1,0 даются следующими соотношениями:
12.1. 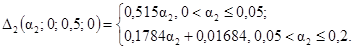
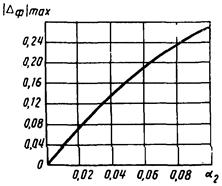
Рис. 1. Зависимость |DΦ|max от a2 для W4(p).
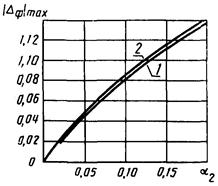
Рис. 2. Зависимость |DΦ|max от a2 для W4(p):
1
- m3 = 0; 0,1; 2 - m2 = 0,3
12.2. 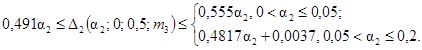
0,1 £ m3 £ 1,0
13. D2(a2; 0; 0,7; 0) = 0,27a2.
14. 0,49a2 £ D2(a2; 0; 0,7;
m3) £ 0,5a2.
0,1 £ m3 £ 1,0
15. D2(a2; 0; 1,0) = 0,315a2.
16. D2(a2; 0; 1,0; m3) = 0,5a2.
0,1 £ m3 £ 1,0
17. 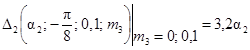
18. 
Значения x1, x2, x3 приведены в табл. 8.
Таблица 8
|
xj
|
m3
|
|
0
|
0,1;
0,3
|
|
x1
|
0,875
|
1,1125
|
|
x2
|
0,7
|
0,91
|
|
x3
|
0,014
|
0,0164
|
Таблица 9
|
xj
|
m3
|
|
0
|
0,1;
0,3
|
0,7;
1,0
|
|
x1
|
0,907
|
1,114
|
1,03
|
|
x2
|
0,72
|
0,917
|
0,806
|
|
x3
|
0,01404
|
0,0152
|
0,0168
|
19. 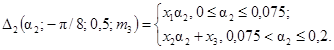
Значения x1, x2, x3 приведены в табл. 9.
20. 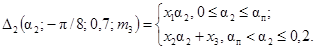
Значения aп, x1, x2, x3 приведены в табл. 10.
Таблица 10
|
aп, xj
|
m3
|
|
0
|
0,1
|
0,3
|
0,7; 1,0
|
|
aп
|
0,09
|
0,1
|
0,1
|
0,09
|
|
x1
|
0,917
|
1,1
|
1,056
|
1,0
|
|
x2
|
0,7043
|
0,845
|
0,814
|
0,7455
|
|
x3
|
0,01915
|
0,0255
|
0,0242
|
0,023
|
Таблица 11
|
xj
|
m3
|
|
0
|
0,1
|
0,3
|
0,7;
1,0
|
|
x1
|
0,947
|
1,12
|
1,067
|
1,02
|
|
x2
|
0,7358
|
0,883
|
0,8238
|
0,764
|
|
x3
|
0,016
|
0,0174
|
0,01824
|
0,0192
|
21. 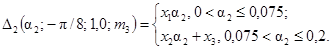
Значения x1, x2, x3 приведены в табл. 11.
22. Зависимость |DΦ|max(a2) = D2(a2; -p/4; 0,1; m3) для m3 = 0; 0,1 представлена на
рис. 3.
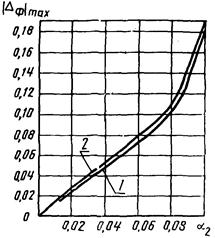
Рис. 3. Зависимость |DΦ|max от a2 для W4(p):
1 - m2 = 0; 2 - m3 = 0,1
23. 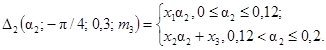
Значения x1, x2, x3 приведены в табл. 12.
Таблица 12
|
xj
|
m3
|
|
0
|
0,1
|
0,3
|
|
x1
|
1,234
|
1,313
|
1,234
|
|
x2
|
1,112
|
1,143
|
1,112
|
|
x3
|
0,0147
|
0,0204
|
0,0147
|
24. 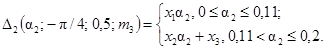
Значения x1, x2, x3 приведены
в табл. 13.
Таблица 13
|
xj
|
m3
|
|
0
|
0,1
|
0,3
|
0,7
|
1,0
|
|
x1
|
1,24
|
1,31
|
1,21
|
1,04
|
0,991
|
|
x2
|
1,107
|
1,1434
|
1,0712
|
0,929
|
0,8855
|
|
x3
|
0,01467
|
0,01834
|
0,01528
|
0,01223
|
0,01162
|
25. 
Значения x1, x2, x3 приведены в табл. 14.
Таблица 14
|
xj
|
m3
|
m2
|
|
0
|
0,1
|
0,3
|
0,7; 1,0
|
|
x1
|
1,250
|
1,31
|
1,187
|
1,015
|
0,7
|
|
x2
|
1,15
|
1,14
|
1,023
|
0,87
|
|
x3
|
0,01
|
0,017
|
0,0164
|
0,0145
|
|
x1
|
1,245
|
1,28
|
1,145
|
0,98
|
0,9
|
|
x2
|
1,135
|
1,12
|
0,975
|
0,91
|
|
x3
|
0,011
|
0,016
|
0,017
|
0,007
|
ПРИМЕРЫ АЛГОРИТМОВ ОБРАБОТКИ ДАННЫХ ПРИ
ОПРЕДЕЛЕНИИ ПОЛНЫХ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК КОСВЕННЫМИ МЕТОДАМИ
1. Метод дискретизации
уравнения свертки
1.1.
Исходные данные.
1.1.1. N* значений испытательного сигнала, взятых с периодом
дискретизации 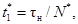
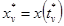 ,
, 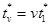 , v = 1, 2
..., N* - 1;
, v = 1, 2
..., N* - 1; 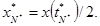
1.1.2. Значения выходного сигнала 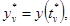 , v
= 1, 2, ..., N*.
, v
= 1, 2, ..., N*.
1.1.3. Верхние границы погрешностей
определения значений испытательного сигнала 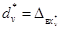 , v = 1, 2, ..., N*.
, v = 1, 2, ..., N*.
1.1.4. Верхние границы погрешностей
определения значений выходного сигнала 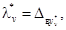 v = 1, 2,
..., N*.
v = 1, 2,
..., N*.
1.2. Последовательность
вычислений.
1.2.1. Определяют момент времени 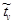 , для
которого выполняется условие
, для
которого выполняется условие 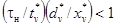 , v = 1, 2,
...;
, v = 1, 2,
...;
вычисляют 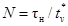 ;
;
принимают новый период
дискретизации: 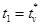 ;
;
выбирают из указанных в п. 1.1 совокупностей 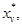
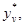
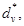
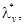
значения, соответствующие моментам
времени ti = it1: [xi = x(ti), i = 1, ..., N - 1; xN = x(tN)/2; yi - y(tt), i = 1, ..., N;  , i
= 1, ..., N;
, i
= 1, ..., N; 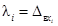 , i = 1, ..., N.
, i = 1, ..., N.
1.2.2. Составляют матрицу
значений испытательного сигнала
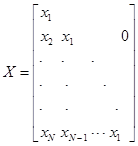
и вектор значений выходного сигнала
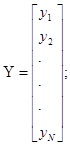
вычисляют обратную матрицу
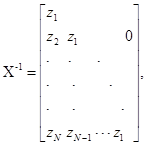
где z1 = 1/x1; 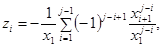 j
= 2, ..., N;
j
= 2, ..., N;
вычисляют вектор оценок значений импульсной
характеристики
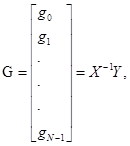
где gi = g(ti), i = 0, 1, ..., N -
1.
1.2.3. Составляют матрицу абсолютных
значений
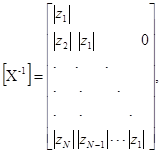
и вектор погрешностей значений
испытательного сигнала

вычисляют вектор
С = |Х-1|Dx;
составляют матрицу
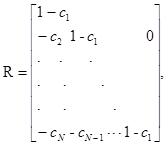
где сi -
элементы вектора С;
вычисляют обратную матрицу
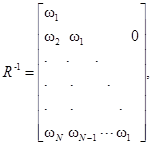
где ω1 = 1/(1 - c1);
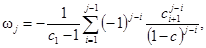 j
= 2, ..., n;
j
= 2, ..., n;
составляют вектор абсолютных значений
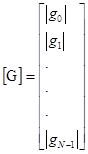
и вектор погрешностей
значений выходного сигнала
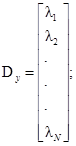
вычисляют вектор оценок
погрешностей определения значений импульсной характеристики  .
.
2. Многократное интегрирование входного и
выходного сигналов
2.1. Исходные данные.
2.1.1. Те же, что в п. 1.1.
2.1.2. Структура дифференциального уравнения
исследуемого средства измерений 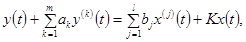 l < m.
l < m.
2.1.3. Статический коэффициент
преобразования средства измерений K.
2.2. Последовательность вычислений.
2.2.1. Вычисляют интегралы от входного и
выходного сигналов на промежутках [0, tr], r
= 1, ..., m + l;

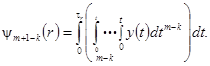
Для приближенного вычисления интеграла Im-j(s
· 2m-j) кратности m - j в
точке 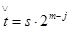 безразмерного
времени
безразмерного
времени  можно
использовать рекуррентную формулу Симпсона:
можно
использовать рекуррентную формулу Симпсона:
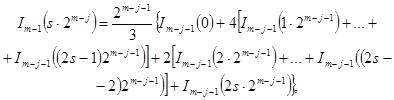
где j = m - 1, ..., 1,0; 
I0(s)
обозначает подынтегральную функцию в точке 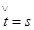 . Для вычисления интеграла
заданной кратности j можно использовать рекуррентную формулу
. Для вычисления интеграла
заданной кратности j можно использовать рекуррентную формулу
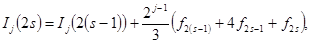
где fs -
значение подынтегральной функции в точке 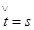 . Верхнюю границу промежутка
интегрирования tm+i
следует выбирать равной времени наблюдений tн. Верхние границы промежутков tr, r
= 1, ..., т + l - 1,
следует выбирать приближенно равномерно в интервале [0, tm+1], при этом должны быть выполнены условия tr-1 < tr. В
случае использования формулы Симпсона количество значений
. Верхнюю границу промежутка
интегрирования tm+i
следует выбирать равной времени наблюдений tн. Верхние границы промежутков tr, r
= 1, ..., т + l - 1,
следует выбирать приближенно равномерно в интервале [0, tm+1], при этом должны быть выполнены условия tr-1 < tr. В
случае использования формулы Симпсона количество значений 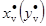 на каждом промежутке
интегрирования должно быть кратно значению 2m+1.
на каждом промежутке
интегрирования должно быть кратно значению 2m+1.
2.2.2. Составляют систему алгебраических
уравнений
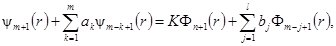 r = 1, ..., m
+ l,
r = 1, ..., m
+ l,
или RиA = F,
где матрица системы
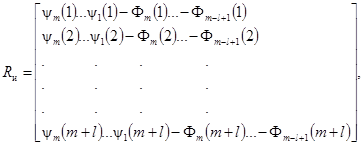
вектор свободных членов

вектор искомых коэффициентов
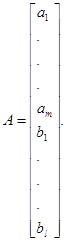
2.2.3. Вычисляют определитель матрицы Rи.
Если detRи ≠ 0, то составляют обратную матрицу
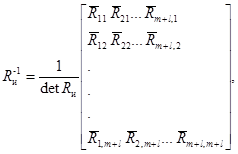
где  - алгебраическое дополнение ij-го элемента матрицы Rи.
- алгебраическое дополнение ij-го элемента матрицы Rи.
Если detRи = 0, то изменяют один из промежутков интегрирования,
вычисляют интегралы Φm+1-j(r),
ψm+1-k(r) на новом промежутке и вычисления по пп. 2.2.2; 2.2.3
повторяют.
2.2.4. Составляют матрицу 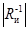 абсолютных
значений элементов
абсолютных
значений элементов 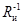 .
.
2.2.5. Составляют матрицу
погрешностей элементов Rи
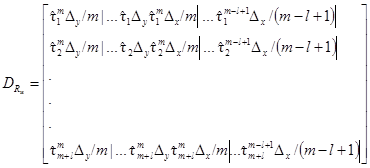
и вектор погрешностей элементов F

где 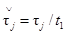 ;
; 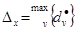 ;
;
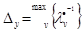 .
.
2.2.6. Вычисляют матрицу
критической обусловленности системы алгебраических уравнений 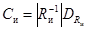 .
.
Вычисляют фактор критической
обусловленности 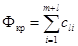 , где cli - диагональный элемент матрицы Cи.
, где cli - диагональный элемент матрицы Cи.
2.2.7. Если Φкр
< 1, то вычисляют вектор  оценок элементов A:
оценок элементов A:
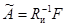 .
.
Если Φкр ³ 1, то увеличивают период дискретизации при разбиении
промежутков интегрирования, и вычисления по пп. 2.2.2 - 2.2.7
повторяют.
2.2.8. Вычисляют вектор погрешностей 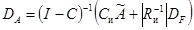 , где
I - единичная матрица.
, где
I - единичная матрица.
3. Адаптивный метод определения полных
динамических характеристик.
3.1. Исходные данные.
3.1.1. Те же, что в п. 1.1,
кроме 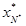 ,
равного
,
равного 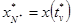 .
Испытательный сигнал может быть задан также аналитическим выражением.
.
Испытательный сигнал может быть задан также аналитическим выражением.
3.1.2. Совокупность
типовых испытательных сигналов, представленных на рисунке:
3.1.4. Иерархическая система
моделей динамических свойств средств измерений с передаточными функциями Wk(p):
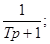
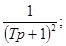
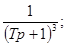
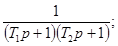

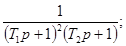
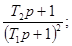
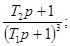
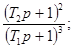
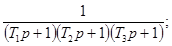
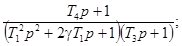
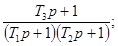
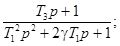
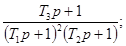
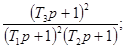
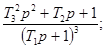
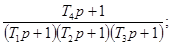
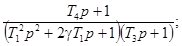
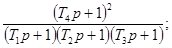

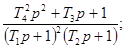
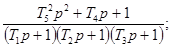

3.2. Принцип алгоритма состоит в
минимизации квадратических функционалов от разности откликов исследуемого
средства измерений и моделей его динамических свойств (выбираемых
последовательно из указанной иерархии) на заданный испытательный сигнал и
нахождении той модели, которая дает значение функционала, не превышающее
заданного.
Комплекс программ, реализующих указанный
выше принцип вычислений, включен в отраслевой фонд алгоритмов и программ
Госстандарта СССР (ФАП АИУС ГИВЦ Госстандарта СССР). Комплекс включает
программы:
для нахождения простейшей по структуре
оптимальной передаточной функции,
для оценивания погрешностей найденных
коэффициентов передаточной функции,
для пересчета найденной передаточной
функции в другие полные динамические характеристики.
УСТАНОВЛЕНИЕ КОЭФФИЦИЕНТА ЗАПАСА Kз
Выбор испытательного сигнала и
установление коэффициента Kз
производят путем последовательных приближений:
принимают Kз0 = 1;
проверяют, удовлетворяет ли сигнал x(t)
неравенствам (13), (14) п. 3.7
рекомендации; при нарушении неравенства выбирают более широкополосный сигнал;
находят требуемую динамическую
характеристику исследуемого средства измерений;
оценивают погрешность
определения динамической характеристики средства измерений;
оценивают неточность DD(t) оценки временной зависимости D(t) искажений испытательного сигнала, обусловленную
погрешностью определения динамической характеристики исследуемого средства
измерений; при условии DDч/Dч £ 0,3 операции выбора заканчивают;
при условии DDч/Dч > 0,3
принимают Kз1 > Kз0 и операции выбора
повторяют.
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК СРЕДСТВ
ИЗМЕРЕНИЙ
1. Контроль нормированной
динамической характеристики
1.1. Исходные данные
Исследуемое средство измерений -
индукционный расходомер с самопишущим измерительным (вторичным) устройством (по
ГОСТ 11988).
Требуемая динамическая характеристика -
переходная характеристика.
Требуемая форма представления
динамической характеристики - графическая.
Предварительная информация - модель
динамических свойств расходомера представляет собой динамическое звено 1-го
порядка с постоянной времени T, номинальное значение которой Tн = 1 с; допускаемые
отклонения переходной характеристики от номинальной по модулю не должны
превышать Dh
= 15 %.
Имеющийся в наличии генератор
испытательного сигнала - мера расхода жидкости, обеспечивающая линейное
нарастание расхода от 0 до 0,03 м3/ч за время tΦ, не
превышающее 0,02 с; погрешность воспроизведения сигнала не превышает 2 %.
Требуемая точность определения
динамической характеристики - не установлена.
Требуемый диапазон частот, в котором
должен быть исследован расходомер, - не установлен.
1.2. Последовательность
операций
1.2.1. Выбор метода контроля
По п. 2.2.1 рекомендации контроль
осуществляется по постоянной времени T.
Допускаемые относительные отклонения
δт параметра T от Tн
определяются условием δh £ eDh/1 - eDh.
Для Dh
= 15 % получается δт £ 69 %, чему
соответствуют пределы допускаемых значений Т:Тmin = 0,31 с, Tmax = 1,69
с.
1.2.2. Выбор испытательного сигнала.
По п. 2.2.3 рекомендации в качестве испытательного выбирается
сигнал, достаточно близкий по форме к единичной ступенчатой функции.
1.2.3. Оценка неидеальности
испытательного сигнала.
Погрешность от неидеальности
испытательного сигнала (приложение 4, 1-я строка таблицы)
вследствие выполнения условия tq
max/Tmin = 0,06 < 0,3 оценивается по формуле 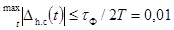 .
.
Значение 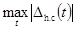 пренебрежимо мало по сравнению
с Dh
и испытательный сигнал можно считать близким к
характеристическому.
пренебрежимо мало по сравнению
с Dh
и испытательный сигнал можно считать близким к
характеристическому.
1.2.4. Проверка требований п. 4.2
рекомендации.
Искажение испытательного сигнала D(t) = 1/k · y(t)
- x(t), где y(t) выходной
сигнал индукционного расходомера; x(t) -
испытательный сигнал,
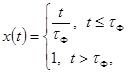
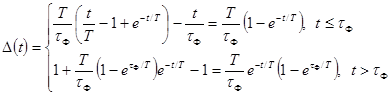
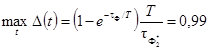 при t = tΦ.
при t = tΦ.
В качестве регистрирующего
используется вторичное устройство расходомера. Таким образом,
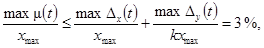
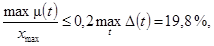
1.2.5. Нахождение контролируемого
параметра.
Исследуемый расходомер подключается к
мере, и выходной сигнал записывается на ленте самопишущего прибора. За начало
отсчета времени принимается момент, смещенный относительно момента включения
меры на время запаздывания. Время запаздывания определяется скоростью движения
жидкости по трубопроводу от меры к расходомеру и
длиной трубопровода.
Оценка 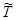 параметра T
находится как длительность интервала времени от начала отсчета до момента,
когда выходной сигнал достигнет уровня, составляющего 63 % от установившегося
значения. Оценка
параметра T
находится как длительность интервала времени от начала отсчета до момента,
когда выходной сигнал достигнет уровня, составляющего 63 % от установившегося
значения. Оценка 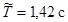 .
.
Найденная оценка сравнивается с границами
диапазона допускаемых значений Т. Пределы
допускаемых отклонений могут быть установлены с учетом и без учета погрешности
контроля. В первом случае найденная оценка удовлетворяет неравенству 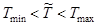 , что
свидетельствует о соответствии динамической характеристики установленным
нормам. Во втором случае диапазон допускаемых значений Т должен быть
сужен на величину погрешности контроля, которая складывается из погрешности от неидеальности испытательного сигнала и
инструментальной погрешности µ(t) и не превышает 5 %.
Поэтому суженный диапазон для Т имеет границы при
, что
свидетельствует о соответствии динамической характеристики установленным
нормам. Во втором случае диапазон допускаемых значений Т должен быть
сужен на величину погрешности контроля, которая складывается из погрешности от неидеальности испытательного сигнала и
инструментальной погрешности µ(t) и не превышает 5 %.
Поэтому суженный диапазон для Т имеет границы при 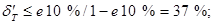
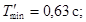
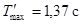 . Оценка
. Оценка 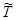 оказывается вне
диапазона допускаемых значений и, следовательно, динамические свойства
расходомера не отвечают установленным нормам.
оказывается вне
диапазона допускаемых значений и, следовательно, динамические свойства
расходомера не отвечают установленным нормам.
2. Определение динамической характеристики
экземпляра средств измерений данного типа
2.1. Исходные данные
Исследуемое средство измерений:
осциллографический гальванометр типа М1013-1800 № 001184.
Требуемая динамическая характеристика -
переходная характеристика.
Требуемая форма представления
динамической характеристики - аналитическая.
Предварительная информация - модель
динамических свойств гальванометра представляет собой колебательное звено 2-го
порядка со степенью успокоения g в пределах 0,1 -
0,4 и собственной частотой f0 не менее
1800 Гц.
Имеющийся в наличии генератор
испытательного сигнала - генератор импульсов точной амплитуды Г5-75, создающий
на согласованной нагрузке прямоугольные импульсы напряжения с длительностью 50
нс - 1 с (в режиме внутреннего запуска) и фронтом не более 10 нс. Погрешность установки
амплитуды импульса: от дискретности установки амплитуды не более 0,5 мВ на
поддиапазоне 1 - 9,9999 В; в динамическом режиме не более (0,01 · 103
+ 2) мВ = 12 мВ; от выбросов на вершине основного импульса - не более 1 % от
амплитуды импульса, что соответствует 10 мВ; от паразитной модуляции параметров
- не более 1 мВ. Результирующая погрешность установки амплитуды импульса с
номинальным значением 1 В равна
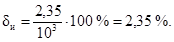
Требуемая точность определения
динамической характеристики - погрешность определения g и f0 не
должны превышать 30 и 25 %, соответственно.
Требуемый диапазон частот, в котором
исследуется гальванометр - от 0 до 1800 Гц.
2.2. Последовательность операций
2.2.1. Выбор метода и испытательного
сигнала
По п.п. 2.2.3, 2.4.2, 2.6
рекомендации выбирается прямой метод определения переходной характеристики с
использованием испытательного сигнала, достаточно близкого к единичной
ступенчатой функции. Длительность импульса выбирается максимальной для данного
генератора и равной 1 с.
2.2.2. Оценка неидеальности
испытательного сигнала
Погрешность от неидеальности
испытательного сигнала (сигнал с линейным нарастанием до установившегося
значения вместо сигнала, описываемого функцией 1(t) -
приложение 3,
последняя строка таблицы):
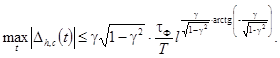
Подставляя 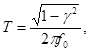 получим
получим
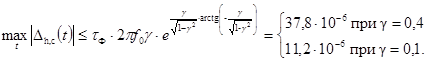
Погрешность Dh,c(t)
пренебрежимо мала, и можно считать, что испытательный сигнал практически
совпадает с характеристическим.
2.2.3. Проверка требований п. 3.3 рекомендации
(приложение 2,
1-я строка таблицы). Поскольку погрешность Dв не задана, принимается максимальное значение δв
= 1. При этом f01 ≈
l МГц. Таким образом, условие f01 > fв выполнено.
2.2.4. Проверка требований п. 4.2
рекомендации
Искажения испытательного сигнала
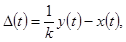
где y(t)
- выходной сигнал;
k -
статический коэффициент преобразования;
x(t) - испытательный сигнал исследуемого средства
измерений.
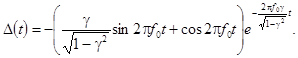
Максимум функции D(t) получим при t = 1/2f0
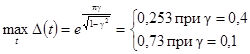
В качестве регистрирующего прибора
используется светолучевой осциллограф типа H115,
амплитудная погрешность которого не превышает 10 %. Учитывая амплитуду входного
сигнала, равную 1 В, получим

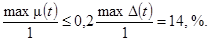
2.2.5. Нахождение параметров g и f0
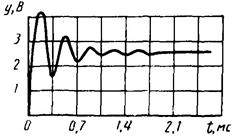
Отклик осциллографического
гальванометра на ступенчатый испытательный сигнал
Ввиду относительно малого успокоения
гальванометра параметры находятся по отклику (см. рисунок) простейшим
графоаналитическим способом с помощью выражений:
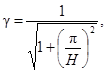
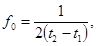
где H = lnξ1/ξ2; ξ1 = ymax - yуст - амплитуда первого
выброса; ymax, yуст, ymin -
максимальное, установившееся и минимальное (не равное нулю) значение отклика; t1, t2 моменты времени,
соответствующие первому и второму пересечениям кривой отклика установившегося
значения.
Значения отклика: yуст = 2,5 В; ymax = 4,5
В; yуст = 1,55
В; на основании чего g = 0,173; f0 = 2857 Гц при t1 = 0,075 мс; t2 = 0,25 мс.
2.2.6. Оценивание погрешностей g и f0
На основании выражений для g и f0 погрешности
их определения равны
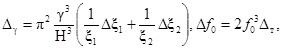
где Dт - погрешность определения интервала времени [t1, t2]; Dξ1 - погрешность определения
амплитуды первого выброса ξ1; Dξ2 - погрешность определения амплитуды ξ2.
Поскольку из ряда осциллографических
гальванометров, входящих в комплект Н115, был выбран гальванометр типа
М014-7000 с рабочей полосой частот 0 - 5000 Гц и собственной частотой fог = 7000 Гц (что намного
больше верхнего предела частотного диапазона, в котором исследуется
гальванометр), причем перед испытаниями он был настроен на оптимальное g, выбранное в соответствии с [1], пренебрегаем погрешностью, вносимой неравномерностью
амплитудно-частотной характеристики гальванометра как пренебрежимо малой по
сравнению со статической погрешностью.
Так как за начало отсчета при определении
отклика осциллографического гальванометра принято установившееся значение
отклика (т.е. измерение амплитуды отклика проводится относительно
установившегося значения), то погрешность измерения
амплитуды по осциллограмме равна
Dξ1 = Dξампл + 2Dотсч.у,
где Dξампл -
погрешность, зависящая от амплитудной погрешности гальванометра,
Dξампл = 0,1ξ;
Dотсч.у -
погрешность отсчитывания по оси y.
Поскольку масштаб по оси y My = 0,05 В/мм (максимальное регистрируемое напряжение 6 В при ширине
фотоленты 120 мм), а погрешность отсчитывания по оси y
при использовании оптических средств достаточно мала, в данном случае она равна
0,125 мм, то Dотсч.у =
0,125 мм´0,05 В/мм = 6,25 мВ. Представляя значение для ξ1 и ξ2 получим
Dξ1 = 0,1ξ1 + 2Dотсч.y = 0,1775
В,
Dξ2 = 0,1ξ2 + 2Dотсч.y = 0,1075
В,
При этом Dj = 0,06; δj = 35,2 %.
Так как полученное значение δj = 35,2 % превышает допустимое значение погрешности определения и нет
возможности использовать осциллограф с меньшим значением амплитудной
погрешности, то возникает необходимость уменьшить статическую погрешность
прибора. Это можно сделать путем коррекции
систематической составляющей погрешности осциллографа: установки нулевой линии,
калибровки, учета погрешности нелинейности прибора [2]. В результате статическая погрешность не
превышает 5 %, а погрешность определения g
Dg £ 0,035; δg £ 20,5 %.
Погрешность Dт
определения интервала времени [t1, t2] определяется,
в основном, погрешностью отсчитывания Dtотсч и
погрешностью развертывания Dр, т.е. Dт = Dtотсч + Dр.
Погрешность отсчитывания Dtотсч зависит от Dt1отсч, Dt2отсч -
погрешностей отсчитывания моментов времени t1, t2, определяющих интервал [t1, t2], т.е. Dtотсч = Dt1отсч + Dt2отсч.
Применение оптических увеличительных устройств позволяет уменьшить погрешность
отсчитывания до значения 0,125 мм, что при скорости v = 104
мм/с соответствует Dt1отсч = Dt2отсч =
12,5 мкс. Отсюда Dотсч = 25
мкс.
Определенная экспериментально [3]
неравномерность движения фотоленты прибора H115 при
скорости v = 104 мм/с на участке l
= 10 мм составляет δ £ 6,5 %, что на интервале [t1, t2] обуславливает
появление погрешности развертывания DР = (t2 - t1) · δ = 0,175 · 0,065
= 0,011 мс. При этом Dт = 0,036
мс, Df0 = 588 Гц, δf0 = 20,6 %. Таким образом, точность определения параметров переходной
характеристики гальванометра (с учетом коррекции систематической составляющей
статической погрешности регистрирующего прибора) удовлетворяет требованиям.
Следует заметить, что экспериментатор не
всегда располагает данными о неравномерности движения носителя для конкретного
типа прибора и соответствующей скорости.
Зная период повторения меток tмет и период повторений T
систематической составляющей Dрс погрешности Dр [4]: T
= pd/v,
где d -
диаметр ведущего. вала лентопротяжного механизма, v - скорость
движения фотоленты, можно получить достаточно близкую оценку «снизу»
погрешности Dт в
следующих случаях:
1) когда определяемый интервал t2 - t1 намного меньше периода Т
(t2 - t1 << T)
и метки времени не позволяют уменьшить систематическую Dрс
составляющую погрешности развертывания на интервале [t1, t2];
2) когда tмет << T
и метки времени позволяют существенно уменьшить Dрс на исследуемом интервале. В примере время затухания
переходного процесса составляет несколько
миллисекунд и максимальная для прибора H115 частота
меток fмет = 500
Гц слишком мала для такого процесса, к тому же с целью получения удобной для
расшифровки осциллограммы выбрана наибольшая скорость движения фотоленты v
= 104 мм/с, поэтому на всей осциллограмме будет не более двух меток,
т.е. имеет место первый случай. Очевидно, что
при выполнении условия t2 - t1 << T,
систематическая составляющая погрешности развертывания на интервале [t1, t2] много меньше максимального значения погрешности Dр.
Пренебрегая случайной и систематической составляющей Dр на
интервале [t1, t2], оценим Dт «снизу» 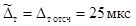 . При этом
получим оценку «снизу» для погрешности определения частоты Df0 = 409 Гц, δf0 = 14,3 %.
. При этом
получим оценку «снизу» для погрешности определения частоты Df0 = 409 Гц, δf0 = 14,3 %.
Рассмотрим второй случай, когда
существенное значение для уменьшения систематической составляющей погрешности
развертывания имеет соотношение периодов tмет и T; т.е. когда выполняется условие tмет << T.
Поскольку наличие меток времени позволяет уменьшить систематическую
составляющую погрешности Dр до
значения, обусловленного нестабильностью скорости протяжки на интервале tмет, то при условии tмет << Т этой
нестабильностью скорости на интервале [t1, t2] можно
пренебречь и тогда, когда t2 - t1 > tмет (при этом
систематическая составляющая погрешности Dр на интервале [t1, t2] равна
систематической составляющей погрешности развертывания на интервале tмет, т.е. пренебрежимо мала
по сравнению с максимальным значением Dр), и тогда, когда t2 - t1 < tмет << T.
Как и в первом случае, погрешность Dт можно оценить «снизу»: Dт = Dtотсч.
1. Бренер М.Д.,
Шкабардня М.С. О погрешности измерений с помощью светолучевых осциллографов в
динамическом режиме. - Метрология, 1980, № 8, с. 22 - 31.
2. Шкабардня М.С.
Теория и принципы построения быстродействующих самопишущих приборов. - М.:
Энергоатомиздат, 1984. - 214 с.
3. Артамонов В.М. и др.
Светолучевые осциллографы. - Л.: Энергоиздат. Ленинградское отделение, 1982. - 104
с.
4. Грановский В.А.
Динамические измерения: Основы метрологического обеспечения. - Л.:
Энергоатомиздат. Ленинградское отделение, 1984. - 224 с.
5. ГОСТ
8.256-77. ГСИ. Нормирование и определение динамических характеристик
аналоговых средств измерений.
6. МИ 1951-88. ГСИ. Динамические
измерения. Термины и определения.
7. ГОСТ
8.207-76. ГСИ. Прямые измерения с многократными наблюдениями. Методы
обработки результатов наблюдений. Основные положения.
8. ГОСТ
8.061-80. ГСИ. Содержание и построение поверочных схем.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНА И ВНЕСЕНА Государственным комитетом СССР по управлению
качеством продукции и стандартам
ИСПОЛНИТЕЛИ
В.А. Грановский, канд. техн. наук (руководитель темы),
Ю.С. Этингер, С.Л. Васильева
2. УТВЕРЖДЕНА ПРИКАЗОМ НПО «Система»
3. ЗАРЕГИСТРИРОВАНА ВНИИМС 04.09.90
4. ВЗАМЕН РД
50-404-83
СОДЕРЖАНИЕ
|
1. Основные положения. 1
2. Выбор методов определения
динамических характеристик исследуемых средств измерений. 2
3. Выбор испытательных сигналов. 5
4. Требования к средствам
измерений, используемым при определении динамических характеристик средств
измерений. 8
5. Алгоритмы обработки данных при
определении динамических характеристик. 10
6. Оценивание погрешностей
определения динамических характеристик. 11
Приложение 1. Соотношения для пересчета полных динамических
характеристик средств измерений. 14
Приложение 2. Аналитические выражения f01
и Dв для распространенных
испытательных сигналов. 16
Приложение 3. Погрешности определения прямыми методами переходной и
импульсной характеристик исследуемого средства измерения, обусловленные
неидеальностью испытательных сигналов, в зависимости от параметров указанных
сигналов, вида и коэффициентов передаточной функции средства измерения
(сигнал с линейным нарастанием до установившегося значения вместо сигнала,
описываемого функцией 1(t),
- для переходной характеристики; импульсный сигнал прямоугольной формы вместо
сигнала, описываемого функцией δ0(t),
- для импульсной характеристики) 16
Приложение 4. Погрешности определения прямым методом переходной
характеристики исследуемого средства измерений, обусловленные неидеальностью
испытательного сигнала, в зависимости от параметра указанного сигнала, вида и
коэффициентов передаточной функции средства измерения (сигнал с
экспоненциальным нарастанием xh(t) = 1 - е-bt вместо сигнала, описываемого функцией 1(t) 18
Приложение 5. Погрешности определения прямым методом переходной
характеристики исследуемого средства измерений, обусловленные неидеальностью
испытательного сигнала, в зависимости от параметра сигнала, вида и
коэффициентов передаточной функции средства измерений. 23
Приложение 6. Погрешности определения прямым методом
амплитудно-частотной характеристики исследуемого средства измерений,
обусловленные неидеальностью испытательного сигнала в зависимости от
параметров сигнала, вида и коэффициентов передаточной функции средства
измерений. 28
Приложение 7. Погрешности определения прямым методом фазочастотной
характеристики исследуемого средства измерения, обусловленные неидеальностью
испытательного сигнала, в зависимости от параметров сигнала, вида и
коэффициентов передаточной функции средства измерений. 37
Приложение 8. Примеры алгоритмов обработки данных при определении
полных динамических характеристик косвенными методами. 43
Приложение 9. Установление коэффициента запаса kз 49
Приложение 10. Примеры определения динамических характеристик средств
измерений. 50
Литература. 55
|
![]() i = 1, ..., m, (2)
i = 1, ..., m, (2)![]() -
характеристика погрешности определения коэффициента vi,
входящего в аналитическое выражение динамической характеристики;
-
характеристика погрешности определения коэффициента vi,
входящего в аналитическое выражение динамической характеристики;![]() - предел допускаемой погрешности определения коэффициента vi; m - число определяемых
коэффициентов.
- предел допускаемой погрешности определения коэффициента vi; m - число определяемых
коэффициентов.![]() изменений во времени
(производная) импульсного испытательного сигнала хg(t) с длительностью tи должна удовлетворять условию
изменений во времени
(производная) импульсного испытательного сигнала хg(t) с длительностью tи должна удовлетворять условию![]() (6)
(6)![]()

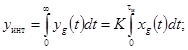
![]()
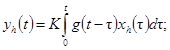
![]()
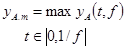

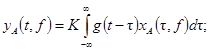
![]()
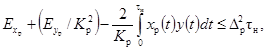 (16)
(16)![]() ;
;![]() ;
;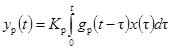 - результат регистрации x(t);
Dp
= Dxч.
- результат регистрации x(t);
Dp
= Dxч.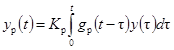 - результат регистрации y(t);
Dр = Dyч.
- результат регистрации y(t);
Dр = Dyч.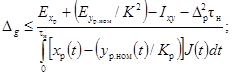 (17)
(17)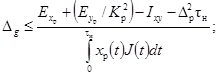 (18)
(18)![]()
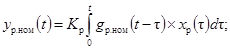
![]()
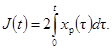
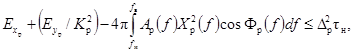 (19)
(19)![]() (20)
(20)![]() (21)
(21)![]()
![]()
![]()
![]()
![]()
![]() (22)
(22)![]() (23)
(23)![]() (24)
(24)![]() (25)
(25)![]() (26)
(26)![]() ;
; ![]() ;
;![]()
![]()
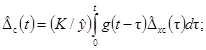
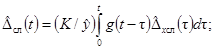
![]() - систематическая составляющая
погрешности
- систематическая составляющая
погрешности ![]() ;
;![]() - случайная составляющая
погрешности
- случайная составляющая
погрешности ![]() ;
;![]() - погрешность определения испытательного
сигнала;
- погрешность определения испытательного
сигнала;![]() - погрешность отсчитывания значений
выходного сигнала (при аналоговой регистрации).
- погрешность отсчитывания значений
выходного сигнала (при аналоговой регистрации).![]() следует находить по ГОСТ
8.207.
следует находить по ГОСТ
8.207.![]() погрешности
погрешности ![]() , обусловленной неидеальностью
испытательного сигнала, для средств измерений с распространенными моделями
динамических свойств и распространенных испытательных сигналов приведены в
приложениях 3
- 5.
, обусловленной неидеальностью
испытательного сигнала, для средств измерений с распространенными моделями
динамических свойств и распространенных испытательных сигналов приведены в
приложениях 3
- 5.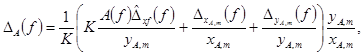 (27)
(27)![]() - погрешность определения xA.т при частоте f;
- погрешность определения xA.т при частоте f;![]() - погрешность определения yA.т при частоте f.
- погрешность определения yA.т при частоте f.![]() (28)
(28)
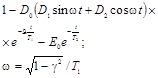
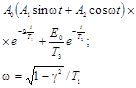
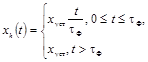
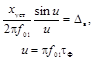
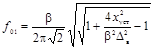
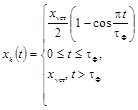
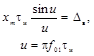
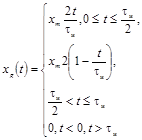
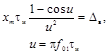
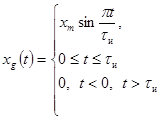
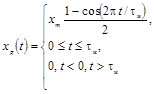
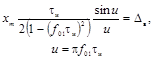
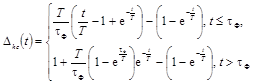
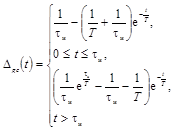
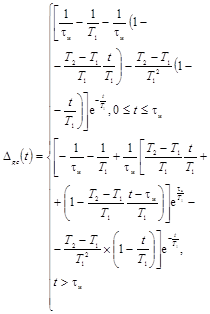
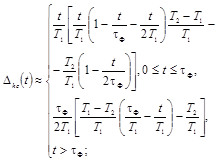
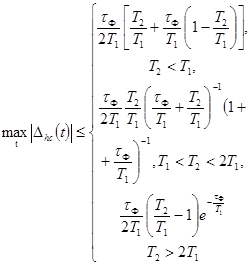
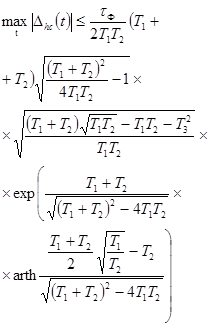

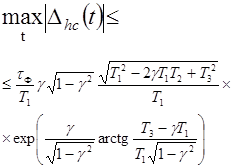
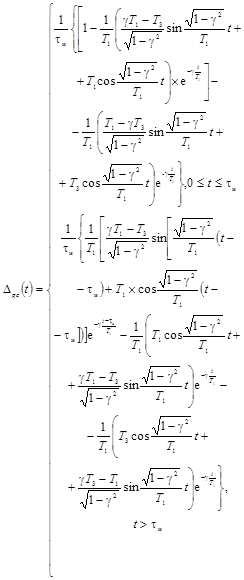
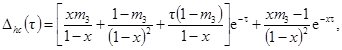
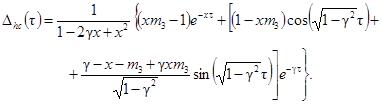
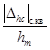 и среднего модуля
и среднего модуля 
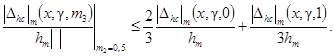





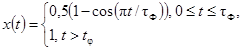
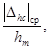









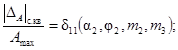
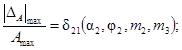
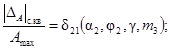

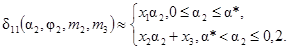




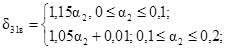
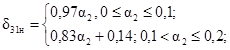
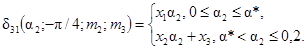
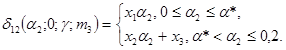
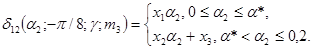
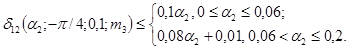
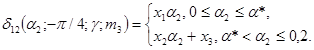
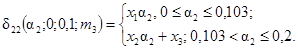

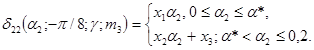
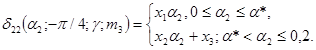
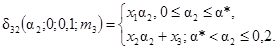


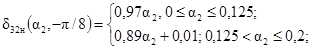
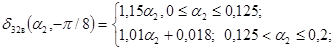
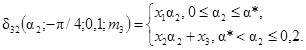

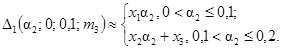

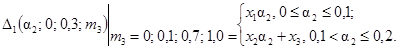
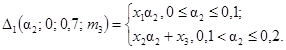
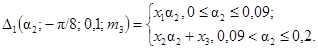
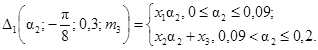
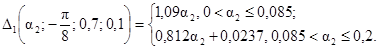
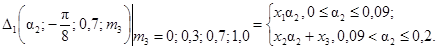
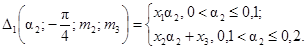
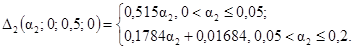


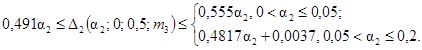
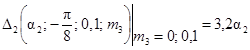

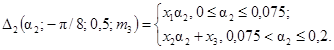
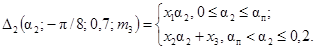
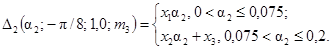

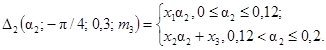
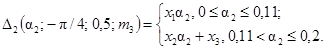

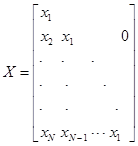
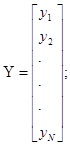
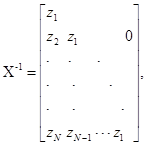
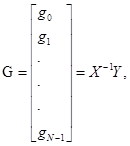
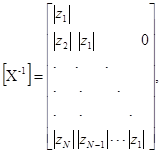

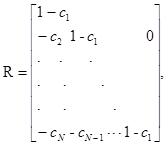
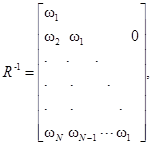
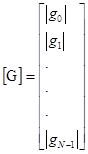
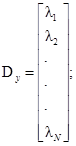

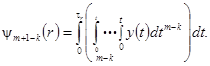
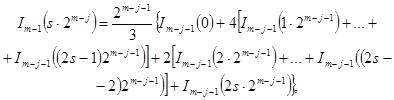

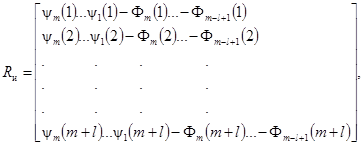

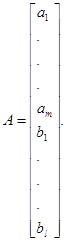
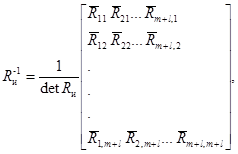
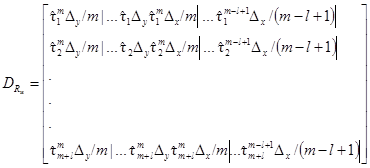

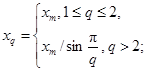
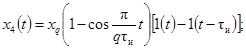
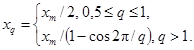
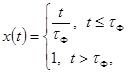
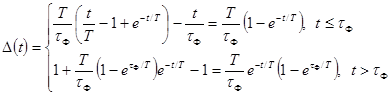
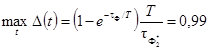 при
при