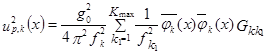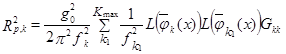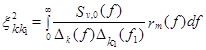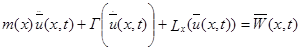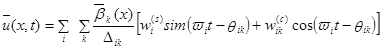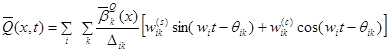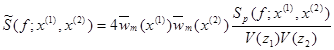ГОССТРОЙ РОССИИ
ГОСУДАРСТВЕННОЕ УНИТАРНОЕ ПРЕДПРИЯТИЕ
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ имени В.А. КУЧЕРЕНКО
ООО ЕВРОСОФТ
Попов Н.А.
РЕКОМЕНДАЦИИ
по уточненному динамическому расчету
зданий и сооружений на действие пульсационной
составляющей ветровой нагрузки
Утверждены Научно-техническим Советом ЦНИИСК 15 декабря 1999г.
Москва 2000 год
"Рекомендации по уточненному динамическому расчету зданий и сооружений на действие пульсационной составляющей ветровой нагрузки" разработаны в развитие главы СНиП 2.01.07-85* "Нагрузки и воздействия" с учетом современных методов численного анализа динамического поведения строительных конструкций и возможностей их программной реализации.
В "Рекомендациях..."
- приведены результаты анализа существующих методов расчета зданий и сооружений на действии пульсационной составляющей ветровой нагрузки;
- описан алгоритм точного решения этой задачи и рассмотрены соотношения, позволяющие реализовать этот алгоритм в численных программных комплексах;
- для четырех типов сооружений проведено сопоставление результатов расчета на это воздействие, полученных по различным методикам.
"Рекомендации..." разработаны в ЦНИИСК им. Кучеренко при участии ООО ЕВРОСОФТ. Их основные положения реализованы в программном комплексе STARK ES семейства программ MicroFe (ООО ЕВРОСОФТ).
Разработка «Рекомендаций...» и методики расчета выполнены к.т.н., ведущим научным сотрудником ЦНИИСК Поповым Н.А.; программирование - Попов Н.А. при участии Лебедева В.Л. (ООО ЕВРОСОФТ).
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ
При взаимодействии ветра со строительными конструкциями в них возбуждаются колебания, которые по своей природе можно разделить на два типа:
- вынужденные колебания, обусловленные непосредственным действием на сооружение пульсаций скорости достаточно сильных, ураганных ветров (в дальнейшем эти воздействия обозначаются как ПВ-нагрузки);
- интенсивные аэроупругие и неустойчивые колебания, которые, как правило, происходят в направлении, перпендикулярном средней скорости ветра (поперечные колебания).
К колебаниям второго типа относятся различные формы аэродинамической неустойчивости сооружений (галопирование, флаттер, параметрический резонанс), а также колебания связанные со срывом вихрей с внешней поверхности сооружений, в том числе и те, которые сопровождаются образованием вихревой дорожки Кармена и приводят к резонансному вихревому возбуждением сооружения на одной из его собственных частот. В настоящих "Рекомендациях..." колебания этого типа не рассматриваются, а основное внимание уделено определению и анализу реакции сооружений на действие ПВ-нагрузки. Кроме того, здесь
- приведены результаты анализа существующих методов расчета зданий и сооружений на действие пулъсационной составляющей ветровой нагрузки;
- описан алгоритм решения задачи о вынужденных случайных колебаниях сооружений при действии ПВ-нагрузок и рассмотрены соотношения, позволяющие реализовать этот алгоритм в численных программных комплексах;
- проведен сравнительный анализ результатов расчета по различным методикам четырех типов сооружений.
Разработка «Рекомендаций...» предпринята с целью расширения нормативно-методической базы, необходимой для численного расчета сооружений на динамическое действие ветра. При этом имелось в виду, что их основные положения, в первую очередь, будут использованы при подготовке соответствующих программных комплексов.
В связи с этим необходимо отметить, что теоретические и экспериментальные основы современных представлений о ПВ-нагрузках и их взаимодействии со зданиями и сооружениями разработаны в конце 50-х - начале 60-х годов и с тех пор принципиально не изменились. В то же время методики расчета сооружений на эти динамические и случайные по своей природе воздействия требовали (и требуют) большого объема численных вычислений, а возможности ЭВМ поколения 60-х - 80-х годов не позволили в полном объеме численно реализовать эти методики. Ситуация коренным образом изменилась в 90-е годы с появлением ПК, процессоров семейства Pentium и развитых Windows-подобных операционных систем (OS/2, Microsoft Windows). Использование этих технологий позволяет достаточно просто создавать адекватные расчетные схемы сложных строительных конструкций и практически реализовать методы структурного анализа их работы и поведения при различных воздействиях, в том числе и динамических. (Подобный подход, в частности, реализован в программных комплексах семейства MicroFe, разработанных "mb Software AG" и "ЕВРОСОФТ".)
Однако, и это тоже необходимо отметить, в настоящее время отсутствуют как нормативная база, позволяющая использовать точные методики расчета сооружений на действие пульсаций ветровой нагрузки, так и публикации в отечественной научно-технической литературе, в которых эти вопросы рассматривались бы в полном, замкнутом объеме. Существующие на русском языке две монографии* написаны в середине 70-х - начале 80-х годов и, что более важно, обе они ориентированны на методы и средства расчета, развитые в то время. Предлагаемые "Рекомендации..." - это 1-ый этап работы по совершенствованию нормативной и методической базы, связанной с расчетом сооружений на динамическое действие ветра.
* В настоящее время существуют две монографии на русском языке, в которых наиболее полно рассмотрены все вопросы, связанные с воздействием ПВ-нагрузок на здания и сооружения. Это - "Руководство по расчету зданий и сооружений на действие ветра" (М., Стройиздат, 1978), подготовленное Барштейном М.Ф., и переводная книга Э. Симиу и Р. Сканлана "Воздействие ветра на здания и сооружения" (М., Стройиздат, 1984). Обе эти работы, базируются на вполне современных представлениях о природе ПВ-нагрузок и достаточно надежных данных натурных и модельных экспериментальных исследований. Однако предлагаемые в них расчетные соотношения, в основном, представлены в той или иной степени в упрощенном виде.
"Рекомендации..." подготовлены институтом ЦНИИСК им. Кучеренко по предложению и при непосредственном участии фирмы «ЕВРОСОФТ»; их основные положения реализованы в программном комплексе proFEt&STARK ES семейства программ MicroFe.
1. Общие положения
1.1. Настоящие "Рекомендации..." разработаны в развитие главы СНиП 2.01.07-85* "Нагрузки и воздействия" и дополняют положения этого нормативного документа. При подготовке "Рекомендаций..." принято во внимание:
a. Изложенная в СниП 2.01.07-85* «Нагрузки и воздействия» методика определения пульсационной составляющей ветровой нагрузки (ПВ-нагрузки) не является универсальной и может быть использована при расчете и проектировании достаточно узкого класса зданий и сооружений, перечисленных в п. 6.7 СНиП;
b. В настоящее время отсутствует нормативно-методическая база по расчету на действие ПВ-нагрузок произвольных сооружений со сложной пространственной расчетной схемой, требующие учета совместных колебаний по различным собственным формам и их взаимной корреляции.
Примечание. В дальнейшем пулъсационная составляющая ветровой нагрузки обозначается как ПВ-нагрузка.
1.2. В "Рекомендациях..." представлена уточненная (по отношению к положениям пп. 6.7 - 6.10 указанного СНиП) методика расчета зданий и сооружений на действие пульсационной составляющей ветровой нагрузки. "Рекомендации..." могут быть использованы при расчете на воздействие ПВ-нагрузок зданий и сооружений произвольного типа с учетом ограничений, перечисленных в п. 1.3
1.3. В "Рекомендациях..." использованы принятые при разработке СНиП подходы и соотношения, описывающие статистические характеристики скорости ветра и ПВ-нагрузок. В связи с этим, положения настоящих "Рекомендаций..." не могут применяться
- для определения реакции сооружений, обусловленной их резонансным вихревым возбуждением;
- для определения реакции покрытий в вертикальном направлении;
- во всех тех случаях, когда основной вклад в динамическую реакцию сооружения вносит воздействие ПВ-нагрузок в зонах с отрицательным средним давлением ветра (в зонах "отсоса").
В этих расчетных случаях необходимо использовать статистически обоснованные результаты натурных или соответствующим образом организованных модельных аэродинамических испытаний сооружения (п. 1.4).
Использование при расчете зданий и сооружений на действие ПВ-нагрузок экспериментальных результатов, полученных при испытаниях в гладких потоках или в потоках с другими типами турбулентности (в частности, в потоках с "решетчатой" турбулентностью) должно быть дополнительно обосновано.
1.5. Результаты расчета зданий и сооружений на действие ПВ-нагрузок, получаемые при использовании численных программных комплексов, должны включать в себя
- усилия и перемещения (суммарные и по формам колебаний), определяемые с учетом положений настоящих "Рекомендаций...".
Кроме того, в структуру численных программных комплексов целесообразно включать:
- определение сил инерции по формам колебаний;
- определение предельных частот колебаний;
- оценку усталостной прочности и выносливости элементов сооружения.
Примечание. Приведенные в п. 6.8 СНиП 2.01.07-85* значения предельных частот f1, получены при наиболее общих предположениях относительно геометрических, конструктивных и динамических свойств сооружений и, в связи с этим, определены с запасом. Как правило, реальные значения f1 значительно меньше тех, которые указаны в СНиП 2.01.07-85*.
1.6. Расчетные значения усилий Qp и перемещений ир, возникающих в элементах зданий и сооружений при действии ПВ-нагрузок, определяются по формулам:
![]() ; (1a)
; (1a)
![]() , (1b)
, (1b)
где
σQ и σu - стандарт усилий и перемещений, соответственно;
γg - коэффициент обеспеченности пульсационной составляющей ветровой нагрузки.
1.7. Коэффициент обеспеченности γg пульсационной составляющей ветровой нагрузки принимается равным 3,0 (γg=3,0), если для сооружений рассматриваемого класса (типа) не оговорены другие значения γg.
1.8. Стандарт перемещений σu, как правило, определяется в результате численного динамического расчета сооружения на действие пульсационной составляющей ветровой нагрузки, статистические характеристики (авто- и взаимные спектральные и корреляционные функции) которой приведены в п.п. 2 и 3 настоящих "Рекомендаций...". Использование для этих функций иных аппроксимирующих соотношений допускается после их соответствующего обоснования.
2. Основные расчетные соотношения
2.1. Расчетные соотношения, представленные в пп. 2 и 3 "Рекомендаций...", соответствуют решению линейной динамической задачи о вынужденных колебаниях сооружений при действии ПВ-нагрузок методом разложения усилий и перемещений в ряды по ортонормированным собственным формам сооружения.
Примечание.
Собственные формы ![]() (k=l,...,) являются ортонормированными, если выполняются
следующие условия:
(k=l,...,) являются ортонормированными, если выполняются
следующие условия:
![]() ; (3а)
; (3а)
![]() , (3b)
, (3b)
где X- область определения переменной х;
т(х) - масса сооружения в точке х.
В этом случае расчетные перемещения ир(х) определяются следующим образом:
где
х=(x1, x2 ,х3) - координаты, описывающие геометрию сооружения;
Ктах - число учитываемых собственных форм;
g0 -расчетные значения коэффициента порывистости (табл. 1);
![]() -
вектор k-oй собственной формы в точке х;
-
вектор k-oй собственной формы в точке х;
fk (Гц) - k-ая собственная частота;
Gкк1 - обобщенное воздействие, учитывающие совместные колебания сооружения по k-oй и ki-oй формам.
2.2. Если усилие (или любая другая расчетная величина)
![]() связана
с перемещением
связана
с перемещением ![]() линейной зависимостью типа
линейной зависимостью типа
![]() , (4)
, (4)
где L(![]() ) - линейная функция,
матрица или оператор (интегральный, дифференциальный, смешанный),
) - линейная функция,
матрица или оператор (интегральный, дифференциальный, смешанный),
то расчетное значение Rp усилий определяется по формуле:
2.3. Обобщенное динамическое воздействие Gkk1 определяется следующим образом:
![]() ; (6b)
; (6b)
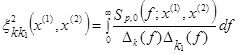 ; (6c)
; (6c)
![]() ; (6d)
; (6d)
![]() . (6e)
. (6e)
Здесь
![]() - вектор
средней составляющей ветровой нагрузки в точке х;
- вектор
средней составляющей ветровой нагрузки в точке х;
А - поверхность сооружения, на которую действует ПВ-нагрузка;
ζ(z) - коэффициент пульсаций скорости ветра (п.2.4);
z - высота над поверхностью земли в точке с координатами х;
Sv,o(f) - нормированный энергетический спектр продольной компоненты скорости вектора (п.2.5);
rv(f; x(1), х(2)) - коэффициент корреляции пульсаций давления (п.2.6) в точках x(1)=(x1(1), x2(1), x3(1)) и x(2)=(x1(2), x2(2), x3(2));
f(Гц) - частота;
σ0 - стандарт спектра скорости ветра;
ξkk1 - коэффициент динамичности, учитывающий совместную реакцию сооружения по k-oй и ki-oй формам.
2.4. Коэффициент пульсаций ζ(z) скорости ветра на высоте z определяется по формуле:
![]() , (7)
, (7)
где значения показателя степени β приведены в табл. 1 в зависимости от типа местности (см. п. 6.5 СНиП).
Таблица 1. Значения коэффициентов go и β
|
Тип местности (см. табл. 7 СНиП 2.01.07-85) |
|||
|
А |
В |
С |
|
|
gо |
0,76 |
1,06 |
1,78 |
|
β |
0,15 |
0,20 |
0,25 |
Примечание. В СНиП 2.01.07-85* приняты следующие типы местности:
А - открытые побережья морей, озер и водохранилищ, пустыни, степи, лесостепи, тундра;
В - городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой более 10 м;
С - городские районы с застройкой зданиями высотой более 25 м.
Сооружение считается расположенным в местности данного типа, если эта местность сохраняется с наветренной стороны сооружения на расстоянии 30h - при высоте сооружения h до 60 м и 2 км - при большей высоте.
2.5. Нормированный энергетический спектр пульсационной составляющей скорости ветра Sv,0(f) описывается соотношением:
![]() ; (8a)
; (8a)
![]() , (8b)
, (8b)
где
λ - безразмерная частота;
f - частота в Гц;
Lx = 1200 м - интегральный продольный масштаб турбулентности:
V0 - базовая скорость ветра на высоте 10м.
2.6. Коэффициент корреляции rv(f;x{1),x(2)) пульсаций скорости ветра в точках x(1)=(x1(1), x2(1), x3(1)) и x(2)=(x1(2), x2(2), x3(2)) определяется по формуле:
![]() ; (9a)
; (9a)
![]() ; (9b)
; (9b)
![]() ;
; ![]() , (9c)
, (9c)
где
Tv(x(I),x(2)) - период корреляции порывов в точках х(1)и х(2);
v0 - базовая скорость ветра на высоте 10м;
Δxi(i=1,2,3) - проекции расстояния между точками х(1) и х(2) на оси правой поточной системы координат, в которой ось Ox1 ориентирована по направлению средней скорости ветра, а ось Ох3 направлена вертикально вверх;
bi(i=1,2,3) - эмпирические константы; b1=20; b2=b3=8.
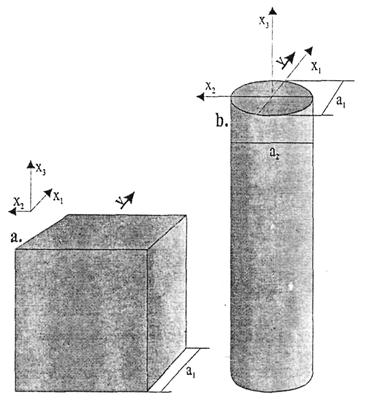
а. Плоская расчетная схема сооружения
В случае, если расчетная схема сооружения (здания,
плоские фермы, щиты) расположена в плоскости Оx2х3, перпендикулярной
вектору средней скорости ветра ![]() , то расстояние Δх1
допускается принимать равным ширине а1 сооружения (рис. 1а), т.е.
, то расстояние Δх1
допускается принимать равным ширине а1 сооружения (рис. 1а), т.е.
Δx1=a1. (10а)
Рис. 1 К определению Δх1 и Δх2 для плоских (а) и линейных (b) расчетных схем
б. Балочная расчетная схема сооружения
Если при проведении расчетов сооружение рассматривается как прямолинейный стержень (башни, мачты, галереи и т.п. сооружения), ось которого параллельна координатной оси Ох3, то
![]() ,
, ![]() ,
,
где
a1 и а2 - размеры поперечного сечения сооружения в направлениях, параллельном и перпендикулярном потоку ветра (рис. 1b);
р - периметр поперечного сечения.
3. Приближенные соотношения
3.1. Формально, соотношения, приведенные в п. 2 полностью определяют (статистически) расчетную динамическую реакцию сооружений при действии пульсаций ветра и могут быть использованы при их расчете, а также при разработке алгоритмов численного решения подобных задач. При практической численной реализации этих соотношений дополнительно должно быть учтено следующее:
a. Необходимо определить верхний предел Ктах суммирования по k в (2а) и (5а) таким образом, чтобы были рассмотрены все гармоники, которые вносят заметный вклад в динамическую реакцию сооружения. По существу, эта задача сводится к нахождению такой предельной частоты flim, что реакцией (в том числе и резонансной) на частотах, превышающих flim, можно было бы пренебречь.
b. Для каждой собственной формы целесообразно уточнить число K1,max£Kmax коррелируемых с ней остальных форм колебаний (т.е., по возможности, уменьшить верхний предел суммирования в (2b) и (5b)).
c. Из соотношений (6) видно, что для определения обобщенного динамического воздействия Gkk1 необходимо вычислить несобственные (с бесконечным верхним пределом) интегралы для каждой пары узлов (или элементов). Для сооружений со сложной расчетной схемой, включающей в себя тысячи узлов и элементов, реализация подобного алгоритма может потребовать многих часов расчетного времени, что, очевидно, неприемлемо при вариантном решении практических задач. В связи с этим желательно упростить процедуру вычисления коэффициента Gkk1, оставаясь при этом в рамках приемлемой точности решения поставленной задачи.
3.2. При реализации общей методики динамического расчета сооружений на действие пульсационной составляющей ветровой нагрузки, изложенной в п.2, допускается использовать единый (осредненный) для всего сооружения период Tv,m корреляции. В этом случае для любых двух собственных форм k и k1 может быть введен общий для всего сооружения коэффициент динамичности ξkk1, а обобщенные динамические силы Gkk1 (п.2.3) определяются следующим образом:
![]() ; (11b)
; (11b)
![]() . (11d)
. (11d)
Примечания.
1. Как правило, методика определения Tv,m должна быть обоснована результатами сравнительного расчета сооружений по точным и приближенным соотношениям.
2.
Коэффициент динамичности ![]() , получаемый из (11с) при k1=k, включает в себя корреляцию порывов ветра и, в связи
с этим, его значения отличаются от тех, что приведены в СНиП [1] и
Руководстве [6].
, получаемый из (11с) при k1=k, включает в себя корреляцию порывов ветра и, в связи
с этим, его значения отличаются от тех, что приведены в СНиП [1] и
Руководстве [6].
Рис. 2. Энергетический спектр динамической реакции сооружений при действии ветра
3.3. Для некоторых расчетных случаев (в частности, при определении предельной частоты flim (п. 3.4), при оценке выносливости и, возможно, в некоторых других случаях) общую реакцию сооружения целесообразно разделить на квазистатическую ио(хп) и динамическую uσ(хn) составляющие (рис. 2). Аналитические выражения для ио(х) и uσ(х) могут быть получены из соотношений (2), (6) и (11), в которых коэффициенты динамичности представлены как сумма двух слагаемых:
![]() . (12)
. (12)
Для приближенных соотношений (11):
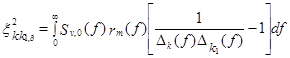 . (13b)
. (13b)
Часть реакции, соответствующая члену v0 обычно называется квазистатической. Она не зависит от динамических свойств сооружения, определяется только турбулентной структурой "свободного" потока ветра и корреляцией давления по поверхности сооружения.
3.4. При проведении как точных (пп. 2), так и приближенных расчетов предельную частоту колебаний flim и соответствующее число Ктах учитываемых форм колебаний допускается определять из условия:
где
![]() -
может быть получено из (11с) при k=k1=Ктах ;
-
может быть получено из (11с) при k=k1=Ктах ;
v0 - задается равенством (13а);
εд £ 0,01 - точность динамического расчета.
По существу, неравенство (14) с некоторым запасом эквивалентно утверждению, что коэффициент динамичности для формы Kmax с точностью до величины εд равен единице.
3.5. При расчете зданий и сооружений на действие ветра корреляцию реакции между k-ой и k1-ой формами допускается не учитывать, если
где
![]() и
и ![]() заданы
соотношениями (11а);
заданы
соотношениями (11а);
εсоr£0,01 - точность определения корреляции реакции по собственным формам.
Если условие (15) выполнено для k и k1-ой форм, то корреляцию реакции можно не учитывать и для всех собственных форм с частотами fk и fk ³ fk1.
ПРИЛОЖЕНИЕ 1
ОБЩИЕ ПРИНЦИПЫ НОРМИРОВАНИЯ ПУЛЬСАЦИОННОЙ СОСТАВЛЯЮЩЕЙ ВЕТРОВОЙ НАГРУЗКИ
П1.1. Определение расчетных усилий и перемещений при случайных воздействиях
Известно (см., например, [6]), что ветер представляет собою нерегулярное, турбулентное движение воздуха и, в связи с этим, при решении большинства прикладных задач, в том числе и проблем строительной динамики, скорость ветра рассматривается как случайный векторный процесс, который, как обычно, описывается своими пространственными и временными статистическими характеристиками: средней величиной, дисперсией, авто- и взаимными спектральными и корреляционными функциями. При таком подходе воздействие ветра w(t,x) на здания и сооружения также может рассматриваться как случайная функция времени t и пространственной координаты х = (x1,x2,x3). При этом w(t,x) достаточно естественно подразделяется [2, 4, 6] на среднюю (wm) и пульсационную (wg) составляющие, т.е.
w(t,x)=wm(х)+wg(t,x). (П1.1)
При проектировании зданий и сооружений средняя составляющая w(t,x) рассматривается как детерминированная (неслучайная) во времени нагрузка, действующая статически. Возникающие при этом в элементах сооружения усилия и перемещения определяются, используя обычные методы строительной механики. Следует отметить, что определение w(t,x) базируется на результатах статистического анализа максимумов (месячных или годовых) средней скорости ветра за достаточно большой (³25 лет) промежуток времени.
Пульсационная составляющая ветровой нагрузки (ПВ-нагрузка) рассматривается как случайная функция времени t и координаты х с известными энергетическим спектром и корреляционной пространственной функцией. Следовательно, задача о вынужденных колебаниях сооружений при этом воздействии может быть решена только статистически. При этом расчетная (максимальная) динамическая реакция сооружения определяется как амплитудное значение перемещения ир, определенное с достаточно большой степенью обеспеченности. При подготовке СНиП "Нагрузки и воздействия" [1] принято, что:
![]() , (П1.2)
, (П1.2)
где
σu - стандарт перемещений;
γg - коэффициент обеспеченности пулъсационной составляющей ветровой нагрузки.
Теоретически, коэффициент γg может быть найден из условия, что реакция и с заданной вероятностью Ри не превышает расчетного значения ир. На практике значение этого коэффициента выбирается на основе экспертных оценок и опыта эксплуатации зданий и сооружений. В нормативных документах различных стран, регулирующих ветровые воздействия, γg изменяется от 2,5 до 4,0; расчетные соотношения СНиП [1] получены для γg = 3,0.
Стандарт реакции σи сооружения определяется в результате решения соответствующей динамической краевой задачи. Как правило, этот расчет проводится численно и в линейной постановке.
П1.2. Качественное описание пульсационной составляющей ветровой нагрузки
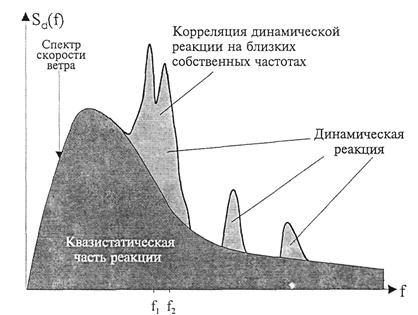
Рис. П1.1. Энергетический спектр скорости ветра и пульсационной составляющей ветровой нагрузки;
выделено элементарное воздействие на частоте f1
Существующие методики [4, 6] нормирования ветровых нагрузок основаны на предположении о том, что энергетический спектр Sw(f) пульсационной составляющей ветровой нагрузки, который характеризует интенсивность воздействия на частоте f, "подобен" спектру Sv(f) продольной компоненты скорости ветра (рис. П1.1), т.е.
Sw(f)~Sv(f).
Кроме того, в этих методиках принимается во внимание, что в один и тот же момент времени интенсивность ПВ-нагрузок различна в точках х(1) и х(2) поверхности сооружения. Этот эффект обычно описывается за счет введения коэффициента корреляции r(f; |x(I) - х(2)|)£1, который зависит от частоты f воздействия и расстояния |х(1) - x(2)| между точками х(1) и х(2).
Таким образом, пульсационная составляющая ветровой нагрузки wg , действующая в каждой точке х на поверхности зданий и сооружений, пропорциональна сумме элементарных воздействий Δws(fi,,x), определенных на всем частотном диапазоне, т.е.
![]() i=1,2…,
i=1,2…,
где
ag,max - точка на поверхности сооружения, в которой пульсации воздействия ветра приняты максимальными;
k(x) - функция пространственной переменной х = (x1,x2,х3), которая зависит от средней составляющей ветровой нагрузки.
Поскольку максимум ПВ-нагрузок может достигаться в любой точке ag,max сооружения, то из соотношения (П1.3) видно, что в общем случае нагрузка Δwg,i=Δwg(fi,х) распределена неравномерно по поверхности сооружений даже для симметричных расчетных схем. Этот эффект приводит к возбуждению "дополнительных" колебаний сооружения по соответствующим (как правило, крутящим) собственным формам. Следовательно, при расчете сооружения на действие ПВ-нагрузок необходимо рассмотреть различные варианты положения точки ag,max и в качестве расчетного выбрать то, при котором реализуется наиболее неблагоприятный вариант ПВ-нагружения.
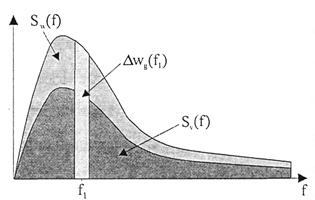
Рис. П 1.2 Энергетический спектр динамической реакции сооружений при действии ветра;
Выделена резонансная реакция на собственной частоте f1
В линейной постановке определение реакции сооружений при действии пульсационной составляющей ветровой нагрузки сводится к решению задачи о вынужденных колебаниях континуальных динамических систем или систем со многим степенями свободы при воздействиях Δwg,i и суперпозиции полученных решений для всех i = 1, 2, ...
Колебания подобных динамических систем давно и подробно исследованы и описаны в литературе. Имея в виду приложение этих результатов к решению поставленной задачи, можно отметить два известных явления, которые во многом определяют реакцию сооружений при действии ПВ-нагрузок:
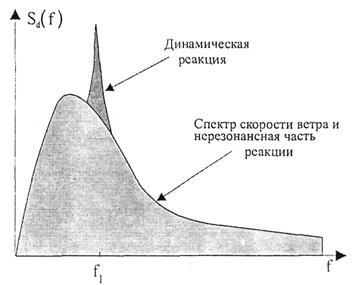
- появление резонансных колебаний на собственных частотах fk (k = 1, 2 ,..) сооружения (рис. П1.2) и
- эффект биения или наложения колебаний, для близких собственных частот fk и fk1, т.е. при fk≈fkl (рис. П1.3). В практике нормирования ПВ-нагрузок это явление, обычно, называется "корреляцией реакции по собственным формам".
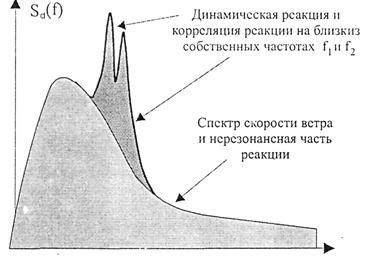
Рис. П 1.3 Энергетический спектр динамической реакции сооружений при действии ветра;
Выделена резонансная реакция на собственных частотах f1 и f2
П1.3. Особенности методики расчета, принятой в СНиП
Существующая методика расчета зданий и сооружений на действие ветра, достаточно подробно описанная в [6], разработана в начале 70-х годов в ЦНИИСК им. Кучеренко и скорректирована в середине 80-х годов при подготовке редакции СНиП 2.-01.07-85 "Нагрузки и воздействия". При проведении этих работ учитывалось, что в соответствии с общими требованиям, предъявляемым к СНиП, эта методика должна включать в себя достаточно простые расчетные формулы и должна быть ориентирована, в первую очередь, на расчет наиболее распространенных типов зданий и сооружений, чувствительных к динамическому воздействию ветра (башни, мачты, высокие жилые и административные здания). В связи с этим, точные соотношения (см., например, [4]), описывающие динамическую реакцию сооружений при действии ветра, были соответствующим образом адаптированы к требованиям СНиП и определенным образом упрощены. В частности,
a. Действие пульсационной составляющей ветровой нагрузки сведено к системе статических сил, определяемых для каждой собственной формы.
b. Для каждой собственной частоты сооружения введен коэффициент динамичности, который определяется без учета корреляции пульсаций давления по поверхности сооружения.
c. Корреляция реакции по собственным формам не учитывается.
d. Для низшей собственной частоты вводится осредненный по всей поверхности сооружения коэффициент корреляции. Для высших собственных форм корреляция порывов ветра не учитывается.
e. Рекомендуемые значения коэффициента корреляции определены в предположении, что низшие собственные формы описываются
- квадратной параболой - для сооружений башенного типа;
- прямой линией - для симметричных в плане зданий.
f. Распределение пульсационной составляющей ветровой нагрузки принято подобным, конгруэнтным распределению ее средней составляющей, т.е. не рассматриваются варианты, соответствующие различным положениям точки ag,max в (П1.2).
g. При разработке последней редакции СНиП "Нагрузки и воздействия", кроме того, были проведены дальнейшие упрощения методики расчета сооружений на действие ПВ-нагрузок:
- область применения принятой здесь методики ограничена зданиями и сооружениями, у которых вторая собственная частота f2 не меньше некоторой предельной частоты flim определяемой в зависимости от демпфирующих свойств сооружения и ветрового района, в котором оно расположено.
- инерционные силы сведены к некоторой статической нагрузке.
Эти упрощения, с одной стороны, вполне соответствуют духу и целям СНиП, а с другой - вносят определенные погрешности (см., например, [4, 7]) в расчетные формулы. По нашим данным, систематических исследований по оценке влияния этих погрешностей на динамическую реакцию сооружений не проводилось. В приложении 2 для некоторых типов сооружений приводятся результаты сравнительного анализа приближенных решений поставленной задачи (получаемых при использовании подхода, принятого в СНиП [1]) с точным, реализованным в расчетном комплексе MicroFE.
Необходимо отметить еще одно обстоятельство, связанное с разработкой и развитием методов динамического расчета сооружений, в т.ч. и на действие ветра. Существующие в 60-80 годы расчетные комплексы, в основном, позволяли достаточно точно и в приемлемые сроки проводить расчет строительных конструкций на действие статических нагрузок. Динамический расчет сооружений, имеющих многие сотни и тысячи степеней свободы, на ЭВМ того поколения требовал большого времени счета, а точность этих расчетов не всегда соответствовала необходимым требованиям. В связи с этим численные динамические расчеты редко включались в подобные программные комплексы тех лет.
В настоящее время ситуация коренным образом изменилась. Современные ПК обладают достаточной памятью и быстродействием для проведения в "разумные" сроки динамического анализа сооружений со сложной расчетной схемой. В частности, в рамках программного комплекса MicroFe существует разработанный на современном уровне блок по определению собственных характеристик (собственных частот и форм) динамических систем с, практически, произвольным числом степеней свободы. Это позволило реализовать в рамках этого же расчетного комплекса алгоритм точного расчета зданий и сооружений на действие пульсационной составляющей ветровой нагрузки.
ПРИЛОЖЕНИЕ 2
ПРИМЕРЫ РАСЧЕТА И СРАВНИТЕЛЬНЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ
Представленная в "Рекомендациях..." методика расчета зданий и сооружений на действие пульсационной составляющей ветровой нагрузки реализована в программном комплексе STARK ES семейства программ MicroFe. Для оценки ее точности и эффективности проведен расчет на действии ПВ-нагрузок некоторых типов сооружений и выполнен сравнительный анализ полученных результатов с данными, соответствующими подходу, принятому в СНиП [1]. При выполнении этих численных исследований рассмотрены:
1. Железобетонная башня (ЖБ) высотой 415 м;
2. Плоская рама (Р2), расположенная в плоскости, параллельной скорости ветра;
3. Пространственная трехмерная расчетная схема (РБ-3) решетчатой башни высотой 180 м;
4. Решетчатая башня (РБ-1), в качестве расчетной схемы которой принят консольный стержень.
Расчет проводился по точной и приближенной методикам (пп. 2 и 3 "Рекомендаций..."), а также используя соотношения принятые в СНиП. Описание расчетных схем сооружений и полученные результаты приведены в пп. П2.1 - П2.4.
П2.1. Воздухоотводящая железобетонная башня (ЖБ)
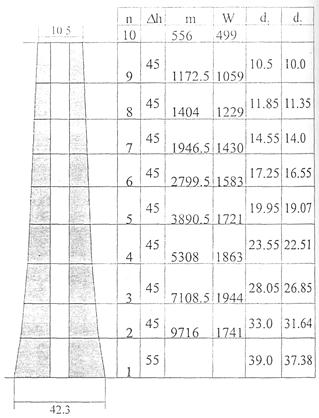
Рассматриваемая воздухоотводящая железобетонная башня имеет высоту 415 м и расположена в 5-ом ветровом районе, на местности типа А. В качестве расчетной схемы этого сооружения принят консольный стержень с переменным поперечным сечением (рис. П2.1). Башня разбита на 10 конечных элементов (КЭ). Основные параметры расчетной схемы: положение узлов, размеры сечения и средняя составляющая ветровой нагрузки приведены в таблице к рис. П2.1, где
п - номер узла или элемента;
Δh(м) - высота участка;
d1 и d2 - соответственно внешний и внутренний диаметр сечения;
W (кН) - средняя составляющая узловой ветровой нагрузки.
Жесткость КЭ определена по геометрическим размерам сечения; инерционные массы сосредоточены в узлах элементов и соответствует плотности материала ρ=3.0 т/м3.
При использовании методики настоящих "Рекомендаций..." получено, что для рассматриваемого железобетонного сооружения, расположенного в 5-ом ветровом районе, предельные частоты
flim=0,43 Гц;
в соответствии с требованиями СНиП
flim(CHиП)=1,6 Гц;
Рис. П2.1 Схема железобетонной башни
Таблица П2.1. Максимальные перемещения (мм) железобетонной башни
|
Форма колебаний |
Частота, Гц |
Метод расчета |
||
|
"Рекомендации..." |
СНиП |
|||
|
Точный |
Приближенный |
|||
|
1 |
0,20 |
517 |
534 |
471 |
|
2 |
0,62 |
23,1 |
22,0 |
29,1 |
|
3 |
1,27 |
4,5 |
1,9 |
2,8 |
При определении реакции башни на действие пульсационной составляющей ветровой нагрузки учитывались ее колебания по трем низшим собственным частотам. Результаты расчета показаны в табл. П2.1.
П2.2. Плоская рама (ПР-2)
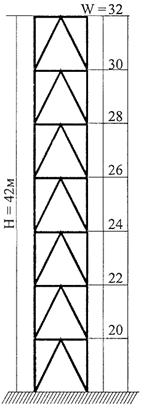
Рассматриваемая плоская металлическая рама расположена
в плоскости, параллельной вектору средней скорости ветра ![]() , и составлена
из элементов с прямоугольным поперечным сечением размером 0,6´0,4 м2. По высоте рама разбита на 7 равных
участков. Средняя составляющая ветровой нагрузки w приложена
в одном из узлов каждого участка. Геометрические размеры сооружения и величины
средней составляющей ветровой нагрузки, приведены на рис П2.2.
Для рассматриваемой металлической рамы, расположенной в 6-ом ветровом районе
, и составлена
из элементов с прямоугольным поперечным сечением размером 0,6´0,4 м2. По высоте рама разбита на 7 равных
участков. Средняя составляющая ветровой нагрузки w приложена
в одном из узлов каждого участка. Геометрические размеры сооружения и величины
средней составляющей ветровой нагрузки, приведены на рис П2.2.
Для рассматриваемой металлической рамы, расположенной в 6-ом ветровом районе
flim=2,22 Гц,
что позволяет учитывать реакцию только по первой низшей форме колебаний. Для сравнения
flim(СНиП) = 5,6 Гц.
Рис. П2.2. Схема рамы (W - в кН)
Таблица П2.2. Максимальные перемещения (мм) плоской металлической рамы ПР-2
|
Частота, Гц |
Метод расчета |
|||
|
"Рекомендации..." |
СНиП |
|||
|
Точный |
Приближенный |
|||
|
1 |
0.82 |
515 |
527 |
560 |
|
2 |
3.7 |
12.6 |
12.2 |
12.5 |
При определении динамической реакции рамы на действие ветра учитывались ее колебания по двум низшим формам. Полученные результаты расчета показаны в табл. П2.2.
П2.3. Решетчатая башня (РБ-3); трехмерная расчетная схема
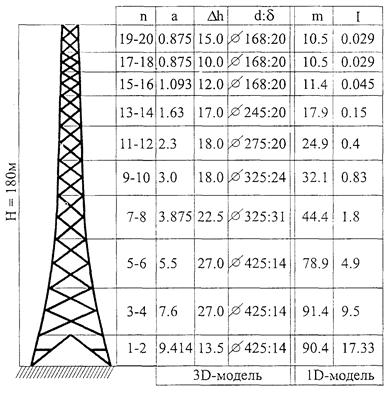
Рис. П2.3. Схема решетчатой башни; 3D- и 1D-модели
Общий вид рассматриваемой решетчатой башни, составленной из трубчатых элементов, показан на рис. П2.3, где
n - номер участка;
Δh (м) - его высота;
а (м) - горизонтальный размер сечения башни;
d и δ - соответственно диаметр и толщина трубчатых элементов.
Масса и жесткость конечных элементов определены по фактическим размерам сечения конструктивных элементов башни. Средняя составляющая ветровой нагрузки, действующей на каждый ее элемент, определялись в соответствии с указаниями СНиП [1]. Для башни (РБ-3), расположенной в 1-ом ветровом районе
flim=0,60 Гц
и, следовательно, при ее динамическом расчете на действие ветра достаточно учитывать колебания по трем низшим собственным формам. Для сравнения можно отметить, что в соответствии с указаниями СниП [1]
flim(СНиП)=2,9 Гц,
что требует учета колебаний по 14-ти собственным формам и численного определения соответствующего числа собственных частот и форм.
Сравнительные результаты динамического расчета сооружения, учитывающие его реакцию по первым двум, основным, формам колебаний, показаны в табл. П2.3. В табл. П2.4 приводятся результаты расчета башни, выполненного в соответствии с требованиями СНиП.
Таблица П2.3. Максимальные перемещения (мм) решетчатой башни РБ-3
|
Частота, Гц |
Метод расчета |
|||
|
"Рекомендации..." |
СНиП |
|||
|
Точный |
Приближенный |
|||
|
1 |
0,26 |
33,9 |
34,7 |
62,9 |
|
2 |
0,26 |
37,4 |
38,3 |
63,1 |
Результаты расчета рассматриваемой решетчатой башни показали, что колебания по первым трем низшим собственным формам коррелированны между собой. При этом реакция по третьей форме, соответствующей кручению сооружения вокруг вертикальной оси, оказалась малой и в табл. П2.3 не приводится.
Таблица П2.4. Результаты расчета башни РБ-3 по методике СНиП.
f (Гц) - собственная частота k ой формы;
итах - максимальное перемещение (мм)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
f,Гц |
0,26 |
0,26 |
0,27 |
0,41 |
0,76 |
1,09 |
1,38 |
|
uтах |
63 |
63 |
0,6 |
0,1 |
0,0 |
0,0 |
4,9 |
|
Форма |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
f,Гц |
1,38 |
1,53 |
1,81 |
1,87 |
2,16 |
2,99 |
2,29 |
|
umах |
4,9 |
0,0 |
0,0 |
0,0 |
0,0 |
0,8 |
0,8 |
П2.4. Решетчатая башня РБ-1; балочная расчетная схема
Рассматриваемая решетчатая башня расположена во втором ветровом районе, в местности типа А. В качестве расчетной схемы этого сооружения принят консольный стержень, который разбит на 20 конечных элементов различной длины и жесткости. Основные параметры принятой расчетной схемы показаны в таблице к рис. П2.3. Средняя составляющая ветровой нагрузки, действующей на каждый участок сооружения, определялась так же, как и для РБ-1 (п. П2.3).
Предельные частоты flim сооружения оказались равными:
flim=0,64 Гц
flim(СНиП)=2,9 Гц
При определении реакции сооружения на действие пульсационной составляющей ветровой нагрузки учитывались его колебания по трем собственным формам. Результаты расчета приведены в табл. П2.5.
Таблица П2.5. Максимальные перемещения (мм) башни РБ-1
|
Частота, Гц |
Метод расчета |
|||
|
"Рекомендации..." |
СНиП |
|||
|
Точный |
Приближенный |
|||
|
1 |
0,49 |
145 |
154 |
199 |
|
2 |
1,34 |
10,0 |
8,4 |
22,7 |
|
3 |
2,87 |
1,4 |
1,4 |
2,3 |
П2.5. Сравнительный анализ
В табл. П2.6 для сооружений, рассмотренных в пп. П2.1 - П2.4 приведены (в процентах) относительные погрешности Δи максимальных перемещений, полученных в результате использования различных методик расчета:
![]() ;
;
![]() - точное
значение максимального перемещения;
- точное
значение максимального перемещения;
umax - максимальные перемещения, полученные при использовании приближенной методики или подхода, принятого в СНиП.
Таблица П2.6. Сравнительные результаты расчета четырех сооружений
|
Метод расчета |
|||
|
"Рекомендации..." (приближенный) |
"Рекомендации..." (точный) |
СНиП |
|
|
ЖБ |
+3,3% |
0 |
-8,9% |
|
Р2 |
+2,3% |
0 |
+8,7% |
|
РБ-3 |
+2,4% |
0 |
+76,5% |
|
РБ-1 |
+6,2% |
0 |
+37,2% |
Полученные результаты показывают:
1. Предлагаемая методика позволяет до 50% повысить точность расчета сооружений на действие пульсаций ветровой нагрузки. При этом усилия и перемещения, получаемые в результате использования положений СНиП, могут как превышать, так и быть меньше их уточненных значений. И если в первом случае использование методики СНиП повышает запас прочности сооружения (хотя может приводить к неоправданному завышению размеров сечения несущих элементов), то во втором случае снижается степень надежности сооружения, а принятые по результатам расчета конструктивные решения могут не обеспечивать его нормальной эксплуатации.
2. Приближенная методика расчета сооружений на действие ветра обеспечивает достаточно высокую (порядка 90-95%) точность получаемых результатов, которая вполне приемлема при проведении инженерных расчетов.
3. Собственные частоты, колебания на которых вносят основной вклад в реакцию сооружений, значительно ниже (см. табл. П2.7) предельных частот flimСНиП, рекомендуемых СНиП.
Снижение предельных частот flim, которое получено при использовании предлагаемой методики, позволяет без потери точности получаемых результатов упростить алгоритм динамического расчета сооружений на действие ветра и снизить ресурсы, необходимые для решения подобных задач.
Таблица П2.7. Предельные частоты flim и число учитываемых форм Ктах
|
Метод расчета |
Сооружение |
||||
|
ЖБ-1 |
Р2 |
РБ-3 |
РБ-1 |
||
|
flim (ГЦ) |
"Рекомендации..." |
0,43 |
2,22 |
0,60 |
0,64 |
|
СНиП |
1,6 |
5,6 |
2,9 |
2,9 |
|
|
Kтах |
"Рекомендации..." |
1 |
1 |
4 |
1 |
|
СНиП |
3 |
2 |
14 |
3 |
|
4. Рекомендуется следующий порядок расчета сооружений на действие ветра:
ü для оценки напряженно-деформированного состояния на начальных этапах проектирования и при проведении вариантных расчетов сооружения, связанных с поиском оптимальных конструктивных решений используется приближенная методика.
ü расчет по точной методике проводится на последней стадии проектирования.
ПРИЛОЖЕНИЕ 3
ДИНАМИЧЕСКАЯ РЕАКЦИЯ СООРУЖЕНИЙ ПРИ ДЕЙСТВИИ ВЕТРА
П3.1. Общее решение задачи о вынужденных колебаниях сооружений
В качестве исходных соотношений, используемых для решения задачи о вынужденных колебаниях сооружений при действии пульсационной составляющей ветровой нагрузки, принимаются:
- линейные уравнения движения сооружения, которые в общем случае могут быть записаны в виде:
- и соответствующие граничные условия:
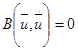 . (П3.1b)
. (П3.1b)
В (П3.1)
![]() -
обобщенный вектор динамических перемещений в точке с координатами х=(x1,х2,х3);
-
обобщенный вектор динамических перемещений в точке с координатами х=(x1,х2,х3);
t - время;
т(х) - масса;
Г( ) и Lx() - линейные дифференциальные операторы, описывающие соответственно диссипативные и упругие свойства сооружения;
![]() (x,t)
- обобщенный вектор ветровой нагрузки;
(x,t)
- обобщенный вектор ветровой нагрузки;
В( ) - линейный оператор (или функция), соответствующие условиям на границе сооружения и условия сопряжения его отдельных элементов;
точкой обозначена операция дифференцирования по времени, т.е.
![]() .
.
Обычно при решении динамических задач строительной механики для описания диссипативных свойств сооружения используется гипотеза Фойхта. Тогда
![]() , (П3.1с)
, (П3.1с)
где ![]() - коэффициент, характеризующий
диссипацию энергии.
- коэффициент, характеризующий
диссипацию энергии.
Величина этого коэффициента зависит от свойств материала, из которого изготовлены элементы сооружения, его конструктивных особенностей, потери энергии в узлах крепления и соединения отдельных элементов, а также от аэродинамического демпфирования и интенсивности колебаний.
В общем случае вектор ![]() (х,t)
включает в себя перемещения и углы
поворота, а вектор
(х,t)
включает в себя перемещения и углы
поворота, а вектор ![]() (x,t)
- действующие силы и моменты.
(x,t)
- действующие силы и моменты.
При решении прикладных задач ветровая нагрузка ![]() (x,t)
рассматривается как векторный
случайный стационарный процесс, который в этом случае может быть разложен в ряд
Фурье
(x,t)
рассматривается как векторный
случайный стационарный процесс, который в этом случае может быть разложен в ряд
Фурье
Тогда решение краевой задачи (П3.2) также ищется в виде ряда Фурье:
![]() , (П3.3)
, (П3.3)
где функции ![]() и
и ![]() удовлетворяют следующей системе
дифференциальных уравнений по пространственным координатам:
удовлетворяют следующей системе
дифференциальных уравнений по пространственным координатам:
![]() ; (П3.4)
; (П3.4)
![]() .
.
Дальнейшее решение рассматриваемой задачи связано с
разложением ![]() в
ряды по некоторой полной (и, как правило, ортогональной) системе функций
в
ряды по некоторой полной (и, как правило, ортогональной) системе функций ![]() . В
качестве такой системы наиболее удобно выбрать собственные функции спектральной
задачи, получаемой из уравнений (П3.1), в которых диссипативные члены и нагрузка (правая
часть) принимаются равными нулю. Тогда перемещение
. В
качестве такой системы наиболее удобно выбрать собственные функции спектральной
задачи, получаемой из уравнений (П3.1), в которых диссипативные члены и нагрузка (правая
часть) принимаются равными нулю. Тогда перемещение ![]() (х,t)
можно представить в виде:
(х,t)
можно представить в виде:
![]() ; (П3.5в)
; (П3.5в)
![]() ; (П3.5с)
; (П3.5с)
![]() ; (П3.5d)
; (П3.5d)
![]() . (П3.5е)
. (П3.5е)
В соотношениях (П3.5):
![]() и
fk (k=l,2,...)
- соответственно собственные функции (формы колебаний) и собственные числа
(частоты, в Гц) рассматриваемой задачи;
и
fk (k=l,2,...)
- соответственно собственные функции (формы колебаний) и собственные числа
(частоты, в Гц) рассматриваемой задачи;
γk - коэффициент неупругого сопротивления для k-ой собственной формы, связанный с логарифмическим декрементом δk соотношением:
![]() ; (П3.5f)
; (П3.5f)
![]() -
коэффициенты разложения функций
-
коэффициенты разложения функций ![]() в ряды по собственным функциям
в ряды по собственным функциям ![]() , т.е.:
, т.е.:
![]() . (П3.5h)
. (П3.5h)
При выводе (П3.5) принято, что собственные функции являются ортогональными с весом т(х) , т.е.
![]() . (П3.6в)
. (П3.6в)
В соотношениях (П3.5g) и (П3.6) интегрирование проводится по всему объему (площади, длине - в зависимости от принятой расчетной схемы) X , занятому сооружением.
П3.2. Статистические характеристики реакции сооружения
П3.2.1. Определение дисперсии перемещений
В том случае, если воздействие ![]() является
детерминированным, соотношения (П3.5) полностью
описывает колебания сооружения. При случайных воздействиях, к которым относится
и ветровая нагрузка, эти выражения служат основой для определения стандарта,
максимальных расчетных и других статистических характеристик, усилий и
перемещений, возникающих в элементах сооружений.
является
детерминированным, соотношения (П3.5) полностью
описывает колебания сооружения. При случайных воздействиях, к которым относится
и ветровая нагрузка, эти выражения служат основой для определения стандарта,
максимальных расчетных и других статистических характеристик, усилий и
перемещений, возникающих в элементах сооружений.
Принимая во внимание данные натурных экспериментальных исследований, пульсационная составляющая ветровой нагрузки может рассматриваться как случайный стационарный и эргодичный процесс. В этом случае параметры wik(s), wik(c), wik и θik в (П3.5) являются случайными величинами со следующими свойствами:
а. Для всех i и k амплитуды wik и фазовые углы θik - статистически независимы; причем wik распределены по закону Релея, а θik - равномерно на интервале (0, 2π);
б. Для i≠i1 коэффициенты wik(s), и wi1k(c) - также являются статистически независимыми и описываются распределением Гаусса.
Тогда, определяя обычным образом дисперсию ![]() перемещения
перемещения
![]() :
:
![]() , (П3.7)
, (П3.7)
ее среднее значение (математическое ожидание) σu2(x) можно представить в виде:
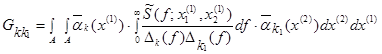 ; (П3.8b)
; (П3.8b)
![]() . (П3.8с)
. (П3.8с)
Здесь
![]() и
и ![]() - соответственно взаимный спектральный
тензор и взаимный корреляционный тензор пулъсационной составляющей ветровой
нагрузки, определенные для точек х(1)=(х1(1),х2(1),х3(1))
и х(2)=(х1(2),х2(2),х3(2));
- соответственно взаимный спектральный
тензор и взаимный корреляционный тензор пулъсационной составляющей ветровой
нагрузки, определенные для точек х(1)=(х1(1),х2(1),х3(1))
и х(2)=(х1(2),х2(2),х3(2));
Е[ ] - оператор осреднения (математическое ожидание) по множеству реализаций;
А - поверхность сооружения, на которую действует пульсационная составляющая ветровой нагрузки.
П3.2.2. Определение дисперсии усилий
Пусть усилие, напряжение или любой другой параметр ![]() , характеризующий
напряженно-деформированное состояние сооружения, связан с перемещением
, характеризующий
напряженно-деформированное состояние сооружения, связан с перемещением ![]() (x,t)
линейным преобразованием типа
(x,t)
линейным преобразованием типа
![]() , (П3.9)
, (П3.9)
где lq( ) - линейная функция или произвольный линейный оператор (интегральный, дифференциальный или смешанный).
Тогда из (П3.5а) следует, что
![]() . (П3.10b)
. (П3.10b)
И, по аналогии с (П3.8), математическое ожидание σ2Q(x) дисперсии параметра Q можно представить в виде:
![]() . (П3.11)
. (П3.11)
Таким образом, для статистического определения
произвольного параметра ![]() , связанного с перемещением
, связанного с перемещением ![]() (x,t)
линейным преобразованием LQ(
(x,t)
линейным преобразованием LQ(![]() ) достаточно
это преобразование применить к базисным функциям
) достаточно
это преобразование применить к базисным функциям ![]() (х) рассматриваемой
задачи.
(х) рассматриваемой
задачи.
П3.2.3. Расчетные значения усилий и перемещений
Из соотношений (П3.2), (П3.5) и (П3.10) видно,
что для фиксированных t=t* и х=х* нагрузка
![]() =
=![]() (x*,t*),
перемещения
(x*,t*),
перемещения ![]() =и(х*,t*)
и усилия
=и(х*,t*)
и усилия ![]() =
=![]() (x*,t*)
являются случайными величинами,
функционально связанными со случайными параметрами wik и
θik, характеризующими
воздействие пульсационной составляющей ветровой нагрузки. При сделанных
предположениях относительно статистического распределения параметров wik и θik,
(п. П3.2.1 а и
b) w*, u* и Q*
будут распределены по закону Релея.
(x*,t*)
являются случайными величинами,
функционально связанными со случайными параметрами wik и
θik, характеризующими
воздействие пульсационной составляющей ветровой нагрузки. При сделанных
предположениях относительно статистического распределения параметров wik и θik,
(п. П3.2.1 а и
b) w*, u* и Q*
будут распределены по закону Релея.
Таблица П3. Обеспеченность Pγ(в %), соответствующая различным γ, для распределения Релея
|
γ |
0,5 |
1 |
2 |
2,5 |
3 |
3,5 |
4 |
|
Pγ |
11,8 |
39,3 |
86,5 |
95,6 |
98,889 |
99,78 |
99,966 |
Тогда можно определить теоретическую вероятность Pγ того, что каждый из этих параметров не превысит величину γσ (см. табл. П3), где γ>0 и σ - стандарт соответствующего параметра w*, и* или Q*; вероятность Рγ называется обеспеченностью воздействия или реакции сооружений.
В практике проектирования в качестве расчетного (максимального) значения перемещений принимается величина
![]() , (П3.12)
, (П3.12)
где
σи - стандарт перемещений;
γр - коэффициент обеспеченности пульсационной составляющей ветровой нагрузки.
Обычно, значение γр назначается на основе экспертных оценок, и с учетом опыта эксплуатации сооружений. В нормативных документах различных стран значение γр изменяется от 2,5 до 4,0; при подготовке СНиП [1] принято γр=3,0, что соответствует теоретической обеспеченности Pγ≈0,9889 ПВ-нагрузок, а также расчетных усилий и перемещений, реализуемых при этом воздействии.
Можно также отметить, что из предположения об эргодичности ПВ-нагрузок следует, что с вероятностью равной 1,0 расчетные значения перемещений и усилий достигаются в некоторые моменты времени tu(x) и tq(x), соответственно, которые, в общем случае, оказываются различными для различных точек (элементов) сооружения и различных параметров (усилий, перемещений, напряжений и т.д.) напряженно-деформированного состояния.
П3.3. Статистическое описание ветровой нагрузки
П3.3.1. Спектральная плотность ветровой нагрузки
При расчете зданий и сооружений на действие
пульсационной составляющей ветровой нагрузки спектральный тензор ![]() , как
правило, описывается (явно или неявно) следующими соотношениями:
, как
правило, описывается (явно или неявно) следующими соотношениями:
![]() , (П3.13b)
, (П3.13b)
где
Sp(f;x(1),x(2)) - взаимный пространственный энергетический спектр пульсаций давлений ветра для точек х(1) и х(2);
Sv(f;z) - энергетический спектр продольной компоненты скорости ветра на высоте;
rv(f;х(1),х(2)) - коэффициент корреляций скорости ветра для точек х(1) и х(2);
rw(f;x(1),х(2)) - коэффициент корреляций пульсаций давления для точек х(1) и х(2).
В качестве обоснования для использования соотношений (П3.13) при динамическом расчете сооружений на действие ветра обычно используются следующие два положения.
1. Данные натурных экспериментальных исследований [2]
показывают, что скорость ветра ![]() можно естественным образом разбить на две
составляющие: среднюю (
можно естественным образом разбить на две
составляющие: среднюю (![]() ), величина которой V определяется
с некоторым осреднением τ=(10÷90) мин., и пульсационную (
), величина которой V определяется
с некоторым осреднением τ=(10÷90) мин., и пульсационную (![]() ), т.е.
), т.е.
![]() . (П3.14a)
. (П3.14a)
Причем в некоторой системе координат (которая называется поточной):
![]() . (П3.14b)
. (П3.14b)
Здесь
V - величина средней скорости ветра;
![]() и
и
![]() -
соответственно продольная, поперечная и вертикальная компоненты пульсаций
скорости ветра.
-
соответственно продольная, поперечная и вертикальная компоненты пульсаций
скорости ветра.
Можно отметить, что в СНиП [1] интервал осреднения τ принят равным 10 мин (τ=10 мин).
2. Принимается, что ветровая нагрузка ![]() , действующая
на сооружения, не зависит от поперечной (
, действующая
на сооружения, не зависит от поперечной (![]() ) и вертикальной (
) и вертикальной (![]() ) компонент
скорости ветра и связана с ее суммарной продольной компонентой (V+v`)
соотношениями:
) компонент
скорости ветра и связана с ее суммарной продольной компонентой (V+v`)
соотношениями:
![]() ; (П3.15а)
; (П3.15а)
![]() ; (П3.15в)
; (П3.15в)
![]() . (П3.15с)
. (П3.15с)
Здесь
![]() и
и
![]() -
соответственно средняя и пульсационная составляющие ветровой нагрузки;
-
соответственно средняя и пульсационная составляющие ветровой нагрузки;
ρа - плотность воздуха;
![]() -
вектор, характеризующий аэродинамические свойства (коэффициенты) сооружения.
-
вектор, характеризующий аэродинамические свойства (коэффициенты) сооружения.
Таким образом, при практических расчетах сооружений на действие ветра принимается, что энергетический спектр (П3.13) этого воздействия "подобен" спектру продольной компоненты скорости ветра, а изменения структуры потока, обусловленные его взаимодействием с сооружением, учитываются только за счет введения в расчетные формулы коэффициента корреляции пульсаций давления (который, кстати, не введен в действующем СНиП [1] и более ранних редакциях этого нормативного документа).
Необходимо отметить, что в целом, такой подход вполне оправдывает себя и оказывается достаточно корректным при расчете на действие пульсаций ветра высоких башенных сооружений, мачт, зданий (в частности тех, у которых оба размера которых в плоскости, перпендикулярной скорости ветра, не превышают 100 м) и многих других подобных строительных конструкций.
В то же время соотношения (П3.13) даже качественно не описывают статистические характеристики ветровых нагрузок, действующих на покрытия и некоторые типы зданий. В подобных случаях приходиться использовать данные соответствующим образом организованных модельных испытаний сооружений в аэродинамических трубах.
П3.3.2. Энергетический спектр скорости ветра
В действующей главе СНиП 2.01.07-85* "Нагрузки и воздействия" принято следующее выражение для энергетического спектра скорости ветра, предложенное Давенпортом [3] в начале 60-х годов:
![]() , (П3.16b)
, (П3.16b)
где
![]() -
дисперсия;
-
дисперсия;
f- частота в Гц;
λ - безразмерная частота;
Lx = 1200 м - интегральный продольный масштаб турбулентности:
v0 - базовая скорость ветра на высоте 10м.
Необходимо отметить, что это соотношение, используемое в отечественной практике нормирования ветровых нагрузок с начала 70-х годов, не совсем точно описывает статистические свойства скорости ветра. В частности, здесь не учитывается зависимость спектра от высоты над поверхностью земли, которая подтверждается многочисленными экспериментальными данными. Результаты сравнительных численных исследований показывают (см., например, [4]), что использование соотношений (П3.16) приводит к заметному завышению динамической реакции большинства сооружений. Поэтому в настоящее время в нормах многих стран для описания энергетического спектра Sv используются иные аппроксимации. В частности, в последней редакции Еврокода
![]() ; (П3.17а)
; (П3.17а)
![]() , (П3.17в)
, (П3.17в)
где Lx(z) и V(z) имеют тот же физический смысл, что и в (П3.16в).
П3.3.3. Коэффициент корреляции скорости ветра
Коэффициент корреляции rv(f;x(1),x(2)) пульсаций скорости ветра для двух произвольных точек x(1) и x(2) обычно аппроксимируется следующим выражением [4,6]:
![]() ; (П3.18а)
; (П3.18а)
![]() ; (П3.18b)
; (П3.18b)
![]() ;
; ![]() , (П3.18с)
, (П3.18с)
где
bi - эмпирические константы;
Δxi - проекции расстояния между точками х(1) и х(2) на оси поточной системы координат (см. (П3.14в))
В СНиП [1]
V=Vo; bi=20; b2=b3=8.
В Еврокоде [5]
V=0,5[V(zl)+V(z2)]; b2=b3=11,5.
Постоянная b1 в Еврокоде не приводится, но по данным авторов этого нормативного документа b1≈30.
П3.3.4. Коэффициент корреляции пульсаций давления
Результаты натурных и модельных экспериментальных исследований показывают, что пульсации давления на различных поверхностях сооружения (наветренных, боковых и подветренных) не полностью коррелированны между собой. В частности, найдено, что корреляция давления между наветренной и подветренной поверхностями достаточно хорошо описывается соотношением [4,5]:
![]() ; (П3.19а)
; (П3.19а)
![]() , (П3.19b)
, (П3.19b)
где
а - характерное расстояние между рассматриваемыми (обычно наветренной и подветренной) поверхностями;
bw - константа.
В СНиП подобные эффекты не учитываются, т.е. пульсации давления на наветренной и подветренной сторонах здания считают полностью коррелированными, что, очевидно, ведет к завышению расчетных ПВ-нагрузок и соответствующей реакции сооружения.
В Еврокоде а=38,5 - расстояние между наветренной и подветренной поверхностями здания.
ЛИТЕРАТУРА.
1. СНиП 2.01.07-85* "Нагрузки и воздействия", М., 1996.
2. А.С. Монин, А.М. Яглом. Статистическая гидромеханика. М., "Наука", 1965.
3. A.G. Davenport, "The Spectrum of Horizontal Gustiness Near the Ground in High Winds", J. Royal Meteorol. Soc., 87, (1961) 194-211.
4. Э. Симиу и Р. Скандлан. Воздействие ветра на здания и сооружения., М., Стройиздат, 1984.
5. Eurocode 1: Basis design and action on structures. Part 2-4: Wind action". ENV 1991-2-4, CEN, 1994.
6. Руководство по расчету зданий и сооружений на действие ветра. М., 1978.
СПИСОК ИСПОЛЬЗОВАННЫХ ОБОЗНАЧЕНИЙ
Латинский алфавит
А - поверхность сооружения, на которую действует ветровая нагрузка.
f (Гц) - частота.
fk (Гц) - k-ая собственная частота.
flim - предельная частота колебаний.
go - расчетные значения коэффициента порывистости.
Gkk1 - обобщенное воздействие, учитывающие совместные колебания сооружения по k-ой и k1-ой формам.
Кmax - число учитываемых собственных форм.
т(х) - масса сооружения в точке х.
Qp - расчетные значения усилий.
rv(f;x(1),x(2)) - коэффициент корреляции пульсаций скорости ветра в точках х(1) и х(2).
rw(f;x(1),х(2)) - коэффициент корреляций пульсаций давления в точек x(1) и х(2).
Sv,0(f) - нормированный энергетический спектр продольной компоненты скорости вектора.
t - время.
Tv(x(1),x(2)) - период корреляции порывов в точках х(1) и х(2).
ир - расчетные значения перемещений.
Vo - базовая скорость ветра на высоте 10м.
wm - средняя составляющая ветровой нагрузки.
wg - пульсационная составляющая ветровой нагрузки.
х=(х1,x2,х3) - координаты, описывающие геометрию сооружения.
z - высота над поверхностью земли в точке с координатами х.
Греческий алфавит
δk - логарифмический декремент.
ε0 - точность динамического расчета.
![]() (х)
- вектор k-ой собственной
формы в точке х.
(х)
- вектор k-ой собственной
формы в точке х.
γg - коэффициент обеспеченности пульсационной составляющей ветровой нагрузки.
γk - коэффициент неупругого сопротивления для k-ой собственной формы.
σ0 - стандарт спектра скорости ветра.
σQ - стандарт усилий.
σи - стандарт перемещений.
v0 - квазистатическая часть реакции.
ξkk1 - коэффициент динамичности, учитывающий совместную реакцию сооружения по k-ой и k1-ой формам.
ξk - коэффициент динамичности для k-ой собственной форме.
ζ(z) - коэффициент пульсаций скорости ветра.