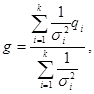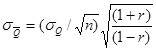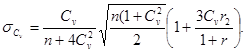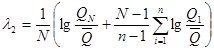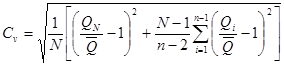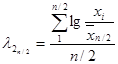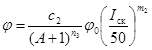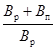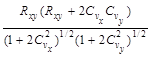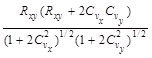СИСТЕМА НОРМАТИВНЫХ ДОКУМЕНТОВ В СТРОИТЕЛЬСТВЕ

СВОД ПРАВИЛ ПО ПРОЕКТИРОВАНИЮ И СТРОИТЕЛЬСТВУ

ОПРЕДЕЛЕНИЕ ОСНОВНЫХ
РАСЧЕТНЫХ ГИДРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК

СП 33-101-2003

ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПО СТРОИТЕЛЬСТВУ И ЖИЛИЩНО-КОММУНАЛЬНОМУ КОМПЛЕКСУ
(ГОССТРОЙ РОССИИ)

Москва

2004

ПРЕДИСЛОВИЕ

1 РАЗРАБОТАН Государственным гидрологическим институтом (ГГИ) Росгидромета, научный руководитель - д-р техн. наук А. В. Рождественский, ответственные исполнители: д-р техн. наук В. А. Бузин, канд. геогр. наук Б. М. Доброумов, канд. техн. наук А. Г. Лобанова, д-р техн. наук В. А. Лобанов, канд. геогр. наук Г. А. Плиткин, канд. техн. наук С. М. Тумановская и Проектным и научно-исследовательским институтом по инженерным изысканиям в строительстве (ПНИИИС) (ответственный исполнитель - д-р техн. наук М. В. Болгов) с участием Российского государственного гидрометеорологического университета (РГГМУ) (ответственный исполнитель - д-р геогр. наук А. М. Владимиров), Института водных проблем (ИВП) (ответственный исполнитель - канд. техн. наук Л. Ф. Сотникова)

2 ВНЕСЕН Управлением технического нормирования, стандартизации и сертификации в строительстве и ЖКХ Госстроя России

3 ОДОБРЕН для применения в качестве нормативного документа постановлением Госстроя России № 218 от 26 декабря 2003 г.

4 ВЗАМЕН СНиП 2.01.14-83

Содержание

СВОД ПРАВИЛ ПО ПРОЕКТИРОВАНИЮ И СТРОИТЕЛЬСТВУ

1 ОБЛАСТЬ ПРИМЕНЕНИЯ

Настоящий Свод правил устанавливает общие положения и требования к организации и порядку проведения инженерных гидрологических расчетов по определению гидрологических характеристик для обоснования проектирования новых, расширения, реконструкции и технического перевооружения действующих предприятий, зданий и сооружений для всех видов строительства и инженерной защиты территорий.

Положения настоящего Свода правил не распространяются на определение расчетных гидрологических характеристик при изысканиях и проектировании объектов, расположенных на участках рек, находящихся в зоне влияния морских приливов, а также на селеопасных реках.

2 НОРМАТИВНЫЕ ССЫЛКИ

СНиП 2.04.02-84* Водоснабжение. Наружные сети и сооружения

СНиП 2.06.04-82* Нагрузки и воздействия на гидротехнические сооружения (волновые, ледовые и от судов)

СНиП 11-02-96 Инженерные изыскания для строительства. Основные положения

СНиП 33-01-2003 Гидротехнические сооружения. Основные положения

СП 11-103-97 Инженерно-гидрометеорологические изыскания для строительства

ГОСТ 19179-73 Гидрология суши. Термины и определения

ГОСТ 27751-88 Надежность строительных конструкций и оснований. Основные положения по расчету

3 ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ

В настоящем Своде правил использованы следующие термины с соответствующими определениями:

гидрологические расчеты: Раздел инженерной гидрологии, в задачи которого входит разработка методов, позволяющих рассчитать значения различных характеристик гидрологического режима.

гидрологические характеристики: Количественные оценки элементов гидрологического режима.

клетчатка вероятностей: Специальные клетчатки с прямоугольной системой координат, построенные таким образом, что на них спрямляются (полностью или частично) различные кривые обеспеченности.

методы гидрологических расчетов: Технические приемы, позволяющие рассчитать, обычно с оценкой вероятности их появления, значения различных характеристик гидрологического режима.

обеспеченность гидрологической характеристики: Вероятность того, что рассматриваемое значение гидрологической характеристики может быть превышено среди совокупности всех возможных ее значений.

расчетная обеспеченность: Обеспеченность гидрологической характеристики, принимаемая при строительном проектировании для установления значения параметров гидрологического режима, определяющих проектные решения.

расчетный расход воды: Расход воды заданной вероятности превышения, принимаемый в качестве исходного значения для определения размеров проектируемых сооружений.

влагоотдача снежного покрова: Процесс поступления на поверхность почвы избыточной (не удерживаемой снегом) гравитационной талой или дождевой воды.

время добегания: Время, в течение которого водная масса проходит заданное расстояние.

запас воды в снежном покрове: Общее количество воды в твердом и жидком состоянии, содержащееся в рассматриваемый момент времени в снежном покрове.

интенсивность дождя: Слой осадков, мм, выпадающих за единицу времени.

интенсивность снеготаяния: Количество воды, мм, образующееся в процессе таяния снега в единицу времени.

коэффициент редукции: Коэффициент, характеризующий интенсивность изменения (убывания) какого-либо одного значения с изменением другого, связанного с ним значения.

объем стока: Количество воды, протекающее через рассматриваемый створ водотока за какой-либо период времени.

редукция интенсивности дождя: Изменение (убывание) средней интенсивности дождя с увеличением его продолжительности.

редукция максимального модуля стока: Изменение (убывание) максимального модуля стока с увеличением площади водосбора.

уклон водной поверхности: Отношение разности отметок уровня воды на рассматриваемом участке к длине этого участка.

водохозяйственный год: Расчетный годичный период, начинающийся с самого многоводного сезона.

лимитирующий период: Часть водохозяйственного года, неблагоприятная для осуществления проектируемых мероприятий либо по водопотреблению и водопользованию, либо по борьбе с наводнениями и осушению болот.

нелимитирующий период: Часть водохозяйственного года за вычетом лимитирующего периода.

свободное состояние русла: Состояние русла, характеризующееся отсутствием препятствий (ледяных образований, водной растительности, сплавного леса и т.д.), которое влияет на зависимость между расходами и уровнями, а также отсутствием подпора.

подпор воды: Повышение уровня воды из-за наличия в русле препятствия для ее движения.

соответственные уровни воды: Уровни воды на двух гидрологических постах, относящиеся к одинаковым фазам уровенного режима, - гребням резко выраженных подъемов или самым низким точкам.

гидрограф: График изменения во времени расходов воды за год или часть года (сезон, половодье или паводок) в данном створе водотока.

4 ОБЩИЕ ПОЛОЖЕНИЯ

4.1 Свод правил (СП) содержит основные методы и схемы расчета средних годовых, максимальных расходов воды и объемов стока весеннего половодья и дождевых паводков, гидрографов, внутригодового распределения стока, отметок наивысших уровней воды рек и озер и минимальных расходов воды.

При применении других методов расчетов, не включенных в СП, следует провести анализ, включающий сравнительную оценку погрешностей расчетов с результатами расчетов по методам, изложенным в настоящем СП.

4.2 Региональные особенности гидрологического режима и соответствующие методы определения расчетных характеристик учитываются и регламентируются территориальными строительными нормами (ТСН), имеющими статус нормативного документа субъекта Российской Федерации.

До разработки ТСН следует использовать методы, изложенные в настоящем Своде правил.

4.3 Определение расчетных гидрологических характеристик должно основываться на данных гидрометеорологических наблюдений, опубликованных в официальных документах Росгидромета, и неопубликованных данных последних лет наблюдений, а также на данных наблюдений, содержащихся в архивах Госгидрометфонда, изыскательских, проектных и других организаций, включая материалы опроса местных жителей. При отсутствии данных гидрометеорологических наблюдений в пункте проектирования необходимо проводить гидрометеорологические изыскания.

Кроме того, следует использовать достоверные данные наблюдений за гидрологическими характеристиками по архивным, литературным и другим материалам, относящимся к периоду до начала регулярных наблюдений. При этом необходимо указать источник, на основании которого установлена гидрологическая информация, и произвести оценку достоверности и точности полученных материалов.

4.4 При гидрологических расчетах следует учитывать материалы инженерно-гидрометеорологических изысканий. Учет кратковременных данных осуществляют методами, изложенными в разделе 6. Изыскания осуществляют в соответствии со СНиП 11-02, СП 11-103.

4.5 Данные гидрометрических наблюдений, вызывающие сомнение, следует подвергать проверке, включающей анализ:

- полноты и надежности наблюдений за уровнями и расходами воды;

- наличия данных о наивысших (мгновенных и среднесуточных) и наинизших уровнях воды за время наблюдений при свободном от льда русле, ледяном покрове, ледоходе, заторе льда, заросшем водной растительностью русле, подпоре от нижерасположенной плотины, сбросах воды выше гидрометрического створа, полноты учета стока воды на поймах и в протоках;

- влияния хозяйственной деятельности на речной сток и другие виды анализа.

Ненадежные данные гидрометрических наблюдений при невозможности их уточнения исключают из расчетного ряда наблюдений. В необходимых случаях должен выполняться пересчет стока воды за отдельные периоды.

4.6 Для рек, в бассейнах которых имеет место интенсивная хозяйственная деятельность, существенно нарушающая естественный гидрологический режим рек, определение расчетных гидрологических характеристик производят по двум расчетным схемам.

Первая расчетная схема предполагает приведение гидрологических рядов наблюдений к естественным однородным стационарным условиям воднобалансовыми и регрессионными методами [1], [2]. В расчетное значение гидрологической характеристики, полученной по естественному ряду в соответствии с разделами 5 - 7 настоящего документа, вводят поправку на влияние хозяйственной деятельности. Численное ежегодное значение поправки представляет собой разность между бытовым и естественным стоками. Значение поправки расчетной вероятности превышения определяют по кривой распределения поправок.

Во второй расчетной схеме гидрологические ряды наблюдений приводят к бытовому стоку за весь период наблюдений в предположении, что сложившийся комплекс хозяйственной деятельности с учетом реальных планов развития народного хозяйства действовал с начала наблюдений. Восстановление бытового стока за весь период наблюдений производят воднобалансовыми и регрессионными методами. Восстановленный ряд проверяют на однородность с использованием генетических и статистических методов. Определение расчетных гидрологических характеристик в этом случае производят по данным за весь период наблюдений без введения поправок на хозяйственную деятельность методами, изложенными в настоящем Своде правил.

Приведение речного стока к естественным условиям не производят, если суммарное значение его изменений не выходит за пределы случайной средней квадратической погрешности исходных данных наблюдений.

Методология предлагаемых двух расчетных схем может быть применена для расчетов основных гидрологических характеристик с учетом влияния возможного регионального антропогенного изменения климата.

4.7 Определение расчетных гидрологических характеристик следует производить по однородным рядам наблюдений. Оценку однородности рядов гидрологических наблюдений осуществляют на основе генетического и статистического анализов исходных данных наблюдений. Генетический анализ условий формирования речного стока заключается в выявлении физических причин, обусловливающих неоднородность исходных данных наблюдений. Для количественной оценки статистической однородности применяют критерии резко отклоняющихся экстремальных значений в эмпирическом распределении (критерии Смирнова - Граббса и Диксона), критерии однородности выборочных дисперсий (критерий Фишера) и выборочных средних (критерий Стьюдента).

Критические значения статистик критериев однородности с учетом автокорреляции между смежными членами анализируемой последовательности и асимметрии эмпирического распределения приведены в Рекомендациях [3].

4.8 Вероятности превышения расчетных гидрологических характеристик для каждого вида строительства устанавливают нормативными документами, утверждаемыми Госстроем России, в зависимости от уровня ответственности сооружений в соответствии с ГОСТ 27751.

4.9 При использовании нескольких независимых (не более трех) методов расчета окончательное расчетное значение рассматриваемой гидрологической характеристики g определяют по формуле

                                                            (4.1)

где q_i - значение рассматриваемой гидрологической характеристики, определенное различными методами;

 - абсолютные дисперсии погрешностей расчетных значений для каждого метода;

k - число методов.

4.10 При выборе рек-аналогов необходимо учитывать следующие условия:

- однотипность стока реки-аналога и исследуемой реки;

- географическую близость расположения водосборов;

- однородность условий формирования стока, сходство климатических условий, однотипность почв (грунтов) и гидрогеологических условий, близкую степень озерности, залесенности, заболоченности и распаханности водосборов;

- средние высоты водосборов не должны существенно отличаться, для горных и полугорных районов следует учитывать экспозицию склона и гипсометрию;

- отсутствие факторов, существенно искажающих естественный речной сток (регулирование стока, сбросы воды, изъятие стока на орошение и другие нужды).

4.11 Гидрологические расчеты для проектируемого сооружения при наличии действующих сооружений на реках должны учитывать возможность их влияния и при необходимости предусматривать согласованные решения по совместной работе вновь проектируемых и существующих сооружений с учетом возможности реконструкции существующих сооружений.

4.12 При проектировании водохозяйственных объектов допускается использование стохастических моделей колебаний стока рек, позволяющих моделировать искусственные ряды гидрометеорологических характеристик требуемой продолжительности. В качестве модели многолетних колебаний стока используют простую цепь Маркова [4], [6].

Моделирование рядов сезонных (месячных) значений стока осуществляют на основе периодических стохастических моделей различной степени сложности. При наличии продолжительных рядов наблюдений допускается использование метода фрагментов с учетом зависимости внутригодового распределения стока от водности года.

4.13 Инженерные гидрологические расчеты для строительного проектирования или отдельные их виды (работы, услуги) должны выполняться специализированными организациями (по видам строительства), имеющими соответствующие лицензии.

4.14 Оценку эффективности полученных эмпирических зависимостей и формул, применяемых в гидрологических расчетах при наличии, недостаточности и отсутствии данных наблюдений, выполняют на основе анализа остатков, оценки устойчивости параметров и коэффициентов этих зависимостей с проверкой на зависимом и независимом от расчетов материалах наблюдений.

4.15 К основным гидрологическим характеристикам относятся:

расход воды Q, м³/с;

объем стока воды W, м³;

модуль стока воды q, м³/с × км²;

слой стока воды h, мм;

уровень воды H, см.

5 ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ГИДРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ПРИ НАЛИЧИИ ДАННЫХ ГИДРОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ

Общие указания

5.1 Определение расчетных гидрологических характеристик при наличии данных гидрометрических наблюдений достаточной продолжительности осуществляют путем применения аналитических функций распределения ежегодных вероятностей превышения - кривых обеспеченностей.

Продолжительность периода наблюдений считают достаточной, если рассматриваемый период репрезентативен (представителен), а относительная средняя квадратическая погрешность расчетного значения исследуемой гидрологической характеристики не превышает 10 % для годового и сезонного стоков и 20 % - для максимального и минимального стоков.

Если относительные средние квадратические погрешности превышают указанные пределы и период наблюдений нерепрезентативен, необходимо осуществить приведение рассматриваемой гидрологической характеристики к многолетнему периоду согласно разделу 6 настоящего Свода правил.

Средние квадратические погрешности расчетного значения исследуемой гидрологической характеристики устанавливают по формулам (5.26) - (5.28) или по специальным таблицам, полученным методом статистических испытаний [4].

5.2 Эмпирическую ежегодную вероятность превышения Р_т,_% гидрологических характеристик определяют по формуле

                                                            (5.1)

где т -    порядковый номер членов ряда гидрологической характеристики, расположенных в убывающем порядке;

п - общее число членов ряда.

Эмпирические кривые распределения ежегодных вероятностей превышения строят на клетчатках вероятностей. Тип клетчатки вероятностей выбирают в соответствии с принятой аналитической функцией распределения вероятностей и полученного отношения коэффициента асимметрии C_s к коэффициенту вариации C_v.

5.3 Для сглаживания и экстраполяции эмпирических кривых распределения ежегодных вероятностей превышения, как правило, применяют трехпараметрические распределения: Крицкого - Менкеля при любом отношении C_s / C_v, распределение Пирсона III типа (биномиальная кривая) при C_s / C_v ≥ 2, лог-нормальное распределение при C_s ≥ (3 C_v + C_v³) и другие распределения, имеющие предел простирания случайной переменной от нуля или положительного значения до бесконечности. При надлежащем обосновании допускается применять двухпараметрические распределения, если эмпирическое отношение C_s / C_v и аналитическое отношение C_s / C_v, свойственные данной функции распределения, приблизительно равны. При неоднородности ряда гидрометрических наблюдений (различные условия формирования стока) применяют усеченные и составные кривые распределения вероятностей.

5.4 Оценки параметров аналитических кривых распределения: среднее многолетнее значение , коэффициент вариации C_v и отношение коэффициента асимметрии к коэффициенту вариации C_s / C_v, устанавливают по рядам наблюдений за рассматриваемой гидрологической характеристикой методом приближенно наибольшего правдоподобия и методом моментов. На начальных стадиях проектирования допускается использование графоаналитического метода (метода квантилей).

5.5 Коэффициент вариации С_v и коэффициент асимметрии С_s для трехпараметрического гамма-распределения Крицкого - Менкеля следует определять методом приближенно наибольшего правдоподобия в зависимости от статистик λ₂ и λ₃, вычисляемых по формулам:

;                                                  (5.2)

,                                                 (5.3)

где k_i - модульный коэффициент рассматриваемой гидрологической характеристики, определяемый по формуле

,                                                                (5.4)

здесь Q_i - погодичные значения расходов воды;

 - среднеарифметическое значение расходов воды, определяемое в зависимости от числа лет гидрометрических наблюдений по формуле

.                                                 (5.5)

По полученным значениям статистик λ₂ и λ₃ определяют коэффициенты вариации и асимметрии по номограммам [5].

5.6 Коэффициенты вариации С_г и асимметрии C_v определяют методом моментов по формулам:

С_v = (а₁ + а₂ / п) + (а₃ + а₄ / n) Č_v + (a₅ + a₆ / п) Č_v²;                            (5.6)

C_s = (b₁ + b₂ / n) + (b₃ + b₄ / n) Č_s + (b₅ + b₆ / п) Č_s², С_s                     (5.7)

где а₁, ..., a₆; b₁, ..., b₆ - коэффициенты, определяемые по приложению Б, таблица Б.1, для распределения Пирсона III типа и с помощью таблицы из [4] - для распределения Крицкого - Менкеля;

Č_v и Č_s - соответственно смешенные оценки коэффициентов вариации и асимметрии, определяемые по формулам:

Č_v 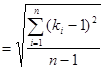,                                                     (5.8)

Č_s 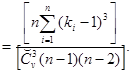                                                    (5.9)

При C_v < 0,6 и C_s < 1,0 коэффициенты вариации и асимметрии допускается определять по формулам (5.8) и (5.9) без введения поправок.

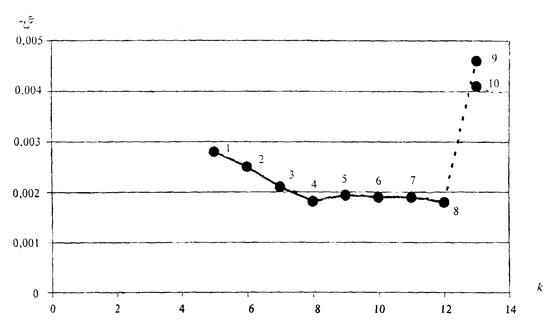
5.7 Расчетные значения отношения коэффициента асимметрии к коэффициенту вариации, а также коэффициента автокорреляции между стоком смежных лет r (1) следует принимать как среднее из значений, установленных по данным группы рек с наиболее продолжительными наблюдениями за рассматриваемой гидрологической характеристикой в гидрологически однородном районе с учетом площадей водосборов и других азональных факторов.

Для проверки однородности эмпирических оценок C_s / C_v и r (1) используют случайные погрешности оценок параметров по специальным таблицам, полученным методом статистических испытаний [4] или по аналитическим формулам. Если рассеяние эмпирических оценок C_s / C_v и r (1) больше теоретического, то принятый район признают неоднородным и он должен быть уменьшен до тех размеров, пока рассеяние эмпирических оценок и теоретические погрешности будут приблизительно равны.

5.8 Уточнение параметров распределений гидрологических характеристик допускается осуществлять методом объединения данных наблюдений по группе станций (постов) в пределах однородных районов. Рассматриваемая гидрологическая характеристика должна быть приведена к единым условиям формирования в однородном гидрологическом районе. Оценка гидрологической характеристики, приведенной к единым условиям формирования, является случайной величиной, распределение которой определяется объемом независимой информации.

Это распределение, называемое выборочным, в гидрологических расчетах характеризуется двумя его параметрами: средним значением и средним квадратическим отклонением (рассеянием).

5.9 Рассеяние оценок, вызванное ограниченностью данных наблюдений, обозначают через ε_случ, а рассеяние, обусловленное не устраненными приводкой различиями между водосборами, - через ε_геогр Полная дисперсия оценки ε_полн состоит из двух компонентов:

ε²_полн = ε²_случ + ε²_геогр                                                   (5.10)

Полную дисперсию оценки ε²_полн определяют по формуле

ε²_полн = 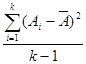,                                                  (5.11)

где i - индекс (номер) объекта. Под объектом понимают либо водосборный бассейн, либо метеорологическую станцию;

k - число совместно анализируемых объектов;

a_i - оценка рассматриваемого параметра по i-му объекту;

 - средняя из оценок по всем объектам.

Случайную составляющую рассеяния оценок ε²_случ вычисляют путем осреднения дисперсий оценок этих параметров по теоретическим формулам, полученным для отдельных объектов (5.26) - (5.28), или по результатам статистических испытаний [4].

Географическую составляющую рассеяния ε²_геогр определяют по (5.10) как разность между полной и случайной дисперсиями. Если оценка ε²_геогр имеет отрицательный знак, то ее принимают равной нулю.

Дисперсию результата совместного расчета определяют по формуле

ε²_ср = .                                                      (5.12)

Соотношение между случайной и географической составляющими определяет целесообразный состав объектов, обрабатываемых методом группового оценивания. При увеличении числа совместно анализируемых водосборов величина случайной составляющей ошибки уменьшается. Географическая составляющая должна увеличиваться за счет вовлечения водосборов, расположенных в пределах более обширной географической области, условия формирования стока которых различаются более существенно. Допустимым (приемлемым) следует считать число водосборов, при котором географическая составляющая не превосходит случайную:

ε_геогр ≤ ε_случ.                                                              (5.13)

Результатом группового анализа является оценка параметра по совокупности собственных и объединенных наблюдений в виде средневзвешенного по точности каждой из оценок:

                                              (5.14)

Стандартную ошибку такой оценки рассчитывают по формуле

.                                                (5.15)

Для оценок асимметрии и коэффициентов автокорреляции результатом группового анализа является средняя из всех индивидуальных оценок в пределах однородного района.

5.10 Порядок выполнения группового анализа (с учетом пространственной скоррелированности данных наблюдений) следующий:

- по каждому водосбору определяют параметры распределения гидрологических характеристик, используемые для совместного анализа и необходимые для вычисления стандартных ошибок параметра А по формулам (5.26), (5.28);

- по каждой паре водосборов оценивают коэффициенты межрядной корреляции R_ij (x);

- по выборке величин A_i оценивают среднее значение параметра

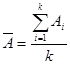                                                          (5.16)

и полную дисперсию ε²_полг по формуле (5.11);

- определяют значения коэффициентов корреляции R_ij (A) между оценками параметра А по теоретическим зависимостям (приложение Б, таблица Б.2);

- определяют стандартное отклонение ε_нез (А) оценок параметра А по выборкам объема п, характеризующее рассеяние оценок для случая независимых выборок и определяемое по формулам (5.26), (5.28) или по результатам статистических испытаний [4];

- стандартное отклонение параметра ε_нез (А), характеризующее независимые выборки, корректируют на величину, учитывающую влияние корреляции между объединяемыми объектами:

ε_случ (А) = ε_нез (А) ,                                     (5.17)

среднее значение коэффициента корреляции между оценками параметра А по всем k водосборам. Найденное значение случайной составляющей используют для вычисления географической составляющей по формуле (5.10);

- если выполняется условие (5.13), то по формулам (5.14) и (5.15) рассчитывают погрешность результата объединенного расчета, средневзвешенную по точности оценку и ее стандартную ошибку.

5.11 На начальных стадиях проектирования допускается определение параметров биномиального распределения графоаналитическим методом по формулам:

S = (Q₅ + Q₉₅ - 2Q₅₀) / (Q₅ - Q₉₅);                                  (5.18)

σ = (Q₅ - Q₉₅) / (Ф₅ - Ф₉₅);                                        (5.19)

 = Q₅₀ - Ф₅₀ σ,                                                      (5.20)

где Q₅, Q₅₀, Q₉₅ - значения расходов воды вероятности превышения соответственно 5 %, 50 %, 95 %, установленные по сглаженной эмпирической кривой распределения;

Ф₅, Ф₅₀, Ф₉₅ - нормированные ординаты биномиальной кривой распределения, соответствующие вычисленному значению коэффициента скошенности S. Значение коэффициента асимметрии C_s определяют по функциональной зависимости от коэффициента S [5].

5.12 В случае неоднородности исходных данных гидрометрических наблюдений, когда рассматриваемый ряд состоит из неоднородных элементов гидрологического режима, эмпирические и аналитические кривые распределения устанавливают отдельно для каждой однородной совокупности.

Общую кривую распределения вероятностей превышения рассчитывают на основе кривых, установленных по однородным элементам одним из двух способов:

а) при наличии в каждом году наблюдений за всеми однородными элементами водного режима реки (n₁, = n₂ = n₃ = n) ежегодную вероятность превышения Р_% рассматриваемой гидрологической характеристики при любом ее значении определяют по формуле

Р = [1 - (1 - Р₁) (1 - Р₂)(1 - Р₃)] 100,                             (5.21)

где Р₁, Р₂, Р₃ - ежегодные вероятности превышения однородных элементов.

Для двух однородных гидрологических характеристик формула (5.21) принимает вид:

P = (Р₁ + Р₂ - Р₁ Р₂) 100;                                           (5.22)

б) если в каждом году имеется лишь одно значение элемента рассматриваемой гидрологической характеристики, ежегодные вероятности превышения при любом ее значении определяют по формуле

,                                               (5.23)

где n₁, n₂, n₃ - число членов однородных элементов. Для двух генетически однородных элементов формула (5.23) принимает вид:

.                                                      (5.24)

При наличии в ряду наблюдений нулевых значений рассматриваемой гидрологической характеристики (например, минимальные расходы воды) ежегодные вероятности превышения определяют по формуле

.                                                        (5.25)

Вероятности превышения Р₁, Р₂, Р₃ в формулах (5.21) и (5.22) выражают в долях единицы, а в формулах (5.23) - (5.25) - в процентах.

Параметры кривых распределения однородных элементов устанавливают согласно требованиям 5.5 - 5.9.

5.13 Для наибольшего или наименьшего члена ряда наблюдений следует указывать доверительные интервалы эмпирической ежегодной вероятности превышения (приложение Б, таблица Б.3).

Если точки эмпирической кривой распределения значительно отклоняются от аналитической кривой, рекомендуется на клетчатке вероятностей для этих точек также указывать доверительные границы и оценивать их однородность в соответствии с 4.6.

5.14 При объединении данных наблюдений по группе станций, а также при оценке достаточной продолжительности рядов наблюдений рассчитывают случайные средние квадратические погрешности выборочных параметров и квантилей распределения.

Случайные средние квадратические погрешности выборочных средних определяют по приближенной зависимости

,                                              (5.26)

которую применяют при коэффициенте автокорреляции между смежными членами ряда r, меньшем 0,5. При больших коэффициентах автокорреляции используют формулу

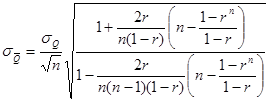.                                (5.27)

Случайные средние квадратические ошибки коэффициентов вариации при C_s = 2Cv определяют по зависимости

                              (5.28)

Случайные погрешности других параметров распределения, квантилей и коэффициентов автокорреляции между стоком смежных лет, рассчитанные методом моментов, следует определять по специальным таблицам, полученным методом статистических испытаний [4].

5.15 При наличии достоверных сведений о случайных относительных средних квадратических погрешностях исходных данных гидрометрических наблюдений оценки коэффициентов вариации и асимметрии уточняют по формулам:

C_v = ;                                          (5.29)

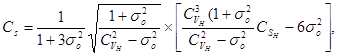                (5.30)

где ,  - соответственно коэффициенты вариации и асимметрии, рассчитанные по наблюденным значениям;

σ_о - случайная относительная (в долях единицы) средняя квадратическая погрешность исходных данных гидрометрических наблюдений.

5.16 Параметры кривых распределения гидрологических характеристик при наличии обоснованных сведений о выдающихся значениях речного стока определяют следующим образом.

При учете одного выдающегося значения гидрологической характеристики, не входящего в непрерывный n-летний ряд данных гидрометрических наблюдении:

а) методом приближенного наибольшего правдоподобия в зависимости от статистик λ₂, и λ₃, определяемых по формулам:

;                                  (5.31)

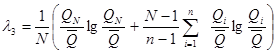;                         (5.32)

б) методом моментов - по формулам:

;                                  (5.33)

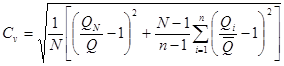.                       (5.34)

При учете одного выдающегося значения гидрологической характеристики, входящего в n-летний ряд данных гидрометрических наблюдений:

а) методом приближенного наибольшего правдоподобия в зависимости от статистик λ₂, и λ₃, определяемых по формулам:

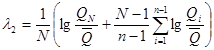;                                 (5.35)

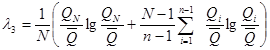;                           (5.36)

б) методом моментов - по формулам:

;                                     (5.37)

.                      (5.38)

В формулах (5.31) - (5.38):

 - среднеарифметическое значение, рассчитанное с учетом выдающегося значения расхода воды;

n - число лет непрерывных наблюдений;

N - число лет, в течение которых выдающееся значение гидрологической характеристики не было превышено.

Использование формул (5.31) - (5.38) допускается лишь в том случае, когда исторические сведения о выдающемся гидрологическом значении и числе лет его непревышения достаточно обоснованы. Произвольное задание Q_N недопустимо.

5.17 Боковую приточность между смежными створами определяют одним из следующих способов:

- суммированием расходов воды притоков с учетом времени добегания, впадающих на участке между двумя створами:

- по разности средних расходов воды в нижнем и верхнем створах участка реки;

- методом руслового водного баланса;

- по модулю стока, определенному по карте для частной площади.

Обработку рядов боковой приточности осуществляют в соответствии с настоящим разделом.

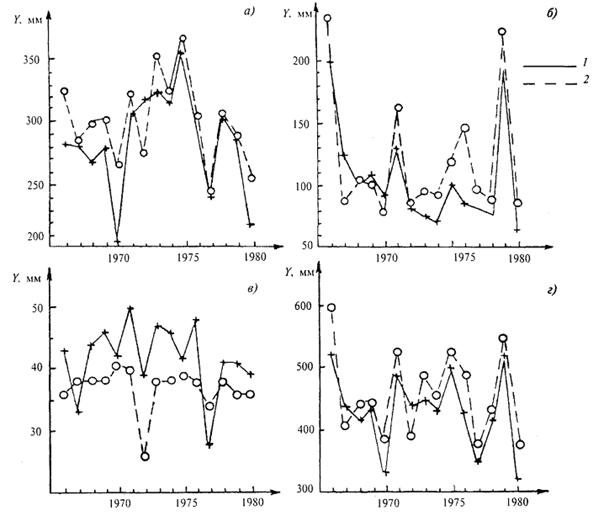
Годовой сток воды и его внутригодовое распределение

5.18 При определении расчетных гидрологических характеристик годового стока воды рек и его внутригодового распределения необходимо выполнять требования, изложенные в 4.3 - 4.15 и 5.1 - 5.16.

5.19 Определение расчетного календарного внутригодового распределения стока при длительности рядов наблюдений n, равной 15 годам и более, производят следующими методами:

- компоновки;

- реального года;

- среднего распределения стока за годы характерной градации водности.

5.20 Расчеты внутригодового распределения стока рек производят по водохозяйственным годам (ВГ), начинающимся с первого месяца многоводного сезона. В отдельных случаях возможно выполнение расчетов внутригодового распределения стока для гидрологических лет, начинающихся с первого месяца периода накопления влаги, или для обычных календарных лет. При расчетах внутригодового распределения стока целесообразно переводить расходы в объемы стока в км³ или в тыс. м³, так как при этом учитывают различие в числе дней не високосных и високосных лет и в числе секунд в разные месяцы года.

В зависимости от типа водного режима реки и преобладающего вида использования стока реки водохозяйственный год делят на два различающихся по длительности периода: лимитирующий (ЛП) и нелимитирующий (НП). а лимитирующий период соответственно на два сезона: лимитирующий (ЛС) и нелимитирующий (НС). Границы сезонов назначают едиными для всех лет с округлением до месяца.

5.21 Расчетное внутригодовое распределение месячного (а в отдельных случаях и декадного) стока определяют для водохозяйственного года расчетной вероятности превышения Р_расч, соответствующей заданной проектной обеспеченности гарантированной отдачи. Длительность п многолетнего периода, необходимая для определения расчетного календарного внутригодового распределения стока, должна удовлетворять требованиям пункта 5.1. В зависимости от достаточной длительности наблюдений п, определенной по указанному критерию точности, выделяют следующие группы лет: по градациям вероятностей превышения стока реки за водохозяйственный год, а в методах компоновки и реального года также и за отдельные расчетные сезоны.

При периоде наблюдений n от 15 до 30 лет выделяют три группы лет: многоводные годы (Р < 33,3 %), средние по водности годы (33,3 % ≤ Р ≤ 66,7 %) и маловодные годы (Р > 66,7 %). При продолжительности наблюдений более 30 лет выделяют пять групп: очень многоводные годы (Р < 16,7 %), многоводные годы (16,7 % ≤ Р < 33,3 %), средние по водности годы (33,3 % ≤ Р < 66,7 %), маловодные годы (66,7 % < Р ≤ 83,3 %) и очень маловодные годы (Р > 83,3 %).

Во всех методах расчета по значениям стока за отдельные водохозяйственные годы (а в методах компоновки и реального года и за расчетные внутригодовые интервалы времени: лимитирующий период, лимитирующий сезон, нелимитирующий сезон, лимитирующий месяц и др.) определяют расчетные квантили. Стандартными квантилями кривых распределения вероятностей стока являются следующие: для многоводных лет, периодов, сезонов и месяцев - 1 %, 3 %, 5 %, 10 % и 25 %; для маловодных лет, периодов, сезонов и месяцев - 75 %, 90 %, 95 %, 97 % и 99 %, для средних по водности лет - 50 %.

5.22 При использовании метода компоновки распределение стока по периодам и сезонам года определяют следующим образом. Расчетные значения стока за водохозяйственный год, лимитирующий период, лимитирующий сезон и лимитирующий месяц определяют по соответствующим аналитическим кривым распределения стока с использованием принципа равенства расчетных вероятностей превышения стока Р_расч за водохозяйственный год Р_вг, лимитирующий период Р_лп, лимитирующий сезон Р_лс и лимитирующий месяц Р_лм. Сток за нелимитирующий период определяют по разности расчетных значений объемов стока за водохозяйственный год и лимитирующий период, сток за нелимитирующий сезон - по разности расчетных объемов стока за лимитирующий период и лимитирующий сезон, а суммарный объем стока всех нелимитирующих месяцев внутри нелимитирующего сезона - по разности расчетных объемов стока за лимитирующий сезон и лимитирующий месяц.

Расчетные значения месячного стока внутри лимитирующего сезона и нелимитирующего сезона определяют с таким расчетом, чтобы получить для этих сезонов наиболее неравномерные распределения стока. С этой целью внутри каждого из этих сезонов, входящих в соответствующую группу водности, месячные объемы стока располагают в убывающем порядке с указанием календарных месяцев, к которым они относятся. Для составного периода (например, для лимитирующего периода), включающего в себя два сезона (лимитирующий сезон и нелимитирующий сезон), месячные объемы стока располагают в порядке убывания отдельно для каждого из составляющих их сезонов (лимитирующий сезон и нелимитирующий сезон). Каждому ранжированному месячному значению каждого из т лет, входящих в рассматриваемую группу водности, присваивают свой порядковый номер. Для всех т лет данной группы водности производят суммирование месячных объемов стока, имеющих одинаковые порядковые номера в полученных ранжированных их внутрисезонных рядах. Путем сложения этих сумм для всех k месяцев, входящих в рассматриваемый сезон, находят их сумму за сезон. Делением сумм стока месяцев, имеющих одинаковые порядковые номера, на их общую сумму за сезон определяют относительное внутрисезонное распределение стока (по месяцам внутри сезона в долях от единицы или в процентах от суммарного объема стока). Полученным средним за т лет месячным долям (или %) вместо присвоенных ранее порядковых номеров присваивают названия того календарного месяца, который встречался наиболее часто при сложении указанных т значений месячного стока одинакового номера из всех лет рассматриваемой градации водности. Таким же или упрощенным способом (без ранжирования и перестановок месячных значений стока, то есть методом расчета средних месячных значений за годы данной градации водности) находят расчетные относительные месячные значения стока внутри нелимитирующего периода.

Расчетные месячные значения стока определяют как произведения их относительных значений (долей от сезонного) на расчетное значение стока соответствующего сезона заданной вероятности превышения. Эти расчеты производят по сезонам для всех месяцев ВГ. Относительное внутригодовое распределение месячного стока в долях (или процентах) от объема стока за водохозяйственный год вычисляют делением расчетных месячных объемов стока на расчетное годовое его значение заданной вероятности превышения.

Примеры расчета внутригодового распределения стока методом компоновки приведены в приложении А и работе [5].

5.23 Определение внутригодового распределения стока методом реального года основано на выборе расчетного водохозяйственного года из числа фактических с использованием принципа наибольшей близости вероятностей превышения стока за водохозяйственный год, лимитирующий период, лимитирующий сезон и лимитирующий месяц к расчетной вероятности превышения. Этот выбор производят из числа j-х лет (от j = 1 до j = т; т - число лет с годовым стоком заданной градации водности) расчетной группы водности с использованием следующего условия:

DP_j = (P_вг - P_расч)² _j + (Р_лп - Р_расч)² _j.+ (Р_лс - Р_расч)² _j + (Р_лм - Р_расч)² _j,                 (5.39)

где                          DP_j - суммарное отклонение, которое определяют для каждого из т j-х исследуемых водохозяйственных лет, вошедших в расчетную группу лет заданной градации водности;

P_расч - расчетная вероятность превышения, принимаемая одинаковой для всех расчетных интервалов времени:

P_вг, Р_лп, Р_лс, Р_лм -        значения вероятностей превышения стока за выбранный водохозяйственный год и его лимитирующий период, лимитирующий сезон и лимитирующий месяц в расчетном створе реки, определяемые по кривой вероятностей превышения соответствующего стокового ряда согласно 5.1 - 5.16.

В качестве расчетного гола принимают тот водохозяйственный год, для которого по формуле (5.39) получено наименьшее значение DP_j. Этот водохозяйственный год принимают в качестве модели относительного внутригодового распределения стока (в долях годового объема стока).

Расчетное распределение стока в этом методе вычисляют путем умножения месячных долей стока на годовой объем стока расчетной вероятности превышения, определяемый по аналитической кривой обеспеченности.

5.24 Метод средних распределений стока за водохозяйственный год заданной градации водности основан на расчете средних относительных распределений месячных объемов стока от годовой их суммы путем осреднения относительных значений стока каждого i-го месяца за все годы, входящие в ту или иную градацию водности. Эти распределения являются типовыми для каждой отдельной группы характерных по водности лет. Расчетное распределение месячного стока вычисляют путем умножения месячных долей стока интересующей градации водности на объем стока за водохозяйственный год заданной вероятности превышения. Последний определяют по аналитической кривой обеспеченности.

Для районов, в которых расчетное распределение стока по сезонам и месяцам практически не зависит от водности года, расчеты рассматриваемым методом сводятся к установлению среднего по всем годам распределения стока по месяцам (декадам) в процентах от годового стока.

5.25 Определение расчетного внутригодового распределения суточного речного стока воды внутри года или характерного его периода, независимо от хронологического хода стока, производят путем построения кривых продолжительности суточных расходов воды. Могут использоваться следующие виды кривых:

а) средняя многолетняя годовая кривая продолжительности суточных расходов воды, дающая характеристику среднего многолетнего типового распределения суточных расходов воды;

б) средняя многолетняя кривая продолжительности суточных расходов воды за тот или иной расчетный период года (навигационный, лесосплавной, вегетационный и т.д.).

Выбор кривой определяют характером решаемой практической задачи. Кривые продолжительности суточных расходов воды строят следующим образом:

а) среднюю многолетнюю годовую кривую продолжительности суточных расходов воды определяют путем осреднения ординат ежегодных кривых среднесуточных расходов воды 30-, 90-, 180-, 270- и 355- суточной продолжительности (или соответствующих относительных продолжительностей стояния, равных 8 %, 25 %, 50 %, 75 % и 97 % обшей длительности года) и абсолютных (срочных) значений максимального и минимального расходов воды за конкретные годы наблюдений. Аналогичным образом строят среднюю многолетнюю кривую продолжительности стояния среднесуточных расходов воды за тот или иной расчетный внутригодовой период. Ее ординаты могут выражаться в долях среднемноголетнего расхода воды за рассматриваемый период (вегетационный, навигационный и т.д.), а абсциссы - в долях его длительности;

б) ежегодную кривую продолжительности суточных расходов воды строят на основе расположенных в убывающем порядке суточных расходов воды конкретного года. Этим ранжированным значениям присваивают порядковые номера с 1-го по 365-й или 366-й. При этом в качестве расходов воды продолжительностью стояния 1 сут и 365 (или 366) сут используют данные соответственно о максимальном и минимальном срочном (а не среднесуточном) расходах воды.

Кривую продолжительности суточных расходов воды для расчетной части конкретного года (вегетационного, навигационного, лесосплавного периода и т.д.) строят аналогичным образом по данным о расположенных в убывающем порядке среднесуточных расходах воды и их порядковых номерах. Эти порядковые номера могут быть заменены их относительными характеристиками, выраженными в долях или в процентах общего числа в расчетном периоде. Выбор указанных расчетных внутригодовых периодов (вегетационный и т.д.) производят с учетом целей проектирования и особенностей изучаемого объекта.

Максимальный сток воды весеннего половодья и дождевых паводков

5.26 Расчетные характеристики максимального стока воды рек весеннего половодья и дождевых паводков следует определять согласно требованиям 5.1 - 5.16.

5.27 Для рек с продолжительностью стояния максимальных расходов воды весеннего половодья и дождевых паводков, равной суткам и более, расчет производят по среднесуточным значениям, менее суток - по срочным расходам воды.

При прохождении максимального расхода воды между сроками наблюдений его значение определяют на основе установления соотношения между мгновенными и среднесуточными его значениями по данным измерений других лет с наибольшими расходами воды или по данным рек-аналогов.

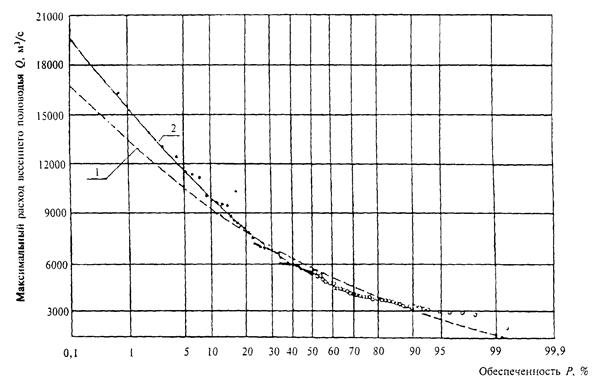
5.28 При невозможности разделения максимальных годовых расходов воды на максимумы дождевых и талых вод допускается построение кривых распределения ежегодных вероятностей превышения максимальных расходов воды независимо от их происхождения.

5.29 При неоднородности максимальных расходов воды используют составные кривые распределения (см. 5.12). Допускается также применение усеченных распределений, которые разработаны для частного случая, - разделение на две однородные совокупности по медианному значению. Сущность усечения кривой распределения состоит в том, что рассматривают только верхнюю часть кривой распределения максимальных расходов воды.

Основное расчетное выражение для оценки среднего х₀ по методу приближенно наибольшего правдоподобия имеет следующий вид:

х₀ =  φ (С_v),                                                     (5.40)

где 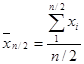 - среднеарифметическое значение верхней половины ранжированного ряда   (5.41);

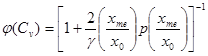.                                     (5.42)

Здесь значения функции φ (С_v) приведены в приложении Б, таблица Б.4;

γ = 1/C_v².

Оценку максимального правдоподобия коэффициента изменчивости C_v определяют через статистику  с помощью табулированной зависимости (приложение Б, таблица Б.5), где - статистика, вычисляемая по верхней половине ранжированного ряда (аналогично полному распределению):

.                                                  (5.43)

Порядок расчетов при использовании усеченного гамма-распределения следующий:

- исходный ряд располагается по убыванию;

- по выражению (5.41) находят среднее значение верхней половины ранжированного ряда x_n/2

- по выражению (5.43) вычисляют статистику ;

- по полученному значению  в соответствии с приложением Б, таблица Б.5 находят значение коэффициента C_v;

- по выражению (5.40) находят оценку x₀;

- отношение C_s / C_v определяют в соответствии с 5.7.

5.30 Расчетные максимальные расходы воды зарегулированных рек определяют исходя из расчетного максимального расхода воды рек в естественном состоянии с учетом изменения его в результате хозяйственной деятельности в бассейне реки и трансформации проектируемыми или действующими водохранилищами.

На реках с каскадным расположением гидроузлов расчетные максимальные расходы воды следует определять с учетом влияния вышележащих гидроузлов на приток к нижерасположенным и боковой приточности между гидроузлами.

5.31 К значениям расчетных максимальных расходов воды Q_p% вероятностью превышения 0,01 % следует прибавлять гарантийную поправку D Q_p%, определяемую по формуле

D Q_0,01% = α E_0,01% Q_0,01% / √N,                                      (5.44)

где α - коэффициент, характеризующий гидрологическую изученность рек; принимают равным 1,0 для гидрологически изученных рек, когда выполняются условия 5.1, во всех остальных случаях - 1,5;

N - число лет наблюдений с учетом приведения к многолетнему периоду;

E_0,01% - величина, характеризующая случайную среднюю квадратическую ошибку расчетного расхода воды ежегодной вероятности превышения Р = 0,01 %, определяемая по приложению Б, таблица Б.6.

Поправка D Q_0,01% должна приниматься равной не более чем 20 % значения максимального расхода воды Q_0,01%. Принимаемый расчетный расход с учетом гарантийной поправки не должен быть меньше, чем наибольший наблюденный расход.

Расчетные гидрографы стока воды рек весеннего половодья и дождевых паводков

5.32 Расчетные гидрографы стока воды весеннего половодья и дождевых паводков необходимо рассчитывать при проектировании водохранилищ, отводе вод от сооружений в период их строительства, расчете затопления пойм и лиманов, пропуске высоких вод через дорожные и другие искусственные сооружения.

5.33 Форму расчетных гидрографов принимают по моделям наблюденных высоких весенних половодий или дождевых паводков с наиболее неблагоприятной их формой, для которых основные элементы гидрографов и их соотношения должны быть близки к расчетным.

Для расчета отверстий дорожных и других искусственных сооружений допускается принимать схематизацию гидрографов стока воды рек весеннего половодья и дождевых паводков по геометрическим формам.

5.34 Гидрографы речного стока следует рассчитывать по равнообеспеченным значениям максимального расхода воды, объема стока воды основной волны и объема всего весеннего половодья (дождевого паводка) расчетной вероятности превышения.

5.35 Расчетные гидрографы стока воды рек определяют:

а) для весеннего половодья - по среднесуточным расходам воды; гидрографы внутрисуточного хода стока воды рассчитывают, если значение максимального мгновенного расхода воды в 1,5 раза больше соответствующего ему среднесуточного расхода воды;

б) для дождевых паводков - по мгновенным расходам воды.

5.36 Выбор метода построения расчетного гидрографа и натурной модели зависит от задач, для решения которых он используется:

а) при проектировании гидротехнических объектов с относительно небольшой регулирующей емкостью водохранилища используют модель одновершинного гидрографа с наибольшим максимальным расходом воды;

б) при больших регулирующих емкостях, сопоставимых с полным объемом половодий (паводков), используют модель с наибольшим объемом половодья (паводка) и наибольшей сосредоточенностью стока в центральной части гидрографа;

в) для рек с многовершинными гидрографами следует выбирать такую модель из числа многоводных лет, в которой наибольшая волна после короткого промежутка следует за меньшей волной;

г) при каскаде водохранилищ строят расчетный гидрограф притока к верхнему гидроузлу и гидрографы боковой приточности между гидроузлами. При этом выбирают модель, общую для всего каскада;

д) для развитых систем инженерной защиты, включающих наряду с водохранилищами обвалование, регулирование русла реки и другие мероприятия, строят расчетные гидрографы во входном створе на основной реке и гидрографы боковой приточности на всем протяжении инженерной защиты по общей для всей системы модели.

5.37 Основные элементы расчетного гидрографа стока воды рек: максимальный расход воды, объем весеннего половодья (дождевого паводка), объем основной волны расчетной вероятности превышения, а также боковую приточность определяют по данным гидрометрических наблюдений согласно требованиям 5.1 - 5.17.

5.38 Общую продолжительность весеннего половодья для больших и средних рек, включая дождевые паводки на спаде половодья, принимают одинаковой для всех лет и створов как на основной реке, так и на притоках при условии включения в ее пределы продолжительности всех половодий.

Назначение периода общей продолжительности весеннего половодья допускается принимать переменным для разных лет, но одинаковым по длине реки.

Продолжительность основной волны, включающей максимальную ординату, следует принимать постоянной в подвижных границах для всех лет исходя из условия наибольшего объема стока (притока) за принятый период.

5.39 Расчет гидрографов весеннего половодья (дождевого паводка) выполняют следующими методами:

а) переходом от гидрографа-модели к расчетному гидрографу путем умножения ординат гидрографа-модели на коэффициенты, определяемые по формулам:

k₁ = Q_p / Q_m;                                                           (5.45)

k₂ = (V_p - 86 400 Q_p) / (V_m - 86 400 Q_m);                                   (5.46)

k₃ = (V′_p - V_p) / (V′_m - V_т),                                                  (5.47)

где Q_m, Q_p - максимальный среднесуточный расход воды весеннего половодья или мгновенный для дождевого паводка соответственно для гидрографа-модели и расчетного гидрографа, м³/с;

V_m и V_p -      объем основной волны соответственно для гидрографа-модели и расчетного гидрографа, м³;

V′_m и V′_p - полный объем весеннего половодья (дождевого паводка) соответственно для гидрографа-модели и расчетного гидрографа, м³;

б) переходом от гидрографа-модели к расчетному гидрографу с применением коэффициента k₁, определяемого по формуле (5.45), и коэффициента k_t определяемого по формуле

k_t = (q_т / h_т) (h_p / q_p),                                                        (5.48)

где q_m, q_p - модуль максимального среднесуточного расхода воды соответственно для гидрографа-модели и расчетного гидрографа, м³/(с × км²);

h_m, h_p - слой стока весеннего половодья (дождевого паводка) соответственно для гидрографа-модели и расчетного гидрографа, мм. Переход от гидрографа-модели к расчетному гидрографу по методу, указанному в пункте

б), возможен только при соблюдении условий:

γ_p = γ_т; k_s,p = k_s,m,

где γ_т, γ_p - коэффициент полноты для гидрографа-модели и расчетного гидрографа γ соответственно, определяемый по формуле

γ = q t / 0,0116 h;                                                       (5.49)

k_s,m, k_s,p - коэффициент несимметричности соответственно для гидрографа-модели и расчетного гидрографа, определяемый по формуле

k_s = h_n / h,                                                            (5.50)

q - модуль максимального среднего суточного расхода воды;

h - слой стока весеннего половодья (дождевого паводка), мм;

t - продолжительность весеннего половодья (дождевого стока), сут;

h_п - слой стока за период подъема весеннего половодья (дождевого паводка), мм.

Координаты расчетного гидрографа определяют в зависимости от коэффициентов k₁ и k_t по формулам:

Q_i = Q_i,m k₁;                                                          (5.51)

t_i = t_i,m k_t,                                                             (5.52)

где Q_i,m, Q_i - расходы воды в i-ю единицу расчетного времени соответственно для гидрографа-модели и расчетного гидрографа, м³;

t_i,m и t_t - ордината времени соответственно для гидрографа-модели и расчетного гидрографа.

За начало отсчета времени t_i,m принимают начало подъема весеннего половодья (дождевого паводка).

5.40 Определение гидрографов внутрисуточного хода стока следует производить по методу, указанному в 5.37; обозначения в формулах (5.48) - (5.50) принимают следующие:

q_m, q_р - модуль максимального мгновенного расхода воды соответственно для гидрографа-модели и расчетного гидрографа, м³/(с × км²);

h_m, h_р - максимальный суточный слой стока весеннего половодья соответственно для гидрографа-модели и расчетного гидрографа, мм;

h_n - слой стока за период подъема максимальной суточной волны весеннего половодья, мм;

t - продолжительность максимальной суточной волны весеннего половодья, сут и менее.

Минимальный сток воды рек

5.41 Определение расчетных минимальных расходов воды при наличии данных гидрометеорологических наблюдений достаточной продолжительности производят по кривым обеспеченности, аппроксимируемым распределением Пирсона III типа или трехпараметрическим распределением Крицкого-Менкеля (см. 5.3). При неоднородности ряда наблюдений применяют усеченные (см. 5.29) или составные (см. 5.12) кривые распределения ежегодных вероятностей превышения.

При значительных расхождениях аналитической кривой и фактических данных в нижней части (резкое отклонение одной - двух последних точек, обусловленное физическими причинами) применяют эмпирические кривые обеспеченности. Такие кривые имеют достаточно плавный вид в основной части и резкий изгиб в нижней. Обычно он приходится на зону обеспеченности в 90 % - 97 %.

При наличии нулевых расходов воды в ряду наблюдений расчеты производят в соответствии с 5.12. а в случае несоответствия полученной аналитической кривой наблюденным значениям - по эмпирической кривой вероятностей превышения.

5.42 Для расчетов используют минимальные среднесуточные, среднемесячные или 30-суточные (не календарные) расходы воды, наблюдавшиеся в зимний и (или) летне-осенний сезоны.

Среднемесячные минимальные расходы используют, если они не превышают 30-суточные более чем на 10 %, в противном случае применяют средние расходы воды за 30 непрерывных суток с наименьшим стоком в рассматриваемом сезоне. При частых паводках и коротких межпаводочных периодах 30-суточный период допускается сокращать до 24 сут, чтобы максимально избежать включения паводковых вод в период минимального стока.

Минимальный суточный расход воды обычно совпадает с 30-суточным (среднемесячным) периодом минимального стока. Однако на реках с частыми паводками их сроки могут значительно различаться.

5.43 Минимальный среднемесячный (календарный) расход воды рекомендуется использовать в расчетах, когда рассматривают сток за зимний сезон для рек, находящихся восточнее границы: Ладожское озеро - верховья рек Днепра и Оки - среднее течение Дона - устье Волги, или сток за летне-осенний сезон для рек, расположенных южнее границы: Санкт-Петербург - Пермь - Магнитогорск - Тюмень - Новосибирск - Барнаул, исключая реки Северного Кавказа. Для остальных районов в расчетах следует использовать минимальные 30-суточные (не календарные) расходы воды.

Наивысшие уровни воды рек и озер

5.44 Расчетные наивысшие уровни воды рек в створе поста определяют по аналитической кривой распределения вероятностей превышения ежегодных наивысших мгновенных или срочных уровней воды за период многолетних наблюдений. При неоднородности наивысших уровней воды допускается использование эмпирических кривых вероятностей распределения.

Для рек, наивысшие уровни которых наблюдаются в разные фазы водного и ледового режимов, производят обработку однородных рядов уровней, соответствующих снеговому половодью, дождевым паводкам и паводкам ледниковых вод при свободном состоянии русла, а также максимальных уровней при зажорах и заторах, осеннем и весеннем ледоходах. Вероятность превышения наивысших годовых уровней воды следует определять в соответствии с 5.2.

При определении вероятности превышения высшего исторического уровня, установленного по данным опроса жителей или архивным источникам, принимают число лет, в течение которых он не был превышен.

Определение расчетных наивысших уровней воды озер следует производить по кривым распределения вероятностей превышения уровней теми же приемами, что и для рек. В засушливой зоне, учитывая наличие длительных квазициклических колебаний уровня воды озер, необходимо выполнять специальные водобалансовые исследования с использованием данных по морфометрии озерной котловины, а также архивных и других материалов.

5.45 Расчетные уровни вверх или вниз по течению реки в случае свободного состояния русла переносят по одному из трех способов:

а) по кривым расходов воды Q = f (H);

б) по кривым связи соответственных уровней воды;

в) по продольному профилю водной поверхности с учетом ее уклона при высоком уровне воды.

Перенос с помощью кривых Q = f (H) осуществляют на бесприточных и малоприточных участках рек значительной протяженности, если для опорного створа имеется надежная кривая расходов воды и данные многолетних наблюдений за стоком, позволяющие определить максимальный расход воды расчетной вероятности превышения. В этом случае на участке проектирования открывают один или несколько временных гидрологических постов и производят параллельные с опорным постом наблюдения за уровнями. Учитывая, что соответственным уровням на участке отвечает один и тот же расход воды, строят в единой системе отметок кривые Q = f (H) для каждого из створов, которые экстраполируют до расчетного максимума расхода. По этим кривым определяют соответствующие ему значения расчетных наивысших уровней в створах временных постов и по ним строят продольный профиль водной поверхности.

Способ переноса расчетного наивысшего уровня воды по связи соответственных уровней требует соблюдения тех же условий, что и в рассмотренном выше способе. Отличие его заключается в том, что экстраполируют не кривые Q = f (H), а кривые связи соответствующих уровней. Характер этих кривых зависит от гидравлических и морфометрических особенностей реки в створах постов и между ними. Поэтому данный способ может быть применен, если параллельными наблюдениями освещено не менее 80 % многолетней амплитуды колебания уровня воды в опорном створе и наличие надежной связи в верхней части кривой выявилось достаточно отчетливо. Кривые связи строят по ежегодным значениям максимальных уровней воды, характерным переломным точкам графиков колебания уровня или ежедневным значениям уровней с учетом времени добегания воды между постами. Связь уровней считают удовлетворительной, если коэффициент корреляции r ≥ 0,8.

Перенос уровней воды по продольному профилю водной поверхности производят в пределах небольших по длине речных участков (1 - 3 км) с учетом зависимости уклона от уровня в условиях установившегося потока.

В устьевых и приустьевых участках рек в отдельные фазы их режима следует учитывать возможность подпора воды со стороны водоприемника. Наивысшие уровни в пределах зон подпора переносят по кривой подпора.

Если наивысшие уровни приходятся на период с ледовыми явлениями, то их перенос осуществляют по графикам связи уровней или кривым Q = f (H) для открытого (свободного) русла и расходам воды, вычисленным по формуле

q′_р% = Q_p% / k_Q,                                                        (5.53)

где Q_p% - расход воды в опорном створе;

k_Q - зимний коэффициент, учитывающий изменения гидравлических характеристик водного потока в результате ледовых явлений (ледохода, ледостава, скопления льда).

Если участок проектирования по условиям ледового режима более или менее однороден, то зимний коэффициент k_Q, характеризующий то или иное явление, может быть принят одинаковым для всех створов. При неоднородном ледовом режиме учитывают различие значений k_Q от створа к створу и значения этого коэффициента определяют путем специальных полевых исследований и расчетов.

Перенос наивысших уровней воды озер от опорного водомерного поста к другим постам производят по графикам связи уровней воды или непосредственно по взаимно увязанным отметкам с учетом волнения и ветрового нагона.

5.46 Продолжительность стояния высоких уровней устанавливают по хронологическим графикам уровней воды в период половодий и паводков, наиболее неблагоприятных по условиям затопления и подтопления застраиваемой территории. Вероятностные значения продолжительности стояния Т_р% определяют по кривой обеспеченности ежегодной длительности превышения той или иной отметки затопления территории (например, отметки выхода воды на пойму). С учетом полученного значения Т_р% строят расчетный график хода уровней по модели одного из наблюдавшихся продолжительных половодий или паводков. Пересчет ординат и абсцисс графика производят с помощью переходных коэффициентов К_Н и К_Т:

К_Н = (Н_р% - Н_Н.З) / (Н_М - Н_Н.З)

и К_Т = Т_р% / Т_М,                                                      (5.54)

где Н_р% и Т_р% - максимальный расчетный уровень воды, см, и расчетная продолжительность стояния уровня, сут;

Н_М и Т_М - максимальный уровень воды, см, и продолжительность для модельного графика колебания уровня воды, сут;

Н_Н.З - отметка начала затопления.

6 ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ГИДРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ПРИ НЕДОСТАТОЧНОСТИ ДАННЫХ ГИДРОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ

Общие положения

6.1 При недостаточности данных гидрометрических наблюдений параметры кривых распределения вероятностей гидрологических характеристик, а также основных элементов расчетного гидрографа необходимо приводить к многолетнему периоду с привлечением данных наблюдений пунктов-аналогов.

6.2 Приведение рассматриваемой гидрологической характеристики осуществляют в случаях, когда средняя квадратическая погрешность расчетного значения гидрологической характеристики превышает 10 % для годового и сезонного стоков, 20 % - для максиматьного и минимального стоков. Случайные средние квадратические погрешности определяют согласно 5.14.

6.3 Основные требования при выборе пунктов-аналогов приведены в 4.11. При выборе пункта-аналога основным критерием является наличие синхронности в колебаниях речного стока расчетного створа и створов-аналогов, которые количественно выражают через коэффициент парной или множественной (при одновременном использовании нескольких аналогов) корреляции между стоком в этих пунктах.

При выборе аналогов следует учитывать как возможно большую продолжительность наблюдений в этих пунктах, так и более тесные связи между стоком в приводимом к многолетнему периоду пункте и стоком в пунктах-аналогах.

При выборе пунктов-аналогов необходимо учитывать пространственную связанность рассматриваемой гидрологической характеристики, которую количественно выражают через матрицу парных коэффициентов корреляции или пространственную корреляционную функцию, представляющую собой зависимость коэффициентов парной корреляции стока рек от расстояния между центрами тяжести водосборов.

Матрицы парных коэффициентов корреляции и корреляционные функции определяют в однородном гидрологическом и физико-географическом районе.

6.4 При восстановлении значений стока за отдельные годы и расчете параметров и квантилей распределения необходимо производить статистическую оценку значимости и устойчивости получаемых решений с определением случайных и систематических погрешностей в соответствии с 6.17.

6.5 При приведении допускается использование гидрометрической информации, а также метеорологической и другой информации, период наблюдений за которой превышает период наблюдений за рассматриваемой гидрологической характеристикой.

При привлечении метеорологической и другой информации могут быть использованы региональные зависимости рассматриваемой гидрологической характеристики от факторов, ее определяющих.

6.6 Приведение гидрологических рядов и их параметров распределения к многолетнему периоду, как правило, осуществляют аналитическими методами. Для предварительного приведения допускается использование графических и графоаналитических методов.

6.7 При расчете параметров распределения и значений стока за отдельные годы Q_i с использованием аналитических методов, основанных на регрессионном анализе, должны соблюдаться следующие условия:

п′ ≥ (6 - 10); R ≥ R_кp; R / σ_R ≥ А_кр; k / σ_k ≥ В_кр,                               (6.1)

где п′ - число совместных лет наблюдений в приводимом пункте и пунктах-аналогах (п′ ≥ 6 при одном аналоге, п′ ≥ 10 при двух и более аналогах) или число пунктов-аналогов при восстановлении с привлечением кратковременных наблюдений (п′ ≥ 6);

R - коэффициент парной или множественной корреляции между значениями стока исследуемой реки и значениями стока в пунктах-аналогах;

k - коэффициент уравнения регрессии;

σ_k - средняя квадратическая погрешность коэффициента регрессии;

R_кp - критическое значение коэффициента парной или множественной корреляции (обычно задается ≥ 0,7);

А_кр, В_кр - критические значения отношений R / σ_R и k / σ_k соответственно (обычно задаются ≥ 2,0).

Если хотя бы один из коэффициентов уравнения регрессии не удовлетворяет условию (6.1), то это уравнение не используют для приведения к многолетнему периоду.

В слабо изученном в гидрологическом отношении районе R_кp, А_кр и В_кр могут быть уменьшены, а в хорошо изученном - увеличены. При увеличении значений R_кp, А_кp и В_кp возрастает точность, но уменьшается объем восстановленных данных.

Методы приведения рядов гидрологических характеристик и их параметров к многолетнему периоду с учетом материалов кратковременных (менее 6 лет) наблюдений

6.8 Методы учета материалов кратковременных полевых гидрометеорологических изысканий предусматривают предварительное приведение к многолетнему периоду погодичных значений, параметров и квантилей распределения речного стока рек исследуемого района согласно 6.15 - 6.23 при п′ ≥ (6 - 10).

6.9 Определение значений стока за каждый год, норм и квантилей распределения речного стока осуществляют по методу отношений, основанному на приблизительном равенстве модульных коэффициентов в пункте с кратковременными наблюдениями и в пунктах-аналогах, по формуле

Q ≈ Q_i (Q_a / Q_ia),                                                     (6.2)

где Q_i и Q_ia - наблюденные значения речного стока соответственно в пункте с кратковременными наблюдениями и в пунктах-аналогах с регулярными наблюдениями;

Q и Q_a        -   в зависимости от требуемых решений могут обозначать восстанавливаемые значения стока за конкретные годы, погодичные значения за пределами гидрометрических наблюдений в пункте проектирования, норму стока или значения стока заданной обеспеченности.

6.10 Метод отношений используют при выполнении условия R ≥ R_кp где R определяют по пространственной корреляционной функции. Пункты-аналоги с регулярными гидрометрическими наблюдениями при расчетах по методу, основанному на равенстве модульных коэффициентов, обычно выбирают по наименьшему расстоянию между центрами тяжести водосборов проектируемого пункта и пунктов-аналогов.

При наличии нескольких пунктов-аналогов расчеты осуществляют последовательно по всем аналогам и результаты осредняют (не более трех аналогов) с учетом случайных средних квадратических погрешностей в соответствии с формулой (4.1).

6.11 Средняя квадратическая погрешность расчета значений стока за каждый год, нормы стока и квантилей распределения определяют по пунктам-аналогам. Для этой цели выбирают два пункта с гидрометрическими наблюдениями в однородном гидрологическом районе проектирования, один из которых условно принимают в качестве исследуемого пункта, а другой - в качестве пункта-аналога. Расчетное значение стока определяют по формуле (6.2) столько раз, сколько имеется наблюдений в створе, принимаемом за исследуемый.

Среднюю квадратическую погрешность погодичного значения или нормы стока, или квантилей распределения по данным одного года наблюдений определяют по формуле

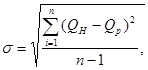                                             (6.3)

где Q_H - наблюденное значение стока за каждый год или норма стока, или квантили распределения;

Q_p - рассчитанное значение стока за каждый год или норма стока, или квантили распределения.

6.12 В соответствии с методикой восстановления значений стока по уравнениям регрессии, когда имеется один год кратковременных наблюдений, строят уравнения между всеми наблюдениями за этот год и последовательно за все остальные годы, в которые имеются наблюдения в пунктах-аналогах, при условии, что количество пунктов должно быть не менее 5 - 6. Уравнения имеют следующий вид:

q_ij = B1_i q_kj + B0_i,                                                   (6.4)

где q_ij - значения стока в j-м пункте в i-и год за пределами кратковременных наблюдений;

q_kj - значения стока в j-м пункте за k-й год, в которым имеются кратковременные наблюдения;

B1_i, B0_i - коэффициенты уравнений регрессий.

6.13 В общем случае, если кратковременные наблюдения проводят в течение нескольких лет, строят зависимости для каждого года кратковременных наблюдений в соответствии с 6.12. При этом результаты восстановления стока за каждый год, полученные по нескольким уравнениям, соответствующим числу лет кратковременных наблюдений, обобщают в соответствии с формулой (4.1).

Предлагаемая схема восстановления погодичных значений стока может применяться не только для приведения к многолетнему периоду наблюдений за речным стоком от одного года до пяти лет, но и для более продолжительных наблюдений.

6.14 Для предварительной оценки коэффициентов вариации и квантилей распределения речного стока может быть использован графический способ: построение кривой обеспеченности рассматриваемой характеристики речного стока на клетчатке вероятностей с фиксированным отношением C_s / C_v, полученным для исследуемого района в соответствии с 5.7. Шкала ординат на клетчатках представлена в виде модульных коэффициентов. Значения модульных коэффициентов определяют по фактическим наблюдениям в проектируемом пункте и норме стока, определенной по методам, рекомендованным в 6.8 - 6.13.

Для определения расчетных значений стока необходимо иметь как минимум два года наблюдений в исследуемом пункте.

По данным пунктов-аналогов рассчитывают эмпирическую обеспеченность значений стока, которые наблюдались в конкретные годы в пункте проектирования. Рассчитанные модульные коэффициенты k_i соответствующей эмпирической обеспеченности наносят на клетчатку вероятностей с выбранным фиксированным значением C_s / C_v Разность между эмпирическими обеспеченностями стока за наблюденные годы должна быть не менее 10 %.

Полученные эмпирические точки аппроксимируют прямой линией, которая продолжается до пересечения со шкалой коэффициентов вариации.

Графический способ рекомендуется и для предварительного определения расчетных значений стока заданной обеспеченности. Для этой цели значения модульных коэффициентов k_i, снятых с кривой распределения, которые рассчитаны по данным двух- или трехлетних наблюдений, умножают на норму стока, определенную с использованием кратковременных наблюдений согласно 6.9.

Методы приведения рядов гидрологических характеристик и их параметров к многолетнему периоду при наличии гидрометрических наблюдений 6 лет и более

6.15 Для расчета параметров распределения и значений стока за отдельные годы используют аналитические методы, основанные на регрессионном анализе с привлечением одного или нескольких пунктов-аналогов на различных временных этапах при соблюдении условий (6.1). Поэтапное использование нескольких аналогов расширяет возможности приведения и делает его более качественным по сравнению с методами, в которых используется дополнительная информация в одном пункте-аналоге. Последовательность приведения к многолетнему периоду состоит в следующем:

- все уравнения, удовлетворяющие условиям (6.1), располагают в порядке убывания коэффициентов корреляции;

- восстанавливают погодичные значения стока приводимого пункта за период совместных наблюдений в пунктах-аналогах по уравнению с наибольшим значением коэффициента корреляции;

- используют уравнения регрессии, коэффициенты корреляции которых меньше предыдущего, но больше всех остальных;

- поэтапное восстановление погодичных значений стока продолжают до тех пор, пока не будут использованы все уравнения регрессии, удовлетворяющие условиям (6.1).

Уравнение множественной линейной регрессии, по которому восстанавливается сток, имеет вид:

q = k₀ + k₁ Q₁ + k₂ Q₂ + ... + k_j Q_j + ... + k_l Q_l,                             (6.5)

где Q - значения стока в приводимом пункте:

Q_j ... Q_l - значения стока в пунктах-аналогах;

k₀ - свободный член;

k_j ... k_l - коэффициенты уравнения регрессии при j = 1,2 ..., l, где l- число пунктов-аналогов.

Коэффициенты и свободный член уравнения (6.5) определяют методом наименьших квадратов (МНК).

6.16 В случае одного пункта-аналога приведение среднего значения к более длительному периоду осуществляют по формуле

                               (6.6)

где ,  - среднеарифметические значения гидрологической характеристики соответственно для исследуемой реки и реки-аналога, вычисленные за период совместных наблюдений;

,  - норма стока за N-летний период соответственно для исследуемой реки и реки-аналога;

, - средние квадратические отклонения гидрологической характеристики за совместный период п лет соответственно для исследуемой реки и реки-аналога.

Относительную среднюю квадратическую погрешность приведенной к многолетнему периоду нормы стока определяют по формуле

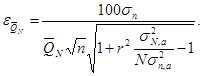                                              (6.7)

Коэффициент вариации C_s,N определяют по формуле

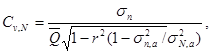                                          (6.8)

где  - среднее квадратическое отклонение гидрологической характеристики реки-аналога за N-летний период, остальные обозначения те же, что и в формуле (6.6).

6.17 Данные, восстановленные по уравнению (6.5), имеют систематически заниженную дисперсию. Исключение систематического уменьшения дисперсии восстановленных данных необходимо осуществлять одним из двух вариантов:

1) введением поправки в погодичные значения стока, полученные по уравнению регрессии:

,                                              (6.9)

где  - погодичные значения гидрологических характеристик, рассчитанные по уравнению регрессии;

 - среднее значение приводимого ряда за совместный с пунктом-аналогом период;

2) с учетом случайной составляющей отклонений наблюденных данных от рассчитанных по уравнению регрессии

                                                  (6.10)

где φ - случайная величина, имеющая нормальный закон распределения с математическим ожиданием, равным нулю, и дисперсией, равной единице; определяют по вероятности Р, которую в свою очередь находят с помощью таблицы равномерно распределенных случайных чисел [4];

σ - среднее квадратическое отклонение исходного ряда наблюдений. Использование этого варианта рекомендуется осуществлять, если число восстановленных значений не менее 30.

Расчет параметров распределения осуществляют по ряду восстановленных значений без поправки (6.9), и он не требует знания параметров ряда-аналога за весь N-летний период наблюдений.

6.18 Норму речного стока, значения стока за каждый год и квантили распределения определяют также по методу, основанному на зависимостях этих значений от стока конкретных лет, при соблюдении условий (6.1), в соответствии с 6.12.

6.19 При восстановлении значений речного стока за отдельные годы по методам, указанным в 6.12 и 6.15, их окончательные значения могут определяться с учетом средних квадратических погрешностей методов по формуле (4.1).

6.20 По восстановленному ряду совместно с наблюденными данными рассчитывают параметры распределения: среднее многолетнее значение, коэффициенты вариации и асимметрии и коэффициент корреляции между стоком смежных лет.

6.21 Расчетные значения коэффициентов асимметрии C_s и автокорреляции r (1) принимают на основании группового анализа отношения C_s / C_v и r (1) по рекам-аналогам в соответствии с 5.7.

6.22 При оценке случайных средних квадратических погрешностей расчетных параметров речного стока необходимо учитывать объем информации, эквивалентной наблюденным данным, который определяют соответственно для нормы  и среднего квадратического отклонения  по формулам:

                                       (6.11)

,                                               (6.12)

где n - число совместных лет наблюдений в приводимом ряду и рядах-аналогах;

N - n - число восстановленных членов ряда по уравнению;

R - коэффициент парной или множественной корреляции.

Так как зависимости между гидрологическими характеристиками не функциональны (R < 1), объем эквивалентно-независимой информации всегда больше п и меньше N, и только при R = 1 N_э = N.

При поэтапном восстановлении значений ряда гидрологических характеристик, т.е. при использовании нескольких уравнений регрессии за разные периоды, общий объем эквивалентно-независимой информации определяют как сумму этой информации за каждый восстановленный период.

6.23 Графический метод приведения к многолетнему периоду допускается применять на начальных стадиях проектирования в основном для определения среднего многолетнего значения (нормы) стока. Графические зависимости могут быть построены при наличии не менее шести соответственных значений речного стока в расчетном створе и створе-аналоге. Зависимости считают удовлетворительными, если коэффициент корреляции между стоком в приводимом пункте и пункте-аналоге не менее 0,7. При прямолинейной зависимости норму стока в приводимом пункте определяют непосредственно по норме стока реки-аналога.

Криволинейные связи значений стока принимают лишь в тех случаях, когда они объясняются не случайным расположением точек, а характером колебания стока в приводимом пункте и пункте-аналоге.

При криволинейной связи по графику для расчетного створа восстанавливают ежегодные значения стока за период наблюдений в пункте-аналоге. По восстановленным значениям определяют расчетные параметры.

6.24 При приведении параметров распределения к многолетнему периоду на начальных стадиях проектирования допускается применять графоаналитический метол. Приведение параметров распределения осуществляют в следующей последовательности:

а) строят график связи между значениями стока приводимого ряда наблюдений и ряда-аналога за совместный период наблюдений;

б) по ряду-аналогу рассчитывают графоаналитическим методом параметры распределения, на основании которых строят аналитическую кривую распределения;

в) с аналитической кривой распределения снимают три квантиля распределения (5 %, 50 %, 95 %). Могут использоваться и схемы с пятью квантилями (1 %, 5 %. 50 %, 95 %, 99 %);

г) по графику равнообеспеченных значений стока определяют квантили 5 %, 50 % и 95 % обеспеченности для короткого ряда наблюдений:

д) на основании приведенных к многолетнему периоду значений 5%, 50 % и 95 % обеспеченности в пункте приведения с помощью графоаналитического метода рассчитывают параметры распределения по формулам (5.18) - (5.20). На их основании строят аналитическую кривую распределения и определяют расчетные значения гидрологических характеристик.

Внутригодовое распределение стока

6.25 Ряды наблюденных значений стока за водохозяйственный год (ВГ), лимитирующий период (ЛП), лимитирующий сезон (ЛС), лимитирующий месяц (ЛМ) и другие месяцы года при недостаточной их длительности приводят к многолетнему периоду методами, изложенными в 6.1 - 6.24 и 7.19 - 7.24. Исходные и приведенные к многолетнему периоду ряды должны проверяться на однородность. Внутригодовые календарные распределения месячного (или декадного) стока в расчетном створе исследуемой реки или реки-аналога определяют методами, изложенными в 5.19 - 5.24.

Расчетные гидрографы стока воды рек весеннего половодья и дождевых паводков

6.26 Для построения расчетных гидрографов боковой приточности должны быть использованы имеющиеся материалы гидрометрических наблюдений по притокам на участках рек или водохранилищ. Если эти материалы освещают режим только наиболее крупных притоков, то сток с остальной части бассейна следует определять по аналогии с гидрологически сходными изученными водосборами.

В зависимости от размеров водохранилища, расположения притоков по его длине и их водности расчетные гидрографы боковой приточности можно строить для всего водохранилища в целом или для его отдельных участков.

6.27 Форму модели расчетного гидрографа стока воды при условии выполнения требований 5.33 принимают согласно 5.39 - 5.40.

6.28 Модель расчетного гидрографа стока воды устанавливают путем осреднения нескольких гидрографов стока воды высоких весенних половодий (дождевых паводков), выраженных в относительных единицах. Координаты натурных гидрографов t′_i и Q′_i из абсолютных значений пересчитывают в относительные (t_i, Q_i) в долях общей продолжительности паводка t_m и максимального расхода Q_m:

t_i = t′_i / t_m;                                                              (6.13)

Q_i = Q′_i /Q_m.                                                            (6.14)

Ординаты совмещают на одном чертеже относительно модальной ординаты. Затем по осредненным значениям ординат строят обобщенный гидрограф, наиболее полно отражающий особенности формы натурных гидрографов. Этот гидрограф и принимают за модель.

Координаты расчетных гидрографов определяют согласно требованиям 5.39 и 5.40.

Минимальный сток воды рек

6.29 В расчетах минимального стока при небольшом числе лет совместных наблюдений (до 6 лет) с рекой-аналогом для более надежного выявления связи в условиях меженных периодов длительностью более двух месяцев рекомендуется использовать значения расходов воды за меженный период или 30-суточные, или среднемесячные расходы воды за все месяцы межени.

Наивысшие уровни воды рек и озер

6.30 На реках, где максимумы уровней однозначно связаны с расходами воды, экстраполяцию эмпирической кривой обеспеченности максимальных уровней за пределы наблюденных значений выполняют с помощью аналитических функций распределения вероятностей превышения расходов воды. Для этого непродолжительные ряды расходов воды приводят к многолетнему периоду в соответствии с 6.1 - 6.24. От расчетного максимального расхода к соответствующему уровню переходят по кривой расходов, координаты верхней части которой рассчитывают по формуле Шези с выделением элементов расходов воды в русле и пойме.

Если под влиянием русловых и гидравлических факторов зависимость между расходами и уровнями воды неоднозначна, то расчетный уровень воды за пределами наблюденных значений определяют по кривой связи уровня и поперечного сечения ω водного потока через значения ω_p%, полученные по аналитической функции распределения вероятностей превышения значений ω.

В случае неоднозначности кривой расходов, обусловленной переменным подпором, для приведения кривых распределения ежегодных вероятностей превышения максимальных уровней воды к многолетнему периоду используют отклонения уровня от стандартной (осредненной) кривой Q = f (H) или от нижней устойчивой кривой. При этом к расчетному уровню воды заданной обеспеченности Н_P%, определенному по Q = f (H) через Q_P%, добавляют значение отклонения DН_Р%, полученное по условному распределению DН при Q_P%.

Если в течение длительного периода наблюдается одностороннее смещение кривой Q = f (H) вверх или вниз, то это свидетельствует о происходящем намыве или размыве русла в исследуемом створе или в створе переката, лимитирующего уровень поста. Для экстраполяции максимальных уровней воды до отметок заданной вероятности превышения изложенным способом на деформируемых участках рек используют отклонения уровня от кривой ω = f (H).

Ряд заторных и зажорных максимумов уровня можно удлинить, если представить их в виде суммы уровня h_q, соответствующего в условиях свободного от льда русла расходу воды в момент вскрытия (замерзания) реки, и превышения над ним DН, что позволяет учесть дополнительную информацию о случаях вскрытия (замерзания), когда скопление льда не формируется на расчетном участке реки. Интегральная кривая распределения вероятностей максимальных заторных (зажорных) уровней совпадает при этом в нижней своей части с кривой обеспеченности уровней вскрытия (замерзания). Точка соединения кривых соответствует повторяемости заторов (зажоров) льда.

Расчетные уровни воды озер редкой повторяемости за пределами наблюденных находят путем экстраполяции аналитической кривой обеспеченности объемов воды V в озере. Необходимые для этого координаты зависимости V = f (H) устанавливают путем производства гидрометрических работ.

7 ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ГИДРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ПРИ ОТСУТСТВИИ ДАННЫХ ГИДРОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ

Общие положения

7.1 При отсутствии данных гидрометрических наблюдений в расчетном створе применяют региональные методы расчета гидрологических характеристик, основанные на результатах обобщения данных гидрометеорологических наблюдений в районе проектирования в соответствии с 4.3.

Оценку точности определения расчетных гидрологических характеристик осуществляют в соответствии с 4.15 и 5.14. Среднюю квадратическую погрешность расчета по региональным зависимостям определяют с учетом отклонений эмпирических точек от этих зависимостей.

Наряду с предлагаемыми в настоящем разделе формулами допускается применять другие региональные формулы при их обосновании (см. 4.15).

7.2 При отсутствии гидрометрических наблюдений в расчетном створе параметры распределения и расчетные значения определяют с помощью следующих основных методов:

- водного баланса;

- гидрологической аналогии;

- осреднения в однородном районе;

- построения карт изолиний;

- построения региональных зависимостей стоковых характеристик от основных физико-географических факторов водосборов;

- построения зависимостей между погодичными стоковыми характеристиками и стокоформирующими факторами.

7.3 Общие условия по выбору рек-аналогов приведены в 4.11. Для каждой гидрологической характеристики должны учитываться дополнительные условия, которые приведены в данном разделе. В качестве одного из основных требований является наличие достаточно продолжительного ряда на реке-аналоге (см. 5.1), который при недостаточности наблюдений приводят к многолетнему периоду в соответствии с разделом 6.

7.4 При статистической однородности параметров распределения в гидрологическом районе расчетное значение параметров в исследуемом створе следует определять как среднеарифметическое значение для рек-аналогов, имеющих наиболее продолжительные ряды наблюдений, или по приведенным к многолетнему периоду данным. Однородность параметров распределения устанавливают по статистическим критериям однородности согласно 4.7.

7.5 При статистической неоднородности значения гидрологических характеристик следует определять по районным картам, которые строят на основе использования всей имеющейся к моменту проектирования гидрологической информации согласно 4.3. Районные карты строят для погодичных гидрологических характеристик (за исключением максимального стока), параметров распределения, расчетных гидрологических характеристик, различных параметров и коэффициентов региональных зависимостей и других уравнений с общей для территории структурой. Наведение изолиний следует осуществлять (сглаживать) с учетом случайных погрешностей исходных данных и случайных погрешностей, обусловленных ограниченностью принятых в расчет выборок. Построение карт изолиний рассматриваемой гидрологической характеристики или параметра осуществляют методами линейной интерполяции, оптимальной интерполяции, основанной на пространственной корреляционной функции, и другими. При этом использование пространственной корреляционной функции включает оценку ее однородности. В случае определяющего влияния других региональных факторов (например, высоты водосборов в горных районах) интерполяцию осуществляют с учетом этих факторов.

7.6 Построение региональных зависимостей для параметров распределения и расчетных гидрологических характеристик включает в себя следующие основные этапы:

- выбор предполагаемых основных физико-географических факторов для исследуемого однородного района (площадь водосбора, средняя высота, уклон водосбора и реки, озерность, заболоченность, залесенность, параметры рядов метеорологических факторов и другие);

- построение и анализ однофакторных зависимостей гидрологических характеристик от региональных факторов с целью выбора основных факторов для исследуемого региона, априорной оценки вида зависимостей и необходимости функциональных преобразований рассматриваемых факторов;

- предварительное формирование общей структуры региональной зависимости на основе генетического анализа и условий формирования стока, результатов анализа однофакторных зависимостей и т.д.;

- построение региональных зависимостей с учетом условий (6.1) и формирование окончательного вида расчетных формул:

- оценку эффективности построенных региональных зависимостей и формул в соответствии с 4.15.

В связи с ограниченностью данных и преобладающим влиянием характеристик физико-географических факторов в однородном районе региональные зависимости, как правило, включают несколько (не более 4 - 5) основных переменных. В приведенных в настоящем разделе пунктах, касающихся конкретных гидрологических характеристик (годовой, максимальный, минимальный стоки, наивысшие уровни воды), даны наиболее распространенные структуры региональных зависимостей и формул, применяющихся в гидрологических расчетах. Параметры этих зависимостей для каждого однородного региона должны определяться на основе всей имеющейся информации, а оценку эффективности получаемых параметров и рассчитываемых по этой зависимости значений осуществляют в соответствии с формулой (6.1) и пунктом 4.15.

7.7 Основными гидрографическими и физико-географическими факторами для построения региональных зависимостей являются следующие:

1) площадь водосбора F, км²;

2) гидрографическая длина водотока L, км;

3) средневзвешенный уклон водотока I, ‰, представляющий собой условный выровненный уклон ломаного профиля, эквивалентный сумме частных средних уклонов профиля водотока, вычисляемый по формуле

,                             (7.1)

где I_i - частный средний уклон отдельных участков продольного профиля водотока, ‰;

l_i - длина частных участков продольного профиля между точками перегиба, км;

L - гидрографическая длина водотока до пункта наблюдений, км.

Средневзвешенный уклон определяют только для незарегулированных водотоков, а также для участков рек, расположенных в нижних бьефах водохранилищ;

4) средняя высота водосбора , м, над уровнем моря; определяют по гипсографической кривой водосбора или по формуле

,                                   (7.2)

где H_в,i - высота поверхности горизонтального сечения (горизонтального), м;

DA_i - площадь между двумя соседними горизонталями, км²;

А - общая площадь водосбора, км²;

5) относительная лесистость водосбора f_л, % общей площади водосбора (лес и кустарники на проходимых болотах в лесные угодья не включают);

6) относительная заболоченность водосбора f_б, % общей площади водосбора; вычисляют с разделением болот на верховые и низинные;

7) относительная озерность водосбора f_оз, %, представляющая собой отношение суммы площадей всех озер, расположенных на водосборе, к общей площади водосбора;

8) средневзвешенная озерность для непроточных озер f′_оз, % общей площади водосбора; вычисляют с учетом расположения озер на водосборе по формуле

,                                                     (7.3)

где S_i - площади озер;

f_i - площади водосборов этих озер;

А - площадь водосбора реки до замыкающего створа;

9) закарстованность водосбора f_к, % общей площади водосбора; определяют отношением закарстованной площади водосбора ко всей его площади;

10) относительная распаханность водосбора f_р % общей площади водосбора; определяют отношением площади распаханных земель под сельскохозяйственные культуры на водосборе ко всей его площади;

11) характеристика типа почвогрунтов, слагающих поверхность водосбора; определяют по почвенным картам, а также выделяют пять групп почвогрунтов по механическому составу: глинистые, суглинистые, песчаные, супесчаные и каменистые;

12) средняя глубина залегания уровня грунтовых вод (первого водоносного горизонта); определяют по гидрогеологическим картам;

13) характеристики зарегулированности речной системы искусственными водоемами (количество, расположение и регулирующие емкости);

14) характеристика рельефа (равнинный - относительное колебание высот в пределах водосбора менее 200 м, горный - относительное колебание высот на водосборе более 200 м).

7.8 Для водотоков малых рек (F < 200 км²) дополнительно определяют следующие характеристики:

1) средний уклон склонов водосбора I_cк, ‰; определяют по картам и планам в горизонталях по формуле

,                                                   (7.4)

где h - высота сечения рельефа, м;

 - сумма длин измеренных горизонталей в пределах водосбора, км;

2) густоту речной сети водосбора ρ_р, км/км²; определяют как отношение суммарной длины всех водотоков (реки, каналы, канавы) на водосборе к общей площади водосбора

,                                                          (7.5)

3) густоту русловой сети водосбора ρ₀, км/км²; определяют как отношение суммарной длины речных долин, сухих русел, оврагов, балок и логов к общей площади водосбора.

Гидрографические характеристики реки и ее водосбора определяют по новейшим топографическим картам, масштабы которых выбирают в зависимости от размера реки и рельефа водосбора по следующим рекомендациям:

а) для определения площадей водосборов, длин рек и уклонов - по таблице 7.1;

б) для определения гидрографических характеристик водоемов - по таблице 7.2;

4) характер почвогрунтов, степень закарстованности, глубину залегания уровня грунтовых вод определяют по специальным картам (почвенно-грунтовым и гидрогеологическим).

Таблица 7.1 - Масштабы карт, используемые для определения площадей водосборов, длин рек и уклонов

Таблица 7.2 - Масштабы карт для определения гидрографических характеристик водоемов

Категории рек (большие, средние, малые) в зависимости от площади водосбора приняты в соответствии с ГОСТ 19179.

7.9 При определении гидрографических характеристик водотока и водосбора выбор масштаба топографических карт, установление местоположения водораздельных линий, истоков, устьев водотоков и картометрические измерения производят в соответствии с таблицами 7.1 и 7.2.

7.10 Для восстановления многолетних рядов гидрологических характеристик при отсутствии данных гидрометрических наблюдений применяют зависимости стока от стокоформирующих факторов, которые строят для продолжительных рядов на реках-аналогах в однородном районе. Основная особенность при построении эмпирических зависимостей - их общая для территории структура, позволяющая интерполировать параметры, коэффициенты и стокоформирующие факторы на неизученный водосбор. Построение и анализ зависимостей осуществляют также в соответствии с требованиями пунктов 4.3, 4.15 и условия (6.1).

Годовой сток

7.11 При отсутствии наблюдений за стоком в расчетном створе параметры распределения (среднее, коэффициент вариации, отношение коэффициента асимметрии к коэффициенту вариации и коэффициент автокорреляции) определяют по рекам-аналогам.

7.12 В значения среднего многолетнего стока (нормы), определенные по районной карте, следует вводить поправки на влияние местных азональных факторов, которые учитывают неполное дренирование реками подземных вод, наличие карста, выходов подземных вод, особенности геологического строения бассейна, характер почв (грунтов), промерзание и пересыхание рек, различие средних высот водосборов и другие особенности. Поправки определяют путем построения зависимостей среднего многолетнего стока от азональных факторов.

7.13 Среднее многолетнее значение стока (в модулях или слоях стока) для расчетного пункта (центра тяжести водосбора) на равнинной территории или при незначительно меняющемся рельефе определяют линейной интерполяцией между изолиниями стока.

В случае пересечения водосбора несколькими изолиниями средневзвешенное значение стока вычисляют по формуле

q_cp = (q₁ A₁ + q₂ A₂ + ... + q_n A_n) / A,                                  (7.6)

где q₁, q₂, ... q_n - средние значения стока между соседними изолиниями, пересекающими водосбор;

А₁, А₂, ..., А_п - соответствующие площади между изолиниями;

А - общая площадь водосбора до расчетного створа.

7.14 Среднее многолетнее значение стока неисследованных горных рек следует определять по районным зависимостям стока от средней высоты водосбора, установленной для изученных рек в районе исследования.

В целях уточнения среднего многолетнего значения стока отдельных горных рек по зависимостям  = f (_%), составленным для достаточно крупных районов, используют дополнительные факторы (экспозицию склонов и др.).

7.15 Значения коэффициента вариации C_v неисследованных рек следует определять по карте изолиний этого параметра или по районным эмпирическим формулам, в которые вводят поправки на азональные факторы.

Коэффициенты вариации по районным эмпирическим формулам определяют в зависимости от среднего многолетнего значения стока, площади водосбора реки или средней высоты бассейна (для горных районов). Эффективность региональных зависимостей определяют условиями (6.1).

На горных реках, в бассейнах которых имеются ледники, занимающие более 10 % их общей площади, устанавливают районные зависимости коэффициента вариации от степени оледенения водосборов рек.

7.16 Коэффициент асимметрии устанавливают в соответствии с 5.7.

7.17 При отсутствии данных наблюдений за годовым стоком в расчетном створе допускается применять эмпирические зависимости от метеорологических и других факторов.

7.18 Годовой сток при наличии продолжительных рядов метеорологических факторов допускается рассчитывать как сумму слоев стока сезонных составляющих за генетически однородные периоды. Для рек с весенним половодьем можно выделить три основных генетически однородных сезона внутри года по условиям формирования стока: сезон весеннего половодья, сезон летне-осенней межени и дождевых паводков и сезон зимней межени. Методика включает следующие основные этапы:

- для каждого водосбора определяют однородные гидрологические сезоны и за каждый сезон рассчитывают слои стока и предполагаемые стокоформирующие факторы;

- для каждого водосбора и каждого гидрологического сезона строят зависимости слоев стока от стокоформирующих факторов и из них выбирают наиболее значимые с общей для территории структурой;

- даты начала и окончания однородных гидрологических сезонов обобщают по территории и их значения определяют для неизученного водосбора;

- в границах полученных сезонов для неизученного водосбора определяют многолетние ряды стокоформирующих факторов, входящие в уравнения территориально-общей структуры;

- коэффициенты уравнений сезонного стока территориально-общей структуры обобщают по территории и их значения определяют для неизученного водосбора;

- на основе рядов стокоформирующих факторов и коэффициентов уравнений для неизученного водосбора вычисляют многолетние ряды сезонного стока;

- слои годового стока определяют как суммы слоев сезонного стока;

- по ряду вычисленного годового стока определяют параметры и квантили распределения как для случая гидрологических расчетов при наличии данных наблюдений (раздел 5).

Внутригодовое распределение стока

7.19 При отсутствии данных гидрометрических наблюдений в створе проектирования расчетное внутригодовое распределение стока определяют по данным рек-аналогов, по районным схемам и по региональным зависимостям.

В первом случае относительные значения стока заданной вероятности превышения за все месяцы водохозяйственного года и соответствующей градации водности определяют путем расчета по данным достаточно длительных наблюдений на реке-аналоге, а во втором - путем составления районной схемы внутригодового распределения стока по результатам расчетов по группе рек-аналогов.

7.20 Применение метода аналогии для расчета внутригодового распределения стока рекомендуется для равнинных территорий и плоскогорий при сравнительно однообразных физико-географических условиях. Допускается при надлежащем обосновании применение этого метода и для горных районов. За аналог принимают реку, удовлетворяющую условиям, приведенным в 4.11.

7.21 Расчет внутригодового распределения стока производят по региональным зависимостям параметров сезонного стока от определяющих факторов: площади водосбора реки, озерности, заболоченности, лесистости, характера почвогрунтов, а в горных условиях - также от средней высоты водосбора и т.д.

7.22 При приведении месячного, сезонного и годового стоков к многолетнему периоду используют рекомендации раздела 6. Определение расчетного внутригодового распределения стока по каждой из рек-аналогов производят согласно рекомендациям 5.19 - 5.24.

7.23 Основным методом обобщения данных по внутригодовому распределению стока как для равнинных, так и для горных районов является составление районных схем межсезонного и внутрисезонного распределений стока, необходимых для определения расчетного календарного распределения месячного стока в характерном по водности году исследуемой неизученной реки. Межсезонное распределение стока выражают в долях годового стока, а внутрисезонное распределение стока - в долях стока соответствующего сезона. В зависимости от характера решаемой практической задачи и принятого в расчетах метода определения внутригодового распределения стока для района исследования (или района проектирования) могут быть построены различные расчетные схемы. Общими при их установлении являются выявление и учет основных природных факторов (площади водосбора и озерности на равнинах и плоскогорьях, средней высоты водосбора - в пересеченных горных районах).

7.24 Построение средней многолетней кривой продолжительности суточных расходов воды производят методом аналогии. Среднюю многолетнюю кривую продолжительности, построенную для реки-аналога в относительных значениях (в долях ее среднемноголетнего годового расхода воды), переносят на неизученную реку с учетом нормы стока неизученной реки, полученной в соответствии с 7.11 - 7.18.

Максимальный сток воды рек

7.25 Методы определения расчетных характеристик максимального стока весеннего половодья и дождевых паводков подразделяют на следующие:

а) при наличии одной или нескольких рек-аналогов;

б) при отсутствии рек-аналогов. Значения параметров и коэффициентов в расчетных формулах следует уточнять на основе использования гидрометеорологической информации за весь период наблюдений, включая последние годы, в соответствии с 4.3.

7.26 Выбор рек-аналогов следует проводить с соблюдением требований, указанных в 4.11, а также при соблюдении условий:

L / A^0,56 ≈ L_a / A_a^0,56;                                                    (7.7)

J A^0,50 ≈ J_a A_a^0,50,                                                       (7.8)

где L и L_a - длина исследуемой реки и реки-аналога соответственно, км;

J и J_a - уклон водной поверхности исследуемой реки и реки-аналога, промилле;

А и A_a - площади водосборов исследуемой реки и реки-аналога соответственно, км².

7.27 При использовании нескольких независимых (но не более трех) региональных методов и схем расчета максимального стока окончательное расчетное значение рассматриваемой характеристики принимают в соответствии с 4.10.

Весеннее половодье

7.28 При наличии рек-аналогов определение максимальных расходов воды весеннего половодья выполняют по редукционной формуле (7.9).

При наличии данных метеорологических наблюдений, позволяющих рассчитывать водоотдачу из снежного покрова, расходы воды весеннего половодья малых рек допускается определять по упрощенным генетическим формулам, структура которых и методы определения параметров регламентируются Территориальными строительными нормами.

7.29 Методы расчета максимальных расходов воды рек весеннего половодья применяют для рек с площадями водосборов от элементарно малых (менее 1 км²) до 20000 км² для европейской части России и до 50000 км² - для азиатской части, за исключением транзитных участков рек, где происходит сильное распластывание волны половодья, вызывающее снижение максимальных расходов воды.

При проектировании сооружений на реках с площадями водосборов, превышающими указанные пределы, максимальные расходы талых вод при отсутствии гидрометрических данных определяют по результатам инженерно-гидрометеорологических изысканий в исследуемом створе.

7.30 Расчетный максимальный расход воды весеннего половодья Q_p%, м³/с, заданной вероятности превышения Р_% при наличии рек-аналогов определяют по редукционной формуле

Q_p% = K₀ h_p% μ δ δ₁ δ₂ A / (A + A₁)ⁿ                                        (7.9)

где K₀ - параметр, характеризующий дружность весеннего половодья; рассчитывают как среднее из значений, определенных по данным нескольких рек-аналогов обратным путем из формулы (7.9);

h_p% - расчетный слой суммарного весеннего стока (без срезки грунтового питания), мм, ежегодной вероятности превышения Р_%; определяют в зависимости от коэффициента вариации C_v и отношения C_s / C_v, a также среднего многолетнего слоя стока h₀;

μ - коэффициент, учитывающий неравенство статистических параметров кривых распределения слоев стока и максимальных расходов воды;

δ, δ₁, δ₂ - коэффициенты, учитывающие влияние водохранилищ, прудов и проточных озер (δ), залесенности (δ₁) и заболоченности речных водосборов (δ₂) на максимальные расходы воды;

А - площадь водосбора исследуемой реки до расчетного створа, км²;

A₁ - дополнительная площадь, учитывающая снижение интенсивности редукции модуля максимального стока с уменьшением площади водосбора, км²;

п - показатель степени редукции.

Показатель степени редукции п и параметр A₁ в формуле (7.9) определяют на основе зависимости q_{max p%} = f (A) по данным наблюдений на изученных реках исследуемого района, где q_{max p%} - модуль максимального стока.

При обосновании в формулу (7.9) допускается введение дополнительных параметров, учитывающих влияние естественных и искусственных факторов на формирование максимального стока воды рек весеннего половодья.

7.31 Средний многолетний слой стока весеннего половодья h₀ следует определять по данным рек-аналогов или интерполяцией по картам, построенным для исследуемого района с учетом последних лет наблюдений. В значение среднего многолетнего слоя весеннего стока вносят поправки на учет влияния местных факторов (площадь водосбора, уклоны склонов на водосборе, озерность, залесенность, заболоченность, распаханность):

а) для рек степной зоны России и полупустынной зоны Западной Сибири с площадями водосборов менее 3000 км² в значения h₀ следует вводить поправки на учет площади водосбора на основе построения зависимости h₀ = f (A) с учетом материалов наблюдений последних лет;

б) для малых равнинных рек с площадями водосборов менее 200 км² лесостепной, степной, полупустынной зон и засушливых степей поправочные коэффициенты устанавливают по зависимости h₀ = f (J_в), где J_в - уклон водосбора;

в) при наличии озер, расположенных на водосборе реки, поправочные коэффициенты к среднему многолетнему слою стока весеннего половодья h₀ определяют по связи слоя стока со значениями средней взвешенной озерности речных бассейнов h₀ = f (A_оз), при этом параметр A_оз, %, определяют по формуле

A_оз = (100 S_i А_i / А²,                                           (7.10)

где S_i - площадь зеркала озера, км²;

А_i - площадь водосбора озера, км²;

А - площадь водосбора в расчетном створе реки;

г) для водосборов с залесенностью, отличной от средней зональной (районной), поправочный коэффициент определяют по соотношению А_л / А_л.р, где А_л - залесенность расчетного водосбора, %; А_л.р - среднее районное значение залесенности, %. Т

Вычисление среднего районного значения залесенности водосборов выполняют как среднеарифметическое из значений залесенности, %, по ближайшим речным водосборам (водосборы с А > 200 км² - для лесной и лесостепной зон и А > 2000 - 3000 км² - для зон степей и полупустынь).

7.32 Коэффициент вариации слоя стока весеннего половодья принимают по рекам-аналогам или интерполяцией по картам изолинии этого параметра, построенным для исследуемого района.

Для рек с площадями водосборов А < 200 км² в значения, полученные интерполяцией по карте, следует вводить поправки, определяемые по зависимостям C_v = f (A) для равнинных рек и C_v = f (H_в) - для горных рек, где H_в - средняя высота речного бассейна, м.

7.33 Расчетное значение отношения коэффициента асимметрии к коэффициенту вариации C_s / C_v устанавливают в соответствии с требованиями 5.7.

7.34 Коэффициент δ, учитывающий снижение максимального расхода воды весеннего половодья на реках, зарегулированных проточными озерами, следует определять по формуле

δ = 1 / (1 + СА_оз),                                                    (7.11)

где С - коэффициент, принимаемый равным 0,2 для лесной и лесостепной зон и 0,4 - для степной зоны.

При наличии в бассейне озер, расположенных вне главного русла и основных притоков, значение коэффициента δ следует принимать для А_оз < 2 % - 1; А_оз > 2 % - 0,8.

Влияние прудов, регулирующих меженный сток, при расчете максимальных расходов воды вероятностью превышения менее 5 % не учитывают, а при Р ≥ 5 % допускается уменьшение расчетного значения до 10 %.

7.35 Коэффициент δ₁, учитывающий снижение максимальных расходов воды в залесенных бассейнах, определяют по формуле

δ₁ = α / (А_л + 1)^n′,                                                     (7.12)

где п - коэффициент редукции; устанавливают по зависимости q_maх = f (A_л) с учетом преобладающих на водосборе почвогрунтов;

α - коэффициент, учитывающий расположение леса на водосборе (в верхней или нижней части водосбора), а также природную зону (лесная или лесостепная).

7.36 Коэффициент δ₂, учитывающий снижение максимальных расходов воды с заболоченных водосборов, определяют по формуле

δ₂ = l - β lg (0,1 А_б + l),                                                 (7.13)

где β - коэффициент, определяемый в зависимости от типа болот и механического состава почвогрунтов вокруг болот и заболоченных земель (со слоем торфа не менее 30 см):

А_б - относительная площадь болот, заболоченных лесов и лугов в бассейне реки, %.

Внутриболотные озера, рассредоточенные по водосбору и расположенные вне главного русла и основных притоков, следует включать в значение относительной площади болот.

При заболоченности менее 3 % или проточной средневзвешенной озерности более 6 % коэффициент δ₂, принимают равным единице.

Для горных рек коэффициенты δ₁, и δ₂ равны единице.

Дождевые паводки

7.37 Выбор типа расчетной формулы для определения максимального срочного расхода воды дождевого паводка заданной вероятности превышения Q_р% следует производить согласно приложению Б, таблица Б.7.

7.38 Расчетная формула типа I (редукционная) для определения Q_р% при наличии одной или нескольких рек-аналогов имеет вид:

Q_р% = q_р%,a φ_м (δ δ₂ / δ_а δ_2а) А,                                         (7.14)

где q_р%,a - модуль максимального срочного расхода воды реки-аналога расчетной вероятности превышения Р_%, м³/с × км²; рассчитывают по формуле

q_р%,a = Q_р%,a / A_a,                                                    (7.15)

где Q_р%,a - максимальный расход воды дождевого паводка вероятности превышения Р_%, м³/с;

А_a - площадь водосбора реки-аналога, км²;

φ_м - коэффициент, учитывающий редукцию максимального модуля стока дождевого паводка (q_1%) с увеличением площади водосбора (А, км²) или продолжительности руслового времени добегания (τ_р, мин); рассчитывают в зависимости от значения коэффициента η_ф, представляющего соотношение коэффициентов формы водосбора исследуемой реки и реки-аналога:

η_ф ≈ L A_a^0,56 / L_a A^0,56,                                              (7.16)

где L и L_a - гидрографическая длина водотока для исследуемой реки и реки-аналога соответственно, км;

А и А_а - площадь водосбора для исследуемой реки и реки-аналога соответственно, км².

При η_ф < 1,5 расчетное значение коэффициента φ_м определяют по формуле (7.17), а при η_ф > 1,5 - по формуле (7.18):

φ_м = (A_a / A)ⁿ;                                                    (7.17)

φ_м = (Ф_а /Ф),                                                  (7.18)

где Ф и Ф_а - гидроморфометрическая характеристика русла для исследуемой реки и реки-аналога соответственно; определяют по формуле

Ф = 1000 L / т_р /  A^0,25,                                   (7.19)

где L и A - тоже, что и в формуле (7.16);

т_р и т - гидравлические параметры, характеризующие состояние и шероховатость русла водотока; определяют согласно приложению Б, таблица Б.8;

I_p - средневзвешенный уклон русла водотока, ‰;

n и n₁ - степенные коэффициенты, отражающие редукцию максимального модуля стока дождевого паводка q_1% соответственно с увеличением площади водосбора А, км², и руслового времени добегания τ_р.

Русловое время добегания τ_р, ч, для гидрологически изученной реки определяют по формуле

τ_р = 1000 L/V = 1000 L / (т_р  ),                           (7.20)

где L            - тоже, что и в формуле (7.16);

V - максимальное значение средней скорости добегания воды по главному водотоку, м/с;

т_р, т и I_p     - то же, что и в формуле (7.19);

δ и δ_а, δ₂ и δ_2а - поправочные коэффициенты, учитывающие для исследуемой реки и реки-аналога регулирующее влияние соответственно озер (прудов, водохранилищ), а также болот и заболоченных земель. При использовании формулы (7.18) значения коэффициентов δ₂ и δ_2а принимают равными единице.

7.39 При установлении степенных коэффициентов редукции n и n₁, а также структуры формул по определению поправочных коэффициентов δ, δ_а, δ₂ и δ_2а порядок выполнения инженерно-гидрологических расчетов по формуле типа I предусматривает последовательность этапов, изложенных в приложении В.

7.40 Расчетный максимальный срочный расход воды дождевого паводка определяют по формуле (7.14) на основе использования одной или нескольких рек-аналогов с учетом полученных значений степенных коэффициентов п и n₁ и формул для учета регулирующего влияния естественных и искусственных факторов.

7.41 При наличии значений степенных коэффициентов n и n₁, а также расчетных формул по определению поправочных коэффициентов δ, δ_а, δ₂ и δ_2а, полученных на основе региональных обобщений, допускается их использование при выполнении расчетов по формуле (7.14).

7.42 Расчетная формула типа II для определения Q_р% при отсутствии рек-аналогов имеет вид:

Q_р% = q₂₀₀ (200 / A)ⁿ δ δ₂ δ₃ λ_р% A,                               (7.21)

где q₂₀₀ - модуль максимального срочного расхода воды ежегодной вероятности превышения Р = 1 %, приведенный к условной площади водосбора, равной 200 км² при δ = δ₂ = δ₃ = 1,0; определяют для исследуемой реки при наличии региональной карты параметра q₂₀₀ интерполяцией, а при отсутствии - на основе использования многолетних данных гидрологически изученных рек;

А - площадь водосбора, км²;

δ и δ₂ - допускается определять соответственно по формулам (В.3), (В.4) приложения В;

δ₃ - поправочный коэффициент, учитывающий изменение параметра q′₂₀₀ с увеличением средней высоты водосбора , м, в полугорных и горных районах;

λ_р% - переходный коэффициент от максимальных срочных расходов воды ежегодной вероятности превышения Р = 1 % к значениям другой вероятности превышения Р < 25 %; назначают на основе установления соотношения (7.22) по данным гидрологически изученных рек в исследуемом районе

λ_р% = Q_р% / Q_1%.                                                    (7.22)

7.43 При отсутствии современной региональной карты параметр q₂₀₀ в формуле (7.21) для исследуемой реки определяют интерполяцией по значениям этой характеристики, определенным для выбранных близко расположенных с исследуемым водотоком гидрологически изученных рек. Для рек полугорных и горных районов на основе анализа графика связи q₂₀₀ = f (, м).

7.44 Расчетная формула типа III для определения Q_p% на водосборах площадью менее 200 км² имеет вид:

Q_p% = q′_1% φ H_1% δ λ _p% A,                                             (7.23)

где q′_1% - относительный модуль максимального срочного расхода воды ежегодной вероятности превышения Р = 1 %, представляющий отношение

q′_1% = q_1% / φ H_1%;                                                 (7.24)

определяют для исследуемого района в зависимости от гидроморфометрической характеристики русла Ф_p и продолжительности склонового добегания τ_ск, мин;

φ - сборный коэффициент стока;

H_1% - максимальный суточный слой осадков вероятности превышения Р = 1 %, мм; определяют по данным ближайших метеорологических станций;

δ, λ_р%, А - то же, что и в формуле (7.21).

Гидроморфометрическую характеристику русла исследуемой реки Ф_p определяют по формуле

Ф_р = 1000 L / [т_р  A^0,25 (φ H_1%)^0,25],                                (7.25)

где т_р, I_p, А - то же, что и в формуле (7.19).

7.45 При расчетах максимального стока по формуле предельной интенсивности следует иметь в виду, что редукционные кривые осадков, приведенные в [5], основаны на данных наблюдений до 60-х годов и требуют обязательного уточнения.

7.46 При наличии реки-аналога порядок расчетов по формуле типа III следующий:

1) для исследуемого водотока устанавливают гидрографические характеристики, тип и механический состав почвогрунтов, слагающих водосбор, а также средний уклон склонов I_ск. ‰, и густоту русловой и овражно-балочной сетей водосбора ρ_р км/км²;

2) в соответствии с рекомендациями (4.11) и (7.26) выбирают реку-аналог (или несколько рек-аналогов), для которой (или которых) в соответствии с требованиями В.3 приложения В определяют значения расчетных максимальных срочных расходов воды дождевого паводка;

3) определяют сборный коэффициент стока φ для равнинных рек по формуле

                    (7.26)

где q_l%,a - модуль максимального срочного расхода воды реки-аналога ежегодной вероятности превышения Р = 1 %, м³/с ×км²;

δ, А, А_a - то же, что и в 7.38;

I_ск, I_ск,а - то же, что и в поз.1);

n₂ - степенной коэффициент, определяемый в зависимости от механического состава почв и природной зоны;

n₃ - степенной коэффициент; принимают для лесотундры и лесной зоны равным 0,07, для остальных природных зон - 0,11;

τ_б - продолжительность бассейнового добегания, мин; определяют по формуле

τ_б = 1,2  + τ_ск,                                                         (7.27)

где τ_р - продолжительность руслового добегания, мин; определяют по формуле (7.20);

16,67  (τ_б) - ордината кривой редукции осадков, приведенная в [5] и уточняемая по 4.3 и приложению Г.

4) продолжительность склонового добегания τ_ск для водотоков, мин, допускается принимать в зависимости от природных зон равной следующим значениям:

тундра и лесная зона:

при заболоченности менее 20 %..................... 60

»                »                20 % - 40 % ........ 100

»                »                более 40 %........... 50

лесостепная зона ............................................. 60

степная зона и зона засушливых степей ......... 30

полупустынная зона ........................................ 10

полугорные и горные районы ........................ 10.

При наличии реки-аналога продолжительность склонового добегания τ_ск определяют в зависимости от района типовой кривой редукции осадков и гидроморфометрической характеристики склонов Ф_ск, которую рассчитывают по формуле

Ф_ск = (1000 L_ск)^0,5 / [т_cк  (φ H_1%)^0,5],                                 (7.28)

где l_ck - средняя длина безрусловых склонов водосбора; определяют по формуле

L_ск = 1 / γ ρ_р,                                                         (7.29)

где ρ_р - то же, что и в поз.1);

γ - коэффициент, принимаемый для односкатных склонов равным 0,9, для двускатных - 1,8;

т_cк - коэффициент, характеризующий шероховатость склонов водосбора; определяют по приложению Б, таблица Б.9;

 - то же, что и в поз.1);

φ - то же, что и в формуле (7.26);

H_1% - то же, что и в формуле (7.23).

Значение τ_ск определяют методом последовательного приближения. По формуле (7.27) определяют бассейновое время добегания τ_б при значении τ_ск, принятом согласно поз. 4). Затем устанавливают значение 16,67  (τ_б) и по формуле (7.26) рассчитывают сборный коэффициент стока φ. По формуле (7.28) определяют значение Ф_ск и далее по таблицам, приведенным в [5], устанавливают значение τ_ск в первом приближении, а затем уточняют в соответствии с 4.3. При значительном расхождении полученного и первоначального значений τ_ск расчеты следует повторить, принимая за исходное последнее вычисленное значение τ_ск;

5) значение H_1% определяют по многолетним данным о максимальных суточных жидких осадках метеорологических станций, ближайших к бассейну исследуемого водотока, которые имеют наибольшую длительность наблюдений, или по региональной карте этой характеристики, построенной с учетом наблюдений последних лет;

6) максимальный срочный расход воды по формуле (7.23) при наличии рек-аналогов определяют с учетом значений параметров и характеристик этой формулы, полученных согласно рекомендациям поз. 1) - 5).

7.47 При отсутствии рек-аналогов расчет по формуле (7.23) производят в последовательности, аналогичной приведенной в 7.46 при определении сборного коэффициента стока ф для равнинных рек по формуле

,                                           (7.30)

где с₂ - эмпирический коэффициент, который для тундры и лесной зоны принимают равным 1,2, для остальных природных зон - 1,3;

φ₀ - сборный коэффициент стока для условного водосбора с площадью А, равной 10 км², и средним уклоном I_ск равным 50 ‰; в первом приближении определяют по [5] и уточняют в соответствии с (4.3);

n₂, n₃, А - то же, что и в 7.46, поз. 3).

Для водотоков со средним уклоном склонов более 150 ‰ сборный коэффициент стока φ рассчитывают по формуле (7.30) при , равном 150 ‰, а для водотоков со средним уклоном склонов менее 15 ‰ - при , равном 15 ‰.

При различной крутизне склонов или значительной пестроте почвогрунтов, слагающих исследуемый водосбор, сборный коэффициент стока φ принимают как средневзвешенное значение.

7.48 Расчетный слой дождевого паводка h_p% для водосборов площадью более 50 км² следует определять по формуле

h_p% = h^*_p% k_H,                                                         (7.31)

где h^*_p% - слой дождевого паводка расчетной вероятности превышения Р_%, мм; принимают по данным реки-аналога или по карте, построенной для гидрологически изученных рек при k_H = 1;

k_H - эмпирический коэффициент, учитывающий уменьшение (редукцию) слоя дождевого паводка с увеличением площади водосбора в засушливых районах; устанавливают на основе исследования зависимости h^*_p% = f (A).

7.49 Расчетный слой дождевого паводка h_p% для водосборов площадью менее 50 км² при наличии рек-аналогов примерно такой же площади следует принимать равным расчетным слоям рек-аналогов.

При отсутствии рек-аналогов расчетные слои дождевого стока следует определять по формуле

h_p% = ψ (τ_{б=150 мин}) φ H_l% λ^*_p%,                                       (7.32)

где ψ (τ_{б=150 мин}) = Hτ / H_p% - относительная интенсивность осадков;

λ^*_p% - переходный коэффициент от слоя стока дождевого паводка вероятности превышения Р = 1 % к слоям других вероятностей превышения; определяют по формуле

λ^*_p% = H_p% / H_l%,                                                       (7.33)

где H_p% и H_l% - слой максимальных суточных осадков вероятности превышения соответственно Р_% и 1 %, мм; определяют по кривым распределения суточных осадков;

φ - сборный коэффициент стока.

Гидрографы стока воды рек весеннего половодья и дождевых паводков

7.50 Параметры основных элементов расчетного гидрографа следует определять согласно 5.32 - 5.40 и 7.28 - 7.49.

7.51 Коэффициент перехода k_t от максимального мгновенного расхода воды весеннего половодья Q′_p к среднесуточному Q_p устанавливают по рекам-аналогам. При их отсутствии для равнинных рек определение коэффициента k_t осуществляют по региональным зависимостям от площади водосбора.

7.52 Одновершинный гидрограф стока воды весеннего половодья (дождевого паводка) рассчитывают согласно приложению Б, таблица Б.10 по значению коэффициента несимметричности k_s, определяемого по формуле (5.50) по данным рек-аналогов или по значению коэффициента формы гидрографа λ определяемого по формуле

λ = q t_п / 0,0116 h.                                                     (7.34)

Ординаты расчетного гидрографа определяют по формуле

Q_i = у Q_p,                                                              (7.35)

абсциссы - по формуле

t_i = х t_п,                                                               (7.36)

где t_п - продолжительность подъема весеннего половодья (дождевого паводка), определяемая по формуле

t_п = 0,0116 λ h_р / q_р;                                                 (7.37)

х, у - относительные координаты расчетного гидрографа стока воды, определяемые по приложению Б. таблица Б.10;

q - расчетный модуль максимального среднего суточного расхода воды весеннего половодья или максимального мгновенного расхода воды дождевого паводка, м³/с × км².

7.53 Внутрисуточный гидрограф стока определяют по формуле (7.35), значения относительных ординат у которого принимают по приложению Б, таблица Б.11.

7.54 Для рек с площадью водосбора менее 200 км² с продолжительностью подъема дождевого паводка 1 сут или менее расчетную продолжительность определяют по формуле

T_п = β λ h_р / q_р,                                                      (7.38)

где β - коэффициент, принимаемый при расчете продолжительности подъема дождевого паводка в часах равным 0,28, в минутах - 16,7.

При определении расчетных гидрографов дождевых паводков согласно требованию 7.52 коэффициент несимметричности k_s следует принимать по рекам-аналогам; при отсутствии аналогов допускается k_s принимать равным 0,30, для рек с площадью менее 1 км² степной и полупустынной зон - равным 0,20.

Минимальный сток воды рек

7.55 Основной расчетной характеристикой является минимальный 30-суточный или среднемесячный расход воды в зимний и (или) летне-осенний сезоны. Минимальный среднесуточный расход определяют по связи с 30-суточным.

Минимальный среднесуточный расход воды обычно используют в случаях, когда не допускаются перерывы в подаче воды.

7.56 Метод определения минимального 30-суточного расхода воды зависит от категории реки: малая, средняя или большая. К малым относят реки, у которых модуль минимального стока изменяется с возрастанием площади водосбора. В зависимости от района к малым относят реки с верхним пределом площади водосбора от 1000 до 5000 км². Наименьшие значения отмечены в зонах избыточного и достаточного увлажнения, наибольшие - в районах с наличием пересыхающих или перемерзающих рек. К средним относят реки с площадью водосбора от вышеуказанных до 50000 - 75000 км². Реки с большей площадью считают большими.

7.57 Минимальные расходы воды на больших и средних реках определяют по интерполяции между пунктами наблюдений с учетом боковой приточности и данных полевых гидрометеорологических изысканий в расчетном створе.

7.58 При невозможности использовать указания 7.57 для расчета минимальных 30-суточных (среднемесячных) расходов применяют методы пространственной интерполяции минимального 30-суточного модуля стока 80 %-ной обеспеченности для зимнего или летне-осеннего сезона.

7.59 Минимальный сток малых равнинных и полугорных рек Q_P%, м³/с, рассчитывают по зависимости минимальных 30-суточных расходов воды 80 %-ной обеспеченности от площади водосбора для районов, однородных по условиям формирования минимального стока. В общем виде эта зависимость имеет вид:

Q_p% = b (A ± A_l)^m δ₁ δ₂ λ_p%,                                       (7.39)

где А - площадь водосбора, км²;

А₁ - дополнительная площадь водосбора: при положительном значении отражает дополнительное питание рек в период минимального стока за счет озерного регулирования при относительной озерности водосбора до 5 %; в случае отрицательного значения показывает площади водосбора с ежегодным отсутствием стока в течение 30 сут;

δ₁ - коэффициент, учитывающий увеличение минимальных расходов воды на озерных реках;

δ₂ - коэффициент, учитывающий увеличение минимальных расходов воды заболоченных водосборов;

λ_p% - переходный коэффициент от минимального 30-суточного расхода воды 80 %-ной обеспеченности к расходу воды расчетной обеспеченности.

7.60 Значение δ₁ определяют по формуле

δ₁ = 1 / (1 - с A_оз),                                                     (7.40)

где с - коэффициент, определяемый в зависимости от среднего многолетнего или 80 %-ной обеспеченности слоя минимального стока;

A_оз - относительная озерность водосбора.

При относительной озерности меньше 2 % и отсутствии ежегодного пересыхания или перемерзания формула (7.39) принимает вид:

Q_p% = b А^т δ₂ λ_p%,                                                       (7.41)

где b, т - районные параметры, определяемые по рекам-аналогам или как средние районные значения с использованием минимальных расходов воды опорной обеспеченности, обычно 80 %.

При относительной озерности водосбора от 5 до 15 % формула (7.39) приобретает вид:

Q_p% = b А^т δ₁ δ₂ λ_p%.                                                    (7.42)

При относительной озерности более 15 % рекомендуется использовать формулу

q₃₀ = а₁ (1 + b₁ A_оз).                                                    (7.43)

где q₃₀ - модуль минимального 30-суточного стока 80 %-ной обеспеченности, л/с ×км²; а₁, b₁, п - районные параметры.

7.61 Коэффициент δ₂ определяют по формуле

δ₂ = l + β^* lg (0,1 A_б + l),                                            (7.44)

где β^* - эмпирический коэффициент, определяемый в зависимости от типа болот;

А_б - относительная площадь болот на водосборе.

При заболоченности водосбора менее 5 % коэффициент δ₂ принимают равным 1.

7.62 Коэффициент λ_p% определяют как средний в однородном районе по данным рек-аналогов с учетом гидрогеологических условий, глубины вреза русла реки и других факторов минимального стока.

7.63 В горных районах минимальный сток следует определять по графической зависимости модуля минимального 30-суточного стока от средней высоты водосбора. Дополнительным параметром для водосборов со средней высотой до 2500 м может служить площадь водосбора.

7.64 Минимальный среднесуточный расход воды расчетной обеспеченности определяют по формуле

Q_сут.р% = k Q_30,80% λ_p%                                              (7.45)

где k - коэффициент, определяемый как средний по району по связи суточных и 30-суточных минимальных расходов.

7.65 Максимальную или среднюю многолетнюю продолжительность ежегодного пересыхания или перемерзания реки в расчетном створе Т, сут, определяют по формуле

T = d₁ (А + 1),                                               (7.46)

где А - площадь бассейна до расчетного створа, км²;

d₁ и m₁ - районные параметры.

7.66 На территории криолитозоны (зоны многолетней мерзлоты) в зимний сезон ежегодно промерзают реки с площадью бассейна до 5000 км². Продолжительность промерзания рекомендуется определять по формуле

T = d₂ (L + 1),                                              (7.47)

где L - длина реки от истока до расчетного створа, км;

d₂ и т₂ - районные параметры.

7.67 Продолжительность эпизодического отсутствия стока в расчетном створе определяют по формуле

T = d₃ ,                                                            (7.48)

где q₃₀ - средний многолетний или 80 %-ной обеспеченности (в зависимости от требований проекта) модуль минимального 30-суточного или среднемесячного стока, л/с × км²;

d₃ и т₃ - районные параметры.

Наивысшие уровни воды рек и озер

7.68 Расчетные наивысшие уровни воды, обусловленные половодьями и паводками, определяют по кривым Q = f (H) через расходы воды Q_p%, рассчитанные способами, изложенными в разделах 5 - 7. При наличии широкой поймы кривые расходов устанавливают отдельно для русла и поймы, а затем их суммируют. Для средних и больших рек расходы воды в пойме могут быть определены с использованием соотношений, приведенных в таблице 7.3.

Таблица 7.3- Зависимость расхода воды в пойме q_п в долях суммарного расхода (Q_p + Q_n) и от отношения общей ширины реки (В_p + В_п) к ширине русла В_p

Кривые расходов строят с помощью формулы

,                                                        (7.49)

где ω - площадь поперечного сечения русла или поймы при отметке уровня H, м²;

п - коэффициент шероховатости, с/м^0,33;

h - средняя глубина воды в русле или пойме, м;

I - уклон водной поверхности.

Кривые ω = f (H) и h = f (H) устанавливают путем промеров глубин в реке ниже уреза воды и нивелирования русла и береговых склонов выше уреза до предполагаемой высоты уровня воды 1 %-ной вероятности превышения плюс один метр.

Коэффициент шероховатости находят по приложению Б, таблица Б.12. Уклон I определяют при высокой воде или в первом приближении по приложению Б, таблица Б.13.

7.69 Исходной характеристикой при расчете подпорных уровней на устьевых участках рек является наивысший уровень водотока или водоема водоприемника расчетной вероятности превышения, определяемый приемами, изложенными выше. Перенос этого уровня вверх от устья реки производят по кривой подпора, которую строят путем соединения плавной вогнутой линией точек продольного профиля, соответствующих расчетному бытовому уровню воды в месте выклинивания подпора и в створе наибольшего подпора у его источника. Дальность распространения подпора L, км, определяют по формуле

L = a(h_Q + Dh) / I_Q,                                                 (7.50)

где I_Q и h_Q - средние уклон водной поверхности, ‰, и глубина реки, м, на расчетном участке при отсутствии подпора;

Dh - наибольший подпор, м;

а - коэффициент, зависящий от отношения Dh / h_Q и определяемый по таблице 7.4.

Таблица 7.4

7.70 Для определения наивысших уровней воды при зажорах и заторах требуется предварительно выполнить специальные исследования с целью установления вероятности образования скоплений льда, их местоположения и мощности.

Возможность образования зажоров определяют следующие признаки:

- замерзание, происходящее путем перемещения кромки ледяного покрова снизу вверх по течению, что имеет место на реках, которые текут с юга на север или выходят с гор на равнину;

- наличие в пределах участка проектирования или непосредственно ниже его перелома продольного профиля его водной поверхности с резким уменьшением к устью уклонов (в 3 раза и более), сужений русла, крутого поворота, островов и других русловых образований, уменьшающих льдопропускную способность русла;

- уклон водной поверхности выше очага зажорообразования, превышающий 0,05 ‰, при котором шуговые скопления вовлекаются под кромку ледяного покрова;

- интенсивный и длительный (6 сут и более) шугоход с расположенного выше по течению участка, что характерно для всех рек, процесс замерзания которых прерывается оттепелями, и для участков рек с большим тепловым стоком из глубоких озер и водохранилищ;

- большая осенняя водность (модуль стока более 3 л/с × км²).

7.71 При оценке возможности формирования заторов учитывают следующие факторы, способствующие заторообразованию:

- более позднее вскрытие участка реки, расположенного ниже по течению, которое имеет место на реках, текущих с юга на север, при выходе рек с гор на равнину и в устьях рек;

- интенсивное снеготаяние и быстрый сброс воды в русловую сеть, чему благоприятствуют большой уклон и малые залесенность, заболоченность и озерность бассейна;

- наличие в пределах участка реки перелома продольного профиля водной поверхности с резким уменьшением уклона и русловых образований, уменьшающих льдопропускную способность русла;

- большая толщина и прочность льда перед вскрытием, наличие зажорных скоплений и наледей в пределах исследуемого участка, интенсивное поступление льда после вскрытия с расположенного выше по течению участка реки, а также с раньше вскрывающихся крупных притоков.

7.72 Расчетный наивысший уровень воды h_з.р.%, обусловленный зажором или затором, вычисляют по формуле

h_з.р.% = (μ  - 1)  + ,                       (7.51)

где μ - коэффициент зажорности или заторности речного участка;

;  и  - уклон водной поверхности, ‰, средняя глубина реки, м, и уровень воды в расчетном створе, м, при расходе Q_з.р.%, и свободном от льда русле;

Q_з.р - расход воды в период зажоро- или заторообразования вероятности превышения Р_%

Коэффициент μ определяют путем полевых исследований, в ходе которых на временном гидрологическом посту ведут учащенные наблюдения за ледовыми явлениями и уровнем воды в период замерзания или вскрытия. Путем измерения скоростей перемещения льдин или расчета модулей стока оценивают расход Q_з и уровень  воды. Последний может быть определен и с помощью графической срезки уровней с учетом данных о стоке воды. Уклон водной поверхности измеряют в период со свободным от льда руслом.

При отсутствии полевых работ значение μ может быть определено по аналогии. При выборе речных участков-аналогов учитывают следующие условия:

- возможную географическую близость расположения;

- однонаправленность течения;

- одни и те же факторы формирования осеннего (весеннего) стока;

- подобие поперечных и плановых форм русла в пределах участков;

- равенство уклонов водной поверхности;

- отсутствие факторов, существенно искажающих естественное развитие процессов зажоро- и заторообразования.

Ориентировочно коэффициент зажорности (заторности) μ может быть определен также по таблице 7.5 в зависимости от вида ледяного образования и приращения ширины реки в пределах подъема уровня от  до h_з.р.%.

Таблица 7.5 - Значения коэффициента μ

Расход воды Q_з рассчитывают через модуль стока, который определяют методом гидрологической аналогии. Помимо обычных требований к реке-аналогу по условиям формирования стока воды в данном случае принимают также во внимание одновременность и направление замерзания (вскрытия) и равенство уклонов.

7.73 Расчетные значения наивысших уровней воды при подвижках льда и ледоходе оценивают по кривой Q = f (H) через расходы, вычисленные по формуле

Q′_P% = (η / K_Q) Q_P%,                                               (7.52)

где η - коэффициент, учитывающий соотношение расходов воды при подвижке (ледоходе) и на пике весеннего половодья Q_P% и несовпадение по годам этих расходов одной вероятности превышения;

k_q - коэффициент, характеризующий изменение гидравлических характеристик водного потока льдом.

Значения коэффициентов η и k_q определяют методом аналогии.

7.74 Для ориентировочных расчетов наивысших уровней воды проточных озер в зоне избыточного увлажнения используют зависимость

H = β (A / Ω)^0,5,                                                 (7.53)

где H - средний многолетний весенне-летний подъем уровня воды в озере над порогом стока, см;

А - площадь водосбора озера, км²;

Ω - площадь зеркала озера, км²;

β - коэффициент, определяемый по данным наблюдений на соседних озерах с близкими соотношениями морфометрических характеристик и режимом стока из водоема.

Для Кольского полуострова и Карелии β принимают равным 20, для озер северных и центральных областей европейской территории России - 32.

Переход от среднего многолетнего подъема уровня к подъему расчетной вероятности превышения производят по кривым обеспеченности с параметрами C_v и отношением C_s / C_v, установленным также по данным наблюдений на соседних, изученных морфологически однородных озерах.

Зависимость (7.52) применима для отношения A / Ω менее 250.

В значения расчетных уровней вводят поправки на нагон DH_н и ветровое волнение DH_в, которые рассчитывают по методикам, приведенным в СНиП 2.06.04. При расчете DH_н учитывают расчетную скорость ветра, среднюю глубину водоема и расстояние пункта, для которого производят расчет, от центра тяжести зеркала водоема. Поправку DH_в определяют с учетом ветровой защищенности исследуемой береговой зоны, длины разгона волны и других факторов.

Для карстовых, периодически исчезающих озер, а также для озер с искаженным естественным режимом обязательно производство полевых исследований.

ПРИЛОЖЕНИЕ А

(рекомендуемое)

ПРИМЕРЫ РАСЧЕТА

А.1 Применение критериев Диксона для анализа резко отклоняющихся значений

Рассматривается ряд наблюдений за среднесуточными максимальными расходами воды весеннего половодья на р. Онега - д. Надпорожский Погост с периодом наблюдений 90 лет. Анализ эмпирической кривой распределения показал, что наибольшее резко отклоняющееся от остальной совокупности значение расхода воды, равное 868 м³/с, может принадлежать иному распределению. Для проверки однородности был применен критерий Диксона и на основе ранжированного ряда определены пять расчетных статистик критерия: D1_N = 0,308, D2_N = 0,311, D3_N = 0,308, D4_N = 0,384 и D5_N = 0,404. Критические значения статистик Диксона без учета асимметрии и автокорреляции при n = 90, С_s = 0 и r (1) = 0 для α = 1 % определены по номограммам [3] и соответственно равны: D1_N^* (0,0) = 0,26, D2_N^* (0,0) = 0,28, D3_N^* (0,0) = 0,29, D4_N^* (0,0) = 0,31 и D5_N^* (0,0) = 0,32. Из сравнения расчетных значений статистик с критическими следует, что D_N > D_N^* (0,0) для всех критериев Диксона. Исходя из вышесказанного гипотезу об отсутствии в ряду наблюдений резко отклоняющегося значения, принадлежащего другому распределению, отклоняют. Поэтому в случае применения «классического» критерия экстремальный расход признают неоднородным и исключают его из ряда наблюдений, если подтвердится, что эта величина имеет большую погрешность, или пересчитывают его эмпирическую обеспеченность для более продолжительного периода.

Если воспользоваться критическими значениями статистик критерия Диксона, обобщенного для асимметричных и автокоррелированных рядов при вычисленных по продолжительному ряду значениях r (1) = 0,19 и С_s = 1,13, то при сравнении расчетных статистик с критическими из номограмм [3] будут иметь место следующие неравенства:

D1_N = 0,308 < D1_N^* = 0,31 при α = 10 %;

D2_N^* = 0,28 при α = 10 % < D2_N = 0,311 < D2_N^* = 0,32 при α = 5 %;

D3_N = 0,308 < D3_N^* = 0,36 при α = 10 %;

D4_N^* = 0,36 при α = 10 % < D4_N = 0,384 < D4_N^* = 0,40 при α = 5 %;

D5_N^* = 0,37 при α = 10 % < D5_N = 0,404 < D5_N^* = 0,41 при α =5 %.

Из неравенств следует, что при α = 5 % гипотезу об «аномальном» экстремуме отклоняют по всем критериям. На этом основании можно сделать вывод, что ряд не содержит неоднородного максимального значения и для определения параметров эмпирического распределения должны быть использованы все данные.

А.2 Применение критерия Смирнова-Граббса для анализа резко отклоняющихся значений

Для анализа выбраны шесть рядов среднесуточных минимальных расходов летне-осеннего сезона в районе Горного Алтая: р. Песчаная - с. Точильное, р. Урсул - с. Онгудай, р. Чарыш - с. Усть-Кумир, р. Ануй - с. Старо-Тырышкино, р. Бухтарма - с. Печи и р. Шаравка - с. Шаравка. Период наблюдений за стоком для выбранных рядов составил от 40 до 49 лет. Значения статистик Смирнова - Граббса, вычисленных для наибольших членов этих рядов, равны: G_N1 = 3,389, G_N2 = 3,394, G_N3 = 2,739, G_N4 = =3,693, G_N5 = 3,522, G_N6 = 3,706. При сравнении расчетных значений статистик с критическими (G_N^* (0,0)) в предположении, что эмпирические ряды соответствуют нормальному распределению и не имеют статистически значимой автокорреляции, т.е. C_s = 0 и r (1) = 0, получаем, что гипотеза о наличии в рядах наблюдений максимального, резко отклоняющегося расхода может быть принята для пяти рядов из шести с вероятностью Р > 99 %.

Однако было установлено, что распределения являются асимметричными и имеет место статистически значимая автокорреляция. Анализ эмпирических распределений минимальных расходов воды, а также метеорологических стокоформирующих факторов (осадков и температуры воздуха) не подтвердил гипотезу о наличии «аномальных» величин в выбранных рядах. Поэтому для проверки гипотезы однородности были использованы критические значения статистик Смирнова-Граббса из таблиц [3], определенные с учетом асимметрии и автокорреляции. Значения коэффициентов r (1) и C_s в связи с ограниченностью выборок были определены по совокупности рядов наблюдений в однородном районе с общим объемом объединенной совокупности в 262 года. В результате получены коэффициент автокорреляции r (1) = 0,26 и коэффициент асимметрии C_s = 1,4. По индивидуальным объемам выборок и обобщенным r (1) и C_s из таблиц [3] были определены критические значения статистик Смирнова-Граббса. Сравнение расчетных значений статистик с критическими, учитывающими асимметрию и автокорреляцию, показало, что G_N < G_N^* при α >10 %, что дает основание отклонить гипотезу о резко выделяющихся максимальных значениях как маловероятную.

А.3 Анализ однородности ряда, содержащего максимальные расходы воды разного генетического происхождения

Ряд наблюдений за максимальными расходами воды р. Абавы у х. Сисени включает 21 расход воды весеннего половодья и 15 расходов дождевых паводков. Оценку однородности средних значений и дисперсий при сравнении двух генетически разнородных выборок осуществляют по критериям Стьюдента и Фишера. Вычисленные расчетные значения статистик критериев соответственно равны: t = 2,52 и F = 1,09. Критические значения статистик F* и t* определяют из таблиц [3] путем интерполяции между табличными значениями при n_x = n_y = 10 и n_x = n_y = 25 для заданного уровня значимости α = 5 %, коэффициента автокорреляции r (1) = 0,2 и коэффициента межрядной корреляции R = 0. В результате получены критические значения t* = 2,04 (для n_x = n_y = 21), t* = 2,06 (для n_x = n_y = 15) и F* = 2,31. При сравнении с расчетными значениями статистик можно сделать вывод, что ряд наблюдений не может рассматриваться как единая совокупность вследствие неоднородности средних значений, так как расчетное значение статистики Стьюдента превышает критическое в обоих случаях (n = 15 и n = 21), при этом гипотеза об однородности дисперсий не отклоняется. Поэтому расчеты необходимо осуществлять отдельно для рядов весеннего половодья и дождевых паводков.

А.4 Оценка эффективности эмпирической зависимости

Для расчетов годового стока и слоя стока весеннего половодья при отсутствии данных гидрометрических наблюдений применяют зависимости от стокоформирующих факторов. Одной из таких существующих зависимостей является уравнение для определения слоя поверхностного стока весеннего половодья Y на р. Оке - с. Половское следующего вида:

Y = 0,8 Х₁ + 0,86 Х₂ - 104, (                                       А.1)

где Х₁ = S + S_л + Х_ос,

S - максимальные запасы воды в снеге, мм;

S_л - запас воды в ледяной корке, мм;

Х_ос - осадки за период половодья, мм;

Х₂ = (L × е) / 50;

здесь L - глубина промерзания почвы, см;

е - величина осеннего увлажнения почвы, см.

Для оценки эффективности эмпирической зависимости в соответствии с 4.15 применен анализ остатков и построены графики, приведенные на рисунке А.1.

Из анализа графиков на рисунке А.1 можно сделать следующие выводы:

- с 1967 г. остатки зависят от времени и имеет место существенное систематическое завышение слоя стока половодья, вычисленного по эмпирической зависимости (рисунок А.1, а);

- наклонная полоса рассеяния на рисунке А.1, б показывает, что отклонения от полученной эмпирической зависимости носят систематический характер: отрицательные остатки соответствуют большим по величине значениям расчетных слоев стока, положительные - малым, что свидетельствует о неточном определении свободного члена в уравнении;

- изгиб полосы рассеяния на рисунке А.1, в показывает, что в уравнении необходимо учесть нелинейность зависимости Y от Х;

- из рисунка А.1, г следует, что коэффициент перед Х₂ также определен неверно.

Для уточнения вида и коэффициентов уравнения была собрана дополнительная информация, проведен анализ однофакторных зависимостей и использованы условия построения регрессионного уравнения (6.1). В результате получена следующая эмпирическая зависимость:

Y = 0,76 Х′₁ + 0,14 × 10^-5 Х₂⁴ + 13,8,                              (А.1, а)

где Х′₁ = Х₁₀ γ_п, здесь Х₁₀ - средний максимальный снегозапас в бассейне, мм, осредненный по 10 метеостанциям, для которых коэффициент корреляции снегозапасов со стоком половодья больше 0,5;

γ_п = К_п × β_п, здесь К_п - модульный коэффициент приведенных запасов влаги в почве;

β_п = sin (α′ + 10°), tg α′ = К_Н, здесь К_Н - модульный коэффициент промерзания;

Х₂ - слой стока за март, мм.

Коэффициент корреляции полученного уравнения равен 0,89. Анализ остатков показал, что полученное эмпирическое уравнение является адекватным.

а) - зависимость остатков от времени (ε = f (t)); б) - зависимость остатков от значений слоя стока, полученного по эмпирической зависимости (ε = f (Y′)); в) - зависимость остатков от первого фактора (ε = f (X₁)); г) - зависимость остатков от второго фактора (ε = f (X₂))

Рисунок A.1 - Анализ остатков эмпирической зависимости для расчета слоев половодья от метеорологических факторов

А.5 Оценка влияния хозяйственной деятельности на параметры ряда годового стока

Рассматривается ряд средних годовых расходов воды на р. Найбе у п. Быково (1951 -1977 гг.). Известно, что начиная с 1966 г. в верховьях бассейна производят вырубку лесов и осуществляют интенсивную распашку земель. Необходимо оценить статистическую однородность ряда, т.е. определить, насколько существенно сказываются отмеченные хозяйственные мероприятия на многолетних колебаниях стока. Для оценки однородности (стационарности) ряд был разбит на две части: естественные колебания до начала влияния хозяйственной деятельности (1951 - 1965 гг.) и колебания стока в условиях влияния хозяйственном деятельности (1966-1977 гг.). Для первой части (n = 15 лет) рассчитано среднее значение Q = 20,0 м³/с. дисперсия σ² = 12,9 (м³/с)² и C_v = 0,18, для второй части (n = 12 лет) - среднее значение Q = 22,3 м³/с, дисперсия σ² = 19,9 (м³/с)² и C_v = 0,20. Полученные по данным параметрам расчетные значения статистик Стьюдента и Фишера соответственно равны: F = 1,54, t = 1,43. Критические значения определены двумя способами: непосредственно по таблицам из [3] и при пересчете степеней свободы также в соответствии с [3]. Коэффициент автокорреляции, определенный по всему ряду, равен 0,2, и уровень значимости назначался в 5 %. В первом случае критические значения статистик были равны: F* = 3,66 и t* = 2,45 при n = 15 и F* = 4,06 и t* = 2,46 при п = 12 и в любом варианте больше расчетных значений, что позволяет принять гипотезу стационарности. По второму способу F* = 3,59 и t* = 2,45 и также превосходят расчетные величины этих статистик. Таким образом, из проведенного анализа стационарности можно сделать вывод о том, что наличие хозяйственной деятельности в данном случае не оказывает существенного влияния на статистическую однородность ряда, а изменение параметров распределения годового стока р. Найбы у п. Быково под влиянием хозяйственной деятельности значительно меньше изменений, происходящих в результате естественных колебаний водности. Поэтому гидрологические расчеты можно осуществлять по всему ряду наблюдений.

А.6 Использование методики совместного анализа

Применение метода группового анализа данных наблюдений иллюстрируется на примере района Приморья.

Для совместного анализа в этом районе были отобраны гидрологические посты, для которых выполнялись следующие условия:

- площадь водосборов не превышает 50000 км²;

- ряды наблюдений за максимальным стоком имеют продолжительность более 30 лет;

- пункты наблюдений относительно равномерно распределены по району;

- данные наблюдений по возможности статистически независимы друг от друга, т.е. отсутствует пространственная корреляция.

В качестве анализируемой характеристики исследуется коэффициент вариации рядов максимальных в году расходов дождевых паводков.

Предварительная разбивка районов на более мелкие подрайоны с относительно близкими значениями коэффициентов вариации производится с использованием карты-схемы пунктов наблюдений с нанесенными значениями характеристик изменчивости стока.

Используя критерий (5.13), проверяют однородность данных, объединяемых в пределах выделяемого подрайона, и оценивают возможность их совместного анализа.

Случайную составляющую ε определяют как среднюю по группе станций выборочную дисперсию моментной оценки коэффициента вариации:

;                                                 (А.2)

.                                                       (А.3)

Географическую составляющую ε определяют как разность между полной и случайной составляющими в соответствии с формулой (5.10). Полную составляющую вычисляют по формуле (5.12).

Если для выделенного подрайона географическая составляющая дисперсии оказывается меньше случайной, то совокупность рядов можно считать однородной, а объединение правомерным. На следующем шаге к однородной группе присоединяют один из ближайших постов и проверяют выполнение условия (5.13). Объединение постов в подрайон заканчивают, когда условие (5.13) перестает выполняться.

Точность расчета статистических характеристик по объединенным данным наблюдений характеризуется стандартной ошибкой ε:

,                                               (А.4)

где k - число совместно анализируемых объектов;

ε / k - стандартное отклонение средней из k оценок.

Погрешность результатов расчетов оценок определяют по формуле (5.14), а их стандартную ошибку - по формуле (5.15).

Исходя из приведенных условий для иллюстрации методики на территории Приморья были отобраны 14 постов и оценена возможность их совместного анализа. Схема расположения постов приведена на рисунке А.2, список постов представлен в таблице А.1.

Рисунок А.2 - Схема расположения гидрологических постов

Таблица А.1 - Список водомерных постов

Коэффициенты вариации рядов максимальных в году расходов дождевых паводков для этих постов приведены в таблице А.1.

В соответствии с рассматриваемой методикой на территории анализируемого района выбирают несколько гидрологических постов с относительно близкими значениями C_v и близким географическим расположением. В данном случае было отобрано пять постов: № 1, 2, 50, 52, 53. Определяют среднее значение, полную, случайную и географическую составляющие, а также дисперсию параметров для объединенной совокупности. Если в результате расчета критерий (5.13) выполняется, то объединение можно считать допустимым.

К полученной группе постов поочередно присоединяют посты, близко к ним расположенные, определяют все вышеперечисленные характеристики (таблица А.2). Результаты отображают в виде графика зависимости ε = f (k) (рисунок А.3).

Таблица А.2 - Результаты расчетов параметров для совместного анализа по группе станций

Рисунок А.3 - График зависимости дисперсии параметров объединенной совокупности от числа совместно анализируемых постов

Результаты расчета погрешностей определения коэффициента вариации приведены в таблице А.3.

Таблица А.3 - Расчет погрешностей определения коэффициентов вариации С_v

Если условие (5.13) выполняется, кривая имеет тенденцию к понижению, если условие нарушается, то следует резкое увеличение значений, а следовательно, такие посты не могут быть присоединены к общей группе (рисунок А.3, точки 9, 10).

А.7 Пример построения усеченного гамма-распределения для вычисления максимальных расходов воды малой вероятности превышения

Рассматриваются данные наблюдений за максимальным расходом воды весеннего половодья р. Белой у г. Уфы с 1878 по 1964 г. (исходные данные приведены в таблице А.4). Требуется вычислить расчетные максимальные расходы воды различной вероятности превышения в этом створе с помощью усеченного гамма-распределения.

По верхней половине ряда, расположенного в убывающем порядке, вычисляют среднее  по формуле (5.41) и статистику  по формуле (5.43). Подготовительные вычисления приведены в таблице А.5.

м³/с;                                 (А.5)

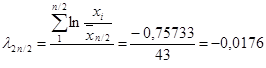.                          (A.6)

По полученному значению  = -0,0176 в соответствии с приложением Б, таблица Б.5 находят значение коэффициента изменчивости = 0,52.

Зная среднее  и определив по вычисленному значению С_v функцию φ (С_v), находим с помощью приложения Б, таблица Б.4 значение среднего :

 =  φ (С_v) = 8132 × 0,715 = 5814 м³/с.

По полученным параметрам Q = 5814 м³/с и = 0,52, используя таблицу ординат гамма-распределения, строят верхнюю часть распределения - усеченное распределение (рисунок А.4). Как следует из рисунка А.4, аналитическая кривая соответствует эмпирическим точкам.

Таблица А.4 - Максимальные расходы воды весеннего половодья X_i р. Белой у г. Уфы

Таблица А5 - Расчет параметров усеченного гамма-распределения по данным наблюдений за максимальными расходами воды р. Белой у г. Уфы

Гамма-распределение: 1 - полное; 2 - усеченное

Рисунок А.4 - Совмещенные кривые распределения вероятностей превышения максимальных расходов весеннего половодья р. Белой у г. Уфы (1878 - 1964 гг.)

А.8 Пример приведения к многолетнему периоду ряда и параметров распределения годового стока р. Сьежа - д. Стан по методике, основанной на одновременном использовании и на различных временных этапах нескольких пунктов-аналогов

По ряду р. Сьежа - д. Стан (площадь водосбора равна 407 км²) имеются наблюдения за 1971 - 1992 гг. (n = 22 года). Для приведения ряда к многолетнему периоду выбраны семь предполагаемых аналогов, имеющих различные периоды наблюдений. Так как многочисленные практические расчеты показали, что число одновременно используемых статистически значимых и устойчивых уравнений не превышает трех, перебор расчетных уравнений регрессии, отвечающих требованиям условий (6.1), начинают с одновременного использования трех аналогов. Индексы при значениях q соответствуют номеру аналога согласно таблице А.6. Сведения о предполагаемых аналогах приведены в таблице А.6.

Таблица А.6

Согласно условиям (6.1) не прошло ни одного уравнения с одновременно используемыми тремя аналогами. С использованием двух аналогов рассчитаны два уравнения, отвечающие этому условию. В данном случае R_кр назначено равным 0,60. По уравнению q = -1,08 + 0,92 q₁ + 0,51 q₃ с R = 0,96 и со средней квадратической погрешностью расчета погодичных значений модулей годового стока, равной 0,85 л/с × км², восстановлено 17 членов ряда (1954 - 1970 гг.). Объем эквивалентно-независимой информации для среднего равен 14 лет, для дисперсии - 12,3 года. По уравнению q = -1,17 + 0,78 q₃+ 0,70 q₄ с R = 0,93 и со средней квадратической погрешностью расчета погодичных значений модулей годового стока, равной 1,08 л/с × км², восстановлено 18 членов ряда (1935 - 1939, 1941 - 1953 гг.). Объем эквивалентно-независимой информации для среднего равен 13,1 года, для дисперсии - 10,6 лет.

При восстановлении погодичных значений модулей стока использованы уравнения с одним аналогом соответственно с меньшим коэффициентом корреляции, чем предыдущие. По уравнению q = -0,59 + 1,30 q₃ с коффициентом корреляции, равным 0,90, и со средней квадратической погрешностью 1,26 л/с × км² восстановлен модуль годового стока за 1940 год, что соответствует объему эквивалентно-независимой информации по среднему - 0,8 года, а по дисперсии - 0,6 года. По уравнению q = 1,19 + 1,15 q₄ с коэффициентом корреляции 0,84 и со средней квадратической погрешностью 1,58 л/с × км² восстановлен сток за 1933, 1934 годы, что соответствует объему эквивалентно-независимой информации соответственно для среднего значения и дисперсии 1,3 и 1,0 лет. По уравнению q = -2,08 + 0,59 q₅ + 0,61 q₇ с коэффициентом корреляции 0,78 и со средней квадратической погрешностью 1,85 л/с × км² восстановлены модули годового стока за 42 года (1891 - 1932 гг.). Объем независимо-эквивалентной информации для среднего значения равен 12,6 лет, а для дисперсии 6,7 лет. По уравнению q = -0,44 + 0,88 q₅ с коэффициентом корреляции 0,68 и со средней квадратической погрешностью 2,15 л/с × км² восстановлены модули годового стока за 1882 - 1890 годы. Объем эквивалентно-независимой информации составил соответственно 2,9 и 1,4 года. Сведения об уравнениях регрессии и их параметрах приведены в таблице А.7.

Таким образом, восстановлены модули годового стока р. Сьежа - д. Стан за период 1882- 1970 годы. Вместе с наблюденными данными имеем период 111 лет, что соответствует объему эквивалентно-независимой информации для среднего значения 66,7 лет, а для дисперсии - 54,6 лет. По ряду, приведенному к многолетнему периоду (таблица А.8), рассчитывают параметры распределения согласно разделу 5.

Таблица А.7- Сведения об уравнениях, по которым восстановлены значения стока р. Сьежа д. Стан

Таблица А.8 - Восстановленные и наблюденные значения модулей годового стока (q, л/с ×км²) р. Сьежа - д. Стан

А.9 Пример восстановления гидрологического ряда с учетом независимой случайной составляющей

В качестве исходной информации взяты среднегодовые расходы воды р. Днепр у г. Орша за 1882 - 1947 гг. (таблица А.9). Восстановление гидрологического ряда производят по уравнению регрессии с учетом отклонений от линии регрессии по нормальному закону распределения.

Для примера разделим исходный ряд на две части. Предположим, что имеются данные за 1882 - 1911 гг. (у_i) и требуется восстановить значения расходов за последующий период с 1912 по 1947 г.

В качестве аналога выбран ряд среднегодовых расходов воды р. Оки у г. Калуги (x_i), коэффициент корреляции r_xy = 0,835. Определяют параметры этих рядов за период наблюдений с 1882 по 1911 г.:

р. Днепр:  = 127 м³/с; σ_у = 33,7: С_vy = 0,27;

р. Ока:  = 307 м³/с; σ_x = 78,9; С_vx = 0,26.

С учетом этих параметров уравнение регрессии примет вид:

                                      (A.7)

у_iрегр = 0,36 x_i + 17,6.                                                 (A.8)

Используя уравнение (А.8) и значения расходов воды реки-аналога x_i за восстанавливаемый период, получаем значения у_iрегр (таблица А.9, столбец 7).

Восстанавливают значения y_i по формуле (А.8). т.е. при условии, что колебания независимой составляющей подчинены нормальному распределению.

Для данного примера в рассчитанные по уравнению (А.8) погодичные значения у_i за период с 1912 по 1947 г. вносят независимую случайную составляющую, определяемую по выражению

.                                     (А.9)

Откорректированные значения у_i определяют по формуле

.                                           (A.10)

Таблицa A.9 - Восстановление гидрологического ряда среднегодовых расходов воды р. Днепра у г. Орши (у_i) с использованием данных о стоке воды реки-аналога (р. Ока - г. Калуга, x_i) и с учетом нормальной случайной составляющей

Расчет производят в следующем порядке (таблица А.9):

1) выписывают из таблицы равномерно распределенных случайных чисел (таблица А.10) 30-членный ряд четырехзначных случайных чисел ξ_i. От значений ξ_i переходят к значениям обеспеченностей Р_i = ξ_i / 100 (таблица А.9, столбец 8);

2) переход от обеспеченностей Р_i к величине отклонения φ_pi осуществляют с помощью стандартного нормативного или гамма-распределения [5]:

3) полученное значение φ_pi относят к стандартному отклонению σ_у, т.е. умножают на σ_у = 18,5 (таблица А.9, столбец 10);

4) суммируя погодичные значения у_iрегр (таблица А.9, столбец 7) и рассчитанные по формуле (А.9) отклонения φ_pi, определяют по формуле (А.10) ряд значений у_i восстановленных с учетом независимой случайной составляющей, распределенной по нормальному закону.

Таблица А.10 - Равномерно распределенные случайные числа ξ_i

А.10 Пример восстановления погодичных значений стока с учетом материалов кратковременных наблюдений

В основе данного способа восстановления погодичных значений стока лежит пространственная связанность рассматриваемой характеристики стока, которая может быть выражена в виде пространственной корреляционной функции (ПКФ). Чем медленнее затухает ПКФ, тем эффективнее будет данный способ восстановления погодичных значений стока. Предлагаемую схему восстановления погодичных значений стока рекомендуется использовать не только для кратковременных наблюдений за речным стоком от одного до пяти лет, но и для более продолжительных наблюдений (см. 6.8).

Рассматривается использование рекомендуемой методики на примере восстановления годового стока р. Сьюча - д. Каменка, имеющей наблюдения с 1972 по 1976 год. Для восстановления привлекались реки-аналоги в исследуемом районе, наблюдения по которым были приведены к многолетнему периоду согласно 6.7. При восстановлении стока использовались уравнения, отвечающие условиям (6.1).

В каждом году использовалось число уравнений от одного до пяти (по ряду р. Сьюча - д. Каменка имелось 5 лет наблюдений). В некоторые годы из-за невыполнения условий (6.1) восстановление значений стока не произведено.

В таблице А.11 представлены восстановленные значения модулей годового стока q, л/с × км², N - число уравнений, используемых при восстановлении модулей годового стока, средние из рассчитанных по уравнениям регрессии коэффициенты корреляции R_ср, средние значения стандартной погрешности для каждого года σ_ср, а также наименьшие σ_мин и наибольшие σ_макс средние квадратические погрешности восстановления погодичных модулей стока.

Таблица А.11 - Результаты восстановления модулей годового стока р. Сьюча - д. Каменка с учетом кратковременных (1972 - 1976 гг.) наблюдений

По восстановленным данным рассчитывают параметры распределения ряда (среднее значение, коэффициент вариации). Отношение коэффициента асимметрии к коэффициенту вариации и коэффициент автокорреляции определяют по групповой оценке согласно 5.7.

А.11 Пример восстановления нормы и квантилей распределения годового стока с учетом кратковременных наблюдений

Рассмотрим пример приведения годового стока р. Пышма - свх. Асбестовский, площадь водосбора которого равна 1480 км² и имеются наблюдения за 1962 год. При восстановлении значений годового стока за все возможные годы использована методика согласно 6.8 - 6.14.

Определяют норму и квантили распределения по погодичному уравнению регрессии, которое рассчитывают по рекам-аналогам за 1962 год. Наблюдения за 1962 год в исследуемом районе имелись по шести пунктам (таблица А.12).

Предварительно по этим пунктам годовой сток был приведен к многолетнему периоду. По полученным параметрам распределения рассчитаны значения стока заданной обеспеченности (P = 10 %, 25 %, 75 %, 90 %, 95 %,99 %). Имея значения годового стока по этим пунктам за 1962 год и среднее многолетнее значение стока, приведенные к многолетнему периоду, рассчитывают уравнение регрессии: у = 0,753 х + 0,510, коэффициент парной корреляции этого уравнения - 0,835, его средняя квадратическая погрешность - 0,135.

При значении модуля годового стока р. Пышма - свх. Асбестовский за 1962 год, равном 3,54 л/с × км², по этому уравнению определяют среднее многолетнее значение, равное 3,18 л/с × км². Абсолютное значение средней квадратической погрешности, определенное по формуле , равно 0,45 л/с × км², относительное - 14,2 %.

Аналогично, используя уравнения связи значений годового стока за 1962 год с расчетными значениями стока заданной обеспеченности рек-аналогов, определяют расчетные квантили для р. Пышма - свх. Асбестовский. В таблице А.13 для различных значений Р_% приведены уравнения регрессии зависимостей Y_p = f (x_i), расчетные значения квантилей Y_p их абсолютные σ_{YP абс} и относительные σ_YP погрешности.

Таблица А.12 - Сведения о пунктах-аналогах

Таблица А.13 - Расчетные значения квантилей распределения х_р р. Пышма - свх. Асбестовский (х₁₉₆₂ = 3,54 л/с × км²,  3,18 л/с × км²)

А.12 Расчет годового стока в виде суммы сезонных составляющих по стокоформирующим факторам при отсутствии данных гидрометрических наблюдений

Выбрано 45 водосборов в районе Северного края, с широким диапазоном площадей от 179 до 220000 км² и с высотами от 68 до 290 м. При этом пять водосборов оставлены для проверки методики на независимом материале. Для всех выбранных водосборов определены даты начала сезонов, слои стока за сезоны и осуществлено обобщение предполагаемых стокоформирующих факторов по водосбору и за каждый сезон. Для каждого водосбора находились регрессионные зависимости для определения слоев стока за каждый сезон. Определялось наиболее эффективное уравнение для каждого сезона и водосбора и результаты обобщались по территории для установления общего уравнения. В результате расчетов были получены следующие уравнения с общей структурой для территории Северного края:

а) сезон весеннего половодья:

Y = b₁ X_тв + b₂ X_вес + b₃ X′_л-о + b₀

с R_ср = 0,75,                                                        (А.11)

где X_тв - твердые осадки;

Х_вес - осадки за половодье;

X′_л-о - осадки за предыдущий летне-осенний сезон;

R_ср - средний коэффициент множественной корреляции для всех водосборов рассматриваемого района

или

Y = а₁ S + а₂ X_вес + а₃ U_осен + а₀

с R_ср = 0,82,                                                          (А.12)

где S - максимальные снегозапасы;

U_осен - предзимнее увлажнение почвы;

а₀, а₁, а₂, а₃ - регрессионные коэффициенты;

б) летне-осенний сезон:

Y = b₁  + b₂  D + b₀

с R_ср = 0,77,                                                             (A.13)

где D - средний дефицит влажности за летне-осенний сезон;

в) период зимней межени:

Y = b₁  + b₂ n + b₃ X_л-о T_зим + b₀

с R_ср = 0,60,                                                          (А.14)

где п - продолжительность зимней межени (в днях);

X_л-о - осадки за текущий летне-осенний сезон;

Т_зим - средняя температура воздуха за зимнюю межень;

b₀, b₁, b₂, b₃ - регрессионные коэффициенты.

Даты начала и окончания однородных сезонов, их продолжительность, коэффициенты уравнений были обобщены по территории различными способами: построение изолиний, осреднение в однородных районах и зависимости с определяющими территориальными факторами, например зависимости продолжительности половодья от площади водосбора, полученные для трех однородных районов на территории. В результате интерполяции и экстраполяции дат сезонов и коэффициентов уравнений на поверочные водосборы были рассчитаны слои стока за каждый сезон и год в виде суммы сезонных слоев. Пример сравнения рассчитанных и фактических слоев сезонного и годового стоков для р. Вага - с. Усть-Сюма показан на рисунке А.5. Как видно на рисунке, рассчитанные слои стока практически полностью отражают динамику колебаний наблюденного стока, имея наибольшие совпадения для годового стока, как интегральной характеристики и наименьшие - для сезона зимней межени. В результате независимой оценки по пяти поверочным водосборам были определены относительные стандартные погрешности: Dε = 24 % - 48 % для периода весеннего половодья, Dε = 20 % - 24 % для летне-осеннего сезона, Dε = 13 % - 33 % для сезона зимней межени и Dε = 8 % - 14 % для годового стока.

а) - весеннее половодье; б) - летне-осенний сезон; в) - сезон зимней межени; г) - годовой сток

Рисунок А.5 - Сравнение фактических (1) и рассчитанных (2) слоев стока р. Вага - с. Усть-Сюма

А.13 Пример расчета внутригодового распределения стока методом компоновки для лет маловодной и очень маловодной градаций водности

Расчет внутригодового распределения стока методом компоновки производят в соответствии с требованиями, изложенными в разделе 5. Ниже приведен пример расчета для р. Унжа - г. Макарьев за расчетный 67-летний период стоковых измерений для лет маловодной и очень маловодной градаций водности. В таблицах А.14 - А. A.18 приведены результаты расчета, характерные для отдельных его этапов.

В таблице А.14 даны результаты расчета сумм месячного стока воды ΣQ_iмес за водохозяйственный год, лимитирующие период, сезон и месяц для конкретных маловодных и очень маловодных лет.

В таблице А.15 приведены результаты расчета абсолютного (в объемных единицах) и относительного (в % объема стока за ВГ) распределения речного стока по водохозяйственным периодам и сезонам в годы маловодной и очень маловодной градаций (групп) водности.

В таблице А. A.16 приведены результаты расчета внутрисезонного распределения речного стока ΣQ_iмес по месяцам Q_iмес на примере лимитирующего сезона. Аналогично выполняют расчеты внутрисезонного распределения стока для других водохозяйственных периодов, в частности для нелимитирующих периода (НП) и сезона (НС). Результаты расчета внутрисезонного относительного (% сезонного) распределения месячного речного стока для маловодной группы водности сезонов приведены в таблице А.17.

В таблице А.18 приведены результаты расчета абсолютного (в 10³ × м³) и относительного (в % годового) внутригодового распределения месячного и сезонного стоков для маловодного (75 %-ной вероятности превышения) и для очень маловодного (95 %-ной обеспеченности) водохозяйственных лет. В основу расчета положены относительные (% объема стока за ВГ) данные о межсезонном (таблица А.15) и внутрисезонном распределениях стока (данные таблиц А.16 и А.17), а также аналогичные данные для НП и НС и для других градаций водности, в частности для группы очень маловодных лет. Этот расчет выполнен умножением относительных значений месячного стока, выраженных в процентах объема стока соответствующего сезона (таблица А.14), на долю стока данного сезона в годовом (таблица А.15).

Таблица А.14 - Расчет сумм месячного стока воды (ΣQ_iмес) за водохозяйственный год, лимитирующие период, сезон и месяц для конкретных маловодных и очень маловодных лет

Таблица А.15 - Расчет абсолютного (в объемных единицах) и относительного (% объема стока за ВГ) межсезонного распределения речного стока в годы маловодной и очень маловодной групп лет

Таблица А.16 - Расчет внутрисезонного распределения речного стока ΣQ_iмес по месяцам Q_iмес на примере лимитирующего сезона

Таблица А.17 - Внутрисезонное относительное (% сезонного) распределение месячного речного стока для маловодной группы водности сезонов

Таблица А.18 - Расчетное распределение стока по месяцам и сезонам года (% годового и м³/с) для маловодного (75 %-ной обеспеченности) и очень маловодного (95 %-ной обеспеченности) периодов водохозяйственных лет

А.14 Расчет максимального заторного уровня воды

Необходимо произвести расчет максимального заторного уровня воды 1 %-ной вероятности превышения для р. Холодной - с. Новое (многолетние гидрометрические наблюдения не производились).

Исходные данные: в ходе полевых исследований установлено, что заторы льда образуются в хвосте сохраняющихся до весны зажоров; наибольший расход весеннего половодья 1 %-ной вероятности превышения, рассчитанный по формулам раздела 7 при отсутствии данных наблюдений, равен 1800 м³/с. На ближайших реках-аналогах отношение Q_з,1% к Q_1% составляет 0,65. Координаты кривых Q = f (H), B = f (H), h = f (H), и I = f (H), определенные путем промеров глубин, нивелирования береговых склонов и продольного уклона водной поверхности с последующим расчетом по формуле Шези, приведены ниже:

H, см ... 500    600    700    800    900

Q, м³/с ...    114    399    788    1180  1800

В, м ...   144    160    176    192    208

h, м ...    2,8     3,4     4,0     4,7     5,3

I, % ...    0,00001 0,00005 0,00013 0,00024 0,00034.

По данным реки-аналога вычисляют значение затороформирующего расхода:

Q_з,1% = 0,65 × 1800 = 1170 м³/с.

Значению Q_з,1% = 1170 м³/с соответствуют следующие значения уровня, ширины реки, глубины и уклона водной поверхности:

H_Qз = 800 см,

В_Qз = 192 м,

h_Qз =4,7 м,

I_Qз = 0,00024.

Заторный максимум уровня воды H_з,р% рассчитывают по формуле (6.51) при DВ / В_Qз = 0:

H_з,р% = (μ  -1) h_Qз,р% + H_Qз,р% = (22,2 × 0,00024^0,3 - 1) × 470 + 800 = 1186 см,

где μ принимают по таблице 7.5.

Рассчитанному значению уровня соответствует ширина реки, равная 265 м. Тогда при DВ / В_Qз = 0,38 получим уточненное значение H_з,р%, т.е.

H_з,р% = (15,2 × 0,00024^0,3 - 1) × 470 + 800 = 916 см.

Далее расчет ведут методом последовательного приближения до тех пор, пока точка с координатами заданного В и вычисленного H_з,р% не попадет на кривую B = f (H), что имеет место в рассматриваемом случае при B = 230 м и DВ / В_Qз = 0,20:

H_з,р% = (18,2 × 0, 00024^0,3 - 1) × 470 + 800 = 1031 см.

А.15 Расчет наивысшего уровня воды в озере

Необходимо рассчитать наивысший уровень воды озера Глубокое в восточной его части повторяемостью один раз в 25 лет. Озеро находится на севере европейской территории России (данные наблюдений отсутствуют).

Исходные данные: плошадь водосбора озера 58,1 км², площадь зеркала 6,5 км². Из озера вытекает ручей Быстрый. Порог стока имеет отметку 2,65 м Балтийской системы. Объем озера в бессточный период относительно постоянен. Ветер над озером преимущественно западного направления. Максимальная скорость ветра - 25 м/с. Озеро вытянуто с юга на север и имеет длину 5 км при ширине 1 км.

Данные расчета элементов водного баланса озера показывают, что осадки, выпадающие на поверхность озера в течение гидрологического года, не превышают 15 % приходной части баланса и равны испарению, поэтому уровенный режим озера находится в прямой зависимости от весеннего притока воды в него. В связи с этим для расчета среднего многолетнего подъема уровня DH используют формулу (7.53) при β = 32:

DH = β (A / Ω)^0,5 = 32 (58,1 / 6,5)^0,5 = 96 см.

Поскольку по данным наблюдений на ближайших озерах-аналогах коэффициент изменчивости H равен 1, то при С_s = 0 ордината кривой распределения, соответствующая 4 %, у = 2,77. Поправка на волнение и нагон H_в.н равна 0,20 м. В этом случае

H_4% = (у × C_v + 1,0) H + Н_в.н + Н_п.ст = (2,77 × 1 + 1,0) × 0,96 + 0,20+ 2,65 = 6,46 м Балтийской системы.

ПРИЛОЖЕНИЕ Б

(обязательное)

ТАБЛИЦЫ ЗНАЧЕНИЙ ПАРАМЕТРОВ РАСЧЕТНЫХ ФОРМУЛ

Таблица Б.1 - Значения коэффициентов a и b в формулах (5.6), (5.7)

Несмещенную оценку коэффициента автокорреляции между смежными членами ряда r (1) определяют по формуле

r (1) = -0,01 + 0,98  (1) - 0,06  (1)² + (l,66 + 6,46  (1) + 5,69  (l)²) ,        (Б.1)

где смещенную оценку определяют по формуле

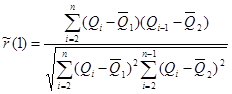,                                             (Б.2)

здесь 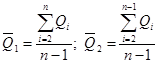                                                .                                           (Б.3)

Таблица Б.2 - Коэффициенты корреляции между оценками параметров распределения

Таблица Б.3 - Доверительные интервалы для эмпирической вероятности превышения

Таблица Б.4 - Значения функции φ (С_v) для вычисления среднего х₀ усеченного гамма-распределения

Таблица Б.5 - Значения зависимости C_v = f (λ_2n/₂) для вычисления коэффициента вариации C_v усеченного гамма-распределения

Таблица Б.6 - Значения Е_P% в формуле (5.44)

Таблица Б.7 - Условия применения расчетных формул по определению максимального расхода воды дождевого паводка заданной вероятности превышения

Таблица Б.8 - Гидравлические параметры, характеризующие состояние и шероховатость русла водотока

Таблица Б.9 - Коэффициент m_cк