РОССИЙСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО
ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ «ЕЭС РОССИИ»
_________
ДЕПАРТАМЕНТ
СТРАТЕГИИ РАЗВИТИЯ
И НАУЧНО-ТЕХНИЧЕСКОЙ ПОЛИТИКИ
МЕТОДИКА
ОПРЕДЕЛЕНИЯ ОБОБЩЕННЫХ МЕТРОЛОГИЧЕСКИХ
ХАРАКТЕРИСТИК ИЗМЕРИТЕЛЬНЫХ КАНАЛОВ
ИИС И АСУ ТП
ПО МЕТРОЛОГИЧЕСКИМ ХАРАКТЕРИСТИКАМ
АГРЕГАТНЫХ СРЕДСТВ ИЗМЕРЕНИЙ
РД 153-34.0-11.201-97
ОРГРЭС
Москва 1999
РОССИЙСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ «ЕЭС РОССИИ»
________
ДЕПАРТАМЕНТ СТРАТЕГИИ РАЗВИТИЯ И НАУЧНО-ТЕХНИЧЕСКОЙ ПОЛИТИКИ
МЕТОДИКА
ОПРЕДЕЛЕНИЯ ОБОБЩЕННЫХ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
ИЗМЕРИТЕЛЬНЫХ КАНАЛОВ ИИС И АСУ ТП ПО МЕТРОЛОГИЧЕСКИМ
ХАРАКТЕРИСТИКАМ АГРЕГАТНЫХ СРЕДСТВ ИЗМЕРЕНИЙ
РД 153-34.0-11.201-97
|
СЛУЖБА ПЕРЕДОВОГО ОПЫТА ОРГРЭС Москва 1999 |
Разработано Открытым акционерным обществом «Фирма по наладке, совершенствованию технологии и эксплуатации электростанций и сетей ОРГРЭС»
Исполнители А.Г. АЖИКИН, В.И. ОСИПОВА, Л.В. СОЛОВЬЕВА
Утверждено Департаментом стратегии развития и научно-технической политики РАО «ЕЭС России» 19.08.97 г.
Первый заместитель начальника А.П. БЕРСЕНЕВ
|
МЕТОДИКА ОПРЕДЕЛЕНИЯ ОБОБЩЕННЫХ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ИЗМЕРИТЕЛЬНЫХ КАНАЛОВ ИИС И АСУ ТП ПО МЕТРОЛОГИЧЕСКИМ ХАРАКТЕРИСТИКАМ АГРЕГАТНЫХ СРЕДСТВ ИЗМЕРЕНИЙ |
РД 153-34.0-11.201-97 |
Вводится в действие
с 01.02.99 г.
Настоящая Методика устанавливает методы расчета обобщенных метрологических характеристик измерительных каналов (ИК) информационно-измерительных систем (ИИС) и АСУ ТП по нормируемым в соответствии с ГОСТ 8.009-84 метрологическим характеристикам агрегатных средств измерений (АСИ), входящих в состав ИК.
Методика предназначена для определения при проектировании ИИС и АСУ ТП обобщенных метрологических характеристик ИК, обеспечивающих измерение параметров технологического процесса с погрешностями, не превышающими установленных норм точности измерений, и расчетной оценки суммарной погрешности ИК ИИС и АСУ ТП, эксплуатируемых на энергопредприятиях, для реальных условий эксплуатации.
Обобщенные метрологические характеристики ИК - метрологические характеристики (математическое ожидание, среднее квадратическое отклонение суммарной погрешности, нижняя и верхняя границы интервала, в котором с вероятностью Р находится суммарная погрешность), определенные для группы каналов. Они должны определяться для стационарного режима работы энергооборудования, для которого установлены нормы точности измерений параметров технологического процесса. В этом режиме работы энергооборудования параметры технологического процесса являются стационарными величинами, поэтому в Методике не рассматривается влияние динамических погрешностей АСИ на суммарную погрешность ИК ИИС и АСУ ТП.
С вводом в действие настоящей Методики утрачивает силу «Методика определения обобщенных метрологических характеристик измерительных каналов ИИС и АСУ ТП по метрологическим характеристикам агрегатных средств измерений: МТ 34-70-038-87» (М: СПО Союзтехэнерго, 1987).
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. В состав ИК входят все средства измерения и линии связи, начиная от первичного измерительного преобразователя до средства представления информации включительно.
математическое ожидание М[Dξ] и среднее квадратическое отклонение s[Dξ] суммарной погрешности ИК для реальных условий эксплуатации;
нижнюю Dикн и верхнюю Dикв границы интервала, в котором с вероятностью Р находится суммарная погрешность ИК.
1.3. Для расчета обобщенных метрологических характеристик следует использовать один из трех методов в зависимости от задач измерений и исходной информации - нормированных в нормативной документации метрологических характеристик средств измерений.
При расчете обобщенных метрологических характеристик ИК следует учитывать в качестве составляющей суммарной погрешности ИК температуры с термоэлектрическими термометрами погрешность от влияния линии связи. Во всех остальных случаях влияние линии связи на погрешность ИК не учитывается вследствие того, что возникающая погрешность будет несоизмеримо мала по сравнению с погрешностями АСИ, входящих в состав ИК.
Первый метод включает в себя определение статических моментов составляющих погрешности ИК и позволяет рассчитывать характеристики погрешности по п. 1.2.
Первый метод расчета используется при нормировании в НД на АСИ (технических условиях, технических описаниях и инструкциях по эксплуатации) раздельно систематической, случайной составляющих основной погрешности, вариации и функций влияния на эти составляющие погрешности.
Второй метод позволяет рассчитать Dикн и Dикв и применяется в том случае, когда в НД на АСИ нормируется основная погрешность и наибольшие допустимые изменения ее или дополнительные погрешности, вызванные изменением влияющих величин.
Если в НД на АСИ нормированы раздельно предел допускаемой основной погрешности и предел допускаемой вариации, то в соответствии с методическим материалом по применению ГОСТ 8.009-84 вариация входит составной частью в предел допускаемой основной погрешности и при расчете суммарной погрешности ИК вторым методом отдельно влияние вариации не учитывается.
Третий метод расчета используется при нормировании в НД на АСИ раздельно систематической, случайной составляющих основной погрешности (причем случайная составляющая основной погрешности является существенной величиной), вариации и функций влияния на эти составляющие погрешности и позволяет рассчитывать характеристики погрешности по п. 1.2.
2. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ
МЕТРОЛОГИЧЕСКИХ
ХАРАКТЕРИСТИК ИК ИИС И АСУ ТП
нормируемые метрологические характеристики АСИ:
предел допускаемой систематической составляющей основной погрешности АСИ - Dios;
предел допускаемого значения среднего квадратического отклонения случайной составляющей основной погрешности АСИ - s[Dio];
предел допускаемой вариации АСИ при нормальных условиях - Hio;
номинальная цена единицы наименьшего разряда кода цифрового измерительного прибора (аналого-цифрового измерительного преобразователя - µ);
номинальная функция влияния на систематическую составляющую погрешности АСИ - ψsi(ξj);
номинальная функция влияния на среднее квадратическое отклонение случайной составляющей погрешности АСИ - ψoi(ξj);
номинальная функция влияния на вариацию АСИ - ψнi(ξj);
характеристики влияющих величин ξj;
математическое ожидание влияющих величин - M[ξj];
наибольшие и наименьшие значения влияющих величин, соответствующие реальным условиям эксплуатации ξsj ξнj.
2.2. Для расчета обобщенных метрологических характеристик ИК для реальных условий эксплуатации вторым методом необходимо иметь следующие исходные данные:
нормируемые метрологические характеристики АСИ:
предел допускаемого значения основной относительной погрешности АСИ - δio %;
наибольшие допускаемые изменения основной погрешности АСИ, вызываемые изменением влияющих величин - ξiн(ξi) %;
дополнительные погрешности, вызываемые изменением влияющих величин - δcij %;
характеристики влияющих величин ξi;
наименьшие и наибольшие значения влияющих величин, соответствующие реальным условиям эксплуатации - ξнj, ξsj;
математическое ожидание влияющих величин - М[ξj].
2.3. Для расчета обобщенных метрологических характеристик ИК для реальных условий эксплуатации третьим методом необходимо иметь исходные данные в соответствии с п. 2.1.
3. РАСЧЕТ ОБОБЩЕННЫХ
МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
ИК ИИС И АСУ ТП ДЛЯ РЕАЛЬНЫХ УСЛОВИЙ ЭКСПЛУАТАЦИИ
3.1. Первый метод расчета
3.1.1. Математическое ожидание суммарной
погрешности ИК для реальных условий эксплуатации ![]() определяется по формуле
определяется по формуле
где М[Dξi] - математическое ожидание погрешности i-гo АСИ, входящего в состав ИК, для реальных условий эксплуатации;
n - количество АСИ, входящих в состав ИК.
Математическое ожидание погрешности i-гo АСИ вычисляется по формуле
![]() (2)
(2)
где М[Dios] - математическое ожидание систематической составляющей основной погрешности i-гo АСИ;
М[ψsi(ξj)] - математическое ожидание функции влияния j-й влияющей величины на систематическую составляющую погрешности i-гo АСИ.
Если для АСИ нормирован симметричный предел Dios допускаемого значения систематической составляющей основной погрешности без указания М[Dios], то для расчетов характеристик погрешности вводится предположение, что М[Dios] = 0.
Для линейных функций влияния:
ψsi(ξj) = Ksij · (ξj - ξoj), (3)
где Ksij - номинальный коэффициент влияния j-й влияющей величины на систематическую составляющую погрешности i-го АСИ;
ξj - значение j-й влияющей величины;
ξoj - нормальное значение j-й влияющей величины.
Математическое ожидание функции влияния j-й влияющей величины на систематическую составляющую погрешности i-го АСИ определяется по формуле
М|ψsi(ξj)| = Ksij · (M|ξj| - ξoj). (4)
Для ступенчатых функций влияния:
ψsi(ξj) = Ksij · Li(ξj), (5)
Математическое ожидание функции влияния j-й влияющей величины на систематическую составляющую погрешности i-гo АСИ определяется по формуле
М[ψsi(ξj)] = 0 (7)
при ξj ≠ ξoj.
При проведении расчетно-экспериментальным методом оценки обобщенных метрологических характеристик ИК эксплуатируемых ИИС и АСУ ТП измеряются влияющие величины в местах установки АСИ. Измерение влияющих величин осуществляется в зимний и летний периоды, так как в это время влияющие величины принимают экстремальные значения, вызывающие наибольшие изменения метрологических характеристик ИК.
Затем вычисляется математическое ожидание влияющей величины по формуле
где i - количество измерений j-й влияющей величины (должно быть не менее 40 в каждый период), i = 1 ÷ k.
При проектировании ИИС и АСУ ТП для j-й влияющей величины известны только ее наименьшее ξнj и наибольшее ξsj значения, соответствующие реальным условиям эксплуатации, и если нет оснований выделить области предпочтительных значений влияющей величины, то вводится предположение, что
М[ξj] = 0,5 · (ξнj + ξsj). (9)
3.1.2. Дисперсия суммарной погрешности ИК для реальных условий эксплуатации D[Dξ] вычисляется по формуле
где D[Dξi] - дисперсия суммарной погрешности i-гo АСИ для реальных условий эксплуатации.
Суммирование осуществляется для n АСИ, входящих в состав ИК.
Дисперсия суммарной погрешности i-гo АСИ для реальных условий эксплуатации определяется по формуле
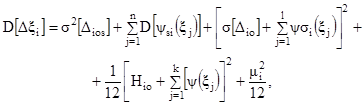 (11)
(11)
где s[Dios] - среднее квадратическое отклонение систематической составляющей основной погрешности i-ro АСИ;
D[ψsi(ξj)] - дисперсия функции влияния j-й влияющей величины на систематическую составляющую погрешности i-гo АСИ.
Для аналоговых АСИ µi = 0.
Если для АСИ нормирован предел Dios систематической составляющей основной погрешности без указания значения s[Dios] и нет оснований предполагать несимметричность и полимодальность распределения указанной погрешности, то для расчета погрешности допускается пользоваться предположением, что
![]() (12)
(12)
Для линейных функций влияния дисперсия вычисляется по формуле
![]() (13)
(13)
Для ступенчатых функций влияния дисперсия вычисляется по формуле
![]() (14)
(14)
При проведении оценки обобщенных метрологических характеристик ИК эксплуатируемых ИИС и АСУ ТП оценка среднего квадратического отклонения j-й влияющей величины определяется по формуле
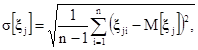 (15)
(15)
где n - количество измерений j-й влияющей величины;
ξji - измеренное значение j-й влияющей величины;
М[ξj] - определяется по формуле (8).
При проектировании ИИС и АСУ ТП, если нет оснований выделять области предпочтительных значений влияющей величины в границах ξнj и ξвj, для расчетов метрологических характеристик ИК вводится предположение, что
3.1.3. Характеристики погрешности ИК ИИС и АСУ ТП для реальных условий эксплуатации:
нижняя и верхняя границы интервала, в котором с вероятностью P находится погрешность ИК, для реальных условий эксплуатации определяются по формулам:
Dикн = М[Dξ] - Kн · s[Dξ]; (17)
Dикs = М[Dξ] + Kн · s[Dξ]; (18)
где М[Dξ] определяется по формуле (1), a
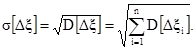 (19)
(19)
Значение коэффициента Kн зависит от вида закона распределения погрешности и выбранного значения доверительной вероятности Р. Для технических измерений обычно принимают значение доверительной вероятности Рi равным 0,95.
При определении суммарной погрешности ИК, если производится суммирование большого количества независимых составляющих погрешности (n > 4), распределенных по различным законам при отсутствии явного доминирования одной или нескольких погрешностей над другими, в соответствии с центральной предельной теоремой теории вероятности допускается, что распределение суммарной погрешности приближается к нормальному.
В этом случае Kн = 1,96 при P = 0,95.
3.2. Второй метод расчета
3.2.1. Если для АСИ, входящих в состав ИК, нормированы метрологические характеристики без разделения их на систематическую и случайную составляющие, то принимается допущение, что погрешности АСИ являются случайными величинами, распределенными по закону равномерной плотности, т.е. внутри интервала, ограниченного предельными значениями погрешностей, все значения погрешностей равновероятны: таким образом, математическое ожидание погрешности АСИ М[δξi] = 0, а следовательно, и математическое ожидание суммарной погрешности ИК М[δξ] = 0.
где n - количество АСИ, входящих в состав ИК;
s[δξi] - среднее квадратическое отклонение случайной погрешности i-го АСИ, %.
3.2.3. Среднее квадратическое отклонение случайной погрешности i-го АСИ определяется по формуле
где s[δio] - среднее квадратическое отклонение основной погрешности i-го АСИ, %;
m - количество влияющих величин, для которых нормированы изменения метрологических характеристик i-гo АСИ;
s[δcij] - среднее квадратическое отклонение дополнительной погрешности i-го АСИ от j-й влияющей величины, %.
3.2.4. Среднее квадратическое отклонение основной погрешности i-го АСИ, распределенной по закону равномерной плотности, определяется по формуле
где δio - предел допускаемого значения основной погрешности i-го АСИ (по НД на конкретное АСИ), %;
Kр - коэффициент, определяемый законом равномерного распределения случайной погрешности при доверительной вероятности Р = 1;
![]()
3.2.5. Среднее квадратическое отклонение дополнительной погрешности i-го АСИ, вызванное j-й влияющей величиной, определяется по формуле
где δcij - наибольшее по абсолютной величине возможное значение дополнительной погрешности i-го АСИ от j-й влияющей величины, %.
3.2.6. Наибольшее возможное значение дополнительной погрешности определяется из НД на АСИ или при задании изменения относительной погрешности от влияющей величины вычисляется по формуле
δcij = ξio(ξj) · K · ξi(ξj) (24)
если диапазон изменения Dξξi влияющей величины, для которого нормированы изменения метрологических характеристик ξio(ξj), равен диапазону рабочих условий применения СИ,
если диапазон изменения Dξξj влияющей величины, для которого нормированы изменения метрологических характеристик ξio(ξj) равен части диапазона рабочих условий применения СИ, причем для любой части рабочих условий нормируется одно и то же значение ξio(ξj);
ξio(ξj) - наибольшее допускаемое изменение погрешности i-го АСИ, вызванное отклонением j-й влияющей величины от нормального значения, %;
Kξi(ξj) - коэффициент, используемый для вычисления δcij;
ξj - j-я влияющая величина;
ξoj - нормальное значение j-й влияющей величины;
Dξξj - приращение j-й влияющей величины, для которой нормирована метрологическая характеристика ξiо(ξj).
3.2.7. При проведении оценки обобщенных метрологических характеристик ИК эксплуатируемых ИИС и АСУ ТП для определения наибольшего по абсолютной величине возможного значения дополнительной погрешности i-го АСИ от j-й влияющей величины в формулах (25) и (26) следует использовать в качестве ξj математическое ожидание j-й влияющей величины, определенное по формуле (6).
3.2.8. При проектировании ИИС и АСУ ТП, когда известны только наибольшее ξвj и наименьшее ξнj значения j-й влияющей величины, соответствующие реальным условиям эксплуатации, для определения δсij в формулах (25) и (26) в качестве ξj следует использовать то значение ξнj или ξвj, которое вызывает появление наибольшей по абсолютной величине дополнительной погрешности.
3.2.9. Характеристики погрешности ИК ИИС и АСУ ТП для реальных условий эксплуатации:
нижняя и верхняя границы интервала, в котором с вероятностью P, равной 0,95, находится суммарная погрешность ИК для реальных условий эксплуатации, определяется по формуле
δик н(в) = ± Kн · s[δξ]. (27)
Для числа измерений больше 4 распределение суммарной погрешности стремится к нормальному (Kн = 1,96).
3.3. Третий метод расчета
3.3.1. При существенной случайной составляющей погрешности АСИ в состав метрологических характеристик (MX), нормируемых по ГОСТ 8.009-84, помимо пределов допускаемой систематической составляющей основной погрешности АСИ + Dios, входит предел допускаемого среднего квадратического отклонения случайной составляющей основной погрешности s[Dio]. По этим двум MX определяют нижнюю и верхнюю границы интервала, в котором с вероятностью P находится погрешность ИК для реальных условий эксплуатации, по формуле
Di(h) = ± (М[Dξ] + Kн · s[Dξ]), (28)
где М[Dξ] - математическое ожидание суммарной погрешности ИК для реальных условий эксплуатации, которое определяется в соответствии с формулами (1 ÷ 9);
Kн - коэффициент Стьюдента;
s[Dξ] - среднее квадратическое отклонение суммарной погрешности для реальных условий эксплуатации, которое определяется в соответствии с формулами (10 ÷ 16).
4. ПРИМЕР РАСЧЕТА
В качестве примера выполнен расчет погрешности ИК температуры информационно-измерительной системы на базе терминала вычислительного связи с объектом (ТВСО) по MX компонентов.
4.1. Метрологические характеристики, подлежащие расчету
4.1.1. Рассчитывается доверительный интервал с предельно допустимыми нижней δик н и верхней δик в границами, в котором с заданной вероятностью P = 0,95 находится погрешность измерительного канала температуры.
4.1.2. Результатами расчета являются численные значения границ доверительного интервала δик н(в).
4.2. Исходные данные для расчета
4.2.1. Диапазон измерений температуры - от 0 до 600 °C.
4.2.2. Первичный измерительный преобразователь - термоэлектрический преобразователь типа ТХА (К), класса допуска 2.
4.2.3. Количество компонентов (АСИ), имеющих нормированные MX, в ИК температуры равно 7. Структурная схема ИК температуры приведена на рисунке. Компонент 8 (средство представления информации) является техническим устройством вычислительной техники, не вносящим погрешность в результат измерения.
4.2.4. Компоненты АСИ, входящие в состав ИК температуры, характеризуются предельными допускаемыми значениями погрешности δio, указанными в разд. 3. Данные о значениях систематической и случайной составляющей погрешности и законе распределения случайной составляющей погрешности отсутствуют.
![]()
Структурная схема ИК температуры:
ПИП - первичный измерительный преобразователь ТП; ЛС - линия
связи; НП - нормирующий преобразователь;
ГрНП - групповой НП; МН - модуль нормализации; МКБ - модуль коммутаций
бесконтактный;
АЦП - аналогово-цифровой преобразователь; СПИ - средство представления
информации
4.2.5. Принимается допущение, что погрешности АСИ являются случайными величинами, распределенными по закону равномерной плотности.
Среднее квадратическое отклонение случайной погрешности i-го АСИ определяется по формуле (21); среднее квадратическое отклонение основной погрешности i-го АСИ определяется по формуле (22).
Среднее квадратическое отклонение дополнительной погрешности i-го АСИ от j-й влияющей величины определяется по формуле (23). В зависимости от вида функции влияния (линейная или ступенчатая) наибольшее возможное значение дополнительной погрешности определяется по формулам (24) и (25) или (24) и (26) и по данным разд. 3.
4.2.6. Среднее квадратическое отклонение случайной погрешности ИК s[δξ] определяется геометрическим суммированием средних квадратических отклонений случайных погрешностей каждого АСИ по формуле (20).
4.2.7. Суммарная погрешность ИК, определяемая геометрическим суммированием большого числа независимых и соизмеримых случайных погрешностей (n > 4), подчиняется нормальному закону распределения.
Таким образом, нижняя и верхняя границы интервала, в котором с доверительной вероятностью P, равной 0,95, находится погрешность ИК, определяется по формуле (27).
4.2.8. Компоненты, входящие в состав ИК температуры, начиная с n = 2 располагаются в кондиционируемых помещениях, т.е. находятся в нормальных условиях:
|
Температура окружающего воздуха .............. |
20 ± 5 °C |
|
Относительная влажность воздуха ................. |
60 ± 20 % |
|
Атмосферное давление ..................................... |
101 ± 10 кПа |
4.3. Расчет погрешности измерительного канала температуры
4.3.1. Среднее квадратическое отклонение случайной составляющей погрешности ИК температуры определяется в соответствии с п. 3.2.2 по формуле (20):

где δТП - основная погрешность термоэлектрического преобразователя, определяемая по ГОСТ Р 50431-92;
Dm = 0,0075´600 °C = 4,5 °C;
![]()
δЛС - дополнительная погрешность от отклонения термо-ЭДС термоэлектродных проводов от номинальной по ГОСТ 24335-80;
DЕЛС = 0,15 мВ, что соответствует DiЛС = ± 3,8 °C,
а ![]()
δНП - основная погрешность измерительного преобразователя типа Ш-79, δНП = ± 0,4 %;
δГрНП - основная погрешность группового нормирующего преобразователя, δГрНП = ± 0,1 %;
δМН - основная погрешность модуля нормализации, δМН = ±0,2 %;
δМКБ - основная погрешность модуля коммутации бесконтактного, δМКБ = ± 0,5 %;
δАЦП - основная погрешность аналогово-цифрового преобразователя, δАЦП = ± 0,5 %.
Таким образом, среднее квадратическое отклонение суммарной погрешности ИК температуры составит:
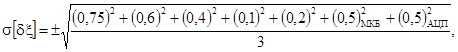
s[δξ] = ±0,74 %.
4.3.2. Предельно допускаемое значение погрешности ИК температуры вычисляется по формуле (27)
δик н(в) = ± (1,96´0,74) = ± 1,45 %.
4.3.3. Принимается значение нижней (верхней) границы доверительного интервала, в котором с вероятностью P, равной 0,95, находится погрешность ИК температуры:
δик н(в) = ± 1,5 %.
СОДЕРЖАНИЕ
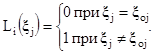 (6)
(6)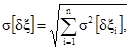
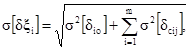
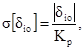
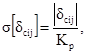
 (25)
(25)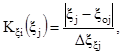 (26)
(26)