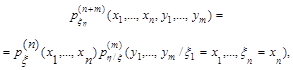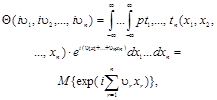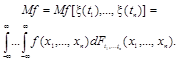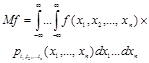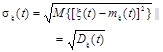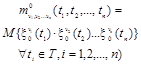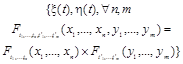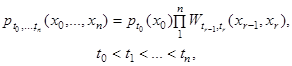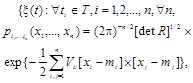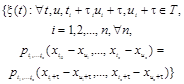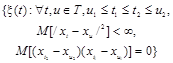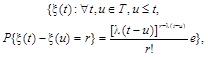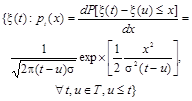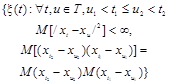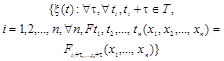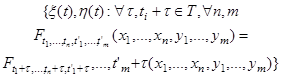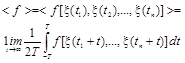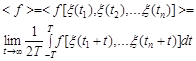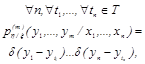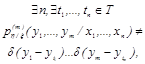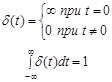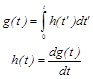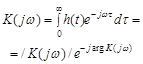ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
СЛУЧАЙНЫЕ ПРОЦЕССЫ
И ДИНАМИЧЕСКИЕ СИСТЕМЫ
ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
ГОСТ 21878-76
государственный комитет стандартов
совета министров ссср
Москва
РАЗРАБОТАН И ВНЕСЕН Всесоюзным научно-исследовательским институтом физико-технических и радиотехнических измерений (ВНИИФТРИ)
Зам. директора по научной работе доктор техн. наук А.М. Трохан
Руководитель темы канд. техн. наук В.Я. Розенберг
Исполнитель Л.М. Юрик
ПОДГОТОВЛЕН К УТВЕРЖДЕНИЮ Всесоюзным научно-исследовательским институтом технической информации, классификации и кодирования (ВНИИКИ)
Зам. директора по научной работе А.А. Саков
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета стандартов Совета Министров СССР от 24 мая 1976 г. № 1268
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
|
СЛУЧАЙНЫЕ ПРОЦЕССЫ И ДИНАМИЧЕСКИЕ СИСТЕМЫ Термины и определения Random processes and dynamical Systems. |
ГОСТ |
Постановлением Государственного комитета стандартов Совета Министров СССР от 24 мая 1976 г. № 1268 срок действия установлен
с 01.07.1977 г.
до 01.07.1982 г.
Настоящий стандарт устанавливает применяемые в науке, технике и производстве термины и определения основных понятий случайных процессов и динамических систем.
Термины, установленные настоящим стандартом, рекомендуются для применения в документации всех видов, учебниках, учебных пособиях, технической и справочной литературе. Приведенные определения можно, при необходимости, изменять по форме изложения, не допуская нарушения границ понятия.
Для каждого понятия установлен один стандартизованный термин. Применение терминов-синонимов стандартизованного термина не рекомендуется. Нерекомендуемые к применению термины-синонимы приведены в стандарте в качестве справочных и обозначены «Нрк».
Для отдельных стандартизованных терминов в стандарте приведены их краткие формы, которые разрешается применять в случаях, исключающих возможность их различного толкования.
В случаях, когда все необходимые и достаточные признаки понятия содержатся в буквальном значении термина, определение не приведено и, соответственно, в графе «Определение» поставлен прочерк.
В стандарте в качестве справочных приведены иностранные эквиваленты на английском языке для стандартизованных терминов и математические формулы и обозначения характеристик случайных процессов и динамических систем.
В стандарте приведены алфавитные указатели содержащихся терминов на русском языке и их иностранных эквивалентов.
Стандартизованные термины набраны полужирным шрифтом, их краткие формы - светлым, а нерекомендуемые синонимы - курсивом.
К стандарту дано справочное приложение, содержащее термины, определения, математические формулы и обозначения характеристик случайных величин.
|
Термин |
Определение |
Математическая формула и обозначение характеристики |
||
|
ОСНОВНЫЕ ПОНЯТИЯ |
||||
|
Семейство скалярных или векторных случайных величин, зависящих от скалярного параметра, имеющего смысл времени, с заданными конечномерными функциями распределения систем случайных величин |
ξ(t) = {ξt, tЄT, xЄX, |
|||
|
Нрк. Стохастический процесс |
||||
|
где символы |
||||
|
Вероятностный процесс |
||||
|
Случайная функция времени |
||||
|
Random process |
Т - область определения случайного процесса; |
|||
|
X - область значений случайного процесса |
||||
|
Примечание. Совокупность числовых значений x(t) = {xt, tЄT}, принимаемых случайным процессом ξ(t) в данном эксперименте, называется реализацией или выборочной функцией случайного процесса, а (х1, х2,,…,хn) - выборкой случайного процесса |
||||
|
Совокупность объектов произвольной природы, объединенных определенными причинно-следственными связями. |
где |
|||
|
Система |
||||
|
Dynamical system |
||||
|
Примечание. Модель системы задают в виде упорядоченной пары (ξt, ηm) двух случайных процессов (где ξn = (ξt, tЄTξ) - входной сигнал системы, а ηm = (ηt, tЄTη) - выходной сигнал системы), описываемой совместной плотностью вероятностей этих сигналов |
||||
|
|
||||
ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ |
||||
|
3. n-мерная функция распределения вероятностей случайного процесса |
Функция векторного аргумента х = (х1, x2,...хп), имеющая смысл вероятности выполнения системы неравенств |
Ft1, t2,..., tn (x1, x2,..., xn) = P{ξ(t1) < x1, ξ(t2) < x2,..., ξ(tn) < xn} |
||
|
Функция распределения случайного процесса. |
||||
|
ξ(t1) < x1, ξ(t2) < x2,..., ξ(tn) < xn |
||||
|
Нрк. п-мерная интегральная функция распределения. Интегральный закон распределения вероятностей |
||||
|
n-dimensional probability distribution function |
||||
|
4. n-мерная плотность распределения вероятностей случайного процесса |
Функция векторного аргумента, равная смешанной частной производной от функции распределения по совокупности n аргументов и имеющая смысл отношения вероятности попадания векторной величины в векторный элементарный интервал к значению этого интервала |
где n - порядок плотности распределения |
||
|
Плотность вероятностей случайного процесса |
||||
|
Нрк. п-мерное распределение |
||||
|
п-мерная дифференциальная функция распределения. Дифференциальный закон распределения |
||||
|
n-dimensional probability density function |
||||
|
5. n-мерная характеристическая функция случайного процесса |
Функция комплексного векторного аргумента, представляющая собой n-кратное преобразование Фурье от n-мерной плотности распределения вероятностей случайного процесса |
|
||
|
Характеристическая функция случайного процесса |
||||
|
Characteristical function |
||||
|
Функция времени, для каждого значения аргумента равная математическому ожиданию случайной величины |
|
|||
|
Нрк. Среднее значение случайного процесса |
||||
|
Первый момент. Статистическое среднее |
||||
|
Mathematical expectation of a random process |
||||
|
7. n-мерное математическое ожидание функции случайного процесса |
Функция для каждого набора значений t1, t2..., tn, равная математическому ожиданию случайной величины |
Если существует плотность распределения
то
|
||
|
Математическое ожидание функции случайного процесса |
f[ξ(t1),..., ξ(tn)] |
|||
|
n-dimensional mathematical expectation of a random process function |
||||
|
Функция времени, для каждого значения аргумента равная дисперсии случайной величины |
Dξ(t) = M{[ξ(t) - mξ(t)]2} |
|||
|
Random process variance |
||||
|
Функция времени, для каждого значения аргумента равная среднему квадратическому отклонению случайной величины |
|
|||
|
Standard deviation of a random process |
||||
|
10. n-мерная начальная моментная функция v-го порядка случайного процесса |
Функция, равная математическому ожиданию произведения п значений случайного процесса в моменты времени ti, взятых в степени vi (i = 1, 2,..., n) |
|
||
|
Начальная моментная функция |
||||
|
Нрк. п-мерный начальный момент v-го порядка случайного процесса |
||||
|
v-й начальный момент распределения случайного процесса |
||||
|
v-th order n-dimensional distribution moment |
||||
|
11. n-мерная центральная моментная функция v-го порядка случайного процесса |
Функция, равная математическому ожиданию произведения п значений центрированного случайного процесса (см. 45) в моменты времени ti, взятых в степени vi (i = 1, 2,..., n) |
|
||
|
Центральная моментная функция |
||||
|
Нрк. п-мерный центральный момент v-го порядка случайного процесса |
||||
|
v-й центральный момент распределения случайного процесса |
||||
|
v-th order n-dimensional distribution central moment |
||||
|
12. n-мерная абсолютная начальная моментная функция v-го порядка случайного процесса |
Функция, равная математическому ожиданию произведения п абсолютных значений случайного процесса в моменты времени ti, взятых в степени vi (i = 1, 2,..., n) |
|
||
|
Абсолютная начальная моментная функция |
||||
|
Нрк. п-мерный абсолютный начальный момент v-го порядка случайного процесса |
||||
|
v-th order n-dimensional distribution absolute moment |
||||
|
13. n-мерная абсолютная центральная моментная функция v-го порядка случайного процесса |
Функция, равная математическому ожиданию произведения п абсолютных значений центрированного случайного процесса (см. п. 45) в моменты времени ti, взятых в степени vi (i = 1, 2,..., n) |
|
||
|
Абсолютная центральная моментная функция |
||||
|
Нрк. п-мерный абсолютный центральный момент v-го порядка случайного процесса |
||||
|
v-th order n-dimensional distribution absolute central moment |
||||
|
14. n+m-мерная взаимная моментная функция v-го порядка двух случайных процессов |
Функция, равная математическому ожиданию произведения vi (i =1, 2,...,п) степеней значений случайного процесса ξ(t) на qj (j = 1, 2,..., т) степени значений случайного процесса η(t) для любых моментов времени из областей определения этих случайных процессов. |
|
||
|
Взаимная моментная функция |
||||
|
Нрк. Совместный, момент случайных процессов |
||||
|
Смешанный момент случайных процессов |
||||
|
Примечание. Размерность моментных функций определяется числом несовпадающих аргументов, а порядок - величиной, равной сумме степеней выборочных значений случайного процесса |
||||
|
Joint v-th order n+m-dimensional distribution moment for two random processes |
||||
|
15. Ковариационная функция случайного процесса |
Функция двух переменных t и и из области определения случайного процесса, равная математическому ожиданию произведения значений случайного процесса в моменты времени t и и |
Kξ (t,
u) = M{ξ(t)ξ(u)}, |
||
|
Нрк. Автоковариационная функция случайного процесса |
||||
|
Корреляционная функция случайного процесса |
||||
|
Autocovariation function |
||||
|
Функция двух переменных t и и, равная ковариационной функции центрированного случайного процесса |
Rξ (t,
u) = M{[ξ(t) - m1]×[ξ(u) - m2]}, |
|||
|
где m1 = M[ξ(t)], m2 = M[ξ(u)] |
||||
|
Нрк. Автокорреляционная функция случайного процесса |
||||
|
Ковариационная функция случайного процесса |
||||
|
Autocorrelation function |
||||
|
17. Нормированная корреляционная функция случайного процесса |
Функция двух переменных t и и, равная отношению корреляционной функции случайного процесса к произведению средних квадратических отклонений случайного процесса в моменты времени t и и |
|
||
|
Нрк. Коэффициент корреляции |
||||
|
Correlation coefficient |
||||
|
Функция двух переменных t и и, равная математическому ожиданию произведения случайных процессов, взятых в любые моменты времени t и u из областей определения этих случайных процессов |
Kξη(t, u) = M{ξ(t)η(u)} |
|||
|
Нрк. Кроссковариационная функция |
||||
|
Кросскорреляционная функция случайных процессов |
||||
|
Cross-covariation function |
||||
|
Функция двух переменных t и u, равная математическому ожиданию произведения значений центрированных случайных процессов, взятых в любые моменты времени t и и из областей определения этих случайных процессов |
Rξη (t,
u) = M{[ξ(t) - mξ]×[η(u) - mη]}, |
|||
|
где mξ = M[ξ(t)], mη = M[η(u)] |
||||
|
Нрк. Кросскорреляционная функция |
||||
|
Кроссковариационная функция случайных процессов |
||||
|
Cross-correlation function |
||||
|
20. Нормированная взаимная корреляционная функция случайных процессов |
Функция двух переменных t и и, равная отношению взаимной корреляционной функции случайных процессов к произведению средних квадратических отклонений этих случайных процессов |
|
||
|
Нрк. Взаимный коэффициент корреляции случайных процессов |
||||
ВИДЫ СЛУЧАЙНЫХ ПРОЦЕССОВ |
||||
|
Случайный процесс, область значений которого есть множество в пространстве действительных чисел R1 |
{ξ(t):xtЄX |
|||
|
Нрк. Одномерный случайный процесс |
||||
|
First-order random process |
||||
|
22. n-мерный векторный случайный процесс |
Случайный процесс, область значений которого есть множество в п-мерном координатном пространстве Rn |
{ξ(t):xtЄX |
||
|
Векторный случайный процесс |
||||
|
Нрк. Многомерный случайный процесс |
||||
|
n-dimensional random process |
||||
|
Случайный процесс, область значений и область определения которого - непрерывные множества |
|
|||
|
Нрк. Случайный процесс с непрерывным временем |
||||
|
Continuous random process |
||||
|
Случайный процесс, у которого область значений - непрерывное множество, а область определения - дискретное |
|
|||
|
Нрк. Временной ряд |
||||
|
Случайный процесс с дискретным временем |
||||
|
Random sequences |
||||
|
Случайный процесс, у которого область значений - дискретное, а область определения - непрерывное множество |
|
|||
|
Нрк. Скачкообразный процесс |
||||
|
Случайный процесс, у которого область значений и область определения - дискретные множества |
|
|||
|
Discrete random sequences |
||||
|
Процесс, значения которого в любой момент времени известны с вероятностью единицы |
{s(t): |
|||
|
Нрк. Регулярный процесс |
||||
|
Абсолютно неслучайный процесс |
||||
|
Процесс нулевого порядка |
||||
|
Determinate process |
||||
|
Процесс, значения которого повторяются через определенные интервалы времени |
{s(t): |
|||
|
Periodic process |
где Т* - период периодического процесса |
|||
|
|
{s(t): |
|||
|
|
||||
|
Nonperiodic process |
|
|||
|
Процесс, реализации которого описываются функциями времени заданного вида s(t, а1, а2...., аn), содержащими один или несколько случайных параметров а = (а1, а2, ..., ап), не зависящих от времени |
{ξ(t):
|
|||
|
Quasi-determinate process |
||||
|
Случайные процессы, у которых совместная функция распределения любого порядка представляет собой произведение функций распределений каждого процесса в отдельности |
|
|||
|
Mutually independent random processes |
||||
|
|
||||
|
Случайный процесс, вполне определяемый своими функциями распределения порядка п, но не определяемый функциями распределения низшего порядка |
|
|||
|
n-order random process |
||||
|
Случайный процесс с независимыми значениями, вполне определяемый одномерной плотностью распределения |
|
|||
|
Белый шум |
||||
|
Нрк. Абсолютно случайный процесс |
||||
|
Чисто случайный процесс |
||||
|
Случайный процесс 1-го порядка |
||||
|
White noise in a narrow sense |
||||
|
Случайный процесс с некоррелированными значениями |
{ξ(t): |
|||
|
White noise in a wide sense |
||||
|
- |
{ξ(t): |
|||
|
Нрк. Небелый шум |
||||
|
Коррелированный шум |
||||
|
Окрашенный шум |
||||
|
Correlated noise |
||||
|
Случайный процесс, для которого при фиксированном ξ(u) = x случайные величины ξ(t), t > u не зависят от ξ(s), s < u |
где |
|||
|
Нрк. Процесс 2-го порядка |
||||
|
Marcovian process |
||||
|
Примечания: 1. Условную
плотность вероятности называют плотностью вероятности перехода из состояния xn-1 в момент времени tn-1 в состояние хп в момент времени tn. Через нее выражаются плотности вероятностей произвольного порядка. 2. Марковский дискретный случайный процесс называется марковской цепью. |
||||
|
Случайный процесс, все n-мерные функции распределения (плотности распределения) вероятностей которого нормальны |
где mi = mi(ti), V = ||Vij|| - матрица, обратная корреляционной матрице R = ||R(ti,tj)||, т.е. подчиняющаяся уравнению
где |
|||
|
Нрк. Нормальный случайный процесс |
||||
|
Gaussian process |
||||
|
38. Случайный процесс со стационарными в узком смысле приращениями |
Случайный процесс, у которого приращения, т.е. разность ξ (t + τ) - ξ (t) для каждого фиксированного τ, есть стационарный в узком смысле процесс |
|
||
|
Random process with stationary in a narrow sense increments |
||||
|
39. Случайный процесс со стационарными в широком смысле приращениями |
Случайный процесс, у которого приращения для каждого фиксированного τ есть стационарный в широком смысле процесс |
|
||
|
Random process with stationary in a wide sense increments |
||||
|
Случайный процесс, абсолютные начальные моментные функции второго порядка приращений которого ограничены, а приращения, отвечающие двум непересекающимся интервалам, ортогональны |
|
|||
|
Random process with orthogonal increments |
||||
|
Случайный процесс, приращения которого, отвечающие двум непересекающимся интервалам, независимы. |
|
|||
|
Additive process |
||||
|
Примечание. Если моментная функция 2-го порядка процесса с независимыми приращениями конечна, то центрированный случайный процесс есть процесс с ортогональными приращениями |
||||
|
Случайный процесс с независимыми стационарными приращениями, распределенными по закону Пуассона |
где λ - параметр пуассоновского процесса |
|||
|
Poisson process |
||||
|
Случайный процесс с независимыми гауссовыми стационарными приращениями |
|
|||
|
Wiener process |
||||
|
Случайный процесс, приращения которого, отвечающие двум непересекающимся интервалам, некоррелированы и абсолютные начальные моментные функции 2-го порядка приращений ограничены |
|
|||
|
Random process with uncorrelated increments |
||||
|
Случайный процесс, представляющий собой разность между случайным процессом и его математическим ожиданием |
ξ0(t) = ξ(t) - mξ(t) |
|||
|
Нрк. Пульсации случайного процесса |
||||
|
Флюктуации случайного процесса |
||||
ВИДЫ СТАЦИОНАРНЫХ ПРОЦЕССОВ И ИХ ХАРАКТЕРИСТИКИ |
||||
|
Случайный процесс, у которого все конечномерные функции распределения вероятностей любого порядка инвариантны относительно сдвига по времени |
|
|||
|
Стационарный процесс |
||||
|
Нрк. Абсолютно стационарный процесс |
||||
|
Строго стационарный процесс |
||||
|
Stationary in a narrow sense random process |
||||
|
Случайный процесс с конечной дисперсией, у которого математическое ожидание и ковариационная функция инвариантны относительно сдвига по времени |
{ξ(t): K(t+ τ, u + τ) = K(t, u) = K(τ) M[ξ(t)] = m, M{/ξ(t) - m/2} < ∞} |
|||
|
Нрк. Стационарный процесс в смысле Хинчина |
||||
|
Слабо стационарный процесс |
||||
|
Стационарный процесс |
||||
|
Stationary in a wide sense random process |
||||
|
Случайные процессы, у которых совместные функции распределения вероятностей любого порядка инвариантны относительно сдвига по времени |
|
|||
|
Нрк. Абсолютно стационарно связанные случайные процессы |
||||
|
Совместно стационарные в узком смысле случайные процессы |
||||
|
Stationary dependent in a narrow sense random process |
||||
|
49. Стационарно связанные в широком смысле случайные процессы |
Случайные процессы, у которых взаимная ковариационная функция инвариантна относительно сдвига по времени |
{ξ(t), η(t): Kξη(t, u) = Kξη (t + τ, u + τ) = Kξη(τ)} |
||
|
Нрк. Совместно стационарные в широком смысле случайные процессы |
||||
|
Stationary dependent in a wide sense random processes |
||||
|
Стационарный случайный процесс, спектральная плотность которого сосредоточена в узкой полосе частот около некоторой фиксированной частоты |
DF << ω0 |
|||
|
Narrow-band stationary random process |
||||
|
- |
DF ≈ ω0 |
|||
|
Wide-band stationary random process |
||||
|
Стационарный случайный процесс, спектр которого равен нулю вне конечного интервала частот |
S(ω) ≡ 0 при /ω/ > 2πВ, |
|||
|
где В - ширина спектра случайного процесса |
||||
|
Random stationary process with boundet spectrum |
||||
|
Случайный процесс, для которого среднее по времени, полученное усреднением на достаточно большом, в пределе бесконечном, интервале по единственной реализации случайного процесса, сходится с вероятностью единица к соответствующей вероятностной характеристике, полученной усреднением по множеству реализаций |
{ξ(t): |
|||
|
Ergodic process |
где
|
|||
|
Два случайных процесса, для которых характеристика, полученная усреднением по времени, произведенным над одной единственной парой реализаций случайных процессов, сходится с вероятностью единица к соответствующей характеристике, полученной усреднением по множеству пар реализаций этих процессов |
{ξ(t), η(t): |
|||
|
где
|
||||
|
Нрк. Взаимно эргодические процессы |
||||
|
Mutually ergodic processes |
||||
|
Длина наибольшего интервала времени, на котором корреляционная связь между значениями случайного процесса существенна для решаемой задачи |
|
|||
|
Нрк. Время корреляции |
||||
|
56. Спектральная плотность стационарного случайного процесса |
Функция частоты, равная преобразованию Фурье ковариационной функции стационарного случайного процесса |
|
||
|
Спектр стационарного случайного процесса |
||||
|
Нрк. Энергетический спектр стационарного случайного процесса |
||||
|
Интенсивность случайного процесса |
||||
|
Спектральная плотность случайного процесса |
||||
|
Спектральная функция распределения случайного процесса |
||||
|
Power spectral density function |
||||
|
Длина наибольшего отрезка на оси частот, на котором спектр случайного процесса имеет существенное для решаемой задачи значение |
|
|||
|
Нрк. Энергетическая ширина спектра |
||||
|
58. Взаимная спектральная плотность стационарно связанных случайных процессов |
Функция частоты, представляющая собой преобразование Фурье взаимной ковариационной функции стационарно связанных случайных процессов |
|
||
|
Cross-power spectral density function of stationary dependent random processes |
||||
ВИДЫ ДИНАМИЧЕСКИХ СИСТЕМ |
||||
|
Система, преобразующая лишь предшествующие и текущие, но не будущие значения входных сигналов |
|
|||
|
Нрк. Динамическая система |
||||
|
Физически реализуемая система |
||||
|
Физически осуществимая система |
||||
|
Nonanticipative dynamical system |
||||
|
- |
|
|||
|
Система, характеризующаяся однозначным или взаимно-однозначным соответствием реализаций входного и выходного сигналов; при этом условная плотность распределения вероятностей выходного сигнала при фиксированной входной реализации xt сосредоточена на реализации yt |
где yt = Ахt , А - оператор системы (см. п. 73) |
|||
|
Нрк. Регулярная система |
||||
|
Determinate system |
||||
|
- |
|
|||
|
Нрк. Недетерминированная система |
||||
|
Нерегулярная система |
||||
|
Рандомизированная система |
||||
|
Стохастическая система |
||||
|
Random system |
||||
|
Система, входной и выходной сигналы которой являются скалярными процессами |
|
|||
|
First-order system |
||||
|
Система, входной и (или) выходной сигналы которой являются векторными процессами |
|
|||
|
Multivariable system |
||||
|
65. Линейная система |
Система, подчиняющаяся принципу суперпозиции |
|
||
|
Linear system |
||||
|
где сv - постоянные коэффициенты; A - оператор системы |
||||
|
- |
|
|||
|
Nonlinear system |
||||
|
Система, значение выходного сигнала которой в некоторый момент времени зависит от значения входного сигнала в тот же момент времени t и от его значений в предшествующие моменты времени |
|
|||
|
Нрк. Система с памятью |
||||
|
Динамическая система |
||||
|
Инерциальная система |
||||
|
Система, в которой значение выходного сигнала в любой момент времени зависит только от значения входного сигнала в этот же момент |
|
|||
|
Нрк. Система без памяти |
||||
|
Неинерционная система |
||||
|
Система, в которой сдвиг входного сигнала во времени приводит к такому же сдвигу выходного сигнала |
Aξδ(t) = ηδ(t) |
|||
|
Нрк. Инвариантная во времени система |
где ξδ(t) = ξ(t - δ) |
|||
|
ηδ(t) = η(t - δ) |
||||
|
Система с постоянными параметрами |
||||
|
Stationary system |
||||
|
- |
Aξδ(t) ≠ ηδ(t) |
|||
|
Нрк. Неинвариантная во времени система |
||||
|
Параметрическая система |
||||
|
Система с переменными параметрами |
||||
|
Nonstationary system |
||||
|
Система, оператор которой может быть представлен в виде одного или системы обыкновенных дифференциальных уравнений |
|
|||
|
Нрк. Непрерывная система |
||||
|
Дифференциальная система |
||||
|
Lumped parameter system |
||||
|
Система, оператор которой может быть представлен в виде одного или системы дифференциальных уравнений в частных производных |
|
|||
|
Нрк. Длинная линия |
||||
|
Long line |
||||
ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ СИСТЕМ |
||||
|
Правило, по которому каждой реализации входного сигнала ставится в однозначное или взаимно-однозначное соответствие реализация выходного сигнала |
yt = Axt |
|||
|
Характеристика линейной системы, представляющая собой выходной сигнал системы при входном сигнале, имеющем вид дельта-функции |
h(t) = y(t)/x(t) = δ(t), |
|||
|
где
|
||||
|
Нрк. Импульсно-переходная функция |
||||
|
Весовая функция |
||||
|
Weight function |
||||
|
(для стационарных систем). Для физически возможных систем h(t) = 0, при t < 0, для устойчивых систем
|
||||
|
Характеристика линейной системы, представляющая собой выходной сигнал системы при входном сигнале, имеющем вид единичной функции |
g(t) = y(t)/x(t) = 1(t), |
|||
|
где
|
||||
|
Unit pulse response |
||||
|
(для стационарных систем), причем |
||||
|
|
||||
|
Характеристика линейной системы, представляющая собой преобразование Лапласа импульсной характеристики системы |
|
|||
|
Trasfer function |
где |
|||
|
s = jω + α |
||||
|
(для стационарных систем) |
||||
|
Характеристика линейной системы, представляющая собой преобразование Фурье импульсной характеристики системы |
|
|||
|
Частотная характеристика |
||||
|
Generalized frequency function |
||||
|
Характеристика линейной системы, представляющая собой модуль комплексной частотной характеристики |
|
|||
|
Gain-frequency characteristic |
||||
|
Характеристика линейной системы, представляющая собой аргумент комплексной частотной характеристики |
|
|||
|
Phase-frequency characteristic |
||||
|
80. Действительная часть комплексной частотной характеристики системы |
- |
ReK(jω) |
||
|
Real frequency response |
||||
|
81. Мнимая часть комплексной частотной характеристики системы |
- |
ImK(jω) |
||
|
Imaginary frequency response |
||||
|
Характеристика безынерционной системы, представляющая собой зависимость между мгновенными значениями входного и выходного сигналов |
y(t*) = f[x(t*)] |
|||
|
где t*ЄT - любой фиксированный момент времени |
||||
|
||||
АЛФАВИТНЫЙ УКАЗАТЕЛЬ ТЕРМИНОВ НА РУССКОМ ЯЗЫКЕ
|
Время корреляции |
(55) |
|
Дисперсия случайного процесса |
|
|
Закон распределения вероятностей интегральный |
(3) |
|
Закон распределения дифференциальный |
(4) |
|
Значение случайного процесса среднее |
(6) |
|
Интенсивность случайного процесса |
(56) |
|
Интервал корреляции стационарного случайного процесса |
|
|
Коэффициент корреляции |
(17) |
|
Коэффициент корреляции случайных процессов взаимный |
(20) |
|
Линия длинная |
(72) |
|
Математическое ожидание случайного процесса |
|
|
Математическое ожидание функции случайного процесса |
|
|
Математическое ожидание функции случайного процесса n-мерное |
|
|
Момент v-го порядка случайного процесса начальный абсолютный п-мерный |
(12) |
|
Момент v-го порядка случайного процесса начальный п-мерный |
(10) |
|
Момент v-го порядка случайного процесса центральный абсолютный п-мерный |
(13) |
|
Момент v-го порядка случайного процесса центральный п-мерный |
(11) |
|
Момент первый |
(6) |
|
Момент распределения случайного процесса v-й начальный |
(10) |
|
Момент распределения случайного процесса центральный v-й |
(11) |
|
Момент случайных процессов смешанный |
(14) |
|
Момент случайных процессов совместный |
(14) |
|
Оператор детерминированной системы |
|
|
Отклонение случайного процесса среднее квадратическое |
|
|
Плотность вероятностей случайного процесса |
|
|
Плотность распределения вероятностей случайного процесса n-мерная |
|
|
Плотность случайного процесса спектральная |
(56) |
|
Плотность стационарно связанных случайных процессов |
|
|
спектральная взаимная |
|
|
Плотность стационарного случайного процесса спектральная |
|
|
Последовательность случайная |
|
|
Последовательность случайная дискретная |
|
|
Процесс абсолютно неслучайный |
(27) |
|
Процесс абсолютно случайный |
(33) |
|
Процесс абсолютно стационарный |
(46) |
|
Процесс вероятностный |
(1) |
|
Процесс Винеровский |
|
|
Процесс 2-го порядка |
(36) |
|
Процесс Гауссовский |
|
|
Процесс детерминированный |
|
|
Процесс квазидетерминированный |
|
|
Процесс Марковский |
|
|
Процесс непериодический |
|
|
Процесс нулевого порядка |
(27) |
|
Процесс периодический |
|
|
Процесс порядка п случайный |
|
|
Процесс Пуассоновский |
|
|
Процесс регулярный |
(27) |
|
Процесс скачкообразный |
(25) |
|
Процесс слабо стационарный |
(47) |
|
Процесс случайный |
|
|
Процесс случайный векторный |
|
|
Процесс случайный векторный n-мерный |
|
|
Процесс случайный дискретный |
|
|
Процесс случайный многомерный |
(22) |
|
Процесс случайный непрерывно-значный |
|
|
Процесс случайный нормальный |
(37) |
|
Процесс случайный одномерный |
(21) |
|
Процесс случайный 1-го порядка |
(33) |
|
Процесс случайный с дискретным временем |
(24) |
|
Процесс случайный скалярный |
|
|
Процесс случайный с коррелированными значениями |
|
|
Процесс случайный с независимыми приращениями |
|
|
Процесс случайный с некоррелированными приращениями |
|
|
Процесс случайный с непрерывным временем |
(23) |
|
Процесс случайный с ортогональными приращениями |
|
|
Процесс случайный со стационарными в узком смысле приращениями |
|
|
Процесс случайный со стационарными в широком смысле приращениями |
|
|
Процесс случайный стационарный в узком смысле |
|
|
Процесс случайный стационарный в широком смысле |
|
|
Процесс случайный стационарный с ограниченным спектром |
|
|
Процесс случайный стационарный узкополосный |
|
|
Процесс случайный центрированный |
|
|
Процесс случайный стационарный широкополосный |
|
|
Процесс стационарный |
|
|
Процесс стационарный |
(47) |
|
Процесс стационарный в смысле Хитина |
(47) |
|
Процесс стохастический |
(1) |
|
Процесс строго стационарный |
(46) |
|
Процесс чисто случайный |
(33) |
|
Процесс эргодический |
|
|
Процессы взаимно эргодические |
(54) |
|
Процессы случайные абсолютно стационарно связанные |
(48) |
|
Процессы случайные независимые |
|
|
Процессы случайные совместно стационарные в узком смысле |
(48) |
|
Процессы случайные совместно стационарные в широком смысле |
(49) |
|
Процессы случайные стационарно связанные в узком смысле |
|
|
Процессы случайные стационарно связанные в широком смысле |
|
|
Процессы совместно эргодические |
|
|
Пульсации случайного процесса |
(45) |
|
Распределение п-мерное |
(4) |
|
Ряд временной |
(24) |
|
Система |
|
|
Система без памяти |
(68) |
|
Система безынерционная |
|
|
Система вероятностная |
|
|
Система детерминированная |
|
|
Система динамическая |
|
|
Система динамическая |
(59) |
|
Система динамическая |
(67) |
|
Система дифференциальная |
(71) |
|
Система инвариантная во времени |
(69) |
|
Система инерциальная |
(67) |
|
Система инерционная |
|
|
Система линейная |
|
|
Система многомерная |
|
|
Система недетерминированная |
(62) |
|
Система неинвариантная во времени |
(70) |
|
Система неинерционная |
(68) |
|
Система нелинейная |
|
|
Система непрерывная |
(71) |
|
Система нерегулярная |
(62) |
|
Система нестационарная |
|
|
Система одномерная |
|
|
Система параметрическая |
(70) |
|
Система рандомизированная |
(62) |
|
Система регулярная |
(61) |
|
Система с памятью |
(67) |
|
Система с переменными параметрами |
(70) |
|
Система с постоянными параметрами |
(69) |
|
Система с распределенными параметрами |
|
|
Система с сосредоточенными параметрами |
|
|
Система стационарная |
|
|
Система стохастическая |
(62) |
|
Система физически возможная |
|
|
Система физически невозможная |
|
|
Система физически осуществимая |
(59) |
|
Система физически реализуемая |
(59) |
|
Спектр стационарного случайного процесса |
|
|
Спектр стационарного случайного процесса энергетический |
(56) |
|
Среднее статистическое |
(6) |
|
Флюктуации случайного процесса |
(45) |
|
Функция весовая |
(74) |
|
Функция времени случайная |
(1) |
|
Функция импульсно-переходная |
(74) |
|
Функция кроссковариационная |
(18) |
|
Функция моментная взаимная |
|
|
Функция моментная начальная |
|
|
Функция моментная начальная абсолютная |
|
|
Функция моментная центральная |
|
|
Функция моментная центральная абсолютная |
|
|
Функция случайных процессов ковариационная взаимная |
|
|
Функция v-го порядка двух случайных процессов моментная |
|
|
взаимная n+m-мерная |
|
|
Функция v-го порядка случайного процесса моментная начальная |
|
|
абсолютная n-мерная |
|
|
Функция v-го порядка случайного процесса моментная начальная n-мерная |
|
|
Функция v-го порядка случайного процесса моментная |
|
|
центральная абсолютная n-мерная |
|
|
Функция v-го порядка случайного процесса моментная центральная |
|
|
n-мерная |
|
|
Функция распределения вероятностей случайного процесса n-мерная |
|
|
Функция распределения дифференциальная п-мерная |
(4) |
|
Функция распределения интегральная п-мерная |
(3) |
|
Функция распределения случайного процесса |
|
|
Функция распределения случайного процесса спектральная |
(56) |
|
Функция системы передаточная |
|
|
Функция случайного процесса автоковариационная |
(15) |
|
Функция случайного процесса автокорреляционная |
(16) |
|
Функция случайного процесса ковариационная |
|
|
Функция случайного процесса ковариационная |
(16) |
|
Функция случайного процесса корреляционная |
|
|
Функция случайного процесса корреляционная |
(15) |
|
Функция случайного процесса корреляционная нормированная |
|
|
Функция случайного процесса характеристическая |
|
|
Функция случайного процесса характеристическая n-мерная |
|
|
Функция случайных процессов кросскорреляционная |
(18) |
|
Функция случайных процессов корреляционная нормированная взаимная |
|
|
Характеристика системы амплитудная |
|
|
Характеристика системы амплитудно-частотная |
|
|
Характеристика системы импульсная |
|
|
Характеристика системы переходная |
|
|
Характеристика системы фазо-частотная |
|
|
Характеристика системы частотная |
|
|
Характеристика системы частотная комплексная |
|
|
Часть комплексной частотной характеристики системы действительная |
|
|
Часть комплексной частотной характеристики системы мнимая |
|
|
Ширина спектра энергетическая |
(57) |
|
Ширина спектра эффективная |
|
|
Шум белый |
|
|
Шум белый в узком смысле |
|
|
Шум белый в широком смысле |
|
|
Шум коррелированный |
(35) |
|
Шум небелый |
(35) |
|
Шум окрашенный |
(35) |
АЛФАВИТНЫЙ УКАЗАТЕЛЬ ТЕРМИНОВ НА АНГЛИЙСКОМ ЯЗЫКЕ
|
Additive process |
|
|
Autocorrelation function |
|
|
Autocovariation function |
|
|
Characteristical function |
|
|
Continuous random process |
|
|
Correlation coefficient |
|
|
Correlation noise |
|
|
Cross-correlation function |
|
|
Cross-covariation function |
|
|
Cross spectral density function of stationary dependent random processes |
|
|
Determinate process |
|
|
Determinate system |
|
|
Discrete random sequences |
|
|
Dynamical system |
|
|
Ergodic process |
|
|
First-order random process |
|
|
First-order system |
|
|
Gain-frecuency characteristic |
|
|
Gaussian process |
|
|
Generalized frecuency function |
|
|
Imaginary frecuency response |
|
|
Joint v-th order n+m dimensional distribution moment for two random processes |
|
|
Linear system |
|
|
Long line |
|
|
Lumped parameter system |
|
|
Marcovian process |
|
|
Mathematical expectation of a random process |
|
|
Multivariable system |
|
|
Mutually ergodic processes |
|
|
Mutually independent random processes |
|
|
n-dimensional mathematical expectation of a random process function |
|
|
n-dimensional probability density function |
|
|
n-dimensional probability distribution function |
|
|
n-dimensional random process |
|
|
n-order random process |
|
|
Narrow-band stationary random process |
|
|
Nonanticipative dynamical system |
|
|
Nonlinear system |
|
|
Nonperiodic process |
|
|
Nonstationary system |
|
|
Periodic process |
|
|
Phase-frecuecy characteristic |
|
|
Poisson process |
|
|
Power spectral density function |
|
|
Quasi-determinate process |
|
|
Random process |
|
|
Random process variance |
|
|
Random process with orthogonal increments |
|
|
Random process with stationary in a narrow sense increments |
|
|
Random process with stationary in a wide sense increments |
|
|
Random process with uncorrelated increments |
|
|
Random sequences |
|
|
Random stationary process with boundet spectrum |
|
|
Random system |
|
|
Real frecuency response |
|
|
Standard deviation of a random process |
|
|
Stationary dependent in a narrow sense random process |
|
|
Stationary dependent in a wide sense random process |
|
|
Stationary in a narrow sense random process |
|
|
Stationary in a wide sense random process |
|
|
Stationary system |
|
|
Trasfer function |
|
|
Unit pulse response |
|
|
Weight function |
|
|
White nois in a narrow sense |
|
|
White noise in a wide sense |
|
|
Wide-band stationary random process |
|
|
Wiener process |
|
|
v-th order n-dimensional distribution absolute central moment |
|
|
v-th order n-dimensional distribution absolute moment |
|
|
v-th order n-dimensional distribution central moment |
|
|
v-th order n-dimensional distribution moment |
ПРИЛОЖЕНИЕ
Справочное
ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
|
Термин |
Определение |
Математическая формула и обозначение характеристики |
|
|
1. Случайная величина |
Числовая величина, значение которой зависит от случая, характеризуемая множеством возможных значений Х = {х} и распределением вероятностей на нем, задаваемым функцией распределения |
|
|
|
Random variable |
|||
|
2. Функция распределения вероятностей случайной величины |
Функция, равная вероятности того, что случайная величина ξ примет значение, меньшее чем х (для всех х на числовой оси) |
Fξ(x) = P{ξ < x}, |
|
|
(-∞ < x < ∞) |
|||
|
Функция распределения случайной величины |
|||
|
Нрк. Интегральная функция распределения. Интегральный закон распределения |
|||
|
Distribution function of a random variable |
|||
|
3. Плотность распределения вероятностей случайной величины |
Функция, определяемая как производная функции распределения |
|
|
|
Плотность вероятностей случайной величины |
|||
|
Нрк. Дифференциальная функция распределения. Дифференциальный закон распределения |
|||
|
Probability density function of a random variable |
|||
|
4. Характеристическая функция случайной величины |
Функция комплексного параметра, равная преобразованию Фурье от плотности распределения вероятностей случайной величины |
|
|
|
Characteristical function |
|||
|
5. Математическое ожидание случайной величины |
Числовая характеристика случайной величины, определяемая как интеграл в бесконечных пределах от произведения случайной величины на плотность распределения вероятностей этой случайной величины |
|
|
|
Main value of a random variable |
|||
|
6. Центрированная случайная величина |
Случайная величина, представляющая собой разность между случайной величиной и ее математическим ожиданием |
ξ0 = ξ - mξ |
|
|
Variable of a random variable |
|||
|
7. Дисперсия случайной величины |
Числовая характеристика случайной величины, равная математическому ожиданию квадрата центрированной случайной величины |
Dξ = M(ξ - mξ) |
|
|
8. Среднее квадратическое отклонение случайной величины |
Величина, равная положительному значению квадратного корня из дисперсии случайной величины |
|
|
|
Нрк. Стандарт случайной величины. Стандартное отклонение случайной величины |
|||
|
Флюктуация случайной величины |
|||
|
Standart deriation |
|||
|
9. Начальный момент v-го порядка случайной величины |
Величина, равная математическому ожиданию v-й степени случайной величины |
|
|
|
Moment of the distribution |
|||
|
10. Центральный момент v-го порядка случайной величины |
Величина, равная математическому ожиданию v-й степени центрированной случайной величины |
|
|
|
11. n-мерный случайный вектор |
Конечное семейство случайных величин |
ξn = (ξ1, ξ2,...,ξn) |
|
|
Случайный вектор |
|||
|
Нрк. п-мерная случайная величина |
|||
|
Случайная векторная величина |
|||
|
n-dimensional random variable |
|||
|
12. Функция распределения вероятностей случайного вектора |
Функция векторного аргумента х = (х1, х2,..., хп), имеющая смысл вероятности совместного выполнения условий |
F (x1, x2,..., xn) = P {ξ1 < x1, ξ2 < x2,...,ξn < xn} |
|
|
Функция распределения случайного вектора |
ξ1 < x1,...., ξn < xn |
||
|
Distribution function of a multidimensional random variable |
|||
|
13. Плотность распределения вероятностей случайного вектора |
Функция векторного аргумента, равная смешанной частной производной от функции распределения по совокупности п аргументов и имеющая смысл отношения вероятности попадания векторной величины |
|
|
|
Плотность вероятностей случайного вектора |
|||
|
Probability density function of a multidimensional random variable |
|||
|
ξn = (ξ1, ξ2,...,ξn) |
|||
|
в векторный элементарный интервал |
|||
|
dx = (dx1, dx2,...,dxn) |
|||
|
к значению этого интервала |
СОДЕРЖАНИЕ
|
Характеристики случайных процессов. 3 Виды стационарных процессов и их характеристики. 10 Характеристики динамических систем.. 13 Алфавитный указатель терминов на русском языке. 15 |