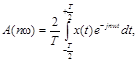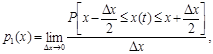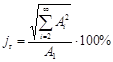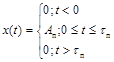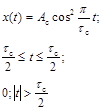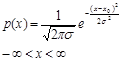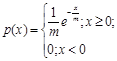МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
|
СИГНАЛЫ РАДИОТЕХНИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ Термины и определения Measuring radiotechnical signals. Terms and definitions |
ГОСТ |
Издание с Изменением № 1, утвержденным в июле 1973 г. (ИУС 8-73).
Постановлением Комитета стандартов, мер и измерительных приборов при Совете Министров СССР от 6 ноября 1970 г. № 1678 дата введения установлена
с 01.07.71
Настоящий стандарт устанавливает термины и определения основных понятий в области измерительных радиотехнических сигналов, получаемых с помощью измерительных генераторов тока и напряжения.
Стандарт не распространяется на сигналы, используемые в радиоэлектронных системах для передачи и приема телевизионной, радиолокационной, телеметрической и другой информации.
Термины, установленные настоящим стандартом, обязательны для применения в документации всех видов, учебниках, учебных пособиях, технической и справочной литературе.
Для каждого понятия установлен один стандартизованный термин, напечатанный полужирным шрифтом. Недопустимые к применению термины-синонимы приведены в стандарте в качестве справочных, обозначены «Ндп» и напечатаны курсивом.
Для отдельных стандартизованных терминов в стандарте приведены в качестве справочных их краткие формы, напечатанные светлым шрифтом, которые разрешается применять в случаях, исключающих возможность различного толкования понятий, установленных настоящим стандартом. Если существенные признаки понятия выражены в самом термине, определение не приведено и в графе «Определение» поставлен прочерк.
Математические формулы и использованные в них буквенные обозначения величин приведены в стандарте в качестве справочных.
|
Определение |
Математическая формула и обозначение величины |
|
|
1. Измерительный радиотехнический сигнал Сигнал Ндп. Тест-сигнал. Тестовый сигнал. Испытательный сигнал. Пробный сигнал. Воздействие. Колебание. Процесс |
Электрическое напряжение или ток, изменяющиеся во времени, с заранее известными характеристиками, используемые для измерения характеристик радиотехнических цепей и их контроля |
x(t), где х - напряжение или ток; t - время |
|
2. Мгновенное значение сигнала Ндп. Отсчет сигнала |
Значение сигнала в заданный момент времени |
х* = х(t*), где t* - заданный момент времени |
|
3. Максимальное значение сигнала Ндп. Амплитуда |
Наибольшее мгновенное значение сигнала на протяжении заданного интервала времени |
xmax = mах x(t), teT* где Т* = t2 - t1 - заданный интервал времени |
|
4. Минимальное значение сигнала |
Наименьшее мгновенное значение сигнала на протяжении заданного интервала времени |
xmin = min x(t) teT* |
|
5. Постоянная составляющая сигнала |
Среднее значение сигнала |
где Тy - интервал времени усреднения |
|
6. Переменная составляющая сигнала Ндп. Центрированный сигнал |
Разность между сигналом и его постоянной составляющей |
x~(t) = x(t) - |
|
7. Пиковое отклонение «вверх» |
Наибольшее мгновенное значение переменной составляющей сигнала на протяжении заданного интервала времени |
xвв = max x~(t) teT* |
|
8. Пиковое отклонение «вниз» |
Наименьшее мгновенное значение переменной составляющей сигнала на протяжении заданного интервала времени, взятое по модулю |
хвн = ômin x~(t)ô teT* |
|
9. Размах сигнала |
Разность между максимальным и минимальным значениями сигнала на протяжении заданного интервала времени |
R = xmax - xmin = xвв + xвн |
|
10. Средневыпрямленное значение сигнала Ндп. Среднее значение сигнала |
Среднее значение модуля сигнала |
|
|
11. Среднеквадратичное значение сигнала Ндп. Среднеквадратичное значение. Действующее значение. Эффективное значение |
Корень квадратный из среднего значения квадрата сигнала |
|
|
12. Средняя мощность сигнала, выделяемая на сопротивлении 1 ом |
Среднее значение квадрата сигнала |
|
|
13. Энергия сигнала, выделяемая на сопротивлении 1 ом |
Интеграл из квадрата сигнала по всей оси времени |
|
|
ХАРАКТЕРИСТИКИ ИМПУЛЬСОВ |
||
|
14. Спектральная функция импульса |
Комплексная функция, представляющая собой преобразование Фурье от импульса |
где x(t) - импульс;
|
|
15. Модуль спектральной функции импульса Ндп. Амплитудный спектр импульса |
- |
|
|
16. Аргумент спектральной функции импульса Ндп. Фазовый спектр импульса |
- |
|
|
Характеристики периодических сигналов |
||
|
17. Период периодического сигнала Период |
Параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала |
T |
|
18. Частота периодического сигнала Частота |
Параметр, представляющий собой величину, обратную периоду периодического сигнала |
|
|
19. Комплексный спектр периодического сигнала |
Комплексная функция дискретного аргумента, равного целому числу значений частоты периодического сигнала, представляющая собой значения коэффициентов комплексного ряда Фурье для периодического сигнала |
где n - любое целое число |
|
20. Амплитудный спектр периодического сигнала Спектр |
Функция дискретного аргумента, представляющая собой модуль комплексного спектра периодического сигнала |
|
|
21. Фазовый спектр периодического сигнала |
Функция дискретного аргумента, представляющая собой аргумент комплексного спектра периодического сигнала |
|
|
22. Гармоника |
Гармонический сигнал с амплитудой и начальной фазой, равными соответственно значениям амплитудного и фазового спектра периодического сигнала при некотором значении аргумента |
где i - номер гармоники |
|
Характеристики случайных сигналов |
||
|
23. Одномерная плотность вероятности Ндп. Дифференциальный закон распределения вероятности. Распределение амплитуд |
Функция, равная пределу отношения вероятности пребывания случайного сигнала в некотором интервале значений к ширине этого интервала при стремлении его к нулю, причем ее аргументом является значение, к которому стягивается интервал |
где P - вероятность; Dx - ширина интервала |
|
24. Корреляционная функция Ндп. Автокорреляционная функция |
Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание. Корреляционная функция характеризует статистическую связь между мгновенными значениями случайного сигнала, разделенными заданным интервалом времени |
где t - время запаздывания (35) |
|
25. Нормированная корреляционная функция Ндп. Коэффициент корреляции |
Функция, равная отношению корреляционной функции случайного сигнала к его дисперсии |
|
|
26. Энергетический спектр Ндп. Спектральная плотность |
Функция, представляющая собой преобразование Фурье от корреляционной функции, аргументом которой является частота |
|
|
Характеристики взаимодействия сигналов |
||
|
27. Отношение сигнал-помеха |
Отношение величин, характеризующих интенсивности сигнала и помехи. Примечание. В качестве величин, характеризующих интенсивности сигнала и помехи, берут их средние мощности, среднеквадратические значения, пиковые отклонения, энергии и т.п. Способ определения этих величин должен всегда оговариваться особо |
|
|
28. Коэффициент модуляции «вверх» Ндп. Коэффициент глубины модуляции «вверх» |
Коэффициент, равный отношению пикового отклонения «вверх» закона модуляции к его постоянной составляющей при амплитудной модуляции |
где
|
|
29. Коэффициент модуляции «вниз» Ндп. Коэффициент глубины модуляции «вниз» |
Коэффициент, равный отношению пикового отклонения «вниз» закона модуляции к его постоянной составляющей при амплитудной модуляции. Примечание. Если Ав = Ав = А, как, например, при гармоническом законе
модуляции, то величина |
где |
|
30. Девиация частоты «вверх» |
Пиковое отклонение «вверх» закона модуляции при частотной модуляции |
где f(t) - закон модуляции при частотной модуляции (мгновенная частота);
|
|
31. Девиация частоты «вниз» |
Пиковое отклонение «вниз» закона модуляции при частотной модуляции. Примечание. Если fgв = fgн = fg как, например, при гармоническом законе модуляции, то величина fg называется девиацией частоты |
|
|
32. Индекс угловой модуляции Индекс модуляции |
Пиковое отклонение закона модуляции фазо-модулированного сигнала при гармоническом законе модуляции |
где W - частота модулирующего сигнала; y - начальная фаза модулирующего сигнала; j0 - начальная фаза модулируемого сигнала |
|
Характеристики взаимосвязи сигналов |
||
|
33. Взаимокорреляционная функция Ндп. Кросскорреляционная функция |
Функция, равная среднему значению произведения переменной составляющей одного случайного сигнала и запаздывающей на заданное время переменной составляющей другого случайного сигнала. Примечание. Взаимнокорреляционная функция характеризует статистическую связь между мгновенными значениями двух случайных сигналов, разделенными заданным интервалом времени |
|
|
34. Взаимный энергетический спектр |
Функция, представляющая собой преобразование Фурье от взаимнокорреляционной функции, аргументом которой является частота |
|
|
35. Время запаздывания |
Параметр, равный значению временного сдвига одного из сигналов, при котором достигается тождественное равенство его другому сигналу с точностью до постоянного множителя и постоянного слагаемого. Примечание. Если формы сигналов различны, определяется эквивалентное время запаздывания: для случайных сигналов как абсцисса максимума взаимнокорреляционной функции, для импульсов как интервал времени между моментами первого достижения каждым из сигналов уровня, равного половине максимального значения |
Параметр t3 > 0 в выражении x2(t) = a1x1(t - t3) + a2, где a1, a2 - константы. Примечание. Параметр t0 = -t3 < 0 называется временем опережения |
|
36. Фазовый сдвиг Ндп. Сдвиг фаз |
Модуль разности начальных фаз двух гармонических сигналов одинаковой частоты |
где j1 и j2 - начальные фазы |
|
Характеристики искажений сигналов |
||
|
37. Коэффициент гармоник Ндп. Коэффициент нелинейных искажений. Клирфактор |
Коэффициент, характеризующий отличие формы данного периодического сигнала от гармонической, равный отношению среднеквадратического напряжения суммы всех гармоник сигнала, кроме первой, к среднеквадратическому напряжению первой гармоники |
где Ai - амплитуда i-й гармоники сигнала |
|
38. Относительное отклонение сигнала от линейного закона |
Коэффициент, равный отношению абсолютного отклонения (40) данного сигнала от прямой линии, соединяющей мгновенные значения сигнала, соответствующие началу и концу заданного интервала времени к максимальному значению сигнала на этом же интервале |
где D - абсолютное отклонение (40) сигналов |
|
39. Коэффициент нелинейности сигнала |
Коэффициент, равный отношению размаха производной сигнала на заданном интервале времени к максимальному значению производной на этом же интервале |
где |
|
40. Абсолютное отклонение сигналов |
Максимальное значение разности мгновенных значений сигналов, взятых в один и тот же момент времени на протяжении заданного интервала времени |
|
АЛФАВИТНЫЙ УКАЗАТЕЛЬ ТЕРМИНОВ
|
(3) |
|
|
Аргумент спектральной функции импульса |
|
|
Воздействие |
(1) |
|
Время запаздывания |
|
|
Гармоника |
|
|
Девиация частоты «вверх» |
|
|
Девиация частоты «вниз» |
|
|
Закон распределения вероятности дифференциальный |
(23) |
|
Значение действующее |
(11) |
|
Значение сигнала максимальное |
|
|
Значение сигнала мгновенное |
|
|
Значение сигнала минимальное |
|
|
Значение сигнала средневыпрямленное |
|
|
Значение сигнала среднее |
(10) |
|
Значение сигнала среднеквадратичное |
|
|
Значение среднеквадратичное |
(11) |
|
Значение эффективное |
(11) |
|
Индекс модуляции |
|
|
Индекс модуляции угловой |
|
|
Клирфактор |
(37) |
|
Колебание |
(1) |
|
Коэффициент гармоник |
|
|
Коэффициент нелинейности сигнала |
|
|
Коэффициент нелинейных искажений |
(37) |
|
Коэффициент корреляции |
(25) |
|
Коэффициент модуляции «вверх» |
(28) |
|
Коэффициент модуляции «вниз» |
|
|
Коэффициент глубины модуляции «вверх» |
(28) |
|
Коэффициент глубины модуляции «вниз» |
(29) |
|
Модуль спектральной функции импульса |
|
|
Мощность сигнала, выделяемая на сопротивлении 1 ом, средняя |
|
|
Отклонение пиковое «вверх» |
|
|
Отклонение пиковое «вниз» |
|
|
Отклонение сигнала от линейного закона относительное |
|
|
Отклонение сигнала абсолютное |
|
|
Отношение сигнал-помеха |
|
|
Отсчет сигнала |
(2) |
|
Период |
|
|
Период периодического сигнала |
|
|
Плотность вероятности одномерная |
|
|
Плотность мощности спектральная |
(26) |
|
Процесс |
(1) |
|
Размах сигнала |
|
|
Распределение амплитуд |
(23) |
|
Сдвиг фазы |
(36) |
|
Сдвиг фазовый |
|
|
Сигнал испытательный |
(1) |
|
Сигнал пробный |
(1) |
|
Сигнал радиотехнический измерительный |
|
|
Сигнал тестовый |
|
|
Сигнал центрированный |
(6) |
|
Составляющая сигнала переменная |
|
|
Составляющая сигнала постоянная |
|
|
Спектр |
|
|
Спектр импульса амплитудный |
(15) |
|
Спектр импульса фазовый |
(16) |
|
Спектр периодического сигнала амплитудный |
|
|
Спектр периодического сигнала комплексный |
|
|
Спектр периодического сигнала фазовый |
|
|
Спектр энергетический |
|
|
Спектр энергетический взаимный |
|
|
Тест-сигнал |
(1) |
|
Функция автокорреляционная |
(24) |
|
Функция взаимнокорреляционная |
|
|
Функция импульса спектральная |
|
|
Функция корреляционная |
|
|
Функция корреляционная нормированная |
|
|
Функция кросскорреляционная |
(33) |
|
Частота |
|
|
Частота периодического сигнала |
|
|
Энергия сигнала, выделяемая на сопротивлении 1 ом |
(Измененная редакция, Изм. № 1).
Справочное
Термины, аналитические и графические определения номинальных форм и параметров некоторых импульсов
|
Графическое определение |
Аналитическое определение |
Параметр |
|
|
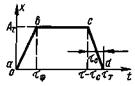
1. Прямоугольный импульс |
|
Ап - амплитуда прямоугольного импульса; tп - длительность прямоугольного импульса. Примечание. Отрезок аb называется фронтом прямоугольного импульса, отрезок bс - вершиной прямоугольного импульса, отрезок cd - срезом прямоугольного импульса |
|
|
2. Трапецеидальный импульс |
|
Ат - амплитуда трапецеидального импульса; tт - длительность трапецеидального импульса; tф - длительность фронта трапецеидального импульса; tс - длительность среза трапецеидального импульса. Примечание. Отрезок аb называется фронтом трапецеидального импульса, отрезок bc - вершиной трапецеидального импульса, отрезок cd - срезом трапецеидального импульса |
|
|
3. Экспоненциальный импульс |
|
Аэ - амплитуда экспоненциального импульса; tэ - постоянная времени экспоненциального импульса |
|
|
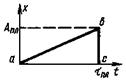
4. Пилообразный импульс |
|
Апл - амплитуда пилообразного импульса; tпл - длительность пилообразного импульса. Примечание. Отрезок аb называется прямым ходом пилообразного импульса, отрезок bc - обратным ходом пилообразного импульса |
|
|
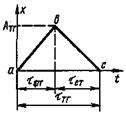
5. Треугольный импульс |
|
Атг - амплитуда треугольного импульса; tфт - длительность фронта треугольного импульса; tст - длительность среза треугольного импульса; tтг - длительность треугольного импульса. Примечания: 1. Отрезок ab называется фронтом треугольного импульса, отрезок bс - срезом треугольного импульса. 2. Интервал времени нарастания фронта между уровнями 0; 1А и 0,9А связан с tфт соотношением tфт (0,1 - 0,9) = 0,8tфт. Интервал времени нарастания среза между уровнями 0,1А и 0,9А связан с tст соотношением tст (0,9 - 0,1) = 0,8tст |
|
|
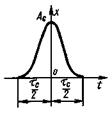
6. Колоколообразный импульс |
|
Ак - амплитуда колоколообразного импульса; 2tк - интервал времени между точками перегиба колоколообразного импульса. Примечания: 1. Значение параметра 2tк определяется также по уровню 0,606Ак. 2. Интервал времени t (0,5) на уровне 0,5Ак связан с tк соотношением tк (0,5) = 2,35tк |
|
|
7. Косинусквадратный импульс |
|
Ас - амплитуда косинусквадратного импульса; tс - длительность косинусквадратного импульса. Примечание. Значение параметра tс определяется также по уровню 0,5Ас |
(Измененная редакция, Изм. № 1).
Справочное
Термины, аналитические и графические определения форм и параметров некоторых периодических сигналов
|
Графическое определение |
Аналитическое определение |
Параметр |
|
|
1. Гармонический сигнал |
|
А - амплитуда гармоничного сигнала; w - круговая частота; j - начальная фаза |
|
|
2. Периодическая последовательность прямоугольных импульсов. Примечание. При
|
|
Ап - амплитуда прямоугольного импульса; tп - длительность прямоугольного импульса; Т - период. Примечание. Отношение |
Примечание. Периодический сигнал может быть образован путем периодического повторения импульсов. Соответствующие термины и определения для такого сигнала вводятся так же, как и для импульсов (см. приложение 1) с добавлением еще одного параметра - значения периода или частоты и указания на периодический характер сигнала.
(Измененная редакция, Изм. № 1).
Справочное
Термины, аналитические и графические определения форм и параметров некоторых одномерных плотностей вероятности
|
Графическое определение |
Аналитическое определение |
Параметр |
|
|
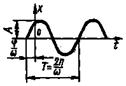
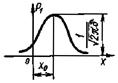
1. Нормальная |
|
s - среднеквадратичное значение сигнала с нормальной плотностью вероятности; х0 - постоянная составляющая сигнала с нормальной плотностью вероятности |
|
|
2. Экспоненциальная |
|
т - постоянная составляющая сигнала с экспоненциальной плотностью вероятности |
|
|
3. Равномерная |
|
|
а - размах сигнала с равномерной плотностью вероятности |
Примечание. Термины и определения одномерных плотностей вероятности других форм вводятся аналогичным образом.
Справочное
Примерные виды осциллограмм некоторых импульсов, способов определения их основных параметров и параметров искажений
|
Примерный вид осциллограммы |
Основные параметры (см. приложение 1) |
Параметры искажений |
|
|
1. Прямоугольный импульс |
Ап, tп |
tфп - длительность фронта прямоугольного импульса; tсп - длительность среза прямоугольного импульса; b1 - выброс на вершине прямоугольного импульса; b2 - выброс в паузе прямоугольного импульса; dп - неравномерность вершины прямоугольного импульса. Примечание. Значение параметра Ап находится путем продления плоской части вершины до пересечения с фронтом прямоугольного импульса |
|
|
2. Трапецеидальный импульс |
Ат, tт, tф, tс |
dт - неравномерность вершины трапецеидального импульса; dф - нелинейность фронта трапецеидального импульса; dс - нелинейность среза трапецеидального импульса |
|
|
3. Экспоненциальный импульс |
Примечание. Значение параметра tэ рассчитывается по формуле
|
Аэ, tэ |
tфэ - длительность фронта экспоненциального импульса; dэ - неэкспоненциальность среза |
|
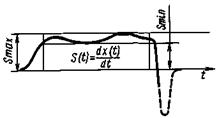
4. Пилообразный импульс |
Апл, tпл |
tобр - длительность обратного хода пилообразного импульса; dпл - нелинейность пилообразного импульса. Примечание. А - вспомогательная величина, используемая при нормировании. К1 < 1; К2 < 1 - заданные коэффициенты |
|
|
Примечание. Если пилообразный сигнал используется для получения развертки, нелинейность определяется в соответствии с определением понятия 39. |
|||
|
|
|
|
|
Примечание. Наряду с параметрами искажений допускается использование безразмерных коэффициентов, представляющих собой отношения приведенных в таблице параметров искажений к соответствующим основным параметрам. Наименования этих коэффициентов образуются путем добавления слова «относительный» (ая) к наименованиям параметров искажений, например:
tфп/tп - относительная длительность фронта прямоугольного импульса;
dп/Ап - относительная неравномерность вершины прямоугольного импульса и т.п.
Справочное
ПОЯСНЕНИЯ К ТЕРМИНАМ, ВСТРЕЧАЮЩИМСЯ В СТАНДАРТЕ
СИГНАЛ - изменяющаяся физическая величина, отображающая сообщение.
Примечания:
1. Особенностью радиотехнических сигналов является использование электрических величин тока, напряжения, напряженности электромагнитного поля. Для этих сигналов характерно то, что они заранее неизвестны получателю сообщения. Особенностью измерительных радиотехнических сигналов, получаемых с помощью измерительных генераторов сигналов, является то, что их свойства известны заранее. После прохождения через исследуемую цепь (с неизвестными характеристиками) сигнал изменяется. Сравнивая сигналы на входе и выходе цепи, можно измерить ее характеристики.
2. В теоретических исследованиях и инженерных расчетах используется математическая модель сигнала, представляющая собой математическое идеализированное описание сигнала, сохраняющее те его свойства, которые являются существенными для решаемой задачи. Для математического описания сигнала используются математические характеристики (П. 2*), представляющие собой функции, параметры функций и их функционалы.
ФУНКЦИЯ - переменная величина у = f(x), зависящая от переменной величины х (аргумента); если при заданном значении х величина у принимает одно определенное значение, функция является однозначной.
СРЕДНЕЕ ЗНАЧЕНИЕ ![]() ФУНКЦИИ
у(t) = j[x(t)]
- величина
ФУНКЦИИ
у(t) = j[x(t)]
- величина  ,
где P1(x)
- одномерная плотность вероятности (23)* сигнала x(t).
,
где P1(x)
- одномерная плотность вероятности (23)* сигнала x(t).
Примечание. Для стационарного эргодического случайного сигнала
также ![]() .
Для периодического сигнала
.
Для периодического сигнала ![]()
где t* - произвольный момент времени; Т - период.
* При ссылках на термины и определения, помещенные в настоящем приложении к стандарту, перед номером в скобках ставится буква П.
ДИСПЕРСИЯ - среднее значение квадрата переменной составляющей случайного сигнала.
ФОРМА ФУНКЦИИ - вид функциональной зависимости f между значениями функции у и аргумента х.
Примечание. Форма функции не изменяется при произвольном
линейном преобразовании осей координат, т.е. все функции вида ![]() при данном f
и произвольных значениях а,b и с имеют одинаковую
форму.
при данном f
и произвольных значениях а,b и с имеют одинаковую
форму.
Рассмотренные выше функции являются, как правило, действительными функциями аргумента, в противном случае сделаны специальные оговорки (см., например, 14.19).
ПАРАМЕТРЫ ФУНКЦИИ f(x, а1, ... аn) - все величины а1, ... ап, кроме аргумента х, от которых зависит значение функции f.
ФУНКЦИОНАЛ F = F{f(x)} - число F, которое по определенному правилу ставится в соответствие с функцией f(х).
Справочное
Классификация измерительных радиотехнических сигналов
Классификация измерительных радиотехнических сигналов
|
Определение |
Математическая формула и обозначение величины |
|
|
1. Характеристики сигналов |
Количественные данные, относящиеся к понятиям, характеризующим данные сигналы |
|
|
2. Математические характеристики сигналов |
Характеристики сигналов, выражаемые с помощью функций, параметров функций и функционалов при математическом описании сигналов |
|
|
3. Общие характеристики сигнала |
Математические характеристики сигнала, рассматриваемого как единое целое |
|
|
4. Детерминированный сигнал |
Сигнал, мгновенные значения которого в любой момент времени известны. Примечание. Общие характеристики детерминированного сигнала могут быть найдены расчетным путем |
|
|
5. Импульсный сигнал Импульс |
Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот сигнал предназначен. Примечания: 1. Сигнал, представляющий собой последовательность конечного известного числа импульсов одинаковой формы, следующих друг за другом через одинаковые интервалы времени, называется пачкой импульсов. 2. Сигнал, состоящий из импульсов, число, форма и значения параметров которых известны, называется кодовой группой импульсов |
где n < ¥ - целое число; ai - высота i-го импульса; Тс - интервал следования
где n < ¥ - целое число |
|
6. Периодический сигнал |
Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени |
x(t) = x(t - iT), где i - любое целое число |
|
7. Случайный сигнал |
Сигнал, мгновенные значения которого являются случайными величинами. Примечание. Случайный сигнал, любая вероятная характеристика которого, полученная усреднением по множеству возможных реализаций с вероятностью, сколь угодно близкой к единице, равна временному среднему, полученному усреднением за достаточно большой промежуток времени одной реализации, называется эргодическим. Рассмотренные выше характеристики случайного сигнала определены для эргодического сигнала |
|
|
8. Стационарный случайный сигнал |
Случайный сигнал, у которого плотность вероятности любой совокупности мгновенных значений не изменяется при любом сдвиге этой совокупности во времени. Примечание. Случайный сигнал, у которого среднее значение и дисперсия не зависят от времени, а корреляционная функция зависит только от времени запаздывания, называется стационарным в широком смысле |
pп(x1, t1; x2, t2; ... ; xn, tn) = pп(x1, t1 + t; x2, t2 + t; ... ; xn, tn + t), где t - произвольный интервал времени |
|
9. Нестационарный случайный сигнал |
Случайный сигнал, у которого плотность вероятности некоторой совокупности мгновенных значений изменяется при некотором сдвиге этой совокупности во времени |
pп(x1, t1; x2, t2; ...; xn, tn) ¹ pп(x1, t1 + t; t2 + t; ...; xn, tn + t) |
|
10. Взаимные характеристики сигналов |
Математические характеристики нескольких сигналов |
|
|
11. Характеристики взаимодействия сигналов |
Взаимные характеристики сигналов, описывающие их взаимодействие при образовании из них нового сигнала. Примечание. Сигнал, образованный в результате взаимодействия нескольких сигналов, является детерминированным, если детерминированы все взаимодействующие сигналы; в противном случае он является случайным |
|
|
12. Аддитивный сигнал |
Сигнал, мгновенные значения которого являются суммой мгновенных значений двух или более сигналов, взятых в один и тот же момент времени. Примечание. Если один из сигналов, образующих аддитивный сигнал, считается полезным, а другие - мешающими, то мешающие сигналы иногда называют помехой или шумом |
где k ³ 2 - целое число |
|
13. Мультипликативный сигнал |
Сигнал, мгновенные значения которого пропорциональны произведению мгновенных значений двух или более сигналов, взятых в один и тот же момент времени |
где k ³ 2 - целое число с = const |
|
14. Модулированный сигнал |
Сигнал, являющийся результатом взаимодействия двух или более сигналов, называемого модуляцией. Примечания: 1. В данном стандарте рассматривается простейший случай взаимодействия двух сигналов с модуляцией по одному параметру |
|
|
2. Модуляцией называется физический процесс получения сигнала, математическое описание которого может быть получено заменой параметра в математическом описании модулируемого сигнала на функцию от модулирующего сигнала. Обычно эта функция (закон модуляции) является линейной. При этом закон модуляции характеризуется такими же параметрами и функционалами, как и модулирующий сигнал |
Пусть x1(t, a1, ... аk, ..., аn) - модулируемый сигнал (переносчик); x2(t) - модулирующий сигнал. Тогда при модуляции по параметру аk(k = 1, ..., аn) x1(t, a1, ..., j[x2(t)], ..., an) - модулированный сигнал; j[x2(t)] - закон модуляции. Если j - линейная функция, то j[x2(t)] = a0 + kx2(t), где а0 = const, например, постоянная составляющая; k = const - коэффициент (крутизна модуляционной характеристики). |
|
|
3. Чаще всего в качестве модулируемого сигнала используется гармонический сигнал или периодическая последовательность прямоугольных импульсов. Если модулируемый сигнал является гармоническим, в зависимости от параметра, подвергаемого воздействию со стороны модулирующего сигнала (амплитуды, частоты, начальной фазы) различают соответственно амплитудную (AM), частотную (ЧМ) и фазовую (ФМ) модуляции. Соответствующие модулированные сигналы называются амплитудно-модулированным (AM - сигнал), частотно-модулированным (ЧМ - сигнал) и фазово-модулированным (ФМ - сигнал). Часто частотная и фазовая модуляция именуются общим термином угловая модуляция |
|
|
|
15. Характеристики взаимосвязи сигналов |
Взаимные характеристики нескольких взаимосвязанных сигналов, не образующих нового сигнала |
|
|
16. Метрологические характеристики сигнала |
Количественные данные, определяемые в результате измерения, устанавливающие степень соответствия сигнала заранее заданному математическому описанию |
|
|
17. Основные параметры |
Метрологические характеристики сигнала, имеющие тот же смысл и наименования, что и параметры математического описания сигнала, для воспроизведения которого предназначен данный измерительный генератор. Примечание. В измерительных генераторах, как правило, допускается возможность произвольной установки основных параметров сигнала в пределах определенных диапазонов значений |
|
|
18. Характеристики искажений |
Метрологические характеристики сигнала, описывающие степень несоответствия сигнала заранее заданному математическому описанию, определяемые таким образом, чтобы их значения обращались в нуль, если сигнал в точности соответствует требуемому математическому описанию |
|
|
19. Коэффициент искажений |
Характеристика искажений, представляющая собой безразмерный коэффициент, описывающий отличие реального сигнала на выходе измерительного генератора от заранее заданного математического описания в целом и зависящий от выбранного критерия сравнения сигналов (критерий абсолютного отклонения, критерий среднеквадратического отклонения и т.п.) |
|
|
20. Параметры искажений |
Характеристики искажений, представляющие собой параметры, отличающиеся от основных параметров, описывающие отличие реального сигнала на выходе измерительного генератора от заранее заданного математического описания более детально, чем коэффициент искажений |
|
СОДЕРЖАНИЕ