МИНИСТЕРСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ СССР
ГЛАВНОЕ ТЕХНИЧЕСКОЕ УПРАВЛЕНИЕ ПО ЭКСПЛУАТАЦИИ ЭНЕРГОСИСТЕМ
ПРОИЗВОДСТВЕННОЕ ОБЪЕДИНЕНИЕ
ПО НАЛАДКЕ, СОВЕРШЕНСТВОВАНИЮ ТЕХНОЛОГИИ
И ЭКСПЛУАТАЦИИ ЭЛЕКТРОСТАНЦИЙ И СЕТЕЙ
«СОЮЗТЕХЭНЕРГО»
ТИПОВАЯ
ИНСТРУКЦИЯ
ПО ОЦЕНКЕ СОСТОЯНИЯ
ГЛАВНОЙ ИЗОЛЯЦИИ ОБМОТОК
СТАТОРОВ ГЕНЕРАТОРОВ
НА ОСНОВЕ ТИПОВЫХ КРИВЫХ
ВЕРОЯТНОСТИ
АВАРИЙНОГО ПРОБОЯ
ТИ 34-70-013-82
Союзтехэнерго
Москва 1983
РАЗРАБОТАНО ВСЕСОЮЗНЫМ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИМ ИНСТИТУТОМ ЭЛЕКТРОЭНЕРГЕТИКИ (ВНИИЭ)
СОСТАВИТЕЛИ Л.А. БЕЛОВА (ВНИИЭИМ), Л.Г. МАЛИКОНЯНЦ (ВНИИЭ), В.Н. ТУТУБАЛИН (МГУ)
СОГЛАСОВАНО СО ВСЕСОЮЗНЫМ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИМ ИНСТИТУТОМ ЭЛЕКТРОИЗОЛЯЦИОННЫХ МАТЕРИАЛОВ И ФОЛЬГИРОВАННЫХ ДИЭЛЕКТРИКОВ (ВНИИЭИМ) И МОСКОВСКИМ ГОСУДАРСТВЕННЫМ УНИВЕРСИТЕТОМ ИМЕНИ М.В. ЛОМОНОСОВА (МГУ)
УТВЕРЖДЕНО Главным техническим управлениям по эксплуатации энергосистем
Заместитель начальника К.М. АНТИПОВ
|
ТИПОВАЯ ИНСТРУКЦИЯ ПО ОЦЕНКЕ СОСТОЯНИЯ ГЛАВНОЙ ИЗОЛЯЦИИ ОБМОТОК СТАТОРОВ ГЕНЕРАТОРОВ НА ОСНОВЕ ТИПОВЫХ КРИВЫХ ВЕРОЯТНОСТИ АВАРИЙНОГО ПРОБОЯ |
ТИ 34-70-013-82 |
Срок действия установлен
с 01.01.83 г.
до 01.01.88 г.
Рассмотрение и анализ отдельных случаев или видов повреждений различных элементов генератора имеют большое техническое значение.
Правильно понятый и своевременно изученный недостаток, переделка неправильно сконструированного узла, естественно, приводят к повышению надежности оборудования. Такой подход к рассмотрению и оценке состояния оборудования и его усовершенствованию необходим и полезен, особенно для приработочного периода.
Вместе с тем полезно иметь практически осуществимую возможность общей оценки состояния всей совокупности работающих генераторов, возможность обоснованного разделения всей совокупности на нормальные и анормальные группы с выполнением более детального анализа для последних с целью ликвидации «узких» мест. Это возможно, если располагать данными, характеризующими общие закономерности поведения отдельных элементов генераторов, закономерности возникновения и развития дефектов.
Подобные закономерности могут быть выявлены лишь на большом экспериментальном материале при использовании математического аппарата теории вероятностей и математической статистики. В качестве экспериментального материала, наряду с другими могут быть использованы эксплуатационные данные.
Как известно, аварийные повреждения корпусной изоляции обмоток статоров генераторов в эксплуатации составляют значительную часть всех повреждений генераторов. Полученные во ВНИИЭ на основе обработки данных об эксплуатационных пробоях корпусной изоляции типовые кривые вероятности аварий описывают закономерности качественного изменения состояния нормальной, удовлетворяющей заданным техническим требованиям, корпусной микалентной изоляции в зависимости от длительности ее эксплуатации. Указанные кривые позволяют получать количественные оценки аварийности, которые помогают в различных ситуациях оценивать состояние машин и анализировать отдельные явления. Практические расчёты по получению количественных оценок аварийности корпусной изоляции при наличии типовой кривой вероятности аварий не требуют больших затрат времени и достаточно просты. Вместе с тем они позволяют анализировать состояние изоляции за прошедший период и прогнозировать возможность возникновения аварий на заданный период в будущем.
В настоящей Типовой инструкции изложены основные положения оценки состояния корпусной изоляции обмоток статоров генераторов по указанной кривой, характеризующей закономерности старения изоляций.
Инструктивной частью являются указания по практическому использованию типовой кривой вероятности для расчетов и область возможных расчетов. Область таких расчетов практически не ограничена и не может быть полностью перечислена в настоящей Типовой инструкции, однако рассмотрение ряда конкретных задач позволяет понять механизм методики количественной оценки состояния корпусной изоляции и использовать ее в любой практической ситуации.
С этой целью в приложении 1 разобрано достаточно большое количество практических примеров.
Так как в процессе практического анализа в ряде случаев требуется сравнение типовой и так называемой текущей1 кривой вероятности аварийного пробоя, для лучшего уяснения изложенных инструктивных указаний в приложении 2 даются основные положения по методике получения текущих кривых вероятности аварийного пробоя изоляции.
1 Кривая называется текущей, так как она вычислена по текущим статистическим данным на определенный момент времени. С поступлением новой информации (другой момент времени, изменение состава совокупности, ее качества и т.п.) эта кривая, в отличие от типовой, может меняться.
1. ОБЩАЯ ЧАСТЬ
1. Причины возникновения аварийных пробоев изоляции различны. В одних случаях можно указать явную причину повреждения изоляции (например, допущенная при сборке или ремонте небрежность, приводящая к механическому повреждению изоляции, воздействие напряжения более высокого класса, ненормальный режим эксплуатации, повреждение при аварии другого элемента, например, короткое замыкание из-за нарушения паянного соединения лобовых частей обмотки и т.п.). В других случаях пробой происходит как бы без всякой видимой причины и в аварийном акте при этом записывается: причиной пробоя является местный дефект изоляции или приводится какая-нибудь малообоснованная или сомнительная причина.
2. С точки зрения применения теории вероятностей и физического смысла задачи оценки состояния изоляции указанные два вида аварий резко различны. В первом случае понятие вероятности не имеет смысла, так как случаи постороннего1 повреждения изоляции разнообразны и вместе с тем сравнительно редки. При таком разнообразии, естественно, не удается получить в каждом отдельном случае необходимую для исследования статистически однородную совокупность и, кроме того, при этом задачей исследования являлось бы изучение природы данного постороннего воздействия, а не свойств собственно изоляции. Поэтому случаи аварийных повреждений, вызванных посторонними причинами при выполнении предлагаемого настоящей Типовой инструкцией характера анализа состояния изоляции не должны привлекаться к исследованию, но в случае потребности они могут быть независимо подвергнуты самостоятельному анализу с соответственно сформулированной задачей и моделью исследования.
1 К таким повреждениям относятся повреждения, вызванные внешними механическими воздействиями, воздействием напряжения более высокого класса, грозовым перенапряжением и т.п.
В случае же обработки данных об аварийных пробоях, происшедших как бы без видимой причины, в первом приближении получается близкая к статистически однородной совокупность, то есть в этом случае можно ставить задачу об определении вероятности аварийного пробоя изоляции, наступающего вследствие развития местных дефектов, и о получении количественной оценки ее состояния.
3. Любая реальная совокупность изоляции состоит из определенной, обычно довольно большой доли так называемых нормальных машин, удовлетворяющих заданным техническим требованиям на конструирование, изготовление и эксплуатацию и сравнительно небольшой доли анормальных машин, отклоняющихся в лучшую или худшую сторону, для которых пробой без явно выраженной причины тем не менее был вызван скрытым дефектом конструирования, изготовления или эксплуатации. Возможность четкого выделения этих отклоняющихся групп и их последующее детальное исследование позволяет выполнить при сравнительно малых затратах достаточно точный анализ состояния изоляции рассматриваемой конкретной совокупности машин (в целом для всей совокупности и вплоть до отдельной конкретной машины) и принять соответствующие технические меры по нормализации возникшей ситуации.
По совокупности нормальных машин (определенных в процессе указанного анализа) предпринимать ничего не следует, можно ограничиться задачей прогнозирования аварийности, т.е. подсчетом предполагаемого числа аварийных пробоев на предстоящий заданный период времени и приготовиться к выполнению ремонтных работ (заготовить резервные стержни, оснастку и т.п.)
4. Подобный анализ возможен, если располагать типовой кривой вероятности аварий корпусной изоляции обмоток статоров генераторов. Такая типовая кривая существует1, она получена на основании обработки данных об аварийных пробоях микалентной изоляции представительной группы генераторов с воздушным и водородным охлаждением за длительный период их эксплуатации.
1 М.: «Электричество», 1979, № 5, стр. 54 - 58.
Эта типовая кривая вероятности аварий корпусной изоляции обмоток статоров характеризует микалентную изоляцию в ее нормальном исполнении и может быть использована в качестве эталона для практического анализа рабочего состояния изоляции любого возможного сочетания групп генераторов: турбо- и гидрогенераторов или отдельных групп, объединенных различными признаками, например уровнем номинального напряжения, территориальным размещением, принадлежностью к заводу-изготовителю и т.п., но с учетом вида охлаждения обмотки статора (от вида охлаждения зависит наклон типовой и текущих кривых).
5. Знание закономерности поведения во времени нормальной изоляции, позволяет получать различные количественные оценки для вышеуказанных разнообразных сочетаний машин в предположении их принадлежности к нормальной (среднестатистической) совокупности.
Сопоставление их фактической повреждаемости с эталонными количественными оценками, полученными по типовым характеристикам, позволяет анализировать состояние оцениваемой изоляции и в ряде случаев прогнозировать опасность появления аварийного пробоя. Это позволяет эффективно решать практические задачи по оценке рабочего состояния изоляции обмоток статоров генераторов в различных реальных ситуациях.
6. К таким практическим задачам относятся:
а) оценка необходимого количества новых машин для достоверного испытания новой изоляции;
б) оценка качества новых видов изоляции на малом экспериментальном материале;
в) оценка степени изношенности изоляции отдельной длительно работавшей машины;
г) возможность выделения из общей совокупности генераторов отдельных типов, видов или групп генераторов с резко большей или резко меньшей аварийностью;
д) осуществление систематического или периодического контроля за состоянием изоляции обмоток статоров наблюдаемой совокупности (контроль стабильности статистической однородности совокупности);
е) анализ состояния изоляции по отдельным энергосистемам или другим территориальным признакам;
ж) оценка качества выпущенной продукции по отдельным заводам-изготовителям;
з) оценка эффективности различных конструктивных решений;
и) сравнительная оценка качества новых видов изоляции (в сравнении с микалентной изоляцией);
к) проверка правильности учета пробоев в работе по отдельным электростанциям или отдельным энергосистемам;
л) прогнозирование аварийности по заданной совокупности на заданный период времени;
м) обоснованное планирование крупных реконструктивных работ (полные перемотки обмоток статоров и т.п.) и регулирование благодаря этому уровня ежегодной удельной аварийности изоляции;
н) определение потребного на планируемый год количества запасных стержней и обмоток с учетом аварийности отдельных типов генераторов.
7. Во всех перечисленных выше и других аналогичных задачах предлагается производить сравнение показателей изоляции анализируемой совокупности с показателями типовой, эталонной кривой вероятности аварийного пробоя, характеризующей нормальное состояние изоляции.
8. Практическое решение перечисленных выше задач требует различного методического подхода.
Вместе с тем общим для всех задач является следующее:
а) практически во всех случаях необходимым, а в некоторых достаточным является определение параметра распределения Пуассона, т.е. определение математического ожидания (МО) возможного числа аварий по типовой кривой и сравнение его с фактическим числом аварий, имевшим место на анализируемой совокупности, или принятие математического ожидания как величины ожидаемой аварийности;
б) в большинстве задач, как например, в задаче систематического статистического контроля за состоянием изоляции наблюдаемой совокупности генераторов требуется также сравнение вновь полученной так называемой, текущей кривой вероятности аварии с типовой кривой;
в) во многих задачах полезным является использование графиков календарной повреждаемости (удельной повреждаемости по годам).
9. В разд. II изложены общие положения методики использования типовой кривой вероятности аварийного пробоя микалентной изоляции для практической оценки состояния корпусной изоляции обмоток статоров генераторов.
10. Типовые кривые вероятности аварийного пробоя для генераторов с новыми видами изоляции и для электродвигателей в настоящей Типовой инструкции не приводятся. Для этих групп машин по приведенной в Типовой инструкции кривой могут быть выполнены только сравнительные расчеты.
2. ИСПОЛЬЗОВАНИЕ ТИПОВОЙ КРИВОЙ ВЕРОЯТНОСТИ АВАРИЙНОГО ПРОБОЯ ДЛЯ ОЦЕНКИ СОСТОЯНИЯ КОРПУСНОЙ ИЗОЛЯЦИИ ОБМОТОК СТАТОРОВ ГЕНЕРАТОРОВ
11. Для практических расчетов в качестве исходных показателей должны быть приняты единица площади и единица времени, так как при принятой статистической модели распределение величины μ(Mi; ti, Ti)* зависит лишь от площади изоляции Si для машины Mi и интервала времени ее эксплуатации (ti, Ti) (предполагается, что число аварийных пробоев изоляции площади S имеет пуассоновское распределение).
12. За единицу площади корпусной изоляции следует принять 100 м2.
13. За единицу времени следует принять 1 · 104 часа, что соответствует примерно 1,5 - 2 годам эксплуатации для базисных электростанций и 2,5 - 3 годам эксплуатации для электростанций, работающих в пиковом режиме.
* Величина μ означает число аварий изоляции, происшедших на машине Mi (Mi есть i-ая машина из рассматриваемой совокупности), в то время как она проходила эксплуатацию от момента ti до момента Ti (время отсчитывается с начала эксплуатации, причем учитывается только рабочее время).
14. Для расчета при анализе выбранной совокупности генераторов в общем случае необходимо иметь следующие данные:
а) паспортные и технические данные, в том числе сведения о перемотках, реконструкциях всех анализируемых машин;
б) количество единиц площади, содержащееся в каждой из рассматриваемых машин и в целом по совокупности;
в) количество единиц времени для каждой машины с момента начала ее эксплуатации или ее полной перемотки до рассматриваемого в задаче времени с делением на календарные периоды. Последнее необходимо для возможности выделения определенных временных периодов, представляющих интерес для расчетчика;
г) фактическая аварийность корпусной изоляции обмоток статоров данных машин за прошедший период.
В отдельных задачах полный объем перечисленных данных не требуется.
15. Для расчетов используются:
- типовая кривая, характеризующая закономерность старения нормальной микалентной изоляции при ее работе с воздушным или водородным охлаждением (независимо от вида, типа генератора, места его установки, завода-изготовителя и т.п.);
- текущие кривые вероятности аварийного пробоя реальных, практически всегда статистически неоднородных совокупностей изоляции (по состоянию на заданный момент времени) из-за наличия в их составе, помимо нормальной изоляции, отдельных групп, выполненных с нарушением принятых правил ее изготовления и эксплуатации: это могут быть ошибки конструирования, нарушения технологии производства или ремонта, нарушения правил эксплуатации и т.п. (методика обработки данных для получения текущих кривых вероятности аварийного пробоя изложена в приложении 2);
- параметр распределения Пуассона (математическое ожидание числа аварийных пробоев - МО).
16. В основе решения практически всех крупных задач лежит сравнение текущей кривой вероятности аварийного пробоя с типовой:
- в случае их совпадения вся процедура анализа может быть закончена, так как анализируемая совокупность должна быть признана однородной, удовлетворяющей нормальным требованиям. В этом случае следует лишь выполнить контрольный тест проверки однородности анализируемой совокупности;
- в случае их несовпадения прежде всего необходимо проанализировать соотношение рассматриваемых кривых. Если текущая кривая лежит на всём диапазоне выше типовой, то текущая исследуемая совокупность содержит группы, отклоняющиеся в худшую сторону; если ниже типовой кривой, то содержит в своем составе группы, отклоняющиеся в лучшую сторону. Текущая кривая может пересекать типовую. В таком случае исследуемая совокупность имеет отклонения как в лучшую, так и худшую сторону.
17. При обнаружении неоднородности совокупности (по отклонению текущей кривой от типовой) следует выполнить ее проверку на однородность с выделением отклоняющихся групп.
Принципиально проверка статистической однородности совокупности состоит в вычислении параметра Пуассона λ, т.е. математического ожидания числа аварий на той или иной совокупности машин или их части, и сравнения этого ожидаемого числа с фактическим числом аварий μ.
При значимом несовпадении этих величин (уровень значимости задается в каждой конкретной задаче) соответствующие группы должны быть выделены в отклоняющиеся.
18. Типовая кривая вероятности аварийного пробоя изоляции позволяет подсчитать для каждого генератора анализируемой совокупности ожидаемое число аварийных пробоев в предположении его соответствия нормальным показателям. Далее путем суммирования λ отдельных машин ожидаемое (соответствующее норме) число аварийных пробоев может быть получено по любым, желательным для анализа перегруппировкам генераторов.
Сравнение расчетного ожидаемого и фактического числа аварийных пробоев данной совокупности, ее отдельных групп или отдельных генераторов позволяет сделать заключение об их соответствии эталону или отклонению от него.
В частности, для оценки возможного влияния различных «сбоев», например:
- технологического - следует произвести сопоставление показателей рассматриваемых генераторов по отдельным заводам;
- конструктивного - по типам;
- эксплуатационного - по электростанциям;
- ремонтного (например, для оценки качества выполненных полных перемоток обмоток статоров) - по генераторам, прошедшим перемотки, можно с подразделением по предприятиям-исполнителям и т.д.
19. Выявленные отклоняющиеся группы исключаются из текущей совокупности. Вновь просчитываются частоты и кривая вероятности аварийного пробоя. Полученная кривая еще раз сравнивается с типовой. Обычно число итераций невелико и совпадение расчетной и типовой кривой достигается сравнительно легко. Затем производится технический анализ отклоняющихся групп и вырабатываются соответствующие рекомендации для воздействия на состояние исследуемой изоляции.
20. Из вышеизложенного видно, что при решении задач практического анализа важное значение имеет параметр распределения Пуассона (λ).
21. В большинстве ситуаций число аварий, рассматриваемых как случайные (согласно принципам классификации, сформулированным в п. 2), представляет собой случайную величину μ, подчиняющуюся распределению вероятностей Пуассона. Это означает, что
![]()
где λ - параметр распределения Пуассона (математическое ожидание случайной величины μ).
22. Число случайных аварийных пробоев μ может относиться к одной машине или к совокупности машин, рассматриваемых в течение определенного периода эксплуатации (период эксплуатации может быть своим для каждой машины и охватывать как все время эксплуатации данной машины, так и любую его часть).
23. Значения параметра λ для конкретной машины, отвечающие заданному интервалу времени, скажем i-ой единице рабочего времени (т.е. времени эксплуатации от [i - 1] · 104 часов до i · 104 часов), получаются умножением площади S изоляции этой машины на число, взятое по типовой кривой, приведенной в табл. 1 (при этом площадь S должна быть измерена в сотнях квадратных метров).
Таблица 1
Типовые значения pi, рассчитанные для единицы площади микалентной изоляции (100 м2) и для интервалов рабочего времени вида [(i - 1) · 104 часов; 1 · 104 часов]
|
Значения pi и их сумм для машин с охлаждением |
||||
|
воздушным |
водородным |
|||
|
pi |
|
pi |
|
|
|
1 |
0,008 |
0,008 |
0,007 |
0,007 |
|
2 |
0,008 |
0,016 |
0,007 |
0,014 |
|
3 |
0,009 |
0,025 |
0,007 |
0,021 |
|
4 |
0,009 |
0,034 |
0,007 |
0,028 |
|
5 |
0,010 |
0,044 |
0,007 |
0,035 |
|
6 |
0,011 |
0,055 |
0,007 |
0,042 |
|
7 |
0,012 |
0,067 |
0,007 |
0,049 |
|
8 |
0,013 |
0,080 |
0,007 |
0,056 |
|
9 |
0,015 |
0,095 |
0,007 |
0,063 |
|
10 |
0,016 |
0,111 |
0,007 |
0070 |
|
11 |
0,018 |
0,129 |
0,007 |
0,077 |
|
12 |
0,020 |
0,149 |
0,007 |
0,084 |
|
13 |
0,022 |
0,171 |
0,007 |
0,091 |
|
14 |
0,024 |
0,195 |
0,007 |
0,098 |
|
15 |
0,026 |
0,221 |
0,007 |
0,105 |
|
16 |
0,029 |
0,250 |
0,007 |
0,112 |
|
17 |
0,031 |
0,281 |
0,007 |
0,119 |
|
18 |
0,034 |
0,315 |
0,007 |
0,126 |
|
19 |
0,037 |
0,352 |
0,007 |
0,133 |
|
20 |
0,040 |
0,392 |
0,007 |
0,140 |
|
21 |
0,044 |
0,436 |
0,007 |
0,147 |
|
32 |
0,047 |
0,483 |
0,007 |
0,154 |
|
23 |
0,051 |
0,534 |
0,007 |
0,161 |
|
24 |
0,054 |
0,588 |
0,007 |
0,168 |
|
25 |
0,058 |
0,646 |
0,007 |
0,175 |
|
26 |
0,062 |
0,708 |
|
|
|
27 |
0,067 |
0,775 |
|
|
|
28 |
0,071 |
0,846 |
|
|
|
29 |
0,079 |
0,925 |
|
|
|
30 |
0,084 |
1,009 |
|
|
|
31 |
0,090 |
1,099 |
|
|
|
32 |
0,096 |
1,195 |
|
|
|
33 |
0,102 |
1,295 |
|
|
|
34 |
0,108 |
1,405 |
|
|
Таблица 1 дается отдельно для машин с воздушным и водородным охлаждением микалентной изоляцией, для машин с термореактивной изоляцией соответствующие данные еще не получены.
Что касается значения параметра λ для каждой машины за период времени эксплуатации (t, T), то оно будет найдено, если разбить период времени (t, T) на части, равные выбранной единице времени, в нашем случае 104 часов, сложить значения pi, отвечающие каждой единице времени (до заданного значения T), и умножить его на площадь S изоляции машины. Для удобства в табл. 1 для всех временных интервалов даны суммы чисел pi.
24. Очевидно, что для совокупности машин параметр λ получается сложением значений этого параметра, вычисленных отдельно для каждой машины из совокупности.
25. Для удобства расчетов и ориентации в их размерах в табл. 2 приведены площади изоляции для некоторых конструктивных типов генераторов.
Таблица 2
Общая площадь изоляции обмоток статоров для некоторых конструктивных типов генераторов
|
Номинальное напряжение, кВ |
Площадь изоляции одной машины, 100 м2 |
Тип генератора |
Номинальное напряжение, кВ |
Площадь изоляции одной машины, 100 м2 |
|
|
ТГВ-300 |
20 |
3,80 |
ТГ 3000/31 |
10,5 |
1,01 |
|
ТВВ-320-2 |
20 |
2,52 |
Т2-25-2 |
10,5/6,3 |
1,01/0,96 |
|
ТГВ-200 |
15,75 |
2,92 |
ТГВ-25 |
10,5/6,3 |
1,01/0,99 |
|
ТВВ-200-2 |
15,75 |
1,06 |
Т-25-2 |
10,5/6,3 |
1,04/0,95 |
|
ТВ-100-2 |
15,75 |
2,30 |
Т2270/98 |
10,5/6,3 |
1,10/1,05 |
|
ТВФ-200 |
10,5 |
3,30 |
Т2-12-2 |
10,5/6,3 |
0,61/0,56 |
|
ТВВ-165-2 |
18,0 |
1,55 |
Т2175/87 |
10,5/6,3 |
0,57/0,53 |
|
ТВ2-150-2 |
18,0 |
2,57 |
СВ1690/175-64 |
15,75 |
5,71 |
|
ТВ2-100-2 |
13,8 |
2,08 |
СВ1190/250-48 |
15,75 |
11,51 |
|
ТВФ-100 |
10,5 |
1,85 |
СВ1100/145-88 |
15,75 |
2,38 |
|
ТВ-60-2 |
10,5/6,3 |
1,52/1,52 |
СВ1500/170-96 |
13,8 |
7,95 |
|
ТВ-50-2 |
10,5/6,3 |
1,52/1,52 |
СВ1160/180-72 |
13,8 |
6,10 |
|
ТГ 1500/62,5 |
10,5 |
2,90 |
СВ465/210-16 |
10,5 |
2,31 |
|
ТГ 1500/58,5 |
10,5 |
2,90 |
СВ840/150-52 |
10,5 |
3,00 |
|
Т2-50-2 |
10,5 |
1,52 |
ВГС1525/135-120 |
10,5 |
5,50 |
|
Т4376/142 |
10,5/6,3 |
2,91/2,98 |
ВГС525/125-28 |
10,5 |
1,80 |
|
ТВ2-30-2 |
10,5/6,3 |
1,01/0,96 |
СВ546/90-40 |
6,3 |
1,63 |
|
ТВС-30 |
10,5/6,3 |
1,01/0,99 |
ВВ-744-300 |
6,3 |
0,89 |
26. Может представиться случай, когда интервал [ti, Ti] не состоит из целого числа интервалов вида [(i - 1) · 104 и i · 104 часов]. В этом случае интервалу вида [(I - α) · 104 и I · 104 часов, где α - число, меньшее единицы, соответствует величина αpi таким же способом, каким величина pi соответствует интервалу [(i - 1) · 104, i · 104 часов].
Пример.
Вычислить pi(ti, Ti),
где ti =
3730 ч; Ti =
33850 ч. Интервал (3730 ч, 33850 ч) разбивается на следующие четыре части (3730; 1 · 104 часов); (1 · 104; 2 · 104 часов); (2 · 104;
3 · 104 часов); (3 · 104; 33850 часов). Первому интервалу
соответствует ![]() второму и третьему интервалу отвечают p2 и p3.
Четвертому интервалу соответствует
второму и третьему интервалу отвечают p2 и p3.
Четвертому интервалу соответствует ![]()
Из табл. 1 имеем:
p1 = 0,008; p2 = 0,008; p3 = 0,009; p4 = 0,009.
Следовательно,
pi(ti, Ti) = 0,63p1 + p2 + p3 + 0,62p4 = (0,63 × 0,008) + 0,008 + 0,009 + (0,62 × 0,009) = 0,005 + 0,008 + 0,009 + 0,006 = 0,028.
27. При решении практических задач в соответствии с вышеизложенным определяется значение параметра Пуассона, а затем по статистическим таблицам (приложение 3) определяется для данной конкретной ситуации вероятность рассматриваемого события.
28. Таблицы распределения Пуассона (по Я. Янко) приведены в приложении для значений параметра λ от 0,1 до 30.
1 В задачах, связанных с прогнозом ожидаемого числа аварий, достаточно определить лишь параметр λK = S · pK, (математическое ожидание).
При λ < 0,1 следует пользоваться приближением e-λ ≈ 1 - λ, а при λ > 30 - нормальным распределением для величины
![]()
Приложение 1
УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАСЧЕТОВ ПО КОНТРОЛЮ И ОЦЕНКЕ СОСТОЯНИЯ КОРПУСНОЙ ИЗОЛЯЦИИ
1. На основе использования типовых кривых вероятности аварийного пробоя, описывающих среднестатическое нормальное состояние изоляции (эталонное), и использования концепции учета отклоняющихся групп можно решать ряд практических задач.
2. Эти задачи могут быть разбиты, по крайней мере, на 2 типа:
а) задачи частного порядка обычно небольшого объема. К таковым, например, относятся задачи п. 6 а, б, в разд. 1 настоящей Типовой инструкции;
б) задачи, требующие больших и точных объемов исходной информации, которые могут решаться один раз или периодически повторяться. Такие задачи могут выполняться отдельными ведомствами, заводами, энергосистемами, ремонтными предприятиями на основе использования типовых кривых вероятности и своих исходных информационных материалов.
В результате рассмотрения таких задач определяется общая картина состояния изучаемого элемента и вместе с тем выделяются отклоняющиеся группы, т.е. определяются так называемые «узкие» места, возникающие вследствие возможного нарушения качества проектирования, изготовления или эксплуатации.
Устранение «узких» мест приводит к нормализации работы изучаемого элемента и тем самым к частичному воздействию на нормализацию работы оборудования в целом. Кроме того, учет допущенных ранее при разработке и выпуске машин ошибок может привести к улучшению их проектирования и изготовления в новых вариантах.
К таким задачам относятся задачи п. 6 г ÷ н разд. 1 настоящей Типовой инструкции.
3. Эти задачи требуют наличия постоянно обновляемого, централизованного, систематизированного исходного материала и по большей части должны решаться ежегодно.
4. При постановке любой статистической задачи, в т.ч. задач анализа состояния изоляции, обычно выдвигается гипотеза (предполагаемый результат расчета), которая подтверждается или отвергается полученной расчетной величиной вероятности при принятых уровнях значимости (за допустимые в задачах п. 6 а, б, в можно принимать уровни значимости 2; 5 или 10 %).
5. Проверка статистической значимости различия между λ и μ, вообще говоря, требует использования таблиц закона Пуассона, но при λ порядка двух - трех десятков и более закон Пуассона с параметром λ близок к нормальному закону, математическое ожидание и дисперсия которого равны λ.
Иными
словами разность (λ - μ) между λ и μ, не превосходящая ![]() , вполне допустимая, разность в 2
, вполне допустимая, разность в 2![]() вызывает сомнение, а
разность в 3
вызывает сомнение, а
разность в 3![]() и более практически указывает
на нарушение предпосылок. Сформулированное правило для определения
существенного различия между λ и μ подлежит корректировке, если таких сравнений проводится много (в
одном случае
из примерно двадцати разность в 2
и более практически указывает
на нарушение предпосылок. Сформулированное правило для определения
существенного различия между λ и μ подлежит корректировке, если таких сравнений проводится много (в
одном случае
из примерно двадцати разность в 2![]() может возникнуть за
счет чисто случайных причин).
может возникнуть за
счет чисто случайных причин).
6. Наряду с общей схемой решения задач практического анализа в каждой задаче очень важна инженерная логика рассуждений, определяющая тактику поиска ответа и глубину проработки. Изложить такой подход к решению задач в виде схемы затруднительно, поэтому наиболее удобным представляется дать изложение путей подхода к решению различных задач на отдельных практических примерах. Ниже рассматривается ряд таких примеров. В некоторых из приведенных примеров (4; 8; 9; 10) мог быть применен и другой более оптимальный и полный путь решения задачи, однако при этом потребовалось бы ввести в условие задачи более точные и более полные исходные данные. А вместе с тем иногда в практической работе требуется быстрая ориентировочная прикидка, в таком случае объем исходного материала и пути решения, изложенные в вышеупомянутых примерах являются вполне приемлемыми.
В качестве примеров использованы конкретные, практические работы, поэтому в каждом из них имеется ссылка на авторов работы.
Пример 1. Оценка необходимого количества машин для достоверного испытания нового вида изоляции1.
1 Тутубалин В.Н.
Постановка задачи.
Допустим, что предложена новая изоляция, которая должна быть абсолютно надежной в работе. Выпускаются машины с новой изоляцией, площадью каждая по 200 м2. Сколько нужно выпустить машин, чтобы через три года безаварийной эксплуатации можно было бы с достаточным основанием сказать, что новая изоляция лучше прежней.
Решение: Необходимо отвергнуть гипотезу о том, что новая изоляция хуже прежней. Для того, чтобы это можно было обоснованно сделать, нужно выпустить столько машин с новой изоляцией, чтобы их безаварийная работа была маловероятной, если качество изоляции такое же, как на прежних машинах.
Пусть, например, вероятность безаварийной работы при прежнем качестве изоляции не превосходит 0,05. Исходя из заданной вероятности, определим число машин с новой изоляцией (L), которое должно находиться в эксплуатации. Для машины площадью 100 м2 с прежней изоляцией из табл. 1 находим
p(0; 3 года) ≈ p(0; 2 · 104 ч) ≈ 0,016,
а для L машин с площадью каждой 2×100 м2 соответствующий параметр Пуассона есть (0,016×2)L = 0,032L.
Вероятность безаварийной эксплуатации L машин равна e-0,032L, и мы требуем, чтобы
e-0,032L ≤ 0,05.
Следовательно,
0,032L ≥ 5,3, т.е. L ≥ 165.
Пример 2. Оценка качества новых видов изоляции на малом экспериментальном материале1
Постановка задачи.
Изготовлены две машины с новой изоляцией площадью каждая по 200 м2, причем в течение первых 2 · 104 часов работы обе машины имели по одной аварии из-за местного дефекта изоляции. Можно ли заключить, что новая изоляция хуже прежней?
Решение: Для прежней (микалентной) изоляции параметр Пуассона для суммарного числа аварий на обеих машинах составляет 0,008 × 2 × 2 = 0,032. По закону Пуассона находим, что вероятность иметь две и более аварий при λ = 0,032 есть
p{μ ≥ 2} = 1 - p{μ = 0} - p{μ - 1} = 1 - e-λ - λe-λ = 1 - (1 + λ)eλ = 1 - (1 + λ) · (1 - λ + λ2/2) = 1 - (1 - λ2)(λ2/2) = λ2/2 = 0,00051.
Эта вероятность очень мала; при таком ее значении следует признать, что среднестатистическая машина, аналогичная рассматриваемой, не могла иметь двух аварий. Отсюда следует, что новая изоляция указанных машин имеет показатели хуже, чем у прежней изоляции.
Пример 3. Оценка степени изношенности изоляции отдельной длительно работавшей машины2
1,2 Тутубалин В.Н.
Постановка задачи.
Некоторая машина площадью 200 м2 имела три аварийных повреждения при эксплуатации в интервале от 15 · 104 до 16 · 104 часов.
Является ли ее изоляция более изношенной, чем это бывает в среднем для машин, проработавших 15 · 104 часов.
Решение: Из табл. 1 мы видим, что в интервале (15 · 104 - 16 · 104 часов) значение p16 составляет 0,029. Поэтому для машины площадью 200 м2 параметр λ не более 0,06, а вероятность трех и более аварий есть
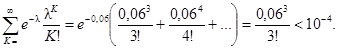
Таким образом, три аварии невероятны, следовательно, изоляция сильно изношена или дефектна.
Пример 4. Оценка аварийности изоляции некоторой совокупности турбогенераторов с воздушным охлаждением1.
1 Белова Л.А., Мамиконянц Л.Г., Тутубалин В.Н.
Постановка задачи.
К рассмотрению принята некоторая совокупность турбогенераторов с воздушным охлаждением, номинальным напряжением 10,5 кВ. Генераторы указанной группы начали эксплуатироваться с 1960 г., точного числа часов работы не имеется. С 1960 г. по 1968 г. включительно на этой группе генераторов имело место 10 аварийных пробоев изоляции, причем нельзя было обнаружить видимую причину разрушения изоляции. Повреждения были классифицированы как происшедшие из-за местных дефектов изоляции. Эти случаи аварийных пробоев характеризуют состояние собственно изоляции и поэтому подлежат исследованию в данной задаче.
Кроме этого, в двух случаях повреждения корпусной изоляции были вызваны попаданием на обмотку статора напряжения более высокого класса и повреждением элементарных проводников. Эти повреждения произошли не из-за дефектов изоляции и соответственно не должны учитываться в рассматриваемом расчете.
Ниже указаны суммарная площадь изоляции обмотки статоров генераторов в 100 м2 и число аварий за каждый год эксплуатации рассматриваемой группы генераторов.
В целом вся группа генераторов за весь рассматриваемый период эксплуатации имела суммарную наработку 609 единиц площади на год, определяемую как сумма единиц площади за каждый год.
Число аварийных пробоев на этой группе генераторов за период с 1960 г. по 1968 г. равнялось 10. Является ли эта аварийность повышенной?
Решение. Необходимо определить значение параметра Пуассона, затем по статистическим таблицам определить для данной конкретной ситуации вероятность рассматриваемых событий. На основании полученных результатов можно сделать соответствующее заключение о состоянии изоляции.
К 1968 г. продолжительность работы генераторов указанной группы составляла примерно от 10000 до 50000 ч*) поэтому при использовании данных табл. 1 должен быть принят интервал времени в пределах 1 · 104 ÷ 5 · 104 часов, для которых значение p1 ÷ p5 равны 0,008 ÷ 0,010.
*) Точное число часов работы каждого генератора за год отсутствует, поэтому время работы за год принято примерно равным 7000 ч.
На типовой кривой вероятности аварийного пробоя единичный интервал времени равен 10000 ч (1 · 104 часов). Если принять время работы генератора за год равным 7000 ч, то суммарную наработку нужно привести к единичному интервалу времени.
В данном конкретном случае это отношение будет определяться следующим образом: 10000/7000 ≈ 1,5.
Приняв указанные положения, определим с помощью типовой кривой параметр Пуассона λK = S · pK:
![]()
![]()
По табл. П3.2 приложения 3 для λ1 = S · p1 и λ5 = S · p5 определим возможную вероятность десяти и более аварий за указанный период (1960 + 1968 гг.) на рассматриваемой группе генераторов.
В таблице суммарных значений функции Пуассона в данном случае под X понимается число аварий (равное 10) и под λ значения
λ1 = S · p1 и λ5 = S · p5.
Как следует из таблицы, вероятность десяти и более аварий при λ = 3,2 ÷ 4,1 равна примерно 0,0018 ÷ 0,0095. Вероятность сравнительно мала, что указывает на некоторую дефектность изоляции турбогенераторов этого типа.
Технический анализ показал, что в данном случае повышенная повреждаемость изоляции была вызвана неудачным креплением крайнего пакета стали на некоторых генераторах этого типа, что приводило к повреждениям изоляции обломившимися лепестками стали.
Пример 5. Оценка качества изоляции группы генераторов с малым сроком эксплуатации1.
1 Тутубалин В.Н.
Постановка задачи.
Изготовлено семь генераторов с компаундированной микалентной изоляцией площадью каждая по 5,71 × 100 м2 (охлаждение стержней непосредственное, водяное).
В течение первых 104 ч работы семь генераторов имело семь аварийных повреждений изоляции (причина повреждения изоляции не могла быть точно названа) и два аварийных повреждения изоляции из-за ее увлажнения. Можно ли заключить, что изоляция этой группы генераторов хуже среднестатистической?
Решение: для микалентной изоляции параметр Пуассона для суммарного числа аварий на семи генераторах составляет
λ1 = p1 · S · L = 0,003×5,71×7 ≈ 0,32.
По табл. П3.2 распределения Пуассона находим, что вероятность семи и более аварий при значении λ, равном 0,32, является практически нулевой.
Следовательно, нужно считать, что повреждаемость этих генераторов является чрезвычайно высокой (необходимо отметить, что на таком количестве генераторов можно было ожидать появления максимум одной аварии).
Пример 6. Оценка аварийной повреждаемости главной изоляции обмоток статоров генераторов одной энергосистемы1.
1 Байкова И.Б., Белова Л.А., Киристая B.C.
Постановка задачи.
Анализу подлежит состояние статорной изоляции 23 турбогенераторов отечественного производства мощностью от 12 до 200 МВт и номинальным напряжением 6,3; 10,5 и 15,75 кВ за период 1952 ÷ 1977 гг. (по состоянию на 01.01.78 г.).
В 8 случаях имело место повреждение главной статорной изоляции, причем в 6 по вине собственно изоляции и 2 было вызвано так называемыми внешними причинами (из-за течи воды в головке стержня).
Решение: произведем обработку исходных данных в зависимости от времени работы генераторов.
Площади всех генераторов расположатся по убывающей с учетом выбывания в каждом интервале более «молодых» генераторов; отметим для каждой аварии, в каком фактическом интервале времени имело место указанное повреждение. Взяв соотношение числа аварий к суммарной площади каждого интервала построим график частот повреждений (см. рис. П1.1, поз. 1). Произведем сглаживание ломанного графика частот повреждений методом наименьших квадратов, в результате получим текущее значение кривой вероятности аварийного пробоя данной совокупности генераторов (поз. 2). На рисунок нанесем также значения типовой кривой (поз. 3).
Из сопоставления текущей и типовой кривых можно сделать вывод, что рассмотренная совокупность генераторов резко неоднородна (в смысле аварийности) и имеет существенно худшие, чем среднестатистические показатели. Все точки текущей кривой лежат значительно выше типовой кривой.
Сравнение ожидаемого (МО) числа аварий, подсчитанного по типовой кривой, и фактического числа аварий выполнено для объединения рассматриваемых генераторов по различным признакам: по заводам-изготовителям (оценка технологических особенностей), типам (оценка конструктивных особенностей) и месту установки (оценка условий эксплуатации).
Рис. П1.1. Сравнение кривых вероятности аварийного пробоя изоляции обмотки статора турбогенераторов рассматриваемой энергосистемы:
1 - фактические данные; 2 - текущая кривая с доверительными интервалами; 3 - типовая кривая
Результаты сравнения ожидаемого и фактического числа аварий по генераторам различных типов и по месту их установки приведены в табл. П1.1 и П1.2
Таблица П1.1
|
Ожидаемое число аварий |
Фактическое число аварий |
|
|
ТВФ-100-2 |
1,1101 |
1 |
|
ТВВ-200-2 |
0,5979 |
5 |
|
Т2-25-2 |
0,3020 |
0 |
|
Т2-12-2 |
0,2678 |
0 |
|
Итого ... |
2,2778 |
6 |
Таблица П1.2
|
Ожидаемое число аварий |
Фактическое число аварий |
|
|
№ 1 |
1,4081 |
3 |
|
№ 2 |
0,2999 |
3 |
|
№ 3 |
0,3020 |
0 |
|
№ 4 |
0,2678 |
0 |
|
Итого ... |
2,2778 |
6 |
Как видно из таблиц, общее фактическое число изоляционных аварий равно 6, что значительно больше суммарного МО, равного 2,2778. В отклоняющиеся должны быть выделены электростанции № 1 и № 2; по типам - генераторы ТВВ-200-2. Оказывается, что генераторы этого типа эксплуатируются именно на электростанциях № 1 и № 2, что и ухудшает их показатели.
Показатели остальных групп машин, как по типам, так и по электростанциям, в том числе и старых генераторов с воздушным охлаждением, удовлетворяют среднестатистическим.
Таким образом, можно констатировать, что на данном этапе в энергосистеме имеется резко отклоняющаяся в худшую сторону группа машин ТВВ-200-2.
Пример 7. Оценка работы главной статорной изоляции турбогенераторов типа ТГВ-200*)
*) Малых В.В., Пидошва В.Г., Пушкарь В.Ф.
Постановка задачи.
Рассматривается совокупность генераторов этого типа (изоляция микалентная компаундированная; охлаждение - водородное) из 72 единиц, установленных на II электростанциях 9 энергосистем.
На всей совокупности генераторов за период с 1960 по 1978 г. имело место 14 аварий изоляции, происшедших без видимых причин, и 8 аварий, вызванных внешними причинами. Произвести анализ и оценку состояния изоляции генераторов этого типа.
Решение: получим календарный график повреждаемости генераторов этой группы (рис. П1.2). Для этого за каждый рассматриваемый год (с 1960 г. по 1978 г.) возьмем отношение числа аварийных пробоев к числу находящейся в эксплуатации в этом году площади. Как видно из рисунка график опасений не вызывает.
Рис. П1.2. Календарный график аварийной повреждаемости изоляции обмоток статоров ТГВ-200
Построим текущую кривую вероятности аварийного пробоя (рис. П1.3) по состоянию на 01.01.79 г. (разъяснение см. в примере 6 и приложении 2). Как видно из рисунка, отмечается практически полное совпадение текущей кривой вероятности аварийного пробоя с типовой.
Для каждой конкретной машины в соответствии с ее числом часов работы определим параметр Пуассона (λ = S · Σpi; Σpi - снято с типовой кривой). Затем по табл. 1 приложения 3 распределения Пуассона определяем вероятность возникновения одной, двух и более аварий. В таблице Пуассона в данном случае под X понимается число аварий (одна, две и т.д.) и под λ значения S · Σpi.
Рис. П1.3. Текущая кривая вероятности аварийного пробоя изоляции обмоток статоров ТГВ-200 (по состоянию на 1.01.1979 г.):
1 - частота повреждений; 2 - текущая кривая; 3 - типовая кривая
Суммируя значения X получаем вероятность возникновения аварии на этой машине (ожидаемое число аварий).
Суммируя ожидаемое число аварий по всей совокупности генераторов получаем: МО - 13,6015. Как отмечалось выше, на всей совокупности генераторов имело место 14 аварий. Совпадение - хорошее.
Попробуем оценить, какова динамика аналогичных соотношений (ΣМО и фактической повреждаемости по всей совокупности) по состоянию на 01.01.1960 г., на 01.01.66 г., на 01.01.71 г., на 01.01.76 г., на 01.01.79 г. (рис. П1.4).
Как видно из рисунка, за весь период эксплуатации отмечалось практически полное совпадение ожидаемого и фактического числа аварийных пробоев.
Если посмотреть распределение ожидаемого и фактического числа аварийных пробоев по отдельным электростанциям по состоянию на 01.01.75 г. табл. П1.3, то обнаруживается что однородность совокупности еще раз подтверждается пропорциональным соотношением рассматриваемых величин практически по всем электростанциям (исключение составляют показатели Бурштынской ГРЭС, которая должна быть выделена в отклоняющуюся группу).
Рис. П1.4. Динамика соотношений ожидаемого и фактического числа аварийных пробоев ТГВ-200 (за период 1960 - 1978 гг.)
![]() ожидаемое значение
ожидаемое значение
![]() фактическое значение
фактическое значение
Из сопоставления всех показателей можно сделать вывод, что генераторы этого типа (за исключением Бурштынской ГРЭС) находятся на среднестатистическом уровне и соответствуют норме, эталону. Учитывая то, что совокупность стабильно за весь период эксплуатации отвечает эталону, можно попытаться осуществить прогноз возникновения последующих аварий. Из табл. П1.3 видно, что ожидаемое число аварий превышает фактическое почти на целую единицу на генераторах Молдавской (0,9208и0) и Верхне-Тагильской ГРЭС (0,8145и0). Очевидно, в первую очередь следует ожидать аварию на Верхне-Тагильской и Молдавской ГРЭС. Так как в настоящее время уже известны последующие данные по возникновению аварий включительно по 1979 г., то можно отметить, что на всей совокупности генераторов ТГВ-200 за период 1975 ÷ 1979 гг. произошли еще три аварийных пробоя: в 1975 г. на Верхне-Тагильской ГРЭС; в 1979 г. на Молдавской ГРЭС; в 1976 г. на Ворошиловградской ГРЭС.
Таблица П1.3
Распределение ожидаемого и фактического числа аварийных пробоев по отдельным электростанциям (по состоянию на 1.01.75)
|
Электростанция |
Ожидаемое число аварий |
Фактическое число аварий |
|
|
Азэнерго |
Северная ГРЭС |
0,1840 |
0 |
|
|
Али-Байрамлинская ГРЭС |
0,6120 |
0 |
|
Львовэнерго |
Бурштынская ГРЭС |
1,3543 |
3 |
|
Мосэнерго |
ГРЭС-5 |
0,1206 |
0 |
|
Молдглавэнерго |
Молдавская ГРЭС |
0,9208 |
0 |
|
Свердловэнерго |
Верхне-Тагильская ГРЭС |
0,8145 |
0 |
|
Татэнерго |
Заинская ГРЭС |
1,3067 |
1 |
|
Харьковэнерго |
Змиевская ГРЭС |
1,1244 |
1 |
|
Южказэнерго |
Джамбульская ГРЭС |
0,2674 |
1 |
|
Донбассэнерго |
Ворошиловградская ГРЭС |
1,1049 |
2 |
|
|
Старобешевская ГРЭС |
1,6138 |
2 |
|
|
Итого... |
9,4234 |
10 |
Пример 8. Сравнение аварийности некоторой совокупности (№ 1) гидрогенераторов за трехлетний период эксплуатации по состоянию на 1 января 1968 г. и 1 января 1970 г.*
* Белова Л.А., Мамиконянц Л.Г., Тутубалин В.Н.
Постановка задачи.
В совокупности рассмотрено 20 генераторов с различной единичной площадью изоляции. Необходимо сравнить математическое ожидание числа аварийных пробоев изоляции обмоток статоров с фактическим числом аварий за трехлетний период эксплуатации для рассматриваемой совокупности гидрогенераторов по состоянию на 1 января 1968 г. (т.е. за 1965, 1966 и 1967 гг.) и на 1 января 1970 г. (т.е. за 1967, 1968, 1969 гг.). Из сопоставления полученных результатов сделать заключение об общем состоянии изоляции и тенденциях в ее изменении.
Решение: Сведем исходные данные по указанной совокупности генераторов в табл. П1.4 и П1.5 и произведем необходимые расчеты.
В табл. П1.4 записаны все генераторы из интересующей нас совокупности по состоянию на 1 января 1968 г. с указанием их единичной площади. Генераторы расположены в порядке, определяемом их возрастом к рассматриваемому периоду (к 1 января 1968 г.). Для каждого из рассматриваемых генераторов значения pi бралось по кривой вероятности аварийного пробоя (в соответствующем интервале) таким, чтобы продолжительность работы генератора соответствовала примерно середине рассматриваемого трехлетнего периода эксплуатации. Например, если на 1 января 1968 г. генератор проработал от 4 · 104 до 5 · 104 часов, то в середине рассматриваемого трехлетнего периода его возраст составляет от 3 · 104 до 4 · 104 часов и соответственно выбирается равным 3 · 104 часов. Значение pi удваивается, так как трехлетний период эксплуатации равен примерно 2 · 104 часов.
По каждой возрастной группе проставлено общее число аварийных пробоев, которые имели место на этих генераторах в 1965, 1966, 1967 гг.
В конце табл. П1.4 произведено суммирование всех полученных значений математического ожидания (МО) числа аварийных пробоев изоляции обмоток статоров за рассматриваемый период (1965, 1966, 1967 гг.) и фактически имевших место аварийных пробоев изоляции на тот же период и произведено их сравнение.
По результатам расчетов по состоянию на 1 января 1968 г. (см. табл. П1.4) следует отметить, что изучаемая совокупность генераторов находится на среднестатистическом уровне и ее состояние не вызывает опасений.
Аналогично вышеизложенному в табл. П1.5 записаны все генераторы интересующей нас совокупности по состоянию на 1 января 1970 г. и выполнены те же расчеты. Фактическая аварийность внесена в каждую возрастную группу соответственно за 1967, 1968, 1969 гг.
За период с 1968 г. по 1970 г. обмотки статоров части генераторов рассматриваемой совокупности подверглись перемотке. В таблице 2 эти генераторы указаны дважды: первый раз в возрастной группе, в которую они должны были бы попасть, если бы не прошли перемотку (о дате перемотки сделаны примечания; математическое ожидание и фактическое число аварий, естественно, отсутствуют), второй раз - в той возрастной группе, к которой они относятся, с учетом продолжительности их работы с момента перемотки (величины математического ожидания числа аварий и фактическое число аварийных пробоев за расчетный период указаны). По результатам расчетов для совокупности генераторов по состоянию на 1 января 1970 г. отмечается некоторое отклонение от среднестатистической нормы, что не наблюдалось по состоянию на 1 января 1968 г.
Таблица П1.4
Сравнение расчетной вероятности аварий и фактического числа аварий для первой группы гидрогенераторов по состоянию на 1 января 1968 г. (за 1965, 1966 и 1967 гг.)
|
Параметр кривой вероятности |
Sген, 100 м2 |
Ожидаемое число аварий |
Фактическое число аварий |
Примечание |
||
|
pi |
2pi |
|||||
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
0 |
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
||
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
||
|
3 · 104 |
0,009 |
0,018 |
2,38 |
0,043 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
2 |
|
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
2 · 104 |
0,008 |
0,016 |
2,38 |
0,038 |
||
|
1 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
2 |
|
|
1 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
1 · 104 |
0,008 |
0,016 |
11,51 |
0,184 |
||
|
1 · 104 |
0,008 |
0,016 |
2,38 |
0,038 |
||
|
1 · 104 |
0,008 |
0,016 |
2,38 |
0,038 |
||
|
1 · 104 |
0,008 |
0,016 |
- |
- |
||
|
1 · 104 |
0,008 |
0,016 |
- |
- |
||
|
|
|
|
|
3,170 |
4 |
Хорошее совпадение математического ожидания аварий и фактического числа аварийных пробоев |
Таблица П1.5
Сравнение расчетной вероятности аварий и фактического числа аварий для первой группы гидрогенераторов по состоянию на 1 января 1970 г. (за 1967, 1968 и 1969 гг.)
|
Параметр кривой вероятности |
Sген 100 м2 |
Ожидаемое число аварий |
Фактическое число аварий |
Примечание |
||
|
pi |
2pi |
|||||
|
5 · 104 |
0,010 |
0,020 |
2,38 |
- |
- |
Обмотка перемотана в 1964 г. |
|
4 · 104 |
0,009 |
0,018 |
2,38 |
- |
- |
Обмотка перемотана в 1962 г. |
|
4 · 104 |
0,009 |
0,018 |
2,38 |
0,043 |
1 |
|
|
4 · 104 |
0,009 |
0,018 |
2,38 |
0,043 |
|
|
|
4 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
4 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
4 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
4 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
4 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
4 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
2,38 |
- |
- |
Обмотка перемотана в 1961 г. |
|
3 · 104 |
0,009 |
0,018 |
2,38 |
0,043 |
4 |
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
3 · 104 |
0,009 |
0,018 |
11,51 |
0,207 |
|
|
|
2 · 104 |
0,008 |
0,016 |
2,38 |
- |
- |
Обмотка перемотана в 1954 г. |
|
2 · 104 |
0,008 |
0,016 |
2,38 |
0,038 |
3 |
|
|
2 · 104 |
0,008 |
0,016 |
2,38 |
0,038 |
|
|
|
1 · 104 |
0,008 |
0,016 |
- |
- |
- |
|
|
1 · 104 |
0,008 |
0,016 |
- |
- |
- |
|
|
1 · 104 |
0,008 |
0,016 |
- |
- |
- |
|
|
|
|
|
|
3,31 |
8 |
Совпадения нет, надо искать причину отклонения фактического числа аварий от математического ожидания |
|
Исключение из рассмотрения одного из генераторов дает следующие результаты |
|
3,11 |
5 |
Хорошее совпадение |
||
При обнаружении такого факта следует попытаться определить, ко всей ли совокупности генераторов относится обнаруженное явление или легко обнаруживается возможность выделения отдельных «худших» или «лучших» генераторов, либо это объясняется возникновением каких-либо внешних влияющих факторов.
В данном конкретном случае при анализе исходных данных легко обнаруживается, что один из 20 генераторов имел за малый промежуток времени три аварийных повреждения.
Площадь и все аварийные повреждения этого генератора были исключены из рассмотрения (из общей суммы), что привело к хорошему совпадению математического ожидания и фактического числа аварий на остальной группе генераторов. Естественно сделать заключение о том, что этот генератор имеет дефектную изоляцию, а остальные 19 соответствуют среднестатистической норме. Однако такая аварийность на одном из 20 генераторов могла быть случайной. В данном конкретном случае проверка обычным статистическим приемом подтверждает случайность этого явления и ставит под сомнение принятые выше объяснения о состоянии всей совокупности.
В таком сомнительном случае, очевидно, нужно рекомендовать до принятия решения, например о срочной перемотке статора дефектного генератора, продолжить наблюдение за указанной совокупностью генераторов и повторить все расчеты через определенный промежуток времени. По результатам повторно произведенных расчетов принять соответствующее решение.
Пример 9. Оценка аварийности некоторой совокупности (№ 1) гидрогенераторов за трехлетний период эксплуатации по состоянию на 1 января 1970 г.1
1 Белова Л.А., Мамиконянц Л.Г., Тутубалин В.Н.
Постановка задачи.
Имеется некоторая другая совокупность гидрогенераторов, по которой также известны все исходные данные по состоянию на 1 января 1970 г. Требуется оценить состояние изоляции.
Решение. По аналогии с примером 8 исходные и расчетные данные по этой совокупности уведены в табл. П1.6.
Результаты расчетов для этой совокупности генераторов значительно отличаются от результатов расчетов предыдущего примера. Повреждаемость этих гидрогенераторов резко отличается от среднестатистической. Указанная группа генераторов должна быть признана дефектной. Причина повышенной повреждаемости должна быть выяснена техническим анализом.
Таблица П1.6
Сравнение расчетной вероятности аварий и фактического числа аварий для второй группы, гидрогенераторов по состоянию на 1 января 1970 г. (за 1967, 1968, 1969 гг.)
|
Параметр кривой вероятности |
Sген 100 м2 |
Ожидаемое число аварий |
Фактическое число аварий |
Примечания |
||
|
pi |
2pi |
|||||
|
1 · 104 |
0,010 |
0,020 |
|
- |
- |
|
|
1 · 104 |
0,010 |
0,020 |
- |
- |
- |
|
|
1 · 104 |
0,010 |
0,020 |
5,71 |
0,114 |
7 |
|
|
1 · 104 |
0,010 |
0,020 |
5,71 |
0,114 |
|
|
|
1 · 104 |
0,010 |
0,020 |
5,71 |
0,114 |
|
|
|
1 · 104 |
0,010 |
0,020 |
5,71 |
0,114 |
|
|
|
1 · 104 |
0,010 |
0,020 |
5,71 |
0,114 |
|
|
|
1 · 104 |
0,010 |
0,020 |
5,71 |
0,114 |
|
|
|
1 · 104 |
0,010 |
0,020 |
5,71 |
0,114 |
|
|
|
|
|
|
|
0,637 |
15 |
Никакого совпадения нет, фактическая повреждаемость значительно превышает ожидание. Причина расхождения должна быть определена методом технического анализа |
Пример 10. Сравнительная оценка качества новых видов изоляции (сравнение с микалентной изоляцией)1.
1 Белова Л.А., Мамиконянц Л.Г., Тутубалин В.Н.
Постановка задачи.
Рассматривается совокупность изоляции новых видов на термореактивных связующих общей суммарной площадью в 1529 × 100 м2.
Изоляция эксплуатируется на турбо- и гидрогенераторах различной единичной мощности, номинальных напряжений, типов и т.п.
Произвести оценку новых видов изоляции.
Решение. Так как по термореактивной изоляции пока отсутствуют типовые, эталонные показатели произведем сравнительную оценку изоляции по отношению к микаленте.
В настоящей задаче ограничимся сравнением ожидаемого и фактического числа аварийных пробоев по однородной совокупности (за минусом отклоняющихся групп).
По типовой кривой для микалентной изоляции для каждой конкретной машины в соответствии с ее числом часов работы на рассматриваемую дату определяем Σpi и соответственно λi = S - Σpi, а затем в табл. 1 приложения 3 распределения Пуассона определяем вероятность возникновения 1-ой, 2-х и т.д. аварий и их общую сумму.
Суммируя общее ожидаемое и фактическое число аварийных пробоев по интересующим нас группам получим следующие соотношения:
|
Вид изоляции |
Ожидаемое число аварийных пробоев |
Фактическое число аварийных пробоев |
Суммарная общая площадь изоляции, 100 м2 |
|
Изоляция из пропитанных лент |
30,9555 |
11 |
856 |
|
В том числе: |
|
|
|
|
слюдотерм |
15,0533 |
3 |
446 |
|
ВЭС |
15,9022 |
8 |
410 |
|
Изоляция из непропитанных лент (монолит) |
16,4640 |
8 |
573 |
|
Общие показатели |
47,4195 |
19 |
1529 |
Как следует из таблицы показатели изоляции на термореактивных связующих лучше показателей микалентной изоляции.
Пример 11. Анализ аварийности статорной микалентной изоляции некоторой совокупности гидрогенераторов 13,8 кВ1
1 Белова Л.А., Мамиконянц Л.Г., Тутубалин В.Н.
Постановка задачи.
В рассматриваемую совокупность входит примерно 150 крупных гидрогенераторов с воздушным охлаждением 9-ти различных типов, изготовленных 4-мя различными заводами (заводы обозначаю индексами А; Б; В и т.д.). Первый гидрогенератор был изготовлен в 1940 г. Генераторы установлены на 19 электростанциях (электростанции обозначены порядковыми номерами) 14 энергосистем.
Удельная повреждаемость на единицу машины и единицу площади изоляции всех гидрогенераторов рассматриваемой группы по годам (календарный график) весьма высока и в последние годы имеет резкую тенденцию к возрастанию. Если бы она отмечалась только для графика на единицу машин, можно было бы размышлять о влиянии (изменении с течением времени и увеличением единичной мощности) габаритных размеров машин. Однако данные графика на единицу площади не позволяют этого сделать. Следовало определить, за счет чего это имеет место - из-за общего чрезмерного старения изоляции рассматриваемой группы генераторов или в последние годы в совокупности просто появились дефектные генераторы? По календарным графикам на этот вопрос ответить нельзя.
Решение: Использована методика статистического анализа, заключающаяся в сравнении текущей кривой вероятности аварийного пробоя с типовой, и концепции выделения отклоняющихся групп. Текущие кривые вероятности аварийного пробоя главной изоляции обмоток статоров в целом для всей совокупности по состоянию на 1 января 1966, 1970, 1972, 1974 и 1975 гг. показаны на рис. П1.5 (средние кривые без указания границ соответствующих доверительных областей). Все эти кривые ложатся выше типовой (показана сплошной линией без точек) и указывают на возникновение значительной неоднородности в указанной совокупности генераторов уже начиная с 1965 г. и соответственно худших показателей состояния изоляции.
Рис. П1.5. Текущие кривые вероятностей аварийного пробоя изоляции всей совокупности гидрогенераторов 13,8 кВ
Сравнение МО количества машин с 1, 2, 3 авариями и т.д. и фактического распределения количества машин с 1, 2, 3 авариями и т.д. за периоды 1940 - 1965 гг. (по состоянию на 1 января 1966 г.); 1940 - 1969 гг. (на 1 января 1970 г.); 1940 - 1974 гг. (по состоянию на 1 января 1975 г.) выполнено для объединения рассматриваемых генераторов по трем различным признакам:
- по заводам-изготовителям (оценка технологических особенностей) в табл. П1.7;
- по типам (оценка конструктивных особенностей) в табл. П1.8;
- по месту установки (оценка условий эксплуатации и т.п.) в табл. П1.9.
Математическое ожидание подсчитано по типовой кривой вероятности аварийного пробоя.
Из сопоставления указанных данных следует, что устойчиво практически за весь рассматриваемый период весьма плохие показатели (суммарное значение МО и суммарной фактической аварийности рассматриваемой группы по состоянию на 1 января 1975 г.) обнаруживает завод В (12,9786 и 61) и лучшие - завод А (81,1317 и 62). Рассмотрение тех же данных по типам показывает, что так же устойчиво из общей совокупности выделяются в худшую сторону тип СВ-1160/180-72 (24,3826 и 82) и в лучшую СВ-1500/200-88 (43,6531 и 32).
По электростанциям выделяются: в худшую сторону - электростанции № 16 и 5, в лучшую - № 3.
Из приведенных данных следует, что ухудшение в каждом из рассмотренных сочетаний (по заводам, типам и электростанциям) определяется одними и теми же показателями. Завод В имеет худшие показатели из-за того, что в выпущенной им продукции имеется тип СВ-1160/180-72. Электростанции № 16 и 5 имеют худшие показатели вследствие того, что на них установлены гидрогенераторы СВ-1160/150-72. В целом тип СВ-1160/180-72 имеет плохие показатели из-за того, что большая часть этих генераторов изготовлена заводом В и установлена на вышеуказанных электростанциях. Генераторы этого же типа, однако, изготовленные заводом А (установлены на электростанции № 6) дают практически нормальные показатели.
Таблица П1.7
Данные об аварийной повреждаемости изоляции гидрогенераторов 13,8 кВ (сравнение по заводам)
|
Расчетное и фактическое значения аварийных повреждений изоляции за периоды |
|||
|
1940 - 1965 гг. (на 1.01.66 г) |
1940 - 1969 гг. (на 1.01.70 г.) |
1940 - 1974 гг. (на 1.01.75 г.) |
|
|
А |
38,7872* 26 |
55,1174 37 |
81,1317 62 |
|
Б |
7,3313 9 |
12,0092 15 |
18,4544 24 |
|
В |
4,3875 7 |
7,5244 21 |
12,9786 61 |
|
Г |
- |
0,5660 1 |
1,1590 1 |
|
Всего... |
50,5060 42 |
75,2170 74 |
113,7237 148 |
|
* В дробном обозначении: числитель - ожидаемое, знаменатель - фактическое число аварийных пробоев.
|
|||
Таблица П1.8
Данные об аварийной повреждаемости изоляции гидрогенераторов 13,8 кВ (сравнение по типам)
|
Расчетное и фактическое значения аварийных повреждений изоляции за периоды |
|||
|
1940 - 1965 гг. (на 1.01.66 г.) |
1940 - 1969 гг. (на 1.01.70 г.) |
1940 - 1974 гг. (на 1.01.75 г.) |
|
|
СВ1500/200-800 |
19,1544* 10 |
29,2497 16 |
43,6531 32 |
|
СВ1160/180-72 |
11,7954 20 |
15,7069 38 |
24,3826 82 |
|
СВ640/170-24 |
- |
- |
0,6322 0 |
|
СВ850/190-48 |
1,1163 1 |
2,3632 2 |
3,7152 3 |
|
СВ1340/150-96 |
10,3715 9 |
16,0073 15 |
24,0134 24 |
|
СВ1250/170-86 |
6,3740 2 |
7,7710 2 |
8,9170 2 |
|
СВ850/235-32 |
- |
- |
0,8116 0 |
|
СВ1500/170-96 |
1,6854 0 |
3,3845 0 |
5,6432 4 |
|
ВГС1225/147 |
- |
0,5660 1 |
1,1590 1 |
|
Всего... |
50,5060 42 |
75,2170 74 |
113,7237 148 |
|
* В дробном обозначении: числитель - ожидаемое, знаменатель - фактическое число аварийных пробоев
|
|||
Таблица П1.9
Данные об аварийной повреждаемости изоляции гидрогенераторов 13,8 кВ (сравнение по электростанциям)
|
Расчетное и фактическое значения аварийных повреждений изоляции за периоды |
|||
|
1940 - 1965 гг. (на 1.01.66 г.) |
1940 - 1969 гг. (на 1.01.70 г.) |
1940 - 1974 гг. (на 1.01.75 г.) |
|
|
1 |
- |
- |
0,8116* 0 |
|
2 |
7,8264 4 |
12,8552 9 |
19,6166 24 |
|
3 |
11,3970 6 |
16,9945 7 |
24,0365 8 |
|
4 |
1,6854 0 |
3,3845 0 |
5,6432 4 |
|
5 |
2,4669 4 |
2,6837 7 |
4,2024 12 |
|
6 |
6,0252 10 |
7,8189 12 |
11,6039 14 |
|
7 |
- |
- |
0,3828 0 |
|
8 |
- |
- |
0,2494 0 |
|
9 |
0,2331 0 |
0,5649 1 |
0,7200 1 |
|
10 |
3,0421 0 |
3,9981 0 |
5,5580 0 |
|
11 |
4,7075 2 |
5,9664 2 |
6,8663 2 |
|
12 |
1,6665 0 |
1,8046 0 |
2,0517 0 |
|
13 |
2,0933 4 |
3,4231 7 |
5,1952 13 |
|
14 |
2,5788 1 |
4,6852 2 |
7,2406 4 |
|
15 |
2,6592 4 |
3,9009 6 |
6,0186 7 |
|
16 |
3,3098 6 |
5,2043 19 |
8,5763 56 |
|
17 |
- |
0,1684 0 |
0,1954 0 |
|
18 |
0,8832 1 |
1,7983 1 |
2,9430 2 |
|
19 |
- |
0,5660 1 |
1,1590 1 |
|
Всего... |
50,5060 42 |
75,2170 74 |
113,7237 178 |
|
* В дробном обозначении: числитель - ожидаемое; знаменатель - фактическое число аварийных пробоев |
|||
Завод А имеет существенно лучшие показатели за счет генераторов СВ-1500/200-88, установленных на электростанциях № 2 и 3. Последняя имеет нормальные показатели, первая - очень хорошие. При анализе показателей электростанции № 3 выяснилось, что по официальным каналам электростанцией была представлена неверная информация об аварийных пробоях. В действительности за рассматриваемый период на электростанции имело место не 8 случаев аварийного пробоя, а 21. Тогда соотношение МО и фактического числа аварийных пробоев выглядит иначе (24,04 и 21 соответственно). В целом по типу соотношение показателей МО и фактического числа аварий также изменяется (43, 64 и 43 соответственно). Отсюда следует, что показатели этой электростанции и показатели завода А должны рассматриваться как нормальные, а не лучшие.
Таким образом, сомнения вызывают только генераторы СВ-1160/180-72, изготовленные заводом В и установленные на электростанциях № 16 и 5. Напрашивается вывод, что либо на заводе В при изготовлении этих генераторов была неудачно модернизирована конструкция или имели место технологические отклонения, либо условия эксплуатации на этих электростанциях привели к значительному ухудшению показателей части машин этого типа. Эта часть работы пока не выполнялась.
Если из всех вышеприведенных расчетных материалов исключить генераторы электростанций № 16 и 5 и внести поправки из-за изменения показателей электростанции № 3, то предположительно текущие кривые вероятности аварийного пробоя должны совпадать с типовой, что будет свидетельствовать о наличии статистической однородности для оставшейся части наблюдаемой совокупности на рассматриваемом этапе. Результаты приведены на рис. П1.6, как видно из рисунка, совпадение кривых идеальное.
Относительная повреждаемость на единицу машины и единицу площади на календарном графике стабилизируется примерно на общих показателях, характеризующих обычный нормальный уровень.
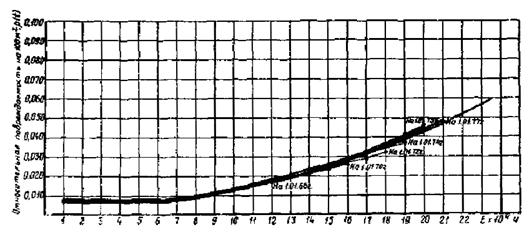
Рис. П1.6. Текущие кривые вероятностей аварийного пробоя изоляции гидрогенераторов 13,8 кВ за минусом генераторов СВ-1160/180-72, установленных на электростанциях № 16 и 5 и с учетом поправки по электростанции № 3
Таким образом, удалось установить, что на данном этапе в рассмотренной совокупности гидрогенераторов 13,8 кВ имеется резко отклоняющаяся группа машин типа СВ-1160/180-72, установленная на электростанциях № 16 и 5. По другим генераторам рассмотренной совокупности пока явления чрезмерного (отклоняющегося от нормального, описываемого типовой кривой) старения главной изоляции в результате ионизационного или теплового воздействия или под влиянием ухудшающегося состояния элементарных проводников (число повреждений в работе собственно элементарных проводников весьма мало - не превышает 7 случаев) не наблюдается. По данной группе гидрогенераторов в 1975 г. проводилось обширное техническое обследование представительной группой экспертов. Результаты технического обследования по оценке состояния главной статорной изоляции совпадают с данными статистического анализа.
Пример 12. К вопросу о целесообразном планировании и качестве выполнения полных перемоток обмоток статоров турбо- и гидрогенераторов1.
1 Кабанов П.С.
Постановка задачи.
Повреждаемость главной статорной изоляции генераторов как в работе, так и при профилактических испытаниях достаточно велика. Однако большая часть аварийных пробоев приводит к незначительному выгоранию обмотки и требует лишь частичного ее ремонта. Тем более это относится к последствиям профилактических пробоев. Вместе с тем возникновение аварийных и профилактических пробоев часто заставляет эксплуатационников ставить вопрос о назначении плановой перемотки обмотки, хотя само по себе большое абсолютное число аварийных и профилактических пробоев еще не говорит о дефектности изоляции, так как оно может соответствовать ожидаемому, (нормальному) уровню. В частности, в системе Минэнерго СССР за весь период эксплуатации группы турбо- и гидрогенераторов, мощностью 10 тыс. кВт и выше по состоянию на 1.01.1975 г. было произведено 333 полных перемотки обмоток статоров генераторов. Если принять в среднем стоимость перемотки одного генератора 200 тыс. руб., то общая сумма затрат составила примерно 70 млн. руб.
Необходимость постановки задачи анализа причин, вызвавших перемотки, целесообразности и своевременности перемоток, а также качества их выполнения очевидна.
Решение
Производится разделение всех рассмотренных работ по полной перемотке обмоток статоров на две группы: группы, где перемотки по техническим последствиям являлись неизбежными, и группы, где перемотки выполнялись в плановом порядке. Подробному анализу подвергается последняя группа.
Нам известно количественное выражение показателей аварийности нормальной микалентной изоляции в виде типовой кривой вероятности аварийного пробоя изоляции. Наличие этого эталона позволяет подсчитать ожидаемое число аварийных пробоев на группе генераторов, предполагаемых к перемотке, сравнить его с фактическим и из их сопоставления сделать оценку целесообразности перемотки. Если соотношения расчетного и фактического числа аварий сопоставлять для различных перегруппировок анализируемой группы генераторов (до ремонта, после ремонта, по работам конкретного предприятия, по типам машин, по территориальному признаку и т.п.), то можно выявить целый ряд технических положений и составить соответствующее заключение по результатам статистического анализа. Очевидно, что результаты статистического анализа должны быть подтверждены и дополнены результатами технического анализа (осмотр, испытания и т.п.) и диагностического анализа (акустические методы, хромотография и т.п.). В практических ситуациях, как показывает опыт, результаты статистического, технического и диагностического исследований совпадают.
Из общего числа 333 выполненных перемоток примерно 83 были вызваны значительным разрушением изоляции под влиянием внешних факторов (разрыв бандажного кольца ротора, нарушение пайки лобовых частей обмотки статора и т.п.). В десяти случаях перемотки были выполнены также после аварий, но вызванных замыканием в обмотке. Последствия аварии разрушительны, со значительным повреждением изоляции. Перемотка в обоих случаях являлась необходимой. Остальные 240 случаев перемоток выполнялись в плановом порядке, в периоды капитальных и реконструктивных ремонтов.
Результат анализа вышеуказанных 240 перемоток показал, что примерно в 40 случаях выполнение перемоток было явно целесообразно и необходимо, так как состояние изоляции было достаточно плохим и затраты на выполнение перемоток окупались ликвидацией аварийных очагов и общим повышением надежности работы генераторов. Подобное заключение можно было сделать опираясь на результаты:
- статистического анализа (сравнение ожидаемого и фактического числа аварийных пробоев главной изоляции обмоток статоров до и после перемоток);
- технического анализа (результаты испытаний и осмотров при капитальных, средних и текущих ремонтах). К сожалению, в данной работе пока не использованы возможности диагностической оценки, но надо полагать, что и они подтвердили бы плохое состояние этих обмоток.
В табл. П1.10 приведены примеры, характеризующие состояние изоляции до перемоток. Как видно из таблицы, перемотки обмоток турбогенераторов ТВВ-200-2, ТВВ-165-2, Т2-25-2, Т-25-2, СВ-1190/250-48, СВ-1100/145-88 (из числа вышеуказанных 40 случаев) были целесообразны. Показатели после перемоток - удовлетворительны (фактическое и ожидаемое число аварий совпадает, технический анализ не указывает сбоев), за исключением генераторов типа ТВВ-200-2.
В остальных 200-х случаях выполнение полных перемоток вызывает сомнение в целесообразности их проведения. По результатам статистического анализа во всех указанных случаях соотношения ожидаемого и фактического числа аварийных пробоев до и после перемоток нормальны, технический анализ не дает достаточных предпосылок для их обоснования.
Очевидно, что среди этих перемоток определенную часть работ следует признать необоснованной, например по генераторам СВ-900/170-80, СВ-1160/180-72* и др. (см. табл. П1.10). Исключение составляют те случаи, где производились перемотки: 1) среднестатистических, нормальных машин с микалентной изоляцией и с воздушным охлаждением, но с большим сроком эксплуатации; 2) с переходом на улучшенные варианты изоляции (от гильзовой к микалентной, от катушечной к стержневой, от микалентной к термореактивной). Общее число таких перемоток - 38. Таким образом, 162 случая плановых перемоток обмоток статоров следует признать необоснованными, затраты по которым составляют примерно 30 ÷ 40 млн. руб.
* Из числа генераторов, установленных на Днепрогэс им. В.И. Ленина.
Таблица П1.10
Сравнение ожидаемого и фактического числа аварийных пробоев изоляции до перемоток обмоток статоров генераторов
|
Ожидаемое число аварий |
Фактическое число аварий |
Технический анализ |
|
|
ТВВ-200-2 ТВВ-165-2 |
0,8944 |
16 |
Дефект конструкции (проседание «корзинки», вымывание компаунда в лобовых частях обмотки, неудовлетворительная подвеска сердечника статора, вибрация стержней и т.п.) |
|
Т-25-2 |
2,7945 |
12 |
Дефект изготовления |
|
СВ-1190/250-48 |
2,4105 |
6 |
То же |
|
Т2-25-2 |
0,9831 |
4 |
-"- |
|
СВ-1100/145-88 |
1,0838 |
4 |
Дефект конструкций |
|
СВ-900/170-80 |
1,4480 1,5338 |
2 3 |
- |
|
Турбогенераторы, установленные на Новомосковской ГРЭС-10 |
2,9048 0,6443 |
3 1 |
- |
|
СВ-1160/180-72 (генераторы, установленные на ДнепроГЭС им. В.И. Ленина) |
1,5255 1,4468 |
1 1 |
- |
|
Т 4376/142 |
16,8325 4,9382 |
10 0 |
- |
|
Примечание. В числителе - до перемотки; в знаменателе - после перемотки. |
|||
Независимо от обоснованности выполненных работ практически все работы (заключение по результатам только статистического анализа) выполнены с достаточно хорошим качеством. Исключение составляют работы, выполненные на генераторах СВ-546/90-40, где показатели ожидаемого и фактического числа аварийных пробоев до перемотки были 0,1091 и 1, после перемотки оказалась 0,5695 и 3 (ожидаемое и фактическое число аварийных пробоев соответственно).
Пример 13. Статистический контроль за состоянием статорной изоляции наблюдаемой совокупности генераторов1.
1 Байкова И.Б., Белова Л.А., Мельниченко Н.А.
Постановка задачи.
При статистическом контроле за состоянием статорной изоляции под наблюдение может быть взята любая совокупность изоляции, работающей в воздушной или водородной среде, например, все генераторы ведомства, все генераторы данной энергосистемы, генераторы одного завода, генераторы с номинальным напряжением 10,5 кВ и т.д.
Для выполнения ежегодного или периодического анализа состояния наблюдаемой совокупности необходимо:
а) располагать «историей жизни» каждого генератора из этой совокупности (год ввода, единичная площадь статорной изоляции, паспортные данные, сведения о перемотках, перестановках, демонтаже, числе часов работы, загрузке, различных режимах: пусках, несинхронных включениях и т.д., которые систематически должны пополняться);
б) иметь типовые кривые вероятности аварийного пробоя для данного вида изоляции с учетом охлаждающей среды.
Например, рассмотрена по состоянию на 1 января 1975 г. некоторая совокупность отечественных турбо- и гидрогенераторов мощностью от 10 до 800 МВт в единице, имеющих микалентную изоляцию. Эта совокупность состоит примерно из 2000 генераторов со сроком эксплуатации от 1 года до 45 лет, установленных примерно на 400 электростанциях. Генераторы (с номинальным напряжением 20; 18; 15,75; 13,8; 10,5 и 6,3 кВ) изготовлены шестью различными заводами, имеют воздушное и водородное охлаждение обмоток статоров.
Турбогенераторы с воздушным охлаждением имеют 14 различных конструктивных типов; гидрогенераторы - 66 типов. Турбогенераторы с водородным охлаждением имеют 22 типа. Генераторы находятся в нормальной эксплуатации при принятой системе профилактического обслуживания; подвергаются плановым перемоткам и т.д. Анализу подвергается лишь один элемент генератора - главная изоляция статоров, так как только по этому элементу известна закономерность старения.
Решение.
Просчитывается относительная повреждаемость изоляции на единицу площади по годам (календарный график) и частоты повреждений в зависимости от времени (учет фактора старения) и их сглаженные значения в виде текущих кривых вероятности аварийного пробоя для всей совокупности в целом и для отдельных вариантов (отдельно для трубо- и гидрогенераторов, с разбивкой по уровню номинального напряжения, по воздушным и водородным машинам и т.п.).
Результаты расчетов в виде текущих кривых вероятности аварийного пробоя для микалентной изоляции в исходном состоянии при ее работе в воздушной среде представлены на рис. П1.7, а. Как видно из рисунка, рассматриваемая реальная совокупность генераторов существенно неоднородна. Весь парк рассмотренных генераторов в начальный период эксплуатации дает завышенные показатели аварийности (сдвиг в худшую сторону), в последующие годы эксплуатации у различных групп показатели различны. Так, гидрогенераторы с номинальным напряжением 15,75 и 13,8 кВ дают худшие показатели, все остальные группы - лучшие. Очевидно, неоднородность достаточно велика и необходимо определить, чем она вызвана. Аналогичный рисунок для микалентной изоляции при ее работе в водородной среде за недостатком места не приводится. Сравнение кривых также указывает на существенную неоднородность в группе генераторов с водородным охлаждением.
Анализ результатов расчетов с использованием значений, снятых с типовой кривой для микалентной изоляции, работающей в воздушной или водородной среде, раздельно по заводам, типам и электростанциям, показывает, что неоднородность в некоторых случаях вызвана отдельными конструктивными типами (одинаково плохими, независимо от завода-изготовителя), так что выделить какой-либо завод, имеющий нарушение в целом по своей продукции, не удается.
Рис. П1.7. Текущие кривые вероятности аварийного пробоя микалентной изоляции генераторов наблюдаемой совокупности, работающей в воздушной среде:
а - до исключения неоднородности; б - после исключения неоднородности
1 - типовая кривая; текущие кривые для гидрогенераторов; 2 - 15,75 кВ; 3 - 13,8 кВ; 4 - 10,5 кВ; 5 - 6,3 кВ; текущие кривые для турбогенераторов; 6 - 10,5; 7 - 6,3 кВ
Анализ результатов расчетов по отдельным электростанциям (всего рассмотрено 289 тепловых электростанций и 107 гидравлических) позволяет выделить 14 электростанций, отклоняющихся в лучшую сторону, и 31 электростанцию, отклоняющуюся в худшую сторону. Более подробное рассмотрение данных по отклоняющимся электростанциям позволяет в 80 % случаев объяснить имеющиеся отклонения наличием на этих электростанциях соответственно лучших или худших типов генераторов. Исключение из показателей каждой электростанции показателей генераторов вышеуказанных типов (их площади и числа аварий) приводит ее показатели к норме. Это указывает на то, что причиной возникновения неоднородности в данных случаях являются особенности конструктивного исполнения, а не условия и режим, в которых эксплуатировались генератора (указанные типы установлены на разных электростанциях и везде имеют одинаково худшие или лучшие показатели, а на одной и той же электростанции генераторы этих типов ведут себя отлично от генераторов других типов). Примерно в 20 % случаев отклонение по показателям электростанций таким образом объяснить не удается. Так, по одной из гидроэлектростанций, имеющей лучшие показатели, тщательное ознакомление с данными повреждаемости показало, что в официальную статистику не попало 11 случаев аварийных пробоев (всего за весь период эксплуатации на всех генераторах электростанции имел место 21 случай аварийного пробоя, а по официальным данным было отмечено только 8). Такое число фактических повреждений при МО 24,3503 заставляет признать состояние изоляции генераторов на этой электростанции нормальным и исключить ее из перечня электростанций, отклоняющихся в лучшую сторону.
В некоторых случаях отклоняющимися должны быть признаны отдельные генераторы. В этом случае наиболее вероятными причинами отклонения являются качество изготовления или эксплуатации.
Таким образом, в целом по исследуемой совокупности генераторов следует признать отклоняющейся лишь небольшую часть генераторов. Подробному техническому анализу теперь должно быть подвергнуто не все огромное количество рассмотренных генераторов, а лишь их незначительная часть. С учетом результатов технического анализа может быть принято необходимое техническое решение по ликвидации «узких» мест.
Аварии и площадь изоляции отклоняющихся групп исключены из общей совокупности, вновь получены частоты для оставшихся совокупностей микалентной изоляции, работающей в воздушной или водородной среде, произведено их сглаживание по методу наименьших квадратов, вновь получены текущие кривые вероятности аварийного пробоя. В результате обнаружено, что вновь полученные текущие кривые практически совпали с типовыми. Результаты расчетов для микалентной изоляции при ее работе в воздушной среде приведены на рис. П1.7, б при ее работе в водородной среде за недостатком места не приведены. В соответствии с этим рассматриваемые оставшиеся совокупности следует признать однородными.
Характер поведения отклоняющихся групп резко отличен от типовой кривой.
Итак, известна значительная доля нормальных машин и некоторая сравнительно небольшая их доля, отклоняющаяся в лучшую или худшую сторону. Но для управления надежностью исследуемого оборудования важно не только выделить отклоняющиеся группы, но и выяснить в каждом случае причины этого отклонения. Это важно и для совершенствования конструктивного исполнения, и для ликвидации аварийного очага в эксплуатации, если причиной являются условия эксплуатации или качество технического обслуживания и ремонта.
В заключение следует еще раз подчеркнуть, что общие показатели подвергнувшейся исследованию эксплуатируемой микалентной изоляции, работающей как в воздушной, так и в водородной среде, являются удовлетворительными. Из общей совокупности в 3486×100 м2 73 % изоляции (2555×100 м2) удовлетворяет нормальным требованиям. По этой совокупности нормальной изоляции осуществлять воздействие на уровень «календарной» аварийности можно только путем ее постоянного «омоложения» (для воздушных генераторов), доводя ее путем перемоток до уровня константы.
Примерно 25 - 27 % (931×100 м2) составляют отклоняющиеся группы. При этом около 10 % отклоняются в лучшую сторону и около 15 % - в худшую. Ориентировочно можно сказать, что отклонения имеют место в результате следующих причин.
|
Причина отклонения |
В лучшую сторону |
В худшую сторону |
|
Конструирование |
90 % |
63 % |
|
Изготовление |
- |
22 % |
|
Условия эксплуатации |
- |
- |
|
Специализированный ремонт |
- |
8 % |
|
Неправильная информация |
10 % |
- |
|
Неясные причины |
- |
7 % |
|
Итого... |
100 % |
100 % |
Часть аварий, которая составляет отклонения, вызывающие возникновение статистической неоднородности в рассматриваемой совокупности, вполне поддается управлению. Для улучшения показателей аварийности главной статорной изоляции генераторов рассмотренной совокупности следует:
а) демонтировать или модернизировать по мере возможности худшие типы (ТВВ-200-2; Т-25-2 и др.);
б) как можно долее продлить эксплуатацию таких типов, как Т-4376/142 и ТВ-50-2;
в) выявить причины повышенной повреждаемости отдельных турбо- и гидрогенераторов (всего - 8) и принять меры к улучшению их показателей;
г) навести порядок в учете аварий (исключить возможности представления неправильной информации об авариях изоляции генераторов).
Периодический статистический контроль на основе использования типовых кривых и концепции выделения отклоняющихся групп позволяет проанализировать состояние наблюдаемой совокупности, выделить отклоняющиеся группы, выполнить анализ причин, вызвавших эти отклонения и принять соответствующие меры.
Такой контроль за наблюдаемой совокупностью генераторов должен производиться периодически, желательно ежегодно, для систематического и своевременного учета всех дополнительно возникающих неоднородностей и принятия соответствующих мер.
Приложение 2
ОБРАБОТКА ИСХОДНЫХ ЭКСПЛУАТАЦИОННЫХ ДАННЫХ ДЛЯ ПОЛУЧЕНИЯ ТЕКУЩИХ КРИВЫХ ВЕРОЯТНОСТИ АВАРИЙНОГО ПРОБОЯ
1. Необходимо выполнить обработку информации по выбранной для анализа совокупности генераторов с целью получения зависимости вероятности возникновения аварии от длительности эксплуатации изоляции.
2. На первом этапе при обработке исходных данных получают значения соответствующих частот аварийных пробоев (отношение числа пробоев к числу единиц площади в каждом из интервалов времени).
3. В качестве примера рассмотрим рис. П2.1. На нем приведены значения частот аварийных пробоев, полученные на основании обработки фактических эксплуатационных данных, как отношение числа аварийных пробоев на единицу площади изоляции1 за интервал времени2 от 1 · 104 до 22 · 104 часов эксплуатации корпусной изоляции обмоток статоров анализируемой группы генераторов. Точки, обозначающие частоты аварийных пробоев за каждый интервал времени, соединены между собой ломаной линией.
1 За единицу площади принято 100 м2.
2 За единицу времени принято 1 · 104 часов.
4. Под каждым значением интервала времени подписана соответствующая данному интервалу площадь изоляции генераторов анализируемой совокупности. С увеличением времени число генераторов последних выпусков постепенно исключается из рассмотрения, поэтому площадь изоляции со временем убывает.
5. Ломаный график частот аварий, представляющий собой случайные колебания рассматриваемой величины, не может быть использован для количественной оценки возможной вероятности пробоя, поэтому следует получить сглаженную кривую. Сглаживание лучше всего производить по методу наименьших квадратов (сглаживание может быть проведено и на глаз, но при этом нельзя оценить ошибку результата).
6. Площади изоляции машин анализируемой группы, эксплуатировавшиеся в интервалах времени [ti-1, ti], ti = 1 · 104 часов обозначаются через Si, соответствующие фактические числа аварий - через μi. Вводится замена временной переменной xi = i/N, причем N = 22 - число интервалов времени, для которых имеются данные.
7. Зависимость pi = p(ti) ищется в виде:
pi = a0 + a1xi2,
поскольку было установлено, что определять более двух коэффициентов методом наименьших квадратов в рассматриваемых задачах нецелесообразно и что член xi2 обеспечивает несколько лучшую точность, чем xi и xi3.
Рис. П2.1. Текущая кривая вероятности аварийного пробоя изоляции некоторой совокупности генераторов с воздушным охлаждением:
1 - p1(t); 2 - p2(t); 3 - ![]() ; 4 - p3(t); 5 - данные
эксплуатации p2(t) - текущая кривая; p1(t) и p3(t) -
доверительные границы для этой кривой;
; 4 - p3(t); 5 - данные
эксплуатации p2(t) - текущая кривая; p1(t) и p3(t) -
доверительные границы для этой кривой; ![]() - кривая для расчетов 1965 г.
- кривая для расчетов 1965 г.
Следовательно, речь идет о сглаженной зависимости вида:
8.
Из предыдущих исследований (см. Электричество, 1965, № 4 и 1967, № 6) известны примерные значения ![]() величин
pi
поэтому дисперсия величин μi/Si
суть примерно
величин
pi
поэтому дисперсия величин μi/Si
суть примерно
![]()
Умножая
обе части (П-1) на ![]() получаем
получаем
Причем дисперсия левой части есть примерно 1.
9.
Обозначая буквами ![]() векторы с компонентами соответственно
векторы с компонентами соответственно
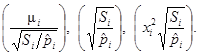 (П-3)
(П-3)
Переписываем (П-2) в виде:
![]()
так, что задача нахождения а0 и а1
сводится к проектированию вектора ![]() на линейную оболочку
векторов
на линейную оболочку
векторов ![]() и
и ![]() Получаемые
так оценки коэффициентов
Получаемые
так оценки коэффициентов ![]() и
и ![]() будут
коррелированны.
будут
коррелированны.
10. Удобнее перейти к ортогональным векторам
![]()
и к записи в форме
где
a1 = b1, ![]() (П-5)
(П-5)
11. Из (П-4) имеем оценки ![]() и
и ![]() для b0 и b1:
для b0 и b1:
Как известно, дисперсия оценок (П-6) суть соответственна:
![]() и
и ![]()
Принимая для величин (П-5) гауссовское распределение получаем, что с вероятностью около 50 % истинное значение пары (b0, b1) лежит внутри прямоугольника с вершинами
12. Далее вопрос состоит в том, чтобы превратить доверительную область (П-7) для чисел b0 и b1 доверительную область для кривой a0 + a1xi2. Поскольку ai связаны с bi линейной заменой (П-5), то a0 + a1xi2 есть в конечном счете при каждом i линейная функция от b0, b1.
13. Простейший способ разыскания ее минимума и максимума на прямоугольнике (П-7) состоит в вычислении ее значений в вершинах этого прямоугольника и в выборе наибольшего и наименьшего из этих четырех чисел.
14. Исходные данные для расчета, т.е. Si, μi, pi, а также найденные значения pi (средняя кривая на рисунке) и границы примерно 50 %-ной доверительной области обозначены на рис. П2.1.
Приложение 3
РАСПРЕДЕЛЕНИЕ ПУАССОНА1
1 Ярослав Янко. Математико-статистические таблицы (Госстатиздат, 1961).
1. Определение
Случайная величина, которая имеет распределение Пуассона, получает значение X = 0, 1, 2, 3 ..., с вероятностями
где λ - константа, λ > 0; это единственный параметр распределения Пуассона. Среднее значение и дисперсия распределения Пуассона равны λ.
2. Описание таблиц
В табл. П3.1 содержатся формулы (П3.1) для разных параметров
λ = 0,1 (0,1) 15,0; 16 (2) 30.
В табл. П3.2 приводятся для тех же значений λ суммы по (П3.2)
которые выражают вероятность того, что случайная величина с распределением Пуассона получит значения X или большие.
Распределение Пуассона
|
x |
λ |
|||||||||
|
0,1 |
0,2 |
0,3 |
04 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
|
0 |
,904837 |
,818731 |
,740818 |
,670320 |
,606531 |
,548812 |
,496585 |
,449329 |
,406570 |
,367879 |
|
1 |
,090484 |
,163746 |
,222245 |
,268128 |
,303265 |
,329287 |
,347610 |
,359463 |
,365913 |
,367879 |
|
2 |
,004524 |
,016375 |
,033337 |
,053626 |
,075816 |
,098786 |
,121663 |
,143785 |
,164661 |
,183940 |
|
3 |
,000151 |
,001092 |
,003334 |
007150 |
,012636 |
,019757 |
,028388 |
,038343 |
,049398 |
,061313 |
|
4 |
,000004 |
,000055 |
,000250 |
,000715 |
,001580 |
,002964 |
,004968 |
,007669 |
,011115 |
,015328 |
|
5 |
- |
,000002 |
,000015 |
,000057 |
,000158 |
,000356 |
,000696 |
,001227 |
,002001 |
,003066 |
|
6 |
- |
- |
,000001 |
,000004 |
,000013 |
,000036 |
,000081 |
,000164 |
,000300 |
,000511 |
|
7 |
- |
- |
- |
- |
,000001 |
,000003 |
,000008 |
,000019 |
,000039 |
,000073 |
|
8 |
- |
- |
- |
- |
- |
- |
,000001 |
,000002 |
,000004 |
,000009 |
|
9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2,0 |
|
|
0 |
,332871 |
,301194 |
,272532 |
,246597 |
,223130 |
,201897 |
,182684 |
,165299 |
,149569 |
,135335 |
|
1 |
,366158 |
,361433 |
,354291 |
,345236 |
,334695 |
,323034 |
,310562 |
,297538 |
,284180 |
,270671 |
|
2 |
,201387 |
,216860 |
,230289 |
,241665 |
,251021 |
,258428 |
,263978 |
,267784 |
,269971 |
,270671 |
|
3 |
,073842 |
,086744 |
,099792 |
,112777 |
,125510 |
,137828 |
,149587 |
,160671 |
,170982 |
,180447 |
|
4 |
,020307 |
,026023 |
,032432 |
,039472 |
,047067 |
,055131 |
,063575 |
,072302 |
,081216 |
,090224 |
|
5 |
,004467 |
,006246 |
,008432 |
,011052 |
,014120 |
,017642 |
,021615 |
,026029 |
,030862 |
,036089 |
|
6 |
,000819 |
,001249 |
,001827 |
,002579 |
,003530 |
,004705 |
,006124 |
,007809 |
,009773 |
,012030 |
|
7 |
,000129 |
,000214 |
,000339 |
,000516 |
,000756 |
,001075 |
,001487 |
,002008 |
,002653 |
,003437 |
|
8 |
,000018 |
,000032 |
,000055 |
,000090 |
,000142 |
,000215 |
,000316 |
,000452 |
,000630 |
,000859 |
|
9 |
,000002 |
,000004 |
,000008 |
,000014 |
,000024 |
,000038 |
,000060 |
,000090 |
,000133 |
,000191 |
|
10 |
- |
,000001 |
,000001 |
,000002 |
,000004 |
,000006 |
,000010 |
,000016 |
,000025 |
,000038 |
|
11 |
- |
- |
- |
- |
- |
,000001 |
,000002 |
,000003 |
,000004 |
,000007 |
|
12 |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
3,0 |
|
|
0 |
,122456 |
,110803 |
,100259 |
,090718 |
,082085 |
,074274 |
,067206 |
,060810 |
,055023 |
,049787 |
|
1 |
,257159 |
,243767 |
,230595 |
,217723 |
,205212 |
,193111 |
,181455 |
,170268 |
,159567 |
,149361 |
|
2 |
,270016 |
,268144 |
,265185 |
,261268 |
,256516 |
,251045 |
,244964 |
,238375 |
,231373 |
,224042 |
|
3 |
,189012 |
,196639 |
,203308 |
,209014 |
,213763 |
,217572 |
,220468 |
,222484 |
,223660 |
,224042 |
|
4 |
,099231 |
,108151 |
,116902 |
,125409 |
,133602 |
,141422 |
,148816 |
,155739 |
,162154 |
,168031 |
|
5 |
,041677 |
,047587 |
,053775 |
,060196 |
,066801 |
,073539 |
,080360 |
,087214 |
,094049 |
,100819 |
|
6 |
,014587 |
,017448 |
,020614 |
,024078 |
,027834 |
,031867 |
,036162 |
,040700 |
,045457 |
,050409 |
|
7 |
,004376 |
,005484 |
,006773 |
,008255 |
,009941 |
,011836 |
,013948 |
,016280 |
,018832 |
,021604 |
|
8 |
,001149 |
,001508 |
,001947 |
,002477 |
,003106 |
,003847 |
,004708 |
,005698 |
,006827 |
,008102 |
|
9 |
,000268 |
,000369 |
,000498 |
,000660 |
,000863 |
,001111 |
,001412 |
,001773 |
,002200 |
,002701 |
|
10 |
,000056 |
,000081 |
,000114 |
,000158 |
,000216 |
,000289 |
,000381 |
,000496 |
,000638 |
,000810 |
|
11 |
,000011 |
,000016 |
,000024 |
,000035 |
,000049 |
,000068 |
,000094 |
,000126 |
,000168 |
,000221 |
|
12 |
,000002 |
,000003 |
,000005 |
,000007 |
,000010 |
,000015 |
,000021 |
,000029 |
,000041 |
,000055 |
|
13 |
- |
,000001 |
,000001 |
,000001 |
,000002 |
,000003 |
,000004 |
,000006 |
,000009 |
,000013 |
|
14 |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000002 |
,000003 |
|
15 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
3,1 |
3,2 |
3,3 |
3,4 |
3,5 |
3,6 |
3,7 |
3,8 |
3,9 |
4,0 |
|
|
0 |
,045049 |
,040762 |
,036883 |
,033373 |
,030197 |
,027324 |
,024724 |
,022371 |
,021242 |
,018316 |
|
1 |
,139653 |
,130439 |
,121714 |
,113469 |
,105691 |
,098365 |
,091477 |
,085009 |
,078943 |
,073263 |
|
2 |
,216461 |
,208702 |
,200829 |
,192898 |
,184959 |
,177058 |
,169233 |
,161517 |
,153940 |
,146525 |
|
3 |
,223677 |
,222616 |
,220912 |
,218617 |
,215785 |
,212469 |
,208720 |
,204588 |
,200122 |
,195367 |
|
4 |
,173350 |
,178093 |
,182252 |
,185825 |
,188812 |
,191222 |
,193066 |
,194359 |
,195119 |
,195367 |
|
5 |
,107477 |
,113979 |
,120286 |
,126361 |
,132169 |
,137680 |
,142869 |
,147713 |
,152193 |
,156293 |
|
6 |
,055530 |
,060789 |
,066158 |
,071604 |
,077098 |
,082608 |
,088102 |
,093551 |
,098925 |
,104196 |
|
7 |
,024592 |
,027789 |
,031189 |
,034779 |
,038549 |
,042484 |
,046568 |
,050785 |
,055115 |
,059540 |
|
8 |
,009529 |
,011116 |
,012865 |
,014781 |
,016865 |
,019118 |
,021538 |
,024123 |
,026869 |
,029770 |
|
9 |
,003282 |
,003932 |
,004714 |
,005584 |
,006559 |
,007647 |
,008854 |
,010185 |
,011643 |
,013231 |
|
10 |
,001018 |
,001265 |
,001557 |
,001899 |
,002296 |
,002753 |
,003276 |
,003870 |
,004541 |
,005292 |
|
11 |
,000287 |
,000368 |
,000467 |
,000587 |
,000730 |
,000901 |
,001102 |
,001337 |
,001610 |
,001925 |
|
12 |
,000074 |
,000098 |
,000128 |
,000166 |
,000213 |
,000270 |
,000340 |
,000423 |
,000523 |
,000642 |
|
13 |
,000018 |
,000024 |
,000033 |
,000043 |
;000057 |
,000075 |
,000097 |
,000124 |
,000157 |
,000197 |
|
14 |
,000004 |
,000006 |
,000008 |
,000011 |
,000014 |
,000019 |
,000026 |
,000034 |
,000044 |
,000056 |
|
15 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
,000005 |
,000006 |
,000009 |
,000011 |
,000015 |
|
16 |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000003 |
,000004 |
|
17 |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
4,1 |
4,2 |
4,3 |
4,4 |
4,5 |
4,6 |
4,7 |
4,8 |
4,9 |
5,0 |
|
|
0 |
,016573 |
,014996 |
,013569 |
,012277 |
,011109 |
,010052 |
,009095 |
,008230 |
,007447 |
,006738 |
|
1 |
,067948 |
,062981 |
,058345 |
,054020 |
,049990 |
,046238 |
,042748 |
,039503 |
,036488 |
,033690 |
|
2 |
,139293 |
,132261 |
,125441 |
,118845 |
,112479 |
,106348 |
,100457 |
,094807 |
,089396 |
,084224 |
|
3 |
,190368 |
,185165 |
,179799 |
,174305 |
,168718 |
,163068 |
,157383 |
,151691 |
,146014 |
,140374 |
|
4 |
,195127 |
,194424 |
,193284 |
,191736 |
,189808 |
,187528 |
,184925 |
,182029 |
,178867 |
,175467 |
|
5 |
,160004 |
,163316 |
,166224 |
,168728 |
,170827 |
,172525 |
,173830 |
,174748 |
,175290 |
,175467 |
|
6 |
,109336 |
,114321 |
,119127 |
,123734 |
,128120 |
,132270 |
,136167 |
,139798 |
,143153 |
,146223 |
|
7 |
,064040 |
,068593 |
,073178 |
,077775 |
,082363 |
,086920 |
,091426 |
,095862 |
,100207 |
,104445 |
|
8 |
,032820 |
,036011 |
,039333 |
,042776 |
,046329 |
,049979 |
,053713 |
,057517 |
,061377 |
,065278 |
|
9 |
,014951 |
,016805 |
,018793 |
,020913 |
,023165 |
,025545 |
,028050 |
,030676 |
,033416 |
,036266 |
|
10 |
,006130 |
,007058 |
,008081 |
,009202 |
,010424 |
,011751 |
,013184 |
,014724 |
,016374 |
,018133 |
|
11 |
,002285 |
,002695 |
,003159 |
,003681 |
,004264 |
,004914 |
,005633 |
,006425 |
,007294 |
,008242 |
|
12 |
,000781 |
,000943 |
,001132 |
,001350 |
,001599 |
,001884 |
,002206 |
,002570 |
,002978 |
,003434 |
|
13 |
,000246 |
,000305 |
,000374 |
,000457 |
,000554 |
,000667 |
,000798 |
,000949 |
,001123 |
,001321 |
|
14 |
,000072 |
,000091 |
,000115 |
,000144 |
,000178 |
,000219 |
,000268 |
,000325 |
,000393 |
,000472 |
|
15 |
,000020 |
,000026 |
,000033 |
,000042 |
,000053 |
,000067 |
,000084 |
,000104 |
,000128 |
,000157 |
|
16 |
,000005 |
,000007 |
,000009 |
,000012 |
,000015 |
,000019 |
,000025 |
,000031 |
,000039 |
,000049 |
|
17 |
,000001 |
,000002 |
,000002 |
,000003 |
,000004 |
,000005 |
,000007 |
,000009 |
,000011 |
,000014 |
|
18 |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
,000004 |
|
19 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
5,1 |
5,2 |
5,3 |
5,4 |
5,5 |
5,6 |
5,7 |
5,8 |
5,9 |
6,0 |
|
|
0 |
,006097 |
,006517 |
,004992 |
,004517 |
,004087 |
,003698 |
,003346 |
,003028 |
,002739 |
,002479 |
|
1 |
,031093 |
,028086 |
,026455 |
,024390 |
,022477 |
,020708 |
,019072 |
,017560 |
,016163 |
,014873 |
|
2 |
,079288 |
,074584 |
,070107 |
,065852 |
,061812 |
,057982 |
,054355 |
,050923 |
,047680 |
,044618 |
|
3 |
,134790 |
,129279 |
,123856 |
,118533 |
,113323 |
,108234 |
,103275 |
,098452 |
,093771 |
,089235 |
|
4 |
,171857 |
,168063 |
,164109 |
,160020 |
,155819 |
,151528 |
,147167 |
,142755 |
,138312 |
,133853 |
|
5 |
,175294 |
,174785 |
,173955 |
,172821 |
,171401 |
,169711 |
,167770 |
,165596 |
,163208 |
,160623 |
|
6 |
,149000 |
,151480 |
,153660 |
,155539 |
,157117 |
,158397 |
,159382 |
,160076 |
,160488 |
,160623 |
|
7 |
,108557 |
,112528 |
,116343 |
,119987 |
,123449 |
126717 |
,129782 |
,132635 |
,135268 |
,137677 |
|
8 |
,069205 |
,073143 |
,077077 |
,080991 |
,084871 |
,088702 |
,092470 |
,096160 |
,099760 |
,103258 |
|
9 |
,039216 |
,042261 |
,045390 |
,046595 |
,051866 |
,055192 |
,058564 |
,061970 |
,065398 |
,068638 |
|
10 |
,020000 |
,021976 |
,024057 |
,026241 |
,028526 |
,030908 |
,033382 |
,035943 |
,038585 |
,041303 |
|
11 |
,009273 |
,010388 |
,011591 |
,012882 |
,014263 |
,015735 |
,017298 |
,018952 |
,020696 |
,022529 |
|
12 |
,003941 |
,004502 |
,005119 |
,005797 |
,006537 |
,007343 |
,008216 |
,009160 |
,010175 |
,011264 |
|
13 |
,001546 |
,001801 |
,002087 |
,002408 |
,002766 |
,003163 |
,003603 |
,004087 |
,004618 |
,005199 |
|
14 |
,000563 |
,000669 |
,000790 |
,000929 |
,001087 |
,001265 |
,001467 |
,001693 |
,001946 |
,002228 |
|
15 |
,000191 |
,000232 |
,000279 |
,000334 |
,000398 |
,000472 |
,000557 |
,000655 |
,000768 |
,000891 |
|
16 |
,000061 |
,000075 |
,000092 |
,000113 |
,000137 |
,000165 |
,000199 |
,000237 |
,000282 |
,000334 |
|
17 |
,000018 |
,000023 |
,000029 |
,000036 |
,000044 |
,000054 |
,000067 |
,000081 |
,000098 |
,000118 |
|
18 |
,000005 |
,000007 |
,000008 |
,000011 |
,000014 |
,000017 |
,000021 |
,000026 |
,000032 |
,000039 |
|
19 |
,000001 |
,000002 |
,000002 |
,000003 |
,000004 |
,000005 |
,000006 |
,000008 |
,000010 |
,000012 |
|
20 |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
,000004 |
|
21 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
6,7 |
6,8 |
6,9 |
7,0 |
|
|
0 |
,002243 |
,002029 |
,001836 |
,001662 |
,001503 |
,001369 |
,001231 |
,001114 |
,001008 |
,000912 |
|
1 |
,013682 |
,012582 |
,011569 |
,010634 |
,009772 |
,008978 |
,008247 |
,007574 |
,006954 |
,006383 |
|
2 |
,041729 |
,039006 |
,036441 |
,034029 |
,031760 |
,029629 |
,027628 |
,025751 |
,023990 |
,022341 |
|
3 |
,084848 |
,080612 |
,076527 |
,072595 |
,068814 |
,065183 |
,061702 |
,058368 |
,055178 |
,052129 |
|
4 |
,129393 |
,124948 |
,120530 |
,116151 |
,111822 |
,107553 |
,103351 |
,099225 |
,095182 |
,091226 |
|
5 |
,157860 |
,154936 |
,151868 |
,148574 |
,145369 |
,141969 |
,138490 |
,134946 |
,131351 |
,127717 |
|
6 |
,160491 |
,160100 |
,159461 |
,158585 |
,157483 |
,156166 |
,154648 |
,152939 |
,151053 |
,149003 |
|
7 |
,139856 |
,141803 |
,143515 |
,144992 |
,146234 |
,147243 |
,148020 |
,148569 |
,148895 |
,149003 |
|
8 |
,106640 |
,109897 |
,113018 |
,115994 |
,118815 |
,121475 |
,123967 |
,126284 |
,128422 |
,130377 |
|
9 |
,072278 |
,075707 |
,079113 |
,082484 |
,085811 |
,089082 |
,092286 |
,095415 |
,098457 |
,101405 |
|
10 |
,044090 |
,046938 |
,049841 |
,052790 |
,055777 |
,058794 |
,061832 |
,064882 |
,067935 |
,070983 |
|
11 |
,024450 |
,026456 |
,028545 |
,030714 |
,082959 |
,035276 |
,037661 |
,040109 |
,042614 |
,045171 |
|
12 |
,012429 |
,013669 |
,014986 |
,016381 |
,017853 |
,019402 |
,021028 |
,022728 |
,024503 |
,026350 |
|
13 |
,005832 |
,006519 |
,007263 |
,008064 |
,008926 |
,009850 |
,010837 |
,011889 |
,013005 |
,014188 |
|
14 |
,002541 |
,002887 |
,003268 |
,003687 |
,004144 |
,004644 |
,005186 |
,005774 |
,006410 |
,007094 |
|
15 |
,001033 |
,001193 |
,001373 |
,001573 |
,001796 |
,002043 |
,002317 |
,002618 |
,002949 |
,003311 |
|
16 |
,000394 |
,000462 |
,000540 |
,600629 |
,000730 |
,000843 |
,000970 |
,001113 |
,001272 |
,001448 |
|
17 |
,000141 |
,000169 |
,000200 |
,000237 |
,000279 |
,000327 |
,000382 |
,000445 |
,000516 |
,000596 |
|
18 |
,000048 |
,000058 |
,000070 |
,000084 |
,000101 |
,000120 |
,000142 |
,000168 |
,000198 |
,000232 |
|
19 |
,000015 |
,000019 |
,000023 |
,000028 |
,000034 |
,000042 |
,000050 |
,000060 |
,000072 |
,000085 |
|
20 |
,000005 |
,000006 |
,000007 |
,000009 |
,000011 |
,000014 |
,000017 |
,000020 |
,000025 |
,000030 |
|
21 |
,000001 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000006 |
,000007 |
,000008 |
,000010 |
|
22 |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
,000003 |
|
23 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
7,1 |
7,2 |
7,3 |
7,4 |
7,5 |
7,6 |
7,7 |
7,8 |
7,9 |
8,0 |
|
|
0 |
,000825 |
,000747 |
,000676 |
,000611 |
,000553 |
,000500 |
,000453 |
,000410 |
,000371 |
,000335 |
|
1 |
,005858 |
,005375 |
,004931 |
,004523 |
,004148 |
,003803 |
,003487 |
,003196 |
,002929 |
,002684 |
|
1 |
,020797 |
,019352 |
,018000 |
,016736 |
,015555 |
,014453 |
,013424 |
,012464 |
,011569 |
,010735 |
|
3 |
,049219 |
,046444 |
,043799 |
,041282 |
,038889 |
,036614 |
,034455 |
,032407 |
,030465 |
,028626 |
|
4 |
,087364 |
,083598 |
,079934 |
,076372 |
,072916 |
,069567 |
,066326 |
,063193 |
,060169 |
057252 |
|
5 |
,124057 |
,120382 |
,116703 |
,113031 |
,109375 |
,105742 |
,102142 |
,098581 |
,095067 |
,091604 |
|
6 |
,146800 |
,144458 |
,141989 |
,139405 |
,136718 |
,133940 |
,131082 |
,128156 |
,125171 |
,122138 |
|
7 |
,148897 |
,148586 |
,148074 |
,147371 |
,146484 |
,145421 |
,144191 |
,142802 |
,141264 |
,139587 |
|
8 |
,132146 |
,133727 |
,135118 |
,136318 |
,137329 |
,138150 |
,138783 |
,139232 |
,139499 |
,139587 |
|
9 |
,104249 |
,106982 |
,109596 |
,112084 |
,114440 |
,116660 |
,118737 |
,120668 |
,122449 |
,124077 |
|
10 |
,074017 |
,077027 |
,080005 |
,082942 |
,085830 |
,088661 |
,091427 |
,094121 |
,096735 |
,099262 |
|
11 |
,047774 |
,050418 |
,053094 |
,055797 |
,058521 |
,061257 |
,063999 |
,066740 |
,069473 |
,072190 |
|
12 |
,028267 |
,030251 |
,032299 |
,034408 |
,036575 |
,038796 |
,041066 |
,043381 |
,045736 |
,048127 |
|
13 |
,015438 |
,016754 |
,018137 |
,019586 |
,021101 |
,022681 |
,024324 |
,026029 |
,027794 |
,029616 |
|
14 |
,007829 |
,008616 |
,009457 |
,010353 |
,011304 |
,012312 |
,013378 |
,014502 |
,015684 |
,016924 |
|
15 |
,003706 |
,004136 |
,004603 |
,005107 |
,005652 |
,006238 |
,006867 |
,007541 |
,008260 |
,009026 |
|
16 |
,001644 |
,001861 |
,002100 |
,002362 |
,002649 |
,002963 |
,003305 |
,003676 |
,004078 |
,004513 |
|
17 |
,000687 |
,000788 |
,000902 |
,001028 |
,001169 |
,001325 |
,001497 |
,001687 |
,001895 |
,002124 |
|
18 |
,000271 |
,000315 |
,000366 |
,000423 |
,000487 |
,000559 |
,000640 |
,000731 |
,000832 |
,000944 |
|
19 |
,000101 |
,000119 |
,000141 |
,000165 |
,000192 |
,000224 |
,000259 |
,000300 |
,000346 |
,000397 |
|
20 |
,000036 |
,000043 |
,000051 |
,000061 |
,000072 |
,000085 |
,000100 |
,000117 |
,000137 |
,000159 |
|
21 |
,000012 |
,000015 |
,000018 |
,000021 |
,000026 |
,000031 |
,000037 |
,000043 |
,000051 |
,000061 |
|
22 |
,000004 |
,000005 |
,000006 |
,000007 |
,000009 |
,000011 |
,000013 |
,000015 |
,000018 |
,000022 |
|
23 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000004 |
,000004 |
,000005 |
,000006 |
,000008 |
|
24 |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
|
25 |
- |
- |
- |
- |
|
- |
- |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
8,1 |
8,2 |
8,3 |
8,4 |
8,5 |
8,6 |
8,7 |
8,8 |
8,9 |
9,0 |
|
|
0 |
,000304 |
,000275 |
,000249 |
,000225 |
,000203 |
,000184 |
,000167 |
,000151 |
,000136 |
,000123 |
|
1 |
,002459 |
,002252 |
,002063 |
,001889 |
,001729 |
,001583 |
,001449 |
,001326 |
,001214 |
,001111 |
|
2 |
,009958 |
,009284 |
,008560 |
,007933 |
,007350 |
,006808 |
,006304 |
,005836 |
,005402 |
,004998 |
|
3 |
,026885 |
,025239 |
,023683 |
,022213 |
,020826 |
,019517 |
,018283 |
,017120 |
,016025 |
,014994 |
|
4 |
,054443 |
,051740 |
,049142 |
,046648 |
,044255 |
,041961 |
,039765 |
,037664 |
,035656 |
,033737 |
|
5 |
,088198 |
,084854 |
,081576 |
,078368 |
,075233 |
,072174 |
,069192 |
,066289 |
,063467 |
,060727 |
|
6 |
,119067 |
,115967 |
,112847 |
,109716 |
,106581 |
,103449 |
,100328 |
,097224 |
,094143 |
,091090 |
|
7 |
,137778 |
,135848 |
,133805 |
,131659 |
,129419 |
,127094 |
,124693 |
,122224 |
,119696 |
,117116 |
|
8 |
,139500 |
,139244 |
,138823 |
,138242 |
,137508 |
,136626 |
,135604 |
,134446 |
,133161 |
,131756 |
|
9 |
,125550 |
,126866 |
,128025 |
,129026 |
,129869 |
,130554 |
,131084 |
,131459 |
,131682 |
,131756 |
|
10 |
,101696 |
,104031 |
,106261 |
,108382 |
,110388 |
,112277 |
,114043 |
,115684 |
,117197 |
,118580 |
|
11 |
,074885 |
,077550 |
,080179 |
,082764 |
,085300 |
,087780 |
,090197 |
,092547 |
,094823 |
,097020 |
|
12 |
,050547 |
,052993 |
,055457 |
,057935 |
,060421 |
,062909 |
,065393 |
,067868 |
,070327 |
,072765 |
|
13 |
,031495 |
,033426 |
,035407 |
,037435 |
,039506 |
,041617 |
,043763 |
,045941 |
,048147 |
,050376 |
|
14 |
,018222 |
,019578 |
,020991 |
,092461 |
,023986 |
,025565 |
,027196 |
,028877 |
,030608 |
,032384 |
|
15 |
,009840 |
,010703 |
,011615 |
,012578 |
,013592 |
,014657 |
,015773 |
,016941 |
,018161 |
,019431 |
|
16 |
,004981 |
,005485 |
,006025 |
,006604 |
,007221 |
,007878 |
,008577 |
,009318 |
010102 |
,010930 |
|
17 |
,002373 |
,002646 |
,002942 |
,003263 |
,003610 |
,003985 |
,004389 |
,004823 |
,005289 |
,005786 |
|
18 |
,001068 |
,001205 |
,001356 |
,001523 |
,001705 |
,001904 |
,002121 |
,002358 |
,002615 |
,002893 |
|
19 |
,000455 |
,000520 |
,000593 |
,000673 |
,000763 |
,000862 |
,000971 |
,001092 |
,001225 |
,001370 |
|
20 |
,000184 |
,000213 |
,000246 |
,000283 |
,000324 |
,000371 |
,000423 |
,000481 |
,000545 |
,000617 |
|
21 |
,000071 |
,000083 |
,000097 |
,000113 |
,000131 |
,000152 |
,000175 |
,000201 |
,000231 |
,000264 |
|
22 |
,000026 |
,000031 |
,000037 |
,000043 |
,000051 |
,000059 |
,000069 |
,000081 |
,000093 |
,000103 |
|
23 |
,000003 |
,000011 |
,000013 |
,000016 |
,000019 |
,000022 |
,000026 |
,000031 |
,000036 |
,000042 |
|
24 |
,000003 |
,000004 |
,000005 |
,000006 |
,000007 |
,000008 |
,000009 |
,000011 |
,000013 |
,000016 |
|
25 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000005 |
,000006 |
|
26 |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
|
27 |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
9,1 |
9,2 |
9,3 |
9,4 |
9,5, |
9,6 |
9,7 |
9,8 |
9,9 |
10,0 |
|
|
0 |
,000112 |
,000101 |
,000091 |
,000083 |
,000075 |
,000063 |
,000061 |
,000055 |
,0000050 |
,000045 |
|
1 |
,001016 |
,000930 |
,000850 |
,000778 |
,000711 |
,000650 |
,000594 |
,000543 |
,000497 |
,000454 |
|
2 |
,004624 |
,004276 |
,003954 |
,003655 |
,003378 |
,003121 |
,002883 |
,002663 |
,002459 |
,002270 |
|
3 |
,014025 |
,013113 |
,012256 |
,011452 |
,010696 |
,009987 |
,009322 |
,008698 |
,008114 |
,007567 |
|
4 |
,031906 |
,030160 |
,028496 |
,026911 |
,025403 |
,023969 |
,022606 |
,021311 |
,020082 |
,018917 |
|
5 |
,058069 |
,055494 |
,053002 |
,050593 |
,048266 |
,046020 |
,043855 |
,041770 |
,039763 |
,037833 |
|
6 |
,088072 |
,085091 |
,082154 |
,079262 |
,076421 |
,073632 |
,070899 |
,068224 |
,065609 |
,063055 |
|
7 |
,114493 |
,111834 |
,106147 |
,106438 |
,103714 |
,100981 |
,098246 |
,095514 |
,092790 |
,090070 |
|
8 |
,130236 |
,128609 |
,126883 |
,125065 |
,123160 |
,121178 |
,119123 |
,117004 |
,114827 |
,112599 |
|
9 |
,131683 |
,131467 |
,131113 |
,130623 |
,130003 |
,129256 |
,128388 |
,127405 |
,126310 |
,125110 |
|
10 |
,119832 |
,120950 |
,121935 |
,122786 |
,123502 |
,124086 |
,124537 |
,124857 |
,125047 |
,125110 |
|
11 |
,099133 |
,101158 |
,103090 |
,104926 |
,106661 |
,108293 |
,109819 |
,111236 |
,112542 |
,113736 |
|
12 |
,075176 |
,077555 |
,079895 |
,082192 |
,084440 |
,086634 |
,088770 |
,090843 |
,092847 |
,094780 |
|
13 |
,052623 |
,054885 |
,057156 |
,059431 |
,061706 |
,063976 |
,066236 |
,068481 |
,070707 |
,072908 |
|
14 |
,034205 |
,036067 |
,037968 |
,039904 |
,041872 |
,043869 |
,045892 |
,047937 |
,050000 |
,052077 |
|
15 |
,020751 |
,022121 |
,023540 |
,025006 |
,026519 |
,028076 |
,029677 |
,031309 |
,033000 |
,034718 |
|
16 |
,011802 |
,012720 |
,013683 |
,014691 |
,015746 |
,016846 |
,017992 |
,019183 |
,020419 |
,021699 |
|
17 |
,006318 |
,006884 |
,007485 |
,008123 |
,008799 |
,009513 |
,010266 |
,011058 |
,011891 |
,012764 |
|
18 |
,003194 |
,003518 |
,003867 |
,004242 |
,004644 |
,005074 |
,005532 |
,006021 |
,006540 |
,007091 |
|
19 |
,001530 |
,001704 |
,001893 |
,002099 |
,002322 |
,002563 |
,002824 |
,003105 |
,003408 |
,003732 |
|
20 |
,000696 |
,000784 |
,000880 |
,000986 |
,001103 |
,001230 |
,001370 |
,001522 |
,001687 |
,001866 |
|
21 |
,000302 |
,000343 |
,000390 |
,000442 |
,000499 |
,000563 |
,000633 |
,000710 |
,000795 |
,000889 |
|
22 |
,000125 |
,000144 |
,000165 |
,000189 |
,000215 |
,000245 |
,000279 |
,000316 |
,000358 |
,000404 |
|
23 |
,000049 |
,000057 |
,000067 |
,000077 |
,000089 |
,000102 |
,000118 |
,000135 |
,000154 |
,000176 |
|
24 |
,000019 |
,000022 |
,000026 |
,000030 |
,000035 |
,000041 |
,000048 |
,000055 |
,000064 |
,000073 |
|
25 |
,000007 |
,000008 |
,000010 |
,000011 |
,000013 |
,000016 |
,000018 |
,000022 |
,000025 |
,000029 |
|
26 |
,000002 |
,000003 |
,000003 |
,000004 |
,000005 |
,000006 |
,000007 |
,000008 |
,000010 |
,000011 |
|
27 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000004 |
,000004 |
|
28 |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
|
29 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
10,1 |
10,2 |
10,3 |
10,4 |
10,5 |
10,6 |
10,7 |
10,8 |
10,9 |
11,0 |
|
|
0 |
,000041 |
,000037 |
000034 |
,000030 |
000028 |
000025 |
,000023 |
,000020 |
,000018 |
,000017 |
|
1 |
,000415 |
,000379 |
,000346 |
,000317 |
,000289 |
,000264 |
,000241 |
,000220 |
,000201 |
,000184 |
|
2 |
,002095 |
,001934 |
,001784 |
,001646 |
,001518 |
,001400 |
,001291 |
,001190 |
,001097 |
,001010 |
|
3 |
,007054 |
,006574 |
,006125 |
,005705 |
,005313 |
,004946 |
,004603 |
,004283 |
,003984 |
,003705 |
|
4 |
,017811 |
,016764 |
,015773 |
,014834 |
,013946 |
,013107 |
,012313 |
,011564 |
,010856 |
,010189 |
|
5 |
,035979 |
,034199 |
,032492 |
,030855 |
,029287 |
,027786 |
,026350 |
,024978 |
,023667 |
,022415 |
|
6 |
,060565 |
,058139 |
,055777 |
,053482 |
,051252 |
,049089 |
,046991 |
,044960 |
,042995 |
,041095 |
|
7 |
,087387 |
,084716 |
,082072 |
,079458 |
,076878 |
,074334 |
,071830 |
,069367 |
,066949 |
,064577 |
|
8 |
,110326 |
,108013 |
,105668 |
,103296 |
,100902 |
,098493 |
,096072 |
,093646 |
,091218 |
,088794 |
|
9 |
,123810 |
,122415 |
,120931 |
,119364 |
,117720 |
,116003 |
,114219 |
,112375 |
,110475 |
,108526 |
|
10 |
,125048 |
,124863 |
,124559 |
,124139 |
,123606 |
,122963 |
,122215 |
,121365 |
,120418 |
,119378 |
|
11 |
,114817 |
,115782 |
,116633 |
,117368 |
,117987 |
,118492 |
,118882 |
,119159 |
,119323 |
,119378 |
|
12 |
,096637 |
,098415 |
,100110 |
,101719 |
,103239 |
,104667 |
,106003 |
,107243 |
,108386 |
,109430 |
|
13 |
,075080 |
,077218 |
,079318 |
,081375 |
,083385 |
,085344 |
,087248 |
,089094 |
,090877 |
,092595 |
|
14 |
,054165 |
,056259 |
,058355 |
,060450 |
,062539 |
,064618 |
,066683 |
,068730 |
,070754 |
,072753 |
|
15 |
,036471 |
,038256 |
,040071 |
,041912 |
,043777 |
,045663 |
,047567 |
,049485 |
,051415 |
,053352 |
|
16 |
,023022 |
,024388 |
,025795 |
,027243 |
,028729 |
,030252 |
,031810 |
,033403 |
,035026 |
,036680 |
|
17 |
,013678 |
,014633 |
,015629 |
,016666 |
,017744 |
,018863 |
,020022 |
,021220 |
,022458 |
,023734 |
|
18 |
,007675 |
,008292 |
,008943 |
,009629 |
,010351 |
,011108 |
,011902 |
,012732 |
,013600 |
,014504 |
|
19 |
,004080 |
,004451 |
,004848 |
,005271 |
,005720 |
,006197 |
,006703 |
,007237 |
,007802 |
,008397 |
|
20 |
,002060 |
,002270 |
,002497 |
,002741 |
,003003 |
,003285 |
,003586 |
,003908 |
,004252 |
,004618 |
|
21 |
,000991 |
,001103 |
,001225 |
,001357 |
,001502 |
,001658 |
,001827 |
,002010 |
,002207 |
,002419 |
|
22 |
,000455 |
,000511 |
,000573 |
,000642 |
,000717 |
,000799 |
,000889 |
,000987 |
,001093 |
,001210 |
|
23 |
,000200 |
,000227 |
,000257 |
,000290 |
,000327 |
,000368 |
,000413 |
,000463 |
,000518 |
,000578 |
|
24 |
,000084 |
,000096 |
,000110 |
,000126 |
,000143 |
,000163 |
,000184 |
,000208 |
,000235 |
,000265 |
|
25 |
,000034 |
,000039 |
,000045 |
,000052 |
,000060 |
,000069 |
,000079 |
,000090 |
,000103 |
,000117 |
|
26 |
,000013 |
,000015 |
,000018 |
,000021 |
,000024 |
,000028 |
,000032 |
,000037 |
,000043 |
,000049 |
|
27 |
,000005 |
,000006 |
,000007 |
,000008 |
,000009 |
,000011 |
,000013 |
,000015 |
,000017 |
,000020 |
|
28 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000004 |
,000005 |
,000006 |
,000007 |
,000008 |
|
29 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
|
30 |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
11,1 |
11,2 |
11,3 |
11,4 |
11,5 |
11,6, |
11,7 |
11,8 |
11,9 |
12,0 |
|
|
0 |
,000015 |
000014 |
000012 |
,000011 |
,000010 |
,000009 |
,000008 |
,000008 |
,000007 |
,000006 |
|
1 |
,000168 |
,000153 |
,000140 |
,000128 |
,000116 |
,000106 |
,000097 |
,000089 |
,000081 |
,000074 |
|
2 |
,000931 |
,000858 |
,000790 |
,000727 |
,000670 |
,000617 |
,000568 |
,000522 |
,000481 |
,000442 |
|
3 |
,003445 |
,003202 |
,002976 |
,002764 |
,002568 |
,002385 |
,002214 |
,002055 |
,001907 |
,001770 |
|
4 |
,009559 |
,008965 |
,008406 |
,007879 |
,007382 |
,006915 |
,006476 |
,006062 |
,005674 |
,005309 |
|
5 |
,021221 |
,020082 |
,018997 |
,017963 |
,016979 |
,016043 |
,015153 |
,014307 |
,013504 |
,012741 |
|
6 |
,039259 |
,037487 |
,035778 |
,034130 |
,032544 |
,031017 |
,029549 |
,028137 |
,026782 |
,025481 |
|
7 |
,062253 |
,059979 |
,057755 |
,055584 |
,053465 |
,051400 |
,049388 |
,047432 |
,045530 |
,043682 |
|
8 |
,086376 |
,083970 |
,081579 |
,079206 |
,076856 |
,074529 |
,072231 |
,069962 |
,067725 |
,065523 |
|
9 |
,106531 |
,104496 |
,102427 |
,100328 |
,098204 |
,096060 |
,093900 |
,091728 |
,089548 |
,087364 |
|
10 |
,118249 |
,117036 |
,115743 |
,114374 |
,112935 |
,111430 |
,109863 |
,108239 |
,106562 |
,104837 |
|
11 |
,119324 |
,119164 |
,118899 |
,118533 |
,118068 |
,117508 |
,116854 |
,116110 |
,115281 |
,114368 |
|
12 |
,110375 |
,111220 |
,111964 |
,112607 |
,113149 |
,113591 |
,113933 |
,114175 |
,114320 |
,114368 |
|
13 |
,094243 |
,095820 |
,097322 |
,098747 |
,100093 |
,101358 |
,102539 |
,103636 |
,104647 |
,105570 |
|
14 |
,074721 |
,076656 |
,078553 |
,080409 |
,082219 |
,083982 |
,085694 |
,087350 |
,088950 |
,090489 |
|
15 |
,055294 |
,057236 |
,059177 |
,061110 |
,063035 |
,064946 |
,066841 |
,068716 |
,070567 |
,072391 |
|
16 |
,038360 |
,040065 |
,041793 |
,043541 |
,045306 |
,047086 |
,048877 |
,050678 |
,052484 |
,054293 |
|
17 |
,025047 |
,026396 |
,027780 |
,029198 |
,030648 |
,032129 |
,033639 |
,035176 |
,036739 |
,038325 |
|
18 |
,015446 |
,016424 |
,017440 |
,018492 |
,019581 |
,020706 |
,021865 |
,023060 |
,024288 |
,025550 |
|
19 |
,009023 |
,009682 |
,010372 |
,011095 |
,011852 |
,012641 |
,013465 |
,014322 |
,015212 |
,016137 |
|
20 |
,005008 |
,005422 |
,005860 |
,006324 |
,006815 |
,007332 |
,007877 |
,008450 |
,009051 |
,009682 |
|
21 |
,002647 |
,002892 |
,003153 |
,003433 |
,003732 |
,004050 |
,004388 |
,004748 |
,005129 |
,005533 |
|
22 |
,001336 |
,001472 |
,001620 |
,001779 |
,001951 |
,002136 |
,002334 |
,002547 |
,002774 |
,003018 |
|
23 |
,000645 |
,000717 |
,000796 |
,000882 |
,000975 |
,001077 |
,001187 |
,001307 |
,001435 |
,001575 |
|
24 |
,000298 |
,000335 |
,000375 |
,000419 |
,000467 |
,000521 |
,000579 |
,000642 |
,000712 |
,000787 |
|
25 |
,000132 |
,000150 |
,000169 |
,000191 |
,000215 |
,000242 |
,000271 |
,000303 |
,000339 |
,000378 |
|
26 |
,000057 |
,000065 |
,000074 |
,000084 |
,000095 |
,000108 |
,000122 |
,000138 |
,000155 |
,000174 |
|
27 |
,000023 |
,000027 |
,000031 |
,000035 |
,000041 |
,000046 |
,000053 |
,000060 |
,000068 |
,000078 |
|
28 |
,000009 |
,000011 |
,000012 |
,000014 |
,000017 |
,000019 |
,000022 |
,000025 |
,000029 |
,000033 |
|
29 |
,000004 |
,000004 |
,000005 |
000006 |
,000007 |
,000008 |
,000009 |
,000010 |
,000012 |
,000014 |
|
30 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
,000003 |
,000004 |
000005 |
,000005 |
|
31 |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
|
32 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
12,1 |
12,2 |
12,3 |
12,4 |
12,5 |
12,6 |
12,7 |
12,8 |
12,9 |
13,0 |
|
|
0 |
,000006 |
,000005 |
,000005 |
,000004 |
,000004 |
,000003 |
,000003 |
,000003 |
,000002 |
,000002 |
|
1 |
,000067 |
,000061 |
,000056 |
,000051 |
,000047 |
,000042 |
,000039 |
,000035 |
,000032 |
,000029 |
|
2 |
,000407 |
,000374 |
,000344 |
,000317 |
,000291 |
,000268 |
,000246 |
,000226 |
,000208 |
,000191 |
|
3 |
,001641 |
,001522 |
,001412 |
,001309 |
,001213 |
,001124 |
,001042 |
,000965 |
,000894 |
,000828 |
|
4 |
,004966 |
,004643 |
,004341 |
,004057 |
,003791 |
,003541 |
,003307 |
,003088 |
,002882 |
,002690 |
|
5 |
,012017 |
,011330 |
,010679 |
,010062 |
,009477 |
,008924 |
,008400 |
,007905 |
,007436 |
,006994 |
|
6 |
,024233 |
,023037 |
0,21892 |
,020794 |
,019744 |
,018740 |
,017781 |
,016864 |
,015988 |
,015153 |
|
7 |
,041889 |
,040151 |
,038467 |
,036836 |
,035258 |
,033733 |
,032259 |
,030837 |
,029464 |
,018141 |
|
8 |
,063358 |
,061230 |
,059142 |
,057095 |
,055091 |
,053129 |
,051212 |
,049339 |
,047511 |
,045730 |
|
9 |
,085181 |
,083000 |
,080828 |
,078665 |
,076515 |
,074381 |
,072266 |
,070171 |
,068100 |
,066054 |
|
10 |
,103069 |
,101261 |
,099418 |
,097544 |
,095644 |
,093720 |
,091777 |
,089819 |
,087849 |
,085870 |
|
11 |
,113376 |
,112308 |
,111168 |
,109959 |
,108686 |
,107352 |
,105961 |
,104516 |
,103023 |
,101483 |
|
12 |
,114321 |
,114180 |
,113947 |
,113624 |
,113215 |
,112720 |
,112142 |
,111484 |
,110749 |
,109940 |
|
13 |
,106406 |
,107153 |
,107811 |
,108380 |
,108860 |
,109251 |
,109554 |
,109769 |
,109897 |
,109940 |
|
14 |
,091965 |
,093376 |
,094720 |
,095994 |
,097197 |
,098326 |
,099381 |
,100360 |
,101263 |
,102087 |
|
15 |
,074185 |
,075946 |
,077670 |
,079355 |
,080997 |
,082594 |
,084143 |
,085641 |
,087086 |
,088475 |
|
16 |
,056103 |
,057909 |
,059709 |
,061500 |
,063279 |
,065043 |
,066788 |
,068513 |
,070213 |
,071886 |
|
17 |
,039932 |
,041558 |
,043201 |
,044859 |
,046529 |
,048208 |
,049895 |
,051586 |
,053279 |
,054972 |
|
18 |
,026843 |
,028167 |
,029521 |
,030903 |
,032312 |
,033746 |
,035204 |
,036683 |
,038183 |
,039702 |
|
19 |
,017095 |
,018086 |
,019111 |
,020168 |
,021258 |
,022379 |
,023531 |
,024713 |
,025925 |
,027164 |
|
20 |
,010342 |
,011033 |
,011753 |
,012504 |
,013286 |
,014099 |
,014942 |
,015816 |
,016721 |
,017657 |
|
21 |
,005959 |
,006409 |
,006884 |
,007383 |
,007908 |
,008459 |
,009036 |
,009640 |
,010272 |
,010930 |
|
22 |
,003278 |
,003554 |
,003849 |
,004162 |
,004493 |
,004845 |
,005216 |
,005609 |
,006023 |
,006459 |
|
23 |
,001724 |
,001885 |
,002058 |
,002244 |
,002442 |
,002654 |
,002880 |
,003122 |
,003378 |
,003651 |
|
24 |
,000869 |
,000958 |
,001055 |
,001159 |
,001272 |
,001393 |
,001524 |
,001665 |
,001816 |
,001977 |
|
25 |
,000421 |
,000468 |
,000519 |
,000575 |
,000636 |
,000702 |
,000774 |
,000852 |
,000937 |
,001028 |
|
26 |
,000196 |
,000219 |
,000246 |
,000274 |
,000306 |
,000340 |
,000378 |
,000420 |
,000465 |
,000514 |
|
27 |
,000088 |
,000099 |
,000112 |
,000126 |
,000142 |
,000159 |
,000178 |
,000199 |
,000222 |
,000248 |
|
28 |
,000038 |
,000043 |
,000049 |
,000056 |
,000063 |
,000071 |
,000081 |
,000091 |
,000102 |
,000115 |
|
29 |
,000016 |
,000018 |
,000021 |
,000024 |
,000027 |
,000031 |
,000035 |
,000040 |
,000046 |
,000052 |
|
30 |
,000006 |
,000007 |
,000009 |
,000010 |
,000011 |
,000013 |
,000015 |
,000017 |
,000020 |
,000022 |
|
31 |
,000002 |
,000003 |
,000003 |
,000004 |
,000005 |
,000005 |
,000006 |
,000007 |
,000008 |
,000009 |
|
32 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
|
33 |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
|
34 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
13,1 |
13,2 |
13,3 |
13,4 |
13,5 |
13,6 |
13,7 |
13,8 |
13,9 |
14,0 |
|
|
0 |
,000002 |
,000002 |
,000002 |
,000002 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
|
1 |
,000027 |
,000024 |
,000022 |
,000020 |
,000019 |
,000017 |
,000015 |
,000014 |
,000013 |
,000012 |
|
2 |
,000175 |
,000161 |
,000148 |
,000136 |
,000125 |
,000115 |
,000105 |
,000097 |
,000089 |
,000081 |
|
3 |
,000766 |
,000709 |
,000657 |
,000608 |
,000562 |
,000520 |
,000481 |
,000445 |
,000411 |
,000380 |
|
4 |
,002510 |
,002341 |
,002183 |
,002035 |
,001897 |
,001768 |
,001648 |
,001535 |
,001429 |
,001331 |
|
5 |
,006575 |
,006180 |
,005807 |
,005455 |
,005123 |
,004810 |
,004514 |
,004236 |
,003974 |
,003727 |
|
6 |
,014356 |
,013596 |
,012872 |
,012183 |
,011526 |
,010902 |
,010308 |
,009743 |
,009206 |
,008696 |
|
7 |
,026867 |
,025639 |
,024458 |
,023322 |
,022230 |
,021181 |
,020173 |
,019207 |
,018280 |
,017392 |
|
8 |
,043994 |
,042304 |
,040661 |
,039064 |
,037512 |
,036007 |
,034547 |
,033132 |
,031762 |
,030435 |
|
9 |
,064036 |
,062046 |
,060088 |
,058161 |
,056269 |
,054410 |
,052588 |
,050802 |
,049054 |
,047344 |
|
10 |
,083887 |
,081901 |
,079916 |
,077936 |
,075963 |
,073998 |
,072046 |
,070107 |
,068185 |
,066282 |
|
11 |
,099901 |
,098281 |
,096626 |
,094940 |
,093227 |
,091489 |
,089730 |
,087953 |
,086162 |
,084359 |
|
12 |
,109059 |
,108109 |
,107094 |
,106017 |
,104880 |
,103687 |
,102441 |
,101146 |
,099804 |
,098418 |
|
13 |
,109898 |
,109773 |
,109566 |
,109279 |
,108914 |
,108473 |
,107957 |
,107370 |
,106713 |
,105989 |
|
14 |
,102833 |
,103500 |
,104087 |
,104595 |
,105024 |
,105373 |
,105644 |
,105836 |
,105951 |
,105989 |
|
15 |
,089807 |
,091080 |
,092291 |
,093439 |
,094522 |
,095539 |
,096488 |
,097369 |
,098181 |
,098923 |
|
16 |
,073530 |
,075141 |
,076717 |
,078255 |
,079753 |
,081208 |
,082618 |
,083981 |
,085295 |
,086558 |
|
17 |
,056661 |
,058345 |
,060019 |
,061683 |
,063333 |
,064966 |
,066180 |
,068173 |
,069741 |
,071283 |
|
18 |
,041237 |
,042786 |
,044348 |
,045920 |
,047500 |
,049086 |
,050675 |
,052266 |
,053856 |
,055442 |
|
19 |
,028432 |
,029725 |
,031043 |
,032385 |
,033750 |
,035135 |
,036539 |
,037962 |
,039400 |
,040852 |
|
20 |
;018623 |
,019619 |
,020644 |
,021698 |
,022781 |
,023892 |
,025030 |
,026193 |
,027383 |
,028597 |
|
21 |
,011617 |
,012332 |
,013074 |
,013846 |
,014645 |
,015473 |
,016329 |
,017213 |
,018125 |
,019064 |
|
22 |
,006917 |
,007399 |
,007904 |
,008433 |
,008987 |
,009565 |
,010168 |
,010797 |
,011452 |
,012132 |
|
23 |
,003940 |
,004246 |
,004571 |
,004913 |
,005275 |
,005656 |
,006057 |
,006478 |
,006921 |
,007385 |
|
24 |
,002151 |
,002336 |
,002533 |
,002743 |
,002967 |
,003205 |
,003457 |
,003725, |
,004008 |
,004308 |
|
25 |
,001127 |
,001233 |
,001348 |
,001470 |
,001602 |
,001744 |
,001895 |
,002056 |
,002229 |
,002412 |
|
26 |
,000568 |
,000626 |
,000689 |
,000758 |
,000832 |
,000912 |
,000998 |
,001091 |
,001191 |
,001299 |
|
27 |
,000275 |
,000306 |
,000340 |
,000376 |
,000416 |
,000459 |
,000507 |
,000558 |
,000613 |
,000674 |
|
28 |
,000129 |
,000144 |
,000161 |
,000180 |
,000201 |
,000223 |
,000248 |
,000275 |
,000305 |
,000337 |
|
29 |
,000058 |
,000066 |
,000074 |
,000083 |
,000093 |
,000105 |
,000117 |
,000131 |
,000146 |
,000163 |
|
30 |
,000025 |
,000029 |
,000033 |
,000037 |
,000042 |
,000047 |
,000053 |
,000060 |
,000068 |
,000076 |
|
31 |
,000011 |
,000012 |
,000014 |
,000016 |
,000018 |
,000021 |
,000024 |
,000027 |
,000030 |
,000034 |
|
32 |
,000004 |
,000005 |
,000006 |
,000007 |
,000008 |
,000009 |
,000010 |
,000012 |
,000013 |
,000015 |
|
33 |
,000002 |
,000002 |
,000002 |
,000030 |
,000003 |
,000004 |
,000004 |
,000005 |
,000006 |
,000006 |
|
34 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
|
35 |
|
|
|
|
|
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||||
|
14,1 |
14,2 |
14,3 |
14,4 |
14,5 |
14,6 |
14,7 |
14,8 |
14,9 |
15,0 |
|
|
0 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
- |
- |
- |
- |
- |
|
1 |
,000011 |
,000010 |
,000009 |
,000008 |
,000007 |
,000007 |
,000006 |
,000006 |
,000005 |
,000005 |
|
2 |
,000075 |
,000069 |
,000063 |
,000058 |
,000053 |
,000049 |
,000045 |
,000041 |
,000038 |
,000034 |
|
3 |
,000352 |
,000325 |
000300 |
,000277 |
,000256 |
,000237 |
,000219 |
,000202 |
,000186 |
,000172 |
|
4 |
,001239 |
,001153 |
,001073 |
,000999 |
,000929 |
,000864 |
,000803 |
,000747 |
,000694 |
,0000645 |
|
5 |
,003494 |
,003275 |
,003070 |
,002876 |
,002694 |
,002523 |
,002362 |
,002211 |
,002069 |
,001936 |
|
6 |
,008212 |
,007752 |
,007316 |
,006902 |
,006510 |
,006139 |
,005787 |
,005454 |
,005138 |
,004839 |
|
7 |
,016541 |
,015726 |
,014946 |
,014199 |
,013486 |
,012804 |
,012152 |
,011530 |
,010937 |
,010370 |
|
8 |
,029153 |
,027913 |
,026715 |
,025559 |
,024443 |
,023367 |
,022330 |
,021331 |
,020370 |
,019444 |
|
9 |
,045673 |
,044040 |
,042447 |
,040894 |
,039380 |
,037907 |
,036472 |
,035078 |
,033723 |
,032407 |
|
10 |
,064399 |
,062537 |
,060700 |
,058887 |
,057101 |
,055343 |
,053614 |
,051915 |
,050247 |
,048611 |
|
11 |
,082547 |
,080730 |
,078910 |
,077089 |
,075270 |
,073456 |
,071648 |
,069850 |
,068062 |
,066287 |
|
12 |
,096993 |
,095530 |
,094034 |
,092507 |
,090951 |
,089371 |
,087769 |
,086148 |
,084510 |
,082859 |
|
13 |
,105200 |
,104349 |
,103437 |
,102489 |
,101446 |
,100371 |
,099247 |
,098076 |
,096862 |
,095807 |
|
14 |
,105951 |
,105839 |
,105654 |
,105396 |
,105069 |
,101672 |
,104209 |
,103681 |
,103089 |
,102436 |
|
15 |
,099594 |
,100196 |
,100723 |
,101181 |
,101567 |
,101881 |
,102125 |
,102298 |
,102402 |
,102436 |
|
16 |
,087768 |
,088923 |
,090021 |
,091063 |
,092045 |
,092967 |
,093827 |
,094626 |
,095361 |
,096034 |
|
17 |
,072795 |
,074277 |
,075724 |
,077135 |
,078509 |
,079842 |
,081133 |
,082380 |
,083581 |
,084736 |
|
18 |
,057023 |
,058596 |
,060158 |
,061708 |
,063243 |
,064761 |
,066259 |
,067735 |
,069187 |
,070613 |
|
19 |
,042317 |
,043793 |
,045277 |
,046768 |
,048264 |
,049763 |
,051263 |
,052762 |
,054257 |
,055747 |
|
20 |
,029834 |
,031093 |
,032373 |
,03 673 |
,034992 |
,030327 |
,037678 |
,039044 |
,040422 |
,041810 |
|
21 |
,020031 |
,021025 |
,022045 |
,023090 |
,024161 |
,025256 |
,026375 |
,027517 |
,028680 |
,029865 |
|
22 |
,012838 |
,013570 |
,014329 |
,015114 |
,015924 |
,016761 |
,017623 |
,018511 |
,019424 |
,020362 |
|
23 |
,007870 |
,008378 |
,008909 |
,009462 |
,010039 |
,010640 |
,011264 |
,011911 |
,012584 |
,013280 |
|
24 |
,004624 |
,004957 |
,005308 |
,005677 |
,006065 |
,006472 |
,006899 |
,007345 |
,007812 |
,008300 |
|
25 |
,002608 |
,002816 |
,003036 |
,003270 |
,003518 |
,003780 |
,004057 |
,004348 |
,004656 |
,004980 |
|
26 |
,001414 |
,001538 |
,001670 |
,001811 |
,001962 |
,002123 |
,002294 |
,002475 |
,002668 |
,002873 |
|
27 |
,000739 |
,000809 |
,000884 |
,000966 |
,001054 |
,001148 |
,001249 |
,001357 |
,001473 |
,001596 |
|
28 |
,000372 |
,000410 |
,000452 |
,000497 |
,000546 |
,000598 |
,000656 |
,000717 |
,000784 |
,000855 |
|
29 |
,000181 |
,000201 |
,000223 |
,000247 |
,000273 |
,000301 |
,000332 |
,000366 |
,000403 |
,000442 |
|
30 |
,000085 |
,000095 |
,000106 |
,000118 |
,000132 |
,000147 |
,000163 |
,000181 |
,000200 |
,000221 |
|
31 |
,000039 |
,000044 |
,000049 |
000055 |
,000062 |
,000069 |
,000077 |
,000086 |
,000096 |
,000107 |
|
32 |
,000017 |
,000019 |
,000022 |
,000025 |
,000028 |
,000032 |
,000035 |
,000040 |
,000045 |
,000050 |
|
33 |
,000007 |
,000008 |
,000009 |
,000011 |
,000012 |
,000014 |
,000016 |
,000018 |
,000020 |
,000023 |
|
34 |
,000003 |
,000003 |
,000004 |
,000005 |
,000005 |
,000006 |
,000007 |
,000008 |
,000009 |
,000010 |
|
35 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000004 |
|
36 |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,00001 |
,000001 |
,000001 |
,000002 |
,000002 |
|
37 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.1
|
x |
λ |
|||||||
|
16 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
|
|
0 |
- |
- |
- |
- |
- |
- |
- |
- |
|
1 |
,000002 |
- |
- |
- |
- |
- |
- |
- |
|
2 |
,000014 |
,000002 |
- |
- |
- |
- |
- |
- |
|
3 |
,000077 |
,000015 |
,000003 |
- |
- |
- |
- |
- |
|
4 |
,000307 |
,000067 |
,000014 |
,000003 |
,000001 |
- |
- |
- |
|
5 |
,000983 |
,000240 |
,000055 |
,000012 |
,000003 |
,000001 |
- |
- |
|
6 |
,002622 |
,000719 |
,000183 |
,000044 |
,000010 |
,000002 |
- |
- |
|
7 |
,005994 |
,001850 |
,000523 |
,000138 |
,000034 |
,000008 |
,000002 |
- |
|
8 |
,011987 |
,004163 |
,001309 |
,000380 |
,000103 |
,000026 |
,000006 |
,000002 |
|
9 |
,021311 |
,008325 |
,002908 |
,000928 |
,000275 |
,000076 |
,000020 |
,000005 |
|
10 |
,034098 |
,014985 |
,005816 |
,002042 |
,000060 |
,000199 |
,000056 |
,000015 |
|
11 |
,049597 |
,024521 |
,010575 |
,004083 |
,001439 |
,000470 |
,000144 |
,000042 |
|
12 |
,066129 |
,036782 |
,017625 |
,007486 |
,002878 |
,001018 |
,000335 |
,000104 |
|
13 |
,081389 |
,050929 |
,027116 |
,012669 |
,005314 |
,002036 |
,000722 |
,000240 |
|
14 |
,093016 |
,065480 |
,038737 |
,019908 |
,009109 |
,003781 |
,001444 |
,000513 |
|
15 |
,099218 |
,078576 |
,051649 |
,029199 |
,014575 |
,006553 |
,002695 |
,001027 |
|
16 |
,099218 |
,088397 |
,064561 |
,040148 |
,021862 |
,010649 |
,004717 |
,001925 |
|
17 |
,093381 |
,093597 |
,075954 |
,051956 |
,030864 |
,016286 |
,007769 |
,003397 |
|
18 |
,083006 |
,093597 |
,084394 |
,063502 |
,041152 |
,023525 |
,012085 |
,005662 |
|
19 |
,069899 |
,088671 |
,088835 |
,073529 |
,051982 |
,032192 |
,017810 |
,008941 |
|
20 |
,055920 |
,079804 |
,088835 |
,080882 |
,062378 |
,041849 |
,024934 |
,013411 |
|
21 |
,042605 |
,068403 |
,084605 |
,084733 |
,071289 |
,051813 |
,033245 |
,019159 |
|
22 |
,030986 |
,055966 |
,076914 |
,084733 |
,077770 |
,061234 |
,042312 |
,026126 |
|
23 |
,021555 |
,043800 |
,066881 |
,081049 |
,081152 |
,069221 |
,051510 |
,034077 |
|
24 |
,014370 |
,032850 |
,055735 |
,074295 |
,081152 |
,074989 |
,060095 |
,042596 |
|
25 |
,009197 |
,023652 |
,044588 |
,065380 |
,077905 |
,077989 |
,067307 |
,051115 |
|
26 |
,005660 |
,016374 |
,034298 |
,055321 |
,071913 |
,077989 |
,072484 |
,058979 |
|
27 |
,003354 |
,010916 |
,025406 |
,045077 |
,063922 |
,075100 |
,075169 |
,065532 |
|
28 |
,001916 |
,007018 |
,018147 |
,035417 |
,054791 |
,069736 |
,075169 |
,070213 |
|
29 |
,001057 |
,004356 |
,012515 |
,026868 |
,045344 |
,062522 |
,072577 |
,072695 |
|
30 |
,000564 |
,002613 |
,008344 |
,019703 |
,036275 |
,054186 |
,067738 |
,072635 |
|
31 |
,000291 |
,001517 |
,005383 |
,013983 |
,028084 |
,045446 |
,061183 |
,070291 |
|
32 |
,000146 |
,000854 |
,003364 |
,009613 |
,021063 |
,036925 |
,053535 |
,065898 |
|
33 |
,000071 |
,000466 |
,002039 |
,006409 |
,015319 |
,029092 |
,045424 |
,059908 |
|
34 |
,000033 |
,000246 |
,001199 |
,004147 |
,010813 |
,022247 |
,037408 |
,052860 |
|
35 |
,000015 |
,000127 |
,000685 |
,002607 |
,007415 |
,016526 |
,029926 |
,045308 |
|
36 |
,000007 |
,000063 |
,000381 |
,001593 |
,004943 |
,011936 |
,023276 |
,037757 |
|
37 |
,000003 |
,000031 |
,000206 |
,000947 |
,003206 |
,008387 |
,017614 |
,030614 |
|
38 |
,000001 |
,000015 |
,000108 |
,000548 |
,002025 |
,005739 |
,012979 |
,024169 |
|
39 |
,000001 |
,000007 |
,000056 |
,000309 |
,001246 |
,003826 |
,009318 |
,018591 |
|
40 |
- |
,000003 |
,000028 |
,000170 |
,000748 |
,002487 |
,006523 |
,013943 |
|
41 |
- |
,000001 |
,000014 |
,000091 |
,000438 |
,001577 |
,004455 |
,010203 |
|
42 |
- |
,000001 |
,000006 |
,000048 |
,000250 |
,000976 |
,002970 |
,007288 |
|
43 |
- |
- |
,000003 |
,000024 |
,000140 |
,000590 |
,001934 |
,005084 |
|
44 |
- |
- |
,000001 |
,000012 |
,000076 |
,000349 |
,001231 |
,003467 |
|
45 |
- |
- |
,000001 |
,000006 |
,000041 |
,000202 |
,000766 |
,002311 |
|
46 |
- |
- |
- |
,000003 |
,000021 |
,000114 |
,000466 |
,001507 |
|
47 |
- |
- |
- |
,000001 |
,000011 |
,000063 |
,000278 |
,000962 |
|
48 |
- |
- |
- |
,000001 |
,000005 |
,000034 |
,000162 |
,000601 |
|
49 |
- |
- |
- |
- |
,000003 |
,000018 |
,000093 |
,000368 |
|
50 |
- |
- |
- |
- |
,000001 |
,000009 |
,000052 |
,000221 |
|
51 |
- |
- |
- |
- |
,000001 |
,000005 |
,000028 |
,000130 |
|
52 |
- |
- |
- |
- |
- |
,000002 |
,000015 |
,000075 |
|
53 |
- |
- |
- |
- |
- |
,000001 |
,000008 |
,000042 |
|
54 |
- |
- |
- |
- |
- |
,000001 |
,000004 |
,000024 |
|
55 |
- |
- |
- |
- |
- |
- |
,000002 |
,000013 |
|
56 |
- |
- |
- |
- |
- |
- |
,000001 |
,000007 |
|
57 |
- |
- |
- |
- |
- |
- |
,000001 |
,000004 |
|
58 |
- |
- |
- |
- |
- |
- |
- |
,000002 |
|
59 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
Суммарные значения функции Пуассона
|
x |
λ |
|||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,095163 |
,181269 |
,259182 |
,329680 |
,393469 |
,451188 |
,503415 |
,550671 |
,593430 |
,632121 |
|
2 |
,004679 |
,017523 |
,036936 |
,061552 |
,090204 |
,121901 |
,155805 |
,191208 |
,227518 |
,264241 |
|
3 |
,000155 |
,001149 |
,003600 |
,007926 |
,014388 |
,023115 |
,034142 |
,047423 |
,062857 |
,080301 |
|
4 |
,000004 |
,000057 |
,000266 |
,000776 |
,001752 |
,003358 |
,005753 |
,009080 |
,013459 |
,018988 |
|
5 |
- |
,000002 |
,000016 |
,000061 |
,000172 |
,000394 |
,000786 |
,001411 |
,002344 |
,003660 |
|
6 |
- |
- |
,000001 |
,000004 |
,000014 |
,000039 |
,000090 |
,000181 |
,000343 |
,000594 |
|
7 |
- |
- |
- |
- |
,000001 |
,000003 |
,000009 |
,000021 |
,000043 |
,000083 |
|
8 |
- |
- |
- |
- |
- |
- |
,000001 |
,000002 |
,000005 |
,000010 |
|
9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,667129 |
,698806 |
,727468 |
,753403 |
,776870 |
,798103 |
,817316 |
,834701 |
,850431 |
,864665 |
|
2 |
,300971 |
,337373 |
,373177 |
,408167 |
,442175 |
,475069 |
,506754 |
,537163 |
,566251 |
,593994 |
|
3 |
,099584 |
,120513 |
,142888 |
,166502 |
,191153 |
,216642 |
,242777 |
,269379 |
,296280 |
,323324 |
|
4 |
,025742 |
,033769 |
,043095 |
,053725 |
,065642 |
,078813 |
,093189 |
,108708 |
,125298 |
,142877 |
|
5 |
,005435 |
,007746 |
,010663 |
,014253 |
,018576 |
,023682 |
,029615 |
,036407 |
,044081 |
,052653 |
|
6 |
,000968 |
,001500 |
,002231 |
,003201 |
,004456 |
,006040 |
,007999 |
,010378 |
,013219 |
,016564 |
|
7 |
,000149 |
,000251 |
,000404 |
,000622 |
,000926 |
,001336 |
,001875 |
,002569 |
,003446 |
,004534 |
|
8 |
,000020 |
,000037 |
,000064 |
,000107 |
,000170 |
,000260 |
,000388 |
,000552 |
,000793 |
,001097 |
|
9 |
,000002 |
,000005 |
,000009 |
,000016 |
,000028 |
,000045 |
,000072 |
,000110 |
,000163 |
,000237 |
|
10 |
- |
,000001 |
,000001 |
,000002 |
,000004 |
,000007 |
,000012 |
,000019 |
,000030 |
,000045 |
|
11 |
- |
- |
- |
- |
,000001 |
,000001 |
,000002 |
,000003 |
,000005 |
,000008 |
|
12 |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
3,0 |
|
|
0 |
1,00000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,877544 |
,889197 |
,899741 |
,909282 |
,917915 |
,925726 |
,932794 |
,939190 |
,944977 |
,950213 |
|
2 |
,620385 |
,645430 |
,669116 |
,691559 |
,712703 |
,732615 |
,751340 |
,768922 |
,785409 |
,800852 |
|
3 |
,350369 |
,377286 |
,403961 |
,430291 |
,456187 |
,481570 |
,506375 |
,530546 |
,554037 |
,576810 |
|
4 |
,161357 |
,180648 |
,200653 |
,221277 |
,242424 |
,263998 |
,285908 |
,308063 |
,330377 |
,352768 |
|
5 |
,062126 |
,072496 |
,083751 |
,095869 |
,108822 |
,122577 |
,137092 |
,152324 |
,168223 |
,184787 |
|
6 |
,020449 |
,024910 |
,029976 |
,035673 |
,042021 |
,049037 |
,056732 |
,065110 |
,074174 |
,083918 |
|
7 |
,005862 |
,007461 |
,009362 |
,011594 |
,014187 |
,017170 |
,020569 |
,024411 |
,028717 |
,033509 |
|
8 |
,001486 |
,001978 |
,002589 |
,003339 |
,004247 |
,005334 |
,006621 |
,008131 |
,009885 |
,011905 |
|
9 |
,000337 |
,000470 |
,000642 |
,000862 |
,001140 |
,001487 |
,001914 |
,002433 |
,003058 |
,003803 |
|
10 |
,000069 |
,000101 |
,000144 |
,000202 |
,000277 |
,000376 |
,000501 |
,000660 |
,000858 |
,001102 |
|
11 |
,000013 |
,000020 |
,000029 |
,000043 |
,000062 |
,000087 |
,000120 |
,000164 |
,000220 |
,000292 |
|
12 |
,000002 |
,000004 |
,000006 |
,000008 |
,000013 |
,000018 |
,000026 |
,000037 |
,000052 |
,000071 |
|
13 |
- |
,000001 |
,000001 |
,000002 |
,000002 |
,000004 |
,000005 |
,000008 |
,000011 |
,000016 |
|
14 |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
|
15 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
3,1 |
3,2 |
3,3 |
3,4 |
3,5 |
3,6 |
3,7 |
3,8 |
3,9 |
4,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,954951 |
,959238 |
,963117 |
,966627 |
,969803 |
,972676 |
,975276 |
,977629 |
,979758 |
,981684 |
|
2 |
,815298 |
,828799 |
,841402 |
,853158 |
,864112 |
,874311 |
,883799 |
,892620 |
,900815 |
,908422 |
|
3 |
,598837 |
,620096 |
,640574 |
,660260 |
,679153 |
,697253 |
,714567 |
,731103 |
,746875 |
,761897 |
|
4 |
,375160 |
,397480 |
,419662 |
,441643 |
,463367 |
,484784 |
,505847 |
,526515 |
,546753 |
,566530 |
|
5 |
,201811 |
,219387 |
,237410 |
,255818 |
,274555 |
,293562 |
,312781 |
,332156 |
,351635 |
,371163 |
|
6 |
,094334 |
,105408 |
,117123 |
,129458 |
,142386 |
,155881 |
,169912 |
,184444 |
,199442 |
,214870 |
|
7 |
,038804 |
,044619 |
,050966 |
,057853 |
,065288 |
,073273 |
,081809 |
,090892 |
,100517 |
,110674 |
|
8 |
,014213 |
,016830 |
,019777 |
,023074 |
,026739 |
,030789 |
,035241 |
,040107 |
,045402 |
,051134 |
|
9 |
,004683 |
,005714 |
,006912 |
,008293 |
,009874 |
,011671 |
,013703 |
,015984 |
,018533 |
,021363 |
|
10 |
,001401 |
,001762 |
,002195 |
,002709 |
,003315 |
,004024 |
,004848 |
,005799 |
,006890 |
,008132 |
|
11 |
,000383 |
,000497 |
,000638 |
,000810 |
,001019 |
,001271 |
,001572 |
,001929 |
,002349 |
,002840 |
|
12 |
,000097 |
,000129 |
,000171 |
,000223 |
,000289 |
,000370 |
,000470 |
,000592 |
,000739 |
,000915 |
|
13 |
,000023 |
,000031 |
,000042 |
,000057 |
,000076 |
,000100 |
,000130 |
,000168 |
,000216 |
,000274 |
|
14 |
,000005 |
,000007 |
,000010 |
,000014 |
,000019 |
,000025 |
,000034 |
,000045 |
,000059 |
,000076 |
|
15 |
,000001 |
,000001 |
,000002 |
,000003 |
,000004 |
,000006 |
,000008 |
,000011 |
,000015 |
,000020 |
|
16 |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000002 |
,000003 |
,000004 |
,000005 |
|
17 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
4,1 |
4,2 |
4,3 |
4,4 |
4,5 |
4,6 |
4,7 |
4,6 |
4,9 |
5,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,983427 |
,985004 |
,986431 |
,987723 |
,988891 |
,989948 |
,990905 |
,991770 |
,992553 |
,993262 |
|
2 |
,915479 |
,922023 |
,928087 |
,933702 |
,938901 |
,943710 |
,948157 |
,952267 |
,956065 |
,959572 |
|
3 |
,776186 |
,789762 |
,802645 |
,814858 |
,826422 |
,837361 |
,847700 |
,857461 |
,866669 |
,875348 |
|
4 |
,585818 |
,604597 |
,622846 |
,640552 |
,657704 |
,674294 |
,690316 |
,705770 |
,720655 |
,734974 |
|
5 |
,390692 |
,410173 |
,429562 |
,448816 |
,467896 |
,486766 |
,505391 |
,523741 |
,541788 |
,559507 |
|
6 |
,230688 |
,246857 |
,263338 |
,280088 |
,297070 |
,314240 |
,331562 |
,348994 |
,366499 |
,384039 |
|
7 |
,121352 |
,132536 |
,144210 |
,156355 |
,168949 |
,181971 |
,195395 |
,209195 |
,223345 |
,237817 |
|
8 |
,057312 |
,063943 |
,071032 |
,078579 |
,086586 |
,095051 |
,103969 |
,113334 |
,123138 |
,133372 |
|
9 |
,024492 |
,027932 |
,031698 |
,035803 |
,040257 |
,045072 |
,050256 |
,055817 |
,061761 |
,068094 |
|
10 |
,009540 |
,011127 |
,012906 |
,014890 |
,017093 |
,019527 |
,022206 |
,025141 |
,028345 |
,031828 |
|
11 |
,003410 |
,004069 |
,004825 |
,005688 |
,006669 |
,007777 |
,009022 |
,010417 |
,011971 |
,013695 |
|
12 |
,001125 |
,001374 |
,001666 |
,002008 |
,002404 |
,002863 |
,003389 |
,003992 |
,004677 |
,005453 |
|
13 |
,000345 |
,000431 |
,000534 |
,000658 |
,000805 |
,000979 |
,001183 |
,001422 |
,001699 |
,002019 |
|
14 |
,000098 |
,000126 |
,000160 |
,000201 |
,000252 |
,000312 |
,000385 |
,000473 |
,000576 |
,000698 |
|
15 |
,000026 |
,000034 |
,000045 |
,000058 |
,000074 |
,000093 |
,000118 |
,000147 |
,000183 |
,000226 |
|
16 |
,000007 |
,000009 |
,000012 |
000016 |
,000020 |
,000026 |
,000034 |
,000043 |
,000055 |
,000069 |
|
17 |
,000002 |
,000002 |
,000003 |
,000004 |
,000005 |
,000007 |
,000009 |
,000012 |
,000015 |
,000020 |
|
18 |
- |
- |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
,000004 |
,000005 |
|
19 |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
5,1 |
5,2 |
5,3 |
5,4 |
5,5 |
5,6 |
5,7 |
5,8 |
5,9 |
6,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,993903 |
,994483 |
,995008 |
,995483 |
,995913 |
,996302 |
,996654 |
,996972 |
,997261 |
,997521 |
|
2 |
,962810 |
,965797 |
,968553 |
,971094 |
,973436 |
,975594 |
,977582 |
,979413 |
,981098 |
,982649 |
|
3 |
,883522 |
,891213 |
,898446 |
,905242 |
,911624 |
,917612 |
,923227 |
,928489 |
,933418 |
,938031 |
|
4 |
,748732 |
,761935 |
,774590 |
,786709 |
,798301 |
,809378 |
,819952 |
,830037 |
,839647 |
,848796 |
|
5 |
,576875 |
,593872 |
,610482 |
,626689 |
,642482 |
,657850 |
,672785 |
,687282 |
,701335 |
,714943 |
|
6 |
,401580 |
,419087 |
,436527 |
,453868 |
,471081 |
,488139 |
,505015 |
,521685 |
,538127 |
,554320 |
|
7 |
,252580 |
,267607 |
,282866 |
,298329 |
,313964 |
,329742 |
,345634 |
,361609 |
,377639 |
,393697 |
|
8 |
,144023 |
,155078 |
,166523 |
,178341 |
,190515 |
,203025 |
,215851 |
,228974 |
,242371 |
,256020 |
|
9 |
,074818 |
,081935 |
,089446 |
,097350 |
,105643, |
,114322 |
,123382 |
,132814 |
,142611 |
,152763 |
|
10 |
,035601 |
,039674 |
,044056 |
,048755 |
,053777 |
,059130 |
,064817 |
,070844 |
,077212 |
,083924 |
|
11 |
,015601 |
,017699 |
,020000 |
,022514 |
,025251 |
,028222 |
,031436 |
,034901 |
,038627 |
,042621 |
|
12 |
,006328 |
,007310 |
,008409 |
,009632 |
,010988 |
,012487 |
,014138 |
,015950 |
,017931 |
,020092 |
|
13 |
,002387 |
,002809 |
,003289 |
,003835 |
,004451 |
,005144 |
,005922 |
,006790 |
,007756 |
,008827 |
|
14 |
,000841 |
,001008 |
,001202 |
,001427 |
,001685 |
,001981 |
,002319 |
,002703 |
,003138 |
,003628 |
|
15 |
,000278 |
,000339 |
,000412 |
,000498 |
,000599 |
,000716 |
,000852 |
,001010 |
,001192 |
,001400 |
|
16 |
,000086 |
,000108 |
,000133 |
,000164 |
,000200 |
,000244 |
,000295 |
,000356 |
,000426 |
,000509 |
|
17 |
,000025 |
,000032 |
,000041 |
,000051 |
,000063 |
,000078 |
,000096 |
,000118 |
,000144 |
,000175 |
|
18 |
,000007 |
,000009 |
,000012 |
,000015 |
,000019 |
,000024 |
,000030 |
,000037 |
,000046 |
,000057 |
|
19 |
,000002 |
,000002 |
,000003 |
,000004 |
,000005 |
,000007 |
,000009 |
,000011 |
,000014 |
,000018 |
|
20 |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
,000004 |
,000005 |
|
21 |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
6,7 |
6,8 |
6,9 |
7,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,997757 |
,997971 |
,998164 |
,998338 |
,998497 |
,998640 |
,998769 |
,998886 |
,998992 |
,999088 |
|
2 |
,984076 |
,985388 |
,986595 |
,987704 |
,988724 |
,989661 |
,990522 |
,991313 |
,992038 |
,992705 |
|
3 |
,942347 |
,946382 |
,950154 |
,953676 |
,956964 |
,960032 |
,962894 |
,965562 |
,968048 |
,970364 |
|
4 |
,857499 |
,865771 |
,873626 |
,881081 |
,888150 |
,894849 |
,901192 |
,907194 |
,912870 |
,918235 |
|
5 |
,728106 |
,740823 |
,753096 |
,764930 |
,776328 |
,787296 |
,797841 |
,807969 |
,817689 |
,827008 |
|
6 |
,570246 |
,585887 |
,601228 |
,616256 |
,630959 |
,645327 |
,659351 |
,673023 |
,686338 |
,699292 |
|
7 |
,409755 |
,425787 |
,441767 |
,457671 |
,473476 |
,489161 |
,504703 |
,520084 |
,535285 |
,550289 |
|
8 |
,269899 |
,283984 |
,298252 |
,312679 |
,327242 |
,341918 |
,356683 |
,371514 |
,386389 |
,401286 |
|
9 |
,163258 |
,174086 |
,185233 |
,196685 |
,208427 |
,220443 |
,232716 |
,245230 |
,257967 |
,270909 |
|
10 |
,090980 |
,098379 |
,106121 |
,114201 |
,122616 |
,131361 |
,140430 |
,149816 |
,150510 |
,169504 |
|
11 |
,046890 |
,051441 |
,056280 |
,061411 |
,066839 |
,072567 |
,078598 |
,084934 |
,091575 |
,098521 |
|
12 |
,022440 |
,024985 |
,027734 |
,030697 |
,033880 |
,037291 |
,040937 |
,044825 |
,048961 |
,053350 |
|
13 |
,010012 |
,011316 |
,012748 |
,014316 |
,016027 |
,017889 |
,019910 |
,022097 |
,024158 |
,027000 |
|
14 |
,004180 |
,004797 |
,005485 |
,006251 |
,007100 |
,008038 |
,009072 |
,010208 |
,011452 |
,012811 |
|
15 |
,001639 |
,001910 |
,002217 |
,002565 |
,002956 |
,003395 |
,003886 |
,004434 |
,005042 |
,005717 |
|
16 |
,000605 |
,000716 |
,000844 |
,000992 |
,001160 |
,001352 |
,001569 |
,001816 |
,002094 |
,002407 |
|
17 |
,000211 |
,000254 |
,000304 |
,000362 |
,000430 |
,000509 |
,000599 |
,000703 |
,000822 |
,000958 |
|
18 |
,000070 |
,000085 |
,000104 |
,000126 |
,000151 |
,000182 |
,000217 |
,000258 |
,000306 |
,000362 |
|
19 |
,000022 |
,000027 |
,000034 |
,000041 |
,000051 |
,000062 |
,000075 |
,000090 |
,000108 |
,000130 |
|
20 |
,000007 |
,000008 |
,000010 |
,000013 |
,000016 |
,000020 |
,000024 |
,000030 |
,000037 |
,000044 |
|
21 |
,000002 |
,000002 |
,000003 |
,000004 |
,000005 |
,000006 |
,000008 |
,000010 |
,000012 |
,000014 |
|
22 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
,000004 |
,000005 |
|
23 |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
7,1 |
7,2 |
7,3 |
7,4 |
7,5 |
7,6 |
7,7 |
7,8 |
7,9 |
8,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,999175 |
,999253 |
,999324 |
,999389 |
,999447 |
,999500 |
,999547 |
,999590 |
,999629 |
,999665 |
|
2 |
,993317 |
,993878 |
,994393 |
,994865 |
,995299 |
,995696 |
,996060 |
,996394 |
,996700 |
,996981 |
|
3 |
,972520 |
,974526 |
,976393 |
,978129 |
,979743 |
,981243 |
,982636 |
,983930 |
,985131 |
,986246 |
|
4 |
,923301 |
,928083 |
,932594 |
,936847 |
,940855 |
,944629 |
,948181 |
,951523 |
,954666 |
,957620 |
|
5 |
,835937 |
,844484 |
,852660 |
,860475 |
,867938 |
,875061 |
,881855 |
,888330 |
,894497 |
,900368 |
|
6 |
,711881 |
,724103 |
,735957 |
3747443 |
,758564 |
,769319 |
,779713 |
,789749 |
,799431 |
,808764 |
|
7 |
,565080 |
,579644 |
,593968 |
,608038 |
,621845 |
,635379 |
,648631 |
,661593 |
,674260 |
,686626 |
|
8 |
,416183 |
,431059 |
,445893 |
,460667 |
,475361 |
,489958 |
,504440 |
,518791 |
,532996 |
,547039 |
|
9 |
,284036 |
,297332 |
,310776 |
,324349 |
,338033 |
,351808 |
,365657 |
,379559 |
,393497 |
,407453 |
|
10 |
,179788 |
,190350 |
,201180 |
,212265 |
,223592 |
,235149 |
,246920 |
,258891 |
,271048 |
,283376 |
|
11 |
,105771 |
,113323 |
,121175 |
,129323 |
,137762 |
,146487 |
,155492 |
,164770 |
,174314 |
,184114 |
|
12 |
,057997 |
,062906 |
,068081 |
,073526 |
,079241 |
,085230 |
,091493 |
,098030 |
,104841 |
,111924 |
|
13 |
,029730 |
,032655 |
,035782 |
,039117 |
,042666 |
,046484 |
,050427 |
,054649 |
,059104 |
,063797 |
|
14 |
,014292 |
,015901 |
,017645 |
,019531 |
,021565 |
,023753 |
,026103 |
,028620 |
,031311 |
,034181 |
|
15 |
,006163 |
,007285 |
,008188 |
,009178 |
,010260 |
,011441 |
,012725 |
,014118 |
,015627 |
,017257 |
|
16 |
,002757 |
,003149 |
,003586 |
,004071 |
,004608 |
,005202 |
,005857 |
,006577 |
,007367 |
,008231 |
|
17 |
,001113 |
,001288 |
,001486 |
,001709 |
,001959 |
,002339 |
,002552 |
,002901 |
,003289 |
,003718 |
|
18 |
,000426 |
,000500 |
,000584 |
,000680 |
,000790 |
,000915 |
,001055 |
,001215 |
,001393 |
,001594 |
|
19 |
,000155 |
,000184 |
,000218 |
,000258 |
,000303 |
,000355 |
,000415 |
,000484 |
,000562 |
,000650 |
|
20 |
,000054 |
,000065 |
,000078 |
,000093 |
,000111 |
,000132 |
,000156 |
,000184 |
,000216 |
,000253 |
|
21 |
,000018 |
,000022 |
,000026 |
,000032 |
,000039 |
,000046 |
,000056 |
,000067 |
,000079 |
,000094 |
|
22 |
,000006 |
,000007 |
,000009 |
,000011 |
,000013 |
,000016 |
,000019 |
,000023 |
,000028 |
,000033 |
|
23 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000005 |
,000006 |
,000008 |
,000009 |
,000011 |
|
24 |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000004 |
|
25 |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
8,1 |
8,2 |
8,3 |
8,4 |
8,5 |
8,6 |
8,7 |
8,8 |
8,9 |
9,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,999696 |
,999725 |
,999754 |
,999775 |
,999797 |
,999816 |
,999833 |
,999849 |
,999864 |
,999877 |
|
2 |
,997238 |
,997437 |
,997689 |
,997886 |
,998067 |
,998233 |
,998384 |
,998523 |
,998650 |
,998766 |
|
3 |
,987280 |
,988239 |
,989129 |
,989953 |
,990717 |
,991424 |
,992080 |
,992686 |
,993248 |
,993768 |
|
4 |
,960395 |
,963000 |
,965446 |
,967740 |
,969891 |
,971907 |
,973797 |
,975566 |
,977223 |
,978774 |
|
5 |
,905951 |
,911260 |
,916303 |
,921092 |
,925636 |
,929946 |
,934032 |
,937902 |
,941567 |
,945036 |
|
6 |
,817753 |
,826406 |
,834727 |
,842723 |
,850403 |
,857772 |
,864840 |
,871613 |
,878100 |
,884309 |
|
7 |
,698686 |
,710438 |
,721879 |
,733007 |
,743822 |
,754324 |
,764512 |
,774390 |
,783958 |
,793219 |
|
8 |
,560908 |
,574591 |
,588074 |
,601348 |
,614403 |
,627229 |
,639819 |
,652166 |
,664262 |
,676103 |
|
9 |
,421408 |
,435347 |
,449252 |
,463106 |
,476895 |
,490603 |
,504216 |
,517719 |
,531101 |
,544347 |
|
10 |
,295858 |
,308481 |
,321226 |
,334080 |
,347026 |
,360049 |
,373132 |
,386260 |
,399419 |
,412592 |
|
11 |
,194163 |
,204450 |
,214965 |
,225699 |
,236638 |
,247772 |
,259089 |
,270577 |
,282222 |
,294012 |
|
12 |
,119278 |
,126900 |
,134787 |
,142934 |
,151338 |
,159992 |
,168892 |
,178030 |
,187399 |
,196992 |
|
13 |
,068731 |
,073907 |
,079330 |
,084999 |
,090917 |
,097081 |
,103499 |
,110162 |
,117072 |
,124227 |
|
14 |
,037236 |
,040481 |
,043923 |
,047564 |
,051411 |
,055467 |
,059736 |
,064221 |
,068925 |
,073851 |
|
15 |
,019014 |
,020903 |
,022931 |
,025103 |
,027425 |
,029902 |
,032540 |
,035343 |
,038317 |
,041466 |
|
16 |
,009174 |
,010201 |
,011316 |
,012525 |
,013833 |
,015245 |
,016767 |
,018402 |
,020157 |
,022036 |
|
17 |
,004192 |
,004715 |
,005291 |
,005922 |
,006613 |
,007367 |
,008190 |
,009084 |
,010055 |
,011106 |
|
18 |
,001819 |
,002070 |
,002349 |
,002659 |
,003002 |
,003382 |
,003800 |
,004261 |
,004766 |
,005320 |
|
19 |
,000751 |
,000864 |
,000992 |
,001136 |
,001297 |
,001478 |
,001679 |
,001903 |
,002151 |
,002426 |
|
20 |
,000296 |
,000344 |
,000400 |
,000463 |
,000535 |
,000616 |
,000707 |
,000811 |
,000926 |
,001056 |
|
21 |
,000111 |
,000131 |
,000154 |
,000180 |
,000211 |
,000245 |
,000285 |
,000330 |
,000381 |
,000439 |
|
22 |
,000040 |
,000048 |
,000057 |
,000067 |
,000079 |
,000094 |
,000110 |
,000129 |
,000150 |
,000175 |
|
23 |
,000014 |
,000017 |
,000020 |
,000024 |
,000029 |
,000034 |
,000041 |
,000048 |
,000057 |
,000067 |
|
24 |
,000005 |
,000006 |
,000007 |
,000008 |
,000010 |
,000012 |
,000014 |
,000017 |
,000021 |
,000025 |
|
25 |
,000001 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000005 |
,000006 |
,000007 |
,000009 |
|
26 |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
|
27 |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
9,1 |
9,2 |
9,3 |
9,4 |
9,5 |
9,6 |
9,7 |
9,8 |
9,9 |
10,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,999888 |
,999899 |
,999909 |
,999917 |
,999925 |
,999932 |
,999939 |
,999945 |
,999950 |
,999955 |
|
2 |
,998872 |
,998969 |
,999058 |
,999140 |
,999214 |
,999282 |
,999344 |
,999401 |
,999453 |
,999501 |
|
3 |
,994249 |
,994693 |
,995105 |
,995485 |
,995836 |
,996161 |
,996461 |
,996738 |
,996994 |
,997231 |
|
4 |
,980224 |
,981580 |
,982848 |
,984033 |
,985140 |
,986174 |
,987139 |
,988040 |
,988880 |
,989664 |
|
5 |
,948318 |
,951420 |
954353 |
,957122 |
,959737 |
,962205 |
,964533 |
,966729 |
,968798 |
,970747 |
|
6 |
,890249 |
,895926 |
,901350 |
,906529 |
,911472 |
,916185 |
,920678 |
,924959 |
,929035 |
,932914 |
|
7 |
,802177 |
,810635 |
,819197 |
,827267 |
,835051 |
,842553 |
,849779 |
,856735 |
,863426 |
,869859 |
|
8 |
,687684 |
,699000 |
,710050 |
,720829 |
,713337 |
,741572 |
,751533 |
,761221 |
,770636 |
,779779 |
|
9 |
,557448 |
,570391 |
,583166 |
,595765 |
,608177 |
,620394 |
,632410 |
,641217 |
,655809 |
,667180 |
|
10 |
,425765 |
,438924 |
,452054 |
,465142 |
,478174 |
,491138 |
,504021 |
,516812 |
,529498 |
,542070 |
|
11 |
,305933 |
,317974 |
,330119 |
,342356 |
,354672 |
,367052 |
,379484 |
,391955 |
,404451 |
,416960 |
|
12 |
,206800 |
,216815 |
,227029 |
,237430 |
,248010 |
,258759 |
,269665 |
,280719 |
,291909 |
,303224 |
|
13 |
,131624 |
,139261 |
,147133 |
,155238 |
,163570 |
,172124 |
,180895 |
,189876 |
,199062 |
,208444 |
|
14 |
,079001 |
,084376 |
,089978 |
,095807 |
,101864 |
,108148 |
,114659 |
,121395 |
,128355 |
,135536 |
|
15 |
,044795 |
,048309 |
,052010 |
,055903 |
,059992 |
,064279 |
,068767 |
,073458 |
,078355 |
,083458 |
|
16 |
,024044 |
,026188 |
,028470 |
,030897 |
,033473 |
,036202 |
,039090 |
,042139 |
,045355 |
,048740 |
|
17 |
,012242 |
,013468 |
,014788 |
,016206 |
,017727 |
,019357 |
,021098 |
,022956 |
,024936 |
,027042 |
|
18 |
,005924 |
,006584 |
,007302 |
,008083 |
,08928 |
,009844 |
,010832 |
,011898 |
,013045 |
,014278 |
|
19 |
,002731 |
,003066 |
,003435 |
,003840 |
,004284 |
,004770 |
,005300 |
,005877 |
,006505 |
,007187 |
|
20 |
,001201 |
,001362 |
,001542 |
,001742 |
,001962 |
,002207 |
,002476 |
,002772 |
,003098 |
,003454 |
|
21 |
,000505 |
,000579 |
,000662 |
,000755 |
,000859 |
,000976 |
,001106 |
,001250 |
,001411 |
,001588 |
|
22 |
,000203 |
,000235 |
,000272 |
,000314 |
,000361 |
,000411 |
,000473 |
,000540 |
,000616 |
,000700 |
|
23 |
,000078 |
,000092 |
,000107 |
,000125 |
,000145 |
,000168 |
,000194 |
,000224 |
,000258 |
,000296 |
|
24 |
,000029 |
,000034 |
,000041 |
,000048 |
,000056 |
,000066 |
,000077 |
,000089 |
,000104 |
,000120 |
|
25 |
,000010 |
,000012 |
,000015 |
,000018 |
,000021 |
,000025 |
,000029 |
,000034 |
,000040 |
,000047 |
|
26 |
,000004 |
,000004 |
,000005 |
,000006 |
,000007 |
,000009 |
,000011 |
,000013 |
,000015 |
,000018 |
|
27 |
,000001 |
,000001 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000004 |
,000005 |
,000006 |
|
28 |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
|
29 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
10,1 |
10,2 |
10,3 |
10,4 |
10,5 |
10,6 |
10,7 |
10,8 |
10,9 |
11,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1000000 |
1,000000 |
|
1 |
,999959 |
,999963 |
,999966 |
,999970 |
,999972 |
,999975 |
,999977 |
,999980 |
,999982 |
,999983 |
|
2 |
,999544 |
,999584 |
,999620 |
,999653 |
,999683 |
,999711 |
,999736 |
,999759 |
,999780 |
,999800 |
|
3 |
,997449 |
,997650 |
,997836 |
,998007 |
,998165 |
,998311 |
,998446 |
,998570 |
,998684 |
,998789 |
|
4 |
,990395 |
,991076 |
,991711 |
,992302 |
,992853 |
,993365 |
,993843 |
,994287 |
,994700 |
,995084 |
|
5 |
,972583 |
,974312 |
,975938 |
,977468 |
,978906 |
,980259 |
,981529 |
,982723 |
,983843 |
,984895 |
|
6 |
,936604 |
,940112 |
,943446 |
,946613 |
,949620 |
,952473 |
,955179 |
,957745 |
,960177 |
,962480 |
|
7 |
,876039 |
,881974 |
,887669 |
,893131 |
,898367 |
,903384 |
,908187 |
,912784 |
,917182 |
,921386 |
|
8 |
,788652 |
,797257 |
,805597 |
,813673 |
,821489 |
,829050 |
,836358 |
,843417 |
,850233 |
,856808 |
|
9 |
,678327 |
,689244 |
,699928 |
,710377 |
,720587 |
,730557 |
,740285 |
,749771 |
,759014 |
,768015 |
|
10 |
,554517 |
,566829 |
,578997 |
,591013 |
,602867 |
,614554 |
,626066 |
,637396 |
,648539 |
,659489 |
|
11 |
,429469 |
,441966 |
,454438 |
,466874 |
,479262 |
,491591 |
,503851 |
,516031 |
,528121 |
,540111 |
|
12 |
,314652 |
,326183 |
,337805 |
,349506 |
,361275 |
,373100 |
,384969 |
,396872 |
,408797 |
,420733 |
|
13 |
,218015 |
,227768 |
,237695 |
,247787 |
,258036 |
,268432 |
,278966 |
,289630 |
,300412 |
,311303 |
|
14 |
,142935 |
,150550 |
,158378 |
,166413 |
,174651 |
,183088 |
,191718 |
,200536 |
,209535 |
,218709 |
|
15 |
,088770 |
,094292 |
,100022 |
,105963 |
,112112 |
,118470 |
,125035 |
,131806 |
,138780 |
,145956 |
|
16 |
,052300 |
,056036 |
,059952 |
,064051 |
,068335 |
,072807 |
,077468 |
,082321 |
,087366 |
,092604 |
|
17 |
,029277 |
,031647 |
,034156 |
,036808 |
,039606 |
,042555 |
,045658 |
,048918 |
,052339 |
,055924 |
|
18 |
,015599 |
,017015 |
,018527 |
,020142 |
,021862 |
,023692 |
,025636 |
,027698 |
,029881 |
,032191 |
|
19 |
,007925 |
,008723 |
,009584 |
,010512 |
,011511 |
,012584 |
,013731 |
,014965 |
,016282 |
,017687 |
|
20 |
,003845 |
,004271 |
,004736 |
,005242 |
,005791 |
,006387 |
,007031 |
,007728 |
,008480 |
,009289 |
|
21 |
,001784 |
,002001 |
,002239 |
,002501 |
,002788 |
,003102 |
,003445 |
,003820 |
,004228 |
,004671 |
|
22 |
,000794 |
,000898 |
,001014 |
,001143 |
,001286 |
,001444 |
,001618 |
,001810 |
,002021 |
,002252 |
|
23 |
,000339 |
,000387 |
,000441 |
,000502 |
,000570 |
,000645 |
,000730 |
,000823 |
,000927 |
,001042 |
|
24 |
,000139 |
,000160 |
,000184 |
,000212 |
,000242 |
,000277 |
,000316 |
,000360 |
,000409 |
,000464 |
|
25 |
,000055 |
,000064 |
,000074 |
,000086 |
,000099 |
,000115 |
,000132 |
,000152 |
,000174 |
,000199 |
|
26 |
,000021 |
,000024 |
,000029 |
,000034 |
,000039 |
,000046 |
,000053 |
,000061 |
,000071 |
,000082 |
|
27 |
,000008 |
,000009 |
,000011 |
,000013 |
,000015 |
,000018 |
,000021 |
,000024 |
,000028 |
,000033 |
|
28 |
,000003 |
,000003 |
,000004 |
,000005 |
,000005 |
,000007 |
,000008 |
,000009 |
,000011 |
,000013 |
|
29 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000005 |
|
30 |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
|
31 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
11,1 |
11,2 |
11,3 |
11,4 |
11,5 |
11,6 |
11,7 |
11,8 |
11,9 |
12,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,999985 |
,999986 |
,999988 |
,999989 |
,999990 |
,999991 |
,999992 |
,999992 |
,999993 |
,999994 |
|
2 |
,999817 |
,999833 |
,999848 |
,999861 |
,999873 |
,999885 |
,999895 |
,999904 |
,999912 |
,999920 |
|
3 |
,999886 |
,998976 |
,999058 |
,999134 |
,999203 |
,999268 |
,999327 |
,999381 |
,999432 |
,999478 |
|
4 |
,995441 |
,995774 |
,996082 |
,996369 |
,996636 |
,996883 |
,997113 |
,997326 |
,997524 |
,997708 |
|
5 |
,985882 |
,986808 |
,987677 |
,988491 |
,989253 |
,989968 |
,990637 |
,991264 |
,991851 |
,992400 |
|
6 |
,964661 |
,966726 |
,968680 |
,970527 |
,972274 |
,973925 |
,975484 |
,976957 |
,978347 |
,979659 |
|
7 |
,925403 |
,929239 |
,932902 |
,936397 |
,939730 |
,942908 |
,945936 |
,948819 |
,951565 |
,954178 |
|
8 |
,863150 |
,869261 |
,875147 |
,880814 |
,886265 |
,891508 |
,896547 |
,901388 |
,906035 |
,910496 |
|
9 |
,776773 |
,785290 |
,793568 |
,801607 |
,809410 |
,816979 |
,824317 |
,831426 |
,838310 |
,844972 |
|
10 |
,670243 |
,680794 |
,691141 |
,701279 |
,711205 |
,720919 |
,730417 |
,739698 |
,748762 |
,757608 |
|
11 |
,551993 |
,563758 |
,575398 |
,586904 |
,598270 |
,609489 |
,620554 |
,631460 |
,642200 |
,652771 |
|
12 |
,432669 |
,444595 |
,456499 |
,468371 |
,480202 |
,491982 |
,503700 |
,515349 |
,526920 |
,538403 |
|
13 |
,322294 |
,333375 |
,344535 |
,355764 |
,367053 |
,378391 |
,389768 |
,401174 |
,412600 |
,424035 |
|
14 |
,228051 |
,237555 |
,247213 |
,257017 |
,266960 |
,277033 |
,287228 |
,296538 |
,307953 |
,318464 |
|
15 |
,153330 |
,160899 |
,168660 |
,176608 |
,184740 |
,193051 |
,201535 |
,210188 |
,219003 |
,227975 |
|
16 |
,098036 |
,103663 |
,109483 |
,115498 |
,121705 |
,128104 |
,134694 |
,141472 |
,148436 |
,155584 |
|
17 |
,059676 |
,063597 |
,067690 |
,071957 |
,076399 |
,081018 |
,085816 |
,090794 |
,095952 |
,101291 |
|
18 |
,034629 |
,037201 |
,039910 |
,042758 |
,045750 |
,048889 |
,052177 |
,055618 |
,059213 |
,062966 |
|
19 |
,019104 |
,020777 |
,022470 |
,024266 |
,026169 |
,028183 |
,030312 |
,032558 |
,034925 |
,037417 |
|
20 |
,010160 |
,011095 |
,012098 |
,013171 |
,014318 |
,015542 |
,016847 |
,018236 |
,019713 |
,021280 |
|
21 |
,005152 |
,005673 |
,006237 |
,006846 |
,007503 |
,008210 |
,008970 |
,009786 |
,010661 |
,011598 |
|
22 |
,002505 |
,002782 |
,003084 |
,003413 |
,003771 |
,004160 |
,004582 |
,005039 |
,005532 |
,006065 |
|
23 |
,001170 |
,001310 |
,001464 |
,001634 |
,001821 |
,002025 |
,002248 |
,002492 |
,002758 |
,003047 |
|
24 |
,000525 |
,000593 |
,000669 |
,000752 |
,000845 |
,000948 |
,001061 |
,001185 |
,001322 |
,001473 |
|
25 |
,000227 |
,000258 |
,000294 |
,000334 |
,000378 |
,000427 |
,000482 |
,000543 |
,000611 |
,000686 |
|
26 |
,000094 |
,000109 |
,000125 |
,000143 |
,000163 |
,000186 |
,000211 |
,000240 |
,000272 |
,000308 |
|
27 |
,000038 |
,000044 |
,000051 |
,000059 |
,000068 |
,000078 |
,000089 |
,000102 |
,000117 |
,000133 |
|
28 |
,000015 |
,000017 |
,000020 |
,000023 |
,000027 |
,000032 |
,000032 |
,000042 |
,000049 |
,000056 |
|
29 |
,000006 |
,000007 |
,000008 |
,000009 |
,000011 |
,000012 |
,000014 |
,000017 |
,000020 |
,000023 |
|
30 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000005 |
,000006 |
,000006 |
,000008 |
,000009 |
|
31 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
|
32 |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
12,1 |
12,2 |
12,3 |
12,4 |
12,5 |
12,6 |
12,7 |
12,8 |
12,9 |
13,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,999994 |
,999995 |
,999995 |
,999996 |
,999996 |
,999997 |
,999997 |
,999997 |
,999997 |
,999998 |
|
2 |
,999927 |
,999934 |
,999939 |
,999945 |
,999950 |
,999954 |
,999958 |
,999962 |
,999965 |
,999968 |
|
3 |
,999520 |
,999559 |
,999595 |
,999628 |
,999659 |
,999686 |
,999712 |
,999736 |
,999757 |
,999777 |
|
4 |
,997879 |
,998037 |
,998183 |
,998319 |
,998445 |
,998562 |
,998670 |
,998771 |
,998864 |
,998950 |
|
5 |
,992913 |
,993393 |
,993842 |
,994262 |
,994655 |
,995021 |
,995363 |
,995683 |
,995981 |
,996260 |
|
6 |
,980897 |
,982064 |
,983164 |
,984200 |
,985177 |
,986097 |
,986963 |
,987778 |
,988545 |
,989266 |
|
7 |
,956663 |
,959026 |
,961272 |
,963406 |
,965433 |
,967356 |
,969182 |
,970914 |
,972556 |
,974113 |
|
8 |
,914774 |
,918875 |
,922806 |
,926570 |
,930175 |
,933624 |
,936923 |
,940077 |
,943092 |
,945972 |
|
9 |
,851416 |
,857645 |
,863663 |
,869475 |
,875084 |
,880494 |
,885711 |
,890738 |
,895580 |
,900242 |
|
10 |
,766235 |
,774644 |
,782835 |
,790810 |
,798569 |
,806114 |
,813446 |
,820567 |
,827481 |
,834188 |
|
11 |
,663166 |
,673383 |
,683417 |
,693266 |
,702925 |
,712394 |
,721669 |
,730749 |
,739632 |
,748318 |
|
12 |
,549790 |
,561075 |
,572250 |
,583307 |
,594239 |
,605042 |
,615708 |
,626232 |
,636609 |
,646835 |
|
13 |
,435470 |
,446896 |
,458303 |
,469682 |
,481025 |
,492322 |
,503566 |
,514748 |
,525860 |
,536895 |
|
14 |
,329064 |
,339743 |
,350492 |
,361302 |
,372165 |
,383071 |
,394012 |
,404979 |
,415963 |
,426955 |
|
15 |
,237099 |
,246366 |
,255772 |
,265308 |
,274968 |
,284745 |
,294631 |
,304619 |
,314700 |
,324868 |
|
16 |
,162913 |
,170420 |
,178101 |
,185953 |
,193971 |
,202151 |
,210488 |
,218978 |
,227615 |
,236393 |
|
17 |
,106811 |
,112511 |
,118392 |
,124453 |
,130692 |
,137108 |
,143700 |
,150465 |
,157402 |
,164507 |
|
18 |
,066879 |
,070953 |
,075191 |
,079594 |
,084163 |
,088900 |
,093805 |
,098879 |
,104122 |
,109535 |
|
19 |
,040036 |
,042786 |
,045670 |
,048691 |
,051852 |
,055154 |
,058602 |
,062196 |
,065939 |
,069833 |
|
20 |
,022941 |
,024700 |
,026559 |
,028523 |
,030694 |
,032776 |
,035071 |
,037483 |
,040014 |
,042669 |
|
21 |
,012599 |
,013667 |
,014806 |
,016019 |
,017308 |
,018677 |
,020129 |
,021667 |
,023293 |
,025012 |
|
22 |
,006640 |
,007258 |
,007922 |
,008635 |
,009400 |
,010218 |
,011093 |
,012026 |
,013021 |
,014081 |
|
23 |
,003362 |
,003703 |
,004073 |
,004474 |
,004906 |
,005373 |
,005876 |
,006417 |
,006999 |
,007622 |
|
24 |
,001638 |
,001818 |
,002015 |
,002230 |
,002464 |
,002719 |
,002996 |
,003290 |
,003620 |
,003972 |
|
25 |
,000768 |
,000860 |
,000960 |
,001071 |
,001192 |
,001326 |
,001471 |
,001631 |
,001805 |
,001994 |
|
26 |
,000348 |
,000392 |
,000441 |
,000496 |
,000557 |
,000623 |
,000697 |
,000778 |
,000868 |
,000966 |
|
27 |
,000152 |
,000173 |
,000196 |
,000222 |
,000251 |
,000283 |
,000319 |
,000359 |
,000403 |
,000452 |
|
28 |
,000064 |
,000073 |
,000084 |
,000096 |
,000109 |
,000124 |
,000141 |
,000160 |
,000181 |
,000204 |
|
29 |
,000026 |
,000030 |
,000035 |
,000040 |
,000046 |
,000053 |
,000060 |
,000069 |
,000079 |
,000089 |
|
30 |
,000010 |
,000012 |
,000014 |
,000016 |
,000019 |
,000022 |
,000025 |
,000029 |
,000033 |
,000038 |
|
31 |
,000004 |
,000005 |
,000005 |
,000006 |
,000007 |
,000009 |
,000010 |
,000012 |
,000013 |
,000016 |
|
32 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000005 |
,000005 |
,000006 |
|
33 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
|
34 |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
13,1 |
13,2 |
13,3 |
13,4 |
13,5 |
13,6 |
13,7 |
13,8 |
13,9 |
14,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
1 |
,999998 |
,999998 |
,999998 |
,999999 |
,999999 |
,999999 |
,999999 |
,999999 |
,999999 |
,999999 |
|
2 |
,999971 |
,999974 |
,999976 |
,999978 |
,999980 |
,999982 |
,999983 |
,999985 |
,999986 |
,999988 |
|
3 |
,999796 |
,999812 |
,999828 |
,999842 |
,999855 |
,999867 |
,999878 |
,999888 |
,999898 |
,999906 |
|
4 |
,999029 |
,999103 |
,999171 |
,999235 |
,999293 |
,999347 |
,999397 |
,999446 |
,999486 |
,999526 |
|
5 |
,996520 |
,996762 |
,996988 |
,997144 |
,997396 |
,997579 |
,997750 |
,997909 |
,998057 |
,998195 |
|
6 |
,989944 |
,990582 |
,991181 |
,991744 |
,992273 |
,992769 |
,993235 |
,993673 |
,994083 |
,994468 |
|
7 |
,975588 |
,976986 |
,978309 |
,979561 |
,980746 |
,981868 |
,982928 |
,983930 |
,984877 |
,985772 |
|
8 |
,948722 |
,951347 |
,953851 |
,956240 |
,958517 |
,960687 |
,962754 |
,964723 |
,966597 |
,968380 |
|
9 |
,904728 |
,909042 |
,913190 |
,917176 |
,921005 |
,924680 |
,928207 |
,931591 |
,934835 |
,937945 |
|
10 |
,840692 |
,846996 |
,853103 |
,859015 |
,864736 |
,870270 |
,875619 |
,880788 |
,885781 |
,890601 |
|
11 |
,756806 |
,765095 |
,773186 |
,781079 |
,788774 |
,796271 |
,803574 |
,810681 |
,817596 |
,824319 |
|
12 |
,656905 |
,666814 |
,676560 |
,686138 |
,695547 |
,704783 |
,713844 |
,722728 |
,731434 |
,739960 |
|
13 |
,547846 |
,558705 |
,569465 |
,580122 |
,590667 |
,601096 |
,611402 |
,621582 |
,631630 |
,641542 |
|
14 |
,437948 |
,448932 |
,459900 |
,470843 |
,481753 |
,492623 |
,503445 |
,514212 |
,524917 |
,535552 |
|
15 |
,335115 |
,345432 |
,355812 |
,366247 |
,376729 |
,387249 |
,397801 |
,408376 |
,418966 |
,429563 |
|
16 |
,245308 |
,254353 |
,263522 |
,272809 |
,282207 |
,291711 |
,301313 |
,311006 |
,320784 |
,330640 |
|
17 |
,171778 |
,179212 |
,186805 |
,194554 |
,202455 |
,210503 |
,218695 |
,227025 |
,235489 |
,244082 |
|
18 |
,115117 |
,120867 |
,126785 |
,132871 |
,139122 |
,145537 |
,152114 |
,158852 |
,165748 |
,172799 |
|
19 |
,073880 |
,078081 |
,082438 |
,086951 |
,091622 |
,096451 |
,101439 |
,106586 |
,111892 |
,117357 |
|
20 |
,045448 |
,048356 |
,051394 |
,054565 |
,057872 |
,061316 |
,064900 |
,068624 |
,072492 |
,076505 |
|
21 |
,026826 |
,028737 |
,030750 |
,032867 |
,035091 |
,037424 |
,039870 |
,042431 |
,045110 |
,047908 |
|
22 |
,015208 |
,016406 |
,017676 |
,019022 |
,020446 |
,021951 |
,023541 |
,025218 |
,026985 |
,028844 |
|
23 |
,008291 |
,009007 |
,009772 |
,010588 |
,011459 |
,012386 |
,013373 |
,014421 |
,015533 |
,016712 |
|
24 |
,004351 |
,004760 |
,005201 |
,005675 |
,006184 |
,006731 |
,007316 |
,007943 |
,008613 |
,009328 |
|
25 |
,002201 |
,002425 |
,002668 |
,002932 |
,003217 |
,003526 |
,003859 |
,004218 |
,004604 |
,005020 |
|
26 |
,001074 |
,001192 |
,001321 |
,001461 |
,001615 |
,001782 |
,001964 |
,002161 |
,002376 |
,002608 |
|
27 |
,000506 |
,000566 |
,000631 |
,000704 |
,000783 |
,000870 |
,000966 |
,001070 |
,001184 |
,001309 |
|
28 |
,000230 |
,000260 |
,000292 |
,000328 |
,000367 |
,000411 |
,000459 |
,000512 |
,000571 |
,000635 |
|
29 |
,000102 |
,000115 |
,000131 |
,000148 |
,000167 |
,000188 |
,000211 |
,000237 |
,000266 |
,000298 |
|
30 |
,000043 |
,000050 |
,000057 |
,000064 |
,000073 |
,000083 |
,000094 |
,000107 |
,000120 |
,000136 |
|
31 |
,000018 |
,000021 |
,000024 |
,000027 |
,000031 |
,000036 |
,000041 |
,000046 |
,000053 |
,000060 |
|
32 |
,000007 |
,000008 |
,000010 |
,000011 |
,000013 |
,000015 |
,000017 |
,000020 |
,000022 |
,000026 |
|
33 |
,000003 |
,000003 |
,000004 |
,000004 |
,000005 |
,000006 |
,000007 |
,000008 |
,000009 |
,000011 |
|
34 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000004 |
|
35 |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
|
36 |
- |
- |
- |
- |
- |
- |
- |
- |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||||
|
14,1 |
14,2 |
14,3 |
14,4 |
14,5 |
14,6 |
14,7 |
14,8 |
14,9 |
15,0 |
|
|
0 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
|
|
|
|
|
|
1 |
,999999 |
,999999 |
999999 |
,999999 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
1,000000 |
|
2 |
,999989 |
,999990 |
,999991 |
,999991 |
,999992 |
,999993 |
,999993 |
,999994 |
,999995 |
,999995 |
|
3 |
,999914 |
,999921 |
,999928 |
,999934 |
,999939 |
,999944 |
,999949 |
,999953 |
,999957 |
,999961 |
|
4 |
,999562 |
,999596 |
,999627 |
,999656 |
,999683 |
,999708 |
,999730 |
,999751 |
,999771 |
,999789 |
|
5 |
,998323 |
,998443 |
,998554 |
,998658 |
,998754 |
,998844 |
,998927 |
,999004 |
,999076 |
,999143 |
|
6 |
,994829 |
,995167 |
,995484 |
,995782 |
,996060 |
,996321 |
,996565 |
,996793 |
,997007 |
,997208 |
|
7 |
,986617 |
,987415 |
,988168 |
,988879 |
,989550 |
,990182 |
,990778 |
,991340 |
,991869 |
,992368 |
|
8 |
,970077 |
,971690 |
,973223 |
,974680 |
,976064 |
,977378 |
,978626 |
,979810 |
,980933 |
,981998 |
|
9 |
,940924 |
,943777 |
,946508 |
,949121 |
,951621 |
,954011 |
,956296 |
,958418 |
,960563 |
,962551 |
|
10 |
,895251 |
,899736 |
,904061 |
,908227 |
,912241 |
,916105 |
,919823 |
,923400 |
,926840 |
,930146 |
|
11 |
,830853 |
,837199 |
,843361 |
,849340 |
,855139 |
,860761 |
,866209 |
,871485 |
,876593 |
,881536 |
|
12 |
,748305 |
,756469 |
,764451 |
,772251 |
,779869 |
,787305 |
,794560 |
,801635 |
,808531 |
,815248 |
|
13 |
,651312 |
,660939 |
,670417 |
,679745 |
,688918 |
,697934 |
,706791 |
,715487 |
,724020 |
,732389 |
|
14 |
,546112 |
,556590 |
,566980 |
,577276 |
,587472 |
,597563 |
,607545 |
,617411 |
,627158 |
,636782 |
|
15 |
,440161 |
,450751 |
,461326 |
,471879 |
,482403 |
,492891 |
,503336 |
,513731 |
,524070 |
,534346 |
|
16 |
,340567 |
,350557 |
,360603 |
,370699 |
,380837 |
,391010 |
,401211 |
,411432 |
,421668 |
,431910 |
|
17 |
,252799 |
,261634 |
,270582 |
,279636 |
,288792 |
,298043 |
,307383 |
,316807 |
,326306 |
,335877 |
|
18 |
,180004 |
,187357 |
,194858 |
,202501 |
,210284 |
,218201 |
,226250 |
,234426 |
,242725 |
,251141 |
|
19 |
,122980 |
,128761 |
,134699 |
,140793 |
,147040 |
,153441 |
,159992 |
,166692 |
,173538 |
,180528 |
|
20 |
,080663 |
,084969 |
,089422 |
,094024 |
,098776 |
,103677 |
,108729 |
,113930 |
,119281 |
,124781 |
|
21 |
,050830 |
,053876 |
,057049 |
,060351 |
,063784 |
,066850 |
,071050 |
,074886 |
,078859 |
,082971 |
|
22 |
,030799 |
,032851 |
,035004 |
,037261 |
,039625 |
,042094 |
,044675 |
,047370 |
,050179 |
,053106 |
|
23 |
,017960 |
,019281 |
,020675 |
,022147 |
,023699 |
,025333 |
,027052 |
,028859 |
,030755 |
,032744 |
|
24 |
,010090 |
010902 |
,011767 |
,012685 |
,013660 |
,014694 |
,015788 |
,016947 |
,018172 |
,019465 |
|
25 |
,005466 |
,005945 |
,006458 |
,007007 |
,007594 |
,008221 |
,008890 |
,009602 |
,010359 |
,011165 |
|
26 |
,002859 |
,003130 |
,003422 |
,003737 |
,004077 |
,004441 |
,004833 |
,005253 |
,005703 |
,006185 |
|
27 |
,001444 |
,001592 |
,001752 |
,001926 |
,002115 |
,002319 |
,002539 |
,002778 |
,003035 |
,003312 |
|
28 |
,000706 |
,000783 |
,000868 |
,000960 |
,001061 |
,001171 |
,001291 |
,001421 |
,001562 |
,001716 |
|
29 |
,000334 |
,000373 |
,000416 |
,000463 |
,000515 |
,000573 |
,000635 |
,000704 |
,000779 |
,000861 |
|
30 |
,000153 |
000172 |
,000193 |
,000217 |
,000243 |
,000271 |
,000303 |
000338 |
,000376 |
,000418 |
|
31 |
,000068 |
,000077 |
,000087 |
,000098 |
,000111 |
,000125 |
,000140 |
,000157 |
,000176 |
,000197 |
|
32 |
,000029 |
,000033 |
,000038 |
,000043 |
,000049 |
,000056 |
,000063 |
,000071 |
,000080 |
,000090 |
|
33 |
,000012 |
,000014 |
,000016 |
,000018 |
,000021 |
,000024 |
,000027 |
,000031 |
,000035 |
,000040 |
|
34 |
,000005 |
,000006 |
,000007 |
,000008 |
,000009 |
,000010 |
,000012 |
,000013 |
,000015 |
,000017 |
|
35 |
,000002 |
,000002 |
,000003 |
,000003 |
,000004 |
,000004 |
,000005 |
,000006 |
,000006 |
,000007 |
|
36 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000002 |
,000002 |
,000002 |
,000003 |
,000003 |
|
37 |
- |
- |
- |
- |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
,000001 |
Продолжение таблицы П3.2
|
x |
λ |
|||||||
|
16 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
1,000000 |
|
|
|
|
|
|
|
|
2 |
,999998 |
1,000000 |
|
|
|
|
|
|
|
3 |
,999984 |
,999997 |
1,000000 |
1,000000 |
|
|
|
|
|
4 |
,999907 |
,999982 |
,999997 |
,999999 |
1,000000 |
|
|
|
|
5 |
,999600 |
,999916 |
,999983 |
,999997 |
,999999 |
1,000000 |
|
|
|
6 |
,998616 |
,999575 |
,999928 |
,999985 |
,999997 |
,999999 |
1,000000 |
|
|
7 |
,995994 |
,998957 |
,999745 |
,999941 |
,999987 |
,999997 |
,999999 |
1,000000 |
|
8 |
,990000 |
,997107 |
,999221 |
,999803 |
,999953 |
,999989 |
,999998 |
,999999 |
|
9 |
,978013 |
,992944 |
,997913 |
,999423 |
,999849 |
,999963 |
,999991 |
,999998 |
|
10 |
,956702 |
,984619 |
,995005 |
,998495 |
,999575 |
,999886 |
,999971 |
,999993 |
|
11 |
,922604 |
,969634 |
,989188 |
,996453 |
,998915 |
,999687 |
,999914 |
,999978 |
|
12 |
,873007 |
,945113 |
,978613 |
,992370 |
,997476 |
,999218 |
,999771 |
,999936 |
|
13 |
,806878 |
,908331 |
,960988 |
,934884 |
,994598 |
,998200 |
,999436 |
,999832 |
|
14 |
,725489 |
,857402 |
,933872 |
,972215 |
,989284 |
,996164 |
,998714 |
,999593 |
|
15 |
,632473 |
,791923 |
,895136 |
,952307 |
,980175 |
,992383 |
,997270 |
,999079 |
|
16 |
,533255 |
,713347 |
,843487 |
,923108 |
,965600 |
,985830 |
,994574 |
,998053 |
|
17 |
,434038 |
,624950 |
,778926 |
,882960 |
,943728 |
,975182 |
,989857 |
,996127 |
|
18 |
,340656 |
,531352 |
,702972 |
,831004 |
,912874 |
,958895 |
,982088 |
,992730 |
|
19 |
,257651 |
,437755 |
,618578 |
,767502 |
,871721 |
,935371 |
,970003 |
,987067 |
|
20 |
,187751 |
,349084 |
,529743 |
,693973 |
,819739 |
,903179 |
,952193 |
,978127 |
|
21 |
,131832 |
,269280 |
,440907 |
,613091 |
,757361 |
,861330 |
,927259 |
,964715 |
|
22 |
,089227 |
,200876 |
,356302 |
,528358 |
,686072 |
,809517 |
,894014 |
,945557 |
|
23 |
,058241 |
,144910 |
,279389 |
,443625 |
,608302 |
,748283 |
,851702 |
,919431 |
|
24 |
,036686 |
,101110 |
,212507 |
,362576 |
,527150 |
,679063 |
,800191 |
,885354 |
|
25 |
,022315 |
,068260 |
,156773 |
,288281 |
,445999 |
,604073 |
,740096 |
,842758 |
|
26 |
,013119 |
,044608 |
,112185 |
,222901 |
,368093 |
,526085 |
,672789 |
,791643 |
|
27 |
,007459 |
,028234 |
,077887 |
,167580 |
,296181 |
,448096 |
,600305 |
,732663 |
|
28 |
,004105 |
,017318 |
,052481 |
,122503 |
,232258 |
,372996 |
,525136 |
,667131 |
|
29 |
,002189 |
,010300 |
,034334 |
,087086 |
,177468 |
,303260 |
,449967 |
,596918 |
|
30 |
,001131 |
,005944 |
,021818 |
,060217 |
,132124 |
,240738 |
,377390 |
,524283 |
|
31 |
,000567 |
,003331 |
,013475 |
,040514 |
,095848 |
,186553 |
,309651 |
,451648 |
|
32 |
,000276 |
,001813 |
,008092 |
,026531 |
,067764 |
,141107 |
,248468 |
,381357 |
|
33 |
,000131 |
,000960 |
,004727 |
,016918 |
,046701 |
,104182 |
,194933 |
,315459 |
|
34 |
,000060 |
,000494 |
,002688 |
,010509 |
,031383 |
,075089 |
,149509 |
,255551 |
|
35 |
,000027 |
,000248 |
,001489 |
,006362 |
,020570 |
,052842 |
,112101 |
,202692 |
|
36 |
,000012 |
,000121 |
,000804 |
,003755 |
,013155 |
,036316 |
,082175 |
,157383 |
|
37 |
,000005 |
,000058 |
,000423 |
,002162 |
,008212 |
,024380 |
,058899 |
,119627 |
|
38 |
,000002 |
,000027 |
,000217 |
,001215 |
,005006 |
,015993 |
,041285 |
,089013 |
|
39 |
- |
,000012 |
,000109 |
,000667 |
,002980 |
,010254 |
,028306 |
,064844 |
|
40 |
- |
,000005 |
,000053 |
,000357 |
,001734 |
,006429 |
,018987 |
,046253 |
|
41 |
- |
,000002 |
,000025 |
,000187 |
,000987 |
,003942 |
,012465 |
,032310 |
|
42 |
- |
,000001 |
,000005 |
,000096 |
,000549 |
,002365 |
,008010 |
,022107 |
|
43 |
- |
- |
,000005 |
,000048 |
,000299 |
,001389 |
,005040 |
,014820 |
|
44 |
- |
- |
,000002 |
,000024 |
,000159 |
,000798 |
,003107 |
,008735 |
|
45 |
- |
- |
,000001 |
,000011 |
,000083 |
,000450 |
,001876 |
,006269 |
|
46 |
- |
- |
- |
,000005 |
,000042 |
,000248 |
,001110 |
,003958 |
|
47 |
- |
- |
- |
,000002 |
,000021 |
,000134 |
,000644 |
,002450 |
|
48 |
- |
- |
- |
,000001 |
,000010 |
,000071 |
,000367 |
,001488 |
|
49 |
- |
- |
- |
- |
,000005 |
,000037 |
,000205 |
,000887 |
|
50 |
- |
- |
- |
- |
,000002 |
,000019 |
,000112 |
,000519 |
|
51 |
- |
- |
- |
- |
,000001 |
,000009 |
,000060 |
,000298 |
|
52 |
- |
- |
- |
- |
- |
,000005 |
,000032 |
,000168 |
|
53 |
- |
- |
- |
- |
- |
,000002 |
,000016 |
,000093 |
|
54 |
- |
- |
- |
- |
- |
,000001 |
,000008 |
,000051 |
|
55 |
- |
- |
- |
- |
- |
- |
,000004 |
,000027 |
|
56 |
- |
- |
- |
- |
- |
- |
,000002 |
,000014 |
|
57 |
- |
- |
- |
- |
- |
- |
,000001 |
,000007 |
|
58 |
- |
- |
- |
- |
- |
- |
- |
,000004 |
|
59 |
- |
- |
- |
- |
- |
- |
- |
,000002 |
|
60 |
- |
- |
- |
- |
- |
- |
- |
,000001 |
СОДЕРЖАНИЕ
|
Приложение 2. Обработка исходных эксплуатационных данных для получения текущих кривых вероятности аварийного пробоя. 31 |
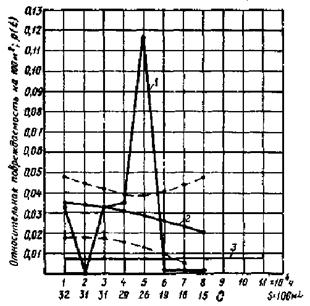
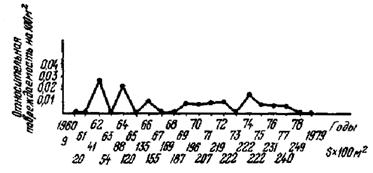
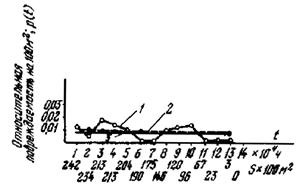
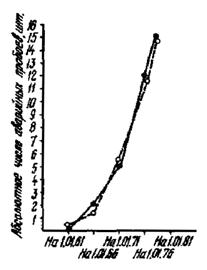
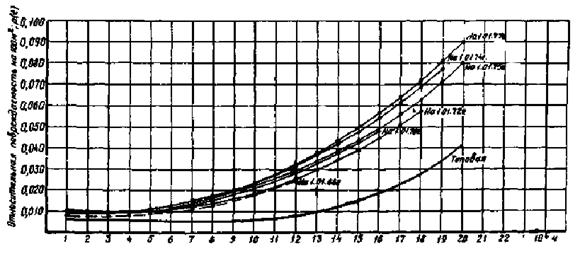
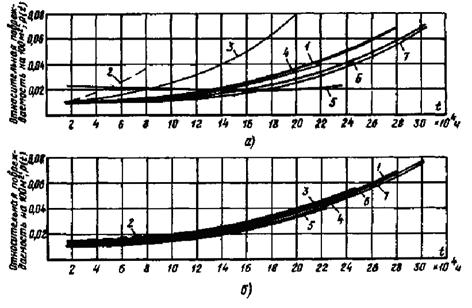
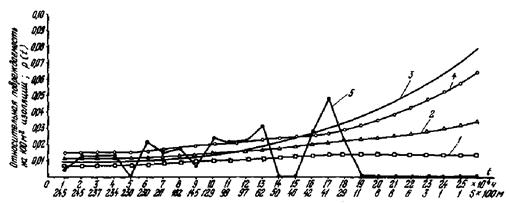
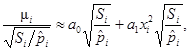 (П-2)
(П-2)