СОЮЗМОРНИИПРОЕКТ
Министерство морского флота
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ОПРЕДЕЛЕНИЮ ВЕТРОВЫХ И ВОЛНОВЫХ УСЛОВИЙ ПРИ ПРОЕКТИРОВАНИИ МОРСКИХ ПОРТОВ
РД 31.33.02-81
РАЗРАБОТАНЫ Государственным проектно-изыскательским и научно-исследовательским институтом морского транспорта "Союзморниипроект". Зам. директора Союзморниипроекта, д. т. н. Костюков В. Д.
Руководитель темы д. ф.-м. н., проф. Крылов Ю. М.
Исполнители: мл. н. с. Галенин Б. Г., вед. инженер Гончаров Е. Н., мл. н. с. Дугинов Б. А., мл. н. с. Кривицкий С. В., ст. н. с., к. г. н. Кузьминская Г. Г., рук. гр. Марков В. В., мл. н. с. Поляков Ю. П., ст. н. с. Попков Р. А., ст. н. с., к. ф.-м. н. Стрекалов С. С.
УТВЕРЖДЕНЫ И. о. гл. инженера Государственного проектно-изыскательского и научно-исследовательского института морского транспорта Т. И. Чодришивили 11 мая 1981 г.
ВВЕДЕНЫ В ДЕЙСТВИЕ с 1 сентября 1981 г. распоряжением гл. инженера Союзморниипроекта № 28 от 5 июня 1981 г.
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ОПРЕДЕЛЕНИЮ ВЕТРОВЫХ И ВОЛНОВЫХ УСЛОВИЙ ПРИ ПРОЕКТИРОВАНИИ МОРСКИХ ПОРТОВ |
РД 31.33.02-81 Вводится впервые |
Вводится в действие с 01.09 1981 г.
Настоящий руководящий документ (РД) служит для определения расчетных характеристик ветра, ветровых волн, штормовых нагонов и элементов низкочастотных колебании, акваторий, являющихся факторами, определяющими надежность и долговечность гидротехнических сооружений. Отдельные положения РД дополняют главы СНиП [1, 2] и "Руководства" [3, 4].
РД предназначен для применения при проектировании морских портов и судоремонтных заводов.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Результаты исследований ветровых и волновых условий в районе строительства или реконструкции объектов морского транспорта представляют в виде режимных функций ветра и волнения, построенных по данным систематических наблюдений. Допускается строить режимные функции элементов волн расчетным путем по ветру; в этом случае обеспеченность волнения определяется по среднему количеству штормовых ситуаций в году.
1.2. Режимные характеристики береговых ветров в удаленном от метеостанции районе, получают по исходной режимной функции ветра на метеостанции с учетом характера местности.
1.3. Режимные характеристики элементов волн в заданной точке акватории получают по режимной функции волнения на подходах к порту с учетов их трансформации в прибрежной мелководной зоне.
1.4. При значительных изменениях ветро-волновых условий в течение года, что выясняется при анализе наблюдений, режимные функции допускается строить для характерных периодов года.
Извещение 1. Раздел 2 заменен РД 31.33.04-84
3. ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ УРОВНЕЙ ВОДЫ И ВЫСОТЫ ВЕТРОВОГО НАГОНА
3.1. Расчетные уровни воды.
3.1.1. Расчетные уровни воды необходимо определять по результатам статистической обработки данных многолетних (не менее 25 лет) рядов наблюдений. При отсутствии данных натурных наблюдений расчетные уровни определяют с учетом приливо-отливных, сгонно-нагонных, сезонных и годовых колебаний уровней.
3.1.2. Максимальный расчетный уровень воды необходимо принимать для сооружения I класса - 1 % (1 раз в 100 лет), II класса 5 % (1 раз в 20 лет), а для III и IV классов - 10 % (1 раз в 10 лет) по наивысшим годовым уровням.
Примечание. При проектировании берегоукрепительных сооружений обеспеченность расчетных уровней воды необходимо принимать в соответствии с требованиями главы СНиП [1].
3.2. Высота ветрового нагона
3.2.1. Высоту ветрового нагона Δh, м, следует, как правило, принимать по данным натурных наблюдении, а при их отсутствии в соответствии с требованиями настоящего раздела.
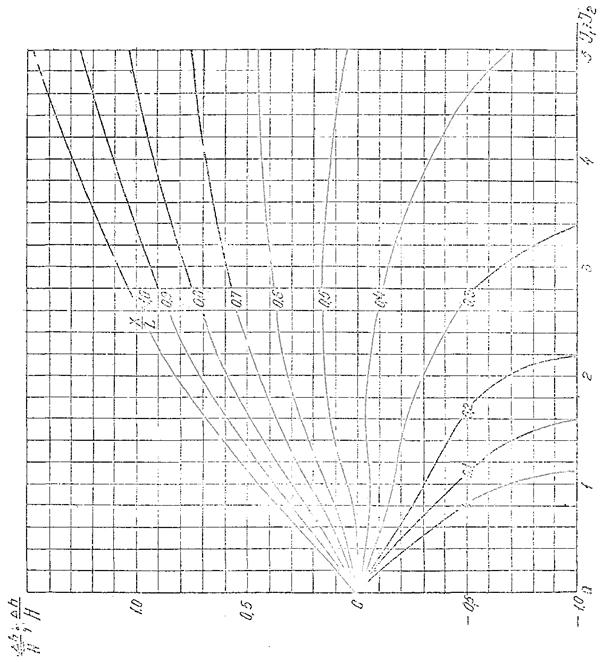
3.2.2. Высоту ветрового нагона для замкнутых водоемов с горизонтальным дном без учета конфигурации береговой линии при ветре, направленном вдоль оси водоема, допускается определять по графику рис. 3.1. По безразмерным величинам:
![]() и
и ![]() ,
,
где Х - расстояние от подветренного берега, м;
L - длина водоема, м;
![]() - средняя
глубина водоема, м;.
- средняя
глубина водоема, м;.
W* - динамическая скорость, м/с,
определяемая по п. 2.2.4 настоящих указаний и
графикам рис. 2.5, получают безразмерную
величину ![]() и
вычисляют высоту ветрового нагона - Δh, м.
и
вычисляют высоту ветрового нагона - Δh, м.
Примечание: Дно считается горизонтальным, если выполняется условие: Нmax/Нmin < 1,5, где Нmax и Нmin - соответственно минимальная и максимальная глубины.
В первом
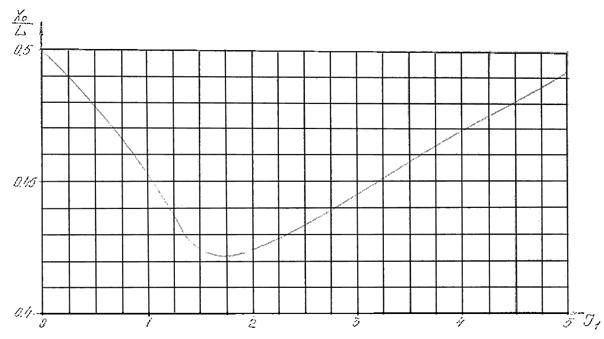
приближении определяют среднюю глубину водоема и по величине I1 и графику рис. 3.2 находят безразмерную
величину![]() и Х0 - положение узловой точки на оси водоема. Величины
Δh, рассчитанные от узловой точки в направлении
действия ветра, принимают положительные значения (нагон), а в противоположном
направлении - отрицательные значения (сгон). Начиная с Х0,
водоем разбивают на отдельные участки таким образом, чтобы учесть изменение его
глубины и конфигурации береговой линии. Безразмерные величины Δhi*/Hi получают
с помощью графика рис. 3.1 по величине Х/L = 1 и величине
и Х0 - положение узловой точки на оси водоема. Величины
Δh, рассчитанные от узловой точки в направлении
действия ветра, принимают положительные значения (нагон), а в противоположном
направлении - отрицательные значения (сгон). Начиная с Х0,
водоем разбивают на отдельные участки таким образом, чтобы учесть изменение его
глубины и конфигурации береговой линии. Безразмерные величины Δhi*/Hi получают
с помощью графика рис. 3.1 по величине Х/L = 1 и величине
![]()
где i = +1; +2; … - номер участка, причем знак соответствует положительным или отрицательным значениям Δh;
Hi - средняя глубина на i-том участке с учетов повышения (понижения) уровня на предыдущем участке, м. Величину нарастания (убывания) уровня на i-том участке. Δhi*, м, вычисляют по отношению Δhi*/Hi. Высоту ветрового нагона (сгона) на i-том участке определяют по формуле:
![]() (3.1.)
(3.1.)
Рис. 3.1. График для определения высоты ветрового нагона.
Рис. 3.2. График для определения положения узловой точки.
Последующие приближения выполняют аналогичным образом, используя для определения положения узловой точки - Х0 соотношения:
V(+) + V(-) = 0, (3.2.)
![]() , (3.3.)
, (3.3.)
где Bi - средняя ширина водоема на i-том участке, а знаки (+) и (-) означают суммирование соответственно с положительными и с отрицательными значениями Δhi. Расчет заканчивают при выполнении требования:
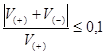 (3.4.)
(3.4.)
3.2.4. Высоту ветрового нагона для замкнутых водоемов при ветре, направленном под углом к оси водоема, допускается рассчитывать согласно требованиям п.п. 3.2.2. и 3.2.3.; вместо величины W*2 принимают ее проекцию на ось водоема.
3.2.5. Расчет высоты ветрового нагона для открытых акваторий допускается выполнять согласно п.п. 3.2.2. - 3.2.4., используя первое приближение. Положение узловой точки в этом случае определяют из условия:
![]() (3.5.)
(3.5.)
где W - расчетная скорость ветра, м/с;
Н0 - глубина, которой соответствует величина Х0 - кратчайшее расстояние от расчетной точки до узловой.
3.2.6. Результаты расчетов допускается корректировать по данным натурных измерений.
4. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ВЕТРОВЫХ ВОЛН
4.1. Расчет характеристик ветровых волн на подходах к порту
4.1.1. Построение режимных функций элементов волн перед портом в тех случаях, когда разгоны волн по всем волноопасным направлениям не превышают 100 км, надлежит выполнять следующим образом.
С графика
режимной функции скорости ветра W, построенной в
соответствии с требованиями п. 2.4.2 и п. 2.4.3., снимают ряд величин Wi
и соответствующих им величин Fi (в % от
общей длительности данного типа штормов и в числе штормовых ситуаций,
когда скорость ветра непрерывно превышает уровень Wi).
По снятым Wi для данного волноопасного
направления с учетом контура береговой черты и в соответствии с требованиями
главы СНиП [1]
и "Руководства" к нему [3] вычисляют соответствующие значения средних высот
hi и средних периодов ![]() в системе волн. Приписав вычисленным элементам волн
обеспеченности Fi, на функциональной сетке (рис. 2.1) строят графики искомых режимных функций.
в системе волн. Приписав вычисленным элементам волн
обеспеченности Fi, на функциональной сетке (рис. 2.1) строят графики искомых режимных функций.
4.1.2. Построение режимных функций элементов волн перед портом в тех случаях, когда разгоны волн перед портом более 100 км, но менее 1000 км, надлежит выполнять следующим образом.
В соответствии с требованиями [1, 3] вычисляют элементы волн в расчетной точке перед портом для каждого типового поля ветра, построенного согласно п. 2.4.6. Вычисленным элементам волн присваивают повторяемости соответствующих типовых полей ветра, и затем строят на функциональной сетке (рис. 2.1) графики режимных функций обеспеченности элементов волн для каждого типа ветровых полей. При этом по горизонтальной оси рис. 2.1 откладывают обеспеченности F в процентах, от общей длительности данного типа, а по вертикали - значения данного элемента волн.
На
горизонтальную ось каждого графика, кроме того, необходимо нанести шкалу
среднего числа штормовых случаев, когда данный элемент волн
непрерывно превышал его фиксированное значение. Переход от F
в % к числу таких случаев осуществляют с помощью построенной согласно
рекомендациям п. 2.4.6. зависимости между скоростью ветра (фиксированного румба
в районе пород портом) и средней продолжительностью штормовой ситуации со
скоростью этого ветра, большей заданного значения. Для этого в расчетной точке
перед портом для каждого типа ветровых полей строят вспомогательную зависимость
скорости ветра от рассматриваемого элемента волн, что позволяет установить
зависимость этого элемента от среднего интервала времени ![]() , в течение которого
элемент превышает заданное значение. Последнюю зависимость используют при
расчете по формуле (2.3) требуемой шкалы.
, в течение которого
элемент превышает заданное значение. Последнюю зависимость используют при
расчете по формуле (2.3) требуемой шкалы.
4.1.2. Среднее значение разгона при предварительном определении элементов волн для заданной расчетной скорости ветра W, м/с, определяют по формуле
![]() (4.1)
(4.1)
где ν - коэффициент кинематической вязкости воздуха, принимаемый 10-5 м2/с.
4.1.3. Значения предельного разгона Dпp, м, допускается принимать по табл. 4.1 для заданной расчетной скорости ветра W, м/c.
Таблица 4.1.
|
Скорость ветра W, м/с |
20 |
25 |
30 |
40 |
50 |
|
Значения предельного разгона Dпp . 10-3, м |
1600 |
1200 |
600 |
200 |
100 |
Примечание. Рассчитанные значения среднего DHB и предельного Dпp разгонов для ограниченных акваторий не должны превышать величины разгона, измеренной по направлению ветра от расчетной точки до береговой черты.
4.1.4. Частотный спектр ветровых волн допускается рассчитывать по формуле:
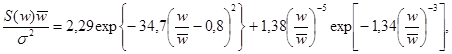 (4.2.)
(4.2.)
где S(w) - спектральная
плотность, (м2с)/рад, w - текущая частота, рад/с; ![]() ,
, ![]() ,
, ![]() и
и ![]() - средние высота и
период волн, определяемые в соответствии с требованиями главы СНиП [1] по
заданной расчетной скорости ветра W и разгону (или
продолжительности t).
- средние высота и
период волн, определяемые в соответствии с требованиями главы СНиП [1] по
заданной расчетной скорости ветра W и разгону (или
продолжительности t).
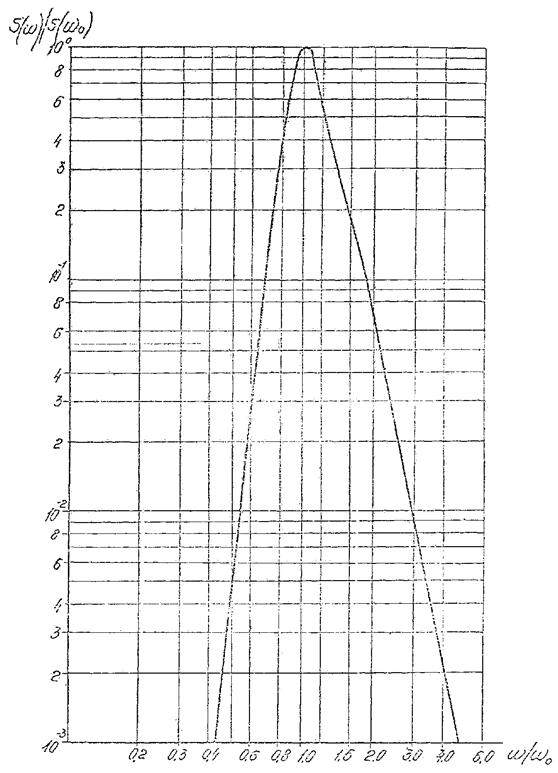
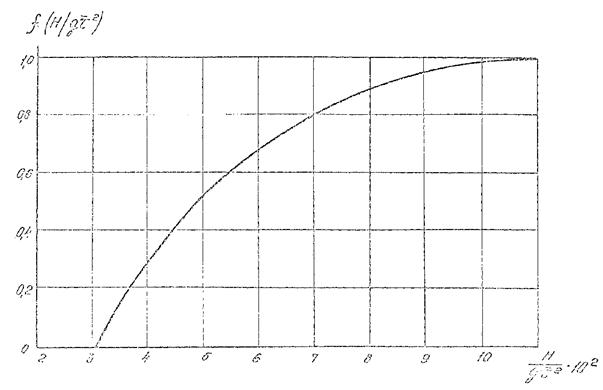
4.1.5. Допускается при расчете частотного спектра ветровых волн использовать график рис. 4.1., причем S(w)/S(w0) определяют по безразмерной частоте w/w0, где S(w0) - спектральная плотность на частоте максимума, (м2с)/рад, w0 - частота максимума, рад/с.
Спектральную плотность S(w0) и частоту максимума определяют по формулам:
![]() (4.3.)
(4.3.)
![]() (4.4.)
(4.4.)
Рис. 4.1. График зависимости безразмерной спектральной плотности S(w)/S(w0) от безразмерной частоты w/w0.
4.1.6. Угловое распределение энергии волн на глубокой воде допускается определять по формуле:
где
n = 0; +1; +2; ... номер луча, знак которого определяет его положение относительного главного луча, проведенного по направлению действия ветра;
j, + 1 - номера лучей, ограничивающих расчетный сектор;
θj - угол между главным и лучом с соответствующим номером; град;
![]() - средние высоты волн,
определяемые в соответствии с требованиями главы СНиП [1] по проекциям разгонов Dn* = Dncosθn.
Величины Dn определяют по направлению
соответствующих лучей.
- средние высоты волн,
определяемые в соответствии с требованиями главы СНиП [1] по проекциям разгонов Dn* = Dncosθn.
Величины Dn определяют по направлению
соответствующих лучей.
4.1.7.
Угловое распределение энергии волн в мелководной зоне допускается -определять
согласно формулам
(4.5.) и (4.6.), в которых величины θj
и ![]() определяют
по результатам расчета рефракции и трансформации волн для каждого луча согласно
положениям [1].
определяют
по результатам расчета рефракции и трансформации волн для каждого луча согласно
положениям [1].
4.1.8. При
определении элементов волн зыби необходимо учитывать элементы ветровых волн в
штормовой зоне - среднюю высоту ![]() и средний период
и средний период ![]() , - определяемые по
требованиям главы СНиП [1] размеры штормовой зоны вдоль направления ветра Dm и расстояние от границы штормовой зоны до
расчетной точки DЗ.
, - определяемые по
требованиям главы СНиП [1] размеры штормовой зоны вдоль направления ветра Dm и расстояние от границы штормовой зоны до
расчетной точки DЗ.
Примечание:
Границы штормовой зоны приближенно оценивают из условия равенства скорости
ветра и фазовой скорости ветровых волн ![]() .
.
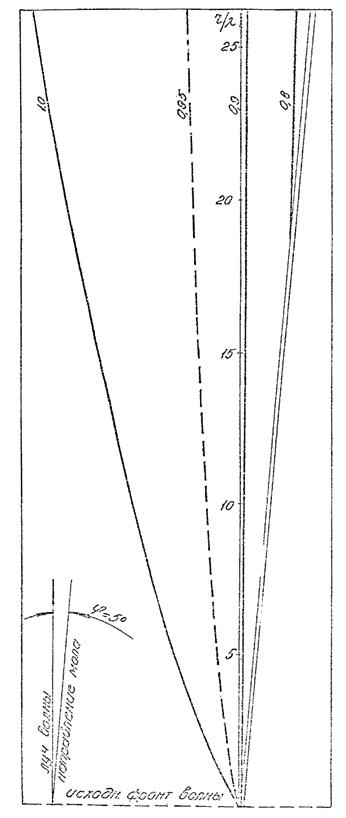
4.1.9.
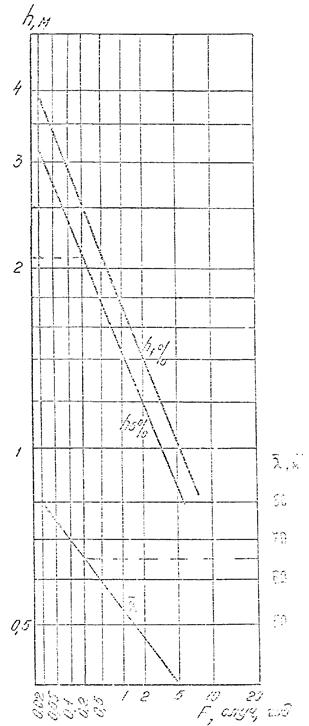
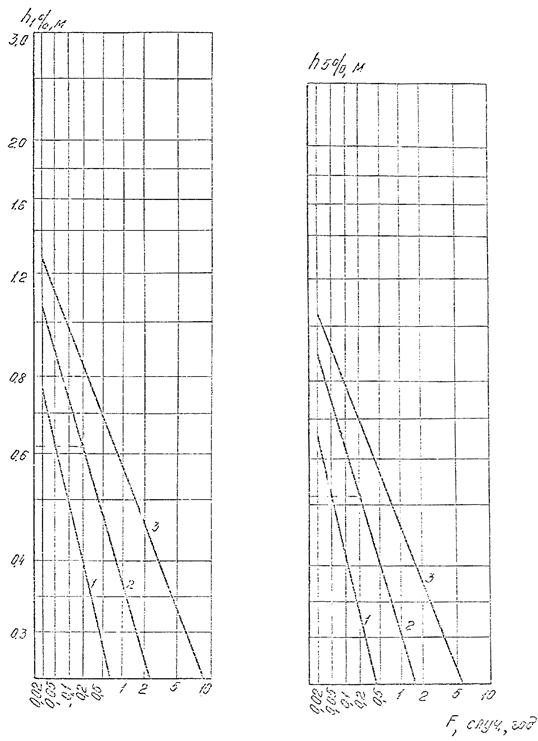
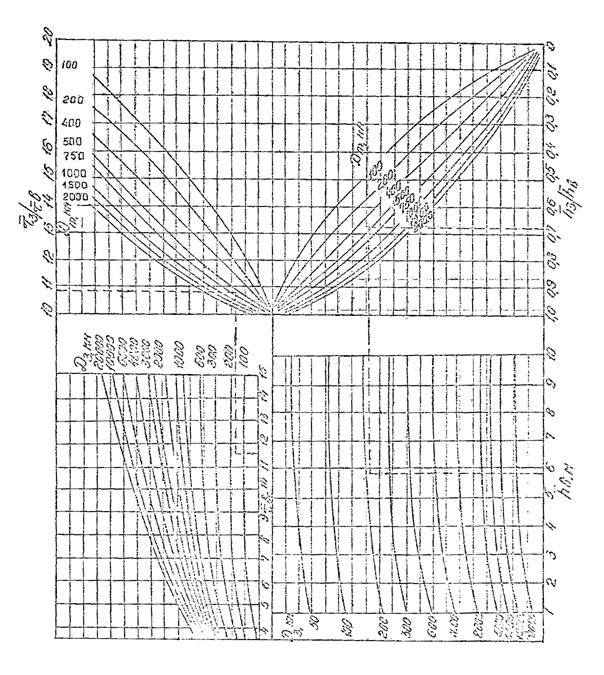
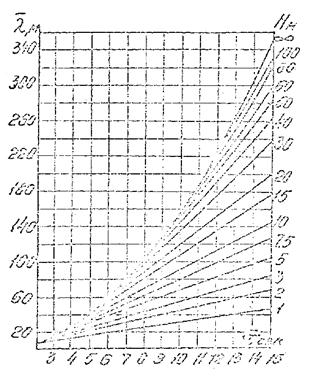
Элементы волн зыби следует определять по рис. 4.2, где верхняя часть
графика служит для определения среднего периода зыби ![]() , нижняя - средней
высоты зыби
, нижняя - средней
высоты зыби ![]() .
.
Рис. 4.2. График для определения периода и высоты волн зыби.
4.1.10. Период зыби получают
путем следующих построений: из точки, соответствующей величине ![]() на верхней
левой горизонтальной шкале, проводят вертикаль до пересечения с кривой,
соответствующей расстоянию DЗ, откуда
проводят горизонтальную прямую до пересечения с линией, отвечающей размеру
штормовой зоны Dm (правая часть графика); из
точки пересечения проводят вертикальную прямую, а затем в верхней части графика
определяют величину
на верхней
левой горизонтальной шкале, проводят вертикаль до пересечения с кривой,
соответствующей расстоянию DЗ, откуда
проводят горизонтальную прямую до пересечения с линией, отвечающей размеру
штормовой зоны Dm (правая часть графика); из
точки пересечения проводят вертикальную прямую, а затем в верхней части графика
определяют величину ![]() /
/![]() и значение
и значение ![]() .
.
4.1.11. Высоту зыби определяют путем аналогичных построений в нижней части графика.
4.1.12. Коэффициент рефракции Кр ветровых волн при угле между волновым лучем и линией берега менее 60° надлежит определять согласно требованиям главы СНиП [1]. В тех случаях, когда угол превышает 60°, определенный в соответствии с [1], коэффициент умножают на поправочный множитель Кпм, принимаемый по данным таблицы 4.2.
Таблица 4.2.
|
Значения коэффициента Кпм при углах αро (при H/λ0 > 0,5) |
||
|
60° < αро < 70° |
75° < αро < 85° |
|
|
0,06 |
1,12 |
1,20 |
|
0,08 |
1,13 |
1,25 |
|
0,1 |
1,13 |
1,3 |
|
0,12 |
1,14 |
1,23 |
|
0,14 |
1,12 |
1,2 |
|
0,16 |
1,10 |
1,18 |
|
0,2 |
1,09 |
1,16 |
|
0,25 |
1,00 |
1,13 |
|
0,3 |
1,00 |
1,07 |
|
> 0,4 |
1,00 |
1,00 |
4.2. Расчет характеристик ветровых волн на акватории порта
4.2.1. Высоту дифрагированной волны hд, м, на акватории, огражденной одиночным молом или двумя сходящимися молами необходимо определять по формуле:
hд = Кд . hi%, (4.7.)
где Кд - коэффициент дифракции волн;
hi% - высота исходной волны i%-ой обеспеченности.
В качестве
исходных элементов волн принимают ![]() и hi на
входе в акваторию. Длину
и hi на
входе в акваторию. Длину ![]() допускается определять по периоду
допускается определять по периоду ![]() и глубине моря
H перед портом с помощью рис. 4.3. Линия фронта
дифрагированной волны должна приниматься:
и глубине моря
H перед портом с помощью рис. 4.3. Линия фронта
дифрагированной волны должна приниматься:
а) в зоне волновой тени - по окружности с центром в голове оградительного сооружения с радиусом, равным расстоянию от головы сооружения до расчетной точки;
б) вне зоны волновой тени (до границы дифракции волн) - по прямой, нормальной к исходному лучу волн.
4.2.2. Коэффициент дифракции волн Кдо для
акватории, огражденной одиночным молом, следует определять с помощью основного
набора диаграмм (приложение 1, рис. 1-9) выполненных на прозрачной
основе (кальке, пленке и т.п.). Набор диаграмм отвечает следующим значениям
угла φ, град., между линией волновой тени и внутренней стороной
оградительного сооружения: 5°, 10°, 15°, 20°, 30°, 45°, 60°, 75° и 90° - и
длине волны ![]() =
100 м в масштабе 1:10000. Для других длин волн диаграммы следует подвергнуть
соответствующему уменьшению или увеличению.
=
100 м в масштабе 1:10000. Для других длин волн диаграммы следует подвергнуть
соответствующему уменьшению или увеличению.
На планах
акватории за одиночным молом наносят расчетные точки и линию исходного
волнового луча, проходящую через оголовок мола. Продолжение линии волнового
луча принимают за границу волновой тени. Между внутренней стороной мола и
границей волновой тени определяют угол φ. По заданным величинам масштаба
плана огражденной акватории, исходной длины волн ![]() и угла φ подбирают
диаграмму, ближайшую к этим величинам. Диаграмму накладывают на план, совмещая
оголовок мола и линию волновой тени на плане и на диаграмме. С диаграммы
снижают значения Кдо для любой заданной точки акватории.
и угла φ подбирают
диаграмму, ближайшую к этим величинам. Диаграмму накладывают на план, совмещая
оголовок мола и линию волновой тени на плане и на диаграмме. С диаграммы
снижают значения Кдо для любой заданной точки акватории.
Рис. 4.3. График для определения средней длины ветровых волн ![]() , м, по среднему
периоду
, м, по среднему
периоду ![]() ,
с, и глубине H, м.
,
с, и глубине H, м.
где Кдо - коэффициент дифракции в заданной точке акватории для случая одиночного мола;
ψсх - поправочный коэффициент, учитывающий наличие двух молов.
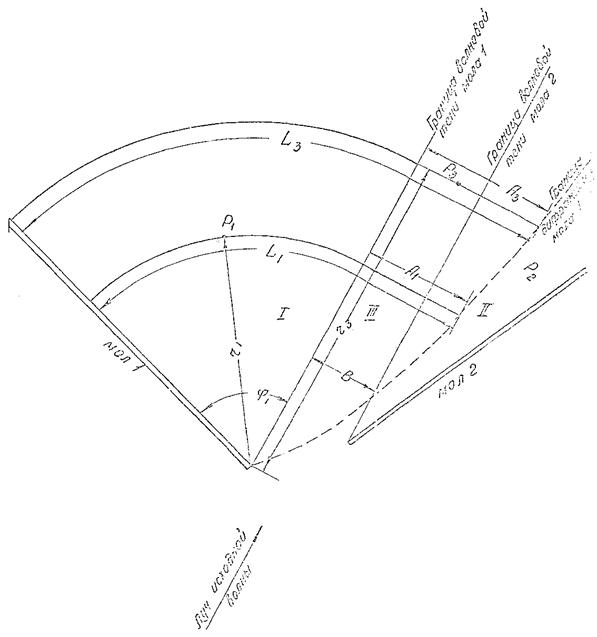
На плане
акватории за двумя молами через их оголовки проводят два луча, параллельных лучу
исходной волны, называемых границами волновой тени молов. Этими лучами
акватория делится на три зоны: зону первого мола (I), зону второго мола (II) и
промежуточную зону (III) (рис. 4.4.). Коэффициент Кдо в
расчетной точке Р1, расположенной в зоне I, надлежит находить по формуле (4.8.).
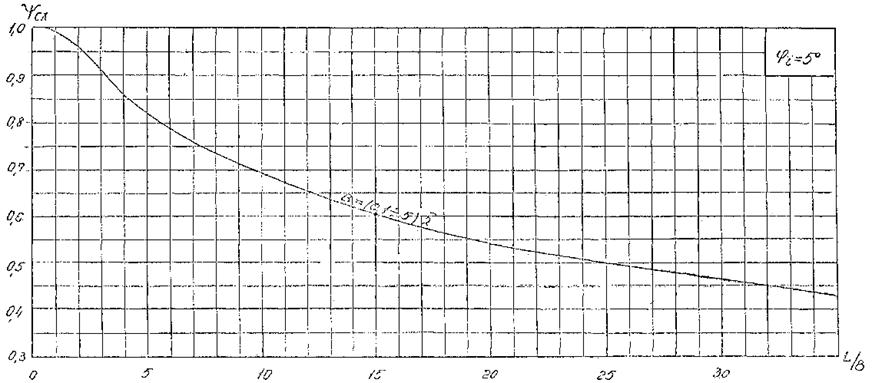
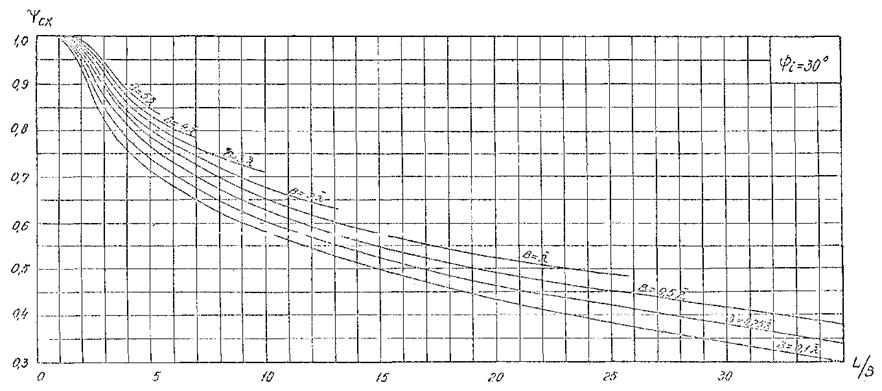
Поправочный коэффициент ψсх в формуле (4.8.) для мола 1
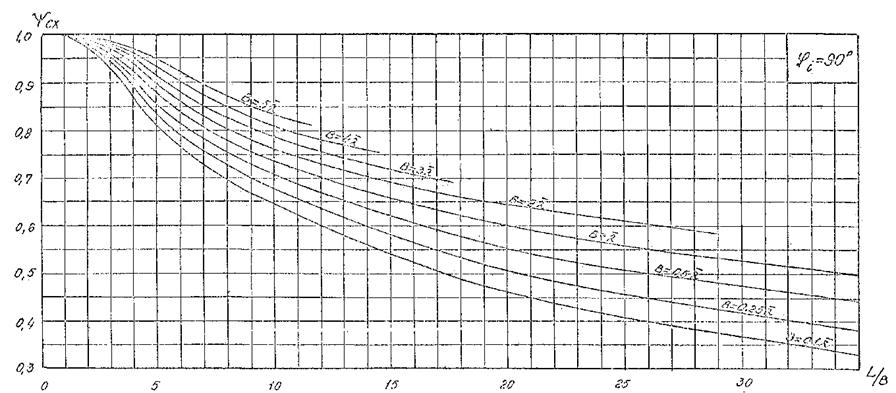
находят по графикам приложения 1 рис. 10 - 18, в зависимости от
безразмерных величин В/![]() , L/B и угла φ1, где B -
проекция отрезка, соединяющая оголовки молов, на фронт исходной волны; L - длина участка фронта волны, проходящего через
расчетную точку, от мола 1 до границы зоны дифракции для этого мола; φ1
- угол между направлением мола и лучом волны.
, L/B и угла φ1, где B -
проекция отрезка, соединяющая оголовки молов, на фронт исходной волны; L - длина участка фронта волны, проходящего через
расчетную точку, от мола 1 до границы зоны дифракции для этого мола; φ1
- угол между направлением мола и лучом волны.
Величину L надлежит вычислять по формуле:
где r - расстояние от оголовка мола 1 до расчетной точки Р1;
А - длина участка фронта между точками его пересечения с границей волновой тени и границей зоны дифракции.
Рис. 4.4. Схема акватории порта, огражденного двумя сходящимися молами.
Коэффициент Кдо в расчетной точке РIII, расположенной в зоне III, находят аналогичным образом.
Коэффициент дифракции Кдс в расчетной точке РIII, расположенной в зоне III, определяют вначале по параметрам мола 1, а затем - мола 2, и в итоге принимают наименьший.
4.2.4. При расчете трансформации нерегулярных волн на акватории порта допускается учитывать угловой спектр на подходах к порту.
4.2.5. Возвышение вершины нерегулярной стоячей волны около вертикальной стенки допекается определять по формуле:
hВ = Kа . h, (4.10)
где h - высота нерегулярной волны около вертикальной стенки;
Ка - коэффициент асимметрии стоячей волны.
При определении возвышения вершины стоячей волны над спокойным уровнем моря следует рассматривать волны обеспеченностью в системе менее 10 %.
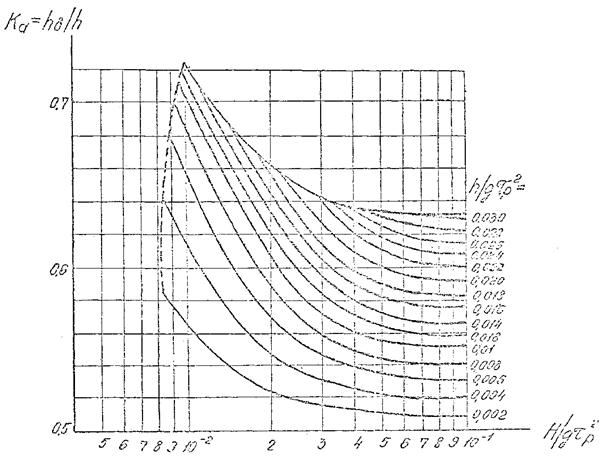
4.2.6.
Коэффициент Ка следует определять по графику рис. 4.5 в
зависимости от безразмерной глубины ![]() и параметра
и параметра ![]() ,
,
где Н - глубина,
g - ускорение свободного падения,
τр - период расчетных волн.
4.2.7. Период расчетных стоячих волн следует определять по формуле:
4.2.8. Режимные функции волнения на огражденной акватории необходимо строить на функциональной сетке (рис. 2.1.) на основании заданных режимных функций волнения на входе в порт. Режимные функции периодов волн в расчетной точке принимают такими же, как и на входе в порт. Режимные функции высот волн трансформируют путем умножения исходных режимных функций на коэффициент дифракции Кд в расчетных точках.
Рис. 4.5. График для определения возвышения вершины стоячей
волны по безразмерной глубине ![]() и параметру
и параметру ![]() .
.
4.3. Определение режима низкочастотных колебаний в порту, вызывающих явление тягуна
4.3.1. Режим элементов низкочастотных колебаний масс воды на подходах и на акватории порта необходимо определять на основе режимных сведений об элементах ветровых волн. Повторяемость и обеспеченность элементов низкочастотных колебаний в режимном плане принимают равным повторяемости и обеспеченности соответствующих элементов ветровых волн.
4.3.2. Средние высоты hn и средние периоды Т низкочастотных колебаний на подходах к порту в узкой прибрежной зоне с уклонами дна 0,01 и более глубоководного водоема необходимо определить по формулам:
при разгонах более
100 км и устойчивых продолжительных ветрах (более суток) со скоростью более 15
м/с. Средний период ![]() и среднюю высоту
и среднюю высоту ![]() ветровых волн
определяют в соответствии с требованиями главы СНиП [1].
ветровых волн
определяют в соответствии с требованиями главы СНиП [1].
4.3.3. Элементы низкочастотных колебаний на подходах к порту в широкой прибрежной зоне при глубине Н (уклоны дна 0,001 и менее) следует вычислять по формулам:
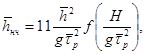 (4.14.)
(4.14.)
![]() (4.15.)
(4.15.)
где значения
функции 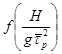 ,
учитывающей влияние дна моря на высоту низкочастотных колебаний, принимают по
графику рис.
4.6.
,
учитывающей влияние дна моря на высоту низкочастотных колебаний, принимают по
графику рис.
4.6.
4.3.4. Среднюю высоту низкочастотных колебаний (ceйшевых) акватории порта необходимо определять по формуле:
где Rн - коэффициент усиления нерегулярных низкочастотных колебаний.
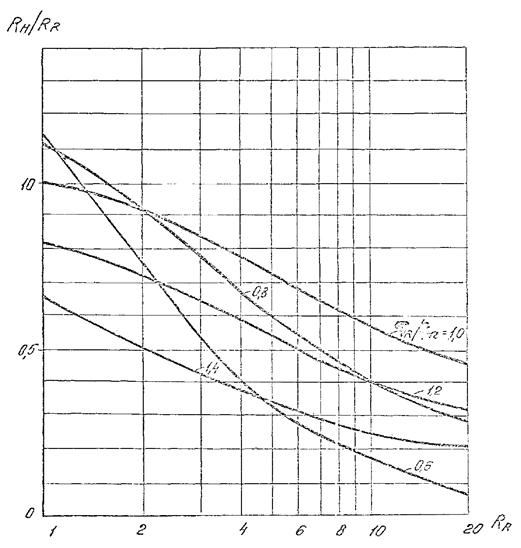
4.3.5.
Коэффициент усиления Rн следует
устанавливать из отношения Rн/RR,
определяемого из графика рис. 4.7 в зависимости от резонансного коэффициента
усиления RR и отношения резонансного периода
τR к периоду ![]() .
.
4.3.6. Резонансный период τR следует принимать равным среднему периоду ceйшевых колебаний и определять по формуле:
где Кр - резонансное волновое число.
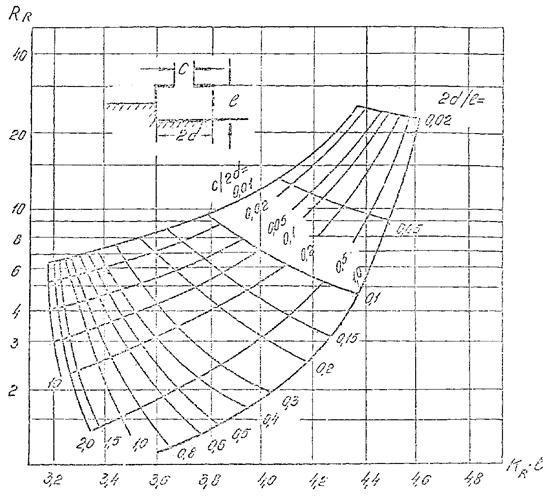
4.3.7. Резонансное волновое число Кр, и резонансный коэффициент усиления RR для портовых акваторий, очертания которых близки к прямоугольным, следует принимать для заданных геометрических параметров порта c/2d и 2d/l в соответствии со схемой и графиками рис. 4.8., где с - ширина входа в порт, 2d и l - размеры порта в плане.
4.3.8. Защищенность порта от тягуна считают
неудовлетворительной, если средний период ceйшевых
колебаний акватории находится в интервале от 0,5 до 2,5 мин., а средняя высота ceйшевых колебаний ![]() превышает 30 см со средней повторяемостью
один раз в год и чаще.
превышает 30 см со средней повторяемостью
один раз в год и чаще.
Рис.
4.6. Зависимость функции 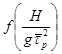 от параметра безразмерной глубины моря.
от параметра безразмерной глубины моря.
Рис.
4.7. Зависимость отношения Rн/RR
от резонансного коэффициента усиления RR при
различных значениях τR/![]() .
.
Рис. 4.8. Номограмма для определения резонансного волнового числа КR и резонансного коэффициента усиления RR для акватории прямоугольной формы по заданным линейным размерам порта.
5. МЕТОДИКА ГИДРАВЛИЧЕСКОГО МОДЕЛИРОВАНИЯ ВЕТРОВЫХ ВОЛН НА ПОРТОВЫХ АКВАТОРИЯХ
5.1. Определение исходных параметров для моделирования
5.1.1. В качестве основного критерия моделирования ветровых волн на акватории порта необходимо использовать критерий Фруда. Согласно этому критерию, размеры сооружений на модели, глубины и элементы волн принимают в линейном масштабе. Время моделируют как квадратный корень из масштаба. На подходах к порту воспроизводится система регулярных волн.
5.1.2. В основу моделирования защищенности портовых акваторий от ветровых волн необходимо класть информацию об угловых спектрах.
5.1.3. Модель акватории порта и подходов к нему необходимо сооружать в масштабе, выбор которого определяется размерами акватории и элементами волн. Обычно масштабы моделирования принимаются равными 1:40 - 1:100.
5.1.4. Дно модели необходимо изготовлять жестким (из цементной стяжки с железнением). Модель рассчитывают таким образом, чтобы на ней разместились подходы к порту, протяженностью не менее 5 длин волн.
5.1.5. Для избежания отражения волн от волнопродуктора вдоль вертикальных стенок оградительных сооружений с внешней их стороны необходимо устраивать гасители из отсыпки камня. Для сохранения аналогии с натурой в явлении дифракции у голов оградительных сооружений отсыпка не устраивается.
5.1.6. Высоты и длины исходных для моделирования волн надлежит получать расчетным путем.
Высоту волны принимают 5 % обеспеченности в системе, длину волны - среднюю в системе.
5.1.7. Необходимо моделировать три волновых режима: максимальный (обеспеченностью 1 раз в 50 лет для сооружений I - II класса и 1 раз в 25 лет для сооружений III - IV класса), средний и минимальный. Последние два режима выбирают таким образом, чтобы охватить весь диапазон волн, возможных на подходах к исследуемому порту.
При расположении входа в порт в прибойной зоне максимальный волновой режим выбирают таким образом, чтобы на модели не происходило забурунивания воды при максимальной высоте волн. Затем по рекомендациям главы СНиП [1] определяют высоту волн, подходящих к воротам порта без забурунивания, а по режимным функциям определяют повторяемость такой высоты и соответствующую длину волн.
5.1.8. Угловой спектр волн в районе установки волнопродуктора для каждого из моделируемых режимов необходимо определять расчетным путем в соответствии с приемами, изложенными в п. 4.1.6 настоящих указаний.
5.1.9. В тех случаях, когда более 90 % энергии исходных волн концентрируется в секторе менее 40° (узкий угловой спектр) моделирование следует выполнять без учета спектральной структуры волн. Если же угловое распределение энергии волн в районе установки волнопродуктора охватывает сектор большей величины (90 % энергии концентрируется в секторе равном или более 40° - широкий угловой спектр), моделирование надлежит выполнять с учетом углового спектра.
5.1.10. При
спектральной методике моделирования каждую систему волн, идущую от
волнопродуктора, рассматривают не в качестве реального волнения в природных
условиях, а как картину деформации отдельных составляющих спектра волн. В
результате моделирования получают коэффициенты изменения высоты составляющих
спектра Kh (отношения высоты волн в данной
точке акватории к высоте волн у входа в порт или бухту). В отдельных случаях
допускается увеличивать высоты исходных волн на модели, чтобы их значения не
были менее 1 см. Коэффициент изменения высоты волн с учетом спектра ![]() вычисляется
по формуле:
вычисляется
по формуле:
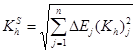 ,
,
где j = 1 - n, номер составляющей;
Еj - доля энергии углового спектра j-ой составляющей.
5.2. Измерения на модели
5.2.1. Измерение высот волн на модели необходимо производить волномерами с записью на осциллограф. Волномеры располагают таким образом, чтобы высота исходных волн измерялась не менее, чем в двух точках, а также чтобы производить измерение высоты волн на входе а порт, на акватории и у причалов.
При производстве записи волнения включают волномеры таким образом, чтобы зафиксировать начало работы волнопродукторов и движение первых волн.
5.2.2. Оптимальное число повторений опыта необходимо устанавливать в лаборатории при многократном (не менее 10) повторении записи в одних и тех же условиях и вычислении ошибок моделирования для 10, 9, 8 и т.д. повторений (запусков).
5.2.3. Запись волнения в бассейне необходимо сопровождать фотографированием и киносъемкой. Длину волн фиксируют съемкой вблизи исходных волномеров на фоне сетки на стене бассейна или на фоне горизонтальной рейки, расположенной выше уровня воды.
Длину волн допускается измерять также специальным прибором, состоящим из рейки с укрепленными на ней двумя электродами, один из которых неподвижен, а второй передвигается. При одновременном соприкосновении гребней волн с обоими электродами цепь замыкается и подается сигнал на измерительный прибор. Отсчет длин производится по расстоянию между электродами в момент сигнала.
5.2.4. Тарировка датчиков высот волн допускается производить путем ступенчатого погружения электродов на определенную глубину, или на специальном приборе, погружающем датчик на заданную глубину с частотой, отвечающей периоду моделируемых волн. Тарировочные зависимости должны быть прямолинейными. Частота тарировок зависит от устойчивости характеристик во времени. Рекомендуется проводить тарировки ежедневно.
5.3. Обработка результатов
5.3.1. Высоту волн следует определять путем обработки осциллограмм. Первым шагом обработки является построение тарировочных зависимостей между отклонением светового луча на записи и глубиной погружения электродов. Если по оси ординат откладывается высота волн (погружение волномера), а по оси абсцисс - отклонение светового луча осциллографа, то крутые тарировочные зависимости допустимы у волномеров перед входом в бухту, где высоты волн велики.
Пологие тарировочные зависимости подбирают предварительно для волномеров, стоящих в глубине бухты или порта. Для остальных волномеров запись производят в масштабе 1:1, т.е., 1 см погружения волномеров соответствует 1 см отклонения светового луча осциллографа, и тарировочная зависимость идет под углом 45°.
5.3.2. При обработке осциллограмм следует прежде всего выделить рабочую часть записи, содержащую 10 - 20 волн, примерно равных по высоте. Рабочая часть записи начинается после прохождение первых волн, идущих по невозмущенной поверхности и имеющих меньшую высоту, и заканчивается до подхода волн, возникающих вследствие отражения от стенок бассейна (так как нет абсолютно надежных гасителей) и от волнопродуктора.
В рабочей части записи пронимают для каждого из волномеров среднюю амплитуду отклонения светового луча, эту величину переносят на тарировочную характеристику волномера, по которой определяют высоту волн h в точке установки волномера.
5.3.3. Вычисление режимных функций высот волн на акватории порта необходимо проводить путем умножения высот волн, снятых с режимных функций волнения на подходах к порту, на коэффициенты изменения высот волн, полученные на модели, для каждого из трех выбранных для моделирования режимов.
5.4. Тарировка модели
5.4.1. Тарировку модели рекомендуется производить с целью доказательства правомерности получения характеристик волнения для проектных вариантов порта.
5.4.2. Сущность тарировки заключается в воспроизводстве условий, при которых проводились наблюдения над волнением в натуре.
С этой целью на модели следует воспроизвести естественный рельеф дна и вид оградительных и причальных сооружений, при которых проводились наблюдения. Затем воспроизводят волны, но не расчетные, которые будут моделироваться далее, а наблюдавшиеся в период конкретных штормов.
5.4.3. В случае совпадения коэффициентов изменения высоты волны на модели и в натуре поправок на приведение лабораторных данных к натуре не вводят. В случаях несовпадения вопрос решается в каждом конкретном случае отдельно. Перед началом моделирования проектного рельефа дна и положения портовых сооружений проводят моделирование тех условий, которые были при натурных наблюдениях над волнением.
Приложение
1
(рекомендуемое)
ГРАФИКИ
для определения коэффициентов дифракции ветровых волн на акватории порта
Рис. 1. График для определения коэффициента дифракции Кдо для угла φ = 5°.
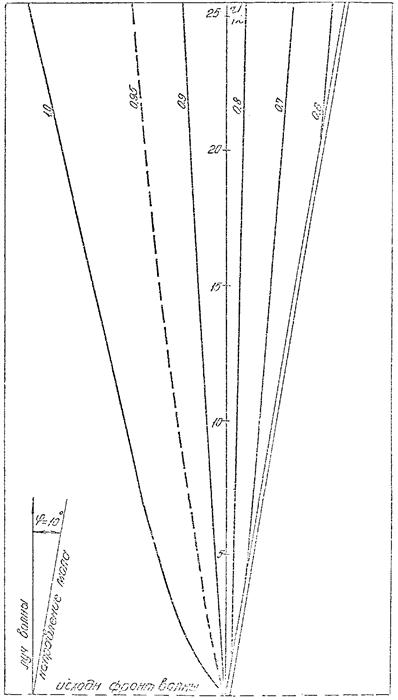
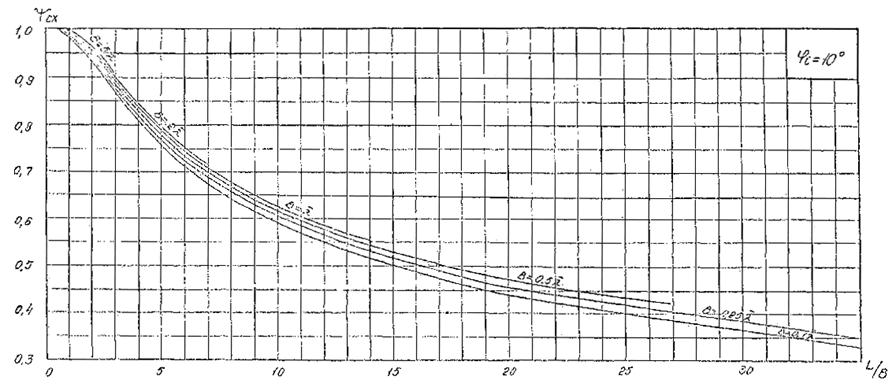
Рис. 2. График для определения коэффициента дифракции Кдо для угла φ = 10°.
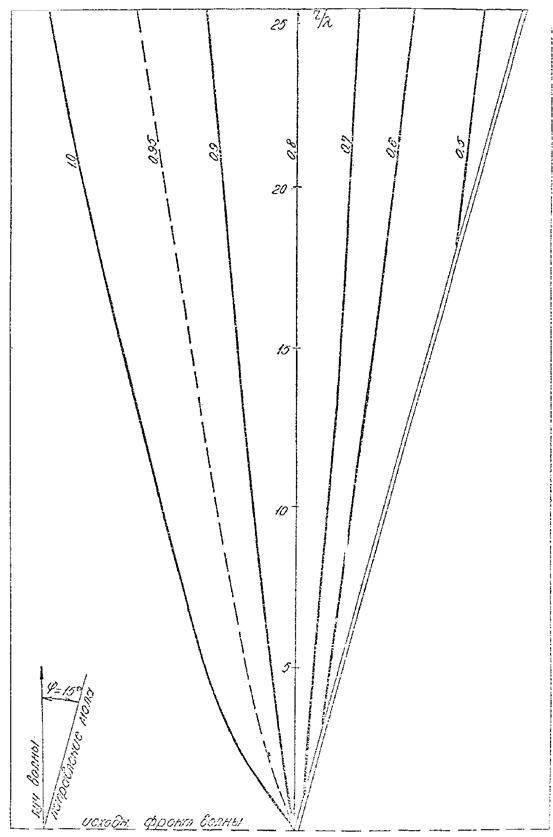
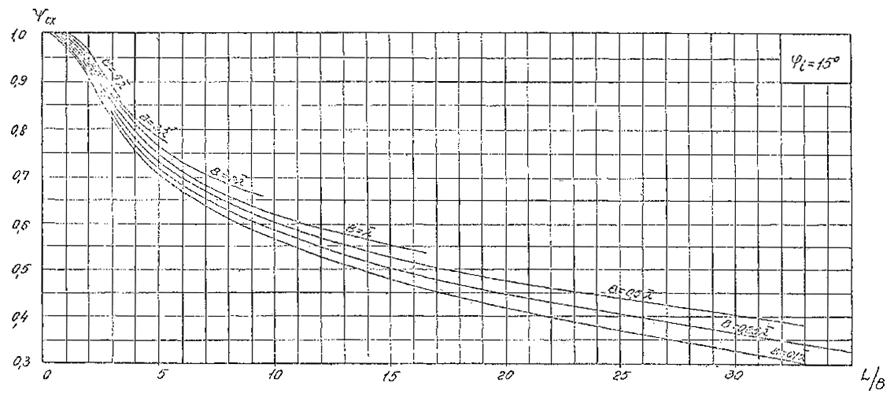
Рис. 3. График для определения коэффициента дифракции Кдо для угла φ = 15°.
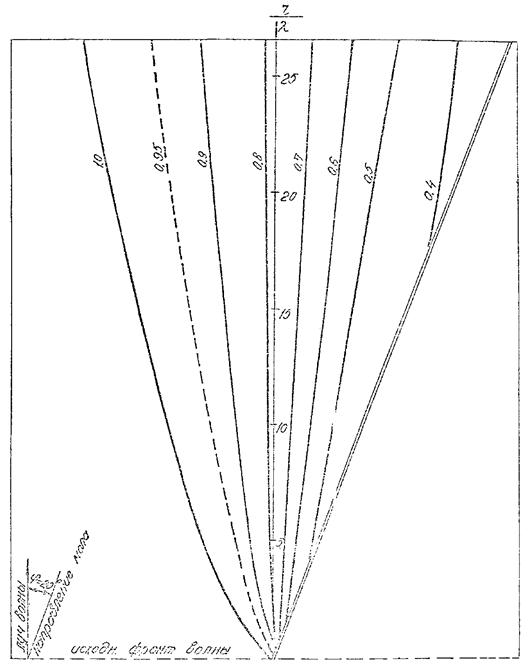
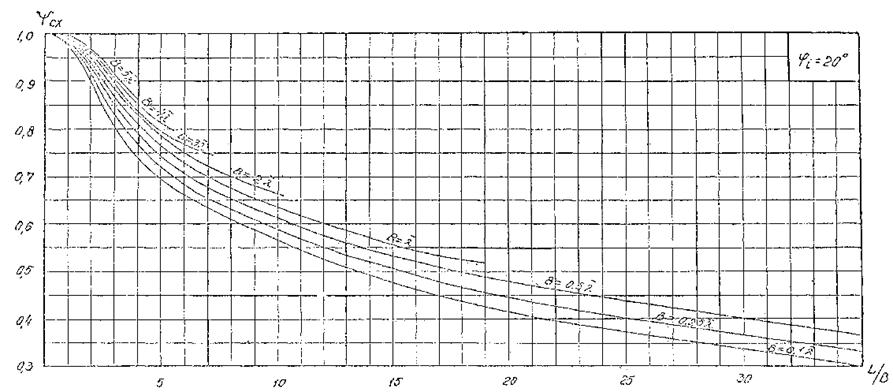
Рис. 4. График для определения коэффициента дифракции Кдо для угла φ = 20°.
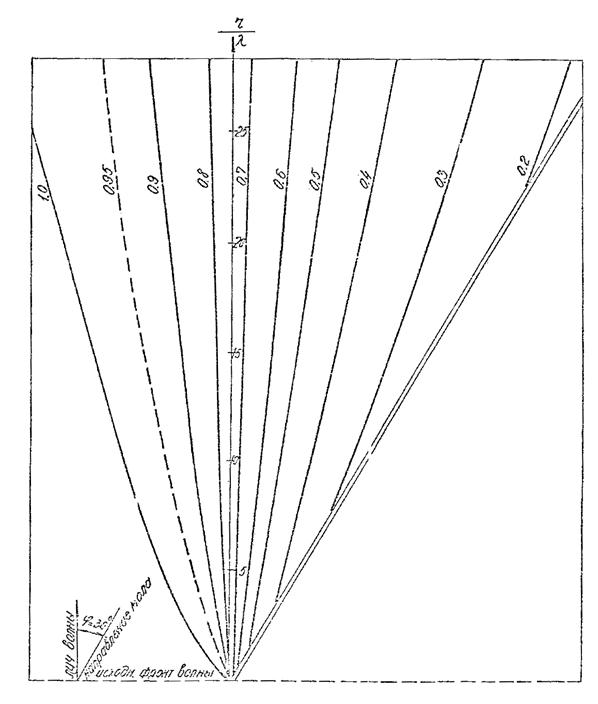
Рис. 5. График для определения коэффициента дифракции Кдо для угла φ = 30°.
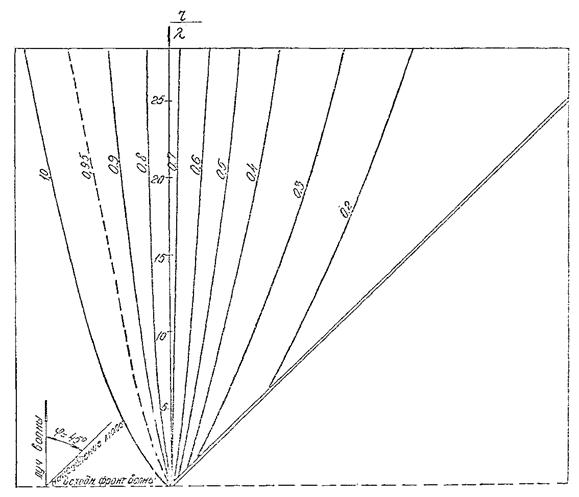
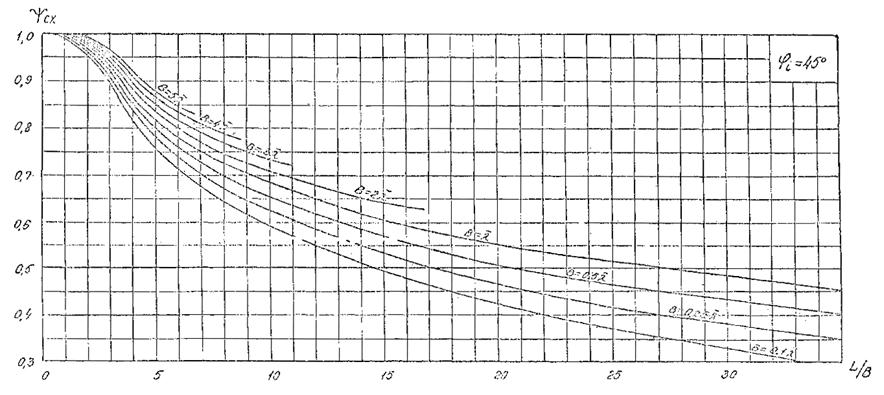
Рис. 6. График для определения коэффициента дифракции Кдо для угла φ = 45°.
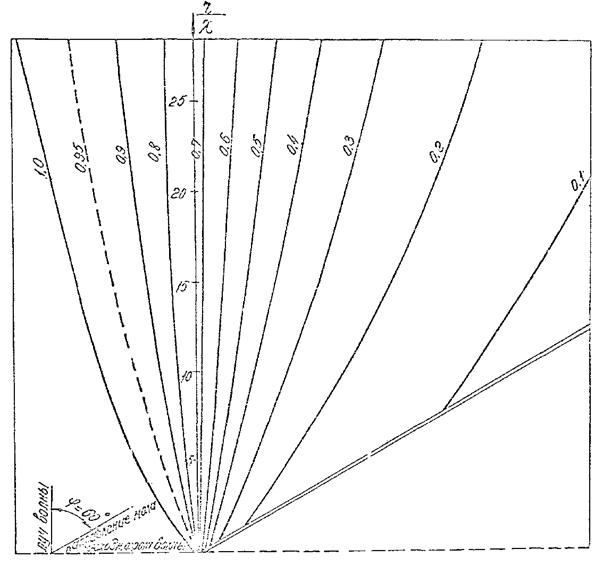
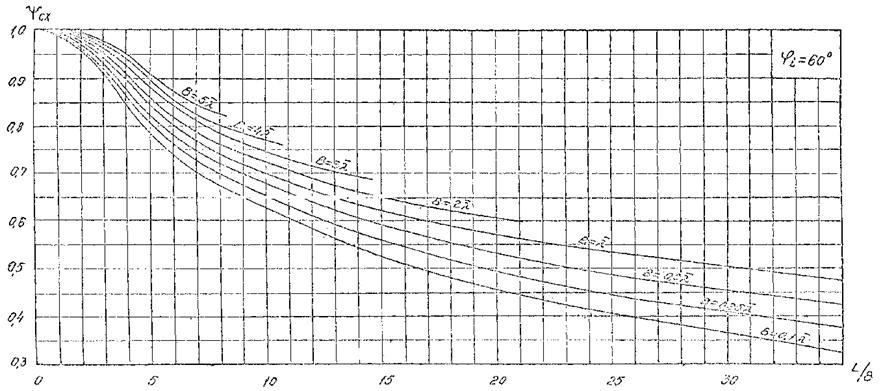
Рис. 7. График для определения коэффициента дифракции Кдо для угла φ = 60°.
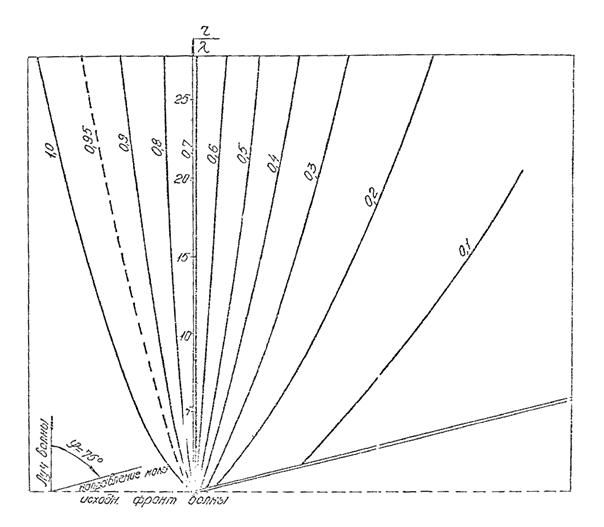
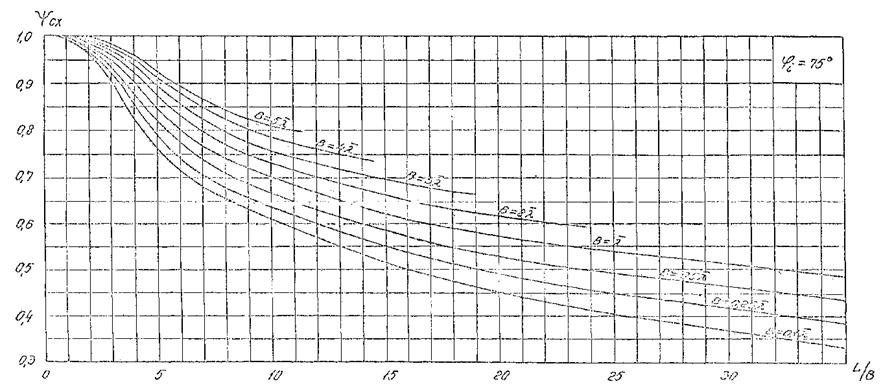
Рис. 8. График для определения коэффициента дифракции Кдо для угла φ = 75°.
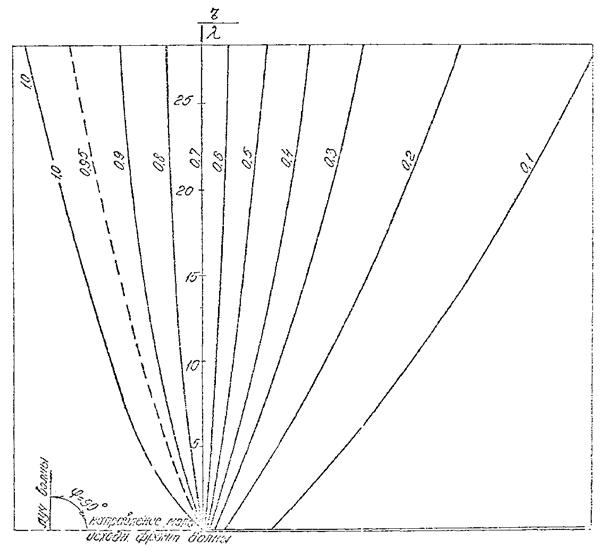
Рис. 9. График для определения коэффициента дифракции Кдо для угла φ = 90°.
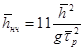
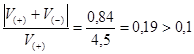 , выполняем
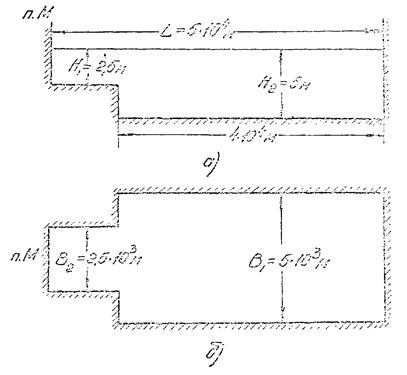
расчет второго приближения. Пусть Xо = 2,2 . 104 м.
В этом случае имеем
, выполняем
расчет второго приближения. Пусть Xо = 2,2 . 104 м.
В этом случае имеем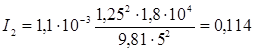 ;
; 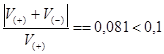 , ограничимся
расчетом второго приближения и принимаем величину нагона в п.М (
, ограничимся
расчетом второго приближения и принимаем величину нагона в п.М (