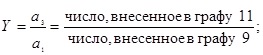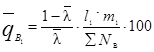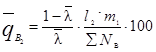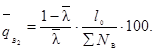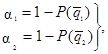ГОСТ 16493-70
МЕЖГОСУДАРСТВЕННЫЙ
СТАНДАРТ
КАЧЕСТВО ПРОДУКЦИИ.
СТАТИСТИЧЕСКИЙ ПРИЕМОЧНЫЙ
КОНТРОЛЬ ПО АЛЬТЕРНАТИВНОМУ
ПРИЗНАКУ
СЛУЧАИ НЕДОПУСТИМОСТИ ДЕФЕКТНЫХ ИЗДЕЛИЙ
В ВЫБОРКЕ
|

|
Москва
Стандартинформ
2011
|
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
|
КАЧЕСТВО ПРОДУКЦИИ
СТАТИСТИЧЕСКИЙ ПРИЕМОЧНЫЙ КОНТРОЛЬ
ПО АЛЬТЕРНАТИВНОМУ ПРИЗНАКУ
Случай недопустимости дефектных изделий в выборке
Product quality. Acceptance statistical
inspection by attributes when acceptable number
of defectives in sample equals 0
|
ГОСТ
16493-70
|
(Переиздание. Февраль
2011 г.)
Постановлением
Государственного комитета стандартов Совета Министров СССР от 15 января 1970г. № 1758 дата введения
установлена
01.01.72
Настоящий стандарт устанавливает планы контроля и
методы вычисления последующих оценок средних уровней входного и выходного
качества в случае, когда приемка партии при наличии дефектных изделий в выборке
является недопустимой по экономическим или иным соображениям.
Стандарт может применяться при статистическом
приемочном контроле по альтернативному признаку для всех видов промышленной
продукции, поступающей на контроль партиями.
Применение стандарта является обязательным, если на
него делаются ссылки в стандартах и технических условиях, устанавливающих
технические требования на продукцию.
Требования разд. 1
и 2 предназначены для контролеров и
других лиц, непосредственно осуществляющих контроль партий продукции, разд. 3 - для лиц, осуществляющих выбор
плана контроля; разд. 4 и 5 - для применения по решению руководителей
служб контроля или других лиц, ответственных за организацию и проведение
контроля.
1.
ПЛАН КОНТРОЛЯ И ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ
1.1. Под планом контроля понимается совокупность
сведений о порядке проведения контроля:
- совокупность значений объема выборки п в
зависимости от объема N контролируемой партии;
- вариант браковки.
1.2. План контроля имеет кодовое обозначение,
состоящее из:
- буквенного обозначения варианта плана контроля (см. п. 1.3);
-значения браковочного уровня качества (см. табл. 1);
-буквенного обозначения варианта браковки (см. п. 2.5). Пример кодового обозначения плана
контроля:
А 5,00 В ГОСТ 16493-70
Таблица 1
|
Браковочный
уровень качества qm,
%
|
А
|
Б
|
|
Объем партии N
|
Объем выборки n
|
Объем партии N
|
Объем выборки n
|
|
10,00
|
1 - 39
|
Все
|
1 - 49
|
Все
|
|
40 - 121
|
20
|
50 - 108
|
25
|
|
122 и более
|
25
|
109 и более
|
30
|
|
8,00
|
1 - 39
|
Все
|
1 - 59
|
Все
|
|
40 - 49
|
20
|
60 - 97
|
30
|
|
50 - 187
|
25
|
98 и более
|
40
|
|
138 и более
|
30
|
|
|
|
6,00
|
1 - 59
|
Все
|
1 - 79
|
Все
|
|
60 - 83
|
30
|
80 - 124
|
40
|
|
84 и более
|
40
|
125 и более
|
50
|
|
5,00
|
1 - 79
|
Все
|
1 - 99
|
Все
|
|
80 - 190
|
40
|
100 - 184
|
50
|
|
191 и более
|
50
|
185 и более
|
60
|
|
4,00
|
1 - 99
|
Все
|
1 - 119
|
Все
|
|
100 - 230
|
50
|
120 - 176
|
60
|
|
231 и более
|
60
|
177 и более
|
75
|
|
3,00
|
1 - 119
|
Все
|
1 - 149
|
Все
|
|
120 - 157
|
60
|
150 - 199
|
75
|
|
158 - 5248
|
75
|
200 и более
|
100
|
|
5249 и более
|
100
|
|
|
|
2,50
|
1 - 149
|
Все
|
1 - 199
|
Все
|
|
150 - 227
|
75
|
200 - 340
|
100
|
|
228 и более
|
100
|
341 и более
|
125
|
|
2,00
|
1 - 199
|
Все
|
1 - 249
|
Все
|
|
200 - 428
|
100
|
250 - 416
|
125
|
|
429 и более
|
125
|
417 и более
|
150
|
|
1,50
|
1 - 249
|
Все
|
1 - 299
|
Все
|
|
250 - 371
|
125
|
300 - 349
|
150
|
|
372 - 4500
|
150
|
350 - 787
|
175
|
|
4501 и более
|
175
|
788 и более
|
200
|
|
1,25
|
1 - 299
|
Все
|
1 - 349
|
Все
|
|
300 - 435
|
150
|
350 - 399
|
175
|
|
436 - 2000
|
175
|
400 - 666
|
200
|
|
2001 и более
|
200
|
667 и более
|
250
|
|
1,00
|
1 - 349
|
Все
|
1 - 499
|
Все
|
|
350 - 403
|
175
|
500 - 833
|
250
|
|
404 - 823
|
200
|
834 и более
|
300
|
|
824 и более
|
250
|
|
|
|
0,80
|
1 - 499
|
Все
|
1 - 599
|
Все
|
|
500 - 1041
|
250
|
600 - 818
|
300
|
|
1042 и более
|
300
|
819 и более
|
400
|
|
0,60
|
1 - 599
|
Все
|
1 - 799
|
Все
|
|
600 - 799
|
300
|
800 - 1111
|
400
|
|
800 и более
|
400
|
1112 и более
|
500
|
|
0,50
|
1 - 799
|
Все
|
1 - 999
|
Все
|
|
800 - 2185
|
400
|
1000 - 1666
|
500
|
|
2186 и более
|
500
|
1667 и более
|
600
|
|
0,40
|
1 - 999
|
Все
|
1 - 1199
|
Все
|
|
1000 - 2000
|
500
|
1200 - 1636
|
600
|
|
2001 и более
|
600
|
1637 и более
|
750
|
|
0,30
|
1 - 1199
|
Все
|
1 - 1499
|
Все
|
|
1200 - 1500
|
600
|
1500 - 1999
|
750
|
|
1501 - 15000
|
750
|
2000 и более
|
1000
|
|
15001 и более
|
1000
|
|
|
|
0,20
|
1 - 1999
|
Все
|
1 - 2499
|
Все
|
|
2000 - 4000
|
1000
|
2500 - 4166
|
1250
|
|
4001 и более
|
1250
|
4167 и более
|
1500
|
|
0,15
|
1 - 2499
|
Все
|
1 - 2999
|
Все
|
|
2500 - 3571
|
1250
|
3000 - 3499
|
1500
|
|
3572 и более
|
1500
|
3500 - 8750
|
1750
|
|
|
8751 и более
|
2000
|
|
0,10
|
1 - 3499
|
Все
|
1 - 4999
|
Все
|
|
3500 - 4375
|
1750
|
5000 - 8333
|
2500
|
|
4376 - 10000
|
2000
|
8334 и более
|
3000
|
|
10001 и более
|
2500
|
|
|
|
Менее 0,10
|
Объем выборки
вычислять по формуле n = 2,3/qm
|
|
Объем выборки
вычислять по формуле n = 3/qm
|
|
Примечание. Если вместо значения объема выборки написано «все»,
то это означает, что объем выборки превышает половину объема партии. В этом
случае выборочный контроль теряет смысл.
1.3. Вариантом плана контроля называется совокупность
зависимостей между объемом выборки п и объемом партии N
(при различных значениях браковочного уровня качества), соответствующая
заданному значению риска потребителя b.
Устанавливается два варианта плана контроля:
А - вариант плана контроля при b = 0,10;
Б - вариант плана контроля при b = 0,05.
1.4. Объем выборки из контролируемой партии определяют
в следующем порядке:
а) по кодовому обозначению плана контроля в табл. 1 отыскивают вертикальную графу,
соответствующую заданному варианту плана контроля, и горизонтальную графу,
соответствующую заданному значению браковочного уровня качества;
б) по значению объема контролируемой партии выбирают
соответствующее ему значение объема выборки (см. примеры 1 и 2
приложения 1).
2. ПОРЯДОК ПРОВЕДЕНИЯ КОНТРОЛЯ
2.1. После определения объема выборки контроль должен
проводиться в следующем порядке:
а) из партии извлекают случайную выборку определенного
объема;
б) проводят контроль изделий в выборке;
в) по результатам контроля принимают решение о партии.
2.2. Извлечение случайной выборки должно проводиться
по специальной методике, устанавливающей порядок случайного отбора изделий из
партии.
2.3. Контроль выборки допускается прекратить после
обнаружения первого дефектного изделия. Если предполагается вычисление
последующих оценок средних уровней входного и выходного качества, то контроль
после обнаружения первого дефектного изделия не должен прекращаться, и выборка
должна контролироваться полностью.
2.4. Решение о партии следует принимать по правилу:
- если в выборке не обнаружено ни одного дефектного
изделия - партия принимается;
- если в выборке обнаружено хотя бы одно дефектное
изделие - партия бракуется в соответствии с вариантом браковки, указанным в
кодовом обозначении плана контроля.
2.5. Предусматривается три варианта браковки:
В - партия возвращается поставщику;
К - проводится сплошной контроль всех изделий в партии
с возвращением всех дефектных изделий поставщику;
КЗ - проводится сплошной контроль всех изделий в
партии с заменой всех дефектных изделий годными.
2.6. Сведения о порядке контроля рекомендуется
заносить в инструкционную карту, которая должна находиться у лица,
осуществляющего контроль.
Форма инструкционной карты контроля приведена в
приложении 2.
2.7. При разделении изделий в выборке на годные и
дефектные необходимо учитывать возможные погрешности измерения контролируемых
характеристик. Величина допустимых погрешностей измерительных средств для
каждой отрасли, конкретной продукции и средств измерения устанавливается
соответствующей технической документацией, утвержденной в установленном
порядке.
3.
ВЫБОР ПЛАНА КОНТРОЛЯ
3.1. Для выбора плана ком роля следует определить:
-значение риска потребителя;
-значение браковочного уровня качества;
- вариант браковки.
3.2. Значение риска потребителя устанавливается
компетентными органами или соглашением между поставщиком и потребителем.
Примечание. Значение риска потребителя 0,05 соответствует более
жестким требованиям потребителя к качеству контролируемой продукции (см. разд. 2 приложения 5).
3.3. Значения браковочного уровня качества следует
выбирать исходя из значения qГ
граничного уровня качества, которое представляет собой максимально допустимую
долю дефектных изделий в партии и устанавливается компетентными органами или
соглашением между поставщиком и потребителем. По табл. 1 отыскивается ближайшее к заданному значению
граничного уровня качества значение браковочного уровня качества. Значение
браковочного уровня качества не должно превышать значения граничного уровня
качества.
3.4. Вариант браковки следует выбирать по правилу:
- если сплошной контроль изделий в партии невозможен,
то следует применять вариант браковки В;
- если сплошной контроль изделий в партии возможен, то
следует применять вариант браковки К или КЗ.
Примечания:
1.
Невозможность сплошного контроля определяется одной из причин:
а) контроль
приводит к разрушению изделия;
б) контроль
не приводит к разрушению изделия, но сплошной контроль изделий в партии
экономически нецелесообразен или технически неосуществим.
2. Конкретный
выбор вариантов браковки К и КЗ определяется практической возможностью замены
дефектных изделий годными
3 Примеры
выбора плана контроля приведены в приложении 1 (примеры 3
и 4).
4. ПОСТРОЕНИЕ ОПЕРАТИВНОЙ ХАРАКТЕРИСТИКИ
4.1. После выборки плана контроля рекомендуется
построить его оперативные характеристики. Оперативная характеристика позволяет
оценить вероятность приемки партии при любой доле дефектных изделий в партии
(см. разд. 2 приложения 5).
4.2. Оперативную характеристику плана контроля следует
строить исходя из кодового обозначения плана контроля и объема контролируемой
партии.
Примечание. Оперативная характеристика плана контроля не зависит
от варианта браковки и определяется двумя первыми позициями кодового
обозначения.
4.3. Построение оперативной характеристики должно
проводиться в следующем порядке:
а) по кодовому обозначению плана контроля и значению
объема партии отыскивается значение объема выборки;
б) вычисляется значение относительного объема выборки
по формуле 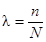 ; вычисление
проводится с точностью до трех цифр после запятой;
; вычисление
проводится с точностью до трех цифр после запятой;
в) из табл. 2
- 20 выбирается таблица,
соответствующая заданному значению объема выборки;
г) по вычисленному значению относительного объема
выборки в выбранной таблице отыскивается графа, содержащая точки оперативной
характеристики, и составляется таблица для построения оперативной
характеристики по форме1; точки с
номерами 1 и 9 одинаковы для любой оперативной характеристики;
д) точки с координатами, записанными в таблице для
построения оперативной характеристики, наносятся на график и соединяются
плавной линией (см. пример 5
приложения 1).
4.4. Если значение браковочного уровня качества менее
0,1 %, то оперативную характеристику следует строить по формуле:
P(q)
» e-nq.
Форма 1
Форма таблицы построения оперативной характеристики
|
Номер точки
|
Значение абсциссы qh, %
|
Значения ординаты P(qh)=h
|
Номер точки
|
Значение абсциссы qh, %
|
Значения ординаты P(qh)=h
|
|
1
|
0,00
|
1,00
|
6
|
q0,20
|
0,20
|
|
2
|
q0,95
|
0,95
|
7
|
q0,10
|
0,10
|
|
3
|
q0,90
|
0,90
|
8
|
q0,05
|
0,05
|
|
4
|
q0,80
|
0,80
|
9
|
q1,00
|
0,00
|
|
5
|
q0,50
|
0,50
|
|
|
|
Примечание. Если вычисленное
значение относительного объема выборки не содержится в верхней строке табл. 2 - 20, то следует брать значения квантилей, соответствующие
значению l, ближайшему к вычисленному,
или вычислять их значения линейной интерполяцией между квантилями,
соответствующими двум значениям l,
ближайшим к вычисленному.
5. ПОСЛЕДУЮЩИЕ ОЦЕНКИ СРЕДНИХ УРОВНЕЙ
ВХОДНОГО И ВЫХОДНОГО КАЧЕСТВА
5.1. Цель вычисления последующих оценок и условия,
необходимые для их вычисления
5.1.1. Последующими оценками средних уровней входного
и выходного качества называются оценки значений средних уровней входного и
выходного качества, вычисленные по результатам контроля нескольких партий.
5.1.2. Последующие оценки средних уровней входного и
выходного качества допускается применять:
- для корректировки плана контроля;
- для вычисления риска поставщика при применении
выбранного плана контроля;
- для надзора за качеством продукции с целью принятия
решения о наладке, настройке или изменении производственного процесса;
- для сравнения качества продукции различных
предприятий, при изменении технологии производства, при использовании разных
материалов и т.п.;
- для экономического стимулирования и подведения
итогов социалистического соревнования;
- для оценки деятельности подразделений,
осуществляющих контроль или несущих ответственность за его проведение;
- для оценки обоснованности претензий потребителя к
поставщику и в других аналогичных случаях.
Примечание. Примеры применения последующих оценок средних уровней
качества приведены в приложении 5
5.1.3. При вычислении, последующих оценок:
а) должны использоваться результаты контроля не менее
чем десяти партий;
б) в каждой выборке должны быть проконтролированы все
изделия.
5.2. Порядок вычисления оценок средних уровней
входного и выходного качества при варианте браковки В.
5.2.1. Для вычисления последующих оценок средних
уровней входного и выходного качества заполняют таблицу по форме 2.
Форма 2
Форма таблицы для последующих оценок
|
Номер партии
|
Исходные данные
|
Результаты
вычислений
|
|
Объем партии N
|
Объем выборки n
|
Число дефектных
изделий в выборке d
|
Решение о партии
|
Число принятых изделий
в партии Nв
|
Относительный
объем выборки l
|
Оценка числа
дефектных изделий в партии
|
|
до контроля Х
|
после контроля Y
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
|
|
|
|
|
|
|
|
5.2.2. В графы 1 - 4 таблицы для последующих оценок
записывают данные контроля по каждой партии.
5.2.3. В графу 5 записывают решение о партии словами:
«принята» или «забракована».
5.2.4. В графу 6 данные записывают по правилу:
если партия принята - значение объема партии;
если партия забракована - нуль.
5.2.5. В графу 7 записывают результат, вычисленный по
формуле:
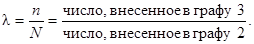
5.2.6. Если партия принимается, то в
графах 8 и 9 проставляют нули.
Если партия бракуется и в выборке обнаружено только
одно дефектное изделие, то графы 8 и 9 заполняют следующим образом:
a) В графе 8 записывают результат, вычисленный по
формуле:

б) в графе 9 записывают результат,
вычисленный по формуле:
Y = X
- 1=(число, внесенное в графу 8) - 1.
Если партия бракуется и в выборке обнаружено больше
одного дефектного изделия, то графы 8 и 9 заполняют следующим образом:
а) в графе 8 записывают результат,
вычисленный по формуле:
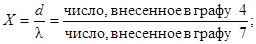
б) в графе 9 проставляют нуль.
5.2.7. Оценки средних уровней входного и выходного
качества вычисляют на основе результатов, внесенных в таблицу:
а) суммируются все числа, внесенные в графу 2 (S N);
б) суммируются все числа, внесенные в графу 8 (S X);
в) вычисляется оценка среднего уровня входного
качества 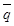 по
формуле:
по
формуле:
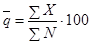 ; (1)
; (1)
г) суммируются все числа, внесенные в
графу 9 (S Y);
д) суммируются все числа, внесенные в графу 6 (S NB);
е) вычисляется оценка среднего уровня выходного
качества 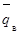 по формуле:
по формуле:
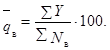 (2)
(2)
Пример вычисления оценки средних уровней
входного и выгодного качества при варианте браковки В приведен в приложении 1 (пример 7).
5.3. Порядок вычисления оценок средних уровней входного и
выходного качества при варианте браковки К
5.3.1. Для вычисления последующих оценок средних
уровней входного и выходного качества заполняют таблицу для последующих оценок
по форме 3.
5.3.2. В графы 1 - 7 записывают исходные данные для
вычисления последующих оценок.
Форма 3
Форма таблицы для последующих оценок
|
Номер партии
|
Исходные данные
|
Результаты
вычислений
|
|
Объем партии N
|
Объем выборки n
|
Число дефектных
изделий в выборке d
|
Решение о партии
|
Общее число
дефектных изделий, обнаруженных в партии, D
|
Число принятых
изделий в партии Nв
|
Относительный
объем выборки l
|
Значение
коэффициента а1
|
Значение
коэффициента а2
|
Значение
коэффициента а3
|
дефектных в партии
|
w2
|
|
после контроля
|
до контроля
|
|
Y
|
X
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графы 4 и 6 заполняют по правилу:
если партия принимается - проставляют нули;
если партия бракуется - в графы 4 записывают число
дефектных изделий, обнаруженных в
выборке, в графе 6 - общее число дефектных изделий во всей разбракованной
партии (включая выборку).
В графе 5 записывают решение о партии словами:
«принята» или «забракована».
В графе 7 записывают число принятых изделий в партии
по правилу:
если партия принимается - значение объема партии,
указанное в графе 2;
если партия бракуется - результат, вычисленный по
формуле:
NB = N - D=(число, внесенное в графу 2) -
(число, внесенное в графу 6).
5.3.3. В графу 8 записывают результат, вычисленный по формуле:
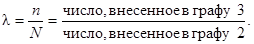
5.3.4. Если партия принимается, графы 9
- 13 заполняют следующим образом:
а) в графах 9 и 11 проставляют прочерк;
б) в графах 10, 12 и 13 проставляют нули.
5.3.5. Если партия бракуется, графы 9 - 13 заполняют
следующим образом:
а) по значению относительного объема выборки,
внесенному в графу 8, в табл. 21
находят значение коэффициента а1; значения относительного
объема выборки до второго знака после запятой указаны в первой графе слева,
значения второго знака после запятой указаны в шапке таблицы, результаты,
найденные в табл. 21, записывают в
графу 9;
б) вычисляют значение коэффициента a2
по формуле:
a = a1
· D = (число, внесенное в графу 9)·(число, внесенное в графу 6);
результат вычисления записывают в графу 10;
в) по значению коэффициента а2 в табл. 22 находят значение коэффициента а3;
целые части значений коэффициента а2 помещены в первой графе
слева, дробные части - в шапке таблицы; результат, найденный в табл. 22, записывают в графу 11;
г) в графе 12 записывают результат, вычисленный по
формуле:
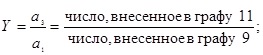
д) в графе 13 записывают результат,
вычисленный по формуле:
X = D
+ Y = (число, внесенное в графу 6) + (число, внесенное в графу 12).
5.3.6. Оценки средних уровней входного и выходного
качества вычисляются на основе результатов, внесенных в таблицу:
а) суммируются все числа, внесенные в графу 2 (S N);
б) суммируются все числа, внесенные в графу 13 (S Y);
в) вычисляется оценка среднего уровня входного
качества 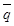 но формуле
но формуле
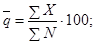 (3)
(3)
г) суммируются все числа, внесенные в графу 7 (S NB);
д) суммируются все числа, внесенные в графу 12 (S Y);
е) вычисляется оценка среднего уровня выходного
качества 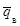 по формуле:
по формуле:
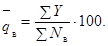 (4)
(4)
Пример оценки средних уровней входного и
выходного качества при варианте браковки К приведен в приложении 1 (пример 8).
Примечание.
Графа 14 заполняется при вычислении доверительных границ для средних уровней
входного и выходного качества (см. приложение 5).
5.4. Порядок вычисления оценок средних уровней
входного и выходного качества при варианте браковки КЗ
5.4.1. Для вычисления оценок средних уровней входного
и выходного качества заполняют таблицу для последующих оценок по форме 3.
542. Таблица заполняется так же, как указано в п. 5.3, со следующими изменениями: в
графе 7 записывают данные, внесенные в графу 2.
5.4.3 Вычисление значений 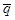 и
и 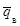 производят по формулам (3) и (4).
производят по формулам (3) и (4).
Таблица 2
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 20
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,19
|
0,20
|
0,20
|
0,21
|
0,22
|
0,22
|
0,23
|
0,23
|
0,24
|
0,25
|
0,26
|
|
q0,90
|
0,39
|
0,41
|
0,42
|
0,44
|
0,45
|
0,46
|
0,47
|
0,49
|
0,50
|
0,51
|
0,53
|
|
q0,80
|
0,81
|
0,85
|
0,88
|
0,91
|
0,91
|
0,97
|
1,00
|
1,03
|
1,06
|
1,08
|
1,11
|
|
q0,50
|
2,50
|
2,60
|
2,70
|
2,80
|
2,89
|
2,98
|
3,07
|
3,16
|
3,24
|
3,32
|
3,41
|
|
q0,20
|
5,67
|
5,90
|
6,13
|
6,35
|
6,56
|
6,77
|
6,97
|
7,17
|
7,36
|
7,54
|
7,73
|
|
q0,10
|
7,97
|
8,30
|
8,62
|
8,92
|
9,22
|
9,51
|
9,80
|
10,08
|
10,37
|
10,63
|
10,89
|
|
q0,05
|
10,21
|
10,63
|
11,05
|
11,44
|
11,82
|
12,19
|
12,56
|
12,91
|
13,26
|
13,59
|
13,92
|
|
qL
|
1,35
|
1,41
|
1,46
|
1,51
|
1,56
|
1,61
|
1,66
|
1,71
|
1,76
|
1,80
|
1,85
|
Таблица 3
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 25
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,15
|
0,16
|
0,16
|
0,17
|
0,17
|
0,18
|
0,18
|
0,19
|
0,19
|
0,20
|
0,20
|
|
q0,90
|
0,31
|
0,32
|
0,33
|
0,35
|
0,36
|
0,37
|
0,38
|
0,39
|
0,40
|
0,41
|
0,42
|
|
q0,80
|
0,65
|
0,68
|
0,70
|
0,73
|
0,75
|
0,78
|
0,80
|
0,83
|
0,85
|
0,87
|
0,89
|
|
q0,50
|
2,00
|
2,08
|
2,16
|
2,24
|
2,32
|
2,39
|
2,46
|
2,53
|
2,60
|
2,67
|
2,73
|
|
q0,20
|
4,56
|
4,74
|
4,92
|
5,10
|
5,28
|
5,45
|
5,61
|
5,77
|
5,93
|
6,08
|
6,24
|
|
q0,10
|
6,43
|
6,70
|
6,96
|
7,21
|
7,45
|
7,69
|
7,92
|
8,12
|
8,37
|
8,59
|
8,80
|
|
q0,05
|
8,24
|
8,58
|
8,92
|
9,24
|
9,56
|
9,88
|
10,19
|
10,48
|
10,77
|
11,05
|
11,32
|
|
qL
|
1,07
|
1,12
|
1,16
|
1,21
|
1,25
|
1,29
|
1,33
|
1,37
|
1,40
|
1,44
|
1,48
|
Таблица 4
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 30
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,12
|
0,13
|
0,13
|
0,14
|
0,14
|
0,15
|
0,15
|
0,16
|
0,16
|
0,17
|
0,17
|
|
q0,90
|
0,26
|
0,27
|
0,28
|
0,29
|
0,30
|
0,31
|
0,32
|
0,33
|
0,33
|
0,34
|
0,35
|
|
q0,80
|
0,54
|
0,57
|
0,59
|
0,61
|
0,63
|
0,65
|
0,67
|
0,69
|
0,70
|
0,72
|
0,74
|
|
q0,50
|
1,67
|
1,74
|
1,80
|
1,87
|
1,93
|
2,00
|
2,06
|
2,11
|
2,17
|
2,23
|
2,28
|
|
q0,20
|
3,81
|
3,97
|
4,12
|
4,27
|
4,42
|
4,56
|
4,70
|
4,84
|
4,97
|
5,09
|
5,22
|
|
q0,10
|
5,39
|
5,61
|
5,83
|
6,04
|
6,25
|
6,45
|
6,65
|
6,84
|
7,02
|
7,21
|
7,39
|
|
q0,05
|
6,92
|
7,21
|
7,50
|
7,77
|
8,04
|
8,30
|
8,55
|
8,80
|
9,04
|
9,27
|
9,50
|
|
qL
|
0,89
|
0,93
|
0,97
|
1,01
|
1,04
|
1,07
|
1,10
|
1,14
|
1,17
|
1,20
|
1,23
|
Таблица 5
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 40
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,09
|
0,10
|
0,10
|
0,11
|
0,11
|
0,11
|
0,12
|
0,12
|
0,12
|
0,13
|
0,13
|
|
q0,90
|
0,19
|
0,20
|
0,21
|
0,22
|
0,22
|
0,23
|
0,24
|
0,25
|
0,25
|
0,26
|
0,26
|
|
q0,80
|
0,40
|
0,42
|
0,44
|
0,46
|
0,47
|
0,49
|
0,50
|
0,52
|
0,53
|
0,54
|
0,56
|
|
q0,50
|
1,25
|
1,30
|
1,34
|
1,40
|
1,45
|
1,50
|
1,54
|
1,59
|
1,60
|
1,68
|
1,72
|
|
q0,20
|
2,87
|
2,99
|
3,11
|
3,22
|
3,33
|
3,44
|
3,54
|
3,65
|
3,75
|
3,85
|
3,94
|
|
q0,10
|
4,07
|
4,24
|
4,41
|
4,57
|
4,73
|
4,88
|
5,03
|
5,18
|
5,32
|
5,46
|
5,59
|
|
q0,05
|
5,24
|
5,46
|
5,68
|
5,89
|
6,09
|
6,29
|
6,48
|
6,67
|
6,86
|
7,04
|
7,22
|
|
qL
|
0,67
|
0,70
|
0,72
|
0,75
|
0,78
|
0,81
|
0,83
|
0,86
|
0,88
|
0,90
|
0,92
|
Таблица 6
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 50
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,07
|
0,08
|
0,08
|
0,09
|
0,09
|
0,09
|
0,09
|
0,10
|
0,10
|
0,10
|
0,10
|
|
q0,90
|
0,15
|
0,16
|
0,17
|
0,18
|
0,18
|
0,19
|
0,19
|
0,20
|
0,20
|
0,21
|
0,21
|
|
q0,80
|
0,32
|
0,34
|
0,35
|
0,37
|
0,38
|
0,39
|
0,40
|
0,41
|
0,42
|
0,43
|
0,45
|
|
q0,50
|
1,00
|
1,04
|
1,08
|
1,12
|
1,16
|
1,20
|
1,24
|
1,28
|
1,31
|
1,34
|
1,38
|
|
q0,20
|
2,30
|
2,40
|
2,49
|
2,58
|
2,67
|
2,76
|
2,85
|
2,93
|
3,01
|
3,09
|
3,17
|
|
q0,10
|
3,27
|
3,41
|
3,54
|
3,67
|
3,80
|
3,92
|
4,04
|
4,16
|
4,28
|
4,39
|
4,50
|
|
q0,05
|
4,22
|
4,40
|
4,58
|
4,75
|
4,91
|
5,07
|
5,22
|
5,38
|
5,53
|
5,67
|
5,81
|
|
qL
|
0,53
|
0,56
|
0,58
|
0,60
|
0,62
|
0,64
|
0,66
|
0,68
|
0,70
|
0,72
|
0,74
|
Таблица 7
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 60
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,06
|
0,06
|
0,07
|
0,07
|
0,07
|
0,08
|
0,08
|
0,08
|
0,08
|
0,08
|
0,09
|
|
q0,90
|
0,13
|
0,14
|
0,14
|
0,15
|
0,15
|
0,16
|
0,16
|
0,16
|
0,17
|
0,17
|
0,18
|
|
q0,80
|
0,27
|
0,28
|
0,29
|
0,30
|
0,31
|
0,32
|
0,33
|
0,34
|
0,35
|
0,36
|
0,37
|
|
q0,50
|
0,83
|
0,87
|
0,90
|
0,94
|
0,97
|
1,00
|
1,03
|
1,06
|
1,09
|
1,12
|
1,15
|
|
q0,20
|
1,92
|
2,00
|
2,08
|
2,16
|
2,23
|
2,30
|
2,37
|
2,44
|
2,51
|
2,59
|
2,67
|
|
q0,10
|
2,72
|
2,84
|
2,96
|
3,07
|
3,18
|
3,28
|
3,38
|
3,48
|
3,58
|
3,68
|
3,77
|
|
q0,05
|
3,53
|
3,68
|
3,83
|
3,97
|
4,11
|
4,24
|
4,37
|
4,50
|
4,63
|
4,75
|
4,87
|
|
qL
|
0,44
|
0,46
|
0,48
|
0,50
|
0,52
|
0,54
|
0,55
|
0,57
|
0,58
|
0,59
|
0,61
|
Таблица 8
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 75
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,05
|
0,05
|
0,05
|
0,06
|
0,06
|
0,06
|
0,06
|
0,06
|
0,06
|
0,07
|
0,07
|
|
q0,90
|
0,10
|
0,11
|
0,11
|
0,12
|
0,12
|
0,13
|
0,13
|
0,13
|
0,13
|
0,14
|
0,14
|
|
q0,80
|
0,22
|
0,23
|
0,23
|
0,24
|
0,25
|
0,26
|
0,27
|
0,28
|
0,28
|
0,29
|
0,30
|
|
q0,50
|
0,67
|
0,70
|
0,72
|
0,75
|
0,78
|
0,81
|
0,83
|
0,85
|
0,87
|
0,90
|
0,92
|
|
q0,20
|
1,54
|
1,61
|
1,67
|
1,73
|
1,79
|
1,85
|
1,91
|
1,97
|
2,02
|
2,07
|
2,12
|
|
q0,10
|
2,19
|
2,29
|
2,38
|
2,47
|
2,55
|
2,63
|
2,71
|
2,79
|
2,87
|
2,95
|
3,02
|
|
q0,05
|
2,84
|
2,36
|
3,08
|
3,19
|
3,30
|
3,41
|
3,51
|
3,62
|
3,72
|
3,82
|
3,92
|
|
qL
|
0,35
|
0,37
|
0,38
|
0,40
|
0,41
|
0,43
|
0,44
|
0,46
|
0,47
|
0,48
|
0,49
|
Таблица 9
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 100
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
|
q0,90
|
0,08
|
0,08
|
0,08
|
0,09
|
0,09
|
0,09
|
0,09
|
0,10
|
0,10
|
0,10
|
0,11
|
|
q0,80
|
0,16
|
0,17
|
0,18
|
0,18
|
0,19
|
0,19
|
0,20
|
0,21
|
0,21
|
0,22
|
0,22
|
|
q0,50
|
0,50
|
0,52
|
0,54
|
0,56
|
0,58
|
0,60
|
0,62
|
0,64
|
0,66
|
0,67
|
0,69
|
|
q0,20
|
1,16
|
1,21
|
1,26
|
1,31
|
1,35
|
1,39
|
1,43
|
1,48
|
1,52
|
1,56
|
1,60
|
|
q0,10
|
1,65
|
1,72
|
1,79
|
1,86
|
1,92
|
1,98
|
2,04
|
2,10
|
2,16
|
2,22
|
2,28
|
|
q0,05
|
2,14
|
2,23
|
2,32
|
2,41
|
2,49
|
2,57
|
2,65
|
2,73
|
2,80
|
2,88
|
2,95
|
|
qL
|
0,27
|
0,28
|
0,29
|
0,30
|
0,31
|
0,32
|
0,33
|
0,34
|
0,35
|
0,36
|
0,37
|
Таблица 10
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 125
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
|
q0,90
|
0,06
|
0,06
|
0,07
|
0,07
|
0,07
|
0,08
|
0,08
|
0,08
|
0,08
|
0,08
|
0,08
|
|
q0,80
|
0,13
|
0,14
|
0,14
|
0,15
|
0,15
|
0,16
|
0,16
|
0,17
|
0,17
|
0,17
|
0,18
|
|
q0,50
|
0,40
|
0,42
|
0,43
|
0,45
|
0,47
|
0,49
|
0,50
|
0,52
|
0,53
|
0,54
|
0,55
|
|
q0,20
|
0,93
|
0,97
|
1,00
|
1,04
|
1,08
|
1,12
|
1,15
|
1,19
|
1,22
|
1,25
|
1,28
|
|
q0,10
|
1,32
|
1,38
|
1,43
|
1,49
|
1,54
|
1,59
|
1,64
|
1,69
|
1,74
|
1,78
|
1,83
|
|
q0,05
|
1,71
|
1,79
|
1,86
|
1,93
|
2,00
|
2,07
|
2,13
|
2,19
|
2,25
|
2,31
|
2,37
|
|
qL
|
0,21
|
0,22
|
0,23
|
0,24
|
0,25
|
0,26
|
0,26
|
0,28
|
0,28
|
0,29
|
0,29
|
Таблица 11
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 150
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,02
|
0,02
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
|
q0,90
|
0,05
|
0,06
|
0,06
|
0,06
|
0,06
|
0,06
|
0,06
|
0,07
|
0,07
|
0,07
|
0,07
|
|
q0,80
|
0,11
|
0,12
|
0,12
|
0,13
|
0,13
|
0,13
|
0,13
|
0,14
|
0,14
|
0,14
|
0,15
|
|
q0,50
|
0,33
|
0,35
|
0,36
|
0,38
|
0,39
|
0,40
|
0,41
|
0,43
|
0,44
|
0,45
|
0,46
|
|
q0,20
|
0,77
|
0,81
|
0,84
|
0,87
|
0,90
|
0,93
|
0,96
|
0,99
|
1,01
|
1,04
|
1,07
|
|
q0,10
|
1,10
|
1,15
|
1,20
|
1,25
|
1,29
|
1,33
|
1,37
|
1,41
|
1,45
|
1,49
|
1,52
|
|
q0,05
|
1,43
|
1,49
|
1,55
|
1,61
|
1,67
|
1,73
|
1,78
|
1,83
|
1,88
|
1,93
|
1,98
|
|
qL
|
0,18
|
0,19
|
0,19
|
0,20
|
0,21
|
0,22
|
0,22
|
0,23
|
0,23
|
0,24
|
0,25
|
Таблица 12
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 175
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
|
q0,90
|
0,04
|
0,04
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,06
|
0,06
|
0,06
|
0,06
|
|
q0,80
|
0,09
|
0,10
|
0,10
|
0,11
|
0,11
|
0,11
|
0,11
|
0,12
|
0,12
|
0,12
|
0,13
|
|
q0,50
|
0,29
|
0,30
|
0,31
|
0,32
|
0,33
|
0,34
|
0,35
|
0,37
|
0,38
|
0,39
|
0,40
|
|
q0,20
|
0,66
|
0,69
|
0,72
|
0,75
|
0,77
|
0,80
|
0,82
|
0,85
|
0,87
|
0,89
|
0,92
|
|
q0,10
|
0,94
|
0,99
|
1,03
|
1,07
|
1,10
|
1,14
|
1,17
|
1,21
|
1,24
|
1,28
|
1,31
|
|
q0,05
|
1,23
|
1,28
|
1,33
|
1,38
|
1,43
|
1,48
|
1,52
|
1,57
|
1,61
|
1,66
|
1,70
|
|
qL
|
0,15
|
0,16
|
0,16
|
0,17
|
0,18
|
0,19
|
0,19
|
0,20
|
0,20
|
0,20
|
0,21
|
Таблица 13
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 200
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,03
|
0,03
|
|
q0,90
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
|
q0,80
|
0,08
|
0,09
|
0,09
|
0,09
|
0,09
|
0,10
|
0,10
|
0,11
|
0,11
|
0,11
|
0,11
|
|
q0,50
|
0,25
|
0,26
|
0,27
|
0,28
|
0,29
|
0,30
|
0,31
|
0,32
|
0,33
|
0,34
|
0,35
|
|
q0,20
|
0,58
|
0,61
|
0,63
|
0,65
|
0,67
|
0,70
|
0,72
|
0,74
|
0,76
|
0,78
|
0,80
|
|
q0,10
|
0,83
|
0,87
|
0,90
|
0,93
|
0,96
|
1,00
|
1,03
|
1,06
|
1,09
|
1,12
|
1,14
|
|
q0,05
|
1,07
|
1,12
|
1,17
|
1,21
|
1,25
|
1,29
|
1,33
|
1,37
|
1,41
|
1,45
|
1,49
|
|
qL
|
0,13
|
0,14
|
0,14
|
0,15
|
0,15
|
0,16
|
0,16
|
0,17
|
0,17
|
0,18
|
0,19
|
Таблица 14
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 250
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,01
|
0,01
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
|
q0,90
|
0,03
|
0,03
|
0,03
|
0,03
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
|
q0,80
|
0,05
|
0,06
|
0,07
|
0,08
|
0,08
|
0,08
|
0,08
|
0,08
|
0,08
|
0,09
|
0,09
|
|
q0,50
|
0,20
|
0,21
|
0,22
|
0,23
|
0,23
|
0,24
|
0,25
|
0,26
|
0,26
|
0,27
|
0,28
|
|
q0,20
|
0,46
|
0,48
|
0,50
|
0,52
|
0,54
|
0,56
|
0,58
|
0,60
|
0,61
|
0,63
|
0,64
|
|
q0,10
|
0,66
|
0,69
|
0,72
|
0,75
|
0,77
|
0,80
|
0,82
|
0,84
|
0,87
|
0,89
|
0,92
|
|
q0,05
|
0,86
|
0,90
|
0,93
|
0,97
|
1,00
|
1,04
|
1,07
|
1,10
|
1,13
|
1,16
|
1,19
|
|
qL
|
0,11
|
0,11
|
0,12
|
0,12
|
0,12
|
0,13
|
0,13
|
0,14
|
0,14
|
0,14
|
0,15
|
Таблица 15
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 300
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
|
q0,90
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,04
|
|
q0,80
|
0,05
|
0,06
|
0,06
|
0,06
|
0,06
|
0,07
|
0,07
|
0,07
|
0,07
|
0,07
|
0,07
|
|
q0,50
|
0,17
|
0,18
|
0,18
|
0,19
|
0,19
|
0,20
|
0,21
|
0,21
|
0,22
|
0,22
|
0,23
|
|
q0,20
|
0,39
|
0,41
|
0,42
|
0,44
|
0,45
|
0,47
|
0,48
|
0,50
|
0,51
|
0,52
|
0,54
|
|
q0,10
|
0,55
|
0,58
|
0,60
|
0,62
|
0,64
|
0,67
|
0,69
|
0,71
|
0,73
|
0,75
|
0,76
|
|
q0,05
|
0,72
|
0,75
|
0,78
|
0,81
|
0,84
|
0,87
|
0,89
|
0,92
|
0,94
|
0,97
|
0,99
|
|
qL
|
0,09
|
0,09
|
0,10
|
0,10
|
0,10
|
0,11
|
0,11
|
0,11
|
0,12
|
0,12
|
0,12
|
Таблица 16
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 400
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
|
q0,90
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,03
|
0,03
|
0,03
|
0,03
|
|
q0,80
|
0,04
|
0,04
|
0,04
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,06
|
|
q0,50
|
0,13
|
0,14
|
0,14
|
0,15
|
0,15
|
0,16
|
0,16
|
0,16
|
0,16
|
0,17
|
0,17
|
|
q0,20
|
0,29
|
0,30
|
0,31
|
0,33
|
0,34
|
0,35
|
0,36
|
0,37
|
0,38
|
0,39
|
0,40
|
|
q0,10
|
0,41
|
0,43
|
0,45
|
0,47
|
0,48
|
0,50
|
0,51
|
0,53
|
0,54
|
0,56
|
0,57
|
|
q0,05
|
0,54
|
0,56
|
0,58
|
0,61
|
0,63
|
0,65
|
0,67
|
0,69
|
0,71
|
0,73
|
0,75
|
|
qL
|
0,07
|
0,07
|
0,07
|
0,08
|
0,08
|
0,08
|
0,08
|
0,09
|
0,09
|
0,09
|
0,09
|
Таблица 17
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 500
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
|
q0,90
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
|
q0,80
|
0,03
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
|
q0,50
|
0,10
|
0,11
|
0,11
|
0,12
|
0,12
|
0,12
|
0,12
|
0,13
|
0,13
|
0,14
|
0,14
|
|
q0,20
|
0,23
|
0,24
|
0,25
|
0,26
|
0,27
|
0,28
|
0,29
|
0,30
|
0,31
|
0,31
|
0,32
|
|
q0,10
|
0,33
|
0,35
|
0,36
|
0,38
|
0,39
|
0,40
|
0,41
|
0,43
|
0,44
|
0,45
|
0,46
|
|
q0,05
|
0,43
|
0,45
|
0,47
|
0,49
|
0,50
|
0,52
|
0,54
|
0,56
|
0,57
|
0,58
|
0,60
|
|
qL
|
0,05
|
0,05
|
0,06
|
0,06
|
0,06
|
0,07
|
0,07
|
0,07
|
0,07
|
0,07
|
0,07
|
Таблица 18
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 600
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
|
q0,90
|
0,01
|
0,01
|
0,01
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
|
q0,80
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,04
|
0,04
|
0,04
|
0,04
|
|
q0,50
|
0,08
|
0,09
|
0,09
|
0,10
|
0,10
|
0,10
|
0,10
|
0,11
|
0,11
|
0,11
|
0,12
|
|
q0,20
|
0,19
|
0,20
|
0,21
|
0,22
|
0,23
|
0,24
|
0,24
|
0,25
|
0,25
|
0,26
|
0,27
|
|
q0,10
|
0,28
|
0,29
|
0,30
|
0,31
|
0,32
|
0,33
|
0,34
|
0,35
|
0,36
|
0,37
|
0,38
|
|
q0,05
|
0,36
|
0,38
|
0,39
|
0,41
|
0,42
|
0,44
|
0,45
|
0,46
|
0,47
|
0,49
|
0,50
|
|
qL
|
0,04
|
0,04
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,06
|
0,06
|
0,06
|
0,06
|
Таблица 19
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 750
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,00
|
0,00
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
|
q0,90
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
|
q0,80
|
0,02
|
0,02
|
0,02
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
|
q0,50
|
0,07
|
0,07
|
0,07
|
0,07
|
0,08
|
0,08
|
0,08
|
0,08
|
0,09
|
0,09
|
0,09
|
|
q0,20
|
0,15
|
0,16
|
0,17
|
0,18
|
0,18
|
0,19
|
0,19
|
0,20
|
0,20
|
0,21
|
0,21
|
|
q0,10
|
0,22
|
0,23
|
0,24
|
0,25
|
0,26
|
0,27
|
0,27
|
0,28
|
0,29
|
0,30
|
0,31
|
|
q0,05
|
0,29
|
0,30
|
0,31
|
0,33
|
0,34
|
0,35
|
0,36
|
0,37
|
0,38
|
0,39
|
0,40
|
|
qL
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,05
|
0,05
|
0,05
|
0,05
|
Таблица 20
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 1000
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,01
|
|
q0,90
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,01
|
0,01
|
0,01
|
0,01
|
|
q0,80
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
|
q0,50
|
0,05
|
0,05
|
0,05
|
0,06
|
0,06
|
0,06
|
0,06
|
0,07
|
0,07
|
0,07
|
0,07
|
|
q0,20
|
0,12
|
0,13
|
0,13
|
0,14
|
0,14
|
0,14
|
0,14
|
0,15
|
0,15
|
0,16
|
0,16
|
|
q0,10
|
0,17
|
0,18
|
0,18
|
0,19
|
0,19
|
0,20
|
0,21
|
0,22
|
0,22
|
0,22
|
0,23
|
|
q0,05
|
0,22
|
0,23
|
0,23
|
0,24
|
0,25
|
0,26
|
0,27
|
0,28
|
0,28
|
0,29
|
0,30
|
|
qL
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,03
|
0,04
|
0,04
|
Примечание. В последней строке табл. 2 - 20 даны значения предела среднего уровня входного
качества qL.
Принципы
применения этого показателя излагаются в приложении 5.
Таблица 21
Значения коэффициента а1
|
Значения
относительного объема выборки до второго знака после запятой
|
Значения
коэффициента а1 при значениях относительного объема
выборки, взятых с точностью до второго знака после запятой
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
0,0
|
0,000
|
0,010
|
0,020
|
0,031
|
0,041
|
0,052
|
0,062
|
0,073
|
0,084
|
0,095
|
|
0,1
|
0,106
|
0,117
|
0,128
|
0,140
|
0,151
|
0,162
|
0,174
|
0,186
|
0,198
|
0,211
|
|
0,2
|
0,224
|
0,236
|
0,249
|
0,261
|
0,274
|
0,288
|
0,301
|
0315
|
0,328
|
0,342
|
|
0,3
|
0,357
|
0,371
|
0,385
|
0,401
|
0,416
|
0,431
|
0,446
|
0,462
|
0,478
|
0,494
|
|
0,4
|
0,512
|
0,528
|
0,545
|
0,562
|
0,580
|
0,598
|
0,516
|
0,635
|
0,654
|
0,673
|
|
0,5
|
0,695
|
0,713
|
0,734
|
0,755
|
0,776
|
0,798
|
0,821
|
0,844
|
0,868
|
0,892
|
Таблица 22
Значения коэффициента а3
|
Целая часть
значения коэффициента а2
|
Значения
коэффициента а3 при значениях коэффициента а2,
взятых с точностью до первого знака после запятой
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
0
|
1,00
|
0,95
|
0,90
|
0,86
|
0,81
|
0,77
|
0,73
|
0,69
|
0,65
|
0,62
|
|
1
|
0,58
|
0,55
|
0,52
|
0,49
|
0,46
|
0,43
|
0,40
|
0,38
|
0,36
|
0,33
|
|
2
|
0,31
|
0,29
|
0,27
|
0,26
|
0,24
|
0,22
|
0,21
|
0,19
|
0,18
|
0,17
|
|
3
|
0,16
|
0,15
|
0,14
|
0,13
|
0,12
|
0,11
|
0,10
|
0,09
|
0,09
|
0,08
|
|
4
|
0,07
|
0,07
|
0,06
|
0,06
|
0,05
|
0,05
|
0,05
|
0,04
|
0,04
|
0,04
|
|
5
|
0,03
|
0,03
|
0,03
|
0,03
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
|
6
|
0,02
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
|
7
|
0,01
|
0,01
|
0,01
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
ПРИЛОЖЕНИЕ 1
Справочное
ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ,
ИЗЛАГАЕМЫХ В СТАНДАРТЕ
Пример 1.
Для плана Б0, 50 В найти объем выборки при N = 2500.
По кодовому обозначению плана в табл. 1 для объема партии N
= 2500 находим n = 600.
Пример 2.
Для плана Б0, 50В найти объем выборки, если объем
партии N =
500.
По кодовому обозначению плана в табл. 1 для объема партии N = 500 находим n = «все».
Следовательно, в данном случае статистический контроль теряет смысл
Пример 3.
Выбрать план контроля при b = 0,05, qг = 0,55
%; контроль приводит к разрушению изделия.
Из табл. 1
находим вариант контроля Б.
В графе «Браковочный уровень качества qm» находим значение, ближайшее к заданному значению граничного уровня
качества, но не превосходящее его: qm = 0,50 %. Определяем вариант браковки (см. п. 3.4 настоящего стандарта): В.
Кодовое обозначение выбранного плана контроля Б0, 50В.
Пример 4.
Выбрать план контроля при b = 0,10, qг = 0,50
%, контроль не приводит к разрушению изделия, возможна замена дефектных изделий
годными.
Из табл. 1
определяем вариант контроля А.
В графе «Браковочный уровень качества qm» находим значение, ближайшее к заданному значению
граничного уровня качества, но не превосходящее его: qm = 0,50 %.
Определяем вариант браковки КЗ. Кодовое обозначение выбранного плана контроля
АО, 50КЗ.
Пример 5.
Построить оперативную характеристику для планов
контроля Б0, 50В, Б0, 50К, Б0, 50КЗ при N
= 2500, n = 600.
Вычисляем l = 600/2500 = 0,24.
Среди табл.
2 - 20 для n = 600 выбираем табл. 18. Для l = 0,25 находим семь значений квантилей и составляем таблицу для
построения оперативной характеристики
|
Номер точки
|
Значение абсциссы qh, %
|
Значения ординаты P(qh)=h
|
Номер точки
|
Значение абсциссы qh, %
|
Значения ординаты P(qh)=h
|
|
1
|
0,00
|
1,00
|
6
|
0,24
|
0,20
|
|
2
|
0,01
|
0,95
|
7
|
0,33
|
0,10
|
|
3
|
0,02
|
0,90
|
8
|
0,41
|
0,05
|
|
4
|
0,03
|
0,80
|
9
|
100,00
|
0,00
|
|
5
|
0,10
|
0,50
|
|
|
|
Пример оперативной характеристики представлен на
чертеже
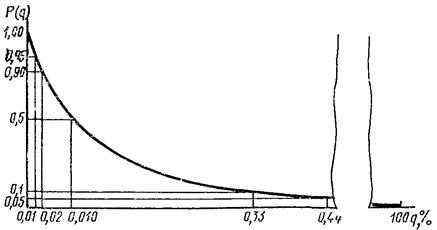
Пример 6
Построить оперативную характеристику для планов Б0,
20В, Б0, 20К, Б0, 20КЗ при N =
10000, n =
1500.
Вычисляем l = 0,15.
Среди табл. 2 - 20 выбираем табл.
11 для n =
1500/10 = 150. Значение квантилей для l = 0,15 делим на
десять. График оперативной характеристики строится по точкам, приведенным в
таблице.
|
Номер точки
|
Значение абсциссы qh, %
|
Значения ординаты P(qh)=h
|
Номер точки
|
Значение абсциссы qh, %
|
Значения ординаты P(qh)=h
|
|
1
|
0
|
1,00
|
6
|
0,093
|
0,20
|
|
2
|
0,003
|
0,95
|
7
|
0,141
|
0,10
|
|
3
|
0,007
|
0,90
|
8
|
0,183
|
0,05
|
|
4
|
0,014
|
0,80
|
9
|
100,000
|
0,00
|
|
5
|
0,043
|
0,50
|
|
|
|
Пример 7.
По результатам контроля (план Б0, 50В)
десяти партий вычислить последующие оценки средних уровней входного и выходного
качества
|
Номер партии
|
Исходные данные
|
Результаты
вычислений
|
|
Объем партии N
|
Объем выборки n
|
Число дефектных
изделий в выборке d
|
Решение о партии
|
Число принятых
изделий в партии Nв
|
Относительный
объем выборки l
|
Оценка числа
дефектных изделий в партии
|
|
до контроля Х
|
после контроля Y
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
|
2500
|
600
|
0
|
Принята
|
2500
|
0,24
|
0
|
0
|
|
2
|
2500
|
600
|
0
|
Принята
|
2500
|
0,24
|
0
|
0
|
|
3
|
2500
|
600
|
2
|
Забракована
|
0
|
0,24
|
8,4
|
0
|
|
4
|
2500
|
600
|
1
|
Забракована
|
0
|
0,24
|
4,2
|
3,2
|
|
5
|
2500
|
600
|
0
|
Принята
|
2500
|
0,24
|
0
|
0
|
|
6
|
2500
|
600
|
1
|
Забракована
|
0
|
0,24
|
4,2
|
3,2
|
|
7
|
2500
|
600
|
0
|
Принята
|
2500
|
0,24
|
0
|
0
|
|
8
|
2500
|
600
|
0
|
Принята
|
2500
|
0,24
|
0
|
0
|
|
9
|
2500
|
600
|
1
|
Забракована
|
0
|
0,24
|
4,2
|
3,2
|
|
10
|
2500
|
600
|
0
|
Принята
|
2500
|
0,24
|
0
|
0
|
|
Всего
|
25000
|
|
5
|
|
15000
|
|
21,0
|
9,6
|
Вычисляем значение l для всех партий:
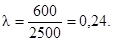
Результат вычисления заносим в графу 7.
Для принятых партий в графах 8 и 9 проставляем нули.
Для партий № 4, 6 и 9 вычисляем значение Х:
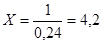 .
.
Результат вычисления записываем в графу 8.
Вычисляем значение Y:
Y = 4,2-1 =
3,2
Результат вычисления записываем в графу 9.
Для партий № 3 вычисляем значение Х:
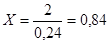 .
.
Результат вычисления записываем в графу 8. В графе 9
проставляем нуль.
Вычисляем значения 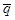 и
и
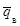 в процентах:
в процентах:
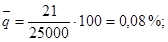
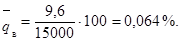
Пример 8.
По результатам контроля (план А2,00К) десяти партий
вычислить последующие оценки средних уровней входного и выходного качества.
В графе 7 таблицы для последующих оценок записываем
число принятых изделий.
Вычисляем значение l для всех партий
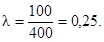
Результат вычисления записываем в графу
8.
Для принятых партий в графах 9 и 11 проставляем
прочерки, в графах 10, 12 и 13 проставляем нули.
В табл. 21
для всех забракованных партий находим значение коэффициента а1=0,288.
Для партий № 3 вычисляем а2=0,288·2=0,58.
Результат вычисления записываем в графу 10. В табл. 22 находим а3=0,74
и записываем в графу 11.
Вычисляем значения Y и Х:
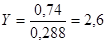 ;
;
X
= 2,6+2 = 4,6.
Результаты вычисления записываем в графы 12 и 13.
Вычисления для остальных забракованных партий
проводятся аналогично.
Вычисляем значения 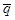 и
и
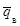 в процентах:
в процентах:
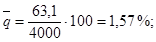
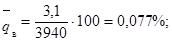
|
Номер партии
|
Исходные данные
|
Результаты
вычислений
|
|
Объем партии N
|
Объем выборки n
|
Число дефектных
изделий в выборке d
|
Решение о партии
|
Общее число
дефектных изделий, обнаруженных в партии, D
|
Число принятых
изделий в партии Nв
|
Относительный
объем выборки l
|
Значение
коэффициента а1
|
Значение
коэффициента а2
|
Значение
коэффициента а3
|
Оценка числа
дефектных изделий в партии
|
|
после контроля Y
|
до контроля X
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
|
1
|
400
|
100
|
0
|
Принята
|
0
|
400
|
0,25
|
-
|
0
|
-
|
0
|
0
|
|
2
|
400
|
100
|
0
|
Принята
|
0
|
400
|
0,25
|
-
|
0
|
-
|
0
|
0
|
|
3
|
400
|
100
|
2
|
Забракована
|
2
|
398
|
0,25
|
0,288
|
0,58
|
074
|
2,6
|
4,6
|
|
4
|
400
|
100
|
5
|
Забракована
|
19
|
381
|
0,25
|
0,288
|
5,5
|
0,02
|
0,1
|
19,1
|
|
5
|
400
|
100
|
0
|
Принята
|
0
|
400
|
0,25
|
-
|
0
|
-
|
0
|
0
|
|
6
|
400
|
100
|
1
|
Забракована
|
27
|
373
|
0,25
|
0,288
|
7,8
|
0
|
0
|
27
|
|
7
|
400
|
100
|
0
|
Принята
|
0
|
400
|
025
|
-
|
0
|
-
|
0
|
0
|
|
8
|
400
|
100
|
0
|
Принята
|
0
|
400
|
0,25
|
-
|
0
|
-
|
0
|
0
|
|
9
|
400
|
100
|
1
|
Забракована
|
12
|
388
|
0,25
|
0,288
|
3,5
|
0,11
|
0,4
|
12,4
|
|
10
|
400
|
100
|
0
|
Принята
|
0
|
400
|
0,25
|
-
|
0
|
-
|
0
|
0
|
|
Всего
|
4000
|
|
9
|
|
60
|
3940
|
|
|
|
|
3,1
|
63,1
|
ПРИЛОЖЕНИЕ
2
Рекомендуемое
Форма инструкционной карты
контроля
|
(предприятие)
|
Инструкционная
карта
№_____________
|
ГОСТ_________
|
|
Цех, участок,
предприятие-поставщик
|
|
|
Номер изделия (или ТУ) и
наименование изделия
|
|
|
Контролируемые
характеристики
|
Характер контроля
|
|
1
...........…………………………………………...........
|
...........……………………………………………….…..
|
|
2
...........………………………………………………...
|
.............……………………………………………….…
|
|
…………………………………………………………
|
...........……………………………………………….…..
|
|
Кодовое обозначение плана
контроля
|
|
План контроля
|
|
Значение риска потребителя
|
|
|
|
|
Значение браковочного уровня
качества
|
|
|
|
|
|
Порядок извлечения
выборки
|
|
Вариант браковки
|
|
|
Примечание.
|
|
|
Начальник технической части
цеха
|
Начальник ОТК цеха:
|
Составил:
|
|
|
|
|
|
Примечания:
1. В графе «Характер
контроля» записывается «сплошной» или «выборочный».
2. В случае, когда производится контроль изделий, полученных от
предприятия-поставщика, в нижней графе карты проставляются подписи лиц,
ответственных за приемку этих изделий.
ПРИЛОЖЕНИЕ
3
Рекомендуемое
ВЫЧИСЛЕНИЕ ДОВЕРИТЕЛЬНЫХ
ГРАНИЦ ДЛЯ СРЕДНИХ УРОВНЕЙ ВХОДНОГО
И ВЫХОДНОГО КАЧЕСТВА
1. Цель вычисления доверительных границ
Вычисление доверительных границ следует проводить в
тех случаях, когда требуется оценить точность последующих оценок средних
уровней входного и выходного качества, вычисленных по методике разд. 5 настоящего стандарта.
2. Исходные данные для вычисления доверительных границ
2.1. Вычисление доверительных границ следует проводить
на основании данных таблицы для вычисления последующих оценок и уровня
доверительной вероятности.
2.2. Если применяется вариант браковки В, то следует
пользоваться таблицей для вычисления последующих оценок по форме 2 настоящего стандарта.
Если применяется вариант браковки К или КЗ, то следует
использовать таблицу для вычисления последующих оценок по форме 3 настоящего стандарта.
2.3. При назначении уровня доверительной вероятности
следует выбирать одно из значений 0,95 или 0,90.
3. Вычисление доверительных границ при варианте
браковки В
3.1. В случае, когда при контроле хотя бы одна партия
была забракована, доверительные границы для среднего уровня входного качества
вычисляют следующим образом:
а) вычисляют сумму чисел (Sd), внесенных в графу 4
таблицы для последующих оценок;
б) вычисляют значение среднего относительного объема
выборок (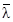 ):
):
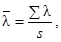 (1)
(1)
где s - число партий;
в) по уровню доверительной вероятности g, суммарному числу дефектных изделий Sd, обнаруженных при контроле, и среднему относительному
объему выборок 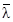 в табл. 2 и 3
отыскивают значения коэффициентов К1 и К2.
в табл. 2 и 3
отыскивают значения коэффициентов К1 и К2.
Примечание. Если в табл. 2
и 3 нет вычислительного значения 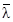 , то значения коэффициентов К1
и К2 вычисляют линейной интерполяцией, либо выбирают
значения, соответствующие ближайшему меньшему значению среднего относительного
объема
, то значения коэффициентов К1
и К2 вычисляют линейной интерполяцией, либо выбирают
значения, соответствующие ближайшему меньшему значению среднего относительного
объема 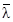 , приведенному в табл. 2 и 3;
, приведенному в табл. 2 и 3;
г) вычисляют сумму чисел (SN),
внесенных в графу 2;
д) вычисляют доверительные границы для среднего уровня
входного качества 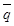 в процентах по формулам:
в процентах по формулам:
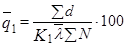 , (2)
, (2)
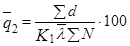 , (3)
, (3)
где
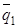 и
и 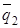 - соответственно
верхняя и нижняя доверительные границы для среднего уровня входного качества.
- соответственно
верхняя и нижняя доверительные границы для среднего уровня входного качества.
3.2. Если при контроле ни одна партия не была
забракована, то нижняя граница для среднего уровня входного качества равна
нулю. Верхнюю границу вычисляют следующим образом:
а) вычисляют сумму чисел (SN), внесенных в графу 2
таблицы для последующих оценок;
б) вычисляют значение среднего относительного объема
выборок (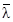 )
)
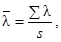 (4)
(4)
где s - число партий;
в) по уровню доверительной вероятности g и значению среднего относительного объема выборок по табл. 1 отыскивают значение коэффициента К0.
Примечание. Если в табл. 1
нет значения 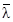 , равного
вычисленному значению
, равного
вычисленному значению 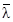 , то
значение КВ вычисляют линейной интерполяцией или выбирают
значение, соответствующее ближайшему меньшему значению
, то
значение КВ вычисляют линейной интерполяцией или выбирают
значение, соответствующее ближайшему меньшему значению 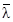 , приведенному в табл. 1;
, приведенному в табл. 1;
г) вычисляют верхнюю доверительную границу 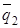 в процентах
для среднего уровня входного качества по формуле:
в процентах
для среднего уровня входного качества по формуле:
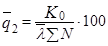 . (5)
. (5)
3.3. Если среди выборок, прошедших контроль, имеются
такие, в которых обнаружено только одно дефектное изделие, доверительные
границы для среднего уровня выходного качества вычисляют следующим образом:
а) вычисляют сумму чисел (SNB), внесенных в графу 6 таблицы для последующих оценок;
б) по данным графы 4 подсчитывают число выборок т1,
в которых при контроле обнаружено только одно дефектное изделие;
в) исходя из уровня доверительной вероятности g, числа партий s и числа выборок т1, в
которых при контроле было обнаружено только одно дефектное изделие, по табл. 5 и 6 отыскивают значения коэффициентов l1 и l2.
Примечание. Если в табл. 5
и 6 нет заданного значения s, то
значения коэффициентов l1 и l2 вычисляют линейной интерполяцией или
выбирают значения коэффициентов, соответствующие ближайшему меньшему значению
s, приведенному в табл. 5 и 6;
г) вычисляют значение среднего относительного объема
выборок (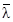 ) по формуле:
) по формуле:
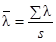 ; (6)
; (6)
д) вычисляют доверительные границы для
среднего уровня выходного качества 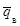 в
процентах по формулам:
в
процентах по формулам:
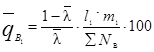 ; (7)
; (7)
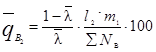 , (8)
, (8)
где 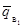 и
и 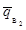 -
соответственно нижняя и верхняя доверительные границы для среднего уровня
выходного качества.
-
соответственно нижняя и верхняя доверительные границы для среднего уровня
выходного качества.
3.4. Если при контроле не оказалось ни одной выборки,
в которой было обнаружено только одно дефектное изделие, нижняя доверительная
граница для среднего уровня выходного качества равна нулю. Верхнюю
доверительную границу следует вычислять следующим образом:
а) вычисляют сумму чисел (SNB), внесенных в графу 6
таблицы для последующих оценок;
б) по уровню доверительной вероятности g и числу партии s в табл. 4
отыскивают значение коэффициента l0.
Примечание. Если в табл. 4
нет заданного значения s, то значение коэффициента l0
вычисляют линейной интерполяцией или выбирают значение соответствующее
ближайшему значению s, приведенному в табл.
4.
б) вычисляют верхнюю доверительную границу для
среднего уровня выходного качества 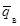 в
процентах по формуле:
в
процентах по формуле:
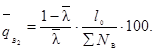 . (9)
. (9)
4. Вычисление доверительных границ при вариантах браковки К и КЗ
4.1. Доверительные границы для среднего уровня входного
качества следует вычислять в следующем порядке:
а) исходя из значения коэффициента а2
в графе 10 таблицы для последующих оценок, в табл.
7 для каждой партии отыскивают значение коэффициента w2;
найденные значения w2
записывают в графу 14;
б) вычисляют сумму чисел SN, SX и Sw2, приведенных в графах 2, 13 и 14;
в) вычисляют величину s по правилу:
если значения относительного объема выборки во всех
партиях одинаковы, то величину s вычисляют по формуле:
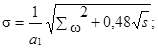 (10)
(10)
если значения относительного объема
выборки для различных партий не одинаковы, то величину о вычисляют по формуле:
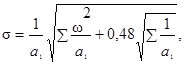 (11)
(11)
где суммирование величин w2/а1
и 1/а1 проводится по всем партиям;
г) по уровню доверительной вероятности выбирают
значения коэффициента u по правилу:
для g = 0,95 u =
1,96;
для g = 0,90 u =
1,64;
д) вычисляют доверительные границы для неизвестного
значения среднего уровня входного качества 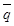 в процентах по формулам:
в процентах по формулам:
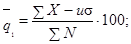 (12)
(12)
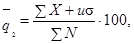 (13)
(13)
где 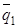 и
и 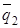 - соответственно нижняя и верхняя
доверительные границы для среднего уровня входного качества.
- соответственно нижняя и верхняя
доверительные границы для среднего уровня входного качества.
Если в результате вычисления по формуле (12) получается отрицательное число, то
нижнюю доверительную границу для среднего уровня входного качества следует
считать равной нулю.
4.2. Доверительные границы для среднего уровня
выходного качества для варианта браковки К вычисляют по методике,
приведенной в п. 4.1, со следующими
изменениями:
а) вместо сумм SN и SХ суммируют значения SNB
и SY,
приведенные в графах 7 и 12;
б) доверительные границы для среднего уровня выходного
качества 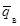 в процентах вычисляют по
формулам:
в процентах вычисляют по
формулам:
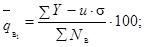 (14)
(14)
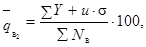 (15)
(15)
где 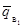 и
и 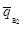 - соответственно нижняя и
верхняя доверительные границы для среднего уровня выходного качества.
- соответственно нижняя и
верхняя доверительные границы для среднего уровня выходного качества.
Если в результате вычисления по формуле (14) получается отрицательное число,
нижнюю доверительную границу для среднего уровня выходного качества следует
считать равной нулю.
4.3. Доверительные границы для среднего уровня
выходного качества для варианта браковки КЗ следует вычислять по методике,
приведенной в п. 4.1, со следующими
изменениями:
а) вместо вычисления суммы SX суммируют значения SY, приведенные в графе 12;
б) доверительные границы для среднего уровня выходного
качества 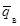 в процентах вычисляют по
формулам:
в процентах вычисляют по
формулам:
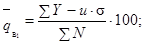 (16)
(16)
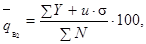 (17)
(17)
где 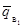 и
и 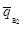 - соответственно нижняя и верхняя
доверительные границы для среднего уровня выходного качества.
- соответственно нижняя и верхняя
доверительные границы для среднего уровня выходного качества.
Если в результате вычисления по формуле (16) получается отрицательное число, то
нижнюю доверительную границу для среднего уровня выходного качества следует
считать равной нулю.
Таблица 1
Значения коэффициента К0
|
Уровни
доверительной вероятности g
|
Значения
коэффициента К0 при среднем относительном объеме выборки 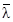
|
|
0,0
|
0,1
|
0,2
|
0,3
|
0.4
|
0,5
|
|
0,90
|
6,4
|
3,8
|
1,9
|
1,5
|
1,3
|
1,2
|
|
0,95
|
9,0
|
5,3
|
2,5
|
1,8
|
1,5
|
1,3
|
Таблица 2
Значения коэффициента K1
|
Суммарное число
дефективных изделий Sd
|
Значения
коэффициента K1 при доверительной вероятности g = 0,90 и среднем относительном объеме
выборки 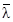
|
Значения
коэффициента K1 при доверительной вероятности g = 0,95 и среднем относительном объеме
выборки 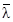
|
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
|
1
|
19,5
|
10,8
|
4,55
|
3,21
|
3,04
|
2,84
|
40
|
26
|
18
|
15
|
12
|
10
|
|
2
|
5,63
|
3,72
|
2,87
|
2,51
|
2,20
|
2,11
|
8,26
|
4,51
|
3,22
|
2,82
|
2,71
|
2,63
|
|
3
|
3,66
|
2,83
|
2,42
|
2,12
|
2,05
|
1,94
|
4,84
|
3,71,
|
2,95
|
2,73
|
2,62
|
2,52
|
|
4
|
2,93
|
2,31
|
2,04
|
1,94
|
1,80
|
1,78
|
3,67
|
3,12
|
2,68
|
2,50
|
2,45
|
2,40
|
|
5
|
2,54
|
2,10
|
1,87
|
1,78
|
1,67
|
1,64
|
3,08
|
2,87
|
2,50
|
2,38
|
2,34
|
2,30
|
|
6
|
2,29
|
2,04
|
1,82
|
1,72
|
1,64
|
1,58
|
2,73
|
2,68
|
2,45
|
2,28
|
2,22
|
2,20
|
|
7
|
2,13
|
1,92
|
1,78
|
1,68
|
1,58
|
1,54
|
2,49
|
2,37
|
2,26
|
2,17
|
2,10
|
2,09
|
|
8
|
2,01
|
1,85
|
1,74
|
1,63
|
1,55
|
1,49
|
2,31
|
2,25
|
2,20
|
2,08
|
1,96
|
1,94
|
|
9
|
1,91
|
1,78
|
1,67
|
1,58
|
1,50
|
1,46
|
2,19
|
2,06
|
1,97
|
1,88
|
1,78
|
1,75
|
|
10
|
1,83
|
1,70
|
1,62
|
1,54
|
1,47
|
1,43
|
2,08
|
1,96
|
1,85
|
1,76
|
1,66
|
1,60
|
|
11
|
1,78
|
1,66
|
1,57
|
1,50
|
1,40
|
1,40
|
2,00
|
1,91
|
1,81
|
1,72
|
1,63
|
1,57
|
|
12
|
1,73
|
1,62
|
1,53
|
1,46
|
1,42
|
1,38
|
1,93
|
1,84
|
1,77
|
1,69
|
1,60
|
1,54
|
|
13
|
1,69
|
1,59
|
1,50
|
1,43
|
1,39
|
1,36
|
1,88
|
1,80
|
1,73
|
1,66
|
1,57
|
1,52
|
|
14
|
1,65
|
1,54
|
1,45
|
1,40
|
1,37
|
1,35
|
1,83
|
1,76
|
1,69
|
1,63
|
1,54
|
1,49
|
|
15
|
1,62
|
1,49
|
1,41
|
1,37
|
1,35
|
1,34
|
1,78
|
1,72
|
1,66
|
1,60
|
1,52
|
1,47
|
|
20
|
1,51
|
1,44
|
1,36
|
1,32
|
1,30
|
1,28
|
1,64
|
1,59
|
1,54
|
1,47
|
1,44
|
1,40
|
|
25
|
1,44
|
1,37
|
1,30
|
1,27
|
1,26
|
1,25
|
1,55
|
1,51
|
1,45
|
1,42
|
1,39
|
1,36
|
|
30
|
1,39
|
1,32
|
1,27
|
1,25
|
1,24
|
1,23
|
1,48
|
1,45
|
1,42
|
1,40
|
1,34
|
1,33
|
|
40
|
1,32
|
1,26
|
1,24
|
1,22
|
1,21
|
1,20
|
1,40
|
1,37
|
1,34
|
1,30
|
1,28
|
1,25
|
|
50
|
1,28
|
1,24
|
1,22
|
1,20
|
1,19
|
1,18
|
1,35
|
1,32
|
1,30
|
1,28
|
1,26
|
1,22
|
|
60
|
1,25
|
1,23
|
1,21
|
1,20
|
1,18
|
1,17
|
1,31
|
1,29
|
1,27
|
1,25
|
1,23
|
1,20
|
|
80
|
1,21
|
1,19
|
1,17
|
1,16
|
1,15
|
1,14
|
1,26
|
1,24
|
1,22
|
1,20
|
1,19
|
1,18
|
|
100
|
1,19
|
1,17
|
1,15
|
1,13
|
1,12
|
1,12
|
1,23
|
1,21
|
1,20
|
1,18
|
1,17
|
1,16
|
|
200
|
1,13
|
1,12
|
1,12
|
1,11
|
1,10
|
1,10
|
1,16
|
1,16
|
1,15
|
1,14
|
1,13
|
1,12
|
|
300
|
1,10
|
1,10
|
1,09
|
1,09
|
1,08
|
1,08
|
1,12
|
1,12
|
1,11
|
1,10
|
1,10
|
1,09
|
Таблица 3
Значения коэффициента К2
|
Суммарное число
дефективных изделий Sd
|
Значения
коэффициента K2 при доверительной вероятности g = 0,90 и среднем относительном объеме
выборки 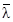
|
Значения
коэффициента К2 при доверительной вероятности g = 0,95 и среднем относительном объеме
выборки 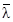
|
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
|
1
|
0,21
|
0,24
|
0,26
|
0,28
|
0,30
|
0,33
|
0,15
|
0,17
|
0,19
|
0,21
|
0,24
|
0,27
|
|
2
|
0,32
|
0,34
|
0,36
|
0,38
|
0,40
|
0,42
|
0,25
|
0,27
|
0,29
|
0,31
|
0,34
|
0,35
|
|
3
|
0,39
|
0,41
|
0,43
|
0,45
|
0,47
|
0,48
|
0,31
|
0,33
|
0,36
|
0,39
|
0,42
|
0,43
|
|
4
|
0,44
|
0,46
|
0,48
|
0,50
|
0,52
|
0,54
|
0,33
|
0,36
|
0,39
|
0,42
|
0,46
|
0,48
|
|
5
|
0,48
|
0,50
|
0,52
|
0,54
|
0,58
|
0,61
|
0,38
|
0,39
|
0,41
|
0,45
|
0,49
|
0,53
|
|
6
|
0,51
|
0,53
|
0,55
|
0,58
|
0,61
|
0,64
|
0,41
|
0,42
|
0,44
|
0,47
|
0,51
|
0,55
|
|
7
|
0,53
|
0,55
|
0,58
|
0,61
|
0,64
|
0,67
|
0,44
|
0,46
|
0,47
|
0,49
|
0,53
|
0,57
|
|
8
|
0,55
|
0,57
|
0,60
|
0,63
|
0,66
|
0,69
|
0,47
|
0,48
|
0,49
|
0,52
|
0,55
|
0,59
|
|
9
|
0,57
|
0,59
|
0,61
|
0,64
|
0,67
|
0,71
|
0,50
|
0,50
|
0,52
|
0,55
|
0,58
|
0,61
|
|
10
|
0,59
|
0,61
|
0,63
|
0,65
|
0,68
|
0,72
|
0,52
|
0,52
|
0,54
|
0,57
|
0,60
|
0,64
|
|
11
|
0,60
|
0,62
|
0,64
|
0,66
|
0,69
|
0,72
|
0,53
|
0,54
|
0,56
|
0,50
|
0,62
|
0,65
|
|
12
|
0,62
|
0,64
|
0,66
|
0,68
|
0,70
|
0,73
|
0,54
|
0,55
|
0,57
|
0,60
|
0,63
|
0,66
|
|
13
|
0,63
|
0,65
|
0,67
|
0,69
|
0,71
|
0,73
|
0,55
|
0,57
|
0,58
|
0,61
|
0,64
|
0,67
|
|
14
|
0,64
|
0,66
|
0,68
|
0,70
|
0,72
|
0,74
|
0,56
|
0,58
|
0,60
|
0,62
|
0,65
|
0,68
|
|
15
|
0,65
|
0,66
|
068
|
0,70
|
0,72
|
0,74
|
0,58
|
0,59
|
0,61
|
0,63
|
0,66
|
0,69
|
|
20
|
0,69
|
0,71
|
0,73
|
0,75
|
0,77
|
0,79
|
0,62
|
0,63
|
0,65
|
0,67
|
0,70
|
0,74
|
|
25
|
0,72
|
0,73
|
0,75
|
0,76
|
0,78
|
0,80
|
0,66
|
0,67
|
0,69
|
0,71
|
0,74
|
0,77
|
|
30
|
0,74
|
0,74
|
0,75
|
0,76
|
0,79
|
0,81
|
0,68
|
0,69
|
0,71
|
0,73
|
0,75
|
0,77
|
|
40
|
0,77
|
0,77
|
0,78
|
0,80
|
0,82
|
0,84
|
0,73
|
0,73
|
0,74
|
0,76
|
0,78
|
0,80
|
|
50
|
0,79
|
0,79
|
0,80
|
0,82
|
0,84
|
0,85
|
0,75
|
0,75
|
0,76
|
0,78
|
0,80
|
0,82
|
|
60
|
0,81
|
0,82
|
0,83
|
0,84
|
0,85
|
0,86
|
0,78
|
0,78
|
0,79
|
0,80
|
0,81
|
0,83
|
|
80
|
0,83
|
0,84
|
0,85
|
0,86
|
0,87
|
0,88
|
0,80
|
0,81
|
0,82
|
0,83
|
0,84
|
0,85
|
|
100
|
0,85
|
0,85
|
0,86
|
0,87
|
0,88
|
0,89
|
0,82
|
0,82
|
0,83
|
0,84
|
0,85
|
0,86
|
|
200
|
0,89
|
0,89
|
0,89
|
0,90
|
0,91
|
0,92
|
0,87
|
0,88
|
0,89
|
0,89
|
0,90
|
0,90
|
|
300
|
0,95
|
0,95
|
0,96
|
0,96
|
0,96
|
0,96
|
0,89
|
0,89
|
0,90
|
0,90
|
0,91
|
0,91
|
Таблица 4
Значения коэффициента l0
|
Уровень
доверительной вероятности g
|
Значения
коэффициента l0 при суммарном
числе партий s
|
|
10
|
30
|
30
|
100
|
200
|
300
|
|
0,90
|
4,0
|
4,4
|
4,9
|
5,5
|
6,4
|
6,7
|
|
0,95
|
5,4
|
5,8
|
6,6
|
7,3
|
8,2
|
8,8
|
Таблица 5
Значения коэффициента l1
|
Число выборок, у
которых d = 1
|
Значения
коэффициента l1 при доверительной
вероятности g = 0,90 и числе партий s
|
Значения
коэффициента l1 при доверительной
вероятности g = 0,95 и числе партий s
|
|
10
|
30
|
50
|
100
|
200
|
300
|
10
|
30
|
50
|
100
|
200
|
300
|
|
4
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
|
5
|
0,10
|
0,04
|
0,00
|
0,00
|
0,00
|
0,00
|
0,01
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
|
6
|
0,18
|
0,13
|
0,10
|
0,08
|
0,01
|
0,00
|
0,03
|
0,01
|
0,00
|
0,00
|
0,00
|
0,00
|
|
7
|
0,23
|
0,19
|
0,16
|
0,09
|
0,04
|
0,01
|
0,14
|
0,03
|
0,01
|
0,00
|
0,00
|
0,00
|
|
8
|
0,28
|
0,25
|
0,23
|
0,19
|
0,14
|
0,09
|
0,15
|
0,12
|
0,09
|
0,01
|
0,00
|
0,00
|
|
9
|
0,33
|
0,29
|
0,27
|
0,23
|
0,20
|
0,17
|
0,22
|
0,19
|
0,16
|
0,03
|
0,02
|
0,00
|
|
10
|
0,36
|
0,33
|
0,31
|
0,29
|
0,25
|
0,22
|
0,24
|
0,22
|
0,20
|
0,16
|
0,12
|
0,10
|
|
11
|
-
|
0,36
|
0,34
|
0,33
|
0,29
|
0,26
|
-
|
0,25
|
0,23
|
0,20
|
0,18
|
0,16
|
|
12
|
-
|
0,38
|
0,37
|
0,35
|
0,32
|
0,30
|
-
|
0,28
|
0,26
|
0,24
|
0,22
|
0,20
|
|
13
|
-
|
0,41
|
0,40
|
0,38
|
0,35
|
0,33
|
-
|
0,31
|
0,29
|
0,28
|
0,26
|
0,24
|
|
14
|
-
|
0,43
|
0,42
|
0,10
|
0,38
|
0,36
|
-
|
0,34
|
0,32
|
0,31
|
0,29
|
0,28
|
|
15
|
-
|
0,45
|
0,44
|
0,43
|
0,41
|
0,39
|
-
|
0,36
|
0,35
|
0,32
|
0,30
|
0,29
|
|
16
|
-
|
0,47
|
0,46
|
0,44
|
0,43
|
0,41
|
-
|
0,38
|
0,37
|
0,36
|
0,35
|
0,32
|
|
17
|
-
|
0,49
|
0,48
|
0,47
|
0,45
|
0,43
|
-
|
0,40
|
0,39
|
0,38
|
0,37
|
0,36
|
|
18
|
-
|
0,50
|
0,49
|
0,48
|
0,46
|
0,45
|
-
|
0,42
|
0,41
|
0,40
|
0,39
|
0,39
|
|
19
|
-
|
0,51
|
0,51
|
0,49
|
0,48
|
0,46
|
-
|
0,43
|
0,42
|
0,42
|
0,42
|
0,41
|
|
20
|
-
|
0,52
|
0,52
|
0,51
|
0,49
|
0,48
|
-
|
0,44
|
0,43
|
0,42
|
0,41
|
0,41
|
|
40
|
-
|
0,66
|
0,66
|
0,66
|
0,65
|
0,64
|
-
|
0,59
|
0,58
|
0,58
|
0,57
|
0,57
|
|
60
|
-
|
-
|
0,72
|
0,72
|
0,71
|
0,70
|
-
|
-
|
0,66
|
0,65
|
0,65
|
0,65
|
|
80
|
-
|
-
|
-
|
0,75
|
0,75
|
0,75
|
-
|
-
|
-
|
0,70
|
0,70
|
0,70
|
|
100
|
-
|
-
|
-
|
0,76
|
0,76
|
0,76
|
-
|
-
|
-
|
0,74
|
0,74
|
0,73
|
Таблица 6
Значения коэффициента l2
|
Число выборок, у
которых d = 1
|
Значения
коэффициента l2 при доверительной
вероятности g = 0,90 и числе партий s
|
Значения
коэффициента l2 при доверительной
вероятности g = 0,95 и числе партий s
|
|
10
|
30
|
50
|
100
|
200
|
300
|
10
|
30
|
50
|
100
|
200
|
300
|
|
1
|
5,94
|
5,31
|
6,72
|
7,35
|
7,73
|
8,12
|
7,42
|
8,02
|
8,52
|
9,00
|
9,50
|
10,2
|
|
2
|
3,75
|
3,98
|
4,11
|
4,35
|
4,65
|
4,85
|
4,71
|
4,87
|
5,03
|
5,32
|
5,61
|
5,90
|
|
3
|
3,04
|
3,12
|
3,24
|
3,36
|
3,54
|
3,66
|
3,72
|
3,81
|
3,91
|
4,11
|
4,27
|
4,42
|
|
4
|
2,68
|
2,74
|
2,80
|
2,87
|
3,04
|
3,12
|
3,21
|
3,29
|
3,36
|
3,44
|
3,51
|
3,61
|
|
5
|
2,42
|
2,48
|
2,54
|
2,60
|
2,68
|
2,78
|
2,81
|
2,88
|
2,95
|
3,02
|
3,11
|
3,20
|
|
6
|
2,26
|
2,30
|
2,33
|
2,38
|
2,45
|
2,53
|
2,61
|
2,67
|
2,73
|
2,80
|
2,85
|
2,92
|
|
7
|
2,14
|
2,18
|
2,21
|
2,24
|
2,28
|
2,33
|
2,42
|
2,47
|
2,52
|
2,58
|
2,63
|
2,70
|
|
8
|
2,04
|
2,07
|
2,10
|
2,15
|
2,19
|
2,22
|
2,36
|
2,40
|
2,44
|
2,33
|
2,48
|
2,53
|
|
9
|
1,95
|
2,00
|
2,03
|
2,07
|
2,10
|
2,14
|
2,23
|
2,26
|
2,29
|
2,32
|
2,35
|
2,42
|
|
10
|
1,90
|
1,92
|
1,95
|
1,97
|
2,00
|
2,04
|
2,16
|
2,19
|
2,21
|
2,24
|
2,27
|
2,30
|
|
11
|
-
|
1,88
|
1,89
|
1,90
|
1,93
|
1,97
|
-
|
2,12
|
2,14
|
2,16
|
2,19
|
2,23
|
|
12
|
-
|
1,84
|
1,85
|
1,86
|
1,89
|
1,92
|
-
|
2,07
|
2,09
|
2,11
|
2,14
|
2,16
|
|
13
|
-
|
1,79
|
1,80
|
1,81
|
1,83
|
1,87
|
-
|
2,02
|
2,04
|
2,05
|
2,07
|
2,10
|
|
14
|
-
|
1,75
|
1,76
|
1,78
|
1,80
|
1,82
|
-
|
1,96
|
1,96
|
1,97
|
2,00
|
2,04
|
|
15
|
-
|
1,73
|
1,74
|
1,75
|
1,76
|
1,78
|
-
|
1,92
|
1,92
|
1,93
|
1,95
|
1,93
|
|
16
|
-
|
1,70
|
1,70
|
1,72
|
1,73
|
1,74
|
-
|
1,88
|
1,89
|
1,90
|
1,92
|
1,93
|
|
17
|
-
|
1,66
|
1,67
|
1,69
|
1,71
|
1,73
|
-
|
1,82
|
1,83
|
1,84
|
1,85
|
1,86
|
|
18
|
-
|
1,64
|
1,65
|
1,65
|
1,66
|
1,69
|
-
|
1,80
|
1,81
|
1,82
|
1,83
|
1,84
|
|
19
|
-
|
1,63
|
1,64
|
1,65
|
1,66
|
1,67
|
-
|
1,78
|
1,79
|
1,80
|
1,82
|
1,83
|
|
20
|
-
|
1,61
|
1,61
|
1,62
|
1,63
|
1,64
|
-
|
1,76
|
1,77
|
1,79
|
1,81
|
1,83
|
|
40
|
-
|
1,41
|
1,41
|
1,41
|
1,42
|
1,42
|
-
|
1,51
|
1,52
|
1,52
|
1,53
|
1,53
|
|
60
|
-
|
-
|
1,32
|
1,32
|
1,33
|
1,34
|
-
|
-
|
1,41
|
1,41
|
1,42
|
1,42
|
|
80
|
-
|
-
|
-
|
1,26
|
1,27
|
1,28
|
-
|
-
|
-
|
1,36
|
1,36
|
1,36
|
|
100
|
-
|
-
|
-
|
1,25
|
1,25
|
1,26
|
-
|
-
|
-
|
1,30
|
1,30
|
1,30
|
Таблица 7
Значения коэффициента w2
|
Целая часть
значения коэффициента а2
|
Значения
коэффициента w2 при
значениях коэффициента а2, взятых с точностью до первого
знака после запятой
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
0,
|
1,00
|
1,00
|
1,00
|
0,99
|
0,99
|
0,98
|
0,97
|
0,96
|
0,95
|
0,94
|
|
1,
|
0,92
|
0,91
|
0,89
|
0,87
|
0,85
|
0,83
|
0,81
|
0,80
|
0,78
|
0,75
|
|
2,
|
0,72
|
0,70
|
0,68
|
0,66
|
0,63
|
0,61
|
0,59
|
0,56
|
0,54
|
0,52
|
|
3,
|
0,50
|
0,47
|
0,45
|
0,43
|
0,41
|
0,39
|
0,37
|
0,36
|
0,34
|
0,32
|
|
4,
|
0,30
|
0,29
|
0,27
|
0,25
|
0,24
|
0,23
|
0,22
|
0,19
|
0,19
|
0,18
|
|
5,
|
0,17
|
0,16
|
0,15
|
0,14
|
0,13
|
0,12
|
0,12
|
0,11
|
0,10
|
0,10
|
|
6,
|
0,09
|
0,08
|
0,08
|
0,07
|
0,07
|
0,06
|
0,06
|
0,06
|
0,05
|
0,05
|
|
7,
|
0,04
|
0,04
|
0,04
|
0,04
|
0,03
|
0,03
|
0,03
|
0,02
|
0,02
|
0,02
|
|
8,
|
0,02
|
0,02
|
0,02
|
0,02
|
0,02
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
|
9,
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,00
|
ПРИЛОЖЕНИЕ 4
Справочное
ТАБЛИЦЫ ОПЕРАТИВНЫХ
ХАРАКТЕРИСТИК ДЛЯ ОБЪЕМОВ ВЫБОРКИ, РАВНЫХ 10 и 15
Настоящим стандартом планы с объемом выборки, меньшим
20, не предусмотрены. Если по каким либо причинам контроль проводится при
объеме выборки, равном 10 или 15, то данные таблиц, приведенных ниже, дадут
возможность построить оперативные характеристики планов контроля и оценить
величины рисков потребления и поставщика
Таблица 1
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 10
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,38
|
0,40
|
0,41
|
0,43
|
0,44
|
0,46
|
0,47
|
0,48
|
0,49
|
050
|
0,51
|
|
q0,90
|
0,78
|
0,81
|
0,84
|
0,87
|
0,90
|
0,93
|
0,95
|
0,98
|
1,00
|
1,03
|
1,05
|
|
q0,80
|
1,65
|
1,71
|
1,77
|
1,83
|
1,89
|
1,95
|
2,00
|
2,06
|
2,11
|
2,16
|
2,21
|
|
q0,50
|
5,00
|
5,19
|
5,38
|
5,56
|
5,73
|
5,90
|
6,07
|
6,23
|
6,39
|
6,54
|
6,70
|
|
q0,20
|
11,08
|
11,52
|
11,93
|
12,33
|
12,73
|
13,11
|
1348
|
13,84
|
14,19
|
14,54
|
14,70
|
|
q0,10
|
15,32
|
15,91
|
16,50
|
17,05
|
17,60
|
18,13
|
18,65
|
19,14
|
19,63
|
20,11
|
20,58
|
|
q0,05
|
19,24
|
19,99
|
20,74
|
21,44
|
22,13
|
22,80
|
23,46
|
24,09
|
24,71
|
25,31
|
25,89
|
|
qL
|
2,73
|
2,84
|
2,95
|
3,06
|
3,16
|
3,26
|
3,36
|
3,46
|
3,55
|
3,64
|
3,73
|
Таблица 2
Квантили оперативных характеристик, в процентах, при
объеме выборки, равном 15
|
l
|
0,50
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
0,15
|
0,10
|
0,05
|
0,00
|
|
q0,95
|
0,25
|
0,26
|
0,27
|
0,28
|
0,29
|
0,30
|
0,31
|
0,32
|
0,33
|
0,33
|
0,34
|
|
q0,90
|
0,52
|
0,54
|
0,56
|
0,58
|
0,60
|
0,62
|
0,63
|
0,65
|
0,66
|
0,68
|
0,70
|
|
q0,80
|
1,09
|
1,14
|
1,18
|
1,22
|
1,26
|
1,30
|
1,33
|
1,37
|
1,41
|
1,44
|
1,48
|
|
q0,50
|
3,35
|
3,48
|
3,60
|
3,72
|
3,84
|
3,96
|
4,08
|
4,19
|
4,30
|
4,41
|
4,52
|
|
q0,20
|
7,50
|
7,80
|
8,10
|
8,38
|
8,66
|
8,93
|
9,19
|
9,41
|
9,62
|
9,93
|
10,19
|
|
q0,10
|
10,51
|
10,93
|
11,34
|
11,73
|
12,11
|
12,49
|
12,86
|
13,22
|
13,57
|
13,91
|
1425
|
|
q0,05
|
13,34
|
13,88
|
14,42
|
14,92
|
15,42
|
15,89
|
16,36
|
16,81
|
17,26
|
17,70
|
18,10
|
|
qL
|
1,80
|
1,88
|
1,95
|
2,02
|
2,09
|
2,16
|
2,22
|
2,29
|
2,35
|
2,41
|
2,47
|
ПРИЛОЖЕНИЕ 5
Рекомендуемое
НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ
ПРИМЕНЕНИЯ ПОСЛЕДУЮЩИХ ОЦЕНОК,
ОПЕРАТИВНЫХ ХАРАКТЕРИСТИК И ПРЕДЕЛА СРЕДНЕГО УРОВНЯ ВЫХОДНОГО КАЧЕСТВА
1. Применение последующих оценок
1.1. Последующие оценки среднего уровня входного
качества следует применять в тех случаях, когда решения, перечисленные в п. 5.1.2 настоящего стандарта,
принимаются на основе информации о качестве продукции, поступающей на контроль.
Последующие оценки среднего уровня выходного качества
следует применять в тех случаях, когда решения, перечисленные в п. 5.1.2 настоящего стандарта
принимаются на основе информации о качестве продукции, прошедшей контроль.
Примечание. Последующие оценки могут вычисляться по методике разд. 5 настоящего стандарта или настоящего
приложения, а также по результатам сплошного контроля ряда партий.
1.2. Последующие оценки средних уровней входного и
выходного качества следует применять одновременно:
- при контроле потребителем полученной продукции;
- при периодическом и летучем контроле принятой
продукции для оценки деятельности служб контроля, и в других случаях, когда
проводится повторный контроль продукции, принятой при первичном контроле.
1.3. Во всех случаях повторного статистического
контроля принятой продукции рекомендуется вычислять оценку среднего уровня
входного качества и сравнивать ее с оценкой среднего уровня выходного качества,
вычисленной при первичном контроле. Для одной из этих оценок следует вычислить
доверительные границы по методике приложения 3. Оценки следует считать совпадающими, если точечная
оценка одного из оцениваемых средних уровней качества находится в пределах
доверительных границ вычисленных для другого среднего уровня качества. Обе
оценки следует вычислять по результатам контроля большого числа партий.
Примечание. Рекомендация основана на том что средний уровень
выходного качества продукции при первичном контроле совпадает со средним
уровнем входного качества при повторном контроле.
1.4. В случае кода оценка среднего уровня входного
качества, вычисленная потребителем не совпадает с оценкой среднего уровня
выходного качества, вычисленной поставщиком, рекомендуется провести контроль
одной или нескольких партий с участием обеих сторон или принять другие меры с
целью выявления причин несовпадения оценок. Такими причинами могут быть:
- недопустимое различие точности средств измерений и
контроля у поставщика и потребителя;
- тенденция у контролеров к необоснованной приемке или
браковке изделий;
- ошибки, допущенные при вычислении последующих
оценок;
- снижение качества продукции при ее транспортировании
от поставщика к потребителю и другие аналогичные причины.
Не рекомендуется предъявлять претензии к поставщику на
основе несовпадения результатов выборочного контроля отдельных партий.
1.5. При оценке деятельности служб контроля на основе
результатов периодического контроля принятой продукции следует
руководствоваться соображениями, аналогичными изложенным в предыдущем пункте.
2. Вычисление и
применение риска поставщика
2.1. Вычисление риска поставщика
Оценка риска поставщика а может быть вычислена
по оперативной характеристике плана контроля, если вычислена оценка среднего
уровня входного качества:
а) точечную оценку риска поставщика а вычисляют
по формуле:
α = 1 - Р(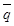 ), (1)
), (1)
где
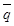 -
точечная оценка среднего уровня входного качества;
-
точечная оценка среднего уровня входного качества;
б) доверительные границы для риска поставщика
вычисляются но формулам:
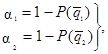 (2)
(2)
где α1 и α2 - соответственно
нижняя и верхняя доверительные границы для риска поставщика;
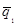 и
и 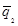 -
соответственно нижняя и верхняя границы для среднего уровня входного качества.
-
соответственно нижняя и верхняя границы для среднего уровня входного качества.
2.2. Применение риска поставщика
2.2.1. Исходя из вычисленного значения риска поставщик
может принять решение о том, насколько гарантированы его интересы при
использовании настоящего стандарта.
2.2.2. Для принятия этого решения поставщик должен
провести технико-экономический анализ с целью установления потерь от браковки
при данном значении риска.
Если эти потери являются недопустимыми, то следует
провести дополнительный анализ с целью проведения одного из следующих
мероприятий:
а) наладка настройка или пересмотр производственного
процесса;
б) проверка деятельности служб контроля;
в) корректировка плана контроля.
2.2.3. Корректировка плана контроля, выбранного в
соответствии с требованиями настоящего стандарта может быть проведена двумя
способами:
- путем выбора нового плана при другом значении риска
потребителя (0,10 вместо 0,05);
- путем выбора нового плана из другого стандарта, если
допускается увеличение приемочного числа.
3. Применение предела среднего уровня выходного
качества
3.1. Предел среднего уровня выходного качества имеет
следующий смысл если используется план контроля, для которого qL
= 3 %, то это значит, что в среднем по
большому количеству партий при использовании этого плана доля дефектных изделии
в принятой продукции будет не более 3 %.
3.2. Значения предела среднего уровня выходного
качества могут быть использованы при выборе плана контроля по методике,
приведенной в разд. 3 настоящего
стандарта при варианте браковки КЗ в случае когда отсутствуют другие конкретные
соображения, позволяющие провести выбор значения риска потребителя. В этом
случае рекомендуется:
а) выбрать планы контроля при b = 0,10 и при b = 0,05 по методике, приведенной в разд. 3;
б) задать значение объема партии и назначить объем
выборки для каждого контроля по методике, приведенной в разд. 1;
в) по заданным значениям объема выборки найти в
настоящем стандарте соответствующие таблицы с квантилями оперативной
характеристики;
г) вычислить значения относительных объемов выборки;
д) в последней строке каждой из найденных таблиц по
назначению относительного объема выборки найти значение предела среднего уровня
выходного качества ql.
Два найденных значения предела среднего уровня
выходного качества следует сравнить и принять решение о выборе значения риска
потребителя по правилу;
если оба значения qL
близки или если оба этих значения удовлетворительны, то следует принять b = 0,10;
если значения qL
существенно отличаются друг от друга и значение qL для плана
при b = 0,10 неудовлетворительно, то следует принять b = 0,05.
Если объем партий, поступающих на контроль, заранее
неизвестен, то следует повторить вычисления для нескольких значений объема партии.
Пример.
Значению браковочного уровня качества qm = 8,00 %
соответствуют планы контроля А8,00КЗ и Б8,001КЗ. Результаты вычислений по
методике настоящего пункта приведены в таблице.
|
Объем партии N
|
Риск потребителя b
|
Объем выборки n
|
Относительный
объем выборки l
|
Предел среднего
уровня выходного качества qL
|
|
60
|
0,10
|
25
|
0,400
|
1,16
|
|
0,05
|
30
|
0,500
|
0,89
|
|
100
|
0,10
|
25
|
0,250
|
1,29
|
|
0,05
|
40
|
0,40
|
0,72
|
|
200
|
0,10
|
30
|
0,150
|
1,14
|
|
0,05
|
40
|
0,200
|
0,83
|
|
300
|
0,10
|
30
|
0,100
|
1,17
|
|
0,05
|
40
|
0,140
|
0,87
|
|
500
|
0,10
|
30
|
0,060
|
1,20
|
|
0,05
|
40
|
0,080
|
0,88
|
|
1000
|
0,10
|
30
|
0,030
|
1,21
|
|
0,05
|
40
|
0,40
|
0,50
|
|
10000
|
0,10
|
30
|
0,003
|
1,23
|
|
0,05
|
40
|
0,004
|
0,92
|
При любом значении объема партии и при (план контроля
А8,00КЗ) b = 0,10 значения qL
превышают 1,00 %; при = 0,05 (план контроля Б8,00КЗ) значения qL меньше 1,00 %.
Если значения предела среднего уровня выходного качества не должны превышать
1,00 %, то следует выбрать план контроля Б8,00КЗ. Если значения предела
среднего уровня выходного качества не должны превышать, например, 1,5 %, то
следует выбрать план А8,00КЗ, поскольку он обеспечивает меньший объем выборки.
ПРИЛОЖЕНИЕ 6
Рекомендуемое
ОЦЕНКА ВЛИЯНИЯ ЧИСЛА
КОНТРОЛИРУЕМЫХ ХАРАКТЕРИСТИК ИЗДЕЛИЯ
НА ПРИМЕНЯЕМОСТЬ СТАТИСТИЧЕСКОГО КОНТРОЛЯ ПО АЛЬТЕРНАТИВНОМУ ПРИЗНАКУ
1. Постановка задачи
1.1. В большинстве практических случаев контроль
изделия проводится по многим характеристикам. Методы, приведенные в настоящем
стандарте, применимы в случае, когда изделие считается годным, если оно
оказалось годным по каждой из контролируемых характеристик, и считается
дефектным, если оно оказалось дефектным хотя бы по одной из контролируемых
характеристик.
1.2. При контроле по многим характеристикам следует
решить вопрос о применимости к данному изделию статистического контроля,
поскольку при увеличении числа контролируемых характеристик может возрасти доля
дефектных изделий и применение статистического контроля потеряет смысл.
1.3. Влияние увеличения числа контролируемых
характеристик на долю дефектных изделий определяется значениями долей дефектных
изделий в партии по каждой контролируемой характеристике и наличием зависимости
между появлениями дефектов по различным характеристикам. Имеют место два
случая:
- дефекты по различным характеристикам независимы или
слабо зависимы;
- между дефектами по различным характеристикам
существует сильная зависимость.
1.4. Сильная зависимость между дефектами по различным
контролируемым характеристикам означает, что появление (или отсутствие)
дефектов по одним характеристикам приводит с большой вероятностью к появлению
(или отсутствию) дефектов по другим характеристикам.
Независимость или слабая зависимость между дефектами
по различным контролируемым характеристикам означает, что появление (или
отсутствие) дефектов по одним контролируемым характеристикам практически не
влияет на появление (или отсутствие) дефектов по другим контролируемым
характеристикам.
1.5. В случае независимости или слабой зависимости
между дефектами по различным характеристикам доля дефектных изделий по всем
контролируемым характеристикам может быть вычислена по формуле:
q = 1 - (1 - q1) · (1 - q2) . . . (1 - qr), (1)
где
q1 - доля
изделий с дефектом по i-й контролируемой характеристике;
r
- общее число контролируемых характеристик.
В частном случае, когда значения долей qi
приблизительно равны,
q » 1 - (1 - q1)r, (2)
где
q1 - значение доли дефектных изделий по одной контролируемой
характеристике.
Результаты вычислений по формуле 2 при различных значениях q1
и r, приведены
в таблице.
1.6. В случае сильной зависимости между дефектами по
различным контролируемым характеристикам значение доли дефектных изделий по
всем контролируемым характеристикам меньше значения, вычисленного по формуле 1 при тех же значениях r
и q1, q2 . . . qr.
Значения доли дефектных изделий q
в процентах.
|
Общее число
контролируемых характеристик r
|
Доля дефектных
изделий q в процентах при значении одной контролируемой
характеристики q1
|
|
0,1
|
0,2
|
0,3
|
0,5
|
0,7
|
1,0
|
2,0
|
3,0
|
|
2
|
0,2
|
0,4
|
0,6
|
1,0
|
1,4
|
2,0
|
4,0
|
5,9
|
|
3
|
0,3
|
0,6
|
0,9
|
1,5
|
2,1
|
3,0
|
6,0
|
8,7
|
|
4
|
0,4
|
0,8
|
1,2
|
2,0
|
2,8
|
4,0
|
8,0
|
11,4
|
|
5
|
0,5
|
1,0
|
1,5
|
2,5
|
3,5
|
5,0
|
9,8
|
14,1
|
|
6
|
0,6
|
1,2
|
1,8
|
3,0
|
4,2
|
6,0
|
11,6
|
16,7
|
|
8
|
0,8
|
1,6
|
2,4
|
4,0
|
5,5
|
7,9
|
15,1
|
21,6
|
|
10
|
1,0
|
2,0
|
3,0
|
5,0
|
6,8
|
9,7
|
18,5
|
26,2
|
|
12
|
1,2
|
2,4
|
3,6
|
6,0
|
8,2
|
11,5
|
21,8
|
30,6
|
|
15
|
1,5
|
3,0
|
4,5
|
7,4
|
10,1
|
14,2
|
26,5
|
36,6
|
|
20
|
2,0
|
4,0
|
5,9
|
9,7
|
13,2
|
18,5
|
33,7
|
45,5
|
|
25
|
2,5
|
5,0
|
7,3
|
12,0
|
16,2
|
22,6
|
40,2
|
53,2
|
|
30
|
3,0
|
6,0
|
8,7
|
14,2
|
19,1
|
26,5
|
46,1
|
59,2
|
|
40
|
4,0
|
7,9
|
11,4
|
18,5
|
21,9
|
30,2
|
56,1
|
70,3
|
|
50
|
5,0
|
9,8
|
14,1
|
22,6
|
24,6
|
33,7
|
64,2
|
78,1
|
|
60
|
6,0
|
11,6
|
16,7
|
29,3
|
27,3
|
43,1
|
70,8
|
83,2
|
|
80
|
7,9
|
15,1
|
21,6
|
36,2
|
36,9
|
48,6
|
80,6
|
91,2
|
|
100
|
9,8
|
18,5
|
26,2
|
42,4
|
45,2
|
53,6
|
87,1
|
95,2
|
2. Исследование применимости статистического контроля
по альтернативному признаку
2.1. Предварительное исследование применимости
статистического контроля по альтернативному признаку рекомендуется проводить в
следующем порядке:
а) проводят сплошной контроль N изделий, число N
должно быть не менее 500;
б) по каждой из г контролируемых характеристик
фиксируют число Di изделий с дефектами по данной
характеристике, фиксируют общее число D дефектных изделий (изделий,
имеющих дефекты хотя бы по одной характеристике);
в) вычисляют долю дефектных изделий по формуле:
q = D/N; (3)
г) выбирают план статистического контроля по методике,
приведенной в разд. 3 настоящего
стандарта;
д) строят оперативную характеристику плана контроля по
методике, приведенной в разд. 4
настоящего стандарта;
е) вычисляют риск поставщика при вычисленной доле
дефектных изделий и проводят анализ вычисленного значения риска по методике,
приведенной в разд. 2 приложения 5
2.2. В случае, если значение риска поставщика является
недопустимо большим, рекомендуется установить наличие или отсутствие
зависимости между дефектами по различным характеристикам. Приближенную проверку
независимости или слабой зависимости между дефектами по различным
характеристикам можно провести по следующей методике:
а) вычисляют фактическую долю дефектных изделий по
формуле (3);
б) вычисляют долю дефектных изделий по каждой
контролируемой характеристике по формулам.
q1 = D1/N;
q2 = D2/N; . . . qr
= Dr/N;
в) вычисляют долю дефектных изделий в предположении о
независимости дефектов по формулам (1)
или (2);
г) сравнивают результаты вычислений по формулам (1) или (2) и (3);
если эти результаты совпадают или близки, дефекты по различным характеристикам
независимы или слабо зависимы, если эти результаты сильно отличаются, то
дефекты по различным характеристикам сильно зависимы.
2.3. После установления наличия или отсутствия
зависимости между дефектами по различным контролируемым характеристикам следует
принять решение о проведении в дальнейшем сплошного контроля по некоторым из
контролируемых характеристик.
2.3.1. В случае независимости дефектов по различным характеристикам
решение о проведении в дальнейшем сплошного контроля должно приниматься исходя
из значений долей дефектных изделий и стоимости или трудоемкости контроля по
каждой контролируемся характеристике.
Сплошной контроль следует применять для характеристик,
по которым значения долей дефектных изделий являются наибольшими.
Если значения долей дефектных изделий приблизительно
равны для всех контролируемых характеристик, то сплошной контроль должен
применяться для характеристик с наименьшими затратами на контроль.
2.3.2. В случае сильной зависимости между дефектами по
различным характеристикам решение о проведении в дальнейшем сплошного контроля
может быть принято по методике, приведенной в п. 2.3.1 настоящего приложения.
Рекомендуется проводить дополнительные исследования
степени и характера зависимости между дефектами с целью разделения всех
контролируемых характеристик на группы таким образом, чтобы зависимость между
дефектами внутри группы была сильной, а для различных групп отсутствовала или
была слабой.
Если такое исследование проведено, решение о
проведении в дальнейшем сплошного контроля следует принимать для характеристик,
выбираемых из различных групп.
2.4. После принятия решения о проведении в дальнейшем
сплошного контроля для некоторых характеристик следует повторить проверку
применимости статистического контроля для остальных характеристик. При
повторном исследовании должны использоваться только результаты контроля
изделий, оказавшихся годными по характеристикам, для которых принято решение о
проведении в дальнейшем сплошного контроля.
СОДЕРЖАНИЕ
![]() ; вычисление
проводится с точностью до трех цифр после запятой;
; вычисление
проводится с точностью до трех цифр после запятой;![]()
![]()
![]()
![]() по
формуле:
по
формуле:![]() ; (1)
; (1)![]() по формуле:
по формуле: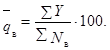 (2)
(2)